

Compact Muon Solenoid
LHC, CERN
| CMS-TOP-20-006 ; CERN-EP-2023-197 | ||
| Differential cross section measurements for the production of top quark pairs and of additional jets using dilepton events from pp collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 13 February 2024 | ||
| JHEP 02 (2025) 064 | ||
| Abstract: Differential cross sections for top quark pair ( $ \mathrm{t} \overline{\mathrm{t}} $) production are measured in proton-proton collisions at a center-of-mass energy of 13 TeV using a sample of events containing two oppositely charged leptons. The data were recorded with the CMS detector at the CERN Large Hadron Collider and correspond to an integrated luminosity of 138 fb$^{-1}$. The differential cross sections are measured as functions of kinematic observables of the $ \mathrm{t} \overline{\mathrm{t}} $ system, the top quark and antiquark and their decay products, as well as of the number of additional jets in the event. The results are presented as functions of up to three variables and are corrected to the parton and particle levels. When compared to standard model predictions based on quantum chromodynamics at different levels of accuracy, it is found that the calculations do not always describe the observed data. The deviations are found to be largest for the multi-differential cross sections. | ||
| Links: e-print arXiv:2402.08486 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Illustration of a pp collision with $ \mathrm{t} \overline{\mathrm{t}} $ plus additional jet production and subsequent dilepton decay of the $ \mathrm{t} \overline{\mathrm{t}} $ system. |

png pdf |
Figure 2:
Distributions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and jet multiplicity (lower right) obtained in selected events with the full kinematic reconstruction. For the first two distributions, ``t'' refers to both top quark and antiquark. The three dilepton channels ($ \mathrm{e}^+\mathrm{e}^- $, $ \mu^{+}\mu^{-} $, and $ \mathrm{e}^\pm\mu^\mp $) are added together. The data with vertical bars corresponding to their statistical uncertainties are plotted together with distributions of simulated signal and background processes. The hatched regions depict the systematic shape uncertainties in the signal and backgrounds (as detailed in Section 8). The lower panel in each plot shows the ratio of the observed data event yields to those expected in the simulation. |

png pdf |
Figure 2-a:
Distributions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and jet multiplicity (lower right) obtained in selected events with the full kinematic reconstruction. For the first two distributions, ``t'' refers to both top quark and antiquark. The three dilepton channels ($ \mathrm{e}^+\mathrm{e}^- $, $ \mu^{+}\mu^{-} $, and $ \mathrm{e}^\pm\mu^\mp $) are added together. The data with vertical bars corresponding to their statistical uncertainties are plotted together with distributions of simulated signal and background processes. The hatched regions depict the systematic shape uncertainties in the signal and backgrounds (as detailed in Section 8). The lower panel in each plot shows the ratio of the observed data event yields to those expected in the simulation. |
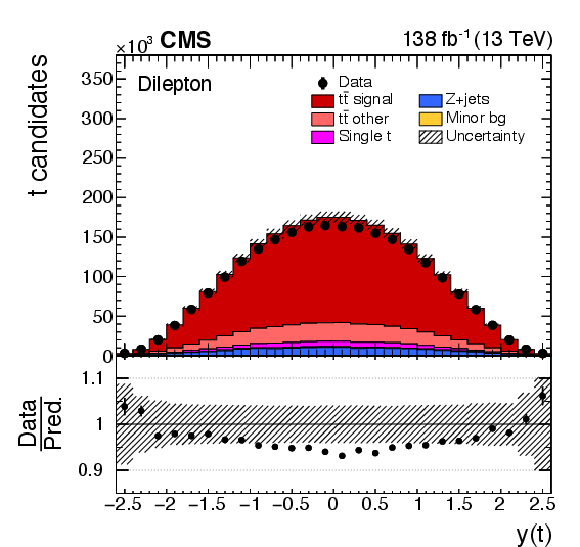
png pdf |
Figure 2-b:
Distributions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and jet multiplicity (lower right) obtained in selected events with the full kinematic reconstruction. For the first two distributions, ``t'' refers to both top quark and antiquark. The three dilepton channels ($ \mathrm{e}^+\mathrm{e}^- $, $ \mu^{+}\mu^{-} $, and $ \mathrm{e}^\pm\mu^\mp $) are added together. The data with vertical bars corresponding to their statistical uncertainties are plotted together with distributions of simulated signal and background processes. The hatched regions depict the systematic shape uncertainties in the signal and backgrounds (as detailed in Section 8). The lower panel in each plot shows the ratio of the observed data event yields to those expected in the simulation. |
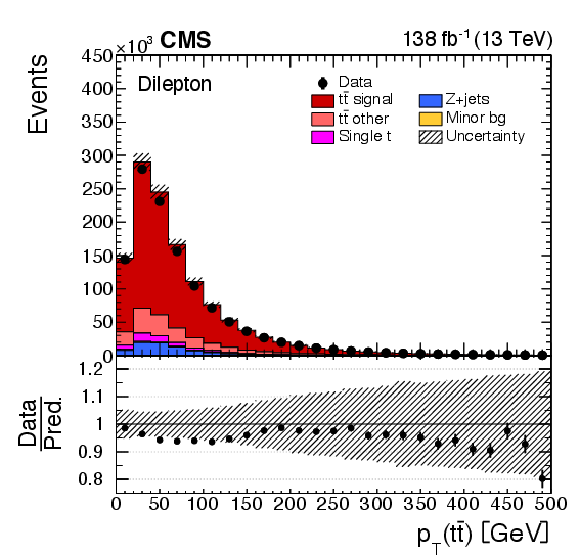
png pdf |
Figure 2-c:
Distributions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and jet multiplicity (lower right) obtained in selected events with the full kinematic reconstruction. For the first two distributions, ``t'' refers to both top quark and antiquark. The three dilepton channels ($ \mathrm{e}^+\mathrm{e}^- $, $ \mu^{+}\mu^{-} $, and $ \mathrm{e}^\pm\mu^\mp $) are added together. The data with vertical bars corresponding to their statistical uncertainties are plotted together with distributions of simulated signal and background processes. The hatched regions depict the systematic shape uncertainties in the signal and backgrounds (as detailed in Section 8). The lower panel in each plot shows the ratio of the observed data event yields to those expected in the simulation. |
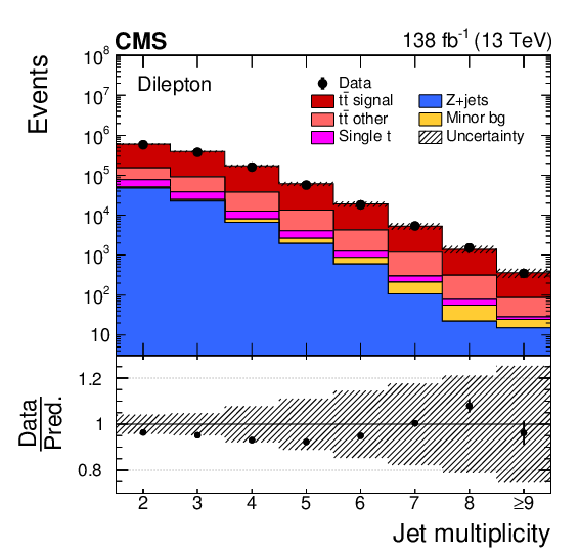
png pdf |
Figure 2-d:
Distributions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and jet multiplicity (lower right) obtained in selected events with the full kinematic reconstruction. For the first two distributions, ``t'' refers to both top quark and antiquark. The three dilepton channels ($ \mathrm{e}^+\mathrm{e}^- $, $ \mu^{+}\mu^{-} $, and $ \mathrm{e}^\pm\mu^\mp $) are added together. The data with vertical bars corresponding to their statistical uncertainties are plotted together with distributions of simulated signal and background processes. The hatched regions depict the systematic shape uncertainties in the signal and backgrounds (as detailed in Section 8). The lower panel in each plot shows the ratio of the observed data event yields to those expected in the simulation. |

png pdf |
Figure 3:
Distributions of $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (left) and $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) obtained in selected events with the full (upper) and the loose kinematic reconstruction (lower). Further details can be found in the caption of Fig. 2. |

png pdf |
Figure 3-a:
Distributions of $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (left) and $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) obtained in selected events with the full (upper) and the loose kinematic reconstruction (lower). Further details can be found in the caption of Fig. 2. |

png pdf |
Figure 3-b:
Distributions of $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (left) and $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) obtained in selected events with the full (upper) and the loose kinematic reconstruction (lower). Further details can be found in the caption of Fig. 2. |
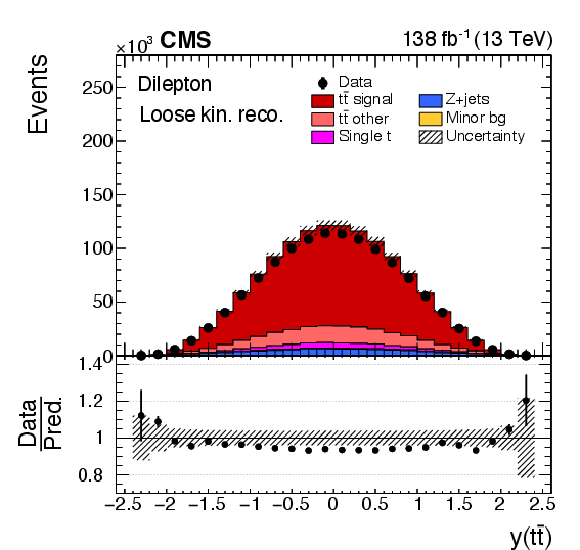
png pdf |
Figure 3-c:
Distributions of $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (left) and $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) obtained in selected events with the full (upper) and the loose kinematic reconstruction (lower). Further details can be found in the caption of Fig. 2. |
png pdf |
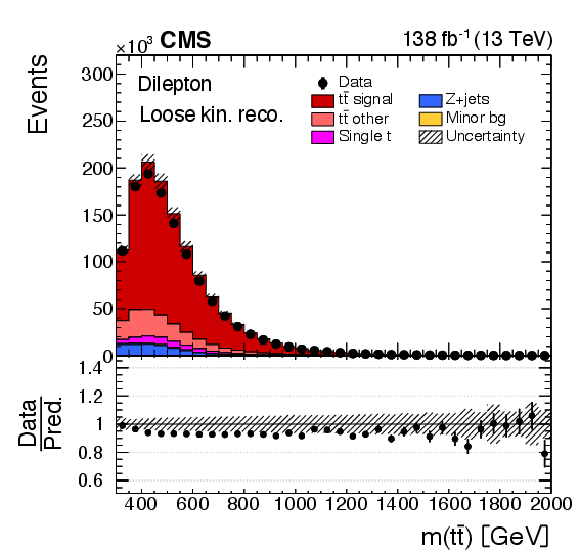
Figure 3-d:
Distributions of $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (left) and $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) obtained in selected events with the full (upper) and the loose kinematic reconstruction (lower). Further details can be found in the caption of Fig. 2. |
png pdf |
Figure 4:
Response matrices for the unfolding of the $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) distributions at the parton level, as extracted from the nominal POWHEG + PYTHIA 8 \ $ \mathrm{t} \overline{\mathrm{t}} $ signal simulation. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 10. |
png pdf |
Figure 4-a:
Response matrices for the unfolding of the $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) distributions at the parton level, as extracted from the nominal POWHEG + PYTHIA 8 \ $ \mathrm{t} \overline{\mathrm{t}} $ signal simulation. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 10. |
png pdf |
Figure 4-b:
Response matrices for the unfolding of the $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (right) distributions at the parton level, as extracted from the nominal POWHEG + PYTHIA 8 \ $ \mathrm{t} \overline{\mathrm{t}} $ signal simulation. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 10. |

png pdf |
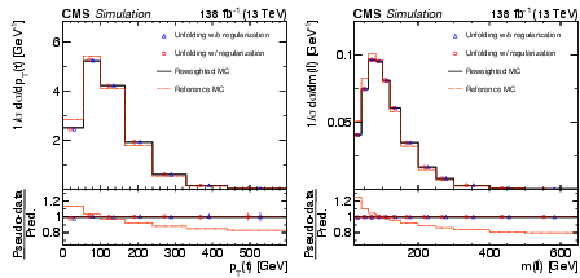
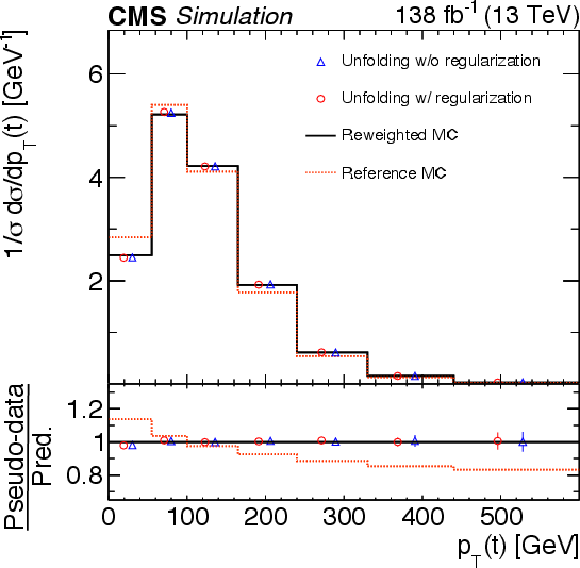
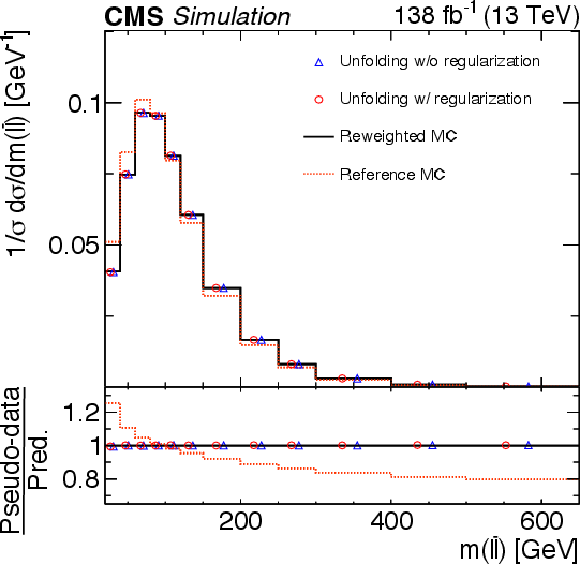
Figure 5:
Reweighting test for the extraction of the normalized differential cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ m(\ell\overline{\ell}) $ (right). The former cross section is measured at the parton level in the full phase space and the latter at the particle level in a fiducial phase space. The nominal $ \mathrm{t} \overline{\mathrm{t}} $ signal MC spectra are shown as dotted red histograms and the assumed true spectra, obtained from reweighting, as solid black histograms. The unfolded spectra, using pseudo-data based on the true spectra but using the nominal spectra for the detector corrections and bias vector in the regularization, are presented as open red circles. The unfolded spectra with the regularization switched off are also shown (open blue triangles). The statistical uncertainties in the unfolded cross sections are represented by a vertical bar on the corresponding points. The lower panel in each plot shows the ratios of the pseudo-data to the predicted spectra. |
png pdf |
Figure 5-a:
Reweighting test for the extraction of the normalized differential cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ m(\ell\overline{\ell}) $ (right). The former cross section is measured at the parton level in the full phase space and the latter at the particle level in a fiducial phase space. The nominal $ \mathrm{t} \overline{\mathrm{t}} $ signal MC spectra are shown as dotted red histograms and the assumed true spectra, obtained from reweighting, as solid black histograms. The unfolded spectra, using pseudo-data based on the true spectra but using the nominal spectra for the detector corrections and bias vector in the regularization, are presented as open red circles. The unfolded spectra with the regularization switched off are also shown (open blue triangles). The statistical uncertainties in the unfolded cross sections are represented by a vertical bar on the corresponding points. The lower panel in each plot shows the ratios of the pseudo-data to the predicted spectra. |
png pdf |
Figure 5-b:
Reweighting test for the extraction of the normalized differential cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (left) and $ m(\ell\overline{\ell}) $ (right). The former cross section is measured at the parton level in the full phase space and the latter at the particle level in a fiducial phase space. The nominal $ \mathrm{t} \overline{\mathrm{t}} $ signal MC spectra are shown as dotted red histograms and the assumed true spectra, obtained from reweighting, as solid black histograms. The unfolded spectra, using pseudo-data based on the true spectra but using the nominal spectra for the detector corrections and bias vector in the regularization, are presented as open red circles. The unfolded spectra with the regularization switched off are also shown (open blue triangles). The statistical uncertainties in the unfolded cross sections are represented by a vertical bar on the corresponding points. The lower panel in each plot shows the ratios of the pseudo-data to the predicted spectra. |
png pdf |
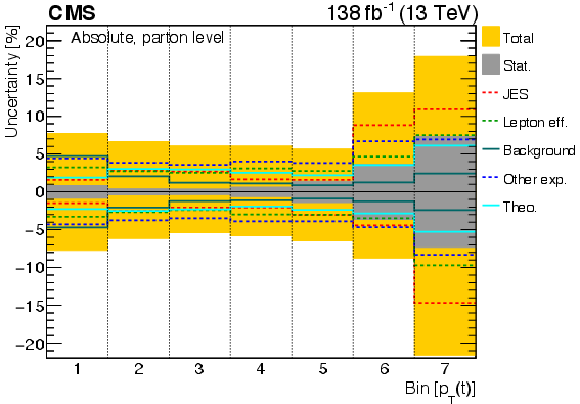
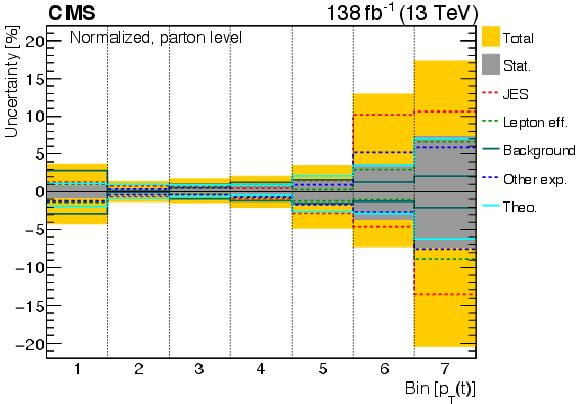
Figure 6:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several parton-level measurements: absolute $ p_{\mathrm{T}}(\mathrm{t}) $ (upper), normalized $ p_{\mathrm{T}}(\mathrm{t}) $ (middle), and normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 17. |
png pdf |
Figure 6-a:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several parton-level measurements: absolute $ p_{\mathrm{T}}(\mathrm{t}) $ (upper), normalized $ p_{\mathrm{T}}(\mathrm{t}) $ (middle), and normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 17. |

png pdf |
Figure 6-b:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several parton-level measurements: absolute $ p_{\mathrm{T}}(\mathrm{t}) $ (upper), normalized $ p_{\mathrm{T}}(\mathrm{t}) $ (middle), and normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 17. |
png pdf |
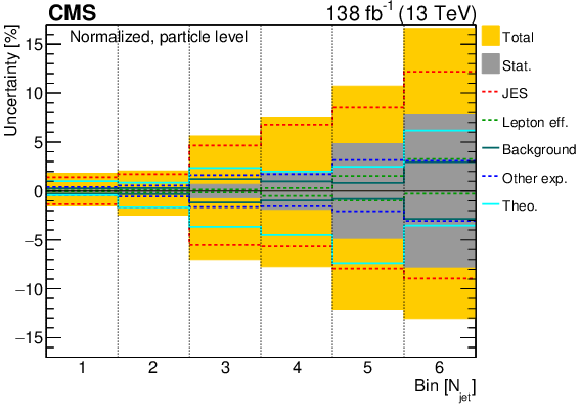
Figure 6-c:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several parton-level measurements: absolute $ p_{\mathrm{T}}(\mathrm{t}) $ (upper), normalized $ p_{\mathrm{T}}(\mathrm{t}) $ (middle), and normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 8 and 17. |
png pdf |
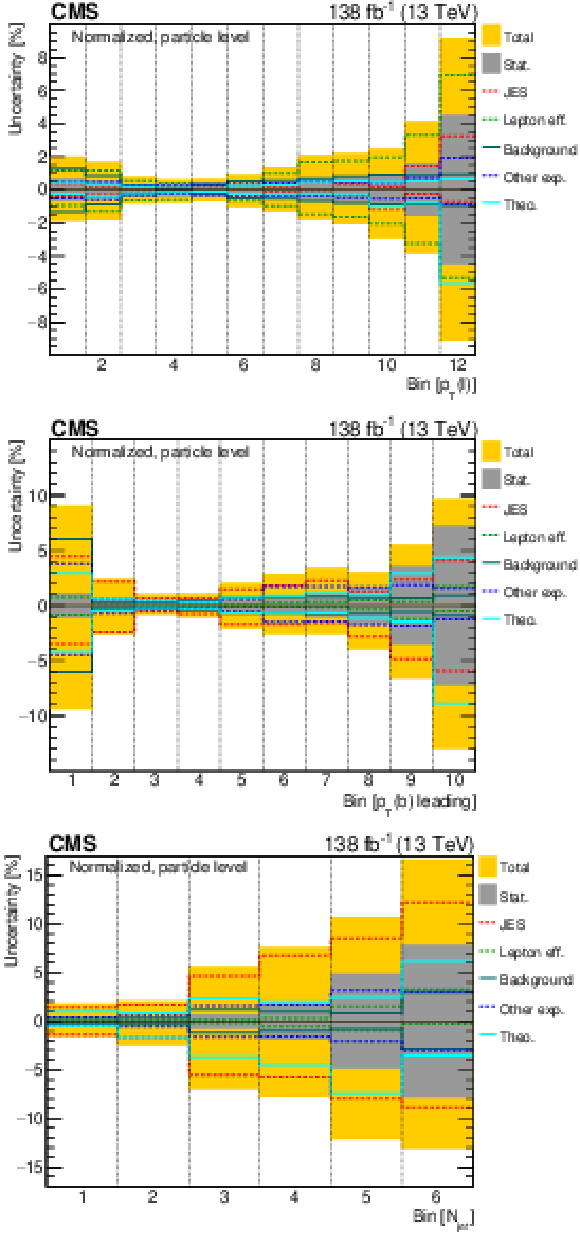
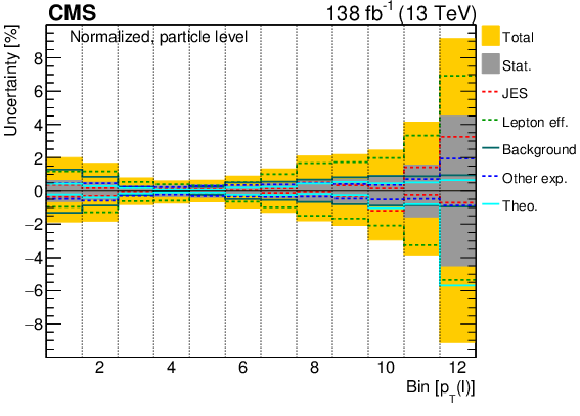
Figure 7:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several normalized particle-level measurements: $ p_{\mathrm{T}} $ of the lepton (upper), $ p_{\mathrm{T}} $ of the leading b jet (middle), and $ N_{\text{jet}} $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 24, 25, and 31. |

png pdf |
Figure 7-a:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several normalized particle-level measurements: $ p_{\mathrm{T}} $ of the lepton (upper), $ p_{\mathrm{T}} $ of the leading b jet (middle), and $ N_{\text{jet}} $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 24, 25, and 31. |
png pdf |
Figure 7-b:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several normalized particle-level measurements: $ p_{\mathrm{T}} $ of the lepton (upper), $ p_{\mathrm{T}} $ of the leading b jet (middle), and $ N_{\text{jet}} $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 24, 25, and 31. |

png pdf |
Figure 7-c:
The various sources of systematic uncertainty and their relative contributions to the overall uncertainty are shown for several normalized particle-level measurements: $ p_{\mathrm{T}} $ of the lepton (upper), $ p_{\mathrm{T}} $ of the leading b jet (middle), and $ N_{\text{jet}} $ (lower). The statistical uncertainties and the total uncertainties (statistical and systematic uncertainties added in quadrature) are shown as grey and yellow bands, respectively. The ranges of the observables for a given bin number can be read off from the corresponding cross section distributions in Figs. 24, 25, and 31. |
png pdf |
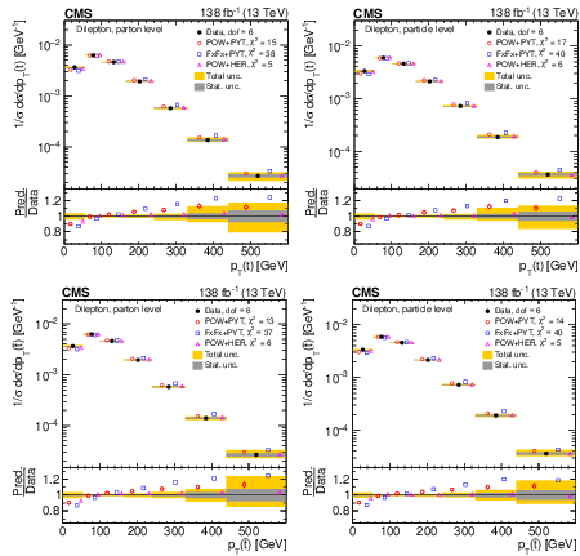
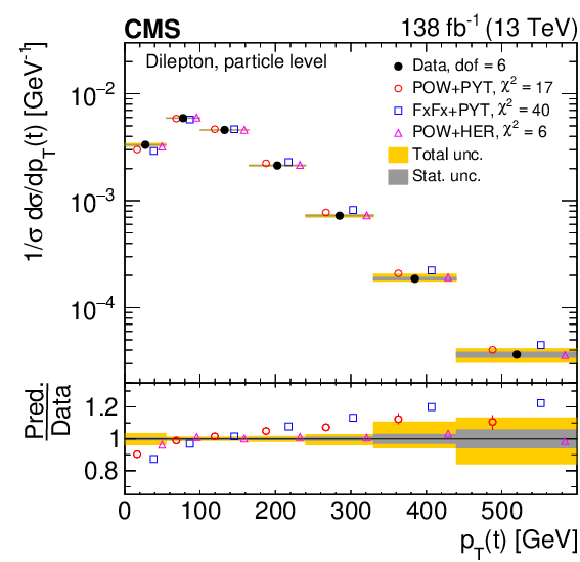
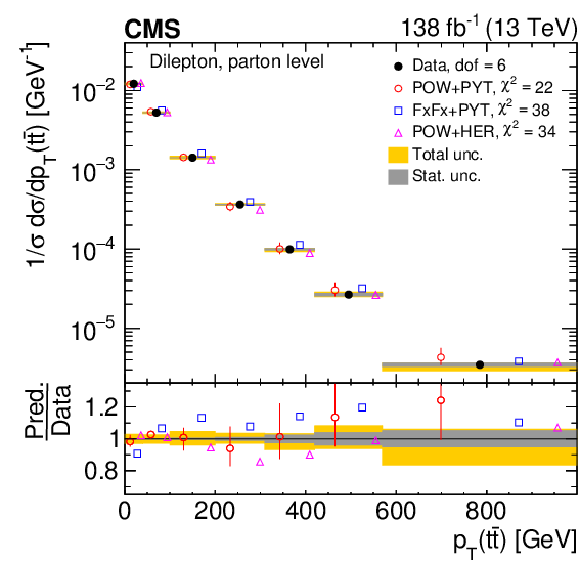
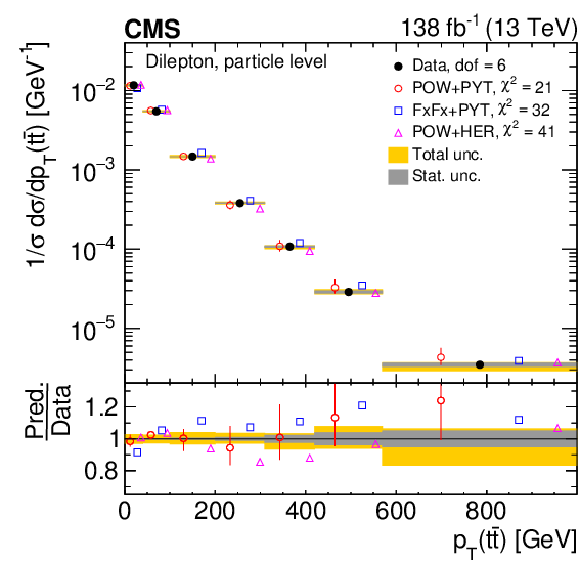
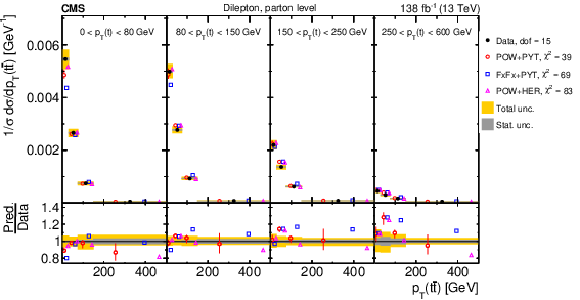
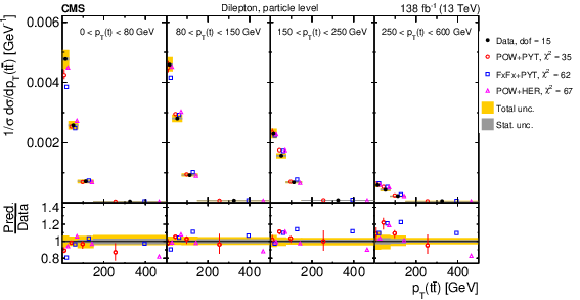
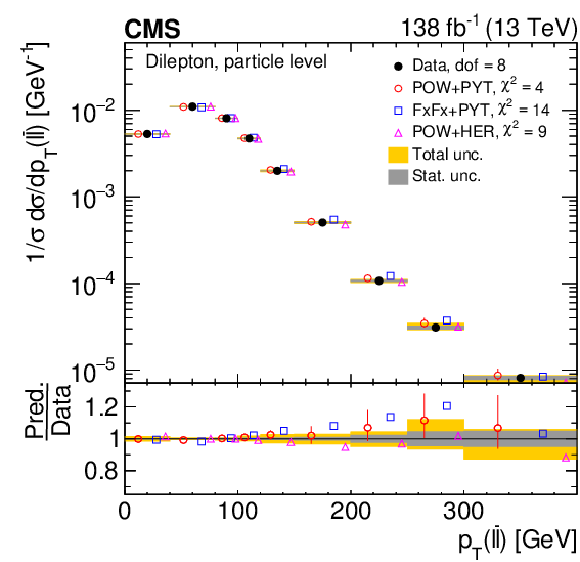
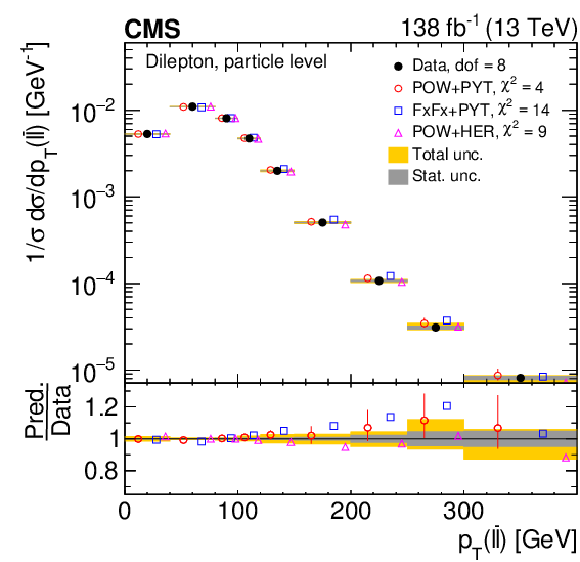
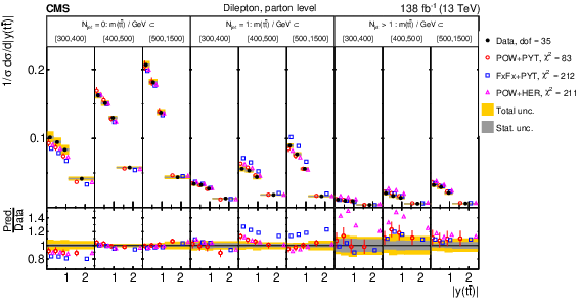
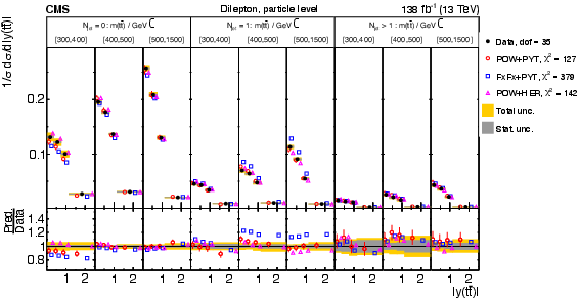
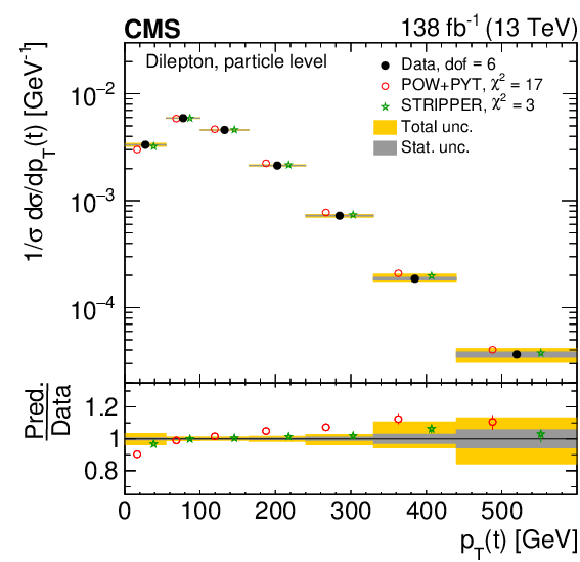
Figure 8:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 8-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 8-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 8-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 8-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
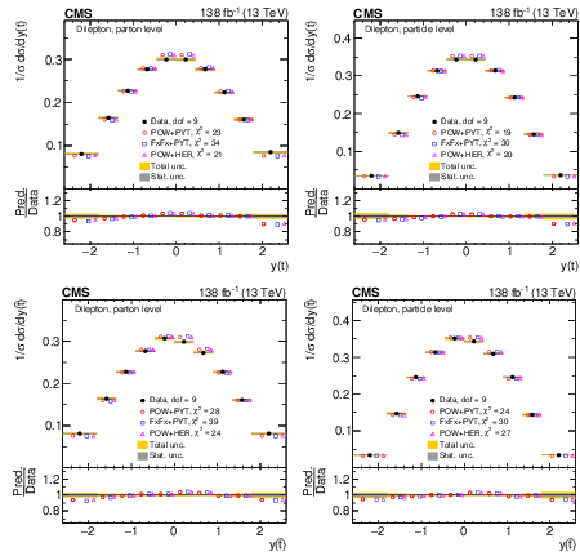
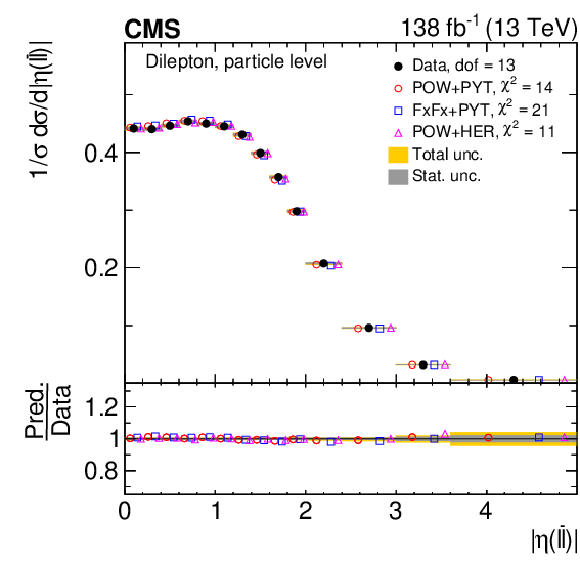
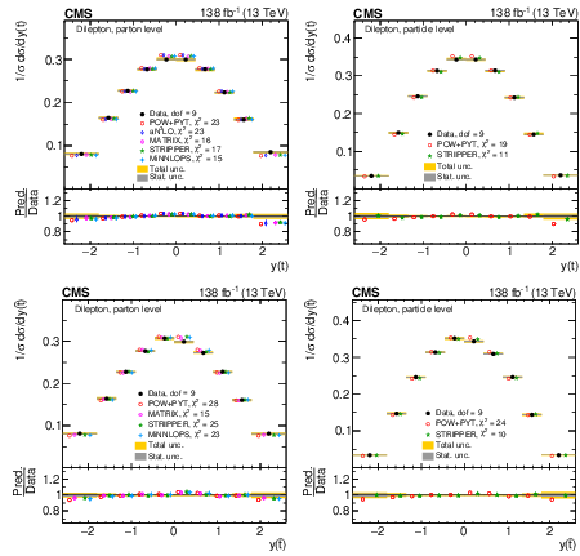
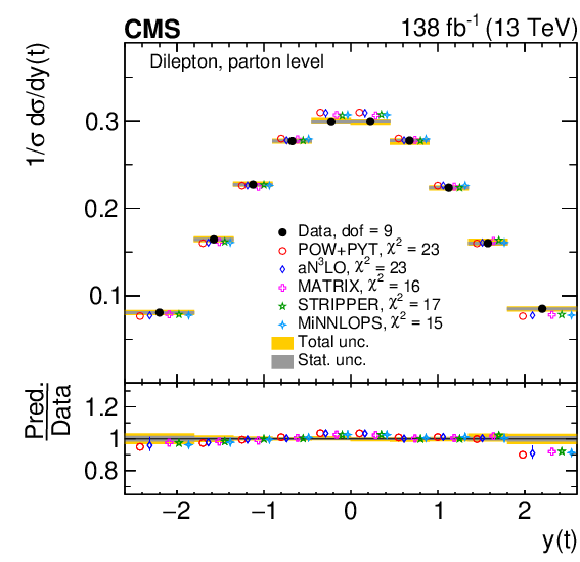
Figure 9:
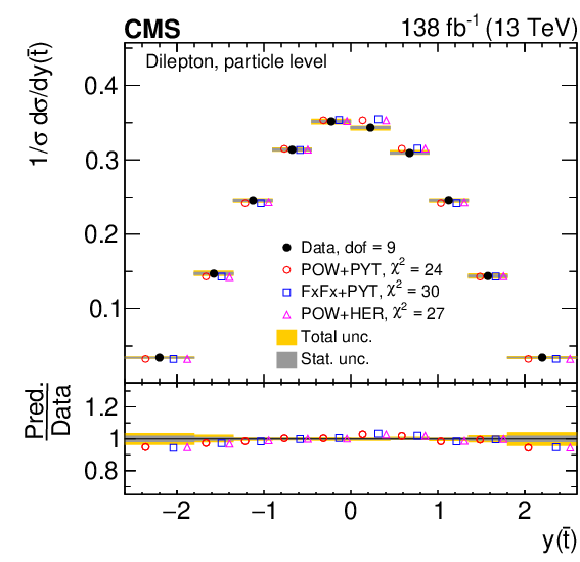
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 9-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 9-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 9-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 9-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
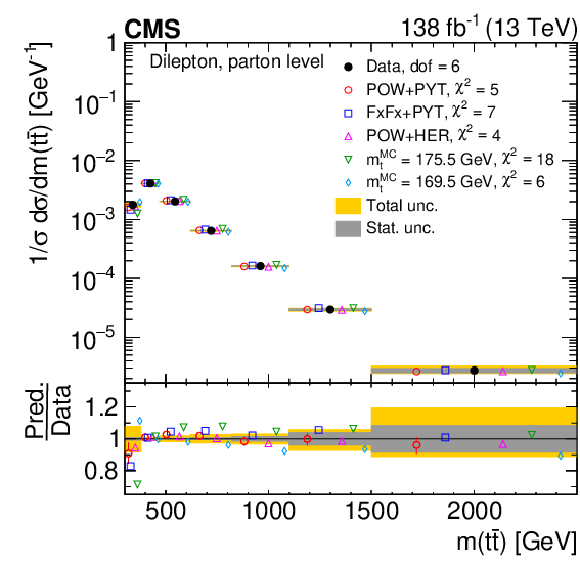
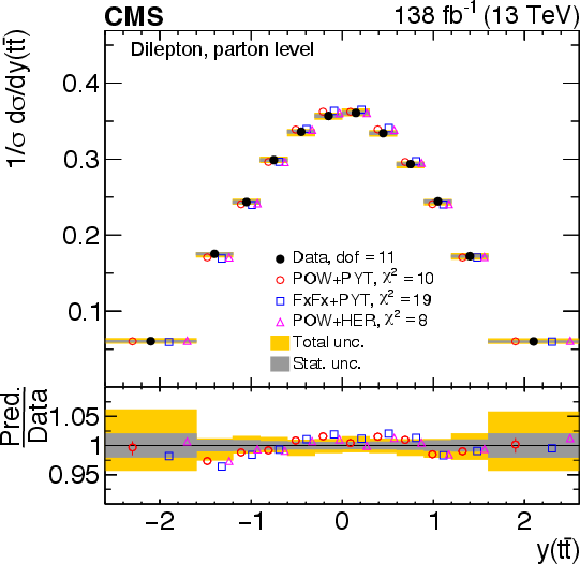
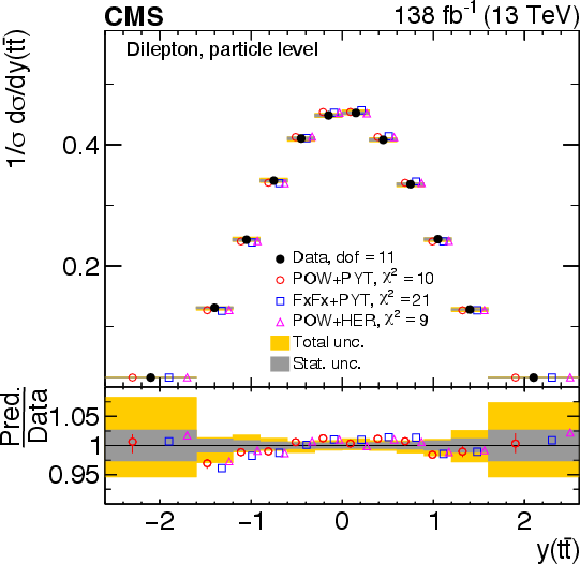
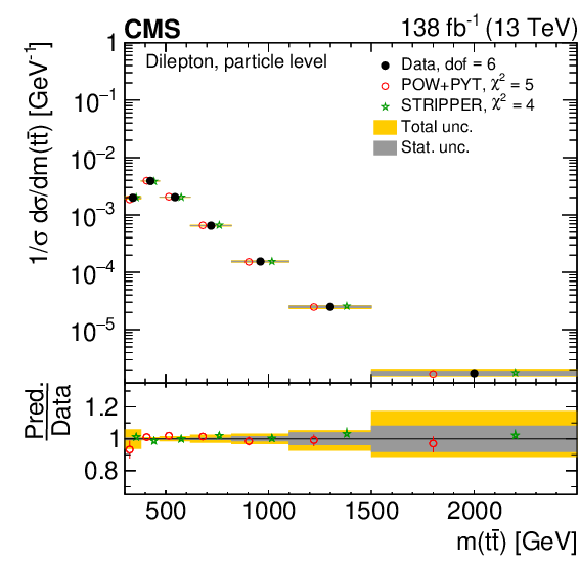
Figure 10:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 10-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 10-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 10-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 10-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 10-e:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 10-f:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 8. |
png pdf |
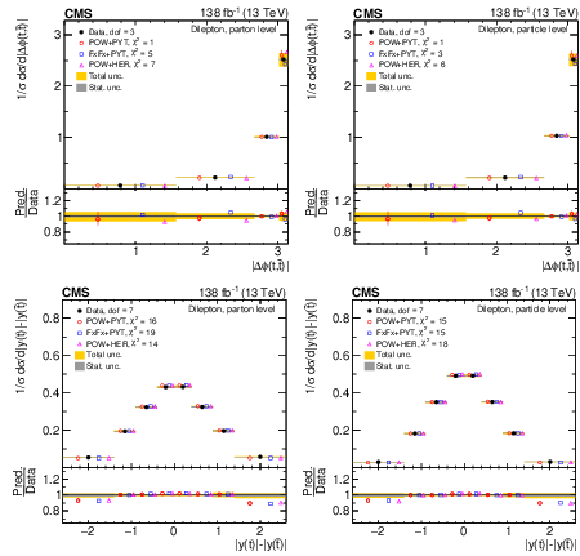
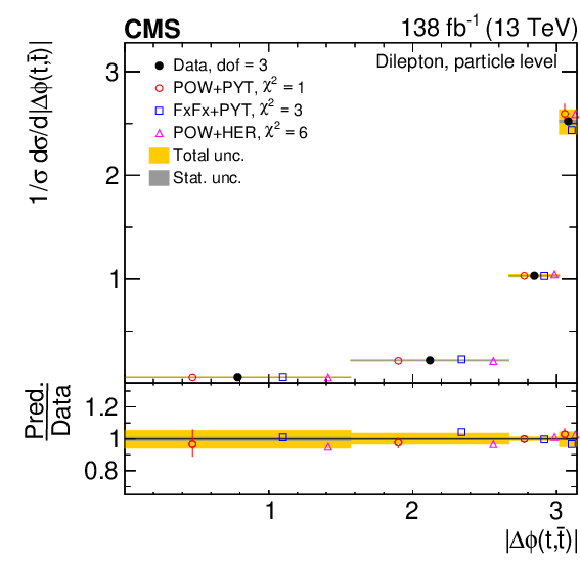
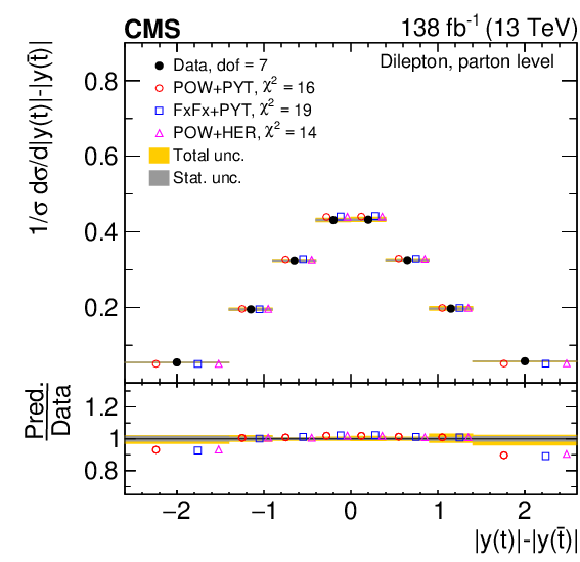
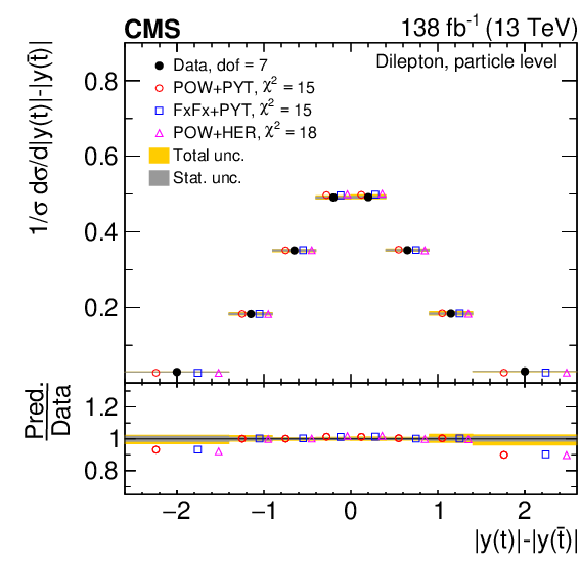
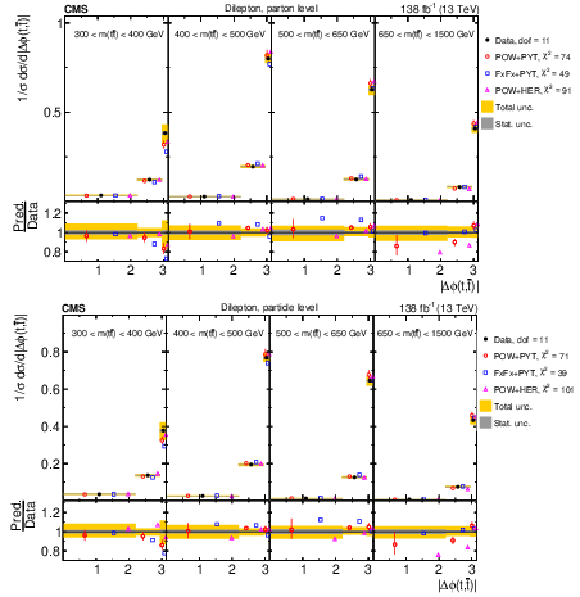
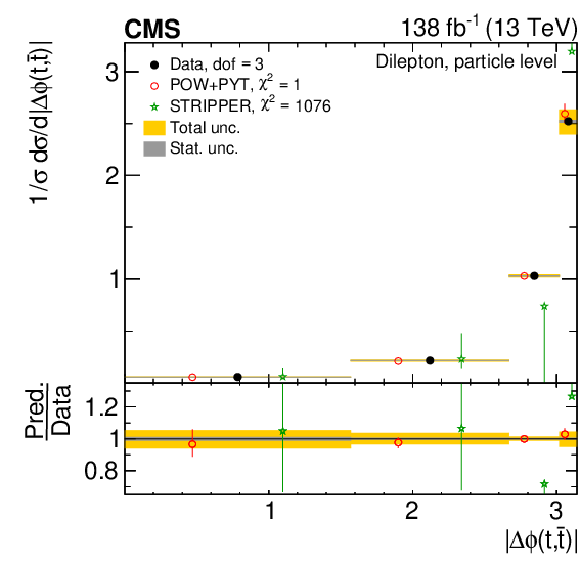
Figure 11:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 11-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 11-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 11-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 11-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
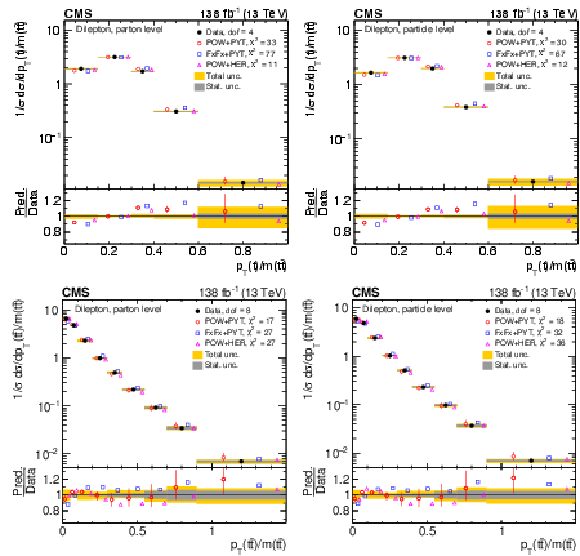
Figure 12:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 12-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 12-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 12-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 12-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
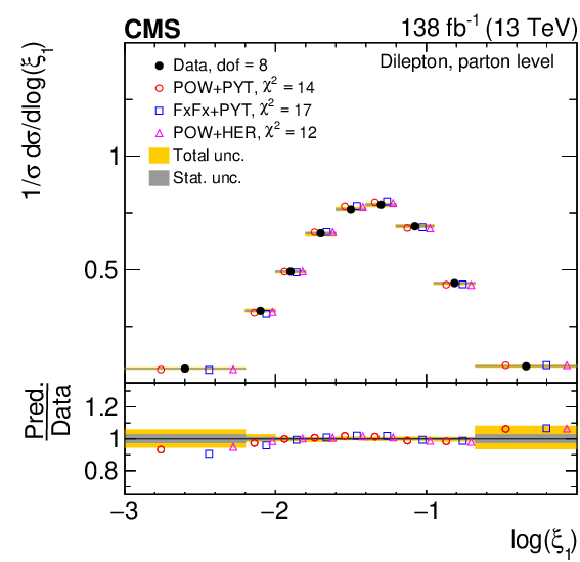
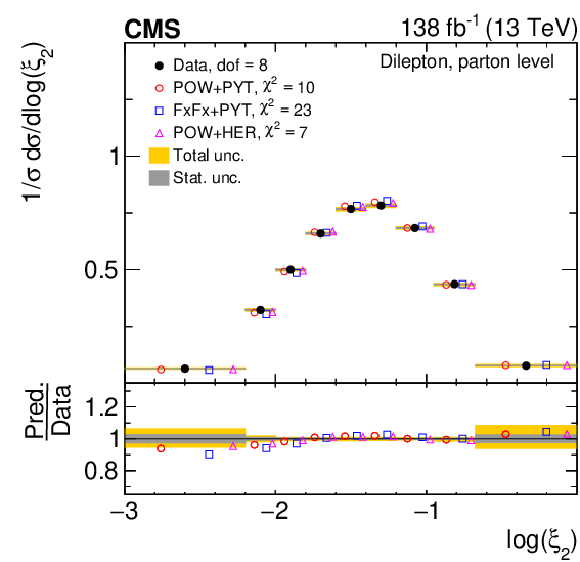
Figure 13:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 13-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 13-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |
png pdf |
Figure 13-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
Figure 13-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 8. |

png pdf |
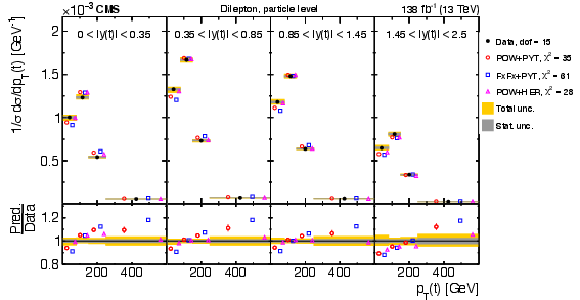
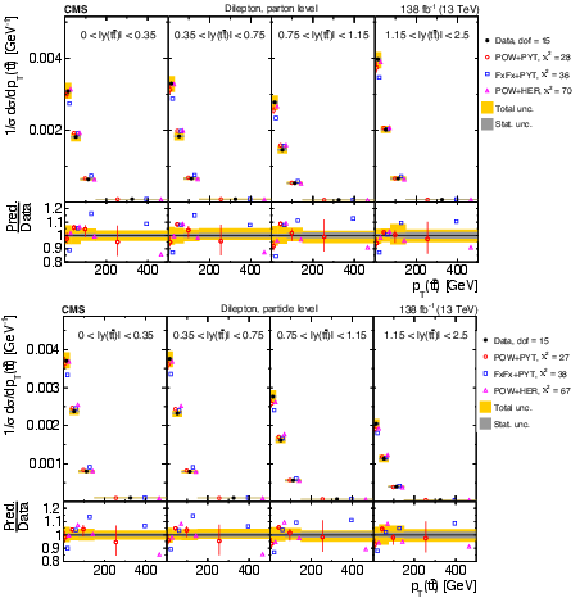
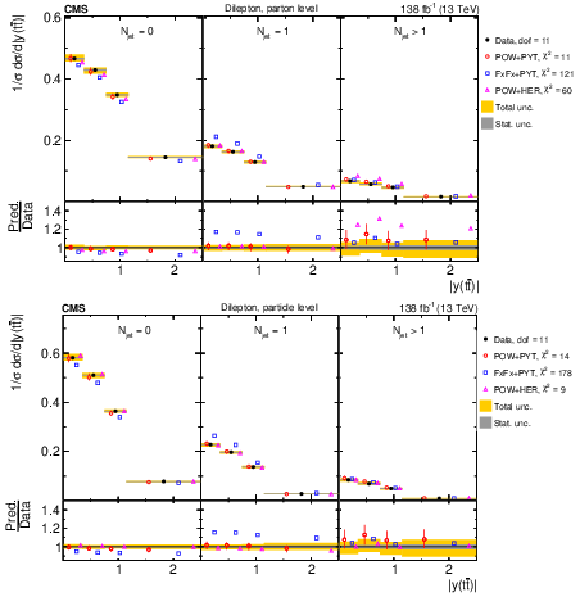
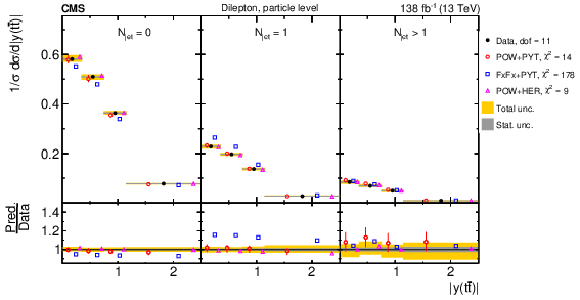
Figure 14:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 14-a:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 14-b:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 15:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 15-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 15-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 16:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 16-a:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 16-b:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
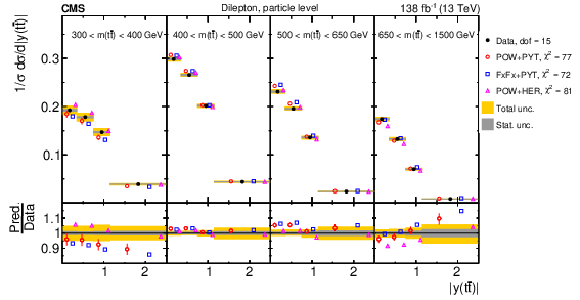
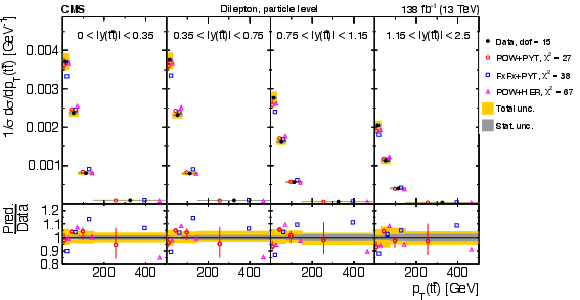
Figure 17:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 17-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 17-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
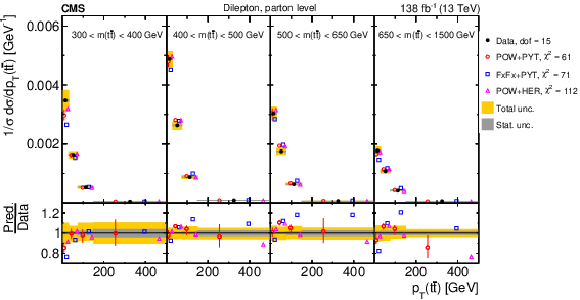
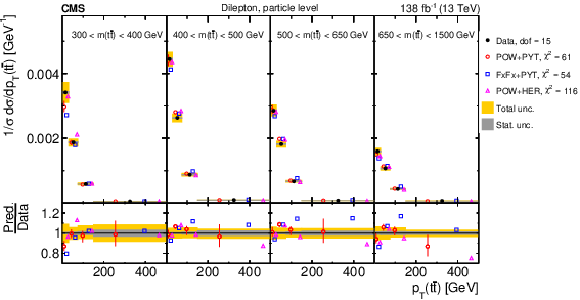
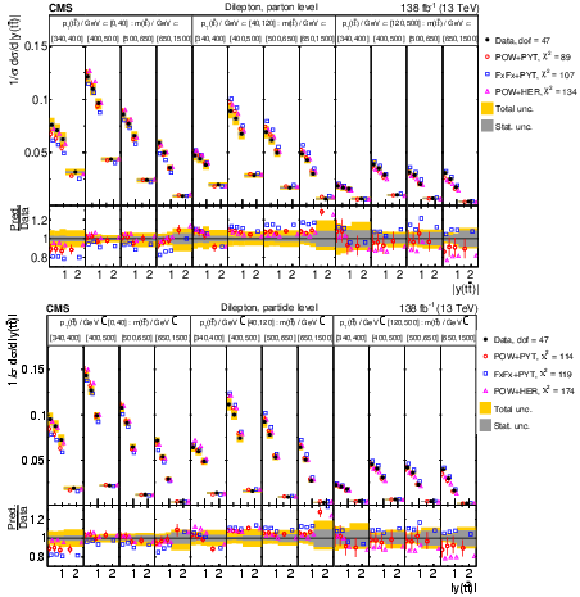
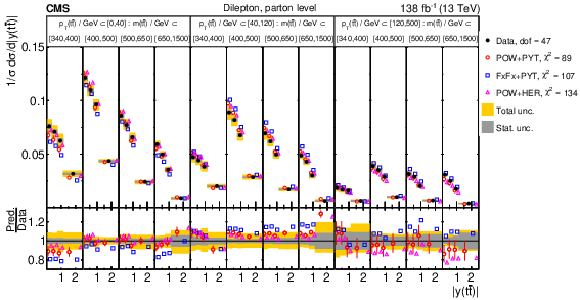
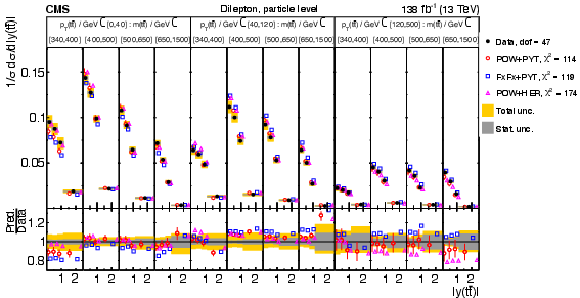
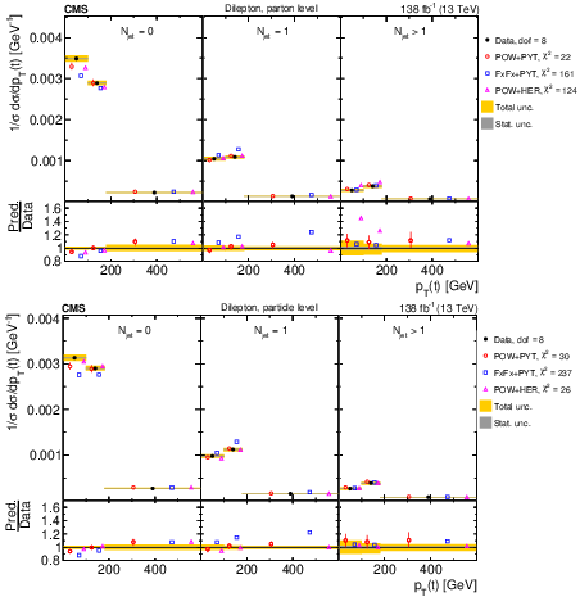
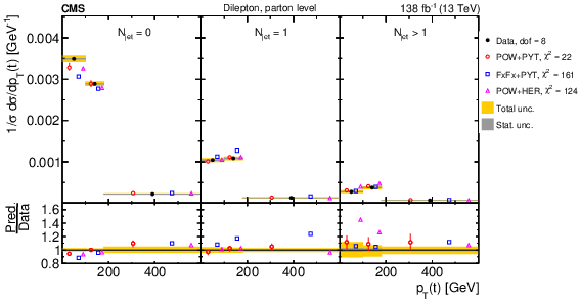
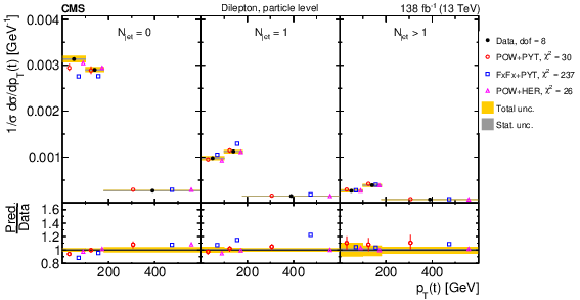
Figure 18:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 18-a:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 18-b:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 19:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 19-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 19-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
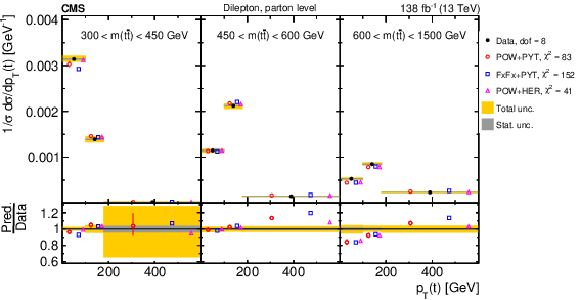
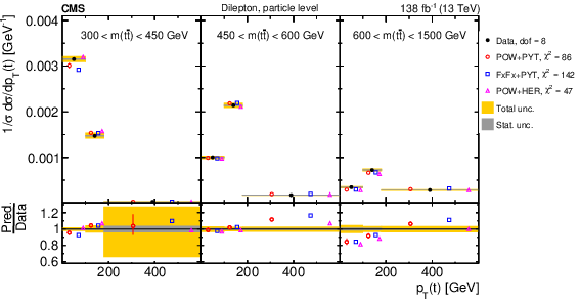
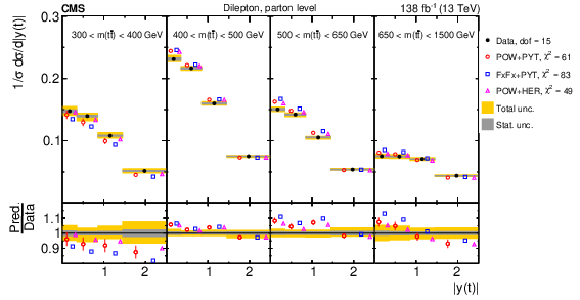
Figure 20:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 20-a:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 20-b:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 21:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 21-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 21-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 22:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 22-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 22-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 23:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
Figure 23-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |
png pdf |
Figure 23-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 14. |

png pdf |
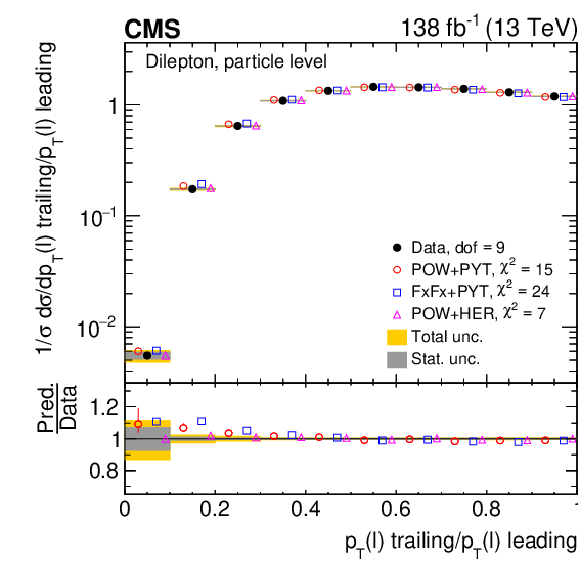
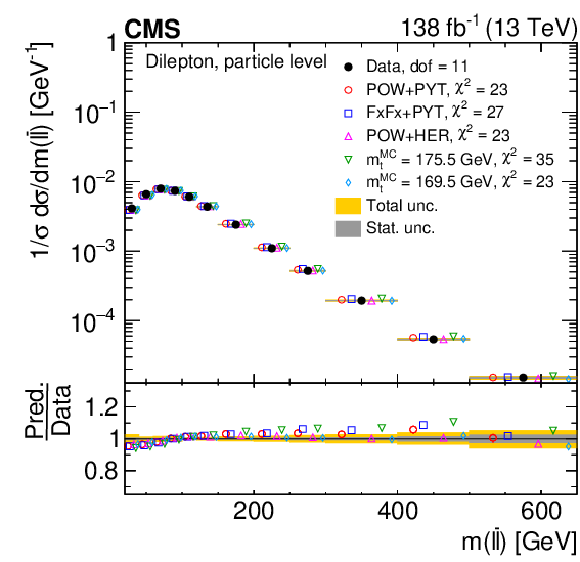
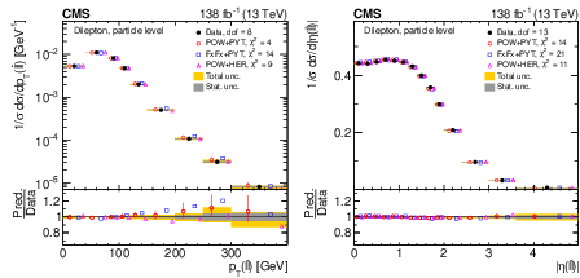
Figure 24:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 24-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 24-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 24-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
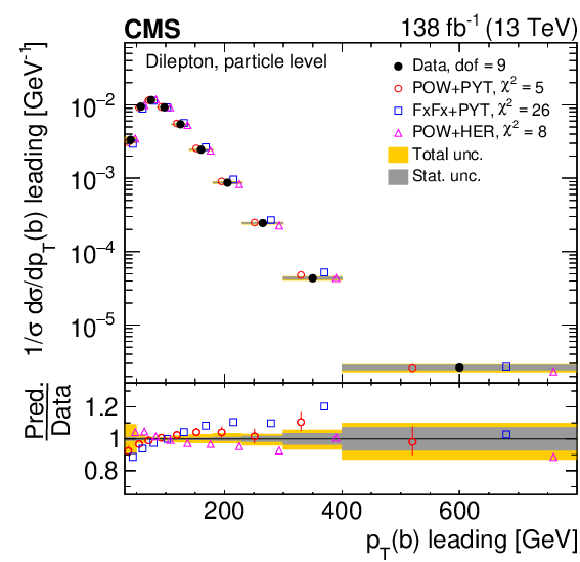
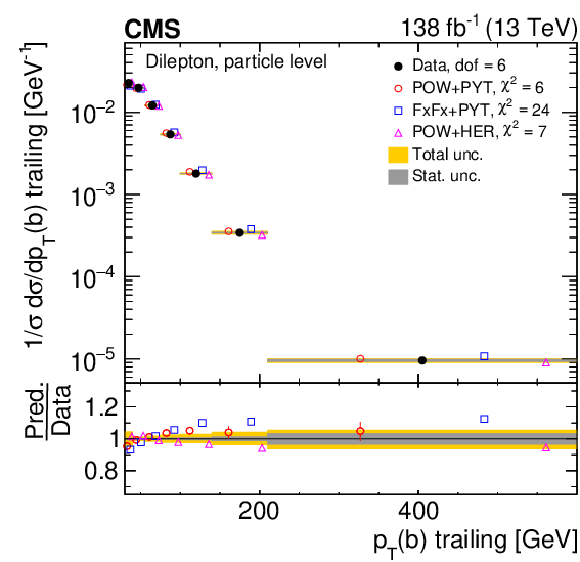
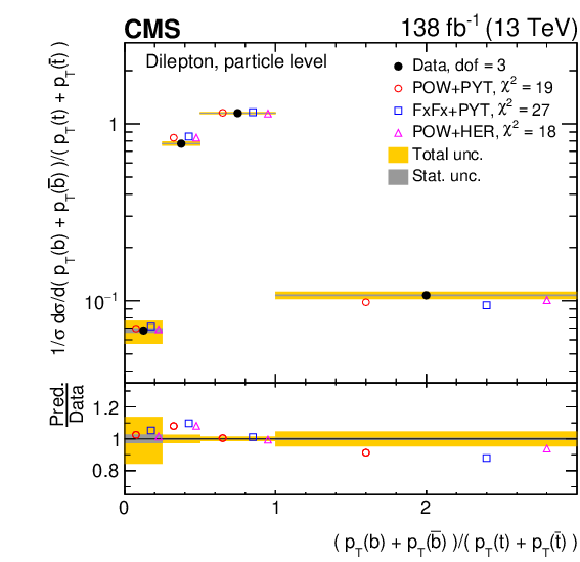
Figure 25:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 25-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 25-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 25-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 24. |
png pdf |
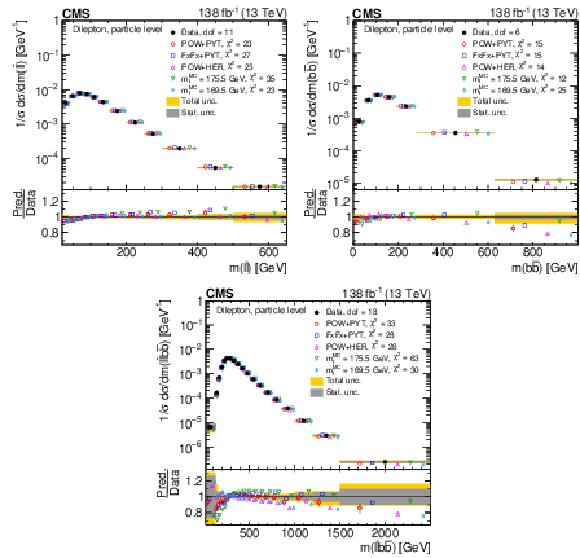
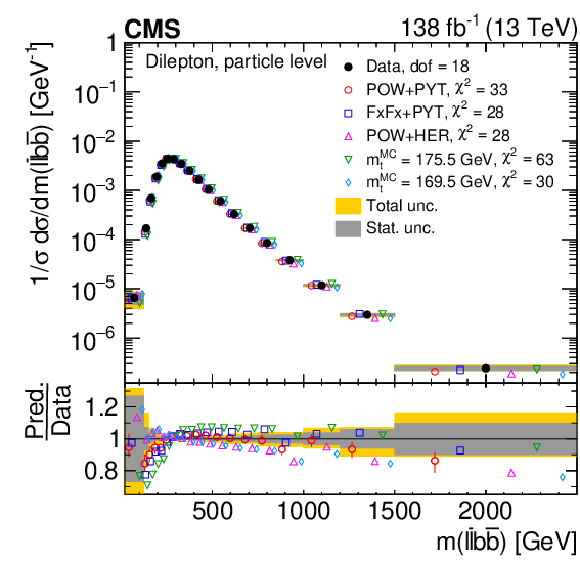
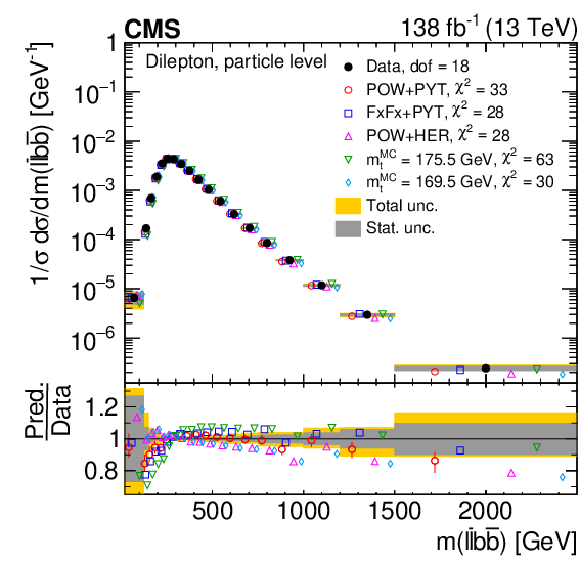
Figure 26:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 26-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 26-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 26-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). The distributions are also compared to POWHEG + PYTHIA 8 (`POW-PYT') simulations with different values of $ m_{\mathrm{t}}^{\text{MC}} $. Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 27:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 27-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |
png pdf |
Figure 27-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 28:
Normalized $ [|\eta(\ell\overline{\ell})|,\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 29:
Normalized $ [|\eta(\ell\overline{\ell})|,\, p_{\mathrm{T}}(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |

png pdf |
Figure 30:
Normalized $ [p_{\mathrm{T}}(\ell\overline{\ell}),\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 24. |
png pdf |
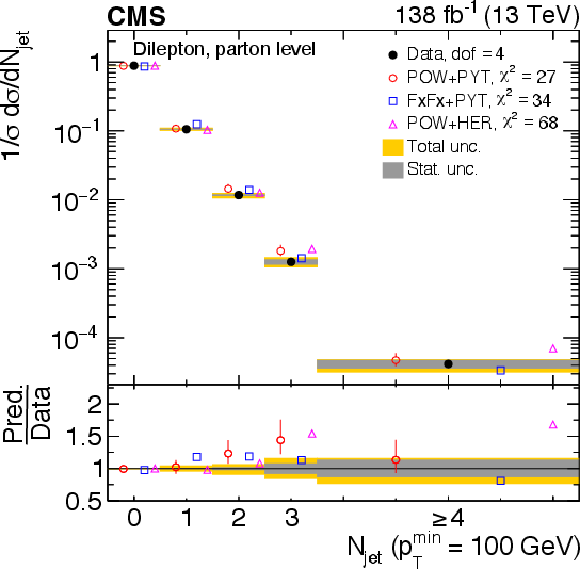
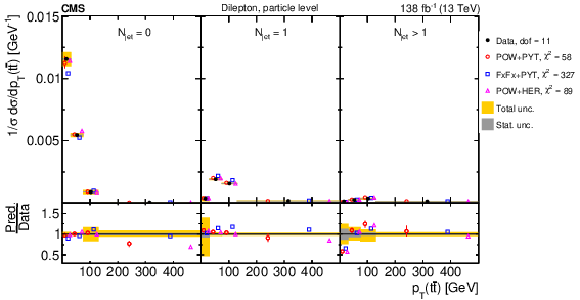
Figure 31:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 31-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 31-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 31-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
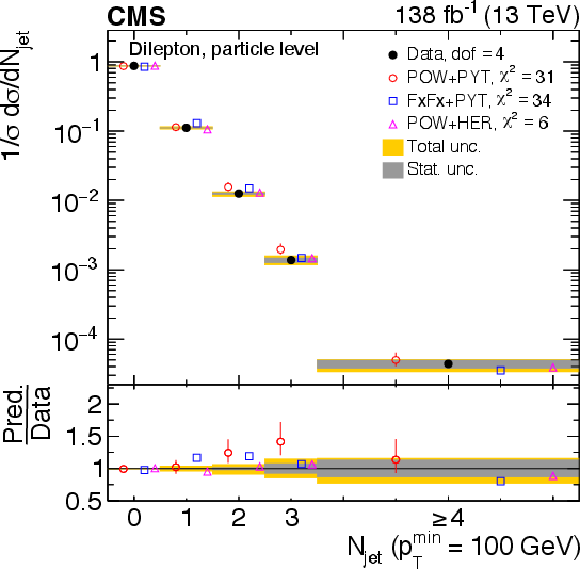
Figure 31-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
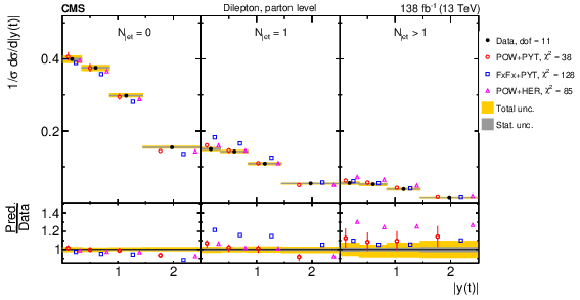
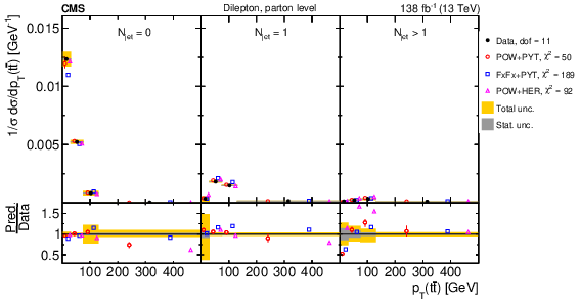
Figure 32:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 32-a:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 32-b:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
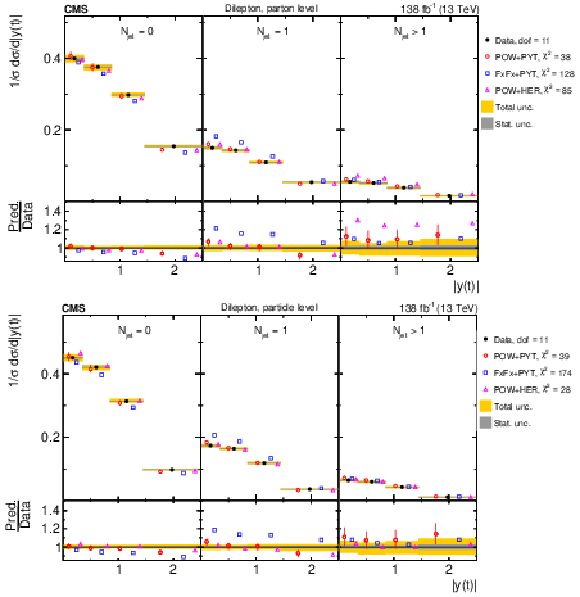
Figure 33:
Normalized $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 33-a:
Normalized $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 33-b:
Normalized $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 34:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 34-a:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 34-b:
Normalized $ [N_{\text{jet}},\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
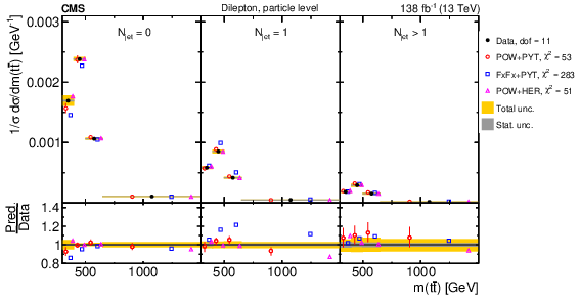
Figure 35:
Normalized $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 35-a:
Normalized $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 35-b:
Normalized $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
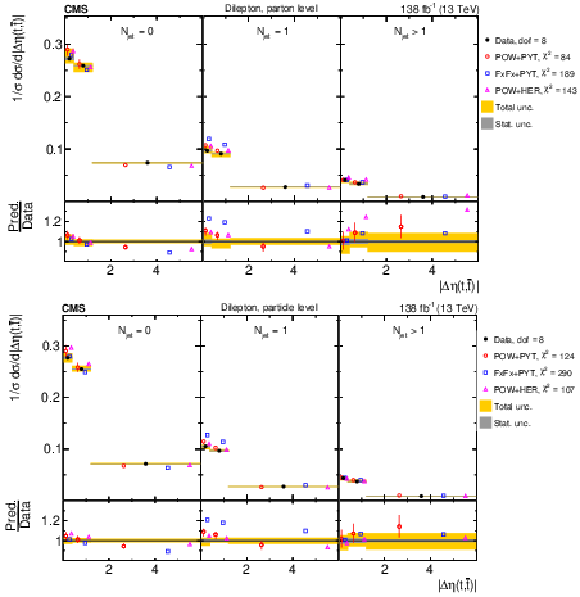
Figure 36:
Normalized $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 36-a:
Normalized $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 36-b:
Normalized $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
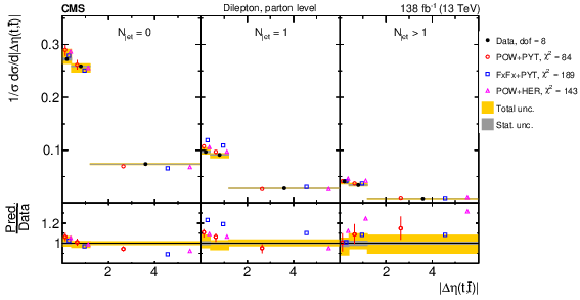
Figure 37:
Normalized $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 37-a:
Normalized $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 37-b:
Normalized $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
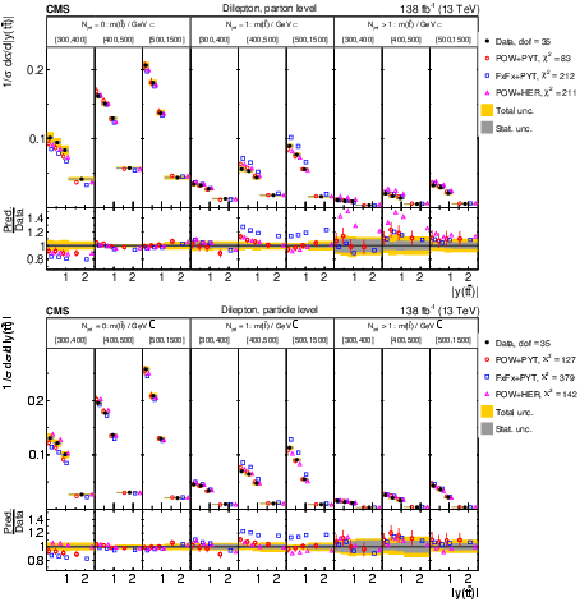
Figure 38:
Normalized $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 38-a:
Normalized $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 38-b:
Normalized $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
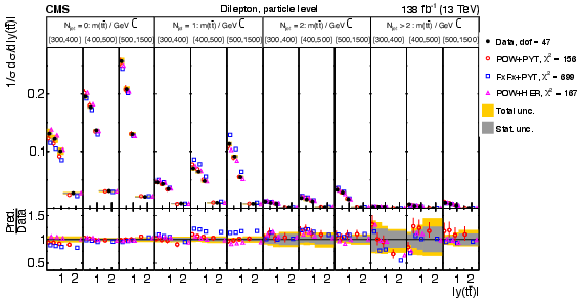
Figure 39:
Normalized $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 39-a:
Normalized $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 39-b:
Normalized $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |

png pdf |
Figure 40:
Normalized $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 40-a:
Normalized $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
Figure 40-b:
Normalized $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 32. |
png pdf |
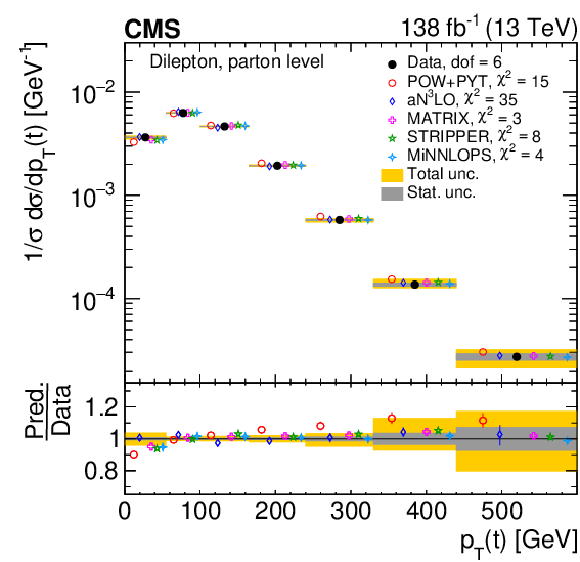
Figure 41:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 41-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 41-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 41-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
png pdf |
Figure 41-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 42:
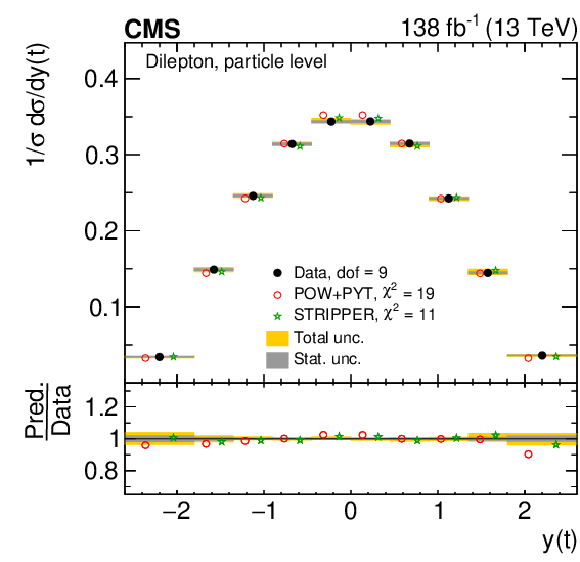
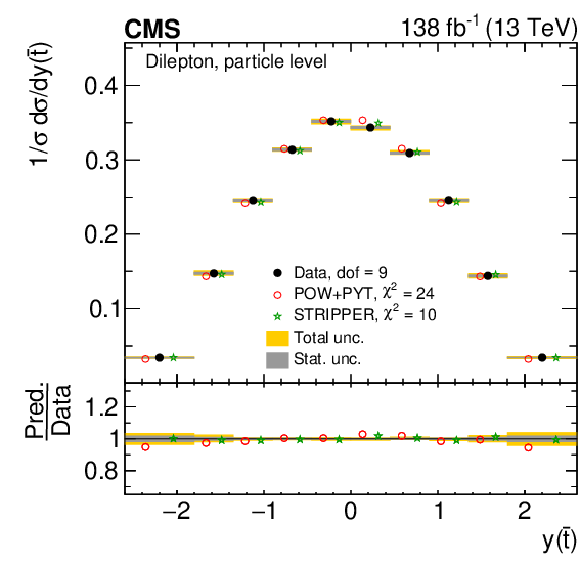
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
png pdf |
Figure 42-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |

png pdf |
Figure 42-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
png pdf |
Figure 42-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
png pdf |
Figure 42-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |

png pdf |
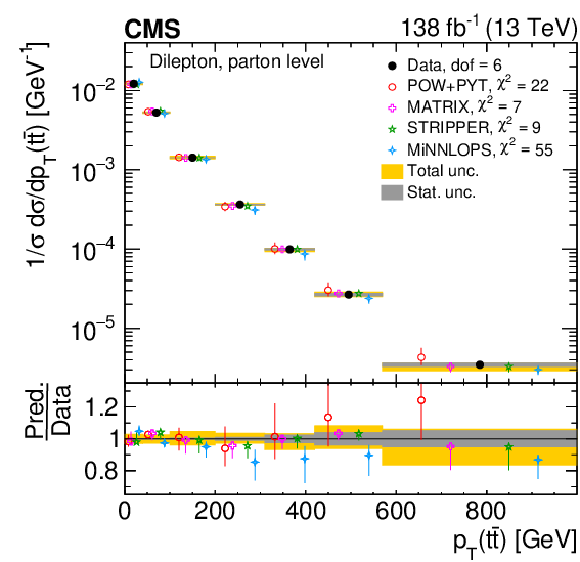
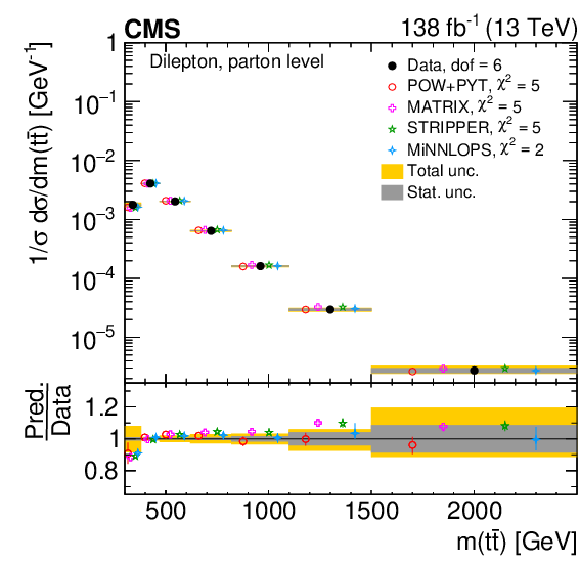
Figure 43:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |

png pdf |
Figure 43-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
png pdf |
Figure 43-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
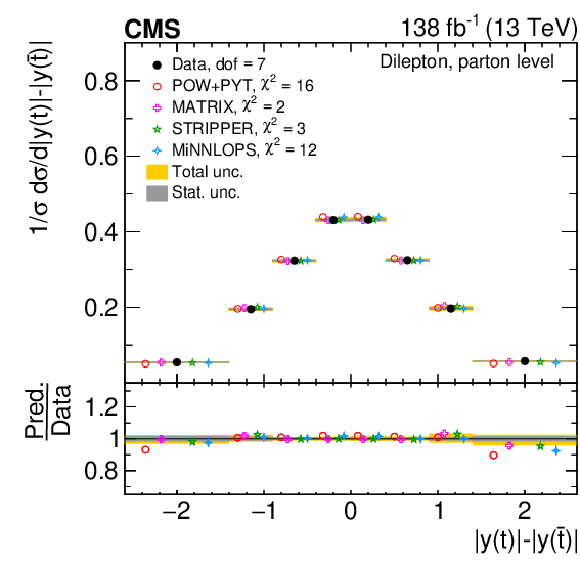
png pdf |
Figure 43-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
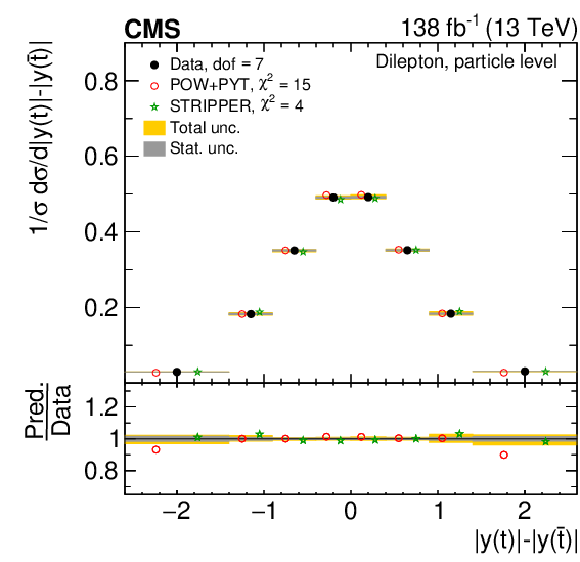
png pdf |
Figure 43-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
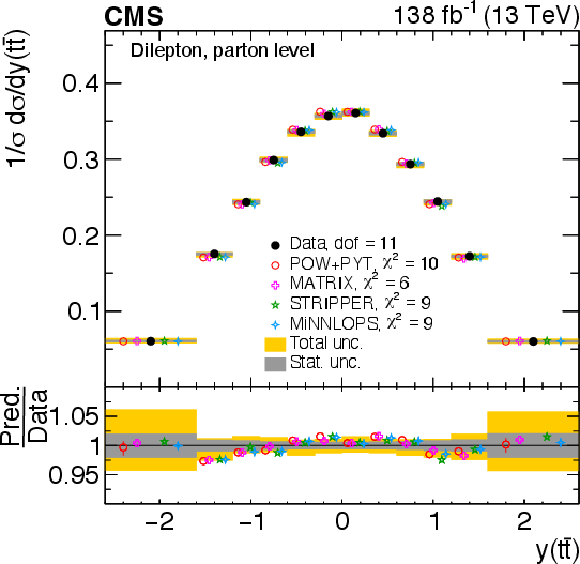
png pdf |
Figure 43-e:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
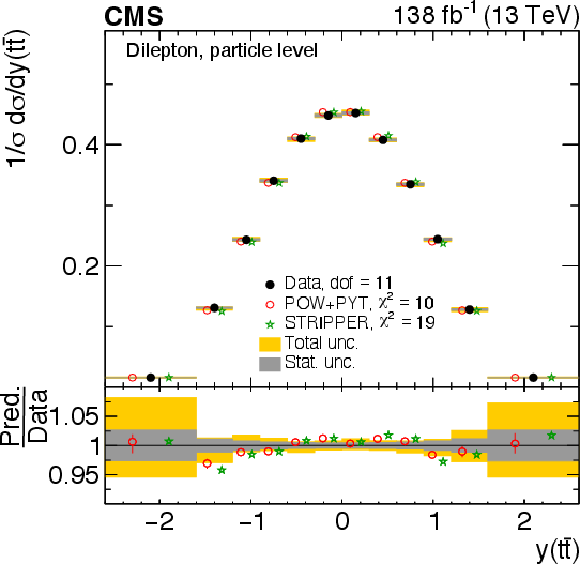
png pdf |
Figure 43-f:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |

png pdf |
Figure 44:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
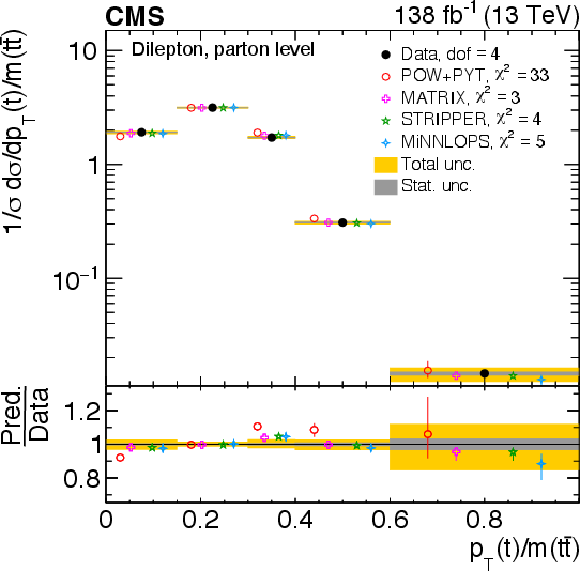
png pdf |
Figure 44-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
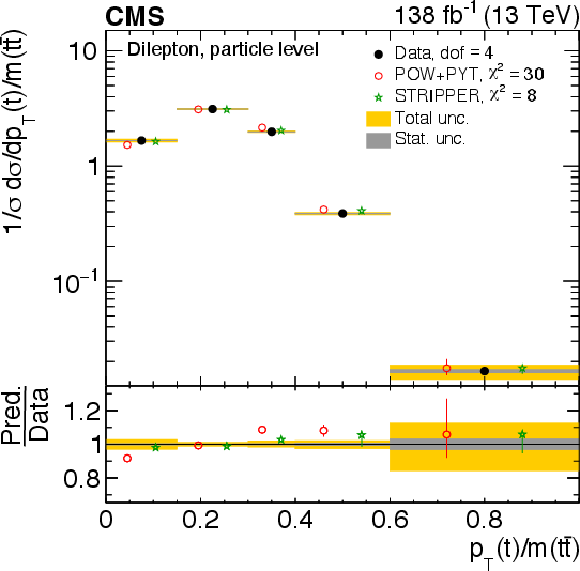
png pdf |
Figure 44-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |

png pdf |
Figure 44-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
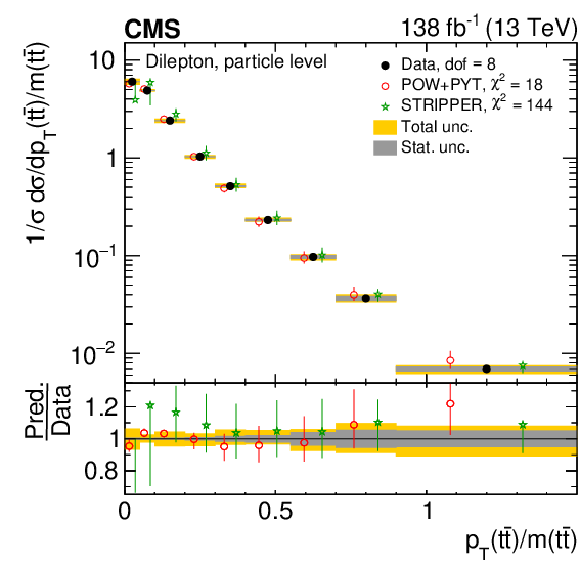
png pdf |
Figure 44-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
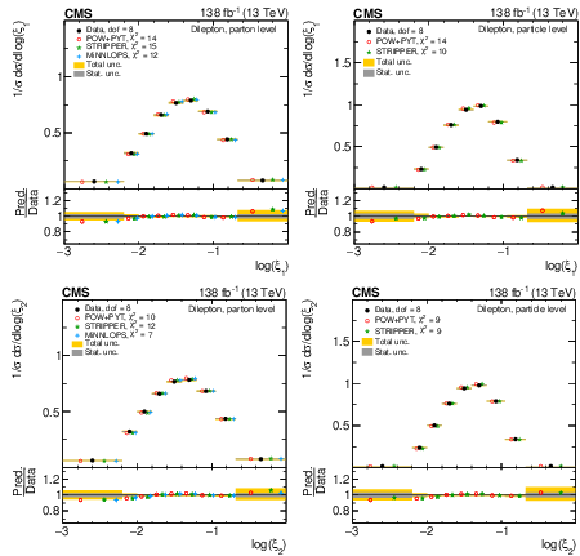
png pdf |
Figure 45:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
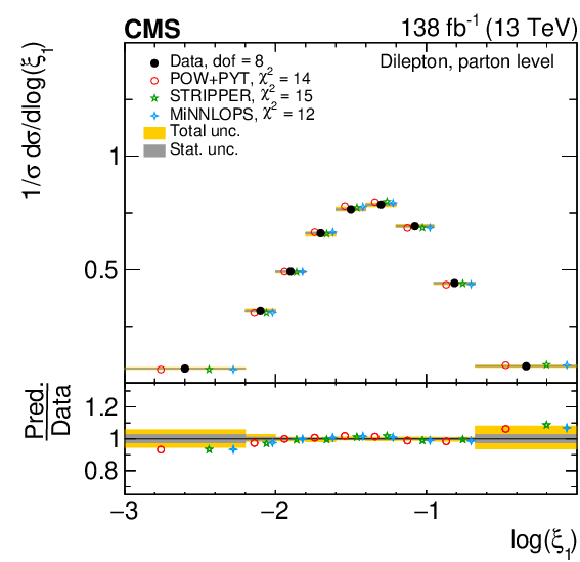
png pdf |
Figure 45-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
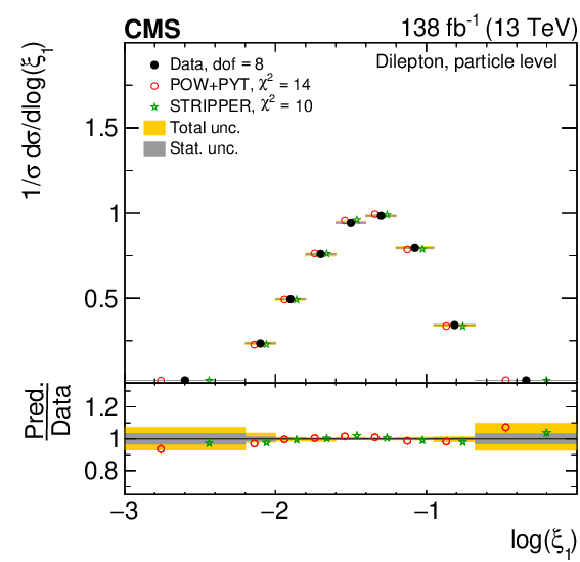
png pdf |
Figure 45-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
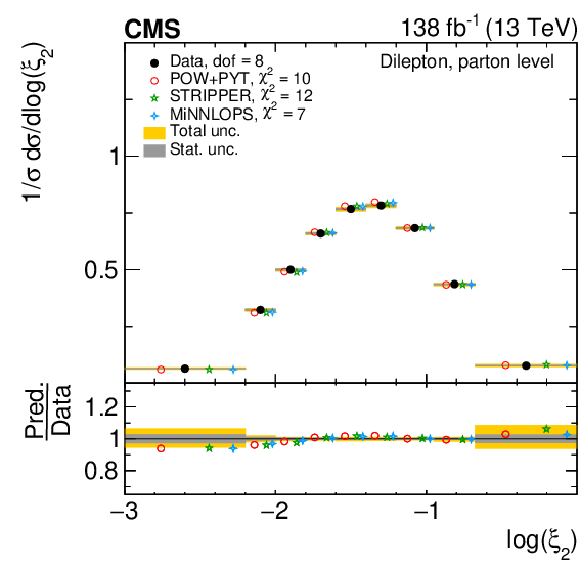
png pdf |
Figure 45-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
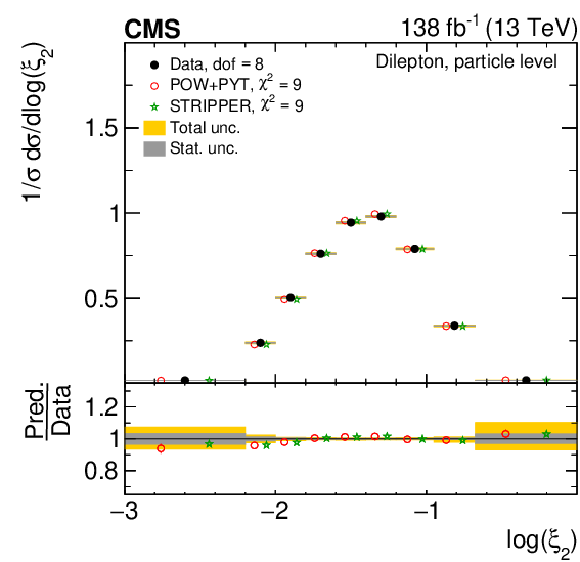
png pdf |
Figure 45-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 41. |
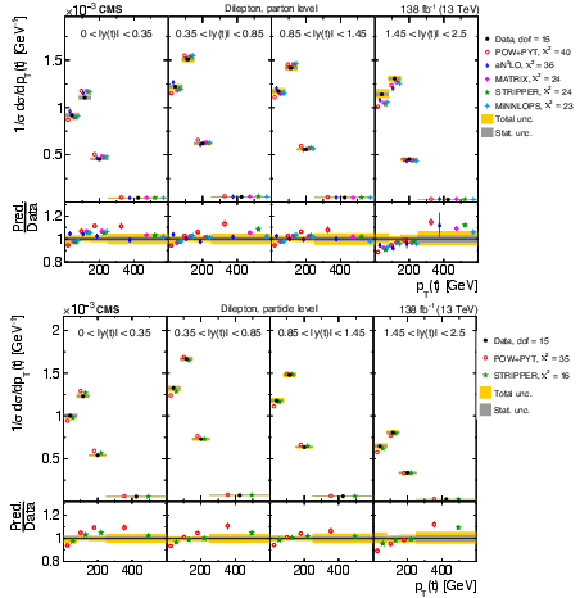
png pdf |
Figure 46:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 41. |
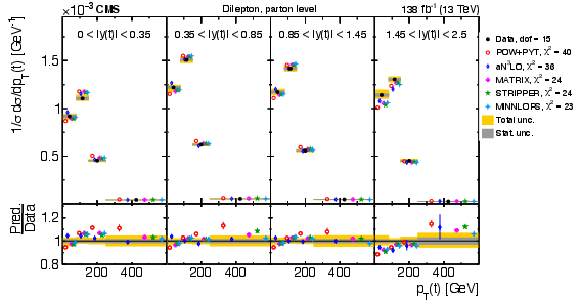
png pdf |
Figure 46-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 41. |
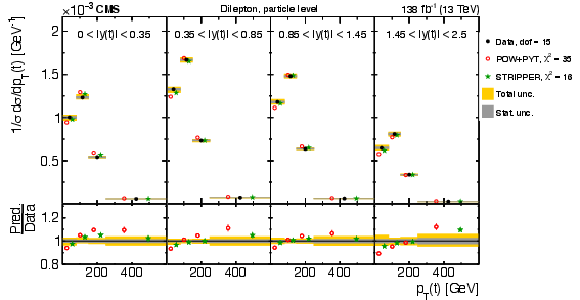
png pdf |
Figure 46-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 41. |
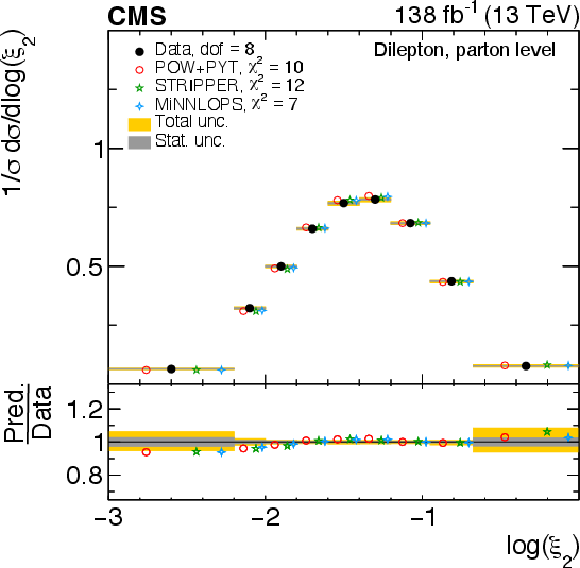
png pdf |
Figure 46-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 41. |
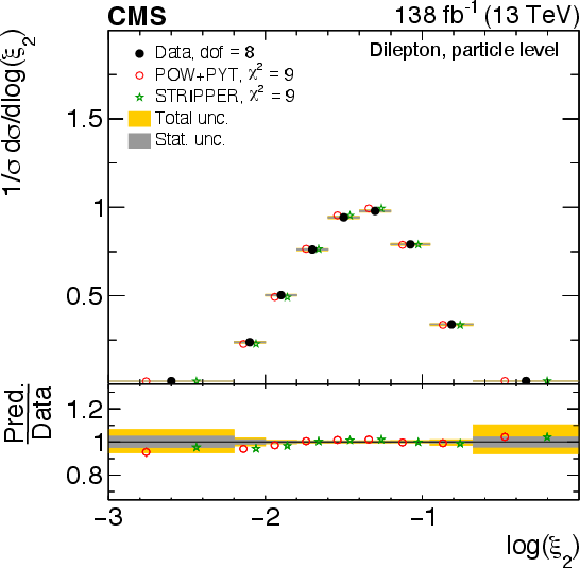
png pdf |
Figure 46-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 41. |
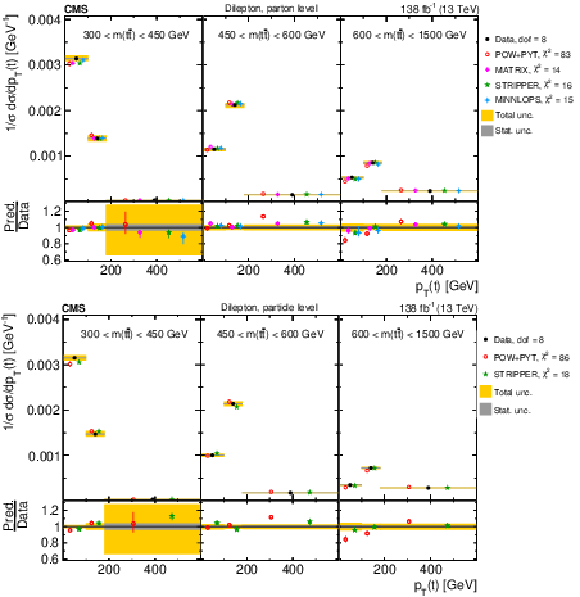
png pdf |
Figure 47:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 47-a:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 47-b:
Normalized $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 48:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 48-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
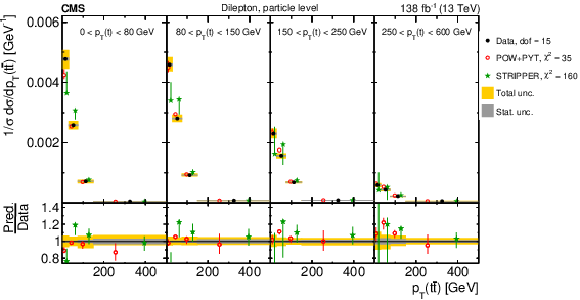
png pdf |
Figure 48-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 49:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
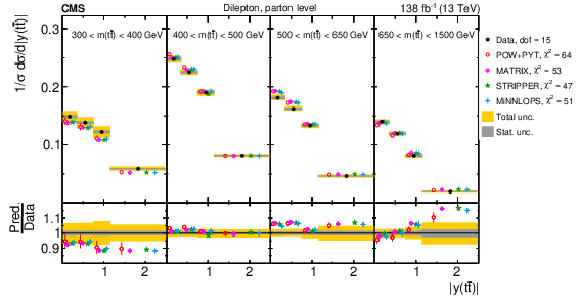
png pdf |
Figure 49-a:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 49-b:
Normalized $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
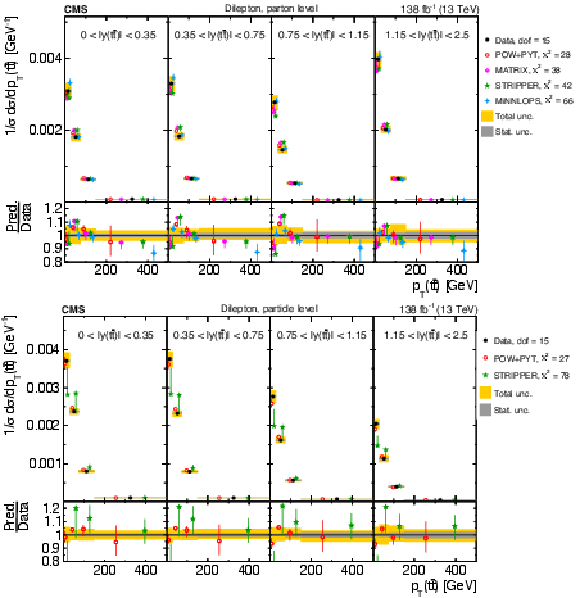
png pdf |
Figure 50:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
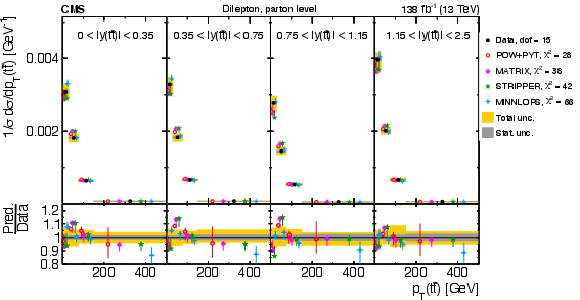
png pdf |
Figure 50-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
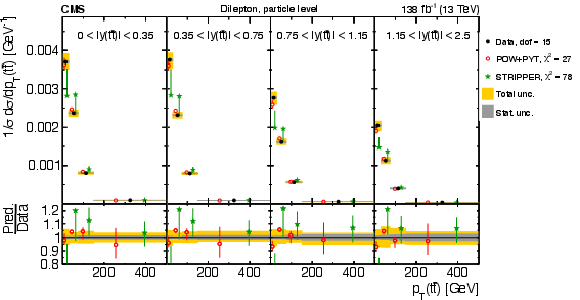
png pdf |
Figure 50-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
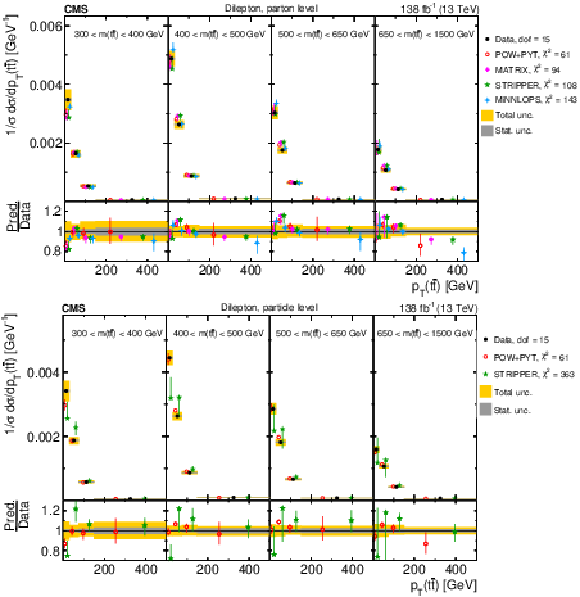
png pdf |
Figure 51:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
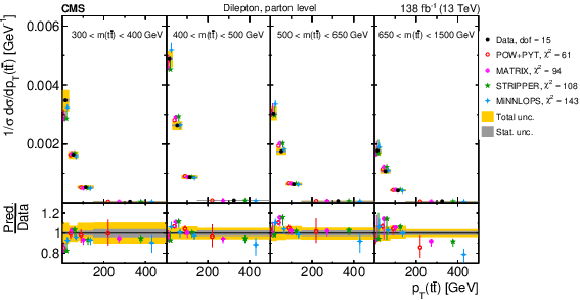
png pdf |
Figure 51-a:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
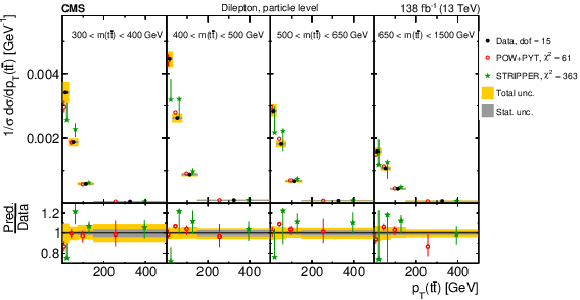
png pdf |
Figure 51-b:
Normalized $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 52:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
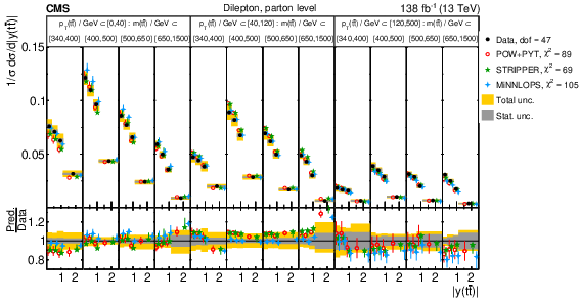
png pdf |
Figure 52-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
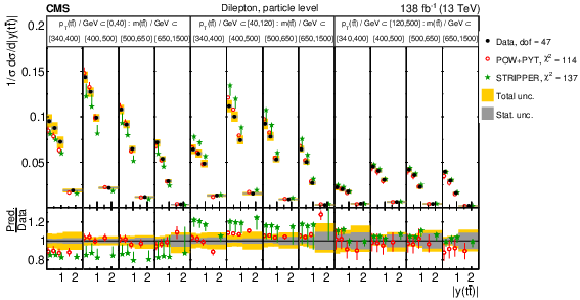
png pdf |
Figure 52-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
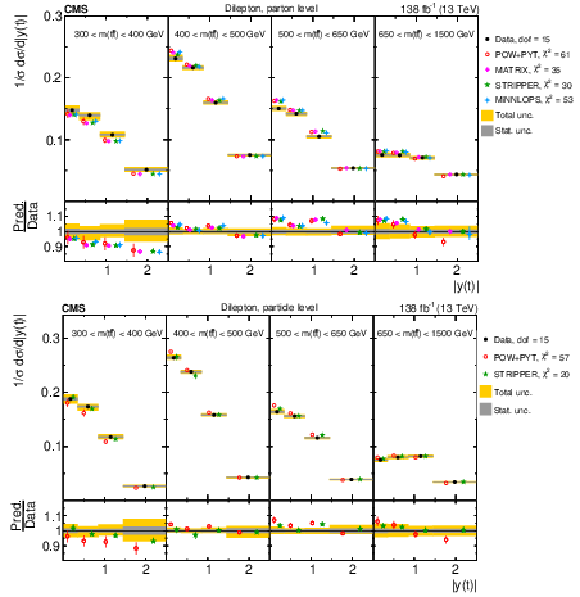
png pdf |
Figure 53:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 53-a:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 53-b:
Normalized $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
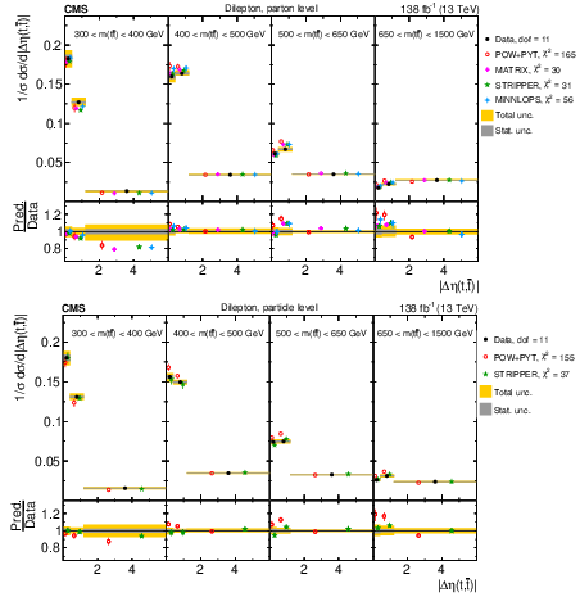
png pdf |
Figure 54:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 54-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 54-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 55:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
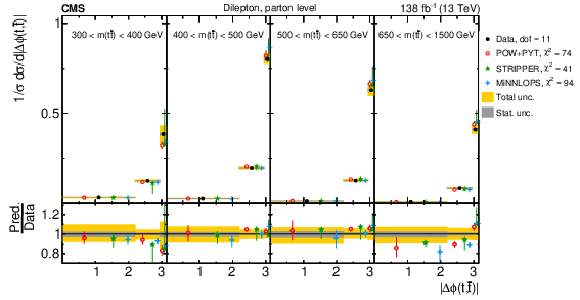
png pdf |
Figure 55-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
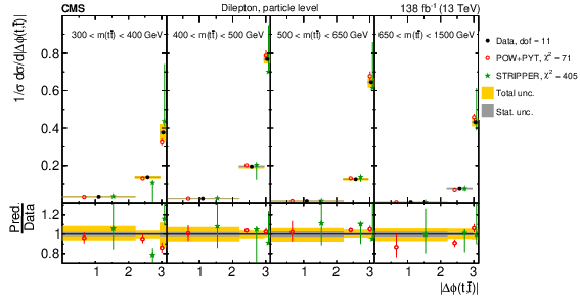
png pdf |
Figure 55-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |

png pdf |
Figure 56:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
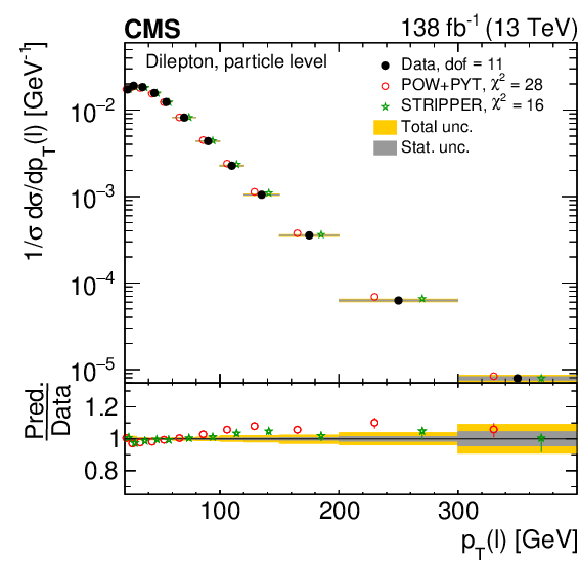
png pdf |
Figure 56-a:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
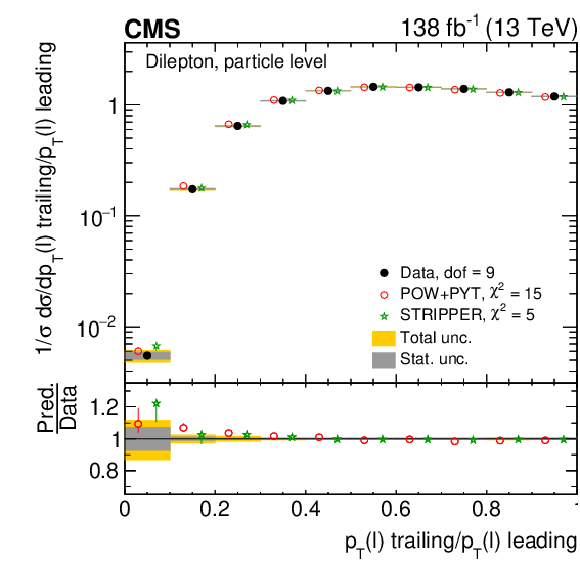
png pdf |
Figure 56-b:
Normalized $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 47. |
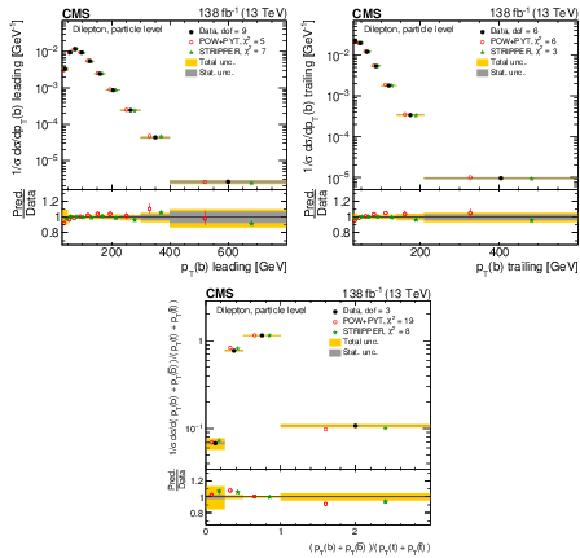
png pdf |
Figure 57:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 57-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
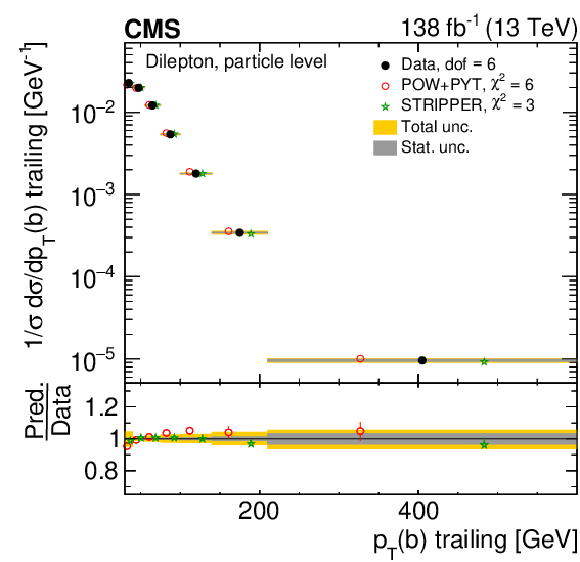
png pdf |
Figure 57-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 57-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the POW+PYT model are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
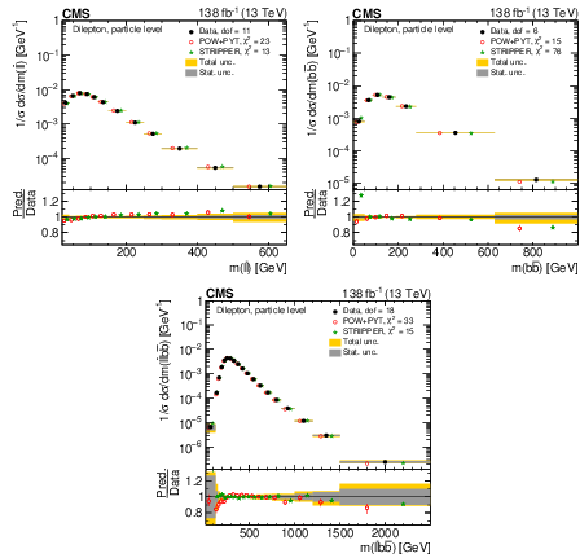
png pdf |
Figure 58:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |

png pdf |
Figure 58-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
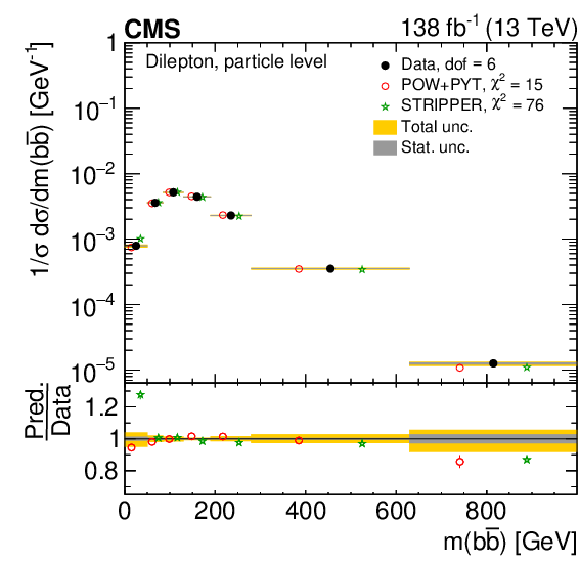
png pdf |
Figure 58-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
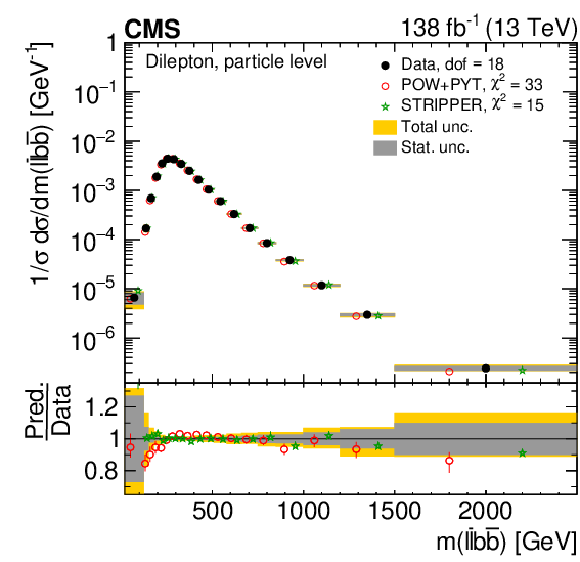
png pdf |
Figure 58-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |

png pdf |
Figure 59:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
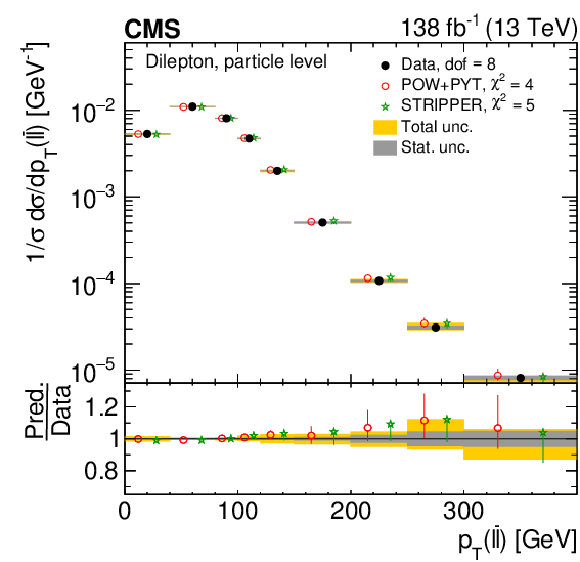
png pdf |
Figure 59-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
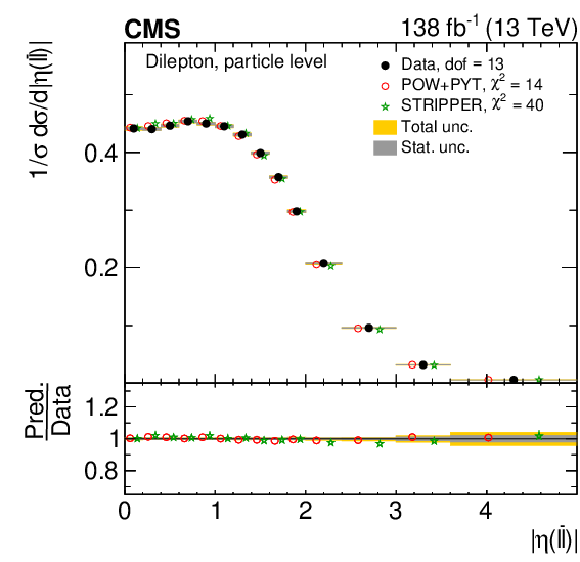
png pdf |
Figure 59-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
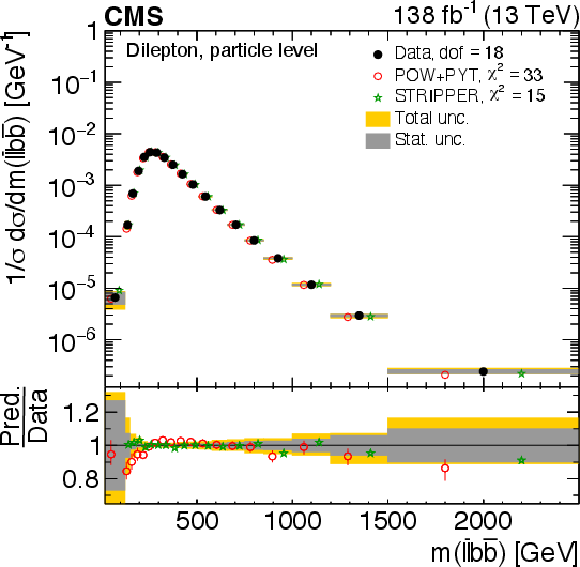
png pdf |
Figure 59-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |

png pdf |
Figure 60:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
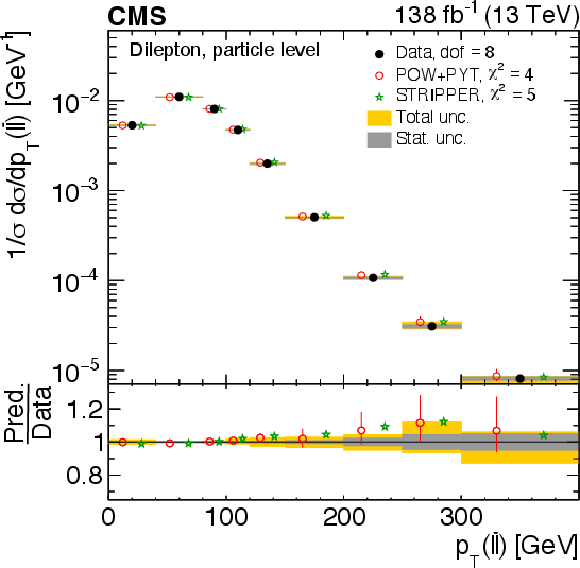
png pdf |
Figure 60-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
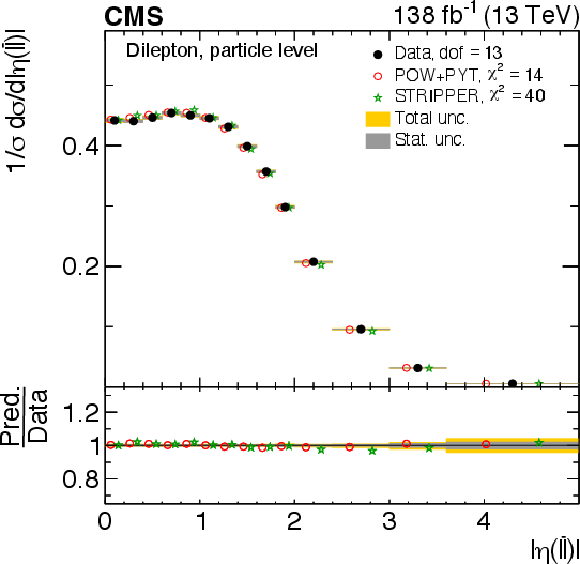
png pdf |
Figure 60-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |

png pdf |
Figure 61:
Normalized $ [|\eta(\ell\overline{\ell})|,\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
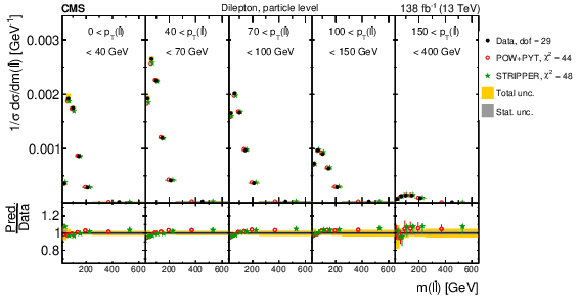
png pdf |
Figure 62:
Normalized $ [|\eta(\ell\overline{\ell})|,\, p_{\mathrm{T}}(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |
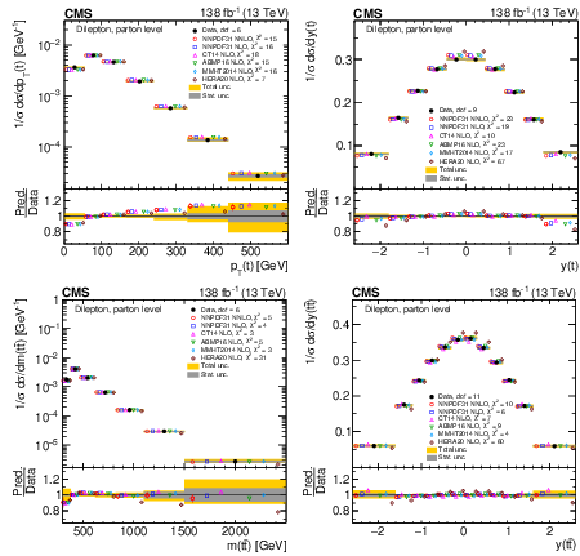
png pdf |
Figure 63:
Normalized $ [p_{\mathrm{T}}(\ell\overline{\ell}),\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 57. |

png pdf |
Figure 64:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower right), measured at the parton level in the full phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets. The nominal prediction (open circles) uses the PDF set NNPDF3.1 at NNLO accuracy, assuming a top quark mass value of 172.5 GeV and $ \alpha_\mathrm{S} = $ 0.118. The alternative PDF sets (other points) constitute NNPDF3.1, CT14, ABMP16, MMHT2014, and HERAPDF2.0 at NLO accuracy and assume the same values for the top quark mass and $ \alpha_\mathrm{S} $ as the nominal NNPDF3.1 NNLO PDF set. The estimated uncertainties in the nominal prediction are represented by vertical bars on the corresponding points. For each PDF set, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
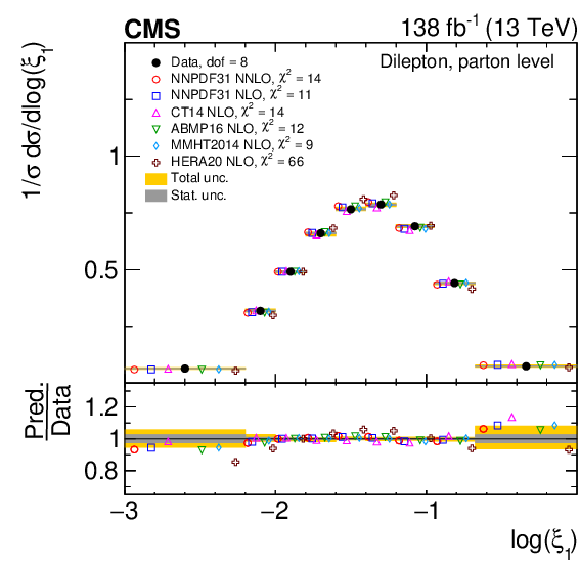
png pdf |
Figure 64-a:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower right), measured at the parton level in the full phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets. The nominal prediction (open circles) uses the PDF set NNPDF3.1 at NNLO accuracy, assuming a top quark mass value of 172.5 GeV and $ \alpha_\mathrm{S} = $ 0.118. The alternative PDF sets (other points) constitute NNPDF3.1, CT14, ABMP16, MMHT2014, and HERAPDF2.0 at NLO accuracy and assume the same values for the top quark mass and $ \alpha_\mathrm{S} $ as the nominal NNPDF3.1 NNLO PDF set. The estimated uncertainties in the nominal prediction are represented by vertical bars on the corresponding points. For each PDF set, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
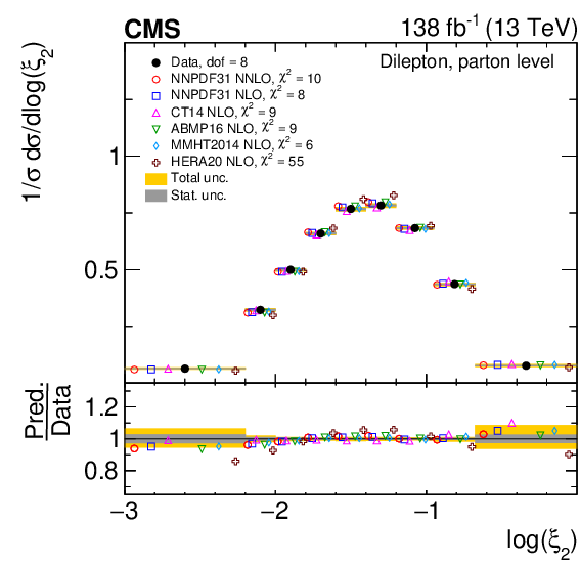
png pdf |
Figure 64-b:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower right), measured at the parton level in the full phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets. The nominal prediction (open circles) uses the PDF set NNPDF3.1 at NNLO accuracy, assuming a top quark mass value of 172.5 GeV and $ \alpha_\mathrm{S} = $ 0.118. The alternative PDF sets (other points) constitute NNPDF3.1, CT14, ABMP16, MMHT2014, and HERAPDF2.0 at NLO accuracy and assume the same values for the top quark mass and $ \alpha_\mathrm{S} $ as the nominal NNPDF3.1 NNLO PDF set. The estimated uncertainties in the nominal prediction are represented by vertical bars on the corresponding points. For each PDF set, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 64-c:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower right), measured at the parton level in the full phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets. The nominal prediction (open circles) uses the PDF set NNPDF3.1 at NNLO accuracy, assuming a top quark mass value of 172.5 GeV and $ \alpha_\mathrm{S} = $ 0.118. The alternative PDF sets (other points) constitute NNPDF3.1, CT14, ABMP16, MMHT2014, and HERAPDF2.0 at NLO accuracy and assume the same values for the top quark mass and $ \alpha_\mathrm{S} $ as the nominal NNPDF3.1 NNLO PDF set. The estimated uncertainties in the nominal prediction are represented by vertical bars on the corresponding points. For each PDF set, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 64-d:
Normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper left), $ y(\mathrm{t}) $ (upper right), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower left), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower right), measured at the parton level in the full phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets. The nominal prediction (open circles) uses the PDF set NNPDF3.1 at NNLO accuracy, assuming a top quark mass value of 172.5 GeV and $ \alpha_\mathrm{S} = $ 0.118. The alternative PDF sets (other points) constitute NNPDF3.1, CT14, ABMP16, MMHT2014, and HERAPDF2.0 at NLO accuracy and assume the same values for the top quark mass and $ \alpha_\mathrm{S} $ as the nominal NNPDF3.1 NNLO PDF set. The estimated uncertainties in the nominal prediction are represented by vertical bars on the corresponding points. For each PDF set, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
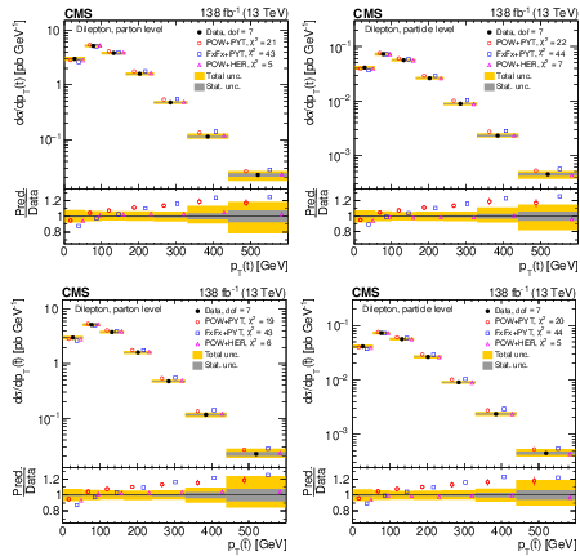
png pdf |
Figure 65:
Normalized $ \log(\xi_{1}) $ (upper left), $ \log(\xi_{2}) $ (upper right), and $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower) cross sections are shown for data (filled circles) and predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets (other points). Further details can be found in the caption of Fig. 64. |
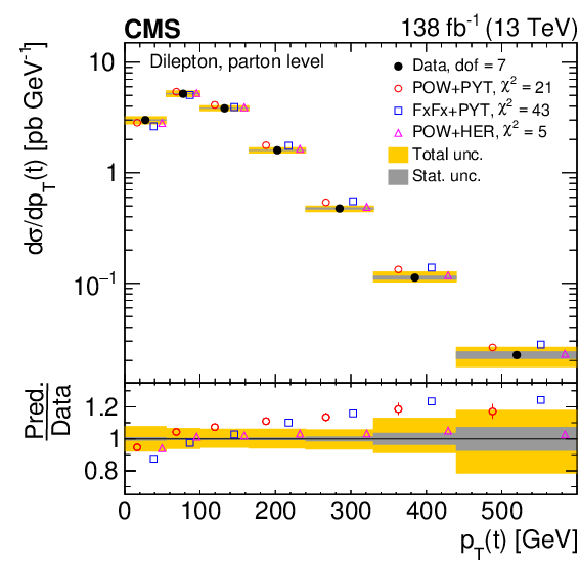
png pdf |
Figure 65-a:
Normalized $ \log(\xi_{1}) $ (upper left), $ \log(\xi_{2}) $ (upper right), and $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower) cross sections are shown for data (filled circles) and predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets (other points). Further details can be found in the caption of Fig. 64. |

png pdf |
Figure 65-b:
Normalized $ \log(\xi_{1}) $ (upper left), $ \log(\xi_{2}) $ (upper right), and $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower) cross sections are shown for data (filled circles) and predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets (other points). Further details can be found in the caption of Fig. 64. |

png pdf |
Figure 65-c:
Normalized $ \log(\xi_{1}) $ (upper left), $ \log(\xi_{2}) $ (upper right), and $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ (lower) cross sections are shown for data (filled circles) and predictions from the POWHEG + PYTHIA 8 (`POW-PYT') simulation with various PDF sets (other points). Further details can be found in the caption of Fig. 64. |
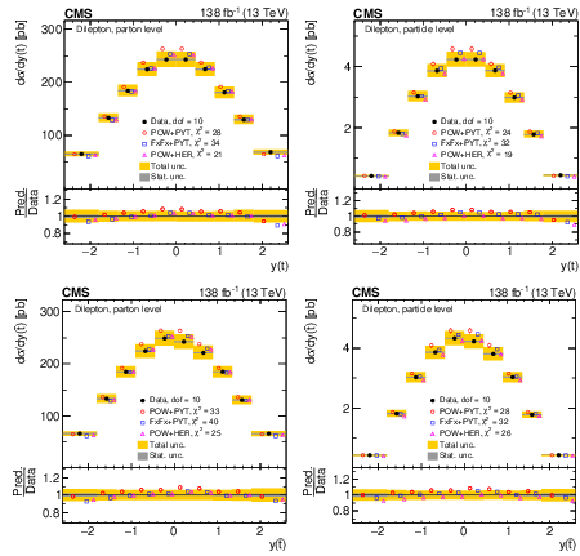
png pdf |
Figure 66:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
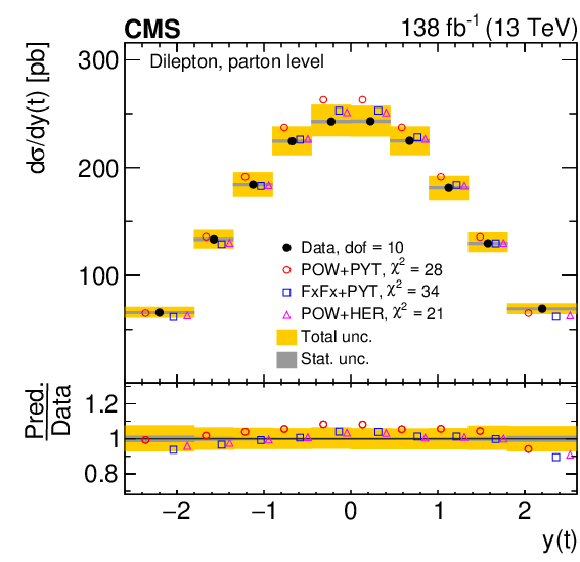
png pdf |
Figure 66-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
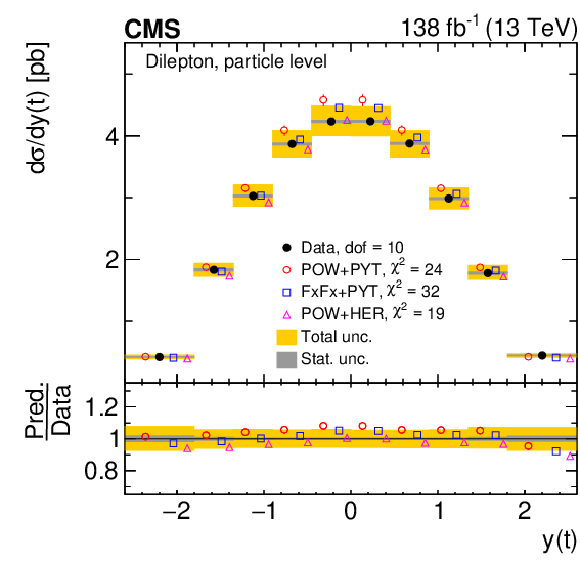
png pdf |
Figure 66-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 66-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
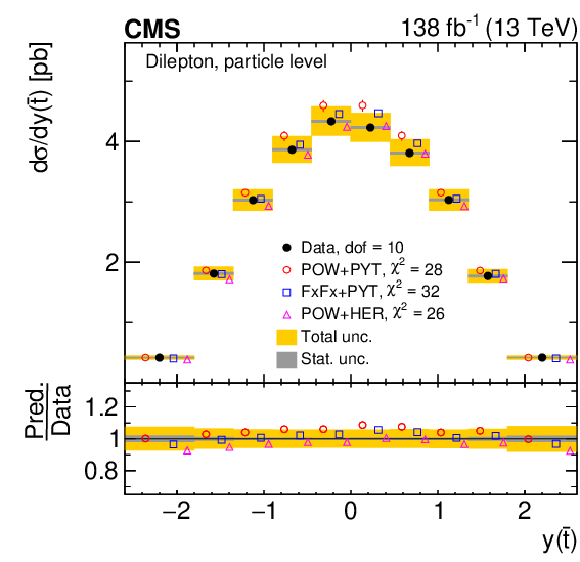
png pdf |
Figure 66-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
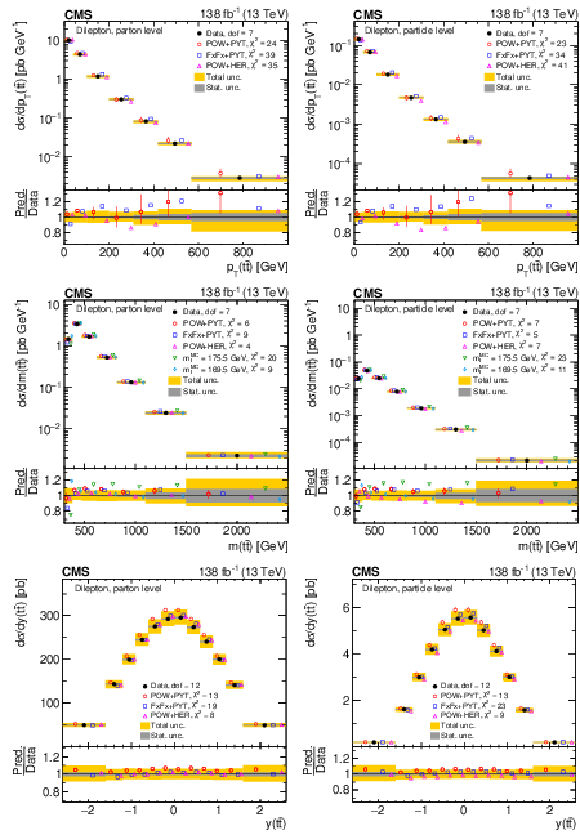
png pdf |
Figure 67:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 67-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 67-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 67-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 67-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
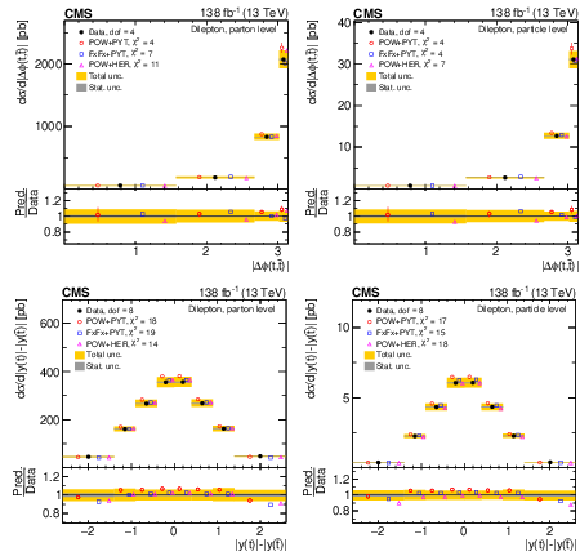
png pdf |
Figure 68:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 68-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 68-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 68-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
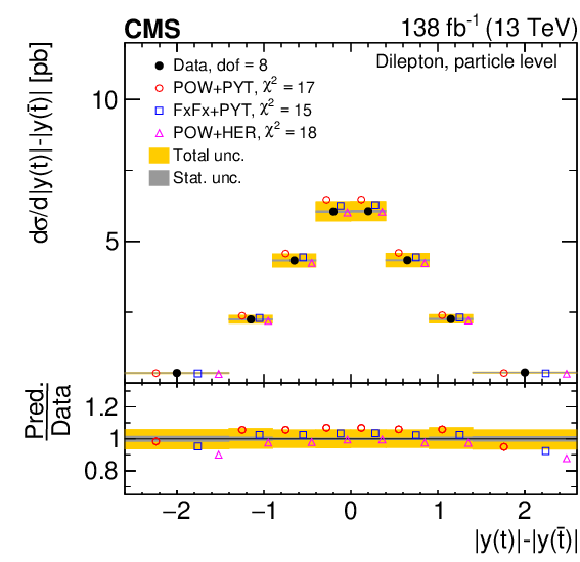
png pdf |
Figure 68-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
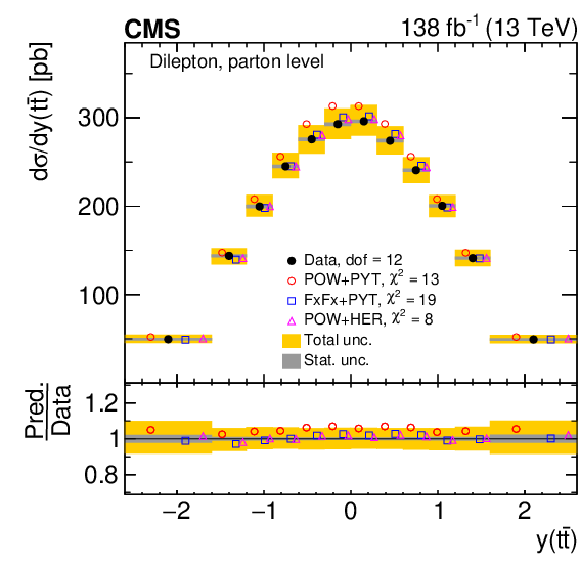
png pdf |
Figure 68-e:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
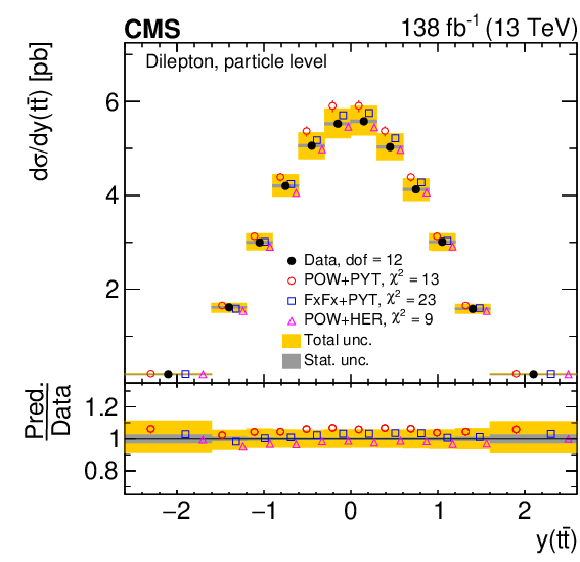
png pdf |
Figure 68-f:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle) and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
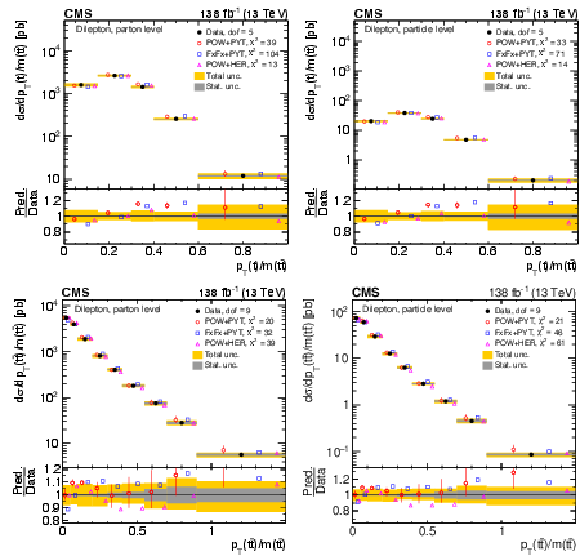
png pdf |
Figure 69:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
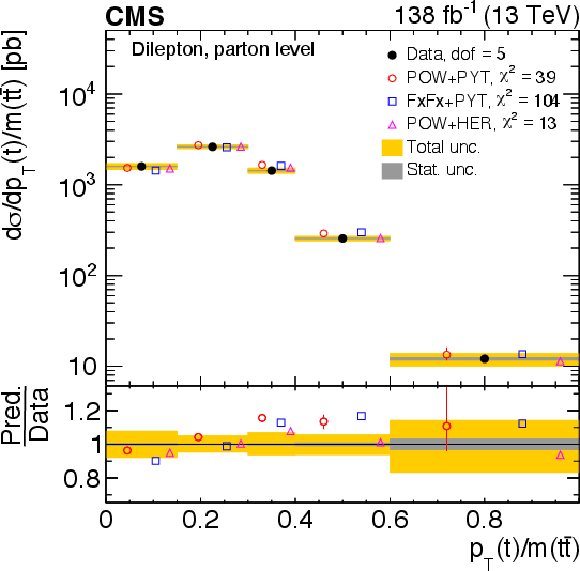
png pdf |
Figure 69-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 69-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 69-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 69-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
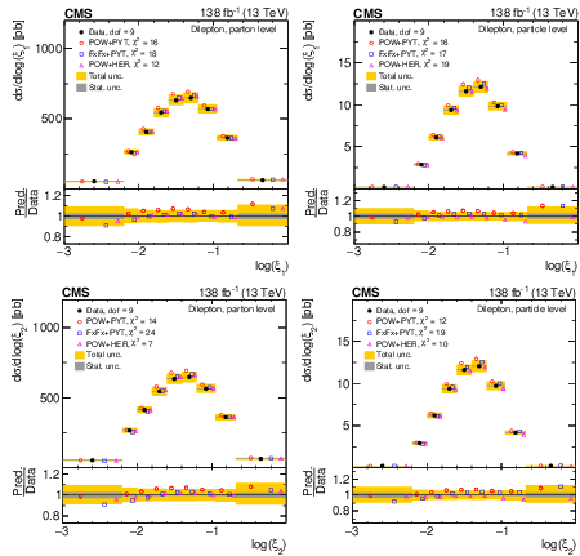
png pdf |
Figure 70:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
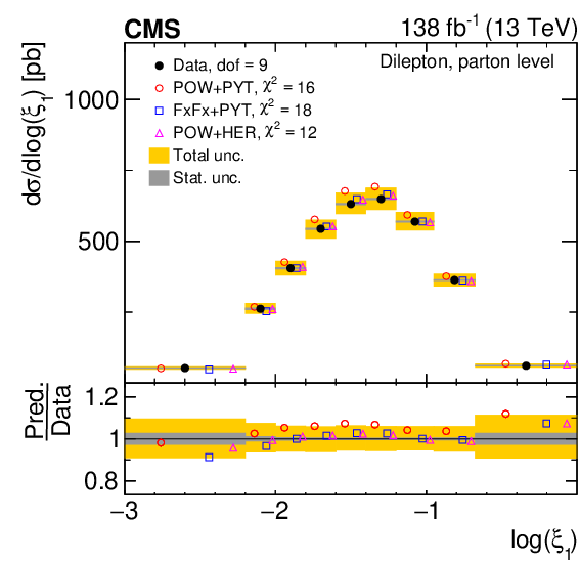
png pdf |
Figure 70-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
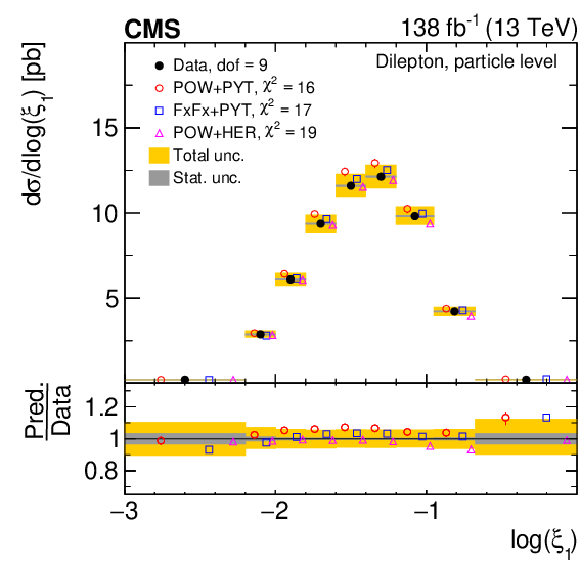
png pdf |
Figure 70-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 70-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
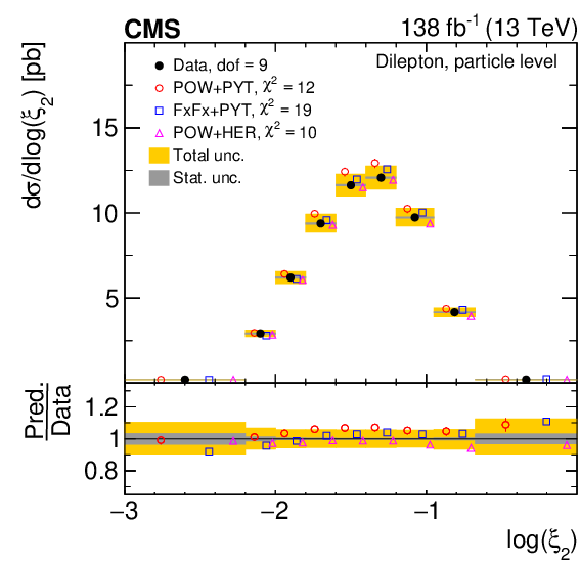
png pdf |
Figure 70-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 71:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
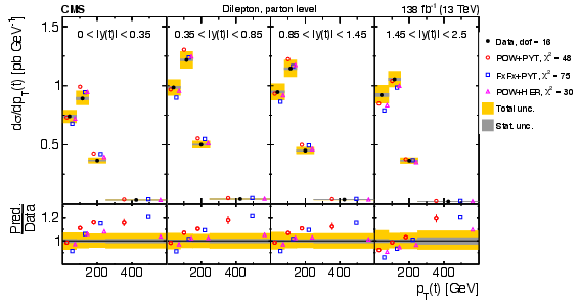
png pdf |
Figure 71-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 71-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
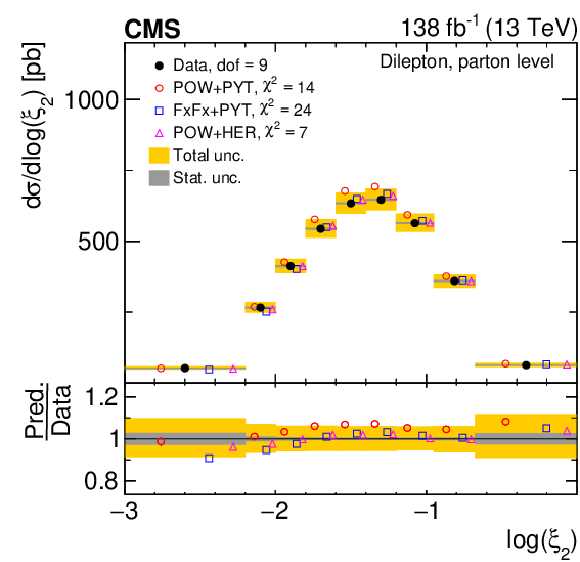
png pdf |
Figure 71-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |
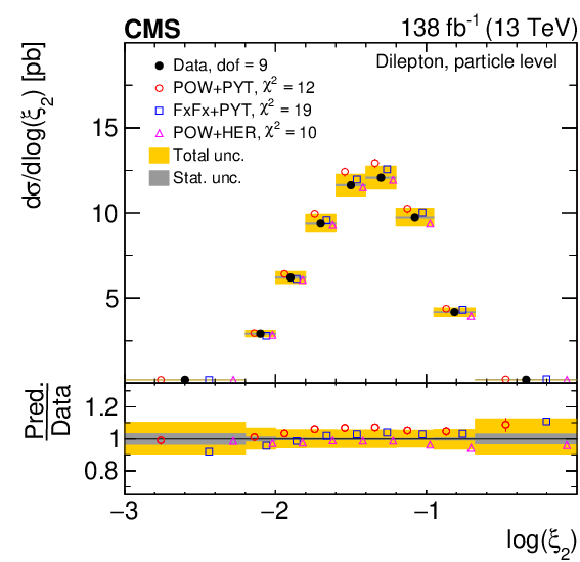
png pdf |
Figure 71-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for the data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 66. |

png pdf |
Figure 72:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 72-a:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 72-b:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 73:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 73-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
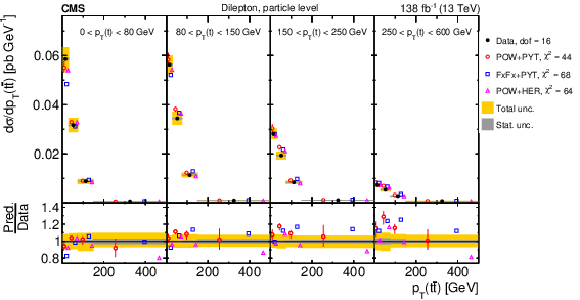
png pdf |
Figure 73-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
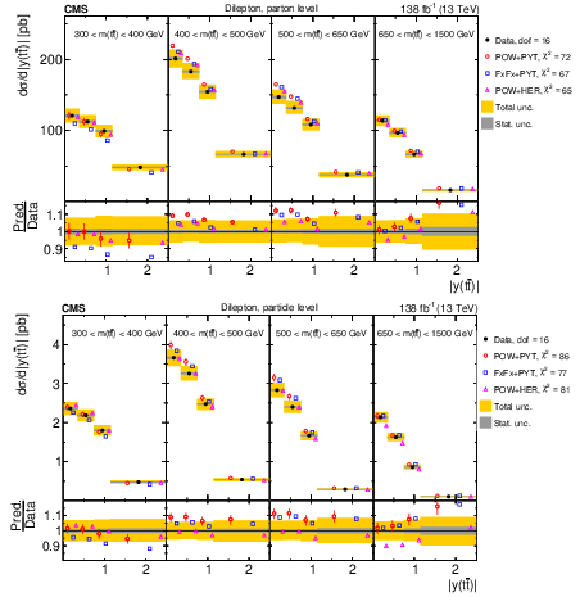
png pdf |
Figure 74:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
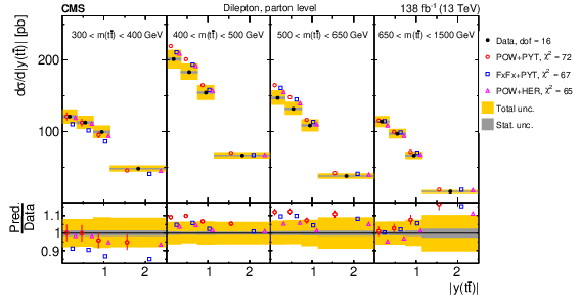
png pdf |
Figure 74-a:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
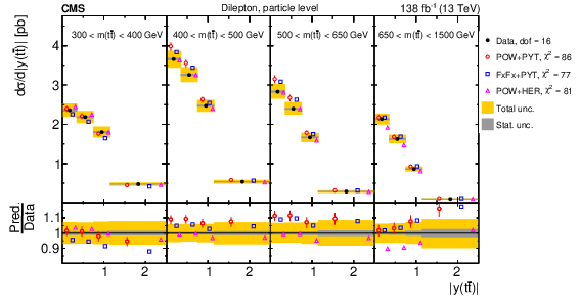
png pdf |
Figure 74-b:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
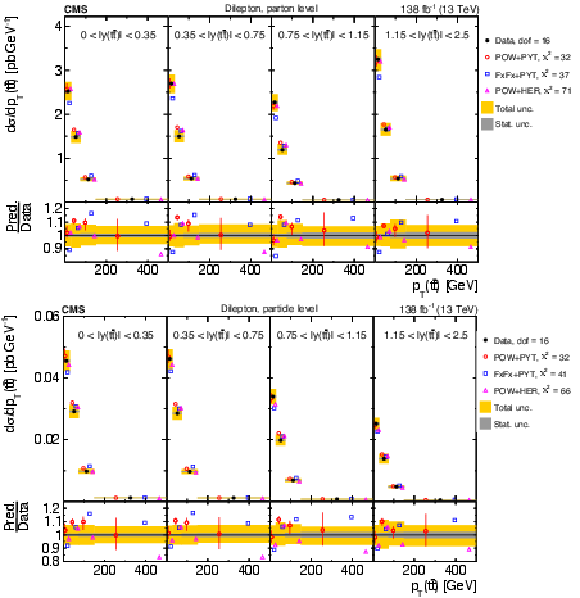
png pdf |
Figure 75:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
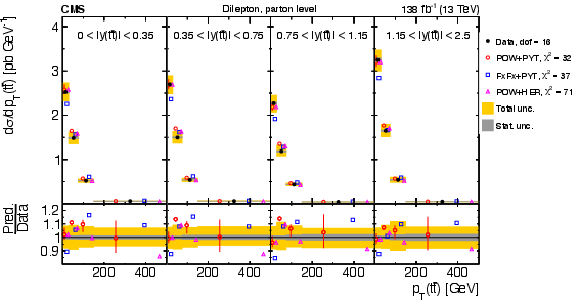
png pdf |
Figure 75-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 75-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
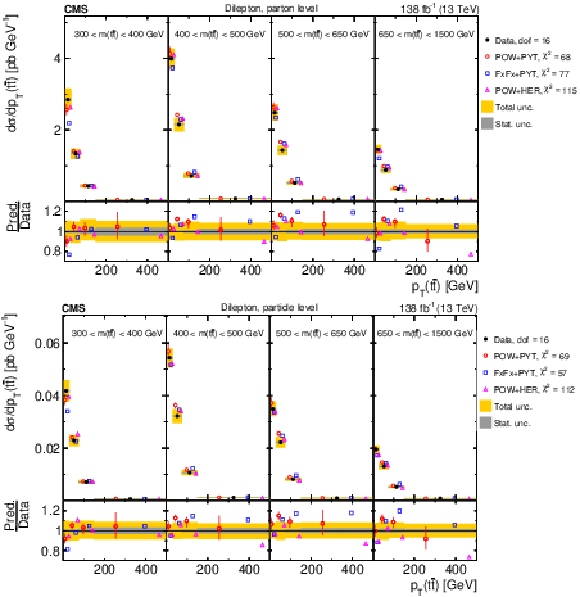
png pdf |
Figure 76:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
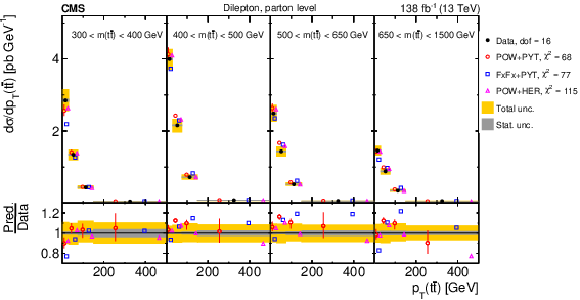
png pdf |
Figure 76-a:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 76-b:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
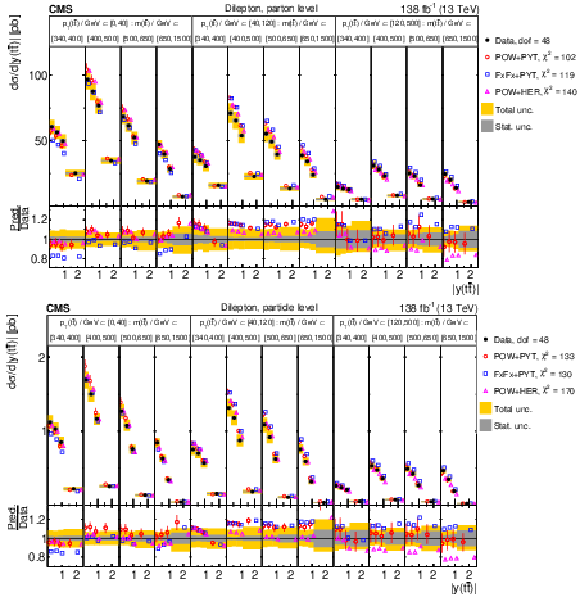
png pdf |
Figure 77:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
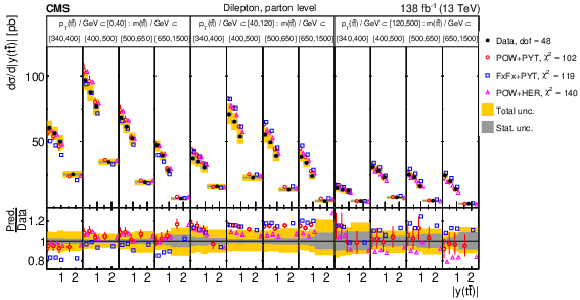
png pdf |
Figure 77-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
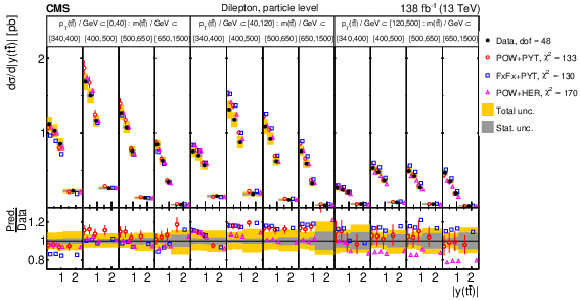
png pdf |
Figure 77-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 78:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 78-a:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
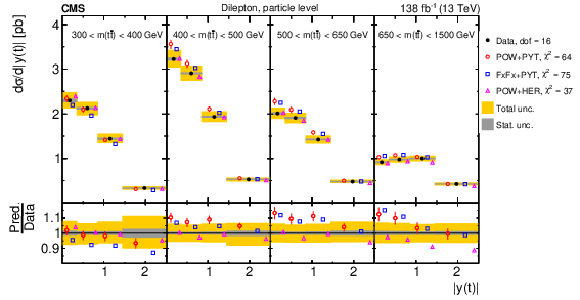
png pdf |
Figure 78-b:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
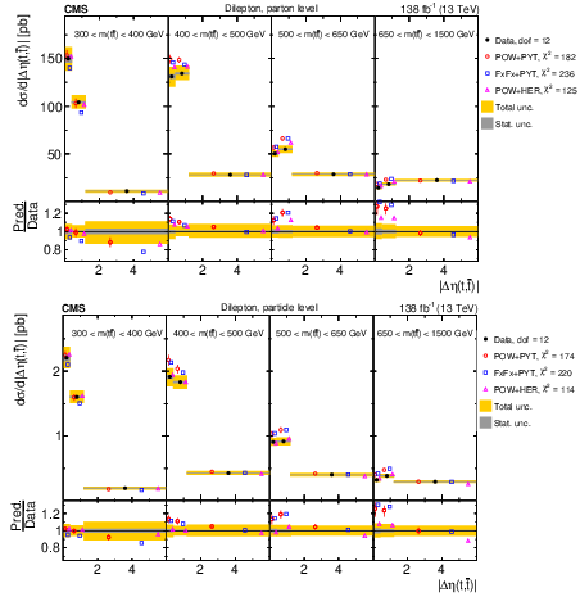
png pdf |
Figure 79:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 79-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 79-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
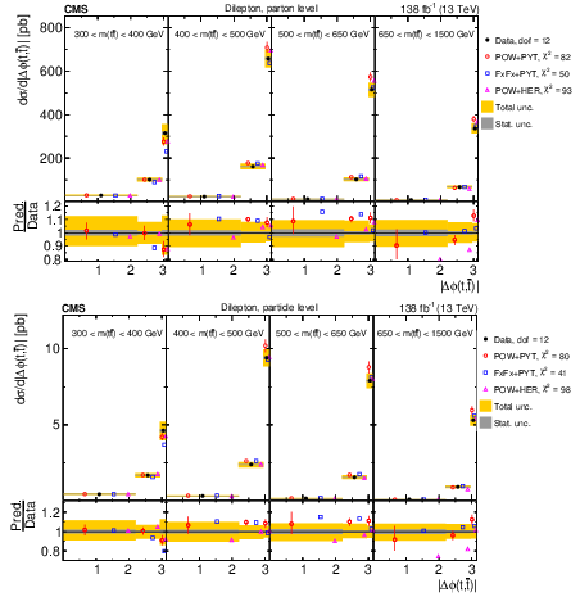
png pdf |
Figure 80:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
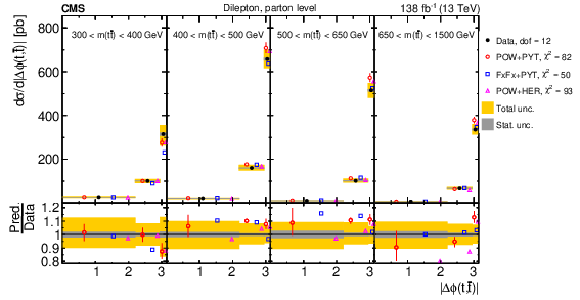
png pdf |
Figure 80-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
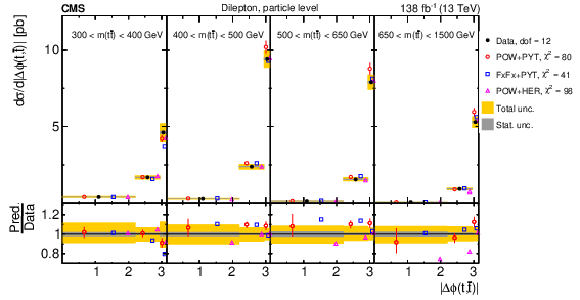
png pdf |
Figure 80-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 81:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |
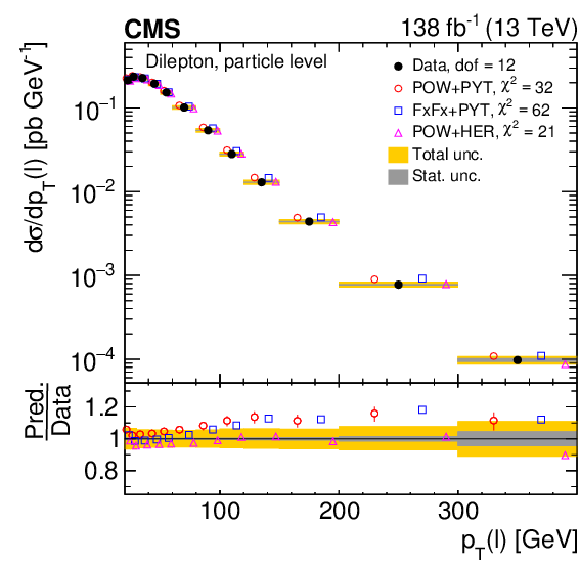
png pdf |
Figure 81-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 81-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 72. |

png pdf |
Figure 82:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
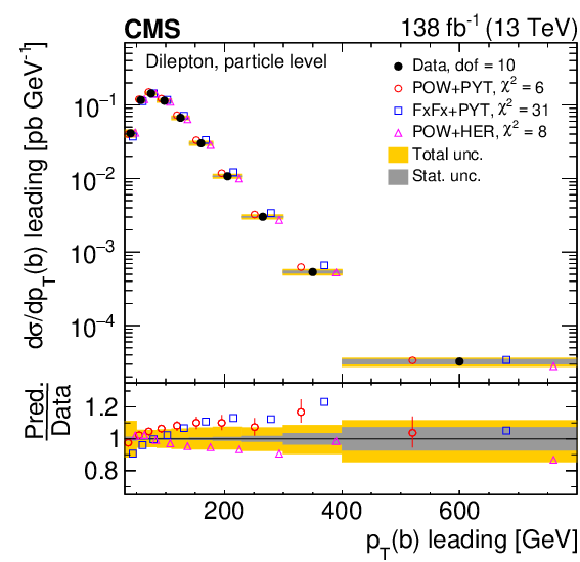
png pdf |
Figure 82-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
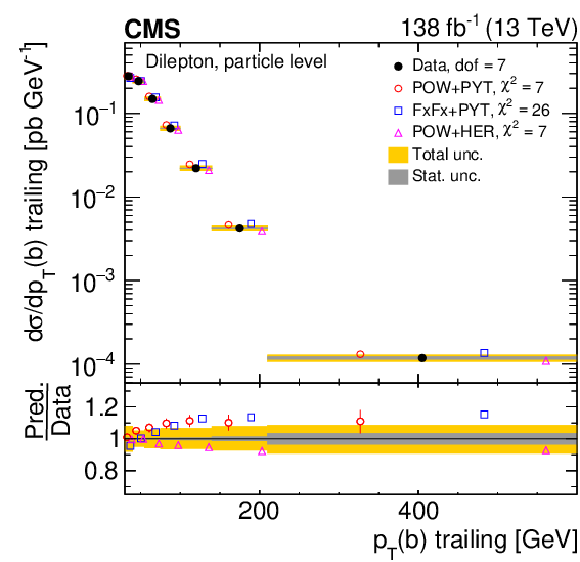
png pdf |
Figure 82-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
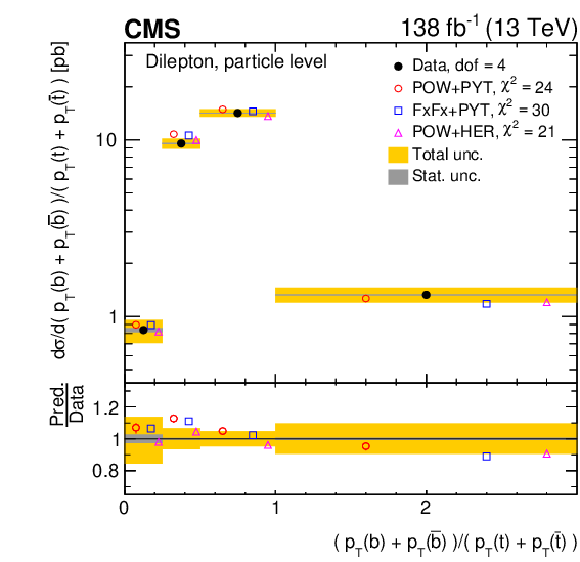
png pdf |
Figure 82-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower middle), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
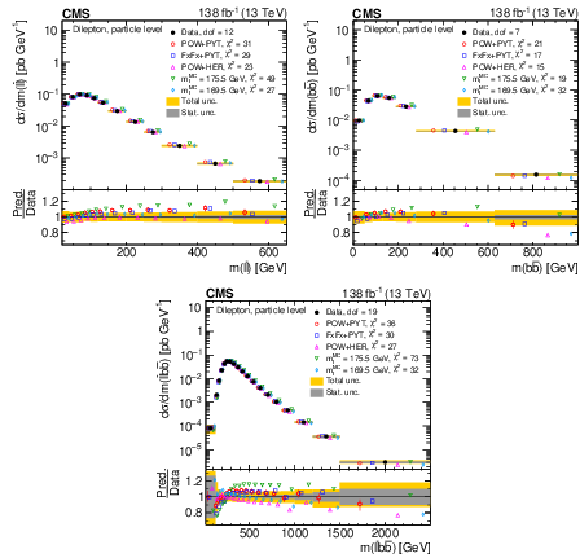
png pdf |
Figure 83:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 83-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 83-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 82. |
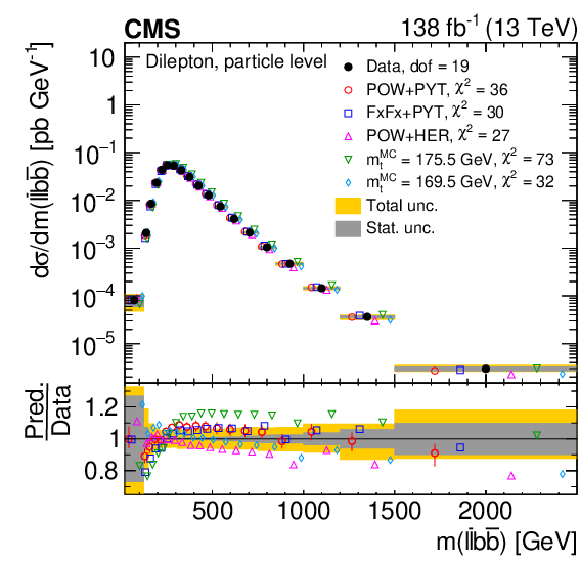
png pdf |
Figure 83-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 84:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right) and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 84-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right) and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 84-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right) and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |
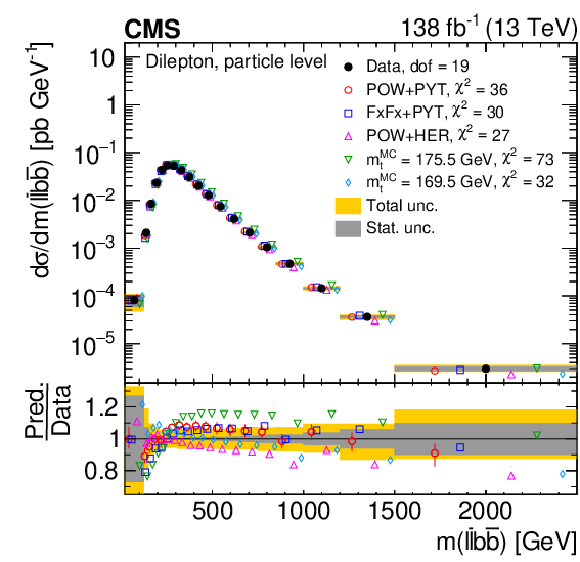
png pdf |
Figure 84-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right) and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |
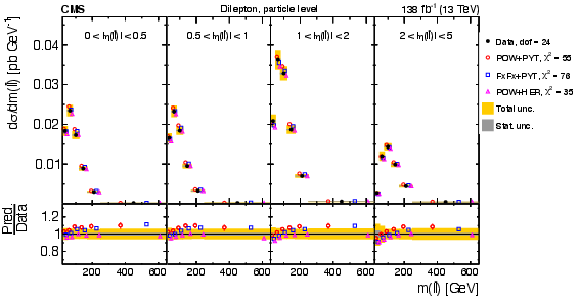
png pdf |
Figure 85:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |
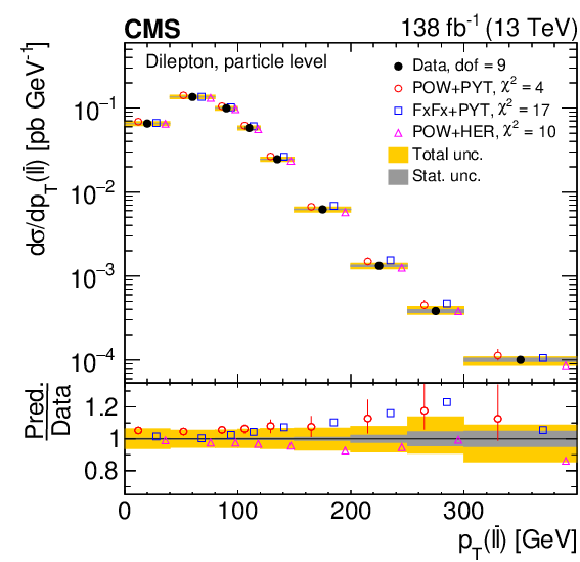
png pdf |
Figure 85-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |
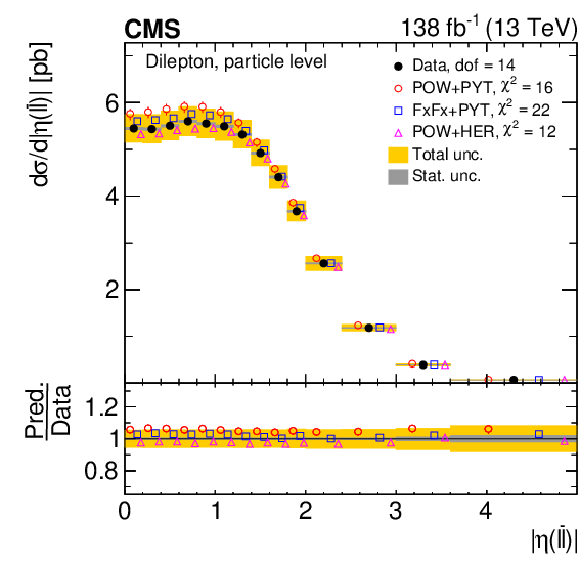
png pdf |
Figure 85-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |
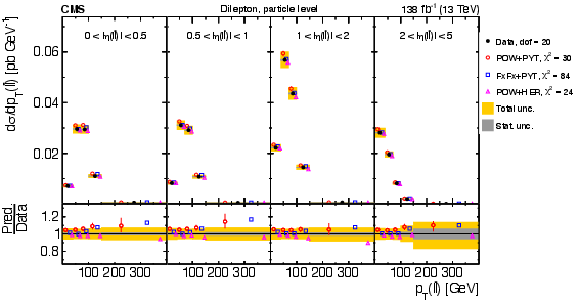
png pdf |
Figure 86:
Absolute $ [|\eta(\ell\overline{\ell})|,\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 87:
Absolute $ [|\eta(\ell\overline{\ell})|,\, p_{\mathrm{T}}(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 88:
Absolute $ [p_{\mathrm{T}}(\ell\overline{\ell}),\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 82. |

png pdf |
Figure 89:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
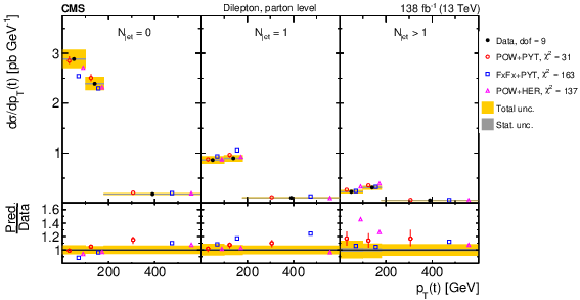
png pdf |
Figure 89-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
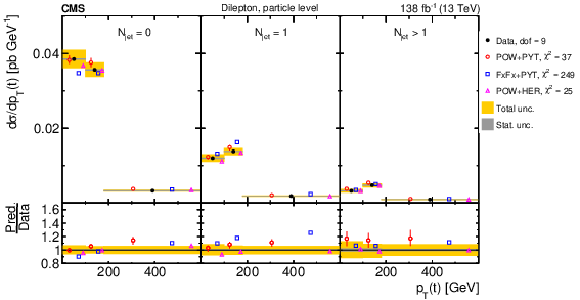
png pdf |
Figure 89-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
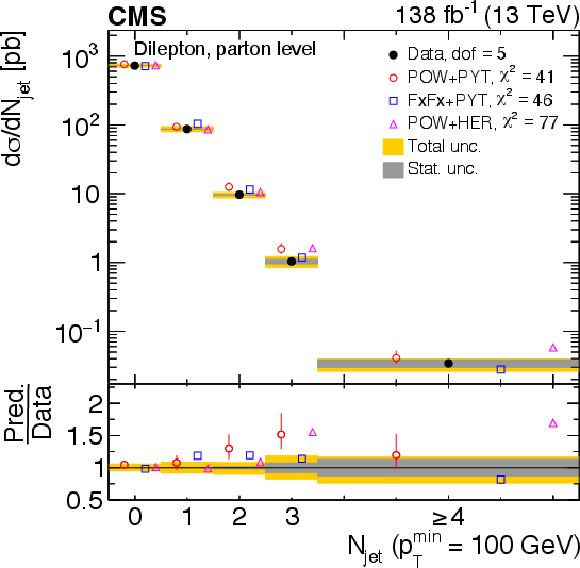
png pdf |
Figure 89-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
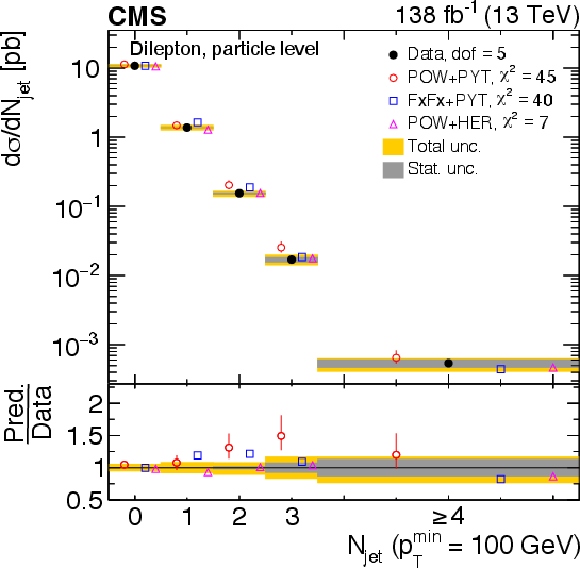
png pdf |
Figure 89-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as a function of $ N_{\text{jet}} $, for a minimum jet $ p_{\mathrm{T}} $ of 40 GeV (upper) and 100 GeV (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
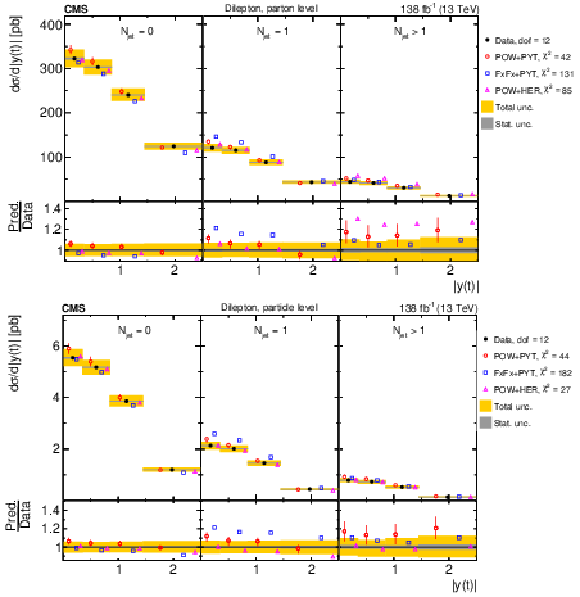
png pdf |
Figure 90:
Absolute $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total (sum in quadrature of statistical and systematic) uncertainties, respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
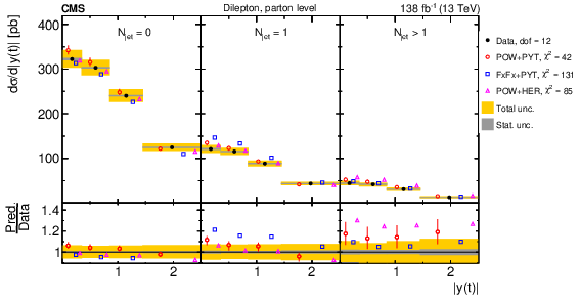
png pdf |
Figure 90-a:
Absolute $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total (sum in quadrature of statistical and systematic) uncertainties, respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
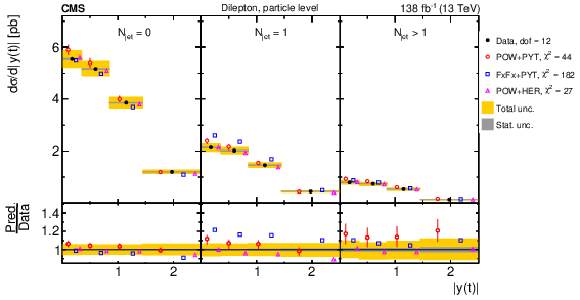
png pdf |
Figure 90-b:
Absolute $ [N_{\text{jet}},\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total (sum in quadrature of statistical and systematic) uncertainties, respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to various MC predictions (other points). The estimated uncertainties in the POWHEG + PYTHIA 8 (`POW-PYT') simulation are represented by vertical bars on the corresponding points. For each MC model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 91:
Absolute $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 91-a:
Absolute $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
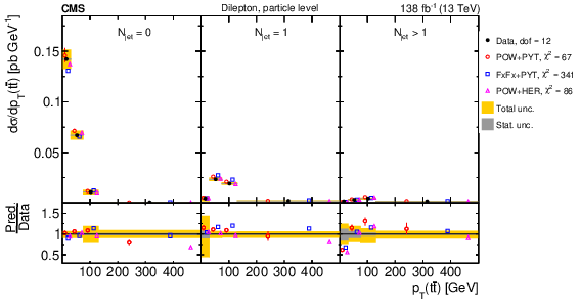
png pdf |
Figure 91-b:
Absolute $ [N_{\text{jet}},\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
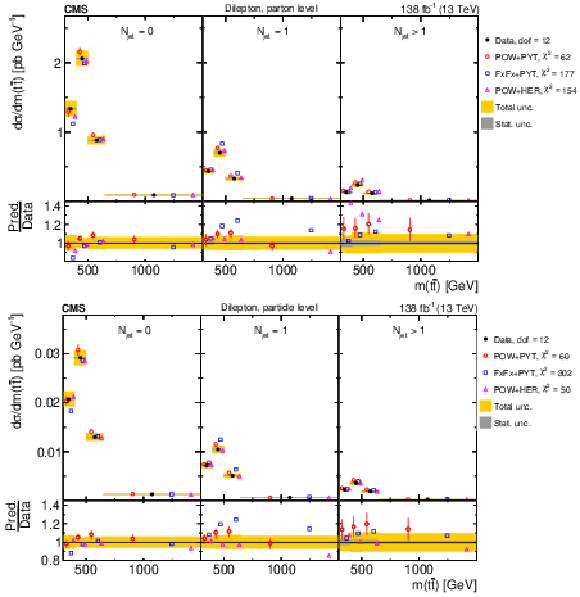
png pdf |
Figure 92:
Absolute $ [N_{\text{jet}},p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 92-a:
Absolute $ [N_{\text{jet}},p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 92-b:
Absolute $ [N_{\text{jet}},p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
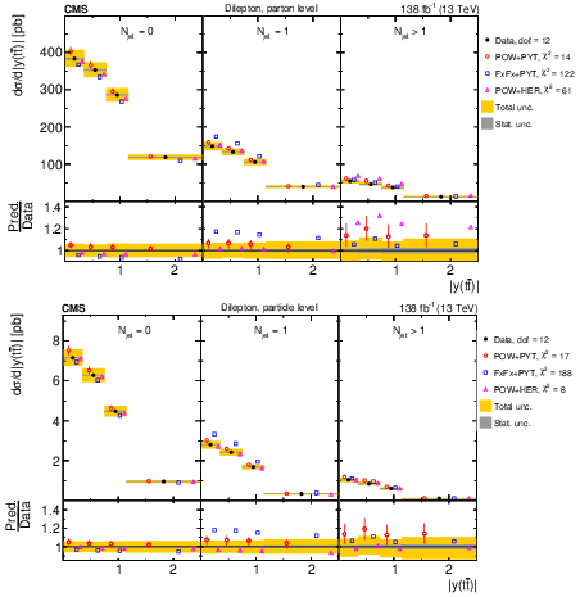
png pdf |
Figure 93:
Absolute $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 93-a:
Absolute $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 93-b:
Absolute $ [N_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 94:
Absolute $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 94-a:
Absolute $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
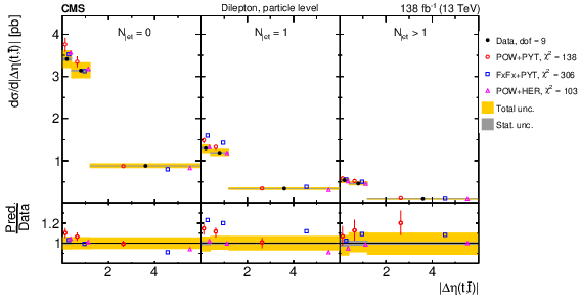
png pdf |
Figure 94-b:
Absolute $ [N_{\text{jet}},\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
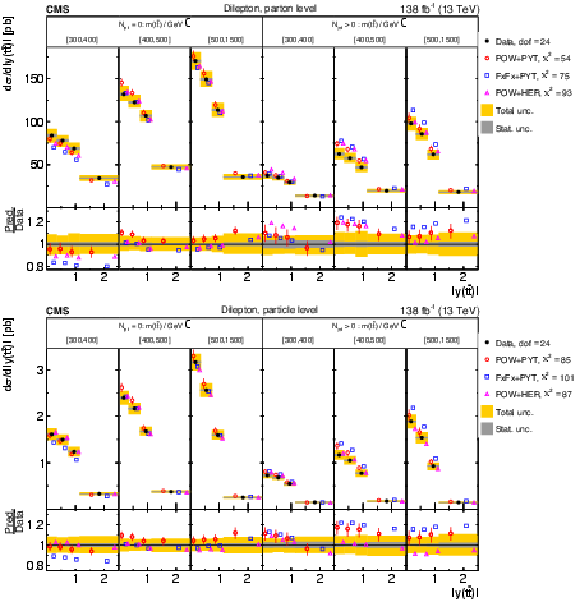
png pdf |
Figure 95:
Absolute $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 95-a:
Absolute $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 95-b:
Absolute $ [N_{\text{jet}},\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
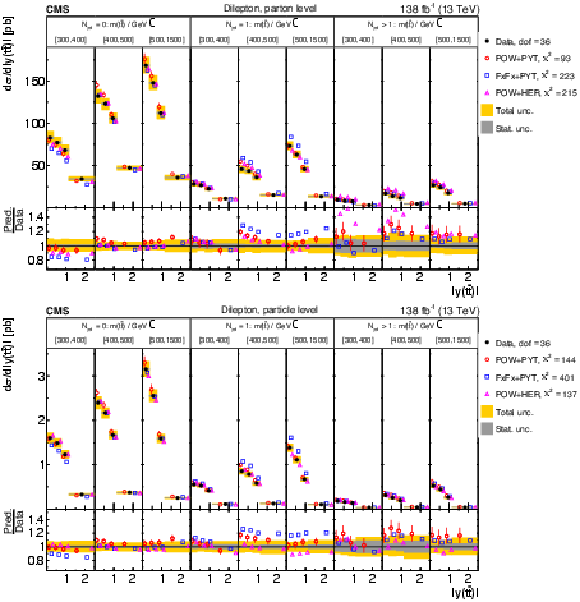
png pdf |
Figure 96:
Absolute $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
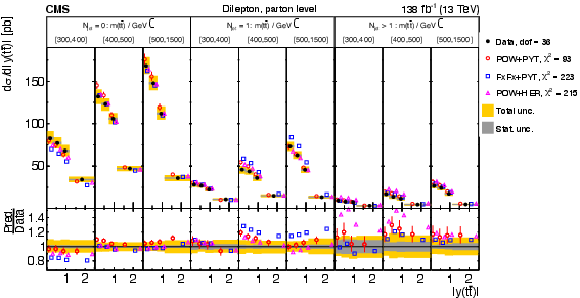
png pdf |
Figure 96-a:
Absolute $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
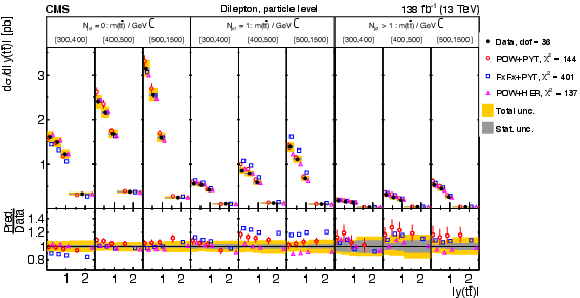
png pdf |
Figure 96-b:
Absolute $ [N^{0,1+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 97:
Absolute $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 97-a:
Absolute $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 97-b:
Absolute $ [N^{0,1,2+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
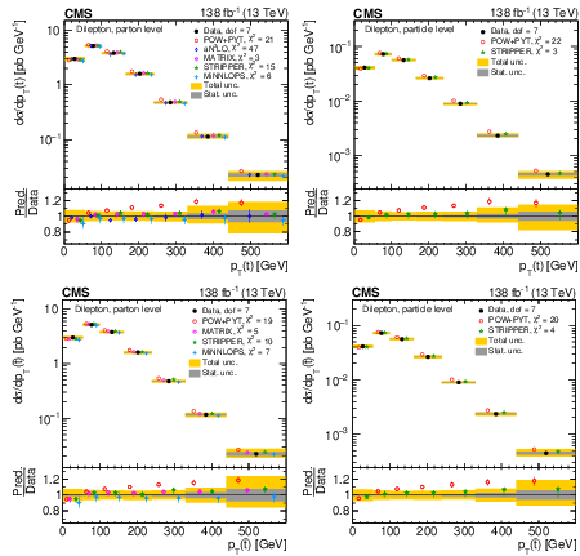
png pdf |
Figure 98:
Absolute $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |

png pdf |
Figure 98-a:
Absolute $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
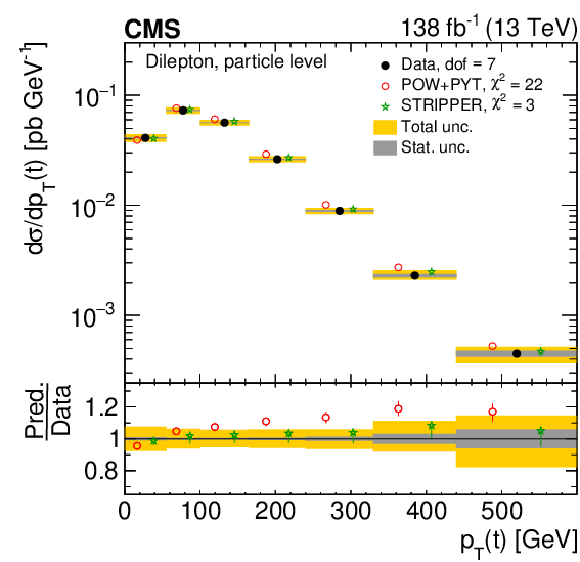
png pdf |
Figure 98-b:
Absolute $ [N^{0,1,2,3+}_{\text{jet}},\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles) and various MC predictions (other points). Further details can be found in the caption of Fig. 90. |
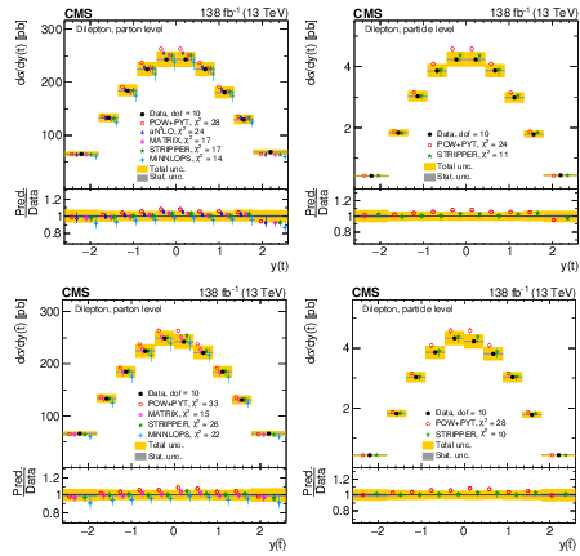
png pdf |
Figure 99:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
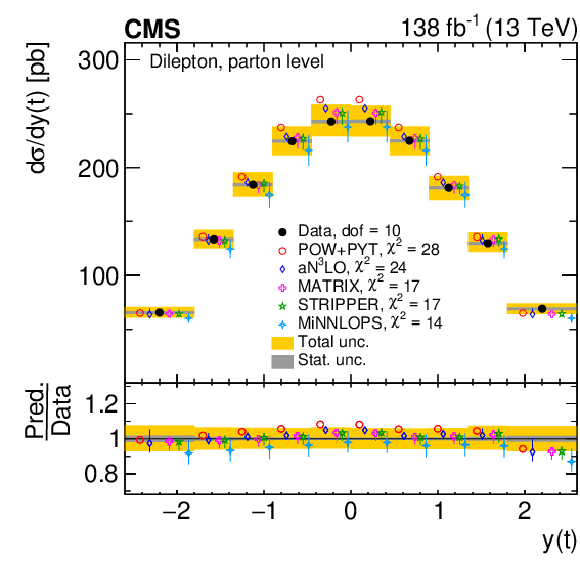
png pdf |
Figure 99-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 99-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 99-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
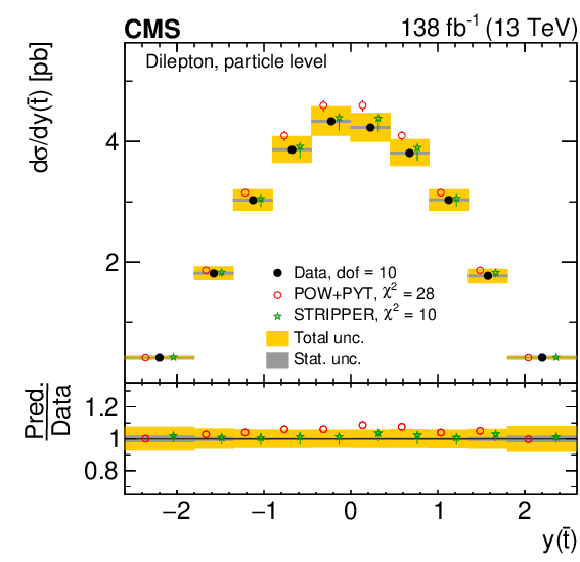
png pdf |
Figure 99-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t}) $ (upper) and $ p_{\mathrm{T}}(\overline{\mathrm{t}}) $ (lower), measured at the parton level in the full phase space (left) and at the particle level in a fiducial phase space (right). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
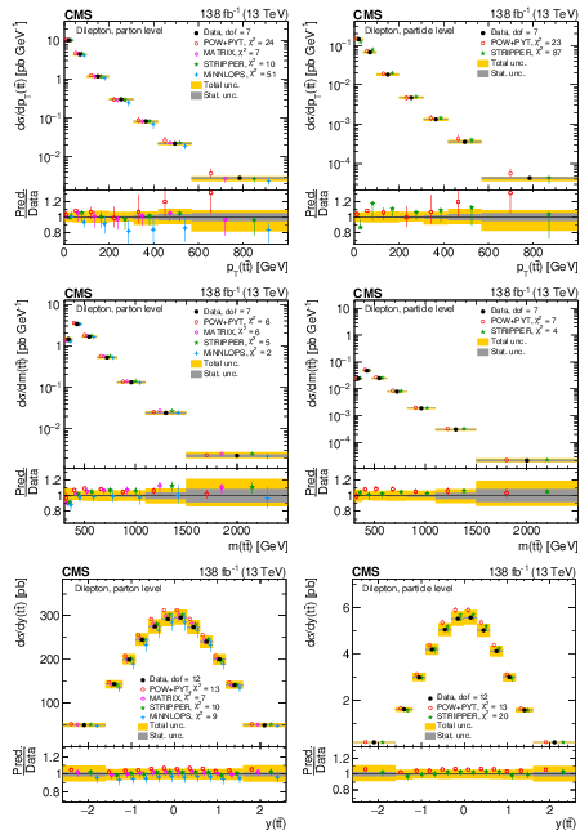
png pdf |
Figure 100:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
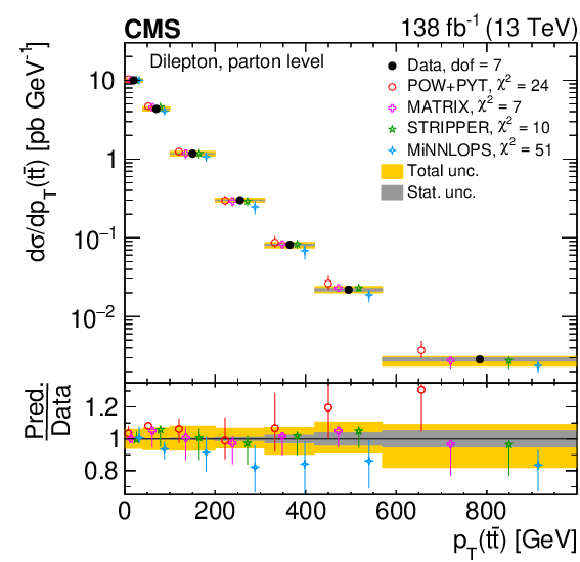
png pdf |
Figure 100-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 100-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
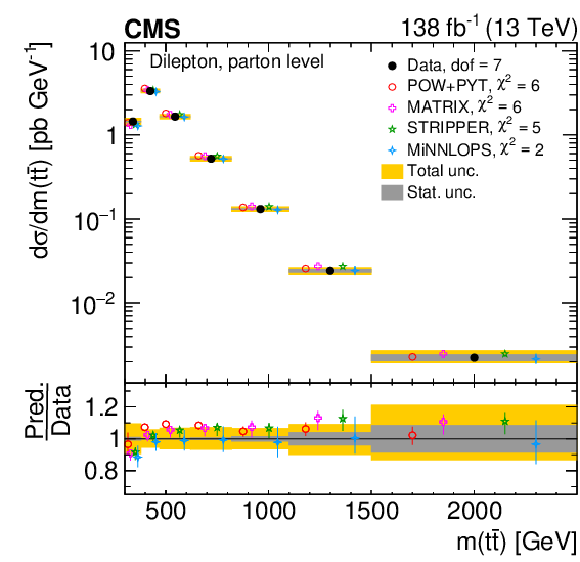
png pdf |
Figure 100-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 100-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ y(\mathrm{t}) $ (upper) and $ y(\overline{\mathrm{t}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 101:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 101-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 101-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 101-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 101-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
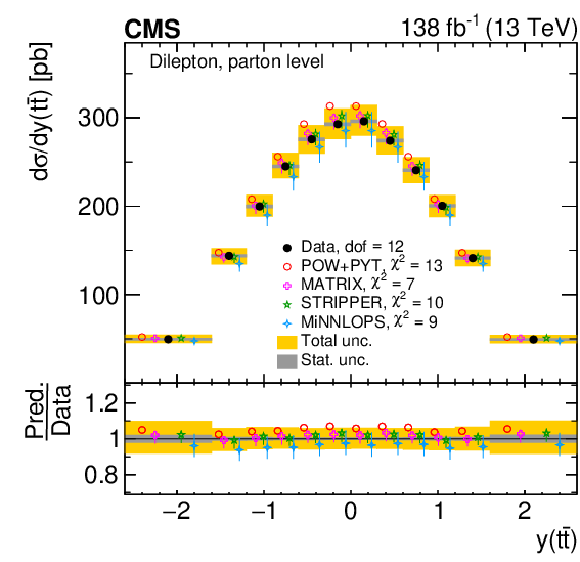
png pdf |
Figure 101-e:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
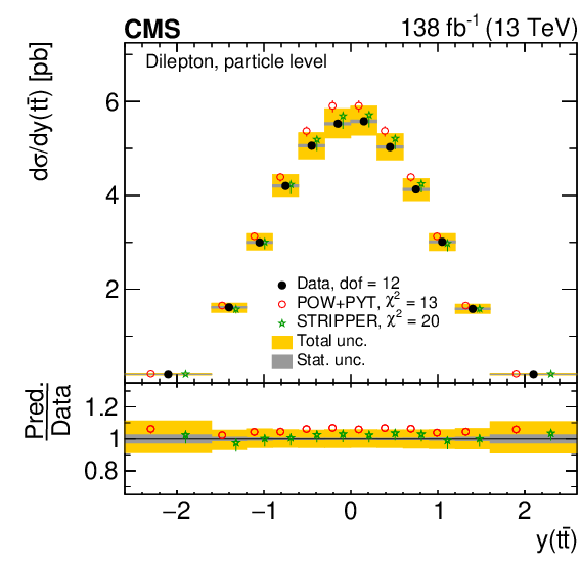
png pdf |
Figure 101-f:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper), $ m({\mathrm{t}\overline{\mathrm{t}}} ) $ (middle), and $ y({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
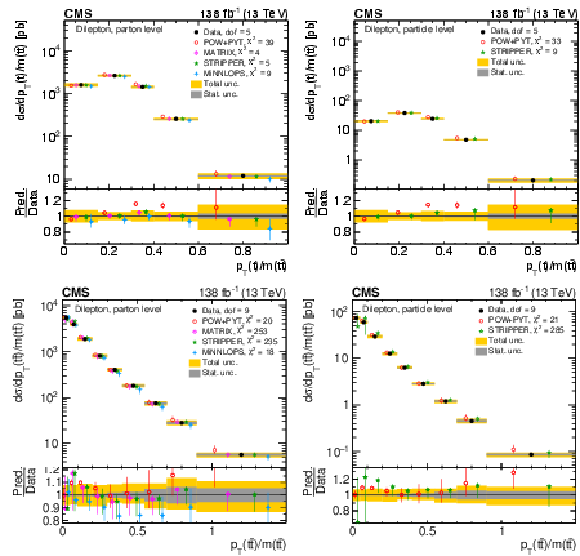
png pdf |
Figure 102:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
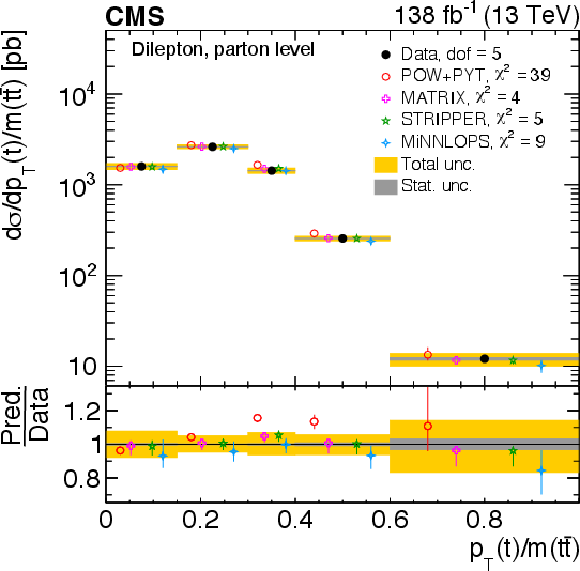
png pdf |
Figure 102-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 102-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
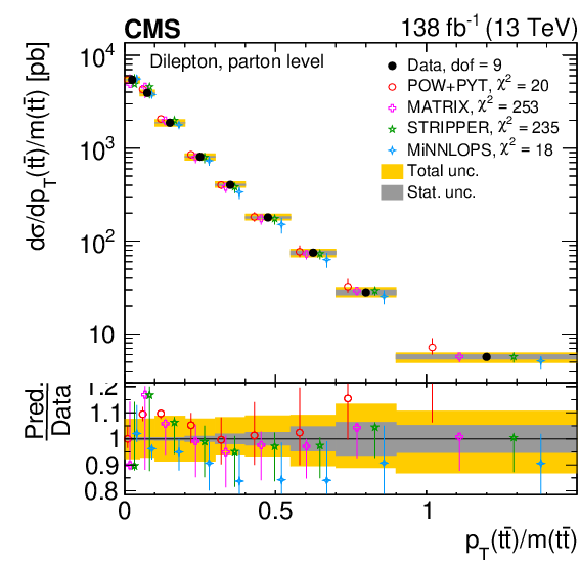
png pdf |
Figure 102-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 102-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})| $ (upper) and $ |y(\mathrm{t})|-|y(\overline{\mathrm{t}})| $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 103:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
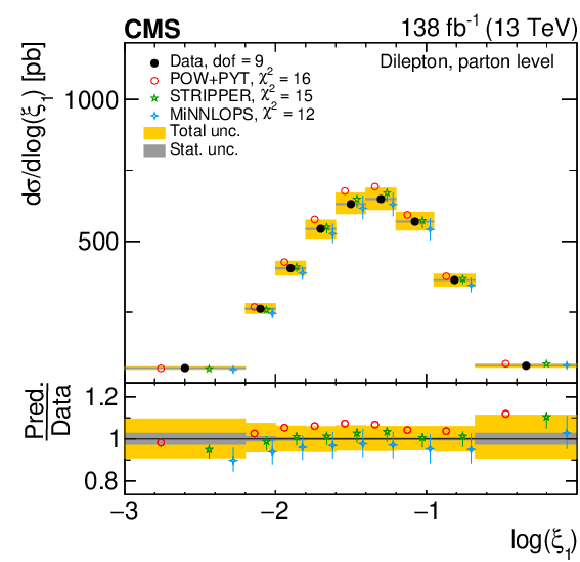
png pdf |
Figure 103-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 103-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 103-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |

png pdf |
Figure 103-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\mathrm{t})/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (upper) and $ p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )/m({\mathrm{t}\overline{\mathrm{t}}} ) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 99. |
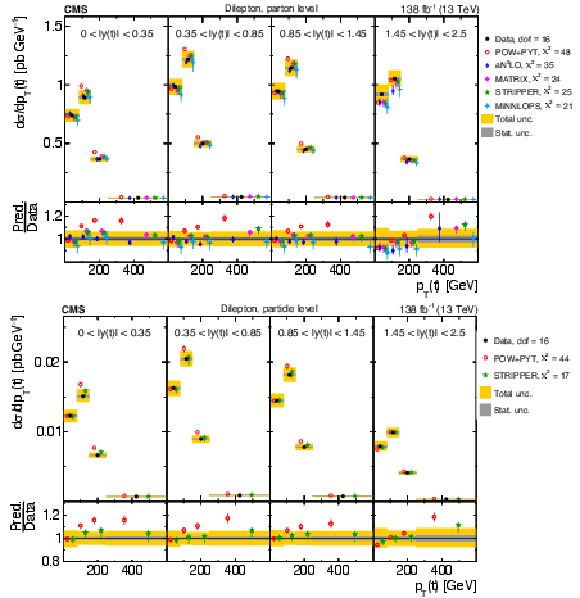
png pdf |
Figure 104:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 99. |
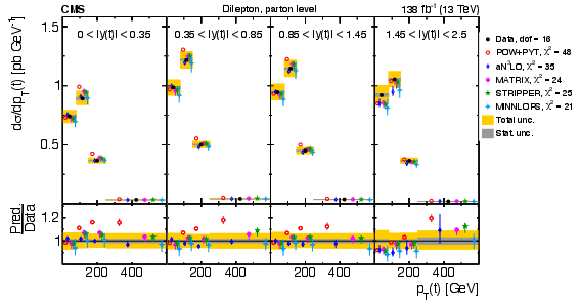
png pdf |
Figure 104-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 99. |
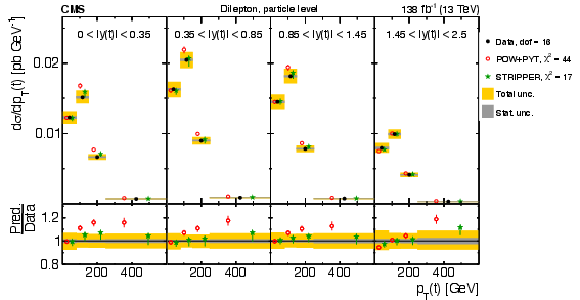
png pdf |
Figure 104-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 99. |
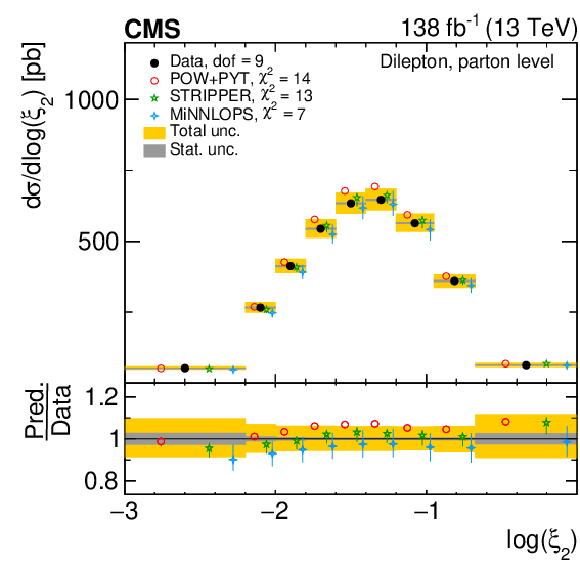
png pdf |
Figure 104-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 99. |
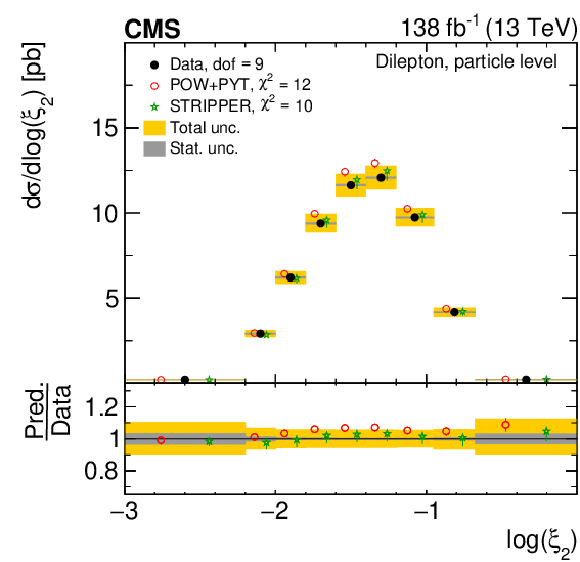
png pdf |
Figure 104-d:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ \log(\xi_{1}) $ (upper) and $ \log(\xi_{2}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 99. |
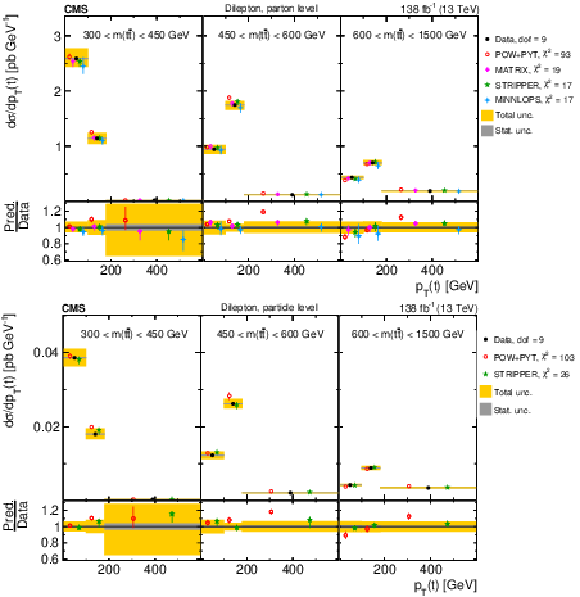
png pdf |
Figure 105:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 105-a:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 105-b:
Absolute $ [|y(\mathrm{t})|,\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections measured at the parton level in the full phase space (upper) and at the particle level in a fiducial phase space (lower). The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and various theoretical predictions with beyond-NLO precision (other points). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 106:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
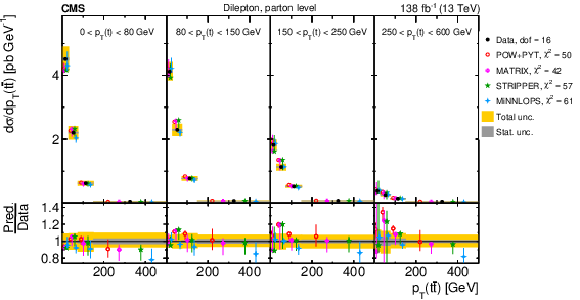
png pdf |
Figure 106-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 106-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}(\mathrm{t})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 107:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 107-a:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 107-b:
Absolute $ [p_{\mathrm{T}}(\mathrm{t}),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 108:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 108-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 108-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
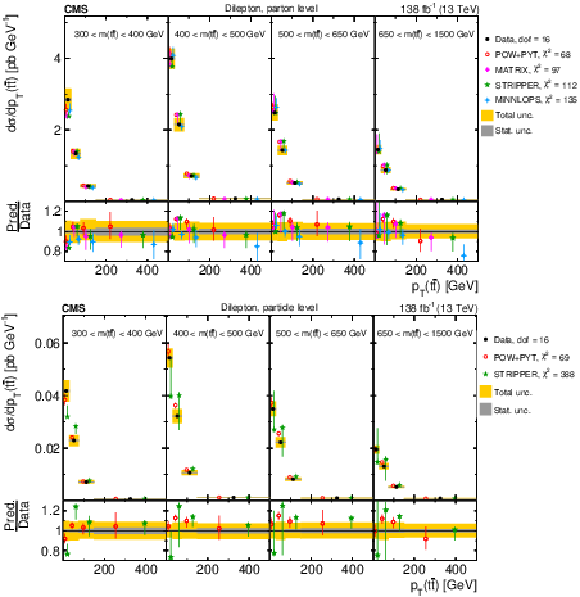
png pdf |
Figure 109:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
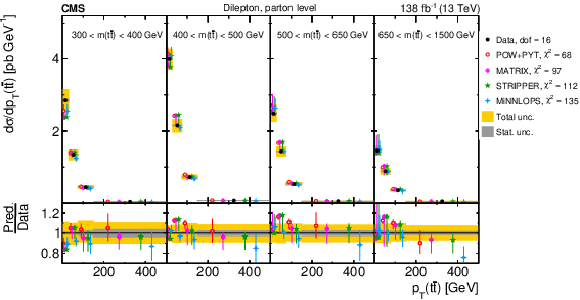
png pdf |
Figure 109-a:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 109-b:
Absolute $ [|y({\mathrm{t}\overline{\mathrm{t}}} )|,\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 110:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
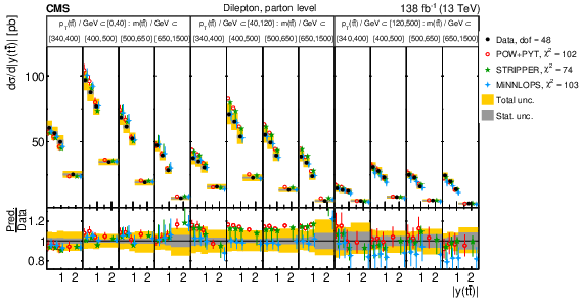
png pdf |
Figure 110-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
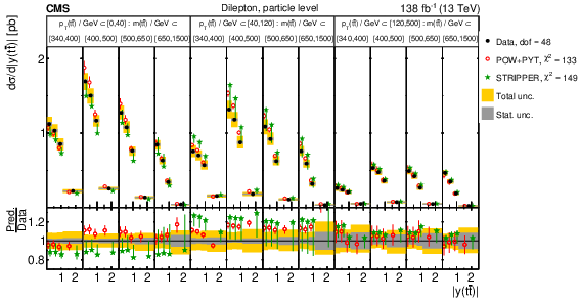
png pdf |
Figure 110-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} )] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
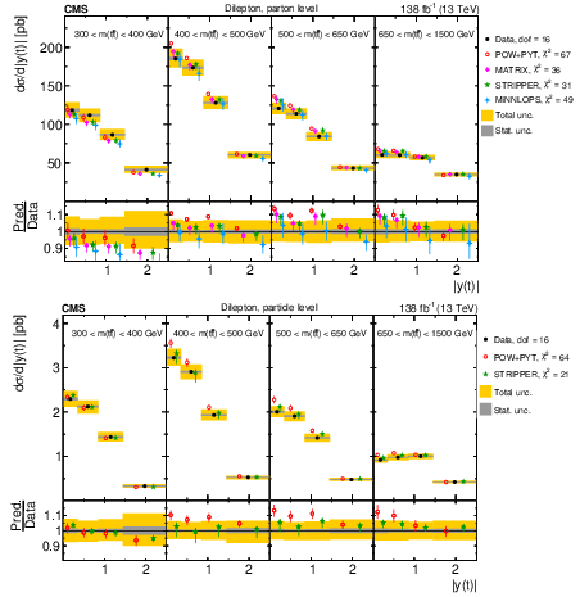
png pdf |
Figure 111:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
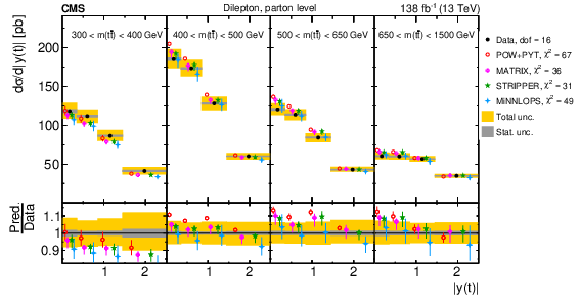
png pdf |
Figure 111-a:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 111-b:
Absolute $ [p_{\mathrm{T}}({\mathrm{t}\overline{\mathrm{t}}} ),\, m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y({\mathrm{t}\overline{\mathrm{t}}} )|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 112:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
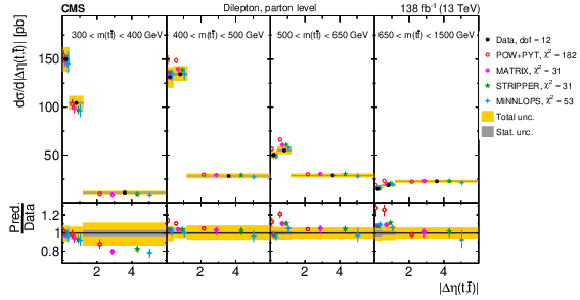
png pdf |
Figure 112-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
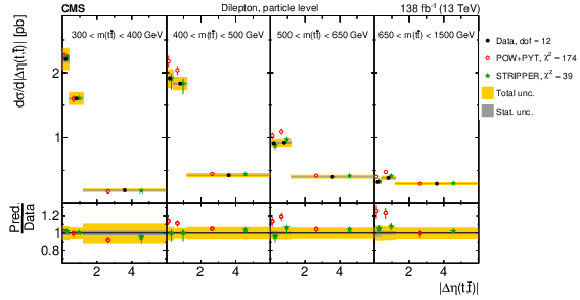
png pdf |
Figure 112-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |y(\mathrm{t})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 113:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
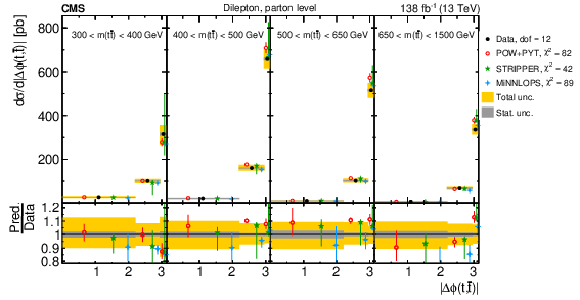
png pdf |
Figure 113-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 113-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \eta(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 114:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |
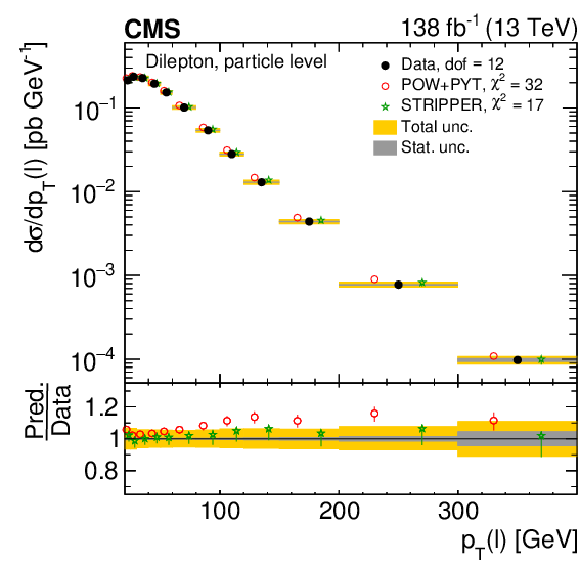
png pdf |
Figure 114-a:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 114-b:
Absolute $ [m({\mathrm{t}\overline{\mathrm{t}}} ),\, |\Delta \phi(\mathrm{t},\overline{\mathrm{t}})|] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and various theoretical predictions with beyond-NLO precision (other points). Further details can be found in the caption of Fig. 105. |

png pdf |
Figure 115:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
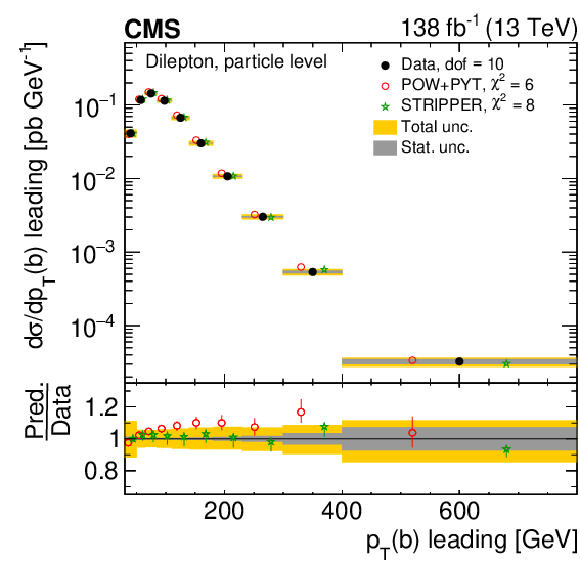
png pdf |
Figure 115-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
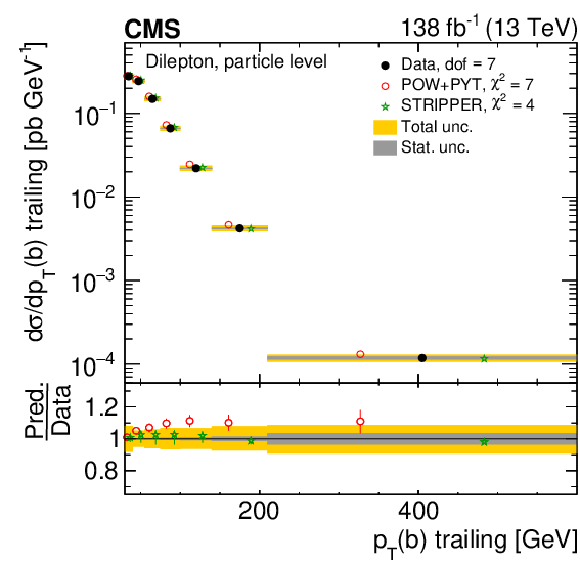
png pdf |
Figure 115-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |
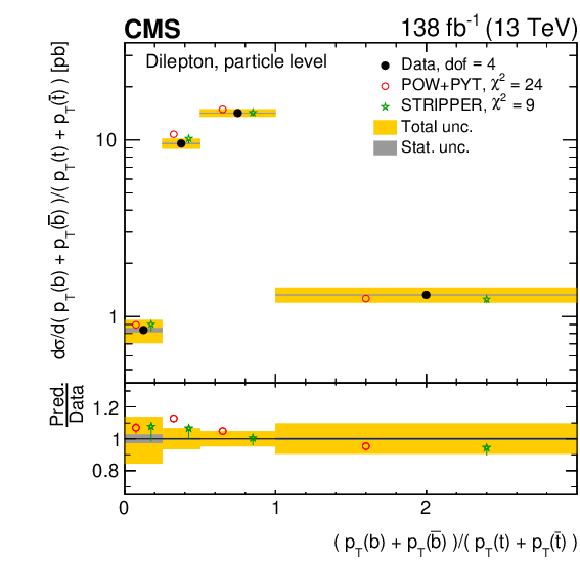
png pdf |
Figure 115-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}} $ of the lepton (upper left), of the ratio of the trailing and leading lepton $ p_{\mathrm{T}} $ (upper right), and of the ratio of lepton and top antiquark $ p_{\mathrm{T}} $ (lower), measured at the particle level in a fiducial phase space. The data are shown as filled circles with grey and yellow bands indicating the statistical and total uncertainties (statistical and systematic uncertainties added in quadrature), respectively. For each distribution, the number of degrees of freedom (dof) is also provided. The cross sections are compared to predictions from the POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation and STRIPPER NNLO calculation (stars). The estimated uncertainties in the predictions are represented by vertical bars on the corresponding points. For each model, a value of $ \chi^2 $ is reported that takes into account the measurement uncertainties. The lower panel in each plot shows the ratios of the predictions to the data. |

png pdf |
Figure 116:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) d-NLO precision (other points). are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
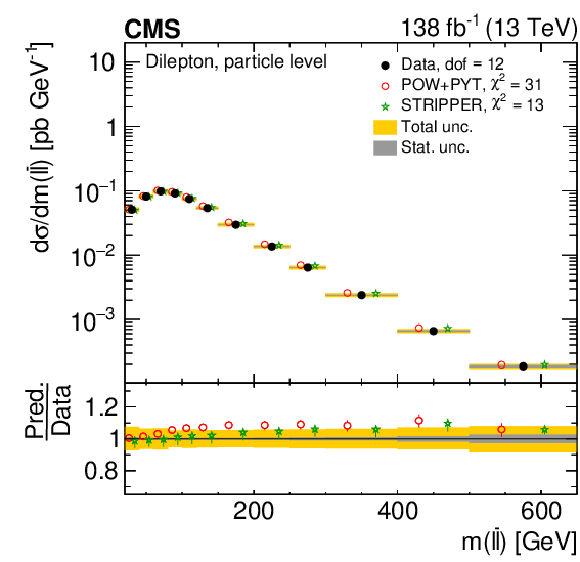
png pdf |
Figure 116-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) d-NLO precision (other points). are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 116-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) d-NLO precision (other points). are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
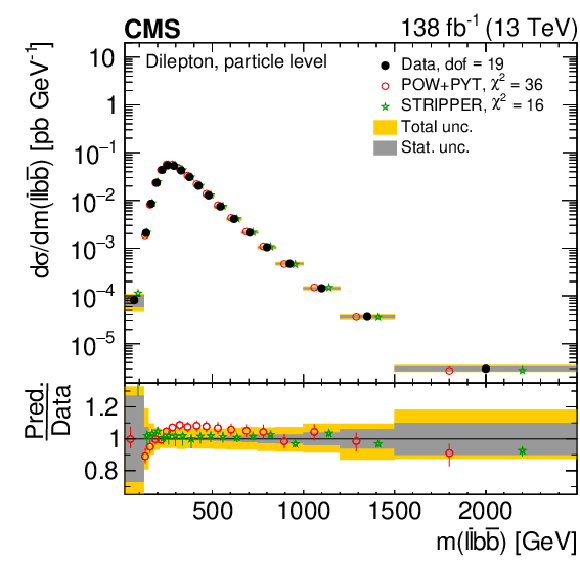
png pdf |
Figure 116-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of the $ p_{\mathrm{T}} $ of the leading (upper left) and trailing (upper right) b jet, and $ (p_{\mathrm{T}}(\mathrm{b}) + p_{\mathrm{T}}(\overline{\mathrm{b}}))/(p_{\mathrm{T}}(\mathrm{t}) + p_{\mathrm{T}}(\overline{\mathrm{t}})) $ (lower) d-NLO precision (other points). are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 117:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
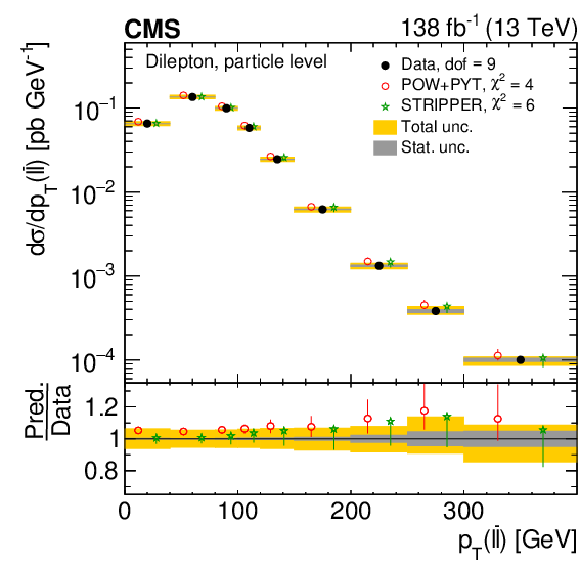
png pdf |
Figure 117-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 117-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
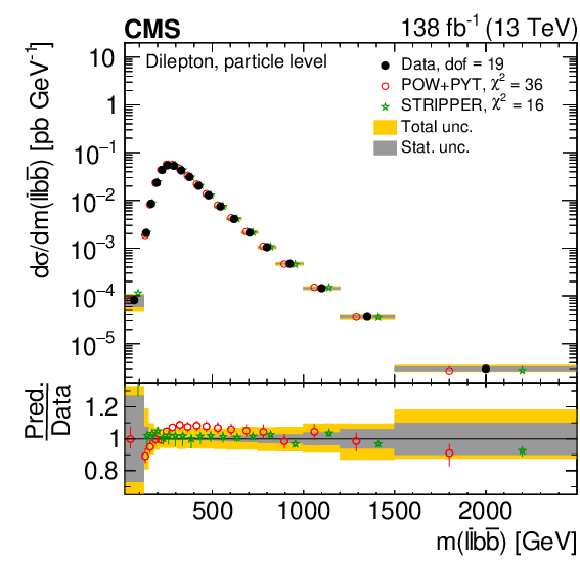
png pdf |
Figure 117-c:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ m(\ell\overline{\ell}) $ (upper left), $ m(\mathrm{b}\overline{\mathrm{b}}) $ (upper right), and $ m(\ell\overline{\ell}\mathrm{b}\overline{\mathrm{b}}) $ (lower) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 118:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
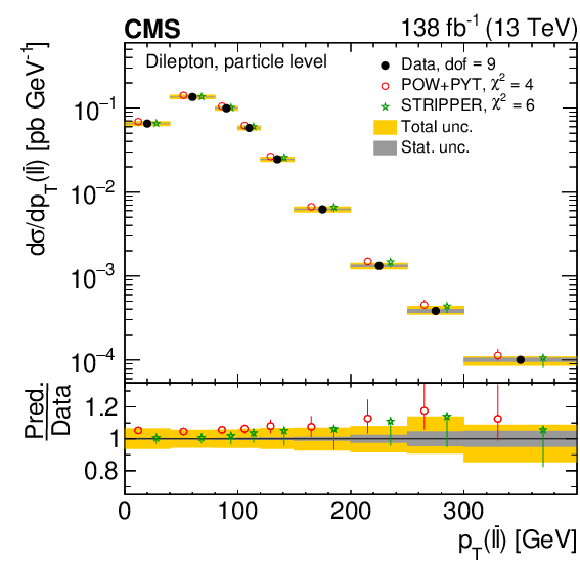
png pdf |
Figure 118-a:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
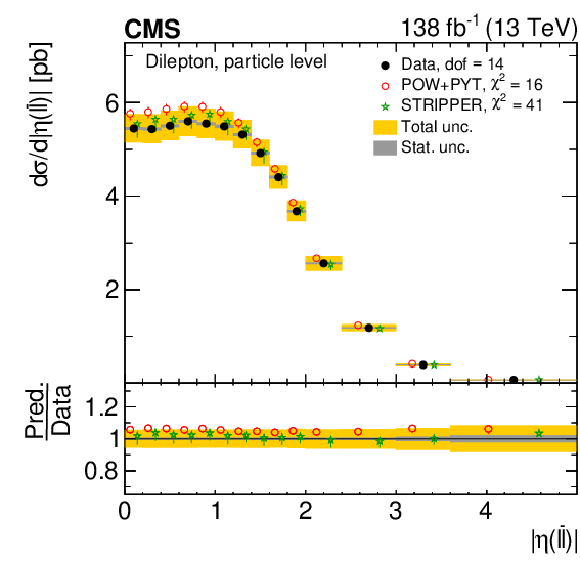
png pdf |
Figure 118-b:
Absolute differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections as functions of $ p_{\mathrm{T}}(\ell\overline{\ell}) $ (left) and $ |\eta(\ell\overline{\ell})| $ (right) are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 119:
Absolute $ [|\eta(\ell\overline{\ell})|,\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |

png pdf |
Figure 120:
Absolute $ [|\eta(\ell\overline{\ell})|,\, p_{\mathrm{T}}(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
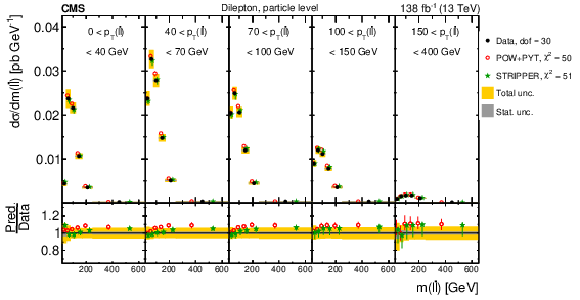
png pdf |
Figure 121:
Absolute $ [p_{\mathrm{T}}(\ell\overline{\ell}),\, m(\ell\overline{\ell})] $ cross sections are shown for data (filled circles), POWHEG + PYTHIA 8 (`POW-PYT', open circles) simulation, and STRIPPER NNLO calculation (stars). Further details can be found in the caption of Fig. 115. |
| Tables | |
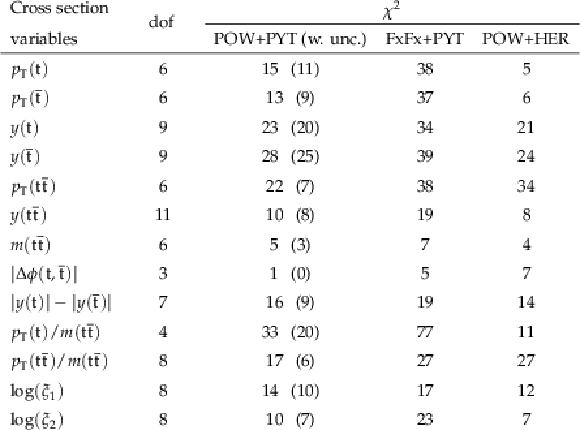
png pdf |
Table 1:
The $ \chi^2 $ values and dof of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 2:
The $ \chi^2 $ values and dof of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 3:
The $ \chi^2 $ values and dof of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 4:
The $ \chi^2 $ values and dof of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 5:
The $ \chi^2 $ values and dof of the measured normalized single-differential cross sections for lepton and b-jet kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 6:
The $ \chi^2 $ values and dof of the measured normalized differential cross sections as a function of the additional-jet multiplicity in the events, at the parton level of the top quark and antiquark, are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
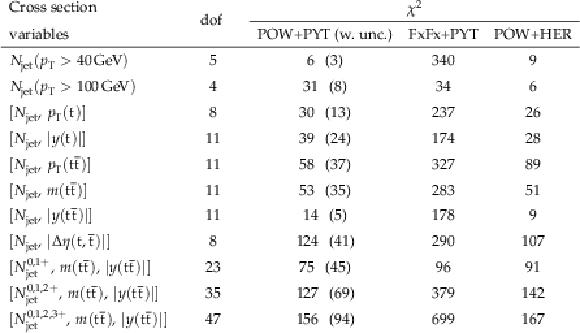
png pdf |
Table 7:
The $ \chi^2 $ values and dof of the measured normalized differential cross sections as a function of the additional-jet multiplicity in the events, at the particle level of the top quark and antiquark, are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
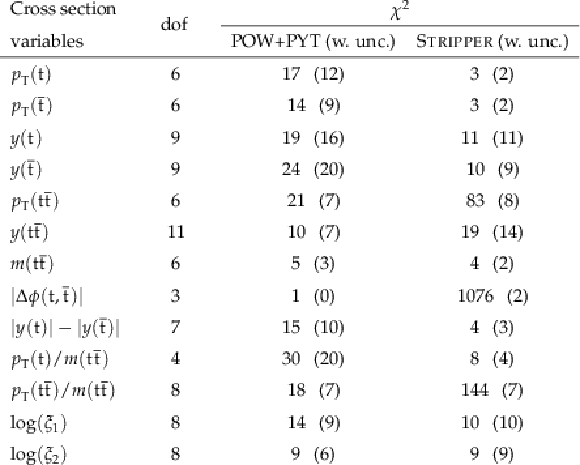
png pdf |
Table 8:
The $ \chi^2 $ values and dof of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 9:
The $ \chi^2 $ values and dof of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 10:
The $ \chi^2 $ values and dof of the measured normalized single-differential cross sections for lepton and b-jet kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
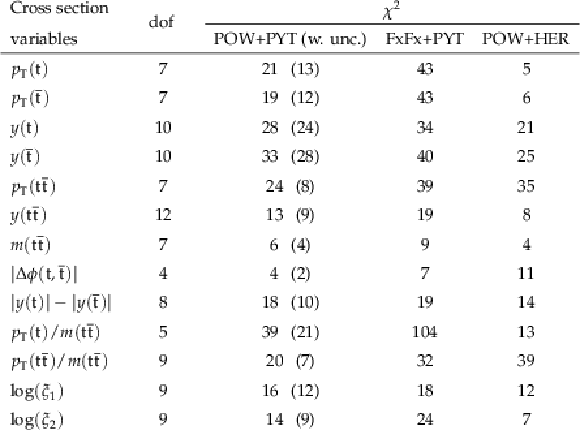
png pdf |
Table 11:
The $ \chi^2 $ values and dof of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 12:
The $ \chi^2 $ values and dof of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
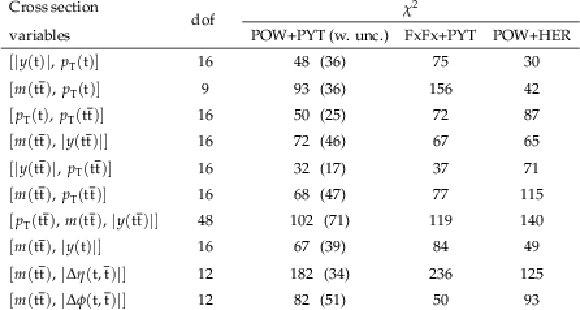
png pdf |
Table 13:
The $ \chi^2 $ values and dof of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 14:
The $ \chi^2 $ values and dof of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
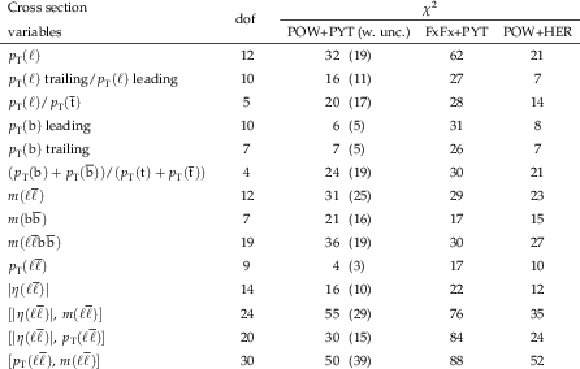
png pdf |
Table 15:
The $ \chi^2 $ values and dof of the measured absolute single-differential cross sections for lepton and b-jet kinematic observables at the particle level are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 16:
The $ \chi^2 $ values and dof of the measured absolute differential cross sections as a function of the additional-jet multiplicity in the events, at the parton level of the top quark and antiquark, are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
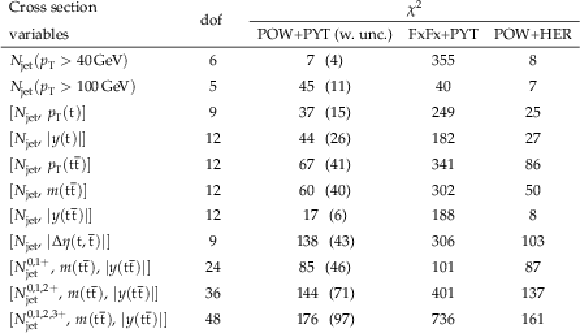
png pdf |
Table 17:
The $ \chi^2 $ values and dof of the measured absolute differential cross sections as a function of the additional-jet multiplicity in the events, at the particle level of the top quark and antiquark, are shown with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 18:
The $ \chi^2 $ values and dof of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
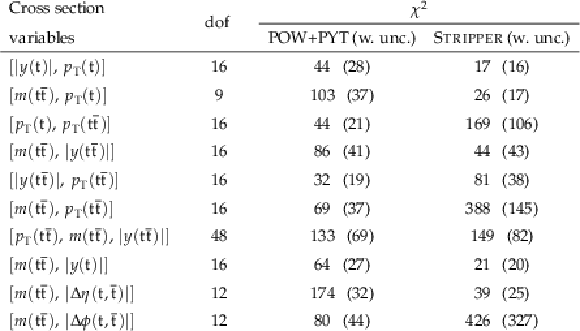
png pdf |
Table 19:
The $ \chi^2 $ values and dof of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
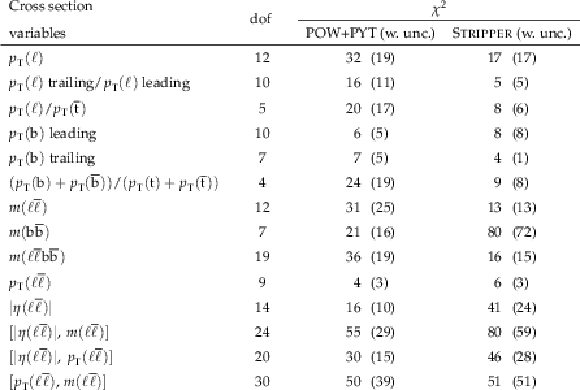
png pdf |
Table 20:
The $ \chi^2 $ values and dof of the measured absolute single-differential cross sections for lepton and b-jet kinematic observables at the particle level are shown with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ \chi^2 $ values including theory uncertainties are indicated with the brackets (w. unc.). |
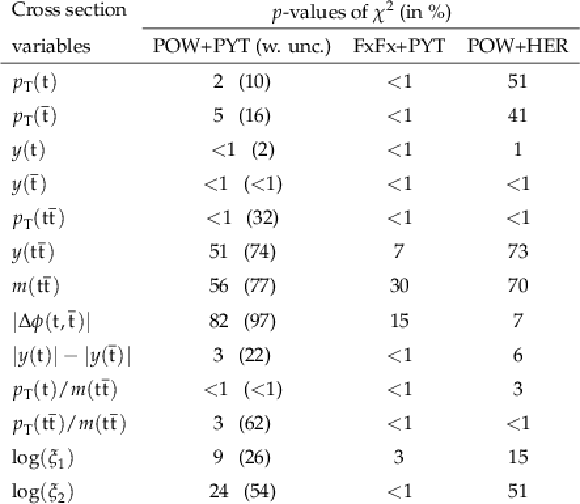
png pdf |
Table 21:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
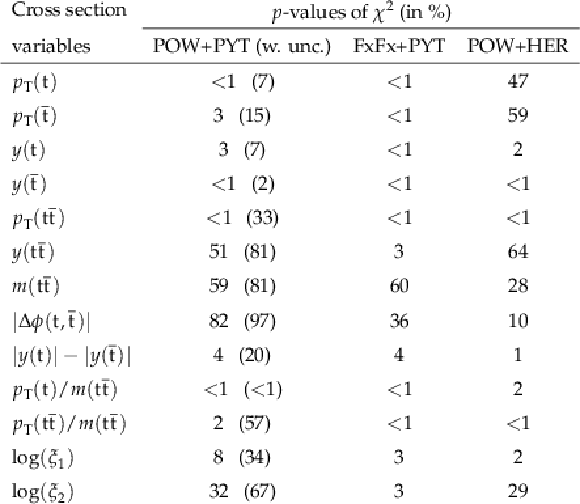
png pdf |
Table 22:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 23:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 24:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
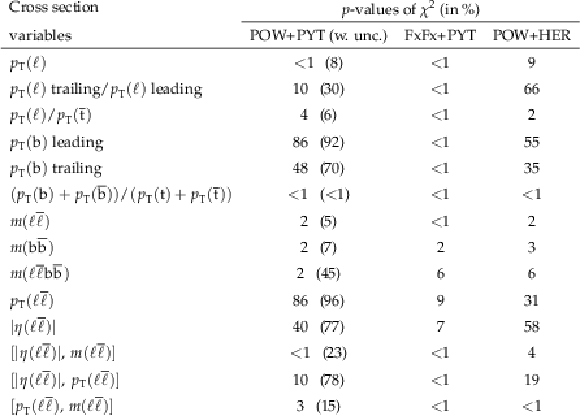
png pdf |
Table 25:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized single-differential cross sections for lepton and b-jet kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 26:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized differential cross sections as a function of the additional-jet multiplicity in the events, at the parton level of the top quark and antiquark, with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
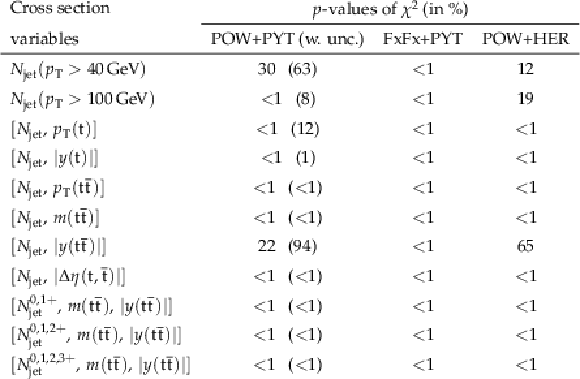
png pdf |
Table 27:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized differential cross sections as a function of the additional-jet multiplicity in the events, at the particle level of the top quark and antiquark, with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
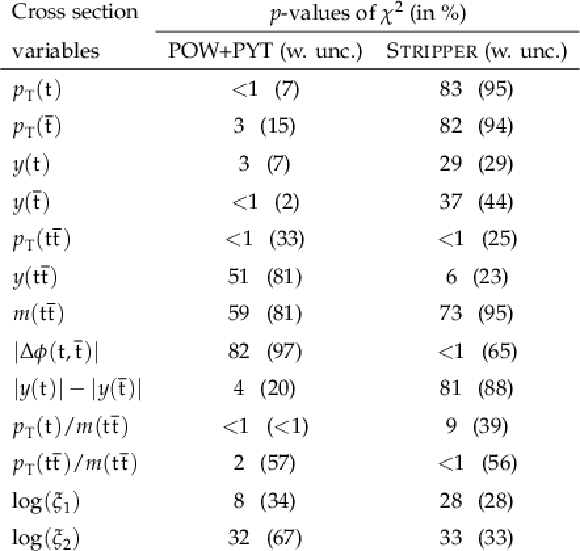
png pdf |
Table 28:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 29:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
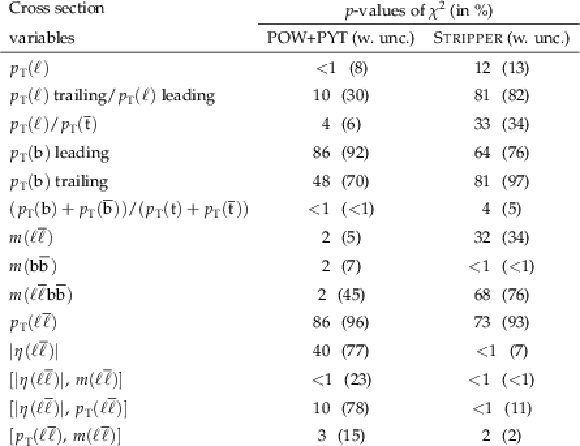
png pdf |
Table 30:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured normalized single-differential cross sections for lepton and b-jet kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 31:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
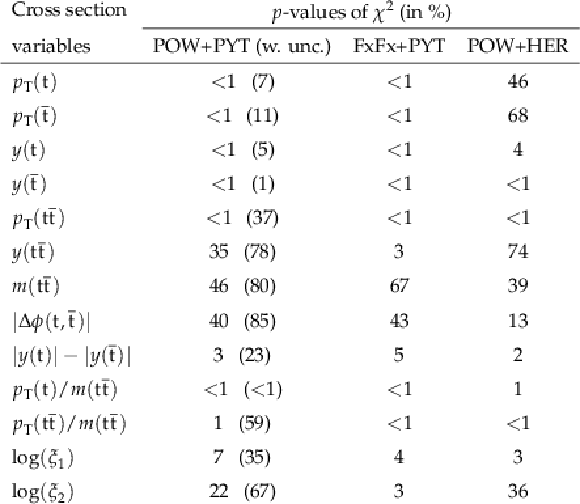
png pdf |
Table 32:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 33:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the parton level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 34:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 35:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute single-differential cross sections for lepton and b-jet kinematic observables at the particle level with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
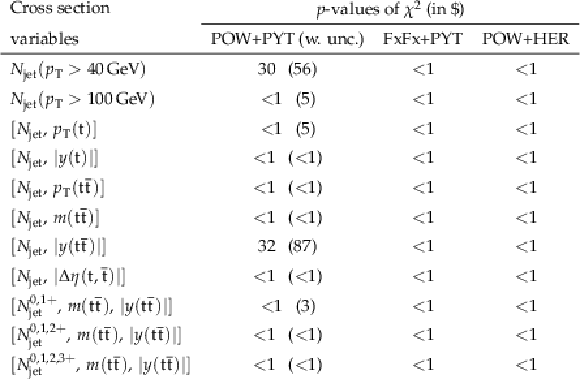
png pdf |
Table 36:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute differential cross sections as a function of the additional-jet multiplicity in the events, at the parton level of the top quark and antiquark, with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 37:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute differential cross sections as a function of the additional-jet multiplicity in the events, at the particle level of the top quark and antiquark, with respect to the predictions of various MC generators. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |

png pdf |
Table 38:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute single-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
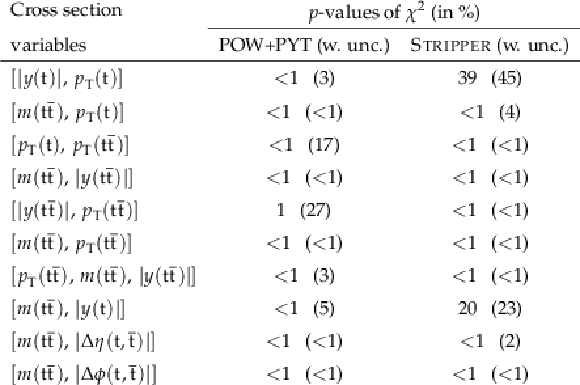
png pdf |
Table 39:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute multi-differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ and top quark kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
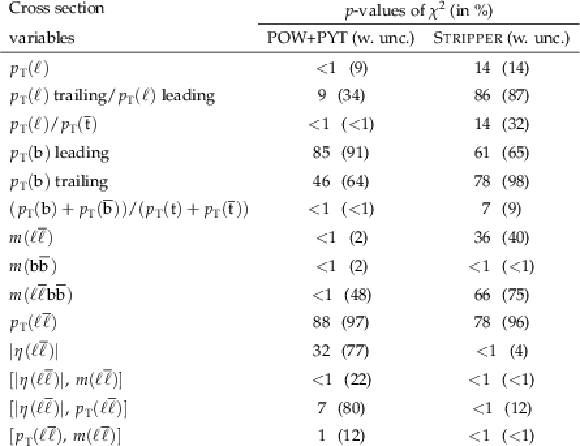
png pdf |
Table 40:
The $ p $-values are shown for the $ \chi^2 $ tests of the measured absolute single-differential cross sections for lepton and b-jet kinematic observables at the particle level with respect to the POWHEG + PYTHIA 8 (`POW-PYT') simulation and the STRIPPER NNLO calculation. The $ \chi^2 $ values are calculated taking only measurement uncertainties into account and excluding theory uncertainties. For POW+PYT, the $ p $-values of the $ \chi^2 $ tests including theory uncertainties are indicated with the brackets (w. unc.). |
| Summary |
| A measurement of differential top quark pair ( $ \mathrm{t} \overline{\mathrm{t}} $) production cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV was presented, performed with events containing two oppositely charged leptons (electrons or muons). The data used in this analysis were recorded in the years 2016 through 2018 with the CMS detector at the LHC and correspond to an integrated luminosity of 138 fb$^{-1}$. Differential cross sections are measured as functions of kinematical observables of the $ \mathrm{t} \overline{\mathrm{t}} $ system, the top quark and antiquark and their decay products, and the total number of additional jets in the event not originating from the $ \mathrm{t} \overline{\mathrm{t}} $ decay. The measurements are performed as functions of single observables, or simultaneously as functions of two or three kinematic variables. The differential cross sections are defined both with particle-level objects in a fiducial phase space close to that of the detector acceptance and with parton-level top quarks in the full phase space. Overall, both the statistical and the systematic uncertainties in the measurements are improved by a factor of about two compared to the previous analyses [38,39] which are based on the 2016 data set. Predictions of several next-to-leading-order (NLO) Monte Carlo (MC) event generators that differ in the hard matrix element, parton shower, and hadronization models were compared to the data. The predictions of these MC models, without taking theoretical uncertainties into account, generally fail to describe many of the measured cross sections in their full kinematic range. The predicted transverse momentum $ p_{\mathrm{T}} $ distributions of the top quark and antiquark are harder than observed in the data, and the rapidity distributions are more central. The invariant mass and rapidity distributions of the $ \mathrm{t} \overline{\mathrm{t}} $ system are reasonably well described by the models overall. The predictions for the $ \mathrm{t} \overline{\mathrm{t}} $ transverse momentum distribution differ from the data even more than the top quark and antiquark distributions do; none of them provides a good description of the data. Double- and triple-differential cross sections show large model-to-data discrepancies, for instance the effect of a harder top quark $ p_{\mathrm{T}} $ spectrum $ p_{\mathrm{T}}(\mathrm{t}) $ in the models is pronounced at high $ m({\mathrm{t}\overline{\mathrm{t}}} ) $. Differential cross sections as functions of kinematic observables of the leptons and b jets originating from the decay of the top quark and antiquark are measured with high precision. Overall, the observed trends for these objects follow those for the top quarks and antiquarks, with the models predicting harder $ p_{\mathrm{T}} $ spectra than seen in the data. For the leptons, this effect is somewhat enhanced and furthermore the dilepton invariant mass spectrum is harder in the models than in the data. The distribution of the multiplicity of additional jets in $ \mathrm{t} \overline{\mathrm{t}} $ events shows varying level of agreement between data and the models. When considered as a function of jet multiplicity, the evolution of the shapes of $ \mathrm{t} \overline{\mathrm{t}} $, top quark and antiquark kinematic distributions is different for the models and for data. There is an indication that the trend of harder $ p_{\mathrm{T}}(\mathrm{t}) $ distributions in the models is localized at small jet multiplicities. Selected kinematic distributions were also compared to a variety of theoretical predictions beyond NLO precision. For observables of the top quark and the $ \mathrm{t} \overline{\mathrm{t}} $ system, these predictions provide descriptions of the data that are of similar or improved quality, compared to the MC model best describing each variable, except for some of the kinematic spectra that are directly sensitive to higher-order QCD effects. For observables associated with the leptons and b jets, the quality of the tested next-to-NLO model is on average comparable to but not better than that of the NLO MC models. Comparing several kinematic distributions of the top quark and the $ \mathrm{t} \overline{\mathrm{t}} $ system to NLO MC models using various parton distribution function (PDF) sets, clear differences are observed which indicate a sensitivity to PDFs that could be exploited in future PDF fits. For each distribution, the quality of the description of the data by the models has been assessed with a $ \chi^2 $ test statistic. When only the measurement uncertainties are taken into account in the calculation (i.e., neglecting the uncertainties on the predictions), the $ p $-values obtained from the $ \chi^2 $ tests are in general close to zero, pointing to a poor description of the data by the nominal models. For the POWHEG + PYTHIA 8 model, additional $ \chi^2 $ values have been evaluated including the uncertainties on the prediction. This inclusion often leads to substantially reduced $ \chi^2 $ values with reasonable $ p $-values. However, for several distributions, and in particular for a larger fraction of the multi-differential distributions, the observed differences between data and simulation still remain significant, providing important input for future theoretical predictions. |
| References | ||||
| 1 | Particle Data Group Collaboration | Review of Particle Physics | PTEP 2022 (2022) 083C01 | |
| 2 | D. Atwood, A. Kagan, and T. G. Rizzo | Constraining anomalous top quark couplings at the Tevatron | PRD 52 (1995) 6264 | hep-ph/9407408 |
| 3 | P. Langacker | The physics of heavy $ Z^\prime $ gauge bosons | Rev. Mod. Phys. 81 (2009) 1199 | 0801.1345 |
| 4 | C. Englert, A. Freitas, M. Spira, and P. M. Zerwas | Constraining the intrinsic structure of top-quarks | PLB 721 (2013) 261 | 1210.2570 |
| 5 | ATLAS Collaboration | Measurement of spin correlation in top-antitop quark events and search for top squark pair production in pp collisions at $ \sqrt{s}= $ 8 TeV using the ATLAS detector | PRL 114 (2015) 142001 | 1412.4742 |
| 6 | A. Albert et al. | Towards the next generation of simplified Dark Matter models | Phys. Dark Univ. 16 (2017) 49 | 1607.06680 |
| 7 | CMS Collaboration | Search for dark matter particles produced in association with a top quark pair at $ \sqrt{s}= $ 13 TeV | PRL 122 (2019) 011803 | CMS-EXO-16-049 1807.06522 |
| 8 | CMS Collaboration | Search for heavy Higgs bosons decaying to a top quark pair in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 04 (2020) 171 | CMS-HIG-17-027 1908.01115 |
| 9 | T. Biekötter et al. | Possible indications for new Higgs bosons in the reach of the LHC: N2HDM and NMSSM interpretations | EPJC 82 (2022) 178 | 2109.01128 |
| 10 | A. Anuar et al. | ALP-ine quests at the LHC: hunting axion-like particles via peaks and dips in $ \mathrm{t} \overline{\mathrm{t}} $ production | 2404.19014 | |
| 11 | N. Kidonakis | NNNLO soft-gluon corrections for the top-quark $ p_{\mathrm{T}} $ and rapidity distributions | PRD 91 (2015) 031501 | 1411.2633 |
| 12 | N. Kidonakis | Top-quark double-differential distributions at approximate N$ ^3 $LO | PRD 101 (2020) 074006 | 1912.10362 |
| 13 | M. Czakon, D. Heymes, and A. Mitov | High-precision differential predictions for top-quark pairs at the LHC | PRL 116 (2016) 082003 | 1511.00549 |
| 14 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 15 | M. Czakon et al. | Resummation for (boosted) top-quark pair production at NNLO+NNLL' in QCD | JHEP 05 (2018) 149 | 1803.07623 |
| 16 | S. Catani et al. | Top-quark pair production at the LHC: Fully differential QCD predictions at NNLO | JHEP 07 (2019) 100 | 1906.06535 |
| 17 | M. Czakon, A. Mitov, and R. Poncelet | NNLO QCD corrections to leptonic observables in top-quark pair production and decay | JHEP 05 (2021) 212 | 2008.11133 |
| 18 | ATLAS Collaboration | Measurements of top quark pair relative differential cross sections with ATLAS in pp collisions at $ \sqrt{s}= $ 7 TeV | EPJC 73 (2013) 2261 | 1207.5644 |
| 19 | CMS Collaboration | Measurement of differential top-quark pair production cross sections in pp collisions at $ \sqrt{s}= $ 7 TeV | EPJC 73 (2013) 2339 | CMS-TOP-11-013 1211.2220 |
| 20 | ATLAS Collaboration | Measurements of normalized differential cross sections for $ \mathrm{t} \overline{\mathrm{t}} $ production in pp collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | PRD 90 (2014) 072004 | 1407.0371 |
| 21 | ATLAS Collaboration | Differential top-antitop cross section measurements as a function of observables constructed from final-state particles using pp collisions at $ \sqrt{s}= $ 7 TeV in the ATLAS detector | JHEP 06 (2015) 100 | 1502.05923 |
| 22 | ATLAS Collaboration | Measurement of top quark pair differential cross sections in the dilepton channel in pp collisions at $ \sqrt{s}= $ 7 and 8 TeV with ATLAS | PRD 94 (2016) 092003 | 1607.07281 |
| 23 | CMS Collaboration | Measurement of the differential cross section for top quark pair production in pp collisions at $ \sqrt{s}= $ 8 TeV | EPJC 75 (2015) 542 | CMS-TOP-12-028 1505.04480 |
| 24 | ATLAS Collaboration | Measurements of top-quark pair differential cross sections in the lepton+jets channel in pp collisions at $ \sqrt{s}= $ 8 TeV using the ATLAS detector | EPJC 76 (2016) 538 | 1511.04716 |
| 25 | ATLAS Collaboration | Measurement of the differential cross section of highly boosted top quarks as a function of their transverse momentum in $ \sqrt{s}= $ 8 TeV proton-proton collisions using the ATLAS detector | PRD 93 (2016) 032009 | 1510.03818 |
| 26 | CMS Collaboration | Measurement of the $ \mathrm{t} \overline{\mathrm{t}} $ production cross section in the all-jets final state in pp collisions at $ \sqrt{s}= $ 8 TeV | EPJC 76 (2016) 128 | CMS-TOP-14-018 1509.06076 |
| 27 | CMS Collaboration | Measurement of the integrated and differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections for high-$ p_{\mathrm{T}} $ top quarks in pp collisions at $ \sqrt{s}= $ 8 TeV | PRD 94 (2016) 072002 | CMS-TOP-14-012 1605.00116 |
| 28 | CMS Collaboration | Measurement of double-differential cross sections for top quark pair production in pp collisions at $ \sqrt{s}= $ 8 TeV and impact on parton distribution functions | EPJC 77 (2017) 459 | CMS-TOP-14-013 1703.01630 |
| 29 | ATLAS Collaboration | Measurement of the top-quark mass in $ {\mathrm{t}\overline{\mathrm{t}}} + $ 1-jet events collected with the ATLAS detector in pp collisions at $ \sqrt{s}= $ 8 TeV | JHEP 11 (2019) 150 | 1905.02302 |
| 30 | CMS Collaboration | Measurement of differential cross sections for top quark pair production using the lepton+jets final state in proton-proton collisions at 13 TeV | PRD 95 (2017) 092001 | CMS-TOP-16-008 1610.04191 |
| 31 | ATLAS Collaboration | Measurement of jet activity produced in top-quark events with an electron, a muon and two b-tagged jets in the final state in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | EPJC 77 (2017) 220 | 1610.09978 |
| 32 | ATLAS Collaboration | Measurements of top-quark pair differential cross sections in the $ {\mathrm{e}}{\mu} $ channel in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | EPJC 77 (2017) 292 | 1612.05220 |
| 33 | ATLAS Collaboration | Measurements of top-quark pair differential cross sections in the lepton+jets channel in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | JHEP 11 (2017) 191 | 1708.00727 |
| 34 | CMS Collaboration | Measurement of normalized differential $ \mathrm{t} \overline{\mathrm{t}} $ cross sections in the dilepton channel from pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 04 (2018) 060 | CMS-TOP-16-007 1708.07638 |
| 35 | ATLAS Collaboration | Measurements of $ t\bar{t} $ differential cross-sections of highly boosted top quarks decaying to all-hadronic final states in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | PRD 98 (2018) 012003 | 1801.02052 |
| 36 | ATLAS Collaboration | Measurements of differential cross sections of top quark pair production in association with jets in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | JHEP 10 (2018) 159 | 1802.06572 |
| 37 | CMS Collaboration | Measurement of differential cross sections for the production of top quark pairs and of additional jets in lepton+jets events from pp collisions at $ \sqrt{s}= $ 13 TeV | PRD 97 (2018) 112003 | CMS-TOP-17-002 1803.08856 |
| 38 | CMS Collaboration | Measurements of $ \mathrm{t} \overline{\mathrm{t}} $ differential cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using events containing two leptons | JHEP 02 (2019) 149 | CMS-TOP-17-014 1811.06625 |
| 39 | CMS Collaboration | Measurement of $ \mathrm{t} \overline{\mathrm{t}} $ normalised multi-differential cross sections in pp collisions at $ \sqrt{s}= $ 13 TeV, and simultaneous determination of the strong coupling strength, top quark pole mass, and parton distribution functions | EPJC 80 (2020) 658 | CMS-TOP-18-004 1904.05237 |
| 40 | ATLAS Collaboration | Measurements of top-quark pair differential and double-differential cross sections in the $ \ell $+jets channel with pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | EPJC 79 (2019) 1028 | 1908.07305 |
| 41 | ATLAS Collaboration | Measurement of the $ \mathrm{t} \overline{\mathrm{t}} $ production cross section and lepton differential distributions in $ {\mathrm{e}}{\mu} $ dilepton events from pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | EPJC 80 (2020) 528 | 1910.08819 |
| 42 | ATLAS Collaboration | Measurements of top-quark pair single- and double-differential cross sections in the all-hadronic channel in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | JHEP 01 (2021) 033 | 2006.09274 |
| 43 | CMS Collaboration | Measurement of differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections using top quarks at large transverse momenta in pp collisions at $ \sqrt{s} = $ 13 TeV | PRD 103 (2021) 052008 | CMS-TOP-18-013 2008.07860 |
| 44 | CMS Collaboration | Measurement of differential $ \mathrm{t} \overline{\mathrm{t}} $ production cross sections in the full kinematic range using lepton+jets events from proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 104 (2021) 092013 | CMS-TOP-20-001 2108.02803 |
| 45 | ATLAS Collaboration | Measurements of differential cross sections in top-quark pair events with a high transverse momentum top quark and limits on beyond the standard model contributions to top-quark pair production with the atlas detector at $ \sqrt{s} = $ 13 TeV | JHEP 06 (2022) 063 | 2202.12134 |
| 46 | ATLAS Collaboration | Differential $ \mathrm{t} \overline{\mathrm{t}} $ cross-section measurements using boosted top quarks in the all-hadronic final state with 139 fb$ ^{-1} $ of ATLAS data | JHEP 04 (2023) 080 | 2205.02817 |
| 47 | ATLAS Collaboration | Inclusive and differential cross sections for dilepton $ \mathrm{t} \overline{\mathrm{t}} $ production measured in $ \sqrt{s} = $ 13 TeV pp collisions with the ATLAS detector | JHEP 07 (2023) 141 | 2303.15340 |
| 48 | CMS Collaboration | HEPData record for this analysis | link | |
| 49 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 50 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 51 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and LO | NPB 855 (2012) 153 | 1107.2652 |
| 52 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 53 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 54 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 55 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 56 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 57 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 58 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 59 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 60 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 61 | CMS Collaboration | Investigations of the impact of the parton shower tuning in PYTHIA in the modelling of $ \mathrm{t} \overline{\mathrm{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS Physics Analysis Summary, 2016 CMS-PAS-TOP-16-021 |
CMS-PAS-TOP-16-021 |
| 62 | P. Artoisenet, R. Frederix, O. Mattelaer, and R. Rietkerk | Automatic spin-entangled decays of heavy resonances in Monte Carlo simulations | JHEP 03 (2013) 015 | 1212.3460 |
| 63 | J. Bellm et al. | HERWIG 7.0/ HERWIG++ 3.0 release note | EPJC 76 (2016) 196 | 1512.01178 |
| 64 | CMS Collaboration | Development and validation of HERWIG 7 tunes from CMS underlying-event measurements | EPJC 81 (2021) 312 | CMS-GEN-19-001 2011.03422 |
| 65 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 66 | R. Frederix, E. Re, and P. Torrielli | Single-top $ t $-channel hadroproduction in the four-flavour scheme with POWHEG and aMC@NLO | JHEP 09 (2012) 130 | 1207.5391 |
| 67 | E. Re | Single-top $ {\mathrm{W}}{\mathrm{t}} $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 68 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 69 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 Tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 70 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 71 | M. L. Mangano, M. Moretti, F. Piccinini, and M. Treccani | Matching matrix elements and shower evolution for top-quark production in hadronic collisions | JHEP 01 (2007) 013 | hep-ex/0611129 |
| 72 | S. Mrenna and P. Richardson | Matching matrix elements and parton showers with HERWIG and PYTHIA | JHEP 05 (2004) 040 | hep-ph/0312274 |
| 73 | P. Kant et al. | HatHor for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | Comput. Phys. Commun. 191 (2015) 74 | 1406.4403 |
| 74 | N. Kidonakis | Two-loop soft anomalous dimensions for single top quark associated production with $ \mathrm{W^-} $ or $ {\mathrm{H}}^- $ | PRD 82 (2010) 054018 | |
| 75 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 76 | J. M. Campbell, R. K. Ellis, and C. Williams | Vector boson pair production at the LHC | JHEP 07 (2011) 018 | 1105.0020 |
| 77 | M. Czakon and A. Mitov | TOP++: a program for the calculation of the top-pair cross section at hadron colliders | Comput. Phys. Commun. 185 (2014) 2930 | 1112.5675 |
| 78 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 79 | P. Bärnreuther, M. Czakon, and A. Mitov | Percent level precision physics at the Tevatron: first genuine NNLO QCD corrections to $ {\mathrm{q}}{\overline{\mathrm{q}}}\rightarrow {\mathrm{t}\overline{\mathrm{t}}} +{\mathrm{X}} $ | PRL 109 (2012) 132001 | 1204.5201 |
| 80 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 81 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 82 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 83 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ \mathcal{O}({\alpha_s}^4) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 84 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 85 | ATLAS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV with the ATLAS detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 86 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 87 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 88 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 89 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 90 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 91 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 92 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 93 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 94 | CMS Collaboration | A Deep Neural Network for simultaneous estimation of b jet energy and resolution | Comput. Softw. Big Sci. 4 (2020) 10 | CMS-HIG-18-027 1912.06046 |
| 95 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 96 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 59 | 1407.6013 |
| 97 | I. Korol | Measurement of Double Differential $ \mathrm{t} \overline{\mathrm{t}} $ Production Cross Sections with the CMS Detector | PhD thesis, Universität Hamburg, 2016 link |
|
| 98 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 99 | R. Brun and F. Rademakers | ROOT: An object oriented data analysis framework | NIM A 389 (1997) 81 | |
| 100 | S. Schmitt | TUnfold: an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 101 | A. N. Tikhonov | Solution of incorrectly formulated problems and the regularization method | Sov. Math. Dokl. 4 (1963) 1035 | |
| 102 | S. Schmitt | Data unfolding methods in high energy physics | Eur. Phys. J. Web Conf. 137 (2017) 11008 | 1611.01927 |
| 103 | CMS Collaboration | Object definitions for top quark analyses at the particle level | CMS Note CERN-CMS-NOTE-2017-004, 2017 CDS |
|
| 104 | M. Cacciari, G. P. Salam, and G. Soyez | The catchment area of jets | JHEP 04 (2008) 005 | 0802.1188 |
| 105 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 106 | CMS Collaboration | CMS Luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 107 | CMS Collaboration | CMS Luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 108 | CMS Collaboration | Measurement of the Drell-Yan cross section in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 10 (2011) 007 | CMS-EWK-10-007 1108.0566 |
| 109 | CMS Collaboration | Measurement of the top quark pair production cross section in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRL 116 (2016) 052002 | CMS-TOP-15-003 1510.05302 |
| 110 | CMS Collaboration | Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at $ \sqrt{s} = $ 13 TeV | EPJC 81 (2021) 378 | CMS-HIG-19-008 2011.03652 |
| 111 | S. Argyropoulos and T. Sjöstrand | Effects of color reconnection on $ \mathrm{t} \overline{\mathrm{t}} $ final states at the LHC | JHEP 11 (2014) 043 | 1407.6653 |
| 112 | J. R. Christiansen and P. Z. Skands | String formation beyond leading colour | JHEP 08 (2015) 003 | 1505.01681 |
| 113 | M. Bähr et al. | HERWIG++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 114 | CMS Collaboration | Running of the top quark mass from proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 803 (2020) 135263 | CMS-TOP-19-007 1909.09193 |
| 115 | T. Chwalek and F. Déliot | Top quark asymmetries | Universe 8 (2022) 622 | |
| 116 | M. Diehl | Theory uncertainties | in Data analysis in high energy physics: A practical guide to statistical methods, O.Behnke, K.Kröninger, T.Schörner-Sadenius, and G.Schott, eds, 2013 link |
|
| 117 | M. Grazzini, S. Kallweit, and M. Wiesemann | Fully differential NNLO computations with MATRIX | EPJC 78 (2018) 537 | 1711.06631 |
| 118 | S. Catani et al. | Top-quark pair hadroproduction at next-to-next-to-leading order in QCD | PRD 99 (2019) 051501 | 1901.04005 |
| 119 | F. Buccioni et al. | OpenLoops 2 | EPJC 79 (2019) 866 | 1907.13071 |
| 120 | F. Cascioli, P. Maierhofer, and S. Pozzorini | Scattering amplitudes with Open Loops | PRL 108 (2012) 111601 | 1111.5206 |
| 121 | A. Denner, S. Dittmaier, and L. Hofer | Collier: a fortran-based Complex One-Loop LIbrary in Extended Regularizations | Comput. Phys. Commun. 212 (2017) 220 | 1604.06792 |
| 122 | S. Catani et al. | Vector boson production at hadron colliders: hard-collinear coefficients at the NNLO | EPJC 72 (2012) 2195 | 1209.0158 |
| 123 | S. Catani and M. Grazzini | An NNLO subtraction formalism in hadron collisions and its application to Higgs boson production at the LHC | PRL 98 (2007) 222002 | hep-ph/0703012 |
| 124 | M. Czakon | A novel subtraction scheme for double-real radiation at NNLO | PLB 693 (2010) 259 | 1005.0274 |
| 125 | M. Czakon and D. Heymes | Four-dimensional formulation of the sector-improved residue subtraction scheme | NPB 890 (2014) 152 | 1408.2500 |
| 126 | M. Czakon | Double-real radiation in hadronic top quark pair production as a proof of a certain concept | NPB 849 (2011) 250 | 1101.0642 |
| 127 | P. F. Monni et al. | MiNNLO$ _{\text {PS}} $: a new method to match NNLO QCD to parton showers | JHEP 05 (2020) 143 | 1908.06987 |
| 128 | P. F. Monni, E. Re, and M. Wiesemann | MiNNLO$ _{\text {PS}} $: optimizing 2 $ \rightarrow $ 1 hadronic processes | EPJC 80 (2020) 1075 | 2006.04133 |
| 129 | J. Mazzitelli et al. | Top-pair production at the LHC with MINNLO$ _{PS} $ | JHEP 04 (2022) 079 | 2112.12135 |
| 130 | K. Hamilton, P. Nason, and G. Zanderighi | MINLO: Multi-scale improved NLO | JHEP 10 (2012) 155 | 1206.3572 |
| 131 | K. Hamilton, P. Nason, C. Oleari, and G. Zanderighi | Merging $ {\mathrm{H}/\mathrm{W}/\mathrm{Z}} $ + 0 and 1 jet at NLO with no merging scale: a path to parton shower + NNLO matching | JHEP 05 (2013) 082 | 1212.4504 |
| 132 | S. Dulat et al. | New parton distribution functions from a global analysis of quantum chromodynamics | PRD 93 (2016) 033006 | 1506.07443 |
| 133 | S. Alekhin, J. Bl \"u mlein, and S. Moch | NLO PDFs from the ABMP16 fit | EPJC 78 (2018) 477 | 1803.07537 |
| 134 | L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne | Parton distributions in the LHC era: MMHT 2014 PDFs | EPJC 75 (2015) 204 | 1412.3989 |
| 135 | H1 and ZEUS Collaborations | Combination of measurements of inclusive deep inelastic $ {\mathrm{e}^\pm\mathrm{p}} $ scattering cross sections and QCD analysis of HERA data | EPJC 75 (2015) 580 | 1506.06042 |
| 136 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 137 | A. Accardi et al. | A critical appraisal and evaluation of modern PDFs | EPJC 76 (2016) 471 | 1603.08906 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|