Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-TOP-21-003 | ||
| Search for new physics using top quark pairs produced in association with a boosted Z or Higgs boson in effective field theory | ||
| CMS Collaboration | ||
| February 2022 | ||
| Abstract: A data sample containing top quark pairs produced in association with a boosted Z or Higgs boson is used to search for signs of new physics. The data correspond to an integrated luminosity of 138 fb$^{-1}$ of proton-proton collisions produced at a center-of-mass energy of 13 TeV at the LHC and collected by the CMS experiment. Selected collision events contain a single lepton and hadronic jets, including two identified with the decay of bottom quarks, plus an additional large-radius jet with high transverse momentum identified as a Z or Higgs boson candidate decaying to a bottom quark pair. Machine learning techniques are employed to discriminate between $\mathrm{t}\bar{\mathrm{t}}$Z or $\mathrm{t}\bar{\mathrm{t}}$H events and events from background processes, which are dominated by $\mathrm{t}\bar{\mathrm{t}}$+jets production. The signal strengths of boosted $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H processes are measured, and upper limits are placed on the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H differential cross sections as functions of the Z or Higgs boson transverse momentum. In addition, effects of physics beyond the standard model are probed using a framework in which the standard model is considered to be the low-energy effective field theory of a higher-scale theory. Eight possible dimension-six operators are added to the standard model Lagrangian and their corresponding coefficients are constrained via a fit to the data. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to PRD. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
Figure 1:
Example tree-level Feynman diagrams for the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H production processes. |
png pdf |
Figure 1-a:
Example tree-level Feynman diagrams for the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H production processes. |
png pdf |
Figure 1-b:
Example tree-level Feynman diagrams for the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H production processes. |
png pdf |
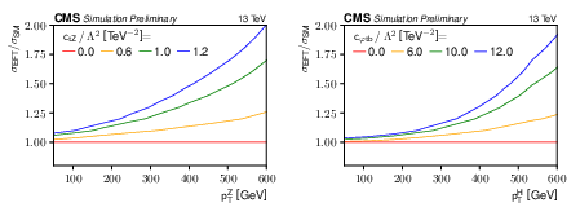
Figure 2:
The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H cross sections in the SM EFT, as ratios to the corresponding SM cross sections, as a function of $ {{c_{{\mathrm {t}} {\mathrm {Z}}}}} /{\Lambda}^{2}$ and the Z boson ${p_{\mathrm {T}}}$ (left), and as a function of $ {{c_{\varphi {\mathrm {t}} {\mathrm {b}}}}} /{\Lambda}^{2}$ and the Higgs boson ${p_{\mathrm {T}}}$ (right). |
png pdf |
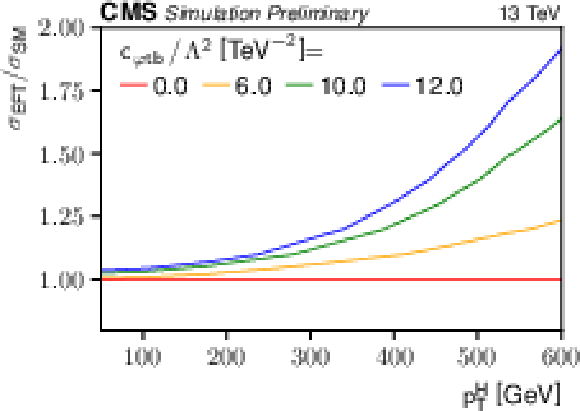
Figure 2-a:
The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H cross sections in the SM EFT, as ratios to the corresponding SM cross sections, as a function of $ {{c_{{\mathrm {t}} {\mathrm {Z}}}}} /{\Lambda}^{2}$ and the Z boson ${p_{\mathrm {T}}}$ (left), and as a function of $ {{c_{\varphi {\mathrm {t}} {\mathrm {b}}}}} /{\Lambda}^{2}$ and the Higgs boson ${p_{\mathrm {T}}}$ (right). |
png pdf |
Figure 2-b:
The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H cross sections in the SM EFT, as ratios to the corresponding SM cross sections, as a function of $ {{c_{{\mathrm {t}} {\mathrm {Z}}}}} /{\Lambda}^{2}$ and the Z boson ${p_{\mathrm {T}}}$ (left), and as a function of $ {{c_{\varphi {\mathrm {t}} {\mathrm {b}}}}} /{\Lambda}^{2}$ and the Higgs boson ${p_{\mathrm {T}}}$ (right). |
png pdf |
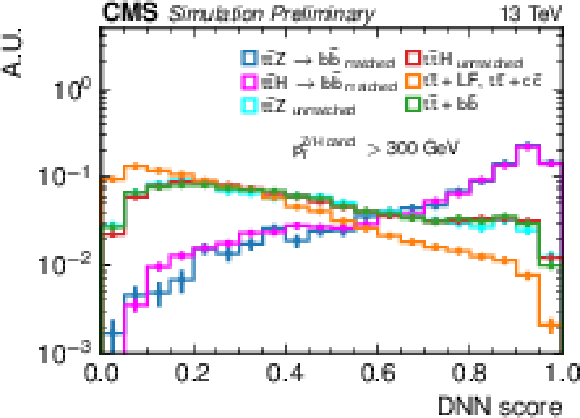
Figure 3:
The DNN score distribution for well-reconstructed $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal events in which the reconstructed Z or Higgs boson candidate is matched to both generator-level daughter b quarks of the Z or Higgs boson, the remaining $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events, and ${{\mathrm {t}\overline {\mathrm {t}}}}$ + ${\mathrm {b}} {\overline {\mathrm {b}}}$, ${{\mathrm {t}\overline {\mathrm {t}}}}$ + ${\mathrm {c}} {\overline {\mathrm {c}}}$, and ${{\mathrm {t}\overline {\mathrm {t}}}}$ + LF background events. The events shown here satisfy the baseline selection requirements described in Section 4 and contain a Z or Higgs boson candidate with $ {p_{\mathrm {T}}} > $ 300 GeV. |
png pdf |
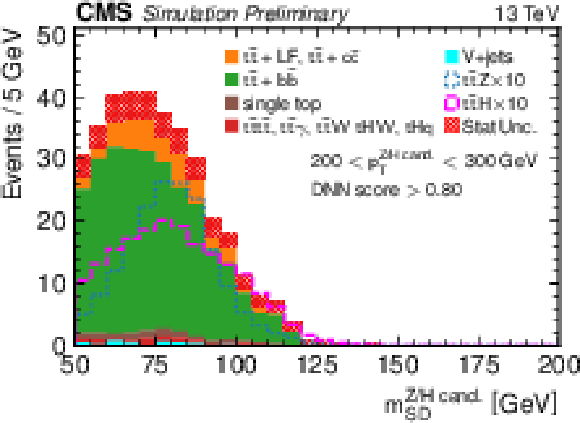
Figure 4:
Soft-drop mass distributions of Z/H $ \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ candidate jets in three ${p_{\mathrm {T}}}$ ranges: 200-300 GeV (upper), 300-450 GeV (middle), and above 450 GeV (lower) in simulated samples. The signal distributions are scaled up by a factor of ten for easier comparison with the backgrounds. The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H distributions include well-reconstructed $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events as well as $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events that either do not contain $ {\mathrm {Z}} / {\mathrm {H}} \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ or are not well reconstructed. The red hatched bands correspond to the statistical uncertainty in the background. |
png pdf |
Figure 4-a:
Soft-drop mass distributions of Z/H $ \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ candidate jets in three ${p_{\mathrm {T}}}$ ranges: 200-300 GeV (upper), 300-450 GeV (middle), and above 450 GeV (lower) in simulated samples. The signal distributions are scaled up by a factor of ten for easier comparison with the backgrounds. The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H distributions include well-reconstructed $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events as well as $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events that either do not contain $ {\mathrm {Z}} / {\mathrm {H}} \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ or are not well reconstructed. The red hatched bands correspond to the statistical uncertainty in the background. |
png pdf |
Figure 4-b:
Soft-drop mass distributions of Z/H $ \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ candidate jets in three ${p_{\mathrm {T}}}$ ranges: 200-300 GeV (upper), 300-450 GeV (middle), and above 450 GeV (lower) in simulated samples. The signal distributions are scaled up by a factor of ten for easier comparison with the backgrounds. The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H distributions include well-reconstructed $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events as well as $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events that either do not contain $ {\mathrm {Z}} / {\mathrm {H}} \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ or are not well reconstructed. The red hatched bands correspond to the statistical uncertainty in the background. |
png pdf |
Figure 4-c:
Soft-drop mass distributions of Z/H $ \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ candidate jets in three ${p_{\mathrm {T}}}$ ranges: 200-300 GeV (upper), 300-450 GeV (middle), and above 450 GeV (lower) in simulated samples. The signal distributions are scaled up by a factor of ten for easier comparison with the backgrounds. The $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H distributions include well-reconstructed $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events as well as $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events that either do not contain $ {\mathrm {Z}} / {\mathrm {H}} \to {{\mathrm {b}} {\overline {\mathrm {b}}}} $ or are not well reconstructed. The red hatched bands correspond to the statistical uncertainty in the background. |
png pdf |
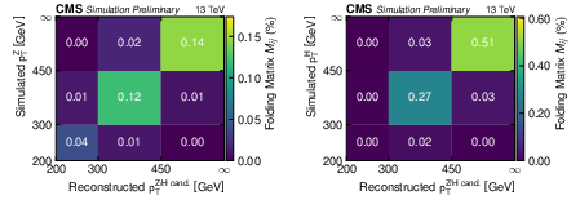
Figure 5:
The percentage of simulated $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) signal events that satisfy the baseline event selection requirements as well as the DNN and mass requirements in bins defined by the reconstructed AK8 jet ${p_{\mathrm {T}}}$ ($x$ axis) and simulated $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ ($y$ axis). The rightmost and topmost bins are unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. The $z$-axis value in each bin is the ratio of the event yield in the bin to the total number of simulated signal events in that $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ bin. |
png pdf |
Figure 5-a:
The percentage of simulated $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) signal events that satisfy the baseline event selection requirements as well as the DNN and mass requirements in bins defined by the reconstructed AK8 jet ${p_{\mathrm {T}}}$ ($x$ axis) and simulated $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ ($y$ axis). The rightmost and topmost bins are unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. The $z$-axis value in each bin is the ratio of the event yield in the bin to the total number of simulated signal events in that $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ bin. |
png pdf |
Figure 5-b:
The percentage of simulated $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) signal events that satisfy the baseline event selection requirements as well as the DNN and mass requirements in bins defined by the reconstructed AK8 jet ${p_{\mathrm {T}}}$ ($x$ axis) and simulated $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ ($y$ axis). The rightmost and topmost bins are unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. The $z$-axis value in each bin is the ratio of the event yield in the bin to the total number of simulated signal events in that $ {p_{\mathrm {T}}} ^{{\mathrm {Z}} / {\mathrm {H}}}$ bin. |
png pdf |
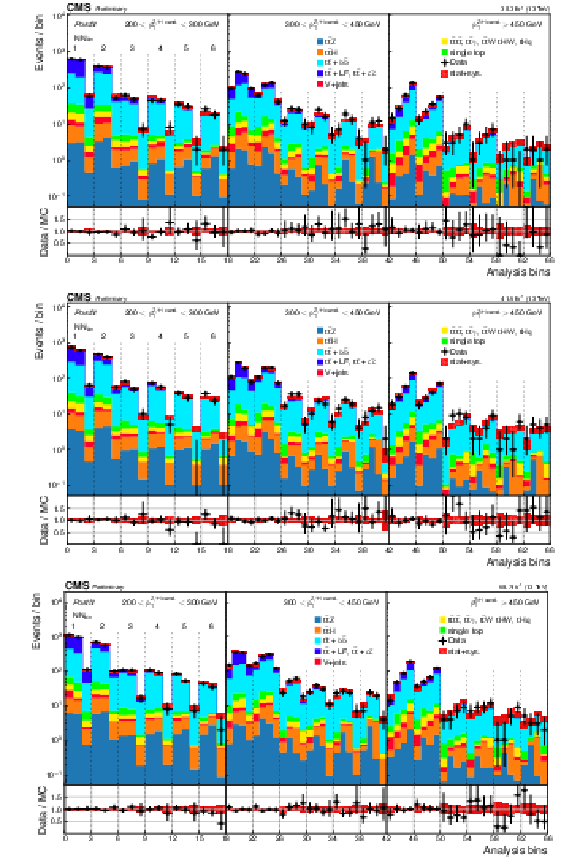
Figure 6:
Post-fit expected and observed yields for the 2016, 2017, and 2018 data-taking periods (from top to bottom) in each analysis bin. In the fit, the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal cross sections are fixed to the SM predictions. The analysis bins are defined as functions of the DNN score, and the ${p_{\mathrm {T}}}$ and ${m_\text {SD}}$ of the boson candidate AK8 jet. The largest groupings of bins are defined by the AK8 jet ${p_{\mathrm {T}}}$. The smaller groups are defined by the DNN score, and the smallest groups, 3 or 4 bins with the same ${p_{\mathrm {T}}}$ and DNN score, correspond to the AK8 jet ${m_\text {SD}}$. |
png pdf |
Figure 6-a:
Post-fit expected and observed yields for the 2016, 2017, and 2018 data-taking periods (from top to bottom) in each analysis bin. In the fit, the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal cross sections are fixed to the SM predictions. The analysis bins are defined as functions of the DNN score, and the ${p_{\mathrm {T}}}$ and ${m_\text {SD}}$ of the boson candidate AK8 jet. The largest groupings of bins are defined by the AK8 jet ${p_{\mathrm {T}}}$. The smaller groups are defined by the DNN score, and the smallest groups, 3 or 4 bins with the same ${p_{\mathrm {T}}}$ and DNN score, correspond to the AK8 jet ${m_\text {SD}}$. |
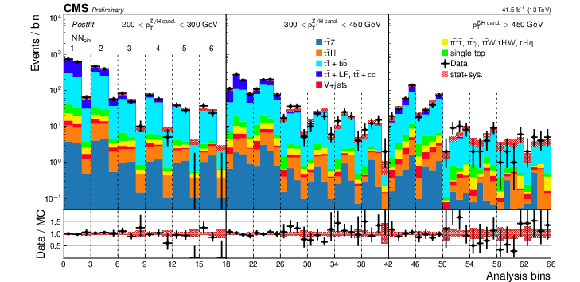
png pdf |
Figure 6-b:
Post-fit expected and observed yields for the 2016, 2017, and 2018 data-taking periods (from top to bottom) in each analysis bin. In the fit, the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal cross sections are fixed to the SM predictions. The analysis bins are defined as functions of the DNN score, and the ${p_{\mathrm {T}}}$ and ${m_\text {SD}}$ of the boson candidate AK8 jet. The largest groupings of bins are defined by the AK8 jet ${p_{\mathrm {T}}}$. The smaller groups are defined by the DNN score, and the smallest groups, 3 or 4 bins with the same ${p_{\mathrm {T}}}$ and DNN score, correspond to the AK8 jet ${m_\text {SD}}$. |
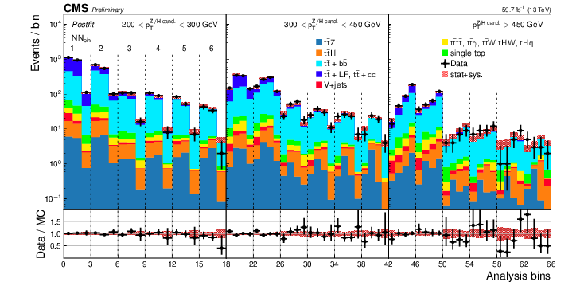
png pdf |
Figure 6-c:
Post-fit expected and observed yields for the 2016, 2017, and 2018 data-taking periods (from top to bottom) in each analysis bin. In the fit, the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal cross sections are fixed to the SM predictions. The analysis bins are defined as functions of the DNN score, and the ${p_{\mathrm {T}}}$ and ${m_\text {SD}}$ of the boson candidate AK8 jet. The largest groupings of bins are defined by the AK8 jet ${p_{\mathrm {T}}}$. The smaller groups are defined by the DNN score, and the smallest groups, 3 or 4 bins with the same ${p_{\mathrm {T}}}$ and DNN score, correspond to the AK8 jet ${m_\text {SD}}$. |
png pdf |
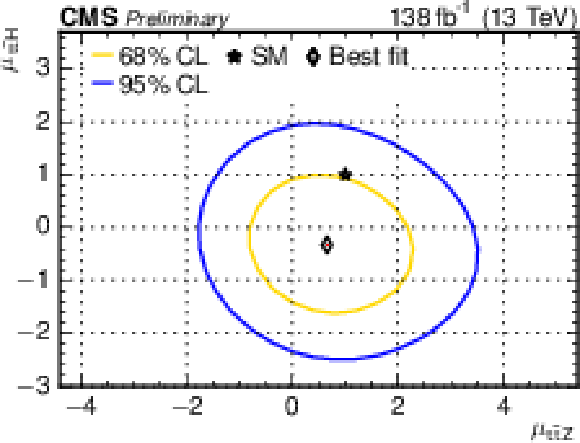
Figure 7:
The observed best-fit signal strengths modifiers $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {Z}}}}$ versus $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {H}}}}$ for simulated Z or Higgs boson $ {p_{\mathrm {T}}} > $ 200 GeV. The contours show the 68 and 95% CL regions. |
png pdf |
Figure 8:
Observed and expected 95% CL upper limits on the $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) differential cross sections as a function of Z and Higgs boson ${p_{\mathrm {T}}}$. The green and yellow bands show the expected 95% CL upper limits while the black lines represent the observed 95% CL upper limits. The magenta lines show the SM predicted differential cross section with PDF + ${\alpha _S} $ and QCD scale uncertainties. The lower panel shows the ratio of the expected and observed upper limits on the differential cross sections to the SM differential cross section. The last bin is unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. |
png pdf |
Figure 8-a:
Observed and expected 95% CL upper limits on the $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) differential cross sections as a function of Z and Higgs boson ${p_{\mathrm {T}}}$. The green and yellow bands show the expected 95% CL upper limits while the black lines represent the observed 95% CL upper limits. The magenta lines show the SM predicted differential cross section with PDF + ${\alpha _S} $ and QCD scale uncertainties. The lower panel shows the ratio of the expected and observed upper limits on the differential cross sections to the SM differential cross section. The last bin is unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. |
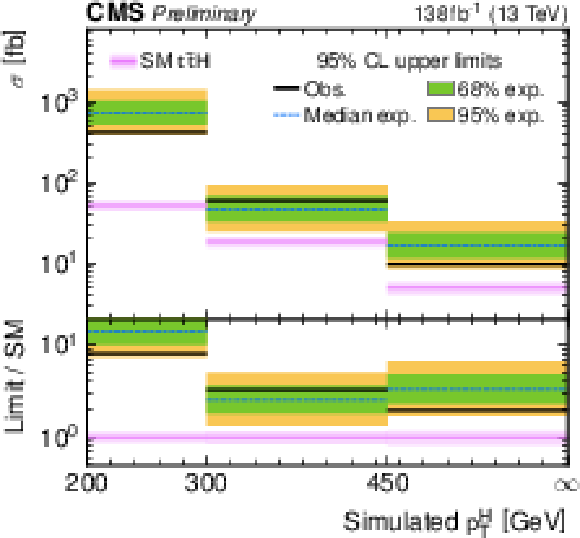
png pdf |
Figure 8-b:
Observed and expected 95% CL upper limits on the $\mathrm{t}\bar{\mathrm{t}}$Z (left) and $\mathrm{t}\bar{\mathrm{t}}$H (right) differential cross sections as a function of Z and Higgs boson ${p_{\mathrm {T}}}$. The green and yellow bands show the expected 95% CL upper limits while the black lines represent the observed 95% CL upper limits. The magenta lines show the SM predicted differential cross section with PDF + ${\alpha _S} $ and QCD scale uncertainties. The lower panel shows the ratio of the expected and observed upper limits on the differential cross sections to the SM differential cross section. The last bin is unbounded, extending to $ {p_{\mathrm {T}}} =\infty $. |
png pdf |
Figure 9:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
Figure 9-a:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
Figure 9-b:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
Figure 9-c:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
Figure 9-d:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
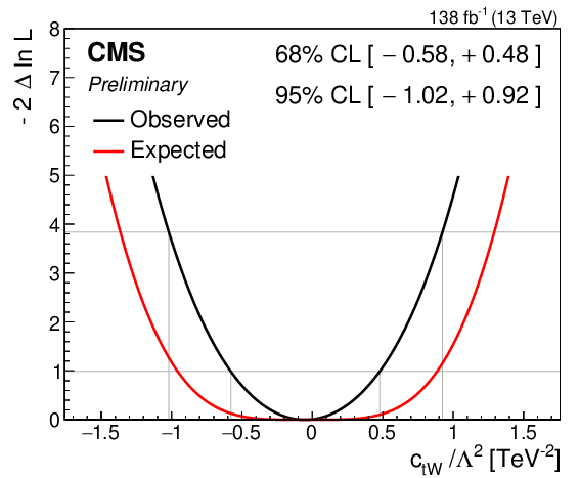
png pdf |
Figure 9-e:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
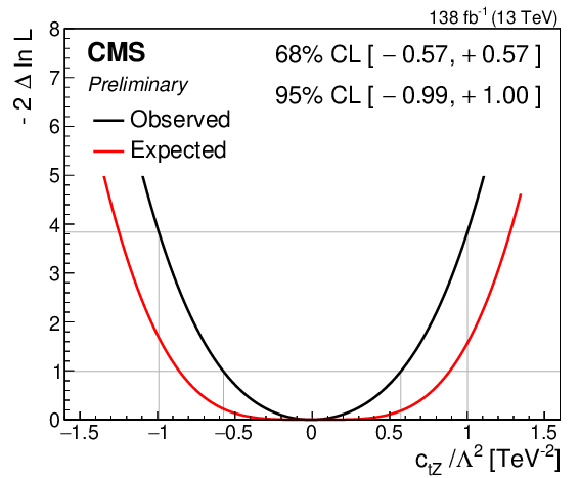
png pdf |
Figure 9-f:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
Figure 9-g:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
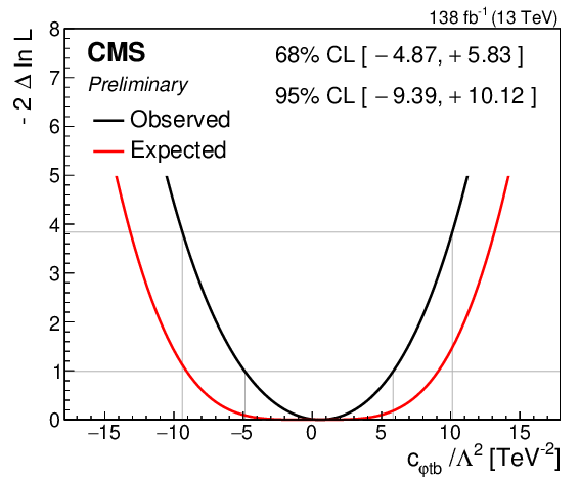
Figure 9-h:
Observed (black) and expected (red) one-dimensional scans of the negative log-likelihood as a function of each of the eight WCs when the seven other WCs are fixed to their SM values. The 68 and 95% CL intervals are indicated by thin gray lines. |
png pdf |
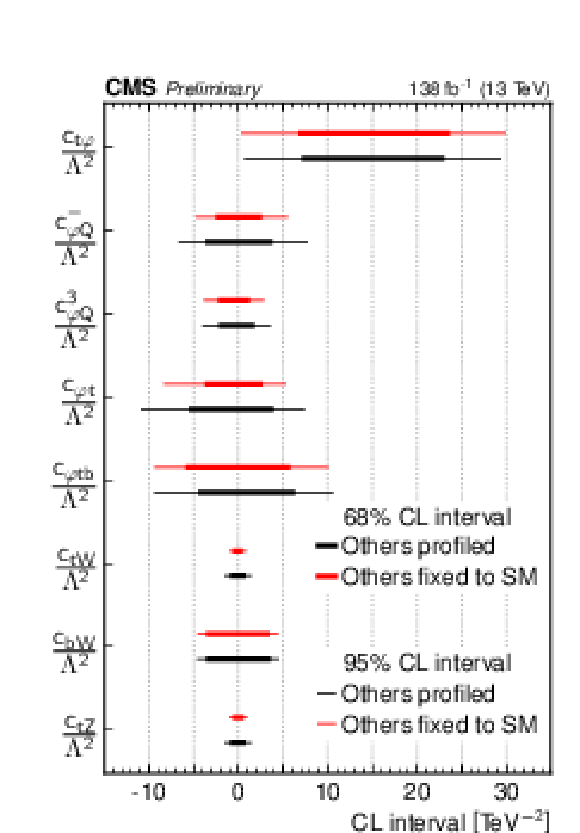
Figure 10:
The observed 68 and 95% CL intervals for the WCs. The intervals are found by scanning over a single WC while either treating the other seven as profiled, or fixing the other seven to the SM value of zero. |
png pdf |
Figure 11:
Observed two-dimensional scans of the negative log-likelihood as a function of two of the eight WCs when all other WCs are fixed to their SM values. The pair of WCs scanned correspond to the three highest observed correlation coefficients out of all pairs. They are ${{c_{\varphi {\mathrm {t}}}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper left), ${{c^{3}_{\varphi Q}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper right), and ${{c_{{\mathrm {t}} {\mathrm {W}}}}}$ versus ${{c_{{\mathrm {t}} {\mathrm {Z}}}}}$ (lower). The 68, 95, and 99.7% CL intervals are indicated by the yellow, blue, and green lines respectively. |
png pdf |
Figure 11-a:
Observed two-dimensional scans of the negative log-likelihood as a function of two of the eight WCs when all other WCs are fixed to their SM values. The pair of WCs scanned correspond to the three highest observed correlation coefficients out of all pairs. They are ${{c_{\varphi {\mathrm {t}}}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper left), ${{c^{3}_{\varphi Q}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper right), and ${{c_{{\mathrm {t}} {\mathrm {W}}}}}$ versus ${{c_{{\mathrm {t}} {\mathrm {Z}}}}}$ (lower). The 68, 95, and 99.7% CL intervals are indicated by the yellow, blue, and green lines respectively. |
png pdf |
Figure 11-b:
Observed two-dimensional scans of the negative log-likelihood as a function of two of the eight WCs when all other WCs are fixed to their SM values. The pair of WCs scanned correspond to the three highest observed correlation coefficients out of all pairs. They are ${{c_{\varphi {\mathrm {t}}}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper left), ${{c^{3}_{\varphi Q}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper right), and ${{c_{{\mathrm {t}} {\mathrm {W}}}}}$ versus ${{c_{{\mathrm {t}} {\mathrm {Z}}}}}$ (lower). The 68, 95, and 99.7% CL intervals are indicated by the yellow, blue, and green lines respectively. |
png pdf |
Figure 11-c:
Observed two-dimensional scans of the negative log-likelihood as a function of two of the eight WCs when all other WCs are fixed to their SM values. The pair of WCs scanned correspond to the three highest observed correlation coefficients out of all pairs. They are ${{c_{\varphi {\mathrm {t}}}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper left), ${{c^{3}_{\varphi Q}}}$ versus ${{c^{-}_{\varphi Q}}}$ (upper right), and ${{c_{{\mathrm {t}} {\mathrm {W}}}}}$ versus ${{c_{{\mathrm {t}} {\mathrm {Z}}}}}$ (lower). The 68, 95, and 99.7% CL intervals are indicated by the yellow, blue, and green lines respectively. |
png pdf |
Figure 12:
The observed 95% CL intervals for the WCs. The intervals are found by scanning over a single WC while fixing the other seven to zero. For comparison, we also show the corresponding 95% CL intervals from Refs. [CMS-TOP-18-009,CMS-TOP-19-001,CMS-TOP-21-001,CMS-TOP-21-004]. |
| Tables | |
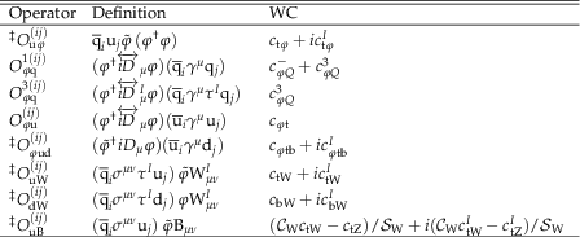
png pdf |
Table 1:
The set of EFT operators considered in this analysis that affect the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H processes at order 1$/\Lambda ^2$. The couplings are restricted to involve only third-generation quarks. The quantity $\gamma ^\mu $ denotes the Dirac matrices, $\sigma ^{\mu \nu}$ denotes the Dirac sigma matrices, and $\tau ^I$ denotes the Pauli matrices. The field $\varphi $ is the Higgs boson doublet, and $\tilde{\varphi}^{j}=\varepsilon _{jk} (\varphi ^{k} )^*$, where $\varepsilon $ is the Levi-Civita symbol and $\varepsilon _{12} = $ $+$1. The quark doublet is represented by q, and u and d represent the right-handed quark singlets. Furthermore, $(\varphi ^{\dagger}i\overleftrightarrow {D}_\mu \varphi) \equiv \varphi ^\dagger (iD_\mu \varphi)-(iD_\mu \varphi ^\dagger)\varphi $ and $(\varphi ^{\dagger}i\overleftrightarrow {D}^I_\mu \varphi) \equiv \varphi ^{\dagger}\tau ^I(iD_\mu \varphi)-(iD_\mu \varphi ^\dagger)\tau ^I\varphi $, where $D_{\mu}$ is the covariant derivative. The symbols $ {\mathrm {W}}_{\mu \nu}^I$ and $ {{\mathrm {B}}}_{\mu \nu}$ denote the field strength tensors for the weak isospin and weak hypercharge gauge fields. The abbreviations ${\mathcal {S}_{\mathrm {W}}}$ and ${\mathcal {C}_{\mathrm {W}}}$ denote the sine and cosine of the weak mixing angle in the unitary gauge, respectively. |
png pdf |
Table 2:
Summary of the reconstructed object and event selection requirements. |
png pdf |
Table 3:
The expected and observed best-fit signal strength modifiers $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {Z}}}}$ and $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {H}}}}$ for simulated Z or Higgs boson $ {p_{\mathrm {T}}} > $ 200 GeV. The observed uncertainties are broken down into the components arising from the limited size of the data, the limited size of the simulation samples, experimental uncertainties, and theoretical uncertainties. |
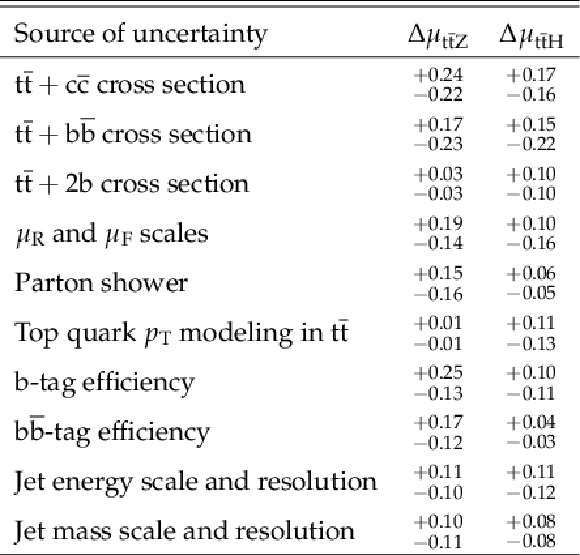
png pdf |
Table 4:
Major sources of uncertainty in the measurement of the signal strength modifiers $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {Z}}}}$ and $\mu _{{{{\mathrm {t}\overline {\mathrm {t}}}} {\mathrm {H}}}}$ for simulated Z or Higgs boson $ {p_{\mathrm {T}}} > $ 200 GeV. |
png pdf |
Table 5:
Observed (median expected ${\pm}$1 standard deviation) 95% CL upper limits for $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H differential cross sections. |
png pdf |
Table 6:
Observed 95% CL intervals on the eight WCs in the EFT model. The intervals are determined by scanning over a single WC while either treating the other seven as profiled, or fixing the other seven to the SM value of zero. |
png pdf |
Table 7:
Comprehensive list of the neural network input variables. The "+'' represents the relativistic four-momentum sum. Some variables are calculated for both the highest ${p_{\mathrm {T}}}$ (leading) and second-highest ${p_{\mathrm {T}}}$ (subleading) jet as indicated. |
| Summary |
|
A measurement of the signal strengths and 95% confidence level (CL) upper limits on the differential cross sections for production of boosted $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H events are presented along with constraints on the parameters of a leading-order effective field theory. The analysis is performed using the $\mathrm{b\bar{b}}$ decay mode of the Z or Higgs boson and the semileptonic decay mode of the associated $\mathrm{t\bar{t}}$ pair. The Z or Higgs boson is required to be highly boosted, with ${p_{\mathrm{T}}} > $ 200 GeV. A deep neural network is employed to discriminate between the $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H signal events and the background, which is dominated by$\mathrm{t}\bar{\mathrm{t}}$+jets production. The data correspond to an integrated luminosity of 138 fb$^{-1}$ collected with the CMS detector at the CERN LHC from 2016 through 2018. The data are binned as a function of the reconstructed ${p_{\mathrm{T}}}$ and mass of the Z or Higgs boson, and the score provided by the global event neural network. Binned maximum likelihood fits are employed to extract the observables from the data. The data are found to be consistent with and fit well to expectations from the standard model. The signal strength modifiers for boosted $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H production are measured to be $\mu_{{\mathrm{t\bar{t}}\mathrm{Z}} } = $ 0.65$^{+1.05}_{-0.98}$ and $\mu_{{\mathrm{t\bar{t}}\mathrm{H}} } = $ $-$0.33$^{+0.87}_{-0.85}$ at the 68% CL. The 95% CL upper limits on the differential $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H cross sections are found to range from 2 to 5 times the SM predicted cross sections when the Z or Higgs boson has ${p_{\mathrm{T}}} > $ 300 GeV. Results are also presented on the eight parameters of a leading-order effective field theory, which have a large impact on the boosted $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H production. These results represent the most restrictive limits to date on the cross sections for the production of $\mathrm{t}\bar{\mathrm{t}}$Z and $\mathrm{t}\bar{\mathrm{t}}$H with Z or Higgs boson ${p_{\mathrm{T}}} > $ 450 GeV, as well as stringent constraints on the Wilson coefficients $c_{\mathrm{t}\varphi}$, $c_{\varphi\mathrm{tb}}$, $c_{\mathrm{bW}}$, and $c_{\mathrm{tW}}$ in effective field theory. |
| References | ||||
| 1 | V. C. Rubin and W. K. Ford, Jr. | Rotation of the Andromeda nebula from a spectroscopic survey of emission regions | Astrophys. J. 159 (1970) 379 | |
| 2 | Planck Collaboration | Planck 2018 results. VI. cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 3 | D. Clowe, A. Gonzalez, and M. Markevitch | Weak lensing mass reconstruction of the interacting cluster 1E0657-558: Direct evidence for the existence of dark matter | Astrophys. J. 604 (2004) 596 | astro-ph/0312273 |
| 4 | R. K. Kaul and P. Majumdar | Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories | NPB 199 (1982) 36 | |
| 5 | R. Barbieri and G. F. Giudice | Upper bounds on supersymmetric particle masses | NPB 306 (1988) 63 | |
| 6 | W. Buchmuller and D. Wyler | Effective Lagrangian analysis of new interactions and flavor conservation | NPB 268 (1986) 621 | |
| 7 | B. Grzadkowski, M. Iskrzynski, M. Misiak, and J. Rosiek | Dimension-six terms in the standard model Lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 8 | A. Falkowski and R. Rattazzi | Which EFT | JHEP 10 (2019) 255 | 1902.05936 |
| 9 | C. Degrande et al. | Effective field theory: a modern approach to anomalous couplings | Annals Phys. 335 (2013) 21 | 1205.4231 |
| 10 | A. Kobach | Baryon number, lepton number, and operator dimension in the standard model | PLB 758 (2016) 455 | 1604.05726 |
| 11 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 12 | J. A. Aguilar-Saavedra et al. | Interpreting top-quark LHC measurements in the standard-model effective field theory | LHC TOP WG note CERN-LPCC-2018-01 | 1802.07237 |
| 13 | ATLAS Collaboration | Measurement of the $ t\bar{t}Z $ and $ t\bar{t}W $ cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 99 (2019) 072009 | 1901.03584 |
| 14 | ATLAS Collaboration | Measurements of the inclusive and differential production cross sections of a top-quark-antiquark pair in association with a $ Z $ boson at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | EPJC 81 (2021) 737 | 2103.12603 |
| 15 | CMS Collaboration | Measurement of the cross section for top quark pair production in association with a W or Z boson in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 08 (2018) 011 | CMS-TOP-17-005 1711.02547 |
| 16 | CMS Collaboration | Measurement of top quark pair production in association with a Z boson in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 56 (2020) 056 | CMS-TOP-18-009 1907.11270 |
| 17 | ATLAS Collaboration | Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector | PLB 784 (2018) 173 | 1806.00425 |
| 18 | ATLAS Collaboration | $ CP $ properties of Higgs boson interactions with top quarks in the $ t\bar{t}H $ and $ tH $ processes using $ H \rightarrow \gamma\gamma $ with the ATLAS detector | PRL 125 (2020) 061802 | 2004.04545 |
| 19 | ATLAS Collaboration | Measurement of Higgs boson decay into $ b $-quarks in associated production with a top-quark pair in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | Submitted to JHEP | 2111.06712 |
| 20 | CMS Collaboration | Observation of $ \mathrm{t\overline{t}} $H production | PRL 120 (2018) 231801 | CMS-HIG-17-035 1804.02610 |
| 21 | CMS Collaboration | Search for $ \mathrm{t}\overline{\mathrm{t}} $H production in the all-jet final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 06 (2018) 101 | CMS-HIG-17-022 1803.06986 |
| 22 | CMS Collaboration | Search for $ \mathrm{t}\overline{\mathrm{t}}\mathrm{H} $ production in the $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ decay channel with leptonic $ \mathrm{t}\overline{\mathrm{t}} $ decays in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 03 (2019) 026 | CMS-HIG-17-026 1804.03682 |
| 23 | CMS Collaboration | Measurements of $ \mathrm{t\bar{t}} $H production and the CP structure of the Yukawa interaction between the Higgs boson and top quark in the diphoton decay channel | PRL 125 (2020) 061801 | CMS-HIG-19-013 2003.10866 |
| 24 | CMS Collaboration | Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at $ \sqrt{s}= $ 13 TeV | EPJC 81 (2021) 378 | CMS-HIG-19-008 2011.03652 |
| 25 | CMS Collaboration | Search for new physics in top quark production with additional leptons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using effective field theory | JHEP 03 (2021) 095 | CMS-TOP-19-001 2012.04120 |
| 26 | CMS Collaboration | Measurement of the inclusive and differential $ \mathrm{t\overline{t}}\gamma $ cross sections in the single-lepton channel and EFT interpretation at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2021) 180 | CMS-TOP-18-010 2107.01508 |
| 27 | CMS Collaboration | Probing effective field theory operators in the associated production of top quarks with a Z boson in multilepton final states at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2021) 083 | CMS-TOP-21-001 2107.13896 |
| 28 | CMS Collaboration | Measurement of the inclusive and differential $ \mathrm{t\bar{t}}\gamma $ cross sections in the dilepton channel and effective field theory interpretation in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | Submitted to JHEP | CMS-TOP-21-004 2201.07301 |
| 29 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 30 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 31 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 32 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 33 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 34 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 35 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 36 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 37 | H. B. Hartanto, B. Jager, L. Reina, and D. Wackeroth | Higgs boson production in association with top quarks in the POWHEG BOX | PRD 91 (2015) 094003 | 1501.04498 |
| 38 | A. Kulesza et al. | Associated production of a top quark pair with a heavy electroweak gauge boson at NLO+NNLL accuracy | EPJC 79 (2019) 249 | 1812.08622 |
| 39 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 4. deciphering the nature of the Higgs sector | CERN Yellow Reports CERN-2017-002-M | 1610.07922 |
| 40 | T. Je\vzo, J. M. Lindert, N. Moretti, and S. Pozzorini | New NLOPS predictions for $ t \bar{t} +b $-jet production at the LHC | EPJC 78 (2018) 502 | 1802.00426 |
| 41 | F. Buccioni, S. Kallweit, S. Pozzorini, and M. F. Zoller | NLO QCD predictions for $ t\bar{t}b\bar{b} $ production in association with a light jet at the LHC | JHEP 12 (2019) 015 | 1907.13624 |
| 42 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 43 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 44 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 45 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 46 | P. Barnreuther, M. Czakon, and A. Mitov | Percent-level-precision physics at the Tevatron: next-to-next-to-leading order QCD corrections to $ \mathrm{q\bar{q}} \to \mathrm{t\bar{t}} + {X} $ | PRL 109 (2012) 132001 | 1204.5201 |
| 47 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 48 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 49 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ O({\alpha_S}^4) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 50 | M. Czakon and A. Mitov | Top++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 51 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 52 | E. Re | Single-top $ Wt $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 53 | S. Quackenbush, R. Gavin, Y. Li, and F. Petriello | W physics at the LHC with FEWZ 2.1 | CPC 184 (2013) 209 | 1201.5896 |
| 54 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in the framework of the FEWZ simulation code | PRD 86 (2012) 094034 | 1208.5967 |
| 55 | N. Kidonakis | Two-loop soft anomalous dimensions for single top quark associated production with a $ \mathrm{W}^- $ or $ \mathrm{H}^- $ | PRD 82 (2010) 054018 | 1005.4451 |
| 56 | M. Aliev et al. | HATHOR: hadronic top and heavy quarks cross section calculator | CPC 182 (2011) 1034 | 1007.1327 |
| 57 | P. Kant et al. | HatHor for single top-quark production: updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | CPC 191 (2015) 74 | 1406.4403 |
| 58 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 59 | M. L. Mangano, M. Moretti, F. Piccinini, and M. Treccani | Matching matrix elements and shower evolution for top-pair production in hadronic collisions | JHEP 01 (2007) 013 | hep-ph/0611129 |
| 60 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 61 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 62 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 63 | NNPDF Collaboration | Parton distributions for the LHC run II | JHEP 04 (2015) 040 | 1410.8849 |
| 64 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 65 | R. Goldouzian et al. | Matching in $ pp\to t\overline{t}W/Z/h+ $ jet SMEFT studies | JHEP 06 (2021) 151 | 2012.06872 |
| 66 | C. Degrande et al. | Automated one-loop computations in the standard model effective field theory | PRD 103 (2021) 096024 | 2008.11743 |
| 67 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 68 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 69 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 70 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 71 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 72 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 73 | CMS Collaboration | Search for supersymmetry in pp collisions at $ \sqrt{s}= $ 13 TeV in the single-lepton final state using the sum of masses of large-radius jets | JHEP 08 (2016) 122 | CMS-SUS-15-007 1605.04608 |
| 74 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 75 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 76 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 77 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 78 | CMS Collaboration | Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques | JINST 15 (2020) P06005 | CMS-JME-18-002 2004.08262 |
| 79 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 80 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 81 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 82 | ATLAS Collaboration | Measurement of event shapes at large momentum transfer with the ATLAS detector in $ pp $ collisions at $ \sqrt{s}= $ 7 TeV | EPJC 72 (2012) 2211 | 1206.2135 |
| 83 | S. Ioffe and C. Szegedy | Batch normalization: accelerating deep network training by reducing internal covariate shift | in Proceedings of Machine Learning Research, volume 37, p. 448 2015 | 1502.03167 |
| 84 | N. Srivastava et al. | Dropout: a simple way to prevent neural networks from overfitting | J. Mach. Learn. Res. 15 (2014) 1929 | |
| 85 | T.-Y. Lin et al. | Focal loss for dense object detection | IEEE Transactions on Pattern Analysis and Machine Intelligence 42 (2020) 318 | 1708.02002 |
| 86 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | CPC 77 (1993) 219 | |
| 87 | J. S. Conway | Incorporating nuisance parameters in likelihoods for multisource spectra | in PHYSTAT 2011 2011 | 1103.0354 |
| 88 | J. Butterworth et al. | PDF4LHC recommendations for LHC run II | JPG 43 (2016) 023001 | 1510.03865 |
| 89 | CMS Collaboration | Measurement of differential cross sections for top quark pair production using the lepton+jets final state in proton-proton collisions at 13 TeV | PRD 95 (2017) 092001 | CMS-TOP-16-008 1610.04191 |
| 90 | G. Ridolfi, M. Ubiali, and M. Zaro | A fragmentation-based study of heavy quark production | JHEP 01 (2020) 196 | 1911.01975 |
| 91 | CMS Collaboration | First measurement of the cross section for top quark pair production with additional charm jets using dileptonic final states in pp collisions at $ \sqrt{s}= $ 13 TeV | PLB 820 (2021) 136565 | CMS-TOP-20-003 2012.09225 |
| 92 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 93 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 94 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 95 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 96 | A. L. Read | Presentation of search results: The CL$ _{\text{s}} $ technique | JPG 28 (2002) 2693 | |
| 97 | ATLAS Collaboration, CMS Collaboration, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 98 | CMS Collaboration | Measurement of the cross section for $ \text{t}\bar{\text{t}} $ production with additional jets and b jets in pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2020) 125 | CMS-TOP-18-002 2003.06467 |
| 99 | CMS Collaboration | Measurement of the $ \mathrm{t\bar{t}}\mathrm{b\bar{b}} $ production cross section in the all-jet final state in pp collisions at $ \sqrt{s} = $ 13 TeV | PLB 803 (2020) 135285 | CMS-TOP-18-011 1909.05306 |
| 100 | CMS Collaboration | Measurement and interpretation of differential cross sections for Higgs boson production at $ \sqrt{s}= $ 13 TeV | PLB 792 (2019) 369 | CMS-HIG-17-028 1812.06504 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|