

Compact Muon Solenoid
LHC, CERN
| CMS-JME-18-002 ; CERN-EP-2020-037 | ||
| Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques | ||
| CMS Collaboration | ||
| 17 April 2020 | ||
| JINST 15 (2020) P06005 | ||
| Abstract: Machine-learning (ML) techniques are explored to identify and classify hadronic decays of highly Lorentz-boosted W/Z/Higgs bosons and top quarks. Techniques without ML have also been evaluated and are included for comparison. The identification performances of a variety of algorithms are characterized in simulated events and directly compared with data. The algorithms are validated using proton-proton collision data at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. Systematic uncertainties are assessed by comparing the results obtained using simulation and collision data. The new techniques studied in this paper provide significant performance improvements over non-ML techniques, reducing the background rate by up to an order of magnitude at the same signal efficiency. | ||
| Links: e-print arXiv:2004.08262 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
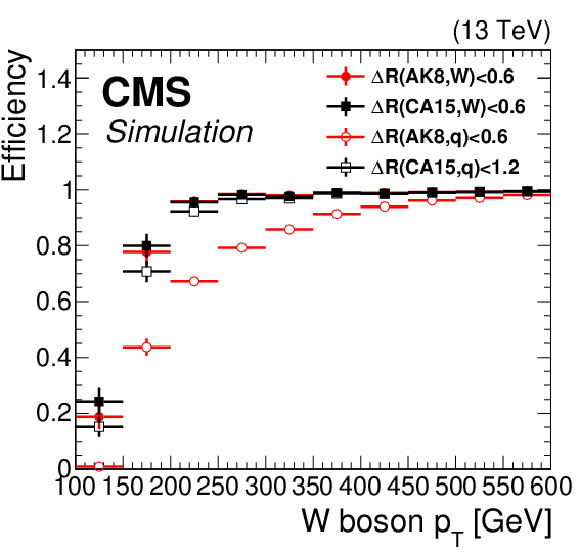
Figure 1:
Matching efficiency as a function of the ${p_{\mathrm {T}}}$ of the generated particle, for hadronically decaying W bosons (left) and t quarks (right). This efficiency is defined as the fraction of the generated particles (t quarks or W bosons) that are within $\Delta R < $ 0.6 with an AK8 or CA15 jet with $ {p_{\mathrm {T}}} > $ 200 GeV and $ {| \eta |} < $ 2.4. Superimposed is the merging efficiency as a function of the generated particle ${p_{\mathrm {T}}}$ when all decay products are within $\smash [b]\Delta R (\text {AK8}, \mathrm{q} _{i}) < $ 0.6 ($\smash [b]\Delta R (\text {CA15}, \mathrm{q} _{i}) < $ 1.2) with an AK8 (CA15) jet. |
png pdf |
Figure 1-a:
Matching efficiency as a function of the ${p_{\mathrm {T}}}$ of the generated particle, for hadronically decaying W bosons (left) and t quarks (right). This efficiency is defined as the fraction of the generated particles (t quarks or W bosons) that are within $\Delta R < $ 0.6 with an AK8 or CA15 jet with $ {p_{\mathrm {T}}} > $ 200 GeV and $ {| \eta |} < $ 2.4. Superimposed is the merging efficiency as a function of the generated particle ${p_{\mathrm {T}}}$ when all decay products are within $\smash [b]\Delta R (\text {AK8}, \mathrm{q} _{i}) < $ 0.6 ($\smash [b]\Delta R (\text {CA15}, \mathrm{q} _{i}) < $ 1.2) with an AK8 (CA15) jet. |

png pdf |
Figure 1-b:
Matching efficiency as a function of the ${p_{\mathrm {T}}}$ of the generated particle, for hadronically decaying W bosons (left) and t quarks (right). This efficiency is defined as the fraction of the generated particles (t quarks or W bosons) that are within $\Delta R < $ 0.6 with an AK8 or CA15 jet with $ {p_{\mathrm {T}}} > $ 200 GeV and $ {| \eta |} < $ 2.4. Superimposed is the merging efficiency as a function of the generated particle ${p_{\mathrm {T}}}$ when all decay products are within $\smash [b]\Delta R (\text {AK8}, \mathrm{q} _{i}) < $ 0.6 ($\smash [b]\Delta R (\text {CA15}, \mathrm{q} _{i}) < $ 1.2) with an AK8 (CA15) jet. |
png pdf |
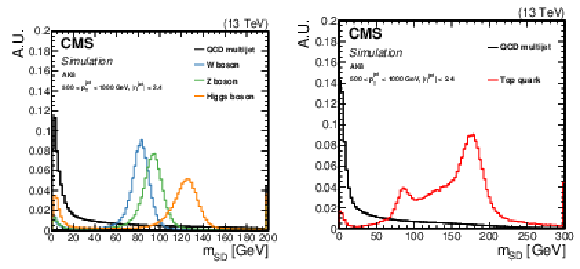
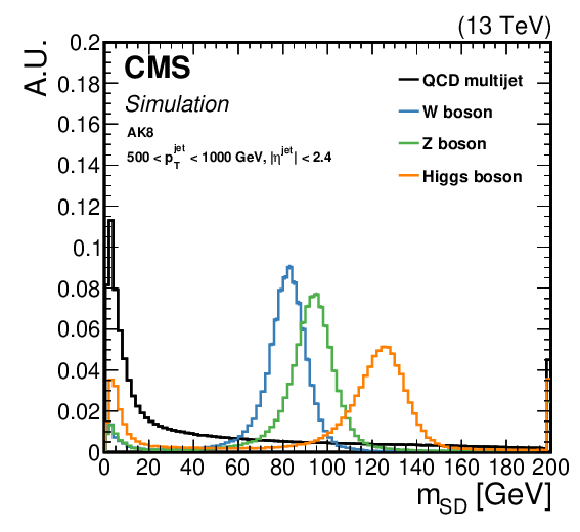
Figure 2:
Comparison of the ${m_{\text {SD}}}$ shape in signal and background AK8 jets in simulation. The fiducial selection on the jets is displayed on the plots. Signal jets are defined as jets arising from hadronic decays of W/Z/H bosons (left) or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |
png pdf |
Figure 2-a:
Comparison of the ${m_{\text {SD}}}$ shape in signal and background AK8 jets in simulation. The fiducial selection on the jets is displayed on the plots. Signal jets are defined as jets arising from hadronic decays of W/Z/H bosons (left) or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |

png pdf |
Figure 2-b:
Comparison of the ${m_{\text {SD}}}$ shape in signal and background AK8 jets in simulation. The fiducial selection on the jets is displayed on the plots. Signal jets are defined as jets arising from hadronic decays of W/Z/H bosons (left) or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |
png pdf |
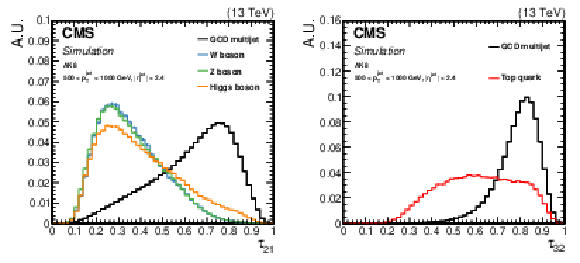
Figure 3:
Comparison of the ${\tau _{21}}$ (left) and ${\tau _{32}}$ (right) shape in signal and background AK8 jets. The fiducial selection on the jets is displayed in the plots. As signal jets we consider jets stemming from hadronic decays of W, Z, or H bosons (left), or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |
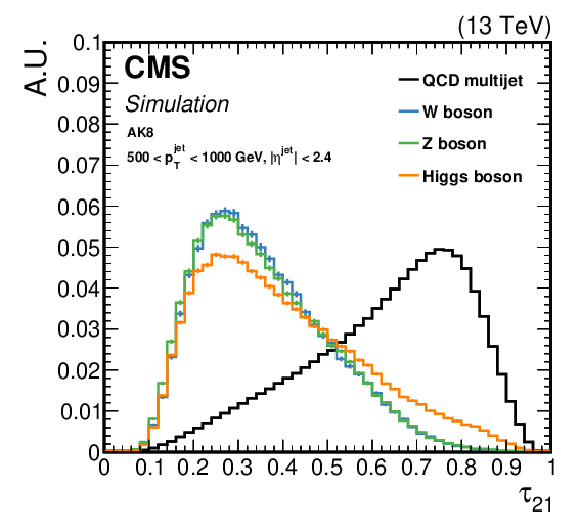
png pdf |
Figure 3-a:
Comparison of the ${\tau _{21}}$ (left) and ${\tau _{32}}$ (right) shape in signal and background AK8 jets. The fiducial selection on the jets is displayed in the plots. As signal jets we consider jets stemming from hadronic decays of W, Z, or H bosons (left), or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |

png pdf |
Figure 3-b:
Comparison of the ${\tau _{21}}$ (left) and ${\tau _{32}}$ (right) shape in signal and background AK8 jets. The fiducial selection on the jets is displayed in the plots. As signal jets we consider jets stemming from hadronic decays of W, Z, or H bosons (left), or t quarks (right), whereas background jets are obtained from the QCD multijet sample. |

png pdf |
Figure 4:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |
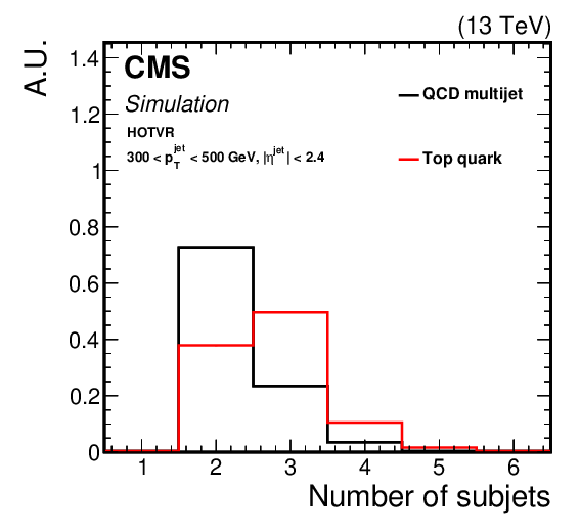
png pdf |
Figure 4-a:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |

png pdf |
Figure 4-b:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |
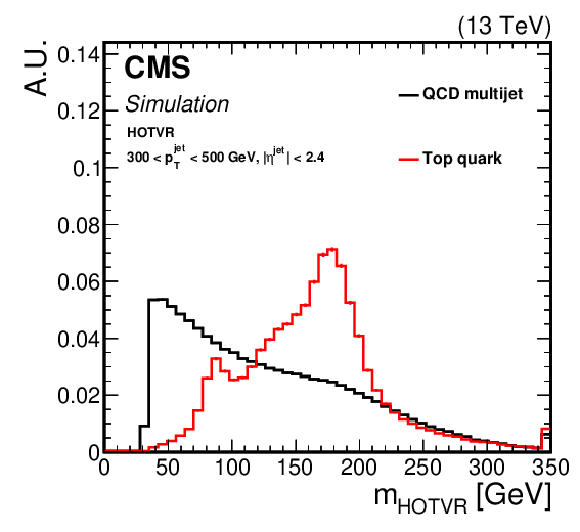
png pdf |
Figure 4-c:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |
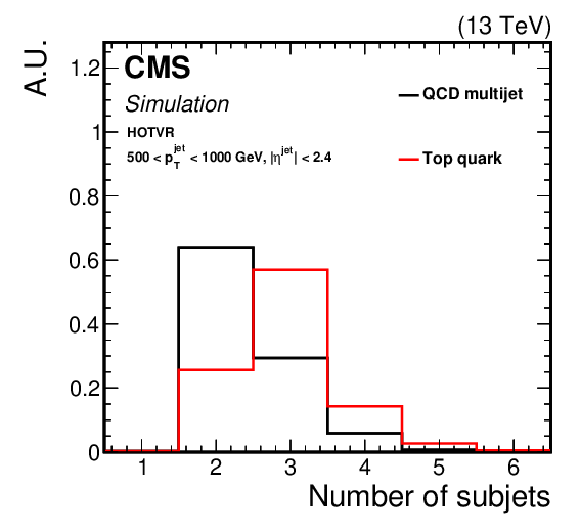
png pdf |
Figure 4-d:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |
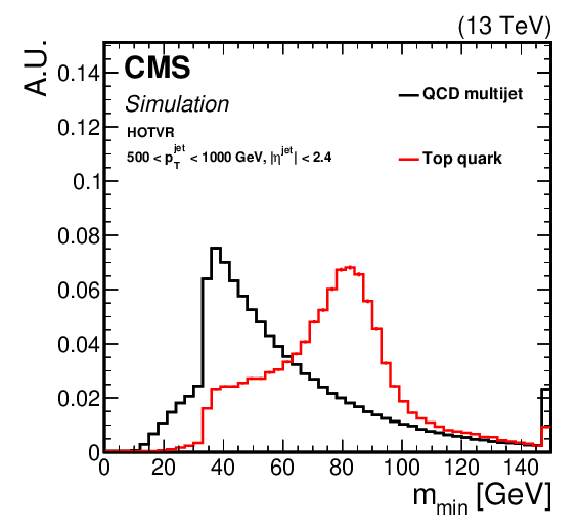
png pdf |
Figure 4-e:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |

png pdf |
Figure 4-f:
Shape comparison of the main variables of the HOTVR algorithm for signal and background jets, in two different regions of the jet ${p_{\mathrm {T}}}$ as displayed in the plots. |
png pdf |
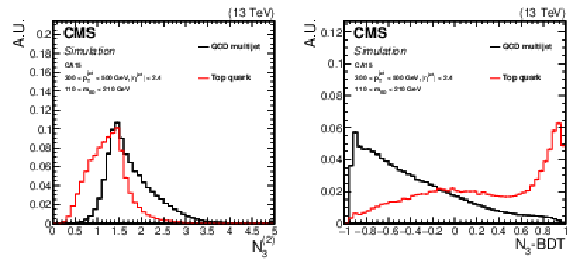
Figure 5:
Comparison of the distribution of $N_3^{(2)}$ (left) and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant (right) in t quarks jets (signal) and jets from QCD multijet processes (background). |
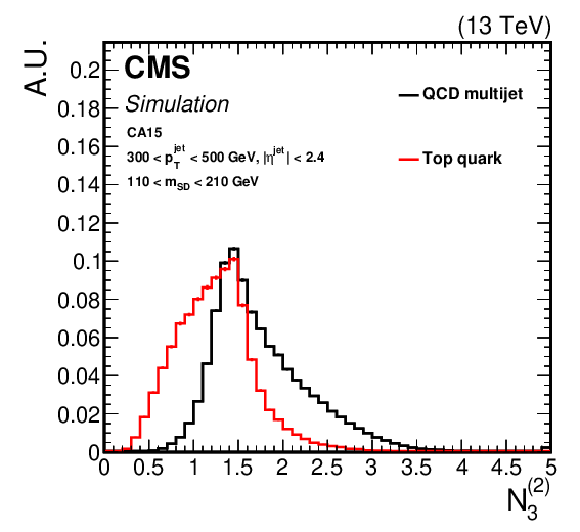
png pdf |
Figure 5-a:
Comparison of the distribution of $N_3^{(2)}$ (left) and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant (right) in t quarks jets (signal) and jets from QCD multijet processes (background). |

png pdf |
Figure 5-b:
Comparison of the distribution of $N_3^{(2)}$ (left) and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant (right) in t quarks jets (signal) and jets from QCD multijet processes (background). |

png pdf |
Figure 6:
Distributions of the ${m_\text {SD}+N_{2}}$ (left) and ${m_\text {SD}+N_{2}^{\text {DDT}}}$ (right) in signal and background jets. |
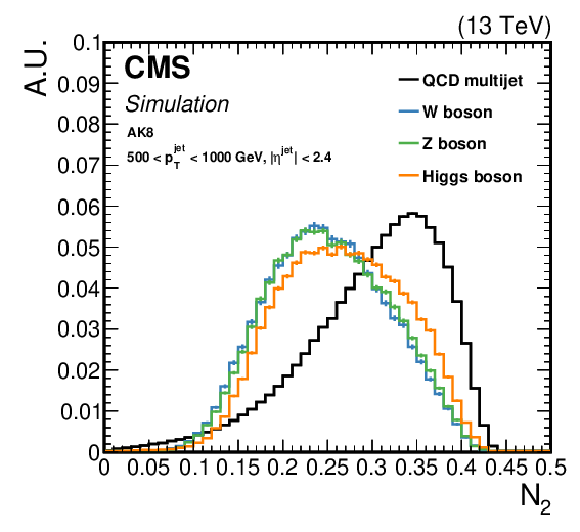
png pdf |
Figure 6-a:
Distributions of the ${m_\text {SD}+N_{2}}$ (left) and ${m_\text {SD}+N_{2}^{\text {DDT}}}$ (right) in signal and background jets. |

png pdf |
Figure 6-b:
Distributions of the ${m_\text {SD}+N_{2}}$ (left) and ${m_\text {SD}+N_{2}^{\text {DDT}}}$ (right) in signal and background jets. |

png pdf |
Figure 7:
The pixelized images used in the ImageTop network with PF candidate colors summed together ("greyscale'') for QCD (left) and t quark (right) jets. The x and y axes are the pixel number, and roughly scale with $\Delta R$. The $z$ axis is the intensity of the greyscale image in the given pixel, related to the PF candidate $ {p_{\mathrm {T}}} $, and has been normalized to unity. This figure shows an ensemble of overlaid images after the image post processing; we can see clear differences between the QCD jet energy and t quark deposition patterns. |

png pdf |
Figure 7-a:
The pixelized images used in the ImageTop network with PF candidate colors summed together ("greyscale'') for QCD (left) and t quark (right) jets. The x and y axes are the pixel number, and roughly scale with $\Delta R$. The $z$ axis is the intensity of the greyscale image in the given pixel, related to the PF candidate $ {p_{\mathrm {T}}} $, and has been normalized to unity. This figure shows an ensemble of overlaid images after the image post processing; we can see clear differences between the QCD jet energy and t quark deposition patterns. |
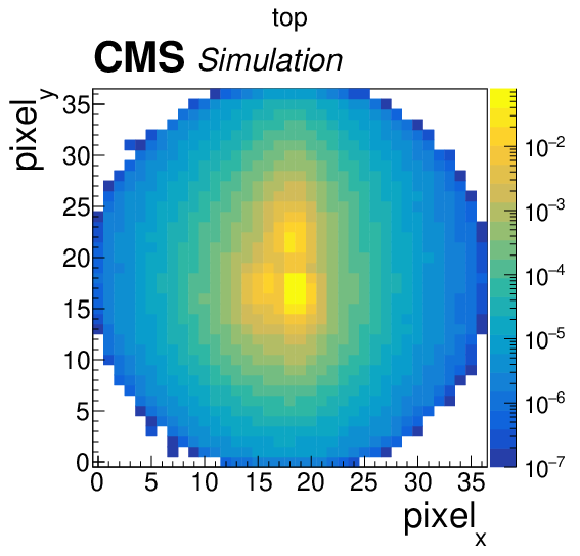
png pdf |
Figure 7-b:
The pixelized images used in the ImageTop network with PF candidate colors summed together ("greyscale'') for QCD (left) and t quark (right) jets. The x and y axes are the pixel number, and roughly scale with $\Delta R$. The $z$ axis is the intensity of the greyscale image in the given pixel, related to the PF candidate $ {p_{\mathrm {T}}} $, and has been normalized to unity. This figure shows an ensemble of overlaid images after the image post processing; we can see clear differences between the QCD jet energy and t quark deposition patterns. |
png pdf |
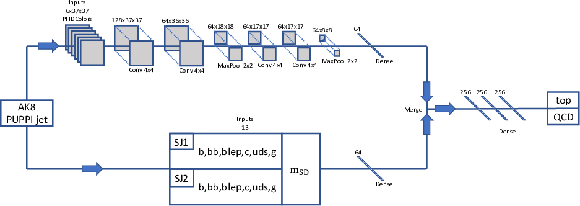
Figure 8:
The ImageTop network architecture. The neural network inputs are the 37x37 pixelized PF candidate ${p_{\mathrm {T}}}$ map, which is split into colors based on the PF candidate flavor, and the DeepFlavor subjet b tags applied to both subjets. The pixelized images are sent through a two-dimensional CNN, and the subjet b tags are inputs to a dense layer. After flattening the CNN, the two networks are taken as input to three dense layers and finally to the two-node output, which is used as the top tagging discriminator. |
png pdf |
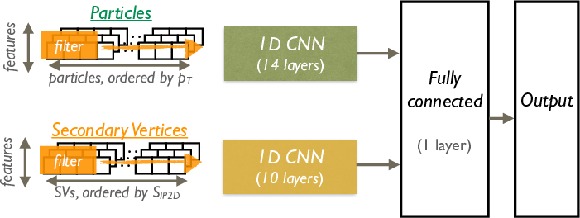
Figure 9:
The network architecture of DeepAK8. |
png pdf |
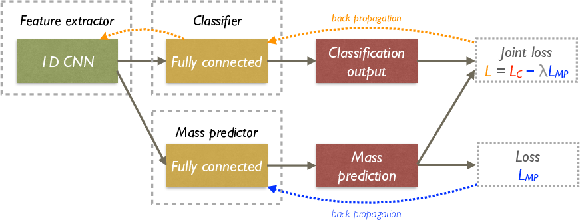
Figure 10:
The network architecture of DeepAK8-MD. |
png pdf |
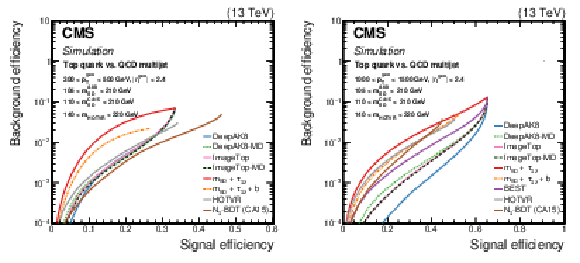
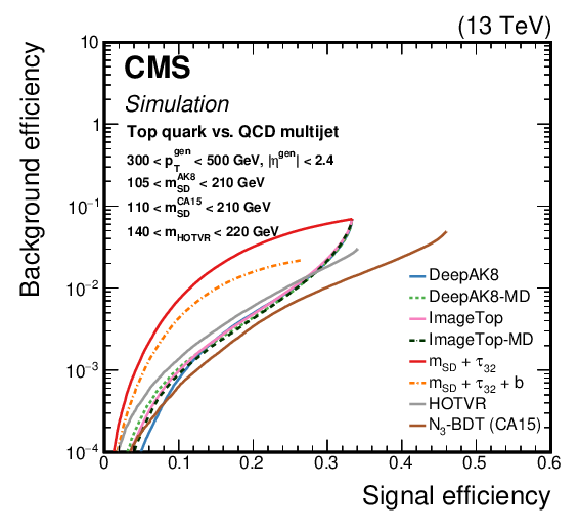
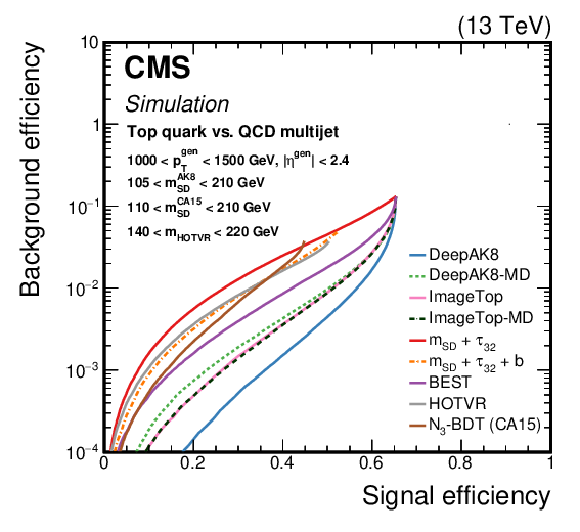
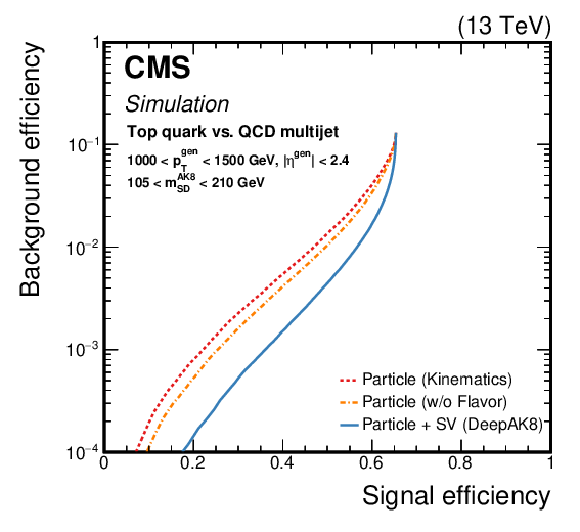
Figure 11:
Comparison of the identification algorithms for hadronically decaying t quark in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
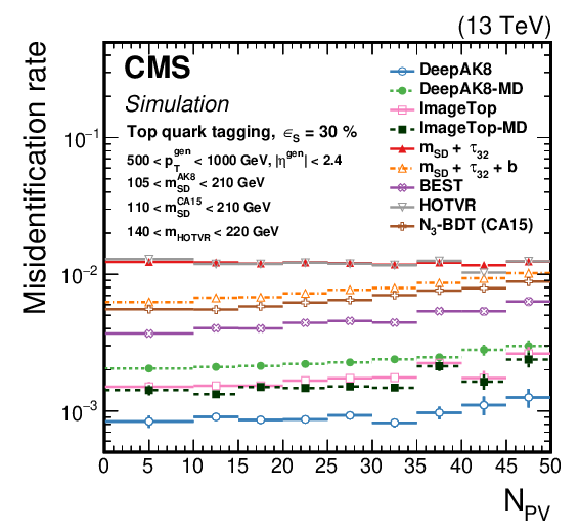
Figure 11-a:
Comparison of the identification algorithms for hadronically decaying t quark in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
Figure 11-b:
Comparison of the identification algorithms for hadronically decaying t quark in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
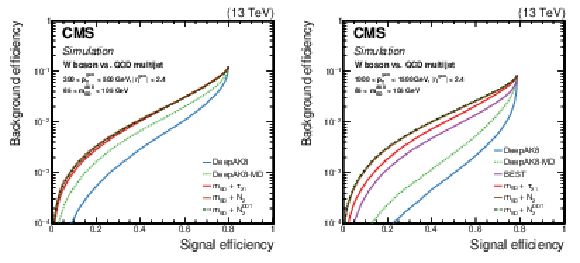
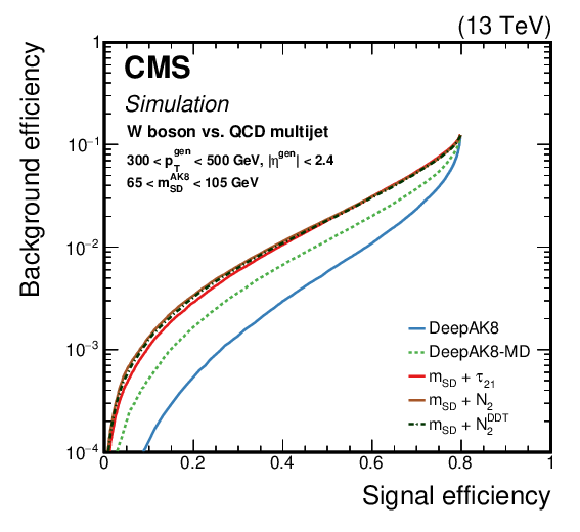
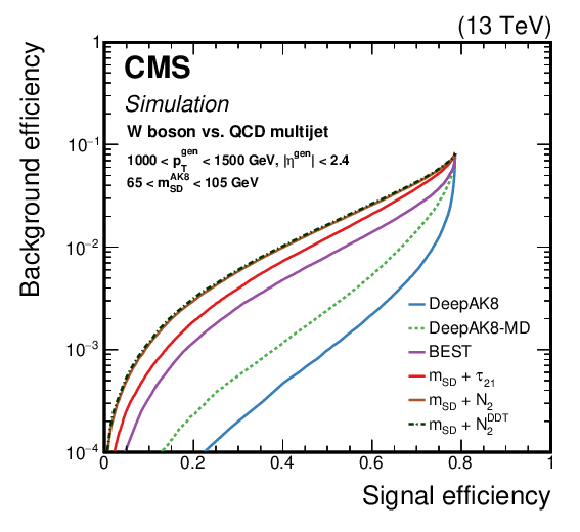
Figure 12:
Comparison of the identification algorithms for hadronically decaying W boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
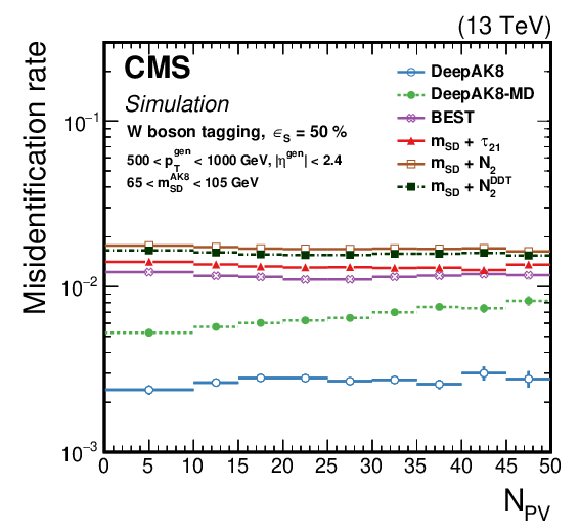
Figure 12-a:
Comparison of the identification algorithms for hadronically decaying W boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
Figure 12-b:
Comparison of the identification algorithms for hadronically decaying W boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
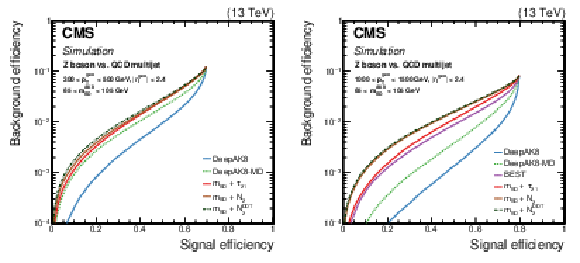
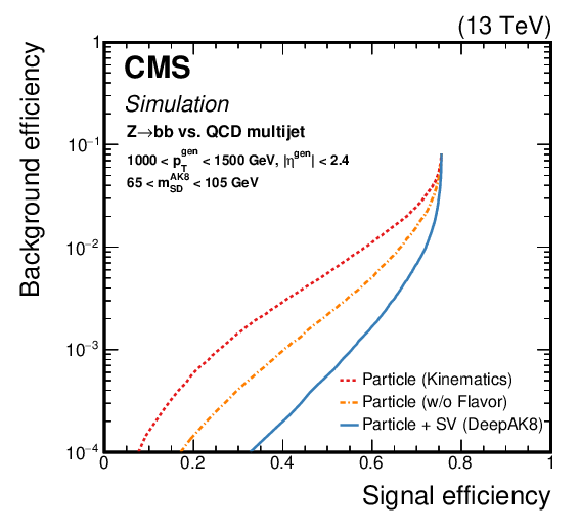
Figure 13:
Comparison of the identification algorithms for hadronically decaying Z boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |

png pdf |
Figure 13-a:
Comparison of the identification algorithms for hadronically decaying Z boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |

png pdf |
Figure 13-b:
Comparison of the identification algorithms for hadronically decaying Z boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
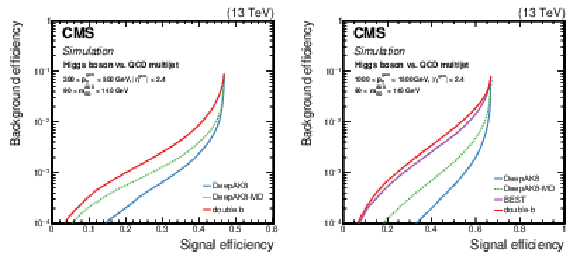
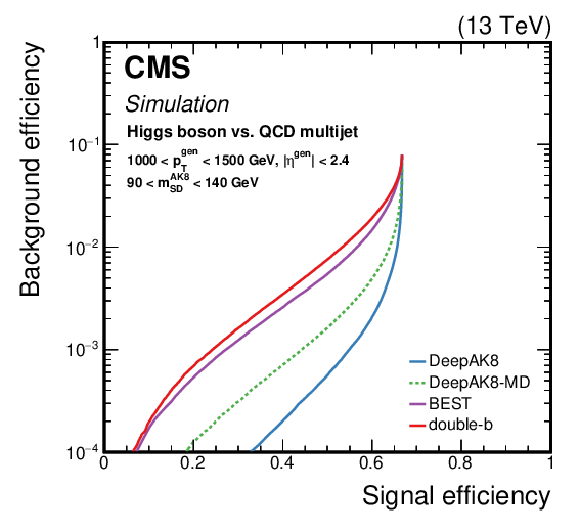
Figure 14:
Comparison of the identification algorithms for hadronically decaying H boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. The H boson decays to a pair of b quarks. Additional fiducial selection criteria applied to the jets are listed on the plots. |

png pdf |
Figure 14-a:
Comparison of the identification algorithms for hadronically decaying H boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. The H boson decays to a pair of b quarks. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
Figure 14-b:
Comparison of the identification algorithms for hadronically decaying H boson in terms of ROC curves in two regions based on the ${p_{\mathrm {T}}}$ of the generated particle; Left: 300 $ < {p_{\mathrm {T}}} < $ 500 GeV, and Right: 1000 $ < {p_{\mathrm {T}}} < $ 1500 GeV. The H boson decays to a pair of b quarks. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
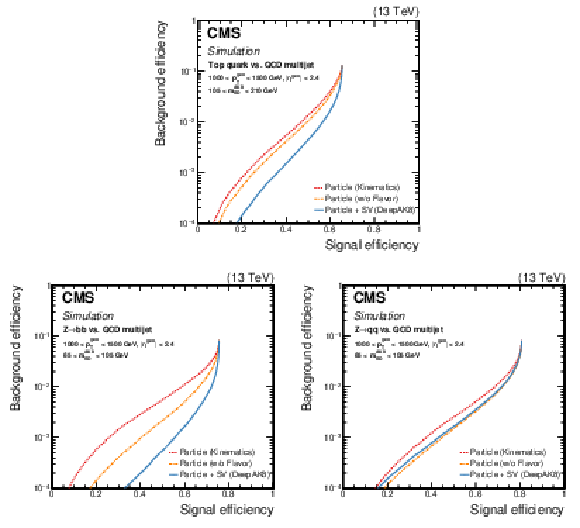
Figure 15:
Alternative versions of DeepAK8 trained using a subset of the input features. The details about each version are discussed in the text. The performances of the three versions of DeepAK8 are compared for t quark (upper) and Z boson (lower) identification. For the latter, the left plot corresponds to Z bosons decaying to a pair of b quarks, and the right plot to a pair of light-flavor quarks. |
png pdf |
Figure 15-a:
Alternative versions of DeepAK8 trained using a subset of the input features. The details about each version are discussed in the text. The performances of the three versions of DeepAK8 are compared for t quark (upper) and Z boson (lower) identification. For the latter, the left plot corresponds to Z bosons decaying to a pair of b quarks, and the right plot to a pair of light-flavor quarks. |
png pdf |
Figure 15-b:
Alternative versions of DeepAK8 trained using a subset of the input features. The details about each version are discussed in the text. The performances of the three versions of DeepAK8 are compared for t quark (upper) and Z boson (lower) identification. For the latter, the left plot corresponds to Z bosons decaying to a pair of b quarks, and the right plot to a pair of light-flavor quarks. |
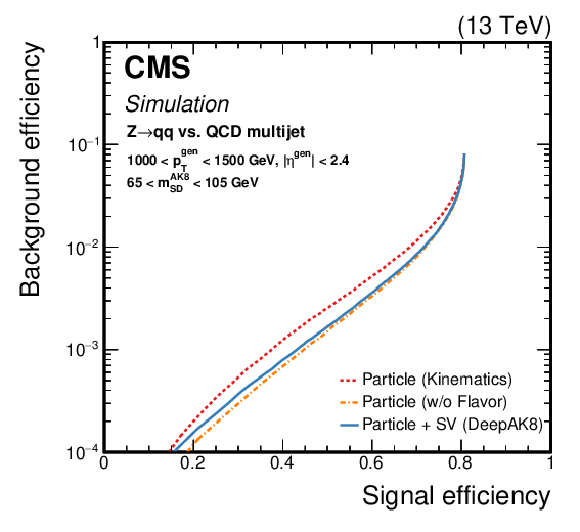
png pdf |
Figure 15-c:
Alternative versions of DeepAK8 trained using a subset of the input features. The details about each version are discussed in the text. The performances of the three versions of DeepAK8 are compared for t quark (upper) and Z boson (lower) identification. For the latter, the left plot corresponds to Z bosons decaying to a pair of b quarks, and the right plot to a pair of light-flavor quarks. |

png pdf |
Figure 16:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
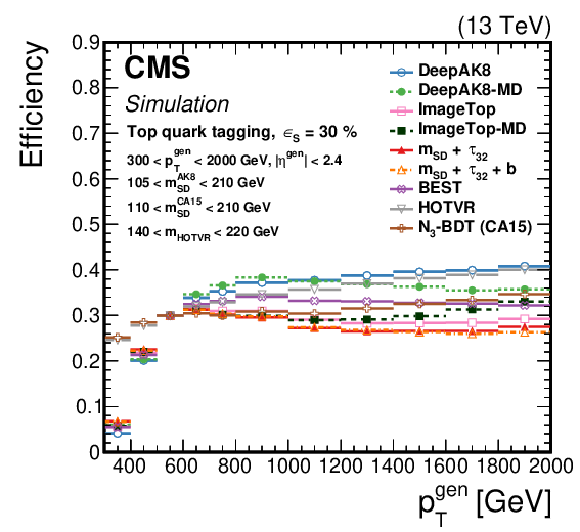
png pdf |
Figure 16-a:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 16-b:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
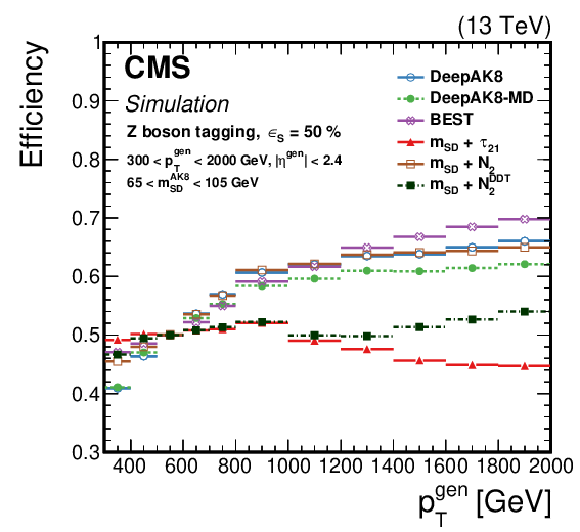
png pdf |
Figure 16-c:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
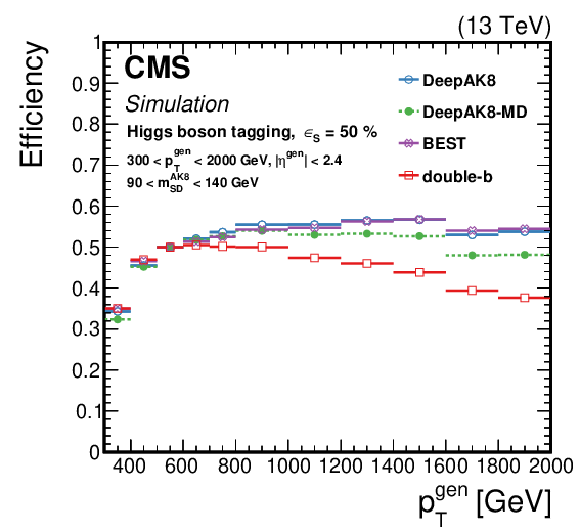
png pdf |
Figure 16-d:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
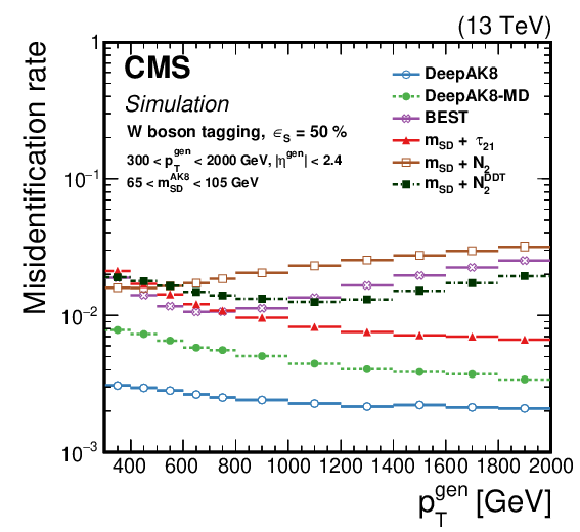
Figure 17:
The distribution of ${\epsilon _{\text {B}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
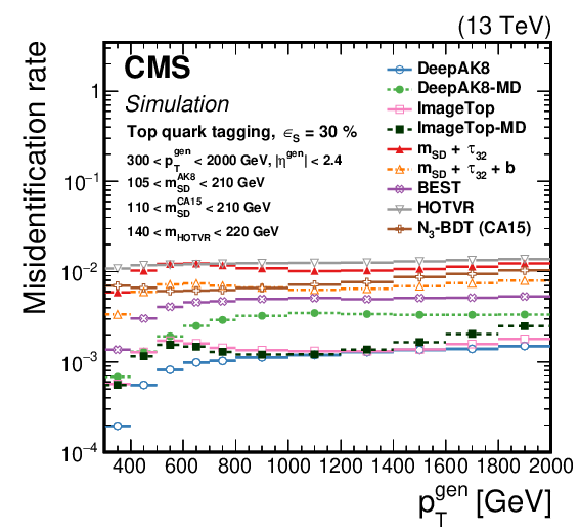
png pdf |
Figure 17-a:
The distribution of ${\epsilon _{\text {B}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 17-b:
The distribution of ${\epsilon _{\text {B}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 17-c:
The distribution of ${\epsilon _{\text {B}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 17-d:
The distribution of ${\epsilon _{\text {B}}}$ as a function of the generated particle ${p_{\mathrm {T}}}$ for a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
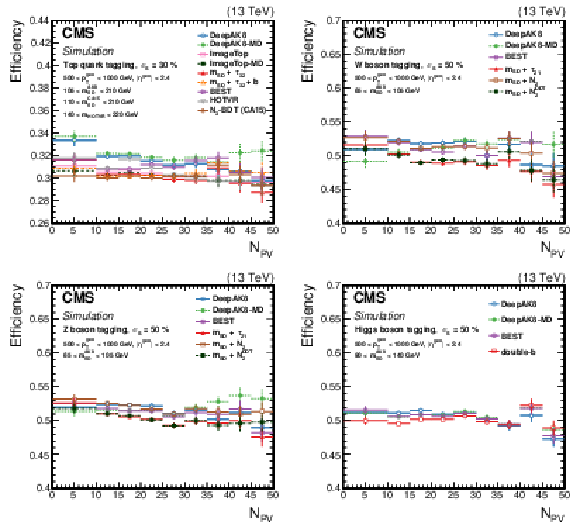
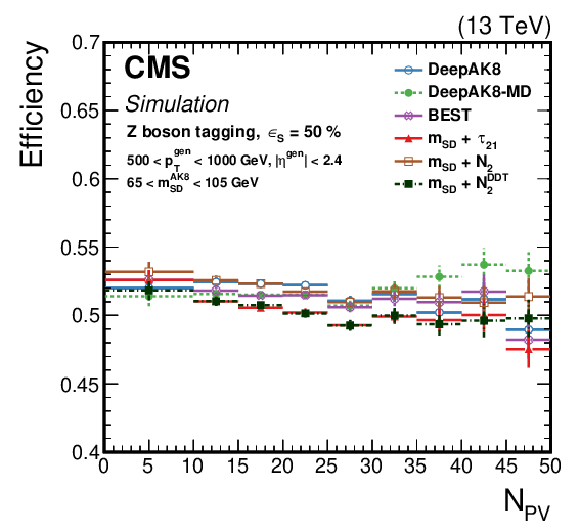
Figure 18:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to a limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 18-a:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to a limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 18-b:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to a limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 18-c:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to a limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
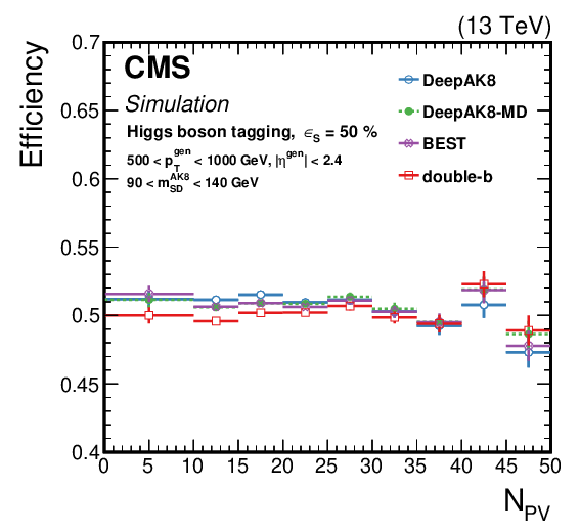
Figure 18-d:
The efficiency ${\epsilon _{\text {S}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to a limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
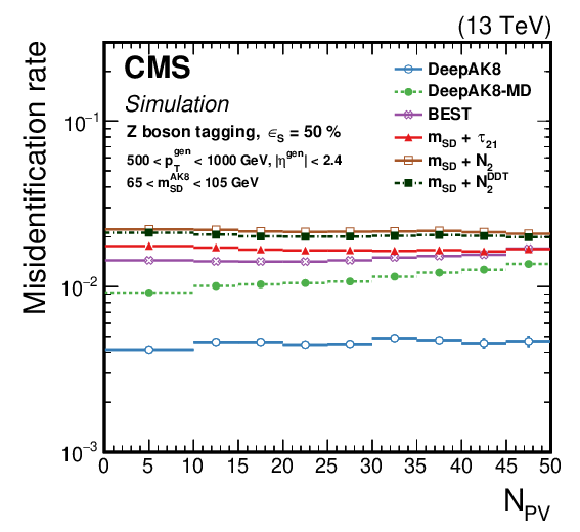
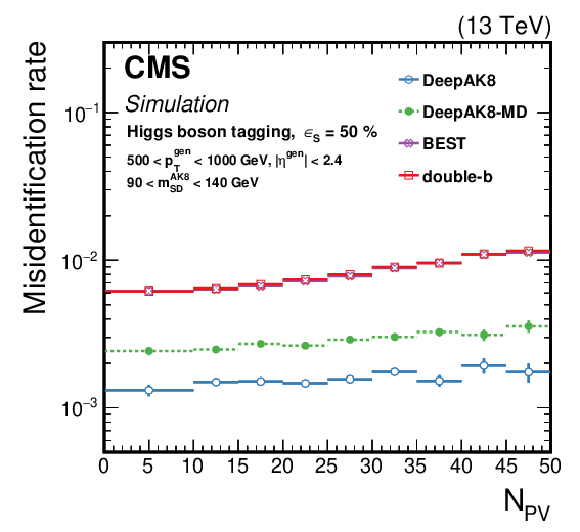
Figure 19:
The efficiency ${\epsilon _{\text {B}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 19-a:
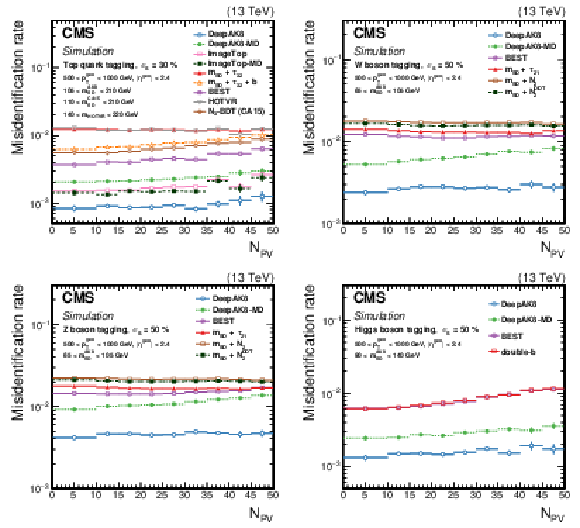
The efficiency ${\epsilon _{\text {B}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 19-b:
The efficiency ${\epsilon _{\text {B}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 19-c:
The efficiency ${\epsilon _{\text {B}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 19-d:
The efficiency ${\epsilon _{\text {B}}}$ as a function of the number of primary vertices (${N_{\text {PV}}}$) for generated particles with 500 $ < {p_{\mathrm {T}}} < $ 1000 GeV at a working point corresponding to $ {\epsilon _{\text {S}}}= $ 30 (50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, due to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
Figure 20:
The normalized ${m_{\text {SD}}}$ distribution for background QCD jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, inclusively and after selection by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
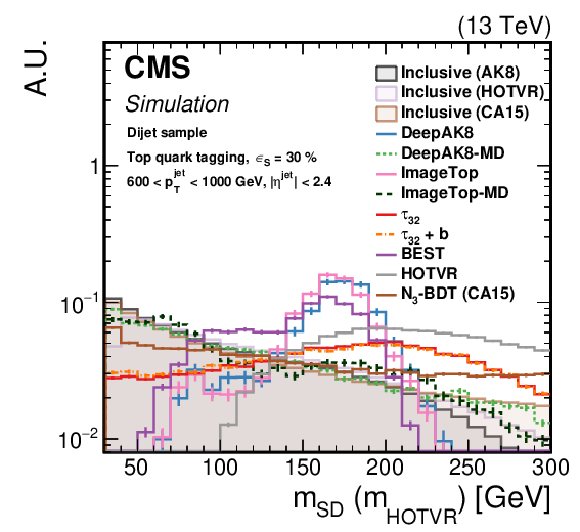
png pdf |
Figure 20-a:
The normalized ${m_{\text {SD}}}$ distribution for background QCD jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, inclusively and after selection by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |

png pdf |
Figure 20-b:
The normalized ${m_{\text {SD}}}$ distribution for background QCD jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, inclusively and after selection by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
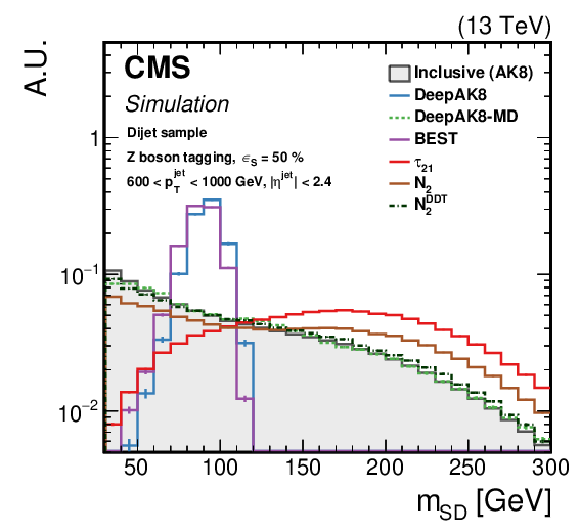
png pdf |
Figure 20-c:
The normalized ${m_{\text {SD}}}$ distribution for background QCD jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, inclusively and after selection by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
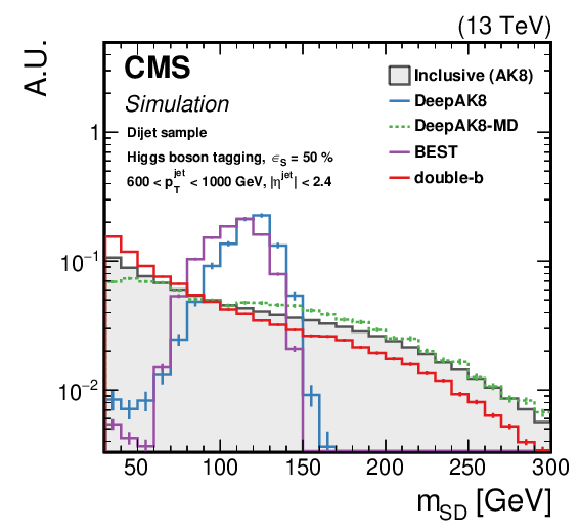
png pdf |
Figure 20-d:
The normalized ${m_{\text {SD}}}$ distribution for background QCD jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, inclusively and after selection by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
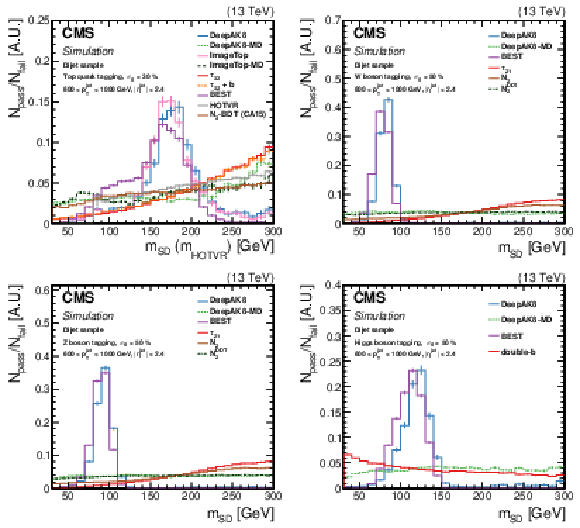
Figure 21:
Normalized ratio of the QCD background jet mass distribution for the passing and failing jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
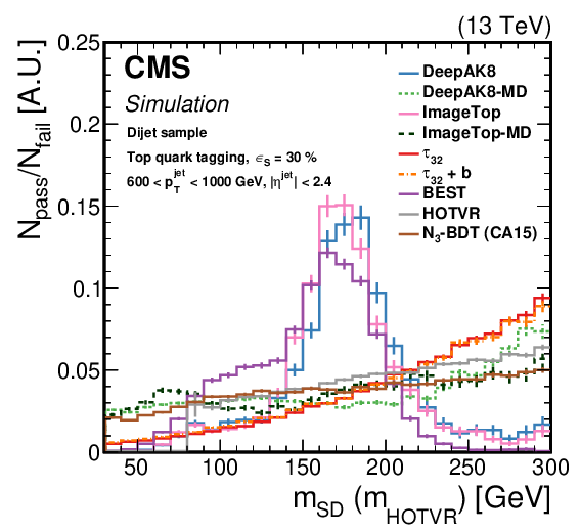
Figure 21-a:
Normalized ratio of the QCD background jet mass distribution for the passing and failing jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
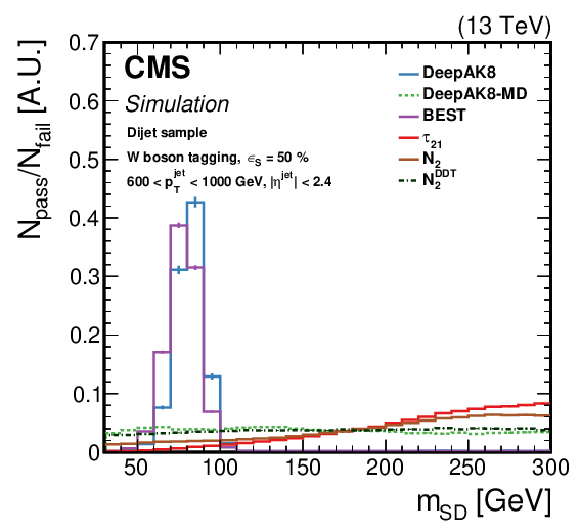
png pdf |
Figure 21-b:
Normalized ratio of the QCD background jet mass distribution for the passing and failing jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
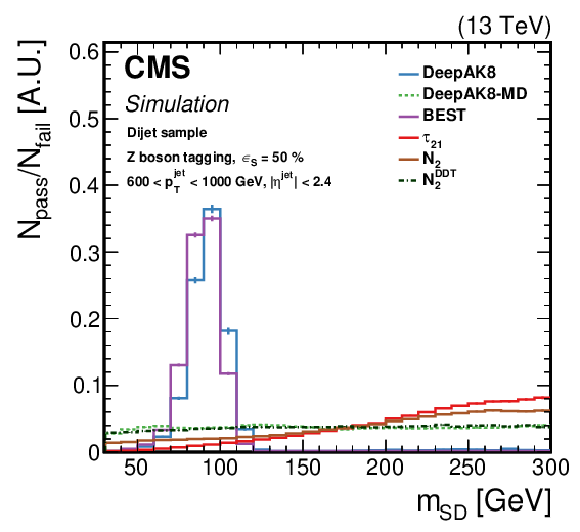
Figure 21-c:
Normalized ratio of the QCD background jet mass distribution for the passing and failing jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
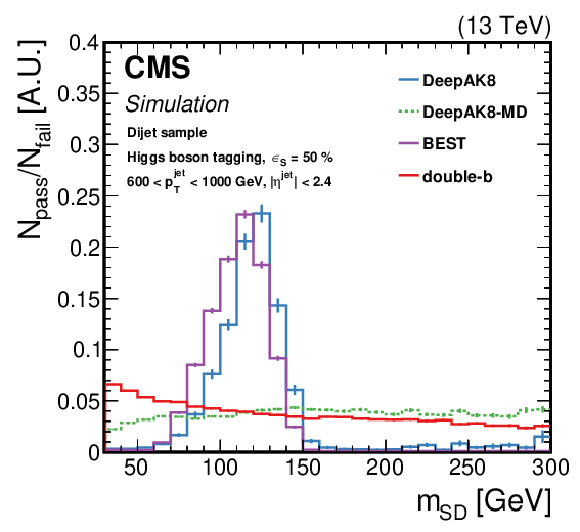
Figure 21-d:
Normalized ratio of the QCD background jet mass distribution for the passing and failing jets with 600 $ < {p_{\mathrm {T}}} < $ 1000 GeV, by each algorithm. The working point chosen corresponds to $ {\epsilon _{\text {S}}}=$ 30 ($ {\epsilon _{\text {S}}}=$ 50)% for t quark (W/Z/H boson) identification. Upper left: t quark, upper right: W boson, lower left: Z boson, lower right: H boson. The error bars represent the statistical uncertainty in each specific bin, which is related to the limited number of simulated events. Additional fiducial selection criteria applied to the jets are listed on the plots. |
png pdf |
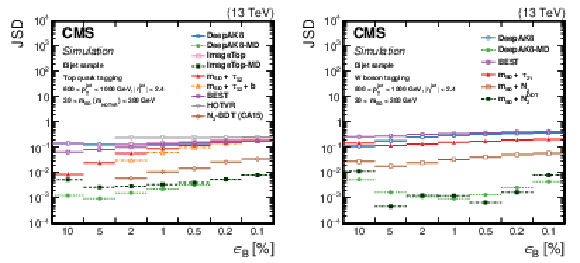
Figure 22:
The JSD as a function of successively tighter selections (expressed in terms of ${\epsilon _{\text {B}}}$) for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
Figure 22-a:
The JSD as a function of successively tighter selections (expressed in terms of ${\epsilon _{\text {B}}}$) for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |
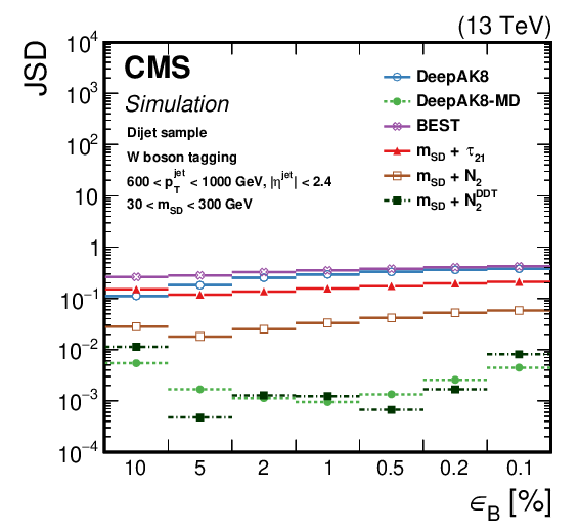
png pdf |
Figure 22-b:
The JSD as a function of successively tighter selections (expressed in terms of ${\epsilon _{\text {B}}}$) for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |

png pdf |
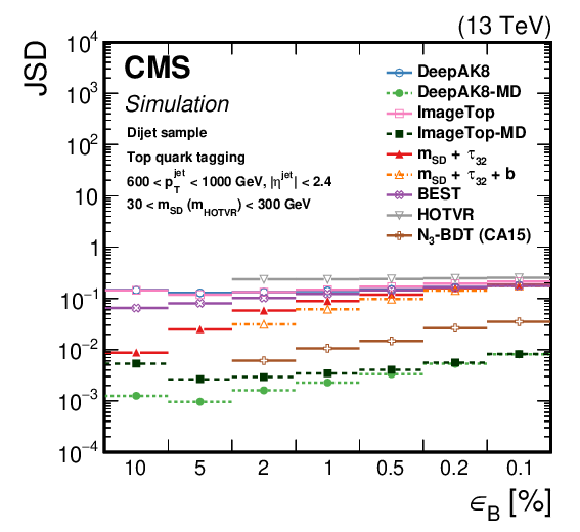
Figure 23:
The JSD, as a function of the jet ${p_{\mathrm {T}}}$ for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |
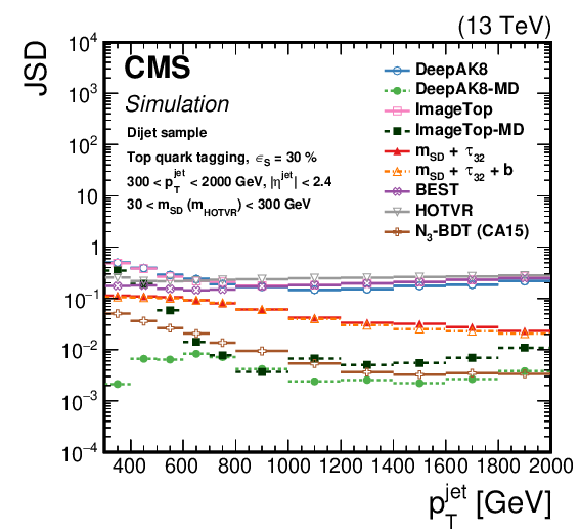
png pdf |
Figure 23-a:
The JSD, as a function of the jet ${p_{\mathrm {T}}}$ for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |
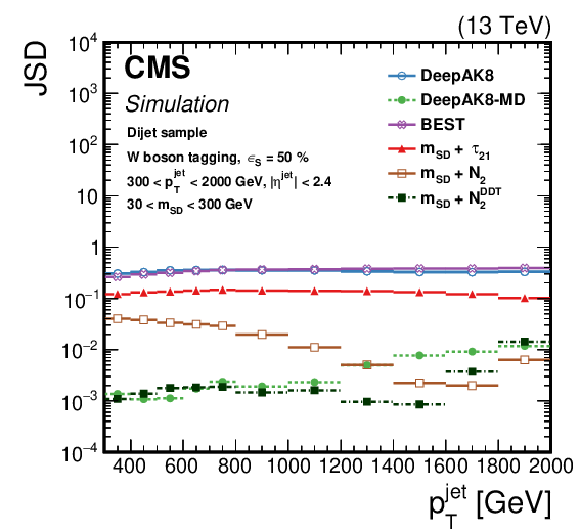
png pdf |
Figure 23-b:
The JSD, as a function of the jet ${p_{\mathrm {T}}}$ for the various t (left) and W (right) tagging algorithms. Lower values of JSD indicate larger similarity of the $m {{}_{\text {SD}}}$ in QCD multijet events passing and failing the selection on the tagging algorithm. Additional fiducial selection criteria applied to the jets are listed in the plots. |
png pdf |
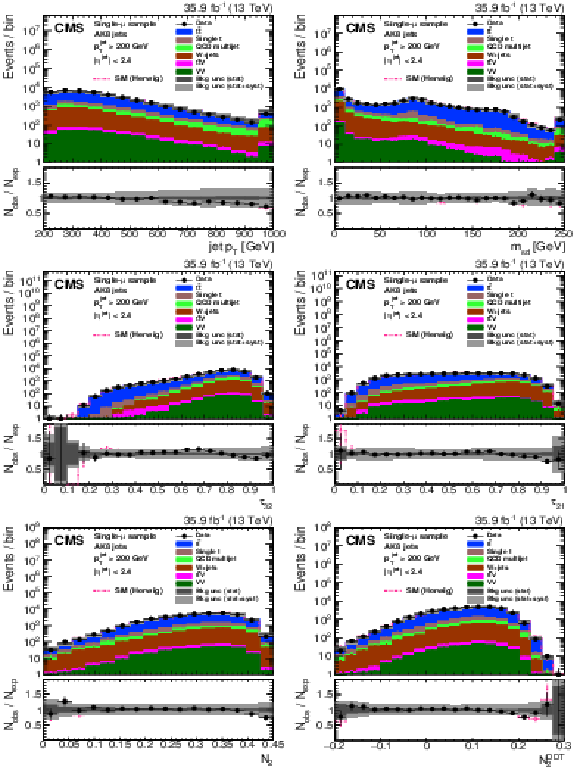
Figure 24:
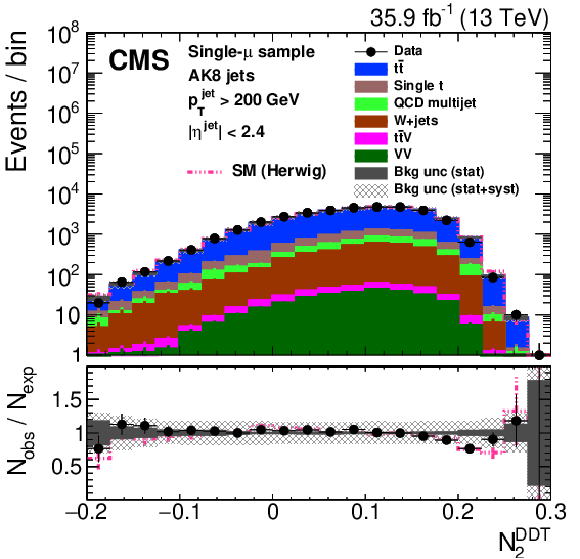
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
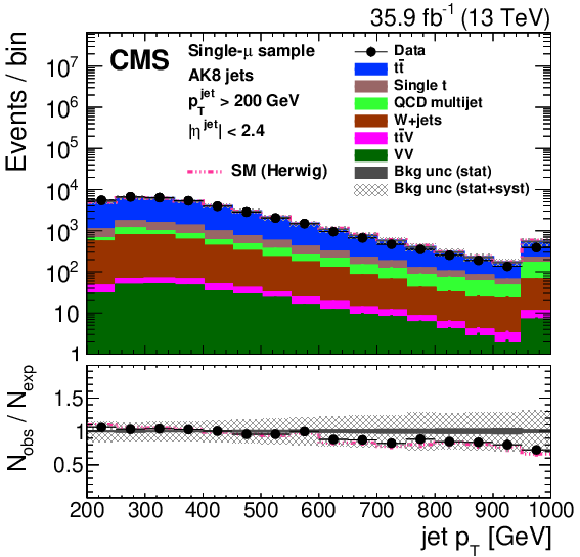
png pdf |
Figure 24-a:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
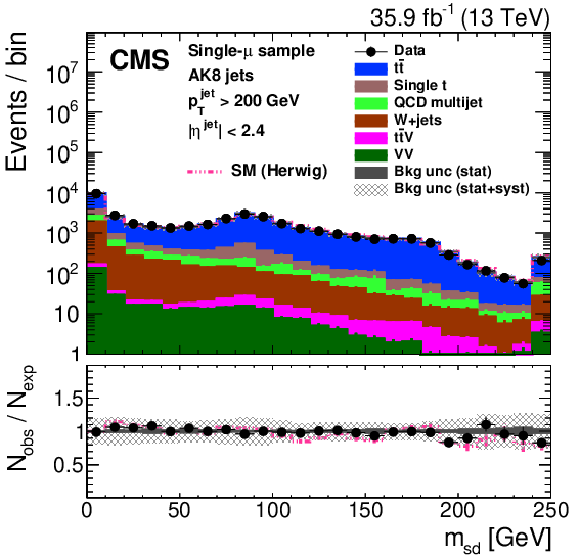
png pdf |
Figure 24-b:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 24-c:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
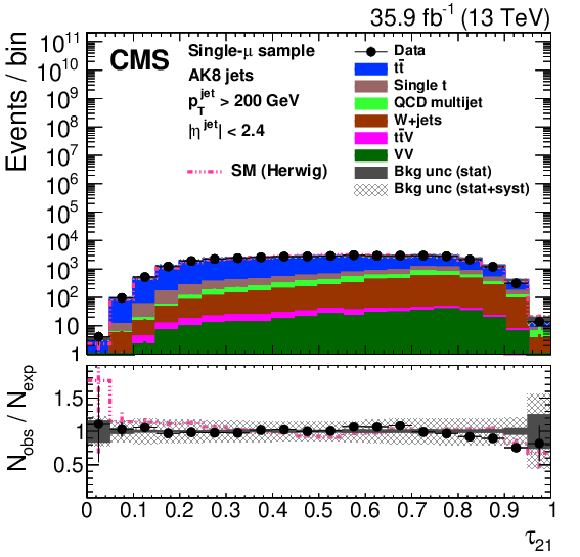
png pdf |
Figure 24-d:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
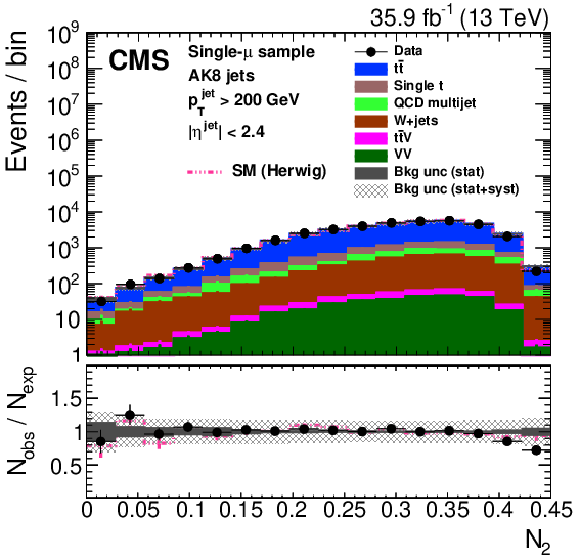
png pdf |
Figure 24-e:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 24-f:
Distribution of the the jet ${p_{\mathrm {T}}}$ (upper left), jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
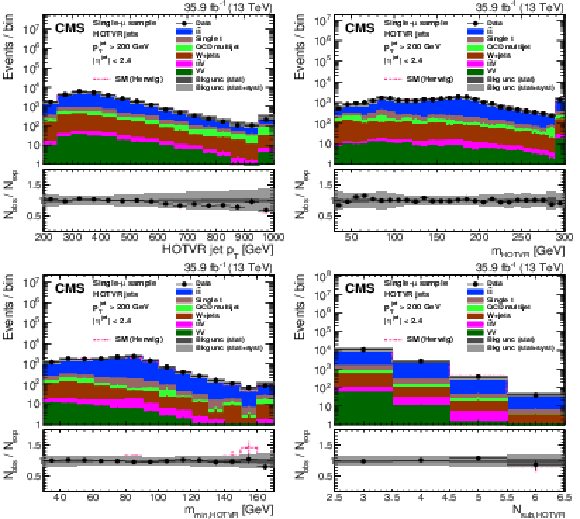
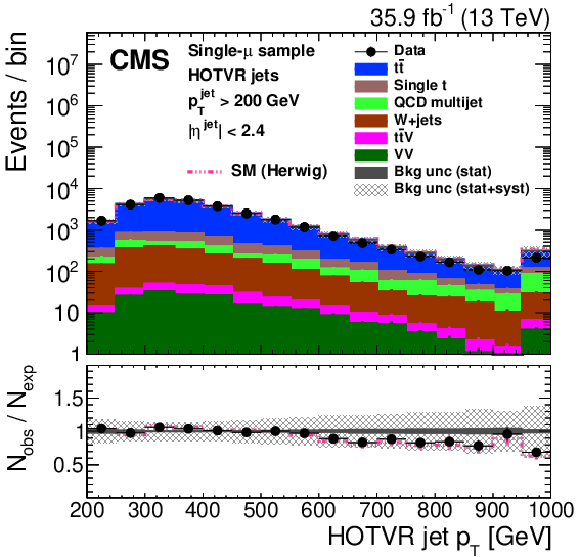
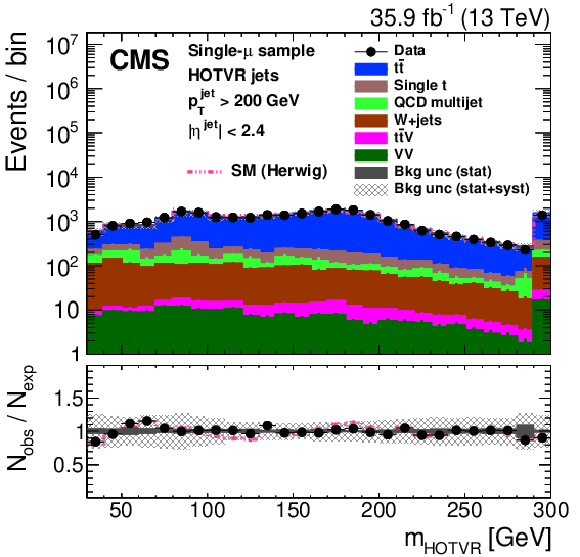
Figure 25:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left), and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 25-a:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left), and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 25-b:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left), and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
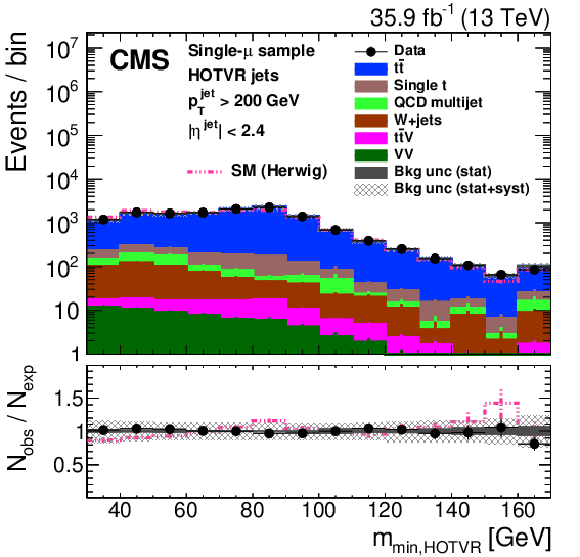
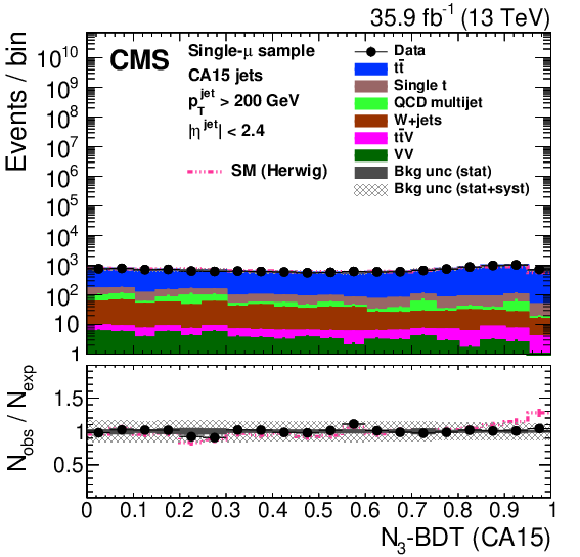
Figure 25-c:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left), and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 25-d:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left), and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 26:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 26-a:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 26-b:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 26-c:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
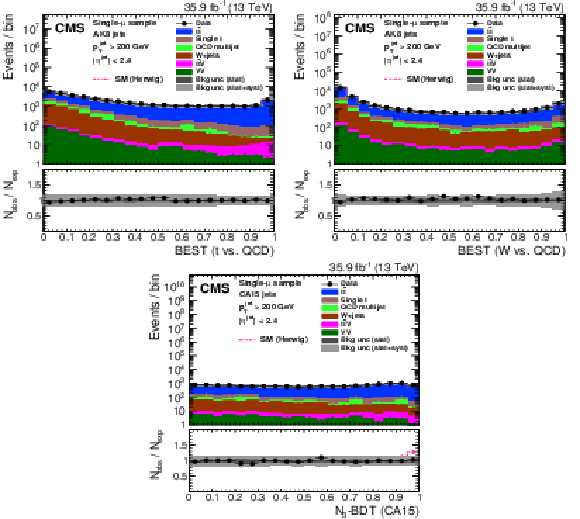
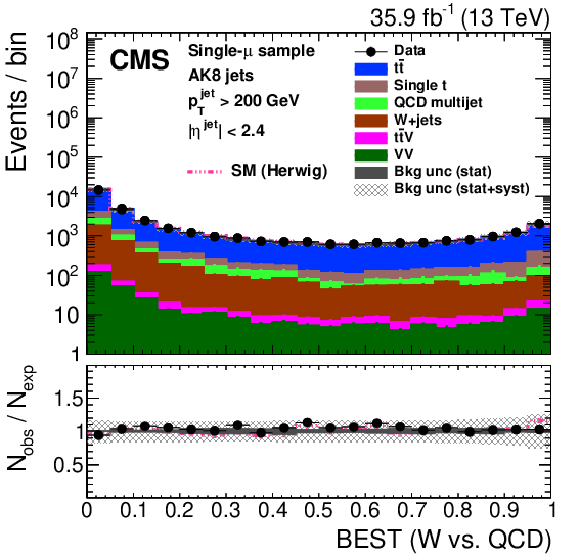
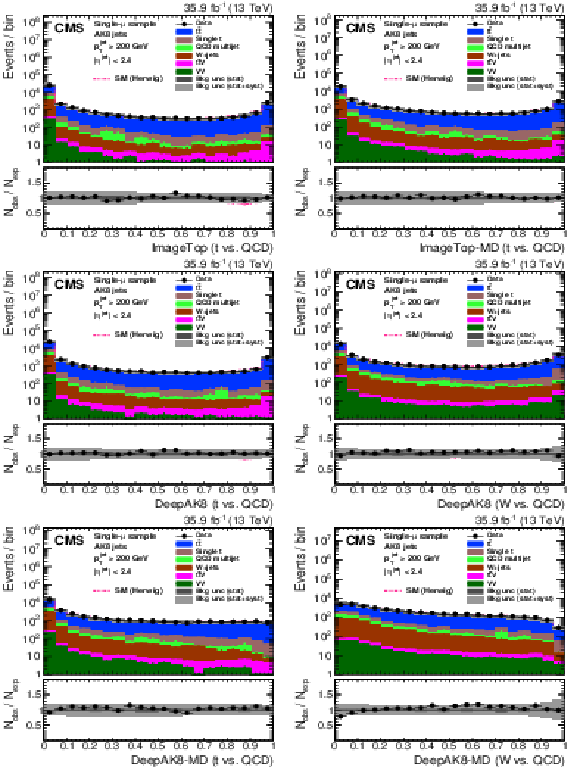
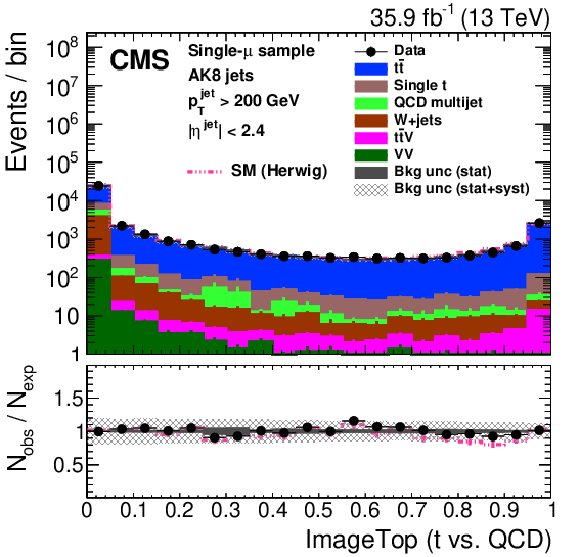
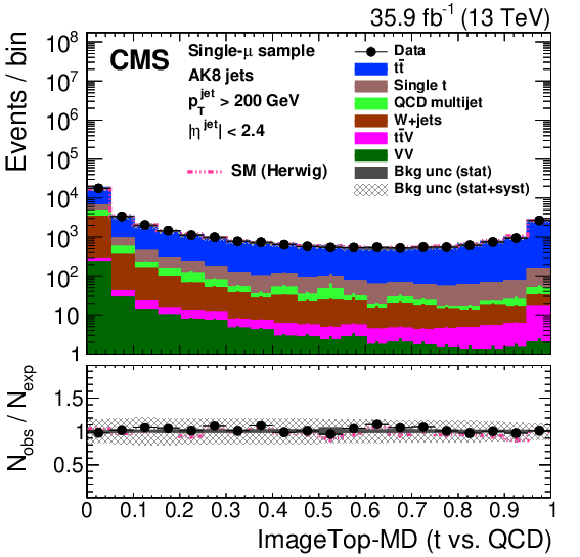
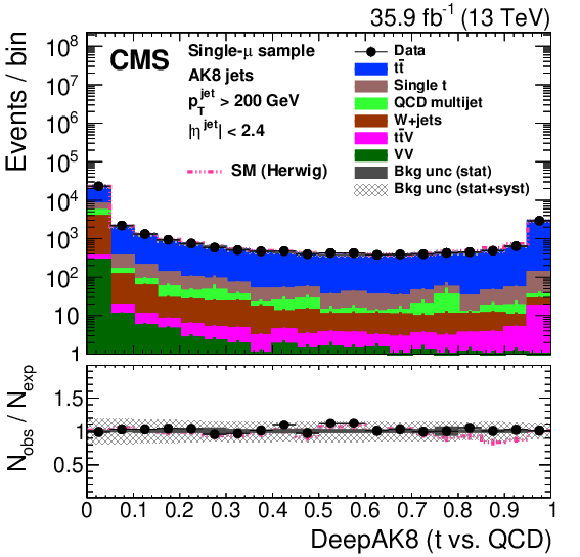
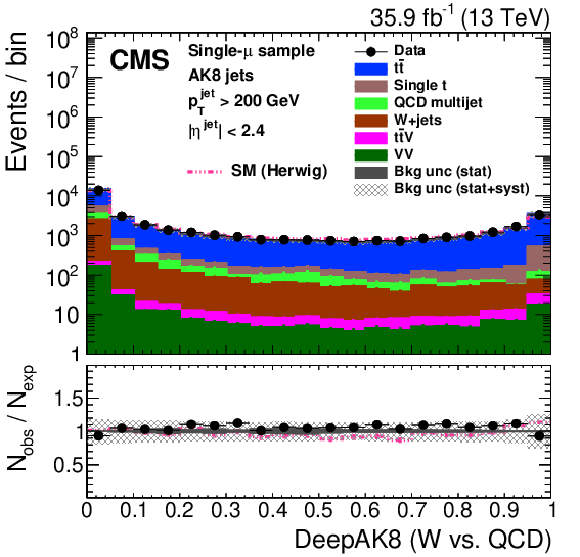
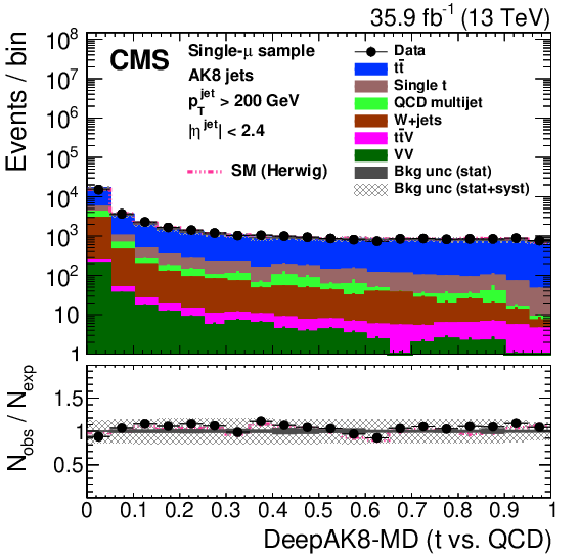
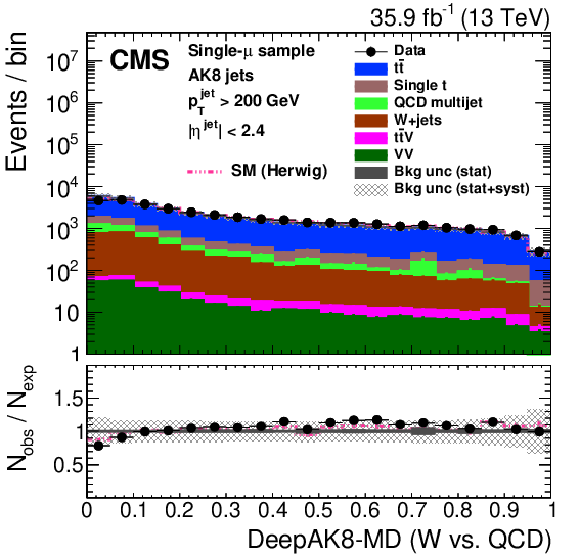
Figure 27:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-a:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-b:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-c:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-d:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-e:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 27-f:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
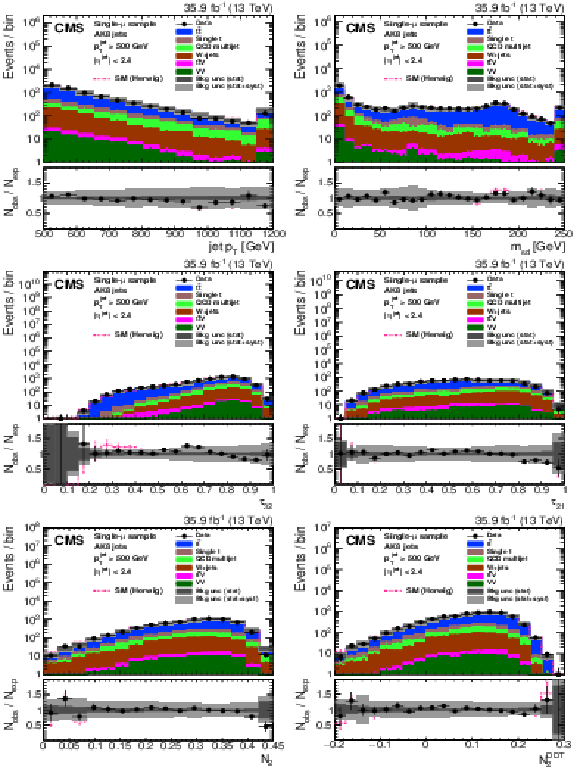
Figure 28:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 28-a:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 28-b:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
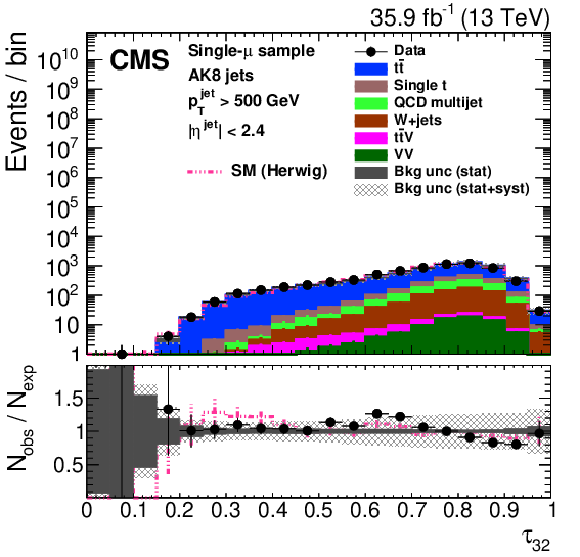
png pdf |
Figure 28-c:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
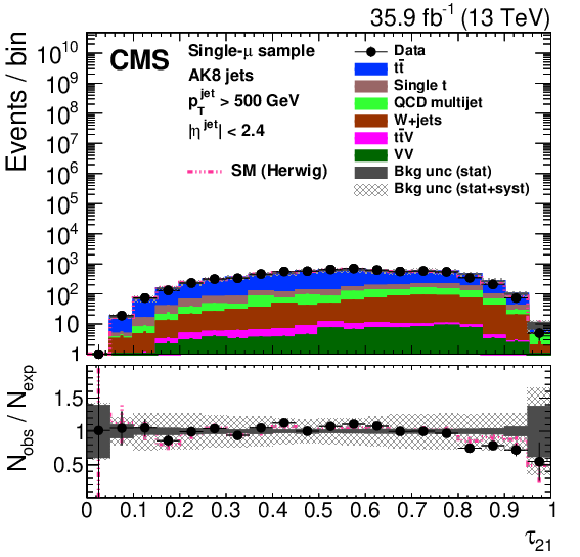
png pdf |
Figure 28-d:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 28-e:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
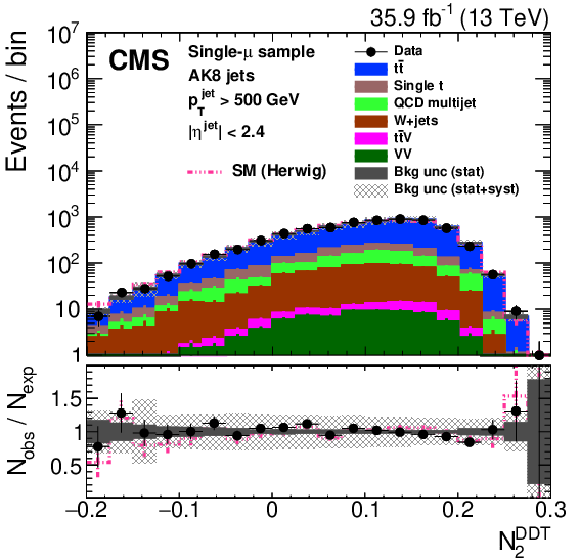
png pdf |
Figure 28-f:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_2^{\text {DDT}}$ (lower right) in data and simulation in the single-$\mu $ signal sample after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
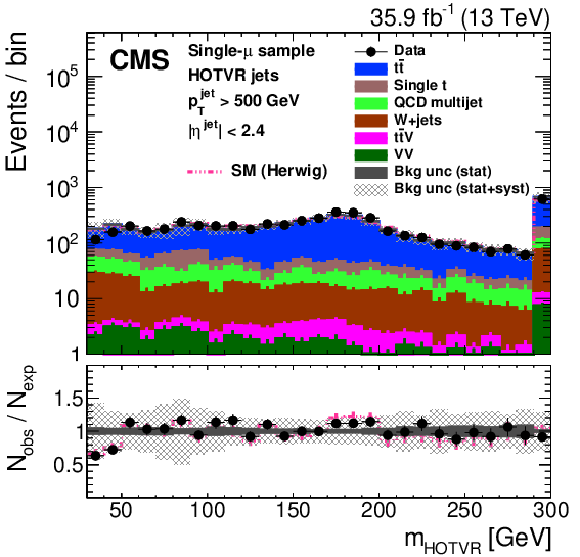
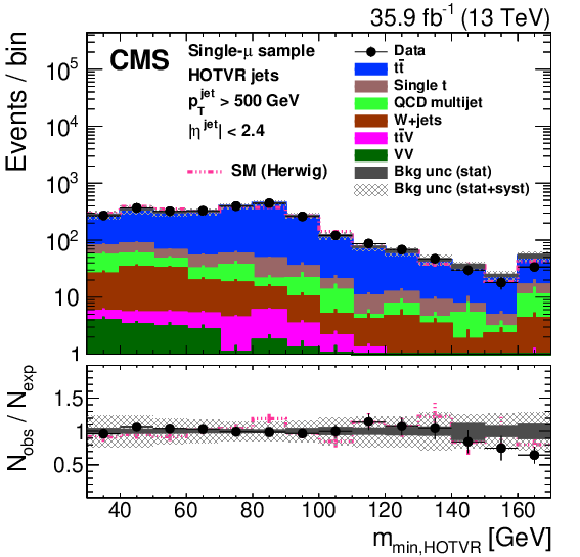
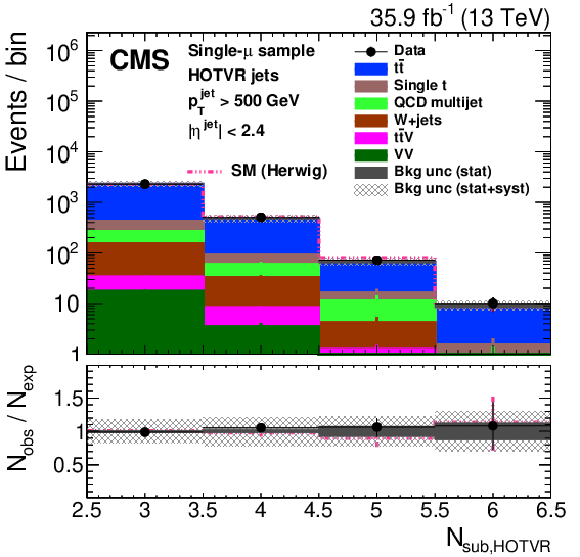
Figure 29:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
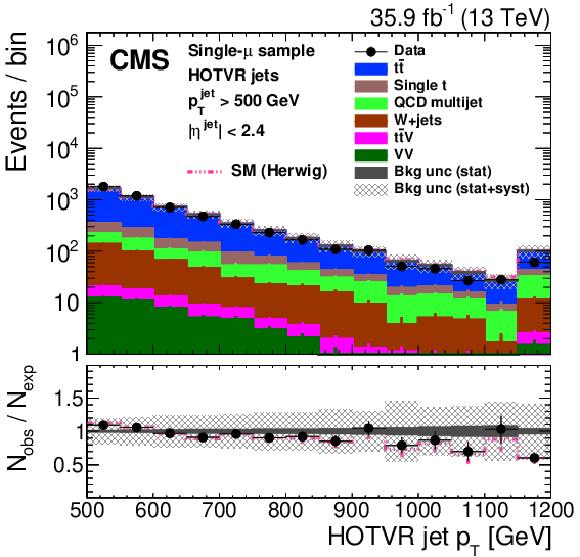
png pdf |
Figure 29-a:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 29-b:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 29-c:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
png pdf |
Figure 29-d:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 30:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
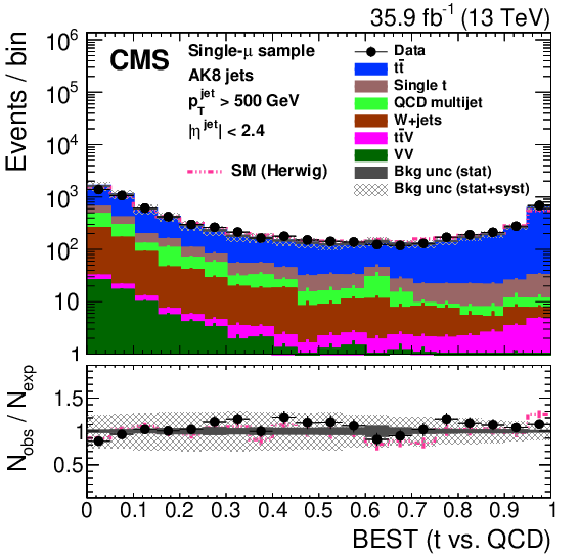
png pdf |
Figure 30-a:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
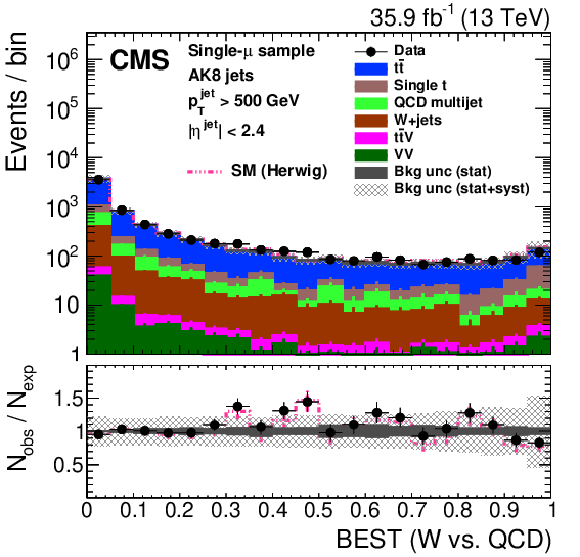
png pdf |
Figure 30-b:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
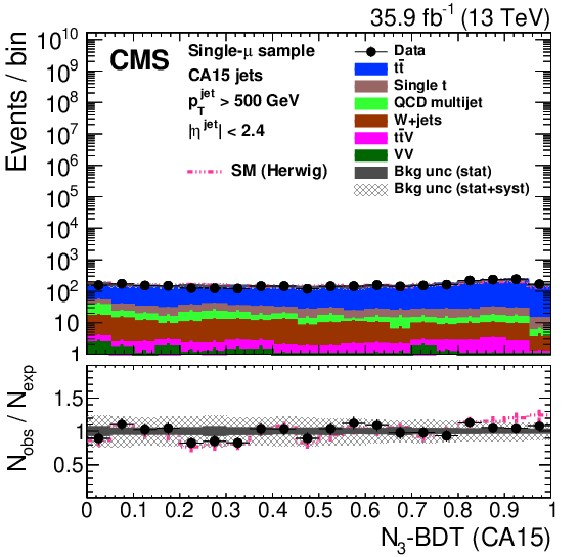
png pdf |
Figure 30-c:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\mu $ signal sample, after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 31:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
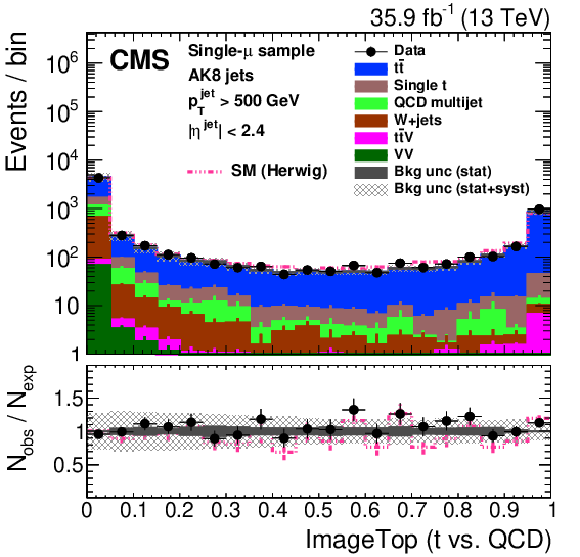
png pdf |
Figure 31-a:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
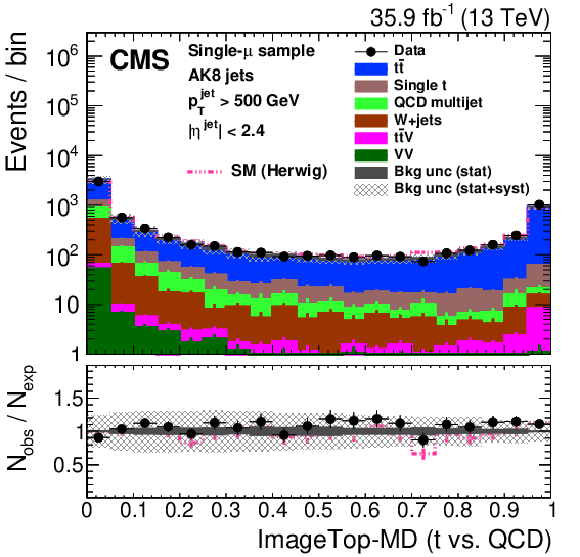
png pdf |
Figure 31-b:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |

png pdf |
Figure 31-c:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
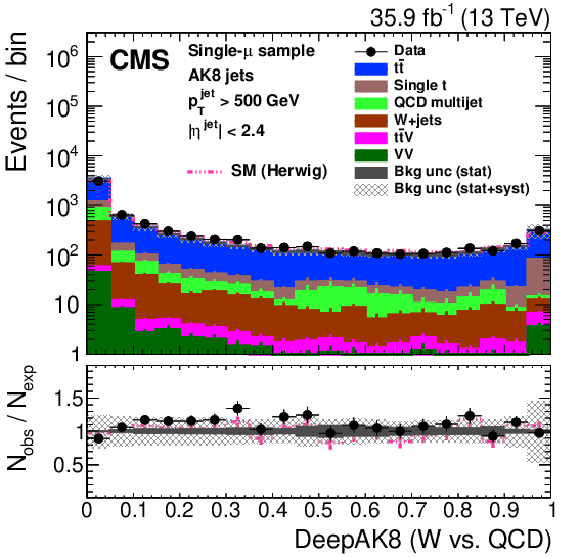
png pdf |
Figure 31-d:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
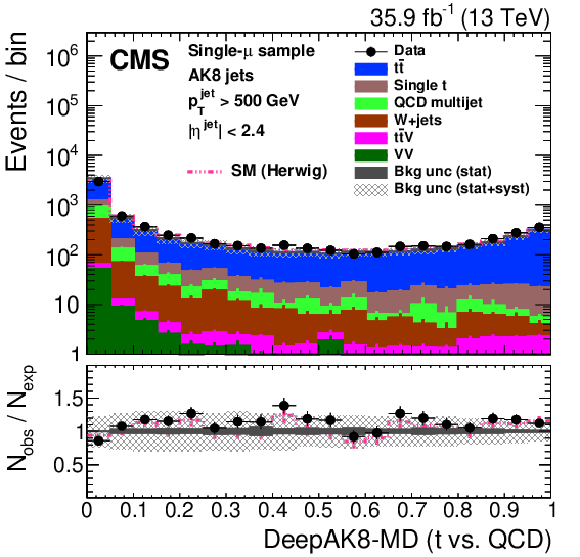
png pdf |
Figure 31-e:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
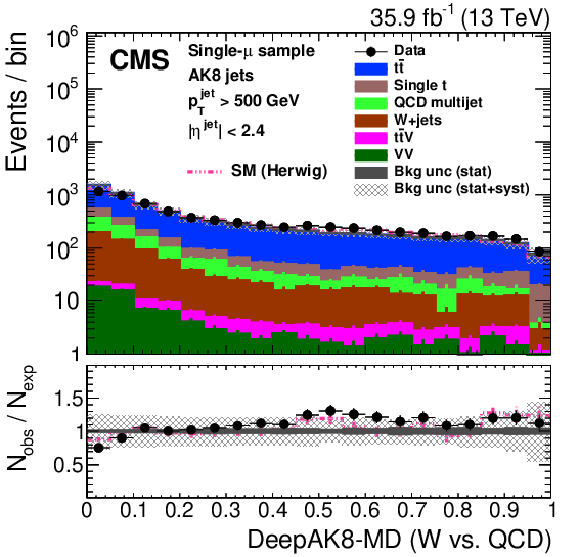
png pdf |
Figure 31-f:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\mu $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm after applying a jet momentum cut $ {p_{\mathrm {T}}} > $ 500 GeV. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative ${\mathrm{t} {}\mathrm{\bar{t}}}$ sample. The distributions are weighted according to the top quark ${p_{\mathrm {T}}}$ weighting procedure described in the text. |
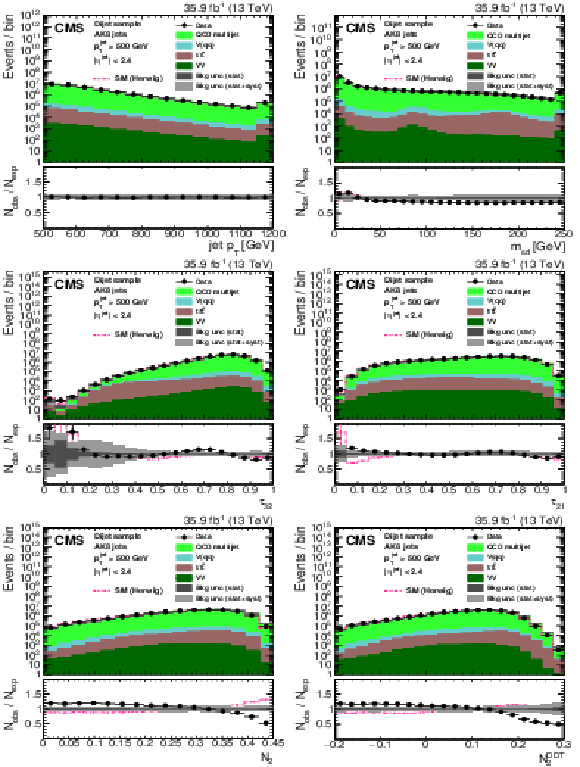
png pdf |
Figure 32:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
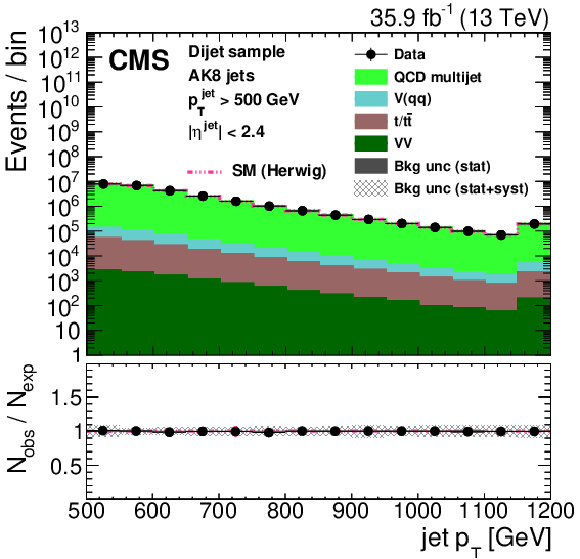
png pdf |
Figure 32-a:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
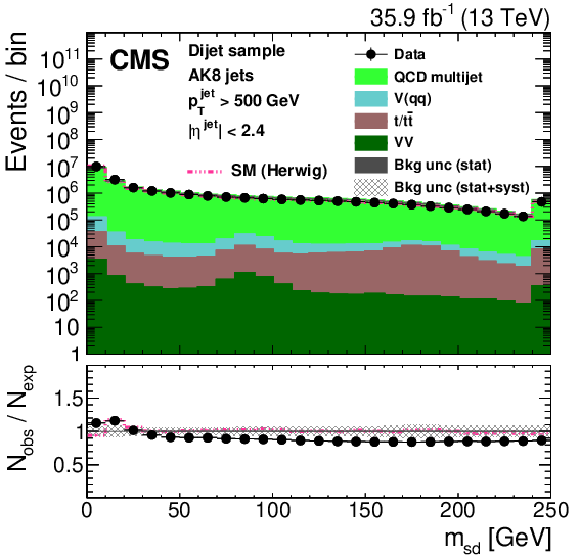
png pdf |
Figure 32-b:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
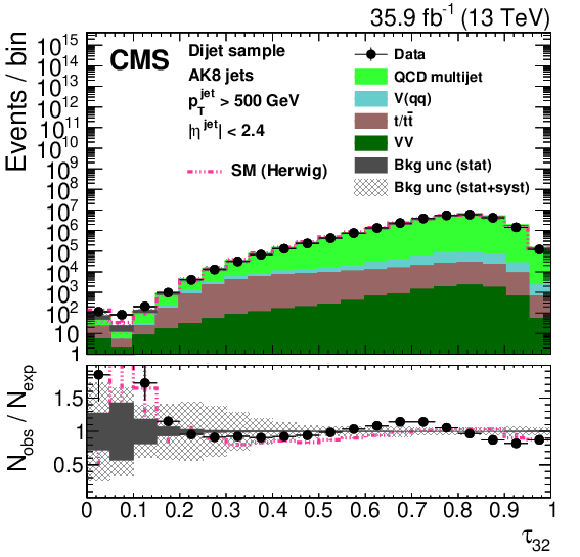
png pdf |
Figure 32-c:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
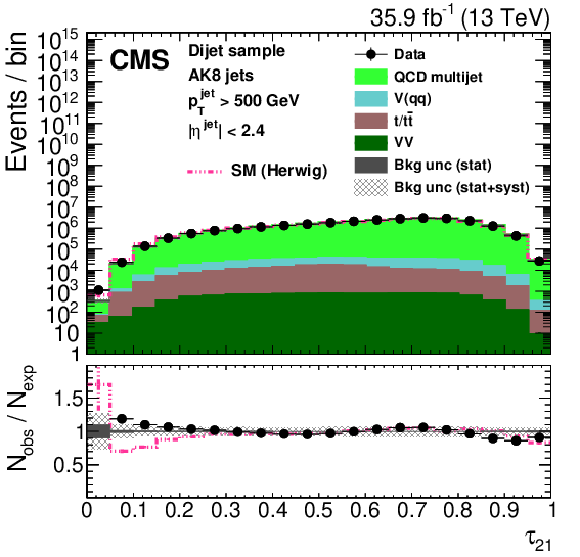
png pdf |
Figure 32-d:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
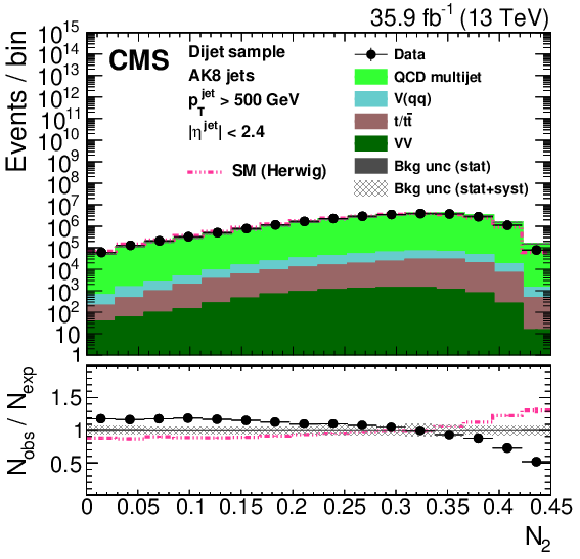
png pdf |
Figure 32-e:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
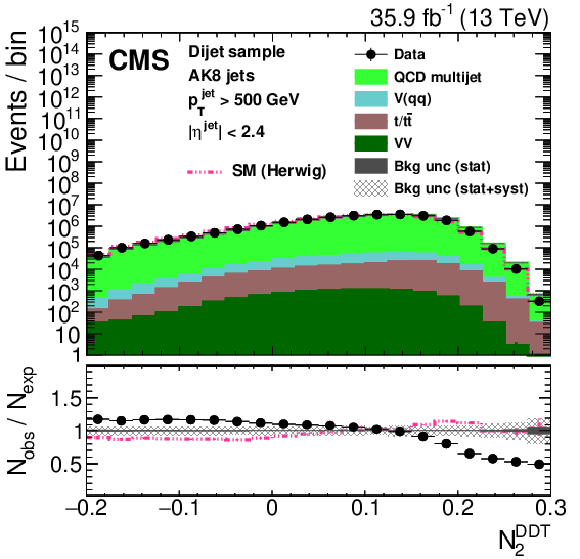
png pdf |
Figure 32-f:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
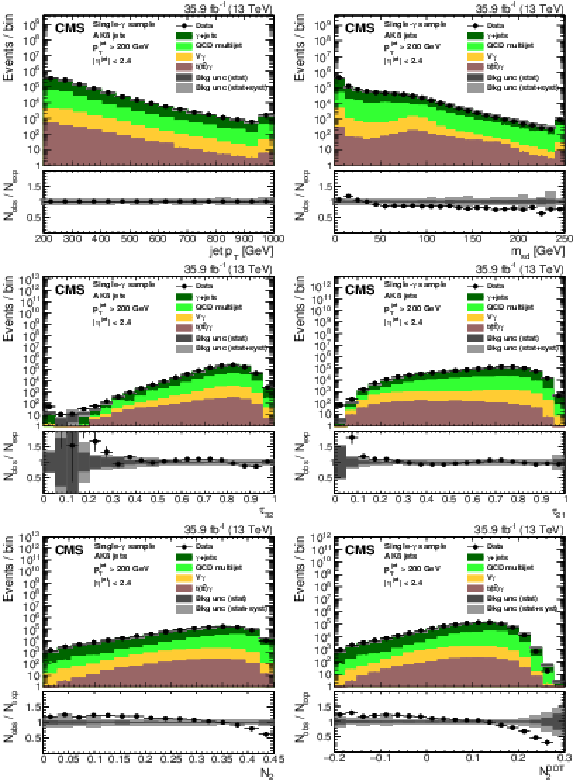
png pdf |
Figure 33:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 33-a:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
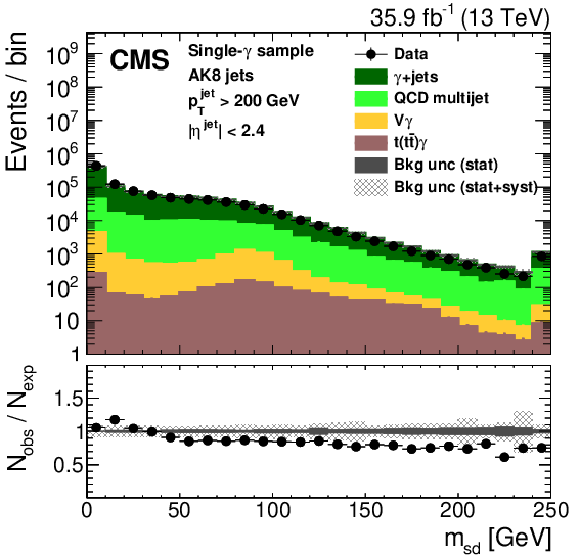
png pdf |
Figure 33-b:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 33-c:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 33-d:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
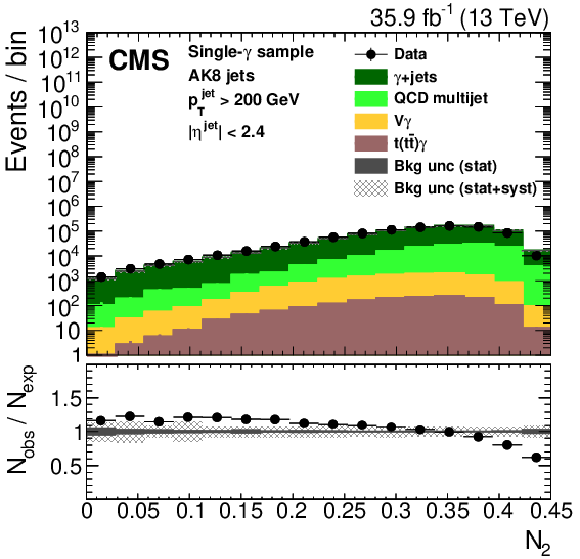
png pdf |
Figure 33-e:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 33-f:
Distribution of the jet ${p_{\mathrm {T}}}$ (upper left), the jet mass, ${m_{\text {SD}}}$ (upper right), the $N$-subjettiness ratios $ {\tau _{32}}$ (middle left) and $ {\tau _{21}}$ (middle right), and the $N_2$ (lower left) and $N_{2}^{\text {DDT}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
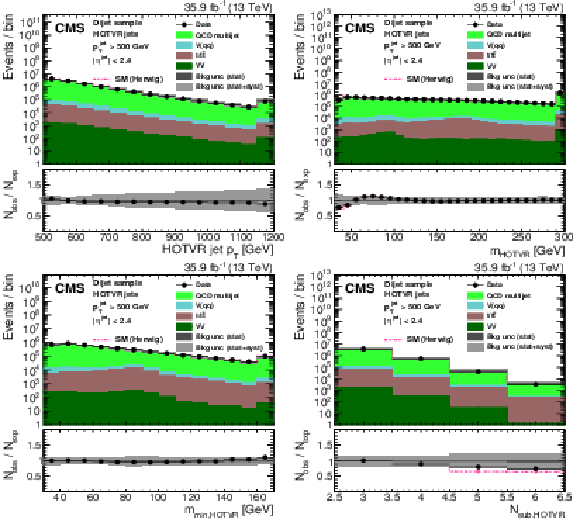
png pdf |
Figure 34:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
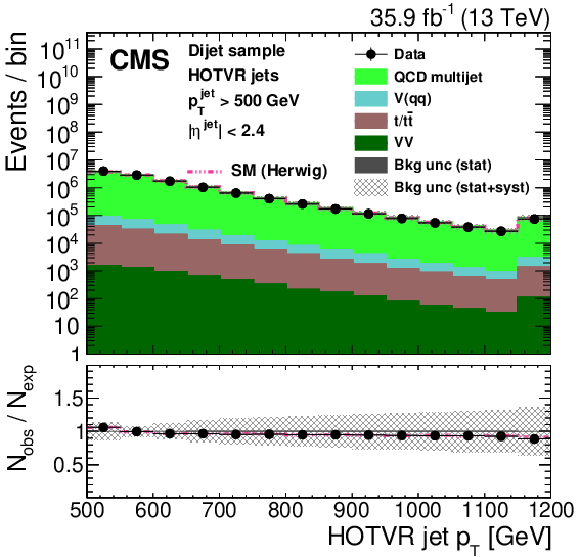
png pdf |
Figure 34-a:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 34-b:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 34-c:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
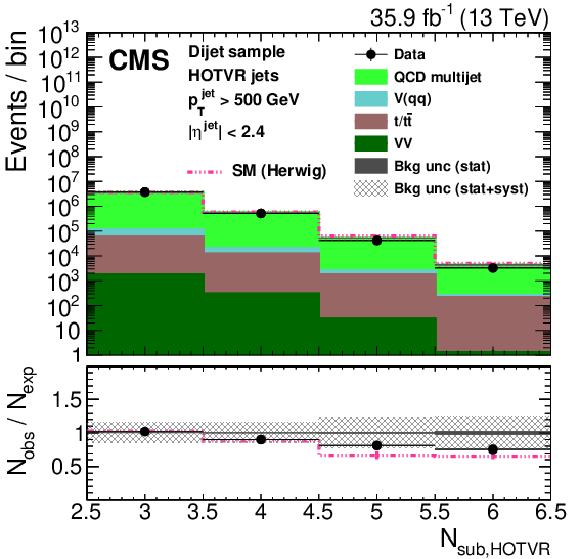
png pdf |
Figure 34-d:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the dijet sample. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
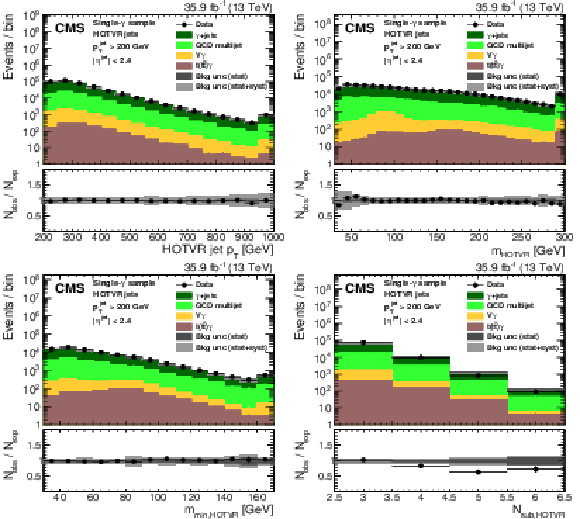
png pdf |
Figure 35:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
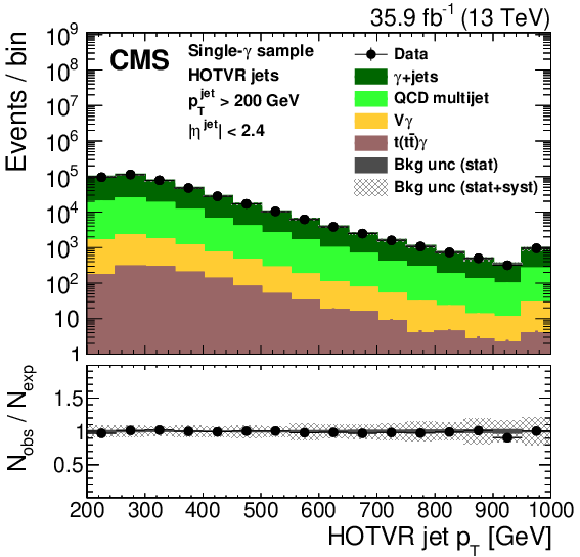
png pdf |
Figure 35-a:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 35-b:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
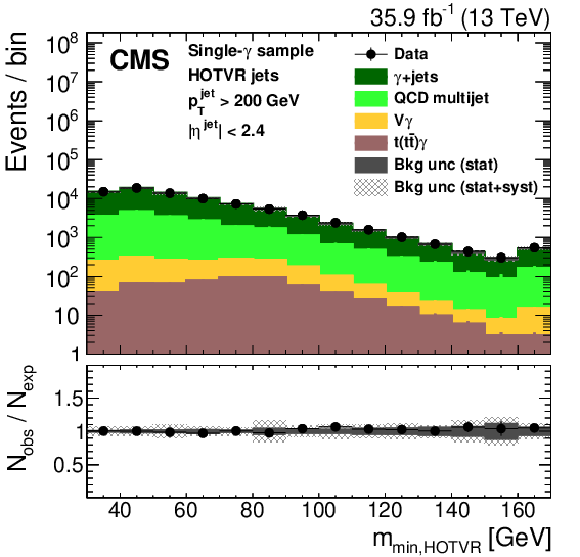
png pdf |
Figure 35-c:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
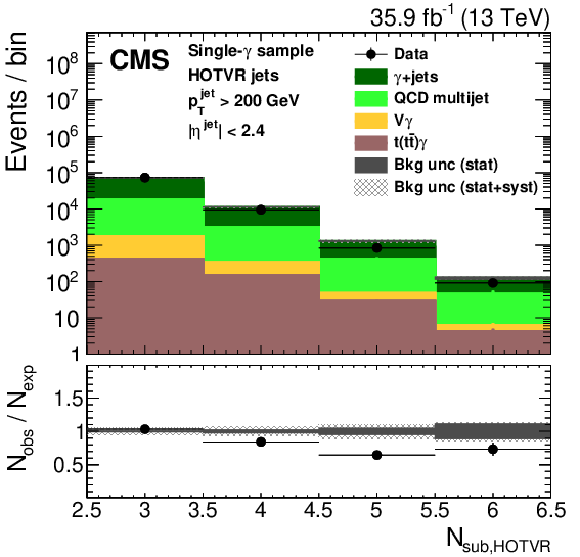
png pdf |
Figure 35-d:
Distribution of the main observables of the HOTVR algorithm, HOTVR jet ${p_{\mathrm {T}}}$ (upper left), $m_{\text {HOTVR}}$ (upper right), $m_{\text {min,HOTVR}}$ (lower left) and $N_{\text {sub,HOTVR}}$ (lower right) in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
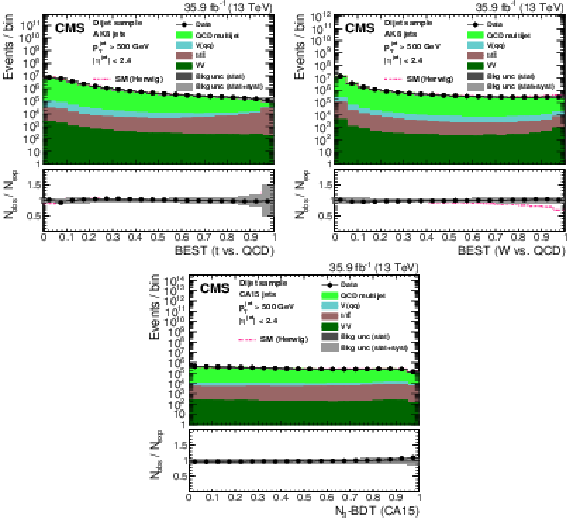
png pdf |
Figure 36:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the dijet sample. The background event yield is normalized to the total observed data yield. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
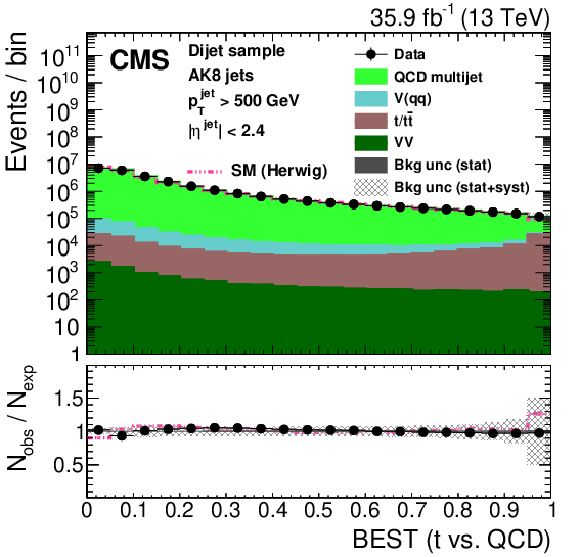
png pdf |
Figure 36-a:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the dijet sample. The background event yield is normalized to the total observed data yield. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
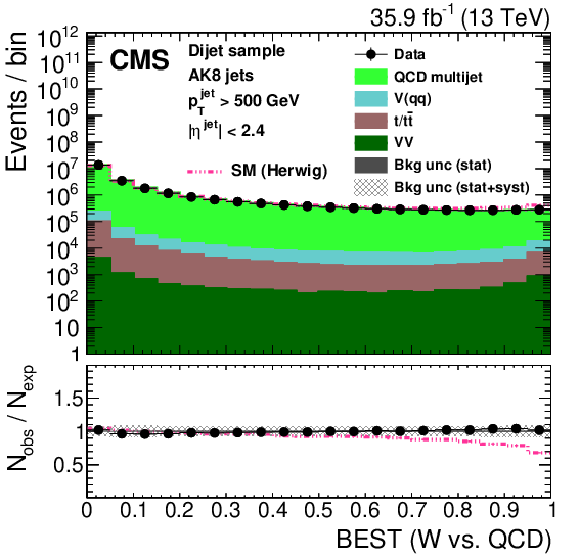
png pdf |
Figure 36-b:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the dijet sample. The background event yield is normalized to the total observed data yield. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
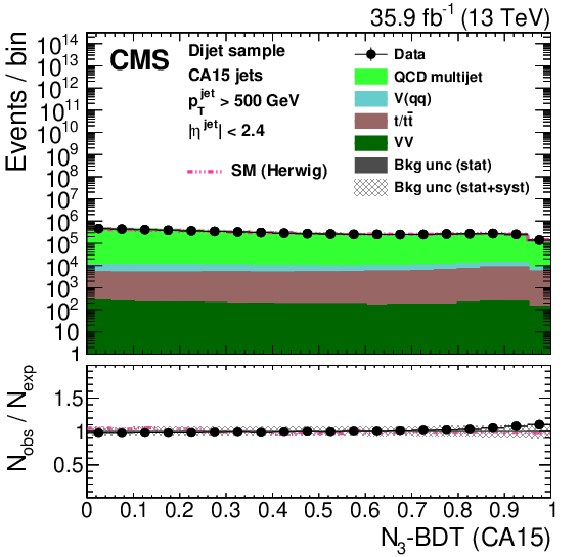
png pdf |
Figure 36-c:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the dijet sample. The background event yield is normalized to the total observed data yield. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 37:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 37-a:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 37-b:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 37-c:
Distribution of the t quark (upper left) and W boson (upper right) identification probabilities for the BEST algorithm, and the ${N_{3}\text {-}\text {BDT} (\text {CA}15)}$ discriminant in data and simulation in the single-$\gamma $ sample. The background event yield is normalized to the total observed data yield. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
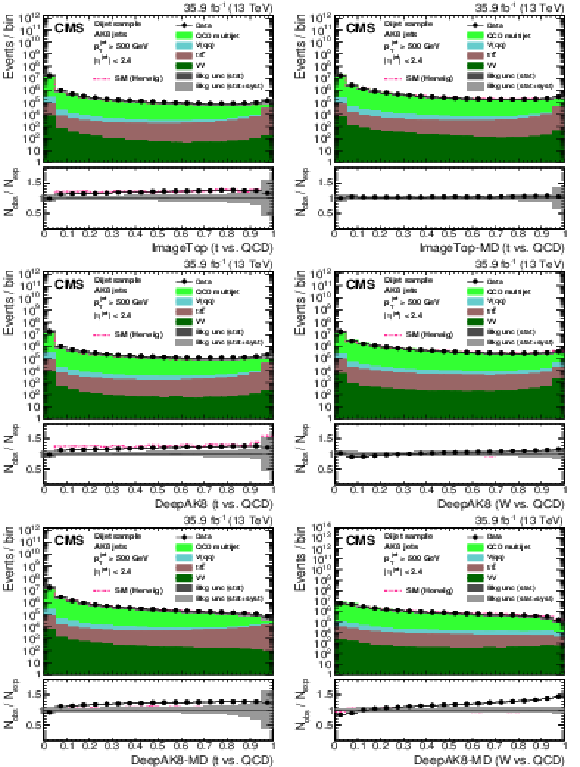
png pdf |
Figure 38:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
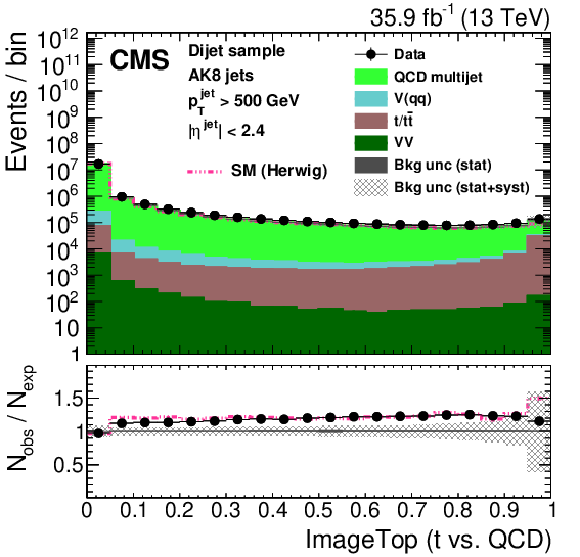
png pdf |
Figure 38-a:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
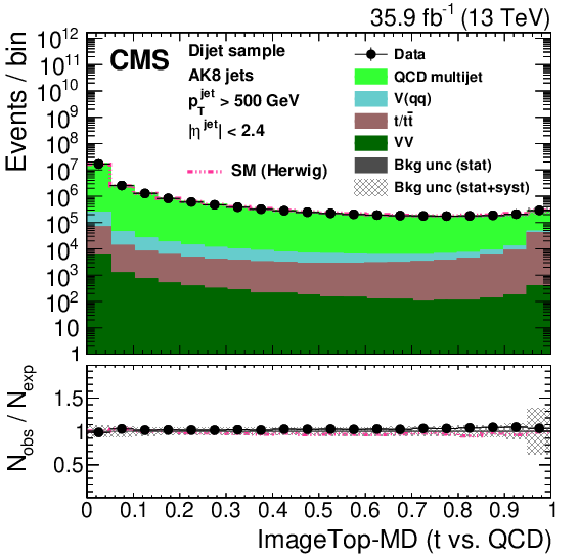
png pdf |
Figure 38-b:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
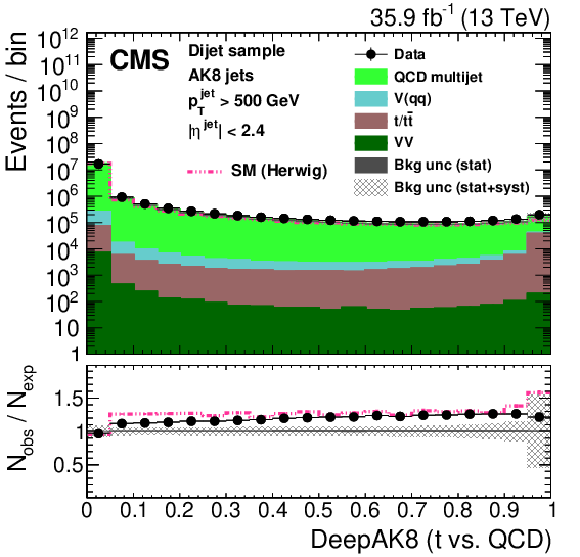
png pdf |
Figure 38-c:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
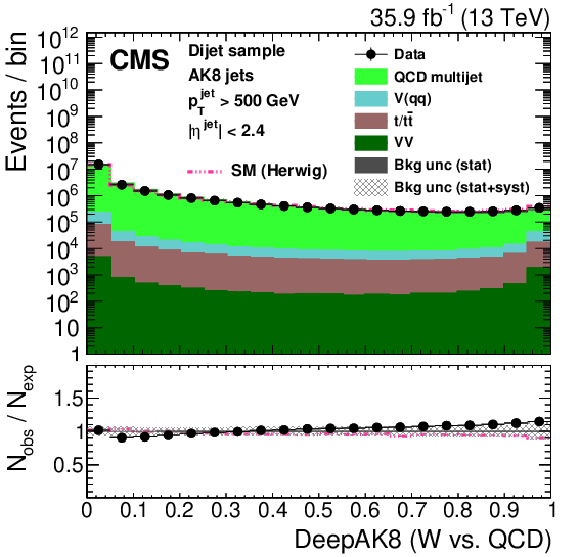
png pdf |
Figure 38-d:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
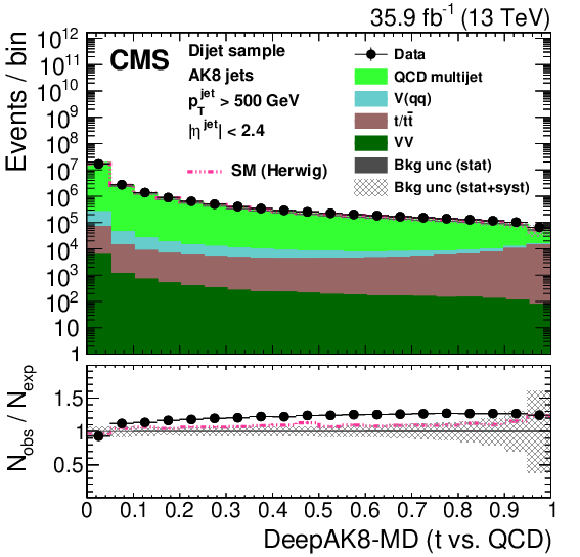
png pdf |
Figure 38-e:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
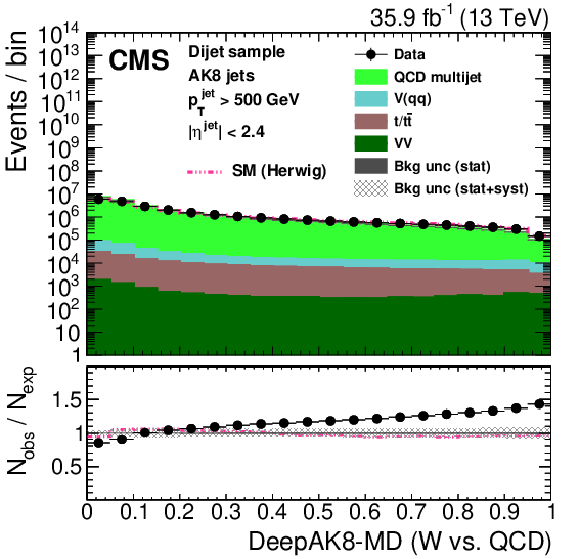
png pdf |
Figure 38-f:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the dijet sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The pink line corresponds to the simulation distribution obtained using the alternative QCD multijet sample. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), the pink line to the data to simulation ratio using the alternative QCD multijet sample, and the vertical black lines correspond to the statistical uncertainty of the data. The vertical pink lines correspond to the statistical uncertainty of the alternative QCD multijet sample. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
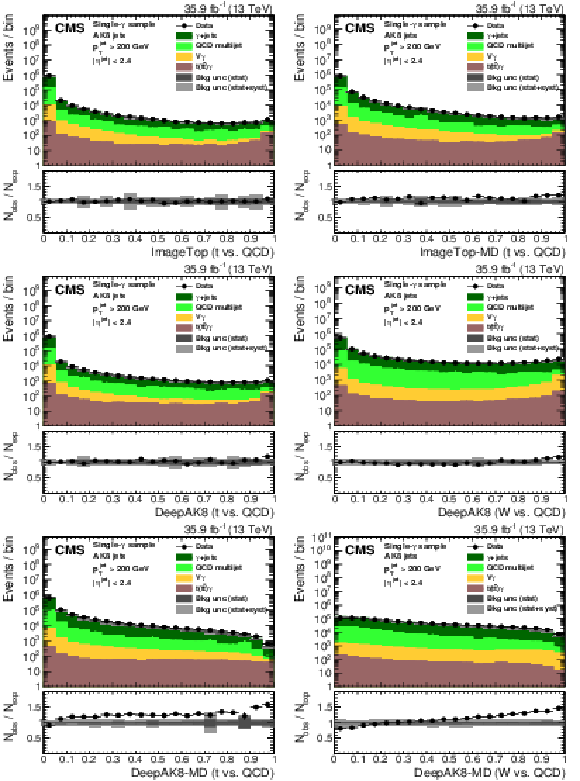
png pdf |
Figure 39:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
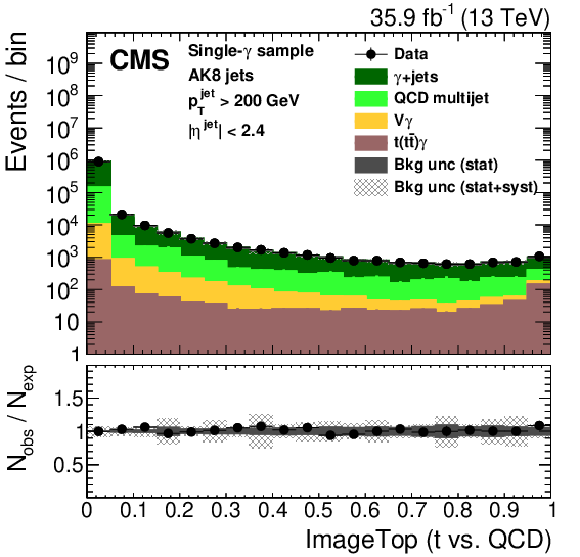
png pdf |
Figure 39-a:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
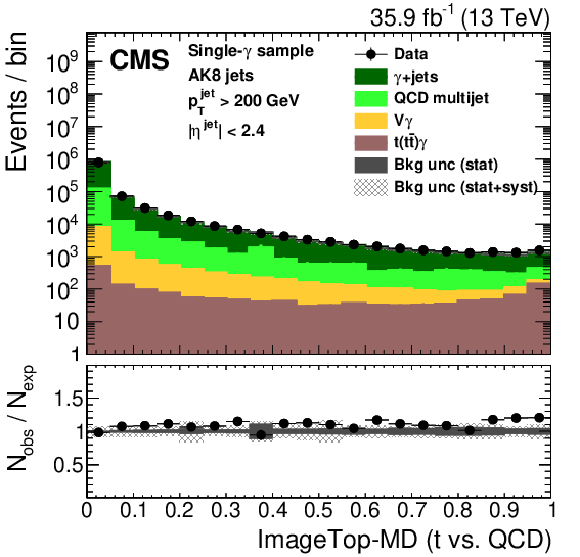
png pdf |
Figure 39-b:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
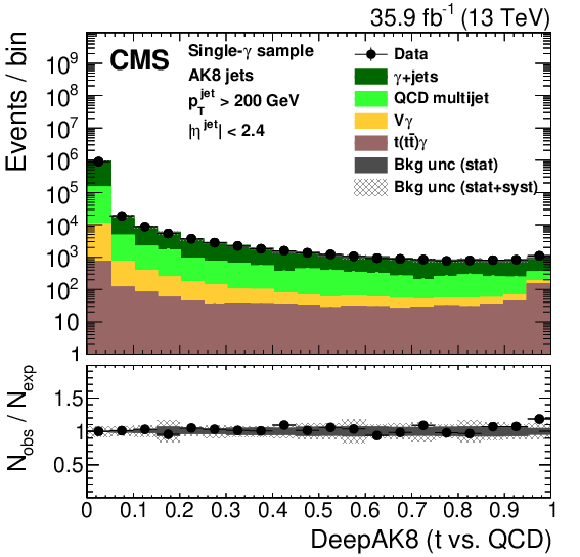
png pdf |
Figure 39-c:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 39-d:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
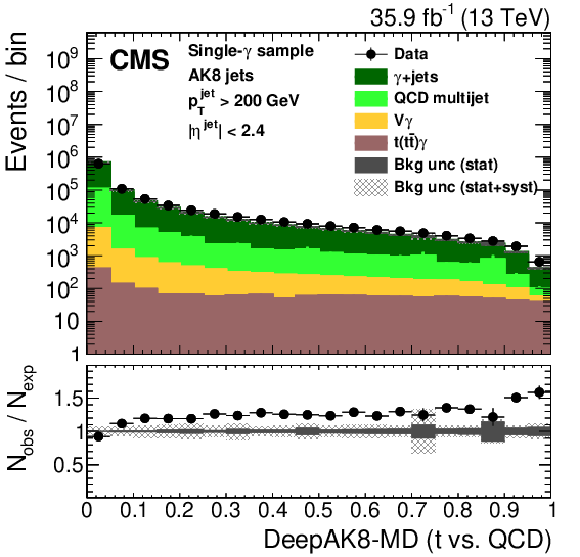
png pdf |
Figure 39-e:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |

png pdf |
Figure 39-f:
Distribution of the ImageTop (upper left) and ImageTop-MD (upper right) discriminant in data and simulation in the single-$\gamma $ sample. The plots in the middle row show the t quark (left) and W boson (right) identification probabilities in data and simulation for the DeepAK8 algorithm. The corresponding plots for DeepAK8-MD are displayed in the lower row. The background event yield is normalized to the total observed data yield. The lower panel shows the data to simulation ratio. The solid dark-gray (shaded light-gray) band corresponds to the total uncertainty (statistical uncertainty of the simulated samples), and the vertical lines correspond to the statistical uncertainty of the data. The distributions are weighted so that the jet ${p_{\mathrm {T}}}$ distribution of the simulation matches the data. |
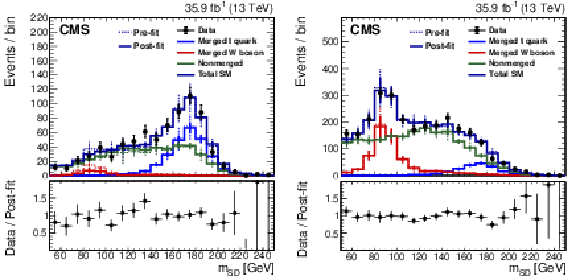
png pdf |
Figure 40:
The ${m_{\text {SD}}}$ distribution in data and simulation in the passing (left) and failing (right) categories for DeepAK8-MD for the jet ${p_{\mathrm {T}}}$ in the 400-800 GeV range. The solid lines correspond to the contribution of each category after performing the maximum likelihood fit as described in the text. The dashed lines are the expectation from simulation before the fit. The lower panel shows the data to simulation ratio. The vertical black lines correspond to the total uncertainty, including the statistical uncertainty of the data, after the fit. |
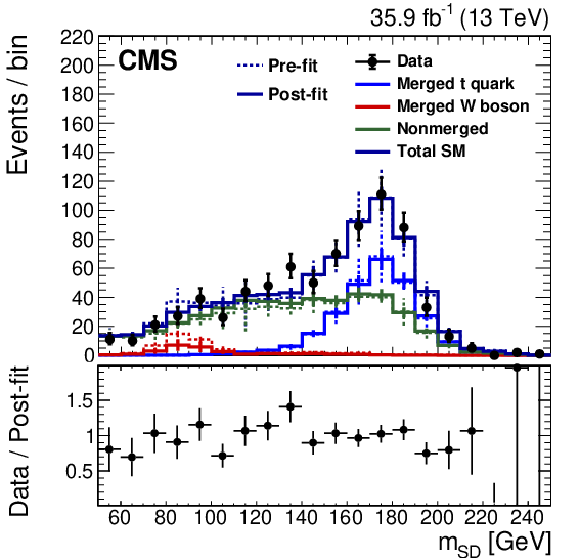
png pdf |
Figure 40-a:
The ${m_{\text {SD}}}$ distribution in data and simulation in the passing (left) and failing (right) categories for DeepAK8-MD for the jet ${p_{\mathrm {T}}}$ in the 400-800 GeV range. The solid lines correspond to the contribution of each category after performing the maximum likelihood fit as described in the text. The dashed lines are the expectation from simulation before the fit. The lower panel shows the data to simulation ratio. The vertical black lines correspond to the total uncertainty, including the statistical uncertainty of the data, after the fit. |

png pdf |
Figure 40-b:
The ${m_{\text {SD}}}$ distribution in data and simulation in the passing (left) and failing (right) categories for DeepAK8-MD for the jet ${p_{\mathrm {T}}}$ in the 400-800 GeV range. The solid lines correspond to the contribution of each category after performing the maximum likelihood fit as described in the text. The dashed lines are the expectation from simulation before the fit. The lower panel shows the data to simulation ratio. The vertical black lines correspond to the total uncertainty, including the statistical uncertainty of the data, after the fit. |
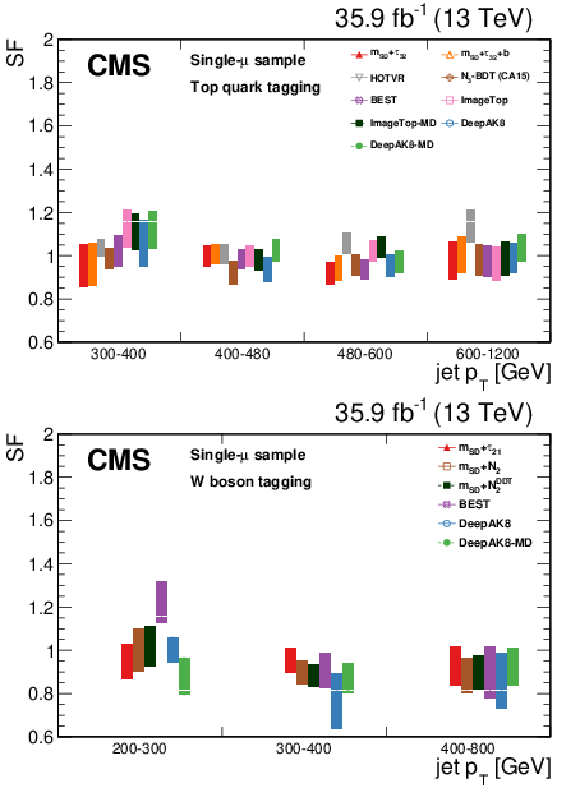
png pdf |
Figure 41:
Summary of the scale factors (SF) measured for each of the t quark (upper) and W boson (lower) identification algorithms. The markers correspond to the SF value, the error bars to the statistical uncertainty on the SF measurement, and the band is the total uncertainty, including the systematic component. |
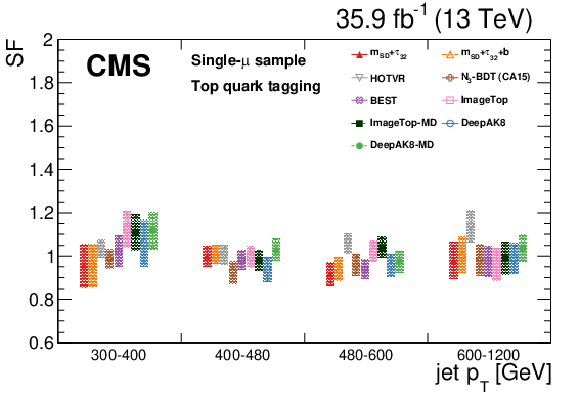
png pdf |
Figure 41-a:
Summary of the scale factors (SF) measured for each of the t quark (upper) and W boson (lower) identification algorithms. The markers correspond to the SF value, the error bars to the statistical uncertainty on the SF measurement, and the band is the total uncertainty, including the systematic component. |

png pdf |
Figure 41-b:
Summary of the scale factors (SF) measured for each of the t quark (upper) and W boson (lower) identification algorithms. The markers correspond to the SF value, the error bars to the statistical uncertainty on the SF measurement, and the band is the total uncertainty, including the systematic component. |
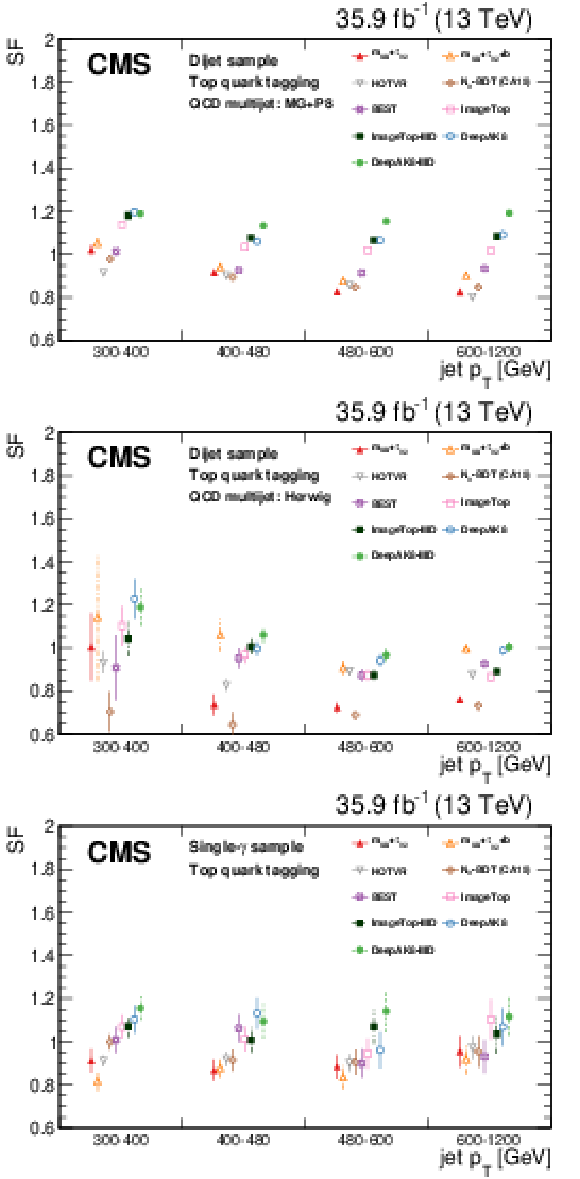
png pdf |
Figure 42:
The ratio of the misidentification rate of t quarks in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
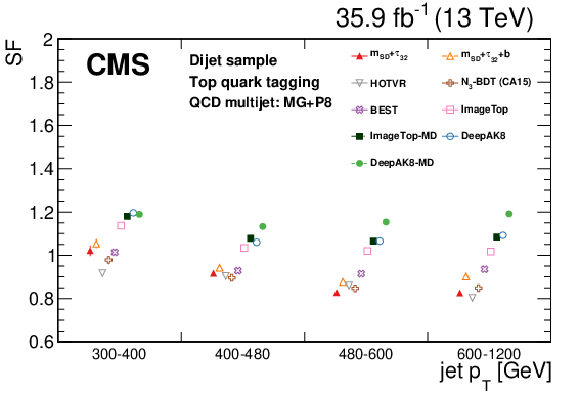
png pdf |
Figure 42-a:
The ratio of the misidentification rate of t quarks in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |

png pdf |
Figure 42-b:
The ratio of the misidentification rate of t quarks in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
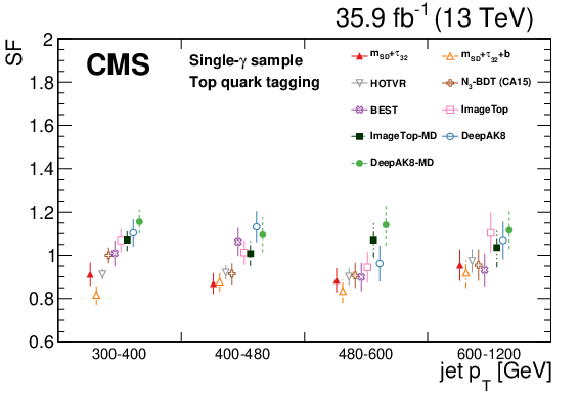
png pdf |
Figure 42-c:
The ratio of the misidentification rate of t quarks in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
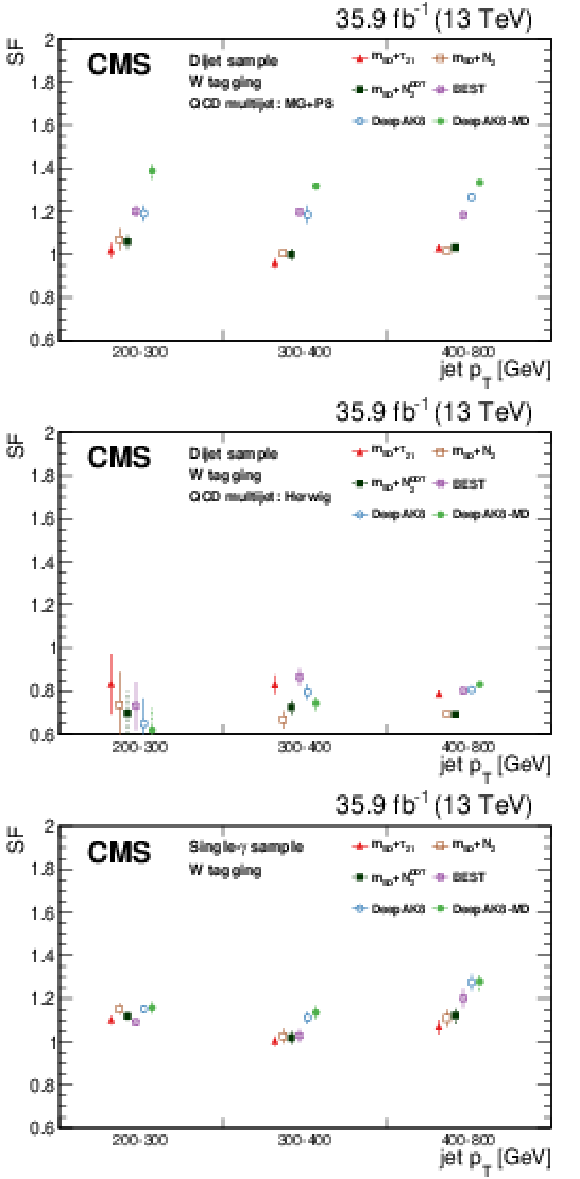
png pdf |
Figure 43:
The ratio of the misidentification rate of W bosons in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |

png pdf |
Figure 43-a:
The ratio of the misidentification rate of W bosons in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
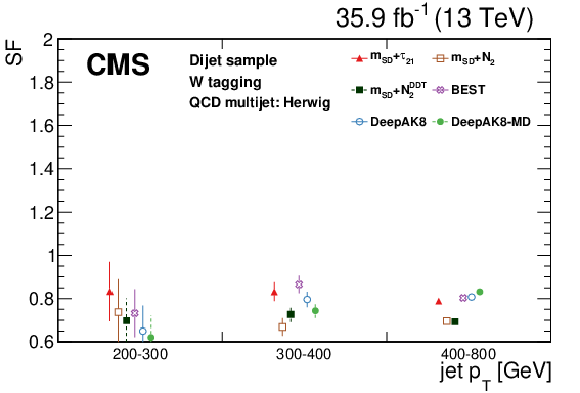
png pdf |
Figure 43-b:
The ratio of the misidentification rate of W bosons in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
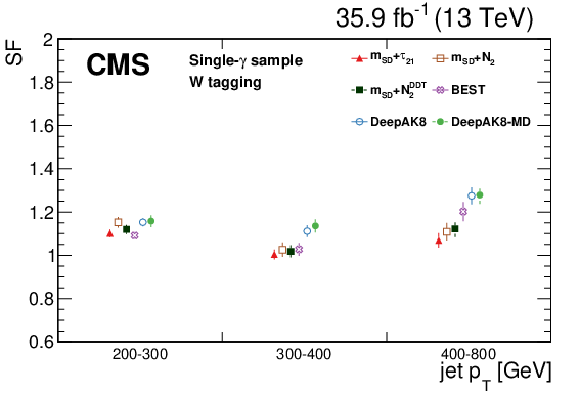
png pdf |
Figure 43-c:
The ratio of the misidentification rate of W bosons in data and simulation in the dijet (upper and middle rows) and the single-$\gamma $ (lower row) samples. The QCD multijet process is simulated using MadGraph for the hard process and {pythia} for parton showering (upper) and {herwig++} for both (middle). The vertical lines correspond to the statistical uncertainty of the data and the simulated samples. |
| Tables | |
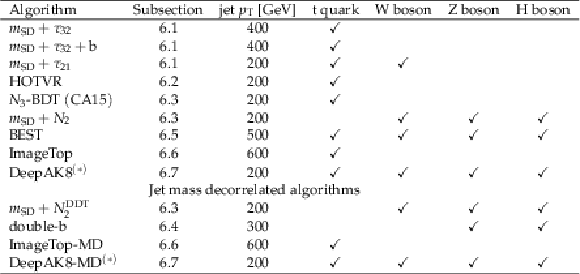
png pdf |
Table 1:
Summary of the CMS algorithms for the identification of hadronically decaying t quarks and W, Z and H bosons. See text for explanation of the algorithm names. The column "Subsection'' indicates the subsection where the algorithm is described, and the column "jet ${p_{\mathrm {T}}}$ [GeV]'' indicates the jet ${p_{\mathrm {T}}}$ threshold to be used in each algorithm. The $^{*}$ in DeepAK8 and DeepAK8-MD algorithms indicates the ability of these algorithm to also identify the decay modes of each particle. |
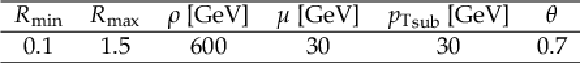
png pdf |
Table 2:
Summary of the HOTVR parameters used in CMS. The $ {p_{\mathrm {T}}} {}_{\text {sub}}$ is the minimum ${p_{\mathrm {T}}}$ threshold of each subjet. |

png pdf |
Table 3:
List of input quantities used for the training and evaluation of the BEST algorithm on AK8 jets. |
| Summary |
|
A review of the heavy-object tagging methods recently developed in CMS has been presented. The variety of tagging strategies is diverse, including algorithms based on more traditional theory-inspired high-level per-jet observables with and without multivariate techniques, as well as methods based on lower-level information from individual particles. New tagging approaches, such as the Energy Correlation Functions (ECF) tagger and the Boosted Event Shape Tagger (BEST), utilize multivariate methods (i.e., boosted decision trees and deep neural networks) on physically motivated high-level observables and attain enhanced performance. Two novel tagging algorithms, ImageTop and DeepAK8, are developed based on candidate-level information, allowing the exploitation of more information, where lower-level information is processed using advanced machine-learning methods. Moreover, the BEST and DeepAK8 algorithms are developed to provide multi-class tagging capabilities. Finally, dedicated versions of the algorithms that are only weakly correlated with the jet mass are developed. Such tools are particularly important for analyses that rely on the jet mass sidebands to estimate the background contribution under the heavy resonance mass. The mass-decorrelated algorithms (${m_\text{SD}+N_{2}^{\text{DDT}}}$, ImageTop-MD, and DeepAK8-MD) typically show weaker discriminating power than their counterparts. However, they can yield better sensitivity in some physics analyses because of smaller uncertainties in background estimations. The performances of the various tagging algorithms are directly compared using simulation in a jet ${p_{\mathrm{T}}}$ range from 200 to 2000 GeV. Overall, the application of machine-learning techniques for jet tagging shows strong improvement compared to cutoff-based methods. The approaches based on low-level information yield the best performance, with as much as an order of magnitude gain in background rejection for the same signal efficiency. Another important aspect essential for the application of the new techniques in physics analysis is the systematic uncertainties associated to each algorithm. Those based on low-level features and advanced machine-learning techniques are typically prone to larger systematic uncertainties. However, these uncertainties are usually small enough to preserve the significant improvements observed. The techniques have also been validated in collision data, with scale factors extracted, including systematic uncertainties. The performances of these tagging algorithms are in good agreement between data and simulation. |
| References | ||||
| 1 | L. Evans and P. Bryant (editors) | LHC machine | JINST 3 (2008) S08001 | |
| 2 | R. Kogler et al. | Jet substructure at the Large Hadron Collider : Experimental review | Rev. Mod. Phys. (2018) | 1803.06991 |
| 3 | A. J. Larkoski, I. Moult, and B. Nachman | Jet substructure at the Large Hadron Collider: a review of recent advances in theory and machine learning | PR (2017) | 1709.04464 |
| 4 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 5 | CMS Collaboration | Measurement of the integrated and differential $ \text{t}\bar{\text{t}} $ production cross sections for high-$ p_t $ top quarks in pp collisions at $ \sqrt s = $ 8 TeV | PRD 94 (2016) 072002 | CMS-TOP-14-012 1605.00116 |
| 6 | CMS Collaboration | Measurement of the jet mass in highly boosted $ {\mathrm{t}}\overline{\mathrm{t}} $ events from pp collisions at $ \sqrt{s}= $ 8 TeV | EPJC 77 (2017) 467 | CMS-TOP-15-015 1703.06330 |
| 7 | CMS Collaboration | Studies of jet mass in dijet and W/Z + jet events | JHEP 05 (2013) 090 | CMS-SMP-12-019 1303.4811 |
| 8 | CMS Collaboration | Measurements of the differential jet cross section as a function of the jet mass in dijet events from proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 11 (2018) 113 | CMS-SMP-16-010 1807.05974 |
| 9 | CMS Collaboration | Measurement of jet substructure observables in $ \mathrm{t\overline{t}} $ events from proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 98 (2018) 092014 | CMS-TOP-17-013 1808.07340 |
| 10 | ATLAS Collaboration | Jet mass and substructure of inclusive jets in $ \sqrt{s}= $ 7 TeV pp collisions with the ATLAS experiment | JHEP 05 (2012) 128 | 1203.4606 |
| 11 | ATLAS Collaboration | Measurement of the soft-drop jet mass in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PRL 121 (2018) 092001 | 1711.08341 |
| 12 | ATLAS Collaboration | Measurement of the cross-section of high transverse momentum vector bosons reconstructed as single jets and studies of jet substructure in pp collisions at $ {\sqrt{s}} = $ 7 TeV with the ATLAS detector | New J. Phys. 16 (2014) 113013 | 1407.0800 |
| 13 | ATLAS Collaboration | Measurements of $ t\bar{t} $ differential cross-sections of highly boosted top quarks decaying to all-hadronic final states in pp collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | PRD 98 (2018) 012003 | 1801.02052 |
| 14 | ATLAS Collaboration | Measurement of jet-substructure observables in top quark, $ W $ boson and light jet production in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | JHEP 08 (2019) 033 | 1903.02942 |
| 15 | J. Dolen et al. | Thinking outside the ROCs: designing decorrelated taggers (DDT) for jet substructure | JHEP 05 (2016) 156 | 1603.00027 |
| 16 | CMS Collaboration | Boosted top jet tagging at CMS | CMS-PAS-JME-13-007 | CMS-PAS-JME-13-007 |
| 17 | CMS Collaboration | Top tagging with new approaches | CMS-PAS-JME-15-002 | CMS-PAS-JME-15-002 |
| 18 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | CMS-PAS-JME-16-003 |
| 19 | CMS Collaboration | Identification techniques for highly boosted W bosons that decay into hadrons | JHEP 12 (2014) 017 | CMS-JME-13-006 1410.4227 |
| 20 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 21 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 22 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 23 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 24 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 25 | L. Randall and R. Sundrum | A large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | hep-ph/9905221 |
| 26 | L. Randall and R. Sundrum | An alternative to compactification | PRL 83 (1999) 4690 | hep-th/9906064 |
| 27 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 28 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A brief introduction to PYTHIA 8.1 | CPC 178 (2008) 852 | 0710.3820 |
| 29 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 30 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 31 | R. D. Ball et al. | Parton distributions with LHC data | NPB 867 (2013) 244 | 1207.1303 |
| 32 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 33 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 34 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 35 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 36 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 37 | M. Bahr et al. | Herwig++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 38 | J. Bellm et al. | Herwig++ 2.7 release note | 1310.6877 | |
| 39 | M. H. Seymour and A. Siodmok | Constraining MPI models using $ \sigma_{eff} $ and recent Tevatron and LHC underlying event data | JHEP 10 (2013) 113 | 1307.5015 |
| 40 | CMS Collaboration | Measurement of differential cross sections for top quark pair production using the $ \text{lepton}+\text{jets} $ final state in proton-proton collisions at 13 TeV | PRD 95 (2017) 092001 | CMS-TOP-16-008 1610.04191 |
| 41 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 42 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 43 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_\text{T} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 44 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 45 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 46 | CMS Collaboration | Pileup removal algorithms | CMS-PAS-JME-14-001 | CMS-PAS-JME-14-001 |
| 47 | Y. L. Dokshitzer, G. D. Leder, S. Moretti, and B. R. Webber | Better jet clustering algorithms | JHEP 08 (1997) 001 | hep-ph/9707323 |
| 48 | M. Wobisch and T. Wengler | Hadronization corrections to jet cross-sections in deep inelastic scattering | in Proceedings of the Workshop on Monte Carlo Generators for HERA Physics, Hamburg, Germany, p. 270 1998 | hep-ph/9907280 |
| 49 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 50 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | Submitted to JINST | CMS-JME-18-001 2003.00503 |
| 51 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 52 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019), no. 07, P07004 | CMS-JME-17-001 1903.06078 |
| 53 | CMS Collaboration | Searches for new physics using the t$ \bar{\text{t}} $ invariant mass distribution in pp collisions at $ \sqrt{s} = $ 8 TeV | PRL 111 (2013) 211804 | CMS-B2G-13-001 1309.2030 |
| 54 | CMS Collaboration | Search for resonant t$ \bar{\text{t}} $ production in proton-proton collisions at $ \sqrt s= $ 8 TeV | PRD 93 (2016) 012001 | CMS-B2G-13-008 1506.03062 |
| 55 | CMS Collaboration | Search for $ \mathrm{t}\overline{\mathrm{t}} $ resonances in highly boosted lepton+jets and fully hadronic final states in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2017) 001 | CMS-B2G-16-015 1704.03366 |
| 56 | CMS Collaboration | Search for resonant $ \mathrm{t}\overline{\mathrm{t}} $ production in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 04 (2019) 031 | CMS-B2G-17-017 1810.05905 |
| 57 | J. Chen, T. Han, and B. Tweedie | Electroweak splitting functions and high energy showering | JHEP 11 (2017) 093 | 1611.00788 |
| 58 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 59 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 60 | C. Frye, A. J. Larkoski, M. D. Schwartz, and K. Yan | Factorization for groomed jet substructure beyond the next-to-leading logarithm | JHEP 07 (2016) 064 | 1603.09338 |
| 61 | S. Marzani, L. Schunk, and G. Soyez | A study of jet mass distributions with grooming | JHEP 07 (2017) 132 | 1704.02210 |
| 62 | J. Thaler and K. Van Tilburg | Identifying boosted objects with $ N $-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 63 | J. Thaler and K. Van Tilburg | Maximizing boosted top identification by minimizing $ N $-subjettiness | JHEP 02 (2012) 093 | 1108.2701 |
| 64 | S. Catani, Y. L. Dokshitzer, M. H. Seymour, and B. R. Webber | Longitudinally invariant $ k_\perp $ clustering algorithms for hadron hadron collisions | NPB 406 (1993) 187 | |
| 65 | S. D. Ellis and D. E. Soper | Successive combination jet algorithm for hadron collisions | PRD 48 (1993) 3160 | hep-ph/9305266 |
| 66 | CMS Collaboration | A multi-dimensional search for new heavy resonances decaying to boosted WW, WZ, or ZZ boson pairs in the dijet final state at 13 TeV | Submitted to EPJC | CMS-B2G-18-002 1906.05977 |
| 67 | CMS Collaboration | Search for heavy resonances that decay into a vector boson and a Higgs boson in hadronic final states at $ \sqrt{s} = $ 13 TeV | EPJC 77 (2017) 636 | CMS-B2G-17-002 1707.01303 |
| 68 | CMS Collaboration | Search for vector-like T and B quark pairs in final states with leptons at $ \sqrt{s} = $ 13 TeV | JHEP 08 (2018) 177 | CMS-B2G-17-011 1805.04758 |
| 69 | CMS Collaboration | Search for pair production of vector-like quarks in the fully hadronic final state | Submitted to PRD | CMS-B2G-18-005 1906.11903 |
| 70 | CMS Collaboration | Search for a W$ ^\prime $ boson decaying to a vector-like quark and a top or bottom quark in the all-jets final state | JHEP 03 (2019) 127 | CMS-B2G-18-001 1811.07010 |
| 71 | CMS Collaboration | Search for a heavy resonance decaying to a top quark and a vector-like top quark in the lepton+jets final state in pp collisions at $ \sqrt{s} = $ 13 TeV | EPJC 79 (2019) 208 | CMS-B2G-17-015 1812.06489 |
| 72 | CMS Collaboration | Searches for W' bosons decaying to a top quark and a bottom quark in proton-proton collisions at 13 TeV | JHEP 08 (2017) 029 | CMS-B2G-16-016 1706.04260 |
| 73 | T. Lapsien, R. Kogler, and J. Haller | A new tagger for hadronically decaying heavy particles at the LHC | EPJC 76 (2016) 600 | 1606.04961 |
| 74 | I. Moult, L. Necib, and J. Thaler | New angles on energy correlation functions | JHEP 12 (2016) 153 | 1609.07483 |
| 75 | T. Plehn, G. P. Salam, and M. Spannowsky | Fat jets for a light Higgs | PRL 104 (2010) 111801 | 0910.5472 |
| 76 | T. Plehn, M. Spannowsky, M. Takeuchi, and D. Zerwas | Stop reconstruction with tagged tops | JHEP 10 (2010) 078 | 1006.2833 |
| 77 | G. Kasieczka et al. | Resonance searches with an updated top tagger | JHEP 06 (2015) 203 | 1503.05921 |
| 78 | H. Voss, A. Hocker, J. Stelzer, and F. Tegenfeldt | TMVA, the toolkit for multivariate data analysis with ROOT | in XIth International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT), p. 40 2007 | physics/0703039 |
| 79 | CMS Collaboration | Search for dark matter in events with energetic, hadronically decaying top quarks and missing transverse momentum at $ \sqrt{s}= $ 13 TeV | JHEP 06 (2018) 027 | CMS-EXO-16-051 1801.08427 |
| 80 | CMS Collaboration | Search for low mass vector resonances decaying into quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 01 (2018) 097 | CMS-EXO-17-001 1710.00159 |
| 81 | CMS Collaboration | Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair | PRL 120 (2018) 071802 | CMS-HIG-17-010 1709.05543 |
| 82 | J. S. Conway, R. Bhaskar, R. D. Erbacher, and J. Pilot | Identification of high-momentum top quarks, Higgs bosons, and W and Z bosons using boosted event shapes | PRD 94 (2016) 094027 | 1606.06859 |
| 83 | G. C. Fox and S. Wolfram | Observables for the analysis of event shapes in $ {\text{e}}^{+}{\text{e}}^{{-}} $ annihilation and other processes | PRL 41 (1978) 1581 | |
| 84 | J. D. Bjorken and S. J. Brodsky | Statistical model for electron-positron annihilation into hadrons | PRD 1 (1970) 1416 | |
| 85 | E. Farhi | Quantum chromodynamics test for jets | PRL 39 (1977) 1587 | |
| 86 | F. Pedregosa et al. | Scikit-learn: Machine learning in Python | J. Mach. Learn. Res. 12 (2011) 2825 | 1201.0490 |
| 87 | V. Nair and G. E. Hinton | Rectified linear units improve restricted Boltzmann machines | in Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML'10, p. 807 Omnipress, USA | |
| 88 | D. P. Kingma and J. Ba | Adam: A method for stochastic optimization | in Proceedings of the 3rd International Conference on Learning Representations, ICLR'15 ICLR, USA | |
| 89 | S. Macaluso and D. Shih | Pulling out all the tops with computer vision and deep learning | JHEP 10 (2018) 121 | 1803.00107 |
| 90 | G. Kasieczka, T. Plehn, M. Russell, and T. Schell | Deep-learning top taggers or the end of QCD? | JHEP 05 (2017) 006 | 1701.08784 |
| 91 | M. Abadi et al. | TensorFlow: Large-scale machine learning on heterogeneous systems | 2015 Software available from tensorflow.org. \url http://tensorflow.org/ | |
| 92 | M. D. Zeiler | ADADELTA: an adaptive learning rate method | CoRR (2012) | 1212.5701 |
| 93 | CMS Collaboration | Performance of b tagging algorithms in proton-proton collisions at 13 TeV with phase 1 CMS detector | CDS | |
| 94 | K. He, X. Zhang, S. Ren, and J. Sun | Deep residual learning for image recognition | CoRR (2015) | 1512.03385 |
| 95 | N. Srivastava et al. | Dropout: A simple way to prevent neural networks from overfitting | J. Mach. Learn. Res 15 (2014) 1929 | |
| 96 | T. Chen et al. | Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems | in Proceedings of the 30th Conference In Neural Information Processing Systems, Workshop on Machine Learning Systems, 2016, NIPS'16 NIPS, Spain | |
| 97 | G. Louppe, M. Kagan, and K. Cranmer | Learning to pivot with adversarial networks | in Advances in Neural Information Processing Systems 30, I. Guyon et al., eds., p. 981 Curran Associates, Inc. | |
| 98 | G. Klambauer, T. Unterthiner, A. Mayr, and S. Hochreiter | Self-normalizing neural networks | in Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS'17, p. 972 Curran Associates Inc., USA | |
| 99 | CMS Collaboration | Search for production of Higgs boson pairs in the four b quark final state using large-area jets in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 01 (2019) 040 | CMS-B2G-17-019 1808.01473 |
| 100 | CMS Collaboration | Search for low-mass resonances decaying into bottom quark-antiquark pairs in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 99 (2019) 012005 | CMS-EXO-17-024 1810.11822 |
| 101 | CMS Collaboration | Search for direct production of supersymmetric partners of the top quark in the all-jets final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 10 (2017) 005 | CMS-SUS-16-049 1707.03316 |
| 102 | J. Lin | Divergence measures based on the Shannon entropy | IEEE Trans. on Inf. Th. 37 (1991) 145 | |
| 103 | S. Kullback and R. A. Leibler | On information and sufficiency | Ann. Math. Statist. 22 (1951) 79 | |
| 104 | CMS Collaboration | Search for the standard model Higgs boson decaying to charm quarks | JHEP 03 (2020) 131 | CMS-HIG-18-031 1912.01662 |
| 105 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 106 | ATLAS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s} = $ 13 TeV with the ATLAS detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 107 | CMS Collaboration | Measurements of inclusive $ W $ and $ Z $ cross sections in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|