Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-HIG-17-031 ; CERN-EP-2018-263

Combined measurements of Higgs boson couplings in proton-proton collisions at $\sqrt{s} = $ 13 TeV

CMS Collaboration

27 September 2018

Eur. Phys. J. C 79 (2019) 421

Abstract: Combined measurements of the production and decay rates of the Higgs boson, as well as its couplings to vector bosons and fermions, are presented. The analysis uses the LHC proton-proton collision data set recorded with the CMS detector in 2016 at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$ . The combination is based on analyses targeting the five main Higgs boson production mechanisms (gluon fusion, vector boson fusion, and associated production with a W or Z boson, or a top quark-antiquark pair) and the following decay modes: $\mathrm{H}\to\gamma\gamma$, $\mathrm{Z}\mathrm{Z}$, $\mathrm{W}\mathrm{W}$, $\tau\tau$, $\mathrm{b}\mathrm{b}$, and $\mu \mu $. Searches for invisible Higgs boson decays are also considered. The best-fit ratio of the signal yield to the standard model expectation is measured to be $\mu= $ 1.17 $\pm$ 0.10, assuming a Higgs boson mass of 125.09 GeV. Additional results are given for parametrizations with varying assumptions on the scaling behavior of the different production and decay modes, including generic ones based on ratios of cross sections and branching fractions or coupling modifiers. The results are compatible with the standard model predictions in all parametrizations considered. In addition, constraints are placed on various two Higgs doublet models.

Links: e-print arXiv:1809.10733 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ;

Figures
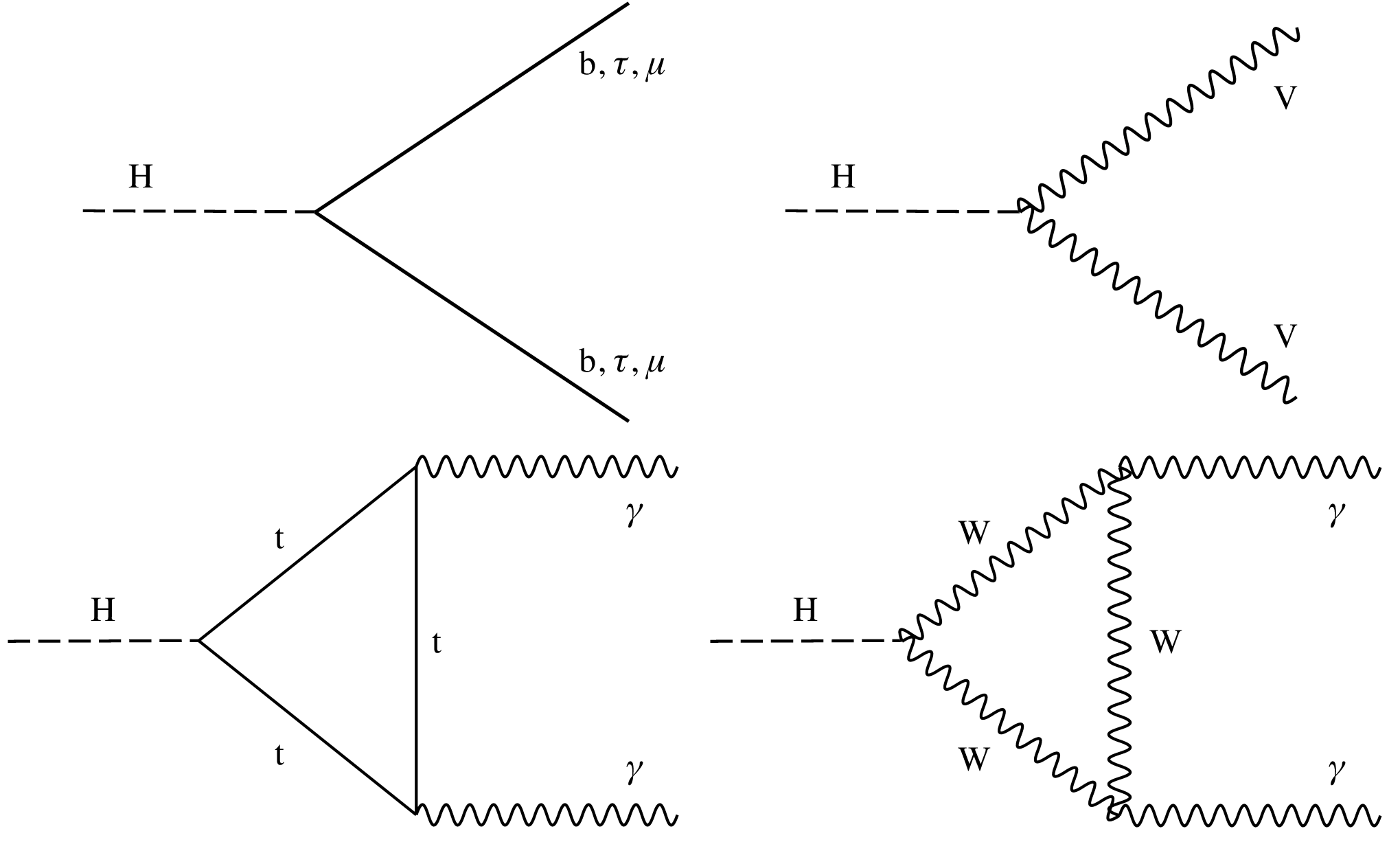
png pdf	Figure 1: Examples of leading-order Feynman diagrams for Higgs boson decays in the $\mathrm{H \to b\bar{b} }$, $\mathrm{H \to \tau\tau }$, and $\mathrm{H \to \mu\mu }$ (upper left); $\mathrm{H \to ZZ }$ and $\mathrm{H \to WW }$ (upper right); and $\mathrm{H \to \gamma\gamma }$ (lower) channels.
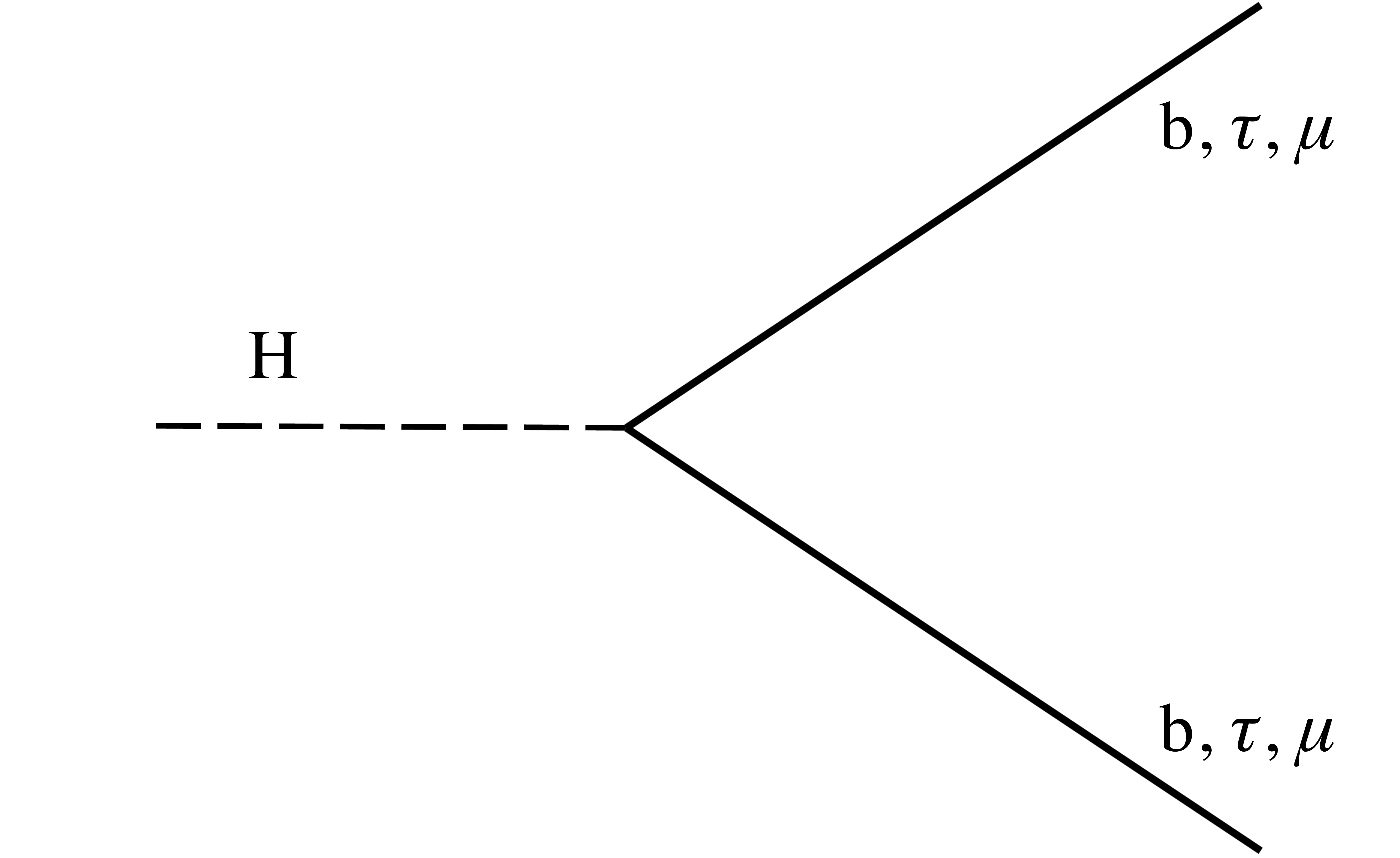
png pdf	Figure 1-a: Example of leading-order Feynman diagram for Higgs boson decays in the $\mathrm{H \to b\bar{b} }$, $\mathrm{H \to \tau\tau }$, and $\mathrm{H \to \mu\mu }$ channels.
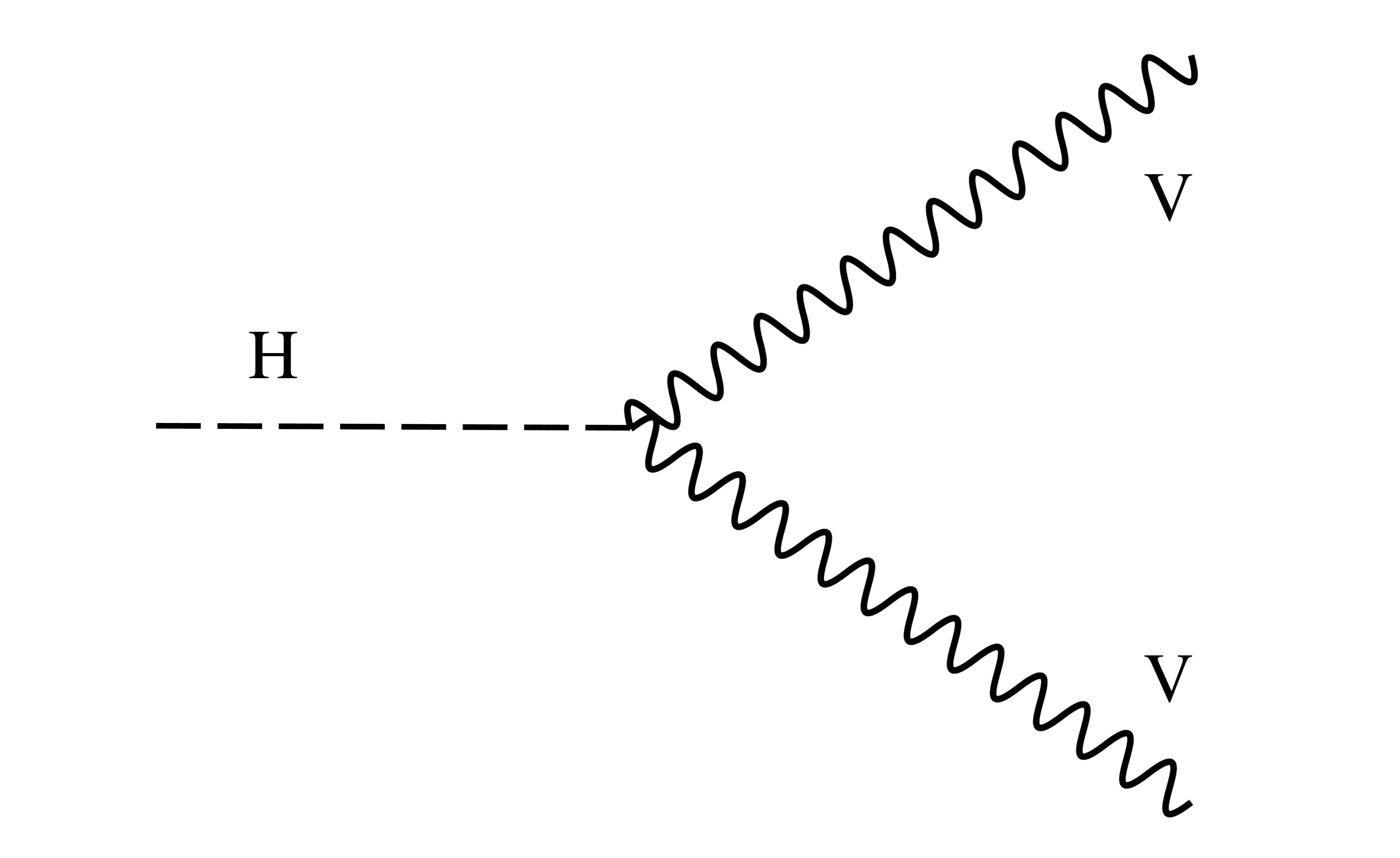
png pdf	Figure 1-b: Example of leading-order Feynman diagram for Higgs boson decays in the $\mathrm{H \to ZZ }$ and $\mathrm{H \to WW }$ channels.
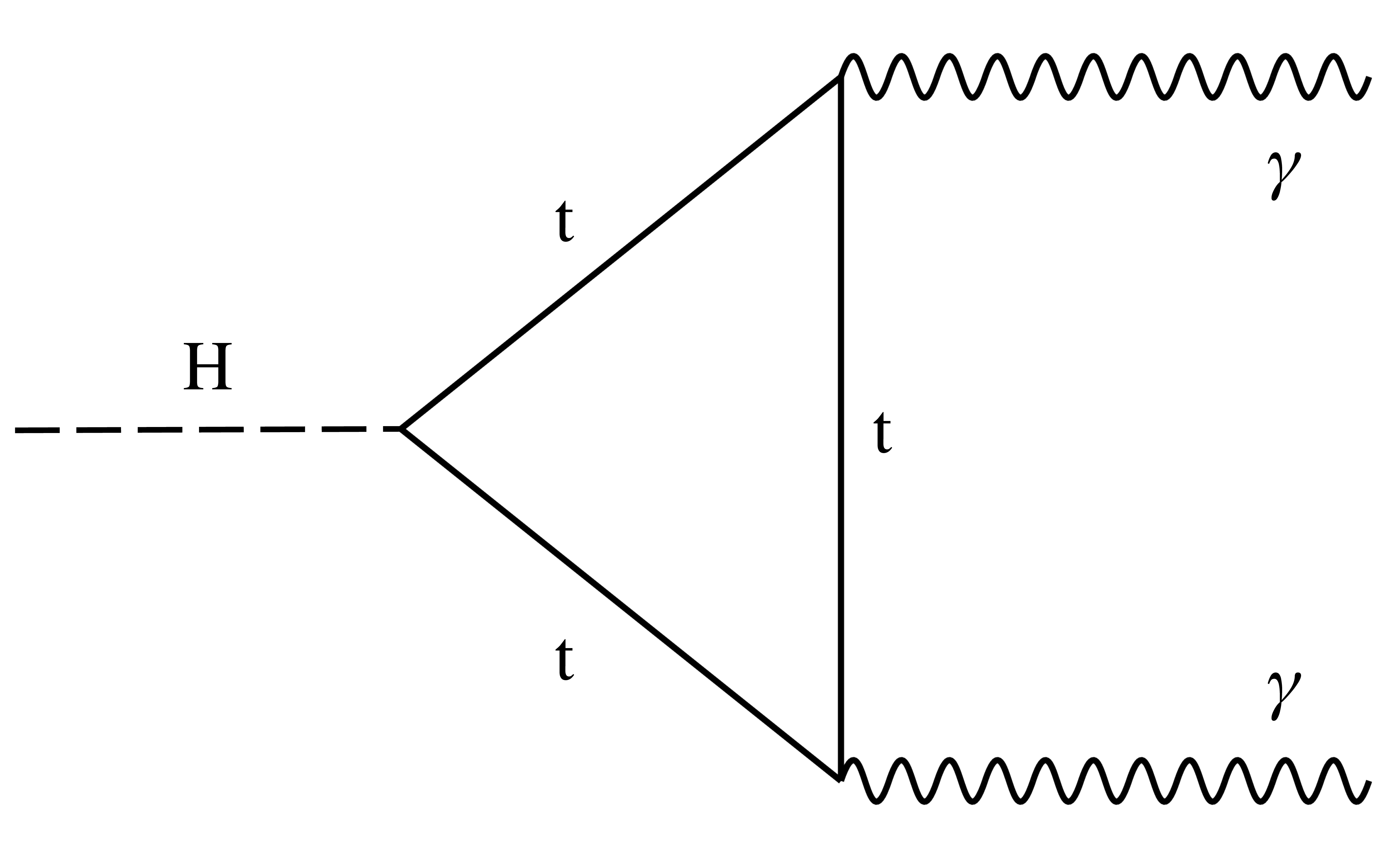
png pdf	Figure 1-c: Example of leading-order Feynman diagram for Higgs boson decays in the $\mathrm{H \to \gamma\gamma }$ channel.
png pdf	Figure 1-d: Example of leading-order Feynman diagram for Higgs boson decays in the $\mathrm{H \to \gamma\gamma }$ channel.
png pdf	Figure 2: Examples of leading-order Feynman diagrams for the ggH (upper left), VBF (upper right), VH (lower left), and ttH (lower right) production modes.
png pdf	Figure 2-a: Example of leading-order Feynman diagram for the ggH production mode.
png pdf	Figure 2-b: Example of leading-order Feynman diagram for the VBF production mode.
png pdf	Figure 2-c: Example of leading-order Feynman diagram for the VH production mode.
png pdf	Figure 2-d: Example of leading-order Feynman diagram for the ttH production mode.
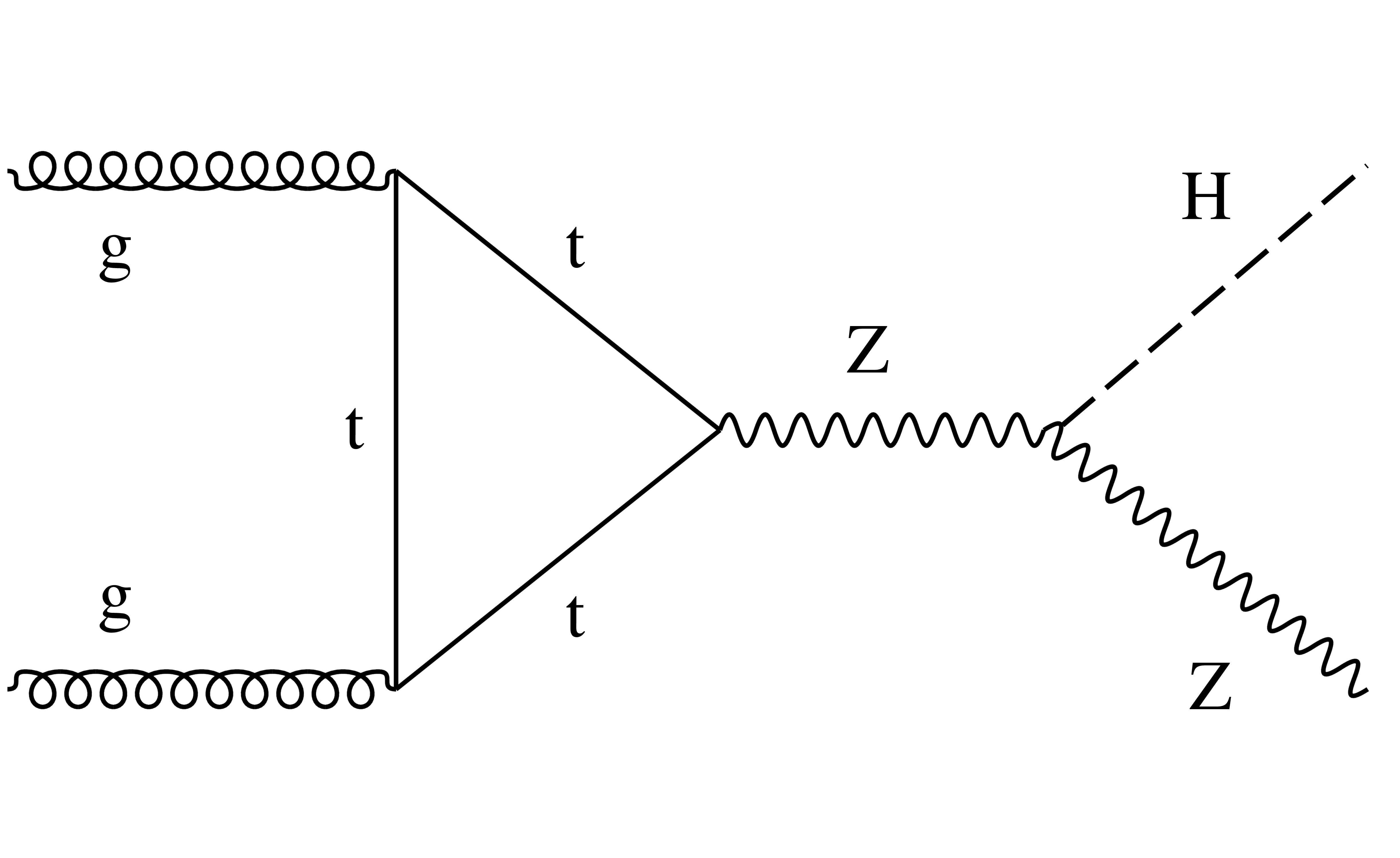
png pdf	Figure 3: Examples of leading-order Feynman diagrams for the $ {\mathrm {g}} {\mathrm {g}} \to {{\mathrm {Z}} {\mathrm {H}}} $ production mode.
png pdf	Figure 3-a: Example of leading-order Feynman diagram for the $ {\mathrm {g}} {\mathrm {g}} \to {{\mathrm {Z}} {\mathrm {H}}} $ production mode.
png pdf	Figure 3-b: Example of leading-order Feynman diagram for the $ {\mathrm {g}} {\mathrm {g}} \to {{\mathrm {Z}} {\mathrm {H}}} $ production mode.
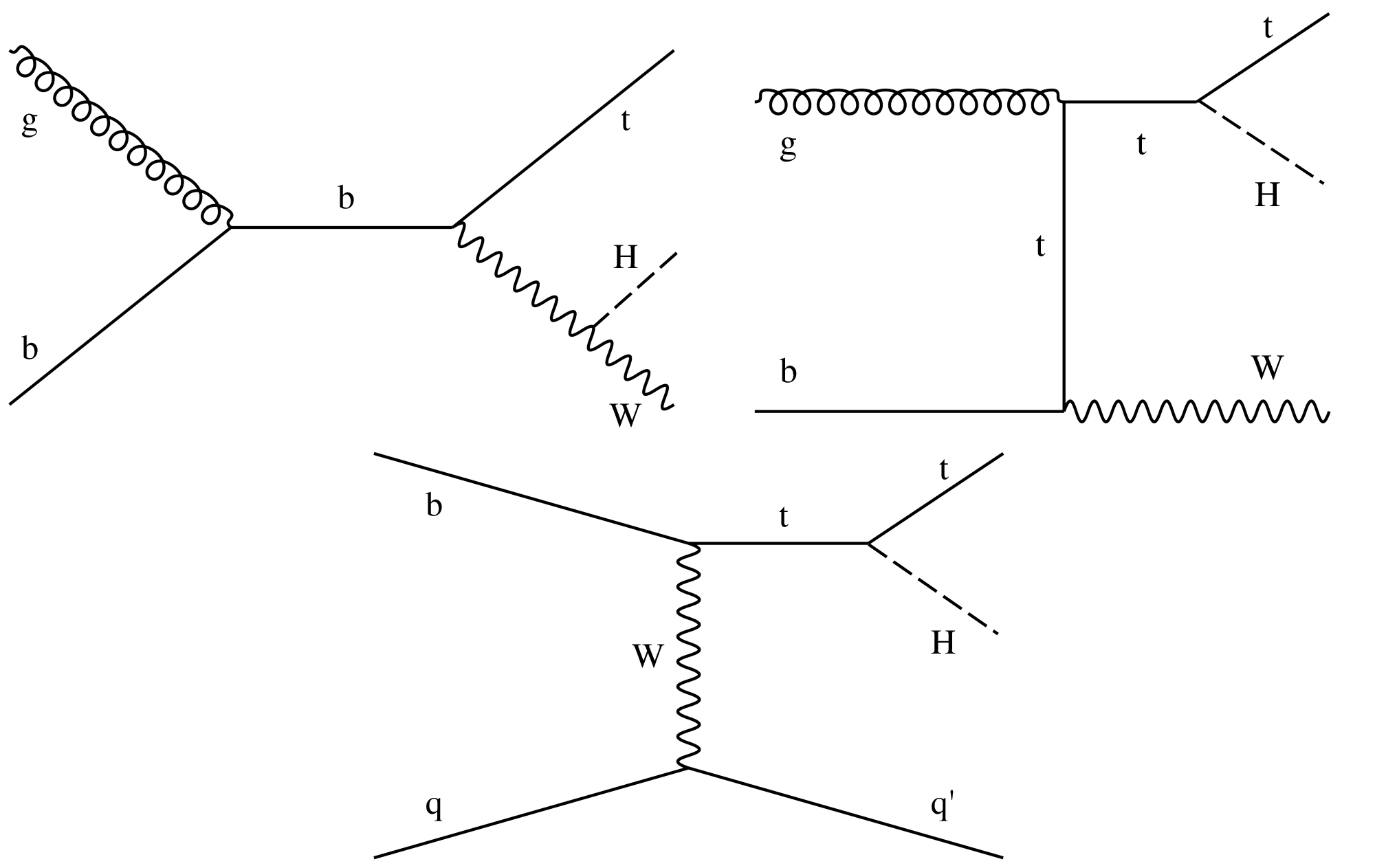
png pdf	Figure 4: Examples of leading-order Feynman diagrams for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ (upper left and right) and ${{\mathrm {t}} {\mathrm {H}} {\mathrm {q}}}$ (lower) modes.
png pdf	Figure 4-a: Example of leading-order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ mode.
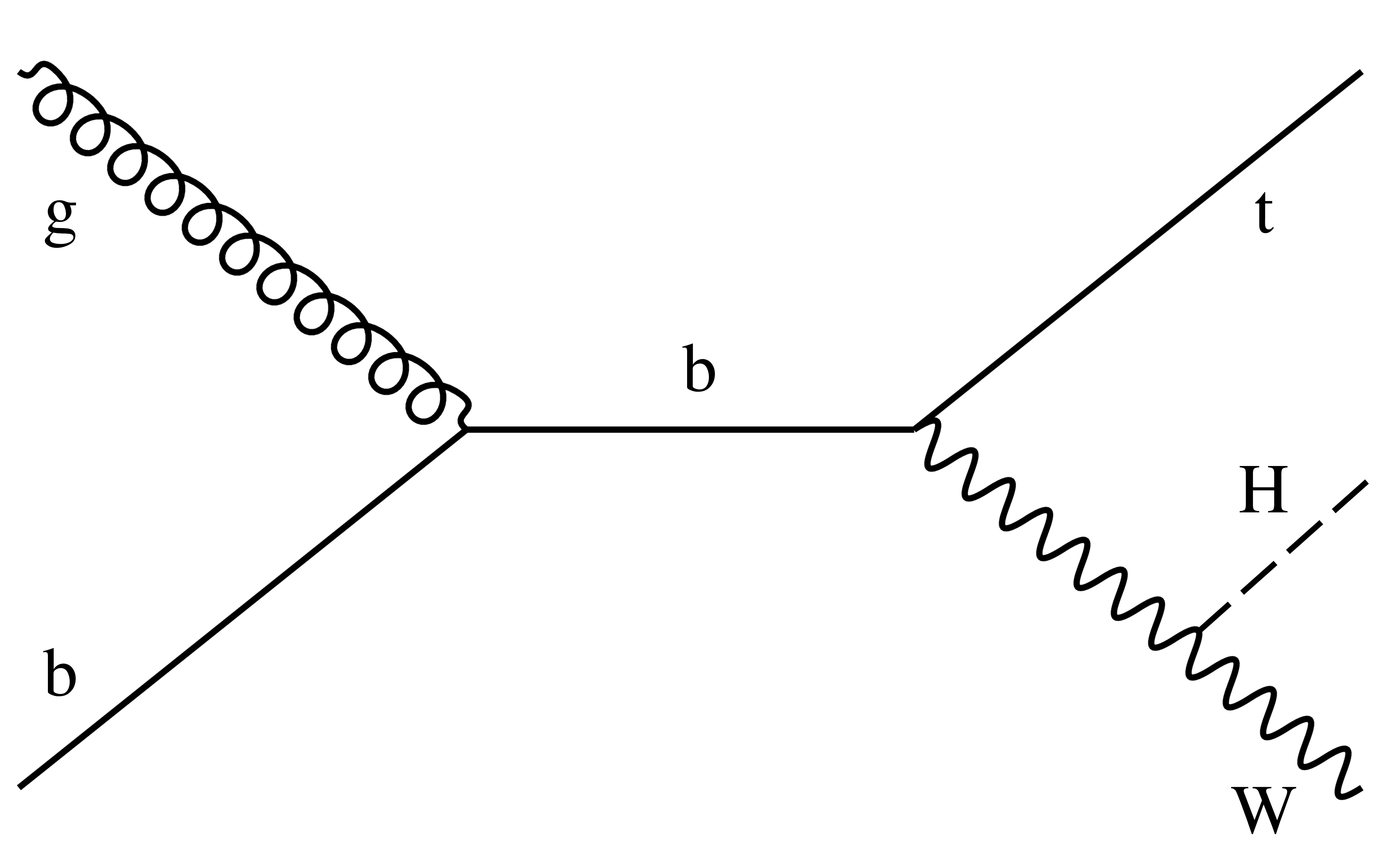
png pdf	Figure 4-b: Example of leading-order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ mode.
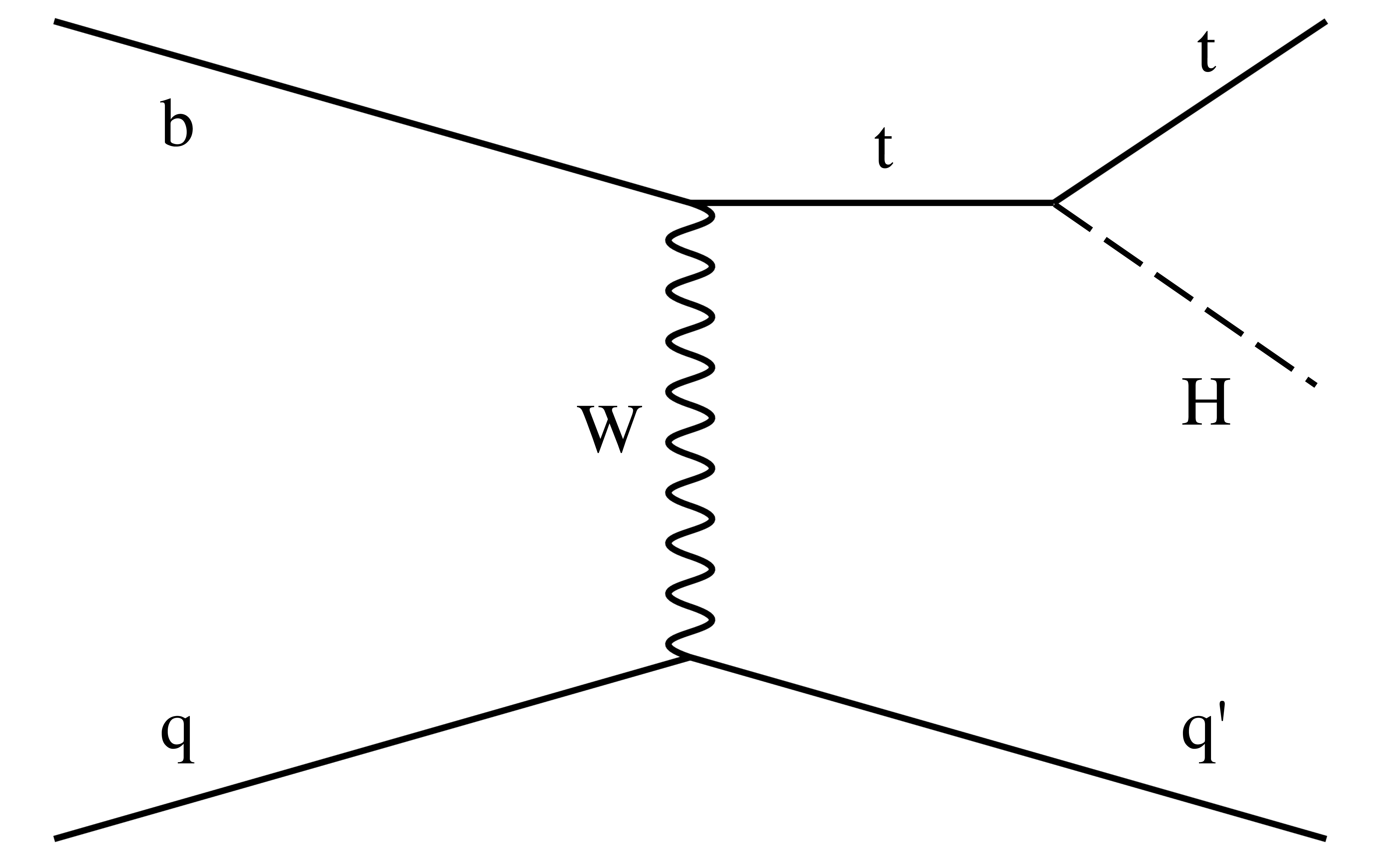
png pdf	Figure 4-c: Example of leading-order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {q}}}$ mode.
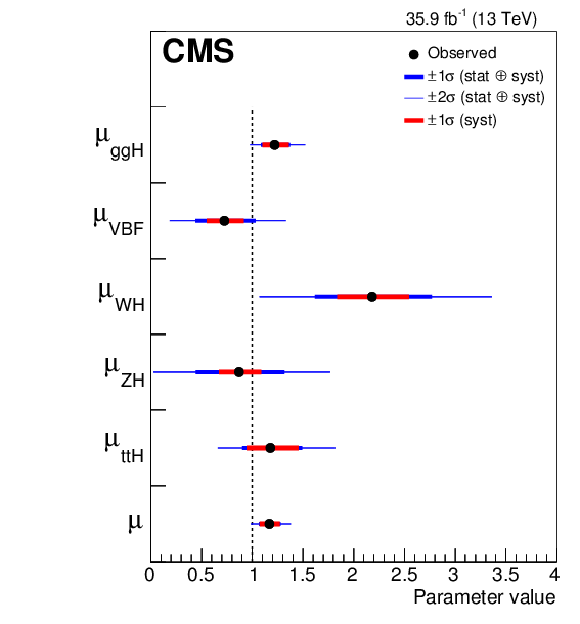
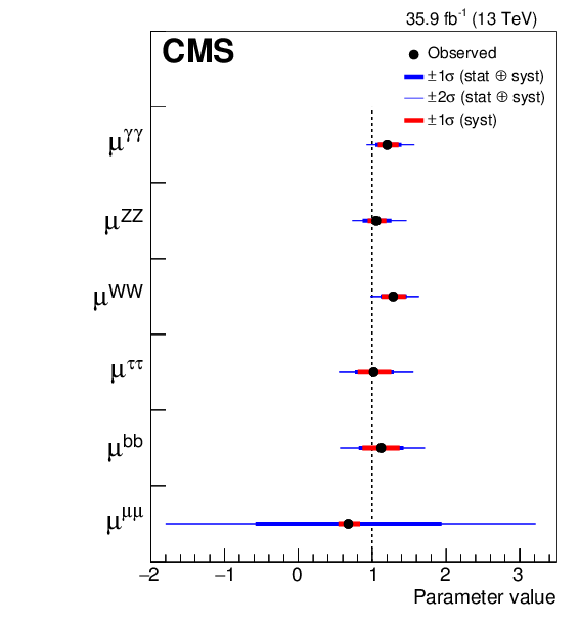
png pdf	Figure 5: Summary plot of the fit to the per-production mode (left) and per-decay mode (right) signal strength modifiers. The thick and thin horizontal bars indicate the $ {\pm} 1 \sigma $ and $ {\pm} 2 \sigma $ uncertainties, respectively. Also shown are the $ {\pm} 1 \sigma $ systematic components of the uncertainties. The last point in the per-production mode summary plot is taken from a separate fit and indicates the result of the combined overall signal strength $\mu $.
png pdf	Figure 5-a: Summary plot of the fit to the per-production mode signal strength modifiers. The thick and thin horizontal bars indicate the $ {\pm} 1 \sigma $ and $ {\pm} 2 \sigma $ uncertainties, respectively. Also shown are the $ {\pm} 1 \sigma $ systematic components of the uncertainties. The last point is taken from a separate fit and indicates the result of the combined overall signal strength $\mu $.
png pdf	Figure 5-b: Summary plot of the fit to the per-decay mode signal strength modifiers. The thick and thin horizontal bars indicate the $ {\pm} 1 \sigma $ and $ {\pm} 2 \sigma $ uncertainties, respectively. Also shown are the $ {\pm} 1 \sigma $ systematic components of the uncertainties.
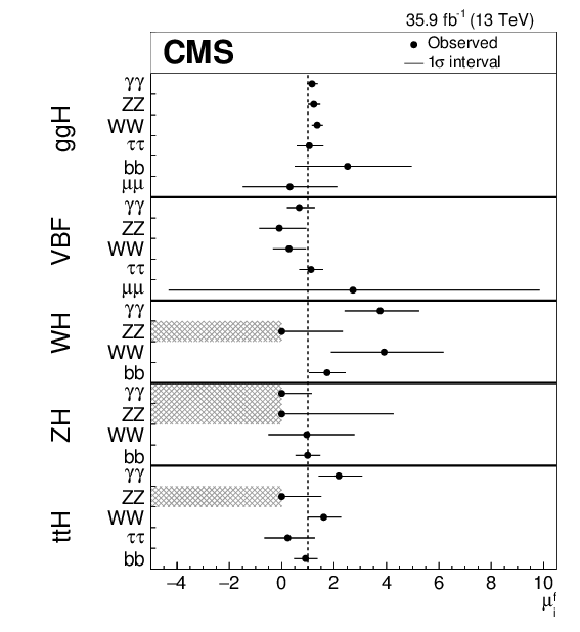
png pdf	Figure 6: Summary plot of the fit to the production-decay signal strength products $\mu _{i}^{f}=\mu _{i} \mu ^{f}$. The points indicate the best fit values while the horizontal bars indicate the $1\sigma $ CL intervals. The hatched areas indicate signal strengths that are restricted to nonnegative values as described in the text.
png pdf	Figure 7: Summary of the cross section and branching fraction ratio model. The thick and thin horizontal bars indicate the $ {\pm} 1 \sigma $ and $ {\pm} 2 \sigma $ uncertainties, respectively. Also shown are the $ {\pm} 1 \sigma $ systematic components of the uncertainties.
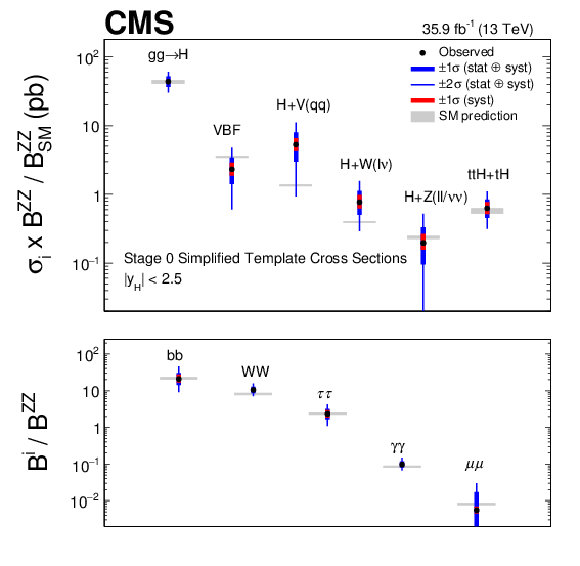
png pdf	Figure 8: Summary of the stage 0 model, ratios of cross sections and branching fractions. The points indicate the best fit values, while the error bars show the $ {\pm} 1 \sigma $ and $ {\pm} 2 \sigma $ uncertainties. The $ {\pm} 1 \sigma $ uncertainties on the measurements considering only the contributions from the systematic uncertainties are also shown. The uncertainties in the SM predictions are indicated.
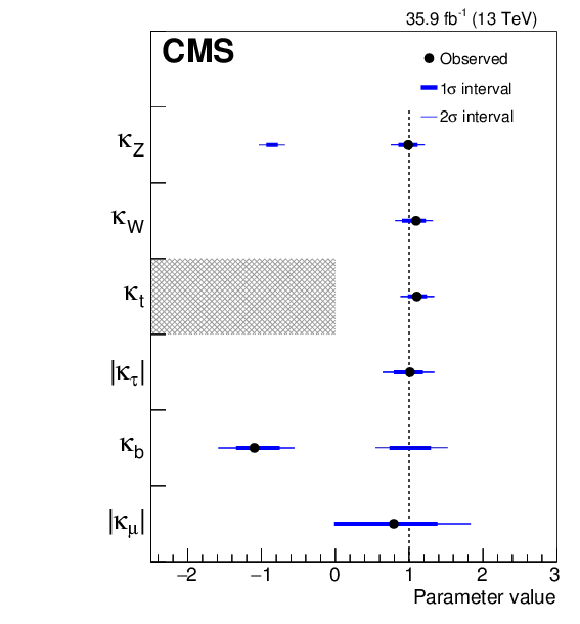
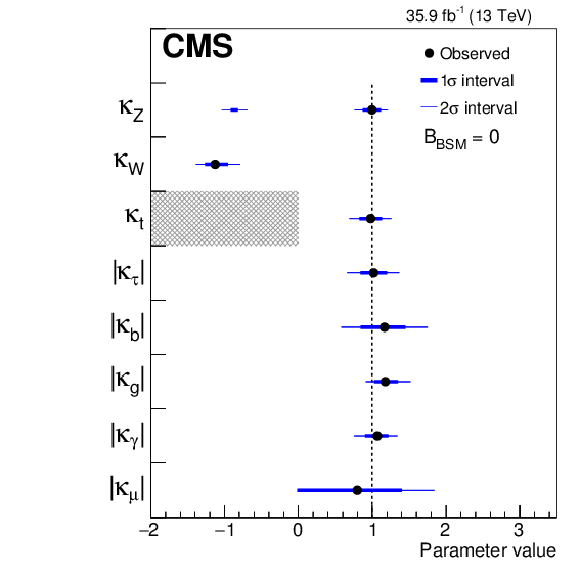
png pdf	Figure 9: Summary of the $\kappa $-framework model assuming resolved loops and $ {{\mathcal {B}} _{\mathrm {BSM}}} =$ 0. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. In this model, the ggH and ${{\mathrm {H}} \to {{\gamma} {\gamma}}}$ loops are resolved in terms of the remaining coupling modifiers. For this model, both positive and negative values of $\kappa _{{\mathrm {W}}}$, $\kappa _{{\mathrm {Z}}}$, and $\kappa _{{\mathrm {b}}}$ are considered. Negative values of $\kappa _{{\mathrm {W}}}$ in this model are disfavored by more than $2\sigma $.
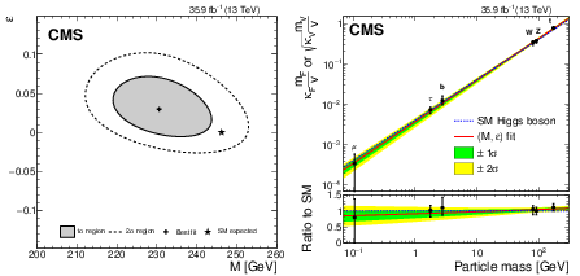
png pdf	Figure 10: Likelihood scan in the $M{\text{-}}\epsilon$ plane (left). The best fit point and the 1$\sigma$ and 2$\sigma$ CL regions are shown, along with the SM prediction. Result of the phenomenological $(M,\,\epsilon)$ fit overlayed with the resolved $\kappa$-framework model (right).
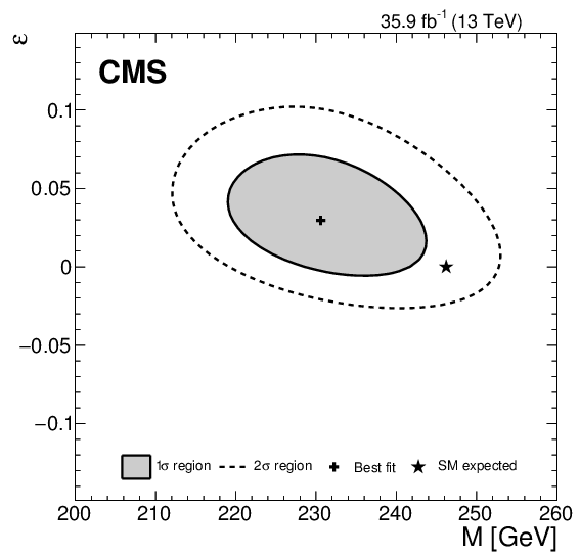
png pdf	Figure 10-a: Likelihood scan in the $M{\text{-}}\epsilon$ plane. The best fit point and the 1$\sigma$ and 2$\sigma$ CL regions are shown, along with the SM prediction.
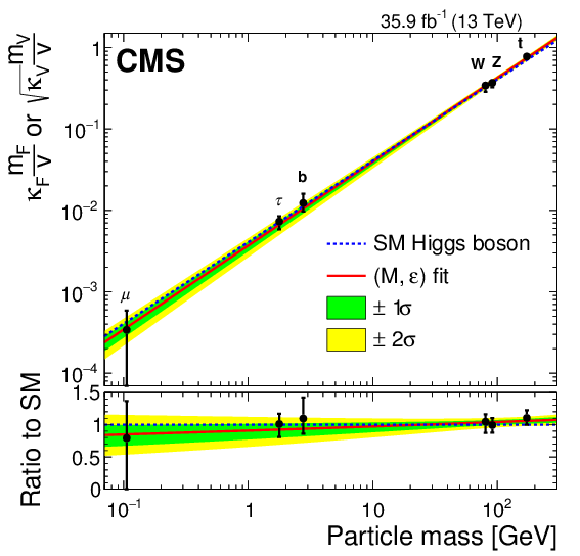
png pdf	Figure 10-b: Result of the phenomenological $(M,\,\epsilon)$ fit overlayed with the resolved $\kappa$-framework model.
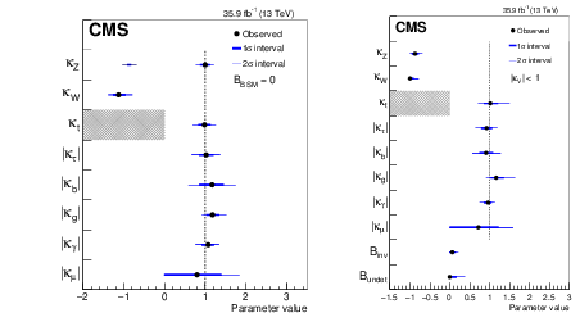
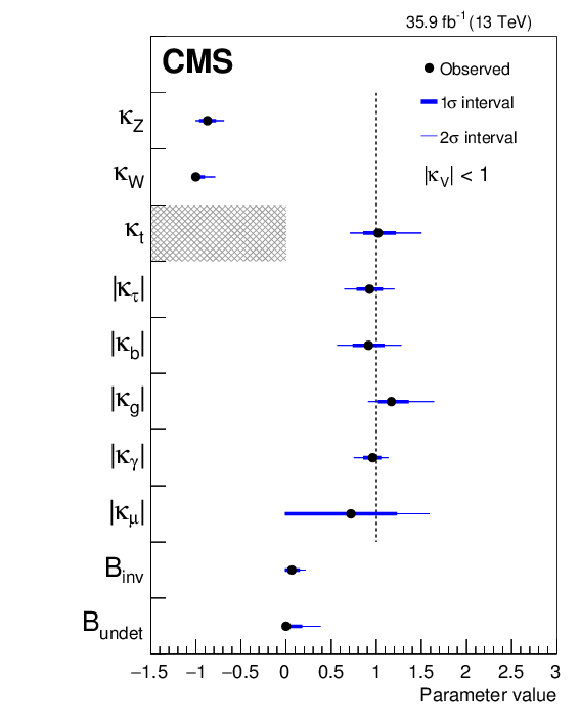
png pdf	Figure 11: Summary plots for the $\kappa $-framework model in which the ggH and ${{\mathrm {H}} \to {{\gamma} {\gamma}}}$ loops are scaled with effective couplings. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. In the left figure the constraint $ {{\mathcal {B}} _{\mathrm {BSM}}} =$ 0 is imposed, and both positive and negative values of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$ are considered. In the right figure a constraint $ {| \kappa _{{\mathrm {W}}} |},\, {| \kappa _{{\mathrm {Z}}} |}\le $ 1 is imposed (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$), while $ {{\mathcal {B}} _{\mathrm {inv}}} > $ 0 and $ {{\mathcal {B}} _{\mathrm {undet}}} > $ 0 are free parameters.
png pdf	Figure 11-a: Summary plot for the $\kappa $-framework model in which the ggH and ${{\mathrm {H}} \to {{\gamma} {\gamma}}}$ loops are scaled with effective couplings. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. In the figure the constraint $ {{\mathcal {B}} _{\mathrm {BSM}}} =$ 0 is imposed, and both positive and negative values of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$ are considered.
png pdf	Figure 11-b: Summary plot for the $\kappa $-framework model in which the ggH and ${{\mathrm {H}} \to {{\gamma} {\gamma}}}$ loops are scaled with effective couplings. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. In the figure a constraint $ {| \kappa _{{\mathrm {W}}} |},\, {| \kappa _{{\mathrm {Z}}} |}\le $ 1 is imposed (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$), while $ {{\mathcal {B}} _{\mathrm {inv}}} > $ 0 and $ {{\mathcal {B}} _{\mathrm {undet}}} > $ 0 are free parameters.
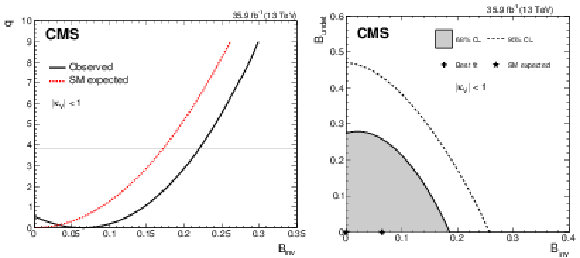
png pdf	Figure 12: Results within the generic $\kappa $-framework model with effective loops and with the constraint $ {| \kappa _{{\mathrm {W}}} |},\, {| \kappa _{{\mathrm {Z}}} |}\le $ 1 (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$), and with $ {{\mathcal {B}} _{\mathrm {inv}}} > $ 0 and $ {{\mathcal {B}} _{\mathrm {undet}}} > $ 0 as free parameters. Scan of the test statistic $q$ as a function of $ {{\mathcal {B}} _{\mathrm {inv}}} $ (left), and 68 and 95% CL regions for $ {{\mathcal {B}} _{\mathrm {inv}}} $ vs. $ {{\mathcal {B}} _{\mathrm {undet}}} $ (right). The scan of the test statistic $q$ as a function of $ {{\mathcal {B}} _{\mathrm {inv}}} $ expected assuming the SM is also shown in the left figure.
png pdf	Figure 12-a: Results within the generic $\kappa $-framework model with effective loops and with the constraint $ {| \kappa _{{\mathrm {W}}} |},\, {| \kappa _{{\mathrm {Z}}} |}\le $ 1 (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$), and with $ {{\mathcal {B}} _{\mathrm {inv}}} > $ 0 and $ {{\mathcal {B}} _{\mathrm {undet}}} > $ 0 as free parameters. Scan of the test statistic $q$ as a function of $ {{\mathcal {B}} _{\mathrm {inv}}} $. The scan of the test statistic $q$ as a function of $ {{\mathcal {B}} _{\mathrm {inv}}} $ expected assuming the SM is also shown.
png pdf	Figure 12-b: Results within the generic $\kappa $-framework model with effective loops and with the constraint $ {| \kappa _{{\mathrm {W}}} |},\, {| \kappa _{{\mathrm {Z}}} |}\le $ 1 (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$), and with $ {{\mathcal {B}} _{\mathrm {inv}}} > $ 0 and $ {{\mathcal {B}} _{\mathrm {undet}}} > $ 0 as free parameters. 68 and 95% CL regions for $ {{\mathcal {B}} _{\mathrm {inv}}} $ vs. $ {{\mathcal {B}} _{\mathrm {undet}}} $.
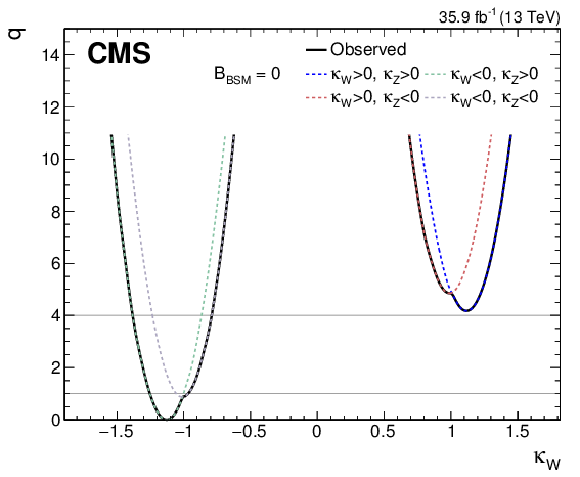
png pdf	Figure 13: Scan of the test statistic $q$ as a function of $\kappa _{{\mathrm {W}}}$ in the generic $\kappa $ model assuming $ {{\mathcal {B}} _{\mathrm {BSM}}} =$ 0 (left) and allowing $ {{\mathcal {B}} _{\mathrm {inv}}} $ and $ {{\mathcal {B}} _{\mathrm {undet}}} $ to float (right). The different colored lines indicate the value of $q$ for different combinations of signs for $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$. The solid black line shows the minimum value of $q(\kappa _{{\mathrm {W}}})$ in each case and is used to determine the best fit point and the $1\sigma $ and $2\sigma $ CL regions. The scan in the right figure is truncated because of the constraints of $ {| \kappa _{{\mathrm {W}}} |}\le $ 1 and $ {| \kappa _{{\mathrm {Z}}} |}\le $ 1, which are imposed in this model.
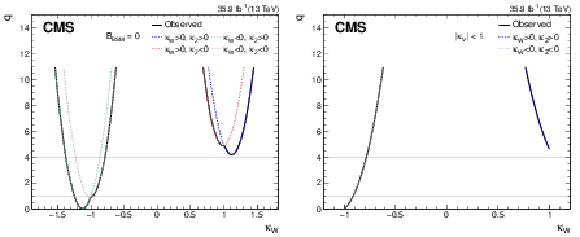
png pdf	Figure 13-a: Scan of the test statistic $q$ as a function of $\kappa _{{\mathrm {W}}}$ in the generic $\kappa $ model assuming $ {{\mathcal {B}} _{\mathrm {BSM}}} =$ 0. The different colored lines indicate the value of $q$ for different combinations of signs for $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$. The solid black line shows the minimum value of $q(\kappa _{{\mathrm {W}}})$ in each case and is used to determine the best fit point and the $1\sigma $ and $2\sigma $ CL regions.
png pdf	Figure 13-b: Scan of the test statistic $q$ as a function of $\kappa _{{\mathrm {W}}}$ in the generic $\kappa $ model allowing $ {{\mathcal {B}} _{\mathrm {inv}}} $ and $ {{\mathcal {B}} _{\mathrm {undet}}} $ to float. The different colored lines indicate the value of $q$ for different combinations of signs for $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$. The solid black line shows the minimum value of $q(\kappa _{{\mathrm {W}}})$ in each case and is used to determine the best fit point and the $1\sigma $ and $2\sigma $ CL regions. The scan is truncated because of the constraints of $ {| \kappa _{{\mathrm {W}}} |}\le $ 1 and $ {| \kappa _{{\mathrm {Z}}} |}\le $ 1, which are imposed in this model.
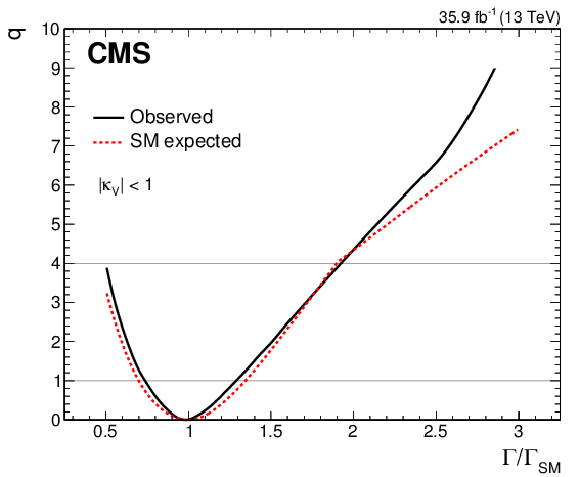
png pdf	Figure 14: The scan of the test statistic $q$ as a function of $\Gamma _{{\mathrm {H}}}/\Gamma _{{\mathrm {H}}}^{\mathrm {SM}}$ obtained by reinterpreting the model allowing for BSM decays of the Higgs boson. The expected scan of $q$ as a function of $\Gamma _{{\mathrm {H}}}/\Gamma _{{\mathrm {H}}}^{\mathrm {SM}}$ assuming the SM is also shown.
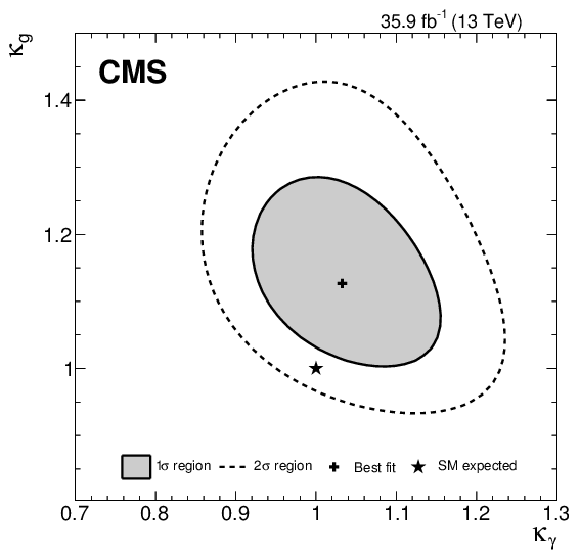
png pdf	Figure 15: The $1\sigma $ and $2\sigma $ CL regions in the $\kappa _{{\mathrm {g}}}$ vs. $\kappa _{{\gamma}}$ parameter space for the model assuming the only BSM contributions to the Higgs boson couplings appear in the loop-induced processes or in BSM Higgs decays.
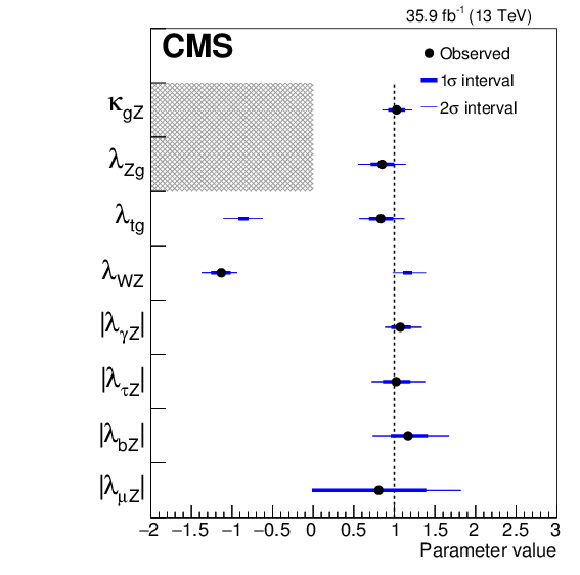
png pdf	Figure 16: Summary of the model with coupling ratios and effective couplings for the ggH and ${{\mathrm {H}} \to {{\gamma} {\gamma}}}$ loops. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. For this model, both positive and negative values of $\lambda _{{\mathrm {W}} {\mathrm {Z}}}$ and $\lambda _{{\mathrm {t}} {\mathrm {g}}}$ are considered.
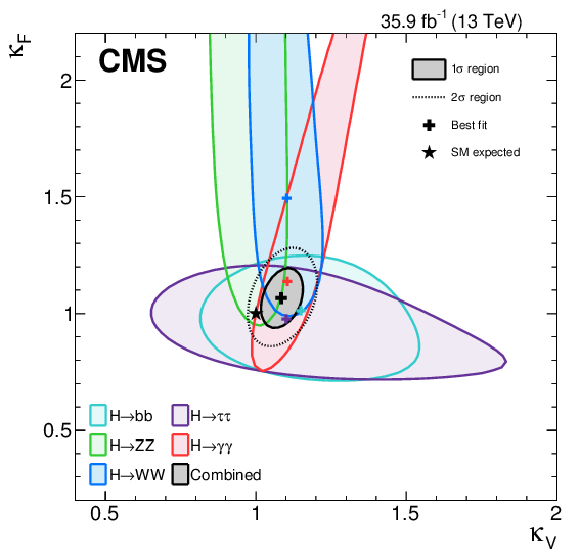
png pdf	Figure 17: The $1\sigma $ and $2\sigma $ CL regions in the $\kappa _{\mathrm {F}}$ vs. $\kappa _{\mathrm {V}}$ parameter space for the model assuming a common scaling of all the vector boson and fermion couplings.
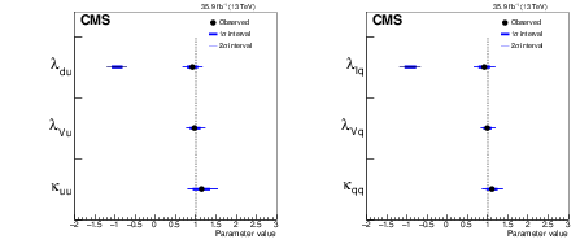
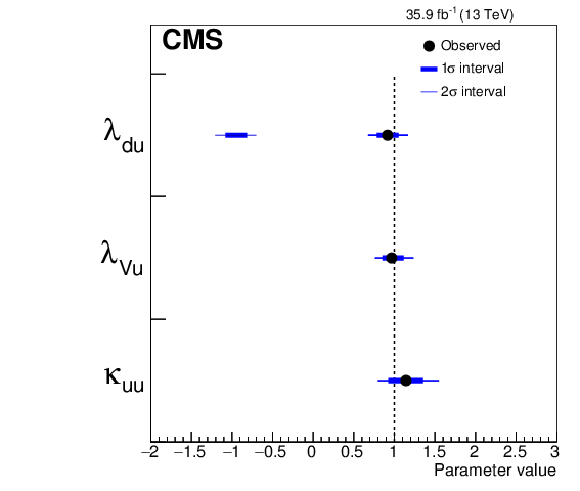
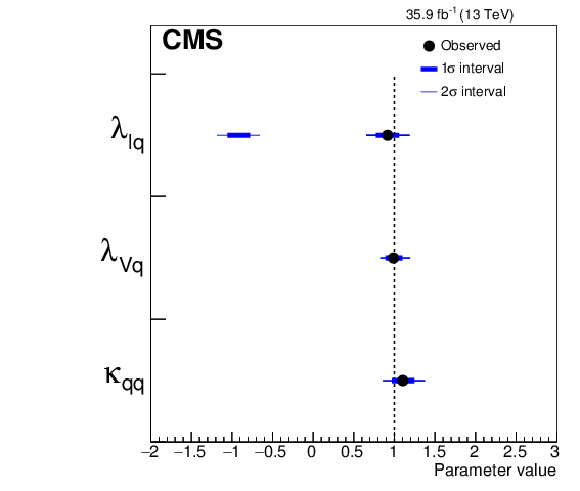
png pdf	Figure 18: Summary plots of the 3-parameter models comparing up- and down-type fermions, and floating the ratio of the vector coupling to the up-type coupling (left) and comparing lepton and quark couplings (right). The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. Both positive and negative values of $\lambda _{{\mathrm {d}} {\mathrm {u}}}$, $\lambda _{\mathrm {V} {\mathrm {u}}}$, $\lambda _{\text {l} {\mathrm {q}}}$, and $\lambda _{\mathrm {V} {\mathrm {q}}}$ are considered.
png pdf	Figure 18-a: Summary plot of the 3-parameter model comparing up- and down-type fermions, and floating the ratio of the vector coupling to the up-type coupling. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. Positive and negative values of $\lambda _{{\mathrm {d}} {\mathrm {u}}}$ and $\lambda _{\mathrm {V} {\mathrm {u}}}$ are considered.
png pdf	Figure 18-b: Summary plot of the 3-parameter models comparing lepton and quark couplings. The points indicate the best fit values while the thick and thin horizontal bars show the $1\sigma $ and $2\sigma $ CL intervals, respectively. Positive and negative values of $\lambda _{\text {l} {\mathrm {q}}}$ and $\lambda _{\mathrm {V} {\mathrm {q}}}$ are considered.
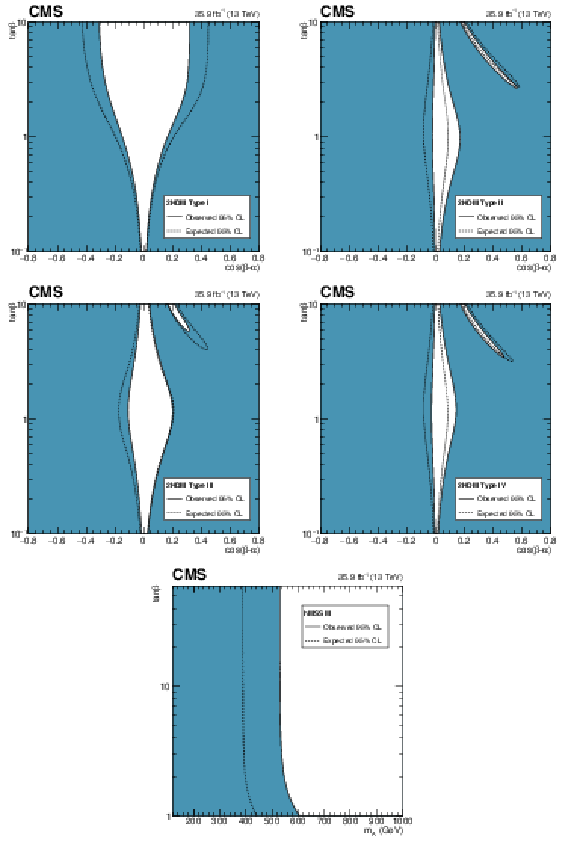
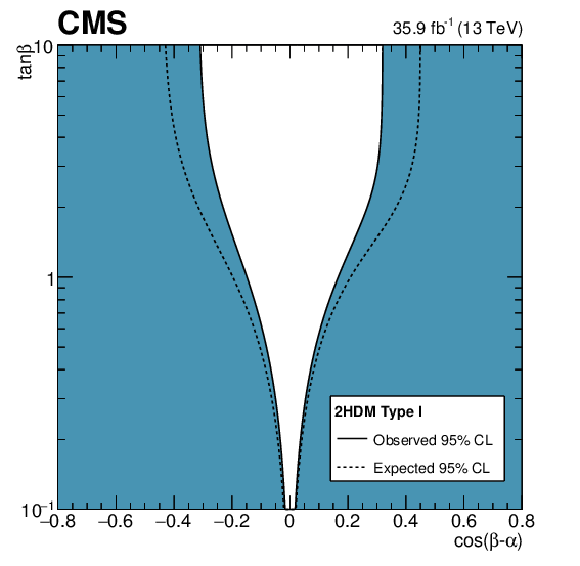
png pdf	Figure 19: Constraints in the $\cos({\beta -\alpha})$ vs. $\tan\beta $ plane for the Types I, II, III, and IV 2HDM, and constraints in the $m_ {\mathrm {A}} $ vs. $\tan\beta $ plane for the hMSSM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.
png pdf	Figure 19-a: Constraints in the $\cos({\beta -\alpha})$ vs. $\tan\beta $ plane for the Types I 2HDM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.
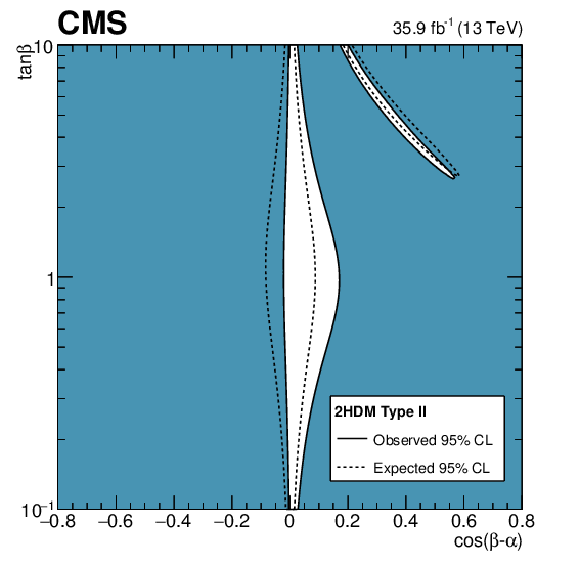
png pdf	Figure 19-b: Constraints in the $\cos({\beta -\alpha})$ vs. $\tan\beta $ plane for the Types II 2HDM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.
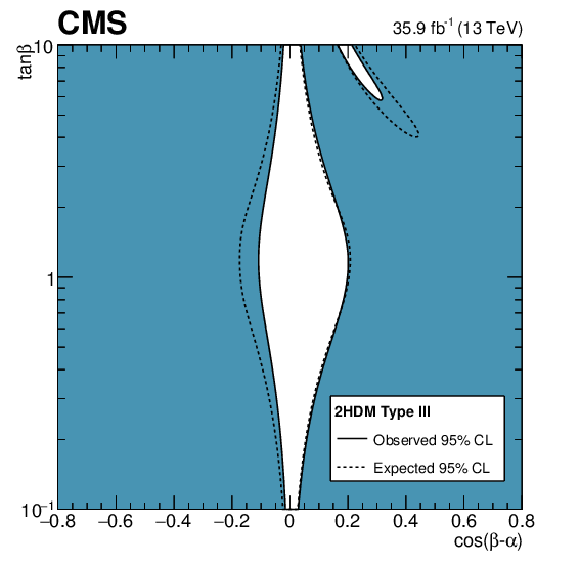
png pdf	Figure 19-c: Constraints in the $\cos({\beta -\alpha})$ vs. $\tan\beta $ plane for the Types III 2HDM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.
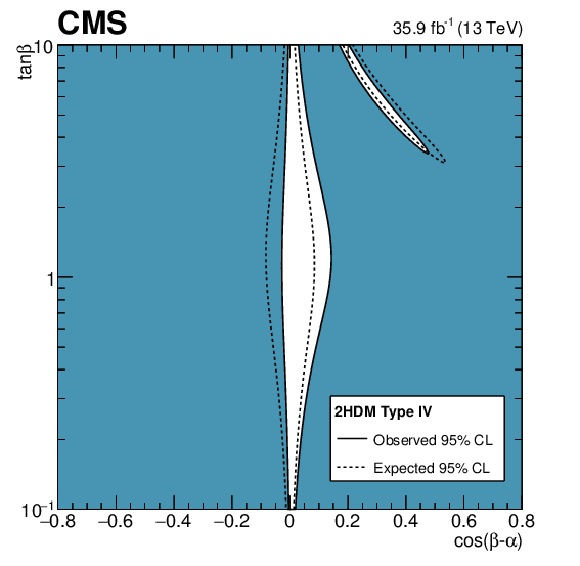
png pdf	Figure 19-d: Constraints in the $\cos({\beta -\alpha})$ vs. $\tan\beta $ plane for the Types IV 2HDM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.
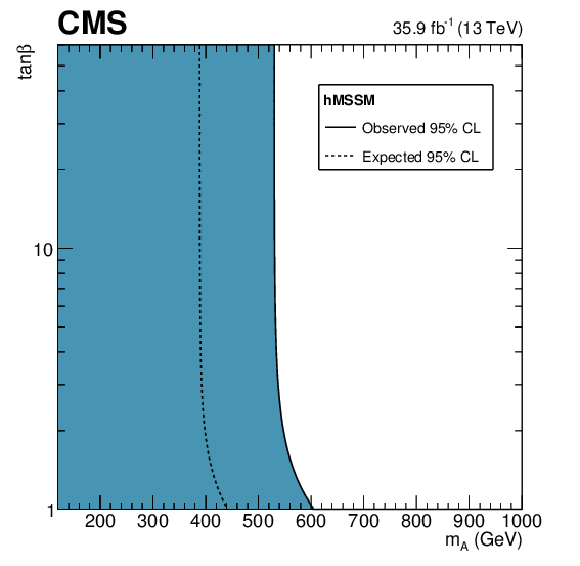
png pdf	Figure 19-e: Constraints in the $m_ {\mathrm {A}} $ vs. $\tan\beta $ plane for the hMSSM. The white regions, bounded by the solid black lines, in each plane represent the regions of the parameter space that are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson.

Tables
png pdf	Table 2: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the parametrizations with per-production mode and per-decay mode signal strength modifiers. The expected uncertainties are given in brackets.
png pdf	Table 3: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the model with one signal strength parameter for each production and decay mode combination. The entries in the table represent the parameter $\mu _{i}^{f}=\mu _{i} \mu ^{f}$, where $i$ is indicated by the column and $f$ by the row. The expected uncertainties are given in brackets. Some of the signal strengths are restricted to nonnegative values, as described in the text.
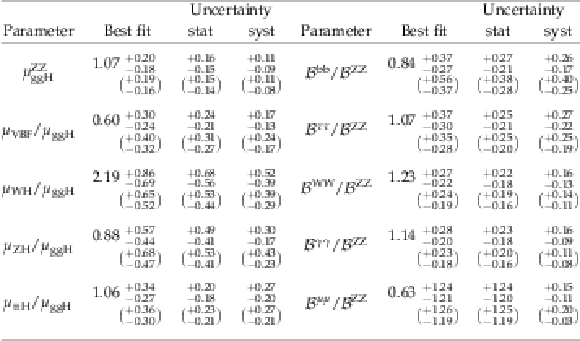
png pdf	Table 4: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the cross section and branching fraction ratio model. The expected uncertainties are given in brackets.
png pdf	Table 5: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the stage 0 simplified template cross section model. The values are all normalized to the SM predictions. The expected uncertainties are given in brackets.
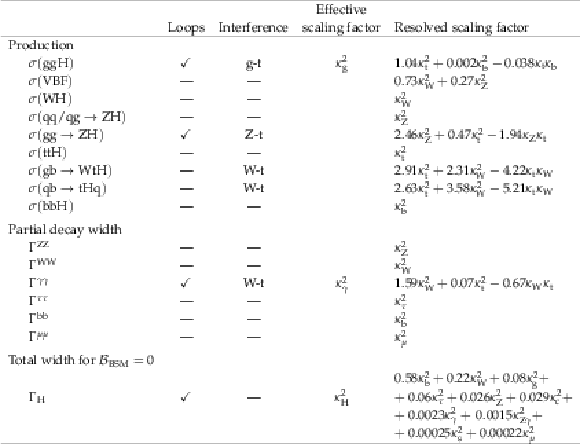
png pdf	Table 6: Normalization scaling factors for all relevant production cross sections and decay partial widths. For the $\kappa $ parameters representing loop processes, the resolved scaling in terms of the fundamental SM couplings is also given.
png pdf	Table 7: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the $\kappa $ model in which the loop processes are resolved. The expected uncertainties are given in brackets.
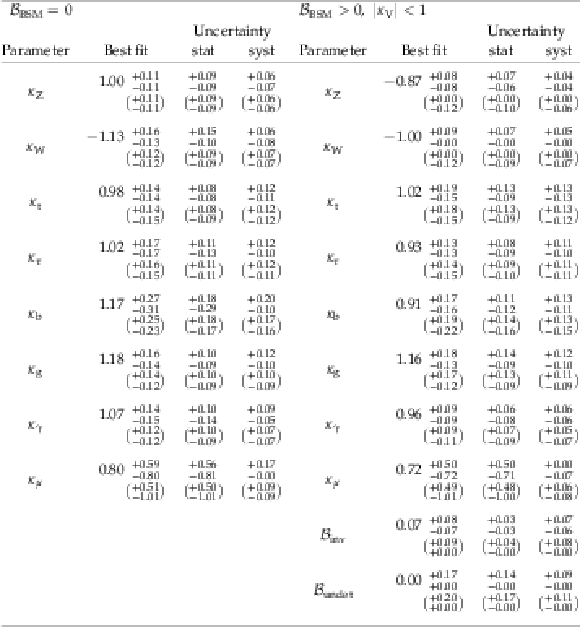
png pdf	Table 8: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the $\kappa $-framework model with effective loops. The expected uncertainties are given in brackets.
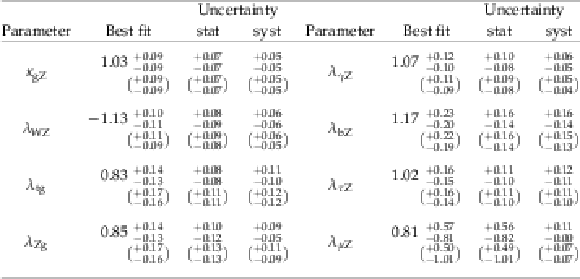
png pdf	Table 9: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the coupling modifier ratio model. The expected uncertainties are given in brackets.
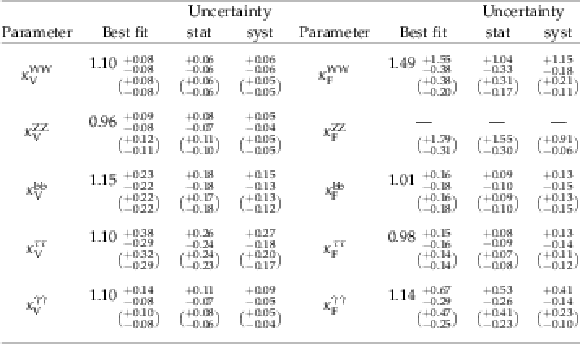
png pdf	Table 10: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the $\kappa _{\mathrm {V}},\kappa _{\mathrm {F}}$ model. The expected uncertainties are given in brackets.
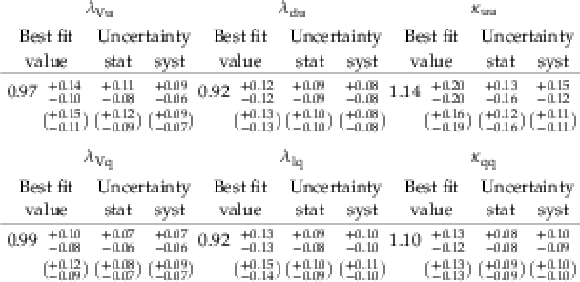
png pdf	Table 11: Best fit values and $ {\pm} 1 \sigma $ uncertainties for the parameters of the two benchmark models with resolved loops to test the symmetry of fermion couplings. The expected uncertainties are given in brackets.
png pdf	Table 12: Compatibility of the fit results with the SM prediction under various signal parametrizations. The value of $q$ at the values of the POIs for which the SM expectation is obtained ($q_{\text {SM}}$) is shown along with the corresponding $p$-value, with respect to the SM, assuming $q$ is distributed according to a $\chi ^{2}$ function with the specified number of degrees of freedom (DOF).
png pdf	Table 13: Modifications to the couplings of the Higgs bosons to up-type ($\kappa _{{\mathrm {u}}}$) and down-type ($\kappa _{{\mathrm {d}}}$) fermions, and vector bosons ($\kappa _{\mathrm {V}}$), with respect to the SM expectation, in 2HDM and for the hMSSM. The coupling modifications for the hMSSM are completed by the expressions for $s_{{\mathrm {u}}}$ and $s_{{\mathrm {d}}}$, as given by Eqs. (8) and (9).

Summary

A set of combined measurements of Higgs boson production and decay rates has been presented, along with the consequential constraints placed on its couplings to standard model (SM) particles, and on the parameter spaces of several beyond the standard model (BSM) scenarios. The combination is based on analyses targeting the gluon fusion and vector boson fusion production modes, and associated production with a vector boson or a pair of top quarks. The analyses included in the combination target Higgs boson decay in the $\mathrm{H} \to \mathrm{Z}\mathrm{Z},\,\mathrm{W}\mathrm{W},\,{\gamma\gamma} ,\,{\tau\tau} $, ${\mathrm{b}\mathrm{b}} $, and $ {\mu \mu } $ channels, using 13 TeV proton-proton collision data collected in 2016 and corresponding to an integrated luminosity of 35.9 fb$^{-1}$. Additionally, searches for invisible Higgs boson decays are included to increase the sensitivity to potential interactions with BSM particles. Measurements of the Higgs boson production cross section times branching fraction in each of the channels are presented, along with a generic parametrization in terms of ratios of production cross sections and branching fractions, which makes no assumptions about the Higgs boson total width. The combined signal yield relative to the SM prediction has been measured as 1.17 $\pm$ 0.10 at $m_{\mathrm{H}} = $ 125.09 GeV. An improvement in the measured precision of the gluon fusion production rate of around $\sim$50% is achieved compared to previous ATLAS and CMS measurements. Additionally, a set of fiducial Higgs boson cross sections, in the context of the simplified template cross section framework, is presented for the first time from a combination of six decay channels. Furthermore, interpretations are provided in the context of a leading-order coupling modifier framework, including variants for which effective couplings to the photon and gluon are introduced. All of the results presented are compatible with the SM prediction. The invisible (undetected) branching fraction of the Higgs boson is constrained to be less than 22 (38%) at 95% Confidence Level. The results are additionally interpreted in two BSM models, the minimal supersymmetric model and the generic two Higgs doublet model. The constraints placed on the parameter spaces of these models are complementary to those that can be obtained from direct searches for additional Higgs bosons.

Additional Figures
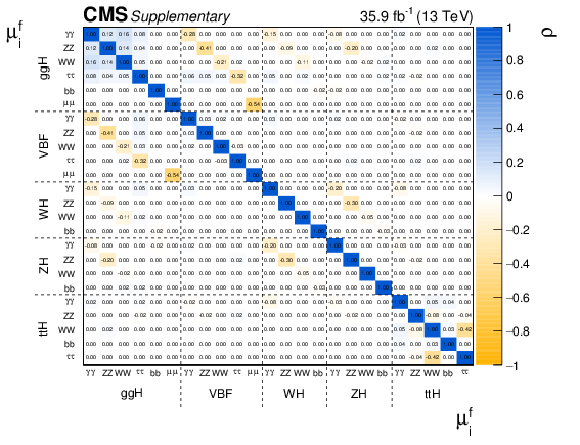
png pdf	Additional Figure 1: The correlation coefficients ($\rho $) obtained from the fit to data for the model with one signal strength parameter for each production and decay mode combination $\mu _{i}^{f}$. The production modes $i$ include gluon fusion (ggH), vector boson fusion (VBF), associated production with a vector boson (WH, ZH) and associated production with a pair of top quarks (ttH). The decay modes $f$ include ZZ, WW, $\gamma \gamma $, $\tau \tau $, bb and $ {{\mu}} {{\mu}}$.
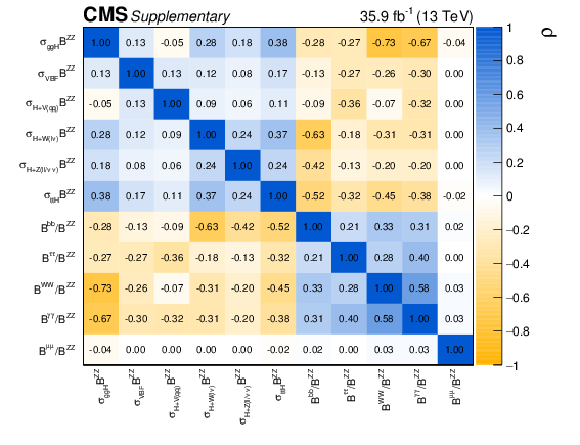
png pdf	Additional Figure 2: The correlation coefficients ($\rho $) obtained from the fit to data for the stage 0 simplified template cross section model. Six of the parameters represent the fiducial cross sections $\sigma _{{{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}}}$, $\sigma _{{\mathrm {VBF}}}$, $\sigma _{{\mathrm {H}} +\rm {V}({\mathrm {q}} {\mathrm {q}})}$, $\sigma _{{\mathrm {H}} + {\mathrm {W}}(\ell \nu)}$, $\sigma _{{\mathrm {H}} +{{\mathrm {Z}}(\ell \ell /\nu \nu)}}$ and $\sigma _{{{\mathrm {t}} {\mathrm {t}} {\mathrm {H}}}}$ multiplied by the branching fraction $\mathcal {B}^{{\mathrm {Z}} {\mathrm {Z}}}$. The remaining five parameters represent the branching fractions for WW, $\gamma \gamma $, $\tau \tau $, $ {{\mathrm {b}} {\mathrm {b}}} $ and $ {{\mu}} {{\mu}}$ divided by $\mathcal {B}^{{\mathrm {Z}} {\mathrm {Z}}}$.

References
1	S. L. Glashow	Partial-symmetries of weak interactions	NP 22 (1961) 579
2	S. Weinberg	A model of leptons	PRL 19 (1967) 1264
3	A. Salam	Weak and electromagnetic interactions	in Elementary particle physics: relativistic groups and analyticity, N. Svartholm, ed., p. 367 Almqvist \& Wiskell, 1968Proceedings of the 8th Nobel symposium
4	G. 't Hooft and M. J. G. Veltman	Regularization and renormalization of gauge fields	NPB 44 (1972) 189
5	F. Englert and R. Brout	Broken symmetry and the mass of gauge vector mesons	PRL 13 (1964) 321
6	P. W. Higgs	Broken symmetries, massless particles and gauge fields	PL12 (1964) 132
7	P. W. Higgs	Broken symmetries and the masses of gauge bosons	PRL 13 (1964) 508
8	G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble	Global conservation laws and massless particles	PRL 13 (1964) 585
9	P. W. Higgs	Spontaneous symmetry breakdown without massless bosons	PR145 (1966) 1156
10	T. W. B. Kibble	Symmetry breaking in non-Abelian gauge theories	PR155 (1967) 1554
11	Y. Nambu and G. Jona-Lasinio	Dynamical model of elementary particles based on an analogy with superconductivity. I	PR122 (1961) 345
12	ATLAS Collaboration	Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC	PLB 716 (2012) 1	1207.7214
13	CMS Collaboration	Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC	PLB 716 (2012) 30	CMS-HIG-12-028 1207.7235
14	CMS Collaboration	Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV	JHEP 06 (2013) 81	CMS-HIG-12-036 1303.4571
15	K. G. Wilson	Renormalization group and strong interactions	PRD 3 (1971) 1818
16	E. Gildener	Gauge-symmetry hierarchies	PRD 14 (1976) 1667
17	S. Weinberg	Gauge hierarchies	PLB 82 (1979) 387
18	G. 't Hooft	Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking	NATO Sci. Ser. B 59 (1980) 135
19	L. Susskind	Dynamics of spontaneous symmetry breaking in the Weinberg-Salam theory	PRD 20 (1979) 2619
20	S. Dimopoulos and H. Georgi	Softly broken supersymmetry and SU(5)	NPB 193 (1981) 150
21	E. Witten	Dynamical breaking of supersymmetry	NPB 188 (1981) 513
22	N. Arkani-Hamed, S. Dimopoulos, and G. Dvali	The hierarchy problem and new dimensions at a millimeter	PLB 429 (1998) 263	hep-ph/9803315
23	L. Randall and R. Sundrum	Large mass hierarchy from a small extra dimension	PRL 83 (1999) 3370	hep-ph/9905221
24	N. Arkani-Hamed, A. G. Cohen, and H. Georgi	Electroweak symmetry breaking from dimensional deconstruction	PLB 513 (2001) 232	hep-ph/0105239
25	G. B\'elanger et al.	The MSSM invisible Higgs in the light of dark matter and g-2	PLB 519 (2001) 93	hep-ph/0106275
26	G. F. Giudice, R. Rattazzi, and J. D. Wells	Graviscalars from higher-dimensional metrics and curvature-Higgs mixing	NPB 595 (2001) 250	hep-ph/0002178
27	D. Dominici and J. F. Gunion	Invisible Higgs decays from Higgs-graviscalar mixing	PRD 80 (2009) 115006	0902.1512
28	C. Bonilla, J. C. Rom\ ao, and J. W. F. Valle	Neutrino mass and invisible Higgs decays at the LHC	PRD 91 (2015) 113015	1502.01649
29	C. Anastasiou et al.	Higgs boson gluon-fusion production in QCD at three loops	PRL 114 (2015) 212001	1503.06056
30	C. Anastasiou et al.	High precision determination of the gluon fusion Higgs boson cross-section at the LHC	JHEP 05 (2016) 58	1602.00695
31	M. Ciccolini, A. Denner, and S. Dittmaier	Strong and electroweak corrections to the production of a Higgs boson+2 jets via weak interactions at the Large Hadron Collider	PRL 99 (2007) 161803	0707.0381
32	M. Ciccolini, A. Denner, and S. Dittmaier	Electroweak and QCD corrections to Higgs production via vector-boson fusion at the LHC	PRD 77 (2008) 013002	0710.4749
33	P. Bolzoni, F. Maltoni, S.-O. Moch, and M. Zaro	Higgs production via vector-boson fusion at NNLO in QCD	PRL 105 (2010) 011801	1003.4451
34	P. Bolzoni, F. Maltoni, S.-O. Moch, and M. Zaro	Vector boson fusion at next-to-next-to-leading order in QCD: Standard model Higgs boson and beyond	PRD 85 (2012) 035002	1109.3717
35	O. Brein, A. Djouadi, and R. Harlander	NNLO QCD corrections to the Higgs-strahlung processes at hadron colliders	PLB 579 (2004) 149	hep-ph/0307206
36	M. L. Ciccolini, S. Dittmaier, and M. Kramer	Electroweak radiative corrections to associated $ WH $ and $ ZH $ production at hadron colliders	PRD 68 (2003) 073003	hep-ph/0306234
37	W. Beenakker et al.	Higgs radiation off top quarks at the Tevatron and the LHC	PRL 87 (2001) 201805	hep-ph/0107081
38	W. Beenakker et al.	NLO QCD corrections to $ \mathrm{t\bar{t}} $ H production in hadron collisions.	NPB 653 (2003) 151	hep-ph/0211352
39	S. Dawson, L. H. Orr, L. Reina, and D. Wackeroth	Associated top quark Higgs boson production at the LHC	PRD 67 (2003) 071503	hep-ph/0211438
40	S. Dawson et al.	Associated Higgs production with top quarks at the Large Hadron Collider: NLO QCD corrections	PRD 68 (2003) 034022	hep-ph/0305087
41	Z. Yu et al.	QCD NLO and EW NLO corrections to $ t\bar{t}H $ production with top quark decays at hadron collider	PLB 738 (2014) 1	1407.1110
42	S. S. Frixione et al.	Weak corrections to Higgs hadroproduction in association with a top-quark pair	JHEP 09 (2014) 65	1407.0823
43	F. Demartin, F. Maltoni, K. Mawatari, and M. Zaro	Higgs production in association with a single top quark at the LHC	EPJC 75 (2015) 267	1504.0611
44	F. Demartin et al.	tWH associated production at the LHC	EPJC 77 (2017) 34	1607.05862
45	A. Denner et al.	Standard model Higgs-boson branching ratios with uncertainties	EPJC 71 (2011) 1753	1107.5909
46	A. Djouadi, J. Kalinowski, and M. Spira	HDECAY: A Program for Higgs boson decays in the standard model and its supersymmetric extension	CPC 108 (1998) 56	hep-ph/9704448
47	A. Djouadi, J. Kalinowski, M. Muhlleitner, and M. Spira	An update of the program HDECAY	in The Les Houches 2009 workshop on TeV colliders: The tools and Monte Carlo working group summary report 2010	1003.1643
48	A. Bredenstein, A. Denner, S. Dittmaier, and M. M. Weber	Precise predictions for the Higgs-boson decay H $ \rightarrow $ WW/ZZ $ \rightarrow $ 4 leptons	PRD 74 (2006) 013004	hep-ph/0604011
49	A. Bredenstein, A. Denner, S. Dittmaier, and M. M. Weber	Radiative corrections to the semileptonic and hadronic Higgs-boson decays H $ \rightarrow $WW/ZZ$ \rightarrow $ 4 fermions	JHEP 02 (2007) 80	hep-ph/0611234
50	S. Boselli et al.	Higgs boson decay into four leptons at NLOPS electroweak accuracy	JHEP 06 (2015) 23	1503.07394
51	S. Actis, G. Passarino, C. Sturm, and S. Uccirati	NNLO computational techniques: the cases $ H \to \gamma \gamma $ and $ H \to g g $	NPB 811 (2009) 182	0809.3667
52	LHC Higgs Cross Section Working Group	Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector		1610.07922
53	ATLAS Collaboration	Measurements of the Higgs boson production and decay rates and coupling strengths using $ pp $ collision data at $ \sqrt{s} = $ 7 and 8 TeV in the ATLAS experiment	EPJC 76 (2016) 6	1507.04548
54	CMS Collaboration	Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV	EPJC 75 (2015) 212	CMS-HIG-14-009 1412.8662
55	ATLAS and CMS Collaborations	Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC $ pp $ collision data at $ \sqrt{s} = $ 7 and 8 TeV	JHEP 08 (2016) 45	1606.02266
56	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
57	CMS Collaboration	Measurements of Higgs boson properties in the diphoton decay channel in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	\emphSubmitted to JHEP	CMS-HIG-16-040 1804.02716
58	B. P. Roe et al.	Boosted decision trees as an alternative to artificial neural networks for particle identification	NIMA 543 (2005) 577	physics/0408124
59	P. D. Dauncey, M. Kenzie, N. Wardle, and G. J. Davies	Handling uncertainties in background shapes: the discrete profiling method	JINST 10 (2015) P04015	1408.6865
60	CMS Collaboration	Measurements of properties of the Higgs boson decaying into the four-lepton final state in pp collisions at $ \sqrt{s}= $ 13 ~TeV	JHEP 11 (2017) 47	CMS-HIG-16-041 1706.09936
61	CMS Collaboration	Measurements of properties of the Higgs boson decaying to a W boson pair in pp collisions at $ \sqrt{s}= $ 13 TeV	Submitted to PLB	CMS-HIG-16-042 1806.05246
62	CMS Collaboration	Observation of the Higgs boson decay to a pair of $ \tau $ leptons with the CMS detector	PLB 779 (2018) 283	CMS-HIG-16-043 1708.00373
63	CMS Collaboration	Evidence for the Higgs boson decay to a bottom quark-antiquark pair	PLB 780 (2018) 501	CMS-HIG-16-044 1709.07497
64	T. Aaltonen et al.	Improved $ b $-jet Energy Correction for $ H \to b\bar{b} $ Searches at CDF		1107.3026
65	CMS Collaboration	Search for the associated production of a Higgs boson with a single top quark in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	JHEP 06 (2016) 177	CMS-HIG-14-027 1509.08159
66	ATLAS Collaboration	Search for the $ \mathrm{b}\overline{\mathrm{b}} $ decay of the Standard Model Higgs boson in associated (W/Z)H production with the ATLAS detector	JHEP 01 (2015) 69	1409.6212
67	CMS Collaboration	Identification of b-quark jets with the CMS experiment	JINST 8 (2013) P04013
68	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV	JINST (2017) P05011	CMS-BTV-16-002 1712.07158
69	CMS Collaboration	Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair	PRL 120 (2018) 071802	CMS-HIG-17-010 1709.05543
70	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm	JHEP 04 (2008) 63	0802.1189
71	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
72	M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam	Towards an understanding of jet substructure	JHEP 09 (2013) 29	1307.0007
73	A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler	Soft drop	JHEP 05 (2014) 146	1402.2657
74	CMS Collaboration	Identification of double-$ \mathrm{b} $ quark jets in boosted event topologies	CMS-PAS-BTV-15-002	CMS-PAS-BTV-15-002
75	CMS Collaboration	Observation of $ \mathrm{t\bar{t}H} $ production	PRL 120 (2018) 231801	CMS-HIG-17-035 1804.02610
76	CMS Collaboration	Evidence for associated production of a Higgs boson with a top quark pair in final states with electrons, muons, and hadronically decaying $ \tau $ leptons at $ \sqrt{s} = $ 13 TeV	JHEP 08 (2018) 066	CMS-HIG-17-018 1803.05485
77	CMS Collaboration	Search for $ \mathrm{t\overline{t}} $H production in the H$ \mathrm{b\overline{b}} $ decay channel with leptonic $ \mathrm{t\overline{t}} $ decays in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Submitted to JHEP	CMS-HIG-17-026 1804.03682
78	CMS Collaboration	Search for $ \mathrm{t}\overline{\mathrm{t}} $H production in the all-jet final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Submitted to JHEP	CMS-HIG-17-022 1803.06986
79	J. Schmidhuber	Deep learning in neural networks: An overview	Neural Networks 61 (2015) 85
80	T. J. Hastie, R. J. Tibshirani, and J. H. Friedman	The elements of statistical learning: data mining, inference, and prediction	Springer series in statistics. Springer, New York, NY, 2nd edition edition
81	P. C. Bhat	Multivariate analysis methods in particle physics	Annu. Rev. Nucl. Part. Sci. 61 (2011) 281
82	P. Speckmayer, A. Hocker, J. Stelzer, and H. Voss	The toolkit for multivariate data analysis, TMVA 4	J. Phys. Conf. Ser. 219 (2010) 032057
83	K. Kondo	Dynamical likelihood method for reconstruction of events with missing momentum. 1: Method and toy models	J. Phys. Soc. Jpn. 57 (1988) 4126
84	D0 Collaboration	A precision measurement of the mass of the top quark	Nature 429 (2004) 638	hep-ex/0406031
85	CMS Collaboration	Performance of quark/gluon discrimination in 8 TeV pp data	CMS-PAS-JME-13-002	CMS-PAS-JME-13-002
86	CMS Collaboration	Performance of quark/gluon discrimination in 13 TeV data	CDS
87	CMS Collaboration	Search for the Higgs boson decaying to two muons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Submitted to PRLett	CMS-HIG-17-019 1807.06325
88	R. E. Shrock and M. Suzuki	Invisible decays of Higgs bosons	PLB 110 (1982) 250
89	CMS Collaboration	Search for invisible decays of a Higgs boson produced through vector boson fusion in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Submitted to PLB	CMS-HIG-17-023 1809.05937
90	CMS Collaboration	Search for new physics in events with a leptonically decaying Z boson and a large transverse momentum imbalance in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	EPJC 78 (2017) 291	CMS-EXO-16-052 1711.00431
91	CMS Collaboration	Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson and transverse momentum imbalance at $ \sqrt{s}= $ 13 TeV	PRD 97 (2018) 092005	CMS-EXO-16-048 1712.02345
92	E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini	Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM	JHEP 02 (2012) 88	1111.2854
93	P. Nason	A New method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
94	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the $ POWHEG $ method	JHEP 11 (2007) 070	0709.2092
95	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
96	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
97	R. Frederix and S. Frixione	Merging meets matching in MC@NLO	JHEP 12 (2012) 61	1209.6215
98	K. Hamilton, P. Nason, E. Re, and G. Zanderighi	NNLOPS simulation of Higgs boson production	JHEP 10 (2013) 222	1309.0017
99	K. Hamilton, P. Nason, and G. Zanderighi	Finite quark-mass effects in the NNLOPS POWHEG+MiNLO Higgs generator		1501.04637
100	R. Barlow and C. Beeston	Fitting using finite Monte Carlo samples	Comp. Phys. Comms. 77 (1993) 219
101	J. S. Conway	Incorporating nuisance parameters in likelihoods for multisource spectra		1103.0354
102	The ATLAS Collaboration, The CMS Collaboration, The LHC Higgs Combination Group	Procedure for the LHC Higgs boson search combination in Summer 2011	CMS-NOTE-2011-005
103	CMS Collaboration	Combined results of searches for the standard model Higgs boson in pp collisions at $ \sqrt{s} = $ 7 TeV	PLB 710 (2012) 26	CMS-HIG-11-032 1202.1488
104	W. Verkerke and D. P. Kirkby	The RooFit toolkit for data modeling	in 13$^\textth$ International Conference for Computing in High Energy and Nuclear Physics (CHEP03) 2003 CHEP-2003-MOLT007	physics/0306116
105	L. Moneta et al.	The RooStats project	in 13th International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT2010) SISSA, 2010 PoS(ACAT2010)057	1009.1003
106	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727
107	ATLAS and CMS Collaborations	Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS and CMS Experiments	PRL 114 (2015) 191803	1503.07589
108	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
109	E. Boos, V. Bunichev, M. Dubinin, and Y. Kurihara	Higgs boson signal at complete tree level in the SM extension by dimension-six operators	PRD 89 (2014) 035001	1309.5410
110	LHC Higgs Cross Section Working Group	Handbook of LHC Higgs Cross Sections: 3. Higgs Properties		1307.1347
111	C. Englert, M. McCullough, and M. Spannowsky	Gluon-initiated associated production boosts Higgs physics	PRD 89 (2014) 013013	1310.4828
112	K. Hagiwara, R. Szalapski, and D. Zeppenfeld	Anomalous Higgs boson production and decay	PLB 318 (1993) 155	hep-ph/9308347
113	C. Arzt, M. B. Einhorn, and J. Wudka	Patterns of deviation from the standard model	NPB 433 (1995) 41	hep-ph/9405214
114	D. Zeppenfeld, R. Kinnunen, A. Nikitenko, and E. Richter-Was	Measuring Higgs boson couplings at the CERN LHC	PRD 62 (2000) 013009	hep-ph/0002036
115	V. Barger et al.	Effects of genuine dimension-six Higgs operators	PRD 67 (2003) 115001	hep-ph/0301097
116	M. Duhrssen et al.	Extracting Higgs boson couplings from CERN LHC data	PRD 70 (2004) 113009	hep-ph/0406323
117	A. Manohar and M. Wise	Modifications to the properties of the Higgs boson	PLB 636 (2006) 107	hep-ph/0601212
118	I. Low, R. Rattazzi, and A. Vichi	Theoretical constraints on the Higgs effective couplings	JHEP 04 (2010) 126	0907.5413
119	J. Ellis and T. You	Global analysis of experimental constraints on a possible Higgs-like particle with mass ~125 GeV	JHEP 06 (2012) 140	1204.0464
120	T. Corbett, O. J. P. Eboli, J. Gonzalez-Fraile, and M. C. Gonzalez-Garcia	Constraining anomalous Higgs boson interactions	PRD 86 (2012) 075013	1207.1344
121	G. Passarino	NLO inspired effective Lagrangians for Higgs physics	NPB 868 (2013) 416	1209.5538
122	M. Klute et al.	Measuring Higgs couplings from LHC data	PRL 109 (2012) 101801	1205.2699
123	R. Contino et al.	Effective Lagrangian for a light Higgs-like scalar	JHEP 07 (2013) 35	1303.3876
124	W.-F. Chang, W.-P. Pan, and F. Xu	Effective gauge-Higgs operators analysis of new physics associated with the Higgs boson	PRD 88 (2013) 033004	1303.7035
125	P. P. Giardino et al.	The universal Higgs fit	JHEP 05 (2014) 46	1303.3570
126	M. Ghezzi, R. Gomez-Ambrosio, G. Passarino, and S. Uccirati	NLO Higgs effective field theory and $ \kappa $-framework	JHEP 07 (2015) 175	1505.03706
127	J. Ellis and T. You	Global analysis of the Higgs candidate with mass $ \sim $ 125 GeV	JHEP 09 (2012) 123	1207.1693
128	J. Ellis and T. You	Updated global analysis of Higgs couplings	JHEP 06 (2013) 103	1303.3879
129	Particle Data Group	Review of particle physics	CPC 40 (2016) 100001
130	G. C. Branco et al.	Theory and phenomenology of two-Higgs-doublet models	PR 516 (2012) 1	1106.0034
131	J. F. Gunion and H. E. Haber	CP-conserving two-Higgs-doublet model: The approach to the decoupling limit	PRD 67 (2003) 075019	hep-ph/0207010
132	L. Maiani, A. D. Polosa, and V. Riquer	Bounds to the Higgs sector masses in minimal supersymmetry from LHC data	PLB 724 (2013) 274	1305.2172
133	A. Djouadi	The Anatomy of electroweak symmetry breaking Tome II. The Higgs bosons in the minimal supersymmetric model	PR 459 (2008) 1	hep-ph/0503173
134	J. F. Gunion and H. E. Haber	Higgs bosons in supersymmetric models (I)	NPB 272 (1986) 1
135	H. E. Haber and G. L. Kane	The search for supersymmetry: Probing physics beyond the standard model	PR 117 (1985) 75
136	H. P. Nilles	Supersymmetry, supergravity and particle physics	PR 110 (1984) 1
137	A. Djouadi et al.	The post-Higgs MSSM scenario: habemus MSSM?	EPJC 73 (2013) 2650	1307.5205
138	A. Djouadi et al.	Fully covering the MSSM Higgs sector at the LHC	JHEP 06 (2015) 168	1502.05653
139	ATLAS Collaboration	Constraints on new phenomena via Higgs boson couplings and invisible decays with the ATLAS detector	JHEP 11 (2015) 206	1509.00672
140	M. Carena et al.	MSSM Higgs boson searches at the LHC: benchmark scenarios after the discovery of a Higgs-like particle	EPJC 73 (2013) 2552	1302.7033
141	ATLAS Collaboration	Search for heavy resonances decaying into $ WW $ in the $ e\nu\mu\nu $ final state in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	EPJC 78 (2018) 24	1710.01123
142	ATLAS Collaboration	Search for additional heavy neutral Higgs and gauge bosons in the ditau final state produced in 36 fb$ ^{-1} $ of pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector	JHEP 01 (2018) 55	1709.07242
143	ATLAS Collaboration	Search for charged Higgs bosons produced in association with a top quark and decaying via $ H^{\pm} \rightarrow \tau\nu $ using $ pp $ collision data recorded at $ \sqrt{s} = $ 13 TeV by the ATLAS detector	PLB 759 (2016) 555	1603.09203
144	CMS Collaboration	Search for neutral MSSM Higgs bosons decaying to a pair of tau leptons in pp collisions	JHEP 10 (2014) 160	CMS-HIG-13-021 1408.3316
145	CMS Collaboration	Search for a standard-model-like Higgs boson with a mass in the range 145 to 1000 GeV at the LHC	EPJC 73 (2013) 2469	CMS-HIG-12-034 1304.0213

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2018 for the benefit of the CMS Collaboration