

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-24-010 | ||
| Improved results on Higgs boson pair production in the 4b final state | ||
| CMS Collaboration | ||
| 2025-10-29 | ||
| Abstract: Measurements of Higgs boson pair (HH) production in the four bottom quark final state are presented using a data set of proton-proton (pp) collisions at $ \sqrt{s}= $ 13.6 TeV collected by the CMS experiment during 2022-2023 and corresponding to an integrated luminosity of 62 fb$ ^{-1} $. Events in which each Higgs boson decay is separately reconstructed as a pair of small-radius jets (resolved), as well as events in which each $ \mathrm{H}\to\mathrm{b}\bar{\mathrm{b}} $ decay is reconstructed as a single large-radius jet (merged) are analyzed exclusively. Benefiting from novel analysis techniques, the combination of resolved and merged channels gives an observed (expected) upper limit at 95% confidence level (CL) on the HH signal strength $ \mu_{\mathrm{HH}} $, defined as the observed HH production cross section divided by the standard model (SM) prediction, of 4.4 (4.4). Compared to previous LHC results, the expected limit with an equivalent integrated luminosity is improved by more than a factor two in the resolved topology and significantly improved in the merged topology as well. The allowed ranges at 95% CL for the Higgs trilinear self-coupling and quartic coupling between two Higgs bosons and two vector bosons, relative to the standard model expectation, are observed (expected, in absence of signal) to be $ [-3.3,9.7] $ ($ [-3.4,10.0] $) and $ [0.63,1.43] $ ($ [0.54,1.51] $), respectively. An updated analysis of the resolved topology using a 13 TeV pp collision data set corresponding to 138 fb$ ^{-1} $ and collected in 2016-2018, reports an observed (expected) 95% CL upper limit on $ \mu_{\mathrm{HH}} $ of 10.0 (5.9), an improvement of about 25% in the expected limit compared to the published results using the same data. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
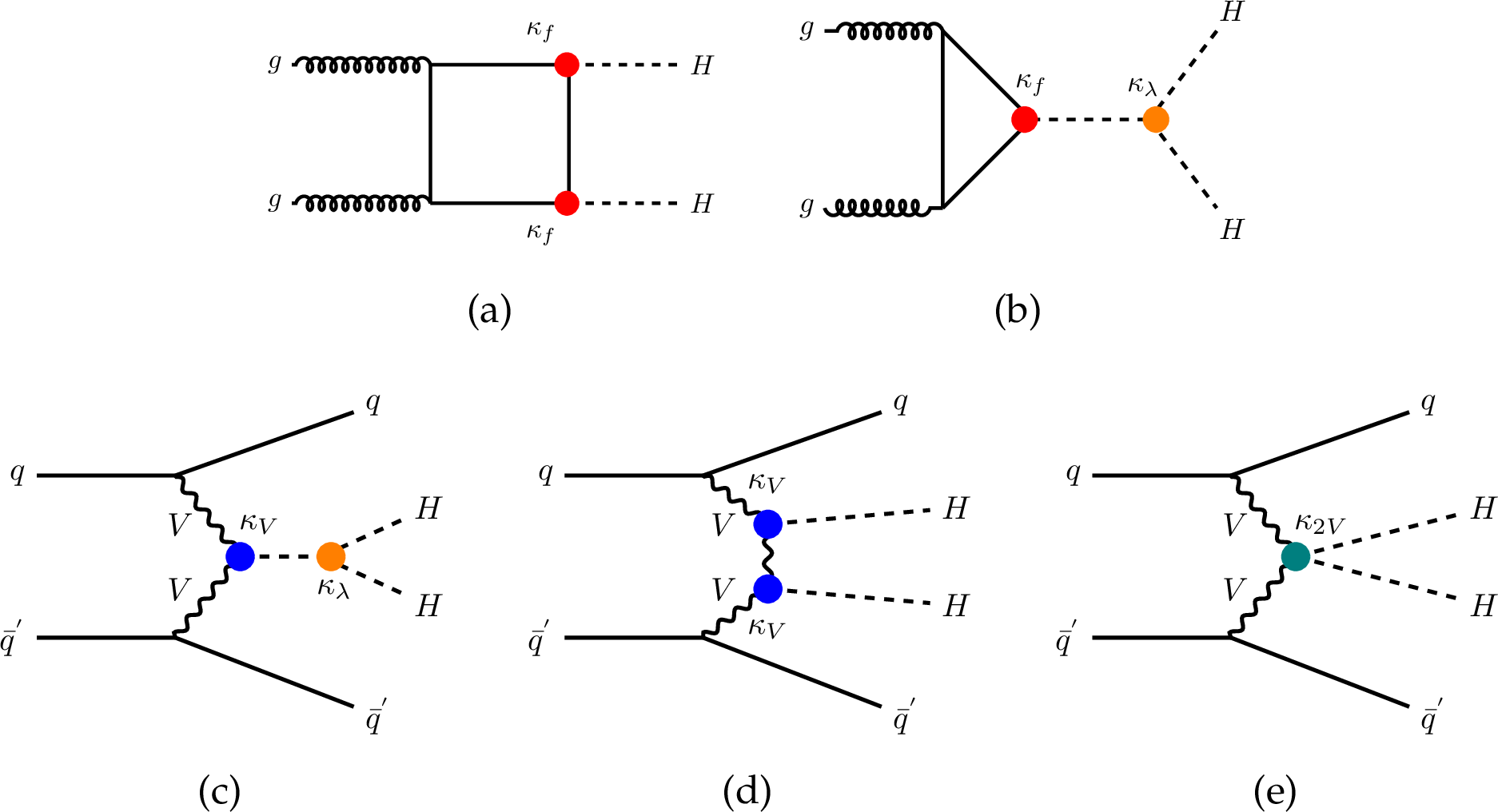
Figure 1:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |
png pdf |
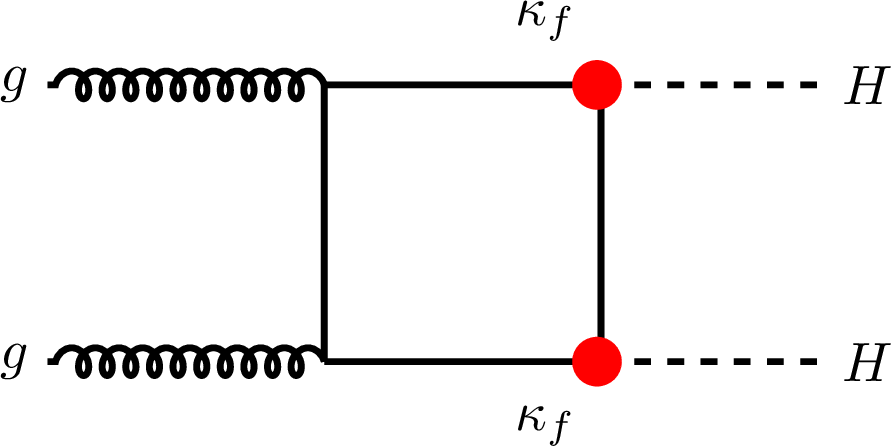
Figure 1-a:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |

png pdf |
Figure 1-b:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |
png pdf |
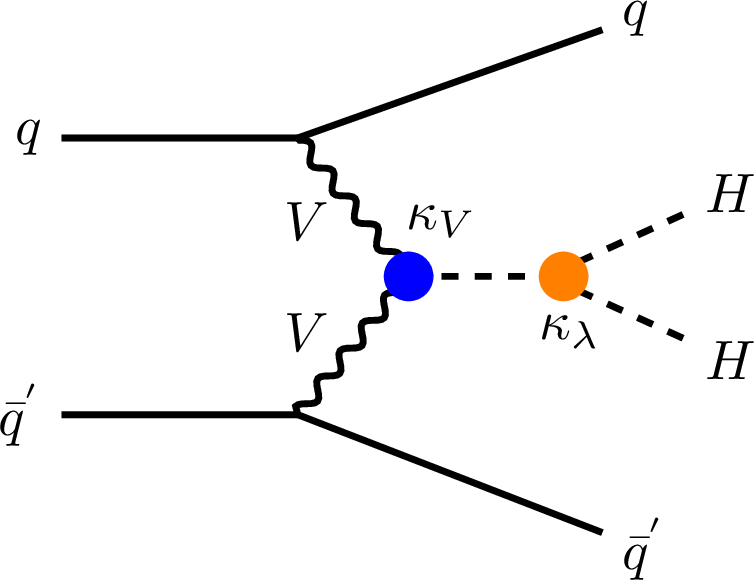
Figure 1-c:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |

png pdf |
Figure 1-d:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |
png pdf |
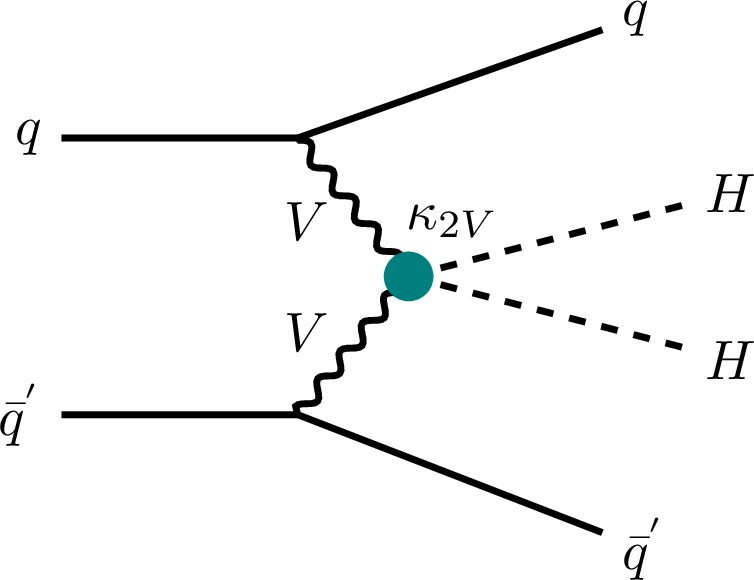
Figure 1-e:
Feynman diagrams that contribute to ggF and VBF HH production at leading order with coupling modifiers affecting the Higgs-to-fermion coupling $ \kappa_f $, to vector-boson coupling $ \kappa_{\text{V}} $, to two-vector-boson vertices $ \kappa_{\text{2V}} $ and self-coupling $ \kappa_{\lambda} $. |
png pdf |
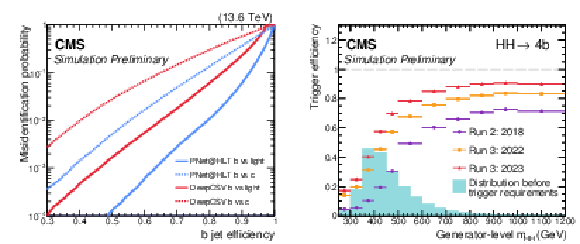
Figure 2:
Left: the b tagging performance of the Run 3 PNET@HLT algorithm (in blue) compared to the best-performing algorithm deployed at HLT in Run 2 (DEEPCSV, in red), as evaluated from $ \mathrm{t} \overline{\mathrm{t}} $ simulation on trigger-level AK4 jets with $ p_{\mathrm{T}} > $ 30 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the triggers targeting the resolved $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ topology as a function of the generator-level $ m_{\mathrm{H}\mathrm{H}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal events in which the generator-level jets from the b quarks produced by $ \mathrm{H}\to \mathrm{b}\overline{\mathrm{b}} $ decays have $ p_{\mathrm{T}} $ larger than 25 GeV and $ {|\eta| < 2.5} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any trigger selections. |

png pdf |
Figure 2-a:
Left: the b tagging performance of the Run 3 PNET@HLT algorithm (in blue) compared to the best-performing algorithm deployed at HLT in Run 2 (DEEPCSV, in red), as evaluated from $ \mathrm{t} \overline{\mathrm{t}} $ simulation on trigger-level AK4 jets with $ p_{\mathrm{T}} > $ 30 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the triggers targeting the resolved $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ topology as a function of the generator-level $ m_{\mathrm{H}\mathrm{H}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal events in which the generator-level jets from the b quarks produced by $ \mathrm{H}\to \mathrm{b}\overline{\mathrm{b}} $ decays have $ p_{\mathrm{T}} $ larger than 25 GeV and $ {|\eta| < 2.5} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any trigger selections. |

png pdf |
Figure 2-b:
Left: the b tagging performance of the Run 3 PNET@HLT algorithm (in blue) compared to the best-performing algorithm deployed at HLT in Run 2 (DEEPCSV, in red), as evaluated from $ \mathrm{t} \overline{\mathrm{t}} $ simulation on trigger-level AK4 jets with $ p_{\mathrm{T}} > $ 30 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the triggers targeting the resolved $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ topology as a function of the generator-level $ m_{\mathrm{H}\mathrm{H}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal events in which the generator-level jets from the b quarks produced by $ \mathrm{H}\to \mathrm{b}\overline{\mathrm{b}} $ decays have $ p_{\mathrm{T}} $ larger than 25 GeV and $ {|\eta| < 2.5} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any trigger selections. |
png pdf |
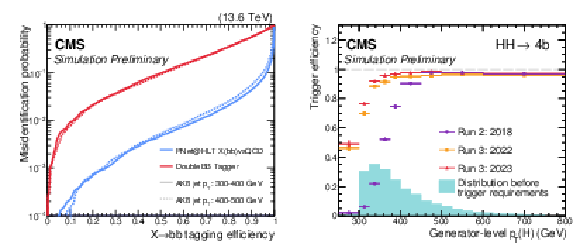
Figure 3:
Left: the $ \mathrm{b}\overline{\mathrm{b}} $ tagging performance of the PNET@HLT algorithm (in blue) compared to the highest-performing Run 2 algorithm (DOUBLEBB, in red), as evaluated on AK8 jets in the HLT from simulated $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ and QCD multijet events with $ p_{\mathrm{T}} > $ 300 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the logical or of the trigger paths developed for the merged topology, as a function of the generator-level leading H candidate $ p_{\mathrm{T}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events in which $ {\Delta R(\mathrm{b},\overline{\mathrm{b}}) < 0.8} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any selections. |
png pdf |
Figure 3-a:
Left: the $ \mathrm{b}\overline{\mathrm{b}} $ tagging performance of the PNET@HLT algorithm (in blue) compared to the highest-performing Run 2 algorithm (DOUBLEBB, in red), as evaluated on AK8 jets in the HLT from simulated $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ and QCD multijet events with $ p_{\mathrm{T}} > $ 300 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the logical or of the trigger paths developed for the merged topology, as a function of the generator-level leading H candidate $ p_{\mathrm{T}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events in which $ {\Delta R(\mathrm{b},\overline{\mathrm{b}}) < 0.8} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any selections. |

png pdf |
Figure 3-b:
Left: the $ \mathrm{b}\overline{\mathrm{b}} $ tagging performance of the PNET@HLT algorithm (in blue) compared to the highest-performing Run 2 algorithm (DOUBLEBB, in red), as evaluated on AK8 jets in the HLT from simulated $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ and QCD multijet events with $ p_{\mathrm{T}} > $ 300 GeV and $ {|\eta| < 2.5} $. Right: efficiency of the logical or of the trigger paths developed for the merged topology, as a function of the generator-level leading H candidate $ p_{\mathrm{T}} $ in simulated SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events in which $ {\Delta R(\mathrm{b},\overline{\mathrm{b}}) < 0.8} $. The teal histogram shows the expected distribution for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal prior to any selections. |

png pdf |
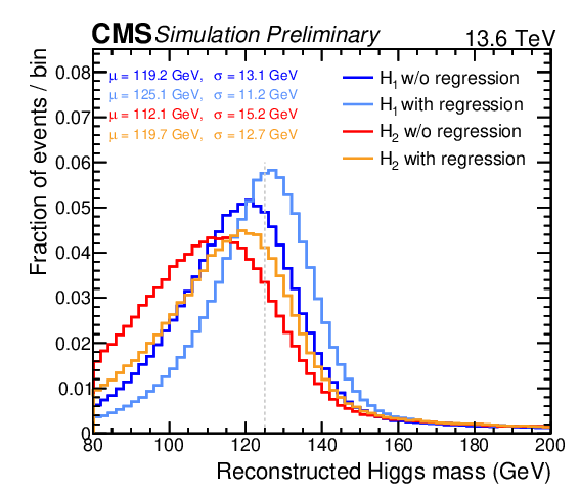
Figure 4:
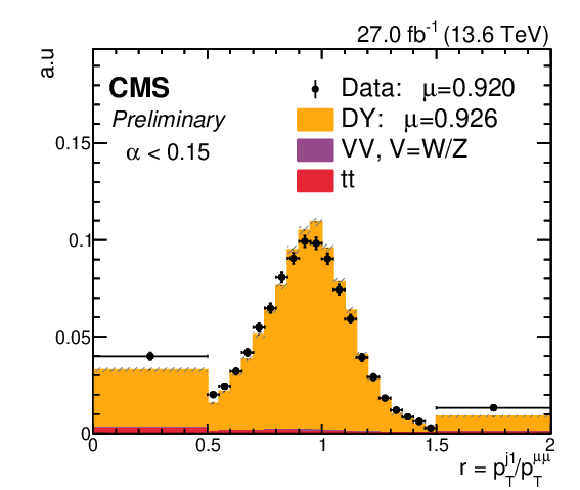
Left: invariant mass distributions for the leading ($ m_{\mathrm{H}_1} $) and subleading ($ m_{\mathrm{H}_2} $) $ p_{\mathrm{T}} \mathrm{H} $ candidates in SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events obtained before and after the application of the PNET jet $ p_{\mathrm{T}} $ regression. Right: distribution of the $ p_{\mathrm{T}} $ balance, $ r=p_{\mathrm{T}}^{\mathrm{j_{1}}}/p_{\mathrm{T}}^{\mu\mu} $, in 2023 data and simulated events for the selected $ \mathrm{Z}(\mu\mu)+\mathrm{b}\text{-jet} $ region with $ \alpha=p_{\mathrm{T}}^{\mathrm{j_{2}}}/p_{\mathrm{T}}^{\mu\mu} < $ 0.15, obtained after applying the PNET jet $ p_{\mathrm{T}} $ regression. The $ \mu $ values quoted in the legend correspond to the mean of the distributions. |
png pdf |
Figure 4-a:
Left: invariant mass distributions for the leading ($ m_{\mathrm{H}_1} $) and subleading ($ m_{\mathrm{H}_2} $) $ p_{\mathrm{T}} \mathrm{H} $ candidates in SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events obtained before and after the application of the PNET jet $ p_{\mathrm{T}} $ regression. Right: distribution of the $ p_{\mathrm{T}} $ balance, $ r=p_{\mathrm{T}}^{\mathrm{j_{1}}}/p_{\mathrm{T}}^{\mu\mu} $, in 2023 data and simulated events for the selected $ \mathrm{Z}(\mu\mu)+\mathrm{b}\text{-jet} $ region with $ \alpha=p_{\mathrm{T}}^{\mathrm{j_{2}}}/p_{\mathrm{T}}^{\mu\mu} < $ 0.15, obtained after applying the PNET jet $ p_{\mathrm{T}} $ regression. The $ \mu $ values quoted in the legend correspond to the mean of the distributions. |
png pdf |
Figure 4-b:
Left: invariant mass distributions for the leading ($ m_{\mathrm{H}_1} $) and subleading ($ m_{\mathrm{H}_2} $) $ p_{\mathrm{T}} \mathrm{H} $ candidates in SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ events obtained before and after the application of the PNET jet $ p_{\mathrm{T}} $ regression. Right: distribution of the $ p_{\mathrm{T}} $ balance, $ r=p_{\mathrm{T}}^{\mathrm{j_{1}}}/p_{\mathrm{T}}^{\mu\mu} $, in 2023 data and simulated events for the selected $ \mathrm{Z}(\mu\mu)+\mathrm{b}\text{-jet} $ region with $ \alpha=p_{\mathrm{T}}^{\mathrm{j_{2}}}/p_{\mathrm{T}}^{\mu\mu} < $ 0.15, obtained after applying the PNET jet $ p_{\mathrm{T}} $ regression. The $ \mu $ values quoted in the legend correspond to the mean of the distributions. |

png pdf |
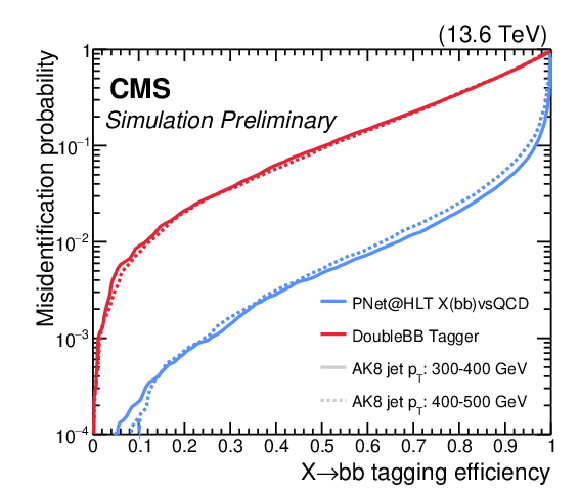
Figure 5:
The ROC curve for GLOPART and PNET for discriminating $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ from QCD jets with 400 $ < p_{\mathrm{T}} < $ 600 GeV, $ |\eta| < $ 2.4, and 60 $ < m_\text{SD} < $ 150 GeV (left). The mass regression performance for GLOPART and PNET for jets with $ p_{\mathrm{T}} > $ 200 GeV, $ |\eta| < $ 2.4, and satisfying a PNET selection corresponding to 30% signal efficiency (right). The conditions correspond to those during data collection in 2023. |

png pdf |
Figure 5-a:
The ROC curve for GLOPART and PNET for discriminating $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ from QCD jets with 400 $ < p_{\mathrm{T}} < $ 600 GeV, $ |\eta| < $ 2.4, and 60 $ < m_\text{SD} < $ 150 GeV (left). The mass regression performance for GLOPART and PNET for jets with $ p_{\mathrm{T}} > $ 200 GeV, $ |\eta| < $ 2.4, and satisfying a PNET selection corresponding to 30% signal efficiency (right). The conditions correspond to those during data collection in 2023. |
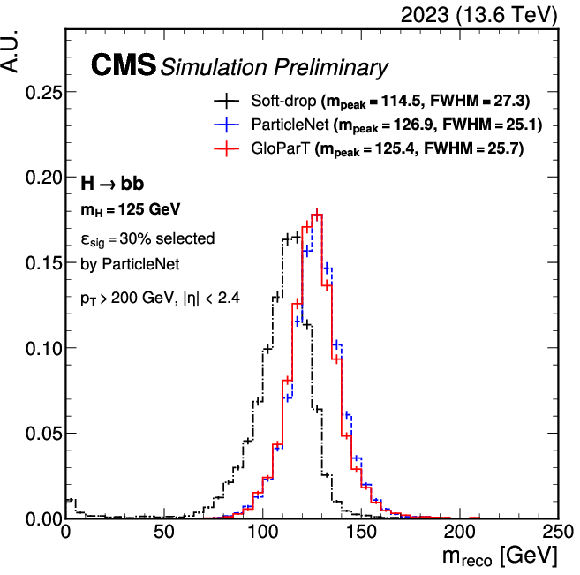
png pdf |
Figure 5-b:
The ROC curve for GLOPART and PNET for discriminating $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ from QCD jets with 400 $ < p_{\mathrm{T}} < $ 600 GeV, $ |\eta| < $ 2.4, and 60 $ < m_\text{SD} < $ 150 GeV (left). The mass regression performance for GLOPART and PNET for jets with $ p_{\mathrm{T}} > $ 200 GeV, $ |\eta| < $ 2.4, and satisfying a PNET selection corresponding to 30% signal efficiency (right). The conditions correspond to those during data collection in 2023. |
png pdf |
Figure 6:
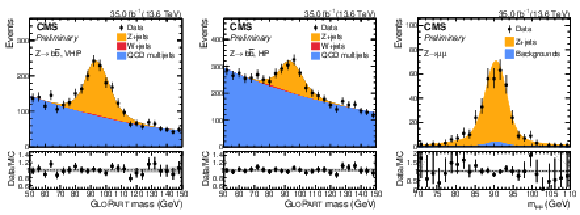
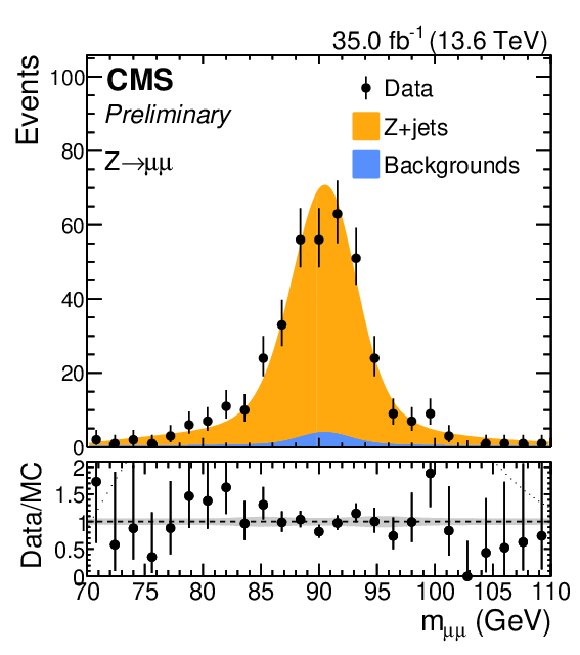
Comparison between data and fit prediction from a simultaneous signal-plus-background fit to the GLOPART regressed jet mass distributions in $ \mathrm{Z} \to \mathrm{b}\overline{\mathrm{b}} $ VHP (left) and HP (middle) categories. Data corresponds to the full integrated luminosity collected by the CMS detector in 2022. The same comparison is performed for the $ m_{\mu\mu} $ distributions in the $ \mathrm{Z} \to \mu\mu $ region (right). Each process considered in the fit is modeled via a parametric function as described in the text. |

png pdf |
Figure 6-a:
Comparison between data and fit prediction from a simultaneous signal-plus-background fit to the GLOPART regressed jet mass distributions in $ \mathrm{Z} \to \mathrm{b}\overline{\mathrm{b}} $ VHP (left) and HP (middle) categories. Data corresponds to the full integrated luminosity collected by the CMS detector in 2022. The same comparison is performed for the $ m_{\mu\mu} $ distributions in the $ \mathrm{Z} \to \mu\mu $ region (right). Each process considered in the fit is modeled via a parametric function as described in the text. |
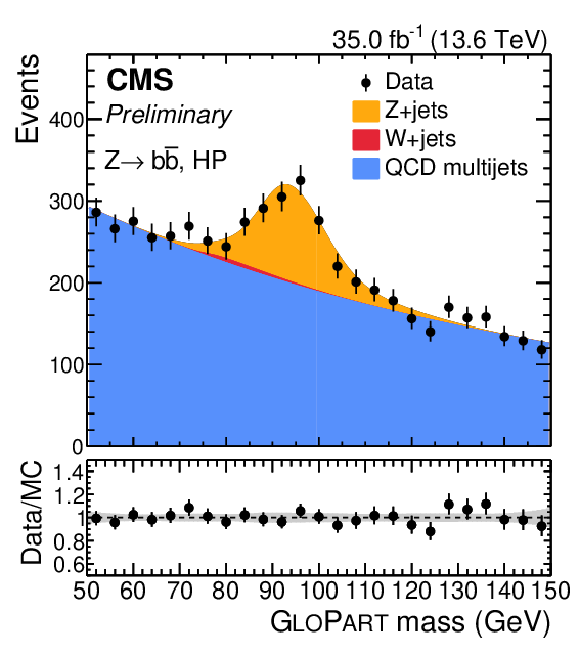
png pdf |
Figure 6-b:
Comparison between data and fit prediction from a simultaneous signal-plus-background fit to the GLOPART regressed jet mass distributions in $ \mathrm{Z} \to \mathrm{b}\overline{\mathrm{b}} $ VHP (left) and HP (middle) categories. Data corresponds to the full integrated luminosity collected by the CMS detector in 2022. The same comparison is performed for the $ m_{\mu\mu} $ distributions in the $ \mathrm{Z} \to \mu\mu $ region (right). Each process considered in the fit is modeled via a parametric function as described in the text. |
png pdf |
Figure 6-c:
Comparison between data and fit prediction from a simultaneous signal-plus-background fit to the GLOPART regressed jet mass distributions in $ \mathrm{Z} \to \mathrm{b}\overline{\mathrm{b}} $ VHP (left) and HP (middle) categories. Data corresponds to the full integrated luminosity collected by the CMS detector in 2022. The same comparison is performed for the $ m_{\mu\mu} $ distributions in the $ \mathrm{Z} \to \mu\mu $ region (right). Each process considered in the fit is modeled via a parametric function as described in the text. |

png pdf |
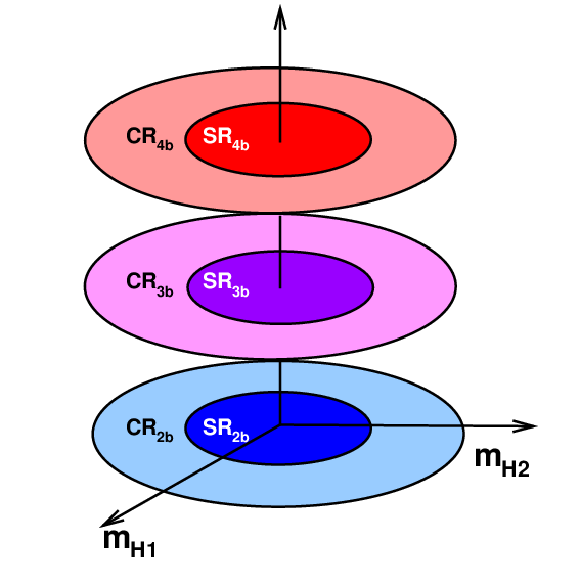
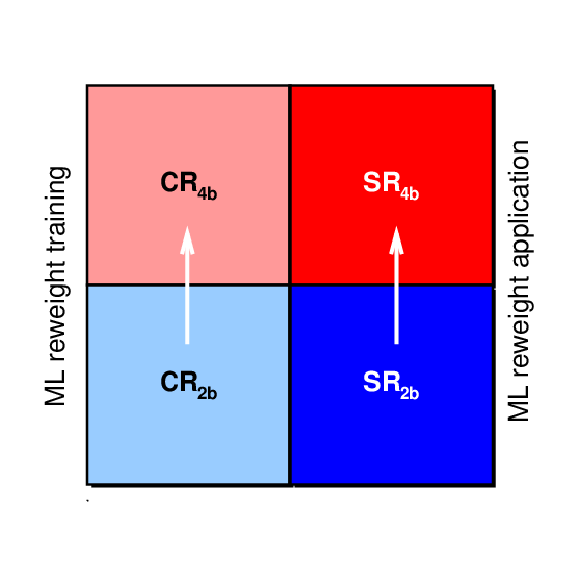
Figure 7:
Left: schematic diagram of the signal regions (dark shaded circles) and control regions (annular regions) in the $ m_{\mathrm{H}_1} $--$ m_{\mathrm{H}_2} $ mass plane as a function of $N_{\mathrm{b jet}}$. Right: schematic diagram showing the background estimation strategy, which applies a multidimensional reweighting of events from $ \mathrm{SR_{2\mathrm{b}}} $ to $ \mathrm{SR_{4\mathrm{b}}} $. |
png pdf |
Figure 7-a:
Left: schematic diagram of the signal regions (dark shaded circles) and control regions (annular regions) in the $ m_{\mathrm{H}_1} $--$ m_{\mathrm{H}_2} $ mass plane as a function of $N_{\mathrm{b jet}}$. Right: schematic diagram showing the background estimation strategy, which applies a multidimensional reweighting of events from $ \mathrm{SR_{2\mathrm{b}}} $ to $ \mathrm{SR_{4\mathrm{b}}} $. |
png pdf |
Figure 7-b:
Left: schematic diagram of the signal regions (dark shaded circles) and control regions (annular regions) in the $ m_{\mathrm{H}_1} $--$ m_{\mathrm{H}_2} $ mass plane as a function of $N_{\mathrm{b jet}}$. Right: schematic diagram showing the background estimation strategy, which applies a multidimensional reweighting of events from $ \mathrm{SR_{2\mathrm{b}}} $ to $ \mathrm{SR_{4\mathrm{b}}} $. |
png pdf |
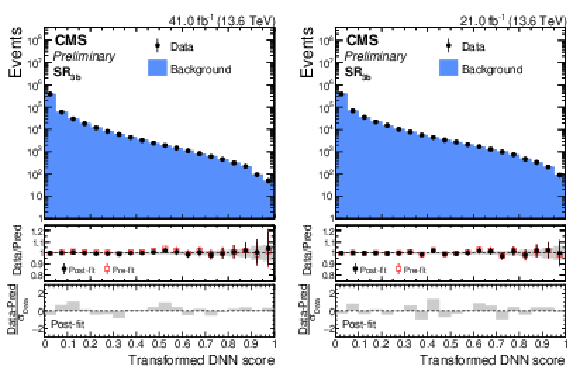
Figure 8:
Distribution of the SvsB classifier score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ category for $ \mathrm{SR_{3\mathrm{b}}} $ data (black points) compared to the data-driven background prediction (blue histogram), for the pre-ParkingHH (left) and post-ParkingHH (right) data sets. The middle panel shows the ratio of data to the pre-fit (red open markers) and post b-only fit (black solid markers) background prediction, with the gray band indicating the background post-fit uncertainty. The lower panel show the distribution of the pulls, defined as the difference between the data and the post-fit background prediction, divided by the statistical uncertainty in the data. |

png pdf |
Figure 8-a:
Distribution of the SvsB classifier score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ category for $ \mathrm{SR_{3\mathrm{b}}} $ data (black points) compared to the data-driven background prediction (blue histogram), for the pre-ParkingHH (left) and post-ParkingHH (right) data sets. The middle panel shows the ratio of data to the pre-fit (red open markers) and post b-only fit (black solid markers) background prediction, with the gray band indicating the background post-fit uncertainty. The lower panel show the distribution of the pulls, defined as the difference between the data and the post-fit background prediction, divided by the statistical uncertainty in the data. |
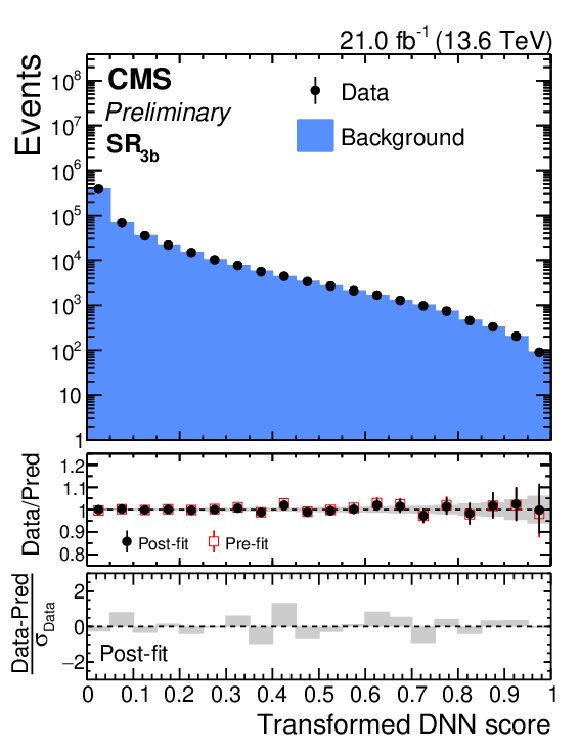
png pdf |
Figure 8-b:
Distribution of the SvsB classifier score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ category for $ \mathrm{SR_{3\mathrm{b}}} $ data (black points) compared to the data-driven background prediction (blue histogram), for the pre-ParkingHH (left) and post-ParkingHH (right) data sets. The middle panel shows the ratio of data to the pre-fit (red open markers) and post b-only fit (black solid markers) background prediction, with the gray band indicating the background post-fit uncertainty. The lower panel show the distribution of the pulls, defined as the difference between the data and the post-fit background prediction, divided by the statistical uncertainty in the data. |
png pdf |
Figure 9:
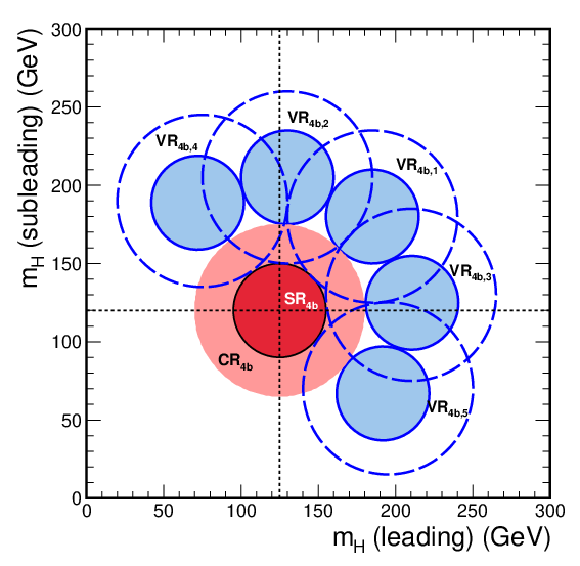
A schematic diagram of the 4b validation regions defined in the $ m_{\mathrm{H}_1} $--$ m_{\mathrm{H}_2} $ mass plane and orthogonal to the $ \mathrm{SR_{4\mathrm{b}}} $. In each validation region, the solid blue area identifies the signal region, while the dashed blue lines indicate the corresponding control region. The ``leading'' H candidate is the one with largest $ p_{\mathrm{T}} $(H). |
png pdf |
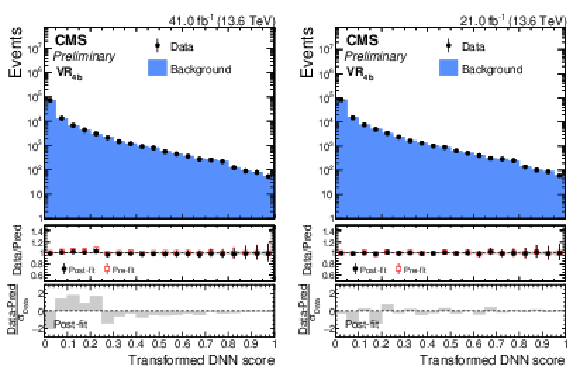
Figure 10:
Pre-fit and post b-only fit distributions of the SvsB classifier output for the sum of all 4b validation regions in pre-ParkingHH (left) and post-ParkingHH (right) data. |

png pdf |
Figure 10-a:
Pre-fit and post b-only fit distributions of the SvsB classifier output for the sum of all 4b validation regions in pre-ParkingHH (left) and post-ParkingHH (right) data. |
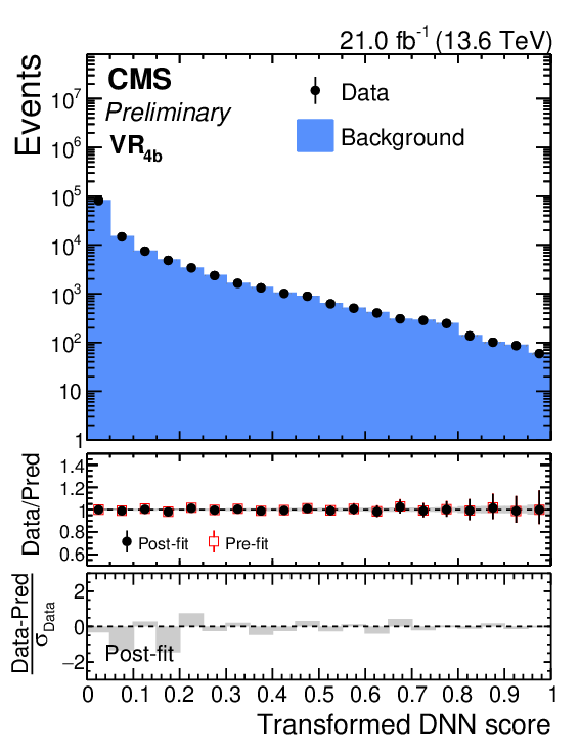
png pdf |
Figure 10-b:
Pre-fit and post b-only fit distributions of the SvsB classifier output for the sum of all 4b validation regions in pre-ParkingHH (left) and post-ParkingHH (right) data. |
png pdf |
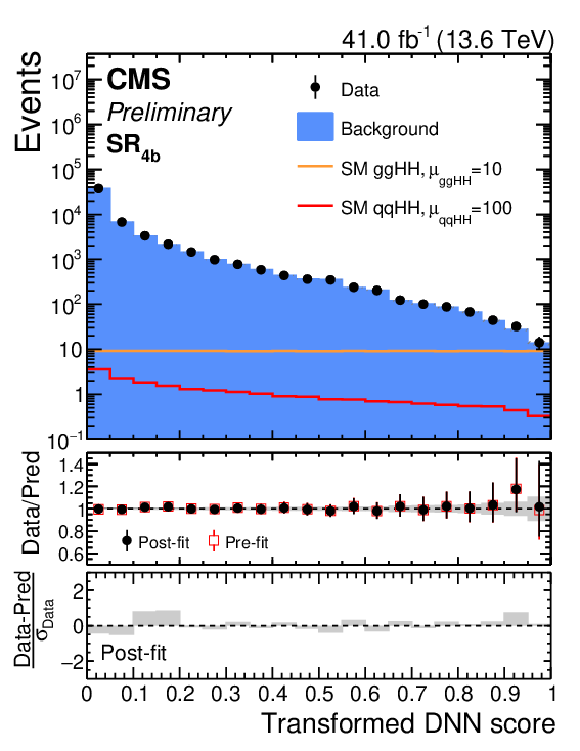
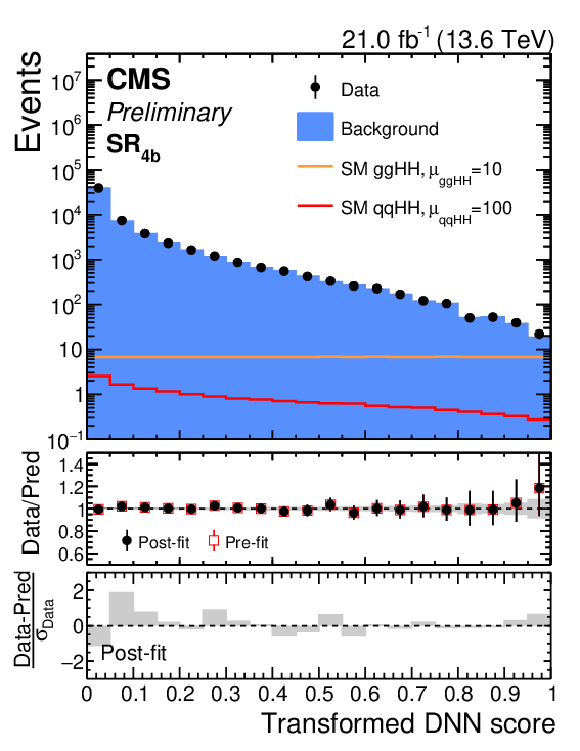
Figure 11:
Post-fit distributions of the SvsB classifier score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ resolved analysis for data (black points) and the predicted background (blue filled histograms), for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red line) signals, scaled to improve their visibility, are overlaid. |
png pdf |
Figure 11-a:
Post-fit distributions of the SvsB classifier score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ resolved analysis for data (black points) and the predicted background (blue filled histograms), for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red line) signals, scaled to improve their visibility, are overlaid. |
png pdf |
Figure 11-b:
Post-fit distributions of the SvsB classifier score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ resolved analysis for data (black points) and the predicted background (blue filled histograms), for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red line) signals, scaled to improve their visibility, are overlaid. |

png pdf |
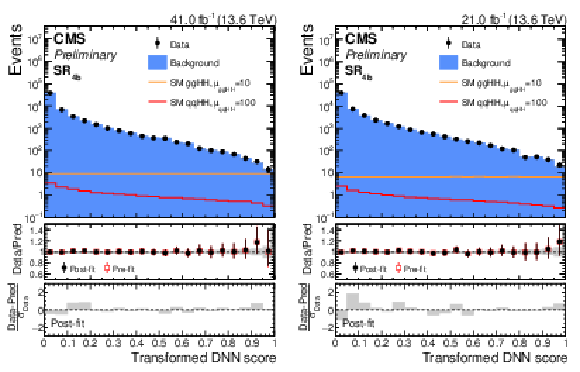
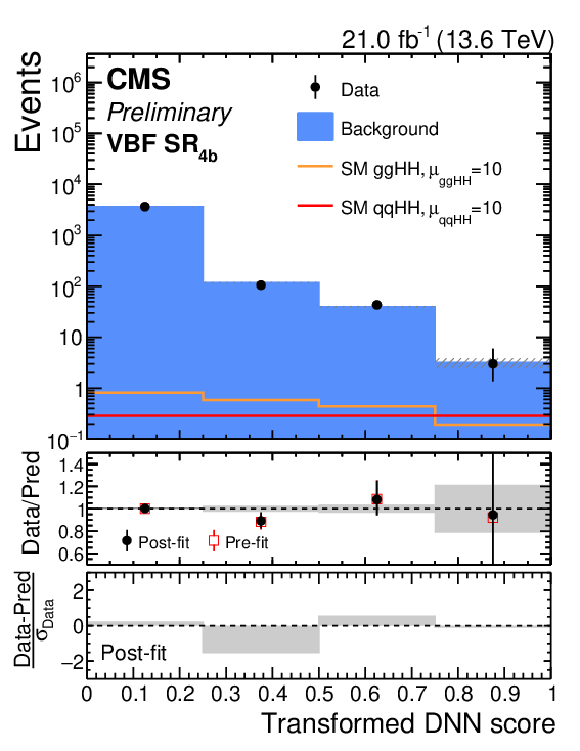
Figure 12:
Post-fit distributions of the SvsB output score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \text{qq}\mathrm{H}\mathrm{H} $ resolved analysis reported for data (black points) and the predicted background (blue filled histograms) for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $(red line) signals, scaled to improve their visibility, are overlaid. |

png pdf |
Figure 12-a:
Post-fit distributions of the SvsB output score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \text{qq}\mathrm{H}\mathrm{H} $ resolved analysis reported for data (black points) and the predicted background (blue filled histograms) for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $(red line) signals, scaled to improve their visibility, are overlaid. |
png pdf |
Figure 12-b:
Post-fit distributions of the SvsB output score in the $ \mathrm{SR_{4\mathrm{b}}} $ of the $ \text{qq}\mathrm{H}\mathrm{H} $ resolved analysis reported for data (black points) and the predicted background (blue filled histograms) for pre-ParkingHH (left) and post-ParkingHH (right) data. The distributions of the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange line) and $ \text{qq}\mathrm{H}\mathrm{H} $(red line) signals, scaled to improve their visibility, are overlaid. |
png pdf |
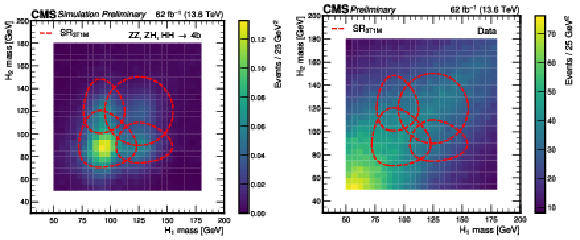
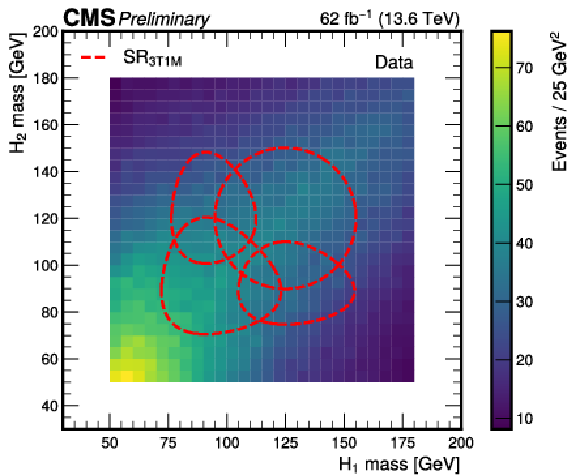
Figure 13:
The expected HH, ZH, and ZZ signal yields as estimated from simulation (left) and the observed data (right) for the Run 3 dataset, in the 3T1M region, as a function of the reconstructed masses of the leading and subleading in $ p_{\mathrm{T}} \mathrm{H} $ candidates. The signal region is defined by the union of the regions enclosed by the dashed red lines. |

png pdf |
Figure 13-a:
The expected HH, ZH, and ZZ signal yields as estimated from simulation (left) and the observed data (right) for the Run 3 dataset, in the 3T1M region, as a function of the reconstructed masses of the leading and subleading in $ p_{\mathrm{T}} \mathrm{H} $ candidates. The signal region is defined by the union of the regions enclosed by the dashed red lines. |
png pdf |
Figure 13-b:
The expected HH, ZH, and ZZ signal yields as estimated from simulation (left) and the observed data (right) for the Run 3 dataset, in the 3T1M region, as a function of the reconstructed masses of the leading and subleading in $ p_{\mathrm{T}} \mathrm{H} $ candidates. The signal region is defined by the union of the regions enclosed by the dashed red lines. |
png pdf |
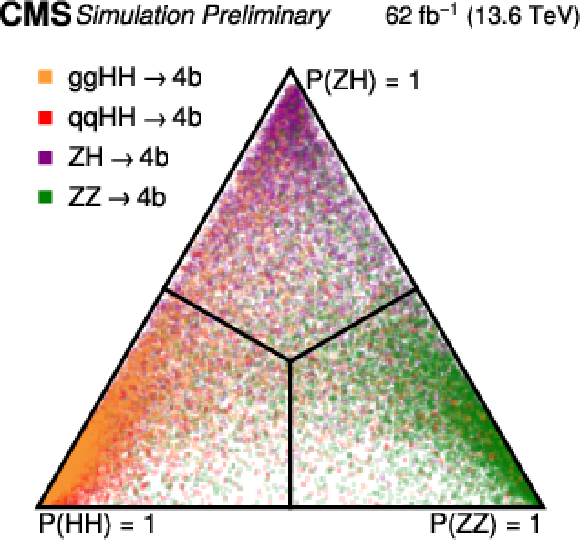
Figure 14:
Distribution of the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $, $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $, ZZ, and ZH signal processes, normalized to unity, as a function of the three FEYNNET probability scores. |
png pdf |
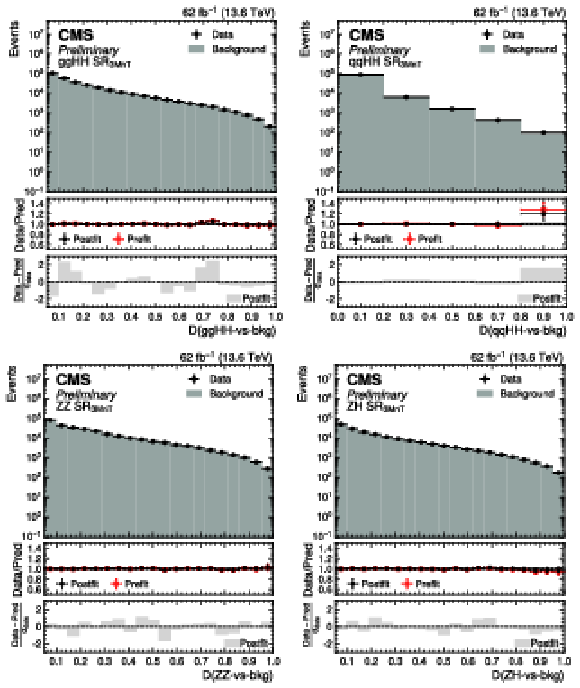
Figure 15:
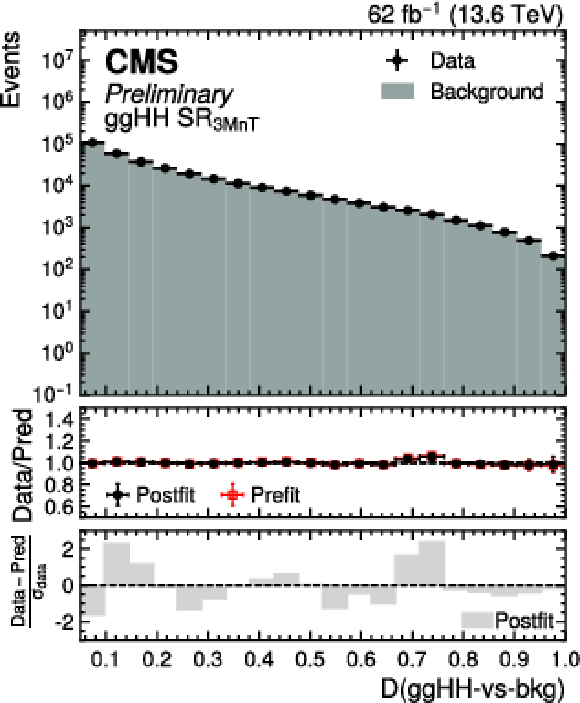
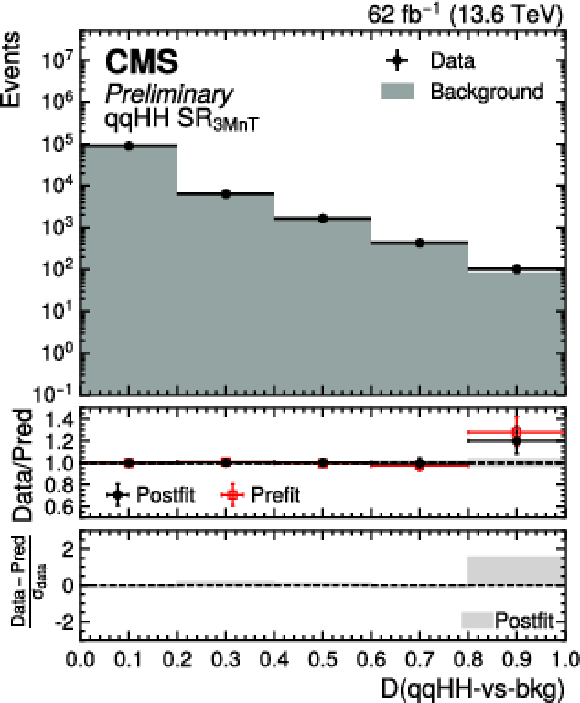
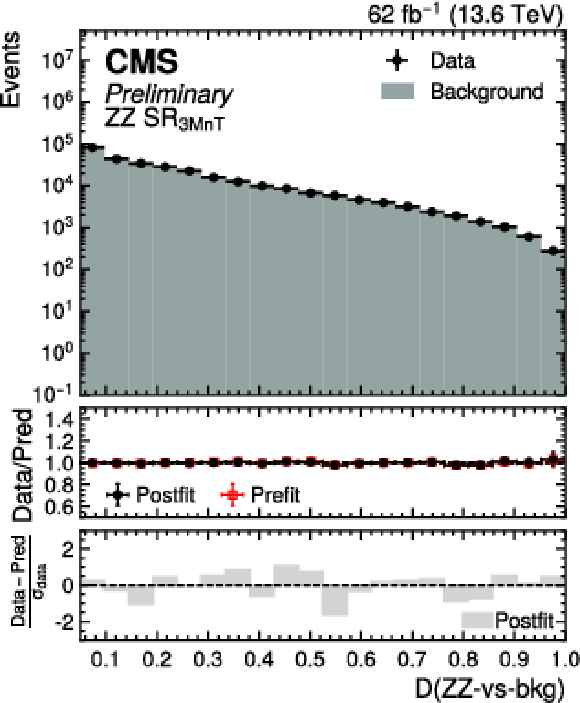
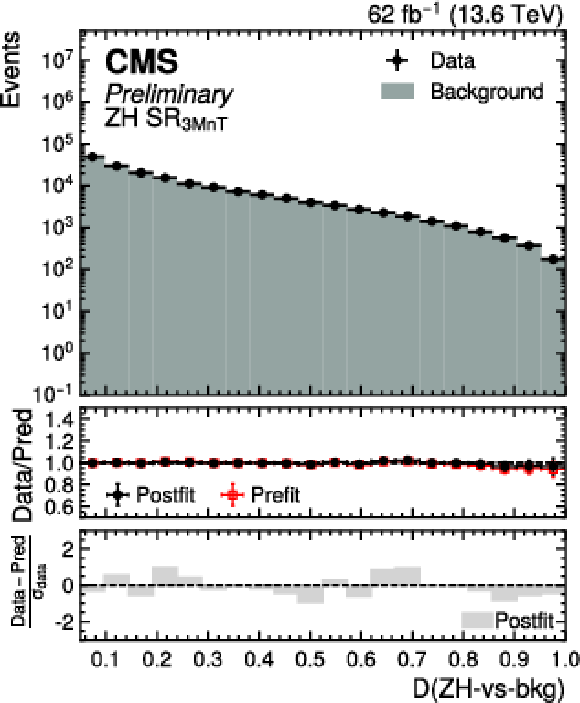
Postfit distribution of the $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) (upper left), $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) (upper right), $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) (lower left), and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) (lower right) scores in the validation region $ \text{SR}_{\text{3MnT}} $ for data (black points) and the predicted background (cyan filled histograms) with the Run 3 dataset. |
png pdf |
Figure 15-a:
Postfit distribution of the $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) (upper left), $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) (upper right), $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) (lower left), and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) (lower right) scores in the validation region $ \text{SR}_{\text{3MnT}} $ for data (black points) and the predicted background (cyan filled histograms) with the Run 3 dataset. |
png pdf |
Figure 15-b:
Postfit distribution of the $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) (upper left), $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) (upper right), $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) (lower left), and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) (lower right) scores in the validation region $ \text{SR}_{\text{3MnT}} $ for data (black points) and the predicted background (cyan filled histograms) with the Run 3 dataset. |
png pdf |
Figure 15-c:
Postfit distribution of the $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) (upper left), $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) (upper right), $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) (lower left), and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) (lower right) scores in the validation region $ \text{SR}_{\text{3MnT}} $ for data (black points) and the predicted background (cyan filled histograms) with the Run 3 dataset. |
png pdf |
Figure 15-d:
Postfit distribution of the $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) (upper left), $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) (upper right), $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) (lower left), and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) (lower right) scores in the validation region $ \text{SR}_{\text{3MnT}} $ for data (black points) and the predicted background (cyan filled histograms) with the Run 3 dataset. |

png pdf |
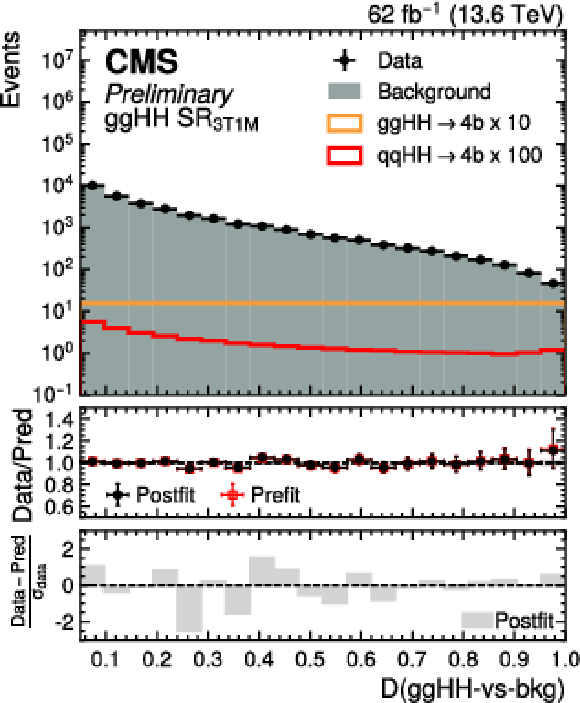
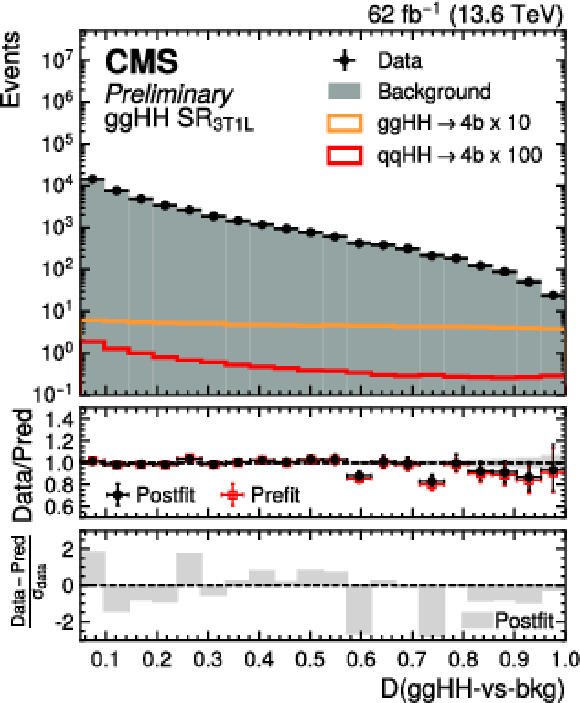
Figure 16:
Postfit distributions of the transformed $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (left) and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1L}} $ (middle) categories, and $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (right) category for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (orange line) and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (red line) signal processes, scaled to improve their visibility, are also overlaid. |
png pdf |
Figure 16-a:
Postfit distributions of the transformed $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (left) and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1L}} $ (middle) categories, and $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (right) category for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (orange line) and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (red line) signal processes, scaled to improve their visibility, are also overlaid. |
png pdf |
Figure 16-b:
Postfit distributions of the transformed $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (left) and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1L}} $ (middle) categories, and $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (right) category for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (orange line) and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (red line) signal processes, scaled to improve their visibility, are also overlaid. |

png pdf |
Figure 16-c:
Postfit distributions of the transformed $ D $ ($\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (left) and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1L}} $ (middle) categories, and $ D $ ($\mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H}$-vs-bkg) score in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} \text{SR}_{\text{3T1M}} $ (right) category for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (orange line) and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ (red line) signal processes, scaled to improve their visibility, are also overlaid. |
png pdf |
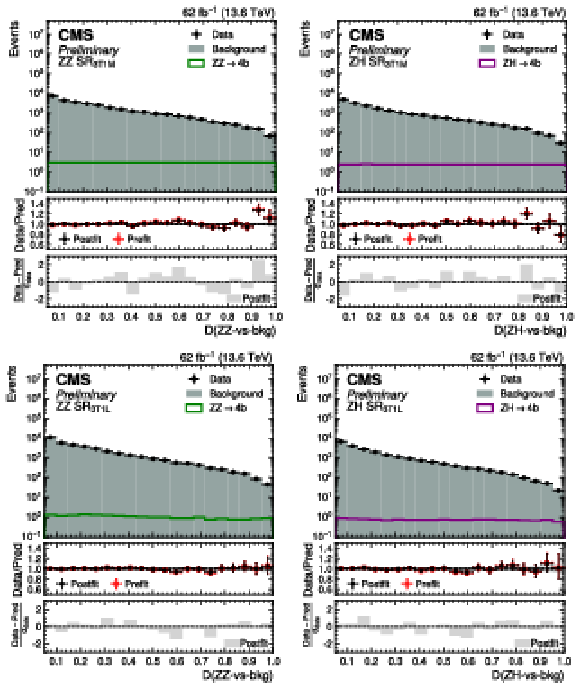
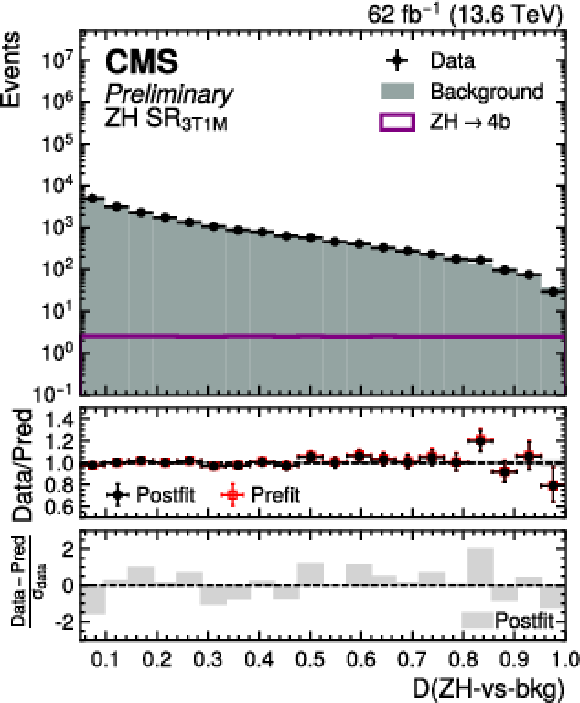
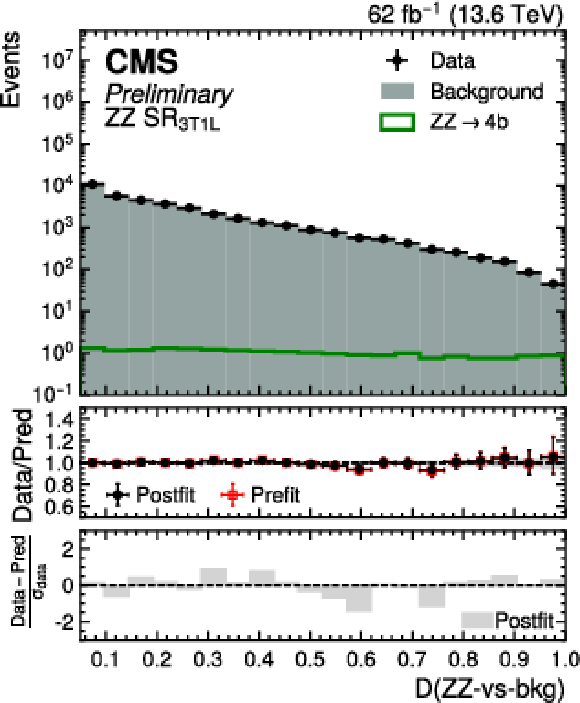
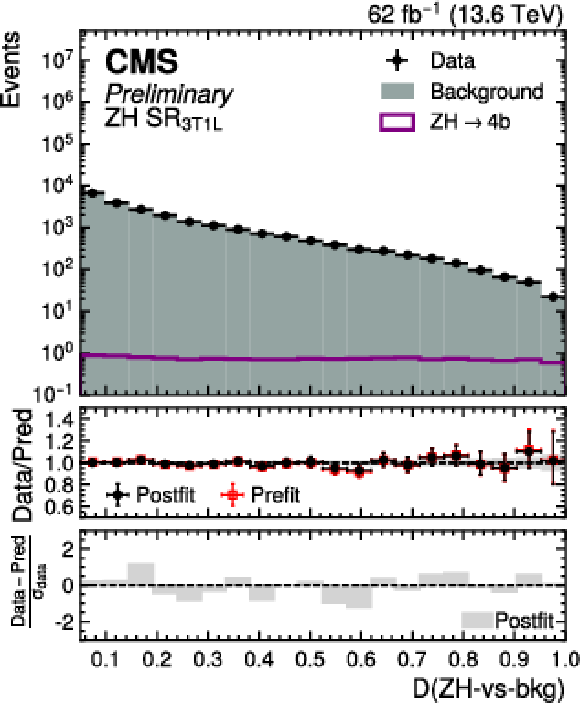
Figure 17:
Postfit distribution of the transformed $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1M}} $ (upper left) and $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1L}} $ (upper right) categories, and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1M}} $ (lower left) and $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1L}} $ (lower right) SR for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM ZZ (green line) and ZH (purple line) processes are also overlaid. |

png pdf |
Figure 17-a:
Postfit distribution of the transformed $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1M}} $ (upper left) and $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1L}} $ (upper right) categories, and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1M}} $ (lower left) and $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1L}} $ (lower right) SR for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM ZZ (green line) and ZH (purple line) processes are also overlaid. |
png pdf |
Figure 17-b:
Postfit distribution of the transformed $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1M}} $ (upper left) and $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1L}} $ (upper right) categories, and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1M}} $ (lower left) and $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1L}} $ (lower right) SR for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM ZZ (green line) and ZH (purple line) processes are also overlaid. |
png pdf |
Figure 17-c:
Postfit distribution of the transformed $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1M}} $ (upper left) and $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1L}} $ (upper right) categories, and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1M}} $ (lower left) and $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1L}} $ (lower right) SR for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM ZZ (green line) and ZH (purple line) processes are also overlaid. |
png pdf |
Figure 17-d:
Postfit distribution of the transformed $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1M}} $ (upper left) and $ \mathrm{Z}\mathrm{Z} \text{SR}_{\text{3T1L}} $ (upper right) categories, and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) score in the $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1M}} $ (lower left) and $ \mathrm{Z}\mathrm{H} \text{SR}_{\text{3T1L}} $ (lower right) SR for data (black points) and the predicted background (cyan filled histograms) for the Run 3 dataset. The distributions of the SM ZZ (green line) and ZH (purple line) processes are also overlaid. |
png pdf |
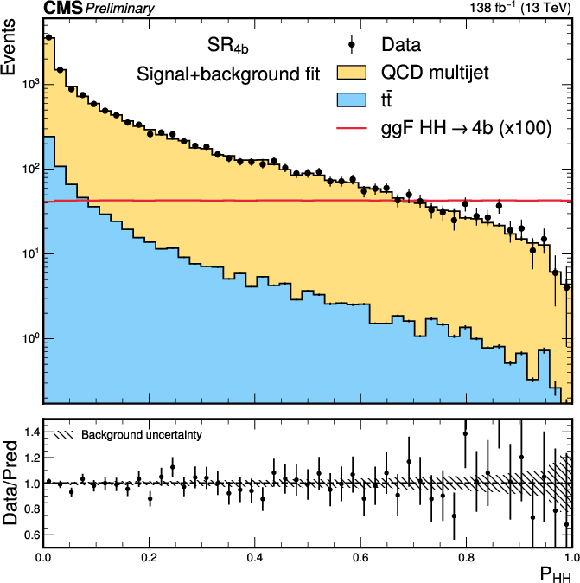
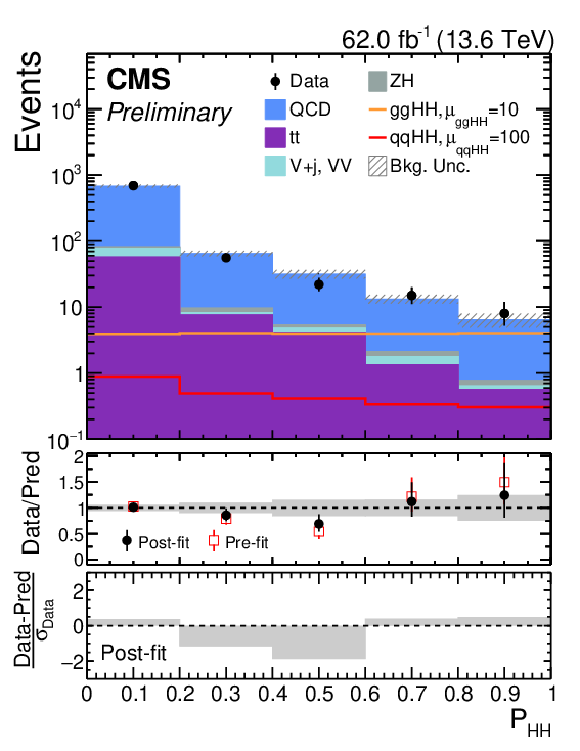
Figure 18:
The fitted signal+background distribution of the signal probability, $ \mathcal{P_{\mathrm{H}\mathrm{H}}} $, in the $ \mathrm{H}\mathrm{H} \mathrm{SR_{4\mathrm{b}}} $. The black points show the 4b events from data. The yellow and blue regions show the predictions from the QCD multijet model and the $ \mathrm{t} \overline{\mathrm{t}} $ simulation, respectively. The prediction for the SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ signal distribution is given by the red histogram, multiplied by 100. The lower panel shows the data-to-background ratio, with the hatched area representing the background uncertainty. |
png pdf |
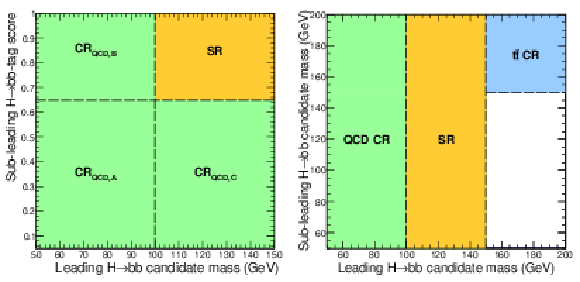
Figure 19:
Left: schematic diagram showing the regions used for the data-driven background estimation strategy used in the merged channel. The purity in QCD multijet events is reported in each of the background-enriched regions ($ \mathrm{CR_{QCD,A}} $, $ \mathrm{CR_{QCD,B}} $, and $ \mathrm{CR_{QCD,C}} $). Right: schematic diagram of the signal (orange area) and control regions (QCD in green, $ \mathrm{t} \overline{\mathrm{t}} $ in azure) in the plane defined by the $ m_\text{reg}({\mathrm{H}_1}) $ and $ m_\text{reg}({\mathrm{H}_2}) $. |

png pdf |
Figure 19-a:
Left: schematic diagram showing the regions used for the data-driven background estimation strategy used in the merged channel. The purity in QCD multijet events is reported in each of the background-enriched regions ($ \mathrm{CR_{QCD,A}} $, $ \mathrm{CR_{QCD,B}} $, and $ \mathrm{CR_{QCD,C}} $). Right: schematic diagram of the signal (orange area) and control regions (QCD in green, $ \mathrm{t} \overline{\mathrm{t}} $ in azure) in the plane defined by the $ m_\text{reg}({\mathrm{H}_1}) $ and $ m_\text{reg}({\mathrm{H}_2}) $. |
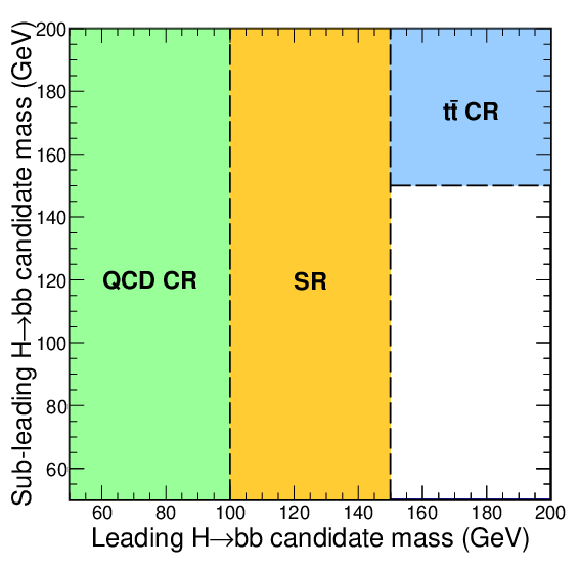
png pdf |
Figure 19-b:
Left: schematic diagram showing the regions used for the data-driven background estimation strategy used in the merged channel. The purity in QCD multijet events is reported in each of the background-enriched regions ($ \mathrm{CR_{QCD,A}} $, $ \mathrm{CR_{QCD,B}} $, and $ \mathrm{CR_{QCD,C}} $). Right: schematic diagram of the signal (orange area) and control regions (QCD in green, $ \mathrm{t} \overline{\mathrm{t}} $ in azure) in the plane defined by the $ m_\text{reg}({\mathrm{H}_1}) $ and $ m_\text{reg}({\mathrm{H}_2}) $. |

png pdf |
Figure 20:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the mass-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
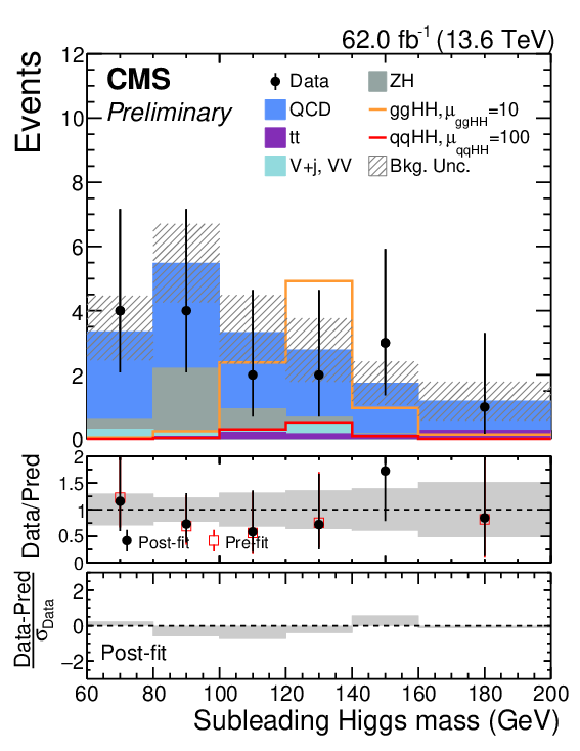
png pdf |
Figure 20-a:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the mass-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
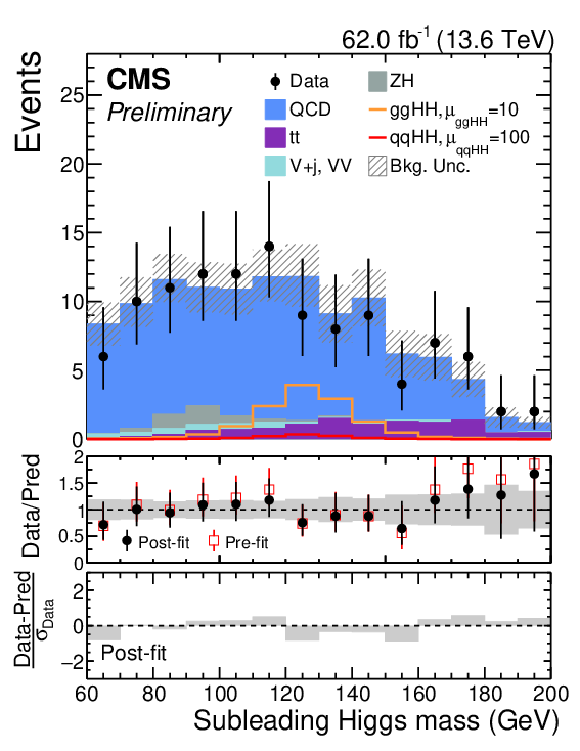
png pdf |
Figure 20-b:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the mass-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |

png pdf |
Figure 21:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the DNN-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
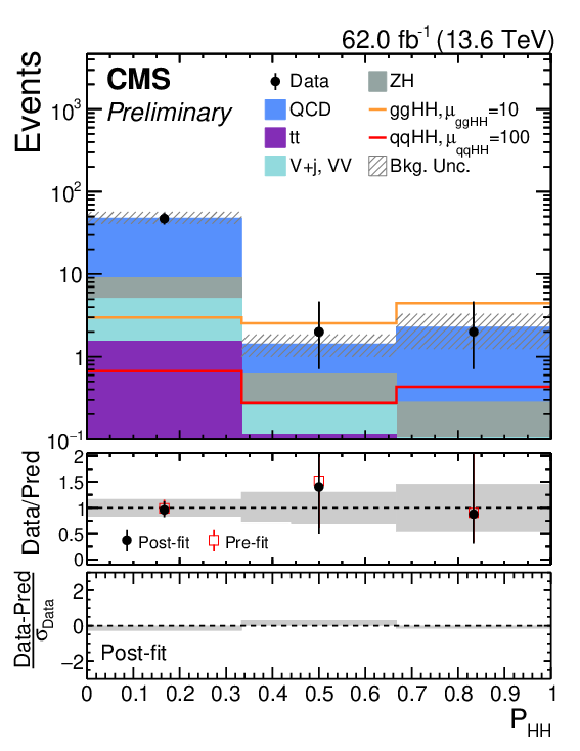
png pdf |
Figure 21-a:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the DNN-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
png pdf |
Figure 21-b:
Pre-fit and post-fit distributions of the fitted observables for the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-inclusive HPSR (left) and LPSR (right) categories of the merged analysis following the DNN-fit method. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
png pdf |
Figure 22:
Pre-fit and post-fit distributions of the fitted observables for the $ \text{qq}\mathrm{H}\mathrm{H} $ HPSR (left) and LPSR (right) categories of the merged analysis. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
png pdf |
Figure 22-a:
Pre-fit and post-fit distributions of the fitted observables for the $ \text{qq}\mathrm{H}\mathrm{H} $ HPSR (left) and LPSR (right) categories of the merged analysis. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |

png pdf |
Figure 22-b:
Pre-fit and post-fit distributions of the fitted observables for the $ \text{qq}\mathrm{H}\mathrm{H} $ HPSR (left) and LPSR (right) categories of the merged analysis. Distributions are shown for data (black points) and the different background contributions from QCD multijet, $ \mathrm{t} \overline{\mathrm{t}} $, $ \mathrm{V}+\text{jets} $, dibosons, and ZH productions. The expected distributions for SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ (orange) and $ \text{qq}\mathrm{H}\mathrm{H} $ (red) signals are overlaid and scaled by a multiplicative factor to improve their visibility. |
png pdf |
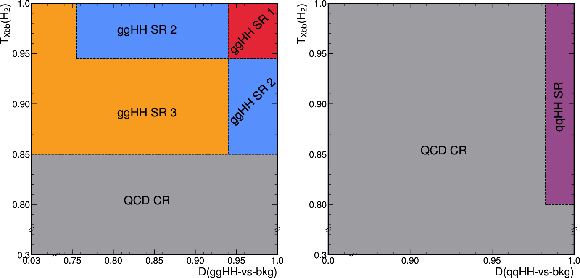
Figure 23:
Schematic diagrams showing the SRs and QCD CR (gray) used in the merged analysis described in Section 6.3. Left: the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (red), 2 (blue), and 3 (orange) are defined based on successively lower selections on the $ T_\text{Xbb} $ score of the \HepParticleHu candidate and the D(\text$ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $-vs-bkg) score. Right: the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (purple) is defined based on a Tight selection on D(\text$ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $-vs-bkg) and a Loose selection on $ T_\text{Xbb} $ of the \HepParticleHu candidate. |
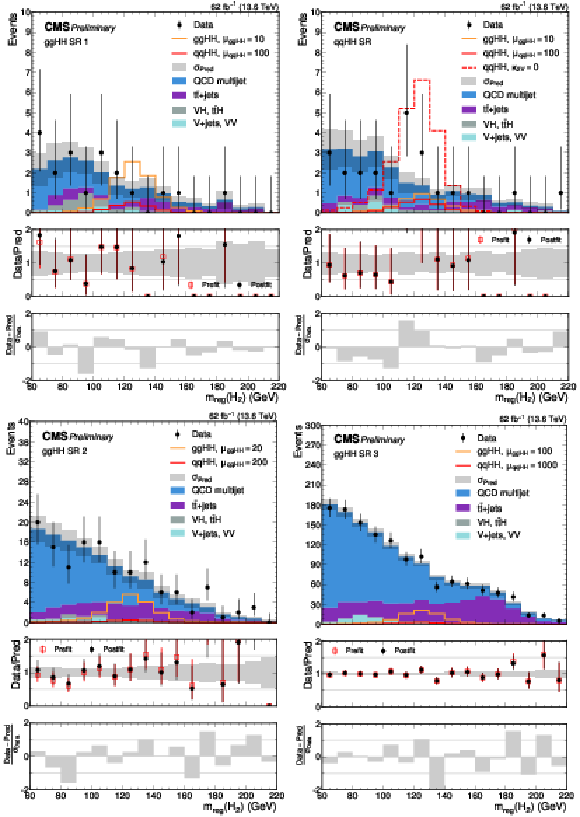
png pdf |
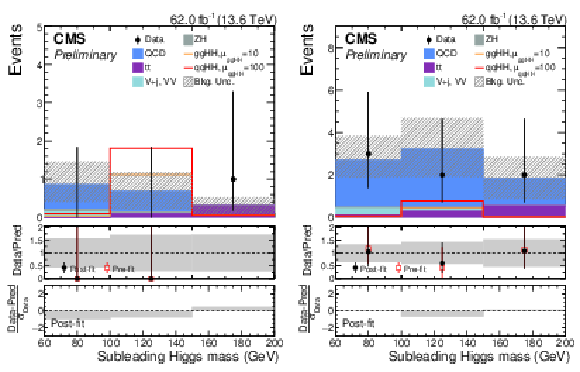
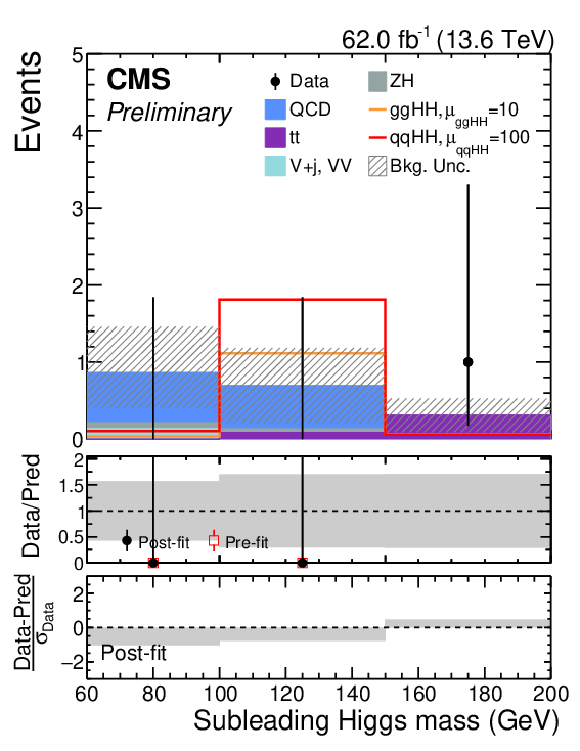
Figure 24:
The fitted signal+background distributions in the regressed mass of the secondary Higgs boson candidate $ m_\text{reg}(\mathrm{H_u}) $ in $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (upper left), the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (upper right), $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 2 (lower left), and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 3 (lower right). The SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal are overlaid in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SRs scaled by different factors. The targeted $ \kappa_{2\mathrm{V}}= $ 0 $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal is also overlaid in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR. |
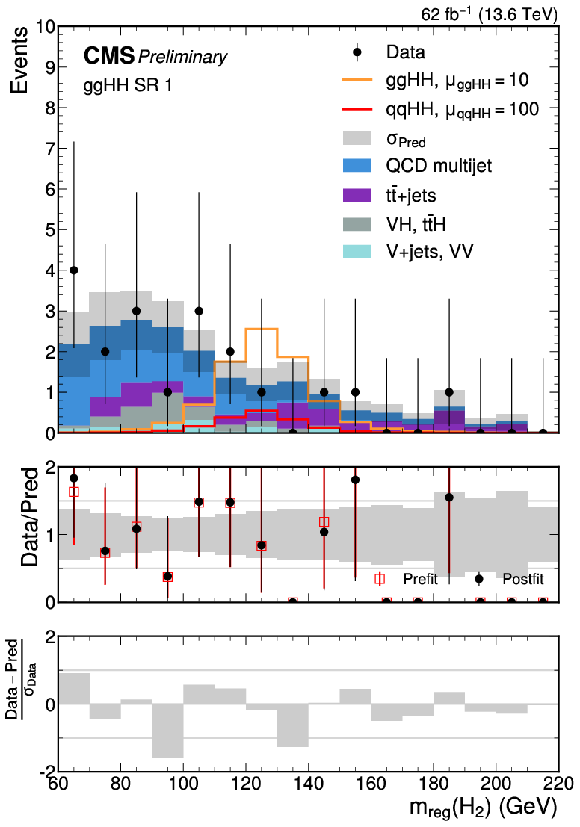
png pdf |
Figure 24-a:
The fitted signal+background distributions in the regressed mass of the secondary Higgs boson candidate $ m_\text{reg}(\mathrm{H_u}) $ in $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (upper left), the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (upper right), $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 2 (lower left), and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 3 (lower right). The SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal are overlaid in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SRs scaled by different factors. The targeted $ \kappa_{2\mathrm{V}}= $ 0 $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal is also overlaid in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR. |
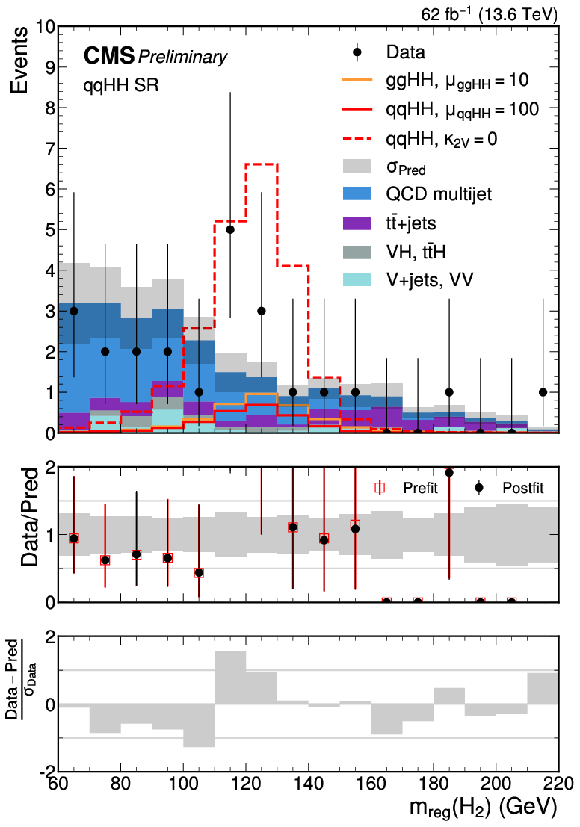
png pdf |
Figure 24-b:
The fitted signal+background distributions in the regressed mass of the secondary Higgs boson candidate $ m_\text{reg}(\mathrm{H_u}) $ in $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (upper left), the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (upper right), $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 2 (lower left), and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 3 (lower right). The SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal are overlaid in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SRs scaled by different factors. The targeted $ \kappa_{2\mathrm{V}}= $ 0 $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal is also overlaid in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR. |

png pdf |
Figure 24-c:
The fitted signal+background distributions in the regressed mass of the secondary Higgs boson candidate $ m_\text{reg}(\mathrm{H_u}) $ in $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (upper left), the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (upper right), $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 2 (lower left), and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 3 (lower right). The SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal are overlaid in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SRs scaled by different factors. The targeted $ \kappa_{2\mathrm{V}}= $ 0 $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal is also overlaid in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR. |
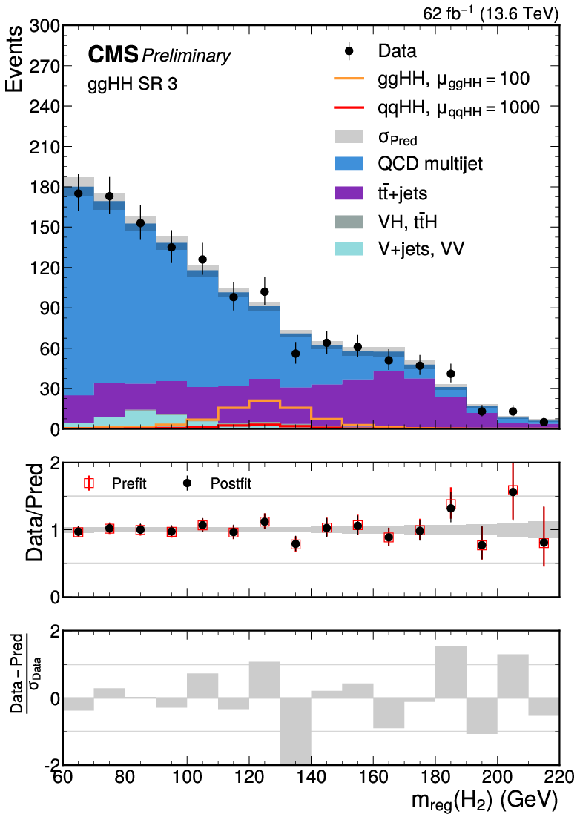
png pdf |
Figure 24-d:
The fitted signal+background distributions in the regressed mass of the secondary Higgs boson candidate $ m_\text{reg}(\mathrm{H_u}) $ in $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 1 (upper left), the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR (upper right), $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 2 (lower left), and $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SR 3 (lower right). The SM $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal are overlaid in the $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $ SRs scaled by different factors. The targeted $ \kappa_{2\mathrm{V}}= $ 0 $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal is also overlaid in the $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ SR. |
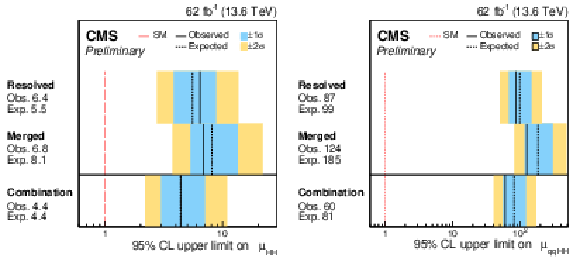
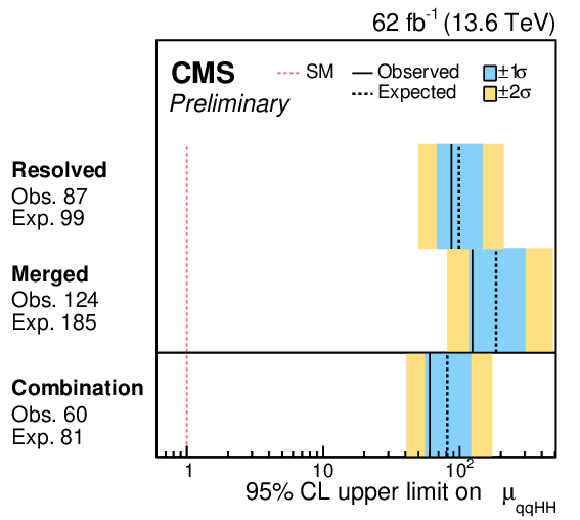
png pdf |
Figure 25:
Left: the observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of HH production from the resolved analysis with overlap removed, the merged HPSR mass-fit category, and their combination. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. Right: the same breakdown of 95% CL upper limits on the signal strength of $ \text{qq}\mathrm{H}\mathrm{H} $ production. |
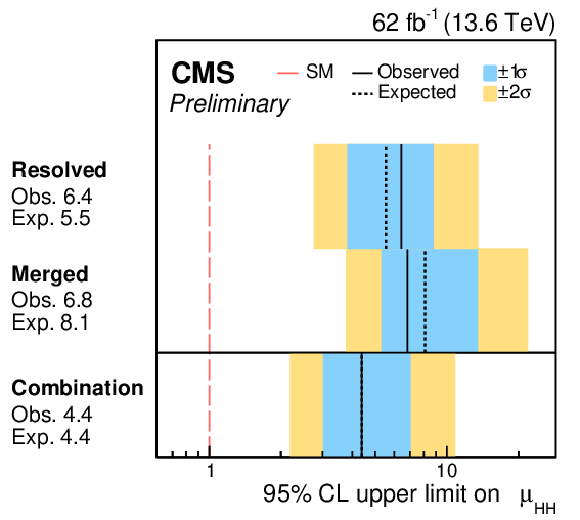
png pdf |
Figure 25-a:
Left: the observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of HH production from the resolved analysis with overlap removed, the merged HPSR mass-fit category, and their combination. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. Right: the same breakdown of 95% CL upper limits on the signal strength of $ \text{qq}\mathrm{H}\mathrm{H} $ production. |
png pdf |
Figure 25-b:
Left: the observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of HH production from the resolved analysis with overlap removed, the merged HPSR mass-fit category, and their combination. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. Right: the same breakdown of 95% CL upper limits on the signal strength of $ \text{qq}\mathrm{H}\mathrm{H} $ production. |
png pdf |
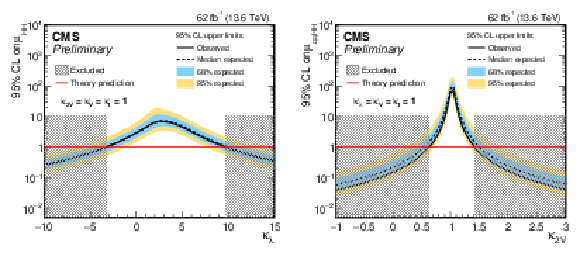
Figure 26:
The observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of the HH production ($ \mu_{\mathrm{H}\mathrm{H}} $) obtained as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. The horizontal red lines indicate the SM prediction. |

png pdf |
Figure 26-a:
The observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of the HH production ($ \mu_{\mathrm{H}\mathrm{H}} $) obtained as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. The horizontal red lines indicate the SM prediction. |
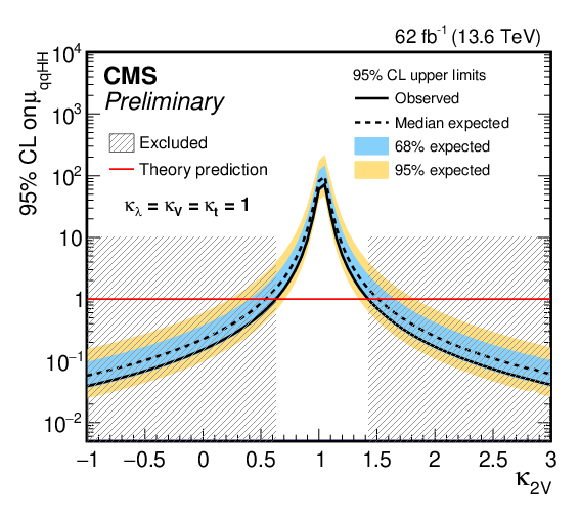
png pdf |
Figure 26-b:
The observed (solid) and expected (dashed) 95% CL upper limits on the signal strength of the HH production ($ \mu_{\mathrm{H}\mathrm{H}} $) obtained as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The cyan and blue bands represent, respectively, the 68 and 95% CL intervals around the expected limit. The horizontal red lines indicate the SM prediction. |

png pdf |
Figure 27:
The observed (solid) and expected (dashed) profile likelihood ratios as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses, where the expected is obtained from an Asimov dataset [100] defined by fixing the nuisances parameters to their maximum likelihood estimate obtained from data in which $ \mu_{\mathrm{H}\mathrm{H}}= $ 1. The 68 and 95% CL levels are indicated with the dashed red lines. |

png pdf |
Figure 27-a:
The observed (solid) and expected (dashed) profile likelihood ratios as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses, where the expected is obtained from an Asimov dataset [100] defined by fixing the nuisances parameters to their maximum likelihood estimate obtained from data in which $ \mu_{\mathrm{H}\mathrm{H}}= $ 1. The 68 and 95% CL levels are indicated with the dashed red lines. |
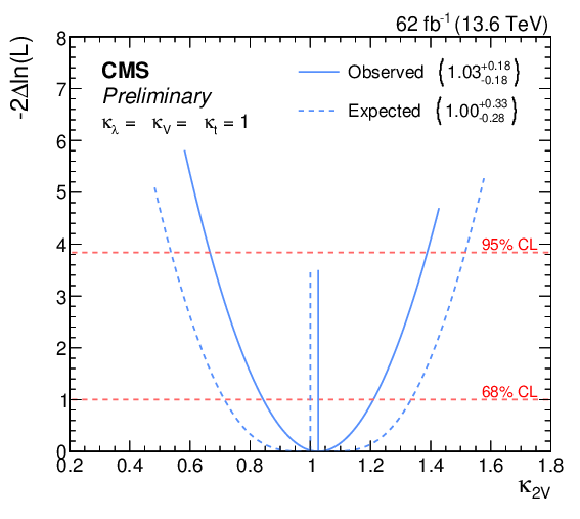
png pdf |
Figure 27-b:
The observed (solid) and expected (dashed) profile likelihood ratios as a function of $ \kappa_{\lambda} $ (left) and $ \kappa_{\text{2V}} $ (right) for the combined fit of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses, where the expected is obtained from an Asimov dataset [100] defined by fixing the nuisances parameters to their maximum likelihood estimate obtained from data in which $ \mu_{\mathrm{H}\mathrm{H}}= $ 1. The 68 and 95% CL levels are indicated with the dashed red lines. |
png pdf |
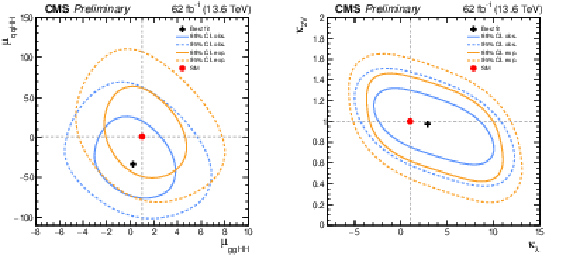
Figure 28:
The observed (blue) and expected (orange) 2D exclusion range for ($ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $, $ \mu_{\text{qq}\mathrm{H}\mathrm{H}} $) (left) and ($ \kappa_{\lambda} $,$ \kappa_{\text{2V}} $) (right) for the combination of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The solid and dashed lines represent the 68 and 95% CL exclusion contours, respectively. The red circle indicates the SM prediction, while the black cross shows the best-fit result. |

png pdf |
Figure 28-a:
The observed (blue) and expected (orange) 2D exclusion range for ($ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $, $ \mu_{\text{qq}\mathrm{H}\mathrm{H}} $) (left) and ($ \kappa_{\lambda} $,$ \kappa_{\text{2V}} $) (right) for the combination of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The solid and dashed lines represent the 68 and 95% CL exclusion contours, respectively. The red circle indicates the SM prediction, while the black cross shows the best-fit result. |
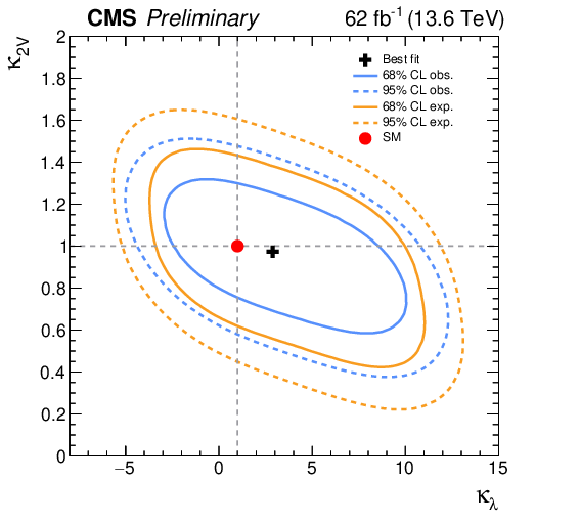
png pdf |
Figure 28-b:
The observed (blue) and expected (orange) 2D exclusion range for ($ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $, $ \mu_{\text{qq}\mathrm{H}\mathrm{H}} $) (left) and ($ \kappa_{\lambda} $,$ \kappa_{\text{2V}} $) (right) for the combination of resolved and merged $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ analyses. The solid and dashed lines represent the 68 and 95% CL exclusion contours, respectively. The red circle indicates the SM prediction, while the black cross shows the best-fit result. |
| Tables | |

png pdf |
Table 1:
The observed (expected) upper limits at 95% CL on the $ \mu_{\mathrm{Z}\mathrm{Z}} $ and $ \mu_{\mathrm{Z}\mathrm{H}} $, observed signal strength and significance. The upper limits are obtained from a fit on the $ D $ ($\mathrm{Z}\mathrm{Z}$-vs-bkg) and $ D $ ($\mathrm{Z}\mathrm{H}$-vs-bkg) scores under the hypothesis of no $ \mathrm{Z}\mathrm{Z} \rightarrow4\mathrm{b} $ or $ \mathrm{Z}\mathrm{H} \rightarrow4\mathrm{b} $ signal. |
png pdf |
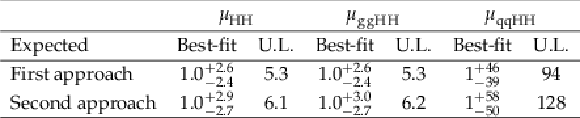
Table 2:
Expected best-fit values and 95% CL upper limits (``U.L.'') for $ \mu_{\mathrm{HH}} $, $ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $, and $ \mu_{\text{qq}\mathrm{H}\mathrm{H}} $ in the $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ resolved analysis following the two approaches described in Secs. 5.2 and 5.3, respectively. The uncertainties given for the best-fit signal strengths correspond to the 68% CL intervals. The best-fit signal strengths are calculated with a SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal injected, while the upper limits are calculated in the absence of signal. |

png pdf |
Table 3:
Observed best-fit values and 95% CL upper limits (``U.L.'') for $ \mu_{\mathrm{HH}} $, $ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $, and $ \mu_{\text{qq}\mathrm{H}\mathrm{H}} $ in the $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ resolved analysis following the two approaches described in Secs. 5.2 and 5.3, respectively. The uncertainties given for the best-fit signal strengths correspond to the 68% CL intervals. |

png pdf |
Table 4:
Observed and expected, in absence of signal, 95% CL intervals for $ \kappa_{\lambda} $ and $ \kappa_{\text{2V}} $ in the $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ resolved analysis, following the two approaches described in Secs. 5.2 and 5.3, respectively. |

png pdf |
Table 5:
Expected and observed $ \mu_{\mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H}} $ and their corresponding upper limits at 95% CL in the $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ resolved channel with Run 2 data (described in Section 5.4). The observed and expected 95% CL intervals for $ \kappa_{\lambda} $ are also reported. |
png pdf |
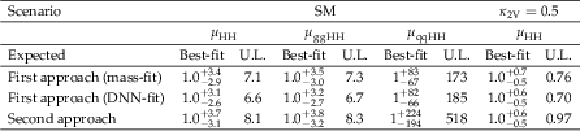
Table 6:
The expected best-fit signal strengths and 95% CL upper limits on the inclusive, $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $, and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal strengths for the SM scenario for the two approaches described in Sections 6.2 and 6.3, respectively. The expected best-fit signal strength and 95% CL upper limit on the HH signal strength for the non-SM $ \kappa_{2\mathrm{V}}= $ 0.5 scenario are also reported. The uncertainties given for the best-fit signal strengths correspond to the 68% CL intervals. The best-fit signal strengths are calculated with a SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal injected, while the upper limits are calculated in the absence of signal. |

png pdf |
Table 7:
The observed best-fit signal strengths and 95% CL upper limits on the inclusive, $ \mathrm{g}\mathrm{g}\mathrm{H}\mathrm{H} $, and $ \mathrm{q}\mathrm{q}\mathrm{H}\mathrm{H} $ signal strengths for the SM scenario for the two approaches described in Sections 6.2 and 6.3, respectively. The best-fit and observed 95% CL upper limits on the HH signal strength for the non-SM $ \kappa_{2\mathrm{V}}= $ 0.5 are also reported. The uncertainties given for the best-fit signal strengths correspond to the 68% CL intervals. |

png pdf |
Table 8:
The observed and expected 95% CL intervals for $ \kappa_\lambda $ and $ \kappa_{2\mathrm{V}} $ in the merged channel for the two approaches described in Sections 6.2 and 6.3, respectively. |

png pdf |
Table 9:
Expected and observed best-fit values for the signal strengths, $ \kappa_{\lambda} $, and $ \kappa_{\text{2V}} $ from the combined fit of the $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ resolved and merged analyses. The uncertainties given correspond to the 68% CL intervals. The expected results are calculated with a SM $ \mathrm{H}\mathrm{H} \to 4\mathrm{b} $ signal injected. |
| Summary |
| Measurements of Higgs boson pair (HH) production in the four bottom quark final state are presented using a data set of proton-proton (pp) collisions at $ \sqrt{s}= $ 13.6 TeV collected by the CMS experiment during 2022-2023 and corresponding to an integrated luminosity of 62 fb$ ^{-1} $. Events in which each Higgs boson decay is separately reconstructed as a pair of small-radius jets (resolved), as well as events in which each $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ decay is reconstructed as a single large-radius jet (merged) are analyzed exclusively. Benefiting from novel analysis techniques, the combination of resolved and merged channels gives an observed (expected) upper limit at 95% confidence level (CL) on the HH signal strength $ \mu_{\mathrm{H}\mathrm{H}} $, defined as the observed HH production cross section divided by the standard model (SM) prediction, of 4.4 (4.4). Compared to previous LHC results, the expected limit with an equivalent integrated luminosity is improved by more than a factor two in the resolved topology and significantly improved in the merged topology as well. The allowed ranges at 95% CL for the Higgs trilinear self-coupling and quartic coupling between two Higgs bosons and two vector bosons, relative to the standard model expectation, are observed (expected, in absence of signal) to be $ [-3.3,9.7] $ ($ [-3.4,10.0] $) and $ [0.63,1.43] $ ($ [0.54,1.51] $), respectively. An updated analysis of the resolved topology using a 13 TeV pp collision data set corresponding to 138 fb$ ^{-1} $ and collected in 2016-2018, reports an observed (expected) 95% CL upper limit on $ \mu_{\mathrm{H}\mathrm{H}} $ of 10.0 (5.9), an improvement of about 25% in the expected limit compared to the published results using the same data. |
| References | ||||
| 1 | F. Englert and R. Brout | Broken symmetry and the mass of gauge vector mesons | PRL 13 (1964) 321 | |
| 2 | P. W. Higgs | Broken symmetries, massless particles and gauge fields | PL 12 (1964) 132 | |
| 3 | P. W. Higgs | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 508 | |
| 4 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global conservation laws and massless particles | PRL 13 (1964) 585 | |
| 5 | P. W. Higgs | Spontaneous symmetry breakdown without massless bosons | PR 145 (1966) 1156 | |
| 6 | T. W. B. Kibble | Symmetry breaking in non-abelian gauge theories | PR 155 (1967) 1554 | |
| 7 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 8 | CMS Collaboration | Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 9 | CMS Collaboration | A portrait of the Higgs boson by the CMS experiment ten years after the discovery. | Nature 607 (2022) 60 | CMS-HIG-22-001 2207.00043 |
| 10 | ATLAS Collaboration | A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery | Nature 607 (2022) 52 | 2207.00092 |
| 11 | J. Alison et al. | Higgs boson potential at colliders: Status and perspectives | Rev. Phys. 5 (2020) 100045 | 1910.00012 |
| 12 | F. Bishara, R. Contino, and J. Rojo | Higgs pair production in vector-boson fusion at the LHC and beyond | EPJC 77 (2017) 481 | 1611.03860 |
| 13 | ATLAS Collaboration | Combination of Searches for Higgs Boson Pair Production in $ pp $ Collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS Detector | PRL 133 (2024) 101801 | 2406.09971 |
| 14 | CMS Collaboration | Combination of searches for nonresonant Higgs boson pair production in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | technical report, 2025 link |
CMS-HIG-20-011 2510.07527 |
| 15 | ATLAS Collaboration | Studies of new Higgs boson interactions through nonresonant HH production in the $ b\overline{b}\gamma \gamma $ final state in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 01 (2024) 066 | 2310.12301 |
| 16 | ATLAS Collaboration | Search for nonresonant pair production of higgs bosons in the $ b\overline{b}b\overline{b} $ final state in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the atlas detector | PRD 108 (2023) 052003 | 2301.03212 |
| 17 | ATLAS Collaboration | Search for the nonresonant production of higgs boson pairs via gluon fusion and vector-boson fusion in the $ b\overline{b}{\tau}^{+}{\tau}^{-} $ final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the atlas detector | PRD 110 (2024) 032012 | 2404.12660 |
| 18 | ATLAS Collaboration | Search for non-resonant Higgs boson pair production in final states with leptons, taus, and photons in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 08 (2024) 164 | 2405.20040 |
| 19 | ATLAS Collaboration | Search for non-resonant Higgs boson pair production in the 2 $ b+2\ell +{E}_{\textrm{T}}^{\textrm{miss}} $ final state in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 02 (2024) 037 | 2310.11286 |
| 20 | CMS Collaboration | Search for nonresonant Higgs boson pair production in final state with two bottom quarks and two tau leptons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 842 (2023) 137531 | CMS-HIG-20-010 2206.09401 |
| 21 | CMS Collaboration | Search for Higgs boson pair production with one associated vector boson in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 10 (2024) 061 | CMS-HIG-22-006 2404.08462 |
| 22 | CMS Collaboration | Search for Higgs boson pairs decaying to WW*WW*, WW*$ \tau\tau $, and $ \tau\tau\tau\tau $ in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2023) 095 | CMS-HIG-21-002 2206.10268 |
| 23 | CMS Collaboration | Search for Higgs boson pair production in the $ \textrm{b}\overline{\textrm{b}}{\textrm{W}}^{+}{\textrm{W}}^{-} $ decay mode in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2024) 293 | CMS-HIG-21-005 2403.09430 |
| 24 | ATLAS Collaboration | Study of Higgs boson pair production in the $ HH \rightarrow b \overline{b} \gamma\gamma $ final state with 308 fb$ ^{-1} $ of data collected at $ \sqrt{s} = $ 13 TeV and 13.6 TeV by the ATLAS experiment | technical report, 2025 link |
2507.03495 |
| 25 | CMS Collaboration | Search for Higgs Boson Pair Production in the Four b Quark Final State in Proton-Proton Collisions at $ \sqrt{s} = $ 13 TeV | PRL 129 (2022) 081802 | CMS-HIG-20-005 2202.09617 |
| 26 | ATLAS Collaboration | Search for pair production of boosted Higgs bosons via vector-boson fusion in the bbbb final state using pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PLB 858 (2024) 139007 | 2404.17193 |
| 27 | CMS Collaboration | Search for Nonresonant Pair Production of Highly Energetic Higgs Bosons Decaying to Bottom Quarks | PRL 131 (2023) 041803 | 2205.06667 |
| 28 | CMS Collaboration | Search for ZZ and ZH Production in the $ \mathrm{b\overline{b}b\overline{b}} $ Final State using Proton-Proton Collisions at $ \sqrt{s} = $ 13 TeV | EPJC 84 (2024) 712 | CMS-HIG-22-011 2403.20241 |
| 29 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 30 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 31 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 32 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 33 | CMS Collaboration | Performance of the CMS high-level trigger during LHC run 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 34 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 35 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 36 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 37 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 38 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 39 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 40 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 02 (2012) 088 | 1111.2854 |
| 41 | G. Heinrich et al. | NLO predictions for Higgs boson pair production with full top quark mass dependence matched to parton showers | JHEP 08 (2017) 088 | 1703.09252 |
| 42 | S. Jones and S. Kuttimalai | Parton shower and NLO-matching uncertainties in Higgs boson pair production | JHEP 02 (2018) 176 | 1711.03319 |
| 43 | G. Buchalla et al. | Higgs boson pair production in non-linear effective field theory with full $ m_\mathrm{t} $-dependence at NLO QCD | JHEP 09 (2018) 057 | 1806.05162 |
| 44 | G. Heinrich et al. | Probing the trilinear Higgs boson coupling in di-Higgs production at NLO QCD including parton shower effects | JHEP 06 (2019) 066 | 1903.08137 |
| 45 | G. Heinrich, S. P. Jones, M. Kerner, and L. Scyboz | A non-linear EFT description of $ \mathrm{g}\mathrm{g}\to\mathrm{H}\mathrm{H} $ at NLO interfaced to POWHEG | JHEP 10 (2020) 021 | 2006.16877 |
| 46 | J. Davies et al. | Double Higgs boson production at NLO: Combining the exact numerical result and high-energy expansion | JHEP 11 (2019) 024 | 1907.06408 |
| 47 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 48 | S. Dawson, S. Dittmaier, and M. Spira | Neutral Higgs boson pair production at hadron colliders: QCD corrections | PRD 58 (1998) 115012 | hep-ph/9805244 |
| 49 | D. Y. Shao, C. S. Li, H. T. Li, and J. Wang | Threshold resummation effects in Higgs boson pair production at the LHC | JHEP 07 (2013) 169 | 1301.1245 |
| 50 | D. de Florian and J. Mazzitelli | Higgs Boson Pair Production at Next-to-Next-to-Leading Order in QCD | PRL 111 (2013) 201801 | 1309.6594 |
| 51 | D. de Florian and J. Mazzitelli | Higgs pair production at next-to-next-to-leading logarithmic accuracy at the LHC | JHEP 09 (2015) 053 | 1505.07122 |
| 52 | S. Borowka et al. | Higgs boson pair production in gluon fusion at next-to-leading order with full top-quark mass dependence | PRL 117 (2016) 012001 | 1604.06447 |
| 53 | M. Grazzini et al. | Higgs boson pair production at NNLO with top quark mass effects | JHEP 05 (2018) 059 | 1803.02463 |
| 54 | J. Baglio et al. | Gluon fusion into Higgs pairs at NLO QCD and the top mass scheme | EPJC 79 (2019) 459 | 1811.05692 |
| 55 | J. Baglio et al. | $ gg \rightarrow HH $: Combined uncertainties | PRD 103 (2021) 056002 | 2008.11626 |
| 56 | F. A. Dreyer and A. Karlberg | Vector-boson fusion Higgs pair production at N$ ^3 $LO | PRD 98 (2018) 114016 | 1811.07906 |
| 57 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 58 | T. Ježo et al. | An NLO+PS generator for $ {\mathrm{t}\overline{\mathrm{t}}} $ and $ \mathrm{W}\mathrm{t} $ production and decay including non-resonant and interference effects | EPJC 76 (2016) 691 | 1607.04538 |
| 58 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | Comput. Phys. Commun. 185 (2014) 2930 | 1112.5675 |
| 60 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 61 | T. Sjostrand et al. | An introduction to PYTHIA8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 62 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 63 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 64 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 65 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 66 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 67 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 68 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 69 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 70 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 71 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 72 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 73 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 74 | H. Qu and L. Gouskos | ParticleNet: Jet Tagging via Particle Clouds | PRD 101 (2020) 056019 | 1902.08570 |
| 75 | CMS Collaboration | Performance of the ParticleNet tagger on small and large-radius jets at High Level Trigger in Run 3 | CMS Detector Performance Note CMS-DP-2023-021, CERN, 2023 CDS |
|
| 76 | CMS Collaboration | Novel strategy targeting HH and HHH production at High Level Trigger in Run 3 | CMS Detector Performance Note CMS-DP-23-050, CERN, 2023 CDS |
|
| 77 | CMS Collaboration | Enriching the physics program of the CMS experiment via data scouting and data parking | Phys. Rept. 1115 (2025) 678 | CMS-EXO-23-007 2403.16134 |
| 78 | CMS Collaboration | Measurement of the Inclusive $ W $ and $ Z $ Production Cross Sections in $ pp $ Collisions at $ \sqrt{s}= $ 7 TeV | JHEP 10 (2011) 132 | CMS-EWK-10-005 1107.4789 |
| 79 | CMS Collaboration | Efficiency of the ParticleNet b-tagging algorithm used in the CMS High-Level Trigger in 2022 and 2023 | CMS Detector Performance Note CMS-DP-2023-089, CERN, 2023 CDS |
|
| 80 | CMS Collaboration | Search for Higgs Boson Decay to a Charm Quark-Antiquark Pair in Proton-Proton Collisions at $ \sqrt{s}= $ 13 TeV | PRL 131 (2023) 061801 | CMS-HIG-21-008 2205.05550 |
| 81 | CMS Collaboration | Performance of heavy-flavour jet identification in boosted topologies in proton-proton collisions at sqrt(s) = 13 TeV | CMS Physics Analysis Summary, CERN, 2023 CMS-PAS-BTV-22-001 |
CMS-PAS-BTV-22-001 |
| 82 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 83 | CMS Collaboration | Run 3 commissioning results of heavy-flavor jet tagging at $ \sqrt{s}= $13.6 TeV with CMS data using a modern framework for data processing | CMS Detector Performance Note CMS-DP-2024-024, CERN, 2024 CDS |
|
| 84 | E. Bols et al. | Jet Flavour Classification Using DeepJet | JINST 15 (2020) P12012 | 2008.10519 |
| 85 | CMS Collaboration | Performance summary of AK4 jet b tagging with data from proton-proton collisions at 13 TeV with the CMS detector | CMS Detector Performance Note CMS-DP-2023-005, CERN, 2023 CDS |
|
| 86 | CMS Collaboration | Performance summary of AK4 jet b tagging with data from 2022 proton-proton collisions at 13.6 TeV with the CMS detector | CMS Detector Performance Note CMS-DP-2024-025, CERN, 2024 CDS |
|
| 87 | CMS Collaboration | A Deep Neural Network for Simultaneous Estimation of b Jet Energy and Resolution | Comput. Softw. Big Sci. 4 (2020) 10 | CMS-HIG-18-027 1912.06046 |
| 88 | H. Qu, C. Li, and S. Qian | Particle Transformer for Jet Tagging | 2202.03772 | |
| 89 | CMS Collaboration | Search for highly energetic double Higgs boson production in the two bottom quark and two vector boson all-hadronic final state | CMS Physics Analysis Summary, CERN, 2024 CMS-PAS-HIG-23-012 |
CMS-PAS-HIG-23-012 |
| 90 | CMS Collaboration | Particle transformers for identifying Lorentz-boosted Higgs bosons decaying to a pair of W bosons | CMS Physics Analysis Summary, CERN, 2025 CMS-PAS-JME-25-001 |
CMS-PAS-JME-25-001 |
| 91 | CMS Collaboration | Identification of highly Lorentz-boosted heavy particles using graph neural networks and new mass decorrelation techniques | CMS Detector Performance Note CMS-DP-2020-002, CERN, 2020 CDS |
|
| 92 | CMS Collaboration | Mass regression of highly-boosted jets using graph neural networks | CMS Detector Performance Note CMS-DP-2021-017, CERN, 2021 CDS |
|
| 93 | J. M. Lindert et al. | Precise predictions for $ V+ $ jets dark matter backgrounds | EPJC 77 (2017) 829 | 1705.04664 |
| 94 | ATLAS Collaboration | Efficiency corrections for a tagger for boosted $ H\rightarrow b\bar{b} $ decays in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | technical report, CERN, Geneva, All figures including auxiliary figures are available at this link |
|
| 95 | R. A. Fisher | On the interpretation of $ \chi^2 $ from contingency tables, and the calculation of p | Journal of the Royal Statistical Society 85 (2018) 87 | |
| 96 | D0 Collaboration | Search for high mass top quark production in $ p\bar{p} $ collisions at $ \sqrt{s} = $ 1.8 TeV | PRL 74 (1995) 2422 | hep-ex/9411001 |
| 97 | R. Kohavi | A study of cross-validation and bootstrap for accuracy estimation and model selection | in Proceedings of the 14th International Joint Conference on Artificial Intelligence - Volume 2, IJCAI'95. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 1995 | |
| 98 | A. Vaswani et al | Attention is all you need | link | |
| 99 | H. A. Panofsky and G. W. G. W. Brier | Some applications of statistics to meteorology | Mineral Industries Extension Services, College of Mineral Industries, Pennsylvania State University, 1st ed. edition, 1958 | |
| 100 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 101 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs Cross Sections: 4. Deciphering the nature of the Higgs sector | CERN Yellow Rep. Monogr. 2 (2017) | 1610.07922 |
| 102 | L.-S. Ling et al. | NNLO QCD corrections to Higgs pair production via vector boson fusion at hadron colliders | PRD 89 (2014) 073001 | 1401.7754 |
| 103 | F. A. Dreyer and A. Karlberg | Fully differential vector-boson fusion Higgs pair production at next-to-next-to-leading order | PRD 99 (2019) 074028 | 1811.07918 |
| 104 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 105 | J. S. Conway | Incorporating Nuisance Parameters in Likelihoods for Multisource Spectra | in PHYSTAT 2011, p. 115. 2011 link |
1103.0354 |
| 106 | R. Barlow and C. Beeston | Fitting using finite monte carlo samples | Computer Physics Communications 77 (1993) 219 | |
| 107 | ATLAS, CMS, LHC Higgs Combination Group Collaboration | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011 | |
| 108 | A. L. Read | Presentation of search results: The $ CL_s $ technique | JPG 28 (2002) 2693 | |
| 109 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 110 | CMS Collaboration | The CMS Statistical Analysis and Combination Tool: Combine | Comput. Softw. Big Sci. 8 (2024) 19 | CMS-CAT-23-001 2404.06614 |
| 111 | W. Verkerke and D. P. Kirkby | The RooFit toolkit for data modeling | technical report, 2003 link |
physics/0306116 |
| 112 | L. Moneta et al. | The RooStats Project | PoS ACAT 057, 2010 link |
1009.1003 |
| 113 | CMS Collaboration | Search for Higgs Boson and Observation of Z Boson through their Decay into a Charm Quark-Antiquark Pair in Boosted Topologies in Proton-Proton Collisions at $ \sqrt{s} = $ 13 TeV | PRL 131 (2023) 041801 | CMS-HIG-21-012 2211.14181 |
| 114 | M. J. Dolan, C. Englert, N. Greiner, and M. Spannowsky | Production of $ \mathrm{H}\mathrm{H} jj $ at the LHC | PRL 112 (2014) 101802 | 1310.1084 |
| 115 | M. J. Dolan et al. | $ \mathrm{H}\mathrm{H} jj $ production at the LHC | EPJC 75 (2015) 387 | 1506.08008 |
| 116 | E. Arganda, C. Garcia-Garcia, and M. J. Herrero | Probing the Higgs self-coupling through double Higgs production in vector boson scattering at the LHC | NPB 945 (2019) 114687 | 1807.09736 |
| 117 | J. Thaler and K. Van Tilburg | Identifying Boosted Objects with N-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 118 | CMS Collaboration | Inclusive search for highly boosted Higgs bosons decaying to bottom quark-antiquark pairs in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 12 (2020) 085 | CMS-HIG-19-003 2006.13251 |
| 119 | CMS Collaboration | Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair | PRL 120 (2018) 071802 | CMS-HIG-17-010 1709.05543 |
| 120 | CMS Collaboration | Search for low mass vector resonances decaying into quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 01 (2018) 097 | CMS-EXO-17-001 1710.00159 |
| 121 | CMS Collaboration | Search for Low Mass Vector Resonances Decaying to Quark-Antiquark Pairs in Proton-Proton Collisions at $ \sqrt{s}= $ 13 TeV | PRL 119 (2017) 111802 | CMS-EXO-16-030 1705.10532 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|