

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-JME-25-001 | ||
| Particle transformers for identifying Lorentz-boosted Higgs bosons decaying to a pair of W bosons | ||
| CMS Collaboration | ||
| 2025-08-03 | ||
| Abstract: A novel deep neural network classifier, the "particle transformer" (ParT), is introduced for the identification of highly Lorentz-boosted, multi-pronged jets in measurements and searches performed with the CMS detector at the LHC. Based on a self-attention mechanism that allows the model to weigh the importance of different particles, ParT is trained on a wide variety of topologies, notably demonstrating strong performance for the first time on jets originating from boosted Higgs boson decays to W bosons. The ParT algorithm achieves a tagging efficiency of $ {>}$50% for such jets at a QCD multijet background efficiency of 1%, while maintaining decorrelation from the jet mass. This performance is calibrated in data collected by CMS from proton-proton collisions at 13 TeV center-of-mass energy, with a dataset corresponding to a total luminosity of 138 fb$ ^{-1} $, using the primary Lund jet planes of individual subjets. Data-to-simulation selection efficiency scale factors are measured to be in the 0.9-1 range, with relative uncertainties ranging between 7 and 23%. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
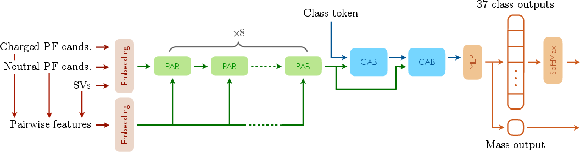
Figure 1:
Diagram of the ParT model architecture. The model processes three different sets of input features per jet, from charged PF candidates, neutral PF candidates, and SVs. These features are embedded using separate MLPs into 128-dimensional representations before being concatenated and passed through eight PABs. Pairwise features are also calculated between each input element, which are embedded using one-dimensional convolutional layers and used as attention biases for each PAB. Two CABs then use the learned features to update a randomly initialized class token, which aggregates these features into a global representation of the jet. Their output is then finally passed through an MLP that outputs the class probabilities, which are normalized by a softmax function, as well as the jet mass. |
png pdf |
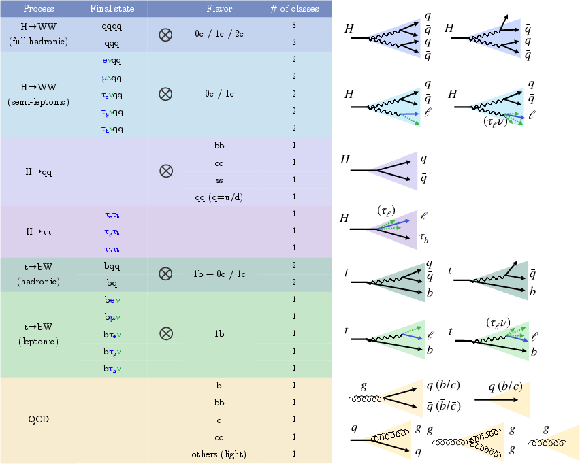
Figure 2:
Full suite of AK8 jet topologies used for the ParT model training. Jet types are first categorized by the number of quarks and leptons in the final state, and then further separated by flavor, as shown in the table on the left. The total number of subclasses for each process, therefore, is given by the tensor product ($ \otimes $) between the different final states and flavors. Diagrams illustrating the corresponding jet topologies are shown on the right. |
png pdf |
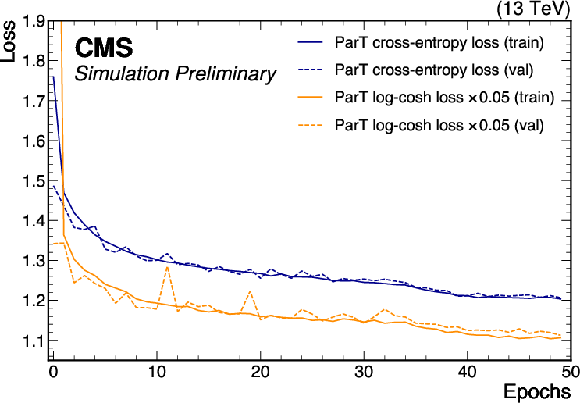
Figure 3:
Evolution of the loss function values for the ParT model on the training and validation datasets over training epochs, shown separately for the classification (cross-entropy) and regression (log-cosh) terms. |
png pdf |
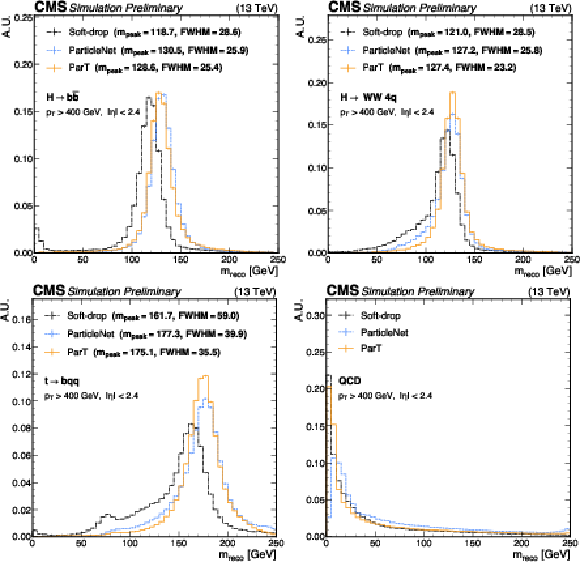
Figure 4:
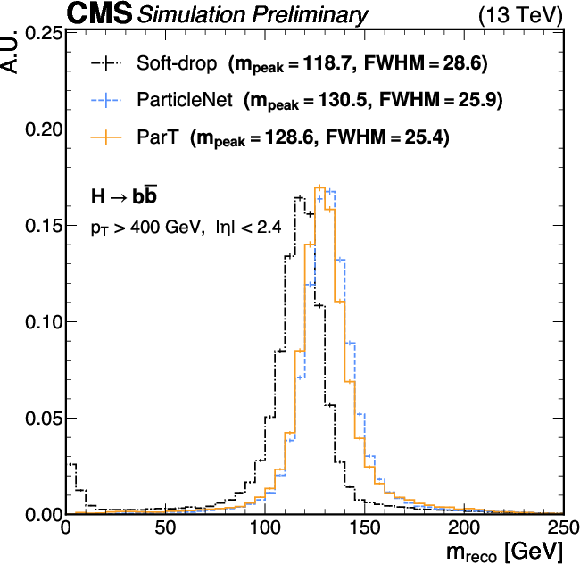
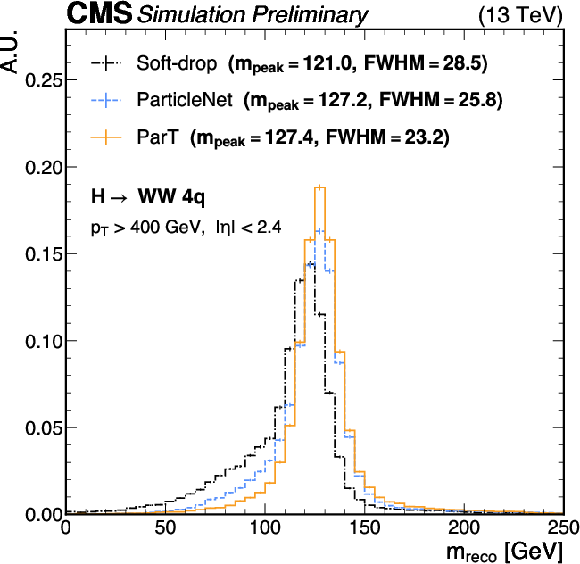
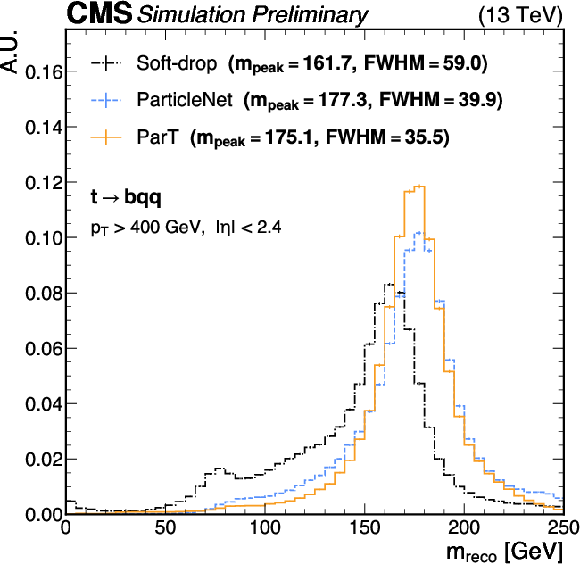
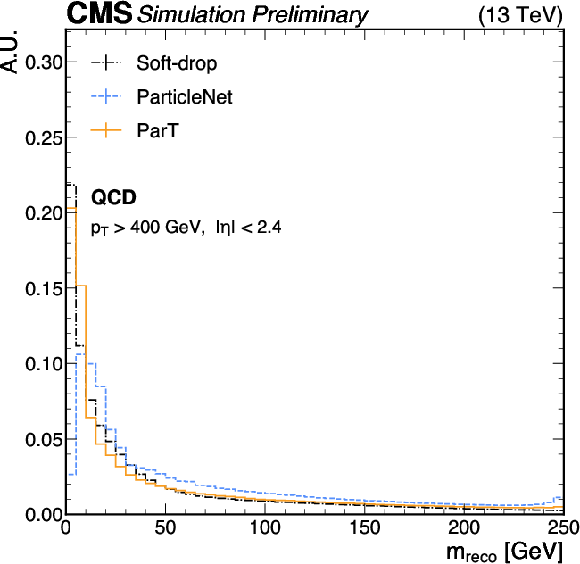
Comparison of jet mass reconstruction ($ {m_\mathrm{reco}} $) using the SD, ParticleNet, and ParT algorithms, for $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ (upper right), $ \mathrm{t}\to\mathrm{b}\mathrm{q}\overline{\mathrm{q}} $(lower left), and QCD (lower right) jets with SM $ {m_\mathrm{H}} $ and $ {m_\mathrm{t}} $. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV and $ |\eta| < $ 2.4. Statistical uncertainties in the bin yields originating from the limited number of simulated events are represented by vertical error bars. The mass at the peak ($ {m_\text{peak}} $) for each algorithm, calculated using Gaussian kernel density estimation, and the mass resolution, quantified by the FWHM of the resonance peak, are shown as well for H and t jets. |
png pdf |
Figure 4-a:
Comparison of jet mass reconstruction ($ {m_\mathrm{reco}} $) using the SD, ParticleNet, and ParT algorithms, for $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ (upper right), $ \mathrm{t}\to\mathrm{b}\mathrm{q}\overline{\mathrm{q}} $(lower left), and QCD (lower right) jets with SM $ {m_\mathrm{H}} $ and $ {m_\mathrm{t}} $. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV and $ |\eta| < $ 2.4. Statistical uncertainties in the bin yields originating from the limited number of simulated events are represented by vertical error bars. The mass at the peak ($ {m_\text{peak}} $) for each algorithm, calculated using Gaussian kernel density estimation, and the mass resolution, quantified by the FWHM of the resonance peak, are shown as well for H and t jets. |
png pdf |
Figure 4-b:
Comparison of jet mass reconstruction ($ {m_\mathrm{reco}} $) using the SD, ParticleNet, and ParT algorithms, for $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ (upper right), $ \mathrm{t}\to\mathrm{b}\mathrm{q}\overline{\mathrm{q}} $(lower left), and QCD (lower right) jets with SM $ {m_\mathrm{H}} $ and $ {m_\mathrm{t}} $. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV and $ |\eta| < $ 2.4. Statistical uncertainties in the bin yields originating from the limited number of simulated events are represented by vertical error bars. The mass at the peak ($ {m_\text{peak}} $) for each algorithm, calculated using Gaussian kernel density estimation, and the mass resolution, quantified by the FWHM of the resonance peak, are shown as well for H and t jets. |
png pdf |
Figure 4-c:
Comparison of jet mass reconstruction ($ {m_\mathrm{reco}} $) using the SD, ParticleNet, and ParT algorithms, for $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ (upper right), $ \mathrm{t}\to\mathrm{b}\mathrm{q}\overline{\mathrm{q}} $(lower left), and QCD (lower right) jets with SM $ {m_\mathrm{H}} $ and $ {m_\mathrm{t}} $. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV and $ |\eta| < $ 2.4. Statistical uncertainties in the bin yields originating from the limited number of simulated events are represented by vertical error bars. The mass at the peak ($ {m_\text{peak}} $) for each algorithm, calculated using Gaussian kernel density estimation, and the mass resolution, quantified by the FWHM of the resonance peak, are shown as well for H and t jets. |
png pdf |
Figure 4-d:
Comparison of jet mass reconstruction ($ {m_\mathrm{reco}} $) using the SD, ParticleNet, and ParT algorithms, for $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ (upper right), $ \mathrm{t}\to\mathrm{b}\mathrm{q}\overline{\mathrm{q}} $(lower left), and QCD (lower right) jets with SM $ {m_\mathrm{H}} $ and $ {m_\mathrm{t}} $. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV and $ |\eta| < $ 2.4. Statistical uncertainties in the bin yields originating from the limited number of simulated events are represented by vertical error bars. The mass at the peak ($ {m_\text{peak}} $) for each algorithm, calculated using Gaussian kernel density estimation, and the mass resolution, quantified by the FWHM of the resonance peak, are shown as well for H and t jets. |
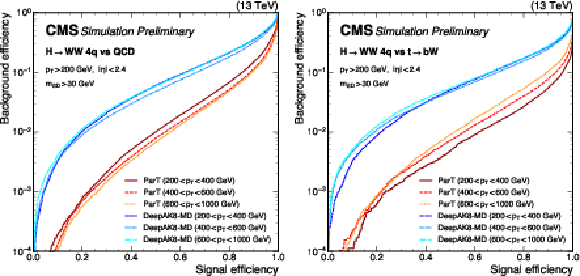
png pdf |
Figure 5:
Receiver operating characteristic curves for $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ signal jets, with SM $ {m_\mathrm{H}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ and the DeepAK8-MD scores in the $ p_{\mathrm{T}} $ ranges 200-400, 400-600, and 600-1000 GeV. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 200 GeV and $ |\eta| < $ 2.4. Signal jets are required to contain all four generator-level quarks from the W boson decays within $ \Delta R $ (jet},\,\mathrm{q) $ < $ 0.8. |
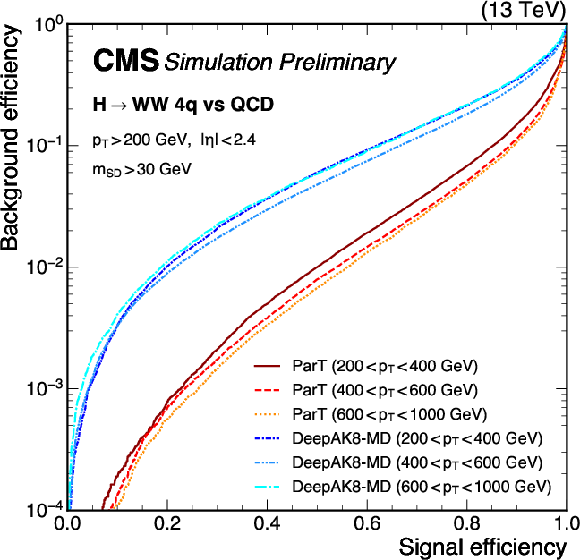
png pdf |
Figure 5-a:
Receiver operating characteristic curves for $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ signal jets, with SM $ {m_\mathrm{H}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ and the DeepAK8-MD scores in the $ p_{\mathrm{T}} $ ranges 200-400, 400-600, and 600-1000 GeV. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 200 GeV and $ |\eta| < $ 2.4. Signal jets are required to contain all four generator-level quarks from the W boson decays within $ \Delta R $ (jet},\,\mathrm{q) $ < $ 0.8. |
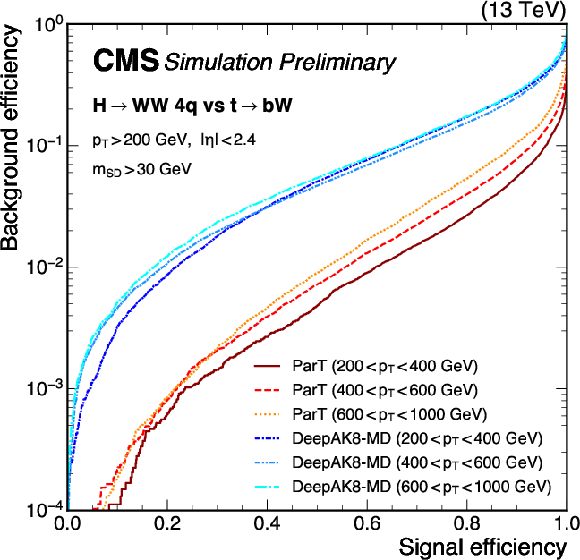
png pdf |
Figure 5-b:
Receiver operating characteristic curves for $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ signal jets, with SM $ {m_\mathrm{H}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ and the DeepAK8-MD scores in the $ p_{\mathrm{T}} $ ranges 200-400, 400-600, and 600-1000 GeV. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 200 GeV and $ |\eta| < $ 2.4. Signal jets are required to contain all four generator-level quarks from the W boson decays within $ \Delta R $ (jet},\,\mathrm{q) $ < $ 0.8. |
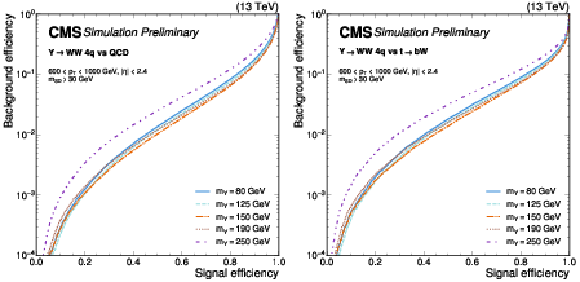
png pdf |
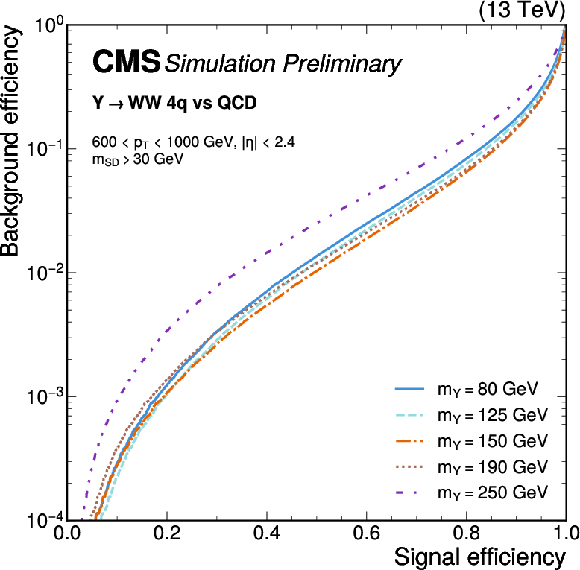
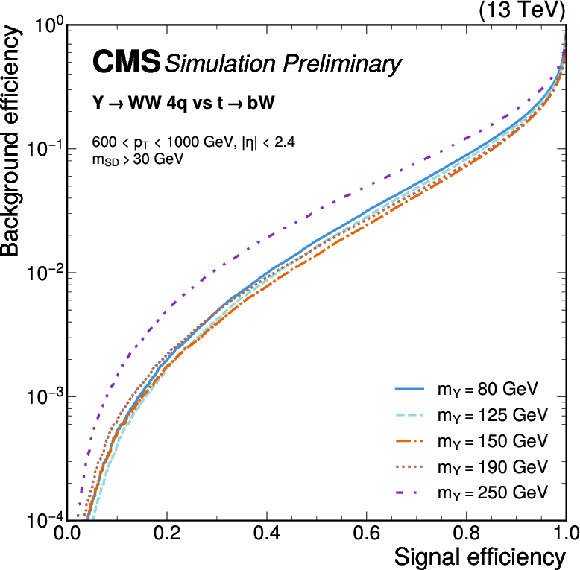
Figure 6:
Receiver operating characteristic curves for $ \mathrm{Y}\to\mathrm{W}\mathrm{W} $ signal jets, with varying $ {m_\mathrm{Y}} $ and SM $ {m_\mathrm{W}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ score. An offline selection is applied to the AK8 jets of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
Figure 6-a:
Receiver operating characteristic curves for $ \mathrm{Y}\to\mathrm{W}\mathrm{W} $ signal jets, with varying $ {m_\mathrm{Y}} $ and SM $ {m_\mathrm{W}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ score. An offline selection is applied to the AK8 jets of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
Figure 6-b:
Receiver operating characteristic curves for $ \mathrm{Y}\to\mathrm{W}\mathrm{W} $ signal jets, with varying $ {m_\mathrm{Y}} $ and SM $ {m_\mathrm{W}} $, versus background jets from simulated QCD multijet (left) and $ \mathrm{t} \overline{\mathrm{t}} $ events (right), for the ParT $T_{\text{HWW}}$ score. An offline selection is applied to the AK8 jets of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |

png pdf |
Figure 7:
Error matrix with each row indicating the fraction of jets per category classified as the column category by PART. An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 200 GeV and $ |\eta| < $ 2.4. |
png pdf |
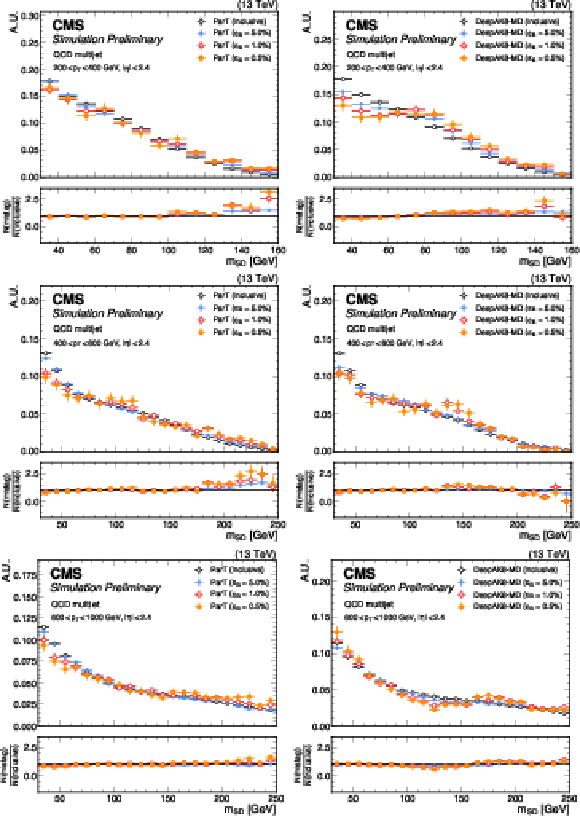
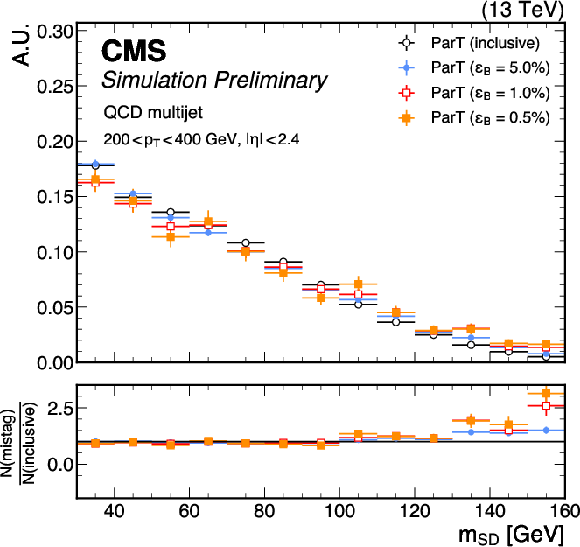
Figure 8:
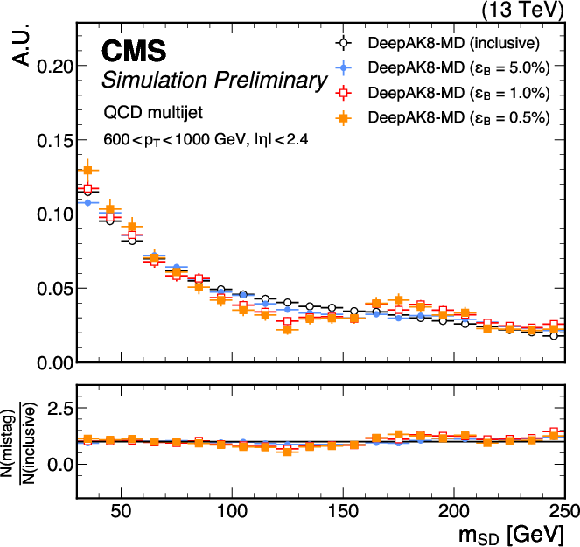
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
Figure 8-a:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
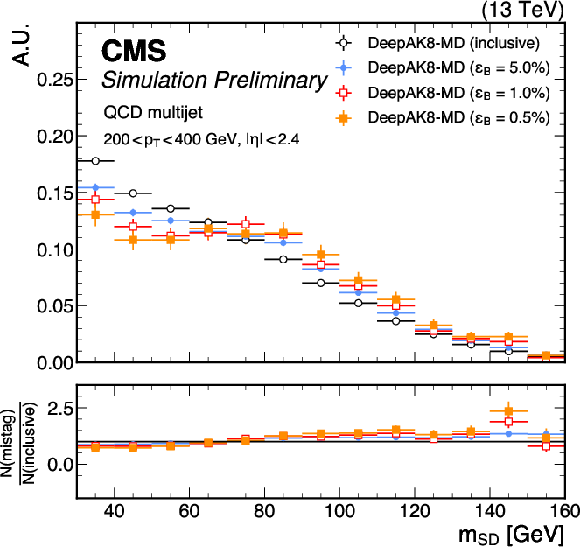
png pdf |
Figure 8-b:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
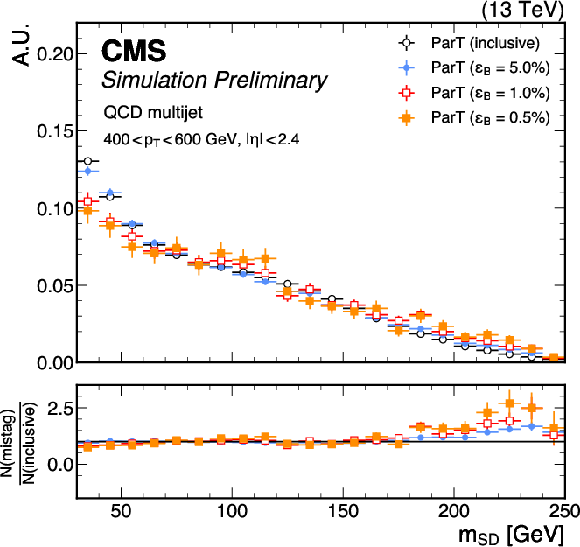
Figure 8-c:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
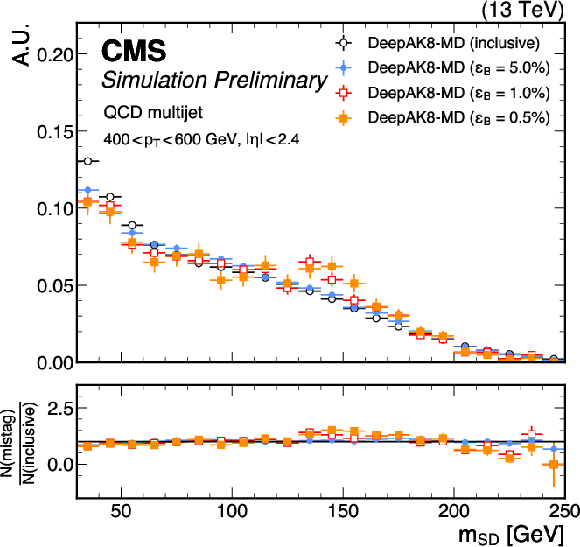
Figure 8-d:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
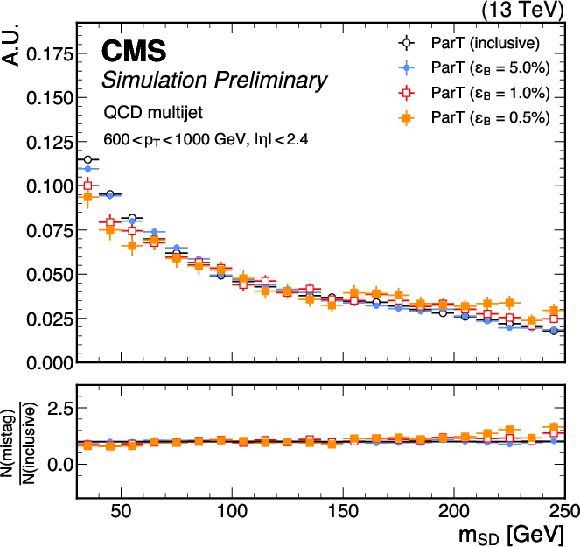
Figure 8-e:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
Figure 8-f:
Distributions of $ {m_\mathrm{SD}} $ for jets from QCD multijet events, in the $ p_{\mathrm{T}} $ ranges 200-400 GeV (top), 400-600 GeV (middle) and 600-1000 GeV (bottom), after no selections (``inclusive'') on the ParT $T_{\text{HWW}}$ score (left) and the DeepAK8-MD score (right) as well as selections corresponding to QCD jet selection efficiencies ($ \epsilon_B $) of 5.0%, 1.0%, and 0.5%. The lower panels display the ratio of the normalized $ {m_\mathrm{SD}} $ distributions for the different selection efficiencies (N(mistag)) to the normalized inclusive $ {m_\mathrm{SD}} $ distribution (N(inclusive)). An offline selection is applied to the AK8 jets of $ p_{\mathrm{T}} > $ 400 GeV, $ |\eta| < $ 2.4, and $ {m_\mathrm{SD}} > $ 30 GeV. |
png pdf |
Figure 9:
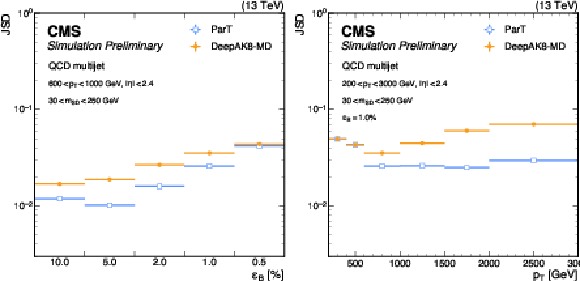
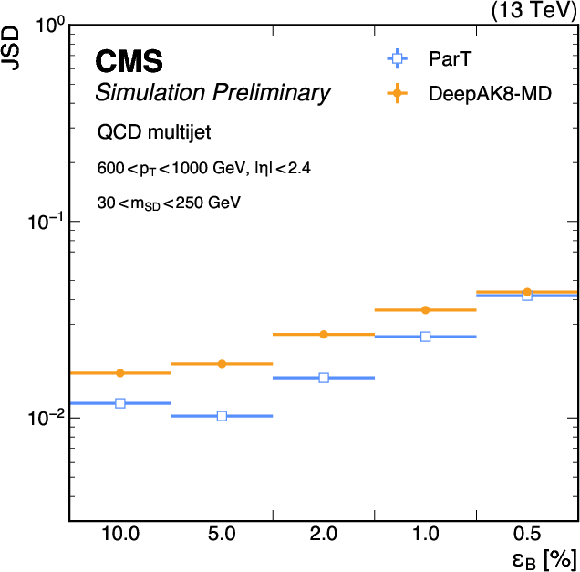
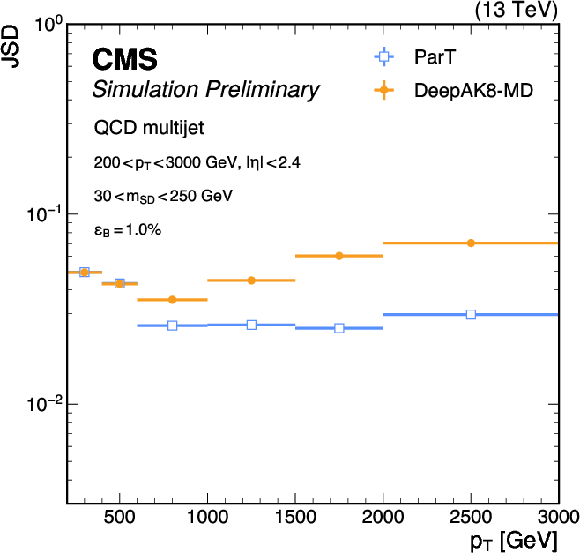
The Jensen-Shannon divergence (JSD) between the $ {m_\mathrm{SD}} $ distribution of jets from QCD multijet events with and without a selection on the ParT and DeepAK8-MD tagger scores. On the left, the JSD is plotted for tagger selections corresponding to different QCD jet selection efficiencies ($ {\epsilon_\mathrm{B}} $), with an offline selection of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and 30 $ < {m_\mathrm{SD}} < $ 250 GeV applied to the jets. On the right, the JSD is plotted for different jet $ p_{\mathrm{T}} $ bins, at a fixed $ {\epsilon_\mathrm{B}} $ of 1%. |
png pdf |
Figure 9-a:
The Jensen-Shannon divergence (JSD) between the $ {m_\mathrm{SD}} $ distribution of jets from QCD multijet events with and without a selection on the ParT and DeepAK8-MD tagger scores. On the left, the JSD is plotted for tagger selections corresponding to different QCD jet selection efficiencies ($ {\epsilon_\mathrm{B}} $), with an offline selection of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and 30 $ < {m_\mathrm{SD}} < $ 250 GeV applied to the jets. On the right, the JSD is plotted for different jet $ p_{\mathrm{T}} $ bins, at a fixed $ {\epsilon_\mathrm{B}} $ of 1%. |
png pdf |
Figure 9-b:
The Jensen-Shannon divergence (JSD) between the $ {m_\mathrm{SD}} $ distribution of jets from QCD multijet events with and without a selection on the ParT and DeepAK8-MD tagger scores. On the left, the JSD is plotted for tagger selections corresponding to different QCD jet selection efficiencies ($ {\epsilon_\mathrm{B}} $), with an offline selection of 600 $ < p_{\mathrm{T}} < $ 1000 GeV, $ |\eta| < $ 2.4, and 30 $ < {m_\mathrm{SD}} < $ 250 GeV applied to the jets. On the right, the JSD is plotted for different jet $ p_{\mathrm{T}} $ bins, at a fixed $ {\epsilon_\mathrm{B}} $ of 1%. |
png pdf |
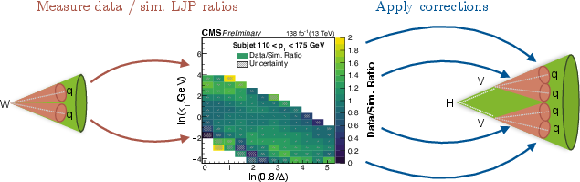
Figure 10:
Schematic of the LJP calibration method for $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ tagging. Ratios of primary LJP densities in data and simulation are first measured per subjet in merged two-pronged W jets, with an example of such a ratio reproduced from Ref. [26]. These are then used to derive correction factors $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ signal jets per prong. |
png pdf |
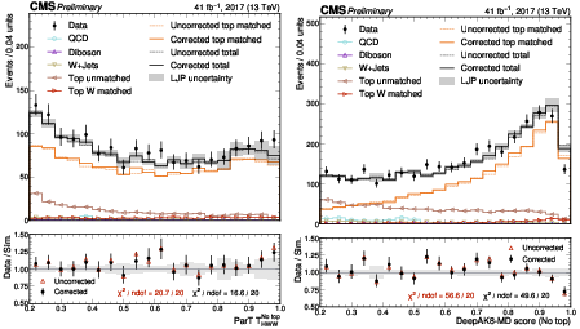
Figure 11:
Distributions of the ParT $T_{\text{HWW}}^{\text{no top}}$ (left) and DeepAK8-MD (No top) (right) discriminants with and without the LJP corrections for top-matched jets for data and individual simulated processes in the top panels, and data versus simulation ratios in the bottom panels. The combined uncertainties from LJP-based SFs per bin are shown in shaded gray, and the statistical uncertainty in the number of data events per bin is represented by vertical error bars in the top and bottom panels. The $ \chi^2 $ test statistic values between data and simulation, normalized to the number of degrees of freedom (ndof), are also shown for both discriminants with and without LJP corrections. |
png pdf |
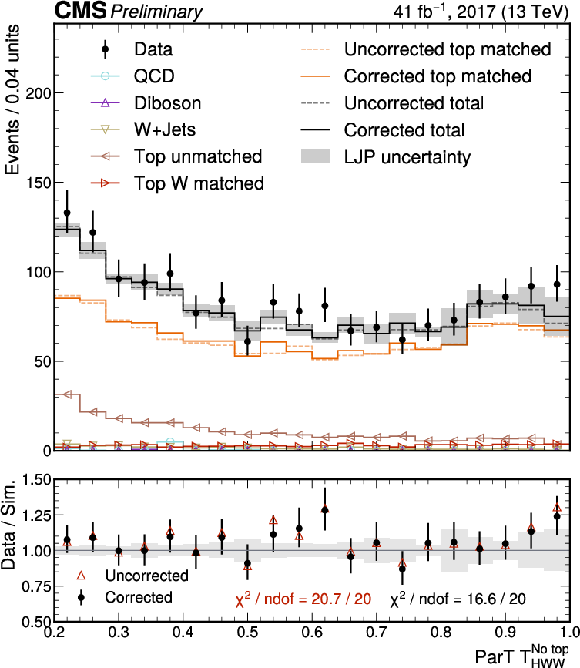
Figure 11-a:
Distributions of the ParT $T_{\text{HWW}}^{\text{no top}}$ (left) and DeepAK8-MD (No top) (right) discriminants with and without the LJP corrections for top-matched jets for data and individual simulated processes in the top panels, and data versus simulation ratios in the bottom panels. The combined uncertainties from LJP-based SFs per bin are shown in shaded gray, and the statistical uncertainty in the number of data events per bin is represented by vertical error bars in the top and bottom panels. The $ \chi^2 $ test statistic values between data and simulation, normalized to the number of degrees of freedom (ndof), are also shown for both discriminants with and without LJP corrections. |
png pdf |
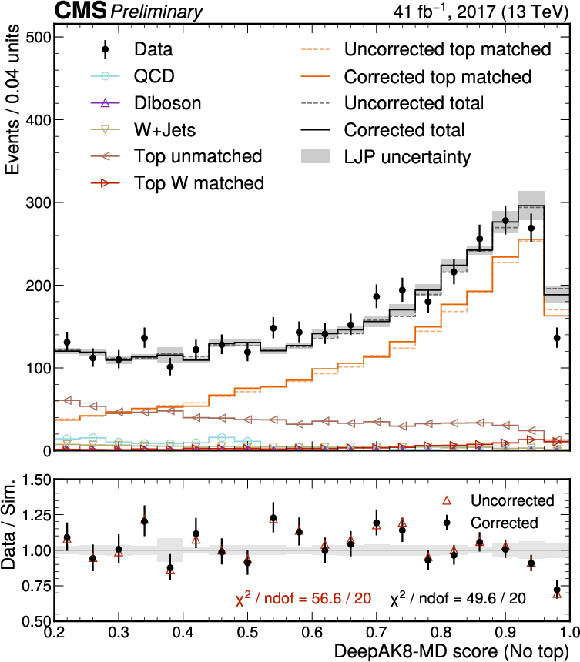
Figure 11-b:
Distributions of the ParT $T_{\text{HWW}}^{\text{no top}}$ (left) and DeepAK8-MD (No top) (right) discriminants with and without the LJP corrections for top-matched jets for data and individual simulated processes in the top panels, and data versus simulation ratios in the bottom panels. The combined uncertainties from LJP-based SFs per bin are shown in shaded gray, and the statistical uncertainty in the number of data events per bin is represented by vertical error bars in the top and bottom panels. The $ \chi^2 $ test statistic values between data and simulation, normalized to the number of degrees of freedom (ndof), are also shown for both discriminants with and without LJP corrections. |
| Tables | |

png pdf |
Table 1:
Summary of particle masses in the ParT training samples. |

png pdf |
Table 2:
The complete set of input features per AK8 jet used for the ParT model training. Three types of inputs are considered: charged PF candidates, neutral PF candidates, and secondary vertices (SVs). |
png pdf |
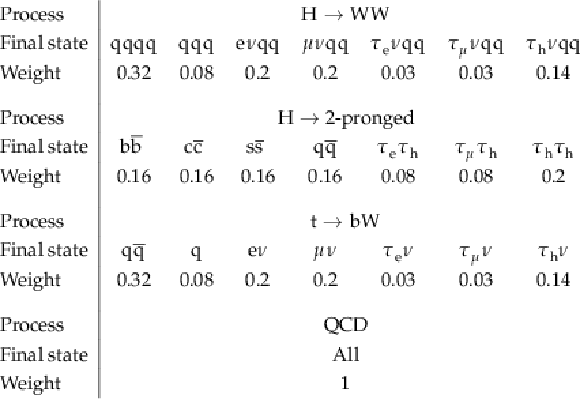
Table 3:
Relative weights of each of the classes used for training the ParT model. Each of the four major processes: $ \mathrm{H}\to\mathrm{W}\mathrm{W} $, $ \mathrm{H}\to $ 2-pronged, $ \mathrm{t}\to\mathrm{b}\mathrm{W} $, and QCD jets, are weighted equally and have one row dedicated to them each. |
png pdf |
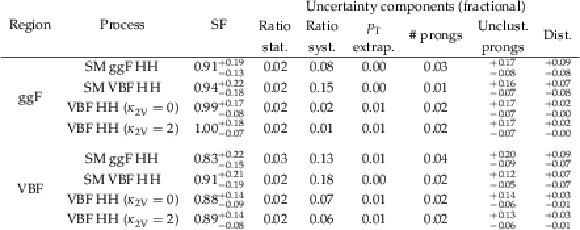
Table 4:
Signal efficiency SFs and uncertainties for BDT selections on the ParT ${\mathrm{H}\to\mathrm{W}\mathrm{W}}$ tagging outputs for the $ {\mathrm{H}\mathrm{H}\to\mathrm{b}\overline{\mathrm{b}}\mathrm{W}\mathrm{W}} $ search, measured using the LJP calibration method for different $ {\mathrm{H}\mathrm{H}} $ signals and analysis regions. Both the total combined uncertainty and the components defined in the text are shown. |
| Summary |
| The particle transformer (ParT) deep neural network for classifying a wide variety of Lorentz-boosted jet topologies has been presented. In particular, ParT enables effective identification of all-hadronic Higgs boson to vector boson ($ \mathrm{H}\to\mathrm{W}\mathrm{W} $) decays by the CMS experiment for the first time. A novel training strategy is used to address challenges pertaining to $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ classification, through which ParT achieves $ > $50% $ \mathrm{H}\to\mathrm{W}\mathrm{W} $ selection efficiency for a QCD multijet background efficiency of 1%, while maintaining decorrelation with the jet mass. The performance is calibrated on data using the primary Lund jet planes of individual subjets, with data-to-simulation scale factors measured in the 0.9-1 range, and relative uncertainties between 7 and 23%. The ParT algorithm represents a significant advancement in CMS' boosted jet identification capabilities, illustrated in the first search for boosted H pair production in the all-hadronic $ \mathrm{b}\overline{\mathrm{b}}\mathrm{W}\mathrm{W} $ channel. |
| References | ||||
| 1 | CMS Collaboration | Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques | JINST 15 (2020) P06005 | CMS-JME-18-002 2004.08262 |
| 2 | CMS Collaboration | Performance of the mass-decorrelated \textscDeepDoubleX classifier for double-b and double-c large-radius jets with the CMS detector | CMS Detector Performance Summary CMS-DP-2022-041, 2022 CDS |
|
| 3 | E. A. Moreno et al. | JEDI-net: a jet identification algorithm based on interaction networks | EPJC 80 (2020) 58 | 1908.05318 |
| 4 | E. A. Moreno et al. | Interaction networks for the identification of boosted $ \mathrm{H}\to\mathrm{b}\overline{\mathrm{b}} $ decays | PRD 102 (2020) 012010 | 1909.12285 |
| 5 | H. Qu and L. Gouskos | PARTICLENET: Jet tagging via particle clouds | PRD 101 (2020) 056019 | 1902.08570 |
| 6 | CMS Collaboration | Identification of highly Lorentz-boosted heavy particles using graph neural networks and new mass decorrelation techniques | CMS Detector Performance Summary CMS-DP-2020-002, 2020 CDS |
|
| 7 | CMS Collaboration | Mass regression of highly-boosted jets using graph neural networks | CMS Detector Performance Summary CMS-DP-2021-017, 2021 CDS |
|
| 8 | CMS Collaboration | Measurement of boosted Higgs bosons produced via vector boson fusion or gluon fusion in the H \textrightarrow$ \textrm{b}\overline{\textrm{b}} $ decay mode using LHC proton-proton collision data at $ \sqrt{s} $ = 13 TeV | JHEP 12 (2024) 035 | CMS-HIG-21-020 2407.08012 |
| 9 | CMS Collaboration | Search for higgs boson decay to a charm quark-antiquark pair in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRL 131 (2023) 061801 | CMS-HIG-21-008 2205.05550 |
| 10 | CMS Collaboration | Search for nonresonant pair production of highly energetic Higgs bosons decaying to bottom quarks | PRL 131 (2023) 041803 | 2205.06667 |
| 11 | CMS Collaboration | Search for a massive scalar resonance decaying to a light scalar and a Higgs boson in the four b quarks final state with boosted topology | PLB 842 (2023) 137392 | 2204.12413 |
| 12 | CMS Collaboration | Search for resonant pair production of Higgs bosons in the $ \textrm{b}\overline{\textrm{b}}\textrm{b}\overline{\textrm{b}} $ final state using large-area jets in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | JHEP 02 (2025) 040 | 2407.13872 |
| 13 | CMS Collaboration | Search for heavy resonances decaying to a pair of Lorentz-boosted Higgs bosons in final states with leptons and a bottom quark pair at $ \sqrt{s} $= 13 TeV | JHEP 05 (2022) 005 | 2112.03161 |
| 14 | CMS Collaboration | Search for resonances decaying to three W bosons in the hadronic final state in proton-proton collisions at $ \sqrt s $ =13 TeV | PRD 106 (2022) 012002 | 2112.13090 |
| 15 | CMS Collaboration | Search for resonances decaying to three W bosons in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | PRL 129 (2022) 021802 | 2201.08476 |
| 16 | A. J. Larkoski, I. Moult, and B. Nachman | Jet Substructure at the Large Hadron Collider: A Review of Recent Advances in Theory and Machine Learning | Phys. Rept. 841 (2020) 1 | 1709.04464 |
| 17 | H. Qu, C. Li, and S. Qian | Particle transformer for jet tagging | in Proc. 39th Int. Conf. on Machine Learning, volume 162, 2022 link |
2202.03772 |
| 18 | G. C. Branco et al. | Theory and phenomenology of two-Higgs-doublet models | Phys. Rept. 516 (2012) 1 | 1106.0034 |
| 19 | N. Craig, J. Galloway, and S. Thomas | Searching for signs of the second Higgs doublet | 1305.2424 | |
| 20 | F. Domingo and S. Pa\ss ehr | About the bosonic decays of heavy Higgs states in the (N)MSSM | EPJC 82 (2022) 962 | 2207.05776 |
| 21 | K. S. Agashe et al. | LHC signals from cascade decays of warped vector resonances | JHEP 05 (2017) 078 | 1612.00047 |
| 22 | K. Agashe et al. | Dedicated strategies for triboson signals from cascade decays of vector resonances | PRD 99 (2019) 075016 | 1711.09920 |
| 23 | H.-Y. Ren, L.-H. Xia, and Y.-P. Kuang | Model-independent probe of anomalous heavy neutral Higgs bosons at the LHC | PRD 90 (2014) 115002 | 1404.6367 |
| 24 | Y.-P. Kuang, H.-Y. Ren, and L.-H. Xia | Further investigation of the model-independent probe of heavy neutral Higgs bosons at LHC Run 2 | Chin. Phys. C 40 (2016) 023101 | 1506.08007 |
| 25 | F. A. Dreyer, G. P. Salam, and G. Soyez | The Lund jet plane | JHEP 12 (2018) 064 | 1807.04758 |
| 26 | CMS Collaboration | A method for correcting the substructure of multiprong jets using the Lund jet plane | CMS-JME-23-001 2507.07775 |
|
| 27 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 28 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 29 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 30 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 31 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 32 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 33 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 34 | CMS Collaboration | Performance of the CMS high-level trigger during LHC run 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 35 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 36 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 37 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 38 | CMS Tracker Group | The CMS phase-1 pixel detector upgrade | JINST 16 (2021) P02027 | 2012.14304 |
| 39 | CMS Collaboration | Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS phase-1 pixel detector | CMS Detector Performance Summary CMS-DP-2020-049, 2020 CDS |
|
| 40 | CMS Collaboration | 2017 tracking performance plots | CMS Detector Performance Summary CMS-DP-2017-015, 2017 CDS |
|
| 41 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 42 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 43 | CMS Collaboration | Offline secondary vertex reconstruction in the CMS detector | PoS LHCP 236, 2025 link |
|
| 44 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 45 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 46 | CMS Collaboration | Pileup removal algorithms | CMS Physics Analysis Summary , CERN, 2014 CMS-PAS-JME-14-001 |
CMS-PAS-JME-14-001 |
| 47 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 48 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 49 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 50 | S. Catani, Y. L. Dokshitzer, M. H. Seymour, and B. R. Webber | Longitudinally invariant $ k_{\mathrm{T}} $ clustering algorithms for hadron hadron collisions | NPB 406 (1993) 187 | |
| 51 | S. D. Ellis and D. E. Soper | Successive combination jet algorithm for hadron collisions | PRD 48 (1993) 3160 | hep-ph/9305266 |
| 52 | Y. L. Dokshitzer, G. D. Leder, S. Moretti, and B. R. Webber | Better jet clustering algorithms | JHEP 08 (1997) 001 | hep-ph/9707323 |
| 53 | M. Wobisch and T. Wengler | Hadronization corrections to jet cross-sections in deep inelastic scattering | in Proc. Workshop on Monte Carlo Generators for HERA Physics (Plenary Starting Meeting), 1998 | hep-ph/9907280 |
| 54 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 55 | E. Bols et al. | Jet flavour classification using DeepJet | JINST 15 (2020) P12012 | 2008.10519 |
| 56 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 57 | S. Bolognesi et al. | On the spin and parity of a single-produced resonance at the LHC | PRD 86 (2012) 095031 | 1208.4018 |
| 58 | T. Sjöstrand et al. | An introduction to PYTHIA8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 59 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 60 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 61 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 62 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG box | JHEP 06 (2010) 043 | 1002.2581 |
| 63 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 02 (2012) 088 | 1111.2854 |
| 64 | M. Grazzini et al. | Higgs boson pair production at NNLO with top quark mass effects | JHEP 05 (2018) 059 | 1803.02463 |
| 65 | S. Dawson, S. Dittmaier, and M. Spira | Neutral Higgs boson pair production at hadron colliders: QCD corrections | PRD 58 (1998) 115012 | hep-ph/9805244 |
| 66 | D. de Florian and J. Mazzitelli | Higgs boson pair production at next-to-next-to-leading order in QCD | PRL 111 (2013) 201801 | 1309.6594 |
| 67 | D. de Florian and J. Mazzitelli | Higgs pair production at next-to-next-to-leading logarithmic accuracy at the LHC | JHEP 09 (2015) 053 | 1505.07122 |
| 68 | J. Baglio et al. | Gluon fusion into Higgs pairs at NLO QCD and the top mass scheme | EPJC 79 (2019) 459 | 1811.05692 |
| 69 | S. Borowka et al. | Higgs boson pair production in gluon fusion at next-to-leading order with full top-quark mass dependence | PRL 117 (2016) 012001 | 1604.06447 |
| 70 | D. Y. Shao, C. S. Li, H. T. Li, and J. Wang | Threshold resummation effects in Higgs boson pair production at the LHC | JHEP 07 (2013) 169 | 1301.1245 |
| 71 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 72 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 73 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 74 | A. Vaswani et al. | Attention is all you need | in Proc. 31st Int. Conf. on Neural Information Processing Systems, NIPS'17, Curran Associates Inc., Red Hook, NY, USA, 2017 | 1706.03762 |
| 75 | H. Touvron et al. | Going deeper with image transformers | in Proc. IEEE/CVF Int. Conf. on Computer Vision (ICCV), 2021 link |
2103.17239 |
| 76 | F. A. Dreyer and H. Qu | Jet tagging in the Lund plane with graph networks | JHEP 03 (2021) 052 | 2012.08526 |
| 77 | H. Qu | Weaver: A machine learning R&D framework for high energy physics applications | https://github.com/hqucms/weaver-core | |
| 78 | A. Paszke et al. | PyTorch: An imperative style, high-performance deep learning library | in Advances in Neural Information Processing Systems 32, Curran Associates, Inc, 2019 link |
1912.01703 |
| 79 | M. Zhang, J. Lucas, J. Ba, and G. E. Hinton | Lookahead optimizer: $ k $ steps forward, 1 step back | in Advances in Neural Information Processing Systems 32, Curran Associates, Inc, 2019 link |
1907.08610 |
| 80 | L. Liu et al. | On the variance of the adaptive learning rate and beyond | in Proc. Int. Conf. on Learning Representations (ICLR), 2020 link |
1908.03265 |
| 81 | J. Lin | Divergence measures based on the Shannon entropy | IEEE Trans. on Inf. Th. 37 (1991) 145 | |
| 82 | S. Kullback and R. A. Leibler | On information and sufficiency | Ann. Math. Statist. 22 (1951) 79 | |
| 83 | ATLAS Collaboration | Search for pair production of boosted Higgs bosons via vector-boson fusion in the $ \mathrm{b}\overline{\mathrm{b}}\mathrm{b}\overline{\mathrm{b}} $ final state using pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PLB 858 (2024) 139007 | 2404.17193 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|