

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-24-008 | ||
| Search for Higgs boson production at high transverse momentum in the $ \mathrm{WW^{*}} $ decay channel in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 21 May 2025 | ||
| Abstract: A search for Higgs boson production at high transverse momentum in the $ \mathrm{WW^{*}} $ decay channel is presented. The analysis uses proton-proton collision data collected with the CMS detector at $ \sqrt{s} = $ 13 TeV during the years 2016--2018, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. Both semileptonic and fully hadronic decay modes are considered, focusing on final states with either one isolated lepton (1 $ \ell $) or none (0 $ \ell $), where the Higgs boson decay products are reconstructed within a single large-radius jet. Higgs boson candidate jets are identified using the particle transformer algorithm, which is calibrated via the Lund jet plane technique and fine-tuned to improve the expected signal significance in the 1 $ \ell $ channel. The 0 $ \ell $ channel considers all Higgs boson production modes inclusively, while the 1 $ \ell $ channel further categorizes events into the two dominant production mechanisms: gluon fusion and vector boson fusion. The signal strength, defined as the ratio of the observed signal to the standard model expectation, is $ \mu_{\mathrm{H}} = $ 0.01 $ ^{+0.63}_{-0.48} $, with no signal observed above the background. The result represents the first measurement in this decay mode and is consistent with those obtained in other final states. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
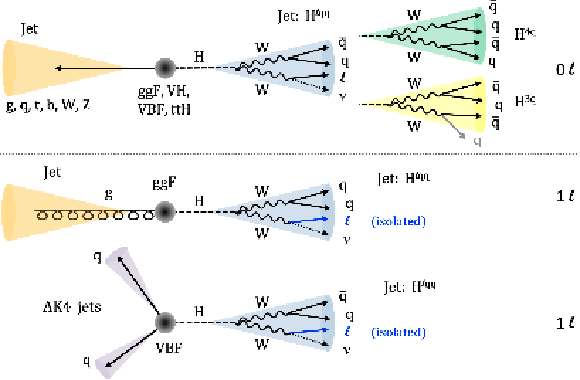
Figure 1:
Illustration of the event topologies analyzed in this study. On the left, the dominant H boson production modes, from top to bottom: gluon fusion (ggF) and vector boson fusion (VBF). Additional jets from initial or final state radiation are shown in yellow cones for 0 $ \ell $ and 1 $ \ell $ ggF, while for 1 $ \ell $ VBF, a pair of extra jets is shown in purple. On the right, the various final states resulting from $ \mathrm{H}\to\mathrm{W}\mathrm{W}^{*}\to\ell\nu\mathrm{q}\mathrm{q}/\mathrm{q} \mathrm{q}\mathrm{q}\mathrm{q} $ decays. |
png pdf |
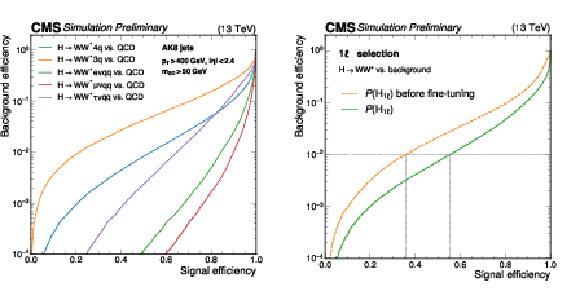
Figure 2:
Performance curves showing the misidentification probability of background jets versus the identification probability of $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ resonance jets for PART and PART-FINETUNED. Left: Discrimination performance of the PART model for various $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ decays against the dominant QCD multijet background, following a selection similar to that of the 0 $ \ell $ channel. Right: Comparison of $ P(\mathrm{H}_{1\ell}) $ before and after fine-tuning, following the event selection in the 1 $ \ell $ channel. After fine-tuning, $ P(\mathrm{H}_{1\ell}) $ provides significantly better discrimination in the 1 $ \ell $ final state, achieving 60% higher signal efficiency at a background misidentification rate of $ 10^{-2} $. The background includes jets originating from QCD multijet events, $ \mathrm{W}(\ell\nu) $+jets, and top quark processes. |
png pdf |
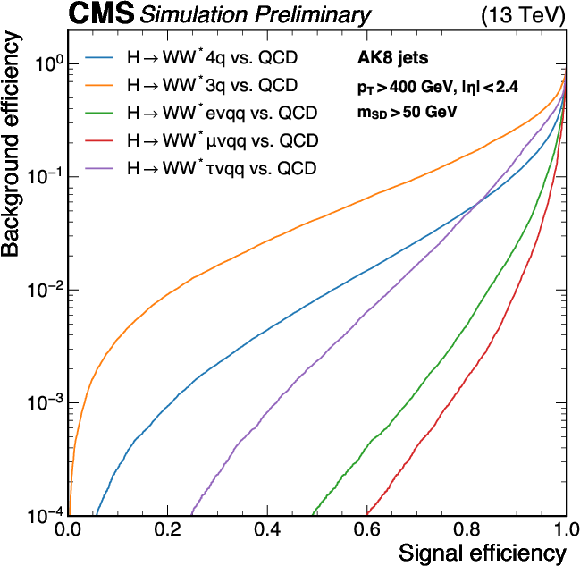
Figure 2-a:
Performance curves showing the misidentification probability of background jets versus the identification probability of $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ resonance jets for PART and PART-FINETUNED. Left: Discrimination performance of the PART model for various $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ decays against the dominant QCD multijet background, following a selection similar to that of the 0 $ \ell $ channel. Right: Comparison of $ P(\mathrm{H}_{1\ell}) $ before and after fine-tuning, following the event selection in the 1 $ \ell $ channel. After fine-tuning, $ P(\mathrm{H}_{1\ell}) $ provides significantly better discrimination in the 1 $ \ell $ final state, achieving 60% higher signal efficiency at a background misidentification rate of $ 10^{-2} $. The background includes jets originating from QCD multijet events, $ \mathrm{W}(\ell\nu) $+jets, and top quark processes. |
png pdf |
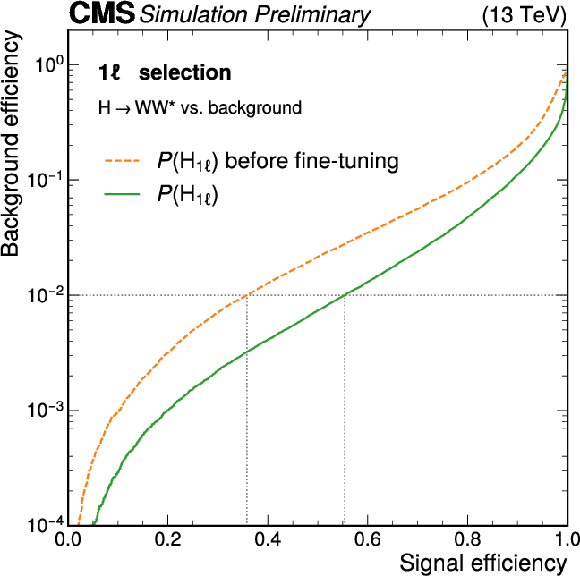
Figure 2-b:
Performance curves showing the misidentification probability of background jets versus the identification probability of $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ resonance jets for PART and PART-FINETUNED. Left: Discrimination performance of the PART model for various $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ decays against the dominant QCD multijet background, following a selection similar to that of the 0 $ \ell $ channel. Right: Comparison of $ P(\mathrm{H}_{1\ell}) $ before and after fine-tuning, following the event selection in the 1 $ \ell $ channel. After fine-tuning, $ P(\mathrm{H}_{1\ell}) $ provides significantly better discrimination in the 1 $ \ell $ final state, achieving 60% higher signal efficiency at a background misidentification rate of $ 10^{-2} $. The background includes jets originating from QCD multijet events, $ \mathrm{W}(\ell\nu) $+jets, and top quark processes. |
png pdf |
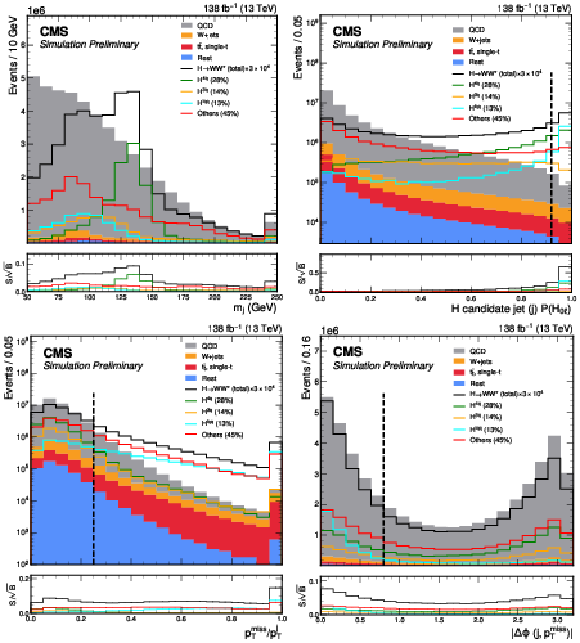
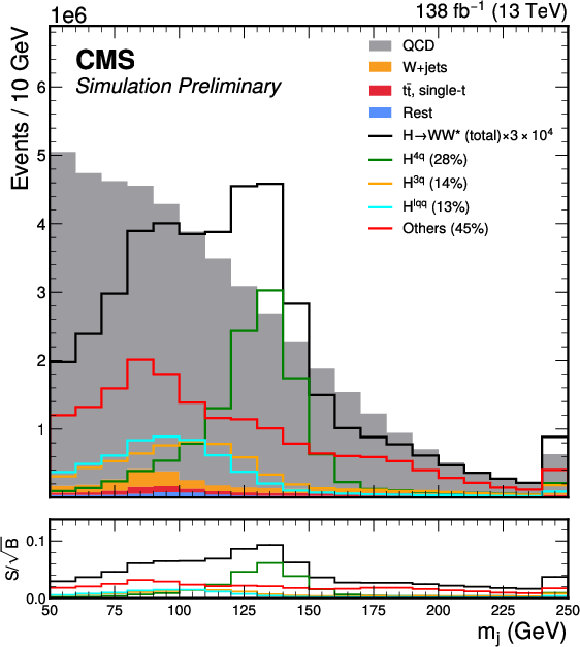
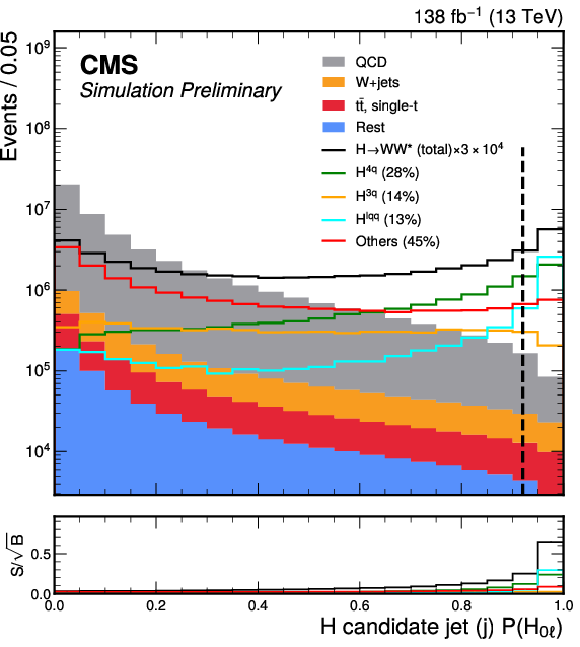
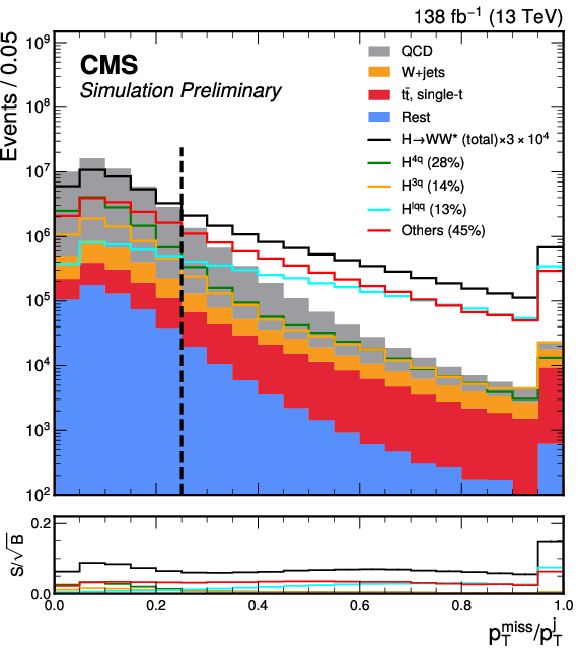
Figure 3:
The event distributions for the total simulated background and total signal (scaled by a factor of 3 $ \times10^4 $) passing the event selection for the 0 $ \ell $ channel. The signal is decomposed into classes as defined in the text. The upper-left and upper-right panels show the soft-drop mass and PART score distributions for the H candidate jet (j) $ P(\mathrm{H}_{0\ell}) $, respectively. The lower-left and lower-right panels display the $ p_{\mathrm{T}}^\text{miss}/p_{\mathrm{T}}^{\text{j}} $ ratio and the angle $ |\Delta\phi (j, {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}) | $, respectively. Vertical lines indicate the selection conditions imposed to define the signal region. |
png pdf |
Figure 3-a:
The event distributions for the total simulated background and total signal (scaled by a factor of 3 $ \times10^4 $) passing the event selection for the 0 $ \ell $ channel. The signal is decomposed into classes as defined in the text. The upper-left and upper-right panels show the soft-drop mass and PART score distributions for the H candidate jet (j) $ P(\mathrm{H}_{0\ell}) $, respectively. The lower-left and lower-right panels display the $ p_{\mathrm{T}}^\text{miss}/p_{\mathrm{T}}^{\text{j}} $ ratio and the angle $ |\Delta\phi (j, {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}) | $, respectively. Vertical lines indicate the selection conditions imposed to define the signal region. |
png pdf |
Figure 3-b:
The event distributions for the total simulated background and total signal (scaled by a factor of 3 $ \times10^4 $) passing the event selection for the 0 $ \ell $ channel. The signal is decomposed into classes as defined in the text. The upper-left and upper-right panels show the soft-drop mass and PART score distributions for the H candidate jet (j) $ P(\mathrm{H}_{0\ell}) $, respectively. The lower-left and lower-right panels display the $ p_{\mathrm{T}}^\text{miss}/p_{\mathrm{T}}^{\text{j}} $ ratio and the angle $ |\Delta\phi (j, {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}) | $, respectively. Vertical lines indicate the selection conditions imposed to define the signal region. |
png pdf |
Figure 3-c:
The event distributions for the total simulated background and total signal (scaled by a factor of 3 $ \times10^4 $) passing the event selection for the 0 $ \ell $ channel. The signal is decomposed into classes as defined in the text. The upper-left and upper-right panels show the soft-drop mass and PART score distributions for the H candidate jet (j) $ P(\mathrm{H}_{0\ell}) $, respectively. The lower-left and lower-right panels display the $ p_{\mathrm{T}}^\text{miss}/p_{\mathrm{T}}^{\text{j}} $ ratio and the angle $ |\Delta\phi (j, {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}) | $, respectively. Vertical lines indicate the selection conditions imposed to define the signal region. |
png pdf |
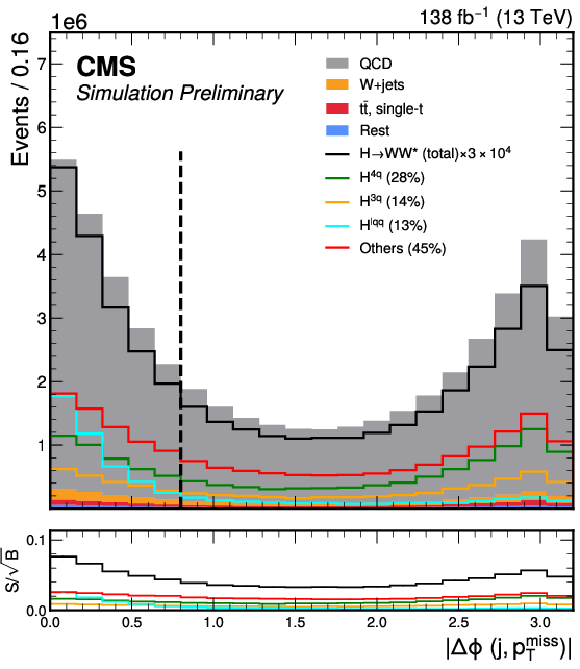
Figure 3-d:
The event distributions for the total simulated background and total signal (scaled by a factor of 3 $ \times10^4 $) passing the event selection for the 0 $ \ell $ channel. The signal is decomposed into classes as defined in the text. The upper-left and upper-right panels show the soft-drop mass and PART score distributions for the H candidate jet (j) $ P(\mathrm{H}_{0\ell}) $, respectively. The lower-left and lower-right panels display the $ p_{\mathrm{T}}^\text{miss}/p_{\mathrm{T}}^{\text{j}} $ ratio and the angle $ |\Delta\phi (j, {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}) | $, respectively. Vertical lines indicate the selection conditions imposed to define the signal region. |
png pdf |
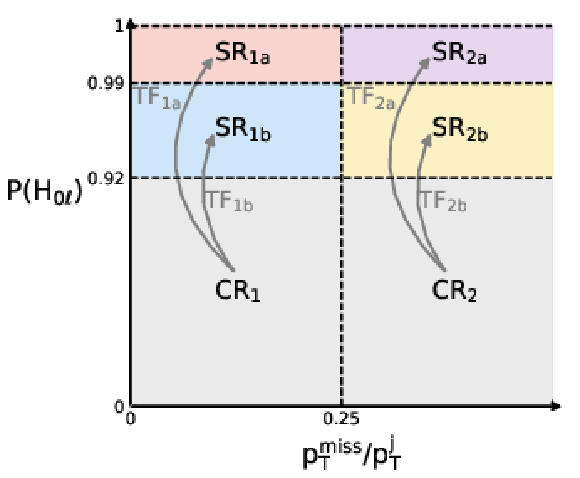
Figure 4:
Illustration of the SRs and CRs, and the TFs used to relate the QCD background in the different regions (left). The TFs used to predict the QCD process in the four SRs as a function of the $ m^*_{\text{j}} $ (right). |
png pdf |
Figure 4-a:
Illustration of the SRs and CRs, and the TFs used to relate the QCD background in the different regions (left). The TFs used to predict the QCD process in the four SRs as a function of the $ m^*_{\text{j}} $ (right). |
png pdf |
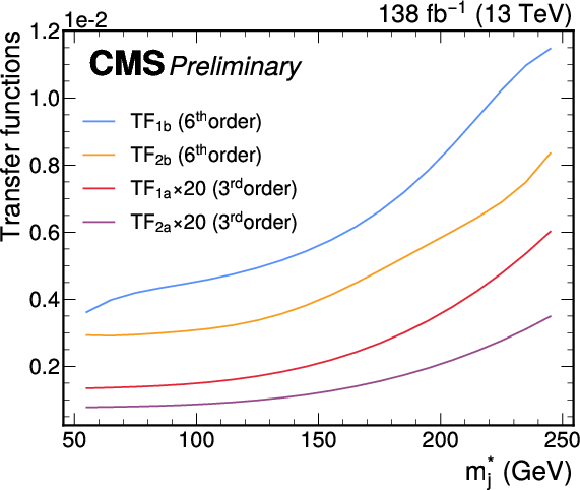
Figure 4-b:
Illustration of the SRs and CRs, and the TFs used to relate the QCD background in the different regions (left). The TFs used to predict the QCD process in the four SRs as a function of the $ m^*_{\text{j}} $ (right). |
png pdf |
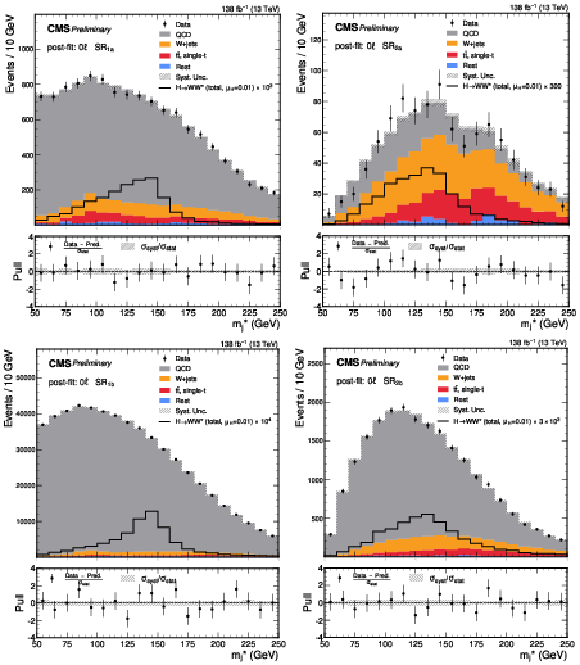
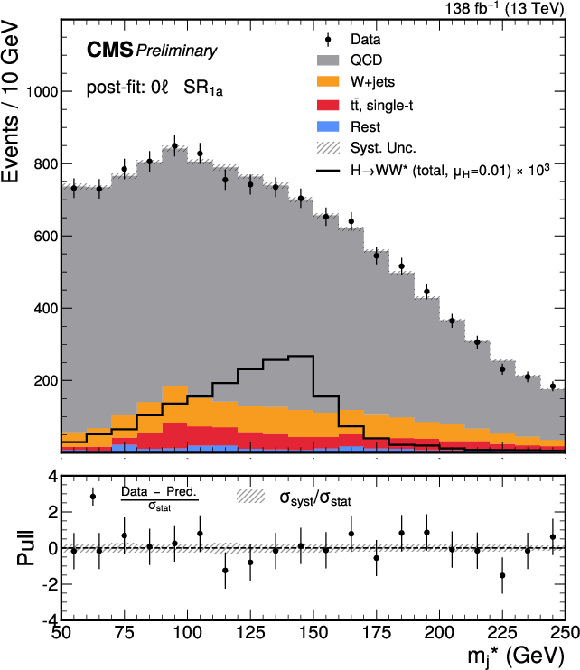
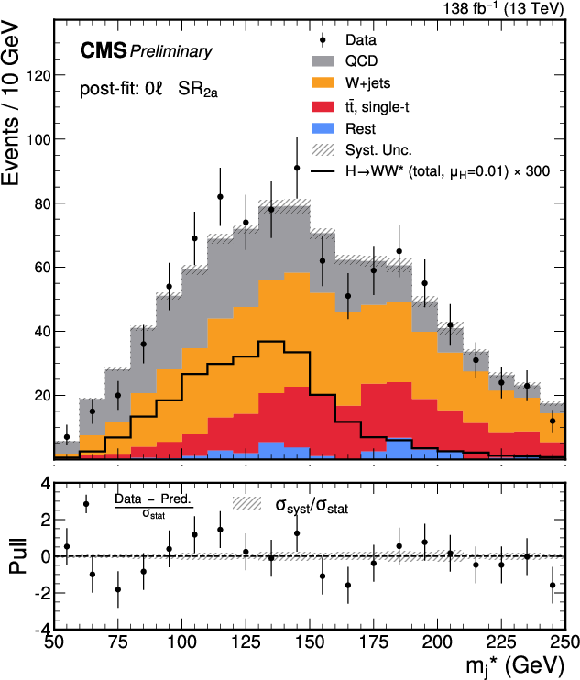
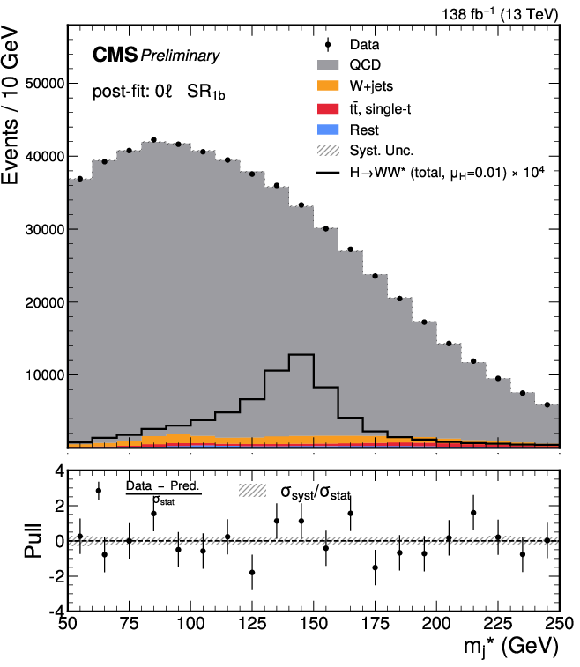
Figure 5:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal in the SRs of the 0 $ \ell $ channel. From upper to lower and left to right, the plots correspond to $ \text{SR}_\text{1a} $, $ \text{SR}_\text{2a} $, $ \text{SR}_\text{1b} $, and $ \text{SR}_\text{2b} $, respectively. The lower panel of each plot presents the pull distribution, as well as the $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility. |
png pdf |
Figure 5-a:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal in the SRs of the 0 $ \ell $ channel. From upper to lower and left to right, the plots correspond to $ \text{SR}_\text{1a} $, $ \text{SR}_\text{2a} $, $ \text{SR}_\text{1b} $, and $ \text{SR}_\text{2b} $, respectively. The lower panel of each plot presents the pull distribution, as well as the $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility. |
png pdf |
Figure 5-b:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal in the SRs of the 0 $ \ell $ channel. From upper to lower and left to right, the plots correspond to $ \text{SR}_\text{1a} $, $ \text{SR}_\text{2a} $, $ \text{SR}_\text{1b} $, and $ \text{SR}_\text{2b} $, respectively. The lower panel of each plot presents the pull distribution, as well as the $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility. |
png pdf |
Figure 5-c:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal in the SRs of the 0 $ \ell $ channel. From upper to lower and left to right, the plots correspond to $ \text{SR}_\text{1a} $, $ \text{SR}_\text{2a} $, $ \text{SR}_\text{1b} $, and $ \text{SR}_\text{2b} $, respectively. The lower panel of each plot presents the pull distribution, as well as the $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility. |
png pdf |
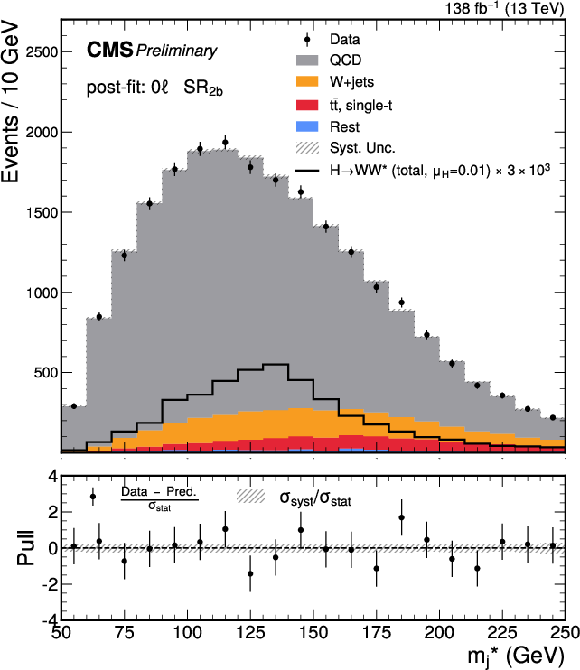
Figure 5-d:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal in the SRs of the 0 $ \ell $ channel. From upper to lower and left to right, the plots correspond to $ \text{SR}_\text{1a} $, $ \text{SR}_\text{2a} $, $ \text{SR}_\text{1b} $, and $ \text{SR}_\text{2b} $, respectively. The lower panel of each plot presents the pull distribution, as well as the $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility. |
png pdf |
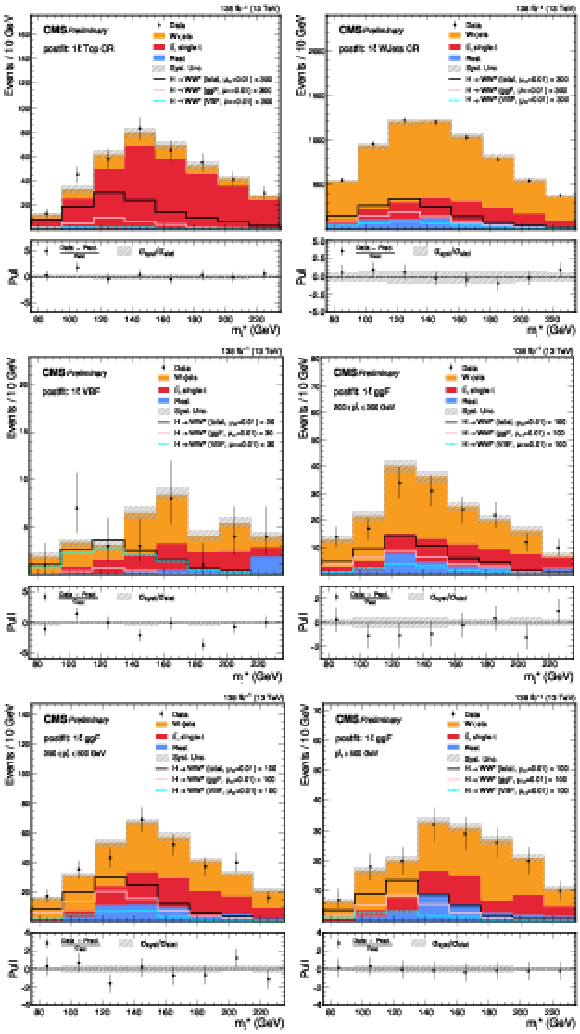
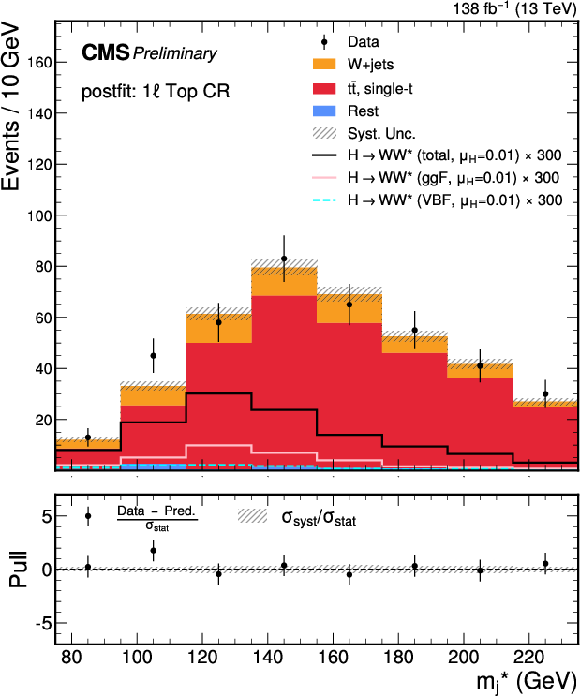
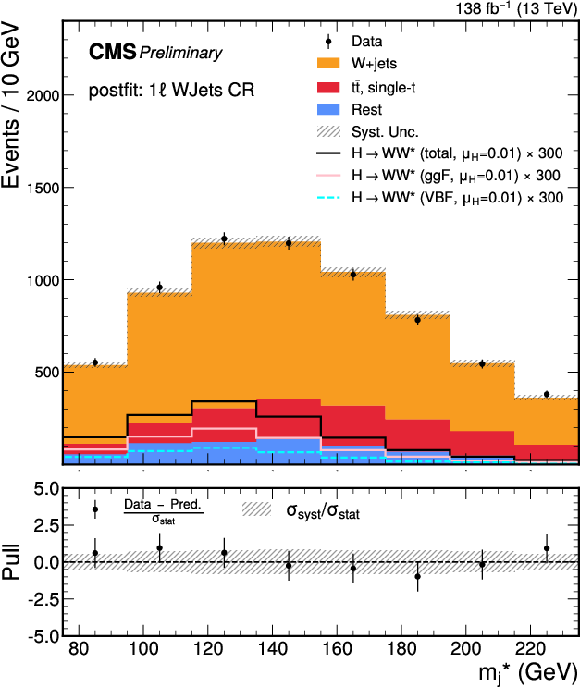
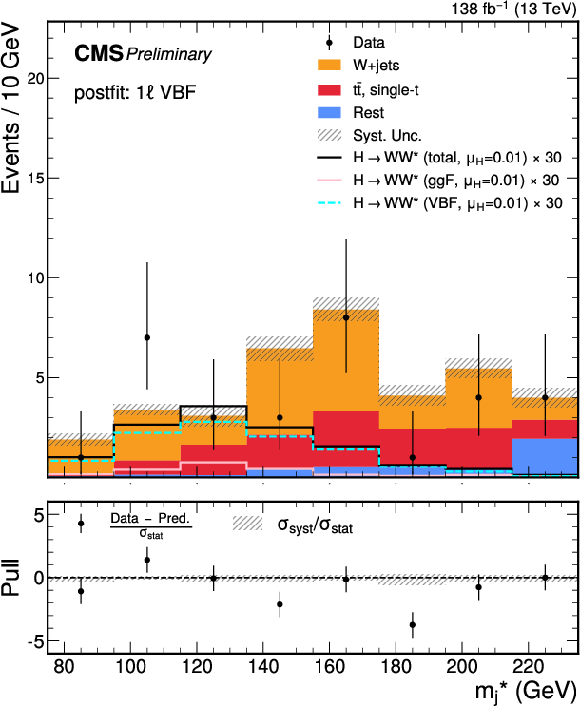
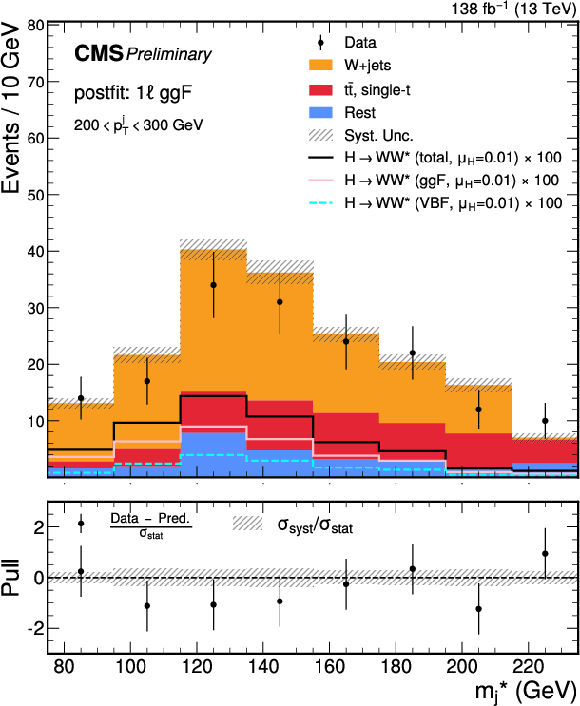
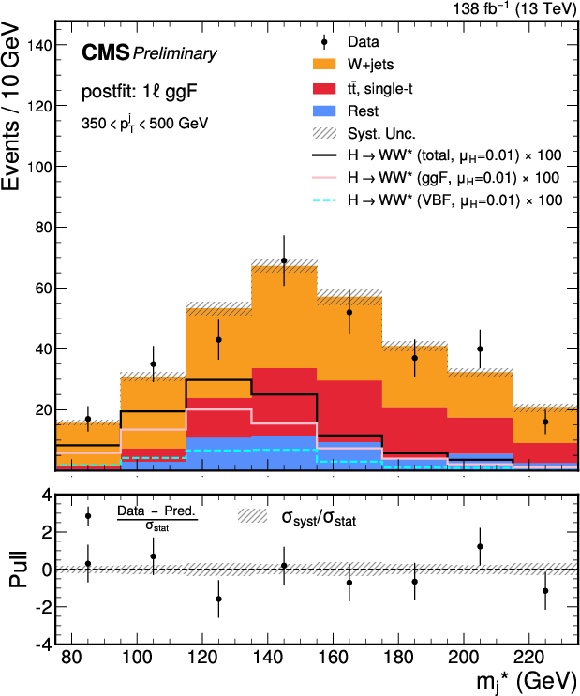
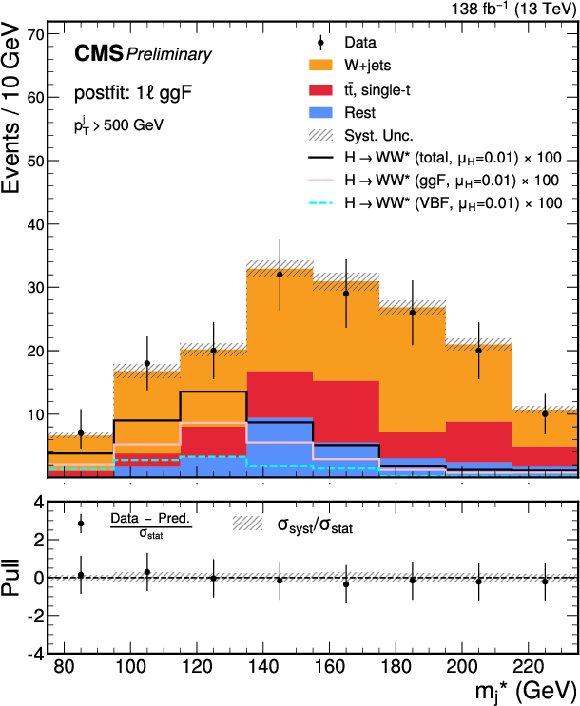
Figure 6:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-a:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-b:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-c:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-d:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-e:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
Figure 6-f:
Post-fit $ m^*_{\text{j}} $ distributions for the predicted background, observed data, and signal, decomposed by production mode, in the SRs of the 1 $ \ell $ channel. Upper to lower row, and left to right: Top CR, W+jets CR, VBF SR, and the ggF SRs binned in $ p_{\mathrm{T}} $ as $ [250,350) $, $ [350,500) $, and $ [500,+\infty) $ GeV, respectively. The lower panel of each plot presents the pull distribution, as well as $ \sigma_\text{syst} $ normalized to the $ \sigma_\text{stat} $. The signal is scaled by its best-fit value, $ \mu_\mathrm{H} = $ 0.01, from the combined 0 $ \ell $ and 1 $ \ell $ channels, and by an additional factor (as labeled) for visibility |
png pdf |
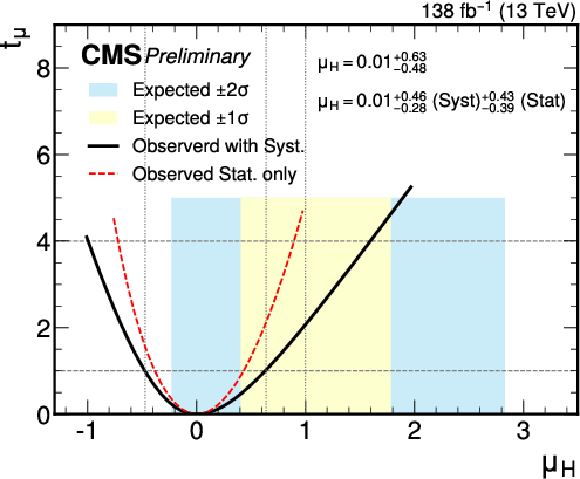
Figure 7:
Observed scan of the profile likelihood test statistic $ t_\mu $ as a function of the signal strength $ \mu_\mathrm{H} $ for the combined 0 $ \ell $ and 1 $ \ell $ channels. The solid lines correspond to profiling all statistical and systematic uncertainties, while the dashed lines correspond to profiling only the statistical uncertainties. |
png pdf |
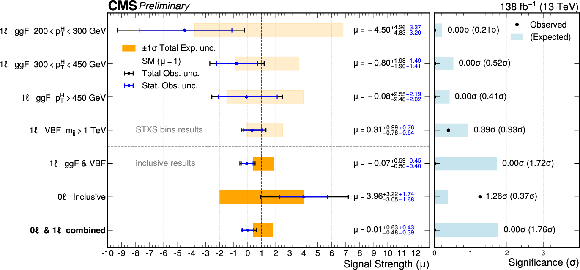
Figure 8:
Fitted signal strength (left) and significance (right) for $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ in the 0 $ \ell $ and 1 $ \ell $ channels using the full dataset. Combined results are presented alongside individual contributions from each channel. For the 1 $ \ell $ channel, results are also shown for an alternative measurement using five independent signal strengths for the ggF and VBF processes, corresponding to different generator-level selections. Expected uncertainties are indicated by yellow (signal strength) and light blue (significance) bands. Blue and black lines represent statistical and total observed uncertainties, respectively. The results are consistent with standard model expectations. |
| Tables | |

png pdf |
Table 1:
The 37 PART jet classification categories. The categories are based on the decay modes of H and V bosons, top quarks, and QCD processes. Numbers in parentheses (e.g., 0 c, 1 c) indicate the number of c quarks present in a given final state in front of it. All listed decay products are assumed to be contained within the jet cone, except for neutrinos. For example, labels such as 3 $ \mathrm{q} $ or $ \mathrm{b}\mathrm{q} $ imply that one quark escapes the jet cone in $ \mathrm{H}\to4\mathrm{q} $ or $ \mathrm{t}\to\mathrm{b}\mathrm{q}\mathrm{q} $ decays, respectively. |

png pdf |
Table 2:
Kinematic requirements used to define the signal regions (SRs) and control regions (CRs) in the 0 $ \ell $ channel. The right columns list the conditions under which the $ m_{\text{j}} $ is replaced by the corrected $ m^*_{\text{j}} $ mass. The ``&" represents the logical ``AND" and $ \Delta\phi $ refers to the azimuthal angle difference between $ {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}} $ and the transverse momentum vector of the H boson candidate. |
png pdf |
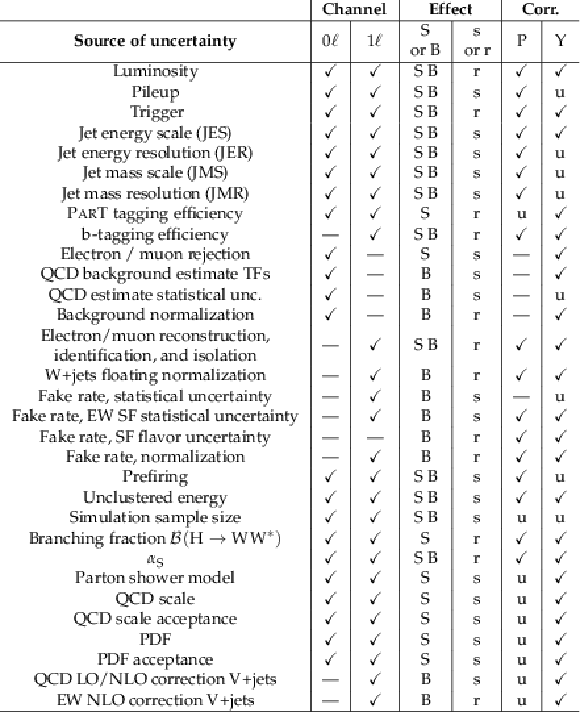
Table 3:
Systematic uncertainty sources considered in the analysis. Left to right columns: the sources, the channels applied, whether the uncertainty affects signal (S) or background (B), its influence on shape (s) or rate (r), whether the nuisances are (un)correlated (u or $ \checkmark $) among different process models (P) or among the data-taking years (Y). |
png pdf |
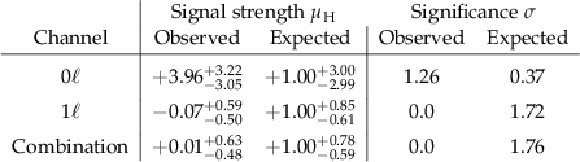
Table 4:
Observed and expected fitted signal strength (second column) and significance (third column) for $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ in the 0 $ \ell $ and 1 $ \ell $ channels, followed by the combined result. |
| Summary |
| A search for Higgs boson (H) production at high transverse momentum in the $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ decay channel is presented. The analysis uses proton-proton collision data collected at $ \sqrt{s} = $ 13 TeV with the CMS experiment, corresponding to an integrated luminosity of 138 fb$^{-1}$, and focuses on semileptonic decays with or without an isolated lepton in the final state. The final states are characterized by a single large-radius jet containing the hadronic decay products of the W bosons, exploiting the jet substructure resulting from the boosted topology of the Higgs boson decay. The 1 $ \ell $ channel categorizes events by the dominant Higgs boson production mechanisms: gluon-gluon fusion and vector boson fusion, while the 0 $ \ell $ channel remains inclusive across all production modes. The particle transformer algorithm leverages advanced machine learning techniques to identify H candidate jets with intricate substructure, missing transverse momentum aligned with the jet, or leptons inside the jet. It is calibrated with the Lund jet plane method, and fine-tuned to optimize the expected signal significance in the 1 $ \ell $ channel. The invariant mass of the Higgs or vector boson candidate jet is used for signal extraction. The expected signal significance is 1.76$ \sigma $, while the observed signal strength relative to the standard model expectation is $ \mu_{\mathrm{H}} = $ 0.01 $ ^{+0.63}_{-0.48} $, showing no evidence of a signal above the background. These measurements represent the first dedicated study of highly Lorentz-boosted $ \mathrm{H} \to \mathrm{W} \mathrm{W}^{*} $ decays, complementing earlier searches in other Higgs boson decay channels and production modes. |
| References | ||||
| 1 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 2 | CMS Collaboration | Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 3 | K. Becker et al. | Precise predictions for boosted Higgs production | SciPost Phys. Core 7 (2024) 001 | 2005.07762 |
| 4 | C. Grojean, E. Salvioni, M. Schlaffer, and A. Weiler | Very boosted Higgs in gluon fusion | JHEP 05 (2014) 22 | 1312.3317 |
| 5 | M. Schlaffer et al. | Boosted Higgs shapes | EPJC 74 (2014) 3120 | 1405.4295 |
| 6 | S. Dawson, I. M. Lewis, and M. Zeng | Usefulness of effective field theory for boosted Higgs production | PRD 91 (2015) 074012 | 1501.04103 |
| 7 | M. Grazzini, A. Ilnicka, M. Spira, and M. Wiesemann | Modeling BSM effects on the Higgs transverse-momentum spectrum in an EFT approach | JHEP 03 (2017) 115 | 1612.00283 |
| 8 | F. Maltoni, K. Mawatari, and M. Zaro | Higgs characterisation via vector-boson fusion and associated production: NLO and parton-shower effects | EPJC 74 (2014) 2710 | 1311.1829 |
| 9 | C. Degrande et al. | Electroweak Higgs boson production in the standard model effective field theory beyond leading order in QCD | EPJC 77 (2017) 262 | 1609.04833 |
| 10 | CMS Collaboration | Measurement of the Higgs boson inclusive and differential fiducial production cross sections in the diphoton decay channel with pp collisions at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2023) 091 | CMS-HIG-19-016 2208.12279 |
| 11 | CMS Collaboration | Measurements of inclusive and differential cross sections for the Higgs boson production and decay to four-leptons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 08 (2023) 040 | CMS-HIG-21-009 2305.07532 |
| 12 | CMS Collaboration | Measurement of the inclusive and differential Higgs boson production cross sections in the leptonic WW decay mode at $ \sqrt{s} = $ 13 TeV | JHEP 03 (2021) 003 | CMS-HIG-19-002 2007.01984 |
| 13 | CMS Collaboration | Measurement of the inclusive and differential Higgs boson production cross sections in the decay mode to a pair of $ \tau $ leptons in pp collisions at $ \sqrt{s} = $ 13 TeV | PRL 128 (2022) 081805 | CMS-HIG-20-015 2107.11486 |
| 14 | CMS Collaboration | Measurement and interpretation of differential cross sections for Higgs boson production at $ \sqrt{s} = $ 13 TeV | PLB 792 (2019) 369 | CMS-HIG-17-028 1812.06504 |
| 15 | CMS Collaboration | Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair | PRL 120 (2018) 071802 | CMS-HIG-17-010 1709.05543 |
| 16 | CMS Collaboration | Inclusive search for highly boosted Higgs bosons decaying to bottom quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2020) 085 | CMS-HIG-19-003 2006.13251 |
| 17 | CMS Collaboration | Search for a boosted Higgs boson decaying to bottom quark pairs in association with a hadronically decaying W or Z boson with the CMS detector using proton-proton collisions at $ \sqrt{s}= $ 13 TeV | Technical Report , CERN, Geneva, 2025 CMS-PAS-HIG-24-017 |
CMS-PAS-HIG-24-017 |
| 18 | ATLAS Collaboration | Constraints on Higgs boson production with large transverse momentum using $ H\rightarrow b\bar{b} $ decays in the ATLAS detector | PRD 105 (2022) 092003 | 2111.08340 |
| 19 | ATLAS Collaboration | Study of High-Transverse-Momentum Higgs Boson Production in Association with a Vector Boson in the qqbb Final State with the ATLAS Detector | PRL 132 (2024) 131802 | 2312.07605 |
| 20 | CMS Collaboration | Measurement of the production cross section of a Higgs boson with large transverse momentum in its decays to a pair of \ensuremath\tau leptons in proton-proton collisions at s=13TeV | PLB 857 (2024) 138964 | CMS-HIG-21-017 2403.20201 |
| 21 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | no. 9, 800, 2021 EPJC 81 (2021) |
CMS-LUM-17-003 2104.01927 |
| 22 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 23 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 24 | H. Qu, C. Li, and S. Qian | Particle Transformer for Jet Tagging | in th International Conference on Machine Learning, K. Chaudhuri et al., eds., volume 162, 2022 Proceedings of the 3 (2022) 18281 |
2202.03772 |
| 25 | CMS Collaboration | Search for highly energetic double Higgs boson production in the two bottom quark and two vector boson all-hadronic final state | CMS Physics Analysis Summary, 2024 CMS-PAS-HIG-23-012 |
CMS-PAS-HIG-23-012 |
| 26 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 27 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 28 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 29 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 30 | CMS Collaboration | Performance of the CMS high-level trigger during LHC run 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 31 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | no. 05, P05014, 2021 JINST 16 (2021) |
CMS-EGM-17-001 2012.06888 |
| 32 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ {\sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 33 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 34 | K. Hamilton, P. Nason, C. Oleari, and G. Zanderighi | Merging H/W/Z + 0 and 1 jet at NLO with no merging scale: a path to parton shower + NNLO matching | JHEP 05 (2013) 082 | 1212.4504 |
| 35 | T. Neumann | NLO Higgs+jet production at large transverse momenta including top quark mass effects | J. Phys. Commun. 2 (2018) 095017 | 1802.02981 |
| 36 | P. Nason and C. Oleari | NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG | JHEP 02 (2010) 037 | 0911.5299 |
| 37 | G. Luisoni, P. Nason, C. Oleari, and F. Tramontano | $ \mathrm{H}\mathrm{W}^{\pm} $/HZ + 0 and 1 jet at NLO with the POWHEG box interfaced to GoSam and their merging within MiNLO | JHEP 10 (2013) 083 | 1306.2542 |
| 38 | H. B. Hartanto, B. Jager, L. Reina, and D. Wackeroth | Higgs boson production in association with top quarks in the POWHEG BOX | PRD 91 (2015) 094003 | 1501.04498 |
| 39 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs Cross Sections: 4. Deciphering the nature of the Higgs sector | CERN Yellow Rep. Monogr. 2 (2017) | 1610.07922 |
| 40 | S. Bolognesi et al. | On the spin and parity of a single-produced resonance at the LHC | PRD 86 (2012) 095031 | 1208.4018 |
| 41 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 42 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 43 | T. Gleisberg et al. | Event generation with SHERPA 1.1 | JHEP 02 (2009) 007 | 0811.4622 |
| 44 | Sherpa Collaboration | Event Generation with Sherpa 2.2 | SciPost Phys. 7 (2019) 034 | 1905.09127 |
| 45 | T. Gleisberg and S. Hoeche | Comix, a new matrix element generator | JHEP 12 (2008) 039 | 0808.3674 |
| 46 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 47 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 48 | S. Kallweit et al. | NLO electroweak automation and precise predictions for W+multijet production at the LHC | JHEP 04 (2015) 012 | 1412.5157 |
| 49 | S. Kallweit et al. | NLO QCD+EW predictions for V+jets including off-shell vector-boson decays and multijet merging | JHEP 04 (2016) 021 | 1511.08692 |
| 50 | S. Kallweit et al. | NLO QCD+EW automation and precise predictions for V+multijet production | in 50th Rencontres de Moriond on QCD and High Energy Interactions, 2015 | 1505.05704 |
| 51 | J. M. Lindert et al. | Precise predictions for V+jets dark matter backgrounds | EPJC 77 (2017) 829 | 1705.04664 |
| 52 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 53 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 54 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 55 | S. Alioli, S.-O. Moch, and P. Uwer | Hadronic top-quark pair-production with one jet and parton showering | JHEP 01 (2012) 137 | 1110.5251 |
| 56 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 57 | R. Frederix, E. Re, and P. Torrielli | Single-top $ t $-channel hadroproduction in the four-flavour scheme with POWHEG and aMC@NLO | JHEP 09 (2012) 130 | 1207.5391 |
| 58 | J. M. Campbell and R. K. Ellis | MCFM for the Tevatron and the LHC | Nucl. Phys. Proc. Suppl. 205 (2010) 10 | 1007.3492 |
| 59 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 60 | J. Allison et al. | GEANT 4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 61 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 62 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 63 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 64 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 65 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 66 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 67 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 68 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 69 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup Per Particle Identification | JHEP 10 (2014) 059 | 1407.6013 |
| 70 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 71 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS Physics Analysis Summary, 2017 CMS-PAS-JME-16-003 |
CMS-PAS-JME-16-003 |
| 72 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 73 | H. Qu and L. Gouskos | ParticleNet: Jet Tagging via Particle Clouds | PRD 101 (2020) 056019 | 1902.08570 |
| 74 | CMS Collaboration | Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques | JINST 15 (2020) P06005 | CMS-JME-18-002 2004.08262 |
| 75 | E. Bols et al. | Jet flavour classification using DeepJet | JINST 15 (2020) P12012 | 2008.10519 |
| 76 | CMS Collaboration | Performance of the DeepJet b tagging algorithm using 41.9 fb$ ^{-1} $ of data from proton-proton collisions at 13 TeV with Phase 1 CMS detector | CMS Detector Performance Note CMS-DP-2018-058, 2018 CDS |
|
| 77 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 78 | K. Rehermann and B. Tweedie | Efficient Identification of Boosted Semileptonic Top Quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 79 | C. Li et al. | Accelerating resonance searches via signature-oriented pre-training | 2405.12972 | |
| 80 | CMS Collaboration | A new method for correcting the substructure of multi-prong jets using Lund jet plane reweighting in the CMS experiment | CMS Physics Analysis Summary, 2025 CMS-PAS-JME-23-001 |
CMS-PAS-JME-23-001 |
| 81 | F. A. Dreyer, G. P. Salam, and G. Soyez | The Lund Jet Plane | JHEP 12 (2018) 064 | 1807.04758 |
| 82 | CMS Collaboration | Lund Plane Reweighting for Jet Substructure Correction | CMS Detector Performance Note CMS-DP-2023-046, 2023 CDS |
|
| 83 | S. Catani, Y. L. Dokshitzer, M. H. Seymour, and B. R. Webber | Longitudinally invariant $ K_t $ clustering algorithms for hadron hadron collisions | --224, 1993 NPB 406 (1993) 187 |
|
| 84 | S. D. Ellis and D. E. Soper | Successive combination jet algorithm for hadron collisions | PRD 48 (1993) 3160 | hep-ph/9305266 |
| 85 | D. Krohn, J. Thaler, and L.-T. Wang | Jet Trimming | JHEP 02 (2010) 084 | 0912.1342 |
| 86 | R. A. Fisher | On the interpretation of $ \chi^{2} $ from contingency tables, and the calculation of P | J. R. Stat. Soc. 85 (1922) 87 | |
| 87 | LHC Higgs Cross Section Working Group | Simplified Template Cross Sections --- Stage 1.1 and 1.2 | Public Note LHCHWG-INT-2025-001, 2025 | |
| 88 | CMS Collaboration | Measurements of properties of the Higgs boson decaying to a W boson pair in pp collisions at $ \sqrt{s}= $ 13 TeV | PLB 791 (2019) 96 | CMS-HIG-16-042 1806.05246 |
| 89 | ATLAS and CMS Collaborations, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011 | |
| 90 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | --228, 1993 Comput. Phys. Commun. 77 (1993) 219 |
|
| 91 | J. S. Conway | Incorporating Nuisance Parameters in Likelihoods for Multisource Spectra | in , volume 1 , p--120, 2019 PHYSTAT 201 (2019) 115 |
1103.0354 |
| 92 | CMS Collaboration | The CMS statistical analysis and combination tool: \textscCombine | Comput. Softw. Big Sci. 8 (2024) 19 | CMS-CAT-23-001 2404.06614 |
| 93 | W. Verkerke and D. P. Kirkby | The RooFit toolkit for data modeling | eConf C0303241 MOLT007, 2003 | physics/0306116 |
| 94 | L. Moneta et al. | The RooStats Project | PoS ACAT 057, 2010 link |
1009.1003 |
| 95 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC 75 (2015) 212 | CMS-HIG-14-009 1412.8662 |
| 96 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|