

Compact Muon Solenoid
LHC, CERN
| CMS-SMP-20-014 ; CERN-EP-2021-163 | ||
| Measurement of the inclusive and differential WZ production cross sections, polarization angles, and triple gauge couplings in pp collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 21 October 2021 | ||
| JHEP 07 (2022) 032 | ||
| Abstract: The associated production of a W and a Z boson is studied in final states with multiple leptons produced in proton-proton (pp) collisions at a centre-of-mass energy of 13 TeV using 137 fb$^{-1}$ of data collected with the CMS detector at the LHC. A measurement of the total inclusive production cross section yields $\sigma_{\textrm{tot}}({\mathrm{p}}{\mathrm{p}}\to{\mathrm{W}\mathrm{Z}} ) = $ 50.6 $\pm$ 0.8 (stat) $\pm$ 1.5 (syst) $\pm$ 1.1 (lumi) $\pm$ 0.5 (theo) pb. Measurements of the fiducial and differential cross sections for several key observables are also performed in all the final-state lepton flavour and charge compositions with a total of three charged leptons, which can be electrons or muons. All results are compared with theoretical predictions computed up to next-to-next-to-leading order in quantum chromodynamics plus next-to-leading order in electroweak theory and for various sets of parton distribution functions. The results include direct measurements of the charge asymmetry and the W and Z vector boson polarization. The first observation of longitudinally polarized W bosons in WZ production is reported. Anomalous gauge couplings are searched for, leading to new constraints on beyond-the-standard-model contributions to the WZ triple gauge coupling. | ||
| Links: e-print arXiv:2110.11231 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
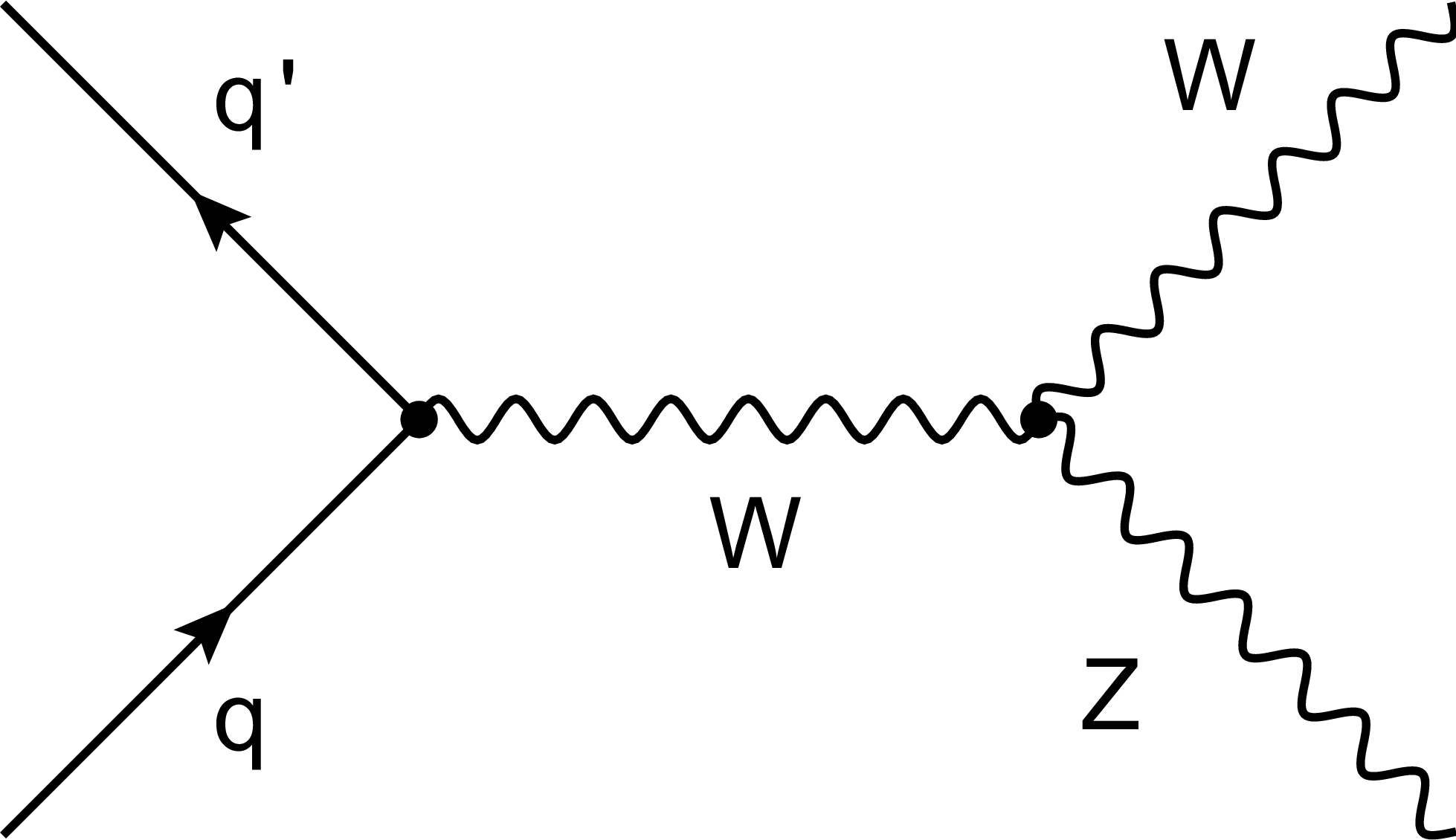
Figure 1:
Feynman diagrams for resonant WZ production at leading order in proton-proton collisions. The contributions from the $s$ channel (left), $t$ channel (middle), and $u$ channel (right) are shown. The contribution from the $s$ channel proceeds through a TGC. |
png pdf |
Figure 1-a:
Feynman diagram for resonant WZ production at leading order in proton-proton collisions. The contribution from the $s$ channel is shown. This contribution proceeds through a TGC. |
png pdf |
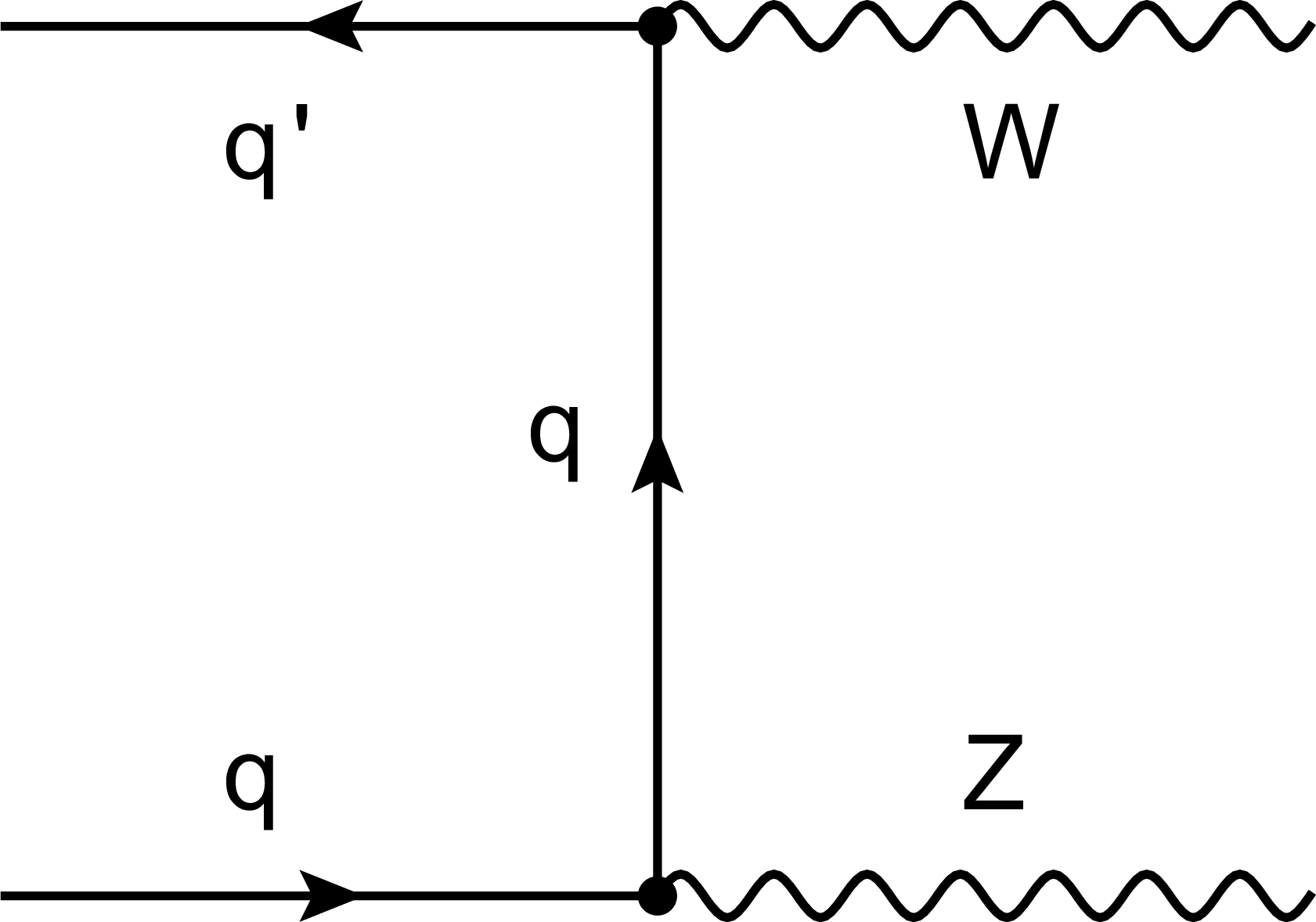
Figure 1-b:
Feynman diagram for resonant WZ production at leading order in proton-proton collisions. The contribution from the $t$ channel is shown. |
png pdf |
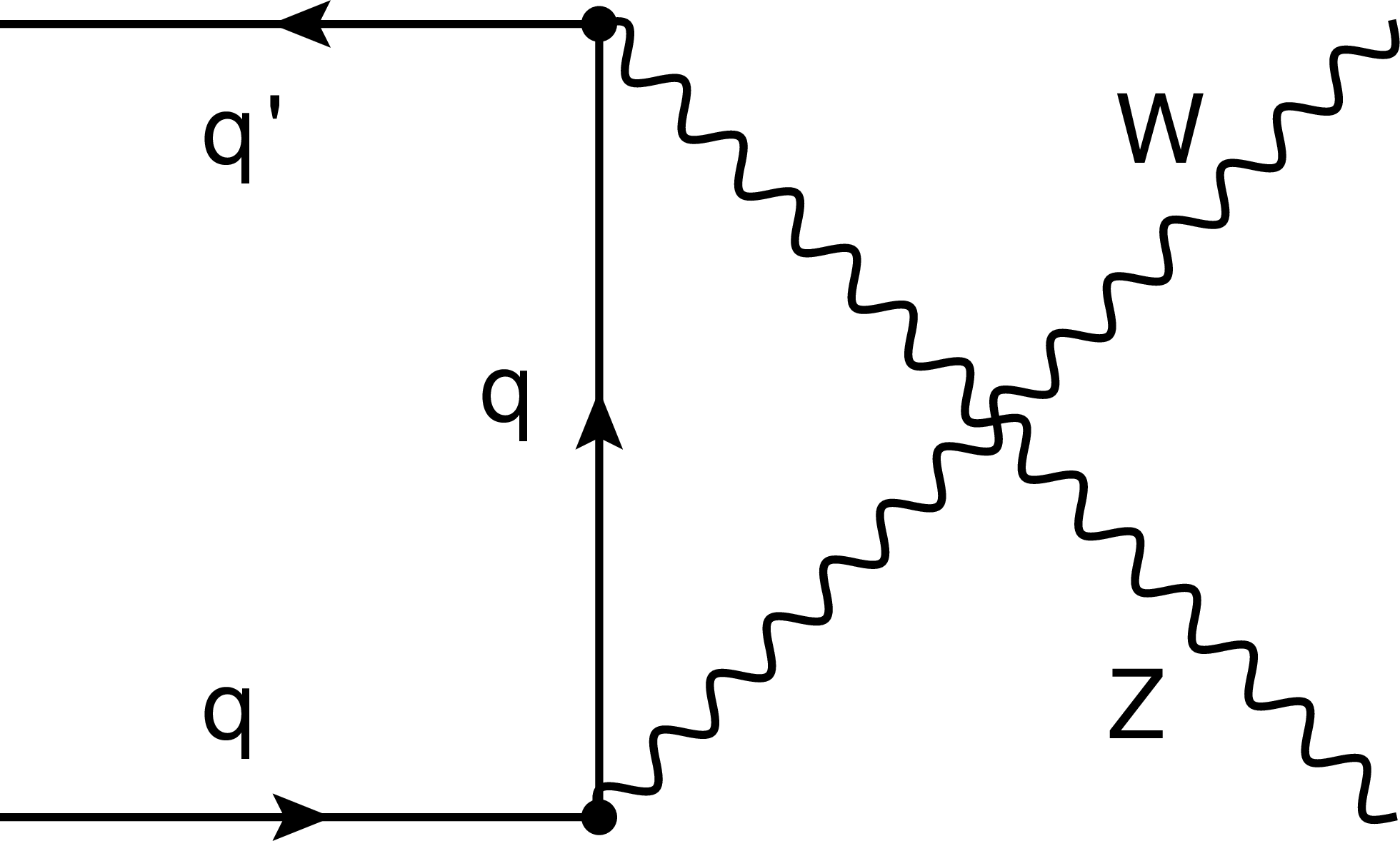
Figure 1-c:
Feynman diagram for resonant WZ production at leading order in proton-proton collisions. The contribution from the $u$ channel is shown. |
png pdf |
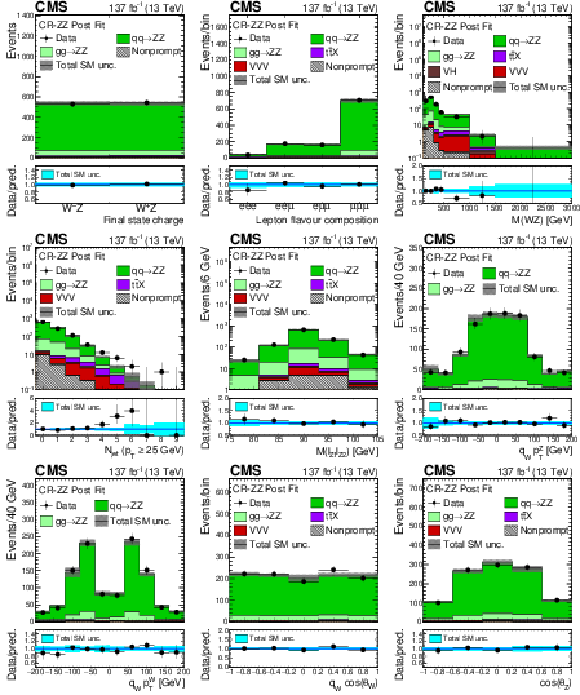
Figure 2:
Distribution of observables in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. From left to right and top to bottom: charge of the system of the three leading leptons, their flavour distribution, invariant mass of the three lepton plus ${{p_{\mathrm {T}}} ^\text {miss}}$ system, number of reconstructed jets, invariant mass of the leptonic pair with mass closest to that of the Z boson, reconstructed ${p_{\mathrm {T}}}$ of the Z boson times charge of the three leading lepton final state, reconstructed ${p_{\mathrm {T}}}$ of the W boson times final-state charge constructed with ${{p_{\mathrm {T}}} ^\text {miss}}$ and the three leading lepton system, cosine of the polarization angle of the W boson multiplied by the boson charge, and cosine of the polarization angle of the Z boson. The polarization angles are described in Sec. 10. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |

png pdf |
Figure 2-a:
Distribution of the charge of the system of the three leading leptons in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
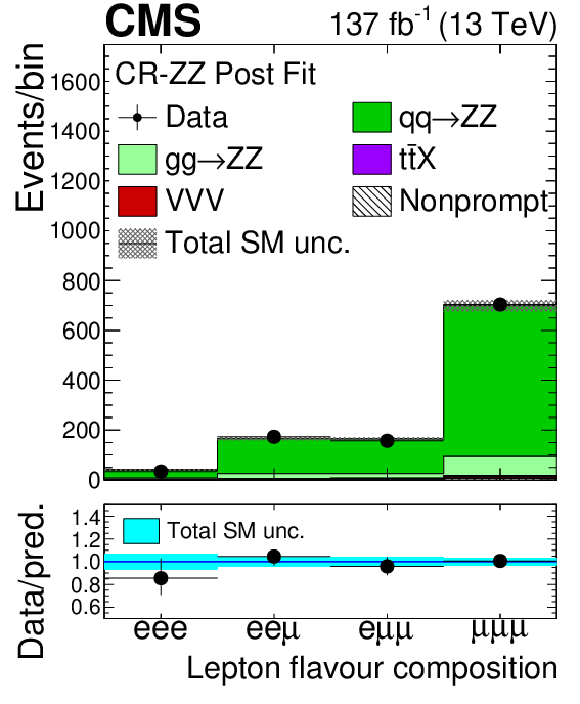
png pdf |
Figure 2-b:
Distribution of the flavour of the system of the three leading leptons in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
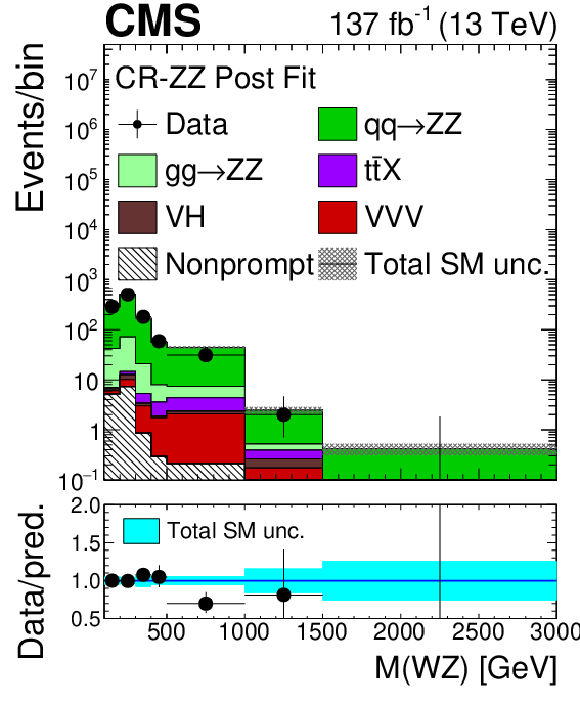
Figure 2-c:
Distribution of the invariant mass of the three lepton plus ${{p_{\mathrm {T}}} ^\text {miss}}$ system in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
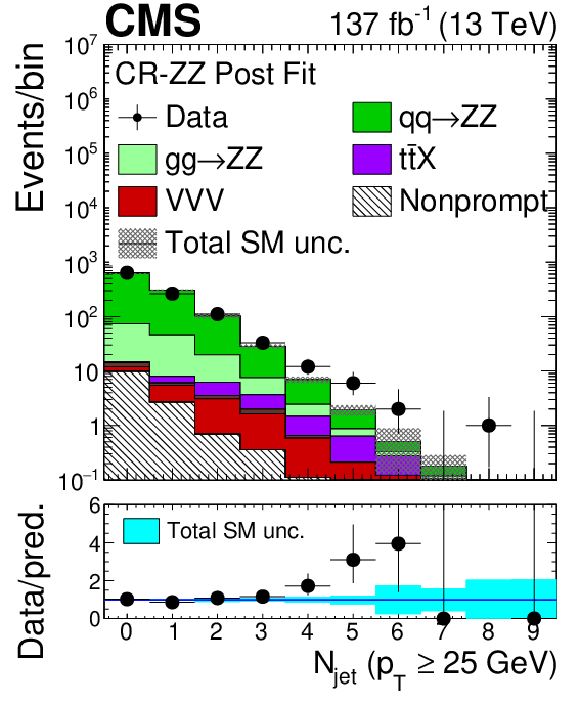
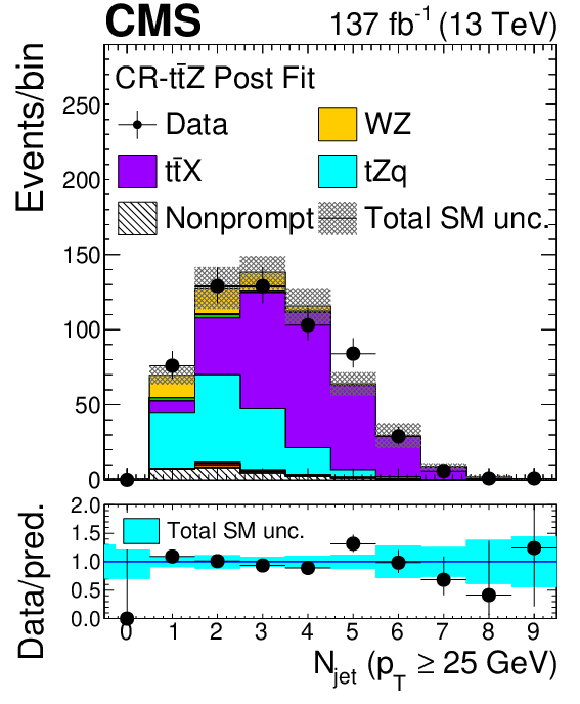
Figure 2-d:
Distribution of the number of reconstructed jets in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
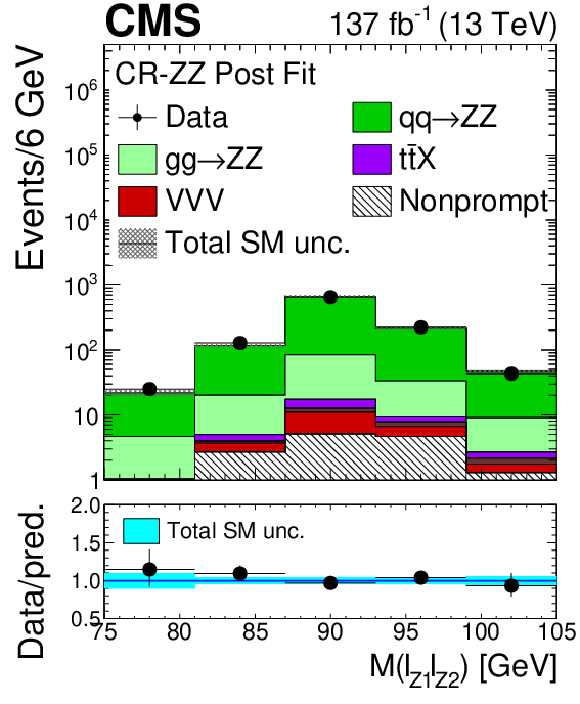
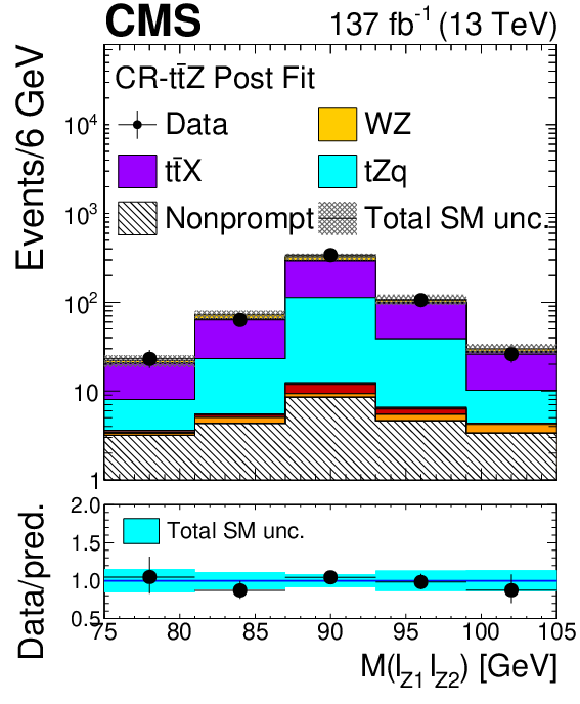
Figure 2-e:
Distribution of the invariant mass of the leptonic pair with mass closest to that of the Z boson in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
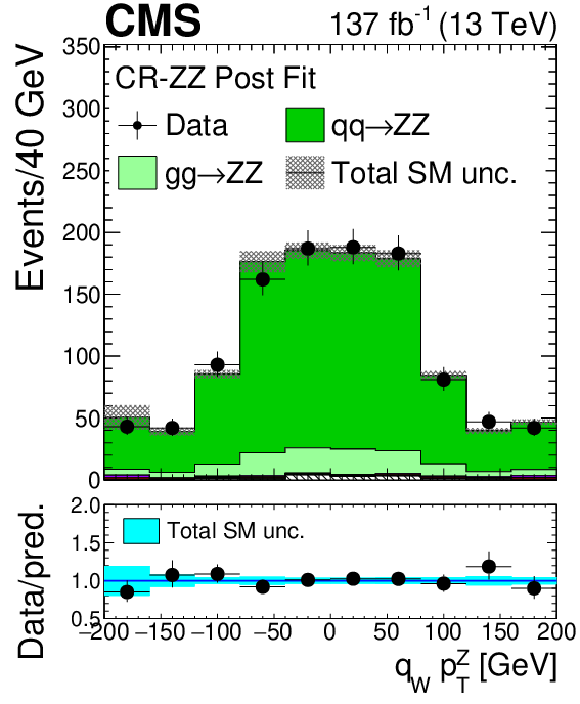
png pdf |
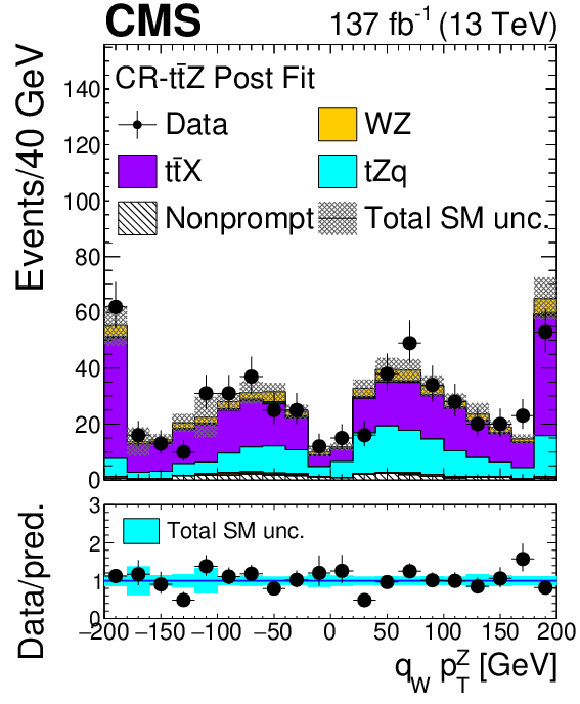
Figure 2-f:
Distribution of the reconstructed ${p_{\mathrm {T}}}$ of the Z boson times charge of the three leading lepton final state in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
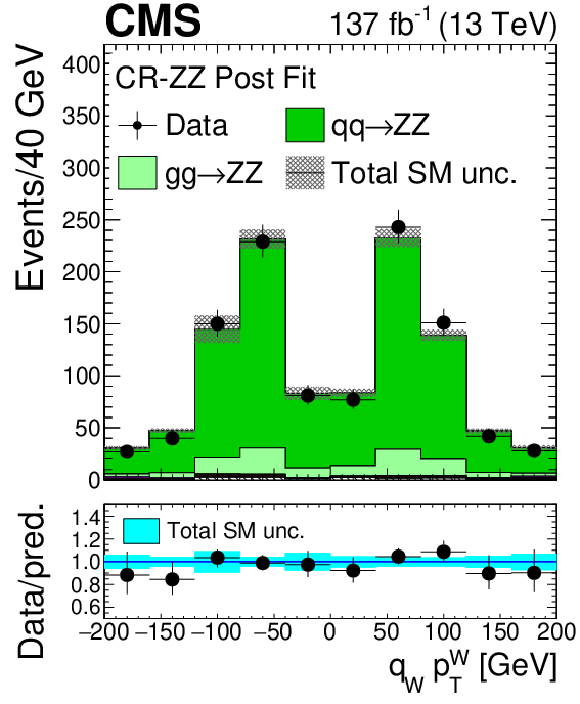
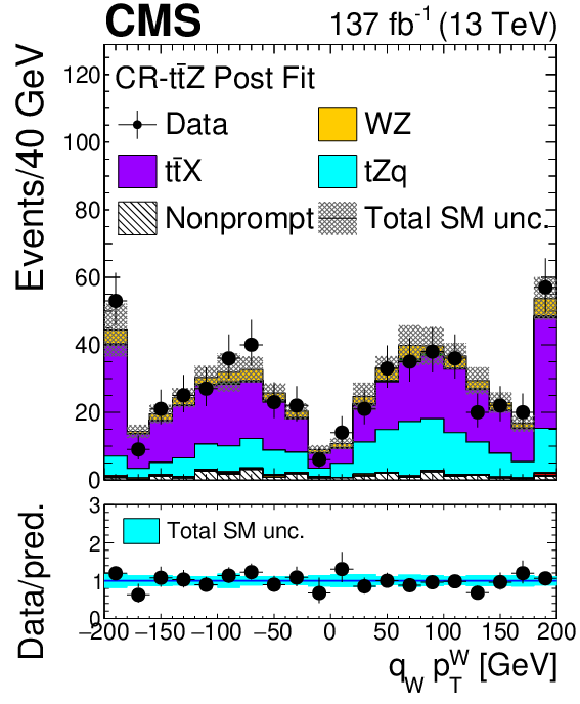
Figure 2-g:
Distribution of the reconstructed ${p_{\mathrm {T}}}$ of the W boson times final-state charge constructed with ${{p_{\mathrm {T}}} ^\text {miss}}$ and the three leading lepton system in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
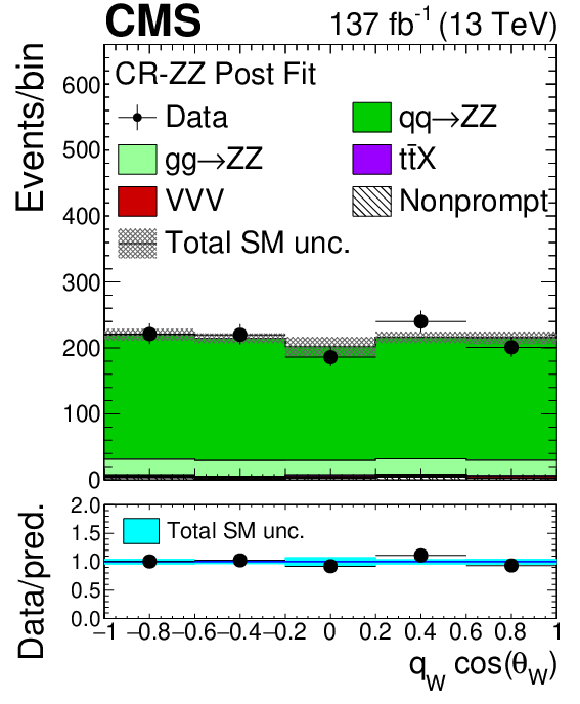
Figure 2-h:
Distribution of the cosine of the polarization angle of the W boson multiplied by the boson charge in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The polarization angles are described in Sec. 10. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
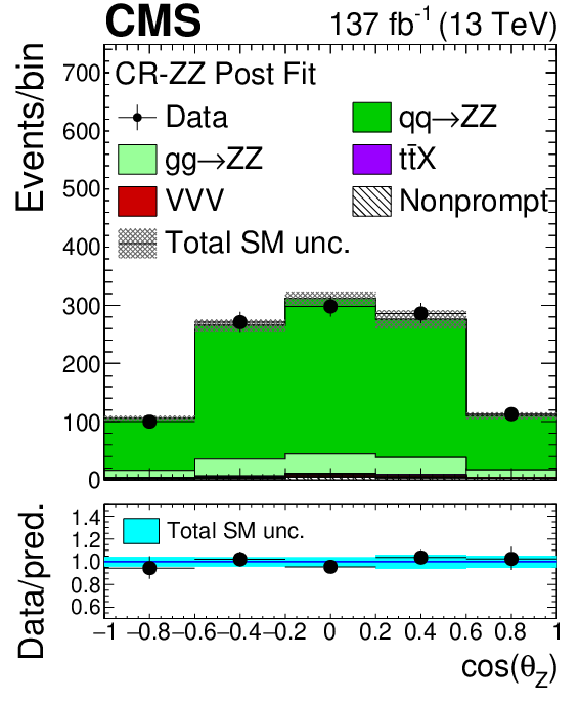
Figure 2-i:
Distribution of the cosine of the polarization angle of the Z boson in the ZZ control region evaluated with the uncertainties obtained after the signal extraction fit described in Section 8. The polarization angles are described in Sec. 10. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin. |
png pdf |
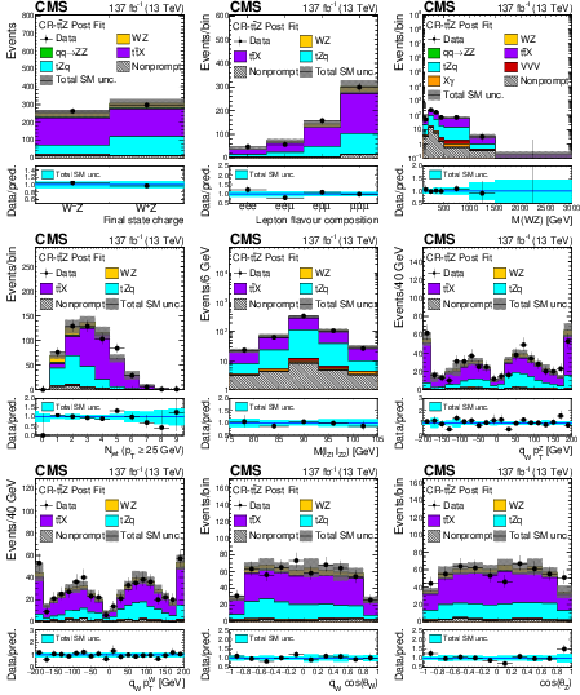
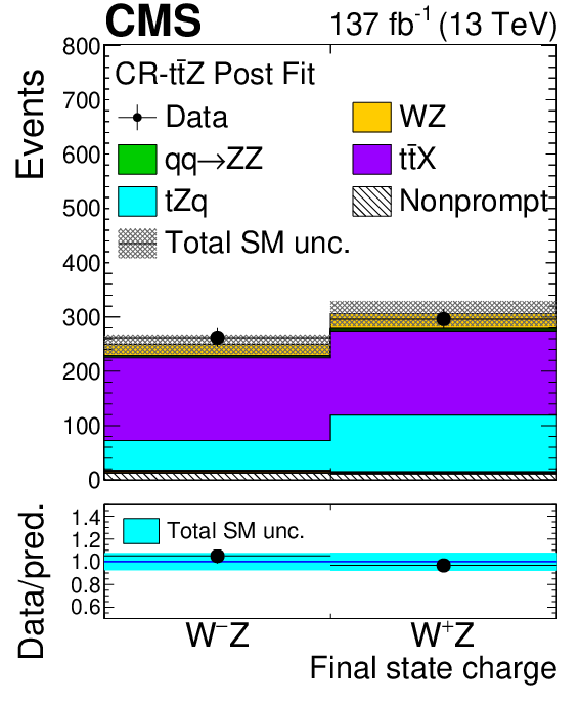
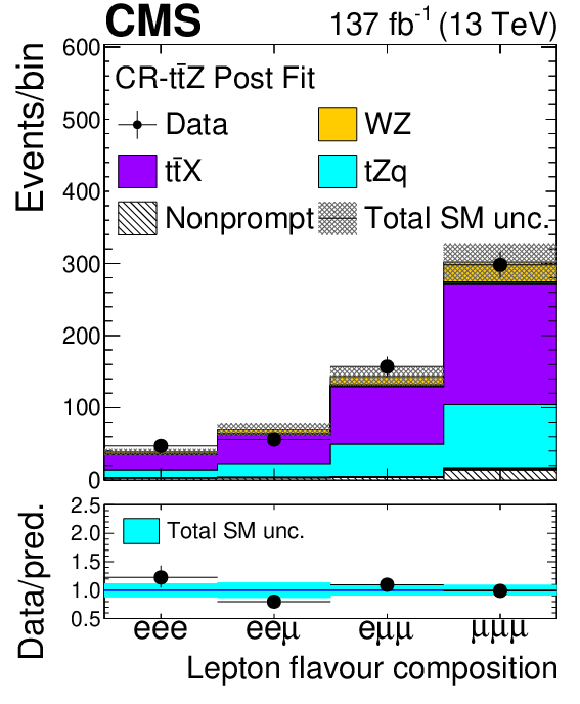
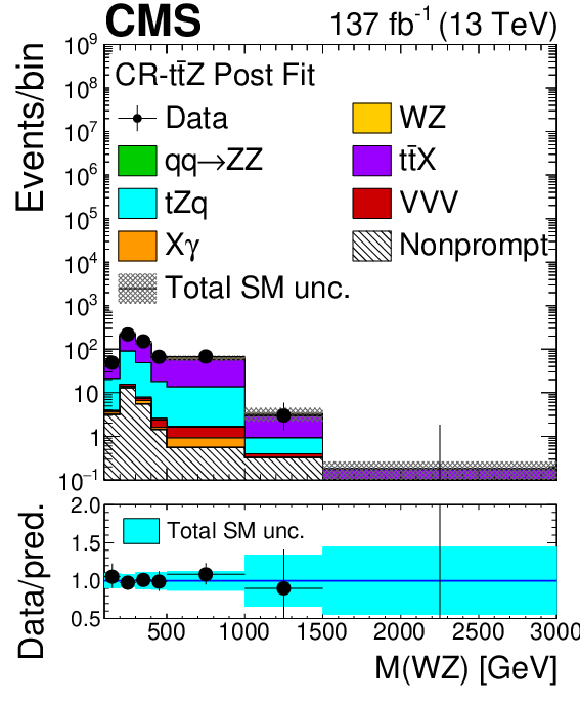
Figure 3:
As in Fig. 2, for the distribution of observables in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-a:
As in Fig. 2-a, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-b:
As in Fig. 2-b, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-c:
As in Fig. 2-c, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-d:
As in Fig. 2-d, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-e:
As in Fig. 2-e, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-f:
As in Fig. 2-f, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
Figure 3-g:
As in Fig. 2-g, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |

png pdf |
Figure 3-h:
As in Fig. 2-h, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |

png pdf |
Figure 3-i:
As in Fig. 2-i, in the ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$ control region. |
png pdf |
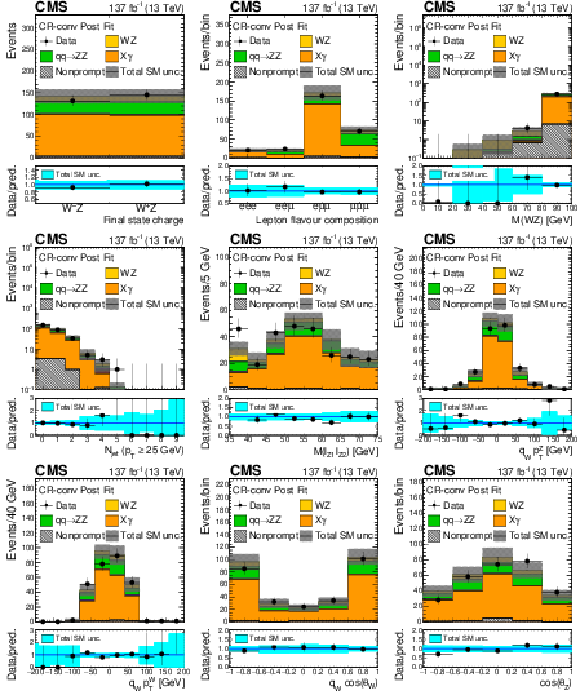
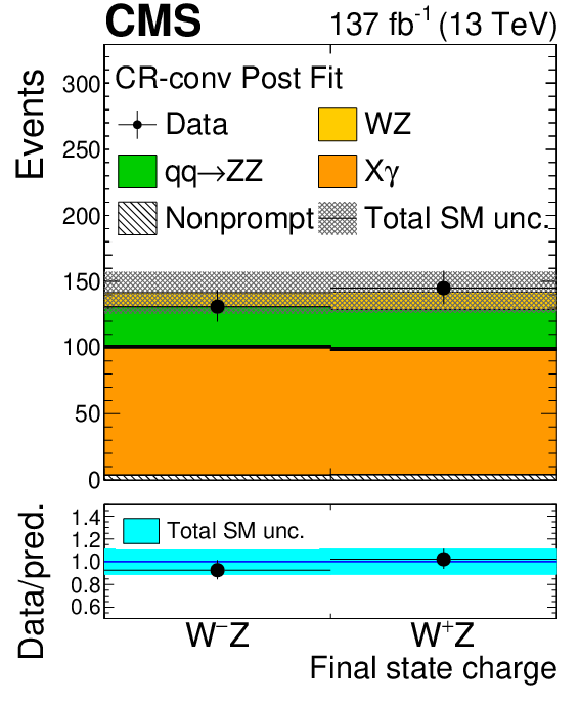
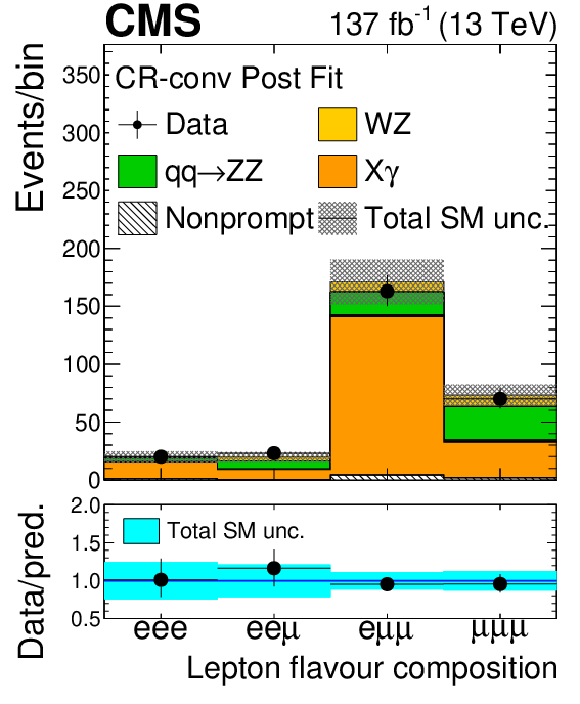
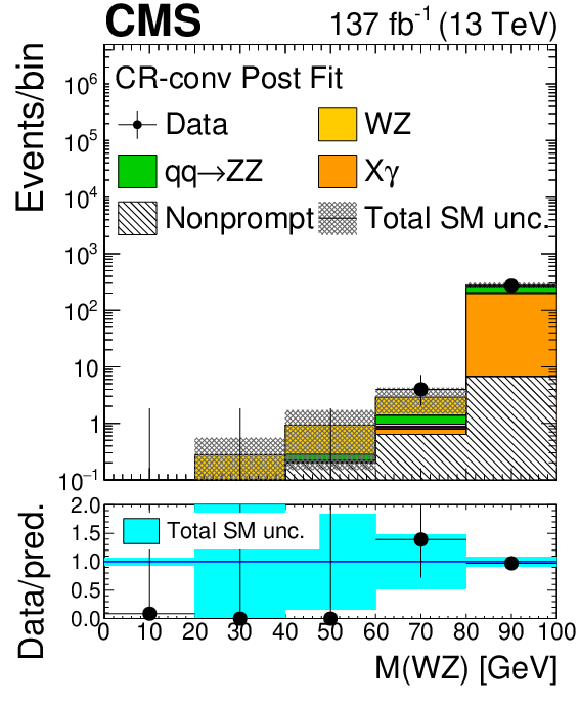
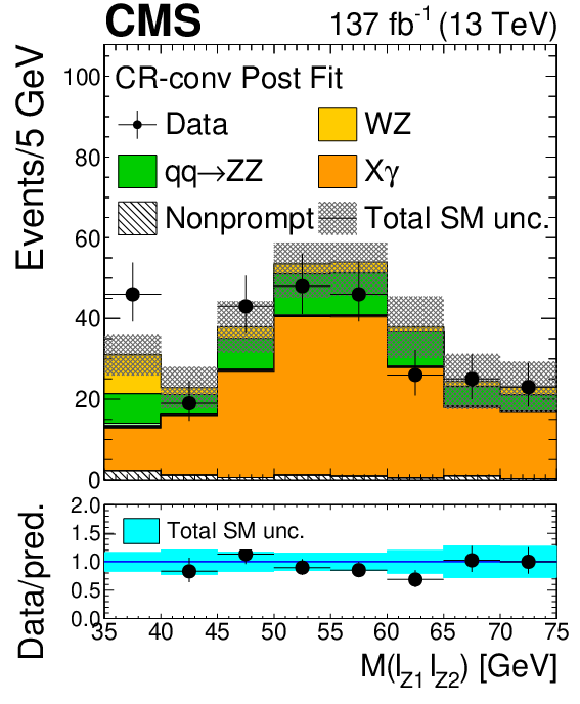
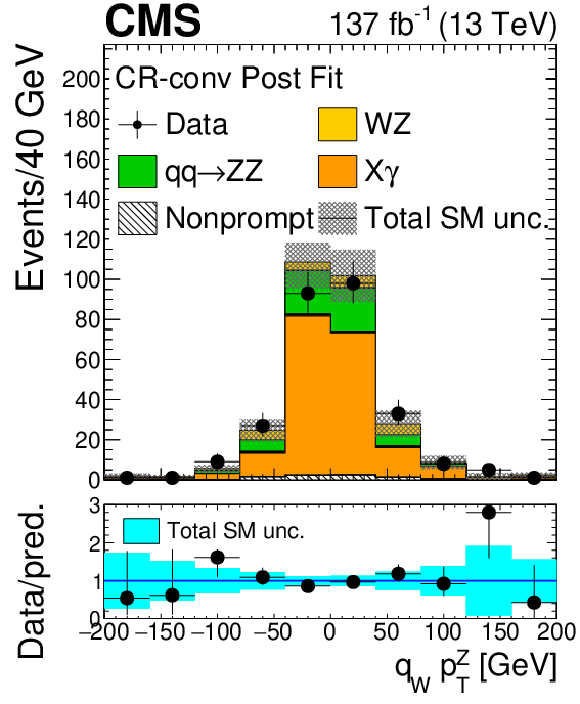
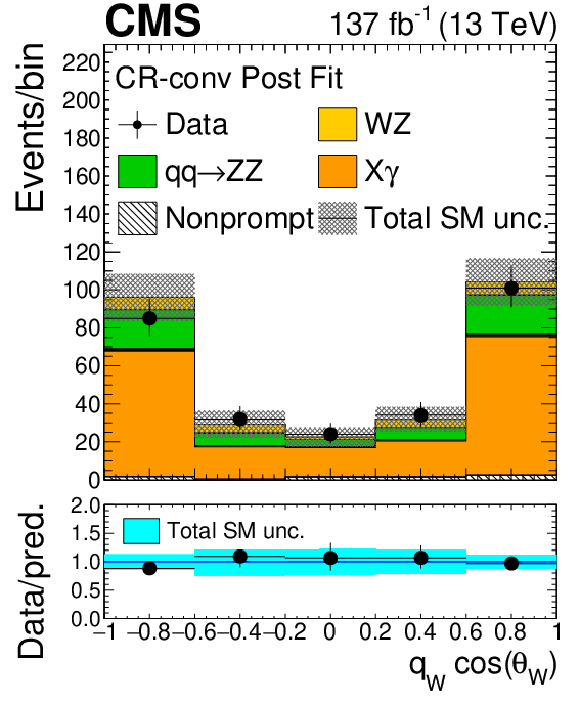
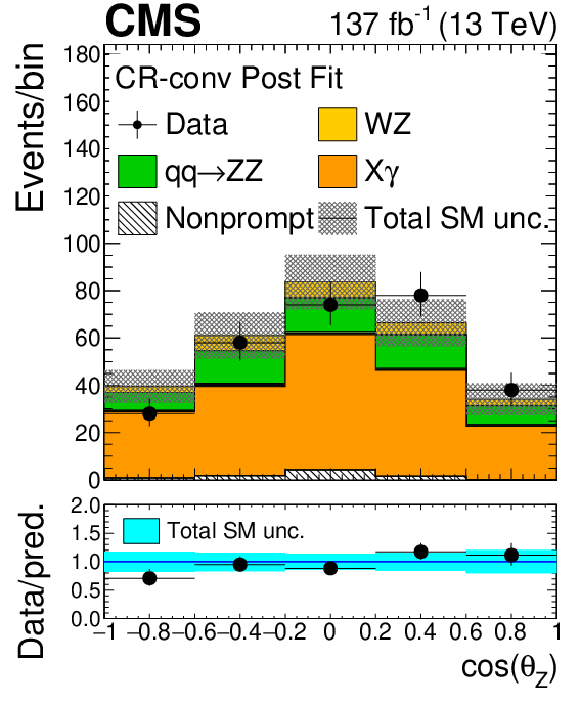
Figure 4:
As in Fig. 2, for the distribution of observables in the conversion control region. |
png pdf |
Figure 4-a:
As in Fig. 2-a, in the conversion control region. |
png pdf |
Figure 4-b:
As in Fig. 2-b, in the conversion control region. |
png pdf |
Figure 4-c:
As in Fig. 2-c, in the conversion control region. |

png pdf |
Figure 4-d:
As in Fig. 2-d, in the conversion control region. |
png pdf |
Figure 4-e:
As in Fig. 2-e, in the conversion control region. |
png pdf |
Figure 4-f:
As in Fig. 2-f, in the conversion control region. |

png pdf |
Figure 4-g:
As in Fig. 2-g, in the conversion control region. |
png pdf |
Figure 4-h:
As in Fig. 2-h, in the conversion control region. |
png pdf |
Figure 4-i:
As in Fig. 2-i, in the conversion control region. |

png pdf |
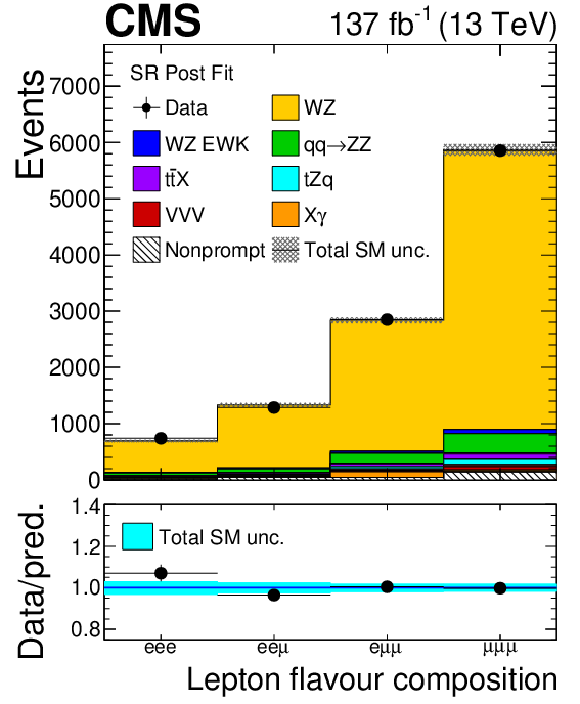
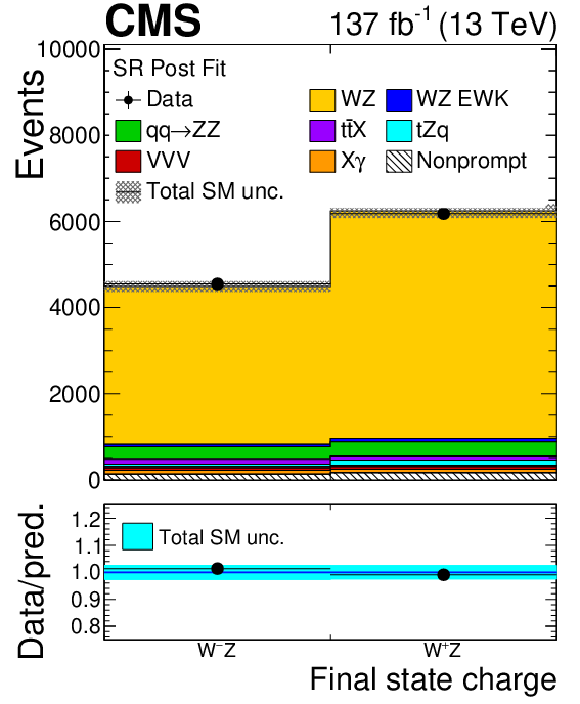
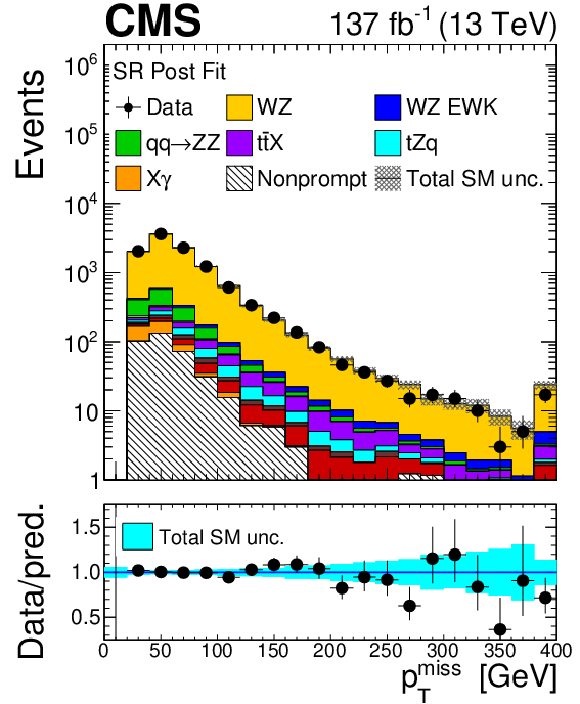
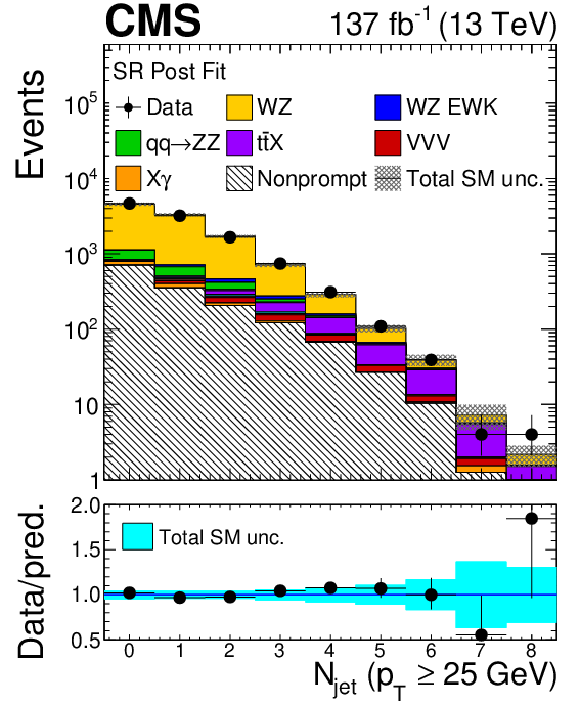
Figure 5:
Distributions of observables in the SR after the combined fit to all data-taking years and flavour final states: flavour composition of the three-lepton final state (top left), sum of charge of the final-state leptons (top right), missing transverse momentum (bottom left), and number of reconstructed jets with ${p_{\mathrm {T}}}$ greater than 25 GeV (bottom right). The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |
png pdf |
Figure 5-a:
Distribution of the flavour composition of the three-lepton final state in the SR after the combined fit to all data-taking years and flavour final states. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |
png pdf |
Figure 5-b:
Distribution of the sum of charge of the final-state leptons in the SR after the combined fit to all data-taking years and flavour final states. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |
png pdf |
Figure 5-c:
Distribution of the missing transverse momentum in the SR after the combined fit to all data-taking years and flavour final states. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |
png pdf |
Figure 5-d:
Distribution of the number of reconstructed jets with ${p_{\mathrm {T}}}$ greater than 25 GeV in the SR after the combined fit to all data-taking years and flavour final states. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the main plot area and the blue band in the ratio show the sum of uncertainties in the signal and background yields. The vertical bars attached to the data points show their associated statistical uncertainty. Underflows (overflows) are included in the first (last) bin shown for each distribution. |
png pdf |
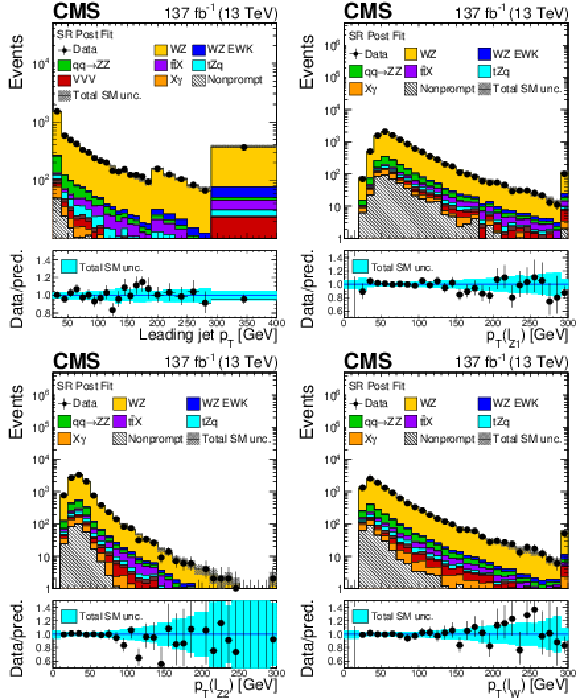
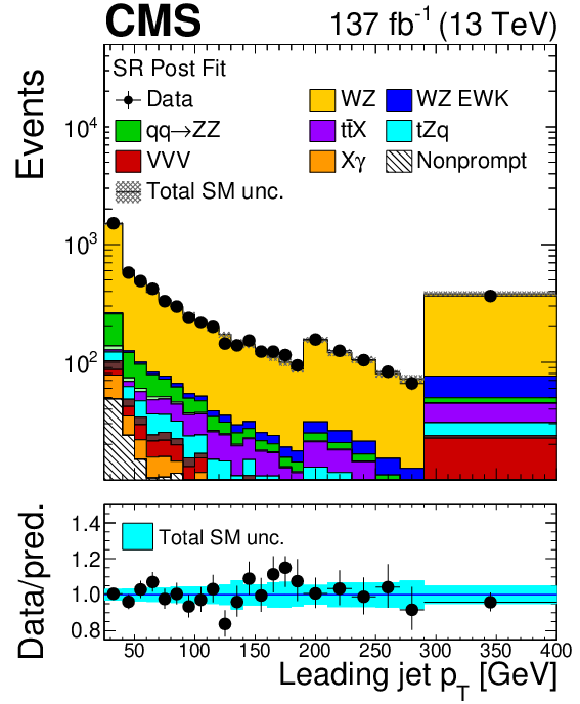
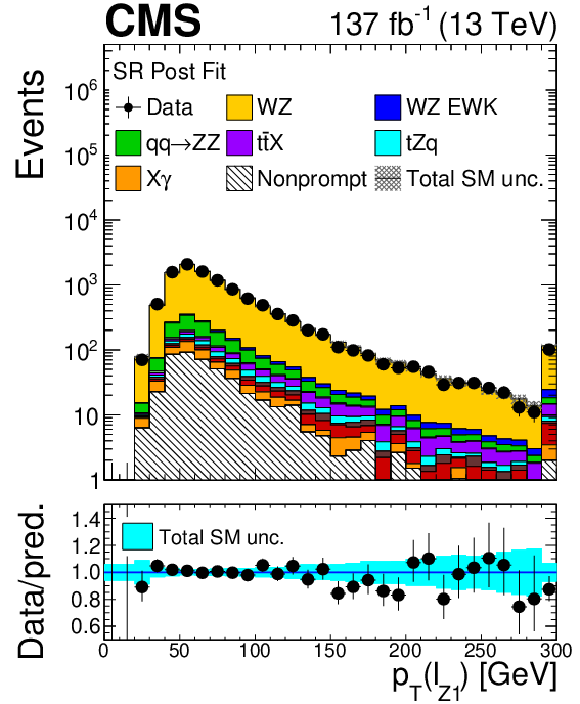
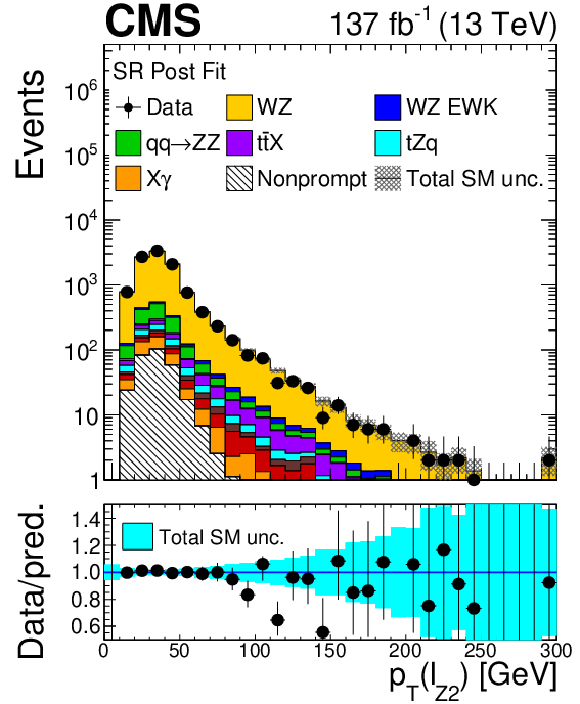
Figure 6:
As in Fig. 5, for: ${p_{\mathrm {T}}}$ of the leading jet with no ${p_{\mathrm {T}}}$ requirements (top left), transverse momentum of the ${\ell _{\mathrm{Z} 1}}$ lepton (top right), transverse momentum of the ${\ell _{\mathrm{Z} 2}}$ lepton (bottom left) and transverse momentum of the ${\ell _{\mathrm{W}}}$ lepton (bottom right). |
png pdf |
Figure 6-a:
As in Fig. 5, for ${p_{\mathrm {T}}}$ of the leading jet with no ${p_{\mathrm {T}}}$ requirements. |
png pdf |
Figure 6-b:
As in Fig. 5, for transverse momentum of the ${\ell _{\mathrm{Z} 1}}$ lepton. |
png pdf |
Figure 6-c:
As in Fig. 5, for transverse momentum of the ${\ell _{\mathrm{Z} 2}}$ lepton. |
png pdf |
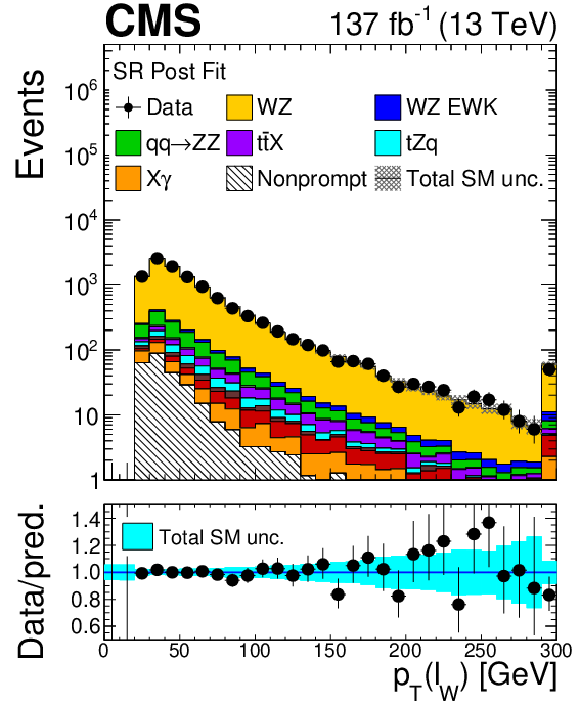
Figure 6-d:
As in Fig. 5, for transverse momentum of the ${\ell _{\mathrm{W}}}$ lepton. |
png pdf |
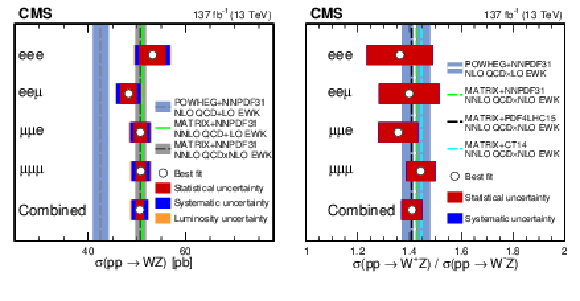
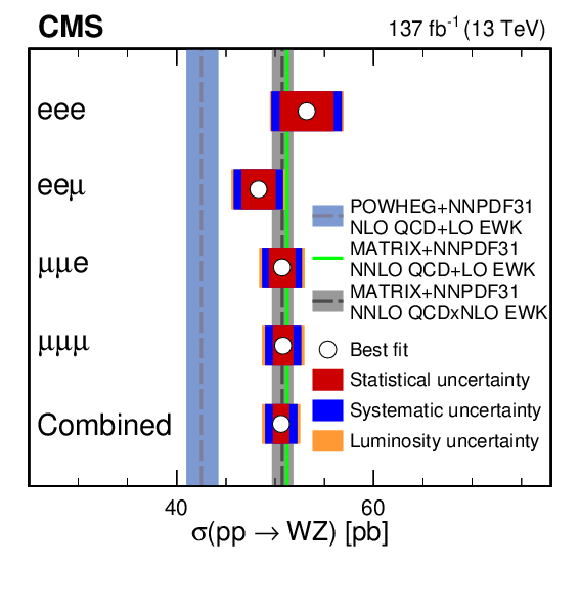
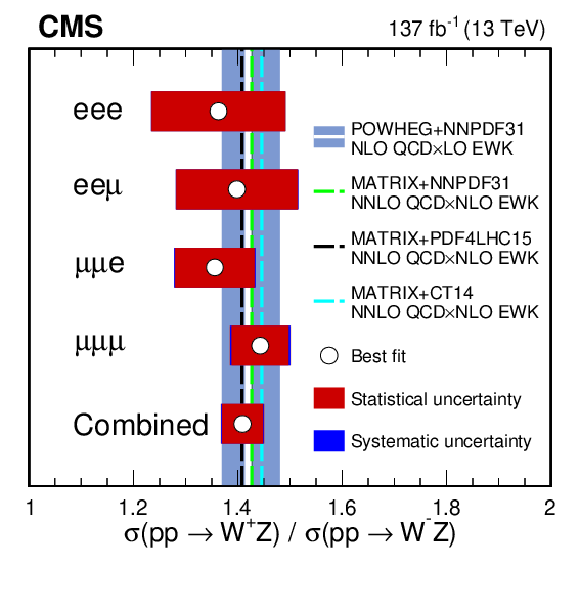
Figure 7:
Total WZ production cross section (left) and charge asymmetry ratio (right) for each of the flavour-exclusive and flavour-inclusive categories. The shaded vertical bands show the theoretical predictions from POWHEG (light blue) and MATRIX (grey). For each of the measurements, the best fit value is denoted with a white point and three main groups of uncertainties (statistical, systematic and luminosity) are denoted as differently coloured (red, blue, and orange) bands with each one being added quadratically on top of the previous one. For the charge asymmetry ratio both POWHEG and MATRIX predictions are close to exact agreement, leading to the blue and grey lines to overlap in the plot. Predictions obtained using MATRIX and several central replicas of different PDF sets are also shown as individual lines in the figure. |
png pdf |
Figure 7-a:
Total WZ production cross section for each of the flavour-exclusive and flavour-inclusive categories. The shaded vertical bands show the theoretical predictions from POWHEG (light blue) and MATRIX (grey). For each of the measurements, the best fit value is denoted with a white point and three main groups of uncertainties (statistical, systematic and luminosity) are denoted as differently coloured (red, blue, and orange) bands with each one being added quadratically on top of the previous one. For the charge asymmetry ratio both POWHEG and MATRIX predictions are close to exact agreement, leading to the blue and grey lines to overlap in the plot. Predictions obtained using MATRIX and several central replicas of different PDF sets are also shown as individual lines in the figure. |
png pdf |
Figure 7-b:
Charge asymmetry ratio for each of the flavour-exclusive and flavour-inclusive categories. The shaded vertical bands show the theoretical predictions from POWHEG (light blue) and MATRIX (grey). For each of the measurements, the best fit value is denoted with a white point and three main groups of uncertainties (statistical, systematic and luminosity) are denoted as differently coloured (red, blue, and orange) bands with each one being added quadratically on top of the previous one. For the charge asymmetry ratio both POWHEG and MATRIX predictions are close to exact agreement, leading to the blue and grey lines to overlap in the plot. Predictions obtained using MATRIX and several central replicas of different PDF sets are also shown as individual lines in the figure. |
png pdf |
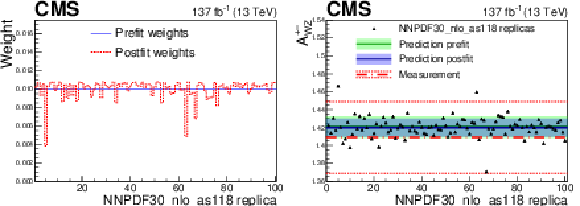
Figure 8:
(Left) Weights associated with each PDF replica in the NNPDF30_nlo_as0118 set before (blue) and after (red) the Bayesian reweighting technique is applied based on the charge asymmetry ratio measurement. (Right) Predictions and updated predictions (using the posterior weights) of the charge asymmetry ratio in WZ production using the nominal POWHEG sample with the NNPDF30_nlo_as0118 PDF set. The central green line gives the nominal predicted values, the shaded bands include the total uncertainty of the PDF set computed using the sample variance of the predictions obtained with each replica, and the triangles are the individual replica predictions. The red dashed and dotted lines are the measured value and uncertainties of the analysis. The blue bands show the predicted central value and uncertainties obtained after the Bayesian reweighting procedure. |
png pdf |
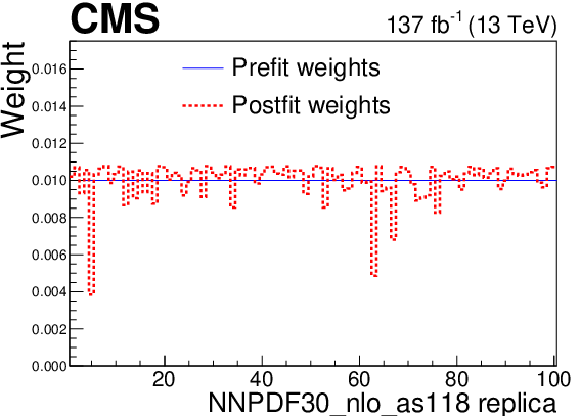
Figure 8-a:
Weights associated with each PDF replica in the NNPDF30_nlo_as0118 set before (blue) and after (red) the Bayesian reweighting technique is applied based on the charge asymmetry ratio measurement. |

png pdf |
Figure 8-b:
Predictions and updated predictions (using the posterior weights) of the charge asymmetry ratio in WZ production using the nominal POWHEG sample with the NNPDF30_nlo_as0118 PDF set. The central green line gives the nominal predicted values, the shaded bands include the total uncertainty of the PDF set computed using the sample variance of the predictions obtained with each replica, and the triangles are the individual replica predictions. The red dashed and dotted lines are the measured value and uncertainties of the analysis. The blue bands show the predicted central value and uncertainties obtained after the Bayesian reweighting procedure. |

png pdf |
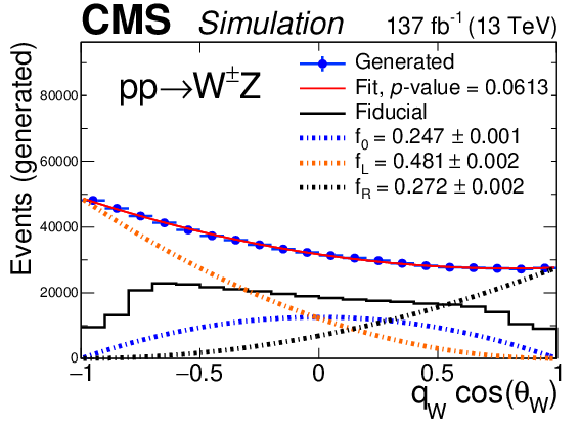
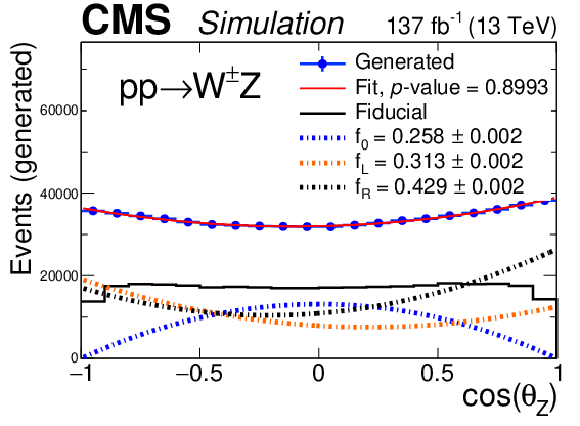
Figure 9:
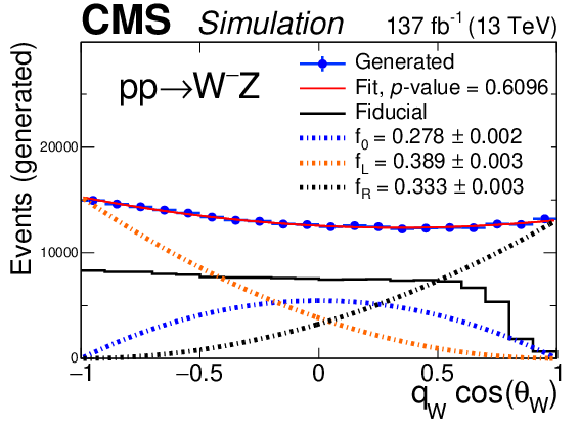
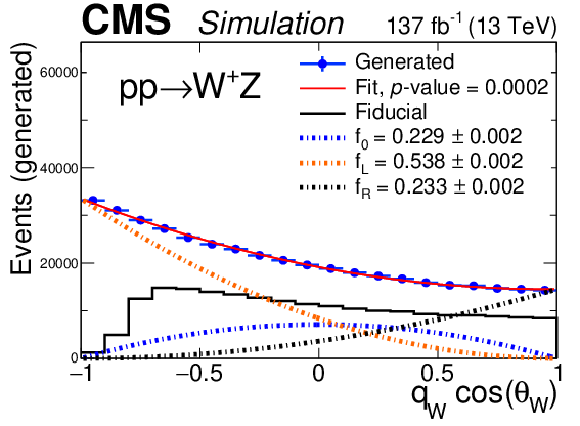
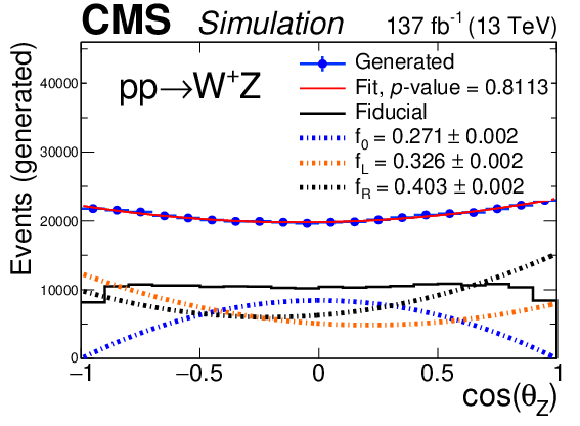
Distribution of the cosine of the polarization angle in the helicity frame at the generator level for the nominal signal sample: from left to right, W and Z bosons; from top to bottom, total (inclusive) final state, negatively charged final state, and positively charged final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |
png pdf |
Figure 9-a:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of W bosons, for the signal sample in the total (inclusive) final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |
png pdf |
Figure 9-b:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of Z bosons, for the signal sample in the total (inclusive) final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |
png pdf |
Figure 9-c:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of W bosons, for the signal sample in the negatively charged final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |

png pdf |
Figure 9-d:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of Z bosons, for the signal sample in the negatively charged final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |
png pdf |
Figure 9-e:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of Z bosons, for the signal sample in the positively charged final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |
png pdf |
Figure 9-f:
Distribution of the cosine of the polarization angle in the helicity frame at the generator level of Z bosons, for the signal sample in the positively charged final state. The blue points are the MC predictions in the total phase space, with vertical bars representing the overall MC statistical uncertainty. The solid red line shows the best quadratic fit to the MC prediction, and the different dashed lines each of the polarization components obtained in the fit. The thick black line shows the distribution of the same variable restricted to the fiducial phase space, showing how kinematic requirements break the quadratic dependence of the differential cross section. The $p$-value, obtained from a $\chi ^2$ test, is included in the legend. |

png pdf |
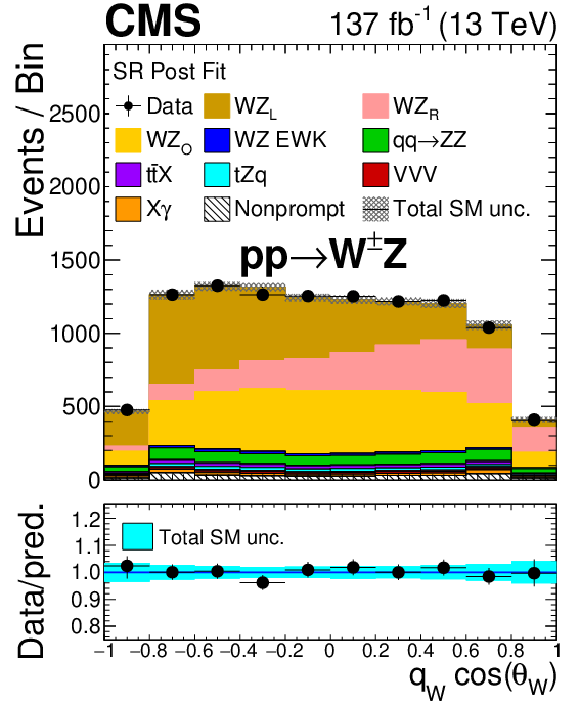
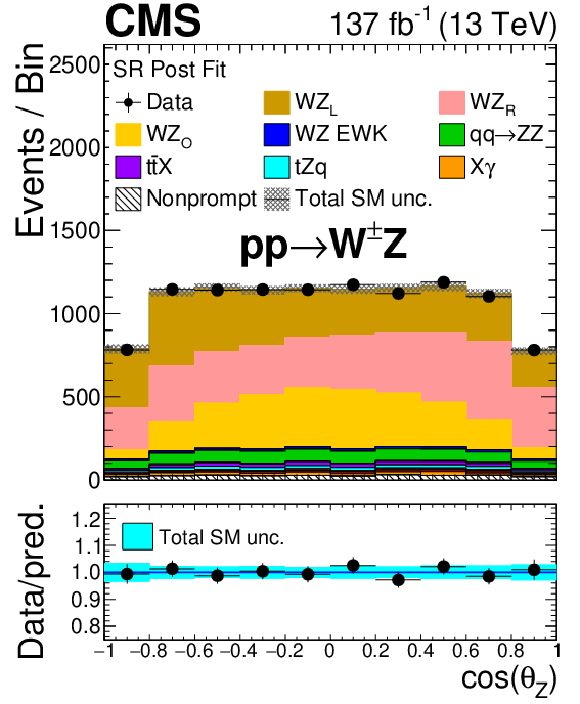
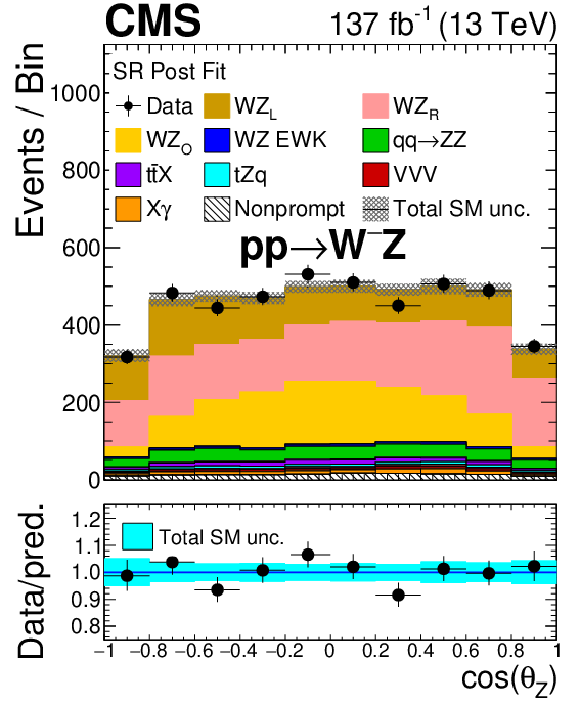
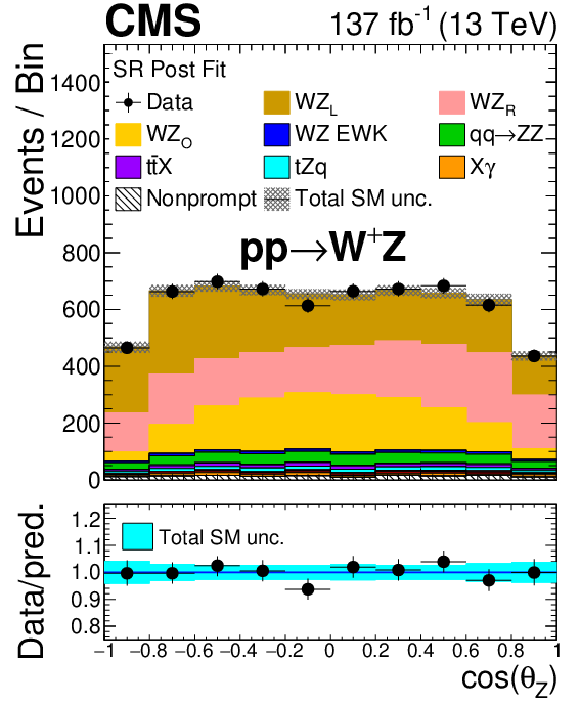
Figure 10:
Distribution of the cosine of the polarization angle for different final-state charges and boson flavours after the fits corresponding to each case. From left to right: W and Z bosons. From top to bottom: charge-inclusive (total), positive final-state charge, and negative final-state charge. The differently polarized final states of the corresponding boson are shown in each of the cases. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |
png pdf |
Figure 10-a:
Distribution of the cosine of the polarization angle of the W boson for the charge-inclusive (total) final-state after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |
png pdf |
Figure 10-b:
Distribution of the cosine of the polarization angle of the Z boson for the charge-inclusive (total) final-state after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |

png pdf |
Figure 10-c:
Distribution of the cosine of the polarization angle of the W boson for the positive final-state charge after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |
png pdf |
Figure 10-d:
Distribution of the cosine of the polarization angle of the Z boson for the positive final-state charge after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |

png pdf |
Figure 10-e:
Distribution of the cosine of the polarization angle of the W boson for the negative final-state charge after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |
png pdf |
Figure 10-f:
Distribution of the cosine of the polarization angle of the Z boson for the negative final-state charge after the corresponding fit. The differently polarized final states of the boson are shown. X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio shows the sum of uncertainties in the signal and background yields. |
png pdf |
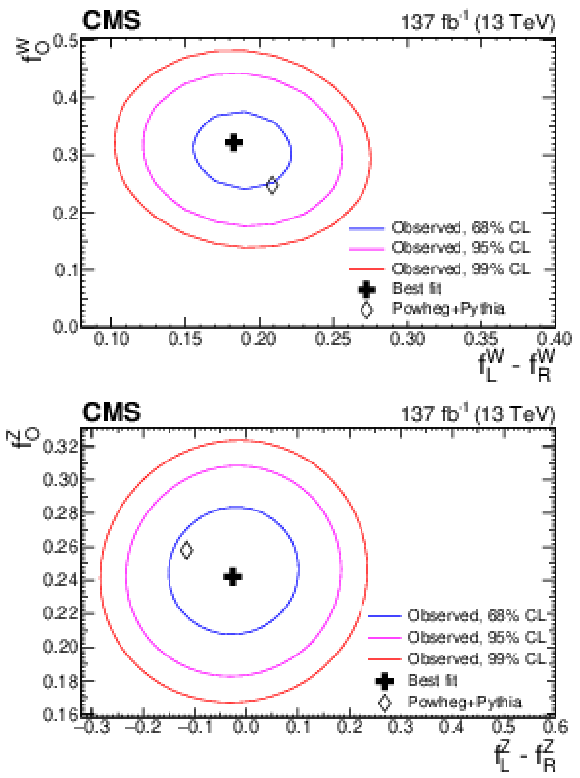
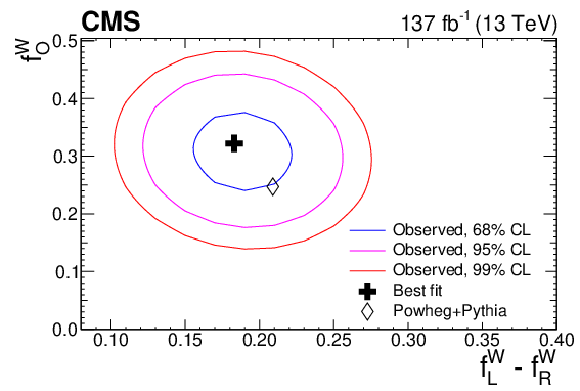
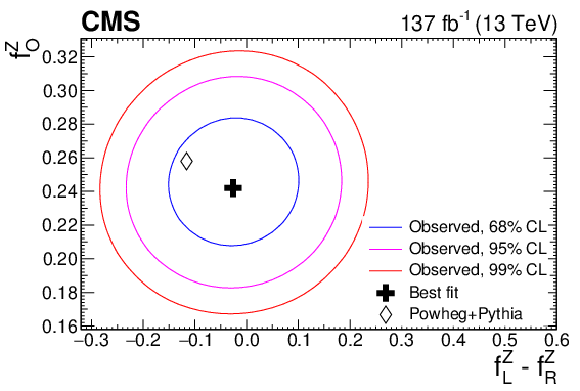
Figure 11:
Confidence regions in the $f_{\mathrm {LR}}$-$f_{0}$ parameter plane for the W (top) and Z (bottom) boson polarization. The results are obtained with no additional requirement for the charge of the W boson. The blue, magenta, and red contours present the 68, 95, and 99% confidence levels, respectively. |
png pdf |
Figure 11-a:
Confidence regions in the $f_{\mathrm {LR}}$-$f_{0}$ parameter plane for the W boson polarization. The results are obtained with no additional requirement for the charge of the W boson. The blue, magenta, and red contours present the 68, 95, and 99% confidence levels, respectively. |
png pdf |
Figure 11-b:
Confidence regions in the $f_{\mathrm {LR}}$-$f_{0}$ parameter plane for the Z boson polarization. The results are obtained with no additional requirement for the charge of the W boson. The blue, magenta, and red contours present the 68, 95, and 99% confidence levels, respectively. |
png pdf |
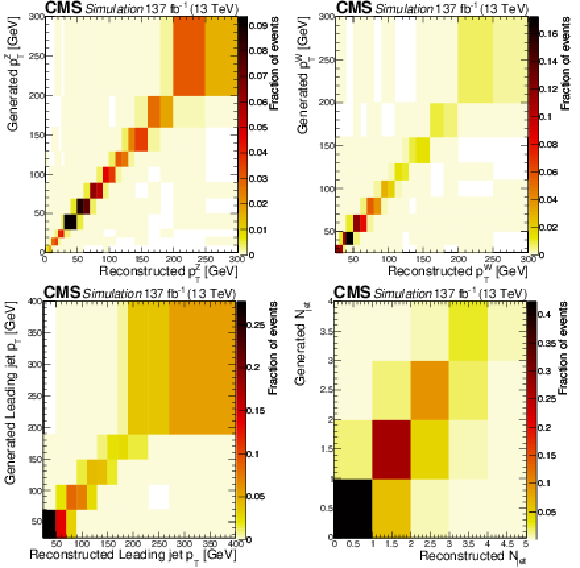
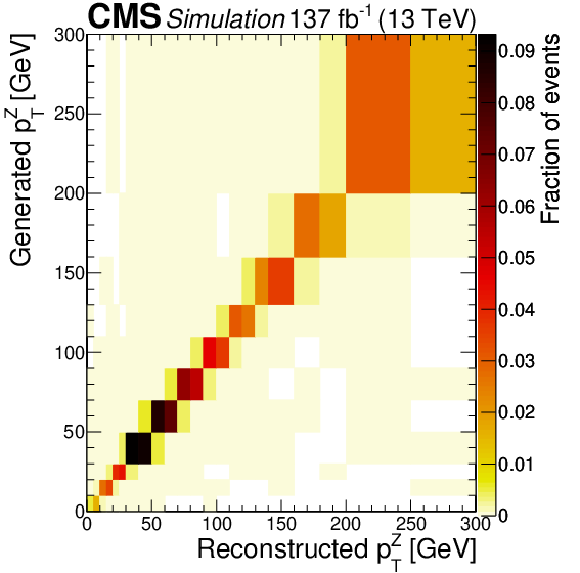
Figure 12:
Response matrices obtained at NLO in QCD using the POWHEG generator. Reconstructed ${p_{\mathrm {T}}}$ of the Z boson (top left, condition number 7.77), ${p_{\mathrm {T}}}$ of the lepton from the W boson decay (top right, condition number 20.9), ${p_{\mathrm {T}}}$ of the leading jet (bottom left, condition number 9.69), and jet multiplicity (bottom right, condition number 16.9). |
png pdf |
Figure 12-a:
Response matrix obtained at NLO in QCD using the POWHEG generator for the reconstructed ${p_{\mathrm {T}}}$ of the Z boson (condition number 7.77). |
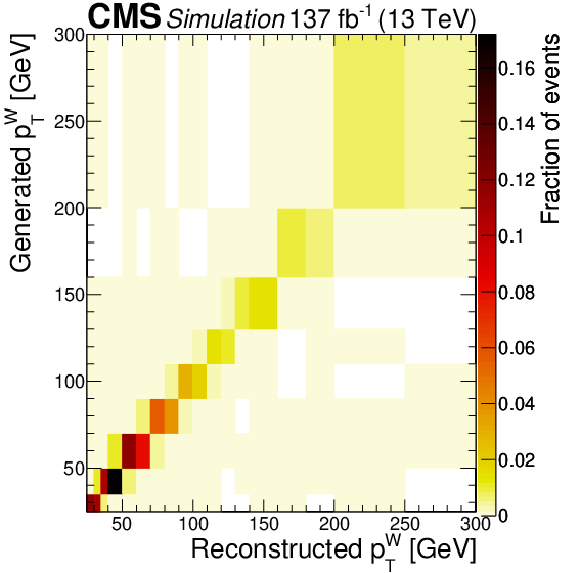
png pdf |
Figure 12-b:
Response matrix obtained at NLO in QCD using the POWHEG generator for the ${p_{\mathrm {T}}}$ of the lepton from the W boson decay (condition number 20.9). |
png pdf |
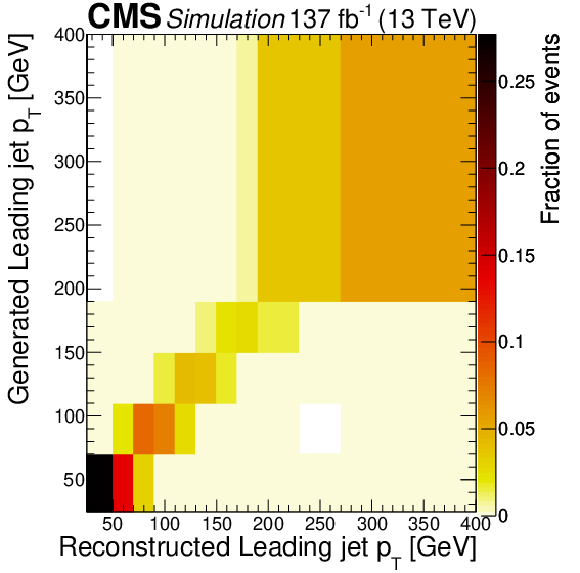
Figure 12-c:
Response matrix obtained at NLO in QCD using the POWHEG generator for the ${p_{\mathrm {T}}}$ of the leading jet (condition number 9.69). |
png pdf |
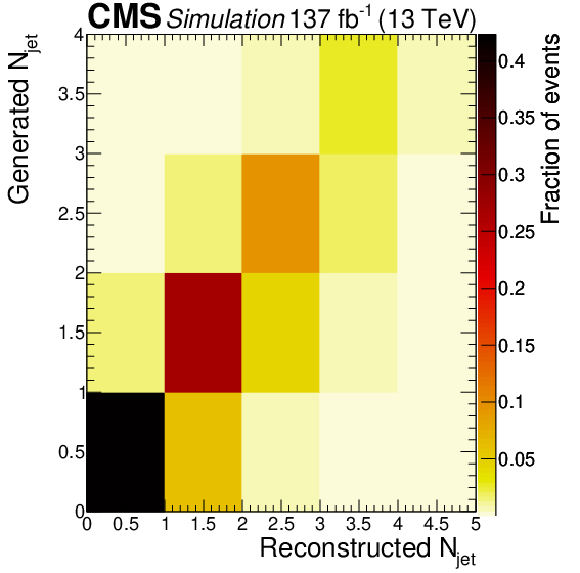
Figure 12-d:
Response matrix obtained at NLO in QCD using the POWHEG generator for the jet multiplicity (condition number 16.9). |
png pdf |
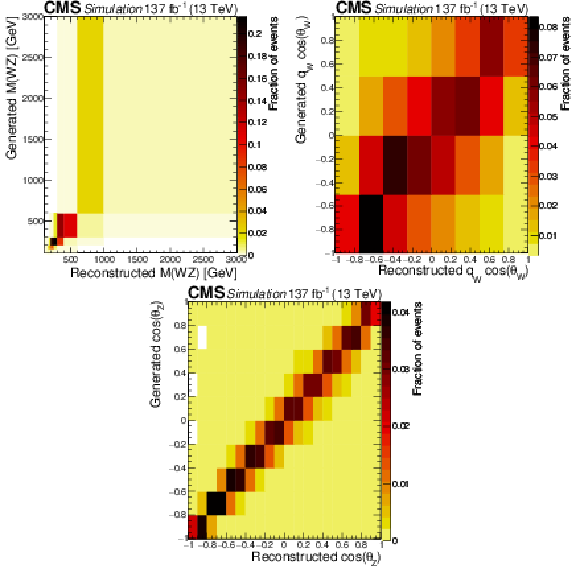
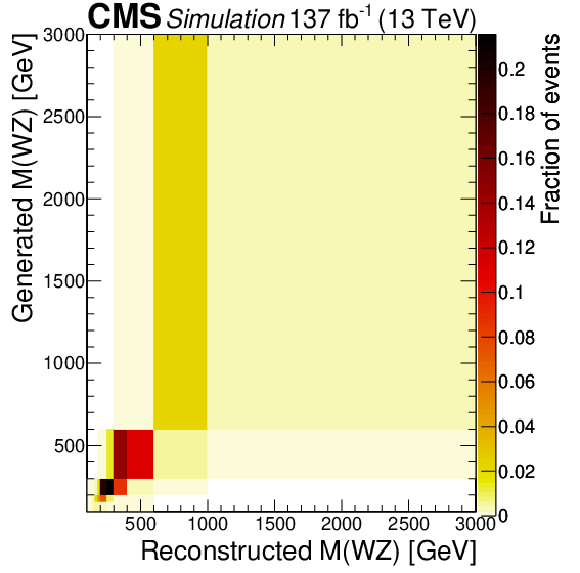
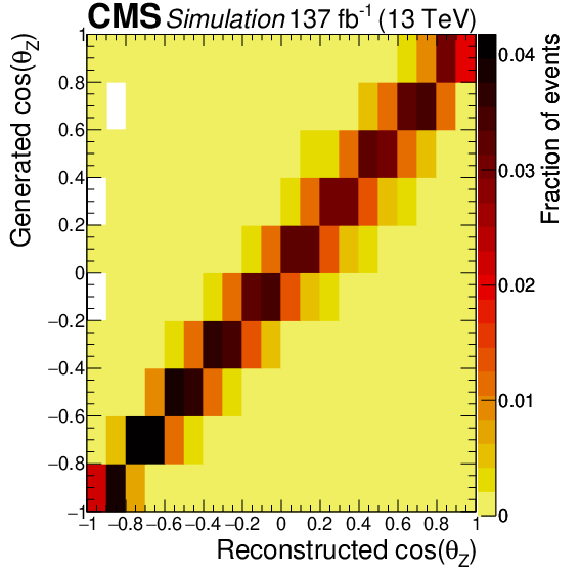
Figure 13:
Response matrices obtained at NLO in QCD using the POWHEG generator. Invariant mass of the WZ system ${M({\mathrm{W} \mathrm{Z}})}$ (top left, condition number 64.0), cosine of the polarization angle ${\theta ^{\mathrm{W}}}$ (top right, condition number 7.84), and cosine of the polarization angle ${\theta ^{\mathrm{Z}}}$ (bottom, condition number 2.94). |
png pdf |
Figure 13-a:
Response matrix obtained at NLO in QCD using the POWHEG generator for the invariant mass of the WZ system ${M({\mathrm{W} \mathrm{Z}})}$ (condition number 64.0). |

png pdf |
Figure 13-b:
Response matrix obtained at NLO in QCD using the POWHEG generator for the cosine of the polarization angle ${\theta ^{\mathrm{W}}}$ (condition number 7.84). |
png pdf |
Figure 13-c:
Response matrix obtained at NLO in QCD using the POWHEG generator for the cosine of the polarization angle ${\theta ^{\mathrm{Z}}}$ (condition number 2.94). |
png pdf |
Figure 14:
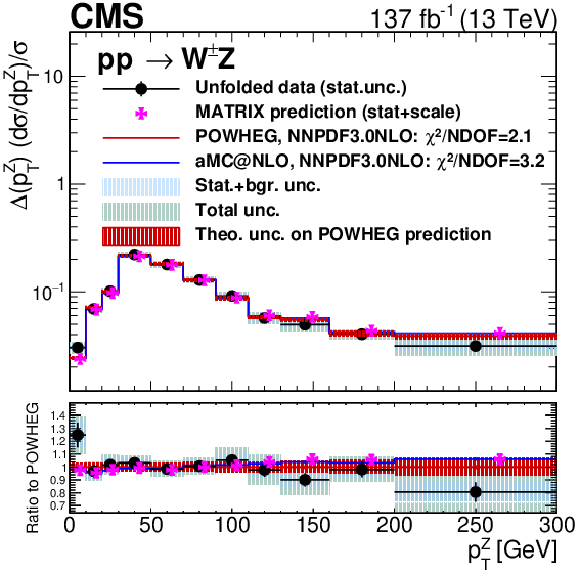
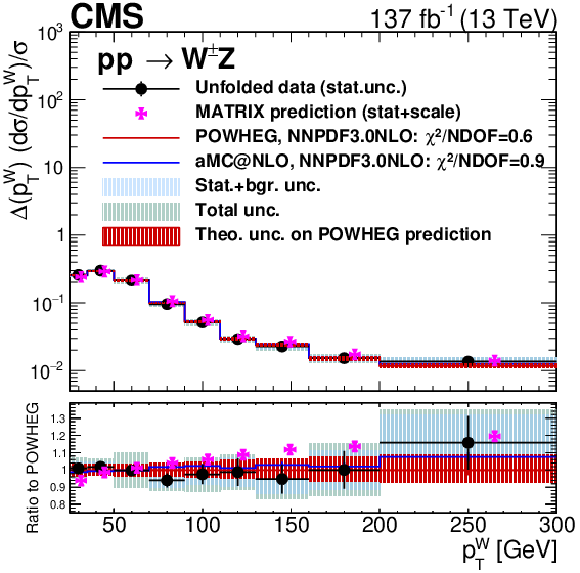
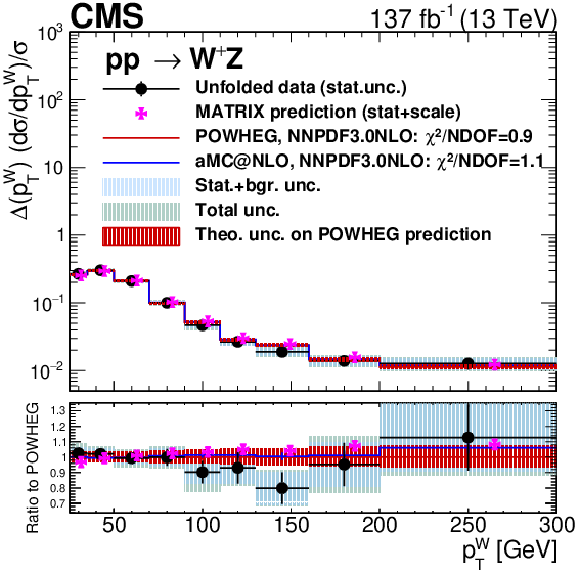
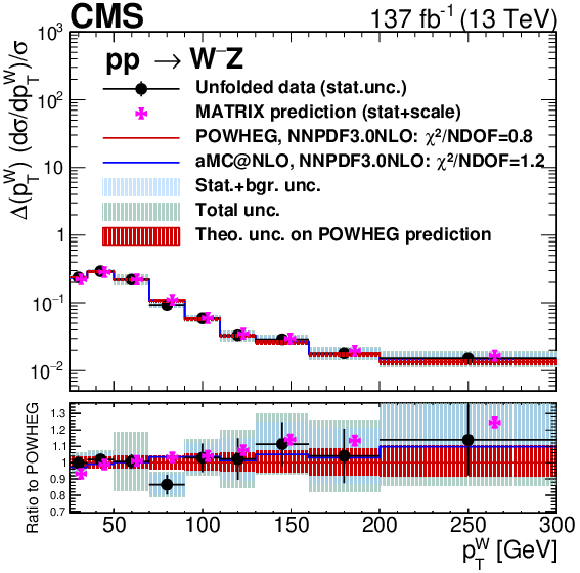
Unfolded results for several variables: the ${p_{\mathrm {T}}}$ value of the Z boson (top left), the ${p_{\mathrm {T}}}$ value of the leading jet in the event (top right), the jet multiplicity (bottom left) and the ${M({\mathrm{W} \mathrm{Z}})}$ variable (bottom right). Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band shows the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. The MATRIX predictions for the jet multiplicity differential cross section are not included as they correspond to a fixed order computation not matched to a parton shower. |
png pdf |
Figure 14-a:
Unfolded results for the ${M({\mathrm{W} \mathrm{Z}})}$. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band shows the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. The MATRIX predictions for the jet multiplicity differential cross section are not included as they correspond to a fixed order computation not matched to a parton shower. |
png pdf |
Figure 14-b:
Unfolded results for several variables: the ${p_{\mathrm {T}}}$ value of the Z boson (top left), the ${p_{\mathrm {T}}}$ value of the leading jet in the event (top right), the jet multiplicity (bottom left) and the ${M({\mathrm{W} \mathrm{Z}})}$ variable (bottom right). Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band shows the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. The MATRIX predictions for the jet multiplicity differential cross section are not included as they correspond to a fixed order computation not matched to a parton shower. |

png pdf |
Figure 14-c:
Unfolded results for several variables: the ${p_{\mathrm {T}}}$ value of the Z boson (top left), the ${p_{\mathrm {T}}}$ value of the leading jet in the event (top right), the jet multiplicity (bottom left) and the ${M({\mathrm{W} \mathrm{Z}})}$ variable (bottom right). Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band shows the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. The MATRIX predictions for the jet multiplicity differential cross section are not included as they correspond to a fixed order computation not matched to a parton shower. |

png pdf |
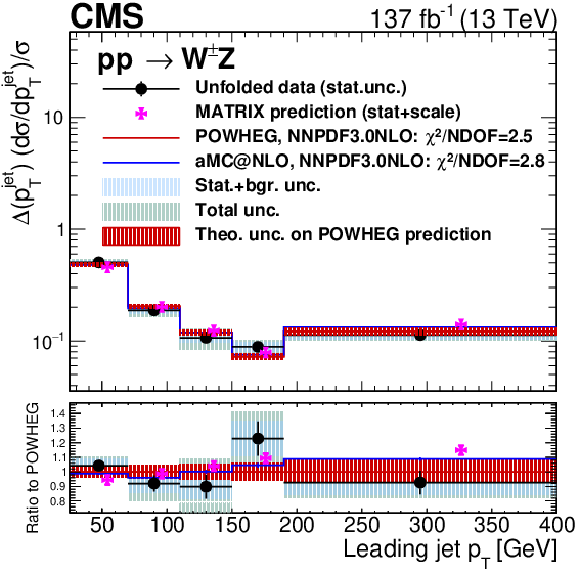
Figure 14-d:
Unfolded results for several variables: the ${p_{\mathrm {T}}}$ value of the Z boson (top left), the ${p_{\mathrm {T}}}$ value of the leading jet in the event (top right), the jet multiplicity (bottom left) and the ${M({\mathrm{W} \mathrm{Z}})}$ variable (bottom right). Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band shows the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. The MATRIX predictions for the jet multiplicity differential cross section are not included as they correspond to a fixed order computation not matched to a parton shower. |
png pdf |
Figure 15:
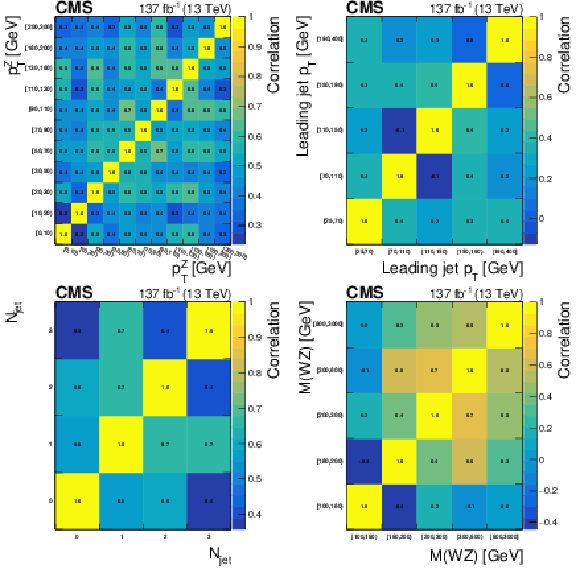
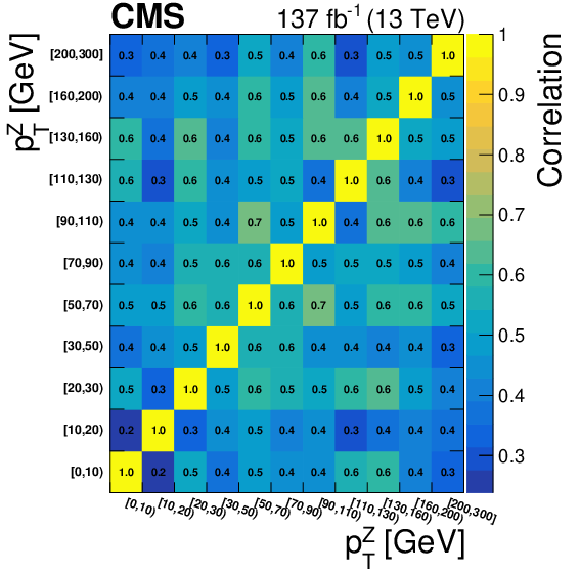
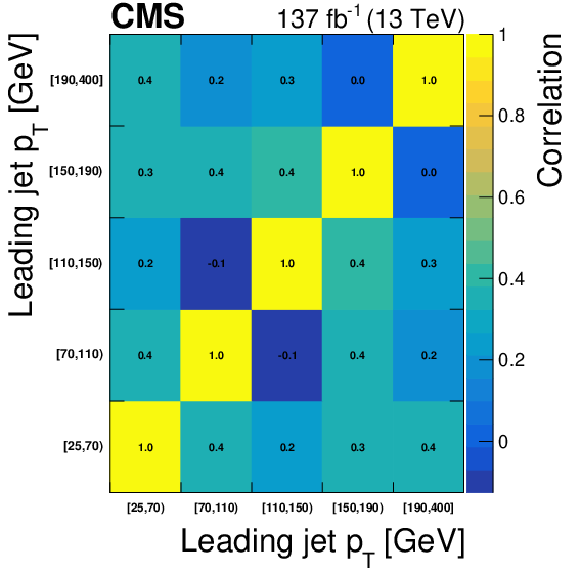
Correlation matrices for the unfolded results obtained using NNLO bias, area constraint, and no additional regularization term for several variables: the ${p_{\mathrm {T}}}$ value of the Z boson (top left), the ${p_{\mathrm {T}}}$ value of the leading jet in the event (top right), the jet multiplicity (bottom left) and the ${M({\mathrm{W} \mathrm{Z}})}$ variable (bottom right). |
png pdf |
Figure 15-a:
Correlation matrix for the unfolded results obtained using NNLO bias, area constraint, and no additional regularization term for the ${p_{\mathrm {T}}}$ value of the Z boson. |
png pdf |
Figure 15-b:
Correlation matrix for the unfolded results obtained using NNLO bias, area constraint, and no additional regularization term for the ${p_{\mathrm {T}}}$ value of the leading jet in the event. |

png pdf |
Figure 15-c:
Correlation matrix for the unfolded results obtained using NNLO bias, area constraint, and no additional regularization term for the jet multiplicity. |
png pdf |
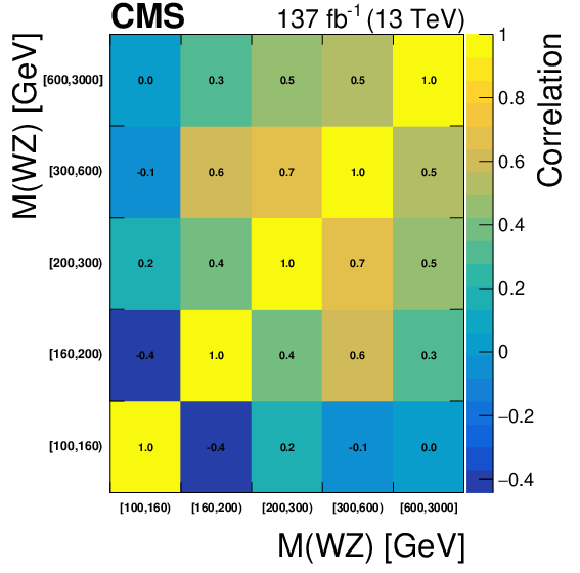
Figure 15-d:
Correlation matrix for the unfolded results obtained using NNLO bias, area constraint, and no additional regularization term for the ${M({\mathrm{W} \mathrm{Z}})}$ variable. |
png pdf |
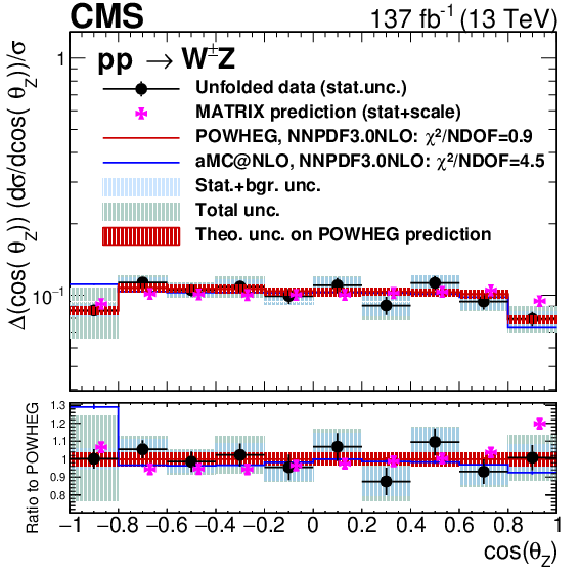
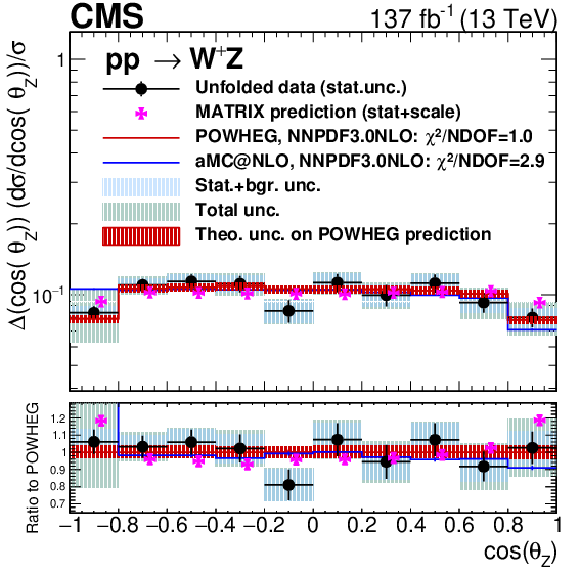
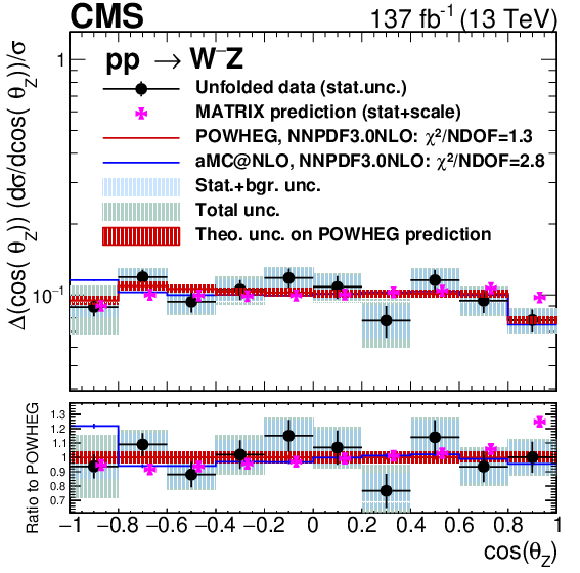
Figure 16:
Unfolded results for several variables and charged final states. From top to bottom: ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, cosine of the polarization angle of the W boson times total leptonic charge, and cosine of the polarization angle of the Z boson. From left to right: charge-inclusive, positive-charge, and negative-charge final states. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-a:
Unfolded results for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the charge-inclusive final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-b:
Unfolded results for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the positive-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-c:
Unfolded results for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the negative-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-d:
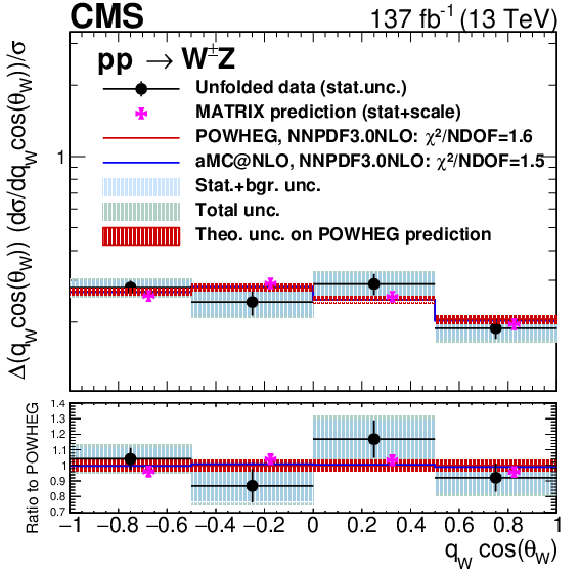
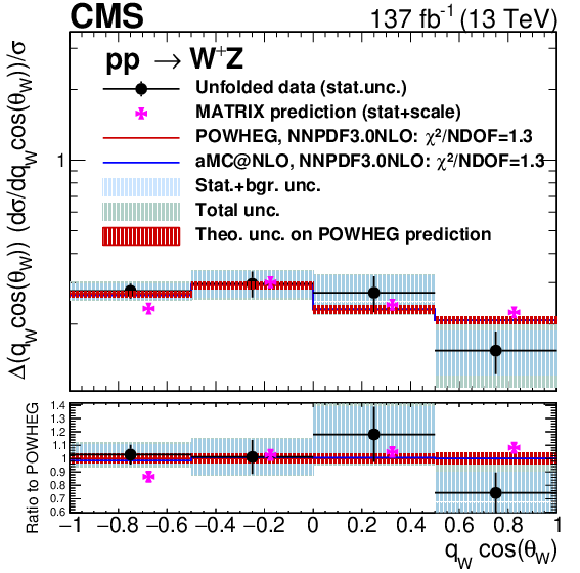
Unfolded results for the cosine of the polarization angle of the W boson times total leptonic charge, in the charge-inclusive final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-e:
Unfolded results for the cosine of the polarization angle of the W boson times total leptonic charge, in the positive-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-f:
Unfolded results for the cosine of the polarization angle of the W boson times total leptonic charge, in the negative-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-g:
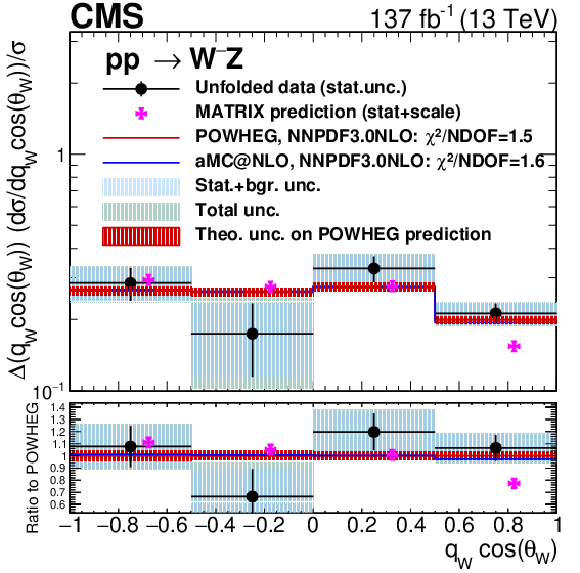
Unfolded results for the cosine of the polarization angle of the Z boson, in the charge-inclusive final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-h:
Unfolded results for the cosine of the polarization angle of the Z boson, in the positive-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
Figure 16-i:
Unfolded results for the cosine of the polarization angle of the Z boson, in the negative-charge final state. Black dots represent unfolded data results, black vertical bars denote statistical uncertainties in the unfolded data results, shaded blue bands represent statistical plus background-related uncertainties, and the green band represent the total unfolding uncertainty. The red histogram and shadow bands are the POWHEG prediction and its theoretical uncertainty. The blue histogram represents the MadGraph 5_aMC@NLO prediction and the violet points show the MATRIX prediction including error bands representing numerical and scale uncertainties. The MATRIX predictions are represented by points with a small offset to the right to improve readability. |
png pdf |
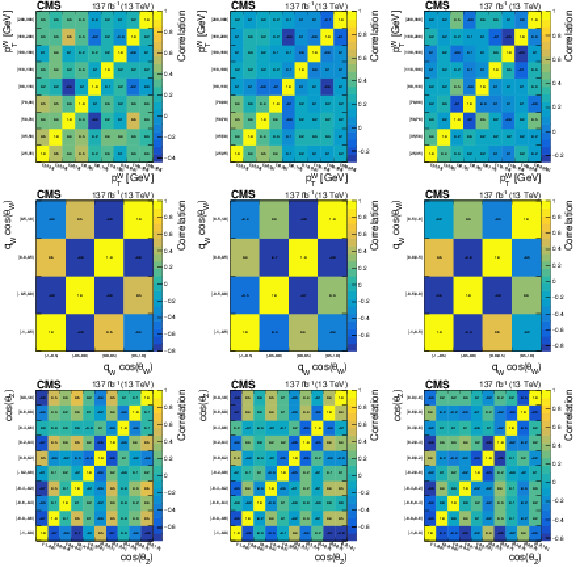
Figure 17:
Correlation matrices for the unfolded results using NNLO bias, area constraint, and no additional regularization term for several variables and charged final states. From top to bottom: ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, cosine of the polarization angle of the W boson, and cosine of the polarization angle of the Z boson. From left to right: charge-inclusive, positive-charge, and negative-charge final states. |
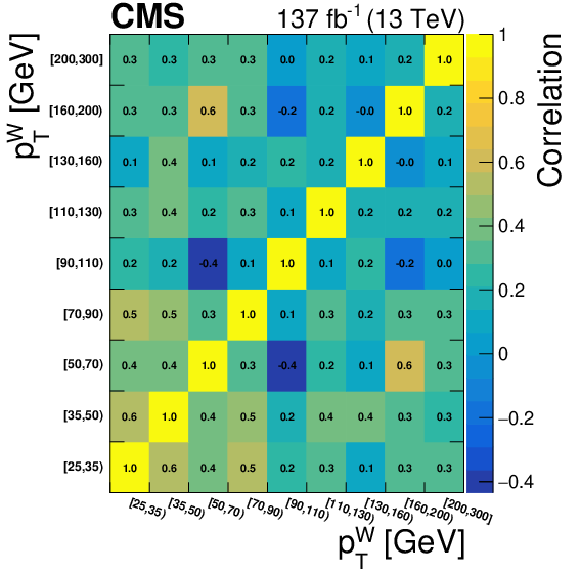
png pdf |
Figure 17-a:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the charge-inclusive final state. |

png pdf |
Figure 17-b:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the positive-charge final state. |
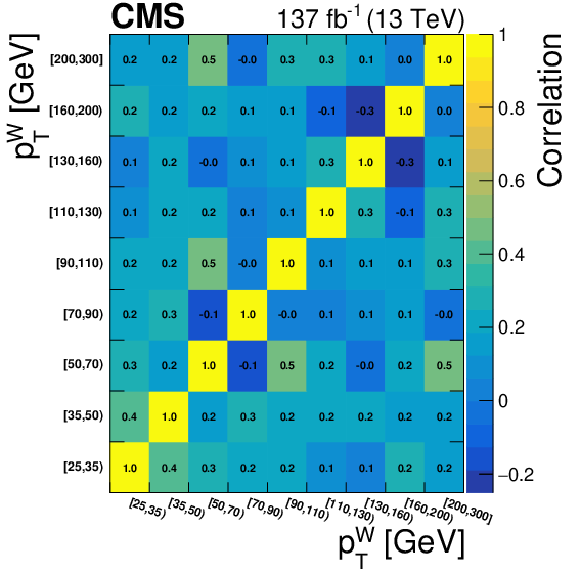
png pdf |
Figure 17-c:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the ${p_{\mathrm {T}}}$ of the lepton in the W boson decay, in the negative-charge final state. |

png pdf |
Figure 17-d:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the W boson, in the charge-inclusive final state. |
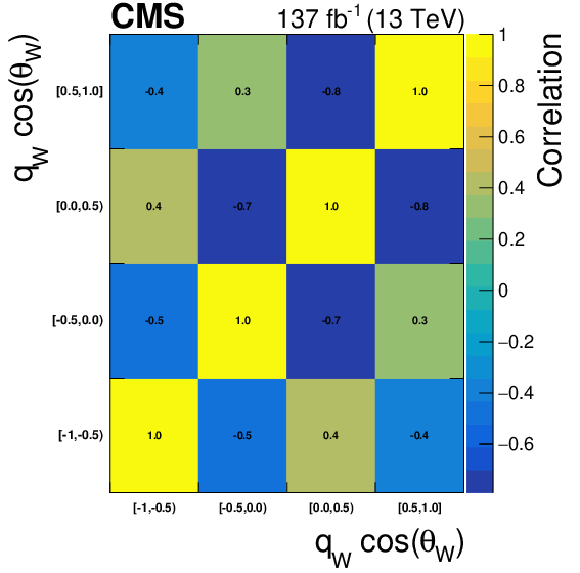
png pdf |
Figure 17-e:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the W boson, in the positive-charge final state. |
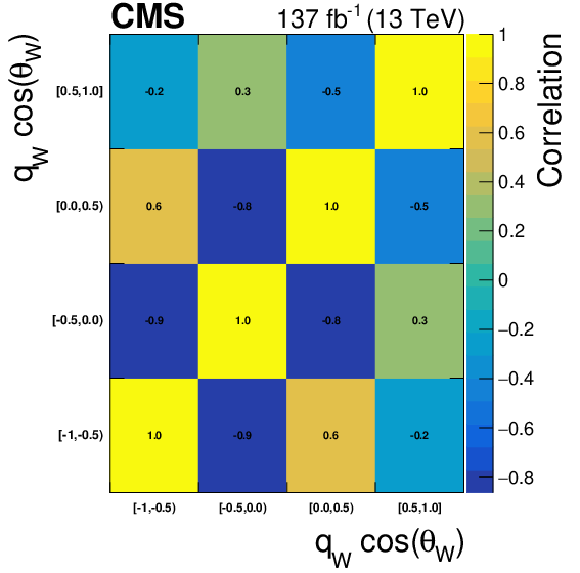
png pdf |
Figure 17-f:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the W boson, in the negative-charge final state. |

png pdf |
Figure 17-g:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the Z boson, in the charge-inclusive final state. |

png pdf |
Figure 17-h:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the Z boson, in the positive-charge final state. |
png pdf |
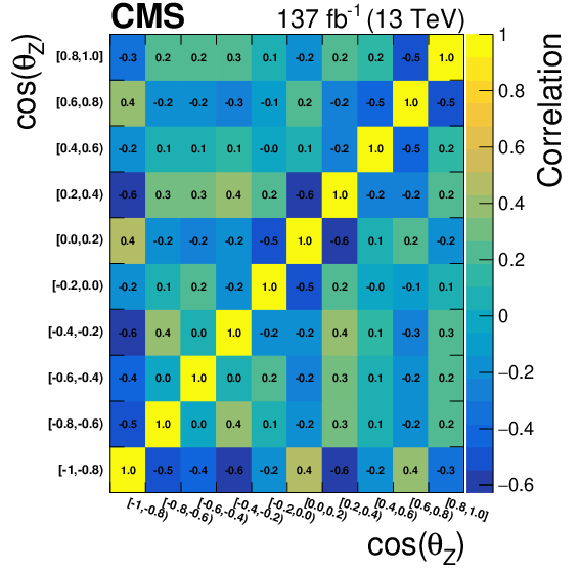
Figure 17-i:
Correlation matrix for the unfolded results using NNLO bias, area constraint, and no additional regularization term for the cosine of the polarization angle of the Z boson, in the negative-charge final state. |
png pdf |
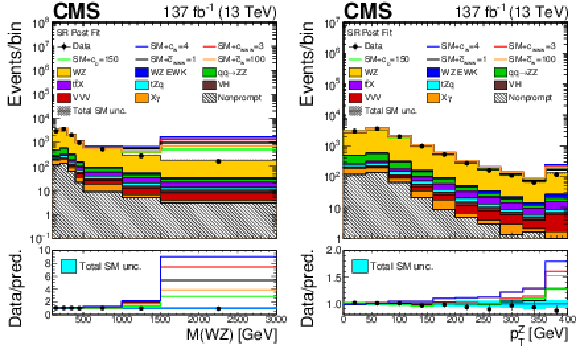
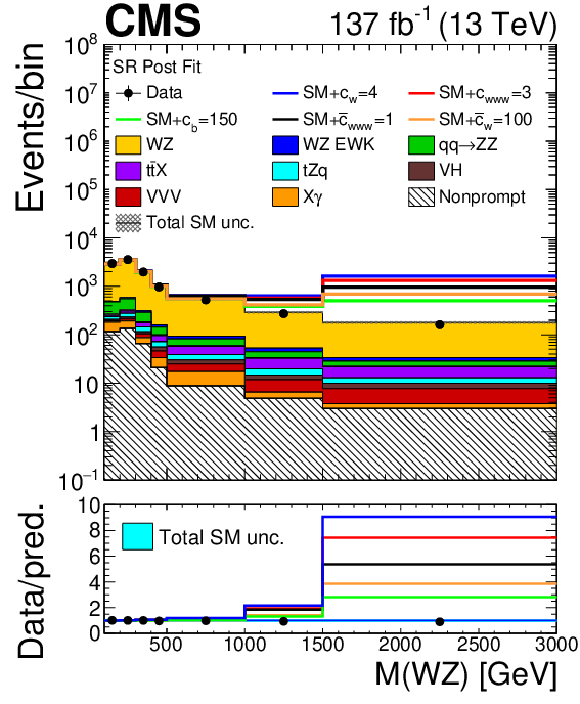
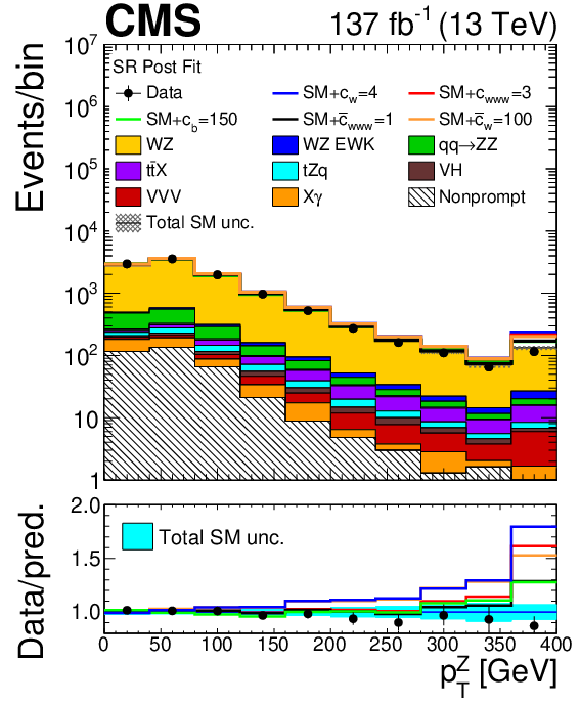
Figure 18:
Distribution of observables in the SR, comparing SM distributions and several possible configurations of EFT parameters after the fit to the SM-only model. Left: invariant mass of the WZ system assuming a neutrino with no longitudinal momentum (${M({\mathrm{W} \mathrm{Z}})}$); right: transverse momentum of the reconstructed Z boson. The SM contributions are shown as the stacked filled histograms, while each of the individual coloured lines shows the expected SM yields plus the contributions from a possible configuration of EFT parameter values. Observed data is shown in black points, with vertical bars representing their statistical uncertainties. The ratio shows the quotient between the BSM contributions and the nominal SM yields. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio presents the total uncertainty in the SM yields. Underflows (overflows) are included in the first (last) bin shown for each distribution. The distribution of the transverse momentum of the Z boson is not used in the BSM interpretation of the analysis and is shown just for illustration. |
png pdf |
Figure 18-a:
Distribution of the invariant mass of the WZ system assuming a neutrino with no longitudinal momentum (${M({\mathrm{W} \mathrm{Z}})}$) in the SR, comparing SM distributions and several possible configurations of EFT parameters after the fit to the SM-only model. The SM contributions are shown as the stacked filled histograms, while each of the individual coloured lines shows the expected SM yields plus the contributions from a possible configuration of EFT parameter values. Observed data is shown in black points, with vertical bars representing their statistical uncertainties. The ratio shows the quotient between the BSM contributions and the nominal SM yields. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio presents the total uncertainty in the SM yields. Underflows (overflows) are included in the first (last) bin. |
png pdf |
Figure 18-b:
Distribution of the transverse momentum of the reconstructed Z boson in the SR, comparing SM distributions and several possible configurations of EFT parameters after the fit to the SM-only model. The SM contributions are shown as the stacked filled histograms, while each of the individual coloured lines shows the expected SM yields plus the contributions from a possible configuration of EFT parameter values. Observed data is shown in black points, with vertical bars representing their statistical uncertainties. The ratio shows the quotient between the BSM contributions and the nominal SM yields. The label X$\gamma$ includes Z$\gamma$, W$\gamma$, ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$, and WZ$ \gamma$ production. The label ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm {X}}$ includes ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{Z}}$, ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{W}}$, and ${{\mathrm{t} \mathrm{\bar{t}}} \mathrm{H}}$ production. The shaded band in the ratio presents the total uncertainty in the SM yields. Underflows (overflows) are included in the first (last) bin. This distribution is not used in the BSM interpretation of the analysis and is shown just for illustration. |

png pdf |
Figure 19:
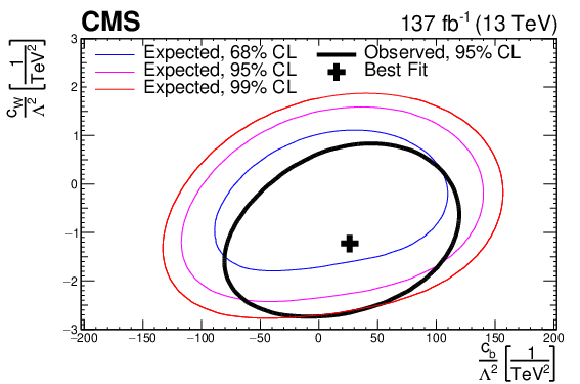
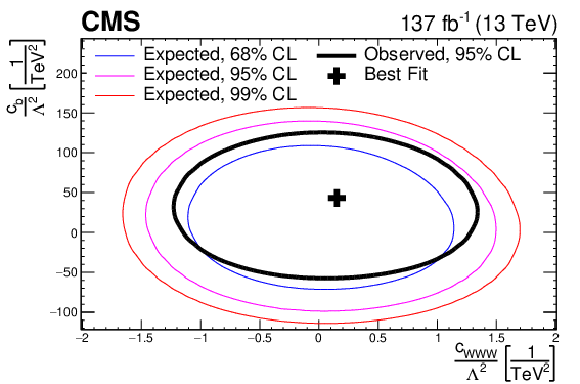
Two-dimensional confidence regions for each of the possible combinations of the considered CP-conserving EFT parameters: $ {c_{\text {w}}}/\Lambda ^2$ vs. $ {c_{\text {www}}}/\Lambda ^2$ (top), $cw/\Lambda ^2$ vs. $ {c_{\text {b}}}/\Lambda ^2$ (middle), and $ {c_{\text {b}}}/\Lambda ^2$ vs. $ {c_{\text {www}}}/\Lambda ^2$ (bottom). The 68, 95, and 99% confidence level contours are presented in each case. |
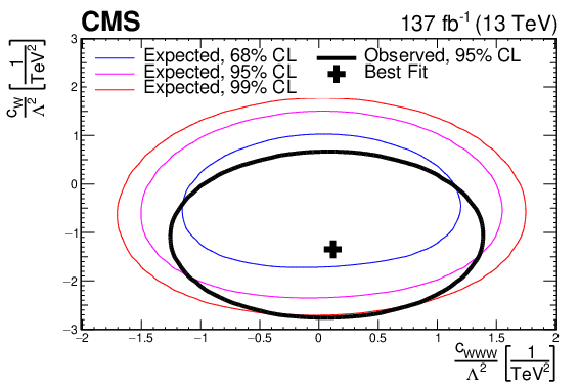
png pdf |
Figure 19-a:
Two-dimensional confidence regions for the $ {c_{\text {w}}}/\Lambda ^2$ vs. $ {c_{\text {www}}}/\Lambda ^2$ combination of CP-conserving EFT parameters. The 68, 95, and 99% confidence level contours are presented. |
png pdf |
Figure 19-b:
Two-dimensional confidence regions for the $cw/\Lambda ^2$ vs. $ {c_{\text {b}}}/\Lambda ^2$ combination of CP-conserving EFT parameters. The 68, 95, and 99% confidence level contours are presented. |
png pdf |
Figure 19-c:
Two-dimensional confidence regions for the $ {c_{\text {b}}}/\Lambda ^2$ vs. $ {c_{\text {www}}}/\Lambda ^2$ combination of CP-conserving EFT parameters. The 68, 95, and 99% confidence level contours are presented. |
png pdf |
Figure 20:
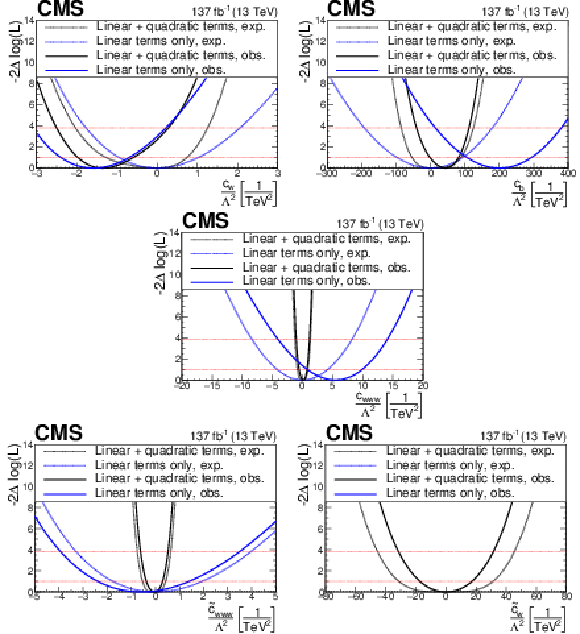
Observed and expected evolution of the log likelihood of the best fit point as a function of each of the considered EFT parameters for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. Very low sensitivity to the interference-only term, ${\tilde{c}_{\text {w}}}/\Lambda ^2$, is observed so the corresponding curve is not shown. |
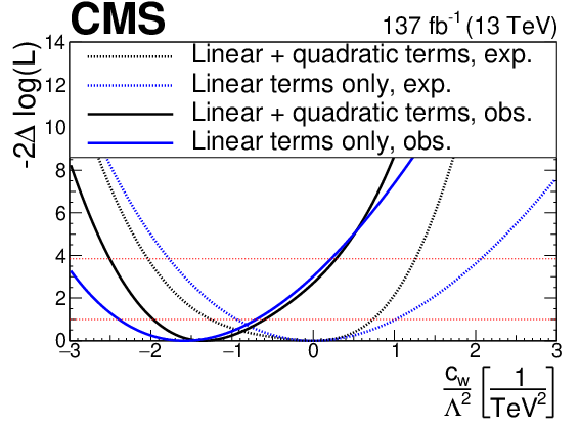
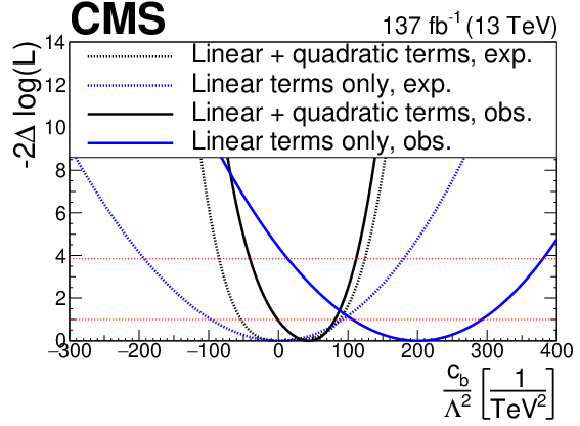
png pdf |
Figure 20-a:
Observed and expected evolution of the log likelihood of the best fit point as a function of the $ {c_{\text {w}}}/\Lambda ^2$ EFT parameter, for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. |
png pdf |
Figure 20-b:
Observed and expected evolution of the log likelihood of the best fit point as a function of the $ {c_{\text {b}}}/\Lambda ^2$ EFT parameter, for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. |
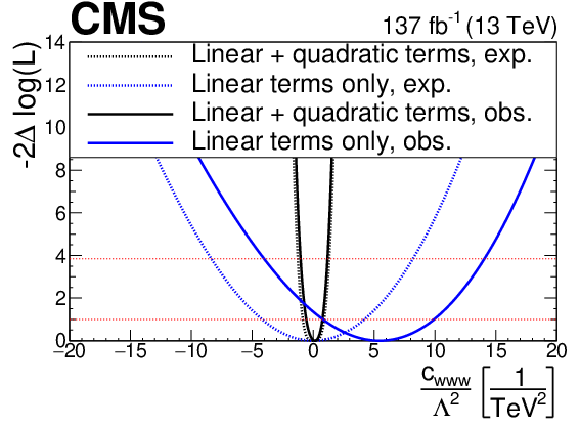
png pdf |
Figure 20-c:
Observed and expected evolution of the log likelihood of the best fit point as a function of the $ {c_{\text {www}}}/\Lambda ^2$ EFT parameter, for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. |
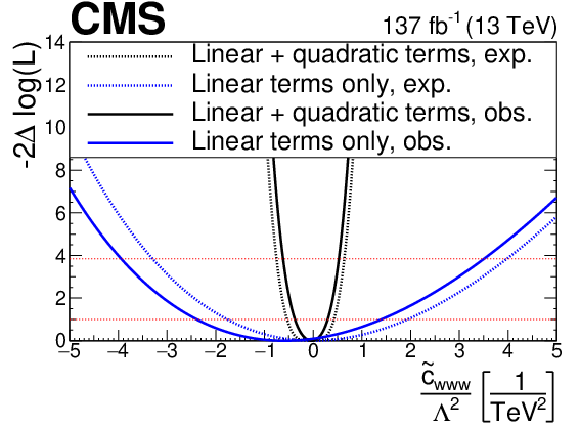
png pdf |
Figure 20-d:
Observed and expected evolution of the log likelihood of the best fit point as a function of the $ {\tilde{c}_{\text {w}}}/\Lambda ^2$ EFT parameter, for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. |

png pdf |
Figure 20-e:
Observed and expected evolution of the log likelihood of the best fit point as a function of the $ {\tilde{c}_{\text {www}}}/\Lambda ^2$ EFT parameter, for both the linear (only interference between SM and BSM physics) and quadratic (both interference and purely BSM term) approaches to the EFT signal modelling. |
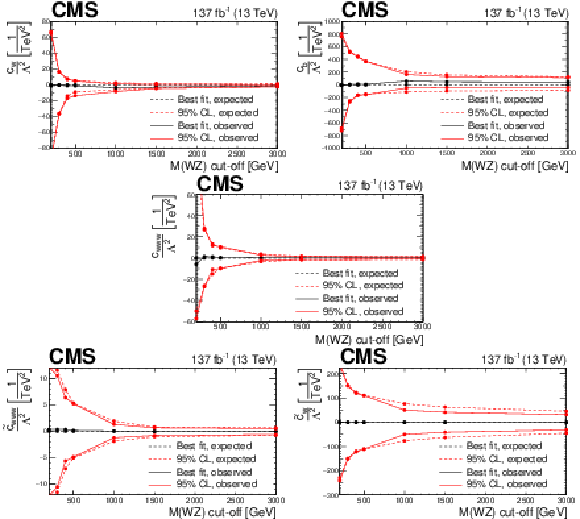
png pdf |
Figure 21:
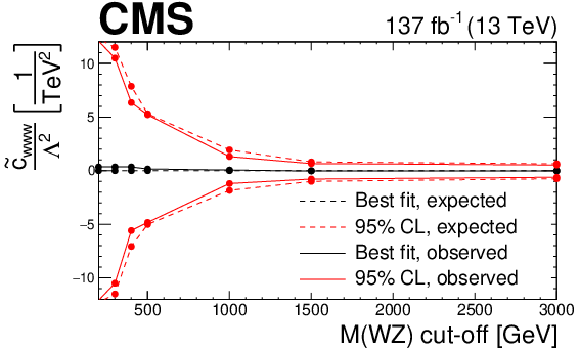
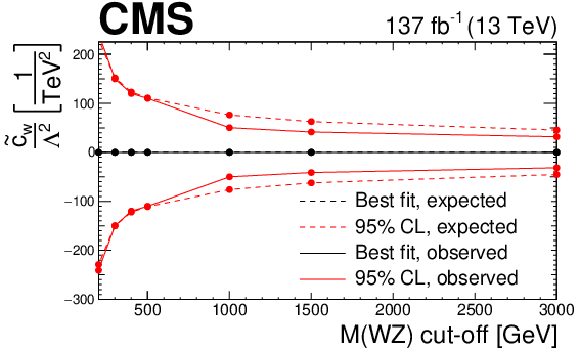
Observed and expected evolution of the confidence intervals in the EFT anomalous coupling parameters in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
png pdf |
Figure 21-a:
Observed and expected evolution of the confidence intervals in the $ {c_{\text {w}}}/\Lambda ^2$ EFT anomalous coupling parameter in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
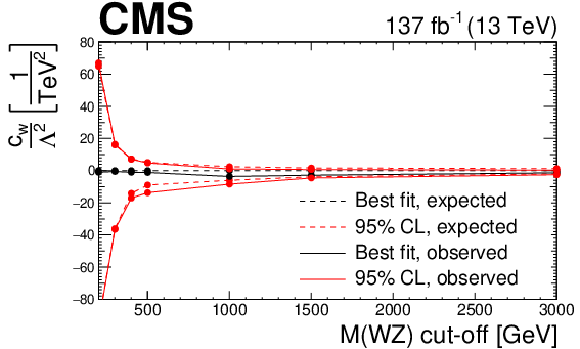
png pdf |
Figure 21-b:
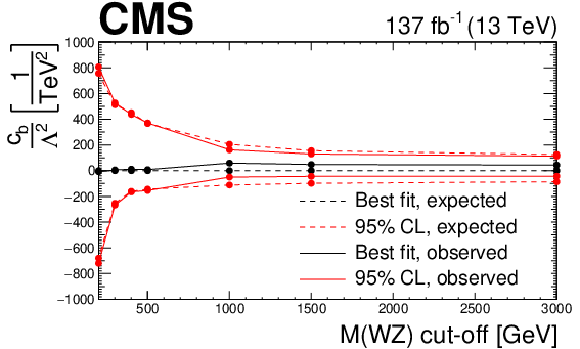
Observed and expected evolution of the confidence intervals in the $ {c_{\text {b}}}/\Lambda ^2$ EFT anomalous coupling parameter in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
png pdf |
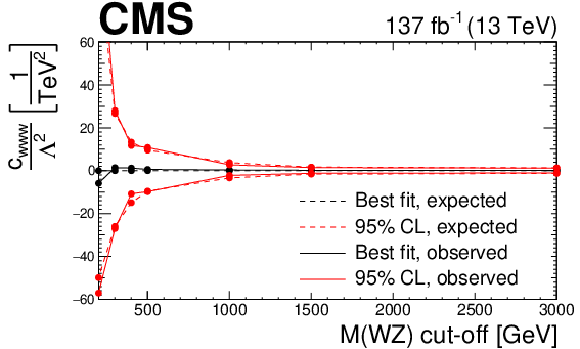
Figure 21-c:
Observed and expected evolution of the confidence intervals in the $ {c_{\text {www}}}/\Lambda ^2$ EFT anomalous coupling parameter in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
png pdf |
Figure 21-d:
Observed and expected evolution of the confidence intervals in the $ {\tilde{c}_{\text {w}}}/\Lambda ^2$ EFT anomalous coupling parameter in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
png pdf |
Figure 21-e:
Observed and expected evolution of the confidence intervals in the $ {\tilde{c}_{\text {www}}}/\Lambda ^2$ EFT anomalous coupling parameter in terms of the cutoff scale given by different restrictions in the ${M({\mathrm{W} \mathrm{Z}})}$ variable. For each point and parameter, the confidence intervals are computed imposing the additional restriction of no anomalous coupling contribution on top of the SM prediction over the given value of ${M({\mathrm{W} \mathrm{Z}})}$. Because of the statistical limitations in our simulation the last point is equivalent to no cut-off requirement being imposed. |
| Tables | |

png pdf |
Table 1:
Requirements for the definition of the SR and the three different CRs designed to estimate the main background sources. The notation $N_{\ell}$ refers to the number of tight leptons, $N_{\mathrm {OSSF}}$ refers to the number of opposite-sign same-flavour lepton pairs, and $N_{\mathrm{b} \mathrm {tag}}$ refers to the number of b-tagged jets. |

png pdf |
Table 2:
Summary of the uncertainties in the analysis, their relative effect for each of the data-taking years, the correlation scheme followed, and which processes are affected by them. Uncertainties related to experimental measurements of efficiencies and energy scales are presented as percentages of the predicted signal yield. Uncertainties related to normalization of specific background processes are described as percentages of the yield of each process or as free if the process is freely floating in the fits. Lepton-related uncertainties are shown as a range as most measurements of the analysis are split in flavour channels, with which the size of these uncertainties is strongly correlated. Systematic uncertainties with an asymmetric effect are marked with a $/$ separating the upwards and downwards variations. |

png pdf |
Table 3:
Expected and observed yields after the combined fit for the relevant SM processes in the SR of the analysis in each of the different lepton flavour combinations for all the data taking years. Total uncertainties affecting each process are included at their postfit values next to the predicted yields. |

png pdf |
Table 4:
Efficiencies, acceptances, and proportion of fiducial signal events in the SR for the combined selection and each of the considered flavour channels separately, as determined using the POWHEG WZ MC sample. Uncertainties are statistical only. Note that while the fiducial region is defined separately per flavour, and thus the inclusive efficiency is a weighted average of the per channel ones, the TR is always flavour-inclusive: the inclusive acceptance is therefore by definition the sum of the ones split by category. |
png pdf |
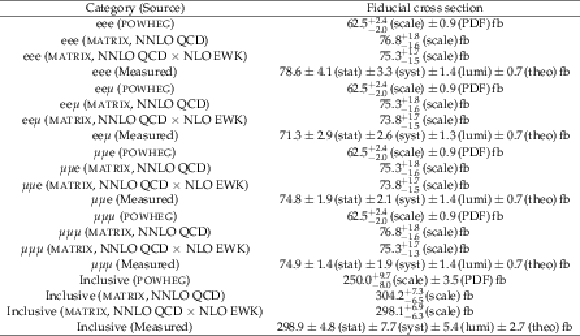
Table 5:
Measured fiducial charge asymmetry ratios and their corresponding uncertainties for the flavour-exclusive and flavour-inclusive categories. The predictions from both POWHEG at NLO in QCD and LO EWK as well as several ones obtained from MATRIX (NNLO QCD, NNLO QCD $\times $ NLO EWK) are also included. |
png pdf |
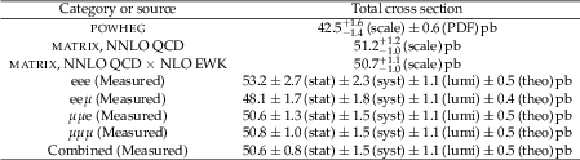
Table 6:
Measured total cross sections and their corresponding uncertainties for the flavour-exclusive and flavour-inclusive categories. The predictions from both POWHEG at NLO in QCD and LO EWK as well as several ones obtained from MATRIX (NNLO QCD, NNLO QCD $\times $ NLO EWK) are also included. |
png pdf |
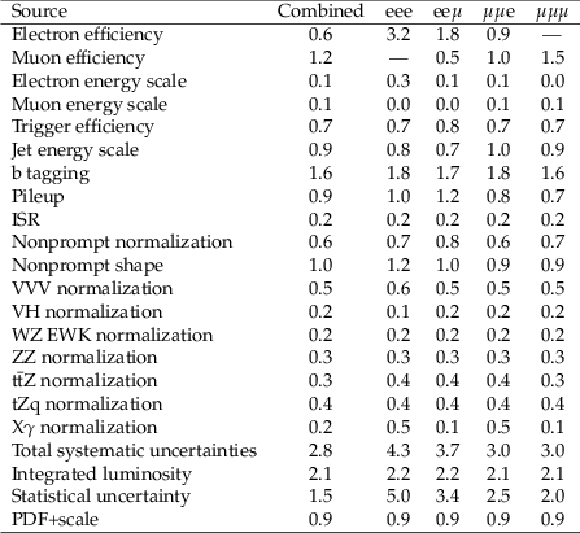
Table 7:
Summary of postfit effects of each uncertainty source in the total WZ cross section measurement separated by flavour categories. Values are given in percentage contribution to the cross section uncertainty. For the scale and PDF uncertainties that are not included in the fit, the effect on the acceptance measurements is shown. |

png pdf |
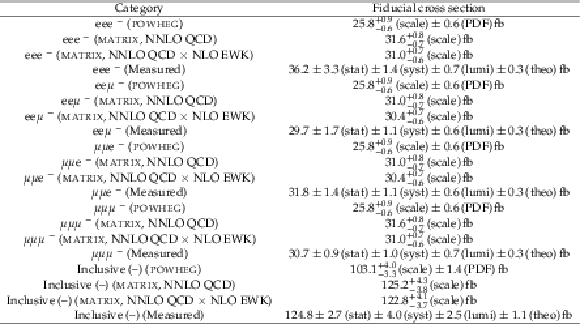
Table 8:
Measured fiducial cross sections and their corresponding uncertainties for each of the individual flavour categories, as well as for their combination, for positively charged final states. The predictions from both MATRIX (at NNLO QCD and NNLO QCD $\times $ NLO EWK) and POWHEG (at NLO QCD) are also included. |
png pdf |
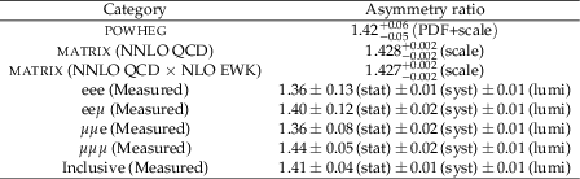
Table 9:
Measured fiducial cross sections and their corresponding uncertainties for each of the individual flavour categories, as well as for their combination, for negatively charged final states. The predictions from both MATRIX (at NNLO QCD and NNLO QCD $\times $ NLO EWK) and POWHEG (at NLO QCD) are also included. |
png pdf |
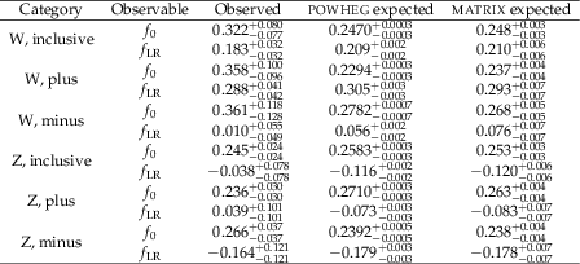
Table 10:
Measured ratios of fiducial cross sections and their corresponding uncertainties for each of the individual flavour categories, as well as for their combination. The predictions from both MATRIX (at NNLO QCD and NNLO QCD $\times $ NLO EWK) and POWHEG (at NLO QCD) are also included. |
png pdf |
Table 11:
Standard model predictions and measured values of the W and Z polarization parameters for inclusive WZ production and each of the charged final states. The label Category indicates the targeted boson and total leptonic charge. The SM values are estimated from the nominal POWHEG sample and the MATRIX shapes by performing a quadratic fit to the generator level cosine of the polarization angle with no fiducial cuts applied and computing the polarization fractions from the fitting parameters. Uncertainties in the POWHEG measurements correspond to the PDF uncertainties, while those included for MATRIX relate to the overall numerical uncertainty. |

png pdf |
Table 12:
Best fit, and expected and observed one-dimensional confidence intervals at 95% confidence level for each of the considered EFT parameters. Both the purely dimension-eight BSM contribution as well as the dimension-six interference term are included to compute the EFT effect in the high tails of ${M({\mathrm{W} \mathrm{Z}})}$ for these results. In computing confidence intervals for each parameter the other ones are fixed to their SM values. |

png pdf |
Table 13:
Best fit, and expected and observed one-dimensional confidence intervals at 95% confidence level for each of the considered EFT parameters. Only the dimension-six interference term is included to compute the EFT effect in the high tails of ${M({\mathrm{W} \mathrm{Z}})}$ for these results. In computing confidence intervals for each parameter the other ones are fixed to their SM values. The -- symbol means no sensitivity is observed for the interference only term for the ${\tilde{c}_{\text {w}}}$ parameter. |
| Summary |
|
The associated production of a W and a Z boson (WZ ) in proton-proton (pp) collisions, denoted ${\mathrm{p}}{\mathrm{p}}\to\mathrm{W}\mathrm{Z}$, is studied in the trilepton final state at $\sqrt{s} = $ 13 TeV, using 137 fb$^{-1}$ of CMS data. The production cross sections in the total and fiducial phase spaces are measured in the inclusive case of final-state charge and in eight different combinations of final-state flavour composition and total final-state charge. The measured total inclusive cross section is $\sigma_{\textrm{tot}}({\mathrm{p}} {\mathrm{p}} \to \mathrm{W}\mathrm{Z}) = $ 50.6 $\pm$ 0.8 (stat) $\pm$ 1.4 (syst) $\pm$ 1.1 (lumi) $\pm$ 0.5 (theo) pb $=$ 50.6 $\pm$ 1.9 pb. This favours the computation performed within the MATRIX computational framework at next-to-next-to-leading order (NNLO) in quantum chromodynamics (QCD) $\times$ next-to-leading order (NLO) in electroweak (EWK) of $\sigma_{\text{MATRIX} } = $ 50.7 $^{+1.1}_{-1.0}$ (scale) pb over the one obtained with the POWHEG event generator at NLO QCD order of $\sigma_{\text{POWHEG}} = $ 42.5 $^{+1.6}_{-1.4}$ (scale) $\pm$ 0.6 (PDF) pb, where PDF stands for parton distribution function. These results are consistent with earlier ATLAS [12] and CMS [22] measurements with a relative precision enhanced down to an overall 4% from the 5 and 6% of the earlier results. The charge asymmetry in the production, resulting from the dominant qq production mode, is also measured in terms of a charge asymmetry ratio of $A^{+-}_{{\mathrm{W}\mathrm{Z}} }= $ 1.41 $\pm$ 0.04 with a relative precision better than 3% and in agreement with the standard model predictions calculated at NLO QCD as $A^{+-,\text{POWHEG}}_{{\mathrm{W}\mathrm{Z}} } = $ 1.42 $\pm$ 0.05. Consistency of the measurement is found with the NNPDF30_nlo_as0118 PDF set. A Bayesian reweighting technique is applied to estimate possible constraints on PDFs that could be derived from this measurement. These results are consistent with previous results by the ATLAS [12] and CMS [22] Collaborations. The polarization of the W and Z bosons in WZ production in the helicity frame is studied in the charge-inclusive and charge-exclusive final states. The observed significance for the presence of longitudinally polarized W bosons is 5.6 standard deviations where 4.3 standard deviations are expected. For the Z boson, both expected and observed significances are well in excess of five standard deviations. Differential distributions are measured, in both the inclusive and the charge-exclusive final states, for several observables: the ${p_{\mathrm{T}}}$ of the Z boson, the ${p_{\mathrm{T}}}$ of the lepton associated with the W boson, the ${p_{\mathrm{T}}}$ of the leading jet of the event, the number of jets, the cosine of the polarization angles$ {\theta^{\mathrm{W}}}$ and ${\theta^{\mathrm{Z}}}$, and the invariant mass of the WZ system. The distributions are compared with predictions at NLO in QCD from POWHEG and MadGraph5+MCatNLO as well as with predictions at NNLO in QCD $\times$ NLO in EWK obtained with MATRIX . The data favour the differential predictions from MATRIX over those from POWHEG. A search for anomalous values of the charged triple gauge coupling WWZ is performed by examining the high-energy tails in the distribution of the mass of the WZ system. The effect of CP-violating dimension-six operators is introduced by CMS for the first time in WZ production, leading to confidence regions similar to those obtained in the CP-conserving case. The results presented are the most precise measurements of the WZ inclusive cross section, charge asymmetry, and polarization fractions in the helicity frame obtained in any energy regime. Longitudinally polarized W and Z bosons in WZ production are observed at the level of five standard deviations for the first time. This search for anomalous triple gauge couplings is better than the best previous limits reported by the LHC experiments, and it provides stronger constraints than previous analyses by a factor of 2. |
| References | ||||
| 1 | UA1 Collaboration | Production of W's with large transverse momentum at the CERN proton-antiproton collider | PLB 193 (1987) 389 | |
| 2 | D0 Collaboration | Measurement of the $ \mathrm{W}\mathrm{Z}\rightarrow \ell\nu\ell\ell $ cross section and limits on anomalous triple gauge couplings in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PLB 695 (2011) 67 | 1006.0761 |
| 3 | CDF Collaboration | Observation of WZ production | PRLett 98 (2007) 161801 | hep-ex/0702027 |
| 4 | ATLAS Collaboration | Measurement of the W$^{\pm}$Z production cross section and limits on anomalous triple gauge couplings in proton-proton collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS detector | PLB 709 (2012) 341 | 1111.5570 |
| 5 | ATLAS Collaboration | Measurement of WZ production in proton-proton collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS detector | EPJC 72 (2012) 2173 | 1208.1390 |
| 6 | ATLAS Collaboration | Measurement of the WW+WZ cross section and limits on anomalous triple gauge couplings using final states with one lepton, missing transverse momentum, and two jets with the ATLAS detector at $ \sqrt{s} = $ 7 TeV | JHEP 01 (2015) 049 | 1410.7238 |
| 7 | ATLAS Collaboration | Measurements of W$^{\pm}$Z production cross sections in pp collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector and limits on anomalous gauge boson self-couplings | PRD 93 (2016) 092004 | 1603.02151 |
| 8 | ATLAS Collaboration | Measurement of the W$^{\pm}$Z boson pair-production cross section in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PLB 762 (2016) 1 | 1606.04017 |
| 9 | ATLAS Collaboration | Search for anomalous electroweak production of WW/WZ in association with a high-mass dijet system in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | PRD 95 (2017) 032001 | 1609.05122 |
| 10 | ATLAS Collaboration | Measurement of $ \mathrm{W}\mathrm{W}/\mathrm{W}\mathrm{Z} \rightarrow \ell \nu q q^{\prime} $ production with the hadronically decaying boson reconstructed as one or two jets in pp collisions at $ \sqrt{s}= $ 8 TeV with ATLAS, and constraints on anomalous gauge couplings | EPJC 77 (2017) 563 | 1706.01702 |
| 11 | ATLAS Collaboration | Search for the electroweak diboson production in association with a high-mass dijet system in semileptonic final states in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 100 (2019) 032007 | 1905.07714 |
| 12 | ATLAS Collaboration | Measurement of W$^{\pm}$Z production cross sections and gauge boson polarisation in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | EPJC 79 (2019) 535 | 1902.05759 |
| 13 | CMS Collaboration | Study of the dijet mass spectrum in $ {\mathrm{p}}{\mathrm{p}} \rightarrow \mathrm{W} + $ jets events at $ \sqrt{s}= $ 7 TeV | PRL 109 (2012) 251801 | CMS-EWK-11-017 1208.3477 |
| 14 | CMS Collaboration | Measurement of the sum of WW and WZ production with W+dijet events in pp collisions at $ \sqrt{s}= $ 7 TeV | EPJC 73 (2013) 2283 | CMS-SMP-12-015 1210.7544 |
| 15 | CMS Collaboration | Measurement of WZ and ZZ production in pp collisions at $ \sqrt{s}= $ 8 TeV in final states with b-tagged jets | EPJC 74 (2014) 2973 | CMS-SMP-13-011 1403.3047 |
| 16 | CMS Collaboration | Measurement of the WZ production cross section in pp collisions at $ \sqrt{s}= $ 13 TeV | PLB 766 (2017) 268 | CMS-SMP-16-002 1607.06943 |
| 17 | CMS Collaboration | Measurement of the WZ production cross section in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV and search for anomalous triple gauge couplings at $ \sqrt{s}= $ 8 TeV | EPJC 77 (2017) 236 | CMS-SMP-14-014 1609.05721 |
| 18 | CMS Collaboration | Search for anomalous couplings in boosted $ \mathrm{W}\mathrm{W}/\mathrm{W}\mathrm{Z}\to\ell\nu\mathrm{q\bar{q}} $ production in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | PLB 772 (2017) 21 | CMS-SMP-13-008 1703.06095 |
| 19 | CMS Collaboration | Search for anomalous electroweak production of vector boson pairs in association with two jets in proton-proton collisions at 13 TeV | PLB 798 (2019) 134985 | CMS-SMP-18-006 1905.07445 |
| 20 | CMS Collaboration | Search for anomalous triple gauge couplings in WW and WZ production in lepton+jet events in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2019) 62 | CMS-SMP-18-008 1907.08354 |
| 21 | CMS Collaboration | Measurement of electroweak WZ boson production and search for new physics in WZ + two jets events in pp collisions at $ \sqrt{s}= $ 13 TeV | PLB 795 (2019) 281 | CMS-SMP-18-001 1901.04060 |
| 22 | CMS Collaboration | Measurements of the pp $ \to $ WZ inclusive and differential production cross section and constraints on charged anomalous triple gauge couplings at $ \sqrt{s} = $ 13 TeV | JHEP 04 (2019) 122 | CMS-SMP-18-002 1901.03428 |
| 23 | CMS Collaboration | HEPData record for this analysis | link | |
| 24 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 25 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 26 | CMS Collaboration | Performance of missing energy reconstruction in 13 TeV pp collision data using the CMS detector | CMS-PAS-JME-16-004 | CMS-PAS-JME-16-004 |
| 27 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 28 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 29 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 30 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W$^{+}$W$^{-}$, WZ, and ZZ production in the POWHEG box | JHEP 11 (2011) 078 | 1107.5051 |
| 31 | P. Nason and G. Zanderighi | W$^{+}$W$^{-}$, WZ and ZZ production in the $ POWHEG-box-v2 | EPJC 74 (2014) 2702 | 1311.1365 |
| 32 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 33 | R. Frederix and S. Frixione | Merging meets matching in MadGraph5+MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 34 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 35 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJ76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 36 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA 8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 37 | O. Mattelaer | On the maximal use of Monte Carlo samples: re-weighting events at NLO accuracy | EPJC 76 (2016) 674 | 1607.00763 |
| 38 | C. Degrande et al. | Effective field theory: A modern approach to anomalous couplings | Annals Phys. 335 (2013) 21 | 1205.4231 |
| 39 | J. M. Campbell and R. K. Ellis | MCFM for the Tevatron and the LHC | NPB Proc. Suppl. 10 (2010) 205 | 1007.3492 |
| 40 | F. Caola, K. Melnikov, R. Rontsch, and L. Tancredi | QCD corrections to ZZ production in gluon fusion at the LHC | PRD 92 (2015) 094028 | 1509.06734 |
| 41 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 42 | M. Grazzini, S. Kallweit, D. Rathlev, and M. Wiesemann | W$^{\pm}$Z production at hadron colliders in NNLO QCD | PLB 761 (2016) 179 | 1604.08576 |
| 43 | M. Grazzini, S. Kallweit, D. Rathlev, and M. Wiesemann | W$^{\pm}$Z production at the LHC: fiducial cross sections and distributions in NNLO QCD | JHEP 05 (2017) 139 | 1703.09065 |
| 44 | M. Grazzini, S. Kallweit, and M. Wiesemann | Fully differential NNLO computations with MATRIX | EPJC 78 (2018) 537 | 1711.06631 |
| 45 | M. Grazzini et al. | NNLO QCD + NLO EW with MATRIX + Open Loops: precise predictions for vector--boson pair production | JHEP 02 (2020) 087 | 1912.00068 |
| 46 | F. Cascioli, P. Maierhofer, and S. Pozzorini | Scattering amplitudes with open loops | PRL 108 (2012) 111601 | 1111.5206 |
| 47 | A. Denner, S. Dittmaier, and L. Hofer | Collier: a fortran-based complex one-loop library in extended regularizations | CPC 212 (2017) 220 | 1604.06792 |
| 48 | S. Catani et al. | Vector boson production at hadron colliders: hard-collinear coefficients at the NNLO | EPJC 72 (2012) 2195 | 1209.0158 |
| 49 | S. Catani and M. Grazzini | An NNLO subtraction formalism in hadron collisions and its application to Higgs boson production at the LHC | PRL 98 (2007) 222002 | hep-ph/0703012 |
| 50 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 51 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 52 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 53 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 54 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 55 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | CMS-PAS-JME-16-003 |
| 56 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 57 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using the CMS detector | JINST 14 (2019) 7004 | CMS-JME-17-001 1903.06078 |
| 58 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 59 | CMS Collaboration | Search for new physics in same-sign dilepton events in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | EPJC 76 (2016) 439 | CMS-SUS-15-008 1605.03171 |
| 60 | CMS Collaboration | Measurements of production cross sections of WZ and same-sign WW boson pairs in association with two jets in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PLB 809 (2020) 135710 | CMS-SMP-19-012 2005.01173 |
| 61 | CMS Collaboration | Observation of Higgs boson decay to bottom quarks | PRL 121 (2018) 121801 | CMS-HIG-18-016 1808.08242 |
| 62 | CMS Collaboration | Measurements of inclusive W and Z cross sections in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |
| 63 | C. J. Clopper and E. S. Pearson | The use of confidence or fiducial limits illustrated in the case of the binomial | Biometrika 26 (1934) 404 | |
| 64 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 65 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 66 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | ||
| 67 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | ||
| 68 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 69 | S. Mrenna and P. Skands | Automated parton-shower variations in PYTHIA-8 | PRD 94 (2016) 074005 | 1605.08352 |
| 70 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 71 | S. Dulat et al. | New parton distribution functions from a global analysis of quantum chromodynamics | PRD 93 (2016) 033006 | 1506.07443 |
| 72 | L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne | Parton distributions in the LHC era: MMHT 2014 PDFs | EPJC 75 (2015) 204 | 1412.3989 |
| 73 | W. T. Giele and S. Keller | Implications of hadron collider observables on parton distribution function uncertainties | PRD 58 (1998) 094023 | hep-ph/9803393 |
| 74 | N. Sato, J. F. Owens, and H. B. Prosper | Bayesian reweighting for global fits | PRD 89 (2014) 114020 | 1310.1089 |
| 75 | J. A. Aguilar-Saavedra and J. Bernabeu | Breaking down the entire W boson spin observables from its decay | PRD 93 (2016) 011301 | 1508.04592 |
| 76 | J. A. Aguilar-Saavedra, J. Bernabeu, V. A. Mitsou, and A. Segarra | The Z boson spin observables as messengers of new physics | EPJC 77 (2017) 234 | 1701.03115 |
| 77 | W. J. Stirling and E. Vryonidou | Electroweak gauge boson polarisation at the LHC | JHEP 07 (2012) 124 | 1204.6427 |
| 78 | Z. Bern et al. | Left-handed W bosons at the LHC | PRD 84 (2011) 034008 | 1103.5445 |
| 79 | G. Cowan | Statistical Data Analysis | Oxford Science Publications | |
| 80 | S. Schmitt | Data unfolding methods in high energy physics | EPJ Web Conf. 137 (2017) 11008 | 1611.01927 |
| 81 | S. Schmitt | TUnfold: an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|