Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-TOP-23-007 | ||
| Measurements of polarization, spin correlations, and entanglement in top quark pairs using lepton+jets events from pp collisions at $ \sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| 13 June 2024 | ||
| Abstract: Measurements of the polarization and spin correlations in top quark pairs ($ \mathrm{t\bar t} $) are presented using events with a single electron or muon and jets in the final state. The measurements are based on proton-proton collision data from the LHC at $ \sqrt{s}= $ 13 TeV collected by the CMS experiment, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. All coefficients of the polarization vectors and the spin correlation matrix are extracted simultaneously by performing a binned likelihood fit to the data. The measurement is performed in bins of additional observables such as the mass of the $ \mathrm{t\bar t} $ system and the top quark scattering angle. Inclusive coefficients are obtained by combining the results of all fitted bins. From the measured spin correlations, conclusions on the $ \mathrm{t\bar t} $ spin entanglement are drawn. The standard model predicts entangled spin $ \mathrm{t\bar t} $ states at the production threshold and at high masses of the $ \mathrm{t\bar t} $ system. Entanglement is observed for the first time in events with high $ \mathrm{t\bar t} $ mass, with an observed (expected) significance of 6.7 (5.6) standard deviations. The observed level of entanglement cannot be explained by classical exchange of information between the two particles alone. The observed (expected) significance for entanglement attributable to space-like separated $ \mathrm{t\bar t} $ pairs is 5.4 (4.1) standard deviations. | ||
|
Links:
CDS record (PDF) ;
Physics Briefing ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to PRD. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
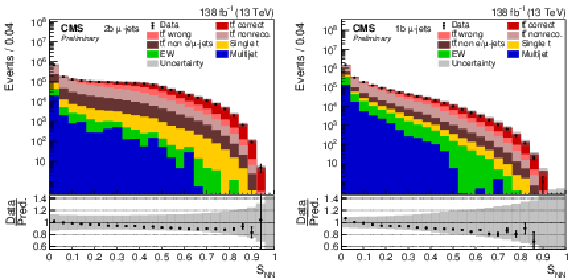
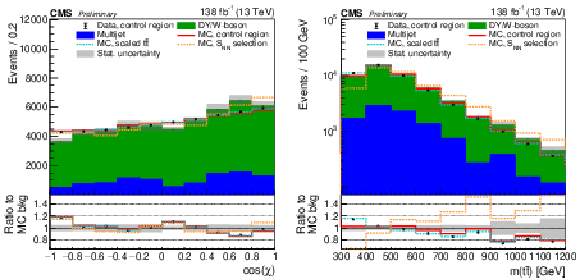
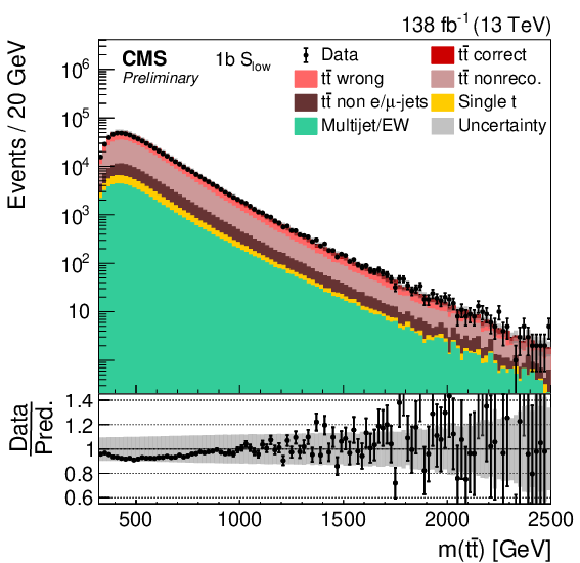
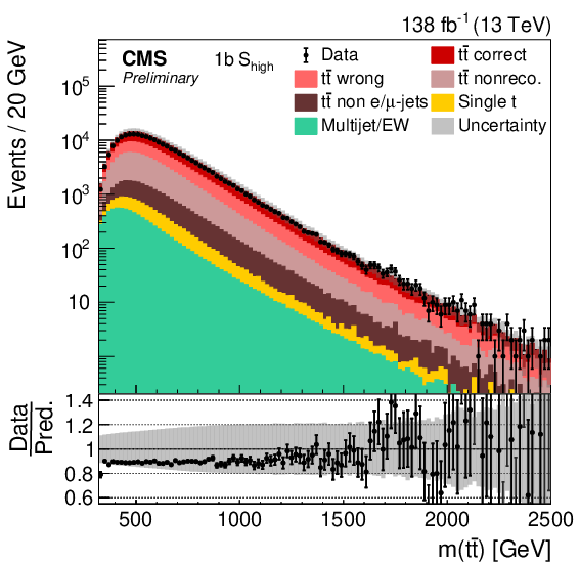
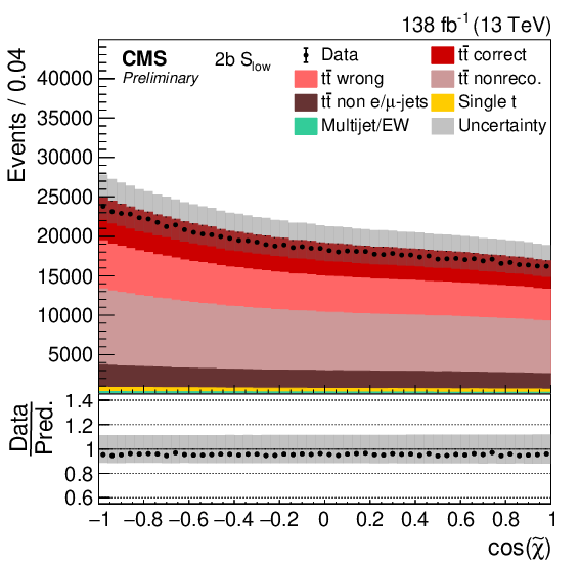
Figure 1:
Distribution of $ S_\mathrm{NN} $ in the 2b (left) and 1b (right) categories for $ \mu $+jets events. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction, while the vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
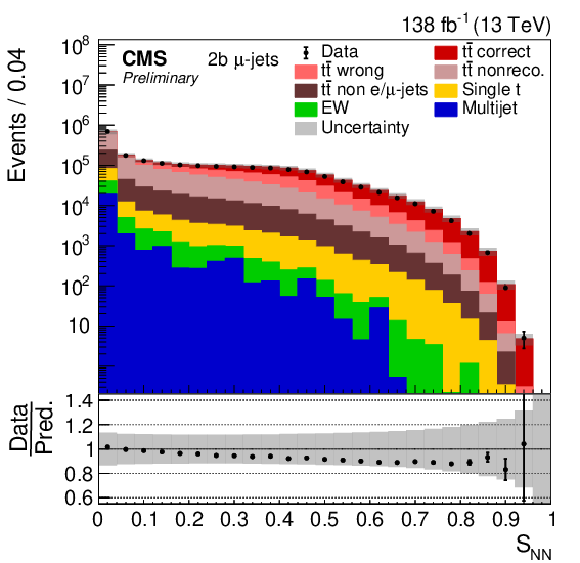
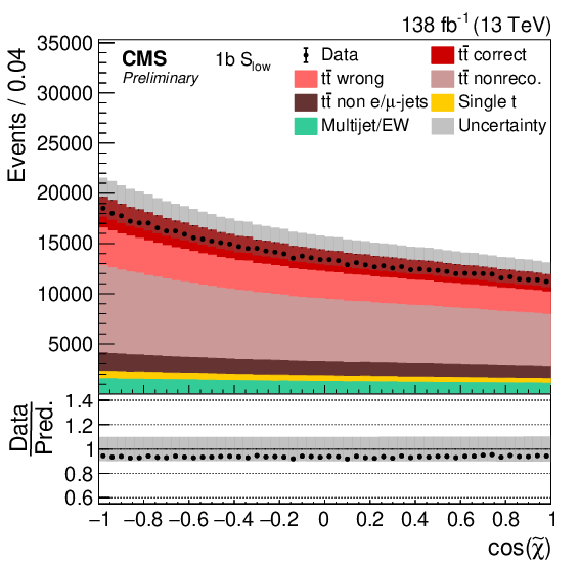
Figure 1-a:
Distribution of $ S_\mathrm{NN} $ in the 2b (left) and 1b (right) categories for $ \mu $+jets events. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction, while the vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
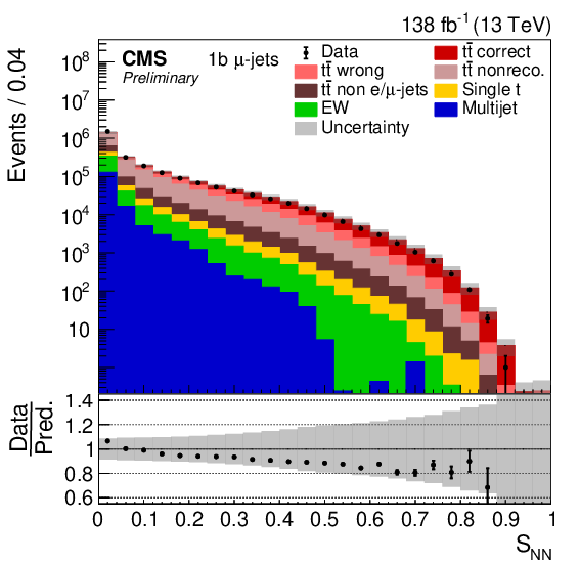
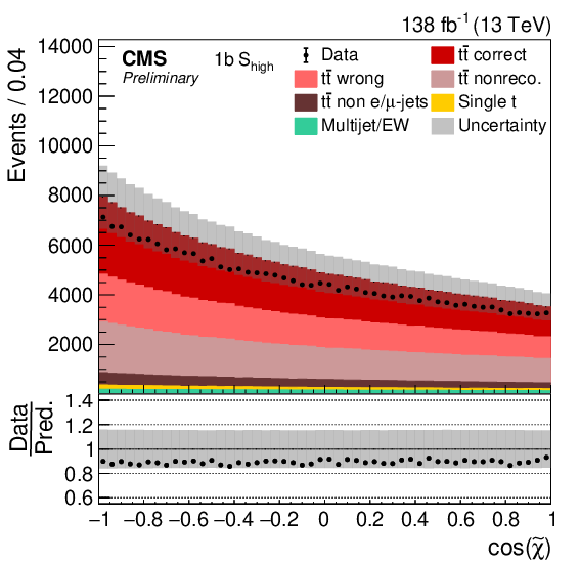
Figure 1-b:
Distribution of $ S_\mathrm{NN} $ in the 2b (left) and 1b (right) categories for $ \mu $+jets events. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction, while the vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
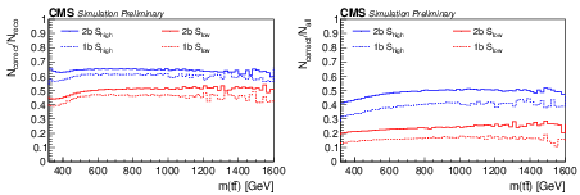
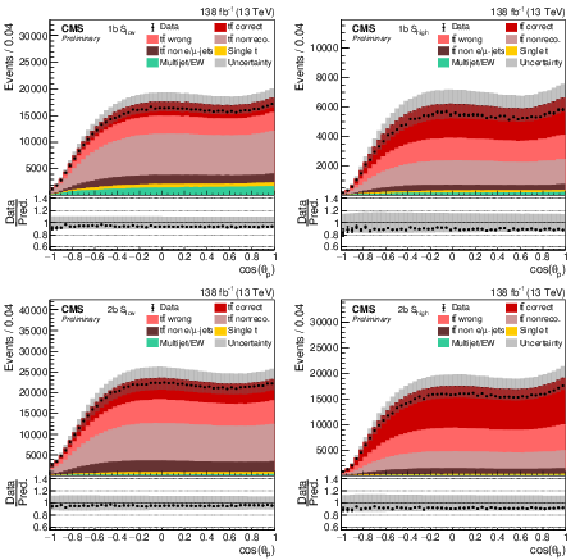
Figure 2:
Reconstruction efficiency of the NN (left) and fraction of correctly reconstructed events (right) as a function of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ estimated from the simulation. The values are shown separately for the 1b and 2b categories with the $ S_\mathrm{low} $ and $ S_\mathrm{high} $ selection. The event counts $ N_\mathrm{correct} $ and $ N_\mathrm{reco} $ refer to the number of correctly reconstructed and ``reconstructable'' $ \mathrm{t \bar{t}} $ events, respectively. All reconstructed events regardless of the process are labeled $ N_\mathrm{all} $. |
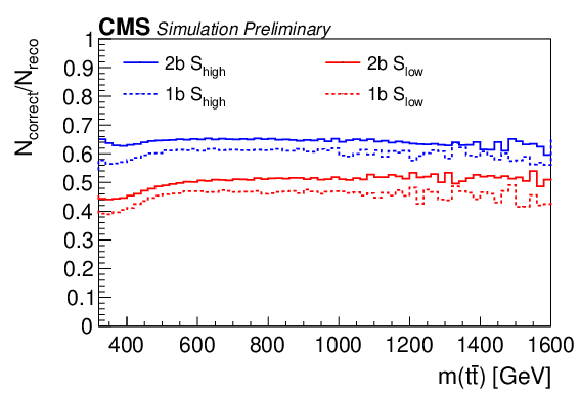
png pdf |
Figure 2-a:
Reconstruction efficiency of the NN (left) and fraction of correctly reconstructed events (right) as a function of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ estimated from the simulation. The values are shown separately for the 1b and 2b categories with the $ S_\mathrm{low} $ and $ S_\mathrm{high} $ selection. The event counts $ N_\mathrm{correct} $ and $ N_\mathrm{reco} $ refer to the number of correctly reconstructed and ``reconstructable'' $ \mathrm{t \bar{t}} $ events, respectively. All reconstructed events regardless of the process are labeled $ N_\mathrm{all} $. |
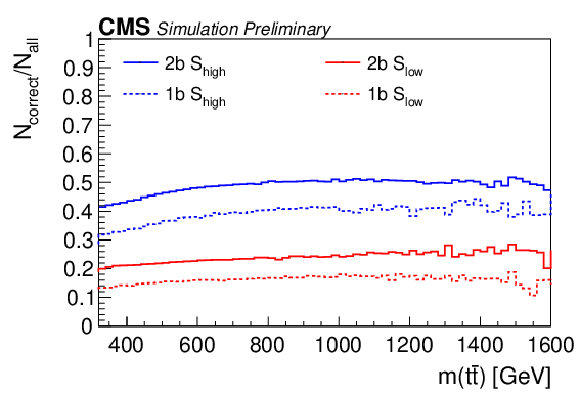
png pdf |
Figure 2-b:
Reconstruction efficiency of the NN (left) and fraction of correctly reconstructed events (right) as a function of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ estimated from the simulation. The values are shown separately for the 1b and 2b categories with the $ S_\mathrm{low} $ and $ S_\mathrm{high} $ selection. The event counts $ N_\mathrm{correct} $ and $ N_\mathrm{reco} $ refer to the number of correctly reconstructed and ``reconstructable'' $ \mathrm{t \bar{t}} $ events, respectively. All reconstructed events regardless of the process are labeled $ N_\mathrm{all} $. |
png pdf |
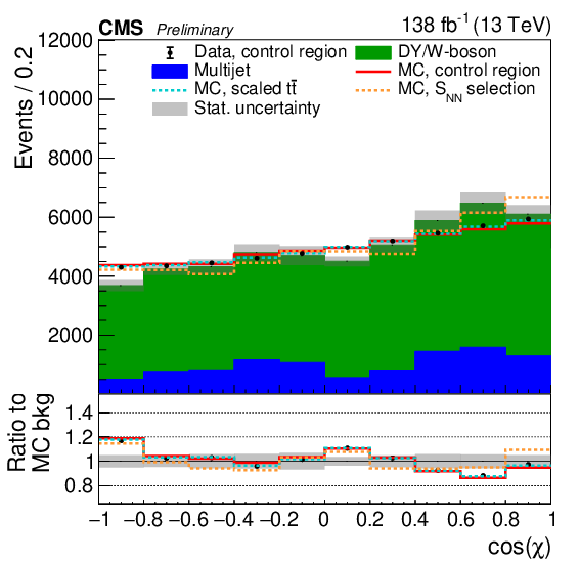
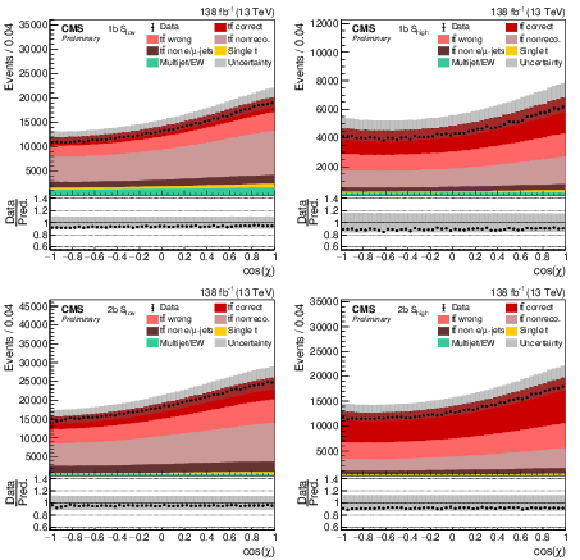
Figure 3:
Comparison of the $ \cos(\chi) $ (left) and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ (right) distributions of the simulated background in the control region (red line) and in the 1b signal category (stacked histograms). The data points show the distribution in the control region after subtracting the predicted $ \mathrm{t \bar{t}} $ and single top contributions. Data to MC agreement in the control region can be seen by comparing the data points to the red line. The dashed orange lines show the distribution after requiring the $ S_\mathrm{NN} $ selections in the control region. The dashed light blue distribution is obtained by taking into account the mismatch of the normalization in the control region when subtracting the $ \mathrm{t \bar{t}} $ and single top contributions. All distributions are normalized to the event yields of the stacked histogram. The gray uncertainty band shows the statistical uncertainties in the prediction. The lower panels show the ratios of the various distributions with respect to the simulated background in the 1b signal category. |
png pdf |
Figure 3-a:
Comparison of the $ \cos(\chi) $ (left) and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ (right) distributions of the simulated background in the control region (red line) and in the 1b signal category (stacked histograms). The data points show the distribution in the control region after subtracting the predicted $ \mathrm{t \bar{t}} $ and single top contributions. Data to MC agreement in the control region can be seen by comparing the data points to the red line. The dashed orange lines show the distribution after requiring the $ S_\mathrm{NN} $ selections in the control region. The dashed light blue distribution is obtained by taking into account the mismatch of the normalization in the control region when subtracting the $ \mathrm{t \bar{t}} $ and single top contributions. All distributions are normalized to the event yields of the stacked histogram. The gray uncertainty band shows the statistical uncertainties in the prediction. The lower panels show the ratios of the various distributions with respect to the simulated background in the 1b signal category. |
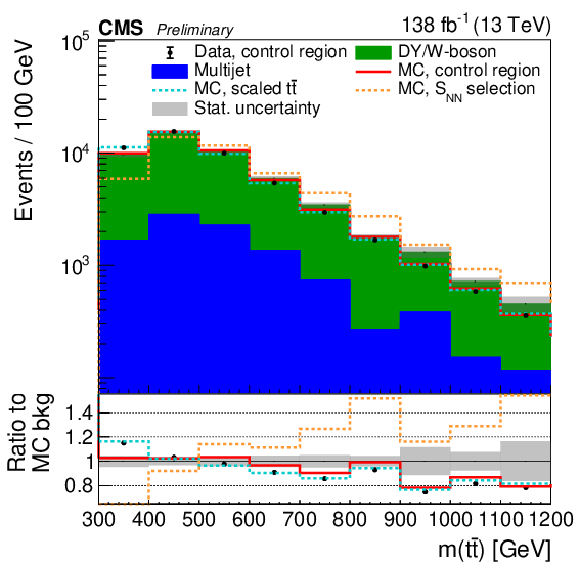
png pdf |
Figure 3-b:
Comparison of the $ \cos(\chi) $ (left) and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ (right) distributions of the simulated background in the control region (red line) and in the 1b signal category (stacked histograms). The data points show the distribution in the control region after subtracting the predicted $ \mathrm{t \bar{t}} $ and single top contributions. Data to MC agreement in the control region can be seen by comparing the data points to the red line. The dashed orange lines show the distribution after requiring the $ S_\mathrm{NN} $ selections in the control region. The dashed light blue distribution is obtained by taking into account the mismatch of the normalization in the control region when subtracting the $ \mathrm{t \bar{t}} $ and single top contributions. All distributions are normalized to the event yields of the stacked histogram. The gray uncertainty band shows the statistical uncertainties in the prediction. The lower panels show the ratios of the various distributions with respect to the simulated background in the 1b signal category. |
png pdf |
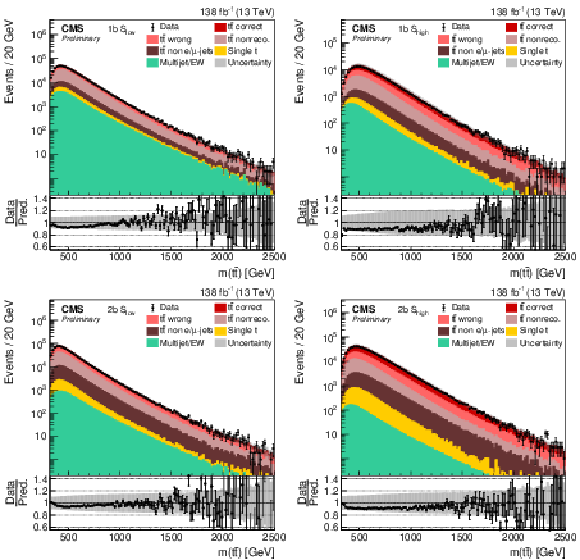
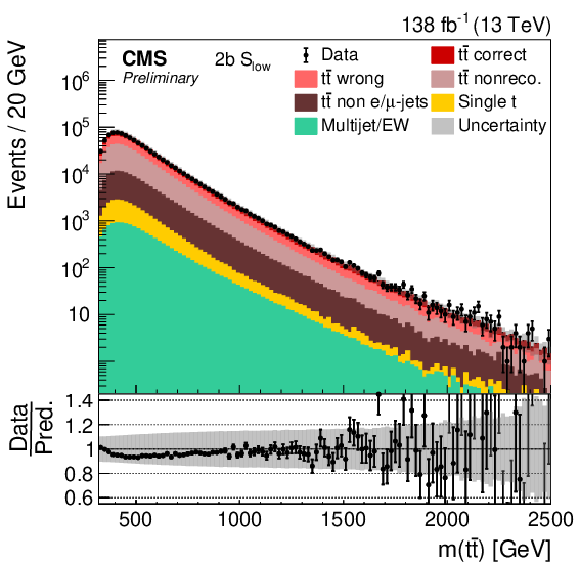
Figure 4:
Distribution in $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 4-a:
Distribution in $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 4-b:
Distribution in $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 4-c:
Distribution in $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 4-d:
Distribution in $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
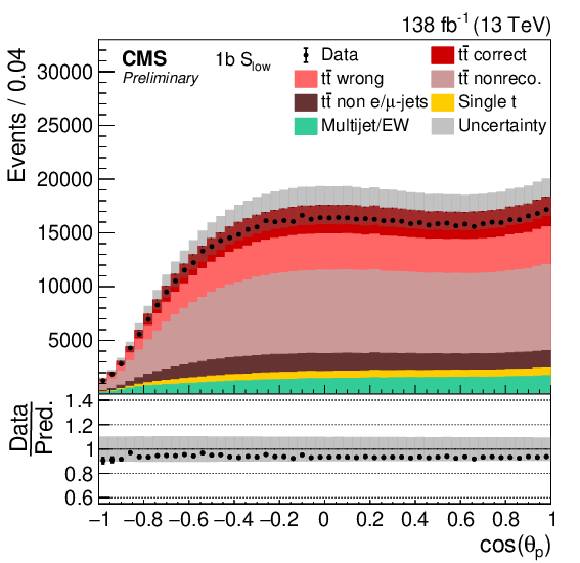
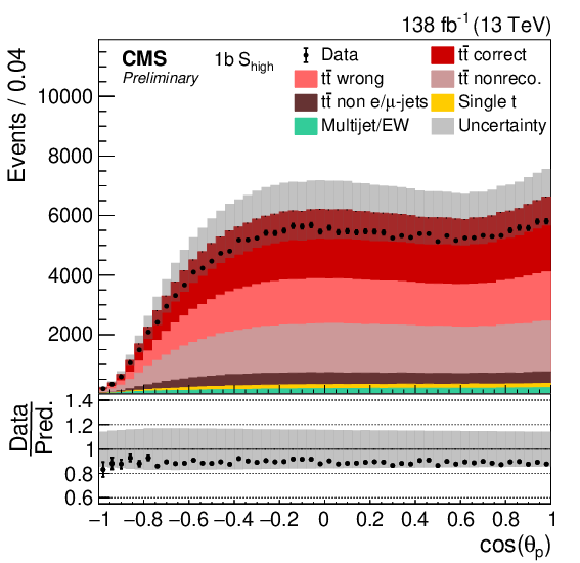
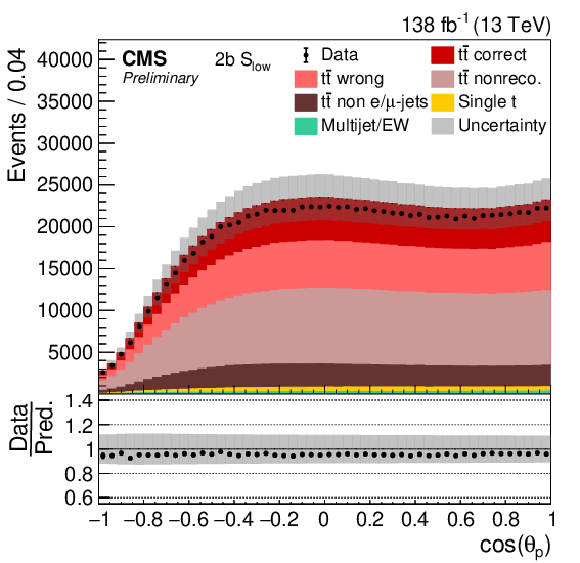
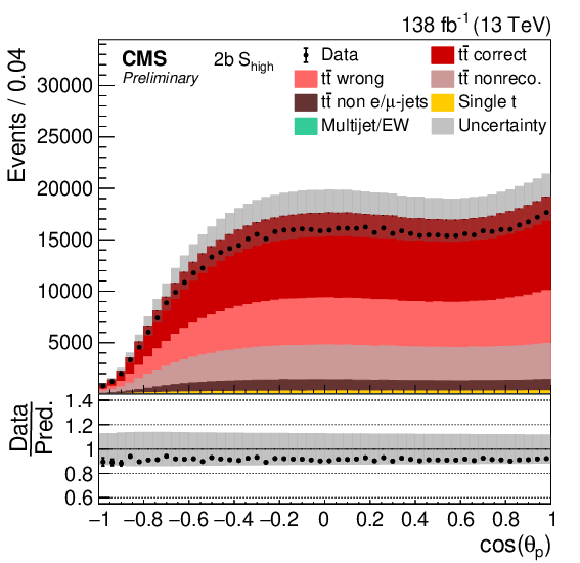
Figure 5:
Distribution in $ \cos(\theta_\mathrm{p}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 5-a:
Distribution in $ \cos(\theta_\mathrm{p}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 5-b:
Distribution in $ \cos(\theta_\mathrm{p}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 5-c:
Distribution in $ \cos(\theta_\mathrm{p}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 5-d:
Distribution in $ \cos(\theta_\mathrm{p}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
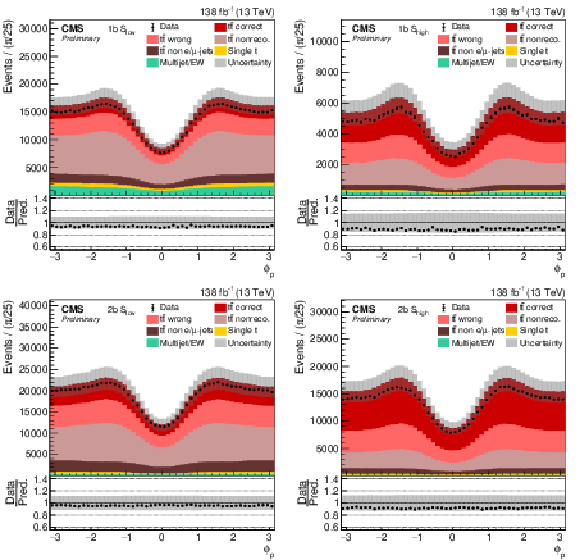
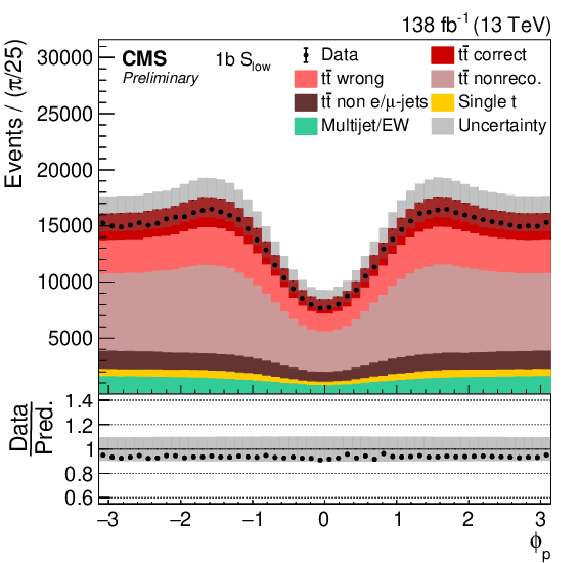
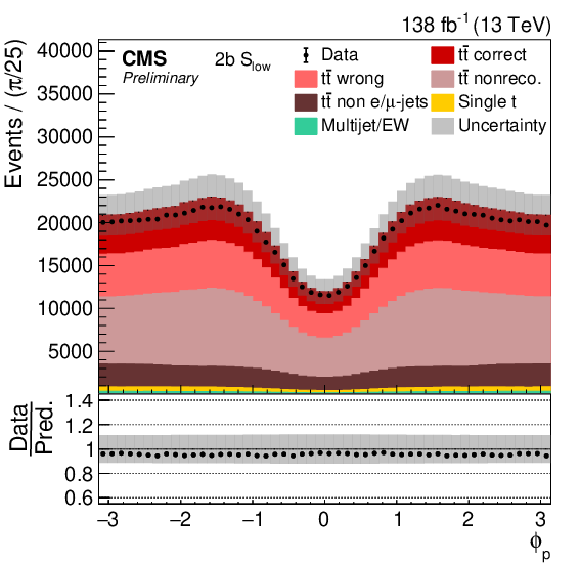
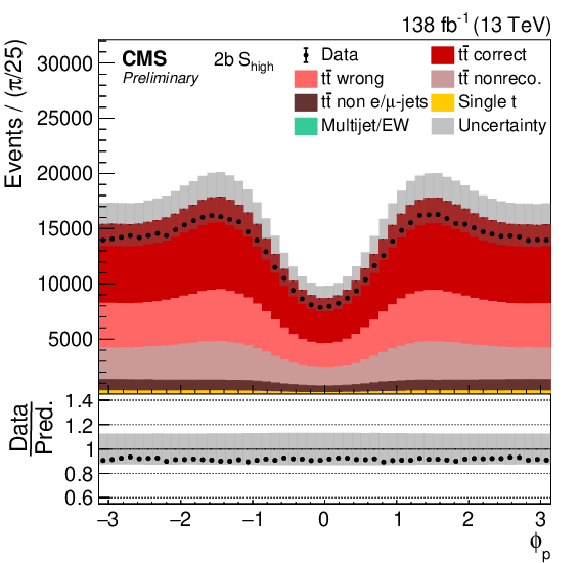
Figure 6:
Distribution in $ \phi_\mathrm{p} $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 6-a:
Distribution in $ \phi_\mathrm{p} $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
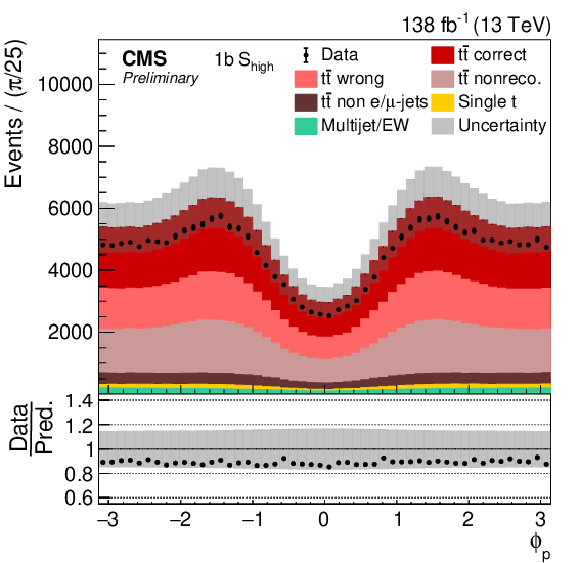
png pdf |
Figure 6-b:
Distribution in $ \phi_\mathrm{p} $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 6-c:
Distribution in $ \phi_\mathrm{p} $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 6-d:
Distribution in $ \phi_\mathrm{p} $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 7:
Distribution of $ \cos(\chi) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
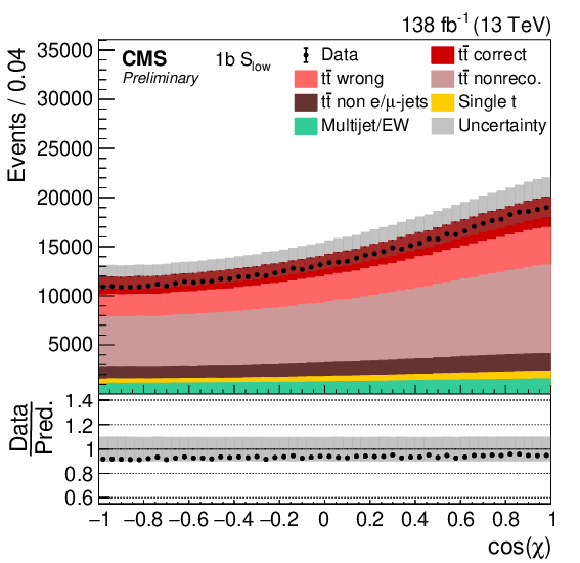
png pdf |
Figure 7-a:
Distribution of $ \cos(\chi) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
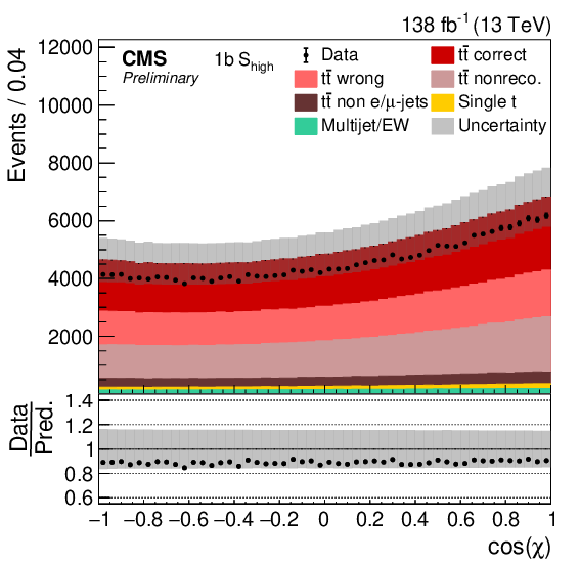
Figure 7-b:
Distribution of $ \cos(\chi) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
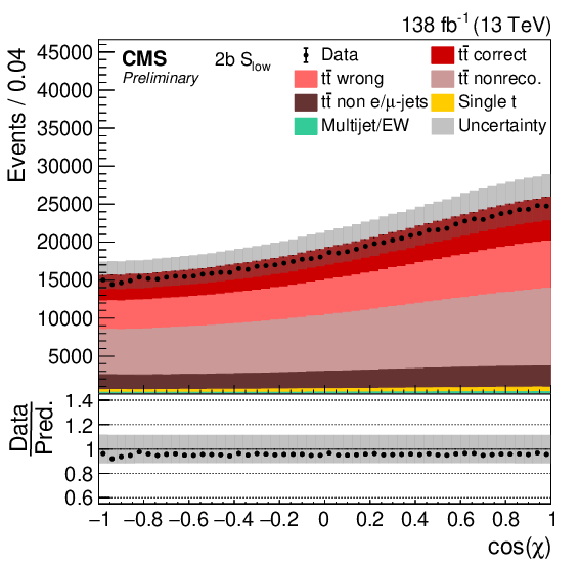
Figure 7-c:
Distribution of $ \cos(\chi) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
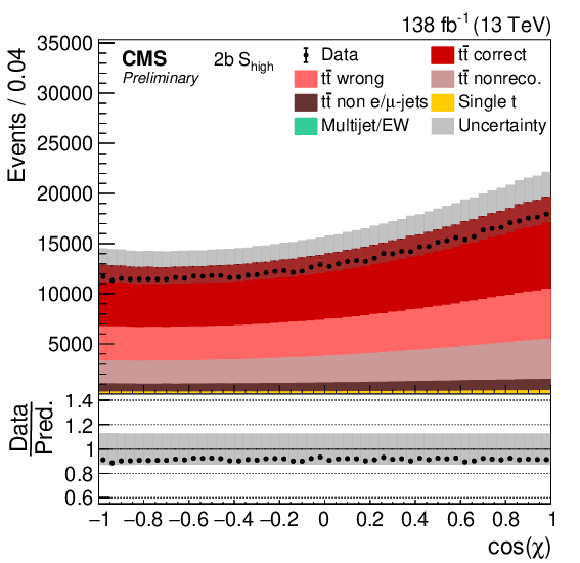
Figure 7-d:
Distribution of $ \cos(\chi) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
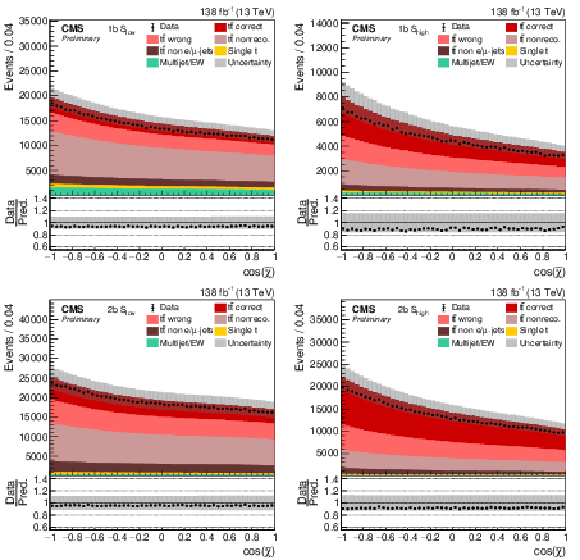
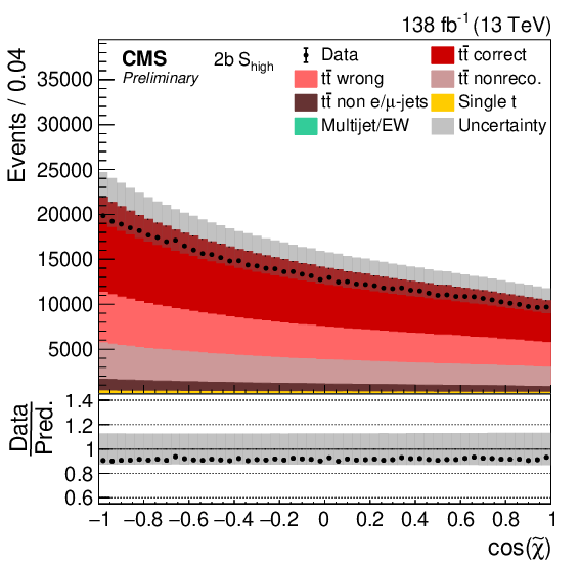
Figure 8:
Distribution of $ \cos(\tilde{\chi}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 8-a:
Distribution of $ \cos(\tilde{\chi}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 8-b:
Distribution of $ \cos(\tilde{\chi}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 8-c:
Distribution of $ \cos(\tilde{\chi}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
Figure 8-d:
Distribution of $ \cos(\tilde{\chi}) $ in all four categories. The data (points) are compared to the prediction (stacked histograms). The $ \mathrm{t \bar{t}} $ and single top components are taken from the prediction, while the multijet/EW background is obtained from a control region. The $ \mathrm{t \bar{t}} $ contribution is split into the correctly and wrongly reconstructed, ``nonreconstructable'', and non $ \mathrm{e}/\mu $+jets events. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty on the data. The ratios of data to the predicted yields are provided in the lower panels. |
png pdf |
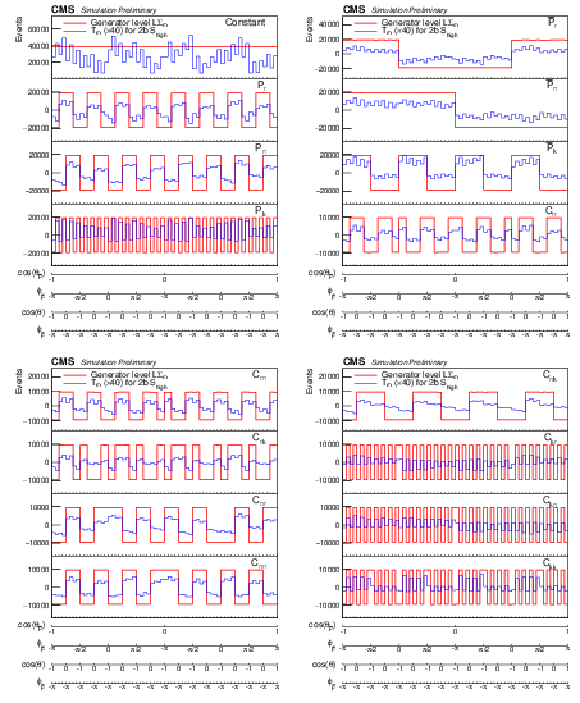
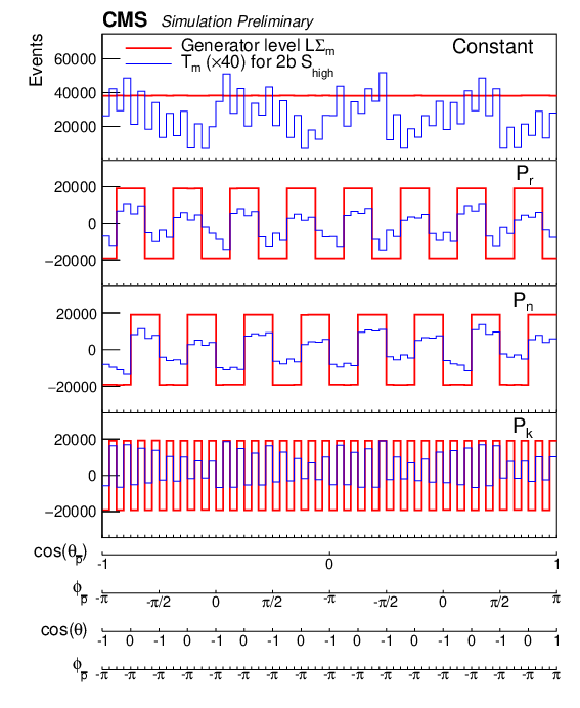
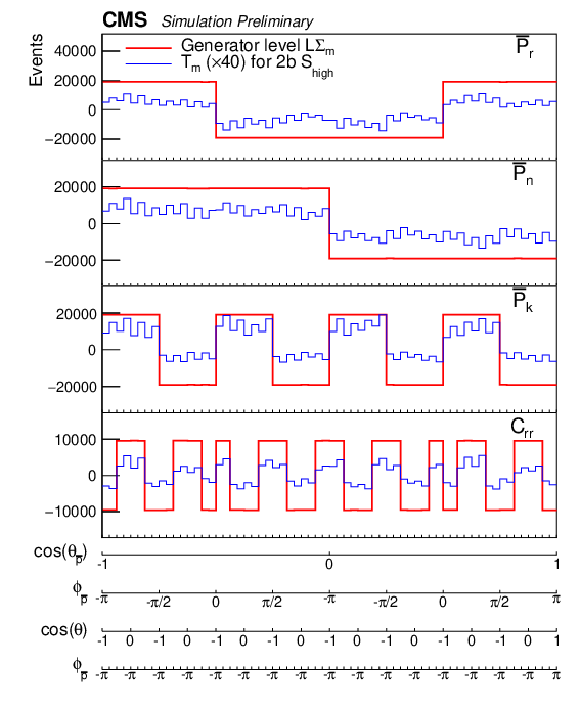
Figure 9:
Examples of unrolled 4-dimensional distributions $ L\Sigma_m $ and $ T_m $ as functions of $ \phi_{p(\bar{p})} $ and $ \theta_{p(\bar{p})} $ for the individual coefficients of the polarization vectors and the spin correlation matrix for events with 400 $ < m({\mathrm{t}\bar{\mathrm{t}}} ) < $ 600 GeV and $ |\cos(\theta)| < $ 0.4. The $ L\Sigma_m $ (red lines) are the distributions at the generator level in the full phase space, and the $ T_m $ (blue lines) are the distributions in the 2b $ S_\mathrm{high} $ category for the 2018 luminosity. The events are required to be reconstructed and generated in the same $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bin. The detector level distributions are enhanced by a factor of 40 to improve their visibility. |
png pdf |
Figure 9-a:
Examples of unrolled 4-dimensional distributions $ L\Sigma_m $ and $ T_m $ as functions of $ \phi_{p(\bar{p})} $ and $ \theta_{p(\bar{p})} $ for the individual coefficients of the polarization vectors and the spin correlation matrix for events with 400 $ < m({\mathrm{t}\bar{\mathrm{t}}} ) < $ 600 GeV and $ |\cos(\theta)| < $ 0.4. The $ L\Sigma_m $ (red lines) are the distributions at the generator level in the full phase space, and the $ T_m $ (blue lines) are the distributions in the 2b $ S_\mathrm{high} $ category for the 2018 luminosity. The events are required to be reconstructed and generated in the same $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bin. The detector level distributions are enhanced by a factor of 40 to improve their visibility. |
png pdf |
Figure 9-b:
Examples of unrolled 4-dimensional distributions $ L\Sigma_m $ and $ T_m $ as functions of $ \phi_{p(\bar{p})} $ and $ \theta_{p(\bar{p})} $ for the individual coefficients of the polarization vectors and the spin correlation matrix for events with 400 $ < m({\mathrm{t}\bar{\mathrm{t}}} ) < $ 600 GeV and $ |\cos(\theta)| < $ 0.4. The $ L\Sigma_m $ (red lines) are the distributions at the generator level in the full phase space, and the $ T_m $ (blue lines) are the distributions in the 2b $ S_\mathrm{high} $ category for the 2018 luminosity. The events are required to be reconstructed and generated in the same $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bin. The detector level distributions are enhanced by a factor of 40 to improve their visibility. |
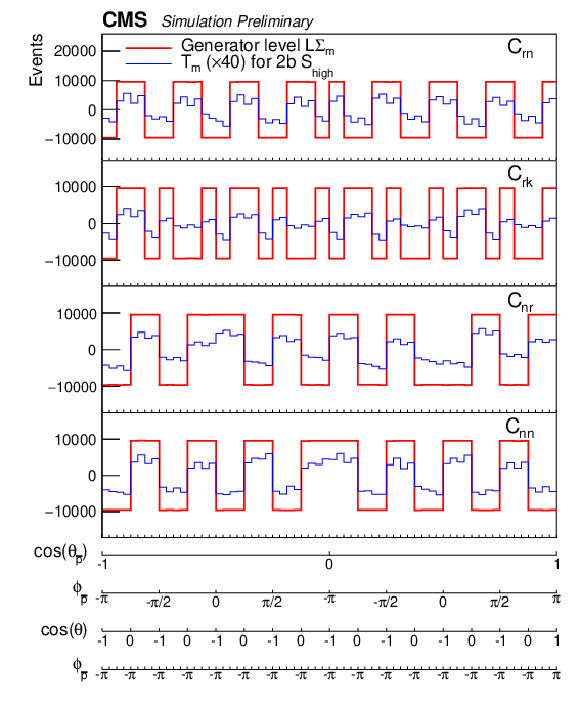
png pdf |
Figure 9-c:
Examples of unrolled 4-dimensional distributions $ L\Sigma_m $ and $ T_m $ as functions of $ \phi_{p(\bar{p})} $ and $ \theta_{p(\bar{p})} $ for the individual coefficients of the polarization vectors and the spin correlation matrix for events with 400 $ < m({\mathrm{t}\bar{\mathrm{t}}} ) < $ 600 GeV and $ |\cos(\theta)| < $ 0.4. The $ L\Sigma_m $ (red lines) are the distributions at the generator level in the full phase space, and the $ T_m $ (blue lines) are the distributions in the 2b $ S_\mathrm{high} $ category for the 2018 luminosity. The events are required to be reconstructed and generated in the same $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bin. The detector level distributions are enhanced by a factor of 40 to improve their visibility. |
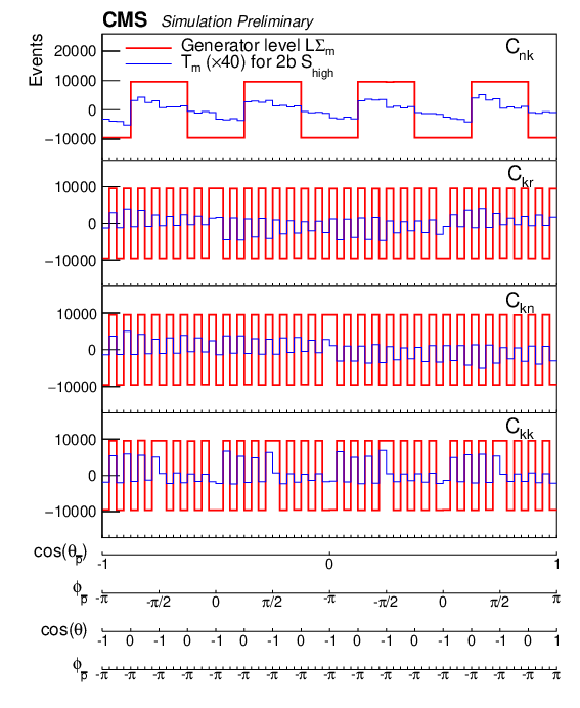
png pdf |
Figure 9-d:
Examples of unrolled 4-dimensional distributions $ L\Sigma_m $ and $ T_m $ as functions of $ \phi_{p(\bar{p})} $ and $ \theta_{p(\bar{p})} $ for the individual coefficients of the polarization vectors and the spin correlation matrix for events with 400 $ < m({\mathrm{t}\bar{\mathrm{t}}} ) < $ 600 GeV and $ |\cos(\theta)| < $ 0.4. The $ L\Sigma_m $ (red lines) are the distributions at the generator level in the full phase space, and the $ T_m $ (blue lines) are the distributions in the 2b $ S_\mathrm{high} $ category for the 2018 luminosity. The events are required to be reconstructed and generated in the same $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bin. The detector level distributions are enhanced by a factor of 40 to improve their visibility. |
png pdf |
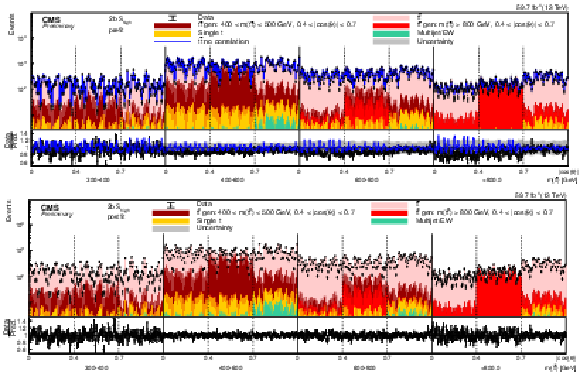
Figure 10:
Pre-fit (upper) and post-fit (lower) distributions comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). The $ x $-axis shows the bin number of the unrolled 4-dimensional distribution of $ \theta_{p} $, $ \phi_{p} $, $ \theta_{\bar{p}} $, and $ \phi_{\bar{p}} $, listed from the inner to the outer most variable in each of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins. For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
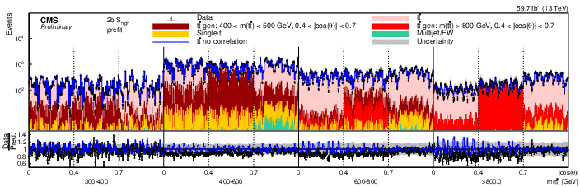
png pdf |
Figure 10-a:
Pre-fit (upper) and post-fit (lower) distributions comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). The $ x $-axis shows the bin number of the unrolled 4-dimensional distribution of $ \theta_{p} $, $ \phi_{p} $, $ \theta_{\bar{p}} $, and $ \phi_{\bar{p}} $, listed from the inner to the outer most variable in each of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins. For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
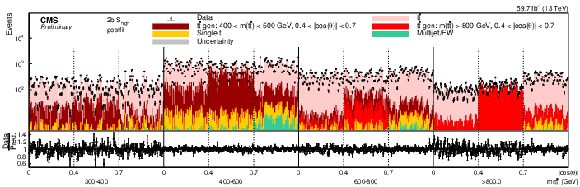
png pdf |
Figure 10-b:
Pre-fit (upper) and post-fit (lower) distributions comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). The $ x $-axis shows the bin number of the unrolled 4-dimensional distribution of $ \theta_{p} $, $ \phi_{p} $, $ \theta_{\bar{p}} $, and $ \phi_{\bar{p}} $, listed from the inner to the outer most variable in each of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins. For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
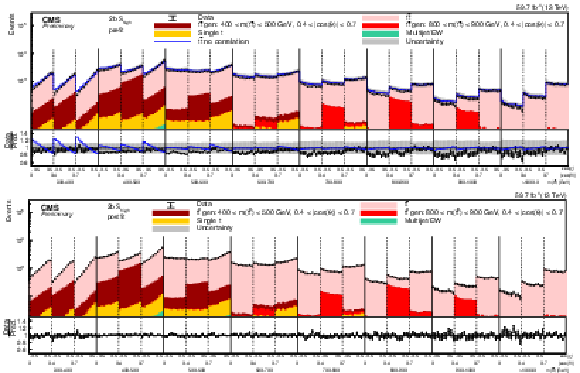
png pdf |
Figure 11:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\chi) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ D $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
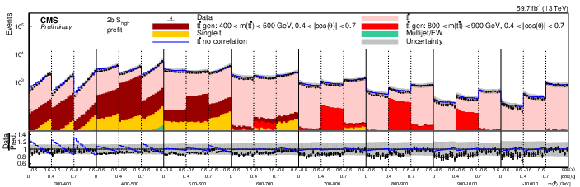
png pdf |
Figure 11-a:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\chi) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ D $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
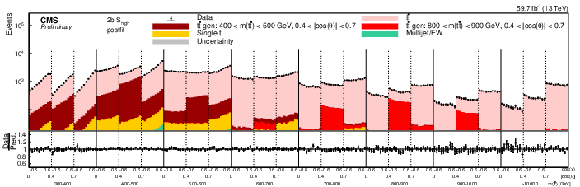
png pdf |
Figure 11-b:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\chi) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ D $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
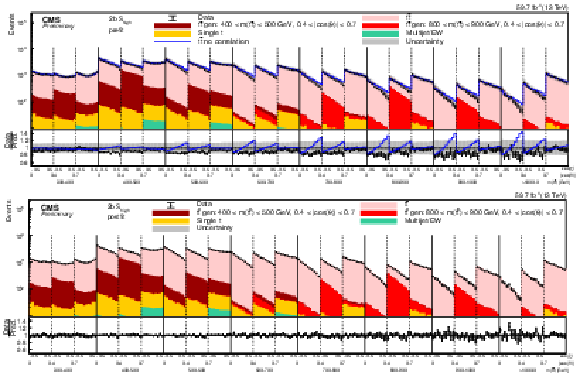
png pdf |
Figure 12:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\tilde{\chi}) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ \tilde{D} $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
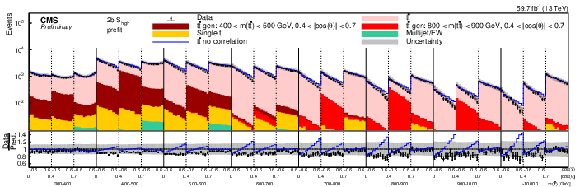
png pdf |
Figure 12-a:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\tilde{\chi}) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ \tilde{D} $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
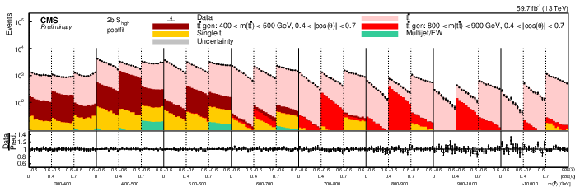
png pdf |
Figure 12-b:
Pre-fit (upper) and post-fit (lower) distributions of $ \cos(\tilde{\chi}) $ comparing the data (points) to the POWHEG +PYTHIA simulation (stacked histograms) for the $ \tilde{D} $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ in the 2b $ S_\mathrm{high} $ category (2018). For the illustration of resolution effects, $ \mathrm{t \bar{t}} $ events generated in two selected $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ bins are shown in different shades of red. All other $ \mathrm{t \bar{t}} $ contributions are shown in light red. A model without any spin polarization and correlations is shown as a blue line. The gray uncertainty band indicates the combined statistical and systematic uncertainties in the prediction. The vertical bars on the points show the statistical uncertainty. The ratios of data to the predicted yields are provided in the lower panels. |
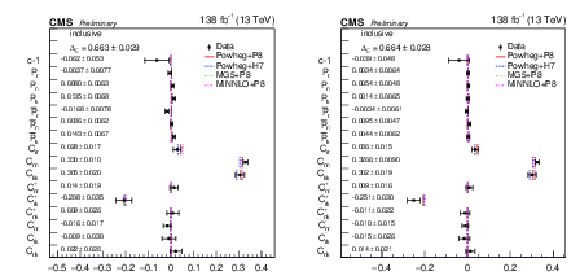
png pdf |
Figure 13:
Results of the inclusive full matrix measurement obtained by combining the bins of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ (left) and $ p_{\mathrm{T}}(\mathrm{t}) $ vs. $ |\cos(\theta)| $ (right) measurements. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
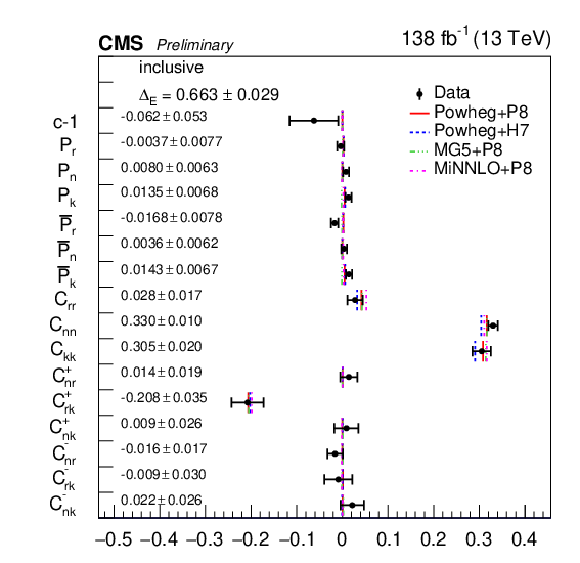
png pdf |
Figure 13-a:
Results of the inclusive full matrix measurement obtained by combining the bins of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ (left) and $ p_{\mathrm{T}}(\mathrm{t}) $ vs. $ |\cos(\theta)| $ (right) measurements. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
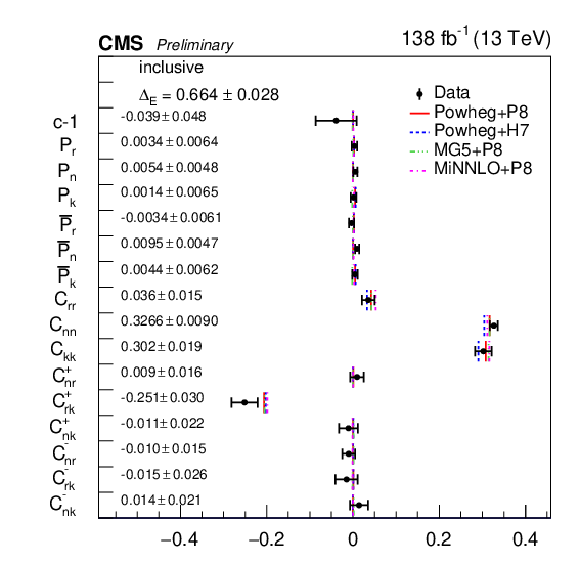
png pdf |
Figure 13-b:
Results of the inclusive full matrix measurement obtained by combining the bins of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ (left) and $ p_{\mathrm{T}}(\mathrm{t}) $ vs. $ |\cos(\theta)| $ (right) measurements. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
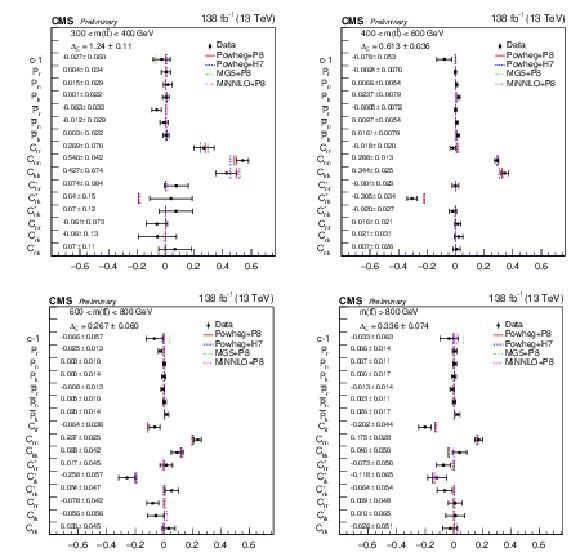
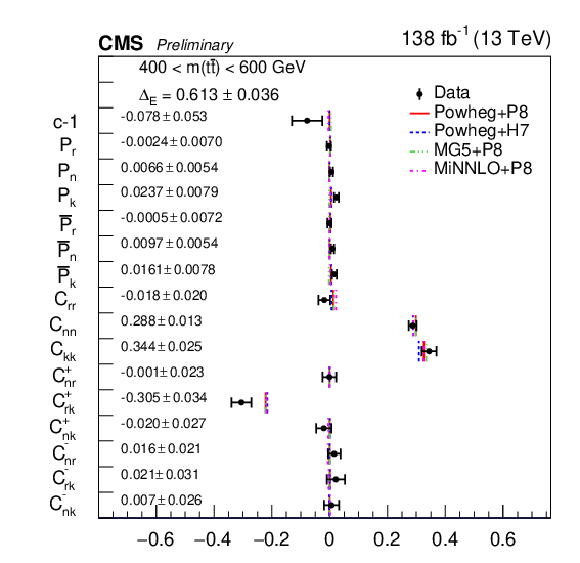
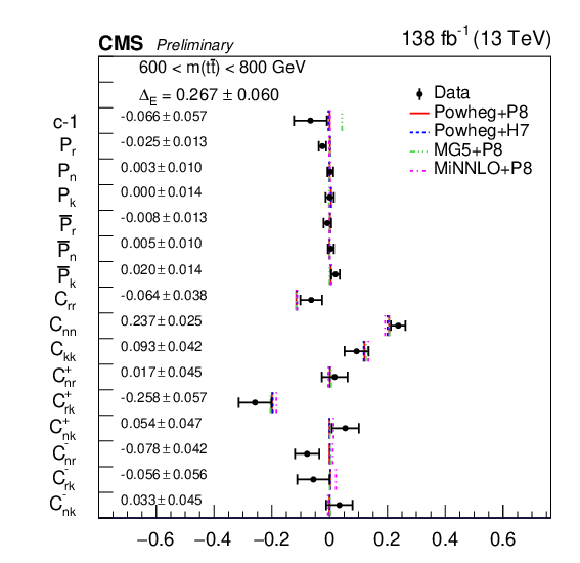
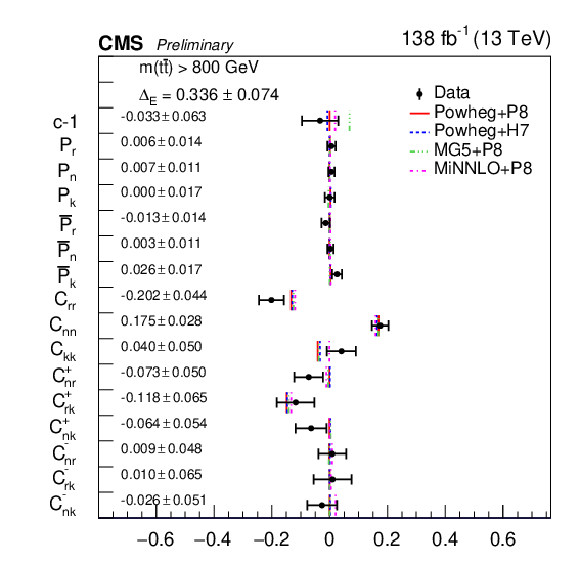
Figure 14:
Results of the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
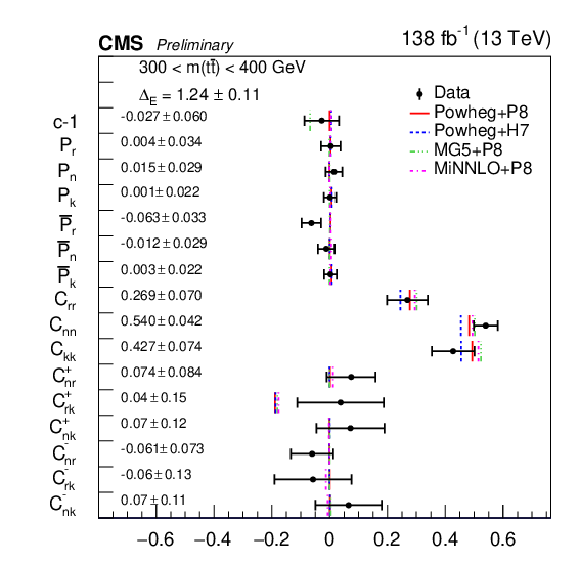
png pdf |
Figure 14-a:
Results of the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
Figure 14-b:
Results of the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
Figure 14-c:
Results of the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
Figure 14-d:
Results of the full matrix measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
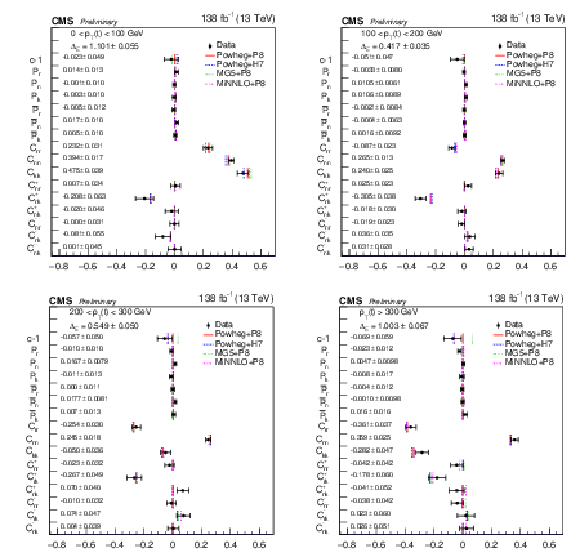
Figure 15:
Results of the full matrix measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
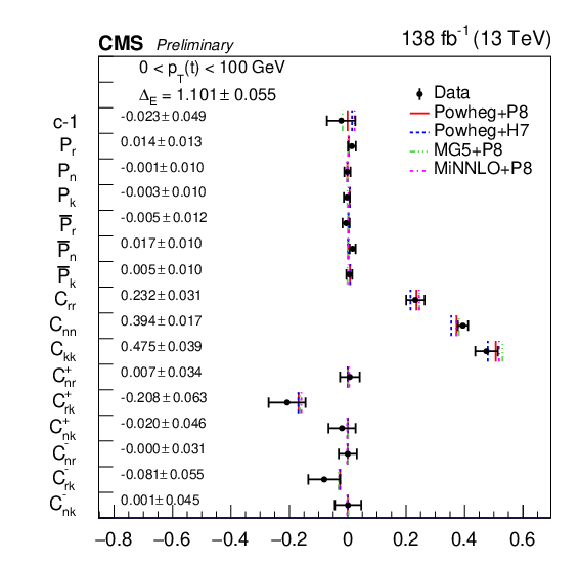
png pdf |
Figure 15-a:
Results of the full matrix measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
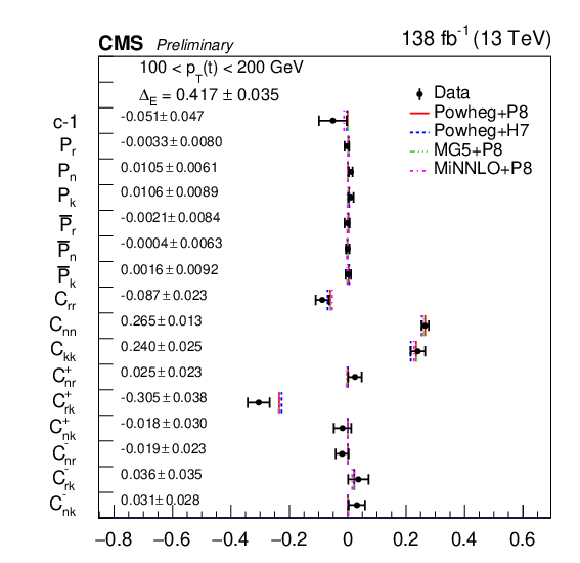
png pdf |
Figure 15-b:
Results of the full matrix measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
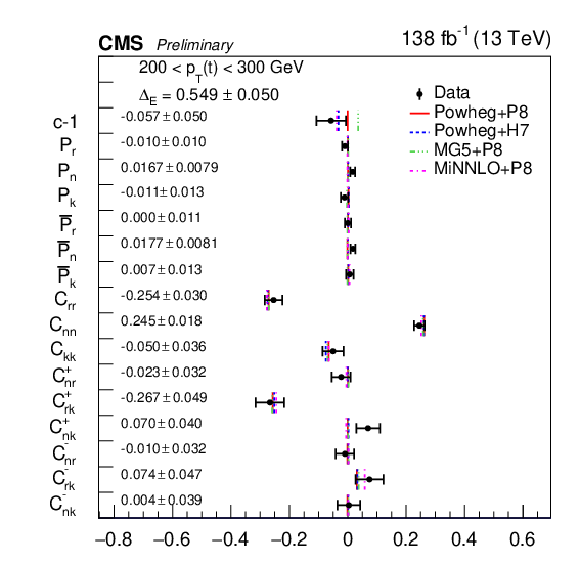
png pdf |
Figure 15-c:
Results of the full matrix measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
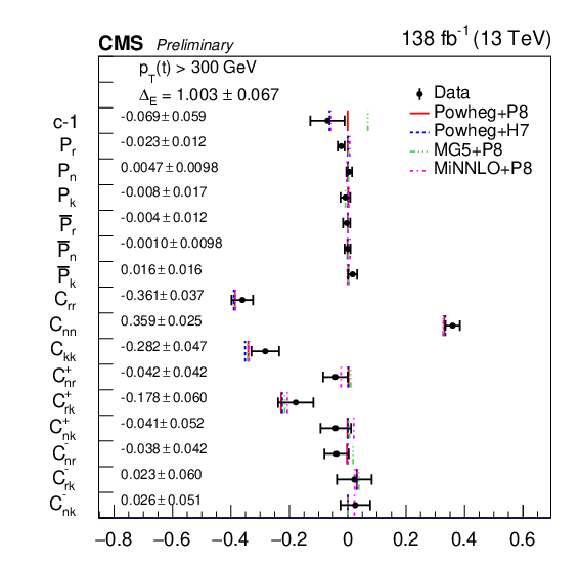
png pdf |
Figure 15-d:
Results of the full matrix measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
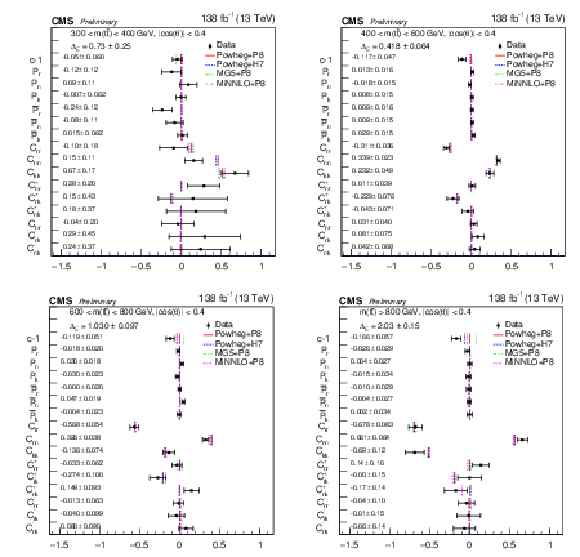
png pdf |
Figure 16:
Results of the full matrix measurement in bins of $ |\cos(\theta)| < $ 0.4 and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
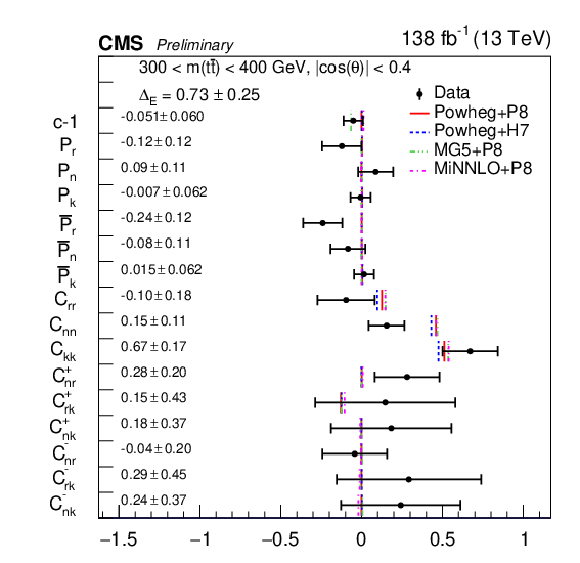
png pdf |
Figure 16-a:
Results of the full matrix measurement in bins of $ |\cos(\theta)| < $ 0.4 and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
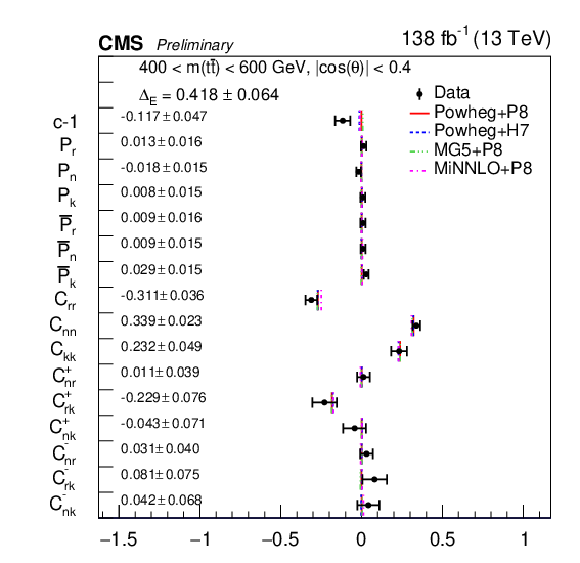
png pdf |
Figure 16-b:
Results of the full matrix measurement in bins of $ |\cos(\theta)| < $ 0.4 and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
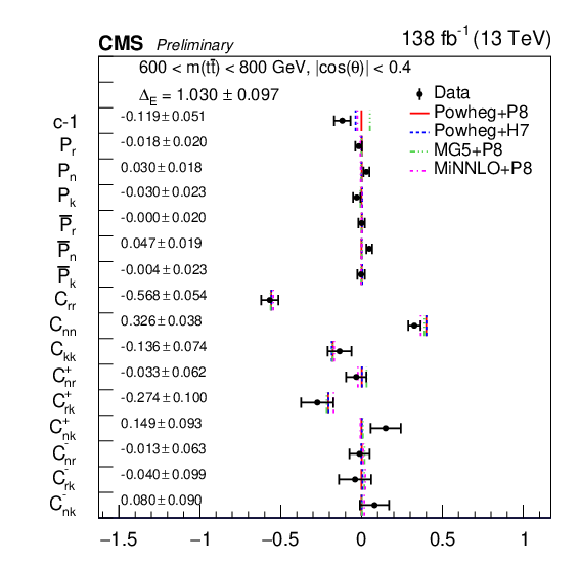
png pdf |
Figure 16-c:
Results of the full matrix measurement in bins of $ |\cos(\theta)| < $ 0.4 and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
png pdf |
Figure 16-d:
Results of the full matrix measurement in bins of $ |\cos(\theta)| < $ 0.4 and $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measurements (markers) are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA and MINNLO+PYTHIA. |
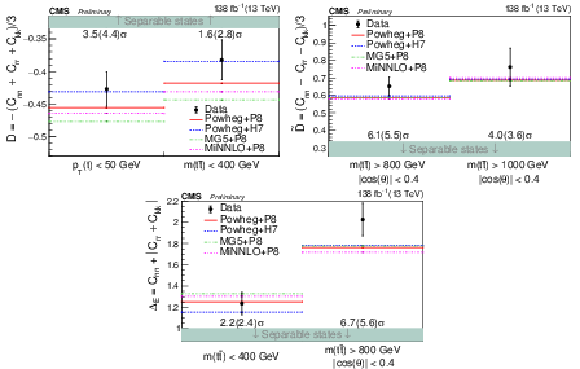
png pdf |
Figure 17:
Entanglement results for the $ D $ measurement in the threshold region (upper left), $ \tilde{D} $ measurement in the high $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ region (upper right), and the full matrix measurement in different $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ regions (lower). The measurements (points) are shown with their uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. The observed (expected) significance to deviate from the boundary of separable states (green region) is quoted in standard deviations. |
png pdf |
Figure 17-a:
Entanglement results for the $ D $ measurement in the threshold region (upper left), $ \tilde{D} $ measurement in the high $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ region (upper right), and the full matrix measurement in different $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ regions (lower). The measurements (points) are shown with their uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. The observed (expected) significance to deviate from the boundary of separable states (green region) is quoted in standard deviations. |
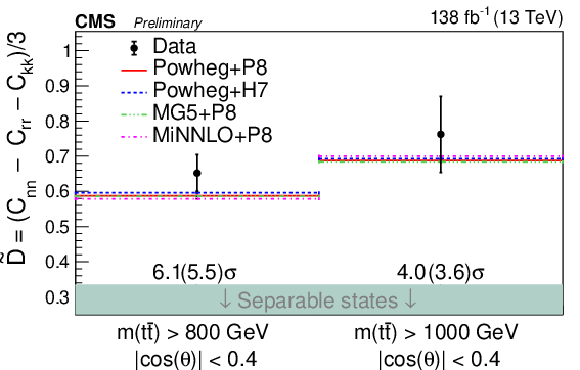
png pdf |
Figure 17-b:
Entanglement results for the $ D $ measurement in the threshold region (upper left), $ \tilde{D} $ measurement in the high $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ region (upper right), and the full matrix measurement in different $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ regions (lower). The measurements (points) are shown with their uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. The observed (expected) significance to deviate from the boundary of separable states (green region) is quoted in standard deviations. |
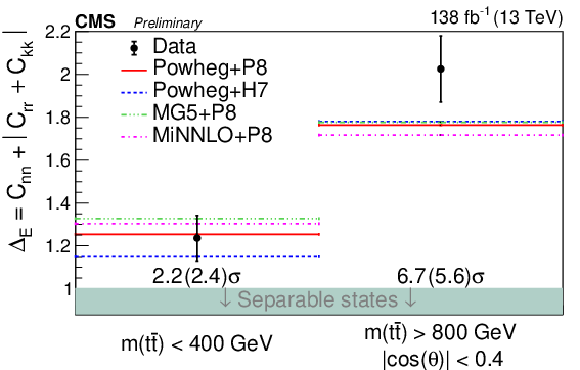
png pdf |
Figure 17-c:
Entanglement results for the $ D $ measurement in the threshold region (upper left), $ \tilde{D} $ measurement in the high $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ region (upper right), and the full matrix measurement in different $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ regions (lower). The measurements (points) are shown with their uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. The observed (expected) significance to deviate from the boundary of separable states (green region) is quoted in standard deviations. |
png pdf |
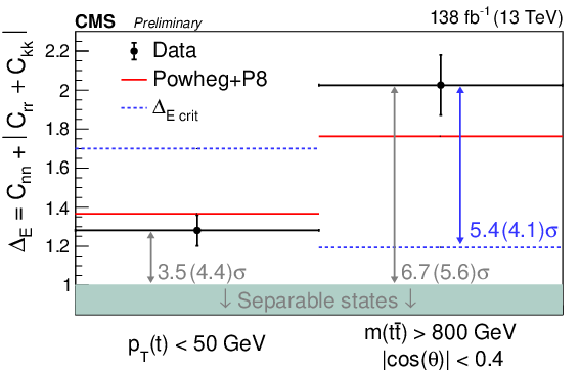
Figure 18:
The observed levels of entanglement characterized by $ \Delta_\mathrm{E} $ are shown in the threshold region using the $ D $ measurement (first bin), and in the high $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ region using the full matrix measurement (second bin). The measurements (points) are shown with their uncertainties and compared to the predictions of POWHEG +PYTHIA. The horizontal blue lines correspond to the maximum level of entanglement $ \Delta_\mathrm{E\,crit} $ that can be explained by the exchange of information between t and $ \bar{\mathrm{t}} $ at the speed of light. The significance in standard deviations by which the measurement exceeds $ \Delta_\mathrm{E\,crit} $ (unity) is quoted in blue (gray) and indicated by corresponding arrows. |
| Tables | |
png pdf |
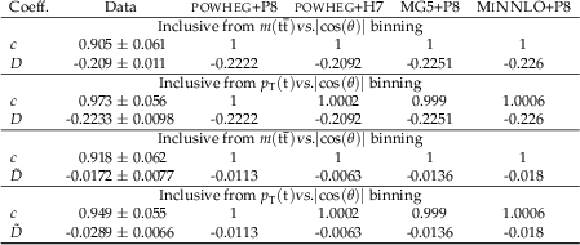
Table 1:
Results of the inclusive $ D $ and $ \tilde{D} $ measurements from the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ vs. $ |\cos(\theta)| $ and $ p_{\mathrm{T}}(\mathrm{t}) $ vs. $ |\cos(\theta)| $ binning. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
png pdf |
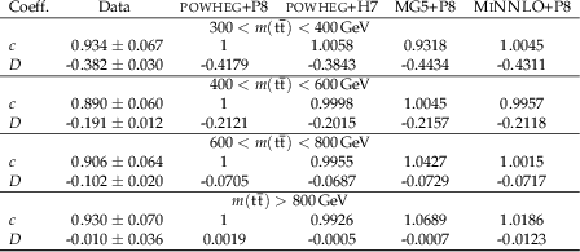
Table 2:
Results of the $ D $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
png pdf |
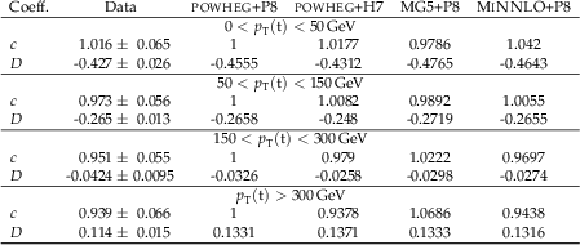
Table 3:
Results of the $ D $ measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
png pdf |
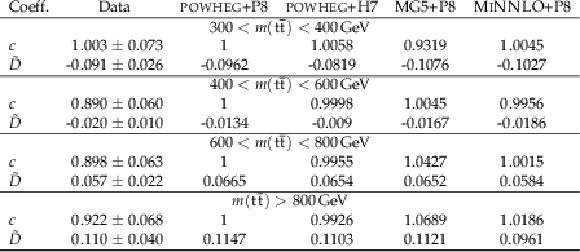
Table 4:
Results of the $ \tilde{D} $ measurement in bins of $ m({\mathrm{t}\bar{\mathrm{t}}} ) $. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
png pdf |
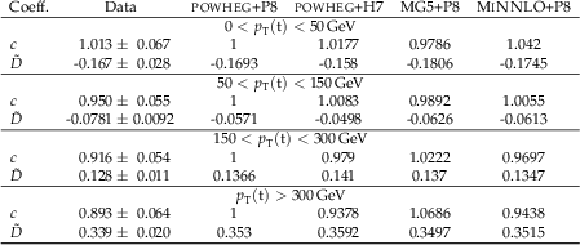
Table 5:
Results of the $ \tilde{D} $ measurement in bins of $ p_{\mathrm{T}}(\mathrm{t}) $. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
png pdf |
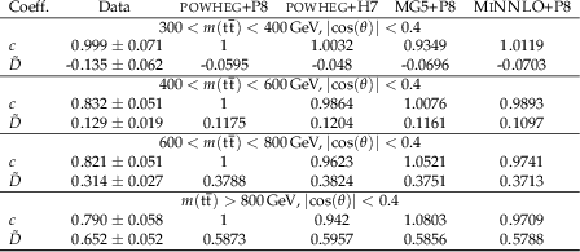
Table 6:
Results of the $ m({\mathrm{t}\bar{\mathrm{t}}} ) $ for $ |\cos(\theta)| < $ 0.4 $ \tilde{D} $ measurement. The measured values are shown with the combined statistical and systematic uncertainties and compared to the predictions of POWHEG +PYTHIA, POWHEG + HERWIG, MadGraph-5_aMC@NLO+PYTHIA, and MINNLO+PYTHIA. |
| Summary |
| The polarization and spin correlations in top quark pair ($ \mathrm{t \bar{t}} $) production are measured in the $ \mathrm{e}/\mu $+jets channels. The entanglement between the spins of the top quark and antiquark is determined from the measured spin correlations. The measurements are based on proton-proton collision data at $ \sqrt{s} = $ 13 TeV collected by the CMS experiment at the LHC, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. The decay products of the top quarks are identified using an artificial neural network. The coefficients of the polarization vectors and the spin correlation matrix are extracted simultaneously from the angular distributions of $ \mathrm{t \bar{t}} $ decay products using a binned likelihood fit. This is done both inclusively and in various regions of the phase space. The standard model predicts entangled $ \mathrm{t \bar{t}} $ states at the production threshold and at high masses of the $ \mathrm{t \bar{t}} $ system. Entanglement is observed in events with high $ \mathrm{t \bar{t}} $ mass, with an observed (expected) significance of 6.7 (5.6) standard deviations, while in events with low transverse momentum of the top quark a significance of 3.5 (4.4) standard deviations is observed (expected). This is the first observation of entanglement at high $ \mathrm{t \bar{t}} $ mass and cannot be explained by classical exchange of information between the two particles alone. The observed (expected) significance for entanglement attributable to space-like separated $ \mathrm{t \bar{t}} $ pairs is 5.4 (4.1) standard deviations. |
| References | ||||
| 1 | Particle Data Group Collaboration | Review of Particle Physics | Prog. Theor. Exp. Phys. 2022 (2022) 083C01 | |
| 2 | G. Mahlon and S. J. Parke | Spin correlation effects in top quark pair production at the LHC | PRD 81 (2010) 074024 | 1001.3422 |
| 3 | CMS Collaboration | Measurement of the top quark polarization and $ \mathrm{t} \overline{\mathrm{t}} $ spin correlations using dilepton final states in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 100 (2019) 072002 | CMS-TOP-18-006 1907.03729 |
| 4 | M. Baumgart and B. Tweedie | A new twist on top quark spin correlations | JHEP 03 (2013) 117 | 1212.4888 |
| 5 | D0 Collaboration | Evidence for spin correlation in $ \mathrm{t} \overline{\mathrm{t}} $ production | PRL 108 (2012) 032004 | 1110.4194 |
| 6 | D0 Collaboration | Measurement of spin correlation between top and antitop quarks produced in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PLB 757 (2016) 199 | 1512.08818 |
| 7 | CMS Collaboration | Measurements of $ \mathrm{t} \overline{\mathrm{t}} $ spin correlations and top-quark polarization using dilepton final states in pp collisions at $ \sqrt{s} = $ 7 TeV | PRL 112 (2014) 182001 | CMS-TOP-13-003 1311.3924 |
| 8 | CMS Collaboration | Measurement of spin correlations in $ \mathrm{t} \overline{\mathrm{t}} $ production using the matrix element method in the muon+jets final state in pp collisions at $ \sqrt{s} = $ 8 TeV | PLB 758 (2016) 321 | CMS-TOP-13-015 1511.06170 |
| 9 | CMS Collaboration | Measurements of $ \mathrm{t} \overline{\mathrm{t}} $ spin correlations and top quark polarization using dilepton final states in pp collisions at $ \sqrt{s} = $ 8 TeV | PRD 93 (2016) 052007 | CMS-TOP-14-023 1601.01107 |
| 10 | ATLAS Collaboration | Observation of spin correlation in $ \mathrm{t} \overline{\mathrm{t}} $ events from pp collisions at $ \sqrt{s} = $ 7 TeV using the ATLAS detector | PRL 108 (2012) 212001 | 1203.4081 |
| 11 | ATLAS Collaboration | Measurement of spin correlation in top-antitop quark events and search for top squark pair production in pp collisions at $ \sqrt{s}= $ 8 TeV using the ATLAS detector | PRL 114 (2015) 142001 | 1412.4742 |
| 12 | ATLAS Collaboration | Measurements of spin correlation in top-antitop quark events from proton-proton collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | PRD 90 (2014) 112016 | 1407.4314 |
| 13 | ATLAS Collaboration | Measurements of top-quark pair spin correlations in the $ \mathrm{e}\mu $ channel at $ \sqrt{s} = $ 13 TeV using pp collisions in the ATLAS detector | EPJC 80 (2020) 754 | 1903.07570 |
| 14 | ATLAS Collaboration | Observation of quantum entanglement in top-quark pairs using the ATLAS detector | Submitted to Nature, 2023 | 2311.07288 |
| 15 | CMS Collaboration | Observation of quantum entanglement in top quark pair production in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | Submitted to ROPP, 2024 | CMS-TOP-23-001 2406.03976 |
| 16 | W. Bernreuther, D. Heisler, and Z.-G. Si | A set of top quark spin correlation and polarization observables for the LHC: Standard Model predictions and new physics contributions | JHEP 12 (2015) 026 | 1508.05271 |
| 17 | A. Brandenburg, Z. G. Si, and P. Uwer | QCD corrected spin analyzing power of jets in decays of polarized top quarks | PLB 539 (2002) 235 | hep-ph/0205023 |
| 18 | Y. Afik and J. R. M. de Nova | Entanglement and quantum tomography with top quarks at the LHC | Eur. Phys. J. Plus 136 (2021) 907 | 2003.02280 |
| 19 | M. Fabbrichesi, R. Floreanini, and E. Gabrielli | Constraining new physics in entangled two-qubit systems: top-quark, tau-lepton and photon pairs | EPJC 83 (2023) 162 | 2208.11723 |
| 20 | M. Fabbrichesi, R. Floreanini, and G. Panizzo | Testing Bell Inequalities at the LHC with Top-Quark Pairs | PRL 127 (2021) 161801 | 2102.11883 |
| 21 | Z. Dong, D. Gon ç alves, K. Kong, and A. Navarro | When the Machine Chimes the Bell: Entanglement and Bell Inequalities with Boosted $ \mathrm{t} \overline{\mathrm{t}} $ | Submitted to Phys. Rev. D., 2023 | 2305.07075 |
| 22 | A. Peres | Separability criterion for density matrices | PRL 77 (1996) 1413 | quant-ph/9604005 |
| 23 | P. Horodecki | Separability criterion and inseparable mixed states with positive partial transposition | Phys. Lett. A 232 (1997) 333 | quant-ph/9703004 |
| 24 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 25 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 26 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 27 | CMS Collaboration | The CMS Experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 28 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 29 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 30 | S. Frixione, P. Nason, and G. Ridolfi | A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 31 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 32 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 33 | J. Mazzitelli et al. | Next-to-Next-to-Leading Order Event Generation for Top-Quark Pair Production | PRL 127 (2021) 062001 | 2012.14267 |
| 34 | M. Aliev et al. | HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR | Comput. Phys. Commun. 182 (2011) 1034 | 1007.1327 |
| 35 | M. Bähr et al. | HERWIG++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 36 | CMS Collaboration | Development and validation of HERWIG 7 tunes from CMS underlying-event measurements | EPJC 81 (2021) 312 | CMS-GEN-19-001 2011.03422 |
| 37 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 38 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | Comput. Phys. Commun. 185 (2014) 2930 | 1112.5675 |
| 39 | CMS Collaboration | Measurement of the top quark mass using proton-proton data at $ {\sqrt{s}} $ = 7 and 8 TeV | PRD 93 (2016) 072004 | CMS-TOP-14-022 1509.04044 |
| 40 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 41 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 42 | M. L. Mangano, M. Moretti, F. Piccinini, and M. Treccani | Matching matrix elements and shower evolution for top-quark production in hadronic collisions | JHEP 01 (2007) 013 | hep-ph/0611129 |
| 43 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 44 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 45 | P. Kant et al. | HatHor for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | Comput. Phys. Commun. 191 (2015) 74 | 1406.4403 |
| 46 | N. Kidonakis | NNLL threshold resummation for top-pair and single-top production | Phys. Part. Nucl. 45 (2014) 714 | 1210.7813 |
| 47 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 48 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical proposal CERN-LHCC-2015-010, CMS-TDR-15-02, CERN, 2015 CDS |
|
| 49 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 50 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 51 | CMS Collaboration | Measurements of inclusive W and Z cross sections in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |
| 52 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 53 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 54 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 55 | E. Bols et al. | Jet Flavour Classification Using DeepJet | JINST 15 (2020) 12012 | 2008.10519 |
| 56 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 57 | D. Kingma and J. Ba | Adam: a method for stochastic optimization | in Proceedings of the 3rd Int. Conf. on Learning Representations, 2015 ICLR 201 (2015) 5 |
1412.6980 |
| 58 | A. Andreassen and B. Nachman | Neural networks for full phase-space reweighting and parameter tuning | PRD 101 (2020) 091901 | 1907.08209 |
| 59 | M. Czakon, P. Fiedler and A. Mitov | The total top quark production cross-section at hadron colliders through O($ \alpha_S^4 $) | PRL 110 (2013) 252004 | 1303.6254 |
| 60 | S. Argyropoulos and T. Sjöstrand | Effects of color reconnection on $ t\bar{t} $ final states at the LHC | JHEP 11 (2014) 043 | 1407.6653 |
| 61 | J. R. Christiansen and P. Z. Skands | String Formation Beyond Leading Colour | JHEP 08 (2015) 003 | 1505.01681 |
| 62 | W.-L. Ju et al. | Top quark pair production near threshold: single/double distributions and mass determination | JHEP 06 (2020) 158 | 2004.03088 |
| 63 | B. Fuks, K. Hagiwara, K. Ma, and Y.-J. Zheng | Signatures of toponium formation in LHC run 2 data | PRD 104 (2021) 034023 | 2102.11281 |
| 64 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 65 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 66 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 67 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 68 | R. Barlow and C. Beeston | Fitting using finite monte carlo samples | Computer Physics Communications 77 (1993) 219 | |
| 69 | W. S. Cleveland | Robust locally weighted regression and smoothing scatterplots | J. Am. Stat. Assoc. 74 (1979) 829 | |
| 70 | C. Severi, C. D. E. Boschi, F. Maltoni, and M. Sioli | Quantum tops at the LHC: from entanglement to Bell inequalities | EPJC 82 (2022) 285 | 2110.10112 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|