

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SMP-23-005 | ||
| Observation of $ \gamma\gamma\rightarrow\tau\tau $ in proton-proton collisions and limits on the anomalous electromagnetic moments of the $ \tau $ lepton | ||
| CMS Collaboration | ||
| 12 March 2024 | ||
| Abstract: The photon-induced production of a pair of $ \tau $ leptons, $ \gamma\gamma\rightarrow\tau\tau $, is observed for the first time in proton-proton collisions. The observation is based on a data set recorded with the CMS detector at the LHC at a center-of-mass energy of 13 TeV and corresponding to an integrated luminosity of 138 fb$ ^{-1} $. Events with a small number of tracks close to the di-$ \tau $ vertex are selected to isolate photon-induced processes. Limits on the anomalous electromagnetic moments of the $ \tau $ lepton originating from potential new physics effects on the $ \gamma\tau\tau $ vertex are also set. | ||
|
Links:
CDS record (PDF) ;
Physics Briefing ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Accepted by ROPP. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |
png pdf |
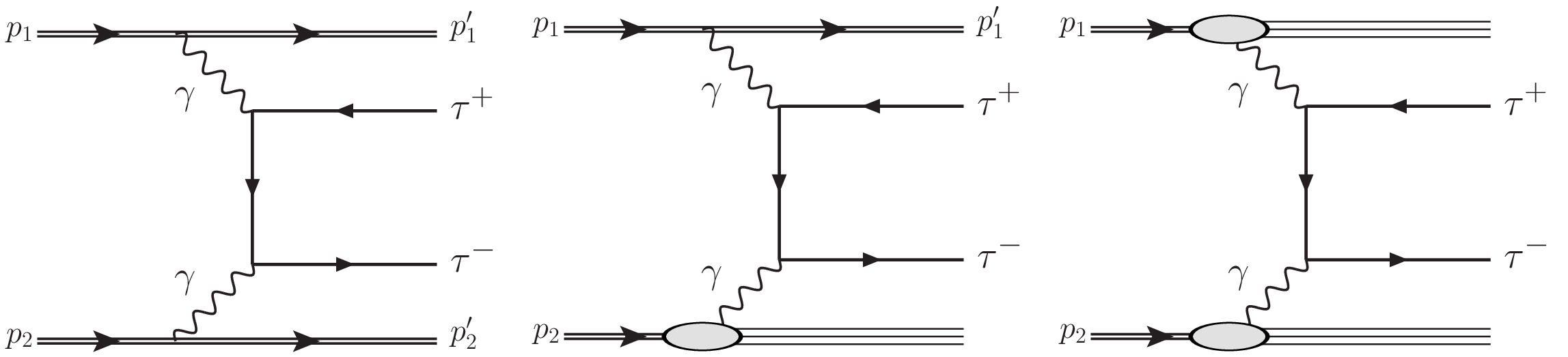
Figure 1:
Production of $ \tau $ lepton pairs by $ \gamma\gamma $ fusion. The exclusive (left), single proton dissociation or semiexclusive (middle), and double proton dissociation (right) topologies are shown. |
png pdf |
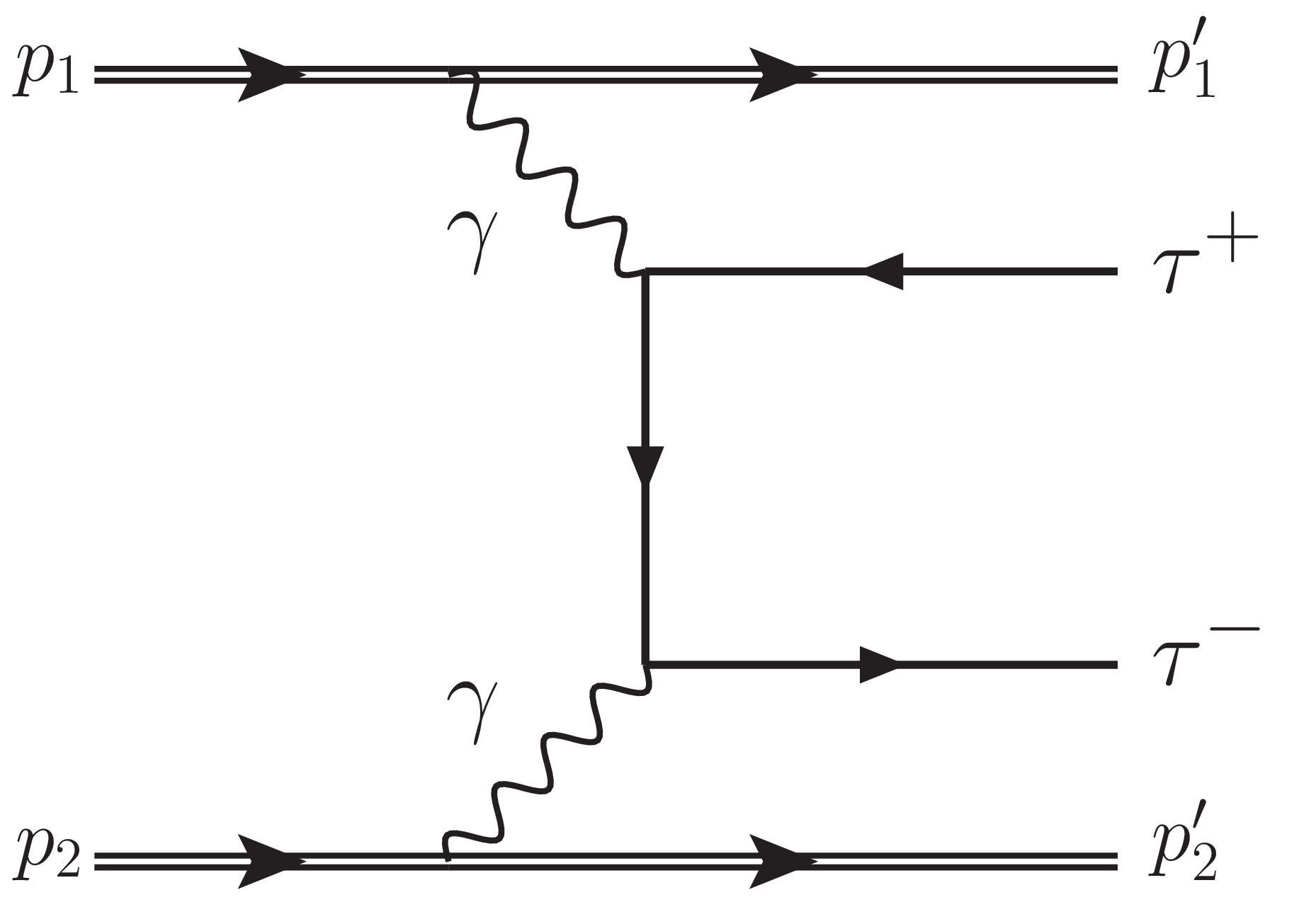
Figure 1-a:
Production of $ \tau $ lepton pairs by $ \gamma\gamma $ fusion. The exclusive (left), single proton dissociation or semiexclusive (middle), and double proton dissociation (right) topologies are shown. |
png pdf |
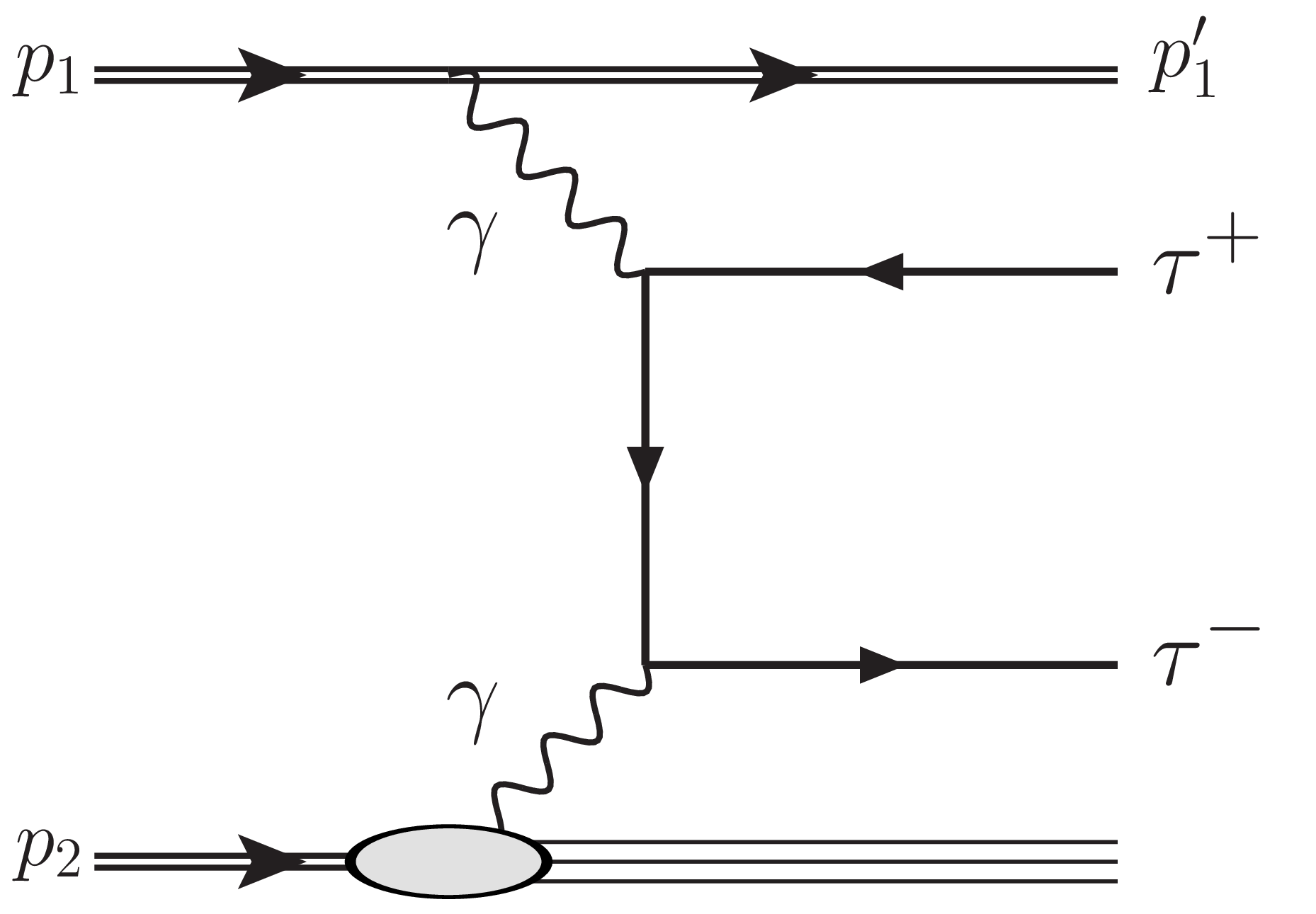
Figure 1-b:
Production of $ \tau $ lepton pairs by $ \gamma\gamma $ fusion. The exclusive (left), single proton dissociation or semiexclusive (middle), and double proton dissociation (right) topologies are shown. |
png pdf |
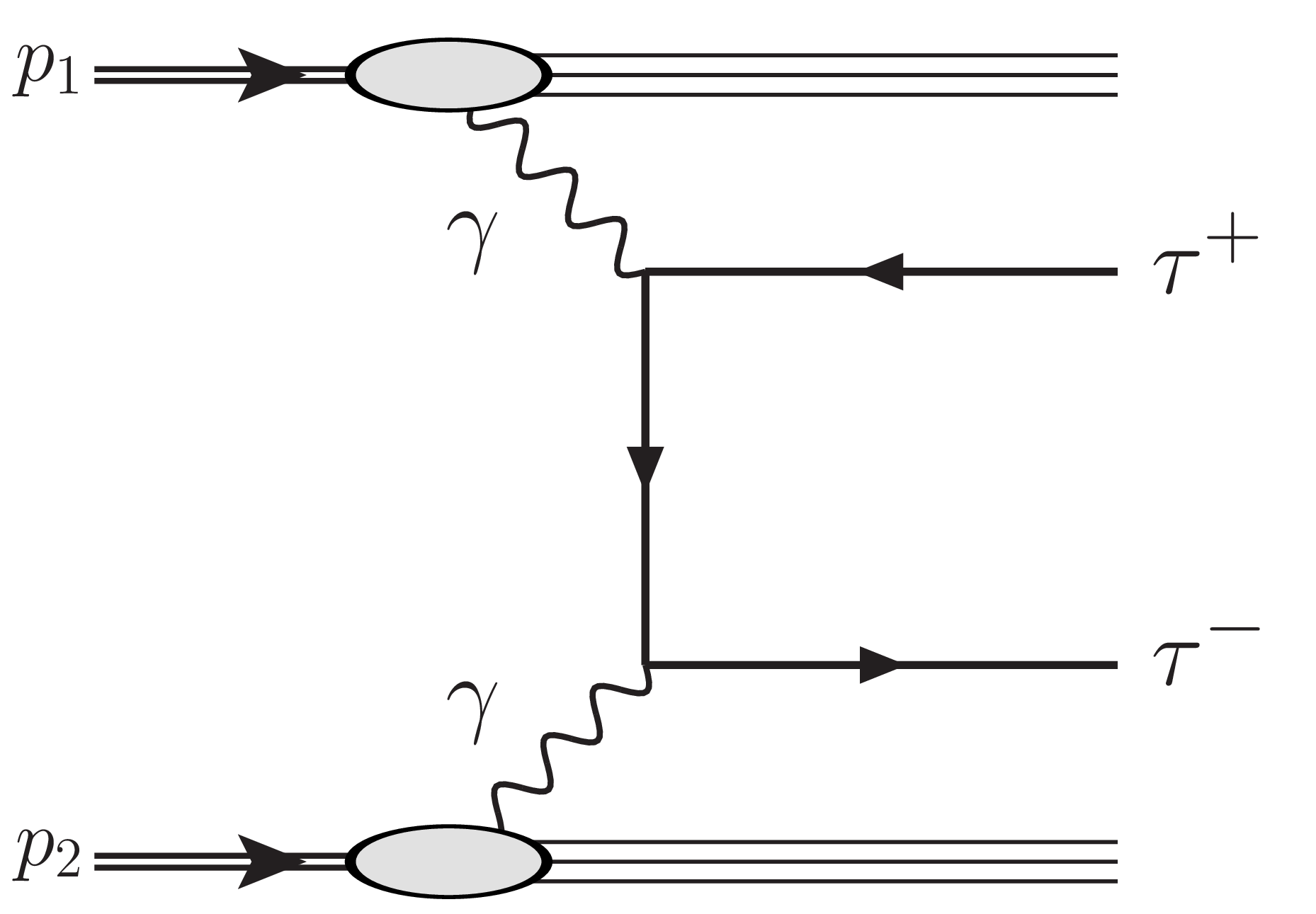
Figure 1-c:
Production of $ \tau $ lepton pairs by $ \gamma\gamma $ fusion. The exclusive (left), single proton dissociation or semiexclusive (middle), and double proton dissociation (right) topologies are shown. |
png pdf |
Figure 2:
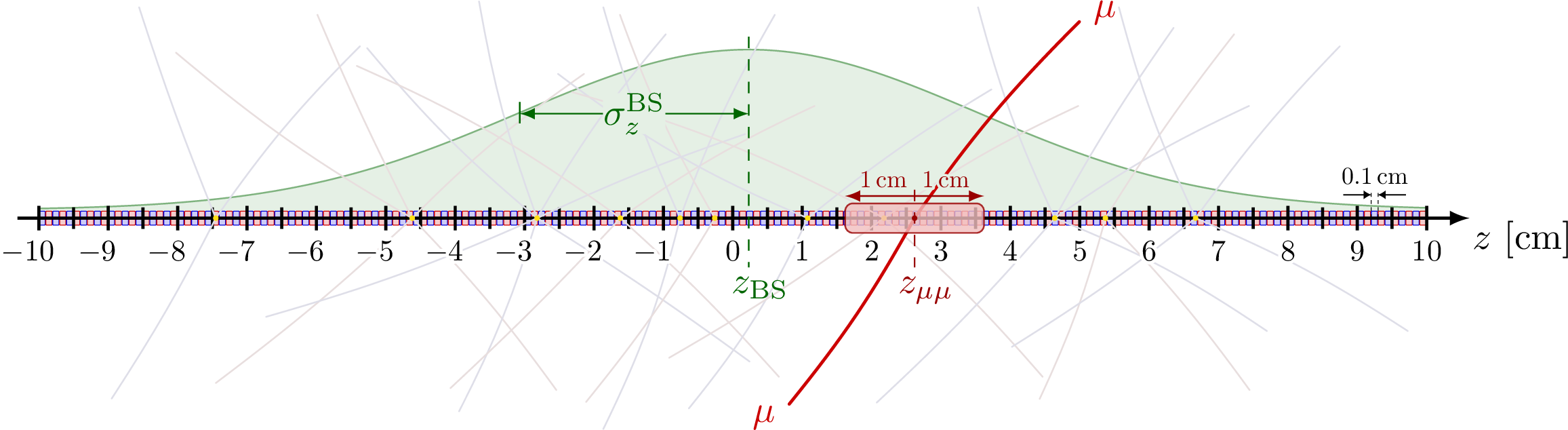
Schematic view of the 0.1 cm-wide windows probed along the $ z $ axis to derive corrections to the PU track density in simulation. Windows within 1 cm from the dimuon vertex, illustrated with the red box, are discarded so as not to count tracks from the hard scattering interaction. The green curve indicates the position and width of the beamspot. |
png pdf |
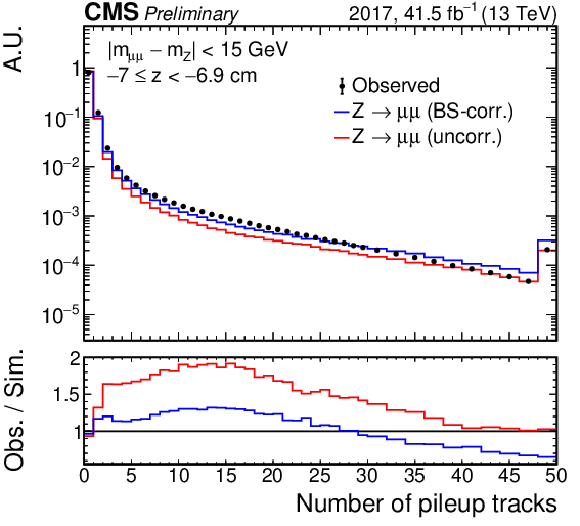
Figure 3:
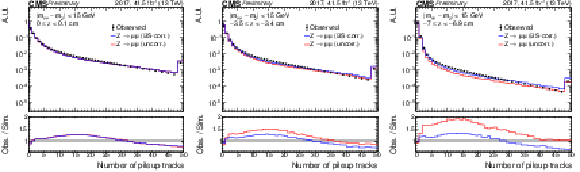
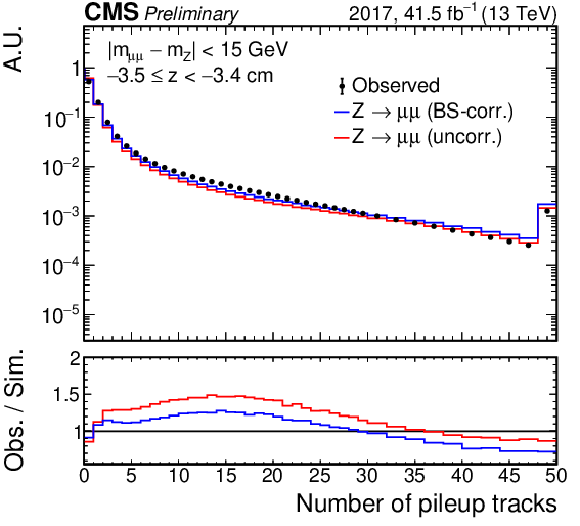
Distribution of $ N_\text{tracks}^\text{PU} $ in windows of 0.1 cm width along the $ z $ axis in data (black), uncorrected simulation (red), and beamspot-corrected simulation (blue) in data collected in 2017. The windows shown here are located at the beamspot center (left), and one (center) or two (right) beamspot widths away from the center. The ratio of corrected simulation to data is taken as a correction to the simulations. |
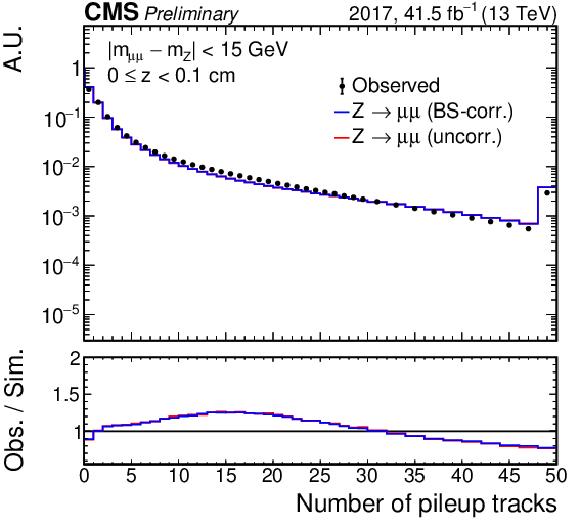
png pdf |
Figure 3-a:
Distribution of $ N_\text{tracks}^\text{PU} $ in windows of 0.1 cm width along the $ z $ axis in data (black), uncorrected simulation (red), and beamspot-corrected simulation (blue) in data collected in 2017. The windows shown here are located at the beamspot center (left), and one (center) or two (right) beamspot widths away from the center. The ratio of corrected simulation to data is taken as a correction to the simulations. |
png pdf |
Figure 3-b:
Distribution of $ N_\text{tracks}^\text{PU} $ in windows of 0.1 cm width along the $ z $ axis in data (black), uncorrected simulation (red), and beamspot-corrected simulation (blue) in data collected in 2017. The windows shown here are located at the beamspot center (left), and one (center) or two (right) beamspot widths away from the center. The ratio of corrected simulation to data is taken as a correction to the simulations. |
png pdf |
Figure 3-c:
Distribution of $ N_\text{tracks}^\text{PU} $ in windows of 0.1 cm width along the $ z $ axis in data (black), uncorrected simulation (red), and beamspot-corrected simulation (blue) in data collected in 2017. The windows shown here are located at the beamspot center (left), and one (center) or two (right) beamspot widths away from the center. The ratio of corrected simulation to data is taken as a correction to the simulations. |
png pdf |
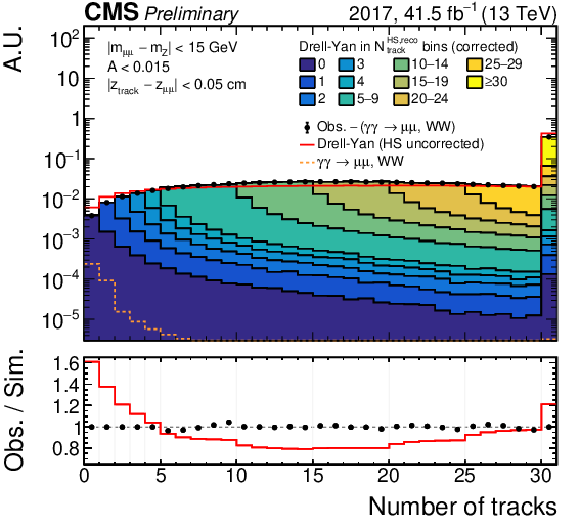
Figure 4:
Distribution of the number of reconstructed tracks in a 0.1 cm-wide window in the $ z $ direction, centered on the dimuon reconstructed vertex, for $ A < $ 0.015. The Drell--Yan simulation is split into several components based on the number of reconstructed tracks originating from the hard interaction. The red line shows the simulation before the correction. The expected contribution from the $ {\gamma\gamma\to\mu\mu} $ and $ \gamma\gamma\to\mathrm{W}\mathrm{W} $ processes (dashed orange line) has been subtracted from observed data. The last bin includes the overflow. |
png pdf |
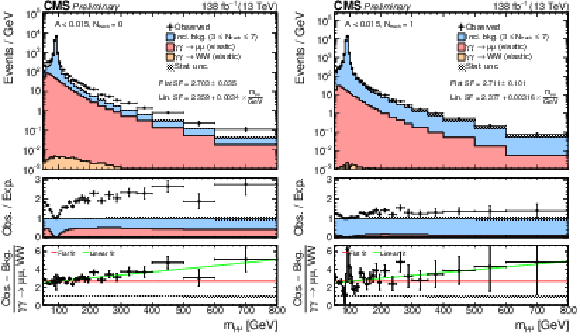
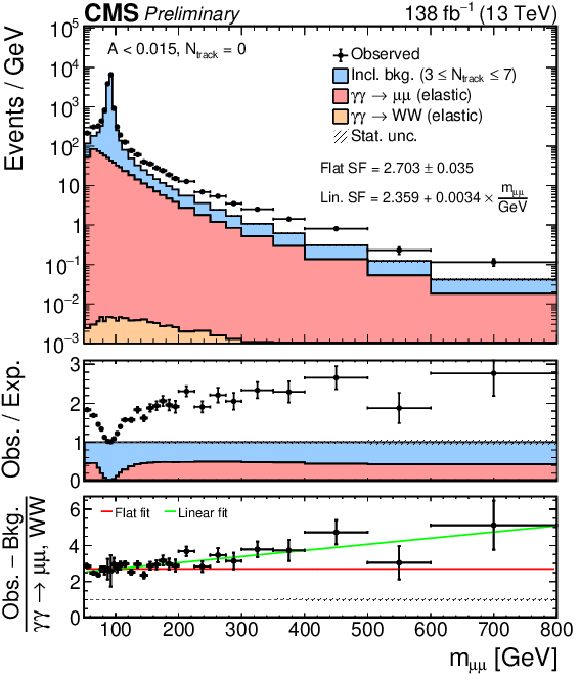
Figure 5:
Measurement of the scaling factor for the elastic-elastic exclusive signal in $ \mu\mu $ events for $ N_\text{tracks}= $ 0 (left) or 1 (right), and $ A < $ 0.015. The shape of the inclusive background (blue) is estimated from the observed data in the 3 $ \leq N_\text{tracks} \leq $ 7 sideband, and rescaled to fit the observed data in 75 $ < m_{\mu\mu} < $ 105 GeV. The scaling factor is fitted in the bottom ratio pad with constant (red) and linear (green) functions. |
png pdf |
Figure 5-a:
Measurement of the scaling factor for the elastic-elastic exclusive signal in $ \mu\mu $ events for $ N_\text{tracks}= $ 0 (left) or 1 (right), and $ A < $ 0.015. The shape of the inclusive background (blue) is estimated from the observed data in the 3 $ \leq N_\text{tracks} \leq $ 7 sideband, and rescaled to fit the observed data in 75 $ < m_{\mu\mu} < $ 105 GeV. The scaling factor is fitted in the bottom ratio pad with constant (red) and linear (green) functions. |
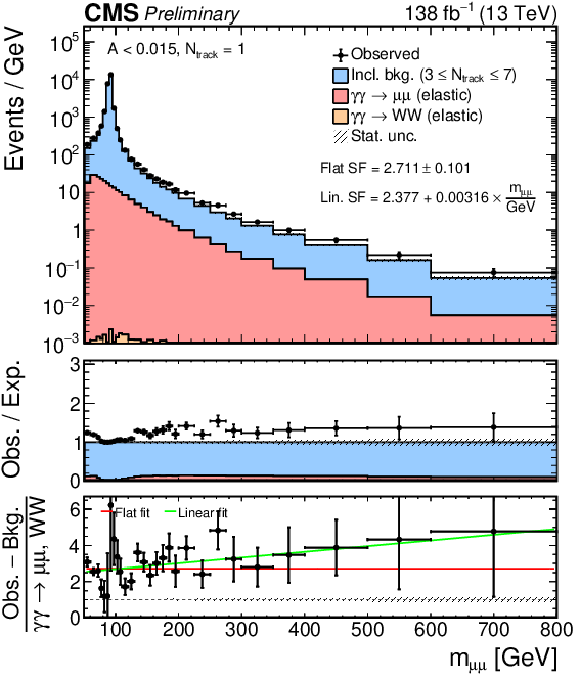
png pdf |
Figure 5-b:
Measurement of the scaling factor for the elastic-elastic exclusive signal in $ \mu\mu $ events for $ N_\text{tracks}= $ 0 (left) or 1 (right), and $ A < $ 0.015. The shape of the inclusive background (blue) is estimated from the observed data in the 3 $ \leq N_\text{tracks} \leq $ 7 sideband, and rescaled to fit the observed data in 75 $ < m_{\mu\mu} < $ 105 GeV. The scaling factor is fitted in the bottom ratio pad with constant (red) and linear (green) functions. |
png pdf |
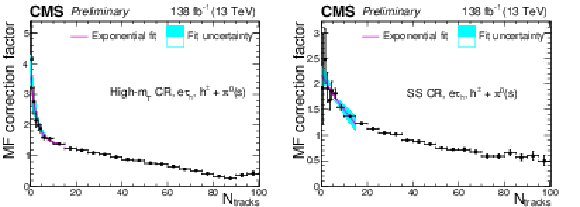
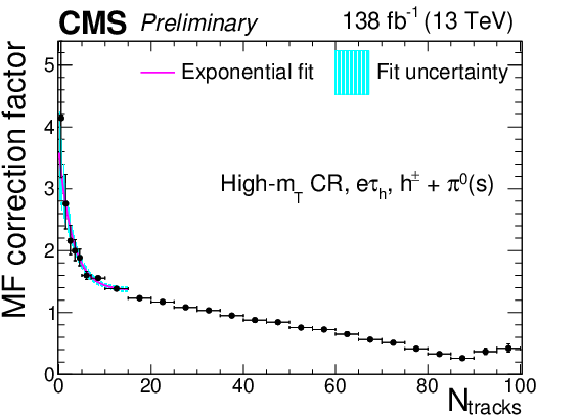
Figure 6:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ MFs, $ \omega(N_\text{tracks}, \textrm{DM}^\tau_\mathrm{h}) $, in the $ \mathrm{e}\tau_\mathrm{h} $ final state, in the high-$ m_\text{T} $ (left) and SS (right) CRs, for the $ h^\pm+\pi^{0} $(s) DM. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Figure 6-a:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ MFs, $ \omega(N_\text{tracks}, \textrm{DM}^\tau_\mathrm{h}) $, in the $ \mathrm{e}\tau_\mathrm{h} $ final state, in the high-$ m_\text{T} $ (left) and SS (right) CRs, for the $ h^\pm+\pi^{0} $(s) DM. The cyan shaded area corresponds to the fit uncertainty. |

png pdf |
Figure 6-b:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ MFs, $ \omega(N_\text{tracks}, \textrm{DM}^\tau_\mathrm{h}) $, in the $ \mathrm{e}\tau_\mathrm{h} $ final state, in the high-$ m_\text{T} $ (left) and SS (right) CRs, for the $ h^\pm+\pi^{0} $(s) DM. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Figure 7:
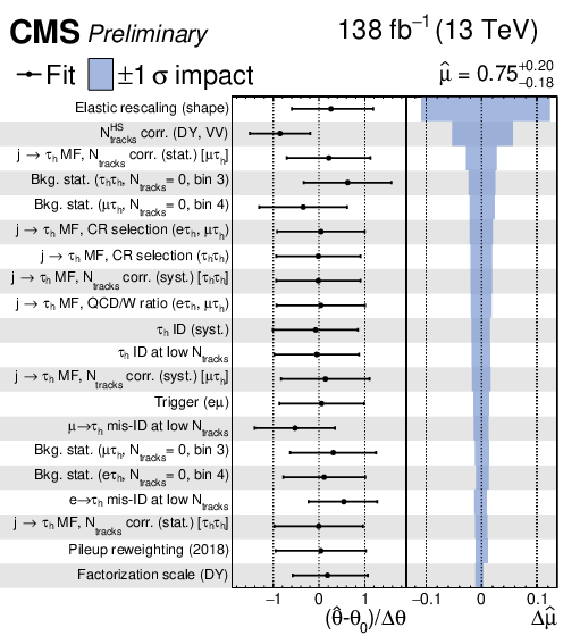
Postfit values of the nuisance parameters (black markers), shown as the difference of their best-fit values, $ \hat{\theta} $, and prefit values, $ \theta_0 $, relative to the prefit uncertainties $ \Delta\theta $. The impact $ \Delta\hat{\mu} $ of the nuisance parameters on the signal strength is computed as the difference of the nominal best fit value of $ \mu $ and the best fit value obtained when fixing the nuisance parameter under scrutiny to its best fit value $ \hat{\theta} $ plus/minus its postfit uncertainty (blue shaded area). The nuisance parameters are ordered by their impact, and only the 20 highest ranked parameters are shown. |
png pdf |
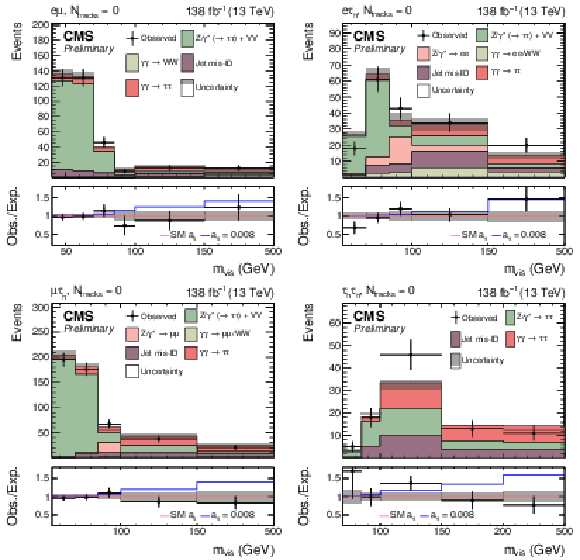
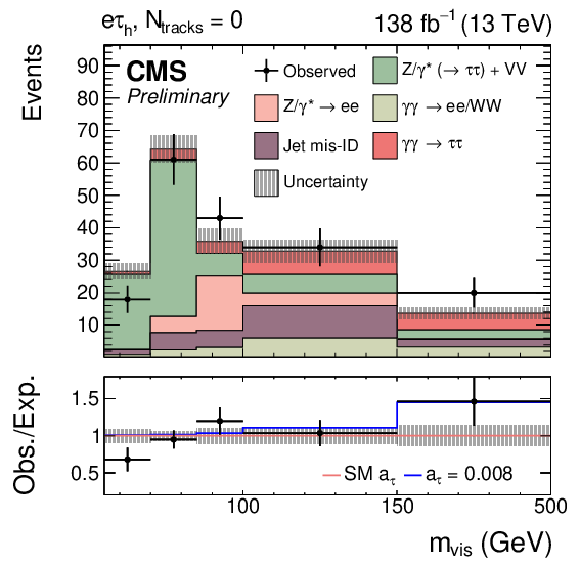
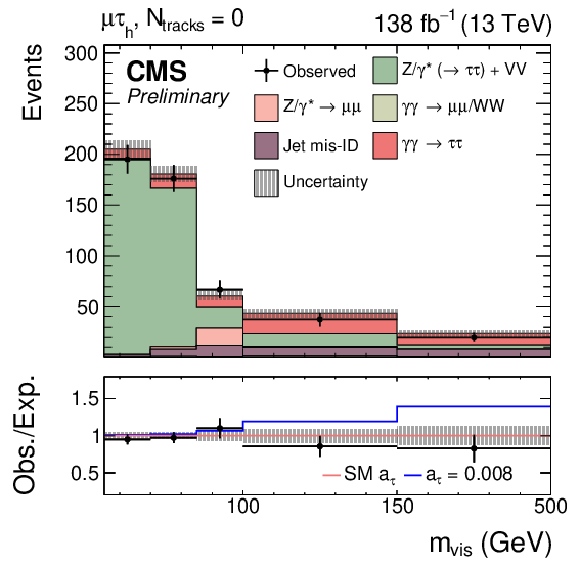
Figure 8:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 0. The minor inclusive diboson background contribution is drawn together with the Drell--Yan background in the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, and $ \mu\tau_\mathrm{h} $ final states. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical, after the global fit. In the fit, $ a_{\tau} $ and $ d_{\tau} $ are fixed to their SM values. The ratio of the total predictions for an illustrative value of $ a_{\tau}= $ 0.008 to those with SM electromagnetic couplings is shown with a blue line in the bottom panel. |

png pdf |
Figure 8-a:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 0. The minor inclusive diboson background contribution is drawn together with the Drell--Yan background in the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, and $ \mu\tau_\mathrm{h} $ final states. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical, after the global fit. In the fit, $ a_{\tau} $ and $ d_{\tau} $ are fixed to their SM values. The ratio of the total predictions for an illustrative value of $ a_{\tau}= $ 0.008 to those with SM electromagnetic couplings is shown with a blue line in the bottom panel. |
png pdf |
Figure 8-b:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 0. The minor inclusive diboson background contribution is drawn together with the Drell--Yan background in the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, and $ \mu\tau_\mathrm{h} $ final states. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical, after the global fit. In the fit, $ a_{\tau} $ and $ d_{\tau} $ are fixed to their SM values. The ratio of the total predictions for an illustrative value of $ a_{\tau}= $ 0.008 to those with SM electromagnetic couplings is shown with a blue line in the bottom panel. |
png pdf |
Figure 8-c:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 0. The minor inclusive diboson background contribution is drawn together with the Drell--Yan background in the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, and $ \mu\tau_\mathrm{h} $ final states. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical, after the global fit. In the fit, $ a_{\tau} $ and $ d_{\tau} $ are fixed to their SM values. The ratio of the total predictions for an illustrative value of $ a_{\tau}= $ 0.008 to those with SM electromagnetic couplings is shown with a blue line in the bottom panel. |

png pdf |
Figure 8-d:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 0. The minor inclusive diboson background contribution is drawn together with the Drell--Yan background in the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, and $ \mu\tau_\mathrm{h} $ final states. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical, after the global fit. In the fit, $ a_{\tau} $ and $ d_{\tau} $ are fixed to their SM values. The ratio of the total predictions for an illustrative value of $ a_{\tau}= $ 0.008 to those with SM electromagnetic couplings is shown with a blue line in the bottom panel. |
png pdf |
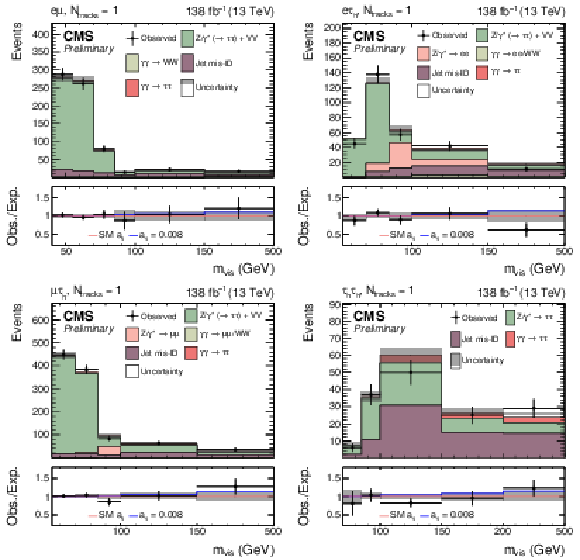
Figure 9:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 1. The description of the histograms is the same as in Fig. 8. |
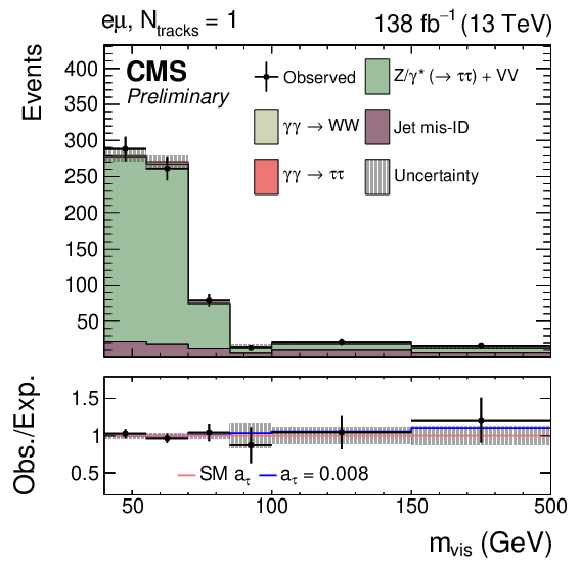
png pdf |
Figure 9-a:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 1. The description of the histograms is the same as in Fig. 8. |
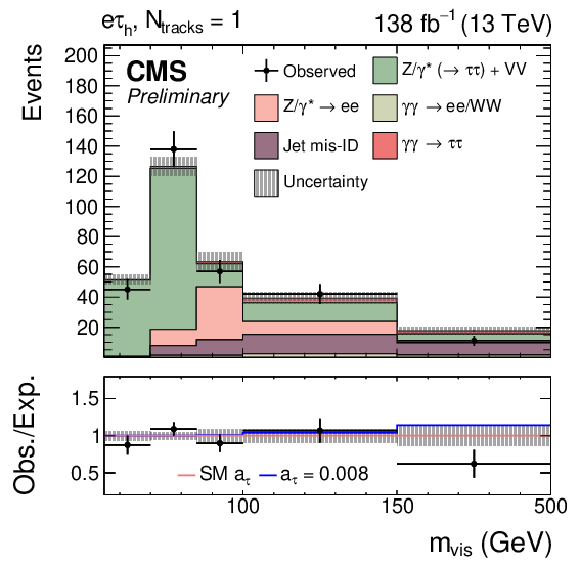
png pdf |
Figure 9-b:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 1. The description of the histograms is the same as in Fig. 8. |
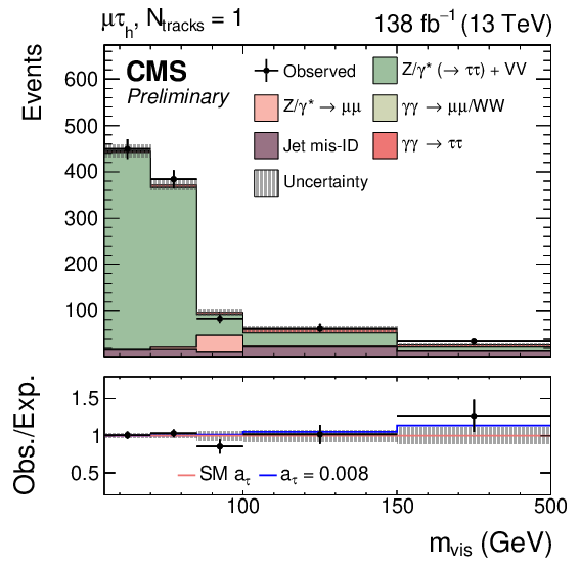
png pdf |
Figure 9-c:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 1. The description of the histograms is the same as in Fig. 8. |
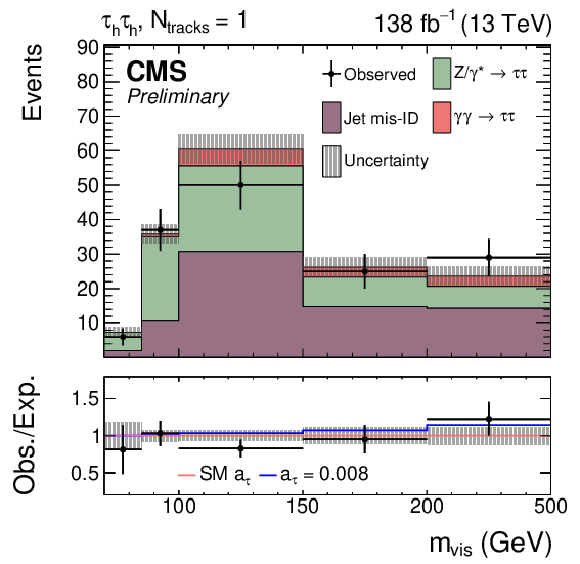
png pdf |
Figure 9-d:
Observed and predicted $ m_\text{vis} $ distributions in the $ \mathrm{e}\mu $ (upper left), $ \mathrm{e}\tau_\mathrm{h} $ (upper right), $ \mu\tau_\mathrm{h} $ (lower left), and $ \tau_\mathrm{h}\tau_\mathrm{h} $ (lower right) final states for events with $ N_\text{tracks}= $ 1. The description of the histograms is the same as in Fig. 8. |
png pdf |
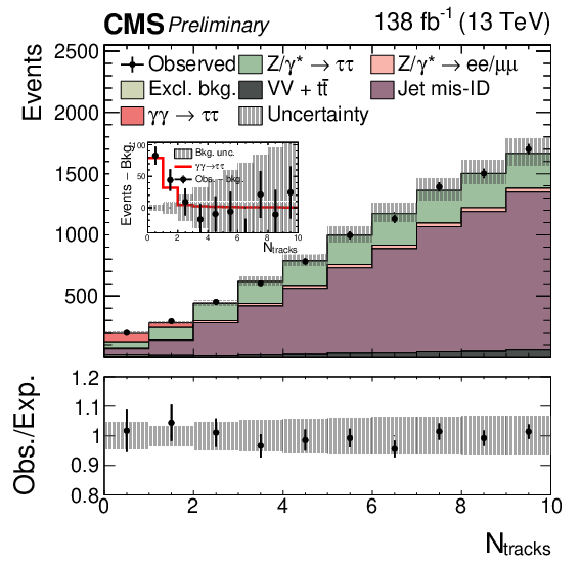
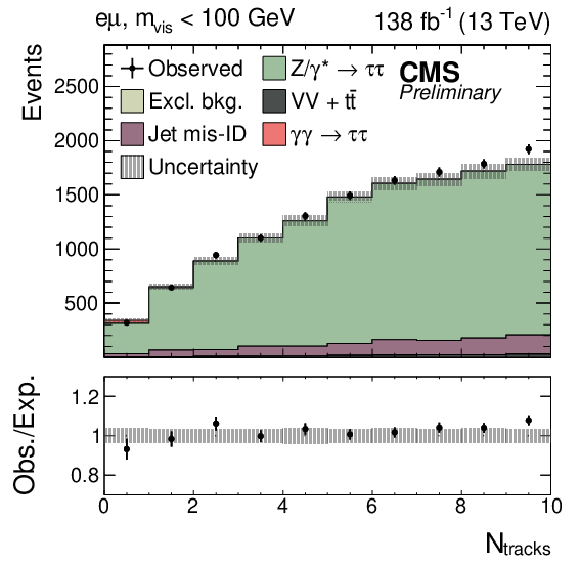
Figure 10:
Observed and predicted $ N_\text{tracks} $ distributions for events passing the SR selection but with the relaxed requirement $ N_\text{tracks} < $ 10 and the additional requirement $ m_\text{vis} > $ 100 GeV, combining the $ \mathrm{e}\mu $, $ \mathrm{e}\tau_\mathrm{h} $, $ \mu\tau_\mathrm{h} $, and $ \tau_\mathrm{h}\tau_\mathrm{h} $ final states together. The inclusive diboson background contribution is drawn together with the $ {\mathrm{t}\overline{\mathrm{t}}} $ process. The predicted distributions are adjusted to the result of the global fit performed with the $ m_\text{vis} $ distributions in the SRs, and the signal distribution is normalized to its best fit signal strength. The inset shows the difference between the observed events and the backgrounds, as well as the signal contribution. Systematic uncertainties are assumed to be uncorrelated between final states to draw the uncertainty band. |
png pdf |
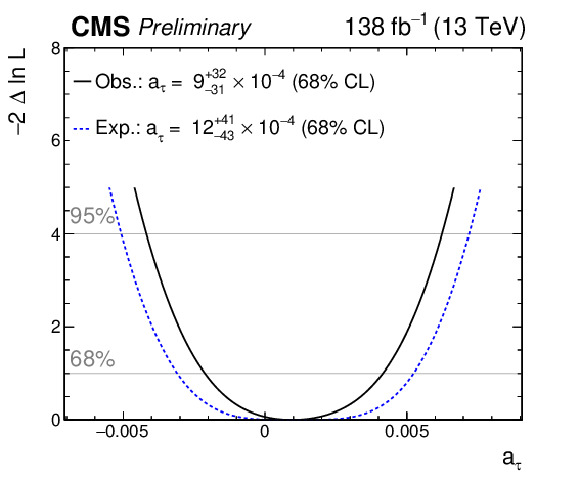
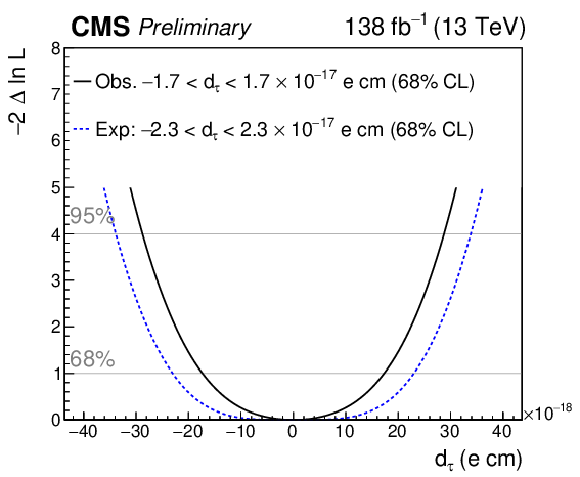
Figure 11:
Expected and observed negative log-likelihood scans as a function of $ a_{\tau} $ (left) and $ d_{\tau} $ (right), for the combination of all SRs in all data-taking periods. |
png pdf |
Figure 11-a:
Expected and observed negative log-likelihood scans as a function of $ a_{\tau} $ (left) and $ d_{\tau} $ (right), for the combination of all SRs in all data-taking periods. |
png pdf |
Figure 11-b:
Expected and observed negative log-likelihood scans as a function of $ a_{\tau} $ (left) and $ d_{\tau} $ (right), for the combination of all SRs in all data-taking periods. |
png pdf |
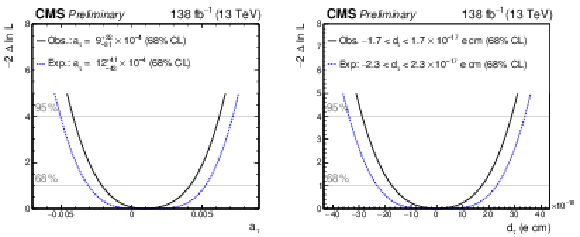
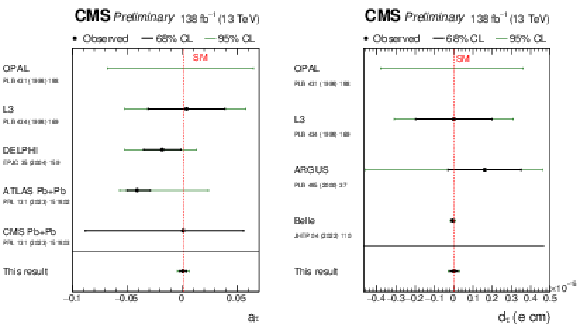
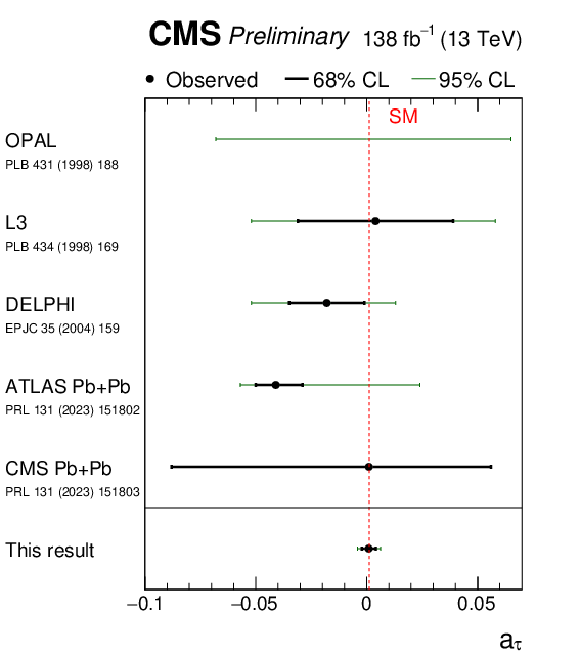
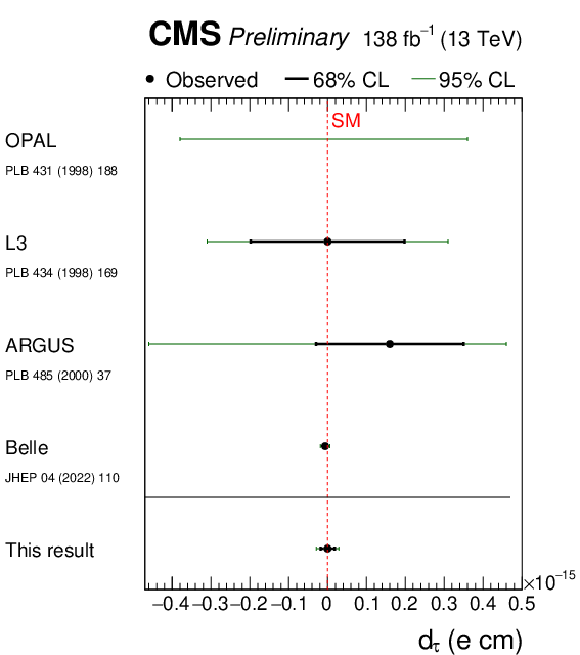
Figure 12:
Measurements of $ a_{\tau} $ (left) and $ d_{\tau} $ (right) performed in this analysis, compared with previous results from the OPAL, L3, ARGUS, Belle, CMS, and ATLAS experiments [15,16,18,17,12,13]. Confidence intervals at 68 and 95% CL are shown with thick black and thin green lines, respectively. |
png pdf |
Figure 12-a:
Measurements of $ a_{\tau} $ (left) and $ d_{\tau} $ (right) performed in this analysis, compared with previous results from the OPAL, L3, ARGUS, Belle, CMS, and ATLAS experiments [15,16,18,17,12,13]. Confidence intervals at 68 and 95% CL are shown with thick black and thin green lines, respectively. |
png pdf |
Figure 12-b:
Measurements of $ a_{\tau} $ (left) and $ d_{\tau} $ (right) performed in this analysis, compared with previous results from the OPAL, L3, ARGUS, Belle, CMS, and ATLAS experiments [15,16,18,17,12,13]. Confidence intervals at 68 and 95% CL are shown with thick black and thin green lines, respectively. |
png pdf |
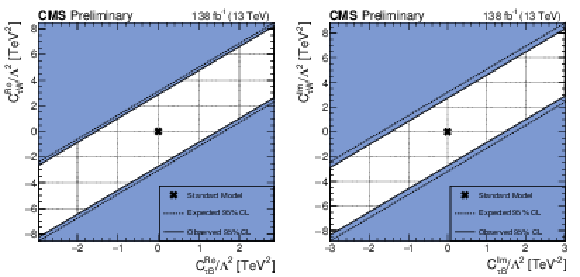
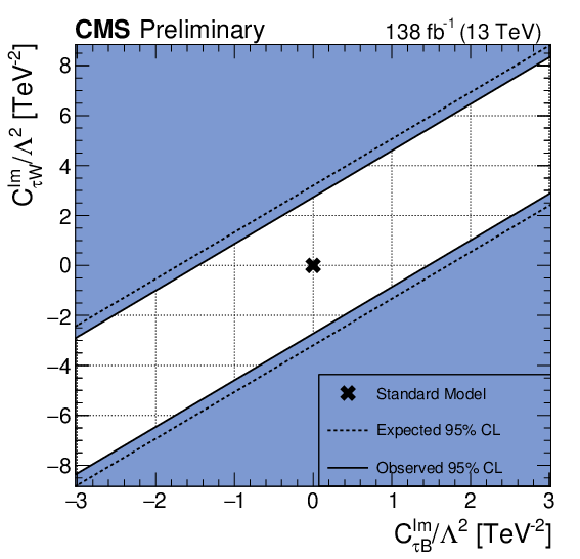
Figure 13:
Expected and observed 95% CL constraints on the real (left) and imaginary (right) parts of the Wilson coefficients $ C_{\tau B} $ and $ C_{\tau W} $ divided by $ \Lambda^2 $. The SM value is indicated with a cross. |
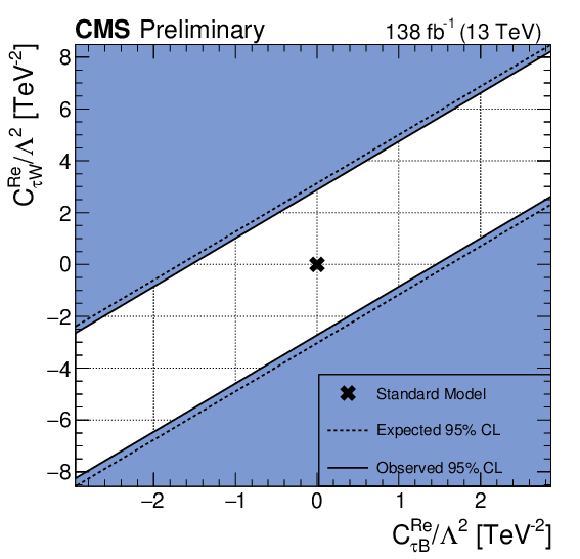
png pdf |
Figure 13-a:
Expected and observed 95% CL constraints on the real (left) and imaginary (right) parts of the Wilson coefficients $ C_{\tau B} $ and $ C_{\tau W} $ divided by $ \Lambda^2 $. The SM value is indicated with a cross. |
png pdf |
Figure 13-b:
Expected and observed 95% CL constraints on the real (left) and imaginary (right) parts of the Wilson coefficients $ C_{\tau B} $ and $ C_{\tau W} $ divided by $ \Lambda^2 $. The SM value is indicated with a cross. |
| Tables | |
png pdf |
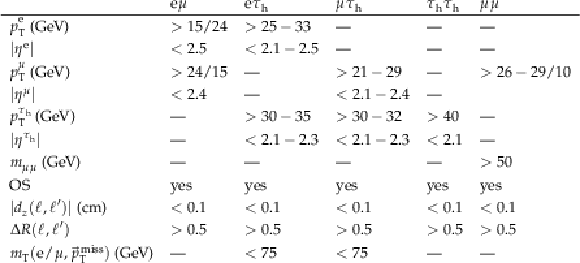
Table 1:
Baseline selection criteria used in the different final states of the SR and in the $ \mu\mu $ CR. The electrons, muons, and $ \tau_\mathrm{h} $ are required to be well identified and isolated. The $ p_{\mathrm{T}} $ and pseudorapidity ranges correspond to different sets of triggers, and different data-taking periods. |
png pdf |
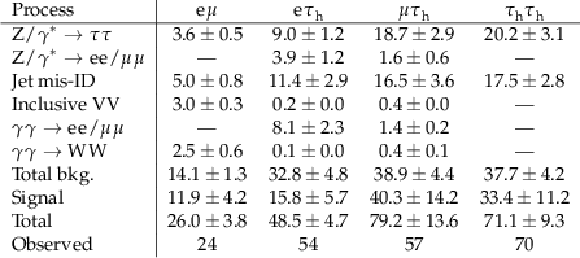
Table 2:
Observed and predicted event yields per final state in the signal-enriched phase space with $ m_\text{vis} > $ 100 GeV and $ N_\text{tracks}= $ 0. The signal and background yields are the result of the global fit including all sources of uncertainties. |
| Summary |
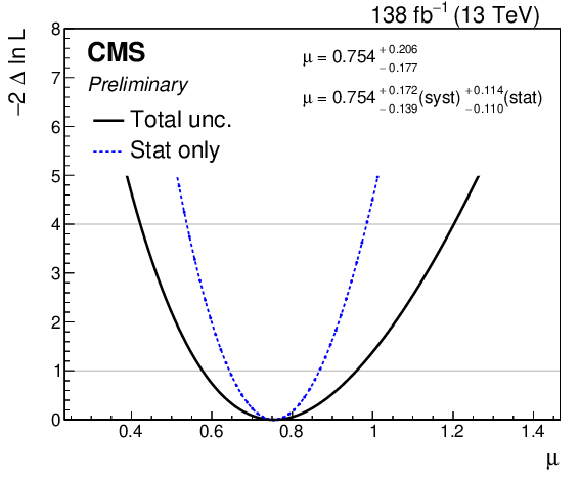
| The exclusive photon-induced production of a pair of $ \tau $ leptons, $ {\gamma\gamma\to\tau\tau} $, has been observed for the first time in proton-proton collisions, with a significance of 5.3 standard deviations (6.5 standard deviations expected). The signal was separated from the inclusive background processes by requiring a low track activity around the di-$ \tau $ vertex and a low acoplanarity between the $ \tau $ candidates. The anomalous $ \tau $ magnetic moment is measured to be $ a_{\tau}= 0.0009_{-0.0031}^{+0.0032} $, while the electric dipole moment of the $ \tau $ lepton is measured to be $ -$1.7 $ < d_{\tau} < $ 1.7 $\times$ 10$^{-17}$ e cm. |
| Additional Figures | |
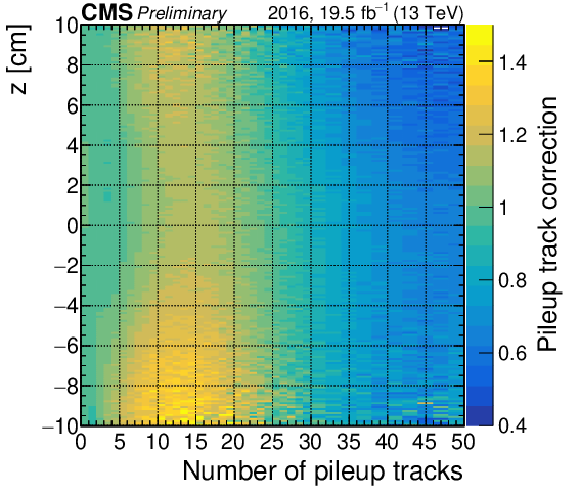
png pdf |
Additional Figure 1:
Event weights applied to simulations in the 2016 pre-VFP data-taking period as a function of the dilepton vertex position along the $ z $ axis and the pileup track multiplicity in a 0.1 cm-wide window around the dilepton vertex, where VFP stands for preamplifier feedback bias corrections due to inefficiencies in the strip modules of the tracker during the 2016 data-taking period. |
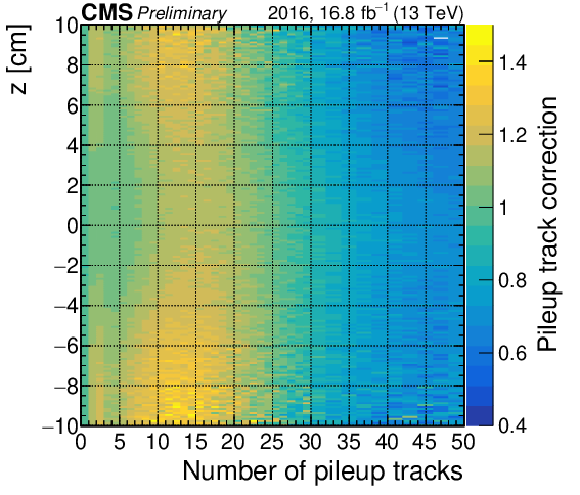
png pdf |
Additional Figure 2:
Event weights applied to simulations in the 2016 post-VFP data-taking period as a function of the dilepton vertex position along the $ z $ axis and the pileup track multiplicity in a 0.1 cm-wide window around the dilepton vertex, where VFP stands for preamplifier feedback bias corrections due to inefficiencies in the strip modules of the tracker during the 2016 data-taking period. |
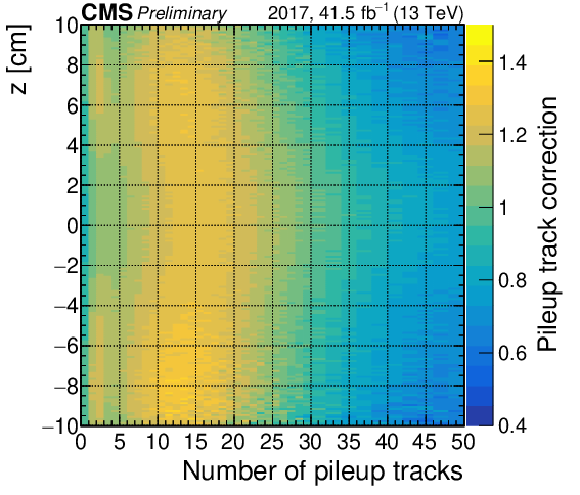
png pdf |
Additional Figure 3:
Event weights applied to simulations in the 2017 data-taking period as a function of the dilepton vertex position along the $ z $ axis and the pileup track multiplicity in a 0.1 cm-wide window around the dilepton vertex. |

png pdf |
Additional Figure 4:
Event weights applied to simulations in the 2018 data-taking period as a function of the dilepton vertex position along the $ z $ axis and the pileup track multiplicity in a 0.1 cm-wide window around the dilepton vertex. |
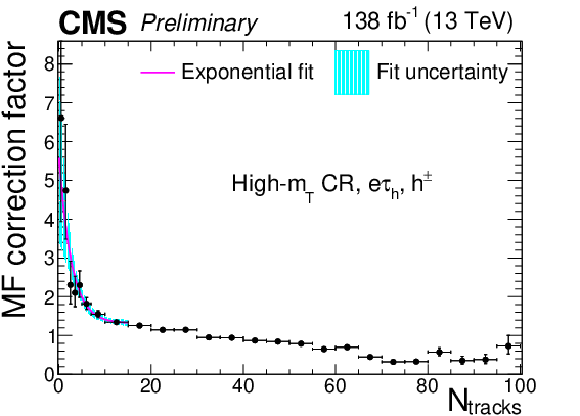
png pdf |
Additional Figure 5:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Additional Figure 6:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
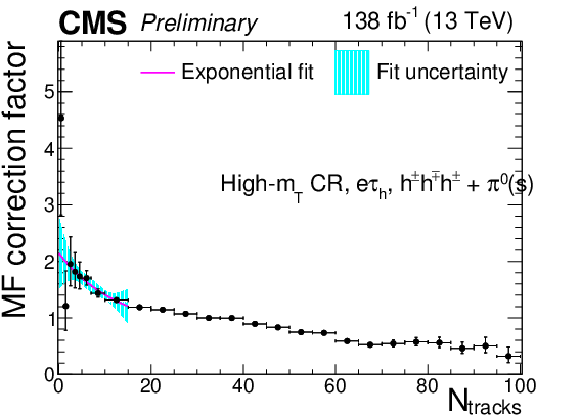
png pdf |
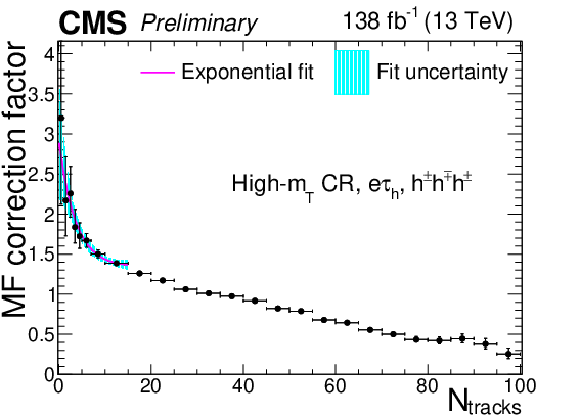
Additional Figure 7:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
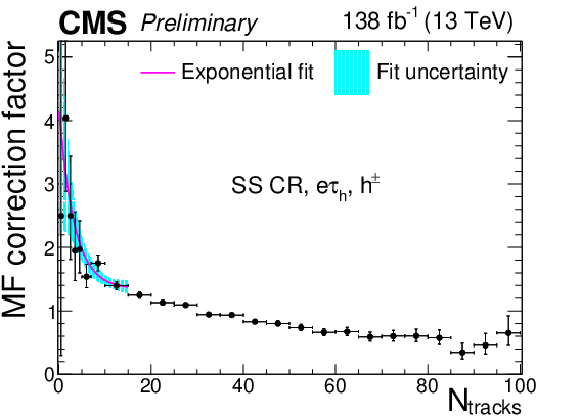
Additional Figure 8:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
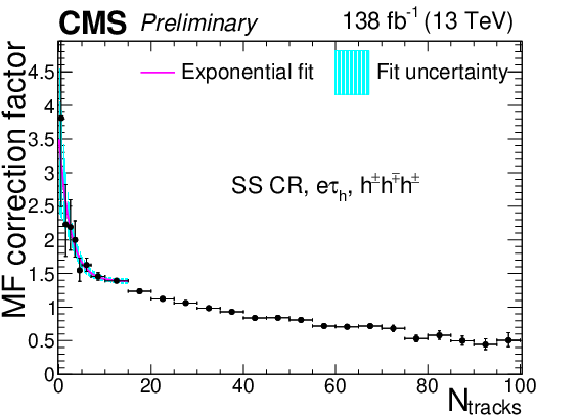
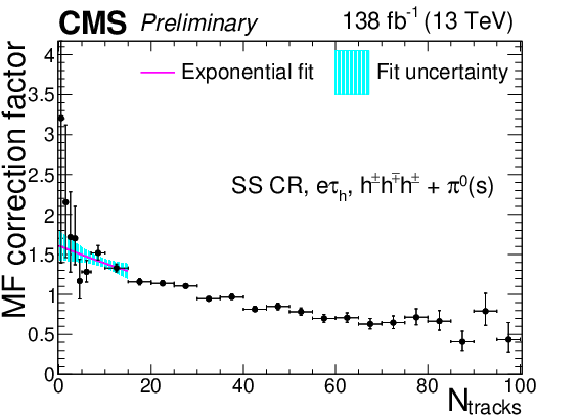
Additional Figure 9:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Additional Figure 10:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mathrm{e}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
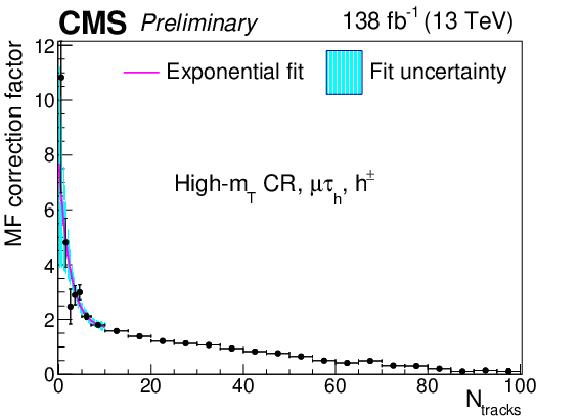
Additional Figure 11:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
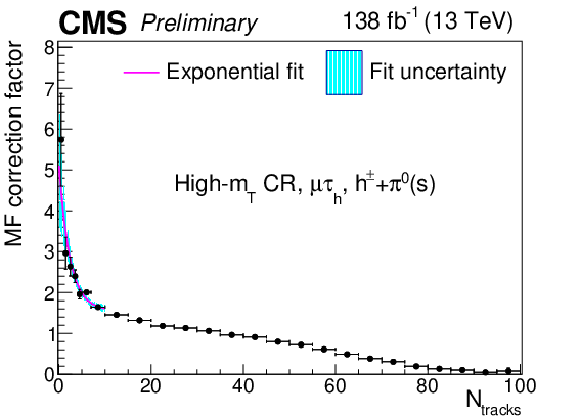
Additional Figure 12:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
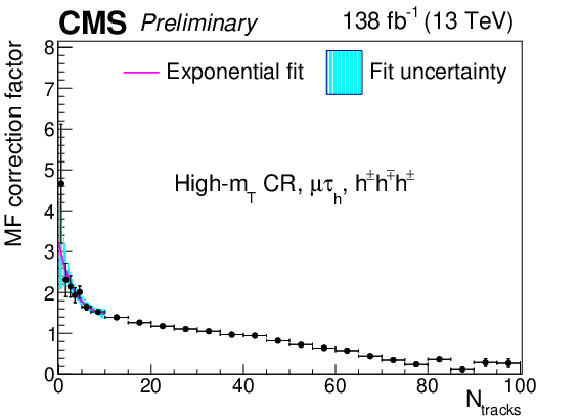
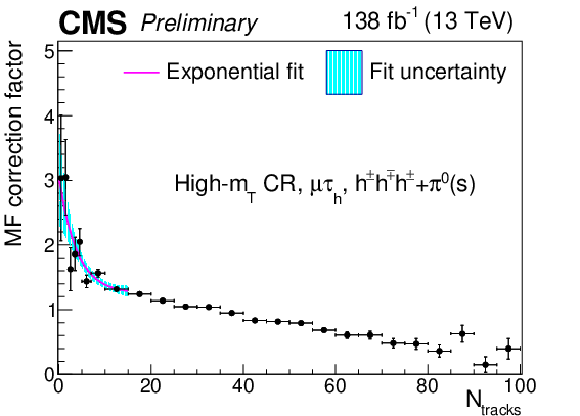
Additional Figure 13:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
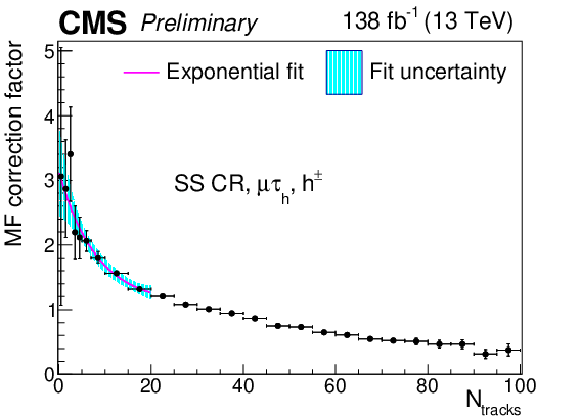
Additional Figure 14:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the high-$ m_\text{T} $ CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Additional Figure 15:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
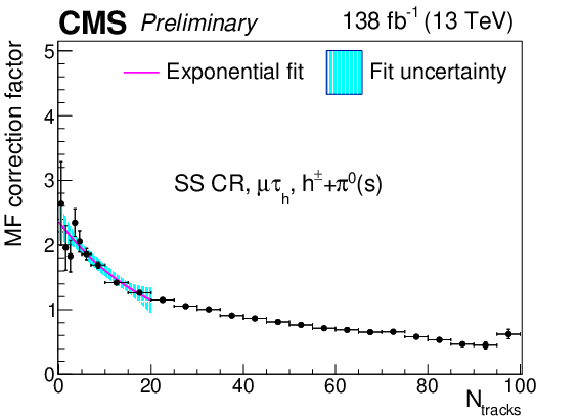
Additional Figure 16:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm+\pi^{0} $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
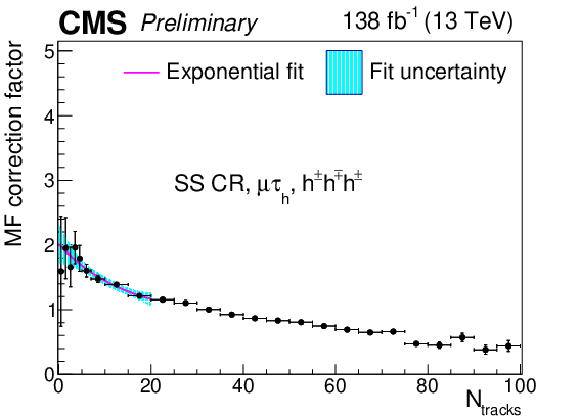
Additional Figure 17:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Additional Figure 18:
Multiplicative $ N_\text{tracks} $-dependent corrections to the $ \tau_\mathrm{h} $ misidentification factors in the $ \mu\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
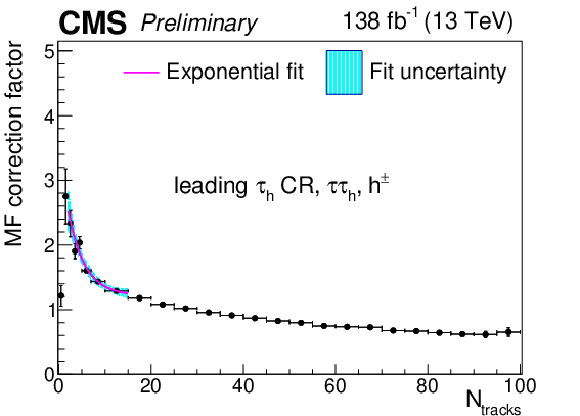
Additional Figure 19:
Multiplicative $ N_\text{tracks} $-dependent corrections to the leading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
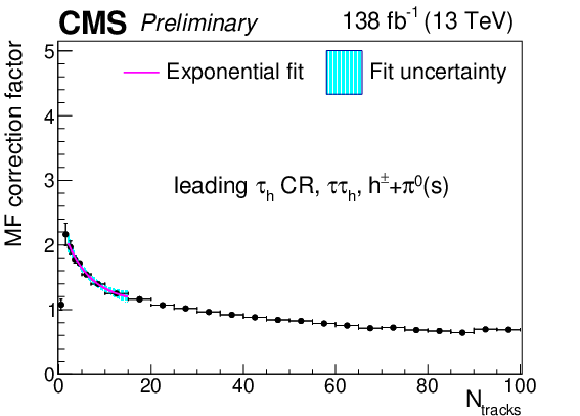
Additional Figure 20:
Multiplicative $ N_\text{tracks} $-dependent corrections to the leading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm+\pi^{0} $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |

png pdf |
Additional Figure 21:
Multiplicative $ N_\text{tracks} $-dependent corrections to the leading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
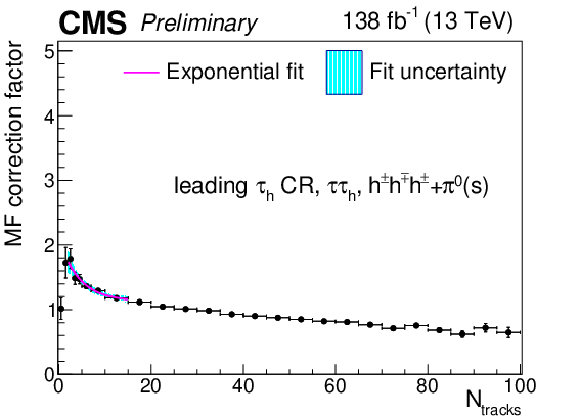
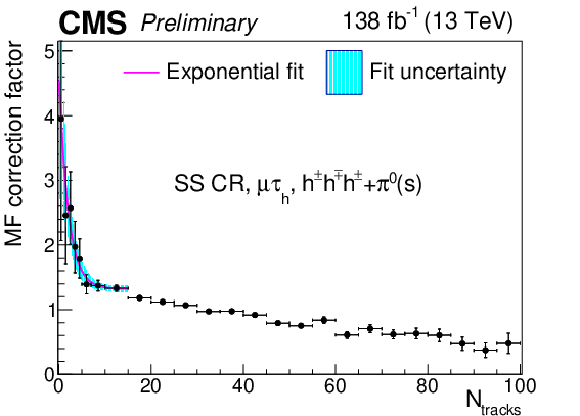
png pdf |
Additional Figure 22:
Multiplicative $ N_\text{tracks} $-dependent corrections to the leading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
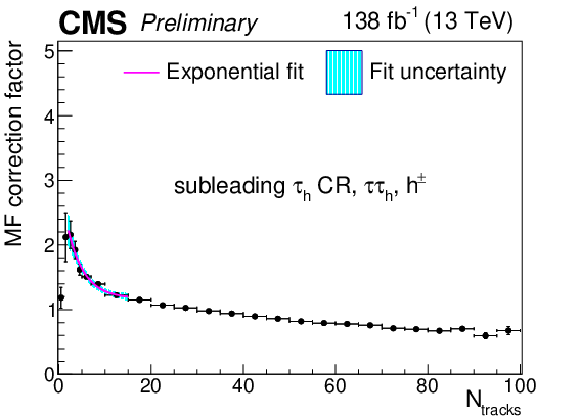
png pdf |
Additional Figure 23:
Multiplicative $ N_\text{tracks} $-dependent corrections to the subleading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
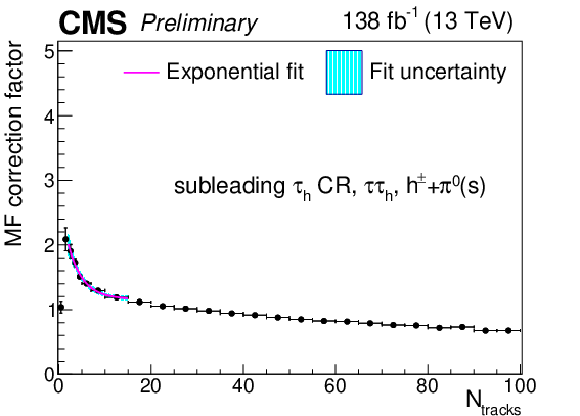
png pdf |
Additional Figure 24:
Multiplicative $ N_\text{tracks} $-dependent corrections to the subleading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm+\pi^{0} $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
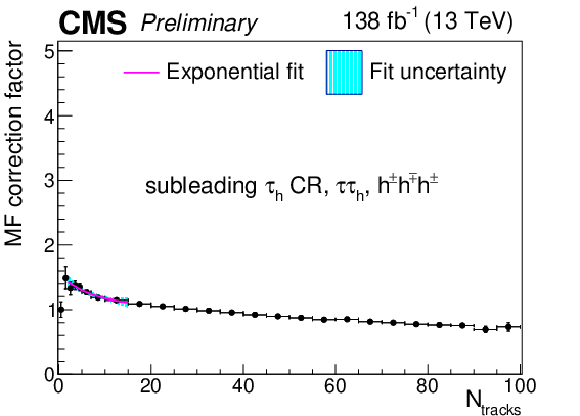
png pdf |
Additional Figure 25:
Multiplicative $ N_\text{tracks} $-dependent corrections to the subleading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm $ decay mode. The cyan shaded area corresponds to the fit uncertainty. |
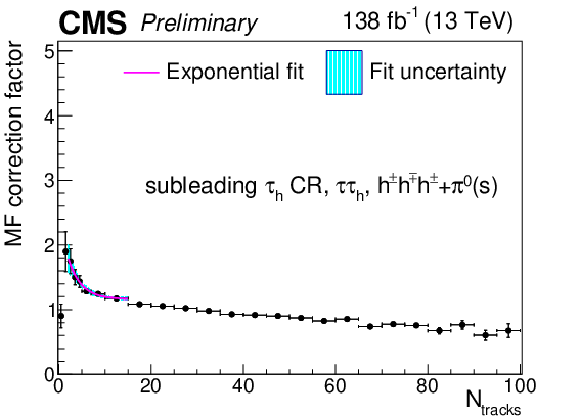
png pdf |
Additional Figure 26:
Multiplicative $ N_\text{tracks} $-dependent corrections to the subleading $ \tau_\mathrm{h} $ misidentification factors in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state in the same-sign CR, for the $ h^\pm h^\mp h^\pm+\pi^{0} $(s) decay mode. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
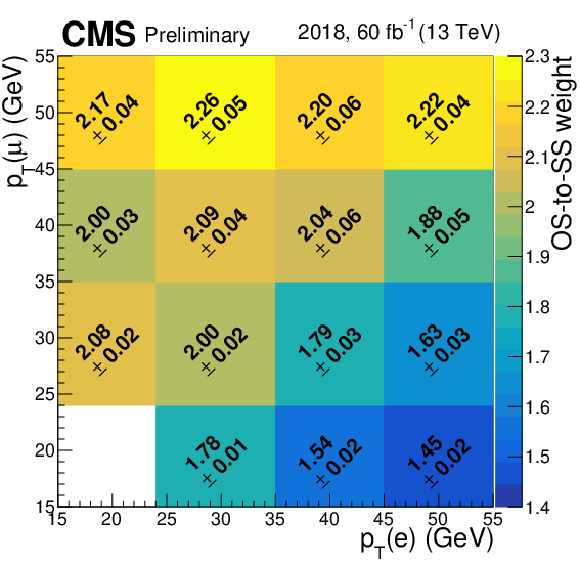
Additional Figure 27:
OS-to-SS scale factors used to estimate the mis-ID background in the $ \mathrm{e}\mu $ final state. They are measured in an $ \mathrm{e}\mu $ CR with inverted muon isolation. |
png pdf |
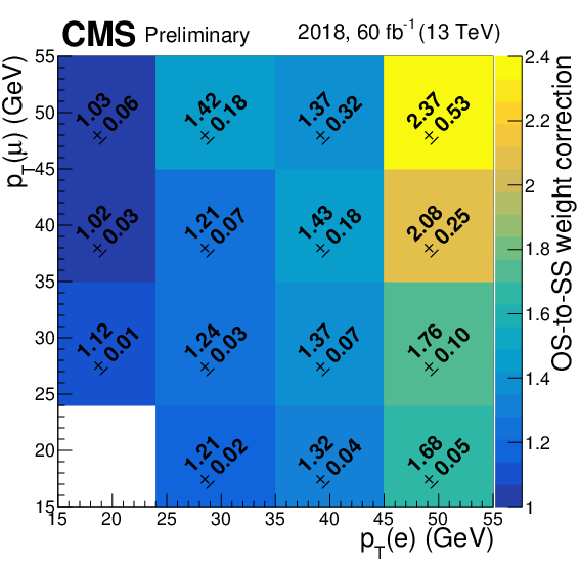
Additional Figure 28:
Correction to the OS-to-SS scale factors in the $ \mathrm{e}\mu $ final state to account for the inversion of the muon isolation. They are measured as the ratio of the OS-to-SS scale factors measured in these two CRs: a CR with inverted electron isolation and nominal muon isolation, and a region with inverted electron and muon isolations. |
png pdf |
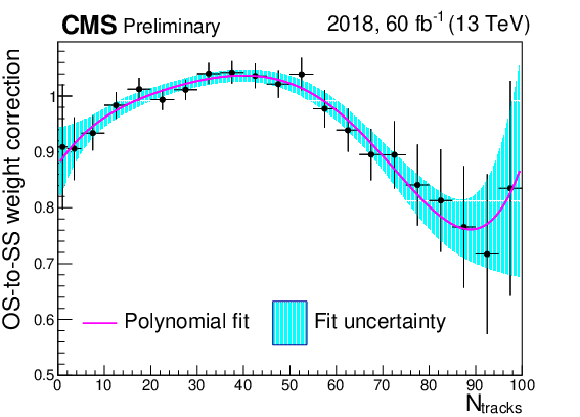
Additional Figure 29:
Multiplicative $ N_\text{tracks} $-dependent correction to the OS-to-SS scale factors used to estimate the jet mis-ID background in the $ \mathrm{e}\mu $ final state. The cyan shaded area corresponds to the fit uncertainty. This correction was measured for the 2018 data-taking period and corrections in the other data-taking periods are similar. The cyan shaded area corresponds to the fit uncertainty. |
png pdf |
Additional Figure 30:
Observed and predicted $ N_\text{tracks} $ distributions in the $ \mathrm{e}\mu $ final state for events passing the SR selection with the additional requirement $ m_\text{vis} < $ 100 GeV. The inclusive diboson background contribution is drawn together with the $ {\mathrm{t}\overline{\mathrm{t}}} $ process. The predicted distributions are adjusted to the result of the global fit performed with the $ m_\text{vis} $ distributions in the SRs, and the signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical. |
png pdf |
Additional Figure 31:
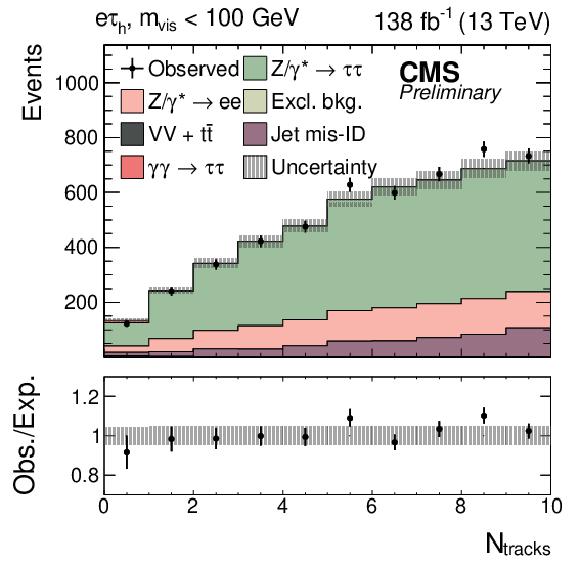
Observed and predicted $ N_\text{tracks} $ distributions in the $ \mathrm{e}\tau_\mathrm{h} $ final state for events passing the SR selection with the additional requirement $ m_\text{vis} < $ 100 GeV. The inclusive diboson background contribution is drawn together with the $ {\mathrm{t}\overline{\mathrm{t}}} $ process. The predicted distributions are adjusted to the result of the global fit performed with the $ m_\text{vis} $ distributions in the SRs, and the signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical. |
png pdf |
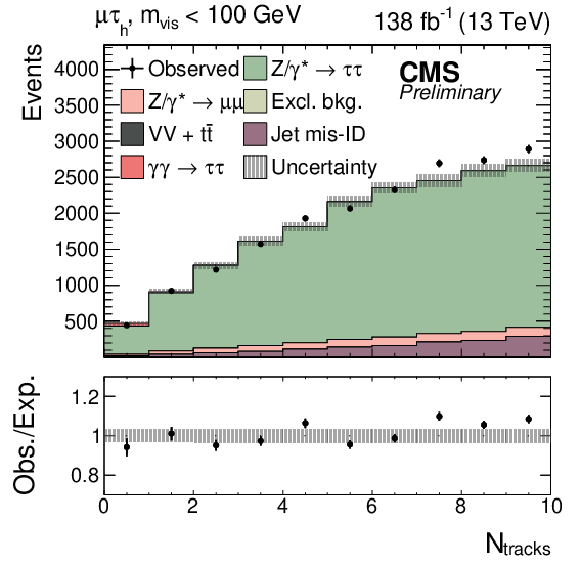
Additional Figure 32:
Observed and predicted $ N_\text{tracks} $ distributions in the $ \mu\tau_\mathrm{h} $ final state for events passing the SR selection with the additional requirement $ m_\text{vis} < $ 100 GeV. The inclusive diboson background contribution is drawn together with the $ {\mathrm{t}\overline{\mathrm{t}}} $ process. The predicted distributions are adjusted to the result of the global fit performed with the $ m_\text{vis} $ distributions in the SRs, and the signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical. |
png pdf |
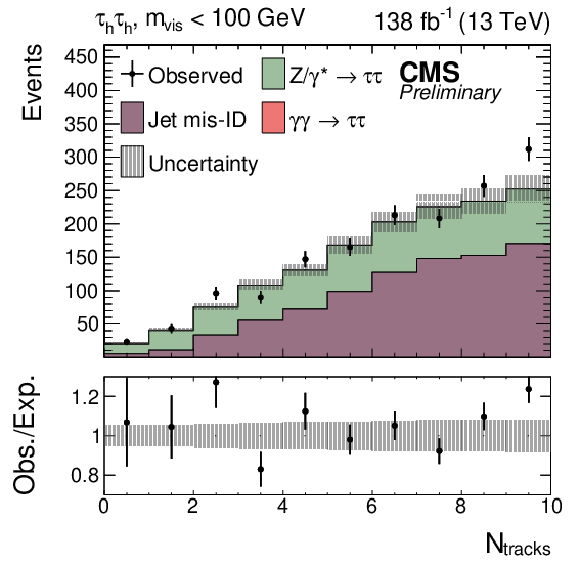
Additional Figure 33:
Observed and predicted $ N_\text{tracks} $ distributions for events in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state passing the SR selection with the additional requirement $ m_\text{vis} < $ 100 GeV. The predicted distributions are adjusted to the result of the global fit performed with the $ m_\text{vis} $ distributions in the SRs, and the signal distribution is normalized to its best fit signal strength. The uncertainty band accounts for all sources of background and signal uncertainty, systematic as well as statistical. |
png pdf |
Additional Figure 34:
Observed negative log-likelihood scans as a function of the signal strength $ \mu $, assuming SM values for $ a_{\tau} $ and $ d_{\tau} $, for the combination of all SRs in all data-taking periods. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
Additional Figure 35:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in all data-taking periods. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
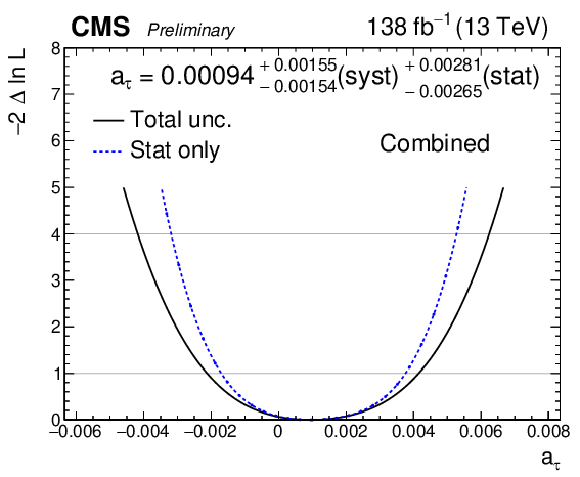
png pdf |
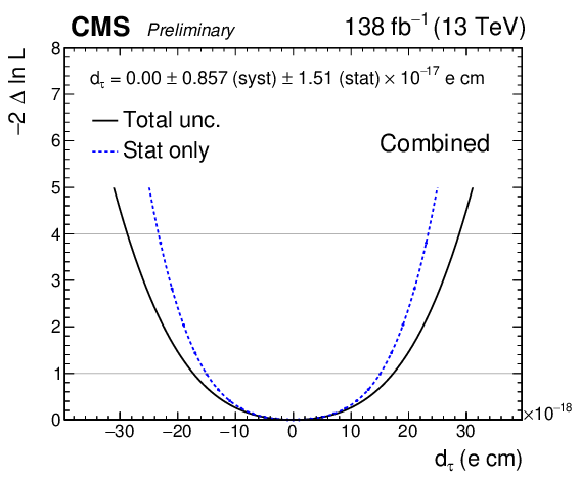
Additional Figure 36:
Observed negative log-likelihood scans as a function of $ d_{\tau} $, for the combination of all SRs in all data-taking periods. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
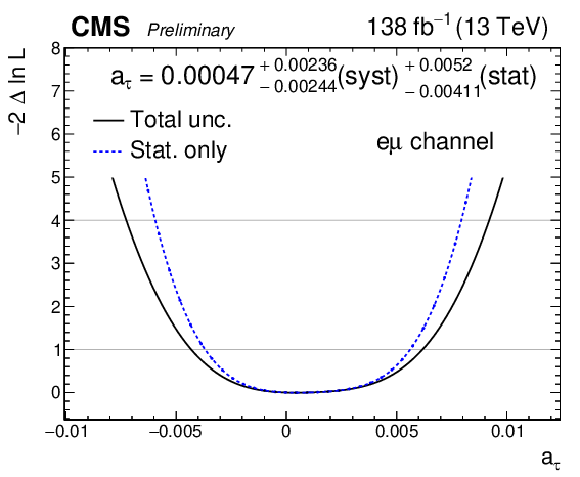
Additional Figure 37:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in the $ \mathrm{e}\mu $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
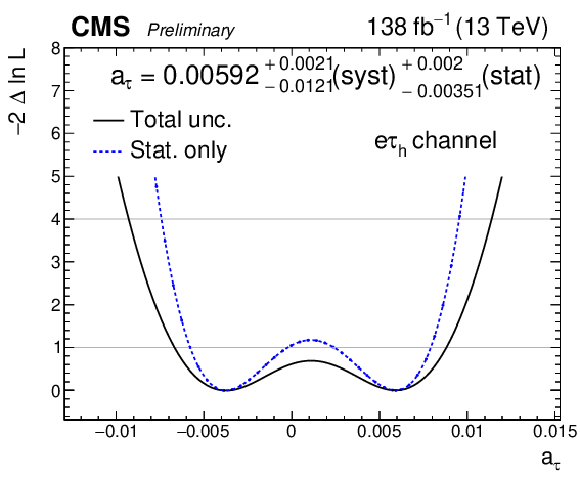
Additional Figure 38:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in the $ \mathrm{e}\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. The double-minimum structure corresponds to an excess of observed events that can be described by non-zero value of $ \deltaa_{\tau} $, where BSM effects only moderately depend on the sign of $ \deltaa_{\tau} $. |

png pdf |
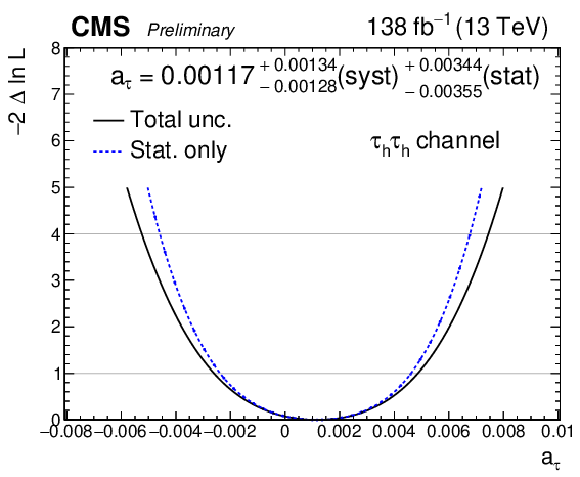
Additional Figure 39:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in the $ \mu\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
Additional Figure 40:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
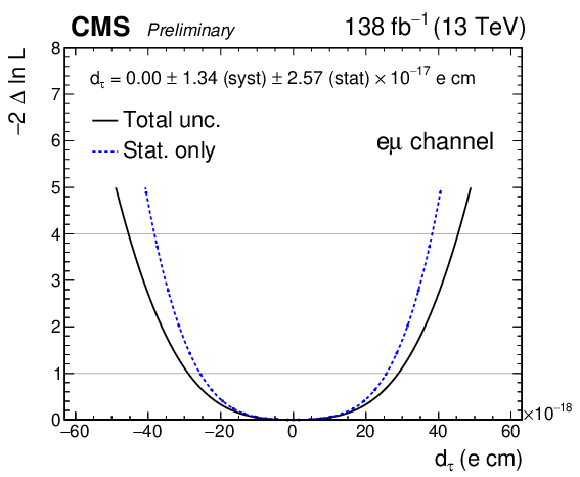
Additional Figure 41:
Observed negative log-likelihood scans as a function of $ d_{\tau} $, for the combination of all SRs in the $ \mathrm{e}\mu $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
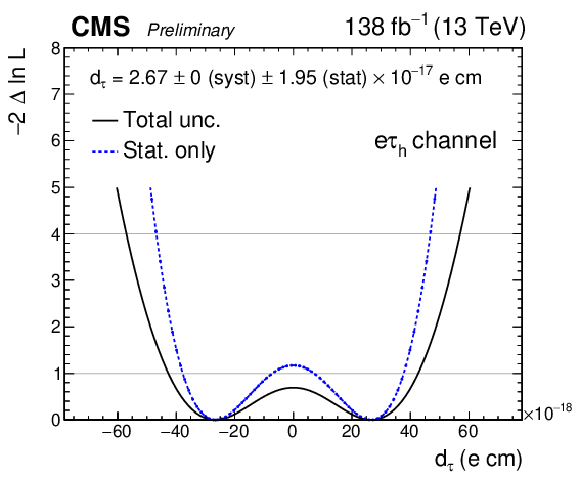
Additional Figure 42:
Observed negative log-likelihood scans as a function of $ a_{\tau} $, for the combination of all SRs in the $ \mathrm{e}\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. The double-minimum structure corresponds to an excess of observed events that can be described by BSM values of $ d_{\tau} $, where BSM effects do not depend on the sign of $ d_{\tau} $. |

png pdf |
Additional Figure 43:
Observed negative log-likelihood scans as a function of $ d_{\tau} $, for the combination of all SRs in the $ \mu\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |
png pdf |
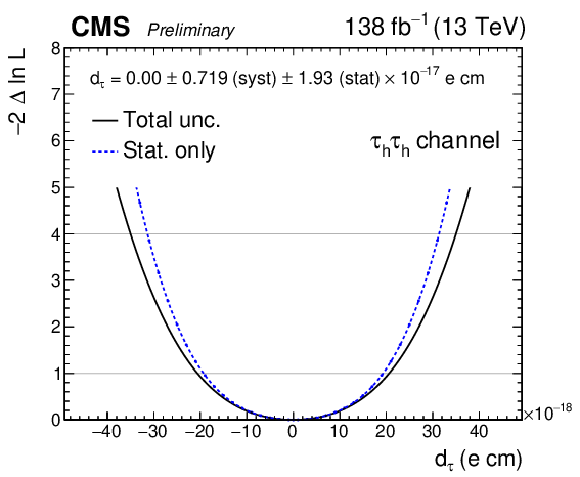
Additional Figure 44:
Observed negative log-likelihood scans as a function of $ d_{\tau} $, for the combination of all SRs in the $ \tau_\mathrm{h}\tau_\mathrm{h} $ final state. The scan with statistical uncertainty in data only is shown with the dashed blue line while the scan including all uncertainties is shown with the solid black line. For the fit with statistical uncertainty only, the nuisance parameters are frozen to their best-fit values. |

png pdf |
Additional Figure 45:
Measured values of $ a_{\tau} $ at 68% CL in the different final states and for the combination of final states. |
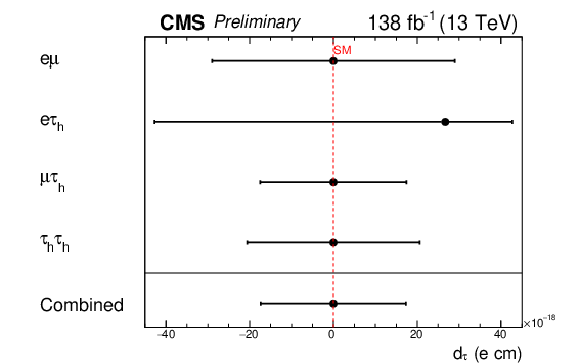
png pdf |
Additional Figure 46:
Measured values of $ d_{\tau} $ at 68% CL in the different final states and for the combination of final states. |
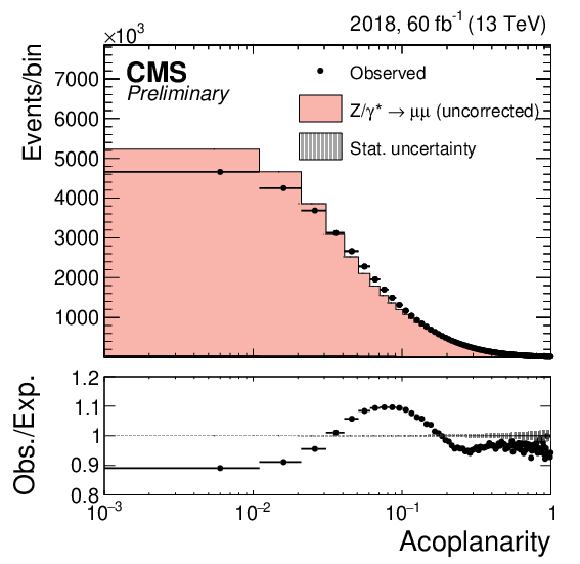
png pdf |
Additional Figure 47:
Acoplanarity distribution in data and in simulation before correction, in the 2018 data-taking period. The background prediction is normalized to match the data yield and only the statistical uncertainty is shown. |
| References | ||||
| 1 | CMS Collaboration | Search for exclusive or semi-exclusive photon pair production and observation of exclusive and semi-exclusive electron pair production in $ pp $ collisions at $ \sqrt{s}= $ 7 TeV | JHEP 11 (2012) 080 | CMS-FWD-11-004 1209.1666 |
| 2 | CMS Collaboration | Exclusive photon-photon production of muon pairs in proton-proton collisions at $ \sqrt{s}= $ 7 TeV | JHEP 01 (2012) 052 | CMS-FWD-10-005 1111.5536 |
| 3 | J. Schwinger | On quantum-electrodynamics and the magnetic moment of the electron | PR 73 (1948) 416 | |
| 4 | R. H. Parker et al. | Measurement of the fine-structure constant as a test of the standard model | Science 360 (2018) 191 | 1812.04130 |
| 5 | X. Fan, T. G. Myers, B. A. D. Sukra, and G. Gabrielse | Measurement of the electron magnetic moment | PRL 130 (2023) 071801 | 2209.13084 |
| 6 | Muon g-2 Collaboration | Measurement of the positive muon anomalous magnetic moment to 0.46 ppm | PRL 126 (2021) 141801 | 2104.03281 |
| 7 | Muon g-2 Collaboration | Measurement of the positive muon anomalous magnetic moment to 0.20 ppm | PRL 131 (2023) 161802 | 2308.06230 |
| 8 | L. Beresford and J. Liu | New physics and tau $ g- $2 using LHC heavy ion collisions | PRD 102 (2020) 113008 | 1908.05180 |
| 9 | S. Eidelman and M. Passera | Theory of the tau lepton anomalous magnetic moment | Mod. Phys. Lett. A 22 (2007) 159 | hep-ph/0701260 |
| 10 | Y. Yamaguchi and N. Yamanaka | Large long-distance contributions to the electric dipole moments of charged leptons in the standard model | PRL 125 (2020) 241802 | 2003.08195 |
| 11 | M. Dyndal, M. Klusek-Gawenda, M. Schott, and A. Szczurek | Anomalous electromagnetic moments of $ \tau $ lepton in $ \gamma \gamma \to \tau^+ \tau^- $ reaction in Pb+Pb collisions at the LHC | PLB 809 (2020) 135682 | 2002.05503 |
| 12 | ATLAS Collaboration | Observation of the $ \gamma\gamma\to\tau\tau $ process in Pb+Pb collisions and constraints on the $\tau$-lepton anomalous magnetic moment with the ATLAS detector | PRL 131 (2023) 151802 | 2204.13478 |
| 13 | CMS Collaboration | Observation of $ \tau $ lepton pair production in ultraperipheral lead-lead collisions at $ \sqrt {\smash [b]{s_{_{\mathrm {NN}}}}} = $ 5.02 TeV | PRL 131 (2023) 151803 | CMS-HIN-21-009 2206.05192 |
| 14 | DELPHI Collaboration | Study of tau-pair production in photon-photon collisions at LEP and limits on the anomalous electromagnetic moments of the tau lepton | EPJC 35 (2004) 159 | hep-ex/0406010 |
| 15 | OPAL Collaboration | An upper limit on the anomalous magnetic moment of the tau lepton | PLB 431 (1998) 188 | hep-ex/9803020 |
| 16 | L3 Collaboration | Measurement of the anomalous magnetic and electric dipole moments of the tau lepton | PLB 434 (1998) 169 | |
| 17 | Belle Collaboration | An improved search for the electric dipole moment of the $ \tau $ lepton | JHEP 04 (2022) 110 | 2108.11543 |
| 18 | ARGUS Collaboration | A search for the electric dipole moment of the tau lepton | PLB 485 (2000) 37 | hep-ex/0004031 |
| 19 | ATLAS Collaboration | Observation of photon-induced $ W^+W^- $ production in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | PLB 816 (2021) 136190 | 2010.04019 |
| 20 | CMS Collaboration | Study of exclusive two-photon production of $ W^+W^- $ in $ pp $ collisions at $ \sqrt{s} = $ 7 TeV and constraints on anomalous quartic gauge couplings | JHEP 07 (2013) 116 | CMS-FSQ-12-010 1305.5596 |
| 21 | CMS Collaboration | Evidence for exclusive $ \gamma\gamma \to W^+ W^- $ production and constraints on anomalous quartic gauge couplings in $ pp $ collisions at $ \sqrt{s}= $ 7 and 8 TeV | JHEP 08 (2016) 119 | CMS-FSQ-13-008 1604.04464 |
| 22 | CMS and TOTEM Collaborations | Observation of proton-tagged, central (semi)exclusive production of high-mass lepton pairs in pp collisions at 13 TeV with the CMS-TOTEM precision proton spectrometer | JHEP 07 (2018) 153 | CMS-PPS-17-001 1803.04496 |
| 23 | ATLAS Collaboration | Measurement of exclusive $ \gamma\gamma\rightarrow W^+W^- $ production and search for exclusive Higgs boson production in $ pp $ collisions at $ \sqrt{s} = $ 8 TeV using the ATLAS detector | PRD 94 (2016) 032011 | 1607.03745 |
| 24 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 25 | CMS Collaboration | Performance of the cms level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 26 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 27 | H.-S. Shao and D. d'Enterria | gamma-UPC: automated generation of exclusive photon-photon processes in ultraperipheral proton and nuclear collisions with varying form factors | JHEP 09 (2022) 248 | 2207.03012 |
| 28 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 29 | J. Alwall et al. | MadGraph/MadEvent v4: the new web generation | JHEP 09 (2007) 028 | |
| 30 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 31 | L. A. Harland-Lang, M. Tasevsky, V. A. Khoze, and M. G. Ryskin | A new approach to modelling elastic and inelastic photon-initiated production at the LHC: SuperChic 4 | EPJC 80 (2020) 925 | 2007.12704 |
| 32 | I. Brivio, Y. Jiang, and M. Trott | The SMEFTsim package, theory and tools | JHEP 12 (2017) 070 | 1709.06492 |
| 33 | I. Brivio | SMEFTsim 3.0 \textemdash a practical guide | JHEP 04 (2021) 073 | 2012.11343 |
| 34 | P. Artoisenet, V. Lemaitre, F. Maltoni, and O. Mattelaer | Automation of the matrix element reweighting method | JHEP 12 (2010) 068 | 1007.3300 |
| 35 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 36 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 37 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 38 | S. Alioli et al. | Jet pair production in POWHEG | JHEP 04 (2011) 081 | 1012.3380 |
| 39 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 40 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 41 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 42 | R. D. Ball et al. | Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO | NPB 855 (2012) 153 | 1107.2652 |
| 43 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 44 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 45 | GEANT4 Collaboration | GEANT 4 --- a simulation toolkit | NIM A 506 (2003) 250 | |
| 46 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 47 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 48 | CMS Collaboration | ECAL 2016 refined calibration and Run2 summary plots | CMS Detector Performance Summary CMS-DP-2020-021, 2020 CDS |
|
| 49 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 50 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 51 | CMS Collaboration | Identification of hadronic tau lepton decays using a deep neural network | JINST 17 (2022) P07023 | CMS-TAU-20-001 2201.08458 |
| 52 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 53 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 54 | CMS Tracker Group Collaboration | The CMS phase-1 pixel detector upgrade | JINST 16 (2021) P02027 | 2012.14304 |
| 55 | CMS Collaboration | Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS phase-1 pixel detector | CMS Detector Performance Summary CMS-DP-2020-049, 2020 CDS |
|
| 56 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 57 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 58 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 59 | R. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 60 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|