Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-TAU-16-003 ; CERN-EP-2018-229

Performance of reconstruction and identification of $\tau$ leptons decaying to hadrons and $\nu_{\tau}$ in pp collisions at $ \sqrt{s} = $ 13 TeV

CMS Collaboration

8 September 2018

JINST 13 (2018) P10005

Abstract: The algorithm developed by the CMS Collaboration to reconstruct and identify $\tau$ leptons produced in proton-proton collisions at $\sqrt{s}= $ 7 and 8 TeV, via their decays to hadrons and a neutrino, has been significantly improved. The changes include a revised reconstruction of $\pi^{0}$ candidates, and improvements in multivariate discriminants to separate $\tau$ leptons from jets and electrons. The algorithm is extended to reconstruct $\tau$ leptons in highly Lorentz-boosted pair production, and in the high-level trigger. The performance of the algorithm is studied using proton-proton collisions recorded during 2016 at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. The performance is evaluated in terms of the efficiency for a genuine $\tau$ lepton to pass the identification criteria and of the probabilities for jets, electrons, and muons to be misidentified as $\tau$ leptons. The results are found to be very close to those expected from Monte Carlo simulation.

Links: e-print arXiv:1809.02816 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ;

Figures
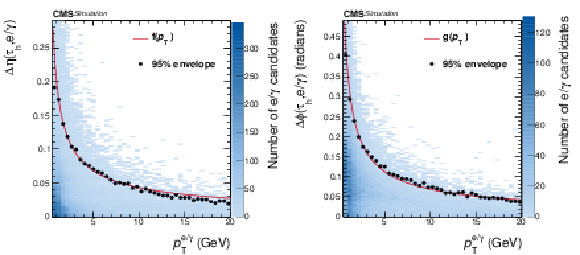
png pdf	Figure 1: Distance in $\eta $ (left) and in $\phi $ (right) between the $ {{\tau} _\mathrm {h}} $ and $ {\mathrm {e}}/ {\gamma} $ candidates for $ {{\tau} _\mathrm {h}} $ decay products, as a function of the $ {p_{\mathrm {T}}} $ of the $ {\mathrm {e}}/ {\gamma} $ candidate, in simulated $ {{\tau} _\mathrm {h}} $ decays. The points show the 95% envelope for a given bin, and the solid red lines represent the fitted functions $f$ and $g$ given in Eq. 3.
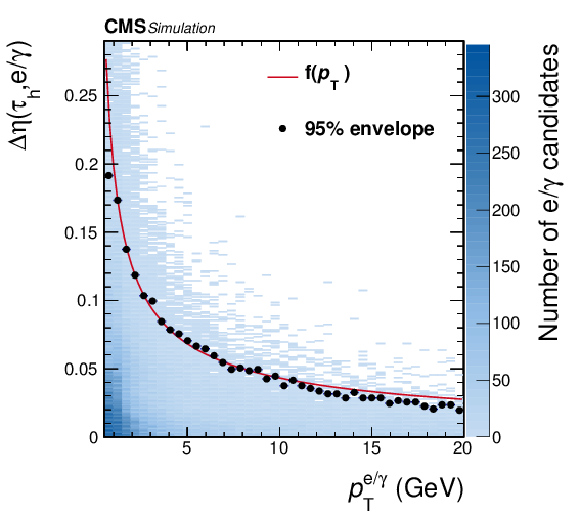
png pdf	Figure 1-a: Distance in $\eta $ between the $ {{\tau} _\mathrm {h}} $ and $ {\mathrm {e}}/ {\gamma} $ candidates for $ {{\tau} _\mathrm {h}} $ decay products, as a function of the $ {p_{\mathrm {T}}} $ of the $ {\mathrm {e}}/ {\gamma} $ candidate, in simulated $ {{\tau} _\mathrm {h}} $ decays. The points show the 95% envelope for a given bin, and the solid red lines represent the fitted functions $f$ and $g$ given in Eq. 3.
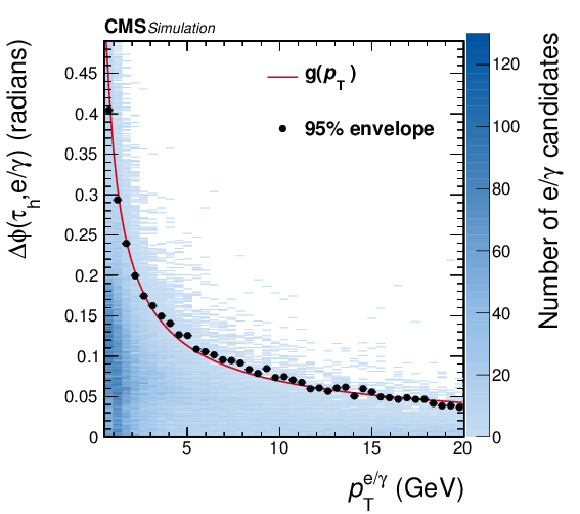
png pdf	Figure 1-b: Distance in $\phi $ between the $ {{\tau} _\mathrm {h}} $ and $ {\mathrm {e}}/ {\gamma} $ candidates for $ {{\tau} _\mathrm {h}} $ decay products, as a function of the $ {p_{\mathrm {T}}} $ of the $ {\mathrm {e}}/ {\gamma} $ candidate, in simulated $ {{\tau} _\mathrm {h}} $ decays. The points show the 95% envelope for a given bin, and the solid red lines represent the fitted functions $f$ and $g$ given in Eq. 3.
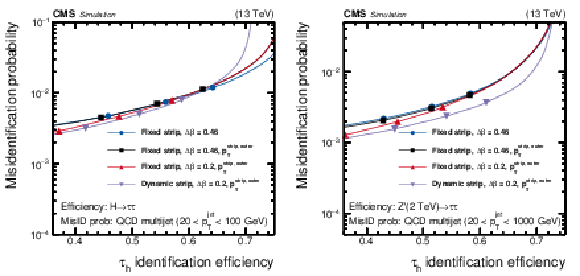
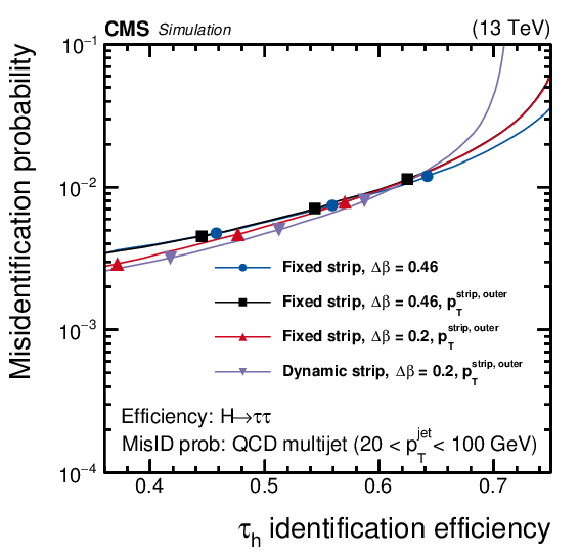
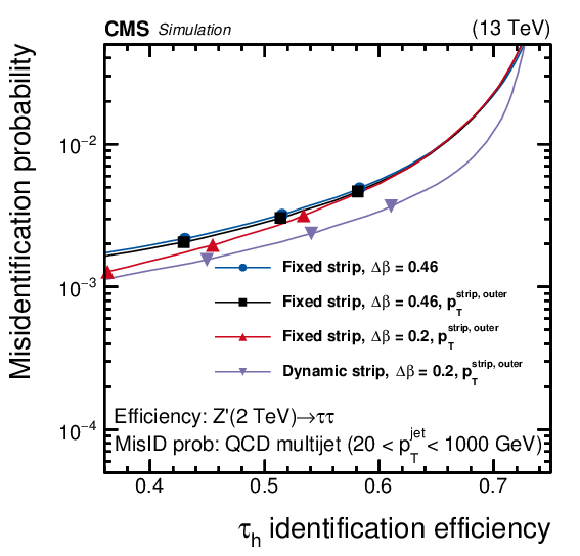
png pdf	Figure 2: Misidentification probabilities as a function of the $ {{\tau} _\mathrm {h}} $ identification efficiencies, evaluated for $ {\mathrm {H}} \to {\tau} {\tau}$ (left) and $ {\mathrm {Z}}^{'}(2 TeV) \to {\tau} {\tau}$ (right), and for QCD multijet MC events. Four configurations of the reconstruction and isolation method are compared. The three points on each curve correspond, from left to right, to the tight, medium, and loose WPs. The solid curves are obtained by imposing cutoffs on $I_{{{\tau} _\mathrm {h}}}$ that decrease linearly from small to large efficiency.
png pdf	Figure 2-a: Misidentification probabilities as a function of the $ {{\tau} _\mathrm {h}} $ identification efficiencies, evaluated for $ {\mathrm {H}} \to {\tau} {\tau}$, and for QCD multijet MC events. Four configurations of the reconstruction and isolation method are compared. The three points on each curve correspond, from left to right, to the tight, medium, and loose WPs. The solid curves are obtained by imposing cutoffs on $I_{{{\tau} _\mathrm {h}}}$ that decrease linearly from small to large efficiency.
png pdf	Figure 2-b: Misidentification probabilities as a function of the $ {{\tau} _\mathrm {h}} $ identification efficiencies, evaluated for $ {\mathrm {Z}}^{'}(2 TeV) \to {\tau} {\tau}$, and for QCD multijet MC events. Four configurations of the reconstruction and isolation method are compared. The three points on each curve correspond, from left to right, to the tight, medium, and loose WPs. The solid curves are obtained by imposing cutoffs on $I_{{{\tau} _\mathrm {h}}}$ that decrease linearly from small to large efficiency.
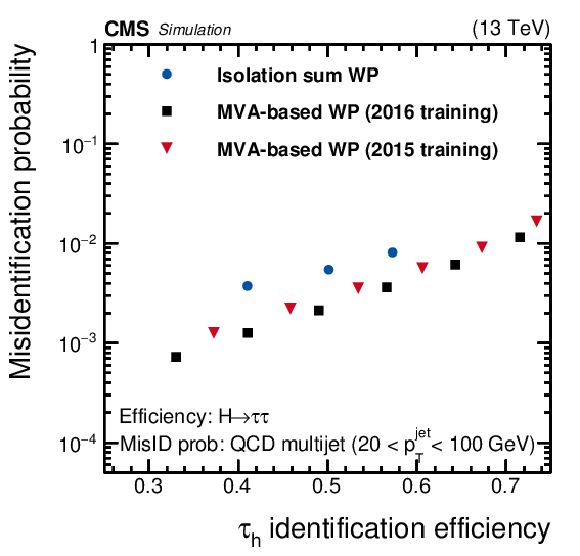
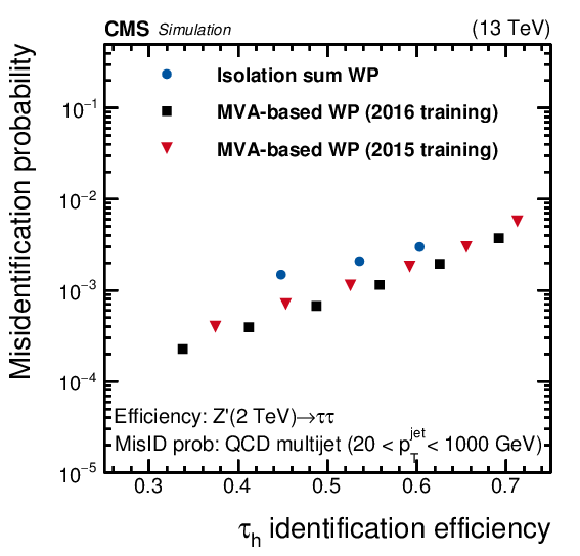
png pdf	Figure 3: Misidentification probabilities for $ {{\tau} _\mathrm {h}} $ as a function of their identification efficiency, evaluated using $ {\mathrm {H}} \to {\tau} {\tau}$ (left), $ {\mathrm {Z}}^{'}(2 TeV) \to {\tau} {\tau}$ (right), and QCD multijet MC events. The MVA-based discriminants trained on their corresponding MC events are compared to each other, as well as to the isolation-sum discriminants. The points correspond to different working points of the discriminants. The three points for the isolation-sum discriminants from left to right correspond to the tight, medium, and loose WPs. Similarly, the six points of the MVA-based discriminants define the WP as very-very tight, very tight, tight, medium, loose, and very loose, respectively.
png pdf	Figure 3-a: Misidentification probabilities for $ {{\tau} _\mathrm {h}} $ as a function of their identification efficiency, evaluated using $ {\mathrm {H}} \to {\tau} {\tau}$ and QCD multijet MC events. The MVA-based discriminants trained on their corresponding MC events are compared to each other, as well as to the isolation-sum discriminants. The points correspond to different working points of the discriminants. The three points for the isolation-sum discriminants from left to right correspond to the tight, medium, and loose WPs. Similarly, the six points of the MVA-based discriminants define the WP as very-very tight, very tight, tight, medium, loose, and very loose, respectively.
png pdf	Figure 3-b: Misidentification probabilities for $ {{\tau} _\mathrm {h}} $ as a function of their identification efficiency, evaluated using $ {\mathrm {Z}}^{'}(2 TeV) \to {\tau} {\tau}$ and QCD multijet MC events. The MVA-based discriminants trained on their corresponding MC events are compared to each other, as well as to the isolation-sum discriminants. The points correspond to different working points of the discriminants. The three points for the isolation-sum discriminants from left to right correspond to the tight, medium, and loose WPs. Similarly, the six points of the MVA-based discriminants define the WP as very-very tight, very tight, tight, medium, loose, and very loose, respectively.
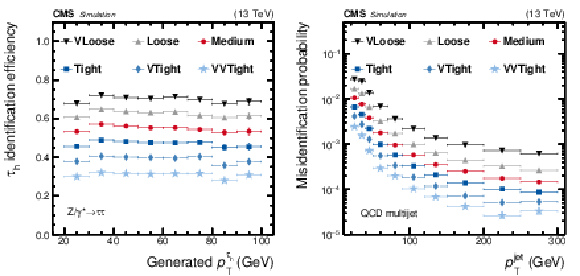
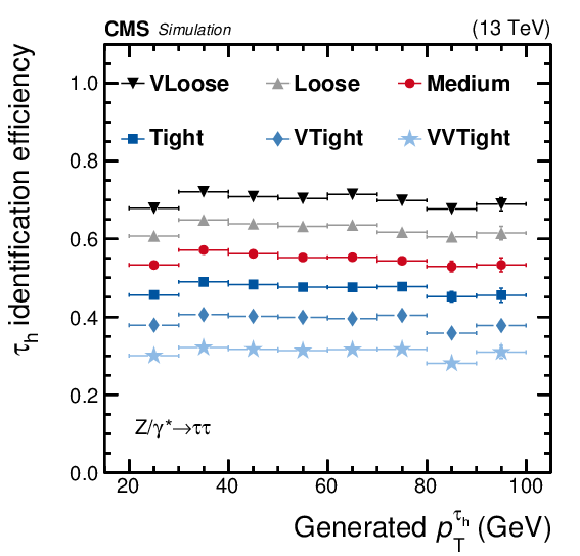
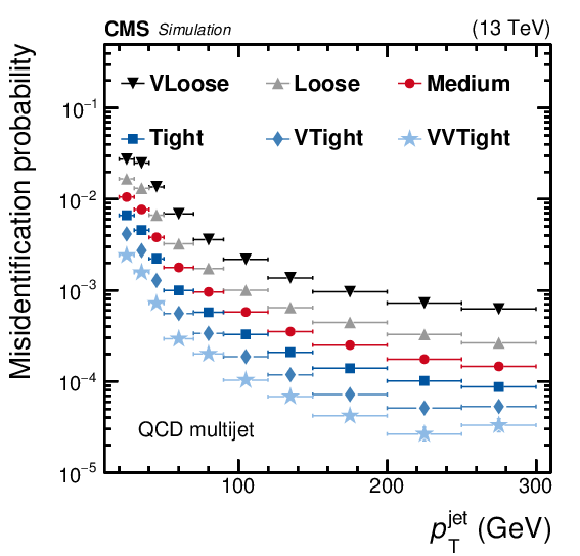
png pdf	Figure 4: Efficiency of $ {{\tau} _\mathrm {h}} $ identification, estimated using simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events (left), and the misidentification probability estimated using simulated QCD multijet events (right) are given, for the very loose, loose, medium, tight, very tight, and very-very tight WPs of the MVA-based $ {{\tau} _\mathrm {h}} $ isolation algorithm. The efficiency and misidentification probabilities are shown as a function of ${p_{\mathrm {T}}}$ of the generated $ {{\tau} _\mathrm {h}} $ and of the reconstructed jet, respectively. Vertical bars (often smaller than the symbol size) correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals [61]), while horizontal bars indicate the bin widths.
png pdf	Figure 4-a: Efficiency of $ {{\tau} _\mathrm {h}} $ identification, estimated using simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events is given, for the very loose, loose, medium, tight, very tight, and very-very tight WPs of the MVA-based $ {{\tau} _\mathrm {h}} $ isolation algorithm. The probability is shown as a function of ${p_{\mathrm {T}}}$ of the generated $ {{\tau} _\mathrm {h}} $ and of the reconstructed jet, respectively. Vertical bars (often smaller than the symbol size) correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals [61]), while horizontal bars indicate the bin widths.
png pdf	Figure 4-b: Misidentification probability estimated using simulated QCD multijet events is given, for the very loose, loose, medium, tight, very tight, and very-very tight WPs of the MVA-based $ {{\tau} _\mathrm {h}} $ isolation algorithm. The probability is shown as a function of ${p_{\mathrm {T}}}$ of the generated $ {{\tau} _\mathrm {h}} $ and of the reconstructed jet, respectively. Vertical bars (often smaller than the symbol size) correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals [61]), while horizontal bars indicate the bin widths.
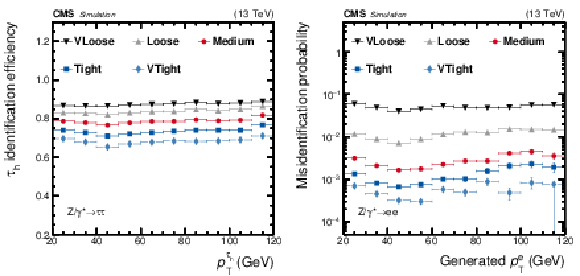
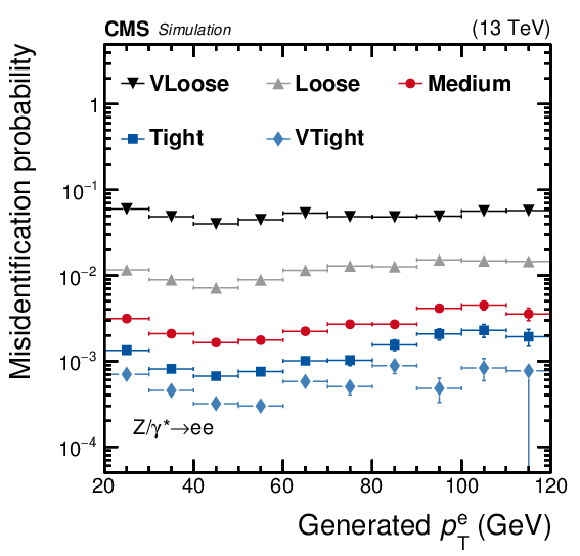
png pdf	Figure 5: Efficiencies of $ {{\tau} _\mathrm {h}} $ identification estimated via simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events (left), and the $ {\mathrm {e}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability estimated using simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\mathrm {e}} {\mathrm {e}}$ events (right) for the very loose, loose, medium, tight, and very tight WPs of the MVA-based electron discrimination algorithm. The efficiency is shown as a function of ${p_{\mathrm {T}}}$ of the reconstructed $ {{\tau} _\mathrm {h}} $ candidate, while the misidentification probability is shown as a function of the generated electron ${p_{\mathrm {T}}}$. The efficiency is calculated for $ {{\tau} _\mathrm {h}} $ candidates with a reconstructed decay mode that pass the loose WP of the isolation-sum discriminant, while the misidentification probability is calculated for generated electrons of $ {p_{\mathrm {T}}} > $ 20 GeV and $ {| \eta |} < 2.3$, excluding the less sensitive detector region of 1.46 $ < {| \eta |} < $ 1.56 between the barrel and endcap ECAL regions. Vertical bars (often smaller than the symbol size) indicate the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
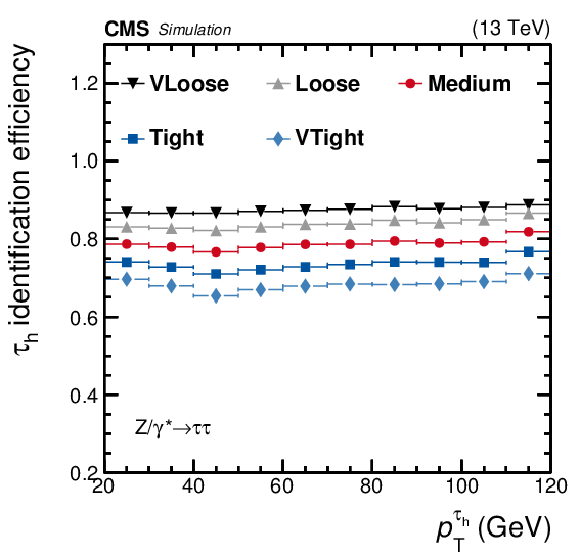
png pdf	Figure 5-a: Efficiencies of $ {{\tau} _\mathrm {h}} $ identification estimated via simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events for the very loose, loose, medium, tight, and very tight WPs of the MVA-based electron discrimination algorithm. The efficiency is shown as a function of ${p_{\mathrm {T}}}$ of the reconstructed $ {{\tau} _\mathrm {h}} $ candidate. The efficiency is calculated for $ {{\tau} _\mathrm {h}} $ candidates with a reconstructed decay mode that pass the loose WP of the isolation-sum discriminant. Vertical bars (often smaller than the symbol size) indicate the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
png pdf	Figure 5-b: The $ {\mathrm {e}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability estimated using simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\mathrm {e}} {\mathrm {e}}$ events for the very loose, loose, medium, tight, and very tight WPs of the MVA-based electron discrimination algorithm. The misidentification probability is shown as a function of the generated electron ${p_{\mathrm {T}}}$. The misidentification probability is calculated for generated electrons of $ {p_{\mathrm {T}}} > $ 20 GeV and $ {| \eta |} < $ 2.3, excluding the less sensitive detector region of 1.46 $ < {| \eta |} < $ 1.56 between the barrel and endcap ECAL regions. Vertical bars (often smaller than the symbol size) indicate the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
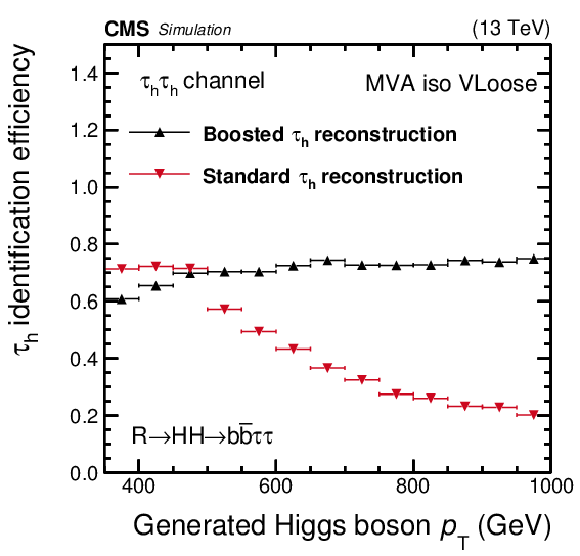
png pdf	Figure 6: Reconstruction and identification efficiencies for the $ {{\tau} _\mathrm {h}} $ in the $ {{\mu}} {{\tau} _\mathrm {h}} $ (upper left) and $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ (upper right) final states, and for the $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ pair (lower left), as a function of the generated $ {p_{\mathrm {T}}} $ of the Higgs boson, and the probability for large-radius jets in QCD multijet events to be misidentified as $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ final states (lower right), as a function of the large-radius jet $ {p_{\mathrm {T}}}$. Vertical bars correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
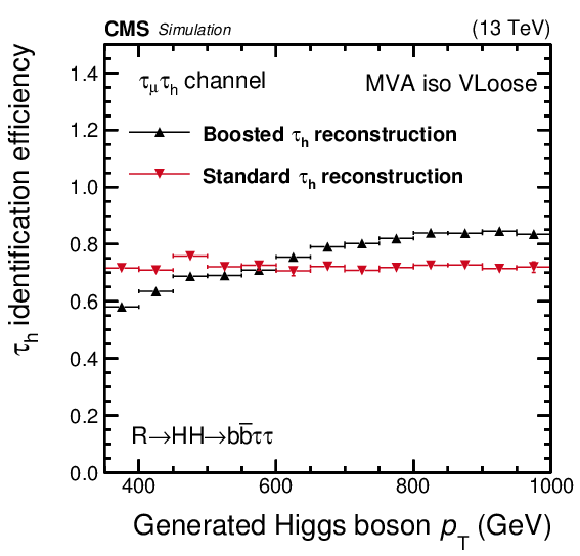
png pdf	Figure 6-a: Reconstruction and identification efficiencies for the $ {{\tau} _\mathrm {h}} $ in the $ {{\mu}} {{\tau} _\mathrm {h}} $ final state, as a function of the generated $ {p_{\mathrm {T}}} $ of the Higgs boson. Vertical bars correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
png pdf	Figure 6-b: Reconstruction and identification efficiencies for the $ {{\tau} _\mathrm {h}} $ in the $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ final state, as a function of the generated $ {p_{\mathrm {T}}} $ of the Higgs boson. Vertical bars correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
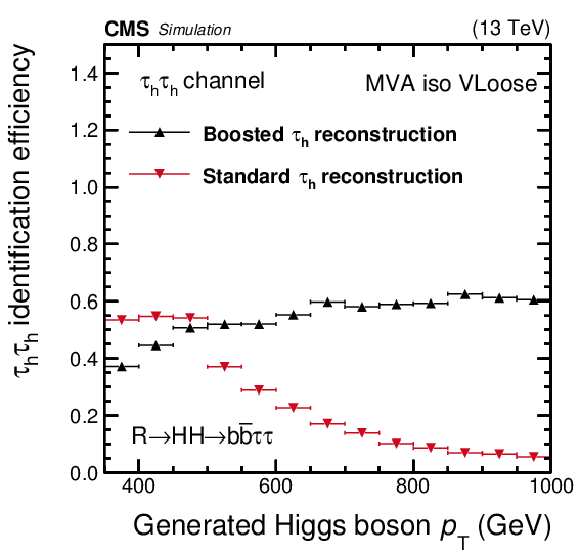
png pdf	Figure 6-c: Reconstruction and identification efficiencies for the $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ pair, as a function of the generated $ {p_{\mathrm {T}}} $ of the Higgs boson. Vertical bars correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
png pdf	Figure 6-d: The probability for large-radius jets in QCD multijet events to be misidentified as $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ final states, as a function of the large-radius jet $ {p_{\mathrm {T}}}$. Vertical bars correspond to the statistical uncertainties (the 68% Clopper-Pearson intervals), while horizontal bars indicate the bin widths.
png pdf	Figure 7: The fitted distribution in $ {m_\text {vis}}$ in the passing (left) and failing (right) categories for the tight WP of the MVA-based isolation. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while shaded bands to the quadratic sum of the fitted statistical and systematic uncertainties.
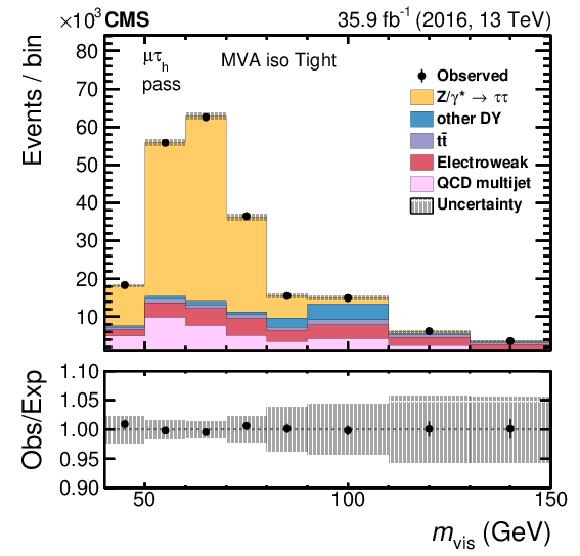
png pdf	Figure 7-a: The fitted distribution in $ {m_\text {vis}}$ in the passing category for the tight WP of the MVA-based isolation. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while shaded bands to the quadratic sum of the fitted statistical and systematic uncertainties.
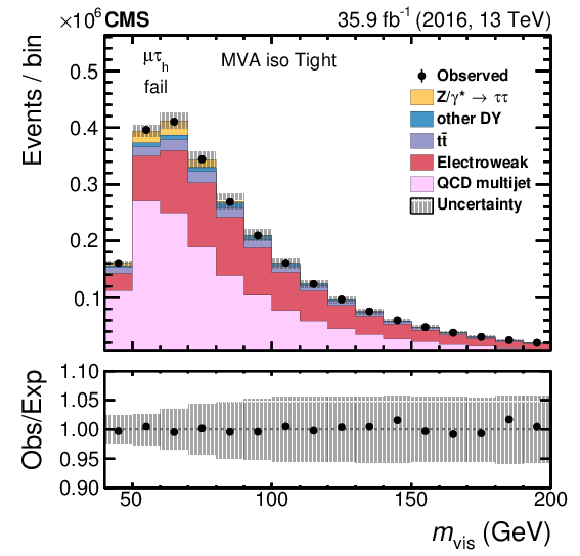
png pdf	Figure 7-b: The fitted distribution in $ {m_\text {vis}}$ in the failing category for the tight WP of the MVA-based isolation. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while shaded bands to the quadratic sum of the fitted statistical and systematic uncertainties.
png pdf	Figure 8: Fitted distributions for the signal (upper), $ {\mathrm {e}} {{\mu}}$ passing (lower left), and the $ {\mathrm {e}} {{\mu}}$ failing (lower right) categories, using the $ {m_{\mathrm {T}}} $ for the $ {\vec{p}_{\mathrm {T}}} ^{\mu}$ and ${\vec{p}_{\mathrm {T}}^{\,\text {miss}}}$ vectors as observables for the tight WP of the MVA-based isolation with $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$ between 30 and 40 GeV. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands reflect the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 8-a: Fitted distribution for the signal category, using the $ {m_{\mathrm {T}}} $ for the $ {\vec{p}_{\mathrm {T}}} ^{\mu}$ and ${\vec{p}_{\mathrm {T}}^{\,\text {miss}}}$ vectors as observables for the tight WP of the MVA-based isolation with $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$ between 30 and 40 GeV. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands reflect the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 8-b: Fitted distribution for the $ {\mathrm {e}} {{\mu}}$ passing category, using the $ {m_{\mathrm {T}}} $ for the $ {\vec{p}_{\mathrm {T}}} ^{\mu}$ and ${\vec{p}_{\mathrm {T}}^{\,\text {miss}}}$ vectors as observables for the tight WP of the MVA-based isolation with $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$ between 30 and 40 GeV. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands reflect the quadratic sum of the statistical and systematic uncertainties after the fit.
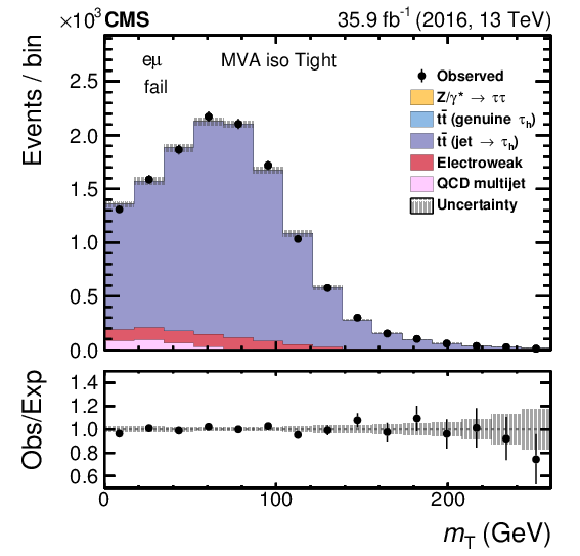
png pdf	Figure 8-c: Fitted distribution for the $ {\mathrm {e}} {{\mu}}$ failing category, using the $ {m_{\mathrm {T}}} $ for the $ {\vec{p}_{\mathrm {T}}} ^{\mu}$ and ${\vec{p}_{\mathrm {T}}^{\,\text {miss}}}$ vectors as observables for the tight WP of the MVA-based isolation with $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$ between 30 and 40 GeV. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands reflect the quadratic sum of the statistical and systematic uncertainties after the fit.
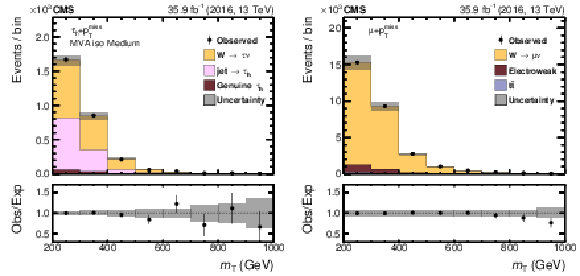
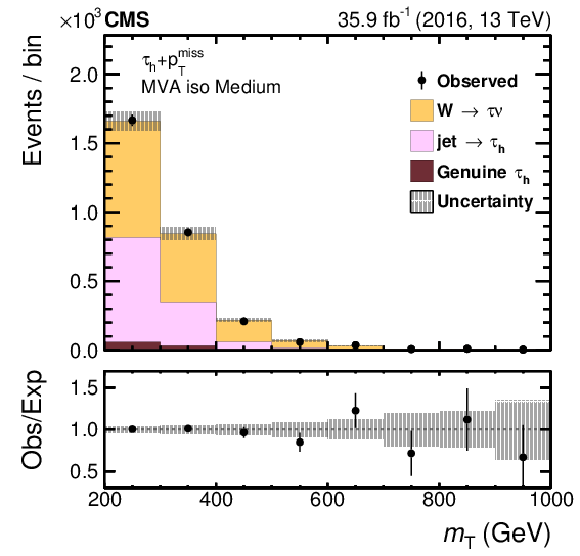
png pdf	Figure 9: The $ {m_{\mathrm {T}}} $ distribution for selected $ {\mathrm {W}}\to {\tau} {\nu}$ (left) and $ {\mathrm {W}}\to {{\mu}} {\nu}$ (right) events after the maximum likelihood fit. The medium WP of the MVA-based isolation discriminant is applied to select $ {\mathrm {W}}\to {\tau} {\nu}$ events. The electroweak background contribution includes diboson and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands to the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 9-a: The $ {m_{\mathrm {T}}} $ distribution for selected $ {\mathrm {W}}\to {\tau} {\nu}$ events after the maximum likelihood fit. The medium WP of the MVA-based isolation discriminant is applied to select $ {\mathrm {W}}\to {\tau} {\nu}$ events. The electroweak background contribution includes diboson and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands to the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 9-b: The $ {m_{\mathrm {T}}} $ distribution for selected $ {\mathrm {W}}\to {{\mu}} {\nu}$ events after the maximum likelihood fit. The electroweak background contribution includes diboson and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands to the quadratic sum of the statistical and systematic uncertainties after the fit.
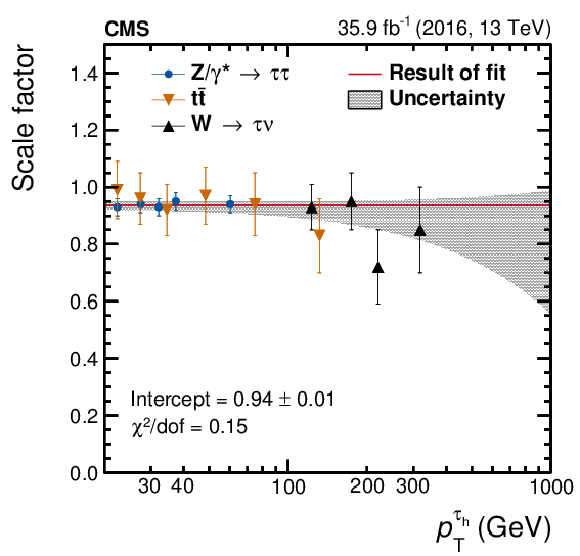
png pdf	Figure 10: Fit of the measured scale factors to a constant value in the $ {{\tau} _\mathrm {h}} $ identification efficiency, for the tight WP of the MVA-based isolation discriminant in $ {\mathrm {Z}}/ {\gamma ^{*}} $, $ {{\mathrm {t}\overline {\mathrm {t}}}} $, and W events, as a function of $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$. The shaded band represents the uncertainties in the fit, where the result is combined with the difference obtained using a first-order polynomial instead of a constant for the downward deviations, which also contain an additional contribution from the uncertainty in track-reconstruction efficiency.
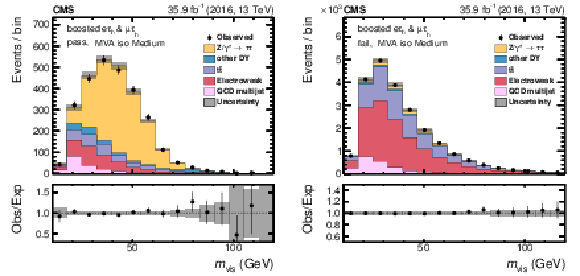
png pdf	Figure 11: Fitted distributions to the passing (left) and failing (right) events for $ {{\tau} _\mathrm {h}} $ from highly boosted $ {\tau}$ lepton pairs that pass the medium WP of the MVA-based isolation discriminant. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 11-a: Fitted distributions to the passing events for $ {{\tau} _\mathrm {h}} $ from highly boosted $ {\tau}$ lepton pairs that pass the medium WP of the MVA-based isolation discriminant. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
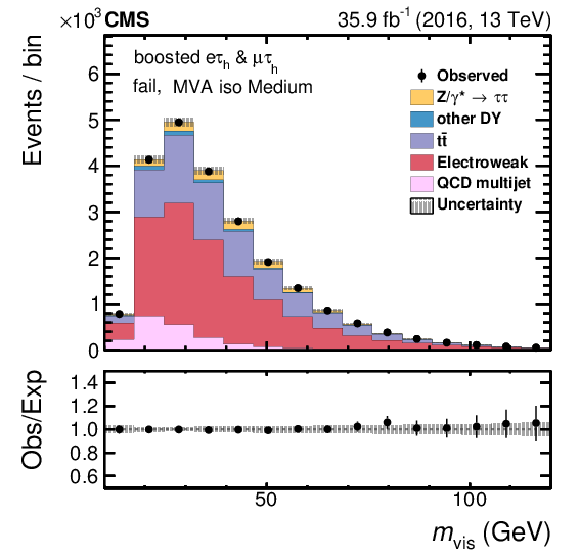
png pdf	Figure 11-b: Fitted distributions to the failing events for $ {{\tau} _\mathrm {h}} $ from highly boosted $ {\tau}$ lepton pairs that pass the medium WP of the MVA-based isolation discriminant. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
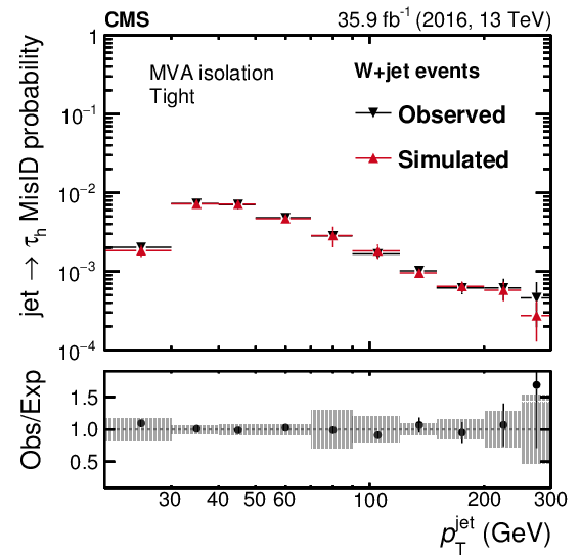
png pdf	Figure 12: Probabilities for quark and gluon jets in W+jet events to pass the loose (uppermost), medium (middle), and tight (lowest) WPs of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$ (left) and $\eta ^\text {jet}$ (right). The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 12-a: Probability for quark and gluon jets in W+jet events to pass the loose WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
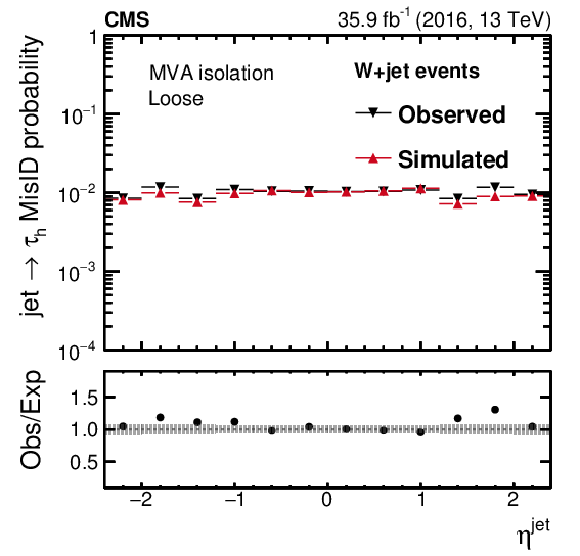
png pdf	Figure 12-b: Probability for quark and gluon jets in W+jet events to pass the loose WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
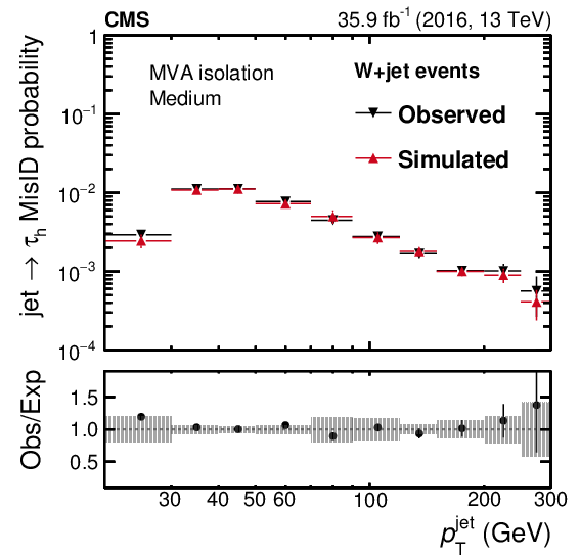
png pdf	Figure 12-c: Probability for quark and gluon jets in W+jet events to pass the medium WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
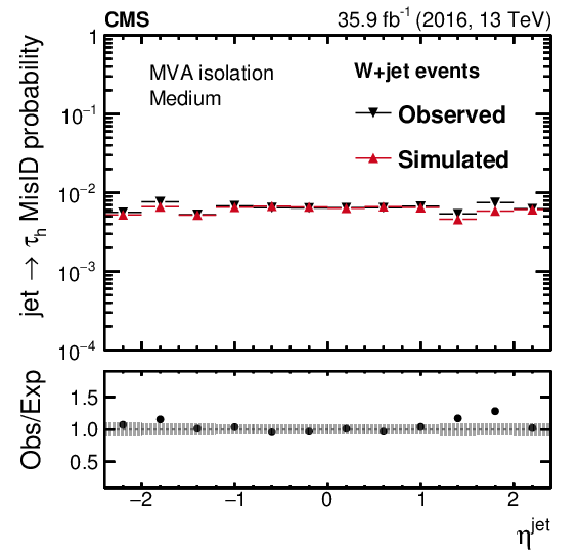
png pdf	Figure 12-d: Probability for quark and gluon jets in W+jet events to pass the medium WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 12-e: Probability for quark and gluon jets in W+jet events to pass the tight WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 12-f: Probability for quark and gluon jets in W+jet events to pass the ltight WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
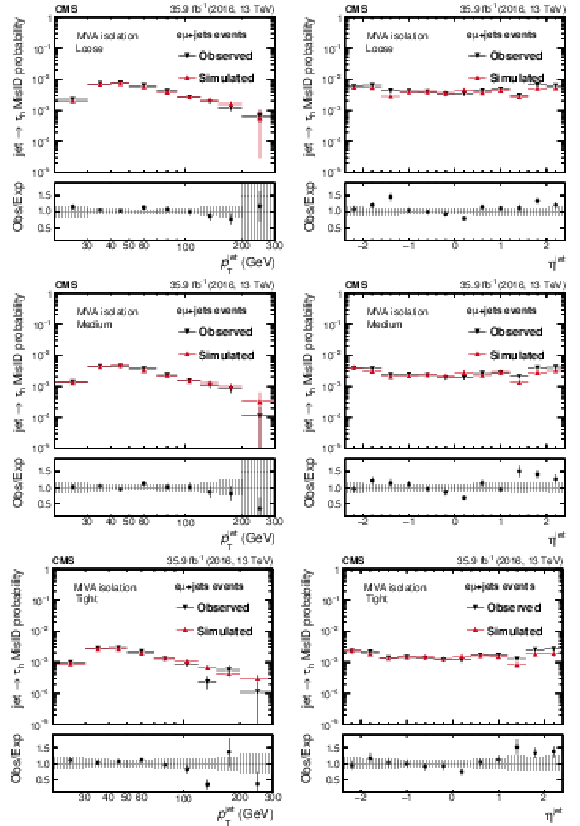
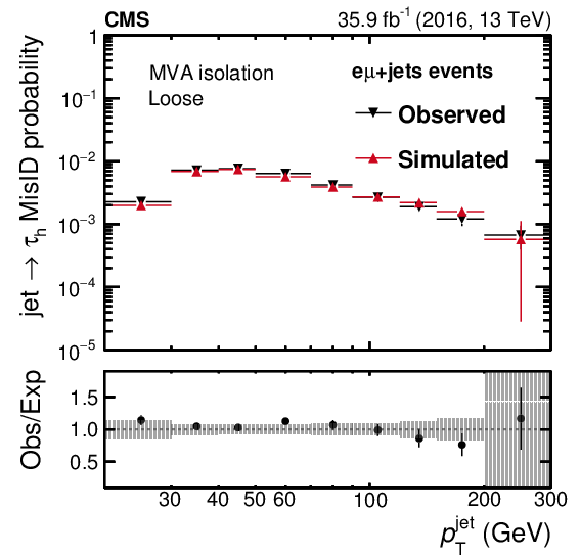
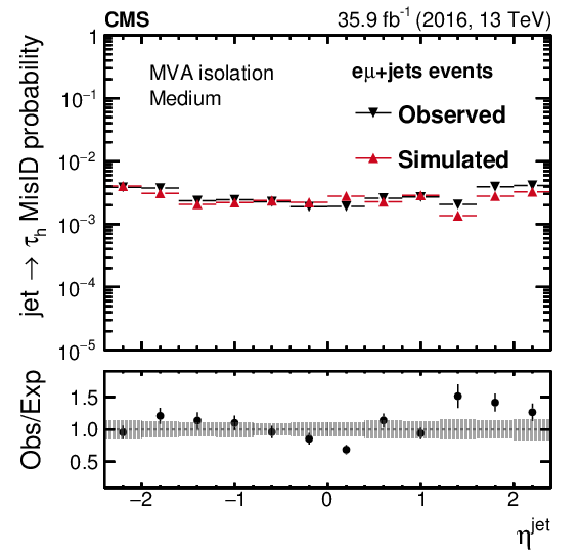
png pdf	Figure 13: Probabilities for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the loose (uppermost), medium (middle), and tight (lowest) WPs of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$ (left) and $\eta ^\text {jet}$ (right). The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 13-a: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the loose WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 13-b: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the loose WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 13-c: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the medium WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
png pdf	Figure 13-d: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the medium WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
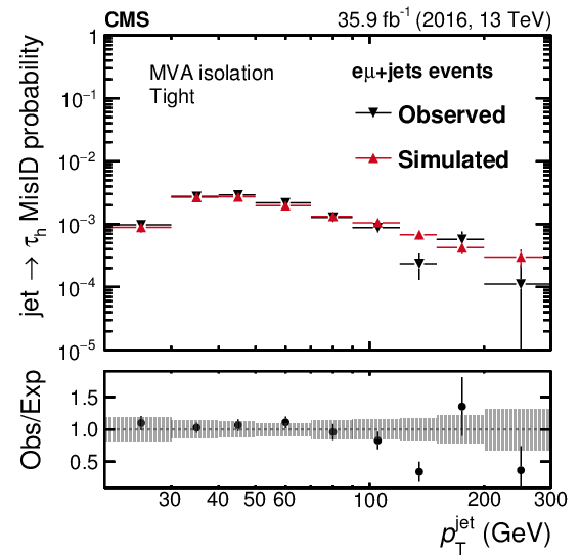
png pdf	Figure 13-e: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the tight WP of the MVA-based isolation discriminant as a function of $ {p_{\mathrm {T}}} ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
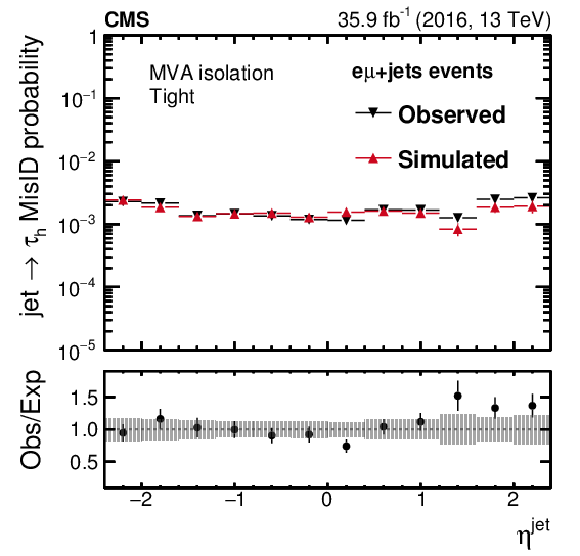
png pdf	Figure 13-f: Probability for quark and gluon jets in $ {\mathrm {e}} {{\mu}}$+jets events to pass the tight WP of the MVA-based isolation discriminant as a function of $\eta ^\text {jet}$. The misidentification probabilities in data are compared to expectations from simulation. The vertical bars in the simulated and observed misidentification probabilities include statistical uncertainties from the limited event count in both data and simulated samples, including the background subtraction. The shaded bands contain the systematic uncertainties related to background subtraction and the jet energy scale.
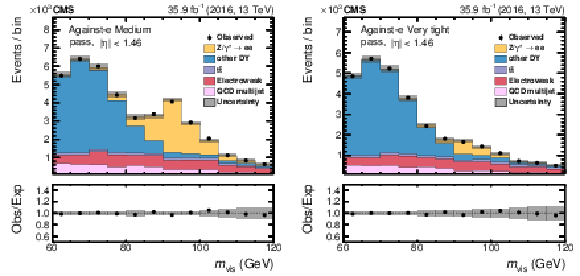
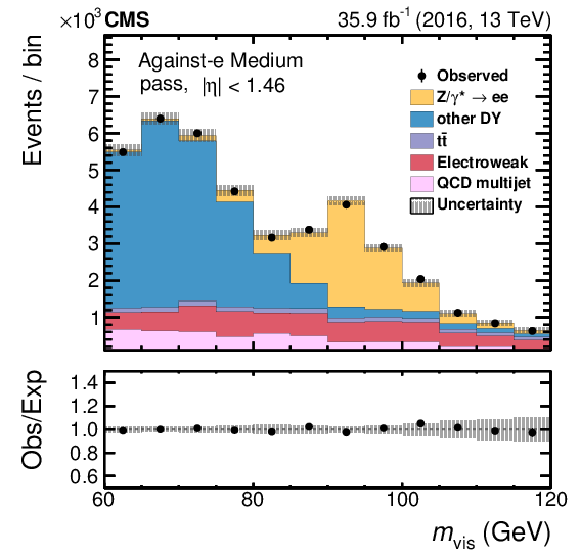
png pdf	Figure 14: Fitted distributions in $ {m_\text {vis}}$ in the passing category for the medium (left) and very tight (right) WPs of the against-$ {\mathrm {e}}$ discriminant in the barrel region. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
png pdf	Figure 14-a: Fitted distribution in $ {m_\text {vis}}$ in the passing category for the medium WP of the against-$ {\mathrm {e}}$ discriminant in the barrel region. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
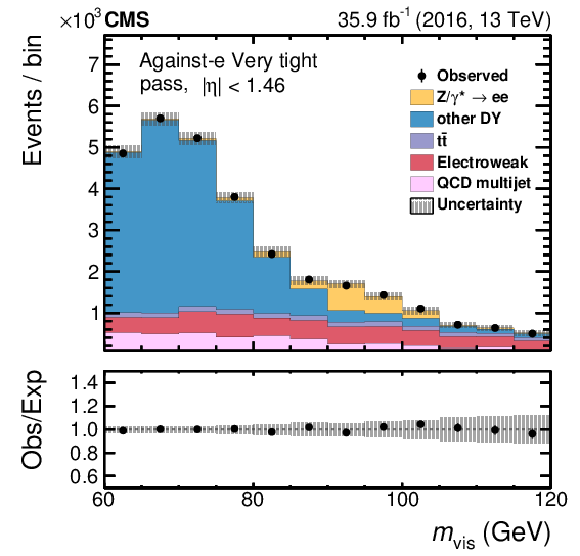
png pdf	Figure 14-b: Fitted distribution in $ {m_\text {vis}}$ in the passing category for the very tight WP of the against-$ {\mathrm {e}}$ discriminant in the barrel region. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
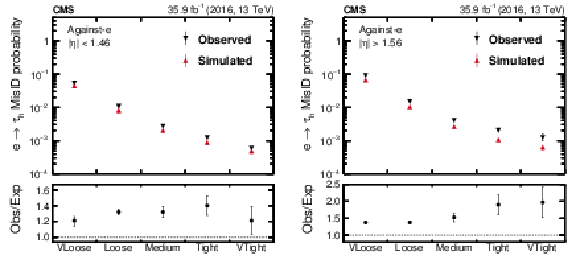
png pdf	Figure 15: Probability for electrons to pass different working points of the against-$ {\mathrm {e}}$ discriminant, split into the barrel (left) and endcap (right) regions. For each working point, the $ {\mathrm {e}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
png pdf	Figure 15-a: Probability for electrons to pass different working points of the against-$ {\mathrm {e}}$ discriminant, in the barrel region. For each working point, the $ {\mathrm {e}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
png pdf	Figure 15-b: Probability for electrons to pass different working points of the against-$ {\mathrm {e}}$ discriminant, in the endcap region. For each working point, the $ {\mathrm {e}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
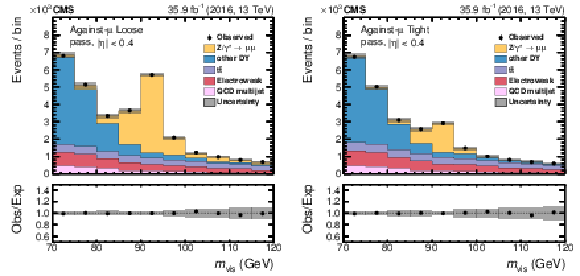
png pdf	Figure 16: Fitted distribution in $ {m_\text {vis}}$ in the passing category for the loose (left) and tight (right) WPs of the against-$ {{\mu}}$ discriminant in the region of $ {| \eta |} < $ 0.4. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
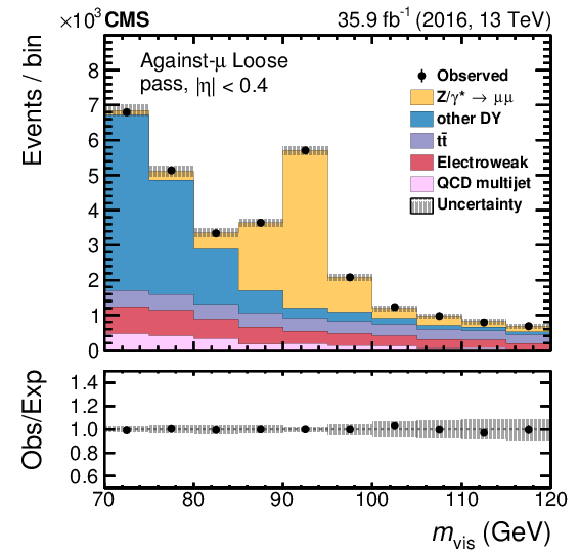
png pdf	Figure 16-a: Fitted distribution in $ {m_\text {vis}}$ in the passing category for the loose WP of the against-$ {{\mu}}$ discriminant in the region of $ {| \eta |} < $ 0.4. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
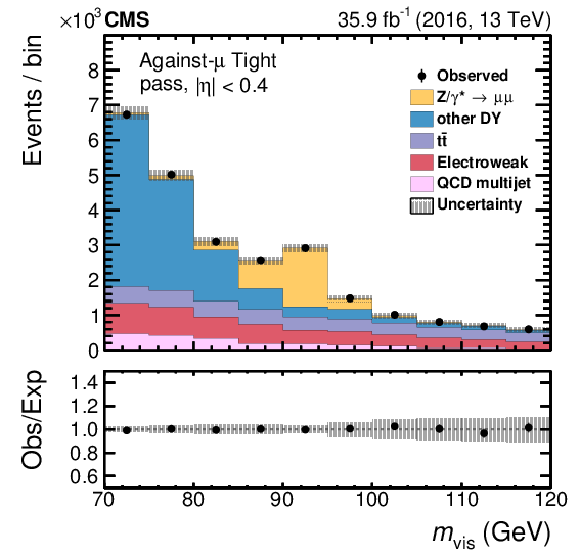
png pdf	Figure 16-b: Fitted distribution in $ {m_\text {vis}}$ in the passing category for the tight WP of the against-$ {{\mu}}$ discriminant in the region of $ {| \eta |} < $ 0.4. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars correspond to the small (not visible) statistical uncertainties in the data points (68% frequentist confidence intervals), while the shaded bands provide the quadratic sum of the statistical and systematic uncertainties after the fit.
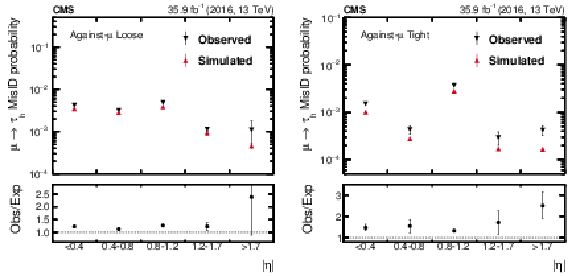
png pdf	Figure 17: Probability for muons to pass the loose (left) and tight (right) WPs of the against-$ {{\mu}}$ discriminant, as a function of the $ {| \eta |}$ of the probe. For each working point, the $ {{\mu}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
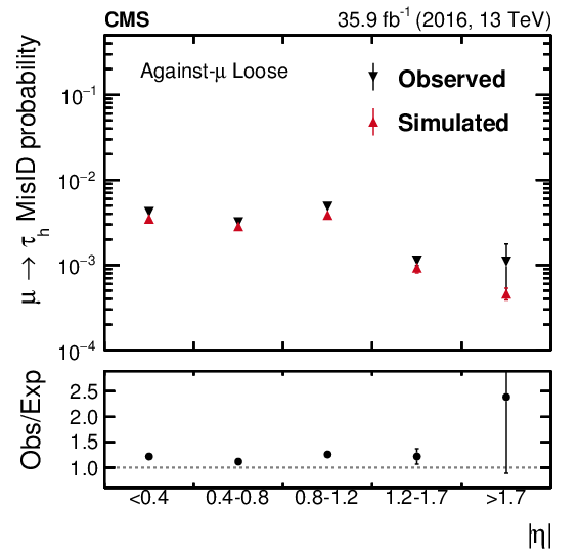
png pdf	Figure 17-a: Probability for muons to pass the loose WP of the against-$ {{\mu}}$ discriminant, as a function of the $ {| \eta |}$ of the probe. The $ {{\mu}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
png pdf	Figure 17-b: Probability for muons to pass the tight WP of the against-$ {{\mu}}$ discriminant, as a function of the $ {| \eta |}$ of the probe. The $ {{\mu}} \rightarrow {{\tau} _\mathrm {h}} $ misidentification probability is defined as the fraction of probes passing that working point relative to the total number of probes. Vertical bars correspond to the statistical and the quadratic sum of the statistical and systematic uncertainties, respectively, for simulated and observed data.
png pdf	Figure 18: The distributions in $m_{{{\tau} _\mathrm {h}}}$ for $ {{\mu}} {{\tau} _\mathrm {h}} $ events in the $ {\mathrm {h}^{\pm} {\pi ^0}} $ decay channel. The data are compared to predictions with different shifts applied to the $ {{\tau} _\mathrm {h}} $ energy scale: 0% (upper), $-$6% (lower left), and $+$6% (lower right). The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars (smaller than the symbol size) correspond to the statistical uncertainty in the data points (68% frequentist confidence intervals), while the shaded bands provide the expected systematic uncertainties.
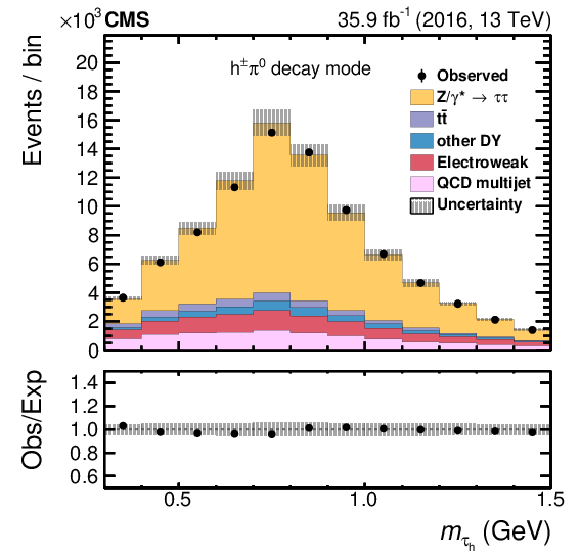
png pdf	Figure 18-a: The distributions in $m_{{{\tau} _\mathrm {h}}}$ for $ {{\mu}} {{\tau} _\mathrm {h}} $ events in the $ {\mathrm {h}^{\pm} {\pi ^0}} $ decay channel. The data are compared to predictions with 0% shift applied to the $ {{\tau} _\mathrm {h}} $ energy scale. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars (smaller than the symbol size) correspond to the statistical uncertainty in the data points (68% frequentist confidence intervals), while the shaded bands provide the expected systematic uncertainties.
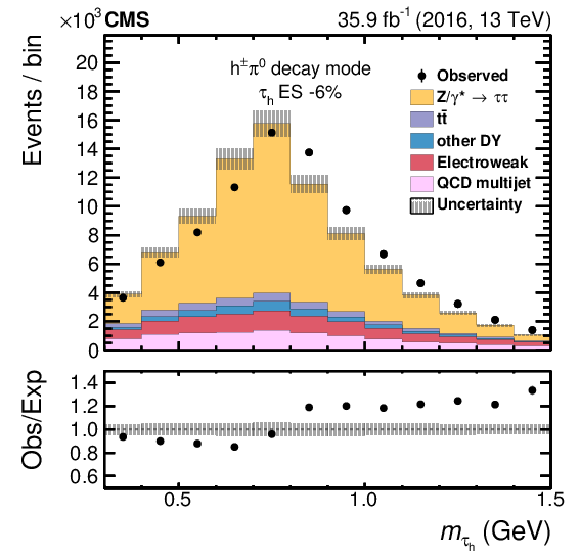
png pdf	Figure 18-b: The distributions in $m_{{{\tau} _\mathrm {h}}}$ for $ {{\mu}} {{\tau} _\mathrm {h}} $ events in the $ {\mathrm {h}^{\pm} {\pi ^0}} $ decay channel. The data are compared to predictions with $-$6% shift applied to the $ {{\tau} _\mathrm {h}} $ energy scale. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars (smaller than the symbol size) correspond to the statistical uncertainty in the data points (68% frequentist confidence intervals), while the shaded bands provide the expected systematic uncertainties.
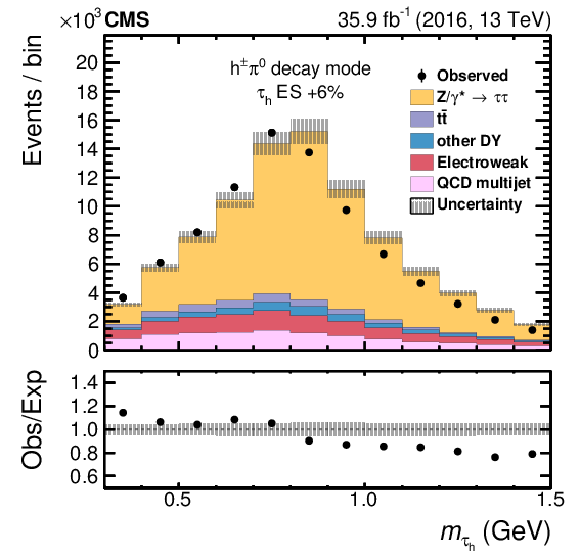
png pdf	Figure 18-c: The distributions in $m_{{{\tau} _\mathrm {h}}}$ for $ {{\mu}} {{\tau} _\mathrm {h}} $ events in the $ {\mathrm {h}^{\pm} {\pi ^0}} $ decay channel. The data are compared to predictions with $+$6% shift applied to the $ {{\tau} _\mathrm {h}} $ energy scale. The electroweak background includes contributions from W+jets (dominating), diboson, and single top quark events. Vertical bars (smaller than the symbol size) correspond to the statistical uncertainty in the data points (68% frequentist confidence intervals), while the shaded bands provide the expected systematic uncertainties.
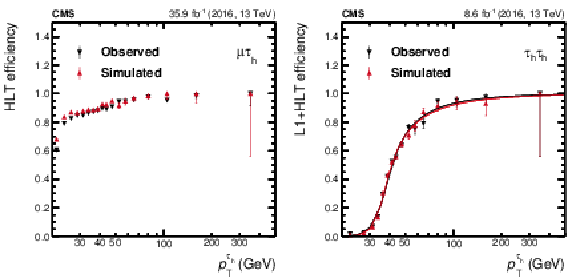
png pdf	Figure 19: Single-$ {{\tau} _\mathrm {h}} $ efficiency of the $ {{\mu}} {{\tau} _\mathrm {h}} $ (left) and $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ (right) triggers. The efficiency is computed per single $ {{\tau} _\mathrm {h}} $, using the tag-and-probe method as a function of the offline-reconstructed $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$. Observed data are compared to simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events selected through the same procedure. Vertical bars correspond to the statistical uncertainties. The plot on the right has data points fitted using a cumulative (integral) distribution of the Crystal Ball function [76].
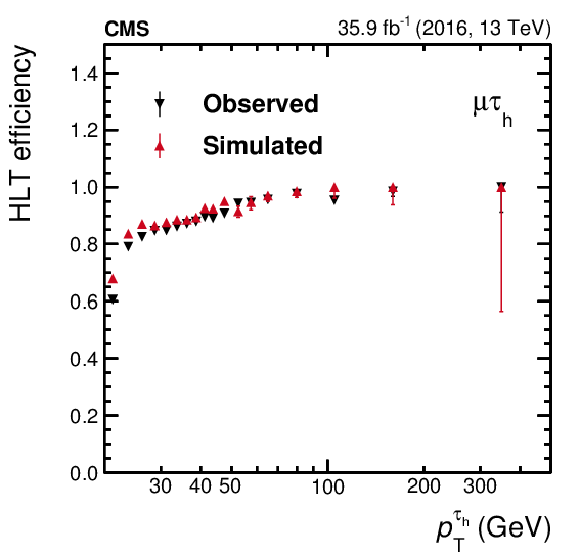
png pdf	Figure 19-a: Single-$ {{\tau} _\mathrm {h}} $ efficiency of the $ {{\mu}} {{\tau} _\mathrm {h}} $ trigger. The efficiency is computed per single $ {{\tau} _\mathrm {h}} $, using the tag-and-probe method as a function of the offline-reconstructed $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$. Observed data are compared to simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events selected through the same procedure. Vertical bars correspond to the statistical uncertainties.
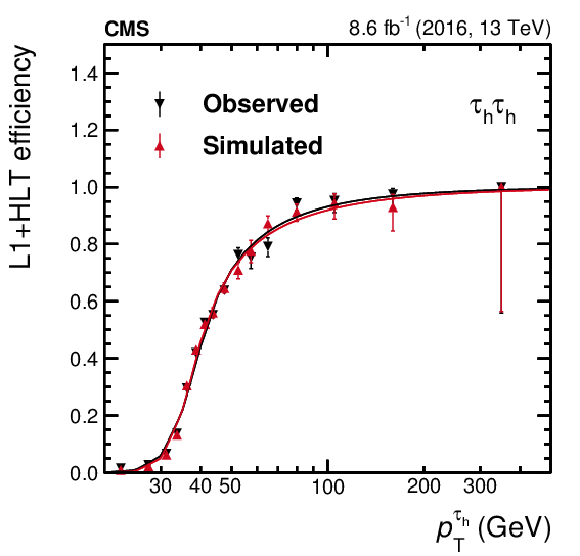
png pdf	Figure 19-b: Single-$ {{\tau} _\mathrm {h}} $ efficiency of the $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ trigger. The efficiency is computed per single $ {{\tau} _\mathrm {h}} $, using the tag-and-probe method as a function of the offline-reconstructed $ {p_{\mathrm {T}}} ^{{{\tau} _\mathrm {h}}}$. Observed data are compared to simulated $ {\mathrm {Z}}/ {\gamma ^{*}} \to {\tau} {\tau}$ events selected through the same procedure. Vertical bars correspond to the statistical uncertainties. Data points are fitted using a cumulative (integral) distribution of the Crystal Ball function [76].

Tables
png pdf	Table 1: Tau lepton decays and their branching fractions.
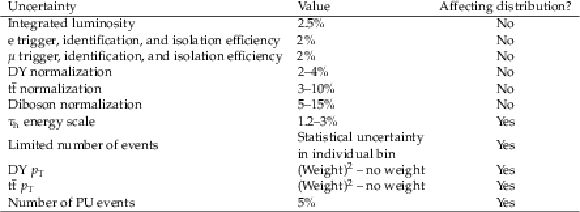
png pdf	Table 2: Systematic uncertainties affecting the measurements described in Sections 9-12. Given are the source of the uncertainty and whether the distribution in question is affected.
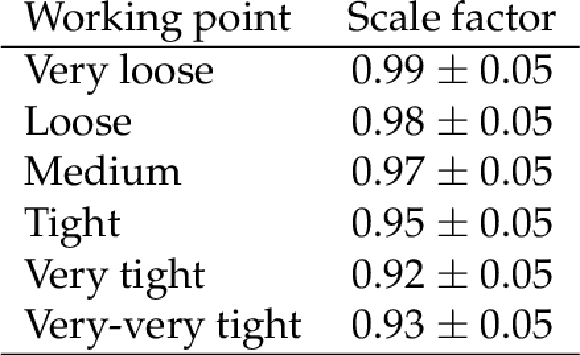
png pdf	Table 3: Data-to-simulation scale factors for different MVA-based isolation working points with $\Delta R=$ 0.5, measured using $ {\mathrm {Z}}/ {\gamma ^{*}} $ events. An uncertainty of 3.9% is added in quadrature to the uncertainty returned by the fit to account for the uncertainty in track reconstruction efficiency.
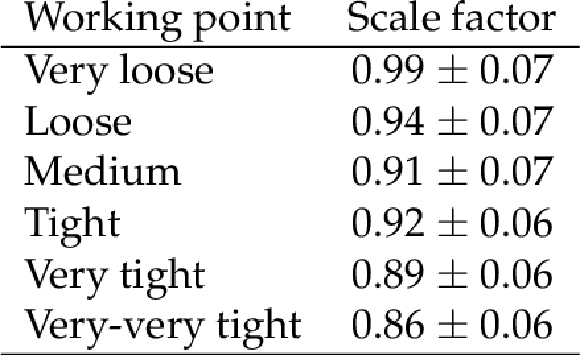
png pdf	Table 4: Data-to-simulation scale factors for different MVA-based isolation working points obtained from $ {{\mathrm {t}\overline {\mathrm {t}}}} $ events.
png pdf	Table 5: The scale factor in the $ {{\tau} _\mathrm {h}} $ identification efficiency, the normalization of W boson production with $m_{{\mathrm {W}}} > $ 200 GeV, $r_{{\mathrm {W}}}$, and the correlation coefficient between the two quantities obtained from the fit, measured for MVA-based discriminants using $\Delta R =$ 0.5 in $ {\mathrm {W}}\to {\tau} {\nu}$ events.
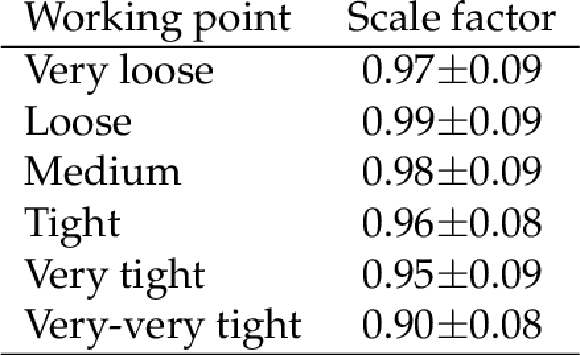
png pdf	Table 6: Data-to-simulation scale factors for different working points of the MVA-based isolation discriminant, using highly boosted $ {\mathrm {Z}}/ {\gamma ^{*}} $ events decaying to $ {\tau}$ lepton pairs.
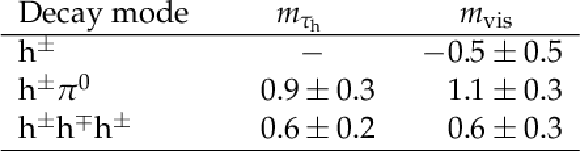
png pdf	Table 7: Numerical results of the tau energy scale measurements.
png pdf	Table 8: Triggers with $ {{\tau} _\mathrm {h}} $ candidates used to record pp collisions in 2016: the final state (Channel), HLT $ {p_{\mathrm {T}}} $ thresholds and $ {{\tau} _\mathrm {h}} $ isolation working point, L1 $ {p_{\mathrm {T}}} $ thresholds, peak instantaneous luminosity ($ {\mathcal {L}} _\text {peak}$) in the period of operation as main trigger, and integrated luminosity (${\mathcal {L}} $) collected with the trigger. The $ {{\tau} _\mathrm {h}} {{\tau} _\mathrm {h}} $ and $ {{\tau} _\mathrm {h}} {{p_{\mathrm {T}}} ^\text {miss}} $ triggers are seeded by sets of L1 triggers with thresholds dynamically adjusted as a function of the instantaneous luminosity to maintain a constant L1 rate, given by the ranges in $ {p_{\mathrm {T}}}$. The trigger $ {p_{\mathrm {T}}} $ thresholds and isolation criteria were successively tightened over the data-taking period to keep the rate of events passing HLT approximately constant with increasing instantaneous luminosity.

Summary

The "hadron-plus-strips'' algorithm developed at the CMS experiment to reconstruct and identify $\tau\to\text{hadrons}+\nu_{\tau}$ decays in proton-proton collisions at $\sqrt{s}=$ 7 and 8 TeV, as presented in Ref. [24], has been improved. The changes include a dynamic strip reconstruction, the reconstruction of highly boosted $\tau$ lepton pairs, and the introduction of additional variables in the multivariate-analysis discriminants used to reject jets and electrons. The isolation discriminants have also been optimized to cope with the large pileup of events in $\sqrt{s} = $ 13 TeV proton-proton runs. The performance of the improved algorithm has been measured using 35.9 fb$^{-1}$ of data recorded during 2016 at $\sqrt{s} = $ 13 TeV. The ${\tau_\mathrm{h}}$ identification efficiency in data at low, intermediate, and high transverse momenta, as well as for highly Lorentz-boosted $\tau$ lepton pairs, is similar to that expected from Monte Carlo simulation, while differences of 10-20% are found between data and simulation for the $\text{jet} \mapsto {\tau_\mathrm{h}}$ misidentification probability. The $\mathrm{e} \mapsto {\tau_\mathrm{h}}$ and $\mu \mapsto {\tau_\mathrm{h}}$ misidentification probabilities are smaller than those of the previous version of the algorithm under the same running conditions, while maintaining a high efficiency for the selection of genuine ${\tau_\mathrm{h}}$ candidates. The corresponding data-to-simulation scale factors have also been determined. The energy scale of ${\tau_\mathrm{h}}$ candidates is measured, and its response relative to Monte Carlo simulation is found to be close to unity. Finally, a specialized ${\tau_\mathrm{h}}$ reconstruction and identification algorithm has been used in the high-level trigger, and its performance has been presented.

References
1	ATLAS, CMS Collaboration	Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}= $ 7 and 8 TeV	JHEP 08 (2016) 045	1606.02266
2	CMS Collaboration	Observation of the Higgs boson decay to a pair of tau leptons	PLB 779 (2018) 283	CMS-HIG-16-043 1708.00373
3	P. Fayet	Supergauge Invariant Extension of the Higgs Mechanism and a Model for the Electron and its Neutrino	NPB 90 (1975) 104
4	P. Fayet	Spontaneously Broken Supersymmetric Theories of Weak, Electromagnetic and Strong Interactions	PLB 69 (1977) 489
5	CMS Collaboration	Search for neutral MSSM Higgs bosons decaying to a pair of tau leptons in pp collisions	JHEP 10 (2014) 160	CMS-HIG-13-021 1408.3316
6	CMS Collaboration	Search for a charged Higgs boson in pp collisions at $ \sqrt{s}= $ 8 TeV	JHEP 11 (2015) 018	CMS-HIG-14-023 1508.07774
7	ATLAS Collaboration	Search for the neutral Higgs bosons of the Minimal Supersymmetric Standard Model in pp collisions at $ \sqrt{s}= $ 7 ~TeV with the ATLAS detector	JHEP 02 (2013) 095	1211.6956
8	CMS Collaboration	Searches for a heavy scalar boson $ \mathrm{H} $ decaying to a pair of 125 GeV Higgs bosons $ \mathrm{hh} $ or for a heavy pseudoscalar boson $ \mathrm{A} $ decaying to $ \mathrm{Zh} $, in the final states with $ \mathrm{h} \to \tau \tau $	PLB 755 (2016) 217	CMS-HIG-14-034 1510.01181
9	CMS Collaboration	Search for lepton flavour violating decays of the Higgs boson to $ \mathrm{e}\tau $ and $ \mathrm{e}\mu $ in proton-proton collisions at $ \sqrt{s}= $ 8 TeV	PLB 763 (2016) 472	CMS-HIG-14-040 1607.03561
10	CMS Collaboration	Search for Lepton-Flavour-Violating Decays of the Higgs Boson	PLB 749 (2015) 337	CMS-HIG-14-005 1502.07400
11	ATLAS Collaboration	Search for additional heavy neutral Higgs and gauge bosons in the ditau final state produced in 36 fb$ ^{-1} $ of pp collisions at $ \sqrt{s}= $ 13 ~TeV with the ATLAS detector	JHEP 01 (2018) 055	1709.07242
12	CMS Collaboration	Search for Third-Generation Scalar Leptoquarks in the t$ \tau $ Channel in Proton-Proton Collisions at $ \sqrt{s} = $ 8 TeV	JHEP 07 (2015) 042	CMS-EXO-14-008 1503.09049
13	CMS Collaboration	Search for electroweak production of charginos in final states with two $ \tau $ leptons in pp collisions at $ \sqrt{s}= $ 8 TeV	JHEP 04 (2017) 018	CMS-SUS-14-022 1610.04870
14	CMS Collaboration	Search for physics beyond the standard model in events with $ \tau $ leptons, jets, and large transverse momentum imbalance in pp collisions at $ \sqrt{s} = $ 7 TeV	EPJC 73 (2013) 2493	CMS-SUS-12-004 1301.3792
15	ATLAS Collaboration	Search for the direct production of charginos and neutralinos in final states with tau leptons in $ \sqrt{s} = $ 13 TeV pp collisions with the ATLAS detector	EPJC 78 (2018) 154	1708.07875
16	ATLAS Collaboration	Search for top squarks decaying to tau sleptons in pp collisions at $ \sqrt{s} = $ 13 ~TeV with the ATLAS detector	PRD 98 (2018) 032008	1803.10178
17	CMS Collaboration	Search for high mass resonances decaying into $ \tau^- $ lepton pairs in pp collisions at $ \sqrt{s}= $ 7 TeV	PLB 716 (2012) 82	CMS-EXO-11-031 1206.1725
18	CMS Collaboration	Search for W' decaying to tau lepton and neutrino in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	PLB 755 (2016) 196	CMS-EXO-12-011 1508.04308
19	ATLAS Collaboration	Search for High-Mass Resonances Decaying to $ \tau\nu $ in pp Collisions at $ \sqrt{s}= $ 13 ~TeV with the ATLAS Detector	PRL 120 (2018) 161802	1801.06992
20	Particle Data Group	Review of Particle Physics	CPC 40 (2016) 100001
21	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s}= $ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
22	CMS Collaboration	Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JINST 13 (2018) P06015	CMS-MUO-16-001 1804.04528
23	CMS Collaboration	Performance of tau-lepton reconstruction and identification in CMS	JINST 7 (2012) P01001	CMS-TAU-11-001 1109.6034
24	CMS Collaboration	Reconstruction and identification of $ \tau $ lepton decays to hadrons and $ \nu_\tau $ at CMS	JINST 11 (2016) P01019	CMS-TAU-14-001 1510.07488
25	CMS Collaboration	CMS Tracking Performance Results from early LHC Operation	EPJC 70 (2010) 1165	CMS-TRK-10-001 1007.1988
26	CMS Collaboration	Description and performance of track and primary-vertex reconstruction with the CMS tracker	JINST 9 (2014) P10009	CMS-TRK-11-001 1405.6569
27	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
28	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
29	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
30	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with Parton Shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
31	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
32	S. Alioli, P. Nason, C. Oleari, and E. Re	NLO Higgs boson production via gluon fusion matched with shower in POWHEG	JHEP 04 (2009) 002	0812.0578
33	P. Nason and C. Oleari	NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG	JHEP 02 (2010) 037	0911.5299
34	T. Sjostrand, S. Mrenna, and P. Z. Skands	A Brief Introduction to PYTHIA 8.1	CPC 178 (2008) 852	0710.3820
35	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
36	J. Alwall et al.	Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions	EPJC 53 (2008) 473	0706.2569
37	S. Alioli, P. Nason, C. Oleari, and E. Re	NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions	JHEP 09 (2009) 111	0907.4076
38	E. Re	Single-top Wt-channel production matched with parton showers using the POWHEG method	EPJC 71 (2011) 1547	1009.2450
39	J. M. Campbell, R. K. Ellis, P. Nason, and E. Re	Top-Pair Production and Decay at NLO Matched with Parton Showers	JHEP 04 (2015) 114	1412.1828
40	R. Frederix and S. Frixione	Merging meets matching in MC@NLO	JHEP 12 (2012) 061	1209.6215
41	P. Nason and G. Zanderighi	$ W^+ W^- $, $ W Z $ and $ Z Z $ production in the POWHEG-BOX-V2	EPJC 74 (2014) 2702	1311.1365
42	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
43	K. Melnikov and F. Petriello	Electroweak gauge boson production at hadron colliders through $ \mathcal{O}(\alpha_{S}^{2}) $	PRD 74 (2006) 114017	hep-ph/0609070
44	K. Melnikov and F. Petriello	$ W $ Boson Production Cross Section at the Large Hadron Collider with $ \mathcal{O}(\alpha^2_s) $ Corrections	PRL 96 (2006) 231803	hep-ph/0603182
45	R. Gavin, Y. Li, F. Petriello, and S. Quackenbush	FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order	CPC 182 (2011) 2388	1011.3540
46	R. Gavin, Y. Li, F. Petriello, and S. Quackenbush	W Physics at the LHC with FEWZ 2.1	CPC 184 (2013) 208	1201.5896
47	Y. Li and F. Petriello	Combining QCD and electroweak corrections to dilepton production in the framework of the FEWZ simulation code	PRD 86 (2012) 094034	1208.5967
48	M. Czakon and A. Mitov	Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders	CPC 185 (2014) 2930	1112.5675
49	M. Czakon, P. Fiedler, and A. Mitov	Total Top-Quark Pair-Production Cross Section at Hadron Colliders Through $ \mathcal{O}(\alpha_{S}^{4}) $	PRL 110 (2013) 252004	1303.6254
50	J. M. Campbell, R. K. Ellis, and C. Williams	Vector boson pair production at the LHC	JHEP 07 (2011) 018	1105.0020
51	S. G. Bondarenko and A. A. Sapronov	NLO EW and QCD proton-proton cross section calculations with mcsanc-v1.01	CPC 184 (2013) 2343	1301.3687
52	J. R. Andersen et al.	Les Houches 2013: Physics at TeV Colliders: Standard Model Working Group Report		1405.1067
53	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
54	GEANT4 Collaboration	$ GEANT4--a $ simulation toolkit	NIMA 506 (2003) 250
55	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
56	M. Cacciari and G. P. Salam	Pileup subtraction using jet areas	PLB 659 (2008) 119	0707.1378
57	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
58	M. Cacciari, G. P. Salam, and G. Soyez	FastJet User Manual	EPJC 72 (2012) 1896	1111.6097
59	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
60	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV	JINST 13 (2018) P05011	CMS-BTV-16-002 1712.07158
61	C. J. Clopper and E. S. Pearson	The use of confidence or fiducial limits illustrated in the case of the binomial	Biometrika 26 (1934) 404
62	G. F. Giudice, R. Rattazzi, and J. D. Wells	Graviscalars from higher dimensional metrics and curvature Higgs mixing	NPB 595 (2001) 250	hep-ph/0002178
63	A. Oliveira	Gravity particles from Warped Extra Dimensions, predictions for LHC		1404.0102
64	M. Wobisch and T. Wengler	Hadronization corrections to jet cross-sections in deep inelastic scattering	in Monte Carlo generators for HERA physics. Proceedings, Workshop, Hamburg, Germany, 1998-1999, p. 270 1998	hep-ph/9907280
65	CMS Collaboration	CMS Technical Design Report for the Level-1 Trigger Upgrade	CDS
66	CMS Collaboration	Level 1 Tau trigger performance in 2016 data and VBF seeds at Level 1 trigger	CDS
67	CMS Collaboration	Electron and photon performance in CMS with first 12.9/fb of 2016 data	CDS
68	CDF Collaboration	Search for neutral MSSM Higgs bosons decaying to tau pairs in $ p\bar{p} $ collisions at $ \sqrt{s} = $ 1.96 TeV	PRL 96 (2006) 011802	hep-ex/0508051
69	CMS Collaboration	Measurements of Inclusive $ W $ and $ Z $ Cross Sections in pp Collisions at $ \sqrt{s}= $ 7 TeV	JHEP 01 (2011) 080	CMS-EWK-10-002 1012.2466
70	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
71	J. M. Campbell and R. K. Ellis	Update on vector boson pair production at hadron colliders	PRD 60 (1999) 113006	hep-ph/9905386
72	J. M. Campbell, R. K. Ellis, and W. T. Giele	A multi-threaded version of MCFM	EPJC 75 (2015) 246	1503.06182
73	R. Barlow and C. Beeston	Fitting using finite Monte Carlo samples	CPC 77 (1993) 219
74	J. S. Conway	Incorporating nuisance parameters in likelihoods for multisource spectra	in Proceedings, PHYSTAT 2011 Workshop on Statistical Issues Related to Discovery Claims in Search Experiments and Unfolding, p. 115 CERN, Geneva, Switzerland, January	1103.0354
75	CMS Collaboration	Measurement of the properties of a Higgs boson in the four-lepton final state	PRD 89 (2014) 092007	CMS-HIG-13-002 1312.5353
76	M. J. Oreglia	A study of the reactions $\psi' \to \gamma\gamma \psi$	PhD thesis, Stanford University, 1980 SLAC Report SLAC-R-236, see Appendix D

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2018 for the benefit of the CMS Collaboration