

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-19-006 | ||
| Search for supersymmetry in proton-proton collisions at 13 TeV in final states with jets and missing transverse momentum | ||
| CMS Collaboration | ||
| July 2019 | ||
| Abstract: Results are reported from a search for supersymmetric particles in the final state with multiple jets and large missing transverse momentum. The search uses a sample of proton-proton collisions at $\sqrt{s}= $ 13 TeV collected with the CMS detector in 2016-2018, corresponding to an integrated luminosity of 137 fb$^{-1}$, representing essentially the full LHC Run 2 data sample. The analysis is performed in a four-dimensional search region defined in terms of the number of jets, the number of tagged bottom quark jets, the scalar sum of jet transverse momenta, and the magnitude of the vector sum of jet transverse momenta. No significant excess in the event yield is observed relative to the expected background contributions from standard model processes. Limits on the pair production of gluinos and squarks are obtained in the framework of simplified models for supersymmetric particle production and decay processes. Assuming the lightest supersymmetric particle to be a neutralino, lower limits on the gluino mass as large as 2000 to 2310 GeV are obtained at 95% confidence level, while lower limits on the squark mass as large as 1190 to 1630 GeV are obtained, depending on the production scenario. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 10 (2019) 244. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
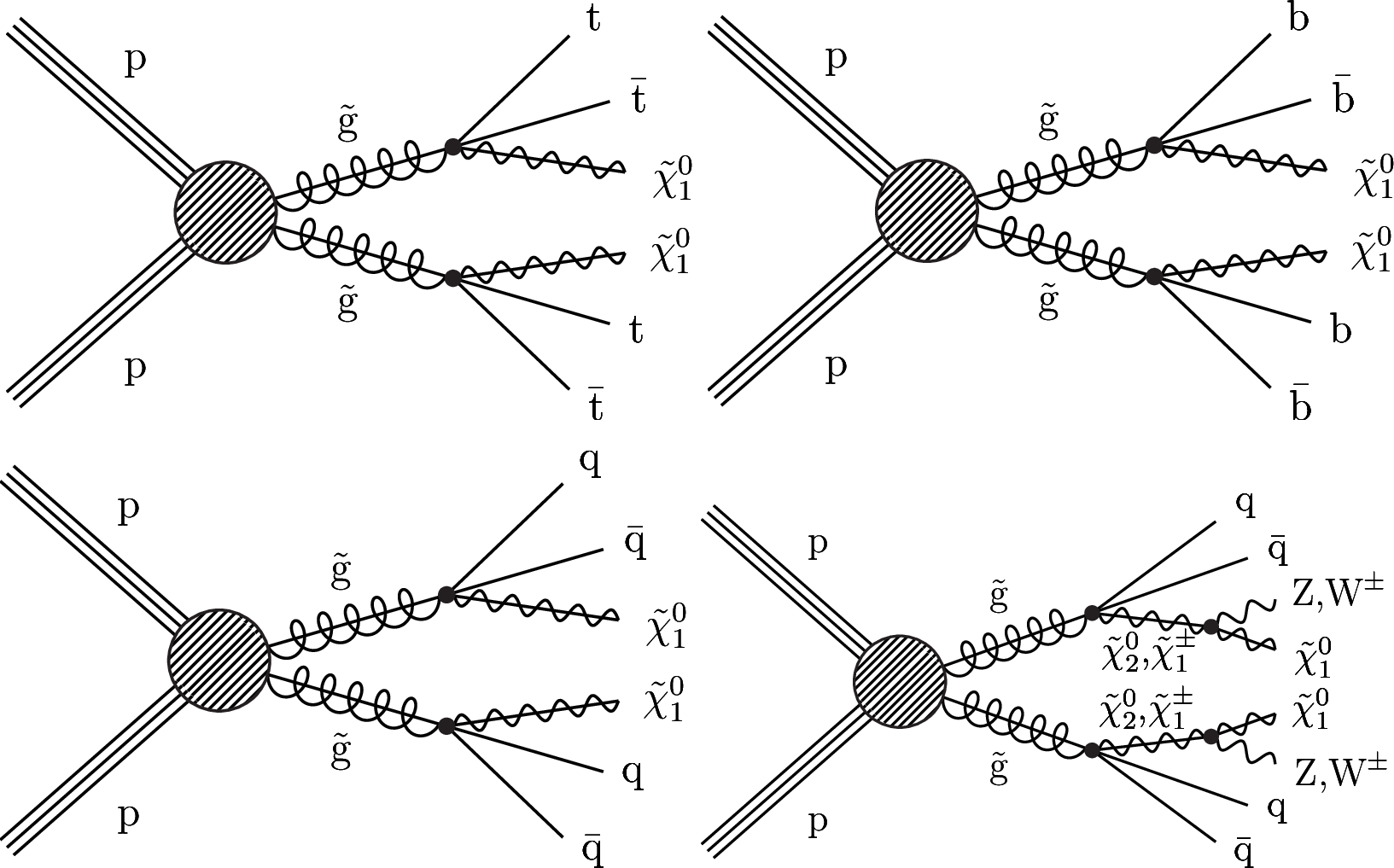
Figure 1:
Diagrams for the simplified models with direct gluino pair production considered in this study: (upper left) T1tttt, (upper right) T1bbbb, (lower left) T1qqqq, and (lower right) T5qqqqVV. |
png pdf |
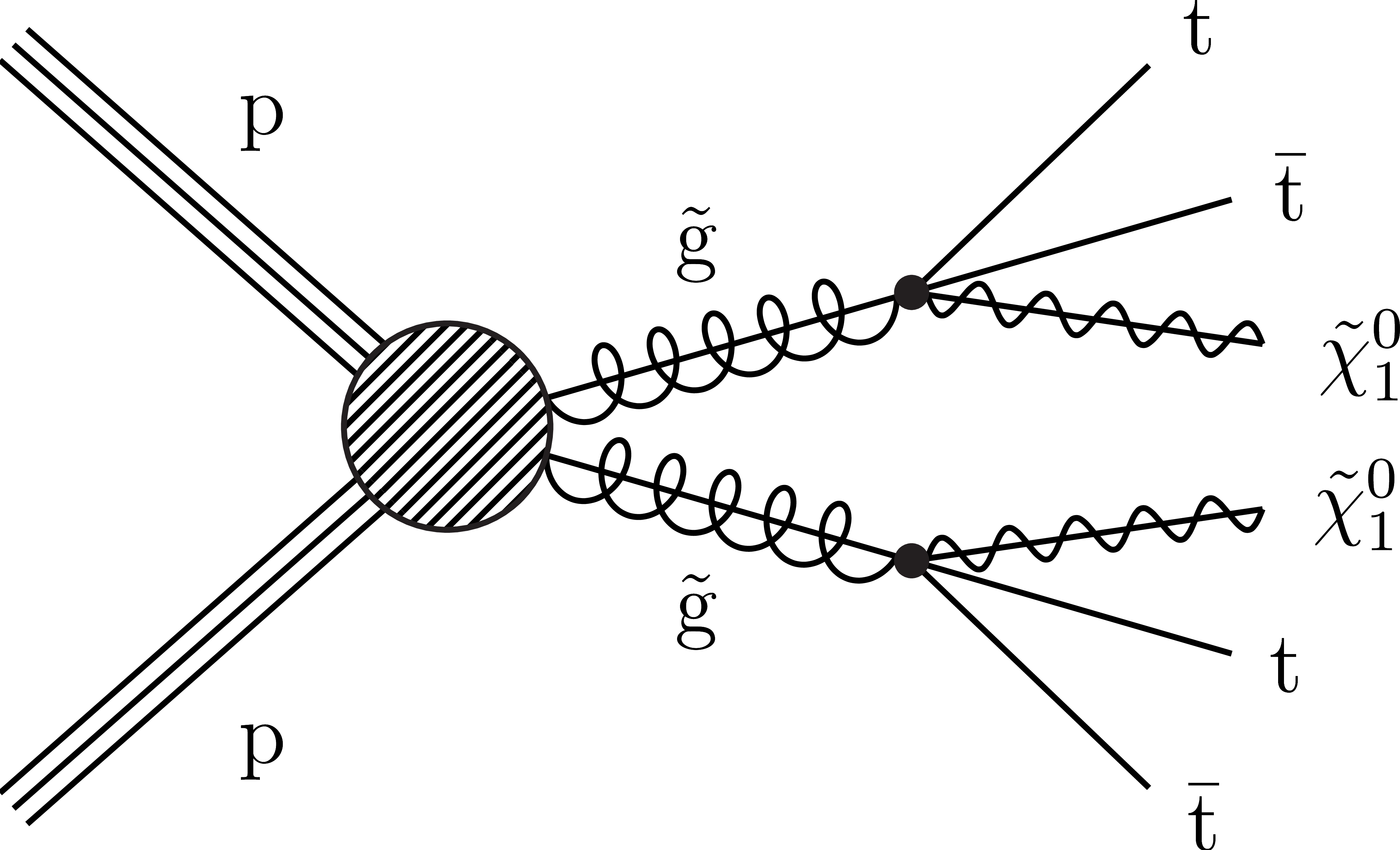
Figure 1-a:
Diagram for the T1tttt simplified model with direct gluino pair production. |

png pdf |
Figure 1-b:
Diagram for the T1bbbb simplified model with direct gluino pair production. |
png pdf |
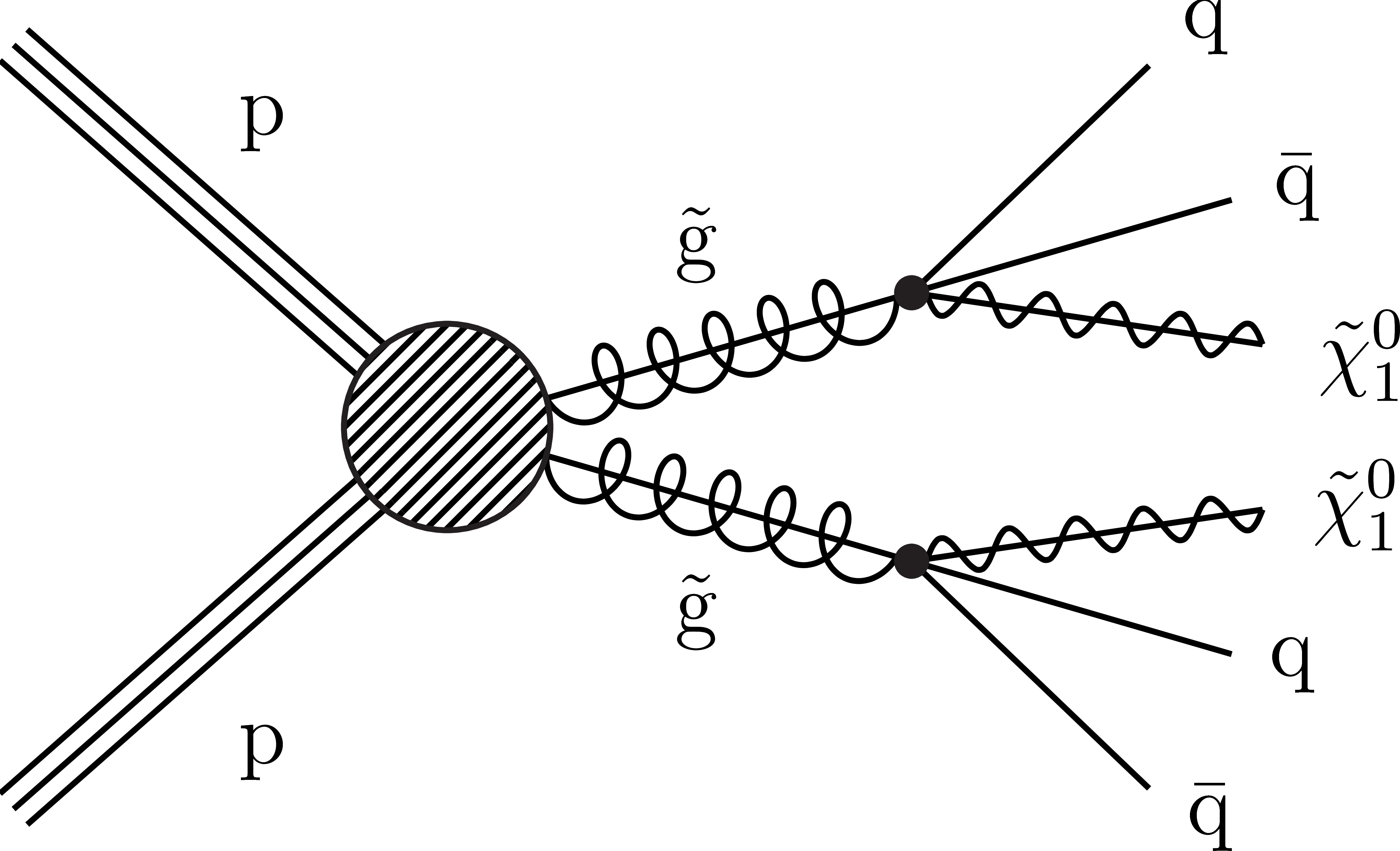
Figure 1-c:
Diagram for the T1qqqq simplified model with direct gluino pair production. |
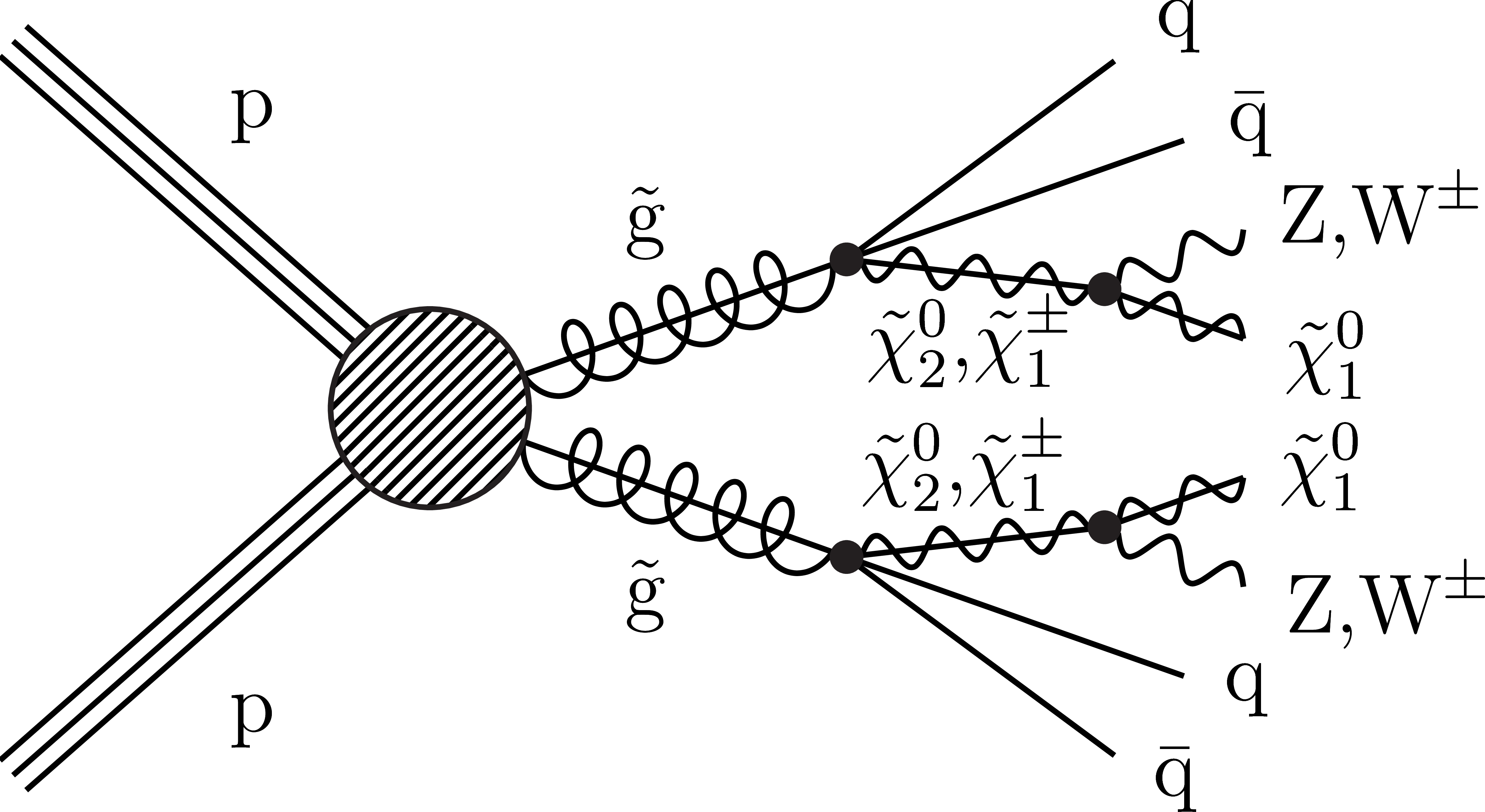
png pdf |
Figure 1-d:
Diagram for the T5qqqqVV simplified model with direct gluino pair production. |

png pdf |
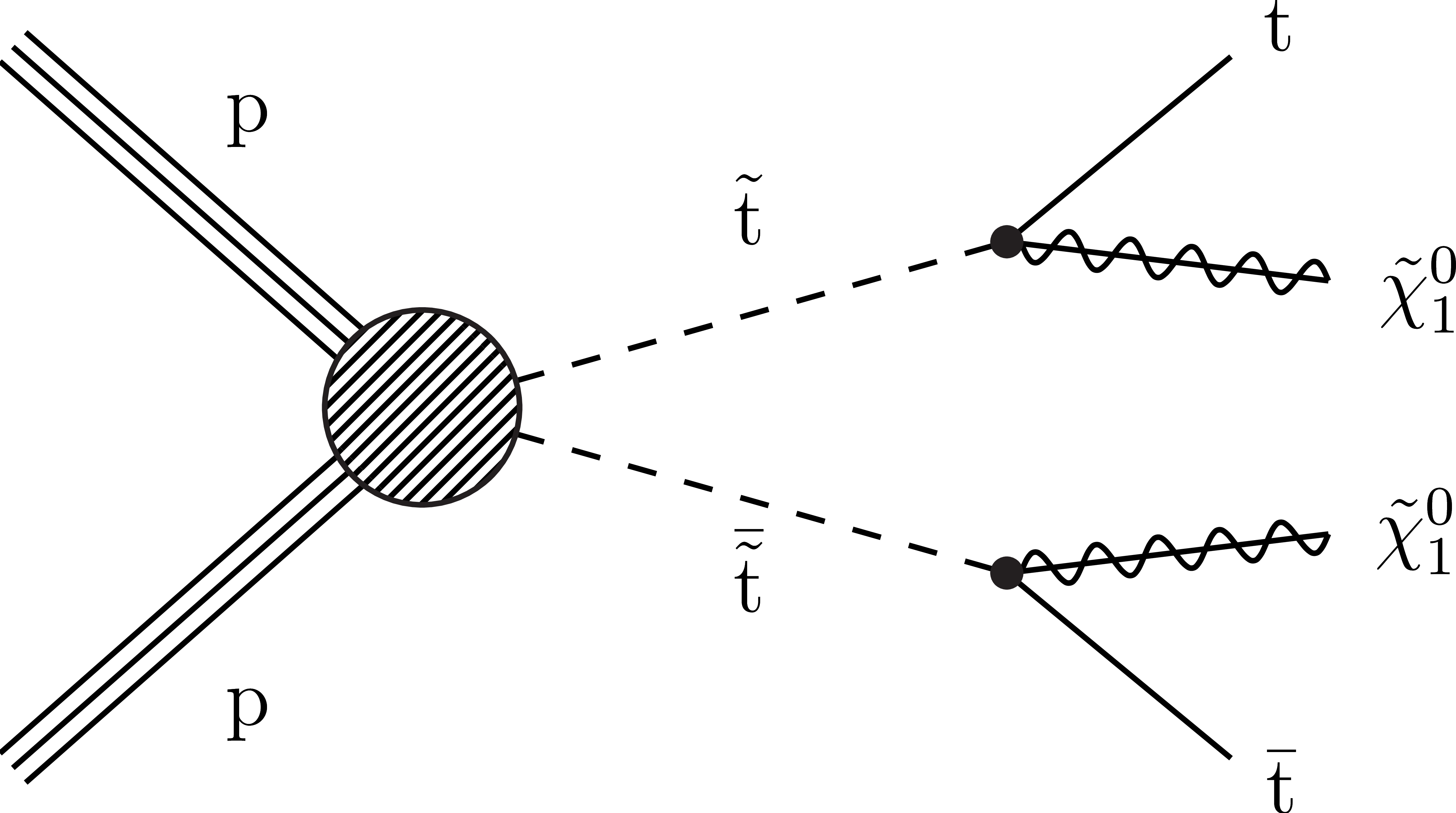
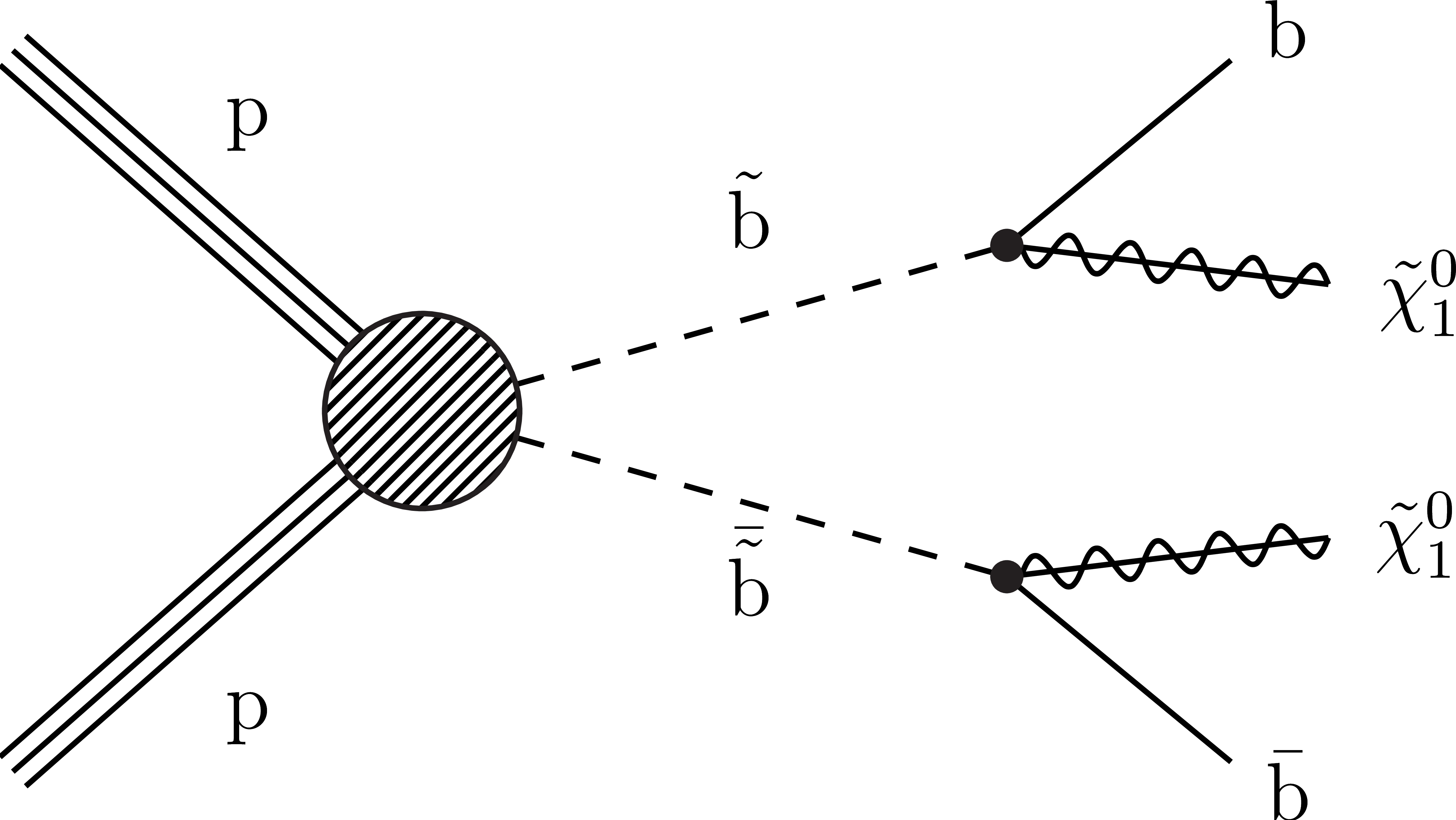
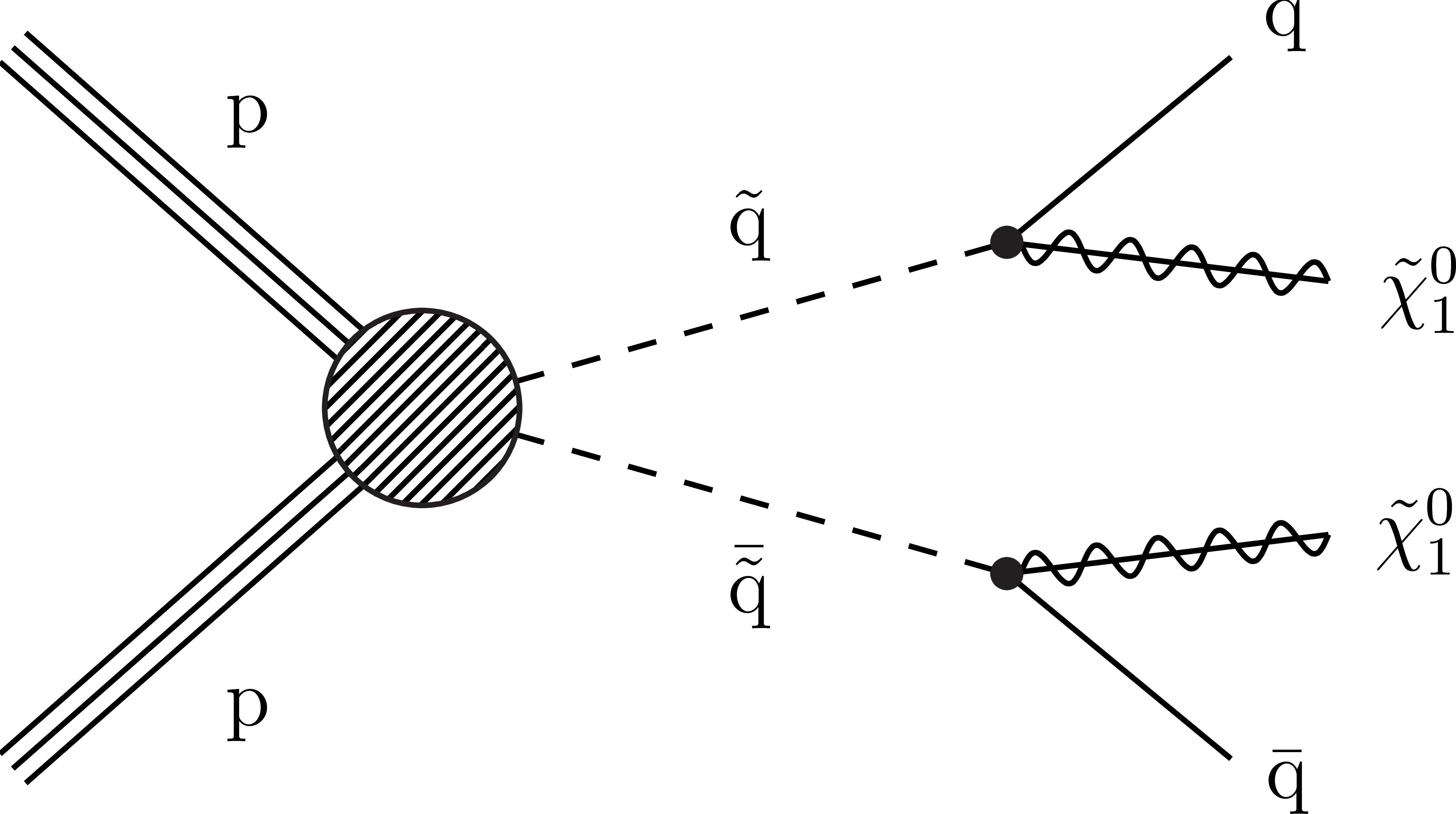
Figure 2:
Diagrams for the simplified models with direct squark pair production considered in this study: (left) T2tt, (middle) T2bb, and (right) T2qq. |
png pdf |
Figure 2-a:
Diagram for the T2tt simplified model with direct squark pair production. |
png pdf |
Figure 2-b:
Diagram for the T2bb simplified model with direct squark pair production. |
png pdf |
Figure 2-c:
Diagram for the T2qq simplified model with direct squark pair production. |
png pdf |
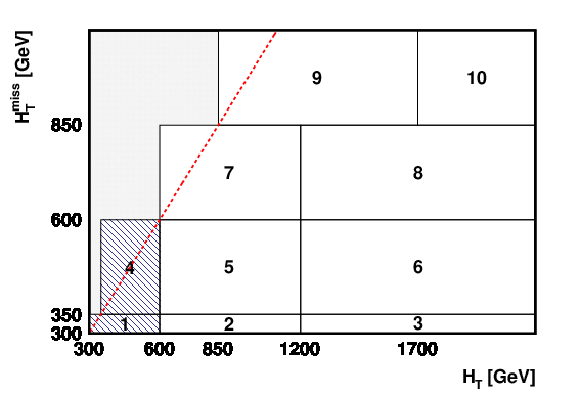
Figure 3:
Schematic illustration of the 10 kinematic search intervals in the ${H_{\mathrm {T}}^{\text {miss}}}$ versus ${H_{\mathrm {T}}}$ plane. The region above the red dashed line is excluded, as are all of regions 1 and 4 for $ {N_{\text {jet}}} \geq $ 8. The rightmost and topmost bins are unbounded, extending to $ {H_{\mathrm {T}}} =\infty $ and $ {H_{\mathrm {T}}^{\text {miss}}} =\infty $, respectively. |
png pdf |
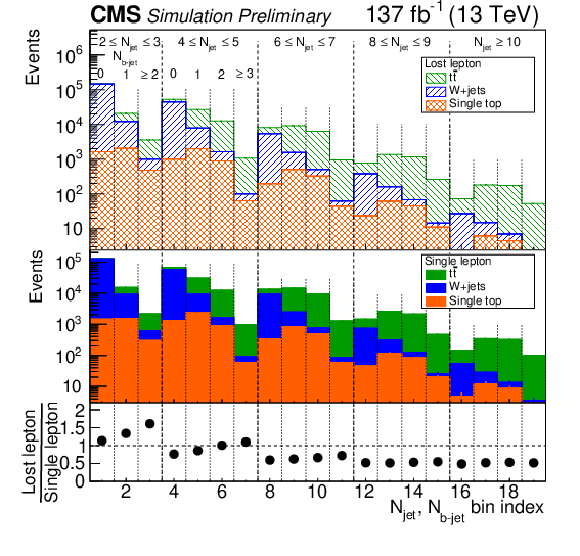
Figure 4:
(upper) The number of lost-lepton events in simulation, integrated over ${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$, as a function of ${N_{\text {jet}}}$ and ${N_{{\mathrm{b}}\text {-jet}}}$. (middle) Corresponding results from simulation for the number of events in the single-lepton control region. (lower) The ratio of the simulated lost-lepton to single-lepton results, with statistical uncertainties (too small to be visible). These ratios are equivalent to the transfer factors used in the evaluation of the lost-lepton background, except integrated over ${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$. |

png pdf |
Figure 5:
Comparison of the directly simulated ${\mathrm{t} {}\mathrm{\bar{t}}}$, single top quark, and W+jets background to the prediction obtained by treating the simulation like data, i.e., by applying the lost-lepton background determination procedure to the simulated single-lepton (e+$\mu$) control region events. The 10 results (8 for $ {N_{\text {jet}}} \geq $ 8) within each region delineated by vertical dashed lines correspond sequentially to the 10 (8) kinematic intervals in ${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$ listed in Table 1 and Fig. 3. The ratio plot in the lower panel is obtained through bin-by-bin division of the corresponding results in the upper panels, including the uncertainties, by the central values of the predicted "treat simulation like data'' results. All uncertainties are statistical only. |
png pdf |
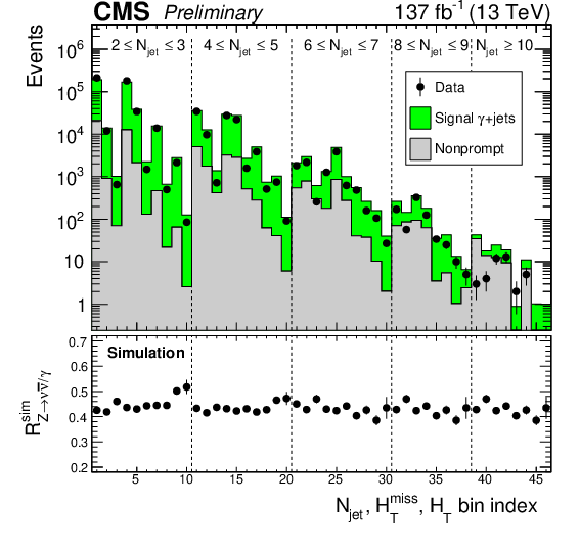
Figure 6:
(upper) The number of events in the ${\gamma}$+jets control region for data and simulation and (lower) the transfer factors ${\mathcal {R}_{{\mathrm{Z} \to \nu \bar{\nu}} /\gamma}^{\text {sim}}}$ from simulation. The respective results are shown for the 46 search bins with $ {N_{{\mathrm{b}}\text {-jet}}}=$ 0. The 10 results (8 for $ {N_{\text {jet}}} \geq $ 8) within each region delineated by vertical dashed lines correspond sequentially to the 10 (8) kinematic intervals in ${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$ listed in Table 1 and Fig. 3. The uncertainties are statistical only. For the upper plot, the simulated results show the stacked event rates for the ${\gamma}$+jets and nonprompt MC event samples, where "nonprompt'' refers to SM MC events other than ${\gamma}$+jets. The simulated nonprompt results are dominated by events from the QCD sample. Because of limited statistic precision in the simulated event samples at large ${N_{\text {jet}}}$, the transfer factors determined for the $8\leq {N_{\text {jet}}} \leq 9$ region are also used for the $ {N_{\text {jet}}} > 10$ region. |
png pdf |
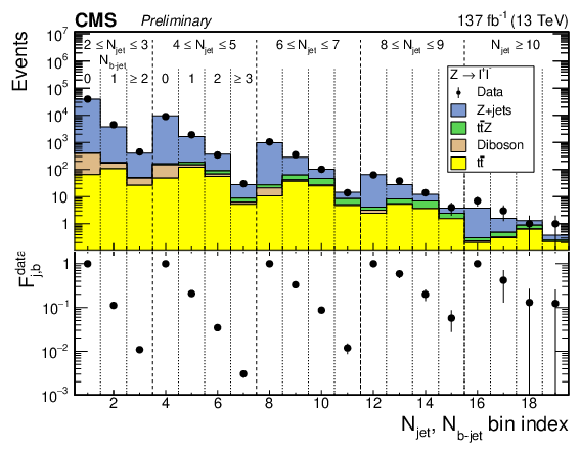
Figure 7:
(upper) The observed event yield in the ${\mathrm{Z} (\to \ell ^{+} \ell ^{-})}$+jets control region, integrated over ${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$, as a function of ${N_{\text {jet}}}$ and ${N_{{\mathrm{b}}\text {-jet}}}$. The uncertainties are statistical only. The stacked histograms show the corresponding results from simulation. (lower) The extrapolation factors ${\mathcal {F}_{\mathrm {j},\mathrm{b}}^{\text {data}}}$ with their statistical uncertainties. |
png pdf |
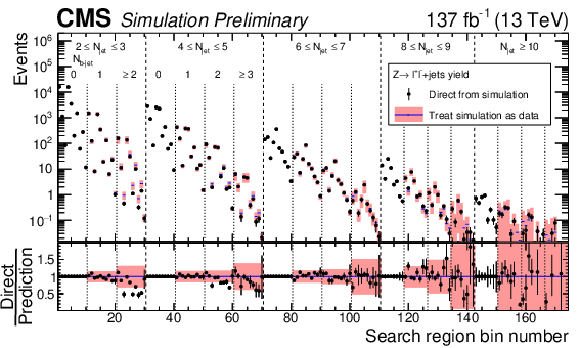
Figure 8:
Prediction from simulation for the ${{\mathrm{Z} (\to \ell ^{+} \ell ^{-})}\,+jets}$ event yields in the 174 search bin space as determined by computing the ${\mathcal {F}_{\mathrm {j},\mathrm{b}}^{\text {data}}}$ factors (Eq. (3)) and the $ {N_{{\mathrm{b}}\text {-jet}}}=$ 0 event yields in the same manner as for data, in comparison to the corresponding direct ${{\mathrm{Z} (\to \ell ^{+} \ell ^{-})}\,+jets}$ prediction from simulation. The labeling of the bin numbers is the same as in Fig. 5. The pink bands show the statistical uncertainties in the prediction combined with the systematic uncertainty attributable to the kinematic (${H_{\mathrm {T}}}$ and ${H_{\mathrm {T}}^{\text {miss}}}$) dependence. For bins corresponding to $ {N_{{\mathrm{b}}\text {-jet}}} = $ 0, the agreement is exact by construction. |
png pdf |
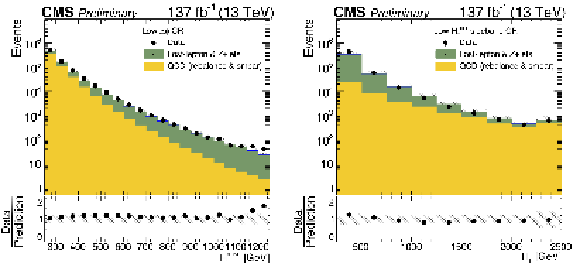
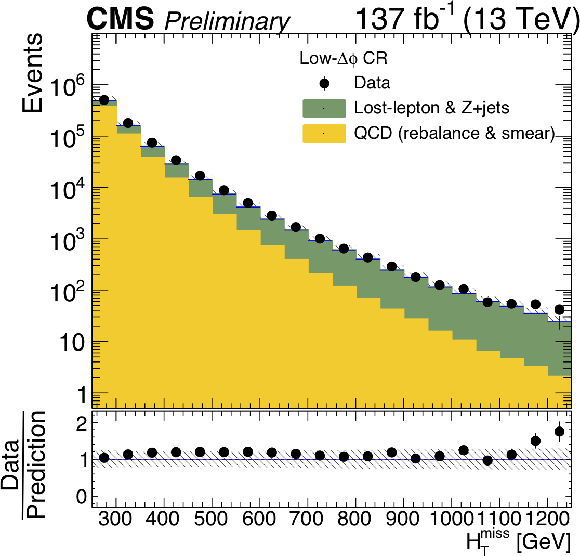
Figure 9:
The observed and predicted distributions of (left) ${H_{\mathrm {T}}^{\text {miss}}}$ in the inverted-$ {\Delta \phi}$ control region and (right) ${H_{\mathrm {T}}}$ in the low- ${H_{\mathrm {T}}^{\text {miss}}}$ sideband. The uncertainties are statistical only. The lower panels show the ratios of the observed to the predicted distributions, with their statistical uncertainties. The hatched regions indicate the total uncertainties in the predictions, with statistical and systematic uncertainties combined in quadrature. |
png pdf |
Figure 9-a:
The observed and predicted distributions of ${H_{\mathrm {T}}^{\text {miss}}}$ in the inverted-$ {\Delta \phi}$ control region. The uncertainties are statistical only. The lower panel shows the ratios of the observed to the predicted distributions, with their statistical uncertainties. The hatched regions indicate the total uncertainties in the predictions, with statistical and systematic uncertainties combined in quadrature. |
png pdf |
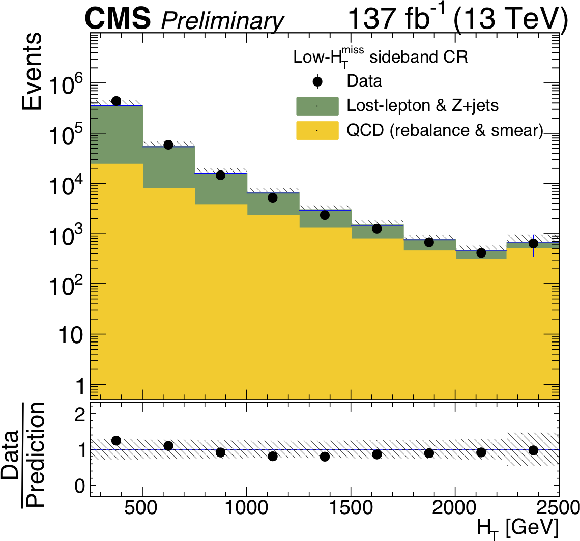
Figure 9-b:
The observed and predicted distributions of ${H_{\mathrm {T}}}$ in the low- ${H_{\mathrm {T}}^{\text {miss}}}$ sideband. The uncertainties are statistical only. The lower panel shows the ratios of the observed to the predicted distributions, with their statistical uncertainties. The hatched regions indicate the total uncertainties in the predictions, with statistical and systematic uncertainties combined in quadrature. |

png pdf |
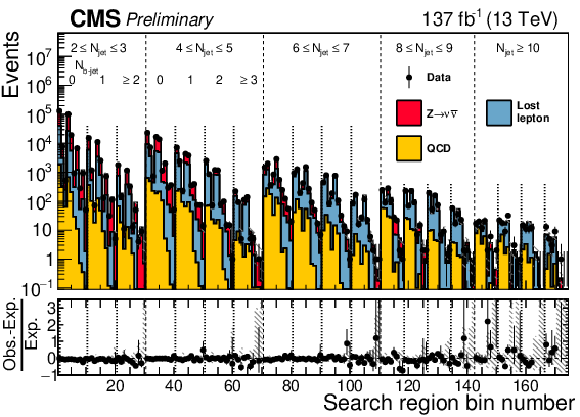
Figure 10:
Distribution of observed and predicted event yields in the inverted-$ {\Delta \phi}$ control region analysis bins. The uncertainties are statistical only. The labeling of the bin numbers is the same as in Fig. 5. The lower panel shows the ratio of the observed to the predicted event yields, with their statistical uncertainties. The hatched region indicates the total uncertainty in the prediction, with statistical and systematic uncertainties combined in quadrature. |
png pdf |
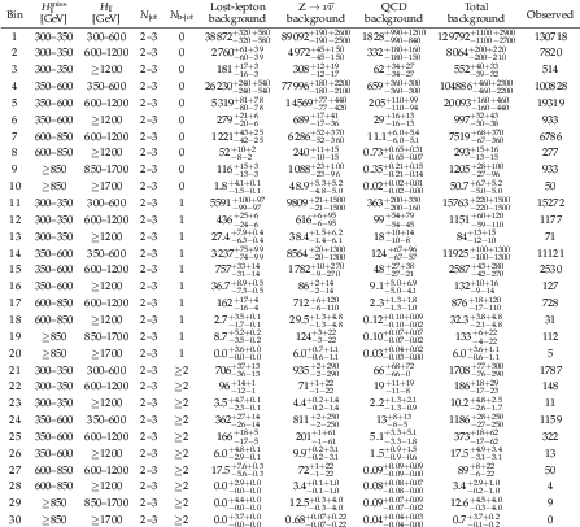
Figure 11:
The observed numbers of events and pre-fit SM background predictions in the 174 search bins of the analysis, where "pre-fit'' means there is no constraint from the likelihood fit. The labeling of the bin numbers is the same as in Fig. 5. Numerical values are given in Appendix A. The hatching indicates the total uncertainty in the background predictions. The lower panel displays the fractional differences between the data and SM predictions. |
png pdf |
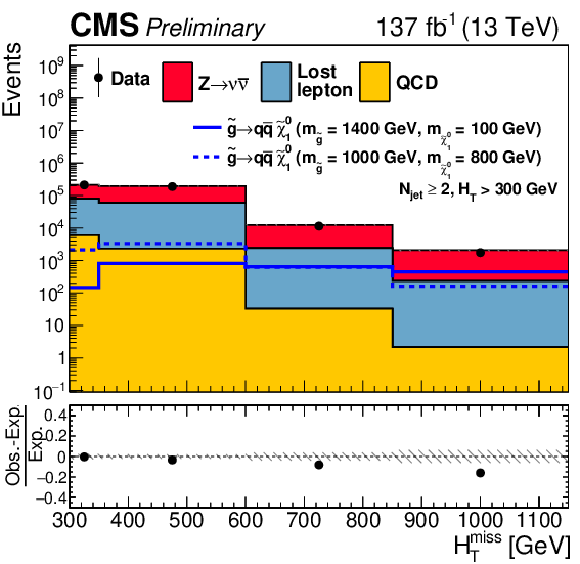
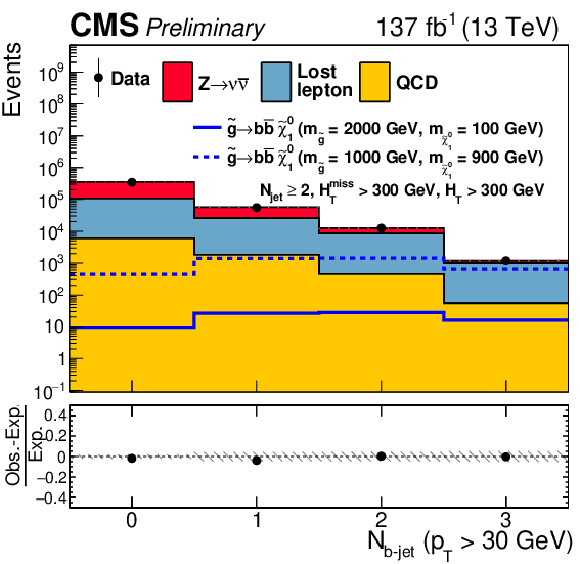
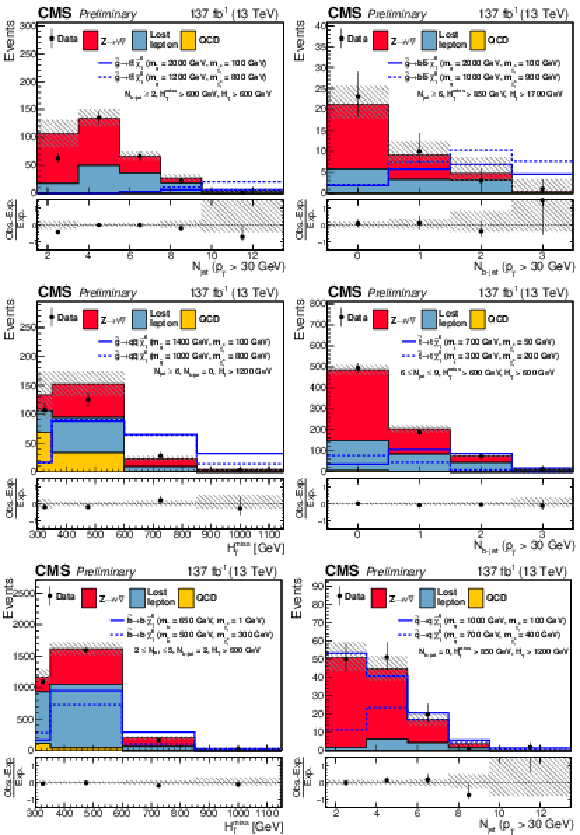
Figure 12:
One-dimensional projections of the data and pre-fit SM predictions in ${H_{\mathrm {T}}^{\text {miss}}}$, ${N_{\text {jet}}}$, and ${N_{{\mathrm{b}}\text {-jet}}}$. The hatched regions indicate the total uncertainties in the background predictions. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
Figure 12-a:
One-dimensional projections of the data and pre-fit SM predictions in ${H_{\mathrm {T}}^{\text {miss}}}$. The hatched regions indicate the total uncertainties in the background predictions. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |

png pdf |
Figure 12-b:
One-dimensional projections of the data and pre-fit SM predictions in ${N_{\text {jet}}}$. The hatched regions indicate the total uncertainties in the background predictions. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
Figure 12-c:
One-dimensional projections of the data and pre-fit SM predictions in ${N_{{\mathrm{b}}\text {-jet}}}$. The hatched regions indicate the total uncertainties in the background predictions. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
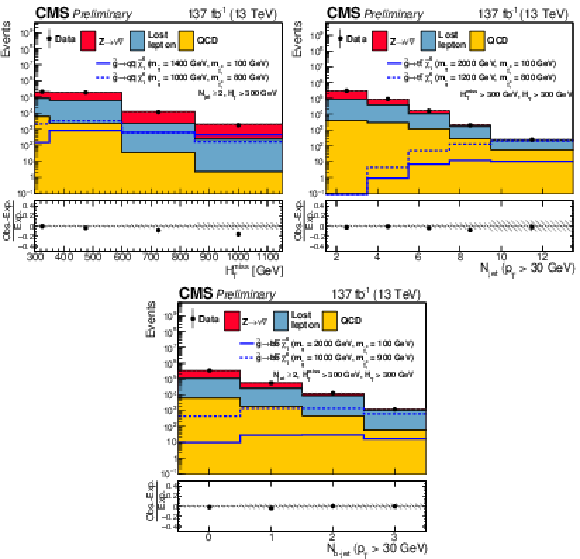
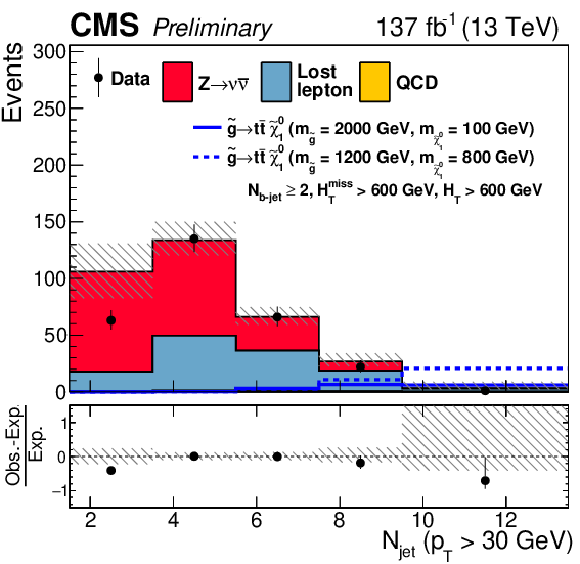
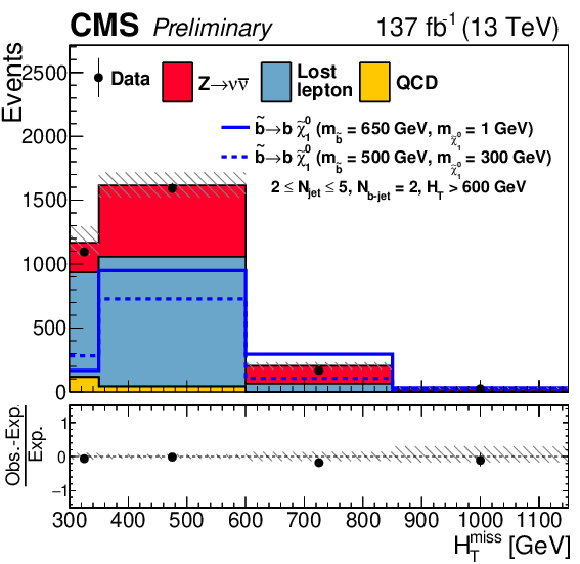
Figure 13:
One-dimensional projections of the data and pre-fit SM predictions in either ${H_{\mathrm {T}}^{\text {miss}}}$, ${N_{\text {jet}}}$, or ${N_{{\mathrm{b}}\text {-jet}}}$ after applying additional selection criteria, given in the figure legends, to enhance the sensitivity to the (upper left) T1tttt, (upper right) T1bbbb, (middle left) T1qqqq, (middle right) T2tt, (lower left) T2bb, and (lower right) T2qq signal processes. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
Figure 13-a:
One-dimensional projection of the data and pre-fit SM prediction in ${N_{\text {jet}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T1tttt signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |

png pdf |
Figure 13-b:
One-dimensional projection of the data and pre-fit SM prediction in ${N_{{\mathrm{b}}\text {-jet}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T1bbbb signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |

png pdf |
Figure 13-c:
One-dimensional projection of the data and pre-fit SM prediction in ${H_{\mathrm {T}}^{\text {miss}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T1qqqq signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |

png pdf |
Figure 13-d:
One-dimensional projection of the data and pre-fit SM prediction in ${N_{{\mathrm{b}}\text {-jet}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T2tt signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
Figure 13-e:
One-dimensional projection of the data and pre-fit SM prediction in ${H_{\mathrm {T}}^{\text {miss}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T2bb signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |

png pdf |
Figure 13-f:
One-dimensional projection of the data and pre-fit SM prediction in ${N_{\text {jet}}}$ after applying additional selection criteria, given in the figure legend, to enhance the sensitivity to the T2qq signal process. The (unstacked) results for two example signal scenarios are shown in each instance, one with $ {\Delta m} \gg $ 0 and the other with $ {\Delta m} \approx $ 0, where ${\Delta m}$ is the difference between the gluino or squark mass and the sum of the masses of the particles into which it decays. |
png pdf |
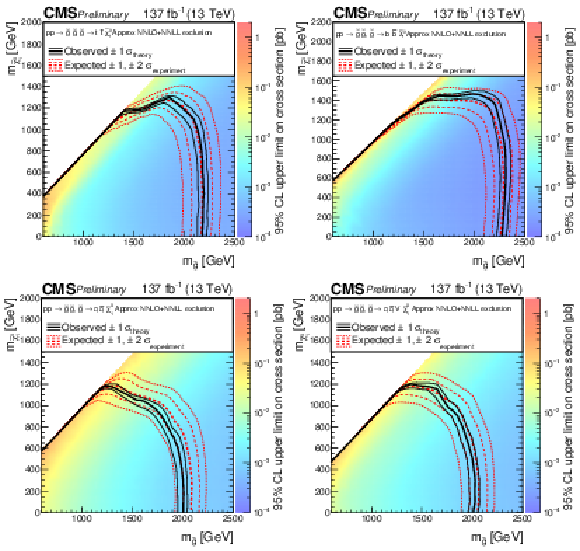
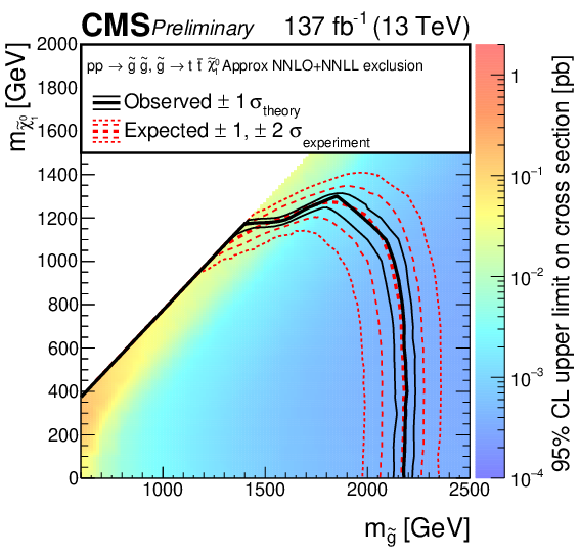
Figure 14:
The 95% CL upper limits on the production cross sections of the (upper left) T1tttt, (upper right) T1bbbb, (lower left) T1qqqq, and (lower right) T5qqqqVV signal models as a function of the gluino and LSP masses ${m_{{\mathrm{\tilde{g}}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The thick solid (black) curves show the observed exclusion limits assuming the approximate-NNLO+NNLL cross sections [70,71,72,73,74]. The thin solid (black) curves show the changes in these limits as the signal cross sections are varied by their theoretical uncertainties [92]. The thick dashed (red) curves present the expected limits under the background-only hypothesis, while the two sets of thin dotted (red) curves indicate the region containing 68 and 95% of the distribution of limits expected under this hypothesis. |
png pdf |
Figure 14-a:
The 95% CL upper limits on the production cross section of the T1tttt signal model as a function of the gluino and LSP masses ${m_{{\mathrm{\tilde{g}}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The thick solid (black) curves show the observed exclusion limits assuming the approximate-NNLO+NNLL cross sections [70,71,72,73,74]. The thin solid (black) curves show the changes in these limits as the signal cross sections are varied by their theoretical uncertainties [92]. The thick dashed (red) curves present the expected limits under the background-only hypothesis, while the two sets of thin dotted (red) curves indicate the region containing 68 and 95% of the distribution of limits expected under this hypothesis. |
png pdf |
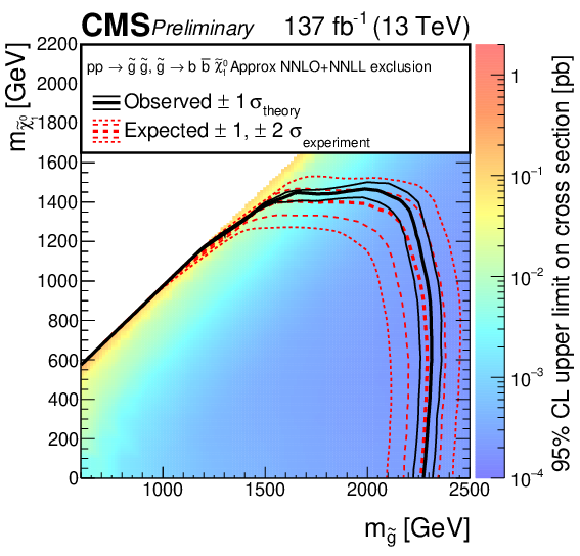
Figure 14-b:
The 95% CL upper limits on the production cross section of the T1bbbb = signal model as a function of the gluino and LSP masses ${m_{{\mathrm{\tilde{g}}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The thick solid (black) curves show the observed exclusion limits assuming the approximate-NNLO+NNLL cross sections [70,71,72,73,74]. The thin solid (black) curves show the changes in these limits as the signal cross sections are varied by their theoretical uncertainties [92]. The thick dashed (red) curves present the expected limits under the background-only hypothesis, while the two sets of thin dotted (red) curves indicate the region containing 68 and 95% of the distribution of limits expected under this hypothesis. |
png pdf |
Figure 14-c:
The 95% CL upper limits on the production cross section of the T1qqqq signal model as a function of the gluino and LSP masses ${m_{{\mathrm{\tilde{g}}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The thick solid (black) curves show the observed exclusion limits assuming the approximate-NNLO+NNLL cross sections [70,71,72,73,74]. The thin solid (black) curves show the changes in these limits as the signal cross sections are varied by their theoretical uncertainties [92]. The thick dashed (red) curves present the expected limits under the background-only hypothesis, while the two sets of thin dotted (red) curves indicate the region containing 68 and 95% of the distribution of limits expected under this hypothesis. |

png pdf |
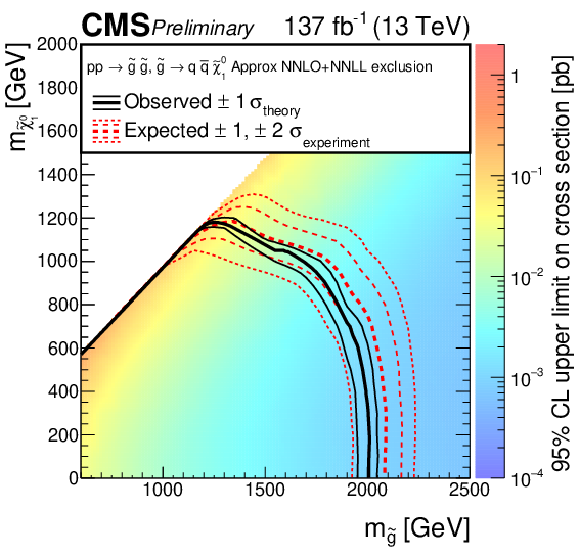
Figure 14-d:
The 95% CL upper limits on the production cross section of the T5qqqqVV signal model as a function of the gluino and LSP masses ${m_{{\mathrm{\tilde{g}}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The thick solid (black) curves show the observed exclusion limits assuming the approximate-NNLO+NNLL cross sections [70,71,72,73,74]. The thin solid (black) curves show the changes in these limits as the signal cross sections are varied by their theoretical uncertainties [92]. The thick dashed (red) curves present the expected limits under the background-only hypothesis, while the two sets of thin dotted (red) curves indicate the region containing 68 and 95% of the distribution of limits expected under this hypothesis. |
png pdf |
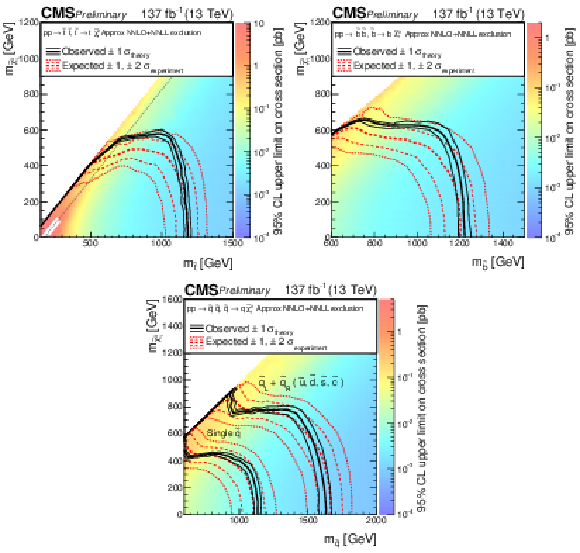
Figure 15:
The 95% CL upper limits on the production cross sections of the (upper left) T2tt, (upper right) T2bb, and (lower) T2qq signal models as a function of the squark and LSP masses ${m_{\tilde{\mathrm{q}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The meaning of the curves is described in the Fig. 14 caption. For the T2tt model, we do not present cross section upper limits in the unshaded diagonal region at low $ {m_{\tilde{\chi}_1^0}}$ for the reason discussed in the text. The diagonal dotted line shown for this model corresponds to $ {m_{\tilde{\mathrm{t}}}} - {m_{\tilde{\chi}_1^0}} = {m_{\mathrm{t}}} $. |
png pdf |
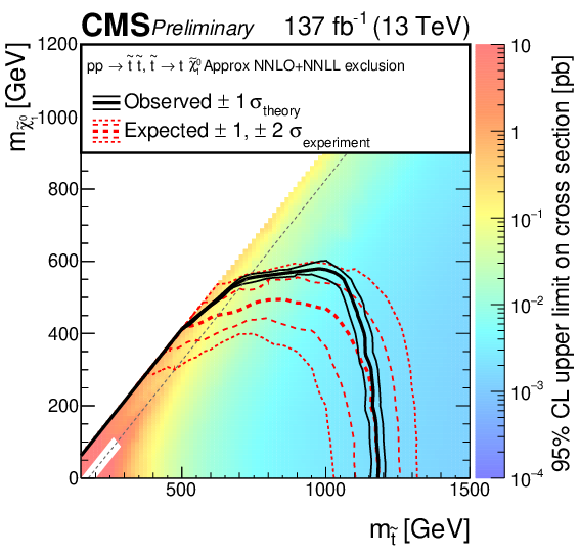
Figure 15-a:
The 95% CL upper limits on the production cross section of the T2tt signal model as a function of the squark and LSP masses ${m_{\tilde{\mathrm{q}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The meaning of the curves is described in the Fig. 14 caption. We do not present cross section upper limits in the unshaded diagonal region at low $ {m_{\tilde{\chi}_1^0}}$ for the reason discussed in the text. The diagonal dotted line shown for this model corresponds to $ {m_{\tilde{\mathrm{t}}}} - {m_{\tilde{\chi}_1^0}} = {m_{\mathrm{t}}} $. |
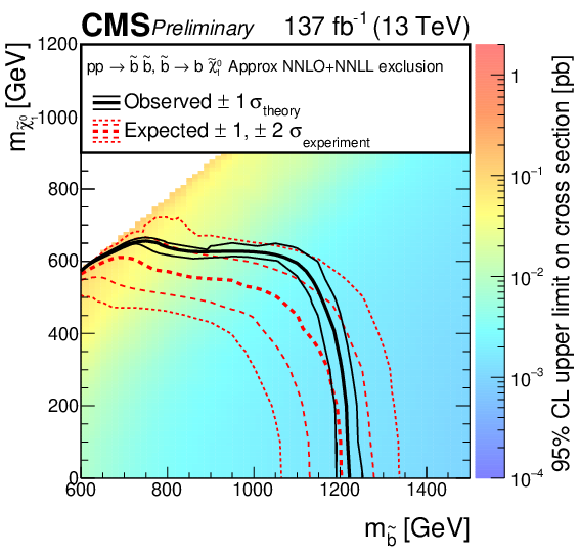
png pdf |
Figure 15-b:
The 95% CL upper limits on the production cross section of the T2bb signal model as a function of the squark and LSP masses ${m_{\tilde{\mathrm{q}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The meaning of the curves is described in the Fig. 14 caption. |

png pdf |
Figure 15-c:
The 95% CL upper limits on the production cross section of the T2qq signal model as a function of the squark and LSP masses ${m_{\tilde{\mathrm{q}}}}$ and $ {m_{\tilde{\chi}_1^0}}$. The meaning of the curves is described in the Fig. 14 caption. |
png pdf |
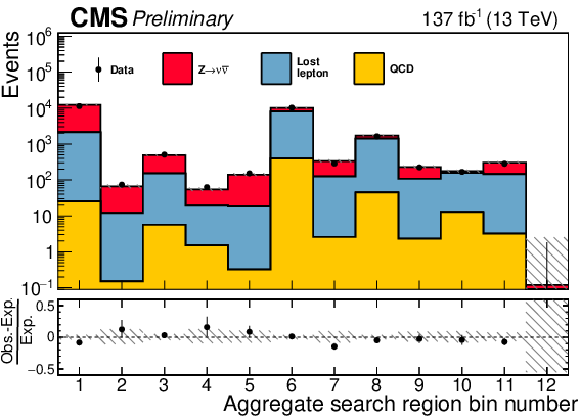
Figure 16:
The observed numbers of events and pre-fit SM background predictions in the aggregate search bins. The total background uncertainty is shown by the hatched regions. The lower panel displays the fractional differences between the data and the SM predictions. |
| Tables | |

png pdf |
Table 1:
Definition of the search intervals in the ${H_{\mathrm {T}}^{\text {miss}}}$ and ${H_{\mathrm {T}}}$ variables. Intervals 1 and 4 are discarded for $ {N_{\text {jet}}} \geq $ 8. |

png pdf |
Table 2:
Systematic uncertainties in the yield of signal events, averaged over all search bins. The variations correspond to different signal models and choices for the SUSY particle masses. Results reported as 0.0 correspond to values less than 0.05%. |
png pdf |
Table 3:
Observed number of events and pre-fit background predictions in the 2 $\leq {N_{\text {jet}}} \leq $ 3 search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |

png pdf |
Table 4:
Observed number of events and pre-fit background predictions in the 4 $\leq {N_{\text {jet}}} \leq $ 5 search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |

png pdf |
Table 5:
Observed number of events and pre-fit background predictions in the 6 $ \leq {N_{\text {jet}}} \leq $ 7 search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |
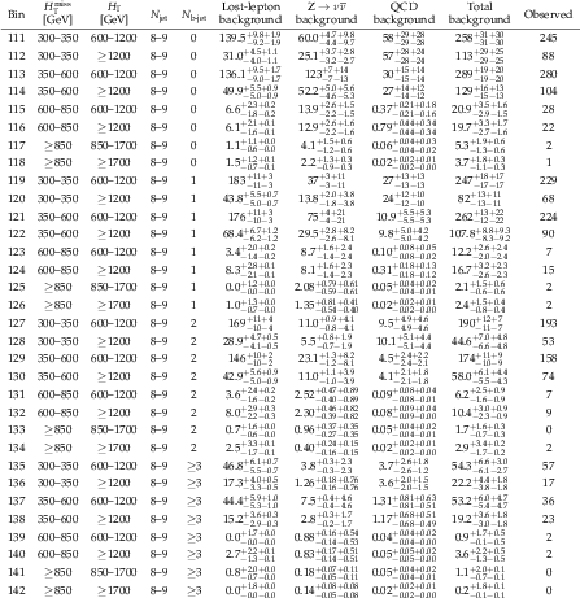
png pdf |
Table 6:
Observed number of events and pre-fit background predictions in the 8 $ \leq {N_{\text {jet}}} \leq $ 9 search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |
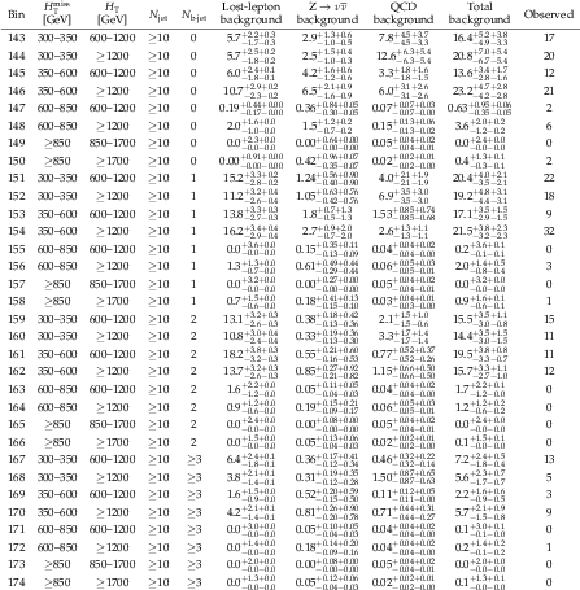
png pdf |
Table 7:
Observed number of events and pre-fit background predictions in the $ {N_{\text {jet}}} \geq $ 10 search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |

png pdf |
Table 8:
Targeted event topologies for the 12 aggregate search bins. |

png pdf |
Table 9:
Selection criteria, pre-fit background predictions, and observed number of events for the 12 aggregate search bins. For the background predictions, the first uncertainty is statistical and the second systematic. |
| Summary |
|
Using essentially the full CMS Run 2 data sample of proton-proton collisions at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 137 fb$^{-1}$ collected in 2016-2018, a search for supersymmetry has been performed based on events containing multiple jets and large missing transverse momentum. The event yields are measured in 174 nonoverlapping search bins defined in a four-dimensional space of missing transverse momentum (${H_{\mathrm {T}}^{\text {miss}}}$), the scalar sum of jet transverse momenta (${H_{\mathrm{T}}}$), the number of jets, and the number of tagged bottom quark jets. The events are required to satisfy ${H_{\mathrm {T}}^{\text {miss}}} > $ 300 GeV, ${H_{\mathrm{T}}} > $ 300 GeV, and to have at least two jets with transverse momentum ${p_{\mathrm{T}}} > $ 30 GeV. Events with isolated high ${p_{\mathrm{T}}}$ leptons or photons are vetoed. The results are compared to the expected number of background events from standard model (SM) processes. The principal backgrounds are from events with neutrino production or jet mismeasurement. The SM background is evaluated using control regions in data supplemented by information from Monte Carlo event simulation. The observed event yields are found to be consistent with the SM background and no evidence for supersymmetry is obtained. The results are interpreted in the context of simplified models for gluino and squark pair production. For the gluino models, each of the produced gluinos decays either to a $\mathrm{t\bar{t}}$ pair and an undetected, stable, lightest-supersymmetric-particle, assumed to be the ${\tilde{\chi}^0_1}$ neutralino (T1tttt model); to a $\mathrm{b\bar{b}}$ pair and the ${\tilde{\chi}^0_1}$ (T1bbbb model); to a light-flavored (u, d, s, c) $\mathrm{q\bar{q}}$ pair and the ${\tilde{\chi}^0_1}$ (T1qqqq model); or to a light-flavored quark and antiquark and either the second-lightest neutralino $\tilde{\chi}^{0}_{2}$ or the lightest chargino $ \tilde{\chi}_1^{\pm}$, followed by decay of the $\tilde{\chi}^{0}_{2}$ ($ \tilde{\chi}_1^{\pm}$) to the $\tilde{\chi}^0_1$ and an on- or off-shell Z (W) boson (T5qqqqVV model). For the squark models, each of the produced squarks decays either to a top quark and the ${\tilde{\chi}^0_1}$ (T2tt model), to a bottom quark and the ${\tilde{\chi}^0_1}$ (T2bb model), or to a light-flavored quark and the ${\tilde{\chi}^0_1}$ (T2qq model). Using the predicted cross sections with next-to-leading order plus next-to-leading logarithm accuracy as a reference, gluinos with masses as large as from 2000 to 2310 GeV are excluded at 95% confidence level, depending on the signal model. The corresponding limits on the masses of directly produced squarks range from 1190 for top squarks to 1630 GeV for light-flavored squarks. The results presented here supersede those of Ref. [7], extending the mass limits of this previous study by, typically, 200 GeV or more. |
| References | ||||
| 1 | ATLAS Collaboration | Search for pair production of gluinos decaying via stop and sbottom in events with b-jets and large missing transverse momentum in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PRD 94 (2016) 032003 | 1605.09318 |
| 2 | ATLAS Collaboration | Search for squarks and gluinos in final states with jets and missing transverse momentum at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | EPJC 76 (2016) 392 | 1605.03814 |
| 3 | CMS Collaboration | Search for supersymmetry in the multijet and missing transverse momentum final state in pp collisions at 13 TeV | PLB 758 (2016) 152 | CMS-SUS-15-002 1602.06581 |
| 4 | CMS Collaboration | Search for new physics with the M$ _{\text{T2}} $ variable in all-jets final states produced in pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 10 (2016) 006 | CMS-SUS-15-003 1603.04053 |
| 5 | CMS Collaboration | Inclusive search for supersymmetry using razor variables in pp collisions at $ \sqrt{s}= $ 13 TeV | PRD 95 (2017) 012003 | CMS-SUS-15-004 1609.07658 |
| 6 | CMS Collaboration | A search for new phenomena in pp collisions at $ \sqrt{s}= $ 13 TeV in final states with missing transverse momentum and at least one jet using the $ {\alpha_{\text{T}}} $ variable | EPJC 77 (2017) 294 | CMS-SUS-15-005 1611.00338 |
| 7 | CMS Collaboration | Search for supersymmetry in multijet events with missing transverse momentum in proton-proton collisions at 13 TeV | PRD 96 (2017) 032003 | CMS-SUS-16-033 1704.07781 |
| 8 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 9 | Y. A. Golfand and E. P. Likhtman | Extension of the algebra of Poincar$ \'e $ group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 10 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 11 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 12 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 13 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 14 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 15 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 16 | S. P. Martin | A supersymmetry primer | Adv. Ser. Direct. High Energy Phys. 21 (2010) 1 | hep-ph/9709356 |
| 17 | B. Gripaios | Composite leptoquarks at the LHC | JHEP 02 (2010) 045 | 0910.1789 |
| 18 | S. Dimopoulos | Technicolored signatures | NPB 168 (1980) 69 | |
| 19 | M. Perelstein | Little Higgs models and their phenomenology | Prog. Part. NP 58 (2007) 247 | hep-ph/0512128 |
| 20 | C. Grojean, E. Salvioni, and R. Torre | A weakly constrained W' at the early LHC | JHEP 07 (2011) 002 | 1103.2761 |
| 21 | L. Lopez-Honorez, T. Schwetz, and J. Zupan | Higgs portal, fermionic dark matter, and a standard model like Higgs at 125 GeV | PLB 716 (2012) 179 | 1203.2064 |
| 22 | J. M. No | Looking through the pseudoscalar portal into dark matter: Novel mono-Higgs and mono-Z signatures at the LHC | PRD 93 (2016) 031701 | 1509.01110 |
| 23 | R. Barbieri and G. F. Giudice | Upper bounds on supersymmetric particle masses | NPB 306 (1988) 63 | |
| 24 | S. Dimopoulos and G. F. Giudice | Naturalness constraints in supersymmetric theories with nonuniversal soft terms | PLB 357 (1995) 573 | hep-ph/9507282 |
| 25 | R. Barbieri and D. Pappadopulo | S-particles at their naturalness limits | JHEP 10 (2009) 061 | 0906.4546 |
| 26 | M. Papucci, J. T. Ruderman, and A. Weiler | Natural SUSY endures | JHEP 09 (2012) 035 | 1110.6926 |
| 27 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 28 | CMS Collaboration | Search for new physics with jets and missing transverse momentum in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 08 (2011) 155 | CMS-SUS-10-005 1106.4503 |
| 29 | CMS Collaboration | Search for new physics in the multijet and missing transverse momentum final state in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JHEP 06 (2014) 055 | CMS-SUS-13-012 1402.4770 |
| 30 | N. Arkani-Hamed et al. | MARMOSET: The path from LHC data to the new standard model via on-shell effective theories | hep-ph/0703088 | |
| 31 | J. Alwall, M.-P. Le, M. Lisanti, and J. G. Wacker | Model-independent jets plus missing energy searches | PRD 79 (2009) 015005 | 0809.3264 |
| 32 | J. Alwall, P. Schuster, and N. Toro | Simplified models for a first characterization of new physics at the LHC | PRD 79 (2009) 075020 | 0810.3921 |
| 33 | D. Alves et al. | Simplified models for LHC new physics searches | JPG 39 (2012) 105005 | 1105.2838 |
| 34 | CMS Collaboration | Interpretation of searches for supersymmetry with simplified models | PRD 88 (2013) 052017 | CMS-SUS-11-016 1301.2175 |
| 35 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 36 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 37 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 38 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 39 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 40 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 41 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 42 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 43 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 44 | K. Rehermann and B. Tweedie | Efficient identification of boosted semileptonic top quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 45 | CMS Collaboration | Jet performance in pp collisions at $ \sqrt{s}= $ 7 ~TeV | CDS | |
| 46 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | CMS-PAS-JME-16-003 |
| 47 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 48 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 49 | UA1 Collaboration | Experimental observation of isolated large transverse energy electrons with associated missing energy at $ \sqrt{s}= $ 540 ~GeV | PLB 122 (1983) 103 | |
| 50 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | Accepted by JINST | CMS-JME-17-001 1903.06078 |
| 51 | CMS Collaboration | Search for supersymmetry in events with a photon, jets, b jets, and missing transverse momentum in proton-proton collisions at 13 TeV | EPJC 79 (2019) 444 | CMS-SUS-18-002 1901.06726 |
| 52 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 53 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 54 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 55 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 56 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 57 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 58 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 59 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 60 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 61 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W$ ^+ $W$ ^- $, WZ and ZZ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 62 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 63 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 64 | P. Barnreuther, M. Czakon, and A. Mitov | Percent level precision physics at the Tevatron: First genuine NNLO QCD corrections to $ \mathrm{q\bar{q}}\to\mathrm{t\bar{t}} +X $ | PRL 109 (2012) 132001 | 1204.5201 |
| 65 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 66 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 67 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ O({\alpha_S}^4) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 68 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | W physics at the LHC with FEWZ 2.1 | CPC 184 (2013) 208 | 1201.5896 |
| 69 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | CPC 182 (2011) 2388 | 1011.3540 |
| 70 | W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas | Squark and gluino production at hadron colliders | NPB 492 (1997) 51 | hep-ph/9610490 |
| 71 | A. Kulesza and L. Motyka | Threshold resummation for squark-antisquark and gluino-pair production at the LHC | PRL 102 (2009) 111802 | 0807.2405 |
| 72 | A. Kulesza and L. Motyka | Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC | PRD 80 (2009) 095004 | 0905.4749 |
| 73 | W. Beenakker et al. | Soft-gluon resummation for squark and gluino hadroproduction | JHEP 12 (2009) 041 | 0909.4418 |
| 74 | W. Beenakker et al. | Squark and gluino hadroproduction | Int. J. Mod. Phys. A 26 (2011) 2637 | 1105.1110 |
| 75 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 76 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 77 | A. Giammanco | The fast simulation of the CMS experiment | J. Phys. Conf. Ser. 513 (2014) 022012 | |
| 78 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 79 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | Submitted to EPJC | CMS-GEN-17-001 1903.12179 |
| 80 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 81 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 82 | A. Kalogeropoulos and J. Alwall | The SysCalc code: A tool to derive theoretical systematic uncertainties | 1801.08401 | |
| 83 | S. Catani, D. de Florian, M. Grazzini, and P. Nason | Soft gluon resummation for Higgs boson production at hadron colliders | JHEP 07 (2003) 028 | hep-ph/0306211 |
| 84 | M. Cacciari et al. | The $ \mathrm{t\bar{t}} $ cross-section at 1.8 TeV and 1.96 TeV: a study of the systematics due to parton densities and scale dependence | JHEP 04 (2004) 068 | hep-ph/0303085 |
| 85 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 86 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 87 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 88 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 89 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 90 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 91 | A. L. Read | Presentation of search results: the CLs technique | JPG 28 (2002) 2693 | |
| 92 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} = $ 13, 14, 33 and 100 TeV | EPJC 74 (2014) 3174 | 1407.5066 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|