

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SMP-18-004 | ||
| Studies of $\mathrm{W^+W^-}$ production at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| April 2020 | ||
| Abstract: A measurement of the $\mathrm{W}^+\mathrm{W}^-$ boson pair production cross section in proton-proton collisions at $\sqrt{s}= $ 13 TeV is presented. The data used in this study were collected with the CMS detector at the LHC and correspond to an integrated luminosity of 35.9 fb$^{-1}$. The $\mathrm{W}^+\mathrm{W}^-$ candidate events are selected by first requiring two oppositely-charged leptons (electrons or muons). Two methods for reducing background contributions are employed. In the first one, a sequence of requirements on kinematic quantities is applied allowing a measurement of the total cross section: 117.6 $\pm$ 6.8 pb which agrees well with the theoretical cross section. Fiducial cross sections are also reported for events with zero jets or one jet, and the change in the zero-jet fiducial cross section with the jet $p_{\mathrm{T}}$ threshold is measured. Normalized differential cross sections are reported within the fiducial region; these are compared to theoretical predictions based on quantum chromodynamics at next-to-next-to-leading-order accuracy. A second method for suppressing background contributions employs two random forest classifiers. The analysis based on this method includes a measurement of the total cross section and also a measurement of the normalized jet multiplicity distribution in $\mathrm{W}^+\mathrm{W}^-$ events. Finally, a dilepton invariant mass distribution is used to probe for physics beyond the standard model in the context of an effective field theory and limits on the presence of dimension-6 operators are derived. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, PRD 102 (2020) 092001. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
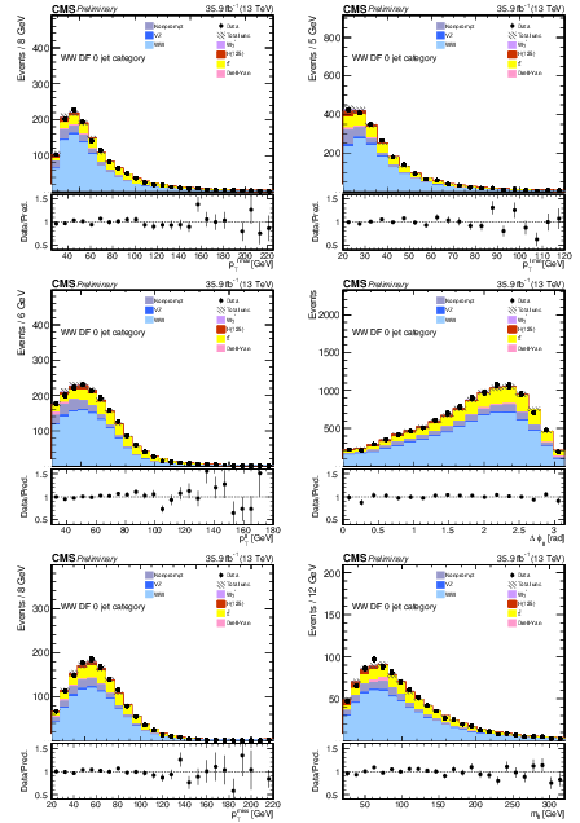
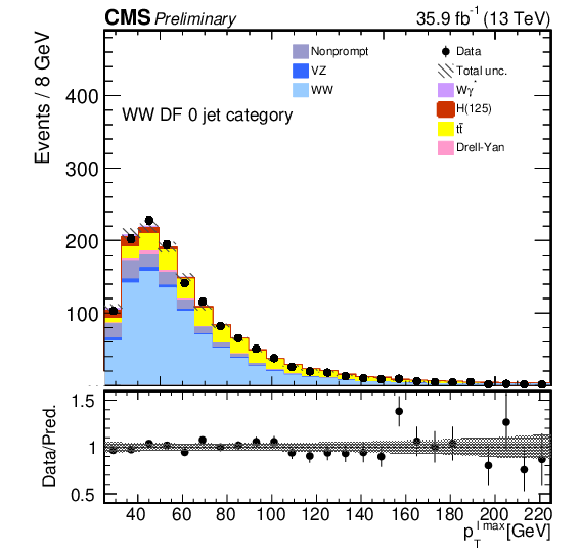
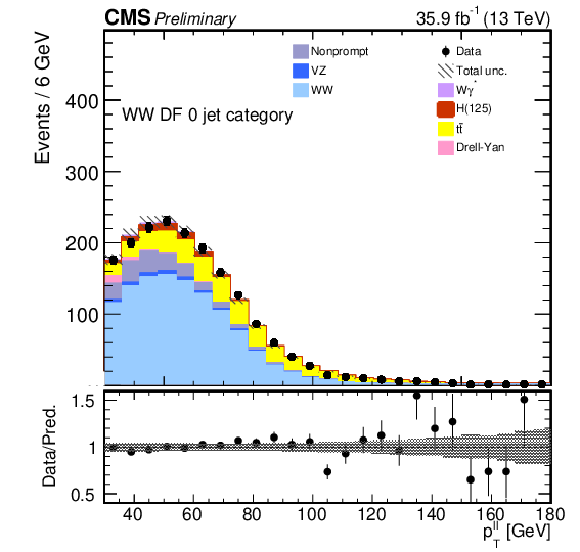
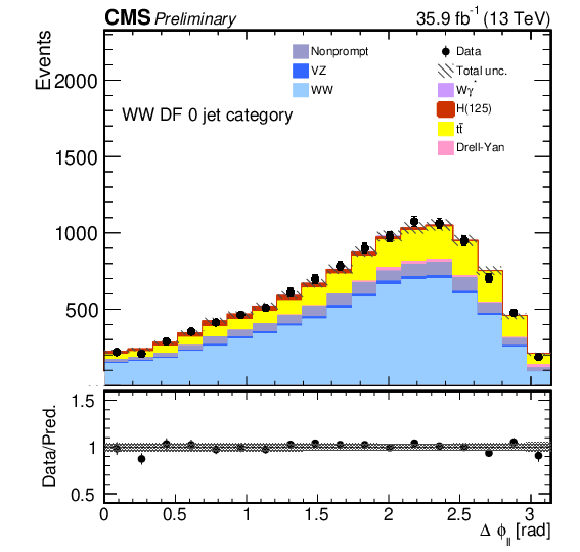
Figure 1:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
png pdf |
Figure 1-a:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |

png pdf |
Figure 1-b:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
png pdf |
Figure 1-c:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
png pdf |
Figure 1-d:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
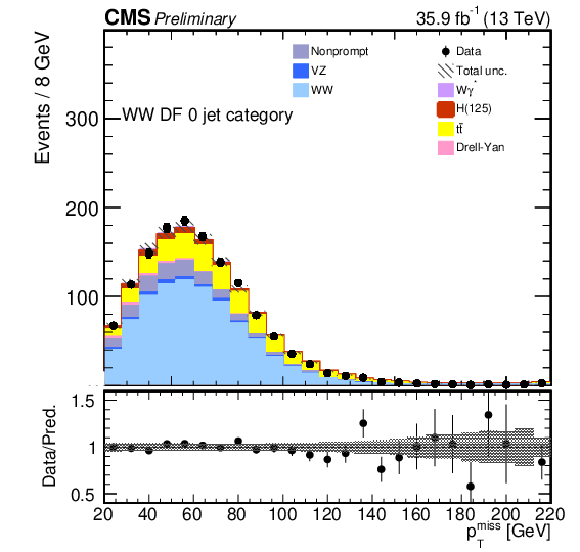
png pdf |
Figure 1-e:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
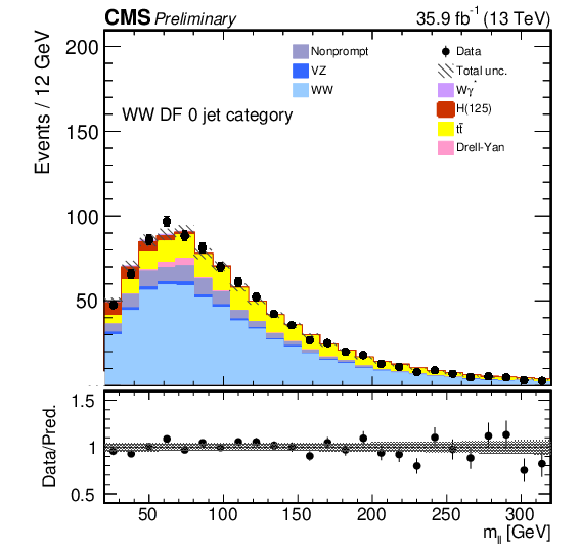
png pdf |
Figure 1-f:
Kinematic distributions for events with zero jets and DF leptons in the sequential cut analysis. The distributions show the leading and trailing lepton $ {p_{\mathrm {T}}} $ ($ {p_{\text {T}}^{\ell \text {\,max}}} $ and $ {p_{\text {T}}^{\ell \text {\,min}}} $), the dilepton transverse momentum $p_{\text {T}}^{\ell \ell}$, the azimuthal angle between the two leptons $ {\Delta \phi _{\ell \ell}} $, the missing transverse momentum $ {{p_{\mathrm {T}}} ^{\mathrm {miss}}}$, and the dilepton invariant mass $ {m_{\ell \ell}}$. The hatched areas represent the combined systematic and statistical uncertainty in each bin. The last bin includes the overflow. |
png pdf |
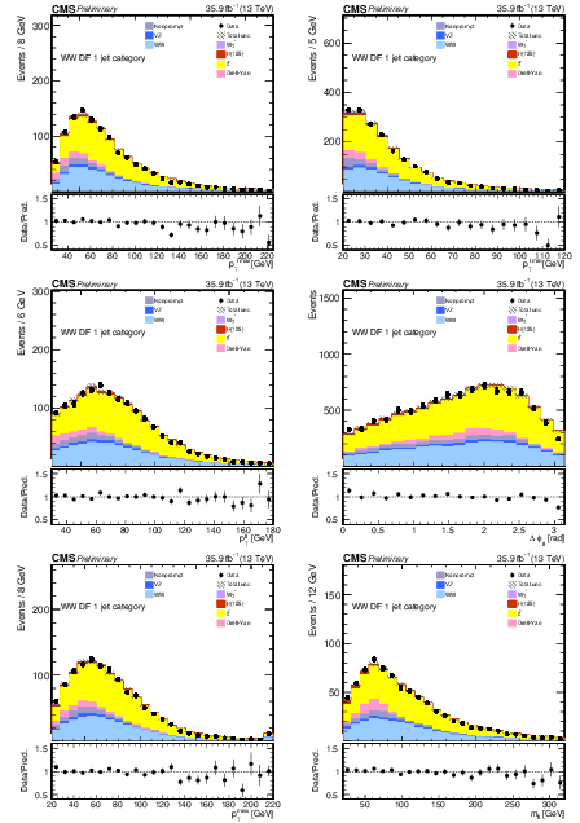
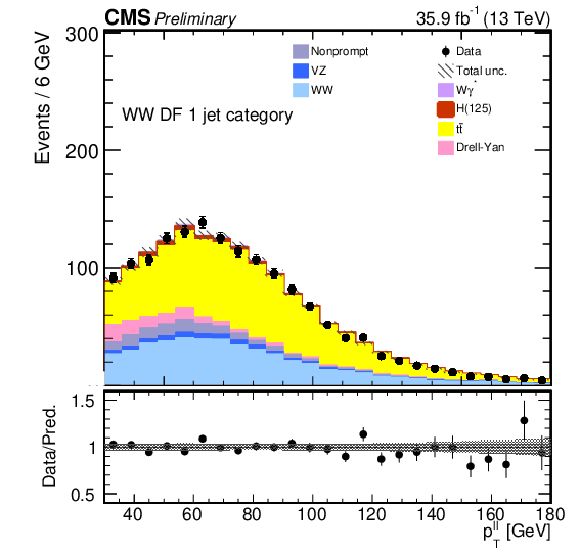
Figure 2:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |
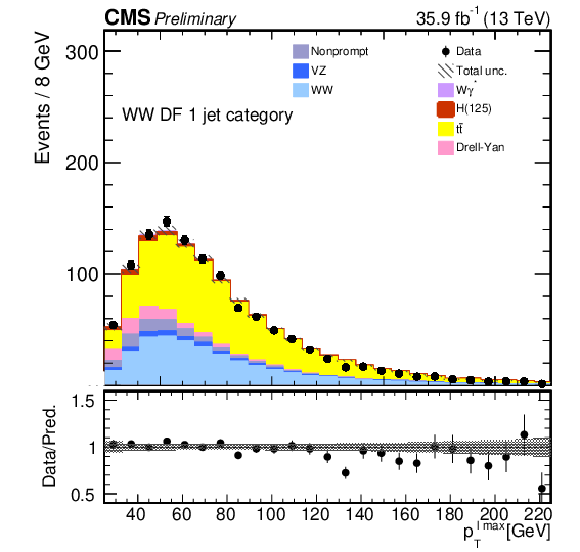
png pdf |
Figure 2-a:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |

png pdf |
Figure 2-b:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |
png pdf |
Figure 2-c:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |
png pdf |
Figure 2-d:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |

png pdf |
Figure 2-e:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |

png pdf |
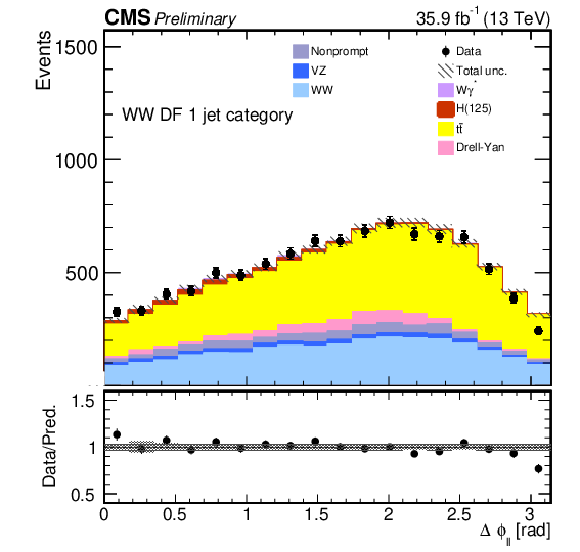
Figure 2-f:
Kinematic distributions for events with one jet and DF leptons in the sequential cut analysis. The quantities and the hatched areas are the same as in Fig. xxxxx. |
png pdf |
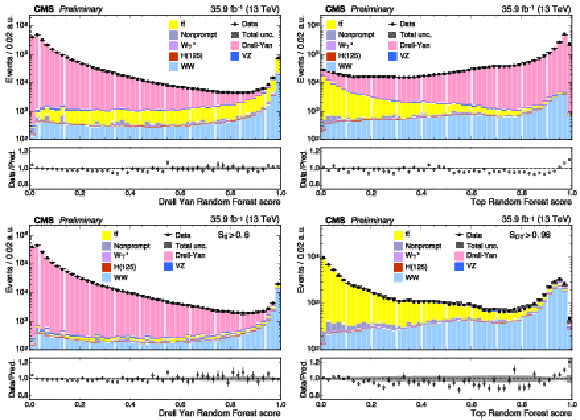
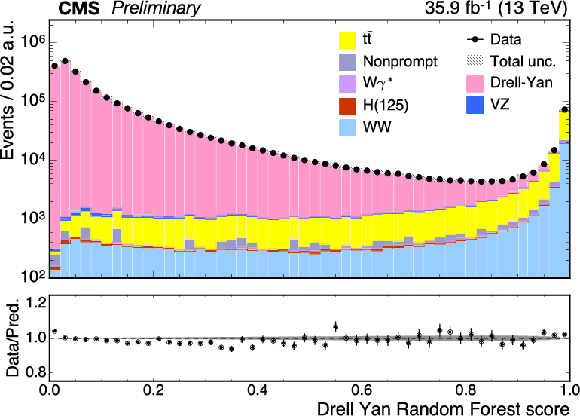
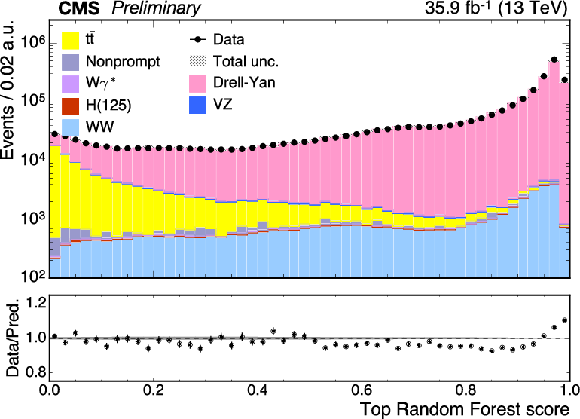
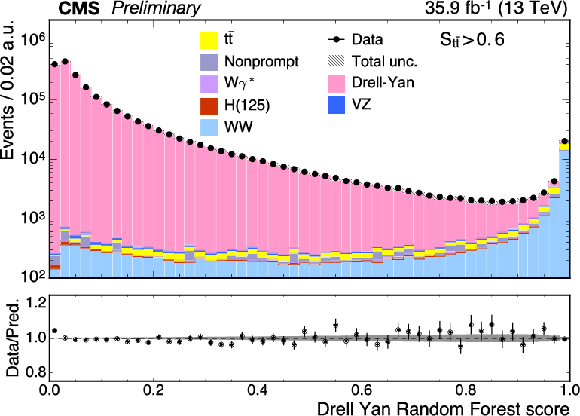
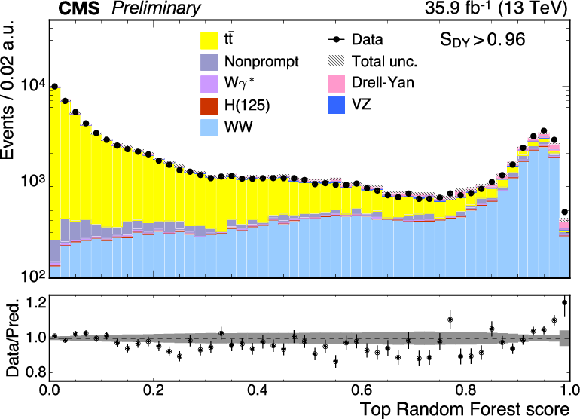
Figure 3:
Top left: score $S_{\text {DY}}$ distribution for the Drell-Yan discriminating random forest discriminant. The Drell-Yan distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ distribution peaks toward one. Top right: score $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution for the top quark random forest discriminant. The ${\mathrm{t} {}\mathrm{\bar{t}}}$ distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ peaks toward one. Bottom left: the $S_{\text {DY}}$ distribution after suppressing top quark events with $S_{{\mathrm{t} {}\mathrm{\bar{t}}}} > S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.6. Bottom right: the $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution after suppressing Drell-Yan events with $S_{\text {DY}} > S_{\text {DY}}^{\text {min}}= $ 0.96. |
png pdf |
Figure 3-a:
Top left: score $S_{\text {DY}}$ distribution for the Drell-Yan discriminating random forest discriminant. The Drell-Yan distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ distribution peaks toward one. Top right: score $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution for the top quark random forest discriminant. The ${\mathrm{t} {}\mathrm{\bar{t}}}$ distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ peaks toward one. Bottom left: the $S_{\text {DY}}$ distribution after suppressing top quark events with $S_{{\mathrm{t} {}\mathrm{\bar{t}}}} > S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.6. Bottom right: the $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution after suppressing Drell-Yan events with $S_{\text {DY}} > S_{\text {DY}}^{\text {min}}= $ 0.96. |
png pdf |
Figure 3-b:
Top left: score $S_{\text {DY}}$ distribution for the Drell-Yan discriminating random forest discriminant. The Drell-Yan distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ distribution peaks toward one. Top right: score $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution for the top quark random forest discriminant. The ${\mathrm{t} {}\mathrm{\bar{t}}}$ distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ peaks toward one. Bottom left: the $S_{\text {DY}}$ distribution after suppressing top quark events with $S_{{\mathrm{t} {}\mathrm{\bar{t}}}} > S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.6. Bottom right: the $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution after suppressing Drell-Yan events with $S_{\text {DY}} > S_{\text {DY}}^{\text {min}}= $ 0.96. |
png pdf |
Figure 3-c:
Top left: score $S_{\text {DY}}$ distribution for the Drell-Yan discriminating random forest discriminant. The Drell-Yan distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ distribution peaks toward one. Top right: score $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution for the top quark random forest discriminant. The ${\mathrm{t} {}\mathrm{\bar{t}}}$ distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ peaks toward one. Bottom left: the $S_{\text {DY}}$ distribution after suppressing top quark events with $S_{{\mathrm{t} {}\mathrm{\bar{t}}}} > S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.6. Bottom right: the $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution after suppressing Drell-Yan events with $S_{\text {DY}} > S_{\text {DY}}^{\text {min}}= $ 0.96. |
png pdf |
Figure 3-d:
Top left: score $S_{\text {DY}}$ distribution for the Drell-Yan discriminating random forest discriminant. The Drell-Yan distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ distribution peaks toward one. Top right: score $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution for the top quark random forest discriminant. The ${\mathrm{t} {}\mathrm{\bar{t}}}$ distribution peaks toward zero and the $ {\mathrm{W} \mathrm{W}} $ peaks toward one. Bottom left: the $S_{\text {DY}}$ distribution after suppressing top quark events with $S_{{\mathrm{t} {}\mathrm{\bar{t}}}} > S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.6. Bottom right: the $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}$ distribution after suppressing Drell-Yan events with $S_{\text {DY}} > S_{\text {DY}}^{\text {min}}= $ 0.96. |
png pdf |
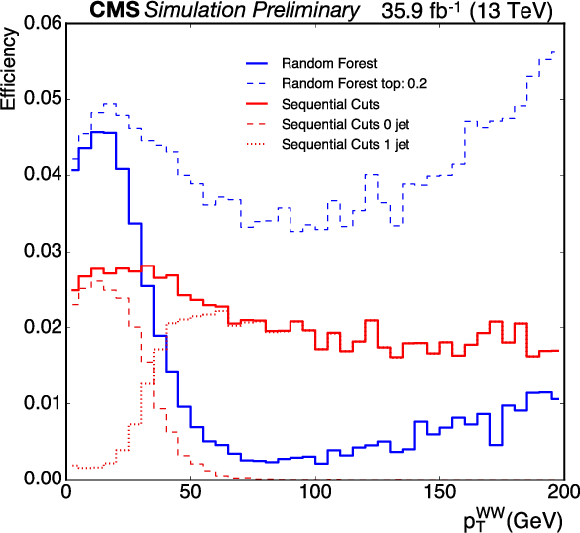
Figure 4:
Comparison of efficiencies for the sequential cut and random forest analyses as a function of $p_{\text {T}}^{\mathrm{W} \mathrm{W}} $. The sequential cut analysis includes 0-jet and 1-jet events from both DF and SF lepton combinations, for which the contribution from 0-jet and 1-jet are shown separately. The efficiency curve for $S_{{\mathrm{t} {}\mathrm{\bar{t}}}}^{\text {min}}= $ 0.2 is also shown; this value is used in measuring the jet multiplicity distribution. |

png pdf |
Figure 5:
The upper panel shows the fiducial cross sections for the production of $ {\mathrm{W^{+}} \mathrm{W^{-}}} $+0-jets as the ${p_{\mathrm {T}}}$ threshold for jets is varied. The fiducial region is defined by two opposite-sign leptons with $ {p_{\mathrm {T}}} > $ 20 GeV and $ {| \eta |} < $ 2.5 excluding the products of $\tau $ lepton decay, and $ {m_{\ell \ell}} > $ 20 GeV, $p_{\text {T}}^{\ell \ell} > $ 30 GeV, and $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 30 GeV. Jets must have $ {p_{\mathrm {T}}} > $ 30 GeV, $ {| \eta |} < $ 4.5, and be separated from each of the two leptons by $\Delta R > $ 0.3. The lower panel shows the ratio of the theoretical prediction to the measurement. The shaded band depicts the uncertainty on the prediction. |
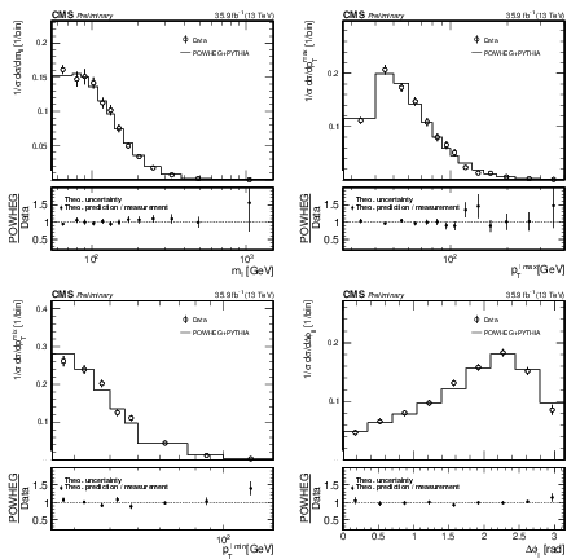
png pdf |
Figure 6:
The upper panels show the normalized differential cross sections with respect to the dilepton invariant mass, leading lepton ${p_{\mathrm {T}}}$, trailing lepton ${p_{\mathrm {T}}}$, and dilepton azimuthal angular separation, compared to POWHEG predictions. The lower panels show the ratio of the theoretical predictions to the measured values. The gray bands around unity in the ratio plots represent the systematic uncertainties, while the error bars on the markers represent the statistical uncertainties. |
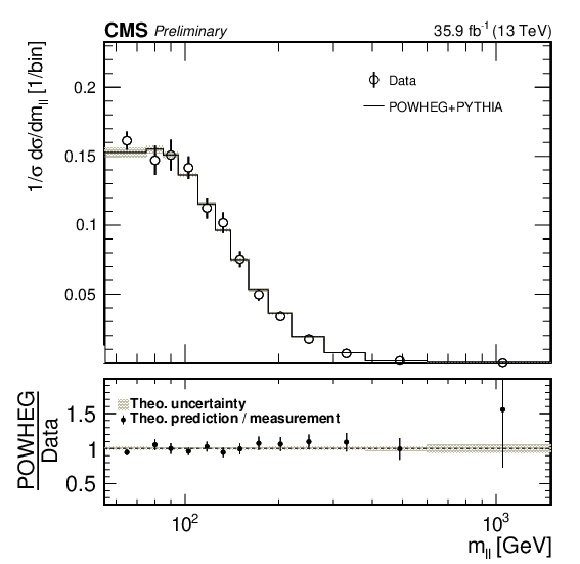
png pdf |
Figure 6-a:
The upper panels show the normalized differential cross sections with respect to the dilepton invariant mass, leading lepton ${p_{\mathrm {T}}}$, trailing lepton ${p_{\mathrm {T}}}$, and dilepton azimuthal angular separation, compared to POWHEG predictions. The lower panels show the ratio of the theoretical predictions to the measured values. The gray bands around unity in the ratio plots represent the systematic uncertainties, while the error bars on the markers represent the statistical uncertainties. |

png pdf |
Figure 6-b:
The upper panels show the normalized differential cross sections with respect to the dilepton invariant mass, leading lepton ${p_{\mathrm {T}}}$, trailing lepton ${p_{\mathrm {T}}}$, and dilepton azimuthal angular separation, compared to POWHEG predictions. The lower panels show the ratio of the theoretical predictions to the measured values. The gray bands around unity in the ratio plots represent the systematic uncertainties, while the error bars on the markers represent the statistical uncertainties. |
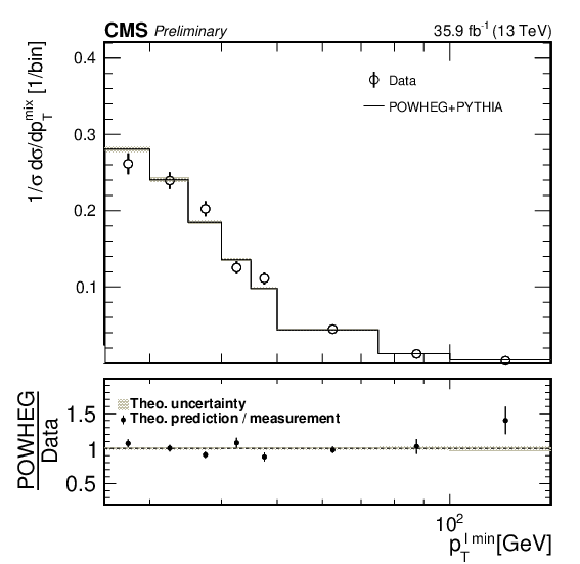
png pdf |
Figure 6-c:
The upper panels show the normalized differential cross sections with respect to the dilepton invariant mass, leading lepton ${p_{\mathrm {T}}}$, trailing lepton ${p_{\mathrm {T}}}$, and dilepton azimuthal angular separation, compared to POWHEG predictions. The lower panels show the ratio of the theoretical predictions to the measured values. The gray bands around unity in the ratio plots represent the systematic uncertainties, while the error bars on the markers represent the statistical uncertainties. |
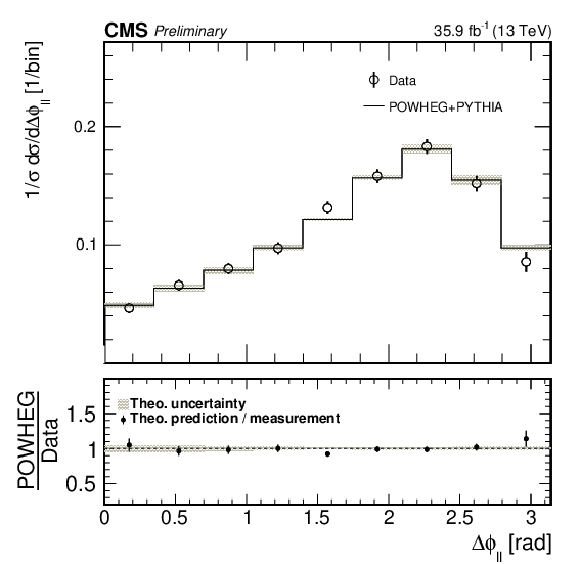
png pdf |
Figure 6-d:
The upper panels show the normalized differential cross sections with respect to the dilepton invariant mass, leading lepton ${p_{\mathrm {T}}}$, trailing lepton ${p_{\mathrm {T}}}$, and dilepton azimuthal angular separation, compared to POWHEG predictions. The lower panels show the ratio of the theoretical predictions to the measured values. The gray bands around unity in the ratio plots represent the systematic uncertainties, while the error bars on the markers represent the statistical uncertainties. |

png pdf |
Figure 7:
The upper panel shows the fractions of events with $ {N_{J}} = $ 0, 1, $\ge $2 jets. The circles represent the data after backgrounds are subtracted and pileup and energy resolution are taken into account. The solid lines represent represent the POWHEG+PYTHIA 8 prediction and an uncertainty represented by the grey band. The lower panel shows the ratio of the theoretical prediction to the measurement. The grey band shows the theoretical uncertainty and the error bars on the markers show the total uncertainty on the measurement. |

png pdf |
Figure 8:
One of the Feynman diagrams through which dimension-6 operators modify the ${\mathrm{p}} {\mathrm{p}} \to {\mathrm{W^{+}} \mathrm{W^{-}}} $ cross section. |
png pdf |
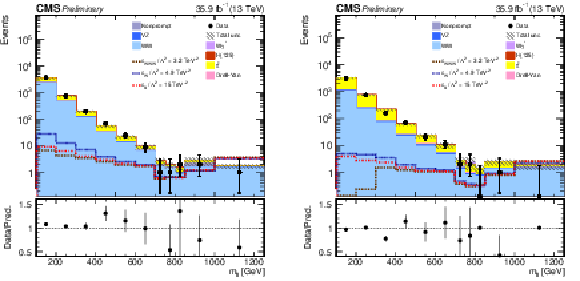
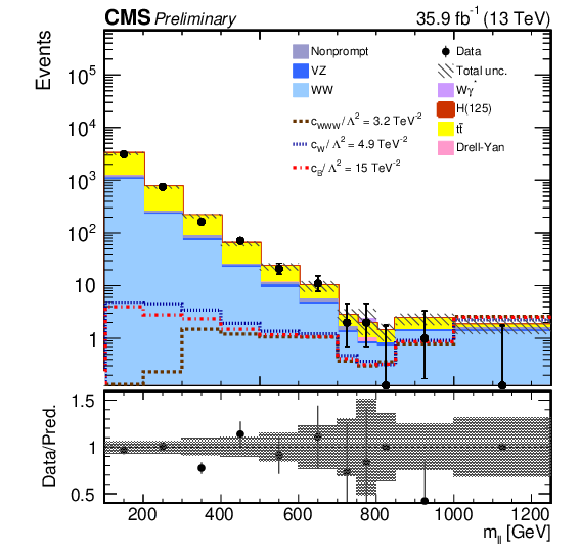
Figure 9:
Comparison of the template fits to the observed $ {m_{\mathrm{e}\mu}} $ distributions in the zero-jet (left) and one-jet (right) categories. The non-SM contributions for $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2 = $ 3.2 TeV$ ^{-2}$, $c_{\mathrm{W}}/\Lambda ^2 = $ 4.9 TeV$ ^{-2}$, and $c_{B}/\Lambda ^2 = $ 15.0 TeV$ ^{-2}$ are shown, not stacked on top of the other contributions. The last bin contains all events with reconstructed $ {m_{\mathrm{e}\mu}} > $ 1 TeV. The hatched areas represents the total uncertainty in the bin yield. |

png pdf |
Figure 9-a:
Comparison of the template fits to the observed $ {m_{\mathrm{e}\mu}} $ distributions in the zero-jet (left) and one-jet (right) categories. The non-SM contributions for $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2 = $ 3.2 TeV$ ^{-2}$, $c_{\mathrm{W}}/\Lambda ^2 = $ 4.9 TeV$ ^{-2}$, and $c_{B}/\Lambda ^2 = $ 15.0 TeV$ ^{-2}$ are shown, not stacked on top of the other contributions. The last bin contains all events with reconstructed $ {m_{\mathrm{e}\mu}} > $ 1 TeV. The hatched areas represents the total uncertainty in the bin yield. |
png pdf |
Figure 9-b:
Comparison of the template fits to the observed $ {m_{\mathrm{e}\mu}} $ distributions in the zero-jet (left) and one-jet (right) categories. The non-SM contributions for $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2 = $ 3.2 TeV$ ^{-2}$, $c_{\mathrm{W}}/\Lambda ^2 = $ 4.9 TeV$ ^{-2}$, and $c_{B}/\Lambda ^2 = $ 15.0 TeV$ ^{-2}$ are shown, not stacked on top of the other contributions. The last bin contains all events with reconstructed $ {m_{\mathrm{e}\mu}} > $ 1 TeV. The hatched areas represents the total uncertainty in the bin yield. |

png pdf |
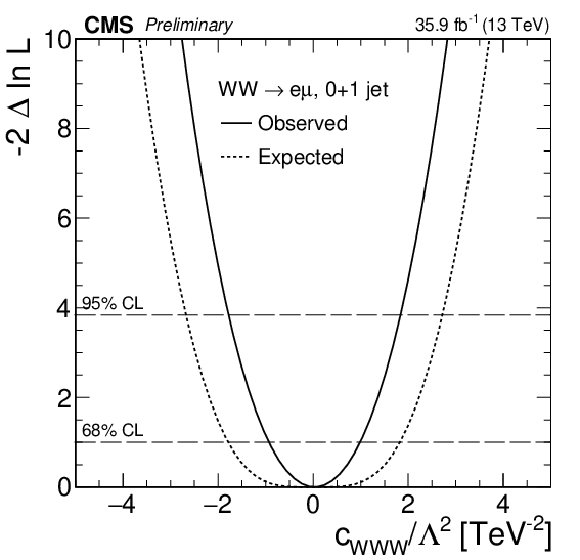
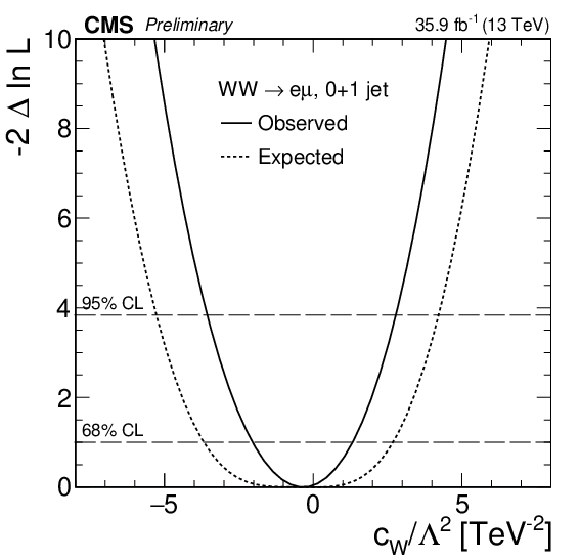
Figure 10:
The expected and observed $-2\Delta \ln L$ curves for the $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2$, $ c_{\mathrm{W}}/\Lambda ^2$, and $c_{\mathrm{W}}/\Lambda ^2$ 1D scans combining the 0-jet and 1-jet categories. |
png pdf |
Figure 10-a:
The expected and observed $-2\Delta \ln L$ curves for the $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2$, $ c_{\mathrm{W}}/\Lambda ^2$, and $c_{\mathrm{W}}/\Lambda ^2$ 1D scans combining the 0-jet and 1-jet categories. |
png pdf |
Figure 10-b:
The expected and observed $-2\Delta \ln L$ curves for the $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2$, $ c_{\mathrm{W}}/\Lambda ^2$, and $c_{\mathrm{W}}/\Lambda ^2$ 1D scans combining the 0-jet and 1-jet categories. |
png pdf |
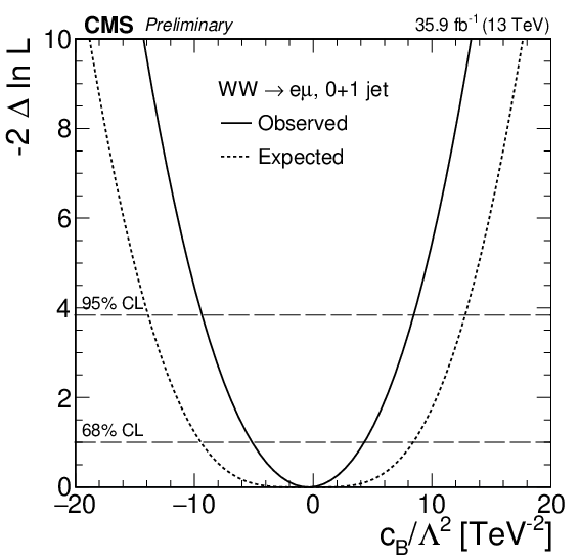
Figure 10-c:
The expected and observed $-2\Delta \ln L$ curves for the $c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2$, $ c_{\mathrm{W}}/\Lambda ^2$, and $c_{\mathrm{W}}/\Lambda ^2$ 1D scans combining the 0-jet and 1-jet categories. |

png pdf |
Figure 11-a:
The expected and observed $-2\Delta \ln L$ contours in the $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{\mathrm{W}}/\Lambda ^2)$, $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$, and $(c_{\mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$ planes combining the 0-jet and 1-jet categories. |

png pdf |
Figure 11-b:
The expected and observed $-2\Delta \ln L$ contours in the $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{\mathrm{W}}/\Lambda ^2)$, $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$, and $(c_{\mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$ planes combining the 0-jet and 1-jet categories. |

png pdf |
Figure 11-c:
The expected and observed $-2\Delta \ln L$ contours in the $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{\mathrm{W}}/\Lambda ^2)$, $(c_{\mathrm{W} \mathrm{W} \mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$, and $(c_{\mathrm{W}}/\Lambda ^2, c_{B}/\Lambda ^2)$ planes combining the 0-jet and 1-jet categories. |
| Tables | |

png pdf |
Table 1:
Summary of event selection criteria for the sequential cut analysis and the random forest analyses. DYMVA refers to an event classifier used in the sequential cut analysis to suppress Drell-Yan background events. RF refers to random forest classifiers. Kinematic quantities are measured in GeV. A dash (--) means no requirement applied. |

png pdf |
Table 2:
Sample composition for the sequential cut and random forest selections after the fits described in Section yyyyy have been executed; the uncertainties shown are based on the total uncertainty obtained from the fit. The purity is the fraction of selected events that are $ {\mathrm{W^{+}} \mathrm{W^{-}}} $ signal events. |

png pdf |
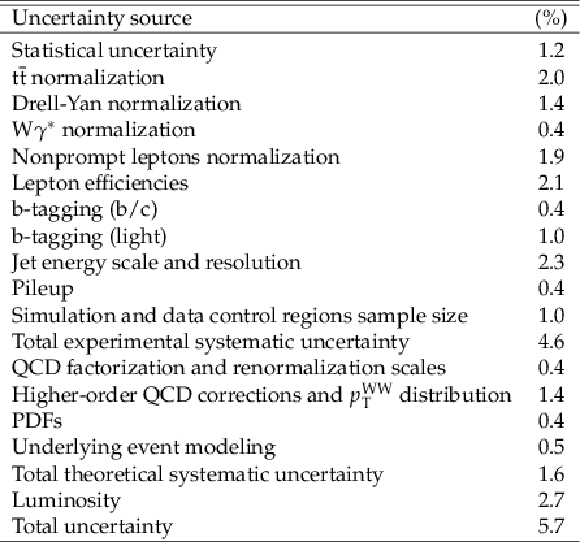
Table 3:
Features used for the random forest classifiers. The first classifier distinguishes Drell-Yan and $ {\mathrm{W^{+}} \mathrm{W^{-}}} $ signal events, and the second one distinguishes top quark events and signal events. |
png pdf |
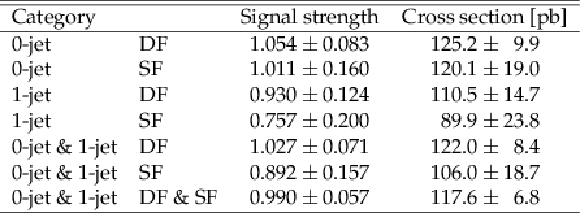
Table 4:
Relative systematic uncertainties of the cross section measurement based on the sequential cut analysis. |
png pdf |
Table 5:
Summary of signal strengths and total cross sections obtained in the sequential cut analysis. The uncertainty listed is the total uncertainty obtained from the fit to the yields. |

png pdf |
Table 6:
Fiducial cross sections for the production of $ {\mathrm{W^{+}} \mathrm{W^{-}}} $+0-jets as the ${p_{\mathrm {T}}}$ threshold for jets is varied. The fiducial region is defined by two opposite-sign leptons with $ {p_{\mathrm {T}}} > $ 20 GeV and $ {| \eta |} < $ 2.5 excluding the products of $\tau $ lepton decay, and $ {m_{\ell \ell}} > $ 20 GeV, $p_{\text {T}}^{\ell \ell} > $ 30 GeV, and $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 30 GeV. Jets must have $ {p_{\mathrm {T}}} > $ 30 GeV, $ {| \eta |} < $ 4.5, and be separated from each of the two leptons by $\Delta R > $ 0.3. |

png pdf |
Table 7:
Efficiency for the random forest selection with respect to preselected events as a function of jet multiplicity. The stated uncertainties are statistical only. |

png pdf |
Table 8:
Fractions of events with $ {N_{J}} = $ 0, 1, $\ge $2 jets. The first uncertainty is statistical and the second combines systematic uncertainties from the response matrix and from the background subtraction. |
png pdf |
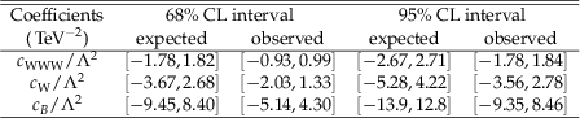
Table 9:
Expected and observed 68% and 95% confidence intervals on the measurement of the Wilson coefficients associated with the three CP-conserving, dimension-6 operators. |
| Summary |
| A study of ${\mathrm{W^{+}}\mathrm{W^{-}}} $ boson pair production in proton-proton collisions at $\sqrt{s} = $ 13 TeV was presented. The measurement is based on data collected with the CMS detector at the LHC correspond to an integrated luminosity of $35.9$ fb$^{-1}$. Candidate events were selected which have two electrons or muons with oppositely-signed charges. Two analysis methods were described. The first method relies on a sequence of requirements on kinematic quantities to suppress backgrounds, while the second uses a pair of random forest classifiers. The total cross section measured in the sequential cut analysis is $\sigma_{\text{SC}}^{\text{tot}} = $ 117.6 $\pm$ 1.4 (stat) $\pm$ 5.5 (syst) $\pm$ 1.9 (theo) $\pm$ 3.2 (lumi) pb $=$ 117.6 $\pm$ 6.8 pb, where the individual uncertainties are statistical, experimental systematic, theoretical, and luminosity; this measured value is consistent with the next-to-next-to-leading order theoretical prediction 118.8 $\pm$ 3.6 pb. The sequential cut analysis was also used to measure fiducial cross sections including the change in the zero-jet fiducial cross section with jet ${p_{\mathrm{T}}}$ threshold. Normalized differential cross sections were reported and compared with next-to-leading order Monte Carlo simulations. Good agreement is observed. The random forest analysis was used to measure the total cross section and to measure the normalized jet multiplicity distribution in ${\mathrm{W^{+}}\mathrm{W^{-}}} $ events. Finally, bounds on coefficients of dimension-6 operators in the context of an effective field theory were set using the electron-muon invariant mass distribution. |
| References | ||||
| 1 | ATLAS Collaboration | Measurement of $ \mathrm{W^{+}}\mathrm{W^{-}} $ production in pp collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector and limits on anomalous WWZ and WW$ \gamma $ couplings | PRD 87 (2013) 112001 | 1210.2979 |
| 2 | CMS Collaboration | Measurement of the $ \mathrm{W^+W^-} $ cross section in pp~collisions at $ \sqrt{s} = $ 7 ~TeV and limits on anomalous WW$ \gamma $ and WWZ couplings | EPJC 73 (2013) 2610 | CMS-SMP-12-005 1306.1126 |
| 3 | CMS Collaboration | Measurement of the $ \mathrm{W^+W^-} $ cross section in pp collisions at $ \sqrt{s} = $ 8 ~TeV and limits on anomalous gauge couplings | EPJC 76 (2016) 401 | CMS-SMP-14-016 1507.03268 |
| 4 | ATLAS Collaboration | Measurement of total and differential $ \mathrm{W^{+}}\mathrm{W^{-}} $ production cross sections in proton-proton collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector and limits on anomalous triple-gauge-boson couplings | JHEP 09 (2016) 029 | 1603.01702 |
| 5 | D0 Collaboration | Measurement of the WW production cross section with dilepton final states in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 ~TeV and limits on anomalous trilinear gauge couplings | PRL 103 (2009) 191801 | 0904.0673 |
| 6 | CDF Collaboration | Measurement of the $ \mathrm{W^{+}}\mathrm{W^{-}} $ production cross section and search for anomalous $ \mathrm{WW}\gamma $ and $ \mathrm{WWZ} $ couplings in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 ~TeV | PRL 104 (2010) 201801 | 0912.4500 |
| 7 | ATLAS Collaboration | Measurement of fiducial and differential $ \mathrm{W^{+}}\mathrm{W^{-}} $ production cross-sections at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | EPJC 79 (2019) 884 | 1905.04242 |
| 8 | T. Gehrmann et al. | $ \mathrm{W^+W^-} $ production at hadron colliders in next to next to leading order QCD | PRL 113 (2014) 212001 | 1408.5243 |
| 9 | F. Caola, K. Melnikov, R. Rantsch, and L. Tancredi | QCD corrections to $ \mathrm{W^{+}}\mathrm{W^{-}} $ production through gluon fusion | PLB 754 (2016) 275 | 1511.08617 |
| 10 | S. Gieseke, T. Kasprzik, and J. H. Kuhn | Vector-boson pair production and electroweak corrections in HERWIG++ | EPJC 74 (2014) 2988 | 1401.3964 |
| 11 | CMS Collaboration | The CMS Experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 12 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 13 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 14 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 15 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 16 | P. Nason and G. Zanderighi | $ \mathrm{W^{+}}\mathrm{W^{-}} $ , WZ and ZZ production in the POWHEG-BOX-V2 | EPJC 74 (2014) 2702 | 1311.1365 |
| 17 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO vector-boson production matched with shower in POWHEG | JHEP 07 (2008) 060 | 0805.4802 |
| 18 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 19 | J. M. Campbell and R. K. Ellis | MCFM for the Tevatron and the LHC | NPPS 205-206 (2010) 10 | 1007.3492 |
| 20 | Y. Gao et al. | Spin determination of single-produced resonances at hadron colliders | PRD 81 (2010) 075022 | 1001.3396 |
| 21 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 22 | J. M. Campbell, R. K. Ellis, P. Nason, and E. Re | Top-pair production and decay at NLO matched with parton showers | JHEP 04 (2015) 114 | 1412.1828 |
| 23 | T. Sjostrand, S. Mrenna, and P. Z. Skands | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | hep-ph/1410.3012 |
| 24 | CMS Collaboration | Investigations of the impact of the parton shower tuning in $ PYTHIA8 $ in the modelling of $ \mathrm{t\overline{t}} $ at $ \sqrt{s} = $ 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 25 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 26 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 27 | NNPDF Collaboration | Parton distributions with LHC data | NPB 867 (2013) 244 | 1207.1303 |
| 28 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 29 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 30 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 31 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 32 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 33 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13~TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 34 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 35 | CMS Collaboration | The performance of the CMS muon detector in proton-proton collisions at $ \sqrt{s} = $ 7 TeV at the LHC | JINST 8 (2013) P11002 | CMS-MUO-11-001 1306.6905 |
| 36 | A. Hoecker et al. | TMVA - toolkit for multivariate data analysis with ROOT | (unpublished) | physics/0703039 |
| 37 | CMS Collaboration | Measurement of Higgs boson production and properties in the WW decay channel with leptonic final states | JHEP 01 (2014) 096 | CMS-HIG-13-023 1312.1129 |
| 38 | L. Breiman | Random Forests | Machine Learning 45 (2001) 5 | |
| 39 | Tin Kam Ho | The random subspace method for constructing decision forests | IEEE Transactions on Pattern Analysis and Machine Intelligence 20 (1998) 832 | |
| 40 | R. Caruana and A. Niculescu-Mizil | An empirical comparison of supervised learning algorithms using different performance metrics | in In Proc. 23 rd Intl. Conf. Machine learning (ICML'06), p. 161 2005 | |
| 41 | CMS Collaboration | Measurements of properties of the Higgs boson decaying to a W boson pair in pp collisions at $ \sqrt{s} = $ 13 TeV | PLB 791 (2019) 96 | CMS-HIG-16-042 1806.05246 |
| 42 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 43 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 44 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 45 | M. Grazzini, S. Kallweit, D. Rathlev, and M. Wiesemann | Transverse-momentum resummation for vector-boson pair production at NNLL+NNLO | JHEP 08 (2015) 154 | 1507.02565 |
| 46 | P. Meade, H. Ramani, and M. Zeng | Transverse momentum resummation effects in $ \mathrm{W^{+}}\mathrm{W^{-}} $ measurements | PRD 90 (2014) 114006 | 1407.4481 |
| 47 | P. Jaiswal and T. Okui | Explanation of the WW excess at the LHC by jet-veto resummation | PRD 90 (2014) 073009 | 1407.4537 |
| 48 | P. Jaiswal, P. Meade, and H. Ramani | Precision diboson measurements and the interplay of $ p_{\mathrm{T}} $ and jet-veto resummations | PRD 93 (2016) 093007 | 1509.07118 |
| 49 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 50 | M. Bahr et al. | Herwig++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 51 | Particle Data Group, M. Tanabashi et al. | Review of particle physics | PRD 98 (2018) 030001 | |
| 52 | W. Buchmuller and D. Wyler | Effective Lagrangian analysis of new interactions and flavor conservation | NPB 268 (1986) 621 | |
| 53 | B. Grzadkowski, M. Iskrzy\'nski, M. Misiak, and J. Rosiek | Dimension-six terms in the standard model Lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 54 | C. Degrande et al. | Effective Field Theory: A Modern Approach to Anomalous Couplings | Annals Phys. 335 (2013) 21 | 1205.4231 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|