

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-EXO-19-020 | ||
| Search for resonant production of strongly-coupled dark matter in proton-proton collisions at 13 TeV | ||
| CMS Collaboration | ||
| August 2021 | ||
| Abstract: The first collider search for dark matter arising from a strongly-coupled hidden sector is presented, using a data sample corresponding to 137 fb$^{-1}$ collected with the CMS detector at the CERN LHC at a center-of-mass energy of 13 TeV. The hidden sector is hypothesized to couple to the standard model (SM) via a heavy leptophobic Z' mediator. The resonant production and decay of such a mediator in proton-proton collisions would result in two "semi-visible'' jets, which contain both visible matter and invisible dark matter. This would lead to moderate missing energy aligned with one of the jets, a signature ignored by most dark matter searches. The observed dijet transverse mass spectrum is smoothly falling, as expected from the SM; no structure compatible with the signal is observed. Assuming the same couplings as the SM Z boson, mediator masses up to 3.9 TeV are excluded at 95% confidence level, depending on the other signal model parameters. To enhance the sensitivity of the search for this particular class of models, a boosted decision tree (BDT) is trained using jet substructure variables to distinguish between semi-visible jets and standard model jets from background processes. When the BDT is employed to select events with jets identified as semi-visible, the mediator mass exclusion increases to 5.1 TeV, for wider ranges of the other signal model parameters. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
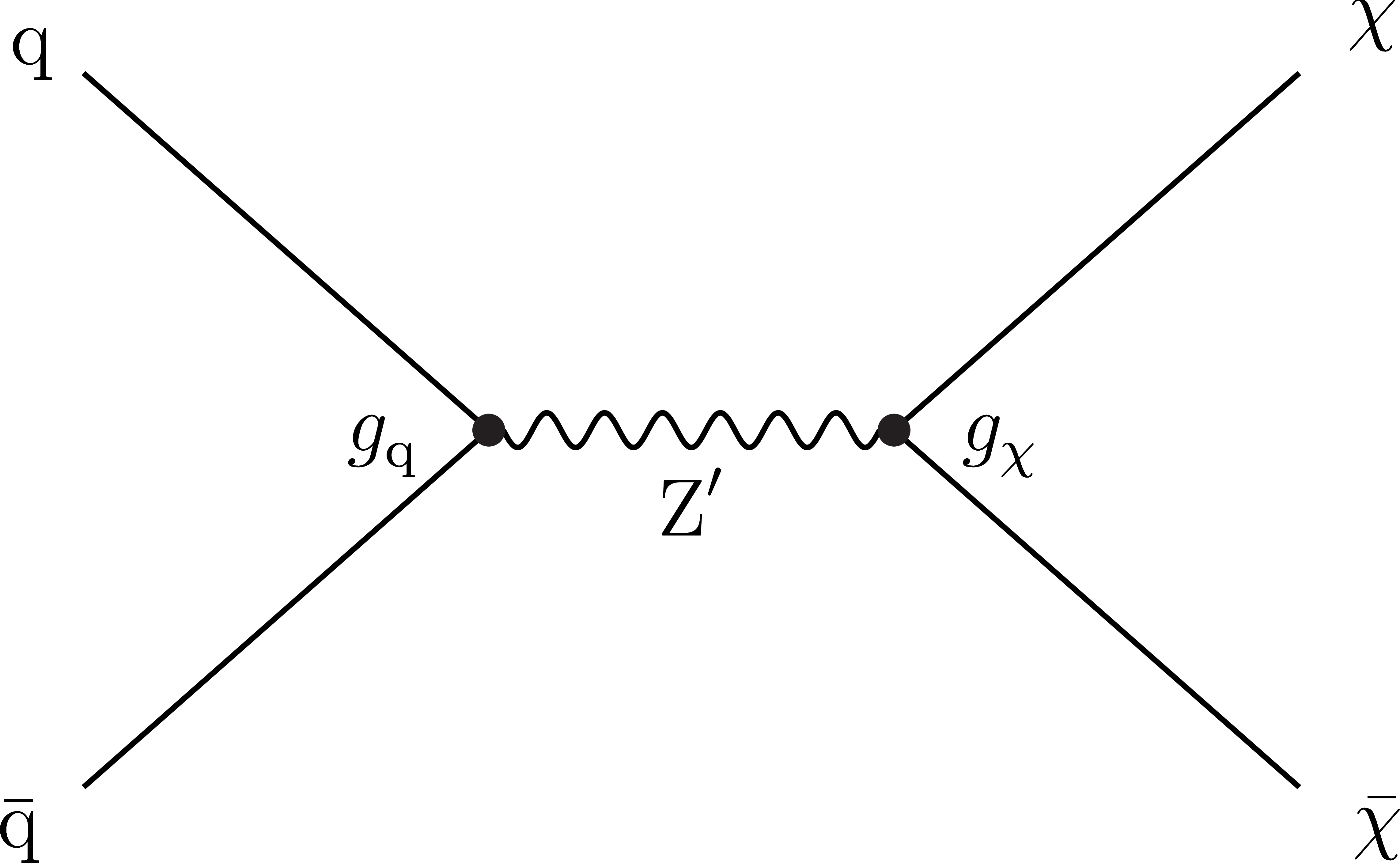
Figure 1:
Diagram of leading-order resonant production of dark quarks through a Z' mediator. The relevant couplings to SM quarks and dark quarks, ${g_{\mathrm{q}}}$ and ${g_{{\chi}}}$, are indicated at the labeled vertices. |

png pdf |
Figure 2:
The normalized distributions of the characteristic variables ${R_{\mathrm {T}}}$ and ${\Delta \phi _{\text {min}}}$ for the simulated SM backgrounds and several signal models. For each variable, the requirement on that variable is omitted, but all other preselection requirements are applied. The black (red) vertical dotted line indicates the preselection (final selection) requirement on the variable, if any. |

png pdf |
Figure 2-a:
The normalized distributions of the characteristic variables ${R_{\mathrm {T}}}$ and ${\Delta \phi _{\text {min}}}$ for the simulated SM backgrounds and several signal models. For each variable, the requirement on that variable is omitted, but all other preselection requirements are applied. The black (red) vertical dotted line indicates the preselection (final selection) requirement on the variable, if any. |

png pdf |
Figure 2-b:
The normalized distributions of the characteristic variables ${R_{\mathrm {T}}}$ and ${\Delta \phi _{\text {min}}}$ for the simulated SM backgrounds and several signal models. For each variable, the requirement on that variable is omitted, but all other preselection requirements are applied. The black (red) vertical dotted line indicates the preselection (final selection) requirement on the variable, if any. |
png pdf |
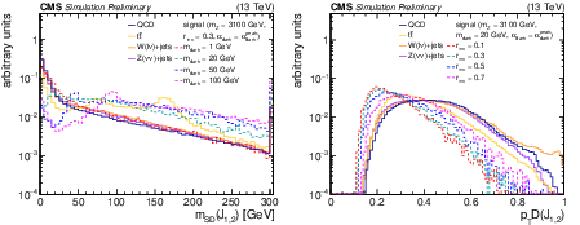
Figure 3:
The normalized distributions of the BDT input variables ${m_{\text {SD}}}$ and ${p_{\text {T}}D}$ for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The jet ${p_{\mathrm {T}}}$ distributions are weighted so that all samples have matching distributions. |

png pdf |
Figure 3-a:
The normalized distributions of the BDT input variables ${m_{\text {SD}}}$ and ${p_{\text {T}}D}$ for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The jet ${p_{\mathrm {T}}}$ distributions are weighted so that all samples have matching distributions. |
png pdf |
Figure 3-b:
The normalized distributions of the BDT input variables ${m_{\text {SD}}}$ and ${p_{\text {T}}D}$ for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The jet ${p_{\mathrm {T}}}$ distributions are weighted so that all samples have matching distributions. |

png pdf |
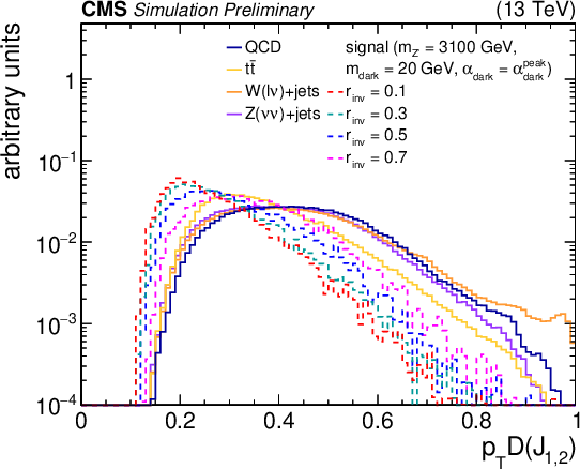
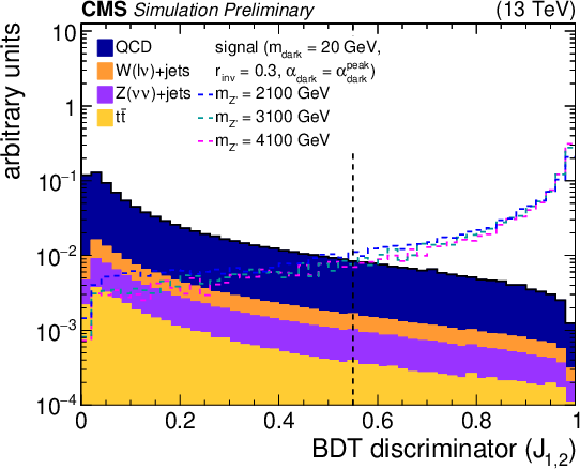
Figure 4:
Left: The normalized BDT discriminator distribution for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The discriminator WP of 0.55 is indicated as a dashed line. Right: The BDT ROC curves for the two highest-${p_{\mathrm {T}}}$ jets, comparing the simulated SM backgrounds with one signal model. The area under the ROC curve is listed for each pairing. The discriminator WP of 0.55 is indicated on each curve as a circle. |
png pdf |
Figure 4-a:
Left: The normalized BDT discriminator distribution for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The discriminator WP of 0.55 is indicated as a dashed line. Right: The BDT ROC curves for the two highest-${p_{\mathrm {T}}}$ jets, comparing the simulated SM backgrounds with one signal model. The area under the ROC curve is listed for each pairing. The discriminator WP of 0.55 is indicated on each curve as a circle. |
png pdf |
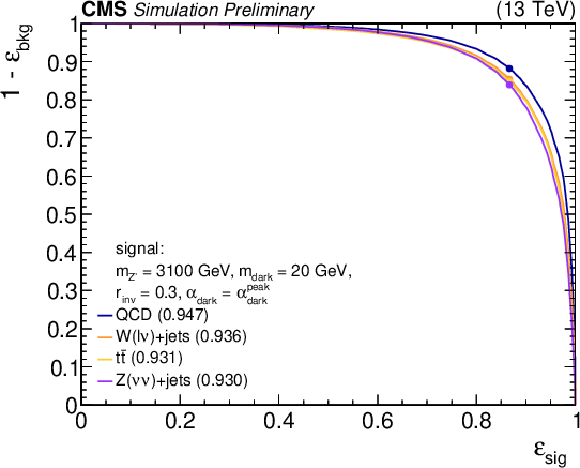
Figure 4-b:
Left: The normalized BDT discriminator distribution for the two highest-${p_{\mathrm {T}}}$ jets from the simulated SM backgrounds and several signal models. The discriminator WP of 0.55 is indicated as a dashed line. Right: The BDT ROC curves for the two highest-${p_{\mathrm {T}}}$ jets, comparing the simulated SM backgrounds with one signal model. The area under the ROC curve is listed for each pairing. The discriminator WP of 0.55 is indicated on each curve as a circle. |
png pdf |
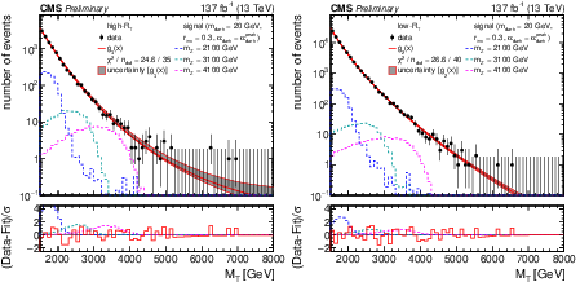
Figure 5:
The ${M_{\mathrm {T}}}$ distribution for the high-${R_{\mathrm {T}}}$ (left) and low-${R_{\mathrm {T}}}$ (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${g_{3}(x) = \exp(p_1 x) x^{p_2 (1 + p_3 \log(x))}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |
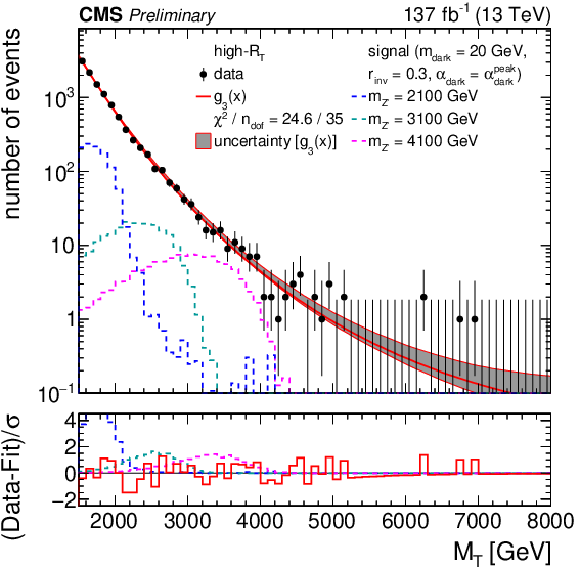
png pdf |
Figure 5-a:
The ${M_{\mathrm {T}}}$ distribution for the high-${R_{\mathrm {T}}}$ (left) and low-${R_{\mathrm {T}}}$ (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${g_{3}(x) = \exp(p_1 x) x^{p_2 (1 + p_3 \log(x))}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |
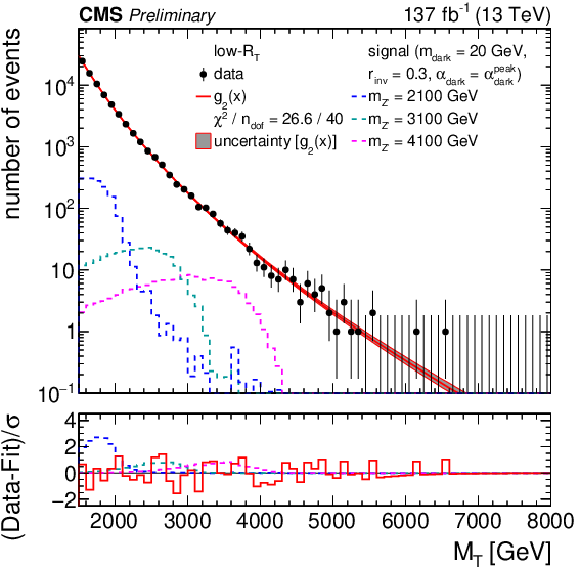
png pdf |
Figure 5-b:
The ${M_{\mathrm {T}}}$ distribution for the high-${R_{\mathrm {T}}}$ (left) and low-${R_{\mathrm {T}}}$ (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${g_{3}(x) = \exp(p_1 x) x^{p_2 (1 + p_3 \log(x))}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |
png pdf |
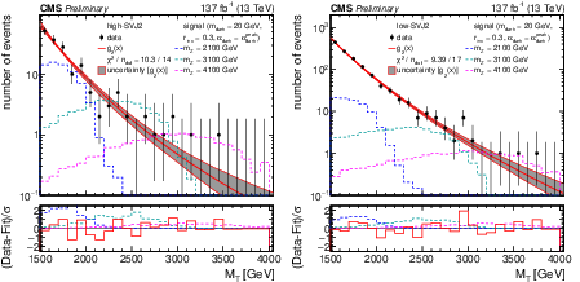
Figure 6:
The ${M_{\mathrm {T}}}$ distribution for the high-SVJ2 (left) and low-SVJ2 (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |
png pdf |
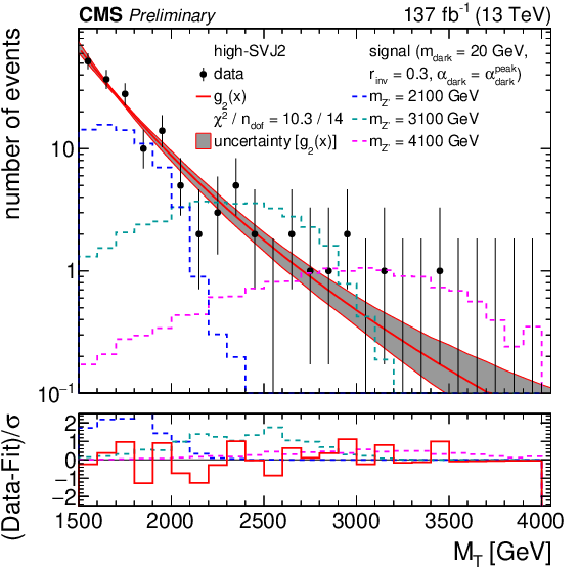
Figure 6-a:
The ${M_{\mathrm {T}}}$ distribution for the high-SVJ2 (left) and low-SVJ2 (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |
png pdf |
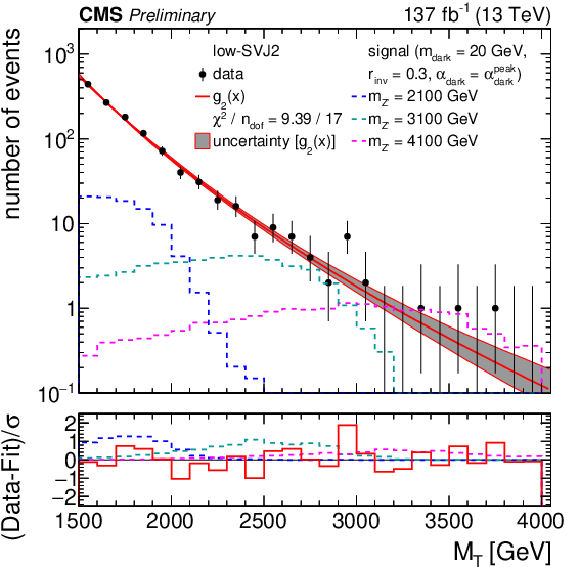
Figure 6-b:
The ${M_{\mathrm {T}}}$ distribution for the high-SVJ2 (left) and low-SVJ2 (right) signal regions, comparing the observed data to the background prediction from the analytic fit (${g_{2}(x) = \exp(p_1 x) x^{p_2}}$, ${x = {M_{\mathrm {T}}} /\,\sqrt {\smash [b]{s}}}$). The lower panel shows the difference between the observation and the prediction divided by the statistical uncertainty in the observation. The distributions from several example signal models, with cross sections corresponding to the observed limits, are superimposed. |

png pdf |
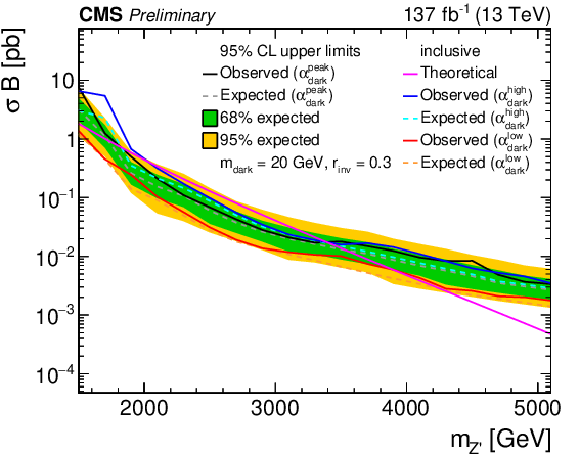
Figure 7:
The 95% CL upper limits on the product of the cross section and branching fraction from the inclusive search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |

png pdf |
Figure 7-a:
The 95% CL upper limits on the product of the cross section and branching fraction from the inclusive search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
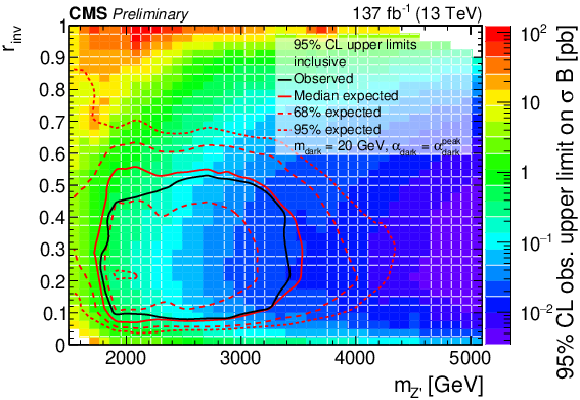
png pdf |
Figure 7-b:
The 95% CL upper limits on the product of the cross section and branching fraction from the inclusive search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
png pdf |
Figure 7-c:
The 95% CL upper limits on the product of the cross section and branching fraction from the inclusive search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
png pdf |
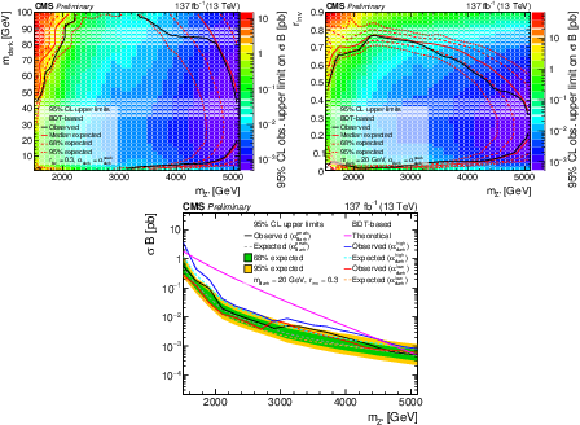
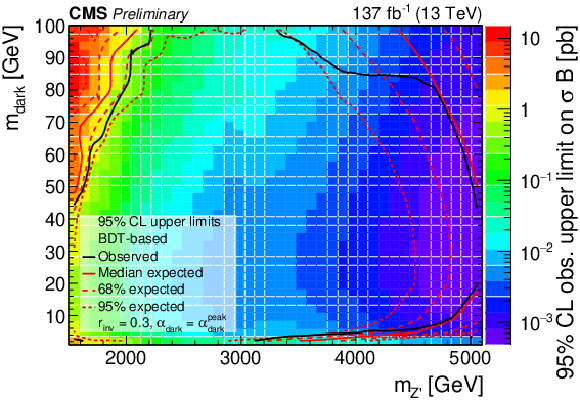
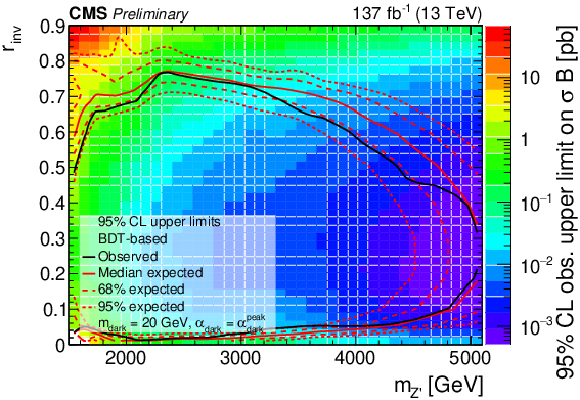
Figure 8:
The 95% CL upper limits on the product of the cross section and branching fraction from the BDT-based search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
png pdf |
Figure 8-a:
The 95% CL upper limits on the product of the cross section and branching fraction from the BDT-based search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
png pdf |
Figure 8-b:
The 95% CL upper limits on the product of the cross section and branching fraction from the BDT-based search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
png pdf |
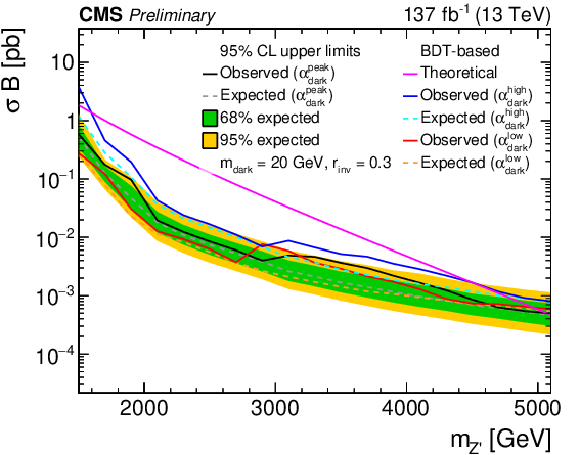
Figure 8-c:
The 95% CL upper limits on the product of the cross section and branching fraction from the BDT-based search for variations of pairs of the signal model parameters. In the upper plots, the filled region indicates the observed upper limit. The solid black curves indicate the observed exclusions for the nominal Z' cross section, while the solid red curves indicate the expected exclusions, and the dashed lines indicate the regions containing 68% and 95% of the distributions of expected exclusions. The lower plot shows the ${\alpha _{\text {dark}}}$ variation as multiple curves in one dimension, because there are only three parameter values considered. The black, blue, and red solid lines show the observed upper limits for each variation, while the dashed lines show the expected limits. The inner (green) and outer (yellow) bands indicate the regions containing 68% and 95%, respectively, of the distributions of expected limits. The purple solid line labeled "Theoretical'' represents the nominal Z' cross section. |
| Tables | |

png pdf |
Table 1:
The three two-dimensional signal model parameter scans. For each scan, the ranges of the parameters that are varied in that scan are given in bold text. |

png pdf |
Table 2:
Summary of the selection requirements. |
png pdf |
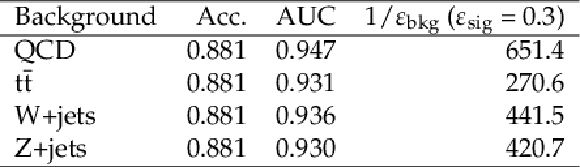
Table 3:
Metrics representing the performance of the BDT for the benchmark signal model ($ {m_{{{\mathrm{Z}}^{\prime}}}} = $ 3100 GeV, $ {m_{\text {dark}}} = $ 20 GeV, $ {r_{\text {inv}}} = $ 0.3, $ {\alpha _{\text {dark}}} = {{\alpha _{\text {dark}}} ^{\text {peak}}} $), compared to each of the major SM background processes. |
| Summary |
| We present the first collider search for resonant production of dark matter from a strongly-coupled hidden sector in the form of semi-visible jets. The search uses the full Run 2 proton-proton collision dataset collected by the CMS detector, which corresponds to an integrated luminosity of 137 fb$^{-1}$ at a center-of-mass energy of 13 TeV. The signal model introduces a dark sector with multiple flavors of dark quarks charged under a dark confining force, which form stable and unstable dark hadrons. The stable dark hadrons constitute dark matter candidates, while the unstable dark hadrons decay promptly to standard model (SM) quarks, forming collimated sprays of both invisible and visible particles known as "semi-visible'' jets. The hidden sector communicates with the SM via a leptophobic Z' boson mediator. |
| References | ||||
| 1 | V. C. Rubin, N. Thonnard, and W. K. Ford, Jr. | Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R = 4 kpc) to UGC 2885 (R = 122 kpc) | Astrophys. J. 238 (1980) 471 | |
| 2 | M. Persic, P. Salucci, and F. Stel | The universal rotation curve of spiral galaxies: 1. the dark matter connection | Mon. Not. Roy. Astron. Soc. 281 (1996) 27 | astro-ph/9506004 |
| 3 | D. Clowe et al. | A direct empirical proof of the existence of dark matter | Astrophys. J. 648 (2006) L109 | astro-ph/0608407 |
| 4 | DES Collaboration | Dark Energy Survey year 1 results: Curved-sky weak lensing mass map | Mon. Not. Roy. Astron. Soc. 475 (2018) 3165 | 1708.01535 |
| 5 | Planck Collaboration | Planck 2018 results. VI. cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 6 | M. Battaglieri et al. | US Cosmic Visions: New Ideas in Dark Matter 2017: Community Report | in U.S. Cosmic Visions: New Ideas in Dark Matter 2017 | 1707.04591 |
| 7 | G. Jungman, M. Kamionkowski, and K. Griest | Supersymmetric dark matter | PR 267 (1996) 195 | hep-ph/9506380 |
| 8 | CMS Collaboration | Search for new particles in events with energetic jets and large missing transverse momentum in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | 2021. Submitted to JHEP | CMS-EXO-20-004 2107.13021 |
| 9 | CMS Collaboration | Search for dark matter produced in association with a Higgs boson decaying to a pair of bottom quarks in proton--proton collisions at $ \sqrt{s}= $ 13 TeV | EPJC 79 (2019) 280 | CMS-EXO-16-050 1811.06562 |
| 10 | CMS Collaboration | Search for dark matter produced in association with a single top quark or a top quark pair in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 03 (2019) 141 | CMS-EXO-18-010 1901.01553 |
| 11 | CMS Collaboration | Search for invisible decays of a Higgs boson produced through vector boson fusion in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 793 (2019) 520 | CMS-HIG-17-023 1809.05937 |
| 12 | ATLAS Collaboration | Search for dark matter in events with a hadronically decaying vector boson and missing transverse momentum in $ pp $ collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 10 (2018) 180 | 1807.11471 |
| 13 | ATLAS Collaboration | Search for top-squark pair production in final states with one lepton, jets, and missing transverse momentum using 36 fb$ ^{-1} $ of $ \sqrt{s}= $ 13 TeV pp collision data with the ATLAS detector | JHEP 06 (2018) 108 | 1711.11520 |
| 14 | ATLAS Collaboration | Search for dark matter and other new phenomena in events with an energetic jet and large missing transverse momentum using the ATLAS detector | JHEP 01 (2018) 126 | 1711.03301 |
| 15 | ATLAS Collaboration | Search for invisible Higgs boson decays in vector boson fusion at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PLB 793 (2019) 499 | 1809.06682 |
| 16 | M. J. Strassler and K. M. Zurek | Echoes of a hidden valley at hadron colliders | PLB 651 (2007) 374 | hep-ph/0604261 |
| 17 | CMS Collaboration | Search for a narrow resonance lighter than 200 GeV decaying to a pair of muons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRL 124 (2020) 131802 | CMS-EXO-19-018 1912.04776 |
| 18 | ATLAS Collaboration | Search for light long-lived neutral particles produced in $ pp $ collisions at $ \sqrt{s} = $ 13 TeV and decaying into collimated leptons or light hadrons with the ATLAS detector | EPJC 80 (2020) 450 | 1909.01246 |
| 19 | CMS Collaboration | Search for dark photons in decays of Higgs bosons produced in association with Z bosons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 10 (2019) 139 | CMS-EXO-19-007 1908.02699 |
| 20 | CMS Collaboration | A search for pair production of new light bosons decaying into muons in proton-proton collisions at 13 TeV | PLB 796 (2019) 131 | CMS-HIG-18-003 1812.00380 |
| 21 | ATLAS Collaboration | Search for long-lived particles in final states with displaced dimuon vertices in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 99 (2019) 012001 | 1808.03057 |
| 22 | LHCb Collaboration | Search for dark photons produced in 13 $ TeV pp $ collisions | PRL 120 (2018) 061801 | 1710.02867 |
| 23 | LHCb Collaboration | Search for $ A'\to\mu^+\mu^- $ Decays | PRL 124 (2020) 041801 | 1910.06926 |
| 24 | LHCb Collaboration | Searches for low-mass dimuon resonances | JHEP 10 (2020) 156 | 2007.03923 |
| 25 | J. Alimena et al. | Searching for long-lived particles beyond the Standard Model at the Large Hadron Collider | JPG 47 (2020) 090501 | 1903.04497 |
| 26 | K. Petraki and R. R. Volkas | Review of asymmetric dark matter | Int. J. Mod. Phys. A 28 (2013) 1330028 | 1305.4939 |
| 27 | Planck Collaboration | Planck 2015 results. XIII. cosmological parameters | Astron. Astrophys. 594 (2016) A13 | 1502.01589 |
| 28 | Y. Bai and P. Schwaller | Scale of dark QCD | PRD 89 (2014) 063522 | 1306.4676 |
| 29 | H. Beauchesne, E. Bertuzzo, and G. Grilli Di Cortona | Dark matter in Hidden Valley models with stable and unstable light dark mesons | JHEP 04 (2019) 118 | 1809.10152 |
| 30 | T. Cohen, M. Lisanti, and H. K. Lou | Semi-visible jets: Dark matter undercover at the LHC | PRL 115 (2015) 171804 | 1503.00009 |
| 31 | T. Cohen, M. Lisanti, H. K. Lou, and S. Mishra-Sharma | LHC searches for dark sector showers | JHEP 11 (2017) 196 | 1707.05326 |
| 32 | CMS Collaboration | Search for high mass dijet resonances with a new background prediction method in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2020) 033 | CMS-EXO-19-012 1911.03947 |
| 33 | ATLAS Collaboration | Search for new resonances in mass distributions of jet pairs using 139 fb$ ^{-1} $ of $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | JHEP 03 (2020) 145 | 1910.08447 |
| 34 | P. Schwaller, D. Stolarski, and A. Weiler | Emerging jets | JHEP 05 (2015) 059 | 1502.05409 |
| 35 | CMS Collaboration | Search for new particles decaying to a jet and an emerging jet | JHEP 02 (2019) 179 | CMS-EXO-18-001 1810.10069 |
| 36 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 37 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 38 | R. K. Ellis, W. J. Stirling, and B. R. Webber | QCD and collider physics | Camb. Monogr. Part. Phys. NP Cosmol. 8 (1996)1 | |
| 39 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 40 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 41 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 42 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 43 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 44 | P. Barnreuther, M. Czakon, and A. Mitov | Percent level precision physics at the Tevatron: First genuine NNLO QCD corrections to $ \mathrm{q\bar{q}}\to\mathrm{t\bar{t}} +X $ | PRL 109 (2012) 132001 | 1204.5201 |
| 45 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 46 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 47 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ O({\alpha_S}^4) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 48 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | W physics at the LHC with FEWZ 2.1 | CPC 184 (2013) 208 | 1201.5896 |
| 49 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | CPC 182 (2011) 2388 | 1011.3540 |
| 50 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 51 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 52 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 53 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 54 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 55 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 56 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 57 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 58 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 59 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 60 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 61 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 62 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | CMS-PAS-JME-16-003 |
| 63 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 64 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 65 | K. Rehermann and B. Tweedie | Efficient identification of boosted semileptonic top quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 66 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 67 | M. Park and M. Zhang | Tagging a jet from a dark sector with jet-substructures at colliders | PRD 100 (2019) 115009 | 1712.09279 |
| 68 | T. Cohen, J. Doss, and M. Freytsis | Jet substructure from dark sector showers | JHEP 09 (2020) 118 | 2004.00631 |
| 69 | E. Bernreuther et al. | Casting a graph net to catch dark showers | SciPost Phys. 10 (2021) 046 | 2006.08639 |
| 70 | J. Thaler and K. Van Tilburg | Identifying boosted objects with $ n $-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 71 | I. Moult, L. Necib, and J. Thaler | New angles on energy correlation functions | JHEP 12 (2016) 153 | 1609.07483 |
| 72 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 73 | J. Gallicchio and M. D. Schwartz | Quark and gluon jet substructure | JHEP 04 (2013) 090 | 1211.7038 |
| 74 | CMS Collaboration | Performance of quark/gluon discrimination in 8 TeV pp data | CMS-PAS-JME-13-002 | CMS-PAS-JME-13-002 |
| 75 | F. Pedregosa et al. | Scikit-learn: Machine learning in Python | J. Mach. Learn. Res. 12 (2011) 2825 | 1201.0490 |
| 76 | T. Likhomanenko et al. | Reproducible Experiment Platform | J. Phys. Conf. Ser. 664 (2015) 052022 | 1510.00624 |
| 77 | UA2 Collaboration | A measurement of two jet decays of the $ w $ and $ z $ bosons at the CERN $ \bar{p} p $ collider | Z. Phys. C 49 (1991) 17 | |
| 78 | UA2 Collaboration | A search for new intermediate vector mesons and excited quarks decaying to two jets at the CERN $ \bar{p} p $ collider | NPB 400 (1993) 3 | |
| 79 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 80 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 81 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 82 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 83 | A. Kalogeropoulos and J. Alwall | The SysCalc code: A tool to derive theoretical systematic uncertainties | 2018 | 1801.08401 |
| 84 | S. Catani, D. de Florian, M. Grazzini, and P. Nason | Soft gluon resummation for Higgs boson production at hadron colliders | JHEP 07 (2003) 028 | hep-ph/0306211 |
| 85 | M. Cacciari et al. | The $ \mathrm{t\bar{t}} $ cross-section at 1.8 TeV and 1.96 TeV: a study of the systematics due to parton densities and scale dependence | JHEP 04 (2004) 068 | hep-ph/0303085 |
| 86 | S. Mrenna and P. Skands | Automated parton-shower variations in Pythia 8 | PRD 94 (2016) 074005 | 1605.08352 |
| 87 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 88 | A. L. Read | Presentation of search results: The CL(s) technique | JPG 28 (2002) 2693 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|