

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-20-004 ; CERN-EP-2021-136 | ||
| Search for new particles in events with energetic jets and large missing transverse momentum in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 27 July 2021 | ||
| JHEP 11 (2021) 153 | ||
| Abstract: A search is presented for new particles produced at the LHC in proton-proton collisions at $\sqrt{s} = $ 13 TeV, using events with energetic jets and large missing transverse momentum. The analysis is based on a data sample corresponding to an integrated luminosity of 101 fb$^{-1}$, collected in 2017-2018 with the CMS detector. Machine learning techniques are used to define separate categories for events with narrow jets from initial-state radiation and events with large-radius jets consistent with a hadronic decay of a W or Z boson. A statistical combination is made with an earlier search based on a data sample of 36 fb$^{-1}$, collected in 2016. No significant excess of events is observed with respect to the standard model background expectation determined from control samples in data. The results are interpreted in terms of limits on the branching fraction of an invisible decay of the Higgs boson, as well as constraints on simplified models of dark matter, on first-generation scalar leptoquarks decaying to quarks and neutrinos, and on models with large extra dimensions. Several of the new limits, specifically for spin-1 dark matter mediators, pseudoscalar mediators, colored mediators, and leptoquarks, are the most restrictive to date. | ||
| Links: e-print arXiv:2107.13021 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Representative Feynman diagrams for a number of signal models: Higgs production in association with an SM vector boson (left), colorless spin-1 and spin-0 mediators (middle left and right, respectively), single leptoquark production (right). In all cases, subdominant production modes not pictured here are taken into account, as described in the text. |
png pdf |
Figure 1-a:
Representative Feynman diagram for a signal model of Higgs production in association with an SM vector boson. |
png pdf |
Figure 1-b:
Representative Feynman diagram for a signal model with colorless spin-1 mediator. |
png pdf |
Figure 1-c:
Representative Feynman diagram for a signal model with colorless spin-0 mediator. |

png pdf |
Figure 1-d:
Representative Feynman diagram for a signal model of single leptoquark production. |

png pdf |
Figure 2:
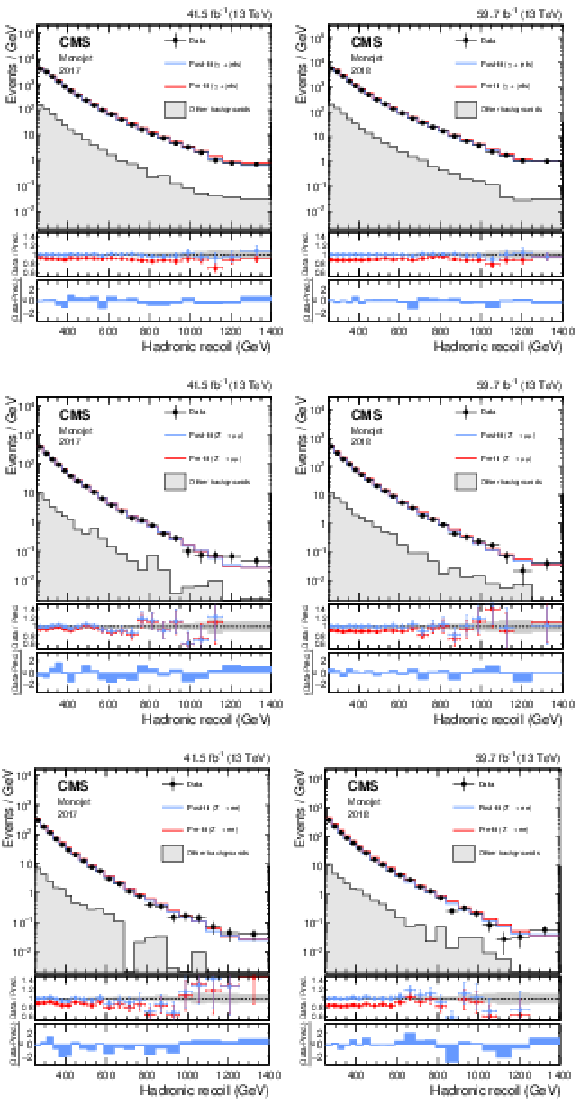
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points). The gray band represents the total uncertainty in the ratio. In the lower panels, the ratio of data over prediction is shown. From upper to lower, the rows show the monojet, low-purity, and high-purity mono-V categories, while the left (right) column represents the 2017 (2018) data set. |
png pdf |
Figure 2-a:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the monojet category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |

png pdf |
Figure 2-b:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the monojet category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
png pdf |
Figure 2-c:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the low-purity mono-V category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
png pdf |
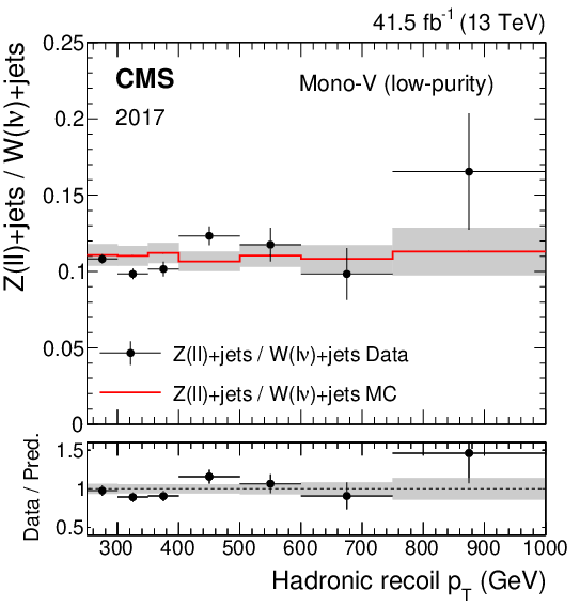
Figure 2-d:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the low-purity mono-V category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
png pdf |
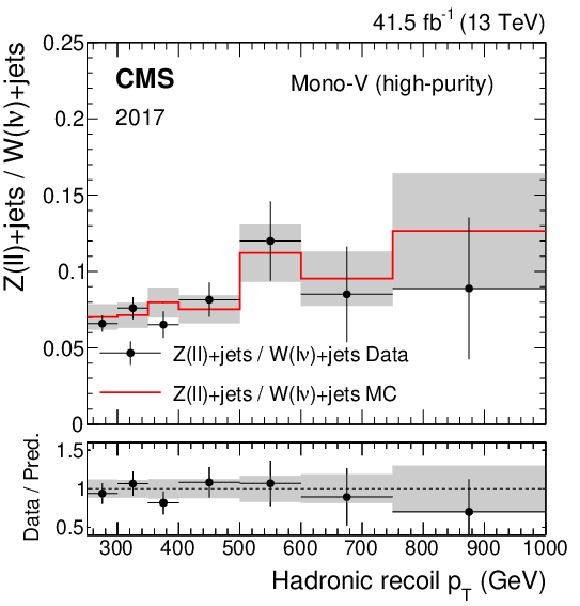
Figure 2-e:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the high-purity mono-V category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |

png pdf |
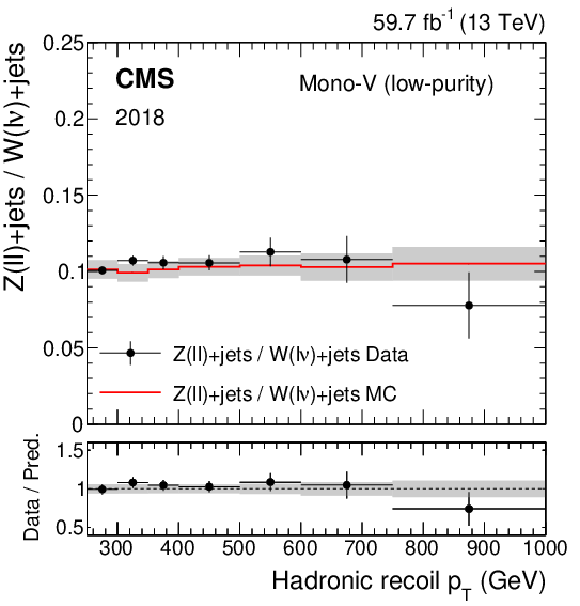
Figure 2-f:
Ratio of the dilepton to single-lepton control region yields predicted using simulation (red solid line), and observed in data (black points) in the high-purity mono-V category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
png pdf |
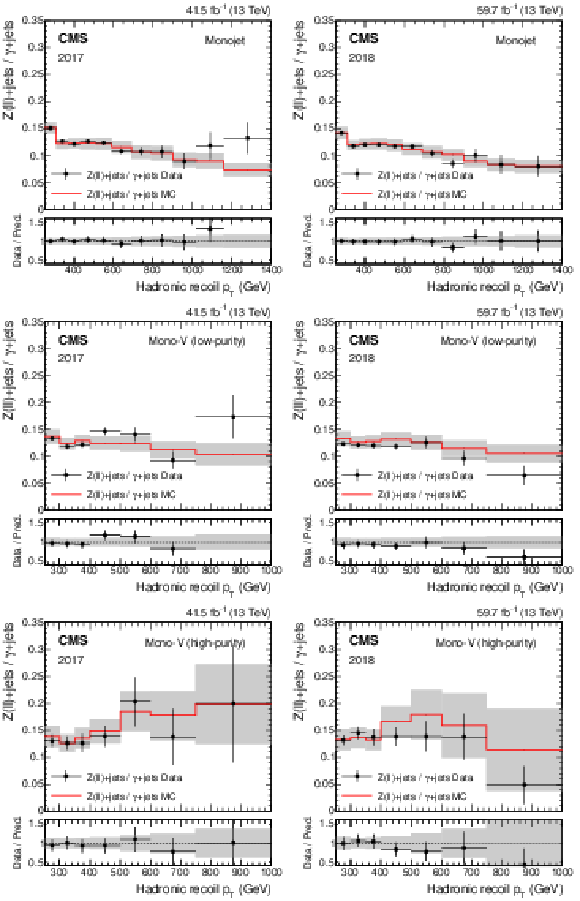
Figure 3:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points). The gray band represents the total uncertainty in the ratio. In the lower panels, the ratio of data over prediction is shown. From upper to lower, the rows show the monojet, low-purity, and high-purity mono-V categories, while the left (right) column represents the 2017 (2018) data set. |

png pdf |
Figure 3-a:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the monojet category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |

png pdf |
Figure 3-b:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the monojet category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
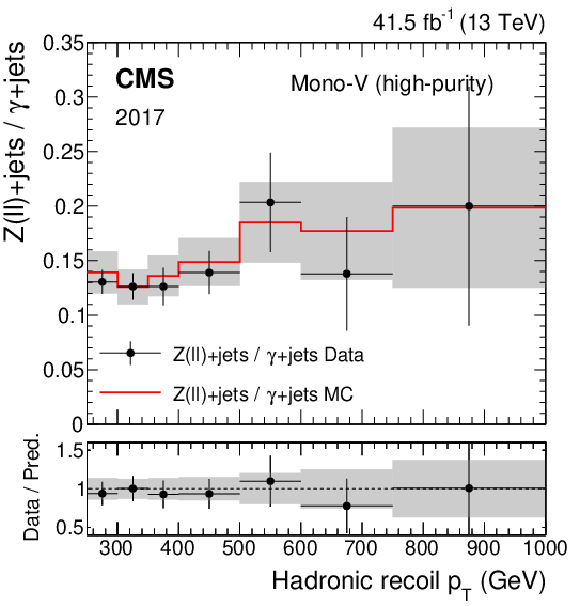
png pdf |
Figure 3-c:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the low-purity mono-V category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
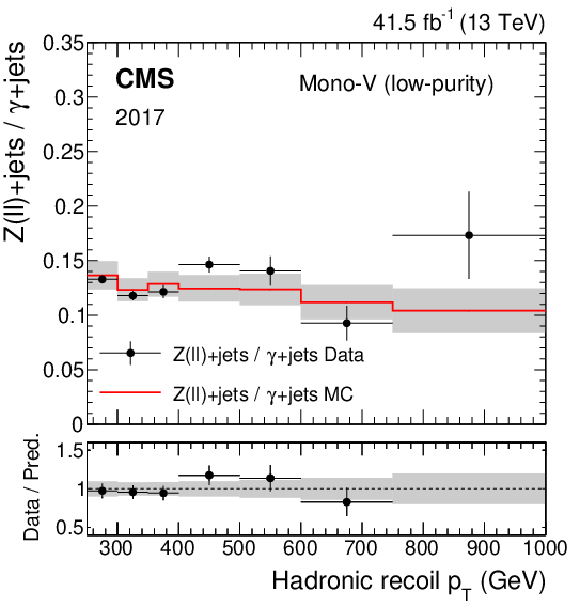
png pdf |
Figure 3-d:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the low-purity mono-V category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
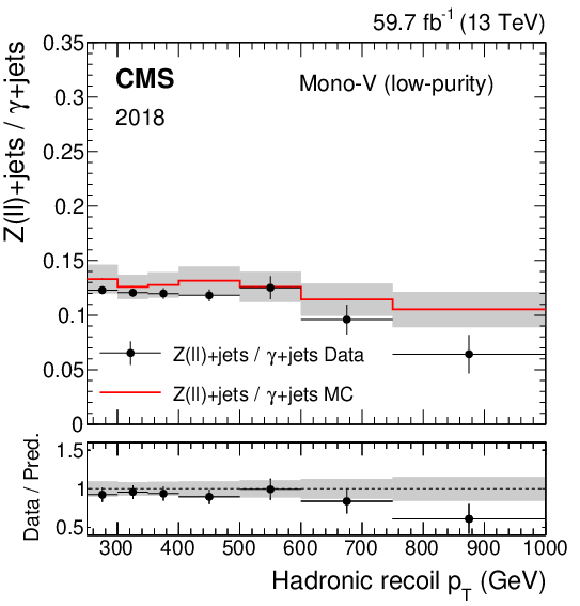
png pdf |
Figure 3-e:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the high-purity mono-V category, for the 2017 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
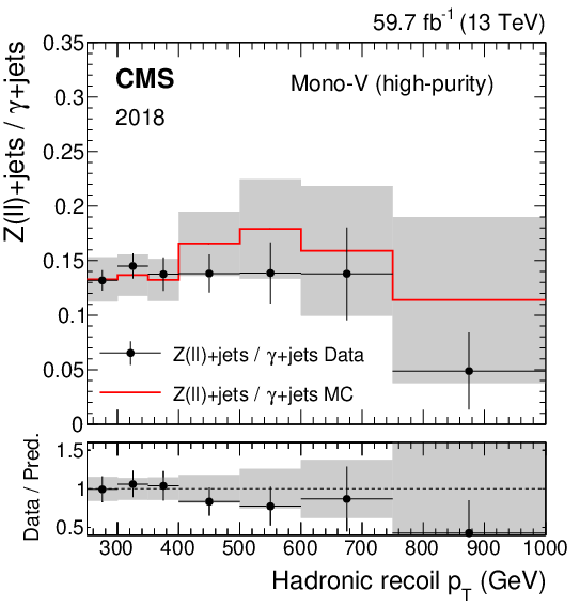
png pdf |
Figure 3-f:
Ratio of the dilepton to photon control region yields predicted using simulation (red solid line), and observed in data (black points) in the high-purity mono-V category, for the 2018 data set. The gray band represents the total uncertainty in the ratio. In the lower panel, the ratio of data over prediction is shown. |
png pdf |
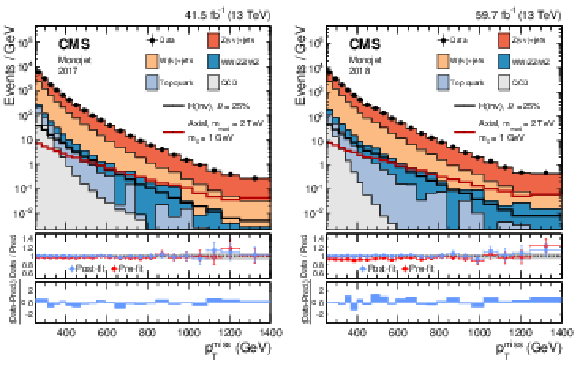
Figure 4:
Comparison between data and the background prediction in the monojet signal region before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2017 (left) and 2018 (right). Templates for two signal hypotheses are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panels, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panels indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panels. |
png pdf |
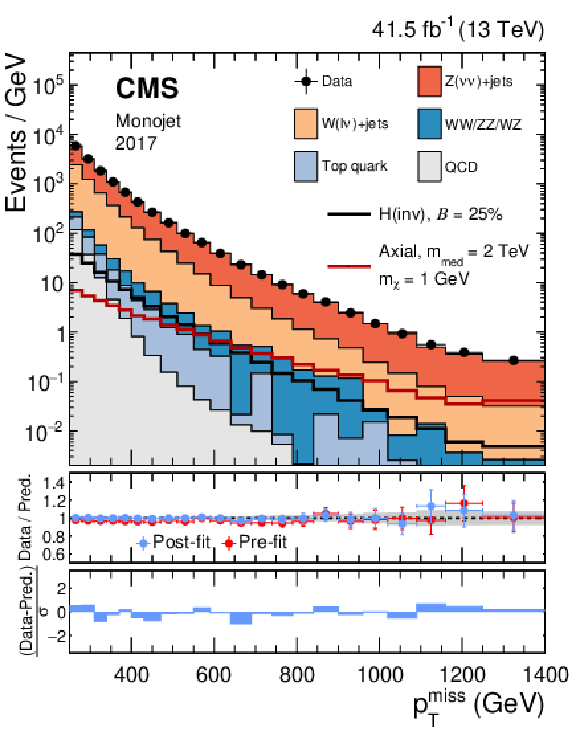
Figure 4-a:
Comparison between data and the background prediction in the monojet signal region before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2017. Templates for two signal hypotheses are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |

png pdf |
Figure 4-b:
Comparison between data and the background prediction in the monojet signal region before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2018. Templates for two signal hypotheses are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |
png pdf |
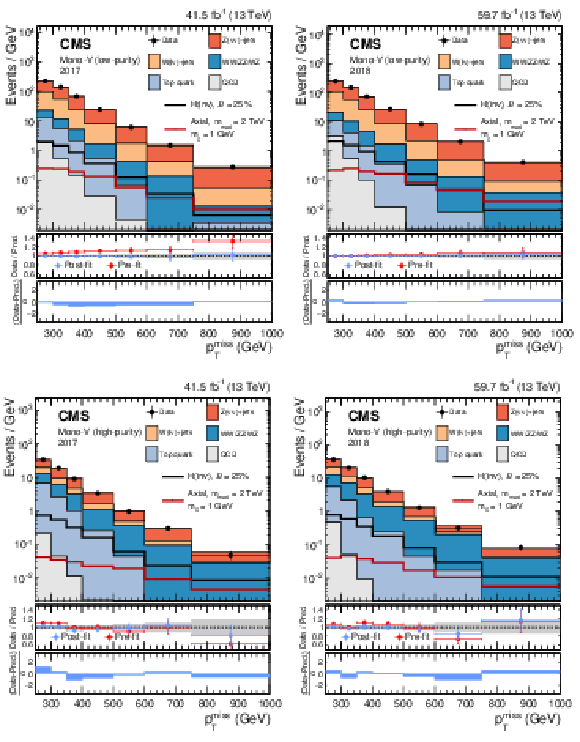
Figure 5:
Comparison between data and the background prediction in the mono-V signal regions before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2017 (left column) and 2018 (right column), as well as for the low- and high-purity categories (upper and lower rows, respectively). Templates for two signal hypothesis are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panels, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panels indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panels. |

png pdf |
Figure 5-a:
Comparison between data and the background prediction in the mono-V signal regions before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2017, as well as for the low-purity category. Templates for two signal hypothesis are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |

png pdf |
Figure 5-b:
Comparison between data and the background prediction in the mono-V signal regions before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2018, as well as for the low-purity category. Templates for two signal hypothesis are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |

png pdf |
Figure 5-c:
Comparison between data and the background prediction in the mono-V signal regions before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2017, as well as for the high-purity category. Templates for two signal hypothesis are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |
png pdf |
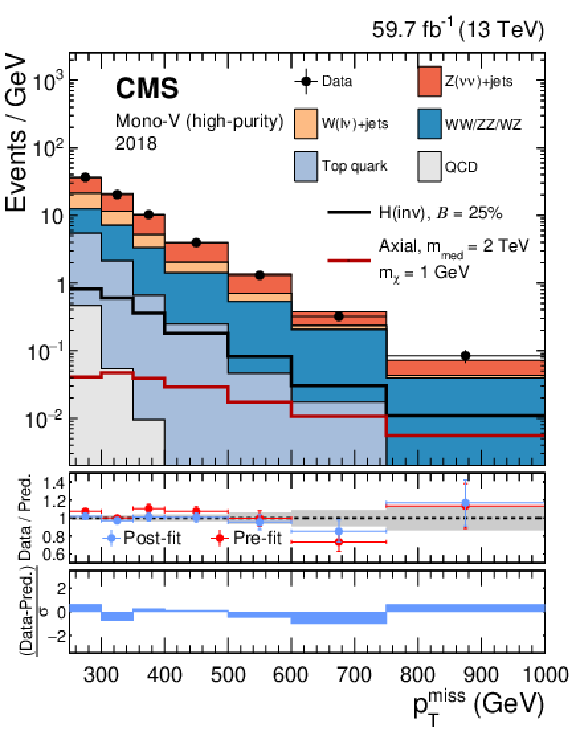
Figure 5-d:
Comparison between data and the background prediction in the mono-V signal regions before and after the simultaneous fit. The fit includes all control regions and the signal region in all categories and both data taking years, and the background-only fit model is used. The resulting distributions are shown separately for 2018, as well as for the high-purity category. Templates for two signal hypothesis are shown overlaid as black and dark red solid lines. The last bin includes the overflow. In the middle panel, ratios of data to the pre-fit background prediction (red solid points) and post-fit background prediction (blue solid points) are shown. The gray band in the middle panel indicates the post-fit uncertainty after combining all the systematic uncertainties. Finally, the distribution of the pulls, defined as the difference between data and the post-fit background prediction divided by the quadratic sum of the post-fit uncertainty in the prediction and statistical uncertainty in data, is shown in the lower panel. |
png pdf |
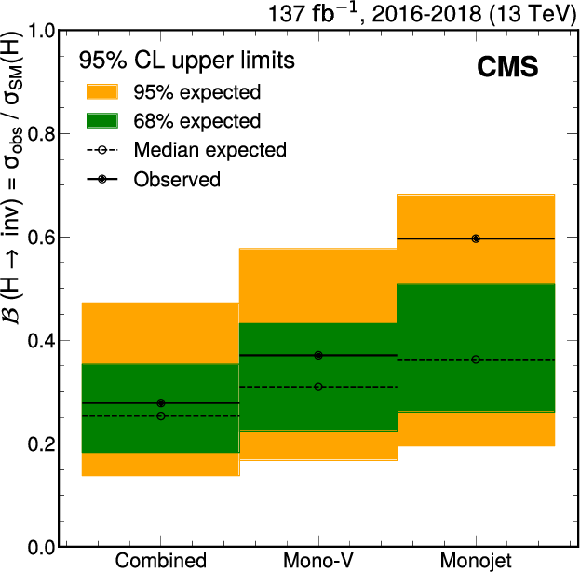
Figure 6:
Upper limits at 95% CL on the branching fraction $\mathcal {B}$ of the Higgs boson to invisible final states. The results are shown separately for the monojet and mono-V categories, as well as for their combination. The final combined limit is 27.8% ($25.3%$ expected). |

png pdf |
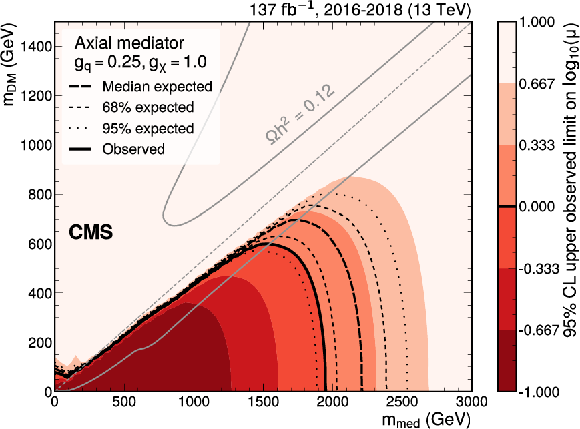
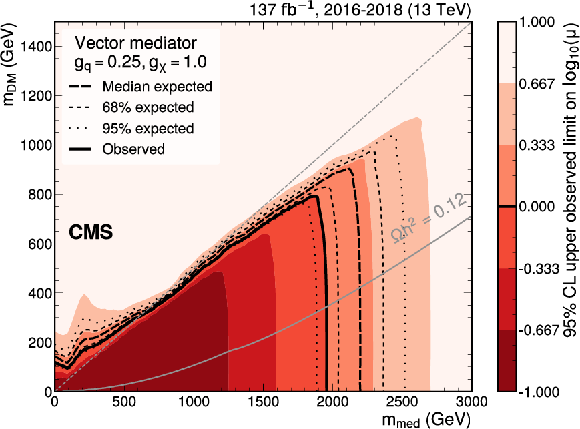
Figure 7:
Exclusion limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ in the ${m_\text {med}} - {m_\text {DM}}$ plane for coupling values of $ {g_\mathrm{q}} =$ 0.25 and $ {g_\chi} =$ 1.0 for an axial-vector (upper) or vector (lower) mediator. The blue solid line indicates the observed exclusion boundary $\mu =$ 1. The black dashed and dotted lines represent the expected exclusion and the 68 and 95% CL intervals around the expected boundary, respectively. Parameter combinations with larger values of $\mu $ (indicated by a darker shade in the color scale) are excluded. The observed exclusion reaches up to $ {m_\text {med}} = $ 1.95 TeV for low values of $ {m_\text {DM}} = $ 1 GeV (2.2 TeV expected). The gray dashed line indicates the diagonal $ {m_\text {med}} = 2 {m_\text {DM}} $, above which only off-shell mediator production contributes to the jet+${{p_{\mathrm {T}}} ^\text {miss}}$ final state. The steep increase of the signal strength limit above the diagonal leads to fluctuations of the exclusion contour, which are due to finite precision in the interpolation method in this region. The gray solid lines represent parameter combinations for which the simplified model reproduces the observed DM relic density in the universe under the assumption of a thermal freeze-out mechanism [63,86]. |
png pdf |
Figure 7-a:
Exclusion limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ in the ${m_\text {med}} - {m_\text {DM}}$ plane for coupling values of $ {g_\mathrm{q}} =$ 0.25 and $ {g_\chi} =$ 1.0 for an axial-vector mediator. The blue solid line indicates the observed exclusion boundary $\mu =$ 1. The black dashed and dotted lines represent the expected exclusion and the 68 and 95% CL intervals around the expected boundary, respectively. Parameter combinations with larger values of $\mu $ (indicated by a darker shade in the color scale) are excluded. The observed exclusion reaches up to $ {m_\text {med}} = $ 1.95 TeV for low values of $ {m_\text {DM}} = $ 1 GeV (2.2 TeV expected). The gray dashed line indicates the diagonal $ {m_\text {med}} = 2 {m_\text {DM}} $, above which only off-shell mediator production contributes to the jet+${{p_{\mathrm {T}}} ^\text {miss}}$ final state. The steep increase of the signal strength limit above the diagonal leads to fluctuations of the exclusion contour, which are due to finite precision in the interpolation method in this region. The gray solid lines represent parameter combinations for which the simplified model reproduces the observed DM relic density in the universe under the assumption of a thermal freeze-out mechanism [63,86]. |
png pdf |
Figure 7-b:
Exclusion limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ in the ${m_\text {med}} - {m_\text {DM}}$ plane for coupling values of $ {g_\mathrm{q}} =$ 0.25 and $ {g_\chi} =$ 1.0 for a vector mediator. The blue solid line indicates the observed exclusion boundary $\mu =$ 1. The black dashed and dotted lines represent the expected exclusion and the 68 and 95% CL intervals around the expected boundary, respectively. Parameter combinations with larger values of $\mu $ (indicated by a darker shade in the color scale) are excluded. The observed exclusion reaches up to $ {m_\text {med}} = $ 1.95 TeV for low values of $ {m_\text {DM}} = $ 1 GeV (2.2 TeV expected). The gray dashed line indicates the diagonal $ {m_\text {med}} = 2 {m_\text {DM}} $, above which only off-shell mediator production contributes to the jet+${{p_{\mathrm {T}}} ^\text {miss}}$ final state. The steep increase of the signal strength limit above the diagonal leads to fluctuations of the exclusion contour, which are due to finite precision in the interpolation method in this region. The gray solid lines represent parameter combinations for which the simplified model reproduces the observed DM relic density in the universe under the assumption of a thermal freeze-out mechanism [63,86]. |
png pdf |
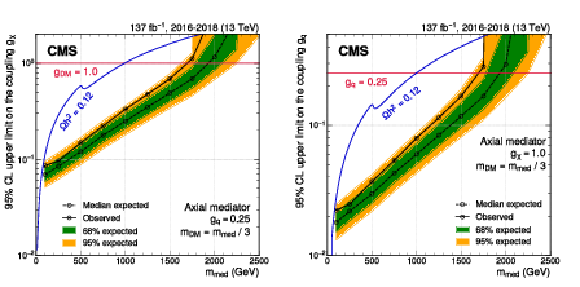
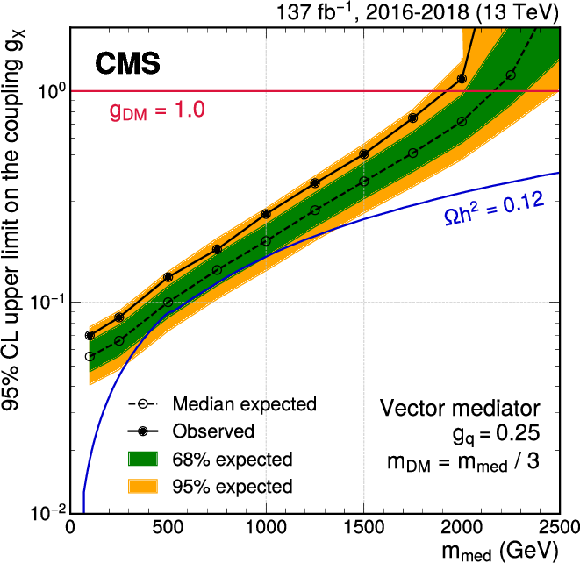
Figure 8:
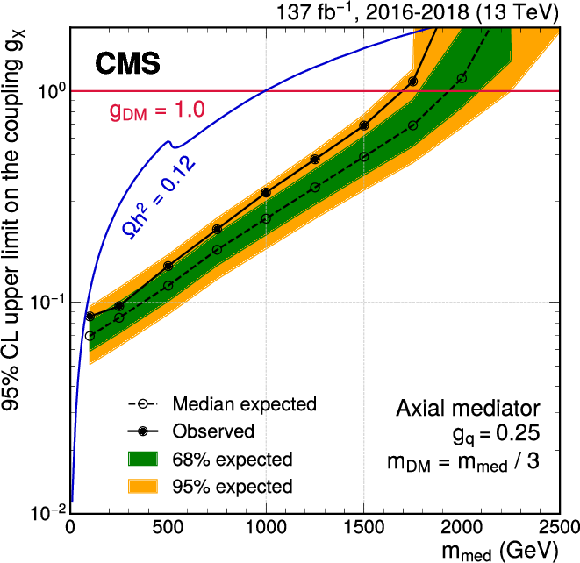
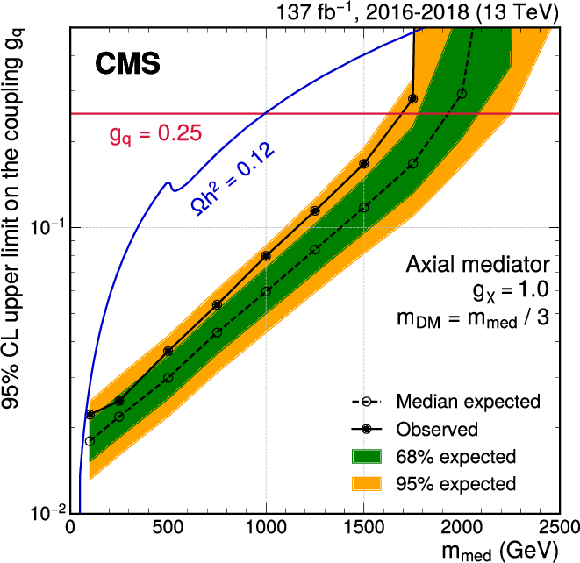
Exclusion limits at 95% CL on the couplings ${g_\chi}$ (left) and ${g_\mathrm{q}}$ (right) for an axial-vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, with the mass of the DM candidate fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. In either case, only one coupling is varied, while the other coupling is fixed at its default value ($ {g_\mathrm{q}} =$ 0.25 or $ {g_\chi} =$ 1.0). The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. The corresponding results for a vector mediator are shown in Fig. 20 in Appendix A.4. |
png pdf |
Figure 8-a:
Exclusion limits at 95% CL on the coupling ${g_\chi}$ for an axial-vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, with the mass of the DM candidate fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. The other coupling is fixed at its default value, $ {g_\mathrm{q}} =$ 0.25. The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. |
png pdf |
Figure 8-b:
Exclusion limits at 95% CL on the coupling ${g_\mathrm{q}}$ for an axial-vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, with the mass of the DM candidate fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. The other coupling is fixed at its default value, $ {g_\chi} =$ 1.0. The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. |
png pdf |
Figure 9:
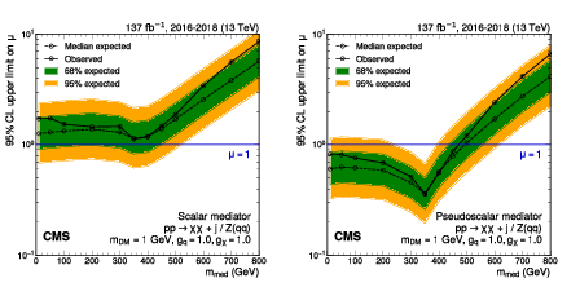
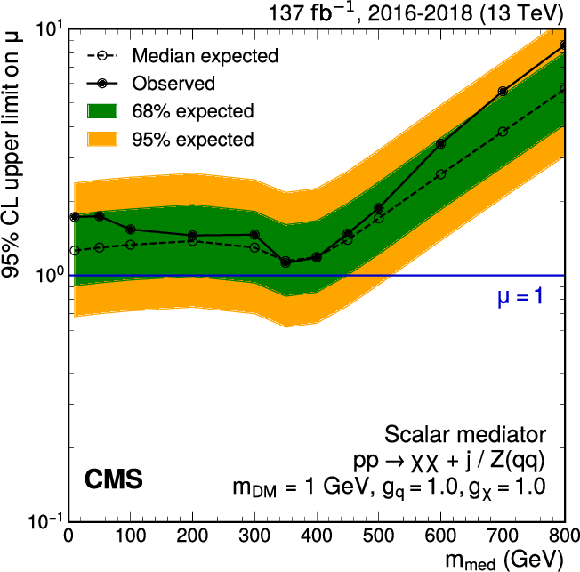
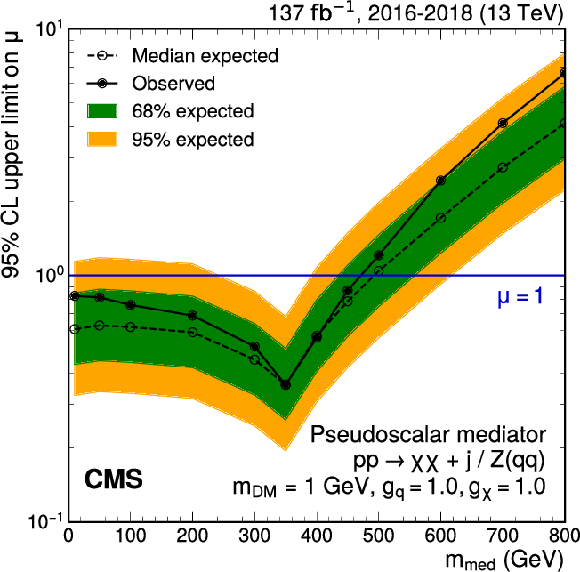
Upper limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ as a function of ${m_\text {med}}$ for scenarios with scalar (left) and pseudoscalar (right) mediators and coupling values of $ {g_\mathrm{q}} =$ 1.0, $ {g_\chi} =$ 1.0, for a constant value of $ {m_\text {DM}} = $ 1 GeV. The blue solid line indicates the exclusion boundary $\mu =$ 1. In the case of a pseudoscalar mediator, ${m_\text {med}}$ values up to 470 GeV are excluded (490 GeV expected). |
png pdf |
Figure 9-a:
Upper limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ as a function of ${m_\text {med}}$ for scenarios with scalar (left) and pseudoscalar (right) mediators and coupling values of $ {g_\mathrm{q}} =$ 1.0, $ {g_\chi} =$ 1.0, for a constant value of $ {m_\text {DM}} = $ 1 GeV. The blue solid line indicates the exclusion boundary $\mu =$ 1. In the case of a pseudoscalar mediator, ${m_\text {med}}$ values up to 470 GeV are excluded (490 GeV expected). |
png pdf |
Figure 9-b:
Upper limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ as a function of ${m_\text {med}}$ for scenarios with scalar (left) and pseudoscalar (right) mediators and coupling values of $ {g_\mathrm{q}} =$ 1.0, $ {g_\chi} =$ 1.0, for a constant value of $ {m_\text {DM}} = $ 1 GeV. The blue solid line indicates the exclusion boundary $\mu =$ 1. In the case of a pseudoscalar mediator, ${m_\text {med}}$ values up to 470 GeV are excluded (490 GeV expected). |

png pdf |
Figure 10:
Exclusion limits at 95% CL in the plane of the mediator mass ${m_{\Phi}}$ and the DM candidate mass ${m_\text {DM}}$ in the fermion portal model. The black solid line indicates the observed exclusion boundary. The black dashed and dotted lines represent the expected exclusion and the 68 and 95% CL intervals around the expected boundary, respectively. |
png pdf |
Figure 11:
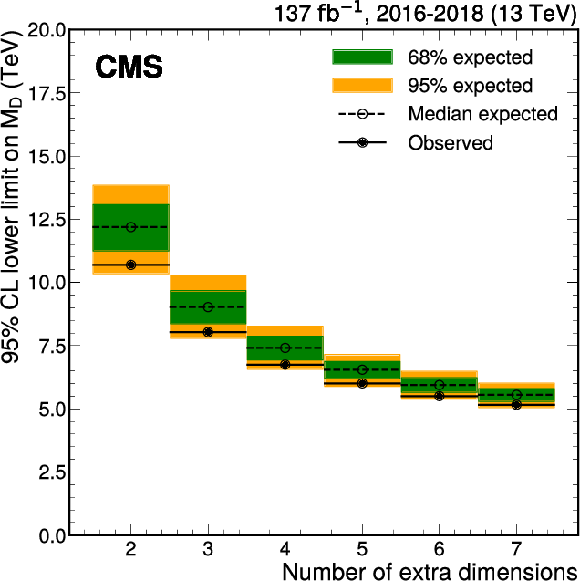
Exclusion limits at 95% CL on ${M_\text {D}}$ in the ADD scenario for different values of the number of extra dimensions $d$. |
png pdf |
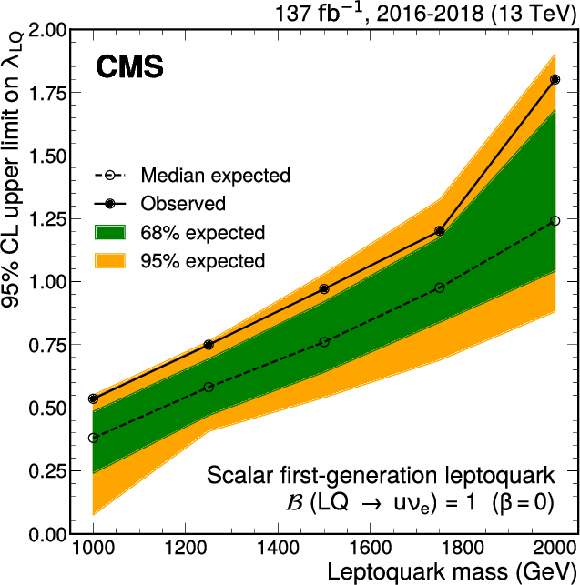
Figure 12:
Upper limits at 95% CL on the leptoquark coupling $ {\lambda _\mathrm {LQ}} $ as a function of the leptoquark mass. The branching fraction for the decay of the leptoquark into an electron neutrino and up quark is assumed to be 100% ($\beta =0$). The dashed line indicates the median expected exclusion contour. |
png pdf |
Figure 13:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 13-a:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 13-b:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
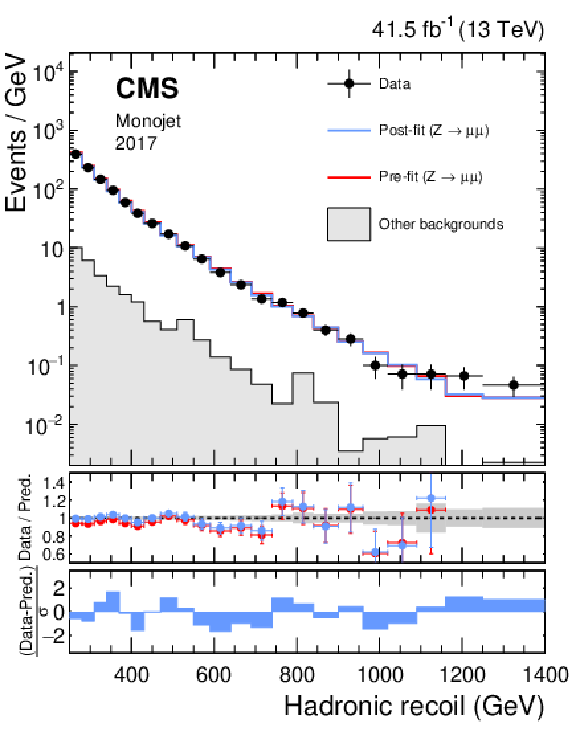
png pdf |
Figure 13-c:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
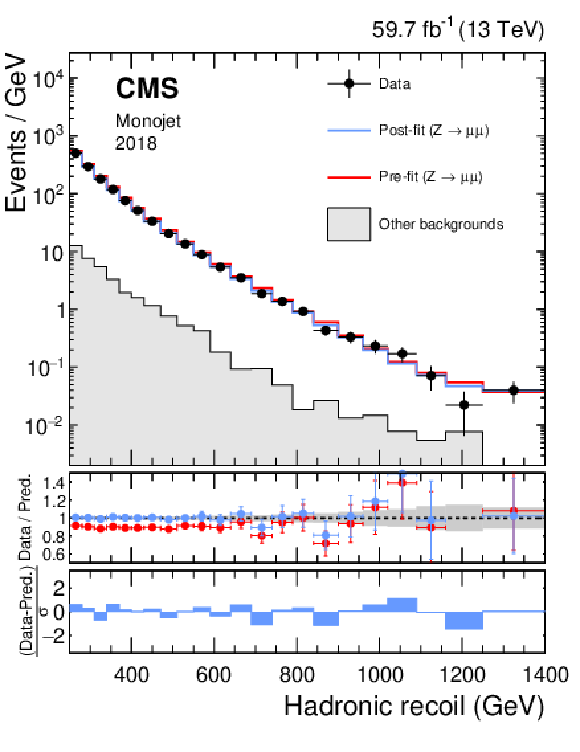
png pdf |
Figure 13-d:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
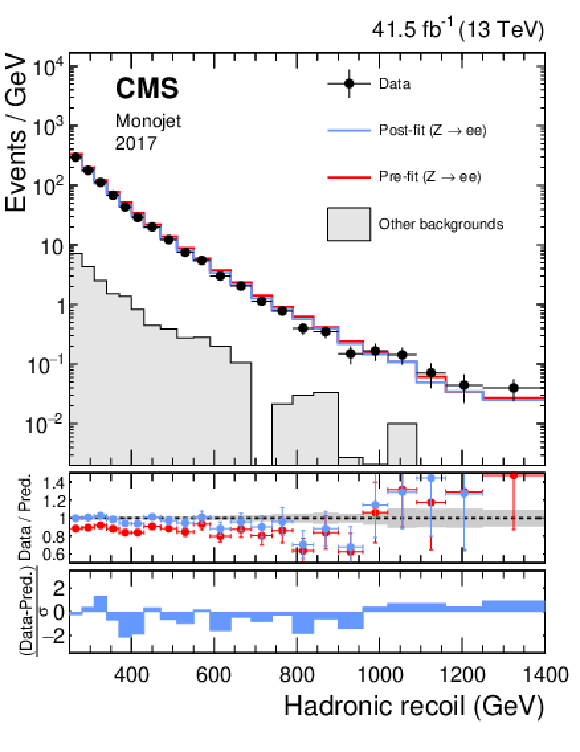
png pdf |
Figure 13-e:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 13-f:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the monojet category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
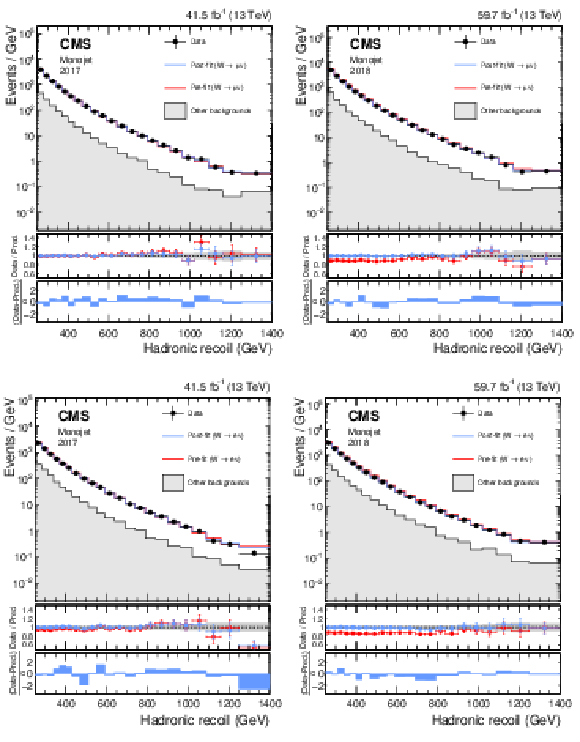
png pdf |
Figure 14:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the monojet category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |

png pdf |
Figure 14-a:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the monojet category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |

png pdf |
Figure 14-b:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the monojet category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
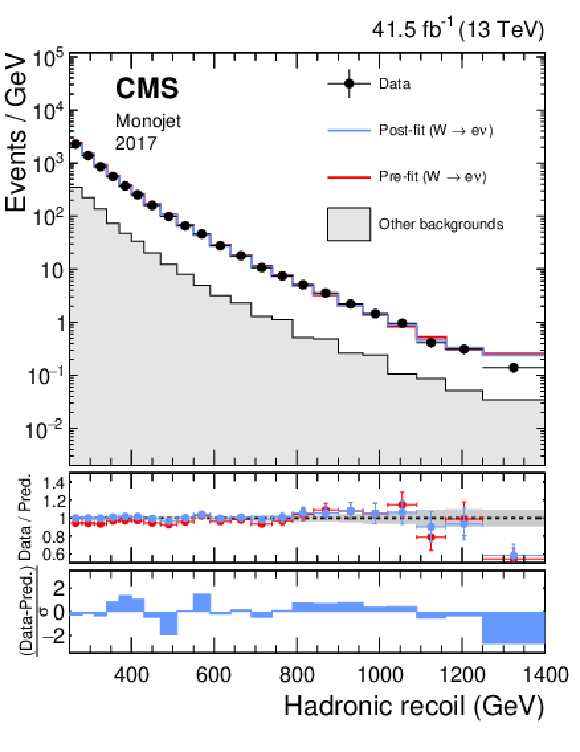
png pdf |
Figure 14-c:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the monojet category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
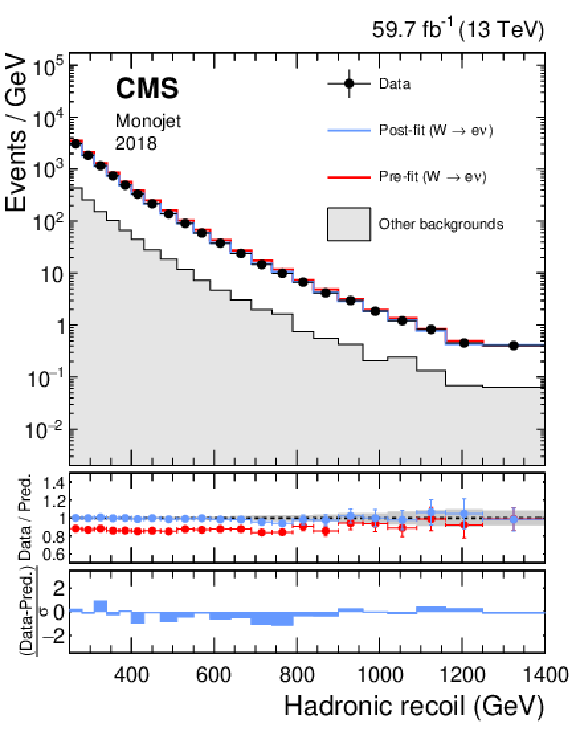
png pdf |
Figure 14-d:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the monojet category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
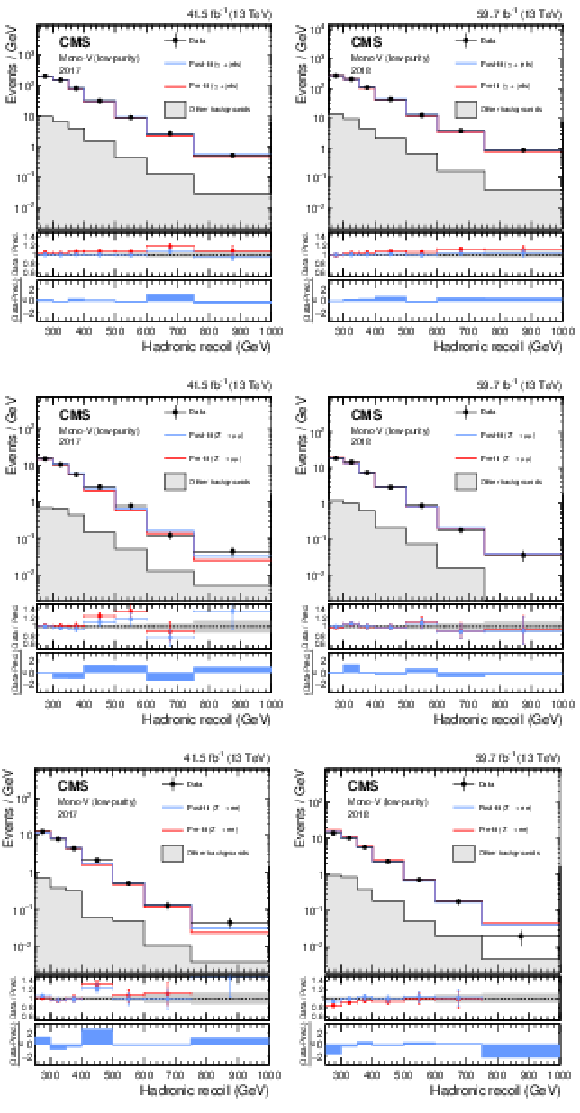
png pdf |
Figure 15:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
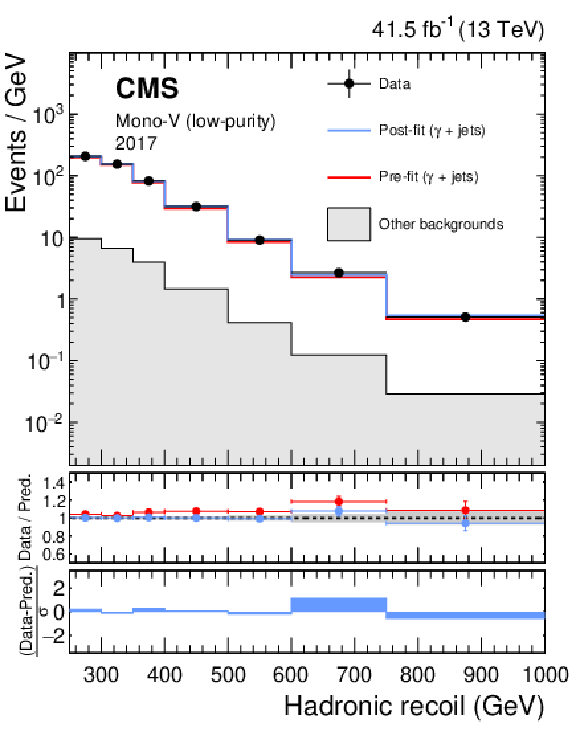
png pdf |
Figure 15-a:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
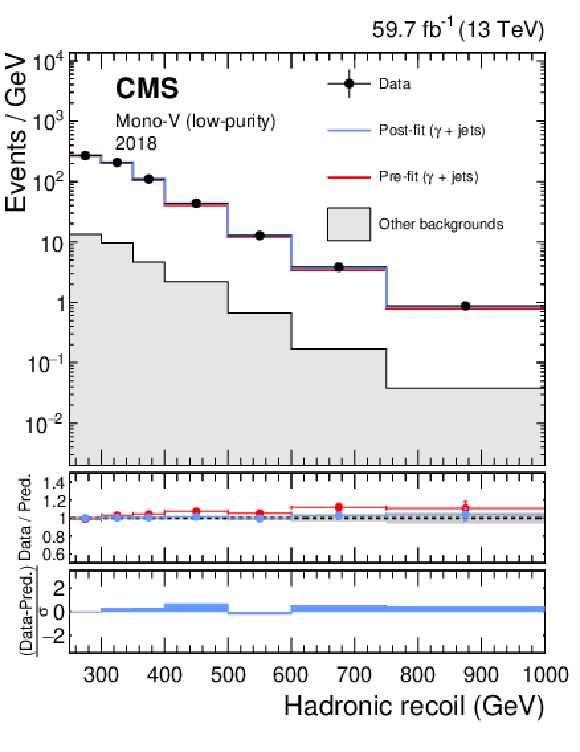
png pdf |
Figure 15-b:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
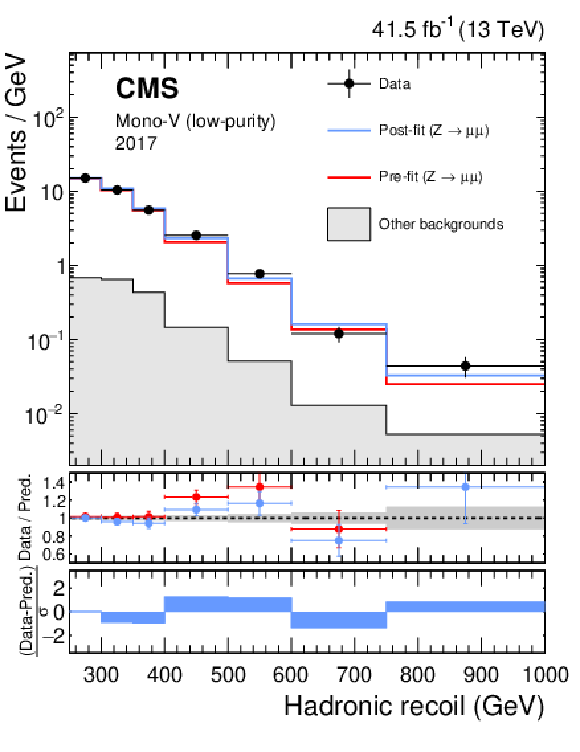
png pdf |
Figure 15-c:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
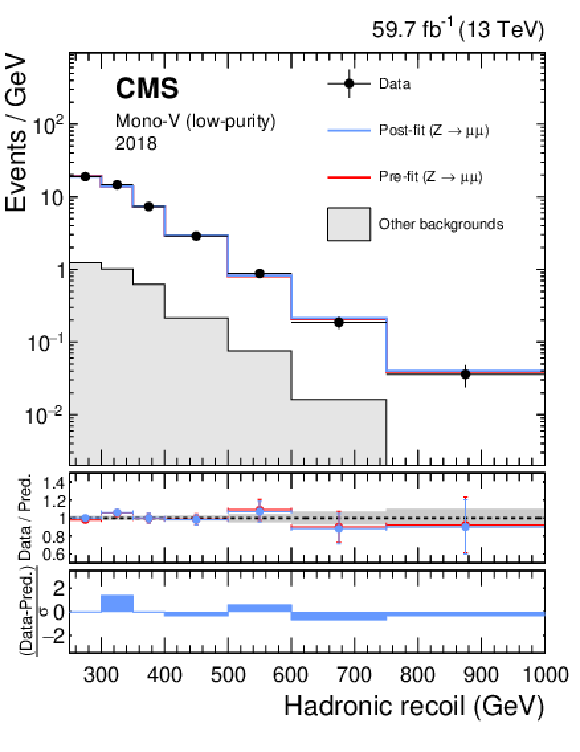
png pdf |
Figure 15-d:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 15-e:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
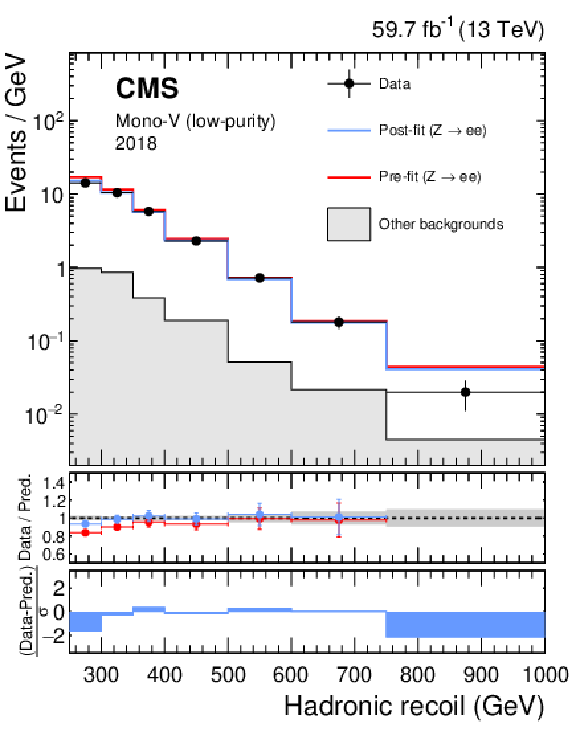
png pdf |
Figure 15-f:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the low-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
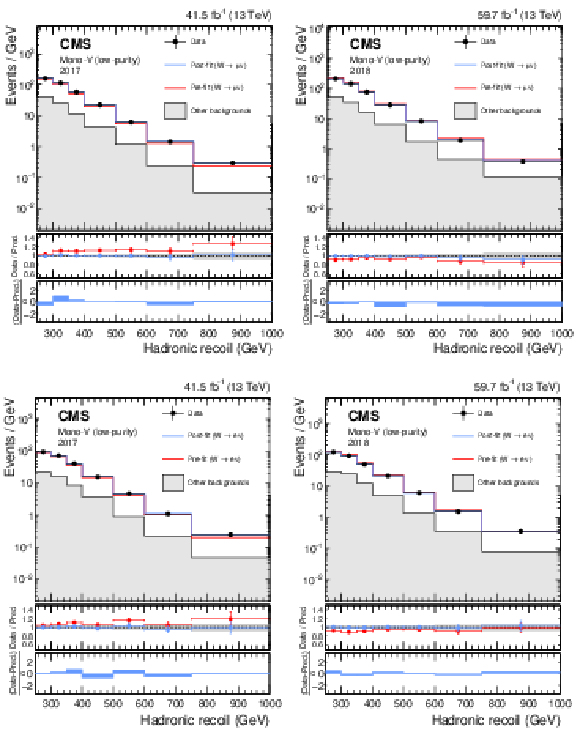
png pdf |
Figure 16:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the low-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |

png pdf |
Figure 16-a:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the low-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |

png pdf |
Figure 16-b:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the low-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
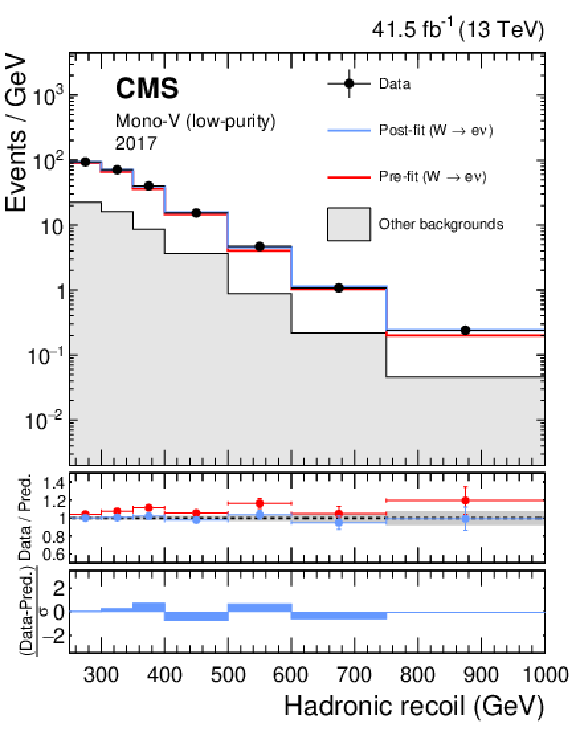
png pdf |
Figure 16-c:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the low-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
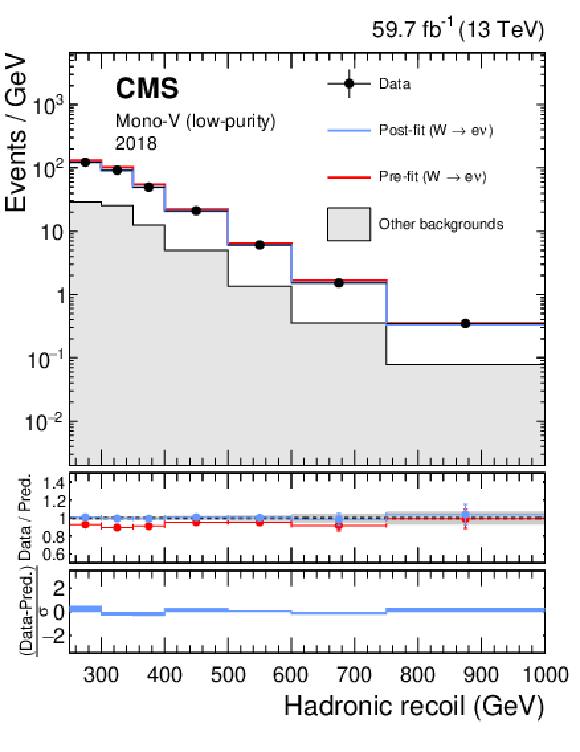
png pdf |
Figure 16-d:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the low-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
png pdf |
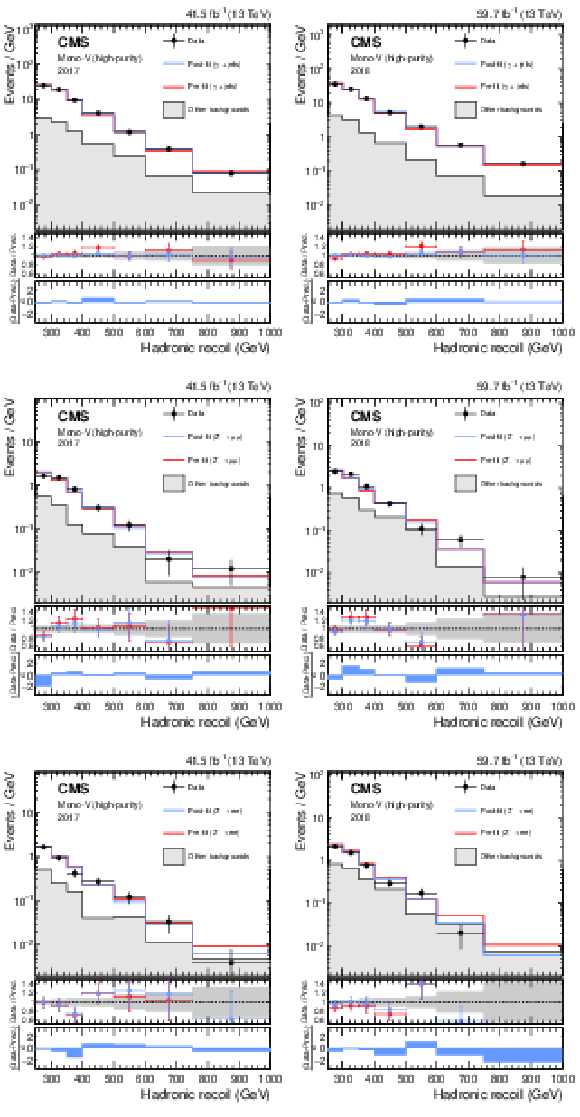
Figure 17:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 17-a:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
Figure 17-b:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
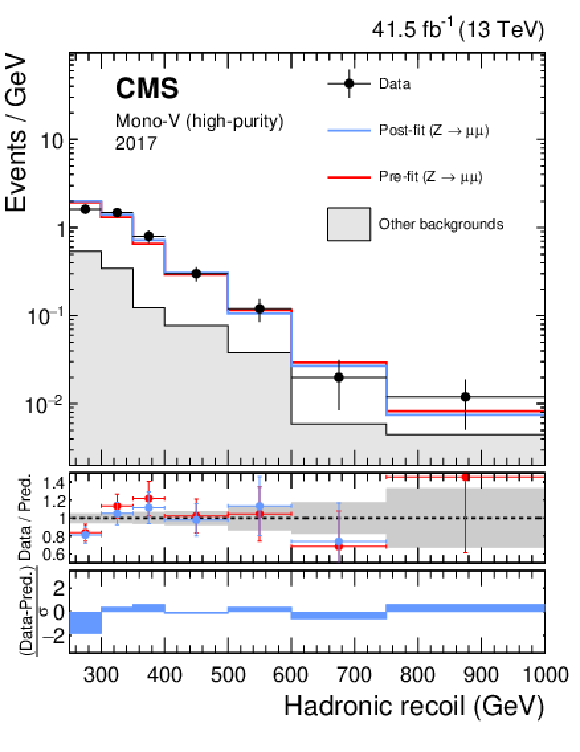
png pdf |
Figure 17-c:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
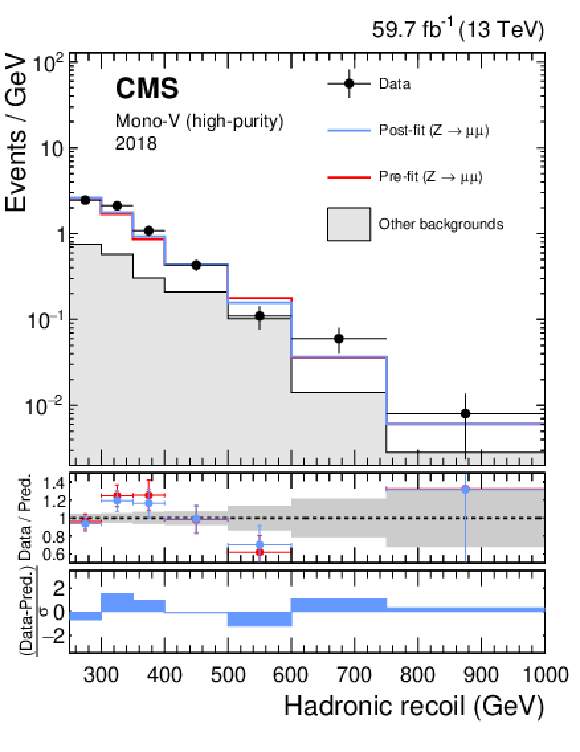
png pdf |
Figure 17-d:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
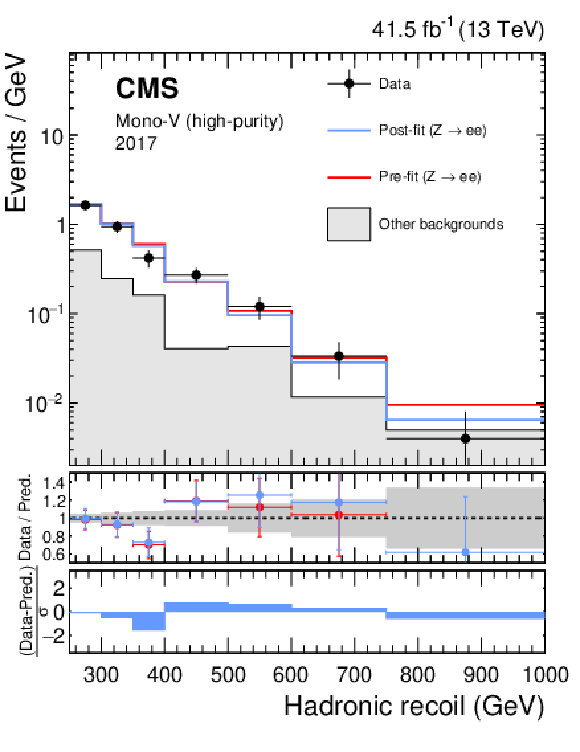
png pdf |
Figure 17-e:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |
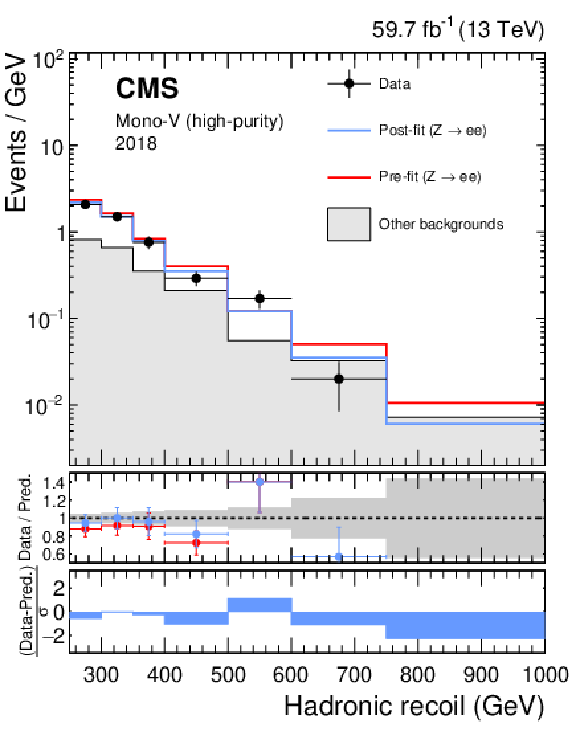
png pdf |
Figure 17-f:
Hadronic recoil distributions in the photon (upper), dimuon (middle) and dielectron control regions (lower) in the high-purity mono-V category. The "Other backgrounds" include QCD multijet production (photon control region), and top quark, diboson, and W+jets processes (dimuon and dielectron control regions). |

png pdf |
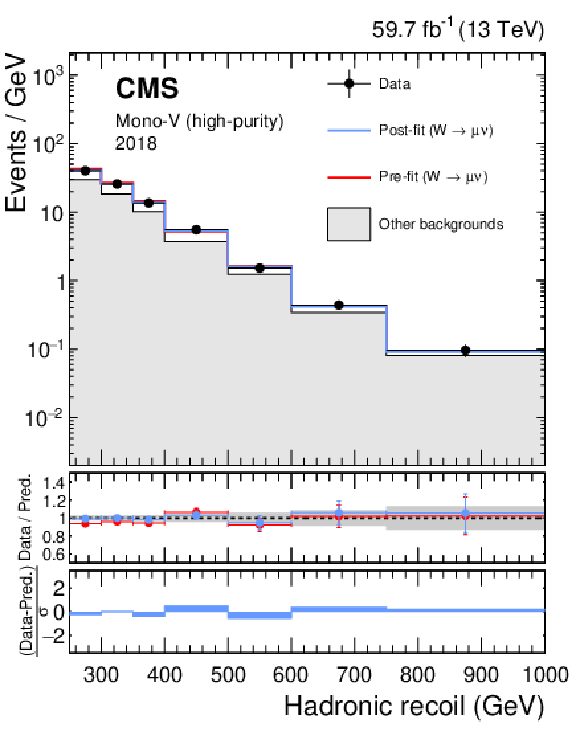
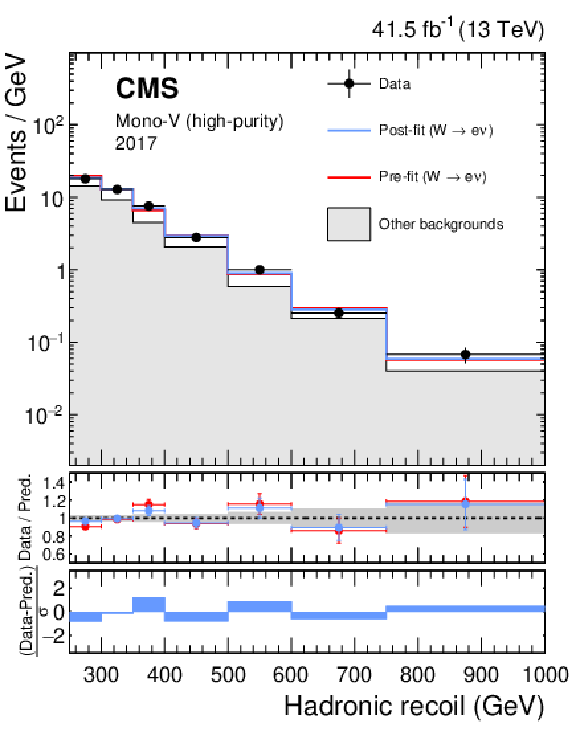
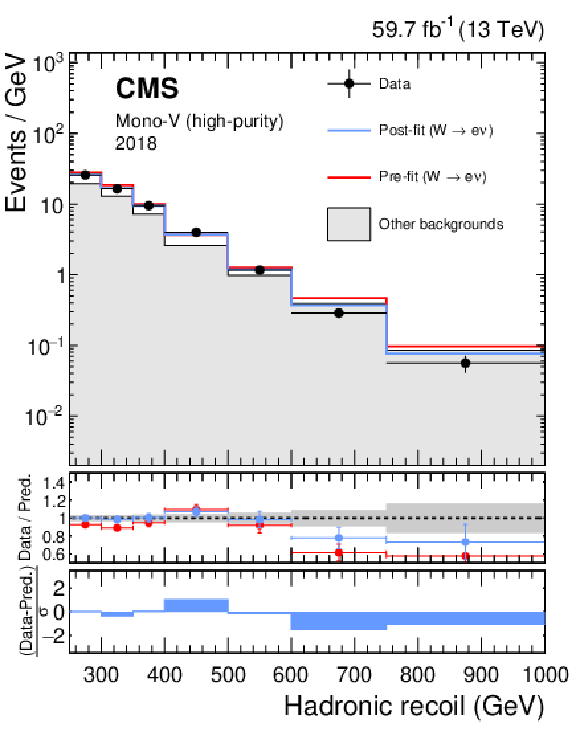
Figure 18:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the high-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
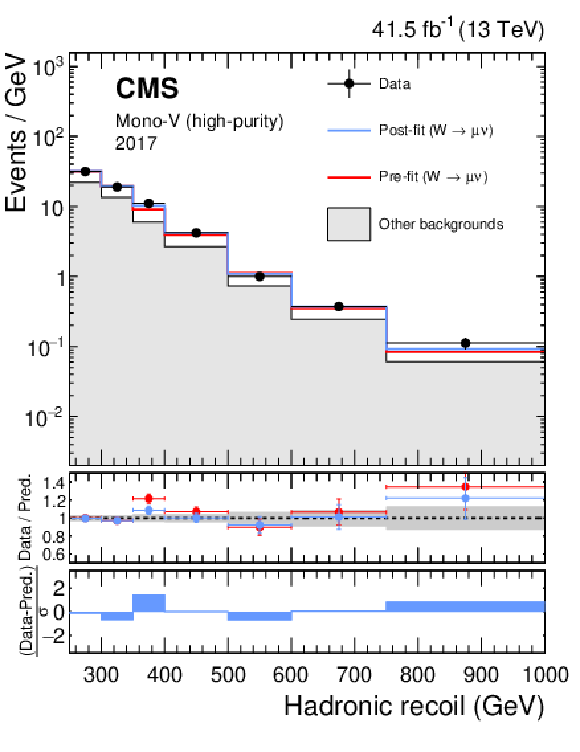
png pdf |
Figure 18-a:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the high-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
png pdf |
Figure 18-b:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the high-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
png pdf |
Figure 18-c:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the high-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
png pdf |
Figure 18-d:
Hadronic recoil distributions in the single muon (upper), and single electron regions (lower) in the high-purity mono-V category. The "Other backgrounds" include top quark, diboson, and QCD multijet processes. |
png pdf |
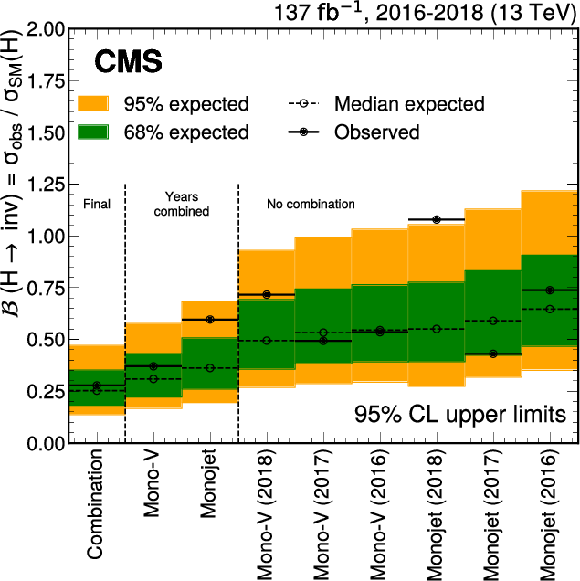
Figure 19:
Exclusion limits at 95% CL on the branching fraction of the Higgs boson to invisible particles. The result is shown separately for the monojet and mono-V categories in each data taking year, as well as their combination. The final combined limit is 27.8% (25.3% expected). |
png pdf |
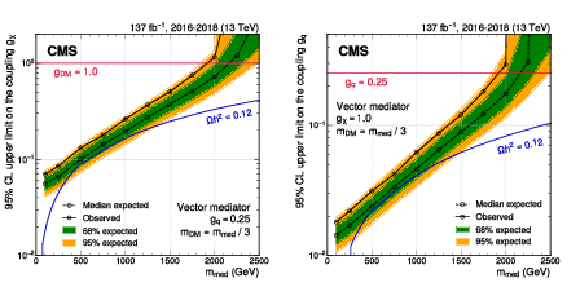
Figure 20:
Exclusion limits at 95% CL on the couplings ${g_\chi}$ (left) and ${g_\mathrm{q}}$ (right) for a vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, and the mass of the DM candidate is fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. In either case, only one coupling is varied, and the respective other coupling is fixed at its default value ($ {g_\mathrm{q}} =$ 0.25, $ {g_\chi} =$ 1.0). The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. |
png pdf |
Figure 20-a:
Exclusion limits at 95% CL on the couplings ${g_\chi}$ (left) and ${g_\mathrm{q}}$ (right) for a vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, and the mass of the DM candidate is fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. In either case, only one coupling is varied, and the respective other coupling is fixed at its default value ($ {g_\mathrm{q}} =$ 0.25, $ {g_\chi} =$ 1.0). The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. |

png pdf |
Figure 20-b:
Exclusion limits at 95% CL on the couplings ${g_\chi}$ (left) and ${g_\mathrm{q}}$ (right) for a vector mediator. In each panel, the result is shown as a function of the mediator mass $ {m_\text {med}} $, and the mass of the DM candidate is fixed to $ {m_\text {DM}} = {m_\text {med}} /3$. In either case, only one coupling is varied, and the respective other coupling is fixed at its default value ($ {g_\mathrm{q}} =$ 0.25, $ {g_\chi} =$ 1.0). The blue solid line indicates the parameter combinations for which the simplified model reproduces the observed DM relic density. Around $ {m_\text {DM}} \approx m_{\text {top}}$, corresponding to $ {m_\text {med}} \approx $ 500 GeV, DM annihilation into top quarks becomes possible, leading to a shift in the relic density. |
png pdf |
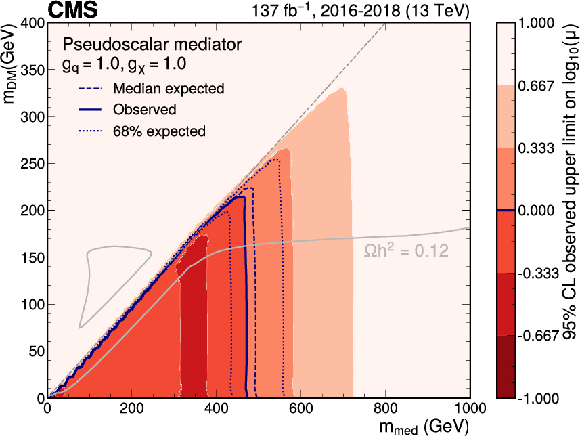
Figure 21:
Exclusion limits at 95% CL on the signal strength $\mu =\sigma /\sigma _\text {theo}$ in the ${m_\text {med}} - {m_\text {DM}}$ plane for coupling values of $ {g_\mathrm{q}} = {g_\chi} =$ 1.0 and a pseudoscalar mediator. The blue solid line indicates the observed exclusion boundary $\mu =$ 1. The blue dashed and dotted lines represent expected exclusion and the 68% CL interval of the expected boundary, respectively. Parameter combinations with larger values of $\mu $ (indicated by a darker shade in the color scale) are excluded. The gray dashed line indicates the diagonal $ {m_\text {med}} =2 {m_\text {DM}} $, above which only off-shell mediator production contributes to the jet+${{p_{\mathrm {T}}} ^\text {miss}}$ final state. The gray solid lines represent parameter combinations for which the simplified model reproduces the observed DM relic density in the universe under the assumption of a thermal freeze-out mechanism [63,86]. |
png pdf |
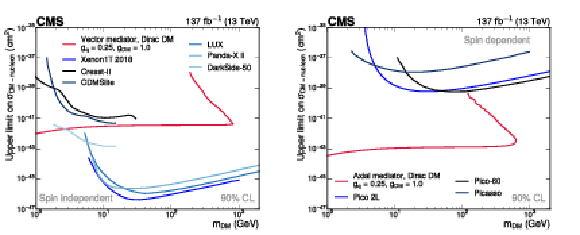
Figure B1:
Comparison of the simplified model constraints from this search (red line) to results from direct-detection experiments (blue lines). The comparison is shown separately for the vector (left) and axial-vector (right) mediators, which translate into spin-independent and spin-dependent DM-nucleon couplings, respectively. In the case of spin-independent couplings, results from CRESST-II [90], CDMSlite [91], LUX [92], DarkSide-50 [93], XENON1T [94], and Panda-X II [95] are shown for comparison. For spin-dependent couplings, PICO-2L [96], PICASSO [97], and PICO-60 [98] limits are displayed. |
png pdf |
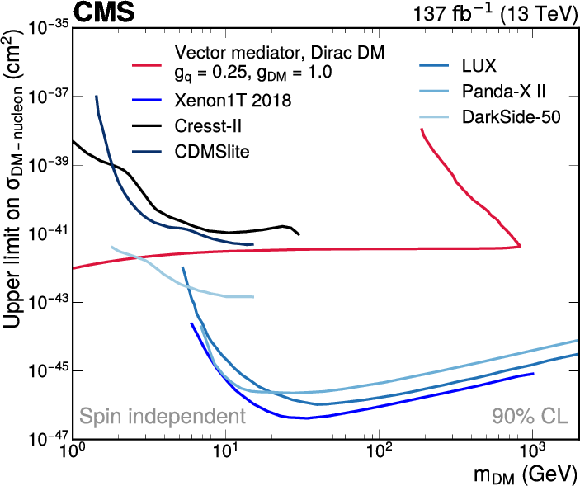
Figure B1-a:
Comparison of the simplified model constraints from this search (red line) to results from direct-detection experiments (blue lines). The comparison is shown for the vector mediator, which translates into spin-independent DM-nucleon couplings. Results from CRESST-II [90], CDMSlite [91], LUX [92], DarkSide-50 [93], XENON1T [94], and Panda-X II [95] are shown for comparison. |
png pdf |
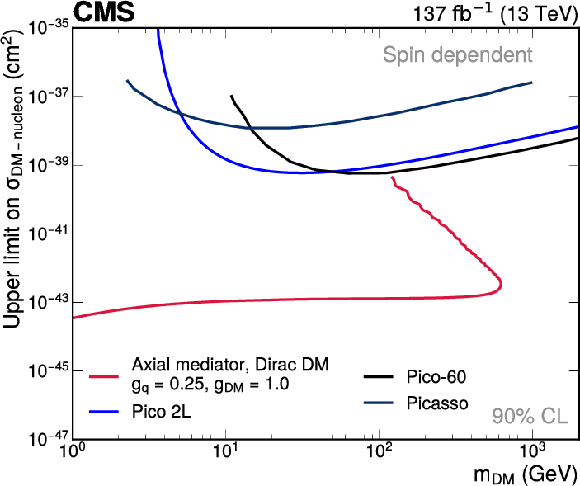
Figure B1-b:
Comparison of the simplified model constraints from this search (red line) to results from direct-detection experiments (blue lines). The comparison is shown for the axial-vector mediator, which translates into spin-dependent DM-nucleon couplings. PICO-2L [96], PICASSO [97], and PICO-60 [98] limits are displayed. |
png pdf |
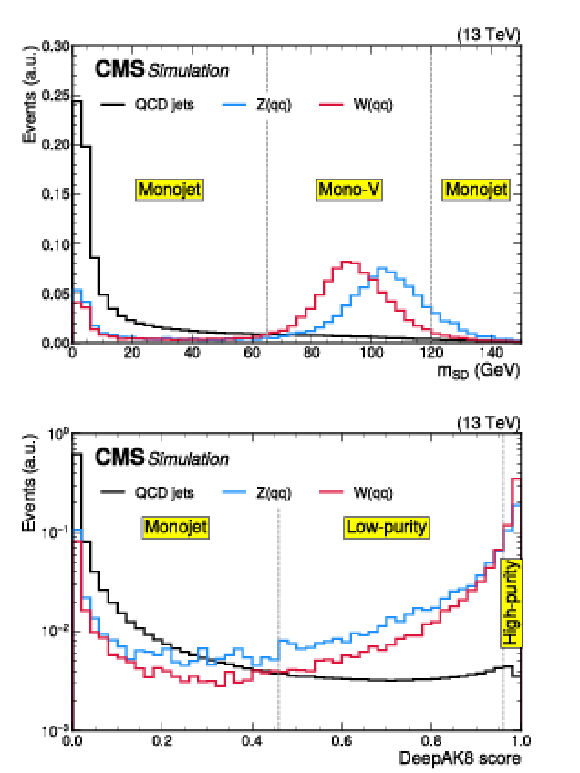
Figure B2:
Distributions of the variables used for the identification of ${\mathrm{V} \to \mathrm{q} \mathrm{q}}$ candidate jets. The upper and lower panels show the SD-corrected jet mass and the DeepAK8 classifier value, respectively. In each panel, the distributions are shown for the ${\mathrm{Z} \to \nu \nu}$ background, as well as the WH(inv.) and ZH(inv.) signals. The distributions are shown after applying the mono-V signal region selection, with the exception of the requirements on the two variables shown here. Vertical dashed lines indicate the acceptance boundaries of different regions. |

png pdf |
Figure B2-a:
Distribution of the the SD-corrected jet mass. The distribution is shown for the ${\mathrm{Z} \to \nu \nu}$ background, as well as the WH(inv.) and ZH(inv.) signals, after applying the mono-V signal region selection, with the exception of the requirements on the variable shown here. Vertical dashed lines indicate the acceptance boundaries of different regions. |
png pdf |
Figure B2-b:
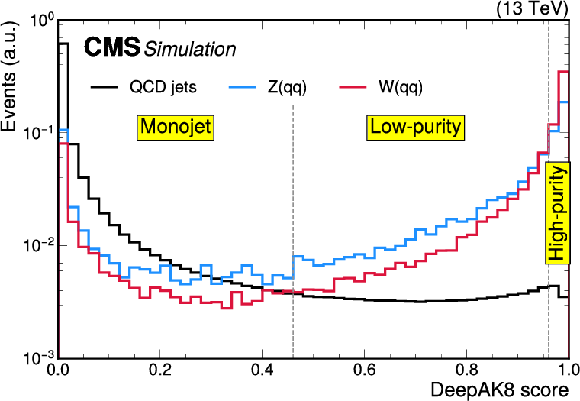
Distribution of the the DeepAK8 classifier value. The distribution is shown for the ${\mathrm{Z} \to \nu \nu}$ background, as well as the WH(inv.) and ZH(inv.) signals, after applying the mono-V signal region selection, with the exception of the requirements on the variable shown here. Vertical dashed lines indicate the acceptance boundaries of different regions. |
png pdf |
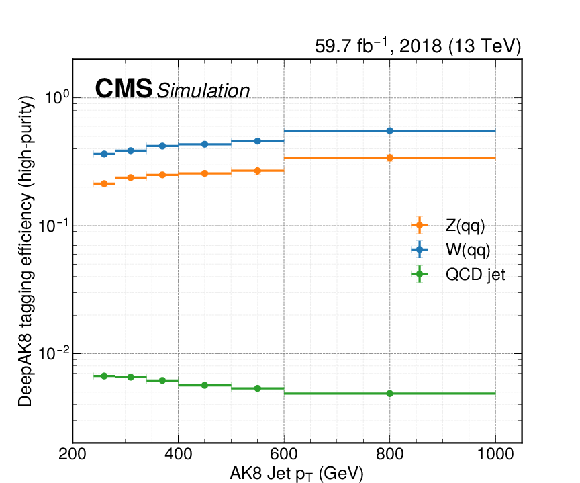
Figure B3:
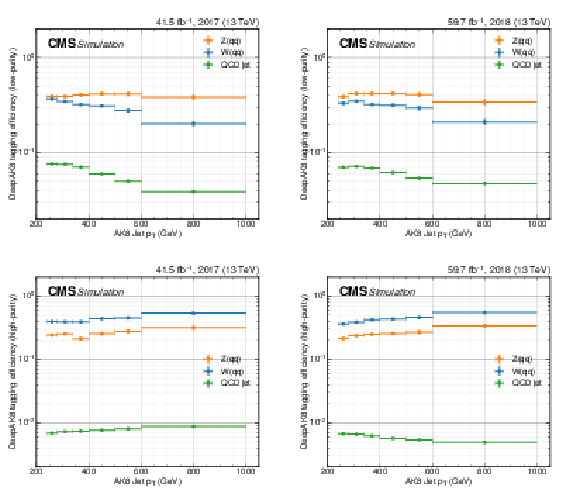
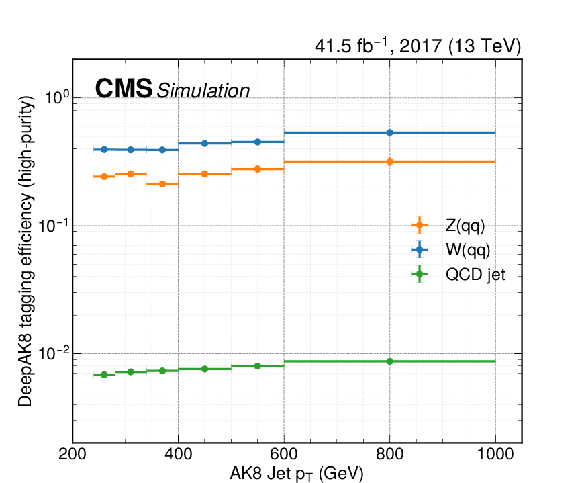
Large-radius jet tagging efficiencies for use in reinterpretation of the results. The efficiencies are shown separately for the low- and high-purity selections in the upper and lower panels, respectively, and for the 2017 (left) and 2018 (right) data taking periods. The efficiencies include the effect of the DeepAK8 tagger, as well as the SD-corrected mass requirement. In each panel, individual curves represent the efficiency for different types of jets, based on whether the jets are matched to a generator-level W boson, Z boson, or neither ("QCD jet''). Simulation-to-data corrections are included. |

png pdf |
Figure B3-a:
Large-radius jet tagging efficiencies for use in reinterpretation of the results. The efficiencies are shown for the low-purity selection, for the 2017 data taking period. The efficiencies include the effect of the DeepAK8 tagger, as well as the SD-corrected mass requirement. Individual curves represent the efficiency for different types of jets, based on whether the jets are matched to a generator-level W boson, Z boson, or neither ("QCD jet''). Simulation-to-data corrections are included. |
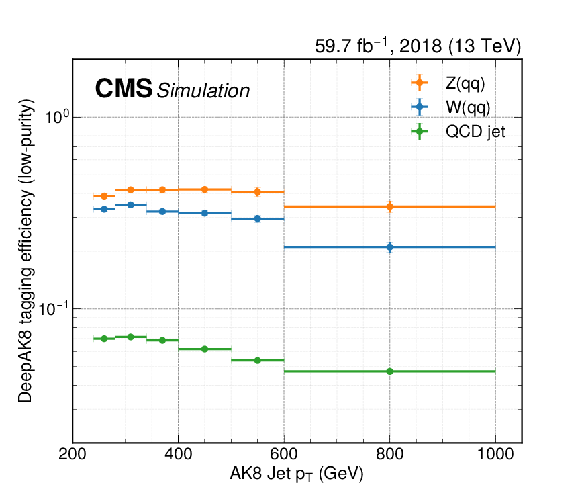
png pdf |
Figure B3-b:
Large-radius jet tagging efficiencies for use in reinterpretation of the results. The efficiencies are shown for the low-purity selection, for the 2018 data taking period. The efficiencies include the effect of the DeepAK8 tagger, as well as the SD-corrected mass requirement. Individual curves represent the efficiency for different types of jets, based on whether the jets are matched to a generator-level W boson, Z boson, or neither ("QCD jet''). Simulation-to-data corrections are included. |
png pdf |
Figure B3-c:
Large-radius jet tagging efficiencies for use in reinterpretation of the results. The efficiencies are shown for the high-purity selection, for the 2017 data taking period. The efficiencies include the effect of the DeepAK8 tagger, as well as the SD-corrected mass requirement. Individual curves represent the efficiency for different types of jets, based on whether the jets are matched to a generator-level W boson, Z boson, or neither ("QCD jet''). Simulation-to-data corrections are included. |
png pdf |
Figure B3-d:
Large-radius jet tagging efficiencies for use in reinterpretation of the results. The efficiencies are shown for the high-purity selection, for the 2018 data taking period. The efficiencies include the effect of the DeepAK8 tagger, as well as the SD-corrected mass requirement. Individual curves represent the efficiency for different types of jets, based on whether the jets are matched to a generator-level W boson, Z boson, or neither ("QCD jet''). Simulation-to-data corrections are included. |

png pdf |
Figure B4:
Distribution of ${{p_{\mathrm {T}}} ^\text {miss}}$ in the monojet category. The distribution is shown including the contributions from all data taking years. It does not directly represent the input to the statistical method, which instead relies on distributions separated by data taking year. The background estimate is obtained from the background-only fit to all data taking periods, regions, and categories, including mono-V. The total uncertainty in the background estimate, shown as a gray band in the middle panel, takes into account all relevant correlations. The signal templates from the Higgs portal and axial-vector mediator hypotheses are overlaid (solid lines). In both cases, contributions from all production modes are taken into account. |

png pdf |
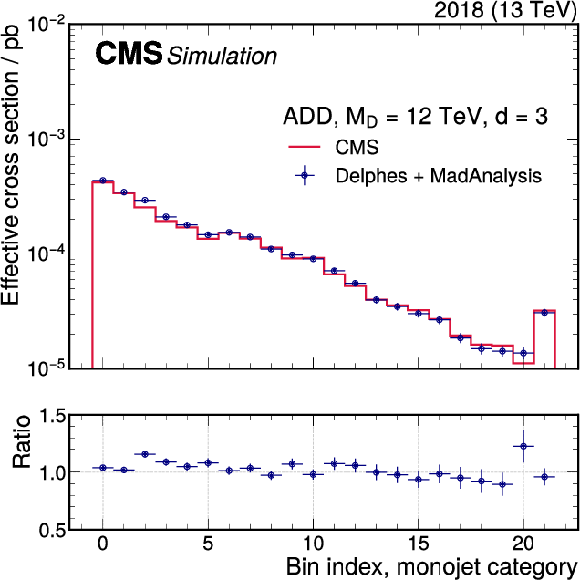
Figure B5:
Comparison of the signal templates derived with DELPHES and MadAnalysis (dark blue points) and the CMS analysis work flow (red solid line). The panels show three example parameter points for the ADD interpretation, and showcase the selection procedure for different years (2016 in the upper left, 2017 in the upper right, and 2018 in the lower panels). The rightmost bin includes the overflow. In all cases, the average agreement is observed to be better than 10%, with maximum deviations up to 20% in single bins. |

png pdf |
Figure B5-a:
Comparison of the signal templates derived with DELPHES and MadAnalysis (dark blue points) and the CMS analysis work flow (red solid line). The panel shows an example parameter point for the ADD interpretation, and showcase the selection procedure for year 2016. The rightmost bin includes the overflow. |

png pdf |
Figure B5-b:
Comparison of the signal templates derived with DELPHES and MadAnalysis (dark blue points) and the CMS analysis work flow (red solid line). The panel shows an example parameter point for the ADD interpretation, and showcase the selection procedure for year 2017. The rightmost bin includes the overflow. |
png pdf |
Figure B5-c:
Comparison of the signal templates derived with DELPHES and MadAnalysis (dark blue points) and the CMS analysis work flow (red solid line). The panel shows an example parameter point for the ADD interpretation, and showcase the selection procedure for year 2018. The rightmost bin includes the overflow. |
png pdf |
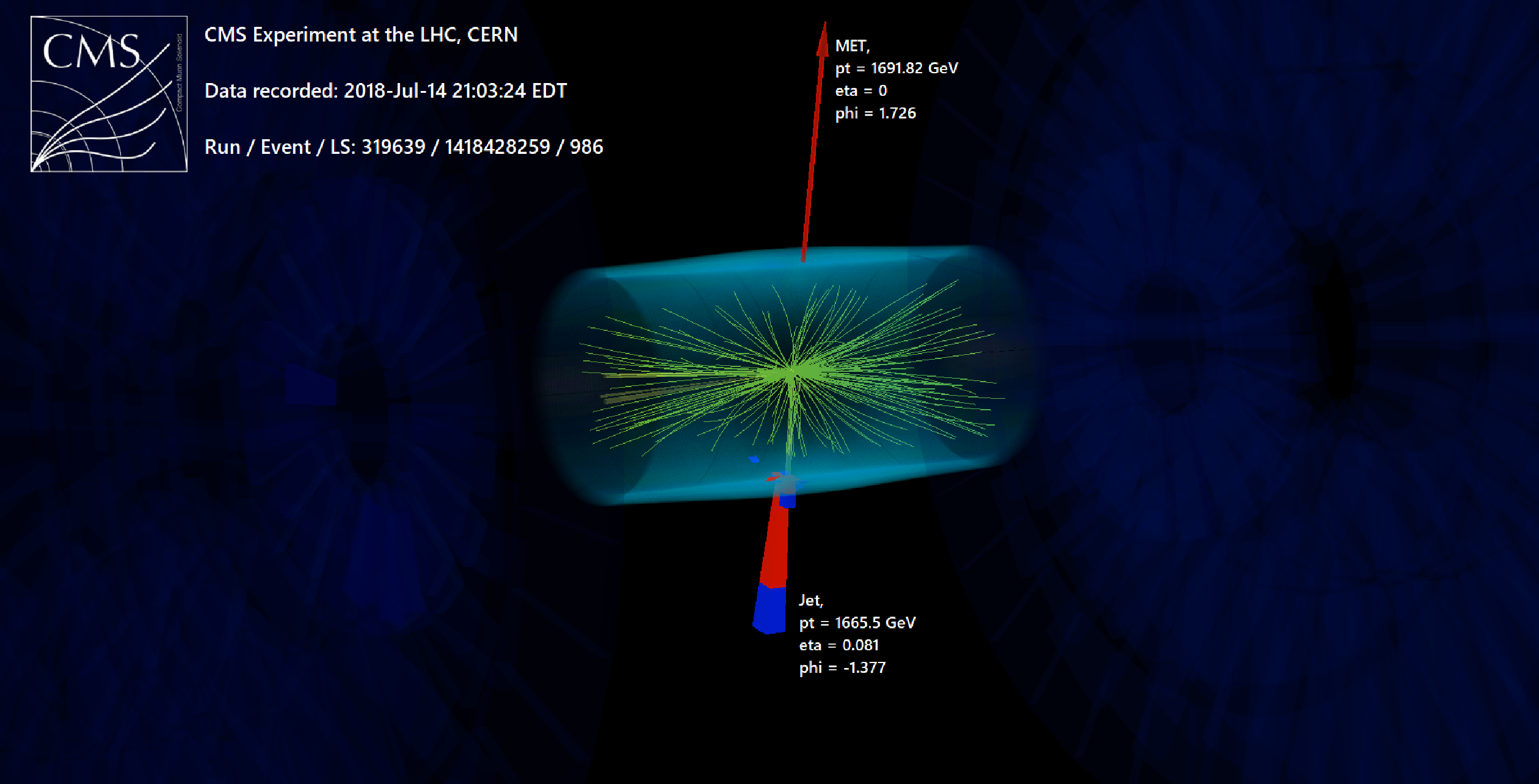
Figure B6:
Display of a representative high-$ {{p_{\mathrm {T}}} ^\text {miss}} $ event from the monojet category in the 2018 data set. In this event, a single high-$ {p_{\mathrm {T}}}$ jet (calorimeter deposits indicated by the red and blue towers) recoils against large ${{p_{\mathrm {T}}} ^\text {miss}}$ (indicated by the red arrow). |
| Tables | |

png pdf |
Table 1:
Summary of the common selection requirements for mono-V and monojet categories. For the control region selections, the requirements on ${{p_{\mathrm {T}}} ^\text {miss}}$ and ${\Delta \phi ({\vec{p}_{\mathrm {T}}^{\, \text {miss}}}}, {\vec{p}_{\mathrm {T}}} ^\text {j})$ are replaced by the equivalent selections based on the hadronic recoil, which is calculated as the vectorial sum of the ${\vec{p}_{\mathrm {T}}^{\, \text {miss}}}$ and the respective lepton or photon transverse momenta used to define the control region selection. The ${\Delta {{p_{\mathrm {T}}} ^\text {miss}} (\text {PF-calorimeter})}$ and ${\Delta \phi (\mathrm {PF},\text {charged})}$ requirements are always evaluated based on ${{p_{\mathrm {T}}} ^\text {miss}}$, and not the hadronic recoil. |

png pdf |
Table 2:
Summary of the topological selections used for different regions in the same category. Note that the trigger-level ${{p_{\mathrm {T}}} ^\text {miss}}$ calculation does not take into account muons, which makes the ${{p_{\mathrm {T}}} ^\text {miss}}$ based trigger equally suitable for the signal region and muon-based control regions. |

png pdf |
Table 3:
Lower limits at 95% CL on the fundamental Planck mass $ {M_\text {D}} $ in TeV as functions of the number of extra dimensions $d$. |
| Summary |
| A search for physics beyond the standard model in events with energetic jets and large missing transverse momentum has been presented. A data set of proton-proton collisions at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 101 fb$^{-1}$ is analyzed, and the analysis results are combined with those of an earlier search using an independent data set collected at the same center-of-mass energy, corresponding to an integrated luminosity of 36 fb$^{-1}$ [21]. Separate analysis categories are defined for events with a large-radius jet consistent with a hadronic decay of a W or a Z boson, and for events without such a jet. A joint maximum likelihood fit over a combination of signal and control regions is used to constrain standard model (SM) background processes and to extract a possible signal. The data are found to be in good agreement with the fit results, with no evidence for a significant signal contribution. The result is interpreted in terms of exclusion limits at 95% confidence level on the parameters of a number of models of beyond-the-SM physics. We constrain the branching fraction of the Higgs boson decay to invisible particles to be below 27.8%. In simplified models of the production of dark matter (DM) candidates via a spin-1 $s$-channel mediator (vector or axial-vector), values of the mediator mass of up to 1.95 TeV are excluded, assuming the couplings of ${g_\mathrm{q}} =$ 0.25 between the mediator and quarks, and ${g_\chi} =$ 1.0 between the mediator and the Dirac fermion DM particles. Assuming a fixed ratio ${m_\text{DM}} = {m_\text {med}}/3$, coupling values as low as ${g_\mathrm{q}} =$ 0.018 and ${g_\chi} =$ 0.070 can be excluded for $ m_\text{med} = $ 100 GeV. In a similar model with a pseudoscalar spin-0 mediator, mmed values less than 470 GeV are excluded. The fermion portal model, in which a colored scalar mediator couples to a DM candidate and a right-handed up quark, is excluded for mediator mass values up to 1.5 TeV at low values of the DM candidate mass ${m_\text{DM}} $, assuming ${\lambda_\mathrm{FP}} =$ 1. In a model of large extra dimensions, values of the fundamental Planck scale below from 10.7 to 5.2 TeV can be excluded, depending on the number of extra dimensions between 2 and 7. Finally, the production of leptoquarks decaying into the up quark and the electron neutrino is excluded for coupling values between the leptoquarks and the SM fermions larger than 0.5 to 1.8, for leptoquark masses between 1.0 and 1.8 TeV. The constraints on ${g_\mathrm{q}} $ in the spin-1 models, on the mediator and dark matter masses in the pseudoscalar and fermion portal models, and on the leptoquark coupling represent the most stringent bounds to date. |
| References | ||||
| 1 | G. Bertone, D. Hooper, and J. Silk | Particle dark matter: evidence, candidates and constraints | PR 405 (2005) 279 | hep-ph/0404175 |
| 2 | S. Kanemura, S. Matsumoto, T. Nabeshima, and N. Okada | Can WIMP dark matter overcome the nightmare scenario? | PRD 82 (2010) 055026 | 1005.5651 |
| 3 | O. Lebedev, H. M. Lee, and Y. Mambrini | Vector Higgs-portal dark matter and the invisible Higgs | PLB 707 (2012) 570 | 1111.4482 |
| 4 | A. Djouadi, O. Lebedev, Y. Mambrini, and J. Quevillon | Implications of LHC searches for Higgs--portal dark matter | PLB 709 (2012) 65 | 1112.3299 |
| 5 | ATLAS Collaboration | Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 6 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 7 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 8 | ATLAS Collaboration | Combination of searches for invisible Higgs boson decays with the ATLAS experiment | PRL 122 (2019) 231801 | 1904.05105 |
| 9 | CMS Collaboration | Search for invisible decays of a Higgs boson produced through vector boson fusion in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 793 (2019) 520 | CMS-HIG-17-023 1809.05937 |
| 10 | D. Abercrombie et al. | Dark matter benchmark models for early LHC run-2 searches: Report of the ATLAS/CMS dark matter forum | Phys. Dark Univ. 27 (2020) 100371 | 1507.00966 |
| 11 | Y. Bai and J. Berger | Fermion portal dark matter | JHEP 11 (2013) 171 | 1308.0612 |
| 12 | N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali | The hierarchy problem and new dimensions at a millimeter | PLB 429 (1998) 263 | hep-ph/9803315 |
| 13 | N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali | Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity | PRD 59 (1999) 086004 | hep-ph/9807344 |
| 14 | CMS Collaboration | Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques | JINST 15 (2020) P06005 | CMS-JME-18-002 2004.08262 |
| 15 | J. C. Pati and A. Salam | Unified lepton-hadron symmetry and a gauge theory of the basic interactions | PRD 8 (1973) 1240 | |
| 16 | J. C. Pati and A. Salam | Lepton number as the fourth color | PRD 10 (1974) 275 | |
| 17 | H. Georgi and S. L. Glashow | Unity of all elementary particle forces | PRL 32 (1974) 438 | |
| 18 | B. Diaz, M. Schmaltz, and Y.-M. Zhong | The leptoquark hunter's guide: Pair production | JHEP 10 (2017) 097 | 1706.05033 |
| 19 | J. L. Hewett and S. Pakvasa | Leptoquark production in hadron colliders | PRD 37 (1988) 3165 | |
| 20 | O. J. P. Eboli and A. V. Olinto | Composite leptoquarks in hadronic colliders | PRD 38 (1988) 3461 | |
| 21 | CMS Collaboration | Search for new physics in final states with an energetic jet or a hadronically decaying $ {\mathrm{W}} $ or $ {\mathrm{Z}} $ boson and transverse momentum imbalance at $ \sqrt{s} = $ 13 TeV | PRD 97 (2018) 092005 | CMS-EXO-16-048 1712.02345 |
| 22 | ATLAS Collaboration | Search for dark matter in events with a hadronically decaying vector boson and missing transverse momentum in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 10 (2018) 180 | 1807.11471 |
| 23 | ATLAS Collaboration | Search for new phenomena in events with an energetic jet and missing transverse momentum in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 103 (2021) 112006 | 2102.10874 |
| 24 | J. Thaler and K. Van Tilburg | Identifying boosted objects with N-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 25 | CMS Collaboration | HEPData record for this analysis | link | |
| 26 | E. Conte, B. Dumont, B. Fuks, and C. Wymant | Designing and recasting LHC analyses with MadAnalysis 5 | EPJC 74 (2014) 3103 | 1405.3982 |
| 27 | B. Dumont et al. | Toward a public analysis database for LHC new physics searches using MadAnalysis 5 | EPJC 75 (2015) 56 | 1407.3278 |
| 28 | A. Albert | Implementation of a search for new phenomena in events featuring energetic jets and missing transverse energy (CMS-EXO-20-004) | 2021 | |
| 29 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 30 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 31 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 32 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 33 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 34 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 35 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 36 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | CMS-PAS-JME-16-003 |
| 37 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 38 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 39 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 40 | J. M. Butterworth, A. R. Davison, M. Rubin, and G. P. Salam | Jet substructure as a new Higgs search channel at the LHC | PRL 100 (2008) 242001 | 0802.2470 |
| 41 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 42 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 43 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 44 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 45 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 46 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 47 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 48 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ o(\alpha^4_s) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 49 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 50 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 51 | N. Kidonakis | Two-loop soft anomalous dimensions for single top quark associated production with a W$ ^{-} $ or H$ ^{-} $ | PRD 82 (2010) 054018 | 1005.4451 |
| 52 | M. Aliev et al. | HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR | CPC 182 (2011) 1034 | 1007.1327 |
| 53 | P. Kant et al. | HATHOR for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | CPC 191 (2015) 74 | 1406.4403 |
| 54 | T. Gehrmann et al. | W$ ^+ $W$ ^- $ production at hadron colliders in next to next to leading order QCD | PRL 113 (2014) 212001 | 1408.5243 |
| 55 | J. M. Campbell and R. K. Ellis | An update on vector boson pair production at hadron colliders | PRD 60 (1999) 113006 | hep-ph/9905386 |
| 56 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 02 (2012) 088 | 1111.2854 |
| 57 | G. Luisoni, P. Nason, C. Oleari, and F. Tramontano | HW$ ^{\pm} $/HZ + 0 and 1 jet at NLO with the POWHEG BOX interfaced to GoSam and their merging within MiNLO | JHEP 10 (2013) 083 | 1306.2542 |
| 58 | P. Nason and C. Oleari | NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG | JHEP 02 (2010) 037 | 0911.5299 |
| 59 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector | CERN-2017-002-M | 1610.07922 |
| 60 | O. Mattelaer and E. Vryonidou | Dark matter production through loop-induced processes at the LHC: the $ s $-channel mediator case | EPJC 75 (2015) 436 | 1508.00564 |
| 61 | M. Backovi\'c et al. | Higher-order QCD predictions for dark matter production at the LHC in simplified models with $ s $-channel mediators | EPJC 75 (2015) 482 | 1508.05327 |
| 62 | M. Neubert, J. Wang, and C. Zhang | Higher-order QCD predictions for dark matter production in mono-$ Z $ searches at the LHC | JHEP 02 (2016) 082 | 1509.05785 |
| 63 | LHC Dark Matter Working Group | Recommendations of the LHC dark matter working group: Comparing LHC searches for dark matter mediators in visible and invisible decay channels and calculations of the thermal relic density | Phys. Dark Univ. 26 (2019) 100377 | 1703.05703 |
| 64 | C. Arina, B. Fuks, and L. Mantani | A universal framework for $ t $-channel dark matter models | EPJC 80 (2020) 409 | 2001.05024 |
| 65 | S. Ask et al. | Real emission and virtual exchange of gravitons and unparticles in Pythia8 | CPC 181 (2010) 1593 | 0912.4233 |
| 66 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 67 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 68 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 69 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 70 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 71 | CMS Collaboration | Search for dark matter produced with an energetic jet or a hadronically decaying $ \mathrm{W} $ or $ \mathrm{Z} $ boson at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2017) 014 | CMS-EXO-16-037 1703.01651 |
| 72 | J. M. Lindert et al. | Precise predictions for V+jets dark matter backgrounds | EPJC 77 (2017) 829 | 1705.04664 |
| 73 | J. Baglio, L. D. Ninh, and M. M. Weber | Massive gauge boson pair production at the LHC: a next-to-leading order story | PRD 88 (2013) 113005 | 1307.4331 |
| 74 | A. Denner, S. Dittmaier, M. Hecht, and C. Pasold | NLO QCD and electroweak corrections to W+$ \gamma $ production with leptonic W-boson decays | JHEP 04 (2015) 018 | 1412.7421 |
| 75 | A. Denner, S. Dittmaier, M. Hecht, and C. Pasold | NLO QCD and electroweak corrections to Z+$ \gamma $ production with leptonic Z-boson decays | JHEP 02 (2016) 057 | 1510.08742 |
| 76 | J. Butterworth et al. | PDF4LHC recommendations for LHC run II | JPG 43 (2016) 023001 | 1510.03865 |
| 77 | S. Dulat et al. | New parton distribution functions from a global analysis of quantum chromodynamics | PRD 93 (2016) 033006 | 1506.07443 |
| 78 | L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne | Parton distributions in the LHC era: MMHT 2014 PDFs | EPJC 75 (2015) 204 | 1412.3989 |
| 79 | NNPDF Collaboration | Parton distributions for the LHC run II | JHEP 04 (2015) 040 | 1410.8849 |
| 80 | M. Czakon, D. Heymes, and A. Mitov | High-precision differential predictions for top-quark pairs at the LHC | PRL 116 (2016) 082003 | 1511.00549 |
| 81 | A. L. Read | Presentation of search results: The CL$ _{\text{s}} $ technique | JPG 28 (2002) 2693 | |
| 82 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 83 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 84 | ATLAS Collaboration | Search for low-mass dijet resonances using trigger-level jets with the ATLAS detector in pp collisions at $ \sqrt{s}= $ 13 TeV | PRL 121 (2018) 081801 | 1804.03496 |
| 85 | CMS Collaboration | Search for low mass vector resonances decaying into quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 100 (2019) 112007 | CMS-EXO-18-012 1909.04114 |
| 86 | Planck Collaboration | Planck 2018 results. VI. cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 87 | CMS Collaboration | Searches for physics beyond the standard model with the $ m_\mathrm{T2} $ variable in hadronic final states with and without disappearing tracks in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | EPJC 80 (2020) 3 | CMS-SUS-19-005 1909.03460 |
| 88 | G. Busoni et al. | Recommendations on presenting LHC searches for missing transverse energy signals using simplified $ s $-channel models of dark matter | Phys. Dark Univ. 27 (2020) 100365 | 1603.04156 |
| 89 | CRESST Collaboration | Results on light dark matter particles with a low-threshold CRESST-II detector | EPJC 76 (2016) 25 | 1509.01515 |
| 90 | SuperCDMS Collaboration | New results from the search for low-mass weakly interacting massive particles with the CDMS low ionization threshold experiment | PRL 116 (2016) 071301 | 1509.02448 |
| 91 | LUX Collaboration | Results from a search for dark matter in the complete LUX exposure | PRL 118 (2017) 021303 | 1608.07648 |
| 92 | DarkSide Collaboration | Low-mass dark matter search with the DarkSide-50 Experiment | PRL 121 (2018) 081307 | 1802.06994 |
| 93 | XENON Collaboration | Dark matter search results from a one ton-year exposure of XENON1T | PRL 121 (2018) 111302 | 1805.12562 |
| 94 | PandaX-II Collaboration | Results of dark matter search using the full PandaX-II exposure | CPC 44 (2020) 125001 | 2007.15469 |
| 95 | PICO Collaboration | Improved dark matter search results from PICO-2L run 2 | PRD 93 (2016) 061101 | 1601.03729 |
| 96 | E. Behnke et al. | Final results of the PICASSO dark matter search experiment | Astropart. Phys. 90 (2017) 85 | 1611.01499 |
| 97 | PICO Collaboration | Dark matter search results from the complete exposure of the PICO-60 C$ _3 $F$ _8 $ bubble chamber | PRD 100 (2019) 022001 | 1902.04031 |
| 98 | DELPHES 3 Collaboration | DELPHES 3, a modular framework for fast simulation of a generic collider experiment | JHEP 02 (2014) 057 | 1307.6346 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|