

Compact Muon Solenoid
LHC, CERN
| CMS-SUS-16-051 ; CERN-EP-2017-109 | ||
| Search for top squark pair production in pp collisions at $ \sqrt{s} = $ 13 TeV using single lepton events | ||
| CMS Collaboration | ||
| 14 June 2017 | ||
| J. High Energy Phys. 10 (2017) 019 | ||
| Abstract: A search for top squark pair production in pp collisions at $ \sqrt{s} = $ 13 TeV is performed using events with a single isolated electron or muon, jets, and a large transverse momentum imbalance. The results are based on data collected in 2016 with the CMS detector at the LHC, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. No significant excess of events is observed above the expectation from standard model processes. Exclusion limits are set in the context of supersymmetric models of pair production of top squarks that decay either to a top quark and a neutralino or to a bottom quark and a chargino. Depending on the details of the model, we exclude top squarks with masses as high as 1120 GeV. Detailed information is also provided to facilitate theoretical interpretations in other scenarios of physics beyond the standard model. | ||
| Links: e-print arXiv:1706.04402 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures & Tables | Summary | Additional Figures & Tables | References | CMS Publications |
|---|
|
Additional information on efficiencies needed for reinterpretation of these results are available here.
Additional technical material for CMS speakers can be found here. |
| Figures | |
png pdf |
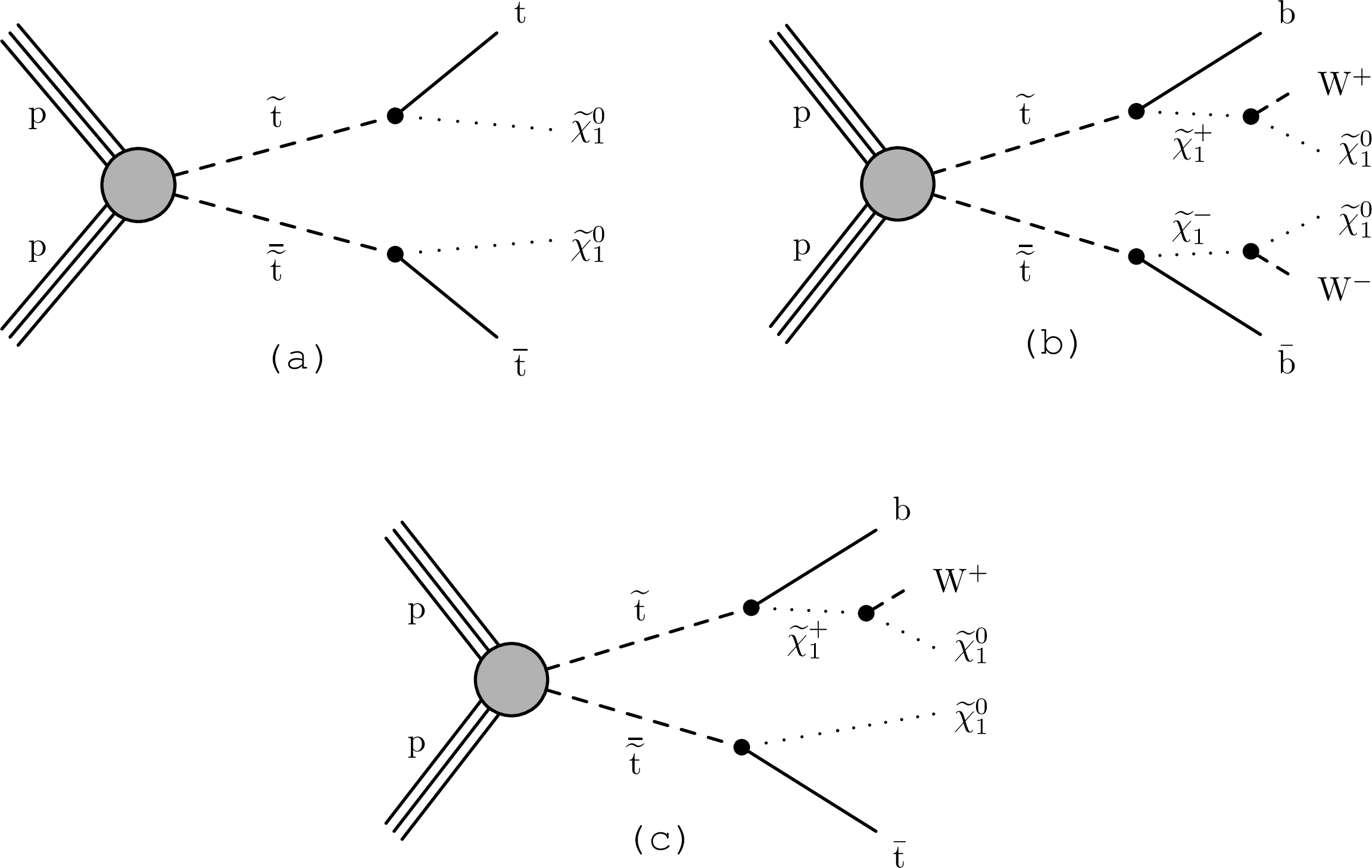
Figure 1:
Simplified-models diagrams corresponding to top squark pair production, followed by the specific decay modes targeted in this paper. (a) $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ t } \tilde{\chi}^0_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $; (b) $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{b} } \tilde{ \chi }^{-}_1 $; (c) $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $. Charge-conjugate decays are implied. |

png pdf |
Figure 1-a:
Simplified-model diagram corresponding to top squark pair-production and decay: $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ t } \tilde{\chi}^0_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $. |

png pdf |
Figure 1-b:
Simplified-model diagram corresponding to top squark pair-production and decay: $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{b} } \tilde{ \chi }^{-}_1 $. Charge-conjugate decays are implied. |

png pdf |
Figure 1-c:
Simplified-model diagram corresponding to top squark pair-production and decay: $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $. Charge-conjugate decays are implied. |
png pdf |
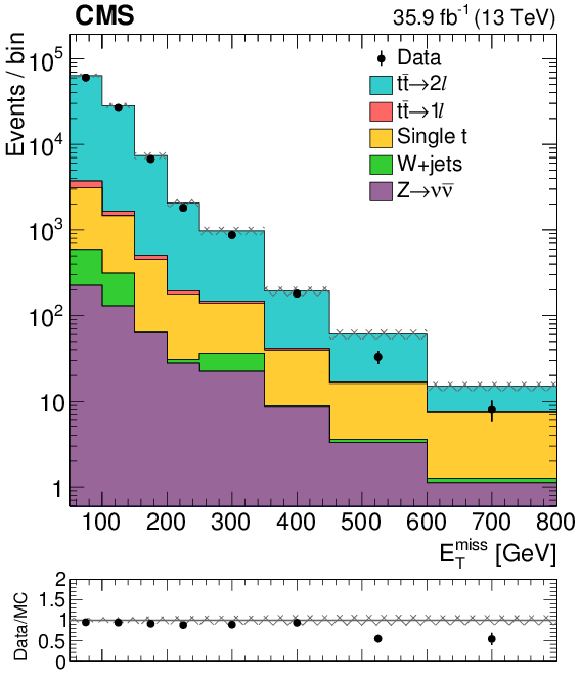
Figure 2:
Distributions in $ {E_{\mathrm {T}}^{\text {miss}}} $ for a top quark enriched control region of e$\mu$ events with at least one b-tagged jet. The ratio of data to simulation as a function of $ {E_{\mathrm {T}}^{\text {miss}}} $ is also shown. |
png pdf |
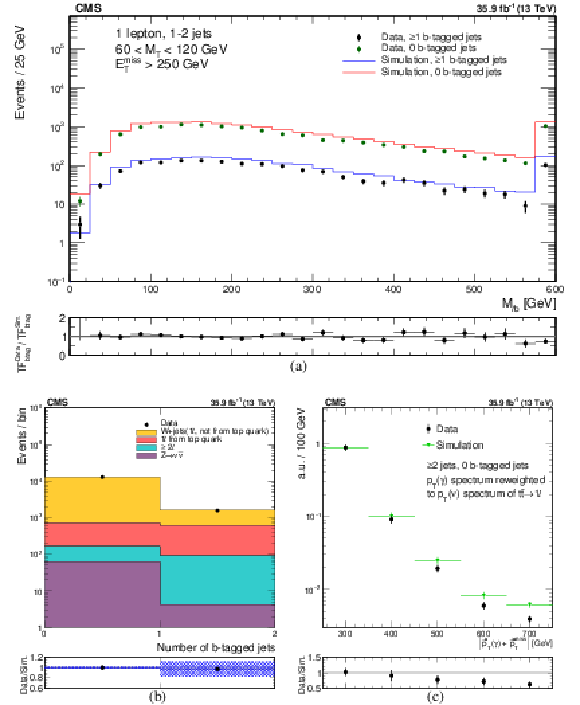
Figure 3:
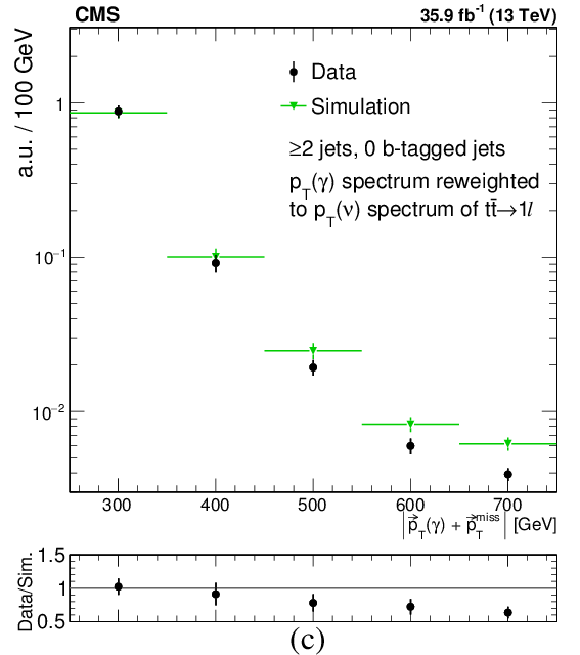
Comparison of the modeling of kinematic distributions in data and simulation relevant for the estimate of the single lepton backgrounds. (a) Distribution in $ {M_{\ell \mathrm{ b } }} $ in a control sample with 1 or 2 jets, with 60 $ < {M_{\mathrm {T}}} < $ 120 GeV and $ E_{\mathrm {T}}^{\text {miss}} > $ 250 GeV. The distribution is shown separately for events with 0 and $\geq $1 jet passing the requirement of the medium b tagging WP. The lower panel shows the ratio of the transfer factors (TF) from the 0 tags to the $\geq $1 tags samples, in data and simulation. The uncertainty shown is statistical only. (b) Distribution in the number of b-tagged jets in the same control sample. The shaded band shows the uncertainty resulting from a 50% systematic uncertainty in the heavy flavor component of the W+jets sample. (c) Comparison of the $ {E_{\mathrm {T}}^{\text {miss}}} $ distribution between data and simulation in the $ \gamma $+jets control region. The uncertainty shown is statistical only. |
png pdf |
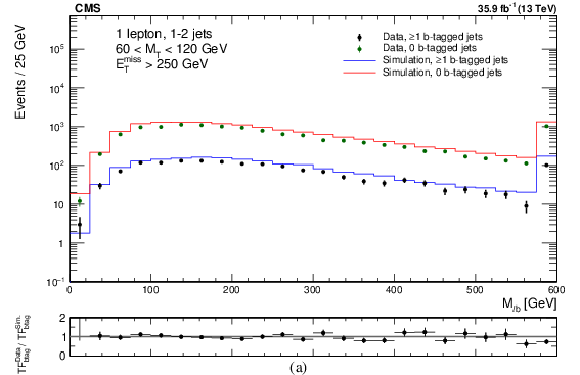
Figure 3-a:
Distribution in $ {M_{\ell \mathrm{ b } }} $ in a control sample with 1 or 2 jets, with 60 $ < {M_{\mathrm {T}}} < $ 120 GeV and $ E_{\mathrm {T}}^{\text {miss}} > $ 250 GeV. The distribution is shown separately for events with 0 and $\geq $1 jet passing the requirement of the medium b tagging WP. The lower panel shows the ratio of the transfer factors (TF) from the 0 tags to the $\geq $1 tags samples, in data and simulation. The uncertainty shown is statistical only. |

png pdf |
Figure 3-b:
Distribution in the number of b-tagged jets in the same control sample. The shaded band shows the uncertainty resulting from a 50% systematic uncertainty in the heavy flavor component of the W+jets sample. |
png pdf |
Figure 3-c:
Distribution in the number of b-tagged jets in the same control sample. The shaded band shows the uncertainty resulting from a 50% systematic uncertainty in the heavy flavor component of the W+jets sample. |
png pdf |
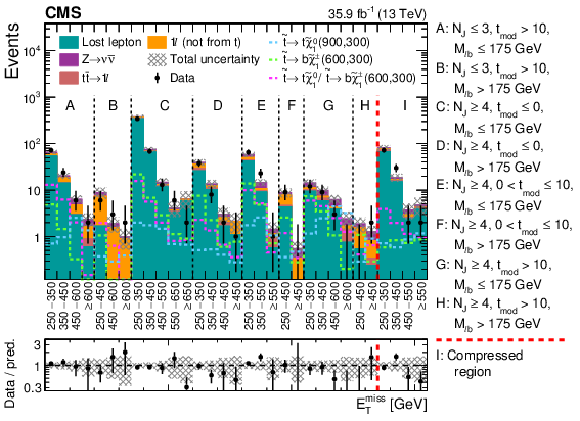
Figure 4:
Observed data yields compared with the SM background estimations for the 31 signal regions of Tables 2 and 3. The total uncertainty in the background estimate, determined as the sum in quadrature of statistical and systematic uncertainties, is shown as a shaded band. The expectations for three signal hypotheses are overlaid. The corresponding numbers in parentheses in the legend refer to the masses in GeV of the top squark and the neutralino. |

png pdf root |
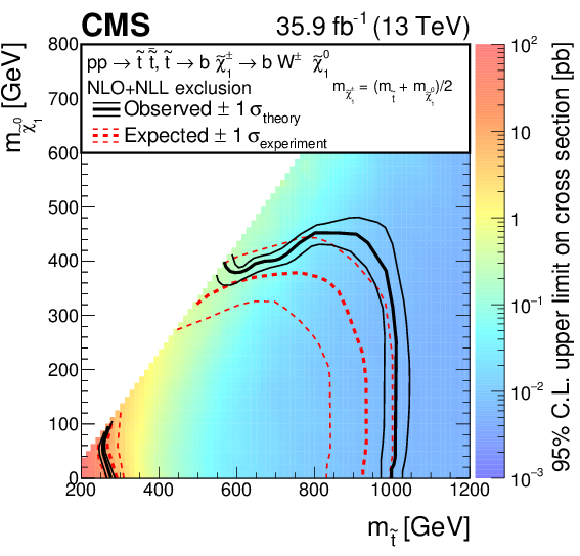
Figure 5:
The exclusion limits at 95% CL for direct top squark pair production with decay $\tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ t } \tilde{\chi}^0_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $. The interpretation is done in the two-dimensional space of $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL assuming 100% branching fraction, while the dashed red lines indicate the expected limits at 95% CL and their ${\pm }$1$\sigma $ experimental standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\text {theory}$) in the signal cross section. The whited out region is discussed in Section 7. |
png pdf root |
Figure 6:
The exclusion limit at 95% CL for direct top squark pair production with decay $\tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{b} } \tilde{ \chi }^{-}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } ^{\pm }\tilde{\chi}^0_1 $. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/$2. The interpretation is done in the two-dimensional space of $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area between the thick black curves represents the observed exclusion region at 95% CL assuming 100% branching fraction, while the dashed red lines indicate the expected limits at 95% CL and their ${\pm }$1$\sigma $ experimental standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\text {theory}$) in the signal cross section. |
png pdf root |
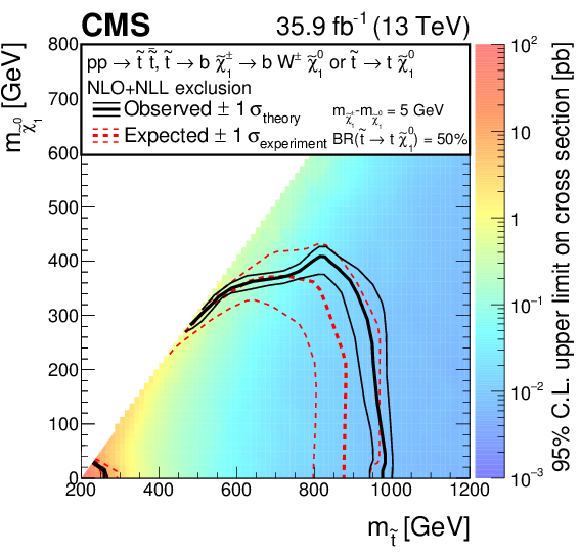
Figure 7:
The exclusion limit at 95% CL for direct top squark pair production with decay $\tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b } \tilde{ \chi }^{+}_1 \mathrm{ \bar{t} } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } ^{\pm }\tilde{\chi}^0_1 $. The mass splitting of the chargino and neutralino is fixed to 5 GeV. The interpretation is done in the two-dimensional space of $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section at each point in the $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area between the thick black curves represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limits at 95% CL and their ${\pm }$1$\sigma $ experimental standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\text {theory}$) in the signal cross section. |

png pdf |
Figure 8:
Correlation matrix for the background predictions for the signal regions for the standard selection (in percent). The labelling of the regions follows the convention of Fig.4. |
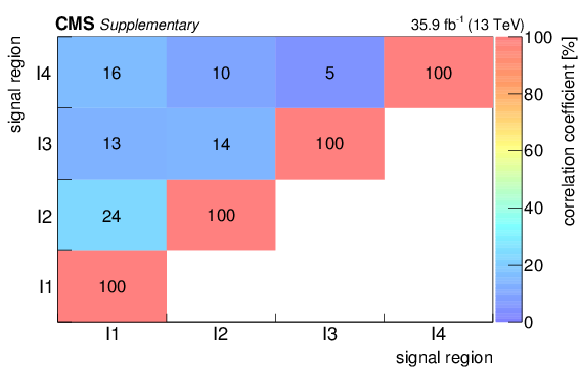
png pdf |
Figure 9:
Correlation matrix for the background predictions for the signal regions for the compressed selection (in percent). The labelling of the regions follows the convention of Fig.4. |
| Tables | |
png pdf |
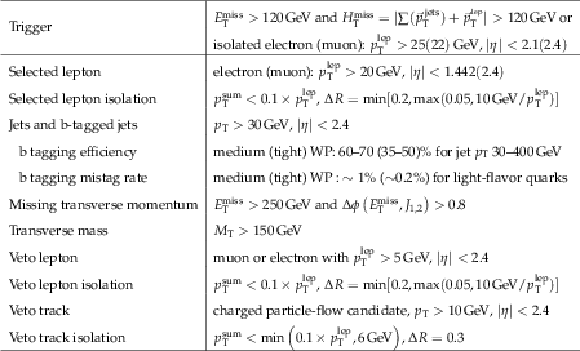
Table 1:
Summary of the event preselection. The symbol $ {p_{\mathrm {T}}} ^{\mathrm {lep}}$ denotes the ${p_{\mathrm {T}}}$ of the lepton, while $ {p_{\mathrm {T}}} ^{\text {sum$ {p_{\mathrm {T}}} $}}$ is the scalar $ {p_{\mathrm {T}}} $ sum of PF candidates in a cone around the lepton but excluding the lepton. For veto tracks this variable is calculated using charged PF candidates, while in the case of selected and veto leptons neutral PF candidates are also included. Light-flavor jets are defined as jets originating from u, d, s quarks or gluons. |
png pdf |
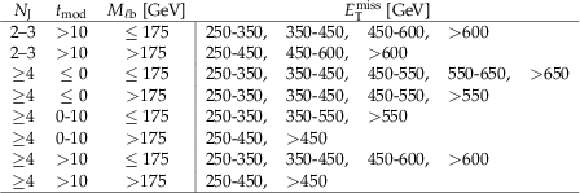
Table 2:
Definitions for the 27 signal regions of the standard selection. At least one b-tagged jet satisfying the medium WP algorithm is required in all search regions. To suppress the W+jets background in signal regions with $ {M_{\ell \mathrm{ b } }} > $ 175 GeV, we instead use the more strict tight WP requirement. |

png pdf |
Table 3:
Summary of the compressed selection and the requirements for the four corresponding signal regions. The symbol $\Delta \phi ( {E_{\mathrm {T}}^{\text {miss}}},\ell ) $ denotes the angle between $ {\vec p}_{\mathrm {T}}^{\, \text {miss}} $ and the $ {\vec p}_{\mathrm {T}}$ of the lepton. |

png pdf |
Table 4:
Dilepton control regions utilizing combined bins in $ {E_{\mathrm {T}}^{\text {miss}}} $. |

png pdf |
Table 5:
Result of the background estimates and data yields corresponding to 35.9 fb$^{-1}$, for the 31 signal regions of Tables 2 and 3. |

png pdf |
Table 6:
Summary of the systematic uncertainties in the signal efficiency. |

png pdf |
Table 7:
Background predictions and yields in data corresponding to 35.9 fb$^{-1}$ for aggregate signal regions. |
| Summary |
| We have reported on a search for top squark pair production in pp collisions at $ \sqrt{s} = $ 13 TeV in events with a single isolated electron or muon, jets, and large missing transverse momentum using data collected with the CMS detector during the 2016 run of the LHC, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. The event data yields are consistent with the expectations from SM processes. The results are interpreted as exclusion limits in the context of supersymmetric models with pair production of top squarks that decay either to a top quark and a neutralino or to a bottom quark and a chargino. Assuming both top squarks decay to a top quark and a neutralino, we exclude at 95% CL top squark masses up to 1120 GeV for a massless neutralino and neutralino masses up to 515 GeV for a 950 GeV top squark mass. For a scenario where both top squarks decay to a bottom quark and a chargino, with the chargino mass the average of the masses of the neutralino and top squark, we exclude at the 95% CL top squark masses up to 1000 GeV for a massless neutralino and neutralino masses up to 450 GeV for a 800 GeV top squark mass. For the mixed decay scenario, with the mass splitting between the chargino and neutralino fixed to be 5 GeV, we exclude at the 95% CL top squark masses up to 980 GeV for a massless neutralino and neutralino masses up to 400 GeV for a 825 GeV top squark mass. |
| Additional Figures | |
png pdf root |
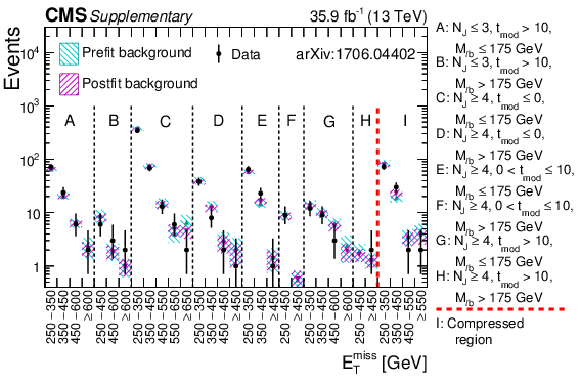
Additional Figure 1:
Comparison between postfit and prefit background predictions and data for 35.9 fb$^{-1}$ collected during 2016 pp collisions. |
png pdf root |
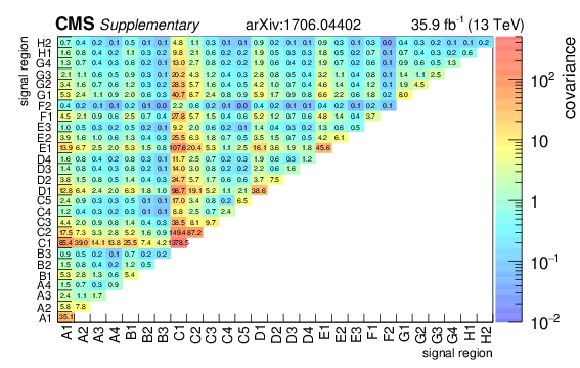
Additional Figure 2:
Covariance matrix for the background predictions for the signal regions for the standard selection. The labelling of the regions follows the convention of correlation matrices in the appendix of the paper. |
png pdf root |
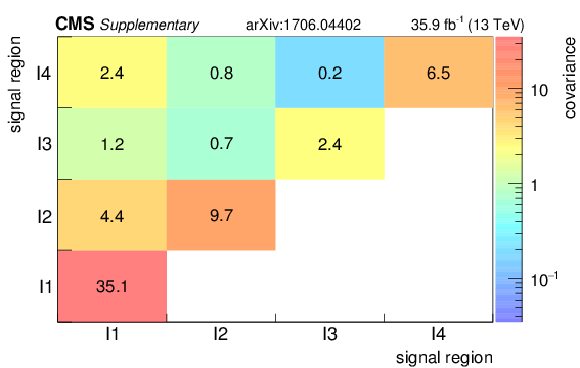
Additional Figure 3:
Covariance matrix for the background predictions for the signal regions for the compressed selection. The labelling of the regions follows the convention of correlation matrices in the appendix of the paper. |
png pdf |
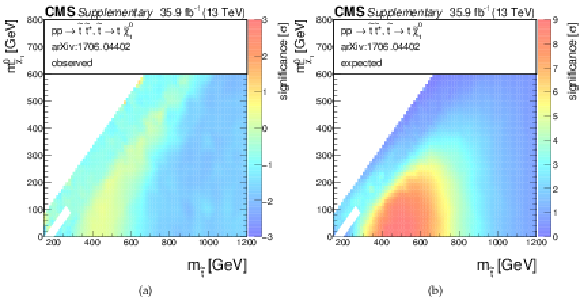
Additional Figure 4:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. Left: Observed, right: expected. |
png pdf |
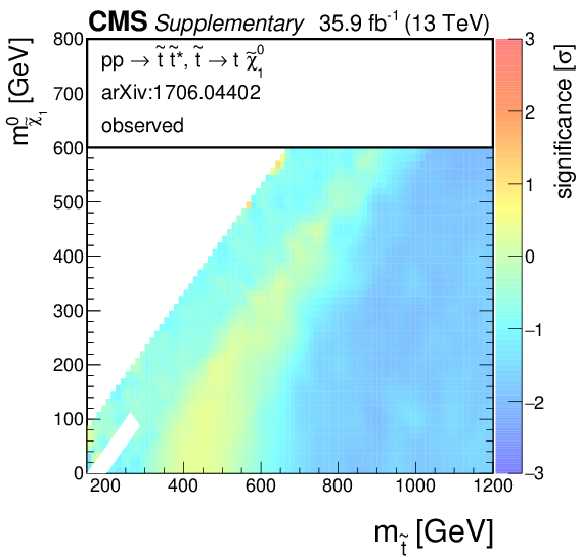
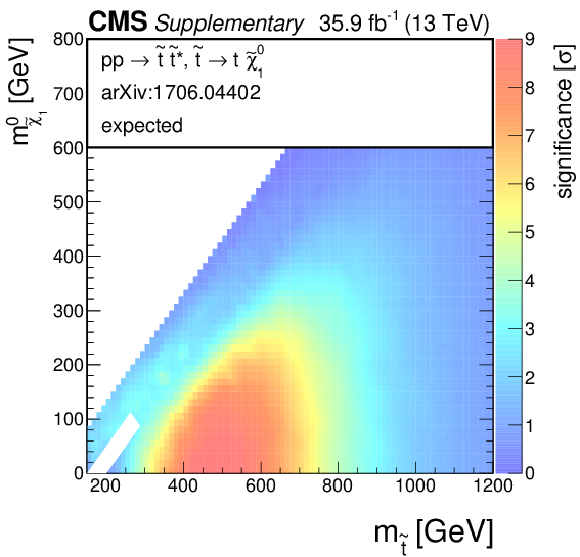
Additional Figure 4-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. |
png pdf |
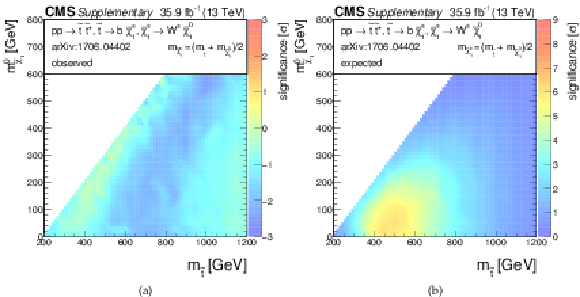
Additional Figure 4-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. |
png pdf |
Additional Figure 5:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$. Left: Observed, right: expected. |

png pdf |
Additional Figure 5-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$. |

png pdf |
Additional Figure 5-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$. |

png pdf |
Additional Figure 6:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. Left: Observed, right: expected. |

png pdf |
Additional Figure 6-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. |
png pdf |
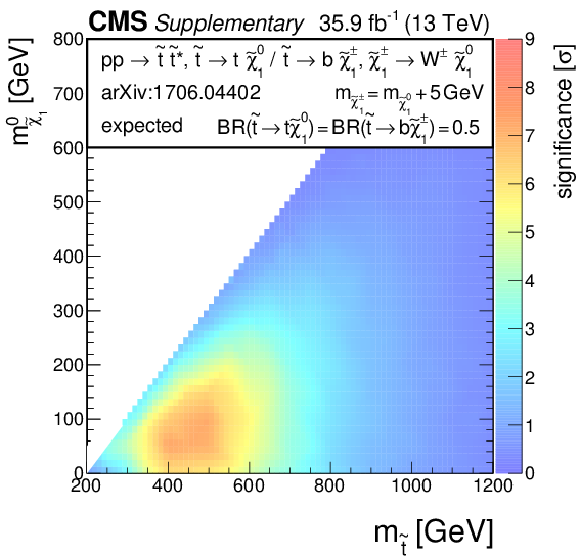
Additional Figure 6-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. |
png pdf root |
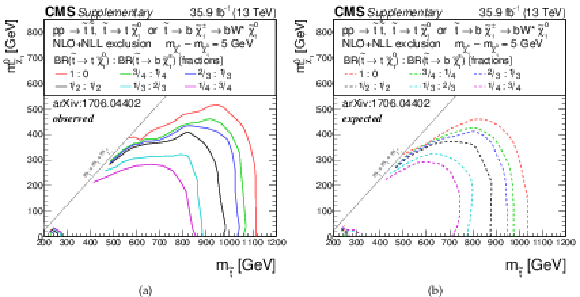
Additional Figure 7:
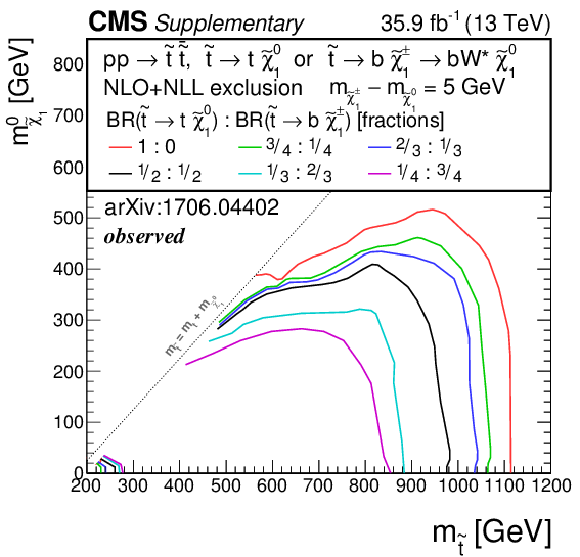
Exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. Left: Observed, right: expected. |
png pdf root |
Additional Figure 7-a:
Observed exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. |
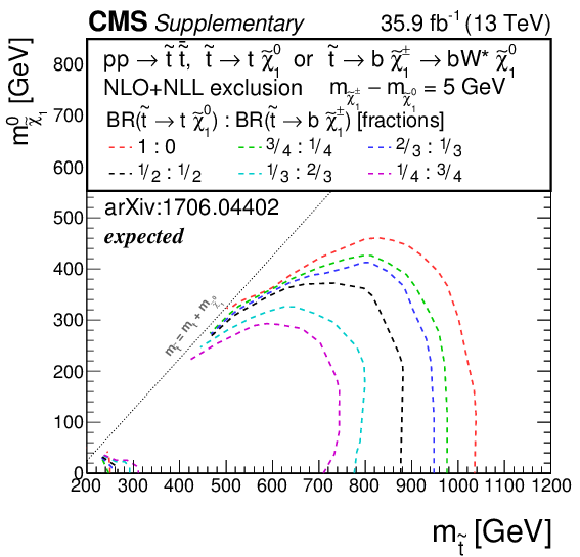
png pdf root |
Additional Figure 7-b:
Expected exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. |
png pdf root |
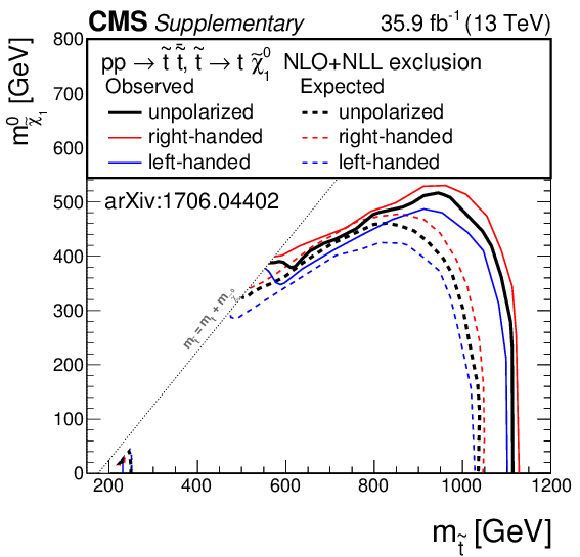
Additional Figure 8:
Exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$ for unpolarized top quarks (black lines), right-handed top quarks (red lines), and left-handed top quarks (blue lines). |
png pdf |
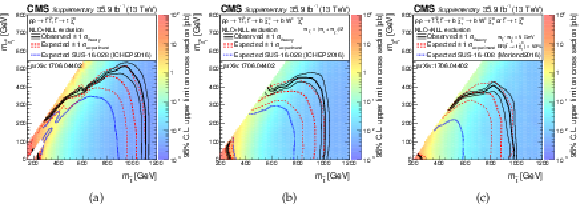
Additional Figure 9:
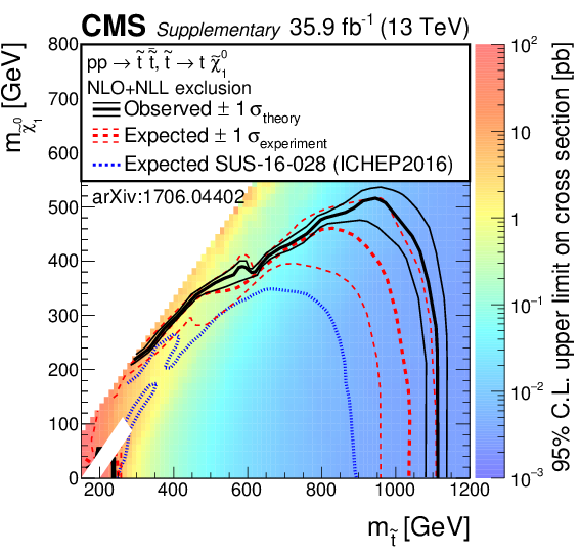
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015. Left: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $, middle: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$, right: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |
png pdf |
Additional Figure 9-a:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $. |
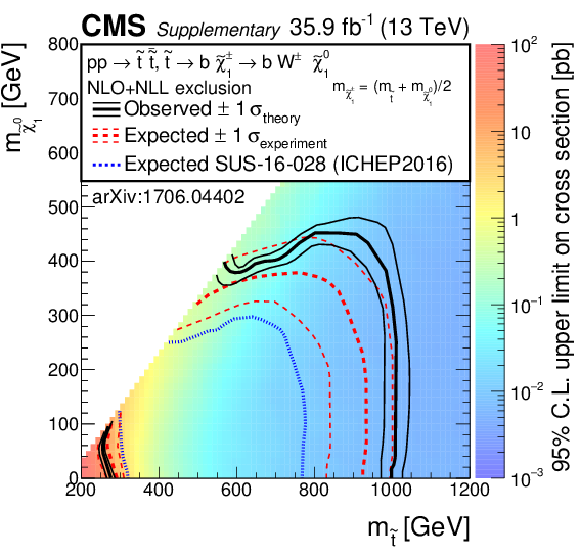
png pdf |
Additional Figure 9-b:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$. |
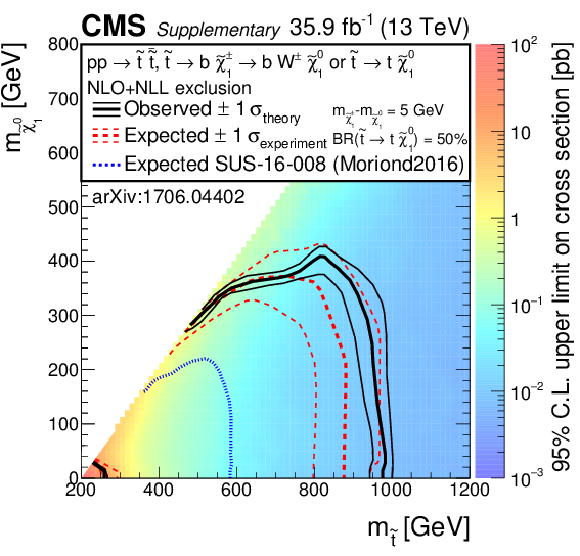
png pdf |
Additional Figure 9-c:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |

png pdf |
Additional Figure 10:
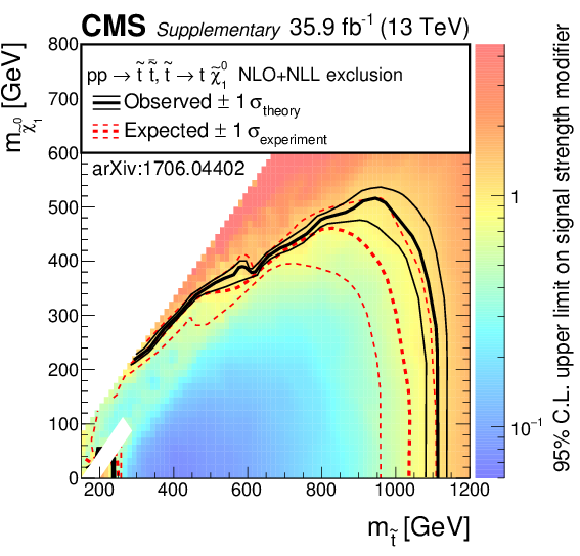
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier. Left: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $, middle: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$, right: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |
png pdf |
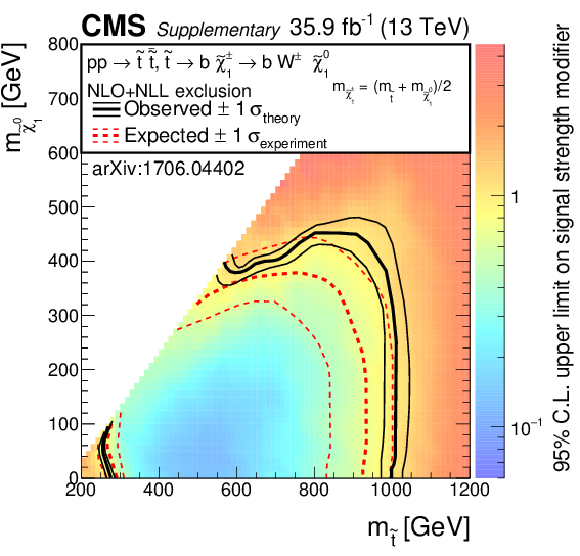
Additional Figure 10-a:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $. |
png pdf |
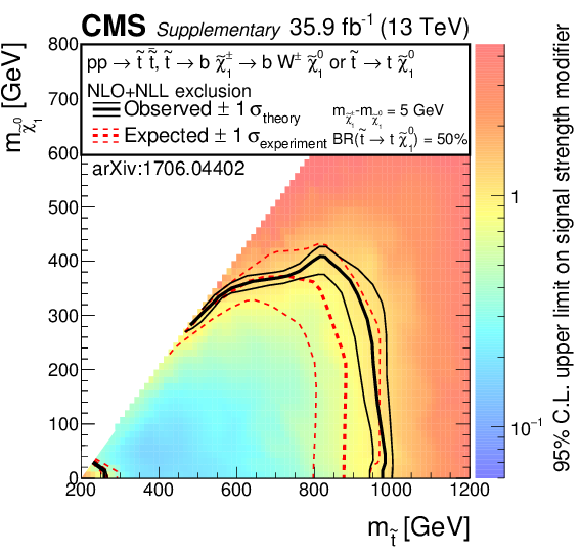
Additional Figure 10-b:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } \to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $m_{\tilde{ \mathrm{ t } } }$ and $m_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } } } + m_{\tilde{\chi}^0_1 })/2$. |
png pdf |
Additional Figure 10-c:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier: for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \bar{ \tilde{ \mathrm{t} } } $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 }$ + 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |
png pdf |
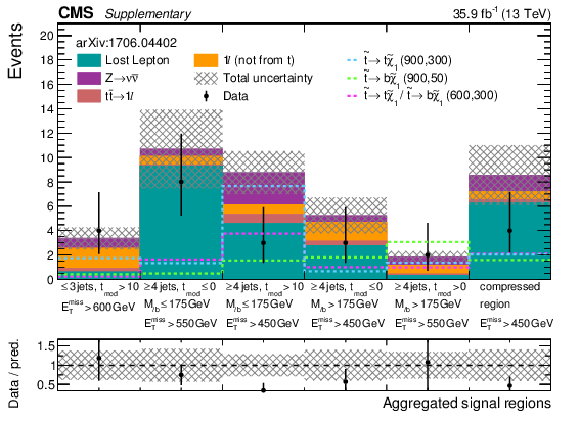
Additional Figure 11:
Background predictions and data for the aggregated signal regions using 35.9 fb$^{-1}$ collected during 2016 pp collisions. |
| Additional Tables | |

png pdf |
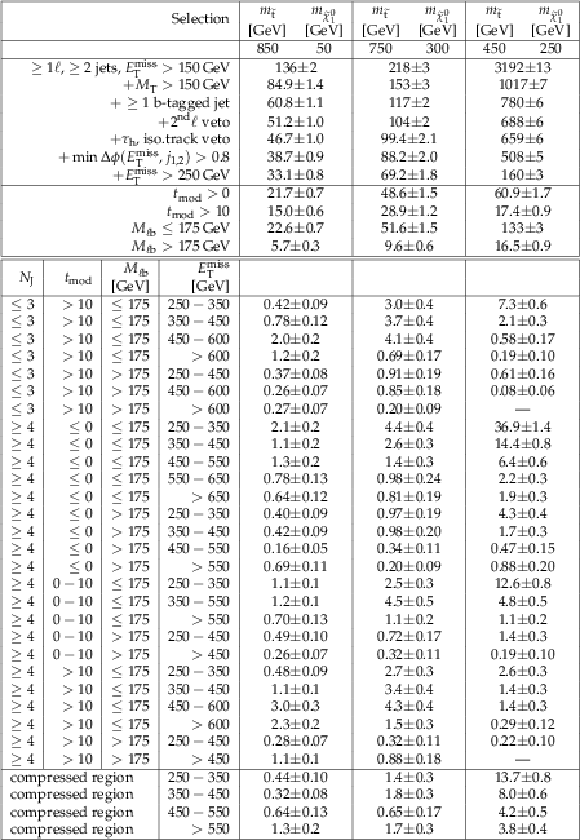
Additional Table 1:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}\to \mathrm{ t \bar{t} } \tilde{\chi}^0_1 \tilde{\chi}^0_1 $ signals for an integrated luminosity of 35.9 fb$^{-1}$. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
png pdf |
Additional Table 2:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}, \tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 / \mathrm{ b } \tilde{ \chi }^{\pm}_1 $ signals for an integrated luminosity of 35.9 fb$^{-1}$. The branching fraction for this model is BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{ \chi }^{\pm}_1 $) = 0.5, and $m_{\tilde{ \chi }^{\pm}_1 } = m_{\tilde{\chi}^0_1 } + 5 GeV $. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
png pdf |
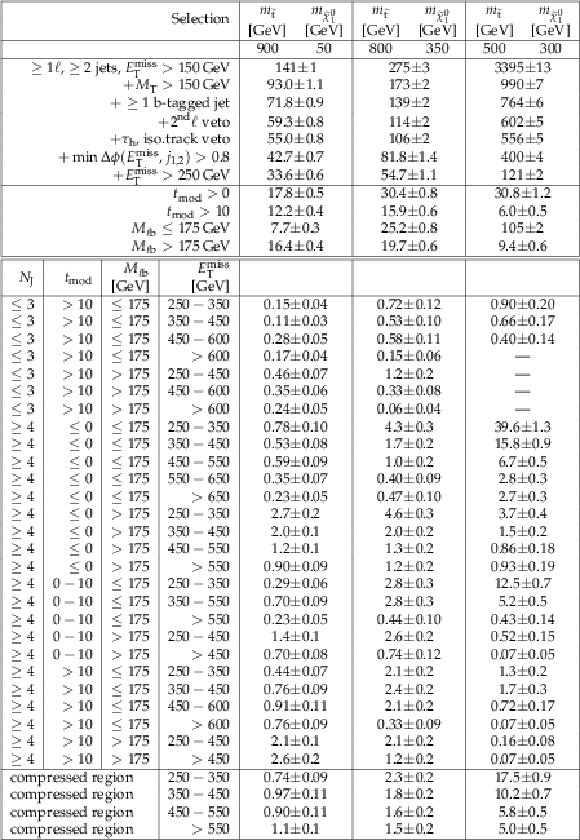
Additional Table 3:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}\to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ signals with $m_{\tilde{ \chi }^{\pm}_1 } = (m_{\tilde{ \mathrm{ t } } }+m_{\tilde{\chi}^0_1 })/2$ for an integrated luminosity of 35.9 fb$^{-1}$. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
|
Electronic version of the limit curves can be found as three rootfiles
here,
here, and
here.
The correlation and covariance matrices can be found as two rootfiles here, and here. A code snippet to calculate the $t_{\text{mod}} $ variables together with an example how to use it is provided here. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Golfand and E. P. Likhtman | Extension of the algebra of Poincare group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | Nucl. Phys. B 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | Nucl. Phys. B 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | Nucl. Phys. B 90 (1975) 104 | |
| 8 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 9 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 10 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 11 | CMS Collaboration | Combined results of searches for the standard model Higgs boson in pp collisions at $ \sqrt{s}=$ 7 TeV | PLB 710 (2012) 26 | CMS-HIG-11-032 1202.1488 |
| 12 | M. Papucci, J. T. Ruderman, and A. Weiler | Natural SUSY endures | JHEP 09 (2012) 035 | 1110.6926 |
| 13 | R. Barbieri and D. Pappadopulo | S-particles at their naturalness limits | JHEP 10 (2009) 061 | 0906.4546 |
| 14 | S. Dimopoulos and G. F. Giudice | Naturalness constraints in supersymmetric theories with nonuniversal soft terms | PLB 357 (1995) 573 | hep-ph/9507282 |
| 15 | ATLAS Collaboration | Search for top squarks in final states with one isolated lepton, jets, and missing transverse momentum in $ \sqrt{s}=$ 13 TeV $ pp $ collisions with the ATLAS detector | PRD 94 (2016) 052009 | 1606.03903 |
| 16 | CMS Collaboration | Searches for pair production for third-generation squarks in $ \sqrt{s} = $ 13 TeV pp collisions | Accepted to EPJC | CMS-SUS-16-008 1612.03877 |
| 17 | CMS Collaboration | Search for supersymmetry in the all-hadronic final state using top quark tagging in pp collisions at $ \sqrt{s} = $ 13 TeV | CMS-SUS-16-009 1701.01954 |
|
| 18 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 19 | N. Arkani-Hamed et al. | MARMOSET: The Path from LHC Data to the New Standard Model via On-Shell Effective Theories | hep-ph/0703088 | |
| 20 | J. Alwall, P. Schuster, and N. Toro | Simplified models for a first characterization of new physics at the LHC | PRD 79 (2009) 075020 | 0810.3921 |
| 21 | J. Alwall, M.-P. Le, M. Lisanti, and J. G. Wacker | Model-Independent Jets plus Missing Energy Searches | PRD 79 (2009) 015005 | 0809.3264 |
| 22 | LHC New Physics Working Group Collaboration | Simplified Models for LHC New Physics Searches | JPG 39 (2012) 105005 | 1105.2838 |
| 23 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 24 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 25 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 26 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 27 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 28 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 29 | E. Re | Single-top $ Wt $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 30 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 31 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 32 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 33 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 34 | CMS Collaboration | Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and $ E_{\mathrm{T}}^{\text{miss}} $ | CDS | |
| 35 | CMS Collaboration | Commissioning of the Particle-flow Event Reconstruction with the first LHC collisions recorded in the CMS detector | CDS | |
| 36 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 37 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}=$ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 38 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 39 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 40 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 41 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 42 | CMS Collaboration | Identification of b quark jets at the CMS Experiment in the LHC Run 2 | CMS-PAS-BTV-15-001 | CMS-PAS-BTV-15-001 |
| 43 | CMS Collaboration | Missing transverse energy performance of the CMS detector | JINST 6 (2011) P09001 | CMS-JME-10-009 1106.5048 |
| 44 | M. L. Graesser and J. Shelton | Hunting Mixed Top Squark Decays | PRL 111 (2013) 121802 | 1212.4495 |
| 45 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 46 | A. L. Read | Presentation of search results: the $ CL_{S} $ technique | JPG 28 (2002) 2693 | |
| 47 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 48 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | ATL-PHYS-PUB 2011-11, CMS NOTE 2011/005 | |
| 49 | C. Borschensky et al. | Squark and gluino production cross sections in $ pp $ collisions at $ \sqrt{s} = $ 13, 14, 33 and 100 TeV | EPJC 74 (2014) 3174 | 1407.5066 |
| 50 | CMS Collaboration | Simplified likelihood for the re-interpretation of public CMS results | CDS | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|