

Compact Muon Solenoid
LHC, CERN
| CMS-SMP-22-005 ; CERN-EP-2024-066 | ||
| Measurement of multijet azimuthal correlations and determination of the strong coupling in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| 24 April 2024 | ||
| Eur. Phys. J. C 84 (2024) 842 | ||
| Abstract: A measurement is presented of a ratio observable that provides a measure of the azimuthal correlations among jets with large transverse momentum $ p_{\mathrm{T}} $. This observable is measured in multijet events over the range of $ p_{\mathrm{T}} = $ 360-3170 GeV based on data collected by the CMS experiment in proton-proton collisions at a centre-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 134 fb$ ^{-1} $. The results are compared with predictions from Monte Carlo parton-shower event generator simulations, as well as with fixed-order perturbative quantum chromodynamics (pQCD) predictions at next-to-leading-order (NLO) accuracy obtained with different parton distribution functions (PDFs) and corrected for nonperturbative and electroweak effects. Data and theory agree within uncertainties. From the comparison of the measured observable with the pQCD prediction obtained with the NNPDF3.1 NLO PDFs, the strong coupling at the Z boson mass scale is $ \alpha_\mathrm{S}(m_{\mathrm{Z}})= $ 0.1177 $ \pm $ 0.0013 (exp) $ _{-0.0073}^{+0.0116} $ (theo) $ = $ 0.1177 $_{-0.0074}^{+0.0117} $, where the total uncertainty is dominated by the scale dependence of the fixed-order predictions. A test of the running of $ \alpha_\mathrm{S} $ in the TeV region shows no deviation from the expected NLO pQCD behaviour. | ||
| Links: e-print arXiv:2404.16082 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
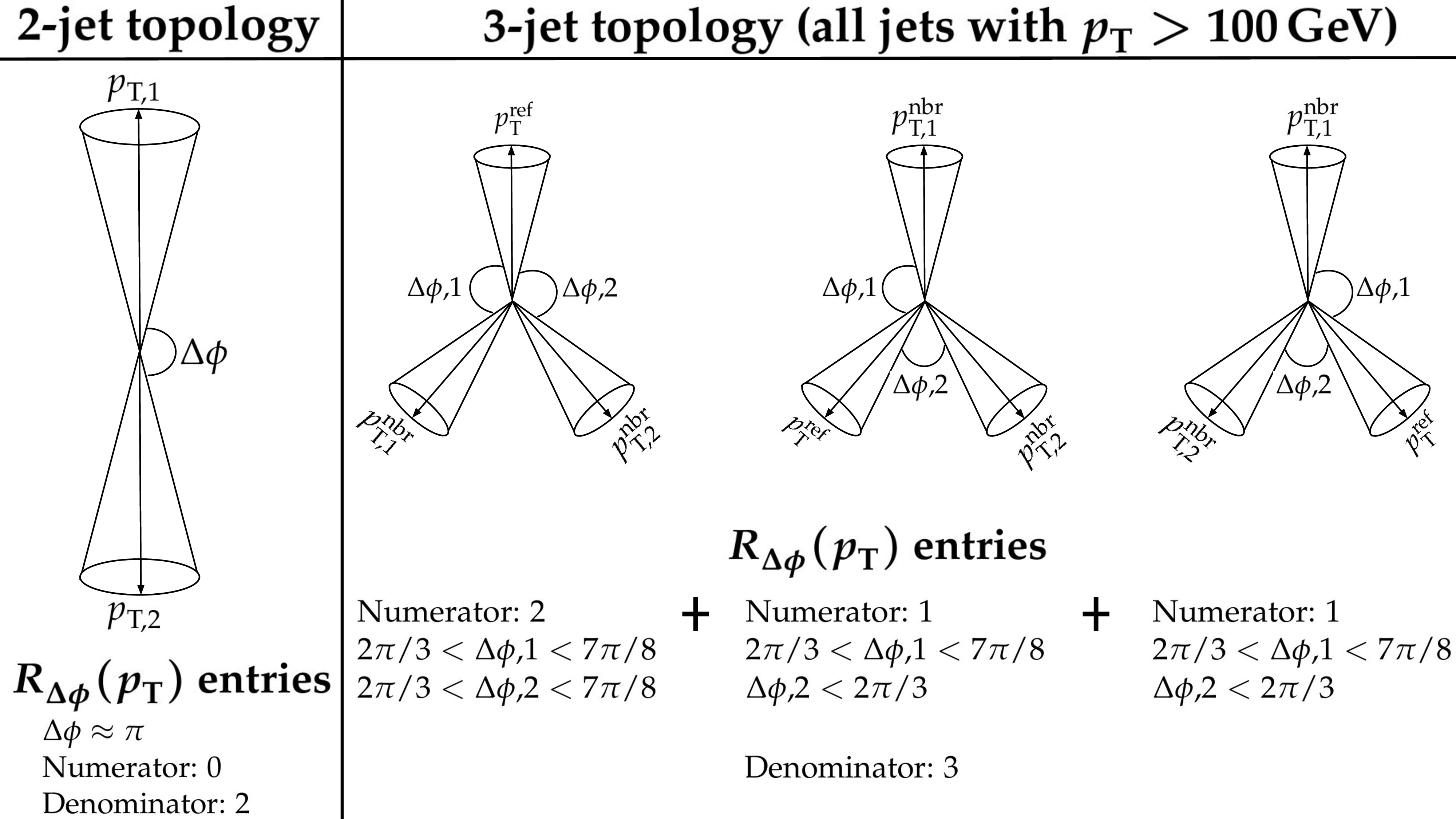
Figure 1:
Example of the number of entries contributing to the numerator and denominator of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio, Eq. (1), for 2-jet (left) and 3-jet (right) events, with all jets having $ p_{\mathrm{T}} > p_{\text{Tmin}}^{\text{nbr}}= $ 100 GeV. The 2-jet topology does not contribute (null numerator) to the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio when the azimuthal distance for neighbouring jets is fixed to 2 $ \pi/3 < \Delta\phi < 7\pi/ $ 8. In the 3-jet topology, each jet is considered as a reference, and its azimuthal separations ($ \Delta\phi{,} $ 1 and $ \Delta\phi{,} $ 2) to other neighbouring jets (with $ p_{\mathrm {T,1}}^{\text {nbr}} $ and $ p_{\mathrm{T,2}}^{\text {nbr}} $) are computed. Each neighbouring jet with $ \Delta\phi $ within the specified interval increments the entries of the numerator, whereas the denominator simply counts the number of jets in the event. |
png pdf |
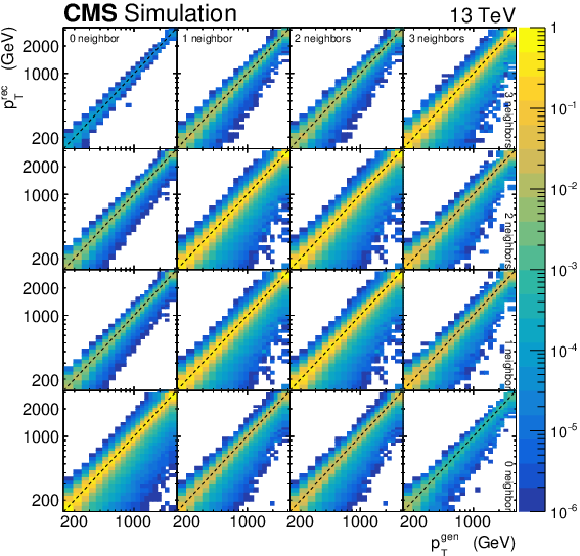
Figure 2:
Probability matrix for the $ N(p_{\mathrm{T}},n) $ distribution built using PYTHIA8 simulated events. The horizontal axis corresponds to the generator-level jet $ p_{\mathrm{T}} $, and the vertical axis to the reconstructed-level jet $ p_{\mathrm{T}} $. The 4 $ \times $ 4 structure of the matrix corresponds to the bins of neighbouring jets $ n $ (labelled in the uppermost row and rightmost column), and indicates migrations among those bins. The horizontal and vertical axes of each cell correspond to the $ p_{\mathrm{T}} $ of the jets, and each cell indicates the migrations among the jet $ p_{\mathrm{T}} $ bins. The range of colours covers from 10$^{-6} $ to 1, and indicates the probability of migrations from a given (generator) particle-level bin to the corresponding (reconstructed) detector-level bin. |

png pdf |
Figure 3:
Bin-to-bin correlation matrix for the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ distribution at the particle level, where the value 1 ($-$1) corresponds to fully (anti)correlated bins. For illustration purposes, only bins with (anti)correlations larger (smaller) than 0.05 ($-$0.05) are shown also as text. |
png pdf |
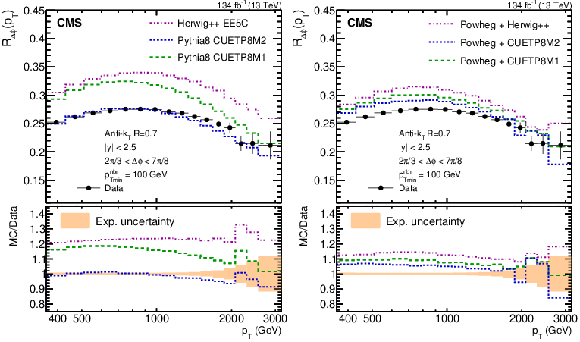
Figure 4:
The $ R_{\Delta\phi}(p_{\mathrm{T}}) $ observable as a function of $ p_{\mathrm{T}} $, compared with MC generator predictions at LO (left) and at NLO (right) accuracy. The LO predictions are obtained with PYTHIA8 tunes CUETP8M1 and CUETP8M2, and HERWIG++ tune UE-EE-5-CTEQ6L1 MC event generators. The NLO predictions are obtained with POWHEG interfaced with each of the aforementioned MC event generators. The experimental data are represented with black dots and the MC predictions with coloured lines. The lower panel of each plot shows the ratio between MC predictions and experimental data. The total experimental uncertainties are indicated by the vertical error bars (upper panels) and coloured band (lower panels) correspondingly. |
png pdf |
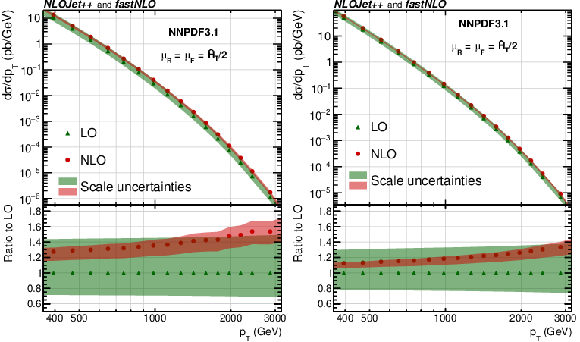
Figure 5:
Theoretical predictions for the cross sections corresponding to the numerator (left) and denominator (right) of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio, Eq. (1), obtained using the NNPDF3.1 NLO PDF set. The coloured bands represent the LO and NLO scale uncertainties derived with a six-point variation of $ \mu_\mathrm{R} $ and $ \mu_\mathrm{F} $ from the central reference value. The lower panels show the ratios to the respective LO predictions. |
png pdf |
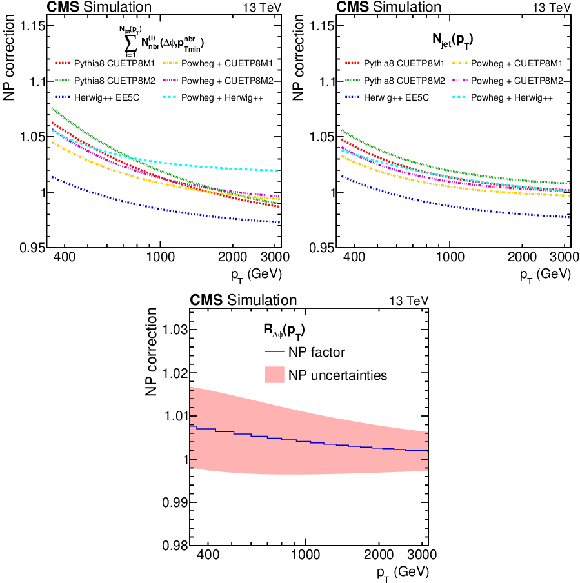
Figure 6:
Nonperturbative correction factors for the numerator (upper left) and denominator (upper right) of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio, Eq. (1), using PYTHIA8 with tunes CUETP8M1 and CUETP8M2, HERWIG++ with tune UE-EE-5-CTEQ6L1, and POWHEG interfaced with each of them. The lower plot shows the NP correction factors (blue line) for $ R_{\Delta\phi}(p_{\mathrm{T}}) $ and their uncertainties. |

png pdf |
Figure 7:
Electroweak corrections for the numerator (blue) and denominator (green) of Eq. (1), and for the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio itself (red). The solid lines correspond to the additive combination of NLO EW corrections to the QCD process (NLO QCD$ \,+\, $EW), and the markers represent the multiplicative combination (NLO QCD$ \,\times\, $EW). |
png pdf |
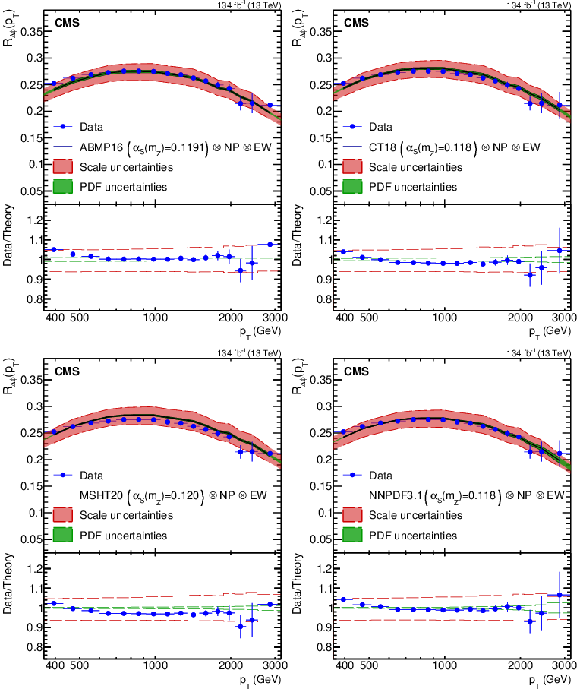
Figure 8:
The $ R_{\Delta\phi}(p_{\mathrm{T}}) $ observable as a function of $ p_{\mathrm{T}} $, compared with fixed-order theoretical calculations at NLO accuracy using the ABMP16 (upper left), CT18 (upper right), MSHT20 (lower left), and NNPDF3.1 (lower right) NLO PDF sets. The experimental data are indicated with blue dots (with error bars representing the total experimental uncertainty), the theoretical prediction for the default $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ for each PDF set with black solid lines, the scale uncertainties with red bands, and the PDF uncertainties with green bands. The lower panel of each plot shows the ratio between experimental data and theoretical predictions. |

png pdf |
Figure 9:
Sensitivity of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio to the strong coupling constant $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $. The data are indicated with blue dots with error bars representing the total experimental uncertainty. In each plot, the lines represent fixed-order NLO theoretical calculations obtained with ABMP16 (upper left), CT18 (upper right), MSHT20 (lower left) and NNPDF3.1 (lower right) NLO PDF sets. Solid green (red) lines indicate maximum (minimum) values, and dotted black lines intermediate values of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ for each PDF set. |

png pdf |
Figure 10:
Minimization of the $ \chi^2 $ between experimental measurements and theoretical predictions for the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio, with respect to $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ for the ABMP16, CT18, MSHT20, and NNPDF3.1 NLO PDF sets. In this plot, only experimental uncertainties are included in the covariance matrix. The minimum value of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ found for each PDF set is indicated with a dashed line and corresponds to the central result. The experimental uncertainty is estimated from the $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ values for which the $ \chi^2 $ is increased by one unit with respect to the minimum value. |
png pdf |
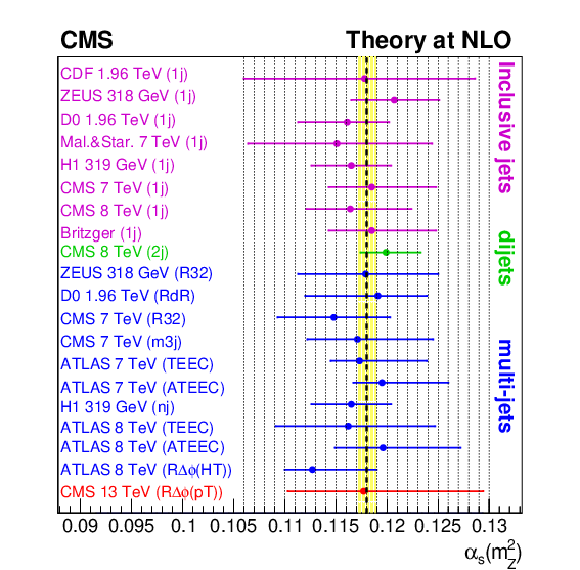
Figure 11:
Determination of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ from the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio with the NNPDF3.1 PDF set (red), in comparison with previous NLO determinations of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ from inclusive jet (magenta), dijet (green), and multijet (blue) measurements. The horizontal error bars indicate the total uncertainty (experimental and theoretical). The world-average $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ value is represented by the vertical dashed black line and its uncertainty by the yellow band. |

png pdf |
Figure 12:
Running of the strong coupling $ \alpha_\mathrm{S}(Q) $ (dashed line) evolved using the current world-average value $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) = $ 0.1180 $ \pm $ 0.0009 [5] together with its associated total uncertainty (yellow band). The four new extractions from the present analysis (Table 5) are shown as filled red circles, compared with results from the H1[93,94,90], ZEUS [95], D0 [11,12], CMS [14],17,18,22], and ATLAS [24,21] experiments. The vertical error bars indicate the total uncertainty (experimental and theoretical). All the experimental results shown in this figure are based on fixed-order predictions at NLO accuracy in pQCD. |
| Tables | |

png pdf |
Table 1:
The different HLT $ p_{\mathrm{T}} $ thresholds used in the measurement and the corresponding integrated luminosities for each data-taking year. |

png pdf |
Table 2:
Values of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ observable in different $ p_{\mathrm{T}} $ intervals, and associated experimental uncertainties. |

png pdf |
Table 3:
Default and range of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ values used in the different NLO PDF sets. |
png pdf |
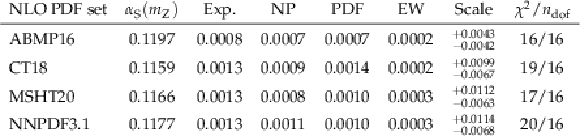
Table 4:
Results for $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $, associated uncertainties, and goodness-of-fit per degree of freedom ($ \chi^2/n_\text{dof} $), obtained from the measured $ R_{\Delta\phi}(p_{\mathrm{T}}) $ distribution compared with theoretical predictions using different NLO PDF sets. |

png pdf |
Table 5:
Values of $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ and $ \alpha_\mathrm{S}(Q) $ determined in four different jet $ p_{\mathrm{T}} $ fitting subregions corresponding to an average scale $ \langle Q \rangle $ over each $ p_{\mathrm{T}} $ interval. |
| Summary |
| A measurement of the $ R_{\Delta\phi}(p_{\mathrm{T}}) $ ratio, sensitive to azimuthal correlations in multijet events, has been presented using proton-proton collision data collected by the CMS experiment at a centre-of-mass energy of 13 TeV and corresponding to an integrated luminosity of 134 fb$ ^{-1} $. The experimental data are compared with predictions from Monte Carlo (MC) event generators, PYTHIA8 with tunes CUETP8M1 and CUETP8M2, HERWIG++ with tune UE-EE-5-CTEQ6L1, and POWHEG interfaced with each one of them. Deviations between data and MC predictions are observed in all cases, except for PYTHIA8 tune CUETP8M2, which gives a good overall description of the measurement. The measurement is also compared with fixed-order perturbative quantum chromodynamics (pQCD) predictions at next-to-leading-order (NLO) accuracy using the NLOJET++ package within the FASTNLO framework. Those predictions are extracted for four different NLO parton distribution function (PDF) sets, ABMP16, CT18, MSHT20, and NNPDF3.1. Corrections for nonperturbative (NP) effects are evaluated using all the aforementioned MC event generators, and are applied to the fixed-order predictions. The predictions are additionally corrected for electroweak (EW) effects that become important at large jet transverse momenta. Generally, the fixed-order predictions are in agreement with the experimental data in the phase space of this analysis, and they provide a good description of the measured $ R_{\Delta\phi}(p_{\mathrm{T}}) $ distribution for all PDF sets. {\tolerance=2400 Based on a comparison of the measured $ R_{\Delta\phi}(p_{\mathrm{T}}) $ distribution and the theoretical predictions, the strong coupling at the scale of the Z boson mass is: $ \alpha_\mathrm{S}(m_{\mathrm{Z}})= $ 0.1177 $_{-0.0068}^{+0.0114} $ (scale) $ \pm $ 0.0013 (exp) $ \pm $ 0.0011 (NP) $ \pm $ 0.0010 (PDF) $ \pm $ 0.0003 (EW) $ \pm $ 0.0020 (PDF choice) $=$ 0.1177 $_{-0.0074}^{+0.0117} $, using calculations based on the NNPDF3.1 NLO PDF set. Alternative $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ results obtained with other PDF sets are compatible among each other, as well as with the central result of this work, and with the current world average, $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) = $ 0.1180 $ \pm $ 0.0009. The spread of the $ \alpha_\mathrm{S}(m_{\mathrm{Z}}) $ values obtained from different PDF sets is used for the assignment of the ``PDF choice'' uncertainty quoted in the final strong coupling constant derived here. The dominant uncertainty in this measurement originates from the scale dependence of the NLO pQCD predictions, and is expected to be significantly reduced with the future inclusion of fixed-order predictions at next-to-NLO accuracy. The evolution of the strong coupling as a function of the energy scale, $ \alpha_\mathrm{S}(Q) $, has been tested up to $ Q\approx $ 2 TeV, a higher scale than that probed in previous H1, ZEUS, D0, CMS, and ATLAS measurements. This test has been performed by choosing as energy scale $ Q $ the average jet transverse momentum in the different intervals considered, and no deviation from the expected NLO pQCD running of the strong coupling is observed. |
| References | ||||
| 1 | C. G. Callan, Jr. | Broken scale invariance in scalar field theory | PRD 2 (1970) 1541 | |
| 2 | K. Symanzik | Small distance behavior in field theory and power counting | Commun. Math. Phys. 18 (1970) 227 | |
| 3 | K. Symanzik | Small distance behavior analysis and Wilson expansion | Commun. Math. Phys. 23 (1971) 49 | |
| 4 | P. A. Baikov, K. G. Chetyrkin, and J. H. K \"u hn | Five-loop running of the QCD coupling constant | PRL 118 (2017) 082002 | 1606.08659 |
| 5 | Particle Data Group , R. L. Workman et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2022 (2022) 083C01 | |
| 6 | D. d'Enterria et al. | The strong coupling constant: State of the art and the decade ahead | Submitted to J. Phys. G, 2022 | 2203.08271 |
| 7 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 8 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 9 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 10 | CDF Collaboration | Measurement of the strong coupling constant from inclusive jet production at the Tevatron $ \mathrm{\bar{p}p} $ collider | PRL 88 (2002) 042001 | hep-ex/0108034 |
| 11 | D0 Collaboration | Determination of the strong coupling constant from the inclusive jet cross section in p$ \bar{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRD 80 (2009) 111107 | 0911.2710 |
| 12 | D0 Collaboration | Measurement of angular correlations of jets at $ \sqrt{s}= $ 1.96 TeV and determination of the strong coupling at high momentum transfers | PLB 718 (2012) 56 | 1207.4957 |
| 13 | B. Malaescu and P. Starovoitov | Evaluation of the strong coupling constant $ \alpha_s $ using the ATLAS inclusive jet cross-section data | EPJC 72 (2012) 2041 | 1203.5416 |
| 14 | CMS Collaboration | Measurement of the ratio of the inclusive 3-jet cross section to the inclusive 2-jet cross section in pp collisions at $ \sqrt{s} = $ 7 TeV and first determination of the strong coupling constant in the TeV range | EPJC 73 (2013) 2604 | CMS-QCD-11-003 1304.7498 |
| 15 | ATLAS Collaboration | Measurement of transverse energy-energy correlations in multi-jet events in pp collisions at $ \sqrt{s} = $ 7 TeV using the ATLAS detector and determination of the strong coupling constant $ \alpha_{\mathrm{s}}(m_Z) $ | PLB 750 (2015) 427 | 1508.01579 |
| 16 | CMS Collaboration | Determination of the top-quark pole mass and strong coupling constant from the $ \rm t \bar{t} $ production cross section in pp collisions at $ \sqrt{s} = $ 7 TeV | PLB 728 (2014) 496 | CMS-TOP-12-022 1307.1907 |
| 17 | CMS Collaboration | Measurement of the inclusive 3-jet production differential cross section in proton-proton collisions at 7 TeV and determination of the strong coupling constant in the TeV range | EPJC 75 (2015) 186 | CMS-SMP-12-027 1412.1633 |
| 18 | CMS Collaboration | Constraints on parton distribution functions and extraction of the strong coupling constant from the inclusive jet cross section in pp collisions at $ \sqrt{s} = $ 7 TeV | EPJC 75 (2015) 288 | CMS-SMP-12-028 1410.6765 |
| 19 | CMS Collaboration | Determination of the strong coupling constant $ \alpha_\mathrm{S}(m_\mathrm{Z}) $ from measurements of inclusive $ \mathrm{W}^{\pm} $ and Z boson production cross sections in proton-proton collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2020) 018 | CMS-SMP-18-005 1912.04387 |
| 20 | D. d'Enterria and A. Poldaru | Extraction of the strong coupling $ \alpha_\mathrm{S}(m_\mathrm{Z}) $ from a combined NNLO analysis of inclusive electroweak boson cross sections at hadron colliders | JHEP 06 (2020) 016 | 1912.11733 |
| 21 | ATLAS Collaboration | Determination of the strong coupling constant $ \alpha _\mathrm{s} $ from transverse energy-energy correlations in multijet events at $ \sqrt{s} = $ 8 TeV using the ATLAS detector | EPJC 77 (2017) 872 | 1707.02562 |
| 22 | CMS Collaboration | Measurement and QCD analysis of double-differential inclusive jet cross sections in pp collisions at $ \sqrt{s}= $ 8 TeV and cross section ratios to 2.76 and 7 TeV | JHEP 03 (2017) 156 | CMS-SMP-14-001 1609.05331 |
| 23 | CMS Collaboration | Measurement of the triple-differential dijet cross section in proton-proton collisions at $ \sqrt{s}= $ 8 TeV and constraints on parton distribution functions | EPJC 77 (2017) 746 | CMS-SMP-16-011 1705.02628 |
| 24 | ATLAS Collaboration | Measurement of dijet azimuthal decorrelations in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector and determination of the strong coupling | PRD 98 (2018) 092004 | 1805.04691 |
| 25 | CMS Collaboration | Measurement of jet substructure observables in $ \mathrm{t\overline{t}} $ events from proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 98 (2018) 092014 | CMS-TOP-17-013 1808.07340 |
| 26 | CMS Collaboration | Measurement of the $ \mathrm{t}\overline{\mathrm{t}} $ production cross section, the top quark mass, and the strong coupling constant using dilepton events in pp collisions at $ \sqrt{s} = $ 13 TeV | EPJC 79 (2019) 368 | CMS-TOP-17-001 1812.10505 |
| 27 | CMS Collaboration | Measurement of $ \mathrm{t\bar t} $ normalised multi-differential cross sections in pp collisions at $ \sqrt s= $ 13 TeV, and simultaneous determination of the strong coupling strength, top quark pole mass, and parton distribution functions | EPJC 80 (2020) 658 | CMS-TOP-18-004 1904.05237 |
| 28 | ATLAS Collaboration | Determination of the strong coupling constant from transverse energy-energy correlations in multijet events at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 07 (2023) 085 | 2301.09351 |
| 29 | CMS Collaboration | Measurement and QCD analysis of double-differential inclusive jet cross sections in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 02 (2022) 142 | CMS-SMP-20-011 2111.10431 |
| 30 | CMS Collaboration | Measurement of multidifferential cross sections for dijet production in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | Submitted to EPJC, 2023 | CMS-SMP-21-008 2312.16669 |
| 31 | CMS Collaboration | Measurement of energy correlators inside jets and determination of the strong coupling $ \alpha_\mathrm{S}(m_\mathrm{Z}) $ | Submitted to Phys. Rev. Lett, 2024 | CMS-SMP-22-015 2402.13864 |
| 32 | CMS Collaboration | HEPData record for this analysis | link | |
| 33 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 34 | CMS Collaboration | Performance of the CMS level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 35 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 36 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 37 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 38 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 39 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 40 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 41 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 42 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS Physics Analysis Summary, 2017 CMS-PAS-JME-16-003 |
CMS-PAS-JME-16-003 |
| 43 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 44 | CMS Collaboration | Performance of the CMS electromagnetic calorimeter in pp collisions at $ \sqrt{s}= $ 13 TeV | Technical Report CERN-EP-2024-014, -003, 2024 CMS-PAS-EGM-18-002 |
|
| 45 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 46 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 47 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 48 | S. Schmitt | TUnfold: an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 49 | V. Blobel | Unfolding | Chapter 6, John Wiley & Sons, Ltd, 2013 link |
|
| 50 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 51 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 52 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 53 | M. Bähr et al. | Herwig++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 54 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 55 | C. Bierlich et al. | Robust independent validation of experiment and theory: Rivet version 3 | SciPost Phys. 8 (2020) 026 | 1912.05451 |
| 56 | B. R. Webber | A QCD model for jet fragmentation including soft gluon interference | NPB 238 (1984) 492 | |
| 57 | M. H. Seymour and A. Siódmok | Constraining MPI models using $ \sigma_{\text{eff}} $ and recent Tevatron and LHC underlying event data | JHEP 10 (2013) 113 | 1307.5015 |
| 58 | D. Stump et al. | Inclusive jet production, parton distributions, and the search for new physics | JHEP 10 (2003) 046 | hep-ph/0303013 |
| 59 | B. Andersson | The Lund model | Volume 7, Cambridge University Press, ISBN~978-0-521-01734-3, 978-0-521-4-5, 978-0-511-88149-7, 2005 link |
|
| 60 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 61 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO | NPB 855 (2012) 153 | 1107.2652 |
| 62 | CMS Collaboration | Investigations of the impact of the parton shower tuning in Pythia 8 in the modelling of $ \mathrm{t\overline{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS Physics Analysis Summary, 2016 CMS-PAS-TOP-16-021 |
CMS-PAS-TOP-16-021 |
| 63 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 64 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 65 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 66 | Z. Nagy | Three-jet cross sections in hadron-hadron collisions at next-to-leading order | PRL 88 (2002) 122003 | hep-ph/0110315 |
| 67 | Z. Nagy | Next-to-leading order calculation of three-jet observables in hadron-hadron collision | PRD 68 (2003) 094002 | hep-ph/0307268 |
| 68 | T. Kluge, K. Rabbertz, and M. Wobisch | FastNLO: Fast pQCD calculations for PDF fits | in 14th International Workshop on Deep Inelastic Scattering, 2006 link |
hep-ph/0609285 |
| 69 | D. Britzger, K. Rabbertz, F. Stober, and M. Wobisch | New features in version 2 of the fastNLO project | fastNLO Collaboration, in 20th International Workshop on Deep-Inelastic Scattering and Related Subjects, 2012 link |
1208.3641 |
| 70 | A. Buckley et al. | LHAPDF6: parton density access in the LHC precision era | EPJC 75 (2015) 132 | 1412.7420 |
| 71 | J. Currie et al. | Infrared sensitivity of single jet inclusive production at hadron colliders | JHEP 10 (2018) 155 | 1807.03692 |
| 72 | M. Czakon, A. Mitov, and R. Poncelet | Next-to-next-to-leading order study of three-jet production at the LHC | PRL 127 (2021) 152001 | 2106.05331 |
| 73 | M. Alvarez et al. | NNLO QCD corrections to event shapes at the LHC | JHEP 03 (2023) 129 | 2301.01086 |
| 74 | M. Cacciari et al. | The top-antitop cross-section at 1.8 TeV and 1.96 TeV: A study of the systematics due to parton densities and scale dependence | JHEP 04 (2004) 068 | hep-ph/0303085 |
| 75 | S. Catani, D. de Florian, M. Grazzini, and P. Nason | Soft gluon resummation for Higgs boson production at hadron colliders | JHEP 07 (2003) 028 | hep-ph/0306211 |
| 76 | A. Banfi, G. P. Salam, and G. Zanderighi | Phenomenology of event shapes at hadron colliders | JHEP 06 (2010) 038 | 1001.4082 |
| 77 | S. Alekhin, J. Blümlein, S. Moch, and R. Plačakyté | Parton distribution functions, $ \alpha_s $, and heavy-quark masses for LHC Run II | PRD 96 (2017) 014011 | 1701.05838 |
| 78 | T.-J. Hou et al. | New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC | PRD 103 (2021) 014013 | 1912.10053 |
| 79 | S. Bailey et al. | Parton distributions from LHC, HERA, Tevatron and fixed target data: MSHT20 PDFs | EPJC 81 (2021) 341 | 2012.04684 |
| 80 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 81 | M. Reyer, M. Schönherr, and S. Schumann | Full NLO corrections to 3-jet production and $ \mathbf {R_{32}} $ at the LHC | EPJC 79 (2019) 321 | 1902.01763 |
| 82 | Sherpa Collaboration | Event generation with Sherpa 2.2 | SciPost Phys. 7 (2019) 034 | 1905.09127 |
| 83 | S. Actis et al. | Recursive generation of one-loop amplitudes in the Standard Model | JHEP 04 (2013) 037 | 1211.6316 |
| 84 | S. Actis et al. | RECOLA: REcursive Computation of One-Loop Amplitudes | Comput. Phys. Commun. 214 (2017) 140 | 1605.01090 |
| 85 | B. Biedermann et al. | Automation of NLO QCD and EW corrections with Sherpa and Recola | EPJC 77 (2017) 492 | 1704.05783 |
| 86 | M. Schönherr | An automated subtraction of NLO EW infrared divergences | EPJC 78 (2018) 119 | 1712.07975 |
| 87 | J. Pumplin et al. | Uncertainties of predictions from parton distribution functions. 2. The Hessian method | PRD 65 (2001) 014013 | hep-ph/0101032 |
| 88 | W. T. Giele, S. A. Keller, and D. A. Kosower | Parton distribution function uncertainties | hep-ph/0104052 | |
| 89 | ZEUS Collaboration | Jet-radius dependence of inclusive-jet cross-sections in deep inelastic scattering at HERA | PLB 649 (2007) 12 | hep-ex/0701039 |
| 90 | H1 Collaboration | Measurement of multijet production in ep collisions at high $ Q^2 $ and determination of the strong coupling $ \alpha_s $ | EPJC 75 (2015) 65 | 1406.4709 |
| 91 | D. Britzger et al. | Determination of the strong coupling constant using inclusive jet cross section data from multiple experiments | EPJC 79 (2019) 68 | 1712.00480 |
| 92 | ZEUS Collaboration | Multijet production in neutral current deep inelastic scattering at HERA and determination of $ \alpha_s $ | EPJC 44 (2005) 183 | hep-ex/0502007 |
| 93 | H1 Collaboration | Jet production in ep collisions at high $ Q^2 $ and determination of $ \alpha_s $ | EPJC 65 (2010) 363 | 0904.3870 |
| 94 | H1 Collaboration | Jet production in ep collisions at low $ Q^2 $ and determination of $ \alpha_s $ | EPJC 67 (2010) 1 | 0911.5678 |
| 95 | ZEUS Collaboration | Inclusive-jet photoproduction at HERA and determination of $ \alpha_s $ | NPB 864 (2012) 1 | 1205.6153 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|