CMS-SMP-16-011

CMS-SMP-16-011 ; CERN-EP-2017-061
Measurement of the triple-differential dijet cross section in proton-proton collisions at $\sqrt{s} =$ 8 TeV and constraints on parton distribution functions
CMS Collaboration
7 May 2017
Eur. Phys. J. C 77 (2017) 746
Abstract: A measurement is presented of the triple-differential dijet cross section at a centre-of-mass energy of 8 TeV using 19.7 fb $^{-1}$ of data collected with the CMS detector in proton-proton collisions at the LHC. The cross section is measured as a function of the average transverse momentum, half the rapidity separation, and the boost of the two leading jets in the event. The cross section is corrected for detector effects and compared to calculations in perturbative quantum chromodynamics at next-to-leading order accuracy, complemented with electroweak and nonperturbative corrections. New constraints on parton distribution functions are obtained and the inferred value of the strong coupling constant is $\alpha_S(M_\text{Z}) =$ 0.1199 $\pm$ 0.0015 (exp) $_{-0.0020}^{+0.0031}$ (theo), where $M_\text{Z}$ is the mass of the Z boson.
Links: e-print arXiv:1705.02628 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ;

Figures & Tables	Summary	References	CMS Publications

Figures
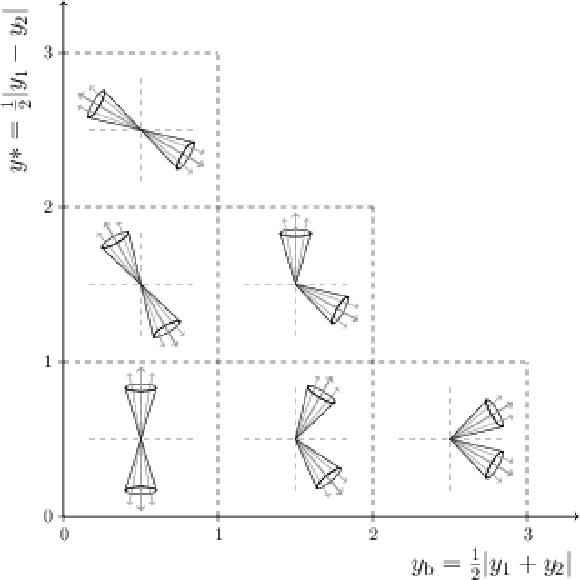
png pdf	Figure 1: Illustration of the dijet event topologies in the ${y^{*}}$ and ${y_{\mathrm {b}}}$ kinematic plane. The dijet system can be classified as a same-side or opposite-side jet event according to the boost of the two leading jets, thereby providing insight into the parton kinematics.
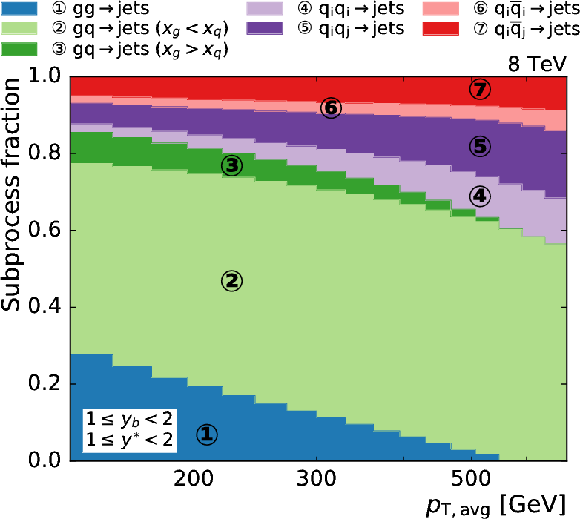
png pdf	Figure 2: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the various ${y^{*}}$ and ${y_{\mathrm {b}}}$ bins. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-a: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 0 $\leq {y^{*}} <$ 1) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-b: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 1 $\leq {y^{*}} <$ 2) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-c: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 2 $\leq {y^{*}} <$ 3) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-d: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 0 $\leq {y^{*}} <$ 1) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-e: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 1 $\leq {y^{*}} <$ 2) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
png pdf	Figure 2-f: Relative contributions of all subprocesses to the total cross section at NLO as a function of ${p_{\mathrm {T,avg}}}$ in the (2 $\leq {{y_{\mathrm {b}}}} <$ 3, 0 $\leq {y^{*}} <$ 1) bin. The subprocess contributions are grouped into seven categories according to the type of the incoming partons. The calculations have been performed with NLOJet++. The notation implies the sum over initial-state parton flavors as well as interchanged quarks and antiquarks.
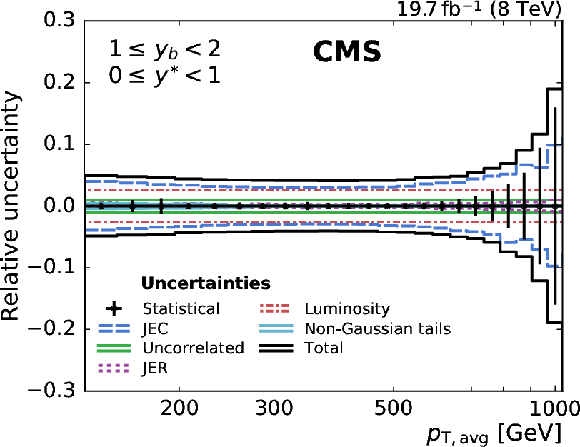
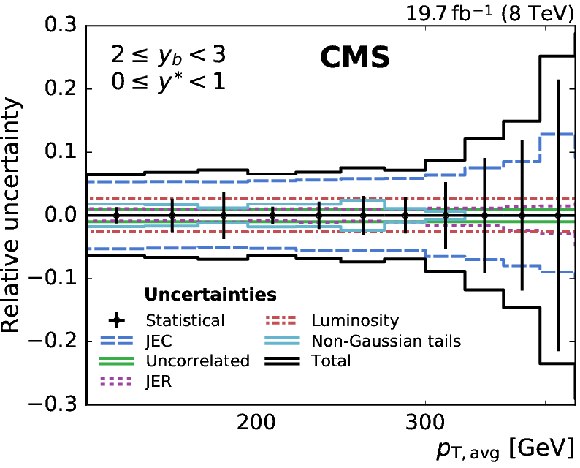
png pdf	Figure 3: Overview of all experimental uncertainties affecting the cross section measurement in six bins of ${y_{\mathrm {b}}}$ and ${y^{*}}$ . The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-a: Overview of all experimental uncertainties affecting the cross section measurement in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 0 $\leq {y^{*}} <$ 1) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-b: Overview of all experimental uncertainties affecting the cross section measurement in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 1 $\leq {y^{*}} <$ 2) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-c: Overview of all experimental uncertainties affecting the cross section measurement in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 2 $\leq {y^{*}} <$ 3) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-d: Overview of all experimental uncertainties affecting the cross section measurement in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 0 $\leq {y^{*}} <$ 1) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-e: Overview of all experimental uncertainties affecting the cross section measurement in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 1 $\leq {y^{*}} <$ 2) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
png pdf	Figure 3-f: Overview of all experimental uncertainties affecting the cross section measurement in the (2 $\leq {{y_{\mathrm {b}}}} <$ 3, 0 $\leq {y^{*}} <$ 1) bin. The error bars indicate the statistical uncertainty after unfolding. The different lines show the uncertainties resulting from jet energy corrections, jet energy resolution, integrated luminosity, non-Gaussian tails in the resolution, and from residual effects included in the uncorrelated uncertainty. The total uncertainty is obtained by adding all uncertainties in quadrature.
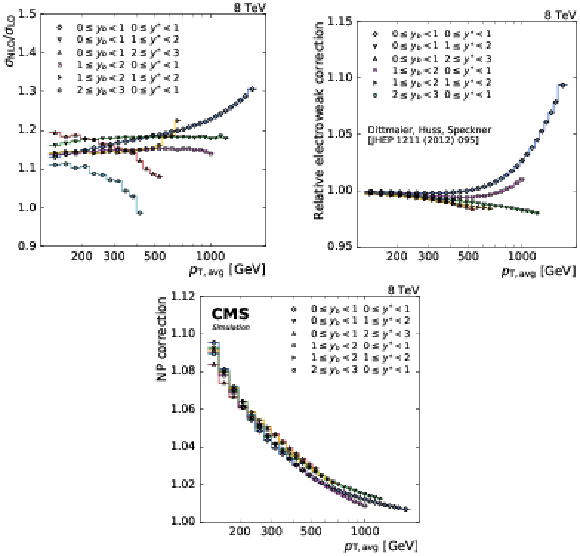
png pdf	Figure 4: Overview of the theoretical correction factors. For each of the six analysis bins the NLO QCD (top left), the electroweak (top right), and the NP correction factor (bottom) are shown as a function of ${p_{\mathrm {T,avg}}}$ . The NLO QCD correction has been derived with the same NLO PDF in numerator and denominator and is included in the NLO prediction by NLOJet++.
png pdf	Figure 4-a: Overview of the theoretical correction factors. For each of the six analysis bins the NLO QCD correction factor is shown as a function of ${p_{\mathrm {T,avg}}}$ . The NLO QCD correction has been derived with the same NLO PDF in numerator and denominator and is included in the NLO prediction by NLOJet++.
png pdf	Figure 4-b: Overview of the theoretical correction factors. For each of the six analysis bins the electroweak correction factor is shown as a function of ${p_{\mathrm {T,avg}}}$ . The NLO QCD correction has been derived with the same NLO PDF in numerator and denominator and is included in the NLO prediction by NLOJet++.
png pdf	Figure 4-c: Overview of the theoretical correction factors. For each of the six analysis bins the NP correction factor is shown as a function of ${p_{\mathrm {T,avg}}}$ . The NLO QCD correction has been derived with the same NLO PDF in numerator and denominator and is included in the NLO prediction by NLOJet++.
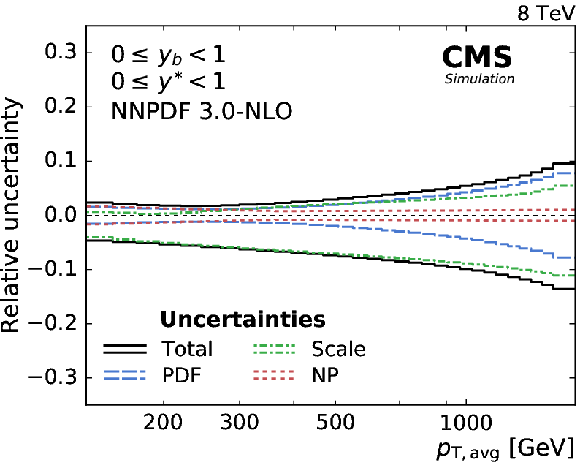
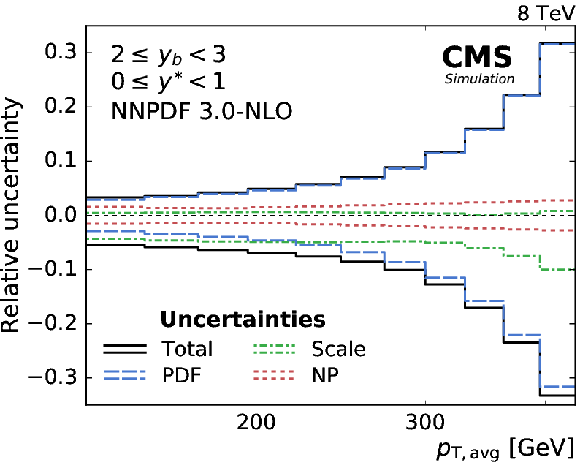
png pdf	Figure 5: Overview of the theoretical uncertainties. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-a: Overview of the theoretical uncertainties in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 0 $\leq {y^{*}} <$ 1) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-b: Overview of the theoretical uncertainties in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 1 $\leq {y^{*}} <$ 2) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-c: Overview of the theoretical uncertainties in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 2 $\leq {y^{*}} <$ 3) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-d: Overview of the theoretical uncertainties in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 0 $\leq {y^{*}} <$ 1) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-e: Overview of the theoretical uncertainties in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 1 $\leq {y^{*}} <$ 2) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 5-f: Overview of the theoretical uncertainties in the (2 $\leq {{y_{\mathrm {b}}}} <$ 3, 0 $\leq {y^{*}} <$ 1) bin. The scale uncertainty dominates in the low- ${p_{\mathrm {T,avg}}}$ region. At high ${p_{\mathrm {T,avg}}}$ , and especially in the boosted region, the PDFs become the dominant source of uncertainty.
png pdf	Figure 6: The triple-differential dijet cross section in six bins of ${y^{*}}$ and ${y_{\mathrm {b}}}$ . The data are indicated by different markers for each bin. The theoretical predictions, obtained with NLOJet++ and NNPDF3.0, and complemented with EW and NP corrections, are depicted by solid lines. Apart from the boosted region, the data are well described by the predictions at NLO accuracy over many orders of magnitude.
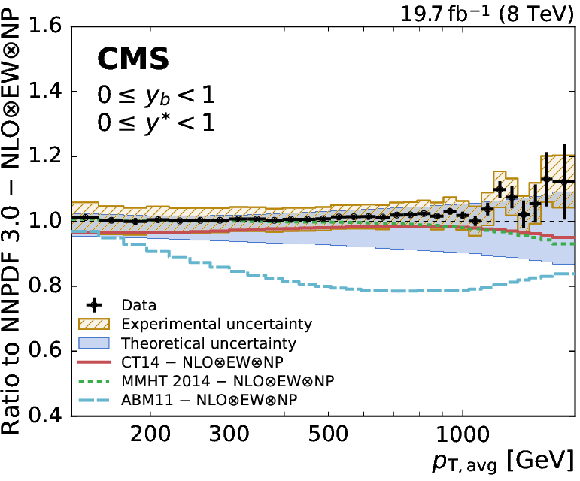
png pdf	Figure 7: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
png pdf	Figure 7-a: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
png pdf	Figure 7-b: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 1 $\leq {y^{*}} <$ 2) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
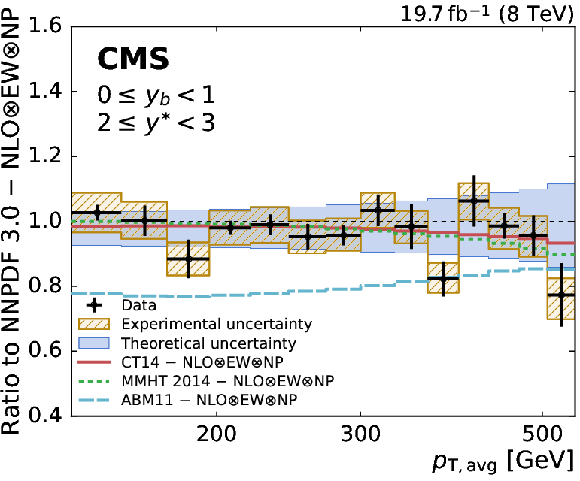
png pdf	Figure 7-c: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 2 $\leq {y^{*}} <$ 3) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
png pdf	Figure 7-d: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
png pdf	Figure 7-e: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 1 $\leq {y^{*}} <$ 2) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
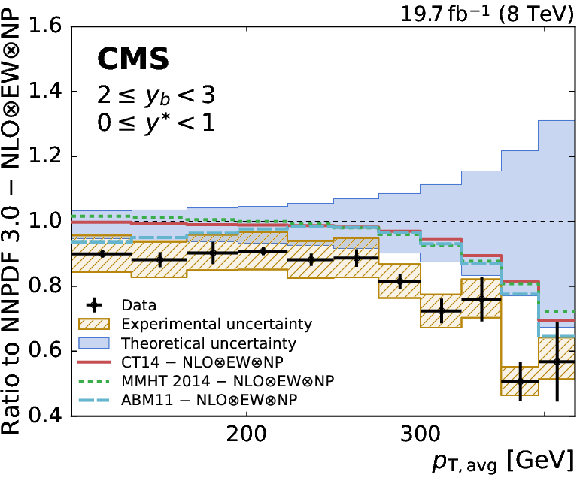
png pdf	Figure 7-f: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (2 $\leq {{y_{\mathrm {b}}}} <$ 3, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added; the solid and dashed lines give the ratios calculated with the predictions for different PDF sets.
png pdf	Figure 8: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
png pdf	Figure 8-a: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
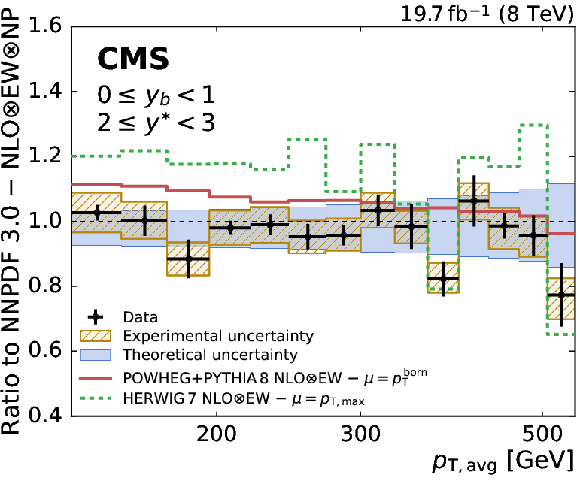
png pdf	Figure 8-b: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 1 $\leq {y^{*}} <$ 2) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
png pdf	Figure 8-c: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (0 $\leq {{y_{\mathrm {b}}}} <$ 1, 2 $\leq {y^{*}} <$ 3) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
png pdf	Figure 8-d: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
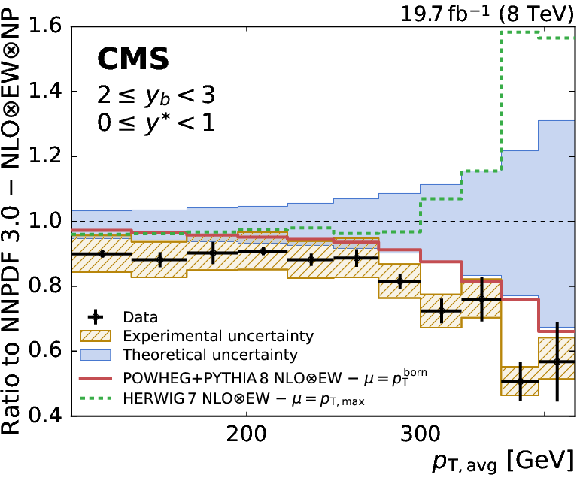
png pdf	Figure 8-e: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (1 $\leq {{y_{\mathrm {b}}}} <$ 2, 1 $\leq {y^{*}} <$ 2) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
png pdf	Figure 8-f: Ratio of the triple-differential dijet cross section to the NLOJet++ prediction using the NNPDF3.0 set in the (2 $\leq {{y_{\mathrm {b}}}} <$ 3, 0 $\leq {y^{*}} <$ 1) bin. The data points including statistical uncertainties are indicated by markers, the systematic experimental uncertainty is represented by the hatched band. The solid band shows the PDF, scale, and NP uncertainties quadratically added. The predictions of the NLO MC event generators POWHEG+PYTHIA-8 and HERWIG-7 are depicted by solid and dashed lines, respectively.
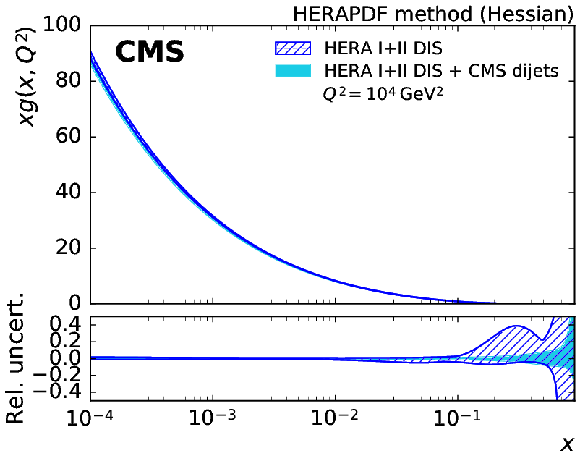
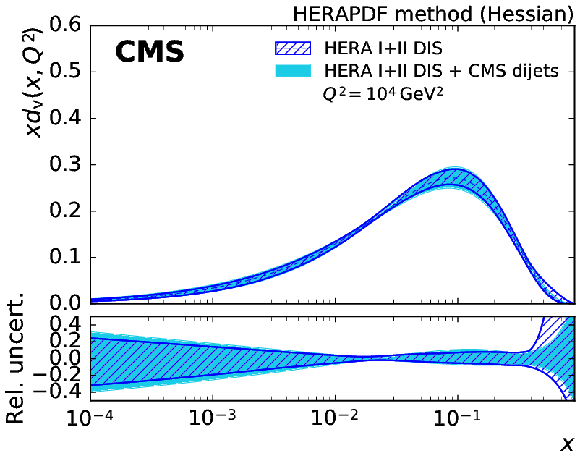
png pdf	Figure 9: The gluon (top left), sea quark (top right), dvalence quark (bottom left), and uvalence quark (bottom right) PDFs as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 9-a: The gluon PDF as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 9-b: The sea quark PDFs as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 9-c: The d-valence quark PDF as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 9-d: The u-valence quark PDF as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 10: The gluon PDF as a function of $x$ as derived from HERA inclusive DIS data alone (hatched band) and in combination with CMS dijet data (solid band). The PDF and its total uncertainty are shown at the starting scale $Q^2 =$ 1.9 GeV $^2$ of the PDF evolution.
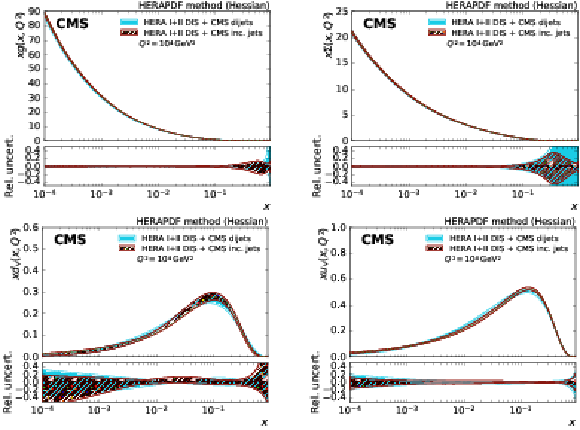
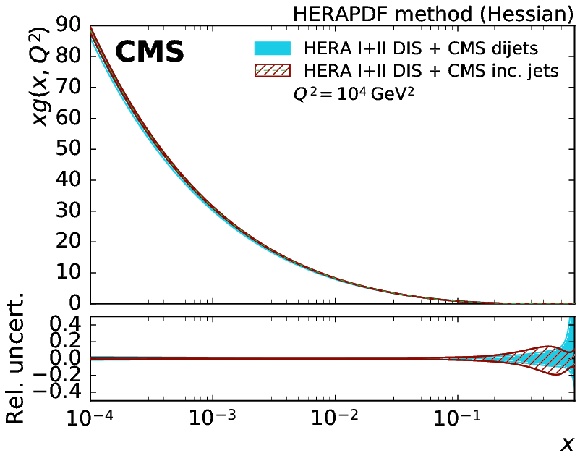
png pdf	Figure 11: The gluon (top left), sea quark (top right), dvalence quark (bottom left), and uvalence quark (bottom right) PDFs as a function of $x$ as derived from a fit of HERA inclusive DIS data in combination with CMS inclusive jet data (solid band) and CMS dijet data (hatched band) at 8 TeV. The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 11-a: The gluon PDF as a function of $x$ as derived from a fit of HERA inclusive DIS data in combination with CMS inclusive jet data (solid band) and CMS dijet data (hatched band) at 8 TeV. The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
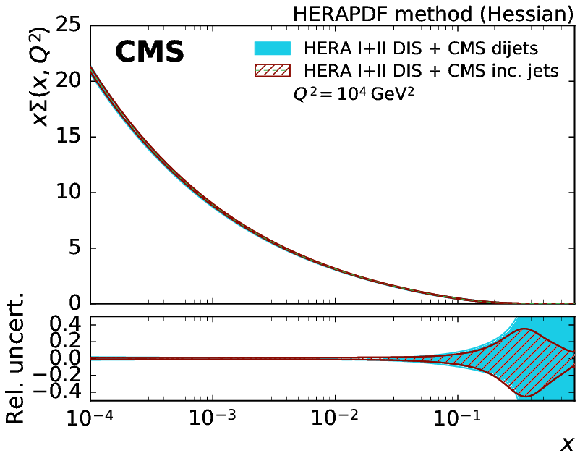
png pdf	Figure 11-b: The sea quark PDF as a function of $x$ as derived from a fit of HERA inclusive DIS data in combination with CMS inclusive jet data (solid band) and CMS dijet data (hatched band) at 8 TeV. The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 11-c: The d-valence quark PDF as a function of $x$ as derived from a fit of HERA inclusive DIS data in combination with CMS inclusive jet data (solid band) and CMS dijet data (hatched band) at 8 TeV. The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.
png pdf	Figure 11-d: The u-valence quark PDF as a function of $x$ as derived from a fit of HERA inclusive DIS data in combination with CMS inclusive jet data (solid band) and CMS dijet data (hatched band) at 8 TeV. The PDFs are shown at the scale $Q^2 = 10^{4}$ GeV $^2$ with their total uncertainties.

Tables
png pdf	Table 1: List of single-jet trigger thresholds used in the analysis.
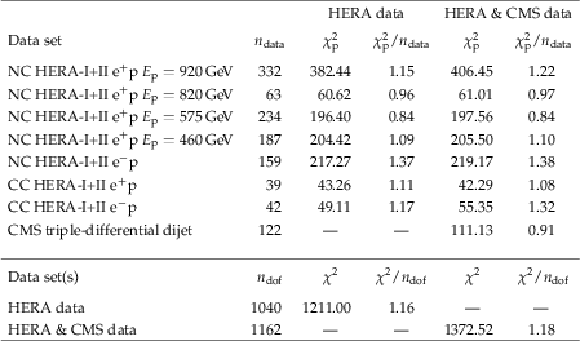
png pdf	Table 2: The partial ${\chi ^2}$ ( ${\chi ^2_\text {p}}$ ) for each data set in the HERA DIS (middle section) or the combined fit including the CMS triple-differential dijet data (right section) are shown. The bottom two lines show the total ${\chi ^2}$ and ${\chi ^2/n_\text {dof}}$ . The difference between the sum of all ${\chi ^2_\text {p}}$ and the total ${\chi ^2}$ for the combined fit is attributed to the nuisance parameters.

Summary

A measurement of the triple-differential dijet cross section is presented for

$\sqrt{s} =$ 8 TeV. The data are found to be well described by NLO predictions corrected for nonperturbative and electroweak effects, except for highly boosted event topologies that suffer from large uncertainties in parton distribution functions (PDFs).

The precise data constrain the PDFs, especially in the highly boosted regime that probes the highest fractions

$x$ of the proton momentum carried by a parton. The impact of the data on the PDFs is demonstrated by performing a simultaneous fit to cross sections of deep-inelastic scattering obtained by the HERA experiments and the dijet cross section measured in this analysis. When including the dijet data, an increased gluon PDF at high

$x$ is obtained and the overall uncertainties of the PDFs, especially those of the gluon distribution, are significantly reduced. In contrast to a fit that uses inclusive jet data, this measurement carries more information on the valence-quark content of the proton such that a more flexible parameterisation is needed to describe the low-

$x$ behaviour of the u and d valence quark PDFs. This higher sensitivity is accompanied by slightly larger uncertainties in the valence quark distributions as a consequence of the greater flexibility in the parameterisation of the PDFs.

In a simultaneous fit the strong coupling constant

$\alpha_S(M_\text{Z})$ is extracted together with the PDFs. The value obtained at the mass of the Z boson is

$\alpha_S(M_\text{Z}) =$ 0.1199

$\pm$ 0.0015 (exp)

$\pm$ 0.0002 (mod)

$_{-0.0004}^{+0.0002}$ (par)

$_{-0.0019}^{+0.0031}$ (scale) = 0.1199

$\pm$ 0.0015 (exp)

$_{-0.0020}^{+0.0031}$ (theo)
and is in agreement with previous measurements at the LHC by CMS [54, 62, 70-72] and ATLAS [73], and with the world average value of

$\alpha_S(M_\text{Z}) =$ 0.1181

$\pm$ 0.0011 [74]. The dominant uncertainty is theoretical in nature and is expected to be reduced significantly in the future using pQCD predictions at next-to-next-to-leading order [75].

References
1	UA2 Collaboration	Observation of very large transverse momentum jets at the CERN $\bar{p}p$ collider	PLB 118 (1982) 203
2	AFS Collaboration	Dijet production cross-section and fragmentation of jets produced in $p p$ collisions at $\sqrt{s} =$ 63 GeV	Z. Phys. C 30 (1986) 27
3	CDF Collaboration	A measurement of the differential dijet mass cross section in $p\bar{p}$ collisions at $\sqrt{s} =$ 1.8 TeV	PRD 61 (2000) 091101	hep-ex/9912022
4	CDF Collaboration	Measurement of the dijet mass distribution in $p\bar{p}$ collisions at $\sqrt{s} =$ 1.8 TeV	PRD 48 (1993) 998
5	CDF Collaboration	Two-jet invariant-mass distribution at $\sqrt{s} =$ 1.8 TeV	PRD 41 (1990) 1722
6	D0 Collaboration	Dijet Mass Spectrum and a Search for Quark Compositeness in $\bar{p}p$ Collisions at $\sqrt{s} =$ 1.8 TeV	PRL 82 (1999) 2457	hep-ex/9807014
7	ATLAS Collaboration	Measurement of inclusive jet and dijet cross sections in proton-proton collisions at 7 TeV centre-of-mass energy with the ATLAS detector	EPJC 71 (2011) 1512	1009.5908
8	CMS Collaboration	Measurement of the differential dijet production cross section in proton-proton collisions at $\sqrt{s} =$ 7 TeV	PLB 700 (2011) 187	CMS-QCD-10-025 1104.1693
9	ATLAS Collaboration	Measurement of inclusive jet and dijet production in $pp$ collisions at $\sqrt{s} =$ 7 TeV using the ATLAS detector	PRD 86 (2012) 014022	1112.6297
10	ATLAS Collaboration	Measurement of dijet cross sections in $pp$ collisions at 7 TeV centre-of-mass energy using the ATLAS detector	JHEP 05 (2014) 059	1312.3524
11	CMS Collaboration	Measurements of differential jet cross sections in proton-proton collisions at $\sqrt{s} =$ 7 TeV with the CMS detector	PRD 87 (2013) 112002	CMS-QCD-11-004 1212.6660
12	CDF Collaboration	Two-Jet Differential Cross-Section in $\bar{p}p$ Collisions at $\sqrt{s} =$ 1.8 TeV	PRL 64 (1990) 157
13	CDF Collaboration	Measurement of the two-jet differential cross section in $p\bar{p}$ collisions at $\sqrt{s} =$ 1800 GeV	PRD 64 (2001) 012001	hep-ex/0012013
14	Z. Nagy	Three Jet Cross-Sections in Hadron Hadron Collisions at Next-To-Leading Order	PRL 88 (2002) 122003	hep-ph/0110315
15	Z. Nagy	Next-to-leading order calculation of three-jet observables in hadron hadron collisions	PRD 68 (2003) 094002	hep-ph/0307268
16	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
17	CMS Collaboration	The CMS high level trigger	EPJC 46 (2006) 605	hep-ex/0512077
18	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
19	CMS Collaboration	Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and MET	CDS
20	CMS Collaboration	Commissioning of the Particle-flow Event Reconstruction with the first LHC collisions recorded in the CMS detector	CDS
21	CMS Collaboration	Pileup Removal Algorithms	CMS-PAS-JME-14-001	CMS-PAS-JME-14-001
22	M. Cacciari, G. P. Salam, and G. Soyez	The anti- $k_t$ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
23	CMS Collaboration	Determination of jet energy calibration and transverse momentum resolution in CMS	JINST 6 (2011) P11002	CMS-JME-10-011 1107.4277
24	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
25	G. D'Agostini	A multidimensional unfolding method based on Bayes' theorem	NIMA 362 (1995) 487
26	L. B. Lucy	An iterative technique for the rectification of observed distributions	Astron. J. 79 (1974) 745
27	W. H. Richardson	Bayesian-Based Iterative Method of Image Restoration	J. Opt. Soc. Am. 62 (1972) 55
28	T. Adye	Unfolding algorithms and tests using RooUnfold	in Proceedings, PHYSTAT 2011 Workshop on Statistical Issues Related to Discovery Claims in Search Experiments and Unfolding, Geneva	1105.1160
29	S. Dulat et al.	New parton distribution functions from a global analysis of quantum chromodynamics	PRD 93 (2016) 033006	1506.07443
30	S. Agostinelli et al.	GEANT4---a simulation toolkit	NIMA 506 (2003) 250
31	T. Sjostrand, S. Mrenna, and P. Z. Skands	PYTHIA 6.4 physics and manual	JHEP 05 (2006) 026	hep-ph/0603175
32	E. Veklerov and J. Llacer	Stopping Rule for the MLE Algorithm Based on Statistical Hypothesis Testing	IEEE Transactions on Medical Imaging MI-6 (1987) 313
33	CMS Collaboration	CMS Luminosity Based on Pixel Cluster Counting - Summer 2013 Update	CMS-PAS-LUM-13-001	CMS-PAS-LUM-13-001
34	T. Kluge, K. Rabbertz, and M. Wobisch	fastNLO: fast pQCD calculations for PDF fits	in 14th International Workshop on Deep Inelastic Scattering (DIS 2006), Tsukuba	hep-ph/0609285
35	D. Britzger, K. Rabbertz, F. Stober, and M. Wobisch	New features in version 2 of the fastNLO project	in Proceedings, XX.\ International Workshop on Deep-Inelastic Scattering and Related Subjects (DIS 2012), Bonn	1208.3641
36	S. D. Ellis, Z. Kunszt, and D. E. Soper	Two-Jet Production in Hadron Collisions at Order $\alpha_s^3$ in QCD	PRL 69 (1992) 1496
37	S. Alekhin, J. Blumlein, and S. Moch	Parton distribution functions and benchmark cross sections at NNLO	PRD 86 (2012) 054009	1202.2281
38	L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne	Parton distributions in the LHC era: MMHT 2014 PDFs	EPJC 75 (2015) 204	1412.3989
39	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
40	M. R. Whalley, D. Bourilkov, and R. C. Group	The Les Houches Accord PDFs (LHAPDF) and LHAGLUE	in Proceedings, HERA and the LHC: A Workshop on the implications of HERA for LHC physics: Vol. B Geneva and Hamburg, 2004	hep-ph/0508110
41	A. Buckley et al.	LHAPDF6: parton density access in the LHC precision era	EPJC 75 (2015) 132	1412.7420
42	T. Sjostrand, S. Mrenna, and P. Z. Skands	A brief introduction to PYTHIA 8.1	CPC 178 (2008) 852	0710.3820
43	M. Bahr et al.	Herwig++ physics and manual	EPJC 58 (2008) 639	0803.0883
44	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2015) 155	CMS-GEN-14-001 1512.00815
45	M. H. Seymour and A. Siodmok	Constraining MPI models using $\sigma_\text{eff}$ and recent Tevatron and LHC underlying event data	JHEP 10 (2013) 113	1307.5015
46	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
47	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with Parton Shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
48	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
49	S. Alioli et al.	Jet pair production in POWHEG	JHEP 04 (2011) 081	1012.3380
50	S. Dittmaier, A. Huss, and C. Speckner	Weak radiative corrections to dijet production at hadron colliders	JHEP 11 (2012) 095	1210.0438
51	R. Frederix et al.	The complete NLO corrections to dijet hadroproduction		1612.06548
52	M. Cacciari et al.	The t anti-t cross-section at 1.8 TeV and 1.96 TeV: a study of the systematics due to parton densities and scale dependence	JHEP 04 (2004) 068	hep-ph/0303085
53	A. Banfi, G. P. Salam, and G. Zanderighi	Phenomenology of event shapes at hadron colliders	JHEP 06 (2010) 038	1001.4082
54	CMS Collaboration	Constraints on parton distribution functions and extraction of the strong coupling constant from the inclusive jet cross section in pp collisions at $\sqrt{s} =$ 7 TeV	EPJC 75 (2015) 288	CMS-SMP-12-028 1410.6765
55	J. Bellm et al.	Herwig 7.0/Herwig++ 3.0 release note	EPJC 76 (2016) 196	1512.01178
56	H1 and ZEUS Collaborations	Combination of measurements of inclusive deep inelastic ${e^{\pm }p}$ scattering cross sections and QCD analysis of HERA data	EPJC 75 (2015) 580	1506.06042
57	S. Alekhin et al.	HERAFitter	EPJC 75 (2015) 304	1410.4412
58	V. N. Gribov and L. N. Lipatov	Deep inelastic ep scattering in perturbation theory	Sov. J. Nucl. Phys. 15 (1972)438
59	G. Altarelli and G. Parisi	Asymptotic freedom in parton language	Nucl. Phys. B 126 (1977) 298
60	Y. L. Dokshitzer	Calculation of the Structure Functions for Deep Inelastic Scattering and $e^+e^-$ Annihilation by Perturbation Theory in Quantum Chromodynamics.	Sov. Phys. JETP 46 (1977)641
61	M. Botje	QCDNUM: fast QCD evolution and convolution	CPC 182 (2011) 490	1005.1481
62	CMS Collaboration	Measurement and QCD analysis of double-differential inclusive jet cross-sections in pp collisions at $\sqrt{s} =$ 8 TeV and ratios to 2.76 and 7 TeV	JHEP 03 (2017) 156	CMS-SMP-14-001 1609.05331
63	R. S. Thorne and R. G. Roberts	An ordered analysis of heavy flavor production in deep inelastic scattering	PRD 57 (1998) 6871	hep-ph/9709442
64	R. S. Thorne	Variable-flavor number scheme for next-to-next-to-leading order	PRD 73 (2006) 054019	hep-ph/0601245
65	CMS Collaboration	Measurement of the differential cross section and charge asymmetry for inclusive $\mathrm {p}\mathrm {p}\rightarrow \mathrm {W}^{\pm }+X$ production at ${\sqrt{s}} =$ 8 TeV	EPJC 76 (2016) 469	CMS-SMP-14-022 1603.01803
66	J. Pumplin et al.	Uncertainties of predictions from parton distribution functions. 2. The Hessian method	PRD 65 (2001) 014013	hep-ph/0101032
67	W. T. Giele and S. Keller	Implications of hadron collider observables on parton distribution function uncertainties	PRD 58 (1998) 094023	hep-ph/9803393
68	CMS Collaboration	Measurement of the muon charge asymmetry in inclusive $pp \to W+X$ production at $\sqrt{s} =$ 7 TeV and an improved determination of light parton distribution functions	PRD 90 (2014) 032004	CMS-SMP-12-021 1312.6283
69	B. J. A. Watt, P. Motylinski, and R. S. Thorne	The effect of LHC jet data on MSTW PDFs	EPJC 74 (2014) 2934	1311.5703
70	CMS Collaboration	Measurement of the ratio of the inclusive 3-jet cross section to the inclusive 2-jet cross section in pp collisions at $\sqrt{s} =$ 7 TeV and first determination of the strong coupling constant in the TeV range	EPJC 73 (2013) 2604	CMS-QCD-11-003 1304.7498
71	CMS Collaboration	Measurement of the inclusive 3-jet production differential cross section in proton-proton collisions at 7 TeV and determination of the strong coupling constant in the TeV range	EPJC 75 (2015) 186	CMS-SMP-12-027 1412.1633
72	CMS Collaboration	Determination of the top-quark pole mass and strong coupling constant from the $\mathrm{t}\bar{\mathrm{t}}$ production cross section in pp collisions at $\sqrt{s} =$ 7 TeV	PLB 728 (2014) 496	CMS-TOP-12-022 1307.1907
73	ATLAS Collaboration	Measurement of transverse energy-energy correlations in multi-jet events in $pp$ collisions at $\sqrt{s} =$ 7 TeV using the ATLAS detector and determination of the strong coupling constant $\alpha_{\mathrm{s}}(m_Z)$	PLB 750 (2015) 427	1508.01579
74	C. Patrignani and others (Particle Data Group)	Review of Particle Physics	CPC 40 (2016) 100001
75	J. Currie, E. W. N. Glover, and J. Pires	Next-to-Next-to Leading Order QCD Predictions for Single Jet Inclusive Production at the LHC	PRL 118 (2017) 072002	1611.01460