

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-24-008 ; CERN-EP-2025-241 | ||
| Search for low-mass hidden-valley dark showers with non-prompt muon pairs in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 14 November 2025 | ||
| Accepted for publication in J. High Energy Phys. | ||
| Abstract: A search for signatures of a dark analog to quantum chromodynamics is performed. The analysis targets long-lived dark mesons that decay into standard-model particles, with a high branching fraction of the dark mesons decaying into muons. The dark mesons are formed by the hadronisation of dark partons, which are produced by a decay of the Higgs boson. The search is performed using a data set corresponding to an integrated luminosity of 41.6 fb$ ^{-1} $, which was collected in proton-proton collisions at $ \sqrt{s}= $ 13 TeV by the CMS experiment at the CERN LHC in 2018 using non-prompt muon triggers. The search is based on resonant muon pair signatures. Machine-learning techniques are employed in the analysis, utilising boosted decision trees to discriminate between signal and background. No significant excess is observed above the standard model expectation. Upper limits on the branching fraction of the Higgs boson decaying to dark partons are determined to be as low as $ 10^{-4} $ at 95% confidence level, surpassing and extending the existing limits on models with dark $ \tilde{\omega} $ mesons for mean proper decay lengths of less than 500 mm and for $ \tilde{\omega} $ masses down to 0.3 GeV. First limits are set for extended dark-shower models with two dark flavours that contain dark photons, probing their masses down to 0.33 GeV. | ||
| Links: e-print arXiv:2511.11888 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Diagram for the vector portal model. An SM Higgs boson decays to dark partons $ \psi\bar{\psi} $, which then hadronise to form dark hadrons including dark vector mesons $ \tilde{\omega} $ and dark pseudoscalar mesons $ \tilde{\eta} $. The $ \tilde{\omega} $ then undergoes displaced decay into SM fermions $ f\bar{f} $. |
png pdf |
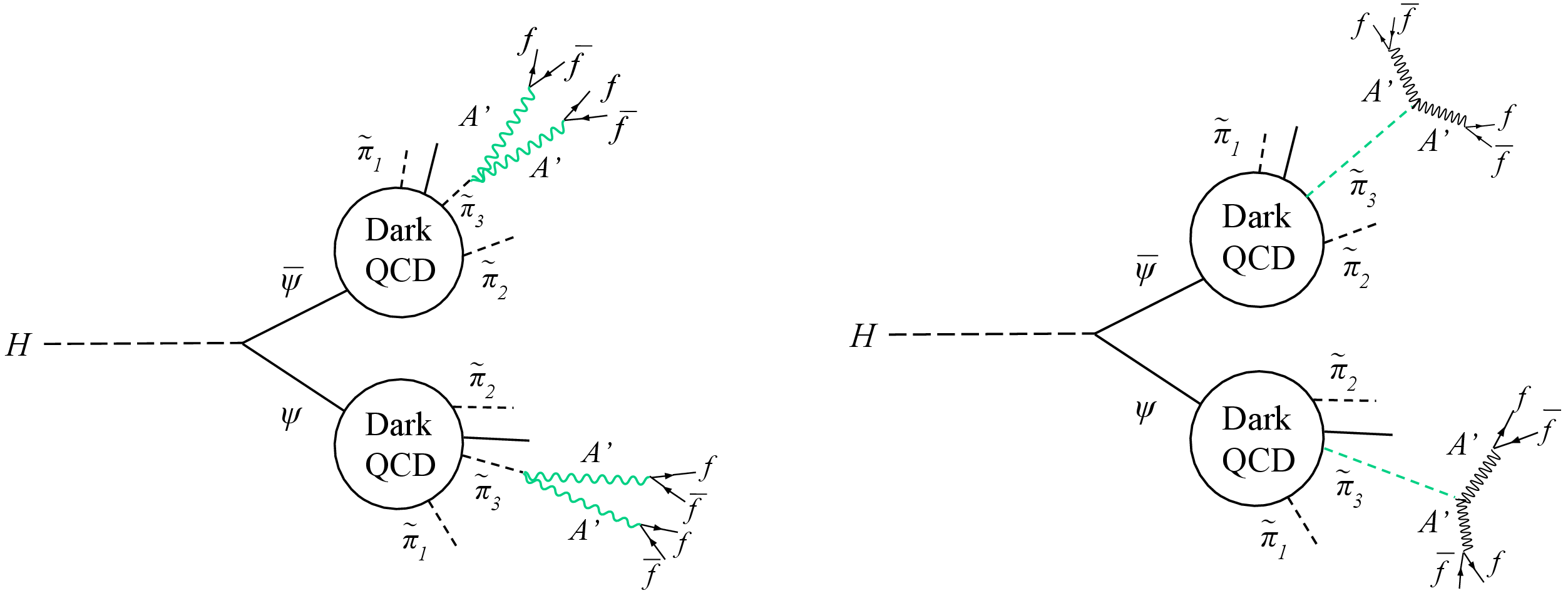
Figure 2:
Diagrams for the Scenario A model (left) and the Scenario B1 model (right). In these extended models the dark hadronisation produces a spectrum of dark mesons, including the dark pions $ \tilde{\pi}_{1} $, $ \tilde{\pi}_{2} $ and $ \tilde{\pi}_{3} $. The $ \tilde{\pi}_{3} $ then decays into SM fermions $ f\bar{f} $ through the dark photon $ \mathrm{A}' $. Green is used to indicate a long-lived particle. The $ \mathrm{A}' $ is a long-lived particle in Scenario A, while $ \tilde{\pi}_{3} $ is a long-lived particle in Scenario B1. |

png pdf |
Figure 2-a:
Diagrams for the Scenario A model (left) and the Scenario B1 model (right). In these extended models the dark hadronisation produces a spectrum of dark mesons, including the dark pions $ \tilde{\pi}_{1} $, $ \tilde{\pi}_{2} $ and $ \tilde{\pi}_{3} $. The $ \tilde{\pi}_{3} $ then decays into SM fermions $ f\bar{f} $ through the dark photon $ \mathrm{A}' $. Green is used to indicate a long-lived particle. The $ \mathrm{A}' $ is a long-lived particle in Scenario A, while $ \tilde{\pi}_{3} $ is a long-lived particle in Scenario B1. |

png pdf |
Figure 2-b:
Diagrams for the Scenario A model (left) and the Scenario B1 model (right). In these extended models the dark hadronisation produces a spectrum of dark mesons, including the dark pions $ \tilde{\pi}_{1} $, $ \tilde{\pi}_{2} $ and $ \tilde{\pi}_{3} $. The $ \tilde{\pi}_{3} $ then decays into SM fermions $ f\bar{f} $ through the dark photon $ \mathrm{A}' $. Green is used to indicate a long-lived particle. The $ \mathrm{A}' $ is a long-lived particle in Scenario A, while $ \tilde{\pi}_{3} $ is a long-lived particle in Scenario B1. |
png pdf |
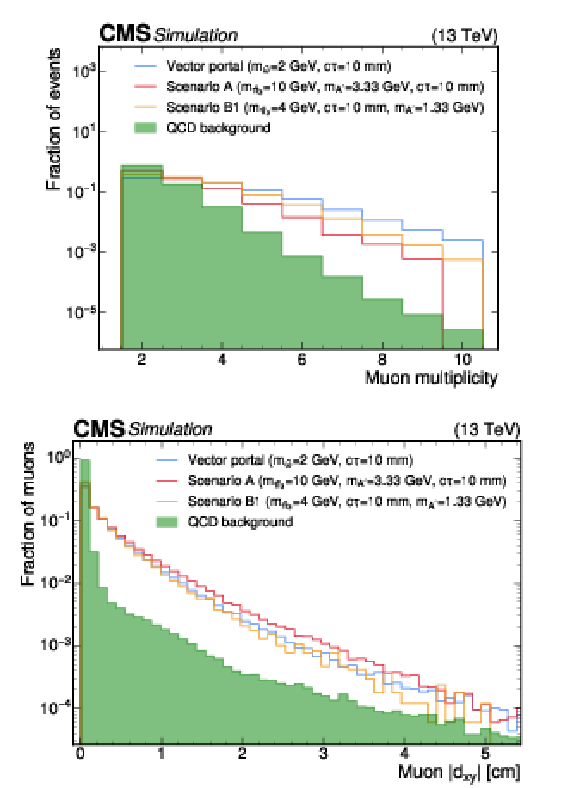
Figure 3:
Distributions of examples of variables that are used in the BDT training for the QCD background and benchmark signal models: muon multiplicity (upper) and muon transverse impact parameter (lower). |

png pdf |
Figure 3-a:
Distributions of examples of variables that are used in the BDT training for the QCD background and benchmark signal models: muon multiplicity (upper) and muon transverse impact parameter (lower). |

png pdf |
Figure 3-b:
Distributions of examples of variables that are used in the BDT training for the QCD background and benchmark signal models: muon multiplicity (upper) and muon transverse impact parameter (lower). |

png pdf |
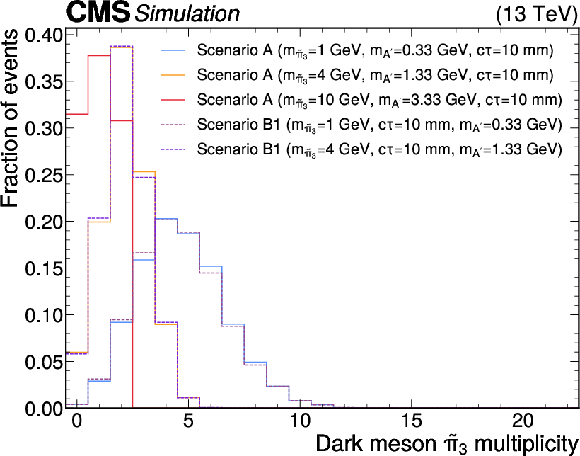
Figure 4:
Distributions of the multiplicity of dark vector mesons $ \tilde{\omega} $ for representative vector portal models (upper), and the multiplicity of dark mesons $ \tilde{\pi}_{3} $ for representative Scenario A and B1 models (lower). |
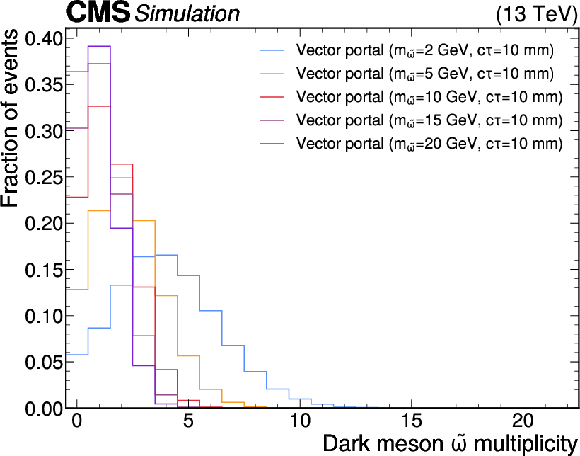
png pdf |
Figure 4-a:
Distributions of the multiplicity of dark vector mesons $ \tilde{\omega} $ for representative vector portal models (upper), and the multiplicity of dark mesons $ \tilde{\pi}_{3} $ for representative Scenario A and B1 models (lower). |
png pdf |
Figure 4-b:
Distributions of the multiplicity of dark vector mesons $ \tilde{\omega} $ for representative vector portal models (upper), and the multiplicity of dark mesons $ \tilde{\pi}_{3} $ for representative Scenario A and B1 models (lower). |
png pdf |
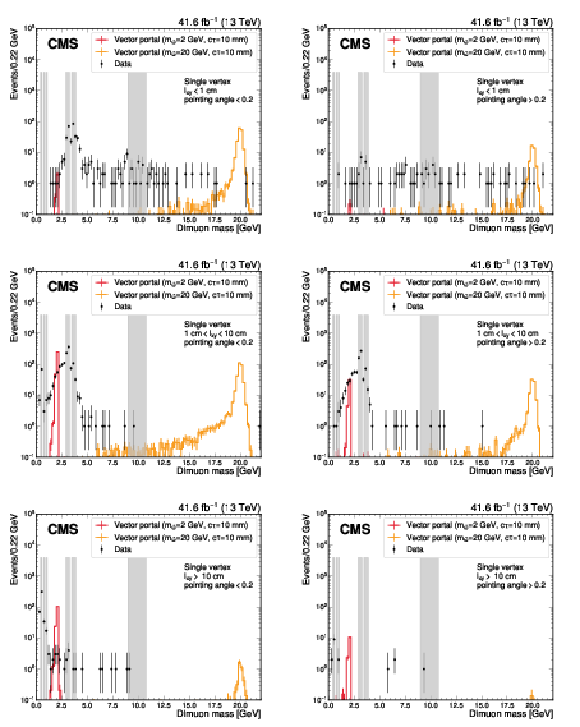
Figure 5:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-a:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-b:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-c:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-d:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-e:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 5-f:
Dimuon invariant mass distributions for each single-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |
png pdf |
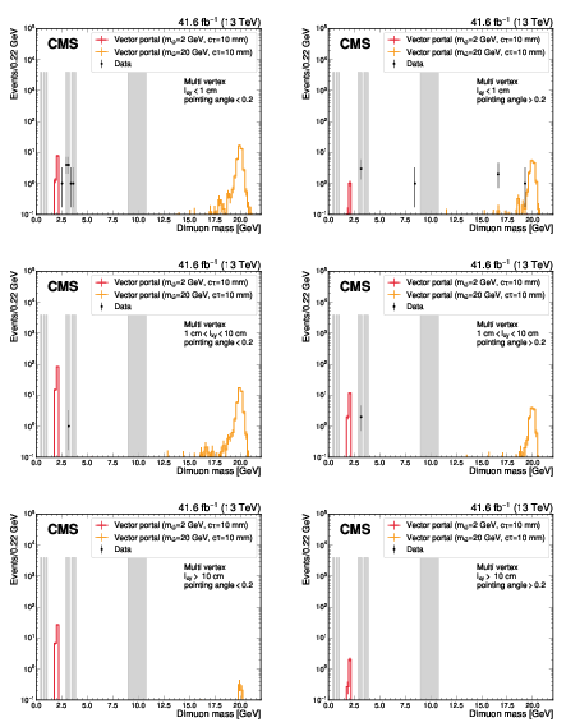
Figure 6:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-a:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-b:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-c:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-d:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-e:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
Figure 6-f:
Dimuon invariant mass distributions for each multi-vertex category for data and two vector portal model signal benchmarks. The shaded regions indicate mass regions of known SM resonances, which are masked in the search. A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. |

png pdf |
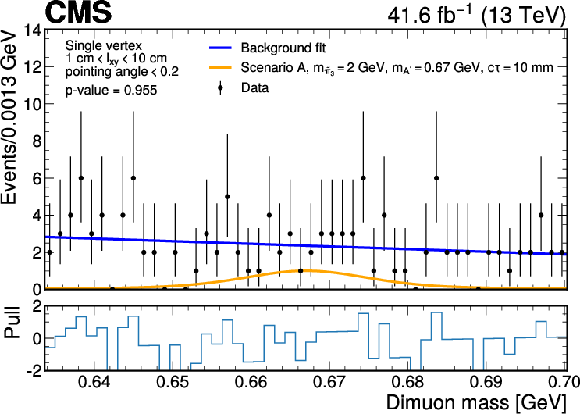
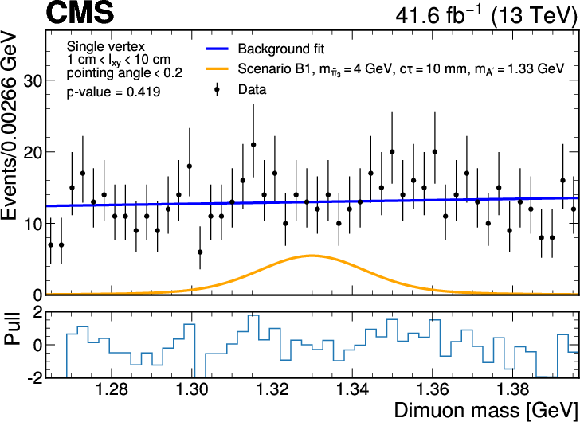
Figure 7:
Dimuon invariant mass distributions in mass windows around 0.67 GeV (upper) and 1.33 GeV (lower), in the single-vertex category with 1 $ \text{cm} < l_{xy} < 10 $ cm and $ \text{pointing angle} < $ 0.2. The background fit is shown together with the signal expected for a representative Scenario A model (upper) and a representative Scenario B1 model (lower). A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. The lower panel in each plot shows the pull distribution, defined as the difference between the data and the background fit in each bin divided by the statistical uncertainty. |
png pdf |
Figure 7-a:
Dimuon invariant mass distributions in mass windows around 0.67 GeV (upper) and 1.33 GeV (lower), in the single-vertex category with 1 $ \text{cm} < l_{xy} < 10 $ cm and $ \text{pointing angle} < $ 0.2. The background fit is shown together with the signal expected for a representative Scenario A model (upper) and a representative Scenario B1 model (lower). A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. The lower panel in each plot shows the pull distribution, defined as the difference between the data and the background fit in each bin divided by the statistical uncertainty. |
png pdf |
Figure 7-b:
Dimuon invariant mass distributions in mass windows around 0.67 GeV (upper) and 1.33 GeV (lower), in the single-vertex category with 1 $ \text{cm} < l_{xy} < 10 $ cm and $ \text{pointing angle} < $ 0.2. The background fit is shown together with the signal expected for a representative Scenario A model (upper) and a representative Scenario B1 model (lower). A branching fraction of 0.01 is assumed for the Higgs boson decaying into dark partons for illustrating the signals. The lower panel in each plot shows the pull distribution, defined as the difference between the data and the background fit in each bin divided by the statistical uncertainty. |

png pdf |
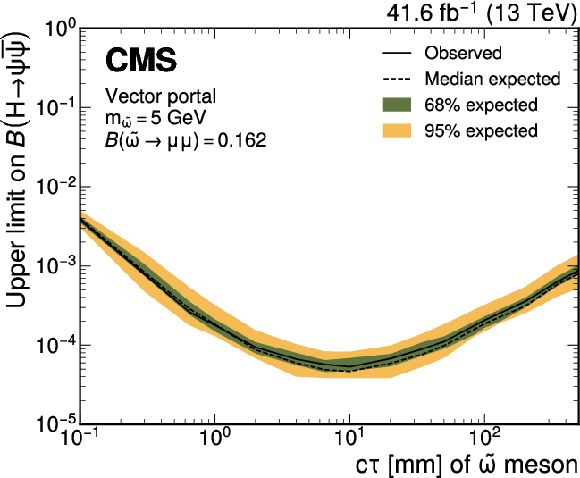
Figure 8:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson $ c\tau $ for representative $ \tilde{\omega} $ mass hypotheses and branching fractions for decaying into a muon pair in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. |

png pdf |
Figure 8-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson $ c\tau $ for representative $ \tilde{\omega} $ mass hypotheses and branching fractions for decaying into a muon pair in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. |
png pdf |
Figure 8-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson $ c\tau $ for representative $ \tilde{\omega} $ mass hypotheses and branching fractions for decaying into a muon pair in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. |

png pdf |
Figure 8-c:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson $ c\tau $ for representative $ \tilde{\omega} $ mass hypotheses and branching fractions for decaying into a muon pair in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. |

png pdf |
Figure 8-d:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson $ c\tau $ for representative $ \tilde{\omega} $ mass hypotheses and branching fractions for decaying into a muon pair in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. |

png pdf |
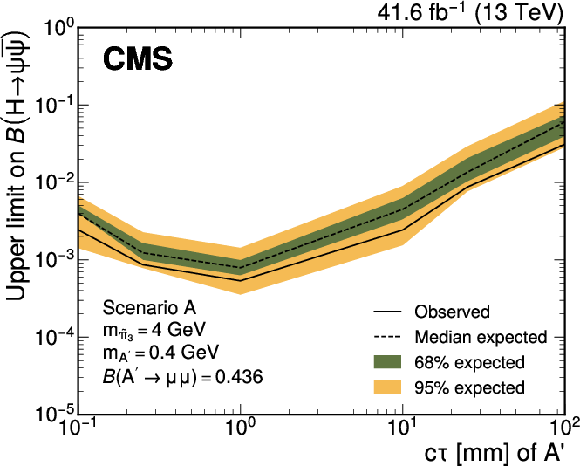
Figure 9:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario A. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 9-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario A. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |
png pdf |
Figure 9-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario A. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 9-c:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario A. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 9-d:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario A. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
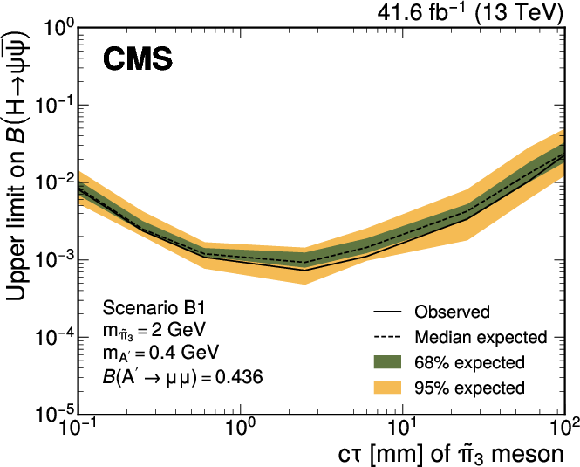
Figure 10:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\pi}_{3} $ meson $ c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario B1. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 10-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\pi}_{3} $ meson $ c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario B1. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |
png pdf |
Figure 10-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\pi}_{3} $ meson $ c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario B1. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 10-c:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\pi}_{3} $ meson $ c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario B1. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |

png pdf |
Figure 10-d:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\pi}_{3} $ meson $ c\tau $ for representative $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ mass hypotheses, and branching fractions of the dark photon decaying into a muon pair in Scenario B1. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. |
png pdf |
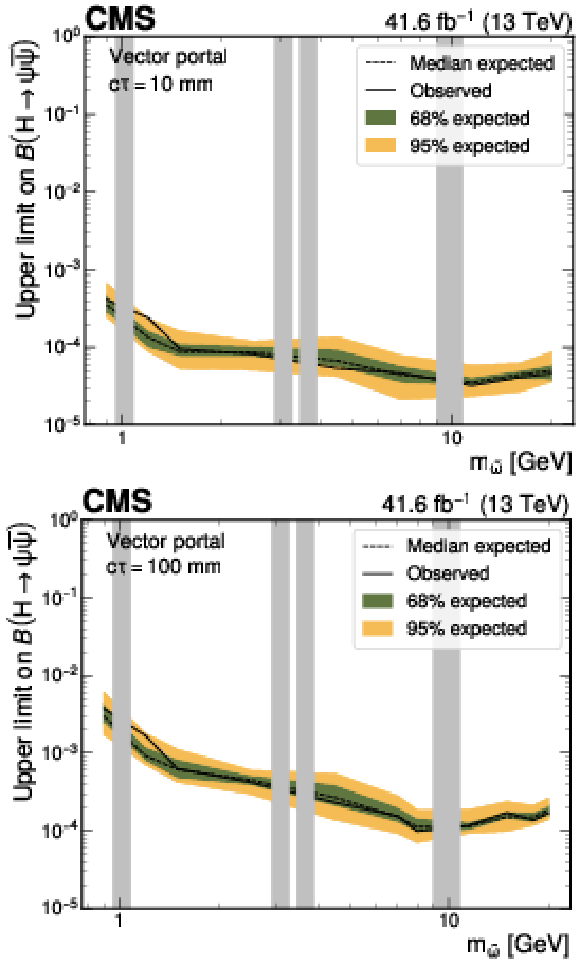
Figure 11:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson mass for representative $ c\tau $ hypotheses in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
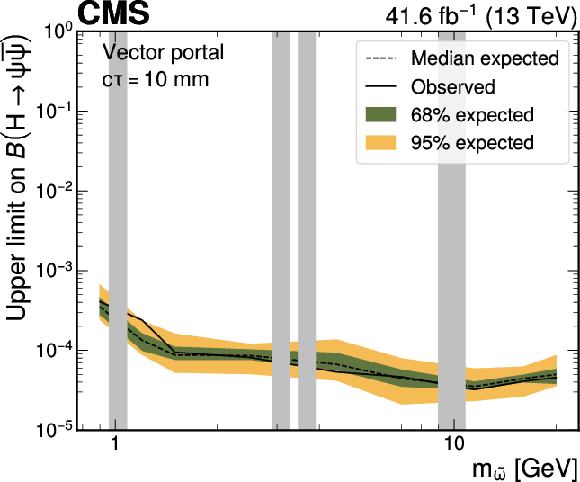
png pdf |
Figure 11-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson mass for representative $ c\tau $ hypotheses in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
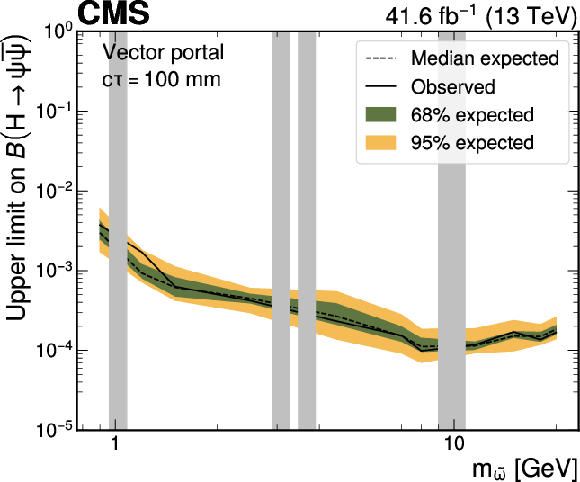
png pdf |
Figure 11-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \tilde{\omega} $ meson mass for representative $ c\tau $ hypotheses in the vector portal model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 12:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario A, for representative $ \mathrm{A}' c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
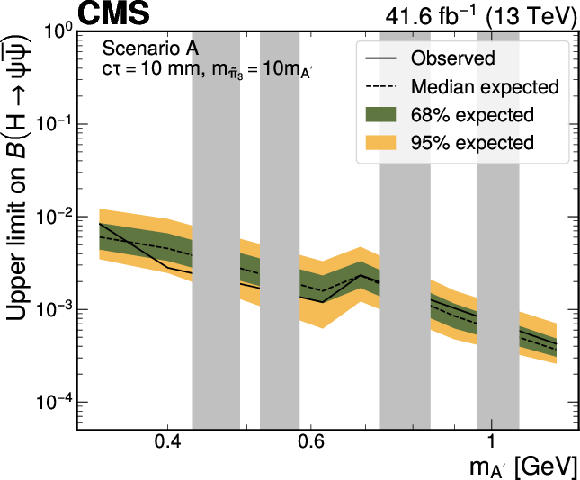
png pdf |
Figure 12-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario A, for representative $ \mathrm{A}' c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
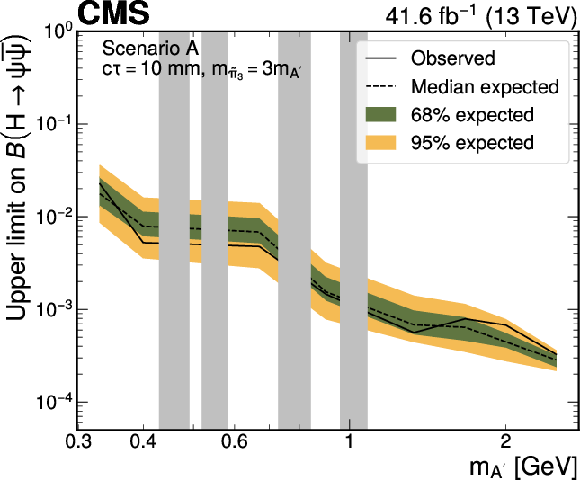
png pdf |
Figure 12-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario A, for representative $ \mathrm{A}' c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 12-c:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario A, for representative $ \mathrm{A}' c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
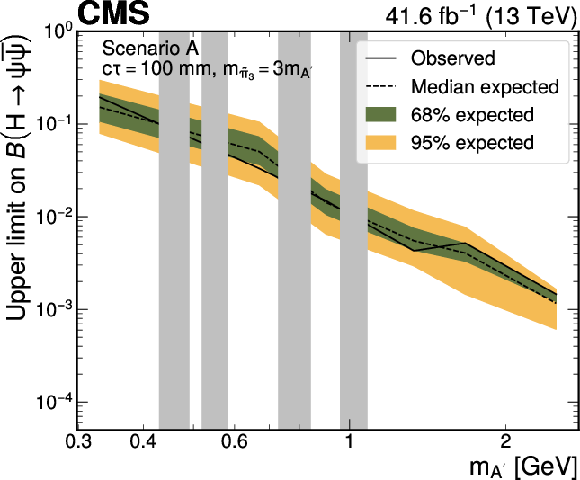
png pdf |
Figure 12-d:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario A, for representative $ \mathrm{A}' c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 13:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario B1, for representative $ \tilde{\pi}_{3} c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 13-a:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario B1, for representative $ \tilde{\pi}_{3} c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
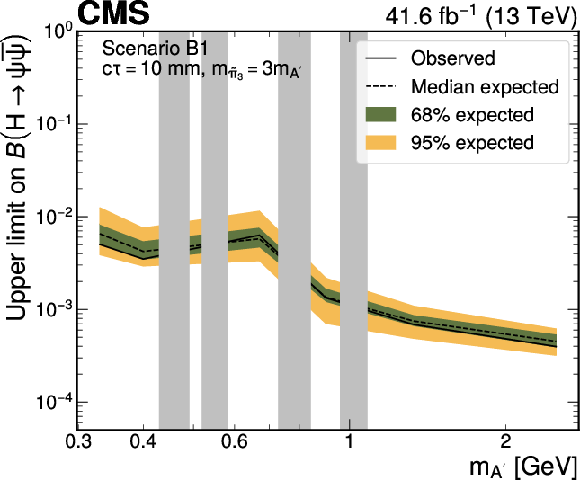
png pdf |
Figure 13-b:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario B1, for representative $ \tilde{\pi}_{3} c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 13-c:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario B1, for representative $ \tilde{\pi}_{3} c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
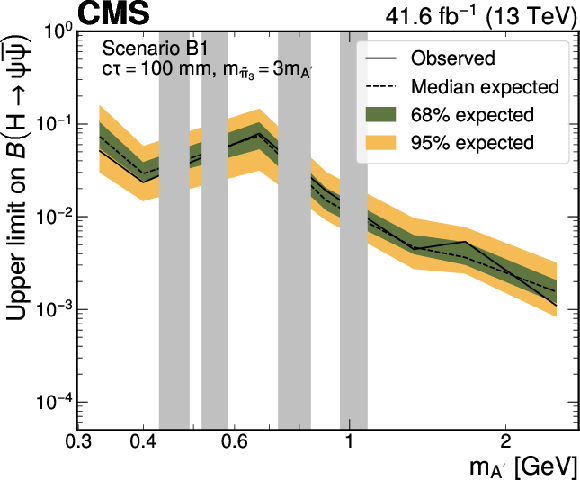
png pdf |
Figure 13-d:
Upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass in Scenario B1, for representative $ \tilde{\pi}_{3} c\tau $ hypotheses, and different ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left column) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right column), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 14:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as a function of the $ \tilde{\omega} $ meson mass and $ c\tau $ in the vector portal model. The parameter space region that is omitted is kinematically forbidden in the model. It is assumed that $ m_{\tilde{\omega}}=\tilde{\Lambda}=m_{\tilde{\eta}} $, where $ m_{\tilde{\omega}} $, $ \tilde{\Lambda} $, and $ m_{\tilde{\eta}} $ are parameters of the dark sector: the mass of the spin-one meson, confinement scale, and the mass of the spin-zero meson, respectively. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 15:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and $ c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario A. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
Figure 15-a:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and $ c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario A. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
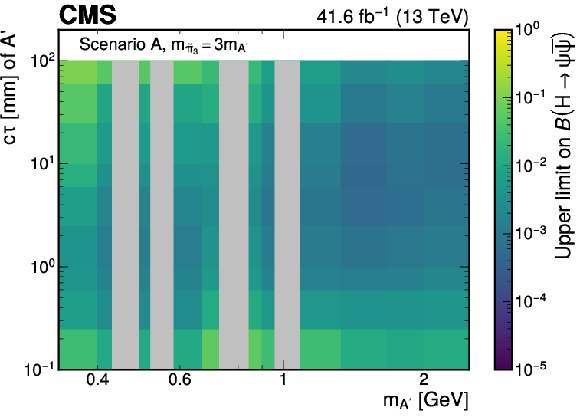
png pdf |
Figure 15-b:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and $ c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario A. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark-sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be 1. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |

png pdf |
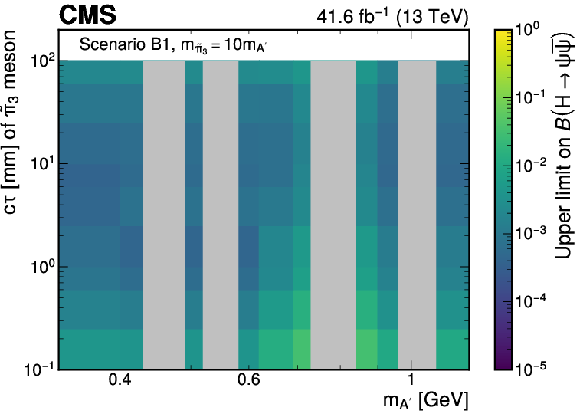
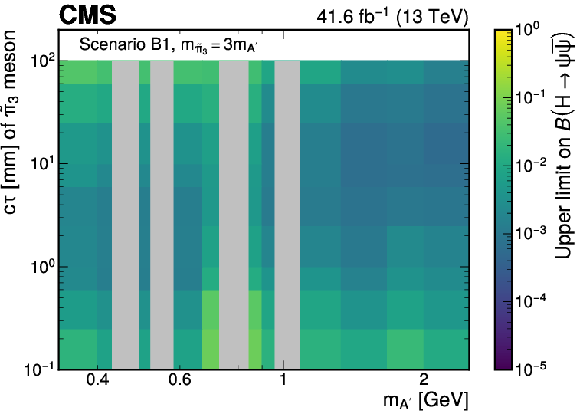
Figure 16:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and the $ \tilde{\pi}_{3} c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario B1. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be one. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
png pdf |
Figure 16-a:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and the $ \tilde{\pi}_{3} c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario B1. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be one. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
png pdf |
Figure 16-b:
Observed upper limits at 95% CL on the branching fraction $ \mathcal{B}(\mathrm{H}\to\psi\overline{\psi}) $ as functions of the $ \mathrm{A}' $ mass and the $ \tilde{\pi}_{3} c\tau $ for representative ratios of the $ \tilde{\pi}_{3} $ and $ \mathrm{A}' $ masses in Scenario B1. The limits are shown for the cases where $ m_{\tilde{\pi}_{3}}=10m_{\mathrm{A}'} $ (left) and $ m_{\tilde{\pi}_{3}}=3m_{\mathrm{A}'} $ (right), respectively. It is assumed that $ m_{\tilde{\eta}}=\tilde{\Lambda}=4m_{\tilde{\pi}_{2}} $ and $ {\sin\theta=0.1} $, where $ m_{\tilde{\eta}} $ is the mass of the dark sector pseudoscalar meson and $ \theta $ is the mixing angle parametrising the isospin violation. The branching fraction $ \mathcal{B}(\tilde{\pi}_{3}\to \mathrm{A}'\mathrm{A}') $ is assumed to be one. The grey bands correspond to mass regions of known SM resonances, which are masked in the search. |
| Tables | |

png pdf |
Table 1:
Model parameters of the different classes of signal models interpreted by the analysis. |

png pdf |
Table 2:
The SM resonances and the corresponding mass windows that are masked in the analysis. |

png pdf |
Table 3:
Summary of the systematic uncertainties in the signal yield expectation. |
| Summary |
| A search for dark showers has been performed with non-prompt muon pairs, using proton-proton collisions at the CERN LHC at a centre-of-mass energy of 13 TeV, collected by the CMS experiment in 2018, corresponding to an integrated luminosity of 41.6 fb$ ^{-1} $. The data set is recorded using the data parking strategy, resulting in a sample of about $ 10^{10} $ recorded events, giving access to masses down to the sub-GeV scale. No significant excess beyond the standard model expectation is observed. Upper limits on the branching fraction of the Higgs boson decaying into dark partons are set as low as $ 10^{-4} $ at 95% confidence level, providing the most stringent limits to date on the vector portal model with dark $ \tilde{\omega} $ mesons of mean proper decay length below 500 mm and masses between 0.3 and 20 GeV. For the first time, limits have been set for extended dark-shower models with two dark flavours (Scenario A and Scenario B1) that contain dark photons, probing their masses down to 0.33 GeV. |
| References | ||||
| 1 | V. C. Rubin, N. Thonnard, and W. K. Ford, Jr. | Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R = 4kpc) to UGC 2885 (R = 122 kpc) | Astrophys. J. 238 (1980) 471 | |
| 2 | M. Markevitch et al. | Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56 | Astrophys. J. 606 (2004) 819 | astro-ph/0309303 |
| 3 | Planck Collaboration | Planck 2018 results. VI. Cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 4 | A. Arbey and F. Mahmoudi | Dark matter and the early universe: a review | Prog. Part. Nucl. Phys. 119 (2021) 103865 | 2104.11488 |
| 5 | M. Persic, P. Salucci, and F. Stel | The universal rotation curve of spiral galaxies: 1. The dark matter connection | Mon. Not. Roy. Astron. Soc. 281 (1996) 27 | astro-ph/9506004 |
| 6 | M. J. Strassler and K. M. Zurek | Echoes of a hidden valley at hadron colliders | PLB 651 (2007) 374 | hep-ph/0604261 |
| 7 | T. Hur, D.-W. Jung, P. Ko, and J. Y. Lee | Electroweak symmetry breaking and cold dark matter from strongly interacting hidden sector | PLB 696 (2011) 262 | 0709.1218 |
| 8 | G. D. Kribs, T. S. Roy, J. Terning, and K. M. Zurek | Quirky composite dark matter | PRD 81 (2010) 095001 | 0909.2034 |
| 9 | H. Beauchesne, E. Bertuzzo, and G. Grilli Di Cortona | Dark matter in Hidden Valley models with stable and unstable light dark mesons | JHEP 04 (2019) 118 | 1809.10152 |
| 10 | A. Francis, R. J. Hudspith, R. Lewis, and S. Tulin | Dark matter from strong dynamics: the minimal theory of dark baryons | JHEP 12 (2018) 118 | 1809.09117 |
| 11 | E. Bernreuther, F. Kahlhoefer, M. Krämer, and P. Tunney | Strongly interacting dark sectors in the early universe and at the LHC through a simplified portal | JHEP 01 (2020) 162 | 1907.04346 |
| 12 | S. Knapen, J. Shelton, and D. Xu | Perturbative benchmark models for a dark shower search program | PRD 103 (2021) 115013 | 2103.01238 |
| 13 | S. Born, R. Karur, S. Knapen, and J. Shelton | Scouting for dark showers at CMS and LHCb | PRD 108 (2023) 035034 | 2303.04167 |
| 14 | D. Curtin et al. | Exotic decays of the 125 GeV Higgs boson | PRD 90 (2014) 075004 | 1312.4992 |
| 15 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 link |
|
| 16 | CMS Collaboration | Enriching the physics program of the CMS experiment via data scouting and data parking | Phys. Rept. 1115 (2025) 678 | CMS-EXO-23-007 2403.16134 |
| 17 | CMS Collaboration | Recording and reconstructing 10 billion unbiased b hadron decays in CMS | Technical Report CMS-CR-2020-081, CERN, Geneva, 2020 link |
|
| 18 | CMS Collaboration | Search for long-lived particles decaying into muon pairs in proton-proton collisions at $ \sqrt{s} = $ 13 TeV collected with a dedicated high-rate data stream | JHEP 04 (2022) 062 | CMS-EXO-20-014 2112.13769 |
| 19 | CMS Collaboration | Search for long-lived particles decaying to final states with a pair of muons in proton-proton collisions at $ \sqrt{s} = $ 13.6 TeV | JHEP 05 (2024) 047 | CMS-EXO-23-014 2402.14491 |
| 20 | ATLAS Collaboration | Search for long-lived particles in final states with displaced dimuon vertices in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 99 (2019) 012001 | 1808.03057 |
| 21 | LHCb Collaboration | Searches for low-mass dimuon resonances | JHEP 10 (2020) 156 | 2007.03923 |
| 22 | CMS Collaboration | Search for long-lived particles decaying in the CMS muon detectors in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 110 (2024) 032007 | CMS-EXO-21-008 2402.01898 |
| 23 | CMS Collaboration | Search for dark QCD with emerging jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2024) 142 | CMS-EXO-22-015 2403.01556 |
| 24 | CMS Collaboration | Search for new particles decaying to a jet and an emerging jet | JHEP 02 (2019) 179 | CMS-EXO-18-001 1810.10069 |
| 25 | P. Schwaller, D. Stolarski, and A. Weiler | Emerging jets | JHEP 05 (2015) 059 | 1502.05409 |
| 26 | S. Renner and P. Schwaller | A flavoured dark sector | JHEP 08 (2018) 052 | 1803.08080 |
| 27 | CMSnoop | none | \hrefHEPData record for this analysis, 2025 link |
|
| 28 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 29 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 30 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 31 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 32 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 33 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 34 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 35 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 36 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 37 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 38 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 39 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 40 | C. Bierlich et al. | A comprehensive guide to the physics and usage of PYTHIA 8.3 | SciPost Phys. Codeb. 2022 (2022) 8 | 2203.11601 |
| 41 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 42 | L. Carloni, J. Rathsman, and T. Sjostrand | Discerning secluded sector gauge structures | JHEP 04 (2011) 091 | 1102.3795 |
| 43 | D. Curtin, R. Essig, S. Gori, and J. Shelton | Illuminating dark photons with high-energy colliders | JHEP 02 (2015) 157 | 1412.0018 |
| 44 | T. Chen and C. Guestrin | XGBoost: A scalable tree boosting system | in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, p. 785. ACM, 2016 link |
|
| 45 | T. Chen et al. | xgboost: Extreme gradient boosting | R package version 2.0.3, 2024 https://github.com/dmlc/xgboost |
|
| 46 | R. Fruhwirth | Application of Kalman filtering to track and vertex fitting | NIM A 262 (1987) 444 | |
| 47 | T. Speer et al. | Vertex fitting in the CMS tracker | Technical Report CMS-NOTE-2006-032, CERN, Geneva, 2006 | |
| 48 | P. D. Dauncey, M. Kenzie, N. Wardle, and G. J. Davies | Handling uncertainties in background shapes: the discrete profiling method | JINST 10 (2015) P04015 | 1408.6865 |
| 49 | CMS Collaboration | Search for a high-mass dimuon resonance produced in association with b quark jets at $ \sqrt{s} = $ 13 TeV | JHEP 10 (2023) 043 | CMS-EXO-22-016 2307.08708 |
| 50 | CMS Collaboration | Measurement of the W and Z inclusive production cross sections at $ \sqrt{s}= $ 7 TeV with the CMS experiment at the LHC | Technical Report, CERN, Geneva, 2011 CMS-PAS-EWK-10-005 |
|
| 51 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 52 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector | Collaboration, D. de Florian et al., CERN Yellow Reports: Monographs. CERN, Geneva, 2017 link |
|
| 53 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 54 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 55 | A. L. Read | Presentation of search results: The $ CL_s $ technique | JPG 28 (2002) 2693 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|