

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-21-008 ; CERN-EP-2024-008 | ||
| Search for long-lived particles decaying in the CMS muon detectors in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| 7 August 2024 | ||
| Phys. Rev. D 110 (2024) 032007 | ||
| Abstract: A search for long-lived particles (LLPs) decaying in the CMS muon detectors is presented. A data sample of proton-proton collisions at $ \sqrt{s}= $ 13 TeV corresponding to an integrated luminosity of 138 fb$ ^{-1} $, recorded at the LHC in 2016-2018, is used. The decays of LLPs are reconstructed as high multiplicity clusters of hits in the muon detectors. In the context of twin Higgs models, the search is sensitive to LLP masses from 0.4 to 55 GeV and a broad range of LLP decay modes, including decays to hadrons, $ \tau $ leptons, electrons, or photons. No excess of events above the standard model background is observed. The most stringent limits to date from LHC data are set on the branching fraction of the Higgs boson decay to a pair of LLPs with masses below 10 GeV. This search also provides the best limits for various intervals of LLP proper decay length and mass. Finally, this search sets the first limits at the LHC on a dark quantum chromodynamic sector whose particles couple to the Higgs boson through gluon, Higgs boson, photon, vector, and dark-photon portals, and is sensitive to branching fractions of the Higgs boson to dark quarks as low as 2 $ \times $ 10$^{-3} $. | ||
| Links: e-print arXiv:2402.01898 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; Physics Briefing ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
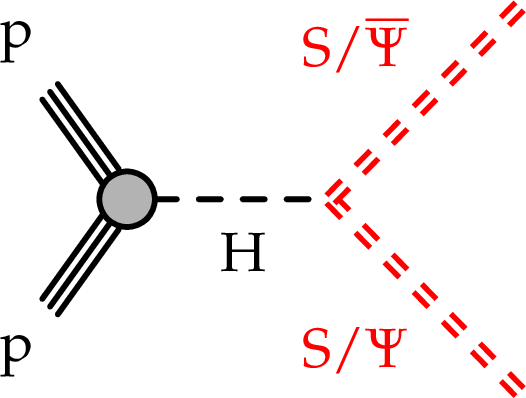
Figure 1:
Diagram representing the twin Higgs and dark-shower models. The SM Higgs boson (H) decays to a pair of neutral long-lived scalars (S) in the twin Higgs model or to a pair of dark-sector quarks (\Psi) in the dark shower model. |
png pdf |
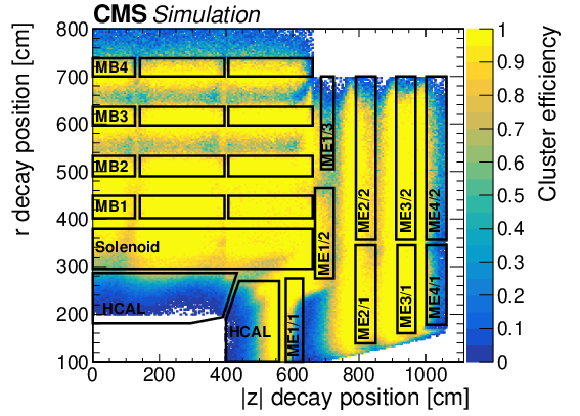
Figure 2:
The cluster reconstruction efficiency, including both DT and CSC clusters, as a function of the simulated $ r $ and $ |z| $ decay positions of the particle S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ in events with $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV, for a mass of 40 GeV and a range of $ c\tau $ values uniformly distributed between 1 and 10 m. The cluster reconstruction efficiency appears to be nonzero beyond MB4 because the MB4 chambers are staggered so that the outer radius of the CMS detector ranges from 738 to 800 cm. The barrel and endcap muon stations are drawn as black boxes and labeled by their station names. The region between labeled sections are mostly steel return yoke. |

png pdf |
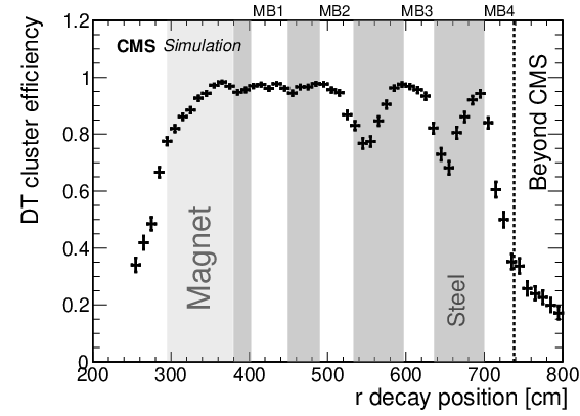
Figure 3:
The DT (left) and CSC (right) cluster reconstruction efficiency as a function of the simulated $ r $ or $ |z| $ decay positions of S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ in events with $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV, for a mass of 40 GeV and a range of $ c\tau $ values between 1 and 10 m. The DT cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |z| < $ 700 cm. The DT cluster reconstruction efficiency appears to be nonzero beyond MB4 because the MB4 chambers are staggered so that the outer radius of the CMS detector ranges from 738 to 800 cm. The CSC cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |r| < $ 700 cm and $ |\eta| < $ 2.6. The clusters are selected from signal events satisfying the $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV requirement. Regions occupied by steel shielding are shaded in gray. |
png pdf |
Figure 3-a:
The DT (left) and CSC (right) cluster reconstruction efficiency as a function of the simulated $ r $ or $ |z| $ decay positions of S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ in events with $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV, for a mass of 40 GeV and a range of $ c\tau $ values between 1 and 10 m. The DT cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |z| < $ 700 cm. The DT cluster reconstruction efficiency appears to be nonzero beyond MB4 because the MB4 chambers are staggered so that the outer radius of the CMS detector ranges from 738 to 800 cm. The CSC cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |r| < $ 700 cm and $ |\eta| < $ 2.6. The clusters are selected from signal events satisfying the $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV requirement. Regions occupied by steel shielding are shaded in gray. |

png pdf |
Figure 3-b:
The DT (left) and CSC (right) cluster reconstruction efficiency as a function of the simulated $ r $ or $ |z| $ decay positions of S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ in events with $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV, for a mass of 40 GeV and a range of $ c\tau $ values between 1 and 10 m. The DT cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |z| < $ 700 cm. The DT cluster reconstruction efficiency appears to be nonzero beyond MB4 because the MB4 chambers are staggered so that the outer radius of the CMS detector ranges from 738 to 800 cm. The CSC cluster reconstruction efficiency is shown for events where the LLP decay occurs at $ |r| < $ 700 cm and $ |\eta| < $ 2.6. The clusters are selected from signal events satisfying the $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV requirement. Regions occupied by steel shielding are shaded in gray. |
png pdf |
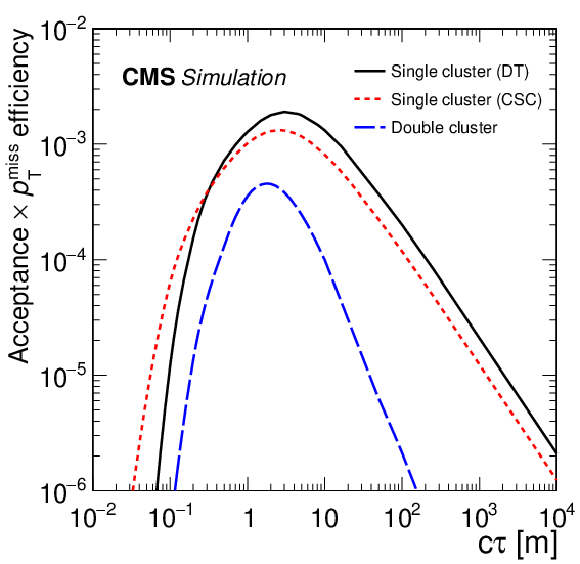
Figure 4:
The geometric acceptance multiplied by the efficiency of the $ p_{\mathrm{T}}^\text{miss} > $ 200 GeV selection, as a function of the proper decay length $ c\tau $ for a scalar particle S with a mass of 40 GeV. |
png pdf |
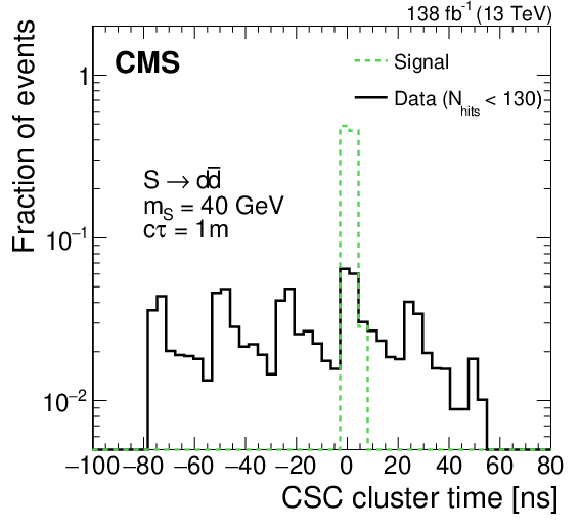
Figure 5:
Distributions of the cluster time ($ t_\text{cluster} $) for signal, where S decays to $ \mathrm{d}\overline{\mathrm{d}} $ with a proper decay length $ c\tau $ of 1 m and mass of 40 GeV, and for a background-enriched sample in data selected by inverting the $ N_\text{hits} $ requirement. |
png pdf |
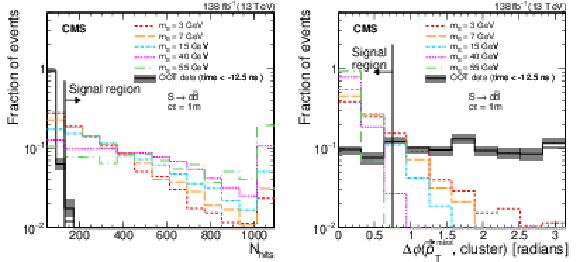
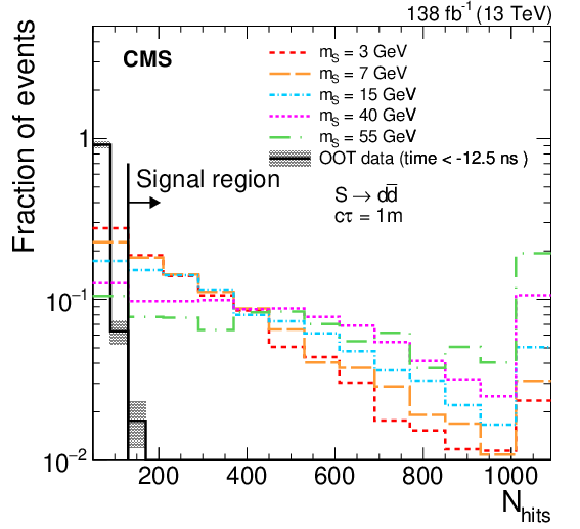
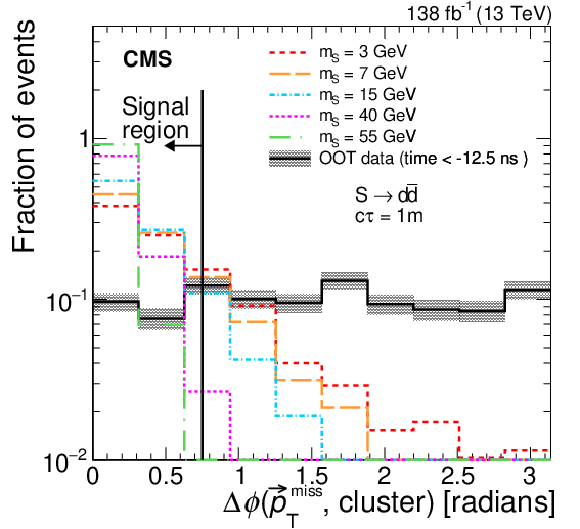
Figure 6:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for single CSC clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the OOT background ($ t_\text{cluster} < -$ 12.5 ns). The OOT background is representative of the overall background shape, because the background passing all the selections described above is dominated by pileup and underlying events. The shaded bands show the statistical uncertainty in the background. |
png pdf |
Figure 6-a:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for single CSC clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the OOT background ($ t_\text{cluster} < -$ 12.5 ns). The OOT background is representative of the overall background shape, because the background passing all the selections described above is dominated by pileup and underlying events. The shaded bands show the statistical uncertainty in the background. |
png pdf |
Figure 6-b:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for single CSC clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the OOT background ($ t_\text{cluster} < -$ 12.5 ns). The OOT background is representative of the overall background shape, because the background passing all the selections described above is dominated by pileup and underlying events. The shaded bands show the statistical uncertainty in the background. |

png pdf |
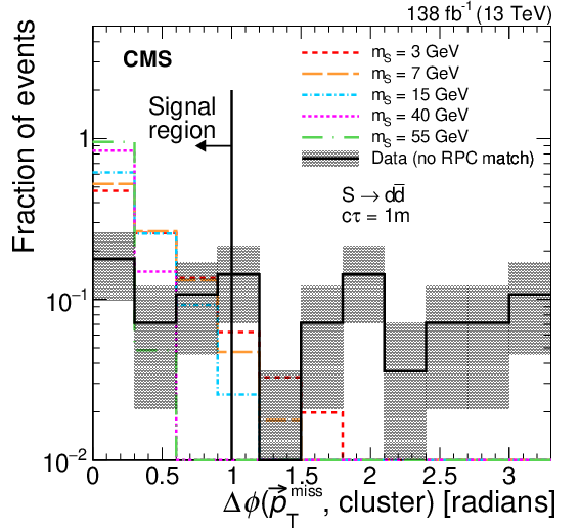
Figure 7:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for DT clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the shape of background in a selection in which the cluster is not matched to any RPC hit and passes all other selections. The background is dominated by clusters from noise and low-$ p_{\mathrm{T}} $ particles. The shaded bands show the statistical uncertainty in the background. |

png pdf |
Figure 7-a:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for DT clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the shape of background in a selection in which the cluster is not matched to any RPC hit and passes all other selections. The background is dominated by clusters from noise and low-$ p_{\mathrm{T}} $ particles. The shaded bands show the statistical uncertainty in the background. |
png pdf |
Figure 7-b:
The distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) for DT clusters are shown for S decaying to $ \mathrm{d}\overline{\mathrm{d}} $ for a proper decay length of 1 m and various masses compared to the shape of background in a selection in which the cluster is not matched to any RPC hit and passes all other selections. The background is dominated by clusters from noise and low-$ p_{\mathrm{T}} $ particles. The shaded bands show the statistical uncertainty in the background. |

png pdf |
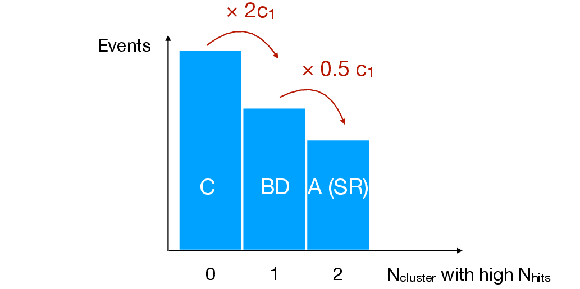
Figure 8:
Diagrams illustrating the ABCD plane for the DT-CSC category (left), and for the DT-DT and CSC-CSC categories (right). The variable $ c_1 $ is the pass-fail ratio of the $ N_\text{hits} $ selection for the background clusters. Bin A is the signal region (SR) for all categories. The size of the blue boxes on the left represents the approximate size of the expected background yield in each bin. |

png pdf |
Figure 8-a:
Diagrams illustrating the ABCD plane for the DT-CSC category (left), and for the DT-DT and CSC-CSC categories (right). The variable $ c_1 $ is the pass-fail ratio of the $ N_\text{hits} $ selection for the background clusters. Bin A is the signal region (SR) for all categories. The size of the blue boxes on the left represents the approximate size of the expected background yield in each bin. |
png pdf |
Figure 8-b:
Diagrams illustrating the ABCD plane for the DT-CSC category (left), and for the DT-DT and CSC-CSC categories (right). The variable $ c_1 $ is the pass-fail ratio of the $ N_\text{hits} $ selection for the background clusters. Bin A is the signal region (SR) for all categories. The size of the blue boxes on the left represents the approximate size of the expected background yield in each bin. |

png pdf |
Figure 9:
Diagram illustrating the ABCD plane for the single-CSC-cluster category, where bin A is the signal region (SR). |
png pdf |
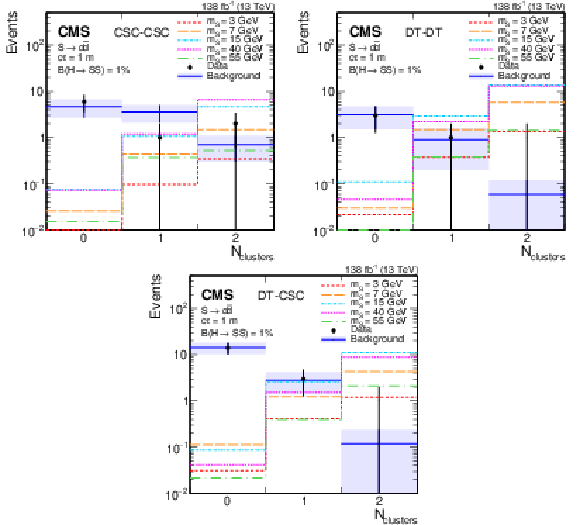
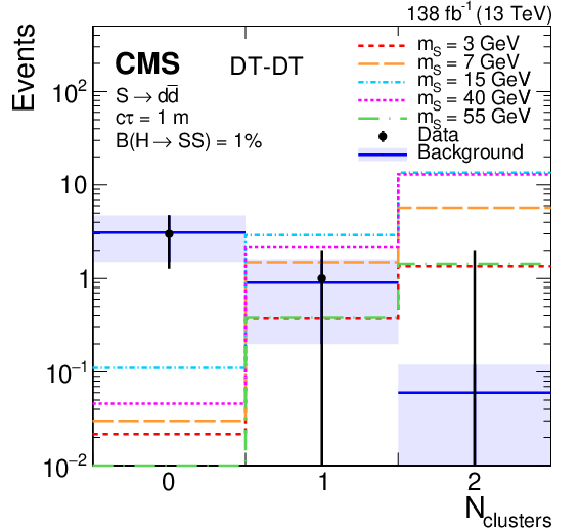
Figure 10:
The signal (assuming $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S} \to \mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m), background, and data distributions of $ N_\text{clusters} $ passing the $ N_\text{hits} $ selection in the search region for CSC-CSC (upper left), DT-DT (upper right), and DT-CSC (lower) categories. The branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ has been set to a specific value purely to allow a visual comparison of the shapes of the signal and background distributions. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. No events are observed in the rightmost bins of the DT-CSC and DT-DT categories, so only the associated uncertainty is shown. |

png pdf |
Figure 10-a:
The signal (assuming $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S} \to \mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m), background, and data distributions of $ N_\text{clusters} $ passing the $ N_\text{hits} $ selection in the search region for CSC-CSC (upper left), DT-DT (upper right), and DT-CSC (lower) categories. The branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ has been set to a specific value purely to allow a visual comparison of the shapes of the signal and background distributions. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. No events are observed in the rightmost bins of the DT-CSC and DT-DT categories, so only the associated uncertainty is shown. |
png pdf |
Figure 10-b:
The signal (assuming $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S} \to \mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m), background, and data distributions of $ N_\text{clusters} $ passing the $ N_\text{hits} $ selection in the search region for CSC-CSC (upper left), DT-DT (upper right), and DT-CSC (lower) categories. The branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ has been set to a specific value purely to allow a visual comparison of the shapes of the signal and background distributions. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. No events are observed in the rightmost bins of the DT-CSC and DT-DT categories, so only the associated uncertainty is shown. |

png pdf |
Figure 10-c:
The signal (assuming $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S} \to \mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m), background, and data distributions of $ N_\text{clusters} $ passing the $ N_\text{hits} $ selection in the search region for CSC-CSC (upper left), DT-DT (upper right), and DT-CSC (lower) categories. The branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ has been set to a specific value purely to allow a visual comparison of the shapes of the signal and background distributions. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. No events are observed in the rightmost bins of the DT-CSC and DT-DT categories, so only the associated uncertainty is shown. |
png pdf |
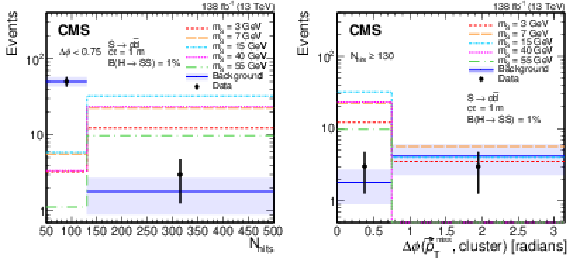
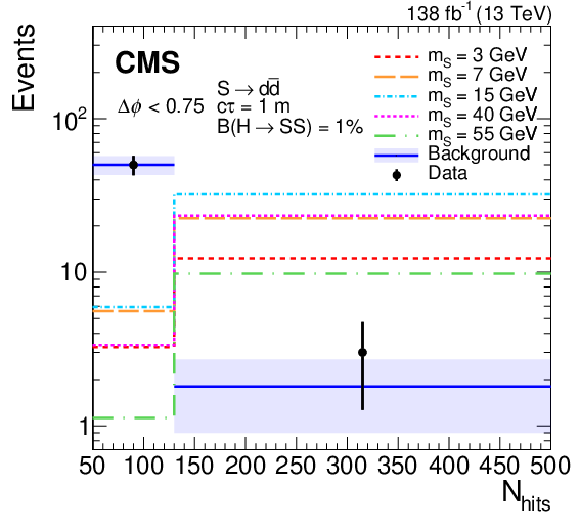
Figure 11:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-CSC-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ distribution includes only events in bins A and B. The rightmost bin in the $ N_\text{hits} $ distribution includes overflow events. |
png pdf |
Figure 11-a:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-CSC-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ distribution includes only events in bins A and B. The rightmost bin in the $ N_\text{hits} $ distribution includes overflow events. |

png pdf |
Figure 11-b:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-CSC-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ distribution includes only events in bins A and B. The rightmost bin in the $ N_\text{hits} $ distribution includes overflow events. |
png pdf |
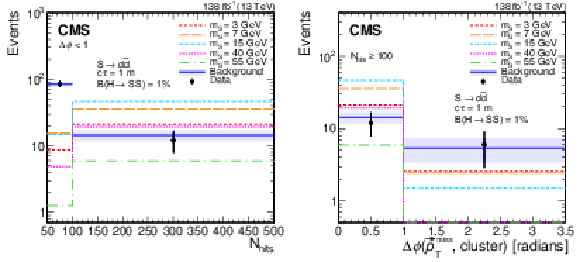
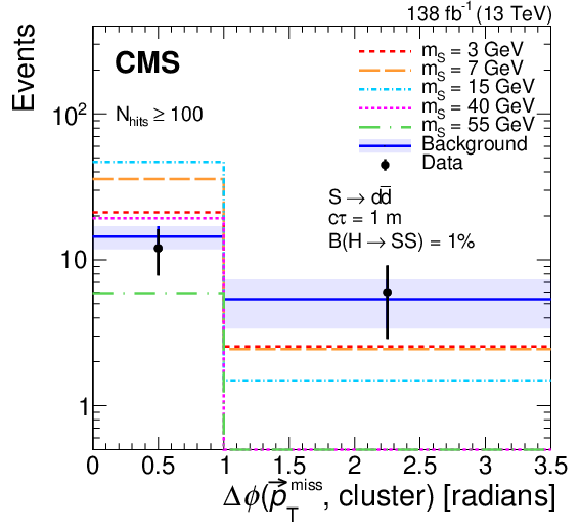
Figure 12:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-DT-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ one includes only events in bins A and B. The right-hand bin in the $ N_\text{hits} $ distribution includes overflow events. |

png pdf |
Figure 12-a:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-DT-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ one includes only events in bins A and B. The right-hand bin in the $ N_\text{hits} $ distribution includes overflow events. |
png pdf |
Figure 12-b:
Distributions of $ N_\text{hits} $ (left) and $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ (right) in the search region of the single-DT-cluster category. The background prediction is obtained from the fit to the observed data assuming no signal contribution, and is shown in blue with the shaded region showing the fitted uncertainty. The expected signal with $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $, $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $, and $ c\tau= $ 1 m is shown for $ m_\mathrm{S} $ of 3, 7, 15, 40, and 55 GeV in various colors and dotted lines. The $ N_\text{hits} $ distribution includes only events in bins A and D, while the $ \Delta\phi{\mathrm{(}{\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}}\mathrm{, cluster)}} $ one includes only events in bins A and B. The right-hand bin in the $ N_\text{hits} $ distribution includes overflow events. |
png pdf |
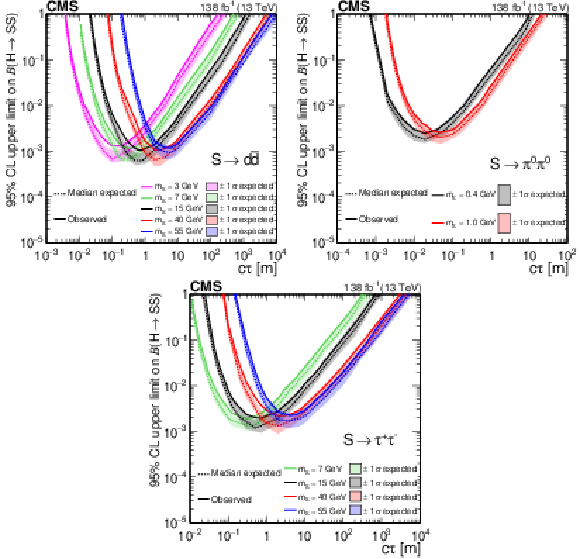
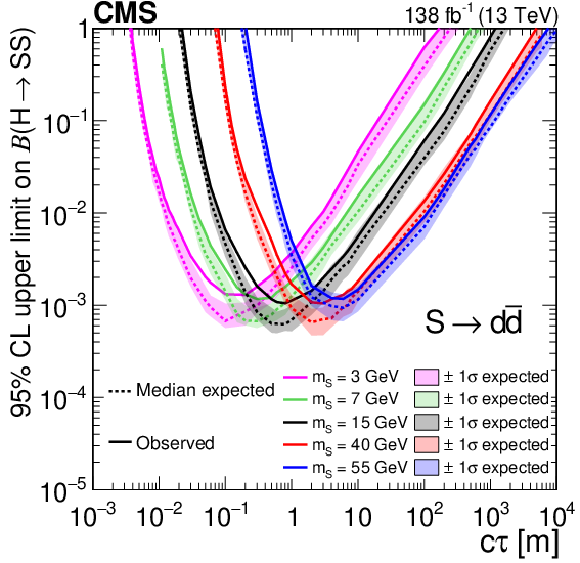
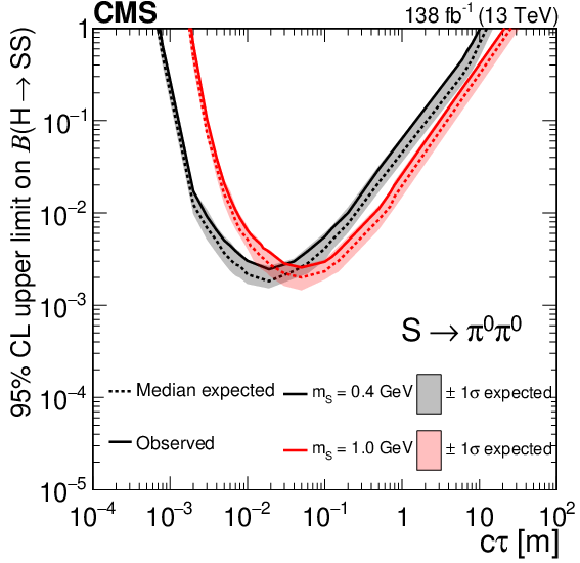
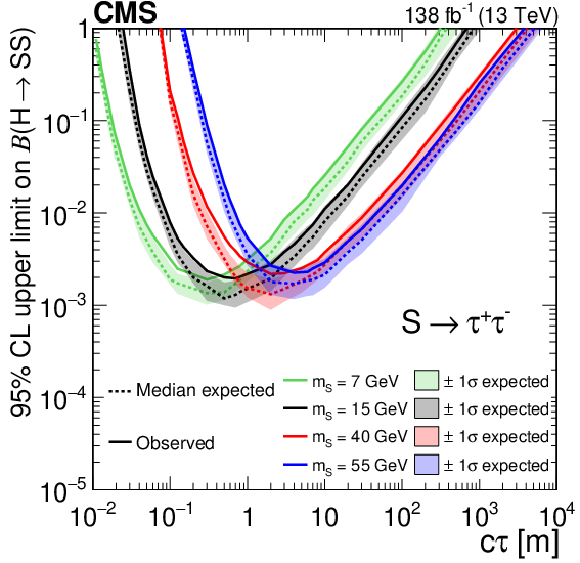
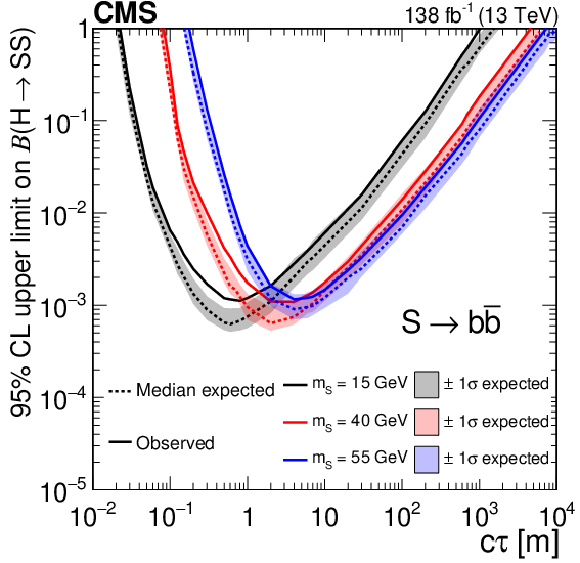
Figure 13:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 13-a:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 13-b:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 13-c:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
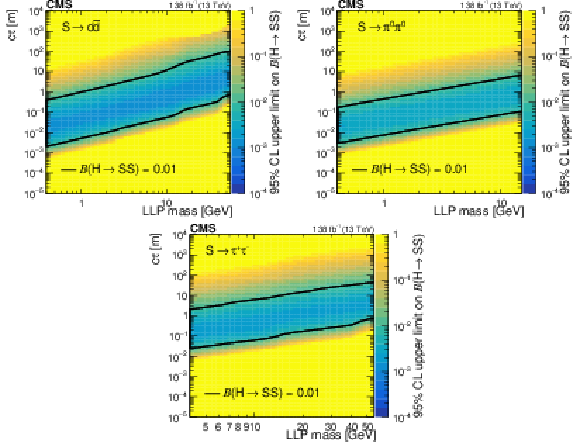
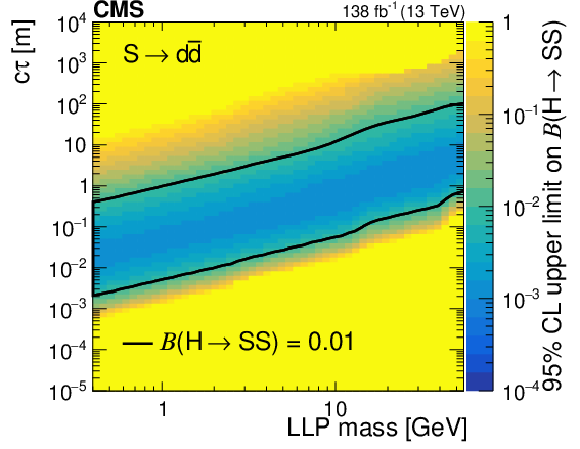
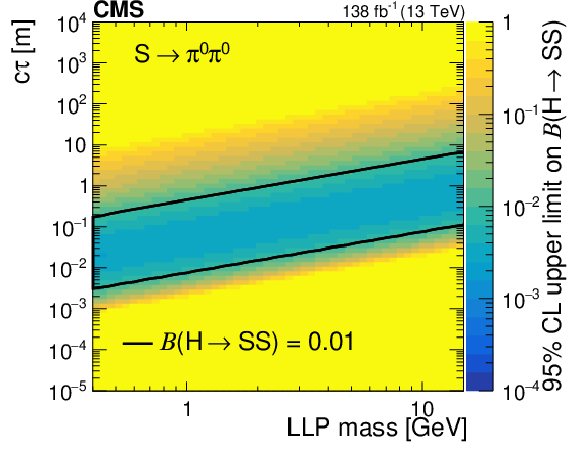
Figure 14:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 14-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 14-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |

png pdf |
Figure 14-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{d}\overline{\mathrm{d}} $ (upper left), $ \mathrm{S}\to\pi^{0}\pi^{0} $ (upper right), and $ \mathrm{S}\to\tau^{+}\tau^{-} $ (lower) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |

png pdf |
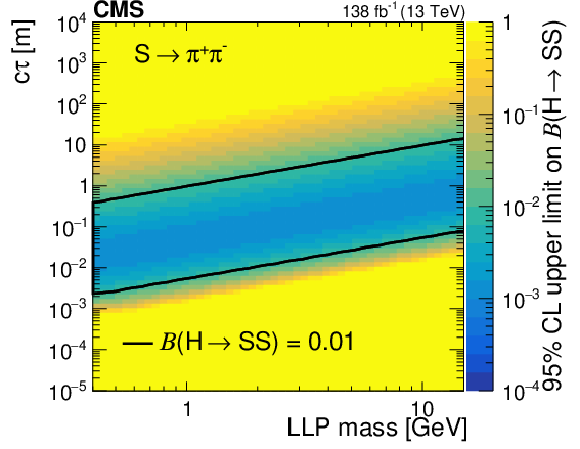
Figure 15:
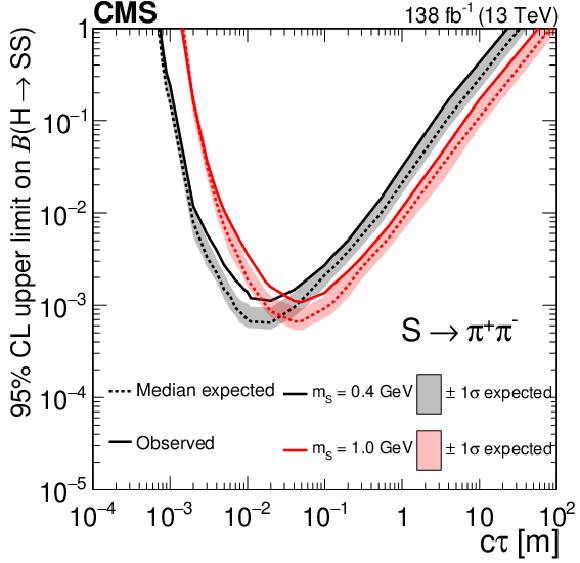
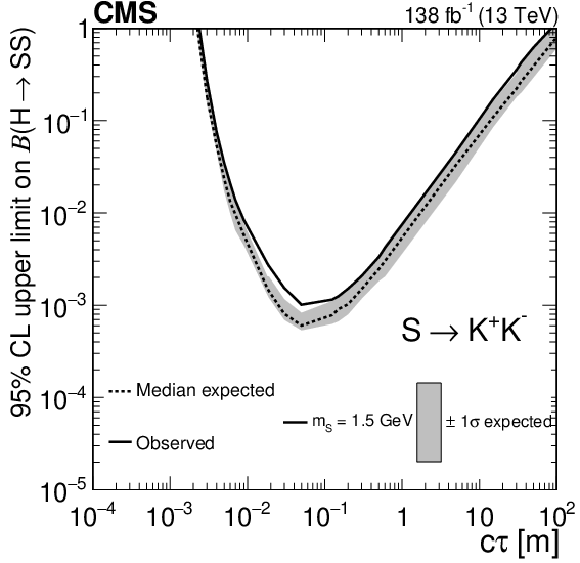
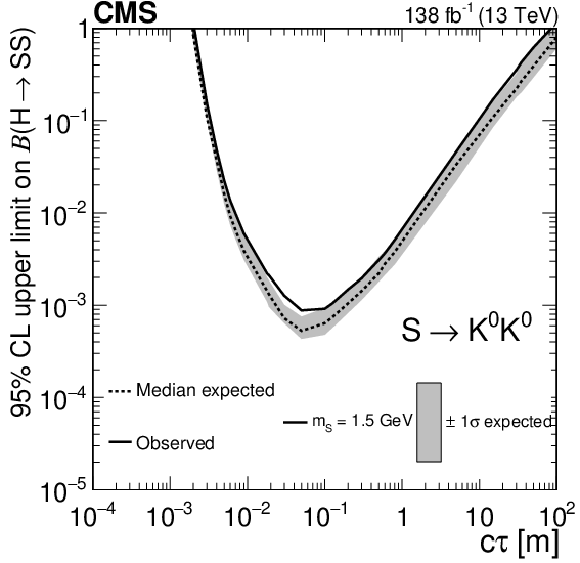
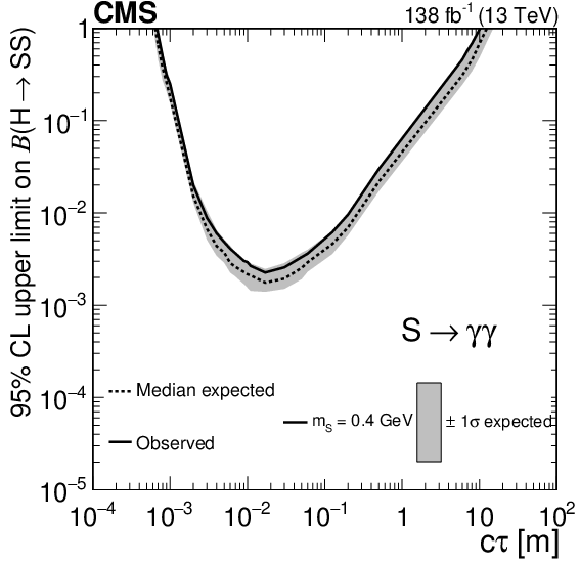
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 15-a:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 15-b:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 15-c:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 15-d:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
Figure 15-e:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
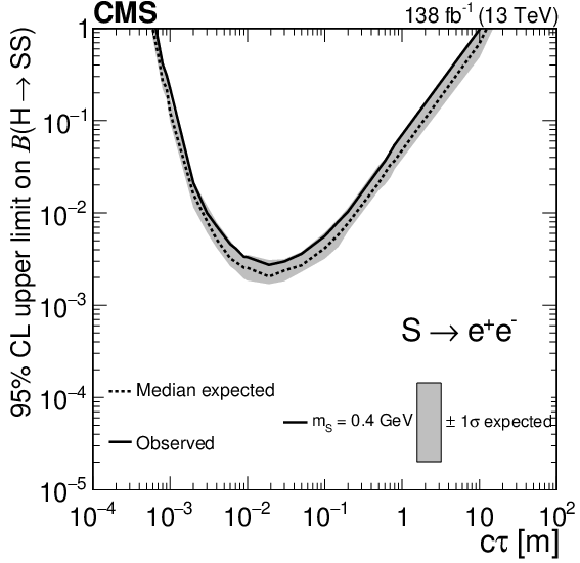
Figure 15-f:
The 95% CL expected (dotted curves) and observed (solid curves) upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to \gamma\gamma $ (lower left), and $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The exclusion limits are shown for different mass hypotheses. |
png pdf |
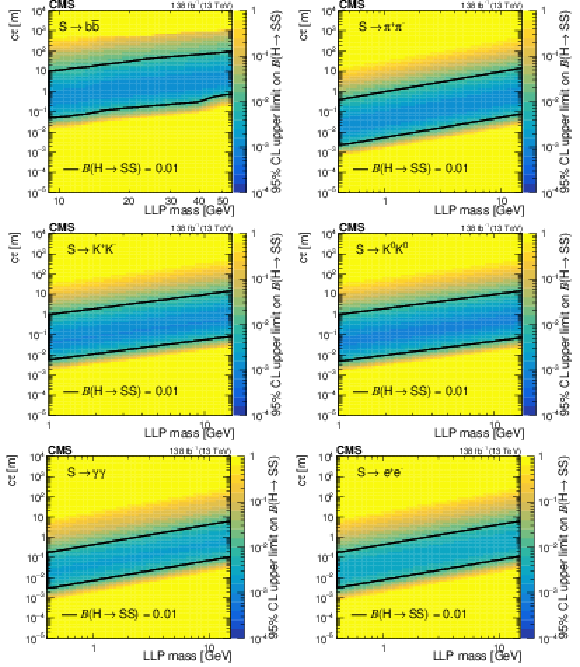
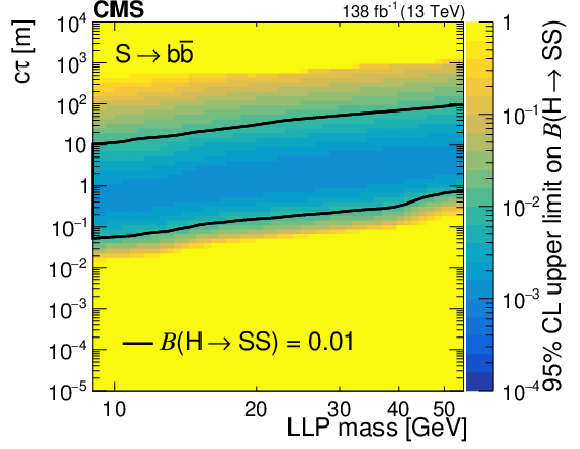
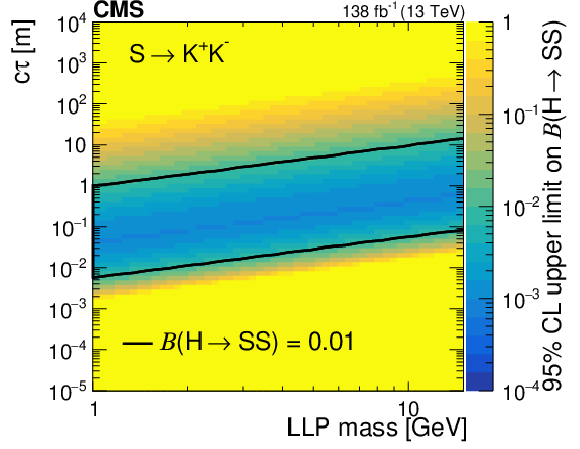
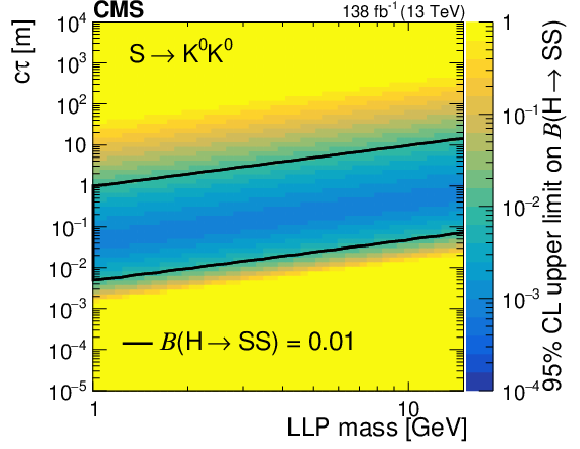
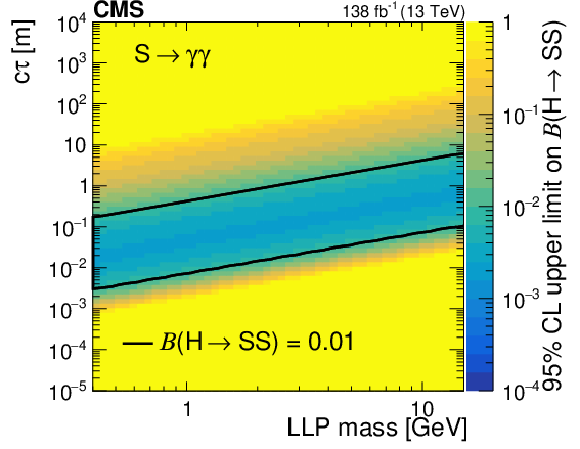
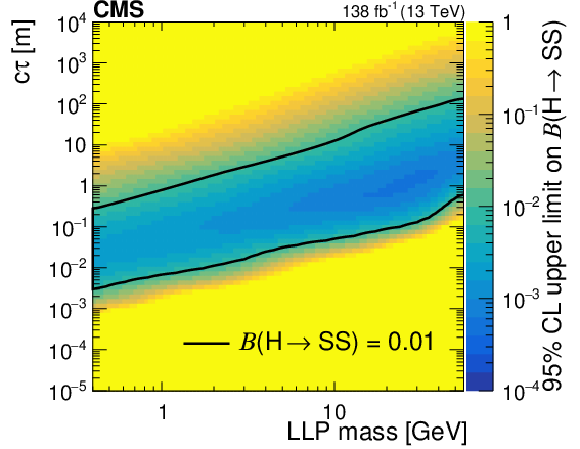
Figure 16:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 16-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 16-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 16-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 16-d:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 16-e:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |

png pdf |
Figure 16-f:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as functions of mass and $ c\tau $ for the $ \mathrm{S}\to\mathrm{b}\overline{\mathrm{b}} $ (upper left), $ \mathrm{S}\to\pi^{+}\pi^{-} $ (upper right), $ \mathrm{S}\to \mathrm{K^+}\mathrm{K^-} $ (middle left), $ \mathrm{S}\to \mathrm{K^0}\mathrm{K^0} $ (middle right), $ \mathrm{S}\to\gamma\gamma $ (lower left), $ \mathrm{S}\to \mathrm{e}^+\mathrm{e}^- $ (lower right) decay modes. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |
png pdf |
Figure 17:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) $ as a function of mass and $ c\tau $, assuming the branching fractions for S are identical to those of a Higgs boson evaluated at $ m_\mathrm{S} $ [66]. The area inside the solid contours represents the region for which the limit is smaller than 0.01. |

png pdf |
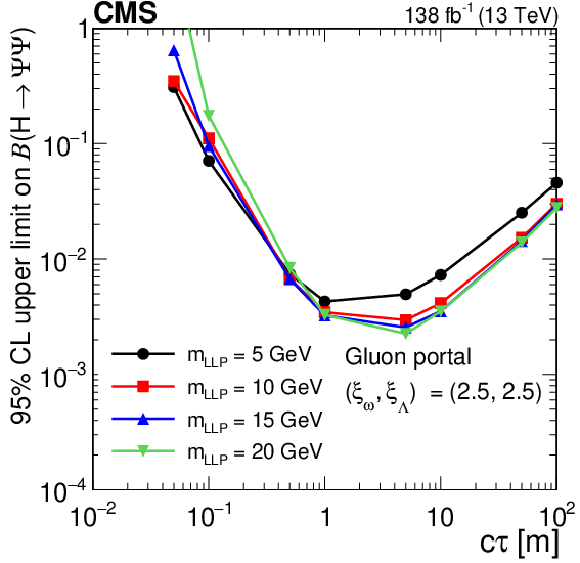
Figure 18:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower vector portal assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $. The exclusion limits are shown for different LLP mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 19:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower gluon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |

png pdf |
Figure 19-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower gluon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |

png pdf |
Figure 19-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower gluon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 19-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower gluon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
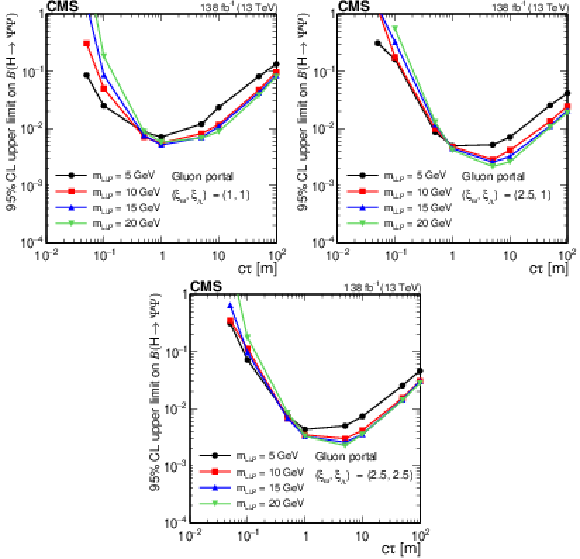
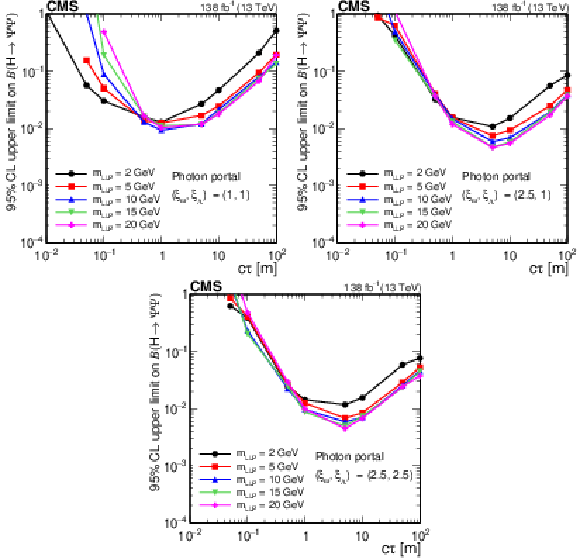
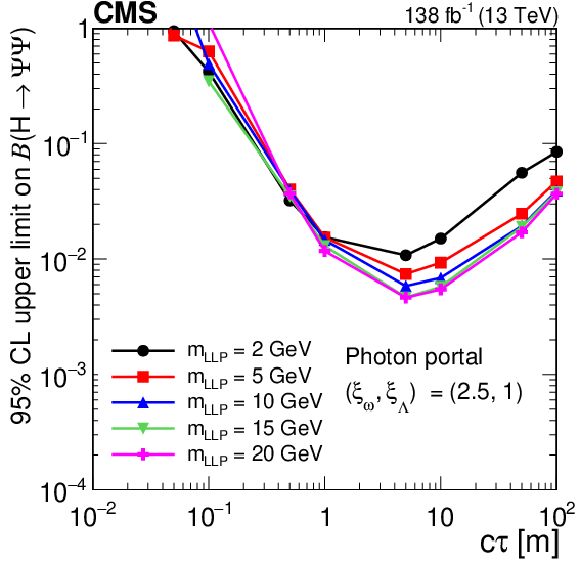
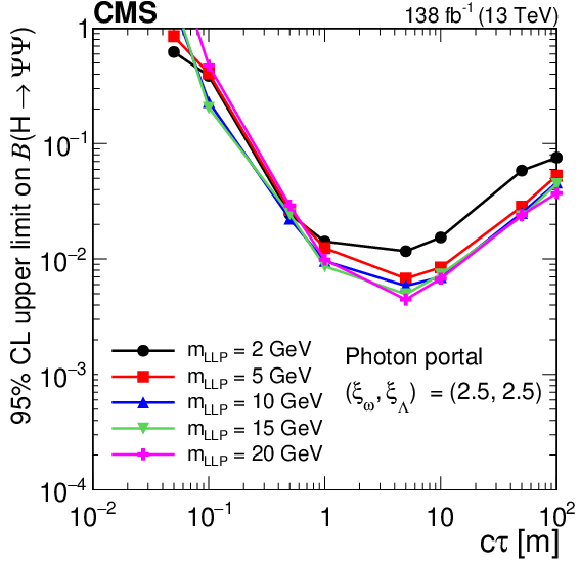
Figure 20:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
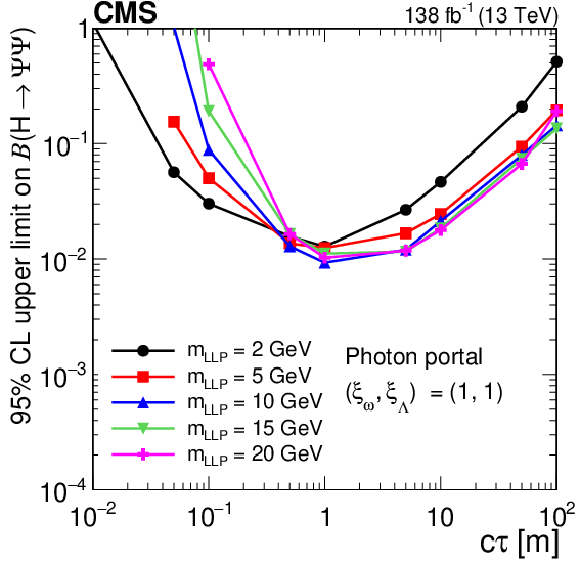
png pdf |
Figure 20-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 20-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 20-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
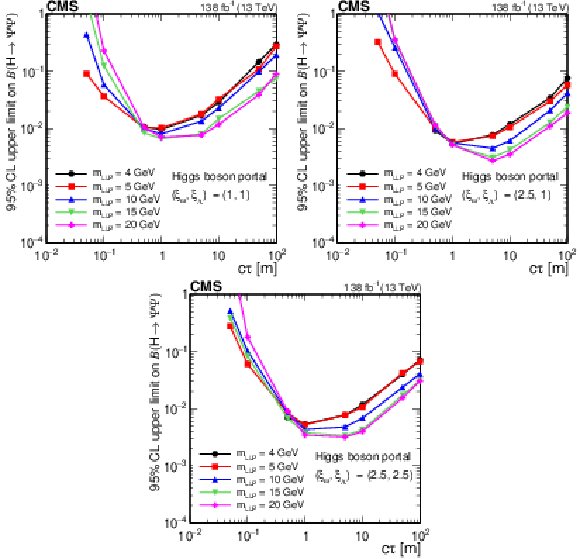
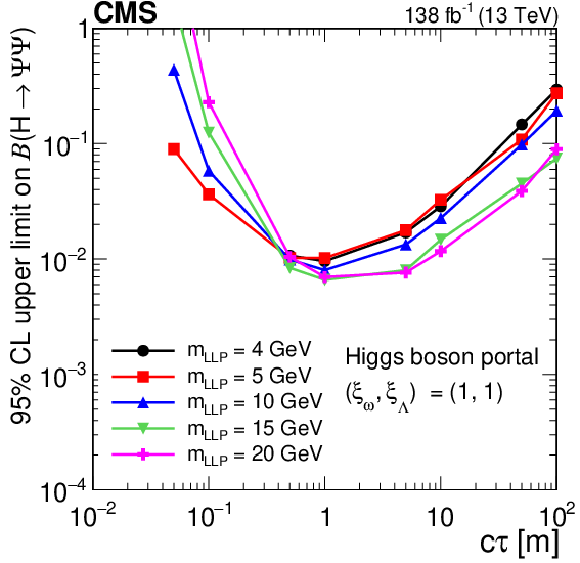
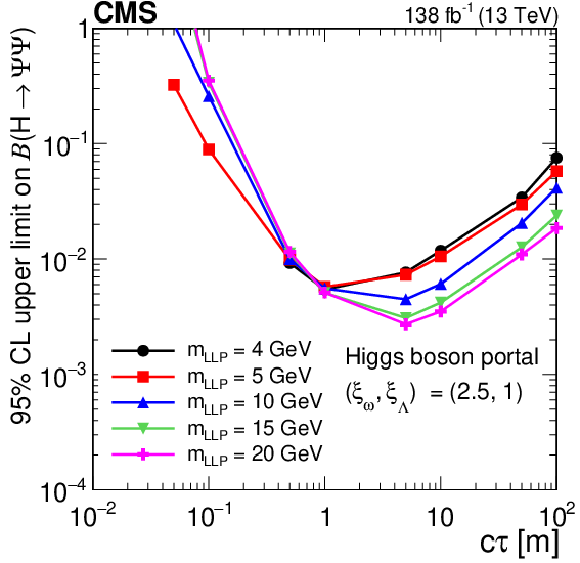
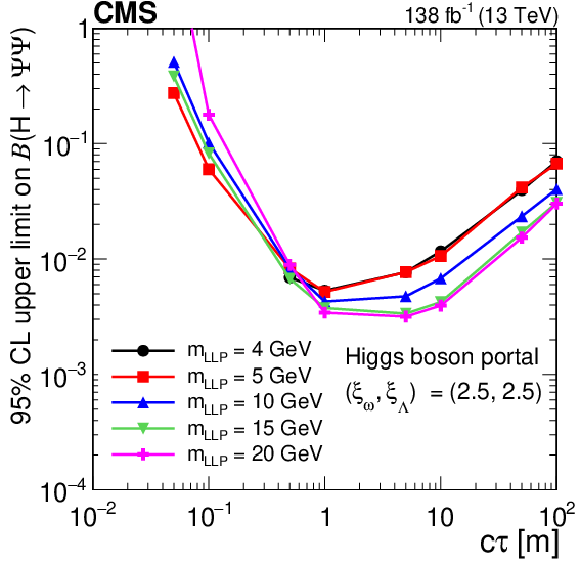
Figure 21:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower Higgs boson portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 21-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower Higgs boson portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 21-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower Higgs boson portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 21-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower Higgs boson portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
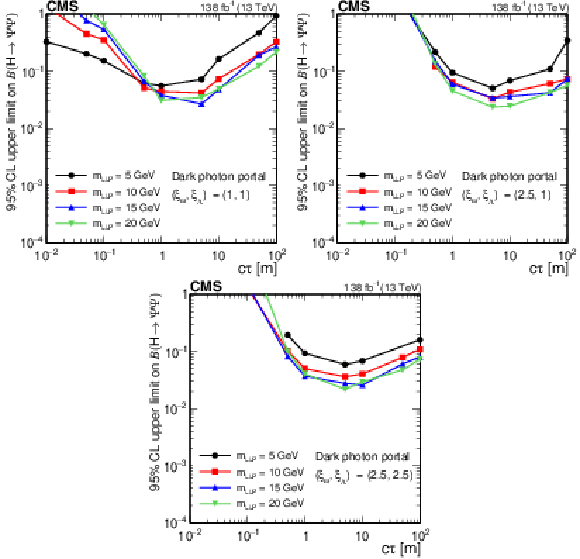
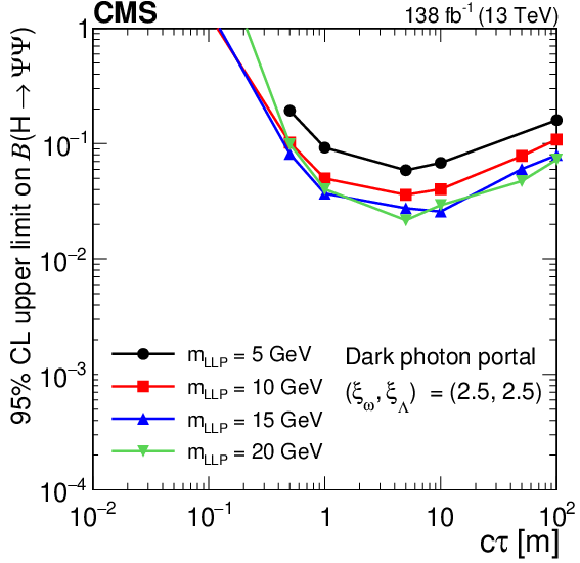
Figure 22:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower dark-photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |

png pdf |
Figure 22-a:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower dark-photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |

png pdf |
Figure 22-b:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower dark-photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
png pdf |
Figure 22-c:
The 95% CL observed upper limits on the branching fraction $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ as functions of $ c\tau $ for the dark shower dark-photon portal, assuming $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (1, 1) $ (upper left), $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 1.0) $ (upper right), and $ (\xi_{\omega} $, $ \xi_{\Lambda}) = (2.5, 2.5) $ (lower). The exclusion limits are shown for different mass hypotheses. The limits are calculated only at the proper decay lengths indicated by the markers and the lines connecting the markers are linear interpolations. The plot is restricted to physical $ \mathcal{B}(\mathrm{H}\to\Psi\Psi) $ values of below 1. |
| Tables | |
png pdf |
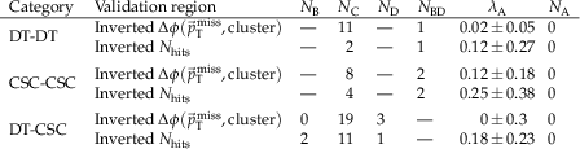
Table 1:
Validation of the ABCD method for the double-cluster category in both VRs. The uncertainty in the prediction is the statistical uncertainty propagated from bins B, C, and D or bins BD and C. The expected background event rate in bin A ($ \lambda_\mathrm{A} $) and the background event rate in bins B, C, D, BD, and A ($ N_\mathrm{B} $, $ N_\mathrm{C} $, $ N_\mathrm{D} $, $ N_\mathrm{BD} $, $ N_\mathrm{A} $) are shown. |

png pdf |
Table 2:
Validation of the ABCD method for the single-CSC-cluster category in both VRs. The uncertainty in the prediction is the statistical uncertainty propagated from bins B, C, and D. The expected background event rate in bin A ($ \lambda_\mathrm{A} $) and the background event rate in bins B, C, D, and A ($ N_\mathrm{B} $, $ N_\mathrm{C} $, $ N_\mathrm{D} $, $ N_\mathrm{A} $) are shown. |

png pdf |
Table 3:
Validation of the ABCD method for the single-DT-cluster category in a pileup-enriched region. The uncertainty in the prediction is the statistical uncertainty propagated from bins B, C, and D. Bins C and D for the MB3 and MB4 categories are combined to reduce the statistical uncertainty in the two regions. The final ABCD fit in the SR will also be performed with those bins combined. |

png pdf |
Table 4:
Validation of the punch-through jet background prediction method for the single-DT-cluster category. The uncertainty in the prediction is the statistical uncertainty propagated from the extrapolated MB1/MB2 hit veto efficiency. |
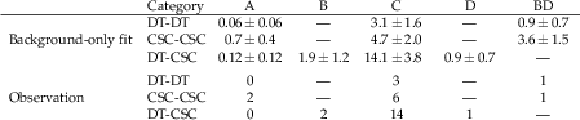
png pdf |
Table 5:
Number of predicted background and observed events in the double-cluster category. The background prediction is obtained from a fit to the observed data assuming no signal contribution. |

png pdf |
Table 6:
Number of predicted background and observed events in the single-CSC-cluster category. The background prediction is obtained from a fit to the observed data assuming no signal contribution. |

png pdf |
Table 7:
Number of predicted background and observed events in the single-DT-cluster category. The background prediction is obtained from a fit to the observed data assuming no signal contribution. |
png pdf |
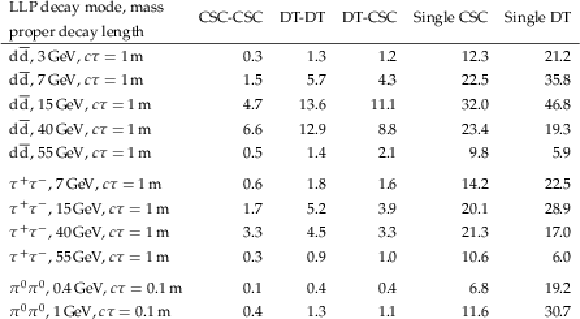
Table 8:
Expected number of signal events in bin A for each category, for a few benchmark signal models assuming $ \mathcal{B}(\mathrm{H}\to\mathrm{S}\mathrm{S}) = 1% $. |
| Summary |
| Data from proton-proton collisions at $ \sqrt{s} = $ 13 TeV recorded by the CMS experiment in 2016-2018, corresponding to an integrated luminosity of 138 fb$ ^{-1} $, have been used to conduct the first search that uses both the barrel and endcap CMS muon detectors to detect hadronic and electromagnetic showers from long-lived particle (LLP) decays. Based on this unique detector signature, the search is largely model-independent, with sensitivity to a broad range of LLP decay modes and masses extending below the GeVns scale. With the excellent shielding provided by the inner CMS detector, the CMS magnet and its steel flux-return yoke, the background is suppressed to a low level and a search for both single and pairs of LLPs decays is possible. No significant deviation from the standard model background is observed. The most stringent LHC constraints to date are set on the branching fraction of the Higgs boson to LLPs with masses below 10 GeV and decaying to particles other than muons. For higher LLP masses the search provides the most stringent branching fraction limits for specific proper decay lengths: 0.04-0.40 m and above 5 m for 15 GeV LLP; 0.3-0.9 m and above 3 m for 40 GeV LLP; and above 0.9 m for 55 GeV LLP. Finally, the first LHC limits on models of dark showers produced via H decay are set, and constrain branching fractions of the H decay to dark quarks as low as 2 $ \times $ 10$^{-3} $ at 95% confidence level. |
| References | ||||
| 1 | G. F. Giudice and A. Romanino | Split supersymmetry | NPB 699 (2004) 65 | hep-ph/0406088 |
| 2 | J. L. Hewett, B. Lillie, M. Masip, and T. G. Rizzo | Signatures of long-lived gluinos in split supersymmetry | JHEP 09 (2004) 070 | hep-ph/0408248 |
| 3 | N. Arkani-Hamed, S. Dimopoulos, G. F. Giudice, and A. Romanino | Aspects of split supersymmetry | NPB 709 (2005) 3 | hep-ph/0409232 |
| 4 | P. Gambino, G. F. Giudice, and P. Slavich | Gluino decays in split supersymmetry | NPB 726 (2005) 35 | hep-ph/0506214 |
| 5 | A. Arvanitaki, N. Craig, S. Dimopoulos, and G. Villadoro | Mini-split | JHEP 02 (2013) 126 | 1210.0555 |
| 6 | N. Arkani-Hamed et al. | Simply unnatural supersymmetry | 1212.6971 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 9 | S. Weinberg | Supersymmetry at ordinary energies. Masses and conservation laws | PRD 26 (1982) 287 | |
| 10 | R. Barbier et al. | $ R $-parity violating supersymmetry | Phys. Rept. 420 (2005) 1 | hep-ph/0406039 |
| 11 | G. F. Giudice and R. Rattazzi | Theories with gauge mediated supersymmetry breaking | Phys. Rept. 322 (1999) 419 | hep-ph/9801271 |
| 12 | P. Meade, N. Seiberg, and D. Shih | General gauge mediation | Prog. Theor. Phys. Suppl. 177 (2009) 143 | 0801.3278 |
| 13 | M. Buican, P. Meade, N. Seiberg, and D. Shih | Exploring general gauge mediation | JHEP 03 (2009) 016 | 0812.3668 |
| 14 | J. Fan, M. Reece, and J. T. Ruderman | Stealth supersymmetry | JHEP 11 (2011) 012 | 1105.5135 |
| 15 | J. Fan, M. Reece, and J. T. Ruderman | A stealth supersymmetry sampler | JHEP 07 (2012) 196 | 1201.4875 |
| 16 | M. J. Strassler and K. M. Zurek | Echoes of a hidden valley at hadron colliders | PLB 651 (2007) 374 | hep-ph/0604261 |
| 17 | M. J. Strassler and K. M. Zurek | Discovering the Higgs through highly-displaced vertices | PLB 661 (2008) 263 | hep-ph/0605193 |
| 18 | T. Han, Z. Si, K. M. Zurek, and M. J. Strassler | Phenomenology of hidden valleys at hadron colliders | JHEP 07 (2008) 008 | 0712.2041 |
| 19 | D. Smith and N. Weiner | Inelastic dark matter | PRD 64 (2001) 043502 | hep-ph/0101138 |
| 20 | Z. Chacko, H.-S. Goh, and R. Harnik | Natural electroweak breaking from a mirror symmetry | PRL 96 (2006) 231802 | hep-ph/0506256 |
| 21 | D. Curtin and C. B. Verhaaren | Discovering uncolored naturalness in exotic Higgs decays | JHEP 12 (2015) 072 | 1506.06141 |
| 22 | H.-C. Cheng, S. Jung, E. Salvioni, and Y. Tsai | Exotic quarks in twin Higgs models | JHEP 03 (2016) 074 | 1512.02647 |
| 23 | CMS Collaboration | Search for long-lived particles decaying in the CMS end cap muon detectors in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRL 127 (2021) 261804 | CMS-EXO-20-015 2107.04838 |
| 24 | CMS Collaboration | The CMS muon project: Technical Design Report | CMS Technical Design Report CERN-LHCC-97-032, 1997 CDS |
|
| 25 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 26 | CMS Collaboration | Search for long-lived particles using displaced jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 104 (2021) 012015 | CMS-EXO-19-021 2012.01581 |
| 27 | ATLAS Collaboration | Search for long-lived particles produced in pp collisions at $ \sqrt{s}= $ 13 TeV that decay into displaced hadronic jets in the ATLAS muon spectrometer | PRD 99 (2019) 052005 | 1811.07370 |
| 28 | ATLAS Collaboration | Search for events with a pair of displaced vertices from long-lived neutral particles decaying into hadronic jets in the ATLAS muon spectrometer in pp collisions at $ \sqrt{s} = $ 13 TeV | PRD 106 (2022) 032005 | 2203.00587 |
| 29 | S. Knapen, J. Shelton, and D. Xu | Perturbative benchmark models for a dark shower search program | PRD 103 (2021) 115013 | 2103.01238 |
| 30 | CMS Collaboration | HEPData record for this analysis | link | |
| 31 | CMS Collaboration | Performance of the CMS drift tube chambers with cosmic rays | JINST 5 (2010) T03015 | CMS-CFT-09-012 0911.4855 |
| 32 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 33 | CMS Collaboration | Performance of the CMS cathode strip chambers with cosmic rays | JINST 5 (2010) T03018 | CMS-CFT-09-011 0911.4992 |
| 34 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 35 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 36 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 37 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 38 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG \textscbox | JHEP 06 (2010) 043 | 1002.2581 |
| 39 | E. Re | Single-top $ \mathrm{W}\mathrm{t} $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 40 | F. Bezrukov and D. Gorbunov | Light inflaton after LHC8 and WMAP9 results | JHEP 07 (2013) 140 | 1303.4395 |
| 41 | M. W. Winkler | Decay and detection of a light scalar boson mixing with the Higgs boson | PRD 99 (2019) 015018 | 1809.01876 |
| 42 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 43 | L. Carloni, J. Rathsman, and T. Sjöstrand | Discerning secluded sector gauge structures | JHEP 04 (2011) 091 | 1102.3795 |
| 44 | L. Carloni and T. Sjöstrand | Visible effects of invisible Hidden Valley radiation | JHEP 09 (2010) 105 | 1006.2911 |
| 45 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 46 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 47 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 48 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 49 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 50 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 51 | CMS Collaboration | Performance of the reconstruction and identification of high-momentum muons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P02027 | CMS-MUO-17-001 1912.03516 |
| 52 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 53 | M. Cacciari, G. P. Salam, and G. Soyez | FASTJET user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 54 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 55 | CMS Collaboration | Missing transverse energy performance of the CMS detector | JINST 6 (2011) P09001 | CMS-JME-10-009 1106.5048 |
| 56 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 57 | M. Ester, H.-P. Kriegel, J. Sander, and X. Xu | A density-based algorithm for discovering clusters in large spatial databases with noise | in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996 link |
|
| 58 | CMS Collaboration | CMS jet algorithms performance in 13 TeV data | CMS Physics Analysis Summary, 2016 CMS-PAS-JME-16-003 |
CMS-PAS-JME-16-003 |
| 59 | G. Kasieczka, B. Nachman, M. D. Schwartz, and D. Shih | Automating the ABCD method with machine learning | PRD 103 (2021) 035021 | 2007.14400 |
| 60 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 61 | CMS Collaboration | CMS luminosity measurements for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2017 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 62 | CMS Collaboration | CMS luminosity measurements for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 63 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 64 | A. L. Read | Presentation of search results: the CL$ _\mathrm{s} $ technique | JPG 28 (2002) 2693 | |
| 65 | ATLAS and CMS Collaborations, The LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011 | |
| 66 | Y. Gershtein, S. Knapen, and D. Redigolo | Probing naturally light singlets with a displaced vertex trigger | PLB 823 (2021) 136758 | 2012.07864 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|