

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-21-011 ; CERN-EP-2024-161 | ||
| Search for long-lived heavy neutral leptons in proton-proton collision events with a lepton-jet pair associated with a secondary vertex at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 15 July 2024 | ||
| JHEP 02 (2025) 036 | ||
| Abstract: A search for long-lived heavy neutral leptons (HNLs) using proton-proton collision data corresponding to an integrated luminosity of 138 fb$ ^{-1} $ collected at $ \sqrt{s} = $ 13 TeV with the CMS detector at the CERN LHC is presented. Events are selected with a charged lepton originating from the primary vertex associated with the proton-proton interaction, as well as a second charged lepton and a hadronic jet associated with a secondary vertex that corresponds to the semileptonic decay of a long-lived HNL. No excess of events above the standard model expectation is observed. Exclusion limits at 95% confidence level are evaluated for HNLs that mix with electron and/or muon neutrinos. Limits are presented in the mass range of 1-16.5 GeV, with excluded square mixing parameter values reaching as low as 2 $ \times $ 10$^{-7} $. For masses above 11 GeV, the presented limits exceed all previous results in the semileptonic decay channel, and for some of the considered scenarios are the strongest to date. | ||
| Links: e-print arXiv:2407.10717 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures & Tables | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |
png pdf |
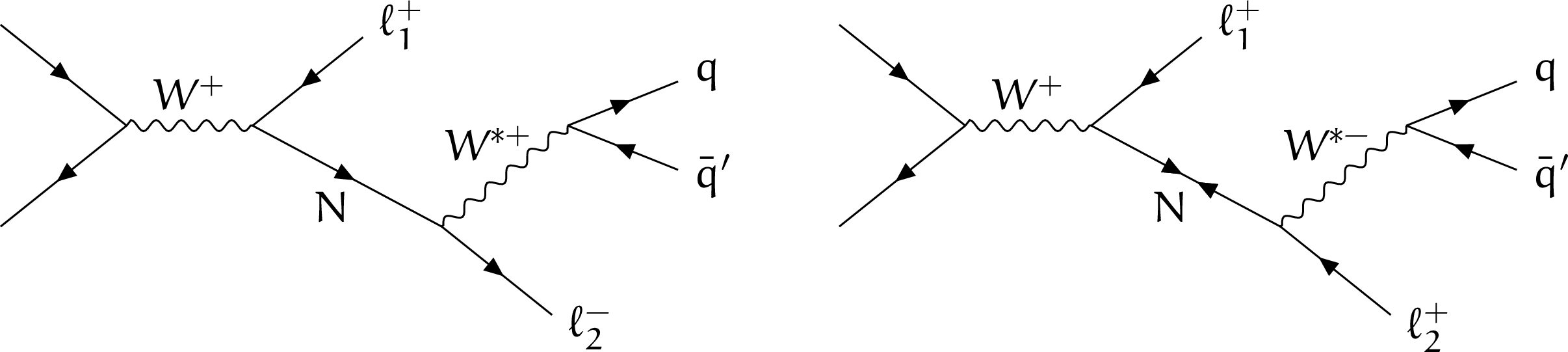
Figure 1:
Examples of LO Feynman diagrams for production and decay of an HNL (indicated with the symbol N) resulting in a final state with two charged leptons and two quarks. In the left diagram, the HNL is a Dirac particle and thus the two charged leptons must have opposite charge. In the right diagram, the HNL is a Majorana particle and the two charged leptons can have the same charge. |
png pdf |
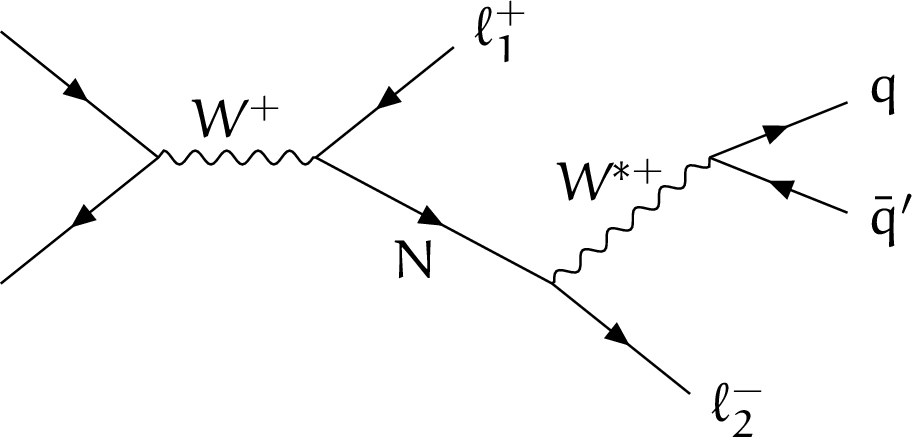
Figure 1-a:
Examples of LO Feynman diagrams for production and decay of an HNL (indicated with the symbol N) resulting in a final state with two charged leptons and two quarks. In the left diagram, the HNL is a Dirac particle and thus the two charged leptons must have opposite charge. In the right diagram, the HNL is a Majorana particle and the two charged leptons can have the same charge. |
png pdf |
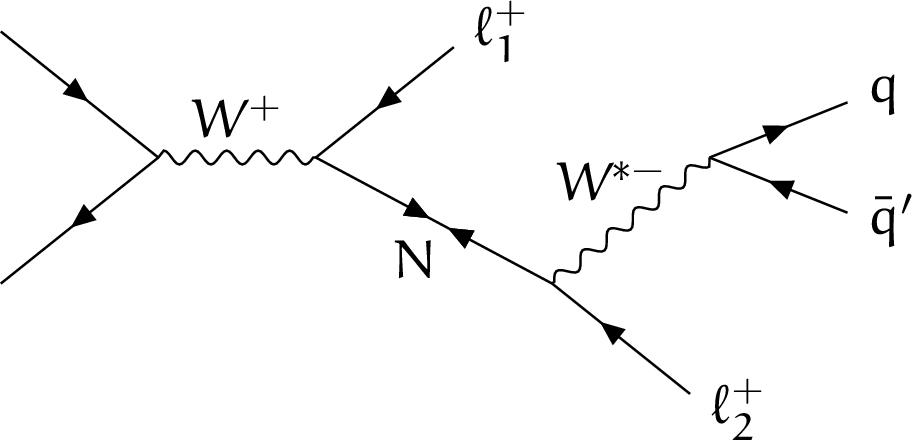
Figure 1-b:
Examples of LO Feynman diagrams for production and decay of an HNL (indicated with the symbol N) resulting in a final state with two charged leptons and two quarks. In the left diagram, the HNL is a Dirac particle and thus the two charged leptons must have opposite charge. In the right diagram, the HNL is a Majorana particle and the two charged leptons can have the same charge. |
png pdf |
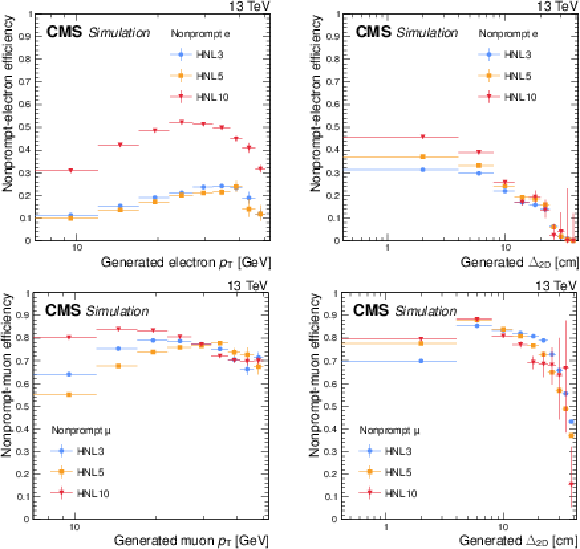
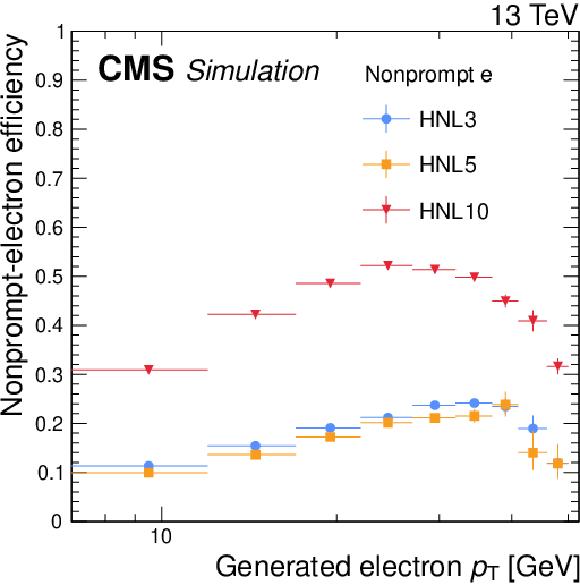
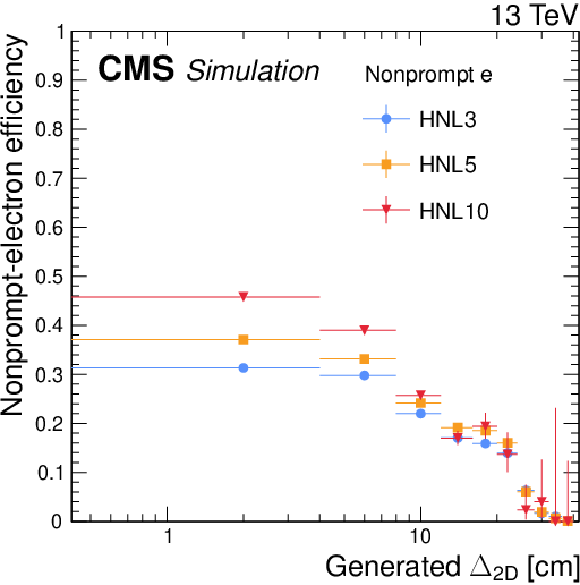
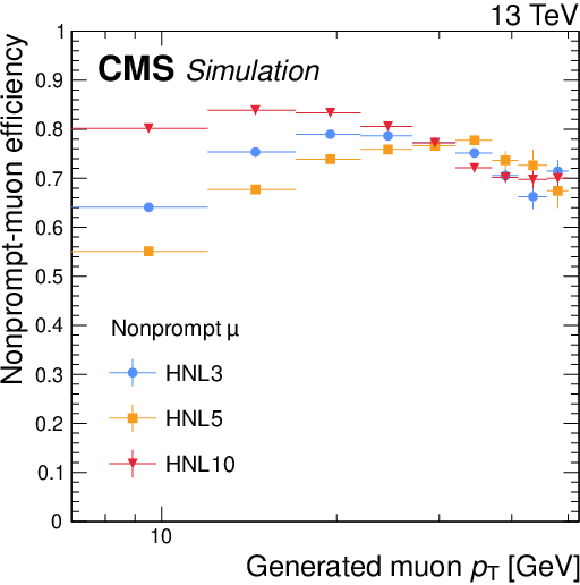
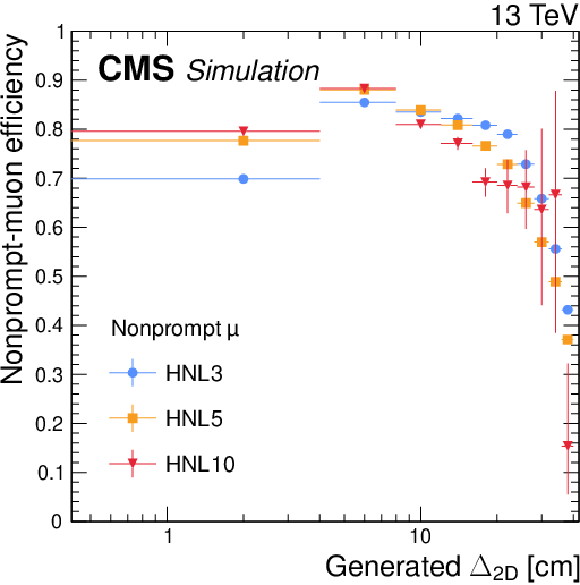
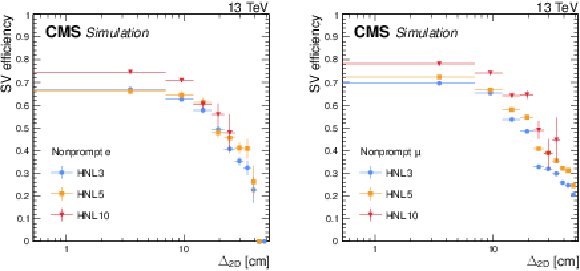
Figure 2:
Selection efficiencies of nonprompt electrons (upper) and muons (lower), evaluated in simulated HNL signal events as functions of the generated lepton $ p_{\mathrm{T}} $ (left) and transverse displacement of the generated SV (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 2-a:
Selection efficiencies of nonprompt electrons (upper) and muons (lower), evaluated in simulated HNL signal events as functions of the generated lepton $ p_{\mathrm{T}} $ (left) and transverse displacement of the generated SV (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 2-b:
Selection efficiencies of nonprompt electrons (upper) and muons (lower), evaluated in simulated HNL signal events as functions of the generated lepton $ p_{\mathrm{T}} $ (left) and transverse displacement of the generated SV (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 2-c:
Selection efficiencies of nonprompt electrons (upper) and muons (lower), evaluated in simulated HNL signal events as functions of the generated lepton $ p_{\mathrm{T}} $ (left) and transverse displacement of the generated SV (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 2-d:
Selection efficiencies of nonprompt electrons (upper) and muons (lower), evaluated in simulated HNL signal events as functions of the generated lepton $ p_{\mathrm{T}} $ (left) and transverse displacement of the generated SV (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
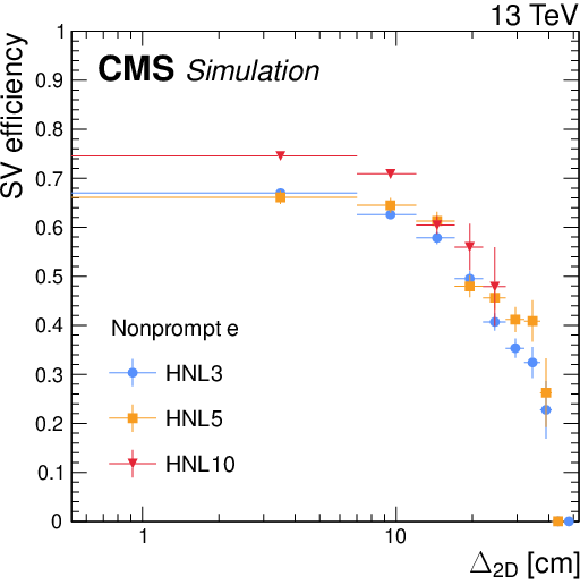
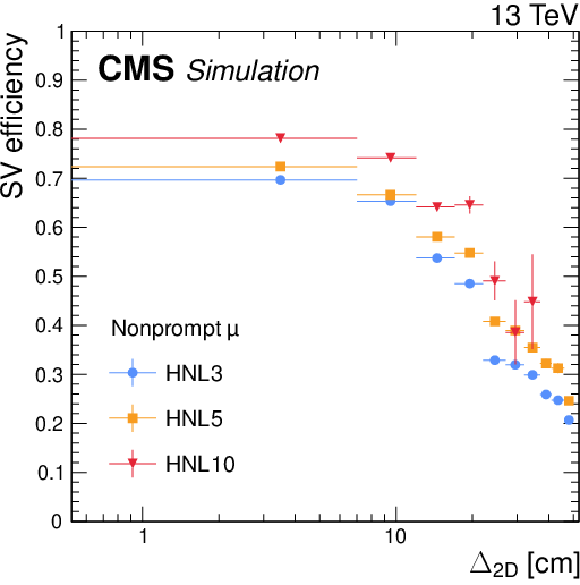
Figure 3:
The SV reconstruction efficiency in simulated HNL signal events as a function of the SV displacement for vertices with a nonprompt electron (left) or muon (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 3-a:
The SV reconstruction efficiency in simulated HNL signal events as a function of the SV displacement for vertices with a nonprompt electron (left) or muon (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
Figure 3-b:
The SV reconstruction efficiency in simulated HNL signal events as a function of the SV displacement for vertices with a nonprompt electron (left) or muon (right). Three HNL signal scenarios are shown, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3, corresponding to $ c\tau_{\mathrm{N}} = $ 23 mm), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 1.6 $\times$ 10$^{-6} $ (HNL5, corresponding to $ c\tau_{\mathrm{N}} = $ 92 mm), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2= $ 5.7 $\times$ 10$^{-7} $ (HNL10, corresponding to $ c\tau_{\mathrm{N}} = $ 7 mm). The error bars in the plot represent statistical uncertainties. |
png pdf |
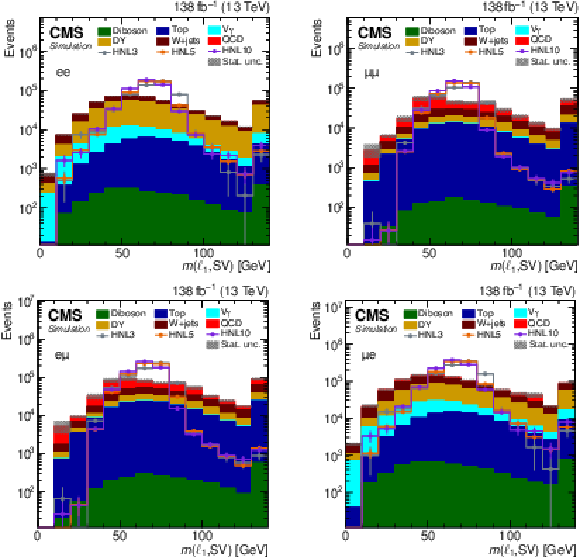
Figure 4:
The $ m(\ell_1,\text{SV}) $ distribution of predicted events yields after applying the selection summarized in Table 1, for the $ \mathrm{e}\mathrm{e} $ (upper left), $ \mu\mu $ (upper right), $ \mathrm{e}\mu $ (lower left), and $ \mu\mathrm{e} $ (lower right) categories. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-5} $ (HNL5), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bins include the overflow. |
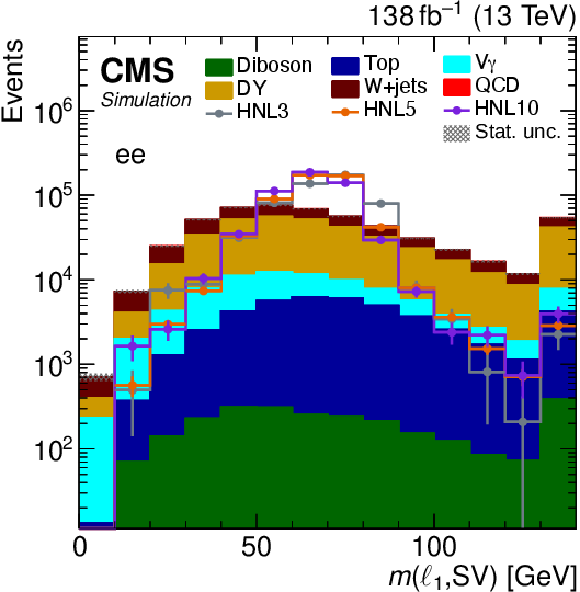
png pdf |
Figure 4-a:
The $ m(\ell_1,\text{SV}) $ distribution of predicted events yields after applying the selection summarized in Table 1, for the $ \mathrm{e}\mathrm{e} $ (upper left), $ \mu\mu $ (upper right), $ \mathrm{e}\mu $ (lower left), and $ \mu\mathrm{e} $ (lower right) categories. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-5} $ (HNL5), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bins include the overflow. |
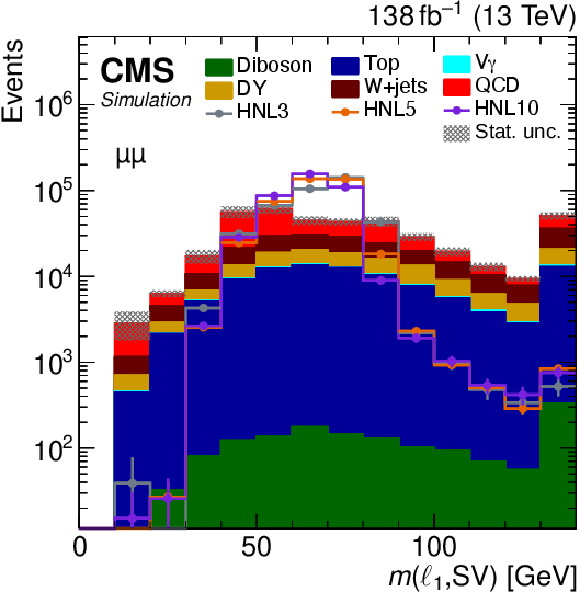
png pdf |
Figure 4-b:
The $ m(\ell_1,\text{SV}) $ distribution of predicted events yields after applying the selection summarized in Table 1, for the $ \mathrm{e}\mathrm{e} $ (upper left), $ \mu\mu $ (upper right), $ \mathrm{e}\mu $ (lower left), and $ \mu\mathrm{e} $ (lower right) categories. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-5} $ (HNL5), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bins include the overflow. |
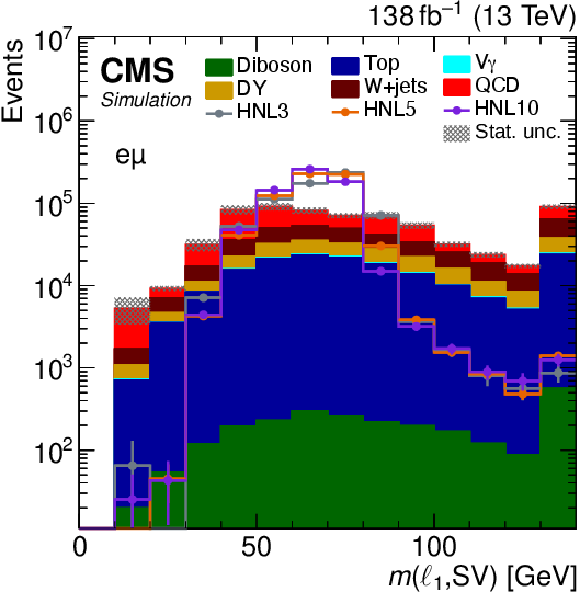
png pdf |
Figure 4-c:
The $ m(\ell_1,\text{SV}) $ distribution of predicted events yields after applying the selection summarized in Table 1, for the $ \mathrm{e}\mathrm{e} $ (upper left), $ \mu\mu $ (upper right), $ \mathrm{e}\mu $ (lower left), and $ \mu\mathrm{e} $ (lower right) categories. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-5} $ (HNL5), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bins include the overflow. |
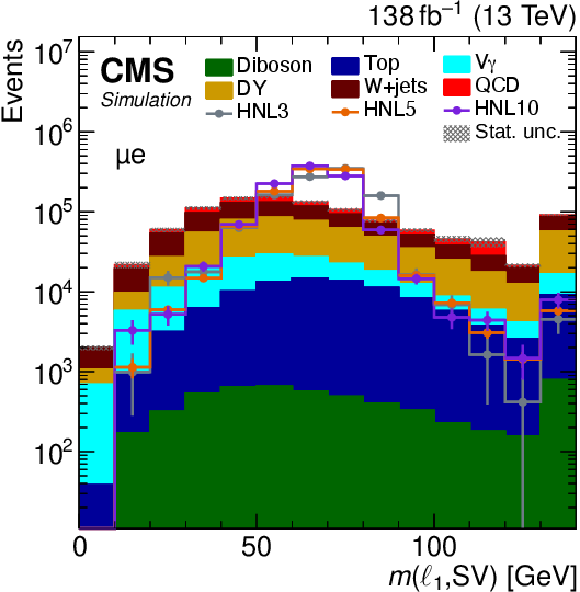
png pdf |
Figure 4-d:
The $ m(\ell_1,\text{SV}) $ distribution of predicted events yields after applying the selection summarized in Table 1, for the $ \mathrm{e}\mathrm{e} $ (upper left), $ \mu\mu $ (upper right), $ \mathrm{e}\mu $ (lower left), and $ \mu\mathrm{e} $ (lower right) categories. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-5} $ (HNL5), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bins include the overflow. |
png pdf |
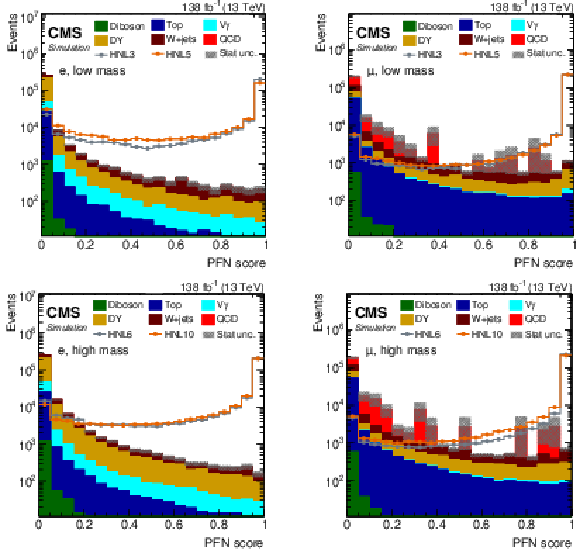
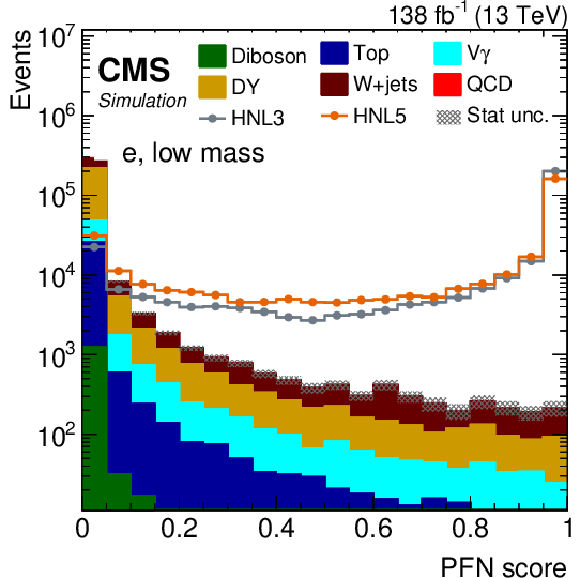
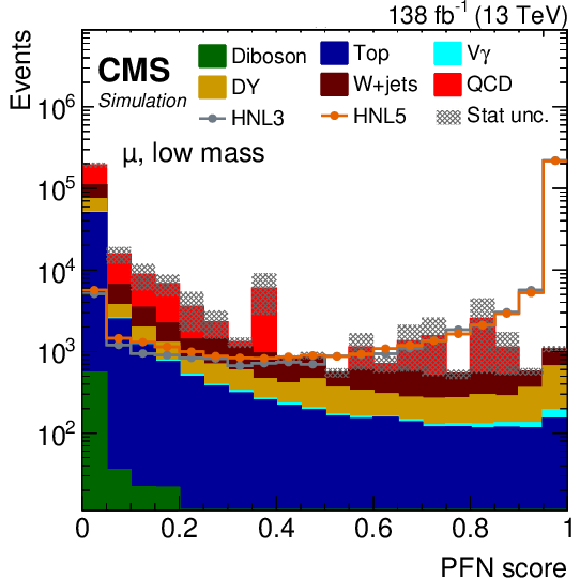
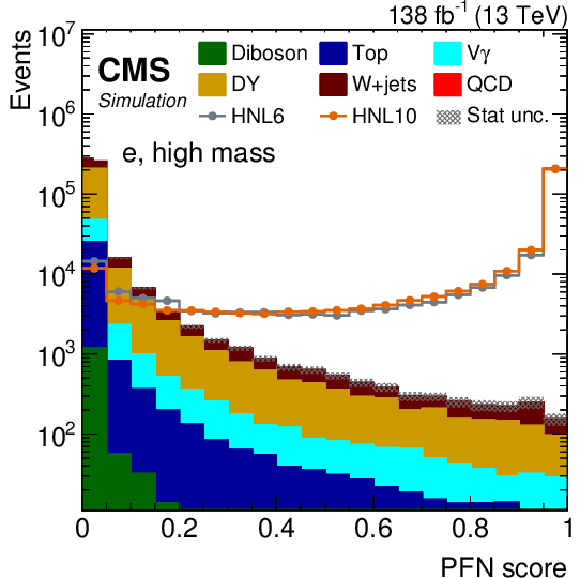
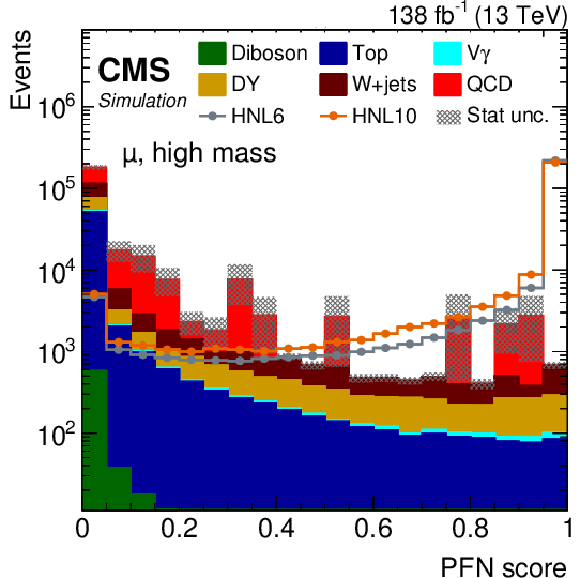
Figure 5:
The PFN score distribution of predicted events yields after applying the selection summarized in Table 1, for the combined $ \mathrm{e}\mathrm{e} $ and $ \mu\mathrm{e} $ (left) or $ \mu\mu $ and $ \mathrm{e}\mu $ (right) categories, using the low-mass (upper) or high-mass (lower) PFNs. The filled histograms display the predicted background yields, where the QCD multijet background displays huge statistical fluctuations for PFN scores above 0.2. The lines show the predicted yields for four HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5), $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-6} $ (HNL6), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
Figure 5-a:
The PFN score distribution of predicted events yields after applying the selection summarized in Table 1, for the combined $ \mathrm{e}\mathrm{e} $ and $ \mu\mathrm{e} $ (left) or $ \mu\mu $ and $ \mathrm{e}\mu $ (right) categories, using the low-mass (upper) or high-mass (lower) PFNs. The filled histograms display the predicted background yields, where the QCD multijet background displays huge statistical fluctuations for PFN scores above 0.2. The lines show the predicted yields for four HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5), $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-6} $ (HNL6), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
Figure 5-b:
The PFN score distribution of predicted events yields after applying the selection summarized in Table 1, for the combined $ \mathrm{e}\mathrm{e} $ and $ \mu\mathrm{e} $ (left) or $ \mu\mu $ and $ \mathrm{e}\mu $ (right) categories, using the low-mass (upper) or high-mass (lower) PFNs. The filled histograms display the predicted background yields, where the QCD multijet background displays huge statistical fluctuations for PFN scores above 0.2. The lines show the predicted yields for four HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5), $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-6} $ (HNL6), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
Figure 5-c:
The PFN score distribution of predicted events yields after applying the selection summarized in Table 1, for the combined $ \mathrm{e}\mathrm{e} $ and $ \mu\mathrm{e} $ (left) or $ \mu\mu $ and $ \mathrm{e}\mu $ (right) categories, using the low-mass (upper) or high-mass (lower) PFNs. The filled histograms display the predicted background yields, where the QCD multijet background displays huge statistical fluctuations for PFN scores above 0.2. The lines show the predicted yields for four HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5), $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-6} $ (HNL6), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
Figure 5-d:
The PFN score distribution of predicted events yields after applying the selection summarized in Table 1, for the combined $ \mathrm{e}\mathrm{e} $ and $ \mu\mathrm{e} $ (left) or $ \mu\mu $ and $ \mathrm{e}\mu $ (right) categories, using the low-mass (upper) or high-mass (lower) PFNs. The filled histograms display the predicted background yields, where the QCD multijet background displays huge statistical fluctuations for PFN scores above 0.2. The lines show the predicted yields for four HNL signal scenarios, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5), $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-6} $ (HNL6), and $ m_{\mathrm{N}} = $ 10 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
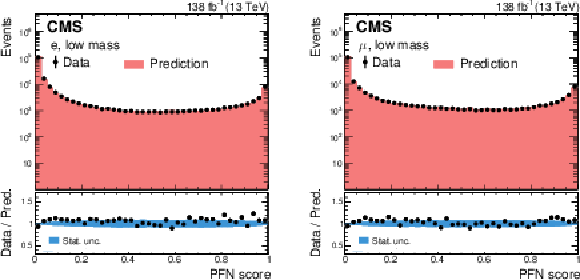
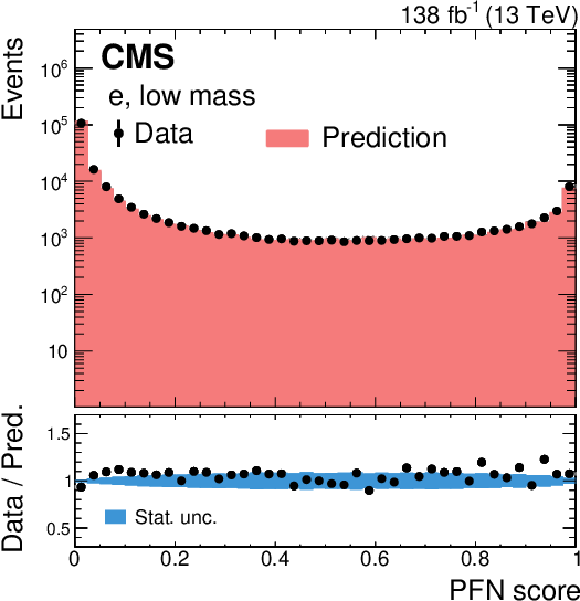
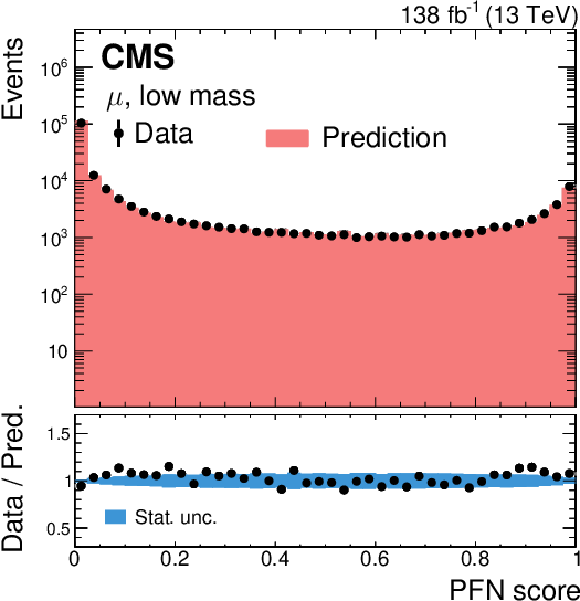
Figure 6:
Predicted and observed event yields in the PFN score distribution for $ \mathrm{K^0_S}\to\pi^{+}\pi^{-} $ decays in $ \mathrm{Z}\to\mu^{+}\mu^{-} $ events, using the low-mass PFNs for the electron (left) and muon (right) channels, where the $ \pi^{\pm} $ with higher $ p_{\mathrm{T}} $ is treated as the lepton. The prediction is scaled to match the overall data yield. The lower panels show the data-to-prediction ratio. |
png pdf |
Figure 6-a:
Predicted and observed event yields in the PFN score distribution for $ \mathrm{K^0_S}\to\pi^{+}\pi^{-} $ decays in $ \mathrm{Z}\to\mu^{+}\mu^{-} $ events, using the low-mass PFNs for the electron (left) and muon (right) channels, where the $ \pi^{\pm} $ with higher $ p_{\mathrm{T}} $ is treated as the lepton. The prediction is scaled to match the overall data yield. The lower panels show the data-to-prediction ratio. |
png pdf |
Figure 6-b:
Predicted and observed event yields in the PFN score distribution for $ \mathrm{K^0_S}\to\pi^{+}\pi^{-} $ decays in $ \mathrm{Z}\to\mu^{+}\mu^{-} $ events, using the low-mass PFNs for the electron (left) and muon (right) channels, where the $ \pi^{\pm} $ with higher $ p_{\mathrm{T}} $ is treated as the lepton. The prediction is scaled to match the overall data yield. The lower panels show the data-to-prediction ratio. |
png pdf |
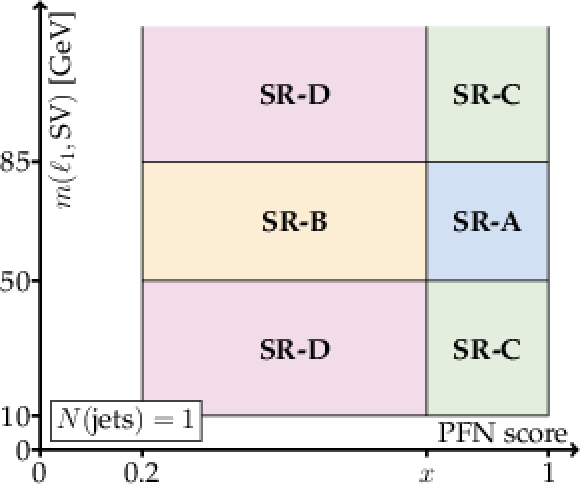
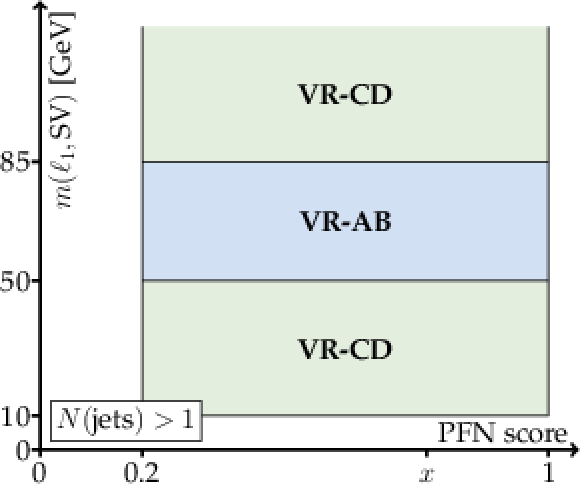
Figure 7:
Illustration of the target and sideband region definitions for the ABCD method applied to the SR, in terms of $ N $ (jets), $ m(\ell_1,\text{SV}) $, and the PFN score. |
png pdf |
Figure 8:
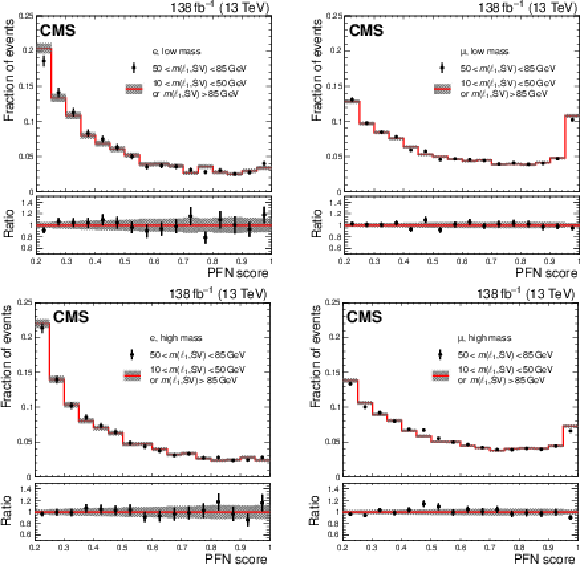
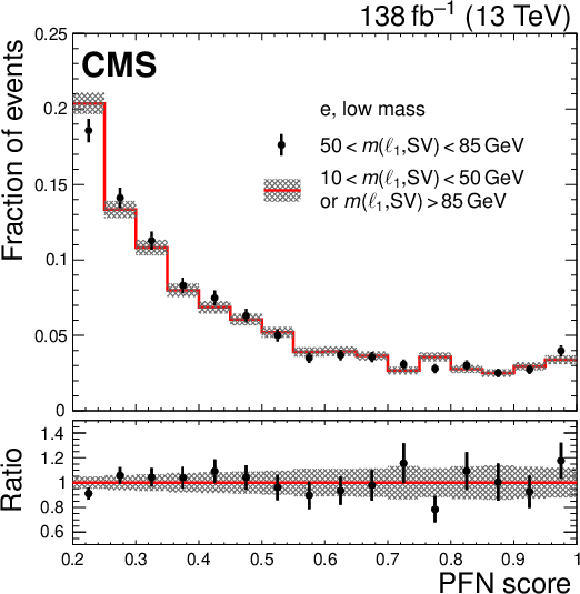
The PFN scores in data in the VR, shown for the electron (left) and muon (right) trainings with the low-mass (upper) and high-mass (lower) samples. The distributions are normalized to unity to facilitate a shape comparison. Statistical uncertainties are indicated with error bars and shaded areas. The lower panels show the ratio of the VR-AB to the VR-CD yields. |
png pdf |
Figure 8-a:
The PFN scores in data in the VR, shown for the electron (left) and muon (right) trainings with the low-mass (upper) and high-mass (lower) samples. The distributions are normalized to unity to facilitate a shape comparison. Statistical uncertainties are indicated with error bars and shaded areas. The lower panels show the ratio of the VR-AB to the VR-CD yields. |
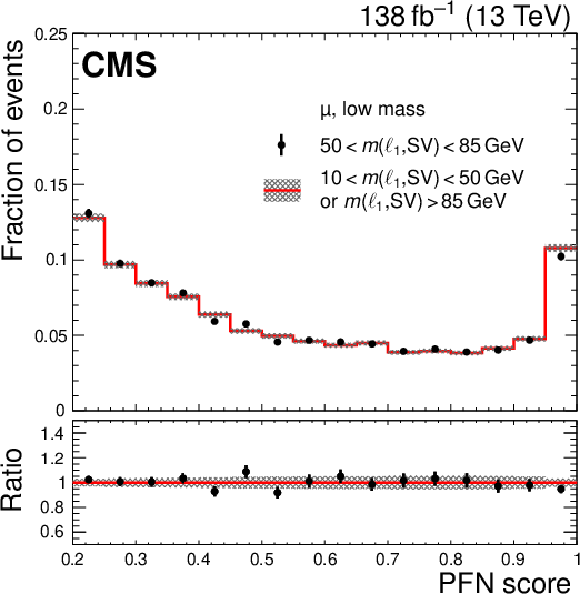
png pdf |
Figure 8-b:
The PFN scores in data in the VR, shown for the electron (left) and muon (right) trainings with the low-mass (upper) and high-mass (lower) samples. The distributions are normalized to unity to facilitate a shape comparison. Statistical uncertainties are indicated with error bars and shaded areas. The lower panels show the ratio of the VR-AB to the VR-CD yields. |
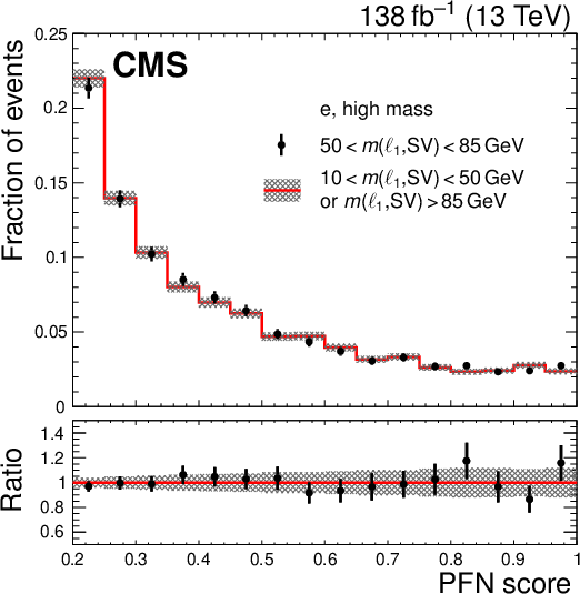
png pdf |
Figure 8-c:
The PFN scores in data in the VR, shown for the electron (left) and muon (right) trainings with the low-mass (upper) and high-mass (lower) samples. The distributions are normalized to unity to facilitate a shape comparison. Statistical uncertainties are indicated with error bars and shaded areas. The lower panels show the ratio of the VR-AB to the VR-CD yields. |
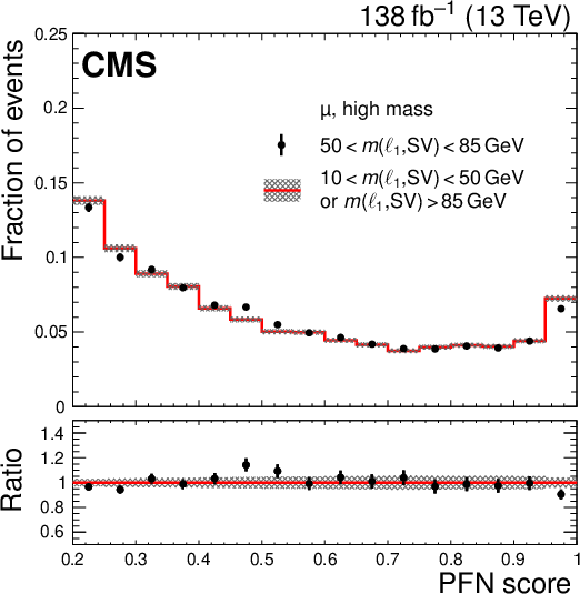
png pdf |
Figure 8-d:
The PFN scores in data in the VR, shown for the electron (left) and muon (right) trainings with the low-mass (upper) and high-mass (lower) samples. The distributions are normalized to unity to facilitate a shape comparison. Statistical uncertainties are indicated with error bars and shaded areas. The lower panels show the ratio of the VR-AB to the VR-CD yields. |
png pdf |
Figure 9:
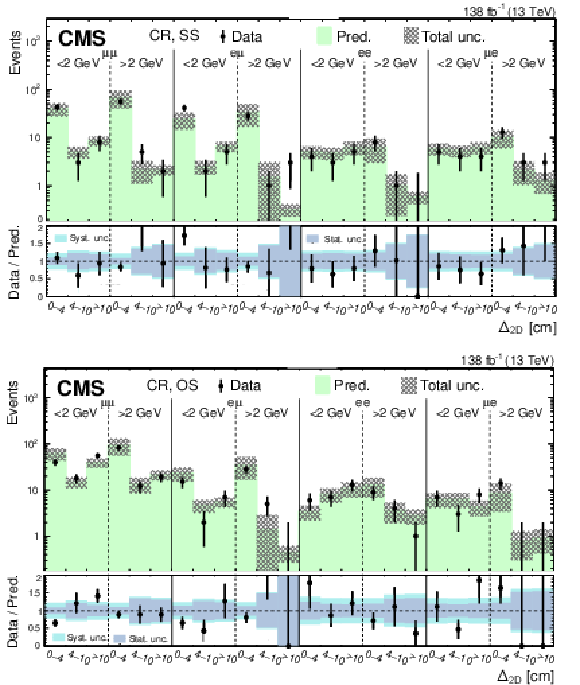
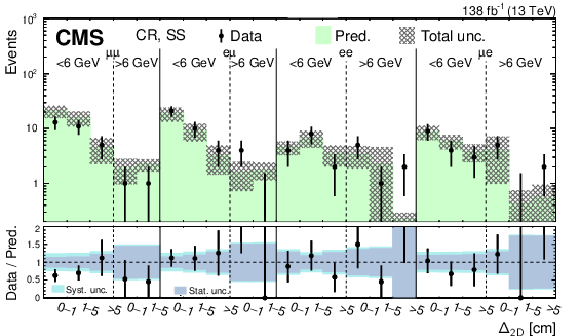
Predicted and observed event yields in the CR for the low-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
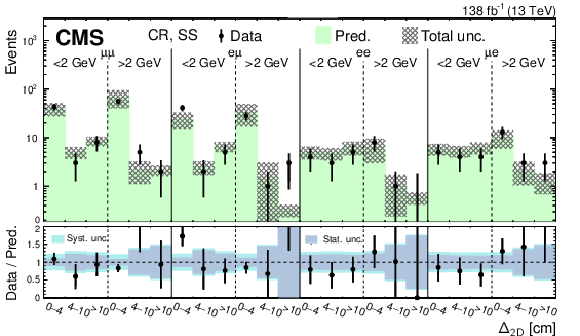
png pdf |
Figure 9-a:
Predicted and observed event yields in the CR for the low-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
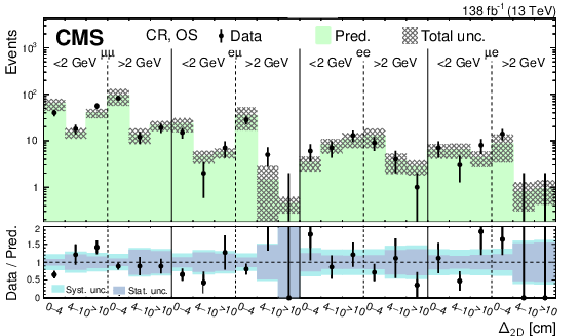
png pdf |
Figure 9-b:
Predicted and observed event yields in the CR for the low-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
png pdf |
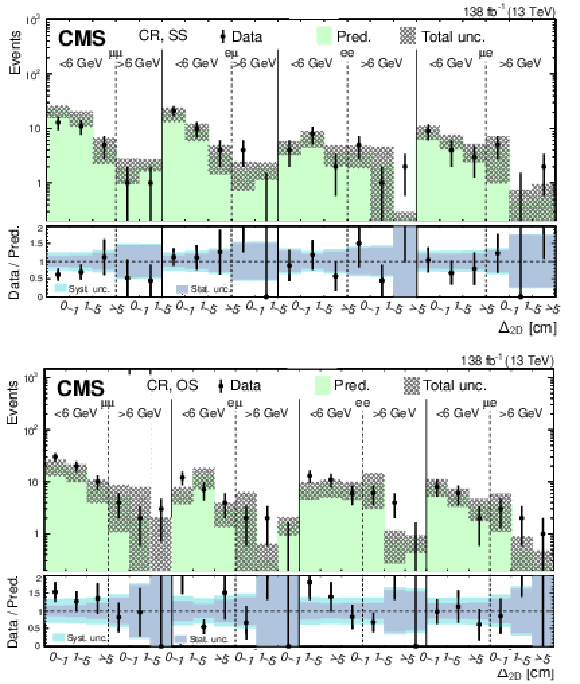
Figure 10:
Predicted and observed event yields in the CR for the high-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
png pdf |
Figure 10-a:
Predicted and observed event yields in the CR for the high-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
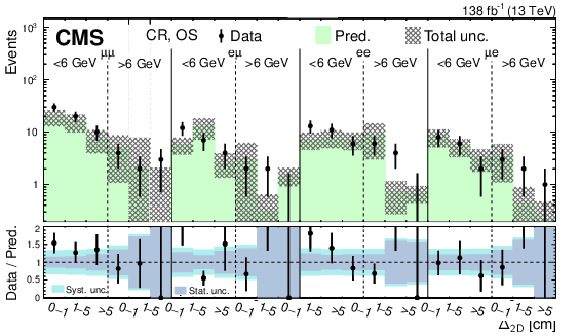
png pdf |
Figure 10-b:
Predicted and observed event yields in the CR for the high-mass PFNs in the SS (upper) and OS (lower) categories, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed bands represent the total uncertainty in the background prediction. The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
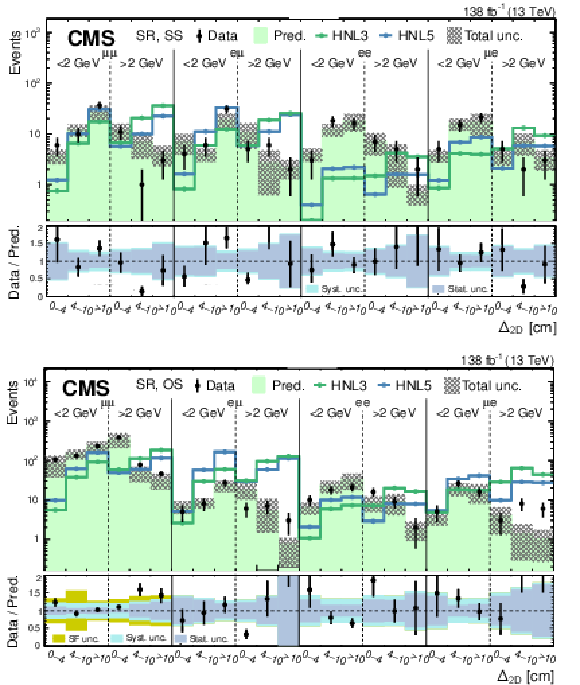
png pdf |
Figure 11:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the low-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), and $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical, main systematic, and DY scale factor contributions. |
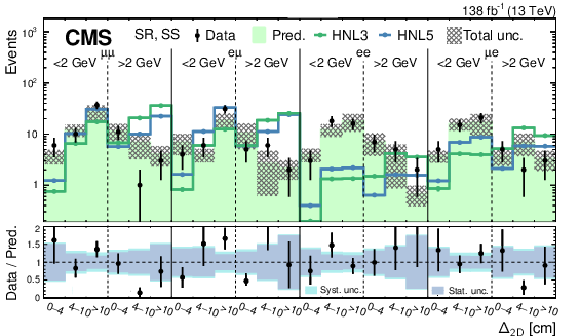
png pdf |
Figure 11-a:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the low-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), and $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical, main systematic, and DY scale factor contributions. |
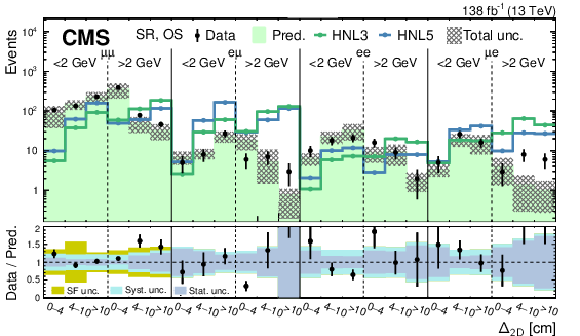
png pdf |
Figure 11-b:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the low-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 3 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 9.9 $\times$ 10$^{-5} $ (HNL3), and $ m_{\mathrm{N}} = $ 5 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 1.6 $\times$ 10$^{-6} $ (HNL5). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical, main systematic, and DY scale factor contributions. |
png pdf |
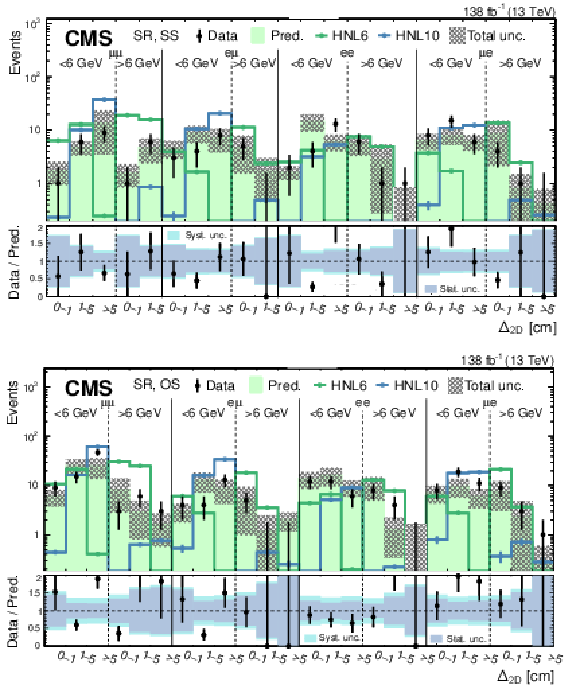
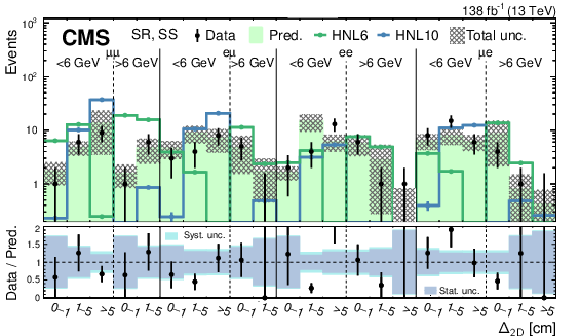
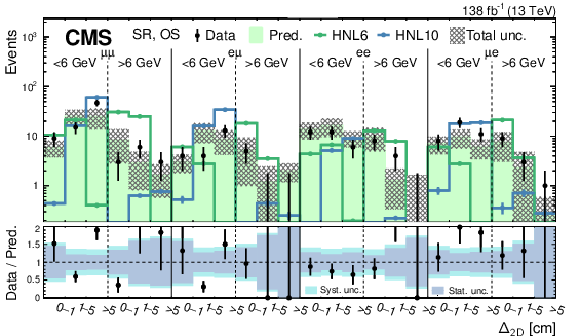
Figure 12:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the high-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-7} $ (HNL6), and $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
png pdf |
Figure 12-a:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the high-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-7} $ (HNL6), and $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
png pdf |
Figure 12-b:
Predicted and observed SR event yields for the SS (upper) and OS (lower) categories of the high-mass PFNs, binned by flavor channel, $ m_{\text{SV}} $ (as specified below the flavor channel), and $ \Delta_{\mathrm{2D}} $. The hashed band represents the total systematic and statistical uncertainty in the background prediction. Signal predictions are shown for two HNL production hypotheses, with $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 2.0 $\times$ 10$^{-7} $ (HNL6), and $ m_{\mathrm{N}} = $ 6 GeV and $ |V_{\ell{\mathrm{N}} }|^2=$ 5.7 $\times$ 10$^{-7} $ (HNL10). The lower panels show the data-to-prediction ratio and the background prediction uncertainty is split into statistical and systematic contributions. |
png pdf |
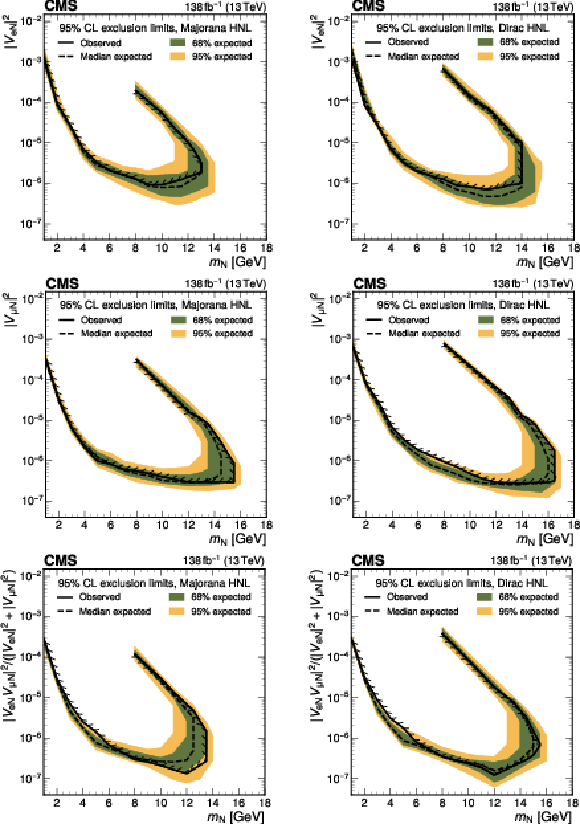
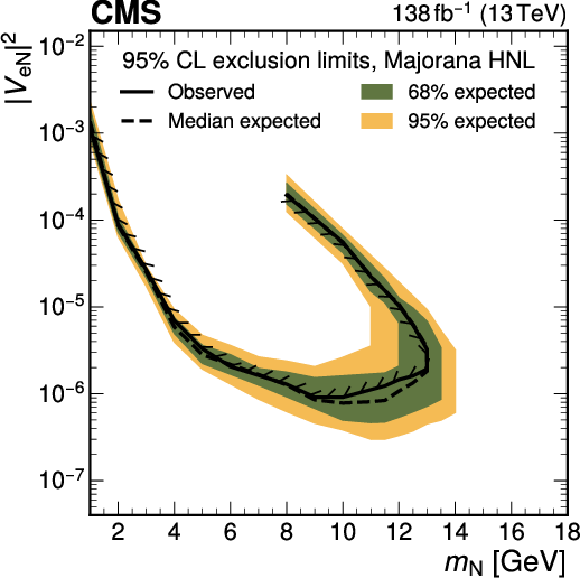
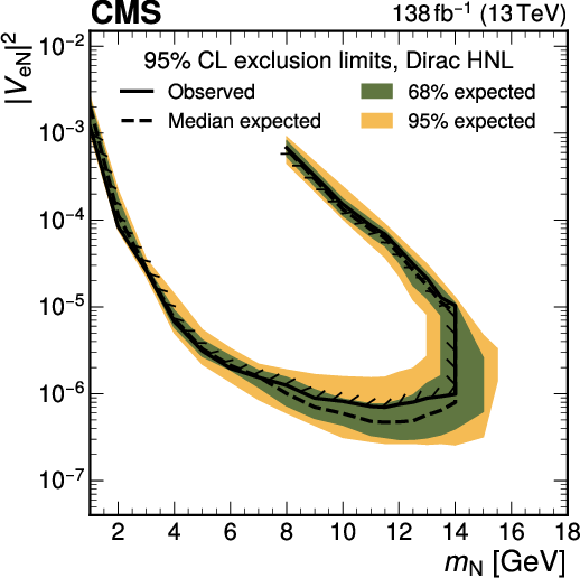
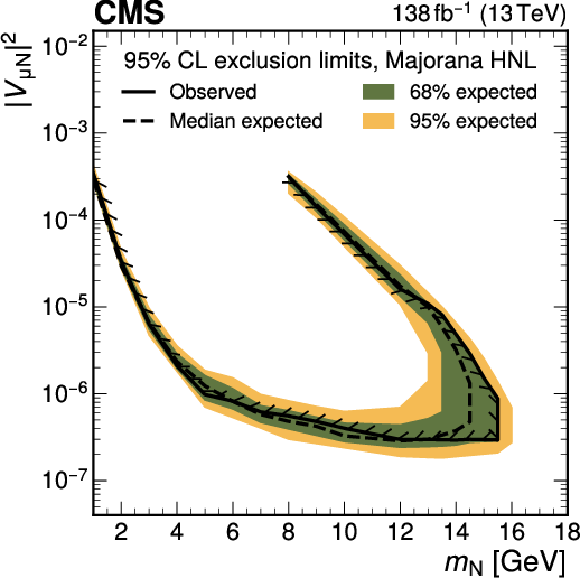
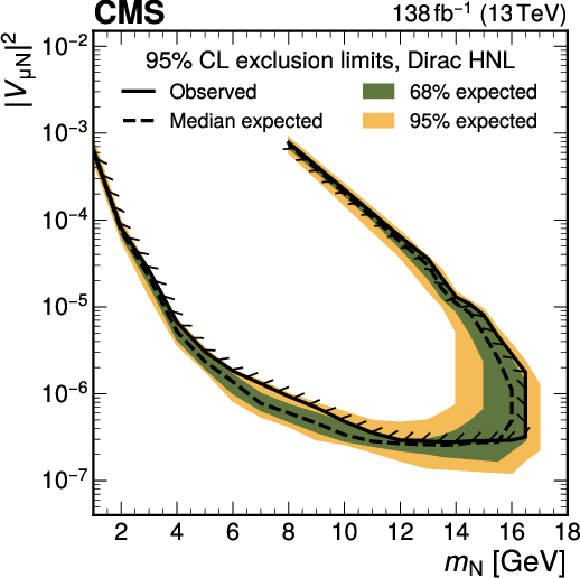
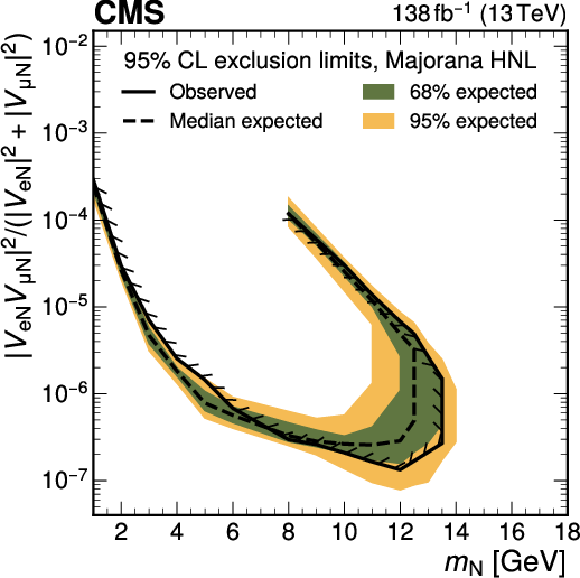
Figure 13:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
png pdf |
Figure 13-a:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
png pdf |
Figure 13-b:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
png pdf |
Figure 13-c:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
png pdf |
Figure 13-d:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
png pdf |
Figure 13-e:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
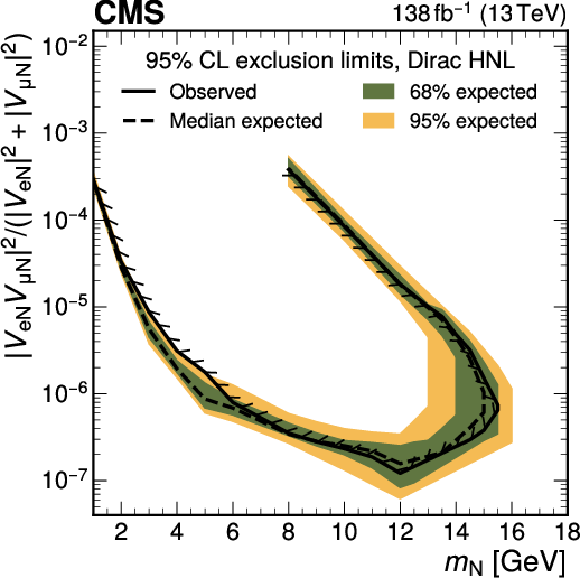
png pdf |
Figure 13-f:
Exclusion limits at 95% CL on $ |V_{\mathrm{e}{\mathrm{N}} }|^2 $ (upper row), $ |V_{\mu{\mathrm{N}} }|^2 $ (middle row), and $ |V_{\mathrm{e}{\mathrm{N}} }V_{\mu{\mathrm{N}} }|^2/(|V_{\mathrm{e}{\mathrm{N}} }|^2+|V_{\mu{\mathrm{N}} }|^2) $ (lower row) as functions of $ m_{\mathrm{N}} $ for a Majorana (left) and Dirac (right) HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. |
| Tables | |

png pdf |
Table 1:
Selection criteria for electrons and muons. Numbers in parentheses indicate values applied in the 2017-2018 data sets, when different from those for 2016. |

png pdf |
Table 2:
Summary of the event selection criteria. |
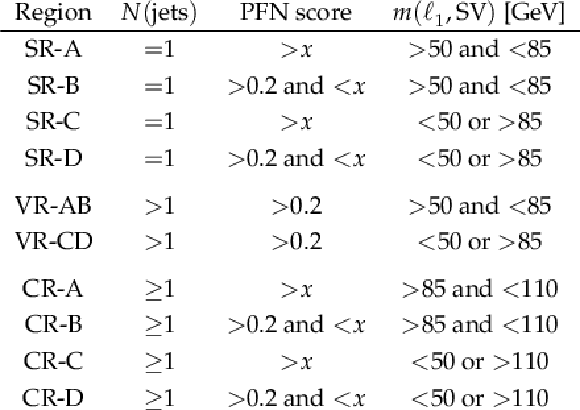
png pdf |
Table 3:
Definition of target and sideband regions used in the ABCD background estimation method for the signal (SR), validation (VR), and control (CR) regions. The threshold value $ x $ is chosen between 0.97 and 0.998 separately for each event category, as described in the text. |
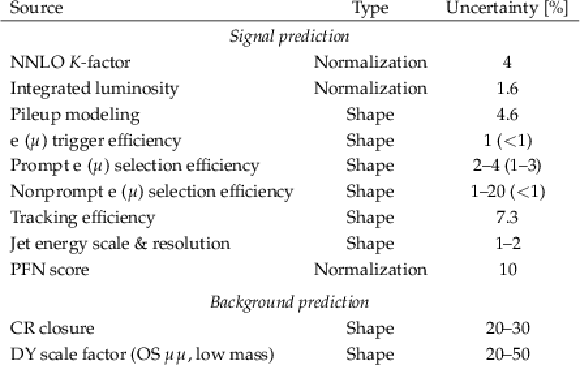
png pdf |
Table 4:
Summary of systematic uncertainty sources in the signal and background predictions. |

png pdf |
Table 5:
Comparison of lowest and highest $ |V_{\ell{\mathrm{N}} }|^2 $ values excluded at 95% CL for Majorana and Dirac HNLs with different coupling scenarios. For each scenario, the $ m_{\mathrm{N}} $ value where the lowest $ |V_{\ell{\mathrm{N}} }|^2 $ value is excluded is shown. |
| Summary |
| A search for long-lived heavy neutral leptons (HNLs) has been presented using proton-proton collision events with one prompt lepton and a system of a nonprompt lepton and a jet associated with a secondary vertex. The data set corresponds to 138 fb$ ^{-1} $ and was collected by the CMS experiment at the LHC in 2016-2018. A dedicated machine-learning method is developed and utilized to identify the secondary vertex associated with the HNL decay. No excess of events above the standard model background prediction obtained from control samples in data is found. Exclusion limits at 95% confidence level are evaluated for different HNL coupling scenarios as functions of the HNL mass and the mixing parameter with standard model neutrinos. The obtained exclusion limits cover HNL masses from 1 to 16.5 GeV and squared mixing parameters as low as 2 $ \times $ 10$^{-7} $, depending on the scenario. These results exceed previous experimental constraints derived in the single-lepton decay channel in the mass range 11-16.5 GeV. For some of the considered coupling scenarios and mass ranges, the presented limits are the strongest to date. |
| Additional Figures | |
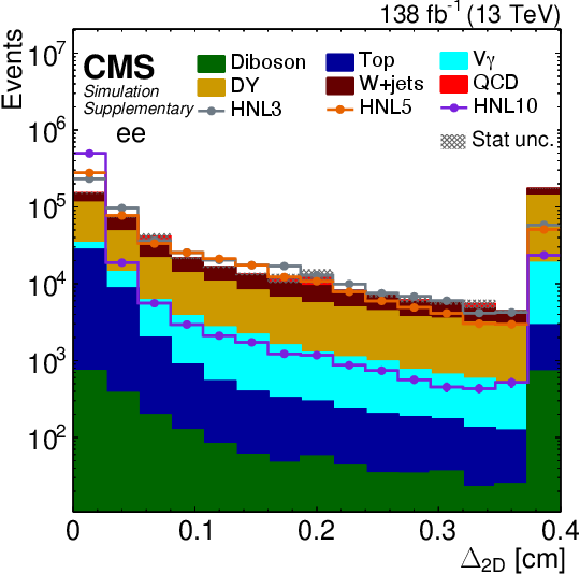
png pdf |
Additional Figure 1:
Distribution of predicted event yields as a function of $ \Delta_{\mathrm{2D}} $ after applying the baseline event selection for the $ \mathrm{ee} $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
Additional Figure 2:
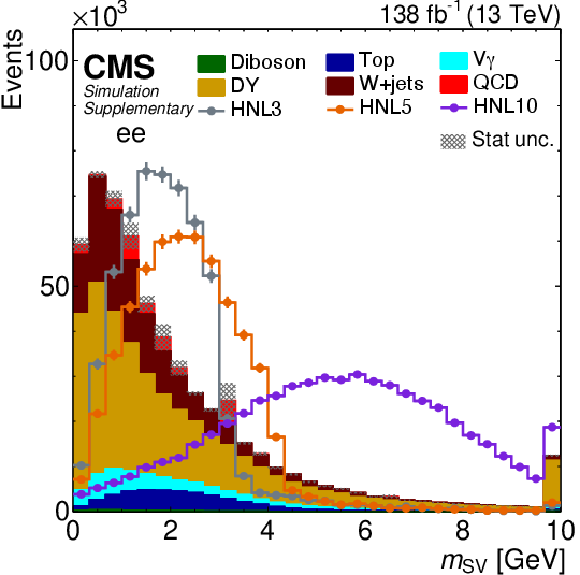
Distribution of predicted event yields as a function of $ m_{\mathrm{SV}} $ after applying the baseline event selection for the $ \mathrm{ee} $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
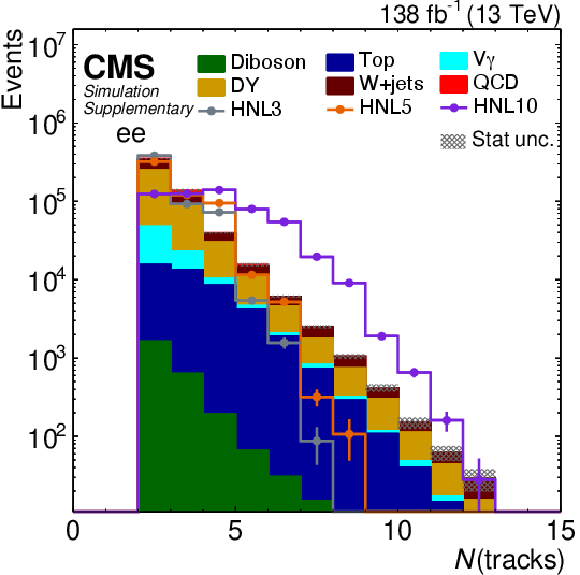
Additional Figure 3:
Distribution of predicted event yields as a function of the track multiplicity after applying the baseline event selection for the $ \mathrm{ee} $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
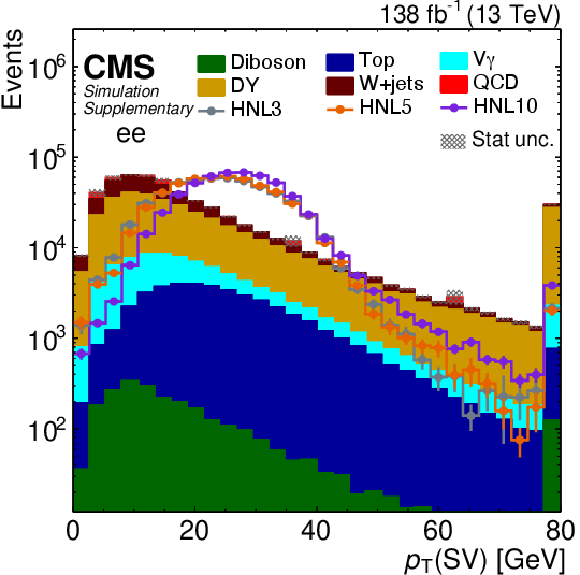
Additional Figure 4:
Distribution of predicted event yields as a function of the $ p_{\mathrm{T}} $ of the SV after applying the baseline event selection for the $ \mathrm{ee} $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
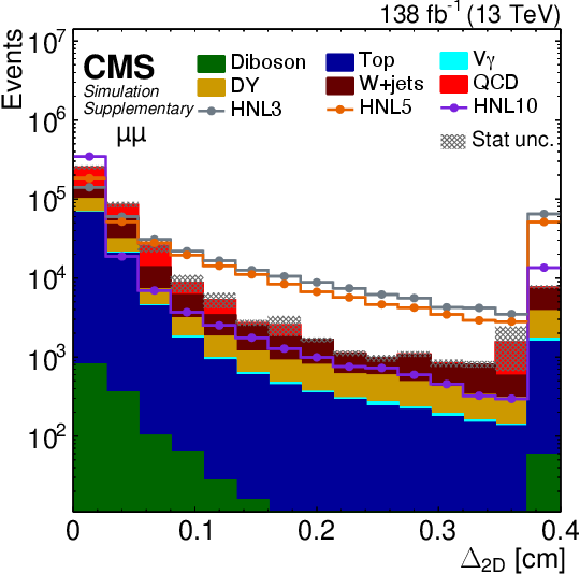
Additional Figure 5:
Distribution of predicted event yields as a function of $ \Delta_{\mathrm{2D}} $ after applying the baseline event selection for the $ \mu\mu $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
Additional Figure 6:
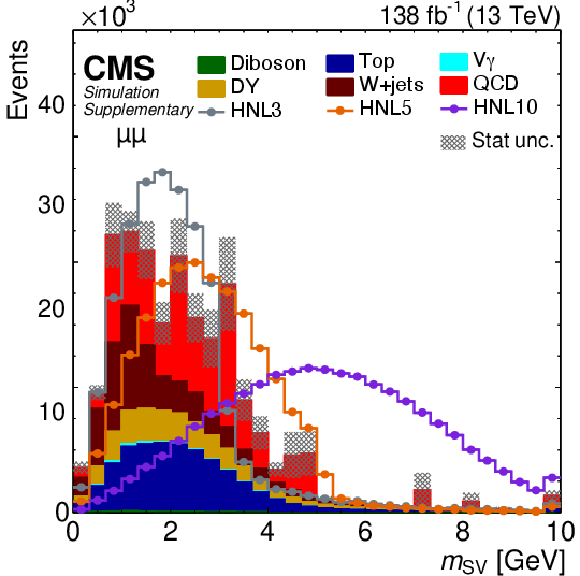
Distribution of predicted event yields as a function of $ m_{\mathrm{SV}} $ after applying the baseline event selection for the $ \mu\mu $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
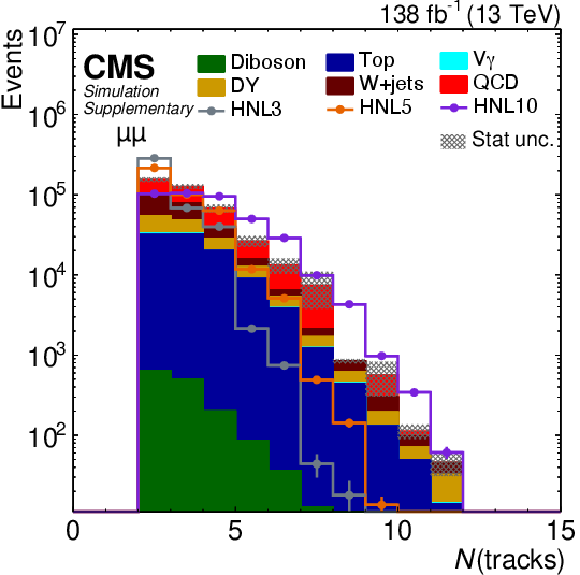
Additional Figure 7:
Distribution of predicted event yields as a function of the track multiplicity after applying the baseline event selection for the $ \mu\mu $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. |
png pdf |
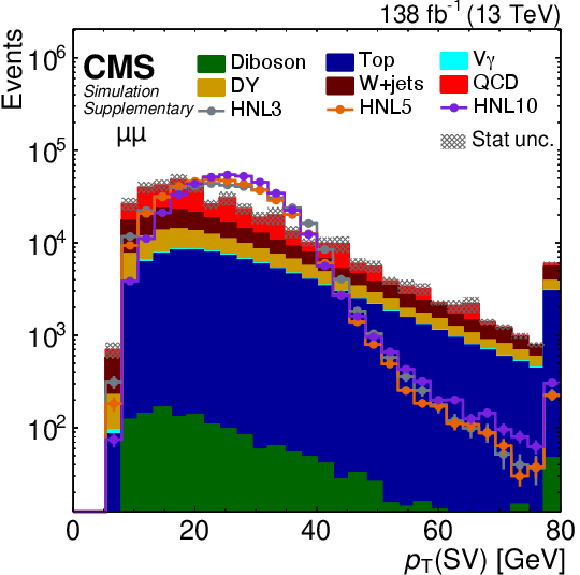
Additional Figure 8:
Distribution of predicted event yields as a function of the $ p_{\mathrm{T}} $ of the SV after applying the baseline event selection for the $ \mu\mu $ category. The filled histograms display the predicted background yields. The lines show the predicted yields for three HNL signal scenarios, with $ m_{\mathrm{N}}= $ 3 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 9.9$\times$10$^{-5} $ (HNL3), $ m_{\mathrm{N}}= $ 5 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 1.6$\times$10$^{-5} $ (HNL5), and $ m_{\mathrm{N}}= $ 10 GeV and $ |V_{\ell\mathrm{N}}|^2=$ 5.7$\times$10$^{-7} $ (HNL10). The HNL signal yield is normalized to the total background yield. The last bin includes the overflow. |
png pdf |
Additional Figure 9:
Illustration of the target and sideband region definitions for the ABCD method applied to the VR in terms of $ N(\mathrm{jets}) $, $ m(\ell_1,\mathrm{SV}) $, and the PFN score. |
png pdf |
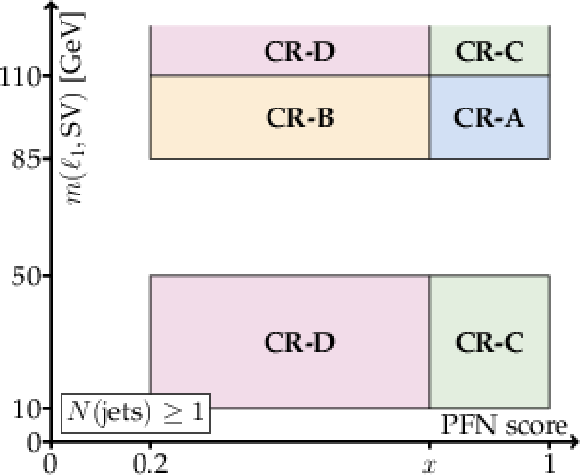
Additional Figure 10:
Illustration of the target and sideband region definitions for the ABCD method applied to the CR in terms of $ N(\mathrm{jets}) $, $ m(\ell_1,\mathrm{SV}) $, and the PFN score. |
png pdf |
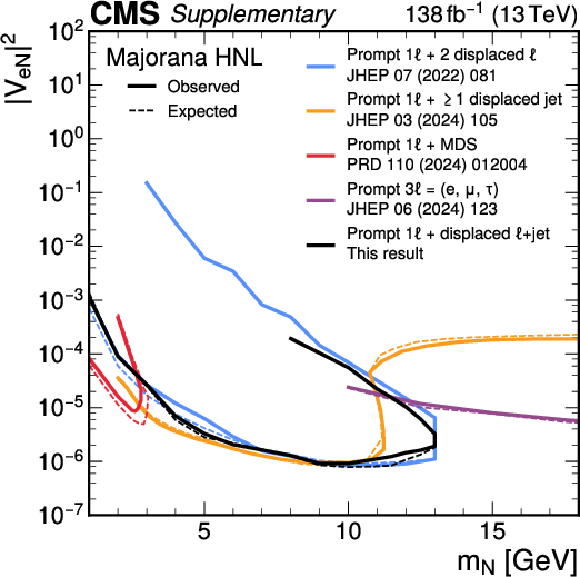
Additional Figure 11:
Exclusion limits at 95% CL on $ |V_{\mathrm{eN}}|^2 $ as functions of $ m_{\mathrm{N}} $ for a Majorana HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. The results from this analysis are shown in black, and the results from earlier CMS analyses that use different channels and/or techniques in different colors. |
png pdf |
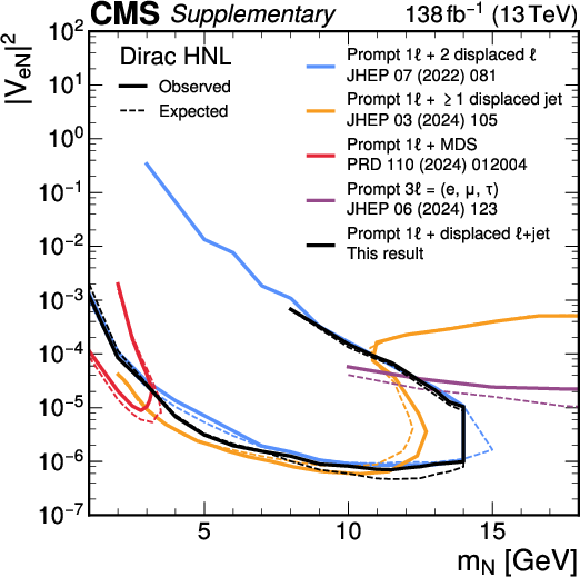
Additional Figure 12:
Exclusion limits at 95% CL on $ |V_{\mathrm{eN}}|^2 $ as functions of $ m_{\mathrm{N}} $ for a Dirac HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. The results from this analysis are shown in black, and the results from earlier CMS analyses that use different channels and/or techniques in different colors. |
png pdf |
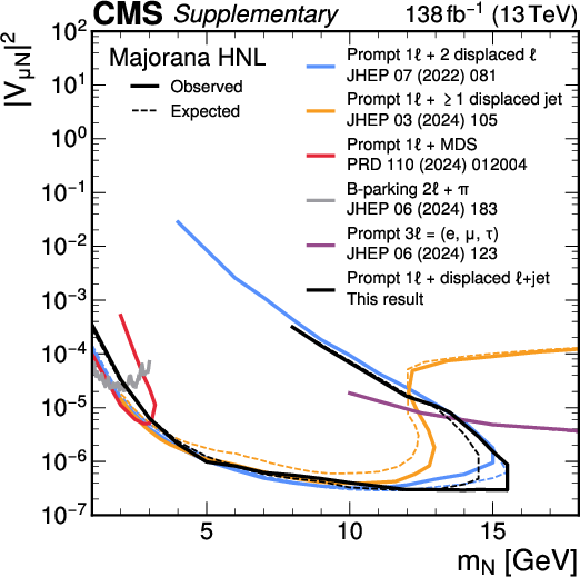
Additional Figure 13:
Exclusion limits at 95% CL on $ |V_{\mu\mathrm{N}}|^2 $ as functions of $ m_{\mathrm{N}} $ for a Majorana HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. The results from this analysis are shown in black, and the results from earlier CMS analyses that use different channels and/or techniques in different colors. |
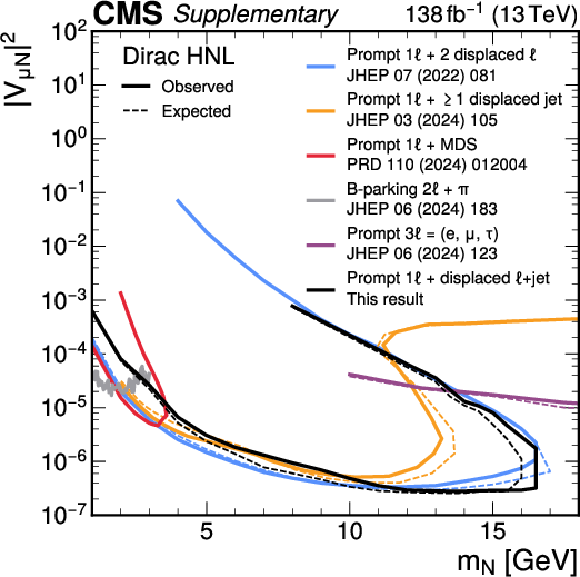
png pdf |
Additional Figure 14:
Exclusion limits at 95% CL on $ |V_{\mu\mathrm{N}}|^2 $ as functions of $ m_{\mathrm{N}} $ for a Dirac HNL. The solid (dashed) black curve indicates the observed (expected) exclusion, where the parameter combinations inside the curve are excluded. The results from this analysis are shown in black, and the results from earlier CMS analyses that use different channels and/or techniques in different colors. |
| References | ||||
| 1 | Super-Kamiokande Collaboration | Evidence for oscillation of atmospheric neutrinos | PRL 81 (1998) 1562 | hep-ex/9807003 |
| 2 | SNO Collaboration | Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory | PRL 89 (2002) 011301 | nucl-ex/0204008 |
| 3 | KamLAND Collaboration | First results from KamLAND: Evidence for reactor antineutrino disappearance | PRL 90 (2003) 021802 | hep-ex/0212021 |
| 4 | S. Bilenky | Neutrino oscillations: From a historical perspective to the present status | NPB 908 (2016) 2 | 1602.00170 |
| 5 | Planck Collaboration | Planck 2018 results. VI. cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 6 | eBOSS Collaboration | Completed SDSS-IV extended baryon oscillation spectroscopic survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory | PRD 103 (2021) 083533 | 2007.08991 |
| 7 | Z. Sakr | A short review on the latest neutrinos mass and number constraints from cosmological observables | Universe 8 (2022) 284 | |
| 8 | J. Formaggio, A. de Gouv \^e a, and R. Robertson | Direct measurements of neutrino mass | Phys. Rept. 914 (2021) 1 | 2102.00594 |
| 9 | KATRIN Collaboration | Direct neutrino-mass measurement with sub-electronvolt sensitivity | Nature Phys. 18 (2022) 160 | 2105.08533 |
| 10 | P. Minkowski | $ {\mu\to\mathrm{e}\gamma} $ at a rate of one out of $ 10^9 $ muon decays? | PLB 67 (1977) 421 | |
| 11 | T. Yanagida | Horizontal gauge symmetry and masses of neutrinos | in Proc. Workshop on the Unified Theories and the Baryon Number in the Universe: Tsukuba, Japan, February 13--14, . . [], 1979 Conf. Proc. C 7902131 (1979) 95 |
|
| 12 | M. Gell-Mann, P. Ramond, and R. Slansky | Complex spinors and unified theories | in Proc. Supergravity Workshop: Stony Brook NY, USA, September 27--28, . . . [], 1979 Conf. Proc. C 790927 (1979) 315 |
1306.4669 |
| 13 | S. Glashow | The future of elementary particle physics | NATO Sci. Ser. B 61 (1980) 687 | |
| 14 | R. Mohapatra and G. Senjanovi \'c | Neutrino mass and spontaneous parity nonconservation | PRL 44 (1980) 912 | |
| 15 | J. Schechter and J. Valle | Neutrino masses in $ \mathrm{SU}(2)\otimes\mathrm{U}(1) $ theories | PRD 22 (1980) 2227 | |
| 16 | R. Shrock | General theory of weak leptonic and semileptonic decays. I. leptonic pseudoscalar meson decays, with associated tests for, and bounds on, neutrino masses and lepton mixing | PRD 24 (1981) 1232 | |
| 17 | Y. Cai, T. Han, T. Li, and R. Ruiz | Lepton number violation: Seesaw models and their collider tests | Front. Phys. 6 (2018) 40 | 1711.02180 |
| 18 | S. Dodelson and L. Widrow | Sterile neutrinos as dark matter | PRL 72 (1994) 17 | hep-ph/9303287 |
| 19 | A. Boyarsky et al. | Sterile neutrino dark matter | Prog. Part. Nucl. Phys. 104 (2019) 1 | 1807.07938 |
| 20 | M. Fukugita and T. Yanagida | Baryogenesis without grand unification | PLB 174 (1986) 45 | |
| 21 | E. Chun et al. | Probing leptogenesis | Int. J. Mod. Phys. A 33 (2018) 1842005 | 1711.02865 |
| 22 | M. Drewes, Y. Georis, and J. Klari \'c | Mapping the viable parameter space for testable leptogenesis | PRL 128 (2022) 051801 | 2106.16226 |
| 23 | T. Asaka, S. Blanchet, and M. Shaposhnikov | The \PGnMSM, dark matter and neutrino masses | PLB 631 (2005) 151 | hep-ph/0503065 |
| 24 | F. del Aguila and J. Aguilar-Saavedra | Distinguishing seesaw models at LHC with multi-lepton signals | NPB 813 (2009) 22 | 0808.2468 |
| 25 | A. Atre, T. Han, S. Pascoli, and B. Zhang | The search for heavy Majorana neutrinos | JHEP 05 (2009) 030 | 0901.3589 |
| 26 | V. Tello et al. | Left-right symmetry: from LHC to neutrinoless double beta decay | PRL 106 (2011) 151801 | 1011.3522 |
| 27 | F. Deppisch, P. Bhupal Dev, and A. Pilaftsis | Neutrinos and collider physics | New J. Phys. 17 (2015) 075019 | 1502.06541 |
| 28 | S. Pascoli, R. Ruiz, and C. Weiland | Heavy neutrinos with dynamic jet vetoes: multilepton searches at $ \sqrt{s}= $ 14, 27, and 100 TeV | JHEP 06 (2019) 049 | 1812.08750 |
| 29 | J. Alimena et al. | Searching for long-lived particles beyond the standard model at the Large Hadron Collider | JPG 47 (2020) 090501 | 1903.04497 |
| 30 | A. Abdullahi et al. | The present and future status of heavy neutral leptons | JPG 50 (2023) 020501 | 2203.08039 |
| 31 | C. Antel et al. | Feebly interacting particles: FIPs 2022 workshop report | EPJC 83 (2023) 1122 | 2305.01715 |
| 32 | CMS Collaboration | Search for heavy Majorana neutrinos in $ {\mu^\pm\mu^\pm}+ $jets and $ {\mathrm{e}^\pm\mathrm{e}^\pm}+ $jets events in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV | PLB 717 (2012) 109 | CMS-EXO-11-076 1207.6079 |
| 33 | CMS Collaboration | Search for heavy Majorana neutrinos in $ {\mu^\pm\mu^\pm}+ $jets events in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | PLB 748 (2015) 144 | CMS-EXO-12-057 1501.05566 |
| 34 | ATLAS Collaboration | Search for heavy Majorana neutrinos with the ATLAS detector in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 8 TeV | JHEP 07 (2015) 162 | 1506.06020 |
| 35 | CMS Collaboration | Search for heavy Majorana neutrinos in $ {\mathrm{e}^\pm\mathrm{e}^\pm}+ $jets and $ {\mathrm{e}^\pm\mu^\pm}+ $jets events in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JHEP 04 (2016) 169 | CMS-EXO-14-014 1603.02248 |
| 36 | CMS Collaboration | Search for heavy neutral leptons in events with three charged leptons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRL 120 (2018) 221801 | CMS-EXO-17-012 1802.02965 |
| 37 | CMS Collaboration | Search for heavy Majorana neutrinos in same-sign dilepton channels in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 01 (2019) 122 | CMS-EXO-17-028 1806.10905 |
| 38 | ATLAS Collaboration | Search for heavy neutral leptons in decays of W bosons produced in 13 TeV $ {\mathrm{p}\mathrm{p}} $ collisions using prompt and displaced signatures with the ATLAS detector | JHEP 10 (2019) 265 | 1905.09787 |
| 39 | LHCb Collaboration | Search for heavy neutral leptons in $ {\mathrm{W^+}\to\mu^{+}\mu^\pm\,\text{jet}} $ decays | EPJC 81 (2021) 248 | 2011.05263 |
| 40 | CMS Collaboration | Search for long-lived heavy neutral leptons with displaced vertices in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2022) 081 | CMS-EXO-20-009 2201.05578 |
| 41 | ATLAS Collaboration | Search for heavy neutral leptons in decays of W bosons using a dilepton displaced vertex in $ \sqrt{s}= $ 13 TeV $ {\mathrm{p}\mathrm{p}} $ collisions with the ATLAS detector | PRL 131 (2023) 061803 | 2204.11988 |
| 42 | CMS Collaboration | Probing heavy Majorana neutrinos and the Weinberg operator through vector boson fusion processes in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRL 131 (2023) 011803 | CMS-EXO-21-003 2206.08956 |
| 43 | ATLAS Collaboration | Search for Majorana neutrinos in same-sign $ {\mathrm{W}\mathrm{W}} $ scattering events from $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 13 TeV | EPJC 83 (2023) 824 | 2305.14931 |
| 44 | CMS Collaboration | Search for long-lived heavy neutral leptons with lepton flavour conserving or violating decays to a jet and a charged lepton | JHEP 03 (2024) 105 | CMS-EXO-21-013 2312.07484 |
| 45 | CMS Collaboration | Search for long-lived heavy neutral leptons decaying in the CMS muon detectors in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 110 (2024) 012004 | CMS-EXO-22-017 2402.18658 |
| 46 | CMS Collaboration | Search for heavy neutral leptons in final states with electrons, muons, and hadronically decaying tau leptons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 06 (2024) 123 | CMS-EXO-22-011 2403.00100 |
| 47 | CMS Collaboration | Search for long-lived heavy neutrinos in the decays of $ {\mathrm{B}} $ mesons produced in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 06 (2024) 183 | CMS-EXO-22-019 2403.04584 |
| 48 | ATLAS Collaboration | Search for heavy Majorana neutrinos in $ {\mathrm{e}^\pm\mathrm{e}^\pm} $ and $ {\mathrm{e}^\pm\mu^\pm} $ final states via $ {\mathrm{W}\mathrm{W}} $ scattering in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PLB 856 (2024) 138865 | 2403.15016 |
| 49 | CMS Collaboration | Review of searches for vector-like quarks, vector-like leptons, and heavy neutral leptons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV at the CMS experiment | Accepted by Phys. Rept, 2024 | CMS-EXO-23-006 2405.17605 |
| 50 | DELPHI Collaboration | Search for neutral heavy leptons produced in Z decays | Z. Phys. C 74 (1997) 57 | |
| 51 | Belle Collaboration | Search for heavy neutrinos at Belle | PRD 87 (2013) 071102 | 1301.1105 |
| 52 | BaBar Collaboration | Search for heavy neutral leptons using tau lepton decays at BaBaR | PRD 107 (2023) 052009 | 2207.09575 |
| 53 | Belle Collaboration | Search for a heavy neutrino in $ \tau $ decays at Belle | PRL 131 (2023) 211802 | 2212.10095 |
| 54 | Belle Collaboration | Search for a heavy neutral lepton that mixes predominantly with the tau neutrino | PRD 109 (2024) L111102 | 2402.02580 |
| 55 | WA66 Collaboration | Search for heavy neutrino decays in the BEBC beam dump experiment | PLB 160 (1985) 207 | |
| 56 | CHARM Collaboration | A search for decays of heavy neutrinos in the mass range 0.5--2.8 GeV | PLB 166 (1986) 473 | |
| 57 | NA3 Collaboration | Mass and lifetime limits on new longlived particles in 300 GeVc $ \pi^{-} $ interactions | Z. Phys. C 31 (1986) 21 | |
| 58 | CHARM II Collaboration | Search for heavy isosinglet neutrinos | PLB 343 (1995) 453 | |
| 59 | A. Vaitaitis et al. | Search for neutral heavy leptons in a high-energy neutrino beam | PRL 83 (1999) 4943 | hep-ex/9908011 |
| 60 | T2K Collaboration | Search for heavy neutrinos with the T2K near detector ND280 | PRD 100 (2019) 052006 | 1902.07598 |
| 61 | NA62 Collaboration | Search for heavy neutral lepton production in $ \mathrm{K^+} $ decays to positrons | PLB 807 (2020) 135599 | 2005.09575 |
| 62 | NA62 Collaboration | Search for $ \mathrm{K^+} $ decays to a muon and invisible particles | PLB 816 (2021) 136259 | 2101.12304 |
| 63 | ArgoNeuT Collaboration | New constraints on tau-coupled heavy neutral leptons with masses $ m_{\mathrm{N}}= $ 280--970 MeV | PRL 127 (2021) 121801 | 2106.13684 |
| 64 | MicroBooNE Collaboration | Search for long-lived heavy neutral leptons and Higgs portal scalars decaying in the MicroBooNE detector | PRD 106 (2022) 092006 | 2207.03840 |
| 65 | MicroBooNE Collaboration | Search for heavy neutral leptons in electron-positron and neutral-pion final states with the MicroBooNE detector | PRL 132 (2024) 041801 | 2310.07660 |
| 66 | A. Abada, N. Bernal, M. Losada, and X. Marcano | Inclusive displaced vertex searches for heavy neutral leptons at the LHC | JHEP 01 (2019) 093 | 1807.10024 |
| 67 | J.-L. Tastet, O. Ruchayskiy, and I. Timiryasov | Reinterpreting the ATLAS bounds on heavy neutral leptons in a realistic neutrino oscillation model | JHEP 12 (2021) 182 | 2107.12980 |
| 68 | I. Boiarska, A. Boyarsky, O. Mikulenko, and M. Ovchynnikov | Constraints from the CHARM experiment on heavy neutral leptons with tau mixing | PRD 104 (2021) 095019 | 2107.14685 |
| 69 | A. Abada, P. Escribano, X. Marcano, and G. Piazza | Collider searches for heavy neutral leptons: beyond simplified scenarios | EPJC 82 (2022) 1030 | 2208.13882 |
| 70 | CMS Collaboration | HEPData record for this analysis | link | |
| 71 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 72 | CMS Collaboration | Development of the CMS detector for the CERN LHC \mboxRun 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 73 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 74 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 75 | CMS Collaboration | Performance of the CMS high-level trigger during LHC \mboxRun 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 76 | CMS Tracker Group Collaboration | The CMS Phase-1 pixel detector upgrade | JINST 16 (2021) P02027 | 2012.14304 |
| 77 | CMS Collaboration | 2017 tracking performance plots | CMS Detector Performance Note CMS-DP-2017-015, 2017 CDS |
|
| 78 | W. Waltenberger, R. Fr \"u hwirth, and P. Vanlaer | Adaptive vertex fitting | JPG 34 (2007) N343 | |
| 79 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 link |
|
| 80 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 81 | CMS Collaboration | Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS Phase-1 pixel detector | CMS Detector Performance Note CMS-DP-2020-049, 2020 CDS |
|
| 82 | CMS Collaboration | Measurement of $ {{\mathrm{B}}\overline{\mathrm{B}}} $ angular correlations based on secondary vertex reconstruction at $ \sqrt{s}= $ 7 TeV | JHEP 03 (2011) 136 | CMS-BPH-10-010 1102.3194 |
| 83 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in $ {\mathrm{p}\mathrm{p}} $ collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 84 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 85 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 86 | M. Cacciari, G. P. Salam, and G. Soyez | FASTJET user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 87 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 88 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in $ {\mathrm{p}\mathrm{p}} $ collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 89 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 90 | CMS Collaboration | ECAL 2016 refined calibration and \mboxRun 2 summary plots | CMS Detector Performance Note CMS-DP-2020-021, 2020 CDS |
|
| 91 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 92 | CMS Collaboration | Single- and double-electron trigger efficiencies using the full \mboxRun 2 data set | CMS Detector Performance Note CMS-DP-2020-016, 2020 CDS |
|
| 93 | CMS Collaboration | Performance of the CMS muon trigger system in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 16 (2021) P07001 | CMS-MUO-19-001 2102.04790 |
| 94 | NNPDF Collaboration | Parton distributions for the LHC run II | JHEP 04 (2015) 040 | 1410.8849 |
| 95 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 96 | T. Sjöstrand et al. | An introduction to PYTHIA8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 97 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 98 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 99 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 100 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 101 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 102 | S. Frixione, G. Ridolfi, and P. Nason | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 103 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 104 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 105 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG \textscbox | JHEP 06 (2010) 043 | 1002.2581 |
| 106 | E. Re | Single-top $ {\mathrm{W}\mathrm{t}} $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 107 | T. Melia, P. Nason, R. Röntsch, and G. Zanderighi | $ {\mathrm{W^+}\mathrm{W^-}} $, $ {\mathrm{W}\mathrm{Z}} $ and $ {\mathrm{Z}\mathrm{Z}} $ production in the POWHEG \textscbox | JHEP 11 (2011) 078 | 1107.5051 |
| 108 | P. Nason and G. Zanderighi | $ {\mathrm{W^+}\mathrm{W^-}} $, $ {\mathrm{W}\mathrm{Z}} $ and $ {\mathrm{Z}\mathrm{Z}} $ production in the POWHEG -\textscbox-v2 | EPJC 74 (2014) 2702 | 1311.1365 |
| 109 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 110 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 111 | D. Alva, T. Han, and R. Ruiz | Heavy Majorana neutrinos from $ {\mathrm{W}\gamma} $ fusion at hadron colliders | JHEP 02 (2015) 072 | 1411.7305 |
| 112 | C. Degrande, O. Mattelaer, R. Ruiz, and J. Turner | Fully-automated precision predictions for heavy neutrino production mechanisms at hadron colliders | PRD 94 (2016) 053002 | 1602.06957 |
| 113 | K. Melnikov and F. Petriello | Electroweak gauge boson production at hadron colliders through $ \mathcal{O}({\alpha_\mathrm{S}^2}) $ | PRD 74 (2006) 114017 | hep-ph/0609070 |
| 114 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | Comput. Phys. Commun. 182 (2011) 2388 | 1011.3540 |
| 115 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | W physics at the LHC with FEWZ 2.1 | Comput. Phys. Commun. 184 (2013) 208 | 1201.5896 |
| 116 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 117 | P. Komiske, E. Metodiev, and J. Thaler | Energy flow networks: deep sets for particle jets | JHEP 01 (2019) 121 | 1810.05165 |
| 118 | et al. | Deep sets | M.~Zaheer in st Conference on Neural Information Processing Systems (NIPS ): Long Beach CA, USA, December 04--09,, 2017 Proc. 3 (2017) 3391 |
1703.06114 |
| 119 | F. Chollet et al. | \textsckeras | Software available from \urlhttps://keras.io, 2015 | |
| 120 | M. Abadi et al. | \textscTensorFlow: Large-scale machine learning on heterogeneous systems | Software available from \urlhttp://tensorflow.org, 2015 link |
|
| 121 | et al. | Dropout: a simple way to prevent neural networks from overfitting | N.~, 2014 Srivastava J. Mach. Learn. Res. 15 (2014) 1929 |
|
| 122 | T. Hastie, R. Tibshirani, and J. Friedman | Model assessment and selection | in The elements of statistical learning. Data mining, inference, and prediction, . Springer Science+Business Media, New York, 2009 link |
|
| 123 | CMS Collaboration | Displaced tracking and vertexing calibration using neutral $ \mathrm{K} $ mesons | CMS Detector Performance Note CMS-DP-2024-010, 2024 CDS |
|
| 124 | Particle Data Group , R. L. Workman et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2022 (2022) 083C01 | |
| 125 | S. Choi and H. Oh | Improved extrapolation methods of data-driven background estimations in high energy physics | EPJC 81 (2021) 643 | 1906.10831 |
| 126 | B. R é millard | Tests of independence | in International encyclopedia of statistical science, M.~Lovric, ed., . Springer-Verlag, Berlin, 2011 link |
|
| 127 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 128 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 129 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 130 | CMS Collaboration | Measurements of inclusive W and Z cross sections in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |
| 131 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 132 | A. L. Read | Presentation of search results: The $ \text{CL}_\text{s} $ technique | JPG 28 (2002) 2693 | |
| 133 | ATLAS and CMS Collaborations, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011 | |
| 134 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 135 | CMS Collaboration | The CMS statistical analysis and combination tool: \textsccombine | Comput. Softw. Big Sci. 8 (2024) 19 | CMS-CAT-23-001 2404.06614 |
| 136 | W. Verkerke and D. Kirkby | The \textscRooFit toolkit for data modeling | in th International Conference on Computing in High Energy and Nuclear Physics (CHEP ): La Jolla CA, United States, March 24--28, . . . [eConf C0303241 MOLT007], 2003 Proc. 1 (2003) 3 |
physics/0306116 |
| 137 | L. Moneta et al. | The \textscRooStats project | in th International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT ): Jaipur, India, February 22--27, . . . [PoS (ACAT) 057], 2010 Proc. 1 (2010) 3 |
1009.1003 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|