Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-EXO-22-017 ; CERN-EP-2024-022

Search for long-lived heavy neutral leptons decaying in the CMS muon detectors in proton-proton collisions at $ \sqrt{s}= $ 13 TeV

CMS Collaboration

28 February 2024

Phys. Rev. D 110 (2024) 012004

Abstract: A search for heavy neutral leptons (HNLs) decaying in the CMS muon system is presented. A data sample is used corresponding to an integrated luminosity of 138 fb$ ^{-1} $ of proton-proton collisions at $ \sqrt{s}= $ 13 TeV, recorded at the CERN LHC in 2016-2018. Decay products of long-lived HNLs could interact with the shielding materials in the CMS muon system and create hadronic and electromagnetic showers detected in the muon chambers. This distinctive signature provides a unique handle to search for HNLs with masses below 4 GeV and proper decay lengths of the order of meters. The signature is sensitive to HNL couplings to all three generations of leptons. Candidate events are required to contain a prompt electron or muon originating from a vertex on the beam axis and a displaced shower in the muon chambers. No significant deviations from the standard model background expectation are observed. In the electron (muon) channel, the most stringent limits to date are set for HNLs in the mass range of 2.1-3.0 (1.9-3.3) GeV, reaching mixing matrix element squared values as low as 8.6 (4.6) $\times$ 10$^{-6} $.

Links: e-print arXiv:2402.18658 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; Physics Briefing ; CADI line (restricted) ;

Figures
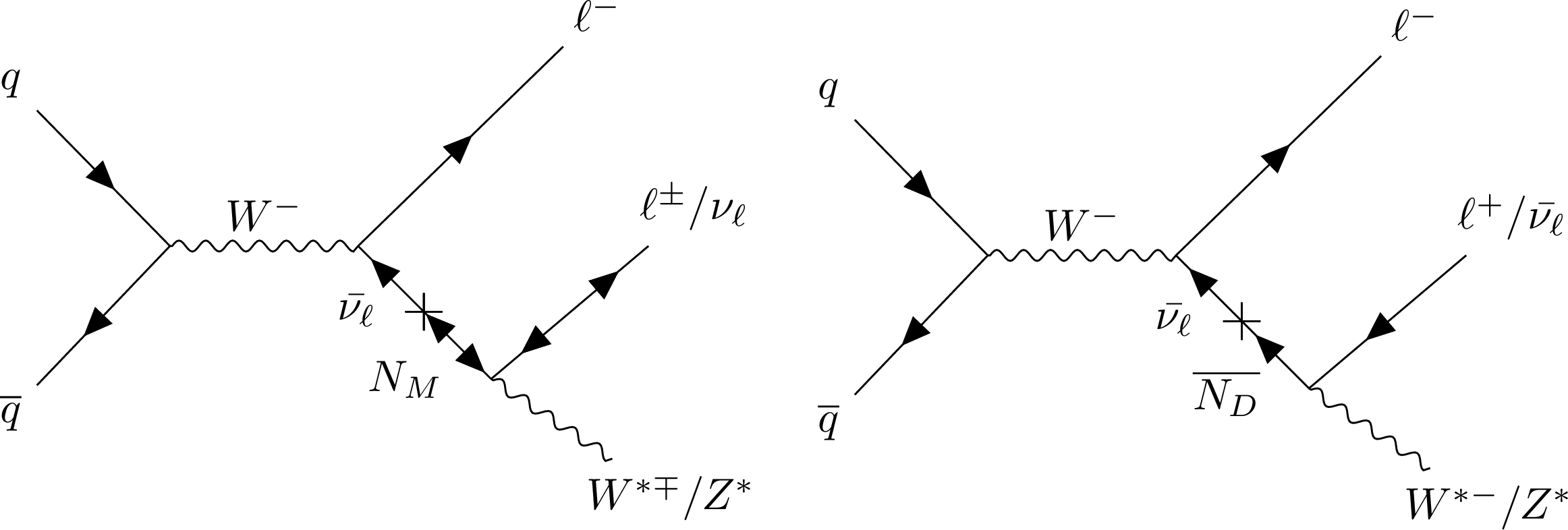
png pdf	Figure 1: Feynman diagrams for the production of a Majorana HNL $ N_M $ (left) and a Dirac HNL $ \overline{N_D} $ (right) via a $ \mathrm{W^-} $ boson decay and through its mixing with an SM neutrino of the same flavor. The prompt lepton from the $ \mathrm{W^-} $ boson serves as a clean signature for triggering, whereas the decay products of the HNL are reconstructed as a cluster of muon detector hits.
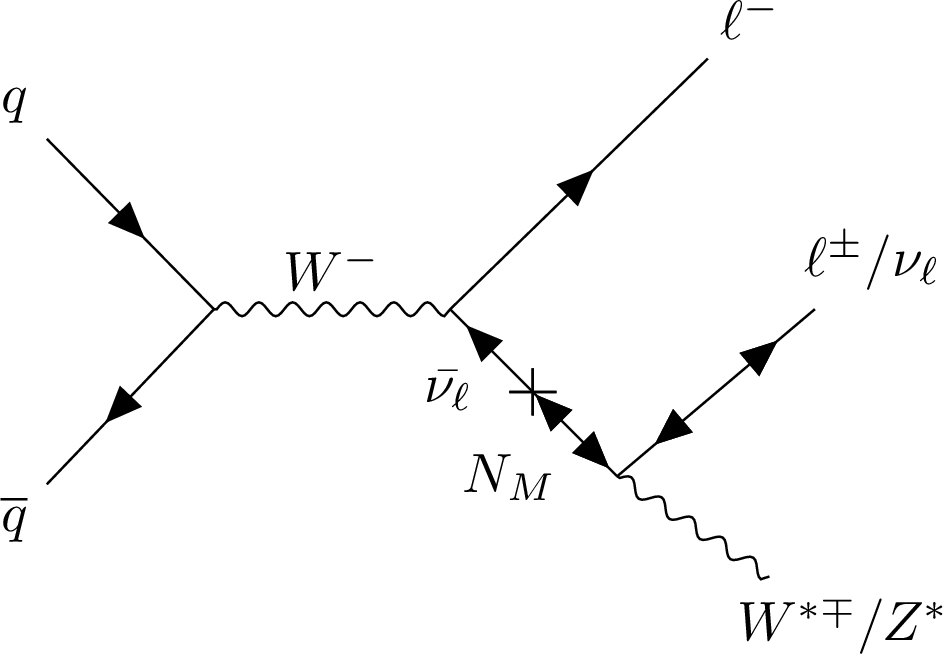
png pdf	Figure 1-a: Feynman diagrams for the production of a Majorana HNL $ N_M $ (left) and a Dirac HNL $ \overline{N_D} $ (right) via a $ \mathrm{W^-} $ boson decay and through its mixing with an SM neutrino of the same flavor. The prompt lepton from the $ \mathrm{W^-} $ boson serves as a clean signature for triggering, whereas the decay products of the HNL are reconstructed as a cluster of muon detector hits.
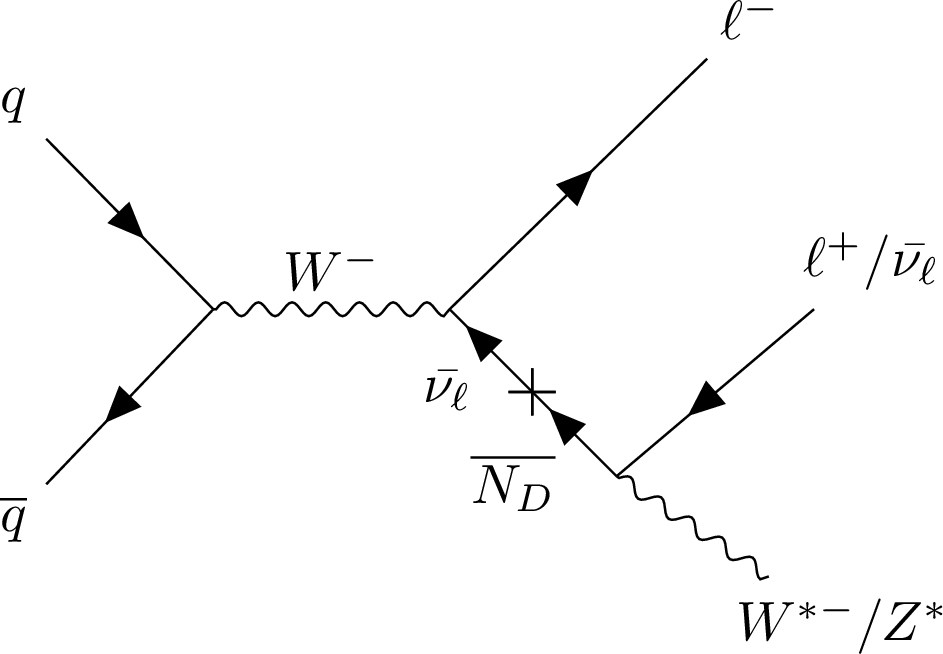
png pdf	Figure 1-b: Feynman diagrams for the production of a Majorana HNL $ N_M $ (left) and a Dirac HNL $ \overline{N_D} $ (right) via a $ \mathrm{W^-} $ boson decay and through its mixing with an SM neutrino of the same flavor. The prompt lepton from the $ \mathrm{W^-} $ boson serves as a clean signature for triggering, whereas the decay products of the HNL are reconstructed as a cluster of muon detector hits.
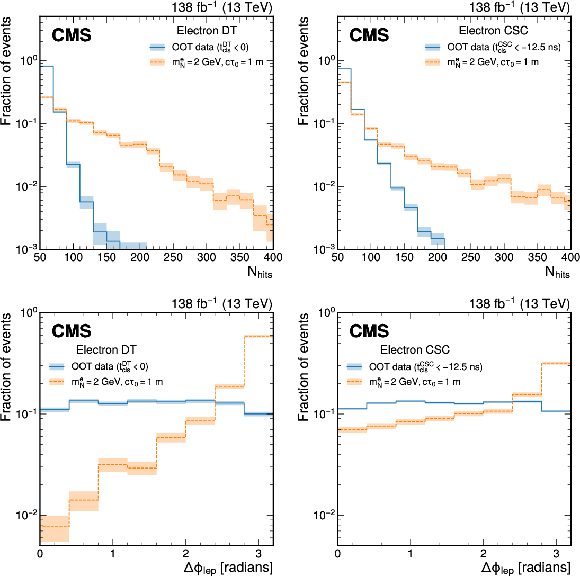
png pdf	Figure 2: Distribution of $ N_{\text{hits}} $ (upper) and $ \Delta\phi_\text{lep} $ (lower) for DT clusters (left) and CSC clusters (right). Signal distributions of a Majorana HNL with $ m_{\mathrm{N}} = $ 2 GeV and $ c\tau_{0}= $ 1 m are compared with the OOT background distributions selected with $ t_\mathrm{cluster}^\mathrm{DT} $ matched to bunch crossings earlier than the PV for DT clusters and $ t_\mathrm{cluster}^\mathrm{CSC} < - $12.5 ns for CSC clusters. The centroids of the clusters in the signal events are required to be within $ \Delta R= $ 0.4 of the HNL's direction. The distributions are normalized to unit area. The shapes of the distributions shown are similar for the electron and muon channels.
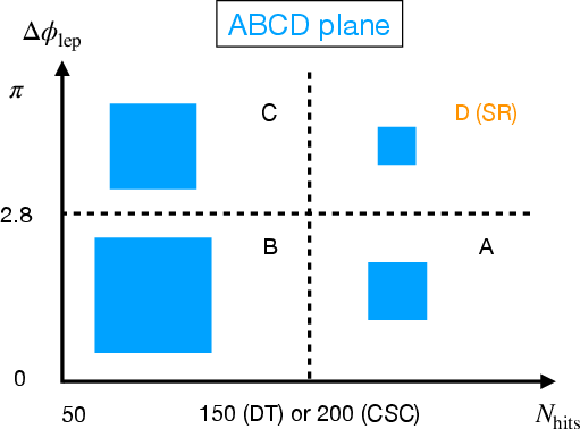
png pdf	Figure 3: Definition of the ABCD plane. The area of the blue squares illustrates the relative amount of expected events in each of the bins, with bins B and C having the majority of the event yields. Bin D is the signal region.
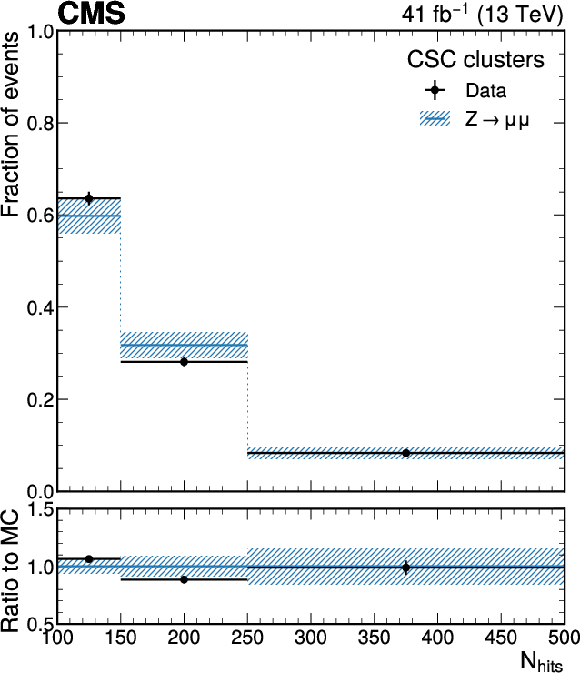
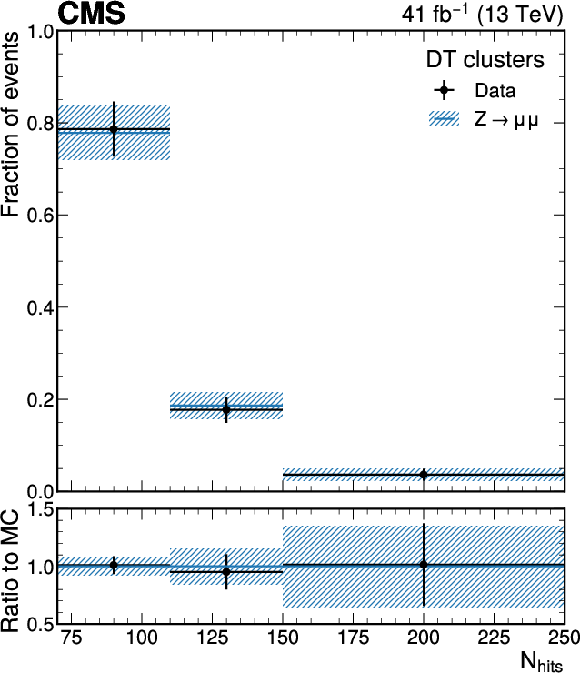
png pdf	Figure 4: Comparison of $ N_{\text{hits}} $ distributions for events with muons from $ \mathrm{Z}\to\mu\mu $ between data and simulation, for CSC clusters (left) and DT clusters (right), using data collected in 2017 and the simulation of the corresponding data-taking conditions. The data sample is selected by requiring a two-muon invariant mass consistent with a Z boson and one of the muons is matched to an MDS cluster. Data-to-simulation correction factors are applied to the $ \mathrm{Z}\to\mu\mu $ simulation. Only statistical uncertainties are included in the figure. Distributions made using data collected in 2016 and 2018 are found to have similar shape as the 2017 data sample.
png pdf	Figure 4-a: Comparison of $ N_{\text{hits}} $ distributions for events with muons from $ \mathrm{Z}\to\mu\mu $ between data and simulation, for CSC clusters (left) and DT clusters (right), using data collected in 2017 and the simulation of the corresponding data-taking conditions. The data sample is selected by requiring a two-muon invariant mass consistent with a Z boson and one of the muons is matched to an MDS cluster. Data-to-simulation correction factors are applied to the $ \mathrm{Z}\to\mu\mu $ simulation. Only statistical uncertainties are included in the figure. Distributions made using data collected in 2016 and 2018 are found to have similar shape as the 2017 data sample.
png pdf	Figure 4-b: Comparison of $ N_{\text{hits}} $ distributions for events with muons from $ \mathrm{Z}\to\mu\mu $ between data and simulation, for CSC clusters (left) and DT clusters (right), using data collected in 2017 and the simulation of the corresponding data-taking conditions. The data sample is selected by requiring a two-muon invariant mass consistent with a Z boson and one of the muons is matched to an MDS cluster. Data-to-simulation correction factors are applied to the $ \mathrm{Z}\to\mu\mu $ simulation. Only statistical uncertainties are included in the figure. Distributions made using data collected in 2016 and 2018 are found to have similar shape as the 2017 data sample.
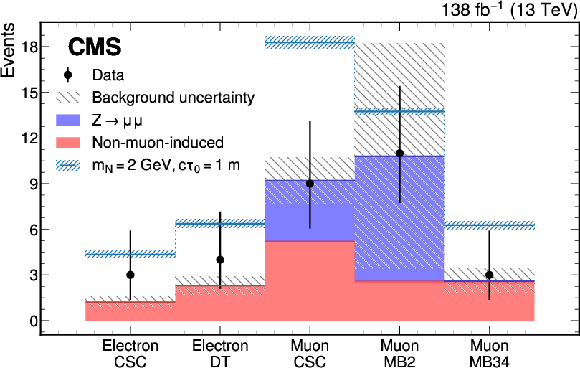
png pdf	Figure 5: The expected and observed number of events in the signal region (bin D) of different event categories. Signal yields of a 2 GeV Majorana HNL with the mean proper decay length of 1 m are added to the expected background.
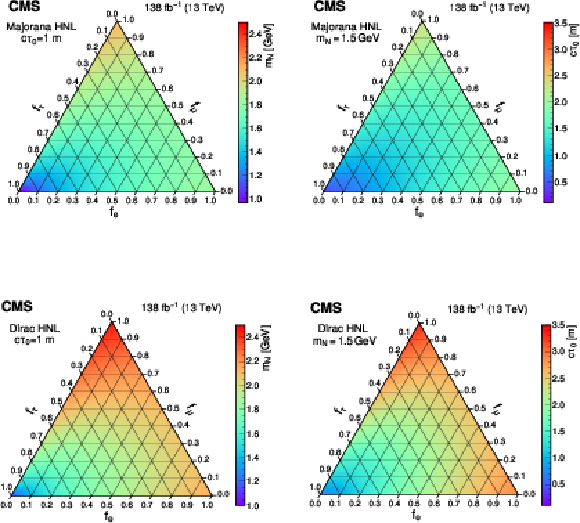
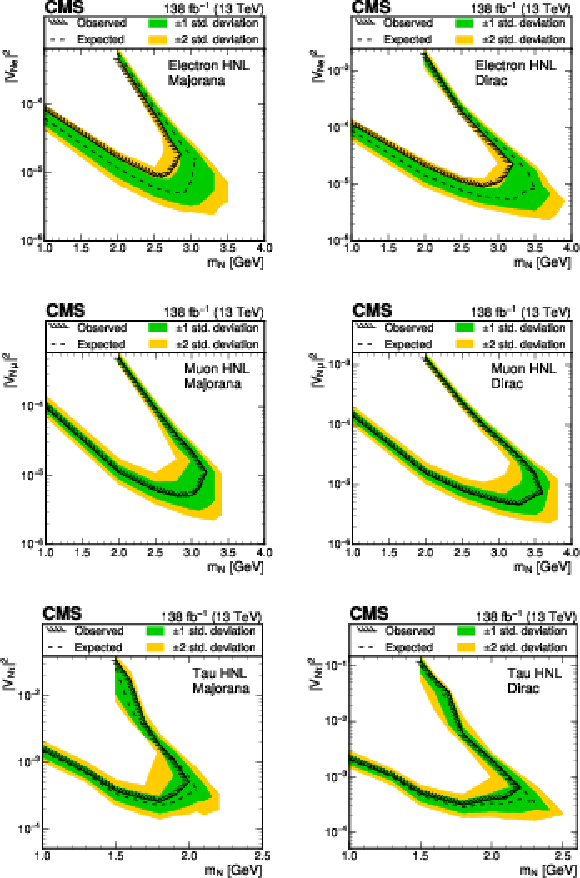
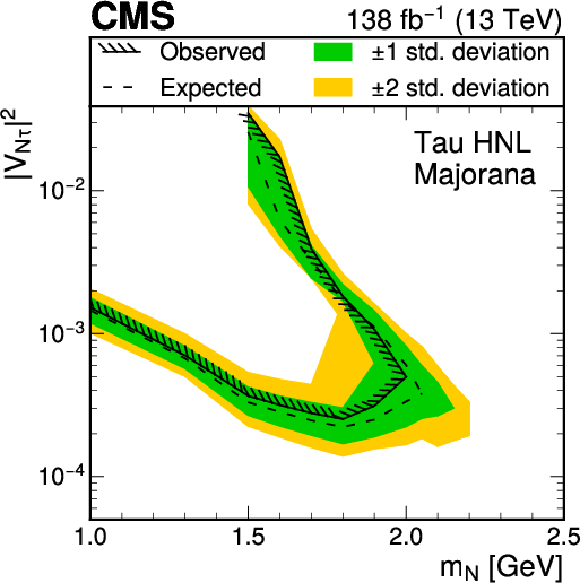
png pdf	Figure 6: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
png pdf	Figure 6-a: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
png pdf	Figure 6-b: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
png pdf	Figure 6-c: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
png pdf	Figure 6-d: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
png pdf	Figure 6-e: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
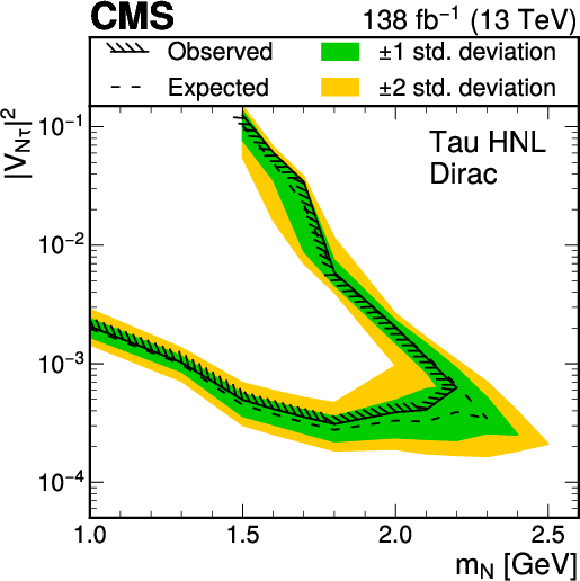
png pdf	Figure 6-f: Expected and observed upper 95% CL limits on $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $ (upper), $ |V_{{\mathrm{N}} \mu}|^2 $ (middle) and $ |V_{{\mathrm{N}} \tau}|^2 $ (lower) as functions of the HNL mass ($ m_{\mathrm{N}} $) for a Majorana (left) and Dirac (right) type HNL. The $ \tau $ neutrino mixing limit is obtained by combining the results from the electron and muon channels. For these limit calculations, the HNL is assumed to mix with a single lepton flavor state only. The differences between the expected and observed limits on $ |V_{{\mathrm{N}} \mu}|^2 $ are not visible in this figure.
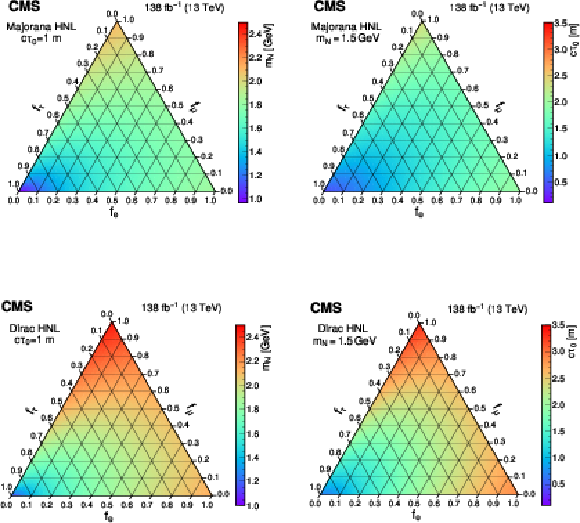
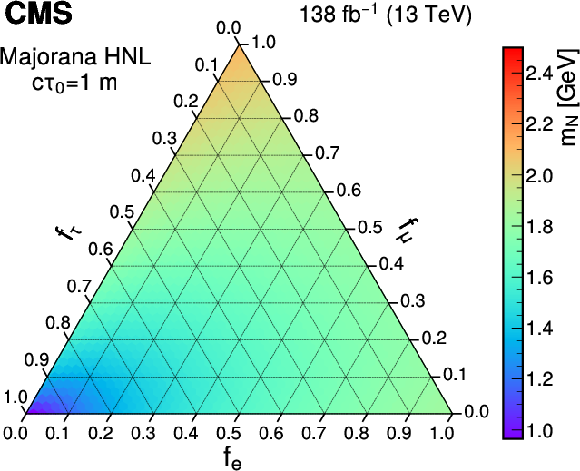
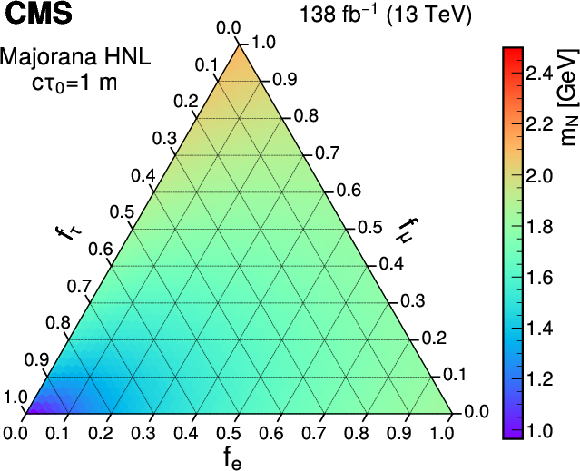
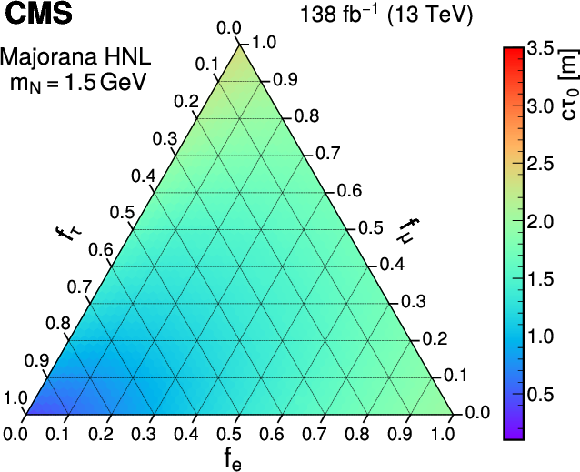
png pdf	Figure 7: The largest values of the Majorana (upper) and Dirac (lower) HNL mass (left) and mean proper decay length (right) parameters that are excluded at 95% CL are shown as a function of the mixing matrix elements squared ratios $ f_\ell $ with the three lepton generations, considering a mean proper decay length of 1 m and a fixed mass of 1.5 GeV, respectively.
png pdf	Figure 7-a: The largest values of the Majorana (upper) and Dirac (lower) HNL mass (left) and mean proper decay length (right) parameters that are excluded at 95% CL are shown as a function of the mixing matrix elements squared ratios $ f_\ell $ with the three lepton generations, considering a mean proper decay length of 1 m and a fixed mass of 1.5 GeV, respectively.
png pdf	Figure 7-b: The largest values of the Majorana (upper) and Dirac (lower) HNL mass (left) and mean proper decay length (right) parameters that are excluded at 95% CL are shown as a function of the mixing matrix elements squared ratios $ f_\ell $ with the three lepton generations, considering a mean proper decay length of 1 m and a fixed mass of 1.5 GeV, respectively.
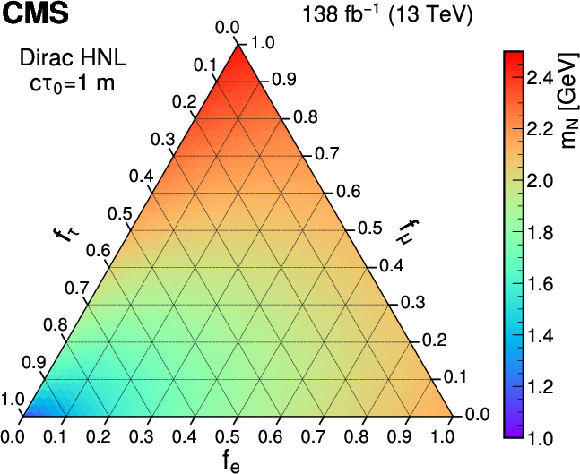
png pdf	Figure 7-c: The largest values of the Majorana (upper) and Dirac (lower) HNL mass (left) and mean proper decay length (right) parameters that are excluded at 95% CL are shown as a function of the mixing matrix elements squared ratios $ f_\ell $ with the three lepton generations, considering a mean proper decay length of 1 m and a fixed mass of 1.5 GeV, respectively.
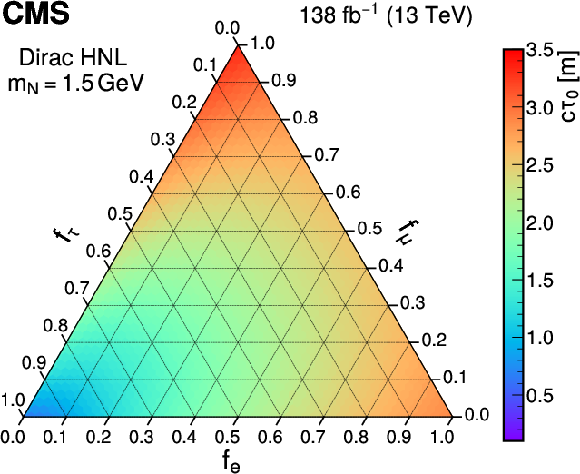
png pdf	Figure 7-d: The largest values of the Majorana (upper) and Dirac (lower) HNL mass (left) and mean proper decay length (right) parameters that are excluded at 95% CL are shown as a function of the mixing matrix elements squared ratios $ f_\ell $ with the three lepton generations, considering a mean proper decay length of 1 m and a fixed mass of 1.5 GeV, respectively.

Tables
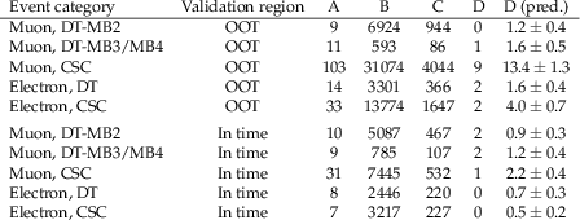
png pdf	Table 1: Validation of the ABCD method in the OOT and in-time validation regions. The predictions of the method for the signal bin (last column) are consistent with the observed number of events, shown in the second-to-last column.
png pdf	Table 2: The event yields in the bins A, B, and C are shown in each of the event categories considered in the search, as well as the prefit prediction for the ABCD background in the signal-enriched bin D.
png pdf	Table 3: Summary of the $ \mathrm{Z}\to\mu\mu $ background estimate in different categories. The first three columns show the estimates in the $ \mathrm{Z}\to\mu\mu $ enriched control region of the total background and its $ \mathrm{Z}\to\mu\mu $ and non-muon-induced components. The fourth column shows the transfer factors $ \zeta $ used to predict the $ \mathrm{Z}\to\mu\mu $ background in the signal region, shown in the fifth column.
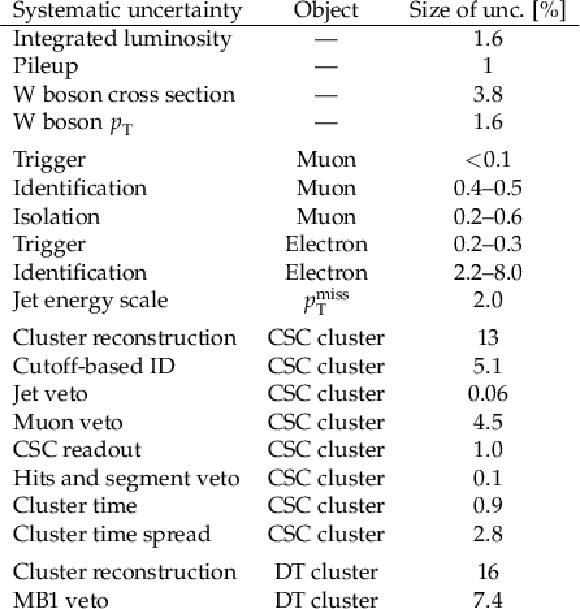
png pdf	Table 4: Summary of systematic uncertainties affecting the signal yield prediction. For DT clusters, the systematic uncertainties due to jet and muon vetoes are found to be negligible and are omitted. The uncertainties are reported relative to their impact on the predicted signal yield.
png pdf	Table 5: Excluded ranges of $ |V_{{\mathrm{N}} \ell}|^2 $ for Majorana and Dirac type HNLs at select HNL masses. The chosen HNL masses are those at which the excluded values of $ |V_{{\mathrm{N}} \ell}|^2 $ have the smallest magnitude.

Summary

A search for long-lived Dirac or Majorana heavy neutral leptons (HNLs) has been performed using proton-proton collision data at $ \sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. The search targets events with one prompt electron or muon and a muon detector shower (MDS) that would result from HNL decays occurring in the CMS muon detector. The presence of the MDS signature along with the associated vetoes and identification criteria suppresses the standard model background by a factor exceeding 10$^{7} $, while maintaining typical signal efficiencies of 25-35%. No significant excess over the standard model background is observed. The results are interpreted as 95% confidence level limits on the HNL mixing matrix elements squared $ |V_{{\mathrm{N}} \mathrm{e}}|^2 $, $ |V_{{\mathrm{N}} \mu}|^2 $, and $ |V_{{\mathrm{N}} \tau}|^2 $. We also present limits on the HNL mass and mean proper decay length as a function of the mixing matrix element squared fractions to the three lepton generations. The most stringent limits to date for HNLs in the mass range of 2.1-3.0 (1.9-3.3) GeV are set, reaching squared mixing matrix element values as low as 8.6 (4.6) $\times$ 10$^{-6} $ in the electron (muon) channel.

Additional Figures
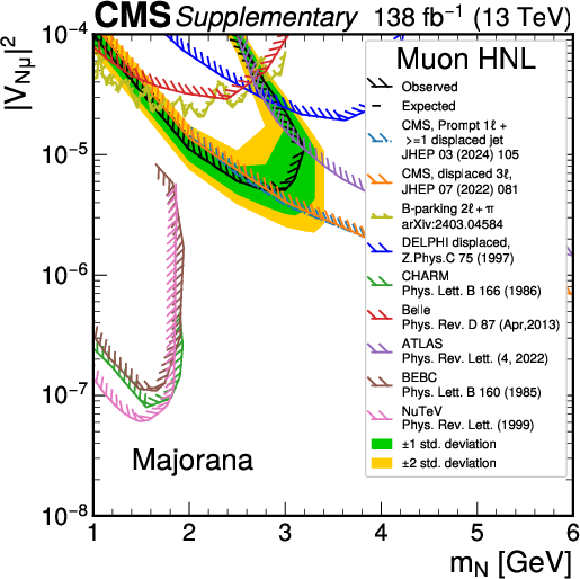
png pdf	Additional Figure 1: Expected and observed upper 95% confidence level (CL) limits on Majorana HNL production as a function of the HNL mass ($ m_{ \mathrm{N}} $) and coupling strengths on pure muon coupling. Results from previous CMS searches [41,38], as well as other experiments, including ATLAS [35], BEBC [27], Belle [31], CHARM [28], DELPHI [29] and NuTeV [30], are shown as reference. The limits from ATLAS, CMS and DELPHI experiments are set at 95% CL, and the other shown limits are set at 90% CL. The hatched side of the lines indicate regions excluded by the other experiments.
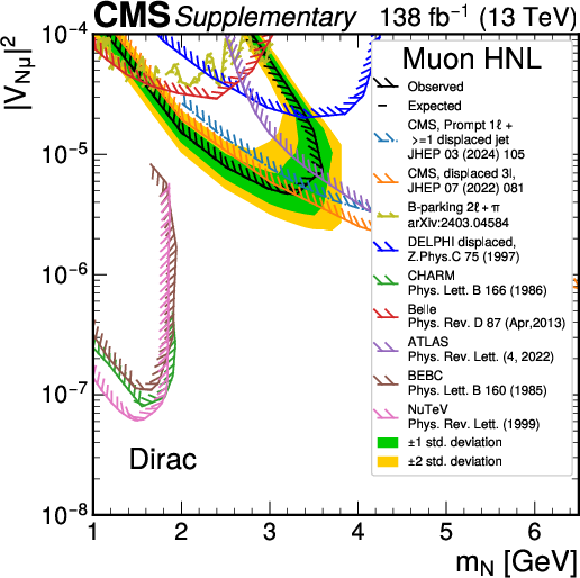
png pdf	Additional Figure 2: Expected and observed upper 95% confidence level (CL) limits on Dirac HNL production as a function of the HNL mass ($ m_{ \mathrm{N}} $) and coupling strengths on pure muon coupling. Results from previous CMS searches [41,38], as well as other experiments, including ATLAS [35], BEBC [27], Belle [31], CHARM [28], DELPHI [29] and NuTeV [30], are shown as reference. The limits from ATLAS, CMS and DELPHI experiments are set at 95% CL, and the other shown limits are set at 90% CL. The hatched side of the lines indicate regions excluded by the other experiments.
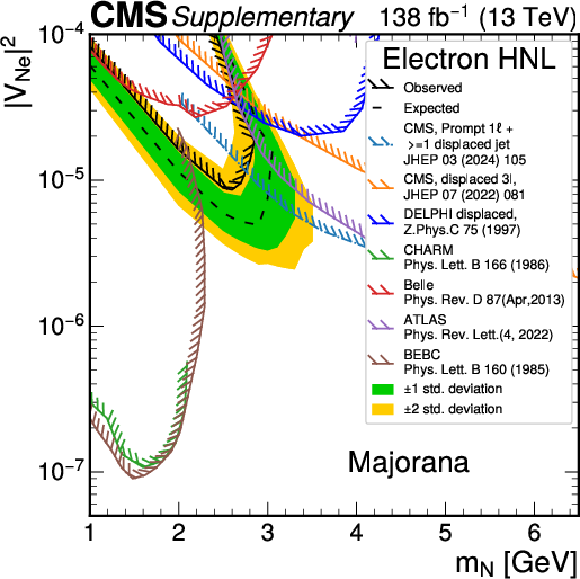
png pdf	Additional Figure 3: Expected and observed upper 95% confidence level (CL) limits on Majorana HNL production as a function of the HNL mass ($ m_{ \mathrm{N}} $) and coupling strengths on pure electron coupling. Results from previous CMS searches [41,38], as well as other experiments, including ATLAS [35], BEBC [27], Belle [31], CHARM [28] and DELPHI [29], are shown as reference. The limits from ATLAS, CMS and DELPHI experiments are set at 95% CL, and the other shown limits are set at 90% CL. The hatched side of the lines indicate regions excluded by the other experiments.
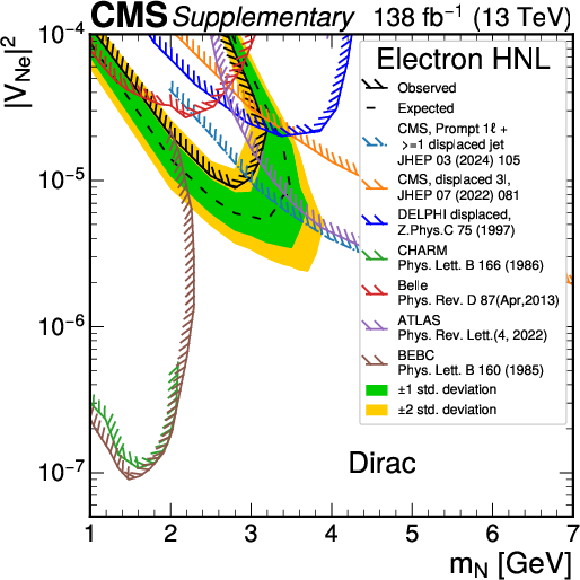
png pdf	Additional Figure 4: Expected and observed upper 95% confidence level (CL) limits on Dirac HNL production as a function of the HNL mass ($ m_{ \mathrm{N}} $) and coupling strengths on pure electron coupling. Results from previous CMS searches [41,38], as well as other experiments, including ATLAS [35], BEBC [27], Belle [31], CHARM [28] and DELPHI [29], are shown as reference. The limits from ATLAS, CMS and DELPHI experiments are set at 95% CL, and the other shown limits are set at 90% CL. The hatched side of the lines indicate regions excluded by the other experiments.

References
1	Super-Kamiokande Collaboration	Evidence for oscillation of atmospheric neutrinos	PRL 81 (1998) 1562	hep-ex/9807003
2	SNO Collaboration	Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory	PRL 89 (2002) 011301	nucl-ex/0204008
3	KamLAND Collaboration	First results from KamLAND: Evidence for reactor antineutrino disappearance	PRL 90 (2003) 021802	hep-ex/0212021
4	S. Bilenky	Neutrino oscillations: From a historical perspective to the present status	NPB 908 (2016) 2	1602.00170
5	S. Roy Choudhury and S. Hannestad	Updated results on neutrino mass and mass hierarchy from cosmology with Planck 2018 likelihoods	JCAP 07 (2020) 037	1907.12598
6	M. Ivanov, M. Simonović , and M. Zaldarriaga	Cosmological parameters and neutrino masses from the final Planck and full-shape BOSS data	PRD 101 (2020) 083504	1912.08208
7	J. Formaggio, A. de Gouvêa, and R. Robertson	Direct measurements of neutrino mass	Phys. Rept. 914 (2021) 1	2102.00594
8	P. Minkowski	$ {\mu\to\mathrm{e}\gamma} $ at a rate of one out of $ 10^{9} $ muon decays?	PLB 67 (1977) 421
9	T. Yanagida	Horizontal symmetry and masses of neutrinos	Prog. of Theo. Phys. 64 (1980) 1103
10	M. Gell-Mann, P. Ramond, and R. Slansky	Complex spinors and unified theories	in Supergravity, North Holland Publishing, 1979	1306.4669
11	S. Glashow	The future of elementary particle physics	NATO Sci. Ser. B 61 (1980) 687
12	R. N. Mohapatra and G. Senjanović	Neutrino mass and spontaneous parity nonconservation	PRL 44 (1980) 912
13	J. Schechter and J. W. F. Valle	Neutrino masses in $ \mathrm{SU}(2)\otimes\mathrm{U}(1) $ theories	PRD 22 (1980) 2227
14	R. E. Shrock	General theory of weak leptonic and semileptonic decays. I. Leptonic pseudoscalar meson decays, with associated tests for, and bounds on, neutrino masses and lepton mixing	PRD 24 (1981) 1232
15	Y. Cai, T. Han, T. Li, and R. Ruiz	Lepton number violation: Seesaw models and their collider tests	Front. Phys. 6 (2018) 40	1711.02180
16	Z. Maki, M. Nakagawa, and S. Sakata	Remarks on the unified model of elementary particles	Prog. Theor. Phys. 28 (1962) 870
17	B. Pontecorvo	Neutrino experiments and the problem of conservation of leptonic charge	Zh. Eksp. Teor. Fiz. 53 (1967) 1717
18	A. Das, P. Konar, and S. Majhi	Production of Heavy neutrino in next-to-leading order QCD at the LHC and beyond	JHEP 06 (2016) 019	1604.00608
19	A. Das and N. Okada	Bounds on heavy Majorana neutrinos in type-I seesaw and implications for collider searches	PLB 774 (2017) 32	1702.04668
20	G. Cottin et al.	Long-lived heavy neutral leptons with a displaced shower signature at CMS	JHEP 02 (2023) 011	2210.17446
21	K. Bondarenko, A. Boyarsky, D. Gorbunov, and O. Ruchayskiy	Phenomenology of GeVns-scale heavy neutral leptons	JHEP 11 (2018) 032	1805.08567
22	M. Fukugita and T. Yanagida	Baryogenesis without grand unification	PLB 174 (1986) 45
23	E. Chun et al.	Probing leptogenesis	Int. J. Mod. Phys. A 33 (2018) 1842005	1711.02865
24	A. Boyarsky et al.	Sterile neutrino dark matter	Prog. Part. Nucl. Phys. 104 (2019) 1
25	V. Cirigliano et al.	Leptonic anomalous magnetic moments in $\nu $SMEFT	JHEP 08 (2021) 103	2105.11462
26	Muon g${-}$2 Collaboration	Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm	PRL 131 (2023) 161802	2308.06230
27	WA66 Collaboration	Search for heavy neutrino decays in the BEBC beam dump experiment	PLB 160 (1985) 207
28	CHARM Collaboration	A search for decays of heavy neutrinos in the mass range 0.5-2.8 GeV	PLB 166 (1986) 473
29	DELPHI Collaboration	Search for neutral heavy leptons produced in Z decays	Z. Phys. C 74 (1997) 57
30	NuTeV(E815) Collaboration	Search for neutral heavy leptons in a high-energy neutrino beam	PRL 83 (1999) 4943	hep-ex/9908011
31	Belle Collaboration	Search for heavy neutrinos at Belle	PRD 87 (2013) 071102	1301.1105
32	F. F. Deppisch, P. S. Bhupal Dev, and A. Pilaftsis	Neutrinos and collider physics	New J. Phys. 17 (2015) 075019	1502.06541
33	J. Beacham et al.	Physics beyond colliders at CERN: Beyond the standard model working group report	JPG 47 (2020) 010501	1901.09966
34	ATLAS Collaboration	Search for heavy neutral leptons in decays of W bosons produced in 13 TeV pp collisions using prompt and displaced signatures with the ATLAS detector	JHEP 10 (2019) 265	1905.09787
35	ATLAS Collaboration	Search for heavy neutral leptons in decays of $ W $ bosons using a dilepton displaced vertex in $ \sqrt{s}= $ 13 TeV pp collisions with the ATLAS detector	PRL 131 (2023) 061803	2204.11988
36	CMS Collaboration	Search for heavy neutral leptons in events with three charged leptons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV	PRL 120 (2018) 221801	CMS-EXO-17-012 1802.02965
37	CMS Collaboration	Search for heavy Majorana neutrinos in same-sign dilepton channels in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 01 (2019) 122	CMS-EXO-17-028 1806.10905
38	CMS Collaboration	Search for long-lived heavy neutral leptons with displaced vertices in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 07 (2022) 081	CMS-EXO-20-009 2201.05578
39	LHCb Collaboration	Search for heavy neutral leptons in $ \textrm{W}^+\to\mu^{+}\mu^{\pm}$jet decays	EPJC 81 (2021) 248	2011.05263
40	LHCb Collaboration	Search for long-lived particles decaying to $ \textrm{e}^\pm \mu^\mp \nu $	EPJC 81 (2021) 261	2012.02696
41	CMS Collaboration	Search for long-lived heavy neutral leptons with lepton flavour conserving or violating decays to a jet and a charged lepton	Submitted to JHEP, 2023	CMS-EXO-21-013 2312.07484
42	CMS Collaboration	Search for long-lived particles decaying in the CMS endcap muon detectors in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	PRL 127 (2021) 261804	CMS-EXO-20-015 2107.04838
43	CMS Collaboration	HEPData record for this analysis	link
44	CMS Collaboration	Performance of the CMS Drift Tube Chambers with Cosmic Rays	JINST 5 (2010) T03015	CMS-CFT-09-012 0911.4855
45	CMS Collaboration	Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV	JINST 15 (2020) P10017	CMS-TRG-17-001 2006.10165
46	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
47	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
48	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
49	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
50	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG box	JHEP 06 (2010) 043	1002.2581
51	R. Gavin, Y. Li, F. Petriello, and S. Quackenbush	FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order	Comput. Phys. Commun. 182 (2011) 2388	1011.3540
52	R. Gavin, Y. Li, F. Petriello, and S. Quackenbush	W physics at the LHC with FEWZ 2.1	Comput. Phys. Commun. 184 (2013) 208	1201.5896
53	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
54	D. Alva, T. Han, and R. Ruiz	Heavy Majorana neutrinos from $ \mathrm{W}\gamma $ fusion at hadron colliders	JHEP 02 (2015) 072	1411.7305
55	C. Degrande, O. Mattelaer, R. Ruiz, and J. Turner	Fully-automated precision predictions for heavy neutrino production mechanisms at hadron colliders	PRD 94 (2016) 053002	1602.06957
56	S. Pascoli, R. Ruiz, and C. Weiland	Heavy neutrinos with dynamic jet vetoes: Multilepton searches at $ \sqrt{s}= $ 14, 27, and 100 TeV	JHEP 06 (2019) 049	1812.08750
57	T. Sjöstrand et al.	An introduction to PYTHIA8.2	Comp. Phys. Comm. 191 (2015) 159	1410.3012
58	Y. Li and F. Petriello	Combining QCD and electroweak corrections to dilepton production in FEWZ	PRD 86 (2012) 094034	1208.5967
59	S. Camarda et al.	DYTurbo: Fast predictions for Drell-Yan processes	EPJC 80 (2020) 251	1910.07049
60	S. Camarda, L. Cieri, and G. Ferrera	Drell-yan lepton-pair production: $ {q}_{T} $ resummation at $ \mathrm{N}^{3}\mathrm{LL} $ accuracy and fiducial cross sections at $ \mathrm{N}^{3}\mathrm{LO} $	PRD 104 (2021) L111503	2103.04974
61	GEANT4 Collaboration	GEANT 4--a simulation toolkit	NIM A 506 (2003) 250
62	CMS Collaboration	Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS	EPJC 81 (2021) 800	CMS-LUM-17-003 2104.01927
63	CMS Collaboration	CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV	CMS Physics Analysis Summary, 2018 link	CMS-PAS-LUM-17-004
64	CMS Collaboration	CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV	CMS Physics Analysis Summary, 2019 link	CMS-PAS-LUM-18-002
65	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
66	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
67	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
68	NNPDF Collaboration	Parton distributions from high-precision collider data	EPJC 77 (2017) 663	1706.00428
69	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
70	CMS Collaboration	Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC	JINST 16 (2021) P05014	CMS-EGM-17-001 2012.06888
71	CMS Collaboration	Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JINST 13 (2018) P06015	CMS-MUO-16-001 1804.04528
72	CMS Collaboration	Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	JINST 10 (2015) P08010	CMS-EGM-14-001 1502.02702
73	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_{\mathrm{T}} $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
74	M. Cacciari, G. P. Salam, and G. Soyez	FASTJET user manual	EPJC 72 (2012) 1896	1111.6097
75	CMS Collaboration	Pileup mitigation at CMS in 13 TeV data	JINST 15 (2020) P09018	CMS-JME-18-001 2003.00503
76	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
77	CMS Collaboration	Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector	JINST 14 (2019) P07004	CMS-JME-17-001 1903.06078
78	CMS Collaboration	Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid	CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS
79	M. Ester, H.-P. Kriegel, J. Sander, and X. Xu	A density-based algorithm for discovering clusters in large spatial databases with noise	in Proc. 2nd Int. Conf. on Knowledge Discovery and Data Mining, Association for the Advancement of Artificial Intelligence, 1996 link
80	CMS Collaboration	Identification of b-quark jets with the CMS experiment	JINST 8 (2013) P04013	CMS-BTV-12-001 1211.4462
81	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV	JINST 13 (2018) P05011	CMS-BTV-16-002 1712.07158
82	T. Junk	Confidence level computation for combining searches with small statistics	NIM A 434 (1999) 435	hep-ex/9902006
83	A. L. Read	Presentation of search results: the $ \text{CL}_\text{s} $ technique	JPG 28 (2002) 2693
84	ATLAS and CMS Collaborations, and the LHC Higgs Combination Group	Procedure for the LHC Higgs boson search combination in Summer 2011	Technical Report CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011
85	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727
86	M. Drewes, J. Klarić, and J. López-Pavón	New benchmark models for heavy neutral lepton searches	EPJC 82 (2022) 1176	2207.02742

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2024 for the benefit of the CMS Collaboration