

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-LUM-20-001 | ||
| Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the CMS detector | ||
| CMS Collaboration | ||
| 2025-08-23 | ||
| Abstract: The measurement of the integrated luminosity recorded by the CMS detector at the LHC in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2017 and 2018 is reported. The absolute luminosity calibration is obtained with the van der Meer (vdM) method through beam-separation scans that were performed in special accelerator conditions. The extrapolation to regular data-taking conditions relies on detector-specific measurements. Multiple independently calibrated luminosity detectors (luminometers) are employed to derive the final integrated luminosity. A relative precision of 0.82 and 0.84% is achieved for the 2017 and 2018 data sets, respectively. Dominant uncertainties are the luminometer nonlinearity and the assumption of transverse factorizability in the vdM method. The consistency of the measurements for 2016, 2017, and 2018 is evaluated using Z boson rates. When combined with the 2015--2016 data sets at the same center-of-mass energy, the relative precision of the total integrated luminosity is 0.73%, representing the most precise luminosity measurement ever achieved at bunched-beam hadron colliders. This is possible due to improved vdM methodology and the combination of results by independent luminometers. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
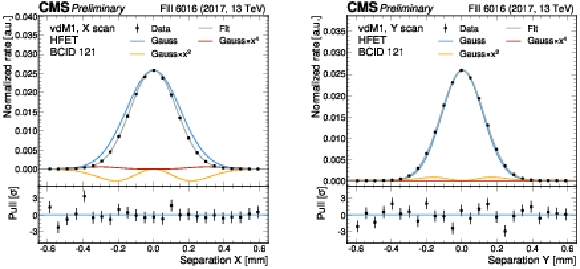
Figure 1:
An illustration of the vdM fit procedure for the HFET method in the 2017 vdM fill after all corrections applied. The luminometer rate (normalized by the product of the bunch proton multiplicity values) is shown for a single bunch crossing location along the orbit (BCID 121) as a function of the transverse separation of the two beams in the horizontal (left) and vertical (right) directions. They are fitted by the product of a fourth order positive symmetric polynomial and a Gaussian. The three additive components as well as the full analytic function are plotted. The widths of the fitted distribution define the beam convolution widths $ \Sigma_x $ and $ \Sigma_y $ and the peak value gives the head-on rate normalized by the bunch intensity ($ R(0,0)/(N_1N_2) $) in Eq. 3. The lower panel shows the difference between the measured data and the fitted function, normalized by the uncertainty. |
png pdf |
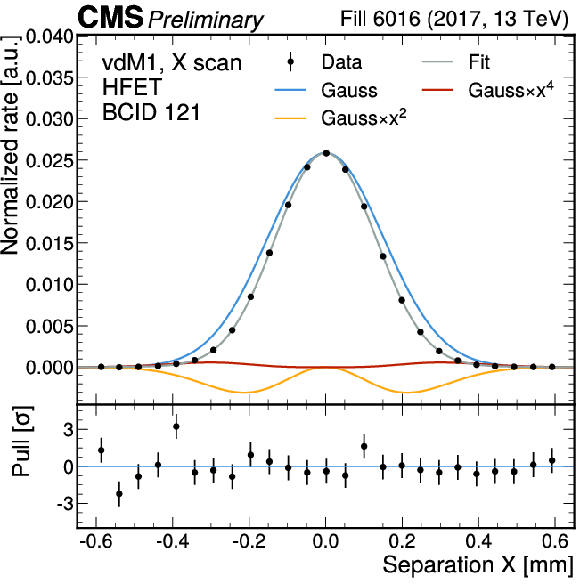
Figure 1-a:
An illustration of the vdM fit procedure for the HFET method in the 2017 vdM fill after all corrections applied. The luminometer rate (normalized by the product of the bunch proton multiplicity values) is shown for a single bunch crossing location along the orbit (BCID 121) as a function of the transverse separation of the two beams in the horizontal (left) and vertical (right) directions. They are fitted by the product of a fourth order positive symmetric polynomial and a Gaussian. The three additive components as well as the full analytic function are plotted. The widths of the fitted distribution define the beam convolution widths $ \Sigma_x $ and $ \Sigma_y $ and the peak value gives the head-on rate normalized by the bunch intensity ($ R(0,0)/(N_1N_2) $) in Eq. 3. The lower panel shows the difference between the measured data and the fitted function, normalized by the uncertainty. |
png pdf |
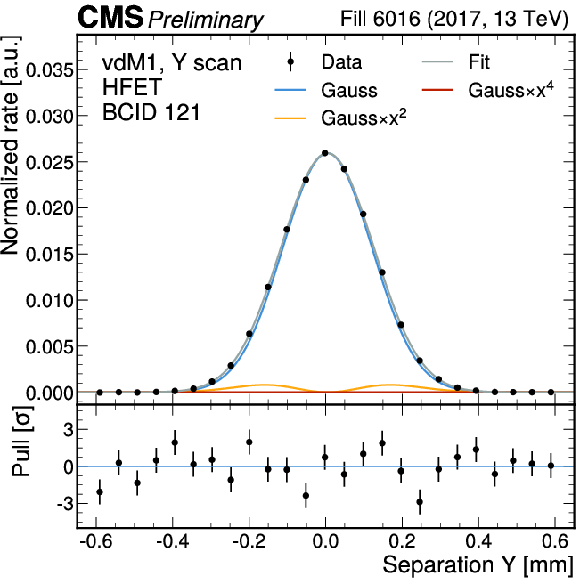
Figure 1-b:
An illustration of the vdM fit procedure for the HFET method in the 2017 vdM fill after all corrections applied. The luminometer rate (normalized by the product of the bunch proton multiplicity values) is shown for a single bunch crossing location along the orbit (BCID 121) as a function of the transverse separation of the two beams in the horizontal (left) and vertical (right) directions. They are fitted by the product of a fourth order positive symmetric polynomial and a Gaussian. The three additive components as well as the full analytic function are plotted. The widths of the fitted distribution define the beam convolution widths $ \Sigma_x $ and $ \Sigma_y $ and the peak value gives the head-on rate normalized by the bunch intensity ($ R(0,0)/(N_1N_2) $) in Eq. 3. The lower panel shows the difference between the measured data and the fitted function, normalized by the uncertainty. |
png pdf |
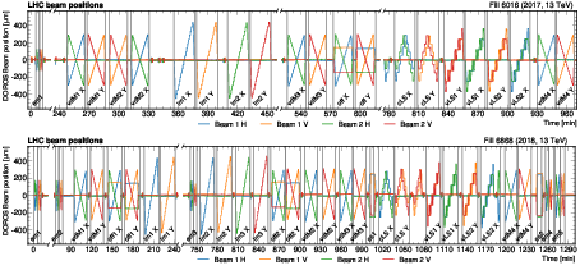
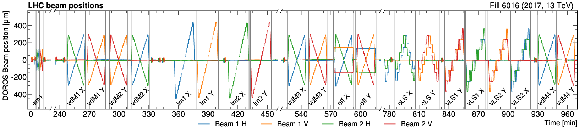
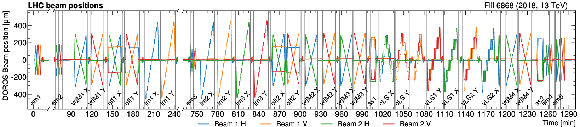
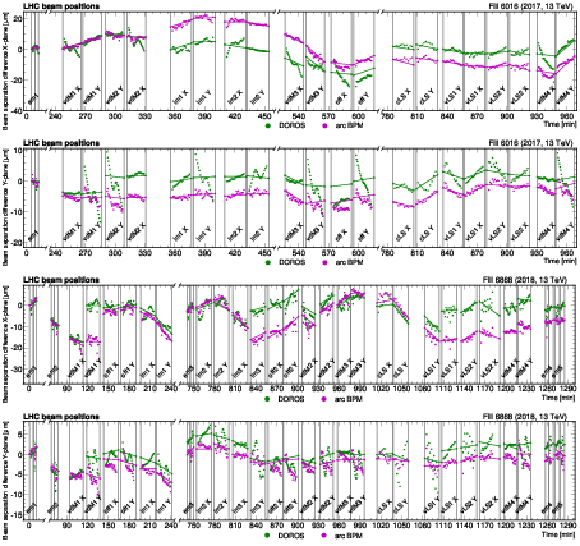
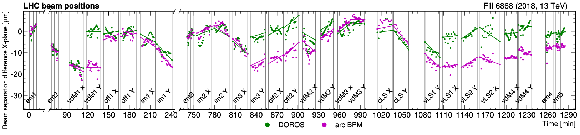
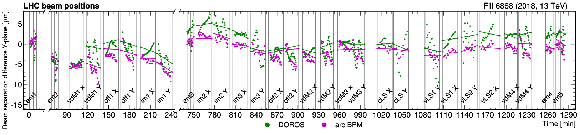
Figure 2:
Vertical (V) and horizontal (H) beam positions as a function of time measured by the DOROS beam position monitors during LHC fill 6016 (upper) and 6868 (lower). The orbit is averaged over the bunches and monitored throughout the scan program with 1\units time granularity. The individual scans are indicated by vertical lines. Each scan pair consists of two scans orthogonal to each other and is labeled with the abbreviation of the specific scan type: ``vdM'', ``em'', ``im'', and ``off'' for vdM, emittance, beam imaging, and offset scans, respectively. Variable- and constant-separation length scale scans are marked with ``vLS'' and ``cLS'', respectively. The super separation periods in 2018 are marked with ``ss''. |
png pdf |
Figure 2-a:
Vertical (V) and horizontal (H) beam positions as a function of time measured by the DOROS beam position monitors during LHC fill 6016 (upper) and 6868 (lower). The orbit is averaged over the bunches and monitored throughout the scan program with 1\units time granularity. The individual scans are indicated by vertical lines. Each scan pair consists of two scans orthogonal to each other and is labeled with the abbreviation of the specific scan type: ``vdM'', ``em'', ``im'', and ``off'' for vdM, emittance, beam imaging, and offset scans, respectively. Variable- and constant-separation length scale scans are marked with ``vLS'' and ``cLS'', respectively. The super separation periods in 2018 are marked with ``ss''. |
png pdf |
Figure 2-b:
Vertical (V) and horizontal (H) beam positions as a function of time measured by the DOROS beam position monitors during LHC fill 6016 (upper) and 6868 (lower). The orbit is averaged over the bunches and monitored throughout the scan program with 1\units time granularity. The individual scans are indicated by vertical lines. Each scan pair consists of two scans orthogonal to each other and is labeled with the abbreviation of the specific scan type: ``vdM'', ``em'', ``im'', and ``off'' for vdM, emittance, beam imaging, and offset scans, respectively. Variable- and constant-separation length scale scans are marked with ``vLS'' and ``cLS'', respectively. The super separation periods in 2018 are marked with ``ss''. |
png pdf |
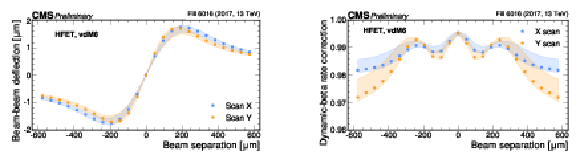
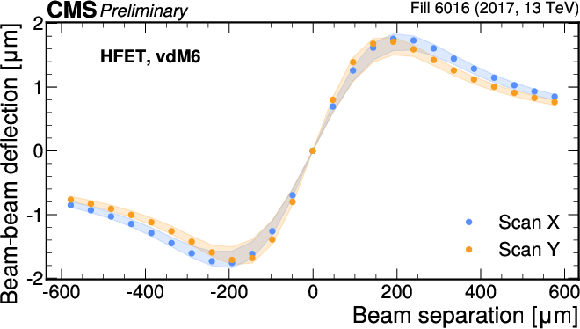
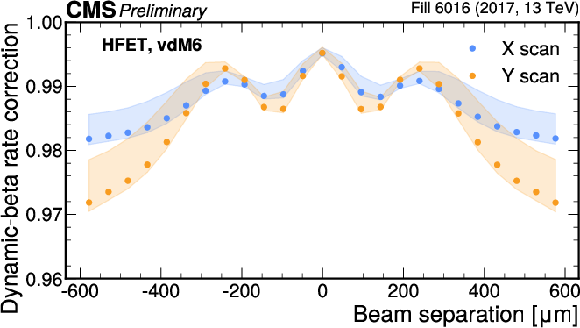
Figure 3:
Beam-beam deflection (left) and dynamic-$ \beta $ correction (right) shown for the last scan pair in fill 6016 for both the $ x $ and $ y $ axes. The values are computed per bunch independently. The points represent the average over the bunches with the shaded area covering the minimum and maximum values. |
png pdf |
Figure 3-a:
Beam-beam deflection (left) and dynamic-$ \beta $ correction (right) shown for the last scan pair in fill 6016 for both the $ x $ and $ y $ axes. The values are computed per bunch independently. The points represent the average over the bunches with the shaded area covering the minimum and maximum values. |
png pdf |
Figure 3-b:
Beam-beam deflection (left) and dynamic-$ \beta $ correction (right) shown for the last scan pair in fill 6016 for both the $ x $ and $ y $ axes. The values are computed per bunch independently. The points represent the average over the bunches with the shaded area covering the minimum and maximum values. |
png pdf |
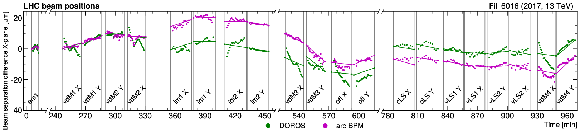
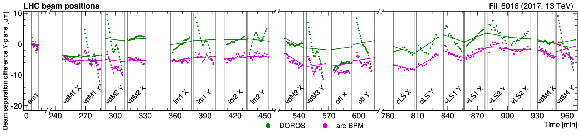
Figure 4:
The difference between nominal and measured beam separations ($ u_{\text{BPM}}-u_{\text{NOM}} $ and $ v_{\text{BPM}}-v_{\text{NOM}} $) per scan step as a function of time for the calibration scans during LHC fills 6016 (upper two figures) and 6868 (lower two figures). The scan boundaries are marked by vertical lines and labeled with the abbreviation of the scan name. The solid green and magenta lines represent the linear interpolation between the head-on reference points before and after the scan, indicating the slow orbit drift component. |
png pdf |
Figure 4-a:
The difference between nominal and measured beam separations ($ u_{\text{BPM}}-u_{\text{NOM}} $ and $ v_{\text{BPM}}-v_{\text{NOM}} $) per scan step as a function of time for the calibration scans during LHC fills 6016 (upper two figures) and 6868 (lower two figures). The scan boundaries are marked by vertical lines and labeled with the abbreviation of the scan name. The solid green and magenta lines represent the linear interpolation between the head-on reference points before and after the scan, indicating the slow orbit drift component. |
png pdf |
Figure 4-b:
The difference between nominal and measured beam separations ($ u_{\text{BPM}}-u_{\text{NOM}} $ and $ v_{\text{BPM}}-v_{\text{NOM}} $) per scan step as a function of time for the calibration scans during LHC fills 6016 (upper two figures) and 6868 (lower two figures). The scan boundaries are marked by vertical lines and labeled with the abbreviation of the scan name. The solid green and magenta lines represent the linear interpolation between the head-on reference points before and after the scan, indicating the slow orbit drift component. |
png pdf |
Figure 4-c:
The difference between nominal and measured beam separations ($ u_{\text{BPM}}-u_{\text{NOM}} $ and $ v_{\text{BPM}}-v_{\text{NOM}} $) per scan step as a function of time for the calibration scans during LHC fills 6016 (upper two figures) and 6868 (lower two figures). The scan boundaries are marked by vertical lines and labeled with the abbreviation of the scan name. The solid green and magenta lines represent the linear interpolation between the head-on reference points before and after the scan, indicating the slow orbit drift component. |
png pdf |
Figure 4-d:
The difference between nominal and measured beam separations ($ u_{\text{BPM}}-u_{\text{NOM}} $ and $ v_{\text{BPM}}-v_{\text{NOM}} $) per scan step as a function of time for the calibration scans during LHC fills 6016 (upper two figures) and 6868 (lower two figures). The scan boundaries are marked by vertical lines and labeled with the abbreviation of the scan name. The solid green and magenta lines represent the linear interpolation between the head-on reference points before and after the scan, indicating the slow orbit drift component. |
png pdf |
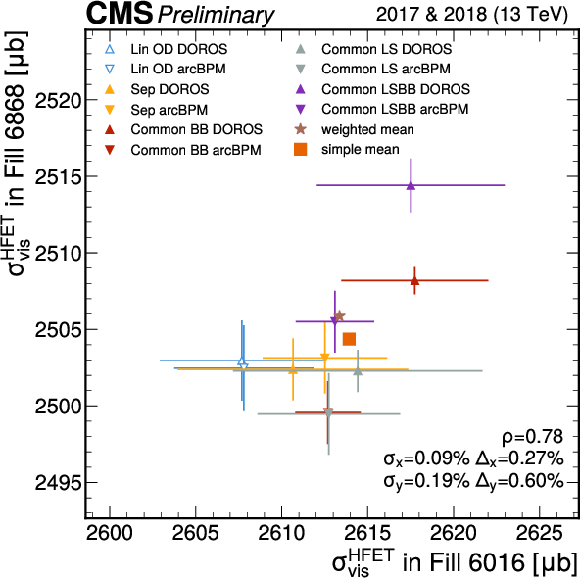
Figure 5:
Visible cross section estimates for the HFET luminometer after applying orbit drift corrections for the 2017 and 2018 calibration fills with different assumptions for the $ \alpha $ and $ \delta $ parameters in the fit which describe the BPM (arc or DOROS) length scale (LS) and the dilution of the beam-beam deflection (BB), respectively. The baseline ``Common LS BB Arc'' method (purple down-facing triangle) uses the arc BPM measurements and assumes a common $ \alpha $ and $ \delta $ for each scan of a given year. Its results are the closest to the means of the various measurements (brown star or orange square) and are used as the central correction values for the calibration. The empty triangles, representing the linear only orbit drift corrections, are not taken into account for the averages, nor for the other metrics on the plot. The observed correlation between the years is large (0.78). The standard deviations and the full range of the measured values are also given. |
png pdf |
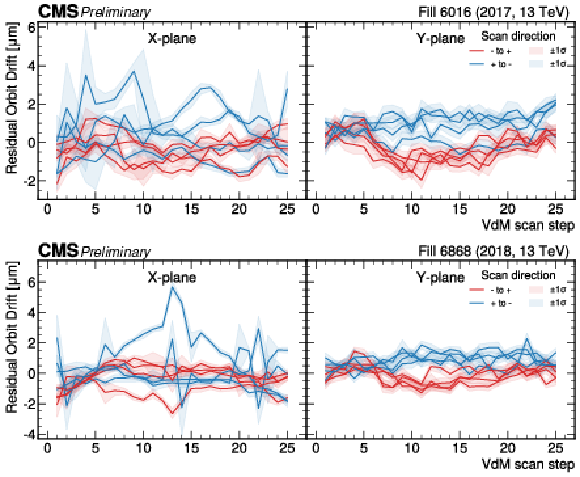
Figure 6:
Residual orbit drift correction on the position of the beams as a function of the scan step number for each regular vdM scan, as calculated using the arc BPM measurements and common $ \alpha $ and $ \delta $ parameters for each scan of a given year for 2017 (upper) and 2018 (lower). The red (blue) lines represent the residuals for the beam moving from the negative (positive) to the positive (negative) direction in the transverse plane with respect to the CMS reference system (see Fig 2). This labeling was chosen to better visualize potential reproducible features due to magnetic non-linearites. The uncertainty bands are derived from the standard deviation of the individual BPM readings within a scan step. |
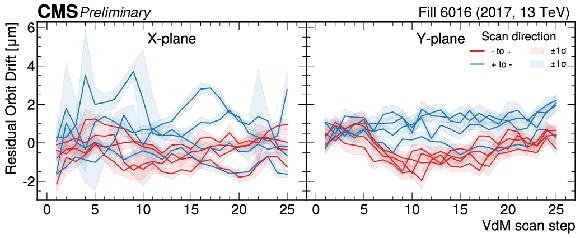
png pdf |
Figure 6-a:
Residual orbit drift correction on the position of the beams as a function of the scan step number for each regular vdM scan, as calculated using the arc BPM measurements and common $ \alpha $ and $ \delta $ parameters for each scan of a given year for 2017 (upper) and 2018 (lower). The red (blue) lines represent the residuals for the beam moving from the negative (positive) to the positive (negative) direction in the transverse plane with respect to the CMS reference system (see Fig 2). This labeling was chosen to better visualize potential reproducible features due to magnetic non-linearites. The uncertainty bands are derived from the standard deviation of the individual BPM readings within a scan step. |
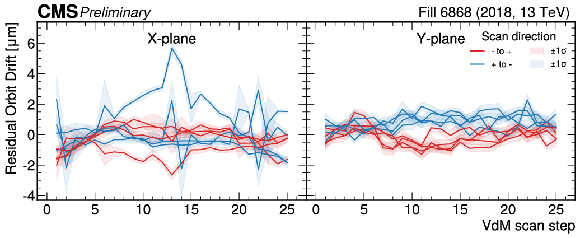
png pdf |
Figure 6-b:
Residual orbit drift correction on the position of the beams as a function of the scan step number for each regular vdM scan, as calculated using the arc BPM measurements and common $ \alpha $ and $ \delta $ parameters for each scan of a given year for 2017 (upper) and 2018 (lower). The red (blue) lines represent the residuals for the beam moving from the negative (positive) to the positive (negative) direction in the transverse plane with respect to the CMS reference system (see Fig 2). This labeling was chosen to better visualize potential reproducible features due to magnetic non-linearites. The uncertainty bands are derived from the standard deviation of the individual BPM readings within a scan step. |
png pdf |
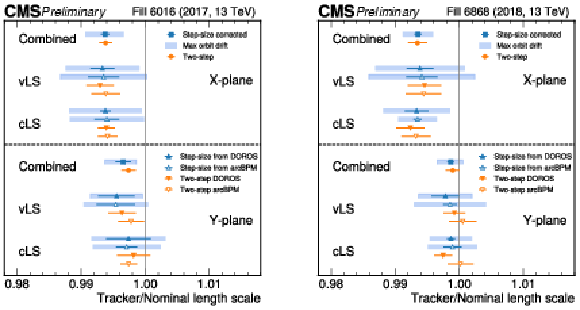
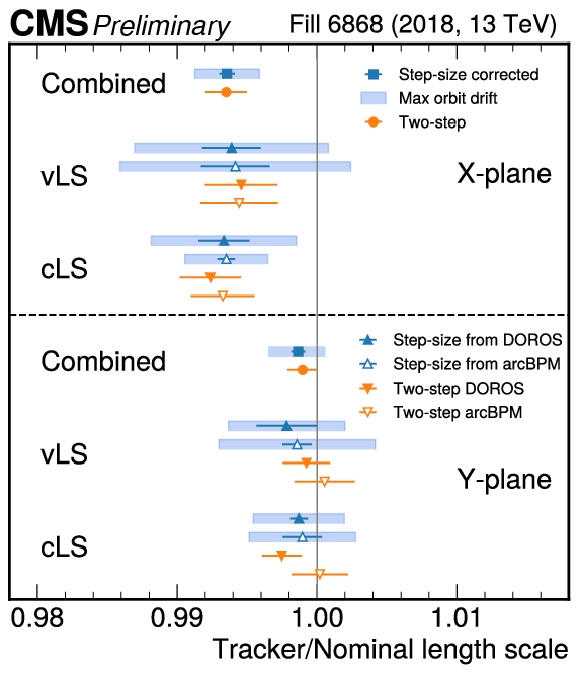
Figure 7:
Two-step and step-size corrected length scale estimates of the nominal position with respect to the the CMS tracker in the 2017 (left) and 2018 (right) vdM fills. Together with the final results, the per-BPM and per-scan results are also shown to illustrate the consistency of the measurements. For the step-size corrected results the error bar shows the uncertainty with two different estimations of the possible bias due to orbit drift: an optimistic expectation comparing the results without and with outlier removal in the average step-size calculation (dark blue), and a more pessimistic scenario as obtained in simulation where the OD is modeled as a Gaussian random walk (light blue band). Since the combination between the vLS and cLS results is a weighted mean, the light blue band is not necessarily centered on the blue points. |
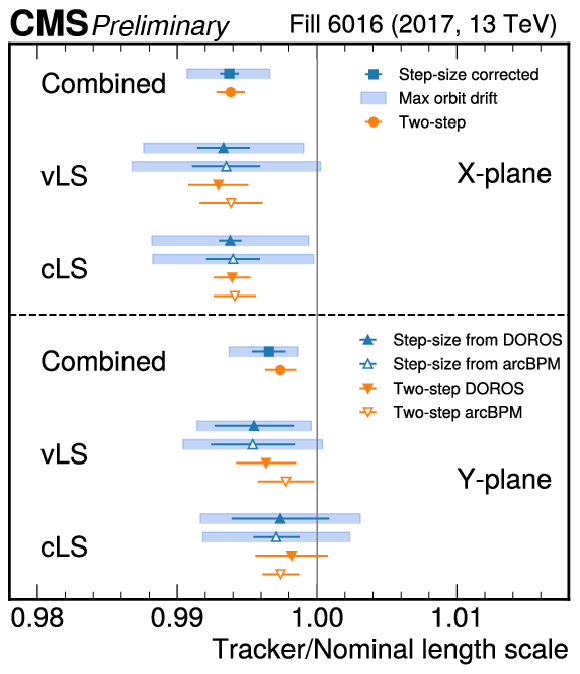
png pdf |
Figure 7-a:
Two-step and step-size corrected length scale estimates of the nominal position with respect to the the CMS tracker in the 2017 (left) and 2018 (right) vdM fills. Together with the final results, the per-BPM and per-scan results are also shown to illustrate the consistency of the measurements. For the step-size corrected results the error bar shows the uncertainty with two different estimations of the possible bias due to orbit drift: an optimistic expectation comparing the results without and with outlier removal in the average step-size calculation (dark blue), and a more pessimistic scenario as obtained in simulation where the OD is modeled as a Gaussian random walk (light blue band). Since the combination between the vLS and cLS results is a weighted mean, the light blue band is not necessarily centered on the blue points. |
png pdf |
Figure 7-b:
Two-step and step-size corrected length scale estimates of the nominal position with respect to the the CMS tracker in the 2017 (left) and 2018 (right) vdM fills. Together with the final results, the per-BPM and per-scan results are also shown to illustrate the consistency of the measurements. For the step-size corrected results the error bar shows the uncertainty with two different estimations of the possible bias due to orbit drift: an optimistic expectation comparing the results without and with outlier removal in the average step-size calculation (dark blue), and a more pessimistic scenario as obtained in simulation where the OD is modeled as a Gaussian random walk (light blue band). Since the combination between the vLS and cLS results is a weighted mean, the light blue band is not necessarily centered on the blue points. |
png pdf |
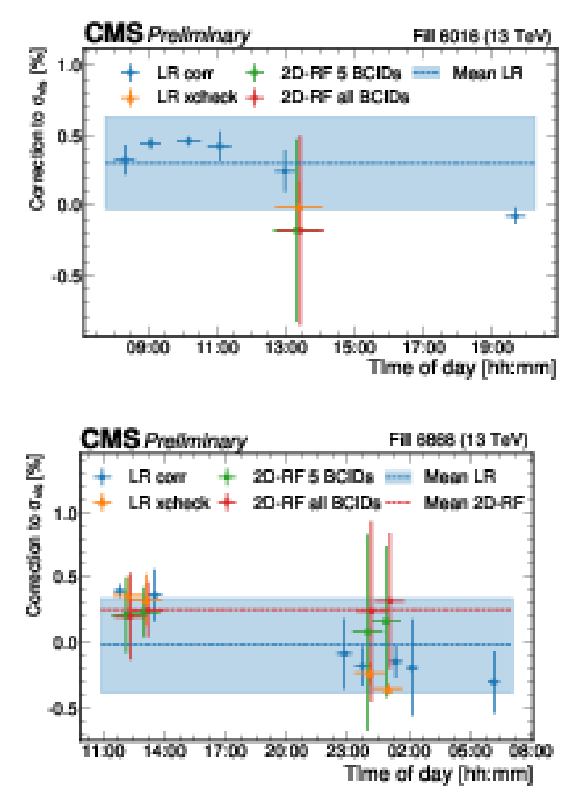
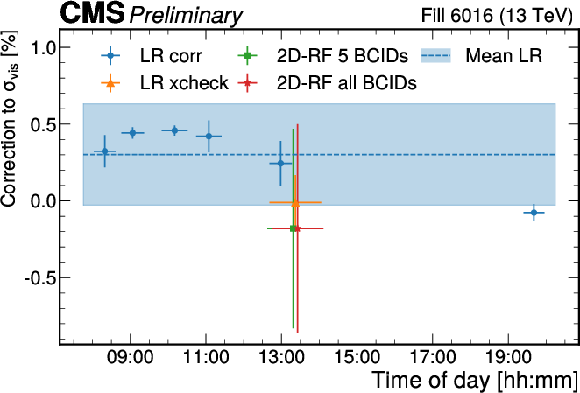
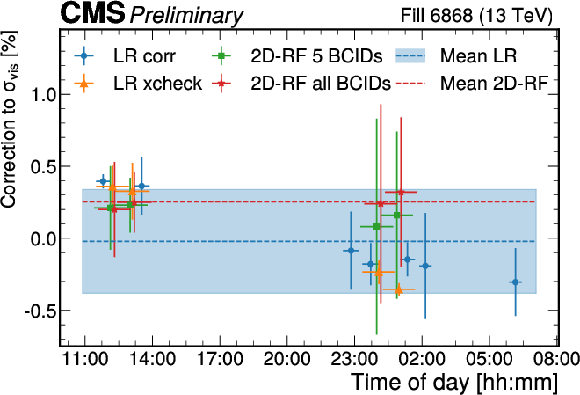
Figure 8:
The final corrections (blue) derived using the best fit luminous region model and the Poly4G vdM model for 2017 (left) and 2018 (right). The horizontal error bars signify the time period during which the input data for the fit is collected. The vertical error bars signify the standard deviation of the BCIDs, while the marker itself shows the average over the BCIDs. The correction to $ \sigma_{\text{vis}} $ is applied scan-by-scan disregarding corrections computed by the combination of multiple scan pairs. A comparison with the 2D rate-fit method is also presented. The orange markers show the LR results using the same input scans, a combination of an on-axis and an off-axis scan pair as the corresponding 2D rate-fit corrections. The red and green markers show the correction derived using the 2D RF method for the five BCIDs where the LR fit is performed and for all colliding BCIDs, respectively, with the vertical error bars indicating the full uncertainty of the method. |
png pdf |
Figure 8-a:
The final corrections (blue) derived using the best fit luminous region model and the Poly4G vdM model for 2017 (left) and 2018 (right). The horizontal error bars signify the time period during which the input data for the fit is collected. The vertical error bars signify the standard deviation of the BCIDs, while the marker itself shows the average over the BCIDs. The correction to $ \sigma_{\text{vis}} $ is applied scan-by-scan disregarding corrections computed by the combination of multiple scan pairs. A comparison with the 2D rate-fit method is also presented. The orange markers show the LR results using the same input scans, a combination of an on-axis and an off-axis scan pair as the corresponding 2D rate-fit corrections. The red and green markers show the correction derived using the 2D RF method for the five BCIDs where the LR fit is performed and for all colliding BCIDs, respectively, with the vertical error bars indicating the full uncertainty of the method. |
png pdf |
Figure 8-b:
The final corrections (blue) derived using the best fit luminous region model and the Poly4G vdM model for 2017 (left) and 2018 (right). The horizontal error bars signify the time period during which the input data for the fit is collected. The vertical error bars signify the standard deviation of the BCIDs, while the marker itself shows the average over the BCIDs. The correction to $ \sigma_{\text{vis}} $ is applied scan-by-scan disregarding corrections computed by the combination of multiple scan pairs. A comparison with the 2D rate-fit method is also presented. The orange markers show the LR results using the same input scans, a combination of an on-axis and an off-axis scan pair as the corresponding 2D rate-fit corrections. The red and green markers show the correction derived using the 2D RF method for the five BCIDs where the LR fit is performed and for all colliding BCIDs, respectively, with the vertical error bars indicating the full uncertainty of the method. |
png pdf |
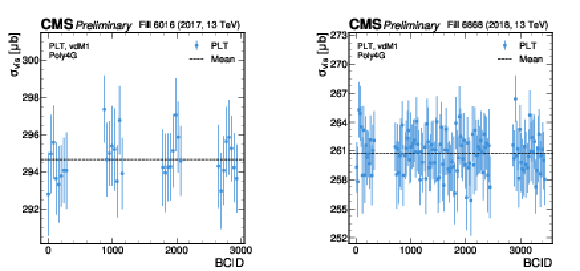
Figure 9:
Per BCID $ \sigma_{\text{vis}} $ values in the first scan in 2017 (left) and 2018 (right) for PLT. The error bars represent the uncertainty propagated from the fit. |
png pdf |
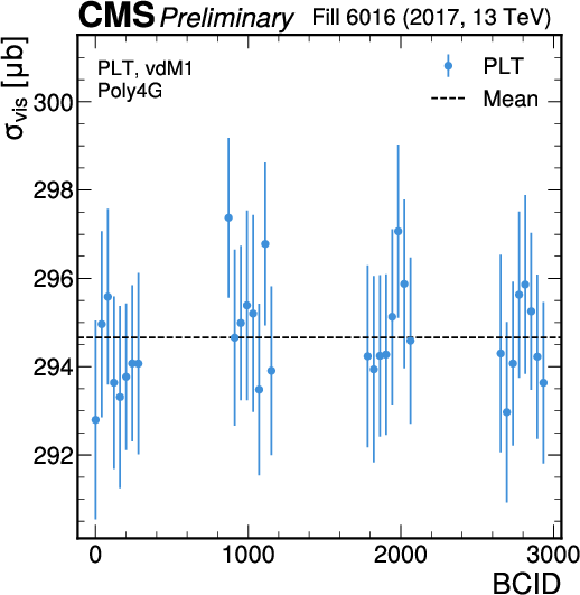
Figure 9-a:
Per BCID $ \sigma_{\text{vis}} $ values in the first scan in 2017 (left) and 2018 (right) for PLT. The error bars represent the uncertainty propagated from the fit. |
png pdf |
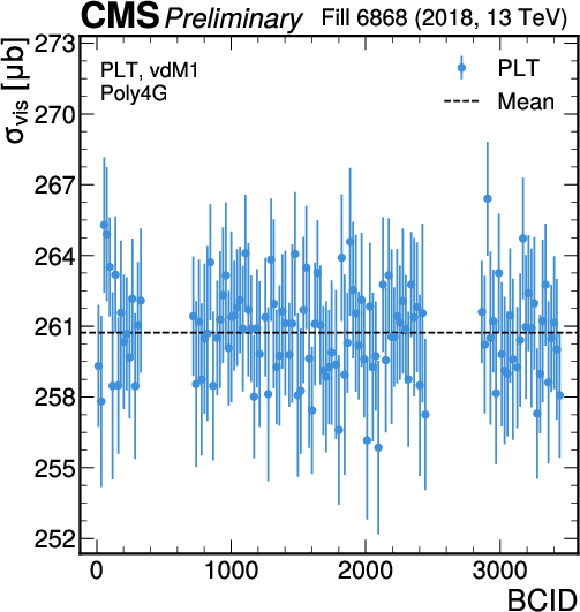
Figure 9-b:
Per BCID $ \sigma_{\text{vis}} $ values in the first scan in 2017 (left) and 2018 (right) for PLT. The error bars represent the uncertainty propagated from the fit. |
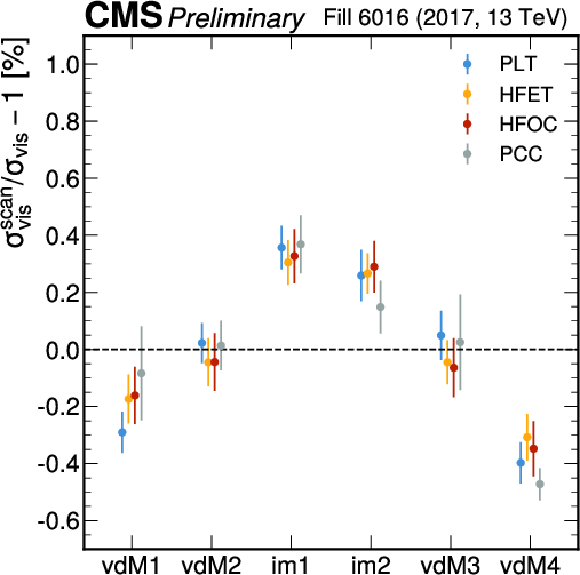
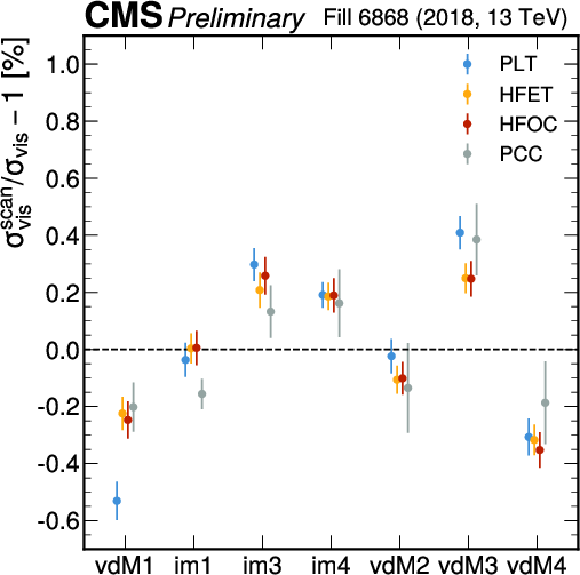
png pdf |
Figure 10:
The BCID averaged $ \sigma_{\text{vis}} $ divided by its average value taken over all scans for all independently calibrated detectors and all scans using the Poly4G fit function in 2017 (left) and 2018 (right). The error bars signify the standard deviation over the BCIDs divided by the square root of the number of BCIDs. |
png pdf |
Figure 10-a:
The BCID averaged $ \sigma_{\text{vis}} $ divided by its average value taken over all scans for all independently calibrated detectors and all scans using the Poly4G fit function in 2017 (left) and 2018 (right). The error bars signify the standard deviation over the BCIDs divided by the square root of the number of BCIDs. |
png pdf |
Figure 10-b:
The BCID averaged $ \sigma_{\text{vis}} $ divided by its average value taken over all scans for all independently calibrated detectors and all scans using the Poly4G fit function in 2017 (left) and 2018 (right). The error bars signify the standard deviation over the BCIDs divided by the square root of the number of BCIDs. |
png pdf |
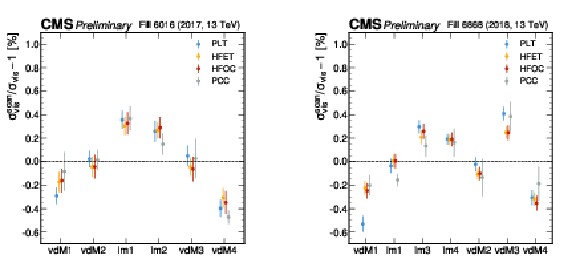
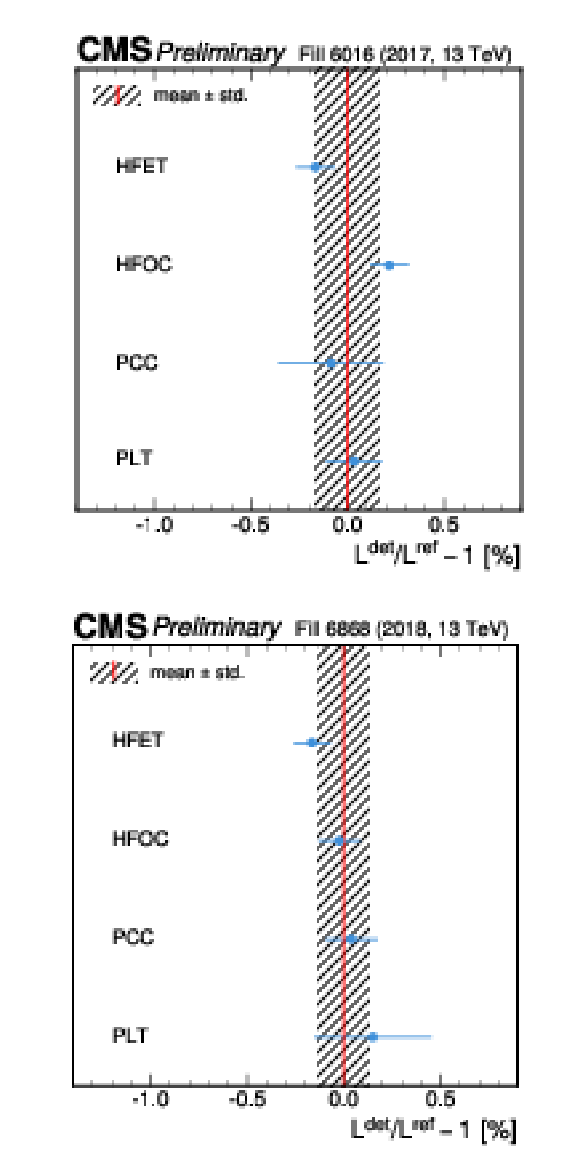
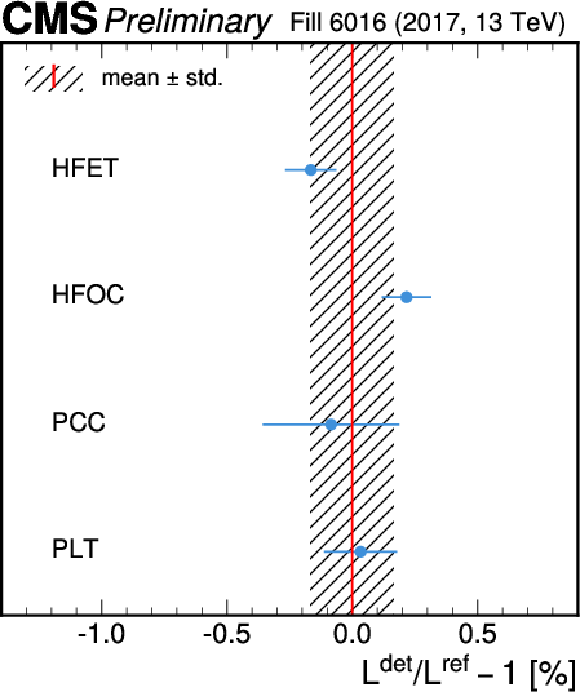
Figure 11:
The ratios of HFET, HFOC, PLT, and PCC luminosity to the detector averaged luminosity in the vdM fill for the head-on periods for 2017 (left) and 2018 (right). The points signify the average ratio, while the error bars represent the standard deviation of the ratio distribution. The shaded area represents the standard deviation of the individual averages. |
png pdf |
Figure 11-a:
The ratios of HFET, HFOC, PLT, and PCC luminosity to the detector averaged luminosity in the vdM fill for the head-on periods for 2017 (left) and 2018 (right). The points signify the average ratio, while the error bars represent the standard deviation of the ratio distribution. The shaded area represents the standard deviation of the individual averages. |
png pdf |
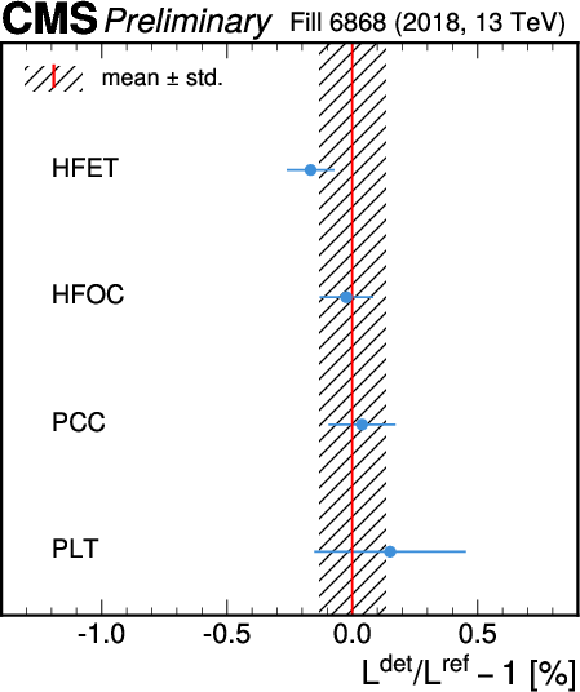
Figure 11-b:
The ratios of HFET, HFOC, PLT, and PCC luminosity to the detector averaged luminosity in the vdM fill for the head-on periods for 2017 (left) and 2018 (right). The points signify the average ratio, while the error bars represent the standard deviation of the ratio distribution. The shaded area represents the standard deviation of the individual averages. |
png pdf |
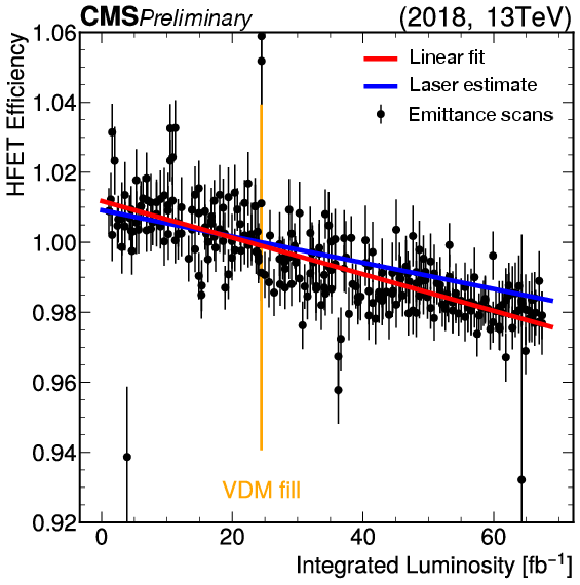
Figure 12:
The aging of HFET in 2018 as measured using emittance scans. The black points represent the efficiency of the HFET counting method, relative to the efficiency close to the time of the vdM scan (indicated by the vertical orange line), as a function of the total integrated luminosity in 2018. The uncertainties are estimated as the standard deviations over the BCIDs. The red line is a linear fit to the data. The expected aging from laser calibration monitoring of the fibers is indicated by a blue line and shows a good agreement with the emittance scan data. |
png pdf |
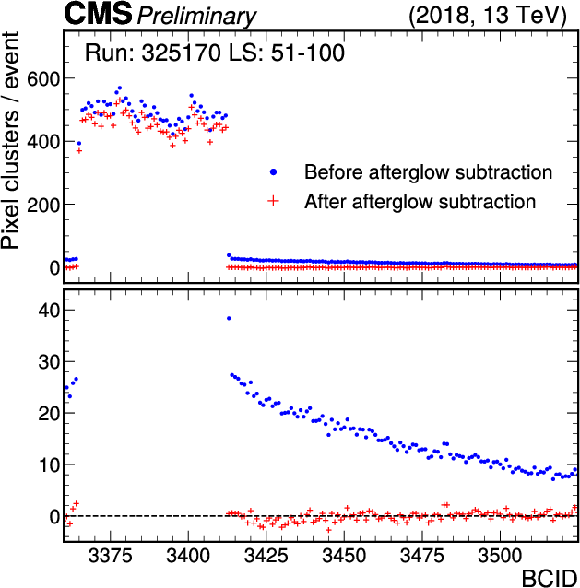
Figure 13:
The number of clusters in the pixel tracker per event is shown as a function of the BCID for the last bunch train of the orbit, with blue points representing the values before correction and red crosses indicating the results after applying out-of-time corrections. The upper panel displays the full count range, encompassing both colliding and empty BCIDs, while the lower panel focuses on empty bunch crossings with a different scale for improved visibility. In the lower panel, the red crosses, which represent the residual rate, are close to zero, demonstrating the excellent performance of the correction. |
png pdf |
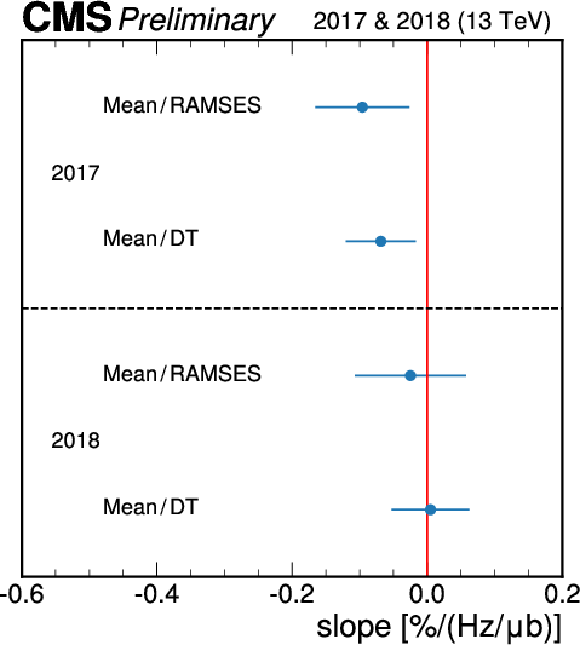
Figure 14:
The luminosity-weighted average of the measured residual nonlinearity between the mean luminosity and DT or RAMSES for 2017 and 2018. The error bars signify the weighted standard deviation over the individual fills. |
png pdf |
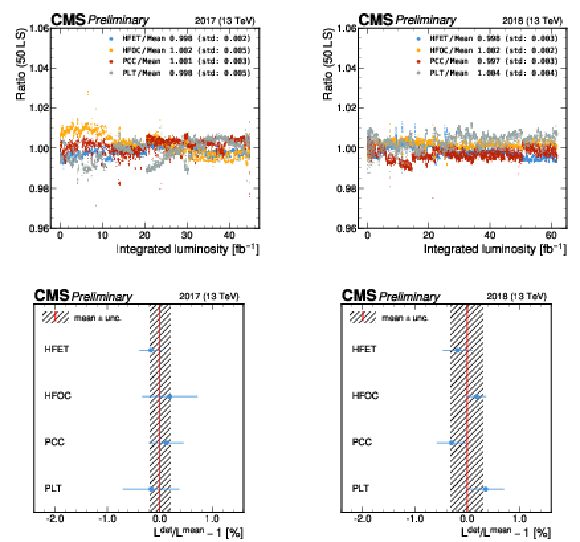
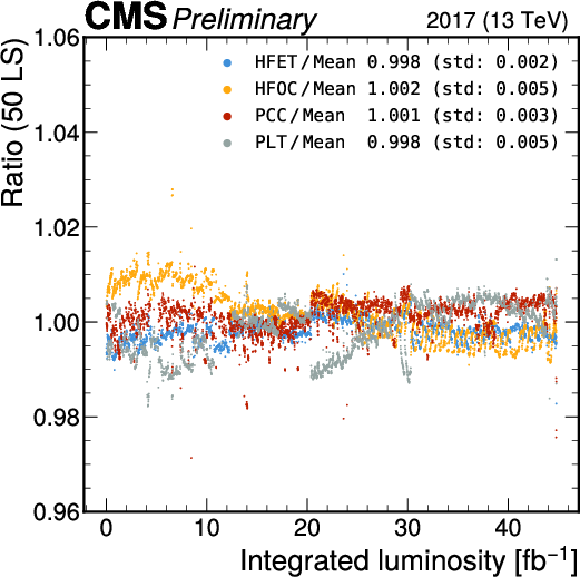
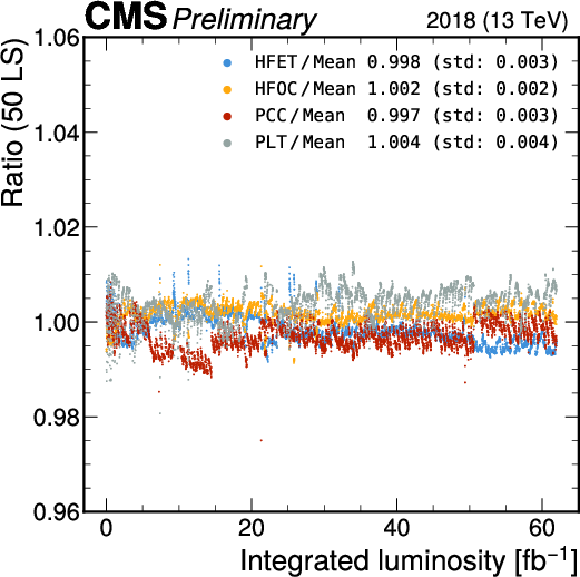
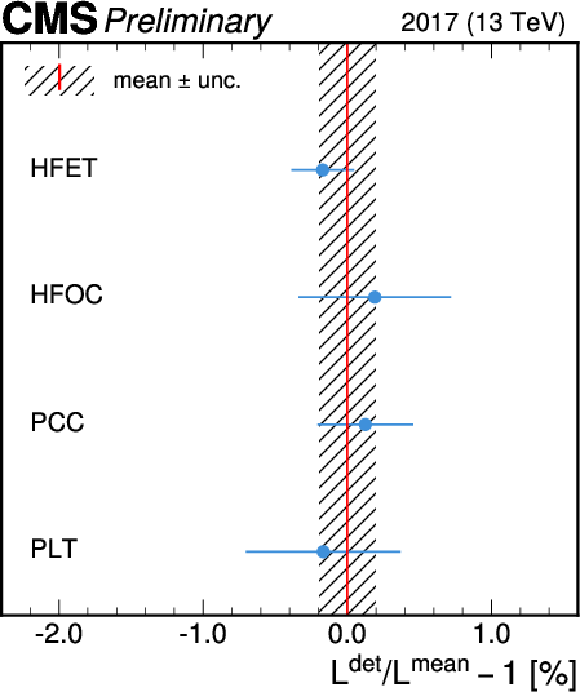
Figure 15:
The ratio of the luminosity measured by HFET, HFOC, PLT, and PCC to their mean per 20-minute blocks for 2017 (left) and 2018 (right). The upper row shows the ratio as a function of integrated luminosity, while the lower row displays the luminosity-weighted average of the ratios. The error bars signify the weighted standard deviation over the 20-minute units. The striped area represents the unweighted standard deviation of the four average ratio values. |
png pdf |
Figure 15-a:
The ratio of the luminosity measured by HFET, HFOC, PLT, and PCC to their mean per 20-minute blocks for 2017 (left) and 2018 (right). The upper row shows the ratio as a function of integrated luminosity, while the lower row displays the luminosity-weighted average of the ratios. The error bars signify the weighted standard deviation over the 20-minute units. The striped area represents the unweighted standard deviation of the four average ratio values. |
png pdf |
Figure 15-b:
The ratio of the luminosity measured by HFET, HFOC, PLT, and PCC to their mean per 20-minute blocks for 2017 (left) and 2018 (right). The upper row shows the ratio as a function of integrated luminosity, while the lower row displays the luminosity-weighted average of the ratios. The error bars signify the weighted standard deviation over the 20-minute units. The striped area represents the unweighted standard deviation of the four average ratio values. |
png pdf |
Figure 15-c:
The ratio of the luminosity measured by HFET, HFOC, PLT, and PCC to their mean per 20-minute blocks for 2017 (left) and 2018 (right). The upper row shows the ratio as a function of integrated luminosity, while the lower row displays the luminosity-weighted average of the ratios. The error bars signify the weighted standard deviation over the 20-minute units. The striped area represents the unweighted standard deviation of the four average ratio values. |
png pdf |
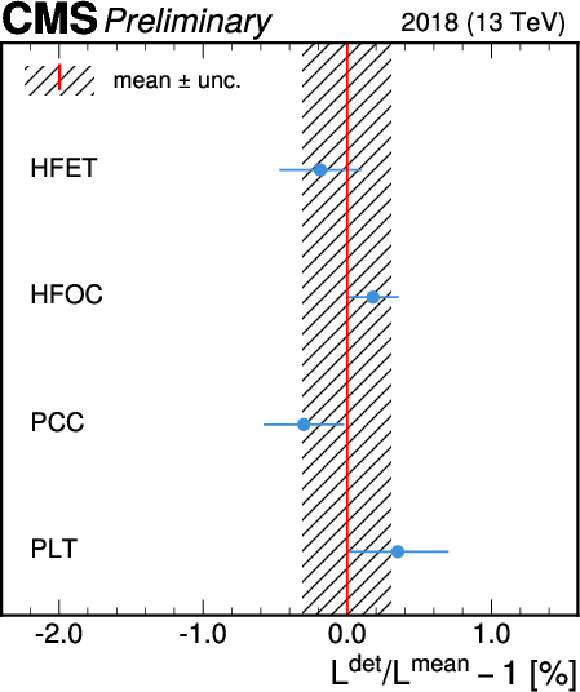
Figure 15-d:
The ratio of the luminosity measured by HFET, HFOC, PLT, and PCC to their mean per 20-minute blocks for 2017 (left) and 2018 (right). The upper row shows the ratio as a function of integrated luminosity, while the lower row displays the luminosity-weighted average of the ratios. The error bars signify the weighted standard deviation over the 20-minute units. The striped area represents the unweighted standard deviation of the four average ratio values. |
png pdf |
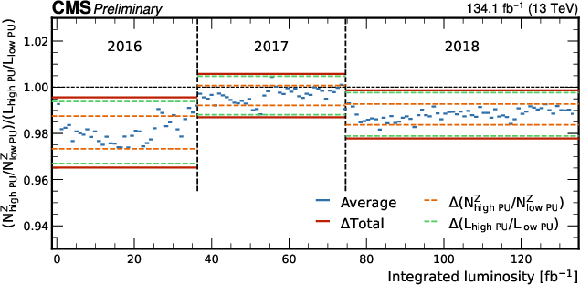
Figure 16:
The luminosity as measured based on Z boson rates divided by the reference luminosity as a function of the reference integrated luminosity for the 2016--2018 high PU data set. Each section corresponds to the luminosity values measured in about 1 fb$ ^{-1} $ of data, used for the measurement of $ N^\mathrm{Z} $. The green and orange dashed lines indicate the uncertainties from the $ N^\mathrm{Z} $ ratio and reference luminosity ratios, respectively, averaged over each year of data taking. Accordingly, the red lines indicate the total uncertainty in the double ratio. The vertical dashed lines separate the 2016, 2017, and 2018 data. |
png pdf |
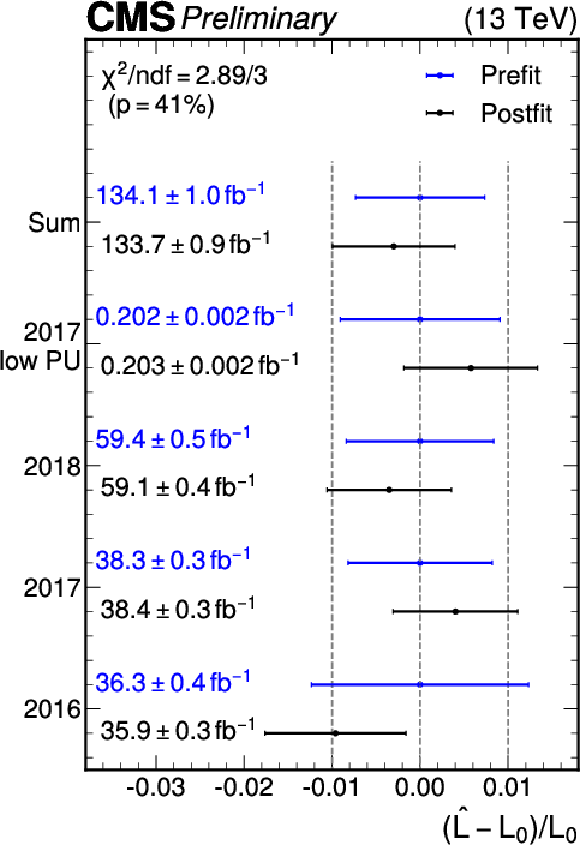
Figure 17:
The uncertainty and the shift of the luminosity values before and after the log-likelihood fit. The prefit (color blue) results originate from the traditional luminosity estimation and the postfit (black) values include the Z boson rate data. Numbers, including their uncertainties, are given for the full 2016--2018 period, and for the individual data sets. The integrated luminosity values are reflective only of the data sets used in this combination. |
png pdf |
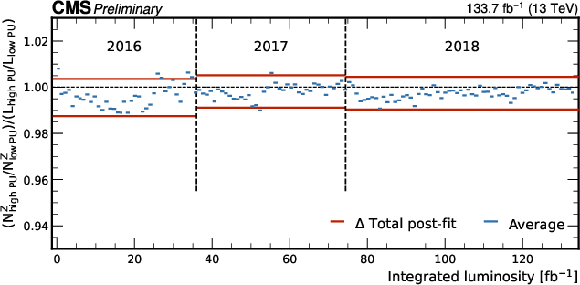
Figure 18:
The postfit ratio of the luminosity as measured based on Z boson rates and the reference luminosity as a function of the reference integrated luminosity for the 2016--2018 high PU data set. Each section corresponds to the luminosity values measured in about 1 fb$ ^{-1} $ of data, used for the measurement of $ N^\mathrm{Z} $. The red lines indicate the total uncertainty in the double ratio. The vertical dashed lines separate the 2016, 2017, and 2018 data. |
| Tables | |
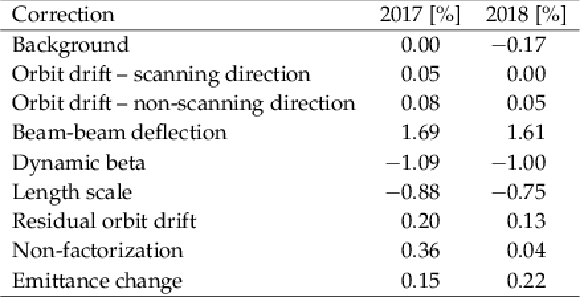
png pdf |
Table 1:
The impact of the corrections applied in the vdM calibration procedure on the final (i.e., bunch- and scan-averaged) $ \sigma_{\text{vis}} $ value for HFET in 2017 and 2018. |
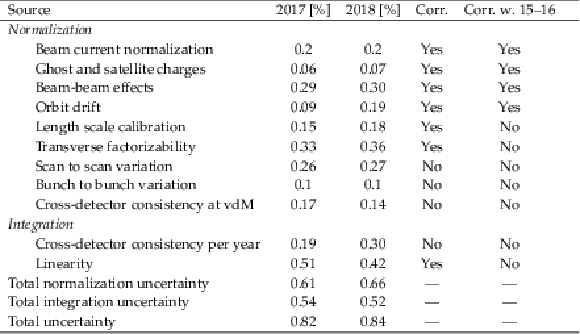
png pdf |
Table 2:
A breakdown of the luminosity uncertainty into its components in 2017, and 2018, divided into two groups affecting the vdM calibration at low luminosity (normalization), and the measurement of the luminosity in physics conditions (integration). The ``Corr.'' column indicates whether the uncertainties are considered fully positively correlated between the two years or independent, while the last column contains the correlation assumption with the 2015--2016 data set. |
| Summary |
| The combination of the total uncertainties across different years reflects the improvement due to the uncorrelated nature of certain systematic effects and results in a relative precision of 0.73% for both the full 2015--2018 and the restricted 2016--2018 data sets. The measured integrated luminosity with high-quality physics data at high PU amounts to 42.12 $ \pm $ 0.34 fb$^{-1}$ in 2017 and 59.45 $ \pm $ 0.50 fb$^{-1}$ in 2018. The total integrated luminosity collected during 2016--2018 (2015--2018) is 137.88 $ \pm $ 1.01 ( 140.15 $ \pm $ 1.03 ) fb$ ^{-1} $. In 2017, CMS also collected 0.2113 $ \pm $ 0.0019 fb$^{-1}$ of data at a PU around 3. Both new and improved methods were utilized to estimate and correct for biases related to micrometer-scale beam position monitoring and the calibration of the length scale of the beam positions with respect to that of the CMS detector, the effect of the assumed factorizability of the transverse beam convolution distribution, and the biases due to beam-beam interactions. Additionally, meticulous adjustments of the luminometer rates for out-of-time contributions, along with the use of emittance scans to monitor luminometer performance, allowed for accurate evaluations of linearity and efficiency changes. The excellent agreement between the results of the four independently calibrated luminometers provides a strong cross check of the measurements. We presented for the first time a combination of these, further improving the precision. Using the rate of Z boson production in the dimuon final state, the consistency of the luminosity calibration was validated across the years. The accuracy of the vdM calibration has reached the target set forward by the CMS collaboration in order to achieve the physics goals of (HL-)LHC [56]. However, luminosity integration is the leading source of uncertainty and will remain challenging with the intensity increase in the HL-LHC data taking. Further improvements to vdM and emittance scan analysis methodology and Z boson rate measurements will play important roles. The precision achieved in the luminosity measurement for the CMS Run 2 proton-proton data is the best at bunched hadron colliders reached to date. |
| References | ||||
| 1 | M. L. Mangano | Motivations and precision targets for an accurate luminosity determination at the LHC | in: Geneva, Switzerland, January 13--14,,. [CERN-Proceedings-2011-001], 2011 LHC Lumi Days 201 (2011) 1 |
|
| 2 | CMS Collaboration | First measurement of the top quark pair production cross section in proton-proton collisions at $ \sqrt{s}= $ 13.6 TeV | JHEP 08 (2023) 204 | CMS-TOP-22-012 2303.10680 |
| 3 | CMS Collaboration | Measurement of the $ \mathrm{t} \overline{\mathrm{t}} $ production cross section, the top quark mass, and the strong coupling constant using dilepton events in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 13 TeV | EPJC 79 (2019) 368 | CMS-TOP-17-001 1812.10505 |
| 4 | CMS Collaboration | Measurement of the inclusive cross sections for W and Z boson production in proton-proton collisions at $ \sqrt{s}= $ 5.02 and 13 TeV | JHEP 04 (2025) 162 | CMS-SMP-20-004 2408.03744 |
| 5 | CMS Collaboration | Measurements of the W boson rapidity, helicity, double-differential cross sections, and charge asymmetry in $ {\mathrm{p}\mathrm{p}} $ collisions at 13 TeV | PRD 102 (2020) 092012 | CMS-SMP-18-012 2008.04174 |
| 6 | CMS Collaboration | Measurements of differential Z boson production cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2019) 061 | CMS-SMP-17-010 1909.04133 |
| 7 | ATLAS and CMS Collaborations | Report on the physics at the HL-LHC and perspectives for the HE-LHC | CERN Report CERN-LPCC-2019-01,, CERN, 2019 link |
1902.10229 |
| 8 | CMS Collaboration | The Phase-2 upgrade of the CMS beam radiation, instrumentation, and luminosity detectors | CMS Technical Proposal CERN-LHCC-2021-008, CMS-TDR-023, CERN, 2021 CDS |
|
| 9 | ATLAS Collaboration | Luminosity determination in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector at the LHC | EPJC 83 (2023) 982 | 2212.09379 |
| 10 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 11 | LHCb Collaboration | Precision luminosity measurements at LHCb | JINST 9 (2014) P12005 | 1410.0149 |
| 12 | ALICE Collaboration | ALICE luminosity determination for PbPb collisions at $ {\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}= $ 5.02 TeV | JINST 19 (2024) P02039 | 2204.10148 |
| 13 | S. van der Meer | Calibration of the effective beam height in the ISR | ISR Report CERN-ISR-PO-68-31, CERN, 1968 | |
| 14 | P. Grafström and W. Kozanecki | Luminosity determination at proton colliders | Prog. Part. Nucl. Phys. 81 (2015) 97 | |
| 15 | M. Guthoff | Instrumentation for beam radiation and luminosity measurement in the CMS experiment using novel detector technologies | CMS Collaboration, in Proc. 14th Vienna Conference on Instrumentation (VCI ): Vienna, Austria, February 15--19,. [], 2017 NIM A 845 (2017) 565 |
|
| 16 | CMS Collaboration | Development of the CMS detector for the CERN LHC \mboxRun 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 17 | J. Salfeld-Nebgen and D. Marlow | Data-driven precision luminosity measurements with Z bosons at the LHC and HL-LHC | JINST 13 (2018) P12016 | 1806.02184 |
| 18 | CMS Collaboration | Luminosity determination using Z boson production at the CMS experiment | EPJC 84 (2024) 26 | CMS-LUM-21-001 2309.01008 |
| 19 | CMS Collaboration | Luminosity measurement for lead-lead collisions at $ {\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}= $ 5.02 TeV in 2015 and 2018 at CMS | Submitted to Eur. Phys. J. C, 2025 | CMS-LUM-20-002 2503.03946 |
| 20 | CMS HCAL Collaboration | Design, performance, and calibration of CMS forward calorimeter wedges | EPJC 53 (2008) 139 | |
| 21 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 22 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 23 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 24 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 25 | CMS Collaboration | CMS technical design report for the Level-1 trigger upgrade | CMS Technical Proposal CERN-LHCC-2013-011, CMS-TDR-012, CERN, 2013 CDS |
|
| 26 | CMS BRIL Collaboration | The pixel luminosity telescope: a detector for luminosity measurement at CMS using silicon pixel sensors | EPJC 83 (2023) 673 | 2206.08870 |
| 27 | G. Segura Millan, D. Perrin, and L. Scibile | RAMSES: the LHC radiation monitoring system for the environment and safety | in Proc. 10th International Conference on Accelerator and Large Experimental Physics Control Systems (ICALEPCS ): Geneva, Switzerland, October 10--14,. [.1-3O], 2005 Conf. Proc. C 051010 (2005) TH3B |
|
| 28 | A. Ledeul, G. Segura Millan, B. Savulescu, A.and Styczen, and D. Vazquez Rivera | CERN supervision, control and data acquisition system for radiation and environmental protection | in th Workshop on Emerging Technologies and Scientific Facilities Controls (PCaPAC): Hsinchu, Taiwan, October 16--19,. [JACoW (PCaPAC) 248], 2018 Proc. 1 (2018) 2 |
|
| 29 | M. Gasior, G. Baud, J. Olexa, and G. Valentino | First operational experience with the LHC diode orbit and oscillation (DOROS) system | in Proc. 5th International Beam Instrumentation Conference (): Barcelona, Spain, September 11--15,. [JACoW (IBIC) 43], 2016 IBIC 201 (2016) 6 |
|
| 30 | et al. | The LHC fast BCT system: A comparison of design parameters with initial performance | D. Belohrad CERN Report CERN-BE-2010-010, CERN, 2010 | |
| 31 | D. Belohrad, D. Esperante Pereira, J. Kral, and S. Pedersen | Upgrade of the LHC bunch by bunch intensity measurement acquisition system | in Proc. 5th International Beam Instrumentation Conference (): Barcelona, Spain, September 11--15,. [JACoW (IBIC) 135], 2016 IBIC 201 (2016) 6 |
|
| 32 | M. Krupa and M. Gasior | The wall current transformer---a new sensor for precise bunch-by-bunch intensity measurements in the LHC | in Proc. 5th International Beam Instrumentation Conference (): Barcelona, Spain, September 11--15,. [JACoW (IBIC) 568], 2016 IBIC 201 (2016) 6 |
|
| 33 | et al. | Results of the LHC DCCT calibration studies | C. Barschel CERN Report CERN-ATS-Note-2012-026 PERF, CERN, 2012 | |
| 34 | A. Jeff et al. | Longitudinal density monitor for the LHC | Phys. Rev. ST Accel. Beams 15 (2012) 032803 | |
| 35 | A. Jeff | A longitudinal density monitor for the LHC | PhD thesis, University of Liverpool, CERN-THESIS-2012-240, 2012 link |
|
| 36 | C. Barschel | Precision luminosity measurement at LHCb with beam-gas imaging | PhD thesis, RWTH Aachen University, CERN-THESIS-2013-301, 2014 link |
|
| 37 | LHCb Collaboration , G. Coombs, M. Ferro-Luzzi, and R. Matev | Beam-gas imaging measurements at LHCb | in Proc. 7th International Beam Instrumentation Conference (): Shanghai, China, September 09--13,. [JACoW (IBIC) 459], 2018 IBIC 201 (2018) 8 |
|
| 38 | A. Babaev et al. | Impact of beam-beam effects on absolute luminosity calibrations at the CERN Large Hadron Collider | EPJC 84 (2024) 17 | 2306.10394 |
| 39 | M. Bassetti and G. A. Erskine | Closed expression for the electrical field of a two-dimensional Gaussian charge | ISR Report CERN-ISR-TH-80-06, CERN, 1980 | |
| 40 | A. Babaev | Coherent deflection of elliptic bunches colliding at crossing angle | 2104.02595 | |
| 41 | V. Balagura | Van der Meer scan luminosity measurement and beam-beam correction | EPJC 81 (2021) 26 | 2012.07752 |
| 42 | J. Wenninger | Operation and configuration of the LHC in \mboxRun 2 | CERN Report CERN-ACC-NOTE-2019-0007, CERN, 2019 | |
| 43 | CERN Accelerators and Beam Physics Computing Working Group (ABP-CWG) | Combi (coherent multibunch beam-beam interactions) | technical report, CERN, 2019 link |
|
| 44 | A. Chmieli \'n ska, L. Fiscarelli, W. Kozanecki, and E. Todesco | Magnetic measurements of MCBC and MCBY orbit correctors under special cycling conditions | CERN Report CERN-ACC-NOTE-2022-0013, CERN, 2022 | |
| 45 | M. Gasior, J. Olexa, and R. Steinhagen | BPM electronics based on compensated diode detectors---results from development systems | in Proc. 15th Beam Instrumentation Workshop (BIW12): Newport News, USA, April 15--19,. [], 2012 Conf. Proc. C 1204151 (2012) 4 |
|
| 46 | J. Olexa | Design and optimization of the beam orbit and oscillation measurement system for the Large Hadron Collider | PhD thesis, Slovenská technická univerzita v Bratislave, CERN-THESIS-2018-185, 2018 link |
|
| 47 | W. Kozanecki, T. Pieloni, and J. Wenninger | Observation of beam-beam deflections with LHC orbit data | CERN Report CERN-ACC-NOTE-2013-0006, CERN, 2013 | |
| 48 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 49 | H. Bartosik and G. Rumolo | Production of single Gaussian bunches for Van der Meer scans in the LHC injector chain | CERN Report CERN-ACC-NOTE-2013-0008, CERN, 2013 | |
| 50 | P. Major | Studies of the factorisation of proton densities in van der Meer scans and its impact on precision luminosity measurements for CMS | CMS Collaboration, in Proc. European Physical Society Conference on High Energy Physics (EPS-): Ghent, Belgium, July 10--17,. [PoS (EPS-HEP) 199], 2019 HEP 201 (2019) 9 |
|
| 51 | P. Major | Probing New Physics: Search for supersymmetry with Higgs particles and high-precision luminosity determination at the CMS experiment | PhD thesis, ELTE Eötvös Loránd University, 2024 link |
|
| 52 | S. N. Webb | Factorisation of beams in van der Meer scans and measurements of the $ \phi^\ast_\eta $ distribution of $ {\mathrm{Z}\to\mathrm{e}^+\mathrm{e}^-} $ events in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | PhD thesis, University of Manchester, CERN-THESIS-2015-054, 2015 link |
|
| 53 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, CERN, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 54 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, CERN, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 55 | T. Becher and T. Neumann | Fiducial $ q_{\mathrm{t}} $ resummation of color-singlet processes at N\textsuperscript3LL+NNLO | JHEP 03 (2021) 199 | 2009.11437 |
| 56 | CMS Collaboration | The Phase-2 upgrade of the CMS beam radiation, instrumentation, and luminosity detectors: conceptual design | CMS Technical Proposal, CERN, 2019 CMS-PAS-TDR-19-003 |
|

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|