CMS-SMP-18-012

CMS-SMP-18-012 ; CERN-EP-2020-116
Measurements of the W boson rapidity, helicity, double-differential cross sections, and charge asymmetry in pp collisions at 13 TeV
CMS Collaboration
10 August 2020
Phys. Rev. D 102 (2020) 092012
Abstract: The differential cross section and charge asymmetry for inclusive W boson production at $\sqrt{s} =$ 13 TeV is measured for the two transverse polarization states as a function of the W boson absolute rapidity. The measurement uses events in which a W boson decays to a neutrino and either a muon or an electron. The data sample of proton-proton collisions recorded with the CMS detector at the LHC in 2016 corresponds to an integrated luminosity of 35.9 fb $^{-1}$ . The differential cross section and its value normalized to the total inclusive W boson production cross section are measured over the rapidity range $\|{y_{\mathrm{W}}}\| <$ 2.5. In addition to the total fiducial cross section, the W boson double-differential cross section, ${\mathrm{d}}^2\sigma/{\mathrm{d}}{p_{\mathrm{T}}}^{\ell}{\mathrm{d}}\|{\eta^{\ell}}\|$ , and the charge asymmetry are measured as functions of the charged lepton transverse momentum and pseudorapidity. The precision of these measurements is used to constrain the parton distribution functions of the proton using the next-to-leading order NNPDF3.0 set.
Links: e-print arXiv:2008.04174 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ;

Figures & Tables	Summary	Additional Figures & Material	References	CMS Publications

Figures
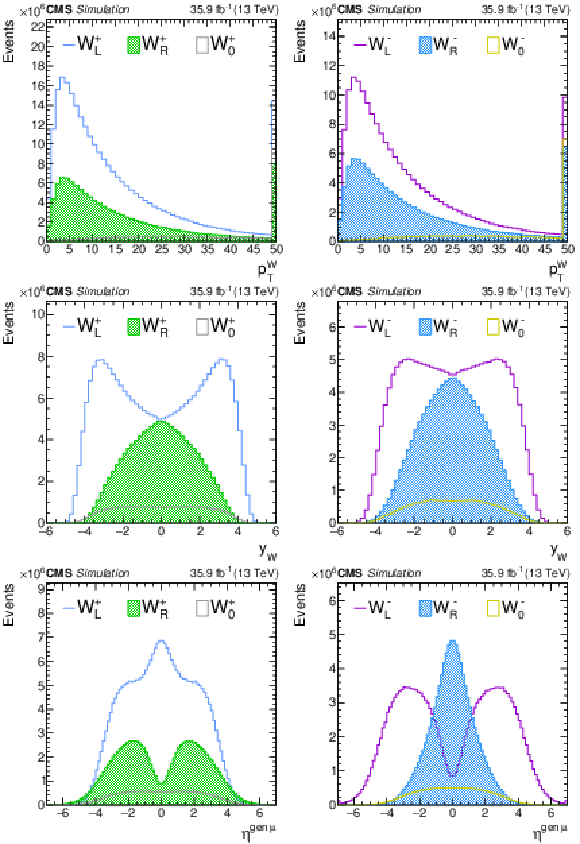
png pdf	Figure 1: Generator-level distributions of the W boson ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ (top), ${{\| y_{\mathrm{W}} \|}}$ (center), and the resulting $\eta$ distribution of the charged lepton (bottom) after reweighting each of the helicity components for positively (left) and negatively (right) charged W bosons.
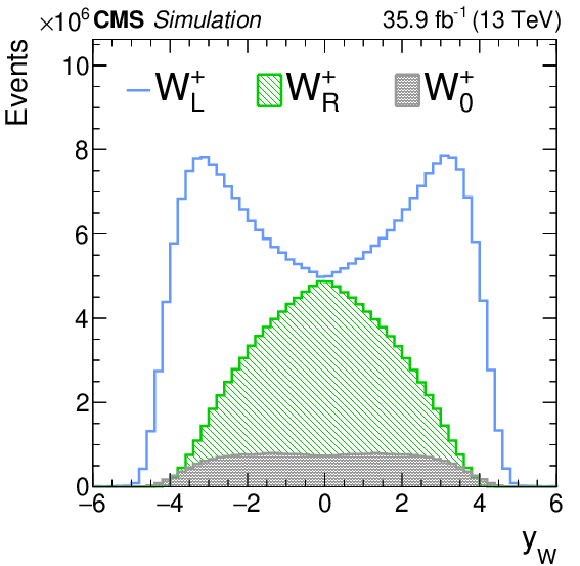
png pdf	Figure 1-a: Generator-level distributions of the W boson ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ after reweighting each of the helicity components for positively charged W bosons.
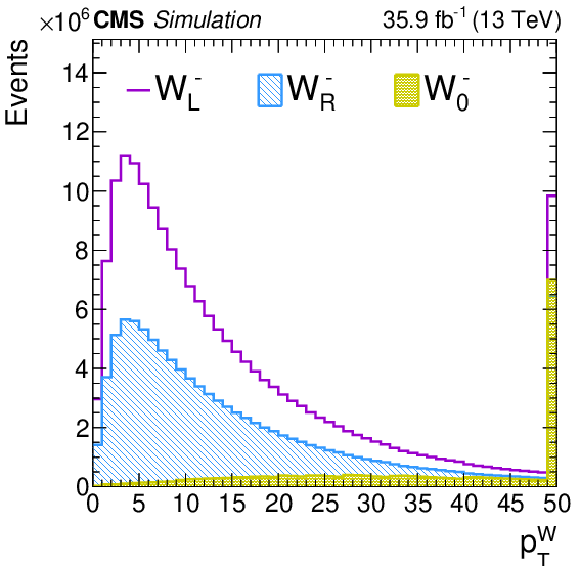
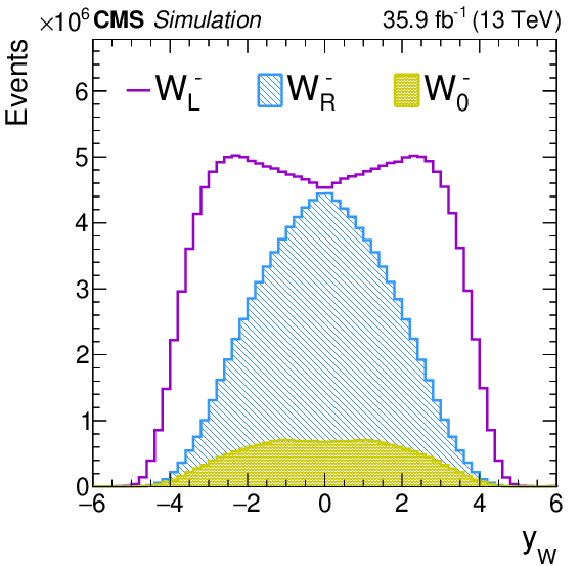
png pdf	Figure 1-b: Generator-level distributions of the W boson ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ after reweighting each of the helicity components for negatively charged W bosons.
png pdf	Figure 1-c: Generator-level distributions of the W boson ${{\| y_{\mathrm{W}} \|}}$ after reweighting each of the helicity components for positively charged W bosons.
png pdf	Figure 1-d: Generator-level distributions of the W boson ${{\| y_{\mathrm{W}} \|}}$ after reweighting each of the helicity components for negatively charged W bosons.
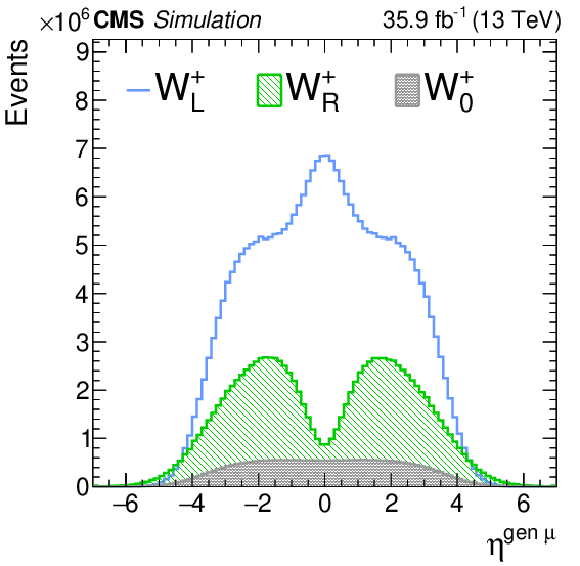
png pdf	Figure 1-e: $\eta$ distributions of the charged lepton after reweighting each of the helicity components for positively charged W bosons.
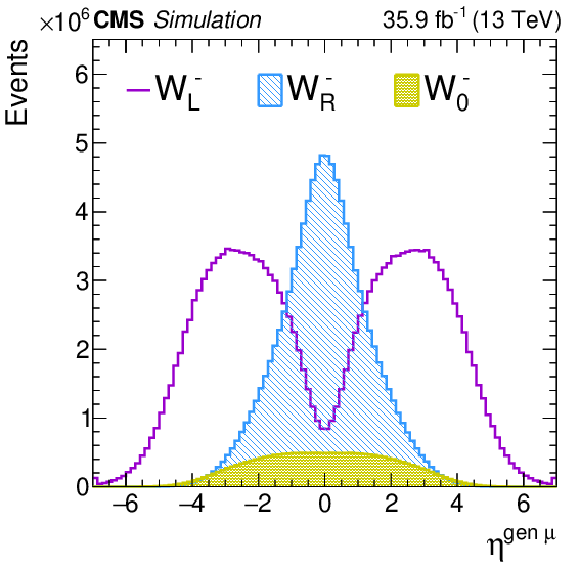
png pdf	Figure 1-f: $\eta$ distributions of the charged lepton after reweighting each of the helicity components for negatively charged W bosons.
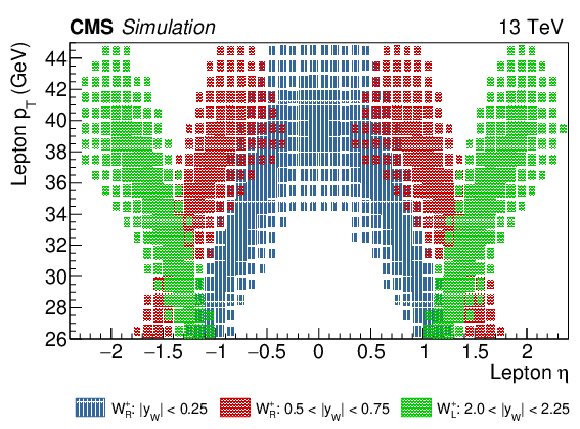
png pdf	Figure 2: Distributions of 2D templates of ${{p_{\mathrm {T}}} ^{\ell}}$ versus ${\eta ^{\ell}}$ , for simulated positively charged W bosons events in different helicity or rapidity bins. Templates for the muon channel are shown. Blue: ${\mathrm{W} ^+_\mathrm {R}}$ with ${{\| y_{\mathrm{W}} \|}} < 0.25$ , red: ${\mathrm{W} ^+_\mathrm {R}}$ with 0.50 $< {{\| y_{\mathrm{W}} \|}} <$ 0.75, green: ${\mathrm{W} ^+_\mathrm {L}}$ with 2.00 $< {{\| y_{\mathrm{W}} \|}} <$ 2.25.
png pdf	Figure 3: Upper: relative impact of groups of uncertainties (as defined in the text) on the normalized signal cross sections as functions of the W boson rapidity for the ${\mathrm{W} ^-_\mathrm {L}}$ case. Lower: absolute impact of uncertainties on the charge asymmetry of the ${\mathrm{W} _\mathrm {L}}$ boson. All impacts are shown for the combination of the muon and electron channels in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure 3-a: Relative impact of groups of uncertainties (as defined in the text) on the normalized signal cross sections as functions of the W boson rapidity for the ${\mathrm{W} ^-_\mathrm {L}}$ case. All impacts are shown for the combination of the muon and electron channels in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
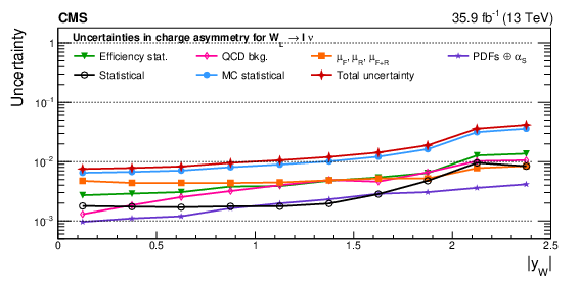
png pdf	Figure 3-b: Absolute impact of uncertainties on the charge asymmetry of the ${\mathrm{W} _\mathrm {L}}$ boson. All impacts are shown for the combination of the muon and electron channels in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
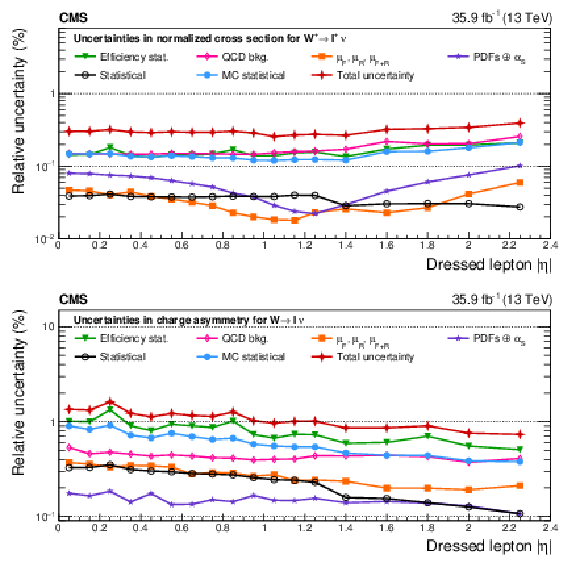
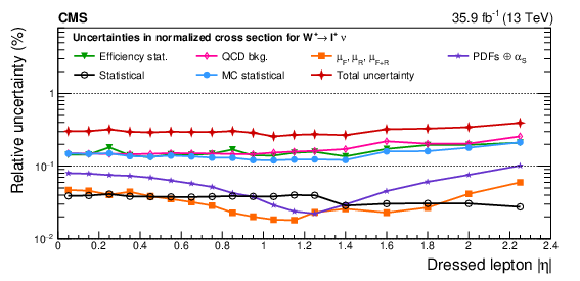
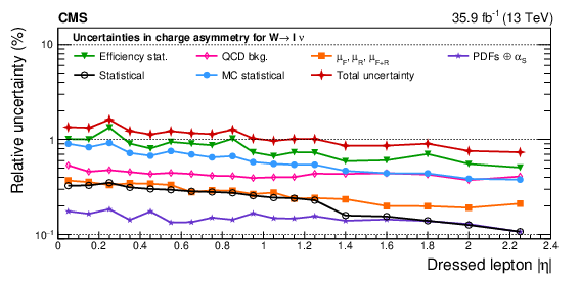
png pdf	Figure 4: Upper: relative impact of groups of systematic uncertainties (as defined in the text) on the normalized cross sections for the ${\mathrm{W^{+}}}$ case as functions of ${{\| \eta ^{\ell} \|}}$ . Lower: relative impact of uncertainties on charge asymmetry. All impacts are shown for the combination of the muon and electron channels in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure 4-a: Relative impact of groups of systematic uncertainties (as defined in the text) on the normalized cross sections for the ${\mathrm{W^{+}}}$ case as functions of ${{\| \eta ^{\ell} \|}}$ . All impacts are shown for the combination of the muon and electron channels in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure 4-b: Relative impact of uncertainties on charge asymmetry. All impacts are shown for the combination of the muon and electron channels in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
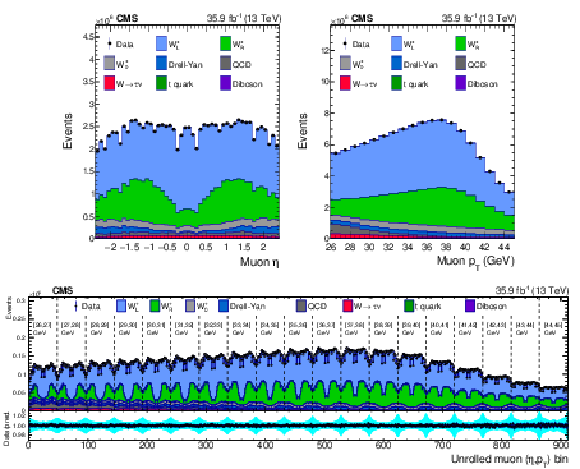
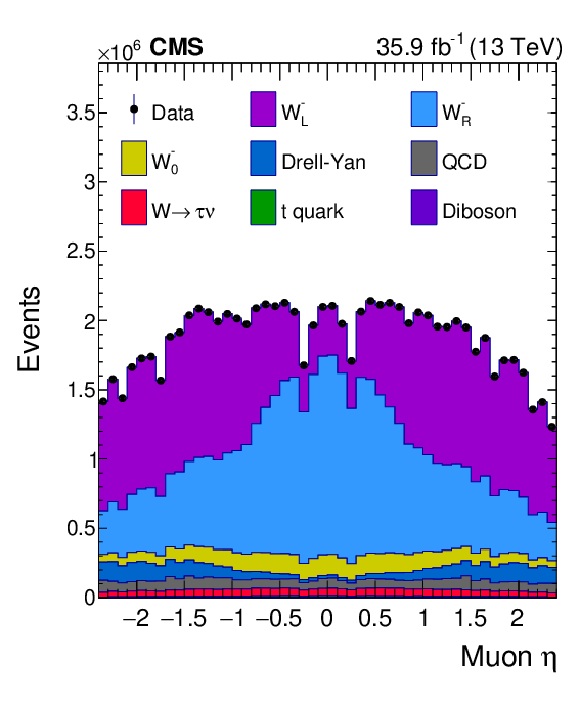
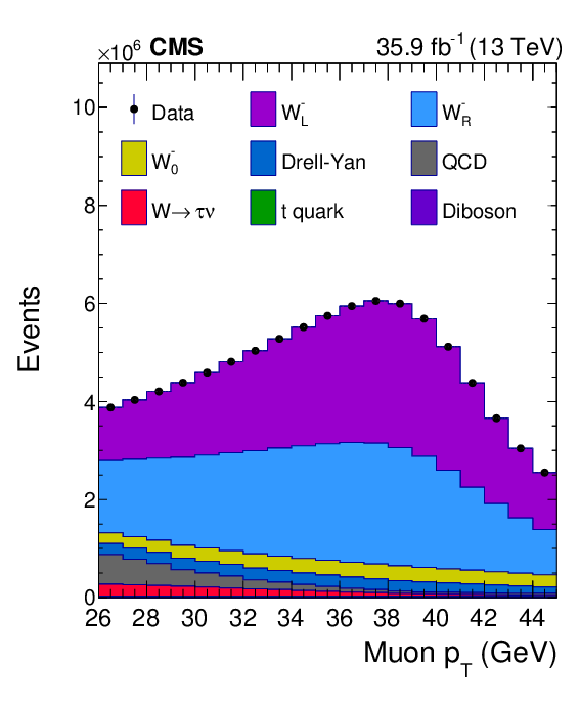
png pdf	Figure 5: Distributions of ${\eta ^{\mu}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mu}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{+}}} \to \mu ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 5-a: Distribution of ${\eta ^{\mu}}$ for ${\mathrm{W^{+}}} \to \mu ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 5-b: Distribution of ${{p_{\mathrm {T}}} ^{\mu}}$ for ${\mathrm{W^{+}}} \to \mu ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 5-c: Distribution of $\mathrm {bin_{unrolled}}$ for ${\mathrm{W^{+}}} \to \mu ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
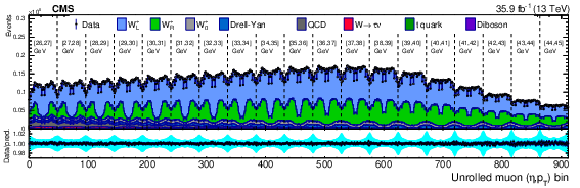
png pdf	Figure 6: Distributions of ${\eta ^{\mu}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mu}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{-}}} \to \mu ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 6-a: Distribution of ${\eta ^{\mu}}$ for ${\mathrm{W^{-}}} \to \mu ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 6-b: Distribution of ${{p_{\mathrm {T}}} ^{\mu}}$ for ${\mathrm{W^{-}}} \to \mu ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
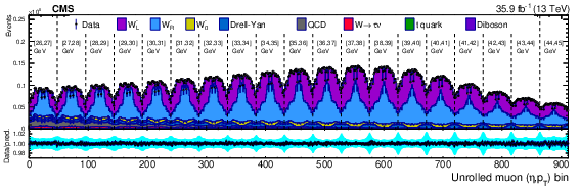
png pdf	Figure 6-c: Distribution of $\mathrm {bin_{unrolled}}$ for ${\mathrm{W^{-}}} \to \mu ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
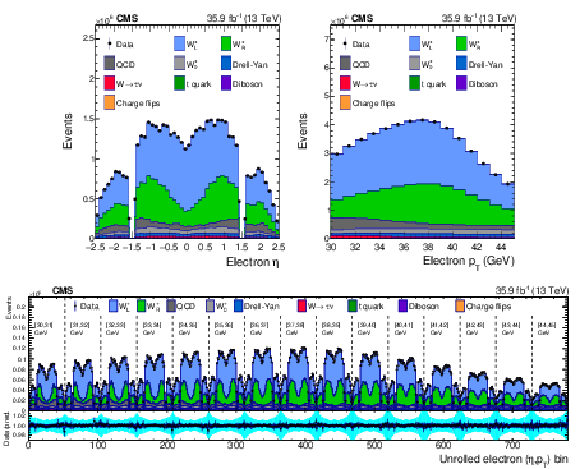
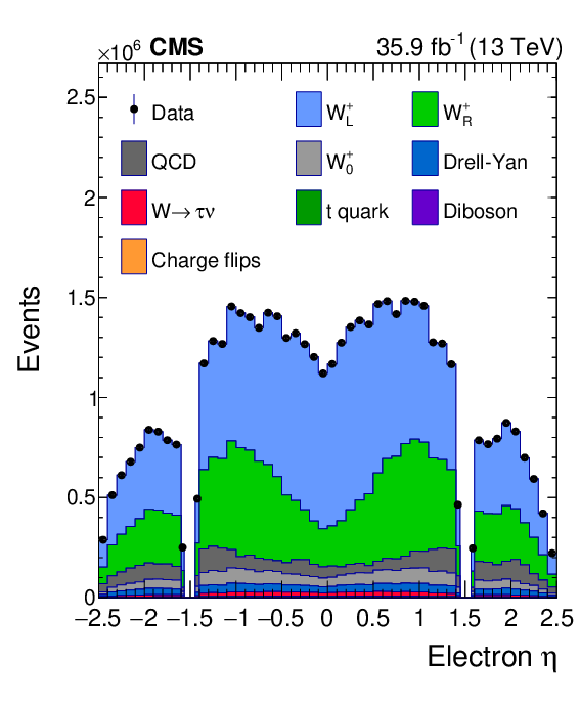
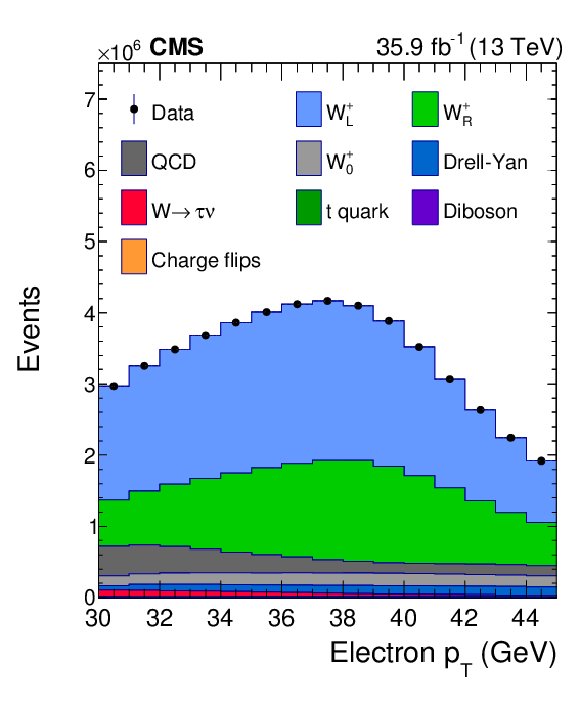
png pdf	Figure 7: Distributions of ${\eta ^{\mathrm{e}}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mathrm{e}}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{+}}} \to \mathrm{e} ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 7-a: Distribution of $\mathrm {bin_{unrolled}}$ for ${\mathrm{W^{+}}} \to \mathrm{e} ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 7-b: Distributions of ${\eta ^{\mathrm{e}}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mathrm{e}}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{+}}} \to \mathrm{e} ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
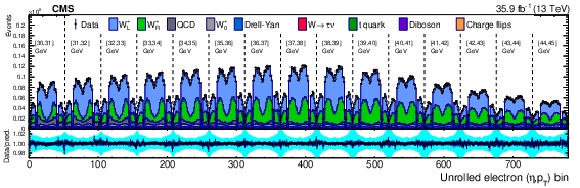
png pdf	Figure 7-c: Distributions of ${\eta ^{\mathrm{e}}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mathrm{e}}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{+}}} \to \mathrm{e} ^+\nu$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
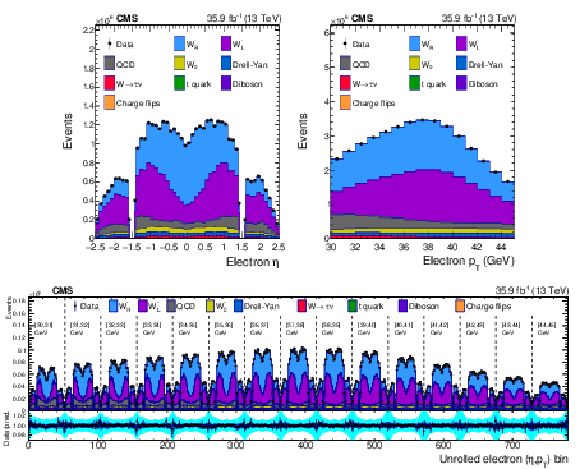
png pdf	Figure 8: Distributions of ${\eta ^{\mathrm{e}}}$ (upper left), ${{p_{\mathrm {T}}} ^{\mathrm{e}}}$ (upper right) and $\mathrm {bin_{unrolled}}$ (lower) for ${\mathrm{W^{-}}} \to \mathrm{e} ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
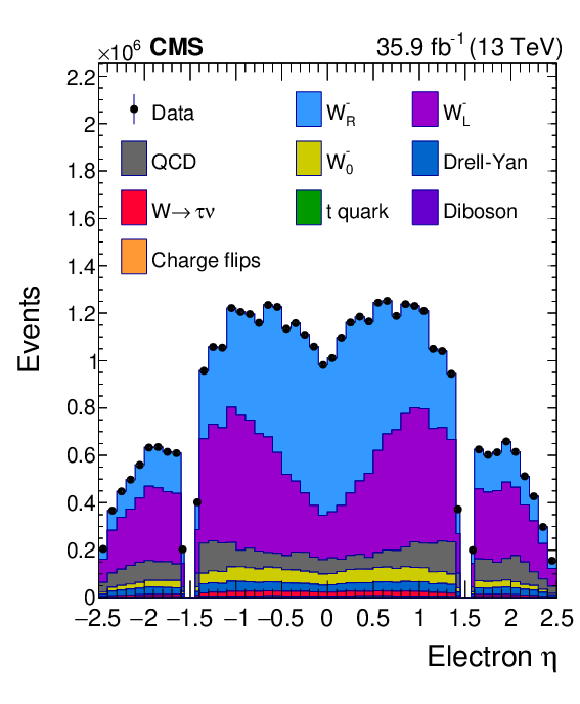
png pdf	Figure 8-a: Distribution of ${\eta ^{\mathrm{e}}}$ for ${\mathrm{W^{-}}} \to \mathrm{e} ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
png pdf	Figure 8-b: Distribution of ${{p_{\mathrm {T}}} ^{\mathrm{e}}}$ for ${\mathrm{W^{-}}} \to \mathrm{e} ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
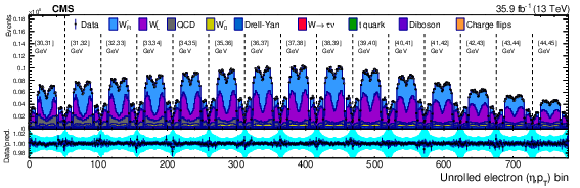
png pdf	Figure 8-c: Distribution of $\mathrm {bin_{unrolled}}$ for ${\mathrm{W^{-}}} \to \mathrm{e} ^-\bar{\nu}$ events for observed data superimposed on signal plus background events. The signal and background processes are normalized to the result of the template fit. The cyan band over the data-to-prediction ratio represents the uncertainty in the total yield in each bin after the profiling process.
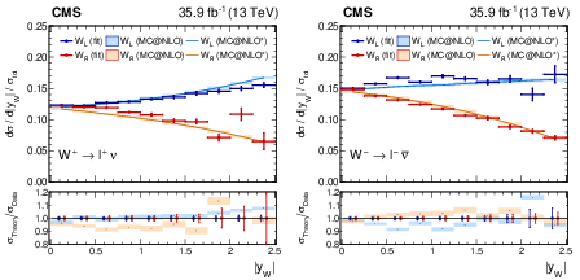
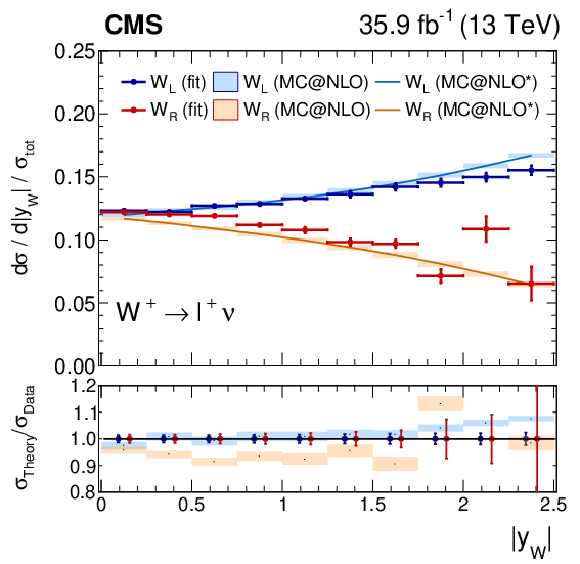
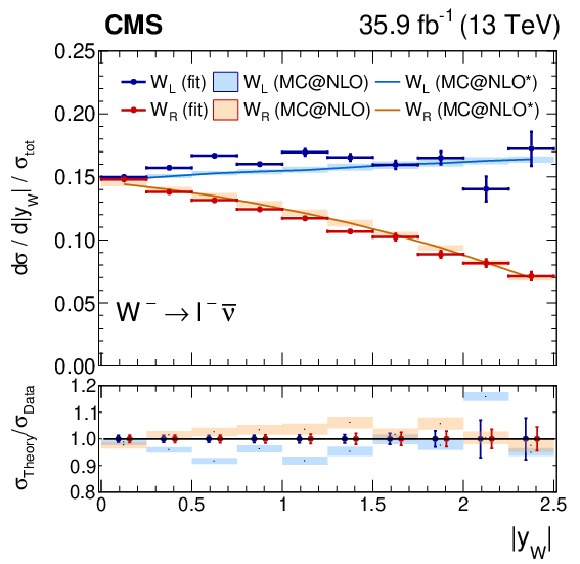
png pdf	Figure 9: Measured normalized ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left plot) or ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right plot) cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of the muon and electron channels, normalized to the total cross section. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure 9-a: Measured normalized ${\mathrm{W^{+}}} \to \ell ^+\nu$ cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of the muon and electron channels, normalized to the total cross section. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure 9-b: Measured normalized ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of the muon and electron channels, normalized to the total cross section. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
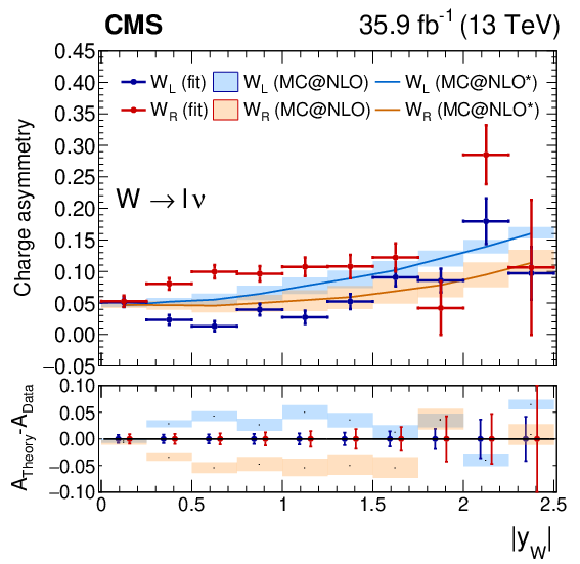
png pdf	Figure 10: Measured W boson charge asymmetry as functions of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of the muon and electron channels. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
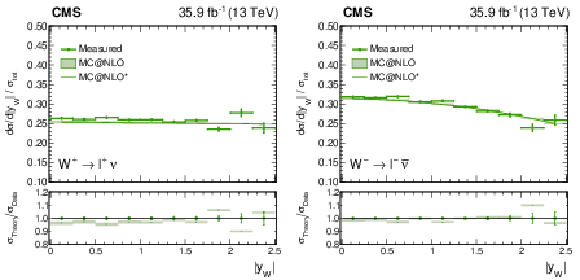
png pdf	Figure 11: Measured normalized ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left plot) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right plot) cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ from the combination of the muon and electron channels, normalized to the total cross section, integrated over the W polarization states. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
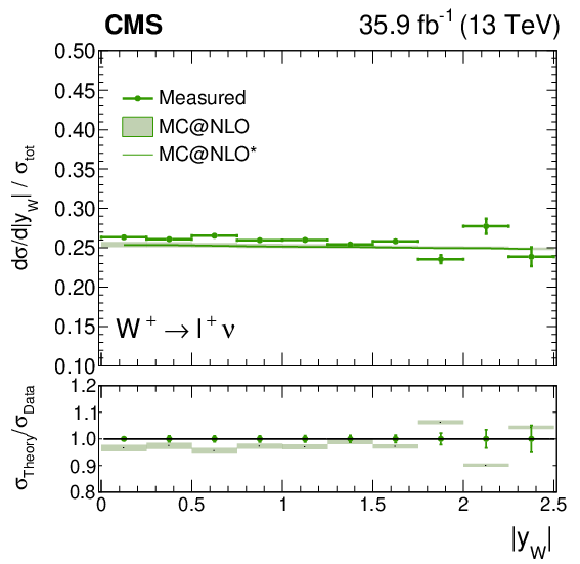
png pdf	Figure 11-a: Measured normalized ${\mathrm{W^{+}}} \to \ell ^+\nu$ cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ from the combination of the muon and electron channels, normalized to the total cross section, integrated over the W polarization states. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
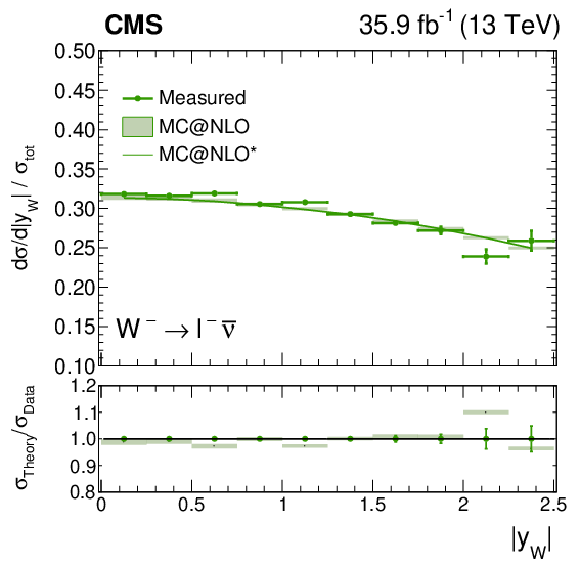
png pdf	Figure 11-b: Measured normalized ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ from the combination of the muon and electron channels, normalized to the total cross section, integrated over the W polarization states. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure 12: Measured W charge asymmetry as a function of ${{\| y_{\mathrm{W}} \|}}$ from the combination of the muon and electron channels, integrated over the W polarization states. Also shown is the ratio of the prediction from MadGraph5_aMC@NLO to the data. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
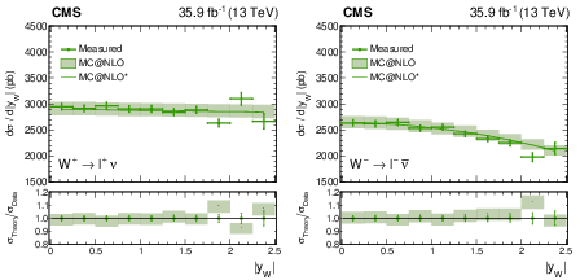
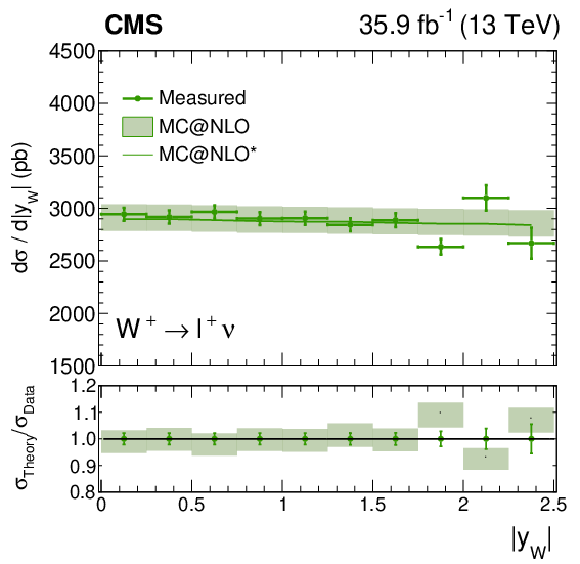
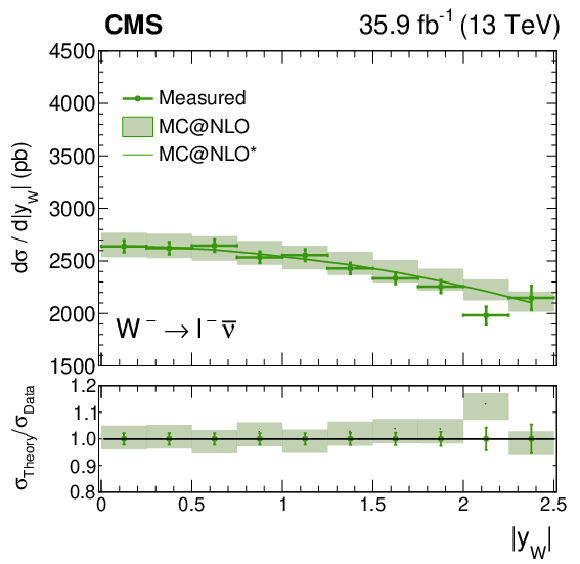
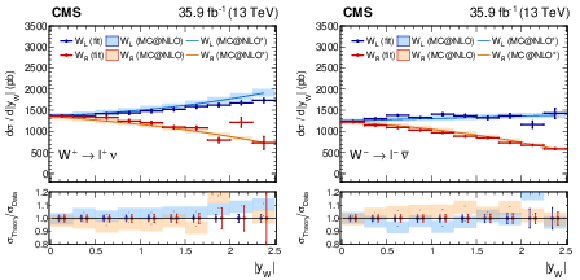
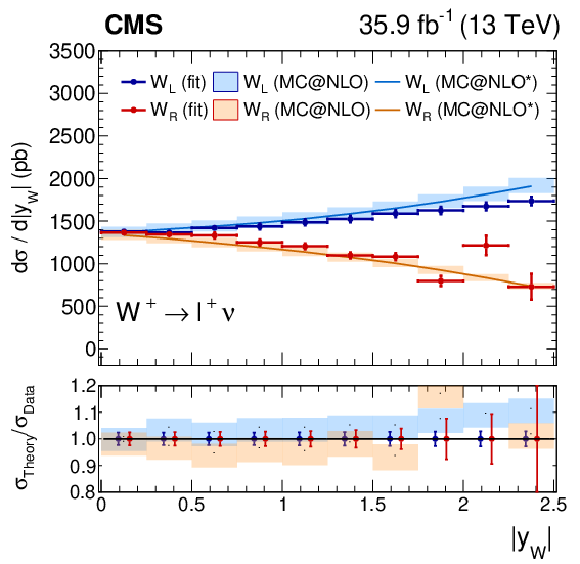
png pdf	Figure 13: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left plot) or ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right plot) cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ from the combined flavor fit. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure 13-a: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ from the combined flavor fit. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure 13-b: Measured absolute ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ cross section as functions of ${{\| y_{\mathrm{W}} \|}}$ from the combined flavor fit. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The MadGraph5_aMC@NLO $^{*}$ spectrum stands for the prediction with the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ weighting applied. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
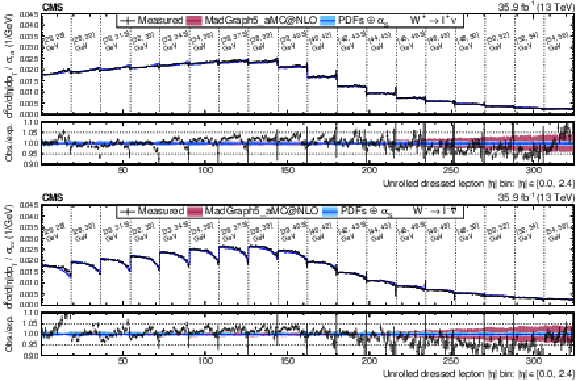
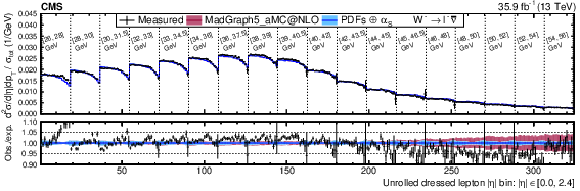
png pdf	Figure 14: Normalized double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{\| \eta ^{\ell} \|}}$ for the positive (negative) charge on the upper (lower) plot. The lower panel in each plot shows the ratio of the observed and expected cross sections. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure 14-a: Normalized double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{\| \eta ^{\ell} \|}}$ for the positive charge. The lower panelshows the ratio of the observed and expected cross sections. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure 14-b: Normalized double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{\| \eta ^{\ell} \|}}$ for the negative charge. The lower panelshows the ratio of the observed and expected cross sections. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
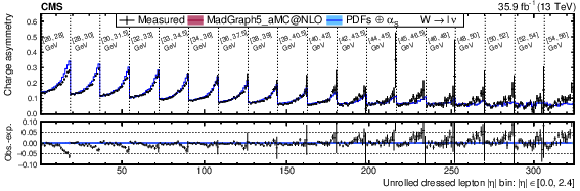
png pdf	Figure 15: Double-differential W boson charge asymmetry as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{\| \eta ^{\ell} \|}}$ . The lower panel shows the difference of the observed and expected charge asymmetry. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
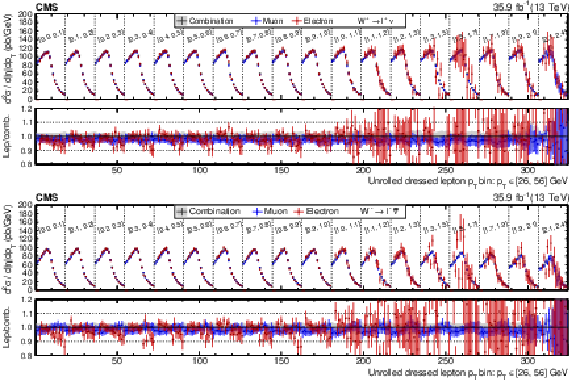
png pdf	Figure 16: Absolute double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for the positive (negative) charge on upper (lower) panel. The combined muon and electron fit is shown in green markers, the muon-only fit in blue markers, and the electron-only fit in red markers. The error bars correspond to the total uncertainty from the respective fits. The filled gray band in the lower panel represents the total uncertainty from the combined fit.
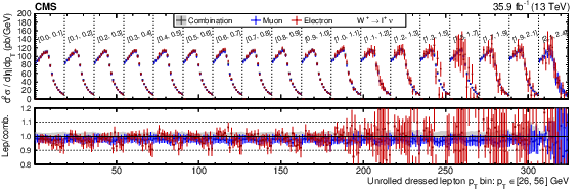
png pdf	Figure 16-a: Absolute double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for the positive charge. The combined muon and electron fit is shown in green markers, the muon-only fit in blue markers, and the electron-only fit in red markers. The error bars correspond to the total uncertainty from the respective fits. The filled gray band in the lower panel represents the total uncertainty from the combined fit.
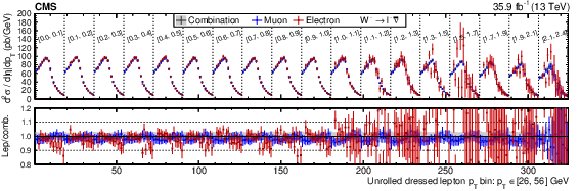
png pdf	Figure 16-b: Absolute double-differential cross section as a function of ${{p_{\mathrm {T}}} ^{\ell}}$ and ${{\| \eta ^{\ell} \|}}$ , unrolled in a 1D histogram along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for the negative charge. The combined muon and electron fit is shown in green markers, the muon-only fit in blue markers, and the electron-only fit in red markers. The error bars correspond to the total uncertainty from the respective fits. The filled gray band in the lower panel represents the total uncertainty from the combined fit.
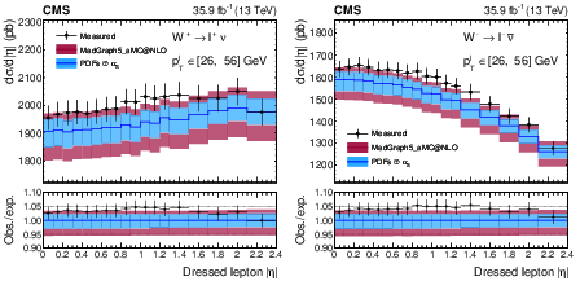
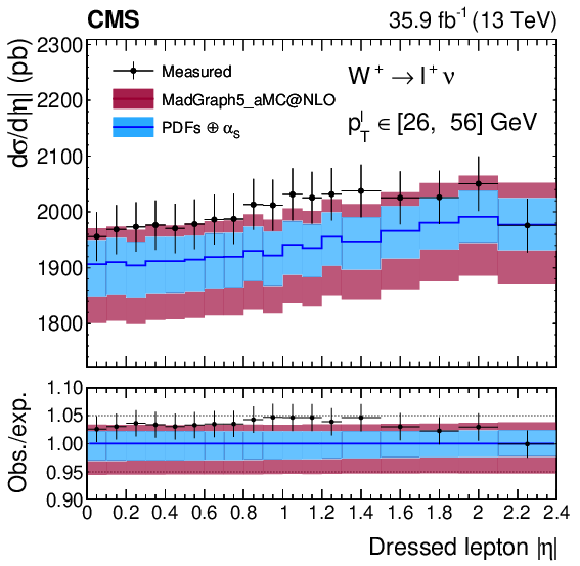
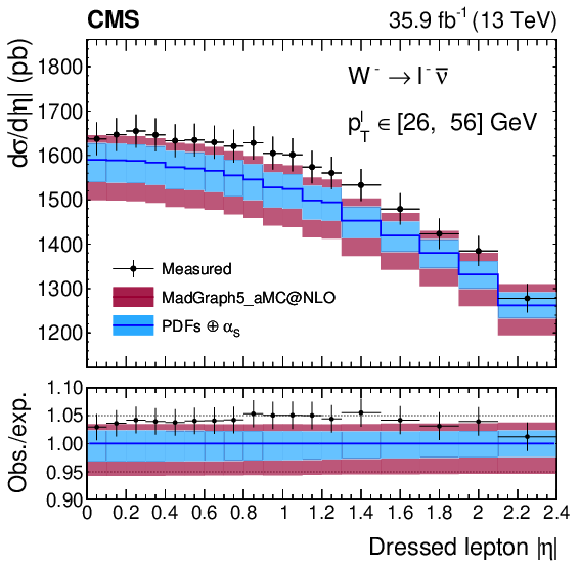
png pdf	Figure 17: Absolute differential cross section as a function of ${{\| \eta ^{\ell} \|}}$ for the ${\mathrm{W^{+}} \to \ell ^+\nu}$ (left) and ${\mathrm{W^{-}} \to \ell ^-\bar{\nu}}$ channel (right). The measurement is the result of the combination of the muon and electron channels. The lower panel in each plot shows the ratio of observed and expected cross section. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure 17-a: Absolute differential cross section as a function of ${{\| \eta ^{\ell} \|}}$ for the ${\mathrm{W^{+}} \to \ell ^+\nu}$ channel. The measurement is the result of the combination of the muon and electron channels. The lower panel shows the ratio of observed and expected cross section. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure 17-b: Absolute differential cross section as a function of ${{\| \eta ^{\ell} \|}}$ for the ${\mathrm{W^{-}} \to \ell ^-\bar{\nu}}$ channel. The measurement is the result of the combination of the muon and electron channels. The lower panel shows the ratio of observed and expected cross section. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
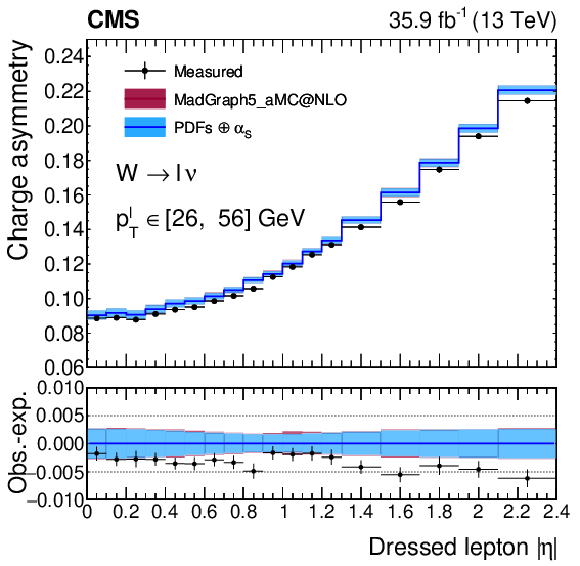
png pdf	Figure 18: Absolute differential W boson charge asymmetry as a function of ${{\| \eta ^{\ell} \|}}$ . The measurement is the result of the combination of the muon and electron channels. The lower panel shows the difference of observed and expected charge asymmetry. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
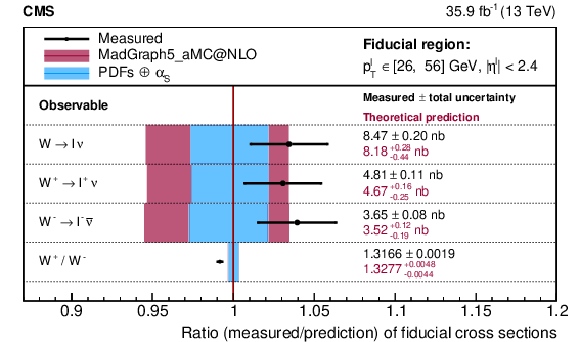
png pdf	Figure 19: Ratio of the measured over predicted absolute inclusive cross section in the fiducial region 26 $< {{p_{\mathrm {T}}} ^{\ell}} <$ 56 GeV and ${{\| \eta ^{\ell} \|}} <$ 2.5, charge-integrated, charge-dependent, and the ratio for ${\mathrm{W^{+}}}$ and ${\mathrm{W^{-}}}$ . The measurement is the result of the combination of the muon and electron channels. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
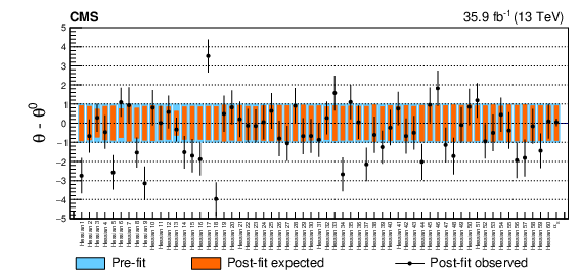
png pdf	Figure 20: Pulls and constraints of the 60 Hessian variations of the NNPDF3.0 PDF set, and of the ${\alpha _S}$ parameter, from the combined fit of muon and electron channels. The underlying fit is performed by fixing the W boson cross sections to their expectation in all helicity and charge processes. The cyan band represents the input values (which all have zero mean and width one), the orange bands show the post-fit expected values, and black points represent the observed pulls and constraint values.
png pdf	Figure A1: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of muon and electron channels. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure A1-a: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of muon and electron channels. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure A1-b: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ for the left-handed and right-handed helicity states from the combination of muon and electron channels. The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
png pdf	Figure A2: Measured absolute ${\mathrm{W^{+}}} \to \ell ^+\nu$ cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ from three distinct fits: the combination of muon and electron channels (green), the muon-only fit (blue), and the electron-only fit (red). The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
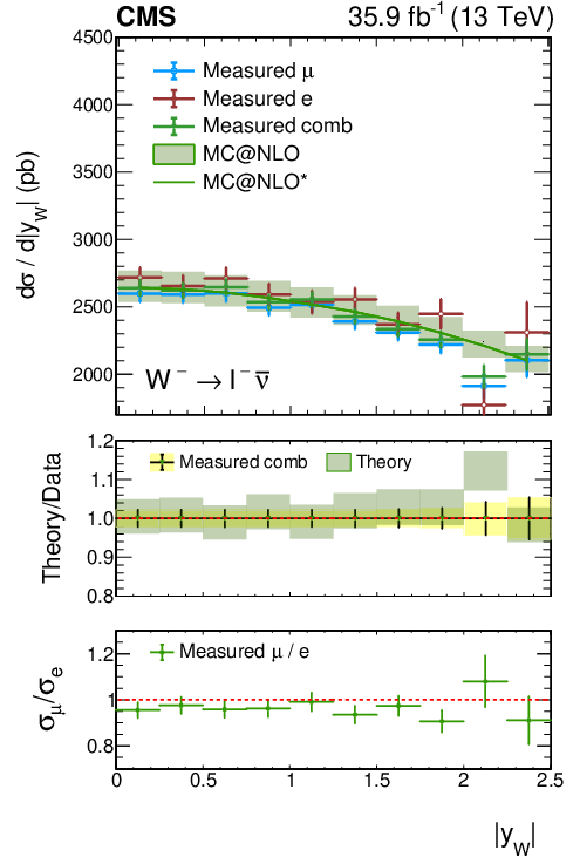
png pdf	Figure A3: Measured absolute ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ cross section as a function of ${{\| y_{\mathrm{W}} \|}}$ from three distinct fits: the combination of muon and electron channels (green), the muon-only fit (blue), and the electron-only fit (red). The ratio of the prediction from MadGraph5_aMC@NLO to the data is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
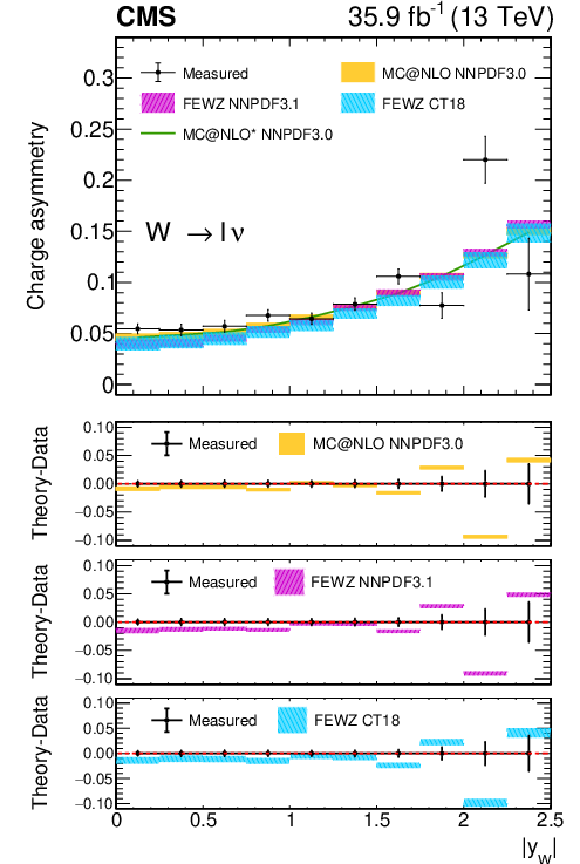
png pdf	Figure A4: Measured W boson charge asymmetry as a function of ${{\| y_{\mathrm{W}} \|}}$ from the combination of the muon and electron channels (black dots), compared with different theoretical predictions. The yellow band represents the default generator used in this analysis, MadGraph5_aMC@NLO with NNPDF3.0 PDF set, the pink band represents the {fewz} generator with NNPDF3.1 PDF set, and the cyan band represents the {fewz} generator with CT18 PDF set. The uncertainty bands of the prediction include PDF uncertainties only, which are dominant with respect to ${\alpha _S}$ or QCD scale variations for this quantity.
png pdf	Figure A5: Measured $A_4$ coefficient for ${\mathrm{W^{+}}} \to \ell ^+\nu$ extracted from the fit of the polarized cross sections to the combined muon and electron channel fit. Note that $A_4$ is negative in this case, and the plotted quantity is $-A_4$ . The difference between the prediction from MadGraph5_aMC@NLO and the measured values is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
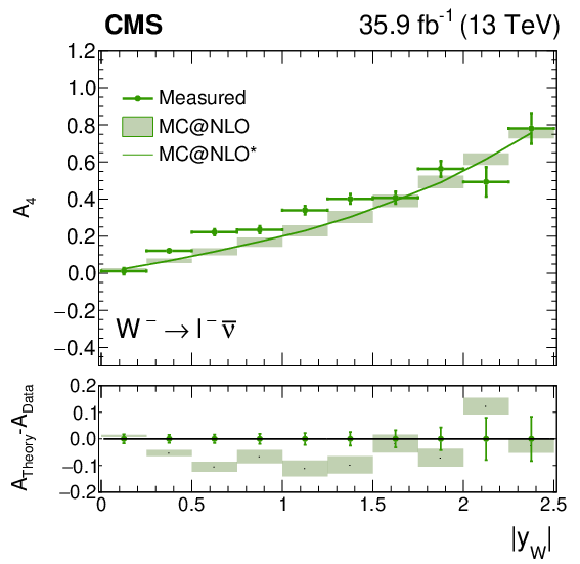
png pdf	Figure A6: Measured $A_4$ coefficient for ${\mathrm{W^{-}}} \to \ell ^-\nu$ extracted from the fit of the polarized cross sections to the combined muon and electron channel fit. The difference between the prediction from MadGraph5_aMC@NLO and the measured values is also shown. The lightly-filled band corresponds to the expected uncertainty from the PDF variations, ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales, and ${\alpha _S}$ .
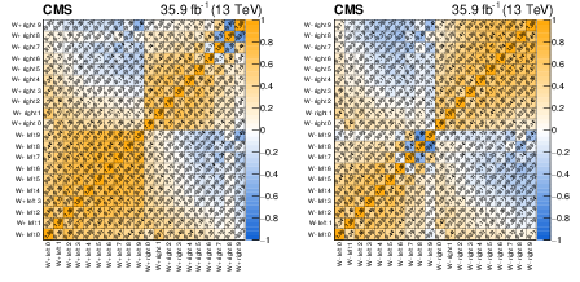
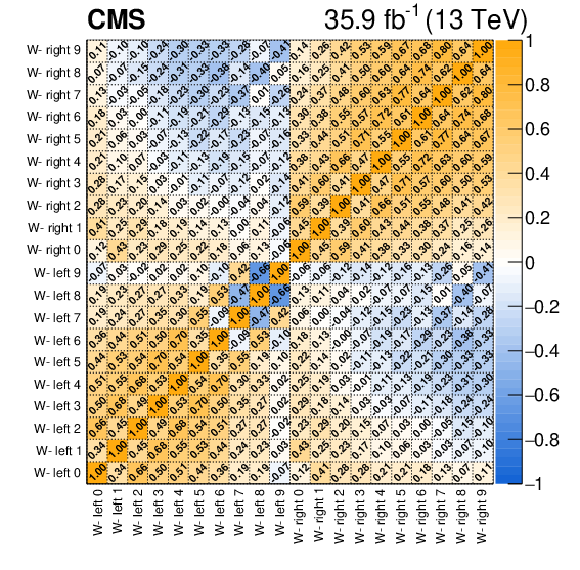
png pdf	Figure A7: Correlation coefficients between the helicity-dependent signal cross sections for ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) extracted from the fit to the combined muon and electron channel fit.
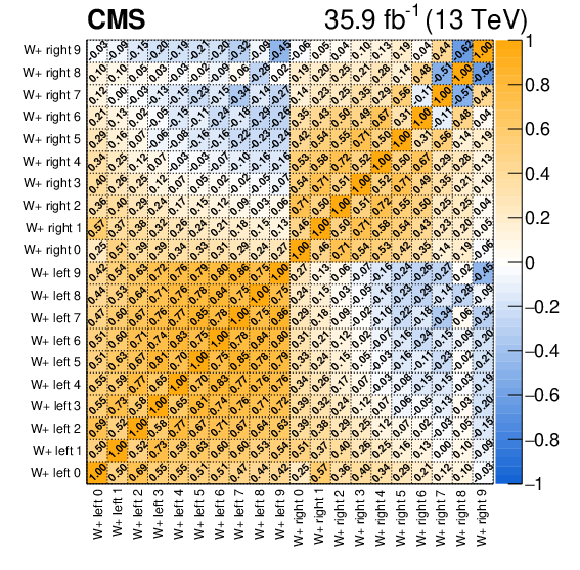
png pdf	Figure A7-a: Correlation coefficients between the helicity-dependent signal cross sections for ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) extracted from the fit to the combined muon and electron channel fit.
png pdf	Figure A7-b: Correlation coefficients between the helicity-dependent signal cross sections for ${\mathrm{W^{+}}} \to \ell ^+\nu$ (left) and ${\mathrm{W^{-}}} \to \ell ^-\bar{\nu}$ (right) extracted from the fit to the combined muon and electron channel fit.
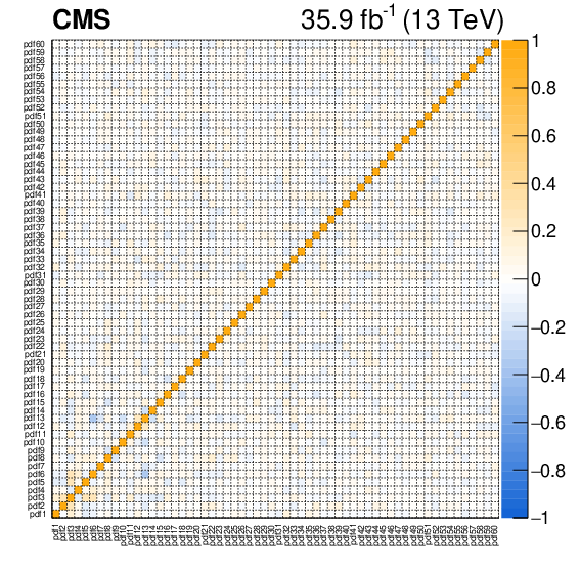
png pdf	Figure A8: Correlation coefficients between the 60 PDF nuisance parameters extracted from the fit to the combined muon and electron channel fit. The underlying fit is performed by fixing the W boson cross sections to their expectation in all helicity and charge processes.
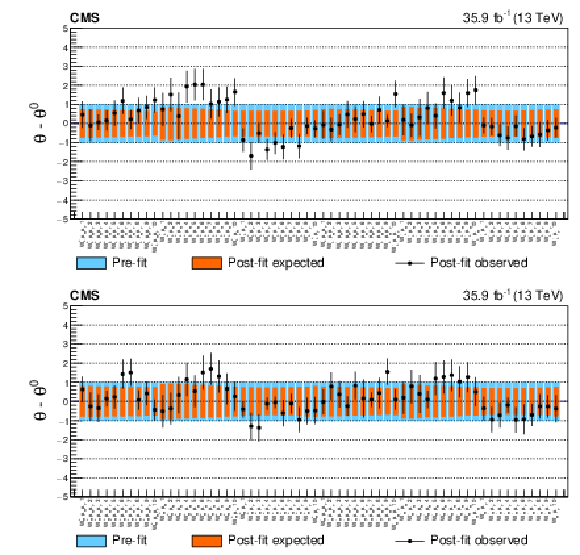
png pdf	Figure A9: Post-fit pulls and constraints of the nuisance parameters associated with the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scale systematic uncertainties. The numbering refers to bins in the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ spectrum in increasing order. The nuisance parameters applied to the "left'' polarization are shown on the upper panel while the ones associated with the "right'' polarization are shown on the lower panel.
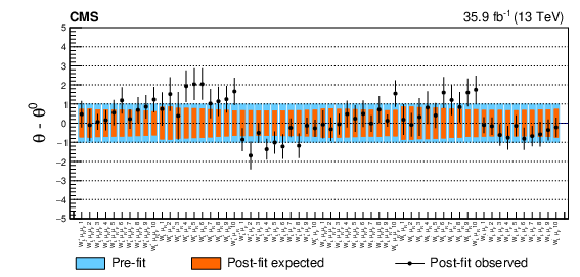
png pdf	Figure A9-a: Post-fit pulls and constraints of the nuisance parameters associated with the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scale systematic uncertainties. The numbering refers to bins in the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ spectrum in increasing order. The nuisance parameters applied to the "left'' polarization are shown on the upper panel while the ones associated with the "right'' polarization are shown on the lower panel.
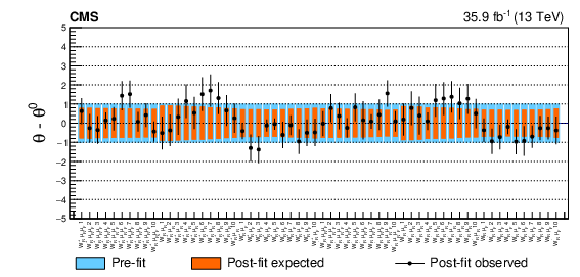
png pdf	Figure A9-b: Post-fit pulls and constraints of the nuisance parameters associated with the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scale systematic uncertainties. The numbering refers to bins in the ${{p_{\mathrm {T}}} ^{\mathrm{W}}}$ spectrum in increasing order. The nuisance parameters applied to the "left'' polarization are shown on the upper panel while the ones associated with the "right'' polarization are shown on the lower panel.
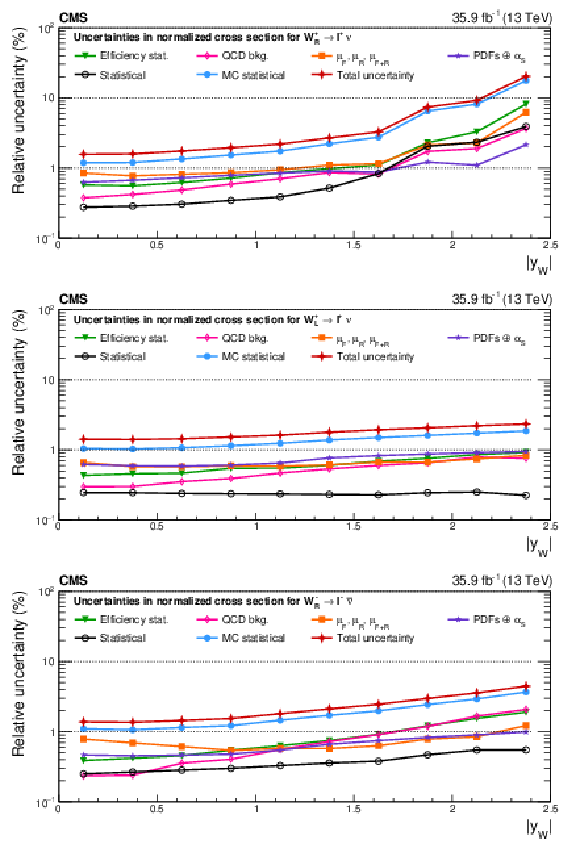
png pdf	Figure A10: Remaining impacts on the normalized polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {R}}$ (upper), ${\mathrm{W} ^+_\mathrm {L}}$ (middle), and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
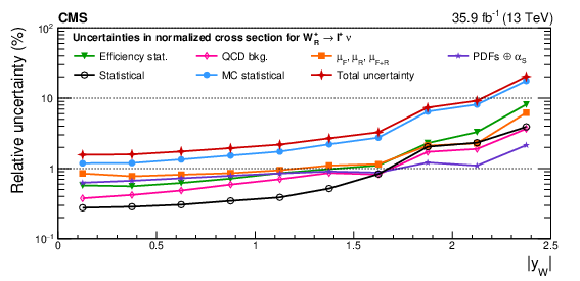
png pdf	Figure A10-a: Remaining impacts on the normalized polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {R}}$ (upper), ${\mathrm{W} ^+_\mathrm {L}}$ (middle), and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
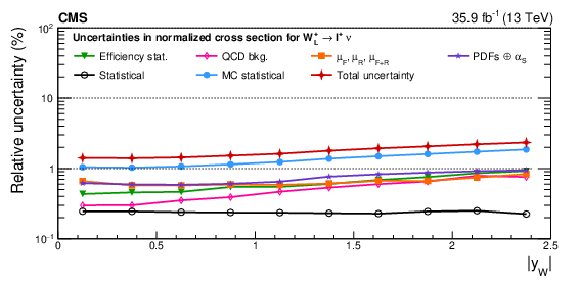
png pdf	Figure A10-b: Remaining impacts on the normalized polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {R}}$ (upper), ${\mathrm{W} ^+_\mathrm {L}}$ (middle), and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A10-c: Remaining impacts on the normalized polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {R}}$ (upper), ${\mathrm{W} ^+_\mathrm {L}}$ (middle), and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
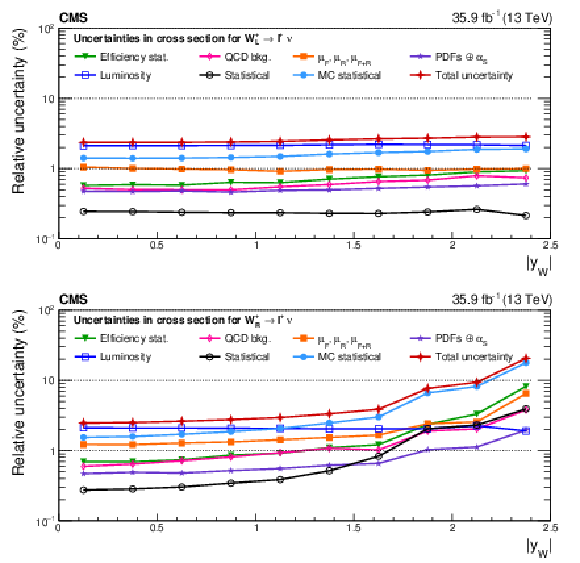
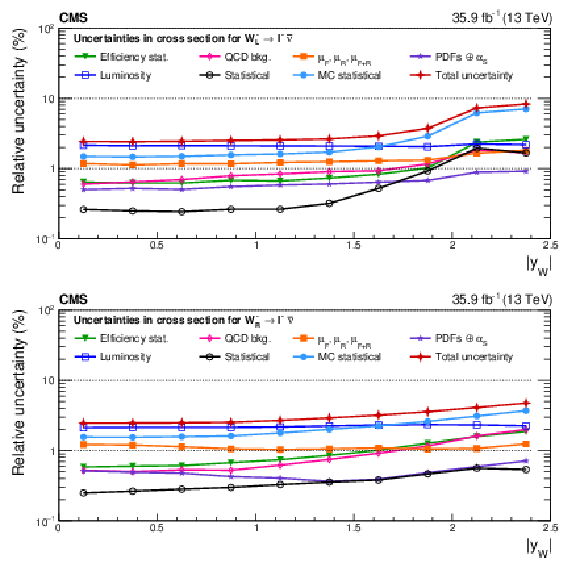
png pdf	Figure A11: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {L}}$ (upper) and ${\mathrm{W} ^+_\mathrm {R}}$ (lower) in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
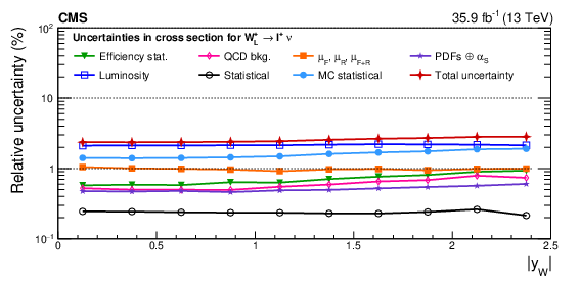
png pdf	Figure A11-a: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {L}}$ (upper) and ${\mathrm{W} ^+_\mathrm {R}}$ (lower) in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
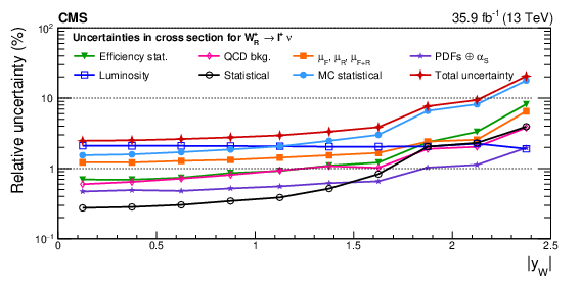
png pdf	Figure A11-b: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^+_\mathrm {L}}$ (upper) and ${\mathrm{W} ^+_\mathrm {R}}$ (lower) in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A12: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^-_\mathrm {L}}$ (upper) and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
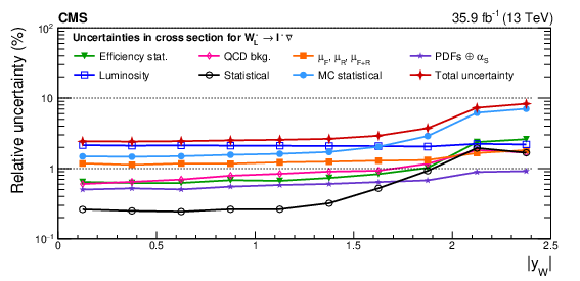
png pdf	Figure A12-a: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^-_\mathrm {L}}$ (upper) and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
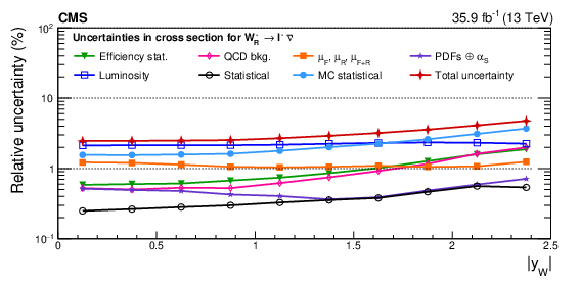
png pdf	Figure A12-b: Impacts on the absolute polarized cross sections as functions of the W boson rapidity. Shown are the impacts of the nuisance groups for ${\mathrm{W} ^-_\mathrm {L}}$ (upper) and ${\mathrm{W} ^-_\mathrm {R}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
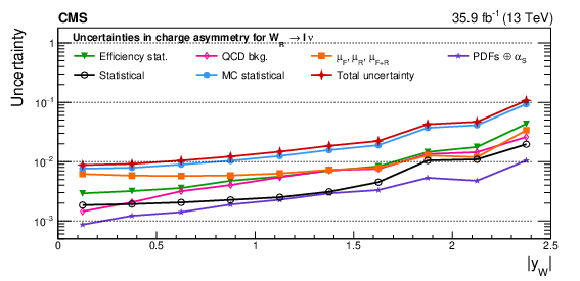
png pdf	Figure A13: Impacts on the charge asymmetry as functions of the W boson rapidity for ${\mathrm{W} _\mathrm {R}}$ bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
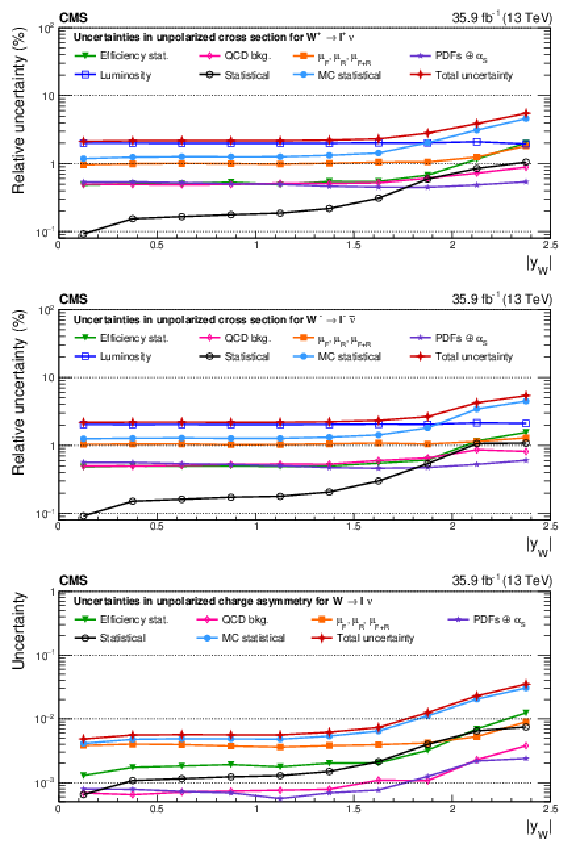
png pdf	Figure A14: Impacts on the unpolarized absolute cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle), and the unpolarized charge asymmetry (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
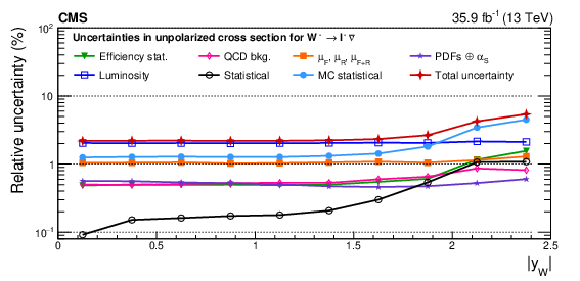
png pdf	Figure A14-a: Impacts on the unpolarized absolute cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle), and the unpolarized charge asymmetry (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
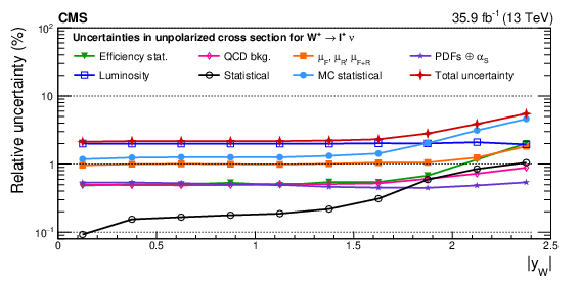
png pdf	Figure A14-b: Impacts on the unpolarized absolute cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle), and the unpolarized charge asymmetry (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
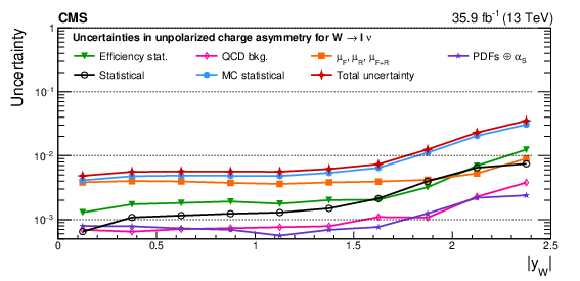
png pdf	Figure A14-c: Impacts on the unpolarized absolute cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle), and the unpolarized charge asymmetry (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
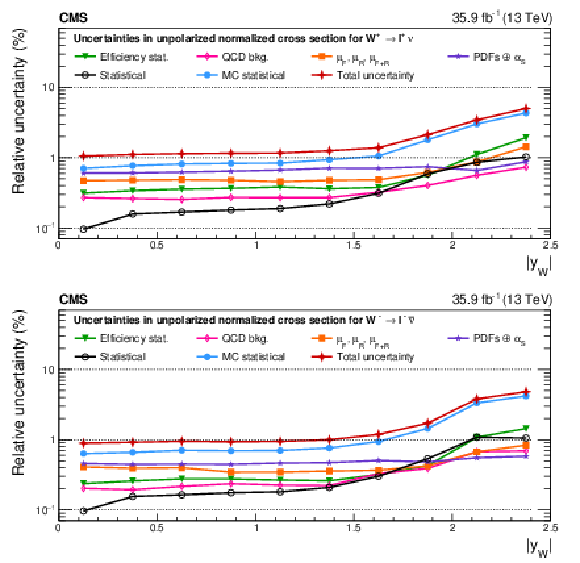
png pdf	Figure A15: Impacts on the unpolarized normalized cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
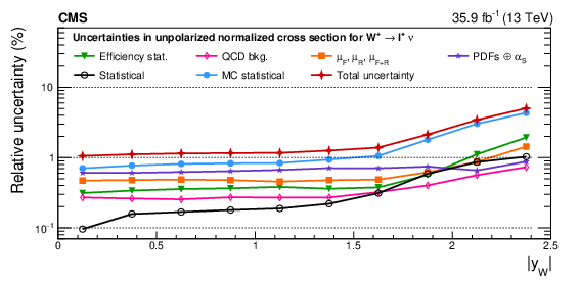
png pdf	Figure A15-a: Impacts on the unpolarized normalized cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
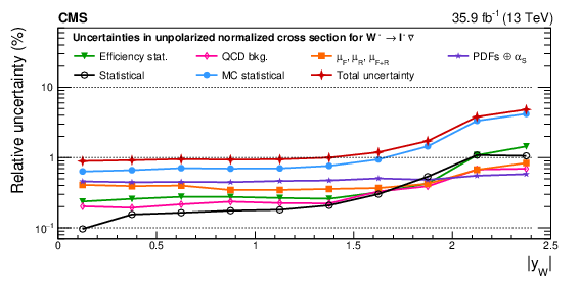
png pdf	Figure A15-b: Impacts on the unpolarized normalized cross sections as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
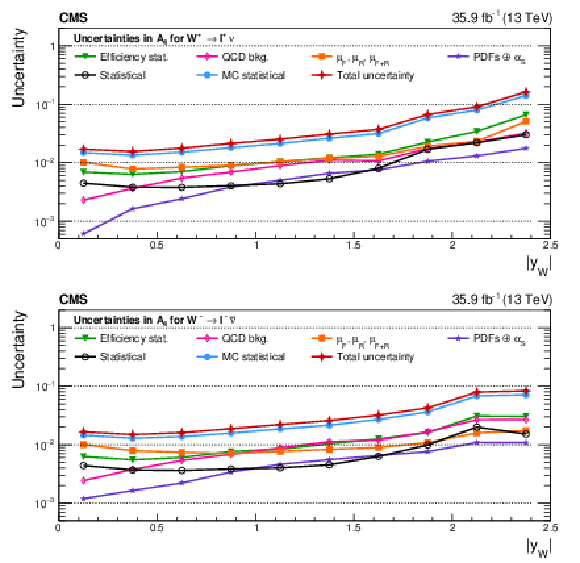
png pdf	Figure A16: Impacts on the A $_4$ coefficient as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
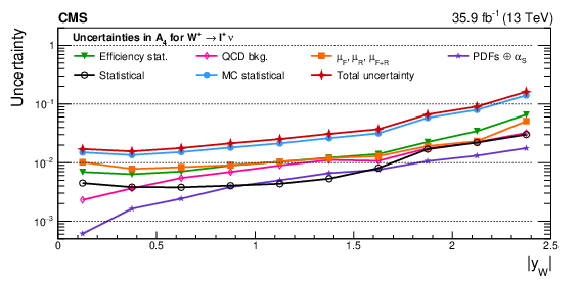
png pdf	Figure A16-a: Impacts on the A $_4$ coefficient as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
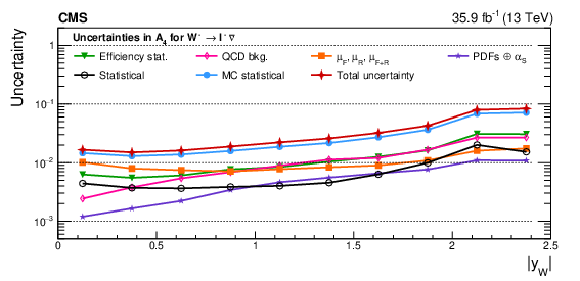
png pdf	Figure A16-b: Impacts on the A $_4$ coefficient as functions of the W boson rapidity for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the helicity fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
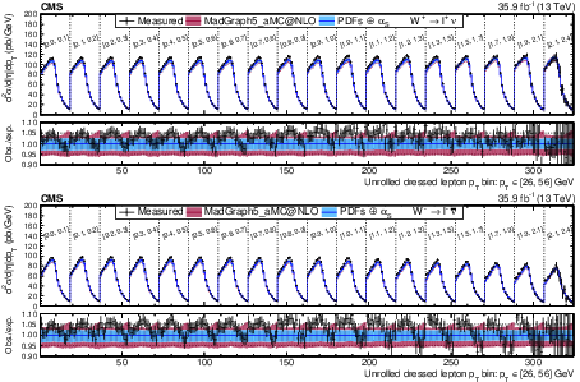
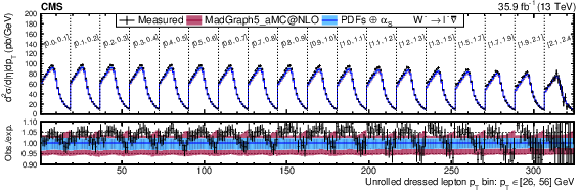
png pdf	Figure A17: Unrolled cross sections for the combined muon and electron channel fit unrolled along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure A17-a: Unrolled cross sections for the combined muon and electron channel fit unrolled along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure A17-b: Unrolled cross sections for the combined muon and electron channel fit unrolled along ${{p_{\mathrm {T}}} ^{\ell}}$ in bins of ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
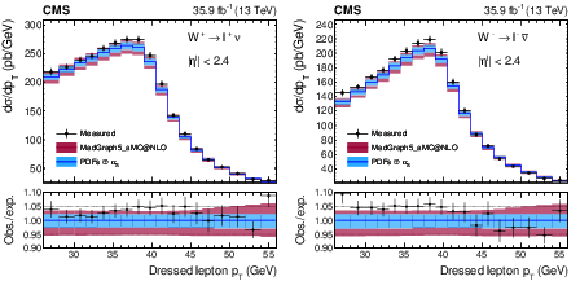
png pdf	Figure A18: Absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure A18-a: Absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
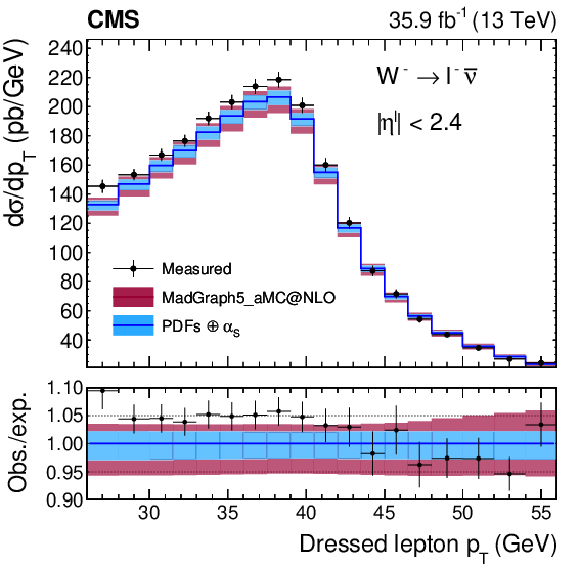
png pdf	Figure A18-b: Absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
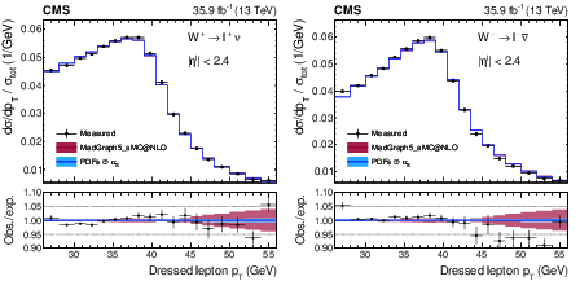
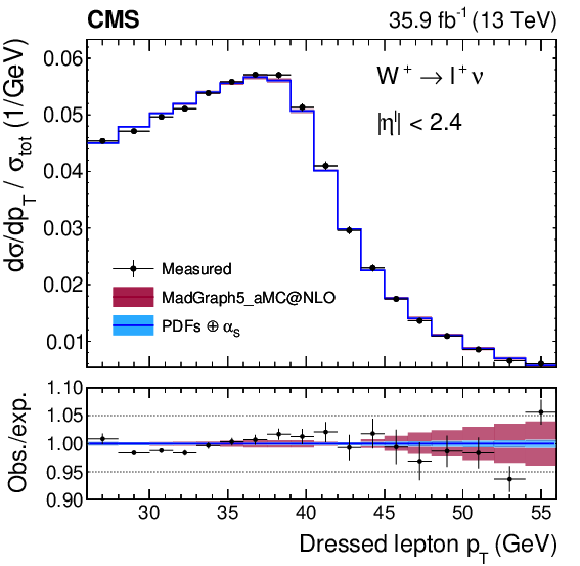
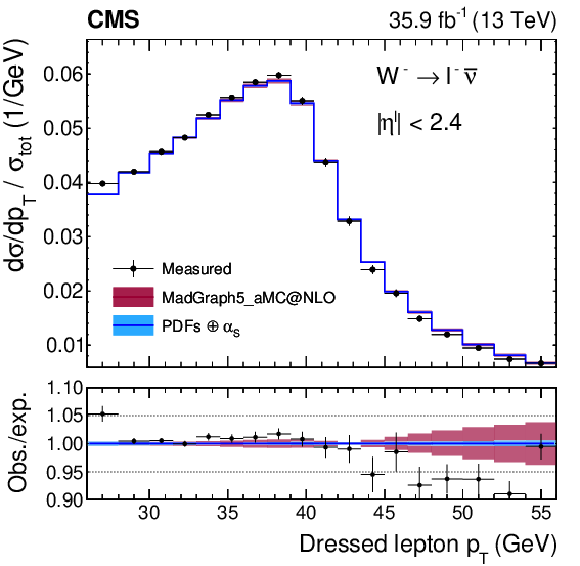
png pdf	Figure A19: Normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure A19-a: Normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
png pdf	Figure A19-b: Normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
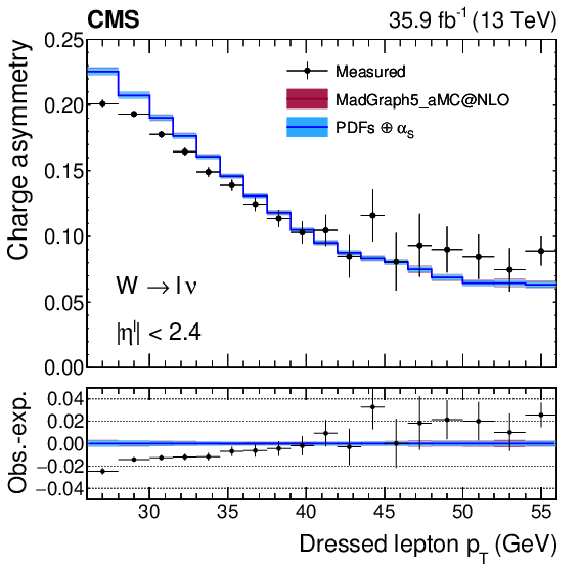
png pdf	Figure A20: W charge asymmetry as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ . The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux).
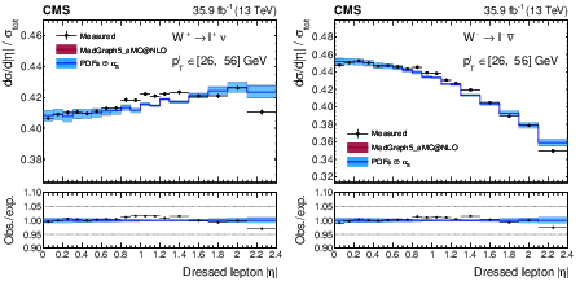
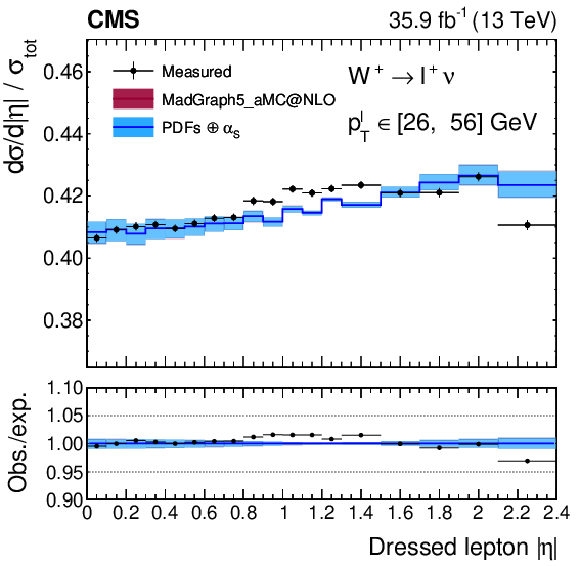
png pdf	Figure A21: Normalized cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated over ${{p_{\mathrm {T}}} ^{\ell}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux). The uncertainty band is almost entirely dominated by the PDF $\oplus {\alpha _S}$ variations, while the missing higher order QCD uncertainties almost perfectly cancel and are therefore invisible.
png pdf	Figure A21-a: Normalized cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated over ${{p_{\mathrm {T}}} ^{\ell}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux). The uncertainty band is almost entirely dominated by the PDF $\oplus {\alpha _S}$ variations, while the missing higher order QCD uncertainties almost perfectly cancel and are therefore invisible.
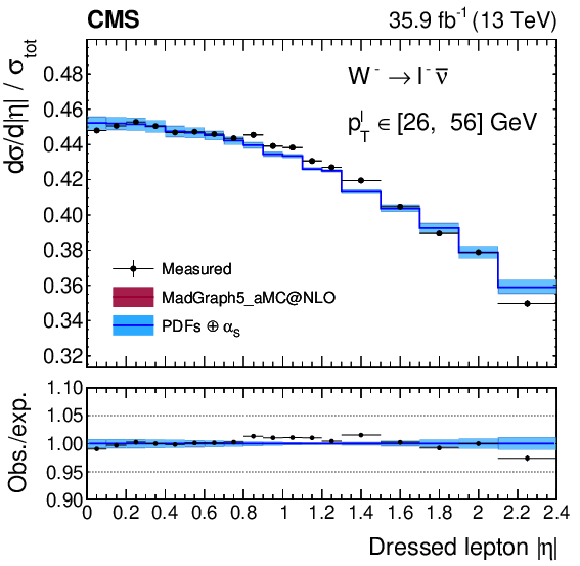
png pdf	Figure A21-b: Normalized cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated over ${{p_{\mathrm {T}}} ^{\ell}}$ for ${\mathrm{W^{+}}}$ (left) and ${\mathrm{W^{-}}}$ (right) bosons. The colored bands represent the prediction from MadGraph5_aMC@NLO with the expected uncertainty from the quadrature sum of the PDF $\oplus {\alpha _S}$ variations (blue) and the ${\mu _\mathrm {F}}$ and ${\mu _\mathrm {R}}$ scales (bordeaux). The uncertainty band is almost entirely dominated by the PDF $\oplus {\alpha _S}$ variations, while the missing higher order QCD uncertainties almost perfectly cancel and are therefore invisible.
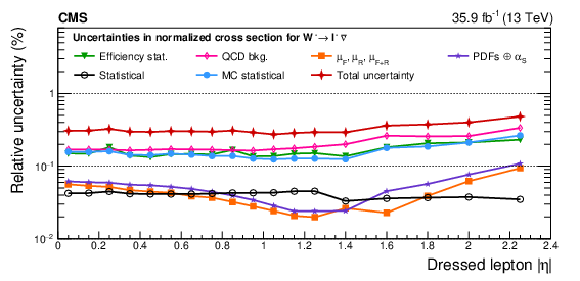
png pdf	Figure A22: Remaining impacts of the nuisance groups on the normalized cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated in ${{p_{\mathrm {T}}} ^{\ell}}$ , for ${\mathrm{W^{-}}}$ bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
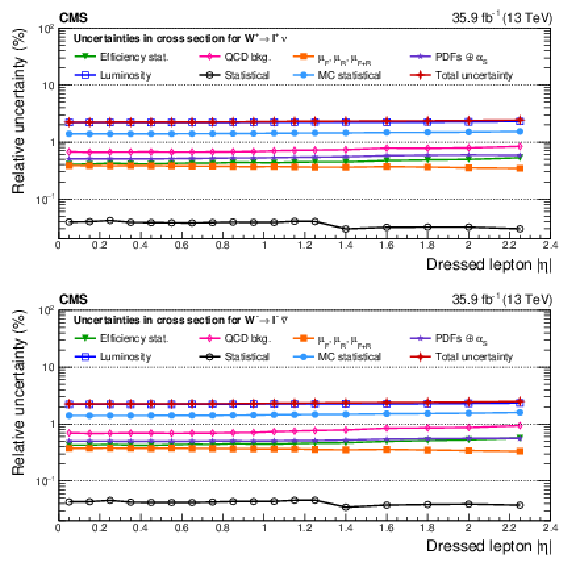
png pdf	Figure A23: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated in ${{p_{\mathrm {T}}} ^{\ell}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A23-a: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated in ${{p_{\mathrm {T}}} ^{\ell}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
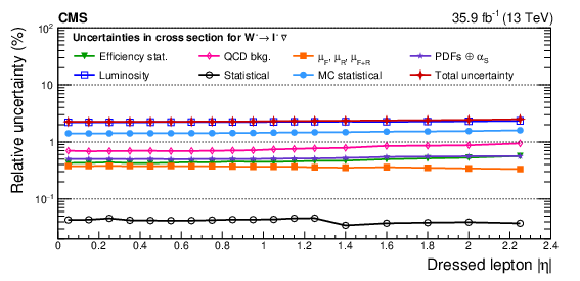
png pdf	Figure A23-b: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{\| \eta ^{\ell} \|}}$ , integrated in ${{p_{\mathrm {T}}} ^{\ell}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
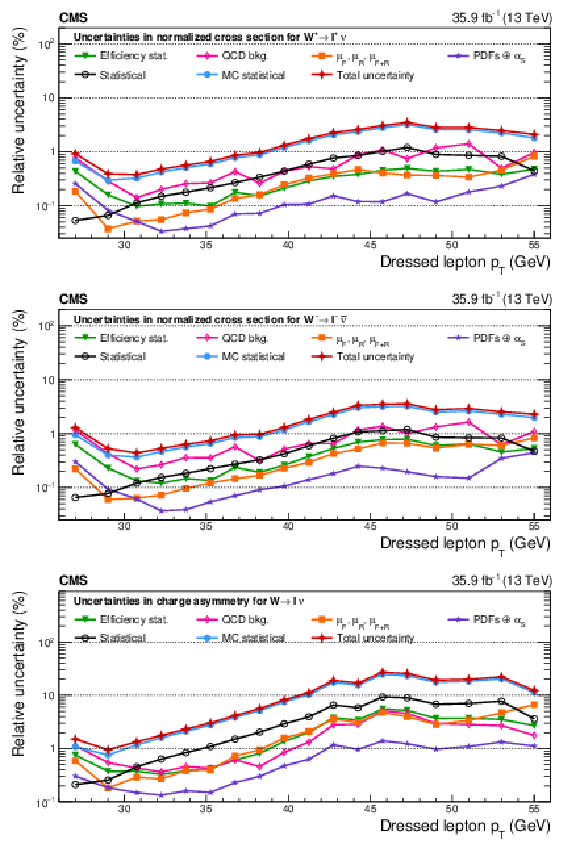
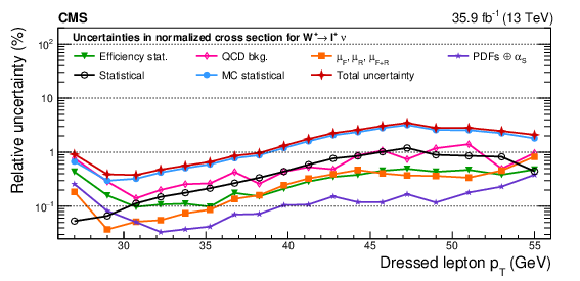
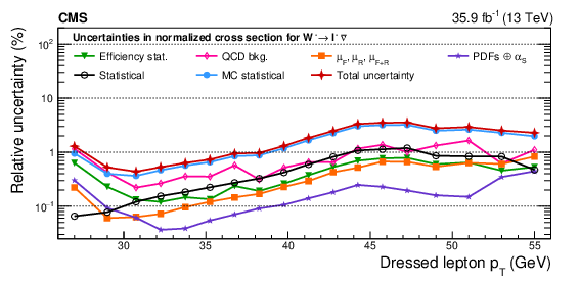
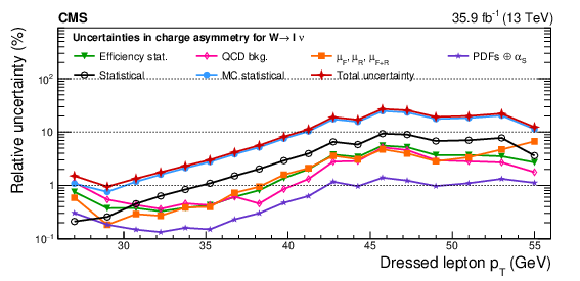
png pdf	Figure A24: Remaining impacts of the nuisance groups on the normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle) bosons, and the resulting charge asymmetry (lower) in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A24-a: Remaining impacts of the nuisance groups on the normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle) bosons, and the resulting charge asymmetry (lower) in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A24-b: Remaining impacts of the nuisance groups on the normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle) bosons, and the resulting charge asymmetry (lower) in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
png pdf	Figure A24-c: Remaining impacts of the nuisance groups on the normalized cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper), ${\mathrm{W^{-}}}$ (middle) bosons, and the resulting charge asymmetry (lower) in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
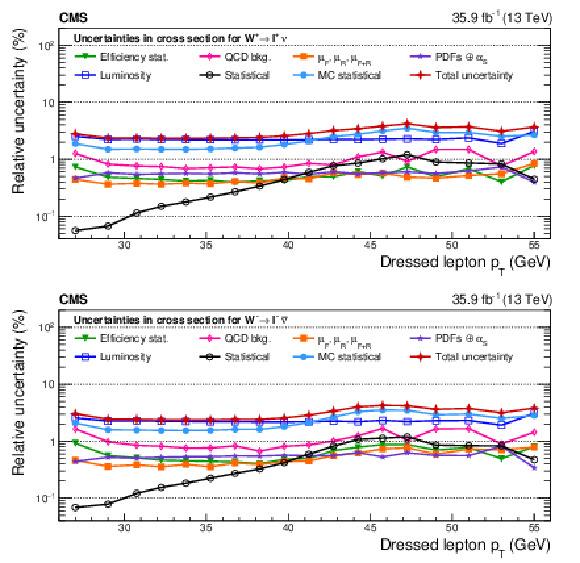
png pdf	Figure A25: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
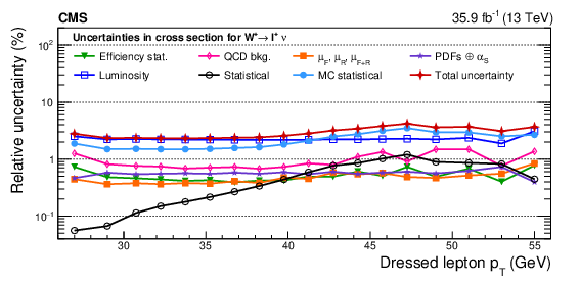
png pdf	Figure A25-a: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.
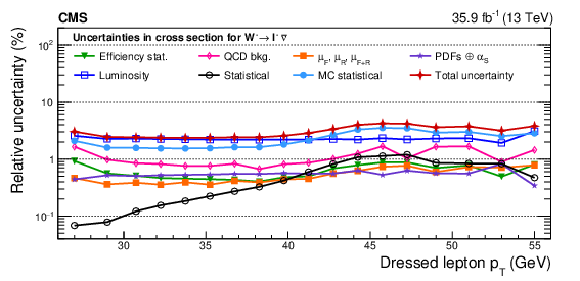
png pdf	Figure A25-b: Remaining impacts of the nuisance groups on the absolute cross sections as functions of ${{p_{\mathrm {T}}} ^{\ell}}$ , integrated over ${{\| \eta ^{\ell} \|}}$ , for ${\mathrm{W^{+}}}$ (upper) and ${\mathrm{W^{-}}}$ (lower) bosons in the double-differential cross section fit. The groups of uncertainties subleading to the ones shown are suppressed for simplicity.

Tables
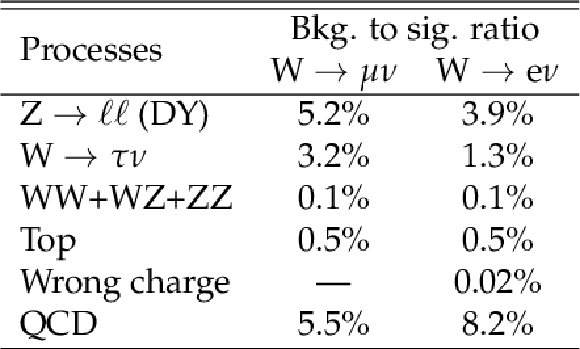
png pdf	Table 1: Estimated background-to-signal ratios in the $\mathrm{W} \to \mu \nu$ and $\mathrm{W} \to \mathrm{e} \nu$ channels. The DY simulation includes $\ell =$ e, $\mu$ , $\tau$ .
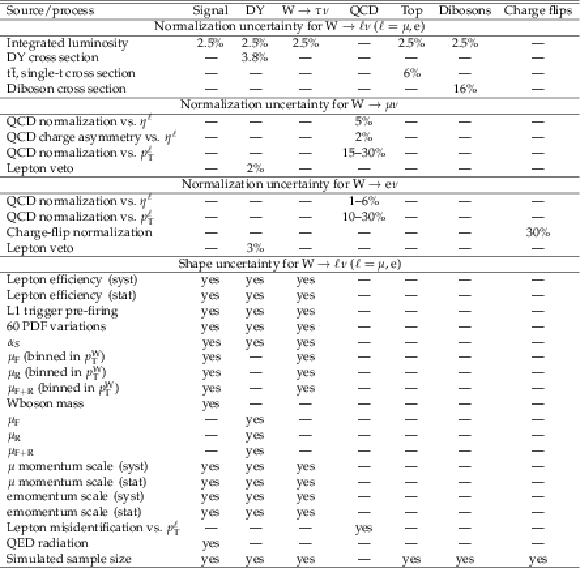
png pdf	Table 2: Systematic uncertainties for each source and process. Quoted numbers correspond to the size of log-normal nuisance parameters applied in the fit, while a "yes'' in a given cell corresponds to the given systematic uncertainty being applied as a shape variation over the full 2D template space.

Summary

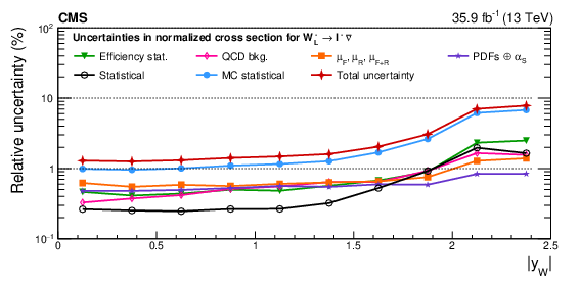
The differential W boson cross sections as functions of the W boson rapidity,

$|{y_{\mathrm{W}}}|$ , and for the two charges separately,

${\mathrm{W^{+}}} \to \ell^+\nu$ and

${\mathrm{W^{-}}} \to \ell^-\bar{\nu}$ , are measured in the W boson helicity states. Double-differential cross sections of the W boson are measured as a function of the charged-lepton transverse momentum

${p_{\mathrm{T}}}^{\ell}$ and absolute pseudorapidity

$|{\eta^{\ell}}|$ . For both

${\mathrm{W^{+}}}$ and

${\mathrm{W^{-}}}$ bosons, the differential charge asymmetry is also extracted.

The measurement is based on data taken in proton-proton collisions at the LHC at a center-of-mass energy of

$\sqrt{s} =$ 13 TeV, corresponding to an integrated luminosity of 35.9 fb

$^{-1}$ . Differential cross sections are presented, both absolute and normalized to the total production cross section within a given acceptance. For the helicity measurement, the range

$|{y_{\mathrm{W}}}| <$ 2.5 is presented, whereas for the double-differential cross section the range

$|{\eta^{\ell}}| <$ 2.4 and 26

$< {p_{\mathrm{T}}}^{\ell} <$ 56 GeV is used. The measurement is performed using both the muon and electron channels, combined together considering all sources of correlated and uncorrelated uncertainties.

The precision in the measurement as a function of

$|{y_{\mathrm{W}}}|$ , using a combination of the two channels, is about 2% in central

$|{y_{\mathrm{W}}}|$ bins, and 5 to 20%, depending on the charge-polarization combination, in the outermost acceptance bins. The precision of the double-differential cross section, relative to the total, is about 1% in the central part of the detector,

$|{\eta^{\ell}}| <$ 1, and better than 2.5% up to

$|{\eta^{\ell}}| <$ 2 for each of the two W boson charges.

Charge asymmetries are also measured, differentially in

$|{y_{\mathrm{W}}}|$ and polarization, as well as in

${p_{\mathrm{T}}}^{\ell}$ and

$|{\eta^{\ell}}|$ . The uncertainties in these asymmetries range from 0.1% in high-acceptance bins to roughly 2.5% in regions of phase space with lower detector acceptance. Furthermore, fiducial cross sections are presented by integrating the two-dimensional differential cross sections over the full acceptance of the analysis.

The measurement of the W boson polarized cross sections as functions of

$|{y_{\mathrm{W}}}|$ is used to constrain the parameters related to parton distribution functions in a simultaneous fit of the two channels and the two W boson charges. The constraints are derived at the detector level on 60 uncorrelated eigenvalues of the NNPDF3.0 set of PDFs within the MadGraph5+MCatNLO event generator, and show a total constraint down to

$\simeq$ 70% of the pre-fit uncertainties for certain variations of the PDF nuisance parameters.

Additional Figures
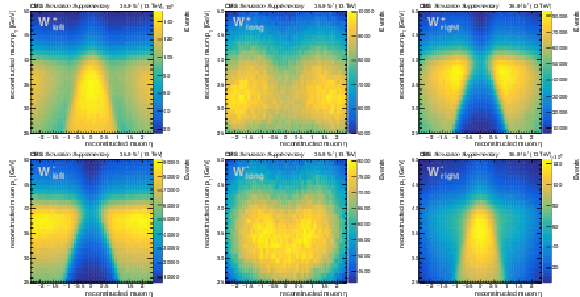
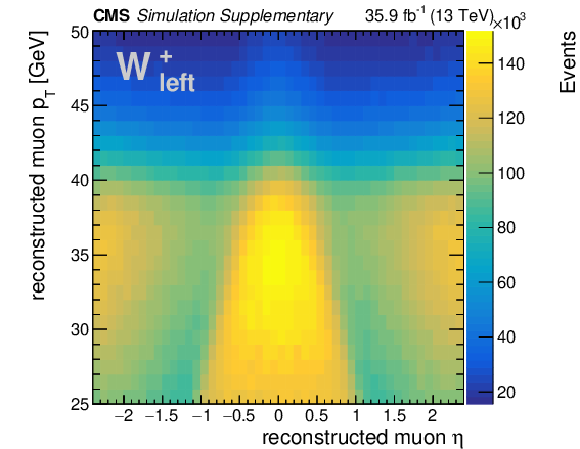
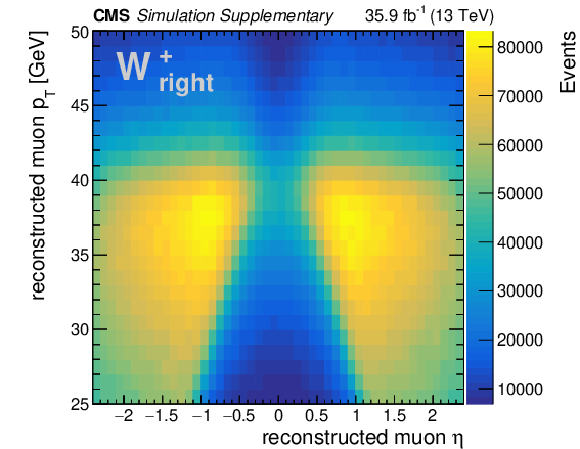
png pdf	Additional Figure 1: Distributions of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, split into W boson charge and polarization (left, longitudinal, right). For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. These distributions are obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
png pdf	Additional Figure 1-a: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for positive charge and left polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
png pdf	Additional Figure 1-b: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for positive charge and longitudinal polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
png pdf	Additional Figure 1-c: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for positive charge and right polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
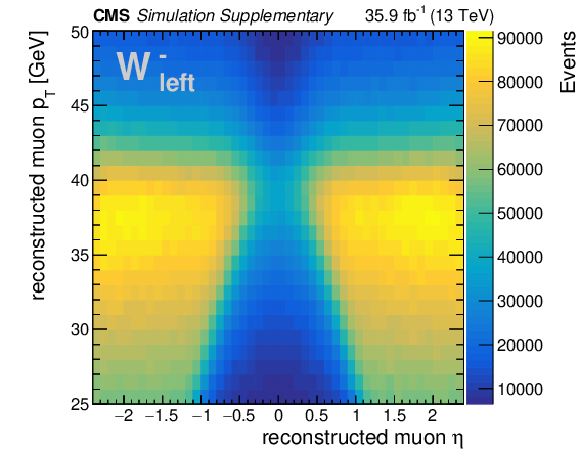
png pdf	Additional Figure 1-d: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for negative charge and left polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
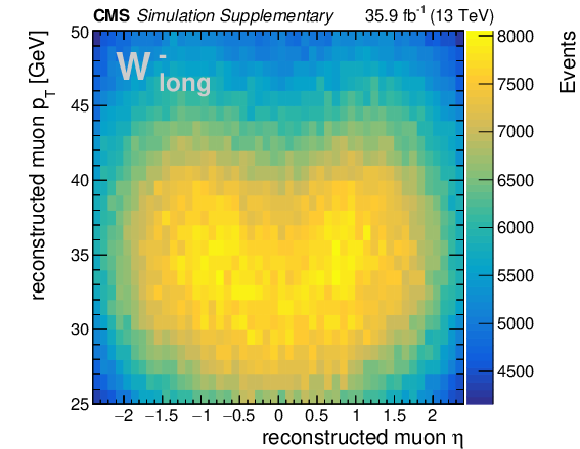
png pdf	Additional Figure 1-e: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for negative charge and longitudinal polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
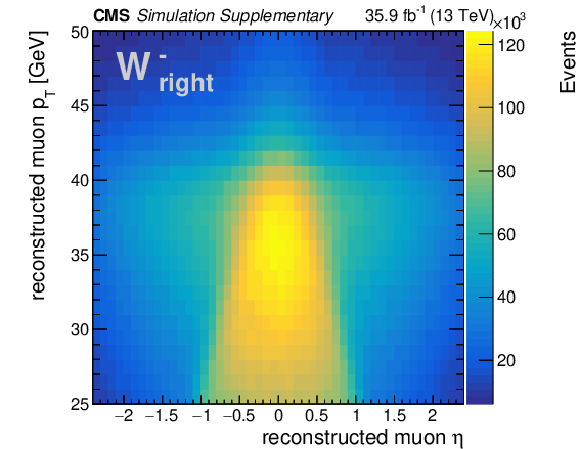
png pdf	Additional Figure 1-f: Distribution of ${\eta ^{\ell}}$ and ${{p_{\mathrm {T}}} ^{\ell}}$ of the reconstructed muon in W boson decays, for negative charge and right polarization. For a given charge and helicity state, the particular shape of each distribution is determined by the underlying W rapidity distribution, which in turn depends on the proton PDFs. This distribution is obtained from simulated $\mathrm{W} \rightarrow \mu \nu$ +jets events at $\sqrt {s} =$ 13 TeV using MadGraph5_aMC@NLO. Event yields are normalized to an integrated luminosity of 35.9 fb $^{-1}$ . No event selection is applied, except for the requirement that a muon is identified and reconstructed within the CMS detector and the plot boundaries in ${{p_{\mathrm {T}}} ^{\ell}}$ from 25 to 50 GeV and $\| \eta ^{\ell} \| <$ 2.4.
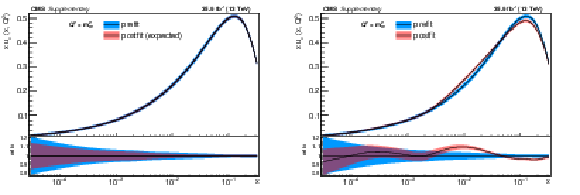
png pdf	Additional Figure 2: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
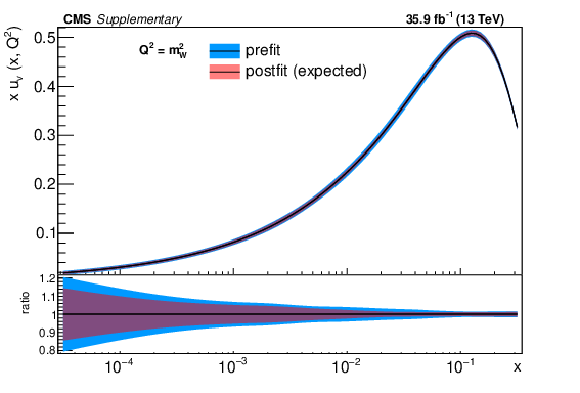
png pdf	Additional Figure 2-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
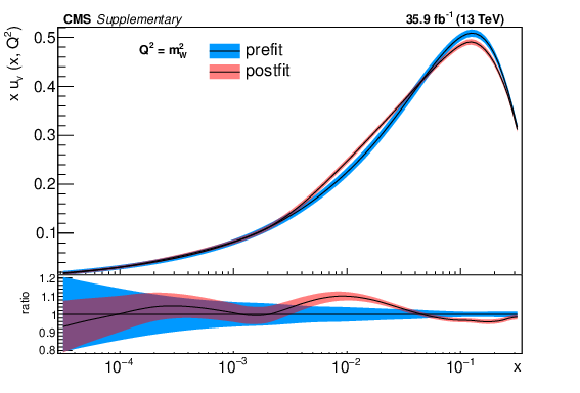
png pdf	Additional Figure 2-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
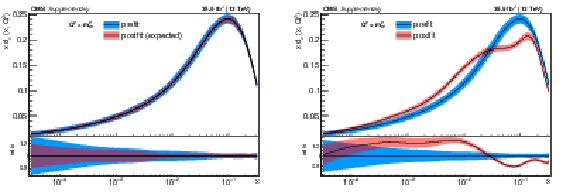
png pdf	Additional Figure 3: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
png pdf	Additional Figure 3-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
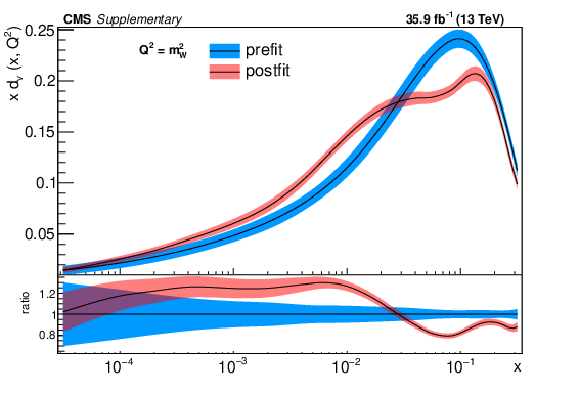
png pdf	Additional Figure 3-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
png pdf	Additional Figure 4: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
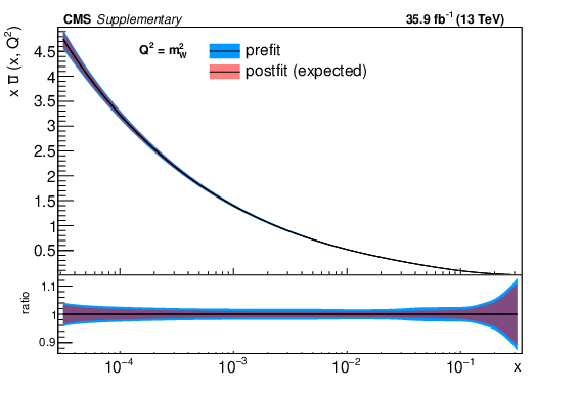
png pdf	Additional Figure 4-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
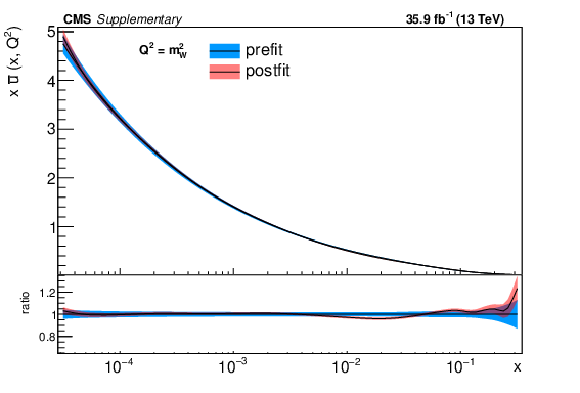
png pdf	Additional Figure 4-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
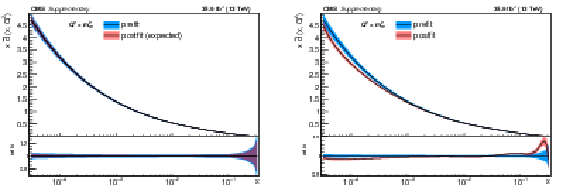
png pdf	Additional Figure 5: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
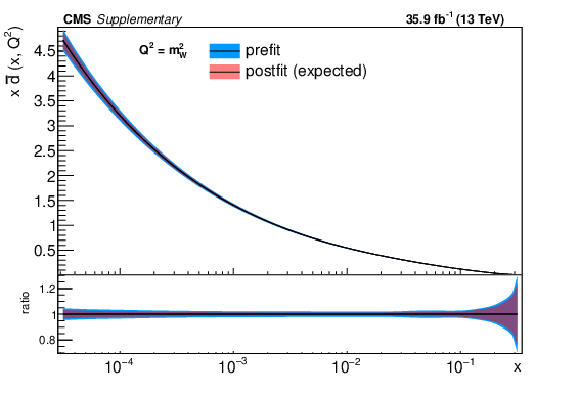
png pdf	Additional Figure 5-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
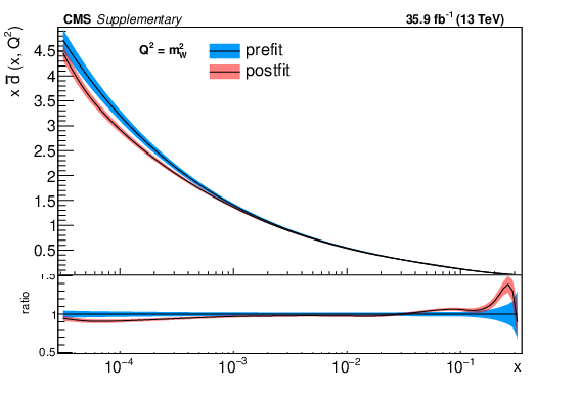
png pdf	Additional Figure 5-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
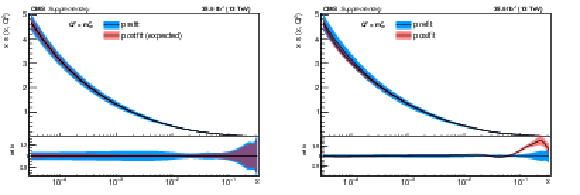
png pdf	Additional Figure 6: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
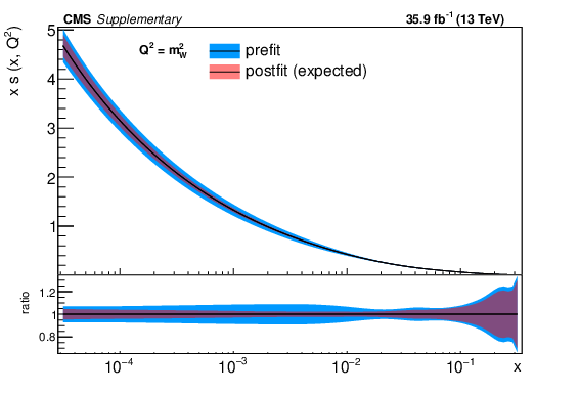
png pdf	Additional Figure 6-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
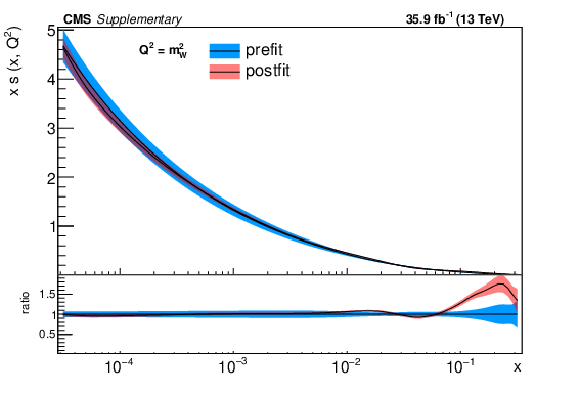
png pdf	Additional Figure 6-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
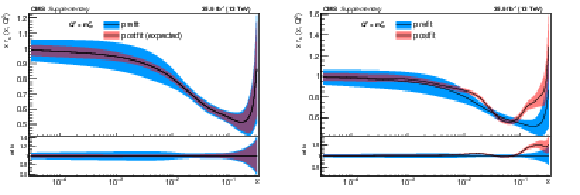
png pdf	Additional Figure 7: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
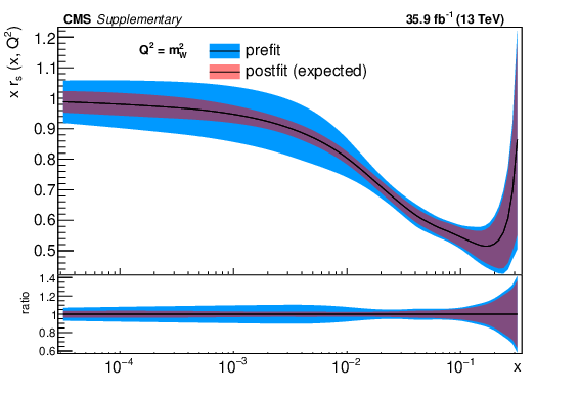
png pdf	Additional Figure 7-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
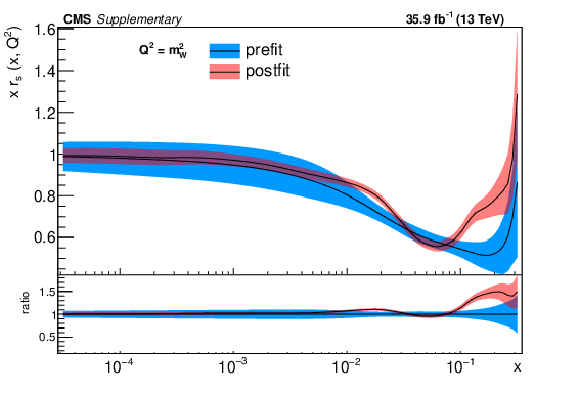
png pdf	Additional Figure 7-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
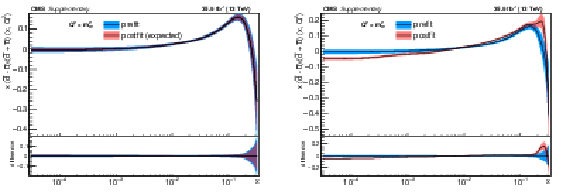
png pdf	Additional Figure 8: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
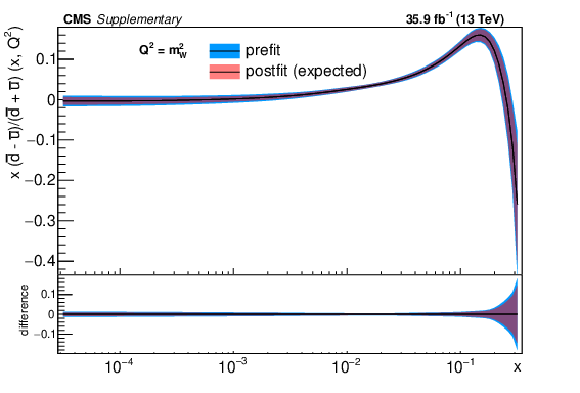
png pdf	Additional Figure 8-a: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.
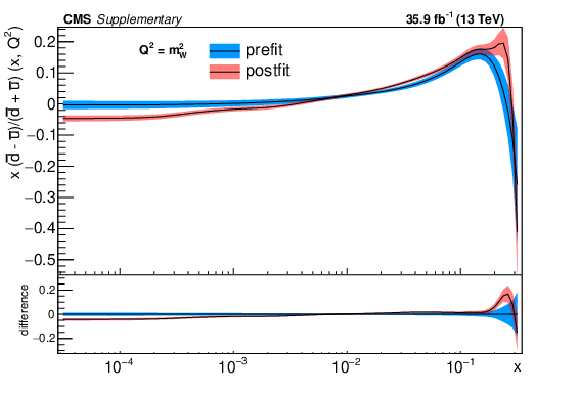
png pdf	Additional Figure 8-b: The post-fit nuisance parameter values and covariance matrix for the PDF and $\alpha _S$ uncertainties from the fixed-parameter-of-interest fit described in Section 8.2 are propagated to the corresponding change in central value and uncertainty with respect to the input NNPDF3.0 NLO PDF set as a function of x for fixed $Q^2=M_\mathrm {W}^2$ . The profiling procedure employed here has the caveat that the results cannot be interpreted as a rigorous PDF determination in case the results are far from the input PDF, and that the measurement under consideration tends to have a larger weight than if it were included in a global PDF determination. Nevertheless the profiling procedure is useful to assess the sensitivity of the different parton distributions to this measurement, and its compatibility with the predictions of the input PDF set. Particular to this result is the fact that constraints are derived only at NLO + parton shower accuracy in QCD, and that there are possible limitations of the PDF set used with respect to newer sets. The presence of oscillatory behaviour in the valence quark distributions is in part related to anti-correlations between different x values arising from the statistical uncertainties in the underlying measurement.

Covariance Matrices among Parameters of Interest and Nuisance Parameters

Compressed tarball (202M) including covariance matrices among parameters of interest (POIs) and nuisance parameters (NPs) in yaml format. The lists of postfit values and uncertainties for POIs and NPs are also included for each matrix. Note that for each of the 3 fits detailed in the paper (double-differential cross section, helicity with floating POIs, and helicity with fixed POIs), the postfit values of NPs and their mutual correlations do not change across different tables.
License cc-by-4.0. The content of this file can be shared and adapted but you must give appropriate credit and cannot restrict access to others.
The list of tables is available in yaml format. The convention adopted to name POIs and NPs in the tables is reported in a glossary of parameters of interest and nuisance parameters.
Below are root files containing the covariance matrices and postfit values for nuisance parameters and parameters of interest. They are equivalent to the yaml tables in the compressed tarball.
chargepois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized charge asymmetry versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.10 in paper.
chargemetapois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized charge asymmetry versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.12 in paper.
polpois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for A4 angular coefficient versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.A5 and A6 in paper.
fixedpoi helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 13M) in the helicity fit with fixed signal cross sections, for combination of muon and electron channel. Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 32k) for nuisance parameters, for combination of muon and electron channel.
pmaskedexpnorm helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized normalized cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.9 in paper.
sumpoisnorm helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized normalized cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.11 in paper.
sumpois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized absolute cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.13 in paper
pmaskedexp helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized absolute cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.A1 in paper.
chargepois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for double differential charge asymmetry versus lepton $\|\eta\|$ - $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.15 in paper.
ratiometapois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 8.2M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 27k) for ratio ( $W^{+}$ / $W{-}$ ) of total fiducial cross sections, for combination of muon and electron channel. The relevant POIs are shown in Fig.19 in paper.
pmaskedexp 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 22M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 39k) for absolute double differential cross section versus lepton $\|\eta\|$ - $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.A17 in paper.
chargemetapois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 8.7M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for single differential charge asymmetry versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.18 and A20 in paper.
sumpoisnorm 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 9.4M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 29k) for normalized single differential cross section versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.A19 and A21 in paper.
sumpois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 9.3M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 29k) for absolute single differential cross section versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , and total fiducial cross section ( $\mathrm{W}^{+}$ , $\mathrm{W}^{-}$ , and charge inclusive), for combination of muon and electron channel. The relevant POIs are shown in Figs.17, 19, and A18 in paper.

Compressed tarball (202M) including covariance matrices among parameters of interest (POIs) and nuisance parameters (NPs) in yaml format. The lists of postfit values and uncertainties for POIs and NPs are also included for each matrix. Note that for each of the 3 fits detailed in the paper (double-differential cross section, helicity with floating POIs, and helicity with fixed POIs), the postfit values of NPs and their mutual correlations do not change across different tables.
License cc-by-4.0. The content of this file can be shared and adapted but you must give appropriate credit and cannot restrict access to others.
The list of tables is available in yaml format. The convention adopted to name POIs and NPs in the tables is reported in a glossary of parameters of interest and nuisance parameters.
Below are root files containing the covariance matrices and postfit values for nuisance parameters and parameters of interest. They are equivalent to the yaml tables in the compressed tarball.
chargepois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized charge asymmetry versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.10 in paper.
chargemetapois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized charge asymmetry versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.12 in paper.
polpois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for A4 angular coefficient versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.A5 and A6 in paper.
fixedpoi helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 13M) in the helicity fit with fixed signal cross sections, for combination of muon and electron channel. Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 32k) for nuisance parameters, for combination of muon and electron channel.
pmaskedexpnorm helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized normalized cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.9 in paper.
sumpoisnorm helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized normalized cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.11 in paper.
sumpois helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for unpolarized absolute cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.13 in paper
pmaskedexp helicity Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for polarized absolute cross section versus $\|y_{\mathrm{W}}\|$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.A1 in paper.
chargepois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 14M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for double differential charge asymmetry versus lepton $\|\eta\|$ - $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.15 in paper.
ratiometapois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 8.2M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 27k) for ratio ( $W^{+}$ / $W{-}$ ) of total fiducial cross sections, for combination of muon and electron channel. The relevant POIs are shown in Fig.19 in paper.
pmaskedexp 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 22M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 39k) for absolute double differential cross section versus lepton $\|\eta\|$ - $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Fig.A17 in paper.
chargemetapois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 8.7M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 33k) for single differential charge asymmetry versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.18 and A20 in paper.
sumpoisnorm 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 9.4M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 29k) for normalized single differential cross section versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , for combination of muon and electron channel. The relevant POIs are shown in Figs.A19 and A21 in paper.
sumpois 2dxsec Covariance matrix among parameters of interest and nuisance parameters (root file, 9.3M) Postfit values and uncertainties for parameters of interest and nuisance parameters (root file, 29k) for absolute single differential cross section versus lepton $\|\eta\|$ or $p_{\mathrm{T}}$ , and total fiducial cross section ( $\mathrm{W}^{+}$ , $\mathrm{W}^{-}$ , and charge inclusive), for combination of muon and electron channel. The relevant POIs are shown in Figs.17, 19, and A18 in paper.

References
1	S. L. Glashow	Partial symmetries of weak interactions	NP 22 (1961) 579
2	S. Weinberg	A model of leptons	PRL 19 (1967) 1264
3	A. Salam and J. C. Ward	Electromagnetic and weak interactions	PL13 (1964) 168
4	J. D. Bjorken and E. A. Paschos	Inelastic electron-proton and ${\gamma}$ -proton scattering and the structure of the nucleon	PR185 (1969) 1975
5	ATLAS Collaboration	Measurement of the W-boson mass in pp collisions at $\sqrt{s}=$ 7 TeV with the ATLAS detector	EPJC 78 (2018) 110	1701.07240
6	W. J. Stirling and A. D. Martin	Parton distribution uncertainty in the measurement of M $_\mathrm{W}$ in proton - anti-proton collisions	PLB 237 (1990) 551
7	ATLAS Collaboration	Measurement of the Drell-Yan triple-differential cross section in pp collisions at $\sqrt{s} =$ 8 TeV	JHEP 12 (2017) 059	1710.05167
8	CMS Collaboration	Measurement of the weak mixing angle using the forward-backward asymmetry of Drell-Yan events in pp collisions at 8 TeV	EPJC 78 (2018) 701	CMS-SMP-16-007 1806.00863
9	CMS Collaboration	Measurement of the differential Drell-Yan cross section in proton-proton collisions at $\sqrt{\mathrm{s}} =$ 13 TeV	JHEP 12 (2019) 059	CMS-SMP-17-001 1812.10529
10	CDF Collaboration	Direct measurement of the W production charge asymmetry in $\mathrm{p}\bar{\mathrm{p}}$ collisions at $\sqrt{s} =$ 1.96 TeV	PRL 102 (2009) 181801	0901.2169
11	D0 Collaboration	Measurement of the muon charge asymmetry in $\mathrm{p}\bar{\mathrm{p}} \to$ W+X $\to \mu \nu$ + X events at $\sqrt{s} =$ 1.96 TeV	PRD 88 (2013) 091102	1309.2591
12	ATLAS Collaboration	Precision measurement and interpretation of inclusive W $^+$ , W $^-$ and $\mathrm{Z}/\gamma ^*$ production cross sections with the ATLAS detector	EPJC 77 (2017) 367	1612.03016
13	ATLAS Collaboration	Measurement of the cross-section and charge asymmetry of W bosons produced in proton-proton collisions at $\sqrt{s}=$ 8 TeV with the ATLAS detector	EPJC 79 (2019) 760	1904.05631
14	CMS Collaboration	Measurement of the electron charge asymmetry in inclusive W production in pp collisions at $\sqrt{s}=$ 7 TeV	PRL 109 (2012) 111806	CMS-SMP-12-001 1206.2598
15	CMS Collaboration	Measurement of the muon charge asymmetry in inclusive pp $\to$ W+X production at $\sqrt s =$ 7 TeV and an improved determination of light parton distribution functions	PRD 90 (2014) 032004	CMS-SMP-12-021 1312.6283
16	CMS Collaboration	Measurement of the differential cross section and charge asymmetry for inclusive $\mathrm {p}\mathrm {p}\rightarrow \mathrm {W}^{\pm}+\mathrm{X}$ production at ${\sqrt{s}} =$ 8 TeV	EPJC 76 (2016) 469	CMS-SMP-14-022 1603.01803
17	LHCb Collaboration	Inclusive W and Z production in the forward region at $\sqrt{s} =$ 7 TeV	JHEP 06 (2012) 058	1204.1620
18	LHCb Collaboration	Measurement of forward W and Z boson production in pp collisions at $\sqrt{s}=$ 8 TeV	JHEP 01 (2016) 155	1511.08039
19	CMS Collaboration	Measurement of associated production of a W boson and a charm quark in proton-proton collisions at $\sqrt{s} =$ 13 TeV	EPJC 79 (2019) 269	CMS-SMP-17-014 1811.10021
20	ATLAS Collaboration	Measurement of the production of a W boson in association with a charm quark in pp collisions at $\sqrt{s} =$ 7 TeV with the ATLAS detector	JHEP 05 (2014) 068	1402.6263
21	LHCb Collaboration	Study of W boson production in association with beauty and charm	PRD 92 (2015) 052001	1505.04051
22	CDF Collaboration	Observation of the production of a W boson in association with a single charm quark	PRL 110 (2013) 071801	1209.1921
23	D0 Collaboration	Measurement of the ratio of the $\mathrm{p} \bar{\mathrm{p}} \to \mathrm{W}^+ \mathrm{c}^-$ jet cross section to the inclusive $\mathrm{p} \bar{\mathrm{p}} \to \mathrm{W} +$ jets cross section	PLB 666 (2008) 23	0803.2259
24	E. Manca, O. Cerri, N. Foppiani, and G. Rolandi	About the rapidity and helicity distributions of the W bosons produced at LHC	JHEP 12 (2017) 130	1707.09344
25	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
26	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
27	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
28	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
29	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
30	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
31	T. Sjostrand et al.	An introduction to PYTHIA 8.2	CPC 191 (2015) 159	1410.3012
32	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
33	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
34	CMS Collaboration	Measurements of differential Z boson production cross sections in proton-proton collisions at $\sqrt{s} =$ 13 TeV	JHEP 12 (2019) 061	CMS-SMP-17-010 1909.04133
35	GEANT4 Collaboration	GEANT4 -- a simulation toolkit	NIMA 506 (2003) 250
36	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
37	CMS Collaboration	Muon identification and isolation efficiency on full 2016 dataset	CDS
38	CMS Collaboration	Energy calibration and resolution of the CMS electromagnetic calorimeter in pp collisions at $\sqrt{s} =$ 7 TeV	JINST 8 (2013) P09009	CMS-EGM-11-001 1306.2016
39	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $\sqrt{s} =$ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
40	CMS Collaboration	Electron and photon performance in CMS with the full 2017 data sample and additional 2016 highlights for the CALOR 2018 conference	CDS
41	CMS Collaboration	Performance of missing transverse momentum reconstruction in proton-proton collisions at $\sqrt{s} =$ 13 TeV using the CMS detector	JINST 14 (2019) P07004	CMS-JME-17-001 1903.06078
42	CMS Collaboration	Measurements of inclusive W and Z cross sections in pp collisions at $\sqrt{s}=$ 7 TeV	JHEP 01 (2011) 080	CMS-EWK-10-002 1012.2466
43	Bern, Z. and Diana, G. and Dixon, L. J. and Cordero, F. Febres and Forde, D. and Gleisberg, T. and Hoche, S. and Ita, H. and Kosower, D. A. and Maître, D. and Ozeren, K.	Left-handed W bosons at the LHC	PRD 84 (2011) 034008	1103.5445
44	J. C. Collins and D. E. Soper	Angular distribution of dileptons in high-energy hadron collisions	PRD 16 (1977) 2219
45	R. K. Ellis, W. J. Stirling, and B. R. Webber	QCD and collider physics	Camb. Monogr. Part. Phys. NP Cosmol. 8 (1996) 1
46	M. Abadi et al.	TensorFlow: Large-scale machine learning on heterogeneous systems	2015 Software available from tensorflow.org. \url https://www.tensorflow.org/
47	ATLAS, CMS, LHC Higgs Combination Group Collaboration	Procedure for the LHC Higgs boson search combination in summer 2011	technical report, CERN
48	A. Bodek et al.	Extracting muon momentum scale corrections for hadron collider experiments	EPJC 72 (2012) 2194	1208.3710
49	B. Efron	Bootstrap methods: Another look at the jackknife	Ann. Statist. 7 (1979) 1
50	S. Carrazza et al.	An unbiased Hessian representation for Monte Carlo PDFs	EPJC 75 (2015) 369	1505.06736
51	M. J. Oreglia	A study of the reactions $\psi' \to \gamma\gamma \psi$	PhD thesis, Stanford University, 1980 SLAC Report SLAC-R-236, see Appendix D
52	J. Gaiser	Charmonium Spectroscopy From Radiative Decays of the $\mathrm{J}/\psi$	PhD thesis, SLAC
53	CMS Collaboration	Measurement of the lepton charge asymmetry in inclusive W production in pp collisions at $\sqrt{s} =$ 7 TeV	JHEP 04 (2011) 050	CMS-EWK-10-006 1103.3470
54	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
55	P. Golonka and Z. Was	PHOTOS Monte Carlo: a precision tool for QED corrections in Z and W decays	EPJC 45 (2006) 97	hep-ph/0506026
56	R. J. Barlow and C. Beeston	Fitting using finite Monte Carlo samples	CPC 77 (1993) 219
57	NNPDF Collaboration	A first determination of parton distributions with theoretical uncertainties	EPJC 79 (2019) 838	1905.04311
58	NNPDF Collaboration	Parton distributions with theory uncertainties: general formalism and first phenomenological studies	EPJC 79 (2019) 931	1906.10698
59	R. Gavin, Y. Li, F. Petriello, and S. Quackenbush	FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order	CPC 182 (2011) 2388	1011.3540
60	Tie-Jiun Hou and Jun Gao and T. J. Hobbs and Keping Xie and Sayipjamal Dulat and Marco Guzzi and Joey Huston and Pavel Nadolsky and Jon Pumplin and Carl Schmidt and Ibrahim Sitiwaldi and Daniel Stump and C. P. Yuan	New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC		1912.10053