

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-17-031 | ||
| Combined measurements of the Higgs boson's couplings at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| March 2018 | ||
| Abstract: Combined measurements of the Higgs boson's production and decay rates, as well its couplings to vector bosons and fermions, are presented. The analysis uses the LHC proton-proton collision data set recorded by the CMS detector in 2016 at $\sqrt{s}= $ 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. The combination is based on the analysis of the production processes gluon fusion, vector boson fusion, and associated production with a W or Z boson or a pair of top quarks, and of the H$\to$ZZ, WW, $\gamma\gamma$, $\tau\tau$, bb, and $\mu\mu$ decay modes. Dedicated searches for invisible Higgs boson decays are also considered. The combined signal strength is measured as $\mu= $ 1.17$^{+0.10}_{-0.10}$. The Higgs boson production and decay rates are combined within the context of two generic parameterizations: one based on the ratios of cross sections and branching ratios, and the other based on the ratios of coupling modifiers. Several interpretations of the results, with more model-dependent parameterizations derived from the generic ones, are also given. The results are compatible with the standard model predictions in all of the parameterizations considered. The results are used to place constraints on the parameter spaces of various two Higgs doublet models. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, EPJC 79 (2019) 421. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
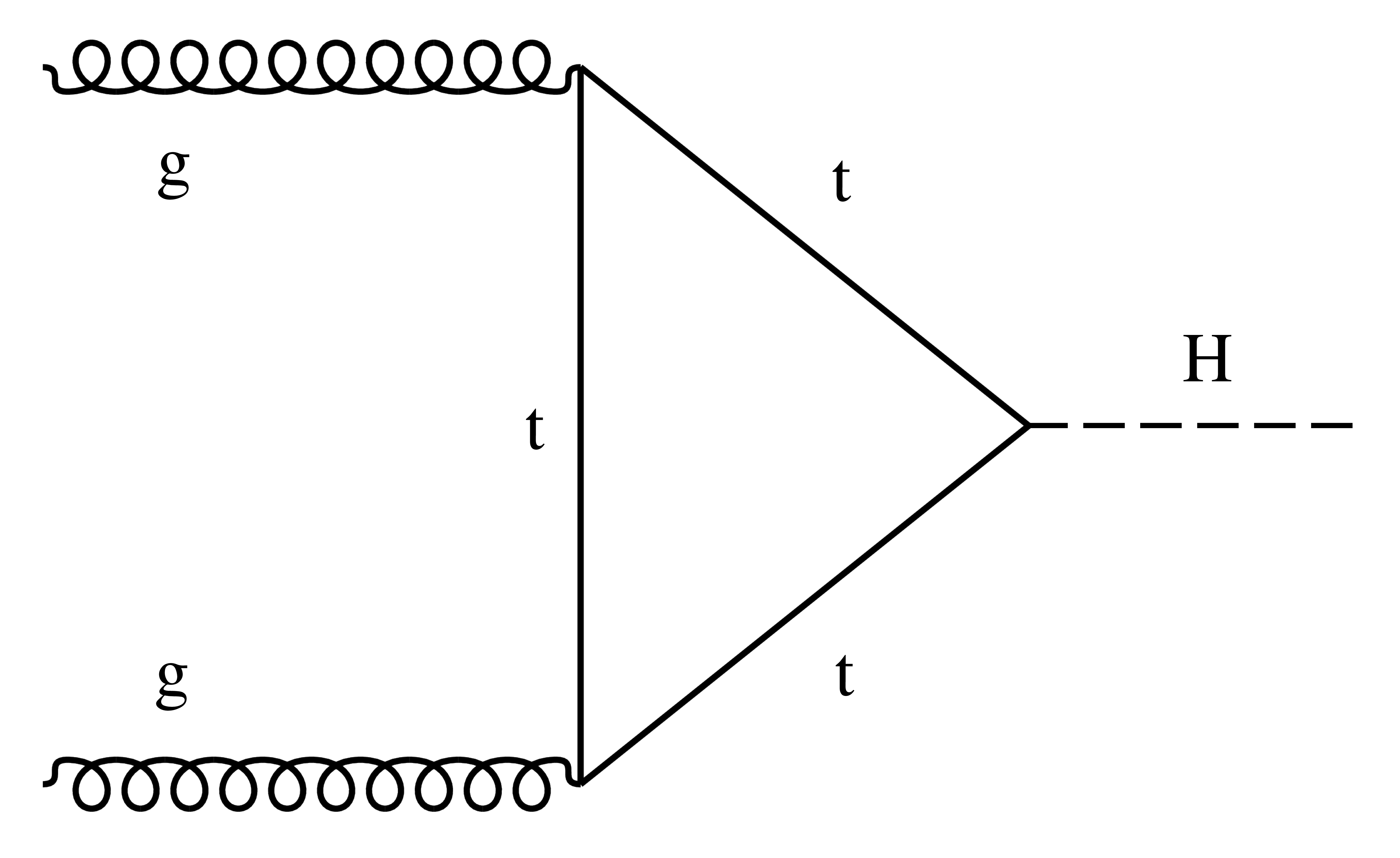
Figure 1:
Examples of leading order Feynman diagrams for the (a) ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}}$, (b) ${\mathrm {VBF}}$, (c) ${\mathrm {V} {\mathrm {H}}}$, and (d) ${{\mathrm {t}} {\mathrm {t}} {\mathrm {H}}}$ production modes. |
png pdf |
Figure 1-a:
Example of leading order Feynman diagram for the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}}$ production mode. |
png pdf |
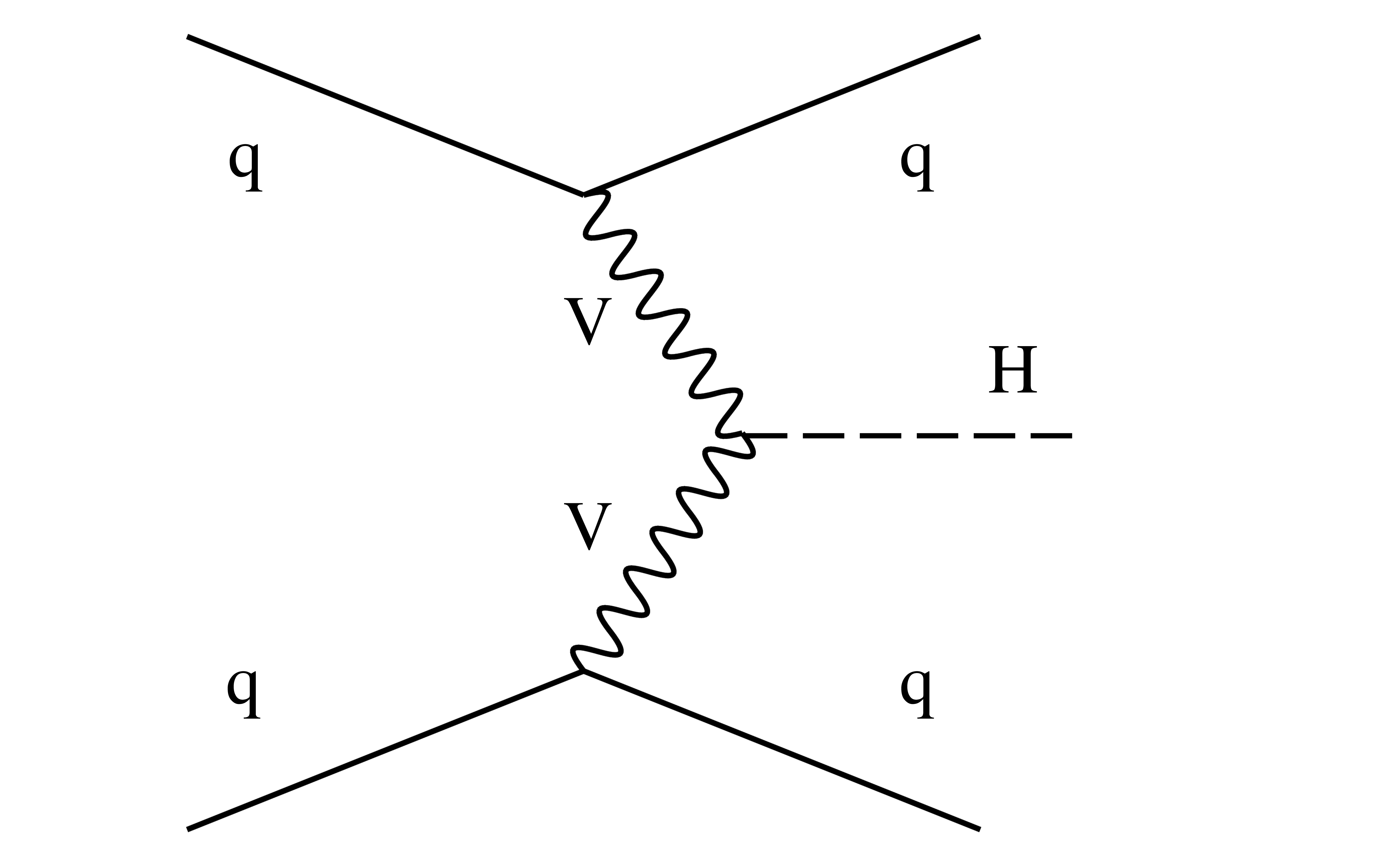
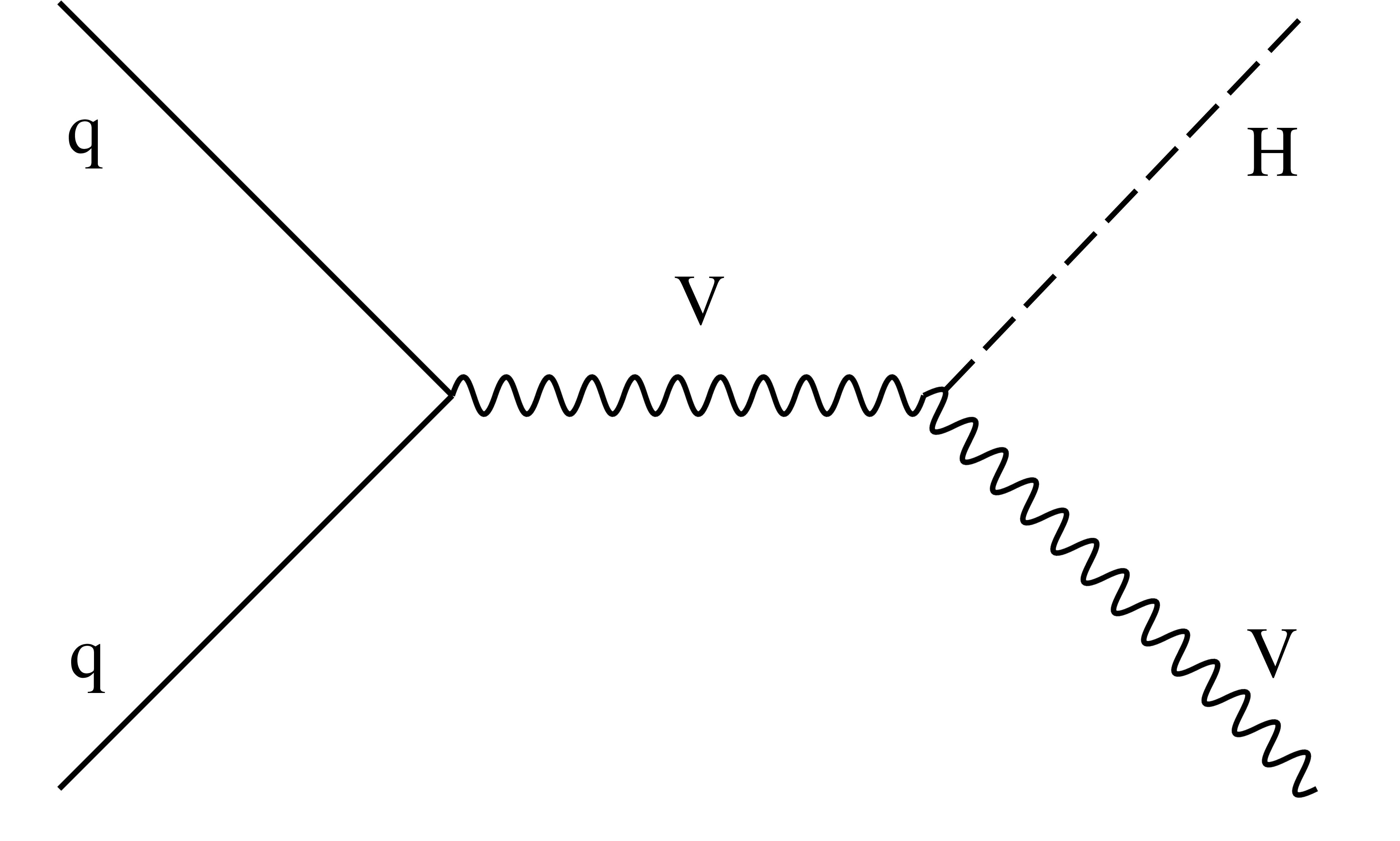
Figure 1-b:
Example of leading order Feynman diagram for the ${\mathrm {VBF}}$, (c) ${\mathrm {V} {\mathrm {H}}}$ production mode. |
png pdf |
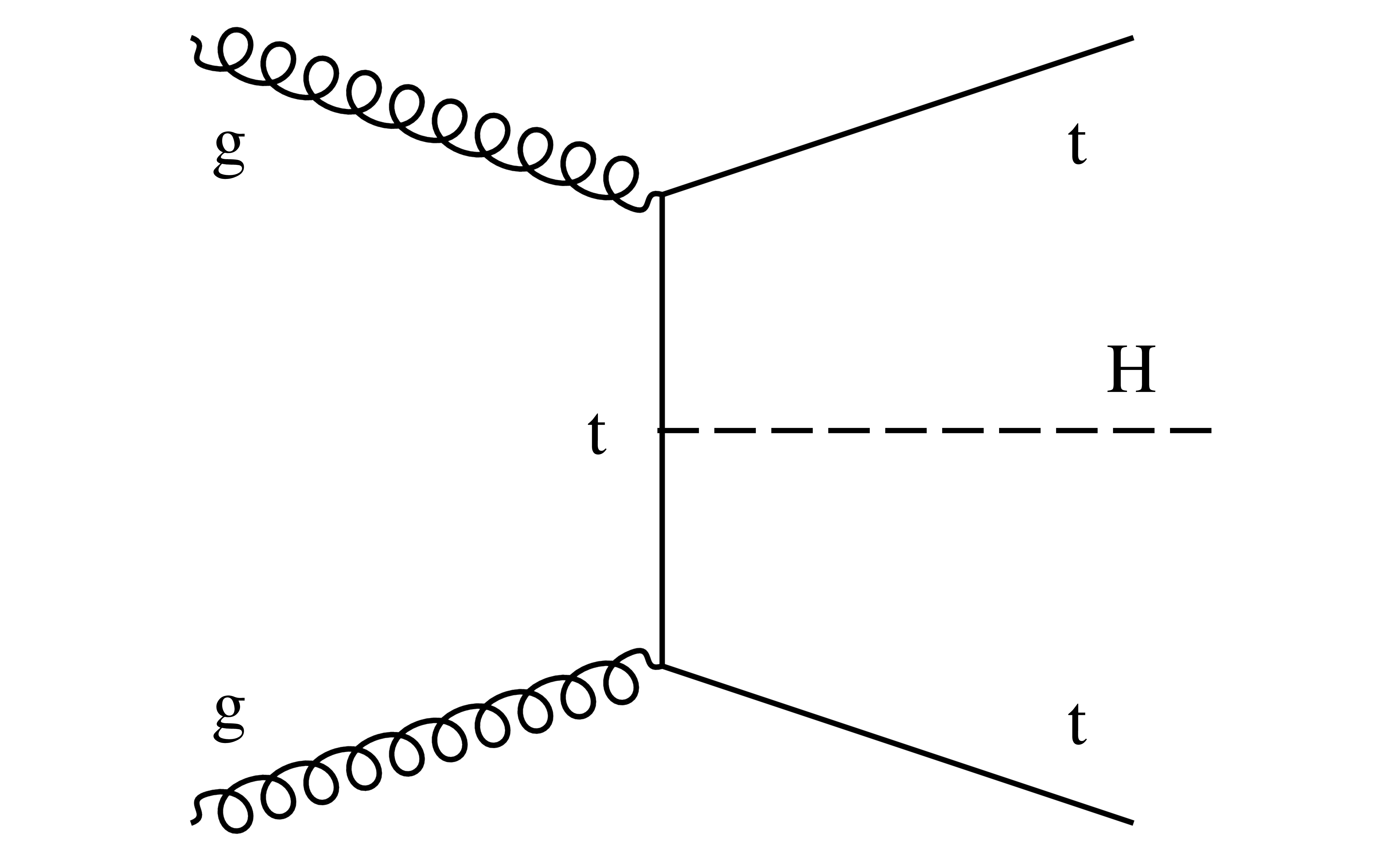
Figure 1-c:
Example of leading order Feynman diagram for the ${{\mathrm {t}} {\mathrm {t}} {\mathrm {H}}}$ production mode. |
png pdf |
Figure 1-d:
Examples of leading order Feynman diagrams for the (a) ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}}$, (b) ${\mathrm {VBF}}$, (c) ${\mathrm {V} {\mathrm {H}}}$, and (d) ${{\mathrm {t}} {\mathrm {t}} {\mathrm {H}}}$ production modes. |
png pdf |
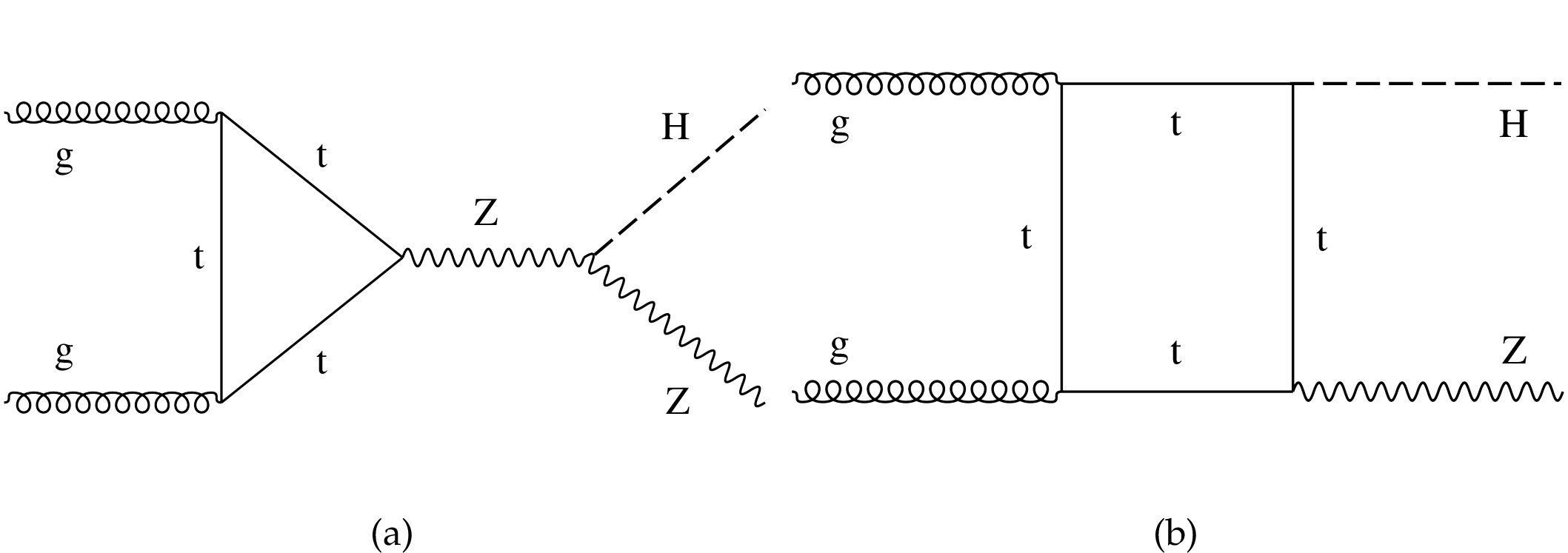
Figure 2:
Examples of leading order Feynman diagrams for the $\text {gg}\to {{\mathrm {Z}} {\mathrm {H}}} $ production mode. |
png pdf |
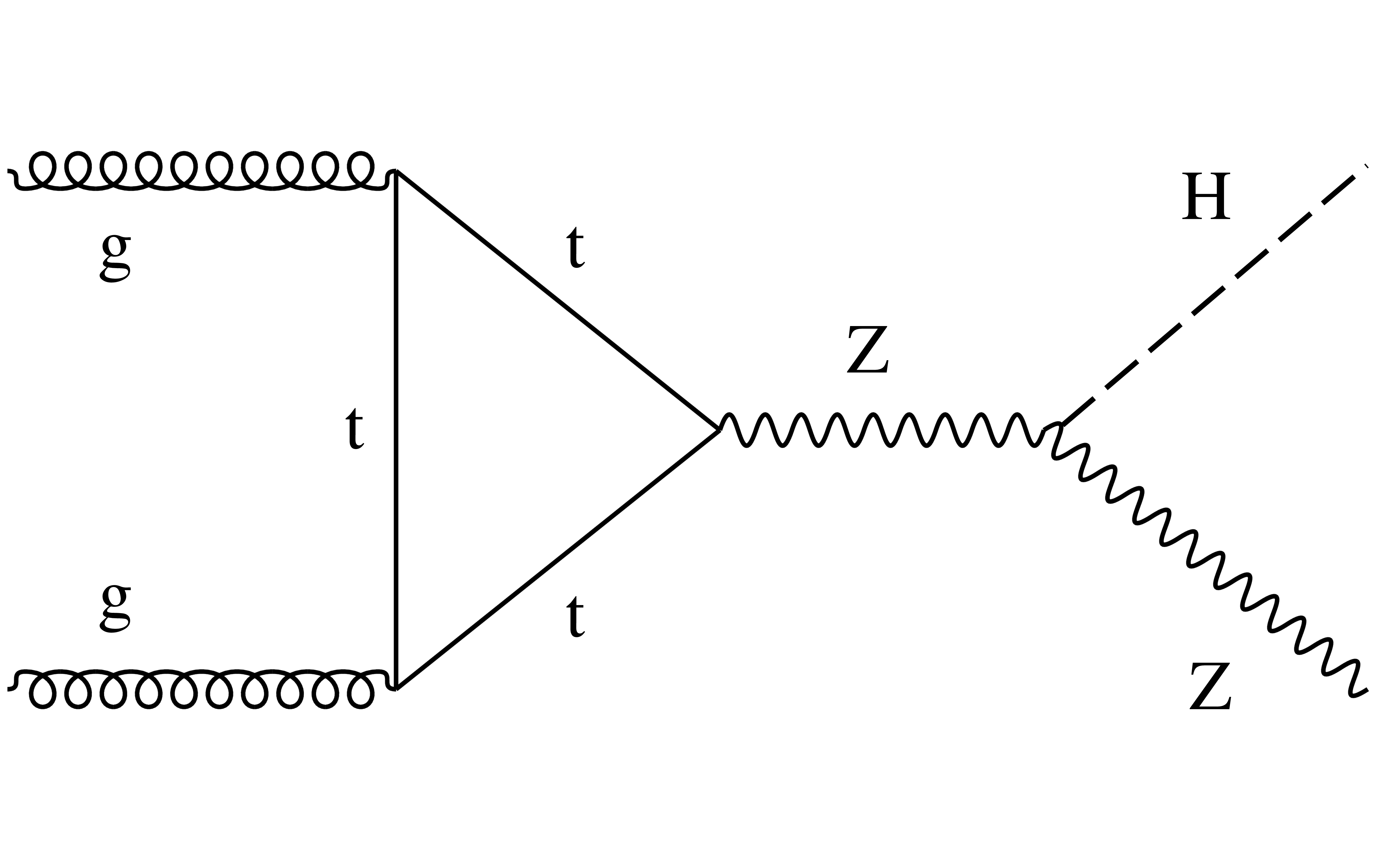
Figure 2-a:
Example of leading order Feynman diagram for the $\text {gg}\to {{\mathrm {Z}} {\mathrm {H}}} $ production mode. |

png pdf |
Figure 2-b:
Example of leading order Feynman diagram for the $\text {gg}\to {{\mathrm {Z}} {\mathrm {H}}} $ production mode. |
png pdf |
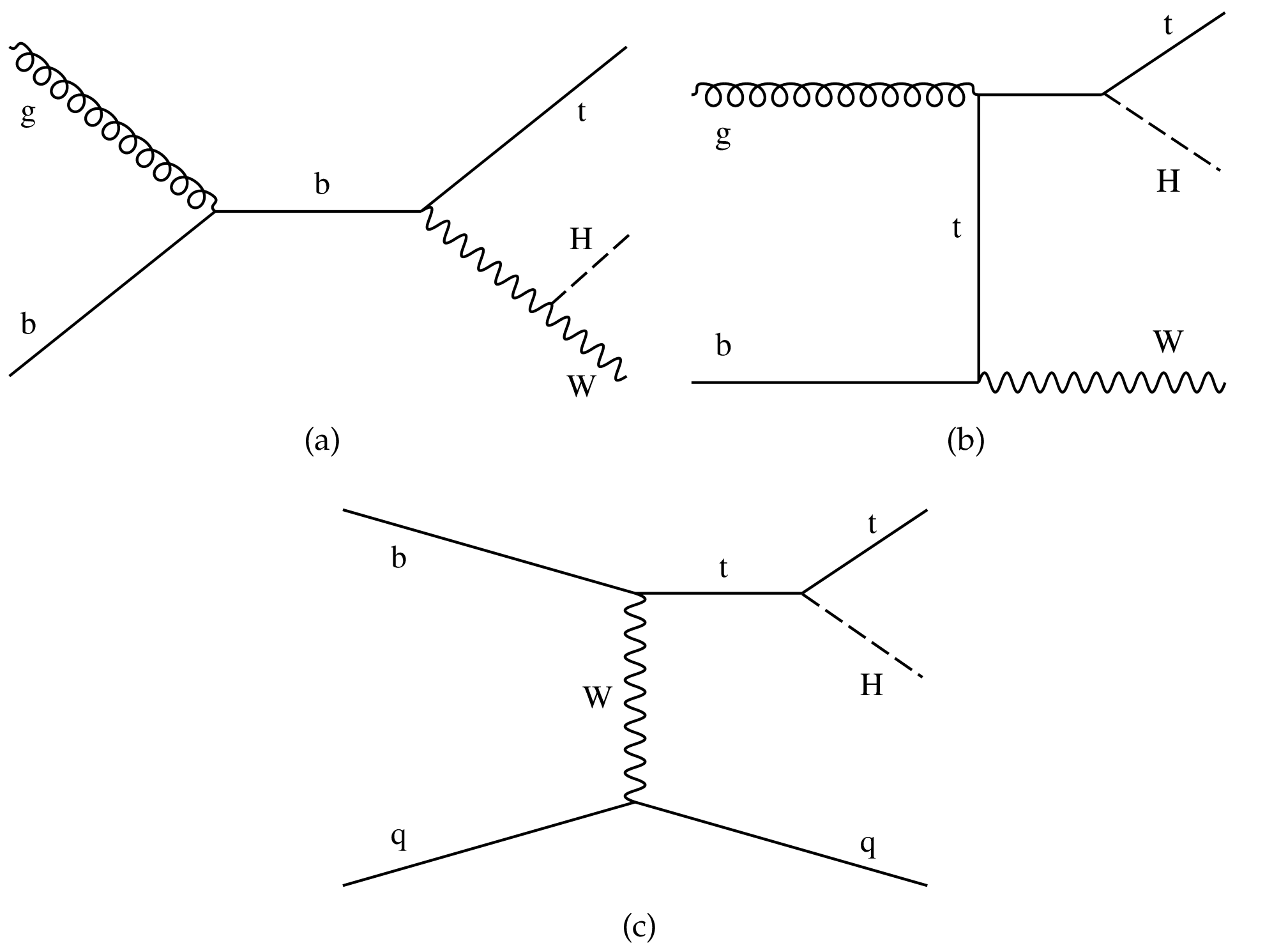
Figure 3:
Examples of leading order Feynman diagrams for ${{\mathrm {t}} {\mathrm {H}}}$ production via the (a,b) ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ and (c) ${{\mathrm {t}} {\mathrm {H}} \mathrm{q}}$ modes. |
png pdf |
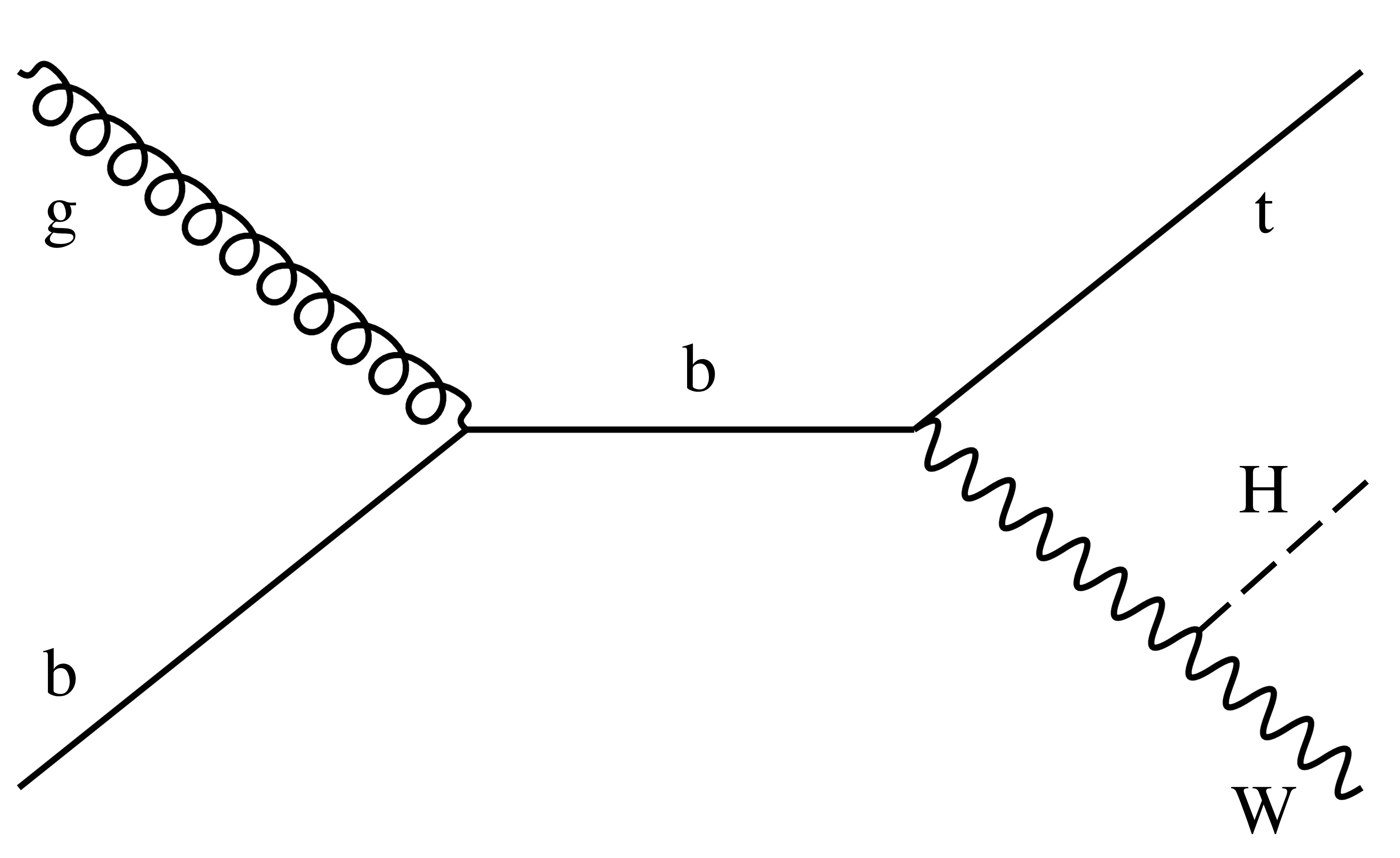
Figure 3-a:
Example of leading order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ mode. |
png pdf |
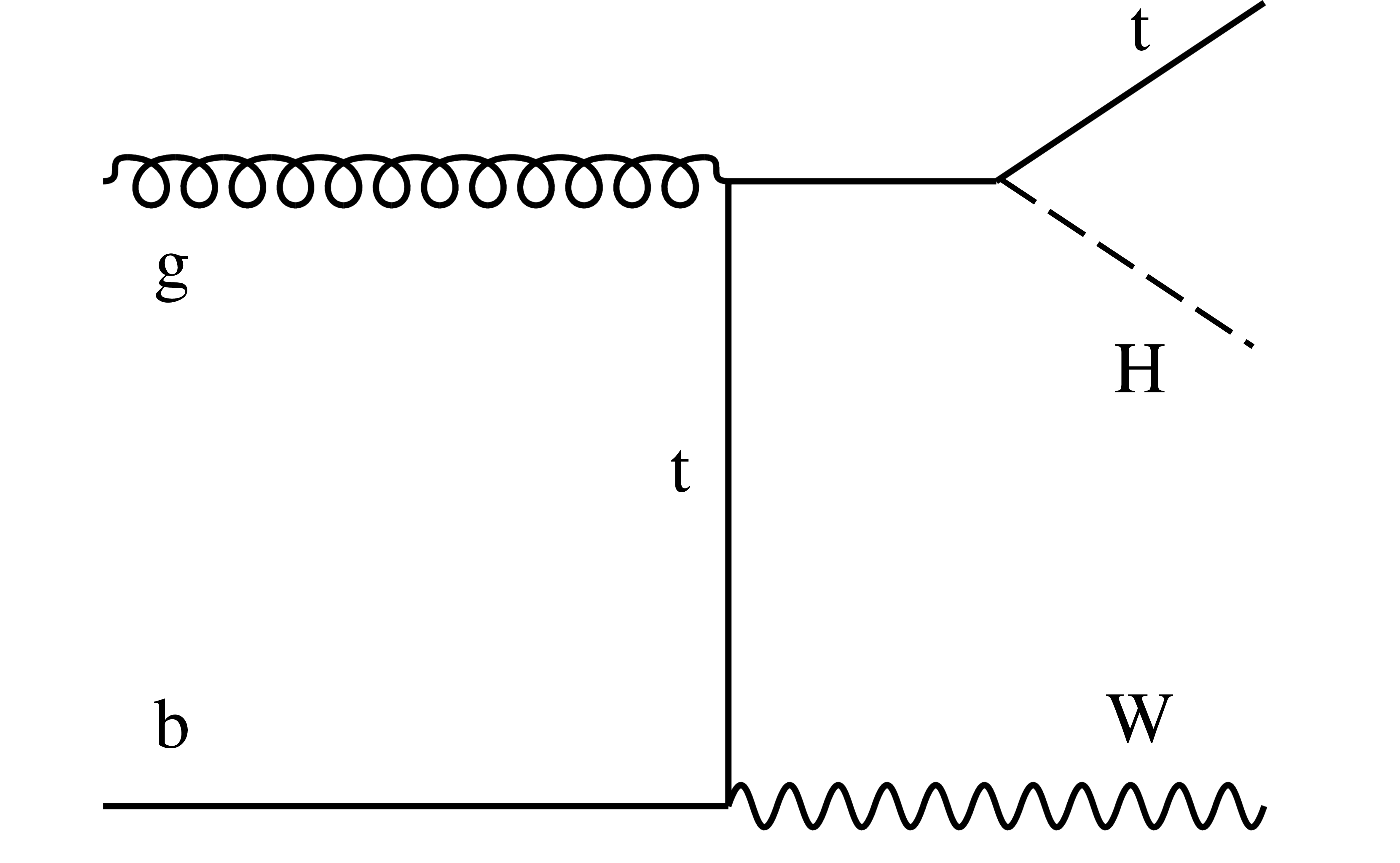
Figure 3-b:
Example of leading order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} {\mathrm {W}}}$ mode. |
png pdf |
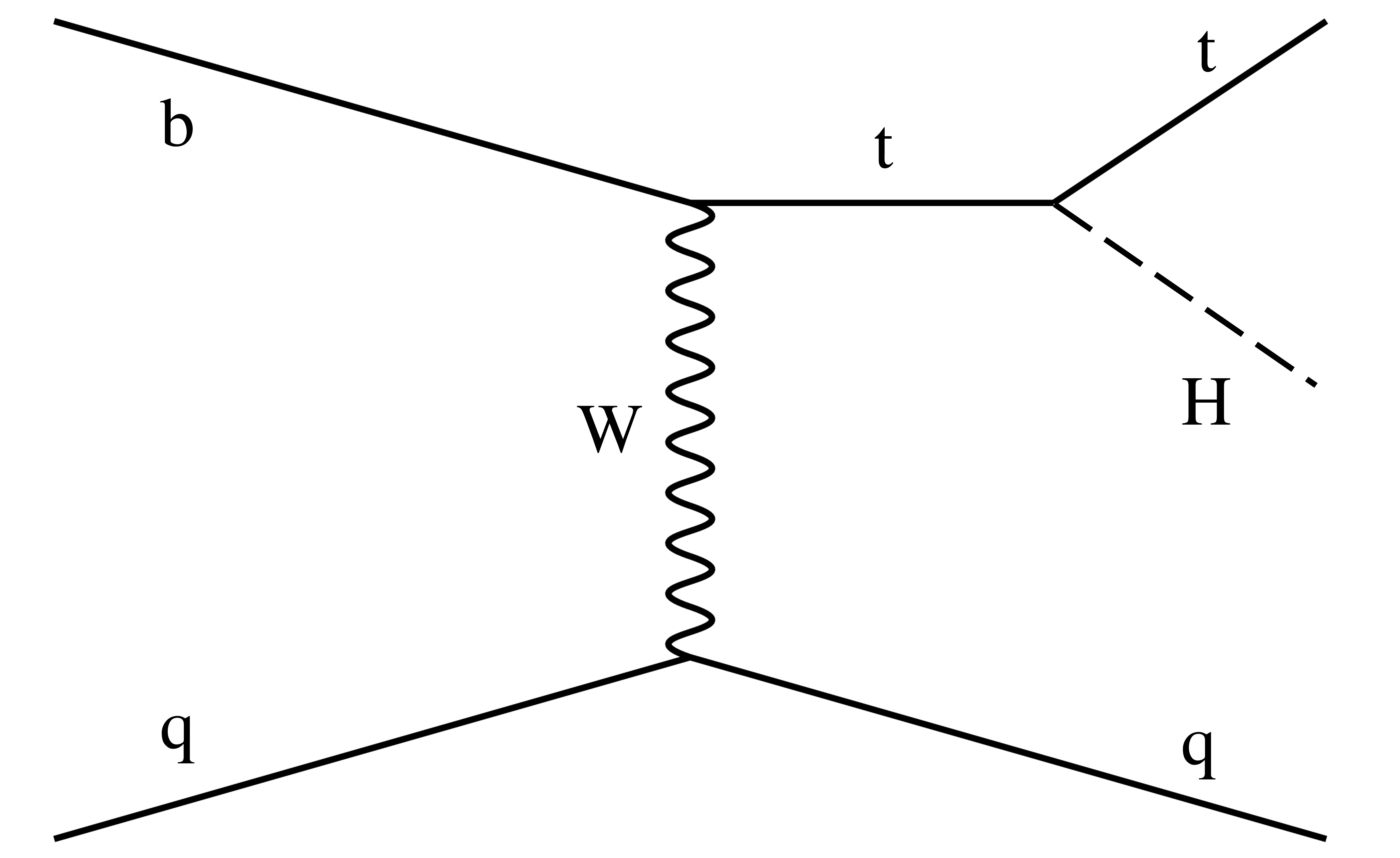
Figure 3-c:
Example of leading order Feynman diagram for ${{\mathrm {t}} {\mathrm {H}}}$ production via the ${{\mathrm {t}} {\mathrm {H}} \mathrm{q}}$ mode. |

png pdf |
Figure 4:
Examples of leading order Feynman diagrams for Higgs boson decay in the (a) bb, $\tau \tau$ and $\mu \mu$, (b) ZZ and WW, (c,d) $\gamma \gamma $ channels. |

png pdf |
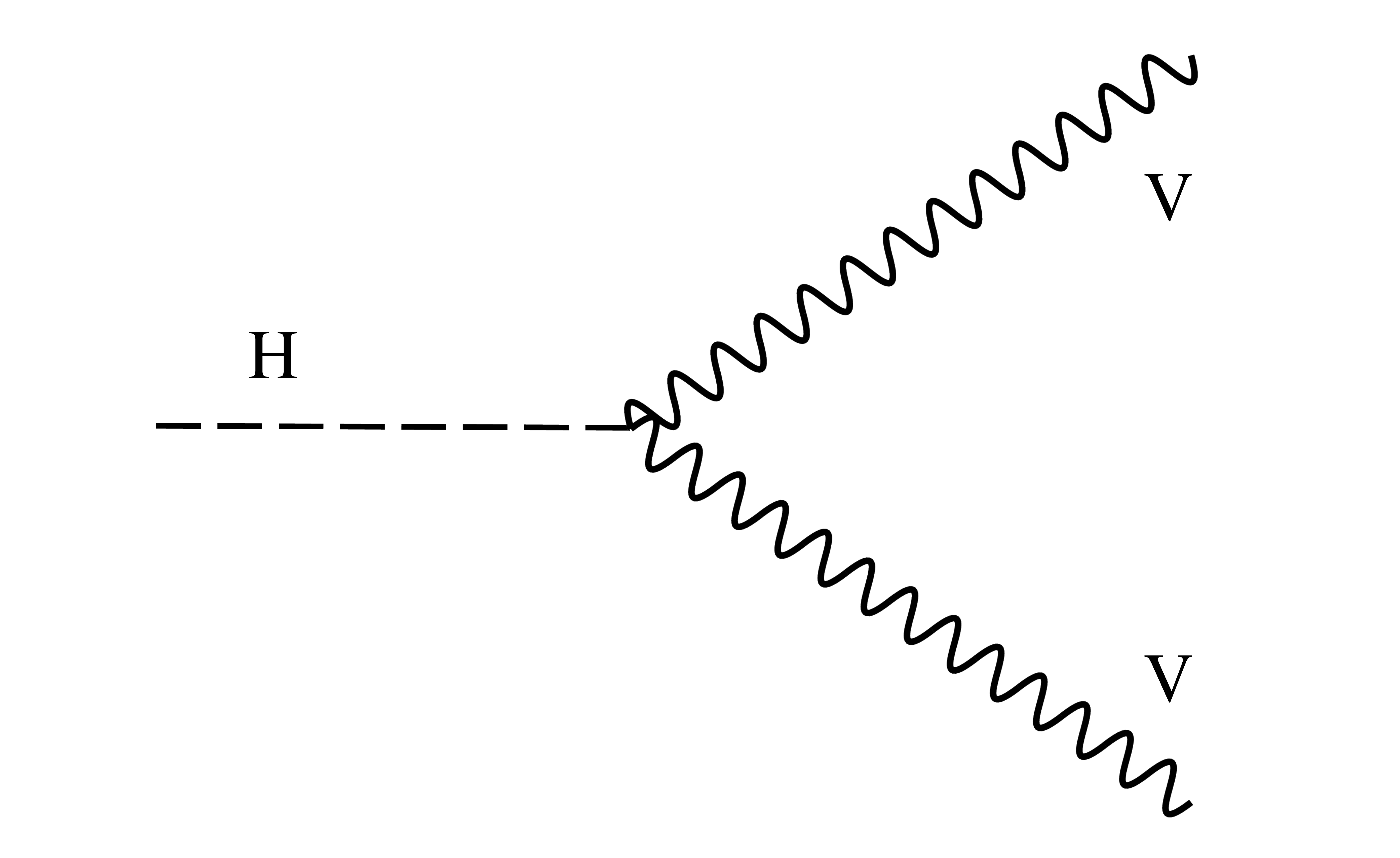
Figure 4-a:
Example of leading order Feynman diagram for Higgs boson decay in the bb, $\tau \tau$ and $\mu \mu$ channels. |
png pdf |
Figure 4-b:
Example of leading order Feynman diagram for Higgs boson decay in the ZZ and WW channels. |

png pdf |
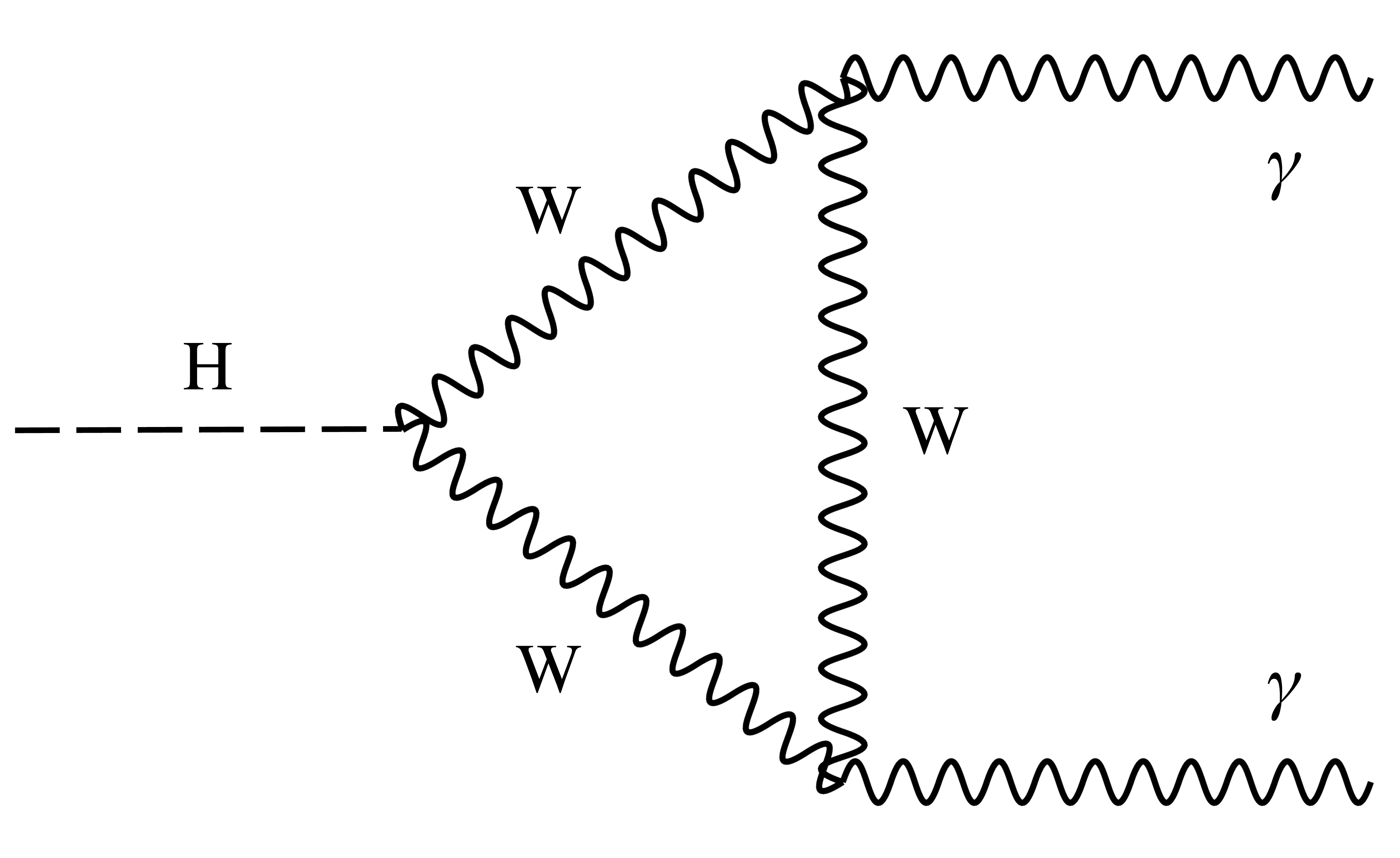
Figure 4-c:
Example of leading order Feynman diagram for Higgs boson decay in the $\gamma \gamma $ channel. |
png pdf |
Figure 4-d:
Example of leading order Feynman diagram for Higgs boson decay in the $\gamma \gamma $ channel. |

png pdf |
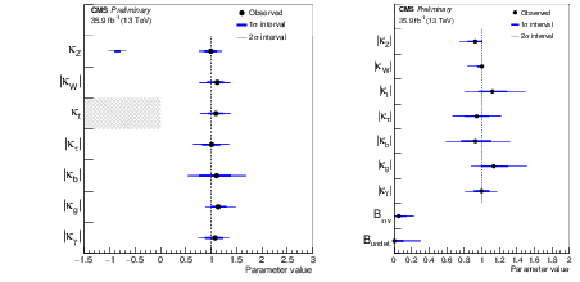
Figure 5:
Summary plot of the fit to the per-production mode (left) and per-decay mode (right) signal strength modifiers $\mu _i$. The thick and thin horizontal bars indicate the $ \pm $1$ \sigma $ and $ \pm $2$ \sigma $ uncertainties, respectively. Also shown are the $ \pm $1$ \sigma $ systematic components of the uncertainties. The last point in the per-production mode summary plot is taken from a separate fit and indicates the result of the combined overall signal strength $\mu $. |
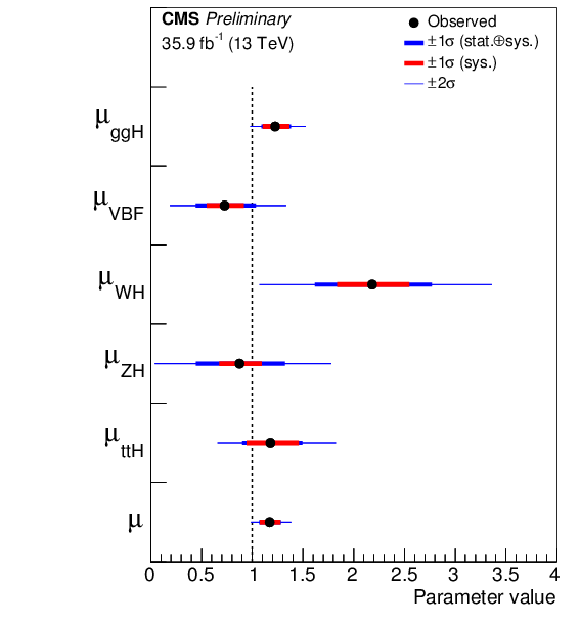
png pdf |
Figure 5-a:
Summary plot of the fit to the per-production mode signal strength modifiers $\mu _i$. The thick and thin horizontal bars indicate the $ \pm $1$ \sigma $ and $ \pm $2$ \sigma $ uncertainties, respectively. Also shown are the $ \pm $1$ \sigma $ systematic components of the uncertainties. The last point is taken from a separate fit and indicates the result of the combined overall signal strength $\mu $. |
png pdf |
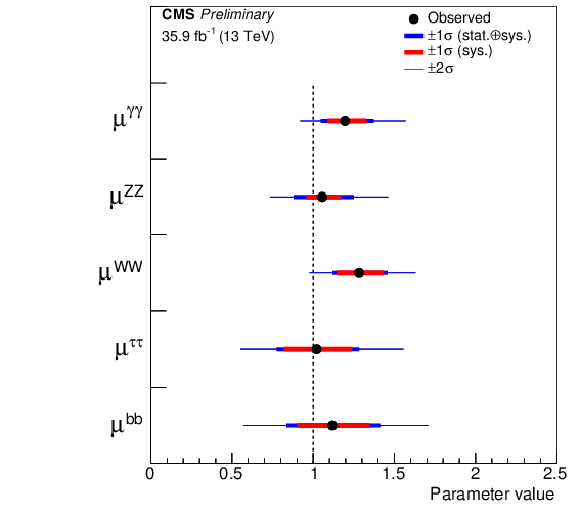
Figure 5-b:
Summary plot of the fit to the per-decay mode signal strength modifiers $\mu _i$. The thick and thin horizontal bars indicate the $ \pm $1$ \sigma $ and $ \pm $2$ \sigma $ uncertainties, respectively. Also shown are the $ \pm $1$ \sigma $ systematic components of the uncertainties. |

png pdf |
Figure 6:
Summary plot of the fit to the production-decay signal strength products $\mu _{i}^{f}=\mu _{i}\times \mu ^{f}$. The points indicate the best-fit values while the horizontal bars indicate the 1$\sigma $ CL intervals. The hatched areas indicate signal strengths which are restricted to positive values due to low background contamination. |
png pdf |
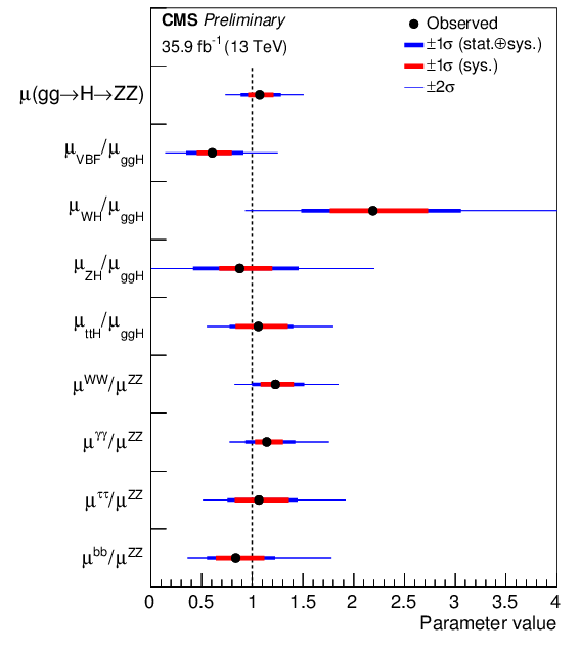
Figure 7:
Summary of the cross section and branching fraction ratio model. The thick and thin horizontal bars indicate the $ \pm $1$ \sigma $ and $ \pm $2$ \sigma $ uncertainties, respectively. Also shown are the $ \pm $1$ \sigma $ systematic components of the uncertainties. |
png pdf |
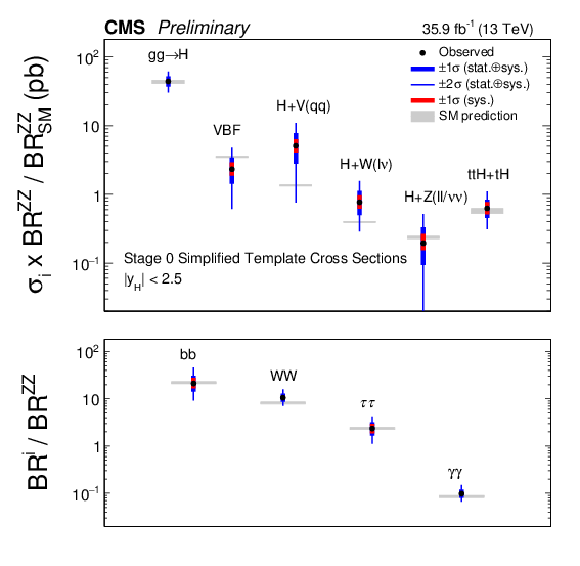
Figure 8:
Summary of the stage 0 model, ratios of cross sections and branching ratios. The points indicate the best-fit values while the error bars show the $ \pm $1$ \sigma $ and $ \pm $2$ \sigma $ uncertainties. Also shown are the $ \pm $1$ \sigma $ uncertainties on the measurements considering only the contributions from the systematic uncertainties. Also shown are the uncertainties on the SM predictions. |

png pdf |
Figure 9:
Summary of the $\kappa $-framework model with $ {\mathrm {BR_{BSM}}} = $ 0. The points indicate the best-fit values while the thick and thin horizontal bars show the 1$\sigma $ and 2$\sigma $ CL intervals, respectively. In this model, the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}} $ and ${{\mathrm {H}} \to {\gamma \gamma}} $ loops are resolved in terms of the remaining coupling modifiers. For this model, both positive and negative values of $\kappa _{{\mathrm {Z}}}$ and $\kappa _{\mathrm{b}}$ are considered while $\kappa _{{\mathrm {W}}}$ is assumed to be positive. |
png pdf |
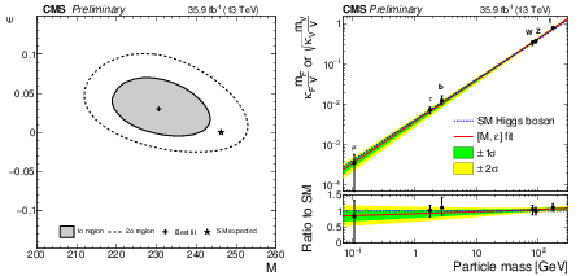
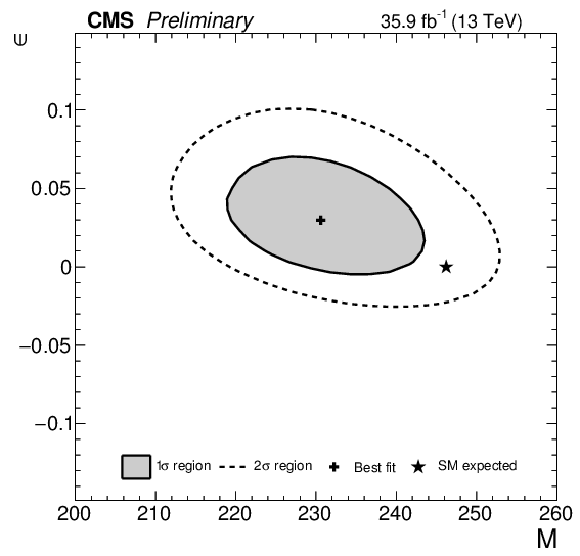
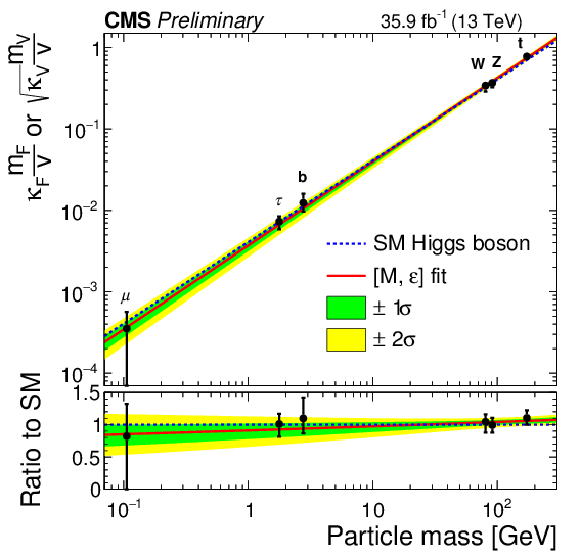
Figure 10:
Left: Likelihood scan in the $\rm{M}$-$\epsilon$ plane. The best-fit point and, 1$\sigma$, 2$\sigma$ CL regions are shown, along with the SM prediction. Right: Result of the phenomenological M, $\epsilon$ fit overlayed with the resolved $\kappa$-framework model. |
png pdf |
Figure 10-a:
Likelihood scan in the $\rm{M}$-$\epsilon$ plane. The best-fit point and, 1$\sigma$, 2$\sigma$ CL regions are shown, along with the SM prediction. |
png pdf |
Figure 10-b:
Result of the phenomenological M, $\epsilon$ fit overlayed with the resolved $\kappa$-framework model. |
png pdf |
Figure 11:
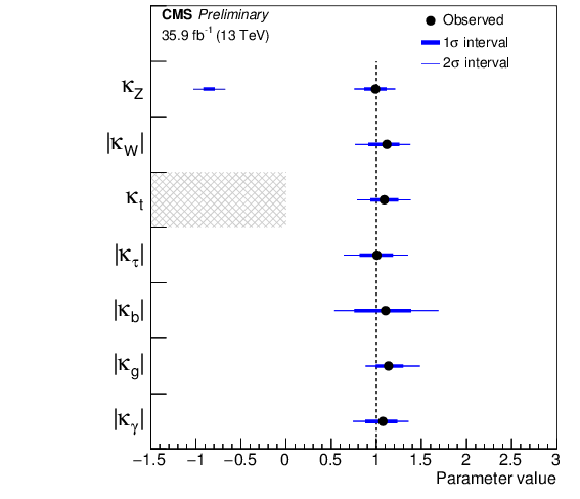
Summary plots of the $\kappa $-framework model in which the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}} $ and ${{\mathrm {H}} \to {\gamma \gamma}} $ loops are scaled with effective couplings. The points indicate the best-fit values while the thick and thin horizontal bars show the 1$\sigma $ and 2$\sigma $ CL intervals, respectively. For the summary plot on the left the constraint $ {\mathrm {BR_{BSM}}} = $ 0 is imposed, and both positive and negative values of $\kappa _{{\mathrm {Z}}}$ are considered while $\kappa _{{\mathrm {W}}}$ is assumed to be positive. For the summary plot on the right, both $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$ are assumed to be positive with the constraint $|\kappa _{{\mathrm {W}}}|, |\kappa _{{\mathrm {Z}}}|\le $ 1, while $ {\mathrm {BR_{inv.}}} > $ 0 and $ {\mathrm {BR_{undet.}}} > $ 0 are free parameters. |
png pdf |
Figure 11-a:
Summary plot of the $\kappa $-framework model in which the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}} $ and ${{\mathrm {H}} \to {\gamma \gamma}} $ loops are scaled with effective couplings. The points indicate the best-fit values while the thick and thin horizontal bars show the 1$\sigma $ and 2$\sigma $ CL intervals, respectively. The constraint $ {\mathrm {BR_{BSM}}} = $ 0 is imposed, and both positive and negative values of $\kappa _{{\mathrm {Z}}}$ are considered while $\kappa _{{\mathrm {W}}}$ is assumed to be positive. |

png pdf |
Figure 11-b:
Summary plot of the $\kappa $-framework model in which the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}} $ and ${{\mathrm {H}} \to {\gamma \gamma}} $ loops are scaled with effective couplings. The points indicate the best-fit values while the thick and thin horizontal bars show the 1$\sigma $ and 2$\sigma $ CL intervals, respectively. Both $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$ are assumed to be positive with the constraint $|\kappa _{{\mathrm {W}}}|, |\kappa _{{\mathrm {Z}}}|\le $ 1, while $ {\mathrm {BR_{inv.}}} > $ 0 and $ {\mathrm {BR_{undet.}}} > $ 0 are free parameters. |
png pdf |
Figure 12:
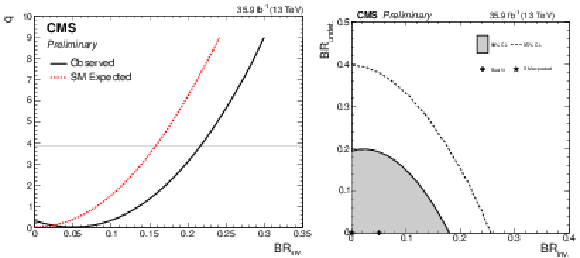
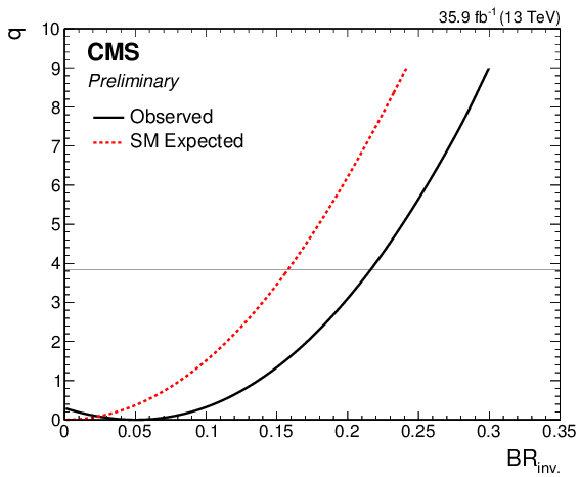
Scans of $q$ as a function of $ {\mathrm {BR_{inv.}}} $ (left), and 68% and 95% CL regions for $ {\mathrm {BR_{inv.}}} $ vs $ {\mathrm {BR_{undet.}}} $ (right), in the model where only positive values of $\kappa _{\rm V}$ (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$) are considered with the constraint $|\kappa _{{\mathrm {W}}}|, |\kappa _{{\mathrm {Z}}}|\le $ 1, and $ {\mathrm {BR_{inv.}}} > $ 0 and $ {\mathrm {BR_{undet.}}} > $ 0 are free parameters. The scan of $q$ as a function of $ {\mathrm {BR_{inv.}}} $ expected assuming the SM is also shown in the left panel. |
png pdf |
Figure 12-a:
Scans of $q$ as a function of $ {\mathrm {BR_{inv.}}} $, in the model where only positive values of $\kappa _{\rm V}$ (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$) are considered with the constraint $|\kappa _{{\mathrm {W}}}|, |\kappa _{{\mathrm {Z}}}|\le $ 1, and $ {\mathrm {BR_{inv.}}} > $ 0 and $ {\mathrm {BR_{undet.}}} > $ 0 are free parameters. The scan of $q$ as a function of $ {\mathrm {BR_{inv.}}} $ expected assuming the SM is also shown. |

png pdf |
Figure 12-b:
68% and 95% CL regions for $ {\mathrm {BR_{inv.}}} $ vs $ {\mathrm {BR_{undet.}}} $, in the model where only positive values of $\kappa _{\rm V}$ (same sign of $\kappa _{{\mathrm {W}}}$ and $\kappa _{{\mathrm {Z}}}$) are considered with the constraint $|\kappa _{{\mathrm {W}}}|, |\kappa _{{\mathrm {Z}}}|\le $ 1, and $ {\mathrm {BR_{inv.}}} > $ 0 and $ {\mathrm {BR_{undet.}}} > $ 0 are free parameters. |
png pdf |
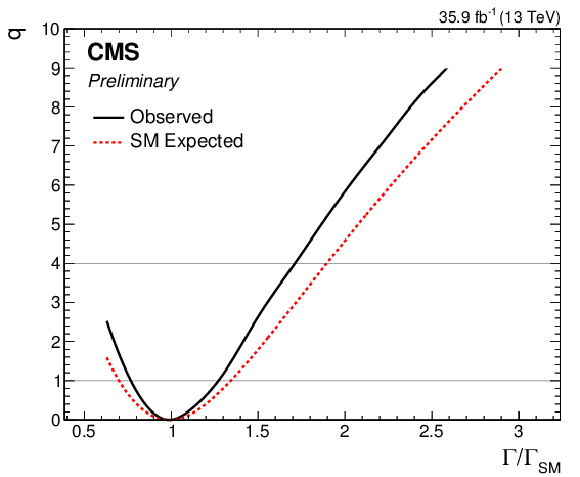
Figure 13:
Scans of $q$ as a function of $\Gamma _{\rm {H}}/\Gamma _{\rm {H}}^{\rm {SM}}$ obtained by reinterpreting the model allowing for BSM decays of the Higgs boson. |
png pdf |
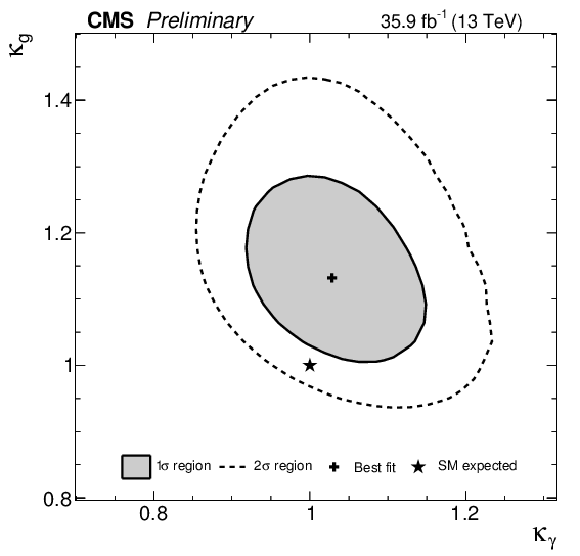
Figure 14:
The 1$\sigma $ and 2$\sigma $ CL regions in the $\kappa _{g}$ vs $\kappa _{\gamma}$ parameter space for the model assuming the only BSM contributions to the Higgs boson couplings appear in the loop-induced processes or in BSM Higgs decays. |
png pdf |
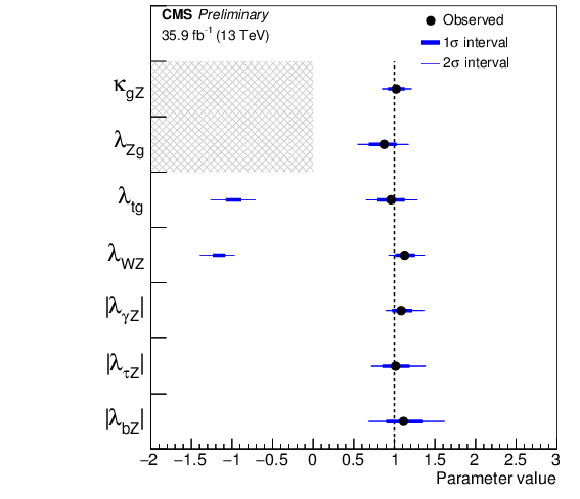
Figure 15:
Summary of the model with coupling ratios and effective couplings for the ${{\mathrm {g}} {\mathrm {g}} {\mathrm {H}}}$ and ${{\mathrm {H}} \to {\gamma \gamma}}$ loops. The points indicate the best-fit values while the thick and thin horizontal bars show the 1$\sigma $ and 2$\sigma $ CL intervals, respectively. For this model, both positive and negative values of $\lambda _{\rm {WZ}}$ and $\lambda _{\mathrm{t} {\mathrm {g}}}$ are considered. |

png pdf |
Figure 16:
The 1$\sigma $ and 2$\sigma $ CL regions in the $\kappa _{\rm {F}}$ vs $\kappa _{\rm {V}}$ parameter space for the model assuming a common scaling of all the vector boson and fermion couplings. |

png pdf |
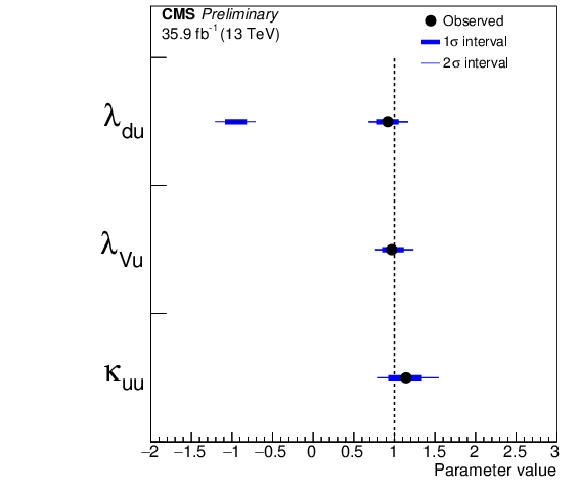
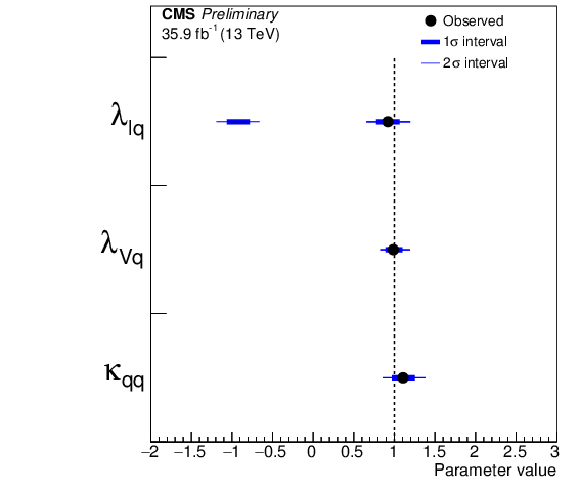
Figure 17:
Summary plots of the 3-parameter models comparing up- and down-type fermions, and floating the ratio of the vector coupling to the up-type coupling (left) and comparing lepton and quark couplings (right). The points indicate the best-fit values while the thick and thin horizontal bars show the $1\sigma $ and 2$\sigma $ CL intervals, respectively. Both positive and negative values of $\lambda _{\rm {du}}$, $\lambda _{\rm {Vu}}$, $\lambda _{\rm {lq}}$, and $\lambda _{\rm {Vq}}$ are considered. |
png pdf |
Figure 17-a:
Summary plot of the 3-parameter models comparing up- and down-type fermions, and floating the ratio of the vector coupling to the up-type coupling. The points indicate the best-fit values while the thick and thin horizontal bars show the $1\sigma $ and 2$\sigma $ CL intervals, respectively. Both positive and negative values of $\lambda _{\rm {du}}$, $\lambda _{\rm {Vu}}$ are considered. |
png pdf |
Figure 17-b:
Summary plot of the 3-parameter models comparing lepton and quark couplings (right). The points indicate the best-fit values while the thick and thin horizontal bars show the $1\sigma $ and 2$\sigma $ CL intervals, respectively. Both positive and negative values of $\lambda _{\rm {lq}}$, and $\lambda _{\rm {Vq}}$ are considered. |
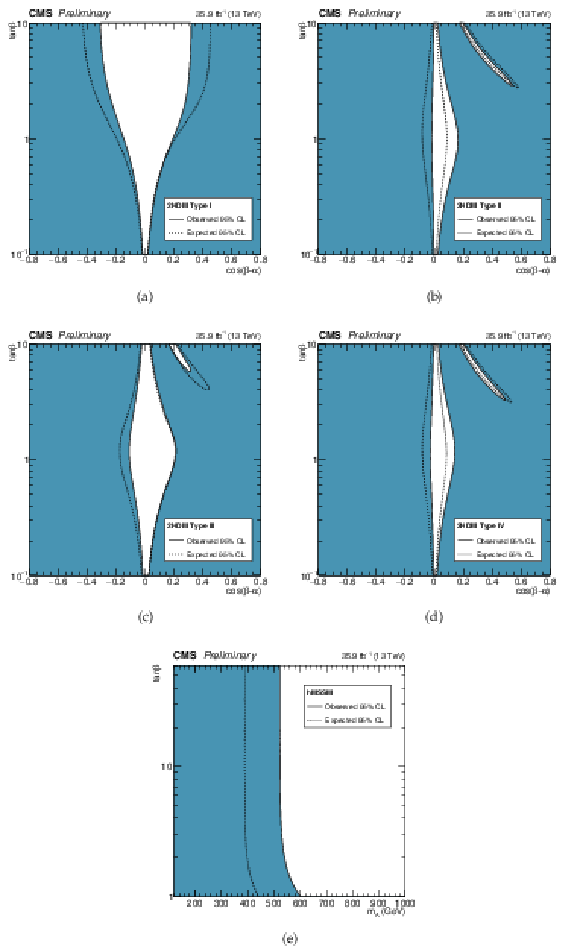
png pdf |
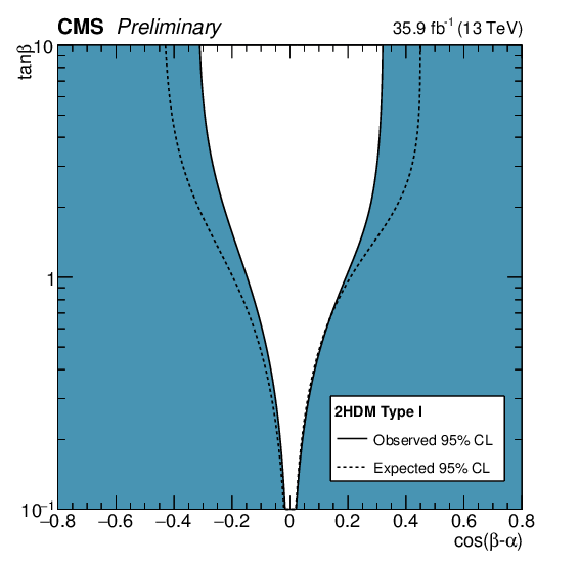
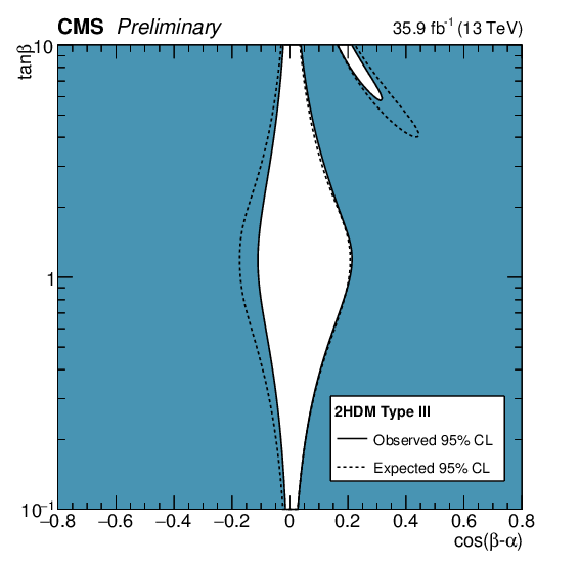
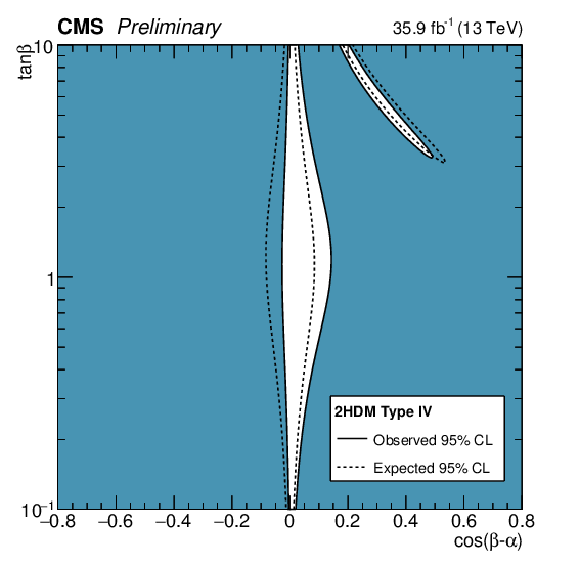
Figure 18:
Constraints in the $\cos({\beta -\alpha})-\tan\beta $ plane for the (a) Type I, (b) Type II, (c) Type III, (d) Type IV 2HDM. (e) Constraints in the $m_{\mathrm {A}}-\tan\beta $ plane for the hMSSM. The white regions, bounded by the solid black lines, in each plane represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |
png pdf |
Figure 18-a:
Constraints in the $\cos({\beta -\alpha})-\tan\beta $ plane for the Type I 2HDM. The white regions, bounded by the solid black lines, represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |

png pdf |
Figure 18-b:
Constraints in the $\cos({\beta -\alpha})-\tan\beta $ plane for the Type II 2HDM. The white regions, bounded by the solid black lines, represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |
png pdf |
Figure 18-c:
Constraints in the $\cos({\beta -\alpha})-\tan\beta $ plane for the Type III 2HDM. The white regions, bounded by the solid black lines, represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |
png pdf |
Figure 18-d:
Constraints in the $\cos({\beta -\alpha})-\tan\beta $ plane for the Type IV 2HDM. The white regions, bounded by the solid black lines, represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |

png pdf |
Figure 18-e:
Constraints in the $m_{\mathrm {A}}-\tan\beta $ plane for the hMSSM. The white regions, bounded by the solid black lines, represents the regions of the parameter space which are allowed at the 95% CL, given the data observed. The dashed lines indicate the boundaries of the allowed regions expected for the SM Higgs boson. |
| Tables | |
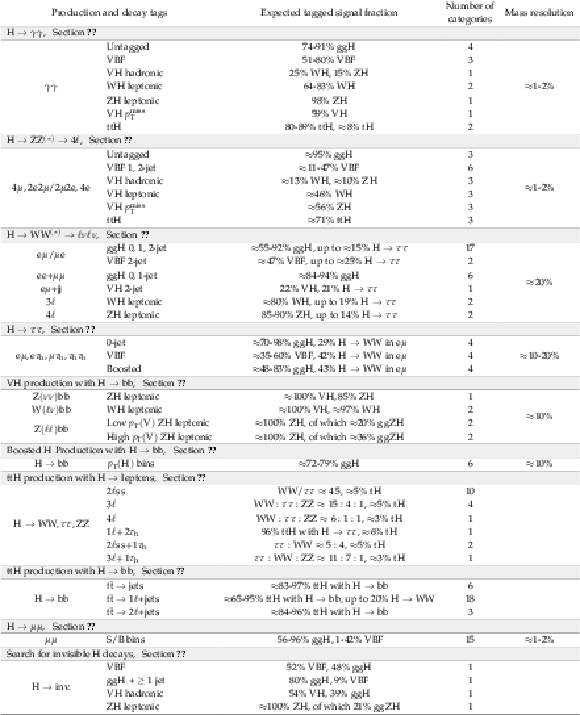
png pdf |
Table 1:
Summary of the channels in the analyses included in this combination. The first and second columns indicate which decay mode and/or production mechanism are targeted by an analysis. |

png pdf |
Table 2:
Compatibility of the fit results with the SM prediction under various signal parameterizations. The value of $q$ at the values of the parameters of interest for which the SM expectation is obtained ($q_{\text {SM}}$) is shown along with the corresponding $p$-value, with respect to the SM, assuming $q$ is distributed according to a $\chi ^{2}$ function with the specified number of degrees of freedom (DOF). |
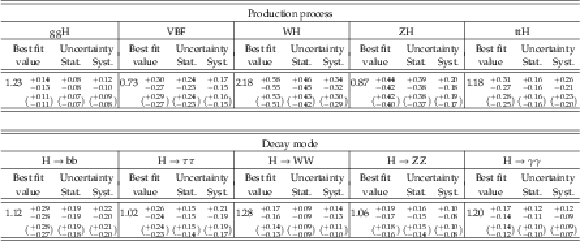
png pdf |
Table 3:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the models with per-production mode and per-decay mode signal strength modifiers. The expected uncertainties are given in brackets. |

png pdf |
Table 4:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the model with one signal strength parameter for each production and decay mode combination. The entries in the table represent the parameter $\mu _{i}^{f}=\mu _{i}\times \mu ^{f}$, where $i$ is indicated by the row and $f$ by the column. The expected uncertainties are given in brackets. Some of the signal strengths are restricted to positive values, as described in the text. |
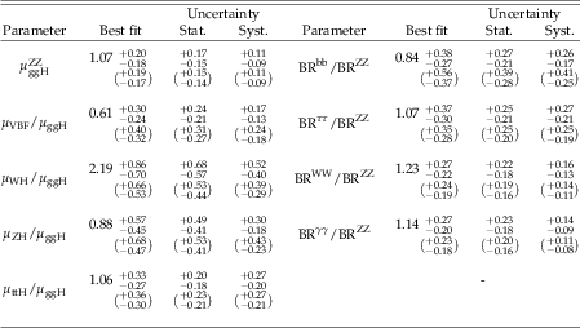
png pdf |
Table 5:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the cross section and branching fraction ratio model. The expected uncertainties are given in brackets. |
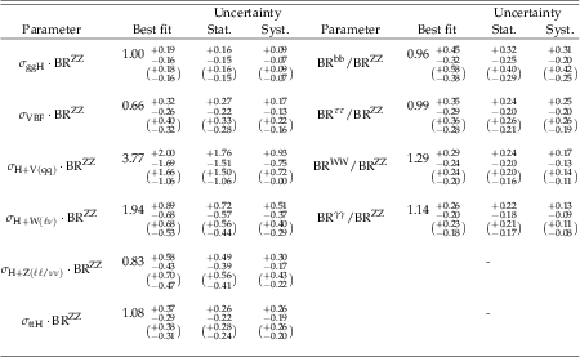
png pdf |
Table 6:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the stage 0 simplified template cross section model. The values are all normalized to the SM predictions. The expected uncertainties are given in brackets. |
png pdf |
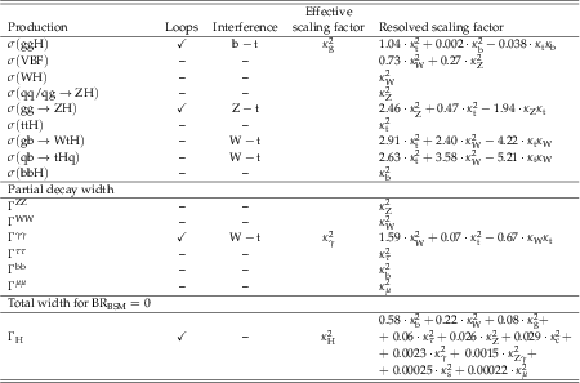
Table 7:
Normalization scaling factors for all relevant production cross sections and decay partial widths. For those $\kappa $ parameters representing loop processes, the resolved scaling in terms of the fundamental SM couplings are also given. |

png pdf |
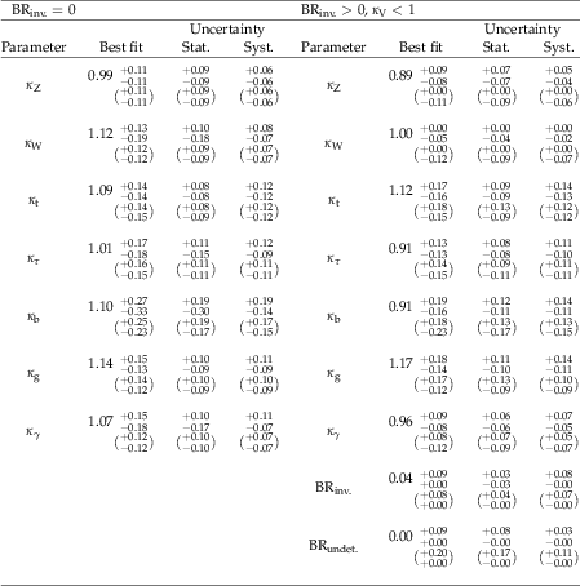
Table 8:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the $\kappa $ model in which the loop processes are resolved. The expected uncertainties are given in brackets. |
png pdf |
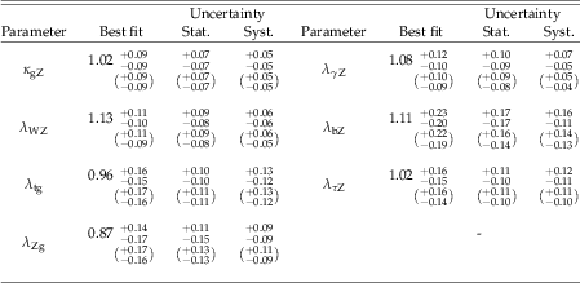
Table 9:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the $\kappa $-framework model with effective loops. The expected uncertainties are given in brackets. |
png pdf |
Table 10:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the coupling modifier ratio model. The expected uncertainties are given in brackets. |

png pdf |
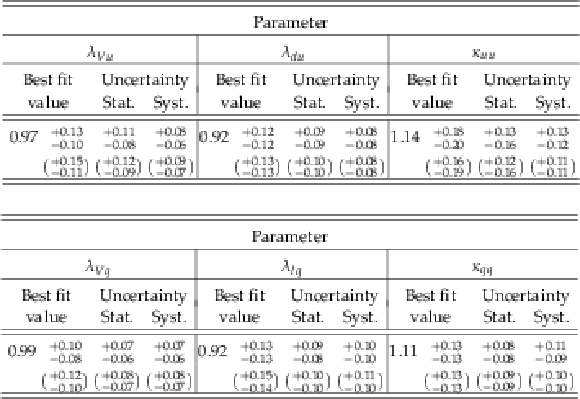
Table 11:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the $\kappa _{\rm {V}},\kappa _{\rm {F}}$ model. The expected uncertainties are given in brackets. |
png pdf |
Table 12:
Best-fit values and $ \pm $1$ \sigma $ uncertainties for the parameters of the benchmark models with resolved loops to test the symmetry of fermion couplings. The expected uncertainties are given in brackets. |

png pdf |
Table 13:
Modifications to the couplings of the Higgs bosons to up-type ($\kappa _{u}$) and down-type ($\kappa _{d}$) fermions, and vector bosons ($\kappa _{V}$), with respect to the SM expectation, in 2HDM and for the hMSSM. The coupling modifications for the hMSSM are completed by the expressions for $s_{u}$ and $s_{d}$, as given in Equation xxxxx. |
| Summary |
|
A set of combined measurements of the Higgs boson's production and decay rates has been presented, along with the consequential constraints placed on its couplings to standard model (SM) particles, and on the parameter spaces of several beyond the standard model (BSM) scenarios. The combination is based on analyses targeting the gluon fusion (${\mathrm{g}\mathrm{g}\mathrm{H}} $), vector boson fusion production modes, and associated production with a vector boson or a pair of top quarks. The analyses included in the combination target Higgs boson decay in one of the $\mathrm{H} \to \mathrm{Z}\mathrm{Z}$, $\mathrm{W}\mathrm{W}$, $\gamma\gamma$, $\tau\tau$, bb, and $\mu\mu$ channels, using 35.9 fb$^{-1}$ of 13 TeV proton-proton collision data. Additionally, searches for invisible Higgs boson decays are included to increase the sensitivity to potential interactions with BSM particles. Measurements of the Higgs boson production cross section times branching ratio, in each of the channels are presented, along with a generic parameterization in terms of ratios of production cross sections and branching ratios, which makes no assumptions about the Higgs boson's total width. The combined signal yield relative to the SM prediction has been measured as $1.17^{+0.10}_{-0.10}$. Improvements in the precision of the ${\mathrm{g}\mathrm{g}\mathrm{H}} $ production rate of around $\sim$50% is achieved compared to previous ATLAS and CMS measurements. Additionally, a set of measurements of fiducial cross sections of Higgs boson processes, in the context of the simplified template cross sections, are presented for the first time from a combination of five decay channels. Furthermore, interpretations are provided in the context of a LO coupling modifier framework, including variants for which effective couplings to the photon and gluon are introduced. All of the results presented are compatible with the SM prediction, and the invisible branching ratio of the Higgs boson is constrained to be less than 22% at 95% CL. The results are additionally interpreted in two BSM models, the minimal supersymmetric model and the generic two Higgs doublet model. The constraints placed in the parameter spaces of these models are complementary to those which can be obtained from direct searches for additional Higgs bosons. |
| References | ||||
| 1 | S. L. Glashow | Partial-symmetries of weak interactions | NP 22 (1961) 579 | |
| 2 | S. Weinberg | A model of leptons | PRL 19 (1967) 1264 | |
| 3 | A. Salam | Weak and electromagnetic interactions | in Elementary particle physics: relativistic groups and analyticity, N. Svartholm, ed., p. 367 Almqvist & Wiskell, 1968Proceedings of the 8th Nobel symposium | |
| 4 | G. 't Hooft and M. Veltman | Regularization and Renormalization of Gauge Fields | NPB 44 (1972) 189 | |
| 5 | F. Englert and R. Brout | Broken symmetry and the mass of gauge vector mesons | PRL 13 (1964) 321 | |
| 6 | P. W. Higgs | Broken symmetries, massless particles and gauge fields | PL12 (1964) 132 | |
| 7 | P. W. Higgs | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 508 | |
| 8 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global conservation laws and massless particles | PRL 13 (1964) 585 | |
| 9 | P. W. Higgs | Spontaneous symmetry breakdown without massless bosons | PR145 (1966) 1156 | |
| 10 | T. W. B. Kibble | Symmetry breaking in non-Abelian gauge theories | PR155 (1967) 1554 | |
| 11 | Y. Nambu and G. Jona-Lasinio | Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I | PR122 (1961) 345 | |
| 12 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 13 | ATLAS Collaboration | Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 14 | K. G. Wilson | Renormalization group and strong interactions | PRD 3 (1971) 1818 | |
| 15 | E. Gildener | Gauge-symmetry hierarchies | PRD 14 (1976) 1667 | |
| 16 | S. Weinberg | Gauge hierarchies | PLB 82 (1979) 387 | |
| 17 | G. 't Hooft | Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking | NATO Sci. Ser. B 59 (1980) 135 | |
| 18 | L. Susskind | Dynamics of spontaneous symmetry breaking in the weinberg-salam theory | PRD 20 (1979) 2619 | |
| 19 | S. Dimopoulos and H. Georgi | Softly broken supersymmetry and su(5) | NPB 193 (1981) 150 | |
| 20 | E. Witten | Dynamical breaking of supersymmetry | NPB 188 (1981) 513 | |
| 21 | N. Arkani-Hamed, S. Dimopoulos, and G. Dvali | The hierarchy problem and new dimensions at a millimeter | PLB 429 (1998) 263 | |
| 22 | L. Randall and R. Sundrum | Large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | |
| 23 | N. Arkani-Hamed, A. G. Cohen, and H. Georgi | Electroweak symmetry breaking from dimensional deconstruction | PLB 513 (2001) 232 | |
| 24 | G. Belanger et al. | The MSSM invisible Higgs in the light of dark matter and g-2 | PLB 519 (2001) 93 | hep-ph/0106275 |
| 25 | G. F. Giudice, R. Rattazzi, and J. D. Wells | Graviscalars from higher-dimensional metrics and curvature-Higgs mixing | NPB 595 (2001) 250 | hep-ph/0002178 |
| 26 | D. Dominici and J. F. Gunion | Invisible Higgs decays from Higgs-graviscalar mixing | PRD 80 (2009) 115006 | 0902.1512 |
| 27 | C. Bonilla, J. W. F. Valle, and J. C. Romão | Neutrino mass and invisible Higgs decays at the LHC | PRD 91 (2015), no. 11, 113015 | 1502.01649 |
| 28 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | Eur Phys. J C 75 (2015) 212 | CMS-HIG-14-009 1412.8662 |
| 29 | ATLAS Collaboration | Measurements of the Higgs boson production and decay rates and coupling strengths using $ pp $ collision data at $ \sqrt{s} = $ 7 and 8 TeV in the ATLAS experiment | Eur Phys. J C 76 (2016) 6 | 1507.04548 |
| 30 | ATLAS, CMS Collaborations | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC $ pp $ collision data at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 08 (2016) 045 | 1606.02266 |
| 31 | C. Anastasiou et al. | High precision determination of the gluon fusion Higgs boson cross-section at the LHC | JHEP 05 (2016) 1 | 1602.00695 |
| 32 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 33 | CMS Collaboration | Measurements of properties of the Higgs boson in the diphoton decay channel with the full 2016 data set | ||
| 34 | B. P. Roe et al. | Boosted decision trees as an alternative to artificial neural networks for particle identification | NIMA 543 (2005) 577 | 0408124 |
| 35 | P. Dauncey, M. Kenzie, N. Wardle, and G. Davies | Handling uncertainties in background shapes: the discrete profiling method | JINST 10 (2015) P04015 | 1408.6865 |
| 36 | CMS Collaboration | Measurements of properties of the Higgs boson decaying into the four-lepton final state in pp collisions at $ \sqrt{s}= $ 13 ~TeV | JHEP 11 (2017) 47 | CMS-HIG-16-041 1706.09936 |
| 37 | CMS Collaboration | Measurements of Higgs boson production and couplings using decays to a W boson pair in pp collisions at 13 TeV | ||
| 38 | CMS Collaboration | Observation of the Higgs boson decay to a pair of tau leptons with the CMS detector | PLB 779 (2018) 283 | CMS-HIG-16-043 1708.00373 |
| 39 | CMS Collaboration | Evidence for the Higgs boson decay to a bottom quark-antiquark pair | \emphAccepted by PLB | CMS-HIG-16-044 1709.07497 |
| 40 | CDF, D0 Collaboration | Improved $ b $-jet Energy Correction for $ H \to b\bar{b} $ Searches at CDF | 1107.3026 | |
| 41 | CMS Collaboration | Search for the associated production of a Higgs boson with a single top quark in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JHEP 06 (2016) 177 | CMS-HIG-14-027 1509.08159 |
| 42 | ATLAS Collaboration | Search for the $ \mathrm{b}\overline{\mathrm{b}} $ decay of the Standard Model Higgs boson in associated (W/Z)H production with the ATLAS detector | JHEP 01 (2015) 069 | 1409.6212 |
| 43 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | |
| 44 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | Submitted to \it JINST | CMS-BTV-16-002 1712.07158 |
| 45 | CMS Collaboration | Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair | PRL 120 (2018) 071802 | CMS-HIG-17-010 1709.05543 |
| 46 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 47 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 48 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 49 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 50 | J. Thaler and K. Van Tilburg | Identifying Boosted Objects with N-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 51 | CMS Collaboration | Evidence for associated production of a Higgs boson with a top quark pair in final states with electrons, muons, and hadronically decaying $ \tau $ leptons at $ \sqrt{s}= $ 13 TeV | CMS-HIG-17-018, 2018 To be submitted to JHEP | |
| 52 | CMS Collaboration | Search for ttH production in the $ $ h \to bb $ $ decay channel in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the CMS detector | ||
| 53 | CMS Collaboration | Search for t$ \bar{\mathrm{t}} $H in all-jet final states in pp collisions at $ \sqrt{s}= $ 13 TeV | CMS-HIG-17-022, 2018 To be submitted to JHEP | |
| 54 | J. Schmidhuber | Deep learning in neural networks: An overview | Neural Networks 61 (2015) 85 | |
| 55 | T. J. Hastie, R. J. Tibshirani, and J. H. Friedman | The elements of statistical learning : data mining, inference, and prediction | Springer series in statistics. Springer, New York, NY, 2. ed., corr. at 10. print. edition, 2013 ISBN 978-0-387-84857-0 | |
| 56 | P. C. Bhat | Multivariate analysis methods in particle physics | Annual Review of Nuclear and Particle Science 61 (2011), no. 1, 281 | |
| 57 | A. Hocker et al. | TMVA: Toolkit for Multivariate Data Analysis | PoS ACAT (2007) 040 | physics/0703039 |
| 58 | K. Kondo | Dynamical Likelihood Method for Reconstruction of Events With Missing Momentum. 1: Method and Toy Models | J. Phys. Soc. Jap. 57 (1988) 4126--4140 | |
| 59 | D0 Collaboration | A precision measurement of the mass of the top quark | Nature 429 (2004) 638--642 | hep-ex/0406031 |
| 60 | CMS Collaboration | Search for the standard model Higgs boson decaying to two muons in pp collisions at $ \sqrt{s}= $ 13 TeV | ||
| 61 | CMS Collaboration | Search for invisible decays of the Higgs boson produced through vector boson fusion at $ \sqrt{s}= $ 13 TeV | ||
| 62 | CMS Collaboration | Search for new physics in events with a leptonically decaying Z boson and a large transverse momentum imbalance in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | \emphSubmitted to EPJC | CMS-EXO-16-052 1711.00431 |
| 63 | CMS Collaboration | Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson and transverse momentum imbalance at $ \sqrt{s}= $ 13 TeV | \emphSubmitted to PRD | CMS-EXO-16-048 1712.02345 |
| 64 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 02 (2012) 088 | 1111.2854 |
| 65 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 66 | R. Frederix and S. Frixione | Merging meets matching in mc@nlo | JHEP 12 (2012) 61 | 1209.6215 |
| 67 | K. Hamilton, P. Nason, E. Re, and G. Zanderighi | NNLOPS simulation of Higgs boson production | JHEP 10 (2013) 222 | 1309.0017 |
| 68 | R. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Computer Physics Communications 77 (1993) 219 | |
| 69 | Conway, J. S. | Incorporating Nuisance Parameters in Likelihoods for Multisource Spectra | 1103.0354 | |
| 70 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | ATL-PHYS-PUB 2011-11, CMS NOTE 2011/005 | |
| 71 | CMS Collaboration | Combined results of searches for the standard model Higgs boson in pp collisions at $ \sqrt{s} = $ 7 TeV | PLB 710 (2012) 26 | CMS-HIG-11-032 1202.1488 |
| 72 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 73 | W. Verkerke and D. P. Kirkby | The RooFit toolkit for data modeling | in 13th International Conference for Computing in High-Energy and Nuclear Physics (CHEP03) 2003 CHEP-2003-MOLT007 | physics/0306116 |
| 74 | L. Moneta et al. | The RooStats Project | PoS ACAT2010 (2010) 057 | 1009.1003 |
| 75 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 76 | ATLAS and CMS Collaborations | Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS and CMS Experiments | Phys.Rev.Lett. 114 (2015) 191803 | 1503.07589 |
| 77 | S. Heinemeyer et al. | Handbook of LHC Higgs Cross Sections: 3. Higgs Properties | 1307.1347 | |
| 78 | C. Englert, M. McCullough, and M. Spannowsky | Gluon-initiated associated production boosts Higgs physics | PRD 89 (2014), no. 1, 013013 | 1310.4828 |
| 79 | J. Ellis and T. You | Global analysis of the Higgs candidate with mass $ \sim $ 125 GeV | JHEP 09 (2012) 123 | 1207.1693 |
| 80 | J. Ellis and T. You | Updated global analysis of Higgs couplings | JHEP 06 (2013) 103 | 1303.3879 |
| 81 | Patrignani et al. (Particle Data Group) | Review of Particle Physics | CPC 40 (2016) 100001 | |
| 82 | G. Branco et al. | Theory and phenomenology of two-Higgs-doublet models | Physics Reports 516 (2012) 1 | 1106.0034 |
| 83 | A. Djouadi | The Anatomy of electro-weak symmetry breaking. II. The Higgs bosons in the minimal supersymmetric model | PR 459 (2008) 1 | hep-ph/0503173 |
| 84 | J. F. Gunion and H. E. Haber | Higgs bosons in supersymmetric models (i) | Nuclear Physics B 272 (1986), no. 1, 1 | |
| 85 | H. Haber and G. Kane | The search for supersymmetry: Probing physics beyond the standard model | Physics Reports 117 (1985), no. 2, 75 | |
| 86 | H. Nilles | Supersymmetry, supergravity and particle physics | Physics Reports 110 (1984), no. 1, 1 -- 162 | |
| 87 | A. Djouadi et al. | The post-Higgs MSSM scenario: Habemus MSSM? | EPJC 73 (2013) 2650 | 1307.5205 |
| 88 | A. Djouadi et al. | Fully covering the MSSM Higgs sector at the LHC | JHEP 06 (2015) 168 | 1502.05653 |
| 89 | ATLAS Collaboration | Constraints on new phenomena via Higgs boson couplings and invisible decays with the ATLAS detector | JHEP 11 (2015) 206 | 1509.00672 |
| 90 | ATLAS Collaboration | Search for heavy resonances decaying into $ WW $ in the $ e\nu\mu\nu $ final state in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | EPJC 78 (2018) | 1710.01123 |
| 91 | ATLAS Collaboration | Search for additional heavy neutral Higgs and gauge bosons in the ditau final state produced in 36 fb$ ^{−1} $ of pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | JHEP 01 (2018) 055 | 1709.07242 |
| 92 | ATLAS Collaboration | Search for charged Higgs bosons produced in association with a top quark and decaying via $ H^{\pm} \rightarrow \tau\nu $ using $ pp $ collision data recorded at $ \sqrt{s} = $ 13 TeV by the ATLAS detector | PLB 759 (2016) 555--574 | 1603.09203 |
| 93 | CMS Collaboration | Search for neutral MSSM Higgs bosons decaying to a pair of tau leptons in pp collisions | JHEP 10 (2014) 160 | CMS-HIG-13-021 1408.3316 |
| 94 | CMS Collaboration | Search for a standard-model-like Higgs boson with a mass in the range 145 to 1000 GeV at the LHC | EPJC 73 (2013) 2469 | CMS-HIG-12-034 1304.0213 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|