Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-TOP-21-004 | ||
| Measurement of the inclusive and differential $\mathrm{t\bar{t}}\gamma$ cross section and EFT interpretation in the dilepton channel at $\sqrt{s}=$ 13 TeV | ||
| CMS Collaboration | ||
| September 2021 | ||
| Abstract: The production cross section of a top quark pair in association with a photon is measured in pp collisions in the decay channel with two oppositely charged leptons ($\text{e}^\pm\mu^\mp$, $\text{e}^+\text{e}^-$, $\mu^+\mu^-$). The data set of 138 fb$^{-1}$ was recorded by the CMS experiment at $\sqrt{s}=$ 13 TeV during the 2016 to 2018 data-taking period of the CERN LHC. A fiducial phase space is defined such that photons radiated by initial-state particles, top quarks, or any of their decay products are included. An inclusive cross section of 174.4 $\pm$ 2.5 (stat) $\pm$ 6.1 (syst) fb is measured in a signal region with at least one b-tagged jet and exactly one photon with transverse momentum above 20 GeV. Differential cross sections are measured as a function of several kinematic observables of the photon, leptons, and jet, and compared to standard model predictions. The measurements are also interpreted in the standard model effective field theory framework, and limits on the relevant Wilson coefficients are combined with a previous CMS measurement of the same production process using single-lepton events. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
Figure 1:
Leading-order Feynman diagrams for ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production with two leptons in the final state, where the photon is radiated by a top quark (left), by an incoming quark (middle), and by one of the charged decay products of a top quark (right). |
png pdf |
Figure 1-a:
Leading-order Feynman diagrams for ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production with two leptons in the final state, where the photon is radiated by a top quark (left), by an incoming quark (middle), and by one of the charged decay products of a top quark (right). |
png pdf |
Figure 1-b:
Leading-order Feynman diagrams for ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production with two leptons in the final state, where the photon is radiated by a top quark (left), by an incoming quark (middle), and by one of the charged decay products of a top quark (right). |
png pdf |
Figure 1-c:
Leading-order Feynman diagrams for ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production with two leptons in the final state, where the photon is radiated by a top quark (left), by an incoming quark (middle), and by one of the charged decay products of a top quark (right). |
png pdf |
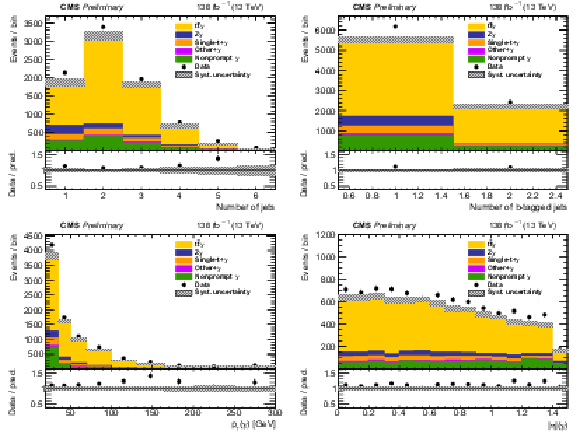
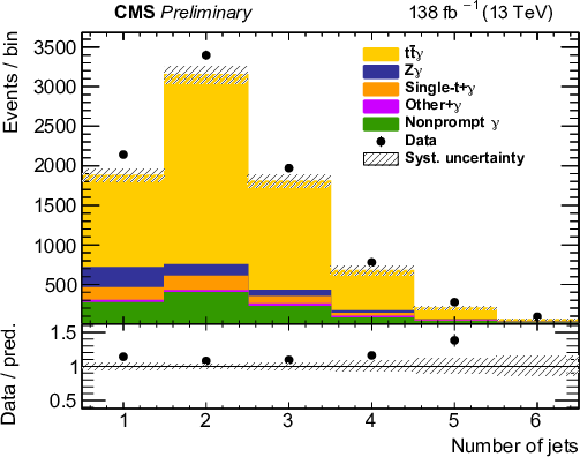
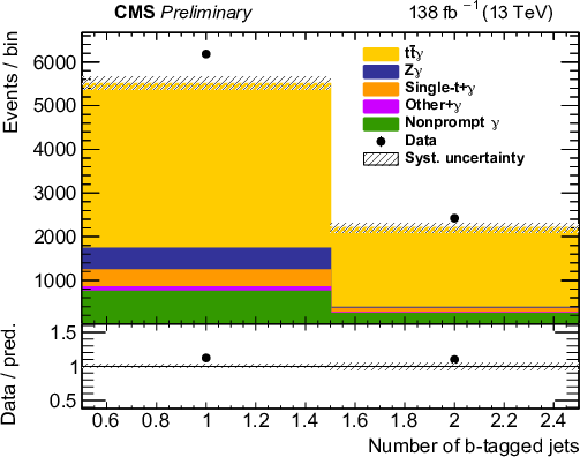
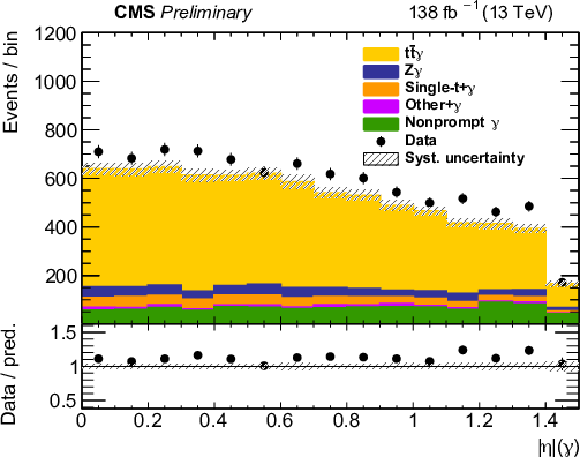
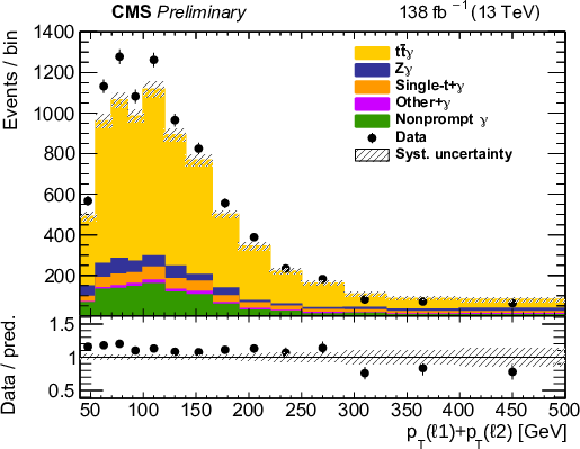
Figure 2:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the number of jets (upper left) and b-tagged jets (upper right), and of the ${p_{\mathrm {T}}}$ (lower left) and $ {| \eta |}$ (lower right) of the photon, after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 2-a:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the number of jets (upper left) and b-tagged jets (upper right), and of the ${p_{\mathrm {T}}}$ (lower left) and $ {| \eta |}$ (lower right) of the photon, after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 2-b:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the number of jets (upper left) and b-tagged jets (upper right), and of the ${p_{\mathrm {T}}}$ (lower left) and $ {| \eta |}$ (lower right) of the photon, after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 2-c:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the number of jets (upper left) and b-tagged jets (upper right), and of the ${p_{\mathrm {T}}}$ (lower left) and $ {| \eta |}$ (lower right) of the photon, after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 2-d:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the number of jets (upper left) and b-tagged jets (upper right), and of the ${p_{\mathrm {T}}}$ (lower left) and $ {| \eta |}$ (lower right) of the photon, after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
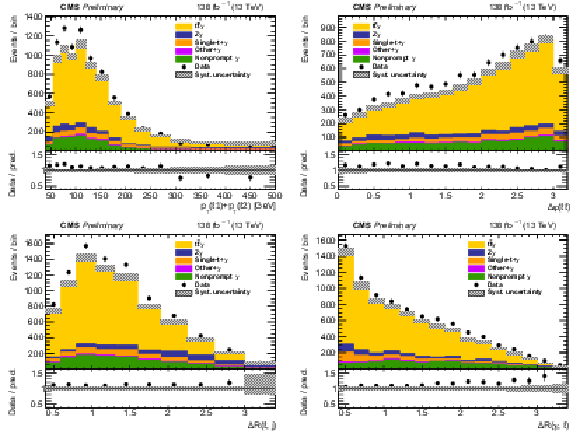
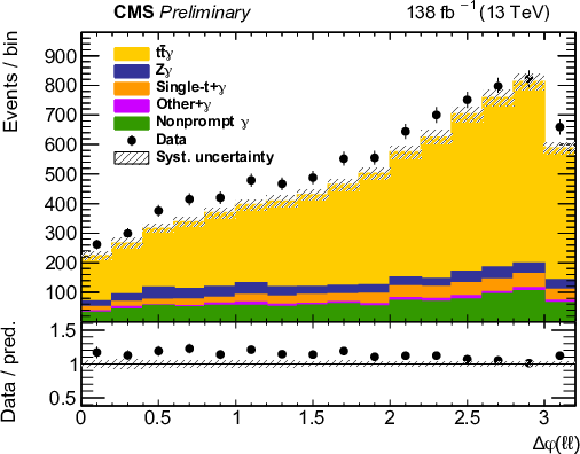
Figure 3:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the scalar ${p_{\mathrm {T}}}$ sum (upper left) and the $\phi $ difference (upper right) of the two leptons, and of the ${\Delta R}$ between the photon and the closest jet (lower left) or the closest lepton (lower right), after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 3-a:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the scalar ${p_{\mathrm {T}}}$ sum (upper left) and the $\phi $ difference (upper right) of the two leptons, and of the ${\Delta R}$ between the photon and the closest jet (lower left) or the closest lepton (lower right), after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 3-b:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the scalar ${p_{\mathrm {T}}}$ sum (upper left) and the $\phi $ difference (upper right) of the two leptons, and of the ${\Delta R}$ between the photon and the closest jet (lower left) or the closest lepton (lower right), after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 3-c:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the scalar ${p_{\mathrm {T}}}$ sum (upper left) and the $\phi $ difference (upper right) of the two leptons, and of the ${\Delta R}$ between the photon and the closest jet (lower left) or the closest lepton (lower right), after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
Figure 3-d:
The observed (points) and the predicted (shaded histograms) signal and background yields as a function of the scalar ${p_{\mathrm {T}}}$ sum (upper left) and the $\phi $ difference (upper right) of the two leptons, and of the ${\Delta R}$ between the photon and the closest jet (lower left) or the closest lepton (lower right), after applying the signal selection. Distributions are shown with all relevant corrections applied, but without scaling of the signal in accordance with the inclusive fit results. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the overall sum of the predictions. |
png pdf |
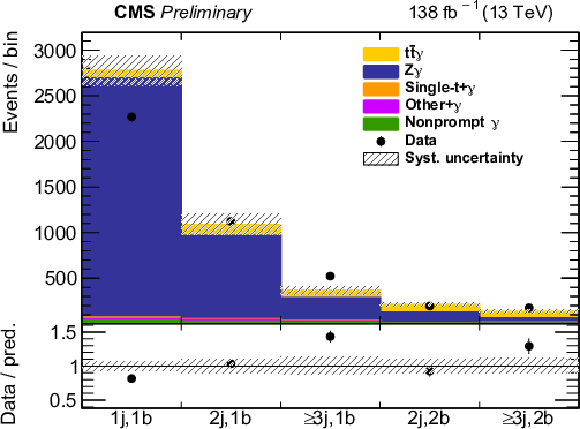
Figure 4:
The observed (points) and predicted (shaded histograms) event yields as a function of ${m(\ell \ell \gamma)}$ (upper left), ${m(\ell \ell)}$ (upper right), photon ${p_{\mathrm {T}}}$ (lower left), and the number of jets and b-tagged jets (lower right), after applying the event selection for the ${\mathrm{Z} \gamma}$ control region. The vertical lines on the points show the statistical uncertainties in the data, and the band the total uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 4-a:
The observed (points) and predicted (shaded histograms) event yields as a function of ${m(\ell \ell \gamma)}$ (upper left), ${m(\ell \ell)}$ (upper right), photon ${p_{\mathrm {T}}}$ (lower left), and the number of jets and b-tagged jets (lower right), after applying the event selection for the ${\mathrm{Z} \gamma}$ control region. The vertical lines on the points show the statistical uncertainties in the data, and the band the total uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 4-b:
The observed (points) and predicted (shaded histograms) event yields as a function of ${m(\ell \ell \gamma)}$ (upper left), ${m(\ell \ell)}$ (upper right), photon ${p_{\mathrm {T}}}$ (lower left), and the number of jets and b-tagged jets (lower right), after applying the event selection for the ${\mathrm{Z} \gamma}$ control region. The vertical lines on the points show the statistical uncertainties in the data, and the band the total uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 4-c:
The observed (points) and predicted (shaded histograms) event yields as a function of ${m(\ell \ell \gamma)}$ (upper left), ${m(\ell \ell)}$ (upper right), photon ${p_{\mathrm {T}}}$ (lower left), and the number of jets and b-tagged jets (lower right), after applying the event selection for the ${\mathrm{Z} \gamma}$ control region. The vertical lines on the points show the statistical uncertainties in the data, and the band the total uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 4-d:
The observed (points) and predicted (shaded histograms) event yields as a function of ${m(\ell \ell \gamma)}$ (upper left), ${m(\ell \ell)}$ (upper right), photon ${p_{\mathrm {T}}}$ (lower left), and the number of jets and b-tagged jets (lower right), after applying the event selection for the ${\mathrm{Z} \gamma}$ control region. The vertical lines on the points show the statistical uncertainties in the data, and the band the total uncertainty in the predictions. The lower panels show the ratio of the event yields in data to the predictions. |
png pdf |
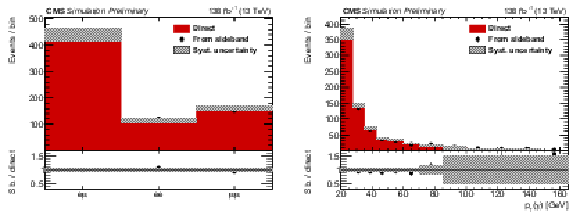
Figure 5:
Event yields in the signal region predicted from a simulated ${\mathrm{t} \mathrm{\bar{t}}}$ event sample (shaded histogram) and estimated from applying the transfer factor to the event yields of the same sample in the sideband region (points), as a function of the lepton flavour (left) and the photon ${p_{\mathrm {T}}}$ (right). The vertical lines on the points show the statistical uncertainties from the simulated event samples, and the band the total systematic uncertainty assigned to the nonprompt photon background estimate. The lower panels show the ratio between the two predictions. |
png pdf |
Figure 5-a:
Event yields in the signal region predicted from a simulated ${\mathrm{t} \mathrm{\bar{t}}}$ event sample (shaded histogram) and estimated from applying the transfer factor to the event yields of the same sample in the sideband region (points), as a function of the lepton flavour (left) and the photon ${p_{\mathrm {T}}}$ (right). The vertical lines on the points show the statistical uncertainties from the simulated event samples, and the band the total systematic uncertainty assigned to the nonprompt photon background estimate. The lower panels show the ratio between the two predictions. |
png pdf |
Figure 5-b:
Event yields in the signal region predicted from a simulated ${\mathrm{t} \mathrm{\bar{t}}}$ event sample (shaded histogram) and estimated from applying the transfer factor to the event yields of the same sample in the sideband region (points), as a function of the lepton flavour (left) and the photon ${p_{\mathrm {T}}}$ (right). The vertical lines on the points show the statistical uncertainties from the simulated event samples, and the band the total systematic uncertainty assigned to the nonprompt photon background estimate. The lower panels show the ratio between the two predictions. |
png pdf |
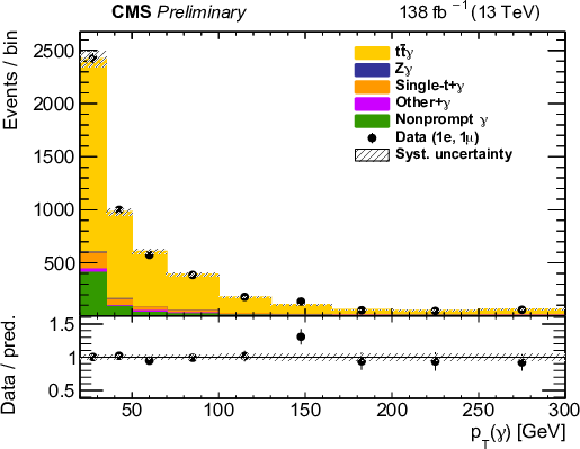
Figure 6:
The observed (points) and predicted (shaded histograms) event yields as a function of the reconstructed photon ${p_{\mathrm {T}}}$ after applying the signal selection, for the ${\mu^{+} \mu^{-}}$ (upper left),$ {\mathrm{e^{\pm}} {\mu ^\mp}}$ (upper right), and ${\mathrm{e^{+}} \mathrm{e^{-}}}$ (lower) channels, after the values of the normalizations and nuisance parameters obtained in the fit are applied. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels of each plot show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 6-a:
The observed (points) and predicted (shaded histograms) event yields as a function of the reconstructed photon ${p_{\mathrm {T}}}$ after applying the signal selection, for the ${\mu^{+} \mu^{-}}$ (upper left),$ {\mathrm{e^{\pm}} {\mu ^\mp}}$ (upper right), and ${\mathrm{e^{+}} \mathrm{e^{-}}}$ (lower) channels, after the values of the normalizations and nuisance parameters obtained in the fit are applied. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels of each plot show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 6-b:
The observed (points) and predicted (shaded histograms) event yields as a function of the reconstructed photon ${p_{\mathrm {T}}}$ after applying the signal selection, for the ${\mu^{+} \mu^{-}}$ (upper left),$ {\mathrm{e^{\pm}} {\mu ^\mp}}$ (upper right), and ${\mathrm{e^{+}} \mathrm{e^{-}}}$ (lower) channels, after the values of the normalizations and nuisance parameters obtained in the fit are applied. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels of each plot show the ratio of the event yields in data to the predictions. |
png pdf |
Figure 6-c:
The observed (points) and predicted (shaded histograms) event yields as a function of the reconstructed photon ${p_{\mathrm {T}}}$ after applying the signal selection, for the ${\mu^{+} \mu^{-}}$ (upper left),$ {\mathrm{e^{\pm}} {\mu ^\mp}}$ (upper right), and ${\mathrm{e^{+}} \mathrm{e^{-}}}$ (lower) channels, after the values of the normalizations and nuisance parameters obtained in the fit are applied. The vertical bars on the points show the statistical uncertainties in the data, and the band the systematic uncertainty in the predictions. The lower panels of each plot show the ratio of the event yields in data to the predictions. |
png pdf |
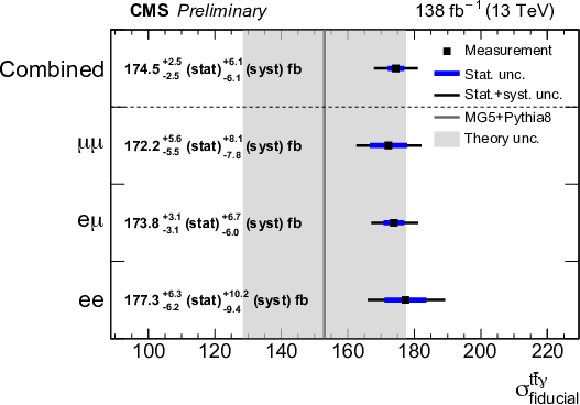
Figure 7:
Fiducial ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross section in the dilepton final state measured for different lepton flavour channels, and the combined result, compared to the SM prediction at NLO accuracy. The shaded band shows the uncertainty in the prediction. |
png pdf |
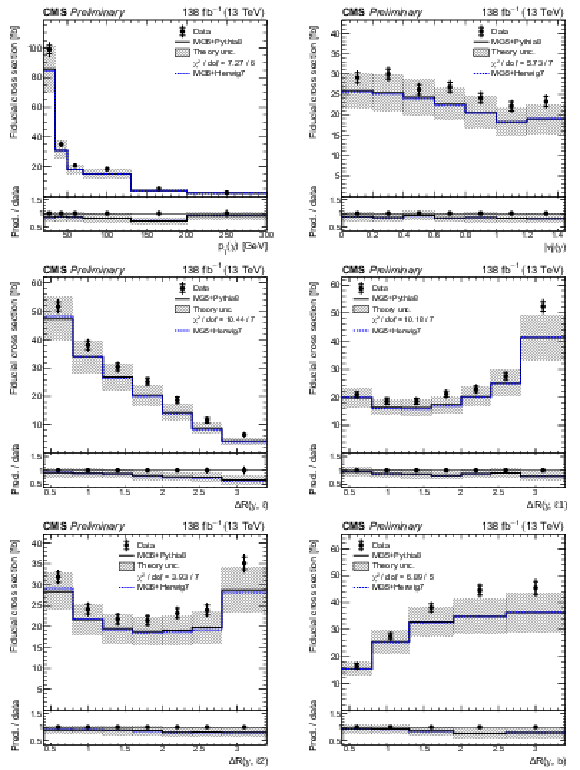
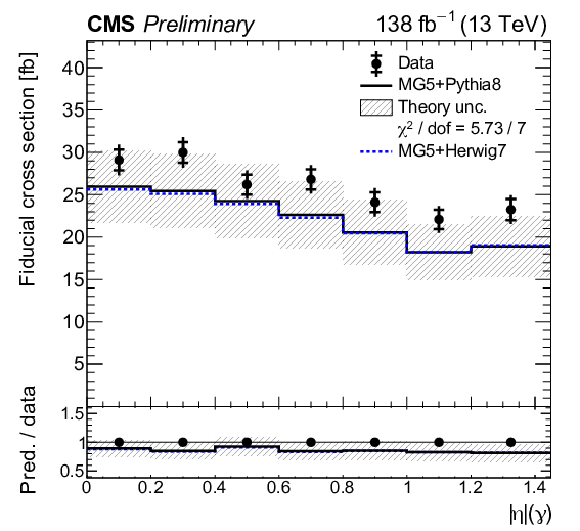
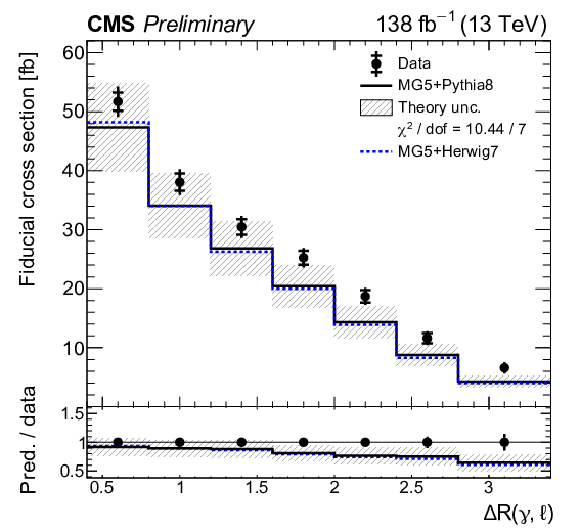
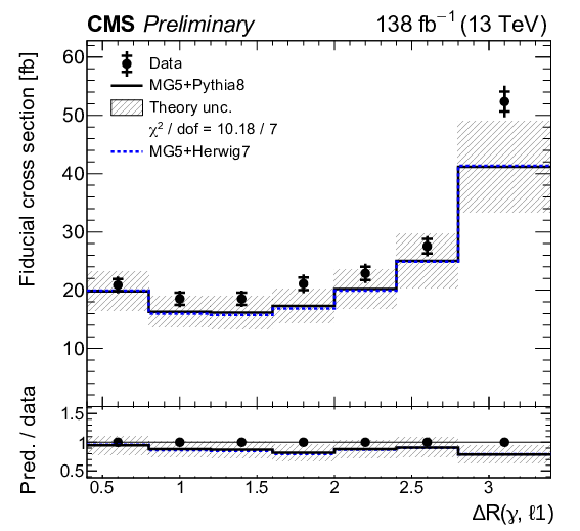
Figure 8:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-a:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-b:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-c:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-d:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-e:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 8-f:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ (lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
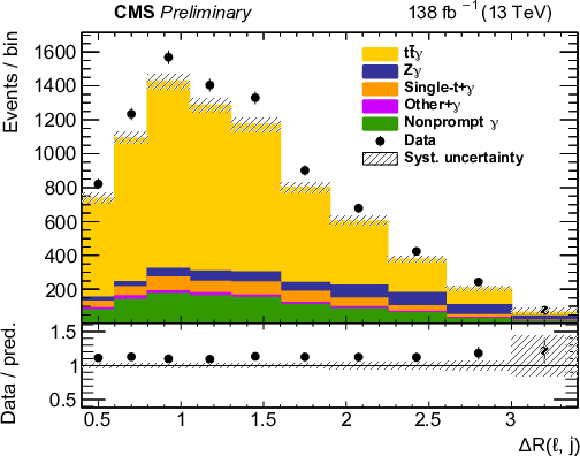
Figure 9:
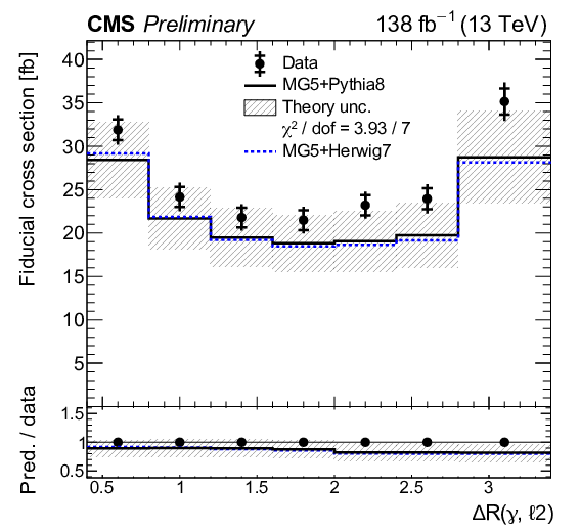
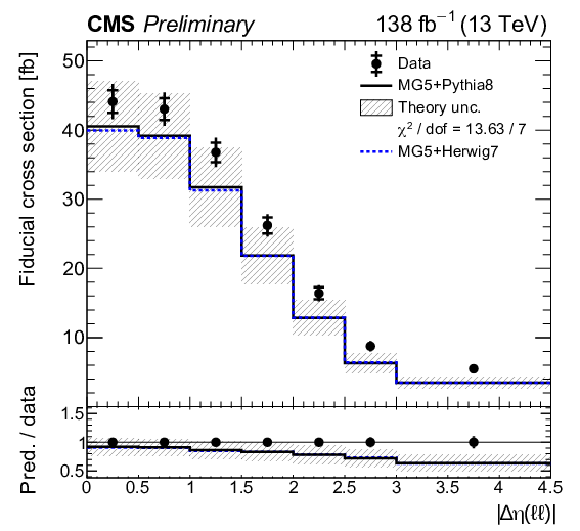
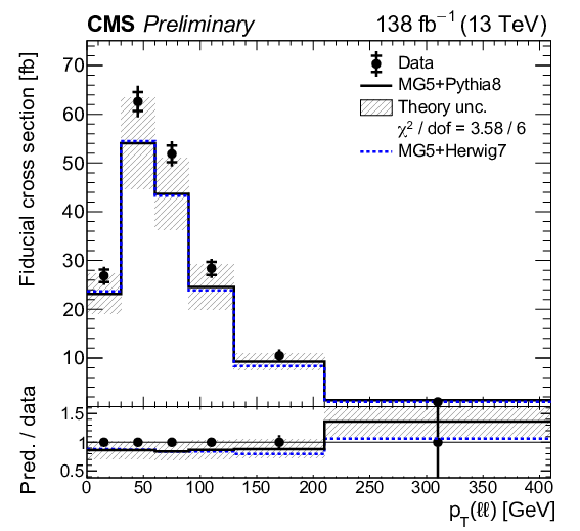
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
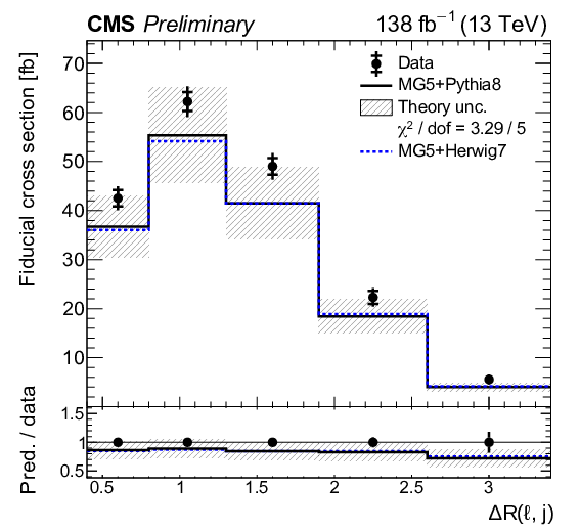
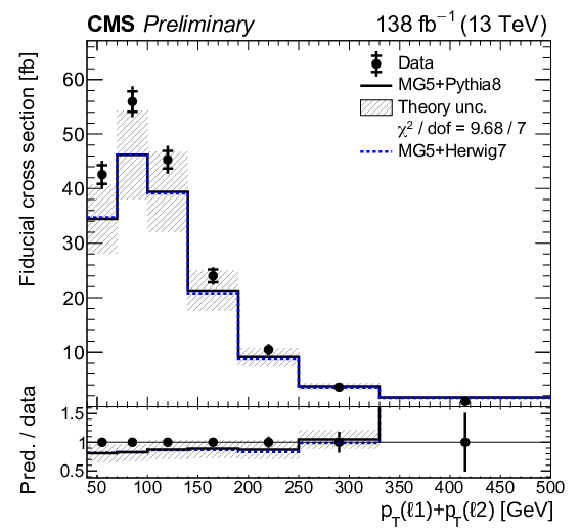
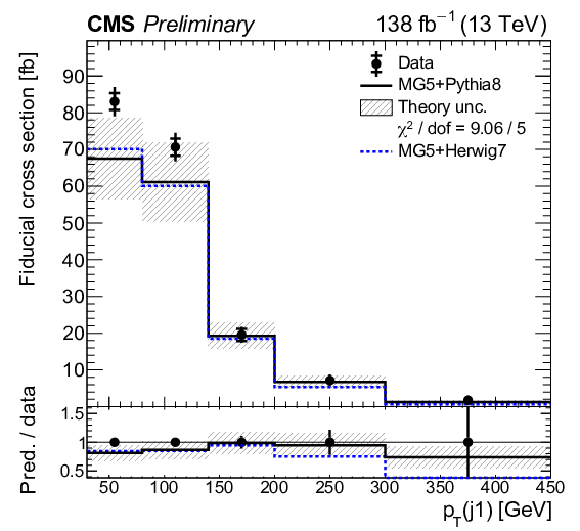
png pdf |
Figure 9-a:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 9-b:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 9-c:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 9-d:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 9-e:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 9-f:
Absolute differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
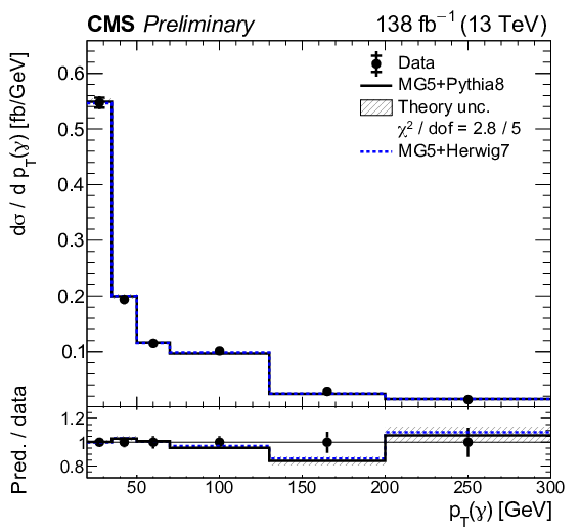
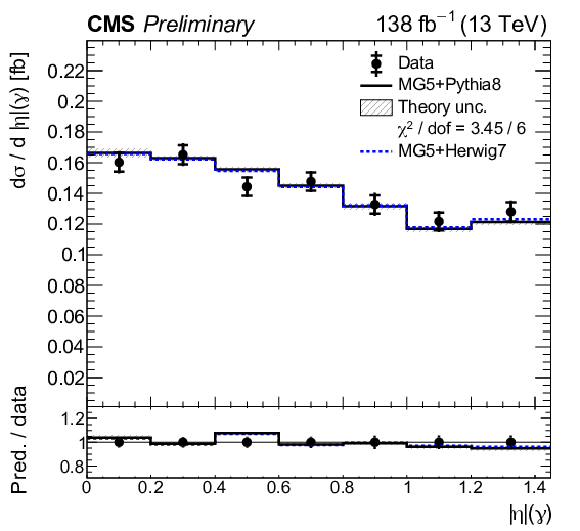
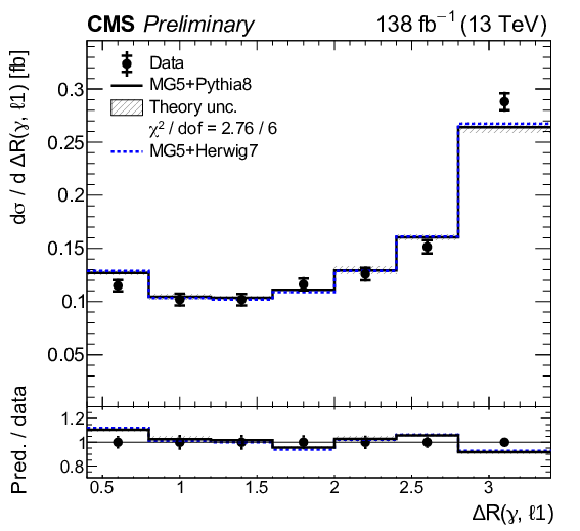
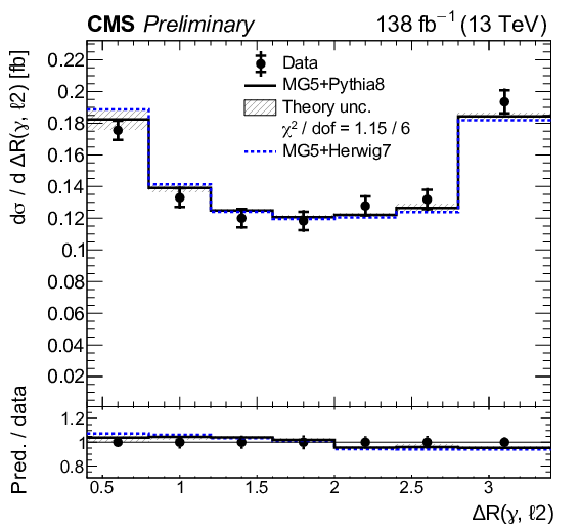
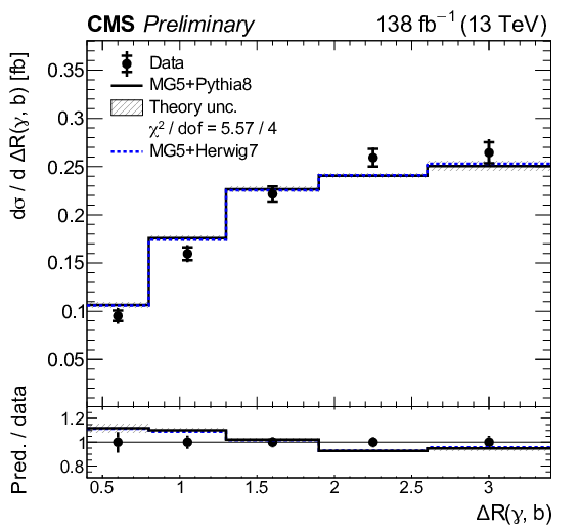
Figure 10:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-a:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-b:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-c:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-d:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-e:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 10-f:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{p_{\mathrm {T}}} (\gamma)}$ (upper left), ${{| \eta |}(\gamma)}$ (upper right), ${{\Delta R} (\gamma,\ell)}$ (middle left), ${{\Delta R} (\gamma,\ell _1)}$ (middle right), ${{\Delta R} (\gamma,\ell _2)}$ lower left), and ${{\Delta R} (\gamma,b)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
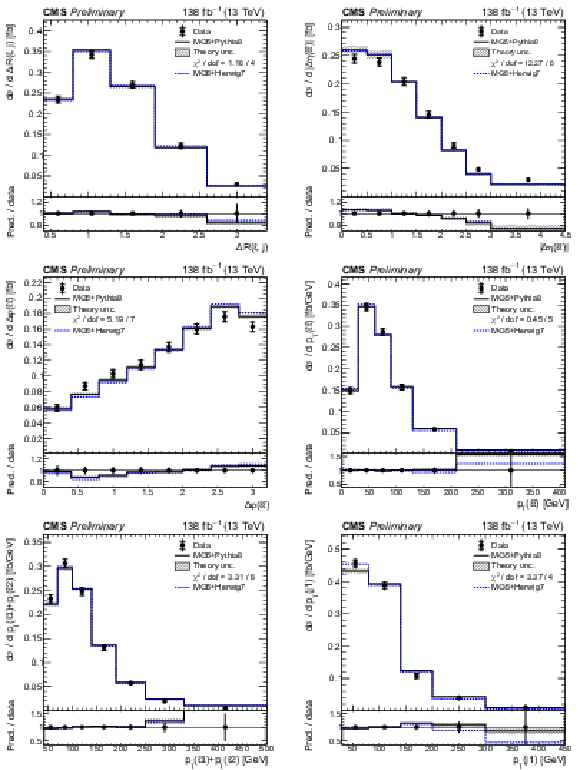
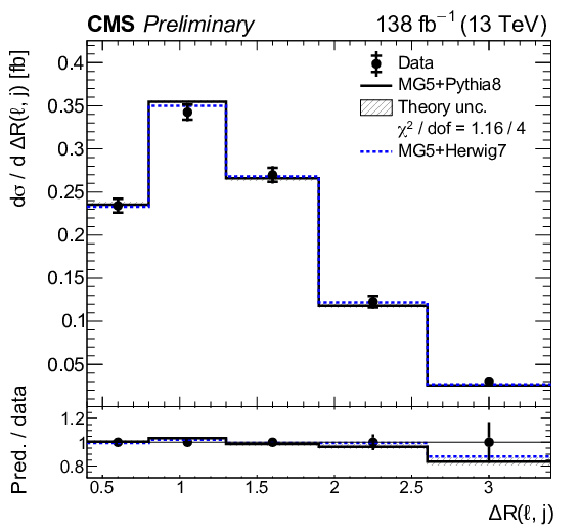
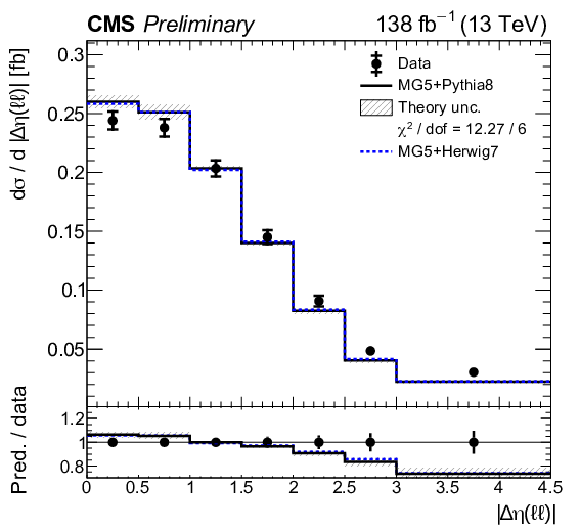
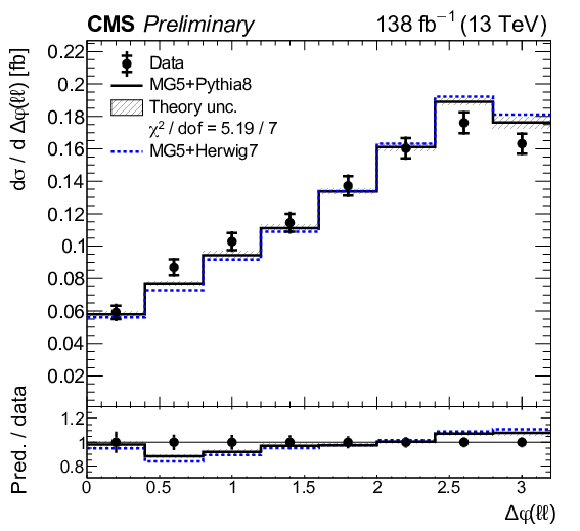
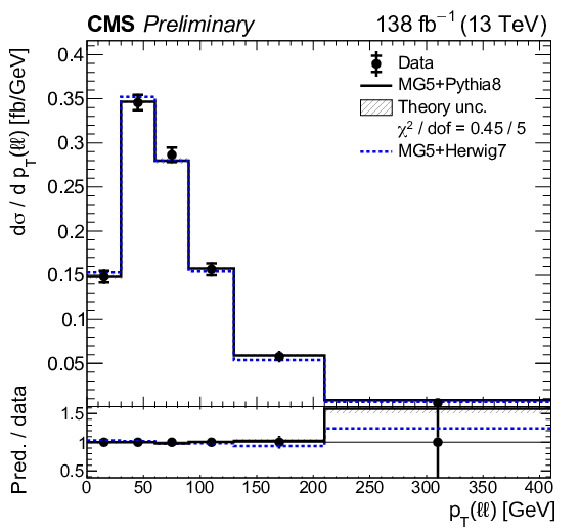
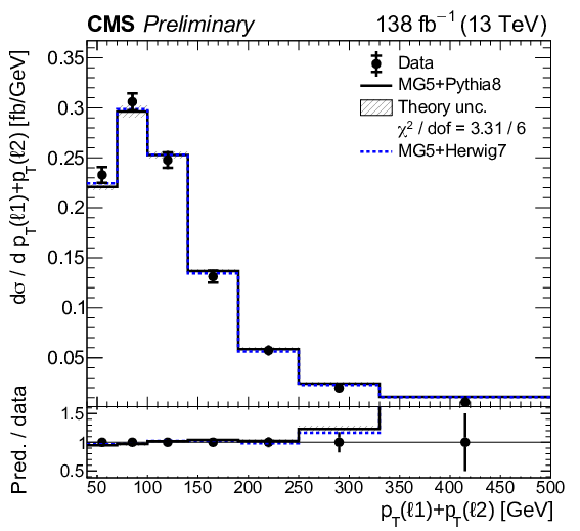
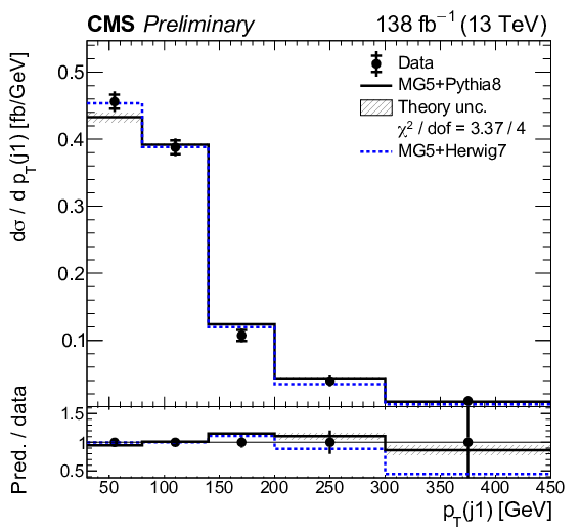
Figure 11:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-a:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-b:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-c:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-d:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-e:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
Figure 11-f:
Normalized differential ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ production cross sections as a function of ${{\Delta R} (\ell,j)}$ (upper left), ${{| {\Delta \eta} (\ell \ell) |}}$ (upper right), ${{\Delta \varphi} (\ell \ell)}$ (middle left), ${{p_{\mathrm {T}}} (\ell \ell)}$ (middle right), ${{p_{\mathrm {T}}} (\ell _1)+ {p_{\mathrm {T}}} (\ell _2)}$ (lower left), and ${{p_{\mathrm {T}}} (j_1)}$ (lower right), as defined in Table xxxxx. The data are represented by points, with inner (outer) vertical bars indicating the statistical (total) uncertainties. The predictions obtained with the MadGraph 5\_aMC@NLO event generator interfaced with different parton shower simulations, as described in the text, are shown as horizontal lines. The theoretical uncertainties in the prediction using PYTHIA 8 are indicated by shaded bands. The lower panels display the ratios of the predictions to the measurement. The values of the ${\chi ^2}$ divided by the number of degrees of freedom (dof) quantifying the agreement between the measurement and the PYTHIA 8 prediction are indicated in the legends. |
png pdf |
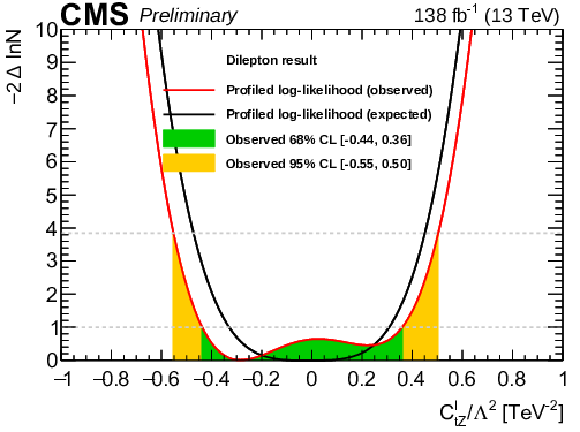
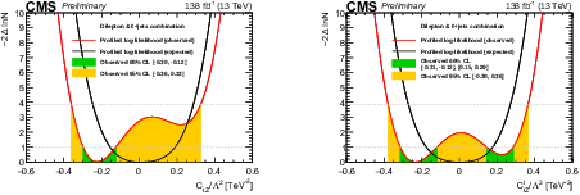
Figure 12:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the interpretation of this result. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
Figure 12-a:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the interpretation of this result. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
Figure 12-b:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the interpretation of this result. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
Figure 13:
Observed result from the two-dimensional scan of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ from the interpretation of this result. The shading quantified by the colour scale on the right reflects the negative log-likelihood ratio with respect to the best fit value that is indicated by the star. The 68% (dashed) and 95% (solid) CL contours are shown with red (black) lines for the observed (expected) result. The triangle indicates the SM prediction. |
png pdf |
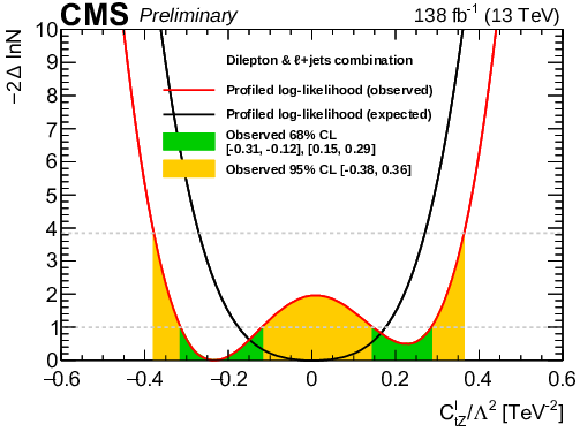
Figure 14:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the combined interpretation of this result and the lepton+jets result from Ref. [7]. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
Figure 14-a:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the combined interpretation of this result and the lepton+jets result from Ref. [7]. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
Figure 14-b:
Expected (black) and observed (red) results from the one-dimensional scans of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ (right) from the combined interpretation of this result and the lepton+jets result from Ref. [7]. In the scans, the other Wilson coefficient is set to zero. The green (yellow) bands indicate the 68% (95%) CL contours of the Wilson coefficients. |
png pdf |
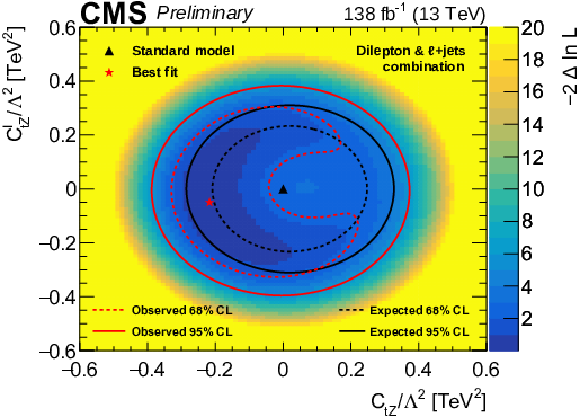
Figure 15:
Observed result from the two-dimensional scan of the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ from the combined interpretation of this result and the lepton+jets result from Ref. [7]. The shading quantified by the colour scale on the right reflects the negative log-likelihood ratio with respect to the best fit value that is indicated by the star. The 68% (dashed) and 95% (solid) CL contours are shown with red (black) lines for the observed (expected) result. The triangle indicates the SM prediction. |
| Tables | |
png pdf |
Table 1:
MC event generators used to simulate events for the signal and background processes. For each simulated process, the order of the cross section normalization calculation, the MC event generator used, and the perturbative order in QCD of the generator calculation are shown. The order is given as LO, NLO, next-to-next-to-leading order (NNLO), and including next-to-next-to-leading-logarithmic (NNLL) corrections. The symbol V refers to W and Z bosons. |
png pdf |
Table 2:
Summary of the fiducial region definition for the various objects at particle level. The "isolated'' definition for the photon requires no stable particle (except neutrinos) with $ {p_{\mathrm {T}}} > $ 5 GeV within a cone of $ {\Delta R} =$ 0.1. The parameters ${N_{\ell}}$, ${N_{\gamma}}$, and ${N_{\mathrm{b}}}$ represent the number of leptons, photons, and b jets, respectively, in the event. |
png pdf |
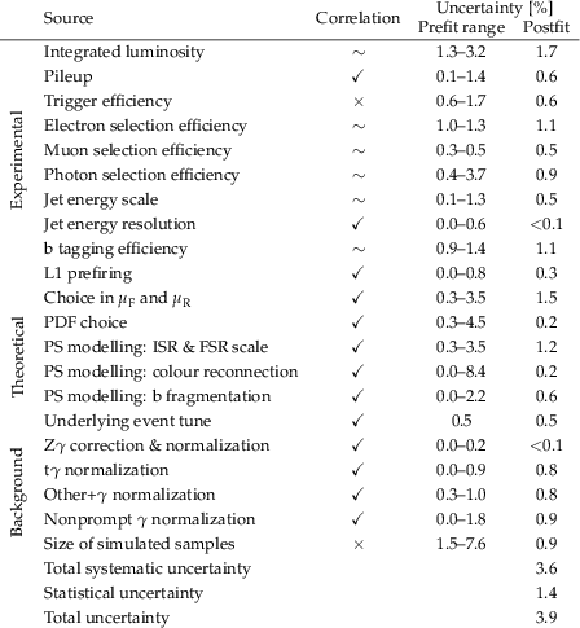
Table 3:
Summary of the sources of statistical and systematic uncertainties in the ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ cross section measurements. The first column lists the source of the uncertainty. The second column indicates the treatment of correlations between the uncertainties in the three years of data taking, where v means fully correlated, ${\sim}$ means partially correlated, and ${\times}$ means uncorrelated. For each systematic source, the uncertainty before applying the fit is estimated from a cut-and-count analysis of the predicted and observed event yields separately in bins of ${{p_{\mathrm {T}}} (\gamma)}$ and for the three years of data taking using the input variations; the typical range across the three years is shown in the third column and can be compared between the different uncertainty sources. The last column gives the impact of each uncertainty on the measured inclusive ${\mathrm{t} \mathrm{\bar{t}}} \gamma$ cross section after the fit to the data, the so-called postfit uncertainties. |
png pdf |
Table 4:
Definition of the observables used in the differential cross section measurement. |
png pdf |
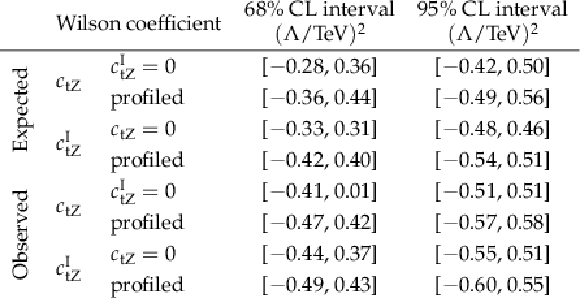
Table 5:
Summary of the one-dimensional CL intervals obtained for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ from the interpretation of this result. The profiled results correspond to the fits where the other Wilson coefficient is left free in the fit, otherwise it is set to zero. |
png pdf |
Table 6:
Summary of the one-dimensional CL intervals obtained for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ and ${c_{\mathrm{t} \mathrm{Z}}^{\mathrm {I}}}$ from the combined interpretation of this result and the lepton+jets result from Ref. [7]. The profiled results correspond to the fits where the other Wilson coefficient is left free in the fit, otherwise it is set to zero. |
| Summary |
|
A cross section measurement of top quark pair production in association with a photon (${\mathrm{t\bar{t}}\gamma} $), using 138 fb$^{-1}$ of proton-proton collision data at $\sqrt{s}=$ 13 TeV recorded with the CMS detector at the CERN LHC, has been presented. The analysis is performed in a fiducial phase space defined by the requirement of exactly one isolated photon, exactly two oppositely charged leptons, and at least one b jet at particle level, including the ${\mathrm{e^{+}}\mathrm{e^{-}}} $, ${\mathrm{e^{\pm}}\mu^{\mp}} $, and $\mu^{+}\mu^{-}$ channels of the $\mathrm{t\bar{t}}$ decay. The inclusive cross section is extracted with a template fit to the transverse momentum distribution of the reconstructed photon, and is measured to be ${\sigma_\text{fid}} (\mathrm{ pp \to t\bar{t}\gamma })=$ 174.4 $\pm$ 2.5 (stat) $\pm$ 6.1(syst) fb, in good agreement with the standard model prediction of ${\sigma_\text{SM}} (\mathrm{ pp \to t\bar{t}\gamma })= $ 153 $\pm$ 25 fb. Differential cross sections are measured as functions of various kinematic properties of the photon, leptons, and jet, and unfolded to particle level. The comparison to standard model predictions is performed using different parton shower algorithms. The measurement is also interpreted in terms of the standard model effective field theory. Constraints are derived on the Wilson coefficients ${c_{\mathrm{t}\mathrm{Z}}}$ and ${c_{\mathrm{t}\mathrm{Z}}^{\mathrm{I}}}$ describing the modifications of the ${\mathrm{t\bar{t}}\mathrm{Z}}$ and ${\mathrm{t\bar{t}}\gamma} $ interaction vertices. From a combined interpretation of this measurement and another CMS measurement of ${\mathrm{t\bar{t}}\gamma} $ production using the single-lepton final state and the same data set, the best limits on these Wilson coefficients to date are derived. |
| References | ||||
| 1 | CDF Collaboration | Evidence for $ \mathrm{t\bar{t}} $ production and measurement of $ \sigma_{\mathrm{t\bar{t}}}/\sigma_{\mathrm{t\bar{t}}} $ | PRD 84 (2011) 031104 | 1106.3970 |
| 2 | ATLAS Collaboration | Observation of top-quark pair production in association with a photon and measurement of the $ \mathrm{t\bar{t}} $ production cross section in $ pp $ collisions at $\sqrt{s} = $ 7 TeV using the ATLAS detector | PRD 91 (2015) 072007 | 1502.00586 |
| 3 | ATLAS Collaboration | Measurement of the $ \mathrm{t\bar{t}} $ production cross section in proton-proton collisions at $\sqrt{s} = $ 8 TeV with the ATLAS detector | JHEP 11 (2017) 086 | 1706.03046 |
| 4 | CMS Collaboration | Measurement of the semileptonic $ \mathrm{t\bar{t}}+{\gamma} $ production cross section in $ pp $ collisions at $\sqrt{s} = $ 8 TeV | JHEP 10 (2017) 006 | CMS-TOP-14-008 1706.08128 |
| 5 | ATLAS Collaboration | Measurements of inclusive and differential fiducial cross-sections of $ \mathrm{t\bar{t}} $ production in leptonic final states at $\sqrt{s} = $ 13 TeV in ATLAS | EPJC 79 (2019) 382 | 1812.01697 |
| 6 | ATLAS Collaboration | Measurements of inclusive and differential cross-sections of combined $ \mathrm{t\bar{t}} $ and $ \mathrm{tW\gamma} $ production in the $ {\mathrm{e}\mu} $ channel at 13 TeV with the ATLAS detector | JHEP 09 (2020) 049 | 2007.06946 |
| 7 | CMS Collaboration | Measurement of the inclusive and differential $ \mathrm{t\bar{t}} $ cross sections in the single-lepton channel and EFT interpretation at $\sqrt{s} = $ 13 TeV | Submitted to JHEP | CMS-TOP-18-010 2107.01508 |
| 8 | J. A. Aguilar-Saavedra et al. | Interpreting top-quark LHC measurements in the standard-model effective field theory | LHC TOP WG note CERN-LPCC-2018-01 | 1802.07237 |
| 9 | P.-F. Duan et al. | QCD corrections to associated production of $ \mathrm{t\bar{t}} $ at hadron colliders | PRD 80 (2009) 014022 | 0907.1324 |
| 10 | K. Melnikov, M. Schulze, and A. Scharf | QCD corrections to top quark pair production in association with a photon at hadron colliders | PRD 83 (2011) 074013 | 1102.1967 |
| 11 | P.-F. Duan et al. | Next-to-leading order QCD corrections to $ \mathrm{t\bar{t}} $ production at the 7 TeV LHC | Chin. PL28 (2011) 111401 | 1110.2315 |
| 12 | A. Kardos and Z. Tr\'ocs\'anyi | Hadroproduction of $ \mathrm{t\bar{t}} $ pair in association with an isolated photon at NLO accuracy matched with parton shower | JHEP 05 (2015) 090 | 1406.2324 |
| 13 | F. Maltoni, D. Pagani, and I. Tsinikos | Associated production of a top-quark pair with vector bosons at NLO in QCD: impact on $ \mathrm{t\bar{t}H} $ searches at the LHC | JHEP 02 (2016) 113 | 1507.05640 |
| 14 | P.-F. Duan et al. | Electroweak corrections to top quark pair production in association with a hard photon at hadron colliders | PLB 766 (2017) 102 | 1612.00248 |
| 15 | G. Bevilacqua et al. | Precise predictions for $ {\mathrm{t\bar{t}}}/\mathrm{t\bar{t}} $ cross section ratios at the LHC | JHEP 01 (2019) 188 | 1809.08562 |
| 16 | G. Bevilacqua et al. | Off-shell vs on-shell modelling of top quarks in photon associated production | JHEP 03 (2020) 154 | 1912.09999 |
| 17 | U. Baur, A. Juste, L. H. Orr, and D. Rainwater | Probing electroweak top quark couplings at hadron colliders | PRD 71 (2005) 054013 | hep-ph/0412021 |
| 18 | A. Bouzas and F. Larios | Electromagnetic dipole moments of the top quark | PRD 87 (2013) 074015 | 1212.6575 |
| 19 | M. Schulze and Y. Soreq | Pinning down electroweak dipole operators of the top quark | EPJC 76 (2016) 466 | 1603.08911 |
| 20 | W. Buchmuller and D. Wyler | Effective lagrangian analysis of new interactions and flavour conservation | NPB 268 (1986) 621 | |
| 21 | B. Grzadkowski, M. Iskrzyński, M. Misiak, and J. Rosiek | Dimension-six terms in the standard model Lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 22 | O. Bessidskaia Bylund et al. | Probing top quark neutral couplings in the standard model effective field theory at NLO in QCD | JHEP 05 (2016) 052 | 1601.08193 |
| 23 | J. A. Aguilar-Saavedra, E. Álvarez, A. Juste, and F. Rubbo | Shedding light on the $ \mathrm{t\bar{t}} $ asymmetry: the photon handle | JHEP 04 (2014) 188 | 1402.3598 |
| 24 | J. Bergner and M. Schulze | The top quark charge asymmetry in $ \mathrm{t\bar{t}} $ production at the LHC | EPJC 79 (2019) 189 | 1812.10535 |
| 25 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 26 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 27 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 28 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 29 | J. M. Campbell, R. K. Ellis, P. Nason, and E. Re | Top-pair production and decay at NLO matched with parton showers | JHEP 04 (2015) 114 | 1412.1828 |
| 30 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 31 | S. Frixione, G. Ridolfi, and P. Nason | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 32 | J. M. Campbell and R. K. Ellis | MCFM for the Tevatron and the LHC | NPB Proc. Suppl. 205-206 (2010) 10 | 1007.3492 |
| 33 | J. M. Campbell, R. K. Ellis, and C. Williams | Bounding the Higgs width at the LHC using full analytic results for $ {\mathrm{g}\mathrm{g}}\to{\mathrm{e^{-}}\mathrm{e^{+}}\mu^{-}\mu^{+}} $ | JHEP 04 (2014) 060 | 1311.3589 |
| 34 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 35 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 36 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A brief introduction to PYTHIA 8.1 | CPC 178 (2008) 852 | 0710.3820 |
| 37 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 38 | CMS Collaboration | Extraction and validation of a new set of CMS $ {PYTHIA8} $ tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 39 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 40 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 41 | CMS Collaboration | Investigations of the impact of the parton shower tuning in Pythia 8 in the modelling of $ \mathrm{t\bar{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 42 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 43 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 44 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 45 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 46 | M. Aliev et al. | HATHOR: Hadronic top and heavy quarks cross section calculator | CPC 182 (2011) 1034 | 1007.1327 |
| 47 | P. Kant et al. | HATHOR for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | CPC 191 (2015) 74 | 1406.4403 |
| 48 | N. Kidonakis | Theoretical results for electroweak boson and single-top production | in XXIII International Workshop on Deep-Inelastic Scattering (DIS2015) 2015 [PoS (DIS2015) 170] | 1506.04072 |
| 49 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 50 | M. Cacciari, G. P. Salam, and G. Soyez | The catchment area of jets | JHEP 04 (2008) 005 | 0802.1188 |
| 51 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 52 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 53 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 54 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 55 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $\sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 56 | CMS Collaboration | Inclusive and differential cross section measurements of single top quark production in association with a $ \mathrm{Z} boson $ in proton-proton collisions at $\sqrt{s} = $ 13 TeV | CMS-PAS-TOP-20-010 | CMS-PAS-TOP-20-010 |
| 57 | A. Hoecker et al. | TMVA - Toolkit for multivariate data analysis | 2007 | physics/0703039 |
| 58 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in $ pp $ collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 59 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in $ pp $ collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 60 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 61 | CMS Collaboration | Search for $ {\mathrm{W}\mathrm{W}\gamma} $ and $ {\mathrm{W}\mathrm{Z}\gamma} $ production and constraints on anomalous quartic gauge couplings in $ pp $ collisions at $\sqrt{s} = $ 8 TeV | PRD 90 (2014) 032008 | CMS-SMP-13-009 1404.4619 |
| 62 | ATLAS Collaboration | Measurements of $ \mathrm{Z}G $ and $ \mathrm{Z}G\gamma $ production in $ pp $ collisions at $\sqrt{s} = $ 8 TeV with the ATLAS detector | PRD 93 (2016) 112002 | 1604.05232 |
| 63 | CMS Collaboration | Measurement of the production cross section for single top quarks in association with W bosons in proton-proton collisions at $\sqrt{s} = $ 13 TeV | JHEP 10 (2018) 117 | CMS-TOP-17-018 1805.07399 |
| 64 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $\sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 65 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $\sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 66 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $\sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 67 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $\sqrt{s} = $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 68 | ATLAS Collaboration | Measurement of the inelastic proton-proton cross section at $\sqrt{s} = $ 13 TeV with the ATLAS detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 69 | S. Argyropoulos and T. Sjostrand | Effects of color reconnection on $ \mathrm{t\bar{t}} $ final states at the LHC | JHEP 11 (2014) 043 | 1407.6653 |
| 70 | J. Christiansen and P. Skands | String formation beyond leading colour | JHEP 08 (2015) 003 | 1505.01681 |
| 71 | M. Bowler | $ {\mathrm{e^{+}}\mathrm{e^{-}}} $ production of heavy quarks in the string model | Z. Phys. C 11 (1981) 169 | |
| 72 | ATLAS Collaboration, CMS Collaboration, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 73 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 74 | G. Cowan | Statistical data analysis | Clarendon Press, Oxford | |
| 75 | S. Schmitt | TUnfold, an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 76 | J. Bellm et al. | $ HERWIG 7.0/HERWIG++ 3.0 $ release note | EPJC 76 (2016) 196 | 1512.01178 |
| 77 | CMS Collaboration | Development and validation of $ HERWIG 7 $ tunes from CMS underlying-event measurements | EPJC 81 (2021) 312 | CMS-GEN-19-001 2011.03422 |
| 78 | J. A. Aguilar-Saavedra | A minimal set of top anomalous couplings | NPB 812 (2009) 181 | 0811.3842 |
| 79 | C. Zhang and S. Willenbrock | Effective-field-theory approach to top-quark production and decay | PRD 83 (2011) 034006 | 1008.3869 |
| 80 | CMS Collaboration | Measurements of $ \mathrm{t\bar{t}} $ differential cross sections in proton-proton collisions at $\sqrt{s} = $ 13 TeV using events containing two leptons | JHEP 02 (2019) 149 | CMS-TOP-17-014 1811.06625 |
| 81 | CMS Collaboration | Measurement of the top quark polarization and $ \mathrm{t\bar{t}} $ spin correlations using dilepton final states in proton-proton collisions at $\sqrt{s} = $ 13 TeV | PRD 100 (2019) 072002 | CMS-TOP-18-006 1907.03729 |
| 82 | ATLAS and CMS Collaborations | Combination of the $ \mathrm{W} $ boson polarization measurements in top quark decays using ATLAS and CMS data at $\sqrt{s} = $ 8 TeV | JHEP 08 (2020) 051 | 2005.03799 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|