Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-SMP-18-010 | ||
| Measurement of the $ \tau $ lepton polarization in Z boson decays | ||
| CMS Collaboration | ||
| 10 February 2023 | ||
| Abstract: The polarization of $ \tau $ leptons is measured using leptonic and hadronic $ \tau $ lepton decays in $ \mathrm{Z}\rightarrow\tau\tau $ events. A sample of pp collisions of an integrated luminosity of 36.3 fb$ ^{-1} $ at $ \sqrt{s}= $ 13 TeV is used. The measured polarization at the Z pole is $ \mathcal{P}_{\tau}(\mathrm{Z}) = - $0.144 $ \pm $ 0.015 $ = - $0.144 $ \pm $ 0.006 (stat) $ \pm $ 0.014 (syst), in good agreement with the standard model value of the lepton asymmetry parameter of $ A_{\ell} = $ 0.1468 $ \pm $ 0.0003. The $ \tau $ polarization is used to determine the ratio of the vector to axial-vector coupling of the $ \tau $ leptons in the neutral current and thus the weak mixing angle independently of the production process of the Z resonance. The obtained value is $ \sin^2\theta^{\mathrm{eff}}_W = $ 0.2319 $ \pm $ 0.0019 $ = $ 0.2319 $ \pm $ 0.0008 (stat) $ \pm $ 0.0018 (syst). | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
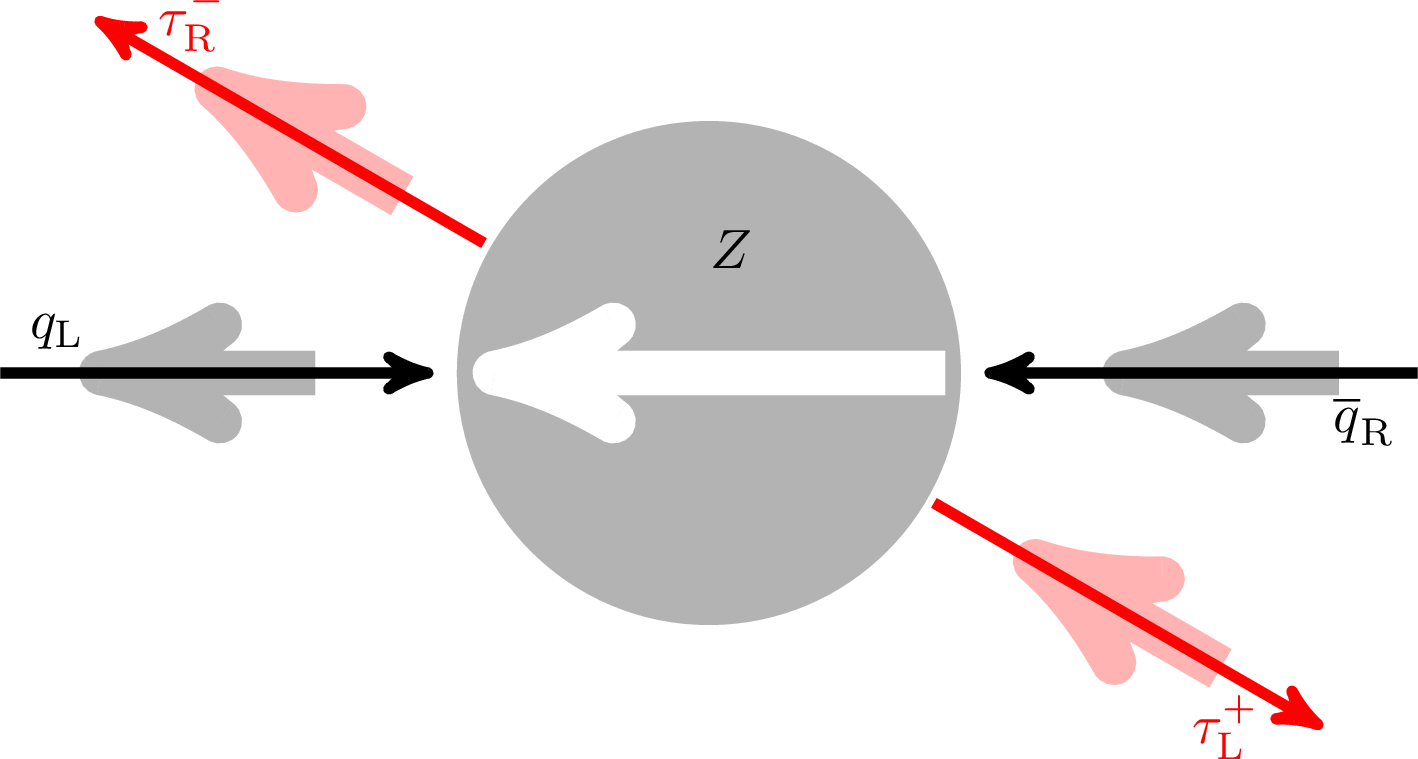
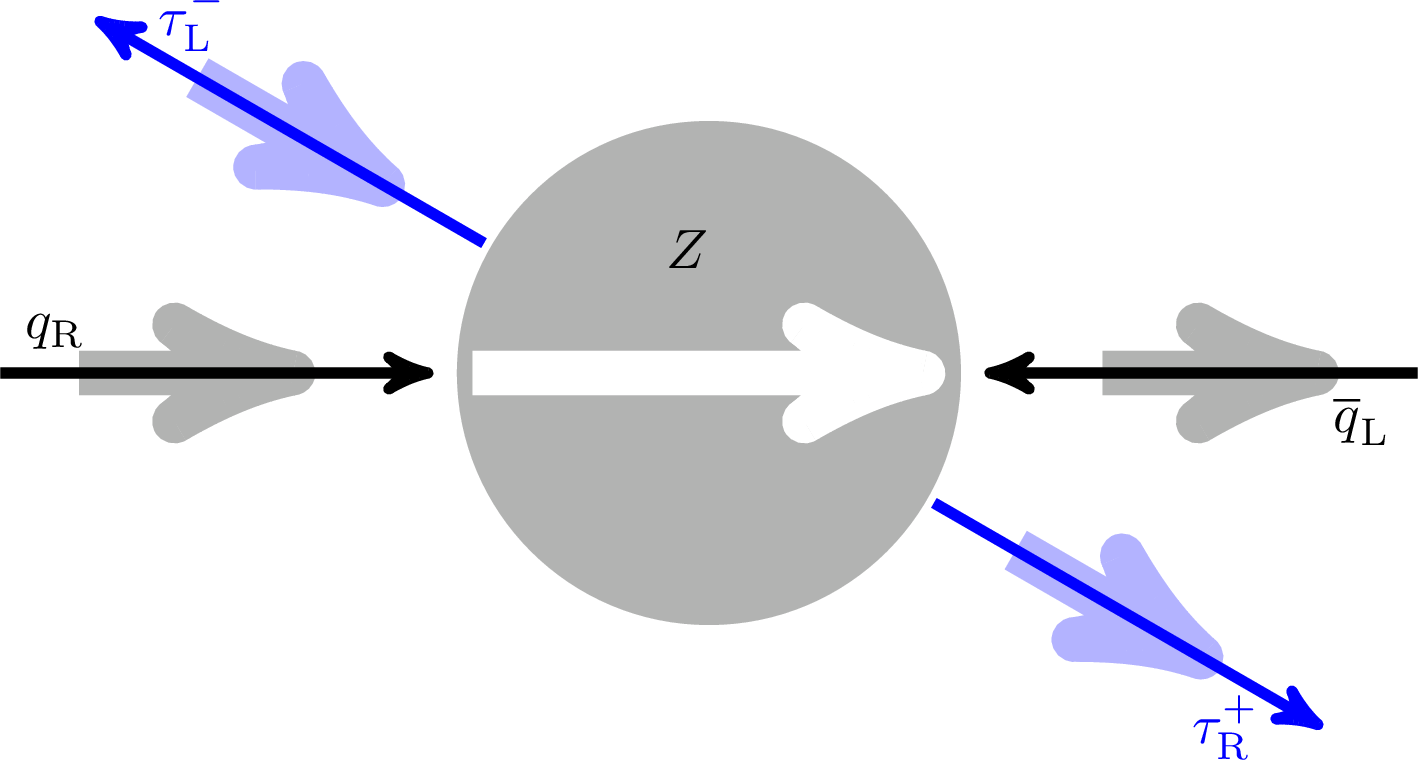
Figure 1:
Four possible helicity states of incoming quarks and outgoing $ \tau $ leptons. Thin arrows depict the direction of movement and the thick arrows show the helicity of the particles. The angle $ \theta_{\tau} $ is the scattering angle of the $ \tau^{-} $ with respect to the quark momentum in the rest frame of the Z boson. |
png pdf |
Figure 1-a:
Four possible helicity states of incoming quarks and outgoing $ \tau $ leptons. Thin arrows depict the direction of movement and the thick arrows show the helicity of the particles. The angle $ \theta_{\tau} $ is the scattering angle of the $ \tau^{-} $ with respect to the quark momentum in the rest frame of the Z boson. |
png pdf |
Figure 1-b:
Four possible helicity states of incoming quarks and outgoing $ \tau $ leptons. Thin arrows depict the direction of movement and the thick arrows show the helicity of the particles. The angle $ \theta_{\tau} $ is the scattering angle of the $ \tau^{-} $ with respect to the quark momentum in the rest frame of the Z boson. |
png pdf |
Figure 1-c:
Four possible helicity states of incoming quarks and outgoing $ \tau $ leptons. Thin arrows depict the direction of movement and the thick arrows show the helicity of the particles. The angle $ \theta_{\tau} $ is the scattering angle of the $ \tau^{-} $ with respect to the quark momentum in the rest frame of the Z boson. |
png pdf |
Figure 1-d:
Four possible helicity states of incoming quarks and outgoing $ \tau $ leptons. Thin arrows depict the direction of movement and the thick arrows show the helicity of the particles. The angle $ \theta_{\tau} $ is the scattering angle of the $ \tau^{-} $ with respect to the quark momentum in the rest frame of the Z boson. |
png pdf |
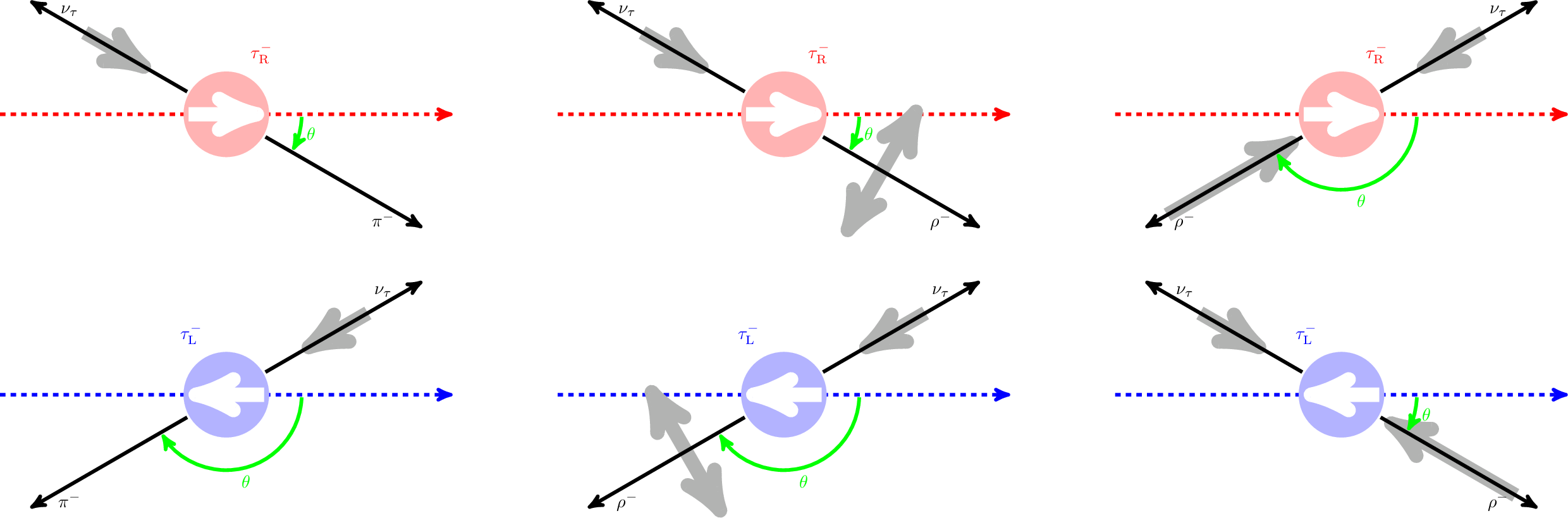
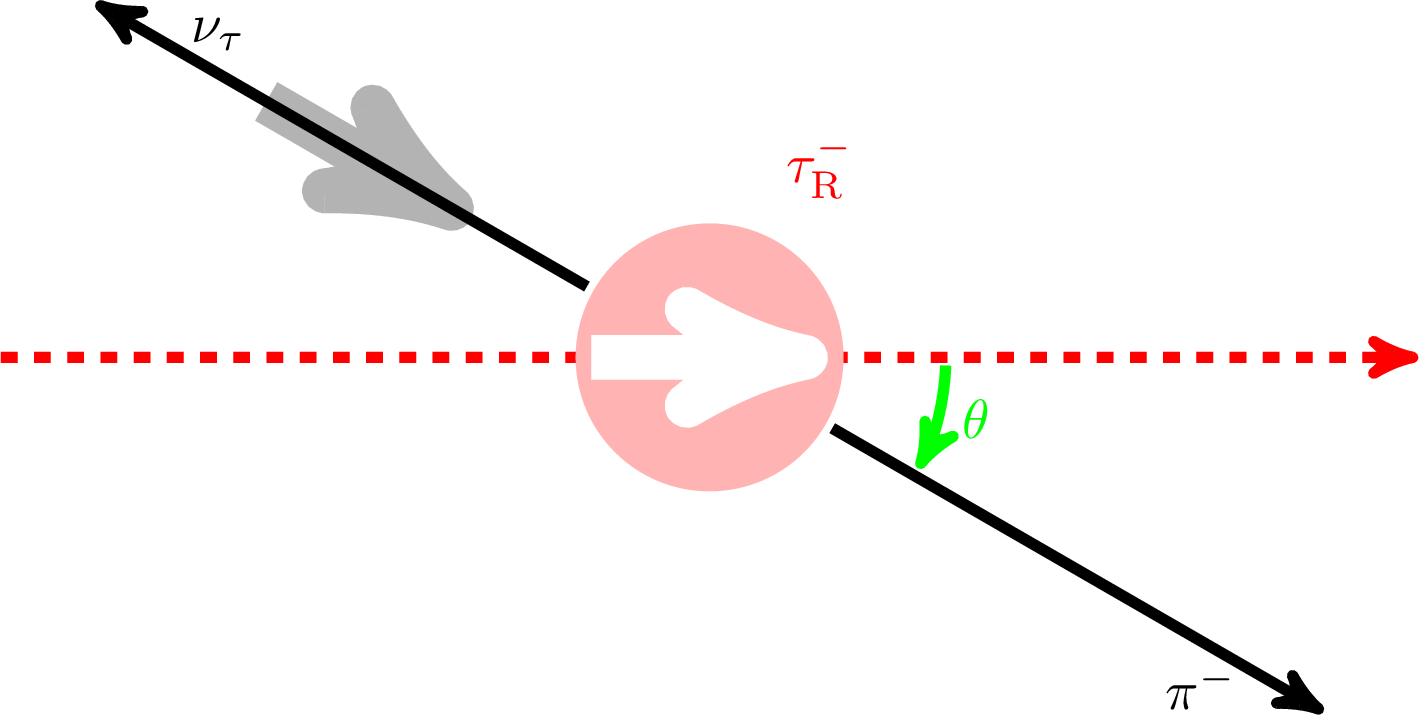
Figure 2:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
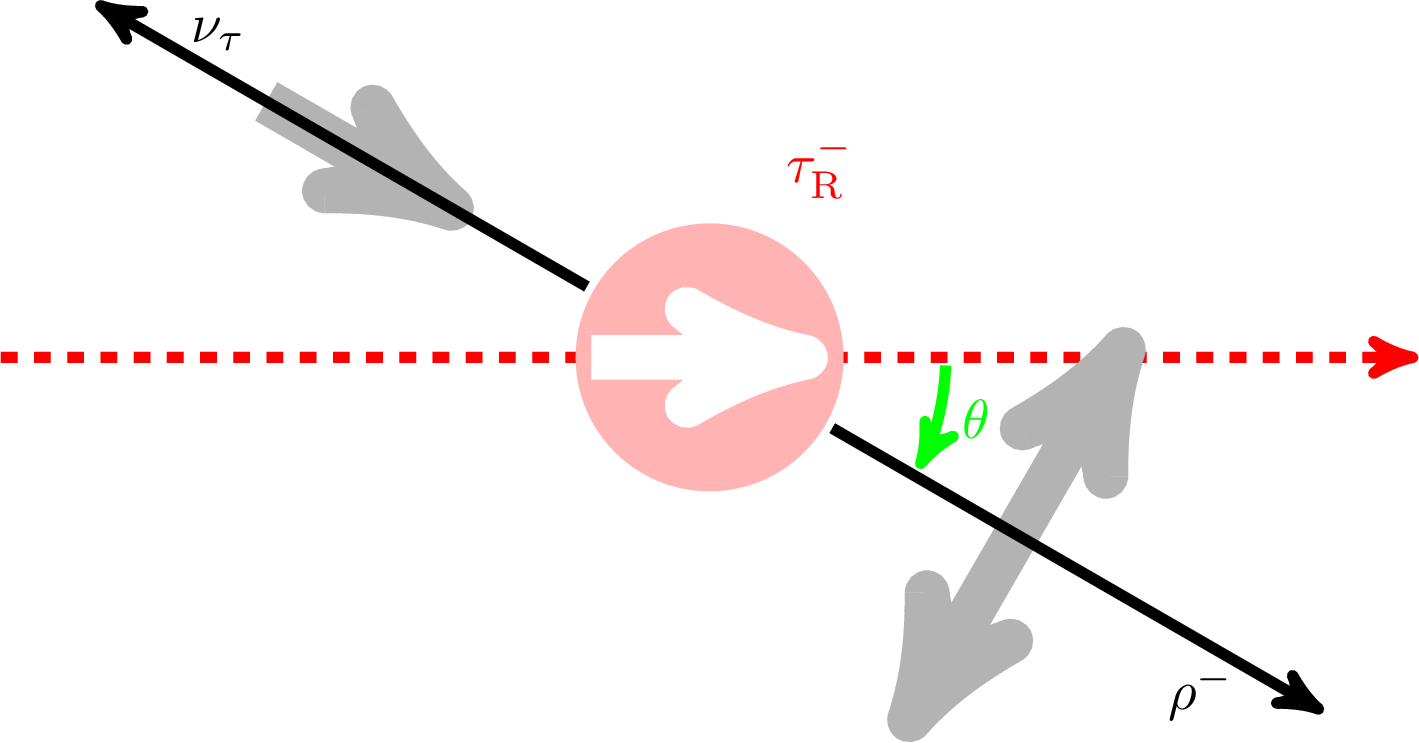
Figure 2-a:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
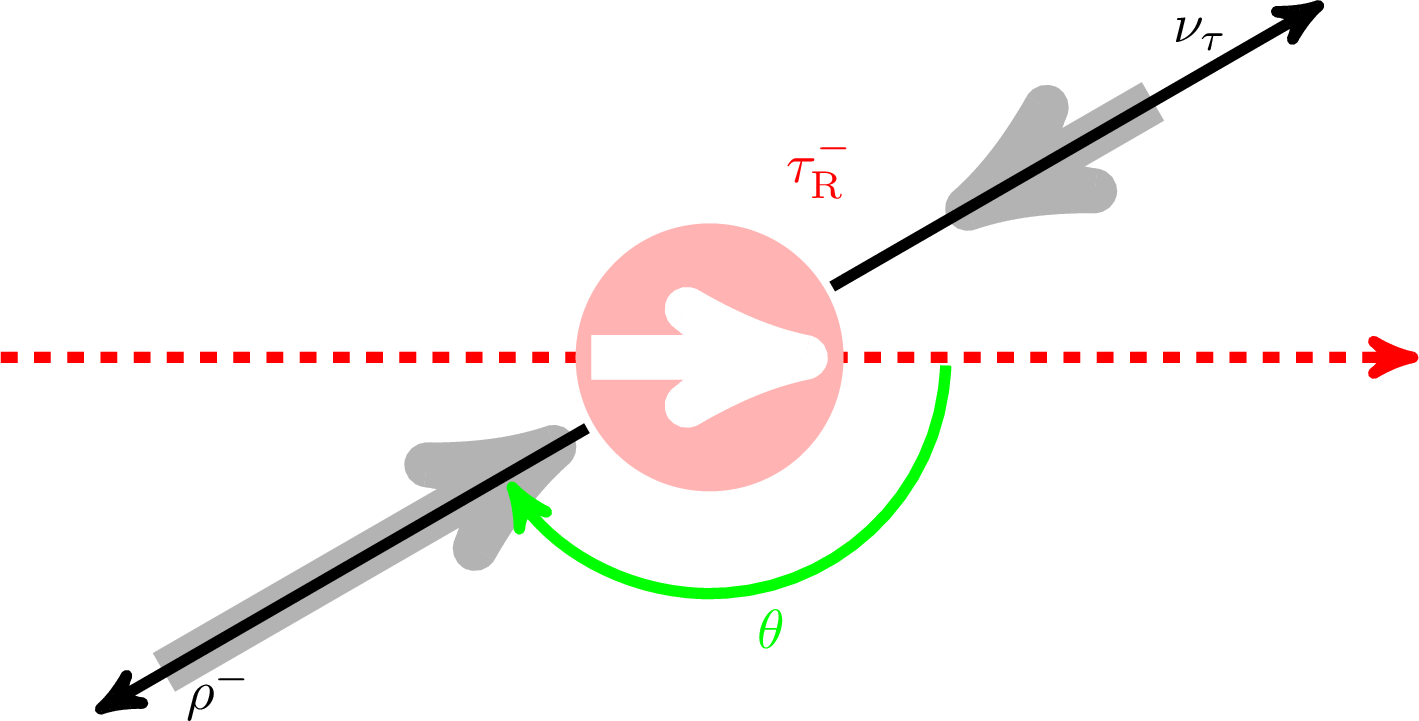
Figure 2-b:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
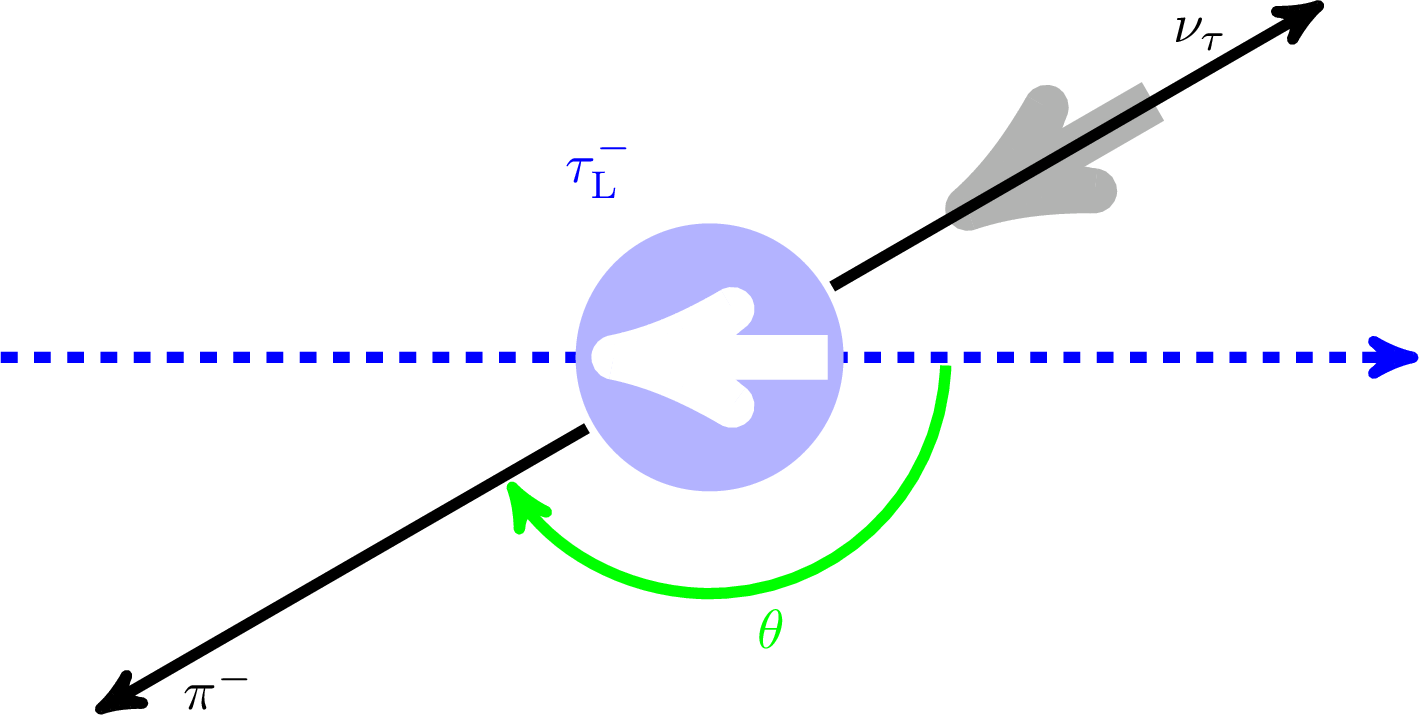
Figure 2-c:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
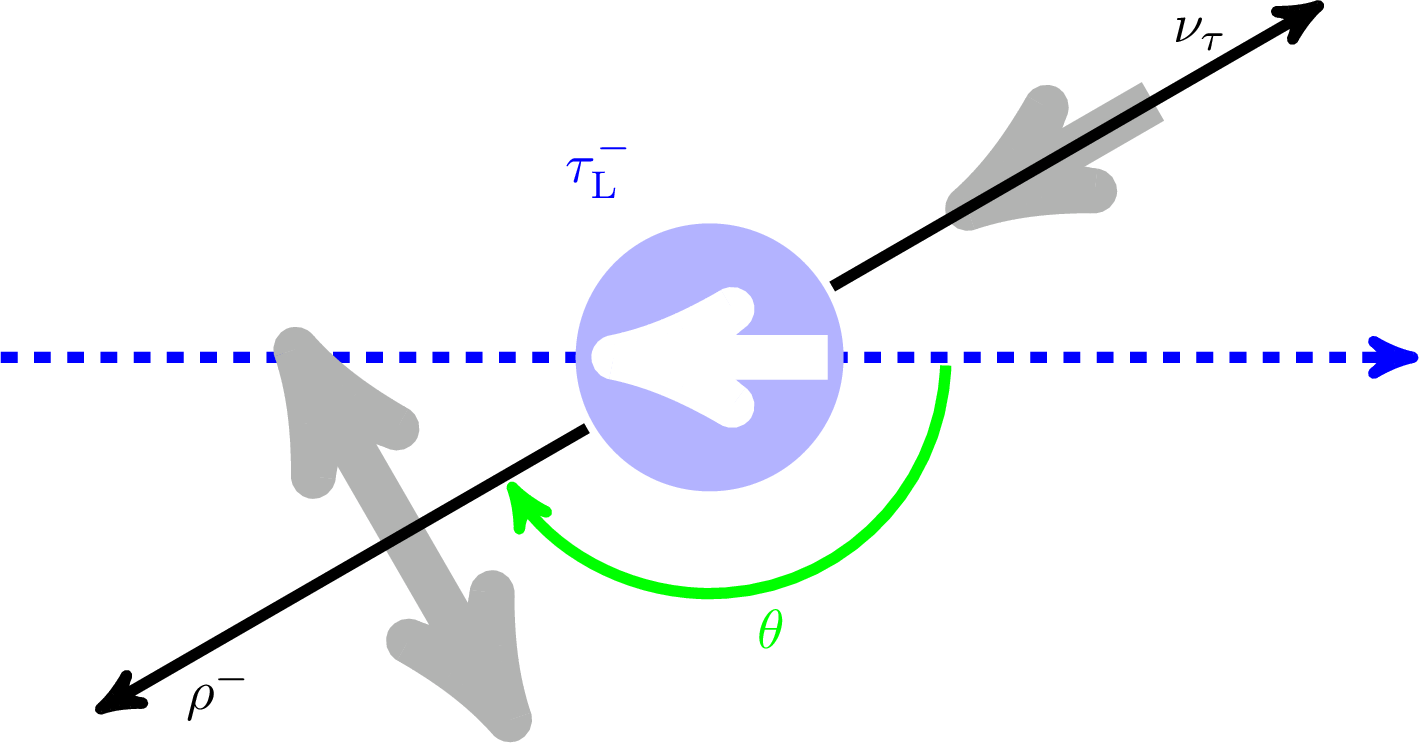
Figure 2-d:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
Figure 2-e:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
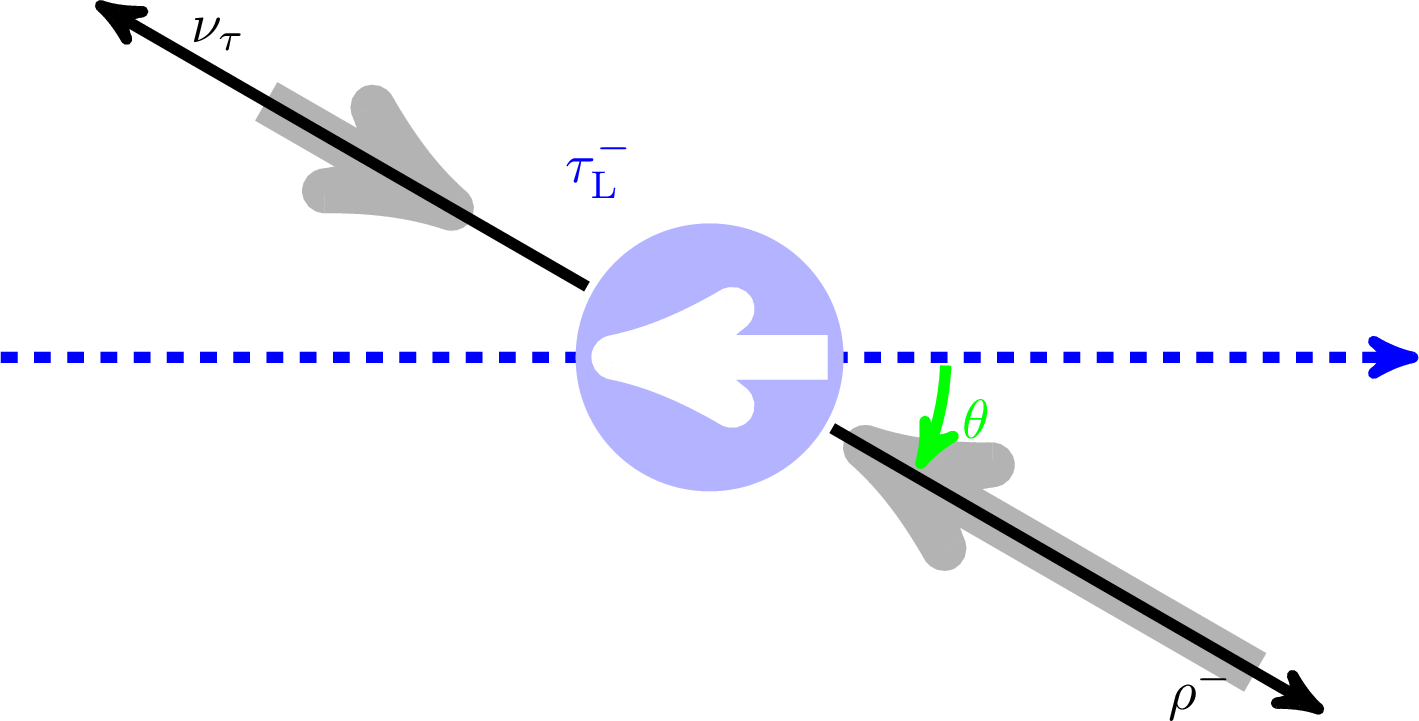
png pdf |
Figure 2-f:
Definition of the angle $ \theta $ in the decays $ \tau \rightarrow h\nu \ \ (h = \pi,\ \ \rho,\ \ a_{1}) $ and $ \tau \rightarrow \mathrm{e}/\mu \nu\overline{\nu} $. Upper row for $ \tau_R $, bottom row for $ \tau_L $. |
png pdf |
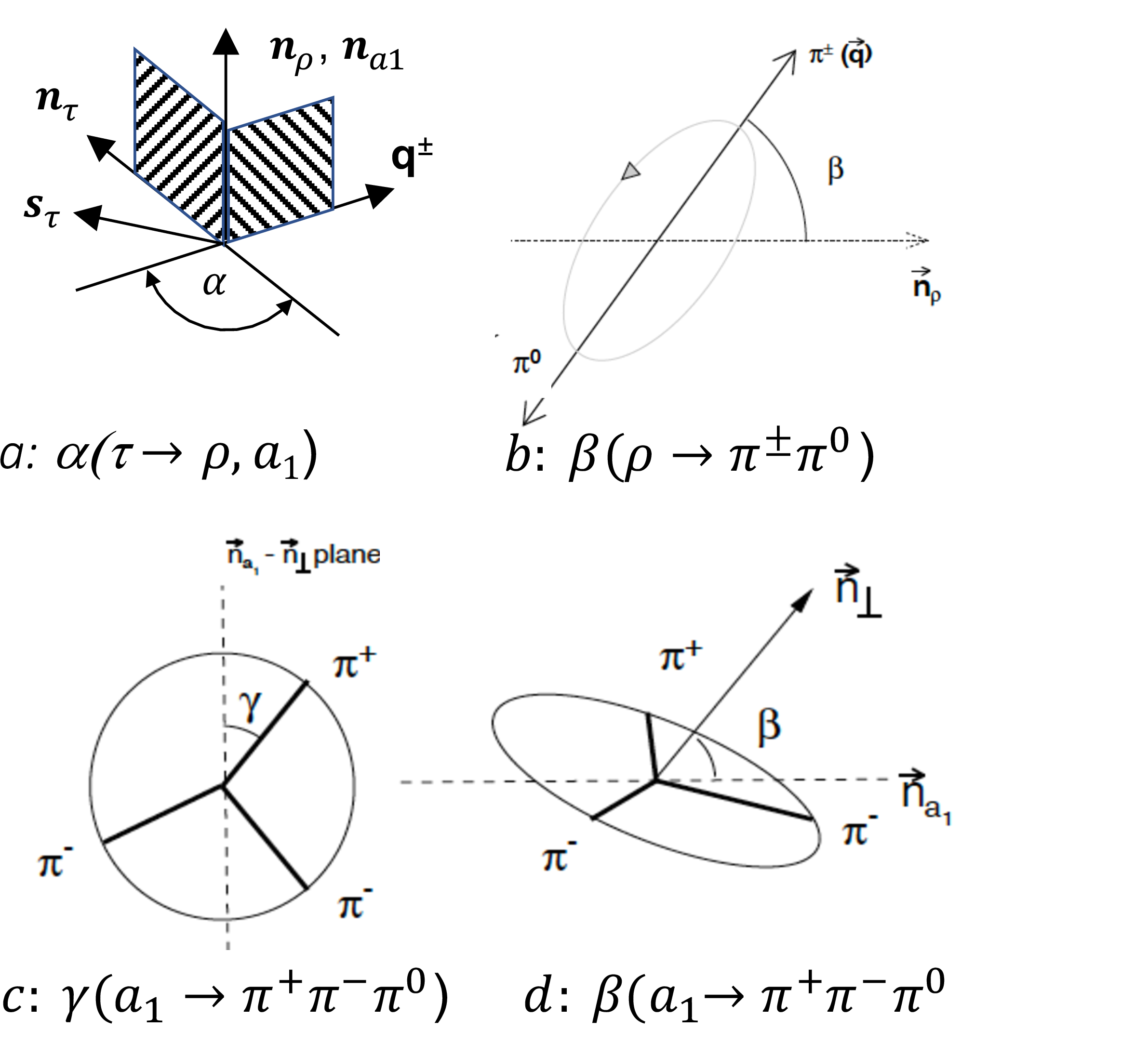
Figure 3:
Definitions of the angles $ \alpha $ in both $ \tau^{-} \rightarrow \rho^{-}\nu $ and $ \tau^{-} \rightarrow a^{-}_1\nu $ (a), the angle $ \beta $ in $ \tau^{-} \rightarrow \rho^{-}\nu $ (b) and for the decay $ \tau^{-} \rightarrow a^{-}_1\nu $ (d) and finally the angle $ \gamma $ (c) for the decay of $ a^{-}_1 \rightarrow \pi^{-}\pi^{+}\pi^{-} $ |
png pdf |
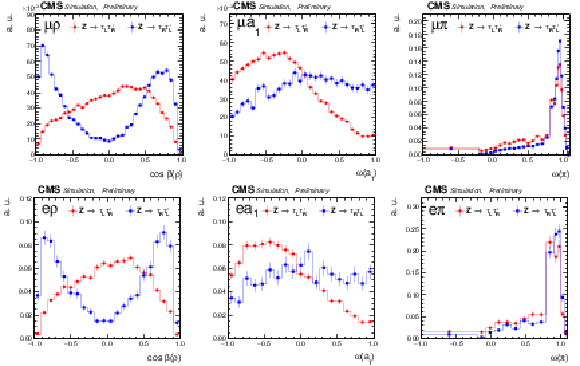
Figure 4:
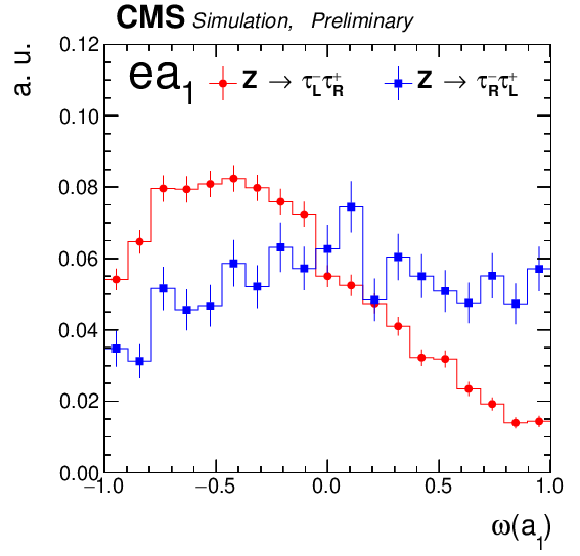
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
png pdf |
Figure 4-a:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
png pdf |
Figure 4-b:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
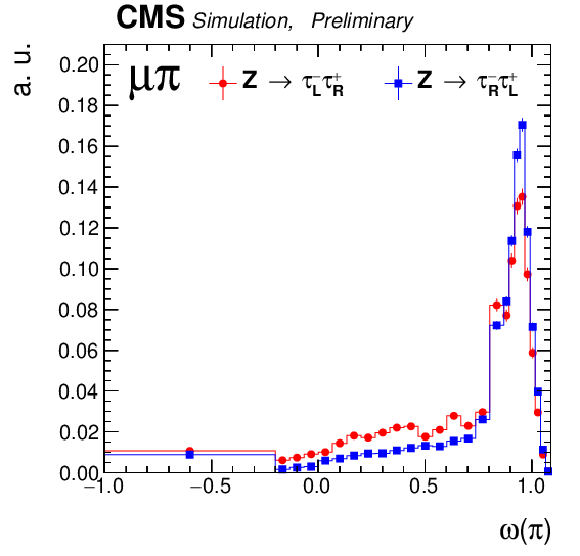
png pdf |
Figure 4-c:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
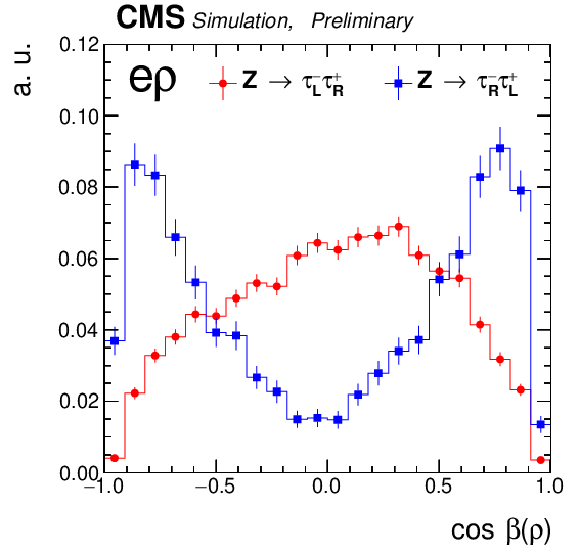
png pdf |
Figure 4-d:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
png pdf |
Figure 4-e:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
png pdf |
Figure 4-f:
Some representative templates for the channels $ \mu+\rho, \mu+a_1, \mu+\pi $ \it (upper row) and $ e+\rho, e+a_1, e+\pi $ \it (lower row), the blue and red lines indicate right and left handed $ \tau $ leptons, respectively. The error bars are statistical only and correspond to the limited MC samples after all selection cuts. |
png pdf |
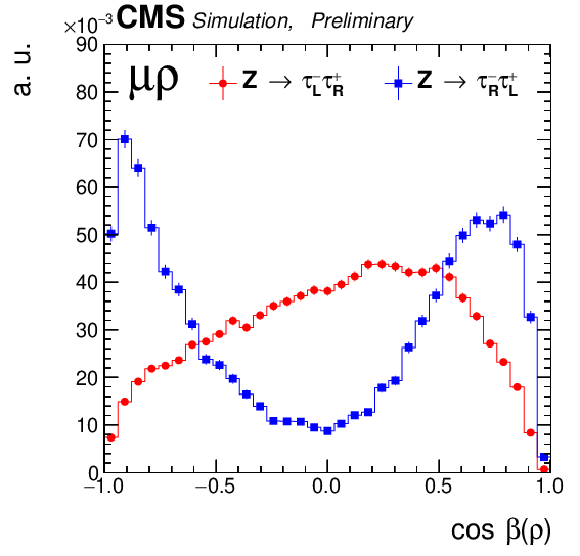
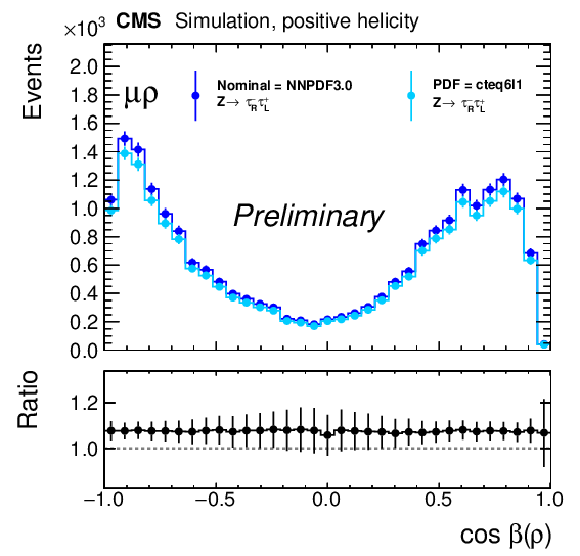
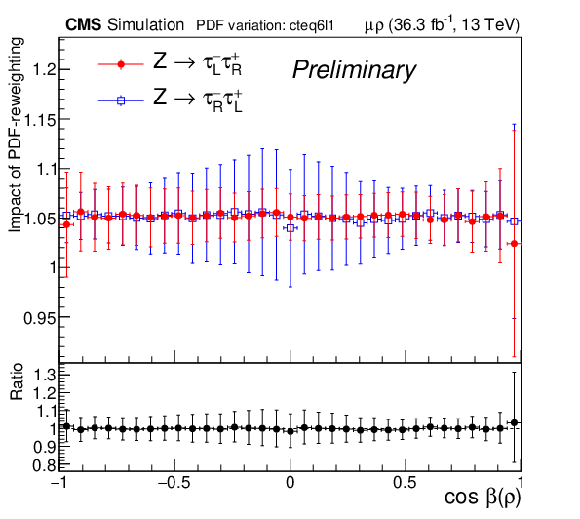
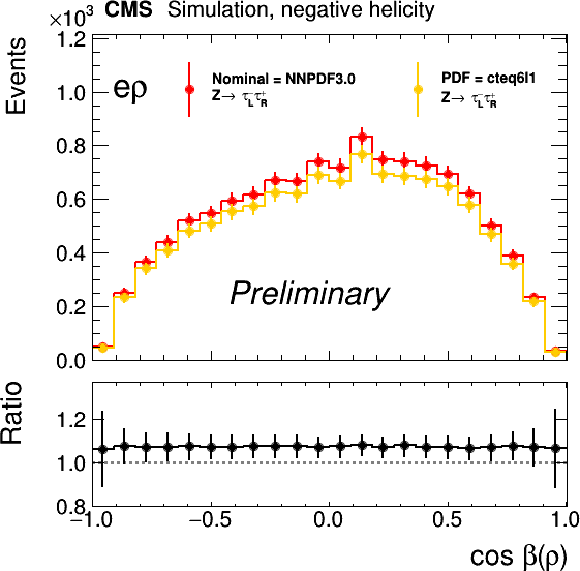
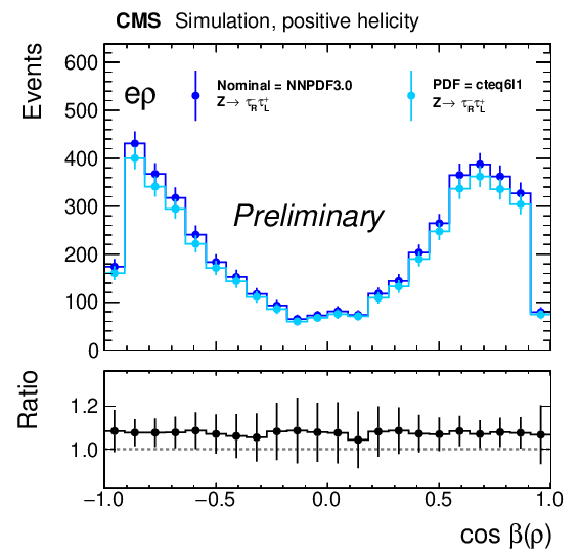
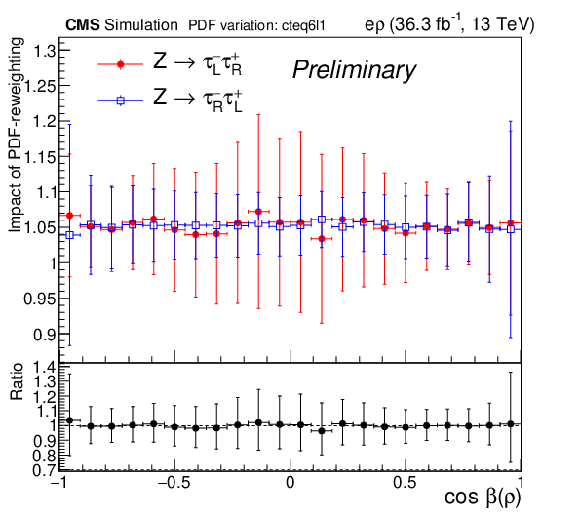
Figure 5:
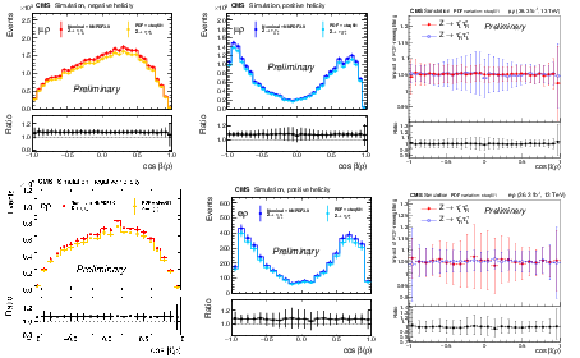
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
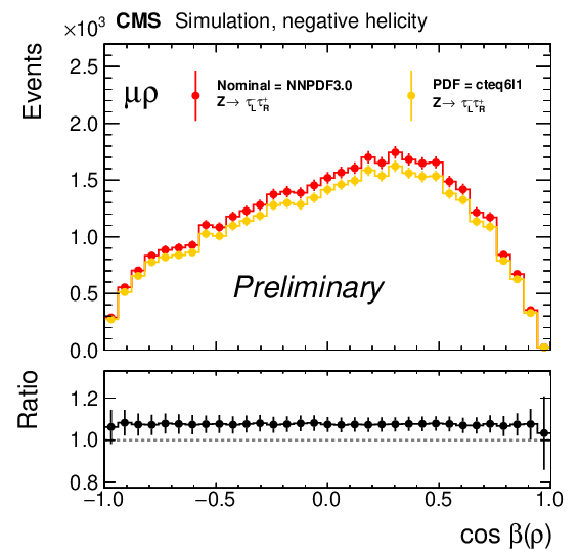
png pdf |
Figure 5-a:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
Figure 5-b:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
Figure 5-c:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
Figure 5-d:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
Figure 5-e:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
Figure 5-f:
Variation of the template for negative (left) and positive (middle) $ \tau $ lepton helicities in the $ \mu+\rho $ and $ e+\rho $ channel under the change of the particle distribution function, here the variation with respect to cteq6l1 parametrization. The plot on the right shows the ratio of the ratios of the changes for negative and positive helicities, which is flat and centered exactly at 1.00 demonstrating that a possible effect on the polarization is much smaller than 1%. |
png pdf |
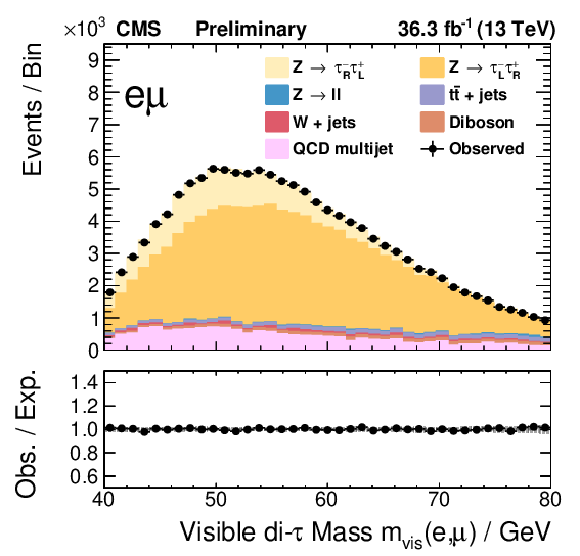
Figure 6:
The final fit of templates to the data for the $ \tau_e\tau_\mu $ channel. |
png pdf |
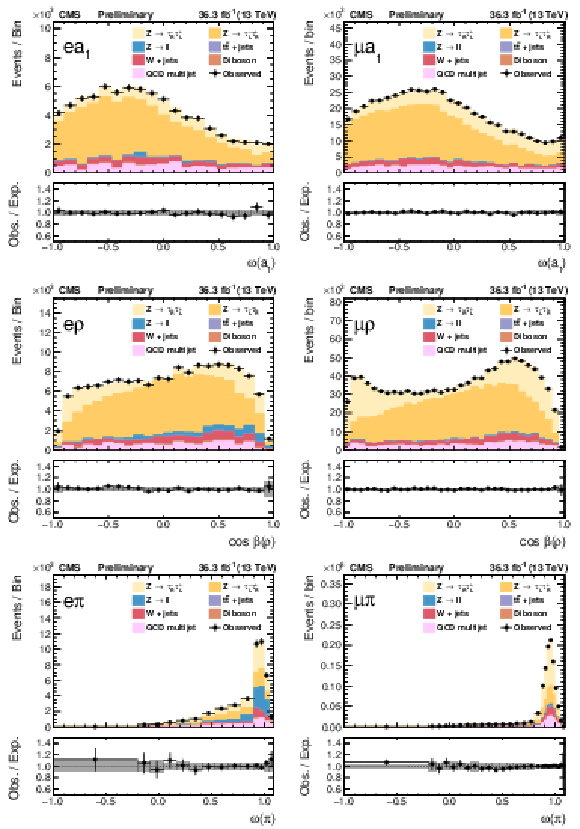
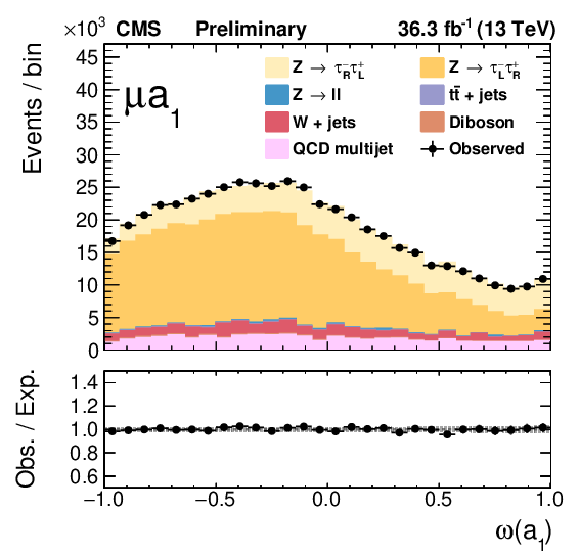
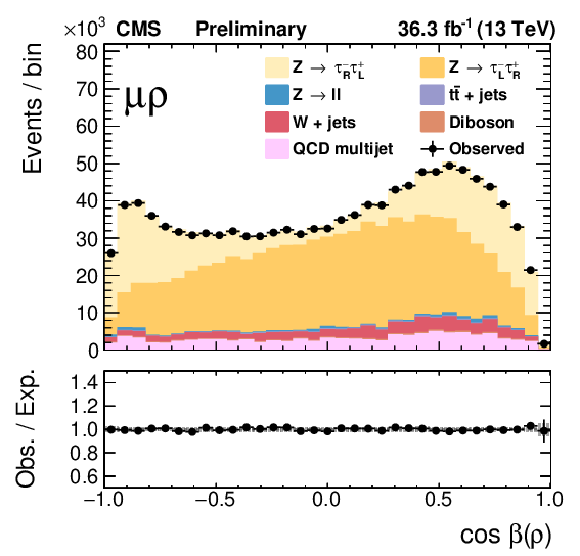
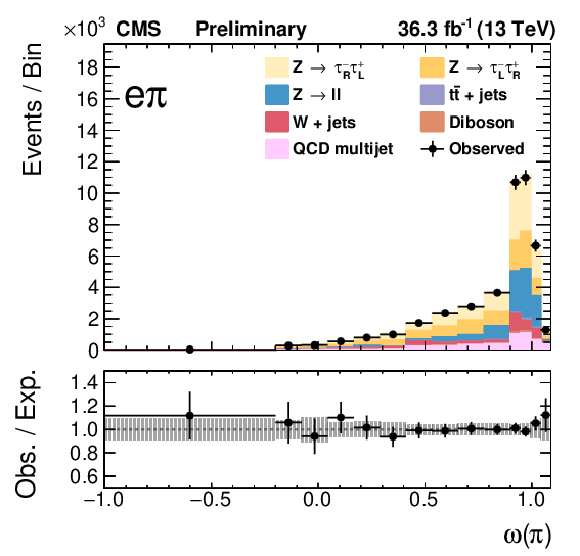
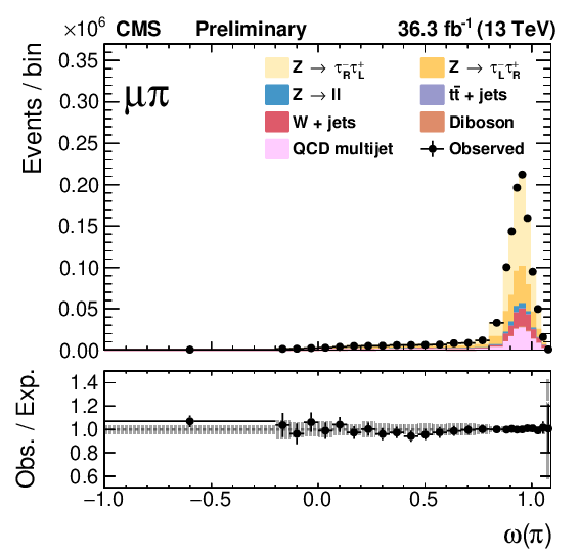
Figure 7:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-a:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-b:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-c:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-d:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-e:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
png pdf |
Figure 7-f:
The final fits of templates to the data for the three $ \tau_e\tau_\mathrm{h} $ (left) and three $ \tau_\mu\tau_\mathrm{h} $ (right) categories. |
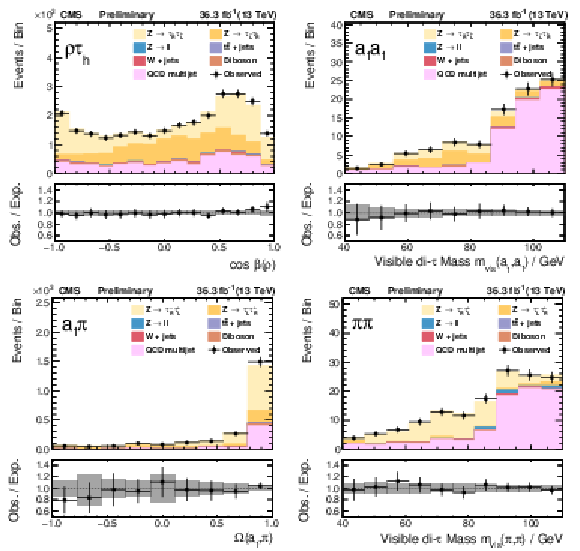
png pdf |
Figure 8:
The final fits of the templates to the data for the $ \tau_\mathrm{h}\tau_\mathrm{h} $ channels. |
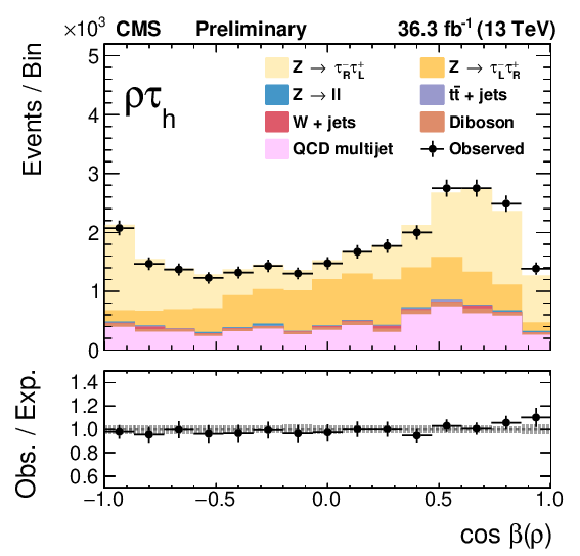
png pdf |
Figure 8-a:
The final fits of the templates to the data for the $ \tau_\mathrm{h}\tau_\mathrm{h} $ channels. |
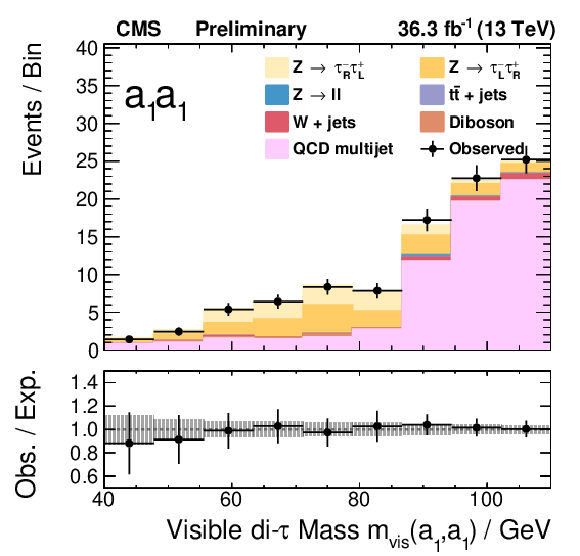
png pdf |
Figure 8-b:
The final fits of the templates to the data for the $ \tau_\mathrm{h}\tau_\mathrm{h} $ channels. |
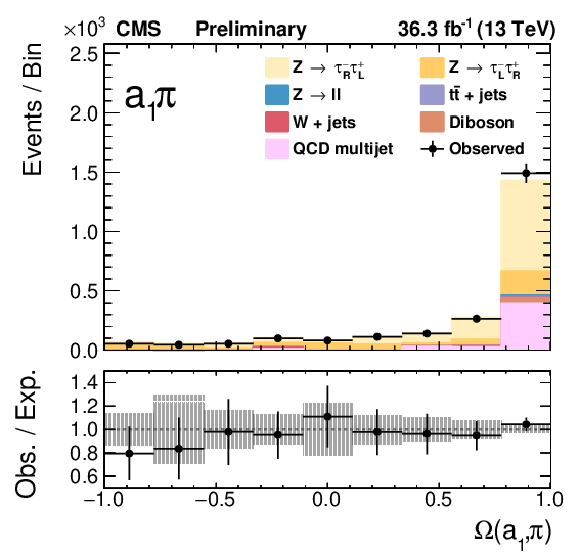
png pdf |
Figure 8-c:
The final fits of the templates to the data for the $ \tau_\mathrm{h}\tau_\mathrm{h} $ channels. |
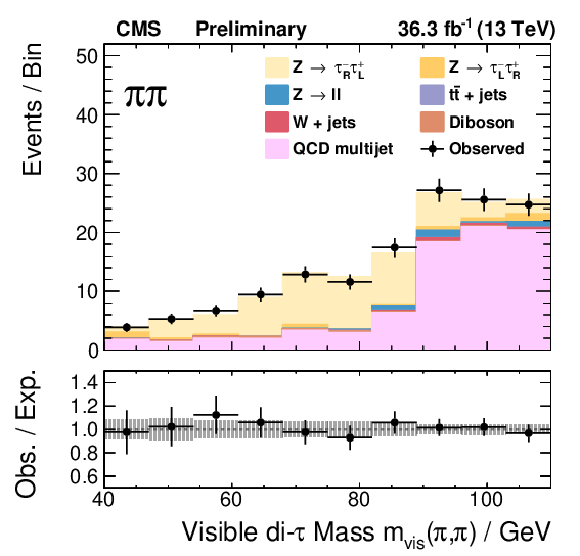
png pdf |
Figure 8-d:
The final fits of the templates to the data for the $ \tau_\mathrm{h}\tau_\mathrm{h} $ channels. |
png pdf |
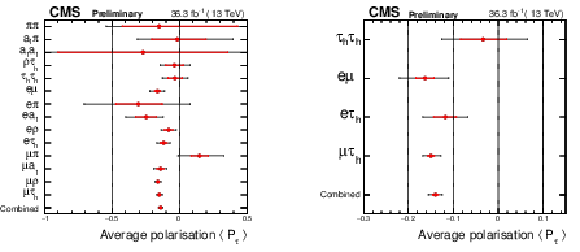
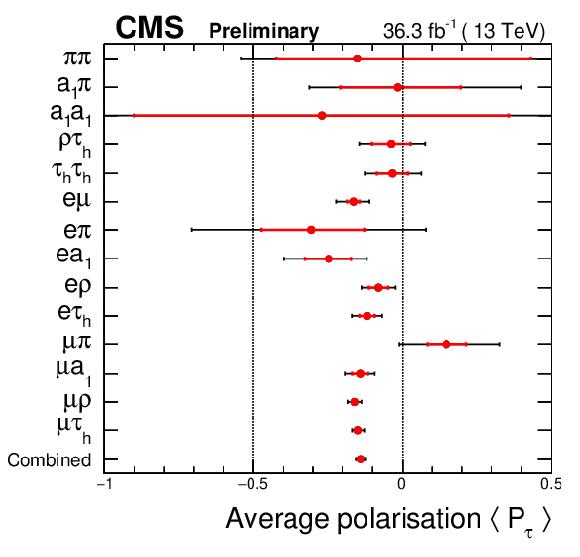
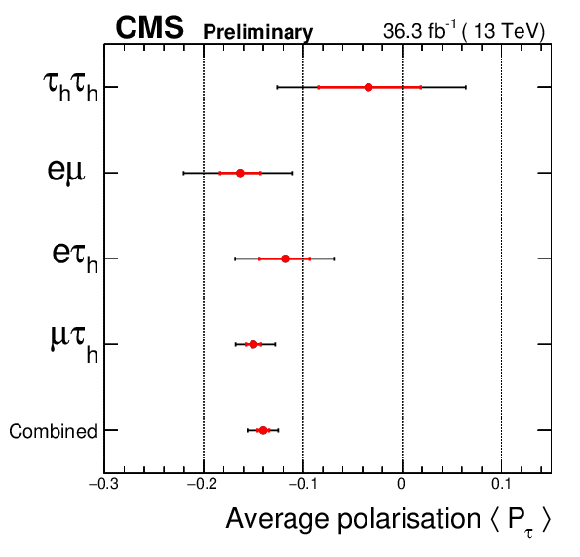
Figure 9:
Fit results for the average $ \tau $ lepton polarization for the 11 event categories on the left and for the 4 channels separately and the combined fit to all channels and categories on the right. The inner error bars represent the statistical uncertainly, the outer bars includes the systematic uncertainty. |
png pdf |
Figure 9-a:
Fit results for the average $ \tau $ lepton polarization for the 11 event categories on the left and for the 4 channels separately and the combined fit to all channels and categories on the right. The inner error bars represent the statistical uncertainly, the outer bars includes the systematic uncertainty. |
png pdf |
Figure 9-b:
Fit results for the average $ \tau $ lepton polarization for the 11 event categories on the left and for the 4 channels separately and the combined fit to all channels and categories on the right. The inner error bars represent the statistical uncertainly, the outer bars includes the systematic uncertainty. |
png pdf |
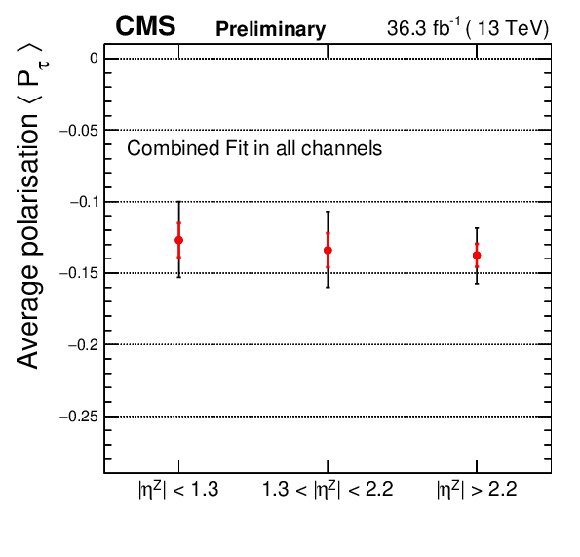
Figure 10:
Final result on the average $ \tau $ polarization in different bins of the Z boson rapidity: $ |\eta | < $ 1.3, 1.3 $ < |\eta | < $ 2.2 and $ |\eta | > $ 2.2. |
png pdf |
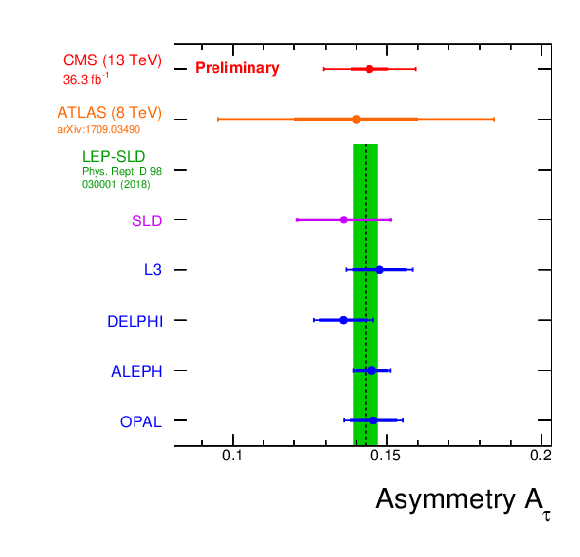
Figure 11:
A comparison of the $ \tau $ asymmetry, $ A_{\tau} $ measured from $ \tau $ polarization at CMS in this work and other experiments. The value of $ A_{\tau} $ for CMS is obtained from the result of Eq. 24 using Eq. 4. The green band indicates the $ \tau $ polarization value obtained by combining the SLD measurement [41] with the measurements performed by L3 [5], DELPHI [42], ALEPH [43], and OPAL [44]. The measurement performed by the ATLAS collaboration at a lower center-of-mass energy of 8 TeV is documented in Ref. [6]. The CMS measurement refers to the result of the analysis presented in this note. The inner error bars represent the statistical uncertainly, the outer bars includes the systematic uncertainty. |
| Tables | |
png pdf |
Table 1:
Selections applied in the data processing of this analysis. |
png pdf |
Table 2:
Final choice of discriminators in the different event categories |
png pdf |
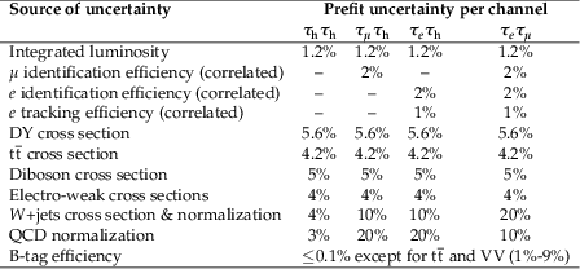
Table 3:
Systematic uncertainties affecting only the normalization of templates. |
png pdf |
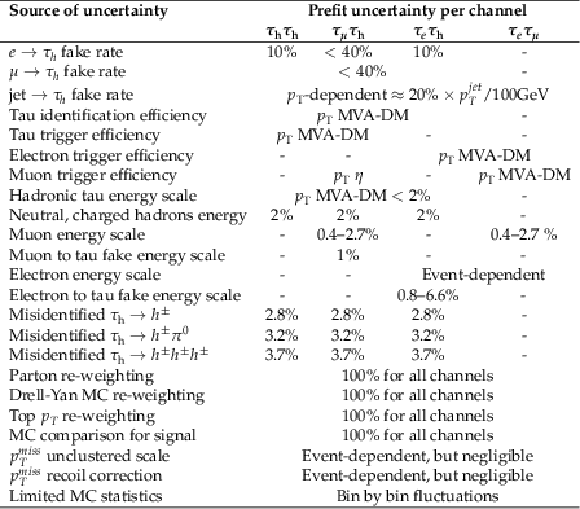
Table 4:
Systematic uncertainties affecting the shapes of templates. The uncertainty magnitudes listed in the Table refer to modifications of the relevant quantity and their dependencies. The comment ''Event-dependent but negligible'' for the $ p_{\mathrm{T}}^\text{miss} $ entries indicate that these corrections are small and vary on an event by event basis due to the event selection. |
| Summary |
| We have used the CMS detector at the LHC to measure the polarization of $ \tau $ leptons in the decay of the Z boson produced in proton-proton collisions at the LHC using nearly all possible decay channels of the $ \tau $ leptons. The measured value for the $ \tau $ polarization, $ \mathcal{P}_{\tau}(Z) = - $0.144 $ \pm $ 0.006 (stat) $ \pm $ 0.014 (syst) $ = - $0.144 $ \pm $ 0.015, is in agreement with values measured by the SLD experiment, at LEP, and by the ATLAS experiment and with the standard model value of the lepton asymmetry parameter $ A_{\ell} $. The uncertainty of the presented measurement is limited by systematic uncertainties. It is more precise than the ATLAS measurement and nearly as precise as single LEP experiments. The measured polarization constrains the effective couplings of $ \tau $ leptons to the Z boson and determines the effective weak mixing angle as $ \sin^{2}\theta_{W}^\mathrm{eff}= $ 0.2319 $ \pm $ 0.0019. This result has a precision of 0.8% and is independent of the production process of the Z boson. This measurement of the $ \tau $ lepton polarization in Z boson decays demonstrates that in the complicated LHC environment the spin of $ \tau $ lepton and spin correlations of $ \tau $ lepton pairs can be determined and be used to explore new physics, for example, for measurements of the CP properties of the Higgs Yukawa coupling to $ \tau $ leptons. |
| References | ||||
| 1 | P. H. Eberhard et al. | The tau polarization measurement at LEP | in LEP Physics Workshop, . . [CERN-EP-89-129], 1989 | |
| 2 | ALEPH Collaboration | Measurement of the tau polarization at LEP | EPJC 20 (2001) 401 | hep-ex/0104038 |
| 3 | DELPHI Collaboration | A precise measurement of the tau polarization at LEP-1 | EPJC 14 (2000) 585 | |
| 4 | OPAL Collaboration | Precision neutral current asymmetry parameter measurements from the tau polarization at LEP | EPJC 21 (2001) 1 | hep-ex/0103045 |
| 5 | L3 Collaboration | Measurement of tau polarization at LEP | PLB 429 (1998) 387 | |
| 6 | ATLAS Collaboration | Measurement of $ \tau $ polarisation in $ Z/\gamma ^{*}\rightarrow \tau \tau $ decays in proton-proton collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | EPJC 78 (2018) 163 | 1709.03490 |
| 7 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 8 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 9 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 10 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 11 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 12 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 13 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 14 | S. Jadach, Z. Was, R. Decker, and J. H. Kuhn | The tau decay library TAUOLA: Version 2.4 | Comput. Phys. Commun. 76 (1993) 361 | |
| 15 | N. Davidson et al. | Universal Interface of TAUOLA Technical and Physics Documentation | Comput. Phys. Commun. 183 (2012) 821 | 1002.0543 |
| 16 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 17 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIM A 506 (2003) 250 | |
| 18 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 19 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: s- and t-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 20 | S. Frixione, P. Nason, and G. Ridolfi | A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 21 | CMS Collaboration | Investigations of the impact of the parton shower tuning in Pythia 8 in the modelling of $ \mathrm{t\overline{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS Physics Analysis Summary, 2016 CMS-PAS-TOP-16-021 |
CMS-PAS-TOP-16-021 |
| 22 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 23 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 24 | CMS Collaboration | Observation of the Higgs boson decay to a pair of $ \tau $ leptons with the CMS detector | PLB 779 (2018) 283 | CMS-HIG-16-043 1708.00373 |
| 25 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 26 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 27 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 28 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 29 | CMS Collaboration | ECAL 2016 refined calibration and run 2 summary plots | CMS Detector Performance Summary CMS-DP-2020-021, 2020 CDS |
|
| 30 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 31 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 32 | CMS Collaboration | Identification of hadronic tau decay channels using multivariate analysis (MVA decay mode) | CMS Detector Performance Summary CMS-DP-2020-041, 2020 CDS |
|
| 33 | CMS Collaboration | Analysis of the $ CP $ structure of the Yukawa coupling between the Higgs boson and $ \tau $ leptons in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | JHEP 06 (2022) 012 | CMS-HIG-20-006 2110.04836 |
| 34 | CMS Collaboration | Identification of hadronic tau lepton decays using a deep neural network | JINST 17 (2022) P07023 | CMS-TAU-20-001 2201.08458 |
| 35 | Y.-S. Tsai | Decay Correlations of Heavy Leptons in $ e^{+}e^{-} \rightarrow \ell^{+}\ell^{-} $ | PRD 4 (1971) 2821 | |
| 36 | M. Davier, L. Duflot, F. Le Diberder, and A. Rouge | The optimal method for the measurement of tau polarization | PLB 306 (1993) 411 | |
| 37 | V. Cherepanov and W. Lohmann | Methods for a measurement of $ \tau $ polarization asymmetry in the decay $ Z\rightarrow \tau\tau $ at LHC and determination of the effective weak mixing angle | 1805.10552 | |
| 38 | CLEO Collaboration | Hadronic structure in the decay $ \tau^{-} \rightarrow \pi^{-}\pi^{0}\pi^{0}\nu_{\tau} $ and the sign of the $ \nu_{\tau} $ helicity | PRD 61 (2000) 012002 | hep-ex/9902022 |
| 39 | L. Bianchini et al. | Reconstruction of the Higgs mass in events with Higgs bosons decaying into a pair of $ \tau $ leptons using matrix element techniques | NIM A 862 (2017) 54 | 1603.05910 |
| 40 | R. Alemany et al. | Tau polarization at the Z peak from the acollinearity between both tau decay products | NPB 379 (1992) 3 | |
| 41 | ALEPH, DELPHI, L3, OPAL, SLD, LEP Electroweak Working Group, SLD Electroweak Group, SLD Heavy Flavour Group Collaboration | Precision electroweak measurements on the $ Z $ resonance | Phys. Rept. 427 (2006) 257 | hep-ex/0509008 |
| 42 | DELPHI Collaboration | A Study of the decays of tau leptons produced on the Z resonance at LEP | Z. Phys. C 55 (1992) 555 | |
| 43 | ALEPH Collaboration | Measurement of the polarization of tau leptons produced in Z decays | PLB 265 (1991) 430 | |
| 44 | OPAL Collaboration | Measurement of branching ratios and tau polarization from $ \tau \rightarrow e $ neutrino anti-neutrino, $ \tau \rightarrow \mu $ neutrino anti-neutrino, and $ \tau \rightarrow \pi (K) $ neutrino decays at LEP | PLB 266 (1991) 201 | |
| 45 | Particle Data Group Collaboration | Review of particle physics | Chin. Phys. C 38 (2014) 090001 | |
| 46 | A. Akhundov, A. Arbuzov, S. Riemann, and T. Riemann | The ZFITTER project | Phys. Part. Nucl. 45 (2014) 529 | 1302.1395 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|