Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-TOP-22-006 ; CERN-EP-2023-124

Search for physics beyond the standard model in top quark production with additional leptons in the context of effective field theory

CMS Collaboration

28 July 2023

JHEP 12 (2023) 068

Abstract: A search for new physics in top quark production with additional final-state leptons is performed using data collected by the CMS experiment in proton-proton collisions at $ \sqrt{s}= $ 13 TeV at the LHC during 2016-2018. The data set corresponds to an integrated luminosity of 138 fb$ ^{-1} $. Using the framework of effective field theory (EFT), potential new physics effects are parametrized in terms of 26 dimension-six EFT operators. The impacts of EFT operators are incorporated through the event-level reweighting of Monte Carlo simulations, which allows for detector-level predictions. The events are divided into several categories based on lepton multiplicity, total lepton charge, jet multiplicity, and b-tagged jet multiplicity. Kinematic variables corresponding to the transverse momentum ($ p_{\mathrm{T}} $) of the leading pair of leptons and/or jets as well as the $ p_{\mathrm{T}} $ of on-shell Z bosons are used to extract the 95% confidence intervals of the 26 Wilson coefficients corresponding to these EFT operators. No significant deviation with respect to the standard model prediction is found.

Links: e-print arXiv:2307.15761 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; Physics Briefing ; CADI line (restricted) ;

Figures
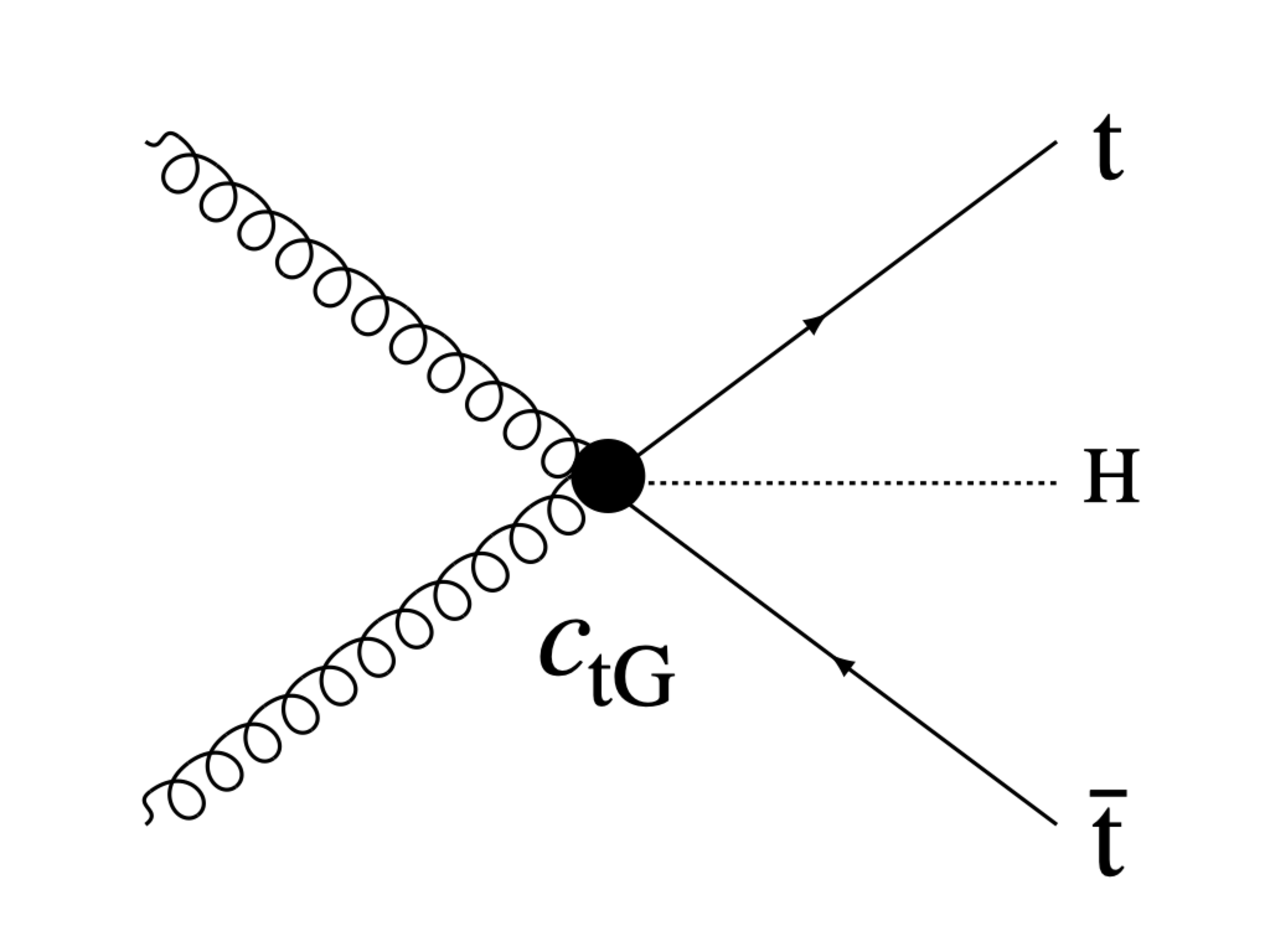
png pdf	Figure 1: Example Feynman diagrams illustrating Wilson coefficients from each of the categories listed in Table 1. From left to right, the diagrams show vertices associated with the $c_{\mathrm{tG}}$, $c_{\mathrm{t\ell}}^{(\ell)}$, $c_{\mathrm{Qq}}^{11}$, and $c_{\mathrm{Qt}}^{1}$.
png pdf	Figure 1-a: Example Feynman diagrams illustrating Wilson coefficients from each of the categories listed in Table 1. From left to right, the diagrams show vertices associated with the $c_{\mathrm{tG}}$, $c_{\mathrm{t\ell}}^{(\ell)}$, $c_{\mathrm{Qq}}^{11}$, and $c_{\mathrm{Qt}}^{1}$.
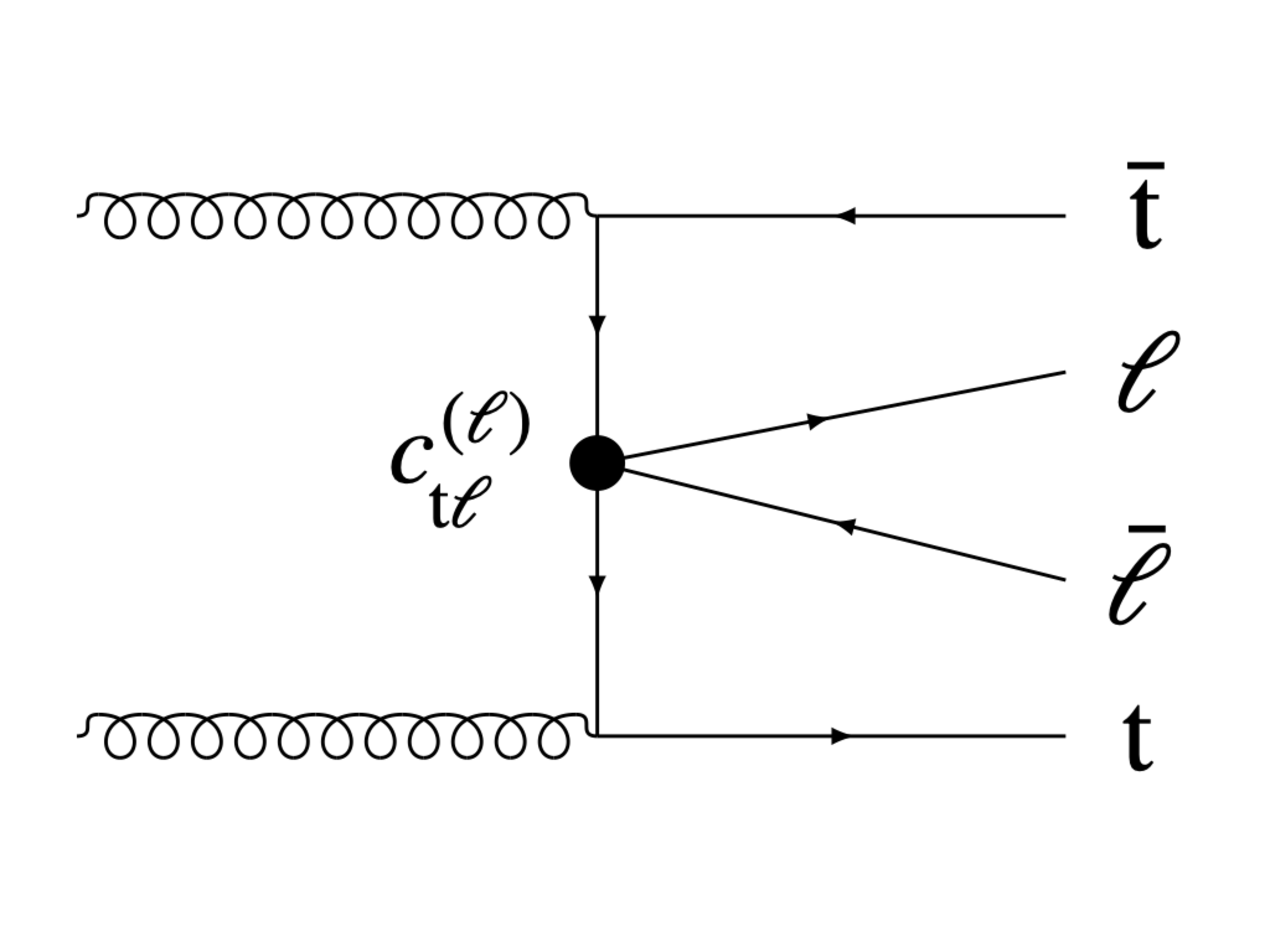
png pdf	Figure 1-b: Example Feynman diagrams illustrating Wilson coefficients from each of the categories listed in Table 1. From left to right, the diagrams show vertices associated with the $c_{\mathrm{tG}}$, $c_{\mathrm{t\ell}}^{(\ell)}$, $c_{\mathrm{Qq}}^{11}$, and $c_{\mathrm{Qt}}^{1}$.
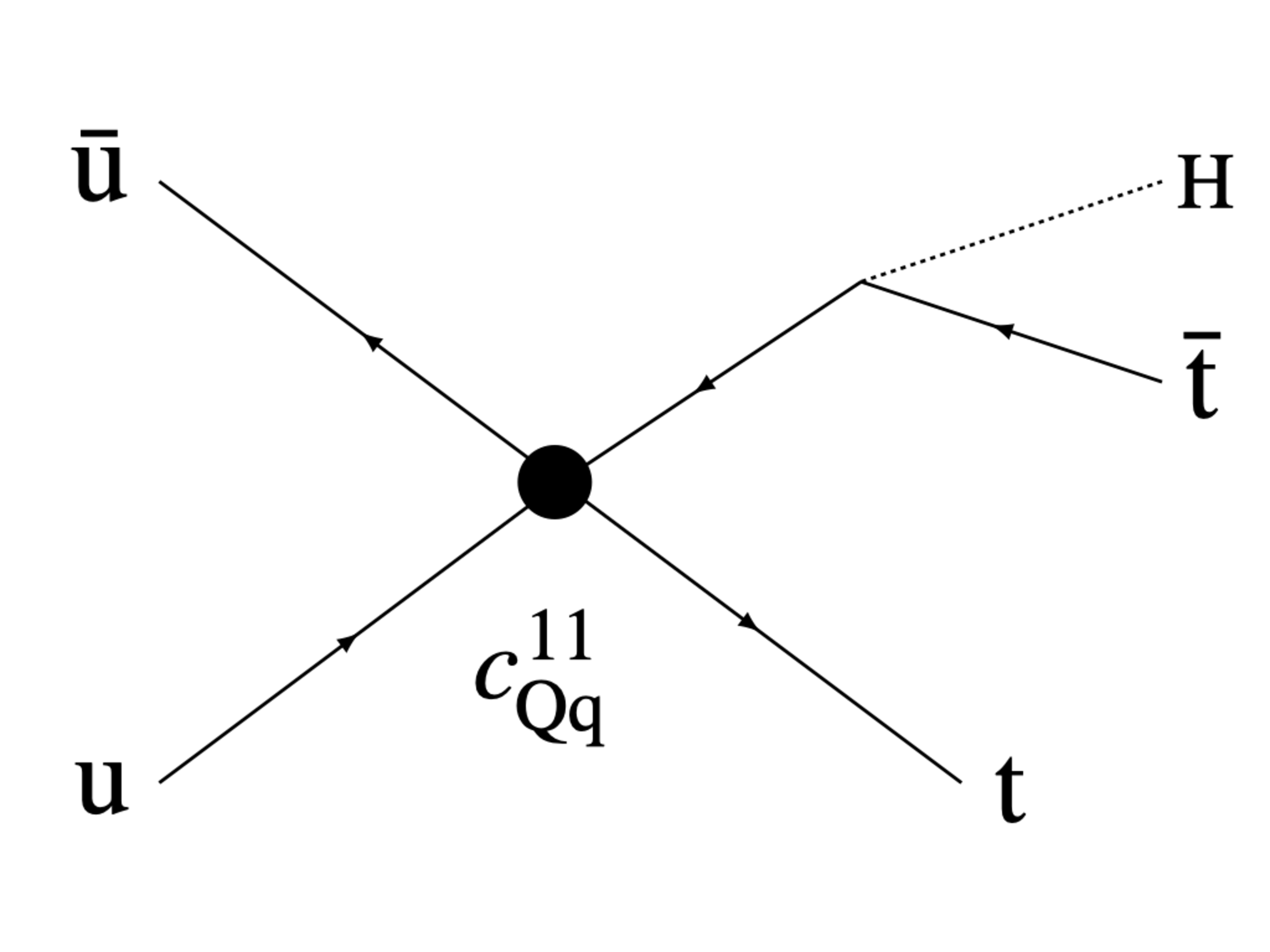
png pdf	Figure 1-c: Example Feynman diagrams illustrating Wilson coefficients from each of the categories listed in Table 1. From left to right, the diagrams show vertices associated with the $c_{\mathrm{tG}}$, $c_{\mathrm{t\ell}}^{(\ell)}$, $c_{\mathrm{Qq}}^{11}$, and $c_{\mathrm{Qt}}^{1}$.
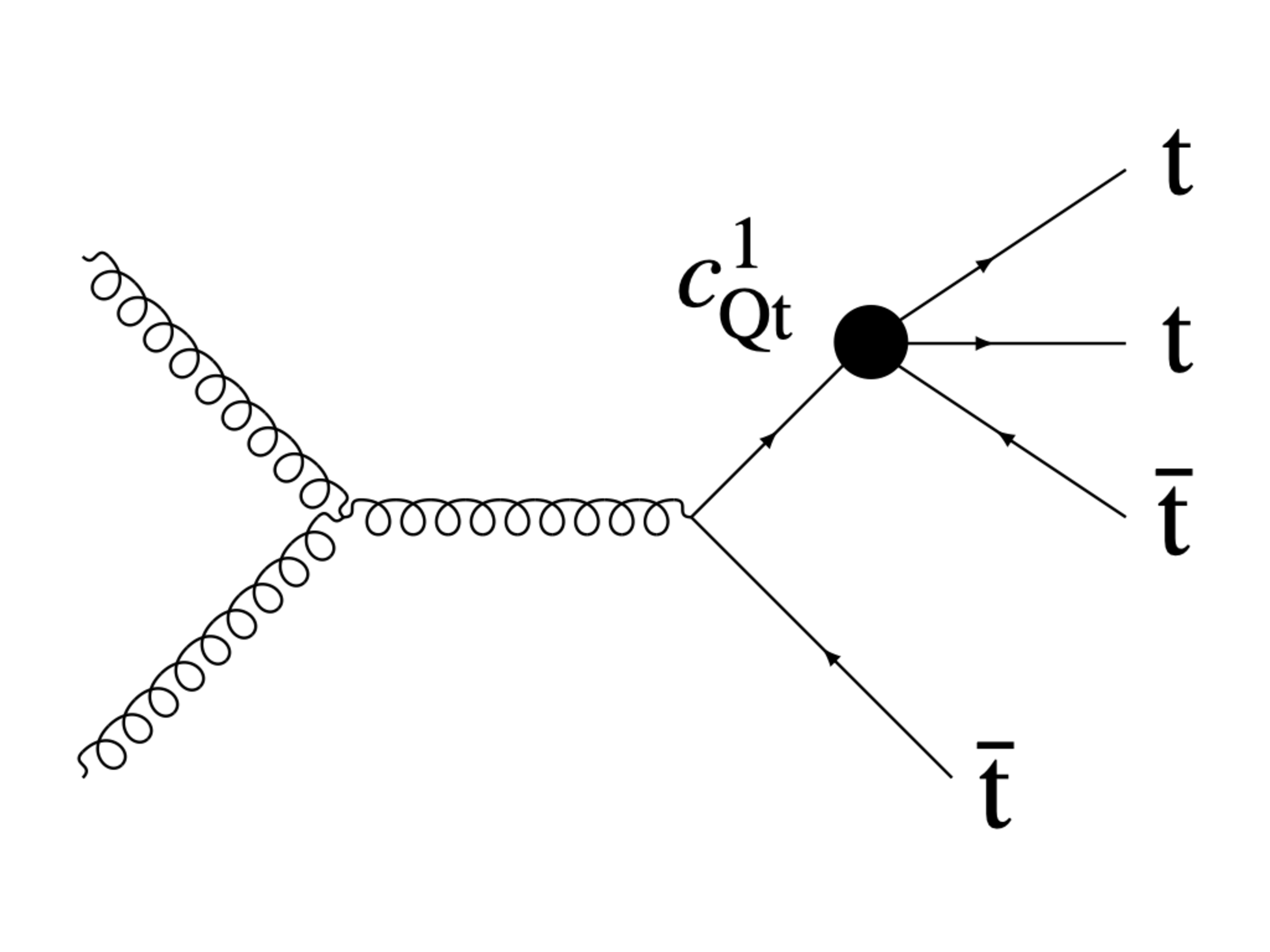
png pdf	Figure 1-d: Example Feynman diagrams illustrating Wilson coefficients from each of the categories listed in Table 1. From left to right, the diagrams show vertices associated with the $c_{\mathrm{tG}}$, $c_{\mathrm{t\ell}}^{(\ell)}$, $c_{\mathrm{Qq}}^{11}$, and $c_{\mathrm{Qt}}^{1}$.
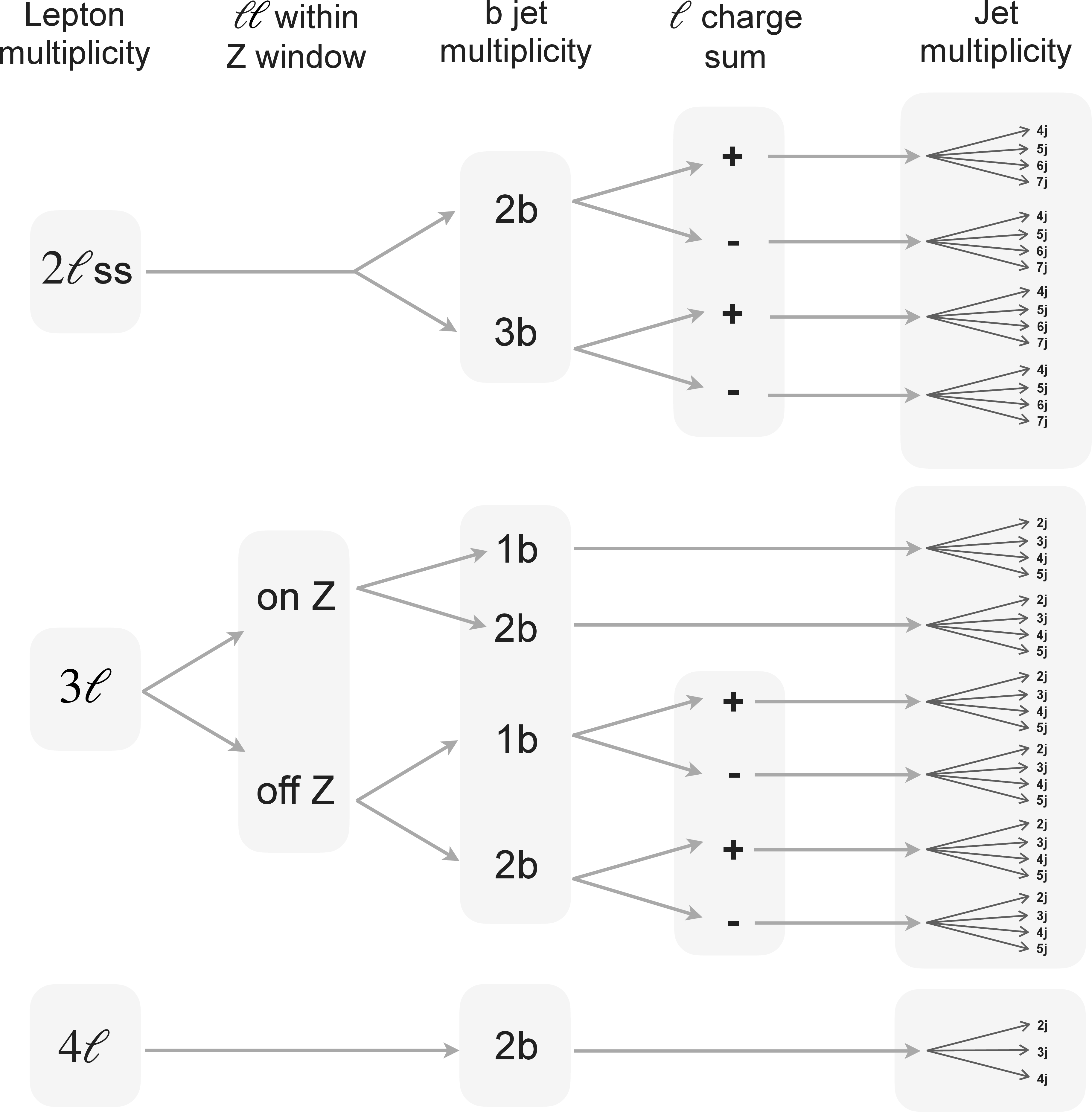
png pdf	Figure 2: Summary of the event selection categorization. The details for the selection requirements are described in Sections 5.1-5.3.
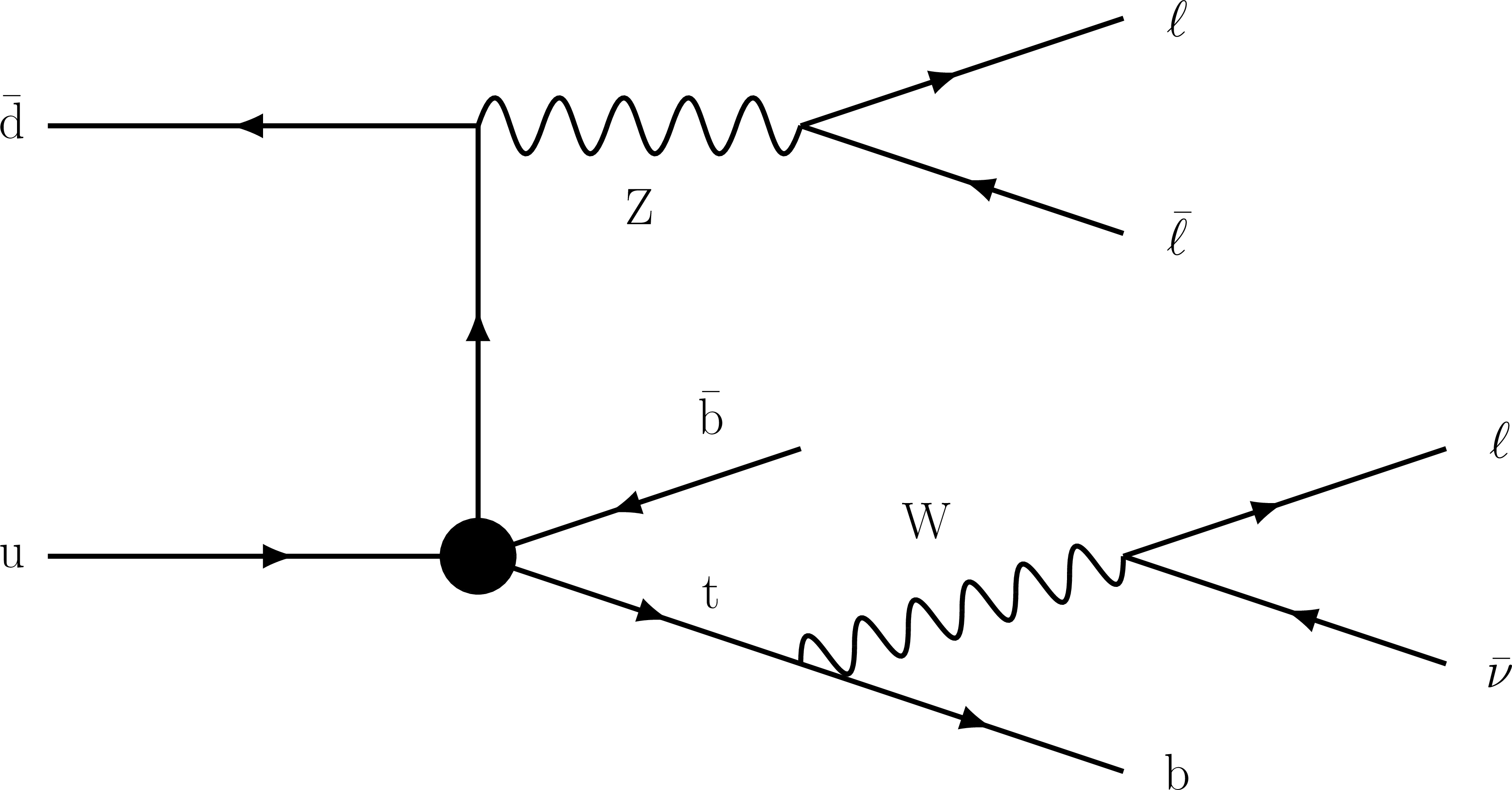
png pdf	Figure 3: Example Feynman diagram illustrating how the $c_{\mathrm{Qq}}^{31}$ and $c_{\mathrm{Qq}}^{38}$ WCs can impact the processes in 3 $ \ell $ categories with two b quarks and an on-shell Z boson. These two WCs are a part of the $ \textrm{2hq2lq} $ group, but unlike the other WCs in this group, these two WCs are associated with operators that have vertices involving a top and bottom quark pair, as pictured in the figure.
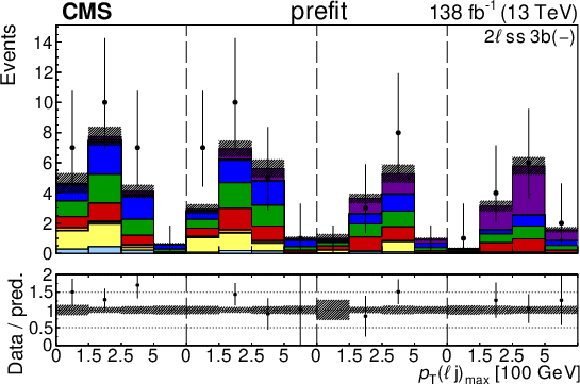
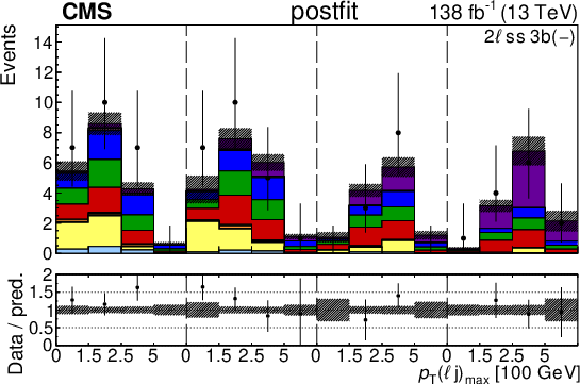
png pdf	Figure 4: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
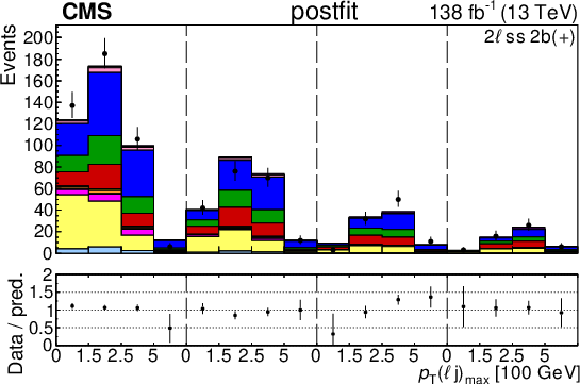
png pdf	Figure 4-a: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
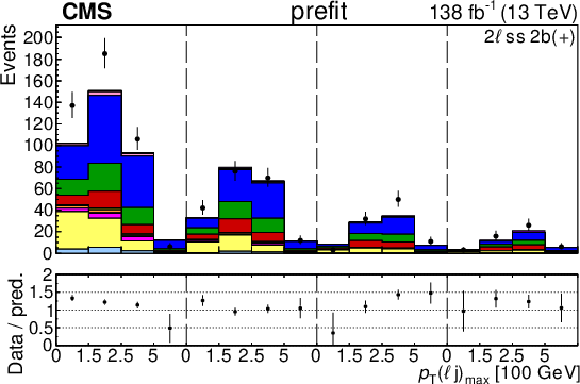
png pdf	Figure 4-b: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
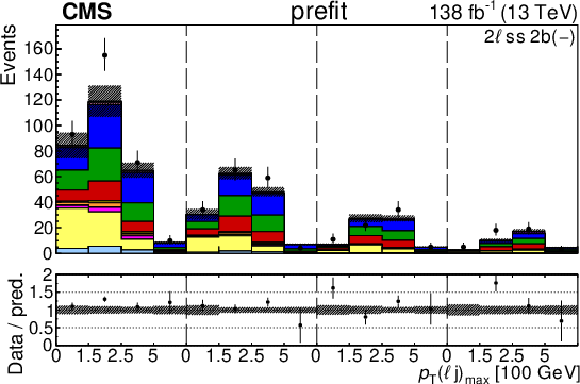
png pdf	Figure 4-c: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
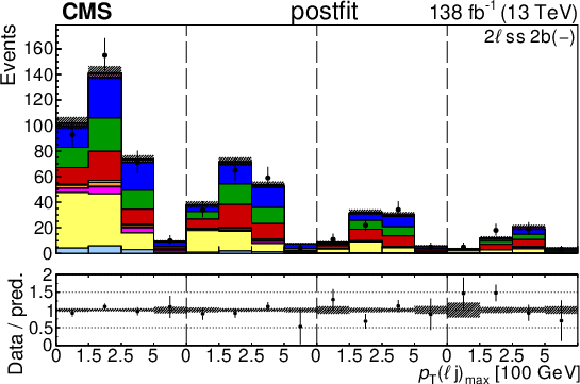
png pdf	Figure 4-d: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
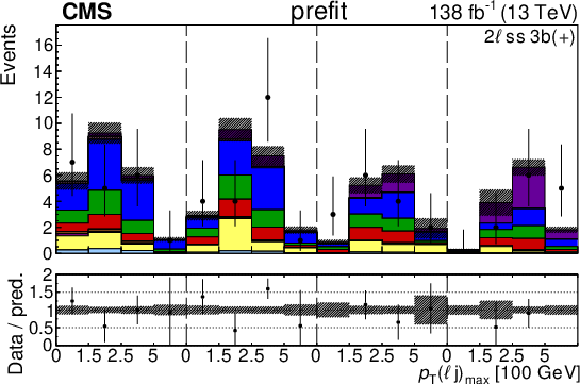
png pdf	Figure 4-e: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
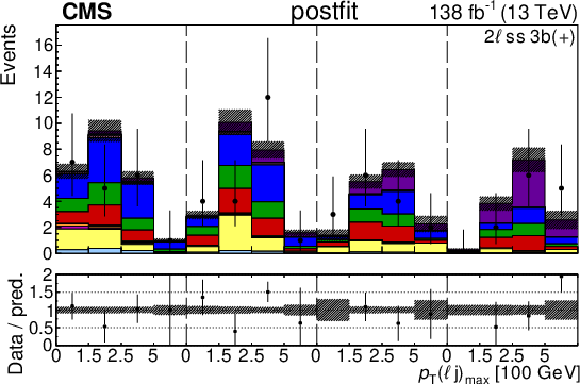
png pdf	Figure 4-f: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
png pdf	Figure 4-g: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
png pdf	Figure 4-h: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
png pdf	Figure 4-i: The categories shown in these plots are 2 $ \ell\text{ss }2\mathrm{b} $ and 2 $ \ell\text{ss }3\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $2\ell\text{ss }2\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $2\ell\text{ss }2\mathrm{b} (+) 4{\mathrm{j}} $, the next four bins are for $2\ell\text{ss }2\mathrm{b} (+) 5{\mathrm{j}} $, etc. The process labeled ``Conv.'' corresponds to the photon conversion background, ``Misid. leptons'' corresponds to misidentified leptons, and ``Charge misid.'' corresponds to leptons with a mismeasured charge.
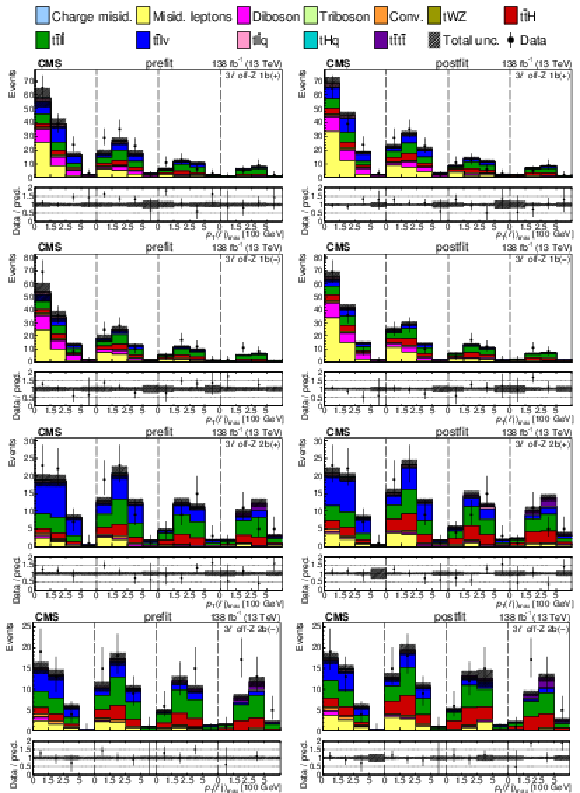
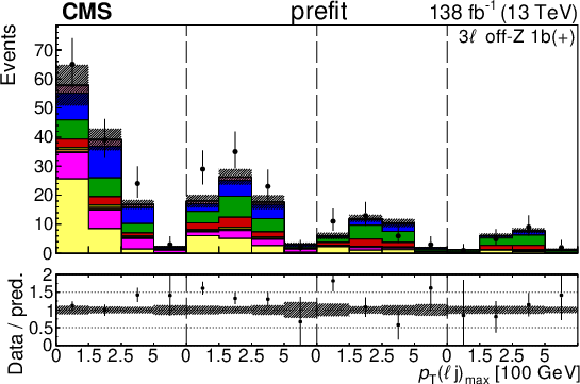
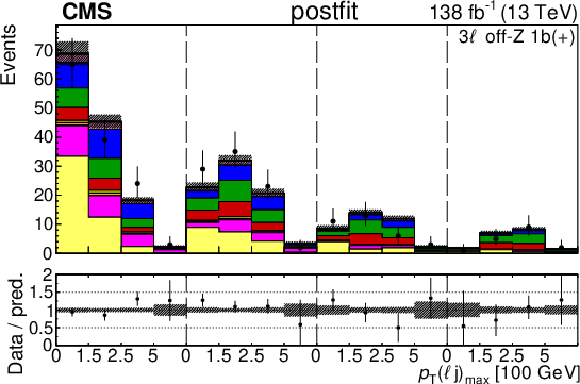
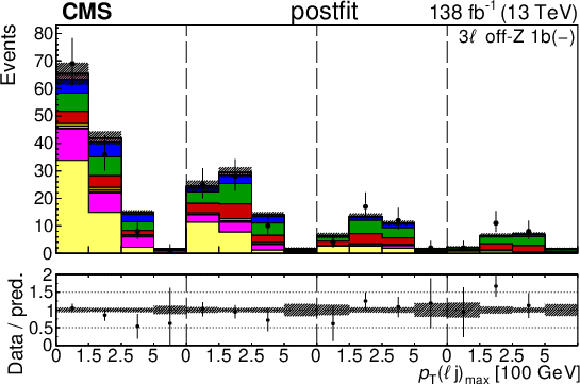
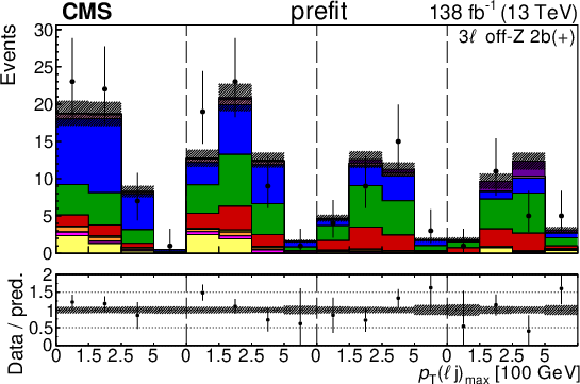
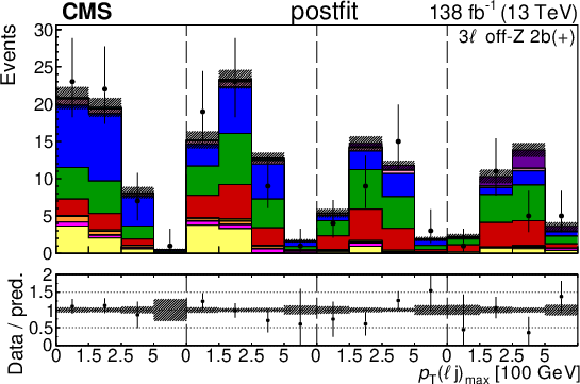
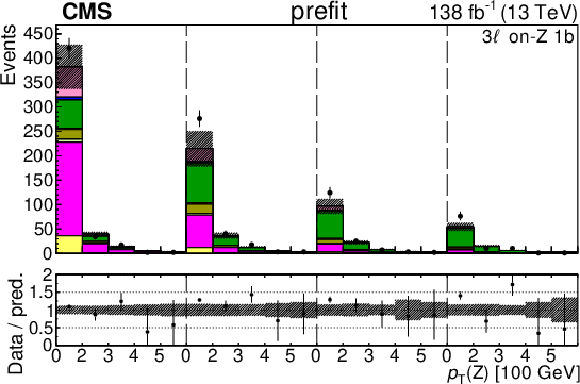
png pdf	Figure 5: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-a: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-b: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-c: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-d: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-e: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-f: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
png pdf	Figure 5-g: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
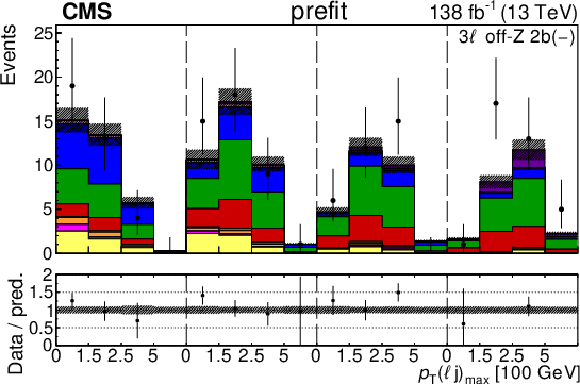
png pdf	Figure 5-h: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
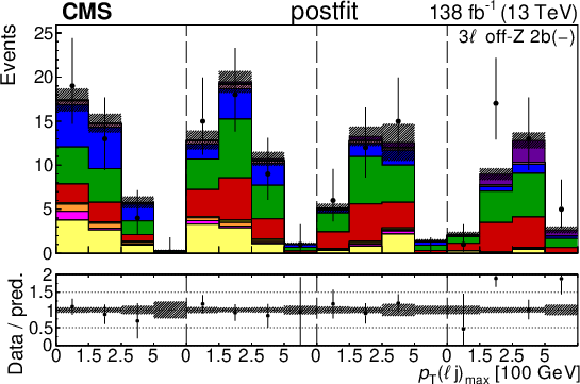
png pdf	Figure 5-i: The categories shown in these plots are 3 $ \ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ off-}\mathrm{Z}\text{ }2\mathrm{b} $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution in the plots is $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+)$ plot, the first four bins are the $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ variable for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 2{\mathrm{j}} $, the next four bins are for $3\ell\text{ off-}\mathrm{Z}\text{ }1\mathrm{b} (+) 3{\mathrm{j}} $, etc.
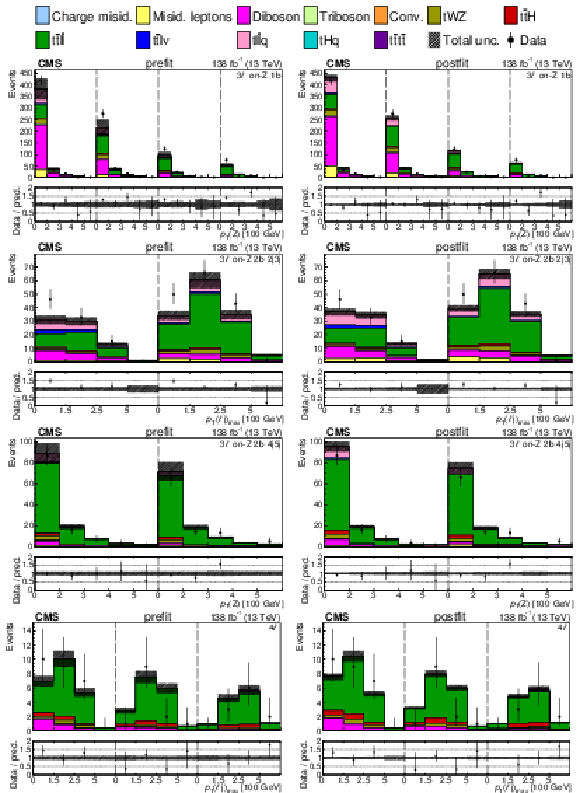
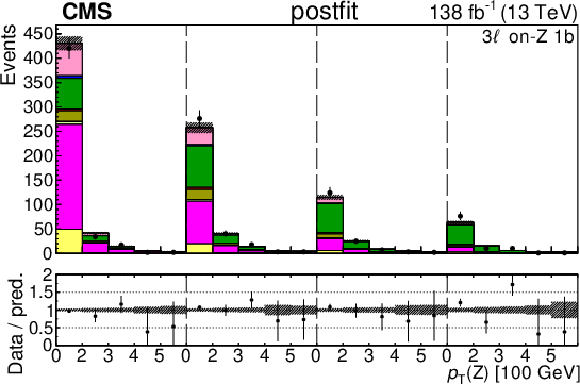
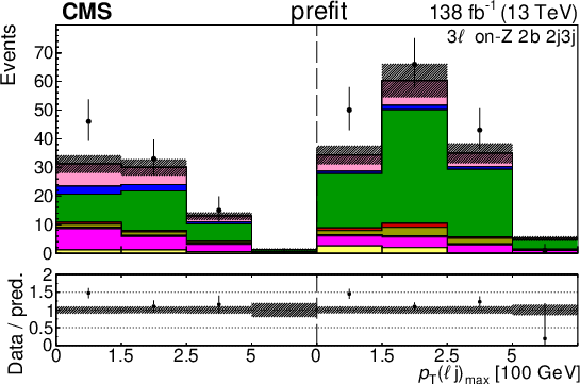
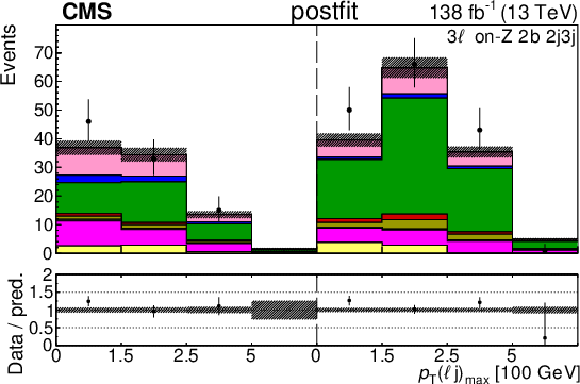
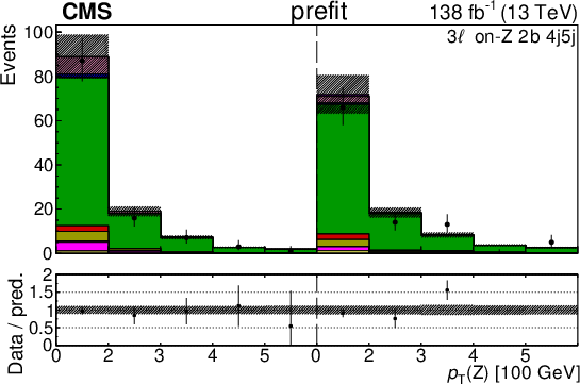
png pdf	Figure 6: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-a: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-b: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-c: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-d: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-e: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-f: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
png pdf	Figure 6-g: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
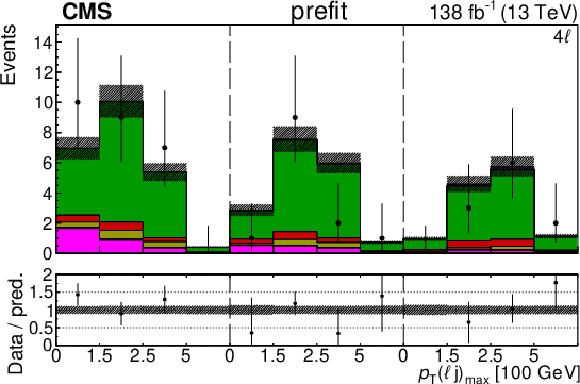
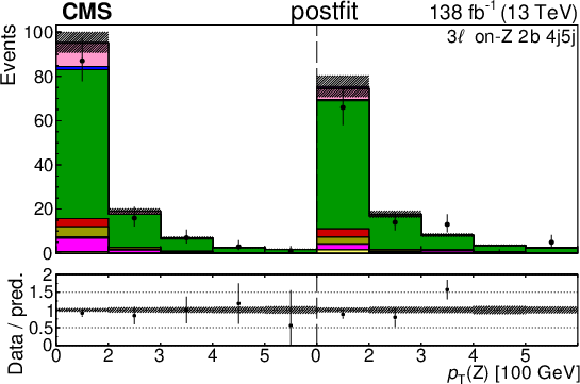
png pdf	Figure 6-h: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
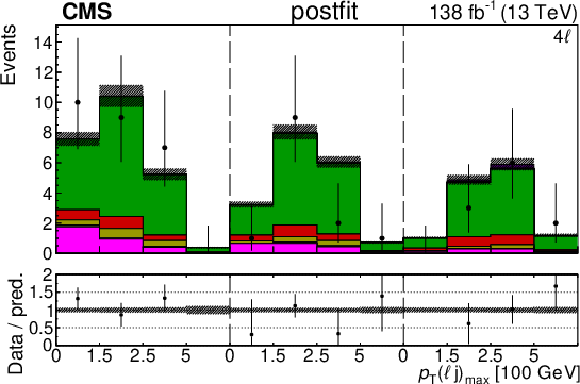
png pdf	Figure 6-i: The categories shown in these plots are 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $, 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $, and 4 $ \ell $. The prefit plots for each category are shown on the left side while the postfit plots are shown on the right side. The differential distribution is $ p_{\mathrm{T}}(\mathrm{Z}) $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ and 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ (4{\mathrm{j}} and 5{\mathrm{j}} ), and $ p_{\mathrm{T}}(\ell{\mathrm{j}} )_{\text{max}} $ in the plots of 3 $ \ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} $ ($2{\mathrm{j}}$ and $3{\mathrm{j}} $) and 4 $ \ell $. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3 $ \ell\text{ on-}\mathrm{Z}\text{ }1\mathrm{b} $ plot, the first five bins are the $ p_{\mathrm{T}}(\mathrm{Z}) $ variable for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 2{\mathrm{j}} $, the next five bins are for $3\ell\text{ on-}\mathrm{Z}\text{ }2\mathrm{b} 3{\mathrm{j}} $, etc.
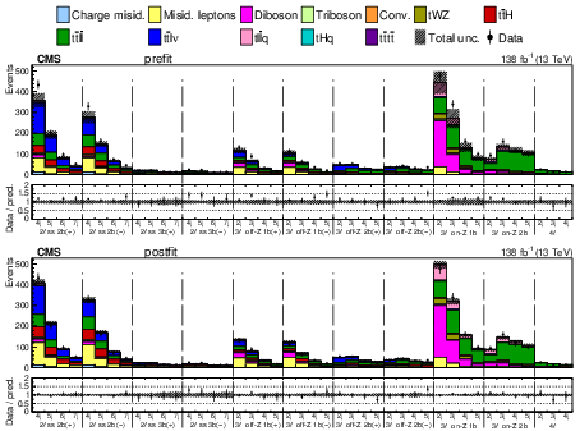
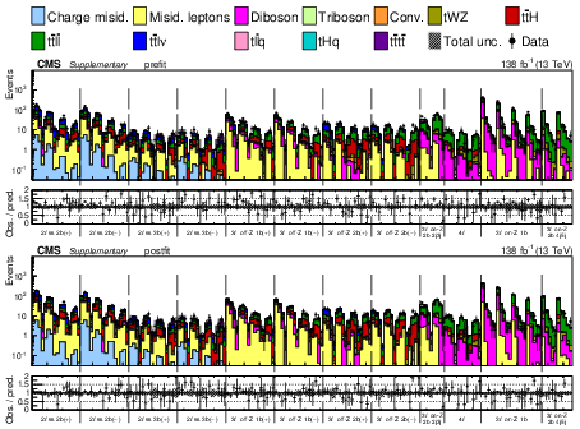
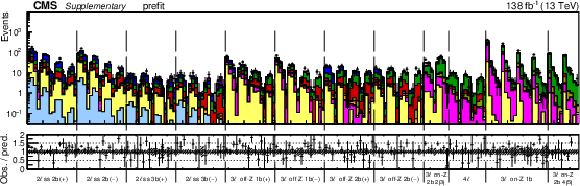
png pdf	Figure 7: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables have been combined, resulting in distributions for the jet multiplicity only. The postfit values are obtained by simultaneously fitting all 26 Wilson coefficients (WCs) and the nuisance parameters (NPs). The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs.
png pdf	Figure 7-a: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables have been combined, resulting in distributions for the jet multiplicity only. The postfit values are obtained by simultaneously fitting all 26 Wilson coefficients (WCs) and the nuisance parameters (NPs). The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs.
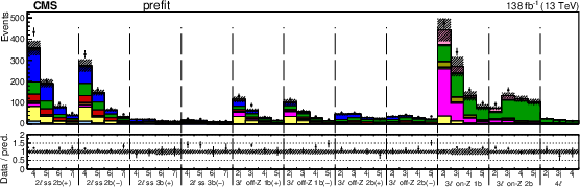
png pdf	Figure 7-b: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables have been combined, resulting in distributions for the jet multiplicity only. The postfit values are obtained by simultaneously fitting all 26 Wilson coefficients (WCs) and the nuisance parameters (NPs). The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs.
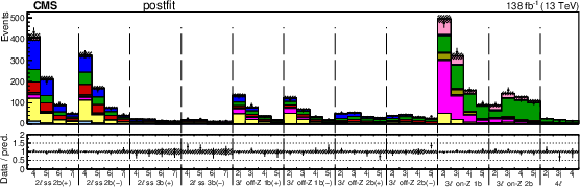
png pdf	Figure 7-c: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables have been combined, resulting in distributions for the jet multiplicity only. The postfit values are obtained by simultaneously fitting all 26 Wilson coefficients (WCs) and the nuisance parameters (NPs). The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs.
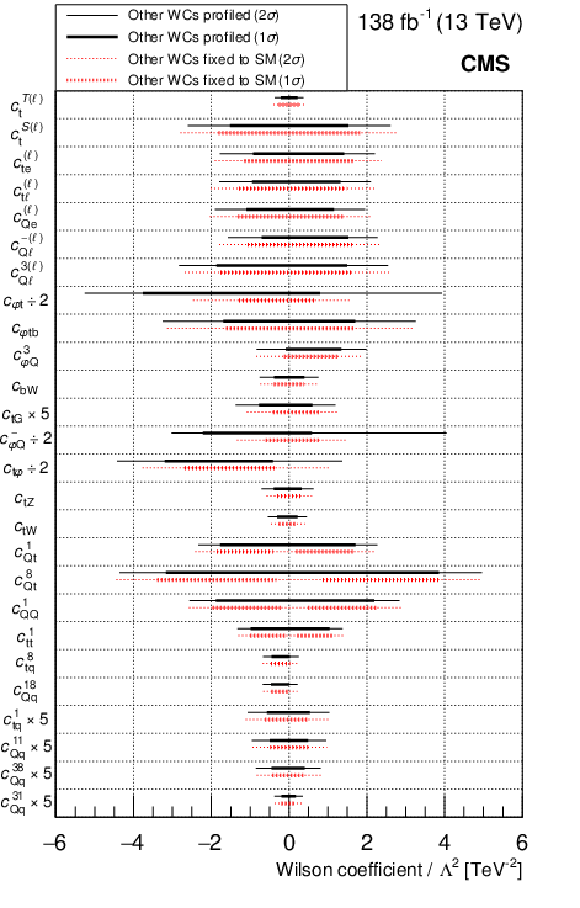
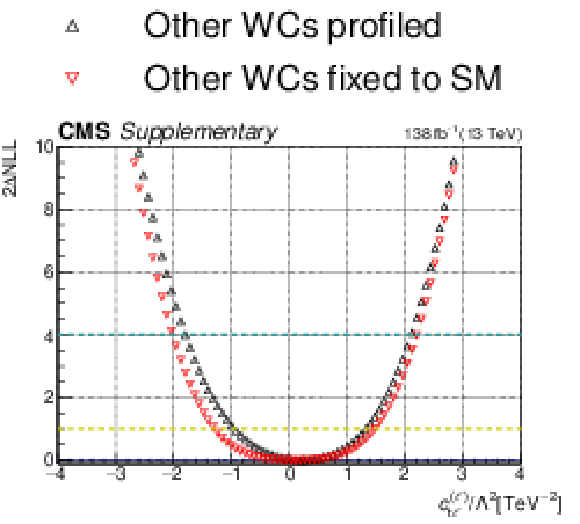
png pdf	Figure 8: Summary of CIs extracted from the likelihood fits described in Section 7. The WC 1$ \sigma $ (thick line) and 2$ \sigma $ (thin line) CIs are shown for the case where the other WCs are profiled (in solid black), and the case where the other WCs are fixed to their SM values of zero (in dashed red). To make the figure more readable, the intervals for $c_{\mathrm{t\varphi}}$, $c_{\mathrm{\varphi t}}$, and $c_{\mathrm{\varphi Q}}^{-}$ were scaled by 0.5, and the intervals for $c_{\mathrm{tG}}$, $c_{\mathrm{tQ}}^{1}$, $c_{\mathrm{Qq}}^{11}$, $c_{\mathrm{Qq}}^{38}$, and $c_{\mathrm{Qq}}^{31}$ were scaled by 5.
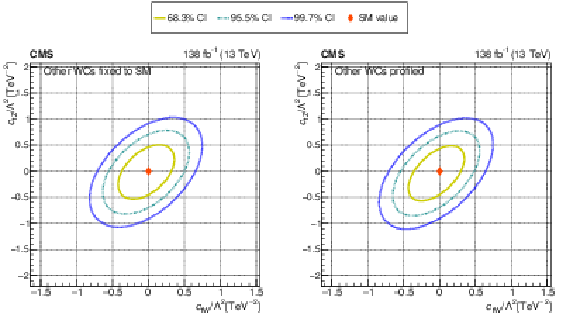
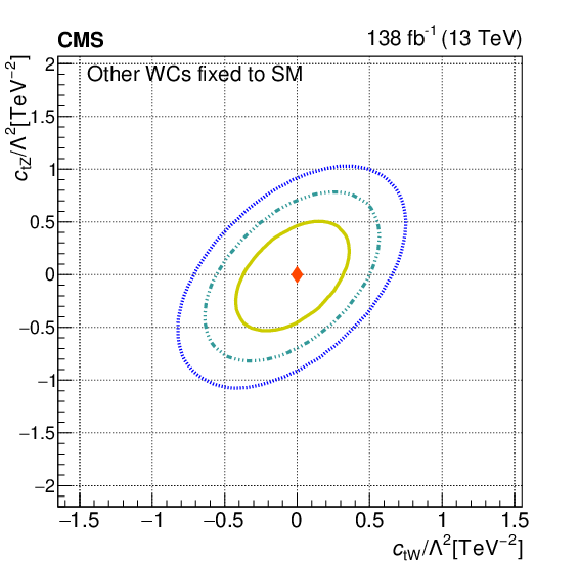
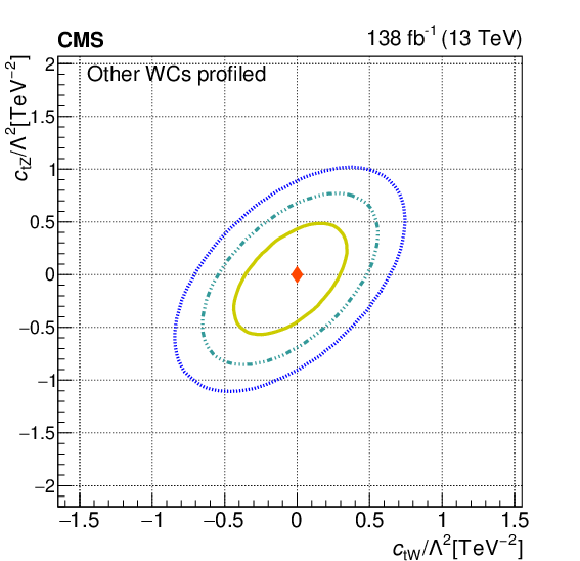
png pdf	Figure 9: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan for $c_{\mathrm{tW}}$ and $c_{\mathrm{tZ}}$ with the other WCs fixed to their SM values (left), and profiled (right). Diamond markers show the SM prediction.
png pdf	Figure 9-a: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan for $c_{\mathrm{tW}}$ and $c_{\mathrm{tZ}}$ with the other WCs fixed to their SM values (left), and profiled (right). Diamond markers show the SM prediction.
png pdf	Figure 9-b: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan for $c_{\mathrm{tW}}$ and $c_{\mathrm{tZ}}$ with the other WCs fixed to their SM values (left), and profiled (right). Diamond markers show the SM prediction.
png pdf	Figure 9-c: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan for $c_{\mathrm{tW}}$ and $c_{\mathrm{tZ}}$ with the other WCs fixed to their SM values (left), and profiled (right). Diamond markers show the SM prediction.
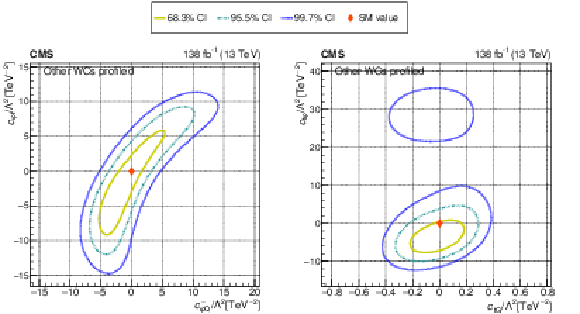
png pdf	Figure 10: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{\varphi Q}}^{-}$ and $c_{\mathrm{\varphi t}}$ (left), and for $c_{\mathrm{tG}}$ and $c_{\mathrm{t\varphi}}$ (right). Diamond markers show the SM prediction.
png pdf	Figure 10-a: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{\varphi Q}}^{-}$ and $c_{\mathrm{\varphi t}}$ (left), and for $c_{\mathrm{tG}}$ and $c_{\mathrm{t\varphi}}$ (right). Diamond markers show the SM prediction.
png pdf	Figure 10-b: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{\varphi Q}}^{-}$ and $c_{\mathrm{\varphi t}}$ (left), and for $c_{\mathrm{tG}}$ and $c_{\mathrm{t\varphi}}$ (right). Diamond markers show the SM prediction.
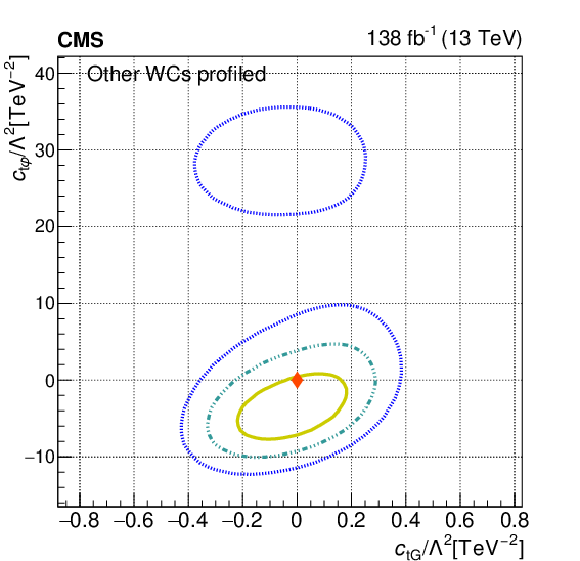
png pdf	Figure 10-c: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{\varphi Q}}^{-}$ and $c_{\mathrm{\varphi t}}$ (left), and for $c_{\mathrm{tG}}$ and $c_{\mathrm{t\varphi}}$ (right). Diamond markers show the SM prediction.
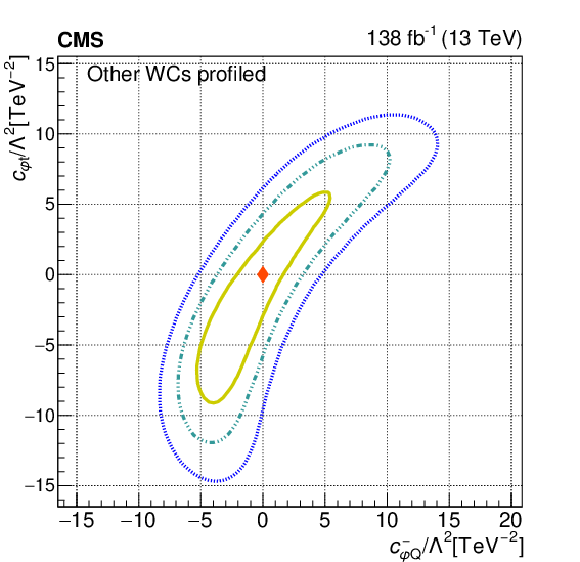
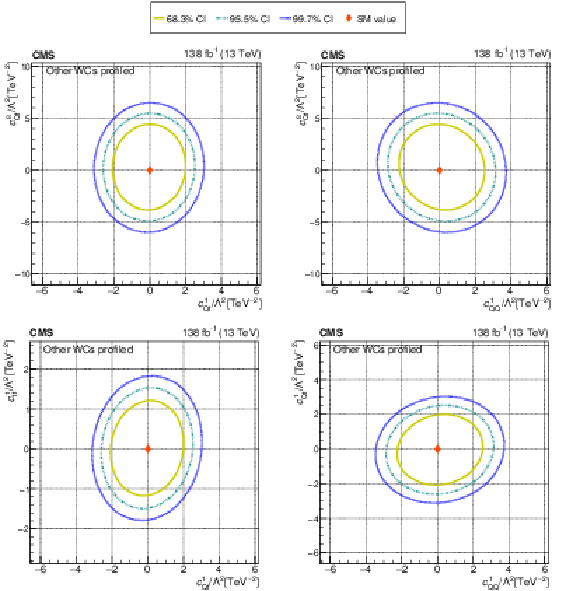
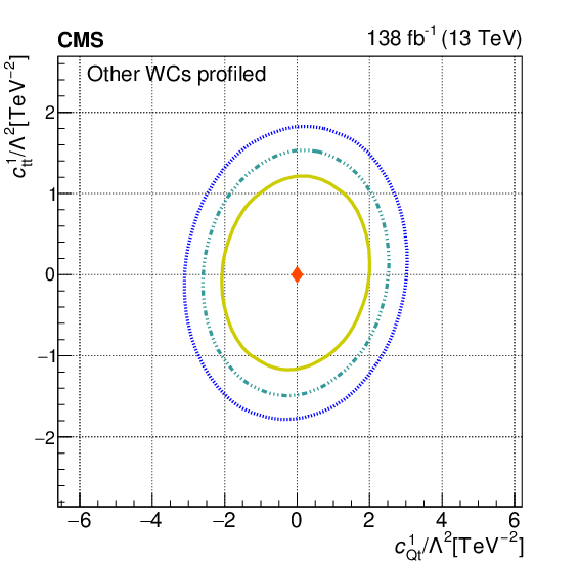
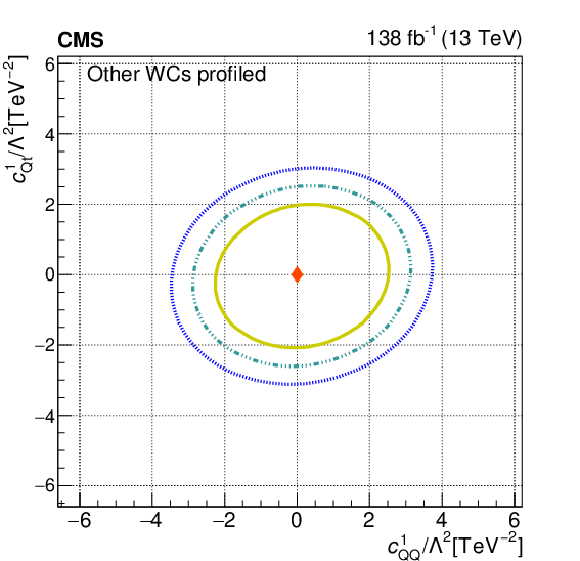
png pdf	Figure 11: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.
png pdf	Figure 11-a: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.
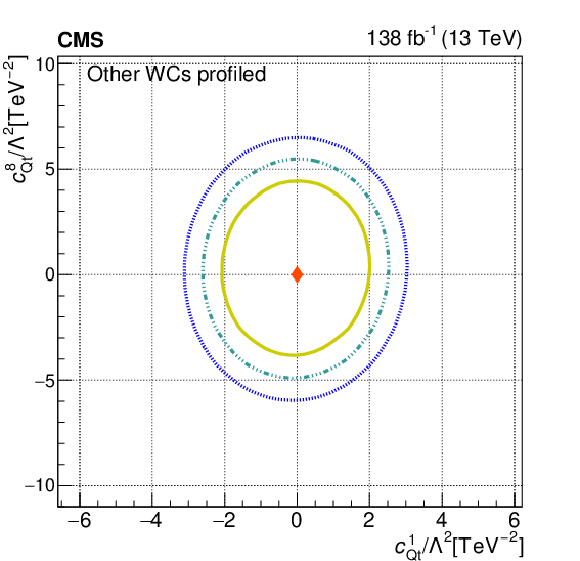
png pdf	Figure 11-b: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.
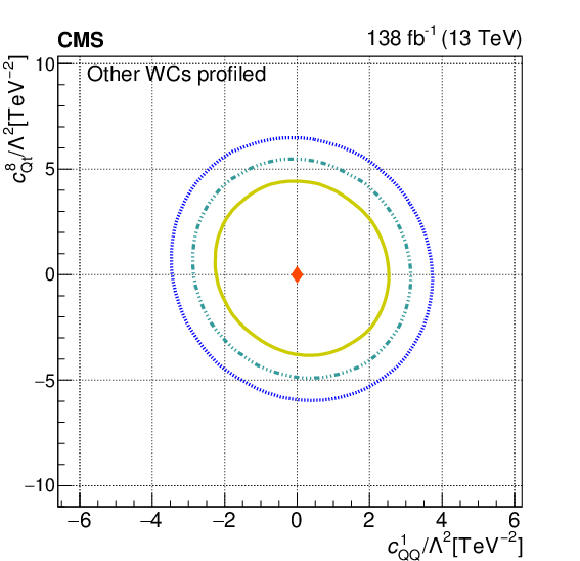
png pdf	Figure 11-c: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.
png pdf	Figure 11-d: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.
png pdf	Figure 11-e: The observed 68.3, 95.5, and 99.7% confidence level contours of a 2D scan with the other WCs profiled, for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{Qt}}^{8}$ (upper left), for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{8}$ (upper right), for $c_{\mathrm{Qt}}^{1}$ and $c_{\mathrm{tt}}^{1}$ (lower left), and for $c_{\mathrm{QQ}}^{8}$ and $c_{\mathrm{Qt}}^{1}$ (lower right). Diamond markers show the SM prediction.

Tables
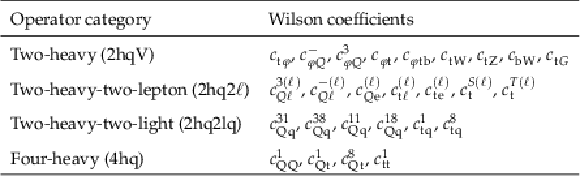
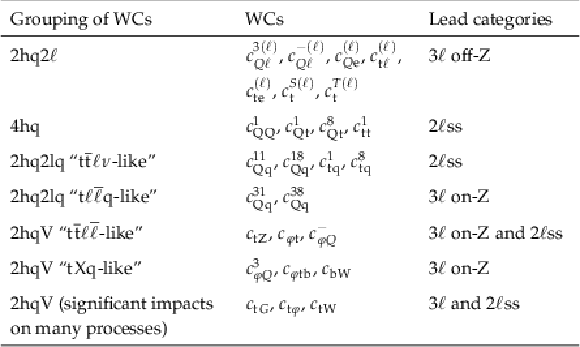
png pdf	Table 1: List of Wilson coefficients (WCs) included in this analysis, grouped according to the categories of WCs defined in Ref. [22]; the abbreviations for the WCs categories used in this paper are noted parenthetically. The definitions of the WCs and the definitions of the corresponding operators can be found in Table 1 of Ref. [22]. An extra factor of the strong coupling is applied to the $c_{\mathrm{tG}}$ coefficient, as explained in the text.
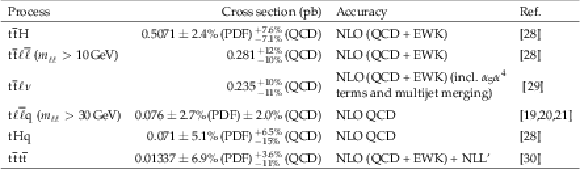
png pdf	Table 2: Theoretical cross sections at next-to-LO (NLO) used for normalization of simulated signal samples. The items are ordered by cross section. The uncertainties are broken into normalization components due to modeling the parton distribution functions (PDFs) and QCD order. Entries without a value are negligible.
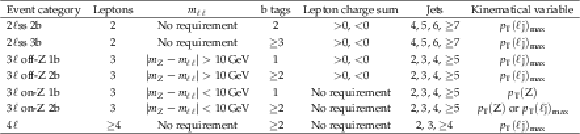
png pdf	Table 3: Object requirements for the 43 event selection categories. Requirements separated by commas indicate a division into subcategories. The kinematical variable that is used in the event category is also listed. Section 5.4 provides further details regarding the kinematical distributions.
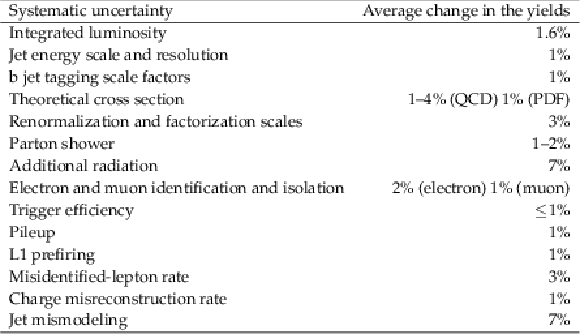
png pdf	Table 4: Summary of systematic uncertainties along with the average change in the SM prediction yields
png pdf	Table 5: The 1$ \sigma $ uncertainty intervals extracted from the likelihood fits described in Section 7. The intervals are shown for the case where the other Wilson coefficients (WCs) are profiled, and the case where the other WCs are fixed to their SM values of zero.
png pdf	Table 6: The 2$ \sigma $ uncertainty intervals extracted from the likelihood fits described in Section 7. The intervals are shown for the case where the other Wilson coefficients (WCs) are profiled, and the case where the other WCs are fixed to their SM values of zero.
png pdf	Table 7: Summary of categories that provide leading contributions to the sensitivity for subsets of the Wilson coefficients (WCs).

Summary

A search for new physics in the production of one or more top quarks with additional leptons, jets, and b jets in the context of effective field theory (EFT) has been performed. Events from proton-proton collisions with a center-of-mass energy of 13 TeV corresponding to an integrated luminosity of 138 fb$ ^{-1} $ are used. EFT effects are incorporated into the event weights of the simulated samples, allowing detector-level predictions that account for correlations and interference effects among EFT operators and between EFT operators and standard model (SM) processes. The Wilson coefficients (WCs) corresponding to 26 EFT operators were simultaneously fit to the data. Confidence intervals were extracted for the WCs either individually or in pairs by scanning the likelihood with the other WCs either profiled or fixed at their SM values of zero. In all cases, the data are found to be consistent with the SM expectations.

Additional Figures
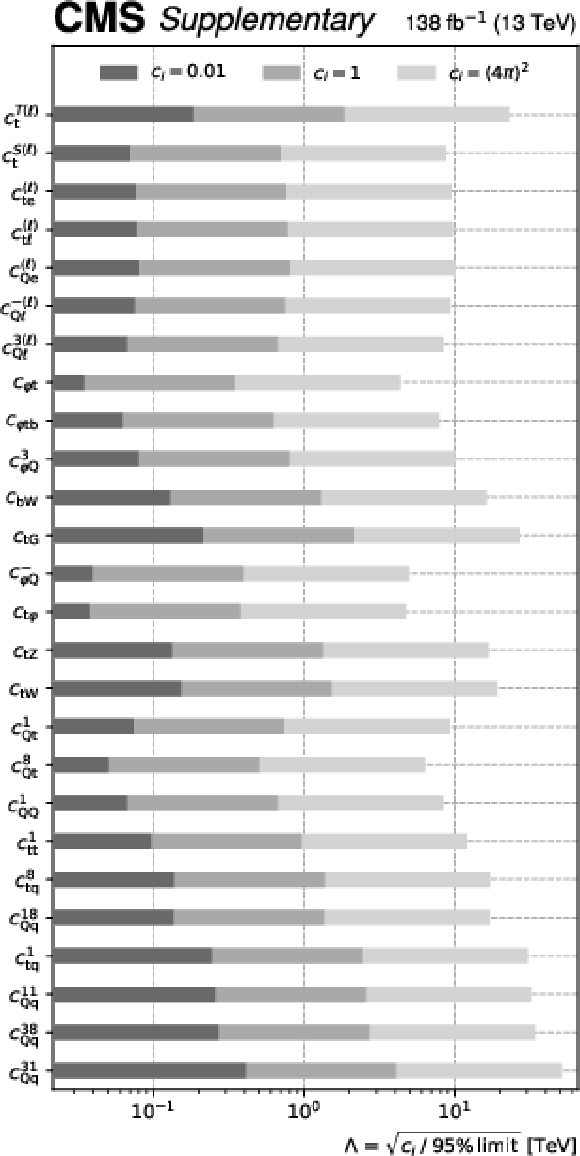
png pdf	Additional Figure 1: The 95% profiled limits for each Wilson coefficient ($ c_i $) interpreted in terms of the energy scale $ \Lambda $ for three different assumptions for the value of the coefficient as indicated in the legend. For limits that are not symmetrical around the SM value of zero, the absolute value of the looser limit is used. The definition of the operator associated with $c_{\mathrm{tG}}$ here includes an explicit factor of the strong coupling constant, which should be accounted for when comparing to results extracted based on other conventions.
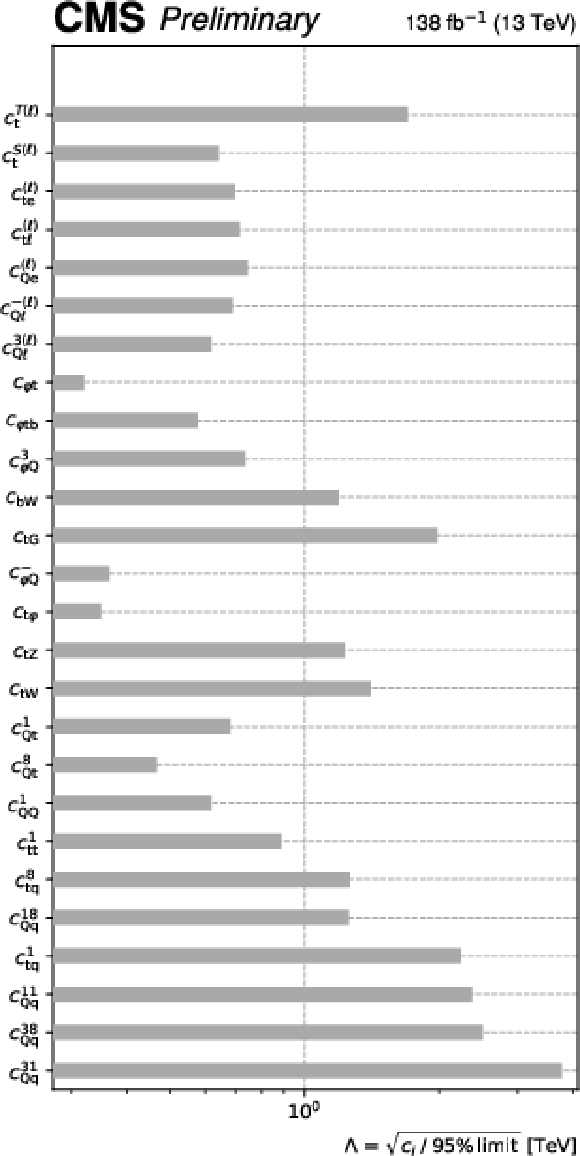
png pdf	Additional Figure 2: The 95% profiled limits for each Wilson coefficient ($ c_i $) interpreted in terms of the energy scale $ \Lambda $ for the value of the coefficient set to 1. For limits that are not symmetrical around the SM value of zero, the absolute value of the looser limit is used. The definition of the operator associated with $c_{\mathrm{tG}}$ here includes an explicit factor of the strong coupling constant, which should be accounted for when comparing to results extracted based on other conventions.
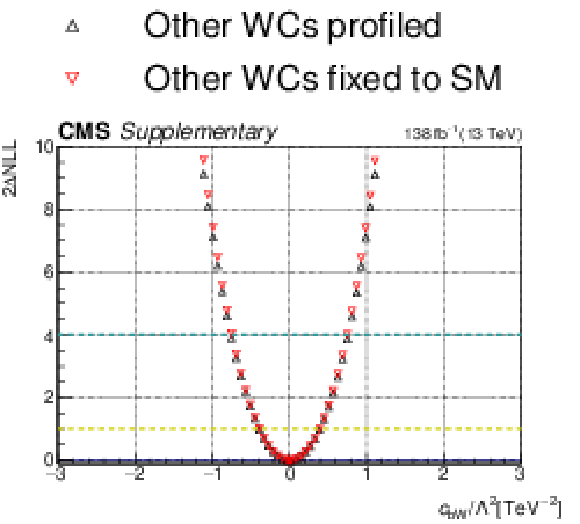
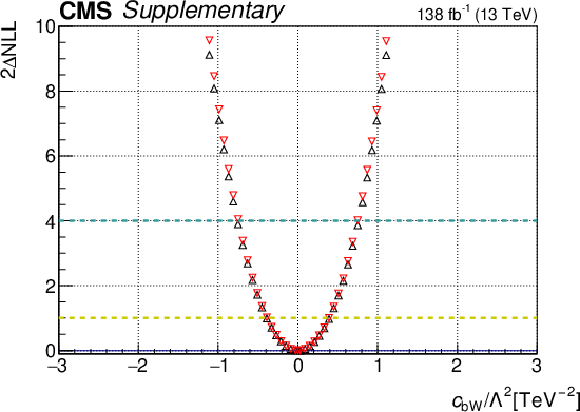
png pdf	Additional Figure 3: One-dimensional scan over the $c_{\mathrm{bW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 3-a: One-dimensional scan over the $c_{\mathrm{bW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 3-b: One-dimensional scan over the $c_{\mathrm{bW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
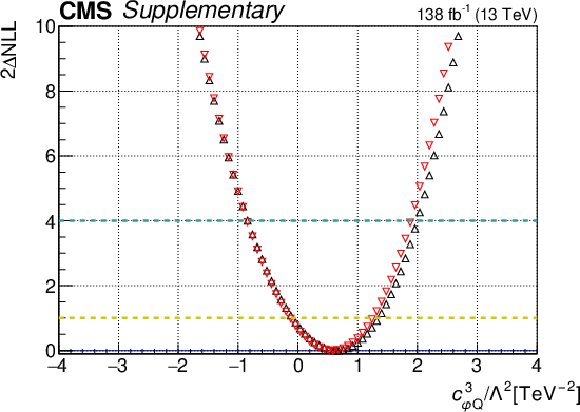
png pdf	Additional Figure 4: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{3}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 4-a: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{3}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 4-b: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{3}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
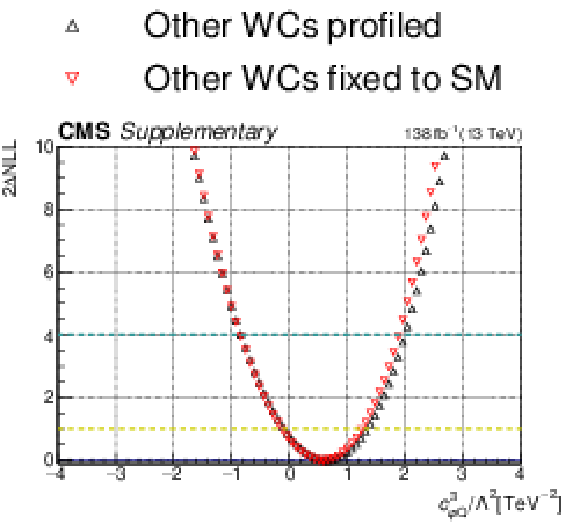
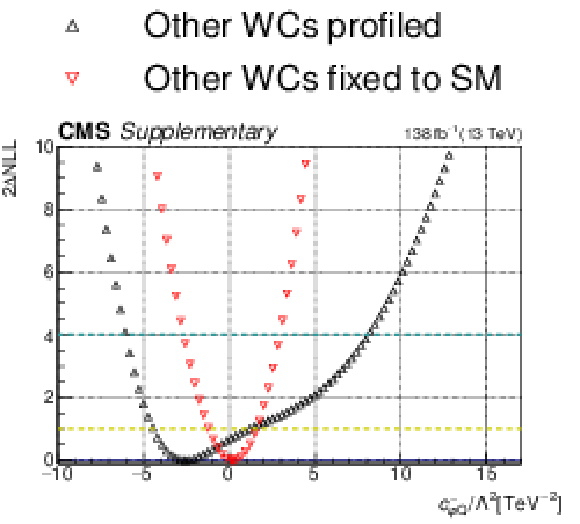
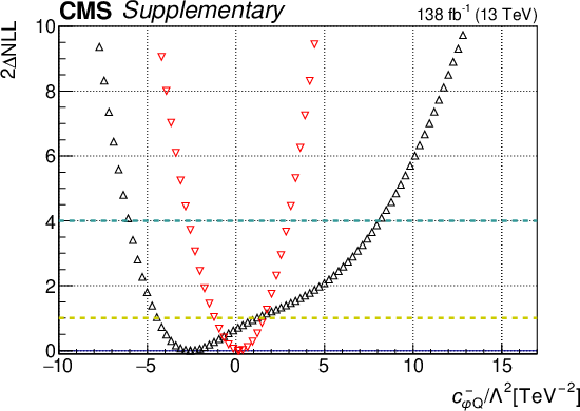
png pdf	Additional Figure 5: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{-}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 5-a: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{-}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 5-b: One-dimensional scan over the $c_{\mathrm{\varphi Q}}^{-}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
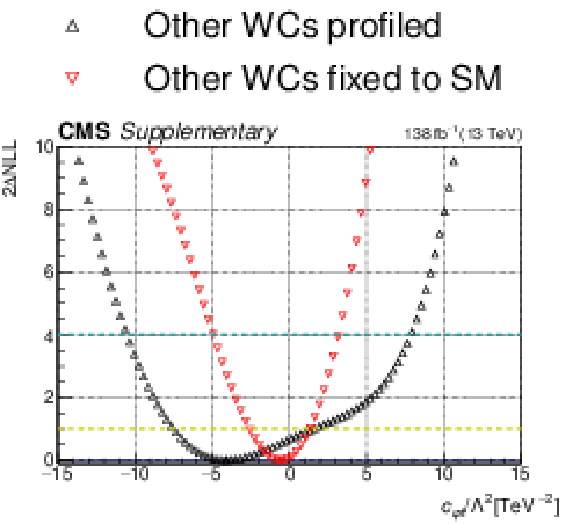
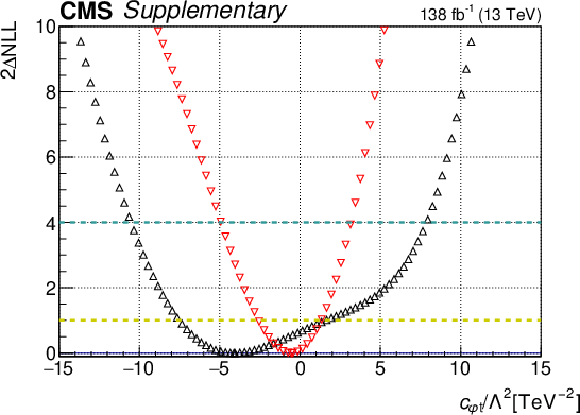
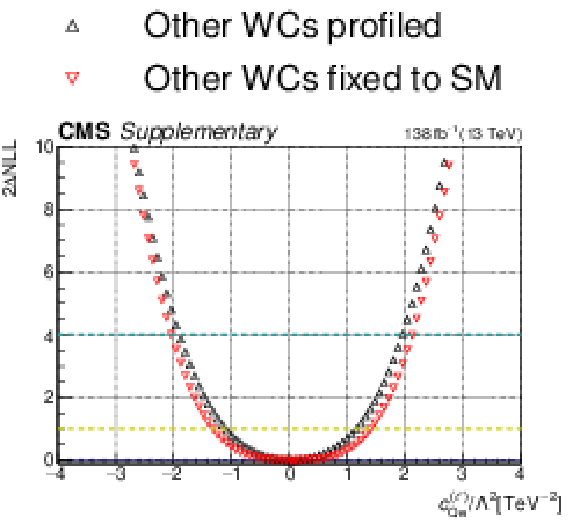
png pdf	Additional Figure 6: One-dimensional scan over the $c_{\mathrm{\varphi t}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 6-a: One-dimensional scan over the $c_{\mathrm{\varphi t}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 6-b: One-dimensional scan over the $c_{\mathrm{\varphi t}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
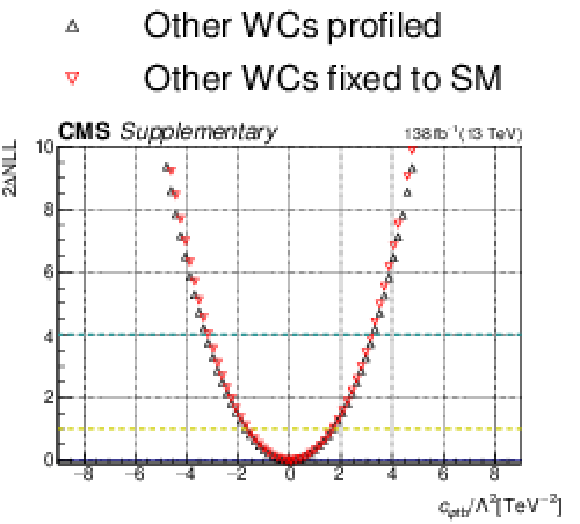
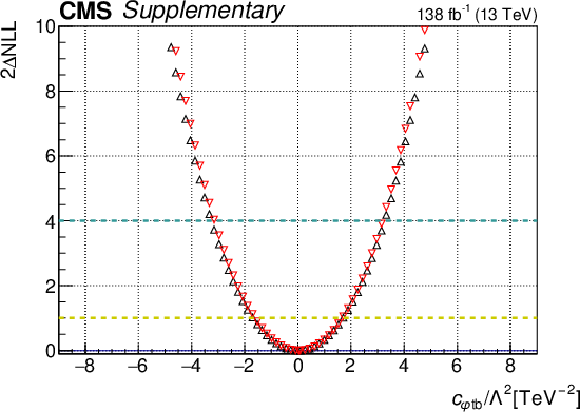
png pdf	Additional Figure 7: One-dimensional scan over the $c_{\mathrm{\varphi tb}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 7-a: One-dimensional scan over the $c_{\mathrm{\varphi tb}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 7-b: One-dimensional scan over the $c_{\mathrm{\varphi tb}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 8: One-dimensional scan over the $c_{\mathrm{qe}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 8-a: One-dimensional scan over the $c_{\mathrm{qe}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
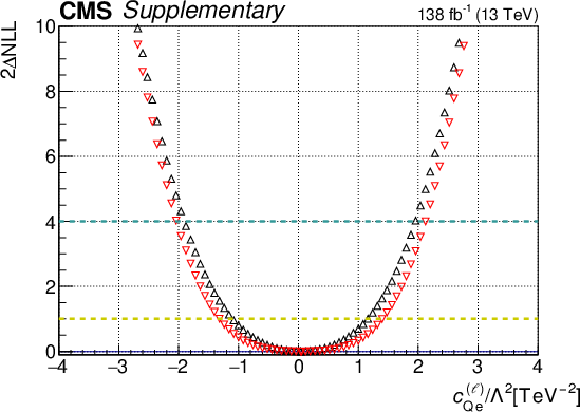
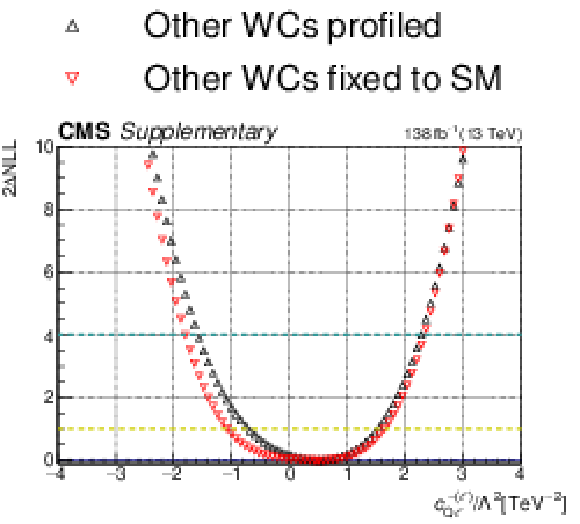
png pdf	Additional Figure 8-b: One-dimensional scan over the $c_{\mathrm{qe}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 9: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{3(\ell)}$Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 9-a: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{3(\ell)}$Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
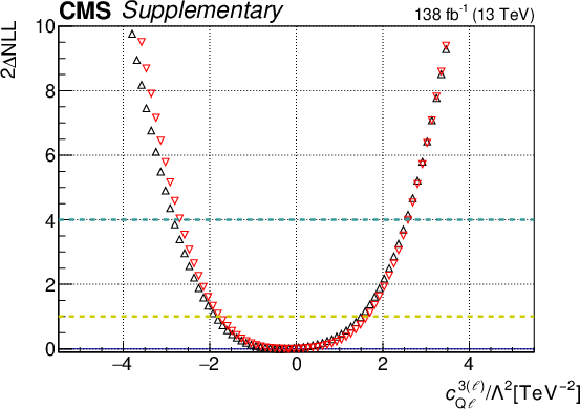
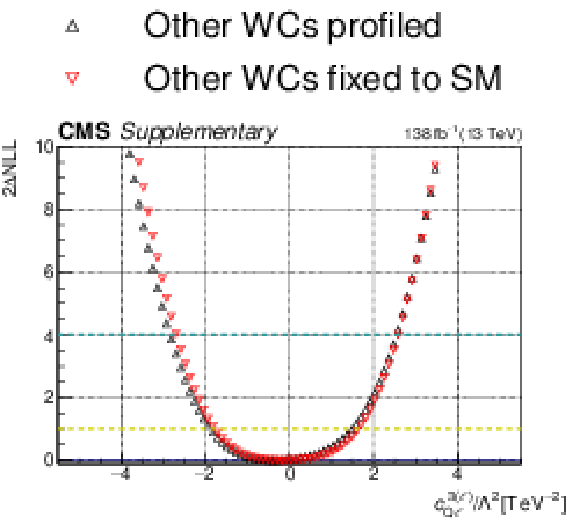
png pdf	Additional Figure 9-b: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{3(\ell)}$Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 10: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{-(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 10-a: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{-(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
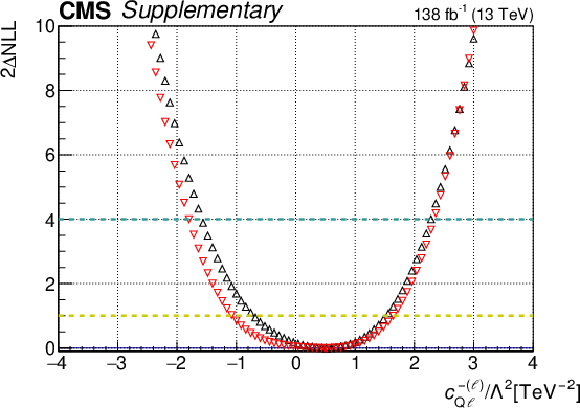
png pdf	Additional Figure 10-b: One-dimensional scan over the $c_{\mathrm{Q\ell}}^{-(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
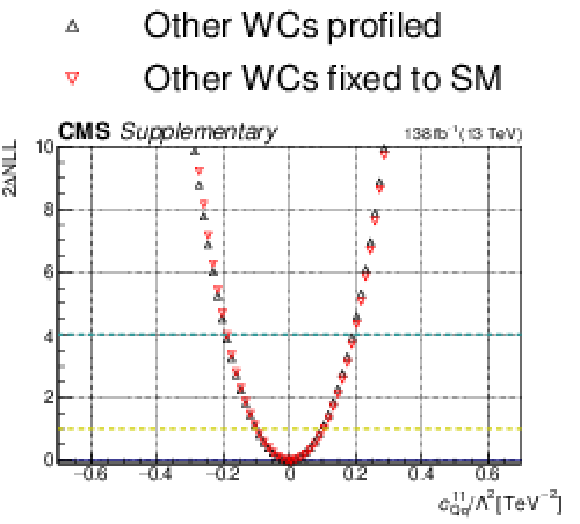
png pdf	Additional Figure 11: One-dimensional scan over the $c_{\mathrm{Qq}}^{11}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 11-a: One-dimensional scan over the $c_{\mathrm{Qq}}^{11}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
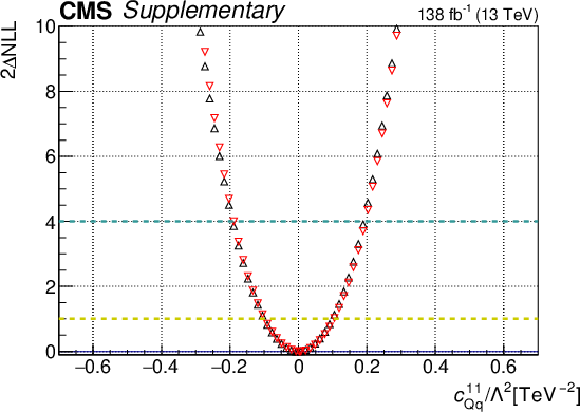
png pdf	Additional Figure 11-b: One-dimensional scan over the $c_{\mathrm{Qq}}^{11}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
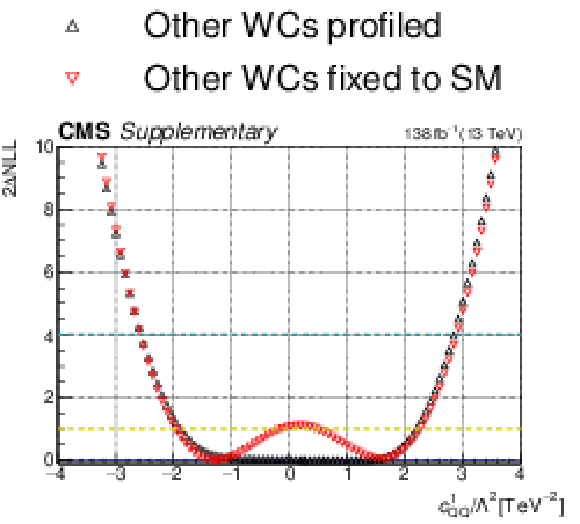
png pdf	Additional Figure 12: One-dimensional scan over the $c_{\mathrm{QQ}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 12-a: One-dimensional scan over the $c_{\mathrm{QQ}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 12-b: One-dimensional scan over the $c_{\mathrm{QQ}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
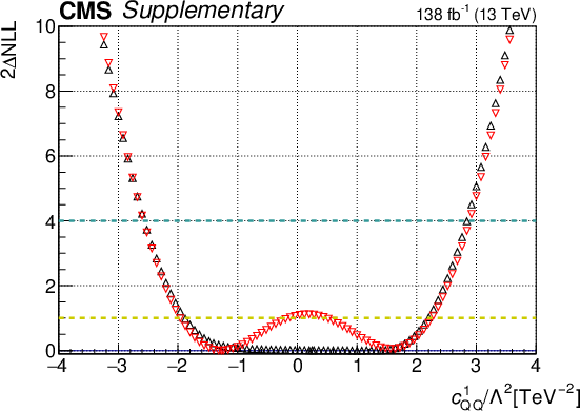
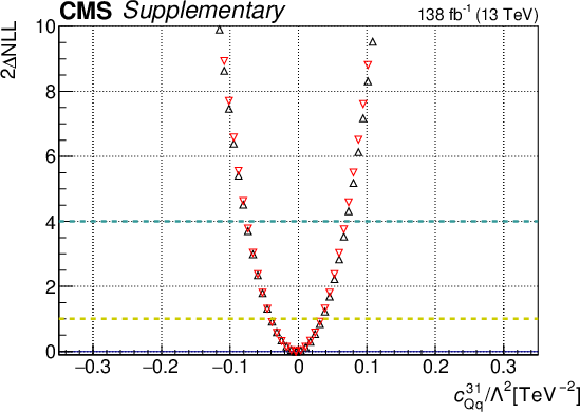
png pdf	Additional Figure 13: One-dimensional scan over the $c_{\mathrm{Qq}}^{31}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 13-a: One-dimensional scan over the $c_{\mathrm{Qq}}^{31}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 13-b: One-dimensional scan over the $c_{\mathrm{Qq}}^{31}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
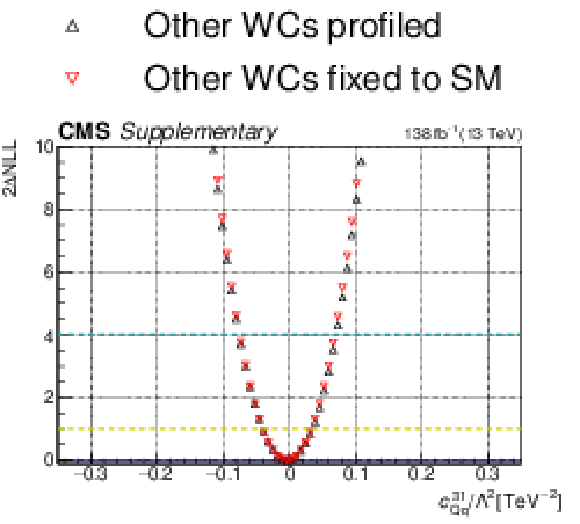
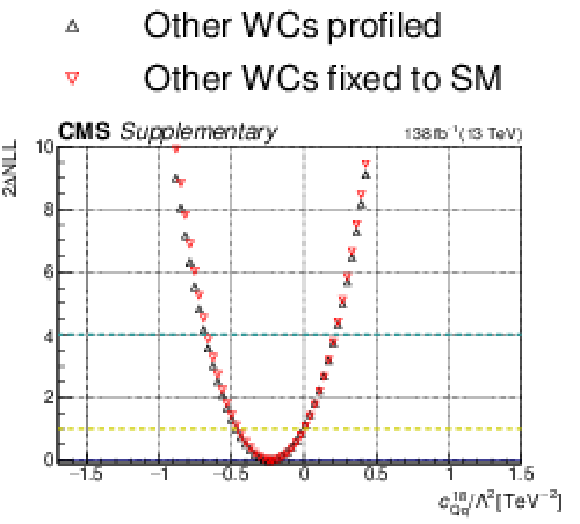
png pdf	Additional Figure 14: One-dimensional scan over the $c_{\mathrm{Qq}}^{18}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 14-a: One-dimensional scan over the $c_{\mathrm{Qq}}^{18}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
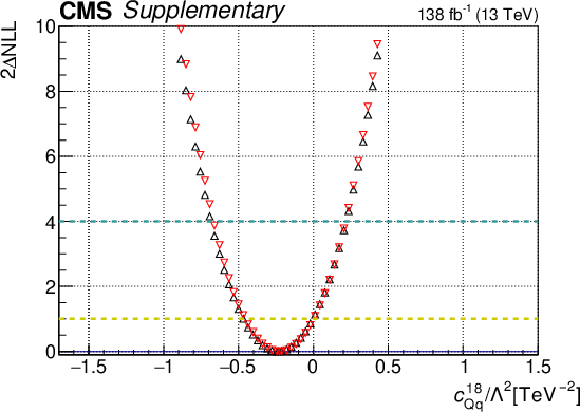
png pdf	Additional Figure 14-b: One-dimensional scan over the $c_{\mathrm{Qq}}^{18}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
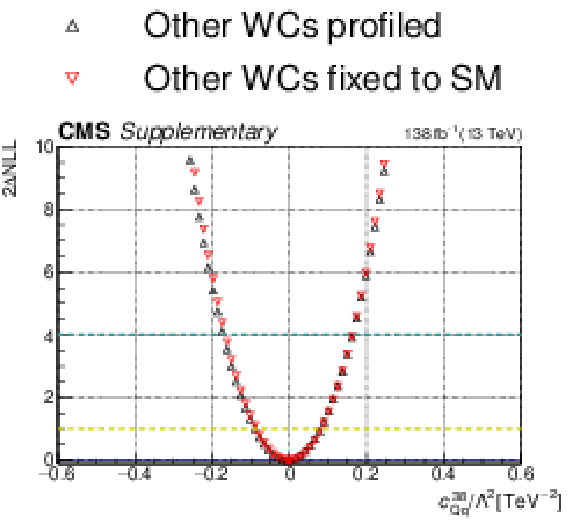
png pdf	Additional Figure 15: One-dimensional scan over the $c_{\mathrm{Qq}}^{38}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 15-a: One-dimensional scan over the $c_{\mathrm{Qq}}^{38}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
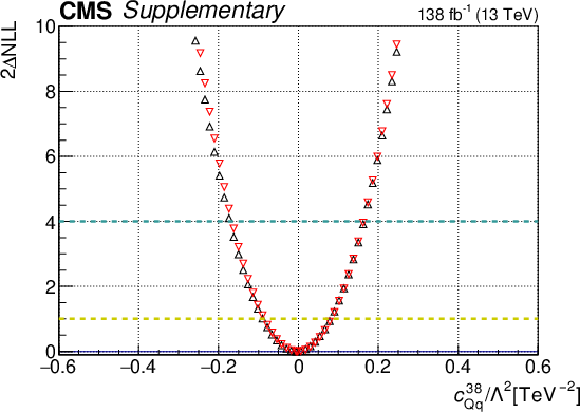
png pdf	Additional Figure 15-b: One-dimensional scan over the $c_{\mathrm{Qq}}^{38}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
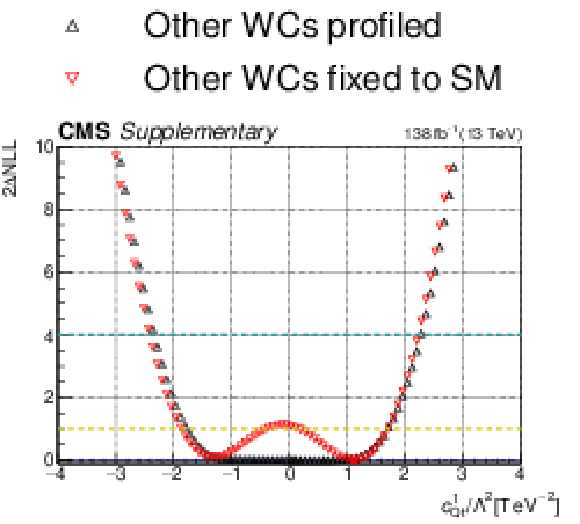
png pdf	Additional Figure 16: One-dimensional scan over the $c_{\mathrm{Qt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 16-a: One-dimensional scan over the $c_{\mathrm{Qt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
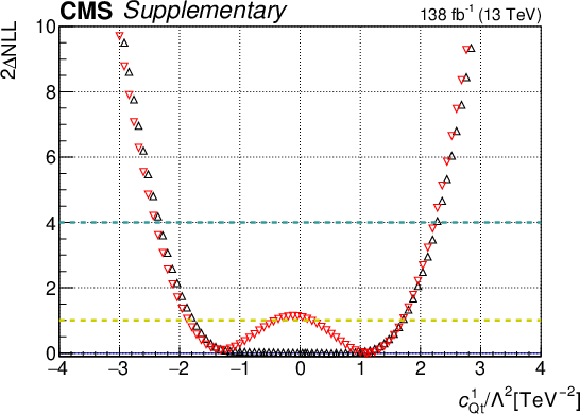
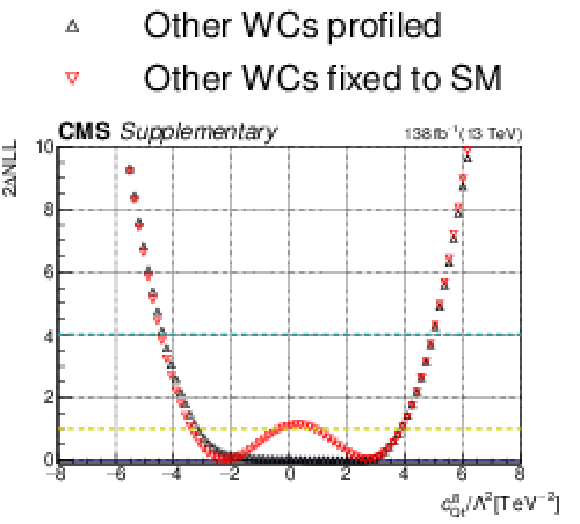
png pdf	Additional Figure 16-b: One-dimensional scan over the $c_{\mathrm{Qt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 17: One-dimensional scan over the $c_{\mathrm{Qt}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 17-a: One-dimensional scan over the $c_{\mathrm{Qt}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
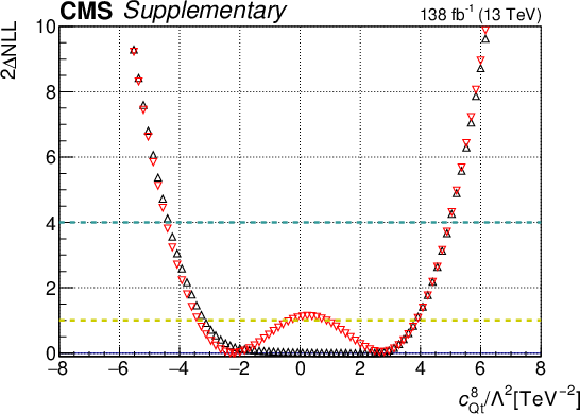
png pdf	Additional Figure 17-b: One-dimensional scan over the $c_{\mathrm{Qt}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
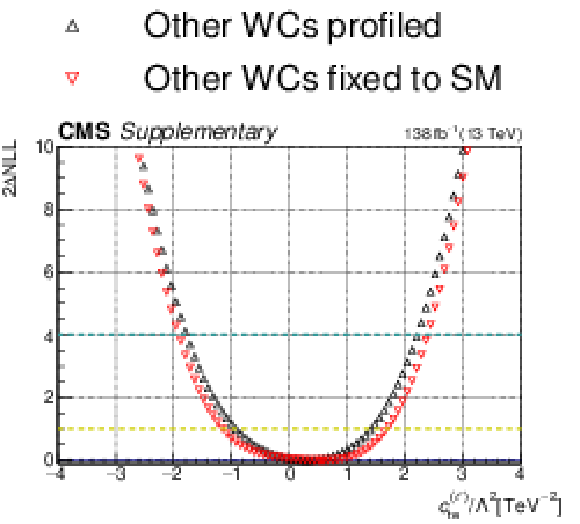
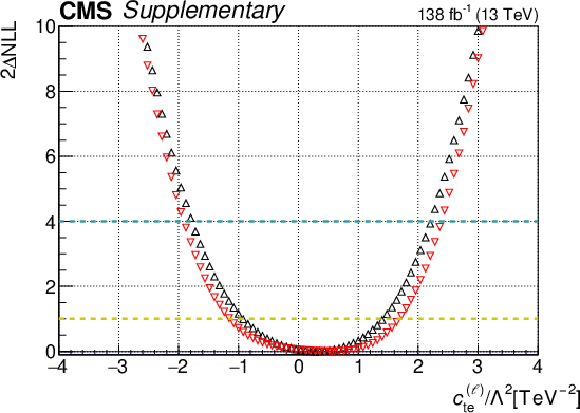
png pdf	Additional Figure 18: One-dimensional scan over the $c_{\mathrm{te}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 18-a: One-dimensional scan over the $c_{\mathrm{te}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 18-b: One-dimensional scan over the $c_{\mathrm{te}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
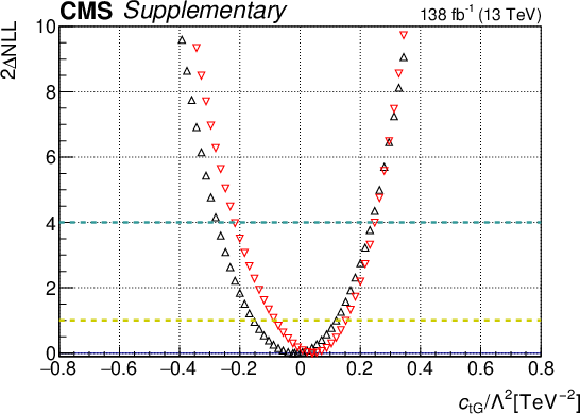
png pdf	Additional Figure 19: One-dimensional scan over the $c_{\mathrm{tG}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 19-a: One-dimensional scan over the $c_{\mathrm{tG}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 19-b: One-dimensional scan over the $c_{\mathrm{tG}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
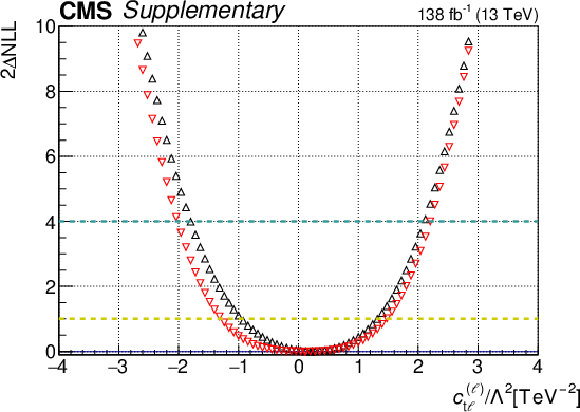
png pdf	Additional Figure 20: One-dimensional scan over the $c_{\mathrm{t\ell}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 20-a: One-dimensional scan over the $c_{\mathrm{t\ell}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 20-b: One-dimensional scan over the $c_{\mathrm{t\ell}}^{(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
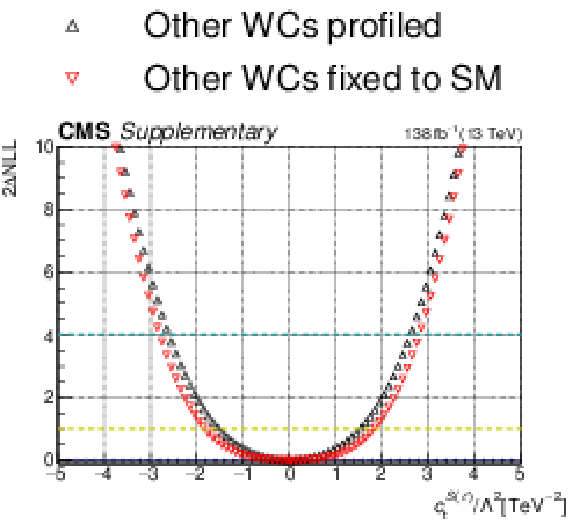
png pdf	Additional Figure 21: One-dimensional scan over the $c_{\mathrm{t}}^{S(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 21-a: One-dimensional scan over the $c_{\mathrm{t}}^{S(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
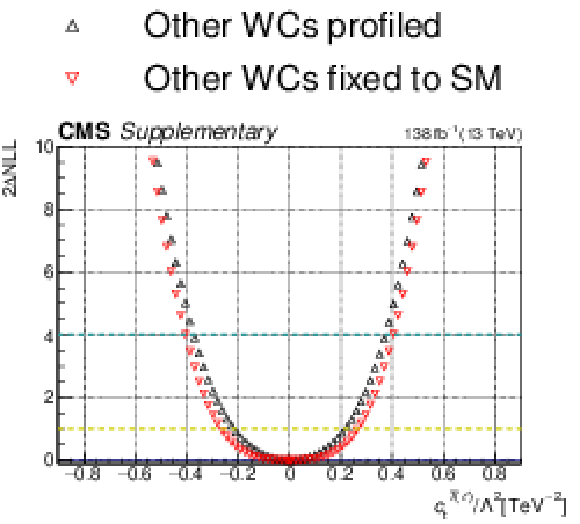
png pdf	Additional Figure 21-b: One-dimensional scan over the $c_{\mathrm{t}}^{S(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
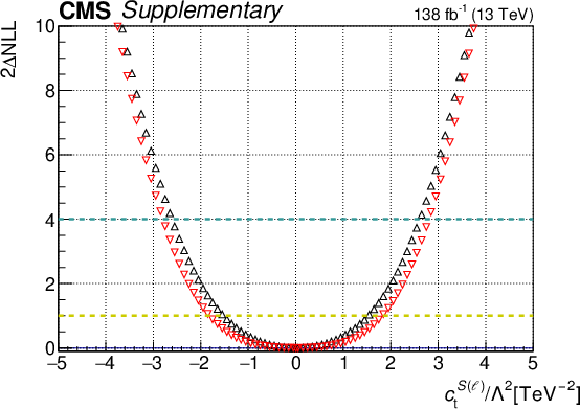
png pdf	Additional Figure 22: One-dimensional scan over the $c_{\mathrm{t}}^{T(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 22-a: One-dimensional scan over the $c_{\mathrm{t}}^{T(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
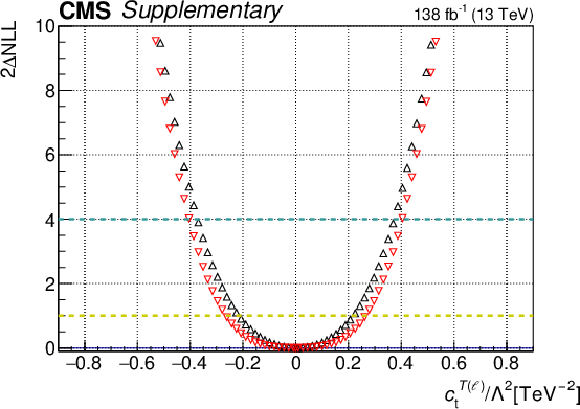
png pdf	Additional Figure 22-b: One-dimensional scan over the $c_{\mathrm{t}}^{T(\ell)}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
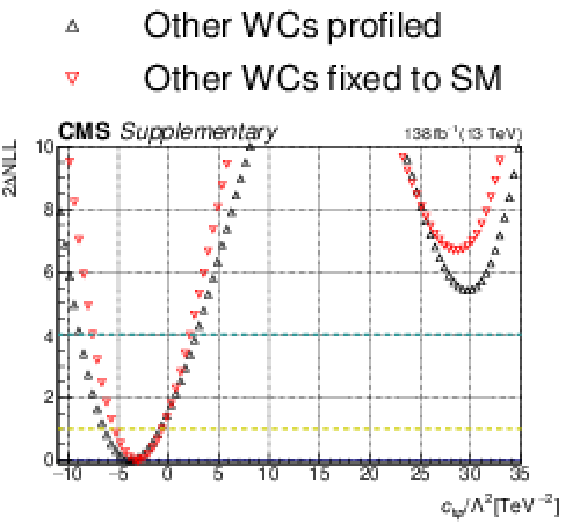
png pdf	Additional Figure 23: One-dimensional scan over the $c_{\mathrm{t\varphi}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 23-a: One-dimensional scan over the $c_{\mathrm{t\varphi}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 23-b: One-dimensional scan over the $c_{\mathrm{t\varphi}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
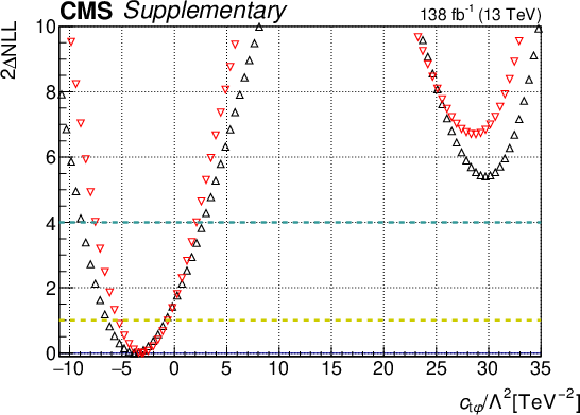
png pdf	Additional Figure 24: One-dimensional scan over the $c_{\mathrm{tQ}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 24-a: One-dimensional scan over the $c_{\mathrm{tQ}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
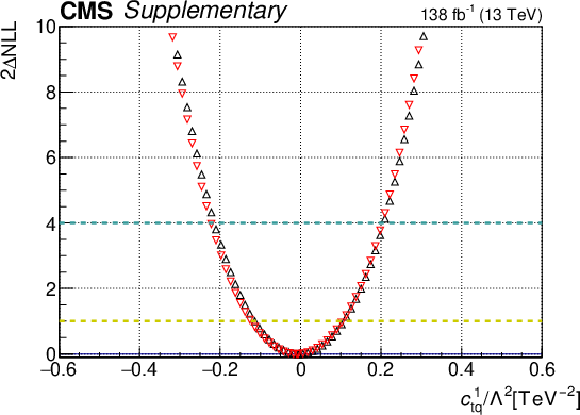
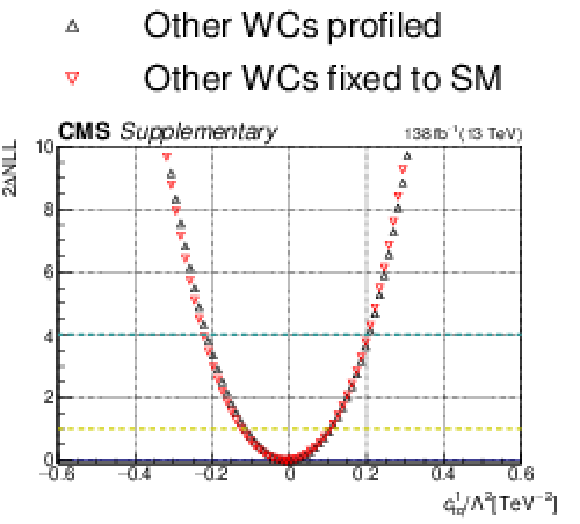
png pdf	Additional Figure 24-b: One-dimensional scan over the $c_{\mathrm{tQ}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
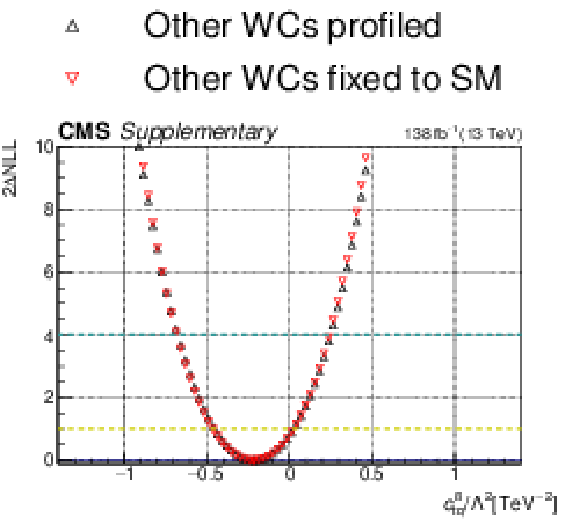
png pdf	Additional Figure 25: One-dimensional scan over the $c_{\mathrm{tq}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 25-a: One-dimensional scan over the $c_{\mathrm{tq}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
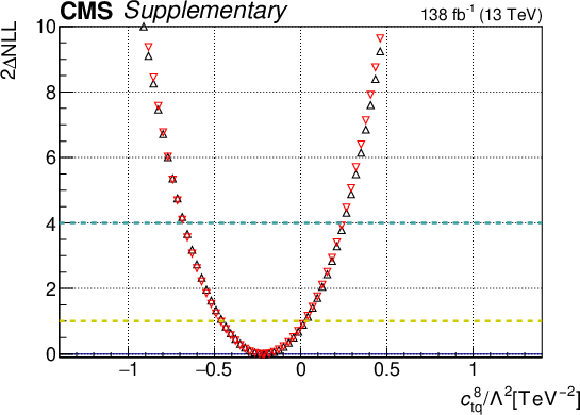
png pdf	Additional Figure 25-b: One-dimensional scan over the $c_{\mathrm{tq}}^{8}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
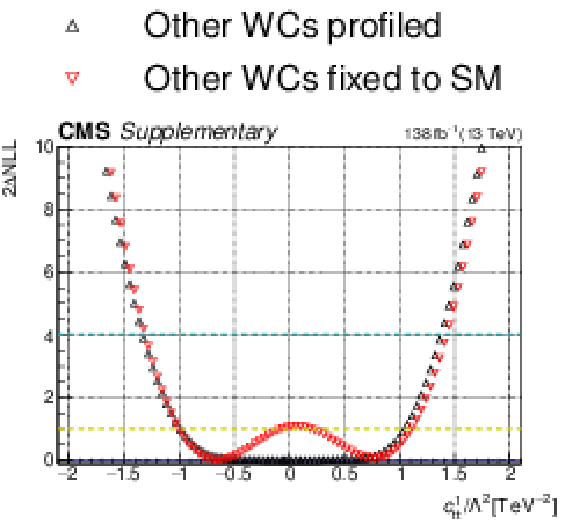
png pdf	Additional Figure 26: One-dimensional scan over the $c_{\mathrm{tt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 26-a: One-dimensional scan over the $c_{\mathrm{tt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 26-b: One-dimensional scan over the $c_{\mathrm{tt}}^{1}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
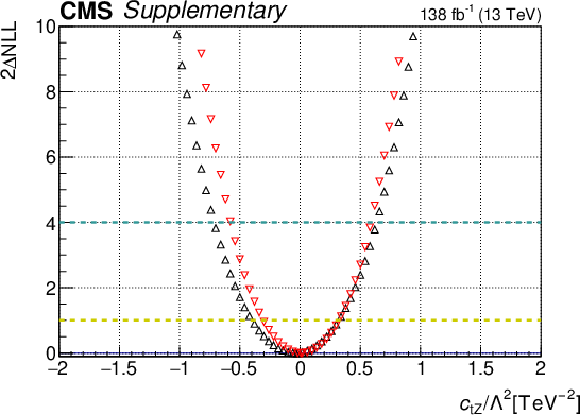
png pdf	Additional Figure 27: One-dimensional scan over the $c_{\mathrm{tW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 27-a: One-dimensional scan over the $c_{\mathrm{tW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
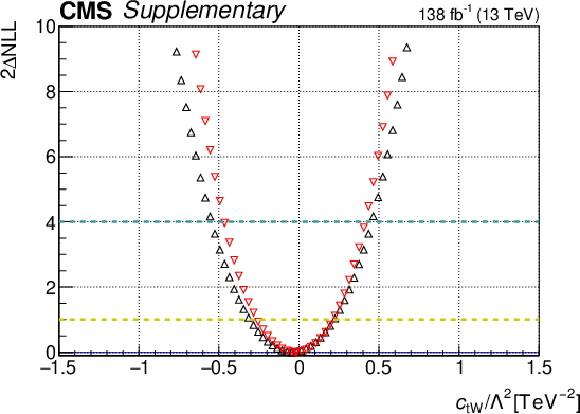
png pdf	Additional Figure 27-b: One-dimensional scan over the $c_{\mathrm{tW}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
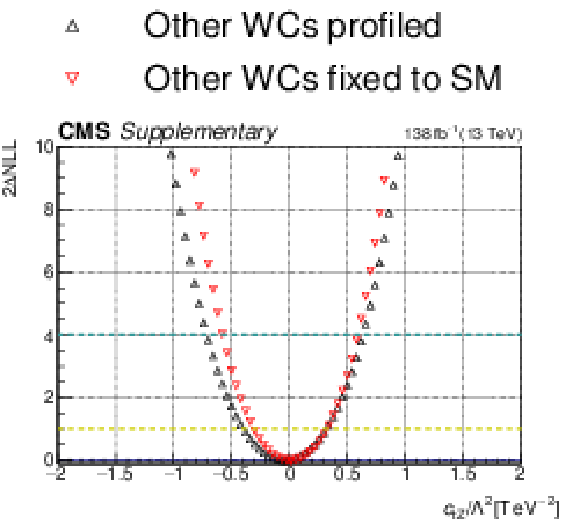
png pdf	Additional Figure 28: One-dimensional scan over the $c_{\mathrm{tZ}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 28-a: One-dimensional scan over the $c_{\mathrm{tZ}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
png pdf	Additional Figure 28-b: One-dimensional scan over the $c_{\mathrm{tZ}}$ Wilson coefficient (WC). The red points correspond to the case where the other WCs are fixed to their SM values of zero, while the black points correspond to the case where the other WCs are profiled.
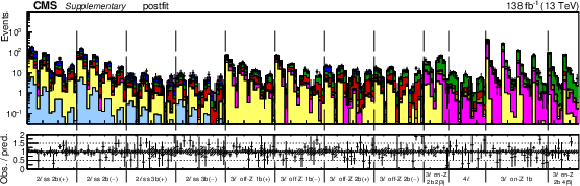
png pdf	Additional Figure 29: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables are shown. The two categories on the right side of the plot (3$ \ell $ on-Z 1b, and the 4 and 5 jet bins of 3$ \ell $ on-Z 2b) use the $ {p_{\mathrm{T}}}\mathrm{(\mathrm{Z})} $ variable, while all the other categories use $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $. Each event category (e.g., 2 $ \ell \textrm{ss} $) is subdivided into its jet multiplcity components. For example, the first four subbins of the 2 $ \ell \textrm{ss} $ bin are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for four jets, the next four subbins are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for 5 jets, etc. The postfit values are obtained by simultaneously fitting all $ \mathrm{26} $ Wilson coefficient (WCs) and the nuisance parameters (NPs). The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs. All yields are plotted on a log scale.
png pdf	Additional Figure 29-a: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables are shown. The two categories on the right side of the plot (3$ \ell $ on-Z 1b, and the 4 and 5 jet bins of 3$ \ell $ on-Z 2b) use the $ {p_{\mathrm{T}}}\mathrm{(\mathrm{Z})} $ variable, while all the other categories use $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $. Each event category (e.g., 2 $ \ell \textrm{ss} $) is subdivided into its jet multiplcity components. For example, the first four subbins of the 2 $ \ell \textrm{ss} $ bin are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for four jets, the next four subbins are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for 5 jets, etc. The postfit values are obtained by simultaneously fitting all $ \mathrm{26} $ Wilson coefficient (WCs) and the nuisance parameters (NPs). The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs. All yields are plotted on a log scale.
png pdf	Additional Figure 29-b: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables are shown. The two categories on the right side of the plot (3$ \ell $ on-Z 1b, and the 4 and 5 jet bins of 3$ \ell $ on-Z 2b) use the $ {p_{\mathrm{T}}}\mathrm{(\mathrm{Z})} $ variable, while all the other categories use $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $. Each event category (e.g., 2 $ \ell \textrm{ss} $) is subdivided into its jet multiplcity components. For example, the first four subbins of the 2 $ \ell \textrm{ss} $ bin are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for four jets, the next four subbins are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for 5 jets, etc. The postfit values are obtained by simultaneously fitting all $ \mathrm{26} $ Wilson coefficient (WCs) and the nuisance parameters (NPs). The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs. All yields are plotted on a log scale.
png pdf	Additional Figure 29-c: Observed data and expected yields in the prefit (upper) and postfit (lower) scenarios. All kinematic variables are shown. The two categories on the right side of the plot (3$ \ell $ on-Z 1b, and the 4 and 5 jet bins of 3$ \ell $ on-Z 2b) use the $ {p_{\mathrm{T}}}\mathrm{(\mathrm{Z})} $ variable, while all the other categories use $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $. Each event category (e.g., 2 $ \ell \textrm{ss} $) is subdivided into its jet multiplcity components. For example, the first four subbins of the 2 $ \ell \textrm{ss} $ bin are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for four jets, the next four subbins are the $ {p_{\mathrm{T}}}\mathrm{(\ell j )_{\rm max}} $ variable for 5 jets, etc. The postfit values are obtained by simultaneously fitting all $ \mathrm{26} $ Wilson coefficient (WCs) and the nuisance parameters (NPs). The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands are computed by propagating the uncertainties from the WCs and NPs. All yields are plotted on a log scale.
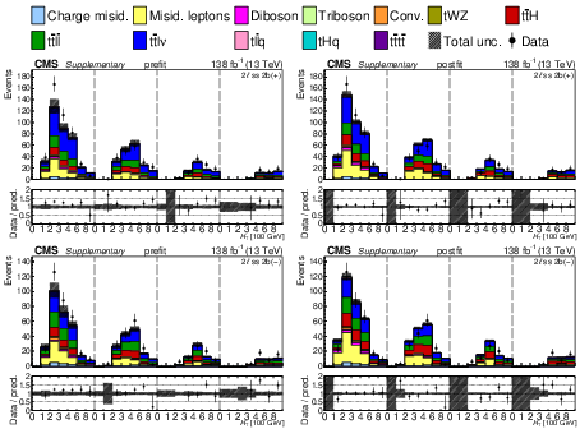
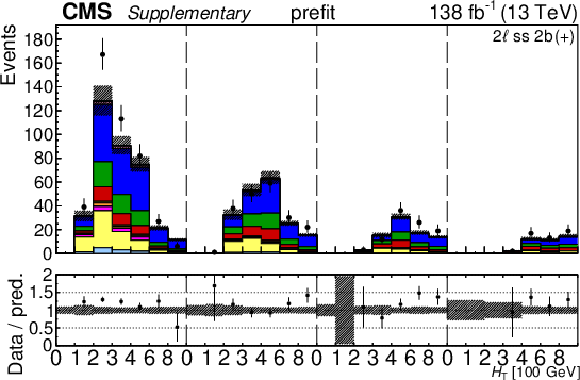
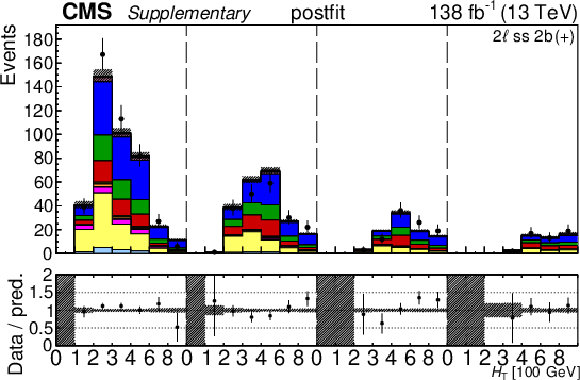
png pdf	Additional Figure 30: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 30-a: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 30-b: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 30-c: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
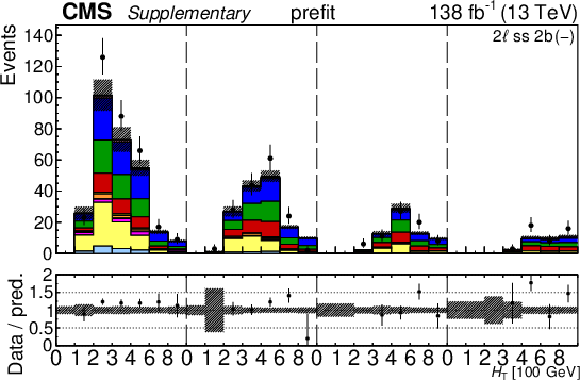
png pdf	Additional Figure 30-d: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
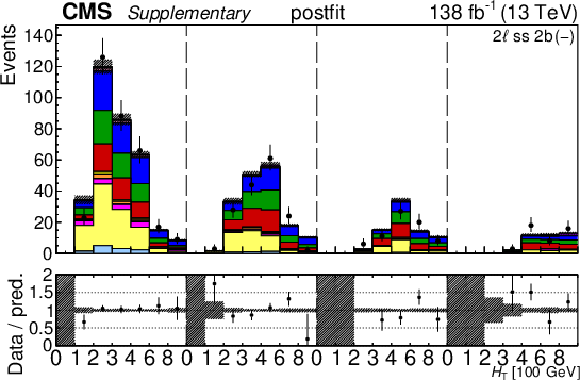
png pdf	Additional Figure 30-e: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 2b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 2b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 2b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
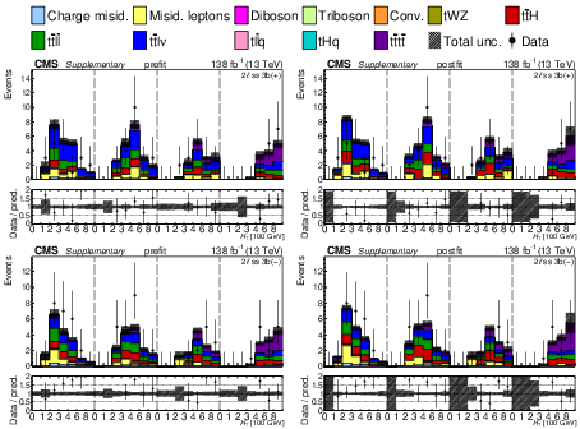
png pdf	Additional Figure 31: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 31-a: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
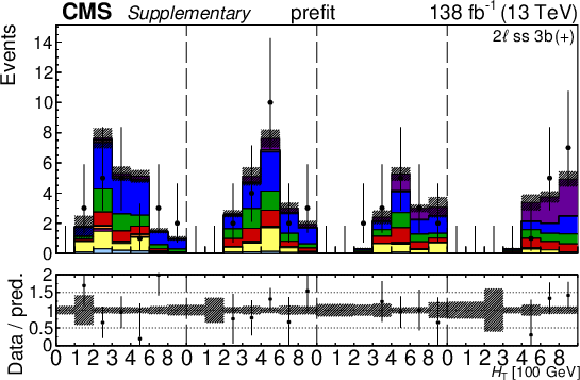
png pdf	Additional Figure 31-b: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 31-c: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
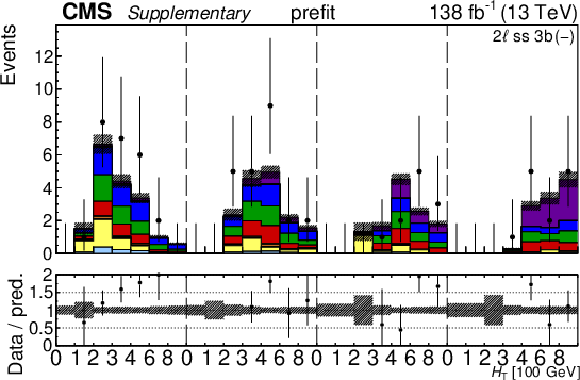
png pdf	Additional Figure 31-d: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 31-e: The top row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 2$ \ell\text{ss 3b} \, (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 2$ \ell\text{ss 3b} \, (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{4j} $, the next seven bins are for 2$ \ell\text{ss 3b} \, (+) \: \mathrm{5j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
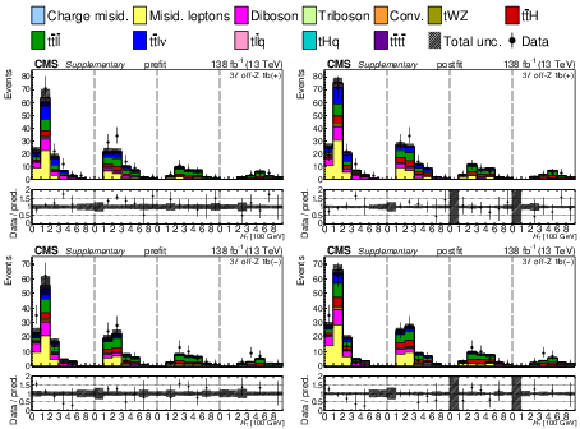
png pdf	Additional Figure 32: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 32-a: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
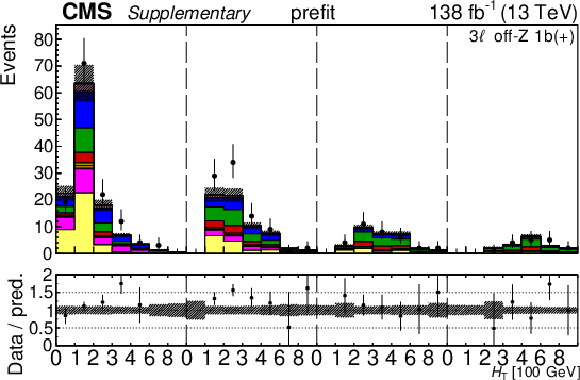
png pdf	Additional Figure 32-b: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
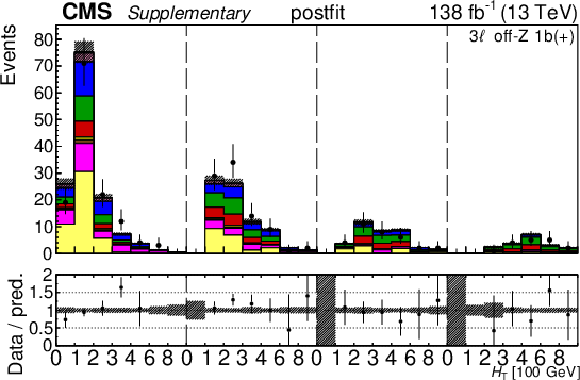
png pdf	Additional Figure 32-c: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
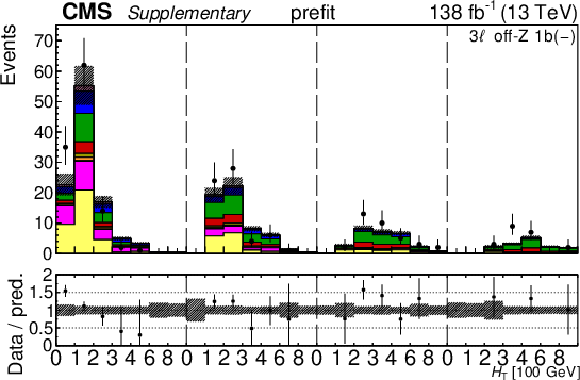
png pdf	Additional Figure 32-d: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
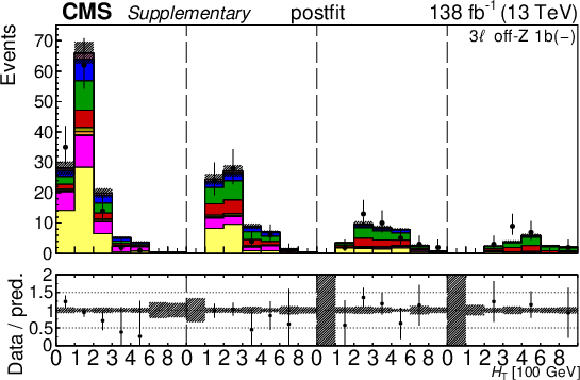
png pdf	Additional Figure 32-e: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 1b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 1b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 1b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
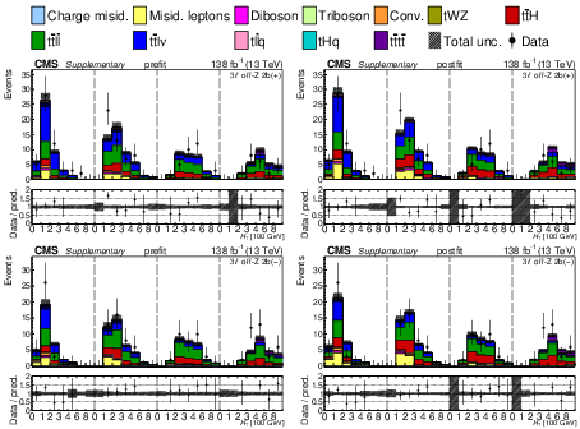
png pdf	Additional Figure 33: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 33-a: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
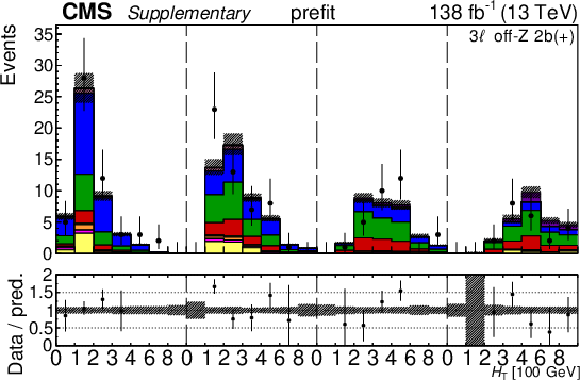
png pdf	Additional Figure 33-b: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
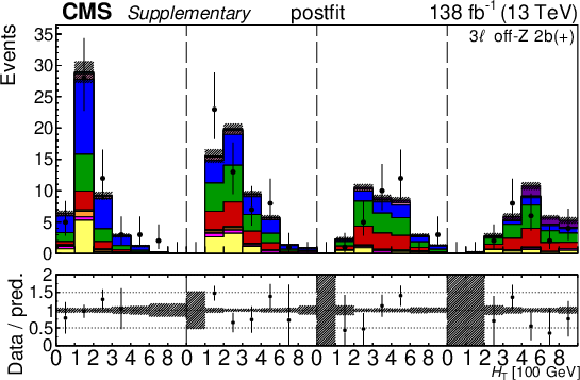
png pdf	Additional Figure 33-c: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
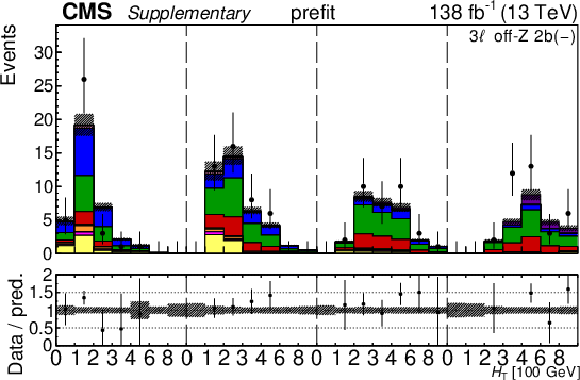
png pdf	Additional Figure 33-d: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
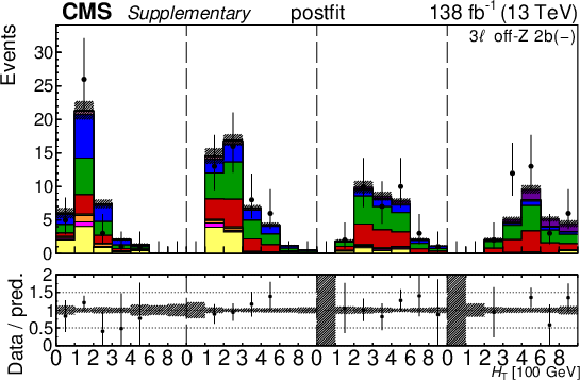
png pdf	Additional Figure 33-e: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (+) $. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ off-Z 2b $ (-) $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ off-Z 2b $ (+) $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{2j} $, the next seven bins are for 3$ \ell $ off-Z 2b $ (+) \: \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
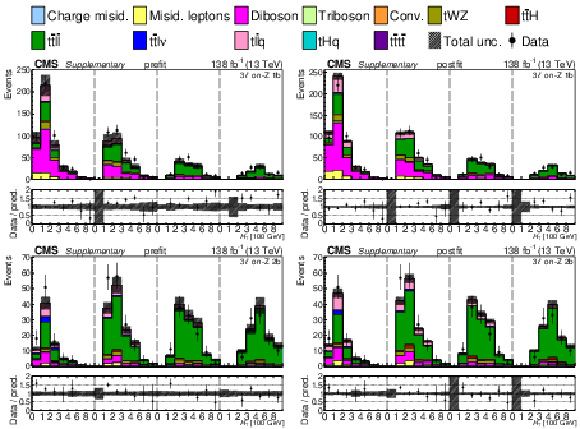
png pdf	Additional Figure 34: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 34-a: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
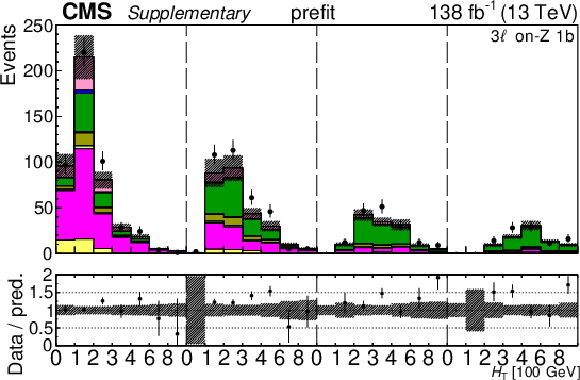
png pdf	Additional Figure 34-b: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
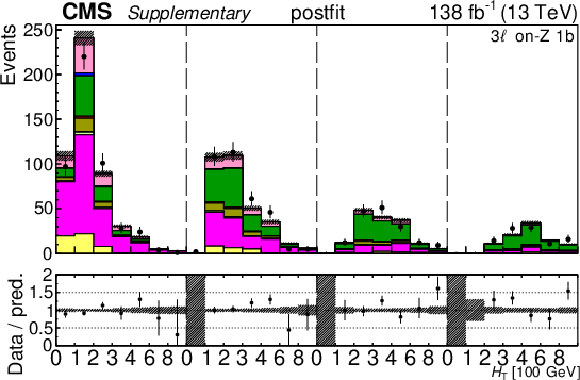
png pdf	Additional Figure 34-c: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
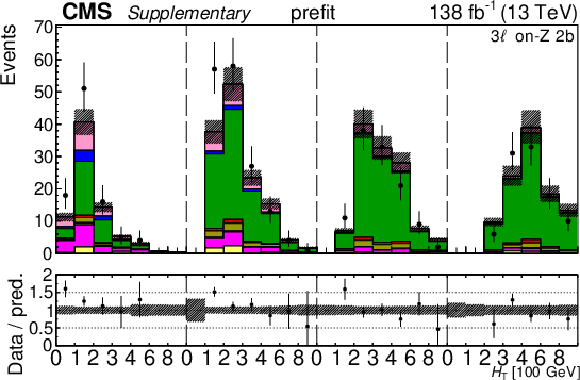
png pdf	Additional Figure 34-d: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
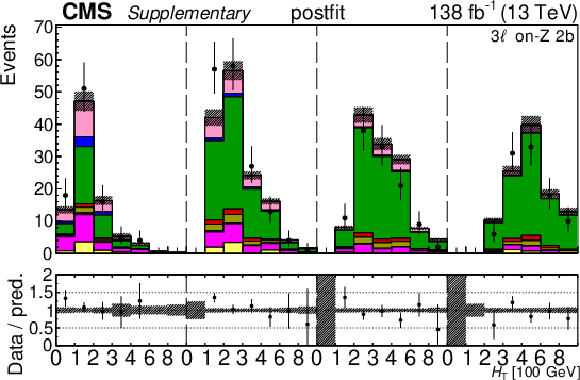
png pdf	Additional Figure 34-e: The top row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 1b. The bottom row shows the prefit (left) and postfit (right) yields of the channel 3$ \ell $ on-Z 2b. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. For example, in the 3$ \ell $ on-Z 1b plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 3$ \ell $ on-Z 1b $ \mathrm{2j} $, the next seven bins are for 3$ \ell $ on-Z 1b $ \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
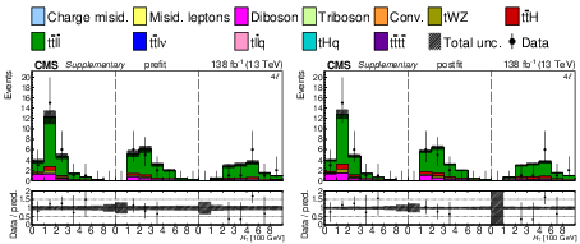
png pdf	Additional Figure 35: Prefit (left) and postfit (right) yields of the channel 4$ \ell $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. In the 4$ \ell $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 4$ \ell \mathrm{2j} $, the next seven bins are for 4$ \ell \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 35-a: Prefit (left) and postfit (right) yields of the channel 4$ \ell $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. In the 4$ \ell $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 4$ \ell \mathrm{2j} $, the next seven bins are for 4$ \ell \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
png pdf	Additional Figure 35-b: Prefit (left) and postfit (right) yields of the channel 4$ \ell $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. In the 4$ \ell $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 4$ \ell \mathrm{2j} $, the next seven bins are for 4$ \ell \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.
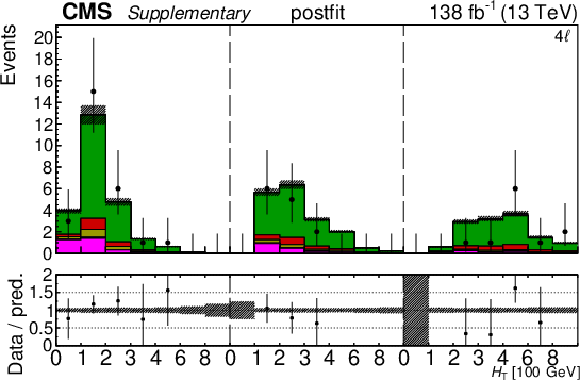
png pdf	Additional Figure 35-c: Prefit (left) and postfit (right) yields of the channel 4$ \ell $. Multiple sets of prefit and postfit plots with the alternative kinematic distribution, including this set of $ H_{\mathrm{T}} $ plots, are used to check the effectiveness of the fit. The jet subcategories are arranged from low jet multiplicity to high jet multiplicity from left to right for each individual plot. In the 4$ \ell $ plot, the first seven bins are the $ H_{\mathrm{T}} $ variable for 4$ \ell \mathrm{2j} $, the next seven bins are for 4$ \ell \mathrm{3j} $, etc. The process labeled ``Conv." corresponds to the photon conversion background, ``Misid. leptons" corresponds to misidentified leptons, and ``Charge misid." corresponds to leptons with a mismeasured charge. The lower panel contains the ratios of the observed yields over the expected. The error bands correspond to nuisance parameter and Wilson coefficient uncertainties added in quadrature.

References
1	J. L. Feng	Dark matter candidates from particle physics and methods of detection	Ann. Rev. Astron. Astrophys. 48 (2010) 495	1003.0904
2	T. A. Porter, R. P. Johnson, and P. W. Graham	Dark matter searches with astroparticle data	Ann. Rev. Astron. Astrophys. 49 (2011) 155	1104.2836
3	C. Degrande et al.	Effective field theory: A modern approach to anomalous couplings	Annals Phys. 335 (2013) 21	1205.4231
4	CDF Collaboration	Observation of top quark production in $ {\overline{\mathrm{p}}\mathrm{p}} $ collisions	PRL 74 (1995) 2626	hep-ex/9503002
5	\DZERO Collaboration	Observation of the top quark	PRL 74 (1995) 2632	hep-ex/9503003
6	Particle Data Group, R. L. Workman et al.	Review of particle physics	Prog. Theor. Exp. Phys. 2022 (2022) 083C01
7	CMS Collaboration	Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at $ \sqrt{s}= $ 13 TeV	EPJC 81 (2021) 378	CMS-HIG-19-008 2011.03652
8	CMS Collaboration	Measurement of the cross section of top quark-antiquark pair production in association with a W boson in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Accepted by JHEP, 2022	CMS-TOP-21-011 2208.06485
9	CMS Collaboration	Measurement of top quark pair production in association with a Z boson in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 03 (2020) 056	CMS-TOP-18-009 1907.11270
10	CMS Collaboration	Inclusive and differential cross section measurements of single top quark production in association with a Z boson in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 02 (2022) 107	CMS-TOP-20-010 2111.02860
11	CMS Collaboration	Evidence for four-top quark production in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	Accepted by PLB, 2023	CMS-TOP-21-005 2303.03864
12	CMS Collaboration	Search for new physics in top quark production with additional leptons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using effective field theory	JHEP 03 (2021) 095	CMS-TOP-19-001 2012.04120
13	CMS Collaboration	Probing effective field theory operators in the associated production of top quarks with a Z boson in multilepton final states at $ \sqrt{s}= $ 13 TeV	JHEP 12 (2021) 083	CMS-TOP-21-001 2107.13896
14	CMS Collaboration	Search for new physics using effective field theory in 13 TeV $ {\mathrm{p}\mathrm{p}} $ collision events that contain a top quark pair and a boosted Z or Higgs boson	Accepted by PRD, 2022	CMS-TOP-21-003 2208.12837
15	CMS Collaboration	HEPData record for this analysis	link
16	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
17	CMS Collaboration	Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JINST 15 (2020) P10017	CMS-TRG-17-001 2006.10165
18	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
19	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
20	R. Frederix and S. Frixione	Merging meets matching in MC@NLO	JHEP 12 (2012) 061	1209.6215
21	J. Alwall et al.	Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions	EPJC 53 (2008) 473	0706.2569
22	J. A. Aguilar-Saavedra et al.	Interpreting top-quark LHC measurements in the standard-model effective field theory	LHC TOP WG note CERN-LPCC-2018-01, 2018	1802.07237
23	B. Grzadkowski, M. Iskrzynski, M. Misiak, and J. Rosiek	Dimension-six terms in the standard model Lagrangian	JHEP 10 (2010) 085	1008.4884
24	R. Goldouzian et al.	Matching in $ {\mathrm{p}\mathrm{p}\to{\mathrm{t}\overline{\mathrm{t}}} \mathrm{W}/\mathrm{Z}/\mathrm{h}} $+jet SMEFT studies	JHEP 06 (2021) 151	2012.06872
25	NNPDF Collaboration	Parton distributions for the LHC run II	JHEP 04 (2015) 040	1410.8849
26	T. Sjöstrand, S. Mrenna, and P. Z. Skands	A brief introduction to PYTHIA8.1	Comput. Phys. Commun. 178 (2008) 852	0710.3820
27	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
28	LHC Higgs Cross Section Working Group , D. de Florian et al.	Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector	CERN Report CERN-2017-002-M, 2016 link	1610.07922
29	R. Frederix and I. Tsinikos	On improving NLO merging for $ {{\mathrm{t}\overline{\mathrm{t}}} \mathrm{W}} $ production	JHEP 11 (2021) 029	2108.07826
30	M. van Beekveld, A. Kulesza, and L. M. Valero	Threshold resummation for the production of four top quarks at the LHC		2212.03259
31	O. Mattelaer	On the maximal use of Monte Carlo samples: re-weighting events at NLO accuracy	EPJC 76 (2016) 674	1607.00763
32	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
33	CMS Collaboration	Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC	JINST 16 (2021) P05014	CMS-EGM-17-001 2012.06888
34	CMS Collaboration	ECAL 2016 refined calibration and Run2 summary plots	CMS Detector Performance Note CMS-DP-2020-021, 2020 CDS
35	CMS Collaboration	Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JINST 13 (2018) P06015	CMS-MUO-16-001 1804.04528
36	CMS Collaboration	Identification of prompt and isolated muons using multivariate techniques at the CMS experiment in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	CMS Physics Analysis Summary, 2023 CMS-PAS-MUO-22-001	CMS-PAS-MUO-22-001
37	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_{\mathrm{T}} $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
38	M. Cacciari, G. P. Salam, and G. Soyez	FASTJET user manual	EPJC 72 (2012) 1896	1111.6097
39	CMS Collaboration	Pileup mitigation at CMS in 13 TeV data	JINST 15 (2020) P09018	CMS-JME-18-001 2003.00503
40	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in $ {\mathrm{p}\mathrm{p}} $ collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
41	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in $ {\mathrm{p}\mathrm{p}} $ collisions at 13 TeV	JINST 13 (2018) P05011	CMS-BTV-16-002 1712.07158
42	E. Bols et al.	Jet flavour classification using DEEPJET	JINST 15 (2020) P12012	2008.10519
43	CMS Collaboration	Performance summary of AK4 jet b tagging with data from proton-proton collisions at 13 TeV with the CMS detector	CMS Detector Performance Note CMS-DP-2023-005, 2023 CDS
44	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
45	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
46	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG \textscbox	JHEP 06 (2010) 043	1002.2581
47	T. Melia, P. Nason, R. Rontsch, and G. Zanderighi	$ {\mathrm{W^+}\mathrm{W^-}} $, $ {\mathrm{W}\mathrm{Z}} $ and $ {\mathrm{Z}\mathrm{Z}} $ production in the POWHEG \textscbox	JHEP 11 (2011) 078	1107.5051
48	S. Frixione, G. Ridolfi, and P. Nason	A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction	JHEP 09 (2007) 126	0707.3088
49	J. M. Campbell and R. K. Ellis	An update on vector boson pair production at hadron colliders	PRD 60 (1999) 113006	hep-ph/9905386
50	M. Grazzini et al.	NNLO QCD + NLO EW with \textscMatrix+\textscOpenLoops: precise predictions for vector-boson pair production	JHEP 02 (2020) 087	1912.00068
51	F. Caola, K. Melnikov, R. Röntsch, and L. Tancredi	QCD corrections to $ {\mathrm{Z}\mathrm{Z}} $ production in gluon fusion at the LHC	PRD 92 (2015) 094028	1509.06734
52	CMS Collaboration	Search for electroweak production of charginos and neutralinos in multilepton final states in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 03 (2018) 166	CMS-SUS-16-039 1709.05406
53	W. Verkerke and D. Kirkby	The RooFit toolkit for data modeling	in 13th Int. Conf. on Computing in High Energy and Nuclear Phys. (CHEP ): La Jolla CA, USA, 2003 Proc. 1 (2003) 3	physics/0306116
54	CMS Collaboration	Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS	EPJC 81 (2021) 800	CMS-LUM-17-003 2104.01927
55	CMS Collaboration	CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s}= $ 13 TeV	CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004	CMS-PAS-LUM-17-004
56	CMS Collaboration	CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV	CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002	CMS-PAS-LUM-18-002
57	CMS Collaboration	Measurements of inclusive W and Z cross sections in $ {\mathrm{p}\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV	JHEP 01 (2011) 080	CMS-EWK-10-002 1012.2466
58	CMS Collaboration	Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV	JHEP 07 (2018) 161	CMS-FSQ-15-005 1802.02613
59	J. Butterworth et al.	PDF4LHC recommendations for LHC Run II	JPG 43 (2016) 023001	1510.03865

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2024 for the benefit of the CMS Collaboration