

Compact Muon Solenoid
LHC, CERN
| CMS-SMP-23-002 ; CERN-EP-2024-308 | ||
| High-precision measurement of the W boson mass with the CMS experiment at the LHC | ||
| CMS Collaboration | ||
| 18 December 2024 | ||
| Submitted to Nature | ||
| Abstract: In the standard model of particle physics, the masses of the carriers of the weak interaction, the W and Z bosons, are uniquely related. Physics beyond the standard model could change this relationship through the effects of quantum loops of virtual particles, thus making it of great importance to measure these masses with the highest possible precision. Although the mass of the Z boson is known to the remarkable precision of 22 parts per million (2.0 MeV), the W boson mass is known much less precisely, given the difficulty of the measurement. A global fit to electroweak data, used to predict the W boson mass in the standard model, yields an uncertainty of 6 MeV. Reaching a comparable experimental precision would be a sensitive and fundamental test of the standard model. Furthermore, a precision measurement of the W boson mass performed by the CDF Collaboration at the Fermilab Tevatron has challenged the standard model by significantly disagreeing with the prediction of the global electroweak fit and the average of other $ m_{\mathrm{W}} $ measurements. We report the first W boson mass measurement by the CMS Collaboration at the CERN LHC, based on a data sample collected in 2016 at the proton-proton collision energy of 13 TeV. The W boson mass is measured using a large sample of $ \mathrm{W}\to\mu\nu $ events via a highly granular binned maximum likelihood fit to the kinematic properties of the muons produced in the $ \mathrm{W^+} $ and $ \mathrm{W^-} $ boson decays. The significant in situ constraints of theoretical inputs and their corresponding uncertainties, together with an accurate determination of the experimental effects, lead to a precise W boson mass measurement, $ m_{\mathrm{W}} = $ 80 360.2 $ \pm $ 9.9 MeV, in agreement with the standard model prediction. | ||
| Links: e-print arXiv:2412.13872 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Covariance matrices can be found here |
| Figures | |

png pdf |
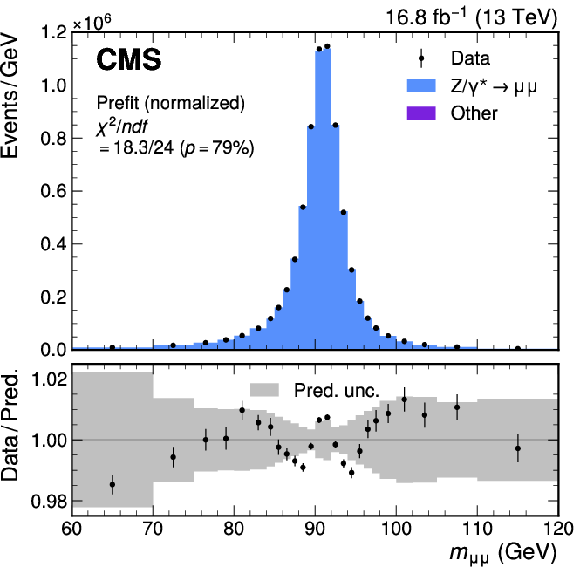
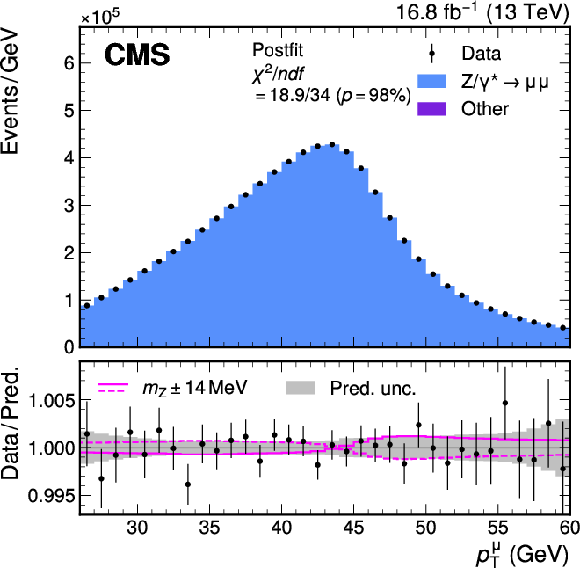
Figure 1:
The Z boson mass measurement. Measured and simulated $ \mathrm{Z}\to\mu\mu $ dimuon mass distributions. The predicted $ \mathrm{Z}\to\mu\mu $ distribution is shown in blue. The small contributions of other processes are included but are not visible. The prediction reflects the best fit parameter values and uncertainties from the maximum likelihood fit. The bottom panel shows the ratio between the number of events observed in data, including variations in the predictions, and the total nominal prediction. The vertical bars represent the statistical uncertainties in the data. The total uncertainty in the prediction after the systematic uncertainty profiling procedure (gray band) and the effect of a $ \pm $4.8 MeV variation of $ m_{\mathrm{Z}} $ (magenta lines) are also shown. |
png pdf |
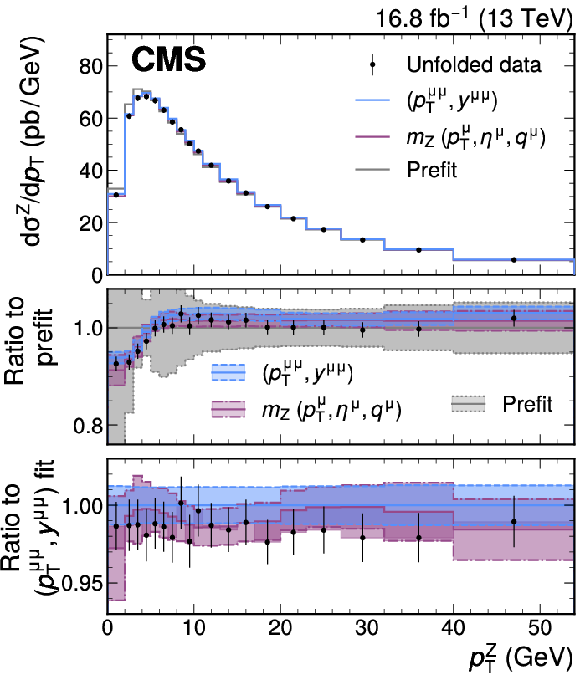
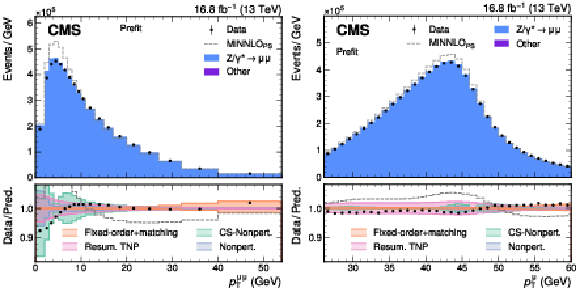
Figure 2:
Validation of the theory model. Unfolded measured $ p_{\mathrm{T}}^{\mathrm{Z}} $ distribution (points) compared with the generator-level SCETLIB $+$ MiNNLO$_{\text{PS}}$ predictions before (prefit, gray) and after adjusting the nuisance parameters to the best fit values obtained from the W-like $ m_{\mathrm{Z}} $ fit (magenta) or from the direct fit to the $ p_{\mathrm{T}}^{\mu\mu} $ distribution (blue). The center panel shows the ratio of the predictions and unfolded data to the prefit prediction. The uncertainty in the prefit prediction is shown by the shaded gray area. The bottom panel shows the ratio of the predictions and unfolded data to the prediction adjusted to the best fit values obtained from the fit to the $ (p_{\mathrm{T}}^{\mu\mu}, y^{\mu\mu}) $ distribution. The uncertainties in the predictions after the maximum likelihood fits are shown in the shaded magenta and blue bands. The vertical bars represent the total uncertainty in the unfolded data. |

png pdf |
Figure 3:
The W boson mass measurement. Measured and predicted $ p_{\mathrm{T}}^{\mu} $ distributions, showing the sensitivity to $ m_{\mathrm{W}} $ from the characteristic Jacobian peak at $ {\sim}m_{\mathrm{W}}/ $ 2. The predicted $ \mathrm{W}\to\mu\nu $ contribution is shown in red, while the background contributions are shown in blue, purple, and yellow. Additional background contributions are included but not visible. The prediction is adjusted to the best fit values of the nuisance parameters and the measured value of $ m_{\mathrm{W}} $. The bottom panel shows the ratio between the number of events observed in data, including variations in the predictions, and the total nominal prediction. The vertical bars represent the statistical uncertainties in the data. A shift in the $ m_{\mathrm{W}} $ value shifts the peak of the distribution, as illustrated by the solid and dashed magenta lines, which show an increase or decrease of $ m_{\mathrm{W}} $ by 9.9 MeV. The total contribution of all theoretical and experimental uncertainties in the predictions, after the systematic uncertainty profiling in the maximum likelihood fit, is shown by the gray band. |
png pdf |
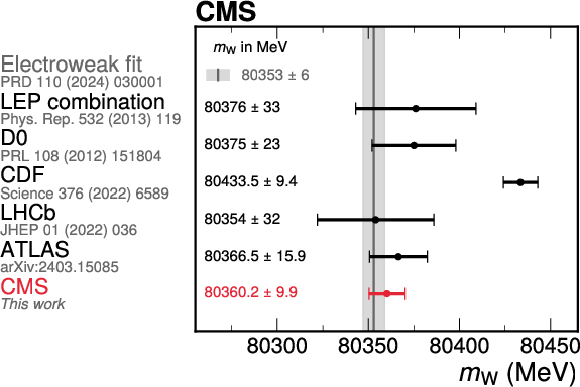
Figure 4:
Comparison with other experiments and the EW fit prediction. The $ m_{\mathrm{W}} $ measurement from this analysis (in red) is compared with the combined measurement of experiments at LEP [54], and with the measurements performed by the D0 [55], CDF [11], LHCb [9], and ATLAS [10] experiments. The global EW fit prediction [5] is represented by the gray vertical band, with the shaded band showing its uncertainty. |

png pdf |
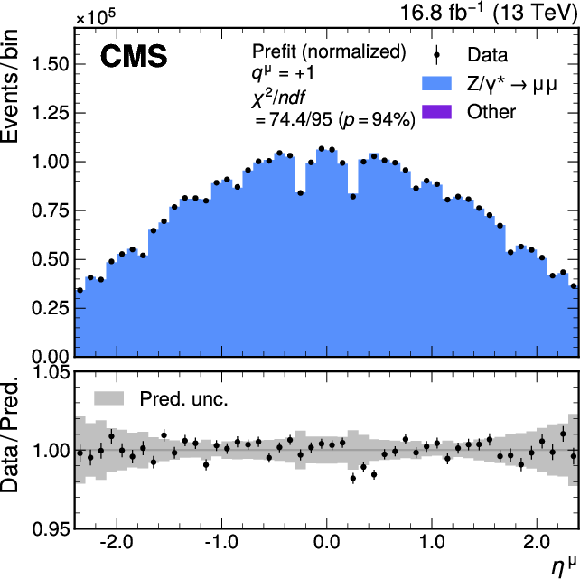
Figure A1:
Measured and predicted $ \eta^{\mu} $ distributions in $ \mathrm{Z}\to\mu\mu $ events with the W-like Z boson selection for positively (left) and negatively (right) charged muons. The total uncertainties (statistical and systematic) are represented by the gray bands and the normalization of the simulated spectrum is scaled to the measured distribution, to better illustrate the level of agreement between the two. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
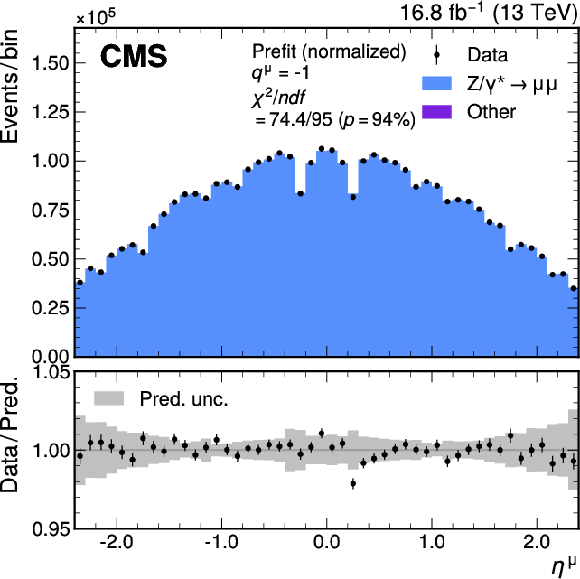
Figure A1-a:
Measured and predicted $ \eta^{\mu} $ distributions in $ \mathrm{Z}\to\mu\mu $ events with the W-like Z boson selection for positively (left) and negatively (right) charged muons. The total uncertainties (statistical and systematic) are represented by the gray bands and the normalization of the simulated spectrum is scaled to the measured distribution, to better illustrate the level of agreement between the two. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
Figure A1-b:
Measured and predicted $ \eta^{\mu} $ distributions in $ \mathrm{Z}\to\mu\mu $ events with the W-like Z boson selection for positively (left) and negatively (right) charged muons. The total uncertainties (statistical and systematic) are represented by the gray bands and the normalization of the simulated spectrum is scaled to the measured distribution, to better illustrate the level of agreement between the two. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
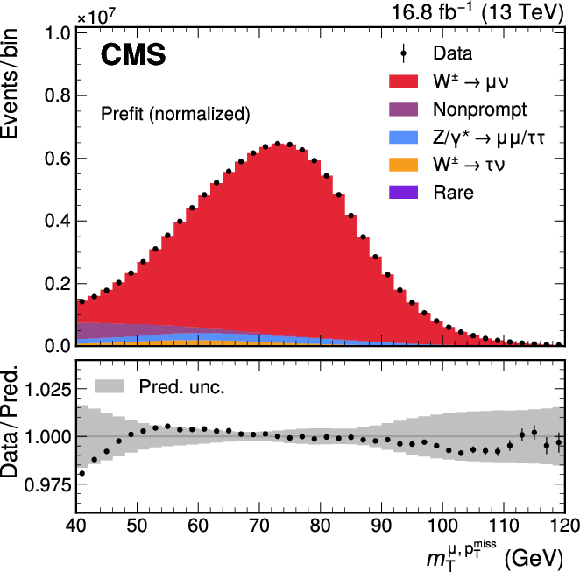
Figure A2:
Measured and predicted $ m_{\mathrm{T}} $ distributions in $ \mathrm{W}\to\mu\nu $ events, after calibrating the hadronic recoil. The predictions are those prior to the fit to data. The total uncertainties (statistical and systematic) are represented by the gray band and the normalization of the simulated spectrum is scaled to the measured distribution to better illustrate their agreement. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
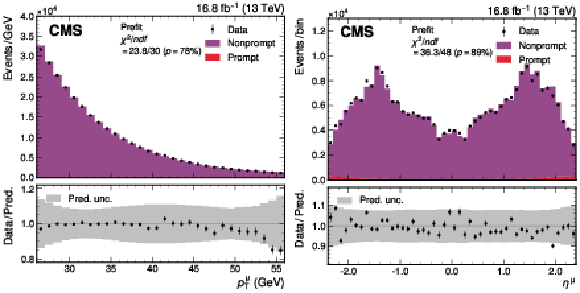
Figure A3:
The observed data and the prediction of the extended ABCD method before the maximum likelihood fit, for the $ p_{\mathrm{T}}^{\mu} $ (left) and $ \eta^{\mu} $ (right) distributions, in a region enriched in events with nonprompt muons obtained by selecting muons compatible with being produced in a secondary vertex. Small contributions from events with a prompt muon, evaluated using simulated samples, are shown by the red histogram. The total uncertainties (statistical and systematic) are represented by the gray bands. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
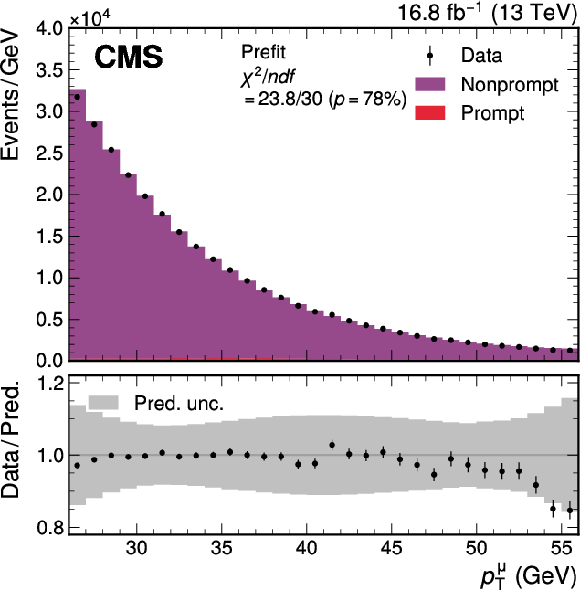
Figure A3-a:
The observed data and the prediction of the extended ABCD method before the maximum likelihood fit, for the $ p_{\mathrm{T}}^{\mu} $ (left) and $ \eta^{\mu} $ (right) distributions, in a region enriched in events with nonprompt muons obtained by selecting muons compatible with being produced in a secondary vertex. Small contributions from events with a prompt muon, evaluated using simulated samples, are shown by the red histogram. The total uncertainties (statistical and systematic) are represented by the gray bands. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
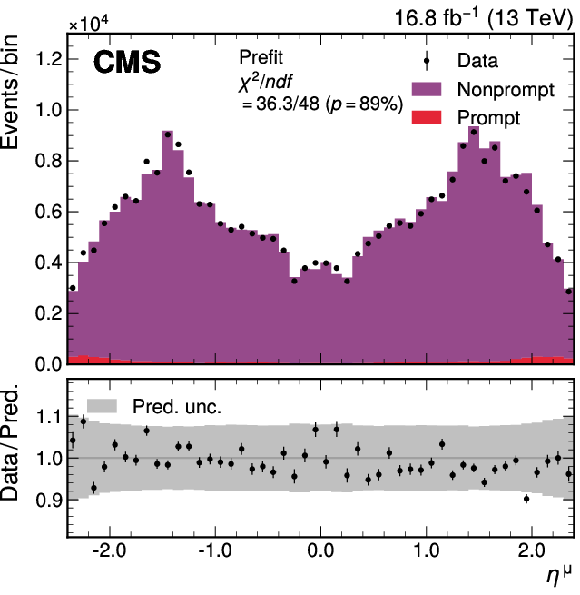
Figure A3-b:
The observed data and the prediction of the extended ABCD method before the maximum likelihood fit, for the $ p_{\mathrm{T}}^{\mu} $ (left) and $ \eta^{\mu} $ (right) distributions, in a region enriched in events with nonprompt muons obtained by selecting muons compatible with being produced in a secondary vertex. Small contributions from events with a prompt muon, evaluated using simulated samples, are shown by the red histogram. The total uncertainties (statistical and systematic) are represented by the gray bands. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |

png pdf |
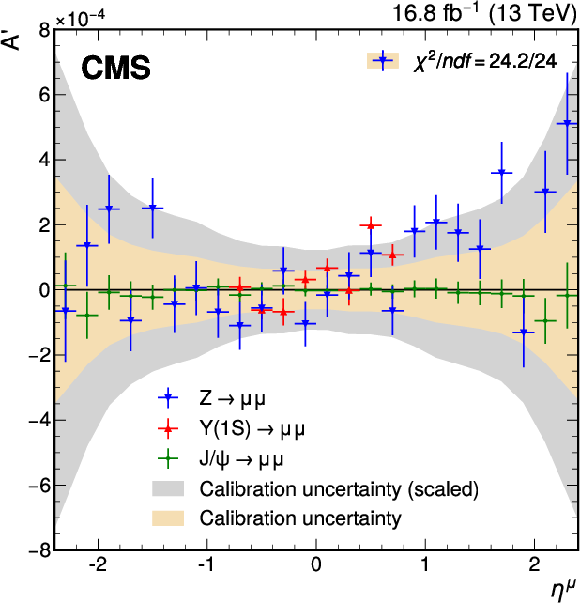
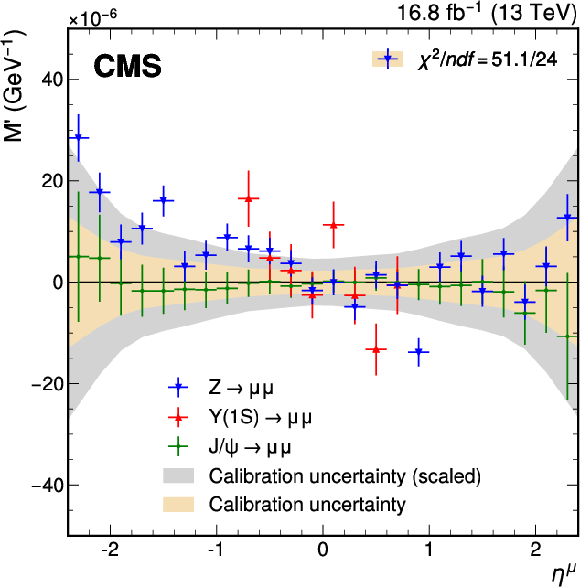
Figure A4:
Charge-independent ($ A^{\prime} $, left) and charge-dependent ($ M^{\prime} $, right) residual scale differences from using $ {\mathrm{J}/\psi} \to\mu\mu $, $ \Upsilon{\textrm{(1S)}}\to\mu\mu $, and $ \mathrm{Z}\to\mu\mu $ events. The charge-independent comparison probes a magnetic-field-like difference, whereas the charge-dependent comparison reflects a misalignment-like term. The points with error bars represent the scale parameters and statistical uncertainties associated with the closure test performed with $ {\mathrm{J}/\psi} \to\mu\mu $ (green), $ \Upsilon{\textrm{(1S)}}\to\mu\mu $ (red), and $ \mathrm{Z}\to\mu\mu $ (blue) events. The yellow band represents the corresponding statistical uncertainty in the calibration parameters derived from the $ \mathrm{J}/\psi $ calibration sample. The filled gray band shows this uncertainty scaled by a factor of 2.1, as described in the text. The $ \chi^2 $ values correspond to the compatibility of the scale parameters with zero for the closure test performed with $ \mathrm{Z}\to\mu\mu $ events and take into account the statistical uncertainties for these parameters, as well as for the calibration parameters derived from the $ \mathrm{J}/\psi $ sample, without additional scaling. The calibration parameter uncertainties are fully uncorrelated from the Z and $ \Upsilon{\textrm{(1S)}} $ closure test uncertainties, but very strongly correlated with the $ \mathrm{J}/\psi $ closure uncertainties, since they use the same data. |
png pdf |
Figure A4-a:
Charge-independent ($ A^{\prime} $, left) and charge-dependent ($ M^{\prime} $, right) residual scale differences from using $ {\mathrm{J}/\psi} \to\mu\mu $, $ \Upsilon{\textrm{(1S)}}\to\mu\mu $, and $ \mathrm{Z}\to\mu\mu $ events. The charge-independent comparison probes a magnetic-field-like difference, whereas the charge-dependent comparison reflects a misalignment-like term. The points with error bars represent the scale parameters and statistical uncertainties associated with the closure test performed with $ {\mathrm{J}/\psi} \to\mu\mu $ (green), $ \Upsilon{\textrm{(1S)}}\to\mu\mu $ (red), and $ \mathrm{Z}\to\mu\mu $ (blue) events. The yellow band represents the corresponding statistical uncertainty in the calibration parameters derived from the $ \mathrm{J}/\psi $ calibration sample. The filled gray band shows this uncertainty scaled by a factor of 2.1, as described in the text. The $ \chi^2 $ values correspond to the compatibility of the scale parameters with zero for the closure test performed with $ \mathrm{Z}\to\mu\mu $ events and take into account the statistical uncertainties for these parameters, as well as for the calibration parameters derived from the $ \mathrm{J}/\psi $ sample, without additional scaling. The calibration parameter uncertainties are fully uncorrelated from the Z and $ \Upsilon{\textrm{(1S)}} $ closure test uncertainties, but very strongly correlated with the $ \mathrm{J}/\psi $ closure uncertainties, since they use the same data. |
png pdf |
Figure A4-b:
Charge-independent ($ A^{\prime} $, left) and charge-dependent ($ M^{\prime} $, right) residual scale differences from using $ {\mathrm{J}/\psi} \to\mu\mu $, $ \Upsilon{\textrm{(1S)}}\to\mu\mu $, and $ \mathrm{Z}\to\mu\mu $ events. The charge-independent comparison probes a magnetic-field-like difference, whereas the charge-dependent comparison reflects a misalignment-like term. The points with error bars represent the scale parameters and statistical uncertainties associated with the closure test performed with $ {\mathrm{J}/\psi} \to\mu\mu $ (green), $ \Upsilon{\textrm{(1S)}}\to\mu\mu $ (red), and $ \mathrm{Z}\to\mu\mu $ (blue) events. The yellow band represents the corresponding statistical uncertainty in the calibration parameters derived from the $ \mathrm{J}/\psi $ calibration sample. The filled gray band shows this uncertainty scaled by a factor of 2.1, as described in the text. The $ \chi^2 $ values correspond to the compatibility of the scale parameters with zero for the closure test performed with $ \mathrm{Z}\to\mu\mu $ events and take into account the statistical uncertainties for these parameters, as well as for the calibration parameters derived from the $ \mathrm{J}/\psi $ sample, without additional scaling. The calibration parameter uncertainties are fully uncorrelated from the Z and $ \Upsilon{\textrm{(1S)}} $ closure test uncertainties, but very strongly correlated with the $ \mathrm{J}/\psi $ closure uncertainties, since they use the same data. |
png pdf |
Figure A5:
Measured and simulated $ \mathrm{Z}\to\mu\mu $ dimuon mass distributions, after applying the muon momentum scale and resolution corrections. The simulated predictions and uncertainties are scaled to match the number of observed data events. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the total nominal prediction. |
png pdf |
Figure A6:
Measured and simulated $ p_{\mathrm{T}}^{\mu\mu} $ (left) and $ p_{\mathrm{T}}^{\mu} $ (right) distributions in selected $ \mathrm{Z}\to\mu\mu $ events. The standalone uncorrected MINNLO$_{\text{PS}}$ predictions are shown by the dashed gray line. The nominal predictions (blue) correct the POWHEG MINNLO$_{\text{PS}}$ $p_{\mathrm{T}}^{\mathrm{V}} $ with SCETLIB $+$ DYTURBO at $ \mathrm{N}^{3}\mathrm{LL}{+}\mathrm{NNLO} $, as described in the text. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data to that of the total nominal prediction, as well as the relative impact of variations of the predictions. Different sources of uncertainty are shown as solid bands in the lower panel: the fixed-order uncertainty and the uncertainty in the resummation and fixed-order matching (orange), resummed prediction using TNPs (pink), the Collins--Soper (CS) kernel nonperturbative uncertainty (green), and other nonperturbative uncertainties (light blue). Additional sources of experimental and theoretical uncertainty that impact the agreement with the data are not shown. |

png pdf |
Figure A6-a:
Measured and simulated $ p_{\mathrm{T}}^{\mu\mu} $ (left) and $ p_{\mathrm{T}}^{\mu} $ (right) distributions in selected $ \mathrm{Z}\to\mu\mu $ events. The standalone uncorrected MINNLO$_{\text{PS}}$ predictions are shown by the dashed gray line. The nominal predictions (blue) correct the POWHEG MINNLO$_{\text{PS}}$ $p_{\mathrm{T}}^{\mathrm{V}} $ with SCETLIB $+$ DYTURBO at $ \mathrm{N}^{3}\mathrm{LL}{+}\mathrm{NNLO} $, as described in the text. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data to that of the total nominal prediction, as well as the relative impact of variations of the predictions. Different sources of uncertainty are shown as solid bands in the lower panel: the fixed-order uncertainty and the uncertainty in the resummation and fixed-order matching (orange), resummed prediction using TNPs (pink), the Collins--Soper (CS) kernel nonperturbative uncertainty (green), and other nonperturbative uncertainties (light blue). Additional sources of experimental and theoretical uncertainty that impact the agreement with the data are not shown. |
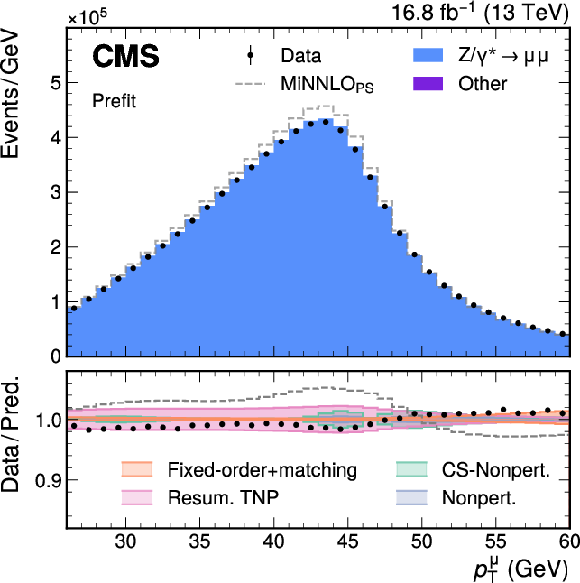
png pdf |
Figure A6-b:
Measured and simulated $ p_{\mathrm{T}}^{\mu\mu} $ (left) and $ p_{\mathrm{T}}^{\mu} $ (right) distributions in selected $ \mathrm{Z}\to\mu\mu $ events. The standalone uncorrected MINNLO$_{\text{PS}}$ predictions are shown by the dashed gray line. The nominal predictions (blue) correct the POWHEG MINNLO$_{\text{PS}}$ $p_{\mathrm{T}}^{\mathrm{V}} $ with SCETLIB $+$ DYTURBO at $ \mathrm{N}^{3}\mathrm{LL}{+}\mathrm{NNLO} $, as described in the text. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data to that of the total nominal prediction, as well as the relative impact of variations of the predictions. Different sources of uncertainty are shown as solid bands in the lower panel: the fixed-order uncertainty and the uncertainty in the resummation and fixed-order matching (orange), resummed prediction using TNPs (pink), the Collins--Soper (CS) kernel nonperturbative uncertainty (green), and other nonperturbative uncertainties (light blue). Additional sources of experimental and theoretical uncertainty that impact the agreement with the data are not shown. |
png pdf |
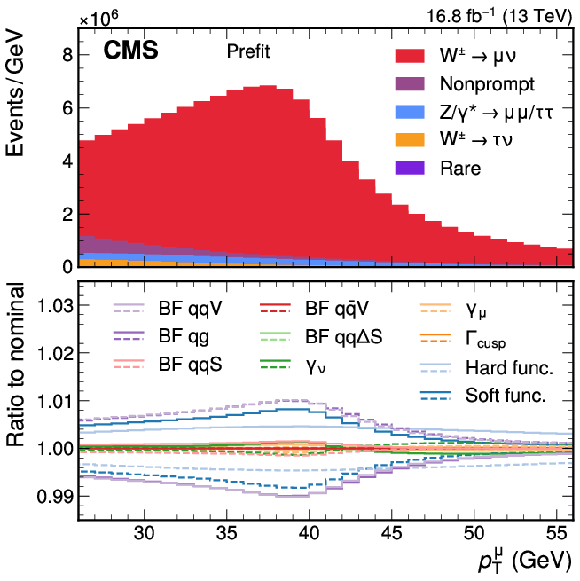
Figure A7:
The predicted $ p_{\mathrm{T}}^{\mu} $ distribution for selected $ \mathrm{W}\to\mu\nu $ events, before the maximum likelihood fit. The lower panel shows the ratio of the ten TNP variations described in the text to the nominal prediction, illustrating their impact on the spectrum. |
png pdf |
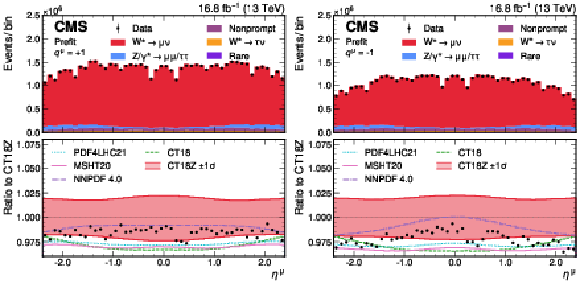
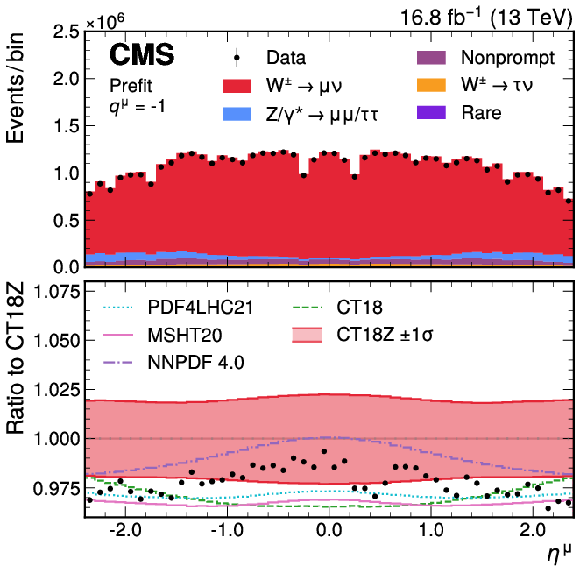
Figure A8:
Measured and predicted $ \eta^{\mu} $ distributions for positively (left) and negatively (right) charged muons. The nominal prediction, obtained with the CT18Z PDF set, is shown in filled light red. The uncertainty, evaluated as the sum of the eigenvector variation sets, is represented by the filled band in the lower panel. The predictions using the PDF4LHC21, MSHT20, NNPDF4.0, and CT18 sets are also shown (without uncertainty bands). The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the nominal prediction. |
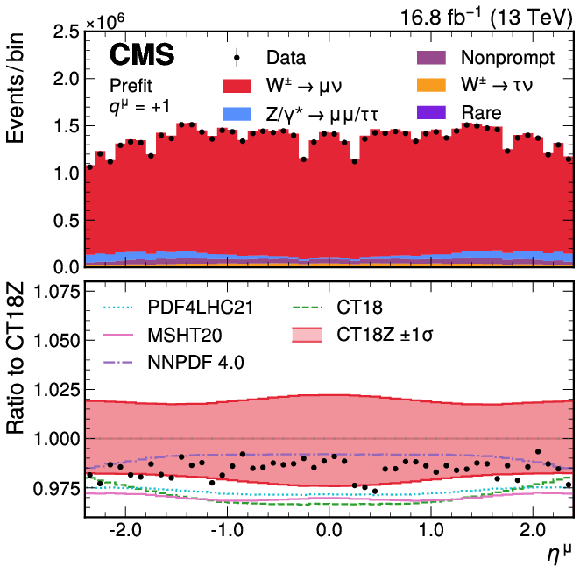
png pdf |
Figure A8-a:
Measured and predicted $ \eta^{\mu} $ distributions for positively (left) and negatively (right) charged muons. The nominal prediction, obtained with the CT18Z PDF set, is shown in filled light red. The uncertainty, evaluated as the sum of the eigenvector variation sets, is represented by the filled band in the lower panel. The predictions using the PDF4LHC21, MSHT20, NNPDF4.0, and CT18 sets are also shown (without uncertainty bands). The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the nominal prediction. |
png pdf |
Figure A8-b:
Measured and predicted $ \eta^{\mu} $ distributions for positively (left) and negatively (right) charged muons. The nominal prediction, obtained with the CT18Z PDF set, is shown in filled light red. The uncertainty, evaluated as the sum of the eigenvector variation sets, is represented by the filled band in the lower panel. The predictions using the PDF4LHC21, MSHT20, NNPDF4.0, and CT18 sets are also shown (without uncertainty bands). The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data and of variations in the predictions to that of the nominal prediction. |

png pdf |
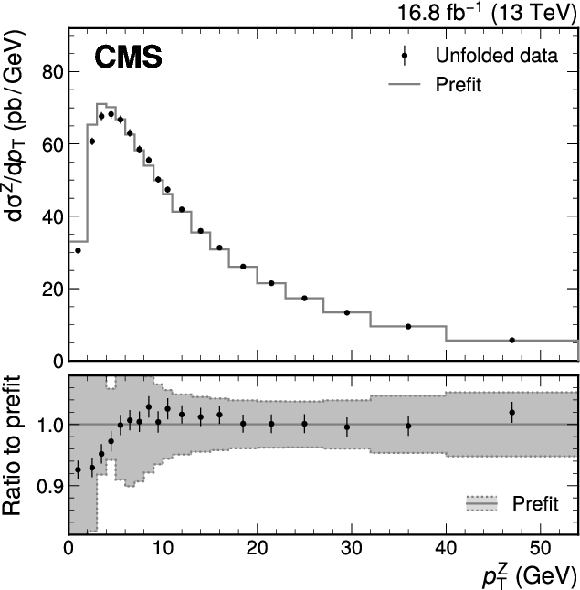
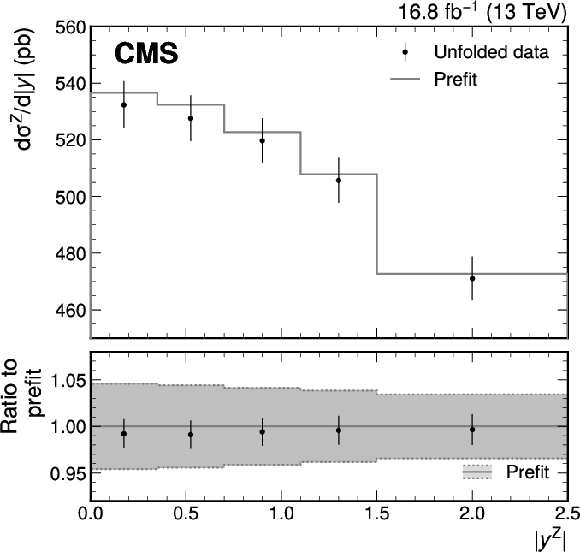
Figure A9:
Unfolded differential cross sections as functions of $ p_{\mathrm{T}}^{\mathrm{Z}} $ (left) and $ |y^{\mathrm{Z}}| $ (right) compared with the prefit prediction from SCETLIB $+$ DYTURBO. The results are obtained with the selection $ |y^{\mathrm{Z}}| < $ 2.5 and $ p_{\mathrm{T}}^{\mathrm{Z}} < $ 54 GeV. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the unfolded data to the SCETLIB $+$ DYTURBO prediction. |
png pdf |
Figure A9-a:
Unfolded differential cross sections as functions of $ p_{\mathrm{T}}^{\mathrm{Z}} $ (left) and $ |y^{\mathrm{Z}}| $ (right) compared with the prefit prediction from SCETLIB $+$ DYTURBO. The results are obtained with the selection $ |y^{\mathrm{Z}}| < $ 2.5 and $ p_{\mathrm{T}}^{\mathrm{Z}} < $ 54 GeV. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the unfolded data to the SCETLIB $+$ DYTURBO prediction. |
png pdf |
Figure A9-b:
Unfolded differential cross sections as functions of $ p_{\mathrm{T}}^{\mathrm{Z}} $ (left) and $ |y^{\mathrm{Z}}| $ (right) compared with the prefit prediction from SCETLIB $+$ DYTURBO. The results are obtained with the selection $ |y^{\mathrm{Z}}| < $ 2.5 and $ p_{\mathrm{T}}^{\mathrm{Z}} < $ 54 GeV. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the unfolded data to the SCETLIB $+$ DYTURBO prediction. |
png pdf |
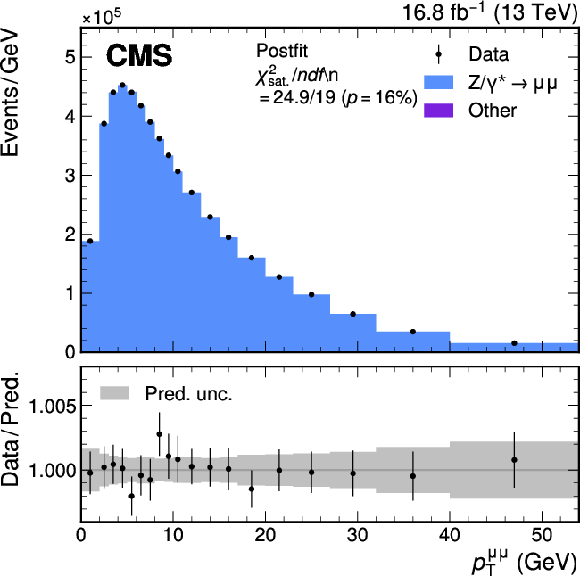
Figure A10:
Measured and simulated $ p_{\mathrm{T}}^{\mu\mu} $ distributions in selected $ \mathrm{Z}\to\mu\mu $ events, with the normalization and uncertainties of the prediction set to the postfit values. The gray band represents the total systematic uncertainty. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio between the number of events observed in data, including variations in the predictions, and the nominal prediction. |
png pdf |
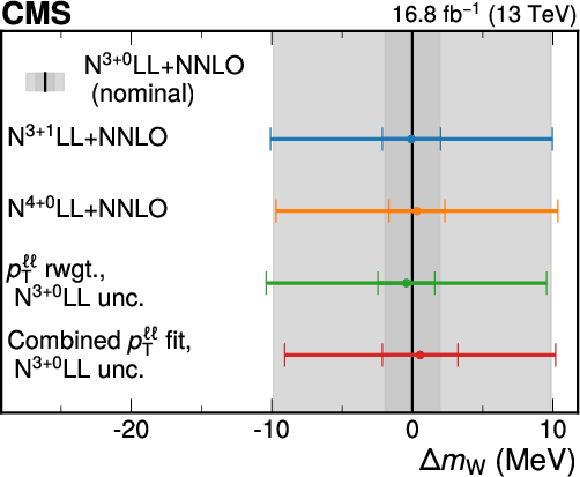
Figure A11:
Comparison of the nominal result and its theory uncertainty, using SCETLIB $+$ DYTURBO at $ \mathrm{N}^{3}\mathrm{LL}{+}\mathrm{NNLO} $, with the difference in $ m_{\mathrm{W}} $ measured when using alternative approaches to the $ p_{\mathrm{T}}^{\mathrm{W}} $ modeling and its uncertainty. The results from alternative approaches to the $ p_{\mathrm{T}}^{\mathrm{W}} $ modeling and uncertainty are shown as points. The solid black line represents the nominal result, the inner shaded gray band shows the $ p_{\mathrm{T}}^{\mathrm{W}} $ modeling uncertainty, and the outer shaded gray band shows the total uncertainty in the nominal result. The $ p_{\mathrm{T}}^{\mathrm{W}} $ modeling uncertainties are shown as the inner bars while the outer bars denote the total uncertainty. |
png pdf |
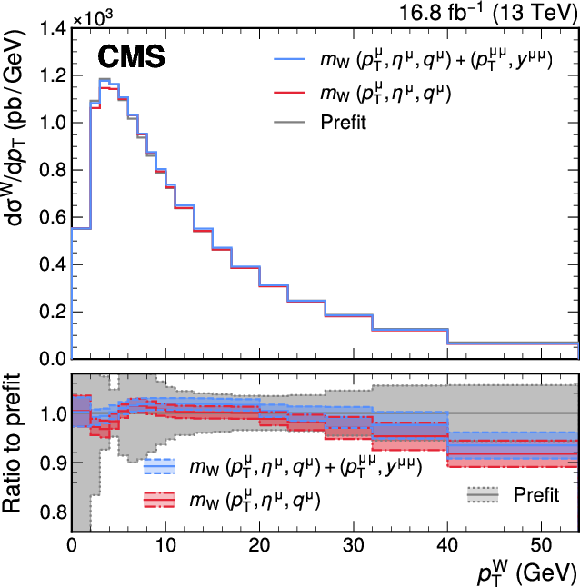
Figure A12:
The generator-level $ p_{\mathrm{T}}^{\mathrm{W}} $ distribution, with three instances of the prediction and their uncertainty: before the maximum likelihood fit (``prefit"), and reflecting the results of the two fits described in the text. The distribution and uncertainties obtained from the combined $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}, q^{\mu}) $ and $ (p_{\mathrm{T}}^{\mu\mu}, y^{\mu\mu}) $ fit is shown in red, whereas the purple band shows the distribution obtained from the nominal $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}, q^{\mu}) $ fit. The generator-level distribution predicted by SCETLIB $+$ DYTURBO before incorporating in situ constraints is shown in gray. The ratio of the postfit predictions to the prefit prediction (in gray), as well as their uncertainties, are shown by the shaded bands in the lower panel. |
png pdf |
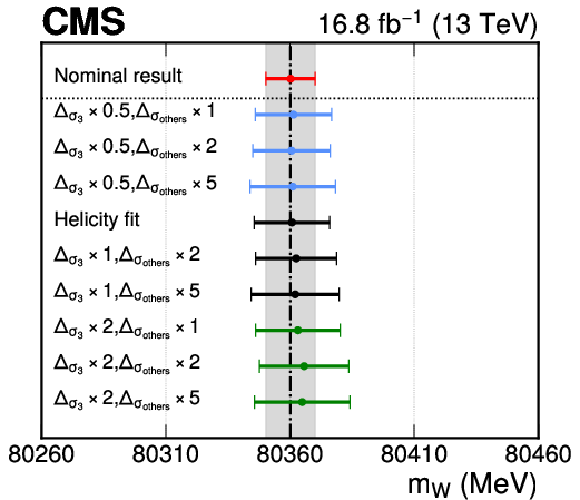
Figure A13:
The W boson mass measured with the helicity fit for different scaling scenarios of the prefit helicity cross section uncertainties, denoted by $ \Delta_{\sigma_3} $ and $ \Delta_{\sigma_{\text{others}}} $ for the $ \sigma_3 $ and the other components, respectively. The points are grouped and colored according to the scaling of $ \sigma_3 $. The black line indicates the nominal result, with its uncertainties shown in the gray band. |
png pdf |
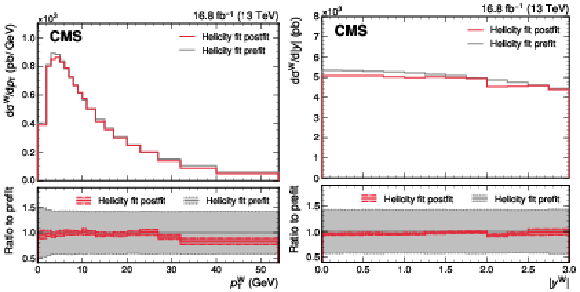
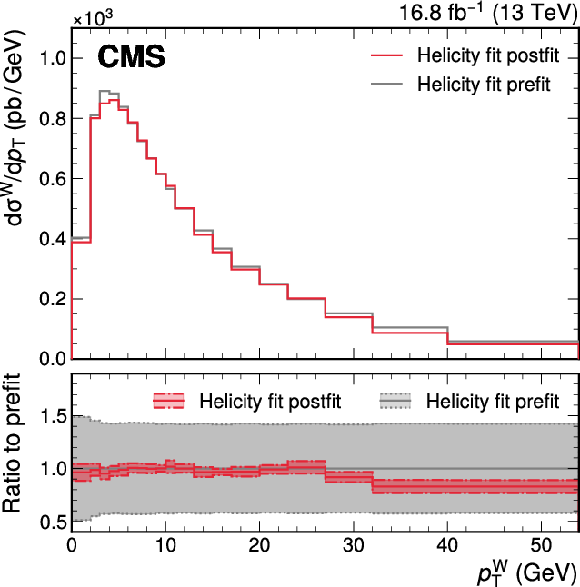
Figure A14:
Differential W boson production cross section, in the $ \mathrm{W}\to\mu\nu $ decay channel, in $ p_{\mathrm{T}}^{\mathrm{W}} $ (left) and $ |y^{\mathrm{W}}| $ (right), measured from the $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}, q^{\mu}) $ distributions using the helicity fit approach (red). The SCETLIB $+$ DYTURBO generator-level predictions, before incorporating in situ constraints, are also shown (in gray). The results are shown for the selection $ |y^{\mathrm{W}}| < $ 3.0 and $ p_{\mathrm{T}}^{\mathrm{W}} < $ 54 GeV. The lower panel shows the ratio between the postfit and prefit spectra. |
png pdf |
Figure A14-a:
Differential W boson production cross section, in the $ \mathrm{W}\to\mu\nu $ decay channel, in $ p_{\mathrm{T}}^{\mathrm{W}} $ (left) and $ |y^{\mathrm{W}}| $ (right), measured from the $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}, q^{\mu}) $ distributions using the helicity fit approach (red). The SCETLIB $+$ DYTURBO generator-level predictions, before incorporating in situ constraints, are also shown (in gray). The results are shown for the selection $ |y^{\mathrm{W}}| < $ 3.0 and $ p_{\mathrm{T}}^{\mathrm{W}} < $ 54 GeV. The lower panel shows the ratio between the postfit and prefit spectra. |

png pdf |
Figure A14-b:
Differential W boson production cross section, in the $ \mathrm{W}\to\mu\nu $ decay channel, in $ p_{\mathrm{T}}^{\mathrm{W}} $ (left) and $ |y^{\mathrm{W}}| $ (right), measured from the $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}, q^{\mu}) $ distributions using the helicity fit approach (red). The SCETLIB $+$ DYTURBO generator-level predictions, before incorporating in situ constraints, are also shown (in gray). The results are shown for the selection $ |y^{\mathrm{W}}| < $ 3.0 and $ p_{\mathrm{T}}^{\mathrm{W}} < $ 54 GeV. The lower panel shows the ratio between the postfit and prefit spectra. |
png pdf |
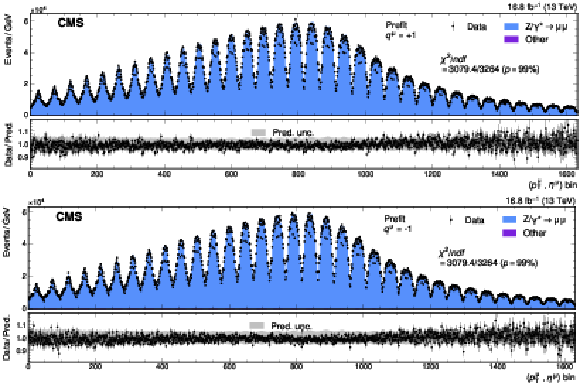
Figure A15:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the W-like $ m_{\mathrm{Z}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |
png pdf |
Figure A15-a:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the W-like $ m_{\mathrm{Z}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |
png pdf |
Figure A15-b:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the W-like $ m_{\mathrm{Z}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |

png pdf |
Figure A16:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the $ m_{\mathrm{W}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |
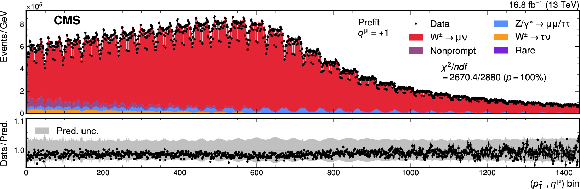
png pdf |
Figure A16-a:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the $ m_{\mathrm{W}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |
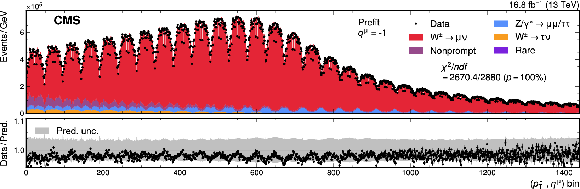
png pdf |
Figure A16-b:
Measured and predicted $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ distributions used in the $ m_{\mathrm{W}} $ measurement, for positively (upper) and negatively (lower) charged muons. The two-dimensional distribution is ``unrolled" such that each bin on the $ x $-axis represents one $ (p_{\mathrm{T}}^{\mu}, \eta^{\mu}) $ cell. The gray band represents the uncertainty in the prediction, before the fit to the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The vertical bars represent the statistical uncertainties in the data. |
png pdf |
Figure A17:
Measured and simulated $ p_{\mathrm{T}}^{\mu} $ distributions, with the prediction adjusted according to the best fit values of nuisance parameters and of $ m_{\mathrm{Z}} $ obtained from the maximum likelihood fit of the W-like $ m_{\mathrm{Z}} $ analysis. The vertical bars represent the statistical uncertainties in the data. The bottom panel shows the ratio of the number of events observed in data to the nominal prediction. The solid and dashed purple lines represent, respectively, the relative impact of an increase and decrease of $ m_{\mathrm{Z}} $ by 14 MeV. The uncertainties in the predictions, after the systematic uncertainty profiling in the maximum likelihood fit, are shown by the shaded band. |

png pdf |
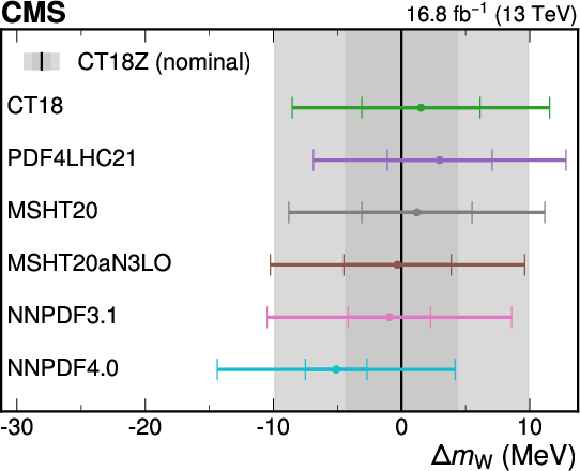
Figure A18:
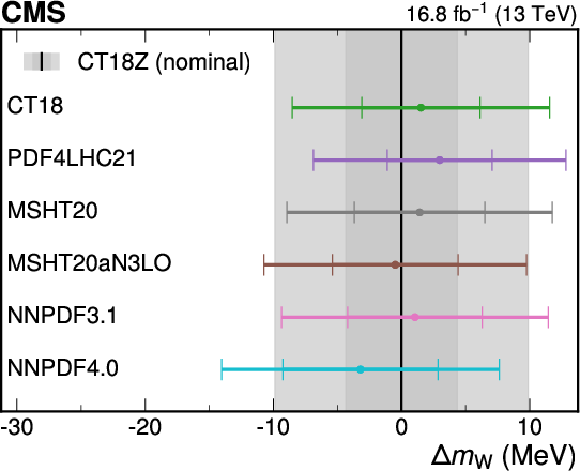
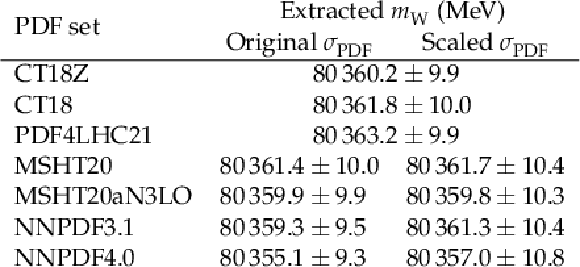
Difference in $ m_{\mathrm{W}} $ values for six alternative recent PDF sets, when using the original uncertainty for the given set (left) and when the uncertainties are scaled to accommodate the central prediction of the other sets (right). Each point corresponds to the result obtained when using the indicated PDF set and its uncertainty for the simulated predictions. The inner bar shows the uncertainty from the PDF, and the outer bar shows the total uncertainty. The nominal result, using CT18Z, is shown by the black line, with the CT18Z PDF and total uncertainty shown in dark and light gray, respectively. The uncertainty scaling procedure described in Section 8.8 improves the consistency of the $ m_{\mathrm{W}} $ values across the PDF sets and with the nominal result. |
png pdf |
Figure A18-a:
Difference in $ m_{\mathrm{W}} $ values for six alternative recent PDF sets, when using the original uncertainty for the given set (left) and when the uncertainties are scaled to accommodate the central prediction of the other sets (right). Each point corresponds to the result obtained when using the indicated PDF set and its uncertainty for the simulated predictions. The inner bar shows the uncertainty from the PDF, and the outer bar shows the total uncertainty. The nominal result, using CT18Z, is shown by the black line, with the CT18Z PDF and total uncertainty shown in dark and light gray, respectively. The uncertainty scaling procedure described in Section 8.8 improves the consistency of the $ m_{\mathrm{W}} $ values across the PDF sets and with the nominal result. |
png pdf |
Figure A18-b:
Difference in $ m_{\mathrm{W}} $ values for six alternative recent PDF sets, when using the original uncertainty for the given set (left) and when the uncertainties are scaled to accommodate the central prediction of the other sets (right). Each point corresponds to the result obtained when using the indicated PDF set and its uncertainty for the simulated predictions. The inner bar shows the uncertainty from the PDF, and the outer bar shows the total uncertainty. The nominal result, using CT18Z, is shown by the black line, with the CT18Z PDF and total uncertainty shown in dark and light gray, respectively. The uncertainty scaling procedure described in Section 8.8 improves the consistency of the $ m_{\mathrm{W}} $ values across the PDF sets and with the nominal result. |
png pdf |
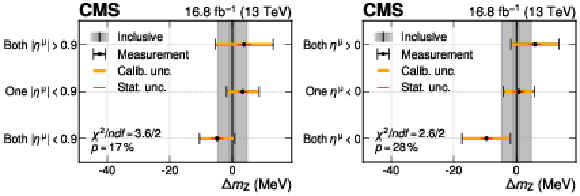
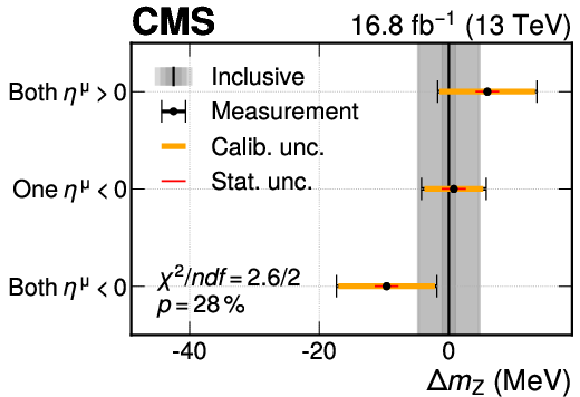
Figure A19:
The difference between the nominal $ m_{\mathrm{Z}} $ value measured from the $ \mathrm{Z}\to\mu\mu $ events and the result where $ m_{\mathrm{Z}} $ is allowed to vary, in three regions of the $ \eta^{\mu} $ of the two muons. The results binned in $ |\eta^{\mu}| $ (both central, one central and one forward, and both forward) are shown on the left and results binned in $ \eta^{\mu} $ (both negative, one positive and one negative, and both positive) are shown on the right. The result of a fit with three $ m_{\mathrm{Z}} $ parameters is compared with the result with a single $ m_{\mathrm{Z}} $ parameter and the compatibility of the results is also shown, as assessed via the saturated goodness-of-fit test. The points show the $ m_{\mathrm{Z}} $ result for the indicated $ \eta^{\mu} $ region and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line represents the result with a single $ m_{\mathrm{Z}} $ parameter, with the three shaded gray bands representing the statistical (dark grey), calibration (intermediate grey), and total (light grey) uncertainties. |

png pdf |
Figure A19-a:
The difference between the nominal $ m_{\mathrm{Z}} $ value measured from the $ \mathrm{Z}\to\mu\mu $ events and the result where $ m_{\mathrm{Z}} $ is allowed to vary, in three regions of the $ \eta^{\mu} $ of the two muons. The results binned in $ |\eta^{\mu}| $ (both central, one central and one forward, and both forward) are shown on the left and results binned in $ \eta^{\mu} $ (both negative, one positive and one negative, and both positive) are shown on the right. The result of a fit with three $ m_{\mathrm{Z}} $ parameters is compared with the result with a single $ m_{\mathrm{Z}} $ parameter and the compatibility of the results is also shown, as assessed via the saturated goodness-of-fit test. The points show the $ m_{\mathrm{Z}} $ result for the indicated $ \eta^{\mu} $ region and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line represents the result with a single $ m_{\mathrm{Z}} $ parameter, with the three shaded gray bands representing the statistical (dark grey), calibration (intermediate grey), and total (light grey) uncertainties. |
png pdf |
Figure A19-b:
The difference between the nominal $ m_{\mathrm{Z}} $ value measured from the $ \mathrm{Z}\to\mu\mu $ events and the result where $ m_{\mathrm{Z}} $ is allowed to vary, in three regions of the $ \eta^{\mu} $ of the two muons. The results binned in $ |\eta^{\mu}| $ (both central, one central and one forward, and both forward) are shown on the left and results binned in $ \eta^{\mu} $ (both negative, one positive and one negative, and both positive) are shown on the right. The result of a fit with three $ m_{\mathrm{Z}} $ parameters is compared with the result with a single $ m_{\mathrm{Z}} $ parameter and the compatibility of the results is also shown, as assessed via the saturated goodness-of-fit test. The points show the $ m_{\mathrm{Z}} $ result for the indicated $ \eta^{\mu} $ region and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line represents the result with a single $ m_{\mathrm{Z}} $ parameter, with the three shaded gray bands representing the statistical (dark grey), calibration (intermediate grey), and total (light grey) uncertainties. |
png pdf |
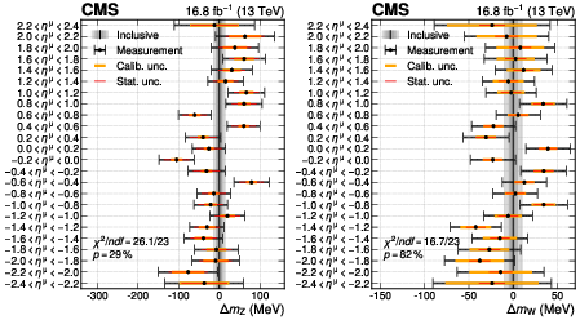
Figure A20:
For the W-like $ m_{\mathrm{Z}} $ analysis (left) and the $ m_{\mathrm{W}} $ measurement (right) the result of a fit with 24 $ m_{\mathrm{V}} $ parameters corresponding to different $ \eta^{\mu} $ ranges is compared with the nominal $ m_{\mathrm{V}} $ fit result. The $ \chi^2 $-like compatibility of the two fits is also shown, assessed via the saturated goodness-of-fit test. The points show $ m_{\mathrm{V}} $ result for the indicated $ \eta^{\mu} $ region, and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line shows the result with a single $ m_{\mathrm{V}} $ parameter, with the shaded gray bands representing its statistical, calibration, and total uncertainties. |
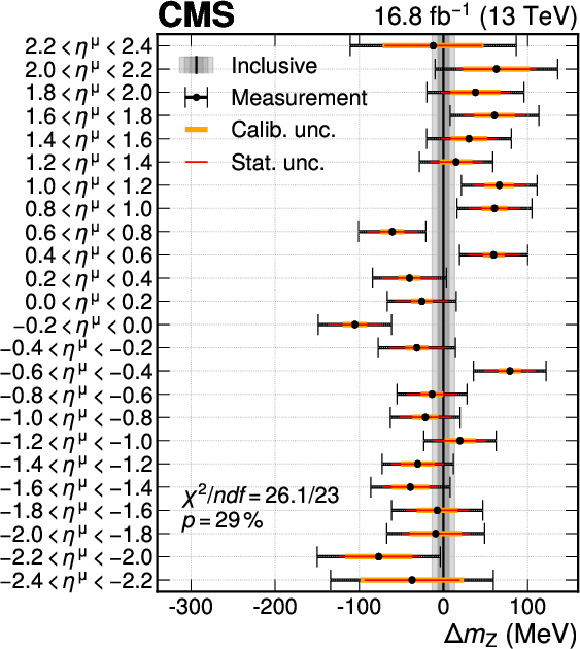
png pdf |
Figure A20-a:
For the W-like $ m_{\mathrm{Z}} $ analysis (left) and the $ m_{\mathrm{W}} $ measurement (right) the result of a fit with 24 $ m_{\mathrm{V}} $ parameters corresponding to different $ \eta^{\mu} $ ranges is compared with the nominal $ m_{\mathrm{V}} $ fit result. The $ \chi^2 $-like compatibility of the two fits is also shown, assessed via the saturated goodness-of-fit test. The points show $ m_{\mathrm{V}} $ result for the indicated $ \eta^{\mu} $ region, and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line shows the result with a single $ m_{\mathrm{V}} $ parameter, with the shaded gray bands representing its statistical, calibration, and total uncertainties. |
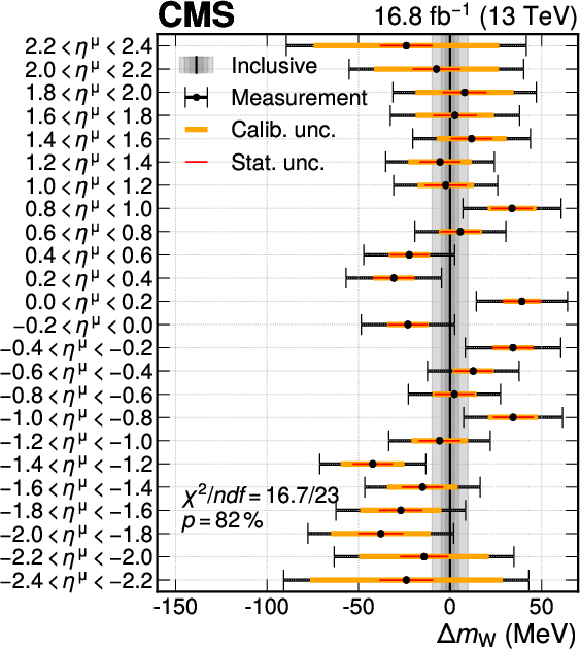
png pdf |
Figure A20-b:
For the W-like $ m_{\mathrm{Z}} $ analysis (left) and the $ m_{\mathrm{W}} $ measurement (right) the result of a fit with 24 $ m_{\mathrm{V}} $ parameters corresponding to different $ \eta^{\mu} $ ranges is compared with the nominal $ m_{\mathrm{V}} $ fit result. The $ \chi^2 $-like compatibility of the two fits is also shown, assessed via the saturated goodness-of-fit test. The points show $ m_{\mathrm{V}} $ result for the indicated $ \eta^{\mu} $ region, and the horizontal bars represent the calibration (orange line), statistical (red line), and total (black line) uncertainties. The black vertical line shows the result with a single $ m_{\mathrm{V}} $ parameter, with the shaded gray bands representing its statistical, calibration, and total uncertainties. |
| Tables | |
png pdf |
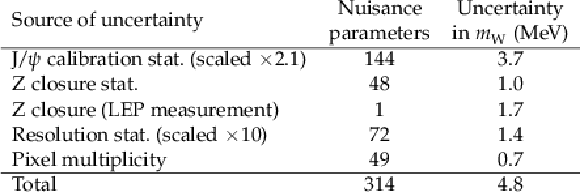
Table A1:
Breakdown of muon momentum calibration uncertainties. |
png pdf |
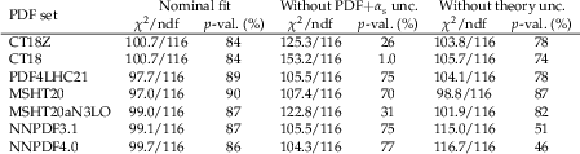
Table A2:
Goodness-of-fit test statistic for different PDF sets when fitting simultaneously the $ \eta^{\mu} $ distributions for selected $ \mathrm{W^+} $ ($ \mathrm{W^-} $) events and the $ y^{\mu\mu} $ distribution for $ \mathrm{Z}\to\mu\mu $ events. The saturated likelihood ratios, which are expected to follow a $ \chi^2 $ distribution with ndf degrees of freedom if the model is an accurate representation of the data, and the associated $ p $-value are both shown. The fit is performed in the nominal configuration with all uncertainties (left column), nominal configuration without PDF and $ \alpha_{s} $ uncertainties (middle column), and nominal configuration without theory uncertainties (right column). |
png pdf |
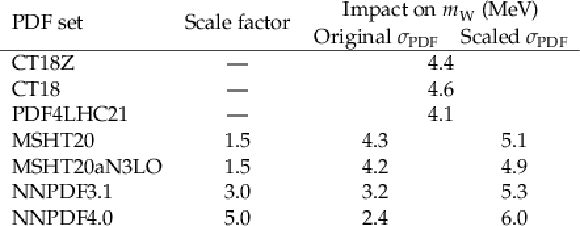
Table A3:
Prefit uncertainty scaling factors required to cover the central predictions of the considered PDF sets and postfit impact on $ m_{\mathrm{W}} $, with and without scaled PDF uncertainties. |
png pdf |
Table A4:
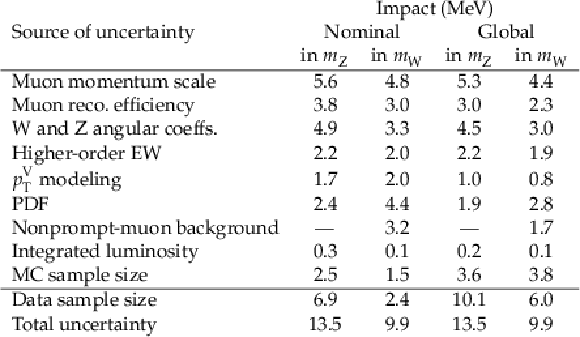
Uncertainties in the W-like $ m_{\mathrm{Z}} $ and $ m_{\mathrm{W}} $ measurements, with contributions to the total uncertainty from individual sources separated according to the ``nominal'' [none-none-none] and ``global'' [97] definitions of the impacts. |

png pdf |
Table A5:
Number of nuisance parameters for the main groups of systematic uncertainties, for the W-like $ m_{\mathrm{Z}} $ and $ m_{\mathrm{W}} $ fits. The number of parameters is displayed only once when it is the same for both fits, while ``$ \text{---} $'' means that this source is not relevant. For completeness, subgroups of parameters are also reported as indented labels for a few groups. |
png pdf |
Table A6:
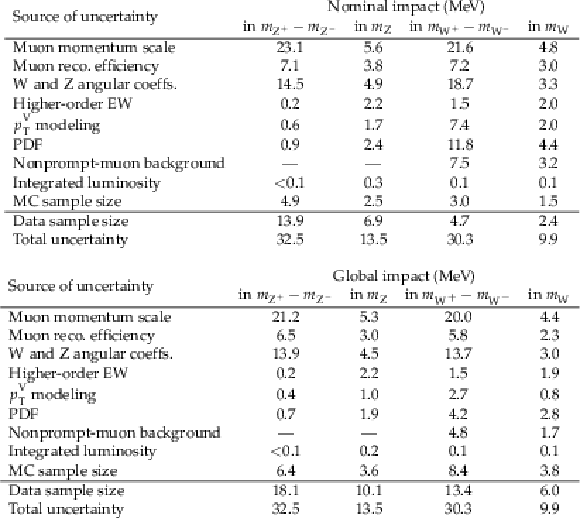
Uncertainties in the W-like $ m_{\mathrm{Z}} $ and $ m_{\mathrm{W}} $ measurements, comparing the mass difference between charges and the nominal charge combination, using nominal (upper) and global (lower) impacts. |
png pdf |
Table A7:
The $ m_{\mathrm{W}} $ values measured for different PDF sets, with uncertainties scaled following the procedure described in Section 8.8 and with the default unscaled uncertainties. |
| Summary |
| In this paper we report the first W boson mass measurement by the CMS Collaboration at the CERN LHC. The result is significantly more precise than previous LHC measurements. The W boson mass is extracted from a sample of 117 million selected $ \mathrm{W}\to\mu\nu $ events, collected in 2016 at the proton-proton collision energy of 13 TeV, via a highly granular binned maximum likelihood fit to the three-dimensional distribution of the muon $ p_{\mathrm{T}}^{\mu} $, $ \eta^{\mu} $, and electric charge. Novel experimental techniques have been used, together with state-of-the-art theoretical models, to improve the measurement accuracy. The muon momentum calibration, based on $ {\mathrm{J}/\psi} \to\mu\mu $ decays, as well as the data analysis methods and the treatment of the theory calculations used in the $ m_{\mathrm{W}} $ measurement have been extensively validated by extracting $ m_{\mathrm{Z}} $ and $ p_{\mathrm{T}}^{\mathrm{Z}} $ both from a direct $ \mathrm{Z}\to\mu\mu $ dimuon analysis and from a W-like analysis of the Z boson data.As shown in Fig. 4, the measured value, $ m_{\mathrm{W}} = $ 80 360.2 $ \pm $ 9.9 MeV, agrees with the standard model expectation from the electroweak fit and is in disagreement with the measurement reported by the CDF Collaboration. Our result has similar precision to the CDF Collaboration measurement and is significantly more precise than all other measurements. The dominant sources of uncertainty are the muon momentum calibration and the parton distribution functions. Uncertainties in the modeling of W boson production are subdominant due to novel approaches used to parameterize and constrain the predictions and their corresponding uncertainties in situ with the data. This result constitutes a significant step towards achieving an experimental measurement of $ m_{\mathrm{W}} $ with a precision matching that of the EW fit. Together with other recent measurements performed by the CMS Collaboration, including the top quark mass [56] and the effective electroweak mixing angle [57], this work demonstrates the power of the CMS detector and of the LHC as instruments for precision measurements of the parameters of the standard model. |
| Covariance Matrices |
|
We provide seven covariance matrices:
|
| References | ||||
| 1 | UA1 Collaboration | Experimental observation of isolated large transverse energy electrons with associated missing energy at $ \sqrt{s} = $ 540 GeV | PLB 122 (1983) 103 | |
| 2 | UA2 Collaboration | Observation of single isolated electrons of high transverse momentum in events with missing transverse energy at the $ \overline{\mathrm{p}}\mathrm{p} $ collider | PLB 122 (1983) 476 | |
| 3 | S. Heinemeyer, W. Hollik, G. Weiglein, and L. Zeune | Implications of LHC search results on the W boson mass prediction in the MSSM | JHEP 12 (2013) 084 | 1311.1663 |
| 4 | D. López-Val and T. Robens | $ \Delta $r and the W-boson mass in the singlet extension of the standard model | PRD 90 (2014) 114018 | 1406.1043 |
| 5 | Particle Data Group, S. Navas et al. | Review of particle physics | PRD 110 (2024) 030001 | |
| 6 | ALEPH, DELPHI, L3, OPAL, SLD, LEP Electroweak Working Group, SLD Electroweak Group, SLD Heavy Flavour Group Collaboration | Precision electroweak measurements on the Z resonance | Phys. Rept. 427 (2006) 257 | hep-ex/0509008 |
| 7 | D0 Collaboration | Measurement of the W boson mass with the D0 detector | PRD 89 (2014) 012005 | 1310.8628 |
| 8 | ATLAS Collaboration | Measurement of the W-boson mass in pp collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | EPJC 78 (2018) 110 | 1701.07240 |
| 9 | LHCb Collaboration | Measurement of the W boson mass | JHEP 01 (2022) 036 | 2109.01113 |
| 10 | ATLAS Collaboration | Measurement of the W-boson mass and width with the ATLAS detector using proton-proton collisions at $ \sqrt{s} = $ 7 TeV | Submitted to Eur. Phys. J. C, 2024 | 2403.15085 |
| 11 | CDF Collaboration | High-precision measurement of the W boson mass with the CDF II detector | Science 376 (2022) 170 | |
| 12 | LHC-TeV MW Working Group, S. Amoroso et al. | Compatibility and combination of world W-boson mass measurements | EPJC 84 (2024) 451 | 2308.09417 |
| 13 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 14 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 15 | CMS Collaboration | Performance of the CMS high-level trigger during LHC Run 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 16 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 17 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 18 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 19 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 20 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 21 | E. Manca, O. Cerri, N. Foppiani, and G. Rolandi | About the rapidity and helicity distributions of the W bosons produced at LHC | JHEP 12 (2017) 130 | 1707.09344 |
| 22 | M. A. Ebert, J. K. L. Michel, I. W. Stewart, and F. J. Tackmann | Drell-Yan $ q_{\mathrm{T}} $ resummation of fiducial power corrections at N$ ^{3} $LL | JHEP 04 (2021) 102 | 2006.11382 |
| 23 | G. Billis, J. K. L. Michel, and F. J. Tackmann | Drell-Yan transverse-momentum spectra at N$ ^3 $LL$ ^\prime $ and approximate N$ ^4 $LL with SCETlib | 2411.16004 | |
| 24 | F. J. Tackmann | Beyond scale variations: perturbative theory uncertainties from nuisance parameters | 2411.18606 | |
| 25 | CMS Collaboration | Measurements of the W boson rapidity, helicity, double-differential cross sections, and charge asymmetry in $ {\mathrm{p}\mathrm{p}} $ collisions at 13 TeV | PRD 102 (2020) 092012 | CMS-SMP-18-012 2008.04174 |
| 26 | E. Mirkes | Angular decay distribution of leptons from W bosons at NLO in hadronic collisions | NPB 387 (1992) 3 | |
| 27 | D. Y. Bardin, A. Leike, T. Riemann, and M. Sachwitz | Energy dependent width effects in $ \mathrm{e}^+\mathrm{e}^- $ annihilation near the Z boson pole | PLB 206 (1988) 539 | |
| 28 | J. R. Klein and A. Roodman | Blind analysis in nuclear and particle physics | Ann. Rev. Nucl. Part. Sci. 55 (2005) 141 | |
| 29 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 30 | CMS Collaboration | Strategies and performance of the CMS silicon tracker alignment during LHC Run 2 | NIM A 1037 (2022) 166795 | CMS-TRK-20-001 2111.08757 |
| 31 | CMSnoop | A new deep-neural-network-based missing transverse momentum estimator, and its application to W recoil | \hrefY. Feng, . PhD thesis, University of Maryland, College Park, 2020 link |
|
| 32 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 33 | P. F. Monni et al. | MiNNLO$ _\mathrm{PS} $: a new method to match NNLO QCD to parton showers | JHEP 05 (2020) 143 | 1908.06987 |
| 34 | P. F. Monni, E. Re, and M. Wiesemann | MiNNLO$ _{\mathrm{PS}} $: optimizing 2 $ \to $ 1 hadronic processes | EPJC 80 (2020) 1075 | 2006.04133 |
| 35 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 36 | P. Golonka and Z. Was | PHOTOS Monte Carlo: a precision tool for QED corrections in Z and W decays | EPJC 45 (2006) 97 | hep-ph/0506026 |
| 37 | N. Davidson, T. Przedzinski, and Z. Was | PHOTOS interface in C++: Technical and physics documentation | Comput. Phys. Commun. 199 (2016) 86 | 1011.0937 |
| 38 | G. Billis, M. A. Ebert, J. K. L. Michel, and F. J. Tackmann | A toolbox for $ q_{\mathrm{T}} $ and 0-jettiness subtractions at N$ ^3 $LO | Eur. Phys. J. Plus 136 (2021) 214 | 1909.00811 |
| 39 | T.-J. Hou et al. | New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC | PRD 103 (2021) 014013 | 1912.10053 |
| 40 | GEANT4 Collaboration | GEANT 4--a simulation toolkit | NIM A 506 (2003) 250 | |
| 41 | S. Choi and H. Oh | Improved extrapolation methods of data-driven background estimations in high energy physics | EPJC 81 (2021) 643 | 1906.10831 |
| 42 | W. Bizon et al. | The transverse momentum spectrum of weak gauge bosons at N$ ^3 $LL+NNLO | EPJC 79 (2019) 868 | 1905.05171 |
| 43 | S. Camarda et al. | DYTurbo: Fast predictions for Drell-Yan processes | EPJC 80 (2020) 251 | 1910.07049 |
| 44 | J. Campbell and T. Neumann | Precision phenomenology with MCFM | JHEP 12 (2019) 034 | 1909.09117 |
| 45 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 46 | J. S. Conway | Incorporating nuisance parameters in likelihoods for multisource spectra | in PHYSTAT 2011 Workshop on statistical issues related to discovery claims in search experiments and unfolding, H.B. Prosper and L.Lyons, eds., CERN Yellow Reports, CERN, Geneva, 2011 link |
1103.0354 |
| 47 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 48 | C.-A. Alexe, J. L. Bendavid, L. Bianchini, and D. Bruschini | Undercoverage in high-statistics counting experiments with finite MC samples | 2401.10542 | |
| 49 | B. Efron | Bootstrap methods: another look at the jackknife | in Breakthroughs in statistics: methodology and distribution, S. Kotz and N. L. Johnson, eds., Springer New York, New York, NY, 1992 link |
|
| 50 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 51 | M. Abadi et al. | TensorFlow: Large-scale machine learning on heterogeneous distributed systems | Software available from tensorflow.org, 2016 | 1603.04467 |
| 52 | A. G. Baydin, B. A. Pearlmutter, A. A. Radul, and J. M. Siskind | Automatic differentiation in machine learning: a survey | Journal of Machine Learning Research, 2018 link |
1502.05767 |
| 53 | J. K. Lindsey | Parametric Statistical Inference | Oxford University Press, ISBN 978023598, 1996 link |
|
| 54 | ALEPH, DELPHI, L3, OPAL, LEP Electroweak Working Group, S. Schael et al. | Electroweak measurements in electron-positron collisions at W-boson-pair energies at LEP | Phys. Rept. 532 (2013) 119 | 1302.3415 |
| 55 | D0 Collaboration | Measurement of the W boson mass with the D0 detector | PRL 108 (2012) 151804 | 1203.0293 |
| 56 | CMS Collaboration | Measurement of the top quark mass using a profile likelihood approach with the lepton$ + $jets final states in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | EPJC 83 (2023) 963 | CMS-TOP-20-008 2302.01967 |
| 57 | CMS Collaboration | Measurement of the Drell-Yan forward-backward asymmetry and of the effective leptonic weak mixing angle in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | Submitted to Physics Letters B, 2024 | CMS-SMP-22-010 2408.07622 |
| 58 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 59 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 60 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 61 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 62 | CMS Collaboration | Measurements of differential Z boson production cross sections in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 12 (2019) 061 | CMS-SMP-17-010 1909.04133 |
| 63 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 64 | NNPDF Collaboration | The path to proton structure at 1\% accuracy | EPJC 82 (2022) 428 | 2109.02653 |
| 65 | S. Bailey et al. | Parton distributions from LHC, HERA, Tevatron and fixed target data: MSHT20 PDFs | EPJC 81 (2021) 341 | 2012.04684 |
| 66 | PDF4LHC Working Group Collaboration | The PDF4LHC21 combination of global PDF fits for the LHC Run III | JPG 49 (2022) 080501 | 2203.05506 |
| 67 | T. Cridge, L. A. Harland-Lang, and R. S. Thorne | Combining QED and approximate N$ ^3 $LO QCD corrections in a global PDF fit: MSHT20qed_an3lo PDFs | SciPost Phys. 17 (2024) 026 | 2312.07665 |
| 68 | NNPDF Collaboration | Illuminating the photon content of the proton within a global PDF analysis | SciPost Phys. 5 (2018) 008 | 1712.07053 |
| 69 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 70 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 71 | CMS Collaboration | Measurements of inclusive W and Z cross sections in pp collisions at $ \sqrt{s} = $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |
| 72 | CMS Collaboration | Performance of the CMS muon trigger system in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 16 (2021) P07001 | CMS-MUO-19-001 2102.04790 |
| 73 | V. Blobel, C. Kleinwort, and F. Meier | Fast alignment of a complex tracking detector using advanced track models | Comput. Phys. Commun. 182 (2011) 1760 | 1103.3909 |
| 74 | V. Blobel | A new fast track-fit algorithm based on broken lines | NIM A 566 (2006) 14 | |
| 75 | CMS Collaboration | Precision measurement of the structure of the CMS inner tracking system using nuclear interactions | JINST 13 (2018) P10034 | CMS-TRK-17-001 1807.03289 |
| 76 | J. Allison et al. | GEANT 4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 77 | J. Allison et al. | Recent developments in GEANT 4 | NIM A 835 (2016) 186 | |
| 78 | V. Klyukhin et al. | The CMS magnetic field measuring and monitoring systems | Symmetry 14 (2022) 169 | 2202.02562 |
| 79 | CMS Collaboration | Alignment of the CMS tracker with LHC and cosmic ray data | JINST 9 (2014) P06009 | CMS-TRK-11-002 1403.2286 |
| 80 | C. W. Bauer, S. Fleming, D. Pirjol, and I. W. Stewart | An effective field theory for collinear and soft gluons: Heavy to light decays | PRD 63 (2001) 114020 | hep-ph/0011336 |
| 81 | C. W. Bauer, D. Pirjol, and I. W. Stewart | Soft collinear factorization in effective field theory | PRD 65 (2002) 054022 | hep-ph/0109045 |
| 82 | J.-Y. Chiu, A. Jain, D. Neill, and I. Z. Rothstein | A formalism for the systematic treatment of rapidity logarithms in quantum field theory | JHEP 05 (2012) 084 | 1202.0814 |
| 83 | S. Camarda, L. Cieri, and G. Ferrera | Drell-Yan lepton-pair production: $ q_{\mathrm{T}} $ resummation at N$ ^3 $LL accuracy and fiducial cross sections at N$ ^3 $LO | PRD 104 (2021) L111503 | 2103.04974 |
| 84 | M. Grazzini, S. Kallweit, and M. Wiesemann | Fully differential NNLO computations with MATRIX | EPJC 78 (2018) 537 | 1711.06631 |
| 85 | T. Becher and T. Neumann | Fiducial $ q_{\mathrm{T}} $ resummation of color-singlet processes at N$ ^3 $LL+NNLO | JHEP 03 (2021) 199 | 2009.11437 |
| 86 | J. C. Collins and D. E. Soper | Back-to-back jets in QCD | NPB 193 (1981) 381 | |
| 87 | M. A. Ebert, J. K. L. Michel, I. W. Stewart, and Z. Sun | Disentangling long and short distances in momentum-space TMDs | JHEP 07 (2022) 129 | 2201.07237 |
| 88 | T. Cridge, L. A. Harland-Lang, A. D. Martin, and R. S. Thorne | An investigation of the $ \alpha_S $ and heavy quark mass dependence in the MSHT20 global PDF analysis | EPJC 81 (2021) 744 | 2106.10289 |
| 89 | J. C. Collins and D. E. Soper | Angular distribution of dileptons in high-energy hadron collisions | PRD 16 (1977) 2219 | |
| 90 | C. M. Carloni Calame, G. Montagna, O. Nicrosini, and M. Treccani | Higher order QED corrections to W boson mass determination at hadron colliders | PRD 69 (2004) 037301 | hep-ph/0303102 |
| 91 | C. M. Carloni Calame, G. Montagna, O. Nicrosini, and M. Treccani | Multiple photon corrections to the neutral-current Drell-Yan process | JHEP 05 (2005) 019 | hep-ph/0502218 |
| 92 | L. Barze et al. | Neutral current Drell-Yan with combined QCD and electroweak corrections in the POWHEG BOX | EPJC 73 (2013) 2474 | 1302.4606 |
| 93 | M. Chiesa, C. L. Del Pio, and F. Piccinini | On electroweak corrections to neutral current Drell-Yan with the POWHEG BOX | EPJC 84 (2024) 539 | 2402.14659 |
| 94 | S. Bondarenko et al. | Hadron-hadron collision mode in ReneSANCe-v1.3.0 | Comput. Phys. Commun. 285 (2023) 108646 | 2207.04332 |
| 95 | L. Barze et al. | Implementation of electroweak corrections in the POWHEG BOX: single W production | JHEP 04 (2012) 037 | 1202.0465 |
| 96 | S. Alioli et al. | Precision studies of observables in $ \mathrm{p}\mathrm{p} \to \mathrm{W} \to l\nu_l $ and $ \mathrm{p}\mathrm{p} \to \gamma,Z \to l^+ l^- $ processes at the LHC | EPJC 77 (2017) 280 | 1606.02330 |
| 97 | A. Pinto et al. | Uncertainty components in profile likelihood fits | EPJC 84 (2024) 593 | 2307.04007 |
| 98 | CMS Collaboration | HEPData record for this analysis | link | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|