

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-19-014 ; CERN-EP-2022-033 | ||
| Search for heavy resonances and quantum black holes in e$\mu$, e$\tau$, and $\mu\tau$ final states in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 13 May 2022 | ||
| JHEP 05 (2023) 227 | ||
| Abstract: A search is reported for heavy resonances and quantum black holes decaying into e$\mu$, e$\tau$, and $\mu\tau$ final states in proton-proton collision data recorded by the CMS experiment at the CERN LHC during 2016-2018 at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 138 fb$^{-1}$. The e$\mu$, e$\tau$, and $\mu\tau$ invariant mass spectra are reconstructed, and no evidence is found for physics beyond the standard model. Upper limits are set at 95% confidence level on the product of the cross section and branching fraction for lepton flavor violating signals. Three benchmark signals are studied: resonant $\tau$ sneutrino production in $R$ parity violating supersymmetric models, heavy Z' gauge bosons with lepton flavor violating decays, and nonresonant quantum black hole production in models with extra spatial dimensions. Resonant $\tau$ sneutrinos are excluded for masses up to 4.2 TeV in the e$\mu$ channel, 3.7 TeV in the e$\tau$ channel, and 3.6 TeV in the $\mu\tau$ channel. A Z' boson with lepton flavor violating couplings is excluded up to a mass of 5.0 TeV in the e$\mu$ channel, up to 4.3 TeV in the e$\tau$ channel, and up to 4.1 TeV in the $\mu\tau$ channel. Quantum black holes in the benchmark model are excluded up to the threshold mass of 5.6 TeV in the e$\mu$ channel, 5.2 TeV in the e$\tau$ channel, and 5.0 TeV in the $\mu\tau$ channel. In addition, model-independent limits are extracted to allow comparisons with other models for the same final states and similar event selection requirements. The results of these searches provide the most stringent limits available from collider experiments for heavy particles that undergo lepton flavor violating decays. | ||
| Links: e-print arXiv:2205.06709 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
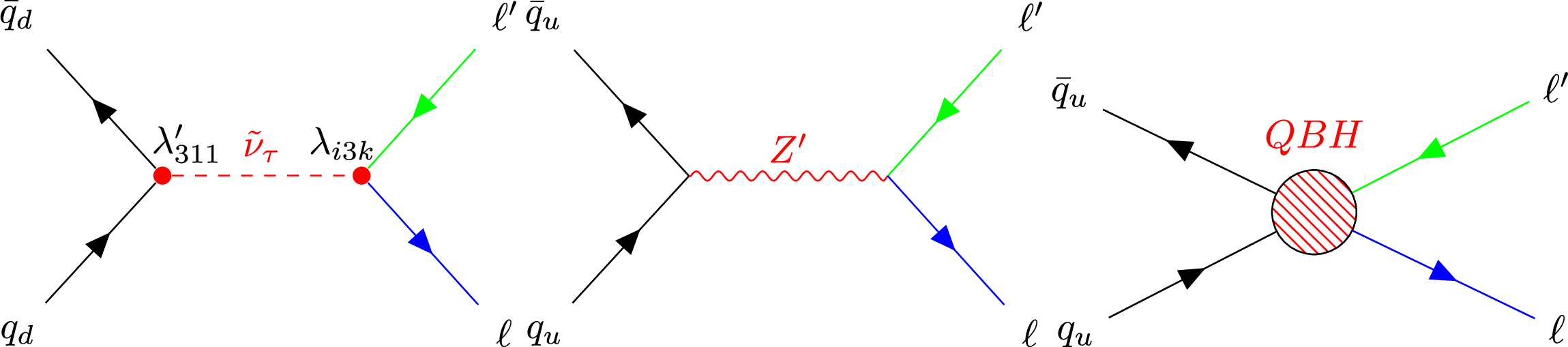
Figure 1:
Leading order Feynman diagrams considered in our search. Left: Resonant production of a $\tau $ sneutrino in an RPV SUSY model that includes the subsequent decay into two leptons of different flavors. The $\nu _\tau $ is produced from the annihilation of two down quarks via the $\lambda '_{311}$ coupling, and then decays via the $\lambda $ couplings. Middle: Resonant production of a Z' boson with subsequent decay into two leptons of different flavors. Right: Production of quantum black holes in a model with extra dimensions that involves subsequent decay into two leptons of different flavors. |

png pdf |
Figure 1-a:
Leading order Feynman diagram considered in our search: Resonant production of a $\tau $ sneutrino in an RPV SUSY model that includes the subsequent decay into two leptons of different flavors. The $\nu _\tau $ is produced from the annihilation of two down quarks via the $\lambda '_{311}$ coupling, and then decays via the $\lambda $ couplings. |
png pdf |
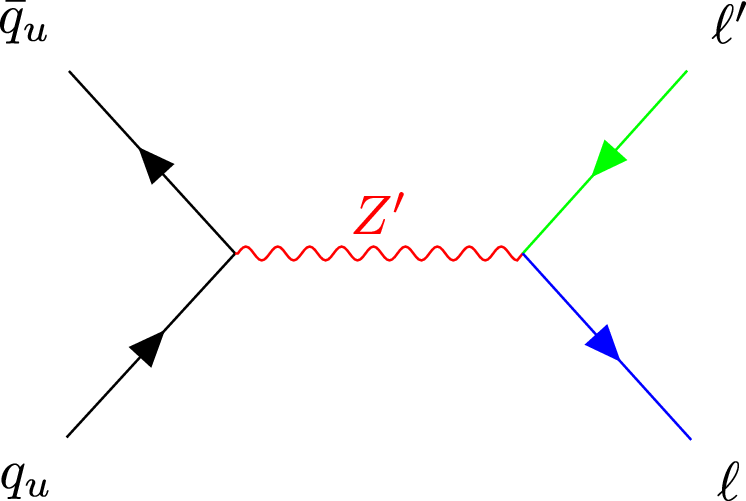
Figure 1-b:
Leading order Feynman diagram considered in our search: Resonant production of a Z' boson with subsequent decay into two leptons of different flavors. |
png pdf |
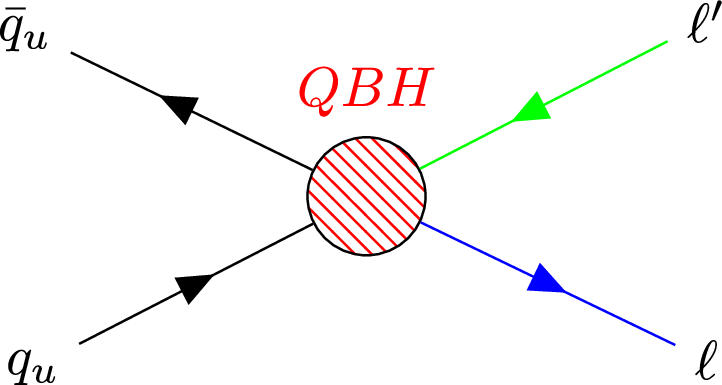
Figure 1-c:
Leading order Feynman diagram considered in our search: Production of quantum black holes in a model with extra dimensions that involves subsequent decay into two leptons of different flavors. |
png pdf |
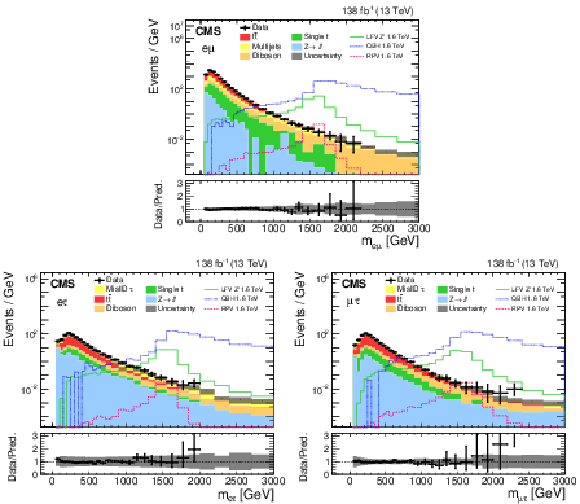
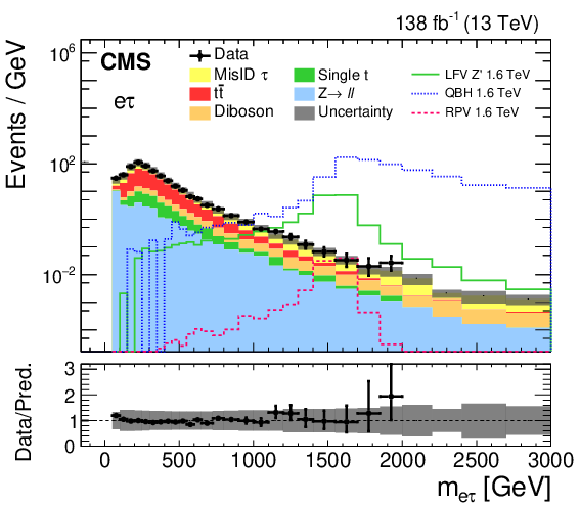
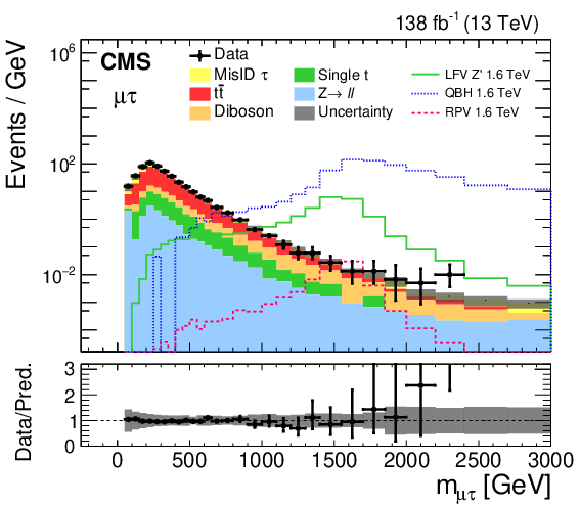
Figure 2:
Invariant mass distributions for the e$ \mu $ channel (upper), and collinear mass distributions for the e$ \tau $ (lower left) and $\mu \tau $ (lower right) channels. In addition to the observed data (black points) and the SM prediction (filled histograms), the expected signal distributions for three models are shown: the RPV SUSY model with $\lambda = \lambda ' = $ 0.01 and $\tau $ sneutrino mass of 1.6 TeV, LFV Z' ($\mathcal {B} = $ 0.1) boson with a mass of 1.6 TeV, and the QBH signal expectation for $n=$ 4 and a threshold mass of 1.6 TeV. The bottom panel of each plot shows the ratio of data and SM prediction. The bin width gradually increases with mass. |

png pdf |
Figure 2-a:
Invariant mass distribution for the e$ \mu $ channel. In addition to the observed data (black points) and the SM prediction (filled histograms), the expected signal distributions for three models are shown: the RPV SUSY model with $\lambda = \lambda ' = $ 0.01 and $\tau $ sneutrino mass of 1.6 TeV, LFV Z' ($\mathcal {B} = $ 0.1) boson with a mass of 1.6 TeV, and the QBH signal expectation for $n=$ 4 and a threshold mass of 1.6 TeV. The bottom panel shows the ratio of data and SM prediction. The bin width gradually increases with mass. |
png pdf |
Figure 2-b:
Collinear mass distribution for the e$ \tau $ $\mu \tau $ channel. In addition to the observed data (black points) and the SM prediction (filled histograms), the expected signal distributions for three models are shown: the RPV SUSY model with $\lambda = \lambda ' = $ 0.01 and $\tau $ sneutrino mass of 1.6 TeV, LFV Z' ($\mathcal {B} = $ 0.1) boson with a mass of 1.6 TeV, and the QBH signal expectation for $n=$ 4 and a threshold mass of 1.6 TeV. The bottom panel shows the ratio of data and SM prediction. The bin width gradually increases with mass. |
png pdf |
Figure 2-c:
Invariant mass distribution for the e$ \mu $ channel. Collinear mass distribution for the e$ \tau $ $\mu \tau $ channel. In addition to the observed data (black points) and the SM prediction (filled histograms), the expected signal distributions for three models are shown: the RPV SUSY model with $\lambda = \lambda ' = $ 0.01 and $\tau $ sneutrino mass of 1.6 TeV, LFV Z' ($\mathcal {B} = $ 0.1) boson with a mass of 1.6 TeV, and the QBH signal expectation for $n=$ 4 and a threshold mass of 1.6 TeV. The bottom panel shows the ratio of data and SM prediction. The bin width gradually increases with mass. |
png pdf |
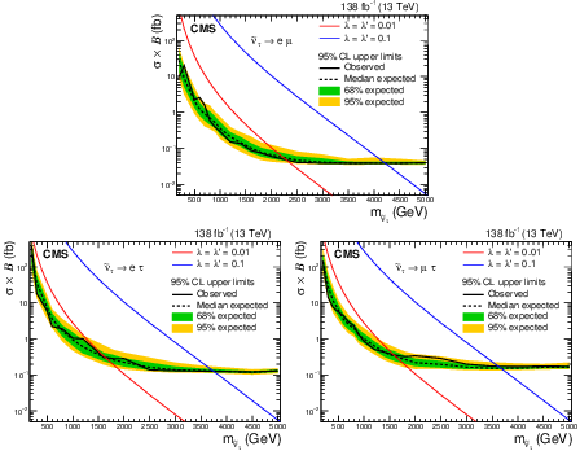
Figure 3:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction as a function of the $\tau $ sneutrino mass in an RPV SUSY model for the e$ \mu $ (upper), e$ \tau $ (lower left), and $\mu \tau $ (lower right) channels. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red and blue solid lines show the predicted product of the cross section and the branching fraction as a function of the tau sneutrino mass for two different values of the couplings. |

png pdf |
Figure 3-a:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction as a function of the $\tau $ sneutrino mass in an RPV SUSY model for the e$ \mu $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red and blue solid lines show the predicted product of the cross section and the branching fraction as a function of the tau sneutrino mass for two different values of the couplings. |

png pdf |
Figure 3-b:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction as a function of the $\tau $ sneutrino mass in an RPV SUSY model for the e$ \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red and blue solid lines show the predicted product of the cross section and the branching fraction as a function of the tau sneutrino mass for two different values of the couplings. |

png pdf |
Figure 3-c:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction as a function of the $\tau $ sneutrino mass in an RPV SUSY model for the $\mu \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red and blue solid lines show the predicted product of the cross section and the branching fraction as a function of the tau sneutrino mass for two different values of the couplings. |
png pdf |
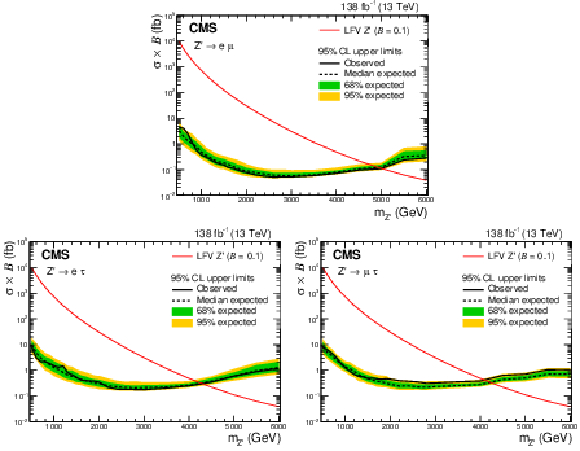
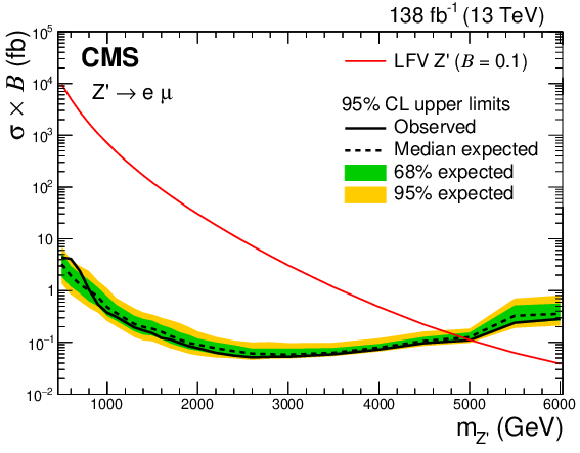
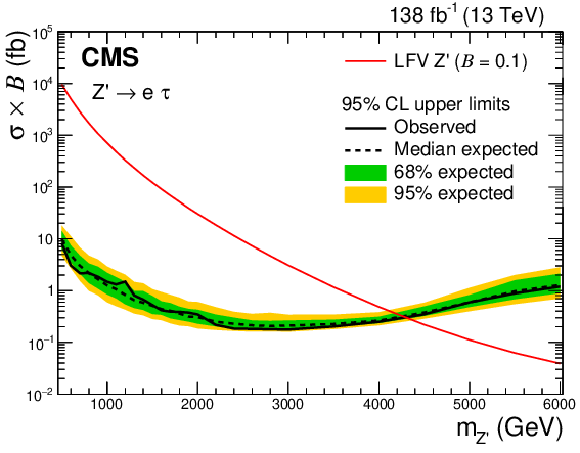
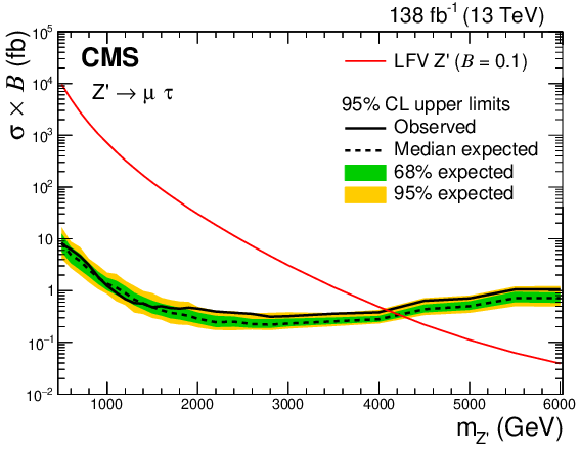
Figure 4:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for a Z' boson with LFV decays, in the e$ \mu $ (upper), e$ \tau $ (lower left), and $\mu \tau $ (lower right) channels. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid lines show the predicted product of the cross section and the branching fraction as a function of the Z' mass assuming $\mathcal {B}=$ 0.1. |
png pdf |
Figure 4-a:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for a Z' boson with LFV decays, in the e$ \mu $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line show2 the predicted product of the cross section and the branching fraction as a function of the Z' mass assuming $\mathcal {B}=$ 0.1. |
png pdf |
Figure 4-b:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for a Z' boson with LFV decays, in the e$ \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line show2 the predicted product of the cross section and the branching fraction as a function of the Z' mass assuming $\mathcal {B}=$ 0.1. |
png pdf |
Figure 4-c:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for a Z' boson with LFV decays, in the $\mu \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line show2 the predicted product of the cross section and the branching fraction as a function of the Z' mass assuming $\mathcal {B}=$ 0.1. |
png pdf |
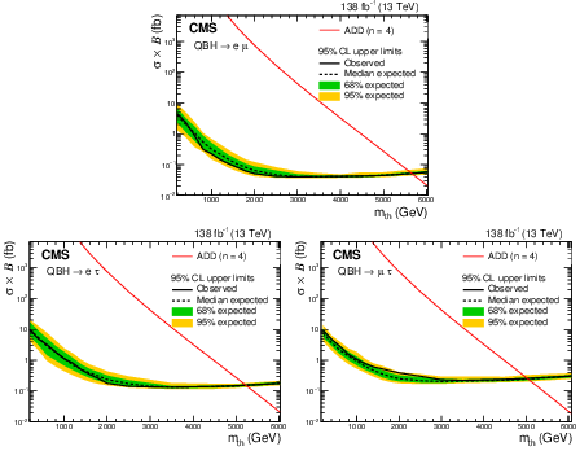
Figure 5:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for quantum black hole production in an ADD model with $n=$ 4 extra dimensions, in the e$ \mu $ (upper), e$ \tau $ (lower left), and $\mu \tau $ (lower right) channels. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid lines show the predicted product of the cross section and the branching fraction as a function of the QBH threshold mass. |

png pdf |
Figure 5-a:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for quantum black hole production in an ADD model with $n=$ 4 extra dimensions, in the e$ \mu $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line shows the predicted product of the cross section and the branching fraction as a function of the QBH threshold mass. |
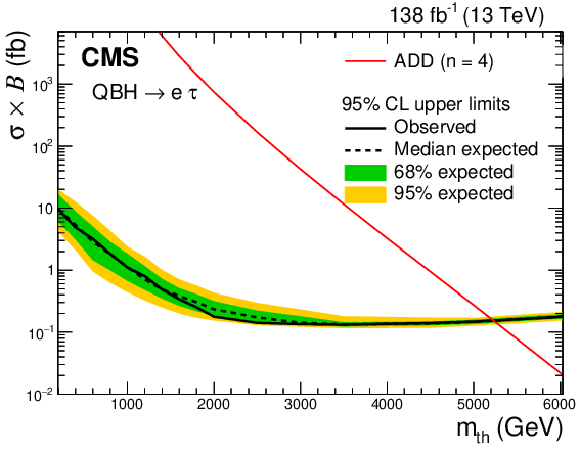
png pdf |
Figure 5-b:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for quantum black hole production in an ADD model with $n=$ 4 extra dimensions, in the e$ \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line shows the predicted product of the cross section and the branching fraction as a function of the QBH threshold mass. |
png pdf |
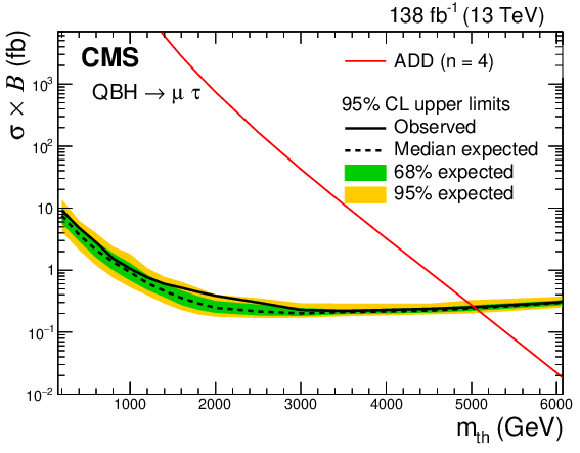
Figure 5-c:
Expected (black dashed line) and observed (black solid line) 95% CL upper limits on the product of the cross section and the branching fraction for quantum black hole production in an ADD model with $n=$ 4 extra dimensions, in the $\mu \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. The red solid line shows the predicted product of the cross section and the branching fraction as a function of the QBH threshold mass. |
png pdf |
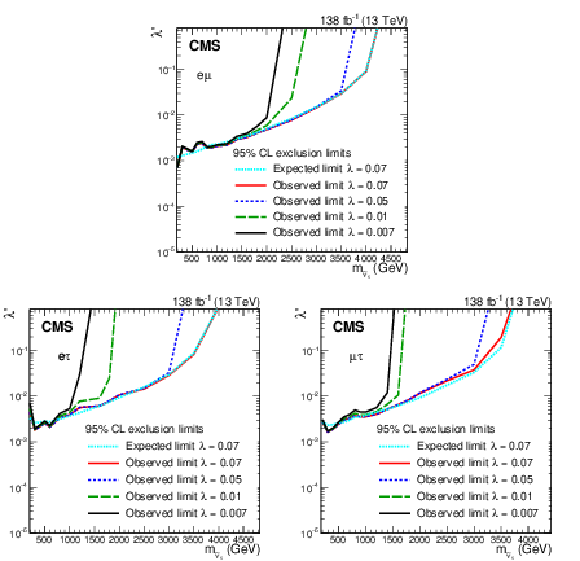
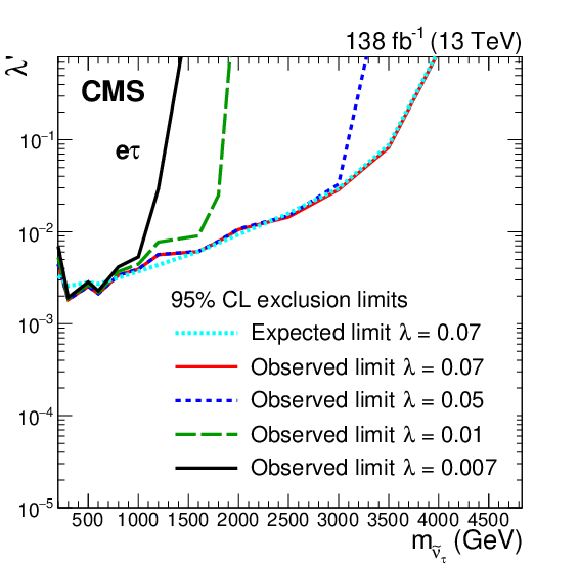
Figure 6:
Exclusion limits at 95% CL on the RPV SUSY model in the plane of $\tau $ sneutrino mass and $\lambda '$ coupling, for four values of $\lambda $ couplings. The regions to the left of and above the curves are excluded. The upper plot corresponds to the e$ \mu $ channel, while the lower left and right plots show the e$ \tau $ and $\mu \tau $ channels, respectively. |
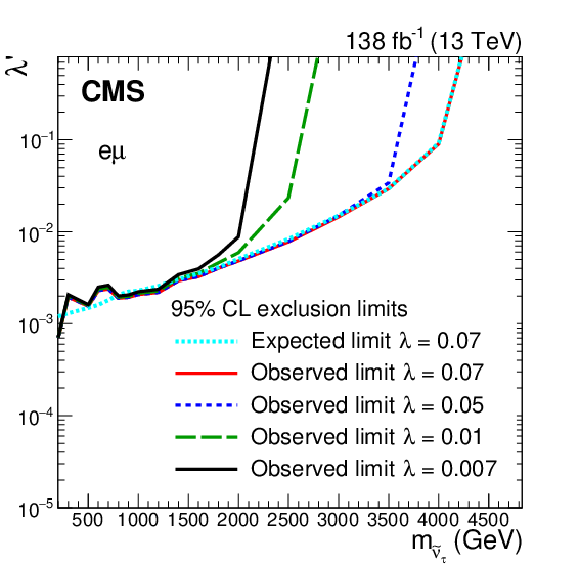
png pdf |
Figure 6-a:
Exclusion limits at 95% CL on the RPV SUSY model in the plane of $\tau $ sneutrino mass and $\lambda '$ coupling, for four values of $\lambda $ couplings. The regions to the left of and above the curves are excluded. The plot corresponds to the e$ \mu $ channel. |
png pdf |
Figure 6-b:
Exclusion limits at 95% CL on the RPV SUSY model in the plane of $\tau $ sneutrino mass and $\lambda '$ coupling, for four values of $\lambda $ couplings. The regions to the left of and above the curves are excluded. The plot corresponds to the e$ \tau $ channel. |

png pdf |
Figure 6-c:
Exclusion limits at 95% CL on the RPV SUSY model in the plane of $\tau $ sneutrino mass and $\lambda '$ coupling, for four values of $\lambda $ couplings. The regions to the left of and above the curves are excluded. The plot corresponds to the $\mu \tau $ channel. |
png pdf |
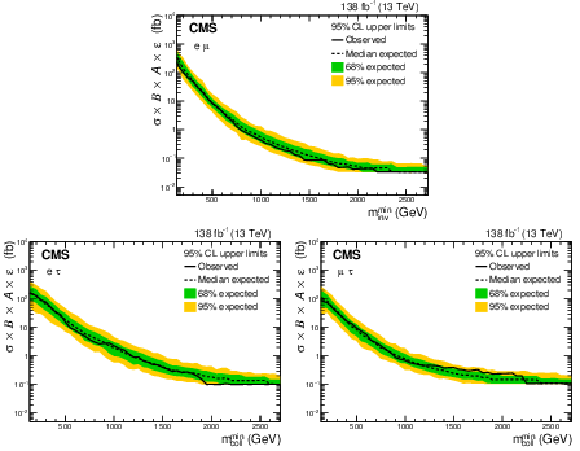
Figure 7:
Model-independent upper limits at 95% CL on the product of the cross section, the branching fraction, acceptance, and efficiency are shown. Observed (expected) limits are shown in black solid (dashed) lines for the e$ \mu $ (upper), e$ \tau $ (lower left), and $\mu \tau $ (lower right) channels. The shaded bands represent 68% and 95% uncertainties in the expected limits. |

png pdf |
Figure 7-a:
Model-independent upper limits at 95% CL on the product of the cross section, the branching fraction, acceptance, and efficiency are shown. Observed (expected) limits are shown in black solid (dashed) lines for the e$ \mu $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. |

png pdf |
Figure 7-b:
Model-independent upper limits at 95% CL on the product of the cross section, the branching fraction, acceptance, and efficiency are shown. Observed (expected) limits are shown in black solid (dashed) lines for the e$ \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. |

png pdf |
Figure 7-c:
Model-independent upper limits at 95% CL on the product of the cross section, the branching fraction, acceptance, and efficiency are shown. Observed (expected) limits are shown in black solid (dashed) lines for the $\mu \tau $ channel. The shaded bands represent 68% and 95% uncertainties in the expected limits. |
| Tables | |
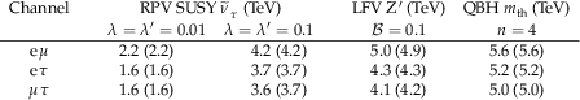
png pdf |
Table 1:
The observed and expected (in parentheses) 95% CL lower mass limits on the RPV SUSY, Z', and QBH signals for the e$ \mu $, e$ \tau $, and $\mu \tau $ channels. |
| Summary |
| A search has been conducted for heavy particles that undergo lepton flavor violating decays into e$\mu$, e$\tau$, and $\mu\tau$ final states. The search is based on proton-proton collision data at $\sqrt{s} = $ 13 TeV recorded during 2016-2018 in the CMS detector at the CERN LHC, corresponding to an integrated luminosity of 138 fb$^{-1}$. The data are consistent with expectations from the standard model. Lower limits at 95% confidence level are set on the mass of supersymmetric $\tau$ sneutrinos at 4.2 TeV in e$\mu$, 3.7 TeV in e$\tau$, and 3.6 TeV in $\mu\tau$ channels. A Z' vector boson with lepton flavor violating couplings is excluded for masses below 5.0, 4.3, and 4.1 TeV in the e$\mu$, e$\tau$, and $\mu\tau$ channels, respectively, assuming a branching fraction of 10%. In the context of the Arkani-Hamed-Dimopoulos-Dvali model with four extra dimensions, values of the threshold mass for quantum black hole production less than 5.6, 5.2, and 5.0 TeV are excluded in the e$\mu$, e$\tau$, and $\mu\tau$ channels, respectively. In addition, model-independent limits are provided allowing the results to be interpreted in other models with the same final states and similar kinematic distributions. Limits in the e$\tau$ and $\mu\tau$ final states, as well as model-independent limits, are reported for the first time in the context of a high-mass lepton flavor violation search. These are the first results of a high-mass lepton flavor violation search using the full Run 2 data set, and they are currently the most stringent limits from any collider experiment. |
| References | ||||
| 1 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 2 | F. de Campos et al. | CERN LHC signals for neutrino mass model in bilinear R-parity violating mAMSB | PRD 77 (2008) 115025 | 0803.4405 |
| 3 | R. Barbier et al. | R-parity violating supersymmetry | PR 420 (2005) 1 | hep-ph/0406039 |
| 4 | P. Langacker | The physics of heavy Z' gauge bosons | Rev. Mod. Phys. 81 (2009) 1199 | 0801.1345 |
| 5 | X. Calmet, W. Gong, and S. D. H. Hsu | Colorful quantum black holes at the LHC | PLB 668 (2008) 20 | 0806.4605 |
| 6 | P. Meade and L. Randall | Black holes and quantum gravity at the LHC | JHEP 05 (2008) 003 | 0708.3017 |
| 7 | S. Dimopoulos and G. Landsberg | Black holes at the LHC | PRL 87 (2001) 161602 | hep-ph/0106295 |
| 8 | S. B. Giddings and S. D. Thomas | High-energy colliders as black hole factories: The end of short distance physics | PRD 65 (2002) 056010 | hep-ph/0106219 |
| 9 | P. W. Graham, D. E. Kaplan, S. Rajendran, and P. Saraswat | Displaced supersymmetry | JHEP 07 (2012) 149 | 1204.6038 |
| 10 | CMS Collaboration | Search for lepton-flavor violating decays of heavy resonances and quantum black holes to e$\mu $ final states in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 04 (2018) 073 | CMS-EXO-16-058 1802.01122 |
| 11 | D. M. Gingrich | Quantum black holes with charge, colour, and spin at the LHC | JPG 37 (2010) 105008 | 0912.0826 |
| 12 | L. Randall and R. Sundrum | A large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | hep-ph/9905221 |
| 13 | N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali | The hierarchy problem and new dimensions at a millimeter | PLB 429 (1998) 263 | hep-ph/9803315 |
| 14 | CDF Collaboration | Search for R-parity violating decays of $ \tau $ sneutrinos to e$\mu $, $ \mu\tau $, and e$\tau $ pairs in $ {\mathrm{p}}\bar{{\mathrm{p}}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRL 105 (2010) 191801 | 1004.3042 |
| 15 | D0 Collaboration | Search for sneutrino production in e$\mu $ final states in 5.3$ fb$^{-1} of $ {\mathrm{p}}\bar{{\mathrm{p}}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRL 105 (2010) 191802 | 1007.4835 |
| 16 | ATLAS Collaboration | Search for a heavy neutral particle decaying to e$\mu $, e$\tau $, or $ \mu\tau $ in pp collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector | PRL 115 (2015) 031801 | 1503.04430 |
| 17 | CMS Collaboration | Search for lepton flavour violating decays of heavy resonances and quantum black holes to an e$\mu $ pair in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | EPJC 76 (2016) 317 | CMS-EXO-13-002 1604.05239 |
| 18 | ATLAS Collaboration | Search for new phenomena in different-flavour high-mass dilepton final states in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | EPJC 76 (2016) 541 | 1607.08079 |
| 19 | ATLAS Collaboration | Search for lepton-flavor violation in different-flavor, high-mass final states in pp collisions at $ \sqrt s = $ 13 TeV with the ATLAS detector | PRD 98 (2018) 092008 | 1807.06573 |
| 20 | CMS Collaboration | Hepdata record for this analysis | doi::10.17182/hepdata.127302 | |
| 21 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 22 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 23 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 24 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 25 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 26 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 27 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 28 | A. Belyaev, N. D. Christensen, and A. Pukhov | CalcHEP 3.4 for collider physics within and beyond the standard model | CPC 184 (2013) 1729 | 1207.6082 |
| 29 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 30 | J. Pumplin et al. | New generation of parton distributions with uncertainties from global QCD analysis | JHEP 07 (2002) 012 | hep-ph/0201195 |
| 31 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 32 | H. K. Dreiner, S. Grab, M. Kramer, and M. K. Trenkel | Supersymmetric NLO QCD corrections to resonant slepton production and signals at the Tevatron and the CERN LHC | PRD 75 (2007) 035003 | hep-ph/0611195 |
| 33 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 34 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 35 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 36 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 37 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 38 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 39 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 40 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 41 | J. Allison et al. | GEANT4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 42 | J. Allison et al. | Recent developments in GEANT4 | NIMA 835 (2016) 186 | |
| 43 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 44 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS-PAS-TDR-15-002 | CMS-PAS-TDR-15-002 |
| 45 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 46 | CMS Collaboration | Identification of hadronic tau lepton decays using a deep neural network | Submitted to JINST | CMS-TAU-20-001 2201.08458 |
| 47 | CMS Collaboration | Search for physics beyond the standard model in dilepton mass spectra in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JHEP 04 (2015) 025 | CMS-EXO-12-061 1412.6302 |
| 48 | B. D. Pecjak, D. J. Scott, X. Wang, and L. L. Yang | Resummed differential cross sections for top-quark pairs at the LHC | PRL 116 (2016) 202001 | 1601.07020 |
| 49 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 50 | CMS Collaboration | Search for resonant and nonresonant new phenomena in high-mass dilepton final states at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2021) 208 | CMS-EXO-19-019 2103.02708 |
| 51 | CMS Collaboration | Performance of the reconstruction and identification of high-momentum muons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P02027 | CMS-MUO-17-001 1912.03516 |
| 52 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 53 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 54 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 55 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 56 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 57 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | CPC 77 (1993) 219 | |
| 58 | G. Cowan, ``Statistics'', Ch. 39 in Particle Data Group, C. Patrignani et al. | Statistics'', Ch. 39 in Particle Data Group, C.~Patrignani et~al., ``Review of particle physics | CPC 40 (2016) 100001 | |
| 59 | ATLAS and CMS Collaborations, and the LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS-NOTE-2011-005 | |
| 60 | M. Baak, S. Gadatsch, R. Harrington, and W. Verkerke | Interpolation between multi-dimensional histograms using a new non-linear moment morphing method | NIMA 771 (2015) 39 | 1410.7388 |
| 61 | B. C. Allanach and C. G. Lester | Sampling using a `bank' of clues | CPC 179 (2008) 256 | 0705.0486 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|