

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-23-014 | ||
| Search for supersymmetry in hadronic and leptonic final states with highly Lorentz-boosted objects at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 20 May 2025 | ||
| Abstract: A search for supersymmetry in final states with highly Lorentz-boosted top quarks, W, Z, Higgs bosons, or leptonic jets is presented. The search is based on proton-proton collision data at a center-of-mass energy of $ \sqrt{s}= $ 13 TeV, collected by the CMS experiment at CERN LHC during 2016, 2017, and 2018, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. Candidates for boosted top quark and W, Z, or Higgs boson decays are identified using jet substructure techniques. In addition, leptonic decays of boosted standard model or supersymmetry particles are explored by identifying boosted leptonic jets. The analysis is performed in channels with zero leptons, an isolated lepton, or a nonisolated lepton. Signal events are discriminated from standard model background events using the razor kinematic variables, which characterize signals with massive particles decaying to visible particles and massive invisible particles as a peak above the smoothly falling background. Standard model backgrounds are estimated by deriving data over simulation correction factors in background-enriched control regions. Data are consistent with standard model expectations. The results are interpreted using several simplified supersymmetry models with pair production of gluinos, top squarks, bottom squarks, and electroweakinos, featuring both $ R $-parity-conserving and $ R $-parity-violating decay chains. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-a:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-b:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-c:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-d:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-e:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |

png pdf |
Figure 1-f:
$ R $-parity conserving signal models considered in this analysis: Gluino pair production T5qqqqWH (top left), T5bbbbZH (top right) and T5ttcc (middle left); top squark pair production T6ttZH (middle right); chargino-neutralino production TChiWZ (bottom left) and chargino-chargino production TChiWW (bottom right). |
png pdf |
Figure 2:
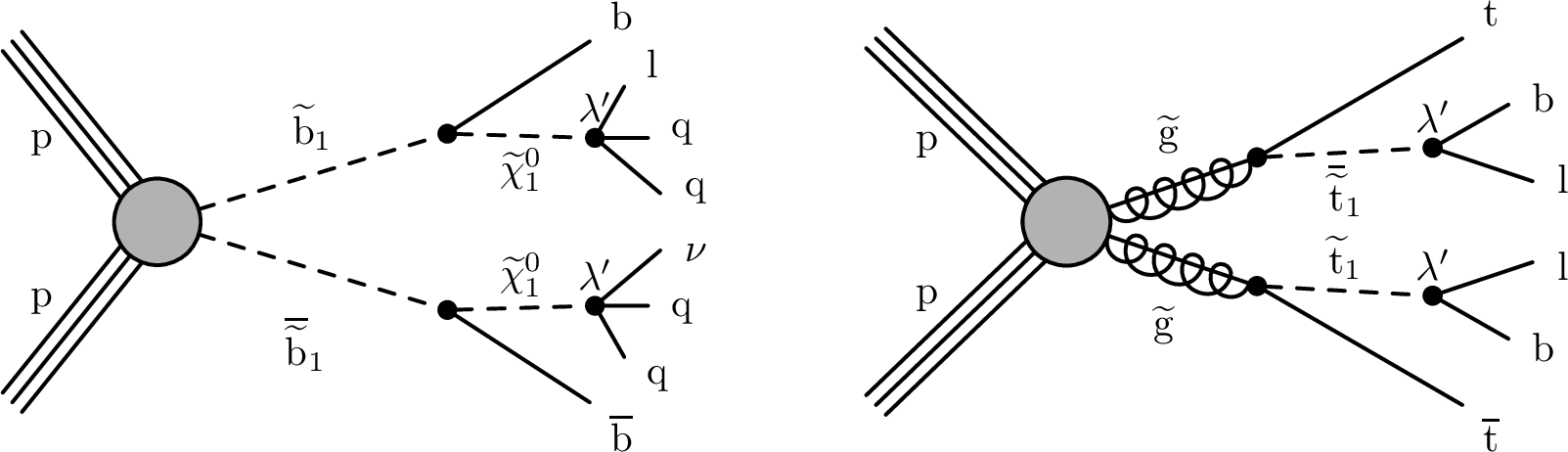
$ R $-parity violating signal models considered in this analysis. Bottom squark pair production decaying to $ R $-parity violating neutralino, R2bbqqlv (left); gluino pair production decaying to $ R $-parity violating top squark, R5ttbl (right). |

png pdf |
Figure 2-a:
$ R $-parity violating signal models considered in this analysis. Bottom squark pair production decaying to $ R $-parity violating neutralino, R2bbqqlv (left); gluino pair production decaying to $ R $-parity violating top squark, R5ttbl (right). |

png pdf |
Figure 2-b:
$ R $-parity violating signal models considered in this analysis. Bottom squark pair production decaying to $ R $-parity violating neutralino, R2bbqqlv (left); gluino pair production decaying to $ R $-parity violating top squark, R5ttbl (right). |

png pdf |
Figure 3:
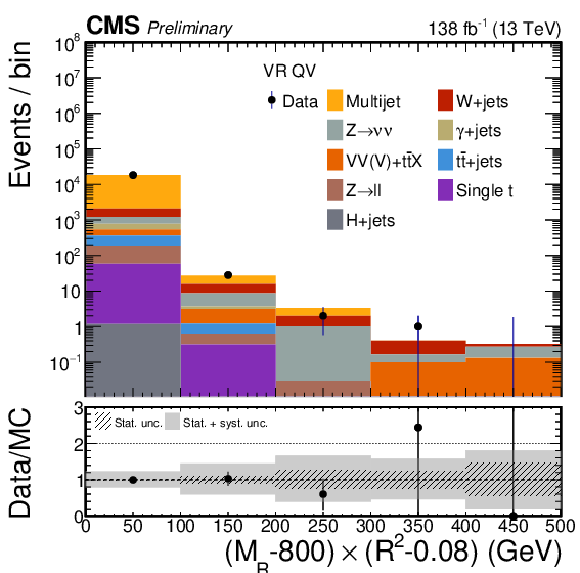
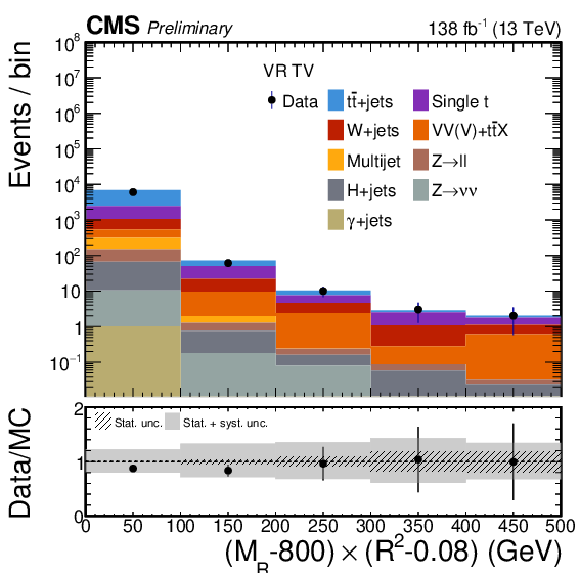
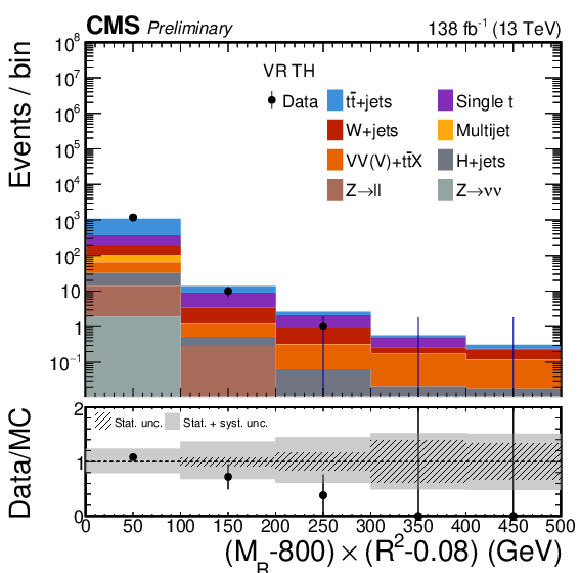
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |
png pdf |
Figure 3-a:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 3-b:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |
png pdf |
Figure 3-c:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 3-d:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |
png pdf |
Figure 3-e:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 3-f:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |
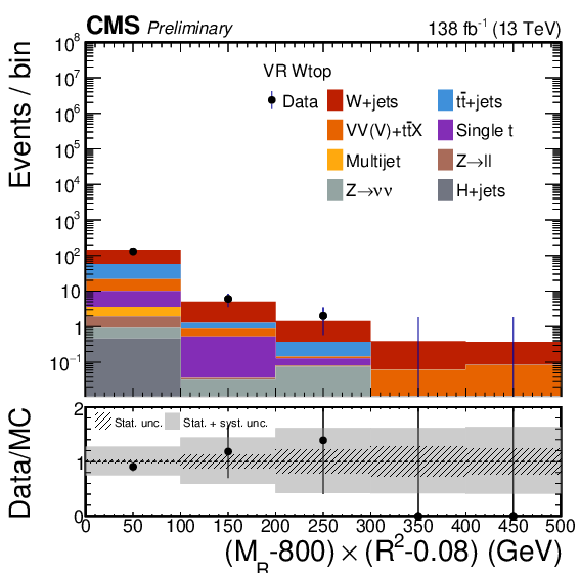
png pdf |
Figure 3-g:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs no 1-7 defined in Table 5, to validate the CFs in cases with explicit boosted object tagging: QV (top left), Qtop (top right), TV (middle left), Ttop (middle center), TH (middle right),.WV (bottom left), and Wtop (bottom right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 4:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs 8, 9, 10 defined in Table 5, to test CF validity under different kinematic conditions: Q' (left), S'V (center), and S'Top (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 4-a:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs 8, 9, 10 defined in Table 5, to test CF validity under different kinematic conditions: Q' (left), S'V (center), and S'Top (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 4-b:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs 8, 9, 10 defined in Table 5, to test CF validity under different kinematic conditions: Q' (left), S'V (center), and S'Top (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 4-c:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ for VRs 8, 9, 10 defined in Table 5, to test CF validity under different kinematic conditions: Q' (left), S'V (center), and S'Top (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 5:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ in VRs no 11, 12 defined in Table 5, to test the validity of CRs in cases with reverted $ \Delta\phi* $ or $ m_\mathrm{T} $, for the nonisolated leptonic regions: low $ \delta\phi^* $ (left), and low $ M_\mathrm{T} $ (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 5-a:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ in VRs no 11, 12 defined in Table 5, to test the validity of CRs in cases with reverted $ \Delta\phi* $ or $ m_\mathrm{T} $, for the nonisolated leptonic regions: low $ \delta\phi^* $ (left), and low $ M_\mathrm{T} $ (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 5-b:
Data and estimated SM background distributions for $ (M_\mathrm{R}-800)\times(R^2-0.08) $ in VRs no 11, 12 defined in Table 5, to test the validity of CRs in cases with reverted $ \Delta\phi* $ or $ m_\mathrm{T} $, for the nonisolated leptonic regions: low $ \delta\phi^* $ (left), and low $ M_\mathrm{T} $ (right). CFs derived for the various background processes are applied event-by-event. Distributions are shown for the complete 2016-2018 data taking period, and include systematic uncertainties. |

png pdf |
Figure 6:
The $ (M_\mathrm{R}-800) $x$ (R^2-0.08) $ distribution observed in data is shown along with the background prediction (post-fit) obtained for the SRs. Data/background prediction ratio is shown in the lower panels, where the gray band is the total (systematic and statistical) uncertainty on the background prediction. |
png pdf |
Figure 7:
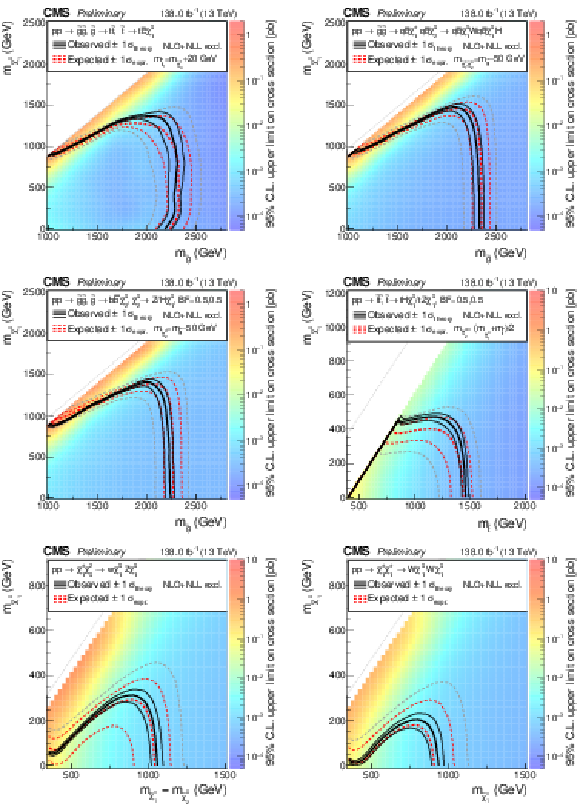
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-a:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-b:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-c:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-d:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-e:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 7-f:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle (lightest neutralino) masses for the $ R $-parity conserving models T5ttcc (top left), T5qqqqWH (top right), T5bbbbZH (middle left), T6ttZH (middle right), TChiWZ (bottom left), and TChiWW (bottom right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
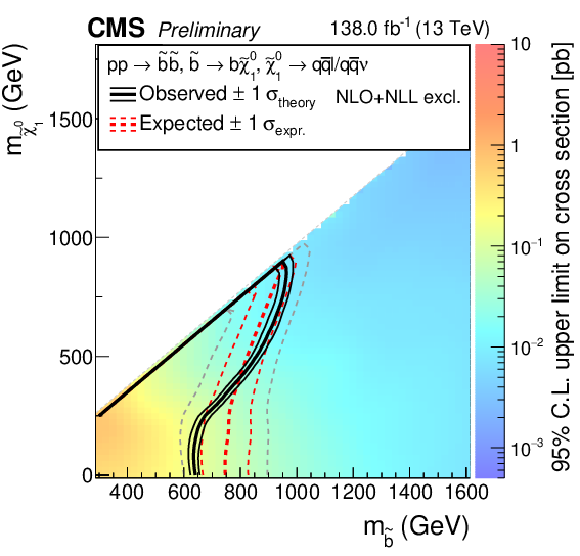
Figure 8:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle masses for the $ R $-parity violating models R2bbqqlv (left), and R5ttbl (right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |
png pdf |
Figure 8-a:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle masses for the $ R $-parity violating models R2bbqqlv (left), and R5ttbl (right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |

png pdf |
Figure 8-b:
Observed 95%CL upper limits on the signal cross sections using asymptotic $ \text{CL}_\text{s} $ versus mother sparticle and lightest supersymmetric particle masses for the $ R $-parity violating models R2bbqqlv (left), and R5ttbl (right). Also shown are the contours corresponding to the observed and expected lower limits, including their uncertainties. |
| Tables | |

png pdf |
Table 1:
Event preselection and SR categories |

png pdf |
Table 2:
SRs and their selection criteria |

png pdf |
Table 3:
SRs and their binning |
png pdf |
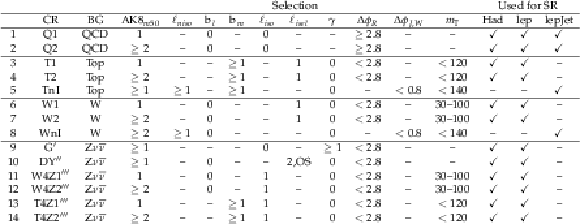
Table 4:
CRs used for background estimation. The region names W4Z and T4Z are abbreviations for WforZ and TforZ. $ \mathrm{b}_l $, $ \mathrm{b}_m $: b-quark jets identified with loose and medium working points. CRs 9-14 have additional selection criteria, corresponding to the $ ' $, $ '' $, and $ ''' $ signs next to the CR name: $ ' $: Photon added to $ {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}} $, $ '' $: Leptons added to $ {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}} $ and $ |\text{mass}(\ell\ell) - \text{mass}(\mathrm{Z})| < $ 10 GeV, $ ''' $: Lepton added to $ {\vec p}_{\mathrm{T}}^{\kern1pt\text{miss}} $. |

png pdf |
Table 5:
Event selection criteria defining the VRs for the CFs used in background estimation. $ \mathrm{b}_l $, $ \mathrm{b}_m $: b-quark jets identified with loose and medium working points. |
| Summary |
| A search for supersymmetry in hadronic and leptonic final states is presented, targeting events containing at least one boosted hadronic top quark, W, Z, or Higgs boson, or a boosted leptonic jet. The analysis is based on proton-proton collision data at $ \sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 138 fb$ ^{-1} $, collected by the CMS experiment. Events are selected using the razor kinematic variables $ M_\mathrm{R} $ and $ R^2 $, and are categorized according to lepton multiplicity, jet and b-tagged jet multiplicities, and the number and type of tagged boosted objects. Standard model backgrounds are estimated using a data-driven method based on control regions, with correction factors derived from simultaneous fits and applied to the background simulation in the signal regions. The background modeling is validated in regions with kinematic properties similar to those of the signal regions. No significant deviations from the standard model expectations are observed. Upper limits at 95% confidence level are set on the production cross sections of various supersymmetric particle pairs. The analysis excludes gluino masses up to 2.35 TeV and top squark masses up to 1.45 TeV in representative $ R $-parity-conserving models. In $ R $-parity-violating scenarios, bottom squark masses are excluded up to 0.97 TeV and gluino masses up to 1.82 TeV. Electroweak production of nearly mass-degenerate charginos and neutralinos is excluded up to 1.05 TeV, depending on the decay topology. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Golfand and E. P. Likhtman | Extension of the algebra of Poincaré group generators and violation of P invariance | JETP Lett. 13 (1971) 323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JETP Lett. 16 (1972) 438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | P. Fayet and S. Ferrara | Supersymmetry | Phys. Rept. 32 (1977) 249 | |
| 9 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 10 | F. Zwicky | On the masses of nebulae and of clusters of nebulae | Astrophys. J. 86 (1937) 217 | |
| 11 | V. C. Rubin and W. K. Ford, Jr. | Rotation of the Andromeda nebula from a spectroscopic survey of emission regions | Astrophys. J. 159 (1970) 379 | |
| 12 | Muon g-2 Collaboration | Detailed report on the measurement of the positive muon anomalous magnetic moment to 0.20 ppm | no. 3, 03, 2024 PRD 110 (2024) |
2402.15410 |
| 13 | Muon g-2 Collaboration | Measurement of the positive muon anomalous magnetic moment to 0.20 ppm | no. 16, 161802, 2023 PRL 131 (2023) |
2308.06230 |
| 14 | ATLAS Collaboration | The ATLAS Experiment at the CERN Large Hadron Collider | JINST 3 (2008) S08003 | |
| 15 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 16 | CMS Collaboration | Search for top squark production in fully-hadronic final states in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | no. 5, 05, 2021 PRD 104 (2021) |
CMS-SUS-19-010 2103.01290 |
| 17 | CMS Collaboration | Search for direct top squark pair production in events with one lepton, jets, and missing transverse momentum at 13 TeV with the CMS experiment | JHEP 05 (2020) 032 | CMS-SUS-19-009 1912.08887 |
| 18 | CMS Collaboration | Search for supersymmetry in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in events with high-momentum Z bosons and missing transverse momentum | JHEP 09 (2020) 149 | CMS-SUS-19-013 2008.04422 |
| 19 | CMS Collaboration | Search for higgsinos decaying to two Higgs bosons and missing transverse momentum in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2022) 014 | CMS-SUS-20-004 2201.04206 |
| 20 | CMS Collaboration | Search for electroweak production of charginos and neutralinos at $ \sqrt{s} = $ 13 TeV in final states containing hadronic decays of WW, WZ, or WH and missing transverse momentum | PLB 842 (2023) 137460 | CMS-SUS-21-002 2205.09597 |
| 21 | CMS Collaboration | Inclusive search for supersymmetry in pp collisions at $ \sqrt{s}= $ 13 TeV using razor variables and boosted object identification in zero and one lepton final states | JHEP 03 (2019) 031 | CMS-SUS-16-017 1812.06302 |
| 22 | C. Rogan | Kinematical variables towards new dynamics at the LHC | 6, 2010 | 1006.2727 |
| 23 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 24 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 25 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | no. 05, P05064, 2024 JINST 19 (2024) |
CMS-PRF-21-001 2309.05466 |
| 26 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 27 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 28 | CMS Collaboration | Performance of the CMS high-level trigger during LHC run 2 | JINST 19 (2024) P11021 | CMS-TRG-19-001 2410.17038 |
| 29 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 30 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 31 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 32 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 33 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 34 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 35 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} $ = 13, 14, 33 and 100 TeV | no. 12, 3174, 2014 EPJC 74 (2014) |
1407.5066 |
| 36 | W. Beenakker et al. | NNLL-fast: predictions for coloured supersymmetric particle production at the LHC with threshold and Coulomb resummation | JHEP 12 (2016) 133 | 1607.07741 |
| 37 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 38 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 39 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 40 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 41 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | Comput. Phys. Commun. 185 (2014) 2930 | 1112.5675 |
| 42 | P. Kant et al. | HatHor for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | Comput. Phys. Commun. 191 (2015) 74 | 1406.4403 |
| 43 | M. Aliev et al. | HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR | Comput. Phys. Commun. 182 (2011) 1034 | 1007.1327 |
| 44 | T. Gehrmann et al. | $ W^+W^- $ production at hadron colliders in next to next to leading order QCD | no. 21, 21, 2014 PRL 113 (2014) |
1408.5243 |
| 45 | J. M. Campbell and R. K. Ellis | An update on vector boson pair production at hadron colliders | PRD 60 (1999) 113006 | hep-ph/9905386 |
| 46 | J. M. Campbell, R. K. Ellis, and C. Williams | Vector boson pair production at the LHC | JHEP 07 (2011) 018 | 1105.0020 |
| 47 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 48 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 49 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 50 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | no. 1, 4, 2020 EPJC 80 (2020) |
CMS-GEN-17-001 1903.12179 |
| 51 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 52 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 53 | A. Giammanco | The fast simulation of the CMS experiment | J. Phys. Conf. Ser. 513 (2014) 022012 | |
| 54 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 55 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 56 | CMS Collaboration | ECAL 2016 refined calibration and Run2 summary plots | CMS Detector Performance Summary CMS-DP-2020-021, 2020 CDS |
|
| 57 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 58 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 59 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | no. 05, P05011, 2018 JINST 13 (2018) |
CMS-BTV-16-002 1712.07158 |
| 60 | E. Bols et al. | Jet flavour classification using DeepJet | JINST 15 (2020) P12012 | 2008.10519 |
| 61 | CMS Collaboration | Performance of the DeepJet b tagging algorithm using 41.9 fb$ ^{-1} $ of data from proton-proton collisions at 13 tev with Phase 1 CMS detector | CMS Detector Performance Summary CMS-DP-2018-058, 2018 CDS |
|
| 62 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 63 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 64 | H. Qu and L. Gouskos | ParticleNet: Jet Tagging via Particle Clouds | no. 5, 056019, 2020 PRD 101 (2020) |
1902.08570 |
| 65 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft Drop | JHEP 05 (2014) 146 | 1402.2657 |
| 66 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 67 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 68 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 69 | R. J. Barlow and C. Beeston | Fitting using finite monte carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 70 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 71 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 72 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 73 | CMS Collaboration | The CMS Statistical Analysis and Combination Tool: Combine | no. 1, 19, 2024 Comput. Softw. Big Sci. 8 (2024) |
CMS-CAT-23-001 2404.06614 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|