

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-TOP-18-010 | ||
| Measurement of the inclusive and differential $\mathrm{t}\bar{\mathrm{t}} + \gamma$ cross section and EFT interpretation in the single lepton channel at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| March 2021 | ||
| Abstract: The production cross section of a top quark pair in association with a photon is measured in proton-proton collisions at the center-of-mass energy of 13 TeV. The data set of 137 fb$^{-1}$ was recorded by the CMS experiment during the LHC Run II. The measurement is performed in events with a well isolated, highly energetic lepton (electron or muon), with at least three jets from the hadronization of quarks and one isolated photon. The photon may be emitted from initial state radiation, from the top quarks, as well as from decay products of the top quarks. The analysis makes use of simultaneous likelihood fits in several signal and control regions to distinguish the $\mathrm{t}\bar{\mathrm{t}} + \gamma$ signal process from various backgrounds. The inclusive cross section for a photon with transverse momentum of $\mathrm{p}_\mathrm{T} \geq$ 20 GeV is measured as 800 $\pm$ 46 (syst) $\pm$ 7 (stat) fb, in good agreement with the prediction from the standard model. The measurement is also carried out differentially in several kinematic observables and interpreted in the framework of the standard model effective field theory. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
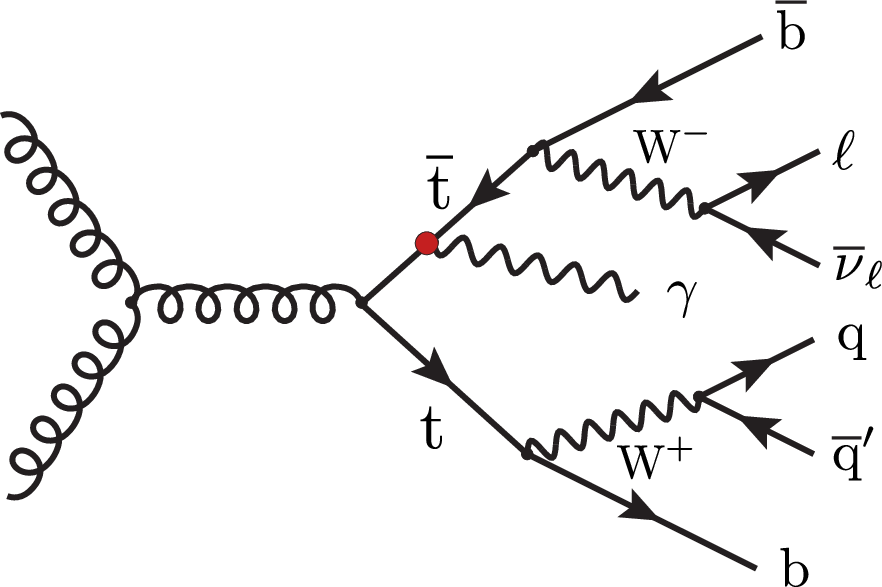
Figure 1:
Representative LO Feynman diagrams for the ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ signal process in the single lepton channel where the high energetic photon originates from the top quark (left, middle), or is emitted from a lepton (right). The $\mathrm{t} \gamma $ interaction is indicated by a circle. |
png pdf |
Figure 1-a:
Representative LO Feynman diagrams for the ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ signal process in the single lepton channel where the high energetic photon originates from the top quark (left, middle), or is emitted from a lepton (right). The $\mathrm{t} \gamma $ interaction is indicated by a circle. |

png pdf |
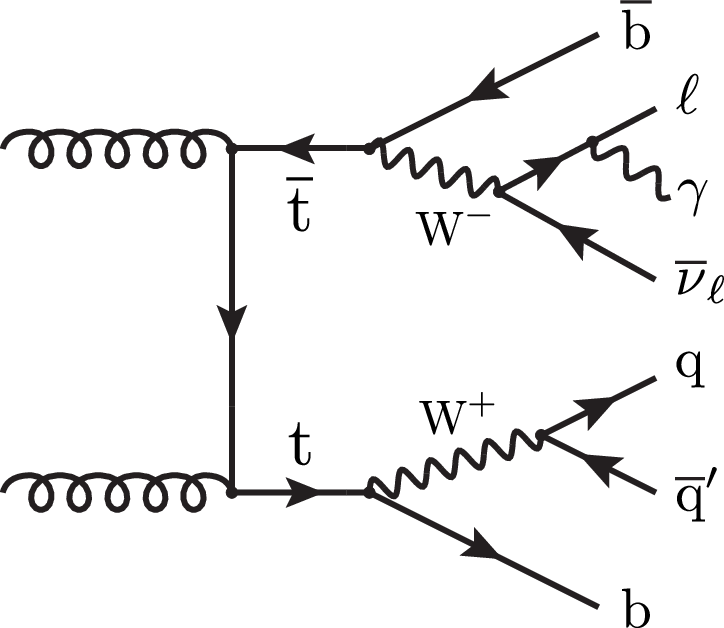
Figure 1-b:
Representative LO Feynman diagrams for the ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ signal process in the single lepton channel where the high energetic photon originates from the top quark (left, middle), or is emitted from a lepton (right). The $\mathrm{t} \gamma $ interaction is indicated by a circle. |
png pdf |
Figure 1-c:
Representative LO Feynman diagrams for the ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ signal process in the single lepton channel where the high energetic photon originates from the top quark (left, middle), or is emitted from a lepton (right). The $\mathrm{t} \gamma $ interaction is indicated by a circle. |
png pdf |
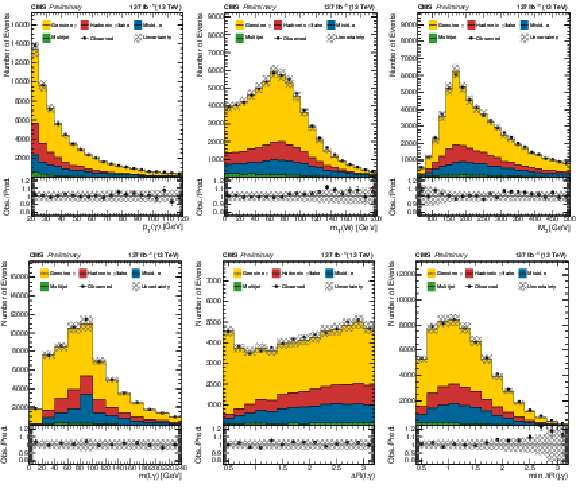
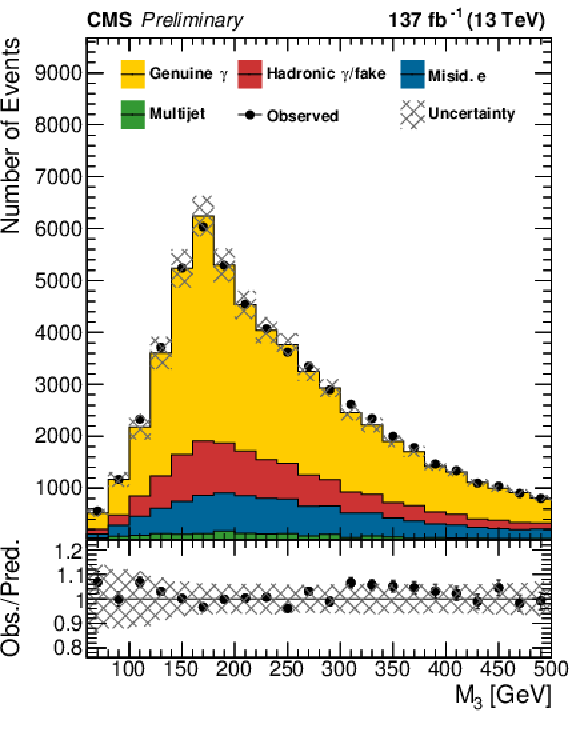
Figure 2:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 2-a:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |
png pdf |
Figure 2-b:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |
png pdf |
Figure 2-c:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 2-d:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 2-e:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 2-f:
Distribution of ${p_{T}(\gamma)}$, the transverse mass ${{m_{\mathrm {T}}} (\mathrm{W})}$ of the W boson candidate, the three-jet invariant mass ${M_3}$ (upper row) and the invariant mass of the lepton and the photon ($m(\ell,\gamma)$), the angular separation of the lepton and the photon ($\Delta R(\ell,\gamma)$), and the angular separation of the leading jet and the photon ($\Delta R(j_1, \gamma)$) (lower row). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
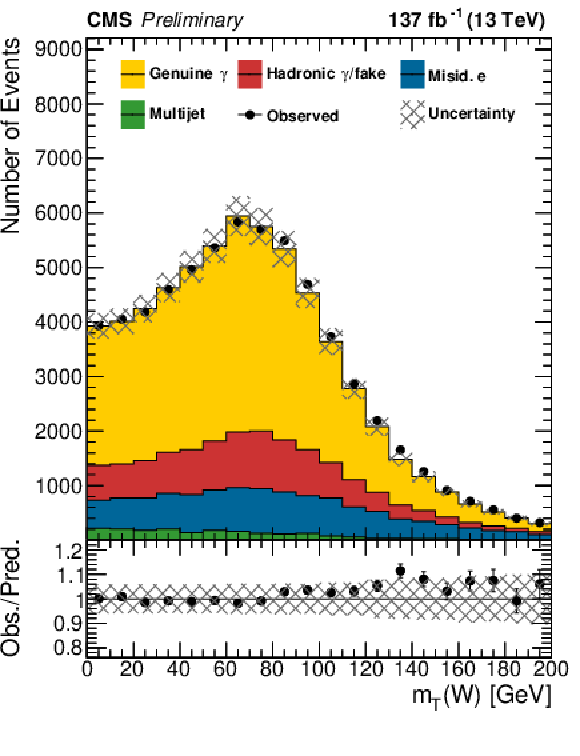
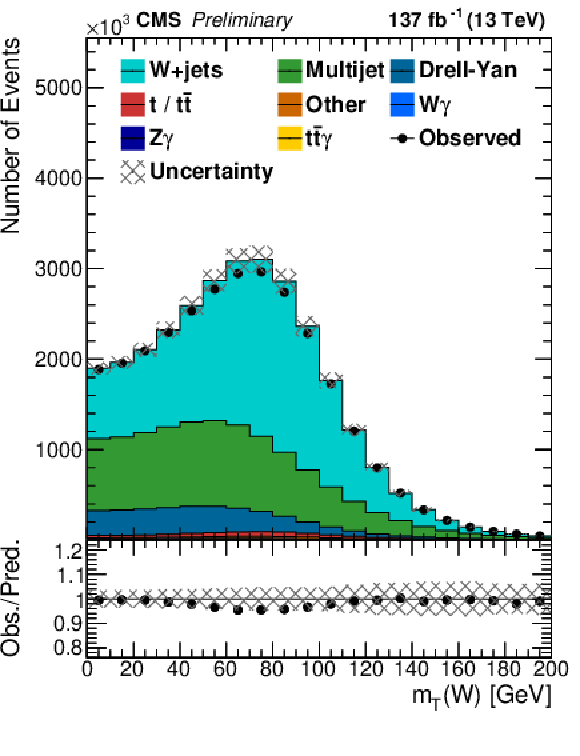
Figure 3:
Fit result of the multijet template obtained with loosely isolated leptons and the electroweak background to the measured ${{m_{\mathrm {T}}} (\mathrm{W})}$ distribution with isolated leptons in the $ {N_\text {jet}} =$ 2, $ {N_\text {b jet}} =$ 0 selection for electrons (left) and muons (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |
png pdf |
Figure 3-a:
Fit result of the multijet template obtained with loosely isolated leptons and the electroweak background to the measured ${{m_{\mathrm {T}}} (\mathrm{W})}$ distribution with isolated leptons in the $ {N_\text {jet}} =$ 2, $ {N_\text {b jet}} =$ 0 selection for electrons (left) and muons (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 3-b:
Fit result of the multijet template obtained with loosely isolated leptons and the electroweak background to the measured ${{m_{\mathrm {T}}} (\mathrm{W})}$ distribution with isolated leptons in the $ {N_\text {jet}} =$ 2, $ {N_\text {b jet}} =$ 0 selection for electrons (left) and muons (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
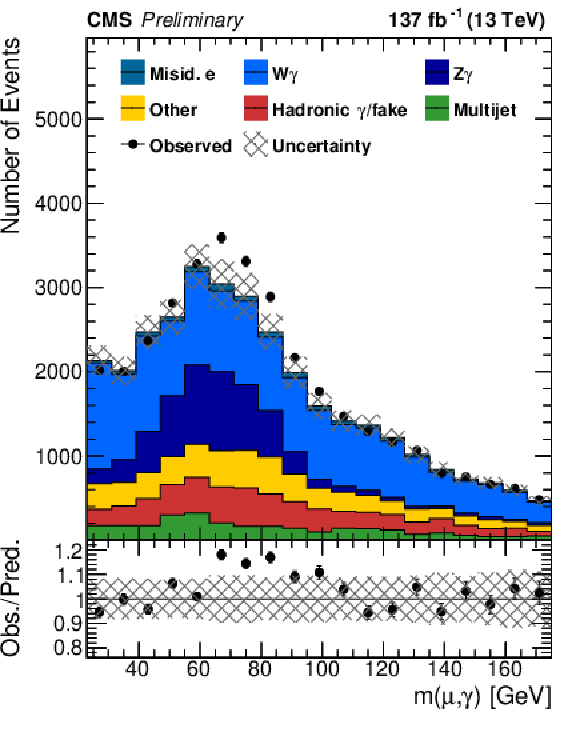
Figure 4:
Distribution of the invariant mass of the lepton and the photon ($m(\ell,\gamma)$) in the $ {N_\text {jet}} \geq $ 3, $ {N_\text {b jet}} =$ 0 selection for the e channel (left) and the $\mu$channel (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
Figure 4-a:
Distribution of the invariant mass of the lepton and the photon ($m(\ell,\gamma)$) in the $ {N_\text {jet}} \geq $ 3, $ {N_\text {b jet}} =$ 0 selection for the e channel (left) and the $\mu$channel (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |
png pdf |
Figure 4-b:
Distribution of the invariant mass of the lepton and the photon ($m(\ell,\gamma)$) in the $ {N_\text {jet}} \geq $ 3, $ {N_\text {b jet}} =$ 0 selection for the e channel (left) and the $\mu$channel (right). The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |

png pdf |
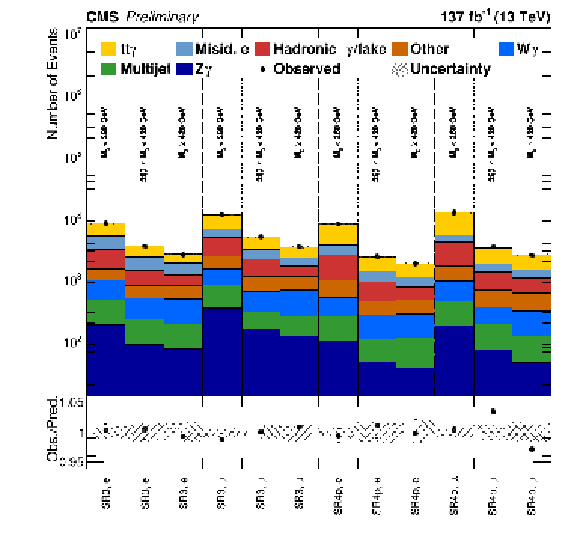
Figure 5:
Predicted yields and observation in the control regions in the $ {N_\text {jet}} =$ 3 and $ {N_\text {jet}} \geq $ 4 selections for post-fit values of the nuisance parameters. The lower panels show the ratio of the observation to the prediction. The shaded bands show the systematic uncertainty in the background prediction. |
png pdf |
Figure 6:
Predicted yields and observation in the signal regions in the $ {N_\text {jet}} =$ 3 and $ {N_\text {jet}} \geq $ 4 selections for post-fit values of the nuisance parameters. The lower panels show the ratio of the observation to the prediction. The systematic uncertainties are shown as a shaded band. |
png pdf |
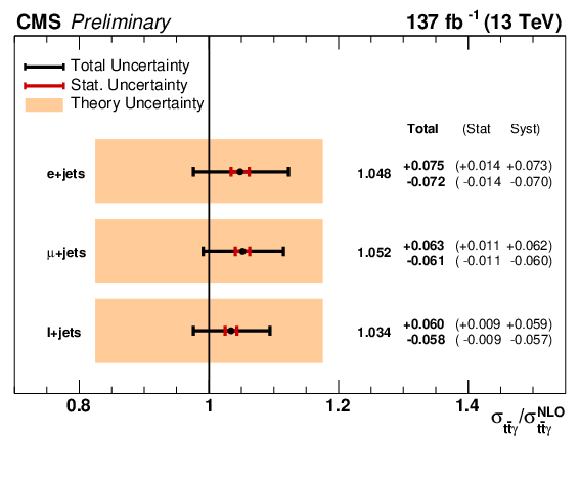
Figure 7:
Summary of the measured cross sections normalized to the NLO cross section prediction for signal regions binned in the e-channel, $\mu $-channel and the combined single lepton measurement. The light brown band indicates the theory uncertainty in the prediction. |
png pdf |
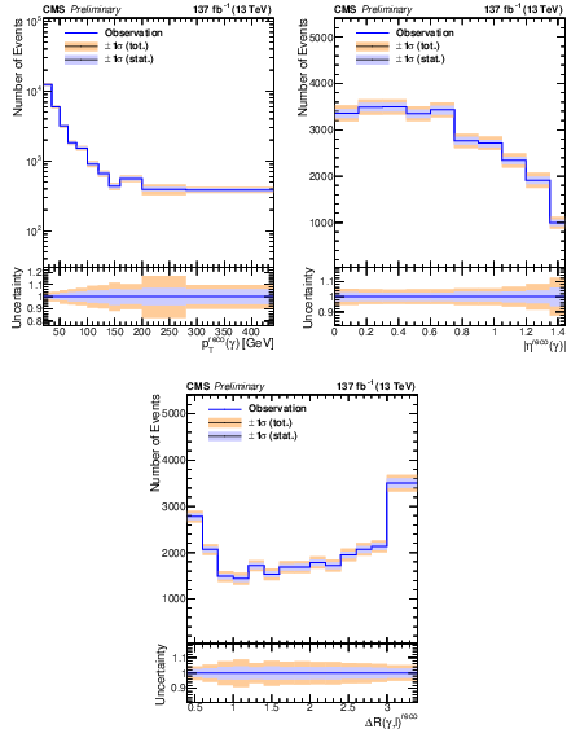
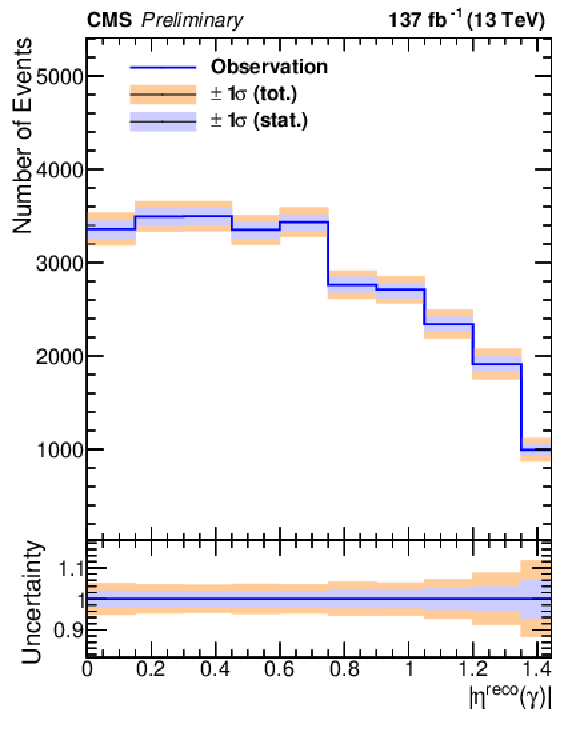
Figure 8:
The distribution of ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom) in the $ {N_\text {jet}} \geq $ 3 selection after background subtraction. The lower panel displays the relative uncertainty, where the inner and outer bands show the statistical and total uncertainties, respectively. |

png pdf |
Figure 8-a:
The distribution of ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom) in the $ {N_\text {jet}} \geq $ 3 selection after background subtraction. The lower panel displays the relative uncertainty, where the inner and outer bands show the statistical and total uncertainties, respectively. |
png pdf |
Figure 8-b:
The distribution of ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom) in the $ {N_\text {jet}} \geq $ 3 selection after background subtraction. The lower panel displays the relative uncertainty, where the inner and outer bands show the statistical and total uncertainties, respectively. |

png pdf |
Figure 8-c:
The distribution of ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom) in the $ {N_\text {jet}} \geq $ 3 selection after background subtraction. The lower panel displays the relative uncertainty, where the inner and outer bands show the statistical and total uncertainties, respectively. |
png pdf |
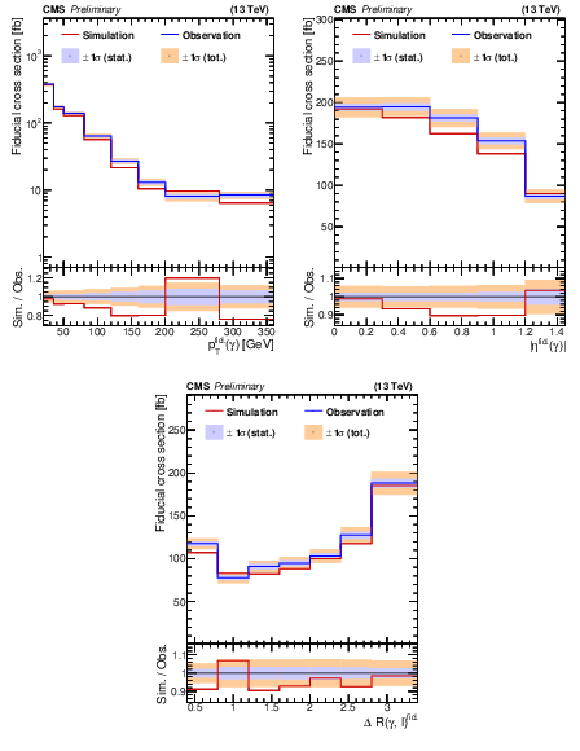
Figure 9:
The unfolded differential cross sections for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). The lower panel displays the ratio of simulation to the observation. The inner and outer bands show the statistical and total uncertainties, respectively. |
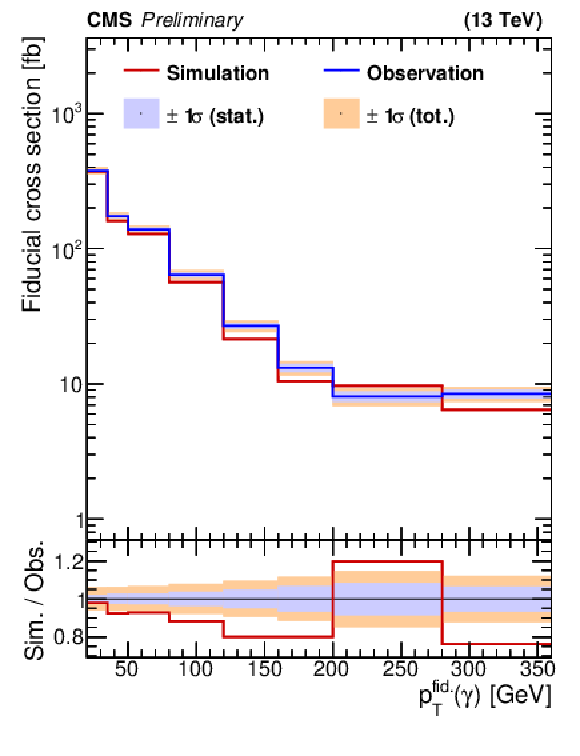
png pdf |
Figure 9-a:
The unfolded differential cross sections for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). The lower panel displays the ratio of simulation to the observation. The inner and outer bands show the statistical and total uncertainties, respectively. |
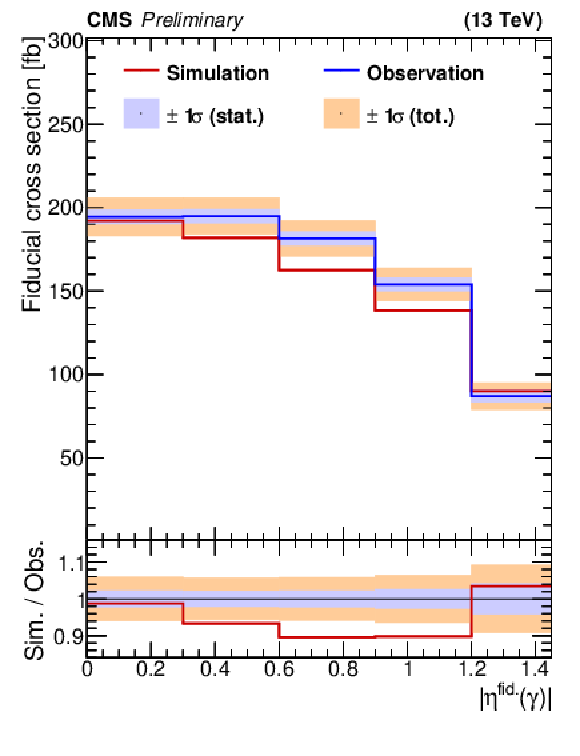
png pdf |
Figure 9-b:
The unfolded differential cross sections for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). The lower panel displays the ratio of simulation to the observation. The inner and outer bands show the statistical and total uncertainties, respectively. |

png pdf |
Figure 9-c:
The unfolded differential cross sections for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). The lower panel displays the ratio of simulation to the observation. The inner and outer bands show the statistical and total uncertainties, respectively. |

png pdf |
Figure 10:
The covariance matrices of the unfolded differential measurement for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). |
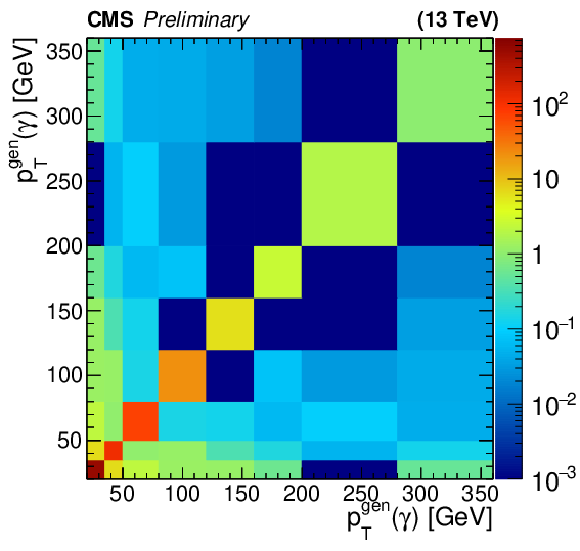
png pdf |
Figure 10-a:
The covariance matrices of the unfolded differential measurement for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). |

png pdf |
Figure 10-b:
The covariance matrices of the unfolded differential measurement for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). |
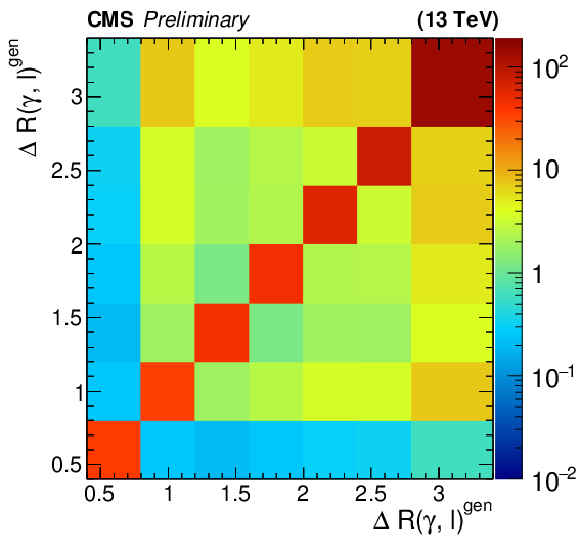
png pdf |
Figure 10-c:
The covariance matrices of the unfolded differential measurement for ${p_{T}(\gamma)}$ (left), ${|\eta (\gamma)|}$ (right), and ${\Delta R(\ell,\gamma)}$ (bottom). |
png pdf |
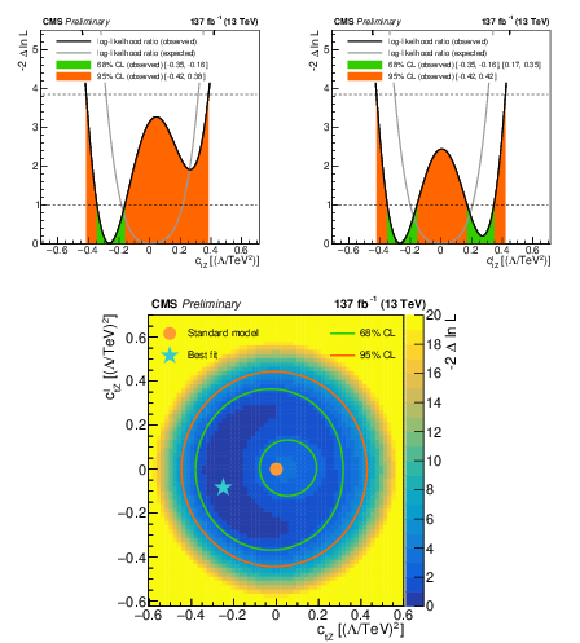
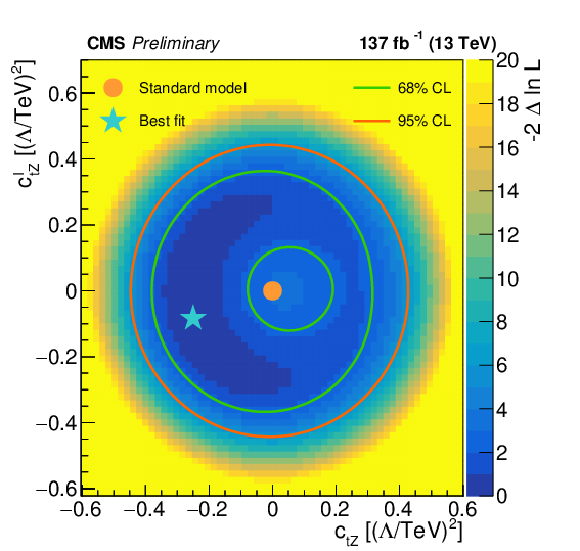
Figure 11:
Results of one-dimensional scans for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{I}}$ (right), and for the two-dimensional plane (bottom). The shading quantified by the color scale on the right reflects the negative log-likelihood ratio with respect to the best-fit value that is designated by the star. The green and orange lines indicate the 68 and 95% CL contours from the fit, respectively. The allowed areas are those between the two green contours and that inside the orange contour. The dot shows the SM prediction. |

png pdf |
Figure 11-a:
Results of one-dimensional scans for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{I}}$ (right), and for the two-dimensional plane (bottom). The shading quantified by the color scale on the right reflects the negative log-likelihood ratio with respect to the best-fit value that is designated by the star. The green and orange lines indicate the 68 and 95% CL contours from the fit, respectively. The allowed areas are those between the two green contours and that inside the orange contour. The dot shows the SM prediction. |

png pdf |
Figure 11-b:
Results of one-dimensional scans for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{I}}$ (right), and for the two-dimensional plane (bottom). The shading quantified by the color scale on the right reflects the negative log-likelihood ratio with respect to the best-fit value that is designated by the star. The green and orange lines indicate the 68 and 95% CL contours from the fit, respectively. The allowed areas are those between the two green contours and that inside the orange contour. The dot shows the SM prediction. |
png pdf |
Figure 11-c:
Results of one-dimensional scans for the Wilson coefficients ${c_{\mathrm{t} \mathrm{Z}}}$ (left) and ${c_{\mathrm{t} \mathrm{Z}}^{I}}$ (right), and for the two-dimensional plane (bottom). The shading quantified by the color scale on the right reflects the negative log-likelihood ratio with respect to the best-fit value that is designated by the star. The green and orange lines indicate the 68 and 95% CL contours from the fit, respectively. The allowed areas are those between the two green contours and that inside the orange contour. The dot shows the SM prediction. |
| Tables | |

png pdf |
Table 1:
Event generator and orders of accuracy for each simulated process. |

png pdf |
Table 2:
Overview of signal and control regions. For ZG, WG, and misDY the regions with suffixes 3 (4p) have a modified jet multiplicity requirement of $ {N_\text {jet}} =$ 3 ($ {N_\text {jet}} \geq $ 4). |

png pdf |
Table 3:
Extracted scale factors for the contribution from misidentified electrons for the three data taking periods, and the ${{\mathrm{Z}} \gamma}, {\mathrm{W} \gamma}$ scale factors. |

png pdf |
Table 4:
Summary of systematic uncertainties. The first column indicates the source of the uncertainty. The second column shows the correlation between the data taking periods, where the check symbol indicates 100% correlation. The third column shows the typical pre-fit uncertainties in the simulated yields of the signal region. The last column gives the corresponding systematic uncertainty in the ${{\mathrm{t} \mathrm{\bar{t}}} \gamma}$ cross section using the fit result. |

png pdf |
Table 5:
Binning choices in the differential measurements. |

png pdf |
Table 6:
Summary of the 1D confidence intervals at 68 and 95% CL. |
| Summary |
|
A measurement of top quark pair production in association with a photon using a data sample of proton-proton collisions at $\sqrt{s} = $ 13 TeV, corresponding to an integrated luminosity of 137 fb$^{-1}$, collected with the CMS detector at the LHC has been presented. The analysis was performed in the three- and at least four-jet final states. A data driven approach is used to estimate the background in the signal regions. The measured inclusive cross section is $\sigma^{\textrm{fid.}}({\mathrm{t\bar{t}}\gamma} ) = $ 800 $\pm$ 46 (syst) $\pm$ 7 (stat) fb and is in good agreement with the standard model prediction. Absolute and normalized differential cross sections for the transverse momentum of the ${p_{\mathrm{T}}}(\gamma)$, ${|\eta(\gamma)|}$, and ${\Delta R(\ell,\gamma)}$ are measured. The measurement is also interpreted in terms of Wilson coefficients in the context of SMEFT. The confidence intervals for the Wilson coefficients ${c_{\mathrm{t}\mathrm{Z}}} $ and ${c_{\mathrm{t}\mathrm{Z}}^{I}} $ are the strongest to date. |
| References | ||||
| 1 | O. Bessidskaia Bylund et al. | Probing top quark neutral couplings in the standard model effective field theory at NLO in QCD | JHEP 05 (2016) 052 | 1601.08193 |
| 2 | CDF Collaboration | Evidence for $ t\bar{t}\gamma $ production and measurement of $ \sigma_{t\bar{t}\gamma}/\sigma_{t\bar{t}} $ | PRD 48 (2011) 031104 | 1106.3970 |
| 3 | ATLAS Collaboration | Observation of top-quark pair production in association with a photon and measurement of the $ \mathrm{t\bar{t}}\gamma $ production cross section in pp collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | PRD 91 (2015) 072007 | 1502.00586 |
| 4 | ATLAS Collaboration | Measurement of the $ t\overline{t}\gamma $ production cross section in proton-proton collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | JHEP 11 (2017) 086 | 1706.03046 |
| 5 | CMS Collaboration | Measurement of the semileptonic $ \mathrm{t}\overline{\mathrm{t}} + \gamma $ production cross section in pp collisions at $ \sqrt{s}= $ 8 TeV | JHEP 10 (2017) 006 | CMS-TOP-14-008 1706.08128 |
| 6 | ATLAS Collaboration | Measurements of inclusive and differential fiducial cross-sections of $ t\bar{t}\gamma $ production in leptonic final states at $ \sqrt{s}= $ 13 TeV in ATLAS | EPJC 79 (2019) 382 | 1812.01697 |
| 7 | ATLAS Collaboration | Measurements of inclusive and differential cross-sections of combined $ t\bar{t}\gamma $ and $ tW\gamma $ production in the $ e\mkern-2mu\mu $ channel at 13 TeV with the ATLAS detector | JHEP 09 (2020) 049 | 2007.06946 |
| 8 | B. Grzadkowski, M. Iskrzynski, M. Misiak, and J. Rosiek | Dimension-six terms in the standard model Lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 9 | D. Barducci et al. | Interpreting top-quark LHC measurements in the standard-model effective field theory | (2, 2018) | 1802.07237 |
| 10 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 11 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 12 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 13 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 14 | J. M. Campbell, R. K. Ellis, P. Nason, and E. Re | Top-pair production and decay at NLO matched with parton showers | JHEP 04 (2015) 114 | 1412.1828 |
| 15 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 16 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 17 | M. Czakon and A. Mitov | Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 18 | S. Dulat et al. | New parton distribution functions from a global analysis of quantum chromodynamics | PRD 93 (2016) 033006 | 1506.07443 |
| 19 | M. Aliev et al. | HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR | CPC 182 (2011) 1034 | 1007.1327 |
| 20 | P. Kant et al. | HATHOR for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | CPC 191 (2015) 74 | 1406.4403 |
| 21 | N. Kidonakis | Theoretical results for electroweak-boson and single-top production | PoS DIS2015 (2015) 170 | 1506.04072 |
| 22 | K. Melnikov and F. Petriello | Electroweak gauge boson production at hadron colliders through $ O(\alpha^2_S) $ | PRD 74 (2006) 114017 | hep-ph/0609070 |
| 23 | S. Catani et al. | Vector boson production at hadron colliders: a fully exclusive QCD calculation at NNLO | PRL 103 (2009) 082001 | 0903.2120 |
| 24 | C. Anastasiou, L. J. Dixon, K. Melnikov, and F. Petriello | High precision QCD at hadron colliders: Electroweak gauge boson rapidity distributions at NNLO | PRD 69 (2004) 094008 | hep-ph/0312266 |
| 25 | S. Dittmaier, A. Huss, and C. Schwinn | Mixed QCD-electroweak $ O(\alpha_S\alpha) $ corrections to Drell-Yan processes in the resonance region: pole approximation and non-factorizable corrections | NPB 885 (2014) 318 | 1403.3216 |
| 26 | J. M. Lindert et al. | Precise predictions for $ V+ $ jets dark matter backgrounds | EPJC 77 (2017) 829 | 1705.04664 |
| 27 | M. V. Garzelli, A. Kardos, C. G. Papadopoulos, and Z. Trocsanyi | $ {\rm t\bar{t}W^{\pm}} $ and $ {\rm t\bar{t}Z} $ hadroproduction at NLO accuracy in QCD with parton shower and hadronization effects | JHEP 11 (2012) 056 | 1208.2665 |
| 28 | S. Frixione et al. | Electroweak and QCD corrections to top-pair hadroproduction in association with heavy bosons | JHEP 06 (2015) 184 | 1504.03446 |
| 29 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 30 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 31 | P. Barnreuther, M. Czakon, and A. Mitov | Percent Level Precision Physics at the Tevatron: First Genuine NNLO QCD Corrections to $ q \bar{q} \to t \bar{t} + X $ | PRL 109 (2012) 132001 | 1204.5201 |
| 32 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 33 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 34 | M. Czakon, P. Fiedler, and A. Mitov | Total Top-Quark Pair-Production Cross Section at Hadron Colliders Through $ O(\alpha^4_S) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 35 | T. Gehrmann et al. | $ W^+W^- $ Production at Hadron Colliders in Next to Next to Leading Order QCD | PRL 113 (2014) 212001 | 1408.5243 |
| 36 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 37 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 38 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 39 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 40 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 41 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 42 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 43 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 44 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 45 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 46 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 47 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 48 | CMS Collaboration | Performance of Photon Reconstruction and Identification with the CMS Detector in Proton-Proton Collisions at sqrt(s) = 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 49 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 50 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet User Manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 51 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | submitted to JINST (2020) | CMS-EGM-17-001 2012.06888 |
| 52 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 53 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 54 | M. Cacciari, G. P. Salam, and G. Soyez | The Catchment Area of Jets | JHEP 04 (2008) 005 | 0802.1188 |
| 55 | CMS Collaboration | CMS luminosity measurement for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 56 | CMS Collaboration | CMS luminosity measurement for the 2017 data taking period | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 57 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 58 | ATLAS Collaboration | Measurement of the Inelastic Proton-Proton Cross Section at $ \sqrt{s}= $ 13 TeV with the ATLAS Detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 59 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 60 | CMS Collaboration | Energy Calibration and Resolution of the CMS Electromagnetic Calorimeter in $ pp $ Collisions at $ \sqrt{s} = $ 7 TeV | JINST 8 (2013) P09009 | CMS-EGM-11-001 1306.2016 |
| 61 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 62 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 63 | R. D. Ball et al. | Parton distributions with LHC data | NPB 867 (2013) 244 | 1207.1303 |
| 64 | A. D. Martin, W. J. Stirling, R. S. Thorne, and G. Watt | Uncertainties on $ \alpha_S $ in global PDF analyses and implications for predicted hadronic cross sections | EPJC 64 (2009) 653 | 0905.3531 |
| 65 | J. Gao et al. | CT10 next-to-next-to-leading order global analysis of QCD | PRD 89 (2014) 033009 | 1302.6246 |
| 66 | S. Argyropoulos and T. Sjostrand | Effects of color reconnection on $ \mathrm{t\bar{t}} $ final states at the LHC | JHEP 11 (2014) 043 | 1407.6653 |
| 67 | J. R. Christiansen and P. Z. Skands | String formation beyond leading colour | JHEP 08 (2015) 003 | 1505.01681 |
| 68 | The ATLAS Collaboration, The CMS Collaboration, The LHC Higgs Combination Group Collaboration | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 69 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 70 | G. Cowan | Statistical data analysis | Clarendon Press, Oxford | |
| 71 | S. Schmitt | TUnfold, an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 72 | W. Hollik et al. | Top dipole form-factors and loop induced CP violation in supersymmetry | NPB 551 (1999) 3 | hep-ph/9812298 |
| 73 | K. Agashe, G. Perez, and A. Soni | Collider Signals of Top Quark Flavor Violation from a Warped Extra Dimension | PRD 75 (2007) 015002 | hep-ph/0606293 |
| 74 | A. L. Kagan, G. Perez, T. Volansky, and J. Zupan | General Minimal Flavor Violation | PRD 80 (2009) 076002 | 0903.1794 |
| 75 | T. Ibrahim and P. Nath | The Top quark electric dipole moment in an MSSM extension with vector like multiplets | PRD 82 (2010) 055001 | 1007.0432 |
| 76 | T. Ibrahim and P. Nath | The Chromoelectric Dipole Moment of the Top Quark in Models with Vector Like Multiplets | PRD 84 (2011) 015003 | 1104.3851 |
| 77 | C. Grojean, O. Matsedonskyi, and G. Panico | Light top partners and precision physics | JHEP 10 (2013) 160 | 1306.4655 |
| 78 | F. Richard | Can LHC observe an anomaly in ttZ production? | 1304.3594 | |
| 79 | C. Zhang and S. Willenbrock | Effective-field-theory approach to top-quark production and decay | PRD 83 (2011) 034006 | 1008.3869 |
| 80 | Rontsch, Raoul and Schulze, Markus | Probing top-Z dipole moments at the LHC and ILC | JHEP 08 (2015) 044 | 1501.05939 |
| 81 | M. Schulze and Y. Soreq | Pinning down electroweak dipole operators of the top quark | EPJC 76 (2016) 466 | 1603.08911 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|