

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-16-051 | ||
| Search for top squark pair production in the single lepton final state in pp collisions at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| March 2017 | ||
| Abstract: A search for top squark pair production in pp collisions at $\sqrt{s}= $ 13 TeV is performed using events with a single isolated electron or muon, jets, and large transverse momentum imbalance. Results are based on a study of data from proton-proton collisions collected in 2016 with the CMS detector at the LHC corresponding to an integrated luminosity of 35.9 fb$^{-1}$. No significant excess of events is observed above the expectation from standard model processes. Exclusion limits are set in the context of supersymmetric models of pair production of top squarks that decay either to a top quark and a neutralino or to a bottom quark and a chargino. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 10 (2017) 019. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures & Tables | References | CMS Publications |
|---|
| Additional information on efficiencies needed for reinterpretation of these results are available here and additional figures for speakers can be found here. |
| Figures | |

png pdf |
Figure 1:
Diagrams corresponding to top squark pair production, followed by the specific decay modes targeted in this note. Top left: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow t^{(*)}\chi ^0_1\bar{t}^{(*)}\chi ^0_1$; top right: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow b\chi ^+_1\bar{b}\chi ^-_1$; bottom: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow t^{(*)}\chi ^0_1b\chi ^+_1$. |

png pdf |
Figure 1-a:
Diagram corresponding to top squark pair production and decay targeted in this note: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow t^{(*)}\chi ^0_1\bar{t}^{(*)}\chi ^0_1$. |

png pdf |
Figure 1-b:
Diagram corresponding to top squark pair production and decay targeted in this note: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow b\chi ^+_1\bar{b}\chi ^-_1$. |

png pdf |
Figure 1-c:
Diagram corresponding to top squark pair production and decay targeted in this note: $pp\rightarrow \tilde{t_1}\tilde{t_1}^*\rightarrow t^{(*)}\chi ^0_1b\chi ^+_1$. |

png pdf |
Figure 2:
Distributions of ${E_{\mathrm {T}}^{\text {miss}}}$ for a top-enriched control region of $\mathrm{ e } \mu$ events with at least one b tagged jet. |
png pdf |
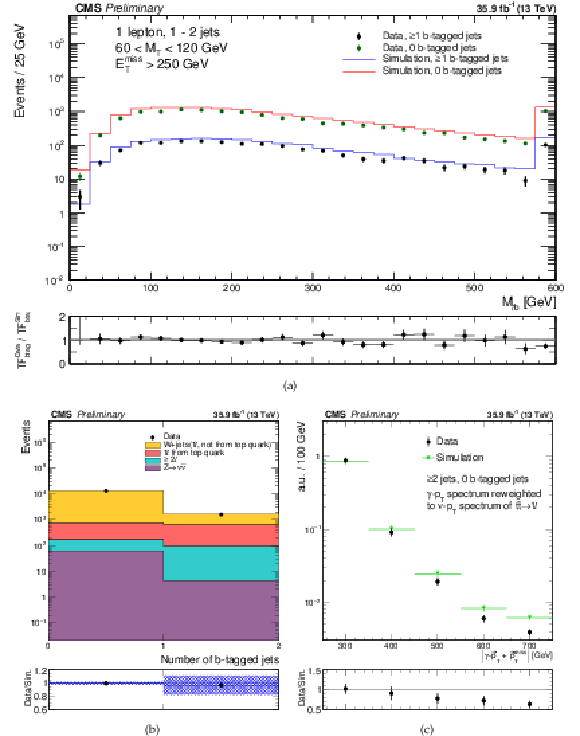
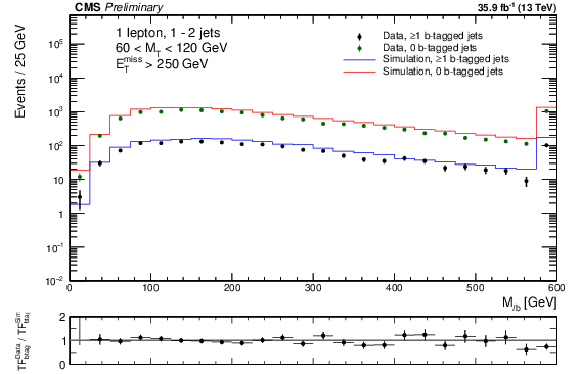
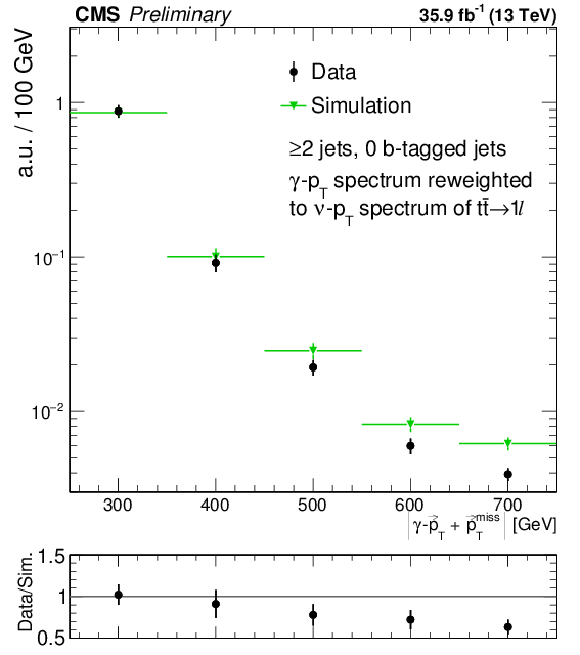
Figure 3:
Comparison of the modeling of kinematic distributions in data and simulation relevant for the estimate of the single lepton backgrounds. (a) Comparison of the ${M_{\mathrm {\ell b}}}$ distribution in a control sample with 1 or 2 jets, with 60 $ < {M_{\mathrm {T}}} < $ 120 GeV. The distribution is shown separately for events with 0 and $\geq $1 jet passing the medium b-tagging working point. The lower panel shows the ratio of the the transfer factors (TF) in data and simulation from the 0 tags to the $\geq 1$ tags samples. (b) The distribution of the number of b-tagged jets in the same control sample after tightening the ${E_{\mathrm {T}}^{\text {miss}}}$ requirement to 250 GeV. The shaded band shows the uncertainty resulting from a 50% systematic uncertainty on the heavy flavor component of the W+jets sample. (c) Comparison of the ${E_{\mathrm {T}}^{\text {miss}}}$ distribution between data and simulation in the $\gamma $+jets control region. The uncertainty shown is statistical-only. |
png pdf |
Figure 3-a:
Comparison of the ${M_{\mathrm {\ell b}}}$ distribution in a control sample with 1 or 2 jets, with 60 $ < {M_{\mathrm {T}}} < $ 120 GeV. The distribution is shown separately for events with 0 and $\geq $1 jet passing the medium b-tagging working point. The lower panel shows the ratio of the the transfer factors (TF) in data and simulation from the 0 tags to the $\geq 1$ tags samples. |

png pdf |
Figure 3-b:
The distribution of the number of b-tagged jets in the same control sample after tightening the ${E_{\mathrm {T}}^{\text {miss}}}$ requirement to 250 GeV. The shaded band shows the uncertainty resulting from a 50% systematic uncertainty on the heavy flavor component of the W+jets sample. |
png pdf |
Figure 3-c:
Comparison of the ${E_{\mathrm {T}}^{\text {miss}}}$ distribution between data and simulation in the $\gamma $+jets control region. The uncertainty shown is statistical-only. |
png pdf |
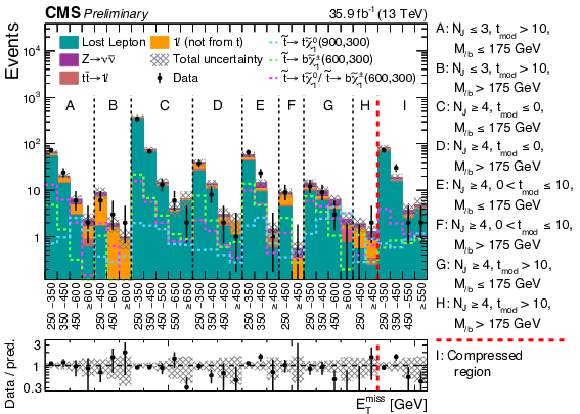
Figure 4:
Observed data yields compared with SM background estimations for the 31 signal regions of Table 2 and 3. The uncertainties, which are the quadratic sums of statistical and systematic uncertainties, are shown as shaded bands. The expectations for three signal hypotheses are overlaid. The corresponding numbers in parentheses in the legend refer to the masses of the top squark and neutralino, respectively. |

png pdf root |
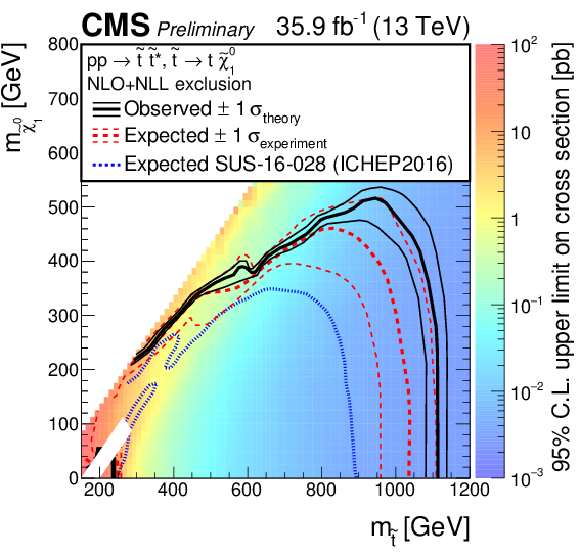
Figure 5:
The exclusion limits at 95% CL for direct top-squark production with decay $\tilde{ \mathrm{ t } }_1 \to \mathrm{ t } \tilde{\chi}^0_1 $. The interpretation is done in the two dimensional space of $m_{\tilde{ \mathrm{ t } } }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } }_1 }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limit at 95% CL and their $\pm$1$ \sigma $ experiment standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\mathrm {theory}$) on the signal cross section. The whited out region is discussed in Sec. 7. |
png pdf root |
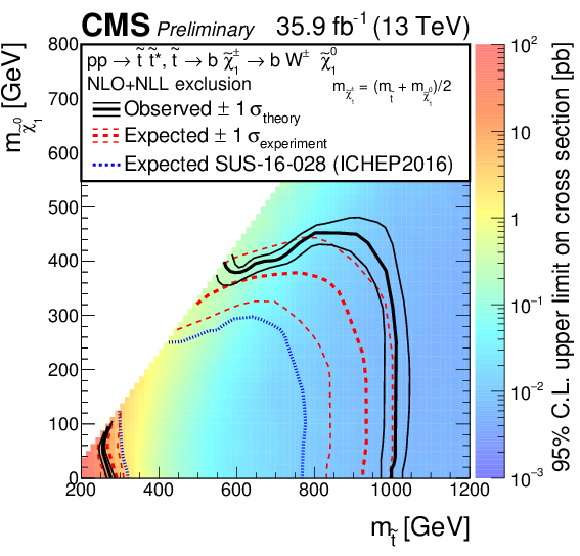
Figure 6:
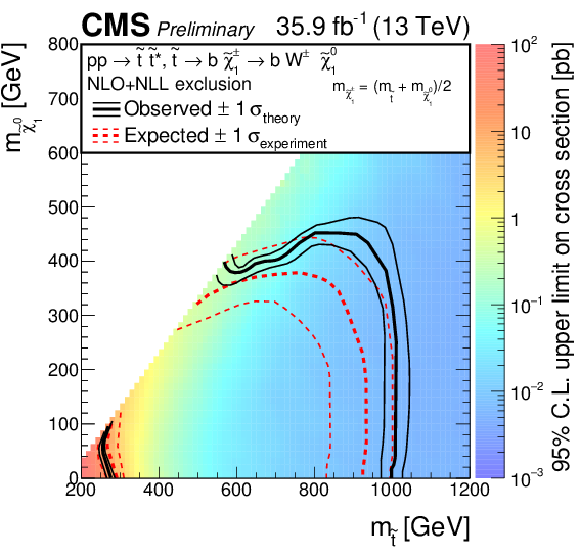
The exclusion limit at 95% CL for direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } }_1 } + m_{\tilde{\chi}^0_1 })/2$. The interpretation is done in the two dimensional space of $m_{\tilde{ \mathrm{ t } }_1 }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } }_1 }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limit at 95% CL and their $\pm$1$ \sigma $ experiment standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\mathrm {theory}$) on the signal cross section. |
png pdf root |
Figure 7:
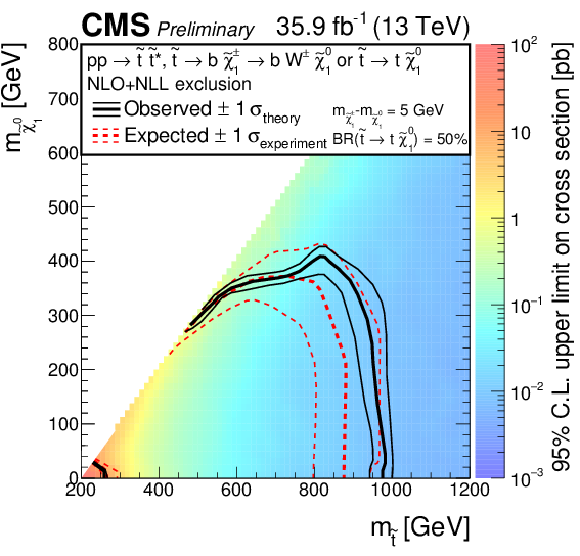
The exclusion limit at 95% CL for direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ t } \mathrm{ b } \tilde{\chi}^{\pm}_1 \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } ^{*}\tilde{\chi}^0_1 $. The mass splitting of the chargino and neutralino is fixed to 5 GeV. The interpretation is done in the two dimensional space of $m_{\tilde{ \mathrm{ t } }_1 }$ vs. $m_{\tilde{\chi}^0_1 }$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } }_1 }$ vs. $m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limit at 95% CL and their $\pm$1$ \sigma $ experiment standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties ($\sigma _\mathrm {theory}$) on the signal cross section. |
png pdf |
Figure 8:
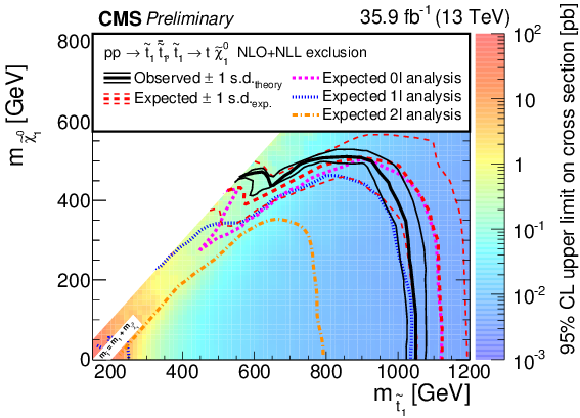
Exclusion limits at 95% CL for direct top squark pair production for the decay mode $\tilde{ \mathrm{ t } }_1 \to \mathrm{ t } \tilde{\chi}^0_1 $. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } }_1 }-m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limits at 95% CL and their $\pm$1$ \sigma $ experiment standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _\mathrm {theory}$ on the signal cross section. The magenta short-dashed, blue dotted, and long-short-dashed orange curves show the expected limits for the fully-hdaronic [27], single-lepton and dilepton [28] analyses, respectively. |
png pdf |
Figure 9:
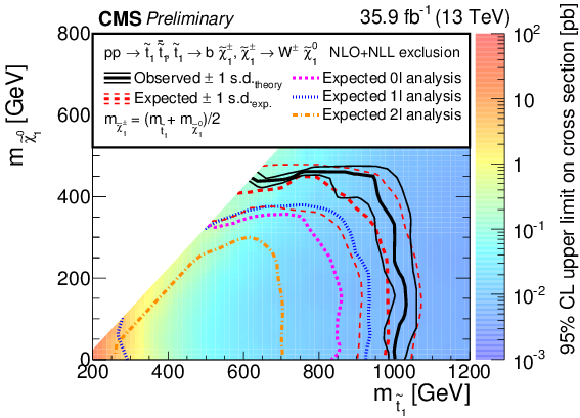
Exclusion limits at 95% CL for direct top squark pair production for the decay mode $\tilde{ \mathrm{ t } }_1 \to \mathrm{ b } \tilde{ \chi }^{+}_1 $, $\tilde{ \chi }^{+}_1 \to \mathrm{ W } ^{+}\tilde{\chi}^0_1 $. The mass of the chargino is chosen to be $(m_{\tilde{ \mathrm{ t } }_1 } + m_{\tilde{\chi}^0_1 })/2$. The color indicates the 95% CL upper limit on the cross section times branching fraction at each point in the $m_{\tilde{ \mathrm{ t } }_1 }-m_{\tilde{\chi}^0_1 }$ plane. The area to the left of and below the thick black curve represents the observed exclusion region at 95% CL, while the dashed red lines indicate the expected limits at 95% CL and their $\pm$1$ \sigma $ experiment standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _\mathrm {theory}$ on the signal cross section. The magenta short-dashed, blue dotted, and long-short-dashed orange curves show the expected limits for the fully-hdaronic [27], single-lepton and dilepton [28] analyses, respectively. |

png pdf root |
Figure 10:
Correlation matrix for the background predictions for the signal regions for the standard selection (in percent). The labelling of the regions follows the convention of Fig. {fig:results}. |

png pdf root |
Figure 11:
Correlation matrix for the background predictions for the signal regions for the compressed selection (in percent). The labelling of the regions follows the convention of Fig. {fig:results}. |
| Tables | |

png pdf |
Table 1:
Summary of the preselection. ${H_{\mathrm {T}}^{\mathrm {miss}}}$ is the magnitude of the vector sum of the transverse momenta of all jets and leptons in the event. The symbol $ {p_{\mathrm {T}}} ^{\mathrm {lep}}$ denotes the transverse momentum of the lepton, while $ {p_{\mathrm {T}}} ^{\mathrm {sum}}$ is the scalar sum of the transverse momenta of all PF candidates in a cone around the lepton but excluding the lepton. The radius of the cone is $\Delta R = $ 0.2 for $ {p_{\mathrm {T}}} ^{\mathrm {lep}} \le $ 50 GeV , and $\Delta R = $ Max(0.05, 10 GeV/$ {p_{\mathrm {T}}} ^{\mathrm {lep}}$) at higher values of lepton transverse momentum. |

png pdf |
Table 2:
Definitions for the 27 signal regions of the standard selection. At least one b-tagged jet (medium WP) is required in all search regions. To suppress the W+jets background in signal regions with $ {M_{\mathrm {\ell b}}} > $ 175 GeV, a more strict requirement that at least one jet satisfies the tight b-tagging WP is made. |
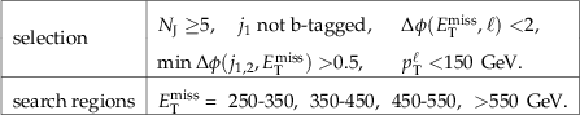
png pdf |
Table 3:
Summary of the compressed selection and the requirements for the four corresponding signal regions. The symbol $\Delta \phi ( {E_{\mathrm {T}}^{\text {miss}}} ,\ell ) $ denotes the angle between $ E_{\mathrm{T}}^{\text{miss}} $ and the $\vec{p}_{\mathrm{T}}$ of the lepton. |

png pdf |
Table 4:
Dilepton control regions that are combined when estimating the LL background. |
png pdf |
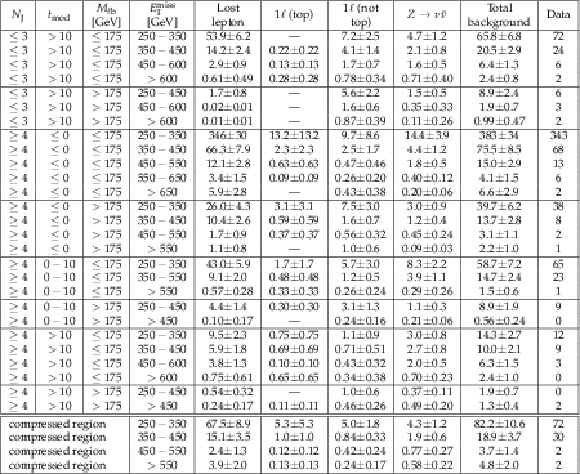
Table 5:
Result of the background estimates and signal region yields corresponding to 35.9 fb${^{-1}} $. |

png pdf |
Table 6:
Summary of the systematic uncertainties for the signal efficiency with their typical values in individual signal regions. |
png pdf |
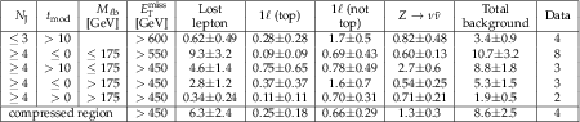
Table 7:
Background predictions and data for aggregated signal regions. |
| Summary |
| We have reported on a search for top squark pair production in pp collisions at $ \sqrt{s} = $ 13 TeV in events with a single isolated electron or muon, jets, and large $E_{\mathrm{T}}^{\text{miss}}$ using 35.9 fb${^{-1}}$ of data collected with the CMS detector during the 2016 run of the LHC. The event data counts are consistent with expectations from SM processes. The results are interpreted as exclusion limits in the context of supersymmetric models with pair production of top squarks that decay either to a top quark and a neutralino or to a bottom quark and a chargino. Assuming both top squarks decay to a top quark and a neutralino, we exclude at the 95% confidence level top squark masses up to 1120 GeV for a massless neutralino and neutralino masses up to 515 GeV for a 950 GeV top squark mass. |
| Additional Figures | |
png pdf root |
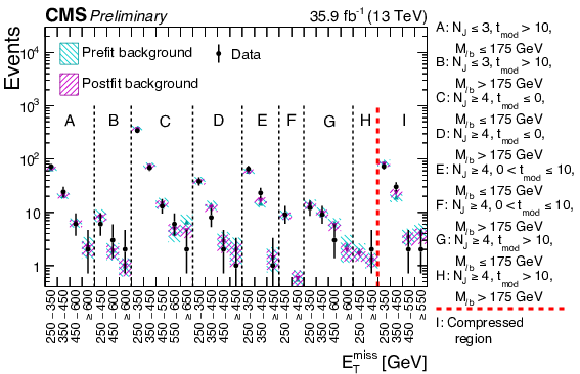
Additional Figure 1:
Comparison between postfit and prefit background predictions and data for 35.9 fb$^{-1}$ collected during 2016 pp collisions. |

png pdf root |
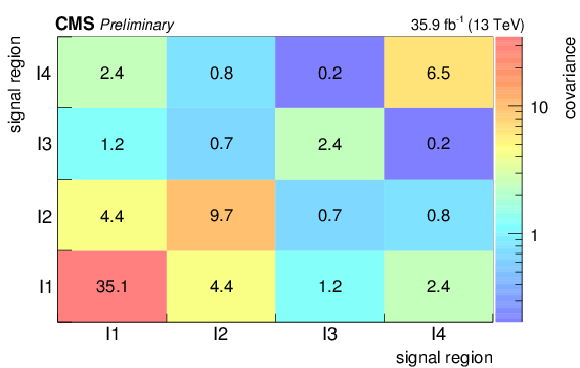
Additional Figure 2:
Covariance matrix for the background predictions for the signal regions for the standard selection. The labelling of the regions follows the convention of correlation matrices in the appendix of the note. |
png pdf root |
Additional Figure 3:
Covariance matrix for the background predictions for the signal regions for the compressed selection. The labelling of the regions follows the convention of correlation matrices in the appendix of the note. |
png pdf |
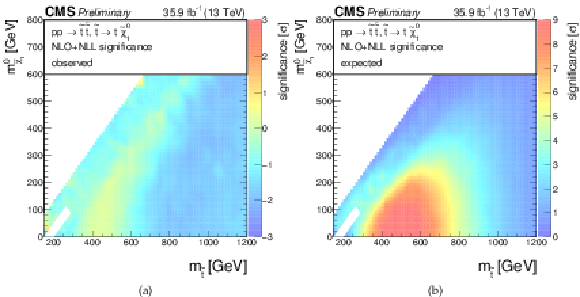
Additional Figure 4:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. (a) Observed, (b) expected. |

png pdf |
Additional Figure 4-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. |
png pdf |
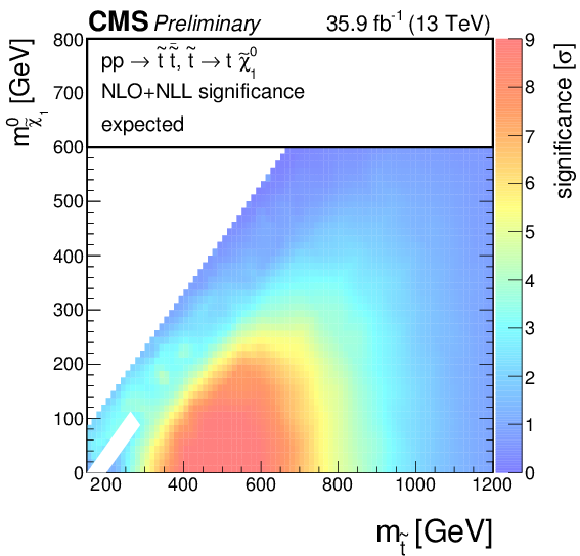
Additional Figure 4-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. |
png pdf |
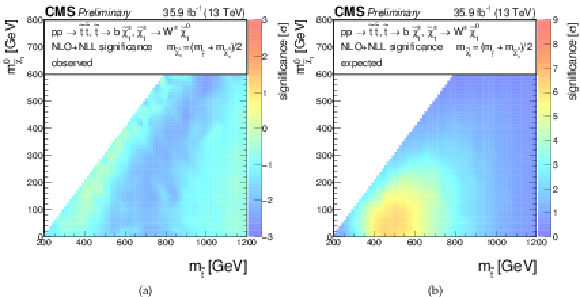
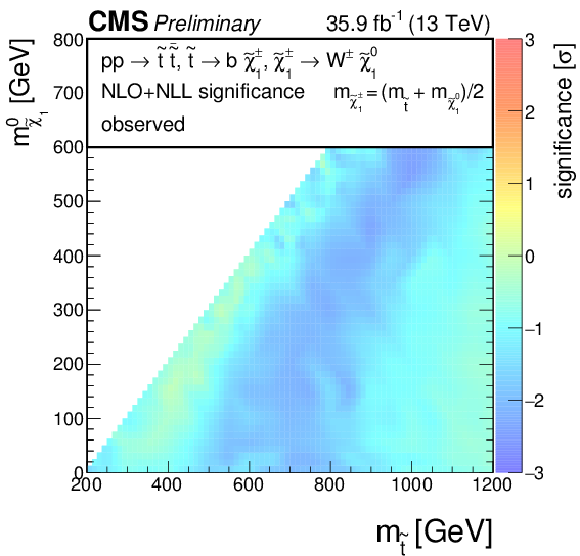
Additional Figure 5:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$. (a) Observed, (b) expected. |
png pdf |
Additional Figure 5-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$. |

png pdf |
Additional Figure 5-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$. |
png pdf |
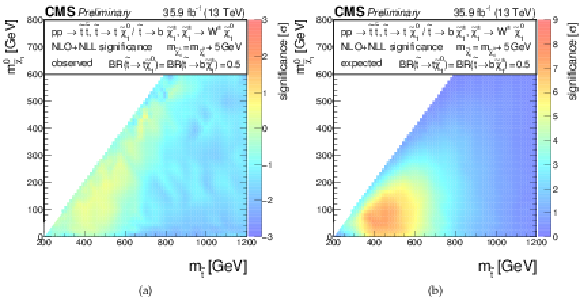
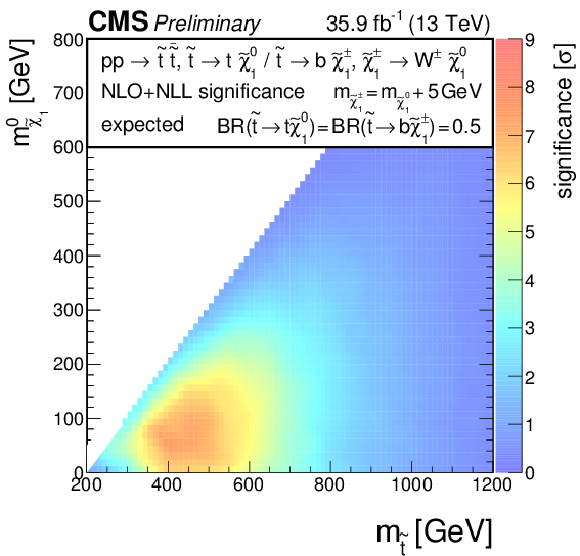
Additional Figure 6:
Significances for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. (a) Observed, (b) expected. |

png pdf |
Additional Figure 6-a:
Observed significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. |
png pdf |
Additional Figure 6-b:
Expected significance for a model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5 as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. |
png pdf root |
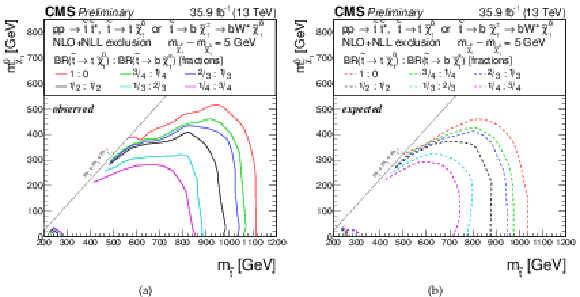
Additional Figure 7:
Exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. (a) Observed, (b) expected. |

png pdf root |
Additional Figure 7-a:
Observed exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. |

png pdf root |
Additional Figure 7-b:
Expected exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$ for various choices of the branching fraction between the two decays. |
png pdf root |
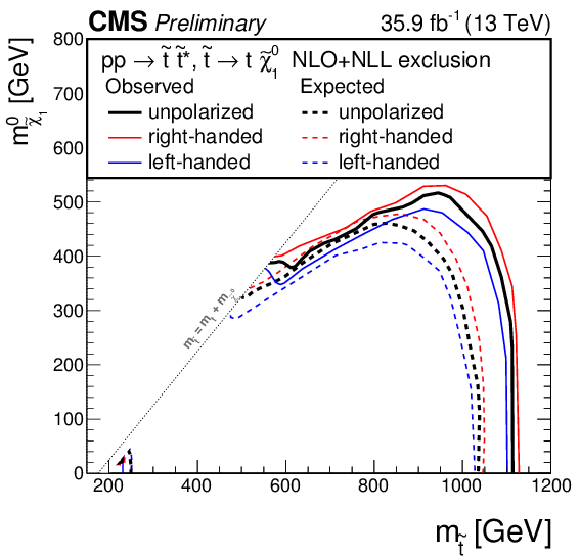
Additional Figure 8:
Exclusion limit for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$ for unpolarized top quarks (black lines), right-handed top quarks (red lines), and left-handed top quarks (blue lines). |
png pdf |
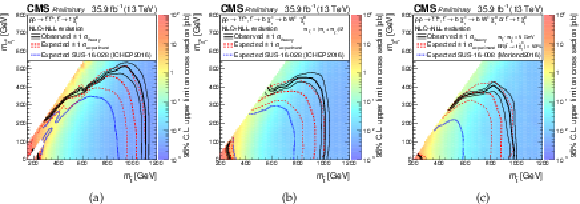
Additional Figure 9:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015. (a): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $, (b): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$, (c): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |
png pdf |
Additional Figure 9-a:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $. |
png pdf |
Additional Figure 9-b:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$. |

png pdf |
Additional Figure 9-c:
Exclusion limits as presented in the note, with the addition of the most recent previous limits as presented during ICHEP 2016 or Moriond 2015, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |

png pdf |
Additional Figure 10:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier. (a): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $, (b): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$, (c): for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |

png pdf |
Additional Figure 10-a:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ t } ^{(*)}\tilde{\chi}^0_1 $, |
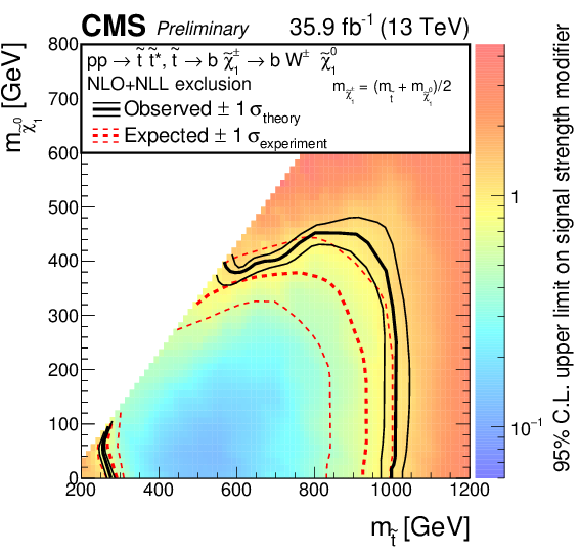
png pdf |
Additional Figure 10-b:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} \to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ as a function of $M_{\tilde{ \mathrm{ t } } }$ and $M_{\tilde{\chi}^0_1 }$. The mass of the chargino is chosen to be $(M_{\tilde{ \mathrm{ t } } } + M_{\tilde{\chi}^0_1 })/2$, |

png pdf |
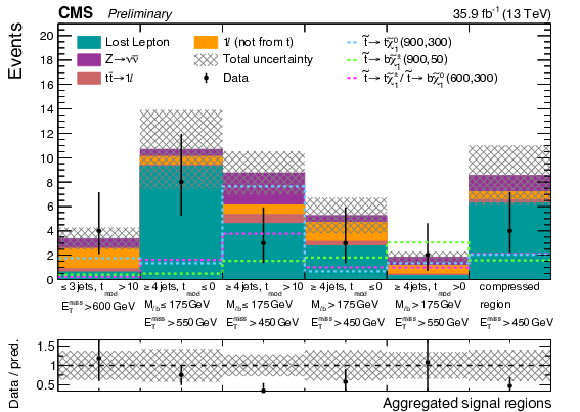
Additional Figure 10-c:
Exclusion limits as presented in the note, however the color map is showing the 95% confidence level on the signal strength modifier, for the model of direct top-squark production with decay $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \overline{\tilde{\mathrm{t}}} $, $\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 / \mathrm{ t } \tilde{\chi}^0_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, $m_{\tilde{\chi}^{\pm}_1 } = m_{\tilde{\chi}^0_1 }+ $ 5 GeV, BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = 0.5. |
png pdf |
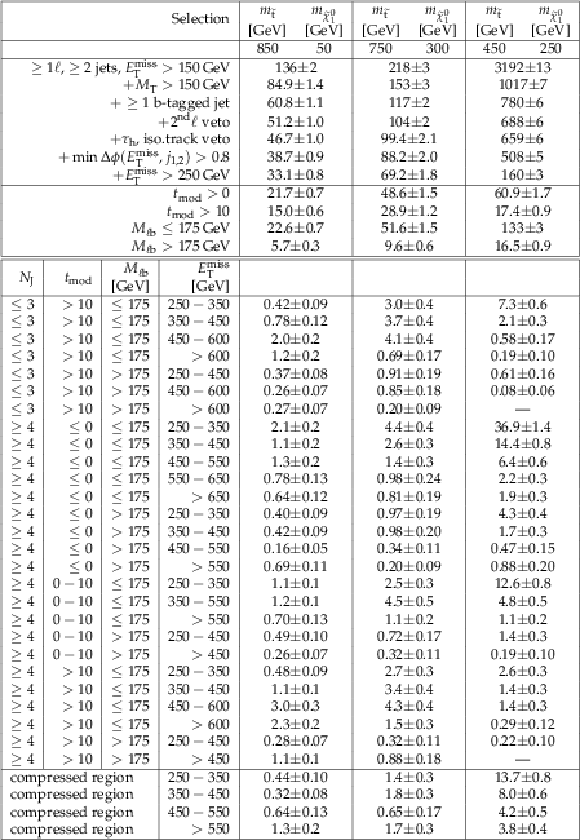
Additional Figure 11:
Background predictions and data for the aggregated signal regions using 35.9 fb$^{-1}$collected during 2016 pp collisions. |
| Additional Tables | |

png pdf |
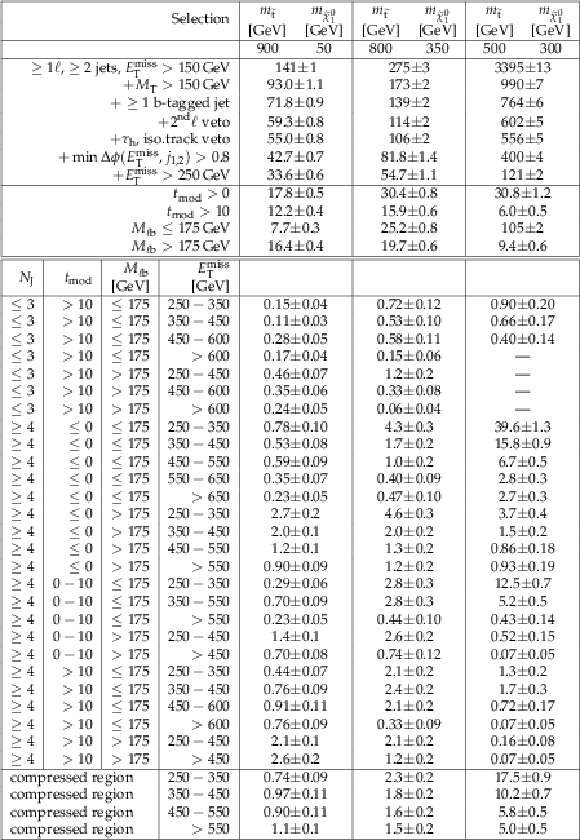
Additional Table 1:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}\to \mathrm{ t \bar{t} } \tilde{\chi}^0_1 \tilde{\chi}^0_1 $ signals for an integrated luminosity of 35.9 fb$^{-1}$. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
png pdf |
Additional Table 2:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}, \tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 / \mathrm{ b } \tilde{\chi}^{\pm}_1 $ signals for an integrated luminosity of 35.9 fb$^{-1}$. The branching fraction for this model is BR($\tilde{ \mathrm{ t } } \to \mathrm{ t } \tilde{\chi}^0_1 $) = BR($\tilde{ \mathrm{ t } } \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $) = 0.5, and $M_{\tilde{\chi}^{\pm}_1 } = M_{\tilde{\chi}^0_1 } + 5 GeV $. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
png pdf |
Additional Table 3:
Cutflow table for $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } } \tilde{ \mathrm{ t } } ^{*}\to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ signals with $M_{\tilde{\chi}^{\pm}_1 } = (M_{\tilde{ \mathrm{ t } } }+M_{\tilde{\chi}^0_1 })/2$ for an integrated luminosity of 35.9 fb$^{-1}$. The uncertainties are purely statistical. No correction for signal contamination in data control regions are applied. |
|
Electronic version of the limit curves can be found as three rootfiles
here,
here, and
here.
The correlation and covariance matrices can be found as two rootfiles here, and here. A code snippet to calculate the tmod variables together with an example how to use it is provided here. |
| References | ||||
| 1 | ATLAS Collaboration | Search for top squarks in final states with one isolated lepton, jets, and missing transverse momentum in $ \sqrt{s}=13 $ TeV $ pp $ collisions with the ATLAS detector | PRD 94 (2016), no. 5, 052009 | 1606.03903 |
| 2 | CMS Collaboration | Searches for pair production for third-generation squarks in sqrt(s)=13 TeV pp collisions | CMS-SUS-16-008 1612.03877 |
|
| 3 | CMS Collaboration | Search for supersymmetry in the all-hadronic final state using top quark tagging in pp collisions at $ \sqrt{s} $ = 13 TeV | CMS-SUS-16-009 1701.01954 |
|
| 4 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 5 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 6 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 7 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 8 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the $ POWHEG $ method | JHEP 11 (2007) 070 | 0709.2092 |
| 9 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the $ POWHEG $ BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 10 | E. Re | Single-top $ Wt $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 11 | T. Sj\"ostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 12 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 13 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 14 | CMS Collaboration | Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and $ E_{\mathrm{T}}^{\text{miss}} $ | CDS | |
| 15 | CMS Collaboration | Commissioning of the Particle-flow Event Reconstruction with the first LHC collisions recorded in the CMS detector | CDS | |
| 16 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = 8 $~TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 17 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}=7 $ TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 18 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_\mathrm{T} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 19 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 20 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 21 | CMS Collaboration | Missing transverse energy performance of the CMS detector | JINST 6 (2011) P09001 | CMS-JME-10-009 1106.5048 |
| 22 | M. L. Graesser and J. Shelton | Hunting Mixed Top Squark Decays | PRL 111 (2013) 121802 | 1212.4495 |
| 23 | A. L. Read | Presentation of search results: the $ CL_{S} $ technique | JPG 28 (2002) 2693 | |
| 24 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 25 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554, , [Erratum: Eur. Phys. J.C73,2501(2013)] | 1007.1727 |
| 26 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report ATL-PHYS-PUB 2011-11, CMS NOTE 2011/005 | |
| 27 | CMS Collaboration | Search for direct top squark pair production in the fully hadronic final state at $ 13 \mathrm{TeV} $ | Technical Report CMS-PAS-SUS-16-049, CERN, Geneva | |
| 28 | CMS Collaboration | Search for direct top squark pair production in the dilepton final state at $ 13 \mathrm{TeV} $ | Technical Report CMS-PAS-SUS-17-001, CERN, Geneva | |
| 29 | CMS Collaboration | Simplified likelihood for the re-interpretation of public CMS results | CDS | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|