

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-20-018 | ||
| A search for light Higgs bosons from supersymmetric cascade decays in proton-proton collisions at 13 TeV | ||
| CMS Collaboration | ||
| September 2021 | ||
| Abstract: A search for pairs of boosted light Higgs bosons ($\mathrm{H}_1$) produced in supersymmetric cascade decays is performed in final states with small missing transverse momentum. The complete LHC Run II proton-proton collision data set is used, recorded with the CMS detector at a centre-of-mass energy of 13 TeV and corresponding to an integrated luminosity of 137 fb$^{-1}$. The search targets events where both $\mathrm{H}_1$ bosons decay into $\mathrm{b}\bar{\mathrm{b}}$ pairs that are reconstructed as large-radius jets using substructure techniques. No evidence is found for any excess of events beyond the background expectations of the standard model (SM). Results from the search are interpreted in the next-to-minimal supersymmetric extension of the SM, where a low-mass singlino leads to multi-step squark and gluino decays that can predominantly end with a boosted singlet-like $\mathrm{H}_1$ boson and a low-momentum singlino-like neutralino. Upper limits are set on the product of the squark or gluino pair-production cross section and the $\mathrm{b}\bar{\mathrm{b}}$ branching ratio of the $\mathrm{H}_1$ for a benchmark model with almost mass-degenerate light flavour squarks and gluinos. Under the assumption of an SM-like $\mathrm{H}_1\to\mathrm{b}\bar{\mathrm{b}}$ branching ratio, $\mathrm{H}_1$ bosons with masses in the range 40-120 GeV, arising from the decays of squarks or gluinos with a mass from 1200-2500 GeV, are excluded at the 95% confidence level. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to EPJC. |
||
| Figures | |

png pdf |
Figure 1:
Diagram of squark pair production and subsequent cascade decay in the benchmark signal model. The particle $\tilde{\chi}^{0}_{2}$ is the NLSP, ${\tilde{\chi} _{\text {S}}^0}$ is the singlino-like LSP, and ${\mathrm{H} _1}$ is the CP-even singlet-like Higgs boson. |

png pdf |
Figure 2:
The normalised ${H_{\mathrm {T}}}$ distribution in signal events with different values of ${M_{\text {SUSY}}}$, and for the simulated SM background processes, as labelled in the legend. The numbers specified in the legend have unit GeV. All events satisfy the pre-selection and have $ {H_{\mathrm {T}}} \ge $ 1200 GeV. |
png pdf |
Figure 3:
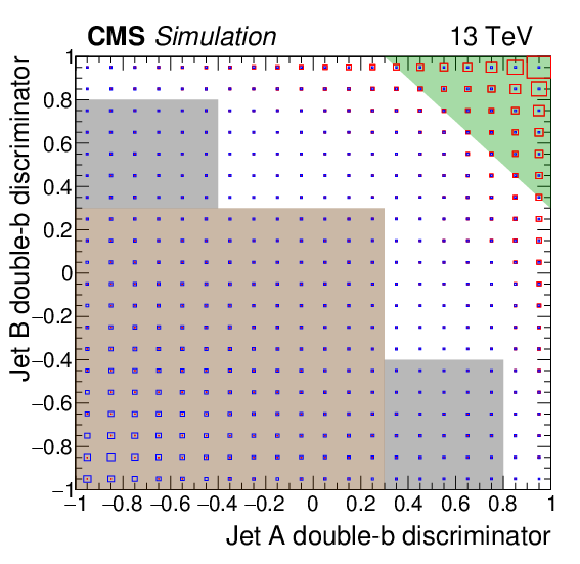
The normalised distributions of simulated signal and multijet events in the 2D double-b-tag discriminator plane, where the event densities in each bin are represented by the areas of red and blue squares, respectively. The signal parameters are $ {M_{\mathrm{H} _1}} = $ 70 GeV and $ {M_{\text {SUSY}}} = $ 2000 GeV. The kinematic event selection is applied, and the masses of the two AK8 jets are required to be within the set of signal and sideband mass regions defined in Figure 4. The green, brown, and grey shaded areas represent the tag region (TR), control region (CR), and validation region (VR), respectively. |
png pdf |
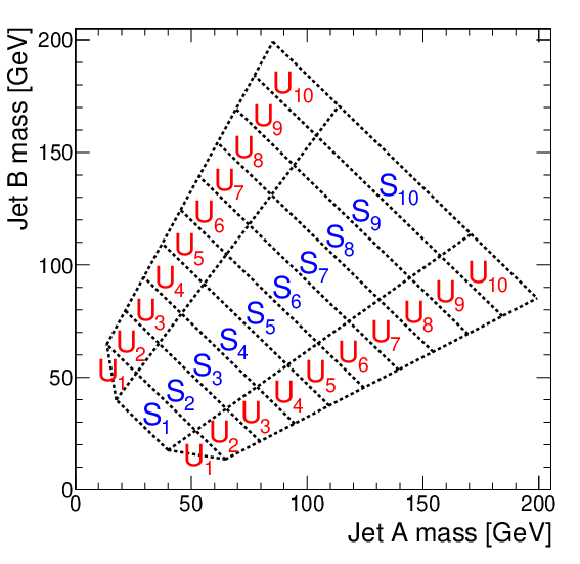
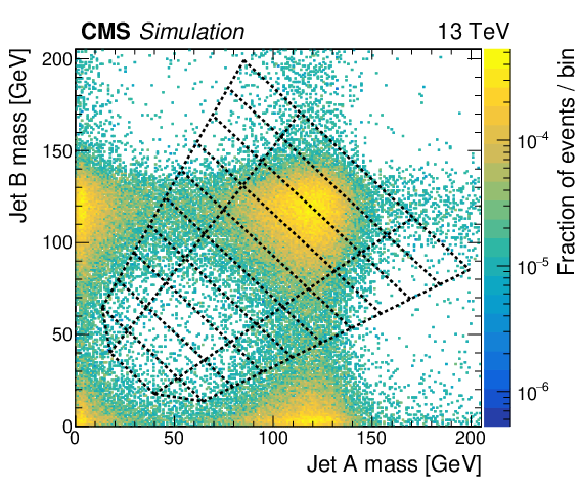
Figure 4:
The mass regions used in the 2D soft-drop mass plane. The regions labelled $S_i$ are the signal mass regions, and the disconnected regions ${U_{i}}$ form the corresponding sidebands. |
png pdf |
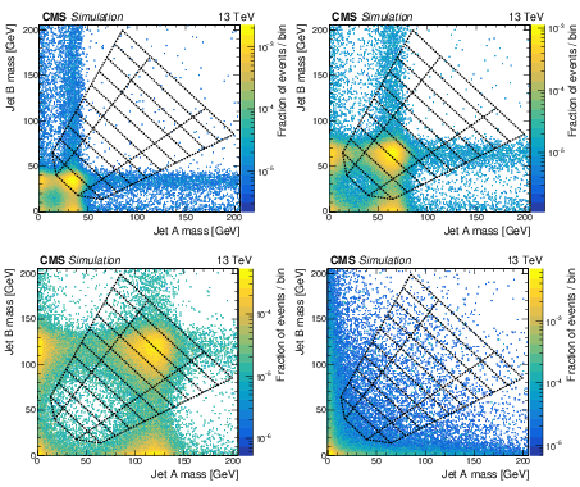
Figure 5:
The normalised distribution of events in the 2D soft-drop mass plane with the mass regions overlaid. The first three sub-figures correspond to signal events with $ {M_{\text {SUSY}}} = $ 2000 GeV and ${M_{\mathrm{H} _1}}$ values of 40, 70, and 125 GeV respectively. The final sub-figure corresponds to simulated multijet events. All events satisfy the TR requirement and the kinematic event selection. |
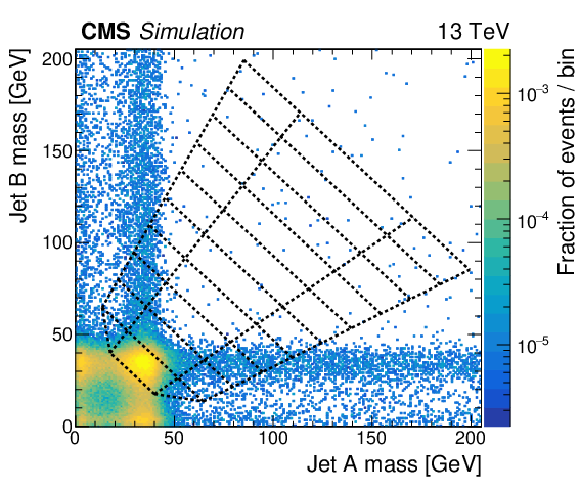
png pdf |
Figure 5-a:
The normalised distribution of events in the 2D soft-drop mass plane with the mass regions overlaid. The first three sub-figures correspond to signal events with $ {M_{\text {SUSY}}} = $ 2000 GeV and ${M_{\mathrm{H} _1}}$ values of 40, 70, and 125 GeV respectively. The final sub-figure corresponds to simulated multijet events. All events satisfy the TR requirement and the kinematic event selection. |

png pdf |
Figure 5-b:
The normalised distribution of events in the 2D soft-drop mass plane with the mass regions overlaid. The first three sub-figures correspond to signal events with $ {M_{\text {SUSY}}} = $ 2000 GeV and ${M_{\mathrm{H} _1}}$ values of 40, 70, and 125 GeV respectively. The final sub-figure corresponds to simulated multijet events. All events satisfy the TR requirement and the kinematic event selection. |
png pdf |
Figure 5-c:
The normalised distribution of events in the 2D soft-drop mass plane with the mass regions overlaid. The first three sub-figures correspond to signal events with $ {M_{\text {SUSY}}} = $ 2000 GeV and ${M_{\mathrm{H} _1}}$ values of 40, 70, and 125 GeV respectively. The final sub-figure corresponds to simulated multijet events. All events satisfy the TR requirement and the kinematic event selection. |

png pdf |
Figure 5-d:
The normalised distribution of events in the 2D soft-drop mass plane with the mass regions overlaid. The first three sub-figures correspond to signal events with $ {M_{\text {SUSY}}} = $ 2000 GeV and ${M_{\mathrm{H} _1}}$ values of 40, 70, and 125 GeV respectively. The final sub-figure corresponds to simulated multijet events. All events satisfy the TR requirement and the kinematic event selection. |
png pdf |
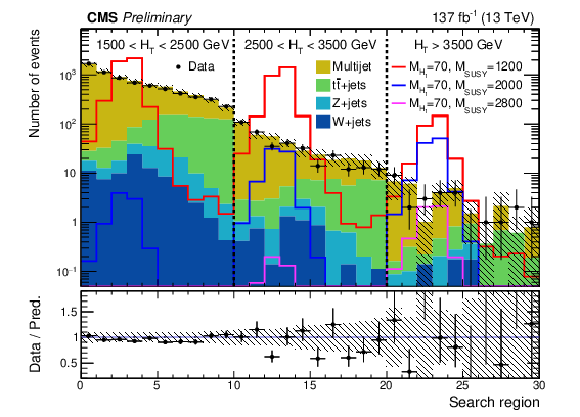
Figure 6:
Observed and predicted yields in the search regions, summed over the three data-taking years. The multijet background is from the data-driven prediction of Section 5, while the other backgrounds are from simulation. Example signal distributions are shown for $ {M_{\mathrm{H} _1}} = $ 70 GeV and ${M_{\text {SUSY}}} = $ 1200, 2000 and 2800 GeV. The numbers specified in the legend have unit GeV. The error bars represent the statistical uncertainties, and the hatched bands the systematic uncertainties. |
png pdf |
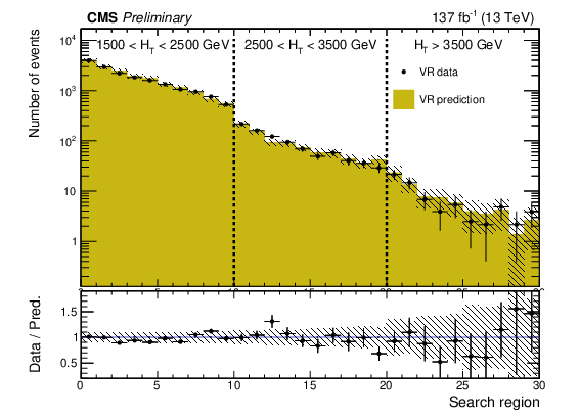
Figure 7:
A comparison of the predicted and observed multijet yields in the validation region (VR), after subtraction of the other simulated backgrounds. The prediction is made separately for the three data-taking years, and the results are summed. The error bars on the data points represent their statistical uncertainties. The uncertainty in the predicted yields (statistical and systematic) is shown by the hatched bands. |
png pdf |
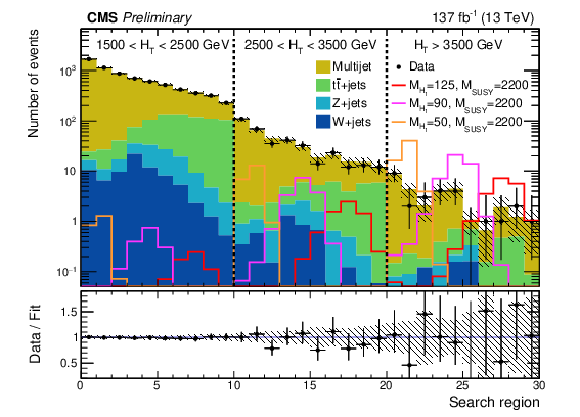
Figure 8:
Search region yields after the background-only fit, summed over the three data-taking years. Example signal contributions used in the signal-plus-background fits are shown for ${M_{\text {SUSY}}} = $ 2200 GeV and ${M_{\mathrm{H} _1}} = $ 50, 90, and 125 GeV. The numbers specified in the legend have unit GeV. |

png pdf |
Figure 9:
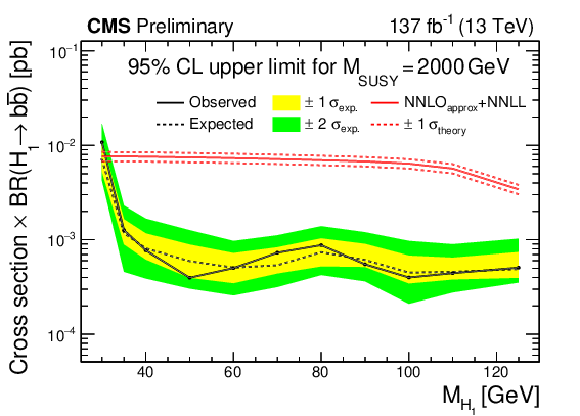
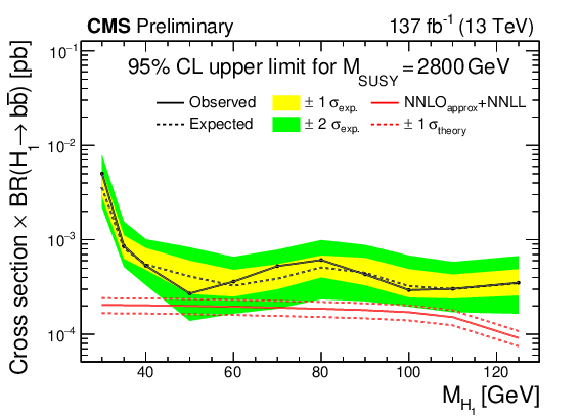
The observed and expected 95% CL upper limit of $\sigma \times \text {BR}$ as a function of ${M_{\mathrm{H} _1}}$. The value of ${M_{\text {SUSY}}}$ is held constant at 1200 GeV (top), 2000 GeV (middle), and 2800 GeV (bottom). The solid (dashed) black line indicates the observed (median expected) limit. The yellow (green) bands indicate the expected limits with $ \pm 1 \sigma $ ($ \pm 2 \sigma $) in experimental uncertainty. The solid and dashed red lines show the theoretical prediction and its uncertainty [16,17,18,19,20,21,22,23,24,25]. The theoretical prediction is not shown in the upper plot, since its value (0.58 pb $\times$ BR) is beyond the upper extent of the vertical axis. |
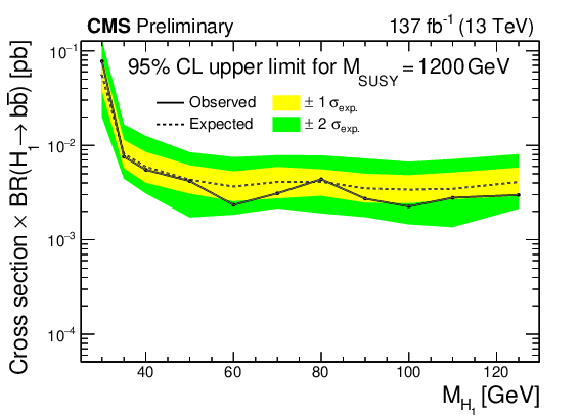
png pdf |
Figure 9-a:
The observed and expected 95% CL upper limit of $\sigma \times \text {BR}$ as a function of ${M_{\mathrm{H} _1}}$. The value of ${M_{\text {SUSY}}}$ is held constant at 1200 GeV (top), 2000 GeV (middle), and 2800 GeV (bottom). The solid (dashed) black line indicates the observed (median expected) limit. The yellow (green) bands indicate the expected limits with $ \pm 1 \sigma $ ($ \pm 2 \sigma $) in experimental uncertainty. The solid and dashed red lines show the theoretical prediction and its uncertainty [16,17,18,19,20,21,22,23,24,25]. The theoretical prediction is not shown in the upper plot, since its value (0.58 pb $\times$ BR) is beyond the upper extent of the vertical axis. |
png pdf |
Figure 9-b:
The observed and expected 95% CL upper limit of $\sigma \times \text {BR}$ as a function of ${M_{\mathrm{H} _1}}$. The value of ${M_{\text {SUSY}}}$ is held constant at 1200 GeV (top), 2000 GeV (middle), and 2800 GeV (bottom). The solid (dashed) black line indicates the observed (median expected) limit. The yellow (green) bands indicate the expected limits with $ \pm 1 \sigma $ ($ \pm 2 \sigma $) in experimental uncertainty. The solid and dashed red lines show the theoretical prediction and its uncertainty [16,17,18,19,20,21,22,23,24,25]. The theoretical prediction is not shown in the upper plot, since its value (0.58 pb $\times$ BR) is beyond the upper extent of the vertical axis. |
png pdf |
Figure 9-c:
The observed and expected 95% CL upper limit of $\sigma \times \text {BR}$ as a function of ${M_{\mathrm{H} _1}}$. The value of ${M_{\text {SUSY}}}$ is held constant at 1200 GeV (top), 2000 GeV (middle), and 2800 GeV (bottom). The solid (dashed) black line indicates the observed (median expected) limit. The yellow (green) bands indicate the expected limits with $ \pm 1 \sigma $ ($ \pm 2 \sigma $) in experimental uncertainty. The solid and dashed red lines show the theoretical prediction and its uncertainty [16,17,18,19,20,21,22,23,24,25]. The theoretical prediction is not shown in the upper plot, since its value (0.58 pb $\times$ BR) is beyond the upper extent of the vertical axis. |
png pdf |
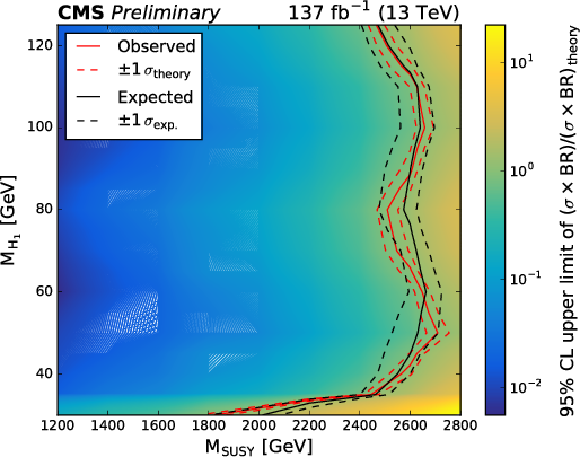
Figure 10:
The observed 95% CL upper limit of $(\sigma \times \text {BR}) / (\sigma \times \text {BR})_{\textrm {theory}}$ (indicated by the colour scale) as a function of ${M_{\mathrm{H} _1}}$ and ${M_{\text {SUSY}}}$. The solid red (black) line delineates the observed (median expected) excluded region. The dashed red (black) line delineates the observed (expected) excluded regions with $ \pm 1 \sigma $ in theoretical (experimental) uncertainty. |
| Tables | |
png pdf |
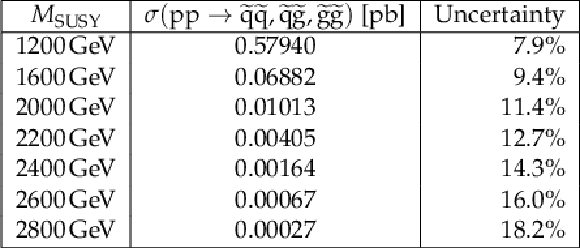
Table 1:
The ${M_{\text {SUSY}}}$ values considered in this search and corresponding production cross sections (the sum of $\mathrm{\tilde{q}} \mathrm{\tilde{q}} $, $\mathrm{\tilde{q}} {\mathrm{\tilde{g}}} $, and ${\mathrm{\tilde{g}}} {\mathrm{\tilde{g}}} $), calculated at approximately NNLO+NNLL in ${\alpha _\mathrm {S}}$ [16,17,18,19,20,21,22,23,24] for a squark mass of ${M_{\text {SUSY}}}$ and a gluino mass 1% larger. The quoted uncertainty is from variations in the choice of scale, parton distribution functions, and ${\alpha _\mathrm {S}}$. |
png pdf |
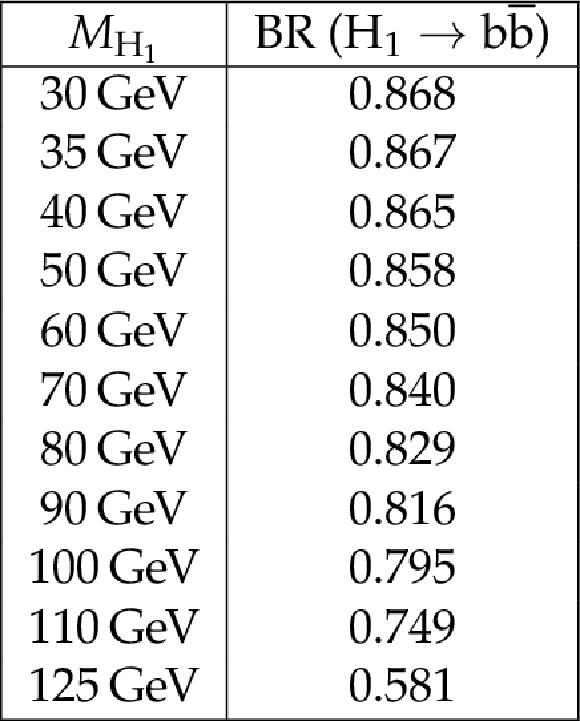
Table 2:
The ${M_{\mathrm{H} _1}}$ values considered in this search and corresponding $ {\mathrm{H} _1} \rightarrow \mathrm{b} {}\mathrm{\bar{b}} $ branching ratios, calculated for a SM-like Higgs boson using the hdecay package [25]. |
| Summary |
|
This note presents a search for pairs of light Higgs bosons (${\mathrm{H}_1} $) produced in supersymmetric cascade decays. The targeted final states have small missing transverse momentum and two ${\mathrm{H}_1} \rightarrow\mathrm{b\bar{b}}$ decays that are reconstructed as large-radius jets using substructure techniques. The search uses a data sample of proton-proton collision events collected by the CMS experiment at centre-of-mass energy $\sqrt s = $ 13 TeV during LHC Run II, corresponding to an integrated luminosity of 137 fb$^{-1}$. No evidence is found for any excess of events beyond the background expectations of the standard model (SM). The results are interpreted in the next-to-minimal supersymmetric extension of the SM, where a low-mass singlino leads to multi-step squark and gluino decays that can predominantly end with a boosted singlet-like ${\mathrm{H}_1}$ boson and a low-momentum singlino-like neutralino. Upper limits are set on the product of the production cross section and the $\mathrm{b\bar{b}}$ branching ratio of the ${\mathrm{H}_1}$ boson for a benchmark model with almost mass-degenerate light flavour squarks and gluinos. Under the assumption of a SM-like ${\mathrm{H}_1} \to\mathrm{b\bar{b}}$ branching ratio, ${\mathrm{H}_1}$ bosons with masses in the range 40-120 GeV, arising from the decays of squarks or gluinos with a mass from 1200-2500 GeV, are excluded at the 95% confidence level. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Golfand and E. P. Likhtman | Extension of the algebra of Poincar$ \'e $ group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 9 | U. Ellwanger, C. Hugonie, and A. M. Teixeira | The next-to-minimal supersymmetric standard model | Physics Reports 496 (2010) 1 | |
| 10 | U. Ellwanger and A. Teixeira | NMSSM with a singlino LSP: possible challenges for searches for supersymmetry at the LHC | JHEP 10 (2014) 113 | |
| 11 | U. Ellwanger and A. Teixeira | Excessive Higgs pair production with little MET from squarks and gluinos in the NMSSM | JHEP 04 (2015) 172 | |
| 12 | A. Titterton et al. | Exploring sensitivity to NMSSM signatures with low missing transverse energy at the LHC | JHEP 10 (2018) 064 | 1807.10672 |
| 13 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 14 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 15 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 16 | W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas | Squark and gluino production at hadron colliders | NPB 492 (1997) 51 | hep-ph/9610490 |
| 17 | A. Kulesza and L. Motyka | Threshold resummation for squark-antisquark and gluino-pair production at the LHC | PRL 102 (2009) 111802 | 0807.2405 |
| 18 | A. Kulesza and L. Motyka | Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC | PRD 80 (2009) 095004 | 0905.4749 |
| 19 | W. Beenakker et al. | Soft-gluon resummation for squark and gluino hadroproduction | JHEP 12 (2009) 041 | 0909.4418 |
| 20 | W. Beenakker et al. | Squark and gluino hadroproduction | Int. J. Mod. Phys. A 26 (2011) 2637 | 1105.1110 |
| 21 | W. Beenakker et al. | NNLL resummation for squark-antisquark pair production at the LHC | JHEP 01 (2012) 076 | 1110.2446 |
| 22 | W. Beenakker et al. | Towards NNLL resummation: hard matching coefficients for squark and gluino hadroproduction | JHEP 10 (2013) 120 | 1304.6354 |
| 23 | W. Beenakker et al. | NNLL resummation for squark and gluino production at the LHC | JHEP 12 (2014) 023 | 1404.3134 |
| 24 | W. Beenakker et al. | NNLL-fast: predictions for coloured supersymmetric particle production at the LHC with threshold and Coulomb resummation | JHEP 12 (2016) 133 | 1607.07741 |
| 25 | A. Djouadi, J. Kalinowski, and M. Spira | HDECAY: a program for Higgs boson decays in the standard model and its supersymmetric extension | Computer Physics Communications 108 (1998) 56 | hep-ph/9704448 |
| 26 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 27 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 28 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 29 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 30 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 31 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 32 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and LO | NPB 855 (2012) 153 | 1107.2652 |
| 33 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 34 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 35 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 36 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 37 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 38 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 39 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA-8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 40 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | CPC 182 (2011) 2388 | 1011.3540 |
| 41 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | W physics at the LHC with FEWZ 2.1 | CPC 184 (2013) 208 | 1201.5896 |
| 42 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 43 | M. Czakon and A. Mitov | TOP++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 44 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 45 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 46 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 47 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 48 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 49 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 50 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 51 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 52 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup Per Particle Identification | JHEP 10 (2014) 059 | 1407.6013 |
| 53 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 54 | CMS Collaboration | Jet energy scale and resolution performance with 13 TeV data collected by CMS in 2016 | CDS | |
| 55 | CMS Collaboration | Identification of double-b quark jets in boosted event topologies | CMS-PAS-BTV-15-002 | CMS-PAS-BTV-15-002 |
| 56 | T. Adams et al. | Beam test evaluation of electromagnetic calorimeter modules made from proton-damaged PbWO$ _4 $ crystals | JINST 11 (2016) P04012 | |
| 57 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft Drop | JHEP 05 (2014) 146 | 1402.2657 |
| 58 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 59 | ATLAS and CMS Collaborations | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS-NOTE-2011-005 | |
| 60 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 61 | A. L. Read | Presentation of search results: The $ CL_{\mathrm{s}} $ technique | JPG 28 (2002) 2693 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|