Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-PAS-HIG-19-001

Measurements of properties of the Higgs boson in the four-lepton final state in proton-proton collisions at $\sqrt{s}= $ 13 TeV

CMS Collaboration

March 2019

Abstract: Properties of the Higgs (H) boson are measured in the $\mathrm{H}\rightarrow{\rm Z}{\rm Z}\rightarrow4\ell$ ($\ell=$ e, $\mu$) decay channel. The full data sample of proton-proton collisions at a center-of-mass energy of 13 TeV is used, corresponding to an integrated luminosity of 137.1 fb$^{-1}$ recorded in 2016, 2017, and 2018 by the CMS detector at the LHC. The signal-strength modifier $\mu$, defined as the ratio of the H boson rate in the 4$\ell$ channel to the Standard Model (SM) expectation, is measured to be $\mu=$ 0.94$^{+0.07}_{-0.07}$(stat.)$^{+0.08}_{-0.07}$(syst.) with the H boson mass profiled in the fit. The signal-strength modifiers for different H boson production modes are also constrained. Measurements of the simplified template cross sections, designed to quantify the different H boson production processes in specific regions of phase space, are reported. The cross section for the production of the $\mathrm{H}\rightarrow4\ell$ in a fiducial region closely matching the experimental selection of the leptons is measured to be $\sigma_{{\rm fid.}}= $ 2.73$^{+0.23}_{-0.22}$(stat.)$^{+0.24}_{-0.19}$(syst.) fb at $m_{\rm H} = $ 125.09 GeV, compared to a SM prediction of 2.76 $\pm$ 0.14 fb. Differential cross sections as a function of the $p_{\rm T}$ and rapidity of the H boson, the number of associated jets, and the $p_{\rm T}$ of the leading associated jet are determined. All results are found to be compatible with the SM predictions, within the measurements precision.

Links: CDS record (PDF) ; CADI line (restricted) ; These preliminary results are superseded in this paper, EPJC 81 (2021) 488. The superseded preliminary plots can be found here.

Figures
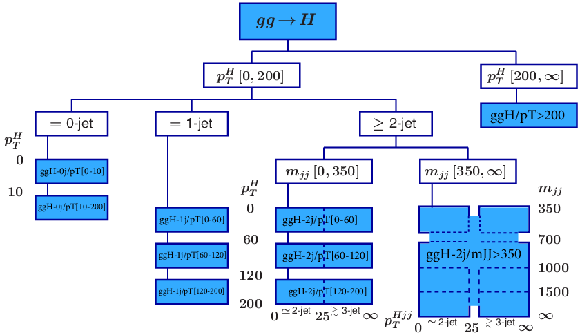
png pdf	Figure 1: Binning of the gluon fusion production in the STXS Stage 1.1 approach [25].
png pdf	Figure 2: Binning of the electroweak production (combines VBF and VH with hadronic V decay) in the STXS Stage 1.1 approach [25].
png pdf	Figure 3: Binning of the VH production with leptonic V decay (combining WH, ZH, and gluon fusion ZH production) in the STXS Stage 1.1 approach [25].
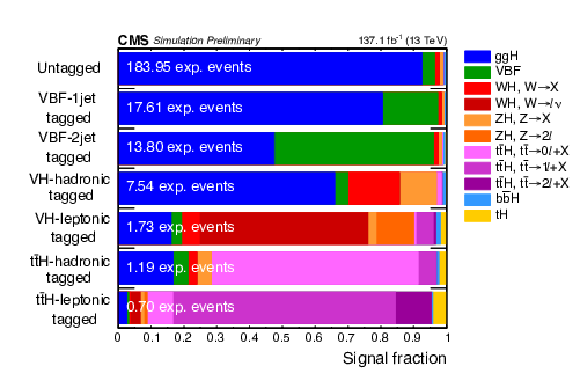
png pdf	Figure 4: Signal relative purity of the event categories in terms of the seven main production mechanisms of the Higgs boson in a 118 $ < {m_{4\ell}} < $ 130 GeV mass window. The $ {\mathrm{W} \mathrm{H}}$, $ {\mathrm{Z} \mathrm{H}}$ and $ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$ processes are split according to the decay of associated objects, whereby X denotes anything other than an electron or muon.
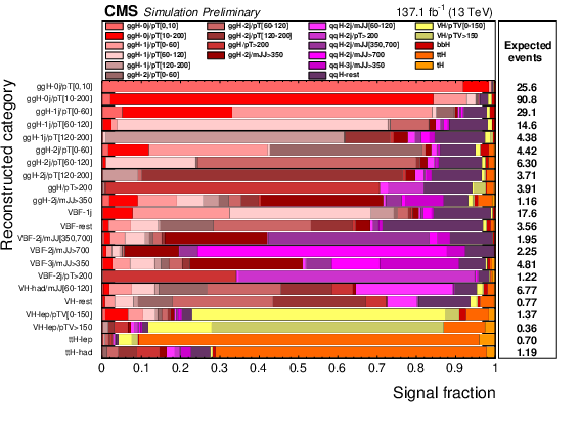
png pdf	Figure 5: Signal relative purity of the 22 event sub-categories in terms of the STXS Stage 1.1 Bins in a 118 $ < {m_{4\ell}} < $ 130 GeV mass window.
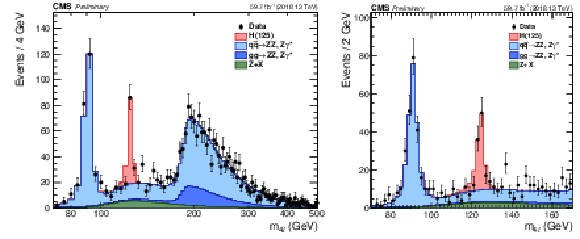
png pdf	Figure 6: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ up to 500 GeV (left) and the low-mass range (right), with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 6-a: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ up to 500 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
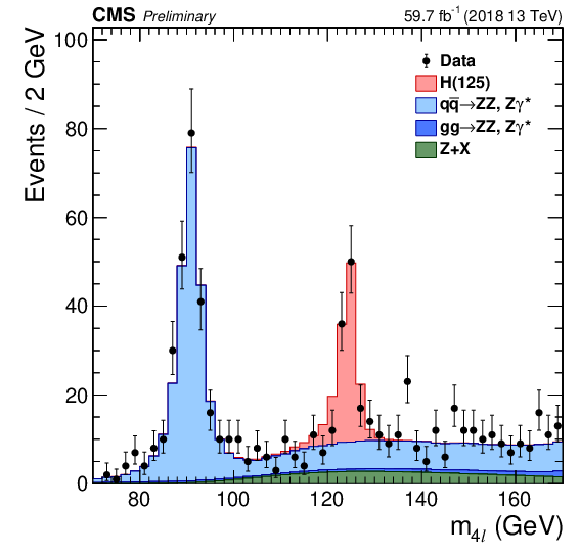
png pdf	Figure 6-b: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ in the low-mass range, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 7: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ up to 500 GeV (left) and the low-mass range (right), with full Run 2 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
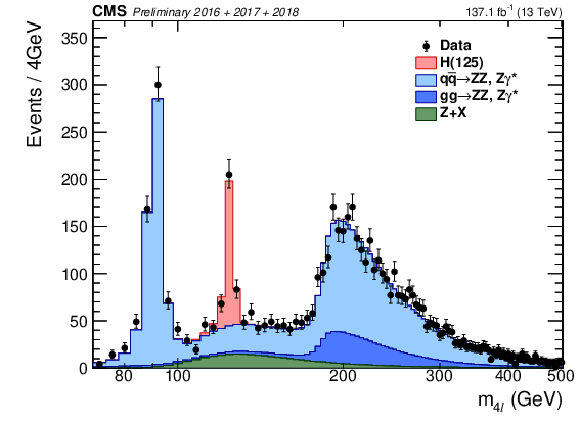
png pdf	Figure 7-a: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ up to 500 GeV, with full Run 2 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
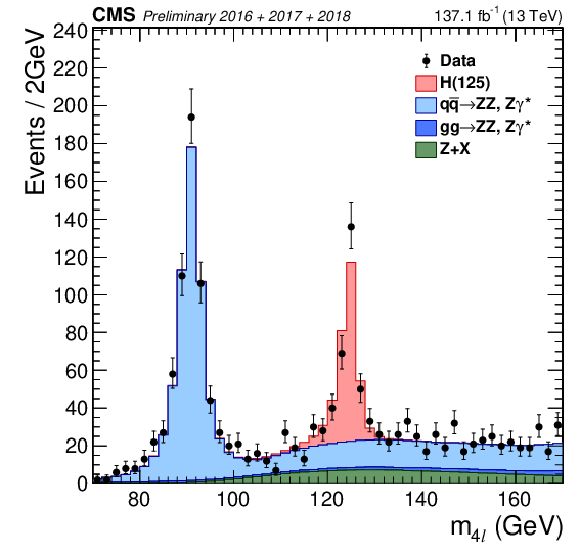
png pdf	Figure 7-b: Distribution of the reconstructed four-lepton invariant mass $ {m_{4\ell}}$ in the low-mass range, with full Run 2 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
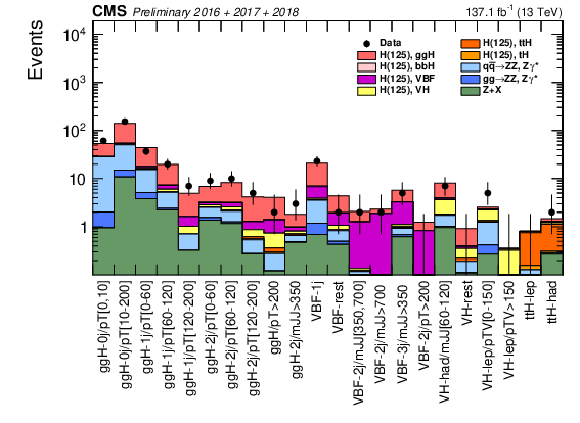
png pdf	Figure 8: Distributions of the expected and observed number of events for all Stage 1.1 sub-categories described in Section 6.2 in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV with Run 2 data. Points with error bars represent the data and stacked histograms represent the expected numbers of the signal and background events. The different SM Higgs boson signal production modes with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
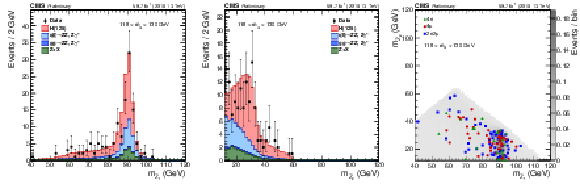
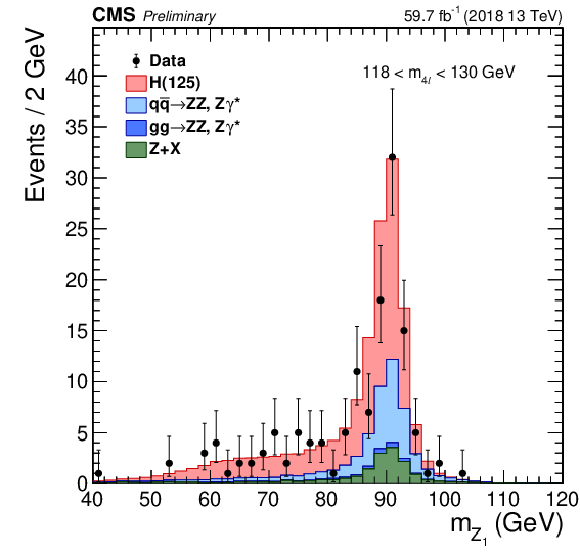
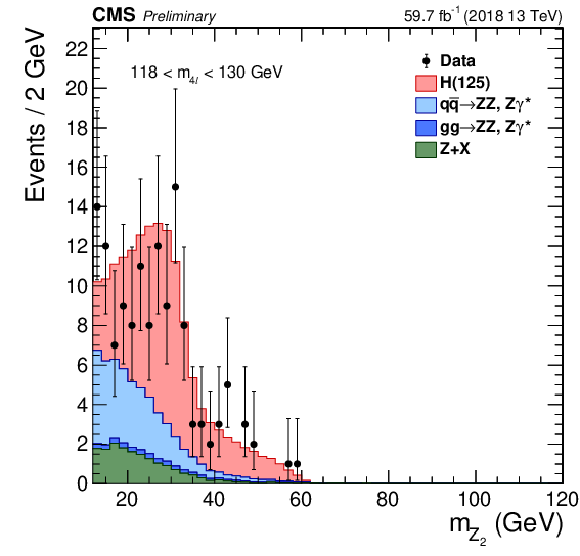
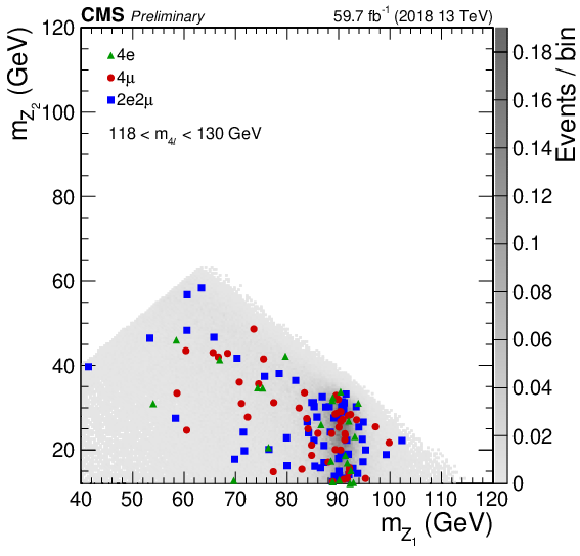
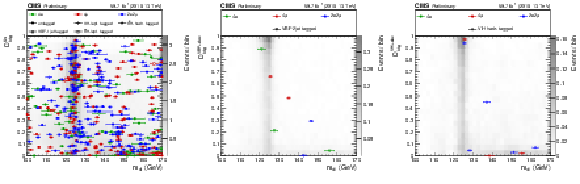
png pdf	Figure 9: Distribution of the $\mathrm{Z} _1$ (left) and $\mathrm{Z} _2$ (center) reconstructed masses and correlation between the two (right) in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. The stacked histograms and the gray scale represent expected distributions of the signal and background processes, and points represent the data. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 9-a: Distribution of the $\mathrm{Z} _1$ reconstructed mass in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. The stacked histograms represent expected distributions of the signal and background processes, and points represent the data. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 9-b: Distribution of the $\mathrm{Z} _2$ reconstructed mass in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. The stacked histograms represent expected distributions of the signal and background processes, and points represent the data. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 9-c: Correlation between $\mathrm{Z} _1$ and $\mathrm{Z} _2$ in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. The gray scale represents the expected distribution of the signal, and points represent the data.
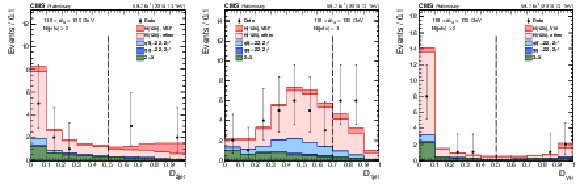
png pdf	Figure 10: Distribution of categorization discriminants in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data: (left) ${{\mathcal D}_{\rm 2jet}}$, (middle) ${{\mathcal D}_{\rm 1jet}}$, (right) ${{\mathcal D}_{\rm VH}} = max({{\mathcal D}_{\rm {\mathrm{W} \mathrm{H}}}}, {{\mathcal D}_{\rm {\mathrm{Z} \mathrm{H}}}})$. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The vertical gray dashed lines denote the working points used in the event categorization. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
png pdf	Figure 10-a: Distribution of the ${{\mathcal D}_{\rm 2jet}}$ categorization discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The vertical gray dashed lines denote the working points used in the event categorization. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
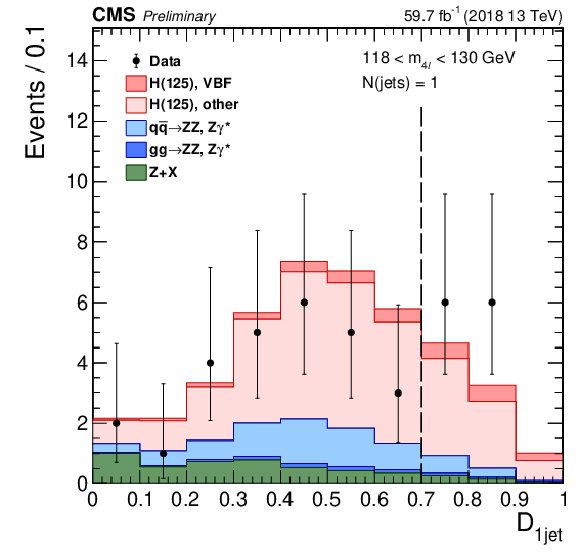
png pdf	Figure 10-b: Distribution of the ${{\mathcal D}_{\rm 1jet}}$ categorization discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The vertical gray dashed lines denote the working points used in the event categorization. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
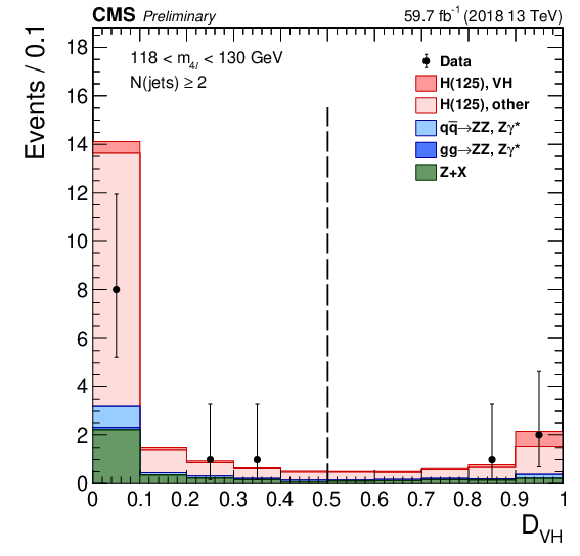
png pdf	Figure 10-c: Distribution of the ${{\mathcal D}_{\rm VH}} = max({{\mathcal D}_{\rm {\mathrm{W} \mathrm{H}}}}, {{\mathcal D}_{\rm {\mathrm{Z} \mathrm{H}}}})$ categorization discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The vertical gray dashed lines denote the working points used in the event categorization. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates. The order in perturbation theory used for the normalization of the irreducible backgrounds is described in Section 7.1.
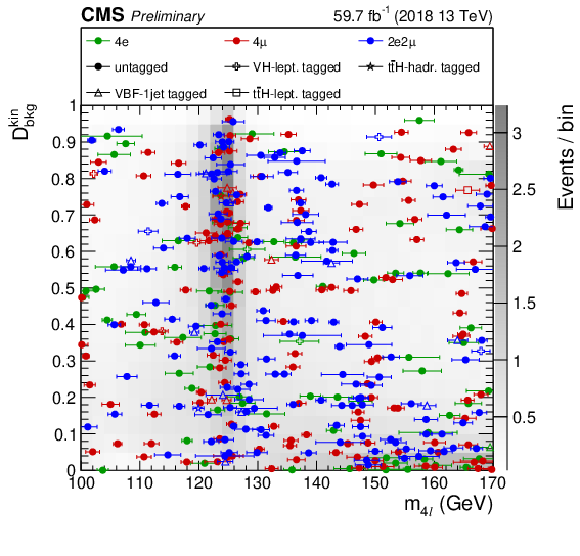
png pdf	Figure 11: Distribution of three different kinematic discriminants versus $ {m_{4\ell}}$, with 2018 data: $ {{\cal D}^{\rm kin}_{\rm bkg}} $ (left), $ {{\mathcal {D}}^{\mathrm {VBF}+\mathrm {dec}}_{\mathrm {bkg}}} $ (middle) and $ {{\mathcal {D}}^{\mathrm {VH}+\mathrm {dec}}_{\mathrm {bkg}}} $ (right) shown in the mass region 100 $ < {m_{4\ell}} < $ 170 GeV. The gray scale represents the expected total number of ZZ and Z+X background and SM Higgs boson signal events for $ {m_{\mathrm{H}}} = $ 125 GeV. The points show the data and the horizontal bars represent the measured event-by-event mass uncertainties. Different marker styles are used to denote the categorization of the events.
png pdf	Figure 11-a: Distribution of the $ {{\cal D}^{\rm kin}_{\rm bkg}} $ kinematic discriminant versus $ {m_{4\ell}}$, with 2018 data, shown in the mass region 100 $ < {m_{4\ell}} < $ 170 GeV. The gray scale represents the expected total number of ZZ and Z+X background and SM Higgs boson signal events for $ {m_{\mathrm{H}}} = $ 125 GeV. The points show the data and the horizontal bars represent the measured event-by-event mass uncertainties. Different marker styles are used to denote the categorization of the events.
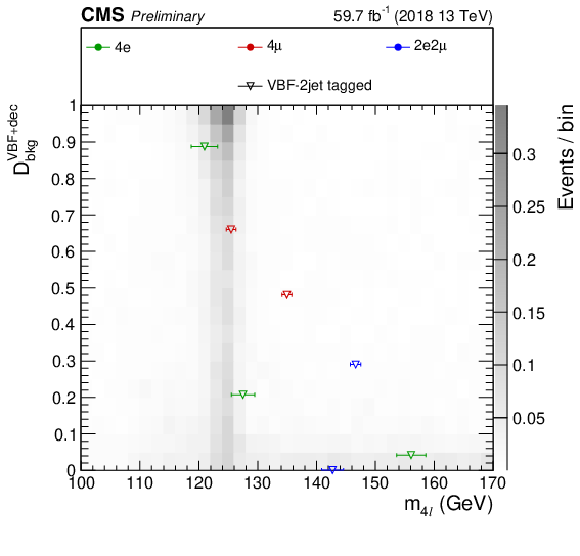
png pdf	Figure 11-b: Distribution of the $ {{\mathcal {D}}^{\mathrm {VBF}+\mathrm {dec}}_{\mathrm {bkg}}} $ kinematic discriminant versus $ {m_{4\ell}}$, with 2018 data, shown in the mass region 100 $ < {m_{4\ell}} < $ 170 GeV. The gray scale represents the expected total number of ZZ and Z+X background and SM Higgs boson signal events for $ {m_{\mathrm{H}}} = $ 125 GeV. The points show the data and the horizontal bars represent the measured event-by-event mass uncertainties. Different marker styles are used to denote the categorization of the events.
png pdf	Figure 11-c: Distribution of the $ {{\mathcal {D}}^{\mathrm {VH}+\mathrm {dec}}_{\mathrm {bkg}}} $ kinematic discriminant versus $ {m_{4\ell}}$, with 2018 data, shown in the mass region 100 $ < {m_{4\ell}} < $ 170 GeV. The gray scale represents the expected total number of ZZ and Z+X background and SM Higgs boson signal events for $ {m_{\mathrm{H}}} = $ 125 GeV. The points show the data and the horizontal bars represent the measured event-by-event mass uncertainties. Different marker styles are used to denote the categorization of the events.
png pdf	Figure 12: Distribution of kinematic discriminants in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data: (left) ${{\cal D}^{\rm kin}_{\rm bkg}}$, (middle) ${{\mathcal {D}}^{\mathrm {VBF}+\mathrm {dec}}_{\mathrm {bkg}}}$, (right) ${{\mathcal {D}}^{\mathrm {VH}+\mathrm {dec}}_{\mathrm {bkg}}}$. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates.
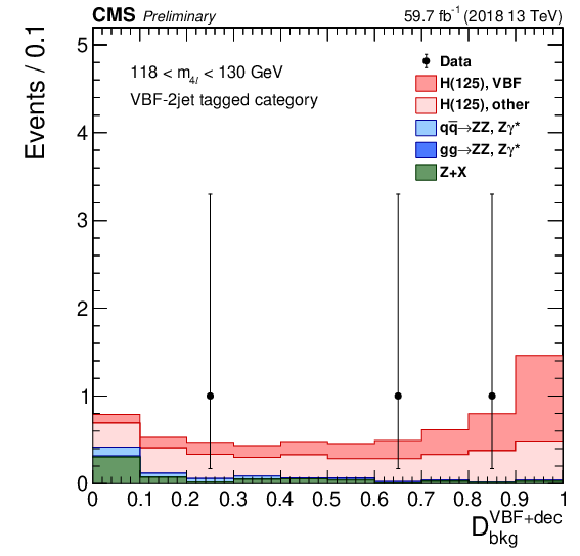
png pdf	Figure 12-a: Distribution of the ${{\cal D}^{\rm kin}_{\rm bkg}}$ kinematic discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates.
png pdf	Figure 12-b: Distribution of the ${{\mathcal {D}}^{\mathrm {VBF}+\mathrm {dec}}_{\mathrm {bkg}}}$ kinematic discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates.
png pdf	Figure 12-c: Distribution of the ${{\mathcal {D}}^{\mathrm {VH}+\mathrm {dec}}_{\mathrm {bkg}}}$ kinematic discriminant in the mass region 118 $ < {m_{4\ell}} < $ 130 GeV, with 2018 data. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The SM Higgs boson signal with $ {m_{\mathrm{H}}} = $ 125 GeV, denoted as ${\rm H}(125)$, and the ZZ backgrounds are normalized to the SM expectation, the Z+X background to the estimation from data. The SM Higgs boson signal is separated into two components: the production mode which is targeted by the specific discriminant, and other production modes, where the gluon fusion process dominates.
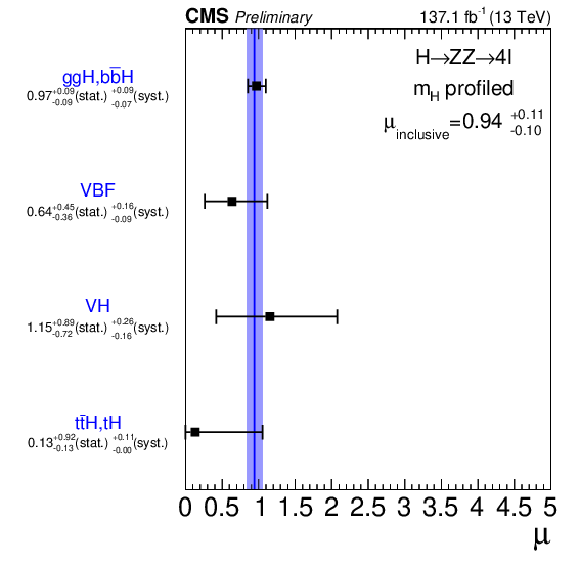
png pdf	Figure 13: (Left) Results of likelihood scans for the signal-strength modifiers corresponding to the main SM Higgs boson production modes, compared to the combined $\mu $ shown as a vertical line. The horizontal bars and the filled band indicate the $\pm $ 1$\sigma $ uncertainties. The uncertainties include both statistical and systematic sources. (Right) Result of the 2D likelihood scan for the $ \mu _{\mathrm{g} \mathrm{g} \mathrm{H}}$, ${\mathrm{t} {}\mathrm{\bar{t}}} \mathrm{H}$, ${\mathrm{b} \bar{\mathrm{b}}\mathrm{H}}$, ${\mathrm{t} \mathrm{H}} $ and $ {\mu _{\mathrm {VBF},\mathrm {V\mathrm{H}}}} $ signal-strength modifiers. The solid and dashed contours show the 68% and 95% CL regions, respectively. The cross indicates the best-fit value, and the diamond represents the expected value for the SM Higgs boson.
png pdf	Figure 13-a: Results of likelihood scans for the signal-strength modifiers corresponding to the main SM Higgs boson production modes, compared to the combined $\mu $ shown as a vertical line. The horizontal bars and the filled band indicate the $\pm $ 1$\sigma $ uncertainties. The uncertainties include both statistical and systematic sources.
png pdf	Figure 13-b: Result of the 2D likelihood scan for the $ \mu _{\mathrm{g} \mathrm{g} \mathrm{H}}$, ${\mathrm{t} {}\mathrm{\bar{t}}} \mathrm{H}$, ${\mathrm{b} \bar{\mathrm{b}}\mathrm{H}}$, ${\mathrm{t} \mathrm{H}} $ and $ {\mu _{\mathrm {VBF},\mathrm {V\mathrm{H}}}} $ signal-strength modifiers. The solid and dashed contours show the 68% and 95% CL regions, respectively. The cross indicates the best-fit value, and the diamond represents the expected value for the SM Higgs boson.
png pdf	Figure 14: The ratios between measured cross sections and the SM prediction for Stage 0 Bins with $ {m_{\mathrm{H}}}$ profiled in the fit. The band around the vertical band shows the theoretical uncertainties on the SM cross section predictions for each Stage 0 Bin. Cross section values are reported for the best fit mass value $ {m_{\mathrm{H}}}= $ 125.1 GeV.
png pdf	Figure 15: The ratios between measured cross sections and the SM prediction for Stage 1.1 Bins with $ {m_{\mathrm{H}}}$ profiled in the fit. The band around the vertical band shows the theoretical uncertainties on the SM cross section predictions for each Stage 1.1 Bin. The cross section ratios are constrained to be non-negative. The parameters whose best-fit values are at zero are known to have 68% CL intervals which slightly under-cover. Cross section values are reported for the best fit mass value $ {m_{\mathrm{H}}}= $ 125.1 GeV.
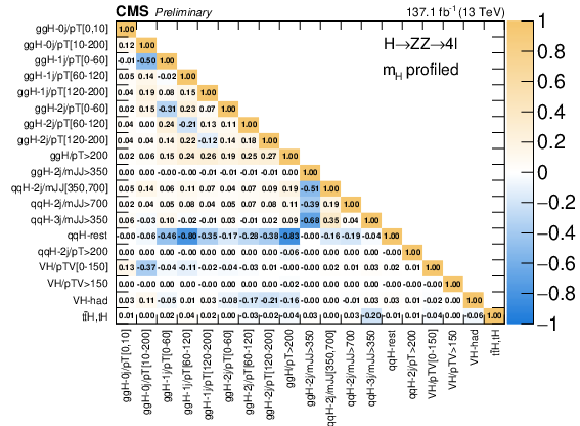
png pdf	Figure 16: Correlation matrix of the fitted signal strengths for Stage 1.1 Bins.
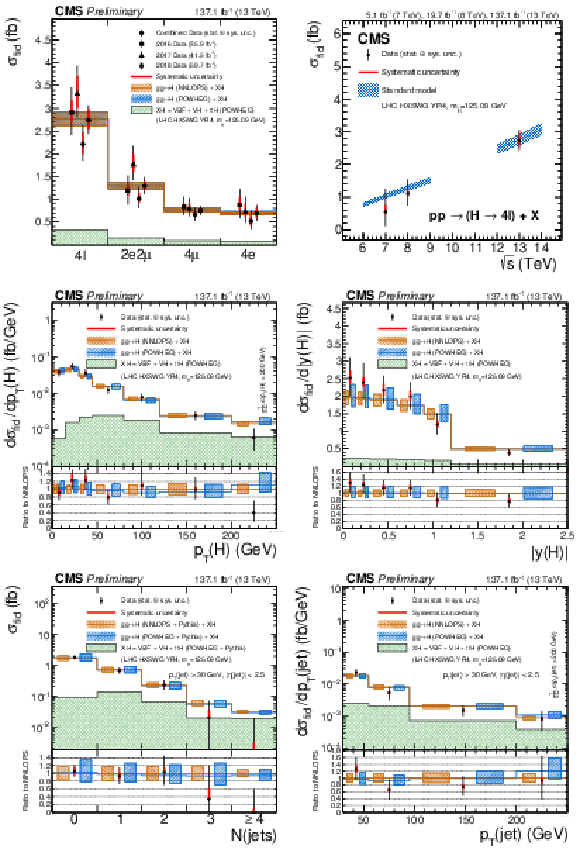
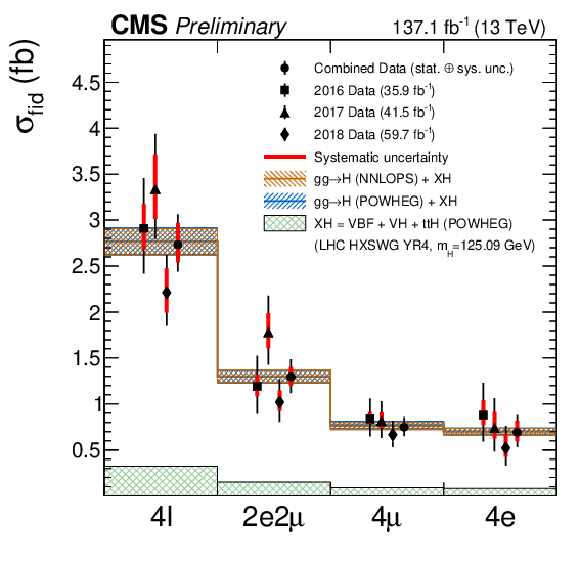
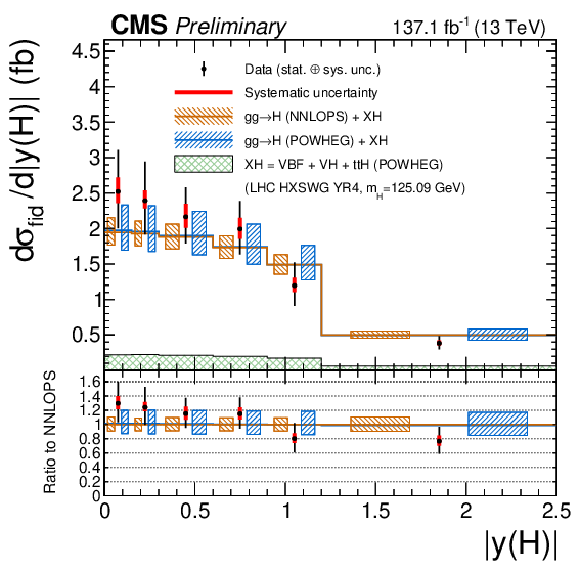
png pdf	Figure 17: The measured inclusive fiducial cross section in different final states (top left). The measured fiducial cross section as a function of $\sqrt {s}$ (top right). The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used. The results of the differential cross section measurement for $ {p_{\mathrm {T}}} ({\rm H})$ (middle left), $|y({\rm H})|$ (middle right) and $N({\text{jets}})$ (bottom left), $p_{\mathrm{T}}$ of the leading jet (bottom right). The acceptance and theoretical uncertainties in the differential bins are are calculated using POWHEG. The sub-dominant component of the the signal (VBF+VH+$ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$) is denoted as XH.
png pdf	Figure 17-a: The measured inclusive fiducial cross section in different final states. The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used.
png pdf	Figure 17-b: The measured fiducial cross section as a function of $\sqrt {s}$. The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used.
png pdf	Figure 17-c: The results of the differential cross section measurement for $p_{\mathrm{T}}$. The acceptance and theoretical uncertainties in the differential bins are are calculated using POWHEG. The sub-dominant component of the the signal (VBF+VH+$ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$) is denoted as XH.
png pdf	Figure 17-d: The measured inclusive fiducial cross section in different final states (top left). The measured fiducial cross section as a function of $\sqrt {s}$ (top right). The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used. The results of the differential cross section measurement for $ {p_{\mathrm {T}}} ({\rm H})$ (middle left), $|y({\rm H})|$ (middle right) and $N({\text{jets}})$ (bottom left), $p_{\mathrm{T}}$ of the leading jet (bottom right). The acceptance and theoretical uncertainties in the differential bins are are calculated using POWHEG. The sub-dominant component of the the signal (VBF+VH+$ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$) is denoted as XH.
png pdf	Figure 17-e: The measured inclusive fiducial cross section in different final states (top left). The measured fiducial cross section as a function of $\sqrt {s}$ (top right). The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used. The results of the differential cross section measurement for $ {p_{\mathrm {T}}} ({\rm H})$ (middle left), $|y({\rm H})|$ (middle right) and $N({\text{jets}})$ (bottom left), $p_{\mathrm{T}}$ of the leading jet (bottom right). The acceptance and theoretical uncertainties in the differential bins are are calculated using POWHEG. The sub-dominant component of the the signal (VBF+VH+$ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$) is denoted as XH.
png pdf	Figure 17-f: The measured inclusive fiducial cross section in different final states (top left). The measured fiducial cross section as a function of $\sqrt {s}$ (top right). The acceptance is calculated using POWHEG at $\sqrt {s}=$ 13 TeV and HRes [63,65] at $\sqrt {s}=$ 7 and 8 TeV and the total gluon fusion cross section and uncertainty are taken from Ref. [32]. The fiducial volume for $\sqrt {s}=$ 6-9 TeV uses the lepton isolation definition from Ref. [21], while for $\sqrt {s}=$ 12-14 TeV the definition described in the text is used. The results of the differential cross section measurement for $ {p_{\mathrm {T}}} ({\rm H})$ (middle left), $|y({\rm H})|$ (middle right) and $N({\text{jets}})$ (bottom left), $p_{\mathrm{T}}$ of the leading jet (bottom right). The acceptance and theoretical uncertainties in the differential bins are are calculated using POWHEG. The sub-dominant component of the the signal (VBF+VH+$ {\mathrm{t} \bar{\mathrm{t}}\mathrm{H}}$) is denoted as XH.

Tables
png pdf	Table 1: The number of expected background and signal events and number of observed candidates after full analysis selection, for each final state, for the full mass range $ {m_{4\ell}} > $ 70 GeV and for an integrated luminosity of 59.7 fb$^{-1}$. Signal and ZZ backgrounds are estimated from Monte Carlo simulation, Z+X is estimated from data. The uncertainties include both statistical and systematic sources.
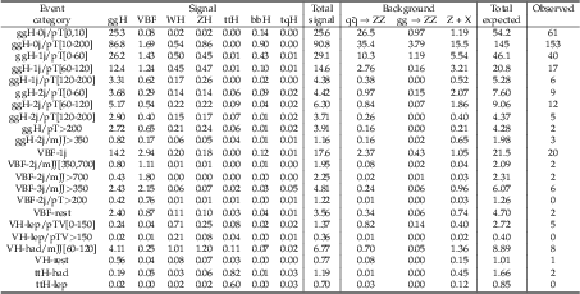
png pdf	Table 2: The number of expected background and signal events and number of observed candidates after full analysis selection, for each event category, for the mass range 118 $ < {m_{4\ell}} < $ 130 GeV and for an integrated luminosity of 137.1 fb$^{-1}$. The yields are given for the different production modes. Signal and ZZ backgrounds are estimated from Monte Carlo simulation, Z+X is estimated from data. The uncertainties include both statistical and systematic sources.
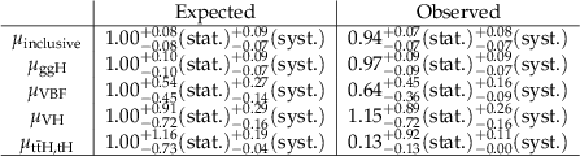
png pdf	Table 3: Expected and observed signal-strength modifiers with Run 2 data. The observed uncertainty numbers are broken into statistical (first) and systematic (second) sources.
png pdf	Table 4: Summary of requirements used in the definition of the fiducial phase space for the $ {\mathrm{H} \to 4\ell}$ cross section measurements.
png pdf	Table 5: Summary of different SM signal models. For all production modes the values given are for $m_{\rm H} = $ 125 GeV. The uncertainties listed are statistical only, and the statistical uncertainty on the acceptance is $\sim $0.001.

Summary

Several measurements of Higgs (H) boson production in the four-lepton final state at $\sqrt{s} = $ 13 TeV have been presented, using data samples corresponding to an integrated luminosity of 137.1 fb$^{-1}$. The measured signal-strength modifier is $\mu=$ 0.94$^{+0.07}_{-0.07}$(stat.)$^{+0.08}_{-0.07}$(syst.) and integrated fiducial cross section is measured to be $\sigma_{{\rm fid.}}= $ 2.73$^{+0.23}_{-0.22}$(stat.)$^{+0.24}_{-0.19}$(syst.) fb. The signal-strength modifiers for the main H boson production modes are also constrained. Measurements of the simplified template cross sections, designed to quantify the different H boson production processes in specific regions of phase space, have been measured for the first time with the Stage 1.1 recommendation. Differential cross sections as a function of the $p_{\rm T}$ and rapidity of the H boson, the number of associated jets, and the $p_{\rm T}$ of the leading associated jet are determined. All results are consistent, within their uncertainties, with the expectations for the Standard Model H boson.

Additional Figures
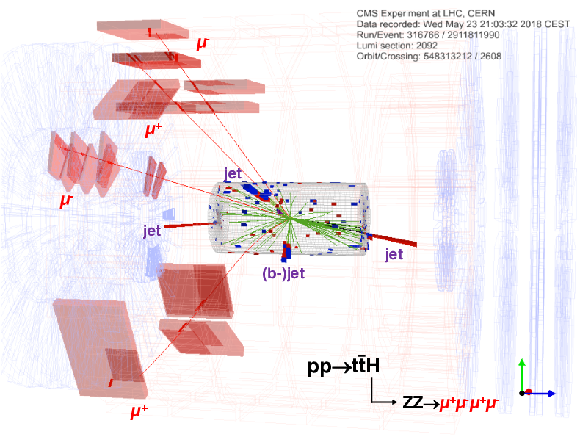
png pdf	Additional Figure 1: Event display for a $\mathrm {t\bar{t}H}$ event candidate.
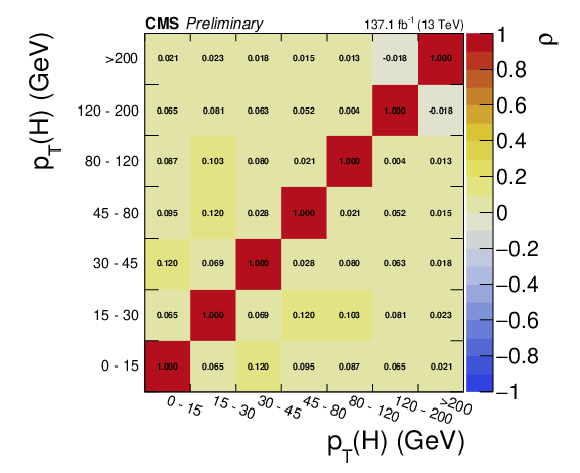
png pdf	Additional Figure 2: Bin-to-bin correlation matrix of the $p_{\mathrm {T}}(\mathrm {H})$ spectrum.
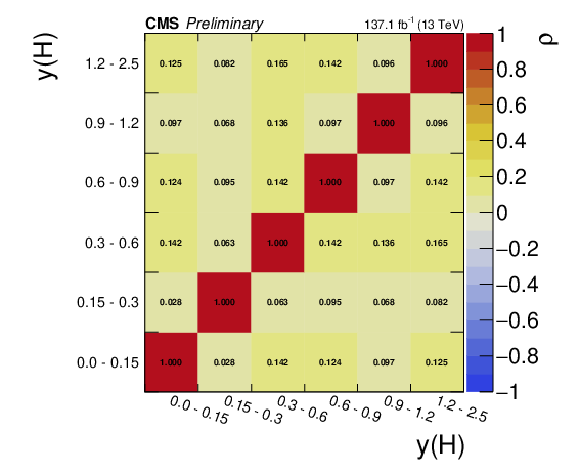
png pdf	Additional Figure 3: Bin-to-bin correlation matrix of the $y(\mathrm {H})$ spectrum.
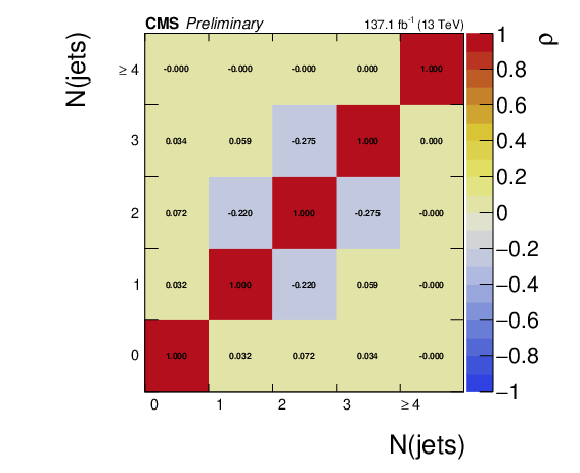
png pdf	Additional Figure 4: Bin-to-bin correlation matrix of the $N(\text{jets})$ spectrum.
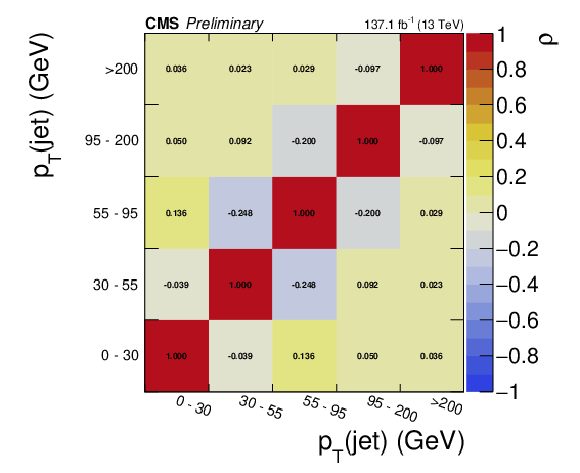
png pdf	Additional Figure 5: Bin-to-bin correlation matrix of the $p_{\mathrm {T}}(\mathrm {jet})$ spectrum.

Additional Tables
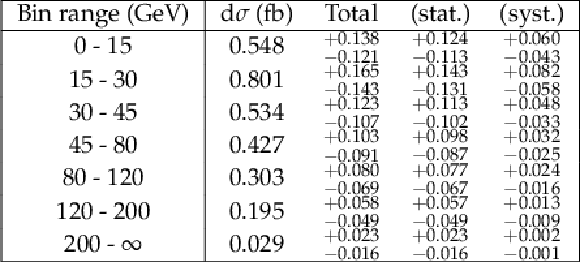
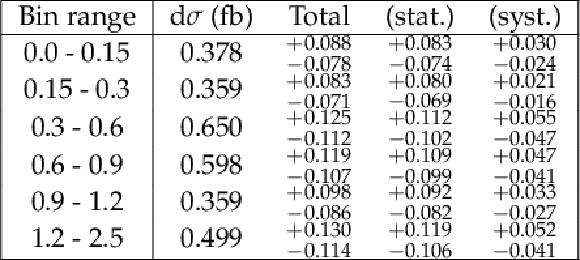
png pdf	Additional Table 1: Differential cross section results for the $p_{\mathrm {T}}(\mathrm {H})$ observable.
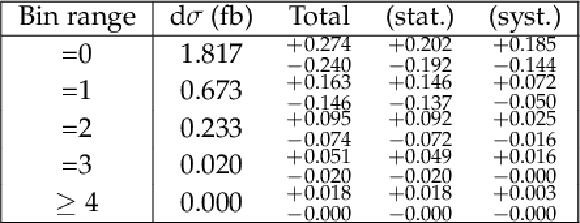
png pdf	Additional Table 2: Differential cross section results for the $y(\mathrm {H})$ observable.
png pdf	Additional Table 3: Differential cross section results for the $N(\text{jets})$ observable.
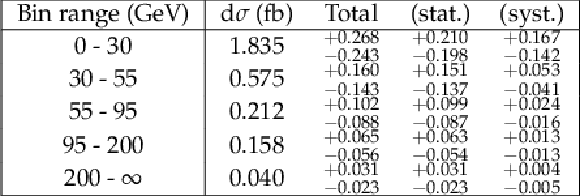
png pdf	Additional Table 4: Differential cross section results for the $p_{\mathrm {T}}(\mathrm {jet})$ observable.

References
1	CMS Collaboration	Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC	PLB 716 (2012) 30	CMS-HIG-12-028 1207.7235
2	ATLAS Collaboration	Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC	PLB 716 (2012) 1	1207.7214
3	F. Englert and R. Brout	Broken Symmetry and the Mass of Gauge Vector Mesons	PRL 13 (1964) 321
4	P. W. Higgs	Broken symmetries, massless particles and gauge fields	PL12 (1964) 132
5	P. W. Higgs	Broken Symmetries and the Masses of Gauge Bosons	PRL 13 (1964) 508
6	G. Guralnik, C. Hagen, and T. Kibble	Global Conservation Laws and Massless Particles	PRL 13 (1964) 585
7	P. W. Higgs	Spontaneous Symmetry Breakdown without Massless Bosons	PR145 (1966) 1156
8	T. Kibble	Symmetry breaking in nonAbelian gauge theories	PR155 (1967) 1554
9	CMS Collaboration	Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV	EPJC 75 (2015) 212	CMS-HIG-14-009 1412.8662
10	ATLAS Collaboration	Measurements of the Higgs boson production and decay rates and coupling strengths using $ pp $ collision data at $ \sqrt{s}= $ 7 and 8 TeV in the ATLAS experiment	EPJC 76 (2016)	1507.04548
11	ATLAS and CMS Collaborations	Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS and CMS Experiments	PRL 114 (2015) 191803	1503.07589
12	ATLAS and CMS Collaborations	Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}= $ 7 and 8 TeV	JHEP 08 (2016) 45	1606.02266
13	CMS Collaboration	Combined meaurements of the Higgs boson's couplings at $ \sqrt{s}= $ 13 TeV
14	CMS Collaboration	Measurements of properties of the Higgs boson decaying into the four-lepton final state in pp collisions at $ \sqrt{s}= $ 13 TeV	JHEP 11 (2017) 047	CMS-HIG-16-041 1706.09936
15	CMS Collaboration	Measurements of properties of the Higgs boson in the four-lepton final state at $ \sqrt{s}= $ 13 TeV	CMS-PAS-HIG 18-001	CMS-PAS-HIG-18-001
16	CMS Collaboration	Measurement of the properties of a Higgs boson in the four-lepton final state	PRD 89 (2014) 092007	CMS-HIG-13-002 1312.5353
17	CMS Collaboration	Study of the Mass and Spin-Parity of the Higgs Boson Candidate via Its Decays to $ Z $ Boson Pairs	PRL 110 (2013) 081803	CMS-HIG-12-041 1212.6639
18	CMS Collaboration	Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV	PRD 92 (2015) 012004	CMS-HIG-14-018 1411.3441
19	CMS Collaboration	Constraints on the Higgs boson width from off-shell production and decay to $ \mathrm{Z} $-boson pairs	PLB 736 (2014) 64	CMS-HIG-14-002 1405.3455
20	CMS Collaboration	Limits on the Higgs boson lifetime and width from its decay to four charged leptons	PRD 92 (2015) 072010	CMS-HIG-14-036 1507.06656
21	CMS Collaboration	Measurement of differential and integrated fiducial cross sections for Higgs boson production in the four-lepton decay channel in pp collisions at $ \sqrt{s}= $ 7 and 8 TeV	JHEP 04 (2016) 005	CMS-HIG-14-028 1512.08377
22	CMS Collaboration	Constraints on anomalous Higgs boson couplings using production and decay information in the four-lepton final state	PLB775 (2017) 1--24	CMS-HIG-17-011 1707.00541
23	CMS Collaboration	Measurements of the Higgs boson width and anomalous HVV couplings from on-shell and off-shell production in the four-lepton final state		CMS-HIG-18-002 1901.00174
24	LHC Higgs Cross Section Working Group	Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector	CERN-2017-002-M (CERN, Geneva, 2016)	1610.07922
25	LHCXSWG	Simplified template cross section, stage 1.1	LHCXSWG Twiki (2018)
26	A. Dominguez et al.	CMS Technical Design Report for the Pixel Detector Upgrade	CERN-LHCC-2012-016. CMS-TDR-11, Sep
27	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
28	S. Alioli, P. Nason, C. Oleari, and E. Re	NLO vector-boson production matched with shower in POWHEG	JHEP 07 (2008) 060	0805.4802
29	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
30	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
31	G. Luisoni, P. Nason, C. Oleari, and F. Tramontano	HW$ ^{\pm} $/HZ + 0 and 1 jet at NLO with the POWHEG BOX interfaced to GoSam and their merging within MiNLO	JHEP 10 (2013) 1	1306.2542
32	C. Anastasiou et al.	High precision determination of the gluon fusion Higgs boson cross-section at the LHC	JHEP 2016 (2016), no. 5, 1	1602.00695
33	Y. Gao et al.	Spin determination of single-produced resonances at hadron colliders	PRD 81 (2010) 075022	1001.3396
34	S. Bolognesi et al.	On the spin and parity of a single-produced resonance at the LHC	PRD 86 (2012) 095031	1208.4018
35	I. Anderson et al.	Constraining anomalous $ HVV $ interactions at proton and lepton colliders	PRD 89 (2014) 035007	1309.4819
36	A. V. Gritsan, R. Roentsch, M. Schulze, and M. Xiao	Constraining anomalous Higgs boson couplings to the heavy flavor fermions using matrix element techniques	PRD94 (2016), no. 5, 055023	1606.03107
37	J. M. Campbell and R. K. Ellis	MCFM for the Tevatron and the LHC	NPPS 205 (2010) 10	1007.3492
38	NNPDF Collaboration	Parton distributions from high-precision collider data	EPJC 77 (2017) 663	1706.00428
39	T. Sjostrand et al.	An introduction to pythia 8.2	Computer Physics Communications 191 (2015) 159
40	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
41	GEANT4 Collaboration	GEANT4: a simulation toolkit	NIMA 506 (2003) 250
42	J. Allison et al.	Geant4 developments and applications	IEEE Trans. Nucl. Sci. 53 (2006) 270
43	CMS Collaboration	Particle-flow reconstruction and global event description with the cms detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
44	CMS Collaboration	Performance of CMS muon reconstruction in $ pp $ collision events at $ \sqrt{s} = $ 7 TeV	JINST 7 (2012) P10002	CMS-MUO-10-004 1206.4071
45	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
46	CMS Collaboration	Electron and Photon performance in CMS with the full 2017 data sample and additional highlights for the CALOR 2018 conference	CMS Detector Performance Summary CMS-DPS-2018/2017
47	T. Chen and C. Guestrin	XGBoost: A Scalable Tree Boosting System		1603.02754
48	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_t $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
49	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
50	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017), no. 02, P02014	CMS-JME-13-004 1607.03663
51	CMS Collaboration	Jet algorithms performance in 13 TeV data	CMS-PAS-JME-16-003	CMS-PAS-JME-16-003
52	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV	JINST 13 (2018), no. 05, P05011	CMS-BTV-16-002 1712.07158
53	Particle Data Group Collaboration	Review of Particle Physics	CPC40 (2016), no. 10, 100001
54	CMS Collaboration	Search for a Higgs Boson in the Mass Range from 145 to 1000 GeV Decaying to a Pair of W or Z Bosons	JHEP 10 (2015) 144	CMS-HIG-13-031 1504.00936
55	M. Grazzini, S. Kallweit, and D. Rathlev	ZZ production at the LHC: Fiducial cross sections and distributions in NNLO QCD	PLB 750 (2015) 407 -- 410	1507.06257
56	A. Bierweiler, T. Kasprzik, and J. H. Kuhn	Vector-boson pair production at the LHC to $ \mathcal{O}(\alpha^3) $ accuracy	JHEP 12 (2013) 071	1305.5402
57	M. Bonvini et al.	Signal-background interference effects in $ gg \to H \to WW $ beyond leading order	PRD 88 (2013) 034032	1304.3053
58	K. Melnikov and M. Dowling	Production of two Z-bosons in gluon fusion in the heavy top quark approximation	PLB 744 (2015) 43	1503.01274
59	C. S. Li, H. T. Li, D. Y. Shao, and J. Wang	Soft gluon resummation in the signal-background interference process of $ gg(\to h^*) \to ZZ $~		1504.02388
60	G. Passarino	Higgs CAT	EPJC 74 (2014) 2866	1312.2397
61	S. Catani and M. Grazzini	An NNLO subtraction formalism in hadron collisions and its application to Higgs boson production at the LHC	PRL 98 (2007) 222002	hep-ph/0703012
62	M. Grazzini	NNLO predictions for the Higgs boson signal in the H $ \to $ WW $ \to\ell\nu\ell\nu $ and H$ \to $ ZZ $ \to4\ell $ decay channels	JHEP 02 (2008) 043	0801.3232
63	M. Grazzini and H. Sargsyan	Heavy-quark mass effects in Higgs boson production at the LHC	JHEP 09 (2013) 129	1306.4581
64	L. Landau	On the energy loss of fast particles by ionization	J. Phys. (USSR) 8 (1944)201
65	D. de Florian, G. Ferrera, M. Grazzini, and D. Tommasini	Higgs boson production at the LHC: transverse momentum resummation effects in the $ H \to \gamma \gamma $, $ H \to WW \to \ell\nu\ell\nu $ and $ H \to ZZ \to 4\ell $ decay modes	JHEP 06 (2012) 132	1203.6321
66	E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini	Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM	JHEP 02 (2012) 088	1111.2854
67	K. Hamilton, P. Nason, E. Re, and G. Zanderighi	NNLOPS simulation of Higgs boson production	JHEP 10 (2013) 222	1309.0017
68	F. Garwood	Fiducial Limits for the Poisson Distribution	Biometrika 28 (1936), no. 3-4, 437
69	ATLAS and CMS Collaborations, LHC Higgs Combination Group	Procedure for the lhc higgs boson search combination in summer 2011	ATL-PHYS-PUB/CMS NOTE 2011-11, 2011/005, CERN
70	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727
71	CMS Collaboration	Measurement of differential cross sections for Higgs boson production in the diphoton decay channel in pp collisions at $ \sqrt{s} = $ 8 TeV	EPJC 76 (2015) 13	CMS-HIG-14-016 1508.07819

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2018 for the benefit of the CMS Collaboration