Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-EXO-19-011 | ||
| A deep neural network-based tagger to search for new long-lived particle states decaying to jets | ||
| CMS Collaboration | ||
| November 2019 | ||
| Abstract: The development of a tagging algorithm to identify jets that are significantly displaced from the luminous regions of LHC proton-proton (pp) collisions is presented. Displaced jets can arise from the decay of a long-lived particle (LLP), which are predicted by several theoretical extensions to the standard model. The tagger is a multiclass classifier based on a deep neural network, which is parameterized according to the proper decay length $\text{c}\tau_0$ of the LLP. A novel scheme is defined to reliably label jets from LLP decays for supervised learning. Samples of both simulated events and pp collision data are used to train the neural network. Domain adaptation by backward propagation is performed to improve the simulation modelling of the jet class probability distributions observed in pp collision data. The tagger is applied in a search for long-lived gluinos, a manifestation of split supersymmetric models. The tagger provides a rejection factor of 10 000 for jets from standard model processes while maintaining an LLP jet tagging efficiency of 30-80% for split supersymmetric models with 1 mm $\leq \text{c}\tau_0 \leq $ 10 m. The expected coverage of the split supersymmetric model parameter space is presented. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, MLST 1 (2020) 035012. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
Figure 1:
Two examples of a ${\mathrm{\tilde{g}}} \to \mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $ decay using truth information from the MadGraph 5\_amc@nlo 2.2.2 [49] and PYTHIA 8.205 [50] programs. The positions of various particles in the $\eta $-$\phi $ plane are shown: the LLP (${\mathrm{\tilde{g}}}$) and its daughter particles ($\mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $) are shown in the lower and middle planes, respectively; the upper plane depicts the location of the stable final-state particles after hadronization, with shaded ellipses overlaid to indicate the reconstructed jets. Each quark and its decay is assigned a unique colour. The dotted lines indicate the links between parent and daughter particles. |
png pdf |
Figure 1-a:
Two examples of a ${\mathrm{\tilde{g}}} \to \mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $ decay using truth information from the MadGraph 5\_amc@nlo 2.2.2 [49] and PYTHIA 8.205 [50] programs. The positions of various particles in the $\eta $-$\phi $ plane are shown: the LLP (${\mathrm{\tilde{g}}}$) and its daughter particles ($\mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $) are shown in the lower and middle planes, respectively; the upper plane depicts the location of the stable final-state particles after hadronization, with shaded ellipses overlaid to indicate the reconstructed jets. Each quark and its decay is assigned a unique colour. The dotted lines indicate the links between parent and daughter particles. |
png pdf |
Figure 1-b:
Two examples of a ${\mathrm{\tilde{g}}} \to \mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $ decay using truth information from the MadGraph 5\_amc@nlo 2.2.2 [49] and PYTHIA 8.205 [50] programs. The positions of various particles in the $\eta $-$\phi $ plane are shown: the LLP (${\mathrm{\tilde{g}}}$) and its daughter particles ($\mathrm{q} \mathrm{\bar{q}} \tilde{\chi}^0_1 $) are shown in the lower and middle planes, respectively; the upper plane depicts the location of the stable final-state particles after hadronization, with shaded ellipses overlaid to indicate the reconstructed jets. Each quark and its decay is assigned a unique colour. The dotted lines indicate the links between parent and daughter particles. |
png pdf |
Figure 2:
An overview of the DNN architecture, which comprises convolutional and dense layers; the number of filters and nodes, respectively, is indicated. Dropout layers and activation functions are not shown. The input features are grouped by object type and ($m \times n$) indicates the maximum number of objects ($m$) and the number of features per object ($n$). The gradients of the class $(L_\text {class})$ and domain $(L_\text {domain})$ losses with respect to the weights $\vec{w}$, used during backward propagation, are shown. |
png pdf |
Figure 3:
A schematic of the input pipeline for training the DNN, which uses the TensorFlow queue system with custom operation kernels for reading ROOT trees from disk, (${p_{\mathrm {T}}}$, $\eta $) resampling for SM jets, and generating random ${c\tau _{0}}$ values for jets from SM backgrounds and data. |
png pdf |
Figure 4:
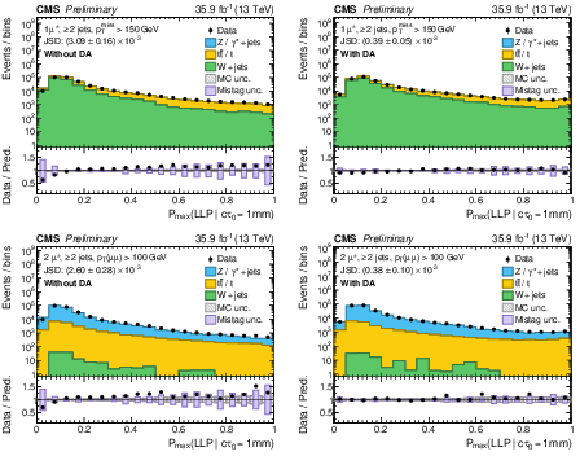
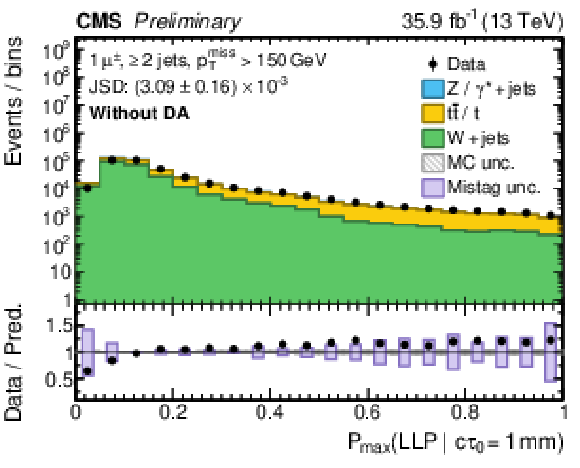
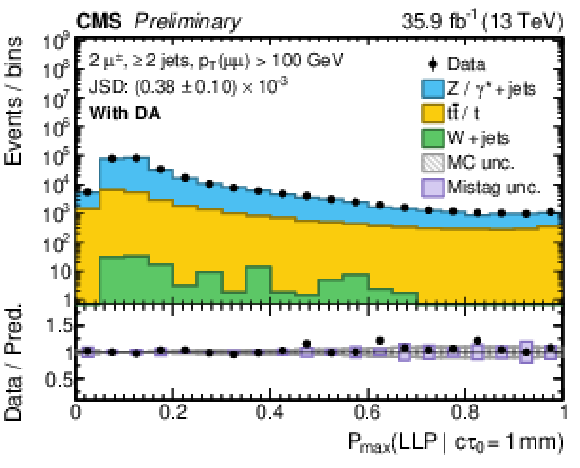
Distributions of the maximum probability for the LLP jet class obtained from all selected jets in a given event, ${P_\text {max}(\text {LLP}| {c\tau _{0}})}$. The distributions from pp collision data (circular marker) and simulated events (histograms) are compared in the $\mu$+jets (upper row) and $\mu\mu$+jets (lower row) CRs, using a DNN trained without (left column) and with (right column) DA. All probabilities are evaluated with $ {c\tau _{0}} = $ 1 mm. The JSD is introduced in the text. |
png pdf |
Figure 4-a:
Distributions of the maximum probability for the LLP jet class obtained from all selected jets in a given event, ${P_\text {max}(\text {LLP}| {c\tau _{0}})}$. The distributions from pp collision data (circular marker) and simulated events (histograms) are compared in the $\mu$+jets (upper row) and $\mu\mu$+jets (lower row) CRs, using a DNN trained without (left column) and with (right column) DA. All probabilities are evaluated with $ {c\tau _{0}} = $ 1 mm. The JSD is introduced in the text. |
png pdf |
Figure 4-b:
Distributions of the maximum probability for the LLP jet class obtained from all selected jets in a given event, ${P_\text {max}(\text {LLP}| {c\tau _{0}})}$. The distributions from pp collision data (circular marker) and simulated events (histograms) are compared in the $\mu$+jets (upper row) and $\mu\mu$+jets (lower row) CRs, using a DNN trained without (left column) and with (right column) DA. All probabilities are evaluated with $ {c\tau _{0}} = $ 1 mm. The JSD is introduced in the text. |
png pdf |
Figure 4-c:
Distributions of the maximum probability for the LLP jet class obtained from all selected jets in a given event, ${P_\text {max}(\text {LLP}| {c\tau _{0}})}$. The distributions from pp collision data (circular marker) and simulated events (histograms) are compared in the $\mu$+jets (upper row) and $\mu\mu$+jets (lower row) CRs, using a DNN trained without (left column) and with (right column) DA. All probabilities are evaluated with $ {c\tau _{0}} = $ 1 mm. The JSD is introduced in the text. |
png pdf |
Figure 4-d:
Distributions of the maximum probability for the LLP jet class obtained from all selected jets in a given event, ${P_\text {max}(\text {LLP}| {c\tau _{0}})}$. The distributions from pp collision data (circular marker) and simulated events (histograms) are compared in the $\mu$+jets (upper row) and $\mu\mu$+jets (lower row) CRs, using a DNN trained without (left column) and with (right column) DA. All probabilities are evaluated with $ {c\tau _{0}} = $ 1 mm. The JSD is introduced in the text. |
png pdf |
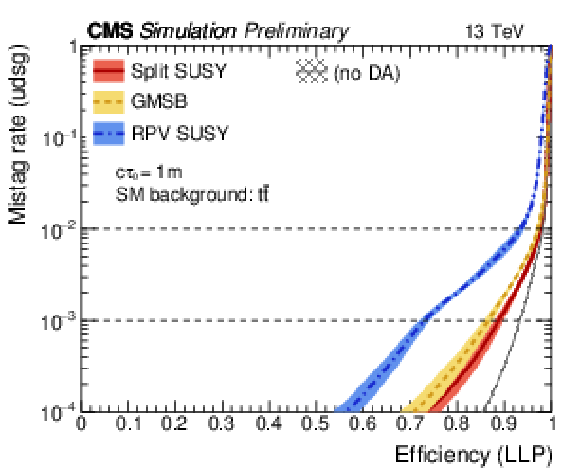
Figure 5:
ROC curves illustrating the tagger performance for the split (solid line), GMSB (dashed), and RPV (dot-dashed) SUSY benchmark models, assuming ${c\tau _{0}}$ values of 1 mm (left) and 1 m (right). The thick and thin solid curves indicate the performance using the DNN trained with and without DA, respectively. The jet sample is defined in the text. |
png pdf |
Figure 5-a:
ROC curves illustrating the tagger performance for the split (solid line), GMSB (dashed), and RPV (dot-dashed) SUSY benchmark models, assuming ${c\tau _{0}}$ values of 1 mm (left) and 1 m (right). The thick and thin solid curves indicate the performance using the DNN trained with and without DA, respectively. The jet sample is defined in the text. |
png pdf |
Figure 5-b:
ROC curves illustrating the tagger performance for the split (solid line), GMSB (dashed), and RPV (dot-dashed) SUSY benchmark models, assuming ${c\tau _{0}}$ values of 1 mm (left) and 1 m (right). The thick and thin solid curves indicate the performance using the DNN trained with and without DA, respectively. The jet sample is defined in the text. |
png pdf |
Figure 6:
The LLP jet tagging efficiency as a function of the jet ${p_{\mathrm {T}}}$, $\eta $, and $N_{\text {SV}}$ using a working point that yields a mistag rate of 0.01% for the udsg jet class, as obtained from an inclusive sample of simulated ${\mathrm{t} \mathrm{\bar{t}}}$ events. The efficiency curves are shown separately for the split (circular marker), GMSB (square), and RPV (triangle) SUSY benchmark models, assuming ${c\tau _{0}}$ values of 1 m (upper row) and 1 mm (lower row). |
png pdf |
Figure 7:
The LLP jet tagging efficiency, using a working point that yields a mistag rate of 0.01% for the udsg jet class obtained from an inclusive sample of simulated ${\mathrm{t} \mathrm{\bar{t}}}$ events, when (left) the DNN is evaluated as a function of the model parameter value ${c\tau _{0}}$ for an uncompressed and a compressed split SUSY model, and (right) the DNN is evaluated over a range of ${c\tau _{0}}$ values for uncompressed split SUSY models generated with $ {c\tau _{0}} = $ 1 mm and 1 m; the dashed vertical lines indicate equality for the evaluated and generated values of ${c\tau _{0}}$ for each model. The fixed model parameters are defined in the legends. |
png pdf |
Figure 7-a:
The LLP jet tagging efficiency, using a working point that yields a mistag rate of 0.01% for the udsg jet class obtained from an inclusive sample of simulated ${\mathrm{t} \mathrm{\bar{t}}}$ events, when (left) the DNN is evaluated as a function of the model parameter value ${c\tau _{0}}$ for an uncompressed and a compressed split SUSY model, and (right) the DNN is evaluated over a range of ${c\tau _{0}}$ values for uncompressed split SUSY models generated with $ {c\tau _{0}} = $ 1 mm and 1 m; the dashed vertical lines indicate equality for the evaluated and generated values of ${c\tau _{0}}$ for each model. The fixed model parameters are defined in the legends. |
png pdf |
Figure 7-b:
The LLP jet tagging efficiency, using a working point that yields a mistag rate of 0.01% for the udsg jet class obtained from an inclusive sample of simulated ${\mathrm{t} \mathrm{\bar{t}}}$ events, when (left) the DNN is evaluated as a function of the model parameter value ${c\tau _{0}}$ for an uncompressed and a compressed split SUSY model, and (right) the DNN is evaluated over a range of ${c\tau _{0}}$ values for uncompressed split SUSY models generated with $ {c\tau _{0}} = $ 1 mm and 1 m; the dashed vertical lines indicate equality for the evaluated and generated values of ${c\tau _{0}}$ for each model. The fixed model parameters are defined in the legends. |
png pdf |
Figure 8:
Expected lower limits (95% CL) on ${m_{{\mathrm{\tilde{g}}}}}$ as a function of ${c\tau _{0}}$ for split SUSY models with an uncompressed (left) and a very compressed (right) mass spectrum. The shaded bands indicate the total uncertainty from both statistical and systematic sources. The model assumptions are indicated by the legends. The results are compared to the expected limits obtained in Ref. [28], indicated by a dashed line. |
png pdf |
Figure 8-a:
Expected lower limits (95% CL) on ${m_{{\mathrm{\tilde{g}}}}}$ as a function of ${c\tau _{0}}$ for split SUSY models with an uncompressed (left) and a very compressed (right) mass spectrum. The shaded bands indicate the total uncertainty from both statistical and systematic sources. The model assumptions are indicated by the legends. The results are compared to the expected limits obtained in Ref. [28], indicated by a dashed line. |
png pdf |
Figure 8-b:
Expected lower limits (95% CL) on ${m_{{\mathrm{\tilde{g}}}}}$ as a function of ${c\tau _{0}}$ for split SUSY models with an uncompressed (left) and a very compressed (right) mass spectrum. The shaded bands indicate the total uncertainty from both statistical and systematic sources. The model assumptions are indicated by the legends. The results are compared to the expected limits obtained in Ref. [28], indicated by a dashed line. |
png pdf |
Figure 9:
The negative log-likelihood of a maximum likelihood fit to the Asimov data set as a function of the expected gluino production cross section for a (left) uncompressed and (right) compressed scenario. The black solid (dashed) line indicate the 68% (95%) CL, while the white dashed lines indicate the SF constraints (68% and 95% CL) at $r = r_\text {UL}$. The product of the LLP jet tagger efficiency and the SF is bound to [0,1]. |
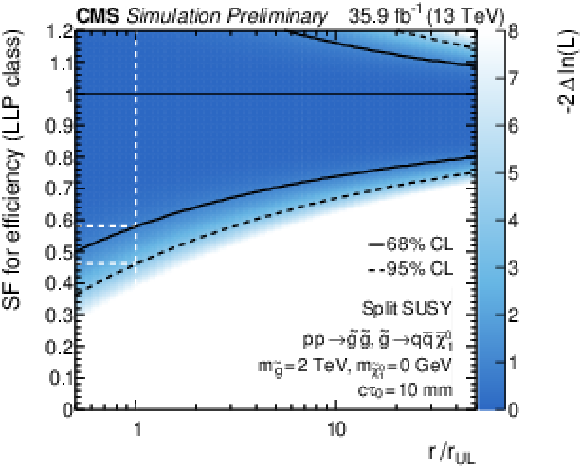
png pdf |
Figure 9-a:
The negative log-likelihood of a maximum likelihood fit to the Asimov data set as a function of the expected gluino production cross section for a (left) uncompressed and (right) compressed scenario. The black solid (dashed) line indicate the 68% (95%) CL, while the white dashed lines indicate the SF constraints (68% and 95% CL) at $r = r_\text {UL}$. The product of the LLP jet tagger efficiency and the SF is bound to [0,1]. |
png pdf |
Figure 9-b:
The negative log-likelihood of a maximum likelihood fit to the Asimov data set as a function of the expected gluino production cross section for a (left) uncompressed and (right) compressed scenario. The black solid (dashed) line indicate the 68% (95%) CL, while the white dashed lines indicate the SF constraints (68% and 95% CL) at $r = r_\text {UL}$. The product of the LLP jet tagger efficiency and the SF is bound to [0,1]. |
| Tables | |
png pdf |
Table 1:
A priori expected counts and uncertainties for SM backgrounds and split SUSY models, as determined from simulation, in categories defined by ${H_\mathrm {T}}$ and (${N_\text {jet}}$, ${N_\text {tag}}$). The uncompressed and compressed split SUSY models are defined in Section 4. The value of ${c\tau _{0}}$ is assumed to be 1 mm. The uncertainties include both statistical and systematic contributions. Expected counts for events that satisfy $ {N_\text {tag}} < $ 2 are not shown. |
| Summary |
|
Many models of new physics beyond the standard model predict the production of long-lived particles (LLPs) in proton-proton (pp) collisions at the LHC. Jets arising from the decay of LLPs (LLP jets) can be appreciably displaced from the pp collisions. The development of a novel tagger to identify LLP jets is presented. The tagger employs a deep neutral network (DNN) using an architecture inspired by the DEEPJET algorithm. Simplified models of split supersymmetry (SUSY), which yield neutralinos and LLP jets from the decay of long-lived gluinos, are used to train the DNN and demonstrate its performance. The application of various techniques related to the tagger are reported. A custom labelling scheme for LLP jets based on truth information from Monte Carlo generator programs is defined. The proper decay length ${c\tau_{0}}$ of the gluino is used as an external parameter to the DNN, which allows hypothesis testing over several orders of magnitude in ${c\tau_{0}}$ with a single DNN. The DNN was trained using both simulated and pp collision data using domain adaptation by backward propagation. This approach significantly improves the agreement between simulation and data, by an order of magnitude according to the Jensen-Shannon divergence, when compared to training the DNN with simulation only. The method is validated using signal-depleted control samples of pp collisions at a centre-of-mass energy of 13 TeV. The samples were recorded by the CMS experiment and correspond to an integrated luminosity of 35.9 fb$^{-1}$. Training the DNN with pp collision data does not significantly degrade the tagger performance. The tagger rejects 99.99% of light-flavour jets from SM processes, as measured in an inclusive $\mathrm{t\bar{t}}$ sample, while retaining approximately 30-80% of LLP jets for split SUSY models with 1 mm $\leq \text{c}\tau_0 \leq$ 10 m and a gluino-neutralino mass difference of at least 200 GeV. Finally, the potential performance of the tagger is demonstrated through its use in a search for split SUSY in final states containing jets and significant transverse missing momentum. Simulated events samples provide the expected contributions from SM background processes. Candidate signal events were categorized according to the scalar sum of jet momenta, the number of jets, and the number of tagged LLP jets. Expected lower limits on the gluino mass (95% CL) are determined with a binned likelihood fit as a function of ${c\tau_{0}}$ in the range from 10 m to 10 m. A procedure to constrain a correction to the LLP jet tagger efficiency in the likelihood fit is introduced. Competitive limits are demonstrated: long-lived gluinos of mass $>$ 2 TeV and proper decay length 1 mm $ \leq {c\tau_{0}} \leq $ 1 m are expected to be excluded by this search. |
| References | ||||
| 1 | K. Albertsson et al. | Machine learning in high energy physics community white paper | J. Phys. Conf. Ser. 1085 (2018) 022008 | 1807.02876 |
| 2 | A. J. Larkoski, I. Moult, and B. Nachman | Jet substructure at the Large Hadron Collider: a review of recent advances in theory and machine learning | Submitted to Phys. Rept | 1709.04464 |
| 3 | ATLAS Collaboration | The ATLAS experiment at the CERN Large Hadron Collider | JINST 3 (2008) S08003 | |
| 4 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 5 | ATLAS Collaboration | ATLAS b-jet identification performance and efficiency measurement with $ \mathrm{t\bar{t}} $ events in pp collisions at $ \sqrt{s} = $ 13 TeV | Submitted to EPJC | 1907.05120 |
| 6 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 7 | M. Stoye | Deep learning in jet reconstruction at CMS | J. Phys. Conf. Ser. 1085 (2018) 042029 | |
| 8 | CMS Collaboration | Performance of the DeepJet b tagging algorithm using 41.9/fb of data from proton-proton collisions at 13 TeV with Phase 1 CMS detector | CDS | |
| 9 | N. Arkani-Hamed and S. Dimopoulos | Supersymmetric unification without low energy supersymmetry and signatures for fine-tuning at the LHC | JHEP 06 (2005) 073 | hep-th/0405159 |
| 10 | G. F. Giudice and A. Romanino | Split supersymmetry | NPB 699 (2004) 65 | hep-ph/0406088 |
| 11 | J. L. Hewett, B. Lillie, M. Masip, and T. G. Rizzo | Signatures of long-lived gluinos in split supersymmetry | JHEP 09 (2004) 070 | hep-ph/0408248 |
| 12 | G. F. Giudice and R. Rattazzi | Theories with gauge mediated supersymmetry breaking | PR 322 (1999) 419 | hep-ph/9801271 |
| 13 | M. J. Strassler and K. M. Zurek | Discovering the Higgs through highly-displaced vertices | PLB 661 (2008) 263 | hep-ph/0605193 |
| 14 | T. Han, Z. Si, K. M. Zurek, and M. J. Strassler | Phenomenology of hidden valleys at hadron colliders | JHEP 07 (2008) 008 | 0712.2041 |
| 15 | D. Alves et al. | Simplified models for LHC new physics searches | JPG 39 (2012) 105005 | 1105.2838 |
| 16 | O. Buchmueller et al. | Simplified models for displaced dark matter signatures | JHEP 09 (2017) 076 | 1704.06515 |
| 17 | J. Alimena et al. | Searching for long-lived particles beyond the standard model at the Large Hadron Collider | 1903.04497 | |
| 18 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 19 | CMS Collaboration | Search for long-lived charged particles in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 94 (2016) 112004 | CMS-EXO-15-010 1609.08382 |
| 20 | LHCb Collaboration | Updated search for long-lived particles decaying to jet pairs | EPJC 77 (2017) 812 | 1705.07332 |
| 21 | ATLAS Collaboration | Search for long-lived neutral particles in pp collisions at $ \sqrt{s} = $ 13 TeV that decay into displaced hadronic jets in the ATLAS calorimeter | EPJC 79 (2019) 481 | 1902.03094 |
| 22 | ATLAS Collaboration | Search for heavy charged long-lived particles in the ATLAS detector in 36.1 fb$ ^{-1} $ of proton-proton collision data at $ \sqrt{s} = $ 13 TeV | PRD 99 (2019) 092007 | 1902.01636 |
| 23 | ATLAS Collaboration | Search for long-lived particles produced in pp collisions at $ \sqrt{s} = $ 13 TeV that decay into displaced hadronic jets in the ATLAS muon spectrometer | PRD 99 (2019) 052005 | 1811.07370 |
| 24 | CMS Collaboration | Search for long-lived particles using nonprompt jets and missing transverse momentum with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 797 (2019) 134876 | CMS-EXO-19-001 1906.06441 |
| 25 | CMS Collaboration | Search for long-lived particles decaying into displaced jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 99 (2019) 032011 | CMS-EXO-18-007 1811.07991 |
| 26 | CMS Collaboration | Search for long-lived particles with displaced vertices in multijet events in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 98 (2018) 092011 | CMS-EXO-17-018 1808.03078 |
| 27 | CMS Collaboration | Search for decays of stopped exotic long-lived particles produced in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2018) 127 | CMS-EXO-16-004 1801.00359 |
| 28 | CMS Collaboration | Search for natural and split supersymmetry in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in final states with jets and missing transverse momentum | JHEP 05 (2018) 025 | CMS-SUS-16-038 1802.02110 |
| 29 | CMS Collaboration | Search for new long-lived particles at $ \sqrt{s} = $ 13 TeV | PLB 780 (2018) 432 | CMS-EXO-16-003 1711.09120 |
| 30 | P. Baldi et al. | Parameterized neural networks for high-energy physics | EPJC 76 (2016) 235 | 1601.07913 |
| 31 | R. Barbier et al. | R-parity violating supersymmetry | PR 420 (2005) 1 | hep-ph/0406039 |
| 32 | Y. Ganin and V. Lempitsky | Unsupervised domain adaptation by backpropagation | 1409.7495 | |
| 33 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 34 | M. Cacciari, G. P. Salam, and G. Soyez | $ FastJet $ user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 35 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 36 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 37 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 38 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 39 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 40 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) 11002 | CMS-JME-10-011 1107.4277 |
| 41 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 42 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 43 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 44 | CMS Collaboration | Search for supersymmetry in pp collisions at 7 TeV in events with jets and missing transverse energy | PLB 698 (2011) 196 | CMS-SUS-10-003 1101.1628 |
| 45 | S. Dimopoulos, S. Raby, and F. Wilczek | Supersymmetry and the scale of unification | PRD 24 (1981) 1681 | |
| 46 | L. E. Ibanez and G. G. Ross | Low-energy predictions in supersymmetric grand unified theories | PLB 105 (1981) 439 | |
| 47 | W. J. Marciano and G. Senjanovi\'c | Predictions of supersymmetric grand unified theories | PRD 25 (1982) 3092 | |
| 48 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 49 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 50 | T. Sjostrand et al. | An introduction to $ PYTHIA $ 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 51 | M. Fairbairn et al. | Stable massive particles at colliders | PR 438 (2007) 1 | hep-ph/0611040 |
| 52 | A. C. Kraan | Interactions of heavy stable hadronizing particles | EPJC 37 (2004) 91 | hep-ex/0404001 |
| 53 | R. Mackeprang and A. Rizzi | Interactions of coloured heavy stable particles in matter | EPJC 50 (2007) 353 | hep-ph/0612161 |
| 54 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 55 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 56 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the $ POWHEG $ method | JHEP 11 (2007) 070 | 0709.2092 |
| 57 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the $ POWHEG $ box | JHEP 06 (2010) 043 | 1002.2581 |
| 58 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 59 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in $ POWHEG: s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 60 | E. Re | Single-top Wt-channel production matched with parton showers using the $ POWHEG $ method | EPJC 71 (2011) 1547 | 1009.2450 |
| 61 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | $ \mathrm{W} $ physics at the LHC with $ FEWZ $ 2.1 | CPC 184 (2013) 208 | 1201.5896 |
| 62 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | $ FEWZ $ 2.0: a code for hadronic $ \mathrm{Z} $ production at next-to-next-to-leading order | CPC 182 (2011) 2388 | 1011.3540 |
| 63 | M. Czakon and A. Mitov | Top++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 64 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} = 13, 14, 33 $ and 100 TeV | EPJC 74 (2014) 3174 | 1407.5066 |
| 65 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 66 | CMS Collaboration | Investigations of the impact of the parton shower tuning in $ PYTHIA $ 8 in the modelling of $ \mathrm{t\bar{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 67 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 68 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 69 | X. Glorot, A. Bordes, and Y. Bengio | Deep sparse rectifier neural networks | in Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, volume 15, p. 315 2011 | |
| 70 | N. Srivastava et al. | Dropout: a simple way to prevent neural networks from overfitting | JMLR 15 (2014) 1929 | |
| 71 | D. P. Kingma and J. Ba | Adam: a method for stochastic optimization | 1412.6980 | |
| 72 | M. Abadi et al. | TensorFlow: large-scale machine learning on heterogeneous systems | 1603.04467 | |
| 73 | F. Chollet | |||
| 74 | R. Brun and F. Rademakers | ROOT: an object oriented data analysis framework | NIMA 389 (1997) 81 | |
| 75 | J. Lin | Divergence measures based on the Shannon entropy | IEEE Trans. Inf. Theor. 37 (2006) 145 | |
| 76 | S. Kallweit et al. | NLO QCD+EW predictions for V+jets including off-shell vector-boson decays and multijet merging | JHEP 04 (2016) 021 | 1511.08692 |
| 77 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s} = $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 78 | A. Kalogeropoulos and J. Alwall | The SysCalc code: a tool to derive theoretical systematic uncertainties | 1801.08401 | |
| 79 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 80 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | CPC 77 (1993) 219 | |
| 81 | ATLAS and CMS Collaborations, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS-NOTE-2011-005 | |
| 82 | T. Junk | Confidence level computation for combining searches with small statistics | Nucl. Instr. Meth. A 434 (1999) 435 | hep-ex/9902006 |
| 83 | A. L. Read | Presentation of search results: the CLs technique | JPG 28 (2002) 2693 | |
| 84 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|