

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-18-007 ; CERN-EP-2018-289 | ||
| Search for long-lived particles decaying into displaced jets in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 19 November 2018 | ||
| Phys. Rev. D 99 (2019) 032011 | ||
| Abstract: A search for long-lived particles decaying into jets is presented. Data were collected with the CMS detector at the LHC from proton-proton collisions at a center-of-mass energy of 13 TeV in 2016, corresponding to an integrated luminosity of 35.9 fb$^{-1}$ . The search examines the distinctive topology of displaced tracks and secondary vertices. The selected events are found to be consistent with standard model predictions. For a simplified model in which long-lived neutral particles are pair produced and decay to two jets, pair production cross sections larger than 0.2 fb are excluded at 95% confidence level for a long-lived particle mass larger than 1000 GeV and proper decay lengths between 3 and 130 mm. Several supersymmetry models with gauge-mediated supersymmetry breaking or $R$-parity violation, where pair-produced long-lived gluinos or top squarks decay to several final-state topologies containing displaced jets, are also tested. For these models, in the mass ranges above 200 GeV, gluino masses up to 2300-2400 GeV and top squark masses up to 1350-1600 GeV are excluded for proper decay lengths approximately between 10 and 100 mm. These are the most restrictive limits to date on these models. | ||
| Links: e-print arXiv:1811.07991 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
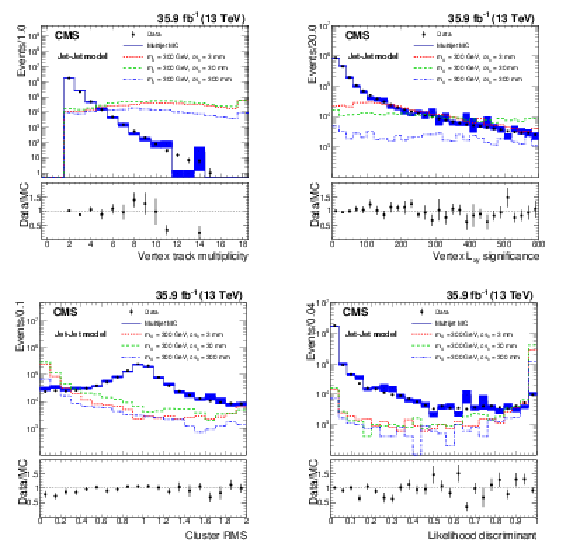
Figure 1:
The distributions of vertex track multiplicity (upper left), vertex $L_{\mathrm {xy}}$ significance (upper right), cluster RMS (lower left), and likelihood discriminant (lower right), for data, simulated QCD multijet events, and simulated signal events. The lower panel of each plot shows the ratio between the data and the simulated QCD multijet events. Data and simulated events are selected with the displaced-jet trigger. The offline $ {H_{\mathrm {T}}} $ is required to be larger than 400 GeV, and the jets are required to have $ {p_{\mathrm {T}}} > $ 50 GeV and $ | \eta | < 2.0$. The error bars and bands represent the statistical uncertainties of each distribution. Three benchmark signal distributions are shown (dashed lines) for the Jet-Jet model with $m_{X} = $ 300 GeV and varying lifetimes. For visualization each signal process is given a cross section, $\sigma $, such that $\sigma \times$ 35.9 fb$^{-1}$ $= 1\times 10^{6}$. |

png pdf |
Figure 1-a:
The distribution of vertex track multiplicity for data, simulated QCD multijet events, and simulated signal events. The lower panel shows the ratio between the data and the simulated QCD multijet events. Data and simulated events are selected with the displaced-jet trigger. The offline $ {H_{\mathrm {T}}} $ is required to be larger than 400 GeV, and the jets are required to have $ {p_{\mathrm {T}}} > $ 50 GeV and $ | \eta | < 2.0$. The error bars and bands represent the statistical uncertainties. Three benchmark signal distributions are shown (dashed lines) for the Jet-Jet model with $m_{X} = $ 300 GeV and varying lifetimes. For visualization each signal process is given a cross section, $\sigma $, such that $\sigma \times$ 35.9 fb$^{-1}$ $= 1\times 10^{6}$. |
png pdf |
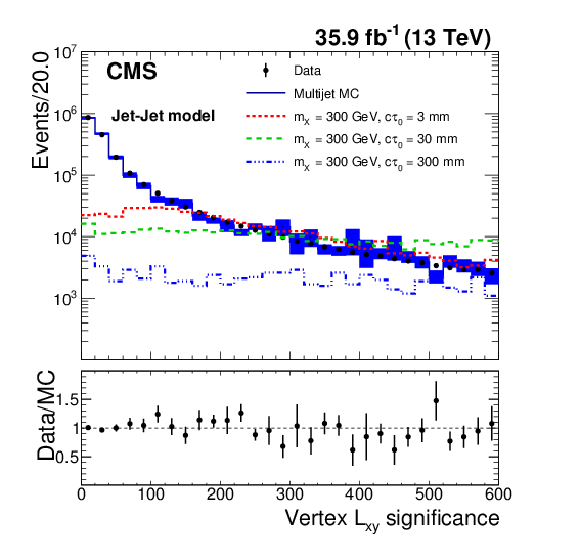
Figure 1-b:
The distribution of vertex $L_{\mathrm {xy}}$ significance for data, simulated QCD multijet events, and simulated signal events. The lower panel shows the ratio between the data and the simulated QCD multijet events. Data and simulated events are selected with the displaced-jet trigger. The offline $ {H_{\mathrm {T}}} $ is required to be larger than 400 GeV, and the jets are required to have $ {p_{\mathrm {T}}} > $ 50 GeV and $ | \eta | < 2.0$. The error bars and bands represent the statistical uncertainties. Three benchmark signal distributions are shown (dashed lines) for the Jet-Jet model with $m_{X} = $ 300 GeV and varying lifetimes. For visualization each signal process is given a cross section, $\sigma $, such that $\sigma \times$ 35.9 fb$^{-1}$ $= 1\times 10^{6}$. |
png pdf |
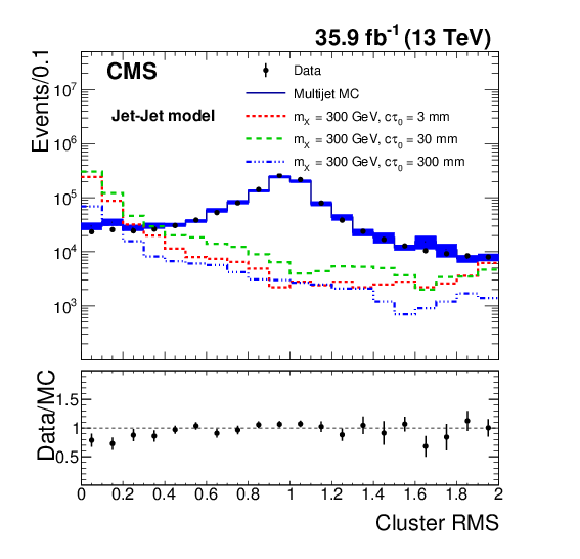
Figure 1-c:
The distribution of cluster RMS for data, simulated QCD multijet events, and simulated signal events. The lower panel shows the ratio between the data and the simulated QCD multijet events. Data and simulated events are selected with the displaced-jet trigger. The offline $ {H_{\mathrm {T}}} $ is required to be larger than 400 GeV, and the jets are required to have $ {p_{\mathrm {T}}} > $ 50 GeV and $ | \eta | < 2.0$. The error bars and bands represent the statistical uncertainties. Three benchmark signal distributions are shown (dashed lines) for the Jet-Jet model with $m_{X} = $ 300 GeV and varying lifetimes. For visualization each signal process is given a cross section, $\sigma $, such that $\sigma \times$ 35.9 fb$^{-1}$ $= 1\times 10^{6}$. |
png pdf |
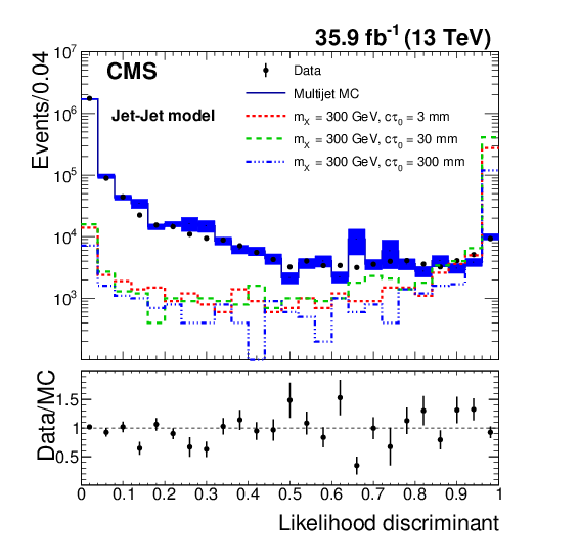
Figure 1-d:
The distribution of likelihood discriminant for data, simulated QCD multijet events, and simulated signal events. The lower panel shows the ratio between the data and the simulated QCD multijet events. Data and simulated events are selected with the displaced-jet trigger. The offline $ {H_{\mathrm {T}}} $ is required to be larger than 400 GeV, and the jets are required to have $ {p_{\mathrm {T}}} > $ 50 GeV and $ | \eta | < 2.0$. The error bars and bands represent the statistical uncertainties. Three benchmark signal distributions are shown (dashed lines) for the Jet-Jet model with $m_{X} = $ 300 GeV and varying lifetimes. For visualization each signal process is given a cross section, $\sigma $, such that $\sigma \times$ 35.9 fb$^{-1}$ $= 1\times 10^{6}$. |

png pdf |
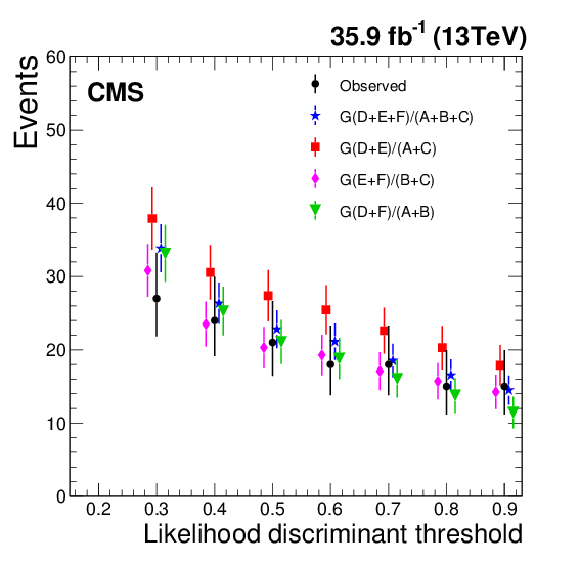
Figure 2:
Numbers of predicted and observed background events for the nominal background method and the three cross checks in the control region. Shown are the comparisons for likelihood discriminant thresholds of 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9 (left); and for thresholds of 0.95, 0.96, 0.97, 0.98, 0.99, and 0.9993 (right). The error bars represent the statistical uncertainties of the predictions and the observations. The data points at different likelihood discriminant thresholds are correlated, since the events passing higher likelihood discriminant thresholds also pass lower likelihood discriminant thresholds. |
png pdf |
Figure 2-a:
Numbers of predicted and observed background events for the nominal background method and the three cross checks in the control region. Shown are the comparisons for likelihood discriminant thresholds of 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9. The error bars represent the statistical uncertainties of the predictions and the observations. The data points at different likelihood discriminant thresholds are correlated, since the events passing higher likelihood discriminant thresholds also pass lower likelihood discriminant thresholds. |

png pdf |
Figure 2-b:
Numbers of predicted and observed background events for the nominal background method and the three cross checks in the control region. Shown are the comparisons for likelihood discriminant thresholds of 0.95, 0.96, 0.97, 0.98, 0.99, and 0.9993. The error bars represent the statistical uncertainties of the predictions and the observations. The data points at different likelihood discriminant thresholds are correlated, since the events passing higher likelihood discriminant thresholds also pass lower likelihood discriminant thresholds. |
png pdf |
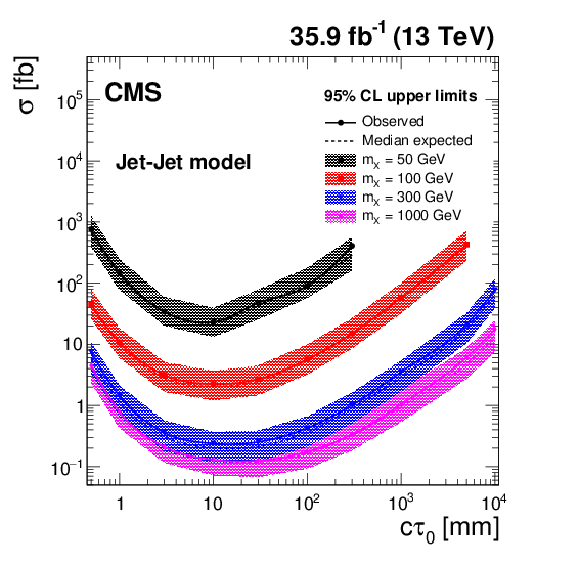
Figure 3:
The expected and observed 95% CL upper limits on the pair production cross section of the long-lived particle X, assuming a 100% branching fraction for X to decay to a quark-antiquark pair, shown at different particle X masses and proper decay lengths for the Jet-Jet model. The solid (dashed) lines represent the observed (median expected) limits. The shaded bands represent the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. |

png pdf |
Figure 4:
Left : the expected and observed 95% CL upper limits on the pair production cross section of the long-lived gluino, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {g}} {\tilde{\mathrm {G}}} $ decays. The horizontal lines indicate the NLO+NLL gluino pair production cross sections for $m_{{\tilde{\mathrm {g}}}} = $ 2400 GeV and $m_{{\tilde{\mathrm {g}}}} = $ 1600 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. Right : the expected and observed 95% CL limits for the long-lived gluino model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {g}} {\tilde{\mathrm {G}}} $ decays, based on the NLO+NLL calculation of the gluino pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distribution of the expected limits under the background-only hypothesis. |

png pdf |
Figure 4-a:
The expected and observed 95% CL upper limits on the pair production cross section of the long-lived gluino, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {g}} {\tilde{\mathrm {G}}} $ decays. The horizontal lines indicate the NLO+NLL gluino pair production cross sections for $m_{{\tilde{\mathrm {g}}}} = $ 2400 GeV and $m_{{\tilde{\mathrm {g}}}} = $ 1600 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. |
png pdf |
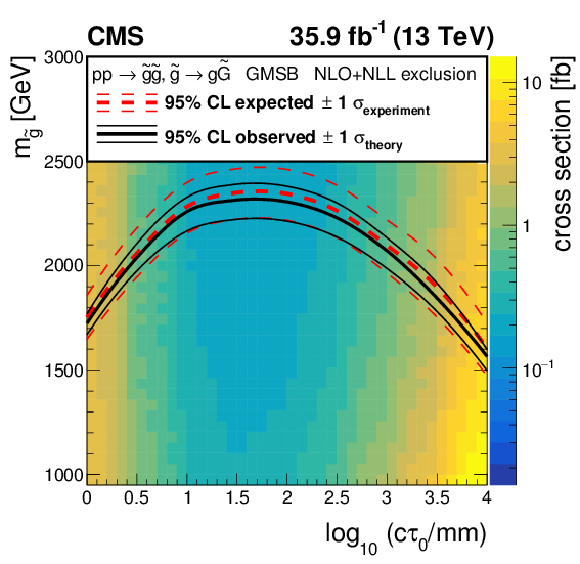
Figure 4-b:
The expected and observed 95% CL limits for the long-lived gluino model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {g}} {\tilde{\mathrm {G}}} $ decays, based on the NLO+NLL calculation of the gluino pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distribution of the expected limits under the background-only hypothesis. |
png pdf |
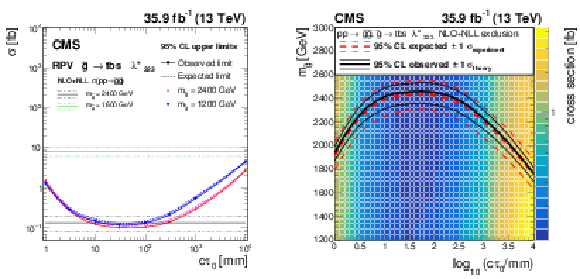
Figure 5:
Left : the expected and observed 95% CL upper limits on the pair production cross section of the long-lived gluino, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ decays. The horizontal lines indicate the NLO+NLL gluino pair production cross sections for $m_{{\tilde{\mathrm {g}}}} = $ 2400 GeV and $m_{{\tilde{\mathrm {g}}}} = $ 1600 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. Right : the expected and observed 95% CL limits for the long-lived gluino model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ decays, based on the NLO+NLL calculation of the gluino pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distributions of the expected limits under the background-only hypothesis. |

png pdf |
Figure 5-a:
The expected and observed 95% CL upper limits on the pair production cross section of the long-lived gluino, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ decays. The horizontal lines indicate the NLO+NLL gluino pair production cross sections for $m_{{\tilde{\mathrm {g}}}} = $ 2400 GeV and $m_{{\tilde{\mathrm {g}}}} = $ 1600 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. |

png pdf |
Figure 5-b:
The expected and observed 95% CL limits for the long-lived gluino model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ decays, based on the NLO+NLL calculation of the gluino pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distributions of the expected limits under the background-only hypothesis. |
png pdf |
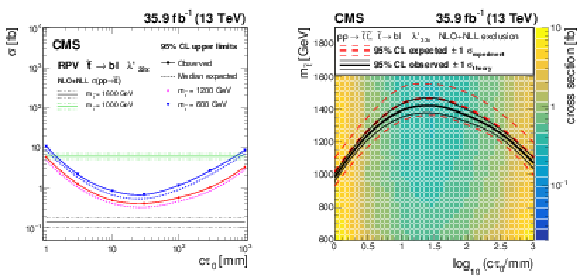
Figure 6:
Left : the expected and observed 95% CL upper limits on the pair production cross section of the long-lived top squark, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\mathrm {b}}\ell $ decays. The horizontal lines indicate the NLO+NLL top squark pair production cross sections for $m_{{\tilde{\mathrm {t}}}} = $ 1600 GeV and $m_{{\tilde{\mathrm {t}}}} = $ 1000 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. Right : the expected and observed 95% limits for the long-lived top squark model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\mathrm {b}}\ell $ decays, based on the NLO+NLL calculation of the top squark pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distributions of the expected limits under the background-only hypothesis. |

png pdf |
Figure 6-a:
The expected and observed 95% CL upper limits on the pair production cross section of the long-lived top squark, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\mathrm {b}}\ell $ decays. The horizontal lines indicate the NLO+NLL top squark pair production cross sections for $m_{{\tilde{\mathrm {t}}}} = $ 1600 GeV and $m_{{\tilde{\mathrm {t}}}} = $ 1000 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. |
png pdf |
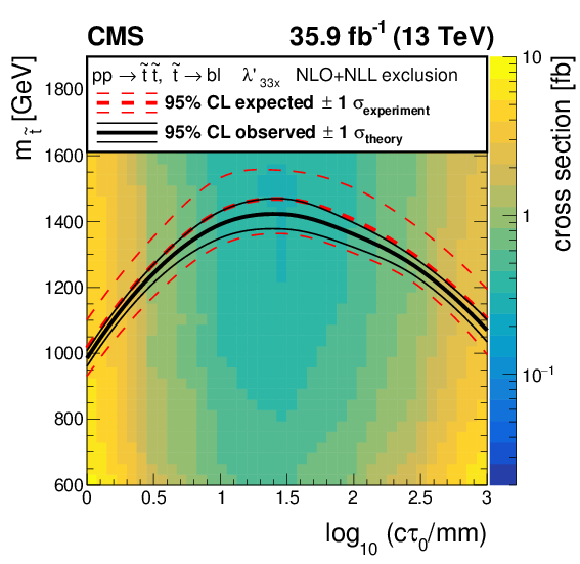
Figure 6-b:
The expected and observed 95% limits for the long-lived top squark model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\mathrm {b}}\ell $ decays, based on the NLO+NLL calculation of the top squark pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distributions of the expected limits under the background-only hypothesis. |
png pdf |
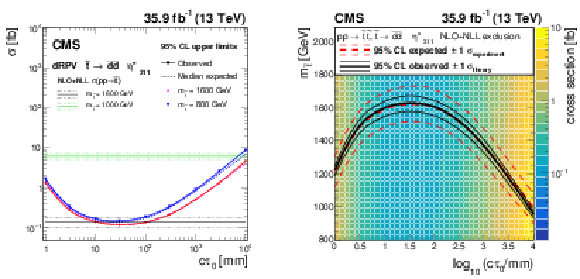
Figure 7:
Left : the expected and observed 95% CL upper limits on the the pair production cross section of the long-lived top squark, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ decays. The horizontal lines indicate the NLO+NLL top squark pair production cross sections for $m_{{\tilde{\mathrm {t}}}} = $ 1600 GeV and $m_{{\tilde{\mathrm {t}}}} = $ 1000 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. Right : the expected and observed 95% limits for the long-lived top squark model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ decays, based on an NLO+NLL calculation of the top squark pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distribution of the expected limits under the background-only hypothesis. |
png pdf |
Figure 7-a:
The expected and observed 95% CL upper limits on the the pair production cross section of the long-lived top squark, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ decays. The horizontal lines indicate the NLO+NLL top squark pair production cross sections for $m_{{\tilde{\mathrm {t}}}} = $ 1600 GeV and $m_{{\tilde{\mathrm {t}}}} = $ 1000 GeV, as well as their variations due to the uncertainties in the choices of renormalization scales, factorization scales, and PDF sets. The solid (dashed) lines represent the observed (median expected) limits, the bands show the regions containing 68% of the distributions of the expected limits under the background-only hypothesis. |

png pdf |
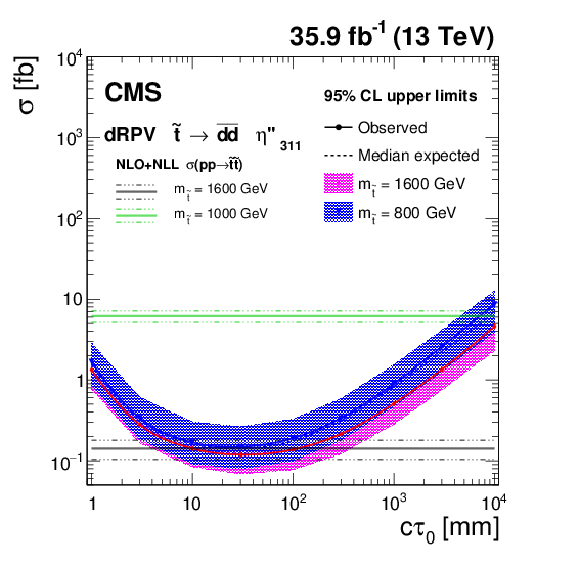
Figure 7-b:
The expected and observed 95% limits for the long-lived top squark model in the mass-lifetime plane, assuming a 100% branching fraction for $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ decays, based on an NLO+NLL calculation of the top squark pair production cross section at $\sqrt {s} = $ 13 TeV. The thick solid black (dashed red) line represents the observed (median expected) limits at 95% CL . The thin black lines represent the change in the observed limit due to the variation of the signal cross sections within their theoretical uncertainties. The thin red lines indicate the region containing 68% of the distribution of the expected limits under the background-only hypothesis. |

png pdf |
Figure 8:
Comparison with search for displaced vertices in multijet events at $\sqrt {s} = $ 13 TeV with the CMS detector [36] (referred to as the CMS DV search) for $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ (left) and $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ (right) models. The CMS DV search looks for a pair of displaced vertices within the beam pipe. The observed limits obtained by the CMS DV search (purple curves) are overlaid with the limits obtained by the search presented in this paper in the mass-lifetime plane, and are good complements for proper decay length $c\tau _{0} < 10 mm $ in these two signal models. |

png pdf |
Figure 8-a:
Comparison with search for displaced vertices in multijet events at $\sqrt {s} = $ 13 TeV with the CMS detector [36] (referred to as the CMS DV search) for the $ {\tilde{\mathrm {g}}} \to {\mathrm {t}} {\mathrm {b}} {\mathrm {s}}$ model. The CMS DV search looks for a pair of displaced vertices within the beam pipe. The observed limits obtained by the CMS DV search (purple curves) are overlaid with the limits obtained by the search presented in this paper in the mass-lifetime plane, and are good complements for proper decay length $c\tau _{0} < 10 mm $ in this model. |

png pdf |
Figure 8-b:
Comparison with search for displaced vertices in multijet events at $\sqrt {s} = $ 13 TeV with the CMS detector [36] (referred to as the CMS DV search) for the $ {\tilde{\mathrm {t}}} \to {\overline {\mathrm {d}}} {\overline {\mathrm {d}}}$ model. The CMS DV search looks for a pair of displaced vertices within the beam pipe. The observed limits obtained by the CMS DV search (purple curves) are overlaid with the limits obtained by the search presented in this paper in the mass-lifetime plane, and are good complements for proper decay length $c\tau _{0} < 10 mm $ in this model. |
| Tables | |

png pdf |
Table 1:
Summary of the preselection criteria |

png pdf |
Table 2:
The definition of the different regions used in the background estimation. |
png pdf |
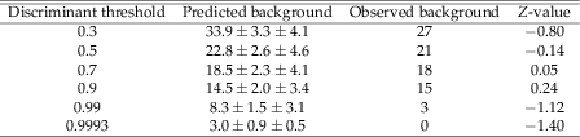
Table 3:
The predicted and observed background in the control region for different likelihood discriminant thresholds. The background predictions are shown together with their statistical (first) and systematic (second) uncertainties (the systematic uncertainties in the background predictions are described in Section xxxxx). The observed significances are also shown in terms of $Z$-values, and are smaller than 1.5 standard deviations. |
png pdf |
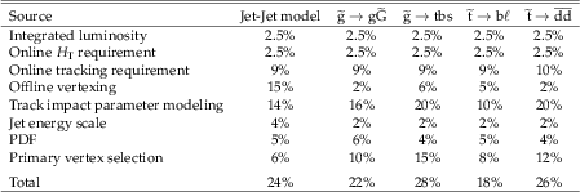
Table 4:
Systematic uncertainties in the signal yields, for each signal model studied. The quoted values reflect the largest variations due to each source for each signal model, in the studied range of masses and proper decay lengths. |

png pdf |
Table 5:
Summary of predicted and observed events in the signal region, for different $ {H_{\mathrm {T}}} $ and number of dijet candidates values. |
png pdf |
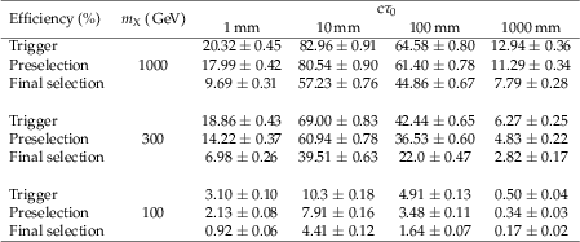
Table 6:
Signal efficiencies (in%) for the Jet-Jet model at different proper decay lengths $c\tau _{0}$ and different masses $m_{\mathrm {X}}$. Selection requirements are cumulative from the first row to the last. Uncertainties are statistical only. |
png pdf |
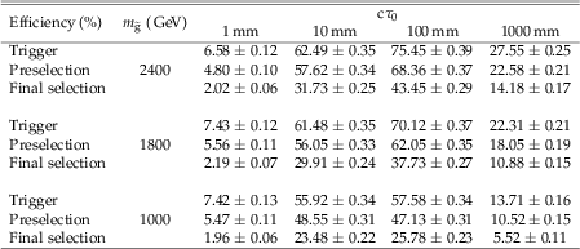
Table 7:
Signal efficiencies (in%) for pair produced long-lived gluinos decaying to a gluon and a gravitino at different proper decay lengths $c\tau _{0}$ and different gluino masses $m_{{\tilde{\mathrm {g}}}}$. Selection requirements are cumulative from the first row to the last. Uncertainties are statistical only. |
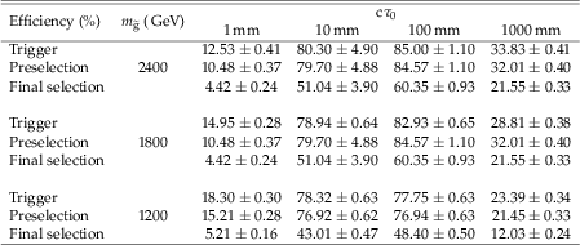
png pdf |
Table 8:
Signal efficiencies (in%) for pair produced long-lived gluinos decaying to top, bottom and strange antiquarks at different proper decay lengths $c\tau _{0}$ and different gluino masses $m_{{\tilde{\mathrm {g}}}}$. Selection requirements are cumulative from the first row to the last. Uncertainties are statistical only. |
png pdf |
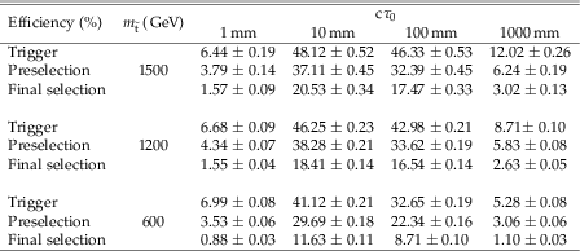
Table 9:
Signal efficiencies (in%) for pair produced long-lived top squarks decaying to a bottom quark and a lepton at different proper decay lengths $c\tau _{0}$ and different top squark masses $m_{{\tilde{\mathrm {t}}}}$. Selection requirements are cumulative from the first row to the last. Uncertainties are statistical only. |

png pdf |
Table 10:
Signal efficiencies (in%) for pair produced long-lived top squarks decaying to two down antiquarks at different proper decay lengths $c\tau _{0}$ and different top squark masses $m_{{\tilde{\mathrm {t}}}}$. Selection requirements are cumulative from the first row to the last. Uncertainties are statistical only. |
| Summary |
| A search for long-lived particles decaying to jets is presented, based on proton-proton collision data collected with the CMS experiment at a center-of-mass energy of 13 TeV in 2016, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. The analysis utilizes a dedicated trigger to capture events with displaced-jet signatures, and exploits jet, track, and secondary vertex information to discriminate displaced-jet candidate events from those produced by the standard model and instrumental backgrounds. The observed yields in data are in agreement with the background predictions. For a variety of models, we set the best limits to date for long-lived particles with proper decay lengths approximately between 5 mm and 10 m. Upper limits are set at 95% confidence level on the pair production cross section of long-lived neutral particles decaying to two jets, for different masses and proper lifetimes, and are as low as 0.2 fb at high mass ($m_{\mathrm{X}} > $ 1000 GeV) for proper decay lengths between 3 and 130 mm. A supersymmetric (SUSY) model with gauge-mediated supersymmetry breaking (GMSB) is also tested, in which the long-lived gluino can decay to one jet and a lightest SUSY particle. Upper limits are set on the pair production cross section of the gluino with different masses and proper decay lengths $c\tau_{0}$. Pair-produced long-lived gluinos lighter than 2300 GeV are excluded for proper decay lengths between 20 and 110 mm. For an $R$-parity violating (RPV) SUSY model, where the long-lived gluino can decay to top, bottom, and strange antiquarks, pair-produced gluinos lighter than 2400 GeV are excluded for decay lengths between 10 and 250 mm. For a second RPV SUSY model, in which the long-lived top squark can decay to one bottom quark and a charged lepton, pair-produced long-lived top squarks lighter than 1350 GeV are excluded for decay lengths between 7 and 110 mm. For another RPV SUSY model where the long-lived top squark decays to two down antiquarks, pair-produced long-lived top squarks lighter than 1600 GeV are excluded for decay lengths between 10 and 110 mm. These are the most stringent limits to date on these models. |
| References | ||||
| 1 | Z. Liu and B. Tweedie | The fate of long-lived superparticles with hadronic decays after LHC Run 1 | JHEP 06 (2015) 042 | 1503.05923 |
| 2 | G. F. Giudice and A. Romanino | Split supersymmetry | NPB 699 (2004) 65 | hep-ph/0406088 |
| 3 | J. L. Hewett, B. Lillie, M. Masip, and T. G. Rizzo | Signatures of long-lived gluinos in split supersymmetry | JHEP 09 (2004) 070 | hep-ph/0408248 |
| 4 | N. Arkani-Hamed, S. Dimopoulos, G. F. Giudice, and A. Romanino | Aspects of split supersymmetry | NPB 709 (2005) 3 | hep-ph/0409232 |
| 5 | P. Gambino, G. F. Giudice, and P. Slavich | Gluino decays in split supersymmetry | NPB 726 (2005) 35 | hep-ph/0506214 |
| 6 | A. Arvanitaki, N. Craig, S. Dimopoulos, and G. Villadoro | Mini-split | JHEP 02 (2013) 126 | 1210.0555 |
| 7 | N. Arkani-Hamed et al. | Simply unnatural supersymmetry | 1212.6971 | |
| 8 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 9 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 10 | S. Weinberg | Supersymmetry at ordinary energies. 1. masses and conservation laws | PRD 26 (1982) 287 | |
| 11 | R. Barbier et al. | $ R $-parity violating supersymmetry | PR 420 (2005) 1 | hep-ph/0406039 |
| 12 | G. F. Giudice and R. Rattazzi | Theories with gauge mediated supersymmetry breaking | PR 322 (1999) 419 | hep-ph/9801271 |
| 13 | P. Meade, N. Seiberg, and D. Shih | General gauge mediation | Prog. Theor. Phys. Suppl. 177 (2009) 143 | 0801.3278 |
| 14 | M. Buican, P. Meade, N. Seiberg, and D. Shih | Exploring general gauge mediation | JHEP 03 (2009) 016 | 0812.3668 |
| 15 | J. Fan, M. Reece, and J. T. Ruderman | Stealth supersymmetry | JHEP 11 (2011) 012 | 1105.5135 |
| 16 | J. Fan, M. Reece, and J. T. Ruderman | A stealth supersymmetry sampler | JHEP 07 (2012) 196 | 1201.4875 |
| 17 | M. J. Strassler and K. M. Zurek | Echoes of a hidden valley at hadron colliders | PLB 651 (2007) 374 | hep-ph/0604261 |
| 18 | M. J. Strassler and K. M. Zurek | Discovering the Higgs through highly-displaced vertices | PLB 661 (2008) 263 | hep-ph/0605193 |
| 19 | T. Han, Z. Si, K. M. Zurek, and M. J. Strassler | Phenomenology of hidden valleys at hadron colliders | JHEP 07 (2008) 008 | 0712.2041 |
| 20 | Y. Cui, L. Randall, and B. Shuve | A WIMPy baryogenesis miracle | JHEP 04 (2012) 075 | 1112.2704 |
| 21 | Y. Cui and R. Sundrum | Baryogenesis for weakly interacting massive particles | PRD 87 (2013) 116013 | 1212.2973 |
| 22 | Y. Cui and B. Shuve | Probing baryogenesis with displaced vertices at the LHC | JHEP 02 (2015) 049 | 1409.6729 |
| 23 | Z. Chacko, H.-S. Goh, and R. Harnik | Natural electroweak breaking from a mirror symmetry | PRL 96 (2006) 231802 | hep-ph/0506256 |
| 24 | D. Curtin and C. B. Verhaaren | Discovering uncolored naturalness in exotic Higgs decays | JHEP 12 (2015) 072 | 1506.06141 |
| 25 | H.-C. Cheng, S. Jung, E. Salvioni, and Y. Tsai | Exotic quarks in twin Higgs models | JHEP 03 (2016) 074 | 1512.02647 |
| 26 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 27 | ATLAS Collaboration | Search for long-lived, weakly interacting particles that decay to displaced hadronic jets in proton-proton collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | PRD 92 (2015) 012010 | 1504.03634 |
| 28 | ATLAS Collaboration | Search for massive, long-lived particles using multitrack displaced vertices or displaced lepton pairs in pp collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector | PRD 92 (2015) 072004 | 1504.05162 |
| 29 | CMS Collaboration | Search for long-lived neutral particles decaying to quark-antiquark pairs in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | PRD 91 (2015) 012007 | CMS-EXO-12-038 1411.6530 |
| 30 | CMS Collaboration | Search for displaced supersymmetry in events with an electron and a muon with large impact parameters | PRL 114 (2015) 061801 | CMS-B2G-12-024 1409.4789 |
| 31 | CMS Collaboration | Search for $ R $-parity violating supersymmetry with displaced vertices in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | PRD 95 (2017) 012009 | CMS-SUS-14-020 1610.05133 |
| 32 | LHCb Collaboration | Search for long-lived particles decaying to jet pairs | EPJC 75 (2015) 152 | 1412.3021 |
| 33 | LHCb Collaboration | Search for Higgs-like bosons decaying into long-lived exotic particles | EPJC 76 (2016) 664 | 1609.03124 |
| 34 | ATLAS Collaboration | Search for long-lived, massive particles in events with displaced vertices and missing transverse momentum in $ \sqrt{s} = $ 13 TeV pp collisions with the ATLAS detector | PRD 97 (2018) 052012 | 1710.04901 |
| 35 | CMS Collaboration | Search for new long-lived particles at $ \sqrt{s} = $ 13 TeV | PLB 780 (2018) 432 | CMS-EXO-16-003 1711.09120 |
| 36 | CMS Collaboration | Search for long-lived particles with displaced vertices in multijet events in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 98 (2018) 092011 | CMS-EXO-17-018 1808.03078 |
| 37 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 38 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 39 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 40 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 41 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 42 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS-PAS-TDR-15-002 | CMS-PAS-TDR-15-002 |
| 43 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 44 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 45 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 46 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 47 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 48 | C. Csaki, Y. Grossman, and B. Heidenreich | MFV SUSY: a natural theory for $ R $-parity violation | PRD 85 (2012) 095009 | 1111.1239 |
| 49 | P. W. Graham, D. E. Kaplan, S. Rajendran, and P. Saraswat | Displaced supersymmetry | JHEP 07 (2012) 149 | 1204.6038 |
| 50 | C. Csaki, E. Kuflik, and T. Volansky | Dynamical $ R $-parity violation | PRL 112 (2014) 131801 | 1309.5957 |
| 51 | C. Csaki, E. Kuflik, O. Slone, and T. Volansky | Models of dynamical $ R $-parity violation | JHEP 06 (2015) 045 | 1502.03096 |
| 52 | C. Csaki et al. | Phenomenology of a long-lived LSP with $ R $-parity violation | JHEP 08 (2015) 016 | 1505.00784 |
| 53 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 54 | G. R. Farrar and P. Fayet | Bounds on $ R $-hadron production from calorimetry experiments | PLB 79 (1978) 442 | |
| 55 | M. Fairbairn et al. | Stable massive particles at colliders | PR 438 (2007) 1 | hep-ph/0611040 |
| 56 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 57 | R. Fruhwirth, W. Waltenberger, and P. Vanlaer | Adaptive vertex fitting | JPG 34 (2007) N343 | |
| 58 | S. C. Johnson | Hierarchical clustering schemes | Psychometrika 32 (1967) 241 | |
| 59 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 60 | S. Dulat et al. | New parton distribution functions from a global analysis of quantum chromodynamics | PRD 93 (2016) 033006 | 1506.07443 |
| 61 | L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne | Parton distributions in the LHC era: MMHT 2014 PDFs | EPJC 75 (2015) 204 | 1412.3989 |
| 62 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 63 | A. Buckley et al. | LHAPDF6: parton density access in the LHC precision era | EPJC 75 (2015) 132 | 1412.7420 |
| 64 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 65 | A. L. Read | Presentation of search results: The CLs technique | JPG 28 (2002) 2693 | |
| 66 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 67 | The ATLAS Collaboration, The CMS Collaboration, The LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 68 | W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas | Squark and gluino production at hadron colliders | NPB 492 (1997) 51 | hep-ph/9610490 |
| 69 | A. Kulesza and L. Motyka | Threshold resummation for squark-antisquark and gluino-pair production at the LHC | PRL 102 (2009) 111802 | 0807.2405 |
| 70 | A. Kulesza and L. Motyka | Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC | PRD 80 (2009) 095004 | 0905.4749 |
| 71 | W. Beenakker et al. | Squark and gluino hadroproduction | Int. J. Mod. Phys. A 26 (2011) 2637 | 1105.1110 |
| 72 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} = $ 13, 14, 33 and 100 TeV | EPJC 74 (2014) 3174 | 1407.5066 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|