

Compact Muon Solenoid
LHC, CERN
| CMS-SUS-19-007 ; CERN-EP-2019-213 | ||
| Search for supersymmetry in pp collisions at $\sqrt{s} = $ 13 TeV with 137 fb$^{-1}$ in final states with a single lepton using the sum of masses of large-radius jets | ||
| CMS Collaboration | ||
| 18 November 2019 | ||
| Phys. Rev. D 1010 (2020) 052010 | ||
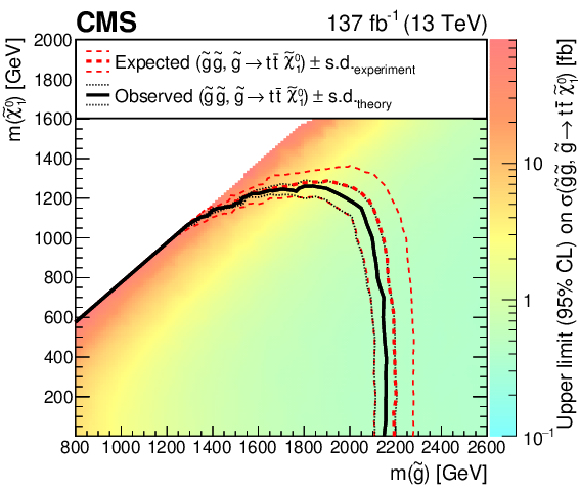
| Abstract: Results are reported from a search for new physics beyond the standard model in proton-proton collisions in final states with a single lepton; multiple jets, including at least one jet tagged as originating from the hadronization of a bottom quark; and large missing transverse momentum. The search uses a sample of proton-proton collision data at $\sqrt{s} = $ 13 TeV, corresponding to 137 fb$^{-1}$, recorded by the CMS experiment at the LHC. The signal region is divided into categories characterized by the total number of jets, the number of bottom quark jets, the missing transverse momentum, and the sum of masses of large-radius jets. The observed event yields in the signal regions are consistent with estimates of standard model backgrounds based on event yields in the control regions. The results are interpreted in the context of simplified models of supersymmetry involving gluino pair production in which each gluino decays into a top quark-antiquark pair and a stable, unobserved neutralino, which generates missing transverse momentum in the event. Scenarios with gluino masses up to about 2150 GeV are excluded at 95% confidence level (or more) for neutralino masses up to 700 GeV. The highest excluded neutralino mass is about 1250 GeV, which holds for gluino masses around 1850 GeV. | ||
| Links: e-print arXiv:1911.07558 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
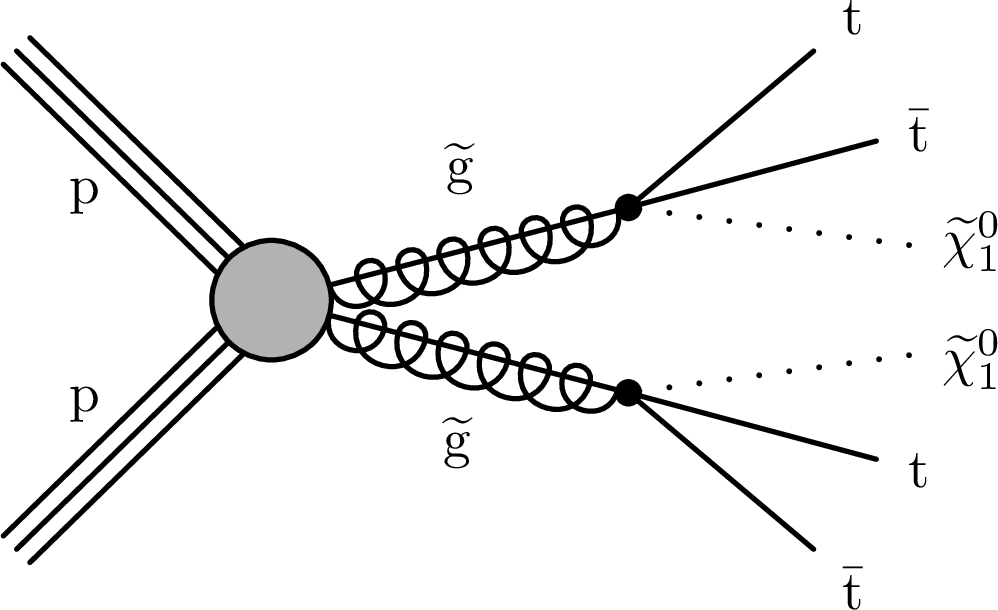
Figure 1:
Gluino pair production and decay for the simplified models T1tttt (left) and T5tttt (right). In T1tttt, the gluino undergoes a three-body decay ${\mathrm{\tilde{g}}} \to {\mathrm{t} {}\mathrm{\bar{t}}} \tilde{\chi}^0_1 $ via a virtual intermediate top squark. In T5tttt, the gluino decays via the sequential two-body process ${\mathrm{\tilde{g}}} \to \tilde{\mathrm{t}} _1\mathrm{\bar{t}} $, $\tilde{\mathrm{t}} _1\to \mathrm{t} \tilde{\chi}^0_1 $. Because gluinos are Majorana fermions, each one can decay to $\tilde{\mathrm{t}} _1\mathrm{\bar{t}} $ and to the charge conjugate final state $\smash {\bar{\tilde{\mathrm{t}}} _1\mathrm{t}}$. The filled circle represents the sum of processes that can lead to gluino pair production. |
png pdf |
Figure 1-a:
Gluino pair production and decay for the simplified model T1tttt. The gluino undergoes a three-body decay ${\mathrm{\tilde{g}}} \to {\mathrm{t} {}\mathrm{\bar{t}}} \tilde{\chi}^0_1 $ via a virtual intermediate top squark. The filled circle represents the sum of processes that can lead to gluino pair production. |

png pdf |
Figure 1-b:
Gluino pair production and decay for the simplified model T5tttt. The gluino decays via the sequential two-body process ${\mathrm{\tilde{g}}} \to \tilde{\mathrm{t}} _1\mathrm{\bar{t}} $, $\tilde{\mathrm{t}} _1\to \mathrm{t} \tilde{\chi}^0_1 $. Because gluinos are Majorana fermions, each one can decay to $\tilde{\mathrm{t}} _1\mathrm{\bar{t}} $ and to the charge conjugate final state $\smash {\bar{\tilde{\mathrm{t}}} _1\mathrm{t}}$. The filled circle represents the sum of processes that can lead to gluino pair production. |

png pdf |
Figure 2:
Analysis regions defined for each bin in ${{p_{\mathrm {T}}} ^\text {miss}}$. For the signal models considered here, the regions R1, R2A, R2B, and R3 are dominated by background, while R4A and R4B would have a significant signal contribution. In the combined fit performed to the event yields observed in these regions, signal contributions are allowed in the background-dominated regions. The R2A, R2B, R4A, and R4B regions are further divided into bins of ${N_{\text {jets}}}$ and ${N_{\text {b}}}$, as discussed in the text. |
png pdf |
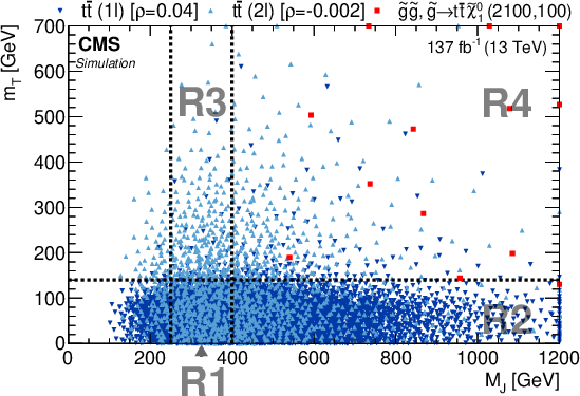
Figure 3:
Distribution of simulated single-lepton ${\mathrm{t} {}\mathrm{\bar{t}}}$ events (dark-blue inverted triangles), dilepton ${\mathrm{t} {}\mathrm{\bar{t}}}$ events (light-blue triangles) in the ${M_J}$-${m_{\mathrm {T}}}$ plane after applying the baseline selection and requiring at least two b jets. A representative random sample of T1tttt events with $ {m({\mathrm{\tilde{g}}})} = $ 2100 GeV and $ {m(\tilde{\chi}^0_1)} = $ 100 GeV is also shown for comparison (red squares). Each marker represents one expected event in the full data sample. Overflow events are placed on the edges of the plot. The values of the correlation coefficients $\rho $ for each of the background process are given in the legend. Region R4, which is further split into smaller bins R4A and R4B, is the nominal signal region, while R1, R2, and R3 serve as control regions. This plot is only illustrative, because the boundary between R1 and R2, as well as between R3 and R4, is ${{p_{\mathrm {T}}} ^\text {miss}}$-dependent. The line shown at 400 GeV corresponds to the value used for the lowest ${{p_{\mathrm {T}}} ^\text {miss}}$ bin. Additional sensitivity is obtained by binning the events in ${{p_{\mathrm {T}}} ^\text {miss}}$, ${N_{\text {jets}}}$, and ${N_{\text {b}}}$. |
png pdf |
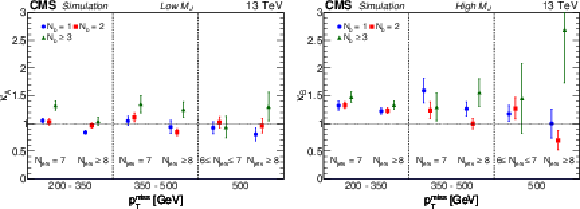
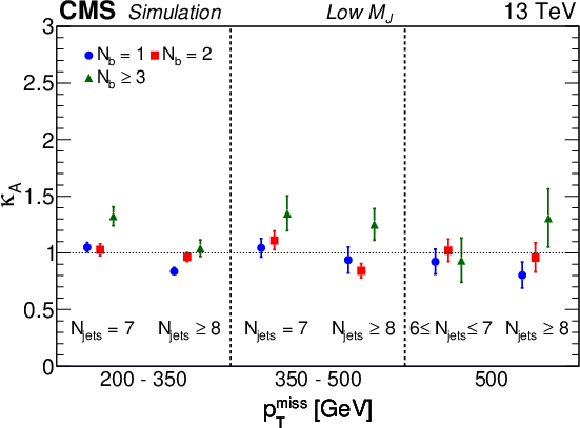
Figure 4:
Values of the double-ratio $\kappa $ for each of the 18 signal bins of the low-${M_J}$ ABCD planes, i.e., R1-R2A-R3-R4A (left), and the 18 signal bins of the high-${M_J}$ ABCD planes, i.e., R1-R2B-R3-R4B (right), calculated using the simulated SM background. The $\kappa $ factors are close to unity, indicating a small correlation between ${M_J}$ and ${m_{\mathrm {T}}}$. The uncertainties shown are statistical only. |
png pdf |
Figure 4-a:
Values of the double-ratio $\kappa $ for each of the 18 signal bins of the low-${M_J}$ ABCD planes, i.e., R1-R2A-R3-R4A, calculated using the simulated SM background. The $\kappa $ factors are close to unity, indicating a small correlation between ${M_J}$ and ${m_{\mathrm {T}}}$. The uncertainties shown are statistical only. |

png pdf |
Figure 4-b:
Values of the double-ratio $\kappa $ for each of the 18 signal bins of the high-${M_J}$ ABCD planes, i.e., R1-R2B-R3-R4B, calculated using the simulated SM background. The $\kappa $ factors are close to unity, indicating a small correlation between ${M_J}$ and ${m_{\mathrm {T}}}$. The uncertainties shown are statistical only. |
png pdf |
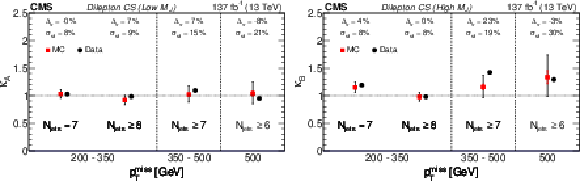
Figure 5:
Dilepton control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for low ${M_J}$ (left) and high ${M_J}$ (right). The data and simulation are shown as black and red points, respectively. No statistical uncertainties are plotted for the data points, but instead, the expected statistical uncertainty for the data points, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points and is quoted as $\sigma _{\mathrm {st}}$. The red portion of the error bar on the red points indicates the contribution from the simulated samples. The quoted values of $\Delta _{\kappa}$ are defined as the relative difference between the $\kappa $ values found in simulation and in data. |
png pdf |
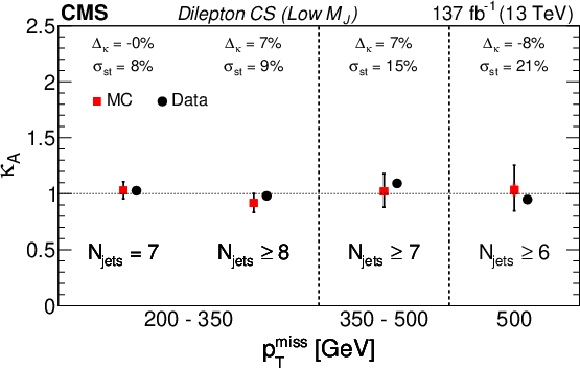
Figure 5-a:
Dilepton control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for low ${M_J}$. The data and simulation are shown as black and red points, respectively. No statistical uncertainties are plotted for the data points, but instead, the expected statistical uncertainty for the data points, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points and is quoted as $\sigma _{\mathrm {st}}$. The red portion of the error bar on the red points indicates the contribution from the simulated samples. The quoted values of $\Delta _{\kappa}$ are defined as the relative difference between the $\kappa $ values found in simulation and in data. |
png pdf |
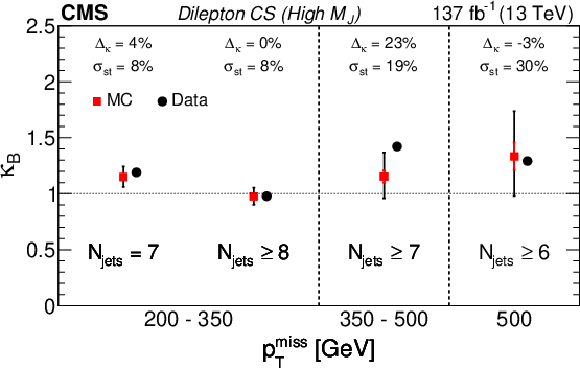
Figure 5-b:
Dilepton control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for high ${M_J}$. The data and simulation are shown as black and red points, respectively. No statistical uncertainties are plotted for the data points, but instead, the expected statistical uncertainty for the data points, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points and is quoted as $\sigma _{\mathrm {st}}$. The red portion of the error bar on the red points indicates the contribution from the simulated samples. The quoted values of $\Delta _{\kappa}$ are defined as the relative difference between the $\kappa $ values found in simulation and in data. |
png pdf |
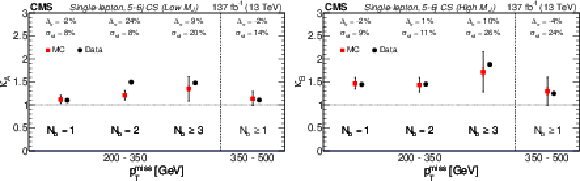
Figure 6:
Single-lepton 5-6 jet control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for low ${M_J}$ (left) and high ${M_J}$ (right). The data and simulation are shown as black and red points, respectively. The expected uncertainty in the data, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points ($\sigma _{\mathrm {st}}$). The red portion of the error bar indicates the contribution from the simulated samples. The values of $\Delta _{\kappa}$ are the relative difference between the $\kappa $ values found in simulation and in data. |
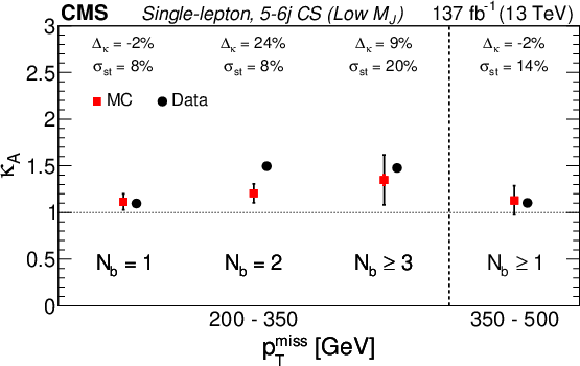
png pdf |
Figure 6-a:
Single-lepton 5-6 jet control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for low ${M_J}$. The data and simulation are shown as black and red points, respectively. The expected uncertainty in the data, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points ($\sigma _{\mathrm {st}}$). The red portion of the error bar indicates the contribution from the simulated samples. The values of $\Delta _{\kappa}$ are the relative difference between the $\kappa $ values found in simulation and in data. |

png pdf |
Figure 6-b:
Single-lepton 5-6 jet control sample (CS): validation of the $\kappa $ factor values found in simulation vs. data for high ${M_J}$. The data and simulation are shown as black and red points, respectively. The expected uncertainty in the data, summed in quadrature with the statistical uncertainty of the simulated samples, is given by the error bar on the red points ($\sigma _{\mathrm {st}}$). The red portion of the error bar indicates the contribution from the simulated samples. The values of $\Delta _{\kappa}$ are the relative difference between the $\kappa $ values found in simulation and in data. |
png pdf |
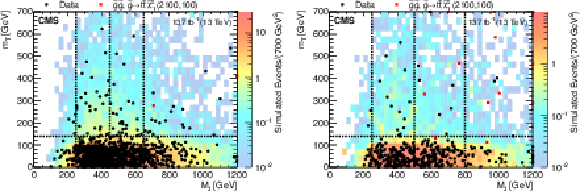
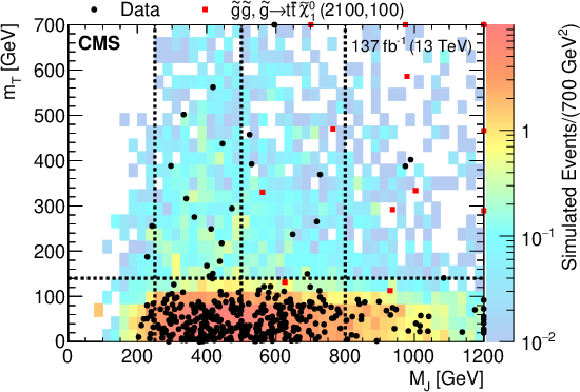
Figure 7:
Two-dimensional distributions in ${M_J}$ and ${m_{\mathrm {T}}}$ for both data and simulated event samples, integrated over the ${N_{\text {jets}}}$ and $ {N_{\text {b}}} \geq $ 2 and shown separately for the 350 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 500 GeV bin (left) and the $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 500 GeV bin (right). The black dots represent events in data, the colored histogram shows the total expected background yield per bin from simulation (not the actual predicted background), and the red squares correspond to a representative random sample of signal events drawn from the simulated distribution for the T1tttt model with $ {m({\mathrm{\tilde{g}}})} = $ 2100 GeV and $ {m(\tilde{\chi}^0_1)} = $ 100 GeV for 137 fb$^{-1}$. Overflow events are shown on the edges of the plot. |

png pdf |
Figure 7-a:
Two-dimensional distributions in ${M_J}$ and ${m_{\mathrm {T}}}$ for both data and simulated event samples, integrated over the ${N_{\text {jets}}}$ and $ {N_{\text {b}}} \geq $ 2 and shown separately for the 350 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 500 GeV bin. The black dots represent events in data, the colored histogram shows the total expected background yield per bin from simulation (not the actual predicted background), and the red squares correspond to a representative random sample of signal events drawn from the simulated distribution for the T1tttt model with $ {m({\mathrm{\tilde{g}}})} = $ 2100 GeV and $ {m(\tilde{\chi}^0_1)} = $ 100 GeV for 137 fb$^{-1}$. Overflow events are shown on the edges of the plot. |
png pdf |
Figure 7-b:
Two-dimensional distributions in ${M_J}$ and ${m_{\mathrm {T}}}$ for both data and simulated event samples, integrated over the ${N_{\text {jets}}}$ and $ {N_{\text {b}}} \geq $ 2 and shown separately for the $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 500 GeV bin. The black dots represent events in data, the colored histogram shows the total expected background yield per bin from simulation (not the actual predicted background), and the red squares correspond to a representative random sample of signal events drawn from the simulated distribution for the T1tttt model with $ {m({\mathrm{\tilde{g}}})} = $ 2100 GeV and $ {m(\tilde{\chi}^0_1)} = $ 100 GeV for 137 fb$^{-1}$. Overflow events are shown on the edges of the plot. |
png pdf |
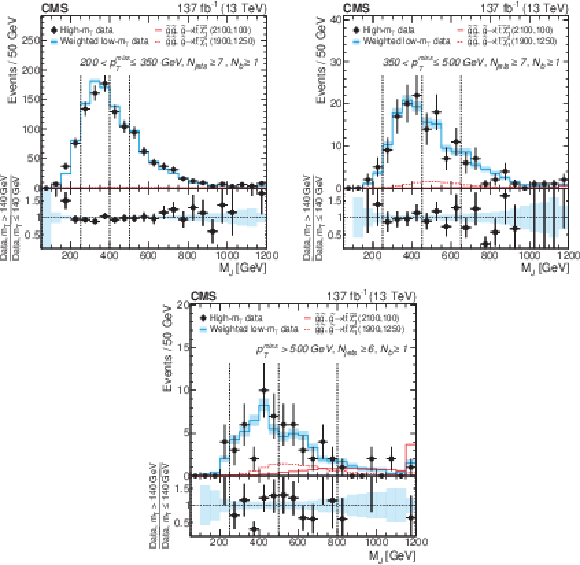
Figure 8:
Distributions of ${M_J}$ observed in data for 200 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 350 GeV (upper left), 350 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 500 GeV (upper right), and $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 500 GeV (lower) in the $1\ell $ data for low- and high-${m_{\mathrm {T}}}$ regions. In each plot, events in the R2A and R2B regions at low ${m_{\mathrm {T}}}$ have been weighted by the relevant $\kappa $ factor and the total low-${m_{\mathrm {T}}}$ yield is normalized to the high-${m_{\mathrm {T}}}$ yield to facilitate comparison of the shapes of the distributions. The vertical dashed line at $ {M_J} = $ 250 GeV shows the lower boundary of regions R1 and R3, while the vertical lines at higher ${M_J}$ values denote the lower ${M_J}$ boundaries of the signal regions R4A and R4B. The data are integrated over the ${N_{\text {b}}}$ and ${N_{\text {jets}}}$ signal bins. Two SUSY benchmark models are shown in the solid and dashed red histograms. |

png pdf |
Figure 8-a:
Distributions of ${M_J}$ observed in data for 200 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 350 GeV in the $1\ell $ data for low- and high-${m_{\mathrm {T}}}$ regions. Events in the R2A and R2B regions at low ${m_{\mathrm {T}}}$ have been weighted by the relevant $\kappa $ factor and the total low-${m_{\mathrm {T}}}$ yield is normalized to the high-${m_{\mathrm {T}}}$ yield to facilitate comparison of the shapes of the distributions. The vertical dashed line at $ {M_J} = $ 250 GeV shows the lower boundary of regions R1 and R3, while the vertical lines at higher ${M_J}$ values denote the lower ${M_J}$ boundaries of the signal regions R4A and R4B. The data are integrated over the ${N_{\text {b}}}$ and ${N_{\text {jets}}}$ signal bins. Two SUSY benchmark models are shown in the solid and dashed red histograms. |
png pdf |
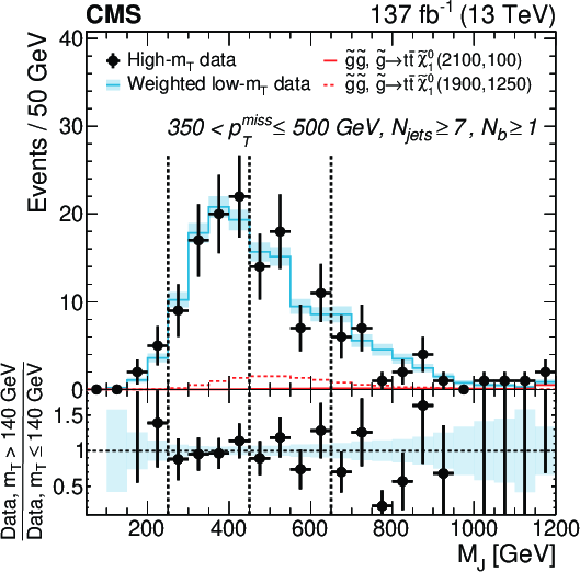
Figure 8-b:
Distributions of ${M_J}$ observed in data for 350 $ < {{p_{\mathrm {T}}} ^\text {miss}} \leq $ 500 GeV in the $1\ell $ data for low- and high-${m_{\mathrm {T}}}$ regions. Events in the R2A and R2B regions at low ${m_{\mathrm {T}}}$ have been weighted by the relevant $\kappa $ factor and the total low-${m_{\mathrm {T}}}$ yield is normalized to the high-${m_{\mathrm {T}}}$ yield to facilitate comparison of the shapes of the distributions. The vertical dashed line at $ {M_J} = $ 250 GeV shows the lower boundary of regions R1 and R3, while the vertical lines at higher ${M_J}$ values denote the lower ${M_J}$ boundaries of the signal regions R4A and R4B. The data are integrated over the ${N_{\text {b}}}$ and ${N_{\text {jets}}}$ signal bins. Two SUSY benchmark models are shown in the solid and dashed red histograms. |
png pdf |
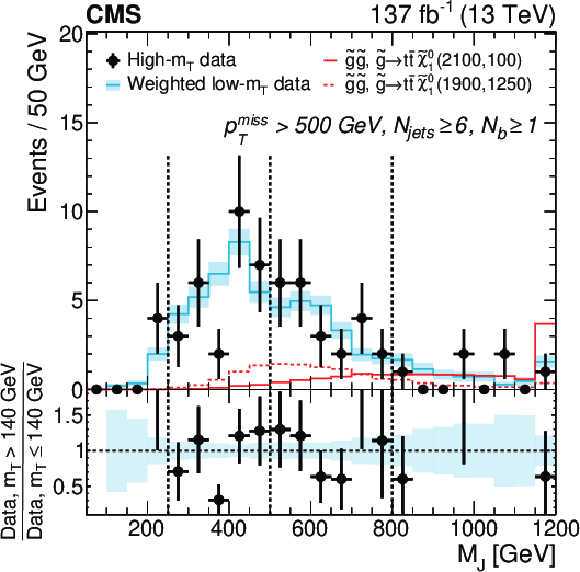
Figure 8-c:
Distributions of ${M_J}$ observed in data for $ {{p_{\mathrm {T}}} ^\text {miss}} > $ 500 GeV in the $1\ell $ data for low- and high-${m_{\mathrm {T}}}$ regions. Events in the R2A and R2B regions at low ${m_{\mathrm {T}}}$ have been weighted by the relevant $\kappa $ factor and the total low-${m_{\mathrm {T}}}$ yield is normalized to the high-${m_{\mathrm {T}}}$ yield to facilitate comparison of the shapes of the distributions. The vertical dashed line at $ {M_J} = $ 250 GeV shows the lower boundary of regions R1 and R3, while the vertical lines at higher ${M_J}$ values denote the lower ${M_J}$ boundaries of the signal regions R4A and R4B. The data are integrated over the ${N_{\text {b}}}$ and ${N_{\text {jets}}}$ signal bins. Two SUSY benchmark models are shown in the solid and dashed red histograms. |

png pdf |
Figure 9:
Observed and predicted event yields in each signal region. The open rectangles represent the prediction and uncertainty obtained using event yields from regions R1, R2, and R3 only (R1-R3 fit), while the hashed rectangles represent the prediction obtained when all regions are included in the fit (R1-R4 fit). The labels 1b, 2b, and $\geq $3b refer to $ {N_{\text {b}}} =$ 1, $ {N_{\text {b}}} =$ 2, and $ {N_{\text {b}}} \geq $ 3 bins, respectively. In both cases, all statistical and systematic uncertainties are included. The bottom panel shows the pulls for both fits, defined as $(N_\text {obs}-N_\text {pred})/\sqrt {\smash [b]{N_\text {pred}+(\sigma ^\text {sys}_\text {pred})^2}}$. |
png pdf |
Figure 10:
Interpretation of the results in the T1tttt model. The colored regions show the upper limits (95% CL) on the production cross section for ${\mathrm{p}} {\mathrm{p}} \to {\mathrm{\tilde{g}}} {\mathrm{\tilde{g}}},{\mathrm{\tilde{g}}} \to {\mathrm{t} {}\mathrm{\bar{t}}} \tilde{\chi}^0_1 $ in the ${m({\mathrm{\tilde{g}}})}$-${m(\tilde{\chi}^0_1)}$ plane. The curves show the expected and observed limits on the corresponding SUSY particle masses obtained by comparing the excluded cross section with theoretical cross sections. |
png pdf |
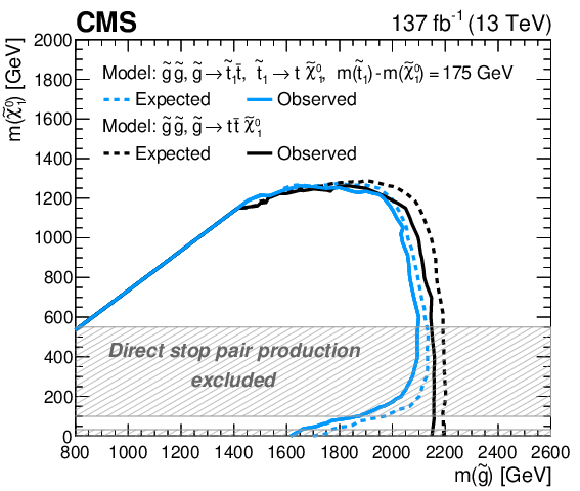
Figure 11:
Interpretation of the results in the T5tttt model. The expected and observed upper limits do not take into account contributions from direct top squark pair production; however, its effect for $m(\tilde{\chi}^0_1) > $ 550 GeV is small. The T1tttt interpretation results are also shown for comparison. |
| Tables | |

png pdf |
Table 1:
Systematic uncertainties in the background correction factors $\kappa $ associated with each signal bin based on the control sample studies described in Sections 7.2 and 7.3 and combined according to Eq.(9). |

png pdf |
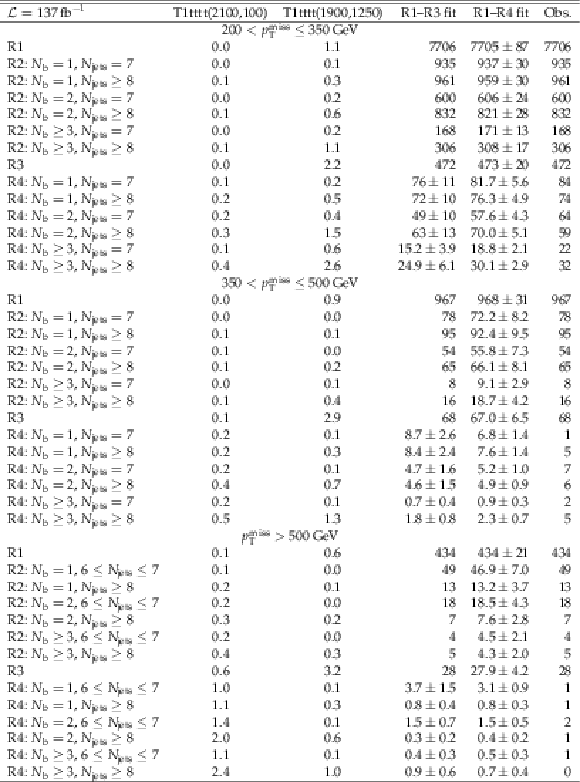
Table 2:
Observed and predicted event yields for the signal regions (R4) and background regions (R1-R3) in the low-${M_J}$ ABCD planes. For the R1-R3 fit, the values given for R1, R2 and R3 correspond to the observed yields in those regions. Expected yields for the two SUSY benchmark scenarios, T1tttt(2100, 100) and T1tttt(1900, 1250), are also given. The uncertainties in the prediction account for the available statistics in the data control samples, the precision of $\kappa $ from MC, and the systematic uncertainties in $\kappa $ assessed from control samples in data. |
png pdf |
Table 3:
Observed and predicted event yields for the signal regions (R4) and background regions (R1-R3) in the high-${M_J}$ ABCD planes. For the R1-R3 fit, the values given for R1, R2 and R3 correspond to the observed yields in those regions. Expected yields for the two SUSY benchmark scenarios, T1tttt(2100, 100) and T1tttt(1900, 1250), are also given. The uncertainties in the prediction account for the available statistics in the data control samples, the precision of $\kappa $ from MC, and the systematic uncertainties in $\kappa $ assessed from control samples in data. |
png pdf |
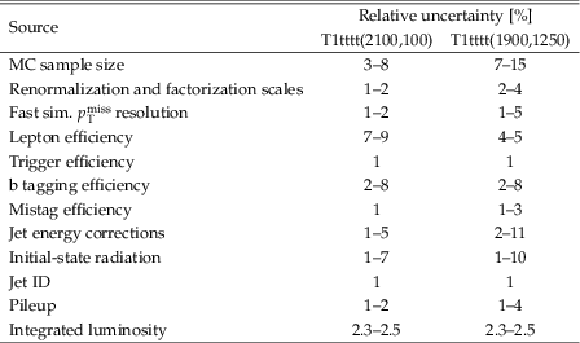
Table 4:
Range of values for the systematic uncertainties in the signal efficiency and acceptance across sensitive bins, specifically across high ${{p_{\mathrm {T}}} ^\text {miss}}$ signal bins for T1tttt(2100,100) and high ${N_{\text {jets}}}$ signal bins for T1tttt(1900,1250). Uncertainties due to a particular source are treated as fully correlated among bins, while uncertainties due to different sources are treated as uncorrelated. |
| Summary |
| A search is performed for an excess event yield above that expected for standard model processes using a data sample of proton-proton collision events with an integrated luminosity of 137 fb$^{-1}$ at $\sqrt{s} = $ 13 TeV. The experimental signature is characterized by a single isolated lepton, multiple jets, at least one b-tagged jet, and large missing transverse momentum. No significant excesses above the standard model backgrounds are observed. The results are interpreted in the framework of simplified models that describe natural supersymmetry scenarios. For gluino pair production followed by the three-body decay ${\mathrm{\tilde{g}}}\to\mathrm{t\bar{t}}\tilde{\chi}^0_1$ (T1tttt model), gluinos with masses below about 2150 GeV are excluded at 95% confidence level for neutralino masses up to 700 GeV. The highest excluded neutralino mass is about 1250 GeV. For the two-body gluino decay ${\mathrm{\tilde{g}}}\to\tilde{\mathrm{t}}_1\bar{\mathrm{t}}$ with $\tilde{\mathrm{t}}_1\to{\mathrm{t}}\tilde{\chi}^0_1$ (T5tttt model), the results are generally similar, except at low neutralino masses, where the excluded gluino mass is somewhat lower. These results extend previous gluino mass limits [19] from this search by about 250 GeV, due to both the data sample increase and the analysis reoptimization enabled by it. These mass limits are among the most stringent constraints on this supersymmetry model to date. |
| References | ||||
| 1 | L. Evans and P. Bryant | LHC machine | JINST 3 (2008) S08001 | |
| 2 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 3 | Y. A. Gol'fand and E. P. Likhtman | Extension of the algebra of Poincar$ \'e $ group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 4 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 5 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 6 | J. Wess and B. Zumino | A lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 7 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 8 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 9 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 10 | ATLAS Collaboration | Search for supersymmetry in final states with jets, missing transverse momentum and one isolated lepton in $ \sqrt{s} = $ 7 TeV pp collisions using 1 fb$ ^{-1} $ of ATLAS data | PRD 85 (2012) 012006 | 1109.6606 |
| 11 | ATLAS Collaboration | Search for squarks and gluinos in events with isolated leptons, jets and missing transverse momentum at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | JHEP 04 (2015) 116 | 1501.03555 |
| 12 | CMS Collaboration | Search for supersymmetry in pp collisions at $ \sqrt{s}= $ 7 TeV in events with a single lepton, jets, and missing transverse momentum | JHEP 08 (2011) 156 | CMS-SUS-10-006 1107.1870 |
| 13 | CMS Collaboration | Search for supersymmetry in pp collisions at $ \sqrt{s} = $ 8 TeV in events with a single lepton, large jet multiplicity, and multiple b jets | PLB 733 (2014) 328 | CMS-SUS-13-007 1311.4937 |
| 14 | ATLAS Collaboration | Search for pair production of gluinos decaying via stop and sbottom in events with b-jets and large missing transverse momentum in pp collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PRD 94 (2016) 032003 | 1605.09318 |
| 15 | ATLAS Collaboration | Search for gluinos in events with an isolated lepton, jets and missing transverse momentum at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | EPJC 76 (2016) 565 | 1605.04285 |
| 16 | ATLAS Collaboration | Search for supersymmetry in final states with missing transverse momentum and multiple $ b $-jets in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | JHEP 06 (2018) 107 | 1711.01901 |
| 17 | CMS Collaboration | Search for supersymmetry in pp collisions at $ \sqrt{s}= $ 13 TeV in the single-lepton final state using the sum of masses of large-radius jets | JHEP 08 (2016) 122 | CMS-SUS-15-007 1605.04608 |
| 18 | CMS Collaboration | Search for supersymmetry in events with one lepton and multiple jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 95 (2017) 012011 | CMS-SUS-15-006 1609.09386 |
| 19 | CMS Collaboration | Search for supersymmetry in $ pp $ collisions at $ \sqrt{s}=13\text{}\text{}\mathrm{TeV} $ in the single-lepton final state using the sum of masses of large-radius jets | PRL 119 (2017) 151802 | CMS-SUS-16-037 1705.04673 |
| 20 | ATLAS Collaboration | Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 21 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 22 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 23 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC 75 (2015) 212 | CMS-HIG-14-009 1412.8662 |
| 24 | ATLAS Collaboration | Measurement of the Higgs boson mass from the $ \textrm{H}\rightarrow \gamma\gamma $ and $ \textrm{H} \rightarrow \textrm{ZZ}^{*} \rightarrow 4\ell $ channels with the ATLAS detector using 25 fb$ ^{-1} $ of $ pp $ collision data | PRD 90 (2014) 052004 | 1406.3827 |
| 25 | ATLAS and CMS Collaborations | Combined measurement of the Higgs boson mass in pp collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS and CMS experiments | PRL 114 (2015) 191803 | 1503.07589 |
| 26 | G. 't Hooft | Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking | NATO Sci. Ser. B 59 (1980) 135 | |
| 27 | E. Witten | Dynamical breaking of supersymmetry | NPB 188 (1981) 513 | |
| 28 | M. Dine, W. Fischler, and M. Srednicki | Supersymmetric technicolor | NPB 189 (1981) 575 | |
| 29 | S. Dimopoulos and S. Raby | Supercolor | NPB 192 (1981) 353 | |
| 30 | S. Dimopoulos and H. Georgi | Softly broken supersymmetry and SU(5) | NPB 193 (1981) 150 | |
| 31 | R. K. Kaul and P. Majumdar | Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories | NPB 199 (1982) 36 | |
| 32 | R. Barbieri and G. F. Giudice | Upper bounds on supersymmetric particle masses | NPB 306 (1988) 63 | |
| 33 | S. Dimopoulos and G. F. Giudice | Naturalness constraints in supersymmetric theories with nonuniversal soft terms | PLB 357 (1995) 573 | hep-ph/9507282 |
| 34 | R. Barbieri and D. Pappadopulo | S-particles at their naturalness limits | JHEP 10 (2009) 061 | 0906.4546 |
| 35 | M. Papucci, J. T. Ruderman, and A. Weiler | Natural SUSY endures | JHEP 09 (2012) 035 | 1110.6926 |
| 36 | J. L. Feng | Naturalness and the status of supersymmetry | Ann. Rev. Nucl. Part. Sci. 63 (2013) 351 | 1302.6587 |
| 37 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 38 | S. P. Martin | A supersymmetry primer | Adv. Ser. Direct. High Energy Phys. 18 (1998) 1 | hep-ph/9709356 |
| 39 | F. Zwicky | Die rotverschiebung von extragalaktischen nebeln | Helv. Phys. Acta 6 (1933)110 | |
| 40 | V. C. Rubin and W. K. Ford Jr | Rotation of the Andromeda nebula from a spectroscopic survey of emission regions | Astrophys. J. 159 (1970) 379 | |
| 41 | Particle Data Group, M. Tanabashi et al. | Review of particle physics | PRD 98 (2018) 030001 | |
| 42 | CMS Collaboration | Interpretation of searches for supersymmetry with simplified models | PRD 88 (2013) 052017 | CMS-SUS-11-016 1301.2175 |
| 43 | J. Alwall, P. C. Schuster, and N. Toro | Simplified models for a first characterization of new physics at the LHC | PRD 79 (2009) 075020 | 0810.3921 |
| 44 | J. Alwall, M.-P. Le, M. Lisanti, and J. G. Wacker | Model-independent jets plus missing energy searches | PRD 79 (2009) 015005 | 0809.3264 |
| 45 | D. Alves et al. | Simplified models for LHC new physics searches | JPG 39 (2012) 105005 | 1105.2838 |
| 46 | A. Hook, E. Izaguirre, M. Lisanti, and J. G. Wacker | High multiplicity searches at the LHC using jet masses | PRD 85 (2012) 055029 | 1202.0558 |
| 47 | T. Cohen, E. Izaguirre, M. Lisanti, and H. K. Lou | Jet substructure by accident | JHEP 03 (2013) 161 | 1212.1456 |
| 48 | S. El Hedri, A. Hook, M. Jankowiak, and J. G. Wacker | Learning how to count: A high multiplicity search for the LHC | JHEP 08 (2013) 136 | 1302.1870 |
| 49 | ATLAS Collaboration | Search for massive supersymmetric particles decaying to many jets using the ATLAS detector in pp collisions at $ \sqrt{s} = $ 8 TeV | PRD 91 (2015) 112016 | 1502.05686 |
| 50 | ATLAS Collaboration | Search for new phenomena in final states with large jet multiplicities and missing transverse momentum at $ \sqrt{s}= $ 8 TeV proton-proton collisions using the ATLAS experiment | JHEP 10 (2013) 130 | 1308.1841 |
| 51 | CMS Collaboration | Commissioning the performance of key observables used in SUSY searches with the first 13 TeV data | CDS | |
| 52 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 53 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 54 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 55 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 56 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 57 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 58 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 59 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | Submitted to EPJC | CMS-GEN-17-001 1903.12179 |
| 60 | GEANT4 Collaboration | GEANT4 --- a simulation toolkit | NIMA 506 (2003) 250 | |
| 61 | CMS Collaboration | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 62 | A. Giammanco | The fast simulation of the CMS experiment | J. Phys. Conf. Ser. 513 (2014) 022012 | |
| 63 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} = $ 13, 14, 33 and 100 TeV | EPJC 74 (2014) 3174 | 1407.5066 |
| 64 | W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas | Squark and gluino production at hadron colliders | NPB 492 (1997) 51 | hep-ph/9610490 |
| 65 | A. Kulesza and L. Motyka | Threshold resummation for squark-antisquark and gluino-pair production at the LHC | PRL 102 (2009) 111802 | 0807.2405 |
| 66 | A. Kulesza and L. Motyka | Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC | PRD 80 (2009) 095004 | 0905.4749 |
| 67 | W. Beenakker et al. | Soft-gluon resummation for squark and gluino hadroproduction | JHEP 12 (2009) 041 | 0909.4418 |
| 68 | W. Beenakker et al. | Squark and gluino hadroproduction | Int. J. Mod. Phys. A 26 (2011) 2637 | 1105.1110 |
| 69 | W. Beenakker et al. | Towards NNLL resummation: hard matching coefficients for squark and gluino hadroproduction | JHEP 10 (2013) 120 | 1304.6354 |
| 70 | W. Beenakker et al. | NNLL resummation for squark and gluino production at the LHC | JHEP 12 (2014) 023 | 1404.3134 |
| 71 | W. Beenakker et al. | NNLL-fast: predictions for coloured supersymmetric particle production at the LHC with threshold and coulomb resummation | JHEP 12 (2016) 133 | 1607.07741 |
| 72 | CMS Collaboration | Search for supersymmetry in proton-proton collisions at 13 tev in final states with jets and missing transverse momentum | Submitted to JHEP | CMS-SUS-19-006 1908.04722 |
| 73 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 74 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 75 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 76 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 77 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 78 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 79 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}= $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 80 | K. Rehermann and B. Tweedie | Efficient identification of boosted semileptonic top quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 81 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 82 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 83 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 tev | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 84 | CMS Collaboration | Jet energy scale and resolution in the cms experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 85 | CMS Collaboration | Performance of missing transverse momentum in pp collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | CMS-PAS-JME-17-001 | CMS-PAS-JME-17-001 |
| 86 | C. G. Lester and D. J. Summers | Measuring masses of semi-invisibly decaying particle pairs produced at hadron colliders | PLB 463 (1999) 5 | hep-ph/9906349 |
| 87 | A. Barr, C. Lester, and P. Stephens | A variable for measuring masses at hadron colliders when missing energy is expected; $ m_{T2} $: the truth behind the glamour | JPG 29 (2003) 2343 | hep-ph/0304226 |
| 88 | CMS Collaboration | CMS luminosity measurement for the 2016 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 89 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 90 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 91 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 92 | A. L. Read | Presentation of search results: the $ CL_s $ technique | in Durham IPPP Workshop: Advanced Statistical Techniques in Particle Physics, p. 2693 Durham, UK, March, 2002 [JPG \bf 28 (2002) 2693] | |
| 93 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 94 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 95 | CMS Collaboration | Search for the pair production of light top squarks in the e$ ^{\pm}\mu^{\mp} $ final state in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 03 (2019) 101 | CMS-SUS-18-003 1901.01288 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|