

Compact Muon Solenoid
LHC, CERN
| CMS-SUS-18-006 ; CERN-EP-2019-154 | ||
| Search for direct pair production of supersymmetric partners to the $\tau$ lepton in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 30 July 2019 | ||
| Eur. Phys. J. C 80 (2020) 189 | ||
| Abstract: A search is presented for $\tau$ slepton pairs produced in proton-proton collisions at a center-of-mass energy of 13 TeV. The search is carried out in events containing two $\tau$ leptons in the final state, on the assumption that each $\tau$ slepton decays primarily to a $\tau$ lepton and a neutralino. Events are considered in which each $\tau$ lepton decays to one or more hadrons and a neutrino, or in which one of the $\tau$ leptons decays instead to an electron or a muon and two neutrinos. The data, collected with the CMS detector in 2016 and 2017, correspond to an integrated luminosity of 77.2 fb$^{-1}$. The observed data are consistent with the standard model background expectation. The results are used to set 95% confidence level upper limits on the cross section for $\tau$ slepton pair production in various models for $\tau$ slepton masses between 90 and 200 GeV and neutralino masses of 1, 10, and 20 GeV. In the case of purely left-handed $\tau$ slepton production and decay to a $\tau$ lepton and a neutralino with a mass of 1 GeV, the strongest limit is obtained for a $\tau$ slepton mass of 125 GeV at a factor of 1.14 larger than the theoretical cross section. | ||
| Links: e-print arXiv:1907.13179 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Diagram for direct $\tilde{\tau}$ pair production, followed by decay of each $\tilde{\tau}$ to a $\tau$ lepton and a $\tilde{\chi}^0_1$. |
png pdf |
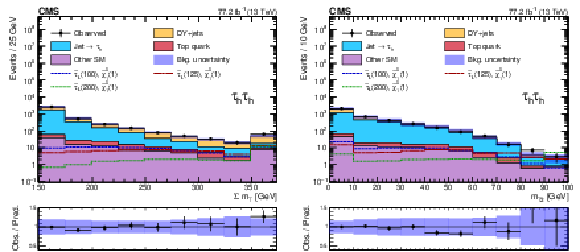
Figure 2:
Distributions in ${\Sigma {m_{\mathrm {T}}}}$ (left) and ${m_{\mathrm {T2}}}$ (right) for events in the combined 2016 and 2017 data sets passing the baseline selection in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for the SM background and three benchmark models for ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV, $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events in each case. The shaded uncertainty bands represent the combined statistical and systematic uncertainties in the background. |
png pdf |
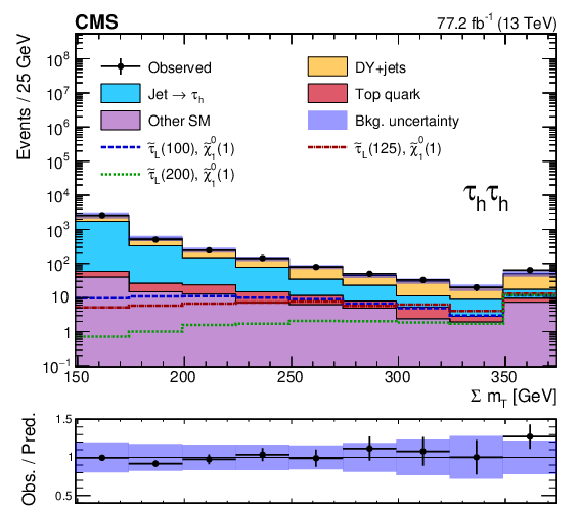
Figure 2-a:
Distribution in ${\Sigma {m_{\mathrm {T}}}}$ for events in the combined 2016 and 2017 data sets passing the baseline selection in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for the SM background and three benchmark models for ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV, $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events. The shaded uncertainty bands represent the combined statistical and systematic uncertainties in the background. |
png pdf |
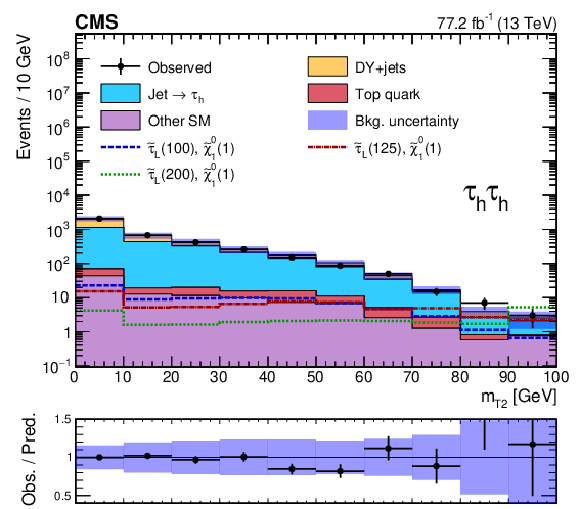
Figure 2-b:
Distribution in ${m_{\mathrm {T2}}}$ for events in the combined 2016 and 2017 data sets passing the baseline selection in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for the SM background and three benchmark models for ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV, $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events. The shaded uncertainty bands represent the combined statistical and systematic uncertainties in the background. |

png pdf |
Figure 3:
Distributions in ${{p_{\mathrm {T}}} ^\text {miss}}$ (left) and $ {m_{\mathrm {T}}} ^{\text {tot}}$ (right) for events in the combined 2016 and 2017 data passing the baseline selections in the ${\mu {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for SM background and three benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events in each case. The shaded uncertainty bands represent the combined statistical and average systematic uncertainties in the background. |

png pdf |
Figure 3-a:
Distribution in ${{p_{\mathrm {T}}} ^\text {miss}}$ for events in the combined 2016 and 2017 data passing the baseline selections in the ${\mu {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for SM background and three benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events. The shaded uncertainty bands represent the combined statistical and average systematic uncertainties in the background. |
png pdf |
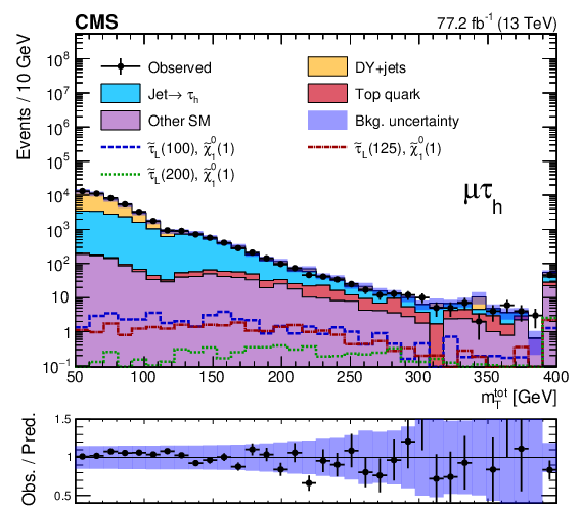
Figure 3-b:
Distribution in $ {m_{\mathrm {T}}} ^{\text {tot}}$ for events in the combined 2016 and 2017 data passing the baseline selections in the ${\mu {\tau _\mathrm {h}}}$ final state, along with the corresponding prediction for SM background and three benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. The numbers within parentheses in the legend correspond to the masses of the ${\tilde{\tau} _{\mathrm {L}}}$ and $\tilde{\chi}^0_1$ in GeV. The last bin includes overflow events. The shaded uncertainty bands represent the combined statistical and average systematic uncertainties in the background. |
png pdf |
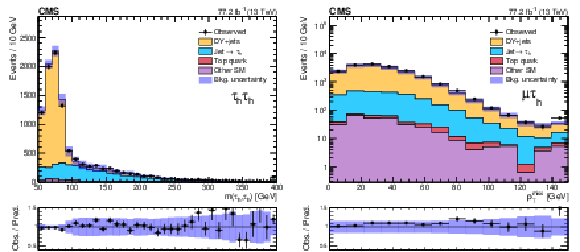
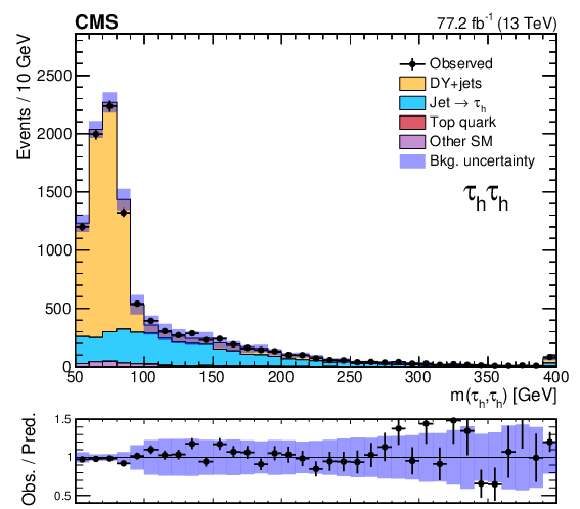
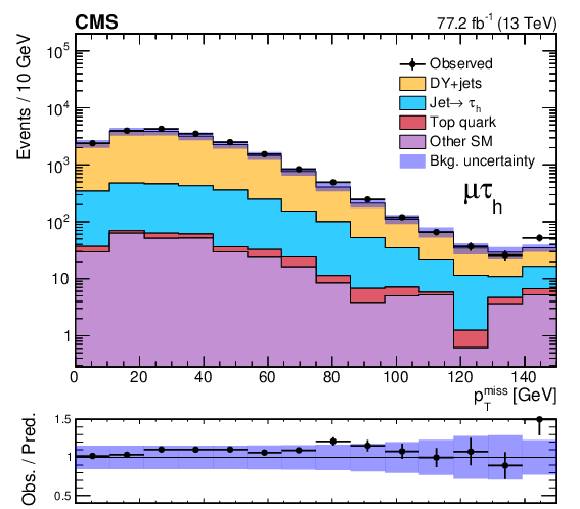
Figure 4:
Visible-mass spectra of $\tau$ lepton pairs in ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ events (left) and ${{p_{\mathrm {T}}} ^\text {miss}}$ distribution in ${\mu {\tau _\mathrm {h}}}$ events (right) in data and the corresponding prediction for SM background in the combined 2016 and 2017 DY+jets validation regions. The last bin includes overflow events in each case. The shaded uncertainty band represents the statistical and systematic uncertainties in the background prediction. For the ${\mu {\tau _\mathrm {h}}}$ distribution, the systematic uncertainty included in each bin corresponds to a single common average value. |
png pdf |
Figure 4-a:
Visible-mass spectra of $\tau$ lepton pairs in ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ events in data and the corresponding prediction for SM background in the combined 2016 and 2017 DY+jets validation regions. The last bin includes overflow events in each case. The shaded uncertainty band represents the statistical and systematic uncertainties in the background prediction. |
png pdf |
Figure 4-b:
${{p_{\mathrm {T}}} ^\text {miss}}$ distribution in ${\mu {\tau _\mathrm {h}}}$ events in data and the corresponding prediction for SM background in the combined 2016 and 2017 DY+jets validation regions. The last bin includes overflow events in each case. The shaded uncertainty band represents the statistical and systematic uncertainties in the background prediction. The systematic uncertainty included in each bin corresponds to a single common average value. |
png pdf |
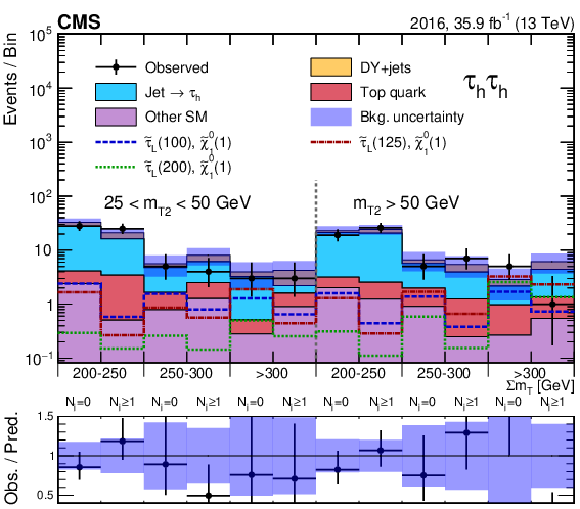
Figure 5:
Event counts and predicted yields for the SM background in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis for the 2016 (left) and 2017 (right) data, before (upper) and after (lower) a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark signal models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
Figure 5-a:
Event counts and predicted yields for the SM background in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis for the 2016 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark signal models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
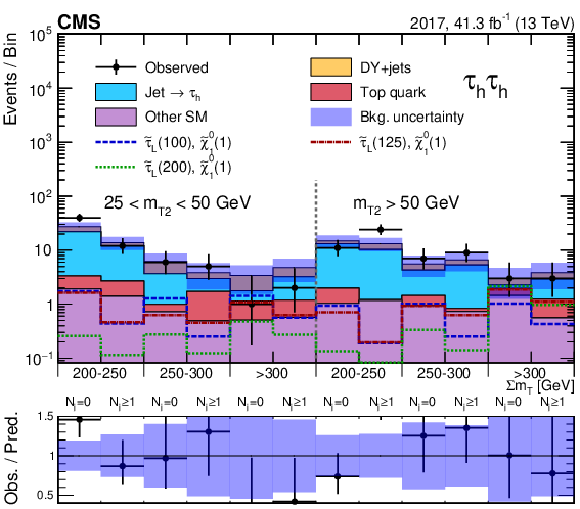
Figure 5-b:
Event counts and predicted yields for the SM background in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis for the 2017 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark signal models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
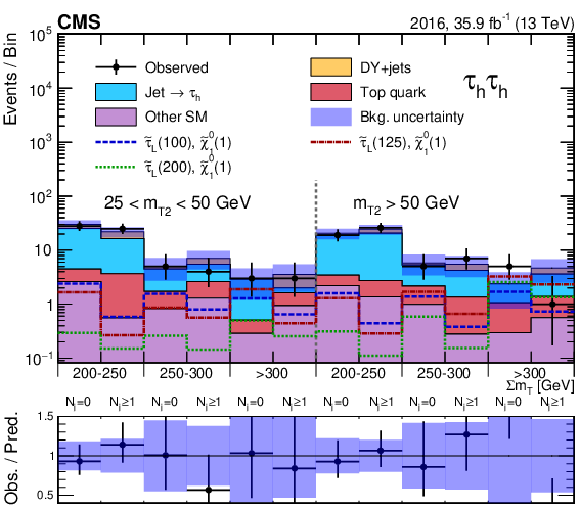
Figure 5-c:
Event counts and predicted yields for the SM background in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis for the 2016 data, after a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark signal models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
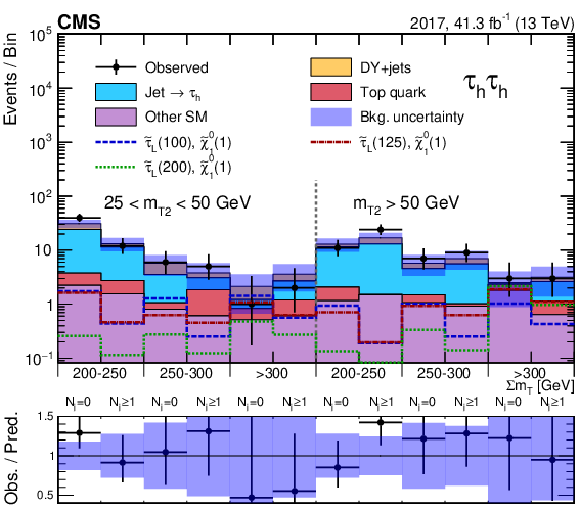
Figure 5-d:
Event counts and predicted yields for the SM background in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis for the 2017 data, after a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark signal models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
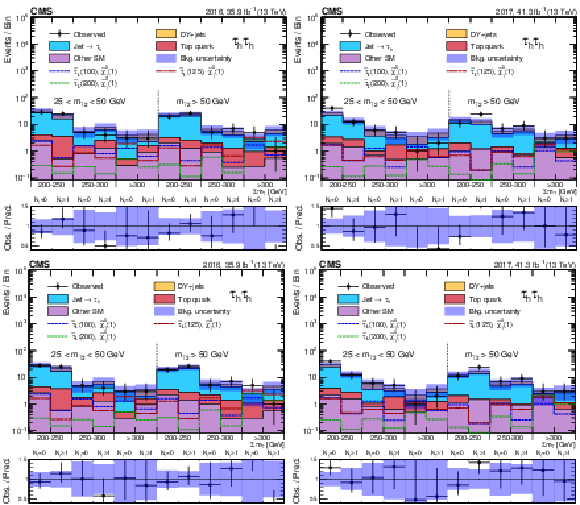
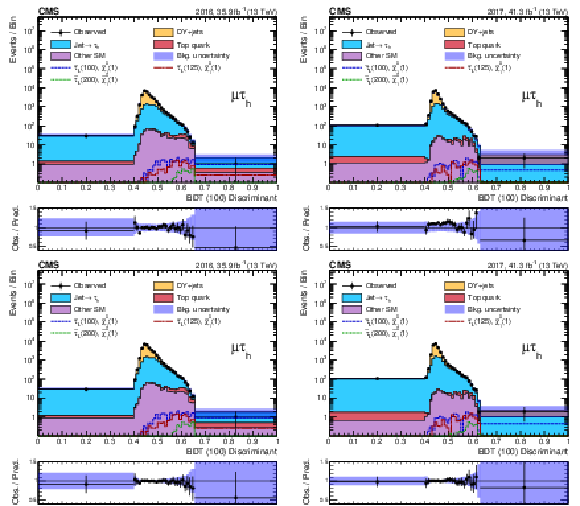
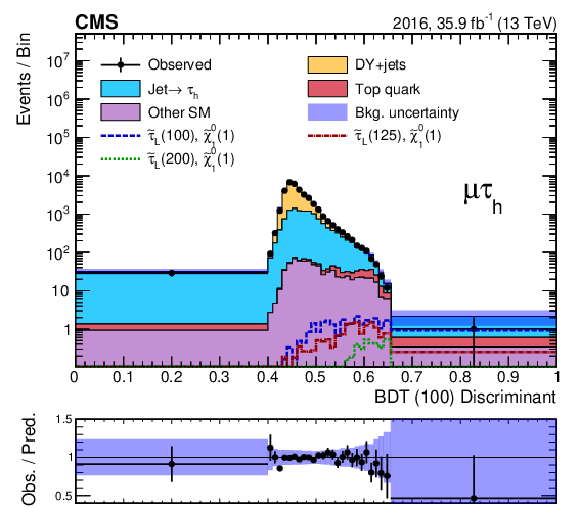
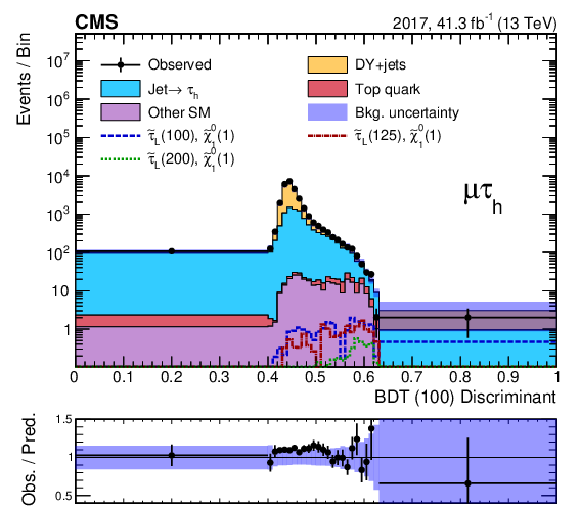
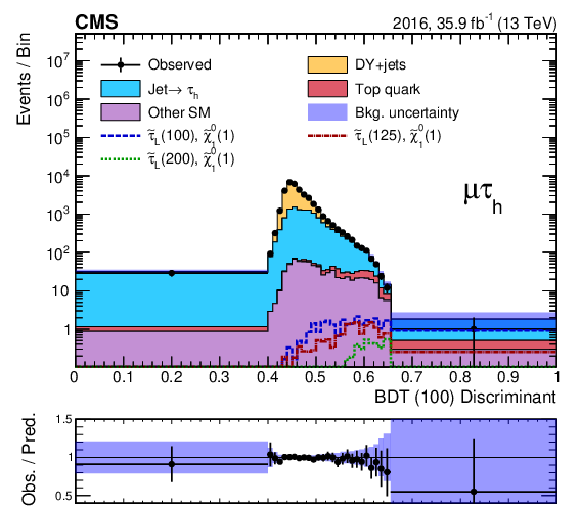
Figure 6:
Discriminant distributions for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mu {\tau _\mathrm {h}}}$ final state for the 2016 (left) and 2017 (right) data, before (upper) and after (lower) a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
Figure 6-a:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mu {\tau _\mathrm {h}}}$ final state for the 2016 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
Figure 6-b:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mu {\tau _\mathrm {h}}}$ final state for the 2017 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
Figure 6-c:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mu {\tau _\mathrm {h}}}$ final state for the 2016 data, after a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
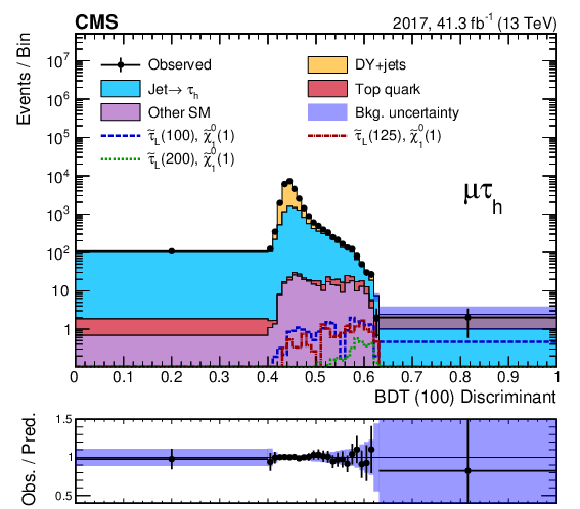
Figure 6-d:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mu {\tau _\mathrm {h}}}$ final state for the 2017 data, after a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
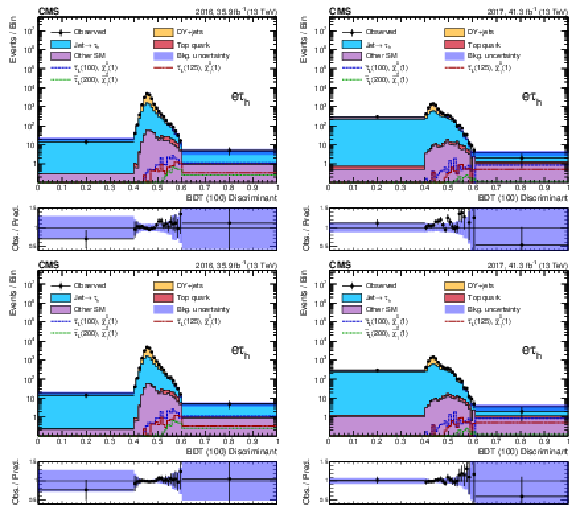
Figure 7:
Discriminant distributions for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mathrm{e} {\tau _\mathrm {h}}}$ final state for the 2016 (left) and 2017 (right) data, before (upper) and after (lower) a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
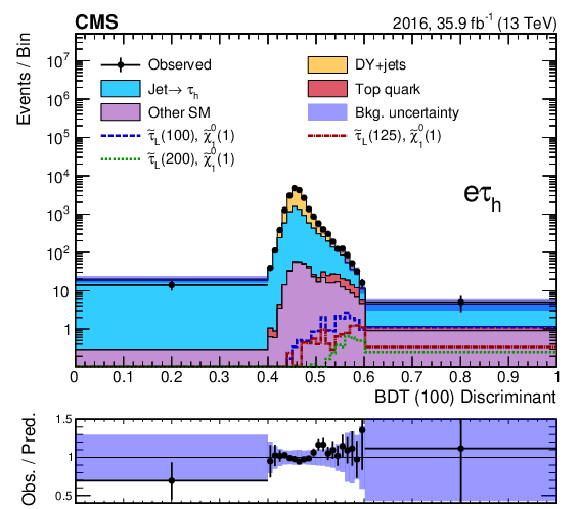
Figure 7-a:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mathrm{e} {\tau _\mathrm {h}}}$ final state for the 2016 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
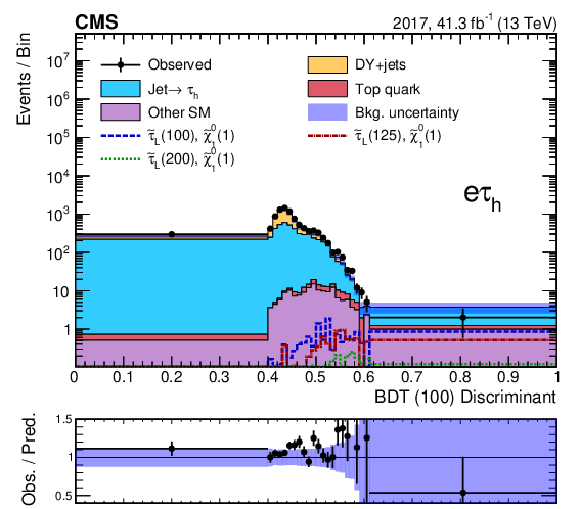
Figure 7-b:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mathrm{e} {\tau _\mathrm {h}}}$ final state for the 2017 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
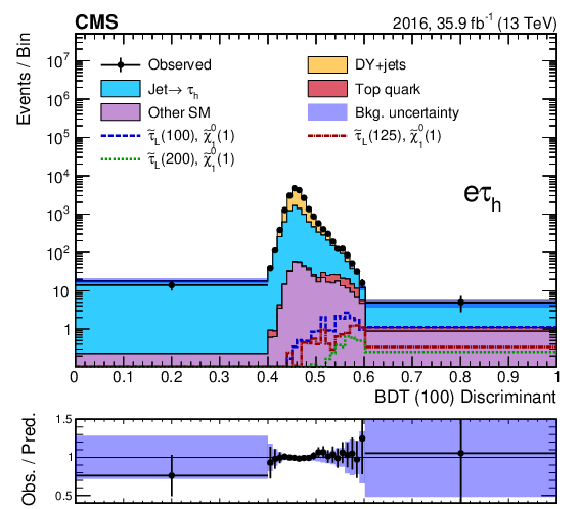
png pdf |
Figure 7-c:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mathrm{e} {\tau _\mathrm {h}}}$ final state for the 2016 data, before a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
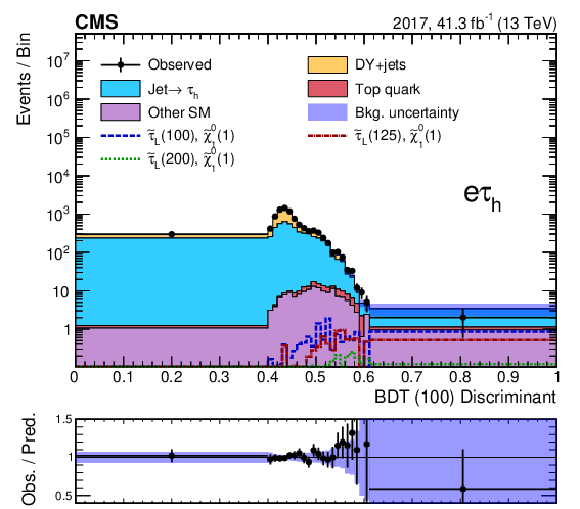
Figure 7-d:
Discriminant distribution for the BDT trained for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV (BDT (100)) in the ${\mathrm{e} {\tau _\mathrm {h}}}$ final state for the 2017 data, after a maximum-likelihood fit to the data. Predicted signal yields are also shown for benchmark models of ${\tilde{\tau} _{\mathrm {L}}}$ pair production with $m({\tilde{\tau} _{\mathrm {L}}})=$ 100, 125, and 200 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. |
png pdf |
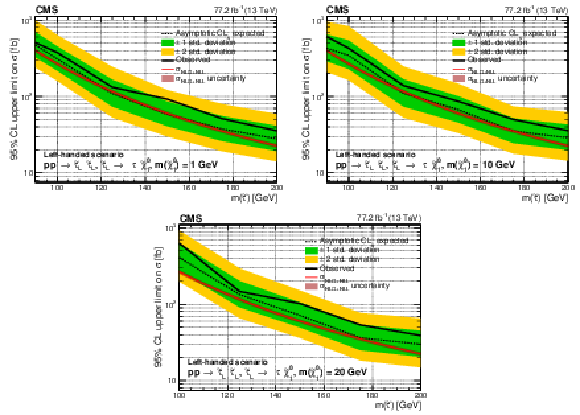
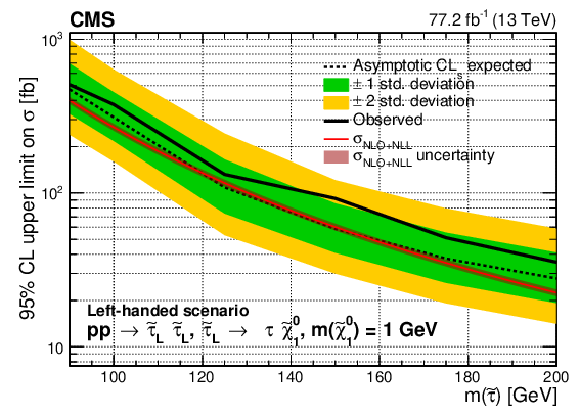
Figure 8:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the purely left-handed $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 1 GeV (upper left), 10 GeV (upper right) and 20 GeV (lower). The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
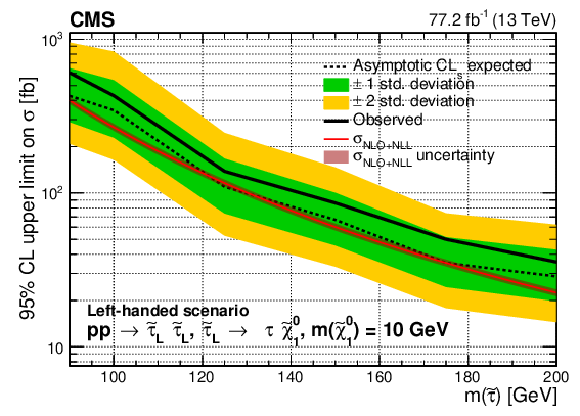
Figure 8-a:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the purely left-handed $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 1 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
Figure 8-b:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the purely left-handed $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 10 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |

png pdf |
Figure 8-c:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the purely left-handed $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 20 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
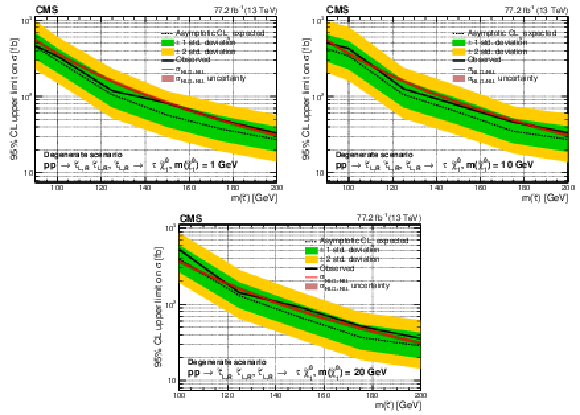
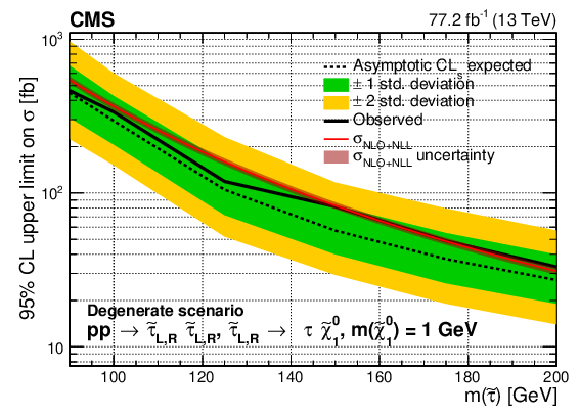
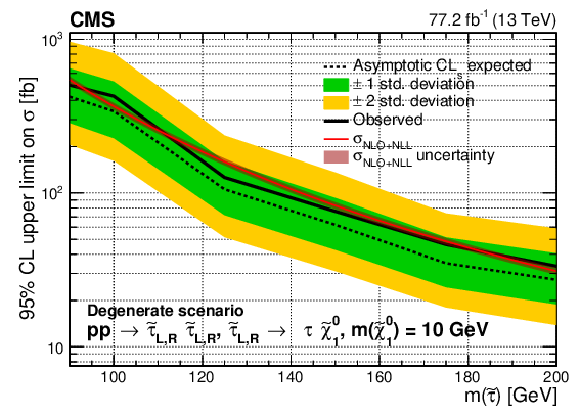
Figure 9:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the degenerate $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 1 GeV (upper left), 10 GeV (upper right) and 20 GeV (lower). The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
Figure 9-a:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the degenerate $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 1 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
Figure 9-b:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the degenerate $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 10 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
png pdf |
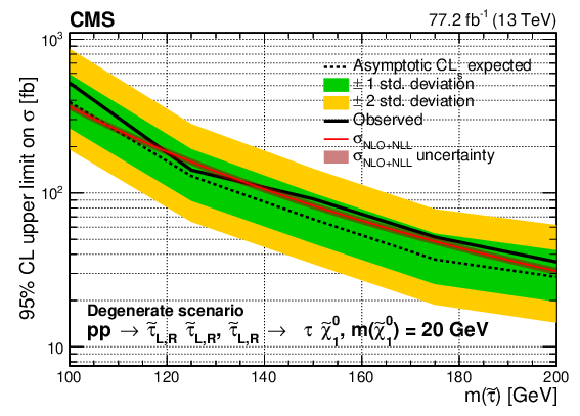
Figure 9-c:
Upper limit on the cross section ($\sigma $) of $\tilde{\tau}$ pair production excluded at 95% CL as a function of the $\tilde{\tau}$ mass in the degenerate $\tilde{\tau}$ models for a $\tilde{\chi}^0_1$ mass of 20 GeV. The results shown are for the statistical combination of the 2016 and 2017 data in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ and ${\ell {\tau _\mathrm {h}}}$ analyses. The inner (green) and outer (yellow) bands indicate the respective regions containing 68 and 95% of the distribution of limits expected under the background-only hypothesis. The solid red line indicates the NLO+NLL prediction for the signal production cross section calculated with Resummino [39], while the red shaded band represents the uncertainty in the prediction. |
| Tables | |
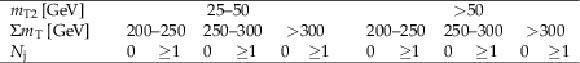
png pdf |
Table 1:
Ranges in ${m_{\mathrm {T2}}}$, ${\Sigma {m_{\mathrm {T}}}}$, and ${N_{\text {j}}}$ used to define the SRs used in the ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ analysis. |
png pdf |
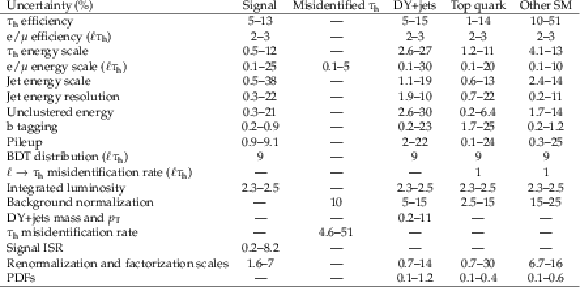
Table 2:
Systematic uncertainties of SM background predictions and a representative signal model, corresponding to a left-handed $\tilde{\tau}$, with $m(\tilde{\tau}) = $ 100 GeV and $m(\tilde{\chi}^0_1) = $ 1 GeV. The uncertainty ranges are given in percent. The spread of values reflects uncertainties in different SRs. |
png pdf |
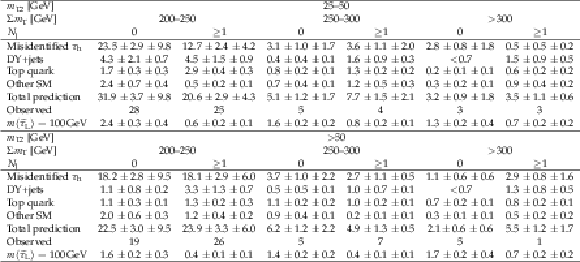
Table 3:
Predicted background yields and observed event counts in ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ SRs in 2016 data. For the background estimates with no events in the sideband or in the simulated sample, we calculate the 68% CL upper limit on the yield. The first and second uncertainties given are statistical and systematic, respectively. We also list the predicted signal yields corresponding to the purely left-handed model for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV. |
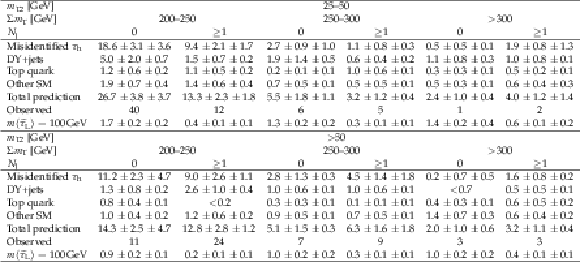
png pdf |
Table 4:
Predicted background yields and observed event counts in ${{\tau _\mathrm {h}} {\tau _\mathrm {h}}}$ SRs in 2017 data. For the background estimates with no events in the sideband or in the simulated sample, we calculate the 68% CL upper limit on the yield. The first and second uncertainties given are statistical and systematic, respectively. We also list the predicted signal yields corresponding to the purely left-handed model for a $\tilde{\tau}$ mass of 100 GeV and a $\tilde{\chi}^0_1$ mass of 1 GeV. |

png pdf |
Table 5:
Predicted background yields and observed event counts in the most sensitive last bins of the BDT distributions in the ${\mathrm{e} {\tau _\mathrm {h}}}$ and ${\mu {\tau _\mathrm {h}}}$ final states, in data collected in 2016. The numbers in parentheses in the first row are the $\tilde{\tau}$ and $\tilde{\chi}^0_1$ masses corresponding to the signal model for left-handed $\tilde{\tau}$ pair production that is used to train the BDT. In the bottom row, we list the corresponding predicted signal yields in the last bin of the BDT distribution. The first and second uncertainties given are statistical and systematic, respectively. |

png pdf |
Table 6:
Predicted background yields and observed event counts in the most sensitive last bins of the BDT distributions in the ${\mathrm{e} {\tau _\mathrm {h}}}$ and ${\mu {\tau _\mathrm {h}}}$ final states, in data collected in 2017. The numbers in parentheses in the first row are the $\tilde{\tau}$ and $\tilde{\chi}^0_1$ masses corresponding to the signal model for left-handed $\tilde{\tau}$ pair production that is used to train the BDT. In the bottom row, we list the corresponding predicted signal yields in the last bin of the BDT distribution. The first and second uncertainties given are statistical and systematic, respectively. |
| Summary |
| A search for direct $\tau$ slepton ($\tilde{\tau}$) pair production has been performed in proton-proton collisions at a center-of-mass energy of 13 TeV in events with a $\tau$ lepton pair and significant missing transverse momentum. Search regions are defined using kinematic observables that exploit expected differences in discriminants between signal and background. The data used for this search correspond to an integrated luminosity of 77.2 fb$^{-1}$ collected in 2016 and 2017 with the CMS detector. No excess above the expected standard model background has been observed. Upper limits have been set on the cross section for direct $\tilde{\tau}$ pair production for simplified models in which each $\tilde{\tau}$ decays to a $\tau$ lepton and the lightest neutralino, with the latter being assumed to be the lightest supersymmetric particle. For purely left-handed $\tilde{\tau}$ pair production, the analysis is most sensitive to a $\tilde{\tau}$ mass of 125 GeV when the neutralino is nearly massless. The observed limit is a factor of 1.14 larger than the expected production cross section in this model. The limits observed for left-handed $\tilde{\tau}$ pair production are the strongest obtained thus far for low values of the $\tilde{\tau}$ mass. In a more optimistic, degenerate production model, in which both left- and right-handed $\tilde{\tau}$ pairs are produced, we exclude $\tilde{\tau}$ masses up to 150 GeV, again under the assumption of a nearly massless neutralino. These results represent the first exclusion reported for this model for low values of the $\tilde{\tau}$ mass between 90 and 120 GeV. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Gol'fand and E. P. Likhtman | Extension of the algebra of Poincaré group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 9 | G. 't Hooft | Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking | NATO Sci. Ser. B 59 (1980)135 | |
| 10 | E. Witten | Dynamical breaking of supersymmetry | NPB 188 (1981) 513 | |
| 11 | M. Dine, W. Fischler, and M. Srednicki | Supersymmetric technicolor | NPB 189 (1981) 575 | |
| 12 | S. Dimopoulos and S. Raby | Supercolor | NPB 192 (1981) 353 | |
| 13 | S. Dimopoulos and H. Georgi | Softly broken supersymmetry and SU(5) | NPB 193 (1981) 150 | |
| 14 | R. K. Kaul and P. Majumdar | Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories | NPB 199 (1982) 36 | |
| 15 | C. Boehm, A. Djouadi, and M. Drees | Light scalar top quarks and supersymmetric dark matter | PRD 62 (2000) 035012 | hep-ph/9911496 |
| 16 | C. Bal\'azs, M. Carena, and C. E. M. Wagner | Dark matter, light stops and electroweak baryogenesis | PRD 70 (2004) 015007 | hep-ph/403224 |
| 17 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 18 | G. Jungman, M. Kamionkowski, and K. Griest | Supersymmetric dark matter | PR 267 (1996) 195 | hep-ph/9506380 |
| 19 | G. Hinshaw et al. | Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological parameter results | Astrophys. J. Suppl. 208 (2013) 19 | 1212.5226 |
| 20 | K. Griest and D. Seckel | Three exceptions in the calculation of relic abundances | PRD 43 (1991) 3191 | |
| 21 | D. A. Vasquez, G. B\'elanger, and C. Boehm | Revisiting light neutralino scenarios in the MSSM | PRD 84 (2011) 095015 | 1108.1338 |
| 22 | S. F. King, J. P. Roberts, and D. P. Roy | Natural dark matter in SUSY GUTs with non-universal gaugino masses | JHEP 10 (2007) 106 | 0705.4219 |
| 23 | M. Battaglia et al. | Proposed post-LEP benchmarks for supersymmetry | EPJC 22 (2001) 535 | hep-ph/0106204 |
| 24 | R. L. Arnowitt et al. | Determining the dark matter relic density in the minimal supergravity stau-neutralino coannihilation region at the Large Hadron Collider | PRL 100 (2008) 231802 | 0802.2968 |
| 25 | G. B\'elanger, S. Biswas, C. Boehm, and B. Mukhopadhyaya | Light neutralino dark matter in the MSSM and its implication for LHC searches for staus | JHEP 12 (2012) 076 | 1206.5404 |
| 26 | E. Arganda, V. Martin-Lozano, A. D. Medina, and N. Mileo | Potential discovery of staus through heavy Higgs boson decays at the LHC | JHEP 09 (2018) 056 | 1804.10698 |
| 27 | J. Alwall, P. Schuster, and N. Toro | Simplified models for a first characterization of new physics at the LHC | PRD 79 (2009) 075020 | 0810.3921 |
| 28 | J. Alwall, M.-P. Le, M. Lisanti, and J. Wacker | Model-independent jets plus missing energy searches | PRD 79 (2009) 015005 | 0809.3264 |
| 29 | LHC New Physics Working Group | Simplified models for LHC new physics searches | JPG 39 (2012) 105005 | 1105.2838 |
| 30 | ALEPH Collaboration | Search for scalar leptons in e$ ^{+} $e$ ^{-} $ collisions at center-of-mass energies up to 209 GeV | PLB 526 (2002) 206 | hep-ex/0112011 |
| 31 | DELPHI Collaboration | Searches for supersymmetric particles in e$ ^{+} $e$ ^{-} $ collisions up to 208 GeV and interpretation of the results within the MSSM | EPJC 31 (2003) 421 | hep-ex/0311019 |
| 32 | L3 Collaboration | Search for scalar leptons and scalar quarks at LEP | PLB 580 (2004) 37 | hep-ex/0310007 |
| 33 | OPAL Collaboration | Search for anomalous production of dilepton events with missing transverse momentum in e$ ^{+} $e$ ^{-} $ collisions at $ \sqrt{s} = $ 183 GeV to 209 GeV | EPJC 32 (2004) 453 | hep-ex/0309014 |
| 34 | ATLAS Collaboration | Search for the direct production of charginos, neutralinos and staus in final states with at least two hadronically decaying taus and missing transverse momentum in pp collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector | JHEP 10 (2014) 96 | 1407.0350 |
| 35 | ATLAS Collaboration | Search for the electroweak production of supersymmetric particles in $ \sqrt{s} = $ 8 TeV pp collisions with the ATLAS detector | PRD 93 (2016) 052002 | 1509.07152 |
| 36 | CMS Collaboration | Search for electroweak production of charginos in final states with two tau leptons in pp collisions at $ \sqrt{s}= $ 8 TeV | JHEP 04 (2017) 018 | CMS-SUS-14-022 1610.04870 |
| 37 | CMS Collaboration | Search for supersymmetry in events with a $ \tau $ lepton pair and missing transverse momentum in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 11 (2018) 151 | CMS-SUS-17-003 1807.02048 |
| 38 | GEANT4 Collaboration | GEANT4 --- a simulation toolkit | NIMA 506 (2003) 250 | |
| 39 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Revisiting slepton pair production at the Large Hadron Collider | JHEP 01 (2014) 168 | 1310.2621 |
| 40 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 41 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 42 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 43 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 44 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 45 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 46 | CMS Collaboration | Study of pileup removal algorithms for jets | CMS-PAS-JME-14-001 | CMS-PAS-JME-14-001 |
| 47 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 48 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 49 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 50 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons decaying to hadrons and $ \nu_\tau $ in pp collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P10005 | CMS-TAU-16-003 1809.02816 |
| 51 | Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner | Gradient-based learning applied to document recognition | in Proceedings of the IEEE, p. 2278 1998 | |
| 52 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 53 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 54 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 55 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 56 | E. Re | Single-top $ Wt $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 57 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 58 | A. Kalogeropoulos and J. Alwall | The SysCalc code: A tool to derive theoretical systematic uncertainties | 1801.08401 | |
| 59 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 60 | CMS Collaboration | Investigations of the impact of the parton shower tuning in Pythia 8 in the modelling of $ \mathrm{t\overline{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 61 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | Submitted to EPJC | CMS-GEN-17-001 1903.12179 |
| 62 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 63 | CMS Collaboration | Search for top-squark pair production in the single-lepton final state in pp collisions at $ \sqrt{s} = $ 8 TeV | EPJC 73 (2013) 2677 | CMS-SUS-13-011 1308.1586 |
| 64 | C. G. Lester and D. J. Summers | Measuring masses of semi-invisibly decaying particle pairs produced at hadron colliders | PLB 463 (1999) 99 | hep-ph/9906349 |
| 65 | A. Barr, C. Lester, and P. Stephens | $ m_{\mathrm{T2}} $: the truth behind the glamour | JPG 29 (2003) 2343 | hep-ph/0304226 |
| 66 | C. G. Lester and B. Nachman | Bisection-based asymmetric $ m_{\mathrm{T2}} $ computation: a higher precision calculator than existing symmetric methods | JHEP 03 (2015) 100 | 1411.4312 |
| 67 | D. Tovey | On measuring the masses of pair-produced semi-invisibly decaying particles at hadron colliders | JHEP 04 (2008) 034 | 0802.2879 |
| 68 | G. Polesello and D. Tovey | Supersymmetric particle mass measurement with boost-corrected contransverse mass | JHEP 03 (2010) 030 | 0910.0174 |
| 69 | C. Cuenca Almenar | Search for the neutral MSSM Higgs bosons in the ditau decay channels at CDF Run II | PhD thesis, Valencia U., IFIC | |
| 70 | CMS Collaboration | Search for neutral MSSM Higgs bosons decaying to a pair of tau leptons in pp collisions | JHEP 10 (2014) 160 | CMS-HIG-13-021 1408.3316 |
| 71 | L. Demortier | P values and nuisance parameters | in Statistical issues for LHC physics. Proceedings, Workshop, PHYSTAT-LHC, Geneva, Switzerland, June 27-29, 2007, p. 23 2008 | |
| 72 | CMS Collaboration | Measurement of the differential Drell-Yan cross section in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | Submitted to JHEP | CMS-SMP-17-001 1812.10529 |
| 73 | CMS Collaboration | Measurements of $ \mathrm{t\overline{t}} $ differential cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using events containing two leptons | JHEP 02 (2019) 149 | CMS-TOP-17-014 1811.06625 |
| 74 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 75 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 76 | CMS Collaboration | Interpretation of searches for supersymmetry with simplified models | PRD 88 (2013) 052017 | CMS-SUS-11-016 1301.2175 |
| 77 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 78 | A. L. Read | Presentation of search results: the $ \text{CL}_\text{s} $ technique | JPG 28 (2002) 2693 | |
| 79 | The ATLAS Collaboration, The CMS Collaboration, The LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 80 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|