

Compact Muon Solenoid
LHC, CERN
| CMS-SMP-23-008 ; CERN-EP-2025-041 | ||
| Measurement of event shapes in minimum-bias events from proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 23 May 2025 | ||
| Phys. Rev. D 112 (2025) 11, 112006 | ||
| Abstract: A measurement of event-shape variables is presented, using a data sample produced in a special run with approximately one inelastic proton-proton collision per bunch crossing. The data were collected with the CMS detector at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 64 $ \mu$b$^{-1} $. A number of observables related to the overall distribution of charged particles in the collisions are corrected for detector effects and compared with simulations. Inclusive event-shape distributions, as well as differential distributions of event shapes as functions of charged-particle multiplicity, are studied. None of the models investigated are able to satisfactorily describe the data. Moreover, there are significant features common amongst all generator setups studied, particularly showing data being more isotropic than any of the simulations. Multidimensional unfolded distributions are provided, along with their correlations. | ||
| Links: e-print arXiv:2505.17850 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
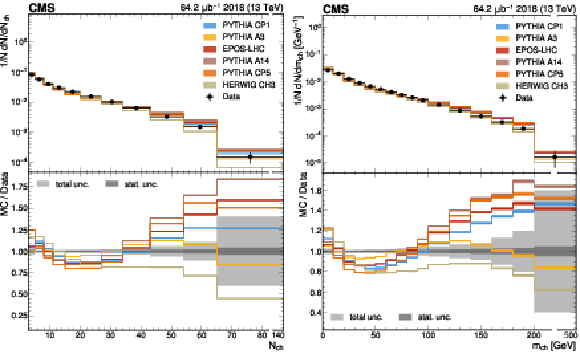
Figure 1:
The unfolded results for (left) the particle multiplicity, and (right) invariant mass, compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
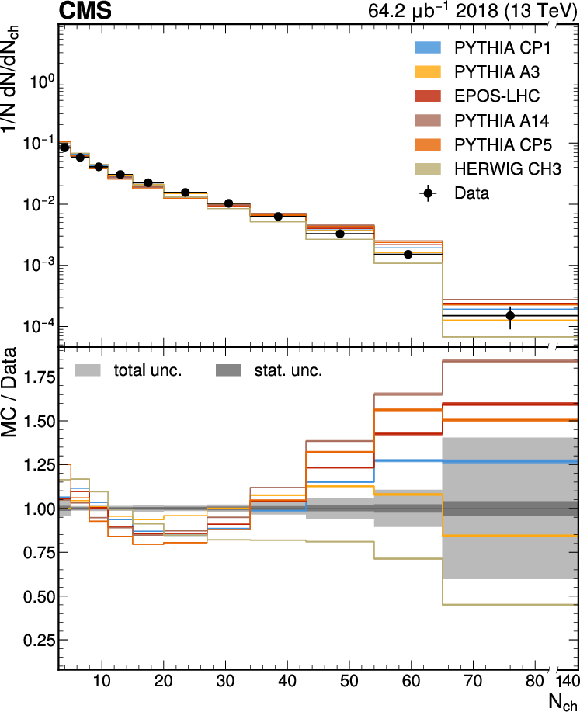
Figure 1-a:
The unfolded results for (left) the particle multiplicity, and (right) invariant mass, compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
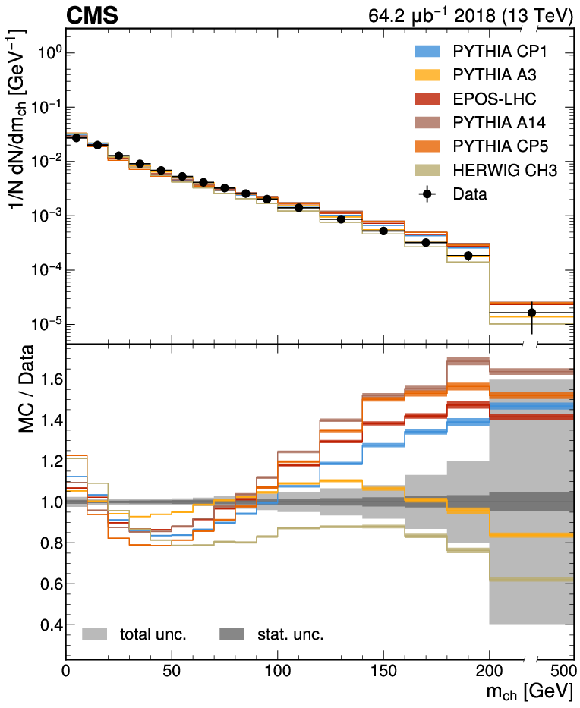
Figure 1-b:
The unfolded results for (left) the particle multiplicity, and (right) invariant mass, compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
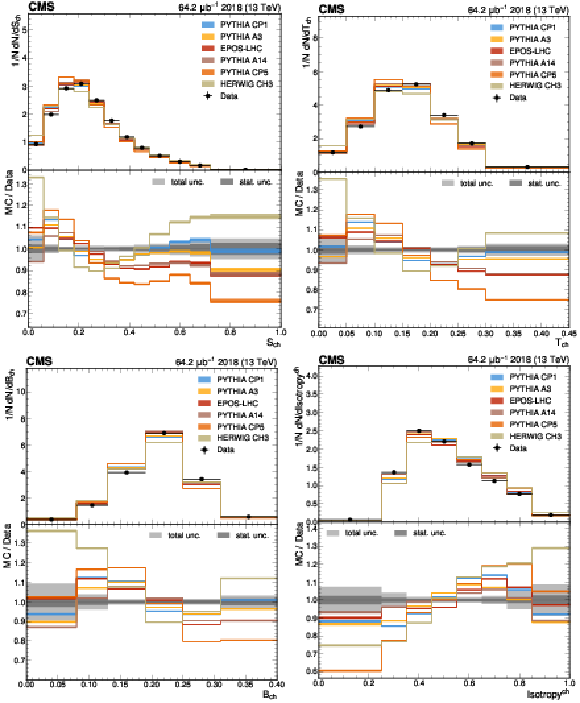
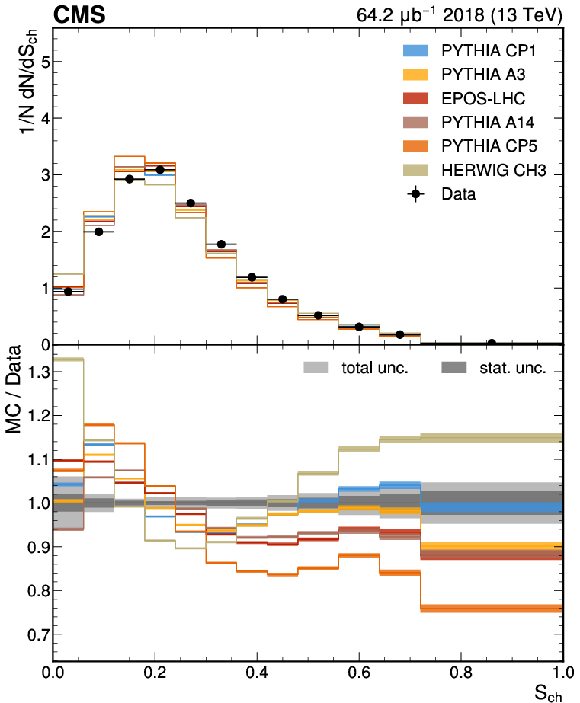
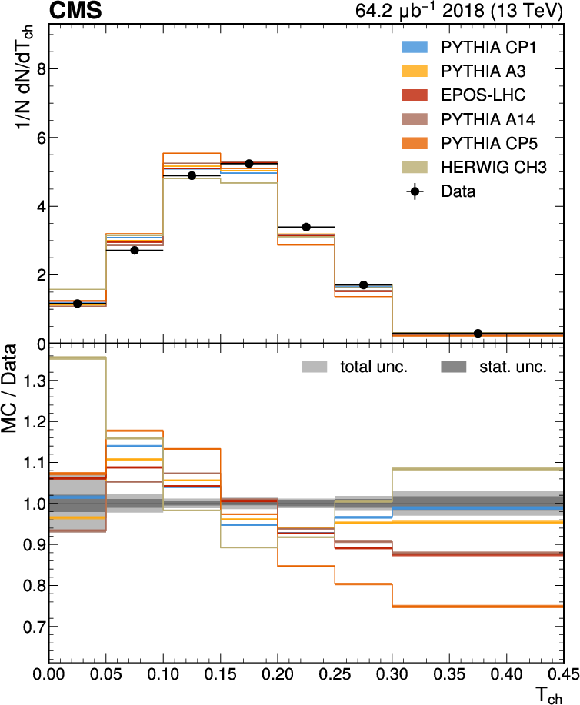
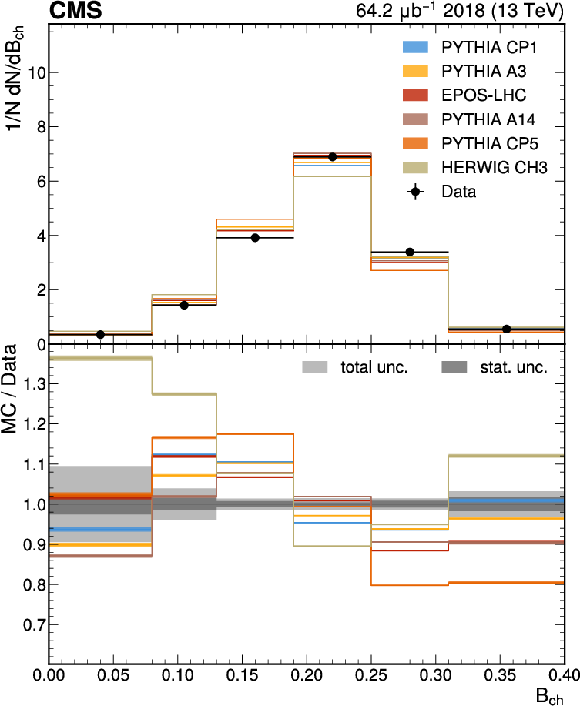
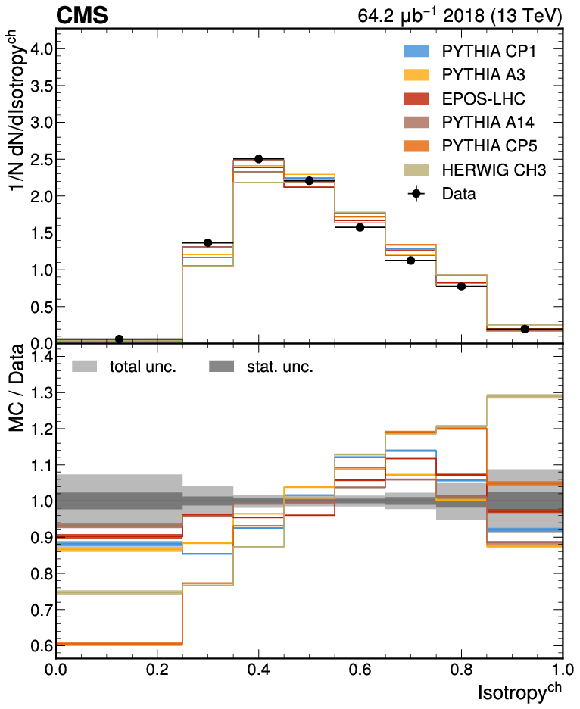
Figure 2:
The unfolded results for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) isotropy compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 2-a:
The unfolded results for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) isotropy compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 2-b:
The unfolded results for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) isotropy compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 2-c:
The unfolded results for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) isotropy compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 2-d:
The unfolded results for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) isotropy compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
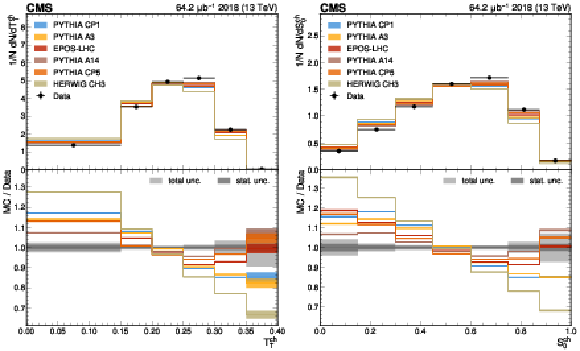
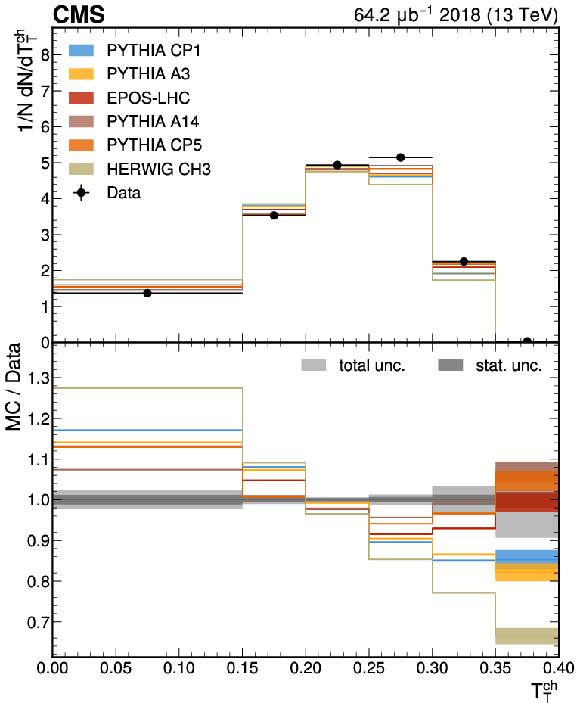
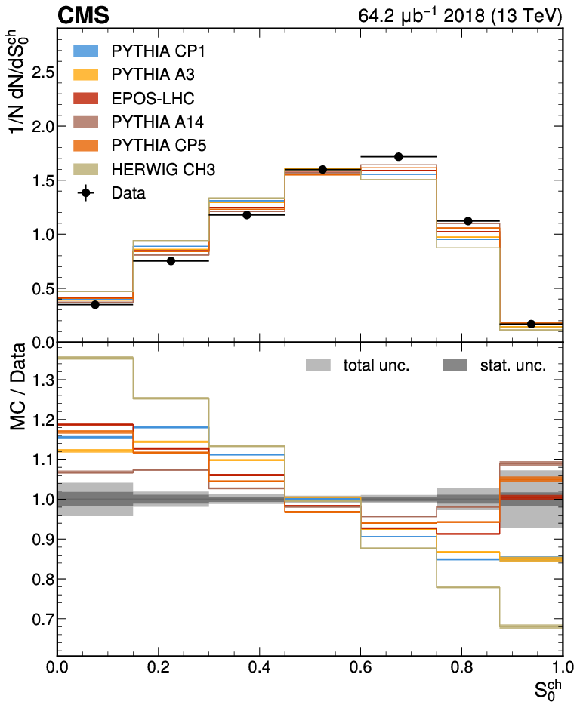
Figure 3:
The unfolded results for (left) transverse thrust, and (right) transverse spherocity compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 3-a:
The unfolded results for (left) transverse thrust, and (right) transverse spherocity compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure 3-b:
The unfolded results for (left) transverse thrust, and (right) transverse spherocity compared with the nominal MC from the PYTHIA CP1 tune and predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
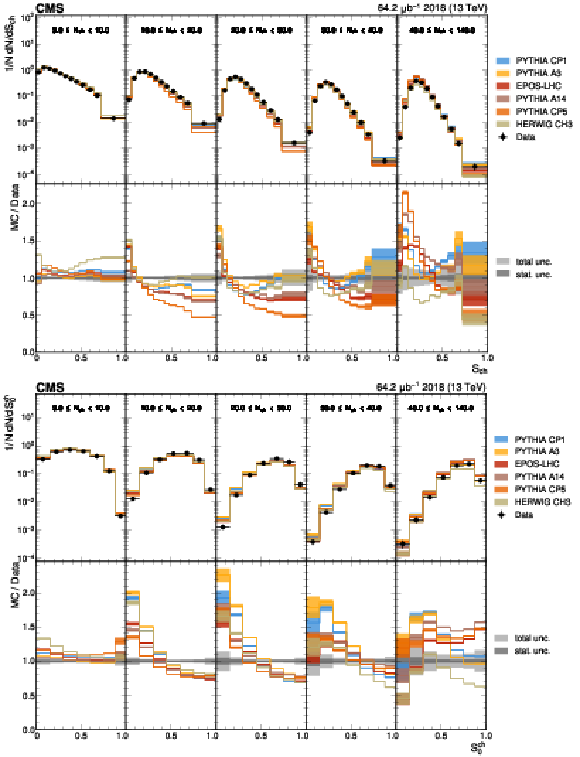
Figure 4:
The unfolded distributions of sphericity (upper) and transverse spherocity (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
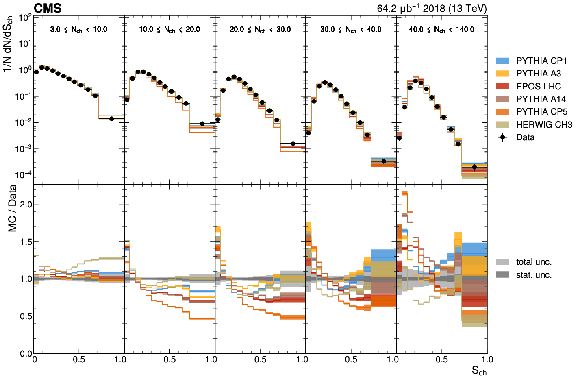
png pdf |
Figure 4-a:
The unfolded distributions of sphericity (upper) and transverse spherocity (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
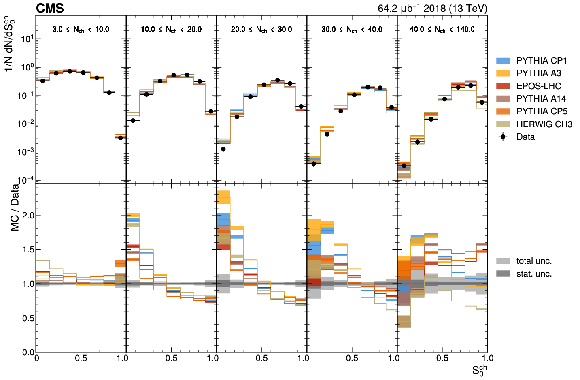
png pdf |
Figure 4-b:
The unfolded distributions of sphericity (upper) and transverse spherocity (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B1:
The unfolded distributions of event isotropy (upper) and broadening (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B1-a:
The unfolded distributions of event isotropy (upper) and broadening (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B1-b:
The unfolded distributions of event isotropy (upper) and broadening (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B2:
The unfolded distributions of thrust (upper) and transverse thrust (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B2-a:
The unfolded distributions of thrust (upper) and transverse thrust (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
Figure B2-b:
The unfolded distributions of thrust (upper) and transverse thrust (lower) in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
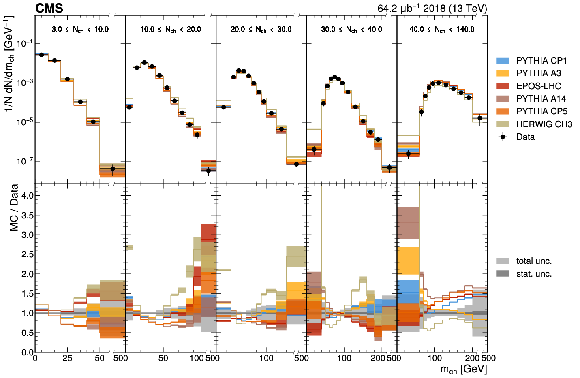
Figure B3:
The unfolded invariant mass of charged particles in slices of charged-particle multiplicity compared with the nominal MC from the PYTHIA CP1 tune and MC predictions from the PYTHIA A14, CP5, A3 tunes, the EPOS-LHC generator, and the HERWIG CH3 tune. The statistical uncertainty on each of the predictions is shown by its shaded band. |
png pdf |
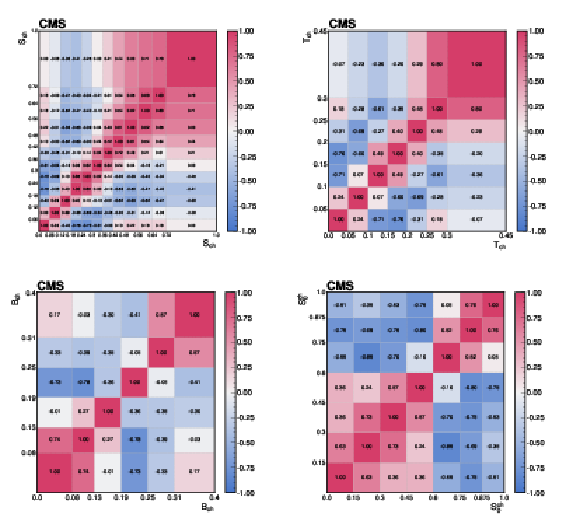
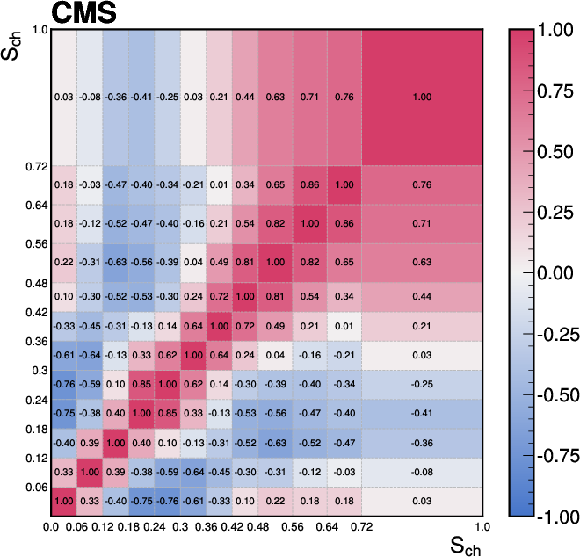
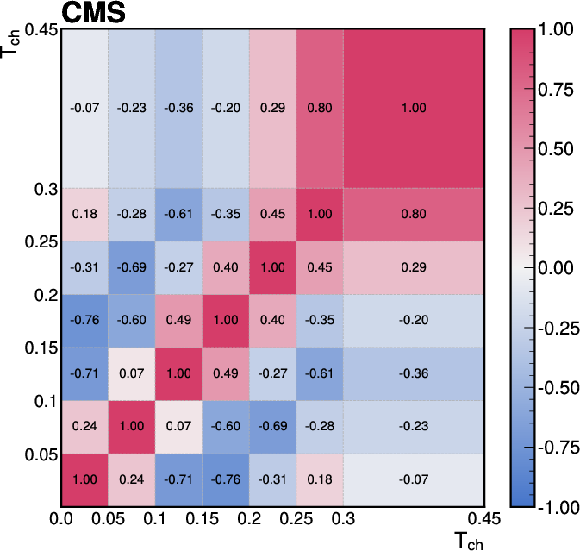
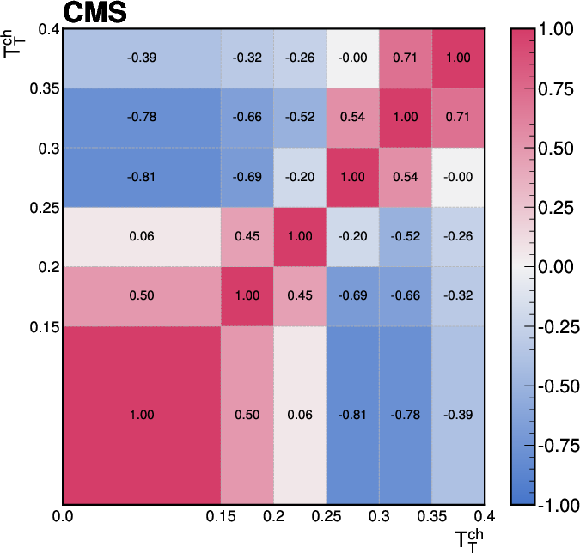
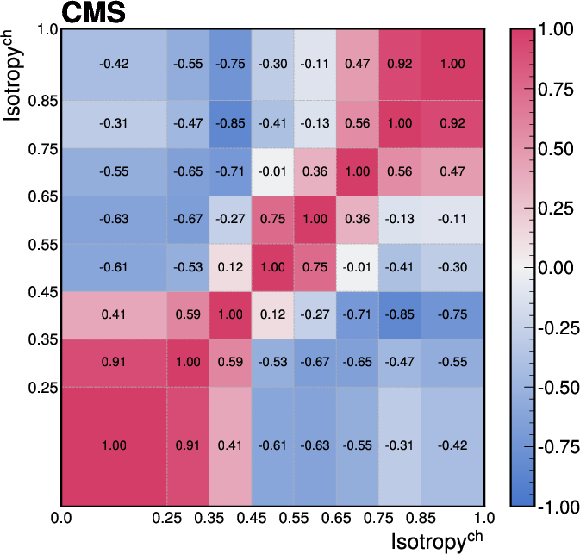
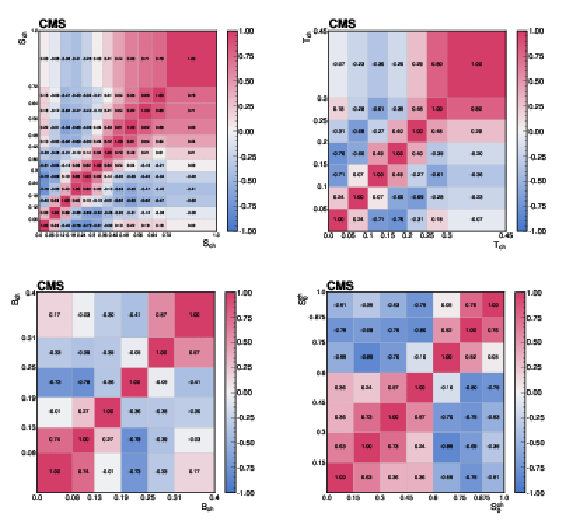
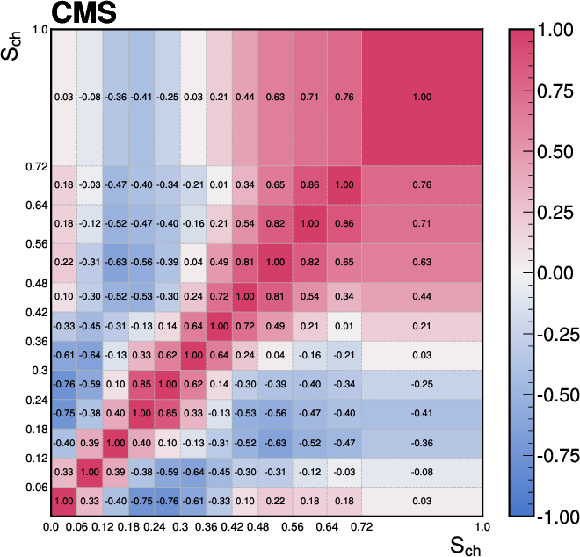
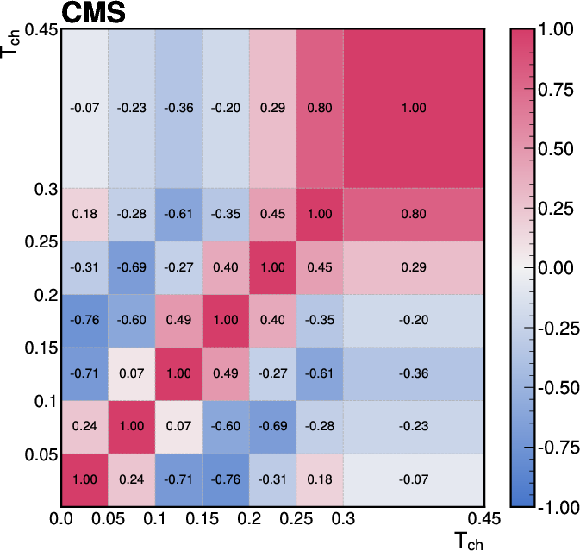
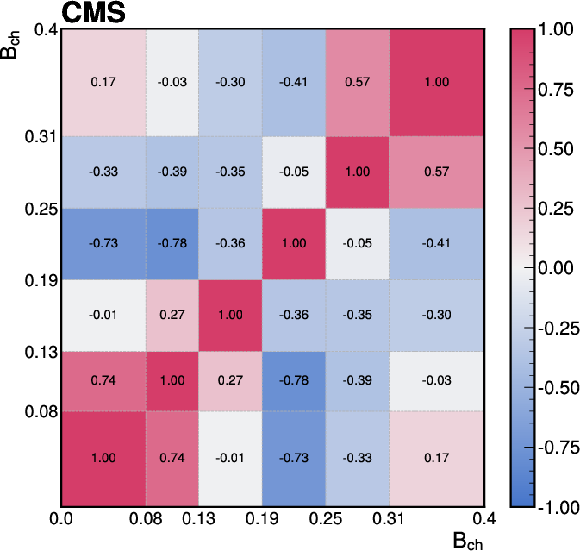
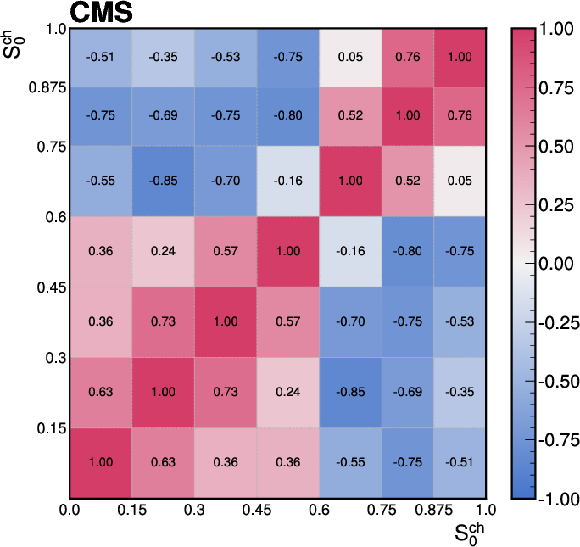
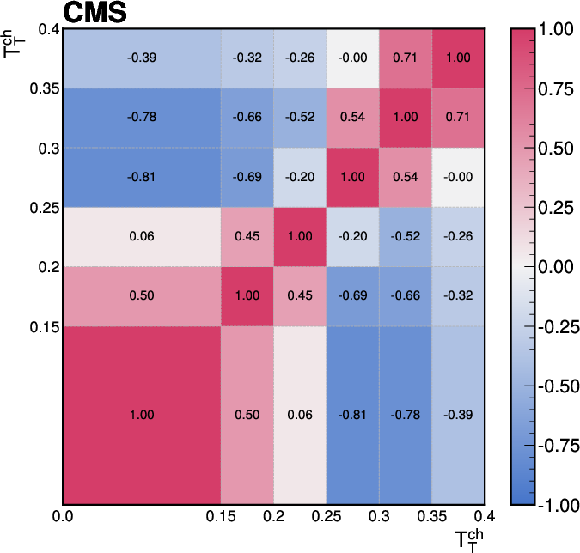
Figure C1:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) transverse spherocity. |
png pdf |
Figure C1-a:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) transverse spherocity. |
png pdf |
Figure C1-b:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) transverse spherocity. |
png pdf |
Figure C1-c:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) transverse spherocity. |
png pdf |
Figure C1-d:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) sphericity, (upper right) thrust, (lower left) broadening, and (lower right) transverse spherocity. |
png pdf |
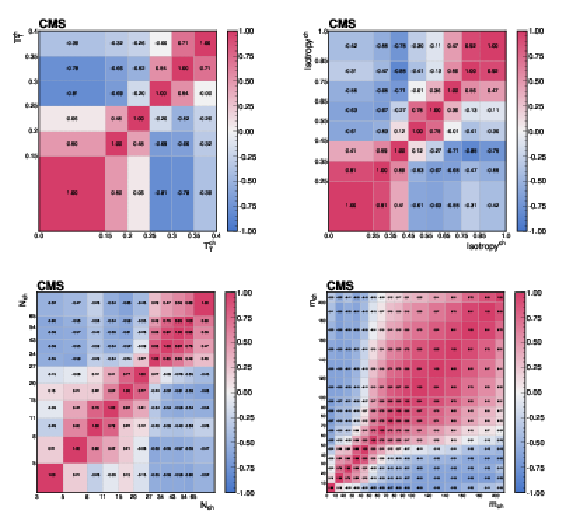
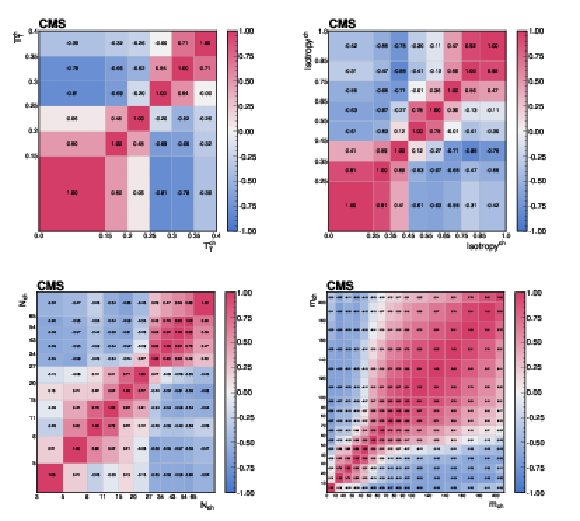
Figure C2:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) transverse thrust, (upper right) isotropy, (lower left) particle multiplicity, and (lower right) invariant mass. |
png pdf |
Figure C2-a:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) transverse thrust, (upper right) isotropy, (lower left) particle multiplicity, and (lower right) invariant mass. |
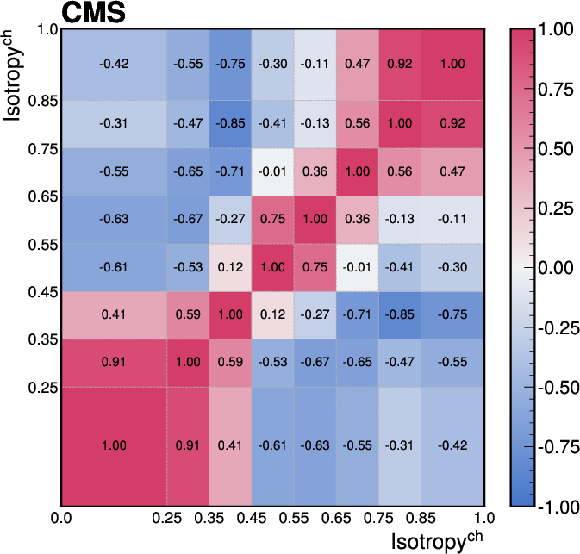
png pdf |
Figure C2-b:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) transverse thrust, (upper right) isotropy, (lower left) particle multiplicity, and (lower right) invariant mass. |

png pdf |
Figure C2-c:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) transverse thrust, (upper right) isotropy, (lower left) particle multiplicity, and (lower right) invariant mass. |

png pdf |
Figure C2-d:
The correlations of the unfolding systematic uncertainty between bins of the event-shape observables shown for (upper left) transverse thrust, (upper right) isotropy, (lower left) particle multiplicity, and (lower right) invariant mass. |
| Tables | |

png pdf |
Table 1:
Samples of simulated minimum-bias events used for the unfolding. The value of the strong coupling constant, $ \alpha_\mathrm{S} $, corresponds to that used in the parton distribution function (PDF) set. The samples are simulated without additional pileup interactions. |

png pdf |
Table A1:
Samples of simulated minimum-bias events used for validation. The value of $ \alpha_\mathrm{S} $ corresponds to that used in the PDF set. |

png pdf |
Table D1:
Relative uncertainties of unfolding from different sources, averaged over bins of transverse sphericity. The uncertainty from regularization and that from the model deficiency of the migration are estimated from the square root of the quadrature sum of the differences between the unfolding result using the nominal MC simulation and those using reweighted MC samples to systematic variations. The MC statistical uncertainty is estimated from the statistical uncertainty of the histogram of weighted MC samples after the unfolding. The data statistical uncertainty is estimated from the standard deviations of the unfolding results to alternative data samples with weight following a Poisson(1) distribution. The average relative uncertainties for the distributions of other observables are similar in size. |
| Summary |
| A measurement of event shapes in a minimum-bias selection of proton-proton collisions at a center-of-mass energy of 13 TeV has been presented. Low-pileup data collected with the CMS detector in 2018 were used, and the kinematics of reconstructed tracks were used to unfold the distributions to the level of stable charged particles. An unbinned multidimensional unfolding algorithm was used to obtain these results. All one- and two-dimensional distributions as well as their covariances are provided. The results show a consistent trend of mismodeling event shapes common across all simulation configurations considered. The simulations under study include several different underlying physics models, from the PYTHIA, EPOS-LHC, and HERWIG generators, as well as a number of tunes of the PYTHIA generator. For each of these simulations, the isotropy of the event shapes is underpredicted across a range of six different event-shape observables. Some mismodeling of the charged-particle multiplicity and the invariant mass of the charged particles is also observed. The interplay between these two trends was investigated by considering the event-shape observables in slices of charged-particle multiplicity. These investigations show that the observed data continue to prefer more isotropic distributions even within slices of charged-particle multiplicity and when considering only the plane transverse to the beam direction. These observations suggest that the mismodeling of event shapes is likely not coming only from the distribution of the number of charged particles or poorly modeled longitudinal components. These event-shape observables are important in probing soft and nonperturbative effects in quantum chromodynamics (QCD) at the LHC. The unfolded data [56,57] should be used by the community to improve and develop existing proton-proton collision models. The continued development of these models will be critical for understanding phenomena such as quark-gluon plasma and topological effects in non-Abelian gauge theories, such as QCD instantons. |
| References | ||||
| 1 | ALICE Collaboration | Long- and short-range correlations and their event-scale dependence in high-multiplicity pp collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2021) 290 | 2101.03110 |
| 2 | CMS Collaboration | Observation of long-range, near-side angular correlations in proton-proton collisions at the LHC | JHEP 09 (2010) 091 | CMS-QCD-10-002 1009.4122 |
| 3 | CMS Collaboration | Evidence for collectivity in pp collisions at the LHC | PLB 765 (2017) 193 | CMS-HIN-16-010 1606.06198 |
| 4 | CMS Collaboration | Multiplicity and rapidity dependence of strange hadron production in pp, pPb, and PbPb collisions at the LHC | PLB 768 (2017) 103 | CMS-HIN-15-006 1605.06699 |
| 5 | ALICE Collaboration | Enhanced production of multi-strange hadrons in high-multiplicity proton-proton collisions | Nat. Phys. 13 (2017) 535 | 1606.07424 |
| 6 | ALICE Collaboration | Studying strangeness and baryon production mechanisms through angular correlations between charged $ \Xi $ baryons and identified hadrons in pp collisions at $ \sqrt{s} $ = 13 TeV | JHEP 09 (2024) 102 | 2308.16706 |
| 7 | T. Pierog et al. | EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider | Phys. Rev. C 92 (2015) 034906 | 1306.0121 |
| 8 | P. Bartalini and J. R. Gaunt, eds. | Multiple parton interactions at the LHC | 'Multiple Scattering in EPOS', 2019 ISBN 978-981-322-775-0, 978-981-322-777-4 |
|
| 9 | K. Werner | Core-corona procedure and microcanonical hadronization to understand strangeness enhancement in proton-proton and heavy ion collisions in the EPOS4 framework | Phys. Rev. C 109 (2024) 014910 | 2306.10277 |
| 10 | K. Werner | Parallel scattering, saturation, and generalized Abramovskii-Gribov-Kancheli (AGK) theorem in the EPOS4 framework, with applications for heavy-ion collisions at $ \sqrt {\smash [b]{s_{_{\mathrm {NN}}}}} $ of 5.02 TeV and 200 GeV | Phys. Rev. C 109 (2024) 034918 | 2310.09380 |
| 11 | K. Werner | Revealing a deep connection between factorization and saturation: New insight into modeling high-energy proton-proton and nucleus-nucleus scattering in the EPOS4 framework | Phys. Rev. C 108 (2023) 064903 | 2301.12517 |
| 12 | K. Werner and B. Guiot | Perturbative QCD concerning light and heavy flavor in the EPOS4 framework | Phys. Rev. C 108 (2023) 034904 | 2306.02396 |
| 13 | C. Bierlich, G. Gustafson, L. Lönnblad, and A. Tarasov | Effects of overlapping strings in pp collisions | JHEP 03 (2015) 148 | 1412.6259 |
| 14 | C. Bierlich | Hadronisation models and colour reconnection | 2016 link |
1606.09456 |
| 15 | C. Bierlich, G. Gustafson, and L. Lönnblad | A shoving model for collectivity in hadronic collisions | 1612.05132 | |
| 16 | Muon g-2 Collaboration | Measurement of the positive muon anomalous magnetic moment to 0.20 ppm | PRL 131 (2023) 161802 | 2308.06230 |
| 17 | S. Borsanyi et al. | Leading hadronic contribution to the muon magnetic moment from lattice QCD | Nature 593 (2021) 51 | 2002.12347 |
| 18 | A. M. Polyakov | Compact gauge fields and the infrared catastrophe | PLB 59 (1975) 82 | |
| 19 | A. A. Belavin, A. M. Polyakov, A. S. Schwartz, and Y. S. Tyupkin | Pseudoparticle solutions of the Yang-Mills equations | PLB 59 (1975) 85 | |
| 20 | G. 't Hooft | Computation of the quantum effects due to a four-dimensional pseudoparticle | PRD 14 (1976) 3432 | |
| 21 | R. Jackiw and C. Rebbi | Vacuum periodicity in a Yang-Mills quantum theory | PRL 37 (1976) 172 | |
| 22 | C. G. Callan, R. F. Dashen, and D. J. Gross | The structure of the gauge theory vacuum | PLB 63 (1976) 334 | |
| 23 | E. Witten | Current algebra theorems for the U(1) `Goldstone boson' | NPB 156 (1979) 269 | |
| 24 | S. Coleman | The uses of instantons | Springer US, Boston, MA, 1979 link |
|
| 25 | E. Shuryak | Lectures on nonperturbative QCD (nonperturbative topological phenomena in QCD and related theories) | 1812.01509 | |
| 26 | V. V. Khoze, F. Krauss, and M. Schott | Large effects from small QCD instantons: making soft bombs at hadron colliders | JHEP 04 (2020) 201 | 1911.09726 |
| 27 | V. A. Khoze, V. V. Khoze, D. Milne, and M. Ryskin | Hunting for QCD instantons at the LHC in events with large rapidity gaps | PRD 104 (2021) 054013 | 2104.01861 |
| 28 | V. A. Khoze, V. V. Khoze, D. Milne, and M. Ryskin | Central instanton production | PRD 105 (2022) 036008 | 2111.02159 |
| 29 | M. Tasevsky, V. A. Khoze, D. Milne, and M. Ryskin | Searches for QCD instantons with forward proton tagging | EPJC 83 (2023) 35 | 2208.14089 |
| 30 | S. Amoroso, D. Kar, and M. Schott | How to discover QCD instantons at the LHC | EPJC 81 (2021) 624 | 2012.09120 |
| 31 | E. Shuryak and I. Zahed | How to observe the QCD instanton/sphaleron processes at hadron colliders? | 2102.00256 | |
| 32 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 33 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 34 | ALEPH Collaboration | Studies of QCD at e+ e- centre-of-mass energies between 91-GeV and 209-GeV | EPJC 35 (2004) 457 | |
| 35 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA 8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 36 | CMS Collaboration | Measurement of charged particle spectra in minimum-bias events from proton-proton collisions at $ \sqrt{s}= $ 13 TeV | EPJC 78 (2018) 697 | CMS-FSQ-16-011 1806.11245 |
| 37 | ALICE Collaboration | Multiplicity dependence of charged-particle production in pp, p-Pb, Xe-Xe and Pb-Pb collisions at the LHC | PLB 845 (2023) 138110 | 2211.15326 |
| 38 | ATLAS Collaboration | Charged-particle distributions at low transverse momentum in $ \sqrt{s} = $ 13 TeV $ pp $ interactions measured with the ATLAS detector at the LHC | EPJC 76 (2016) 502 | 1606.01133 |
| 39 | CMS Collaboration | Study of the underlying event in top quark pair production in pp collisions at 13 TeV | EPJC 79 (2019) | CMS-TOP-17-015 1807.02810 |
| 40 | ATLAS Collaboration | Measurements of multijet event isotropies using optimal transport with the ATLAS detector | JHEP 10 (2023) 060 | 2305.16930 |
| 41 | CMS Collaboration | First measurement of hadronic event shapes in pp collisions at $ \sqrt {s}= $ 7 TeV | PLB 699 (2011) 48 | CMS-QCD-10-013 1102.0068 |
| 42 | ALICE Collaboration | Transverse sphericity of primary charged particles in minimum bias proton-proton collisions at $ \sqrt{s}= $ 0.9, 2.76 and 7 TeV | EPJC 72 (2012) 2124 | 1205.3963 |
| 43 | ATLAS Collaboration | Measurement of charged-particle event shape variables in $ \sqrt{s}= $ 7 TeV proton-proton interactions with the ATLAS detector | PRD 88 (2013) 032004 | 1207.6915 |
| 44 | G. Parisi | Superinclusive cross sections | PLB 74 (1978) 65 | |
| 45 | J. F. Donoghue, F. E. Low, and S.-Y. Pi | Tensor analysis of hadronic jets in quantum chromodynamics | PRD 20 (1979) 2759 | |
| 46 | S. Brandt and H. Dahmen | Axes and scalar measures of two-jet and three-jet events | Z. Phys. C 1 (1979) 61 | |
| 47 | P. T. Komiske, E. M. Metodiev, and J. Thaler | Energy flow networks: deep sets for particle jets | JHEP 01 (2019) 121 | 1810.05165 |
| 48 | C. Cesarotti and J. Thaler | A robust measure of event isotropy at colliders | JHEP 08 (2020) 084 | 2004.06125 |
| 49 | C. Cesarotti, M. Reece, and M. J. Strassler | The efficacy of event isotropy as an event shape observable | JHEP 07 (2021) 215 | 2011.06599 |
| 50 | M. Bähr et al. | HERWIG++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 51 | J. Bellm et al. | HERWIG 7.0/ HERWIG++ 3.0 release note | EPJC 76 (2016) 196 | 1512.01178 |
| 52 | T. Sjöstrand et al. | An introduction to PYTHIA8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 53 | A. Andreassen et al. | Omnifold: A method to simultaneously unfold all observables | PRL 124 (2020) 182001 | 1911.09107 |
| 54 | A. Andreassen et al. | Scaffolding simulations with deep learning for high-dimensional deconvolution | 2105.04448 | |
| 55 | CMS Collaboration | HEPData record for this analysis | link | |
| 56 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 57 | CMS Collaboration | Development of the CMS detector for the CERN LHC Run 3 | JINST 19 (2024) P05064 | CMS-PRF-21-001 2309.05466 |
| 58 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 59 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 60 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 61 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 62 | GEANT4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 63 | ATLAS Collaboration | The PYTHIA 8 A3 tune description of ATLAS minimum bias and inelastic measurements incorporating the Donnachie-Landshoff diffractive model | ATLAS Note ATL-PHYS-PUB-2016-017, 2016 | |
| 64 | CMS Collaboration | Development and validation of HERWIG 7 tunes from CMS underlying-event measurements | EPJC 81 (2021) 312 | CMS-GEN-19-001 2011.03422 |
| 65 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 66 | CMS Collaboration | Investigations of the impact of the parton shower tuning in PYTHIA 8 in the modelling of $ \mathrm{t\overline{t}} $ at $ \sqrt{s}= $ 8 and 13 TeV | CMS Physics Analysis Summary, 2016 CMS-PAS-TOP-16-021 |
CMS-PAS-TOP-16-021 |
| 67 | CMS Collaboration | CMS pythia 8 colour reconnection tunes based on underlying-event data | EPJC 83 (2023) 587 | CMS-GEN-17-002 2205.02905 |
| 68 | ATLAS Collaboration | ATLAS PYTHIA 8 tunes to 7 TeV data | ATLAS Note ATL-PHYS-PUB-2014-021, 2014 | |
| 69 | A. Buckley et al. | The HepMC3 event record library for Monte Carlo event generators | Comput. Phys. Comm. 260 (2021) 107310 | 1912.08005 |
| 70 | W. H. Richardson | Bayesian-based iterative method of image restoration | J. Opt. Soc. Am. 62 (1972) 55 | |
| 71 | L. B. Lucy | An iterative technique for the rectification of observed distributions | Astronomical Journal 79 (1974) 745 | |
| 72 | G. D'Agostini | A multidimensional unfolding method based on Bayes' theorem | NIM A 362 (1995) 487 | |
| 73 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s} $ = 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 74 | R. D. Cousins, S. J. May, and Y. Sun | Should unfolded histograms be used to test hypotheses? | 1607.07038 | |
| 75 | S. M. S. Lee and G. A. Young | Parametric bootstrapping with nuisance parameters | Stat. Probab. Lett. 71 (2005) 143 | |
| 76 | R. J. Tibshirani and B. Efron | An introduction to the bootstrap | Chapman and Hall New York, 1993 Monographs on statistics and applied probability 5 (1993) 7 |
|
| 77 | CMS Collaboration | Tracking performance for charged pions with Run2 Legacy data | CMS Detector Performance Note CMS-DP-2022-012, 2022 link |
|
| 78 | CMS Collaboration | Muon tracking efficiency for 2018 dataset using tag and probe method | CMS Detector Performance Note CMS-DP-2020-013, 2019 CDS |
|
| 79 | CMS Collaboration | Measurement of the underlying event activity at the lhc with $ \sqrt{s}= $ 7 TeV and comparison with $ \sqrt{s} = $ 0.9 TeV | JHEP 09 (2011) 109 | CMS-QCD-10-010 1107.0330 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|