CMS-HIG-17-002

CMS-HIG-17-002 ; CERN-EP-2017-126
Search for Higgs boson pair production in events with two bottom quarks and two tau leptons in proton-proton collisions at $\sqrt{s} =$ 13 TeV
CMS Collaboration
10 July 2017
Phys. Lett. B 778 (2018) 101
Abstract: A search for the production of Higgs boson pairs in proton-proton collisions at a centre-of-mass energy of 13 TeV is presented, using a data sample corresponding to an integrated luminosity of 35.9 fb $^{-1}$ collected with the CMS detector at the LHC. Events with one Higgs boson decaying into two bottom quarks and the other decaying into two $\tau$ leptons are explored to investigate both resonant and nonresonant production mechanisms. The data are found to be consistent, within uncertainties, with the standard model background predictions. For resonant production, upper limits at the 95% confidence level are set on the production cross section for Higgs boson pairs as a function of the hypothesized resonance mass and are interpreted in the context of the minimal supersymmetric standard model. For nonresonant production, upper limits on the production cross section constrain the parameter space for anomalous Higgs boson couplings. The observed (expected) upper limit at 95% confidence level corresponds to about 30 (25) times the prediction of the standard model.
Links: e-print arXiv:1707.02909 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ;

Figures & Tables	Summary	Additional Figures & Tables	References	CMS Publications

Figures
png pdf	Figure 1: Feynman diagrams contributing to Higgs pair production via gluon-gluon fusion at leading order at the LHC.
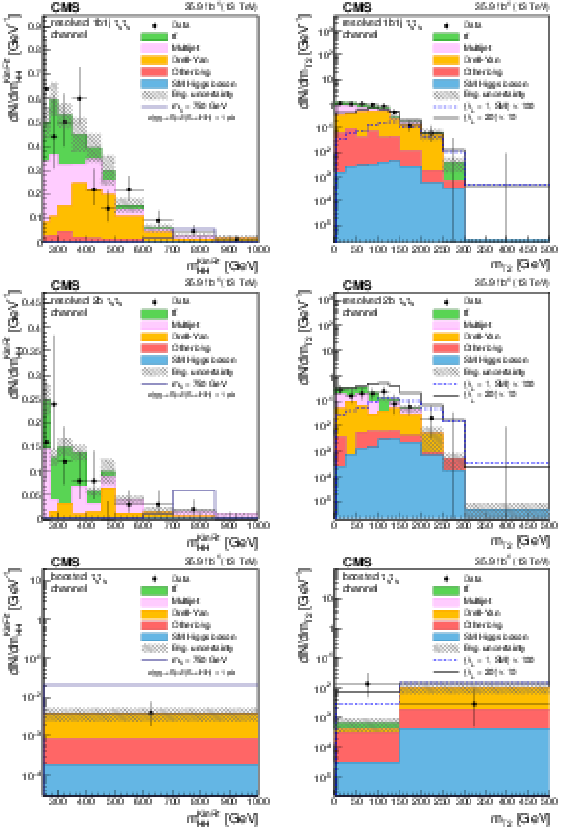
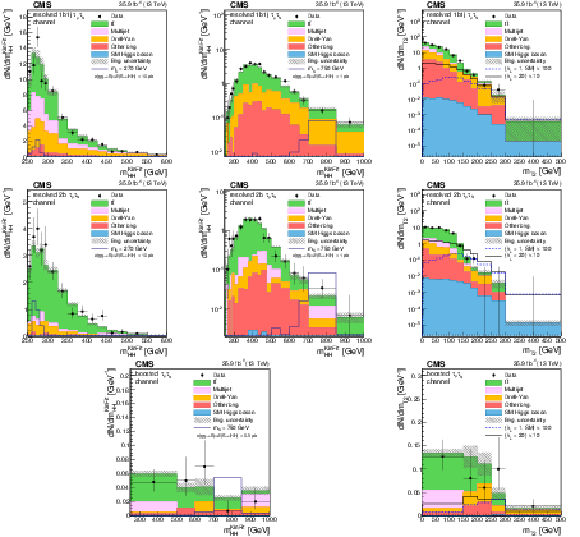
png pdf	Figure 2: Distributions of the events observed in the signal regions of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. The first, second, and third rows show the resolved 1b1j, 2b, and boosted regions, respectively. Panels in the right column show the distribution of the ${m_\text {T2}}$ variable, while the other panels show the distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable, separated in the low-mass (LM, left panels) and high-mass (HM, central panels) regions for the resolved event categories. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 2-a: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 1b1j signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. The distribution is shown in the low-mass (LM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
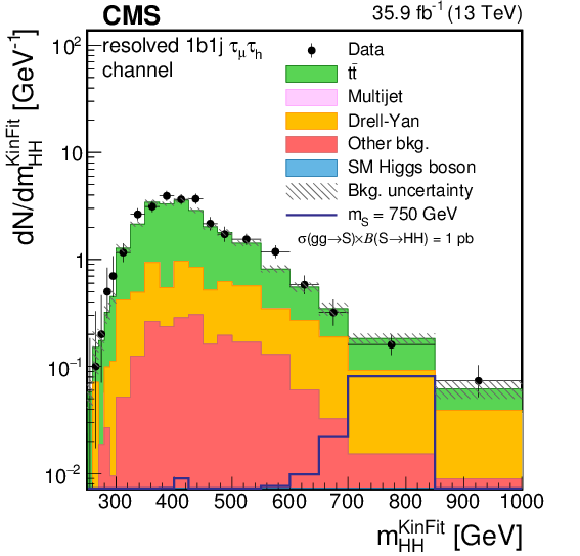
png pdf	Figure 2-b: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 1b1j signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. The distribution is shown in the high-mass (HM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 2-c: Distribution of the ${m_\text {T2}}$ variable for events observed in the resolved 1b1j signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
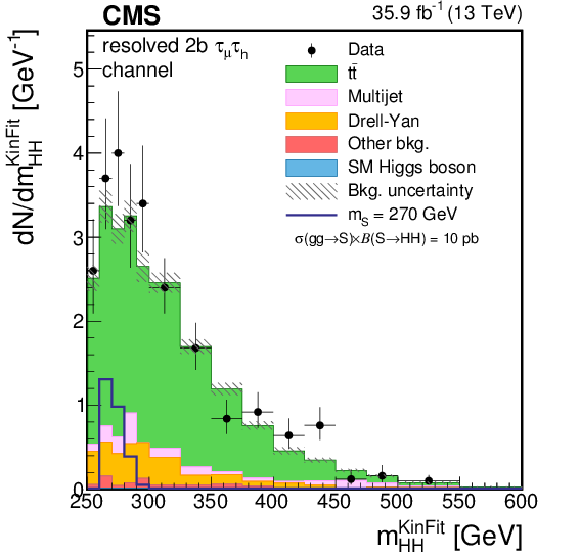
png pdf	Figure 2-d: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 2b signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. The distribution is shown in the low-mass (LM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
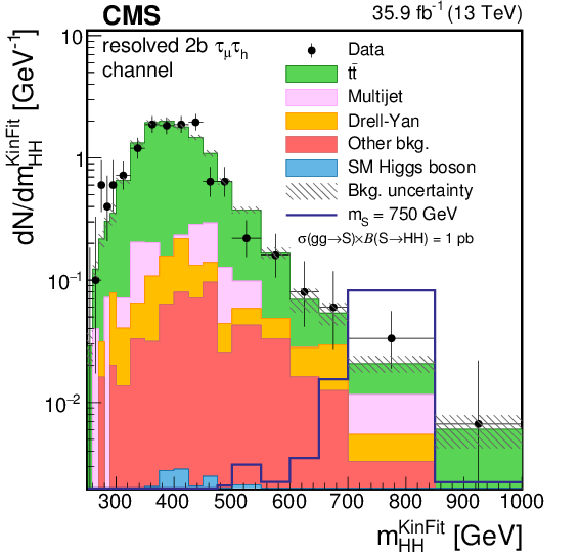
png pdf	Figure 2-e: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 2b signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. The distribution is shown in the high-mass (HM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 2-f: Distribution of the ${m_\text {T2}}$ variable for events observed in the resolved 2b signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
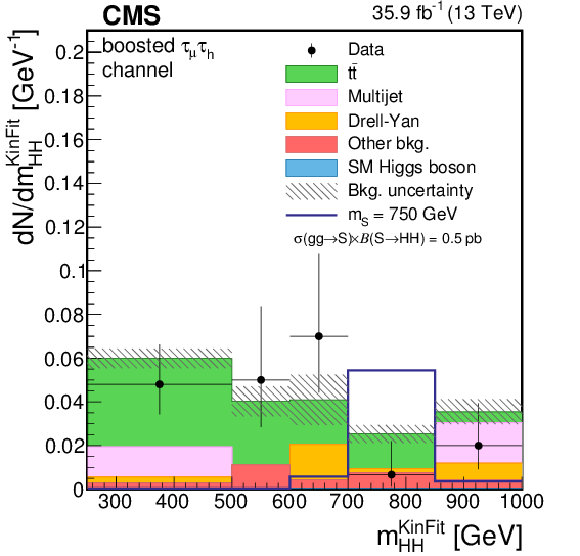
png pdf	Figure 2-g: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the boosted signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 2-h: Distribution of the ${m_\text {T2}}$ variable for events observed in the boosted signal region of the ${\tau _\mu {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 3: Distributions of the events observed in the signal regions of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. The first, second, and third rows show the resolved 1b1j, 2b, and boosted regions, respectively. Panels in the right column show the distribution of the ${m_\text {T2}}$ variable, while the other panels show the distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable, separated in the low-mass (LM, left panels) and high-mass (HM, central panels) regions for the resolved event categories. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
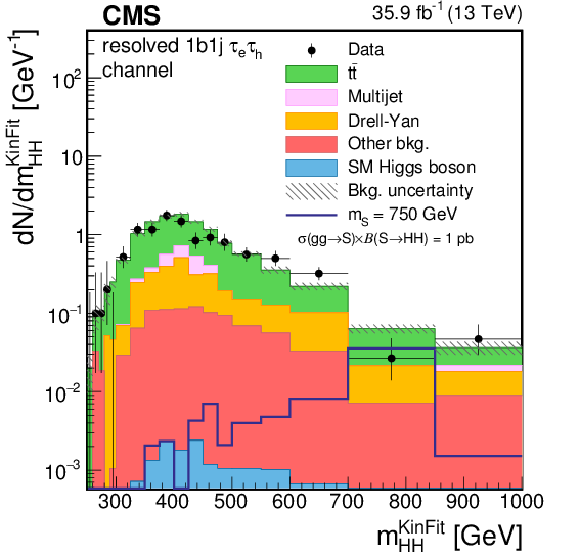
png pdf	Figure 3-a: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 1b1j signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. The distribution is shown in the low-mass (LM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 3-b: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 1b1j signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. The distribution is shown in the high-mass (HM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 3-c: Distribution of the ${m_\text {T2}}$ variable for events observed in the resolved 1b1j signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
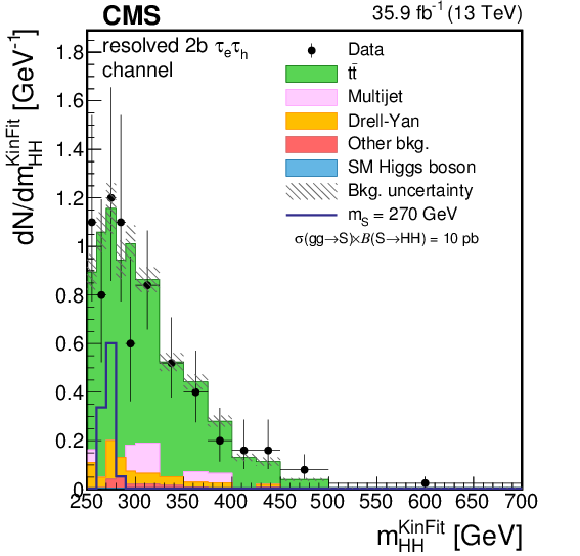
png pdf	Figure 3-d: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 2b signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. The distribution is shown in the low-mass (LM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
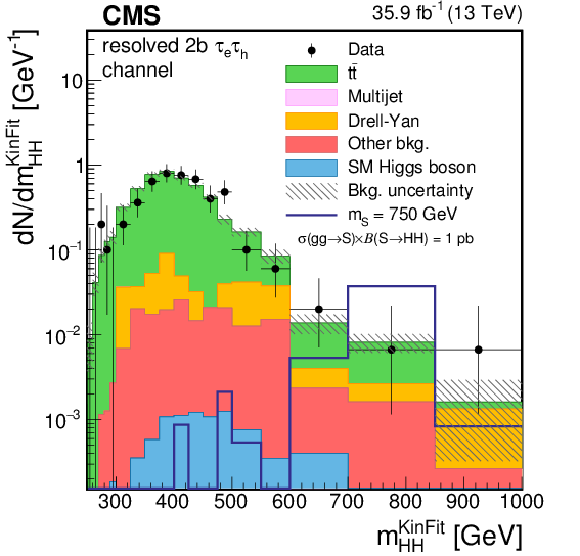
png pdf	Figure 3-e: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the resolved 2b signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. The distribution is shown in the high-mass (HM) region. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
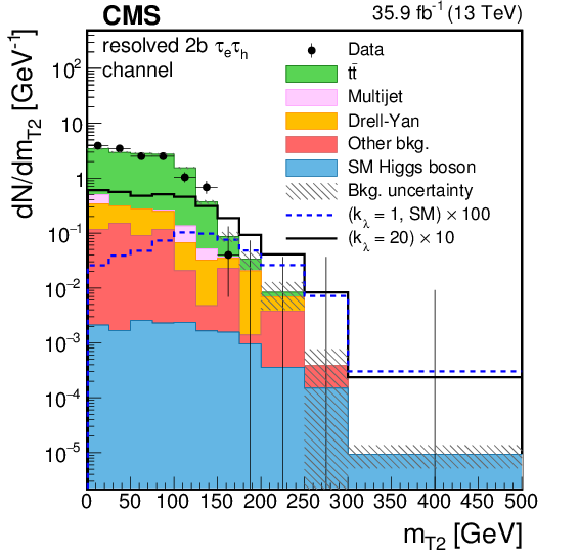
png pdf	Figure 3-f: Distribution of the ${m_\text {T2}}$ variable for events observed in the resolved 2b signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 3-g: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable for events observed in the boosted signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
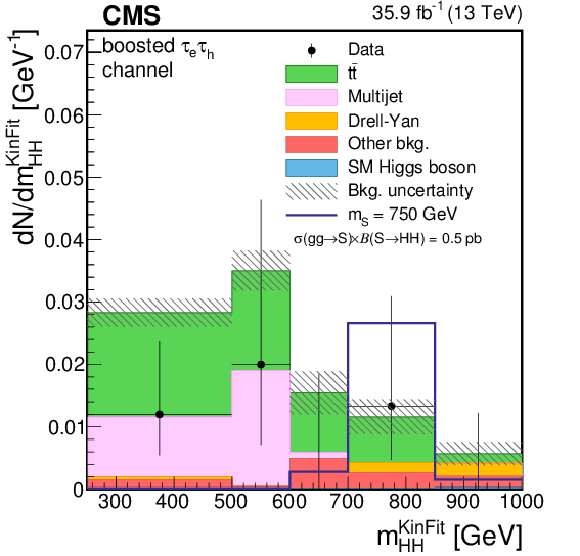
png pdf	Figure 3-h: Distribution of the ${m_\text {T2}}$ variable for events observed in the boosted signal region of the ${\tau _{\mathrm{e}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 4: Distributions of the events observed in the signal regions of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. The first, second, and third rows show the resolved 1b1j, 2b, and boosted regions, respectively. Panels in the left column show the distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ variable and panels in the right column show the distribution of the ${m_\text {T2}}$ variable. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
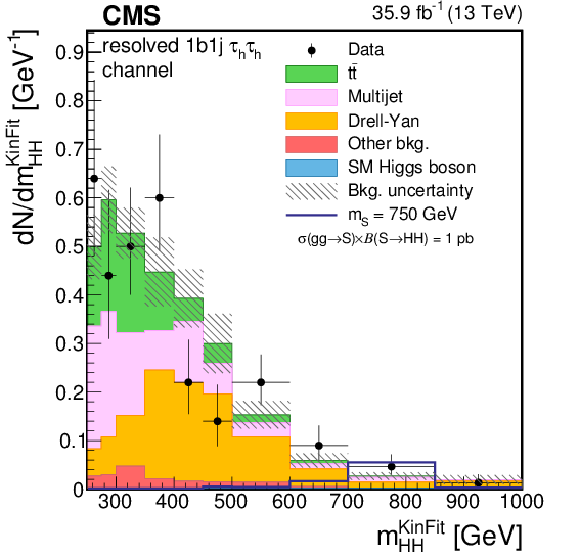
png pdf	Figure 4-a: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ for events observed in the resolved 1b1j region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
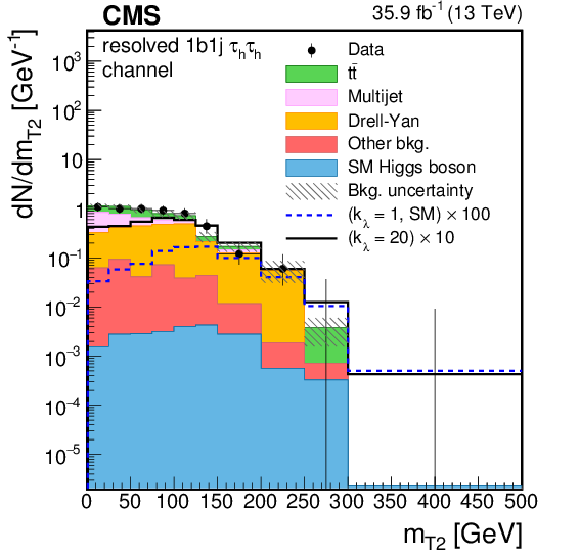
png pdf	Figure 4-b: Distribution of the ${m_\text {T2}}$ for events observed in the resolved 1b1j region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
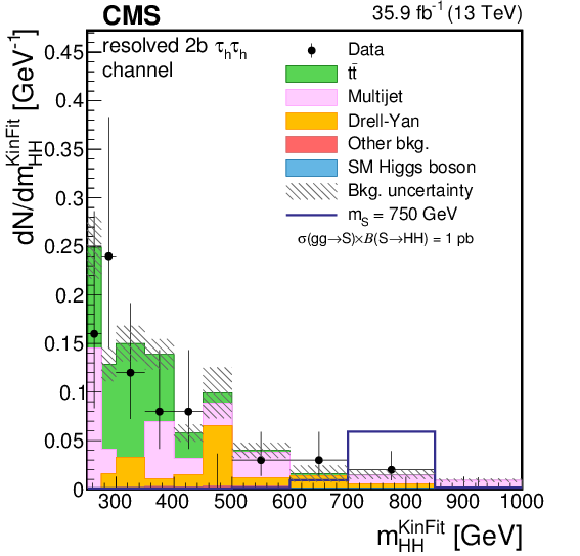
png pdf	Figure 4-c: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ for events observed in the resolved 2b region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 4-d: Distribution of the ${m_\text {T2}}$ for events observed in the resolved 2b region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
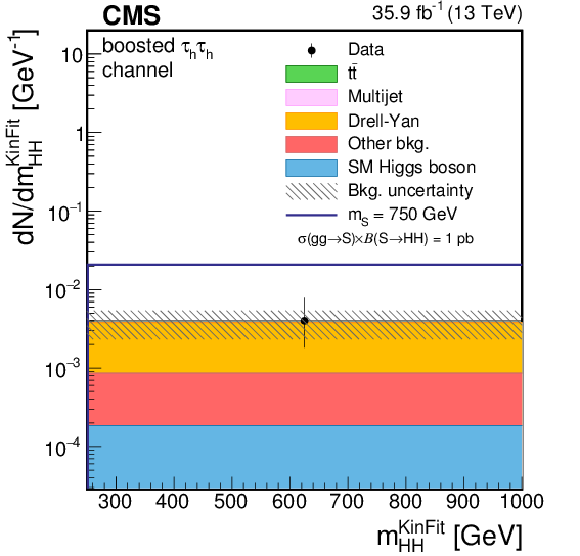
png pdf	Figure 4-e: Distribution of the ${m_{ {\mathrm{ H } \mathrm{ H } } }^\text {KinFit} }$ for events observed in the boosted region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
png pdf	Figure 4-f: Distribution of the ${m_\text {T2}}$ for events observed in the boosted region of the ${ {\tau _\mathrm {h}} {\tau _\mathrm {h}} }$ final state. Data are represented by points with error bars and expected signal contributions are represented by the solid (BSM HH signals) and dashed (SM nonresonant HH signal) lines. Expected background contributions (shaded histograms) and associated systematic uncertainties (dashed areas) are shown as obtained after the maximum likelihood fit to the data under the background-only hypothesis. The background histograms are stacked while the signal histograms are not stacked.
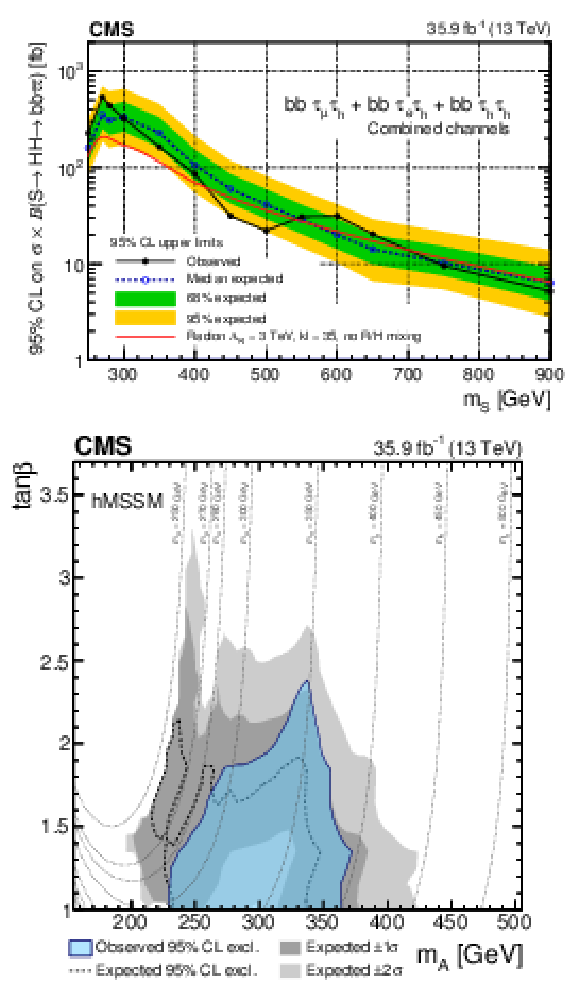
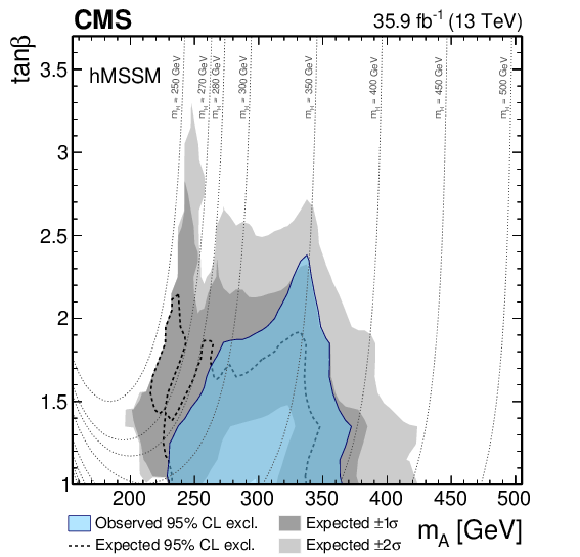
png pdf	Figure 5: (upper) Observed and expected 95% CL upper limits on cross section times branching fraction as a function of the mass of the resonance ${m_\mathrm {S} }$ under the hypothesis that its intrinsic width is negligible with respect to the experimental resolution. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The red line denotes the expectation for the production of a radion, a spin-0 state predicted in WED models, for the parameters $\Lambda _\text {R} =$ 3 TeV (mass scale) and $\text {kL} =$ 35 (size of the extra dimension), assuming the absence of mixing with the Higgs boson. (lower) Interpretation of the exclusion limit in the context of the hMSSM model, parametrized as a function of the $\tan\beta$ and $m_\mathrm {A}$ parameters. In this model, the CP-even lighter scalar is assumed to be the observed 125 GeV Higgs boson and is denoted as h, while the CP-even heavier scalar is denoted as H and the CP-odd scalar is denoted as A. The dotted lines indicate trajectories in the plane corresponding to equal values of the mass of the CP-even heavier scalar of the model, $m_\text {H}$ .
png pdf	Figure 5-a: Observed and expected 95% CL upper limits on cross section times branching fraction as a function of the mass of the resonance ${m_\mathrm {S} }$ under the hypothesis that its intrinsic width is negligible with respect to the experimental resolution. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The red line denotes the expectation for the production of a radion, a spin-0 state predicted in WED models, for the parameters $\Lambda _\text {R} =$ 3 TeV (mass scale) and $\text {kL} =$ 35 (size of the extra dimension), assuming the absence of mixing with the Higgs boson.
png pdf	Figure 5-b: Interpretation of the exclusion limit in the context of the hMSSM model, parametrized as a function of the $\tan\beta$ and $m_\mathrm {A}$ parameters. In this model, the CP-even lighter scalar is assumed to be the observed 125 GeV Higgs boson and is denoted as h, while the CP-even heavier scalar is denoted as H and the CP-odd scalar is denoted as A. The dotted lines indicate trajectories in the plane corresponding to equal values of the mass of the CP-even heavier scalar of the model, $m_\text {H}$ .
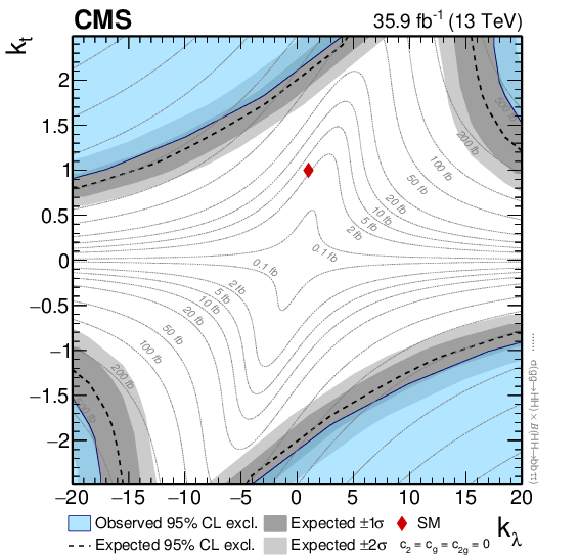
png pdf	Figure 6: Test of $k_\lambda$ and $k_\mathrm{ t }$ anomalous couplings. The blue region denotes the parameters excluded by the data at 95% CL, while the dashed black line and the grey regions denote the expected exclusions and the 1 $\sigma$ and 2 $\sigma$ bands. The dotted lines indicate trajectories in the plane with equal values of cross section times branching fraction that are displayed in the associated labels. The diamond-shaped symbol denotes the couplings predicted by the SM. The theory predictions and the expected and observed limits are symmetric through a $(k_\lambda$ , $k_\mathrm{ t } ) \leftrightarrow (-k_\lambda , -k_\mathrm{ t } )$ transformation. The couplings that are not explicitly tested are assumed to correspond to the SM prediction.
png pdf	Figure 6-a: Observed and expected 95% CL upper limits on cross section times branching fraction as a function of $k_\lambda /k_\mathrm{ t }$ . The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The two red bands show the theoretical cross section expectations and the corresponding uncertainties for $k_\mathrm{ t } =$ 1 and $k_\mathrm{ t } =$ 2. The couplings that are not explicitly tested are assumed to correspond to the SM prediction.
png pdf	Figure 6-b: Test of $k_\lambda$ and $k_\mathrm{ t }$ anomalous couplings. The blue region denotes the parameters excluded by the data at 95% CL, while the dashed black line and the grey regions denote the expected exclusions and the 1 $\sigma$ and 2 $\sigma$ bands. The dotted lines indicate trajectories in the plane with equal values of cross section times branching fraction that are displayed in the associated labels. The diamond-shaped symbol denotes the couplings predicted by the SM. The theory predictions and the expected and observed limits are symmetric through a $(k_\lambda$ , $k_\mathrm{ t } ) \leftrightarrow (-k_\lambda , -k_\mathrm{ t } )$ transformation. The couplings that are not explicitly tested are assumed to correspond to the SM prediction.

Tables
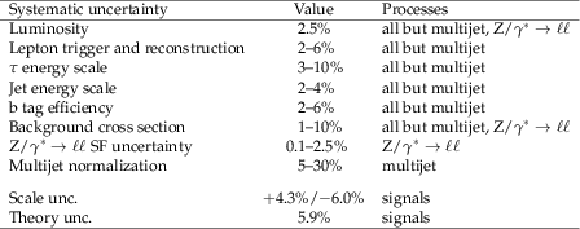
png pdf	Table 1: Systematic uncertainties affecting the normalization of the different processes.

Summary

A search for resonant and nonresonant Higgs boson pair (HH) production in the

$\mathrm{ b\bar{b} } \tau\tau$ final state is presented. This search uses a data sample collected in proton-proton collisions at

$\sqrt{s} =$ 13 TeV that corresponds to an integrated luminosity of 35.9 fb

$^{-1}$ . The three most sensitive decay channels of the

$\tau$ lepton pair, requiring the decay of one or both

$\tau$ leptons into final-state hadrons and a neutrino, are used. The results are found to be statistically compatible with the expected standard model (SM) background contribution, and upper limits at the 95% confidence level are set on the HH production cross sections.

For the resonant production mechanism, upper exclusion limits at 95% confidence level (CL) are obtained for the production of a narrow resonance of mass

$m_{\mathrm{X}}$ ranging from 250 to 900 GeV. These model-independent results are interpreted in the context of the hMSSM scenario, where a region in the parameter space corresponding to values of

$m_\mathrm{A}$ between 230 and 360 GeV and

$\tan \beta \lesssim 2$ is excluded at 95% CL.

For the nonresonant production mechanism, the theoretical framework of an effective Lagrangian is used to parametrize the cross section as a function of anomalous couplings of the Higgs boson. Upper limits at 95% CL on the HH cross section are obtained as a function of

$k_\lambda = \lambda_{\mathrm{HHH}}/\lambda_{\mathrm{HHH}}^\text{SM}$ and

$k_\mathrm{ t } = y_\mathrm{ t }/y^\text{SM}_\mathrm{ t }$ . The observed 95% CL upper limit corresponds to approximately 30 times the theoretical prediction for the SM cross section, and the expected limit is about 25 times the SM prediction. This is the highest sensitivity achieved so far for SM HH production at the LHC.

Additional Figures
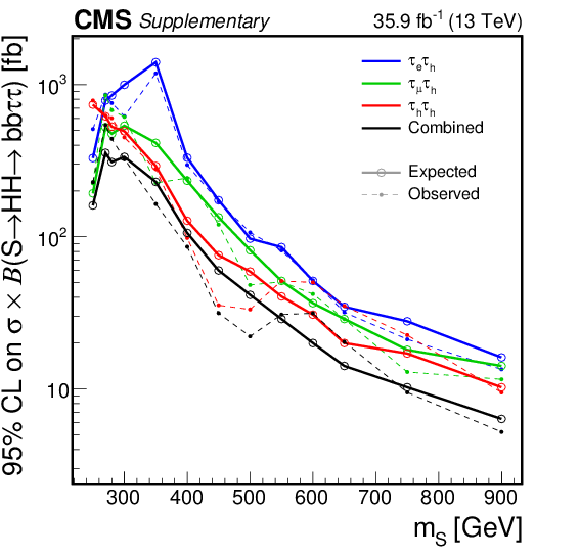
png pdf	Additional Figure 1: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \text {S})\times \mathcal {B}(\text {S}\to \mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three event categories. The dashed and solid lines denote respectively the observed and expected upper limits.
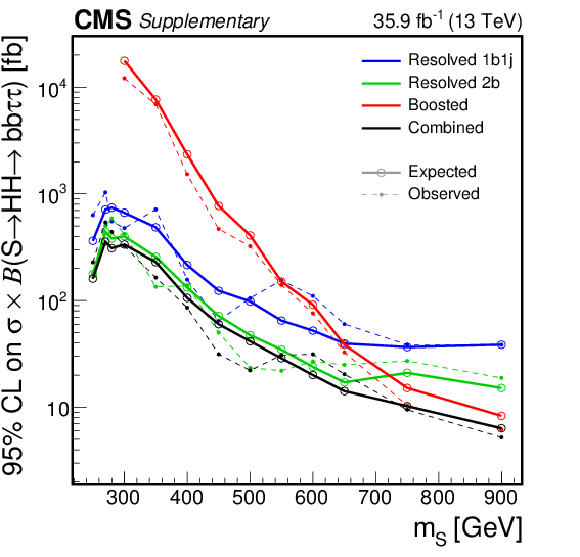
png pdf	Additional Figure 1-a: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \text {S})\times \mathcal {B}(\text {S}\to \mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three decay channels. The dashed and solid lines denote respectively the observed and expected upper limits.
png pdf	Additional Figure 1-b: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \text {S})\times \mathcal {B}(\text {S}\to \mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three event categories. The dashed and solid lines denote respectively the observed and expected upper limits.
png pdf	Additional Figure 2: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \mathrm{H} \mathrm{H})\times \mathcal {B}(\mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three decay channels (a) and the three event categories (b). The dashed and solid lines denote respectively the observed and expected upper limits.
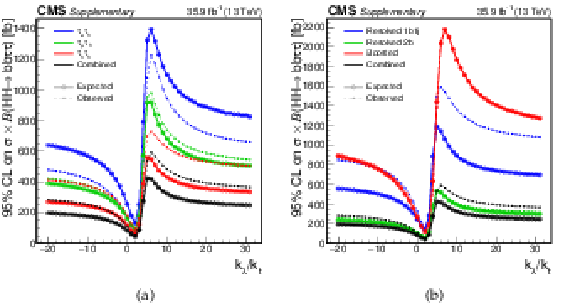
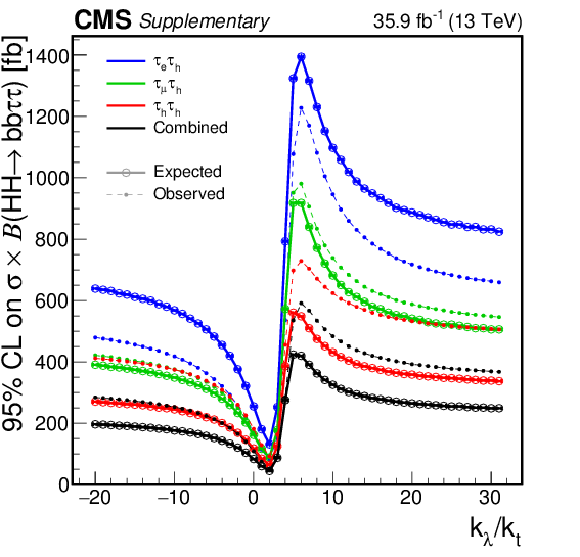
png pdf	Additional Figure 2-a: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \mathrm{H} \mathrm{H})\times \mathcal {B}(\mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three decay channels. The dashed and solid lines denote respectively the observed and expected upper limits.
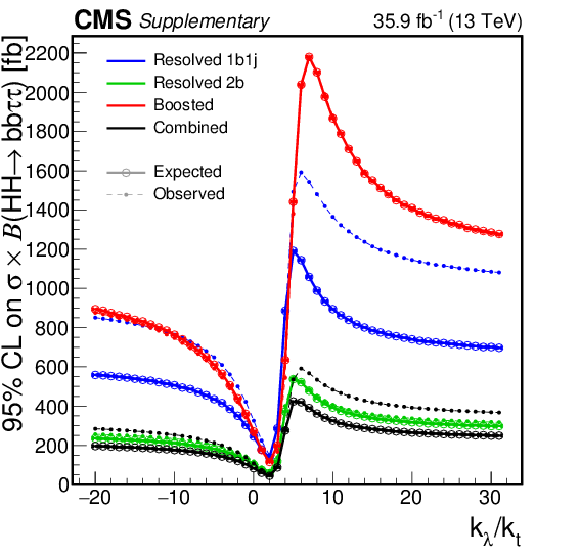
png pdf	Additional Figure 2-b: Upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \mathrm{H} \mathrm{H})\times \mathcal {B}(\mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ , shown for the three event categories. The dashed and solid lines denote respectively the observed and expected upper limits.
png pdf	Additional Figure 3: Observed and expected 95% CL upper limits on cross section times branching fraction for different combinations of Higgs boson couplings in the effective Lagrangian parametrization. The numbers from 1 to 12 denote the shape benchmarks defined in Ref. [1], corresponding to points in the five-dimensional parameter space with characteristic kinematic properties of the HH system. Also shown are the SM signal and the case where all couplings except $y_\text {t}$ vanish. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis.
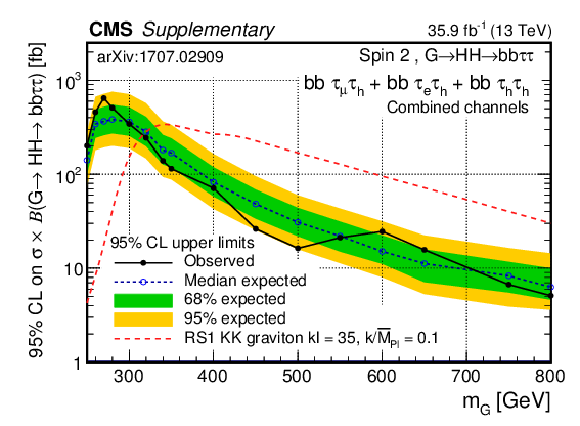
png pdf	Additional Figure 4: Observed and expected 95% CL upper limits on cross section times branching fraction as a function of the mass of the spin-2 resonance $m_\text {G}$ under the hypothesis that its intrinsic width is negligible with respect to the experimental resolution. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The red line denotes the expectation for the production of a graviton, a spin-2 state predicted in WED models, for the parameters $\text {kl} =$ 35 (size of the extra dimension) and $k/\overline {M}_\text {pl} =$ 0.1 (coupling to matter fields, where $\overline {M}_\text {pl} = M_\text {pl}/\sqrt {8\pi}$ ). The absence of mixing with the Higgs boson is assumed.

Additional Tables
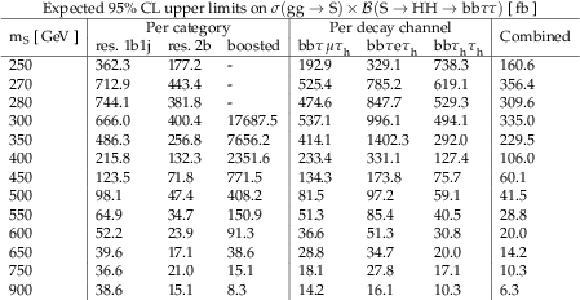
png pdf	Additional Table 1: Expected upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \text {S})\times \mathcal {B}(\text {S}\to \mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ . The limits are computed for a spin-0 resonance, and are shown separately for the three decay channels (combining the three event categories) and for the three event categories (combining the three decay channels). The combined upper limit is also shown.
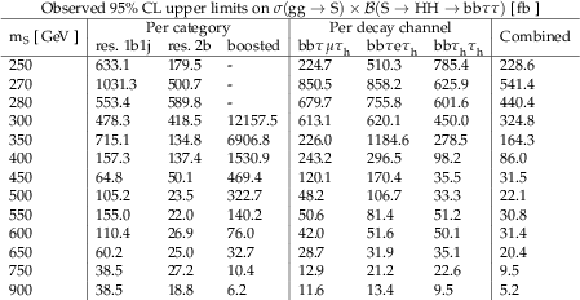
png pdf	Additional Table 2: Observed upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \text {S})\times \mathcal {B}(\text {S}\to \mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ . The limits are computed for a spin-0 resonance, and are shown separately for the three decay channels (combining the three event categories) and for the three event categories (combining the three decay channels). The combined upper limit is also shown.
png pdf	Additional Table 3: Expected upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \mathrm{H} \mathrm{H})\times \mathcal {B}(\mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ . The limits are computed for different $k_\lambda /k_\text {t}$ hypotheses, and are shown separately for the three decay channels (combining the three event categories) and for the three event categories (combining the three decay channels). The combined upper limit is also shown.
png pdf	Additional Table 4: Observed upper limits at the 95% confidence level on $\sigma (\mathrm{g} \mathrm{g} \to \mathrm{H} \mathrm{H})\times \mathcal {B}(\mathrm{H} \mathrm{H} \to {\mathrm{b} \mathrm{b} \tau \tau})$ . The limits are computed for different $k_\lambda /k_\text {t}$ hypotheses, and are shown separately for the three decay channels (combining the three event categories) and for the three event categories (combining the three decay channels). The combined upper limit is also shown.

References
1	ATLAS Collaboration	Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC	PLB 716 (2012) 1	1207.7214
2	CMS Collaboration	Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC	PLB 716 (2012) 30	CMS-HIG-12-028 1207.7235
3	CMS Collaboration	Observation of a new boson with mass near 125 GeV in pp collisions at $\sqrt{s} =$ 7 and 8 TeV	JHEP 06 (2013) 081	CMS-HIG-12-036 1303.4571
4	ATLAS and CMS Collaborations	Combined measurement of the Higgs boson mass in $pp$ collisions at $\sqrt{s}=$ 7 and 8 TeV with the ATLAS and CMS experiments	PRL 114 (2015) 191803	1503.07589
5	ATLAS and CMS Collaborations	Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $\sqrt{s}=$ 7 and 8 TeV	JHEP 08 (2016) 045	1606.02266
6	J. Baglio et al.	The measurement of the Higgs self-coupling at the LHC: theoretical status	JHEP 04 (2013) 151	1212.5581
7	D. de Florian et al.	Handbook of LHC Higgs cross sections: 4. deciphering the nature of the Higgs sector	CERN Report CERN-2017-002-M	1610.07922
8	T. Binoth and J. J. van der Bij	Influence of strongly coupled, hidden scalars on Higgs signals	Z. Phys. C 75 (1997) 17	hep-ph/9608245
9	R. M. Schabinger and J. D. Wells	Minimal spontaneously broken hidden sector and its impact on Higgs boson physics at the CERN Large Hadron Collider	PRD 72 (2005) 093007	hep-ph/0509209
10	B. Patt and F. Wilczek	Higgs-field portal into hidden sectors		hep-ph/0605188
11	G. C. Branco et al.	Theory and phenomenology of two-Higgs-doublet models	PR 516 (2012) 1	1106.0034
12	P. Fayet	Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino	Nucl. Phys. B 90 (1975) 104
13	P. Fayet	Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions	PLB 69 (1977) 489
14	K. Agashe, H. Davoudiasl, G. Perez, and A. Soni	Warped gravitons at the CERN LHC and beyond	PRD 76 (2007) 036006	hep-ph/0701186
15	A. L. Fitzpatrick, J. Kaplan, L. Randall, and L.-T. Wang	Searching for the Kaluza-Klein graviton in bulk RS models	JHEP 09 (2007) 013	hep-ph/0701150
16	F. Goertz, A. Papaefstathiou, L. L. Yang, and J. Zurita	Higgs boson pair production in the D=6 extension of the SM	JHEP 04 (2015) 167	1410.3471
17	A. Carvalho et al.	Higgs pair production: choosing benchmarks with cluster analysis	JHEP 04 (2016) 126	1507.02245
18	ATLAS Collaboration	Searches for Higgs boson pair production in the $hh {\rightarrow}bb {\tau} {\tau}$ , ${\gamma} {\gamma}{W}{W}^{*}$ , ${\gamma} {\gamma}bb$ , $bbbb$ channels with the ATLAS detector	PRD 92 (2015) 092004	1509.04670
19	ATLAS Collaboration	Search for pair production of Higgs bosons in the $b\bar{b}b\bar{b}$ final state using proton--proton collisions at $\sqrt{s} = 13$ TeV with the ATLAS detector	PRD 94 (2016) 052002	1606.04782
20	CMS Collaboration	Search for two Higgs bosons in final states containing two photons and two bottom quarks in proton-proton collisions at 8 TeV	PRD 94 (2016) 052012	CMS-HIG-13-032 1603.06896
21	CMS Collaboration	Search for resonant pair production of Higgs bosons decaying to two bottom quark-antiquark pairs in proton-proton collisions at 8 TeV	PLB 749 (2015) 560	CMS-HIG-14-013 1503.04114
22	CMS Collaboration	A search for Higgs boson pair production in the $bb\tau\tau$ final state in proton-proton collisions at $\sqrt{s} =$ 8TeV	Submitted to PRD	CMS-HIG-15-013 1707.00350
23	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
24	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
25	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
26	A. Carvalho et al.	Analytical parametrization and shape classification of anomalous HH production in the EFT approach		1608.06578
27	J. Alwall et al.	Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions	EPJC 53 (2008) 473	0706.2569
28	E. Re	Single-top $Wt$ -channel production matched with parton showers using the POWHEG method	EPJC 71 (2011) 1547	1009.2450
29	J. M. Campbell, R. K. Ellis, P. Nason, and E. Re	Top-pair production and decay at NLO matched with parton showers	JHEP 04 (2015) 114	1412.1828
30	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
31	T. Sjostrand et al.	An introduction to PYTHIA 8.2	CPC 191 (2015) 159	1410.3012
32	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
33	M. Czakon and A. Mitov	Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders	CPC 185 (2014) 2930	1112.5675
34	Y. Li and F. Petriello	Combining QCD and electroweak corrections to dilepton production in FEWZ	PRD 86 (2012) 094034	1208.5967
35	N. Kidonakis	Top quark production	in Proceedings, Helmholtz International Summer School on Physics of Heavy Quarks and Hadrons (HQ 2013), Dubna	1311.0283
36	J. M. Campbell, R. K. Ellis, and C. Williams	Vector boson pair production at the LHC	JHEP 07 (2011) 018	1105.0020
37	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	Submitted to JINST	CMS-PRF-14-001 1706.04965
38	M. Cacciari, G. P. Salam, and G. Soyez	The anti- $k_t$ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
39	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
40	J. M. Butterworth, A. R. Davison, M. Rubin, and G. P. Salam	Jet substructure as a new Higgs-search channel at the Large Hadron Collider	PRL 100 (2008) 242001	0802.2470
41	A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler	Soft drop	JHEP 05 (2014) 146	1402.2657
42	CMS Collaboration	Determination of jet energy calibration and transverse momentum resolution in CMS	JINST 6 (2011) P11002	CMS-JME-10-011 1107.4277
43	CMS Collaboration	Performance of missing energy reconstruction in 13 TeV pp collision data using the CMS detector	CMS-PAS-JME-16-004	CMS-PAS-JME-16-004
44	CMS Collaboration	Reconstruction and identification of $\tau$ lepton decays to hadrons and $\nu_\tau$ at CMS	JINST 11 (2016) P01019	CMS-TAU-14-001 1510.07488
45	CMS Collaboration	Performance of reconstruction and identification of tau leptons in their decays to hadrons and tau neutrino in LHC Run-2	CMS-PAS-TAU-16-002	CMS-PAS-TAU-16-002
46	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $\sqrt{s} =$ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
47	CMS Collaboration	Performance of CMS muon reconstruction in pp collision events at $\sqrt{s}=$ 7 TeV	JINST 7 (2012) P10002	CMS-MUO-10-004 1206.4071
48	CMS Collaboration	Identification of b-quark jets with the CMS experiment	JINST 8 (2013) P04013	CMS-BTV-12-001 1211.4462
49	CMS Collaboration	Identification of b quark jets at the CMS Experiment in the LHC Run 2	CMS-PAS-BTV-15-001	CMS-PAS-BTV-15-001
50	L. Bianchini, J. Conway, E. K. Friis, and C. Veelken	Reconstruction of the Higgs mass in $H \to \tau\tau$ events by dynamical likelihood techniques	J. Phys. Conf. Ser. 513 (2014) 022035
51	H. Voss, A. Hocker, J. Stelzer, and F. Tegenfeldt	TMVA, the toolkit for multivariate data analysis with ROOT	in XIth International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT) 2007	physics/0703039
52	J. H. Friedman	Greedy function approximation: A gradient boosting machine	Ann. Statist. 29 (2001) 1189
53	CMS Collaboration	Searches for a heavy scalar boson H decaying to a pair of 125 GeV Higgs bosons hh or for a heavy pseudoscalar boson A decaying to Zh, in the final states with $h \to \tau \tau$	PLB 755 (2016) 217	CMS-HIG-14-034 1510.01181
54	C. G. Lester and D. J. Summers	Measuring masses of semiinvisibly decaying particles pair produced at hadron colliders	PLB 463 (1999) 99	hep-ph/9906349
55	A. Barr, C. Lester, and P. Stephens	A variable for measuring masses at hadron colliders when missing energy is expected; $m_{T2}$ : the truth behind the glamour	JPG 29 (2003) 2343	hep-ph/0304226
56	A. J. Barr, M. J. Dolan, C. Englert, and M. Spannowsky	Di-Higgs final states augMT2ed -- selecting $hh$ events at the high luminosity LHC	PLB 728 (2014) 308	1309.6318
57	C. G. Lester and B. Nachman	Bisection-based asymmetric MT2 computation: a higher precision calculator than existing symmetric methods	JHEP 03 (2015) 100	1411.4312
58	CMS Collaboration	Measurements of differential production cross sections for a Z boson in association with jets in pp collisions at $\sqrt{s}=$ 8 TeV	JHEP 04 (2017) 022	CMS-SMP-14-013 1611.03844
59	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
60	CMS Collaboration	Measurement of differential cross sections for top quark pair production using the lepton+jets final state in proton-proton collisions at 13 TeV	PRD 95 (2017) 092001	CMS-TOP-16-008 1610.04191
61	T. Junk	Confidence level computation for combining searches with small statistics	NIMA 434 (1999) 435	hep-ex/9902006
62	A. L. Read	Presentation of search results: the $CL_s$ technique	JPG 28 (2002) 2693
63	A. Oliveira	Gravity particles from Warped Extra Dimensions, predictions for LHC		1404.0102
64	A. Djouadi et al.	The post-Higgs MSSM scenario: habemus MSSM?	EPJC 73 (2013) 2650	1307.5205
65	A. Djouadi et al.	Fully covering the MSSM Higgs sector at the LHC	JHEP 06 (2015) 168	1502.05653