CMS-PAS-B2G-24-015

CMS-PAS-B2G-24-015
Search for resonances decaying to a Higgs boson in the bb final state and an anomalous jet
CMS Collaboration
28 March 2025

Abstract: This note presents an analysis searching for new physics through the process where a new massive particle, X, decays into a Higgs boson and a second particle, Y. The Higgs boson subsequently decays into a pair of b-quarks and the decay products of Y are assumed to produce a non-QCD-like, e.g. anomalous, jet. In the benchmark process, Y decays into $\text W^+ \text W^-$ forming one large-area jet. A second benchmark process is also considered, where Y is a hadronically decaying top quark, originating from a vector-like quark decaying into a top quark and a Higgs boson. CMS data recorded at a centre-of-mass energy of 13 TeV in 2016-2018 and corresponding to 138 fb $^{-1}$ are analysed. In this analysis, the identification of the Y particle is enhanced by computing the anomaly score of its candidate jet using an autoencoder, allowing the simultaneous search for multiple Y decay modes with a single analysis. No significant excesses are observed and upper limits on the signal cross section for various masses of X and Y, at 95% confidence level, are placed.
Links: CDS record (PDF) ; CADI line (restricted) ;

Figures	Summary	References	CMS Publications

Figures
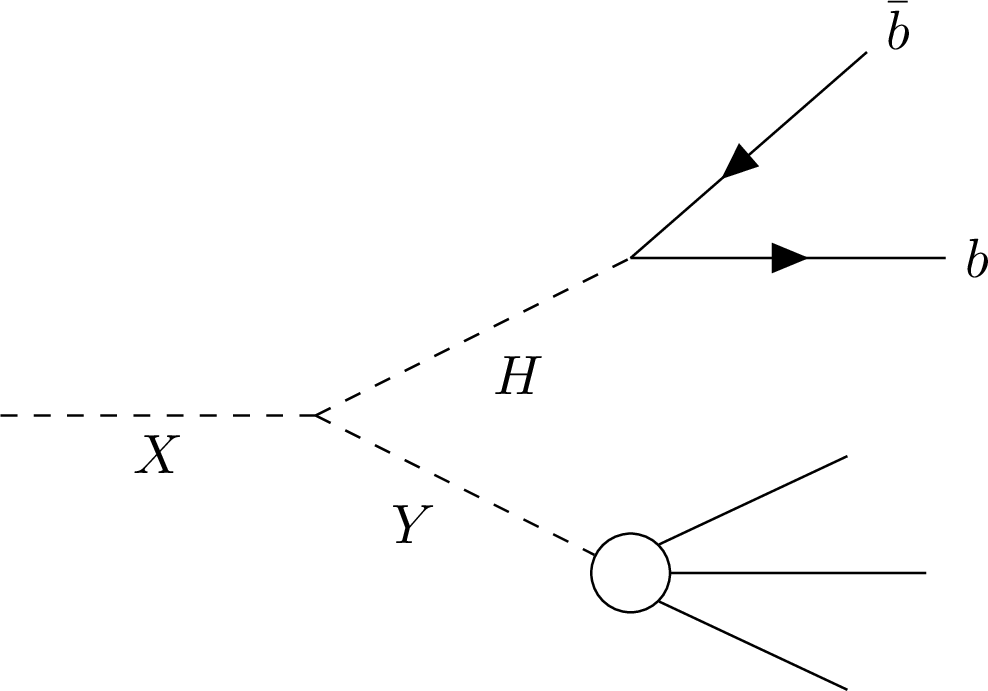
png pdf	Figure 1: An illustration showing the signal targeted by this analysis. The final state consists of a boosted jet originated from H decaying to $\mathrm{b} \overline{\mathrm{b}}$ and another boosted jet originating from the decay of a second particle, $\mathrm{Y}$ .
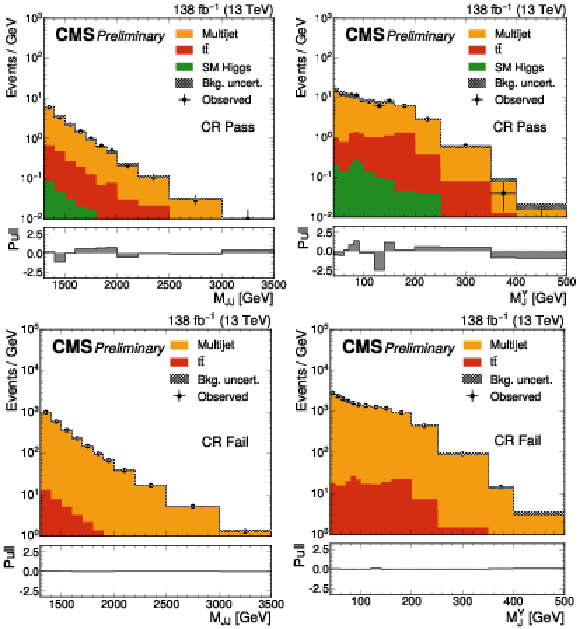
png pdf	Figure 2: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the CR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate. The lower panels show the ``Pull'' defined as (observed events $-$ expected events) $/\sqrt{\smash[b]{\sigma_{\text{obs}}^{2} + \sigma_{\text{exp}}^{2}}}$ , where $\sigma_{\text{obs}}$ and $\sigma_{\text{exp}}$ are the total uncertainties in the observation and the background estimation, respectively.
png pdf	Figure 2-a: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the CR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate. The lower panels show the ``Pull'' defined as (observed events $-$ expected events) $/\sqrt{\smash[b]{\sigma_{\text{obs}}^{2} + \sigma_{\text{exp}}^{2}}}$ , where $\sigma_{\text{obs}}$ and $\sigma_{\text{exp}}$ are the total uncertainties in the observation and the background estimation, respectively.
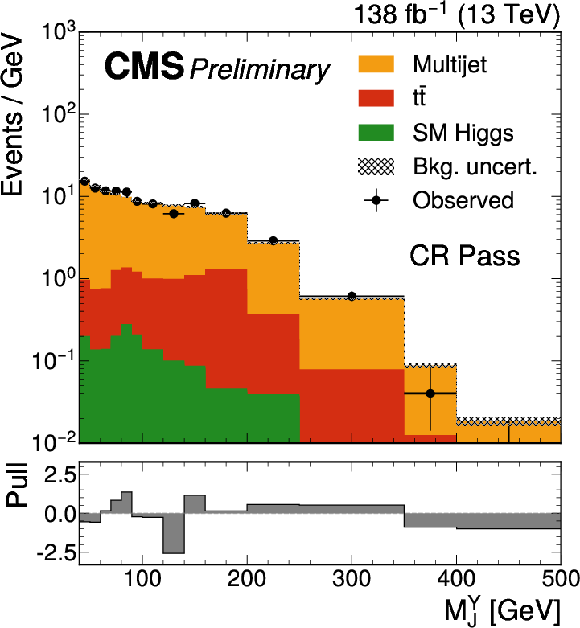
png pdf	Figure 2-b: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the CR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate. The lower panels show the ``Pull'' defined as (observed events $-$ expected events) $/\sqrt{\smash[b]{\sigma_{\text{obs}}^{2} + \sigma_{\text{exp}}^{2}}}$ , where $\sigma_{\text{obs}}$ and $\sigma_{\text{exp}}$ are the total uncertainties in the observation and the background estimation, respectively.
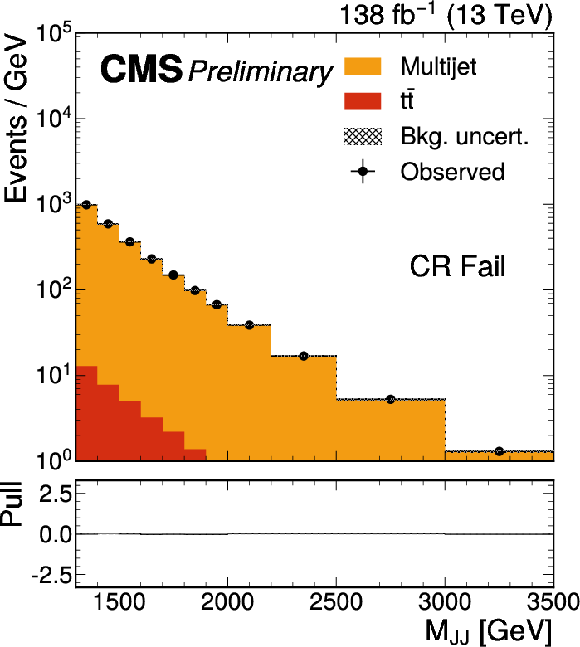
png pdf	Figure 2-c: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the CR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate. The lower panels show the ``Pull'' defined as (observed events $-$ expected events) $/\sqrt{\smash[b]{\sigma_{\text{obs}}^{2} + \sigma_{\text{exp}}^{2}}}$ , where $\sigma_{\text{obs}}$ and $\sigma_{\text{exp}}$ are the total uncertainties in the observation and the background estimation, respectively.
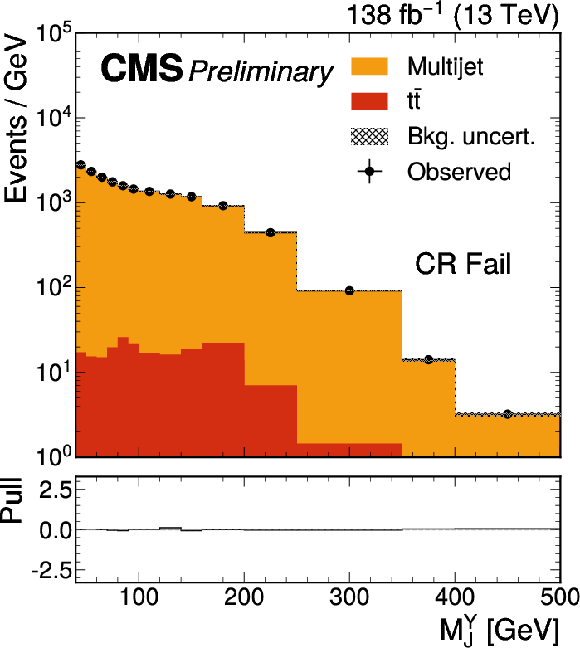
png pdf	Figure 2-d: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the CR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate. The lower panels show the ``Pull'' defined as (observed events $-$ expected events) $/\sqrt{\smash[b]{\sigma_{\text{obs}}^{2} + \sigma_{\text{exp}}^{2}}}$ , where $\sigma_{\text{obs}}$ and $\sigma_{\text{exp}}$ are the total uncertainties in the observation and the background estimation, respectively.
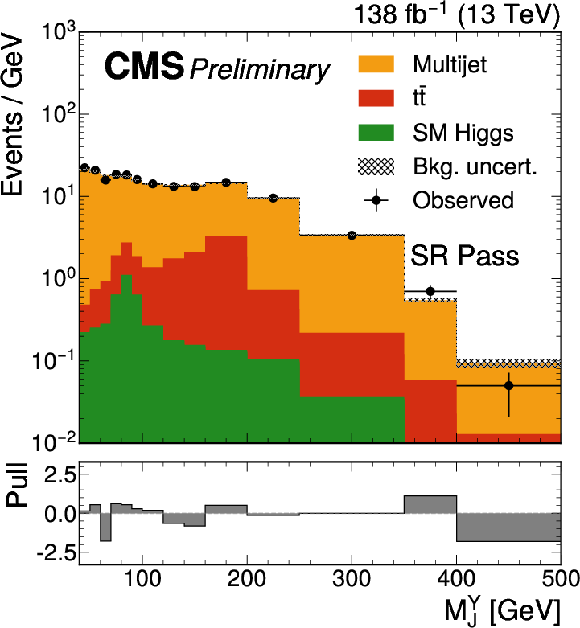
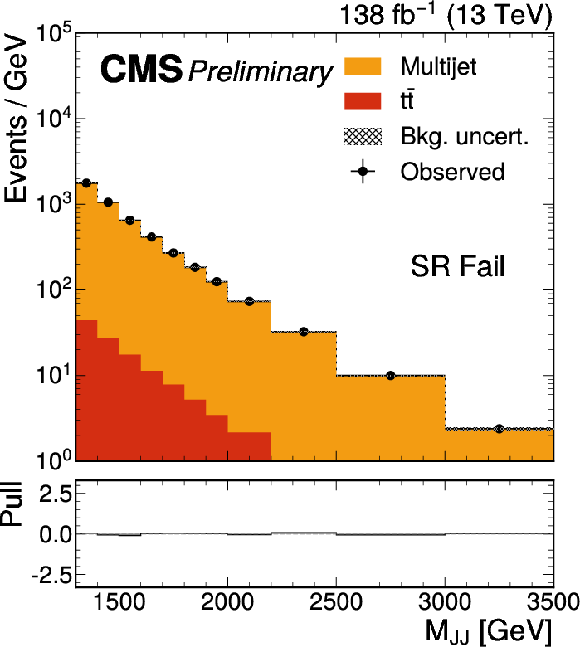
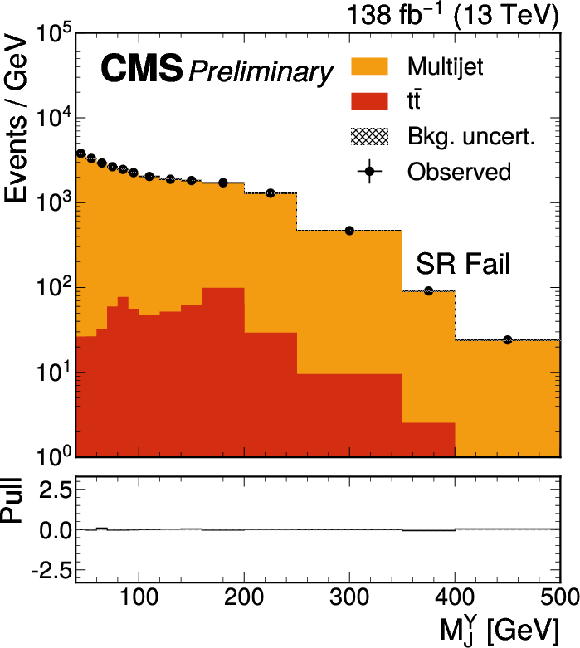
png pdf	Figure 3: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the SR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate.
png pdf	Figure 3-a: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the SR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate.
png pdf	Figure 3-b: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the SR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate.
png pdf	Figure 3-c: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the SR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate.
png pdf	Figure 3-d: The $M_\mathrm{jj}$ (left) and $M_\mathrm{j}^{\mathrm{Y}}$ (right) projections for the number of observed events (black markers) compared with the backgrounds estimated in the fit to the data (filled histograms) in the SR. Pass (upper) and fail (lower) control region categories are shown. The high level of agreement between the model and the data in the fail region is due to the nature of the background estimate.
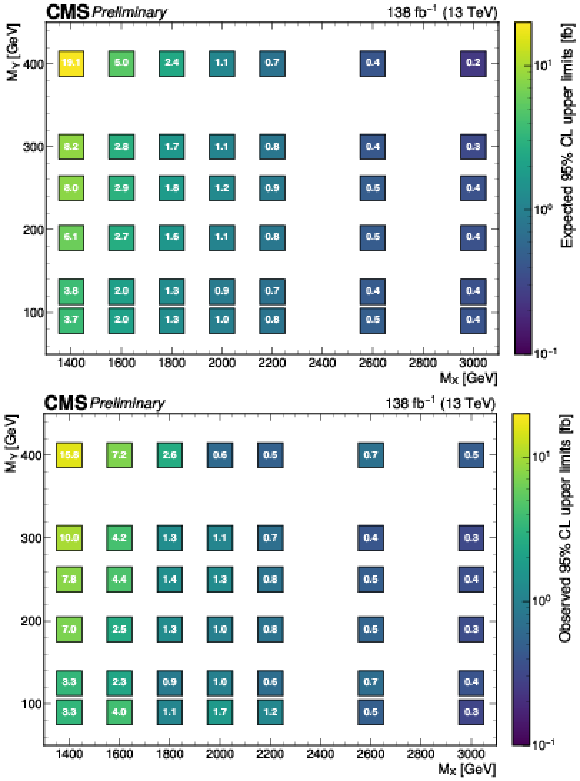
png pdf	Figure 4: The expected (upper) and observed (lower) 95% confidence level upper limits on $\sigma(\mathrm{p}\mathrm{p} \to {\mathrm{X}\to(\mathrm{H}\to\mathrm{b} \overline{\mathrm{b}})(\mathrm{Y}\to\mathrm{W}\mathrm{W}\to4\mathrm{q})})$ for different values of $\mathrm{M}_\mathrm{X}$ and $\mathrm{M}_\mathrm{Y}$ . The limits have been evaluated in discrete steps corresponding to the centers of the boxes. The numbers in the boxes are given in fb.
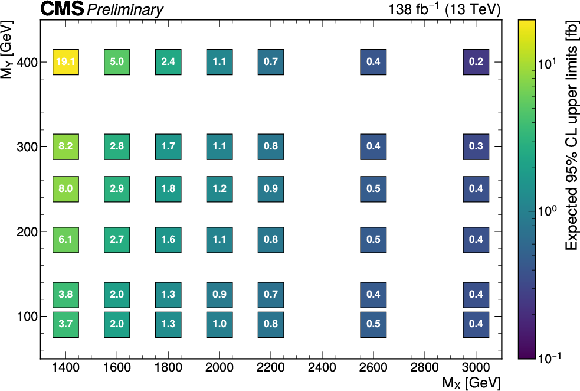
png pdf	Figure 4-a: The expected (upper) and observed (lower) 95% confidence level upper limits on $\sigma(\mathrm{p}\mathrm{p} \to {\mathrm{X}\to(\mathrm{H}\to\mathrm{b} \overline{\mathrm{b}})(\mathrm{Y}\to\mathrm{W}\mathrm{W}\to4\mathrm{q})})$ for different values of $\mathrm{M}_\mathrm{X}$ and $\mathrm{M}_\mathrm{Y}$ . The limits have been evaluated in discrete steps corresponding to the centers of the boxes. The numbers in the boxes are given in fb.
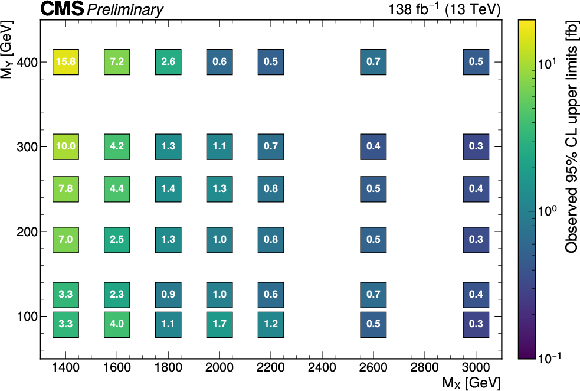
png pdf	Figure 4-b: The expected (upper) and observed (lower) 95% confidence level upper limits on $\sigma(\mathrm{p}\mathrm{p} \to {\mathrm{X}\to(\mathrm{H}\to\mathrm{b} \overline{\mathrm{b}})(\mathrm{Y}\to\mathrm{W}\mathrm{W}\to4\mathrm{q})})$ for different values of $\mathrm{M}_\mathrm{X}$ and $\mathrm{M}_\mathrm{Y}$ . The limits have been evaluated in discrete steps corresponding to the centers of the boxes. The numbers in the boxes are given in fb.
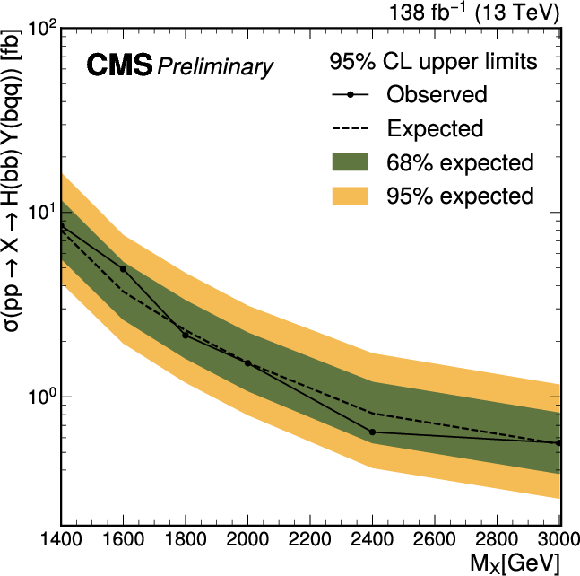
png pdf	Figure 5: The median expected (dashed line) and observed (solid line) 95% confidence level upper limits on $\sigma(\mathrm{p}\mathrm{p} \to {\mathrm{X}\to(\mathrm{H}\to\mathrm{b} \overline{\mathrm{b}})(\mathrm{Y}\to\mathrm{b} \mathrm{q} \overline{\mathrm{q}})})$ for different values of $\mathrm{M}_\mathrm{X}$ . The inner (green) band and the outer (yellow) band indicate the regions containing 68% and 95%, respectively, of the distribution of limits expected under the background-only hypothesis.

Summary

A search for new physics through the process where a resonant particle decays into a Higgs boson and an additional particle

$\mathrm{Y}$ is presented. The Higgs boson subsequently decays into a pair of b-quarks, and both resultant particles are reconstructed as large-area jets in the Lorentz-boosted regime. H candidate jets are tagged using the ParticleNet tagger that is designed to recognize jets originating from a decay of a massive particle into

$\mathrm{b} \overline{\mathrm{b}}$ . The identification of the second particle is enhanced by computing the anomaly score of its candidate jet using an autoencoder, allowing the simultaneous search for multiple Y decay modes with a single analysis. The analysis considers two benchmark models. The main benchmark assumes

$\mathrm{Y} \to \mathrm{W}^+\mathrm{W}^-$ , with further hadronic decays of the W bosons. It is simulated for 42 different

$\mathrm{M}_\mathrm{X}$ and

$\mathrm{M}_\mathrm{Y}$ hypotheses. The largest local significance of 2.06

$\sigma$ is observed for

$\mathrm{M}_\mathrm{X}=$ 1600 GeV and

$\mathrm{M}_\mathrm{Y}=$ 90 GeV, with a

$p$ value of 0.019. This corresponds to a global significance of 0.13

$\sigma$ after accounting for the look-elsewhere effect. Exclusion limits, at 95% confidence level, are set in the 0.3--16 fb range, depending on the mass hypothesis. Exclusion limits are also placed on a second benchmark that assumes the

$\mathrm{Y} \to \mathrm{b} \mathrm{q} \overline{\mathrm{q}}$ decay mode, originating from a vector-like quark decaying into a top quark and a Higgs boson, with

$\mathrm{M}_\mathrm{X}$ ranging from 1400 to 3000 GeV while

$\mathrm{M}_\mathrm{Y}$ is set to the mass of the top quark.

References
1	Particle Data Group Collaboration	Review of particle physics	PRD 110 (2024) 030001
2	Planck Collaboration	Planck 2013 results. I. Overview of products and scientific results	Astron. Astrophys. 571 (2014)	1303.5062
3	M. Dine and A. Kusenko	Origin of the matter-antimatter asymmetry	Rev. Mod. Phys. 76 (2003)	hep-ph/0303065
4	P. Fayet	Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino	NPB 90 (1975) 104
5	P. Fayet	Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions	PLB 69 (1977) 489
6	L. Randall and R. Sundrum	A large mass hierarchy from a small extra dimension	PRL 83 (1999) 3370	hep-ph/9905221
7	L. Randall and R. Sundrum	An Alternative to compactification	PRL 83 (1999) 4690	hep-th/9906064
8	T. Robens, T. Stefaniak, and J. Wittbrodt	Two-real-scalar-singlet extension of the SM: LHC phenomenology and benchmark scenarios	EPJC 80 (2020) 151	1908.08554
9	U. Ellwanger, C. Hugonie, and A. M. Teixeira	The next-to-minimal supersymmetric standard model	Phys. Rept. 496 (2010) 1	0910.1785
10	CMS Collaboration	Searches for Higgs boson production through decays of heavy resonances	Phys. Rept. 1115 (2025) 368	2403.16926
11	A. Carvalho et al.	Single production of vectorlike quarks with large width at the large hadron collider	Physical Review D 98 (2018)	1805.06402
12	G. Kasieczka et al.	The LHC olympics 2020: A community challenge for anomaly detection in high energy physics	Rept. Prog. Phys. 84 (2021) 124201	2101.08320
13	CMS Collaboration	Model-agnostic search for dijet resonances with anomalous jet substructure in proton-proton collisions at $\sqrt{s}$ = 13 TeV	CMS Physics Analysis Summary, 2024 CMS-PAS-EXO-22-026	CMS-PAS-EXO-22-026
14	CMS Collaboration	Identification of highly Lorentz-boosted heavy particles using graph neural networks and new mass decorrelation techniques	CMS Detector Performance Summary CMS-DP-2020-002, 2020 CDS
15	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
16	CMS Collaboration	Development of the CMS detector for the CERN LHC Run 3	JINST 19 (2024) P05064	CMS-PRF-21-001 2309.05466
17	CMS Collaboration	Performance of the CMS Level-1 trigger in proton-proton collisions at $\sqrt{s} =$ 13\,TeV	JINST 15 (2020) P10017	CMS-TRG-17-001 2006.10165
18	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
19	CMS Collaboration	Performance of the CMS high-level trigger during LHC Run 2	JINST 19 (2024) P11021	CMS-TRG-19-001 2410.17038
20	CMS Collaboration	Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC	JINST 16 (2021) P05014	CMS-EGM-17-001 2012.06888
21	CMS Collaboration	Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $\sqrt{s}=$ 13 TeV	JINST 13 (2018) P06015	CMS-MUO-16-001 1804.04528
22	CMS Collaboration	Description and performance of track and primary-vertex reconstruction with the CMS tracker	JINST 9 (2014) P10009	CMS-TRK-11-001 1405.6569
23	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
24	M. Cacciari, G. P. Salam, and G. Soyez	The anti- $k_{\mathrm{T}}$ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
25	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
26	CMS Collaboration	Pileup mitigation at CMS in 13 TeV data	JINST 15 (2020) P09018	CMS-JME-18-001 2003.00503
27	D. Bertolini, P. Harris, M. Low, and N. Tran	Pileup per particle identification	JHEP 10 (2014) 059	1407.6013
28	G. P. Salam	Towards jetography	EPJC 67 (2010) 637	0906.1833
29	M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam	Towards an understanding of jet substructure	JHEP 09 (2013) 029	1307.0007
30	A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler	Soft drop	JHEP 05 (2014) 146	1402.2657
31	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
32	D. Curtin et al.	Exotic decays of the 125 GeV Higgs boson	PRD 90 (2014) 075004	1312.4992
33	A. Alloul et al.	FeynRules 2.0 --- a complete toolbox for tree-level phenomenology	Comput. Phys. Commun. 185 (2014) 2250	1310.1921
34	S. Frixione, G. Ridolfi, and P. Nason	A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction	JHEP 09 (2007) 126	0707.3088
35	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
36	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
37	P. Nason	A new method for combining NLO QCD with shower monte carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
38	M. Czakon and A. Mitov	Top++: A program for the calculation of the top-pair cross-section at hadron colliders	Comput. Phys. Commun. 185 (2014) 2930	1112.5675
39	P. F. Monni et al.	MiNNLO $_{\text {PS}}$ : a new method to match NNLO QCD to parton showers	JHEP 05 (2020) 143	1908.06987
40	P. F. Monni, E. Re, and M. Wiesemann	MiNNLO $_{\text {PS}}$ : optimizing 2 $\rightarrow$ 1 hadronic processes	EPJC 80 (2020) 1075	2006.04133
41	P. Nason and C. Oleari	NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG	JHEP 02 (2010) 037	0911.5299
42	G. Luisoni, P. Nason, C. Oleari, and F. Tramontano	$\mathrm{H}\mathrm{W}^{\pm}$ /HZ+0 and 1 jet at NLO with the POWHEG box interfaced to GoSam and their merging within MiNLO	JHEP 10 (2013) 083	1306.2542
43	NNPDF Collaboration	Parton distributions from high-precision collider data	EPJC 77 (2017) 663	1706.00428
44	A. Buckley et al.	LHAPDF6: parton density access in the LHC precision era	EPJC 75 (2015) 132	1412.7420
45	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
46	J. Allison et al.	GEANT 4 developments and applications	IEEE Trans. Nucl. Sci. 53 (2006) 270
47	CMS Collaboration	Measurement of the inelastic proton-proton cross section at $\sqrt{s} =$ 13 TeV	JHEP 07 (2018) 161	CMS-FSQ-15-005 1802.02613
48	D. P. Kingma and M. Welling	Auto-encoding variational bayes	\url https://arxiv.org/abs/1312.6114, 2022 link
49	CMS Collaboration	Lund Plane Reweighting for Jet Substructure Correction	CMS Detector Performance Summary CMS-DP-2023-046, 2023 CDS
50	R. G. Lomax and D. L. Hahs	Statistical concepts: a second course	-Vaughn, . Taylor and Francis, 2012
51	CMS Collaboration	Precision luminosity measurement in proton-proton collisions at $\sqrt{s} =$ 13 TeV in 2015 and 2016 at CMS	EPJC 81 (2021) 800	CMS-LUM-17-003 2104.01927
52	CMS Collaboration	CMS luminosity measurement for the 2017 data-taking period at $\sqrt{s}$ = 13 TeV	CMS Physics Analysis Summary, 2018 link	CMS-PAS-LUM-17-004
53	CMS Collaboration	CMS luminosity measurement for the 2018 data-taking period at $\sqrt{s}$ = 13 TeV	CMS Physics Analysis Summary, 2019 link	CMS-PAS-LUM-18-002
54	CMS Collaboration	The CMS statistical analysis and combination tool: COMBINE	Comput. Softw. Big Sci. 8 (2024) 19	CMS-CAT-23-001 2404.06614
55	A. L. Read	Presentation of search results: the CL $_s$ technique	JPG 28 (2002) 2693
56	T. Junk	Confidence level computation for combining searches with small statistics	NIM A 434 (1999) 435	hep-ex/9902006
57	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727