CMS-PAS-TOP-19-007

CMS-PAS-TOP-19-007
First measurement of the running of the top quark mass
CMS Collaboration
August 2019

Abstract: The first measurement of the running of the top quark mass is presented. The mass of the top quark in the modified minimal subtraction renormalization scheme is extracted from the differential $\mathrm{t\bar{t}}$ cross section as a function of the invariant mass of the $\mathrm{t\bar{t}}$ system via a $\chi^2$ fit to next-to-leading-order differential theory predictions. The differential cross section is measured at the parton level by means of a maximum-likelihood fit to multidifferential distributions of final state observables. The analysis is performed using $\mathrm{t\bar{t}}$ candidate events in the $\mathrm{e}^\pm \mu^\mp$ final state, using data recorded by the CMS experiment at the CERN LHC in 2016 corresponding to an integrated luminosity of 35.9 fb $^{-1}$ . The observed running is found to be compatible with the scale dependence predicted by the renormalization group equation.
Links: CDS record (PDF) ; CADI line (restricted) ; These preliminary results are superseded in this paper, PLB 803 (2020) 135263. The superseded preliminary plots can be found here.

Figures & Tables	Summary	Additional Figures	References	CMS Publications

Figures
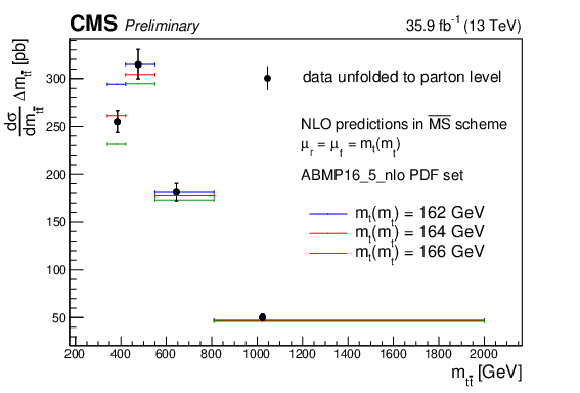
png pdf	Figure 1: Measured values of ${\sigma _{\mathrm{t} \mathrm{\bar{t}}} ^{(\mu _k)}}$ (dots) and their uncertainties (vertical error bars) compared to NLO predictions in the ${\mathrm {\overline {MS}}}$ scheme obtained with different values of ${{m_\mathrm {\mathrm{t}}} ({m_\mathrm {\mathrm{t}}})}$ (lines of different colours). The values of ${\sigma _{\mathrm{t} \mathrm{\bar{t}}} ^{(\mu _k)}}$ are shown at the central scale of the process $\mu _k$ , defined as the centre-of-gravity of the ${m_{\mathrm{t} \mathrm{\bar{t}}}}$ spectrum of each bin.
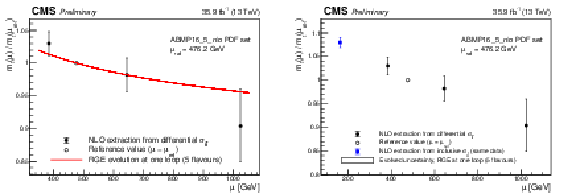
png pdf	Figure 2: Left: measured running of the top quark mass ${{m_\mathrm {\mathrm{t}}} (\mu)}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ compared to the prediction from RGE solved with one-loop precision assuming five active flavours. The reference scale $\mu _\text {ref}$ corresponds to 476.2 GeV. Right: comparison of the result with the value of ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ , where ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ is extracted from the inclusive ${\mathrm{t} \mathrm{\bar{t}}}$ cross section measurement of Ref. [7] at NLO. The uncertainty in ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ includes experimental, extrapolation and PDF uncertainties. The measurement of the inclusive ${\sigma _{\mathrm{t} \mathrm{\bar{t}}}}$ uses the same data as this analysis.
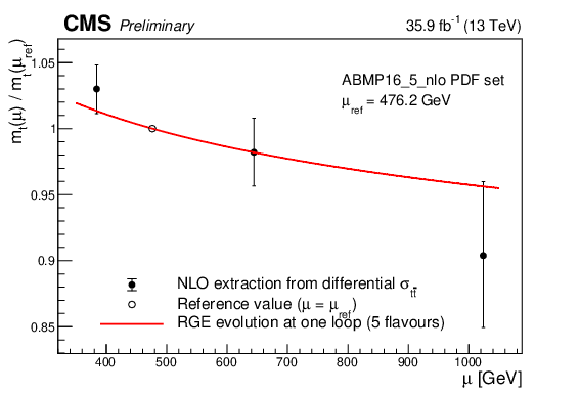
png pdf	Figure 2-a: Left: measured running of the top quark mass ${{m_\mathrm {\mathrm{t}}} (\mu)}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ compared to the prediction from RGE solved with one-loop precision assuming five active flavours. The reference scale $\mu _\text {ref}$ corresponds to 476.2 GeV. Right: comparison of the result with the value of ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ , where ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ is extracted from the inclusive ${\mathrm{t} \mathrm{\bar{t}}}$ cross section measurement of Ref. [7] at NLO. The uncertainty in ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ includes experimental, extrapolation and PDF uncertainties. The measurement of the inclusive ${\sigma _{\mathrm{t} \mathrm{\bar{t}}}}$ uses the same data as this analysis.
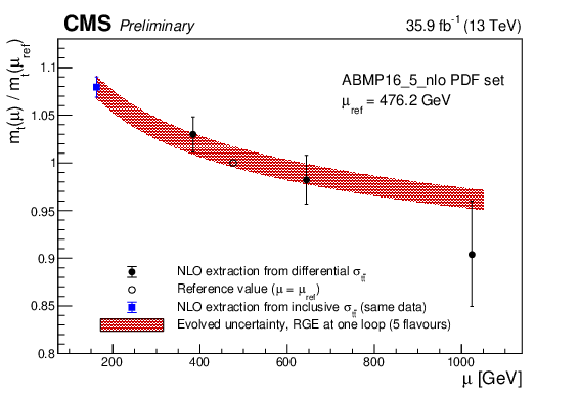
png pdf	Figure 2-b: Left: measured running of the top quark mass ${{m_\mathrm {\mathrm{t}}} (\mu)}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ compared to the prediction from RGE solved with one-loop precision assuming five active flavours. The reference scale $\mu _\text {ref}$ corresponds to 476.2 GeV. Right: comparison of the result with the value of ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ / ${m_\mathrm {\mathrm{t}}} (\mu _\text {ref})$ , where ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ is extracted from the inclusive ${\mathrm{t} \mathrm{\bar{t}}}$ cross section measurement of Ref. [7] at NLO. The uncertainty in ${{m_\mathrm {\mathrm{t}}} ^\text {incl}({m_\mathrm {\mathrm{t}}})}$ includes experimental, extrapolation and PDF uncertainties. The measurement of the inclusive ${\sigma _{\mathrm{t} \mathrm{\bar{t}}}}$ uses the same data as this analysis.

Tables
png pdf	Table 1: Bins of ${m_{\mathrm{t} \mathrm{\bar{t}}}}$ , the corresponding fraction of events in the POWHEG simulation, and the representative scale $\mu _k$ .

Summary

In this note, the first measurement of the running of the top quark mass is presented. The running of

${m_{\mathrm{t}} (\mu)}$ is extracted at next-to-leading order as a function of the invariant mass of the

$\mathrm{t\bar{t}}$ system,

${m_{\mathrm{t\bar{t}}}}$ , from a measurement of the differential

$\mathrm{t\bar{t}}$ cross section obtained using proton-proton collision data recorded by the CMS experiment at the centre-of-mass energy of 13 TeV. The measurement is performed using

$\mathrm{t\bar{t}}$ candidate events in the final state with an electron and a muon of opposite charge.

The differential

$\mathrm{t\bar{t}}$ cross section is measured at the parton level as a function of

${m_{\mathrm{t\bar{t}}}}$ using a maximum-likelihood fit to multidifferential distributions of final state observables. This technique, known as maximum-likelihood unfolding, allows constraining the nuisance parameters simultaneously with the differential cross section and therefore provides results with significantly improved precision compared to conventional procedures in which the unfolding is performed as a separate step.

The

${\mathrm{\overline{MS}}}$ mass of the top quark

$m_{\mathrm{t}} (m_{\mathrm{t}} )$ is determined independently in each

${m_{\mathrm{t\bar{t}}}}$ bin via a

${\chi^2}$ fit to theory predictions at next-to-leading order. The extracted masses are then evolved to the representative scale of the process in each bin. The observed evolution of

${m_{\mathrm{t}} (\mu)}$ is found to be in agreement with the prediction from the renormalization group equation at one-loop precision, within {1.3} standard deviations, and the significance of the observed running is found to be 2.6 standard deviations with respect to the no-running hypothesis.

Additional Figures
png pdf	Additional Figure 1: Distribution of the reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system after the fit to the data, with the same binning as used in the fit. The hatched band corresponds to the total systematic uncertainty including all correlations, while the solid gray band represents the contribution of the statistical uncertainty in the MC simulation. The $\mathrm{t\bar{t}}$ MC sample is split into four subsamples, denoted with "Signal ( $\mu_k$ )'', corresponding to the bins in invariant mass of the $\mathrm{t\bar{t}}$ system at the parton level.
png pdf	Additional Figure 2: Post-fit distribution of fit input in the category with less than two jets and zero or more than two b-tagged jets.
png pdf	Additional Figure 3: Post-fit distribution of fit input in the category with zero or more than two b-tagged jets and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system below 420 GeV.
png pdf	Additional Figure 4: Post-fit distribution of fit input in the category with zero or more than two b-tagged jets and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 420 and 550 GeV.
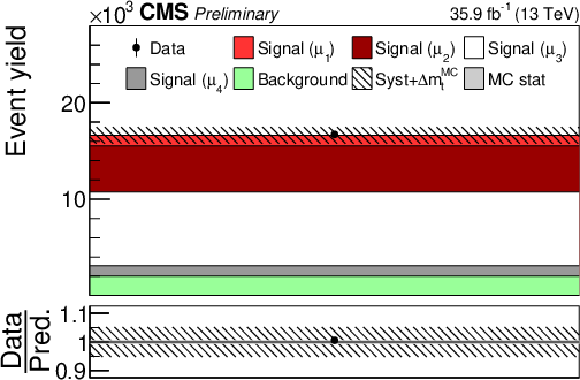
png pdf	Additional Figure 5: Post-fit distribution of fit input in the category with zero or more than two b-tagged jets and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 550 and 810 GeV.
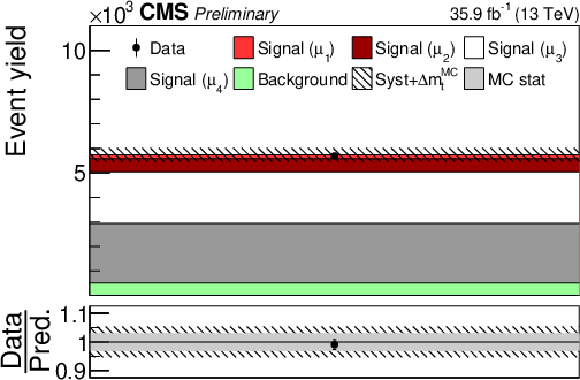
png pdf	Additional Figure 6: Post-fit distribution of fit input in the category with zero or more than two b-tagged jets and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system above 810 GeV.
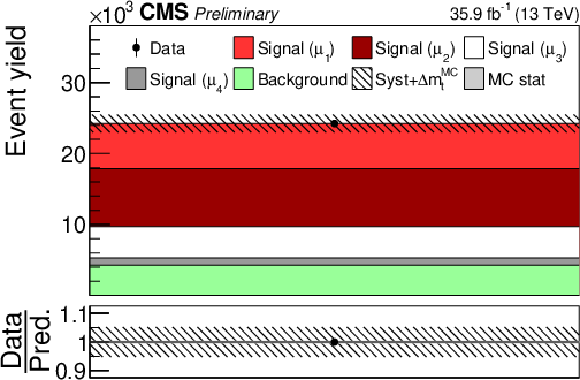
png pdf	Additional Figure 7: Post-fit distribution of fit input in the category with less than two jets and one b-tagged jet.
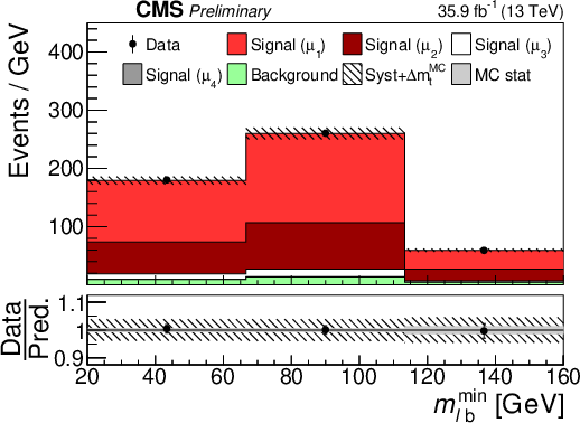
png pdf	Additional Figure 8: Post-fit distribution of fit input in the category with one b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system below 420 GeV.
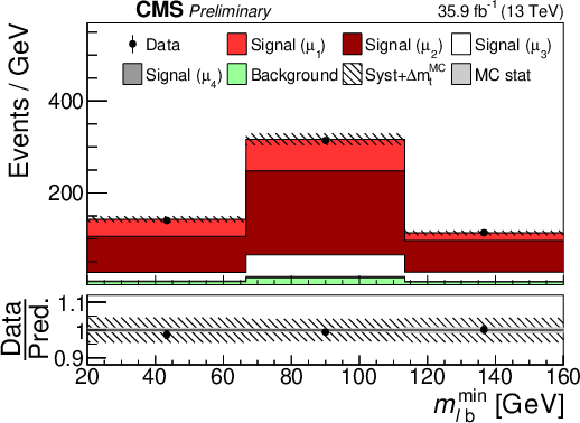
png pdf	Additional Figure 9: Post-fit distribution of fit input in the category with one b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 420 and 550 GeV.
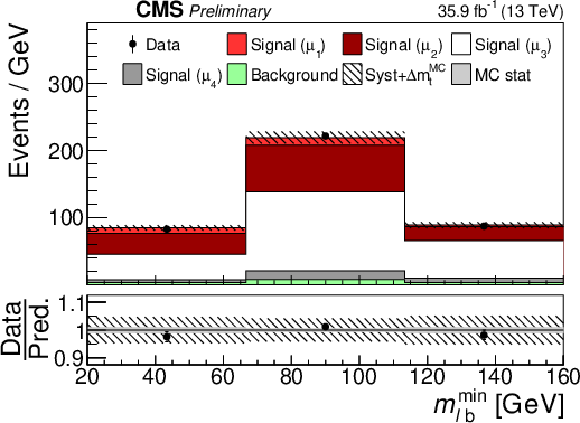
png pdf	Additional Figure 10: Post-fit distribution of fit input in the category with one b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 550 and 810 GeV.
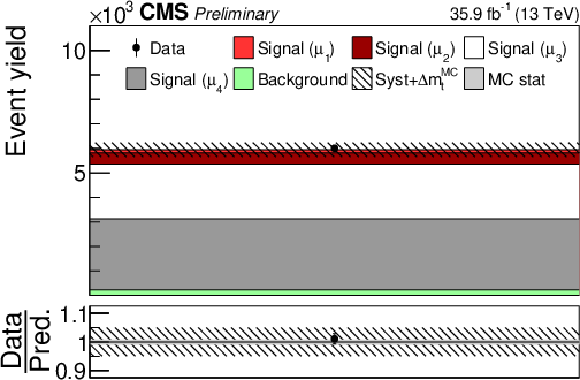
png pdf	Additional Figure 11: Post-fit distribution of fit input in the category with one b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system above 810 GeV.
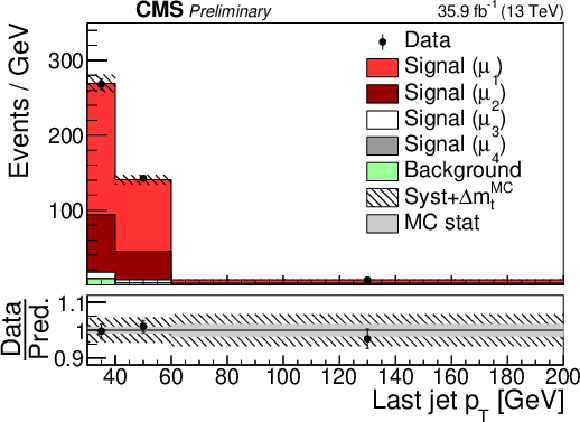
png pdf	Additional Figure 12: Post-fit distribution of fit input in the category with two b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system below 420 GeV.
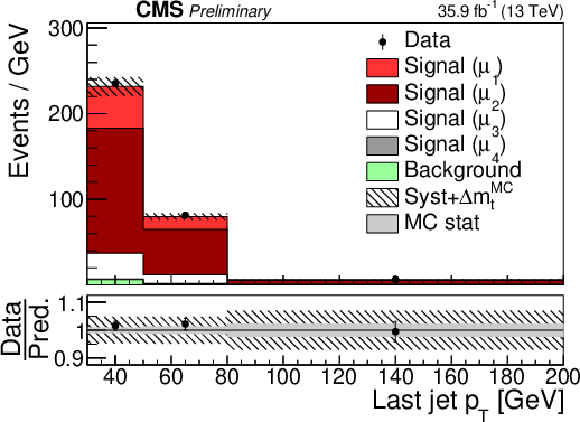
png pdf	Additional Figure 13: Post-fit distribution of fit input in the category with two b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 420 and 550 GeV.
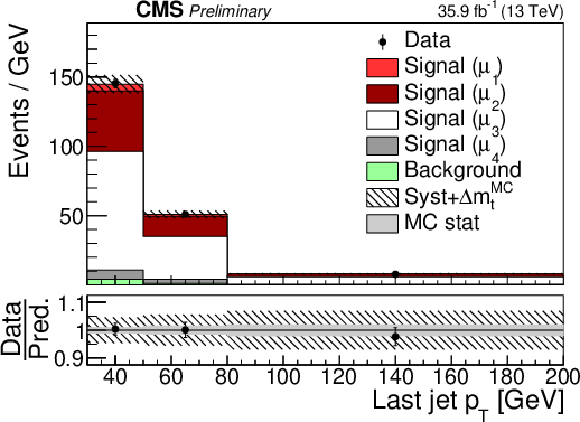
png pdf	Additional Figure 14: Post-fit distribution of fit input in the category with two b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system between 550 and 810 GeV.
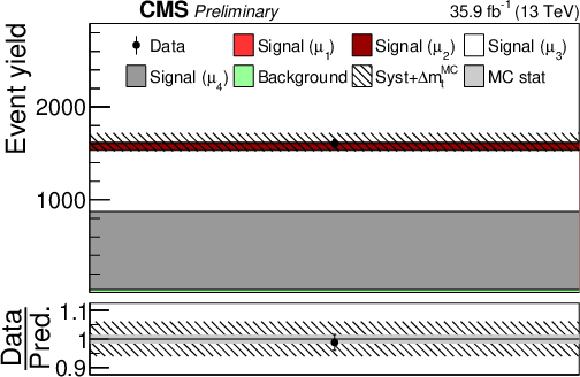
png pdf	Additional Figure 15: Post-fit distribution of fit input in the category with two b-tagged jet and reconstructed invariant mass of the $\mathrm{t\bar{t}}$ system above 810 GeV.

References
1	A. Deur, S. J. Brodsky, and G. F. de Teramond	The QCD Running Coupling	Prog. Part. NP 90 (2016) 1	1604.08082
2	CMS Collaboration	Measurement and QCD analysis of double-differential inclusive jet cross sections in pp collisions at $\sqrt{s}=$ 8 TeV and cross section ratios to 2.76 and 7 TeV	JHEP 03 (2017) 156	CMS-SMP-14-001 1609.05331
3	P. A. Baikov, K. G. Chetyrkin, and J. H. Kuhn	Quark Mass and Field Anomalous Dimensions to ${\cal O}(\alpha_s^5)$	JHEP 10 (2014) 076	1402.6611
4	T. Luthe, A. Maier, P. Marquard, and Y. Schroder	Five-loop quark mass and field anomalous dimensions for a general gauge group	JHEP 01 (2017) 081	1612.05512
5	DELPHI Collaboration	Study of b-quark mass effects in multijet topologies with the DELPHI detector at LEP	EPJC 55 (2008) 525	0804.3883
6	A. Gizhko et al.	Running of the charm-quark mass from HERA Deep-Inelastic Scattering data	PLB 775 (2017) 233	1705.08863
7	CMS Collaboration	Measurement of the $\mathrm{t\bar{t}}$ production cross section, the top quark mass, and the strong coupling constant using dilepton events in $pp$ collisions at $\$ \sqrt{s} =$ $ 13 TeV	EPJC 79 (2019) 368	CMS-TOP-17-001 1812.10505
8	P. Nason	A New method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
9	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with Parton Shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
10	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
11	S. Frixione, P. Nason, and G. Ridolfi	A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction	JHEP 09 (2007) 126	0707.3088
12	J. M. Campbell and R. K. Ellis	MCFM for the Tevatron and the LHC	NPPS 205-206 (2010)	1007.3492
13	J. M. Campbell and R. K. Ellis	Top-Quark Processes at NLO in Production and Decay	JPG 42 (2015) 015005	1204.1513
14	M. Dowling and S.-O. Moch	Differential distributions for top-quark hadro-production with a running mass	EPJC 74 (2014) 3167	1305.6422
15	S. Alekhin, J. Blumlein, and S. Moch	NLO PDFs from the ABMP16 fit	EPJC 78 (2018) 477	1803.07537
16	T. Sjostrand et al.	An introduction to $PYTHIA 8.2$	CPC 191 (2015) 159	1410.3012
17	CMS Collaboration	Investigations of the impact of the parton shower tuning in $PYTHIA 8$ in the modelling of $\mathrm{t\bar{t}}$ at $\sqrt{s}=$ 8 and 13 TeV	CMS-PAS-TOP-16-021	CMS-PAS-TOP-16-021
18	P. Skands, S. Carrazza, and J. Rojo	Tuning $PYTHIA 8.1:$ the Monash 2013 Tune	EPJC 74 (2014) 3024	1404.5630
19	CMS Collaboration	Measurements of $\mathrm{t\bar{t}}$ differential cross sections in proton-proton collisions at $\$ \sqrt{s} =$ $ 13 TeV using events containing two leptons	JHEP 02 (2019) 149	CMS-TOP-17-014 1811.06625
20	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
21	CMS Collaboration	Jet algorithms performance in 13 TeV data	CMS-PAS-JME-16-003	CMS-PAS-JME-16-003
22	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in $pp$ collisions at 13 TeV	JINST 13 (2018) P05011	CMS-BTV-16-002 1712.07158
23	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
24	M. Cacciari et al.	The $\mathrm{t\bar{t}}$ cross-section at 1.8 TeV and 1.96 $TeV:$ a study of the systematics due to parton densities and scale dependence	JHEP 04 (2004) 068	hep-ph/0303085
25	S. Catani, D. de Florian, M. Grazzini, and P. Nason	Soft gluon resummation for Higgs boson production at hadron colliders	JHEP 07 (2003) 028	hep-ph/0306211
26	S. Dulat et al.	New parton distribution functions from a global analysis of quantum chromodynamics	PRD 93 (2016) 033006	1506.07443
27	M. G. Bowler	$\mathrm{e^{+}e^{-}}$ production of heavy quarks in the string model	Z. Phys. C 11 (1981) 169
28	C. Peterson, D. Schlatter, I. Schmitt, and P. M. Zerwas	Scaling violations in inclusive $\mathrm{e^{+}e^{-}}$ annihilation spectra	PRD 27 (1983) 105
29	S. Argyropoulos and T. Sjostrand	Effects of color reconnection on $\mathrm{t\bar{t}}$ final states at the LHC	JHEP 11 (2014) 043	1407.6653
30	J. R. Christiansen and P. Z. Skands	String formation beyond leading colour	JHEP 08 (2015) 003	1505.01681
31	CMS Collaboration	Measurement of normalized differential $\mathrm{t\bar{t}}$ cross sections in the dilepton channel from $pp$ collisions at $\sqrt{s}=$ 13 TeV	JHEP 04 (2018) 060	CMS-TOP-16-007 1708.07638
32	CMS Collaboration	Measurement of differential cross sections for top quark pair production using the lepton+jets final state in proton-proton collisions at 13 TeV	PRD 95 (2017) 092001	CMS-TOP-16-008 1610.04191
33	CMS Collaboration	Measurement of inclusive and differential Higgs boson production cross sections in the diphoton decay channel in proton-proton collisions at $\sqrt{s}=$ 13 TeV	JHEP 01 (2019) 183	CMS-HIG-17-025 1807.03825
34	F. James and M. Roos	Minuit: a system for function minimization and analysis of the parameter errors and correlations	CPC 10 (1975) 343
35	R. Barlow	Asymmetric errors	eConf C030908 (2003) WEMT002	physics/0401042
36	B. Schmidt and M. Steinhauser	CRunDec: a C++ package for running and decoupling of the strong coupling and quark masses	CPC 183 (2012) 1845	1201.6149
37	M. Aliev et al.	Hathor: HAdronic Top and Heavy quarks crOss section calculatoR	CPC 182 (2011) 1034	1007.1327