Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-SUS-18-004 | ||
| Search for physics beyond the standard model in final states with two or three soft leptons and missing transverse momentum in proton-proton collisions at 13 TeV | ||
| CMS Collaboration | ||
| March 2021 | ||
| Abstract: A search for new physics is performed using events with two or three low-momentum (soft) leptons and missing transverse momentum. These signatures are motivated by theoretical models predicting new weakly interacting massive particles with nearly degenerate mass. The search results are based on data collected by the CMS experiment at the LHC from 2016 to 2018, corresponding to an integrated luminosity of up to 137 fb$^{-1}$. The observed event yields are in agreement with the standard model expectations. The results are interpreted in terms of pair produced electroweakinos ($\tilde{\chi}_{1}^{\pm}$,$\tilde{\chi}_{2}^{0}$) with compressed mass spectra, which are present in natural supersymmetry models with light higgsinos, as well as in terms of the pair production of top squarks nearly mass-degenerate with the lightest neutralino (LSP). For the electroweakino interpretation, two simplified models are considered: a wino-bino model and a higgsino model. In the framework of the wino-bino simplified model, the search probes $\tilde{\chi}_{2}^{0}/\tilde{\chi}_{1}^{\pm}$ masses up to 280 GeV for a mass difference of 10 GeV relative to the LSP, at 95% confidence level. Considering the higgsino model, the probed masses reach up to 215 GeV for a mass difference of 7.5 GeV and 150 GeV in the highly compressed region with a mass difference of 3 GeV. The higgsino search results are further interpreted using a phenomenological MSSM model probing the higgsino mass parameter $\mu$ up to 190 GeV with the bino mass parameter $M_1 = 0.5 M_2$ set to 1000 GeV, where $M_2$ is the wino mass parameter. In the top squark interpretation, masses up to 550 GeV are probed for a mass difference of 30 GeV relative to the LSP in the scenario of four-body top squark decay and in the scenario of a chargino-mediated decay, masses up to 475 GeV are probed for the same mass difference. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
Figure 1:
Production and decay of electroweakinos in the TChiWZ model (left) and a top squark pair in the chargino-mediated T2bw model (right). |
png pdf |
Figure 1-a:
Production and decay of electroweakinos in the TChiWZ model (left) and a top squark pair in the chargino-mediated T2bw model (right). |
png pdf |
Figure 1-b:
Production and decay of electroweakinos in the TChiWZ model (left) and a top squark pair in the chargino-mediated T2bw model (right). |
png pdf |
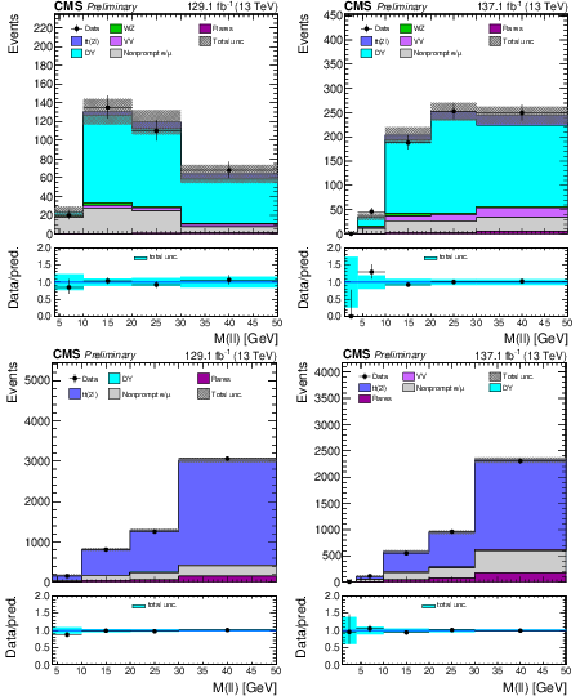
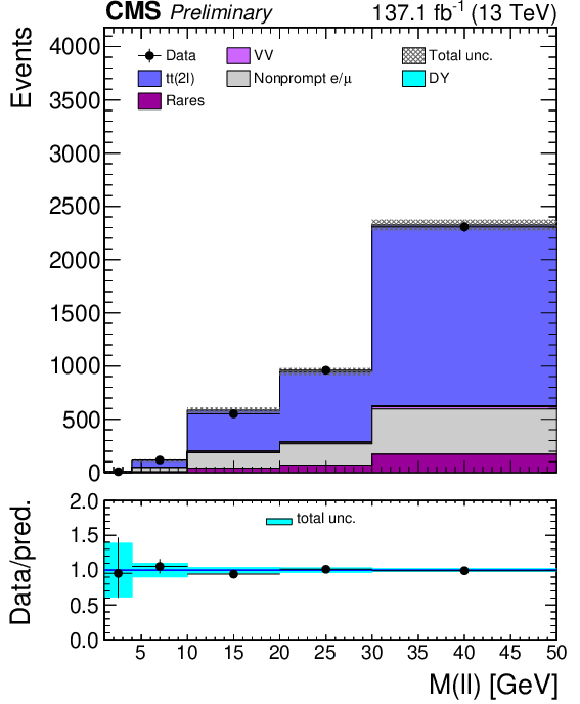
Figure 2:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the DY (top) and ${\mathrm{t} {}\mathrm{\bar{t}}}$ (bottom) control regions. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 2-a:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the DY (top) and ${\mathrm{t} {}\mathrm{\bar{t}}}$ (bottom) control regions. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 2-b:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the DY (top) and ${\mathrm{t} {}\mathrm{\bar{t}}}$ (bottom) control regions. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 2-c:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the DY (top) and ${\mathrm{t} {}\mathrm{\bar{t}}}$ (bottom) control regions. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 2-d:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the DY (top) and ${\mathrm{t} {}\mathrm{\bar{t}}}$ (bottom) control regions. Uncertainties include both the statistical and systematic components. |
png pdf |
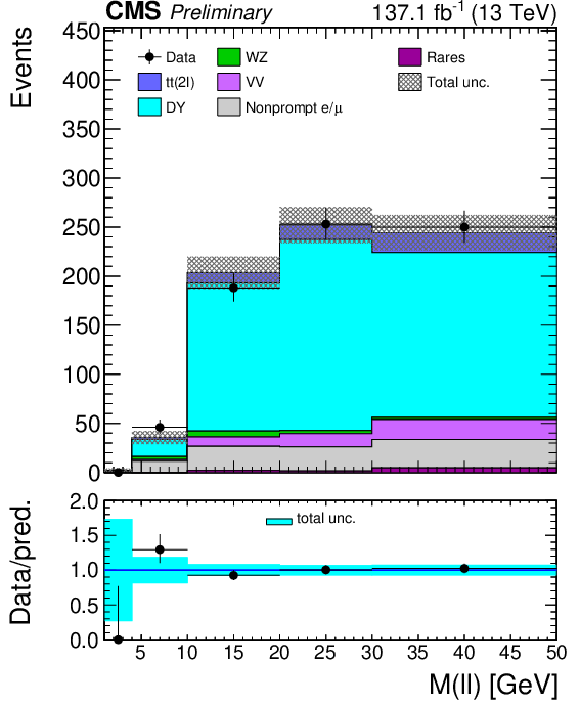
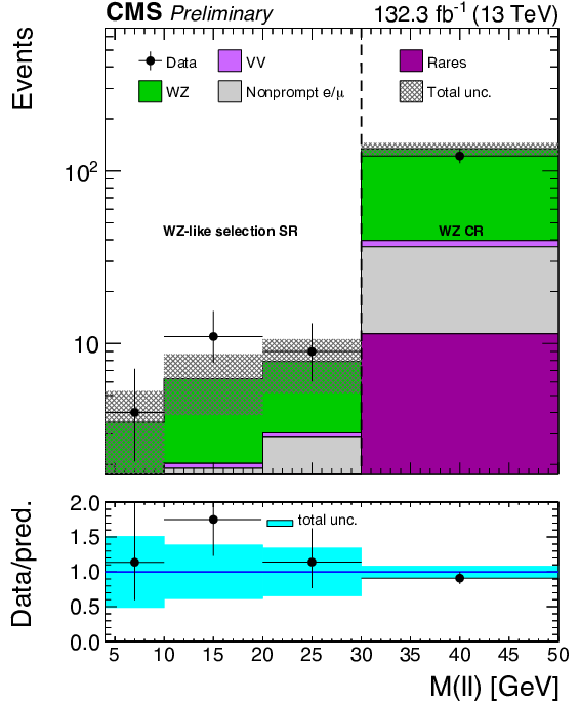
Figure 3:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the WZ enriched region. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 3-a:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the WZ enriched region. Uncertainties include both the statistical and systematic components. |
png pdf |
Figure 3-b:
The distribution of the $M(\ell \ell)$ variable is shown for the low (left) and high (right) MET bins for the WZ enriched region. Uncertainties include both the statistical and systematic components. |
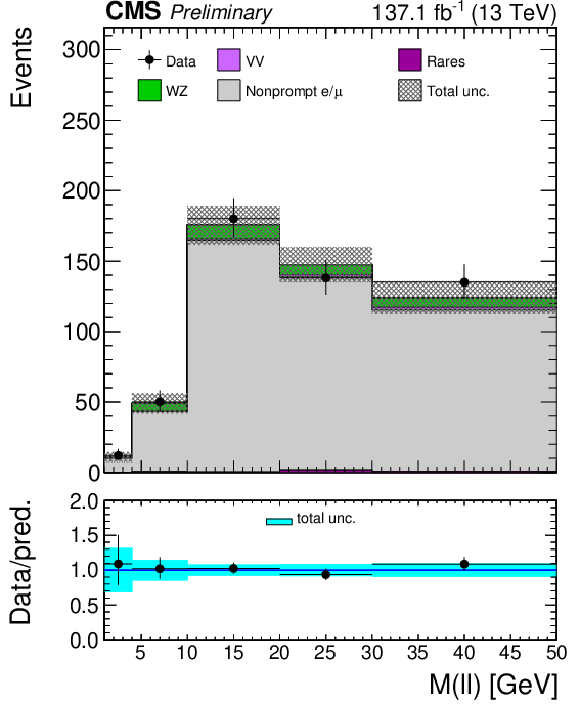
png pdf |
Figure 4:
The distribution of the $M(\ell \ell)$ variable is shown for the high MET bin for the SS control region. Uncertainties include both the statistical and systematic components. |
png pdf |
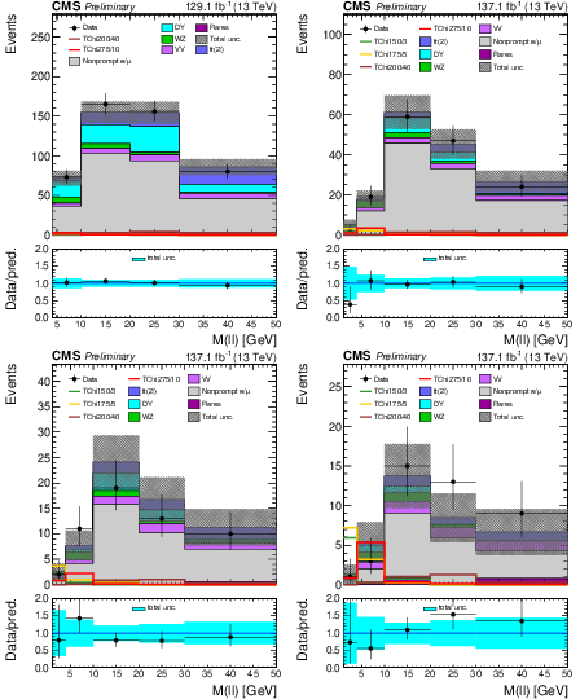
Figure 5:
The 2$\ell $ Ewk search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 5-a:
The 2$\ell $ Ewk search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 5-b:
The 2$\ell $ Ewk search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 5-c:
The 2$\ell $ Ewk search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 5-d:
The 2$\ell $ Ewk search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
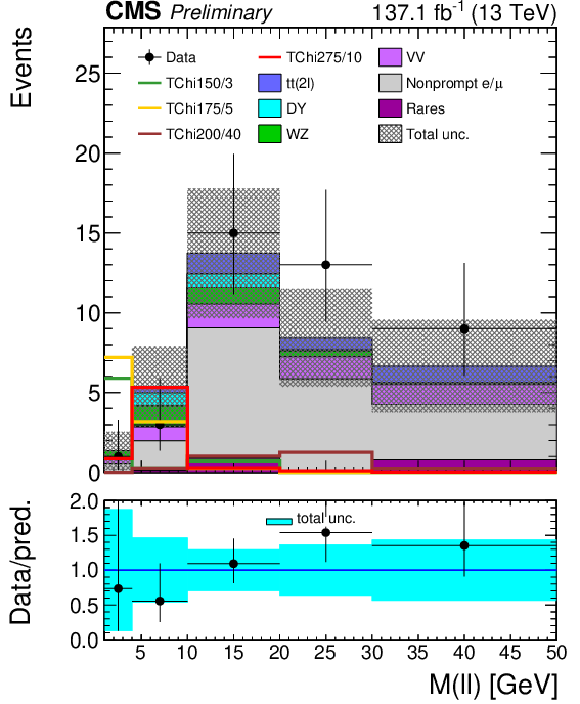
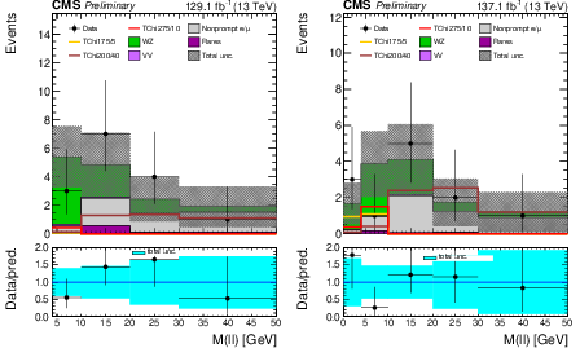
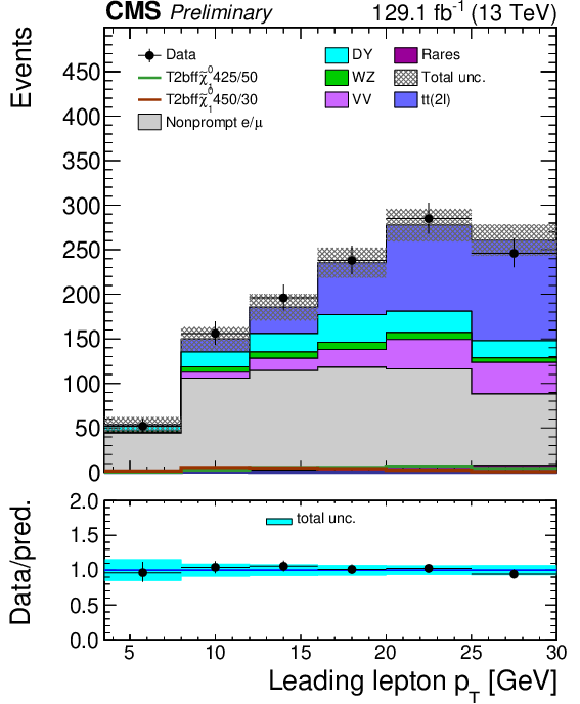
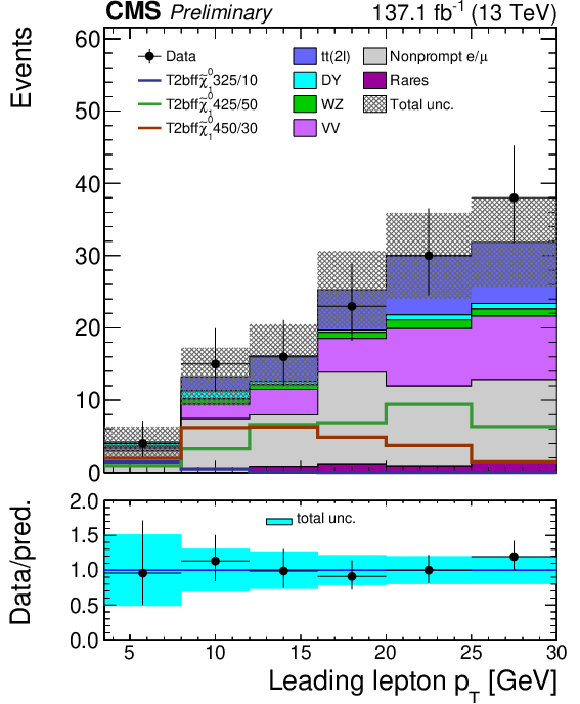
Figure 6:
The 3$\ell $ Ewk search regions: the distribution of the $m^{min}_{\ell \ell \text {,SFOS}}$ variable is shown for the low (left) and medium (right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 6-a:
The 3$\ell $ Ewk search regions: the distribution of the $m^{min}_{\ell \ell \text {,SFOS}}$ variable is shown for the low (left) and medium (right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
Figure 6-b:
The 3$\ell $ Ewk search regions: the distribution of the $m^{min}_{\ell \ell \text {,SFOS}}$ variable is shown for the low (left) and medium (right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the TChiWZ model in the scenario where the product of $m_{\tilde{\chi}^0_1} m_{\tilde{\chi}^{0}_2} $ eigenvalues is positive. The numbers after the model name in the legend indicate the mass of the NLSP and the mass splitting between the NLSP and the LSP. |
png pdf |
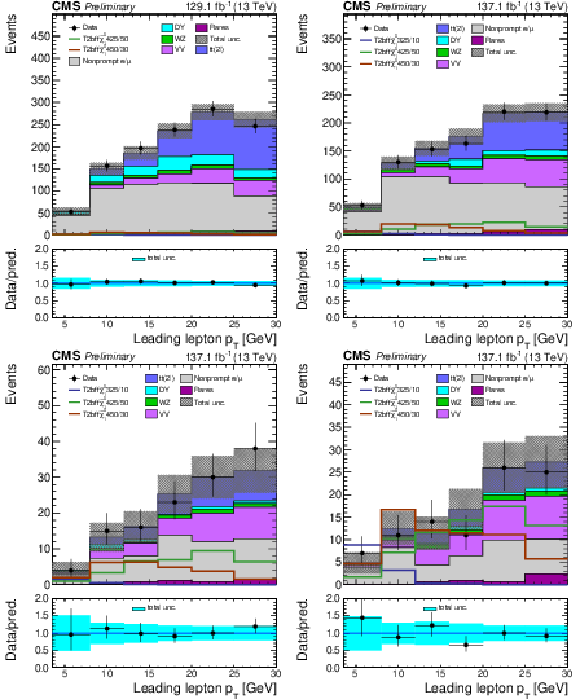
Figure 7:
The 2$\ell $ Stop search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the T2b$ff\tilde{\chi}^0_1 $ model. The numbers after the model name in the legend indicate the mass of the top squark and the mass splitting between the top squark and the LSP. |
png pdf |
Figure 7-a:
The 2$\ell $ Stop search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the T2b$ff\tilde{\chi}^0_1 $ model. The numbers after the model name in the legend indicate the mass of the top squark and the mass splitting between the top squark and the LSP. |
png pdf |
Figure 7-b:
The 2$\ell $ Stop search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the T2b$ff\tilde{\chi}^0_1 $ model. The numbers after the model name in the legend indicate the mass of the top squark and the mass splitting between the top squark and the LSP. |
png pdf |
Figure 7-c:
The 2$\ell $ Stop search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the T2b$ff\tilde{\chi}^0_1 $ model. The numbers after the model name in the legend indicate the mass of the top squark and the mass splitting between the top squark and the LSP. |
png pdf |
Figure 7-d:
The 2$\ell $ Stop search regions: the distribution of the $M(\ell \ell)$ variable is shown for the low (top left), medium (top right), high (bottom left) and ultra (bottom right) MET bins. Uncertainties include both the statistical and systematic components. The signal distributions overlaid on the plot are from the T2b$ff\tilde{\chi}^0_1 $ model. The numbers after the model name in the legend indicate the mass of the top squark and the mass splitting between the top squark and the LSP. |
png pdf |
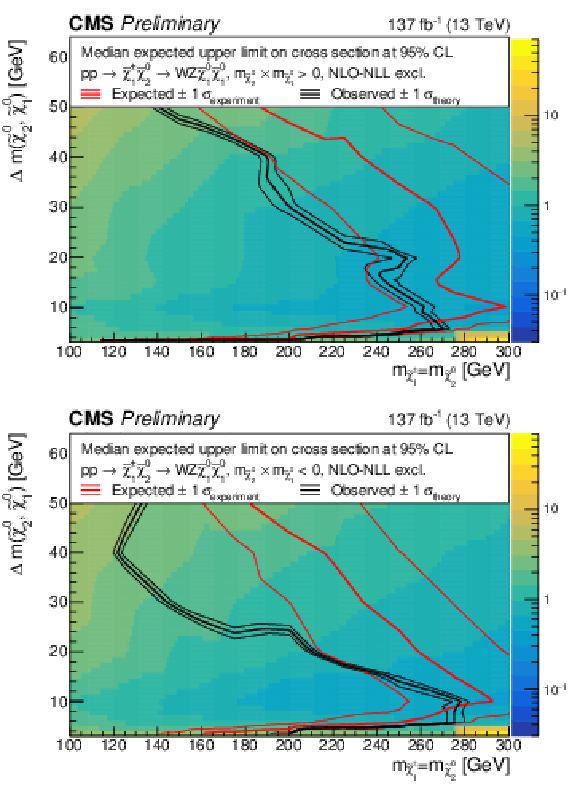
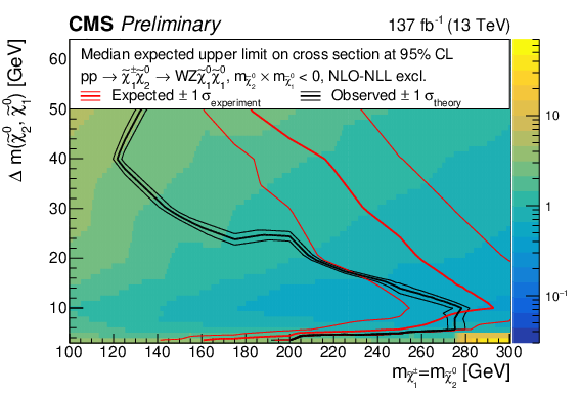
Figure 8:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the TChiWZ model. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. Results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} > $ 0 reweighting scenario on the top and the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario on the bottom. |
png pdf |
Figure 8-a:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the TChiWZ model. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. Results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} > $ 0 reweighting scenario on the top and the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario on the bottom. |
png pdf |
Figure 8-b:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the TChiWZ model. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. Results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} > $ 0 reweighting scenario on the top and the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario on the bottom. |
png pdf |
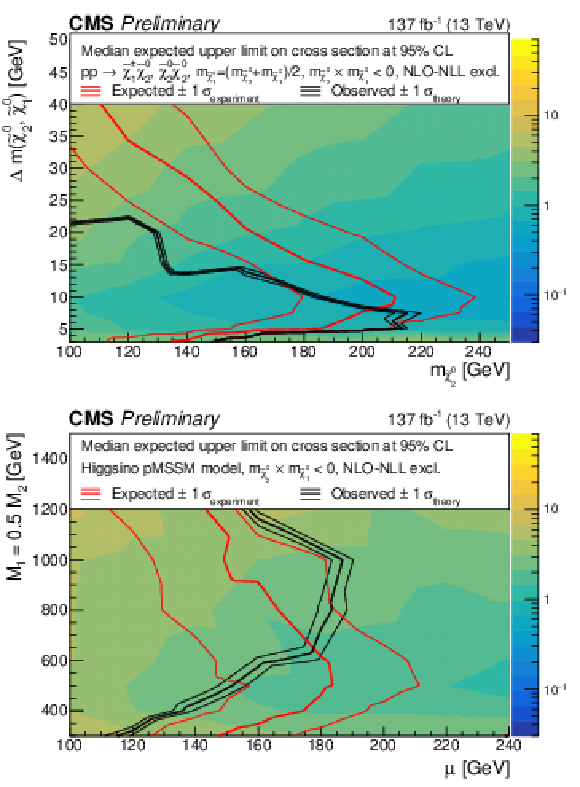
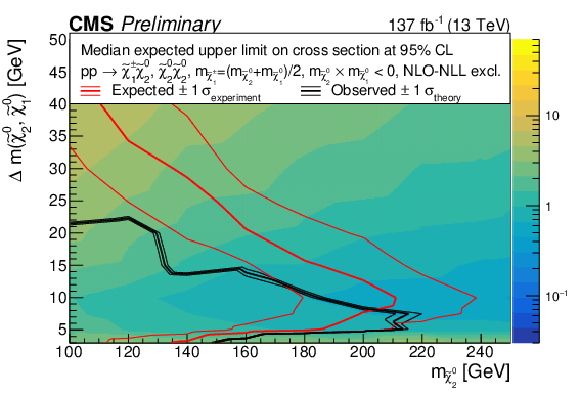
Figure 9:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the simplified (top) and the pMSSM (bottom) higgsino model. The simplified model includes both neutralino pair and neutralino-chargino production modes, while the pMSSM one includes all possible production modes. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. The results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario. |
png pdf |
Figure 9-a:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the simplified (top) and the pMSSM (bottom) higgsino model. The simplified model includes both neutralino pair and neutralino-chargino production modes, while the pMSSM one includes all possible production modes. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. The results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario. |
png pdf |
Figure 9-b:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the simplified (top) and the pMSSM (bottom) higgsino model. The simplified model includes both neutralino pair and neutralino-chargino production modes, while the pMSSM one includes all possible production modes. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. The results are reported for the $m_{\tilde{\chi}^{0}_2}m_{\tilde{\chi}^0_1} < $ 0 reweighting scenario. |
png pdf |
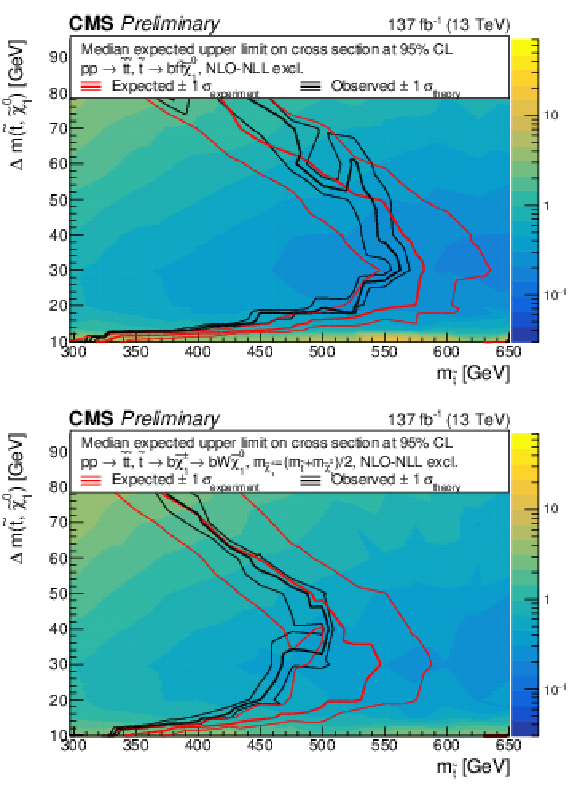
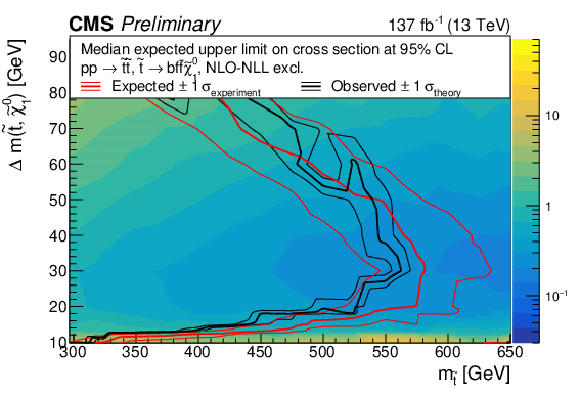
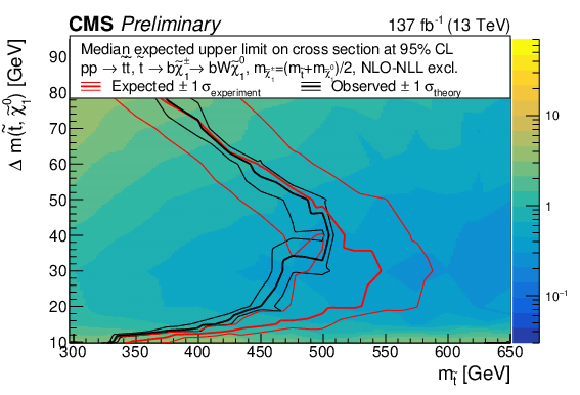
Figure 10:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the T2b$ff\tilde{\chi}^0_1 $ (top) and T2bW (bottom) simplified models. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. |
png pdf |
Figure 10-a:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the T2b$ff\tilde{\chi}^0_1 $ (top) and T2bW (bottom) simplified models. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. |
png pdf |
Figure 10-b:
The observed 95% CL exclusion contours (black curves) assuming the NLO+NLL cross sections, with the variations (thin lines) corresponding to the uncertainty in the cross section for the T2b$ff\tilde{\chi}^0_1 $ (top) and T2bW (bottom) simplified models. The red curves present the 95% CL expected limits with the band (thin lines) covering 68% of the limits in the absence of signal. |
| Tables | |
png pdf |
Table 1:
Definition of the MET bins of the SRs. The boundaries (in GeV) of ${{p_{\mathrm {T}}} ^\text {miss}}$ and ${{p_{\mathrm {T}}} ^\text {miss,corr}}$ of every bin are described. |
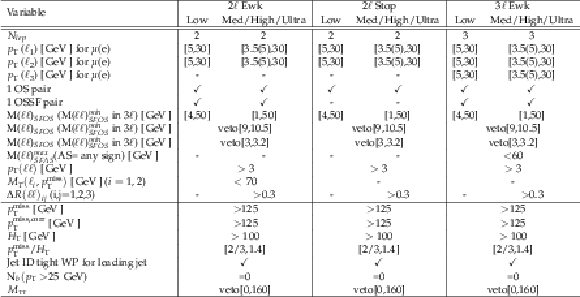
png pdf |
Table 2:
List of all criteria that events must satisfy in order to be selected in one of the SRs. |
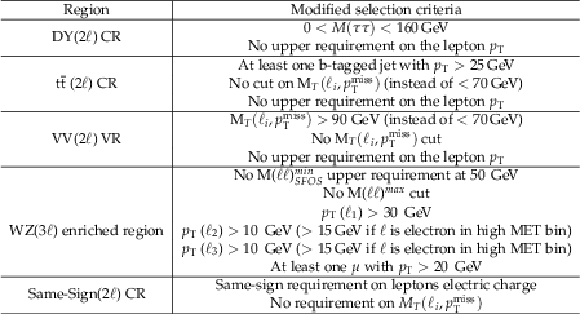
png pdf |
Table 3:
Summary of changes in the selection criteria with respect to the search regions for all the background regions. |
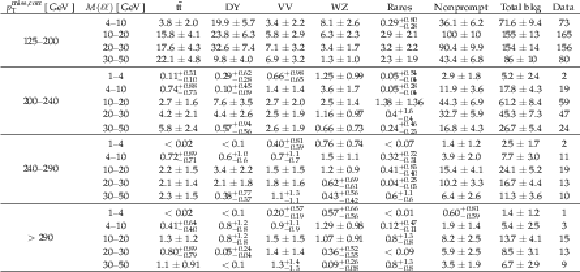
png pdf |
Table 4:
Observed and predicted yields as extracted from the final fit, in the 2$\ell $ Ewk search regions. Uncertainties include both the statistical and systematic components. |
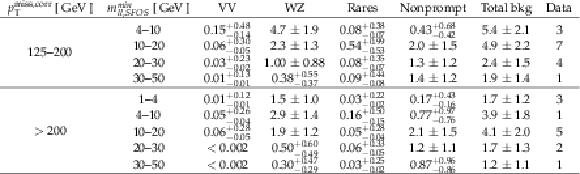
png pdf |
Table 5:
Observed and predicted yields as extracted from the final fit, in the 3$\ell $ Ewk search regions. Uncertainties include both the statistical and systematic components. |
png pdf |
Table 6:
Observed and predicted yields as extracted from the final fit, in the 2$\ell $ Stop search regions. Uncertainties include both the statistical and systematic components. |
| Summary |
|
A search for new physics is performed using events with two or three soft leptons and missing transverse momentum. These signatures are motivated by models predicting a hypothetical Weakly Interacting Massive Particle which originates from the decay of another new particle with nearly degenerate mass. The results are based on data collected by the CMS experiment at the LHC during 2016-2018, corresponding to an integrated luminosity of up to 137 fb$^{-1}$. The observed event yields are in agreement with the standard model expectations. The results are interpreted in the framework of supersymmetric simplified models targeting electroweakino mass-degenerate spectra and $\tilde{\mathrm{t}}$-$\tilde{\chi}^0_1$ mass-degenerate benchmark models. An interpretation of the analysis is performed also in the pMSSM framework. In particular, in the simplified wino-bino model, the $\tilde{\chi}^{0}_2\tilde{\chi}^{\pm}_1\to \mathrm{Z}^{*}\mathrm{W}^{*}\tilde{\chi}^0_1\tilde{\chi}^0_1$ process is explored for mass differences ($\Delta m$) between $\tilde{\chi}^{0}_2$ and $\tilde{\chi}^0_1$ of less than 50 GeV, assuming wino production cross sections. At 95% confidence level, wino-like $\tilde{\chi}^{\pm}_1$/$\tilde{\chi}^{0}_2$ masses are excluded up to 280 GeV for a mass difference of 10 GeV relative to the lightest neutralino. The higgsino simplified model is of particular interest; mass-degenerate electroweakinos are expected in natural supersymmetry, which predicts light higgsinos. In this model excluded masses reach up to 215 GeV for $\Delta m$ of 7.5 GeV and 150 GeV for a highly compressed scenario with $\Delta m$ of 3 GeV. In the pMSSM higgsino model, the limits are presented in the higgsino-bino mass parameters $\mu$-$M_1$ plane. The higgsino mass parameter $\mu$ is excluded up to 160 GeV, when the bino mass parameter $M_1$ is 600 GeV and the wino mass parameter $M_2$ is 1200 GeV. For larger values of $M_1$ and $M_2$, the mass splitting $\Delta m (\tilde{\chi}^{0}_2, \tilde{\chi}^0_1)$ becomes smaller and the sensitivity is increased. For $M_1 = $ 1000 GeV, $\mu$ is excluded up to 190 GeV. Finally, two $\tilde{\mathrm{t}}$-$\tilde{\chi}^0_1$ mass-degenerate benchmark models are considered. For the four-body top squark decay model, limits for the $m_{\tilde{\mathrm{t}}}$ at 550 GeV are set with a ($\tilde{\mathrm{t}}$-$\tilde{\chi}^0_1$) mass splitting at 30 GeV, while for the model of a chargino-mediated top squark decay, the mass of the $\tilde{\mathrm{t}}$ is excluded up to 475 GeV for the same mass splitting. |
| References | ||||
| 1 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 2 | H. P. Nilles | Supersymmetry, supergravity and particle physics | PR 110 (1984) 1 | |
| 3 | H. E. Haber and G. L. Kane | The search for supersymmetry: Probing physics beyond the standard model | PR 117 (1985) 75 | |
| 4 | R. Barbieri, S. Ferrara, and C. A. Savoy | Gauge models with spontaneously broken local supersymmetry | PLB 119 (1982) 343 | |
| 5 | S. Dawson, E. Eichten, and C. Quigg | Search for supersymmetric particles in hadron-hadron collisions | PRD 31 (1985) 1581 | |
| 6 | R. Barbieri and G. Giudice | Upper bounds on supersymmetric particle masses | NPB 306 (1988) 63 | |
| 7 | E. Witten | Dynamical breaking of supersymmetry | NPB 188 (1981) 513 | |
| 8 | S. Dimopoulos and H. Georgi | Softly broken supersymmetry and SU(5) | NPB 193 (1981) 150 | |
| 9 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 10 | Particle Data Group, P. A. Zyla et al. | Review of particle physics | Prog. Theor. Exp. Phys. 2020 (2020) 083C01 | |
| 11 | B. de Carlos and J. Casas | One-loop analysis of the electroweak breaking in supersymmetric models and the fine-tuning problem | PLB 309 (1993) 320 | hep-ph/9303291 |
| 12 | M. Dine, W. Fischler, and M. Srednicki | Supersymmetric technicolor | NPB 189 (1981) 575 | |
| 13 | S. Dimopoulos and S. Raby | Supercolor | NPB 192 (1981) 353 | |
| 14 | N. Sakai | Naturalness in supersymmetric GUTS | Z. Phys. C 11 (1981) 153 | |
| 15 | R. K. Kaul and P. Majumdar | Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories | NPB 199 (1982) 36 | |
| 16 | K. Griest and D. Seckel | Three exceptions in the calculation of relic abundances | PRD 43 (1991) 3191 | |
| 17 | J. Edsjo and P. Gondolo | Neutralino relic density including coannihilations | PRD 56 (1997) 1879 | hep-ph/9704361 |
| 18 | H. Baer, A. Mustafayev, and X. Tata | Monojet plus soft dilepton signal from light higgsino pair production at LHC14 | PRD 90 (2014) 115007 | 1409.7058 |
| 19 | C. Han et al. | Probing light higgsinos in natural SUSY from monojet signals at the LHC | JHEP 02 (2014) 049 | 1310.4274 |
| 20 | Z. Han, G. D. Kribs, A. Martin, and A. Menon | Hunting quasidegenerate Higgsinos | PRD 89 (2014) 075007 | 1401.1235 |
| 21 | C. Bal\'azs, M. Carena, and C. E. M. Wagner | Dark matter, light stops and electroweak baryogenesis | PRD 70 (2004) 015007 | hep-ph/0403224 |
| 22 | CMS Collaboration | Search for new physics in events with two soft oppositely charged leptons and missing transverse momentum in proton--proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 782 (2018) 440 | CMS-SUS-16-048 1801.01846 |
| 23 | ATLAS Collaboration | Searches for electroweak production of supersymmetric particles with compressed mass spectra in $ \sqrt{s}=$ 13 TeV pp collisions with the ATLAS detector | PRD 101 (2020) 052005 | 1911.12606 |
| 24 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 25 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 26 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 27 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 28 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 29 | P. Nason | A new method for combining NLO QCD with shower monte carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 30 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 31 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower monte carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 32 | T. Melia, P. Nason, and G. Rontsch, Raoul andZanderighi | $ \mathrm{W}^+\mathrm{W}^- $, $ \mathrm{W}\mathrm{Z} $ and $ \mathrm{Z}\mathrm{Z} $ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 33 | P. Nason and G. Zanderighi | $ \mathrm{W}^+ \mathrm{W}^- $, $ \mathrm{W}\mathrm{Z} $ and $ \mathrm{Z}\mathrm{Z} $ production in the POWHEG-BOX-V2 | EPJC 74 (2014) 2702 | 1311.1365 |
| 34 | E. Re | Single-top $ wt $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 35 | NNPDF Collaboration | Parton distributions for the LHC run II | JHEP 04 (2015) 040 | 1410.8849 |
| 36 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 37 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 38 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 39 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | The European Physical Journal C 80 (2020), no. 1 | CMS-GEN-17-001 1903.12179 |
| 40 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 41 | W. Beenakker et al. | Production of charginos, neutralinos, and sleptons at hadron colliders | PRL 83 (1999) 3780 | hep-ph/9906298 |
| 42 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Gaugino production in proton-proton collisions at a center-of-mass energy of 8 TeV | JHEP 10 (2012) 081 | 1207.2159 |
| 43 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Precision predictions for electroweak superpartner production at hadron colliders with resummino | EPJC 73 (2013) 2480 | 1304.0790 |
| 44 | MSSM Working Group | The minimal supersymmetric standard model: Group summary report | hep-ph/9901246 | |
| 45 | W. Beenakker, R. Hopker, and M. Spira | PROSPINO: A program for the production of supersymmetric particles in next-to-leading order QCD | hep-ph/9611232 | |
| 46 | A. Djouadi, J.-L. Kneur, and G. Moultaka | SuSpect: A fortran code for the supersymmetric and higgs particle spectrum in the MSSM | CPC 176 (2007) 426 | hep-ph/0211331 |
| 47 | M. Muhlleitner, A. Djouadi, and Y. Mambrini | SDECAY: A fortran code for the decays of the supersymmetric particles in the MSSM | CPC 168 (2005) 46 | hep-ph/0311167 |
| 48 | A. Djouadi, J. Kalinowski, and M. Spira | HDECAY: A program for higgs boson decays in the standard model and its supersymmetric extension | CPC 108 (1998) 56 | hep-ph/9704448 |
| 49 | M. M. Muhlleitner, A. Djouadi, and M. Spira | Decays of supersymmetric particles: The program SUSY-HIT | in Physics at LHC. Proceedings, 3rd Conference, volume 38, p. 635 Cracow, Poland, 2006 Acta Phys. Polon. B 38 (2007) 635 | hep-ph/0609292 |
| 50 | P. Z. Skands et al. | SUSY Les Houches accord: Interfacing SUSY spectrum calculators, decay packages, and event generators | JHEP 07 (2004) 036 | hep-ph/0311123 |
| 51 | U. De Sanctis, T. Lari, S. Montesano, and C. Troncon | Perspectives for the detection and measurement of supersymmetry in the focus point region of mSUGRA models with the ATLAS detector at LHC | EPJC 52 (2007) 743 | 0704.2515 |
| 52 | R. Grober, M. M. Muhlleitner, E. Popenda, and A. Wlotzka | Light stop decays: Implications for LHC searches | EPJC 75 (2015) 420 | 1408.4662 |
| 53 | CMS Collaboration | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 54 | A. Giammanco | The fast simulation of the CMS experiment | J. Phys. Conf. Ser. 513 (2014), no. 2, 022012 | |
| 55 | CMS Collaboration | Identification of b quark jets at the CMS experiment in the LHC run 2 | CMS-PAS-BTV-15-001 | CMS-PAS-BTV-15-001 |
| 56 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) 10003 | CMS-PRF-14-001 1706.04965 |
| 57 | N. E. E. Chabanat | Deterministic annealing for vertex finding at CMS | ||
| 58 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) 10009 | CMS-TRK-11-001 1405.6569 |
| 59 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020), no. 09, P09018 | CMS-JME-18-001 2003.00503 |
| 60 | G. P. S. Matteo Cacciari | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 61 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 62 | CMS Collaboration | Performance of electron reconstruction and selection with the cms detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 63 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 64 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 65 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) 5011 | CMS-BTV-16-002 1712.07158 |
| 66 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 67 | A. Elagin, P. Murat, A. Pranko, and A. Safonov | A new mass reconstruction technique for resonances decaying to $ \tau\tau $ | Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 654 (2011) 481 | 1012.4686 |
| 68 | CMS Collaboration | Performance of methods for data-driven background estimation in SUSY searches | CMS-PAS-SUS-10-001 | |
| 69 | CMS Collaboration | Search for new physics with same-sign isolated dilepton events with jets and missing transverse energy at the LHC | Journal of High Energy Physics 2011 (2011), no. 6 | |
| 70 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 71 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 72 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-17-004 | CMS-PAS-LUM-17-004 |
| 73 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS-PAS-LUM-18-002 | CMS-PAS-LUM-18-002 |
| 74 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 75 | A. L. Read | Presentation of search results: the $ CL_s $ technique | JPG 28 (2002) 2693 | |
| 76 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 77 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in summer 2011 | ATL-PHYS-PUB/2011-11, CMS NOTE 2011/005 | |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|