

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-16-036 | ||
| Search for new physics in the all-hadronic final state with the $M_{\mathrm{T2}}$ variable | ||
| CMS Collaboration | ||
| March 2017 | ||
| Abstract: A search for new physics is performed using events with jets and a large transverse momentum imbalance, as measured through the $M_{\mathrm{T2}}$ variable. The results are based on a sample of proton-proton collisions collected in 2016 at a center-of-mass energy of 13 TeV with the CMS detector and corresponding to an integrated luminosity of 35.9 fb$^{-1}$. No excess above the standard model background is observed. The results are interpreted as limits on the masses of potential new particles in a variety of simplified models of R-parity conserving supersymmetry. Depending on the details of the model, 95% CL lower limits on the gluino and squark mass are placed up to 2025 and 1550 GeV, respectively. In the case of top (bottom) squarks, the mass limits are as high as 1070 (1175) GeV. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, EPJC 77 (2017) 710. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures & Tables | References | CMS Publications |
|---|
| Additional information on efficiencies needed for reinterpretation of these results are available here. Additional technical material for CMS speakers can be found here. |
| Figures | |

png pdf |
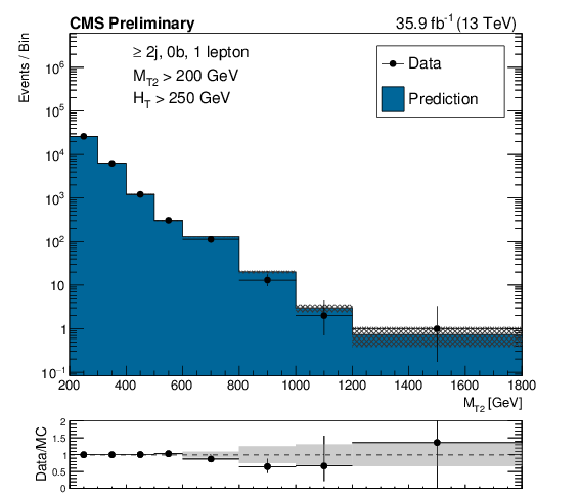
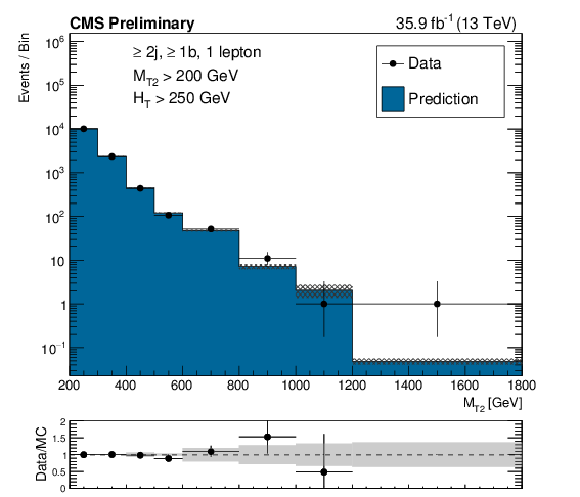
Figure 1:
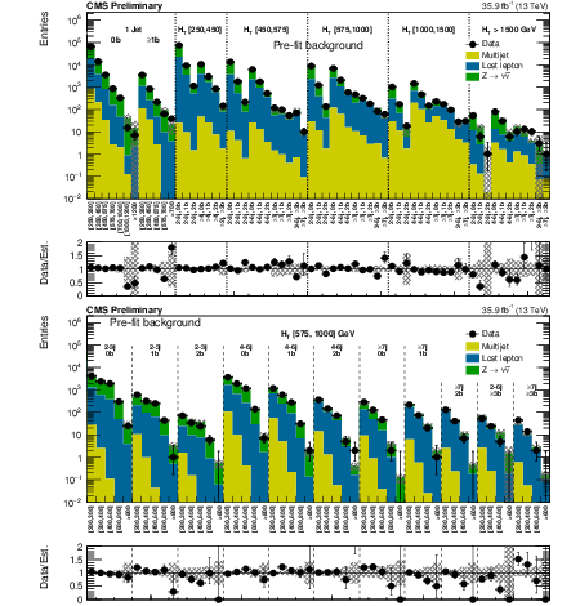
Distributions of data and MC predictions for the single lepton control region selection, after MC is normalized to data in the control region bins of $ {H_{\mathrm {T}}} $, $ {N_{\mathrm {j}}} $, and $ {N_{\mathrm {b}}} $, and $ {M_{\mathrm {T2}}} $ shapes are used, for events with no b-tags (left), and events with at least one b-tag (right). The hashed bands on the lost lepton histogram show the MC statistical uncertainty, while the solid gray band on the ratio plot shows the systematic uncertainty on the $ {M_{\mathrm {T2}}} $ shape. |
png pdf |
Figure 1-a:
Distributions of data and MC predictions for the single lepton control region selection, after MC is normalized to data in the control region bins of $ {H_{\mathrm {T}}} $, $ {N_{\mathrm {j}}} $, and $ {N_{\mathrm {b}}} $, and $ {M_{\mathrm {T2}}} $ shapes are used, for events with no b-tags. The hashed bands on the lost lepton histogram show the MC statistical uncertainty, while the solid gray band on the ratio plot shows the systematic uncertainty on the $ {M_{\mathrm {T2}}} $ shape. |
png pdf |
Figure 1-b:
Distributions of data and MC predictions for the single lepton control region selection, after MC is normalized to data in the control region bins of $ {H_{\mathrm {T}}} $, $ {N_{\mathrm {j}}} $, and $ {N_{\mathrm {b}}} $, and $ {M_{\mathrm {T2}}} $ shapes are used, for events with at least one b-tag. The hashed bands on the lost lepton histogram show the MC statistical uncertainty, while the solid gray band on the ratio plot shows the systematic uncertainty on the $ {M_{\mathrm {T2}}} $ shape. |
png pdf |
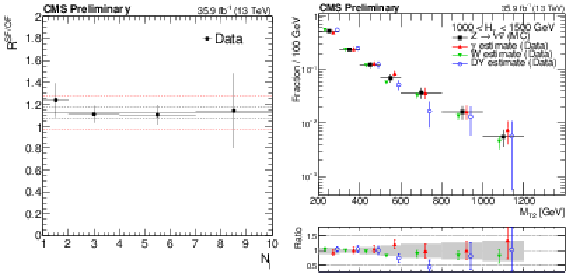
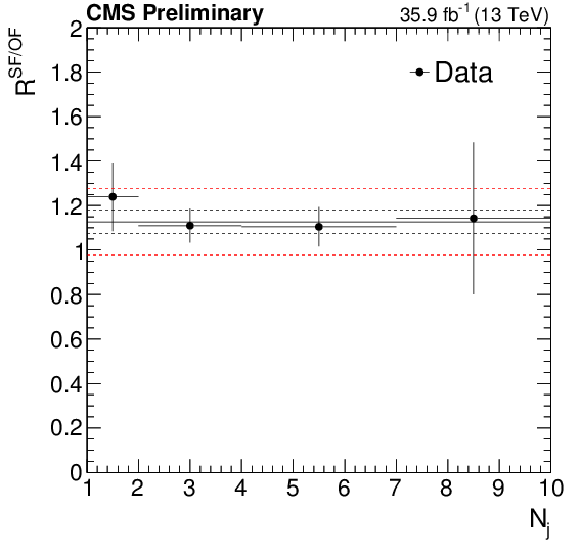
Figure 2:
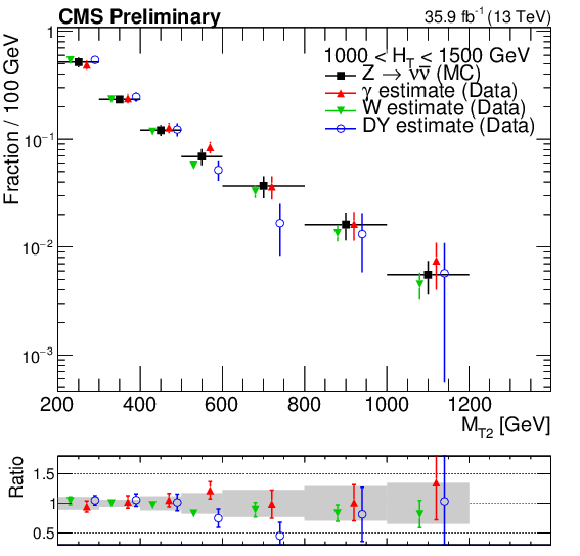
(Left) Ratio $R^{\mathrm {SF}/\mathrm {OF}}$ in data as a function of $ {N_{\mathrm {j}}} $. The solid black line enclosed by the red band corresponds to a value of 1.13$\pm $0.15 that is observed to be stable with respect to event kinematics, while the two dashed black lines denote the statistical uncertainty on the $R^{\mathrm {SF}/\mathrm {OF}}$ value. (Right) The shape of the $ {M_{\mathrm {T2}}} $distribution from ${Z\rightarrow \nu \overline {\nu }}$ simulation compared to shapes from $\gamma $, W, and Z data control samples in a region with 1000 $ < {H_{\mathrm {T}}} < $ 1500 GeV and $ {N_{\mathrm {j}}} \ge $ 2, and inclusive in $ {N_{\mathrm {b}}} $. The solid gray band on the ratio plot shows the systematic uncertainty on the $ {M_{\mathrm {T2}}} $ shape. |
png pdf |
Figure 2-a:
Ratio $R^{\mathrm {SF}/\mathrm {OF}}$ in data as a function of $ {N_{\mathrm {j}}} $. The solid black line enclosed by the red band corresponds to a value of 1.13$\pm $0.15 that is observed to be stable with respect to event kinematics, while the two dashed black lines denote the statistical uncertainty on the $R^{\mathrm {SF}/\mathrm {OF}}$ value. |
png pdf |
Figure 2-b:
The shape of the $ {M_{\mathrm {T2}}} $distribution from ${Z\rightarrow \nu \overline {\nu }}$ simulation compared to shapes from $\gamma $, W, and Z data control samples in a region with 1000 $ < {H_{\mathrm {T}}} < $ 1500 GeV and $ {N_{\mathrm {j}}} \ge $ 2, and inclusive in $ {N_{\mathrm {b}}} $. The solid gray band on the ratio plot shows the systematic uncertainty on the $ {M_{\mathrm {T2}}} $ shape. |

png pdf |
Figure 3:
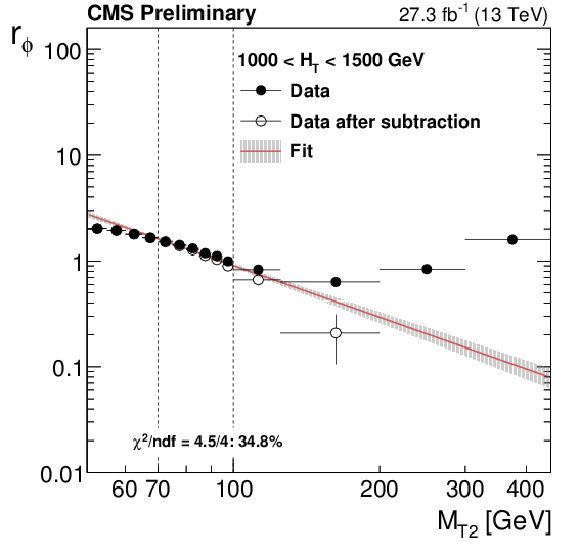
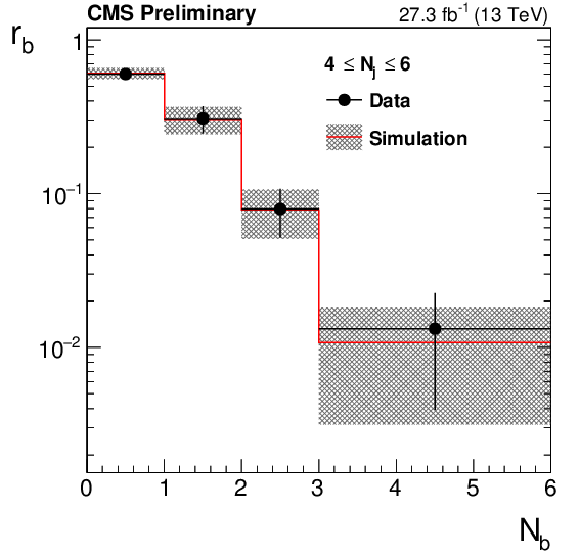
Distribution of the ratio $r_{\phi }$ as a function of $ {M_{\mathrm {T2}}} $ for the region 1000 $< {H_{\mathrm {T}}} <$ 1500 GeV (left). The fit is performed to the hollow, background-subtracted data points. The full points represent the data before subtracting non-QCD backgrounds using simulation. Data point uncertainties are statistical only. The red line and the band around it show the result of the fit to a power-law function perfomed in the window 70 $ < {M_{\mathrm {T2}}} < $ 100 GeV and the associated fit uncertainty. Values of $f_j$, the fraction of events in bin $ {N_{\mathrm {j}}} $, (center) and $r_b$, the fraction of events that fall in bin $ {N_{\mathrm {b}}} $, (right) are measured in data after requiring ${\Delta \phi _{\mathrm {min}}} < $ 0.3 radians and 100 $ < {M_{\mathrm {T2}}} < $ 200 GeV. The bands represent both statistical and systematic uncertainties. |
png pdf |
Figure 3-a:
Distribution of the ratio $r_{\phi }$ as a function of $ {M_{\mathrm {T2}}} $ for the region 1000 $< {H_{\mathrm {T}}} <$ 1500 GeV. The fit is performed to the hollow, background-subtracted data points. The full points represent the data before subtracting non-QCD backgrounds using simulation. Data point uncertainties are statistical only. The red line and the band around it show the result of the fit to a power-law function perfomed in the window 70 $ < {M_{\mathrm {T2}}} < $ 100 GeV and the associated fit uncertainty. |

png pdf |
Figure 3-b:
Values of $f_j$, the fraction of events in bin $ {N_{\mathrm {j}}} $, is measured in data after requiring ${\Delta \phi _{\mathrm {min}}} < $ 0.3 radians and 100 $ < {M_{\mathrm {T2}}} < $ 200 GeV. The bands represent both statistical and systematic uncertainties. |
png pdf |
Figure 3-c:
Values of $r_b$, the fraction of events that fall in bin $ {N_{\mathrm {b}}} $, is measured in data after requiring ${\Delta \phi _{\mathrm {min}}} < $ 0.3 radians and 100 $ < {M_{\mathrm {T2}}} < $ 200 GeV. The bands represent both statistical and systematic uncertainties. |
png pdf |
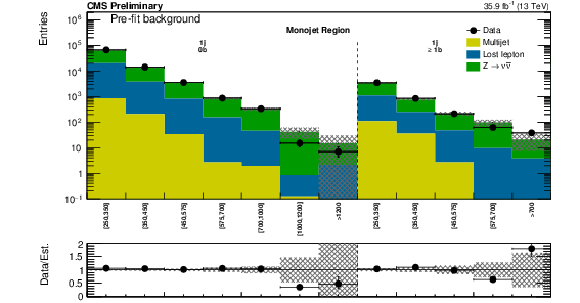
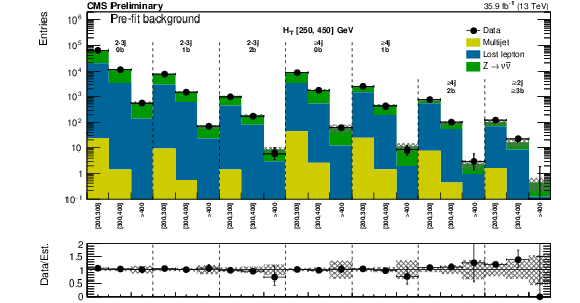
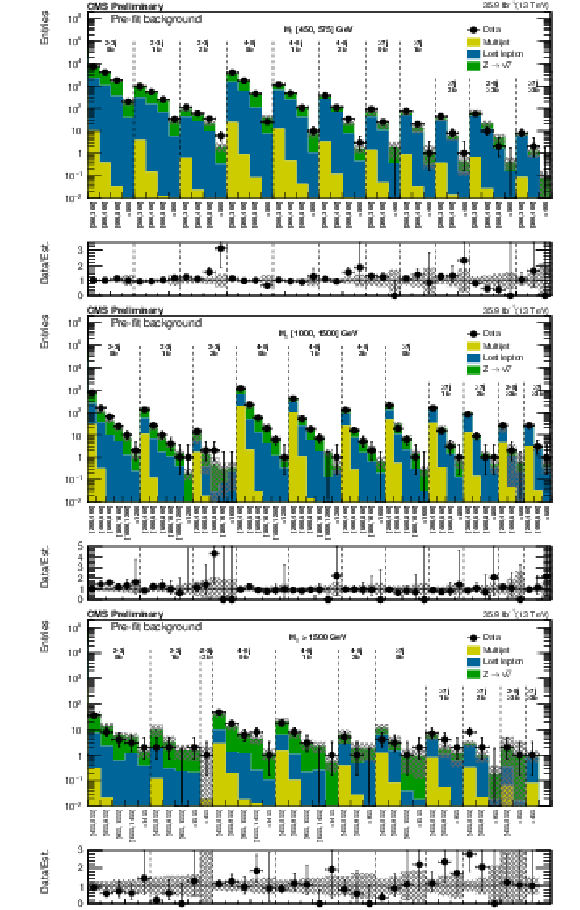
Figure 4:
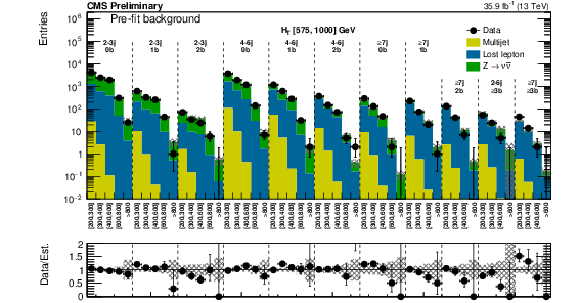
(Above) Comparison of estimated (pre-fit) background and observed data events in each topological region. Hatched bands represent the full uncertainty on the background estimate. The results shown for $ {N_{\mathrm {j}}} = $ 1 correspond to the monojet search regions binned in jet ${p_{\mathrm {T}}} $, whereas for the multijet signal regions, the notations j, b indicate $ {N_{\mathrm {j}}} $, $ {N_{\mathrm {b}}} $ labeling. (Below) Same for individual $ {M_{\mathrm {T2}}} $ signal bins in the medium $ {H_{\mathrm {T}}} $ region. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. |
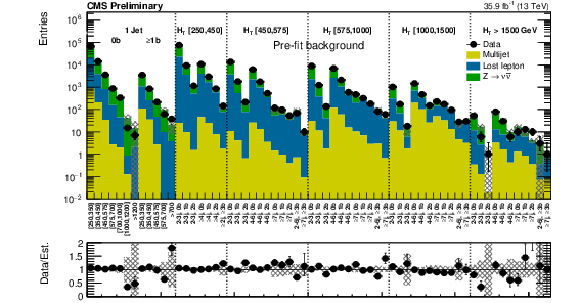
png pdf |
Figure 4-a:
Comparison of estimated (pre-fit) background and observed data events in each topological region. Hatched bands represent the full uncertainty on the background estimate. The results shown for $ {N_{\mathrm {j}}} = $ 1 correspond to the monojet search regions binned in jet ${p_{\mathrm {T}}} $, whereas for the multijet signal regions, the notations j, b indicate $ {N_{\mathrm {j}}} $, $ {N_{\mathrm {b}}} $ labeling. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. |
png pdf |
Figure 4-b:
Same as Fig. 4-a for individual $ {M_{\mathrm {T2}}} $ signal bins in the medium $ {H_{\mathrm {T}}} $ region. |
png pdf |
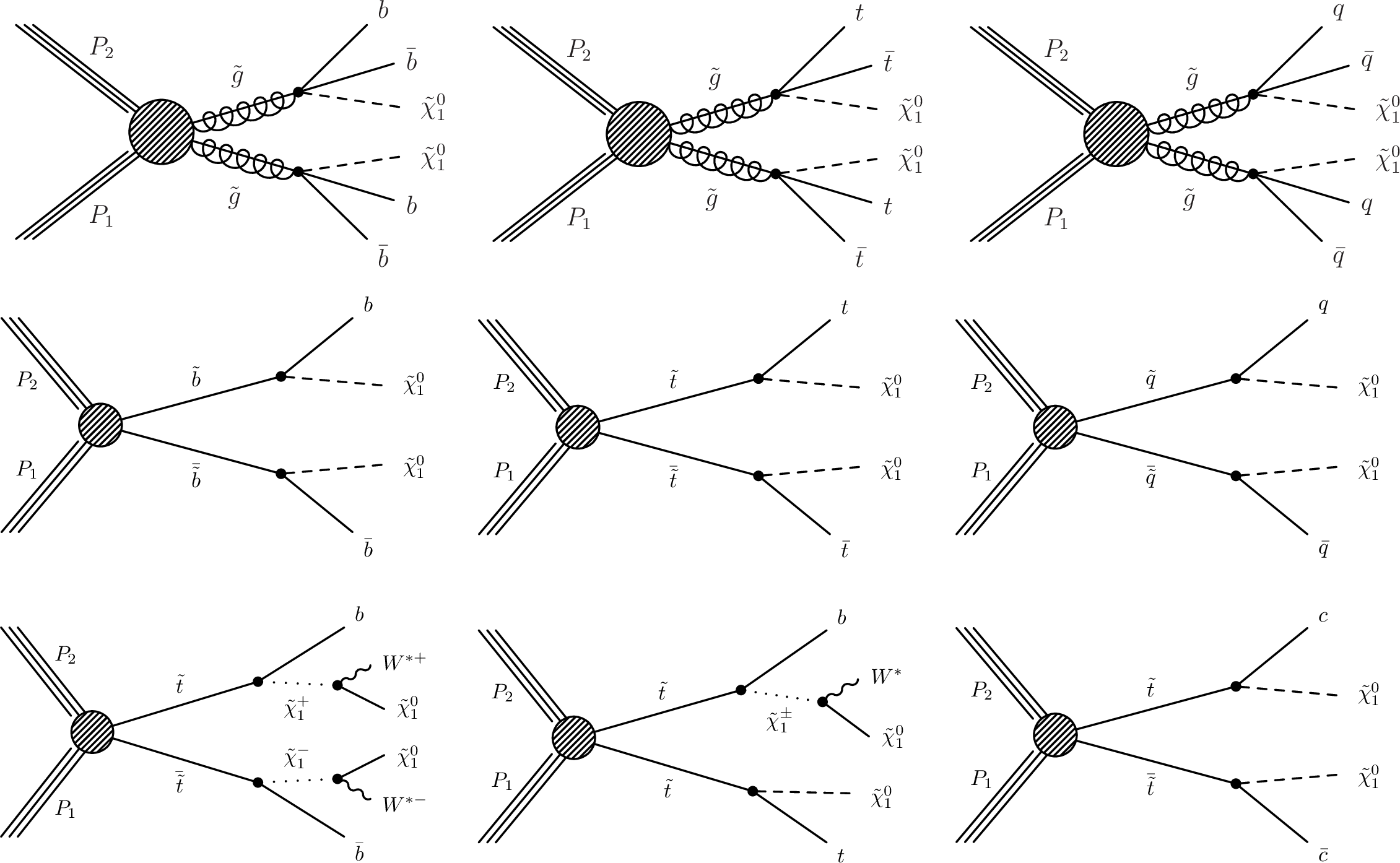
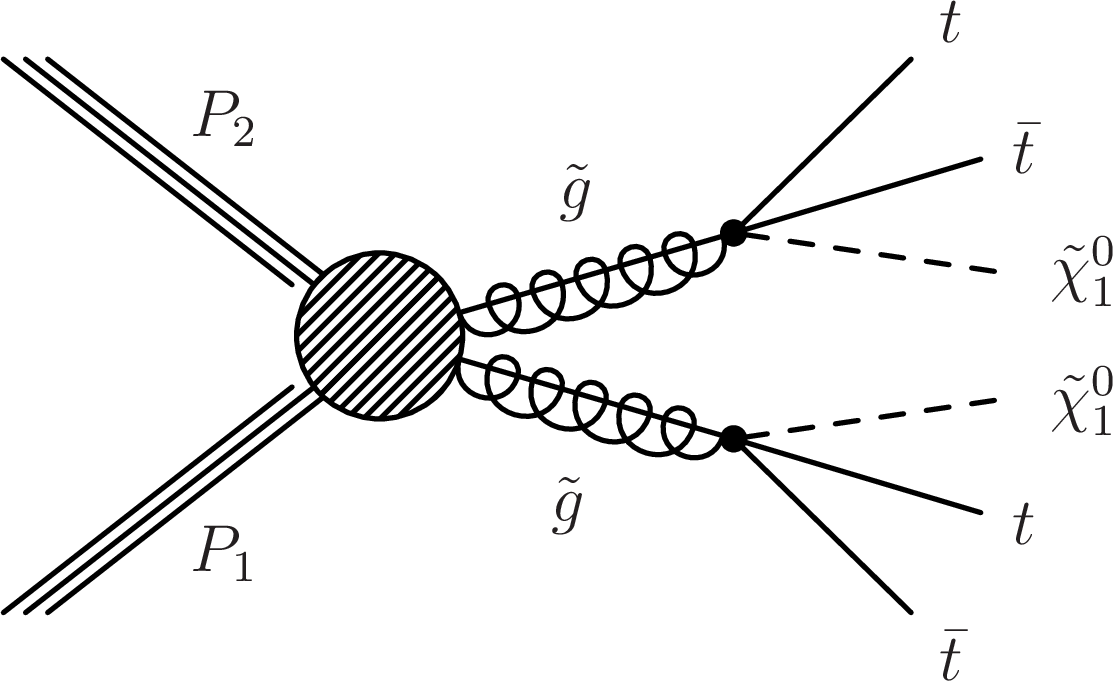
Figure 5:
(Top) Diagrams for the three scenarios of gluino mediated bottom squark, top squark and light flavor squark production considered. (Middle) Similar diagrams for the direct production of bottom, top and light flavor squark pairs. (Bottom) Similar diagrams for three alternate scenarios of direct top squark production with different decay modes. For mixed decay scenarios, a 50% branching fraction for each decay is assumed. |

png pdf |
Figure 5-a:
Diagram for the scenario of gluino mediated bottom squark production considered. |
png pdf |
Figure 5-b:
Diagram for the scenario of gluino mediated top squark production considered. |
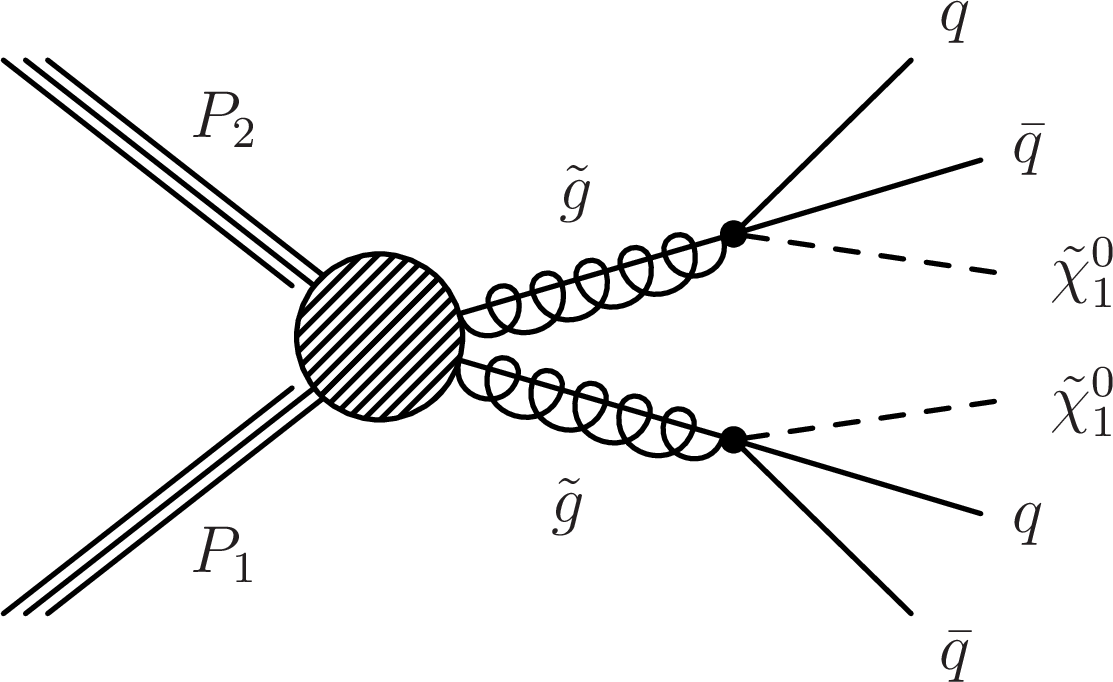
png pdf |
Figure 5-c:
Diagram for the scenario of gluino mediated light flavor squark production considered. |

png pdf |
Figure 5-d:
Diagram for the direct production of bottom squark pairs. |

png pdf |
Figure 5-e:
Diagram for the direct production of top squark pairs. |

png pdf |
Figure 5-f:
Diagram for the direct production of light flavor squark pairs. |

png pdf |
Figure 5-g:
Diagram for an alternate scenario of direct top squark production with identical decay modes. |

png pdf |
Figure 5-h:
Diagram for an alternate scenario of direct top squark production with identical decay modes. |

png pdf |
Figure 5-i:
Diagram for an alternate scenario of direct top squark production with mixed decay modes. A 50% branching fraction for each decay is assumed. |
png pdf |
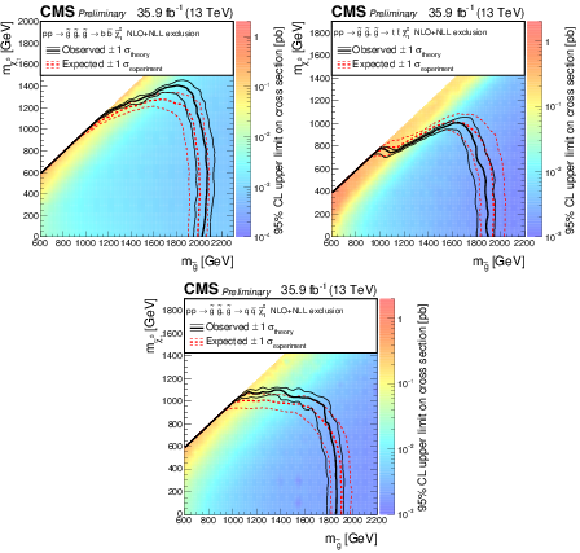
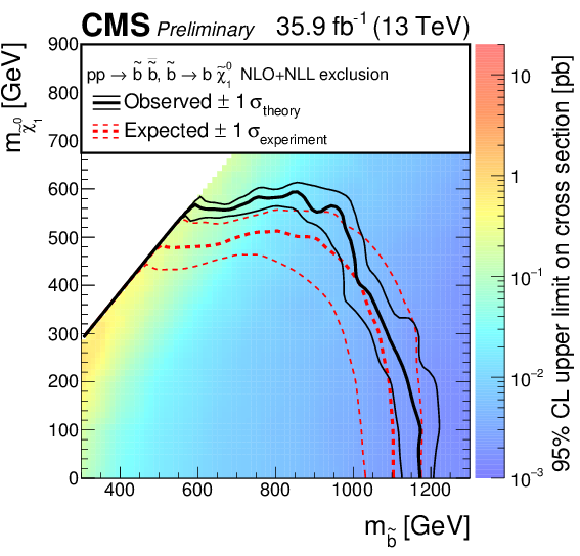
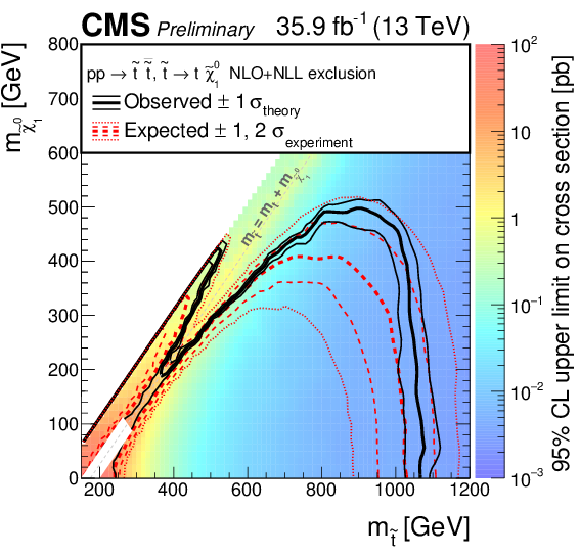
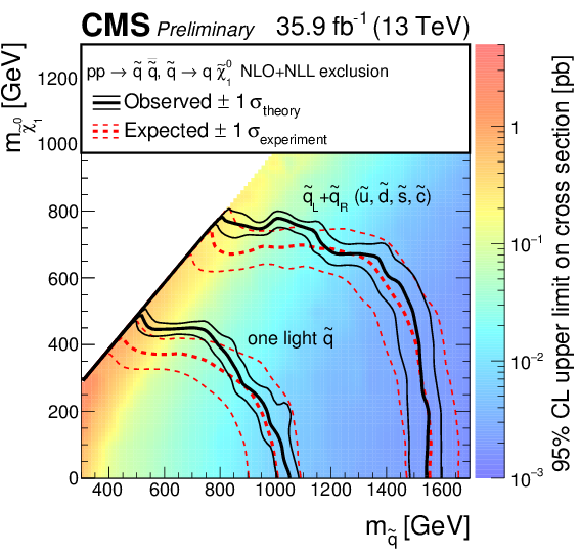
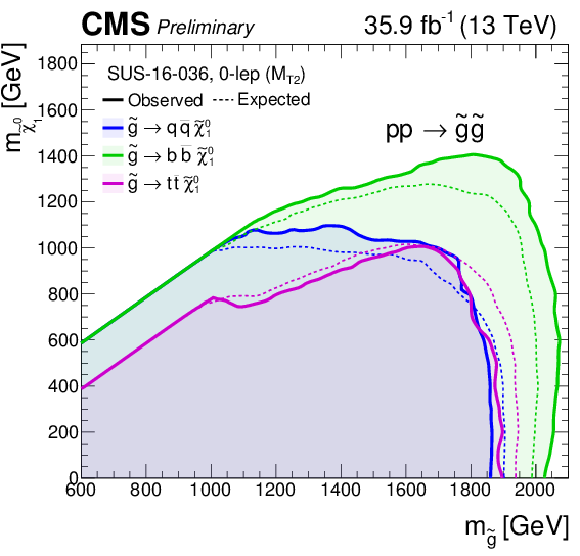
Figure 6:
Exclusion limits at 95% CL on the cross sections for gluino-mediated bottom squark production (above left), gluino-mediated top squark production (above right), and gluino-mediated light-flavor squark production (below). The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |

png pdf root |
Figure 6-a:
Exclusion limits at 95% CL on the cross sections for gluino-mediated bottom squark production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf root |
Figure 6-b:
Exclusion limits at 95% CL on the cross sections for gluino-mediated top squark production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf root |
Figure 6-c:
Exclusion limits at 95% CL on the cross sections for gluino-mediated light-flavor squark production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf |
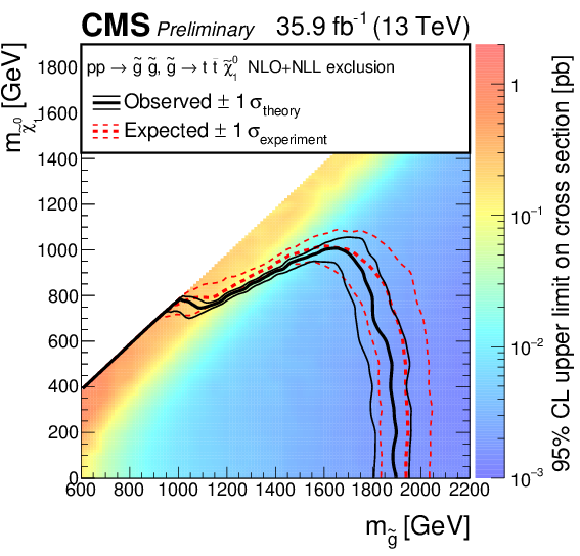
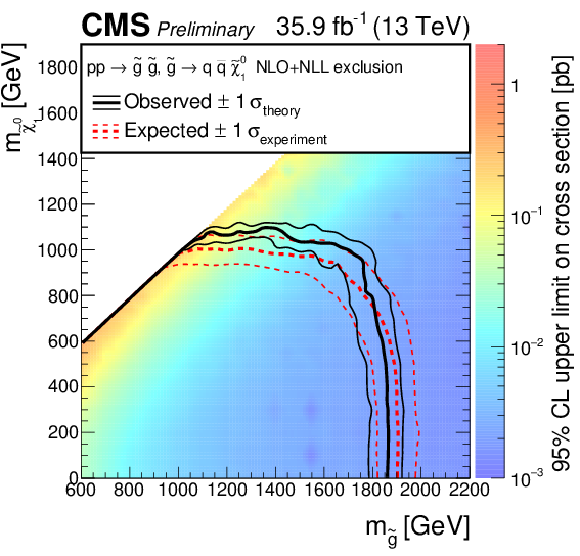
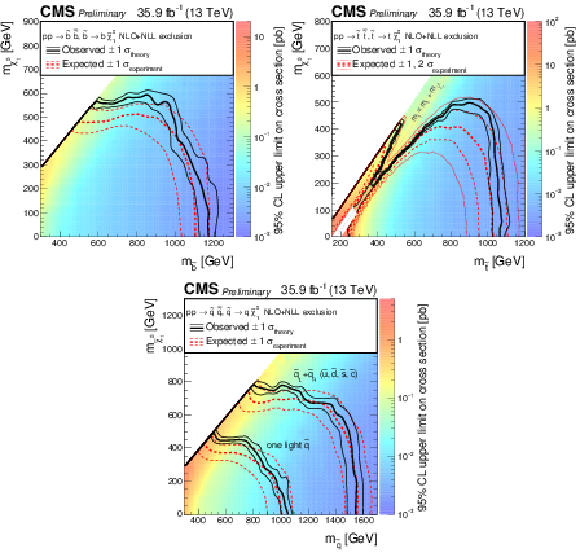
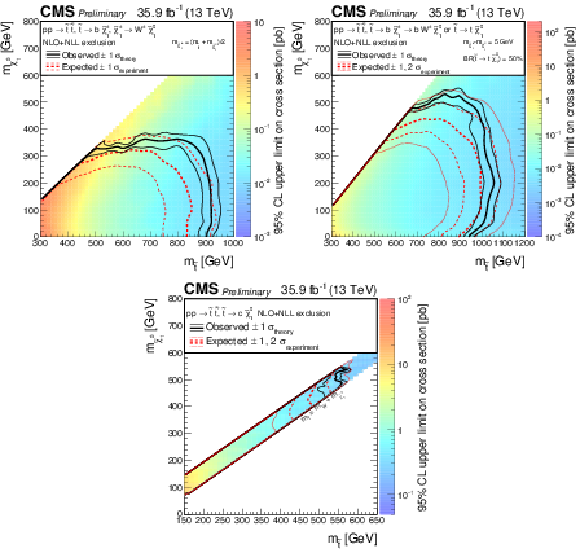
Figure 7:
Exclusion limit at 95% CL on the cross sections for bottom squark pair production (above left), top squark pair production (above right), and light-flavor squark pair production (below). The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. For the top squark-pair production plot, the $\pm $2 standard deviation uncertainties are also shown. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. The white diagonal band in the upper right plot corresponds to the region $ {| m_{\tilde{\mathrm {t}}}-m_{\mathrm {t}}-m_{\mathrm {LSP}} | } < $ 25 GeV, and small $m_{\mathrm {LSP}}$. Here the efficiency of the selection is a strong function of $m_{\tilde{\mathrm {t}}}-m_{\mathrm {LSP}}$, and as a result the precise determination of the cross section upper limit is uncertain because of the finite granularity of the available MC samples in this region of the ($m_{\tilde{\mathrm {t}}}$, $m_{\mathrm {LSP}}$) plane. |
png pdf root |
Figure 7-a:
Exclusion limit at 95% CL on the cross sections for bottom squark pair production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. For the top squark-pair production plot, the $\pm $2 standard deviation uncertainties are also shown. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. The white diagonal band in the upper right plot corresponds to the region $ {| m_{\tilde{\mathrm {t}}}-m_{\mathrm {t}}-m_{\mathrm {LSP}} | } < $ 25 GeV, and small $m_{\mathrm {LSP}}$. Here the efficiency of the selection is a strong function of $m_{\tilde{\mathrm {t}}}-m_{\mathrm {LSP}}$, and as a result the precise determination of the cross section upper limit is uncertain because of the finite granularity of the available MC samples in this region of the ($m_{\tilde{\mathrm {t}}}$, $m_{\mathrm {LSP}}$) plane. |
png pdf root |
Figure 7-b:
Exclusion limit at 95% CL on the cross sections for top squark pair production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. For the top squark-pair production plot, the $\pm $2 standard deviation uncertainties are also shown. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. The white diagonal band in the upper right plot corresponds to the region $ {| m_{\tilde{\mathrm {t}}}-m_{\mathrm {t}}-m_{\mathrm {LSP}} | } < $ 25 GeV, and small $m_{\mathrm {LSP}}$. Here the efficiency of the selection is a strong function of $m_{\tilde{\mathrm {t}}}-m_{\mathrm {LSP}}$, and as a result the precise determination of the cross section upper limit is uncertain because of the finite granularity of the available MC samples in this region of the ($m_{\tilde{\mathrm {t}}}$, $m_{\mathrm {LSP}}$) plane. |
png pdf root |
Figure 7-c:
Exclusion limit at 95% CL on the cross sections for light-flavor squark pair production. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1$\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. For the top squark-pair production plot, the $\pm $2 standard deviation uncertainties are also shown. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. The white diagonal band in the upper right plot corresponds to the region $ {| m_{\tilde{\mathrm {t}}}-m_{\mathrm {t}}-m_{\mathrm {LSP}} | } < $ 25 GeV, and small $m_{\mathrm {LSP}}$. Here the efficiency of the selection is a strong function of $m_{\tilde{\mathrm {t}}}-m_{\mathrm {LSP}}$, and as a result the precise determination of the cross section upper limit is uncertain because of the finite granularity of the available MC samples in this region of the ($m_{\tilde{\mathrm {t}}}$, $m_{\mathrm {LSP}}$) plane. |
png pdf |
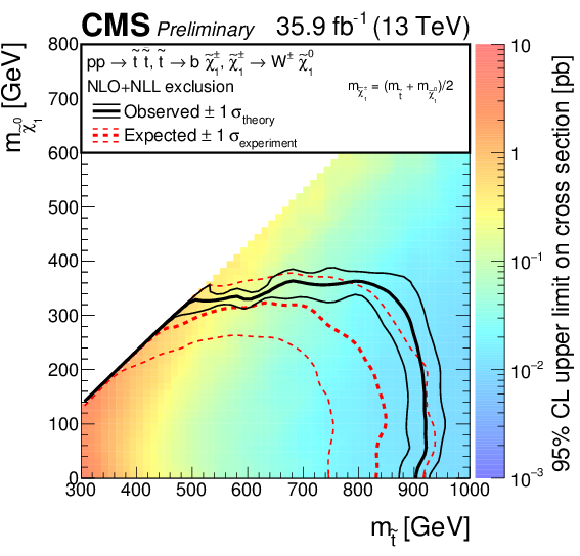
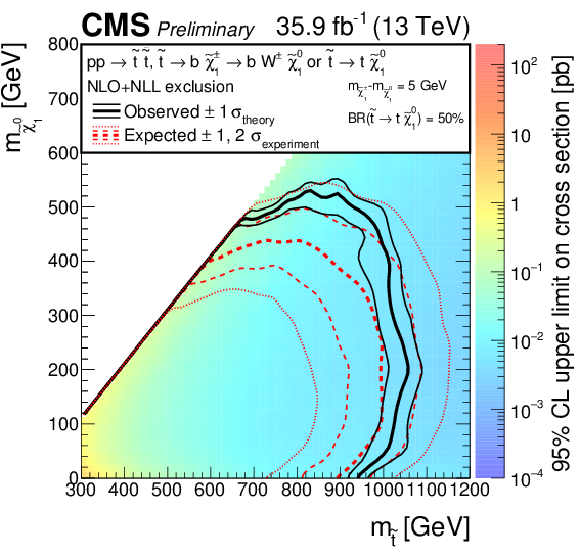
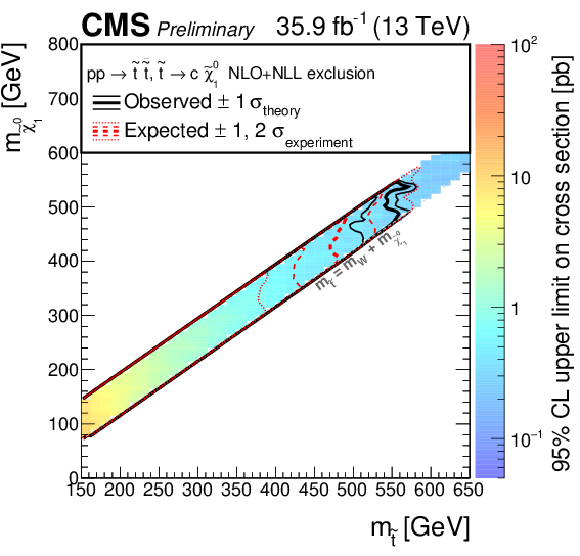
Figure 8:
Exclusion limit at 95% CL on the cross sections for top squark pair production for different decay modes of the top squark. For the scenario where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1\tilde{ \mathrm{ t } }_1^*\to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $ (above left), the mass of the chargino is chosen to be half way in between the masses of the top squark and the neutralino. A mixed decay scenario (above right), $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*$ with equal branching fractions for the top squark decays $\tilde{ \mathrm{ t } }_1 \to \mathrm{ t } \tilde{\chi}^0_1 $ and $\tilde{ \mathrm{ t } }_1 \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } ^{*}\tilde{\chi}^0_1 $, is also considered with the chargino mass chosen such that $\Delta m\left (\tilde{\chi}^{\pm}_1,\tilde{\chi}^0_1 \right ) = $ 5 GeV. A compressed scenario (below) is also considered where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ c \bar{c} } \tilde{\chi}^0_1 \tilde{\chi}^0_1 $. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1 $\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf root |
Figure 8-a:
Exclusion limit at 95% CL on the cross sections for top squark pair production for the scenario where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1\tilde{ \mathrm{ t } }_1^*\to \mathrm{ b \bar{b} } \tilde{\chi}^{\pm}_1 \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $. The mass of the chargino is chosen to be half way in between the masses of the top squark and the neutralino. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1 $\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf root |
Figure 8-b:
Exclusion limit at 95% CL on the cross sections for top squark pair production for a mixed decay scenario, $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*$ with equal branching fractions for the top squark decays $\tilde{ \mathrm{ t } }_1 \to \mathrm{ t } \tilde{\chi}^0_1 $ and $\tilde{ \mathrm{ t } }_1 \to \mathrm{ b } \tilde{\chi}^{\pm}_1 $, $\tilde{\chi}^{\pm}_1 \to \mathrm{ W } ^{*}\tilde{\chi}^0_1 $, with the chargino mass chosen such that $\Delta m\left (\tilde{\chi}^{\pm}_1,\tilde{\chi}^0_1 \right ) = $ 5 GeV. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1 $\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf root |
Figure 8-c:
Exclusion limit at 95% CL on the cross sections for top squark pair production for a compressed scenario, where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ c \bar{c} } \tilde{\chi}^0_1 \tilde{\chi}^0_1 $. The area to the left of and below the thick black curve represents the observed exclusion region, while the dashed red lines indicate the expected limits and their $\pm $1 $\sigma _{\mathrm {experiment}}$ standard deviation uncertainties. The thin black lines show the effect of the theoretical uncertainties $\sigma _{\mathrm {theory}}$ on the signal cross section. |
png pdf |
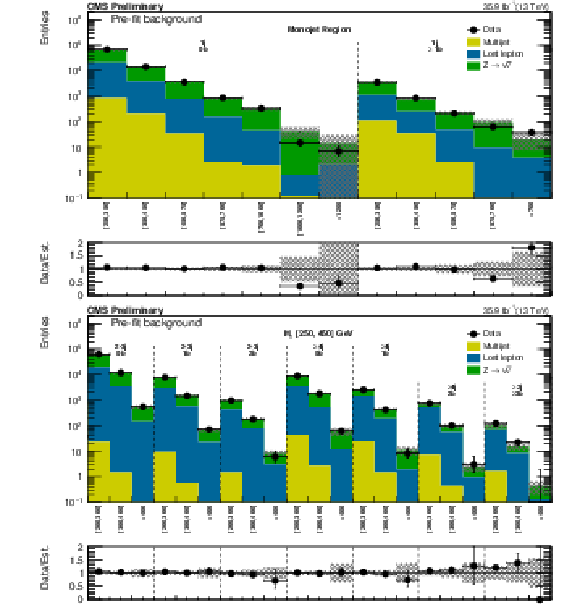
Figure 9:
(Above) Comparison of the estimated background and observed data events in each signal bin in the monojet region. On the $x$-axis, the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning is shown (in GeV). Hatched bands represent the full uncertainty on the background estimate. (Below) Same for the very low $ {H_{\mathrm {T}}} $ region. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. |
png pdf |
Figure 9-a:
Comparison of the estimated background and observed data events in each signal bin in the monojet region. On the $x$-axis, the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning is shown (in GeV). Hatched bands represent the full uncertainty on the background estimate. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. |
png pdf |
Figure 9-b:
Same as Fig.9-a for the very low $ {H_{\mathrm {T}}} $ region. |
png pdf |
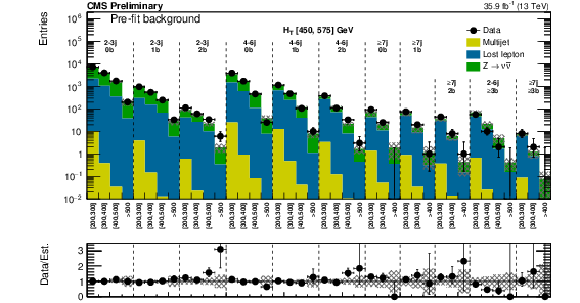
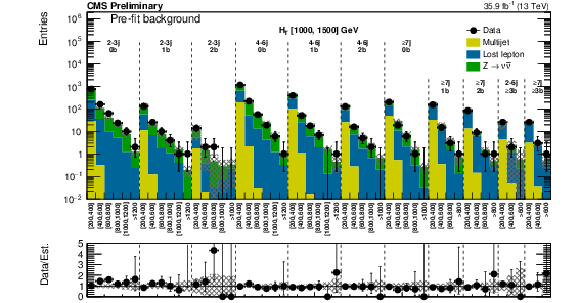
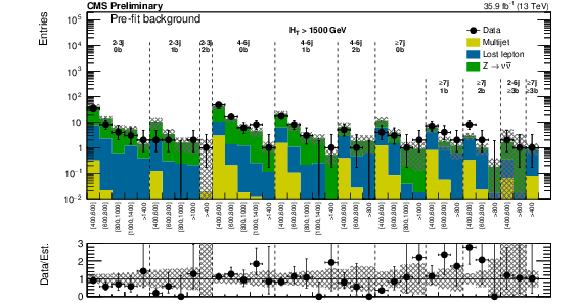
Figure 10:
(Top) Comparison of the estimated background and observed data events in each signal bin in the low $ {H_{\mathrm {T}}} $ region. Hatched bands represent the full uncertainty on the background estimate. Same for the high (middle) and extreme (bottom) $ {H_{\mathrm {T}}} $ regions. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. For the extreme $ {H_{\mathrm {T}}} $ region, the last bin is left empty for visualization purposes. |
png pdf |
Figure 10-a:
Comparison of the estimated background and observed data events in each signal bin in the low $ {H_{\mathrm {T}}} $ region. Hatched bands represent the full uncertainty on the background estimate. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. |
png pdf |
Figure 10-b:
Same as Fig. 10-a for the high $ {H_{\mathrm {T}}} $ region. |
png pdf |
Figure 10-c:
Same as Fig. 10-a for the extreme $ {H_{\mathrm {T}}} $ region. The last bin is left empty for visualization purposes. |
png pdf |
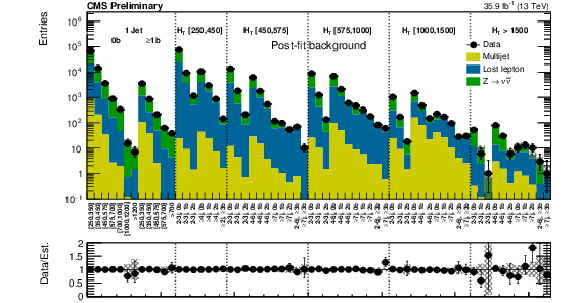
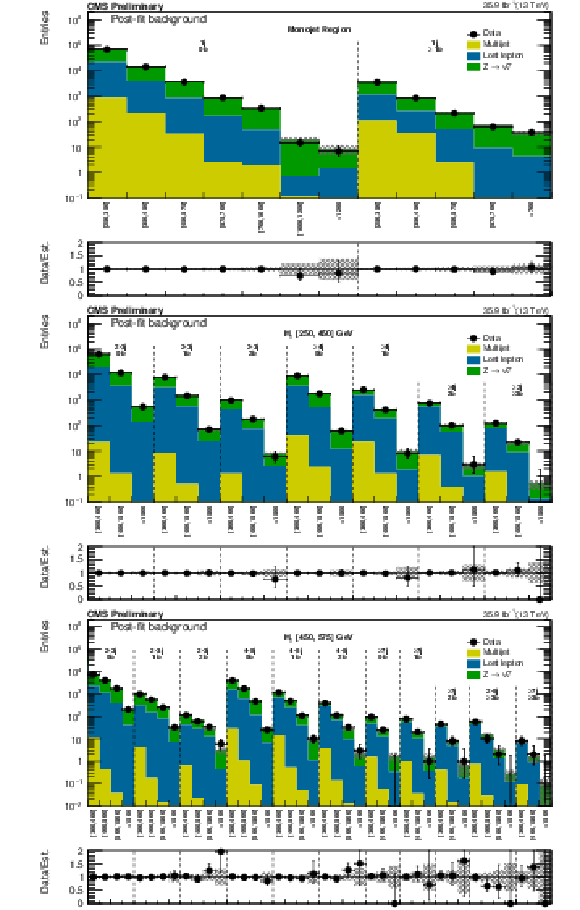
Figure 11:
Comparison of post-fit background prediction and observed data events in each topological region. Hatched bands represent the post-fit uncertainty on the background prediction. For the monojet, on the $x$-axis the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning is shown (in GeV), whereas for the multijet signal regions, the notations j, b indicate $ {N_{\mathrm {j}}} $, $ {N_{\mathrm {b}}} $ labeling. |
png pdf |
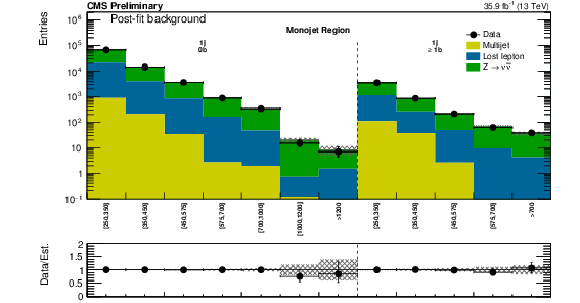
Figure 12:
(Top) Comparison of the post-fit background prediction and observed data events in each signal bin in the monojet region. On the $x$-axis, the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning is shown (in GeV). (Medium) and (bottom): Same for the very low and low $ {H_{\mathrm {T}}} $ region. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. In these Figures, the hatched bands represent the post-fit uncertainty on the background prediction. |
png pdf |
Figure 12-a:
Comparison of the post-fit background prediction and observed data events in each signal bin in the monojet region. On the $x$-axis, the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. The hatched bands represent the post-fit uncertainty on the background prediction. |
png pdf |
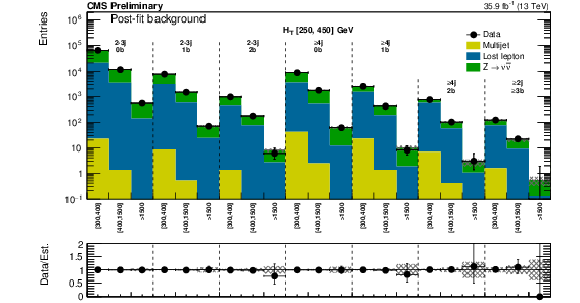
Figure 12-b:
Same as Fig. 12-a for the very low $ {H_{\mathrm {T}}} $ region. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). |
png pdf |
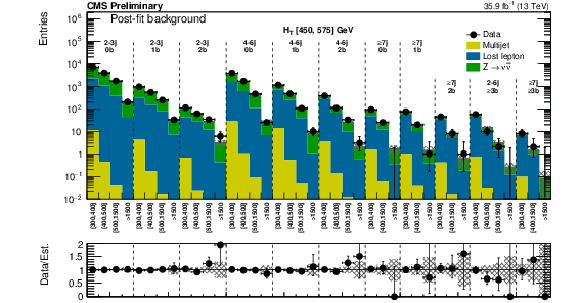
Figure 12-c:
Same as Fig. 12-b for the low $ {H_{\mathrm {T}}} $ region. |
png pdf |
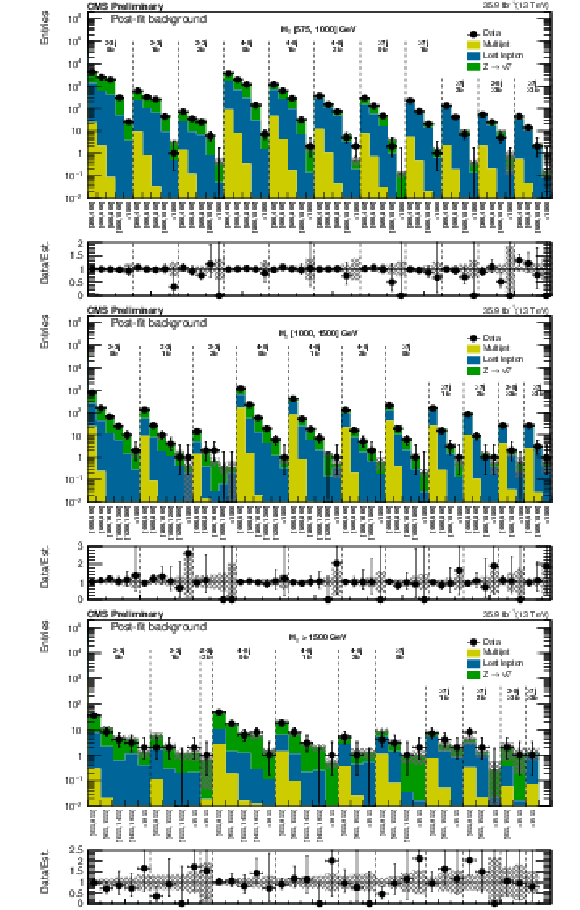
Figure 13:
(Top) Comparison of the post-fit background prediction and observed data events in each signal bin in the medium $ {H_{\mathrm {T}}} $ region. Same for the high (middle) and extreme (bottom) $ {H_{\mathrm {T}}} $ regions. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. In these Figures, the hatched bands represent the post-fit uncertainty on the background prediction. For the extreme $ {H_{\mathrm {T}}} $ region, the last bin is left empty for visualization purposes. |
png pdf |
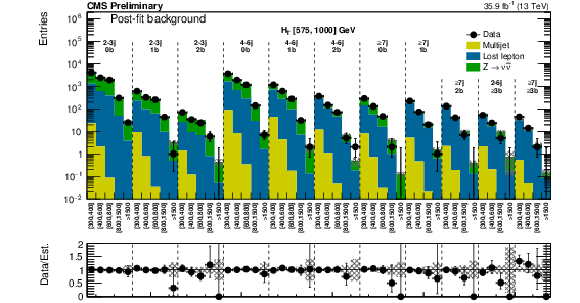
Figure 13-a:
Comparison of the post-fit background prediction and observed data events in each signal bin in the medium $ {H_{\mathrm {T}}} $ region. On the $x$-axis, the $ {M_{\mathrm {T2}}} $ binning is shown (in GeV). Bins with no entry for data have an observed count of 0. In these Figures, the hatched bands represent the post-fit uncertainty on the background prediction. |
png pdf |
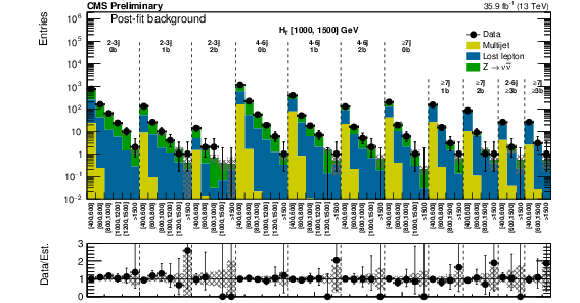
Figure 13-b:
Same as Fig. 13-a for the high $ {H_{\mathrm {T}}} $ region. |
png pdf |
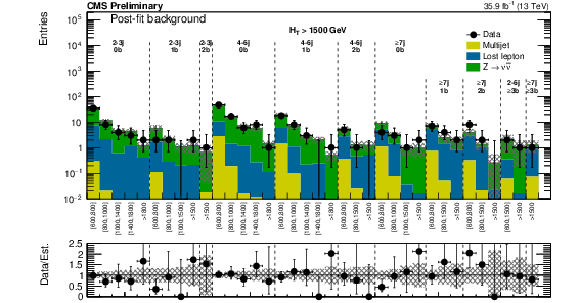
Figure 13-c:
Same as Fig. 13-a for the high extreme $ {H_{\mathrm {T}}} $ region. The last bin is left empty for visualization purposes. |
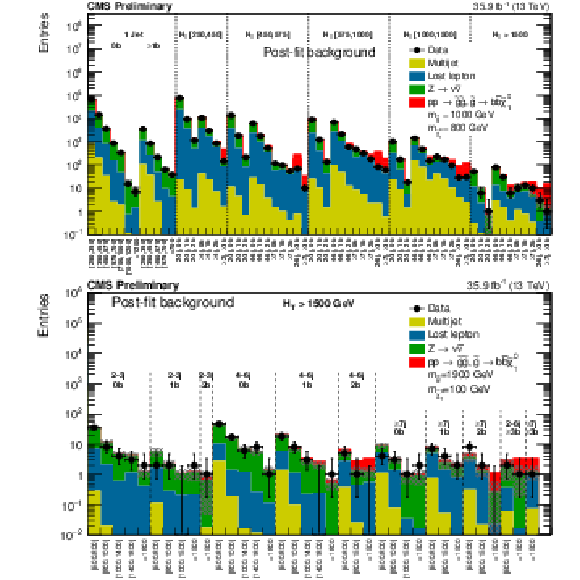
png pdf |
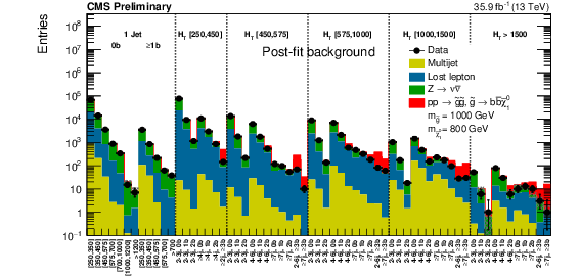
Figure 14:
(Above) The post-fit background prediction and observed data events in the analysis binning, for all topological regions with the expected yield for the signal model of gluino mediated bottom-squark production ($m_{\tilde{ \mathrm{g} } }=$ 1000 GeV, $m_{\tilde{\chi}^0_1 }=$ 800 GeV ) stacked on top of the expected background. For the monojet regions, on the $x$-axis is shown the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning (in GeV). (Below) Same for the extreme $ {H_{\mathrm {T}}} $ region for the same signal with ($m_{\tilde{ \mathrm{g} } }=$ 1900 GeV, $m_{\tilde{\chi}^0_1 }=$ 100 GeV). In these Figures, the hatched bands represent the post-fit uncertainty on the background prediction. For the extreme $ {H_{\mathrm {T}}} $ region, the last bin is left empty for visualization purposes. |
png pdf |
Figure 14-a:
The post-fit background prediction and observed data events in the analysis binning, for all topological regions with the expected yield for the signal model of gluino mediated bottom-squark production ($m_{\tilde{ \mathrm{g} } }=$ 1000 GeV, $m_{\tilde{\chi}^0_1 }=$ 800 GeV ) stacked on top of the expected background. For the monojet regions, on the $x$-axis is shown the ${ {p_{\mathrm {T}}} ^{\mathrm {jet1}}}$ binning (in GeV). The hatched bands represent the post-fit uncertainty on the background prediction. |
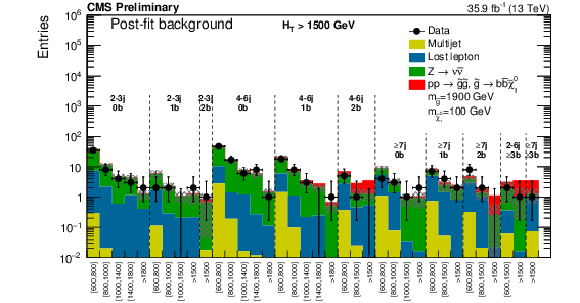
png pdf |
Figure 14-b:
Same for the extreme $ {H_{\mathrm {T}}} $ region for the same signal with ($m_{\tilde{ \mathrm{g} } }=$ 1900 GeV, $m_{\tilde{\chi}^0_1 }=$ 100 GeV). The last bin is left empty for visualization purposes. |
| Tables | |
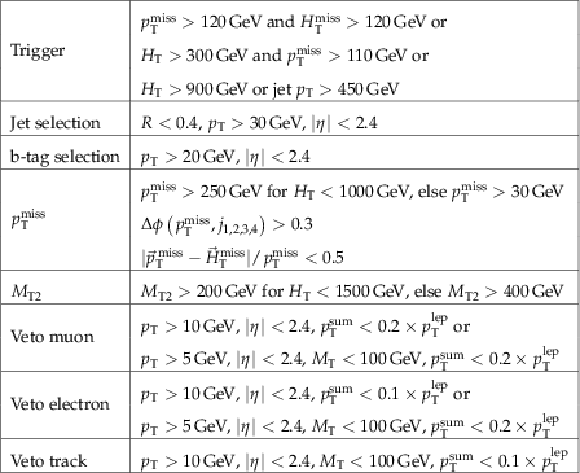
png pdf |
Table 1:
Summary of objects and preselection. For veto leptons and tracks, the ${M_{\mathrm {T}}}$ is determined using the veto object and the ${ {p_{\mathrm {T}}} ^\text {miss}} $, while $ {p_{\mathrm {T}}} ^{\mathrm {sum}}$ denotes the sum of the transverse momenta of all the particle candidates around the lepton or track. Details of the lepton selection are described in Ref. [5]. The i$^{th}$ highest $ {p_{\mathrm {T}}} $ jet is denoted as $j_{\mathrm {i}}$. |
png pdf |
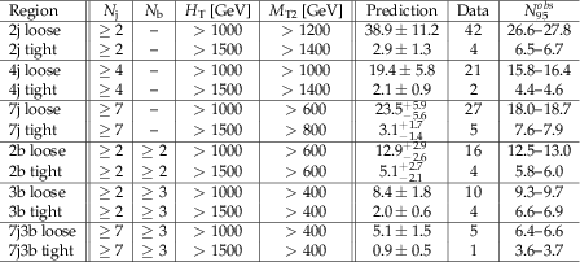
Table 2:
Definitions of super signal regions, along with predictions, observed data, and the observed 95% CL limit on the number of signal events contributing to each region ($N_{95}^{obs}$). No uncertainty on the signal acceptance is assumed in calculating these limits. A dash in the selections means that no cut is applied. |
png pdf |
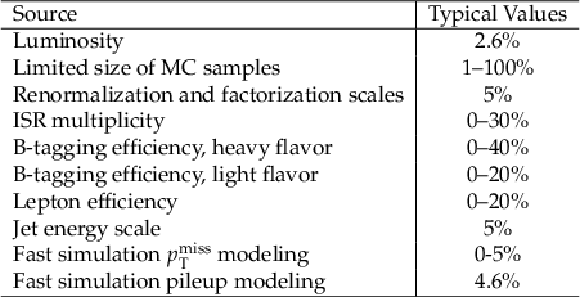
Table 3:
Typical values of the signal systematic uncertainties as evaluated for the simplified signal model of gluino mediated bottom squark production, $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{g} } \tilde{ \mathrm{g} },\, \tilde{ \mathrm{g} } \to {\mathrm{ b \bar{b} } } \tilde{\chi}^0_1 $. Uncertainties evaluated on other signal models are consistent with these ranges of values. |
png pdf |
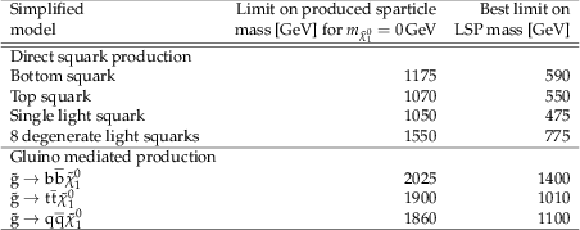
Table 4:
Summary of 95% CL observed exclusion limits for different SUSY simplified model scenarios. The limit on the mass of the produced sparticle is quoted for a massless LSP, while for the lightest neutralino the best limit on its mass is quoted. |

png pdf |
Table 5:
Summary of signal regions for the monojet selection. |

png pdf |
Table 6:
Adopted $ {M_{\mathrm {T2}}} $ binning in each topological region of the multi-jet search regions, for the very low, low and medium $ {H_{\mathrm {T}}} $regions. |

png pdf |
Table 7:
Adopted $ {M_{\mathrm {T2}}} $ binning in each topological region of the multi-jet search regions, for the high and extreme $ {H_{\mathrm {T}}} $regions. |
| Summary |
| This paper presents the result of a search for new physics using events with jets and the $M_{\mathrm{T2}}$ variable. Results are based on a 35.9 fb$ {^{-1}} $ data sample of proton-proton collisions at $\sqrt{s} =$ 13 TeV collected in 2016 with the CMS detector. No significant deviations from the standard model expectations are observed. The results are interpreted as limits on the production of new, massive colored particles in simplified models of supersymmetry. We probe gluino masses up to 2025 GeV and LSP masses up to 1400 GeV. Additional interpretations in the context of the pair production of light flavor, bottom, and top squarks are performed, probing masses up to 1550, 1175, and 1070 GeV, respectively, and LSP masses up to 775, 590, and 550 GeV in each scenario. |
| Additional Figures | |
png pdf root |
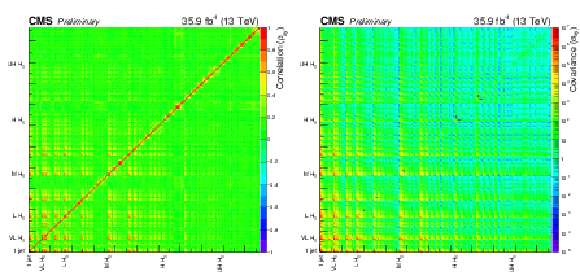
Additional Figure 1:
Full correlation (a) and covariance (b) matrices. |
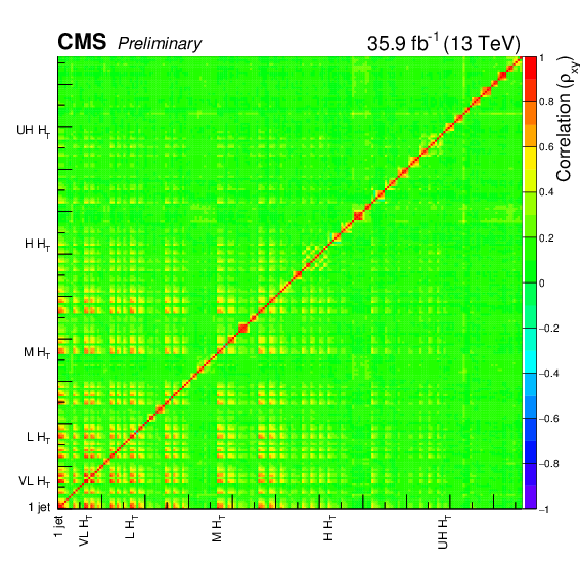
png pdf root |
Additional Figure 1-a:
Full correlation matrix. |
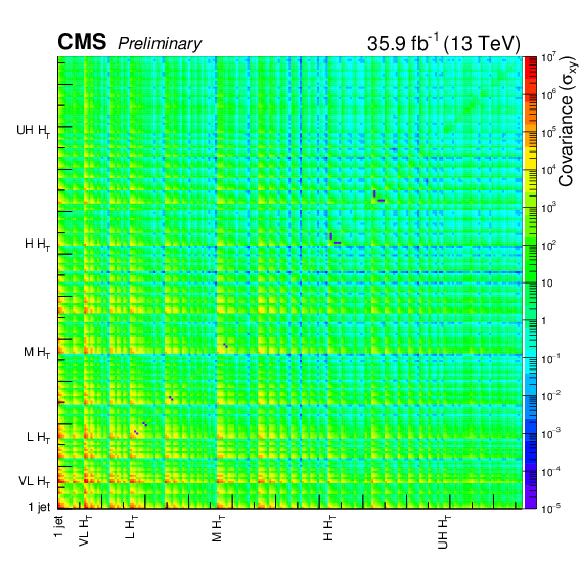
png pdf root |
Additional Figure 1-b:
Full covariance matrix. |
png pdf root |
Additional Figure 2:
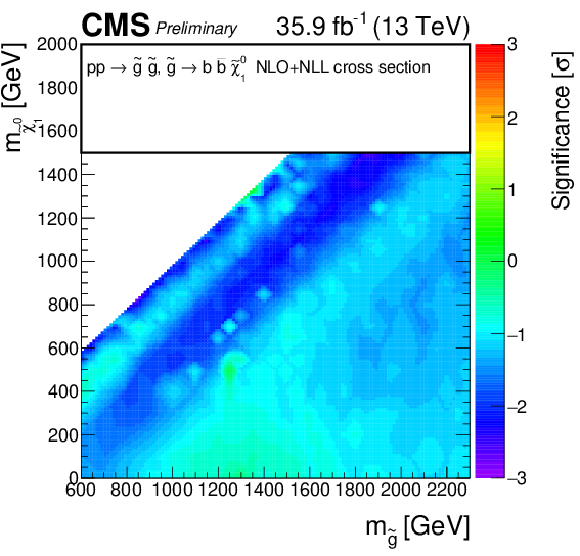
Observed significance for gluino-mediated bottom squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
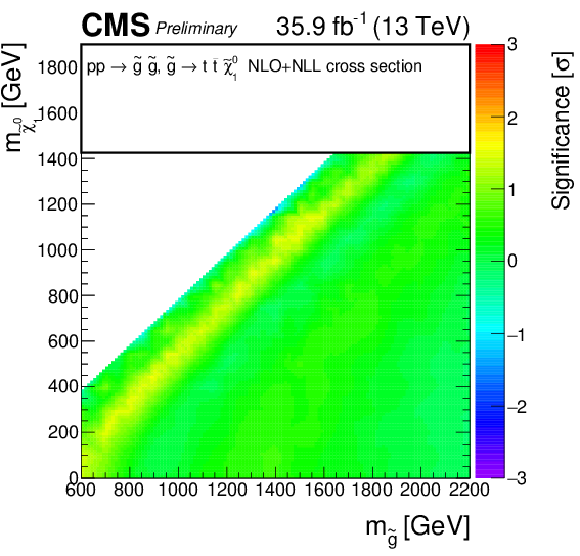
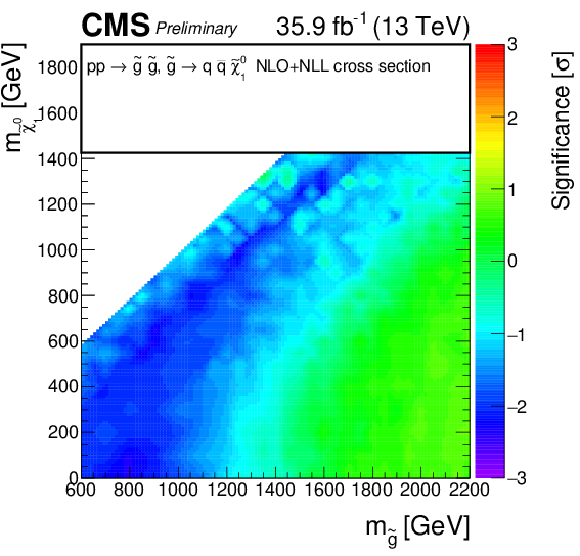
Additional Figure 3:
Observed significance for gluino-mediated top squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
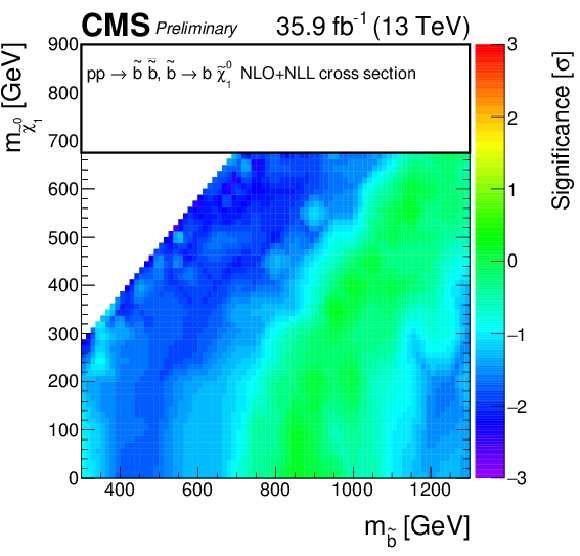
Additional Figure 4:
Observed significance for gluino-mediated light squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
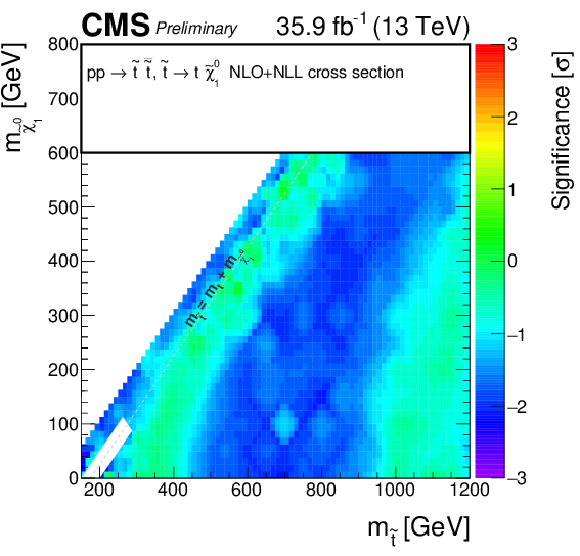
Additional Figure 5:
Observed significance for direct bottom squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
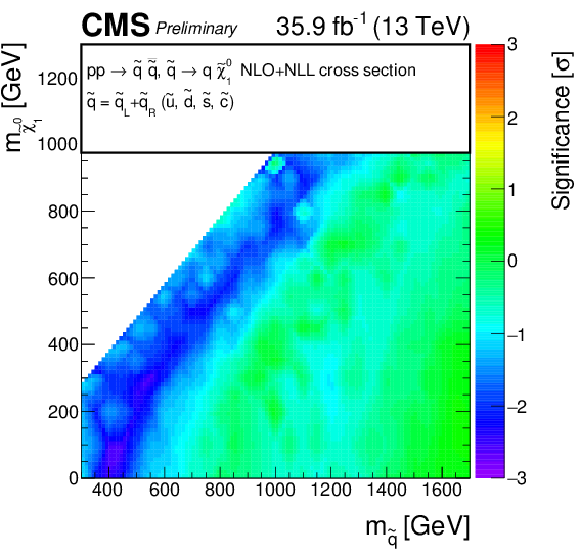
Additional Figure 6:
Observed significance for direct top squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
Additional Figure 7:
Observed significance for direct light squark production model. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
png pdf root |
Additional Figure 8:
Observed significance for direct top squark pair production model, for the scenario where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ b \bar{b} } \tilde{ \chi }^{\pm}_1 \tilde{ \chi }^{\pm}_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } \tilde{\chi}^0_1 $, with the mass of the chargino chosen to be half way in between the masses of the top squark and the neutralino. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
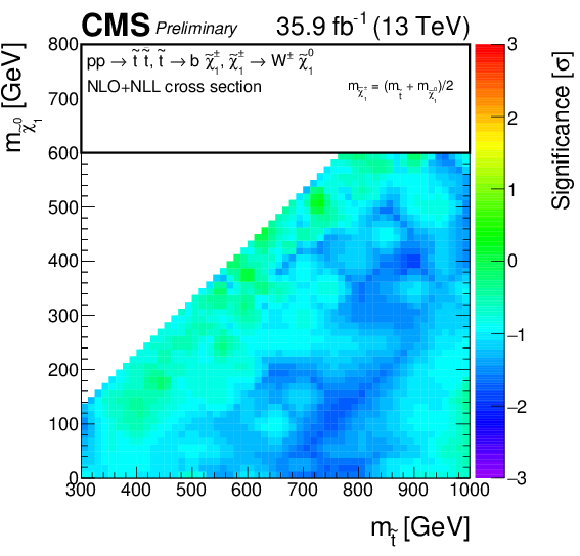
png pdf root |
Additional Figure 9:
Observed significance for direct top squark pair production model, for the scenario where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ t } \mathrm{ b } \tilde{ \chi }^{\pm}_1 \tilde{\chi}^0_1 $, $\tilde{ \chi }^{\pm}_1 \to \mathrm{ W } ^{*}\tilde{\chi}^0_1 $, with the chargino mass chosen such that $\Delta m (\tilde{ \chi }^{\pm}_1 ,\tilde{\chi}^0_1 ) = $ 5 GeV. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
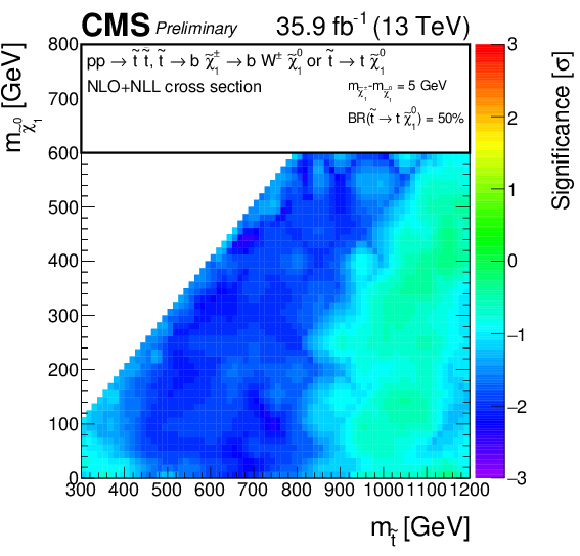
png pdf root |
Additional Figure 10:
Observed significance for direct top squark pair production model, for a compressed scenario where $\mathrm{ p } \mathrm{ p } \to \tilde{ \mathrm{ t } }_1 \tilde{ \mathrm{ t } }_1 ^*\to \mathrm{ c } \bar{ \mathrm{ c } } \tilde{\chi}^0_1 \tilde{\chi}^0_1 $. A linear interpolation is performed across the plane, to account for the limited granularity of the simulated samples. Due to the non-linear nature of the significance, small fluctuations for single signal points may result into a visible effect on the plane. |
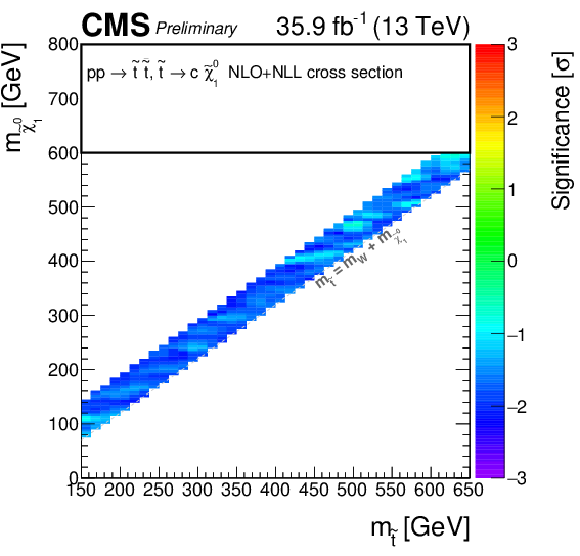
png pdf |
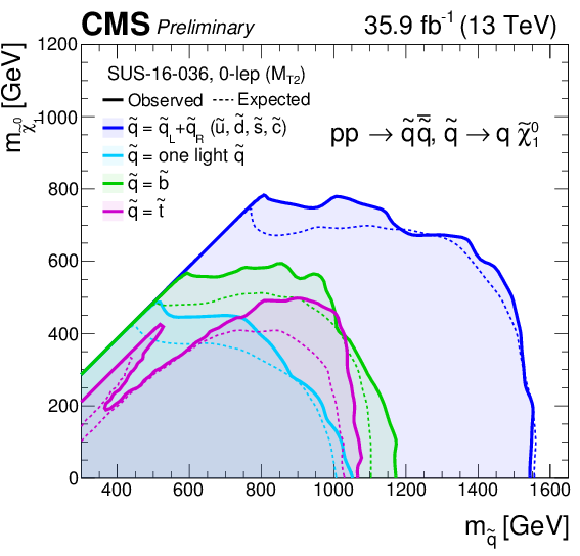
Additional Figure 11:
Summary of exclusion limits for gluino production models. |
png pdf |
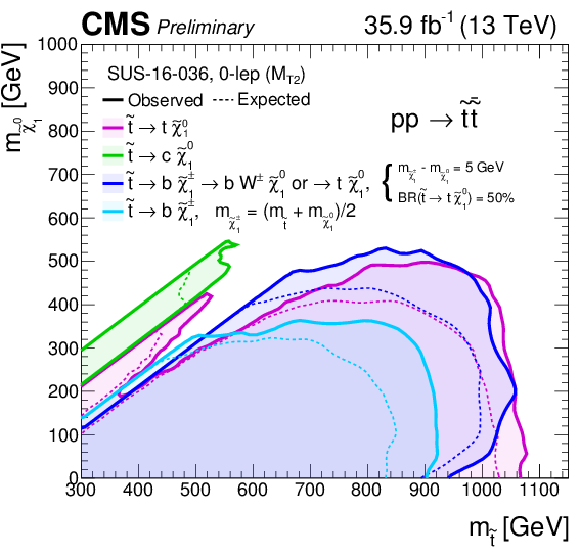
Additional Figure 12:
Summary of exclusion limits for direct squark production models. |
png pdf |
Additional Figure 13:
Summary of exclusion limits for direct stop production models. |
| Additional Tables | |
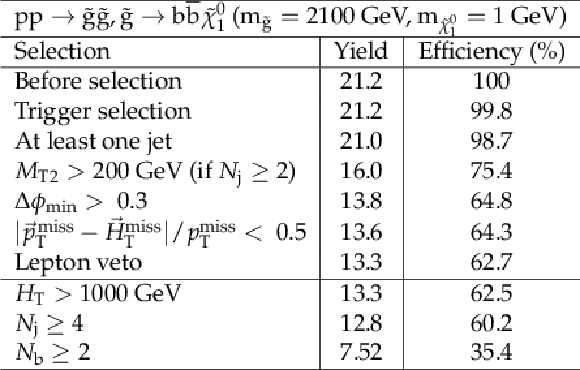
png pdf |
Additional Table 1:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated bottom squark production with the mass of the gluino and the LSP equal to 2100 and 1 GeV, respectively. Theory cross section for this signal is 0.59 fb. |

png pdf |
Additional Table 2:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated bottom squark production with the mass of the gluino and the LSP equal to 1800 and 1300 GeV, respectively. Theory cross section for this signal is 2.76 fb. |
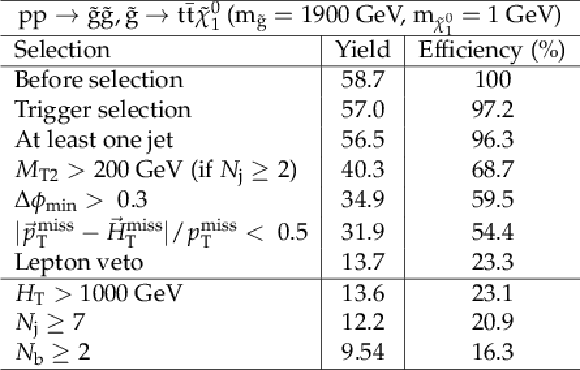
png pdf |
Additional Table 3:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated top squark production with the mass of the gluino and the LSP equal to 1900 and 1 GeV, respectively. Theory cross section for this signal is 1.64 fb. |
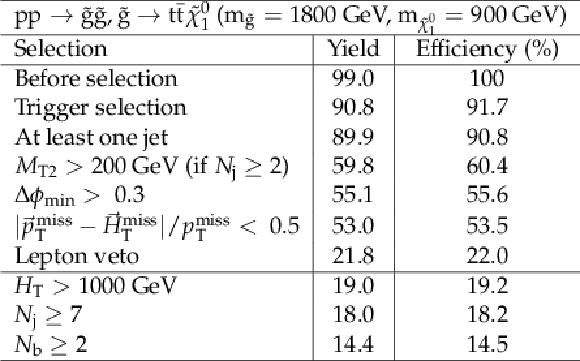
png pdf |
Additional Table 4:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated top squark production with the mass of the gluino and the LSP equal to 1800 and 900 GeV, respectively. Theory cross section for this signal is 2.76 fb. |
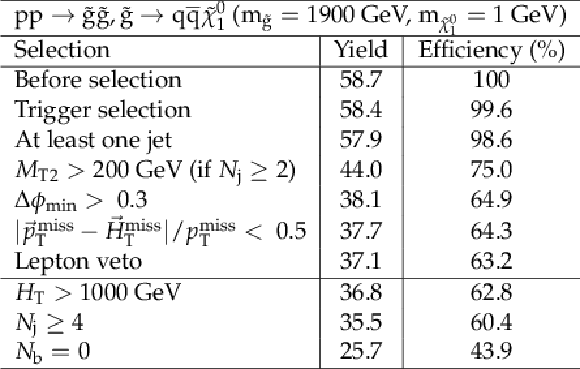
png pdf |
Additional Table 5:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated light squark production with the mass of the gluino and the LSP equal to 1900 and 1 GeV, respectively. Theory cross section for this signal is 1.64 fb. |
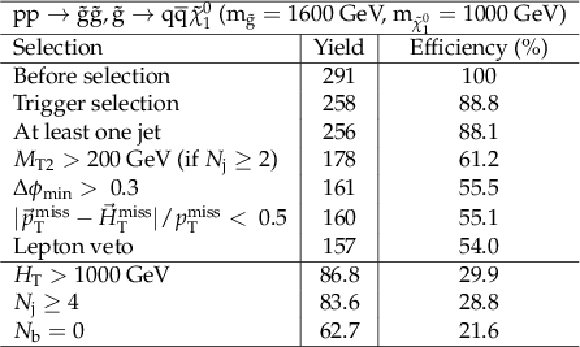
png pdf |
Additional Table 6:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of gluino-mediated light squark production with the mass of the gluino and the LSP equal to 1600 and 1000 GeV, respectively. Theory cross section for this signal is 8.10 fb. |
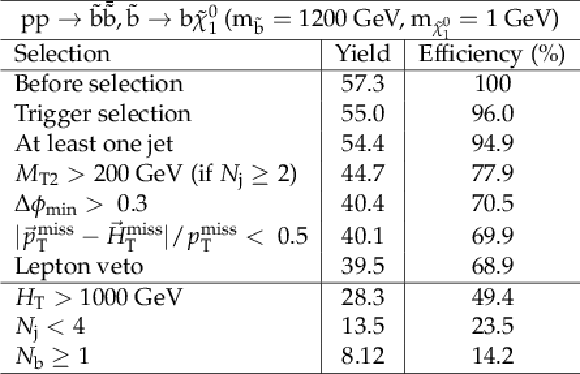
png pdf |
Additional Table 7:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct bottom squark production with the mass of the squark and the LSP equal to 1200 and 1 GeV, respectively. Theory cross section for this signal is 1.60 fb. |
png pdf |
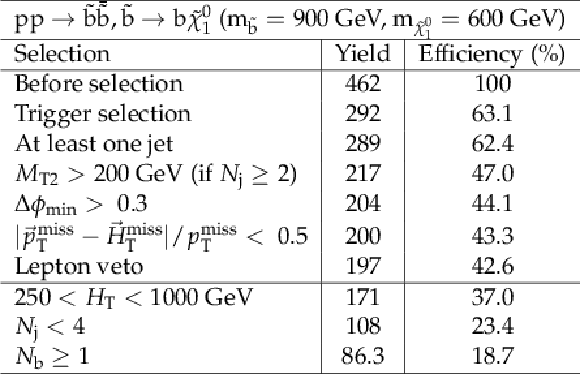
Additional Table 8:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct bottom squark production with the mass of the squark and the LSP equal to 900 and 600 GeV, respectively. Theory cross section for this signal is 12.9 fb. |
png pdf |
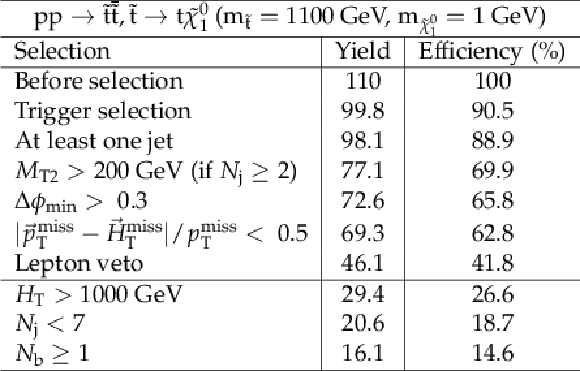
Additional Table 9:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production with the mass of the squark and the LSP equal to 1100 and 1 GeV, respectively. Theory cross section for this signal is 3.07 fb. |
png pdf |
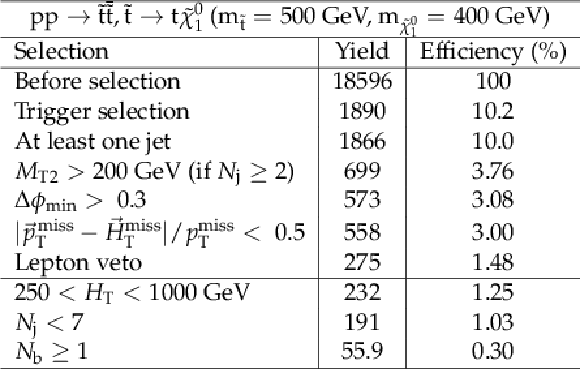
Additional Table 10:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production with the mass of the squark and the LSP equal to 500 and 400 GeV, respectively. Theory cross section for this signal is 518 fb. |
png pdf |
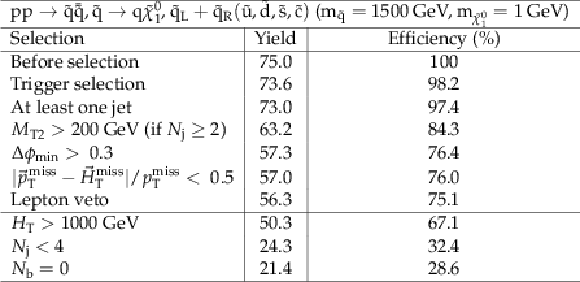
Additional Table 11:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct light squark production with the mass of the squark and the LSP equal to 1500 and 1 GeV, respectively. Theory cross section for this signal is 2.09 fb. |
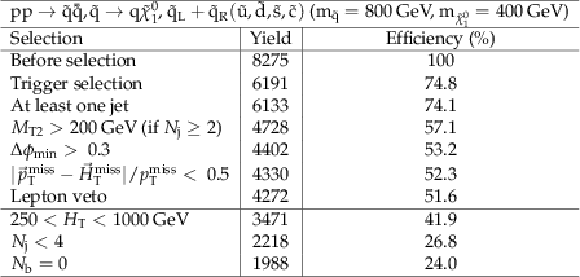
png pdf |
Additional Table 12:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct light squark production with the mass of the squark and the LSP equal to 800 and 400 GeV, respectively. Theory cross section for this signal is 231 fb. |
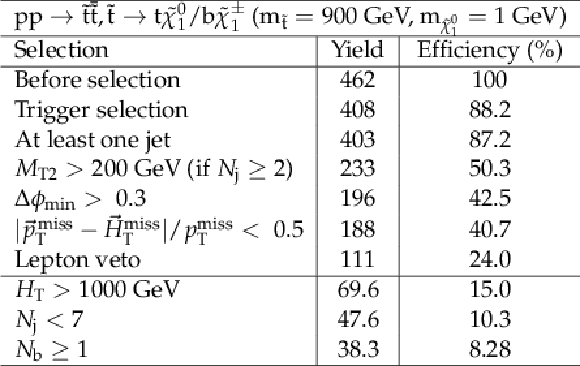
png pdf |
Additional Table 13:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where one top squark decays via a bottom quark while the other decays via a top quark, with the mass of the squark and the LSP equal to 900 and 1 GeV, respectively. Theory cross section for this signal is 12.9 fb. |
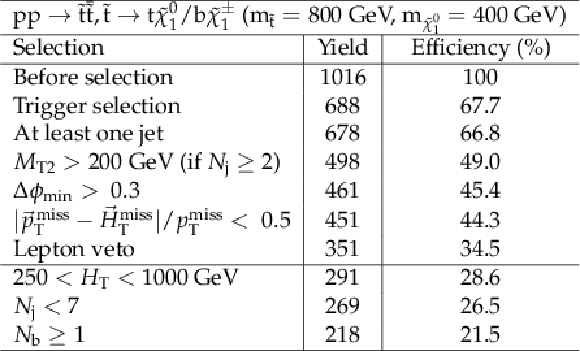
png pdf |
Additional Table 14:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where one top squark decays via a bottom quark while the other decays via a top quark, with the mass of the squark and the LSP equal to 800 and 400 GeV, respectively. Theory cross section for this signal is 28.3 fb. |
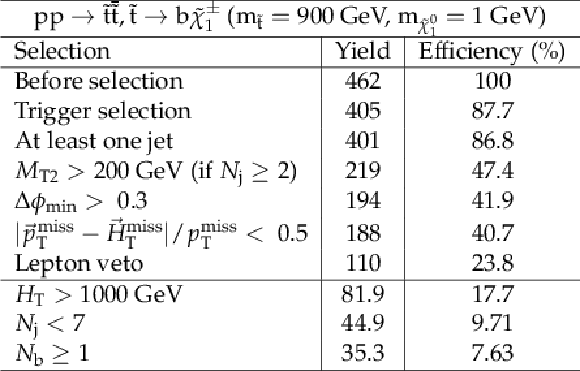
png pdf |
Additional Table 15:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where the top squark decays via a bottom quark, with the mass of the squark and the LSP equal to 900 and 1 GeV, respectively. Theory cross section for this signal is 12.9 fb. |
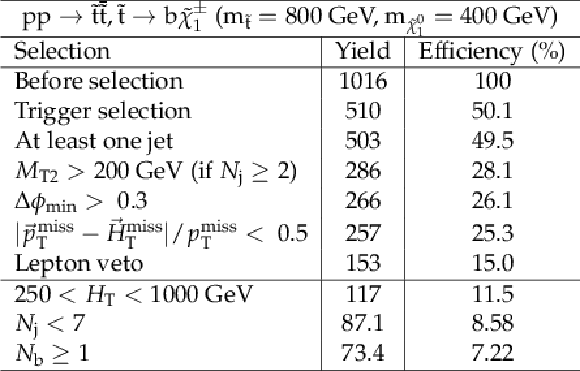
png pdf |
Additional Table 16:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where the top squark decays via a bottom quark, with the mass of the squark and the LSP equal to 800 and 400 GeV, respectively. Theory cross section for this signal is 28.3 fb. |
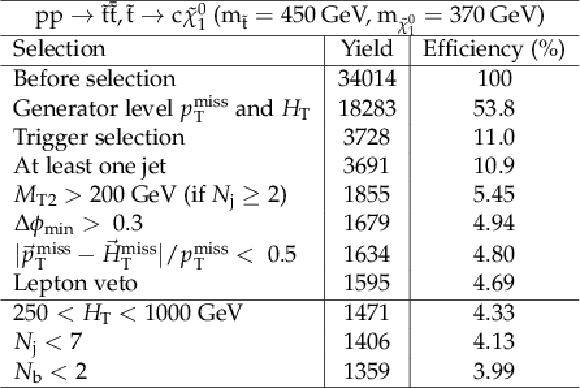
png pdf |
Additional Table 17:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where the top squark decays via a charm quark, with the mass of the squark and the LSP equal to 450 and 370 GeV, respectively. Theory cross section for this signal is 948 fb. |

png pdf |
Additional Table 18:
Cut flow table for baseline selection and several sample additional kinematic selections for a signal model of direct top squark production, where the top squark decays via a charm quark, with the mass of the squark and the LSP equal to 450 and 440 GeV, respectively. Theory cross section for this signal is 948 fb. |
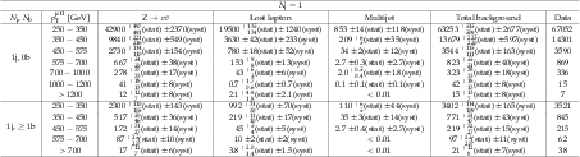
png pdf |
Additional Table 19:
Background estimate and observation in bins of jet $p_{\mathrm {T}}$ for the monojet regions. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
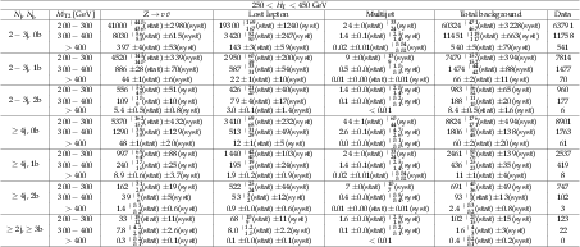
png pdf |
Additional Table 20:
Background estimate and observation in bins of $M_{\mathrm {T2}}$ for 250 $ < H_{\mathrm {T}} < $ 450 GeV. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
png pdf |
Additional Table 21:
Background estimate and observation in bins of $M_{\mathrm {T2}}$ for 450 $ < H_{\mathrm {T}} < $ 575 GeV. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
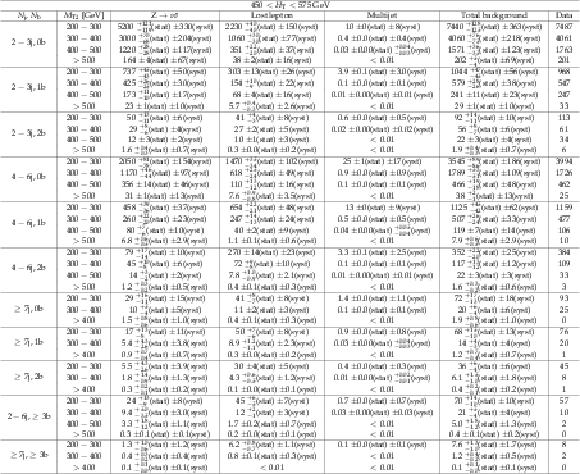
png pdf |
Additional Table 22:
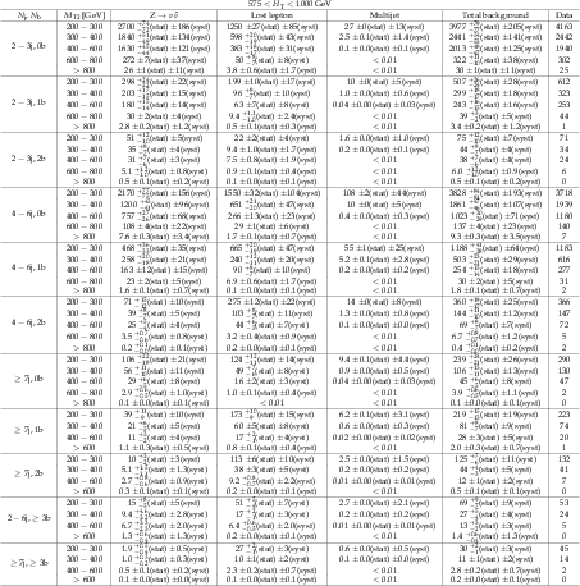
Background estimate and observation in bins of $M_{\mathrm {T2}}$ for 575 $ < H_{\mathrm {T}} < $ 1000 GeV. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
png pdf |
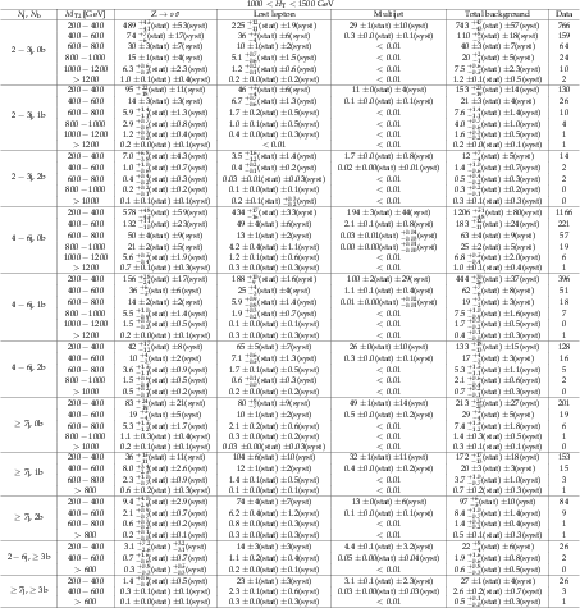
Additional Table 23:
Background estimate and observation in bins of $M_{\mathrm {T2}}$ for 1000 $ < H_{\mathrm {T}} < $ 1500 GeV. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
png pdf |
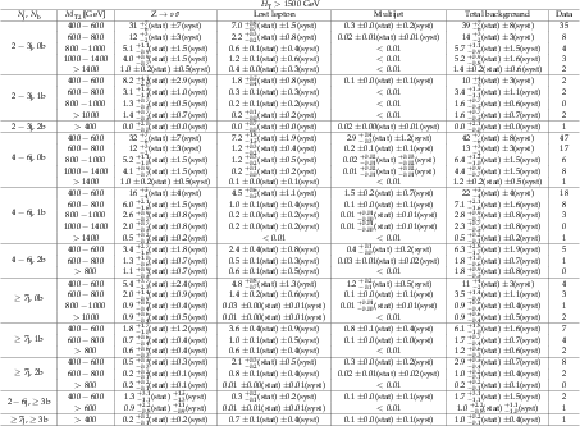
Additional Table 24:
Background estimate and observation in bins of $M_{\mathrm {T2}}$ for $ H_{\mathrm {T}} > $ 1500 GeV. The yields correspond to an integrated luminosity of 35.9 fb$^{-1}$. |
|
Additional code to compute hemispheres and MT2 and an example of usage is available here.
The code available here also include python scripts to facilitate the access to the full covariance (correlation) matrix. One script allows to retrive the bin number on the covariance matrix axes for a given kinematic selection: python getBinNumber_CMS-SUS-16-036.py Nj Nb HT (jet pT) [MT2] with HT, jet pT, and/or MT2 expressed in GeV will return the bin number corresponding to the kinematic selection, together with the corresponding background predictions and observation. A second script allows to retrieve the kinematic selection corresponding to one bin number on the covariance matrix axes: python getRegionFromBinNumber_CMS-SUS-16-036.py binNumber (1..213) will return the kinematic selection corresponding to the input bin number, together with the corresponding background predictions and observation. |
| References | ||||
| 1 | ATLAS Collaboration | Search for new phenomena in final states with large jet multiplicities and missing transverse momentum with ATLAS using $ \sqrt{s} = $ 13 TeV proton-proton collisions | PLB757 (2016) 334--355 | 1602.06194 |
| 2 | ATLAS Collaboration | Search for new phenomena in final states with an energetic jet and large missing transverse momentum in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV using the ATLAS detector | 1604.07773 | |
| 3 | ATLAS Collaboration | Search for squarks and gluinos in final states with jets and missing transverse momentum at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | 1605.03814 | |
| 4 | ATLAS Collaboration | Search for pair production of gluinos decaying via stop and sbottom in events with $ b $-jets and large missing transverse momentum in $ pp $ collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | 1605.09318 | |
| 5 | CMS Collaboration | Search for new physics with the MT2 variable in all-jets final states produced in pp collisions at $ \sqrt{s}= $ 13 TeV | CMS-SUS-15-003 1603.04053 |
|
| 6 | CMS Collaboration | Search for supersymmetry in the multijet and missing transverse momentum final state in pp collisions at 13 TeV | PLB758 (2016) 152--180 | CMS-SUS-15-002 1602.06581 |
| 7 | CMS Collaboration | Inclusive search for supersymmetry using razor variables in pp collisions at $ \sqrt{s}= $ 13 TeV | PRD95 (2017), no. 1, 012003 | CMS-SUS-15-004 1609.07658 |
| 8 | CMS Collaboration | A search for new phenomena in pp collisions at $ \sqrt{s}= $ 13 TeV in final states with missing transverse momentum and at least one jet using the $ {\alpha_{\mathrm{T}}} $ variable | Submitted to: EPJC (2016) | CMS-SUS-15-005 1611.00338 |
| 9 | C. G. Lester and D. J. Summers | Measuring masses of semiinvisibly decaying particles pair produced at hadron colliders | PLB 463 (1999) 99 | hep-ph/9906349 |
| 10 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 11 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 12 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 13 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 14 | CMS Collaboration | Missing transverse energy performance of the CMS detector | JINST 6 (2011) P09001 | CMS-JME-10-009 1106.5048 |
| 15 | J. Alwall et al. | MadGraph 5: going beyond | JHEP 06 (2011) 128 | 1106.0522 |
| 16 | A. L. Read | Presentation of search results: The $ CL_{s} $ technique | JPG 28 (2002) 2693 | |
| 17 | A. L. Read | Modified frequentist analysis of search results (The $ CL_{s} $ method) | CERN-OPEN 205(2000) | |
| 18 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 19 | ATLAS and CMS Collaborations | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS-NOTE-2011-005 | |
| 20 | W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas | Squark and gluino production at hadron colliders | Nucl. Phys. B 492 (1997) 51 | hep-ph/9610490 |
| 21 | A. Kulesza and L. Motyka | Threshold resummation for squark-antisquark and gluino-pair production at the LHC | PRL 102 (2009) 111802 | 0807.2405 |
| 22 | A. Kulesza and L. Motyka | Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC | PRD 80 (2009) 095004 | 0905.4749 |
| 23 | W. Beenakker et al. | Soft-gluon resummation for squark and gluino hadroproduction | JHEP 12 (2009) 041 | 0909.4418 |
| 24 | W. Beenakker et al. | Squark and gluino hadroproduction | Int. J. Mod. Phys. A 26 (2011) 2637 | 1105.1110 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|