

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SMP-21-004 | ||
| Nonresonant central exclusive production of charged hadron pairs in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| TOTEM and CMS Collaborations | ||
| 20 August 2023 | ||
| Abstract: The central exclusive production of charged hadron pairs in pp collisions at a centre-of-mass energy of 13 TeV is examined, based on data collected in a special high-$ \beta^* $ run of the LHC. Events are selected by requiring both scattered protons detected in the TOTEM Roman pots, exactly two oppositely charged identified particles in the CMS silicon tracker, and the energy-momentum balance of these four particles. The nonresonant continuum processes are studied with the invariant mass of the centrally produced two-pion system in the resonance-free region, $ m < $ 0.7 GeV or $ m > $ 1.8 GeV. Differential cross sections as functions of the azimuthal angle between the surviving protons, squared four-momenta, and two-hadron invariant mass are measured in a wide region of scattered proton transverse momenta 0.2 $ \mathrm{GeV} < p_\text{1,T}, p_\text{2,T} < $ 0.8 GeV and for hadron rapidities $ |y| < $ 2. A rich structure of interactions related to double pomeron exchange emerges. The parabolic minimum in the distribution of the two-proton azimuthal angle is observed for the first time. It can be understood as an effect of additional pomeron exchanges between the protons from the interference between the bare and the rescattered amplitudes. After model tuning, various physical quantities related to the pomeron cross section, proton-pomeron and hadron-pomeron form factors, trajectory slopes and intercepts, as well as coefficients of diffractive eigenstates of the proton are determined. | ||
|
Links:
CDS record (PDF) ;
Physics Briefing ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Accepted by PRD. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
Figure 1:
Born-level Feynman diagrams for central exclusive production of hadron pairs via double pomeron exchange, depicting resonant (left) and nonresonant continuum (rightmost two) contributions. |
png pdf |
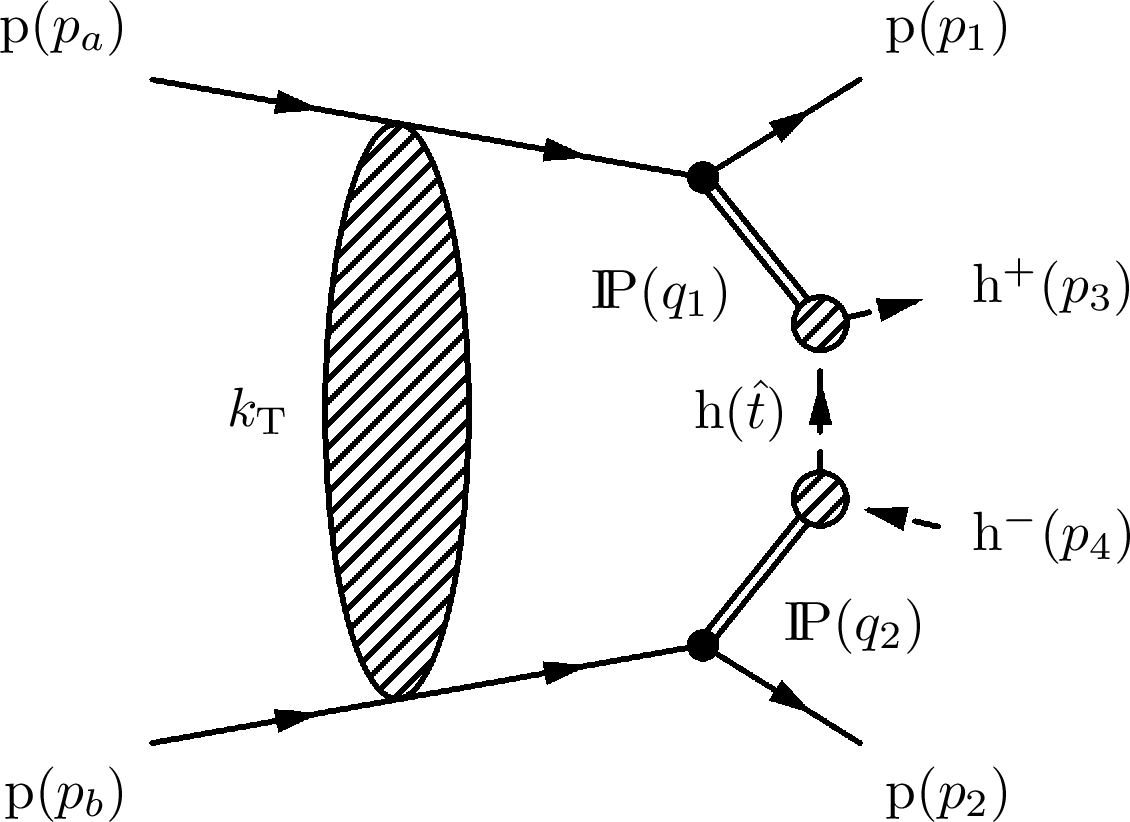
Figure 2:
Feynman diagram for the nonresonant continuum of central exclusive production of hadron pairs via double pomeron exchange, including the rescattering correction. |
png pdf |
Figure 3:
Left: Calculated suppression efficiency of the elastic-like events as functions of momentum components in the $ y $ direction in arms 1 and 2, shown here for the two diagonal trigger configurations (pots 2B with 1T, and 2T with 1B). Boxes with short dashed lines indicate regions not taken into account in the comparison of the expected and detected number of events. Centre and right: Measured correlation of detected proton momenta $ (p_{1,y},p_{2,y}) $ in arms 1 and 2 for all four trigger configurations. Limits of single-proton acceptance are indicated with long dashed lines. |
png pdf |
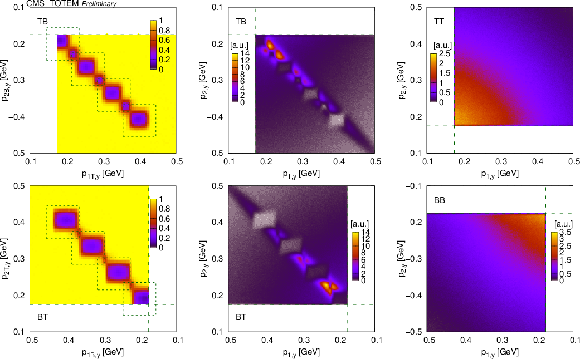
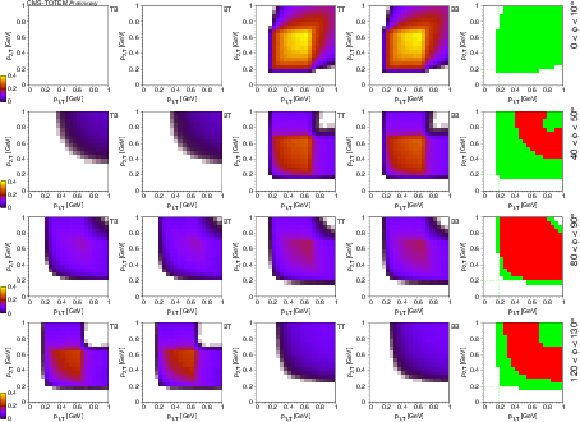
Figure 4:
Calculated detection efficiencies for the pair of scattered protons as a function of their transverse momenta $ (p_\text{1,T}, p_\text{2,T}) $, in some selected bins of the proton-proton azimuthal angle $ \phi $ (indicated on the right side of each row). While the first four subfigures in each row show the efficiencies for each trigger configuration, the rightmost subfigure displays the coverage of the measurement with colour codes (white: not covered; green: covered by at least one configuration; red: covered by all configurations). The lines corresponding to 0.2 GeV are drawn in the rightmost subfigures. |

png pdf |
Figure 4-a:
Calculated detection efficiencies for the pair of scattered protons as a function of their transverse momenta $ (p_\text{1,T}, p_\text{2,T}) $, in some selected bins of the proton-proton azimuthal angle $ \phi $ (indicated on the right side of each row). While the first four subfigures in each row show the efficiencies for each trigger configuration, the rightmost subfigure displays the coverage of the measurement with colour codes (white: not covered; green: covered by at least one configuration; red: covered by all configurations). The lines corresponding to 0.2 GeV are drawn in the rightmost subfigures. |

png pdf |
Figure 4-b:
Calculated detection efficiencies for the pair of scattered protons as a function of their transverse momenta $ (p_\text{1,T}, p_\text{2,T}) $, in some selected bins of the proton-proton azimuthal angle $ \phi $ (indicated on the right side of each row). While the first four subfigures in each row show the efficiencies for each trigger configuration, the rightmost subfigure displays the coverage of the measurement with colour codes (white: not covered; green: covered by at least one configuration; red: covered by all configurations). The lines corresponding to 0.2 GeV are drawn in the rightmost subfigures. |
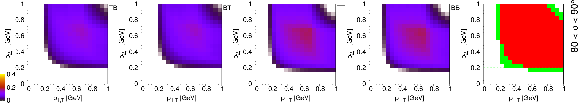
png pdf |
Figure 4-c:
Calculated detection efficiencies for the pair of scattered protons as a function of their transverse momenta $ (p_\text{1,T}, p_\text{2,T}) $, in some selected bins of the proton-proton azimuthal angle $ \phi $ (indicated on the right side of each row). While the first four subfigures in each row show the efficiencies for each trigger configuration, the rightmost subfigure displays the coverage of the measurement with colour codes (white: not covered; green: covered by at least one configuration; red: covered by all configurations). The lines corresponding to 0.2 GeV are drawn in the rightmost subfigures. |
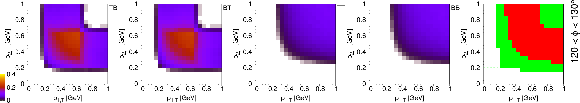
png pdf |
Figure 4-d:
Calculated detection efficiencies for the pair of scattered protons as a function of their transverse momenta $ (p_\text{1,T}, p_\text{2,T}) $, in some selected bins of the proton-proton azimuthal angle $ \phi $ (indicated on the right side of each row). While the first four subfigures in each row show the efficiencies for each trigger configuration, the rightmost subfigure displays the coverage of the measurement with colour codes (white: not covered; green: covered by at least one configuration; red: covered by all configurations). The lines corresponding to 0.2 GeV are drawn in the rightmost subfigures. |
png pdf |
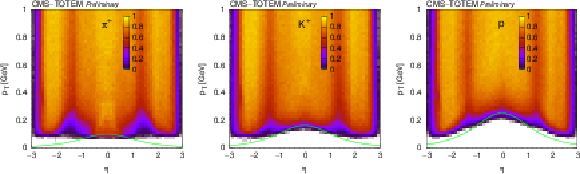
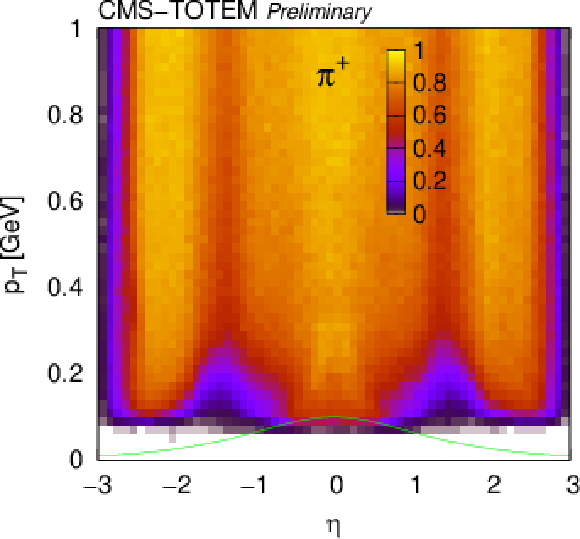
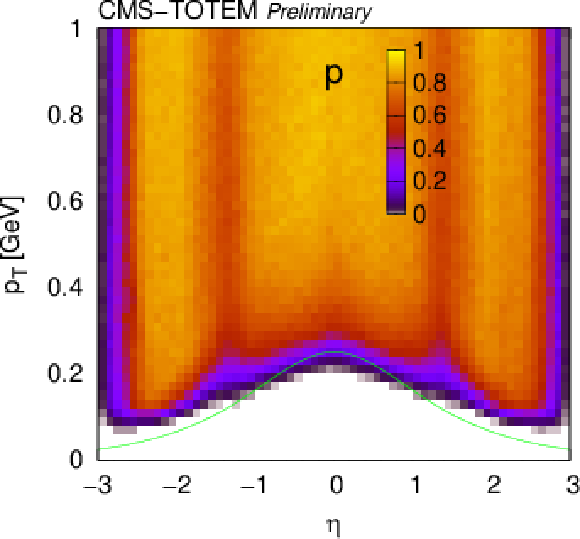
Figure 5:
The combined reconstruction and HLT efficiency (reconstructed and fired HLT), for positively charged pions, kaons, and protons as functions of $ (\eta,p_{\mathrm{T}}) $. Curves indicate constant total momentum ($ p = $ 0.1 GeV for pions, 0.16 GeV for kaons, 0.25 GeV for protons). Plots for negatively charged particles are similar. |
png pdf |
Figure 5-a:
The combined reconstruction and HLT efficiency (reconstructed and fired HLT), for positively charged pions, kaons, and protons as functions of $ (\eta,p_{\mathrm{T}}) $. Curves indicate constant total momentum ($ p = $ 0.1 GeV for pions, 0.16 GeV for kaons, 0.25 GeV for protons). Plots for negatively charged particles are similar. |

png pdf |
Figure 5-b:
The combined reconstruction and HLT efficiency (reconstructed and fired HLT), for positively charged pions, kaons, and protons as functions of $ (\eta,p_{\mathrm{T}}) $. Curves indicate constant total momentum ($ p = $ 0.1 GeV for pions, 0.16 GeV for kaons, 0.25 GeV for protons). Plots for negatively charged particles are similar. |
png pdf |
Figure 5-c:
The combined reconstruction and HLT efficiency (reconstructed and fired HLT), for positively charged pions, kaons, and protons as functions of $ (\eta,p_{\mathrm{T}}) $. Curves indicate constant total momentum ($ p = $ 0.1 GeV for pions, 0.16 GeV for kaons, 0.25 GeV for protons). Plots for negatively charged particles are similar. |
png pdf |
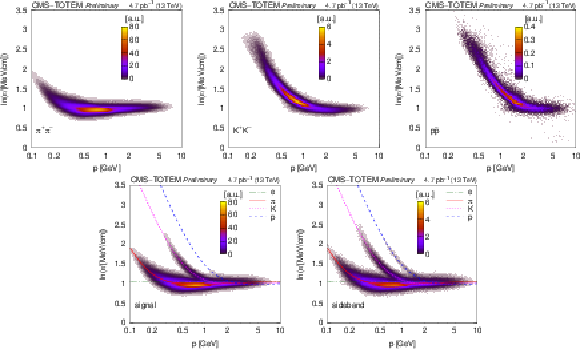
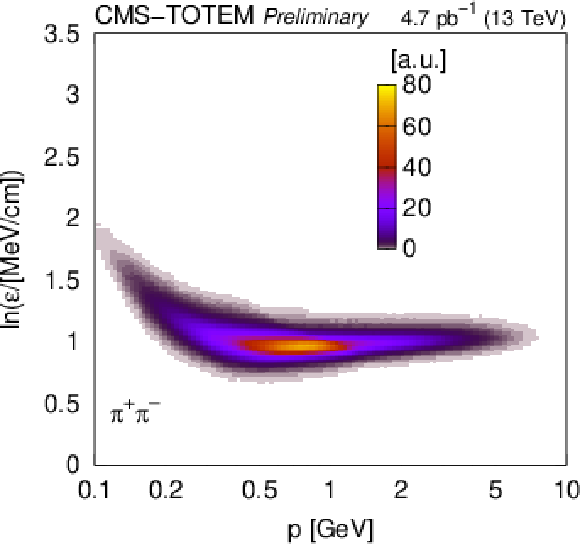
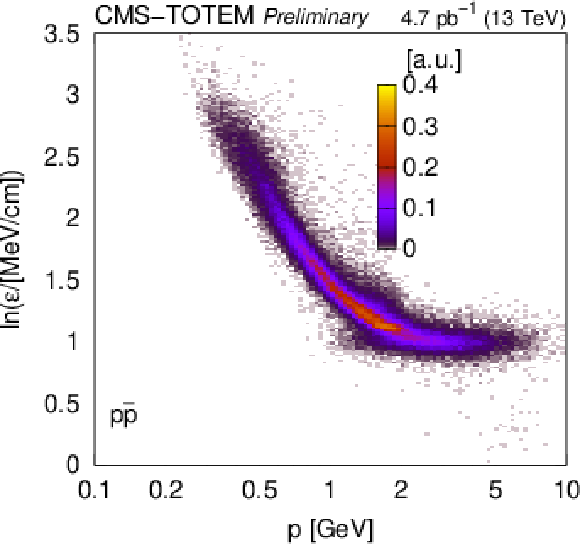
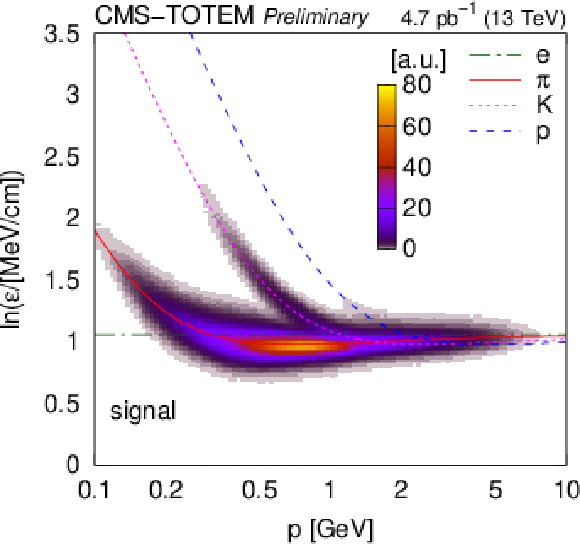
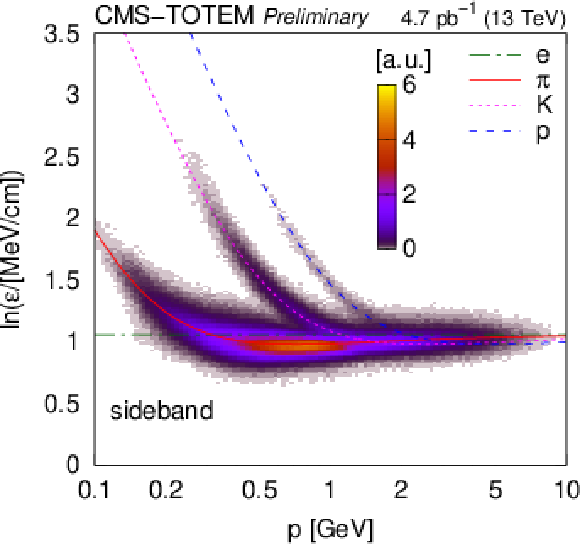
Figure 6:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |
png pdf |
Figure 6-a:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |

png pdf |
Figure 6-b:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |
png pdf |
Figure 6-c:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |
png pdf |
Figure 6-d:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |
png pdf |
Figure 6-e:
Distribution of $ \ln\varepsilon $ as a function of total momentum, for reconstructed charged particles in selected two-track events (identified $ \pi^{+}\pi^{-} $, $ \mathrm{K^+}\mathrm{K^-} $, $ \mathrm{p}\overline{\mathrm{p}} $, signal, and sideband; Section 5). The variable $ \varepsilon $ is the most probable energy loss rate at a reference path length $ l_0 = $ 450 m. The colour scale is shown in arbitrary units and is linear. The curves show the expected $ \ln\varepsilon $ for electrons, pions, kaons, and protons (Eq. (34.12) in Ref. [1]). |
png pdf |
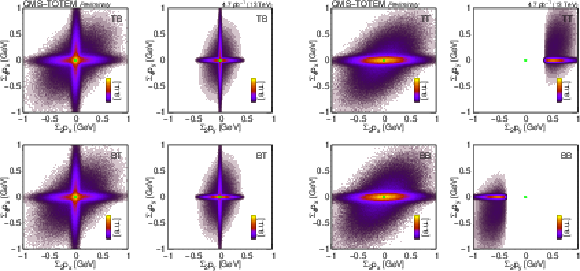
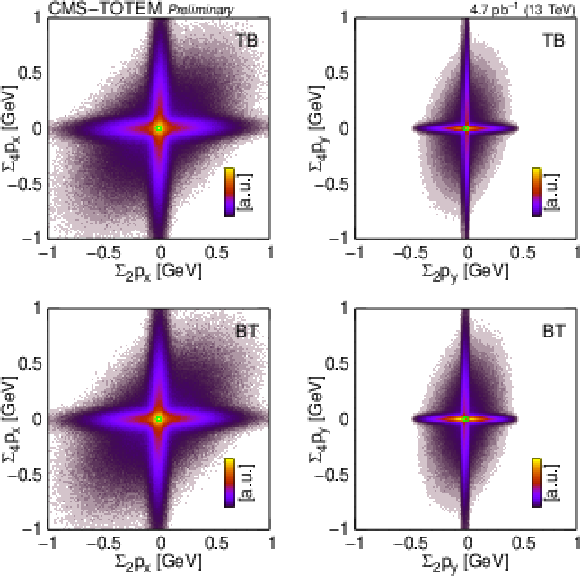
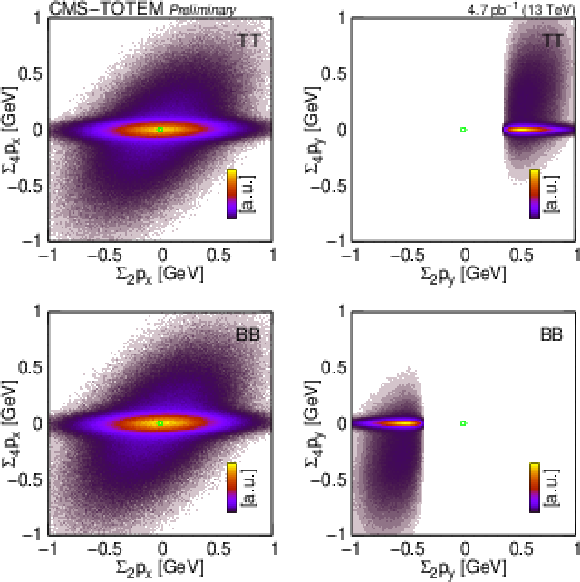
Figure 7:
Distribution of the sum of the scattered proton momenta and the sum of the scattered proton and central hadron momenta ($ \sum_4 p_x $ vs. $ \sum_2 p_x $, $ \sum_4 p_y $ vs. $ \sum_2 p_y $) shown for various trigger configurations (TB, BT, TT, and BB) for 2-track events. |
png pdf |
Figure 7-a:
Distribution of the sum of the scattered proton momenta and the sum of the scattered proton and central hadron momenta ($ \sum_4 p_x $ vs. $ \sum_2 p_x $, $ \sum_4 p_y $ vs. $ \sum_2 p_y $) shown for various trigger configurations (TB, BT, TT, and BB) for 2-track events. |
png pdf |
Figure 7-b:
Distribution of the sum of the scattered proton momenta and the sum of the scattered proton and central hadron momenta ($ \sum_4 p_x $ vs. $ \sum_2 p_x $, $ \sum_4 p_y $ vs. $ \sum_2 p_y $) shown for various trigger configurations (TB, BT, TT, and BB) for 2-track events. |
png pdf |
Figure 8:
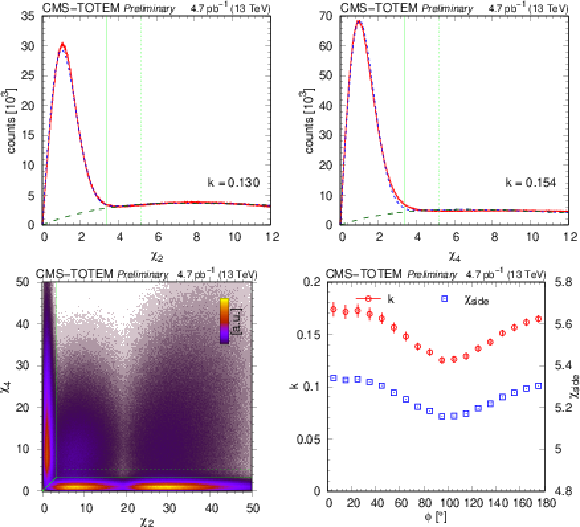
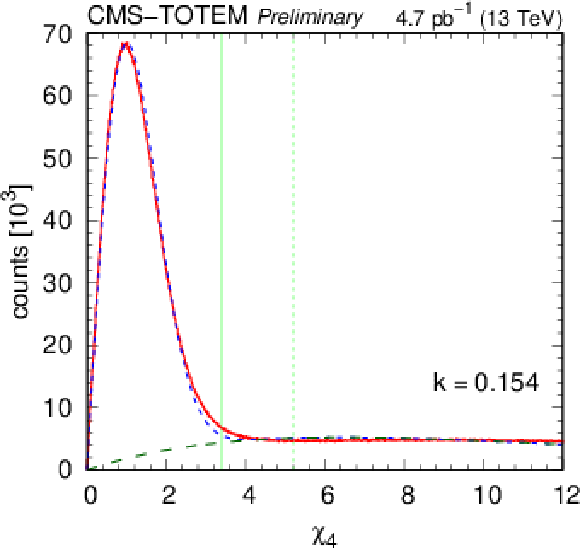
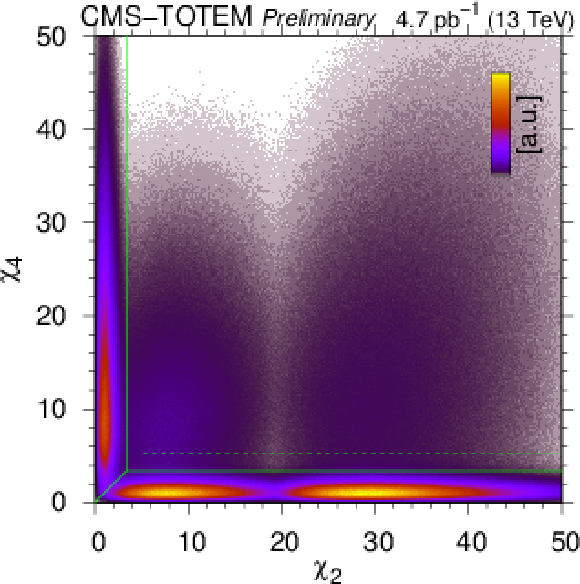
Top: Distribution of the classification variables $ \chi_2 $ (left) and $ \chi_4 $ (right). Fits using a two-component model are indicated. The distributions are integrated over the angle between the scattered protons $ \phi $. Selection lines at 3.4 (green solid) and 5.2 (green dotted) are also plotted. Bottom left: Joint distributions of classification variables $ \chi_2 $ and $ \chi_4 $. Central exclusive signal events are at the bottom while elastic events are at the left margin. Bottom right: Coefficient $ k $ and the position of the upper cut $ \chi_\text{side} $ for the description of the background component as a function of the angle between the scattered protons $ \phi $ in the plane transverse to the beam direction. |

png pdf |
Figure 8-a:
Top: Distribution of the classification variables $ \chi_2 $ (left) and $ \chi_4 $ (right). Fits using a two-component model are indicated. The distributions are integrated over the angle between the scattered protons $ \phi $. Selection lines at 3.4 (green solid) and 5.2 (green dotted) are also plotted. Bottom left: Joint distributions of classification variables $ \chi_2 $ and $ \chi_4 $. Central exclusive signal events are at the bottom while elastic events are at the left margin. Bottom right: Coefficient $ k $ and the position of the upper cut $ \chi_\text{side} $ for the description of the background component as a function of the angle between the scattered protons $ \phi $ in the plane transverse to the beam direction. |
png pdf |
Figure 8-b:
Top: Distribution of the classification variables $ \chi_2 $ (left) and $ \chi_4 $ (right). Fits using a two-component model are indicated. The distributions are integrated over the angle between the scattered protons $ \phi $. Selection lines at 3.4 (green solid) and 5.2 (green dotted) are also plotted. Bottom left: Joint distributions of classification variables $ \chi_2 $ and $ \chi_4 $. Central exclusive signal events are at the bottom while elastic events are at the left margin. Bottom right: Coefficient $ k $ and the position of the upper cut $ \chi_\text{side} $ for the description of the background component as a function of the angle between the scattered protons $ \phi $ in the plane transverse to the beam direction. |
png pdf |
Figure 8-c:
Top: Distribution of the classification variables $ \chi_2 $ (left) and $ \chi_4 $ (right). Fits using a two-component model are indicated. The distributions are integrated over the angle between the scattered protons $ \phi $. Selection lines at 3.4 (green solid) and 5.2 (green dotted) are also plotted. Bottom left: Joint distributions of classification variables $ \chi_2 $ and $ \chi_4 $. Central exclusive signal events are at the bottom while elastic events are at the left margin. Bottom right: Coefficient $ k $ and the position of the upper cut $ \chi_\text{side} $ for the description of the background component as a function of the angle between the scattered protons $ \phi $ in the plane transverse to the beam direction. |

png pdf |
Figure 8-d:
Top: Distribution of the classification variables $ \chi_2 $ (left) and $ \chi_4 $ (right). Fits using a two-component model are indicated. The distributions are integrated over the angle between the scattered protons $ \phi $. Selection lines at 3.4 (green solid) and 5.2 (green dotted) are also plotted. Bottom left: Joint distributions of classification variables $ \chi_2 $ and $ \chi_4 $. Central exclusive signal events are at the bottom while elastic events are at the left margin. Bottom right: Coefficient $ k $ and the position of the upper cut $ \chi_\text{side} $ for the description of the background component as a function of the angle between the scattered protons $ \phi $ in the plane transverse to the beam direction. |
png pdf |
Figure 9:
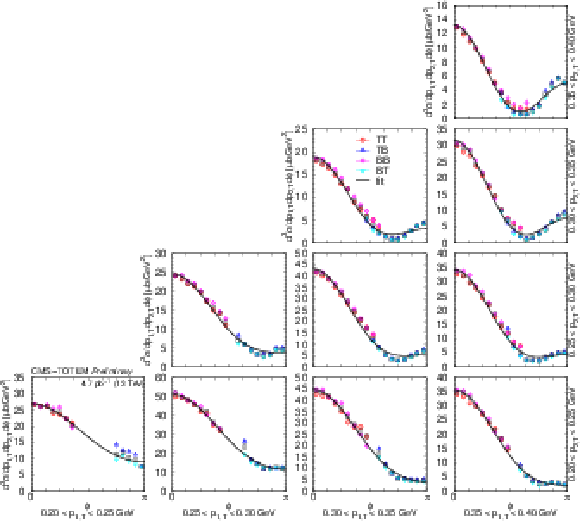
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $ \mu\mathrm{b}/$ GeV$^2 $. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 10:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
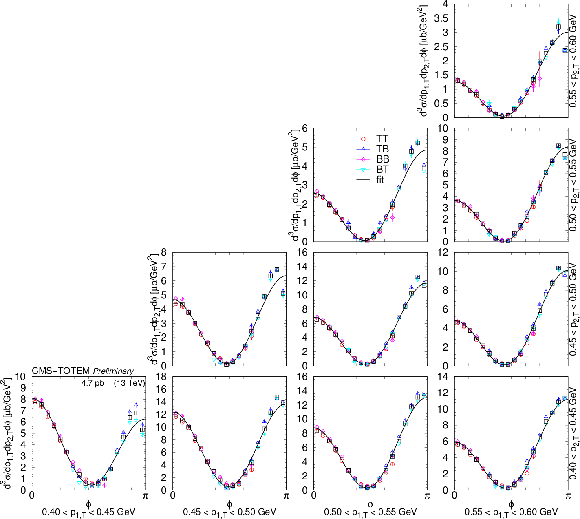
png pdf |
Figure 10-a:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
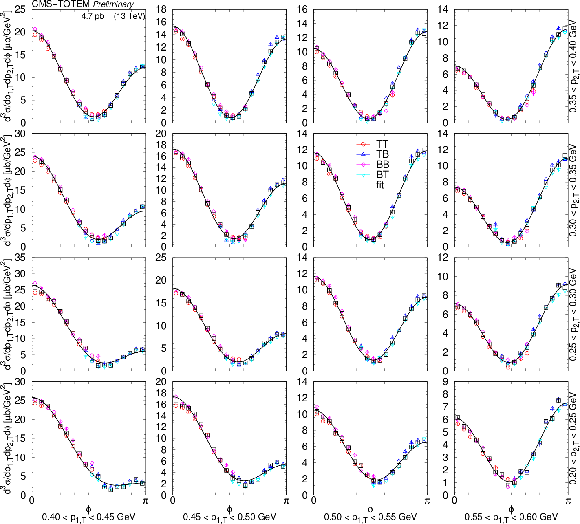
png pdf |
Figure 10-b:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 11:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
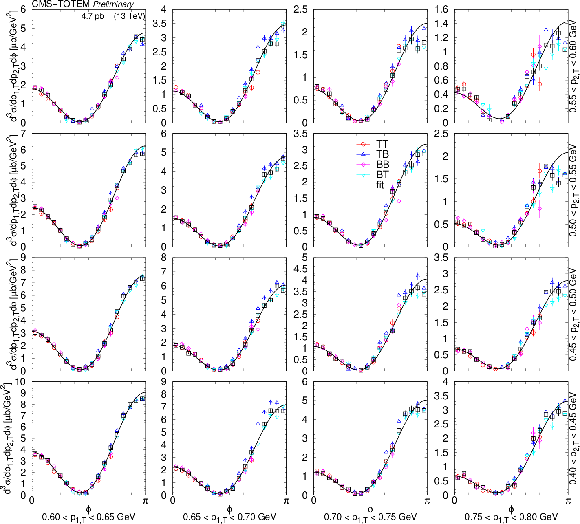
png pdf |
Figure 11-a:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 11-b:
Distributions of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in the $ \pi^{+}\pi^{-} $ nonresonant region (0.35 $ < m < $ 0.65 GeV) in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Values based on data from each RP trigger configuration (TB, BT, TT, and TT) are shown separately with coloured symbols, while the weighted average is indicated with black symbols. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
png pdf |
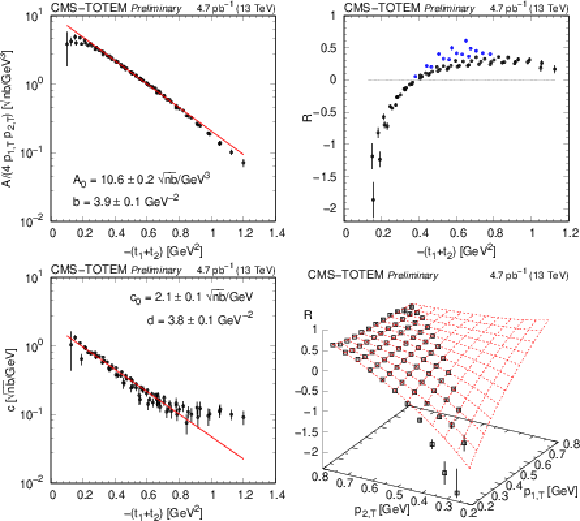
Figure 12:
Dependence of the parameters $ A $, $ R $, and $ c $ (Eq. \eqrefeq:ARc) on $ (t_1,t_2) $. The fits correspond to the functional forms displayed in Eqs. \eqrefeq:A-\eqrefeq:c. In the top right plot, points with significantly differing proton transverse momenta ($ |p_\text{1,T} - p_\text{2,T}| > $ 0.35 GeV) are coloured blue. |

png pdf |
Figure 12-a:
Dependence of the parameters $ A $, $ R $, and $ c $ (Eq. \eqrefeq:ARc) on $ (t_1,t_2) $. The fits correspond to the functional forms displayed in Eqs. \eqrefeq:A-\eqrefeq:c. In the top right plot, points with significantly differing proton transverse momenta ($ |p_\text{1,T} - p_\text{2,T}| > $ 0.35 GeV) are coloured blue. |
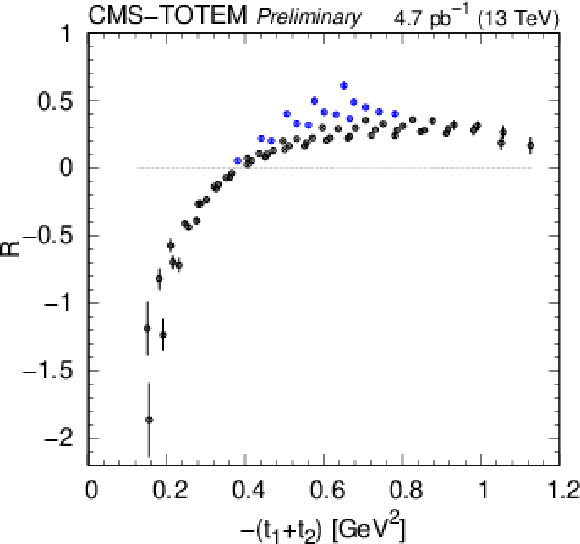
png pdf |
Figure 12-b:
Dependence of the parameters $ A $, $ R $, and $ c $ (Eq. \eqrefeq:ARc) on $ (t_1,t_2) $. The fits correspond to the functional forms displayed in Eqs. \eqrefeq:A-\eqrefeq:c. In the top right plot, points with significantly differing proton transverse momenta ($ |p_\text{1,T} - p_\text{2,T}| > $ 0.35 GeV) are coloured blue. |
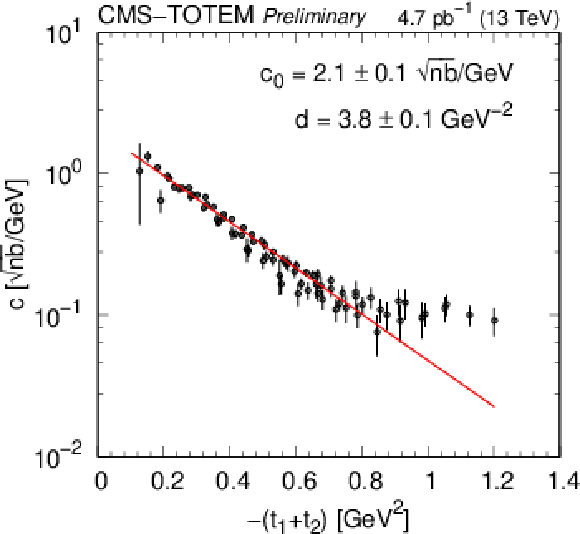
png pdf |
Figure 12-c:
Dependence of the parameters $ A $, $ R $, and $ c $ (Eq. \eqrefeq:ARc) on $ (t_1,t_2) $. The fits correspond to the functional forms displayed in Eqs. \eqrefeq:A-\eqrefeq:c. In the top right plot, points with significantly differing proton transverse momenta ($ |p_\text{1,T} - p_\text{2,T}| > $ 0.35 GeV) are coloured blue. |
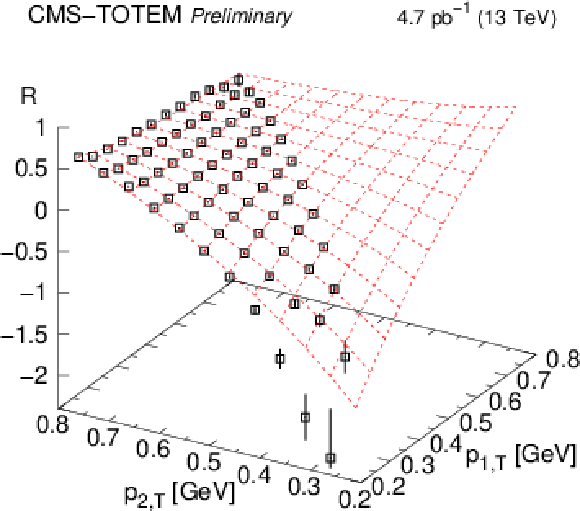
png pdf |
Figure 12-d:
Dependence of the parameters $ A $, $ R $, and $ c $ (Eq. \eqrefeq:ARc) on $ (t_1,t_2) $. The fits correspond to the functional forms displayed in Eqs. \eqrefeq:A-\eqrefeq:c. In the top right plot, points with significantly differing proton transverse momenta ($ |p_\text{1,T} - p_\text{2,T}| > $ 0.35 GeV) are coloured blue. |
png pdf |
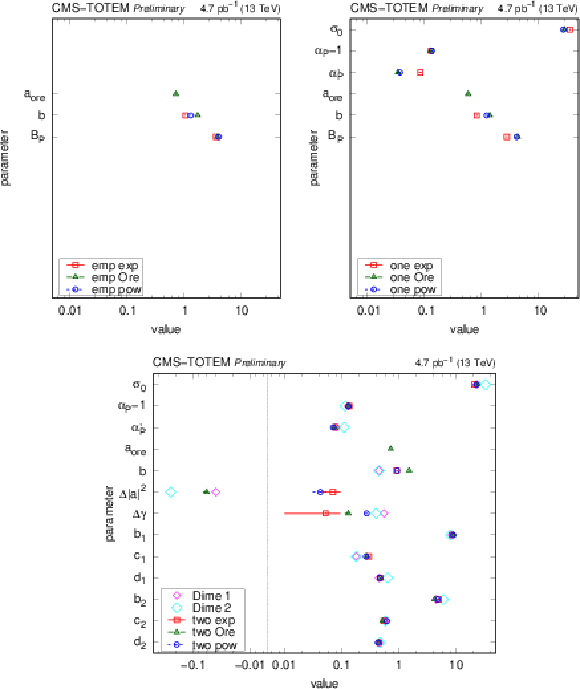
Figure 13:
Values of best parameters for the empirical (top left), one-channel (top right), and two-channel (bottom) models with several choices of the proton-pomeron form factor (exponential, Orear-type, power-law). In the case of the two-channel model, parameter values of models describing the elastic differential proton-proton cross section from Ref. [26] are also indicated (DIME 1 and 2). |
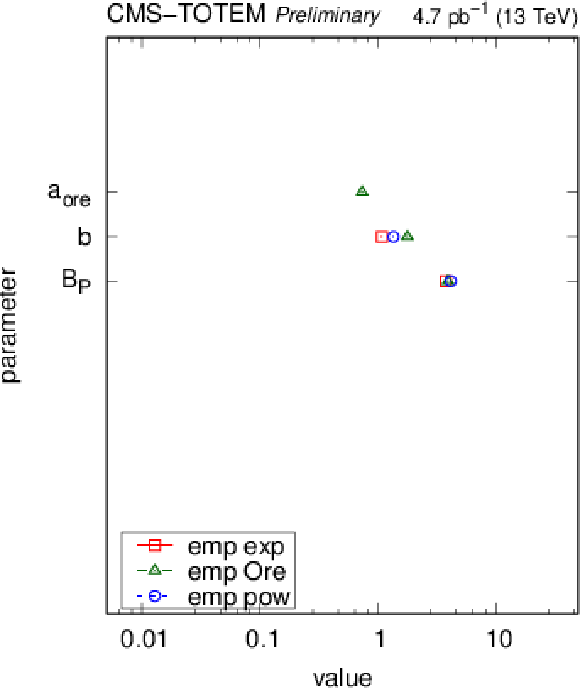
png pdf |
Figure 13-a:
Values of best parameters for the empirical (top left), one-channel (top right), and two-channel (bottom) models with several choices of the proton-pomeron form factor (exponential, Orear-type, power-law). In the case of the two-channel model, parameter values of models describing the elastic differential proton-proton cross section from Ref. [26] are also indicated (DIME 1 and 2). |

png pdf |
Figure 13-b:
Values of best parameters for the empirical (top left), one-channel (top right), and two-channel (bottom) models with several choices of the proton-pomeron form factor (exponential, Orear-type, power-law). In the case of the two-channel model, parameter values of models describing the elastic differential proton-proton cross section from Ref. [26] are also indicated (DIME 1 and 2). |
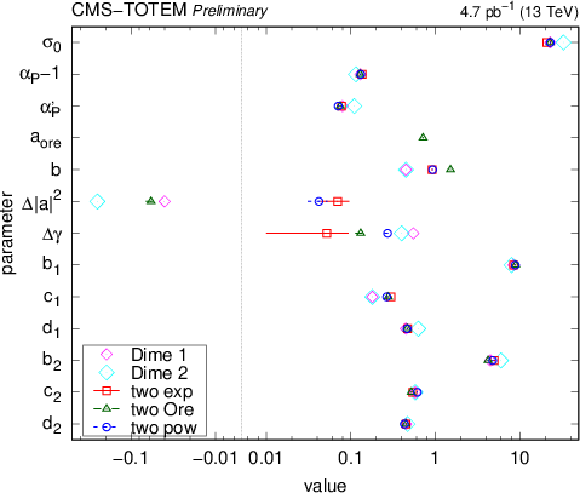
png pdf |
Figure 13-c:
Values of best parameters for the empirical (top left), one-channel (top right), and two-channel (bottom) models with several choices of the proton-pomeron form factor (exponential, Orear-type, power-law). In the case of the two-channel model, parameter values of models describing the elastic differential proton-proton cross section from Ref. [26] are also indicated (DIME 1 and 2). |

png pdf |
Figure 14:
Correlation coefficients among values of best parameters for the two-channel model, in the case of exponential (left), Orear-type (centre), and power-law (right) parametrisations of the proton-pomeron form factor. |

png pdf |
Figure 14-a:
Correlation coefficients among values of best parameters for the two-channel model, in the case of exponential (left), Orear-type (centre), and power-law (right) parametrisations of the proton-pomeron form factor. |
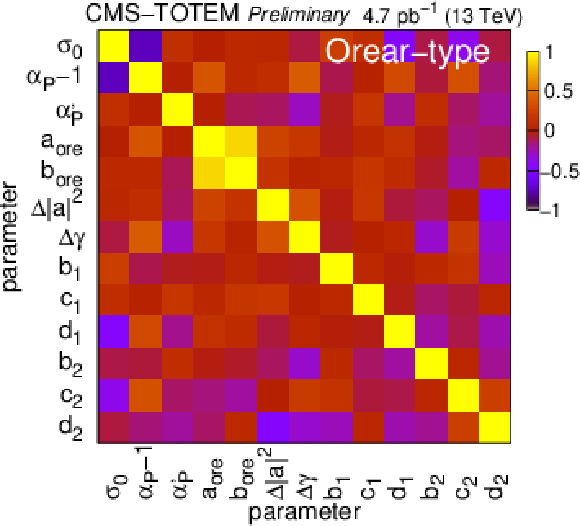
png pdf |
Figure 14-b:
Correlation coefficients among values of best parameters for the two-channel model, in the case of exponential (left), Orear-type (centre), and power-law (right) parametrisations of the proton-pomeron form factor. |
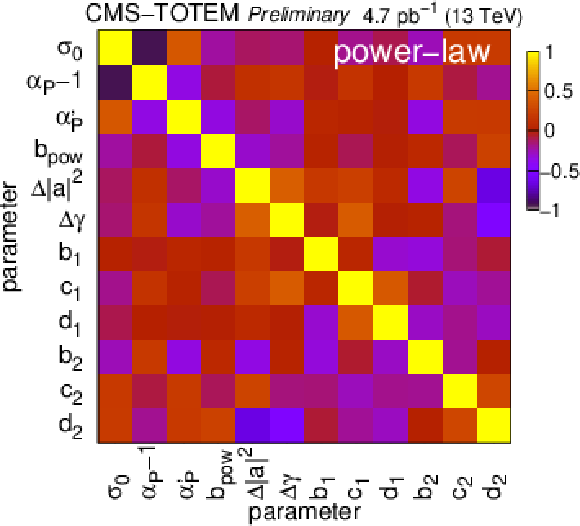
png pdf |
Figure 14-c:
Correlation coefficients among values of best parameters for the two-channel model, in the case of exponential (left), Orear-type (centre), and power-law (right) parametrisations of the proton-pomeron form factor. |

png pdf |
Figure 15:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 16:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
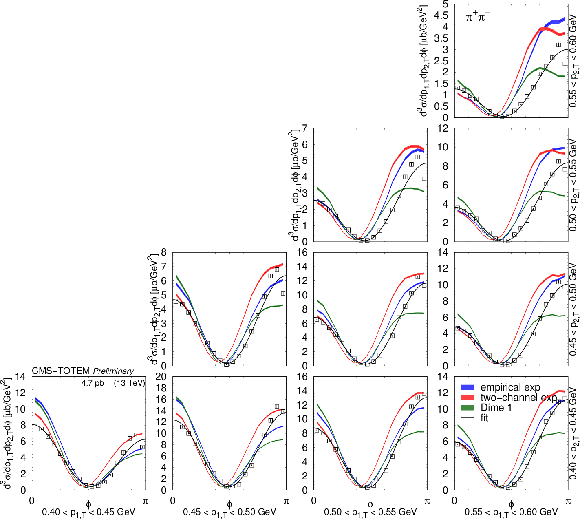
png pdf |
Figure 16-a:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
png pdf |
Figure 16-b:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
png pdf |
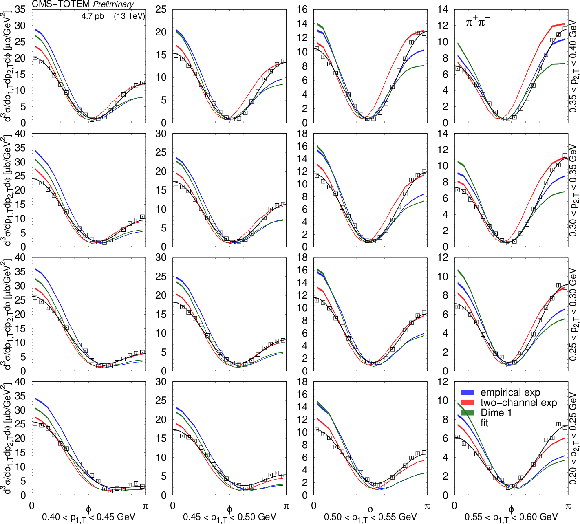
Figure 17:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 17-a:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 17-b:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d}\phi $ as a function of $ \phi $ in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^2$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. Results of fits with the form $ [A(R - \cos\phi)]^2 + c^2 $ are plotted with curves. The error bars indicate the statistical uncertainties. |
png pdf |
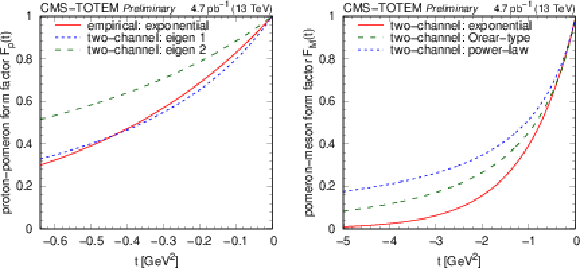
Figure 18:
Results of model tuning. Left: The plain exponential proton-pomeron form factor compared to those of the two diffractive proton eigenstates. Right: Various options of the meson-pomeron form factor, shown for the exponential, power-law, and the Orear-type parametrisations. |
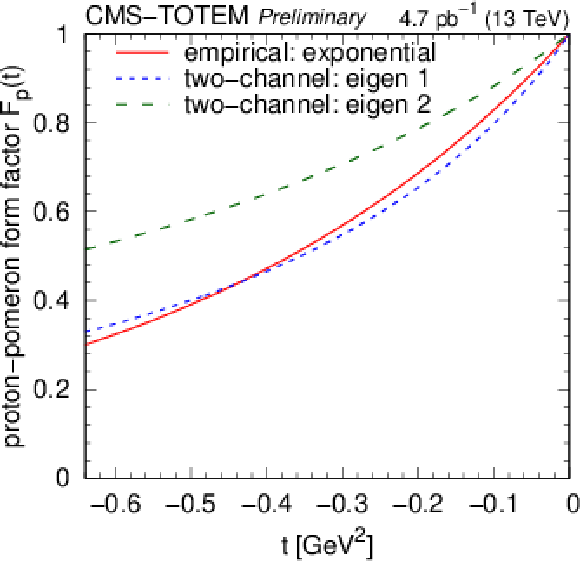
png pdf |
Figure 18-a:
Results of model tuning. Left: The plain exponential proton-pomeron form factor compared to those of the two diffractive proton eigenstates. Right: Various options of the meson-pomeron form factor, shown for the exponential, power-law, and the Orear-type parametrisations. |
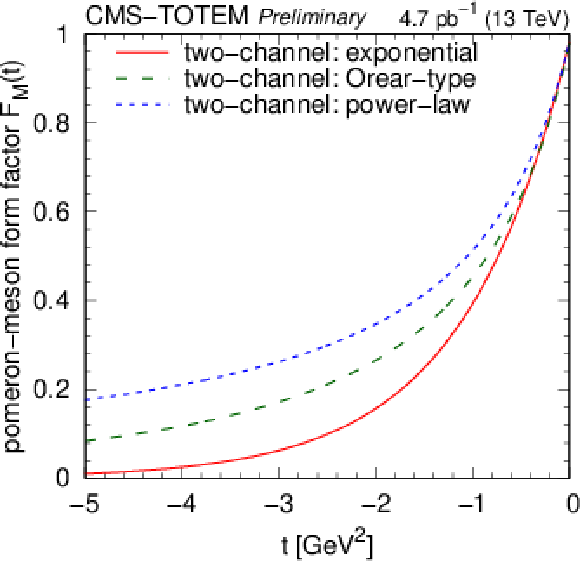
png pdf |
Figure 18-b:
Results of model tuning. Left: The plain exponential proton-pomeron form factor compared to those of the two diffractive proton eigenstates. Right: Various options of the meson-pomeron form factor, shown for the exponential, power-law, and the Orear-type parametrisations. |
png pdf |
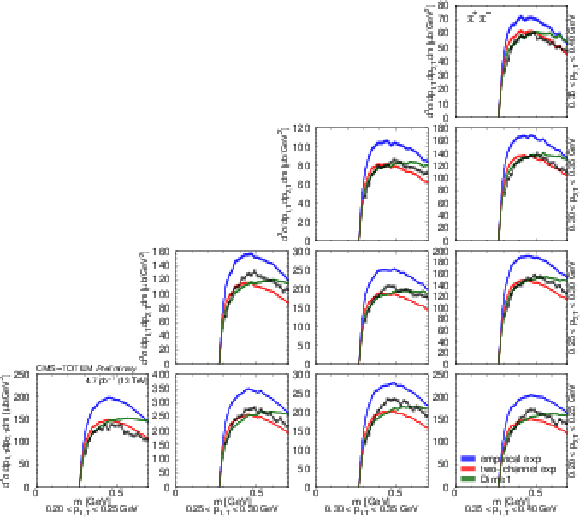
Figure 19:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |
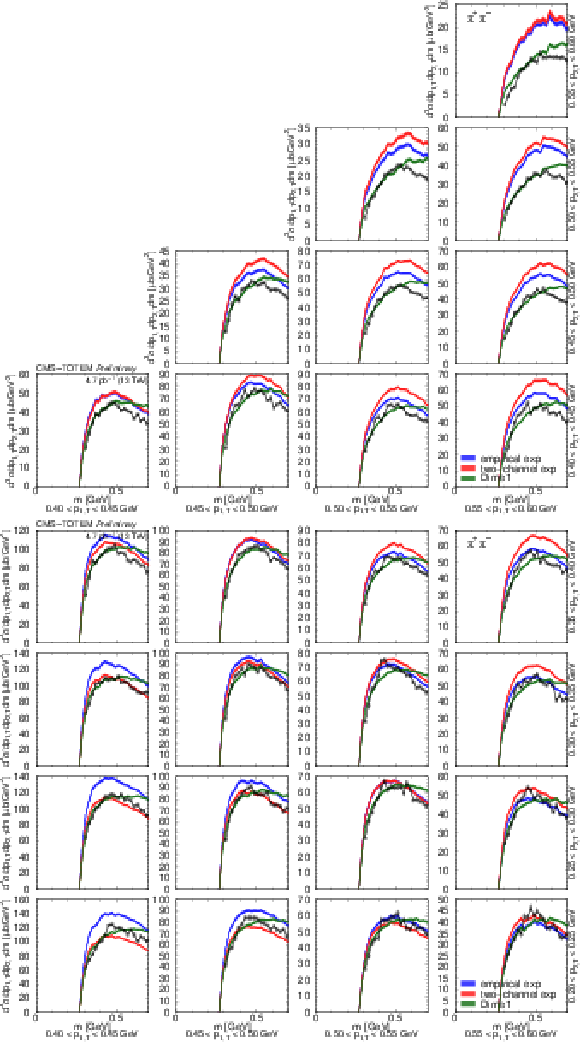
png pdf |
Figure 20:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |

png pdf |
Figure 20-a:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |
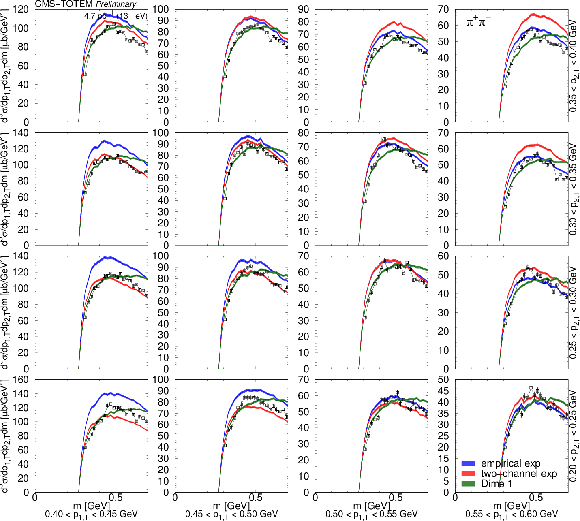
png pdf |
Figure 20-b:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |
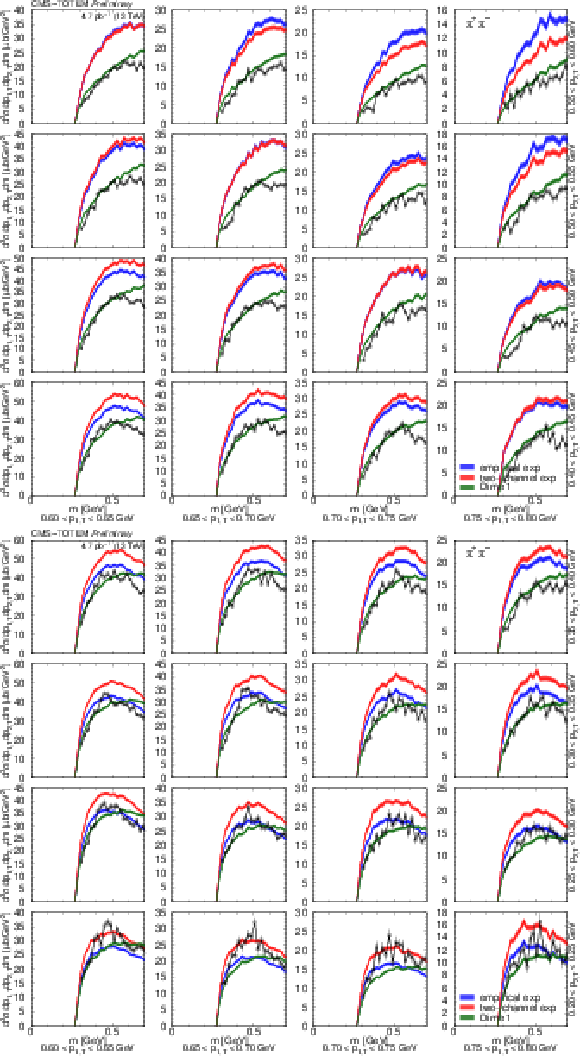
png pdf |
Figure 21:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |

png pdf |
Figure 21-a:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |

png pdf |
Figure 21-b:
Distribution of $ {\mathrm d}^3\sigma/{\mathrm d} p_\text{1,T} {\mathrm d} p_\text{2,T} {\mathrm d} m $ as a function of $ m $ for $ \pi^{+}\pi^{-} $ pairs in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1) are also plotted. The error bars indicate the statistical uncertainties. Lines connecting the data points are drawn to guide the eye. |
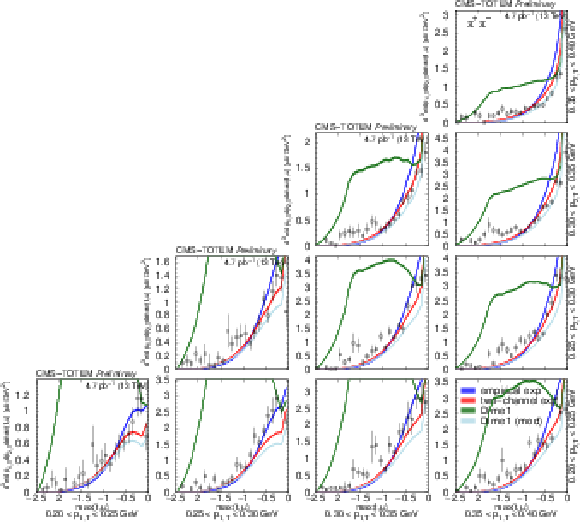
png pdf |
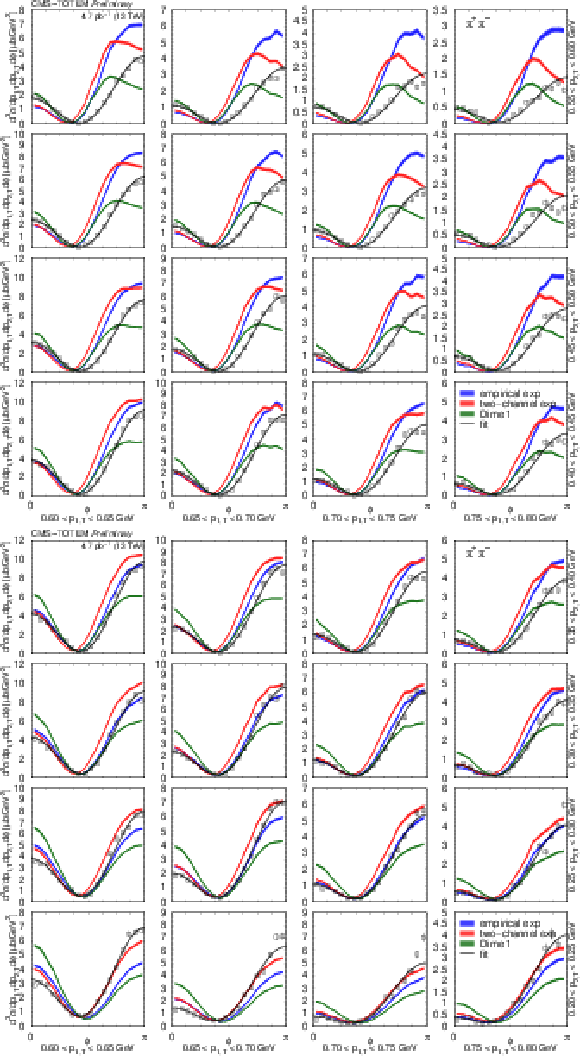
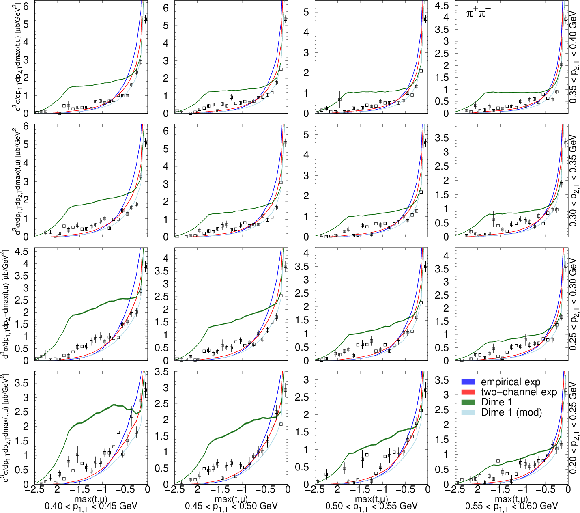
Figure 22:
Distribution of the squared momentum transfer of the virtual meson in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1, ``Dime 1'') and its modification (labelled ``Dime 1 (mod)'') with $ b_\text{exp} = $ 0.9 GeV$^{-2}$ are also plotted. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 23:
Distribution of the squared momentum transfer of the virtual meson in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1, ``Dime 1'') and its modification (labelled ``Dime 1 (mod)'') with $ b_\text{exp} = $ 0.9 GeV$^{-2}$ are also plotted. The error bars indicate the statistical uncertainties. |

png pdf |
Figure 23-a:
Distribution of the squared momentum transfer of the virtual meson in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1, ``Dime 1'') and its modification (labelled ``Dime 1 (mod)'') with $ b_\text{exp} = $ 0.9 GeV$^{-2}$ are also plotted. The error bars indicate the statistical uncertainties. |
png pdf |
Figure 23-b:
Distribution of the squared momentum transfer of the virtual meson in several $ (p_\text{1,T},p_\text{2,T}) $ bins, in units of $\mu$b GeV$^{3}$. Measured values (black symbols) are shown together with the predictions of the empirical and the two-channel models (coloured symbols) using the tuned parameters for the exponential proton-pomeron form factors (see text for details). Curves corresponding to DIME (model 1, ``Dime 1'') and its modification (labelled ``Dime 1 (mod)'') with $ b_\text{exp} = $ 0.9 GeV$^{-2}$ are also plotted. The error bars indicate the statistical uncertainties. |
| Tables | |

png pdf |
Table 1:
Bias and resolution of the reconstructed transverse momentum and the two-hadron invariant mass, shown for pions, kaons, and protons. |

png pdf |
Table 2:
List of systematic uncertainties: the sources and the systematic uncertainties propagated to the final differential cross sections. |
png pdf |
Table 3:
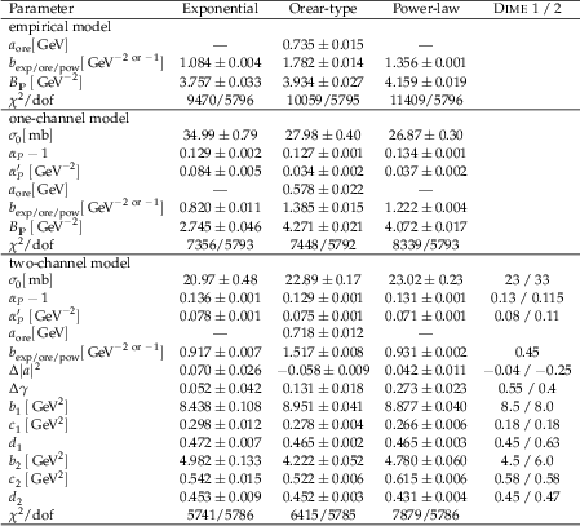
Values and statistical uncertainties of the parameters tuned with the \sc Professor\ tool, given for the empirical, one-channel, and two-channel model along with DIME\ soft models 1 and 2 with the exponential, power-law, and the Orear-type parametrisations of the proton-pomeron form factor. Goodness-of-fit ($ \chi^2/\mathrm{dof} $) values are also listed. |
| Summary |
| We have examined the central exclusive production of charged hadron pairs in pp collisions at a centre-of-mass energy of 13 TeV. Events were selected by requiring both scattered protons detected in the TOTEM Roman pots, exactly two oppositely charged identified pions in the CMS silicon tracker, and the energy-momentum balance of these four particles. The process was studied in the resonance-free region, for invariant masses of the centrally produced two-hadron system $ m < $ 0.7 GeV or $ m > $ 1.8 GeV. Differential cross sections are measured as functions of the azimuthal angle between the surviving protons in a wide region of scattered proton transverse momenta, 0.2 GeV $< p_\text{1,T},p_\text{2,T} < $ 0.8 GeV and for hadron rapidities $ |y| < $ 2. A rich structure of nonperturbative interactions related to double pomeron exchange emerges, measured with good precision. The parabolic minimum in the distribution of the two-proton azimuthal angle is measured for the first time. It can be understood as an effect of additional pomeron exchanges between the incoming protons, resulting from the interference of the bare and the rescattered amplitudes. With help of model tuning, various physical quantities related to the pomeron cross section, proton-pomeron and hadron-pomeron form factors, trajectory slopes and intercepts, as well as coefficients of diffractive eigenstates of the proton are determined. |
| References | ||||
| 1 | Particle Data Group Collaboration | Review of Particle Physics | PTEP 2022 (2022) 083C01 | |
| 2 | V. Berestetsky and I. Pomeranchuk | On the asymptotic behaviour of cross sections at high energies | NP 22 (1961) 629 | |
| 3 | D. Amati, A. Stanghellini, and S. Fubini | Theory of high-energy scattering and multiple production | Nuovo Cim. 26 (1962) 896 | |
| 4 | S. Donnachie, H. G. Dosch, O. Nachtmann, and P. Landshoff | Pomeron physics and QCD | ISBN~978-0-511-06050-2, 978-0-521-78039-1, 978-0-521-67570-3, 2004 | |
| 5 | H. B. Meyer and M. J. Teper | Glueball Regge trajectories and the pomeron: A Lattice study | PLB 605 (2005) 344 | hep-ph/0409183 |
| 6 | D0 and TOTEM Collaborations | Odderon Exchange from Elastic Scattering Differences between $ pp $ and $ p \bar{p} $ Data at 1.96 TeV and from pp Forward Scattering Measurements | PRL 127 (2021) 062003 | 2012.03981 |
| 7 | M. Albrow, T. Coughlin, and J. Forshaw | Central Exclusive Particle Production at High Energy Hadron Colliders | Prog. Part. Nucl. Phys. 65 (2010) 149 | 1006.1289 |
| 8 | W. Ochs | The Status of Glueballs | JPG 40 (2013) 043001 | 1301.5183 |
| 9 | WA76 Collaboration | Study of the centrally produced $ \pi\pi $ and $ \mathrm{K\overline{K}} $ systems at 85-GeV/c and 300-GeV/c | Z. Phys. C 51 (1991) 351 | |
| 10 | WA91 Collaboration | A further study of the centrally produced $ \pi^{+}\pi^{-} $ and $ \pi^{+}\pi^{-}\pi^{+}\pi^{-} $ channels in pp interactions at 300 and 450 GeV/c | PLB 353 (1995) 5894 | |
| 11 | F. E. Close and G. A. Schuler | Evidence that the pomeron transforms as a nonconserved vector current | PLB 464 (1999) 279 | hep-ph/9905305 |
| 12 | WA102 Collaboration | Experimental evidence for a vector like behavior of Pomeron exchange | PLB 467 (1999) 165 | hep-ex/9909013 |
| 13 | F. E. Close, A. Kirk, and G. Schuler | Dynamics of glueball and $ \mathrm{q\overline{q}} $ production in the central region of pp collisions | PLB 477 (2000) 13 | hep-ph/0001158 |
| 14 | A. Kirk | Resonance production in central pp collisions at the CERN Omega spectrometer | PLB 489 (2000) 29 | hep-ph/0008053 |
| 15 | CDF Collaboration | Measurement of central exclusive $ \pi^+ \pi^- $ production in $ p\bar{p} $ collisions at $ \sqrt{s} = $ 0.9 and 1.96 TeV at CDF | PRD 91 (2015) 091101 | 1502.01391 |
| 16 | STAR Collaboration | Measurement of the central exclusive production of charged particle pairs in proton-proton collisions at $ \sqrt{s} = $ 200 GeV with the STAR detector at RHIC | JHEP 07 (2020) 178 | 2004.11078 |
| 17 | ATLAS Collaboration | Measurement of exclusive pion pair production in proton-proton collisions at $ \sqrt{s}={7}\,\text {TeV} $ with the ATLAS detector | EPJC 83 (2023) 627 | 2212.00664 |
| 18 | CMS Collaboration | Study of central exclusive $ \pi^+\pi^- $ production in proton-proton collisions at $ \sqrt{s} = $ 5.02 and 13 TeV | EPJC 80 (2020) 718 | CMS-FSQ-16-006 2003.02811 |
| 19 | P. Lebiedowicz and A. Szczurek | Exclusive $ pp \to pp \pi^{+}\pi^{-} $ reaction: From the threshold to LHC | PRD 81 (2010) 036003 | 0912.0190 |
| 20 | P. Lebiedowicz and A. Szczurek | Revised model of absorption corrections for the $ p p \to p p \pi^{+} \pi^{-} $ process | PRD 92 (2015) 054001 | 1504.07560 |
| 21 | P. Lebiedowicz, O. Nachtmann, and A. Szczurek | Central exclusive diffractive production of $ \pi^{+}\pi^{-} $ continuum, scalar and tensor resonances in $ pp $ and $ p \bar{p} $ scattering within tensor pomeron approach | PRD 93 (2016) 054015 | 1601.04537 |
| 22 | P. Lebiedowicz, O. Nachtmann, and A. Szczurek | Towards a complete study of central exclusive production of $ K^{+}K^{-} $ pairs in proton-proton collisions within the tensor Pomeron approach | PRD 98 (2018) 014001 | 1804.04706 |
| 23 | P. Lebiedowicz, O. Nachtmann, and A. Szczurek | Central exclusive diffractive production of $ p \bar{p} $ pairs in proton-proton collisions at high energies | PRD 97 (2018) 094027 | 1801.03902 |
| 24 | M. Ryskin, A. Martin, and V. Khoze | Proton Opacity in the Light of LHC Diffractive Data | EPJC 72 (2012) 1937 | 1201.6298 |
| 25 | L. A. Harland-Lang, V. A. Khoze, M. G. Ryskin, and W. J. Stirling | The Phenomenology of Central Exclusive Production at Hadron Colliders | EPJC 72 (2012) 2110 | 1204.4803 |
| 26 | V. Khoze, A. Martin, and M. Ryskin | Diffraction at the LHC | EPJC 73 (2013) 2503 | 1306.2149 |
| 27 | L. A. Harland-Lang, V. A. Khoze, and M. G. Ryskin | Modelling exclusive meson pair production at hadron colliders | EPJC 74 (2014) 2848 | 1312.4553 |
| 28 | A. Grau, S. Pacetti, G. Pancheri, and Y. N. Srivastava | Checks of Asymptotia in pp Elastic Scattering at LHC | PLB 714 (2012) 70 | 1206.1076 |
| 29 | D. A. Fagundes et al. | Elastic $ pp $ scattering from the optical point to past the dip: An empirical parametrization from ISR to the LHC | PRD 88 (2013) 094019 | 1306.0452 |
| 30 | A. Donnachie and P. Landshoff | Total cross-sections | PLB 296 (1992) 227 | hep-ph/9209205 |
| 31 | J. Cudell et al. | Hadronic scattering amplitudes: Medium-energy constraints on asymptotic behavior | PRD 65 (2002) 074024 | hep-ph/0107219 |
| 32 | CMS Collaboration | Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS Phase-1 Pixel detector | CMS Detector Performance Note CMS-DP-2020-049, Oct, 2020 CDS |
|
| 33 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 34 | TOTEM Collaboration | The TOTEM experiment at the CERN Large Hadron Collider | JINST 3 (2008) S08007 | |
| 35 | TOTEM Collaboration | Performance of the TOTEM Detectors at the LHC | Int. J. Mod. Phys. A 28 (2013) 1330046 | 1310.2908 |
| 36 | S. Agostinelli et al. | Geant4 --- a simulation toolkit | NIM A 506 (2003) 250 | |
| 37 | K. Gottfried and J. D. Jackson | On the Connection between production mechanism and decay of resonances at high-energies | Nuovo Cim. 33 (1964) 309 | |
| 38 | ATLAS Collaboration | Measurement of the Inelastic Proton-Proton Cross Section at $ \sqrt{s} = $ 13 TeV with the ATLAS Detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 39 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 40 | LHCb Collaboration | Measurement of the inelastic $ pp $ cross-section at a centre-of-mass energy of 13 TeV | JHEP 06 (2018) 100 | 1803.10974 |
| 41 | TOTEM Collaboration | First measurement of elastic, inelastic and total cross-section at $ \sqrt{s}= $ 13 TeV by TOTEM and overview of cross-section data at LHC energies | EPJC 79 (2019) 103 | 1712.06153 |
| 42 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 43 | CMS and TOTEM Collaborations | Study of proton reconstruction using the TOTEM Roman pot detectors during the high-$ \beta^* $ data taking period | CMS DN-2013/014, 2023 | |
| 44 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 45 | CMS Collaboration | Measurement of Tracking Efficiency | CMS Physics Analysis Summary, 2010 CMS-PAS-TRK-10-002 |
|
| 46 | CMS Collaboration | Measurement of charged pion, kaon, and proton production in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | PRD 96 (2017) 112003 | CMS-FSQ-16-004 1706.10194 |
| 47 | R. Sternheimer, M. Berger, and S. Seltzer | Density effect for the ionization loss of charged particles in various substances | Atom.\ Data Nucl.\, 1984 Data Tabl. 30 (1984) 261 |
|
| 48 | L. A. Harland-Lang, V. A. Khoze, and M. G. Ryskin | Exclusive physics at the LHC with SuperChic 2 | EPJC 76 (2016) 9 | 1508.02718 |
| 49 | R. Kycia, J. Chwastowski, R. Staszewski, and J. Turnau | GenEx: A simple generator structure for exclusive processes in high energy collisions | Commun. Comput. Phys. 24 (2018) 860 | 1411.6035 |
| 50 | M. Mieskolainen | GRANIITTI: A Monte Carlo Event Generator for High Energy Diffraction | 1910.06300 | |
| 51 | TOTEM Collaboration | First determination of the $ {\rho } $ parameter at $ {\sqrt{s} = 13} $ TeV: probing the existence of a colourless C-odd three-gluon compound state | EPJC 79 (2019) 785 | 1812.04732 |
| 52 | TOTEM Collaboration | Elastic differential cross-section measurement at $ \sqrt{s}= $ 13 TeV by TOTEM | EPJC 79 (2019) 861 | 1812.08283 |
| 53 | V. A. Khoze, A. D. Martin, and M. G. Ryskin | t dependence of the slope of the high energy elastic pp cross section | JPG 42 (2015) 025003 | 1410.0508 |
| 54 | A. Buckley et al. | Systematic event generator tuning for the LHC | EPJC 65 (2010) 331 | 0907.2973 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|