Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-SMP-19-006 | ||
| Study of hard color singlet exchange in dijet events with proton-proton collisions at $\sqrt{s}= $ 13 TeV | ||
| CMS and TOTEM Collaborations | ||
| April 2020 | ||
| Abstract: This note presents a study of proton-proton collision events where the two leading jets are separated by a large pseudorapidity interval devoid of particle activity, known as jet-gap-jet events. Both jets have transverse momentum $p_\text{T, jet} > $ 40 GeV and pseudorapidity 1.4 $ < |\eta_\text{jet}| < $ 4.7, with $\eta_\text{jet-1}\times \eta_\text{jet-2} < $ 0. The analysis is based on data collected by the CMS experiment in proton-proton collisions during a low luminosity, high-$\beta^*$ run in 2015 at $\sqrt{s} = $ 13 TeV, with an integrated luminosity of 0.66 pb$^{-1}$. The number of charged particles detected with transverse momentum $p_\text{T} > $ 200 MeV in the fixed pseudorapidity interval $-1 < \eta < 1$ between the jets is used to discriminate jet-gap-jet events from color exchange dijet events. The fraction of jet-gap-jet events to all dijet events with similar kinematics, $f_\text{CSE}$, is presented as a function of the pseudorapidity difference between the leading two jets, the transverse momentum of the subleading jet, and the azimuthal angle separation between the leading two jets. The results are compared to previous measurements and to perturbative quantum chromodynamics predictions. In addition, the note presents the first study of jet-gap-jet events with a leading proton, interpreted as a proton-gap-jet-gap-jet topology, using a subsample of events collected by the CMS and TOTEM experiments with an integrated luminosity of 0.40 pb$^{-1}$. The leading protons are detected with the Roman pot detectors of the TOTEM experiment. The ratio $f_\text{CSE}$ in this sample is found to be 2.91 $\pm$ 0.70 (stat) $^{+ 1.02}_{- 0.94}$ (syst) times larger than that for inclusive dijet production for dijets with similar kinematics. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Accepted by PRD. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
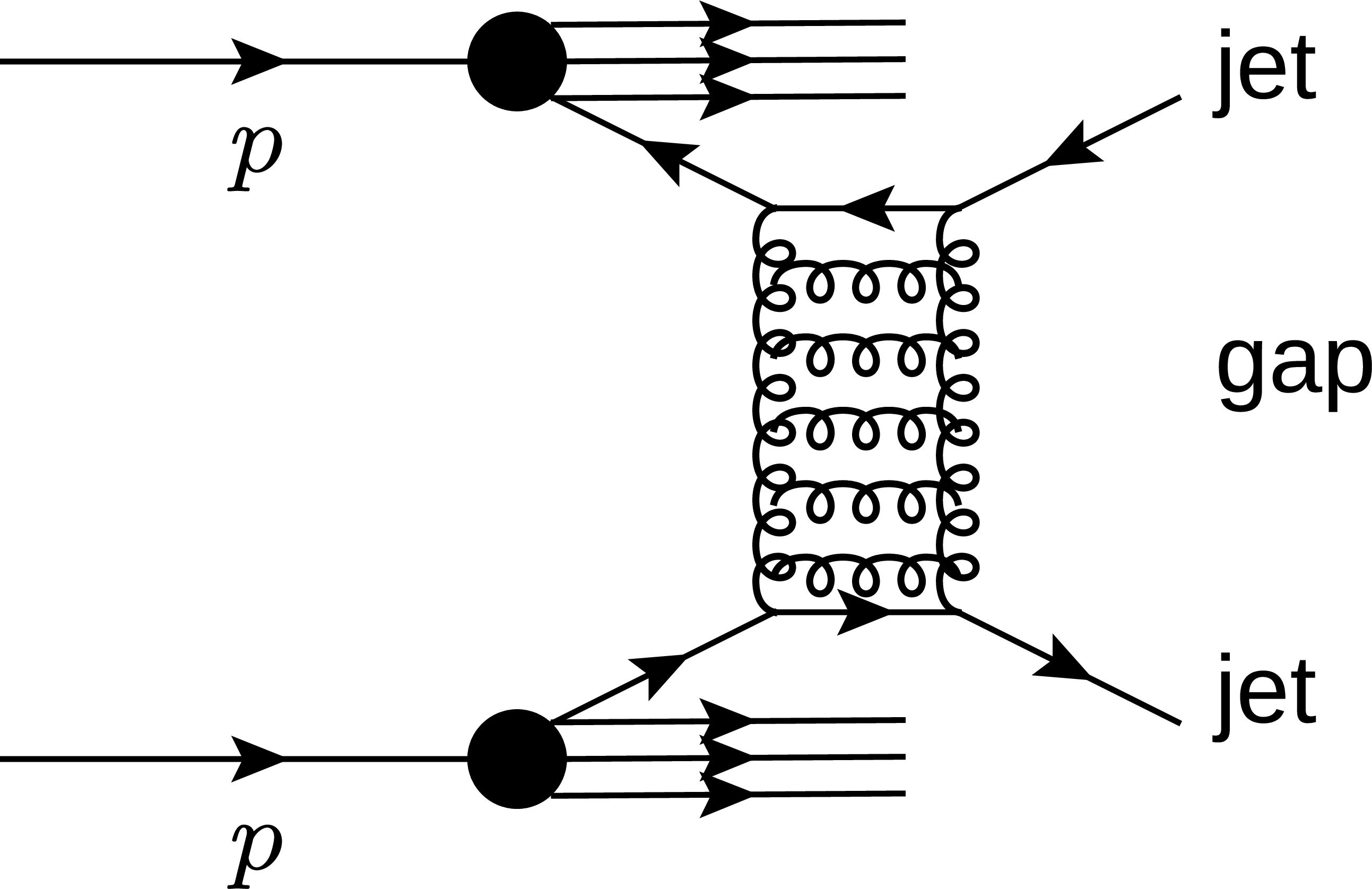
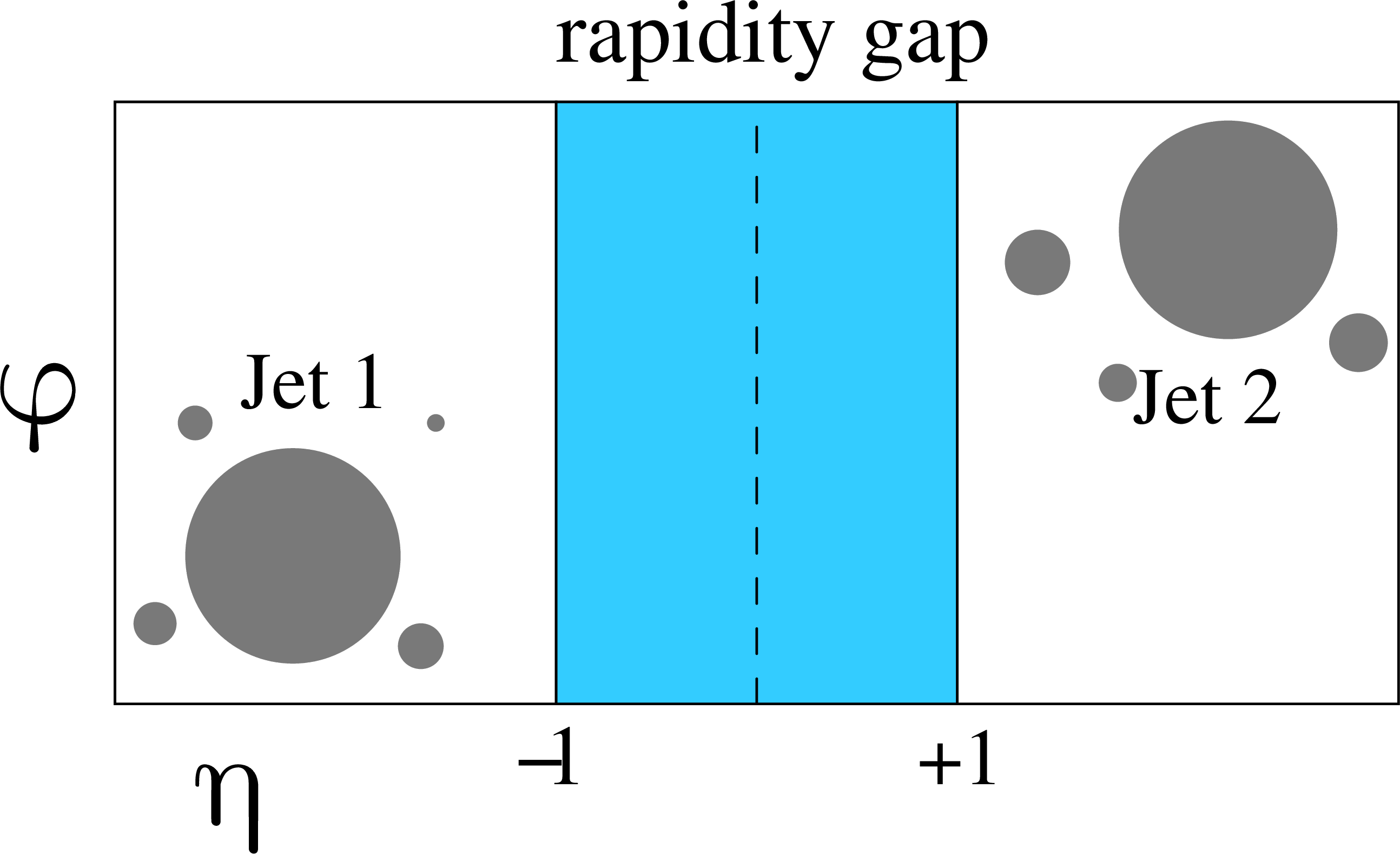
Figure 1:
(Left) Schematic diagram of $t$-channel two-gluon exchange in pp collisions, which yields the jet-gap-jet signature reconstructed in the CMS detector. The lines adjacent to the protons represent the proton breakup. (Right) Jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled area between the jets denotes the fixed pseudorapidity region $|\eta | < $ 1 devoid of charged particle tracks. |
png pdf |
Figure 1-a:
(Left) Schematic diagram of $t$-channel two-gluon exchange in pp collisions, which yields the jet-gap-jet signature reconstructed in the CMS detector. The lines adjacent to the protons represent the proton breakup. (Right) Jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled area between the jets denotes the fixed pseudorapidity region $|\eta | < $ 1 devoid of charged particle tracks. |
png pdf |
Figure 1-b:
(Left) Schematic diagram of $t$-channel two-gluon exchange in pp collisions, which yields the jet-gap-jet signature reconstructed in the CMS detector. The lines adjacent to the protons represent the proton breakup. (Right) Jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled area between the jets denotes the fixed pseudorapidity region $|\eta | < $ 1 devoid of charged particle tracks. |
png pdf |
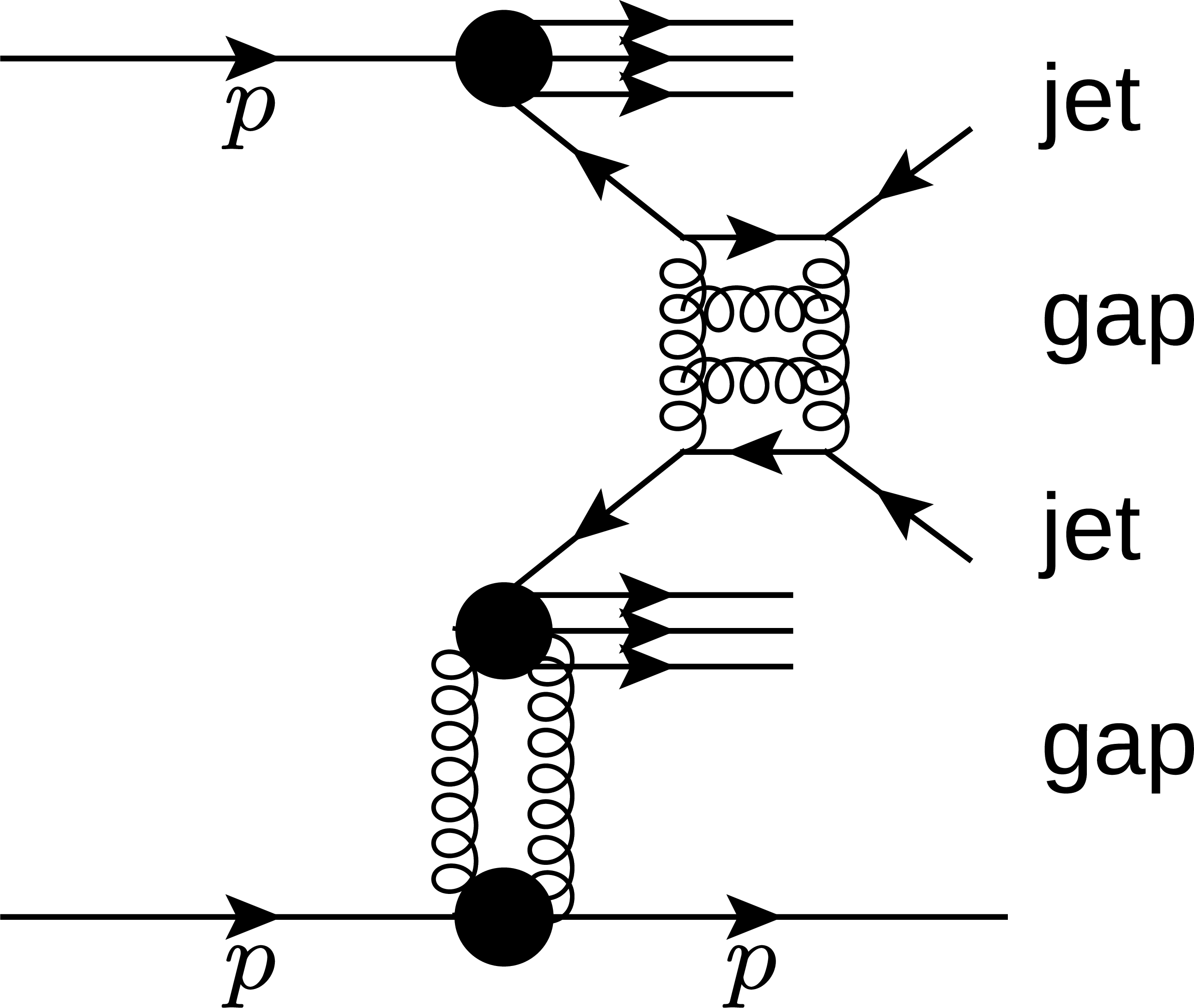
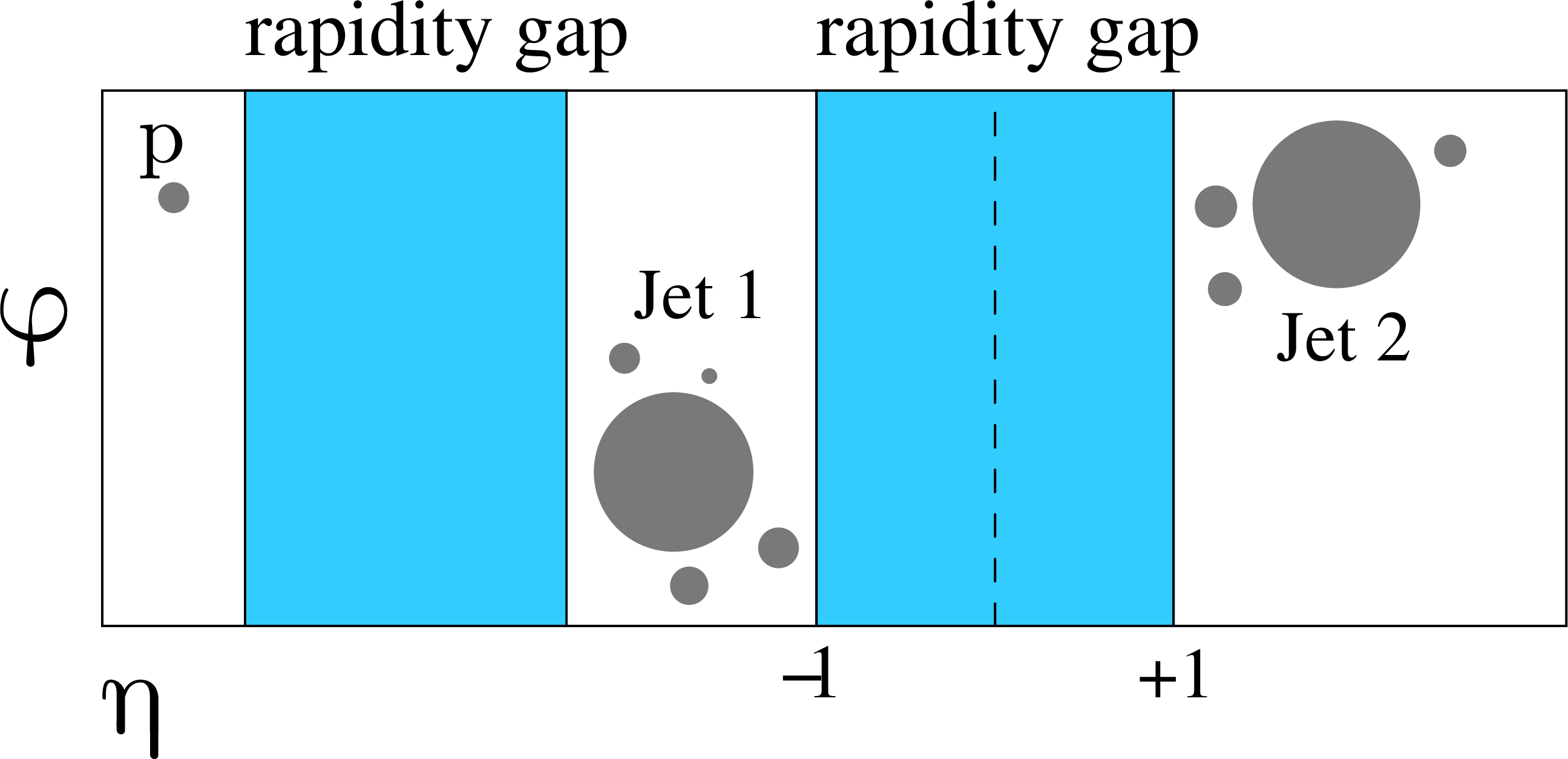
Figure 2:
(Left) Schematic diagram of the production of jet-gap-jet event with a leading proton in pp collisions. The jet-gap-jet signature is observed in the CMS detector, while the leading proton is detected with the forward proton spectrometer of the TOTEM experiment. (Right) Proton-gap-jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled areas denote the central gap region $|\eta | < $ 1 where the charged particle track multiplicity is measured, and the forward rapidity gap which is inferred from the forward proton detection. |
png pdf |
Figure 2-a:
(Left) Schematic diagram of the production of jet-gap-jet event with a leading proton in pp collisions. The jet-gap-jet signature is observed in the CMS detector, while the leading proton is detected with the forward proton spectrometer of the TOTEM experiment. (Right) Proton-gap-jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled areas denote the central gap region $|\eta | < $ 1 where the charged particle track multiplicity is measured, and the forward rapidity gap which is inferred from the forward proton detection. |
png pdf |
Figure 2-b:
(Left) Schematic diagram of the production of jet-gap-jet event with a leading proton in pp collisions. The jet-gap-jet signature is observed in the CMS detector, while the leading proton is detected with the forward proton spectrometer of the TOTEM experiment. (Right) Proton-gap-jet-gap-jet event signature in the $\eta $-$\phi $ plane. The filled circles represent final-state particles. The filled areas denote the central gap region $|\eta | < $ 1 where the charged particle track multiplicity is measured, and the forward rapidity gap which is inferred from the forward proton detection. |
png pdf |
Figure 3:
Side-view of detectors configuration during the 2015 CMS-TOTEM combined run. The horizontal dashed line indicates the beamline. The CMS detector is denoted by the filled circle in the center. The leading proton(s) are transported via the accelerator magnetic fields (blue rectangles), eventually passing through the silicon detectors housed in the Roman pots (black rectangles) of the TOTEM experiment. Sector 45 and sector 56 are located towards the positive and negative pseudorapidities in the CMS coordinate system, respectively. |
png pdf |
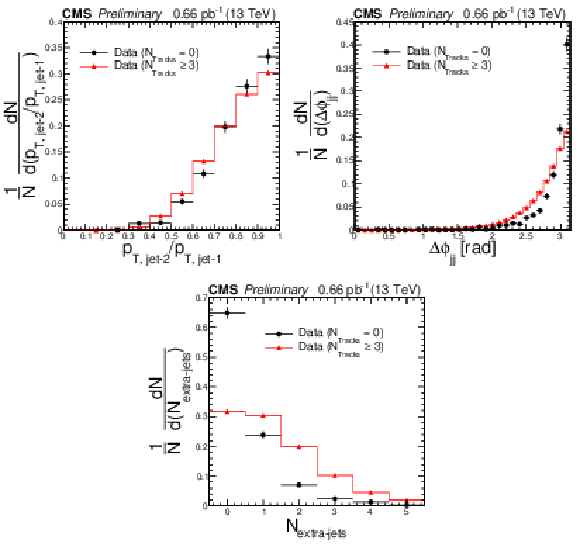
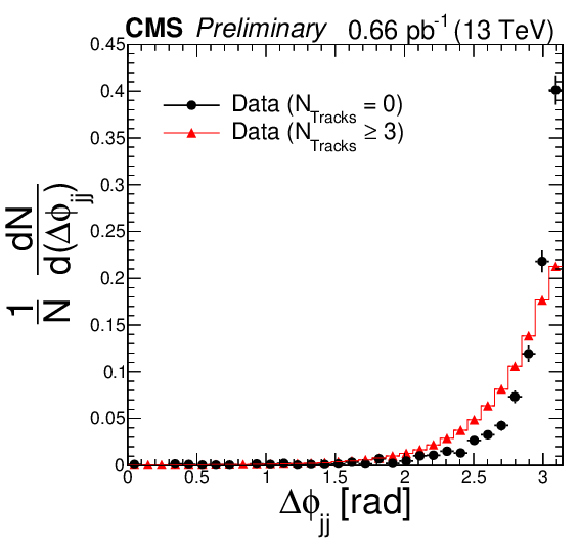
Figure 4:
Distributions of the ratio of subleading jet transverse momentum to leading jet transverse momentum $p_\text {T, jet-2}/p_\text {T, jet-1}$ (left), azimuthal angle separation between leading two jets $\Delta \phi _\text {jj}$(right), and number of additional jets $N_\text {extra-jets}$ with $p_\text {T,extra-jet} > $ 15 GeV (bottom), for jet-gap-jet candidates with $N_\text {Tracks} = $ 0 in $|\eta | < $ 1 (black) and the color exchange dijet candidates $N_\text {Tracks} \geq $ 3 in $|\eta | < $ 1 (red). The distributions are normalized to unity. |
png pdf |
Figure 4-a:
Distributions of the ratio of subleading jet transverse momentum to leading jet transverse momentum $p_\text {T, jet-2}/p_\text {T, jet-1}$ (left), azimuthal angle separation between leading two jets $\Delta \phi _\text {jj}$(right), and number of additional jets $N_\text {extra-jets}$ with $p_\text {T,extra-jet} > $ 15 GeV (bottom), for jet-gap-jet candidates with $N_\text {Tracks} = $ 0 in $|\eta | < $ 1 (black) and the color exchange dijet candidates $N_\text {Tracks} \geq $ 3 in $|\eta | < $ 1 (red). The distributions are normalized to unity. |
png pdf |
Figure 4-b:
Distributions of the ratio of subleading jet transverse momentum to leading jet transverse momentum $p_\text {T, jet-2}/p_\text {T, jet-1}$ (left), azimuthal angle separation between leading two jets $\Delta \phi _\text {jj}$(right), and number of additional jets $N_\text {extra-jets}$ with $p_\text {T,extra-jet} > $ 15 GeV (bottom), for jet-gap-jet candidates with $N_\text {Tracks} = $ 0 in $|\eta | < $ 1 (black) and the color exchange dijet candidates $N_\text {Tracks} \geq $ 3 in $|\eta | < $ 1 (red). The distributions are normalized to unity. |
png pdf |
Figure 4-c:
Distributions of the ratio of subleading jet transverse momentum to leading jet transverse momentum $p_\text {T, jet-2}/p_\text {T, jet-1}$ (left), azimuthal angle separation between leading two jets $\Delta \phi _\text {jj}$(right), and number of additional jets $N_\text {extra-jets}$ with $p_\text {T,extra-jet} > $ 15 GeV (bottom), for jet-gap-jet candidates with $N_\text {Tracks} = $ 0 in $|\eta | < $ 1 (black) and the color exchange dijet candidates $N_\text {Tracks} \geq $ 3 in $|\eta | < $ 1 (red). The distributions are normalized to unity. |
png pdf |
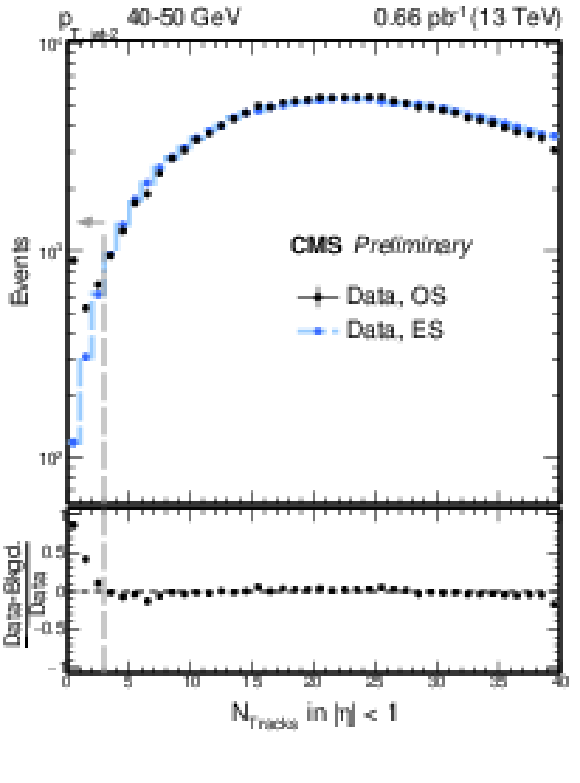
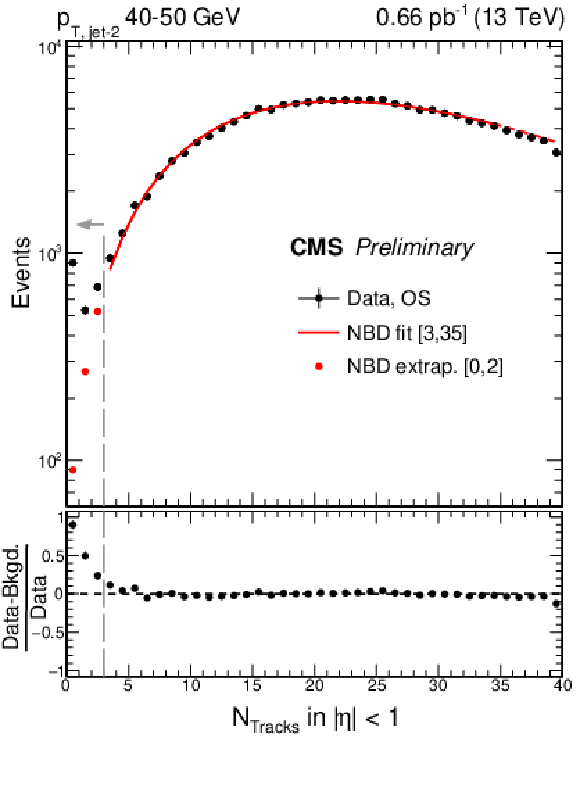
Figure 5:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 for charged particle tracks with ${p_{\mathrm {T}}} > $ 200 MeV for dijet events with 40 $ < p_\text {T, jet-2} < $ 50 GeV. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars, which represent statistical uncertainties, are smaller than the markers for most data points. Results from color exchange dijet background estimation based on the equal side (ES) dijet events and the negative binomial distribution (NBD) function fit are shown on the left and right panels, respectively. The NBD function is fit in 3 $ \leq N_\text {Tracks} \leq $ 35, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 3. The fraction $f_\text {CSE}$ corresponds to the ratio of the excess of events at low multiplicities relative to the integrated number of events, as described in text. The dashed curve in $N_\text {Tracks} > $ 35 on the right panel is an extrapolation of the NBD fit. |
png pdf |
Figure 5-a:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 for charged particle tracks with ${p_{\mathrm {T}}} > $ 200 MeV for dijet events with 40 $ < p_\text {T, jet-2} < $ 50 GeV. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars, which represent statistical uncertainties, are smaller than the markers for most data points. Results from color exchange dijet background estimation based on the equal side (ES) dijet events and the negative binomial distribution (NBD) function fit are shown on the left and right panels, respectively. The NBD function is fit in 3 $ \leq N_\text {Tracks} \leq $ 35, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 3. The fraction $f_\text {CSE}$ corresponds to the ratio of the excess of events at low multiplicities relative to the integrated number of events, as described in text. The dashed curve in $N_\text {Tracks} > $ 35 on the right panel is an extrapolation of the NBD fit. |
png pdf |
Figure 5-b:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 for charged particle tracks with ${p_{\mathrm {T}}} > $ 200 MeV for dijet events with 40 $ < p_\text {T, jet-2} < $ 50 GeV. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars, which represent statistical uncertainties, are smaller than the markers for most data points. Results from color exchange dijet background estimation based on the equal side (ES) dijet events and the negative binomial distribution (NBD) function fit are shown on the left and right panels, respectively. The NBD function is fit in 3 $ \leq N_\text {Tracks} \leq $ 35, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 3. The fraction $f_\text {CSE}$ corresponds to the ratio of the excess of events at low multiplicities relative to the integrated number of events, as described in text. The dashed curve in $N_\text {Tracks} > $ 35 on the right panel is an extrapolation of the NBD fit. |
png pdf |
Figure 6:
Distribution of $\xi _p(\text {PF}) - \xi _p(\text {RP})$ in sector 45 (left) and sector 56 (right) in data, where $\xi _p(\text {PF})$ and $\xi _p(\text {RP})$ denote the fractional momentum loss of the proton reconstructed with the particle-flow (PF) candidates of CMS and the Roman pots (RP) of TOTEM, respectively. Vertical bars indicate statistical uncertainties only. The estimated background contamination (beam background events) is represented by the filled histogram, and is estimated from the data, as described in text. No central pseudorapidity gap is required for this plot. The vertical dashed line represents the requirement applied in the analysis to remove most of the beam background contribution. |
png pdf |
Figure 6-a:
Distribution of $\xi _p(\text {PF}) - \xi _p(\text {RP})$ in sector 45 (left) and sector 56 (right) in data, where $\xi _p(\text {PF})$ and $\xi _p(\text {RP})$ denote the fractional momentum loss of the proton reconstructed with the particle-flow (PF) candidates of CMS and the Roman pots (RP) of TOTEM, respectively. Vertical bars indicate statistical uncertainties only. The estimated background contamination (beam background events) is represented by the filled histogram, and is estimated from the data, as described in text. No central pseudorapidity gap is required for this plot. The vertical dashed line represents the requirement applied in the analysis to remove most of the beam background contribution. |
png pdf |
Figure 6-b:
Distribution of $\xi _p(\text {PF}) - \xi _p(\text {RP})$ in sector 45 (left) and sector 56 (right) in data, where $\xi _p(\text {PF})$ and $\xi _p(\text {RP})$ denote the fractional momentum loss of the proton reconstructed with the particle-flow (PF) candidates of CMS and the Roman pots (RP) of TOTEM, respectively. Vertical bars indicate statistical uncertainties only. The estimated background contamination (beam background events) is represented by the filled histogram, and is estimated from the data, as described in text. No central pseudorapidity gap is required for this plot. The vertical dashed line represents the requirement applied in the analysis to remove most of the beam background contribution. |
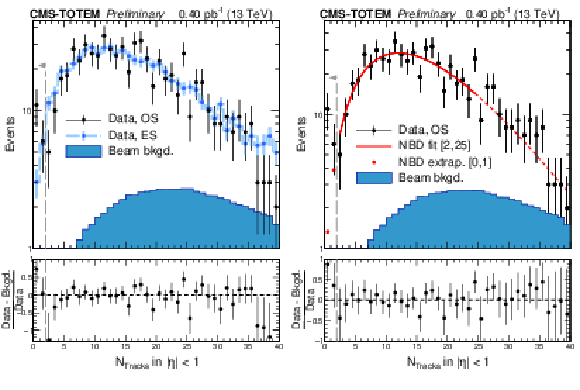
png pdf |
Figure 7:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 after the dijet selection and proton selection. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars indicate statistical uncertainties. The filled histogram represents the residual beam related contamination. The contribution of proton-gap-jet-jet events which feature a central gap is modeled with the equal side (ES) dijet events (left) and with the negative binomial distribution (NBD) function fit (right), as described in text. The NBD function is fit in 2 $ \leq N_\text {Tracks} \leq $ 25, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 2. An excess is observed in the lowest charged particle multiplicity bins, which corresponds to the presence of proton-gap-jet-gap-jet events in the sample. The dashed curve on the right panel represents an extrapolation of the NBD fit to $N_\text {Tracks} > $ 25. |
png pdf |
Figure 7-a:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 after the dijet selection and proton selection. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars indicate statistical uncertainties. The filled histogram represents the residual beam related contamination. The contribution of proton-gap-jet-jet events which feature a central gap is modeled with the equal side (ES) dijet events (left) and with the negative binomial distribution (NBD) function fit (right), as described in text. The NBD function is fit in 2 $ \leq N_\text {Tracks} \leq $ 25, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 2. An excess is observed in the lowest charged particle multiplicity bins, which corresponds to the presence of proton-gap-jet-gap-jet events in the sample. The dashed curve on the right panel represents an extrapolation of the NBD fit to $N_\text {Tracks} > $ 25. |
png pdf |
Figure 7-b:
Charged particle multiplicity distribution in the fixed pseudorapidity region $|\eta | < $ 1 after the dijet selection and proton selection. Opposite side (OS) dijet events satisfy $\eta _\text {jet-1}\times \eta _\text {jet-2} < $ 0. Vertical bars indicate statistical uncertainties. The filled histogram represents the residual beam related contamination. The contribution of proton-gap-jet-jet events which feature a central gap is modeled with the equal side (ES) dijet events (left) and with the negative binomial distribution (NBD) function fit (right), as described in text. The NBD function is fit in 2 $ \leq N_\text {Tracks} \leq $ 25, and extrapolated down to $N_\text {Tracks} = $ 0. The vertical dashed line represents the jet-gap-jet signal region used in the analysis, $N_\text {Tracks} < $ 2. An excess is observed in the lowest charged particle multiplicity bins, which corresponds to the presence of proton-gap-jet-gap-jet events in the sample. The dashed curve on the right panel represents an extrapolation of the NBD fit to $N_\text {Tracks} > $ 25. |
png pdf |
Figure 8:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$, $p_\text {T,jet-2}$, and $\Delta \phi _\text {jj}$ in pp collisions at $\sqrt {s} = $ 13 TeV. Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The results are plotted at the mean values of $\Delta \eta _\text {jj}$, $p_\text {T, jet-2}$, and $\Delta \phi _\text {jj}$ in the bin. The results on $f_\text {CSE}$ versus $\Delta \eta _\text {jj}$ and $p_\text {T,jet-2}$ are integrated over $\Delta \phi _\text {jj}$. The solid curve corresponds to theoretical predictions by the Royon, Marquet, Kepka (RMK) model [70,71] with survival probability of $|\mathcal {S}|^2 = $ 10%. The hatched band represents the associated theoretical uncertainties. |
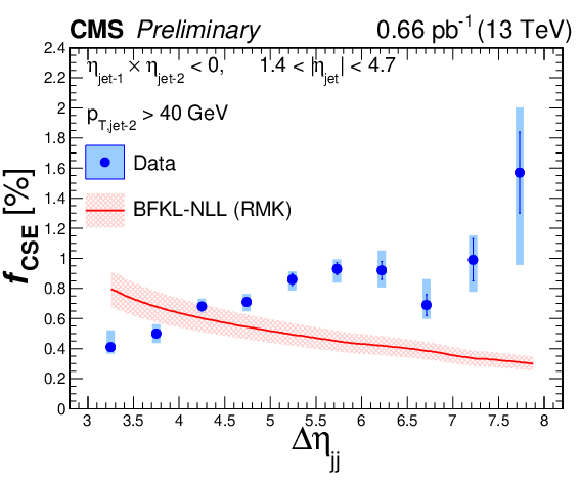
png pdf |
Figure 8-a:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$, $p_\text {T,jet-2}$, and $\Delta \phi _\text {jj}$ in pp collisions at $\sqrt {s} = $ 13 TeV. Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The results are plotted at the mean values of $\Delta \eta _\text {jj}$, $p_\text {T, jet-2}$, and $\Delta \phi _\text {jj}$ in the bin. The results on $f_\text {CSE}$ versus $\Delta \eta _\text {jj}$ and $p_\text {T,jet-2}$ are integrated over $\Delta \phi _\text {jj}$. The solid curve corresponds to theoretical predictions by the Royon, Marquet, Kepka (RMK) model [70,71] with survival probability of $|\mathcal {S}|^2 = $ 10%. The hatched band represents the associated theoretical uncertainties. |
png pdf |
Figure 8-b:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$, $p_\text {T,jet-2}$, and $\Delta \phi _\text {jj}$ in pp collisions at $\sqrt {s} = $ 13 TeV. Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The results are plotted at the mean values of $\Delta \eta _\text {jj}$, $p_\text {T, jet-2}$, and $\Delta \phi _\text {jj}$ in the bin. The results on $f_\text {CSE}$ versus $\Delta \eta _\text {jj}$ and $p_\text {T,jet-2}$ are integrated over $\Delta \phi _\text {jj}$. The solid curve corresponds to theoretical predictions by the Royon, Marquet, Kepka (RMK) model [70,71] with survival probability of $|\mathcal {S}|^2 = $ 10%. The hatched band represents the associated theoretical uncertainties. |
png pdf |
Figure 8-c:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$, $p_\text {T,jet-2}$, and $\Delta \phi _\text {jj}$ in pp collisions at $\sqrt {s} = $ 13 TeV. Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The results are plotted at the mean values of $\Delta \eta _\text {jj}$, $p_\text {T, jet-2}$, and $\Delta \phi _\text {jj}$ in the bin. The results on $f_\text {CSE}$ versus $\Delta \eta _\text {jj}$ and $p_\text {T,jet-2}$ are integrated over $\Delta \phi _\text {jj}$. The solid curve corresponds to theoretical predictions by the Royon, Marquet, Kepka (RMK) model [70,71] with survival probability of $|\mathcal {S}|^2 = $ 10%. The hatched band represents the associated theoretical uncertainties. |
png pdf |
Figure 9:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of the subleading jet transverse momentum $p_\text {T,jet-2}$ by the D0 and CDF Collaborations [42,43,40] at $\sqrt {s} = $ 0.63 (red symbols) and 1.8 TeV (green symbols), and by the CMS Collaboration [44] at 7 TeV (magenta symbol) and the present results at 13 TeV (blue band). The central gap is defined by means of the particle activity in the fixed pseudorapidity interval $|\eta | < $ 1 in these measurements. |
png pdf |
Figure 10:
Fraction of color singlet exchange dijet events, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$ by CMS at 7 TeV [44] and the present measurement at 13 TeV. The 7 TeV measurement was performed in three bins of the transverse momentum of the subleading jet $p_\text {T, jet-2} = $ 40-60, 60-100, 100-200 GeV, which are represented by the open circle, square, and cross symbols, respectively. |
png pdf |
Figure 11:
Gap fraction, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in inclusive dijet event production (labeled CMS, represented by the circle marker) and in dijet events with a leading proton at 13 TeV (labeled CMS-TOTEM, represented by the cross marker). Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The CMS-TOTEM results are plotted at the mean values of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in the bin. Most of the CMS-TOTEM events considered here have separations 3 $ < \Delta \eta _\text {jj} < $ 6.5, and transverse momenta 40 $ < p_\text {T, jet-2} < $ 100 GeV, as indicated in the figure. |
png pdf |
Figure 11-a:
Gap fraction, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in inclusive dijet event production (labeled CMS, represented by the circle marker) and in dijet events with a leading proton at 13 TeV (labeled CMS-TOTEM, represented by the cross marker). Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The CMS-TOTEM results are plotted at the mean values of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in the bin. Most of the CMS-TOTEM events considered here have separations 3 $ < \Delta \eta _\text {jj} < $ 6.5, and transverse momenta 40 $ < p_\text {T, jet-2} < $ 100 GeV, as indicated in the figure. |
png pdf |
Figure 11-b:
Gap fraction, $f_\text {CSE}$, measured as a function of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in inclusive dijet event production (labeled CMS, represented by the circle marker) and in dijet events with a leading proton at 13 TeV (labeled CMS-TOTEM, represented by the cross marker). Vertical bars represent statistical uncertainties, while boxes represent the combination of statistical and systematic uncertainties in quadrature. The CMS-TOTEM results are plotted at the mean values of $\Delta \eta _\text {jj}$ and $p_\text {T, jet-2}$ in the bin. Most of the CMS-TOTEM events considered here have separations 3 $ < \Delta \eta _\text {jj} < $ 6.5, and transverse momenta 40 $ < p_\text {T, jet-2} < $ 100 GeV, as indicated in the figure. |
| Tables | |
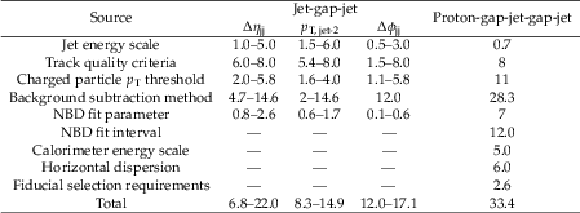
png pdf |
Table 1:
Relative systematic uncertainties in percentage for the measurements of $f_\text {CSE}$ in jet-gap-jet events and proton-gap-jet-gap-jet events. The jet-gap-jet results summarize the systematic uncertainties found in bins of the kinematic variables of interest $p_\text {T, jet-2}$, $\Delta \eta _\text {jj}$, and $\Delta \phi _\text {jj}$. When an uncertainty range is given, the range of values is representative of the variation found in the jet-gap-jet fraction in bins of the kinematic variables of interest. |
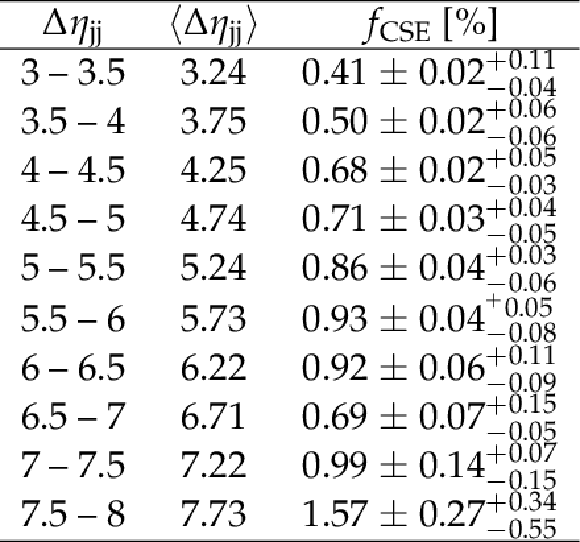
png pdf |
Table 2:
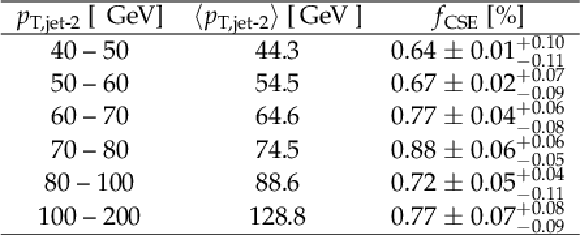
Measured values of the jet-gap-jet fraction $f_\text {CSE}$ in bins of pseudorapidity difference between the leading two jets $\Delta \eta _\text {jj}$. The first column indicates the $\Delta \eta _\text {jj}$ intervals and the last column represents the measured fraction. The first and second uncertainties correspond to the statistical and systematic components, respectively. The results are for jets satisfying $p_\text {T, jet} > $ 40 GeV and 0 $ < \Delta \phi _\text {jj} < \pi $. The mean values of $\Delta \eta _\text {jj}$ in the bin are given in the middle column. |
png pdf |
Table 3:
Measured values of the jet-gap-jet fraction $f_\text {CSE}$ in bins of the subleading jet transverse momentum $p_\text {T,jet-2}$. The first column indicates the $p_\text {T,jet-2}$ bin intervals and the last column represents the measured fraction. The first and second uncertainties correspond to the statistical and systematic components, respectively. The results are for jets satisfying 1.4 $ < |\eta _\text {jet}| < $ 4.7 and 0 $ < \Delta \phi _\text {jj} < \pi $. The mean values of $p_\text {T,jet-2}$ in the bin are given in the middle column. |
png pdf |
Table 4:
Measured values of the jet-gap-jet fraction $f_\text {CSE}$ in bins of azimuthal angle difference between the leading two jets $\Delta \phi _\text {jj}$. The first column indicates the $\Delta \phi _\text {jj}$ bin intervals and the last column represents the measured fraction. The first and second uncertainties correspond to the statistical and systematic components, respectively. The results are for jets satisfying $p_\text {T, jet} > $ 40 GeV and 1.4 $ < |\eta _\text {jet} | < $ 4.7. The mean values of $\Delta \phi _\text {jj}$ in the bin are given in the middle column. |
| Summary |
|
Events with two leading jets separated by a large pseudorapidity gap have been studied in pp collisions at $\sqrt{s}=$ 13 TeV with the CMS detector. The "gap'' is determined by the absence of charged particles with ${p_{\mathrm{T}}} > $ 200 MeV in the pseudorapidity range $|\eta| < $ 1 produced in the collision. Each of the two leading jets has pseudorapidity values of 1.4 $ < |\eta_\text{jet}| < $ 4.7 and transverse momentum of $p_\text{T, jet} > $ 40 GeV, with $\eta_\text{jet-1} \times \eta_\text{jet-2} < $ 0. The pseudorapidity gap signature is indicative of an underlying hard color singlet exchange, which is described in terms of two-gluon exchange in perturbative quantum chromodynamics. Jet-gap-jet events appear as an excess of events over the expected charged particle multiplicity of color exchange dijet events at the lowest charged particle multiplicity counts. The fraction of jet-gap-jet events to events where the two jets have similar kinematics, $f_\text{CSE}$, has been measured as a function of the pseudorapidity difference between the leading two jets, $\Delta\eta_\text{jj} \equiv |\eta_\text{jet-1} - \eta_\text{jet-2}|$, the transverse momentum of the subleading jet, $p_\text{T, jet-2}$, and the azimuthal angle separation between the leading two jets, $\Delta\phi_\text{jj} \equiv |\phi_\text{jet-1} - \phi_\text{jet-2}|$. The fraction $f_\text{CSE}$ has values of 0.6-1%. It increases with $\Delta\eta_\text{jj}$, is only weakly dependent on $p_\text{T, jet-2}$, and increases as $\Delta\phi_\text{jj}$ approaches $\pi$. No significant difference in $f_\text{CSE}$ is observed comparing the present results at 13 TeV with those presented by the CMS Collaboration at 7 TeV. This is in contrast to the trend found at lower collision energies of 0.63 and 1.8 TeV by the D0 and CDF Collaborations, where a significant decrease with increasing energy was observed. The results are compared with calculations based on the Balitsky-Fadin-Kuraev-Lipatov framework with resummation of large logarithms of energy at next-to-leading logarithm accuracy, leading order impact factors, and a constant survival probability factor. The implementation by Royon, Marquet, and Kepka describes some features of the data, but is not able to simultaneously describe all aspects of the measurement. The present disagreement between theory and data provides guidance for further improvements on the perturbative and nonperturbative treatment for pseudorapidity gap formation and destruction mechanisms. Complementary to the jet-gap-jet study, a sample of dijet events with leading protons collected by the CMS and TOTEM experiments in 2015 is used to study jet-gap-jet events with leading protons, which correspond to proton-gap-jet-gap-jet topologies. This is the first study of this diffractive event topology. The gap fraction extracted in this sample is found to be 2.91 $\pm$ 0.70 (stat) $^{+ 1.02}_{- 0.94}$ (syst) times larger than that found in inclusive dijet production, pointing to a larger abundance of jets with a central gap in events with leading protons. This can be interpreted in terms of a lower spectator parton activity in events with leading protons, which decreases the likelihood of the central gap signature being spoiled. |
| References | ||||
| 1 | Particle Data Group Collaboration | Review of Particle Physics | PRD 98 (2018) 030001 | |
| 2 | E. A. Kuraev, L. N. Lipatov, and V. S. Fadin | The Pomeranchuk singularity in nonabelian gauge theories | Sov. Phys. JETP 45 (1977)199 | |
| 3 | I. I. Balitsky and L. N. Lipatov | The Pomeranchuk singularity in quantum chromodynamics | Sov. J. NP 28 (1978)822 | |
| 4 | L. N. Lipatov | The bare pomeron in quantum chromodynamics | Sov. Phys. JETP 63 (1986)904 | |
| 5 | V. S. Fadin and L. N. Lipatov | BFKL pomeron in the next-to-leading approximation | PLB 429 (1998) 127 | hep-ph/9802290 |
| 6 | M. Ciafaloni and G. Camici | Energy scale(s) and next-to-leading BFKL equation | PLB 430 (1998) 349 | hep-ph/9803389 |
| 7 | CMS Collaboration | Azimuthal decorrelation of jets widely separated in rapidity in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 08 (2016) 139 | CMS-FSQ-12-002 1601.06713 |
| 8 | LHCb Collaboration | Updated measurements of exclusive $ \mathrm{J}/\psi $ and $ \psi $(2S) production cross-sections in pp collisions at $ \sqrt{s}= $ 7 TeV | JPG 41 (2014) 055002 | 1401.3288 |
| 9 | LHCb Collaboration | Measurement of the exclusive Y production cross-section in pp collisions at $ {\sqrt{s}=7} $ TeV and 8 TeV | JHEP 09 (2015) 084 | 1505.08139 |
| 10 | ALICE Collaboration | Coherent $ J/\psi $ photoproduction in ultra-peripheral Pb-Pb collisions at $ \sqrt{s_{NN}} = $ 2.76 TeV | PLB 718 (2013) 1273 | 1209.3715 |
| 11 | ALICE Collaboration | Exclusive $ \mathrm{J/}\psi $ photoproduction off protons in ultra-peripheral p-Pb collisions at $ \sqrt{s_{\rm NN}}= $ 5.02 TeV | PRL 113 (2014) 232504 | 1406.7819 |
| 12 | ALICE Collaboration | Coherent $ \rho^{0} $ photoproduction in ultra-peripheral Pb-Pb collisions at $ \sqrt{s_{\mathrm{NN}}}= $ 2.76 TeV | JHEP 09 (2015) 095 | 1503.09177 |
| 13 | CMS Collaboration | Measurement of exclusive $ \Upsilon $ photoproduction from protons in pPb collisions at $ \sqrt{s_\mathrm{NN}} = $ 5.02 TeV | EPJC 79 (2019) 277 | CMS-FSQ-13-009 1809.11080 |
| 14 | CMS Collaboration | Measurement of exclusive $ \rho(770)^0 $ photoproduction in ultraperipheral pPb collisions at $ \sqrt{s_\mathrm{NN}} = $ 5.02 TeV | EPJC 79 (2019) 702 | CMS-FSQ-16-007 1902.01339 |
| 15 | V. N. Gribov and L. N. Lipatov | Deep inelastic ep scattering in perturbation theory | Sov. J. NP 15 (1972)438 | |
| 16 | G. Altarelli and G. Parisi | Asymptotic freedom in parton language | NPB 126 (1977) 298 | |
| 17 | Y. L. Dokshitzer | Calculation of the structure functions for deep inelastic scattering and e$ ^{+} $ e$ ^{-} $ annihilation by perturbation theory in quantum chromodynamics | Sov. Phys. JETP 46 (1977)641 | |
| 18 | CMS Collaboration | Measurement of the differential dijet production cross section in proton-proton collisions at $ \sqrt{s}= $ 7 TeV | PLB 700 (2011) 187 | CMS-QCD-10-025 1104.1693 |
| 19 | CMS Collaboration | Measurement of the inclusive production cross sections for forward jets and for dijet events with one forward and one central jet in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 06 (2012) 036 | CMS-FWD-11-002 1202.0704 |
| 20 | CMS Collaboration | Ratios of dijet production cross sections as a function of the absolute difference in rapidity between jets in proton-proton collisions at $ \sqrt{s}= $ 7 TeV | EPJC 72 (2012) 2216 | CMS-FWD-10-014 1204.0696 |
| 21 | CMS Collaboration | Measurement of the inclusive jet cross section in pp collisions at $ \sqrt{s} = $ 2.76 TeV | EPJC 76 (2016) 265 | CMS-SMP-14-017 1512.06212 |
| 22 | CMS Collaboration | Measurement of dijet azimuthal decorrelation in pp collisions at $ \sqrt{s}= $ 8 TeV | EPJC 76 (2016) 536 | CMS-SMP-14-015 1602.04384 |
| 23 | CMS Collaboration | Measurement of the double-differential inclusive jet cross section in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | EPJC 76 (2016) 451 | CMS-SMP-15-007 1605.04436 |
| 24 | CMS Collaboration | Measurement and QCD analysis of double-differential inclusive jet cross sections in pp collisions at $ \sqrt{s}= $ 8 TeV and cross section ratios to 2.76 and 7 TeV | JHEP 03 (2017) 156 | CMS-SMP-14-001 1609.05331 |
| 25 | CMS Collaboration | Azimuthal correlations for inclusive 2-jet, 3-jet, and 4-jet events in pp collisions at $ \sqrt{s}= $ 13 TeV | EPJC 78 (2018) 566 | CMS-SMP-16-014 1712.05471 |
| 26 | CMS Collaboration | Measurement of inclusive very forward jet cross sections in proton-lead collisions at $ \sqrt{s_{\mathrm{NN}}} = $ 5.02 TeV | JHEP 05 (2019) 043 | CMS-FSQ-17-001 1812.01691 |
| 27 | ATLAS Collaboration | Measurement of inclusive jet and dijet cross sections in proton-proton collisions at 7 TeV centre-of-mass energy with the ATLAS detector | EPJC 71 (2011) 1512 | 1009.5908 |
| 28 | ATLAS Collaboration | Measurement of dijet production with a veto on additional central jet activity in pp collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | JHEP 09 (2011) 053 | 1107.1641 |
| 29 | ATLAS Collaboration | Measurement of inclusive jet and dijet production in pp collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | PRD 86 (2012) 014022 | 1112.6297 |
| 30 | ATLAS Collaboration | Measurement of dijet cross sections in pp collisions at 7 TeV centre-of-mass energy using the ATLAS detector | JHEP 05 (2014) 059 | 1312.3524 |
| 31 | ATLAS Collaboration | Measurements of jet vetoes and azimuthal decorrelations in dijet events produced in pp collisions at $ \sqrt{s}= $ 7 TeV using the ATLAS detector | EPJC 74 (2014) 3117 | 1407.5756 |
| 32 | ATLAS Collaboration | Measurement of the inclusive jet cross-sections in proton-proton collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | JHEP 09 (2017) 020 | 1706.03192 |
| 33 | ATLAS Collaboration | Measurement of dijet azimuthal decorrelations in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector and determination of the strong coupling | PRD 98 (2018) 092004 | 1805.04691 |
| 34 | R. D. Ball et al. | Parton distributions with small-$ x $ resummation: evidence for BFKL dynamics in HERA data | EPJC 78 (2018) 321 | 1710.05935 |
| 35 | A. Mueller and W.-K. Tang | High energy parton-parton elastic scattering in QCD | PLB 284 (1992) 123 | |
| 36 | H1 Collaboration | Energy flow and rapidity gaps between jets in photoproduction at HERA | EPJC 24 (2002) 517 | hep-ex/0203011 |
| 37 | ZEUS Collaboration | Rapidity gaps between jets in photoproduction at HERA | PLB 369 (1996) 55 | hep-ex/9510012 |
| 38 | D0 Collaboration | Rapidity gaps between jets in p$ \bar{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 1.8 TeV | PRL 72 (1994) 2332 | |
| 39 | D0 Collaboration | Jet production via strongly-interacting color-singlet exchange in p$ \bar{\mathrm{p}} $ collisions | PRL 76 (1996) 734 | hep-ex/9509013 |
| 40 | D0 Collaboration | Probing hard color-singlet exchange in p$ \bar{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 630 GeV and 1800 GeV | PLB 440 (1998) 189 | hep-ex/9809016 |
| 41 | CDF Collaboration | Observation of rapidity gaps in $ \bar{\mathrm{p}} $p collisions at 1.8 TeV | PRL 74 (1995) 855 | |
| 42 | CDF Collaboration | Dijet production by color-singlet exchange at the Fermilab Tevatron | PRL 80 (1998) 1156 | |
| 43 | CDF Collaboration | Events with a rapidity gap between jets in $ \bar{\mathrm{p}} $p collisions at $ \sqrt{s} = $ 630 GeV | PRL 81 (1998) 5278 | |
| 44 | CMS Collaboration | Study of dijet events with a large rapidity gap between the two leading jets in pp collisions at $ \sqrt{s}= $ 7 TeV | EPJC 78 (2018) 242 | CMS-FSQ-12-001 1710.02586 |
| 45 | J. D. Bjorken | Rapidity gaps and jets as a new-physics signature in very-high-energy hadron-hadron collisions | PRD 47 (1993) 101 | |
| 46 | V. Barone and E. Predazzi | High-energy particle diffraction | Springer, Berlin | |
| 47 | S. Donnachie, G. Dosch, P. Landshoff, and O. Nachtmann | Pomeron physics and QCD | Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press | |
| 48 | J. R. Forshaw and D. A. Ross | Quantum chromodynamics and the pomeron | Cambridge Lecture Notes in Physics. Cambridge University Press | |
| 49 | J. Bjorken | A full-acceptance detector for SSC physics at low and intermediate mass scales: an expression of interest to the SSC | International Journal of Modern Physics A 07 (1992) 4189 | |
| 50 | E. Gotsman, E. Levin, and U. Maor | Energy dependence of the survival probability of large rapidity gaps | PLB 438 (1998) 229 | hep-ph/9804404 |
| 51 | V. A. Khoze, A. D. Martin, and M. G. Ryskin | Diffraction at the LHC | EPJC 73 (2013) 2503 | 1306.2149 |
| 52 | E. Gotsman, E. Levin, and U. Maor | CGC/saturation approach for soft interactions at high energy: survival probability of central exclusive production | EPJC 76 (2016) 177 | 1510.07249 |
| 53 | V. A. Khoze, A. D. Martin, and M. G. Ryskin | Multiple interactions and rapidity gap survival | JPG 45 (2018) 053002 | 1710.11505 |
| 54 | R. Enberg, G. Ingelman, and L. Motyka | Hard color singlet exchange and gaps between jets at the Tevatron | PLB 524 (2002) 273 | hep-ph/0111090 |
| 55 | I. Babiarz, R. Staszewski, and A. Szczurek | Multi-parton interactions and rapidity gap survival probability in jet-gap-jet processes | PLB 771 (2017) 532 | 1704.00546 |
| 56 | C. Marquet, C. Royon, M. Trzebi\ifmmode \acuten\else \'n\fiski, and R. \ifmmode \checkZ\else \vZ\fileb\ifmmode \checkc\else \vc\fi\'\ik | Gaps between jets in double-Pomeron-exchange processes at the LHC | PRD 87 (2013) 034010 | 1212.2059 |
| 57 | TOTEM Collaboration | The TOTEM experiment at the CERN Large Hadron Collider | Journal of Instrumentation 3 (2008) S08007 | |
| 58 | O. S. Broning et al. | LHC design report | CERN Yellow Reports: Monographs. CERN | |
| 59 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 60 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 61 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 62 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 63 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 64 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 65 | TOTEM Collaboration | LHC optics measurement with proton tracks detected by the Roman pots of the TOTEM experiment | New J. Phys. 16 (2014) 103041 | 1406.0546 |
| 66 | TOTEM Collaboration | Performance of the TOTEM detectors at the LHC | Int. J. Mod. Phys. A 28 (2013) 1330046 | 1310.2908 |
| 67 | H. Niewiadomski | Reconstruction of protons in the TOTEM Roman pot detectors at the LHC | PhD thesis, Manchester U., 2008 CERN-THESIS-2008-080 | |
| 68 | CMS and TOTEM Collaborations | Measurement of single-diffractive dijet production in proton-proton collisions at $ \sqrt{s} = $ 8 TeV with the CMS and TOTEM experiments | Submitted to EPJC | 2002.12146 |
| 69 | B. Cox, J. R. Forshaw, and L. Lonnblad | Hard color singlet exchange at the Tevatron | JHEP 10 (1999) 023 | hep-ph/9908464 |
| 70 | F. Chevallier, O. Kepka, C. Marquet, and C. Royon | Gaps between jets at hadron colliders in the next-to-leading BFKL framework | PRD 79 (2009) 094019 | 0903.4598 |
| 71 | O. Kepka, C. Marquet, and C. Royon | Gaps between jets in hadronic collisions | PRD 83 (2011) 034036 | 1012.3849 |
| 72 | A. Giovannini and L. Van Hove | Negative binomial multiplicity distributions in high energy hadron collisions | Zeitschrift f\"ur Physik C Particles and Fields 30 (1986) 391 | |
| 73 | P. Ghosh | Negative binomial multiplicity distribution in proton-proton collisions in limited pseudorapidity intervals at LHC up to $ \sqrt{s} = $ 7 TeV and the clan model | PRD 85 (2012) 054017 | 1202.4221 |
| 74 | UA5 Collaboration | Multiplicity distributions in different pseudorapidity intervals at a c.o.m. energy of 540 GeV | PLB 160 (1985) 193 | |
| 75 | UA5 Collaboration | Charged particle multiplicity distributions at 200 GeV and 900 GeV c.m. energy | Z. Phys. C 43 (1989) 357 | |
| 76 | ALICE Collaboration | Charged-particle multiplicities in proton-proton collisions at $ \sqrt{s} = $ 0.9 to 8 TeV | EPJC 77 (2017) 33 | 1509.07541 |
| 77 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 78 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO | NPB 855 (2012) 153 | 1107.2652 |
| 79 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 80 | B. Andersson, G. Gustafson, G. Ingelman, and T. Sjostrand | Parton fragmentation and string dynamics | PR 97 (1983) 31 | |
| 81 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 82 | G. Corcella et al. | HERWIG 6: an event generator for hadron emission reactions with interfering gluons (including supersymmetric processes) | JHEP 01 (2001) 010 | hep-ph/0011363 |
| 83 | J. Pumplin et al. | New generation of parton distributions with uncertainties from global QCD analysis | JHEP 07 (2002) 012 | hep-ph/0201195 |
| 84 | B. R. Webber | A QCD model for jet fragmentation including soft gluon interference | NPB 238 (1984) 492 | |
| 85 | J. M. Butterworth, J. R. Forshaw, and M. H. Seymour | Multiparton interactions in photoproduction at HERA | Z. Phys. C 72 (1996) 637 | hep-ph/9601371 |
| 86 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 87 | D0 Collaboration | Hard single diffraction in $ \mathrm{\bar{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 630 GeV and 1800 GeV | PLB 531 (2002) 52 | hep-ex/9912061 |
| 88 | CDF Collaboration | Diffractive dijets with a leading antiproton in $ \mathrm{\bar{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 1800 GeV | PRL 84 (2000) 5043 | |
| 89 | CDF Collaboration | Diffractive dijet production at $ \sqrt{s} = $ 630 GeV and 1800 GeV at the Fermilab Tevatron | PRL 88 (2002) 151802 | hep-ex/0109025 |
| 90 | CDF Collaboration | Observation of exclusive dijet production at the Fermilab Tevatron $ \mathrm{\bar{p}}{\mathrm{p}} $ Collider | PRD 77 (2008) 052004 | 0712.0604 |
| 91 | CDF Collaboration | Diffractive Dijet Production in $ \mathrm{\bar{p}}{\mathrm{p}} $ Collisions at $ \sqrt{s}= $ 1.96 TeV | PRD 86 (2012) 032009 | 1206.3955 |
| 92 | H1 Collaboration | Diffractive dijet production with a leading proton in $ \rm{e}{\mathrm{p}} $ collisions at HERA | JHEP 05 (2015) 056 | 1502.01683 |
| 93 | P. \ifmmode \acuteS\else \'S\fiwierska and M. Trzebi\ifmmode \acuten\else \'n\fiski | BFKL amplitude parametrization for the jet-gap-jet events at the LHC energies | Acta Phys. Polon. B 46 (2015) 2477 | 1504.06271 |
| 94 | M. Hentschinski, J. D. Madrigal Mart\ifmmode \acutei\else \'i\finez, B. Murdaca, and A. Sabio Vera | The next-to-leading order vertex for a forward jet plus a rapidity gap at high energies | PLB 735 (2014) 168 | 1404.2937 |
| 95 | M. Hentschinski, J. D. Madrigal Mart\ifmmode \acutei\else \'i\finez, B. Murdaca, and A. Sabio Vera | The gluon-induced Mueller-Tang jet impact factor at next-to-leading order | Nuclear Physics B 889 (2014) 549 | 1409.6704 |
| 96 | CDF Collaboration | Dijet production by double pomeron exchange at the Fermilab Tevatron | PRL 85 (2000) 4215 | |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|