

Compact Muon Solenoid
LHC, CERN
| CMS-FSQ-12-002 ; CERN-PH-EP-2015-309 | ||
| Azimuthal decorrelation of jets widely separated in rapidity in pp collisions at $\sqrt{s} =$ 7 TeV | ||
| CMS Collaboration | ||
| 25 January 2016 | ||
| J. High Energy Phys. 08 (2016) 139 | ||
| Abstract: The decorrelation in the azimuthal angle between the most forward and the most backward jets (Mueller-Navelet jets) is measured in data collected in pp collisions with the CMS detector at the LHC at $\sqrt{s} =$ 7 TeV. The measurement is presented in the form of distributions of azimuthal-angle differences, $ \Delta \phi $, between the Mueller-Navelet jets, the average cosines of $ ( \pi- \Delta \phi) $, $ 2 ( \pi-\Delta\phi) $, and $ 3 ( \pi-\Delta\phi) $, and ratios of these cosines. The jets are required to have transverse momenta, $p_{\mathrm{T}}$, in excess of 35 GeV and rapidities, $| y |$, of less than 4.7. The results are presented as a function of the rapidity separation, $\Delta{y}$, between the Mueller-Navelet jets, reaching $\Delta{y}$ up to 9.4 for the first time. The results are compared to predictions of various Monte Carlo event generators and to analytical predictions based on the DGLAP and BFKL parton evolution schemes. | ||
| Links: e-print arXiv:1601.06713 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Left: Distributions of the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity intervals $ \Delta {y} < $ 3.0 (top row), 3.0 $ < \Delta {y} < $ 6.0 (centre row), and 6.0 $ < \Delta {y} < $ 9.4 (bottom row). Right: Ratios of predictions to the data in the corresponding rapidity intervals. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |

png pdf |
Figure 1-a:
Distribution of the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval $ \Delta {y} < $ 3.0. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |

png pdf |
Figure 1-b:
Ratio of predictions to the data for the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval $ \Delta {y} < $ 3.0. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |
png pdf |
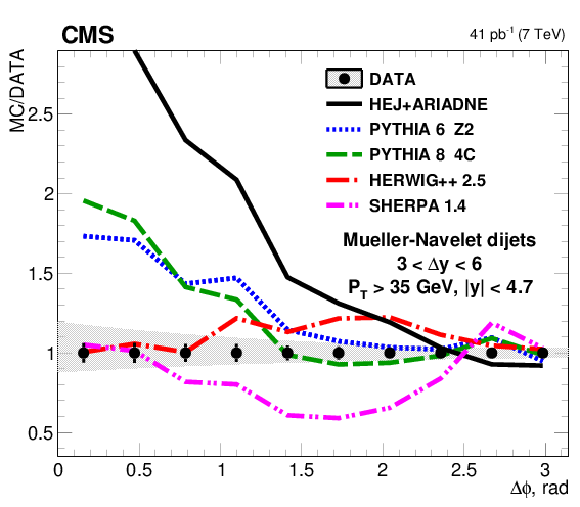
Figure 1-c:
Distribution of the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval 3.0 $ < \Delta {y} < $ 6.0. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |
png pdf |
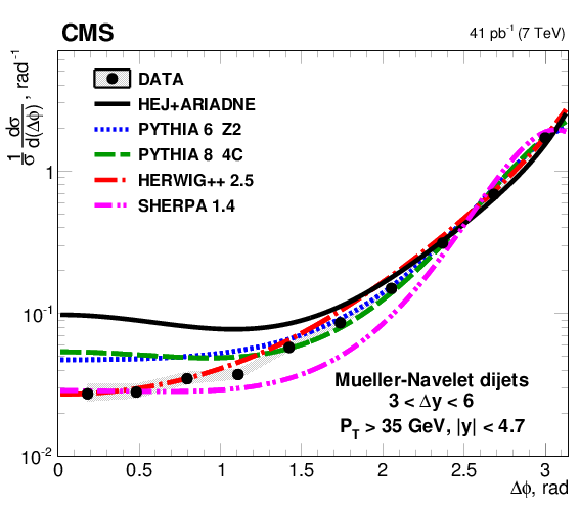
Figure 1-d:
Ratio of predictions to the data for the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval 3.0 $ < \Delta {y} < $ 6.0. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |
png pdf |
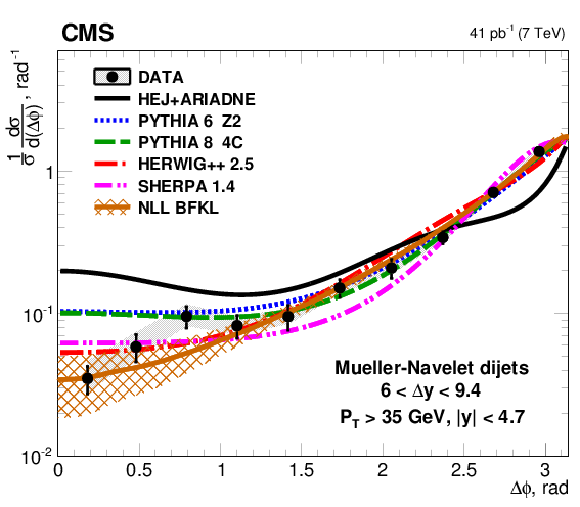
Figure 1-e:
Distribution of the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval 6.0 $ < \Delta {y} < $ 9.4. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |

png pdf |
Figure 1-f:
Ratio of predictions to the data for the azimuthal-angle difference, $\Delta \phi $, between MN jets in the rapidity interval 6.0 $ < \Delta {y} < $ 9.4. The data (points) are plotted with experimental statistical (systematic) uncertainties indicated by the error bars (the shaded band), and compared to predictions from the LL DGLAP-based MC generators PYTHIA 6, PYTHIA 8, HERWIG++, and SHERPA, and to the LL BFKL-motivated MC generator HEJ with hadronisation performed with ARIADNE (solid line). |
png pdf |
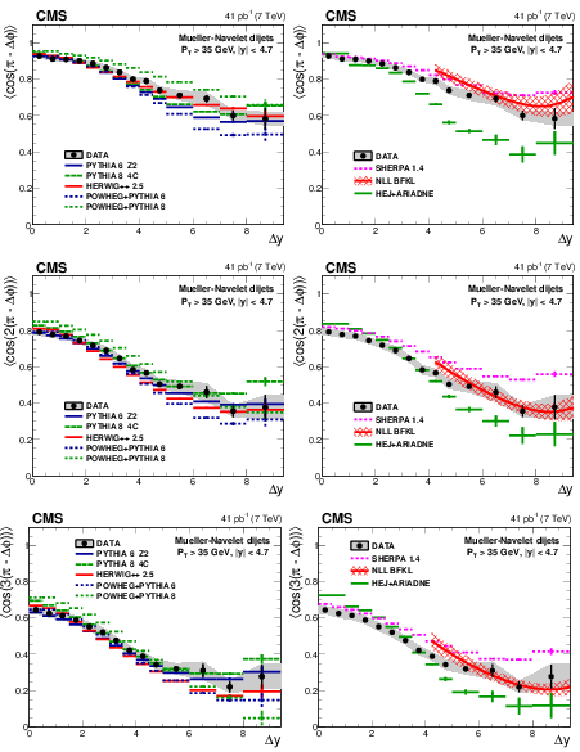
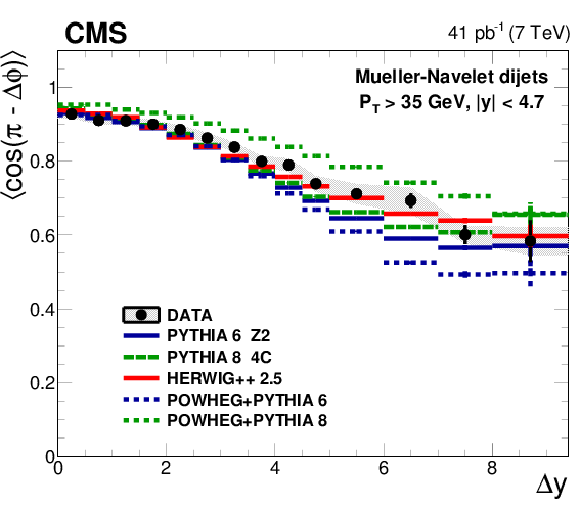
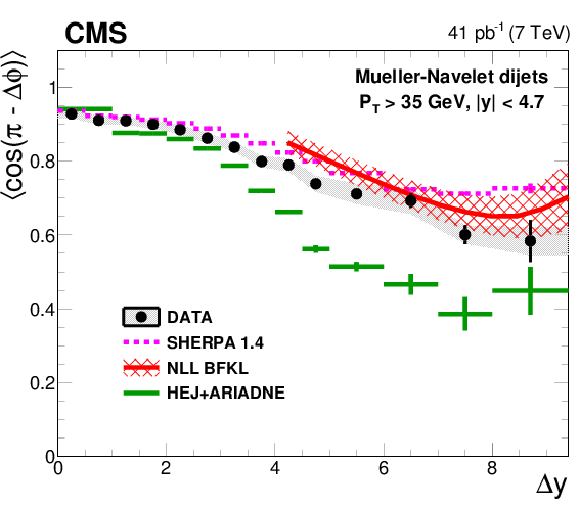
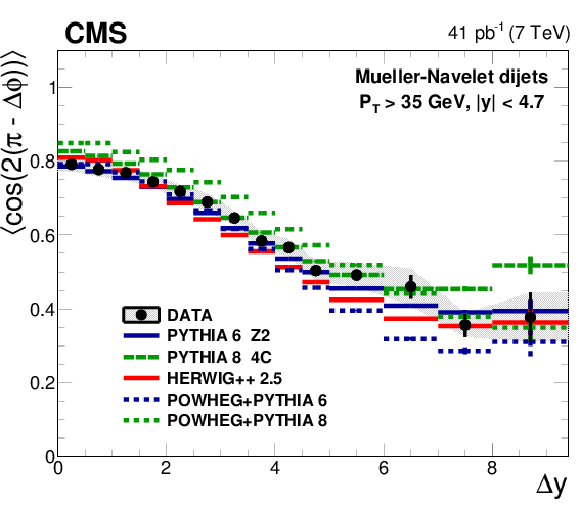
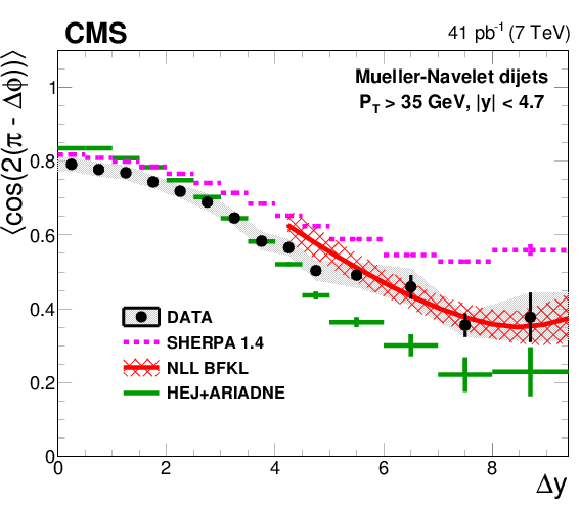
Figure 2:
Left: Average $< \cos(n(\pi -\Delta \phi )) >$ ($n =$ 1, 2, 3) as a function of $ \Delta {y} $ compared to LL DGLAP MC generators. In addition, the predictions of the NLO generator POWHEG interfaced with the LL DGLAP generators PYTHIA 6 and PYTHIA 8 are shown. Right: Comparison of the data to the MC generator SHERPA with parton matrix elements matched to a LL DGLAP parton shower, to the LL BFKL inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level (4.0 $< \Delta {y} <$ 9.4). |
png pdf |
Figure 2-a:
Average $< \cos(\pi -\Delta \phi ) >$ as a function of $ \Delta {y} $ compared to LL DGLAP MC generators. In addition, the predictions of the NLO generator POWHEG interfaced with the LL DGLAP generators PYTHIA 6 and PYTHIA 8 are shown. |
png pdf |
Figure 2-b:
Average $< \cos(\pi -\Delta \phi ) >$ as a function of $ \Delta {y} $ compared to the MC generator SHERPA with parton matrix elements matched to a LL DGLAP parton shower, to the LL BFKL inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level (4.0 $< \Delta {y} <$ 9.4). |
png pdf |
Figure 2-c:
Average $< \cos(2(\pi -\Delta \phi )) >$ as a function of $ \Delta {y} $ compared to LL DGLAP MC generators. In addition, the predictions of the NLO generator POWHEG interfaced with the LL DGLAP generators PYTHIA 6 and PYTHIA 8 are shown. |
png pdf |
Figure 2-d:
Average $< \cos(2(\pi -\Delta \phi )) >$ as a function of $ \Delta {y} $ compared to the MC generator SHERPA with parton matrix elements matched to a LL DGLAP parton shower, to the LL BFKL inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level (4.0 $< \Delta {y} <$ 9.4). |
png pdf |
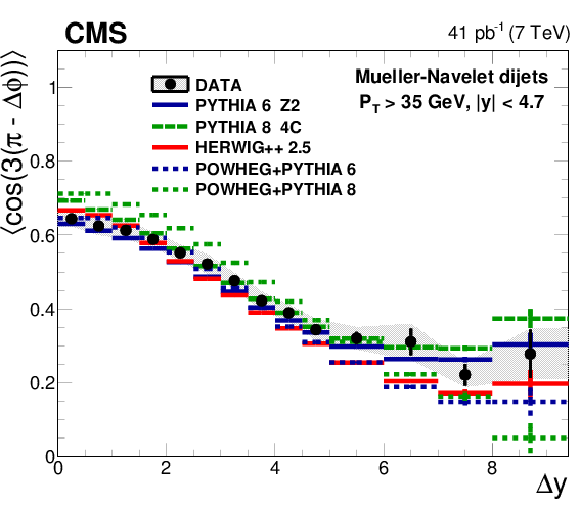
Figure 2-e:
Average $< \cos(3(\pi -\Delta \phi )) >$ as a function of $ \Delta {y} $ compared to LL DGLAP MC generators. In addition, the predictions of the NLO generator POWHEG interfaced with the LL DGLAP generators PYTHIA 6 and PYTHIA 8 are shown. |
png pdf |
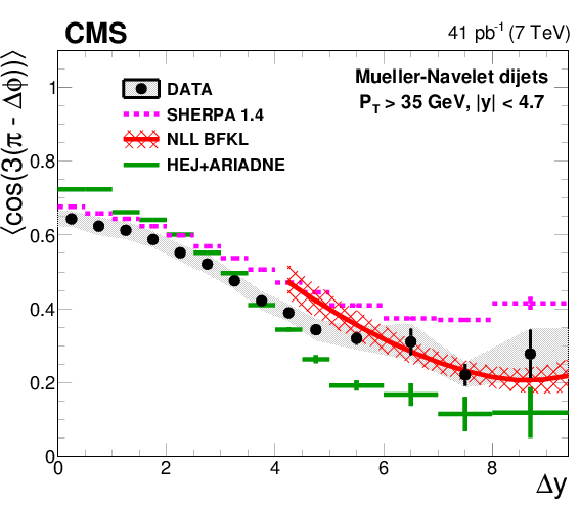
Figure 2-f:
Average $< \cos(3(\pi -\Delta \phi )) >$ as a function of $ \Delta {y} $ compared to the MC generator SHERPA with parton matrix elements matched to a LL DGLAP parton shower, to the LL BFKL inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level (4.0 $< \Delta {y} <$ 9.4). |
png pdf |
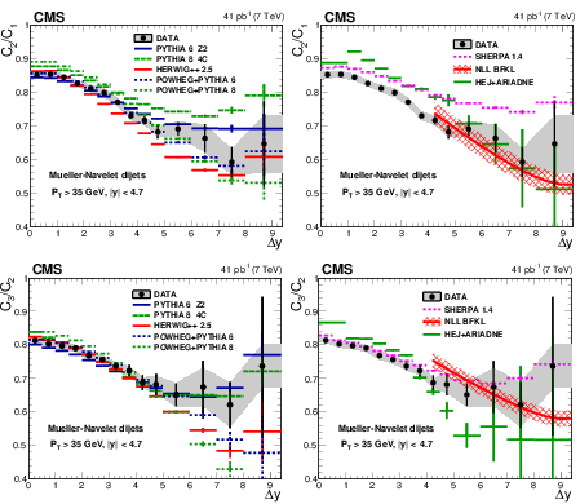
Figure 3:
Left: The measured ratios $C_2/C_1$ (top row) and $C_3/C_2$ (bottom row) as a function of rapidity difference $ \Delta {y} $ are compared to LL DGLAP parton shower generators and to the NLO generator POWHEG interfaced with PYTHIA 6 and PYTHIA 8. Right: Comparison of the ratios to the MC generator SHERPA with parton matrix element matched to a LL DGLAP parton shower, to the LL BFKL-inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level. |

png pdf |
Figure 3-a:
The measured ratio $C_2/C_1$ as a function of rapidity difference $ \Delta {y} $ are compared to LL DGLAP parton shower generators and to the NLO generator POWHEG interfaced with PYTHIA 6 and PYTHIA 8. |
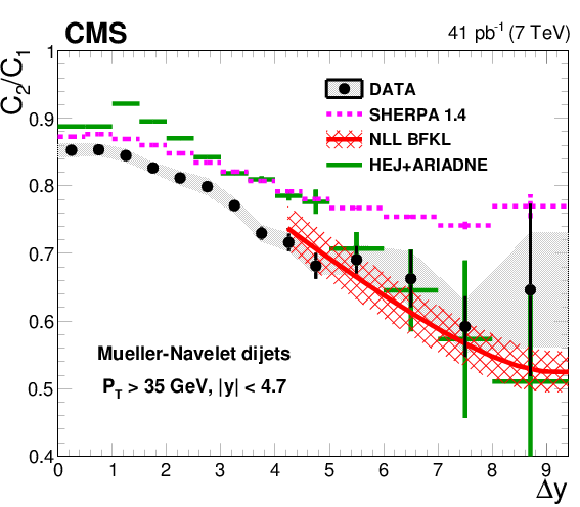
png pdf |
Figure 3-b:
The measured ratio $C_2/C_1$ as a function of rapidity difference $ \Delta {y} $ are compared to the MC generator SHERPA with parton matrix element matched to a LL DGLAP parton shower, to the LL BFKL-inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level. |

png pdf |
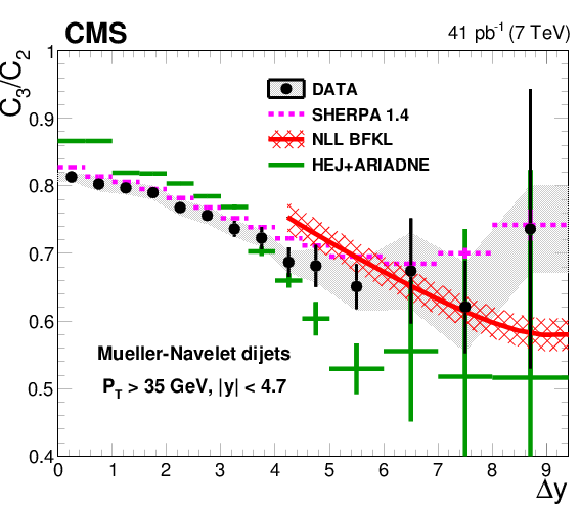
Figure 3-c:
The measured ratio $C_3/C_2$ as a function of rapidity difference $ \Delta {y} $ are compared to LL DGLAP parton shower generators and to the NLO generator POWHEG interfaced with PYTHIA 6 and PYTHIA 8. |
png pdf |
Figure 3-d:
The measured ratio $C_3/C_2$ as a function of rapidity difference $ \Delta {y} $ are compared to the MC generator SHERPA with parton matrix element matched to a LL DGLAP parton shower, to the LL BFKL-inspired generator HEJ with hadronisation by ARIADNE, and to analytical NLL BFKL calculations at the parton level. |
png pdf |
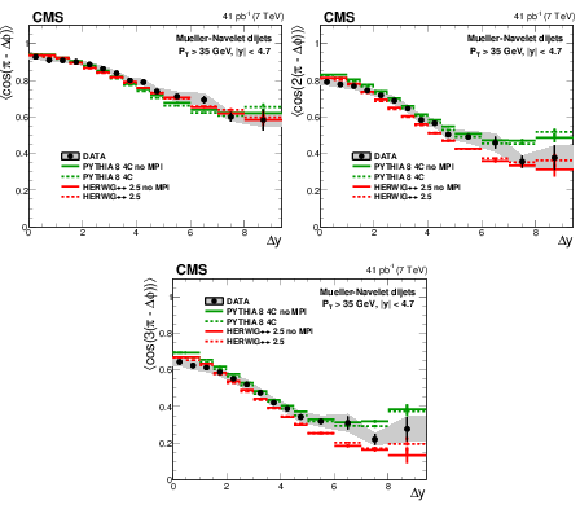
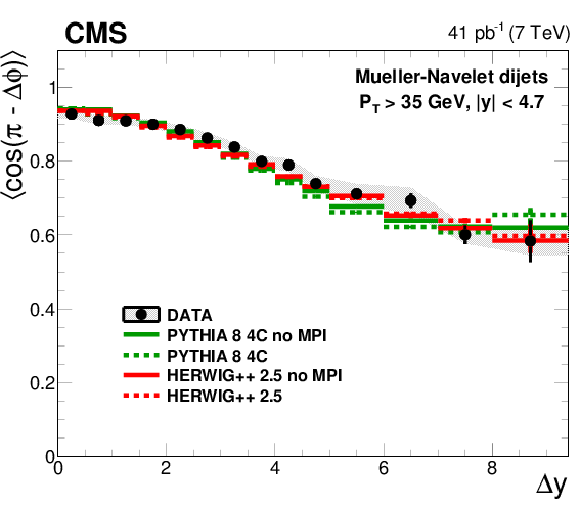
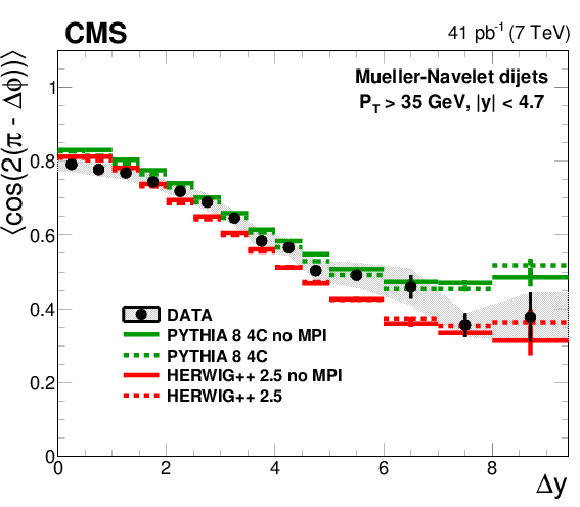
Figure 4:
Average $< \cos{(\pi - \Delta \phi )}> $, $< \cos{2(\pi - \Delta \phi )}> $ and $< \cos{3(\pi - \Delta \phi )} > $ compared to PYTHIA 6 with and without MPI. |
png pdf |
Figure 4-a:
Average $< \cos{(\pi - \Delta \phi )}> $ compared to PYTHIA 6 with and without MPI. |
png pdf |
Figure 4-b:
Average $< \cos{2(\pi - \Delta \phi )}> $ compared to PYTHIA 6 with and without MPI. |
png pdf |
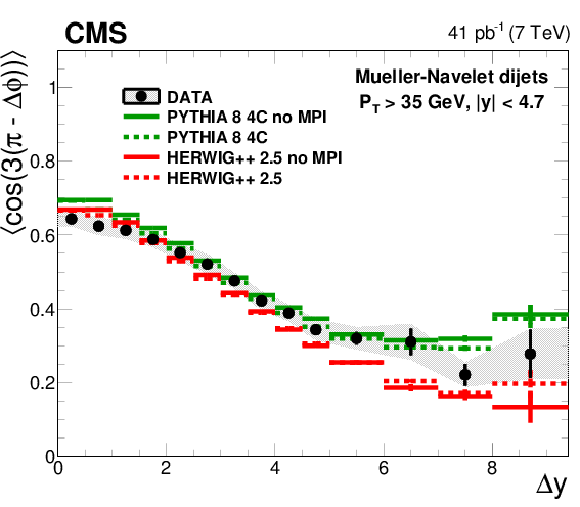
Figure 4-c:
Average $< \cos{3(\pi - \Delta \phi )} > $ compared to PYTHIA 6 with and without MPI. |
png pdf |
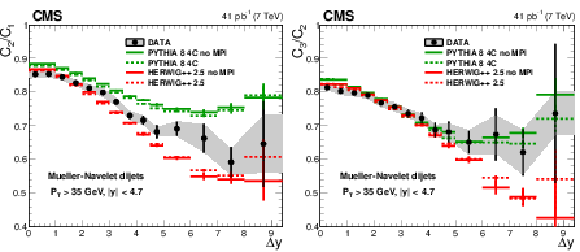
Figure 5:
Measured ratios $C_2/C_1$ (left) and $C_3/C_2$ (right) compared to PYTHIA 8 with and without MPI. |
png pdf |
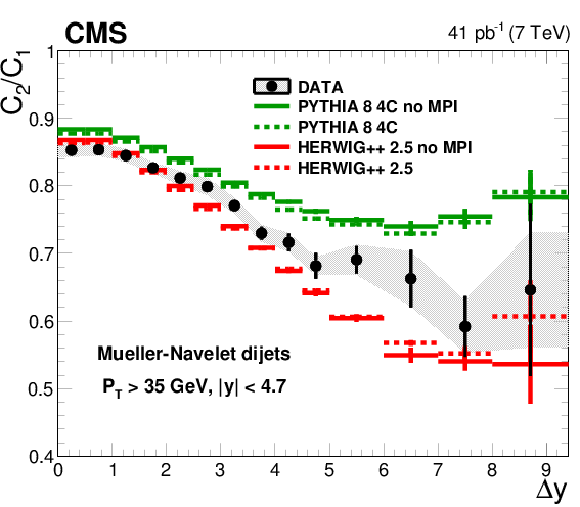
Figure 5-a:
Measured ratios $C_2/C_1$ compared to PYTHIA 8 with and without MPI. |

png pdf |
Figure 5-b:
Measured ratios $C_3/C_2$ compared to PYTHIA 8 with and without MPI. |
| Tables | |

png pdf |
Table 1:
Systematic and statistical uncertainties (%) of the observables measured in this work. |
| Summary |
|
The first measurement of the azimuthal decorrelation of the most-forward and backward jets in the event (called Mueller-Navelet dijets), with rapidity separations up to $\Delta{y}=$ 9.4, is presented for proton-proton collisions at $\sqrt{s}=$ 7 TeV. The measured observables include azimuthal-angle distributions, moments of the average cosines of the decorrelation angle, $< \cos(n(\pi - \Delta \phi)) >$ for $n=$ 1, 2, 3, as well as ratios of the average cosines, as a function of the rapidity separation $\Delta{y}$ between the MN jets. The predictions of the DGLAP-based MC generator HERWIG++ 2.5, improved with leading-log (LL) parton showers and colour-coherence effects, exhibit satisfactory agreement with the data for all measured observables. Other MC generators of this type, such as PYTHIA 6 Z2, PYTHIA 8 4C, and SHERPA 1.4, provide a less accurate description of all measurements. The MC generator POWHEG, with NLO matrix elements interfaced with the LL parton shower of PYTHIA 6 and PYTHIA 8, does not improve the overall agreement with the data compared to the description provided by PYTHIA 6 and 8 alone. The MC generator HEJ, based on LL BFKL matrix elements combined with ARIANDE for parton shower and hadronisation, predicts a stronger decorrelation than observed in the data. An analytical BFKL calculation at next-to-leading logarithmic (NLL) accuracy with an optimised renormalisation scheme and scale, provides a satisfactory description of the data for the measured jet observables at $\Delta{y}>$ 4. The observed sensitivity to the implementation of the colour-coherence effects in the DGLAP MC generators and the reasonable data-theory agreement shown by the NLL BFKL analytical calculations at large $\Delta{y}$, may be considered as indications that the kinematical domain of the present study lies in between the regions described by the DGLAP and BFKL approaches. Possible manifestations of BFKL signatures are expected to be more pronounced at increasing collision energies. |
| References | ||||
| 1 | V. N. Gribov and L. N. Lipatov | Deep inelastic ep scattering in perturbation theory | Sov. J. Nucl. Phys. 15 (1972) 438 | |
| 2 | V. N. Gribov and L. N. Lipatov | $ \mathrm{ e^{+}e^{-} } $ pair annihilation and deep inelastic ep scattering in perturbation theory | Sov. J. Nucl. Phys. 15 (1972) 675 | |
| 3 | L. N. Lipatov | The parton model and perturbation theory | Sov. J. Nucl. Phys. 20 (1975) 94 | |
| 4 | G. Altarelli and G. Parisi | Asymptotic freedom in parton language | Nucl. Phys. B 126 (1977) 298 | |
| 5 | Y. L. Dokshitzer | Calculation of the structure functions for deep inelastic scattering and $ \mathrm{ e^+ e^-} $ annihilation by perturbation theory in quantum chromodynamics | Sov. Phys. JETP 46 (1977) 641 | |
| 6 | E. A. Kuraev, L. N. Lipatov and V. S. Fadin | Multi-reggeon processes in the Yang-Mills theory | Sov. Phys. JETP 44 (1976) 443 | |
| 7 | E. A. Kuraev, L. N. Lipatov and V. S. Fadin | The Pomeranchuk singularity in nonabelian gauge theories | Sov. Phys. JETP 45 (1977) 199 | |
| 8 | I. I. Balitsky and L. N. Lipatov | The Pomeranchuk singularity in quantum chromodynamics | Sov. J. Nucl. Phys. 28 (1978) 822 | |
| 9 | A. H. Mueller and H. Navelet | An inclusive minijet cross-section and the bare pomeron in QCD | Nucl. Phys. B 282 (1987) 727 | |
| 10 | V. Del Duca and C. R. Schmidt | Mini-jet corrections to Higgs production | PRD 49 (1994) 177 | hep-ph/9305346 |
| 11 | W. J. Stirling | Production of jet pairs at large relative rapidity in hadron hadron collisions as a probe of the perturbative pomeron | Nucl. Phys. B 423 (1994) 56 | hep-ph/9401266 |
| 12 | V. S. Fadin and L. N. Lipatov | BFKL pomeron in the next-to-leading approximation | PLB 429 (1998) 127 | hep-ph/9802290 |
| 13 | M. Ciafaloni and G. Camici | Energy scale(s) and next-to-leading BFKL equation | PLB 430 (1998) 349 | hep-ph/9803389 |
| 14 | S. J. Brodsky et al. | The QCD pomeron with optimal renormalization | JEPTL 70 (1999) 155 | hep-ph/9901229 |
| 15 | M. Ciafaloni, D. Colferai, and G. P. Salam | Renormalization group improved small-$ x $ equation | PRD 60 (1999) 114036 | hep-ph/9905566 |
| 16 | DZERO Collaboration | The azimuthal decorrelation of jets widely separated in rapidity | PRL 77 (1996) 595 | hep-ex/9603010 |
| 17 | DZERO Collaboration | Probing BFKL dynamics in the dijet cross section at large rapidity intervals in $ \mathrm{ p\bar{p} } $ collisions at $ \sqrt{s} =$ 1800 GeV and 630 GeV | PRL 84 (2000) 5722 | hep-ex/9912032 |
| 18 | ATLAS Collaboration | Measurement of dijet production with a veto on additional central jet activity in $ \mathrm{ pp } $ collisions at $ \sqrt{s} = $ 7 TeV using the ATLAS detector | JHEP 09 (2011) 053 | 1107.1641 |
| 19 | CMS Collaboration | Ratios of dijet production cross sections as a function of the absolute difference in rapidity between jets in $ \mathrm{ pp } $ collisions at $ \sqrt{s} = $ 7 TeV | EPJC 72 (2012) 2216 | CMS-FWD-10-014 1204.0696 |
| 20 | A. Sabio Vera and F. Schwennsen | The azimuthal decorrelation of jets widely separated in rapidity as a test of the BFKL kernel | Nucl. Phys. B 776 (2007) 170 | hep-ph/0702158 |
| 21 | ATLAS Collaboration | Measurements of jet vetoes and azimuthal decorrelations in dijet events produced in $ pp $ collisions at $ \sqrt{s}=7\,\mathrm{TeV} $ using the ATLAS detector | EPJC 74 (2014), no. 11 | 1407.5756 |
| 22 | V. T. Kim and G. B. Pivovarov | Balitskii-Fadin-Kuraev-Lipatov QCD Pomeron in high energy hadron collisions: Inclusive dijet production | PRD 53 (1996) 6 | hep-ph/9506381 |
| 23 | M. Angioni, G. Chachamis, J. D. Madrigal, and A. Sabio Vera | Dijet production at large rapidity separation in $ N=4 $ SYM | PRL 107 (2011) 191601 | hep-th/1106.6172 |
| 24 | D. Colferai, F. Schwennsen, L. Szymanowski, and S. Wallon | Mueller-Navelet jets at LHC: complete NLL BFKL calculation | JHEP 12 (2010) 026 | 1002.1365 |
| 25 | B. Duclou\'e, L. Szymanowski, and S. Wallon | Mueller-Navelet jets at LHC: the first complete NLL BFKL study | in Sixth International Conference on Quarks and Nuclear Physics 2012 PoS QNP2012 165 | 1208.6111 |
| 26 | B. Duclou\'e, L. Szymanowski, and S. Wallon | Confronting Mueller--Navelet jets in NLL BFKL with LHC experiments at 7 TeV | JHEP 05 (2013) 096 | 1302.7012 |
| 27 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 28 | M. Cacciari and G. P. Salam | Dispelling the $ N^3 $ myth for the $ k_t $ jet-finder | PLB 641 (2006) 57 | hep-ph/0512210 |
| 29 | T. Sj\"ostrand, S. Mrenna and P. Skands | PYTHIA 6.4 physics and manual | JHEP 05 (2006) 026 | hep-ph/0603175 |
| 30 | R. Field | Min-bias and the underlying event at the LHC | in 51$^\text st$ Cracow School of Theoretical Physics 2011 Acta Phys. Polon. B 42 (2011) 2631 | 1110.5530 |
| 31 | M. B\"ahr et al. | Herwig++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 32 | T. Sj\"ostrand, S. Mrenna, and P. Skands | A brief introduction to PYTHIA 8.1 | CPC 178 (2008) 852 | 0710.3820 |
| 33 | R. Corke and T. Sj\"ostrand | Interleaved parton showers and tuning prospects | JHEP 03 (2011) 32 | 1011.1759 |
| 34 | P. Nason | A New method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 35 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 36 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 37 | J. Pumplin et al. | New generation of parton distributions with uncertainties from global QCD analysis | JHEP 07 (2002) 012 | hep-ph/0201195 |
| 38 | T. Gleisberg et al. | Event generation with SHERPA 1.1 | JHEP 02 (2009) 007 | 0811.4622 |
| 39 | B. Duclou\'e, L. Szymanowski, and S. Wallon | Evidence for high-energy resummation effects in Mueller-Navelet jets at the LHC | PRL 112 (2013) 082003 | 1309.3229 |
| 40 | J. Andersen, L. Lonnblad, and J. Smillie | A parton shower for high energy jets | JHEP 07 (2011) 110 | 1104.1316 |
| 41 | J. R. Andersen and J. M. Smillie | Multiple jets at the LHC with high energy jets | JHEP 06 (2011) 010 | 1101.5394 |
| 42 | L. L\"onnblad | Ariadne version 4: A program for simulation of QCD cascades implementing the colour dipole model | CPC 71 (1992) 15 | |
| 43 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 44 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 45 | CMS Collaboration | Zero bias and HF-based minimum bias triggering for pp collisions at 14 TeV in CMS | CDS | |
| 46 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 47 | CMS Collaboration | Jet performance in $ \mathrm{ pp } $ collisions at $ \sqrt{s} = $ 7 TeV | CDS | |
| 48 | CMS Collaboration | Measurement of the inclusive production cross sections for forward jets and for dijet events with one forward and one central jet in pp collisions at $ \sqrt{s} = $ 7 TeV | JHEP 06 (2012) 036 | CMS-FWD-11-002 1202.0704 |
| 49 | CMS Collaboration | Alignment of the CMS tracker with LHC and cosmic ray data | JINST 9 (2014) P06009 | CMS-TRK-11-002 1403.2286 |
| 50 | CMS Collaboration | Calorimeter jet quality criteria for the first CMS collision data | CDS | |
| 51 | G. D'Agostini | A multidimensional unfolding method based on Bayes' theorem | NIMA 362 (1995) 487 | |
| 52 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 53 | F. Caporale, D. Y. Ivanov, B. Murdaca, and A. Papa | Mueller-Navelet small-cone jets at LHC in next-to-leading BFKL | Nucl. Phys. B 877 (2013) 73 | 1211.7225 |
| 54 | S. J. Brodsky, G. P. Lepage, and P. B. Mackenzie | On the elimination of scale ambiguities in perturbative quantum chromodynamics | PRD 28 (1983) 228 | |
| 55 | F. Caporale, D. Y. Ivanov, B. Murdaca, and A. Papa | Mueller-Navelet jets in next-to-leading order BFKL: theory versus experiment | EPJC 74 (2014) 3084 | 1407.8431 |
| 56 | H. Jung et al. | The CCFM Monte Carlo generator CASCADE version 2.2.03 | EPJC 70 (2010) 1237 | 1008.0152 |
| 57 | H. Jung and G. P. Salam | Hadronic final state predictions from CCFM: The hadron level Monte Carlo generator CASCADE | EPJC 19 (2001) 351 | hep-ph/0012143 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|