

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-EXO-23-014 | ||
| Search for long-lived particles decaying to a pair of muons in pp collisions at $ \sqrt{s}= $ 13.6 TeV with 2022 data | ||
| CMS Collaboration | ||
| 23 August 2023 | ||
| Abstract: An inclusive search for long-lived exotic particles decaying to a pair of muons is presented. The search uses data collected by the CMS experiment at the CERN LHC in proton-proton collisions at $ \sqrt{s}= $ 13.6 TeV in 2022 and corresponding to an integrated luminosity of 36.7 fb$ ^{-1} $. The experimental signature is a pair of oppositely charged muons originating from a common secondary vertex spatially separated from the pp interaction point by distances ranging from several hundred $ \mu $m to several meters. The results are interpreted in the frameworks of the hidden Abelian Higgs model, in which the Higgs boson decays to a pair of long-lived dark photons; and of an $ R $-parity violating supersymmetry model, in which long-lived neutralinos decay to a pair of muons and a neutrino. The results show substantial improvements as compared to the analysis performed using data taken at $ \sqrt{s}= $ 13 TeV, particularly at low masses and long lifetimes, mainly because of improved triggers for displaced muons and offline analysis refinements. | ||
|
Links:
CDS record (PDF) ;
Physics Briefing ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Accepted by JHEP. The superseded preliminary plots can be found here. |
||
| Figures | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |

png pdf |
Figure 1:
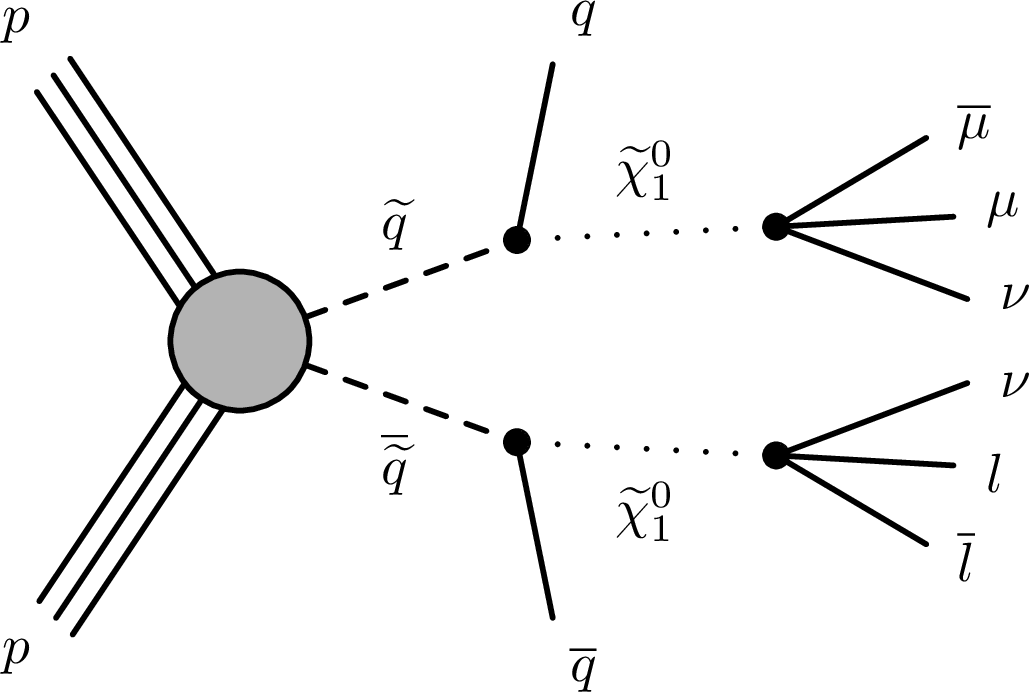
Feynman diagrams for (left) the HAHM model, showing the production of long-lived dark photons $ \mathrm{Z}\mathrm{_{D}} $ via the Higgs portal, through $\mathrm{H}$-$ \mathrm{H}\mathrm{_{D}} $ mixing with the parameter $ \kappa $, with subsequent decays to pairs of muons or other fermions via the vector portal; and (right) pair production of squarks followed by $ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} $ decay, where the RPV neutralino is assumed to be a long-lived particle that decays into a neutrino and two charged leptons. |

png pdf |
Figure 1-a:
Feynman diagrams for (left) the HAHM model, showing the production of long-lived dark photons $ \mathrm{Z}\mathrm{_{D}} $ via the Higgs portal, through $\mathrm{H}$-$ \mathrm{H}\mathrm{_{D}} $ mixing with the parameter $ \kappa $, with subsequent decays to pairs of muons or other fermions via the vector portal; and (right) pair production of squarks followed by $ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} $ decay, where the RPV neutralino is assumed to be a long-lived particle that decays into a neutrino and two charged leptons. |
png pdf |
Figure 1-b:
Feynman diagrams for (left) the HAHM model, showing the production of long-lived dark photons $ \mathrm{Z}\mathrm{_{D}} $ via the Higgs portal, through $\mathrm{H}$-$ \mathrm{H}\mathrm{_{D}} $ mixing with the parameter $ \kappa $, with subsequent decays to pairs of muons or other fermions via the vector portal; and (right) pair production of squarks followed by $ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} $ decay, where the RPV neutralino is assumed to be a long-lived particle that decays into a neutrino and two charged leptons. |
png pdf |
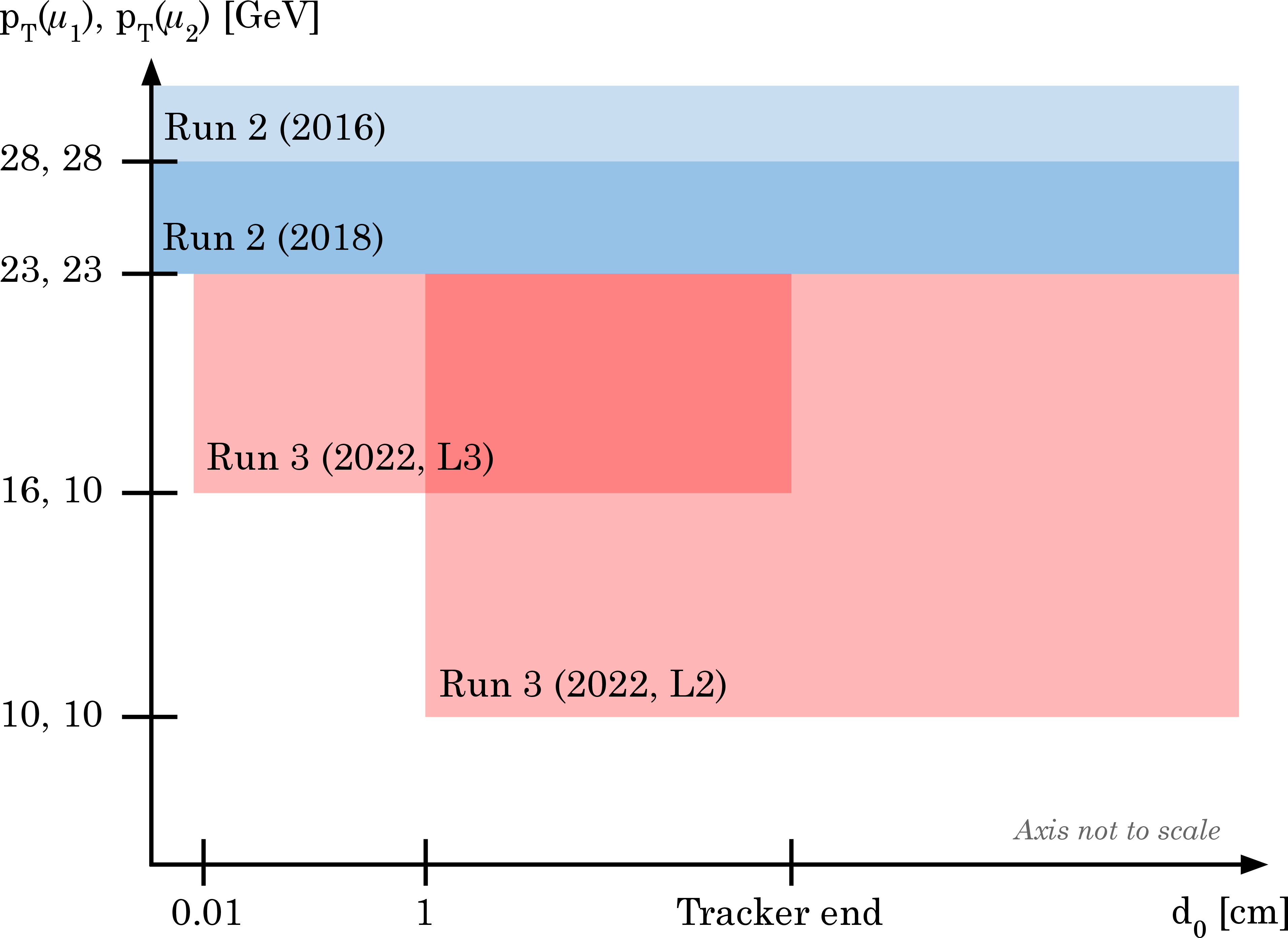
Figure 2:
The $ p_{\mathrm{T}} $ and $ d_{\mathrm{0}} $ coverage of the 2016 Run 2 triggers (light blue), 2018 Run 2 triggers (blue), and 2022 Run 3 triggers (red). |
png pdf |
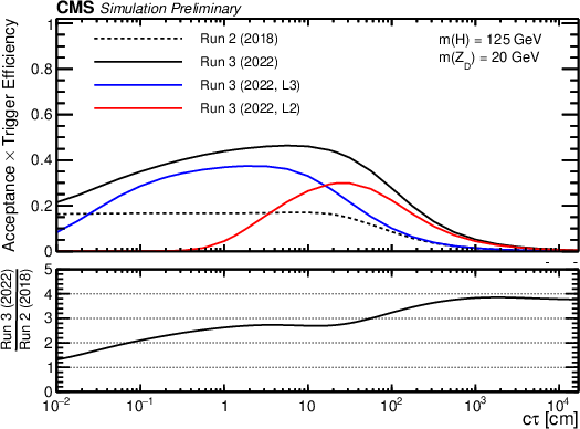
Figure 3:
Efficiencies of the Run 2 and Run 3 triggers as a function of $ c\tau $. The efficiency is defined as the fraction of simulated HAHM events with $ m(\mathrm{Z}\mathrm{_{D}}) = $ 20 GeV that satisfy the requirements of the following sets of trigger paths: the Run 2 (2018) triggers (dashed black); the Run 3 (2022, L3) triggers (blue); the Run 3 (2022, L2) triggers (red); and the OR of all Run 3 (2022) triggers (black). The lower panel shows the ratio of the overall Run 3 (2022) efficiency to the Run 2 (2018) efficiency. |
png pdf |
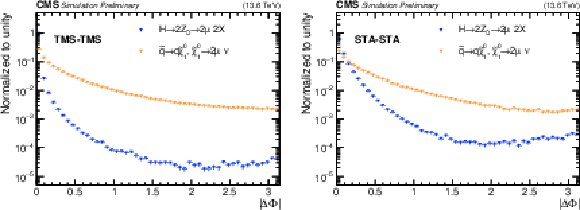
Figure 4:
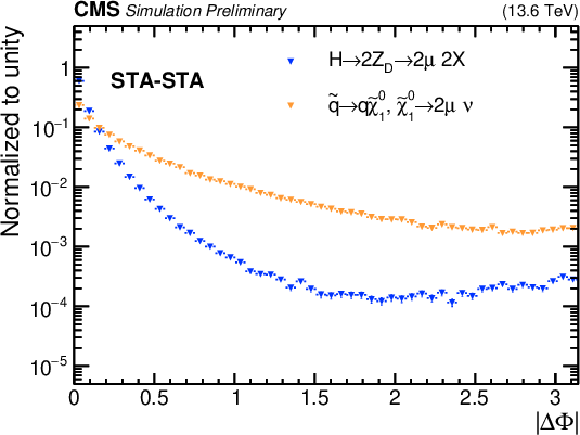
Distribution of $ |\Delta\Phi| $ for (left) TMS-TMS and (right) STA-STA dimuons passing the full selection except for a requirement on $ |\Delta\Phi| $ in all HAHM (blue) and RPV SUSY (orange) signal samples combined. All distributions are normalized to a unit area. |
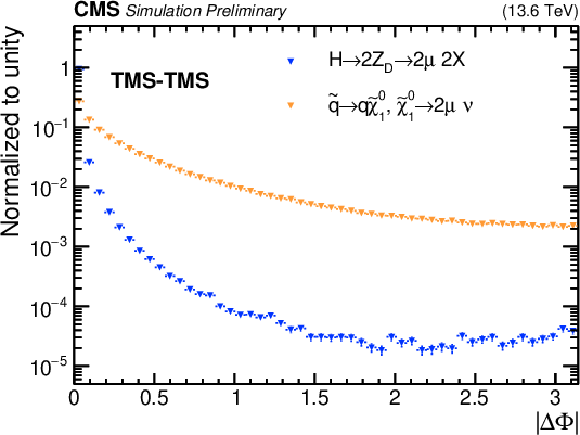
png pdf |
Figure 4-a:
Distribution of $ |\Delta\Phi| $ for (left) TMS-TMS and (right) STA-STA dimuons passing the full selection except for a requirement on $ |\Delta\Phi| $ in all HAHM (blue) and RPV SUSY (orange) signal samples combined. All distributions are normalized to a unit area. |
png pdf |
Figure 4-b:
Distribution of $ |\Delta\Phi| $ for (left) TMS-TMS and (right) STA-STA dimuons passing the full selection except for a requirement on $ |\Delta\Phi| $ in all HAHM (blue) and RPV SUSY (orange) signal samples combined. All distributions are normalized to a unit area. |
png pdf |
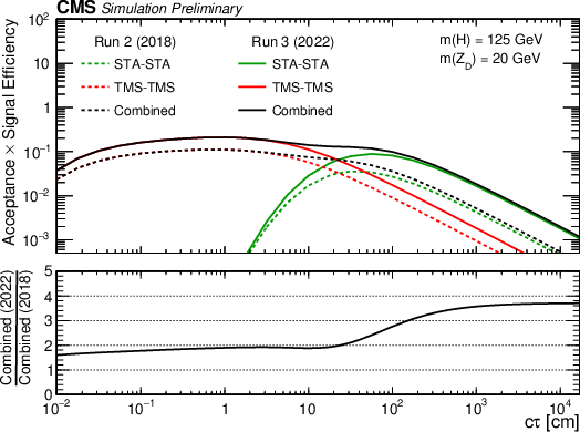
Figure 5:
Signal efficiencies in the TMS-TMS (red) and STA-STA (green) dimuon categories as well as their combination (black) as a function of $ c\tau $ for the HAHM signal with $ m(\mathrm{Z}\mathrm{_{D}})= $ 20 GeV. Solid curves show efficiencies achieved with the Run 3 triggers, whereas dashed curves show efficiencies for the subset of events selected by the triggers used in the 2018 Run 2 search. The efficiency is defined as the fraction of signal events that passed the criteria of the indicated trigger as well as the full set of offline selection criteria. The lower panel shows the relative improvement of the overall signal efficiency brought in by improvements in the trigger. |
png pdf |
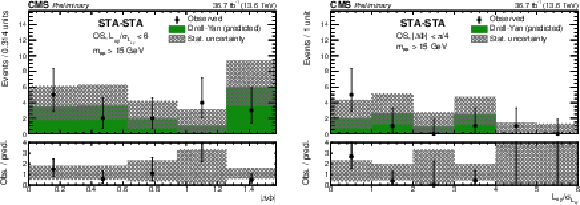
Figure 6:
Example of background prediction checks for STA-STA dimuons: (left) $ |\Delta\Phi| $ and (right) $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with $ m_{\mu\mu} > $ 15 GeV in the $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 6 VR in data (black circles), compared to the background predictions (histograms). The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |

png pdf |
Figure 6-a:
Example of background prediction checks for STA-STA dimuons: (left) $ |\Delta\Phi| $ and (right) $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with $ m_{\mu\mu} > $ 15 GeV in the $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 6 VR in data (black circles), compared to the background predictions (histograms). The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |

png pdf |
Figure 6-b:
Example of background prediction checks for STA-STA dimuons: (left) $ |\Delta\Phi| $ and (right) $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with $ m_{\mu\mu} > $ 15 GeV in the $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 6 VR in data (black circles), compared to the background predictions (histograms). The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |

png pdf |
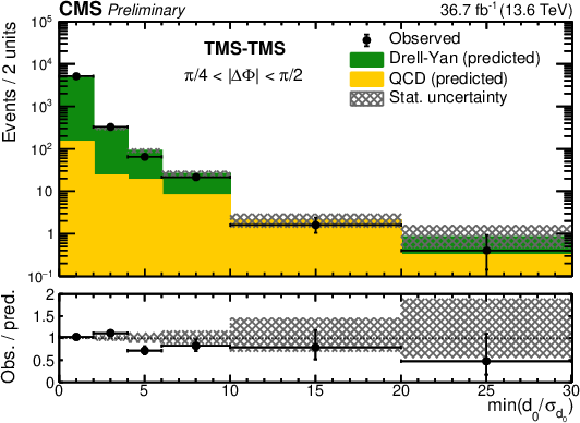
Figure 7:
Example of background prediction checks for TMS-TMS dimuons: $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with (left) $ |\Delta\Phi| < \pi/ $ 4 and (right) $ |\Delta\Phi| < \pi/ $ 30 in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR, compared with the outcome of the background prediction method. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin contains the overflow. The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |
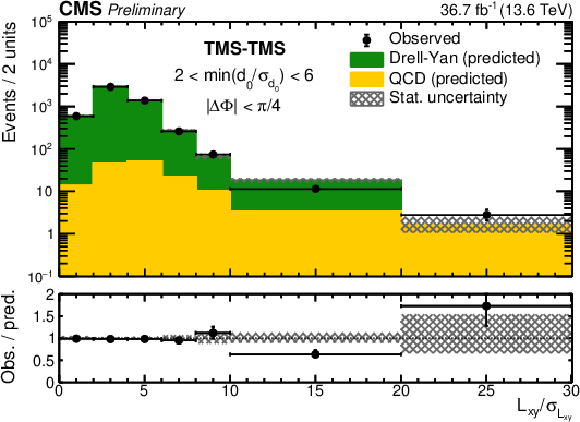
png pdf |
Figure 7-a:
Example of background prediction checks for TMS-TMS dimuons: $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with (left) $ |\Delta\Phi| < \pi/ $ 4 and (right) $ |\Delta\Phi| < \pi/ $ 30 in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR, compared with the outcome of the background prediction method. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin contains the overflow. The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |
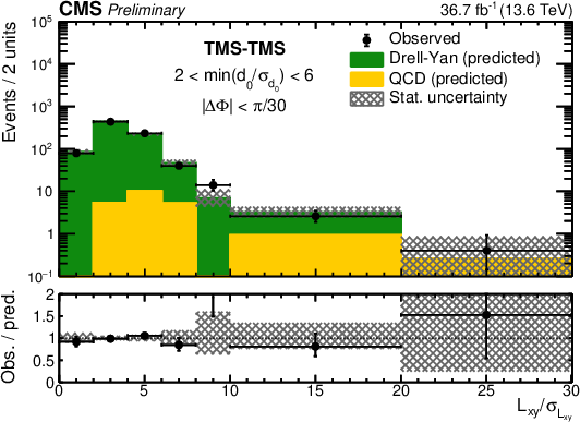
png pdf |
Figure 7-b:
Example of background prediction checks for TMS-TMS dimuons: $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} $ distributions for events with (left) $ |\Delta\Phi| < \pi/ $ 4 and (right) $ |\Delta\Phi| < \pi/ $ 30 in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR, compared with the outcome of the background prediction method. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin contains the overflow. The lower panels show the ratio of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |
png pdf |
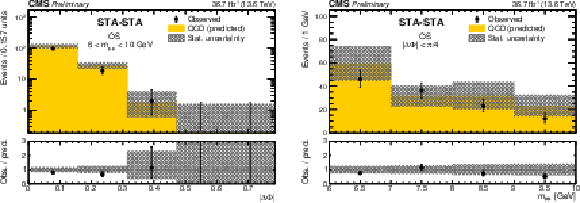
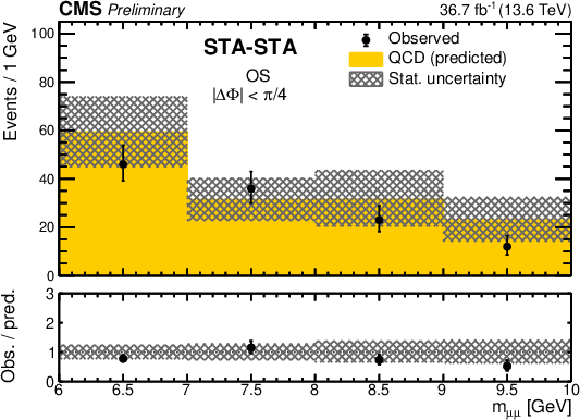
Figure 8:
Distributions of (left) $ |\Delta\Phi| $ and (right) dimuon invariant mass for STA-STA dimuons in the low-mass validation region (6 GeV $ < m_{\mu\mu} < $ 10 GeV) in data (black circles) compared to the background prediction (histograms). The lower panels show the ratio of the observed to predicted number of events. All uncertainties are statistical only. |
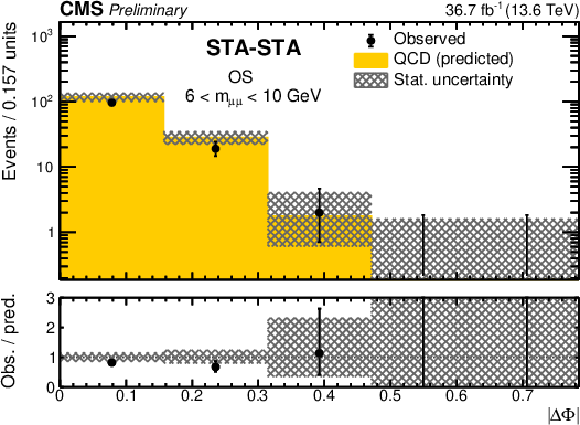
png pdf |
Figure 8-a:
Distributions of (left) $ |\Delta\Phi| $ and (right) dimuon invariant mass for STA-STA dimuons in the low-mass validation region (6 GeV $ < m_{\mu\mu} < $ 10 GeV) in data (black circles) compared to the background prediction (histograms). The lower panels show the ratio of the observed to predicted number of events. All uncertainties are statistical only. |
png pdf |
Figure 8-b:
Distributions of (left) $ |\Delta\Phi| $ and (right) dimuon invariant mass for STA-STA dimuons in the low-mass validation region (6 GeV $ < m_{\mu\mu} < $ 10 GeV) in data (black circles) compared to the background prediction (histograms). The lower panels show the ratio of the observed to predicted number of events. All uncertainties are statistical only. |
png pdf |
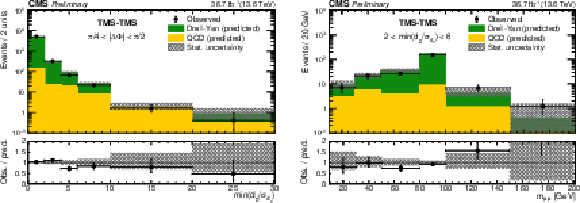
Figure 9:
(left) Comparison of the number of TMS-TMS dimuons in data with the results of the background prediction method: (left) as a function of min($ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $) for events in the $ \pi/4 < |\Delta\Phi| < \pi/ $ 2 VR; (right) as a function of $ m_{\mu\mu} $ for events in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin includes events in the overflow. The lower panels show the ratios of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |
png pdf |
Figure 9-a:
(left) Comparison of the number of TMS-TMS dimuons in data with the results of the background prediction method: (left) as a function of min($ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $) for events in the $ \pi/4 < |\Delta\Phi| < \pi/ $ 2 VR; (right) as a function of $ m_{\mu\mu} $ for events in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin includes events in the overflow. The lower panels show the ratios of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |

png pdf |
Figure 9-b:
(left) Comparison of the number of TMS-TMS dimuons in data with the results of the background prediction method: (left) as a function of min($ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $) for events in the $ \pi/4 < |\Delta\Phi| < \pi/ $ 2 VR; (right) as a function of $ m_{\mu\mu} $ for events in the 2 $ < \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) < $ 6 VR. The number of observed events (black circles) is overlaid with stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. The last bin includes events in the overflow. The lower panels show the ratios of the observed to predicted number of events. Hatched histograms show the statistical uncertainty in the background prediction. |
png pdf |
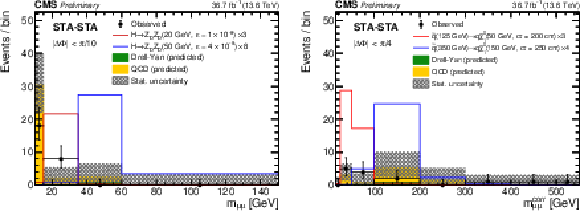
Figure 10:
Comparison of observed (black points) and expected (histograms) numbers of events in non-overlapping (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ intervals in the STA-STA dimuon category, in the signal regions optimized for the (left) HAHM and (right) RPV SUSY model. Yellow and green stacked histograms represent mean expected background contributions from QCD and DY, respectively, while statistical uncertainties in the total expected background are shown as hatched histograms. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. The last bin includes events in the overflow. |
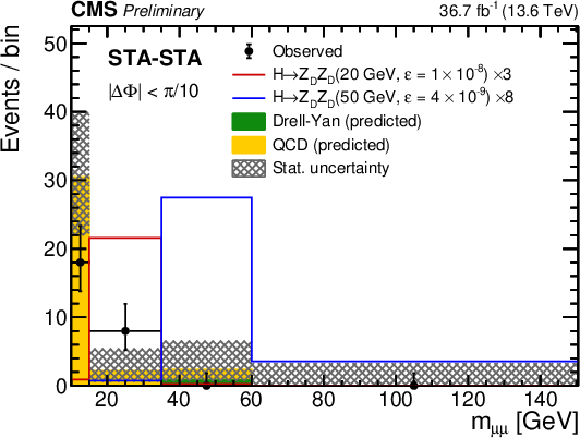
png pdf |
Figure 10-a:
Comparison of observed (black points) and expected (histograms) numbers of events in non-overlapping (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ intervals in the STA-STA dimuon category, in the signal regions optimized for the (left) HAHM and (right) RPV SUSY model. Yellow and green stacked histograms represent mean expected background contributions from QCD and DY, respectively, while statistical uncertainties in the total expected background are shown as hatched histograms. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. The last bin includes events in the overflow. |
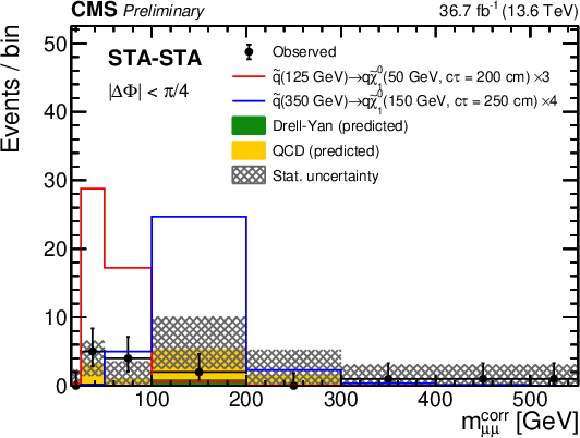
png pdf |
Figure 10-b:
Comparison of observed (black points) and expected (histograms) numbers of events in non-overlapping (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ intervals in the STA-STA dimuon category, in the signal regions optimized for the (left) HAHM and (right) RPV SUSY model. Yellow and green stacked histograms represent mean expected background contributions from QCD and DY, respectively, while statistical uncertainties in the total expected background are shown as hatched histograms. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. The last bin includes events in the overflow. |
png pdf |
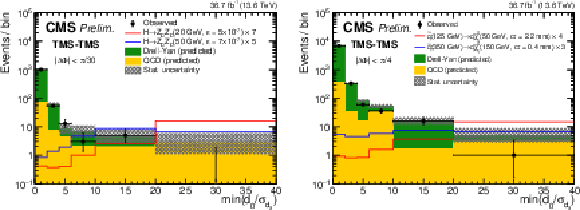
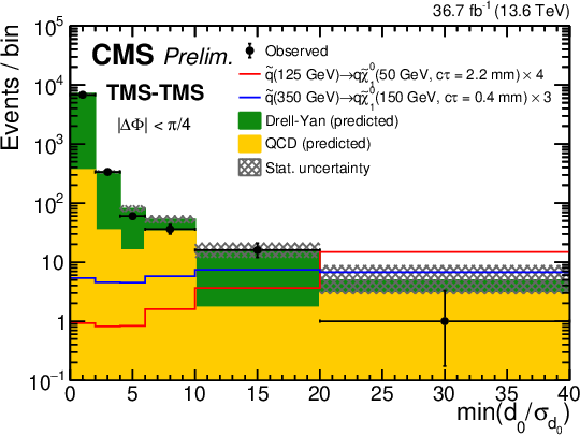
Figure 11:
Distributions of $ \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) $ for TMS-TMS dimuons with (left) $ |\Delta\Phi| < \pi/ $ 30 and (right) $ |\Delta\Phi| < \pi/ $ 4, for events in all mass intervals combined. The number of observed events (black circles) is overlaid with the stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. Events are required to satisfy all nominal selection criteria with the exception of the $ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $ requirement. The last bin includes events in the overflow. All uncertainties shown are statistical only. |
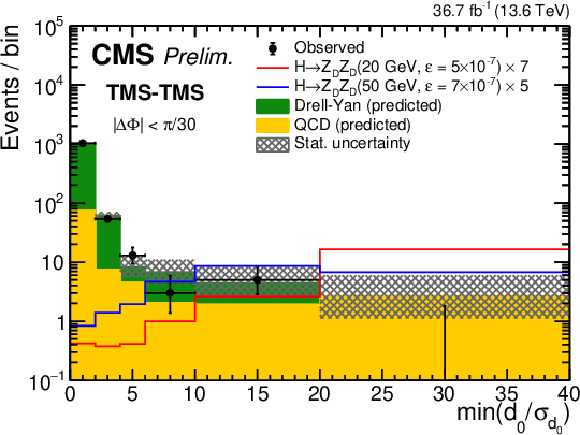
png pdf |
Figure 11-a:
Distributions of $ \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) $ for TMS-TMS dimuons with (left) $ |\Delta\Phi| < \pi/ $ 30 and (right) $ |\Delta\Phi| < \pi/ $ 4, for events in all mass intervals combined. The number of observed events (black circles) is overlaid with the stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. Events are required to satisfy all nominal selection criteria with the exception of the $ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $ requirement. The last bin includes events in the overflow. All uncertainties shown are statistical only. |
png pdf |
Figure 11-b:
Distributions of $ \text{min}(d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}}) $ for TMS-TMS dimuons with (left) $ |\Delta\Phi| < \pi/ $ 30 and (right) $ |\Delta\Phi| < \pi/ $ 4, for events in all mass intervals combined. The number of observed events (black circles) is overlaid with the stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events. Signal contributions expected from simulated signals indicated in the legends are shown in red and blue. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. Events are required to satisfy all nominal selection criteria with the exception of the $ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $ requirement. The last bin includes events in the overflow. All uncertainties shown are statistical only. |
png pdf |
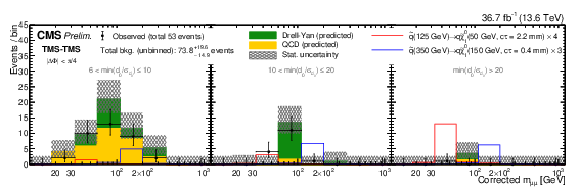
Figure 12:
Comparison of observed and expected numbers of events in the TMS-TMS dimuon category, in the RPV SUSY study that requires $ |\Delta\Phi| < \pi/ $ 4, in bins of $ m^\text{corr}_{\mu\mu} $. The number of observed events (black circles) is overlaid with the stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events in bins of $ m^\text{corr}_{\mu\mu} $ in three min($ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $) bins: (left) 6-10, (center) 10-20, and (right) $ > $ 20. Contributions expected from signal events predicted by the RPV SUSY model with the parameters indicated in the legends are shown as red and blue histograms. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. The last bin includes events in the overflow. All uncertainties shown are statistical only. |
png pdf |
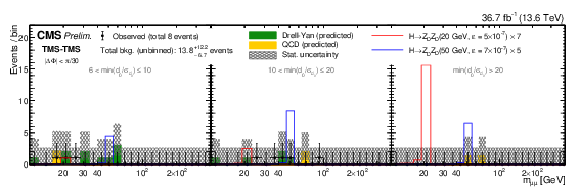
Figure 13:
Comparison of observed and expected numbers of events in the TMS-TMS dimuon category, in the HAHM study that requires $ |\Delta\Phi| < \pi/ $ 30, in bins of $ m_{\mu\mu} $. The number of observed events (black circles) is overlaid with the stacked histograms showing the expected numbers of QCD (yellow) and DY (green) background events in bins of $ m_{\mu\mu} $ in three min($ d_{\mathrm{0}}/\sigma_{d_{\mathrm{0}}} $) bins: (left) 6-10, (center) 10-20, and (right) $ > $ 20. Signal contributions expected from simulated $ \mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}} $ events with the parameters indicated in the legends are shown as red and blue histograms. Their yields are set to the corresponding median expected 95% CL exclusion limits obtained from the ensemble of both dimuon categories, scaled up as indicated in the legend to improve visibility. The last bin includes events in the overflow. All uncertainties shown are statistical only. |
png pdf |
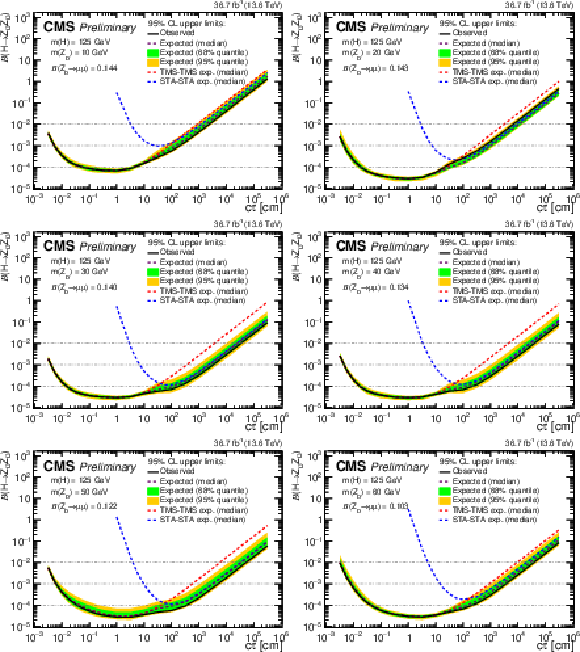
Figure 14:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
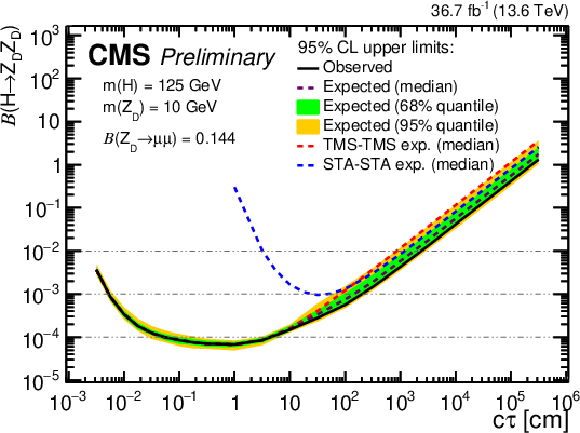
png pdf |
Figure 14-a:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
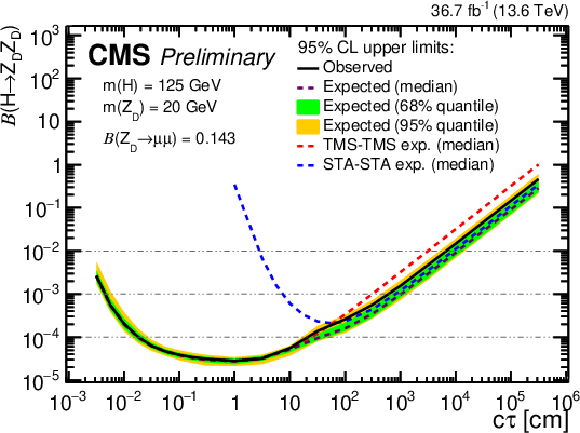
png pdf |
Figure 14-b:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
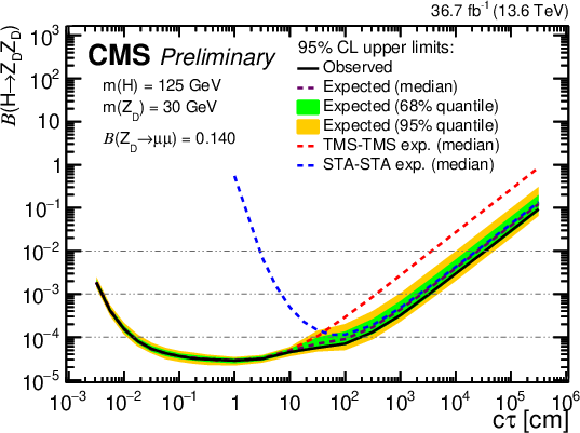
png pdf |
Figure 14-c:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
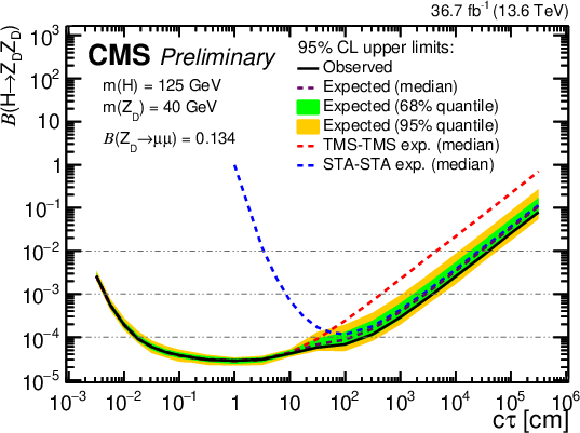
png pdf |
Figure 14-d:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
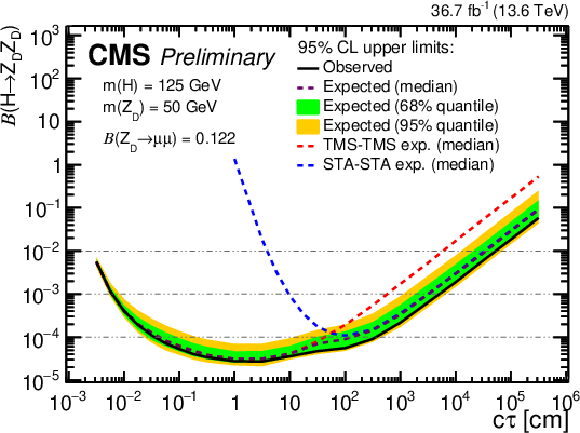
png pdf |
Figure 14-e:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
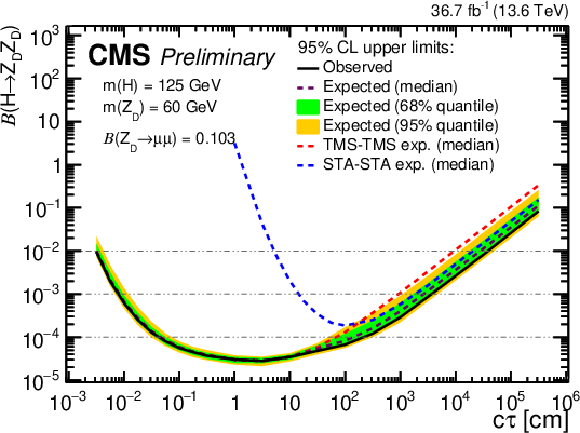
png pdf |
Figure 14-f:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, in the STA-STA and TMS-TMS dimuon categories in 2022 data and their combination. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the combined median expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
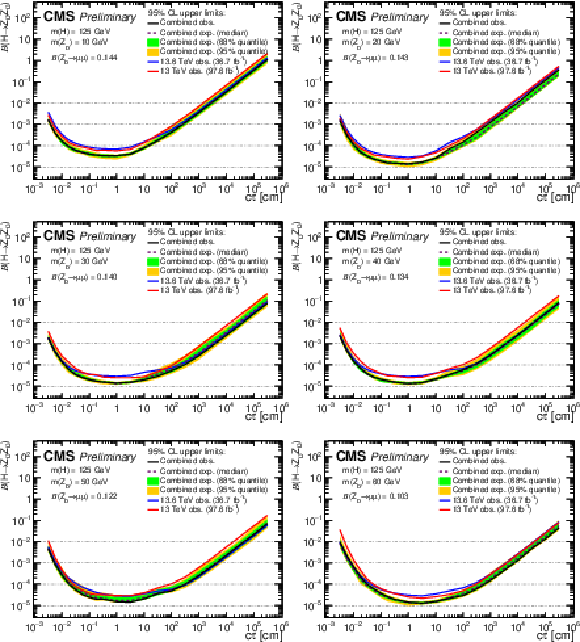
png pdf |
Figure 15:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
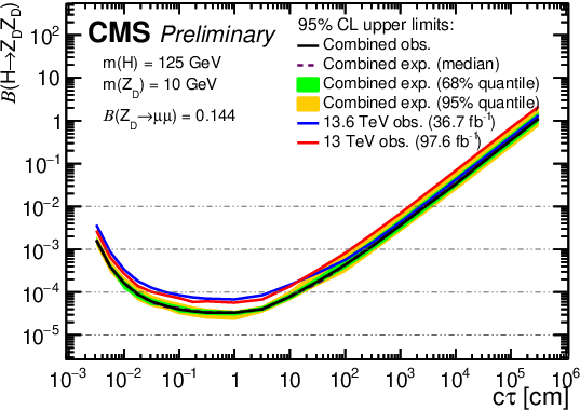
png pdf |
Figure 15-a:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
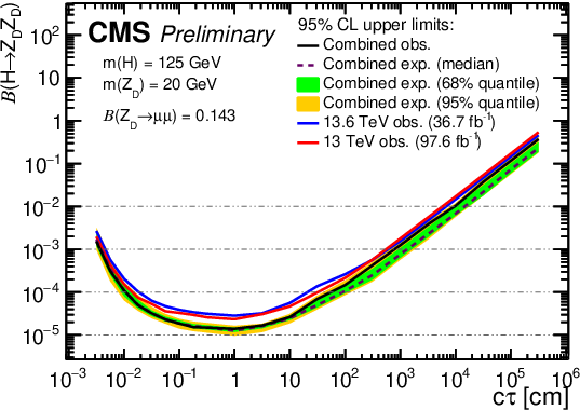
png pdf |
Figure 15-b:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
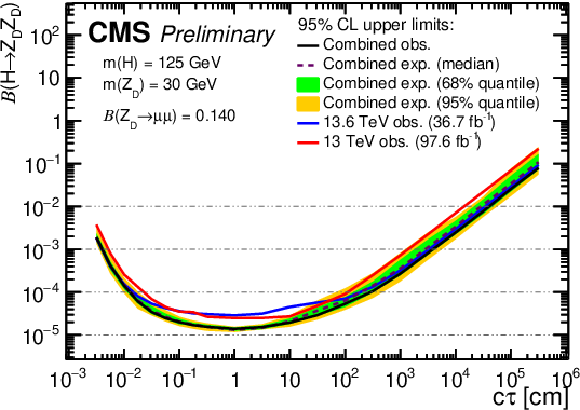
png pdf |
Figure 15-c:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
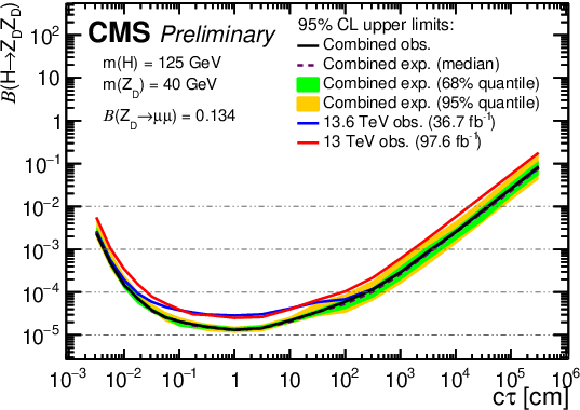
png pdf |
Figure 15-d:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
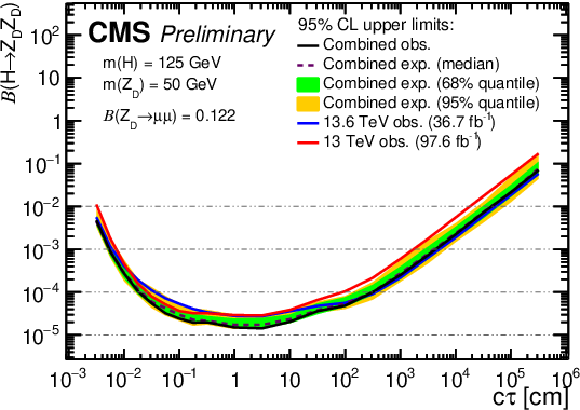
png pdf |
Figure 15-e:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |
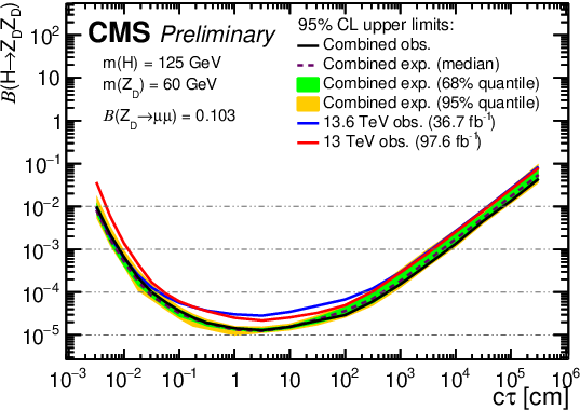
png pdf |
Figure 15-f:
The 95% CL upper limits on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ as a function of $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ in the HAHM model, for $ m(\mathrm{Z}\mathrm{_{D}}) $ ranging from (upper left) 10 GeV to (lower right) 60 GeV, obtained in this analysis, the Run 2 analysis [6], and their combination. The observed limits in this analysis and in the Run 2 analysis [6] are shown as blue and red curves, respectively; the combined expected limits are shown as dashed black curves; and the combined observed limits are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the combined expected limits. |

png pdf |
Figure 16:
The 95% CL upper limits on $ \sigma({ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} } ) $ as a function of $ c\tau(\tilde{\chi}_{1}^{0}) $ in the RPV SUSY model, for $ \mathcal{B}({ \tilde{\chi}_{1}^{0} $\to$ \mu \mu \nu } ) = $ 0.5 and various combinations of $ m(\tilde{\mathrm{q}}) $ and $ m(\tilde{\chi}_{1}^{0}) $ indicated in the legends. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the median expected limits in the ensemble of both categories are shown as dashed black curves; and the observed limits in the ensemble of both categories are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the expected limits in the ensemble of both categories. |
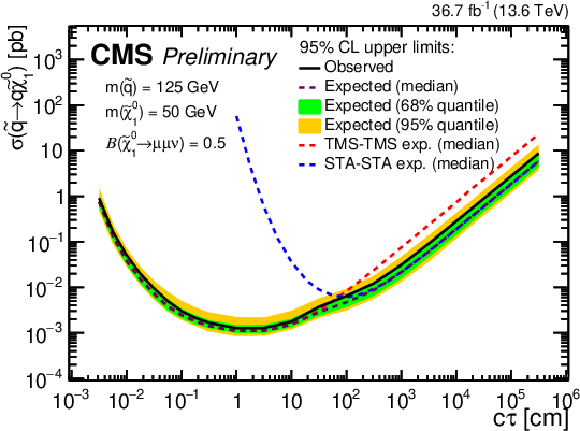
png pdf |
Figure 16-a:
The 95% CL upper limits on $ \sigma({ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} } ) $ as a function of $ c\tau(\tilde{\chi}_{1}^{0}) $ in the RPV SUSY model, for $ \mathcal{B}({ \tilde{\chi}_{1}^{0} $\to$ \mu \mu \nu } ) = $ 0.5 and various combinations of $ m(\tilde{\mathrm{q}}) $ and $ m(\tilde{\chi}_{1}^{0}) $ indicated in the legends. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the median expected limits in the ensemble of both categories are shown as dashed black curves; and the observed limits in the ensemble of both categories are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the expected limits in the ensemble of both categories. |
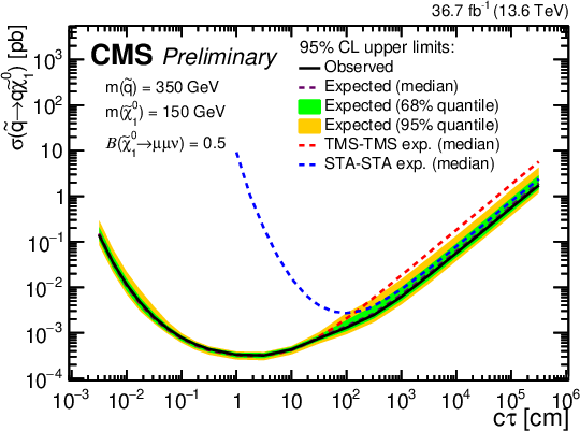
png pdf |
Figure 16-b:
The 95% CL upper limits on $ \sigma({ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} } ) $ as a function of $ c\tau(\tilde{\chi}_{1}^{0}) $ in the RPV SUSY model, for $ \mathcal{B}({ \tilde{\chi}_{1}^{0} $\to$ \mu \mu \nu } ) = $ 0.5 and various combinations of $ m(\tilde{\mathrm{q}}) $ and $ m(\tilde{\chi}_{1}^{0}) $ indicated in the legends. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the median expected limits in the ensemble of both categories are shown as dashed black curves; and the observed limits in the ensemble of both categories are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the expected limits in the ensemble of both categories. |
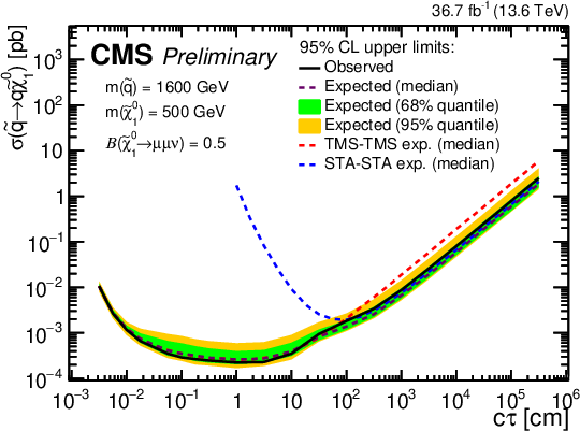
png pdf |
Figure 16-c:
The 95% CL upper limits on $ \sigma({ \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}_{1}^{0} } ) $ as a function of $ c\tau(\tilde{\chi}_{1}^{0}) $ in the RPV SUSY model, for $ \mathcal{B}({ \tilde{\chi}_{1}^{0} $\to$ \mu \mu \nu } ) = $ 0.5 and various combinations of $ m(\tilde{\mathrm{q}}) $ and $ m(\tilde{\chi}_{1}^{0}) $ indicated in the legends. The median expected limits obtained from the STA-STA and TMS-TMS dimuon categories are shown as dashed blue and red curves, respectively; the median expected limits in the ensemble of both categories are shown as dashed black curves; and the observed limits in the ensemble of both categories are shown as solid black curves. The green and yellow bands correspond, respectively, to the 68 and 95% quantiles for the expected limits in the ensemble of both categories. |
| Summary |
| Data collected by the CMS experiment in proton-proton collisions at $ \sqrt{s} = $ 13.6 TeV in 2022 and corresponding to an integrated luminosity of 36.7 fb$ ^{-1} $ have been used to conduct an inclusive search for long-lived exotic neutral particles (LLPs) decaying to a pair of oppositely charged muons. The search is largely model-independent and is sensitive to a broad range of LLP lifetimes and masses. No significant excess of events above the standard model background is observed. The results are interpreted as limits on the parameters of the hidden Abelian Higgs model, in which the Higgs boson decays to a pair of long-lived dark photons $ \mathrm{Z}\mathrm{_{D}} $, and of an $ R $-parity violating SUSY model, in which long-lived neutralinos decay to a pair of muons and a neutrino. Even though the size of the data sample used by this analysis is a factor of 2.5 smaller than that in the search for displaced dimuons in pp collisions at $ \sqrt{s} = $ 13 TeV, the constraints on the parameters of the HAHM model are comparable or tighter in a significant fraction of the parameter space, thanks mainly to recent improvements in the trigger algorithms for displaced muons. The combination of the results of this analysis with the results obtained at $ \sqrt{s} = $ 13 TeV improves the constraints on a branching fraction of the Higgs boson to dark photons $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ by approximately a factor of 2. In the $ m(\mathrm{Z}\mathrm{_{D}}) $ range of 10-60 GeV, $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ of 1% is excluded at 95% confidence level in the range of proper decay length $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ from a few tens of $\mu$m to 30 m (at $ m(\mathrm{Z}\mathrm{_{D}}) $ = 10 GeV) and 700 m (at $ m(\mathrm{Z}\mathrm{_{D}}) $ = 60 GeV). For $ m(\mathrm{Z}\mathrm{_{D}}) $ greater than 20 GeV and less than $ m(\mathrm{H})/ $ 2, the combined limits provide the best limits to date on $ \mathcal{B}(\mathrm{H} \to \mathrm{Z}\mathrm{_{D}} \mathrm{Z}\mathrm{_{D}}) $ for $ c\tau(\mathrm{Z}\mathrm{_{D}}) $ (varying with $ m(\mathrm{Z}\mathrm{_{D}}) $) between 300 $\mu$m and $ {\approx}$0.1cm, and above $ {\approx}$10 cm. |
| Additional Figures | |
png pdf |
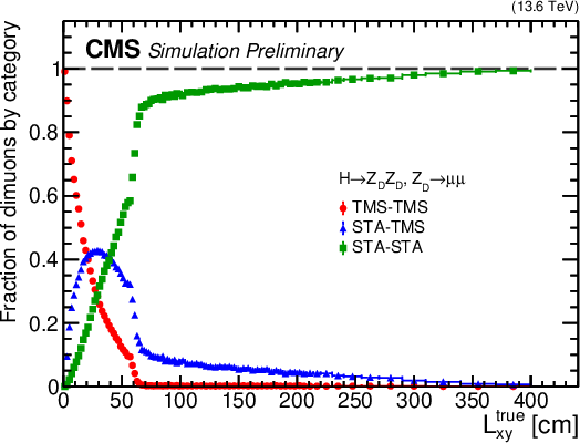
Additional Figure 1:
Fractions of signal events with zero (green), one (blue), and two (red) STA muons matched to TMS muons by the STA to TMS association procedure, as a function of generated $ L_{\mathrm{xy}} $, in all HAHM signal samples combined. |
png pdf |
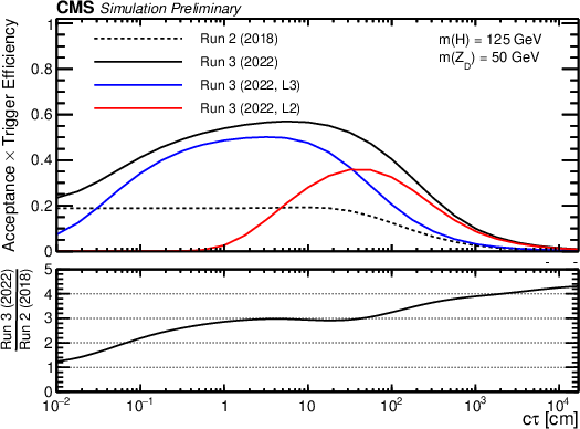
Additional Figure 2:
Efficiencies of the Run 2 and Run 3 triggers as a function of $ c\tau $. The efficiency is defined as the fraction of simulated HAHM events with $ m(\mathrm{Z}\mathrm{_{D}}) = $ 50 GeV that satisfy the requirements of the following sets of trigger paths: the Run 2 (2018) triggers (dashed black); the Run 3 (2022, L3) triggers (blue); the Run 3 (2022, L2) triggers (red); and the OR of all Run 3 (2022) triggers (black). The lower panel shows the ratio of the overall Run 3 (2022) efficiency to the Run 2 (2018) efficiency. |
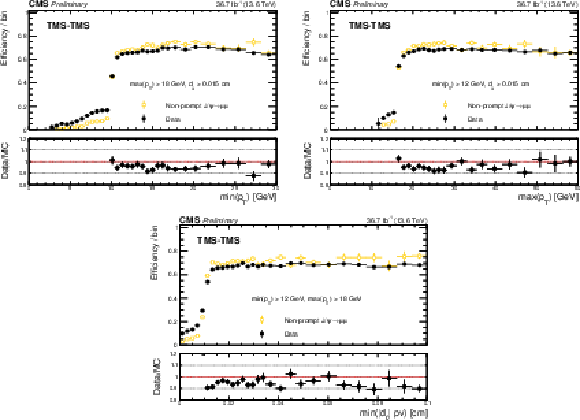
png pdf |
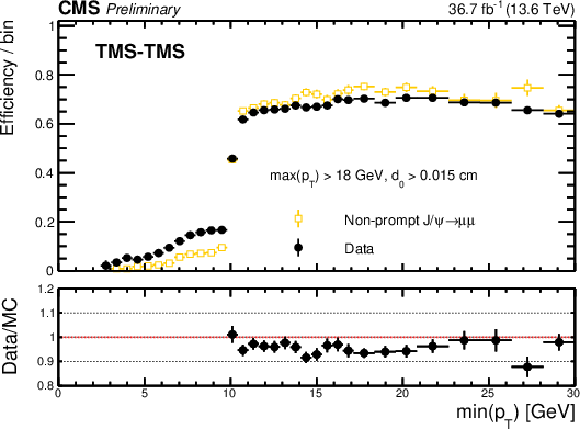
Additional Figure 3:
Trigger efficiency (black), defined as the fraction of events recorded by the triggers based on the information from jets and missing transverse energy that also satisfy the requirements of the Run 3 (2022, L3) triggers, as a function of min($ p_{\mathrm{T}} $) (upper left), max($ p_{\mathrm{T}} $) (upper right), and min($ d_{\mathrm{0}} $) (lower) in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Efficiencies in data are compared to efficiencies from a combination of simulated samples of non-prompt $ {\mathrm{J}/\psi} \to\mu\mu $ produced in B hadron decays (yellow). |
png pdf |
Additional Figure 3-a:
Trigger efficiency (black), defined as the fraction of events recorded by the triggers based on the information from jets and missing transverse energy that also satisfy the requirements of the Run 3 (2022, L3) triggers, as a function of min($ p_{\mathrm{T}} $) (upper left), max($ p_{\mathrm{T}} $) (upper right), and min($ d_{\mathrm{0}} $) (lower) in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Efficiencies in data are compared to efficiencies from a combination of simulated samples of non-prompt $ {\mathrm{J}/\psi} \to\mu\mu $ produced in B hadron decays (yellow). |
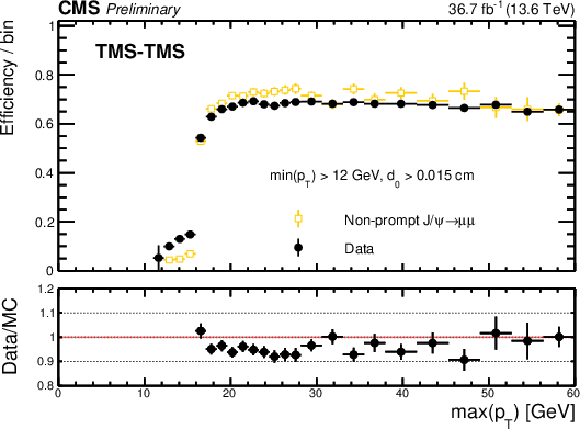
png pdf |
Additional Figure 3-b:
Trigger efficiency (black), defined as the fraction of events recorded by the triggers based on the information from jets and missing transverse energy that also satisfy the requirements of the Run 3 (2022, L3) triggers, as a function of min($ p_{\mathrm{T}} $) (upper left), max($ p_{\mathrm{T}} $) (upper right), and min($ d_{\mathrm{0}} $) (lower) in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Efficiencies in data are compared to efficiencies from a combination of simulated samples of non-prompt $ {\mathrm{J}/\psi} \to\mu\mu $ produced in B hadron decays (yellow). |
png pdf |
Additional Figure 3-c:
Trigger efficiency (black), defined as the fraction of events recorded by the triggers based on the information from jets and missing transverse energy that also satisfy the requirements of the Run 3 (2022, L3) triggers, as a function of min($ p_{\mathrm{T}} $) (upper left), max($ p_{\mathrm{T}} $) (upper right), and min($ d_{\mathrm{0}} $) (lower) in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Efficiencies in data are compared to efficiencies from a combination of simulated samples of non-prompt $ {\mathrm{J}/\psi} \to\mu\mu $ produced in B hadron decays (yellow). |
png pdf |
Additional Figure 4:
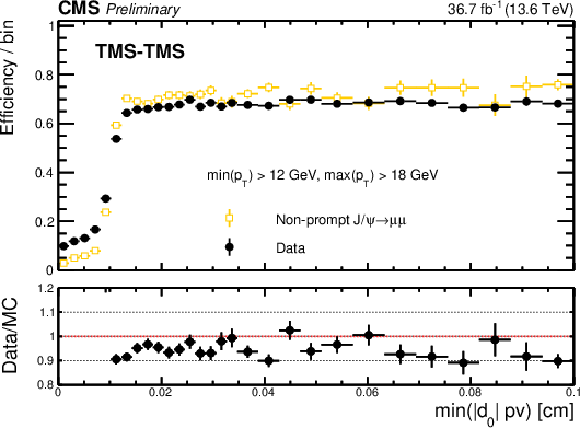
Left: Invariant mass distribution for TMS-TMS dimuons with $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 1 in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L3) triggers (blue), illustrating the background rejection of the Run 3 (2022, L3) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L3) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for TMS-TMS dimuons in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For dimuons with offline $ \text{min}(d_{\mathrm{0}}) > $ 0.012 cm, the combined efficiency of the L3 muon reconstruction and the online min($ d_{\mathrm{0}} $) requirement is larger than 90% in all data taking periods. |

png pdf |
Additional Figure 4-a:
Left: Invariant mass distribution for TMS-TMS dimuons with $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 1 in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L3) triggers (blue), illustrating the background rejection of the Run 3 (2022, L3) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L3) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for TMS-TMS dimuons in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For dimuons with offline $ \text{min}(d_{\mathrm{0}}) > $ 0.012 cm, the combined efficiency of the L3 muon reconstruction and the online min($ d_{\mathrm{0}} $) requirement is larger than 90% in all data taking periods. |
png pdf |
Additional Figure 4-b:
Left: Invariant mass distribution for TMS-TMS dimuons with $ L_{\mathrm{xy}}/\sigma_{L_{\mathrm{xy}}} < $ 1 in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L3) triggers (blue), illustrating the background rejection of the Run 3 (2022, L3) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L3) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for TMS-TMS dimuons in events enriched in $ {\mathrm{J}/\psi} \to\mu\mu $. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For dimuons with offline $ \text{min}(d_{\mathrm{0}}) > $ 0.012 cm, the combined efficiency of the L3 muon reconstruction and the online min($ d_{\mathrm{0}} $) requirement is larger than 90% in all data taking periods. |

png pdf |
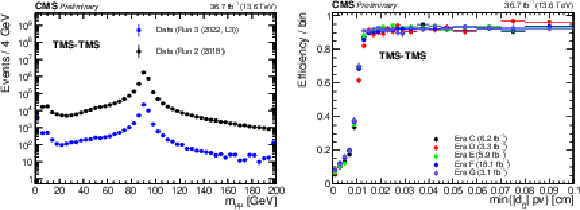
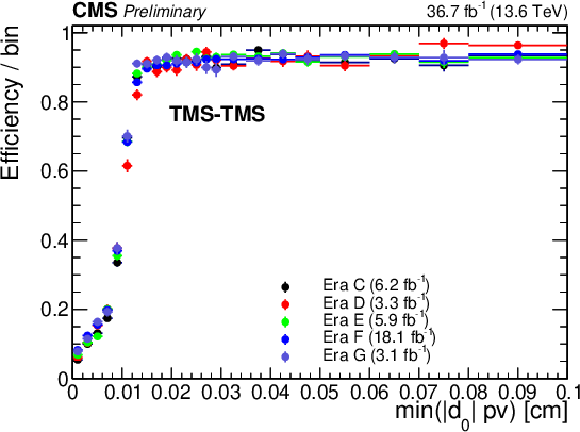
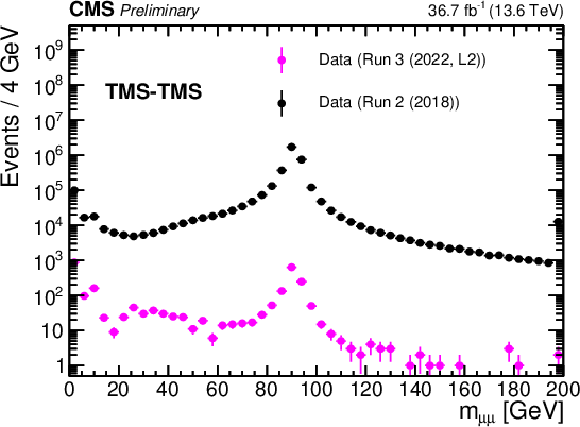
Additional Figure 5:
Left: Invariant mass distribution of TMS-TMS dimuons in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L2) triggers (pink), illustrating the background rejection of the Run 3 (2022, L2) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L2) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for STA-STA dimuons in events enriched in cosmic ray muons. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For displaced muons, the efficiency of the online min($ d_{\mathrm{0}} $) requirement is larger than 95% in all data taking periods. |
png pdf |
Additional Figure 5-a:
Left: Invariant mass distribution of TMS-TMS dimuons in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L2) triggers (pink), illustrating the background rejection of the Run 3 (2022, L2) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L2) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for STA-STA dimuons in events enriched in cosmic ray muons. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For displaced muons, the efficiency of the online min($ d_{\mathrm{0}} $) requirement is larger than 95% in all data taking periods. |
png pdf |
Additional Figure 5-b:
Left: Invariant mass distribution of TMS-TMS dimuons in events recorded by the Run 2 (2018) triggers in 2022 data (black), and in the subset of events also selected by the Run 3 (2022, L2) triggers (pink), illustrating the background rejection of the Run 3 (2022, L2) triggers. Right: Trigger efficiency, defined as the fraction of events recorded by the Run 2 (2018) triggers that also satisfied the requirements of the Run 3 (2022, L2) triggers, as a function of offline-reconstructed min($ d_{\mathrm{0}} $) for STA-STA dimuons in events enriched in cosmic ray muons. Different symbols show efficiencies in different periods of the 2022 data taking corresponding to the integrated luminosities indicated in the legend. For displaced muons, the efficiency of the online min($ d_{\mathrm{0}} $) requirement is larger than 95% in all data taking periods. |
png pdf |
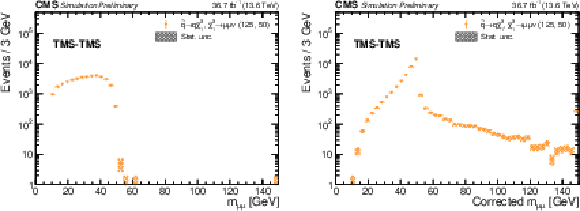
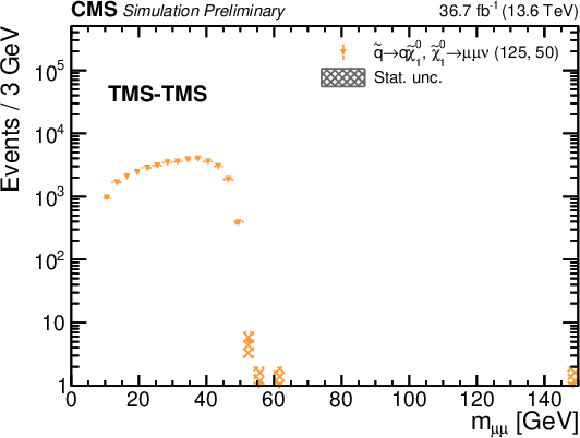
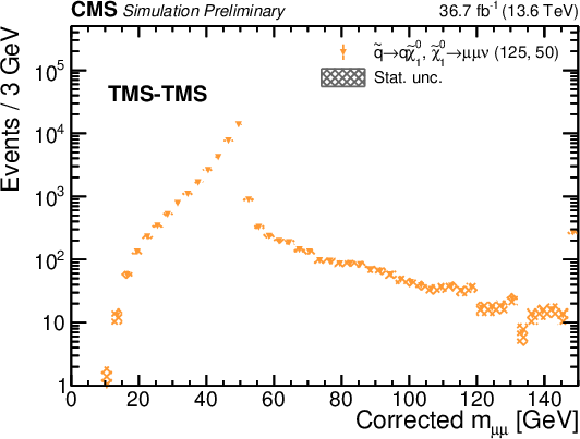
Additional Figure 6:
Distributions of (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ in the TMS-TMS dimuon category, for simulated signal events with $ m(\tilde{q}) = $ 125 GeV and $ m(\tilde{\chi}^{0}_{1}) = $ 50 GeV in the RPV SUSY model. |
png pdf |
Additional Figure 6-a:
Distributions of (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ in the TMS-TMS dimuon category, for simulated signal events with $ m(\tilde{q}) = $ 125 GeV and $ m(\tilde{\chi}^{0}_{1}) = $ 50 GeV in the RPV SUSY model. |
png pdf |
Additional Figure 6-b:
Distributions of (left) $ m_{\mu\mu} $ and (right) $ m^\text{corr}_{\mu\mu} $ in the TMS-TMS dimuon category, for simulated signal events with $ m(\tilde{q}) = $ 125 GeV and $ m(\tilde{\chi}^{0}_{1}) = $ 50 GeV in the RPV SUSY model. |
png pdf |
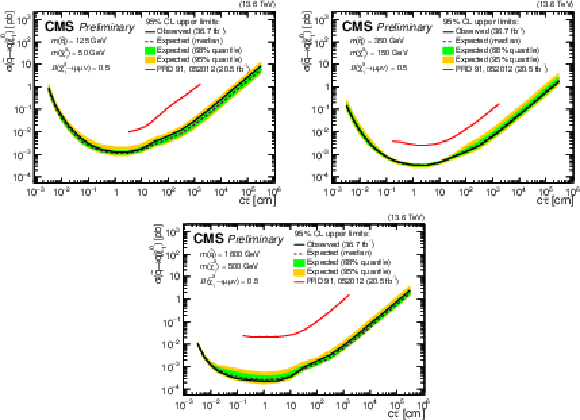
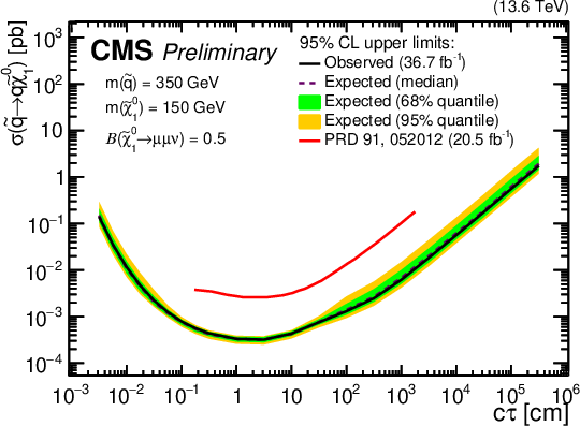
Additional Figure 7:
Observed (solid) and expected (dashed) 95% CL upper limits on $ \sigma( \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ as a function of $ c\tau(\tilde{\chi}^{0}_{1}) $ for $ \mathcal{B}( \tilde{\chi}^{0}_{1} \to \mu \mu \nu ) = $ 0.5 in the RPV SUSY model, for various combinations of $ m(\tilde{q}) $ and $ m(\tilde{\chi}^{0}_{1}) $ indicated in the legends. The limits obtained in this analysis (black) are compared with the corresponding limits in the analysis of Run 1 data rescaled by the ratio of $ \sigma( \tilde{q} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ at 13 TeV and 8 TeV (red). |

png pdf |
Additional Figure 7-a:
Observed (solid) and expected (dashed) 95% CL upper limits on $ \sigma( \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ as a function of $ c\tau(\tilde{\chi}^{0}_{1}) $ for $ \mathcal{B}( \tilde{\chi}^{0}_{1} \to \mu \mu \nu ) = $ 0.5 in the RPV SUSY model, for various combinations of $ m(\tilde{q}) $ and $ m(\tilde{\chi}^{0}_{1}) $ indicated in the legends. The limits obtained in this analysis (black) are compared with the corresponding limits in the analysis of Run 1 data rescaled by the ratio of $ \sigma( \tilde{q} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ at 13 TeV and 8 TeV (red). |
png pdf |
Additional Figure 7-b:
Observed (solid) and expected (dashed) 95% CL upper limits on $ \sigma( \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ as a function of $ c\tau(\tilde{\chi}^{0}_{1}) $ for $ \mathcal{B}( \tilde{\chi}^{0}_{1} \to \mu \mu \nu ) = $ 0.5 in the RPV SUSY model, for various combinations of $ m(\tilde{q}) $ and $ m(\tilde{\chi}^{0}_{1}) $ indicated in the legends. The limits obtained in this analysis (black) are compared with the corresponding limits in the analysis of Run 1 data rescaled by the ratio of $ \sigma( \tilde{q} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ at 13 TeV and 8 TeV (red). |

png pdf |
Additional Figure 7-c:
Observed (solid) and expected (dashed) 95% CL upper limits on $ \sigma( \tilde{\mathrm{q}} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ as a function of $ c\tau(\tilde{\chi}^{0}_{1}) $ for $ \mathcal{B}( \tilde{\chi}^{0}_{1} \to \mu \mu \nu ) = $ 0.5 in the RPV SUSY model, for various combinations of $ m(\tilde{q}) $ and $ m(\tilde{\chi}^{0}_{1}) $ indicated in the legends. The limits obtained in this analysis (black) are compared with the corresponding limits in the analysis of Run 1 data rescaled by the ratio of $ \sigma( \tilde{q} \to \mathrm{q} \tilde{\chi}^{0}_{1} ) $ at 13 TeV and 8 TeV (red). |
| References | ||||
| 1 | R. Barbier et al. | $ R $-parity-violating supersymmetry | Phys. Rept. 420 (2005) 1 | hep-ph/0406039 |
| 2 | J. L. Hewett, B. Lillie, M. Masip, and T. G. Rizzo | Signatures of long-lived gluinos in split supersymmetry | JHEP 09 (2004) 070 | hep-ph/0408248 |
| 3 | M. J. Strassler and K. M. Zurek | Echoes of a hidden valley at hadron colliders | PLB 651 (2007) 374 | hep-ph/0604261 |
| 4 | T. Han, Z. Si, K. M. Zurek, and M. J. Strassler | Phenomenology of hidden valleys at hadron colliders | JHEP 07 (2008) 008 | 0712.2041 |
| 5 | D. Curtin, R. Essig, S. Gori, and J. Shelton | Illuminating dark photons with high-energy colliders | JHEP 02 (2015) 157 | 1412.0018 |
| 6 | CMS Collaboration | Search for long-lived particles decaying to a pair of muons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2023) 228 | CMS-EXO-21-006 2205.08582 |
| 7 | CMS Collaboration | Search for long-lived particles decaying into muon pairs in proton-proton collisions at $ \sqrt{s} $ = 13 TeV collected with a dedicated high-rate data stream | JHEP 04 (2022) 062 | CMS-EXO-20-014 2112.13769 |
| 8 | CMS Collaboration | Search for long-lived particles that decay into final states containing two electrons or two muons in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | PRD 91 (2015) 052012 | CMS-EXO-12-037 1411.6977 |
| 9 | CMS Collaboration | Search for long-lived particles that decay into final states containing two muons, reconstructed using only the CMS muon chambers | CMS Physics Analysis Summary, 2015 CMS-PAS-EXO-14-012 |
CMS-PAS-EXO-14-012 |
| 10 | ATLAS Collaboration | Search for long-lived particles in final states with displaced dimuon vertices in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PRD 99 (2019) 012001 | 1808.03057 |
| 11 | ATLAS Collaboration | Search for displaced vertices of oppositely charged leptons from decays of long-lived particles in $ pp $ collisions at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | PLB 801 (2020) 135114 | 1907.10037 |
| 12 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 13 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 14 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 15 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 16 | J. D. Wells | How to find a hidden world at the Large Hadron Collider | in Perspectives on LHC Physics, Kane and Pierce, eds., World Scientific, 2008 link |
0803.1243 |
| 17 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 18 | M. Cepeda et al. | Report from working group 2: Higgs physics at the HL-LHC and HE-LHC | in Proceedings of the HL/HE-LHC Workshop, Dainese et al., eds., CERN Yellow Rep. Monogr., 2019 link |
1902.00134 |
| 19 | LHC Higgs Cross Section Working Group | Ad Interim 13.6 TeV cross sections | link | |
| 20 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 21 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 22 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 23 | GEANT 4 Collaboration | GEANT 4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 24 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 25 | CMS Collaboration | Performance of the CMS muon trigger system in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 16 (2021) P07001 | CMS-MUO-19-001 2102.04790 |
| 26 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}= $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 27 | LHCb Collaboration | Identification of beauty and charm quark jets at LHCb | JINST 10 (2015) P06013 | 1504.07670 |
| 28 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 29 | A. L. Read | Presentation of search results: The CL$ _{\text{s}} $ technique | JPG 28 (2002) 2693 | |
| 30 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 31 | ATLAS and CMS Collaborations, and LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report CMS-NOTE-2011-005. ATL-PHYS-PUB-2011-11, 2011 | |
| 32 | CMS Collaboration | A search for decays of the Higgs boson to invisible particles in events with a top-antitop quark pair or a vector boson in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | Submitted to EPJC, 2023 | CMS-HIG-21-007 2303.01214 |
| 33 | CMS Collaboration | Search for invisible decays of a Higgs boson produced through vector boson fusion in proton--proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 105 (2022) 092007 | CMS-HIG-20-003 2201.11585 |
| 34 | CMS Collaboration | Combined measurements of Higgs boson couplings in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | EPJC 79 (2019) 421 | CMS-HIG-17-031 1809.10733 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|