

Compact Muon Solenoid
LHC, CERN
| CMS-TOP-22-010 ; CERN-EP-2023-234 | ||
| Search for new Higgs bosons via same-sign top quark pair production in association with a jet in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| 6 November 2023 | ||
| Phys. Lett. B 850 (2024) 138478 | ||
| Abstract: A search is presented for new Higgs bosons in proton-proton (pp) collision events in which a same-sign top quark pair is produced in association with a jet, via the $ \mathrm{p}\mathrm{p}\to \mathrm{t}\mathrm{H}/\mathrm{A} \to\mathrm{t}\mathrm{t}\overline{\mathrm{c}} $ and $ \mathrm{p}\mathrm{p}\to \mathrm{t}\mathrm{H}/\mathrm{A} \to\mathrm{t}\mathrm{t}\overline{\mathrm{u}} $ processes. Here, H and A represent the extra scalar and pseudoscalar boson, respectively, of the second Higgs doublet in the generalized two-Higgs-doublet model (g2HDM). The search is based on pp collision data collected at a center-of-mass energy of 13 TeV with the CMS detector at the LHC, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. Final states with a same-sign lepton pair in association with jets and missing transverse momentum are considered. New Higgs bosons in the 200--1000 GeV mass range and new Yukawa couplings between 0.1 and 1.0 are targeted in the search, for scenarios in which either H or A appear alone, or in which they coexist and interfere. No significant excess above the standard model prediction is observed. Exclusion limits are derived in the context of the g2HDM. | ||
| Links: e-print arXiv:2311.03261 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; Physics Briefing ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
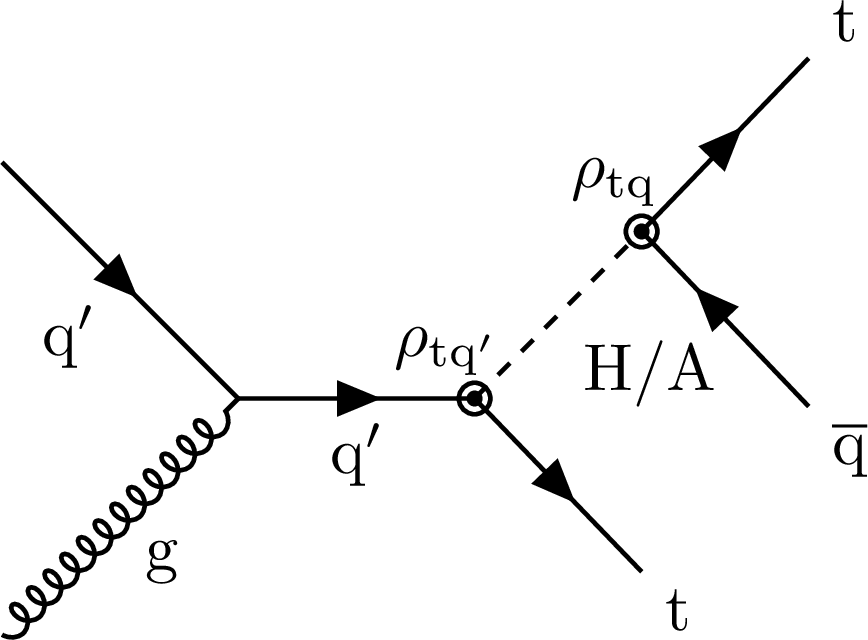
Figure 1:
Representative Feynman diagram for $ \mathrm{t}\mathrm{t}\overline{\mathrm{q}} $ ($ \mathrm{q} = $ u, c) production through a new scalar (H) or pseudoscalar (A) Higgs boson. In this analysis, events with $ \mathrm{q}=\mathrm{q}' $ are considered. |
png pdf |
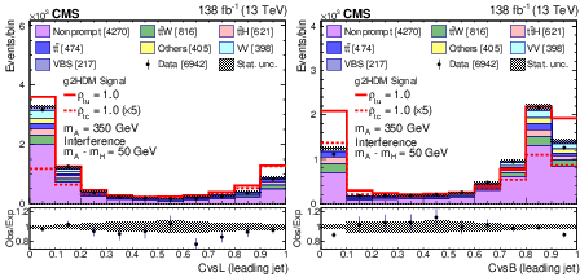
Figure 2:
The pre-fit CvsL (left) and CvsB (right) distributions for the selected highest $ p_{\mathrm{T}} $ jet. The predictions for $ m_{\mathrm{A} } = $ 350 GeV with A-H interference assuming $ m_{\mathrm{A} } -m_{\mathrm{H}}= $ 50 GeV for $ \rho_{\mathrm{t}\mathrm{u}}= $ 1.0 (solid blue line) and $ \rho_{\mathrm{t}\mathrm{c}}= $ 1.0 (dashed red line) are also displayed. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points and the hatched bands represent the statistical uncertainties in the data and in the background predictions, respectively. Beneath each plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plots include statistical uncertainties in the data and in the background predictions. |
png pdf |
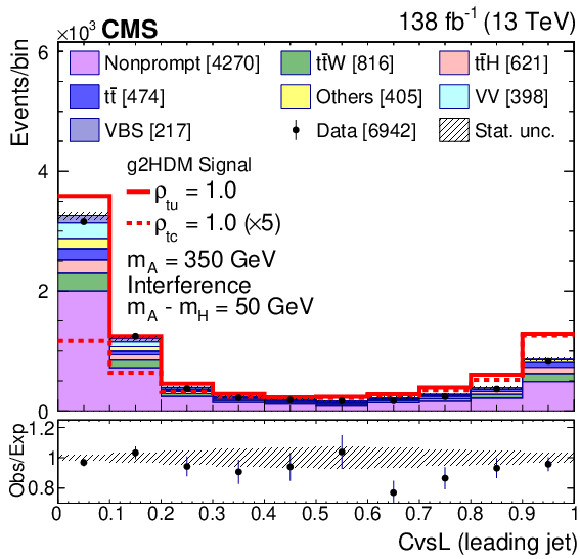
Figure 2-a:
The pre-fit CvsL distribution for the selected highest $ p_{\mathrm{T}} $ jet. The predictions for $ m_{\mathrm{A} } = $ 350 GeV with A-H interference assuming $ m_{\mathrm{A} } -m_{\mathrm{H}}= $ 50 GeV for $ \rho_{\mathrm{t}\mathrm{u}}= $ 1.0 (solid blue line) and $ \rho_{\mathrm{t}\mathrm{c}}= $ 1.0 (dashed red line) are also displayed. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points and the hatched bands represent the statistical uncertainties in the data and in the background predictions, respectively. Beneath the plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plot include statistical uncertainties in the data and in the background predictions. |
png pdf |
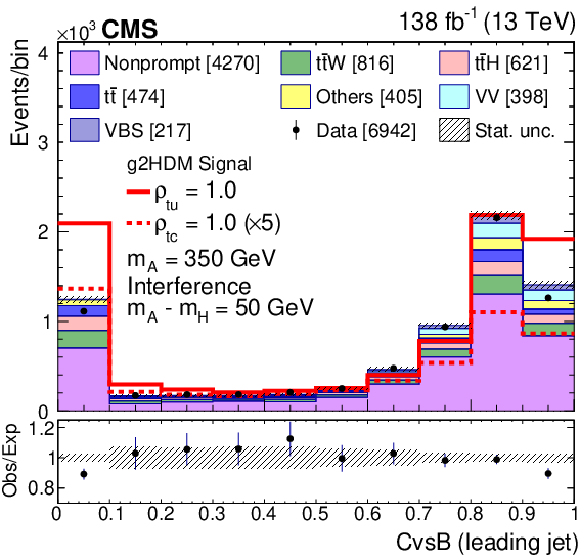
Figure 2-b:
The pre-fit CvsB distribution for the selected highest $ p_{\mathrm{T}} $ jet. The predictions for $ m_{\mathrm{A} } = $ 350 GeV with A-H interference assuming $ m_{\mathrm{A} } -m_{\mathrm{H}}= $ 50 GeV for $ \rho_{\mathrm{t}\mathrm{u}}= $ 1.0 (solid blue line) and $ \rho_{\mathrm{t}\mathrm{c}}= $ 1.0 (dashed red line) are also displayed. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points and the hatched bands represent the statistical uncertainties in the data and in the background predictions, respectively. Beneath the plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plot include statistical uncertainties in the data and in the background predictions. |
png pdf |
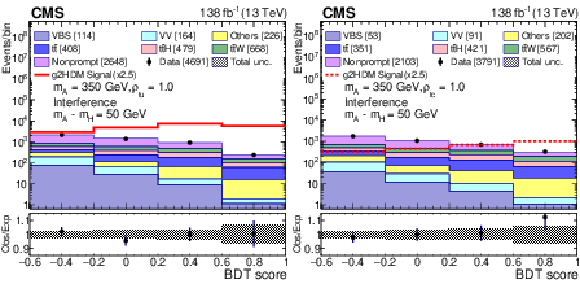
Figure 3:
Post-fit distributions of the BDT discriminants combining the categories $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $, for $ m_{\mathrm{A} }= $ 350 GeV with $ \rho_{\mathrm{t}\mathrm{u}}= $ 1.0 (left), and $ \rho_{\mathrm{t}\mathrm{c}}= $ 1.0 (right) with the A-H interference. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points represent the statistical uncertainties in the data. Beneath each plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plots include statistical uncertainties in the data and the total uncertainty in the background predictions, and the hatched bands represent the total uncertainty in the background predictions. |
png pdf |
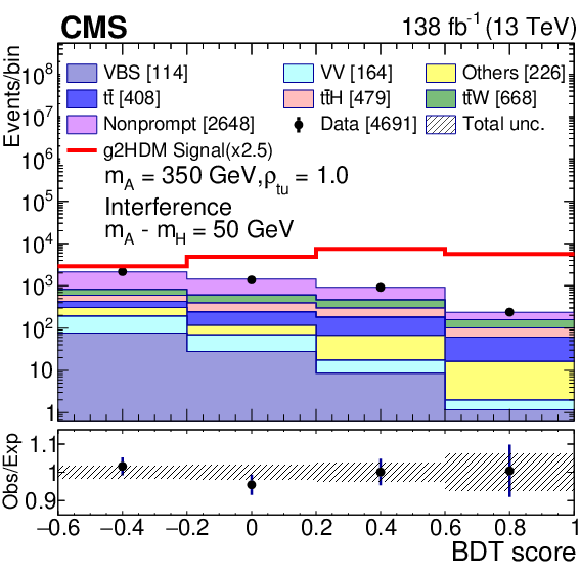
Figure 3-a:
Post-fit distribution of the BDT discriminants combining the categories $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $, for $ m_{\mathrm{A} }= $ 350 GeV with $ \rho_{\mathrm{t}\mathrm{u}}= $ 1.0 with the A-H interference. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points represent the statistical uncertainties in the data. Beneath the plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plot include statistical uncertainties in the data and the total uncertainty in the background predictions, and the hatched bands represent the total uncertainty in the background predictions. |
png pdf |
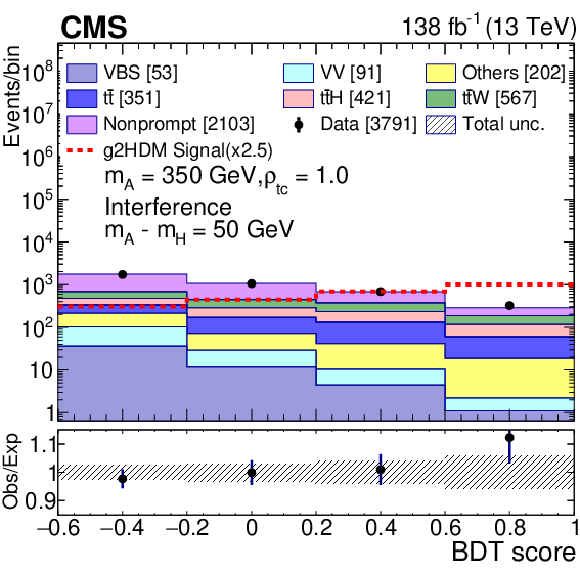
Figure 3-b:
Post-fit distribution of the BDT discriminants combining the categories $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $, for $ m_{\mathrm{A} }= $ 350 GeV with $ \rho_{\mathrm{t}\mathrm{c}}= $ 1.0 with the A-H interference. The numbers in square brackets represent the yields for each sample. The uncertainty bars on the points represent the statistical uncertainties in the data. Beneath the plot the ratio of data to predictions is shown. The uncertainty bars in the ratio plot include statistical uncertainties in the data and the total uncertainty in the background predictions, and the hatched bands represent the total uncertainty in the background predictions. |

png pdf |
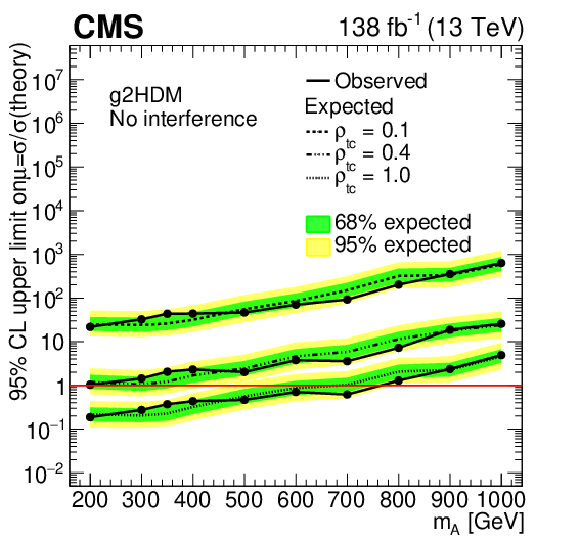
Figure 4:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{u}} = $ 0.1, 0.4, 1.0 (left) and $ \rho_{\mathrm{t}\mathrm{c}} = $ 0.1, 0.4, 1.0 (right) without interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |

png pdf |
Figure 4-a:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{u}} = $ 0.1, 0.4, 1.0 without interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |
png pdf |
Figure 4-b:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{c}} = $ 0.1, 0.4, 1.0 without interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |
png pdf |
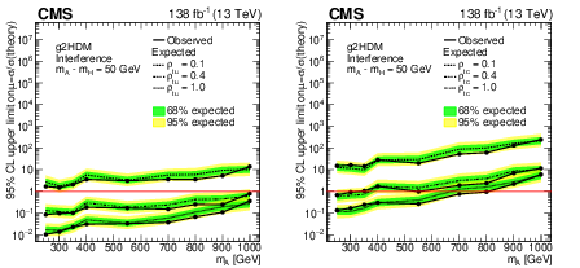
Figure 5:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{u}} = $ 0.1, 0.4, 1.0 (left) and $ \rho_{\mathrm{t}\mathrm{c}} = $ 0.1, 0.4, 1.0 (right) with A-H interference assuming $ m_{\mathrm{A} } - m_{\mathrm{H}} = $ 50 GeV, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |

png pdf |
Figure 5-a:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{u}} = $ 0.1, 0.4, 1.0 with A-H interference assuming $ m_{\mathrm{A} } - m_{\mathrm{H}} = $ 50 GeV, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |

png pdf |
Figure 5-b:
Observed and expected 95% CL upper limits on the signal strength as functions of $ m_{\mathrm{A} } $ for g2HDM using different coupling assumptions: $ \rho_{\mathrm{t}\mathrm{c}} = $ 0.1, 0.4, 1.0 with A-H interference assuming $ m_{\mathrm{A} } - m_{\mathrm{H}} = $ 50 GeV, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. |

png pdf |
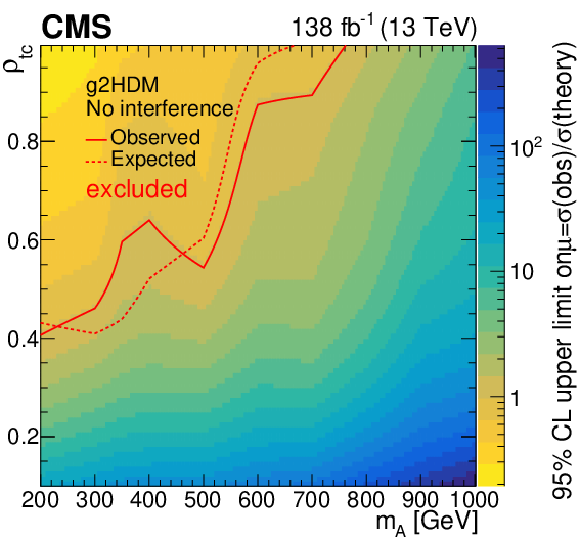
Figure 6:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{u}} $ (left) and $ \rho_{\mathrm{t}\mathrm{c}} $ (right) for g2HDM without the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |

png pdf |
Figure 6-a:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{u}} $ for g2HDM without the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |
png pdf |
Figure 6-b:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{c}} $ for g2HDM without the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |
png pdf |
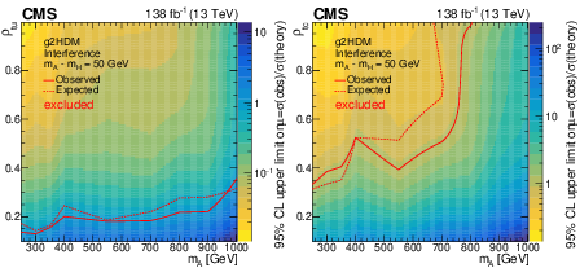
Figure 7:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{u}} $ (left) and $ \rho_{\mathrm{t}\mathrm{c}} $ (right) for g2HDM signal model with the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |

png pdf |
Figure 7-a:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{u}} $ for g2HDM signal model with the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |

png pdf |
Figure 7-b:
Observed 95% CL upper limit on the signal strength as a function of $ m_{\mathrm{A} } $ and $ \rho_{\mathrm{t}\mathrm{c}} $ for g2HDM signal model with the A-H interference, for the combination of the $ \mathrm{e}^\pm\mathrm{e}^\pm $, $ \mu^\pm\mu^\pm $, and $ \mathrm{e}^\pm\mu^\pm $ categories. The color axis represents the observed upper limit on the signal strength. Expected (dashed lines) and observed (solid lines) exclusion contours are also shown. |
| Tables | |

png pdf |
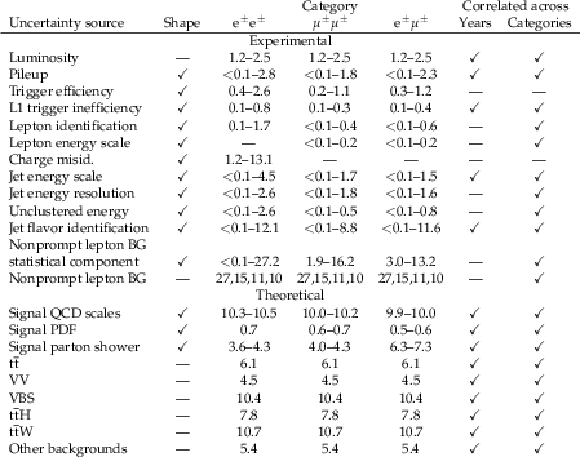
Table 1:
Input variables of the BDT. Jets and leptons are ordered by $ p_{\mathrm{T}} $. |
png pdf |
Table 2:
Summary of systematic uncertainties for $ \rho_{\mathrm{t}\mathrm{c}}= $ 0.4 and $ m_{\mathrm{A} } = $ 350 GeV with A-H interference assuming $ m_{\mathrm{A} } -m_{\mathrm{H}}= $ 50 GeV. The first column indicates the source of uncertainty. The second column specifies whether the shape of the fit discriminant is affected by the nuisance parameter (checkmark) or not (dash). The impact in percent of these nuisance parameters on the pre-fit expected event yields is displayed in the third column. This column is subdivided into three event categories representing the analysis channels. The percentage impacts are given as a range of values representing the minimum and maximum differences obtained in the different bins of the BDT distribution through the four data-taking periods. The numbers for the normalization component of the nonprompt lepton background represent the uncertainties used for each data-taking period. Whether or not a nuisance parameter is taken correlated across years and categories is specified in the last two columns. The luminosity and jet flavor identification nuisances are only partially correlated across years. |
png pdf |
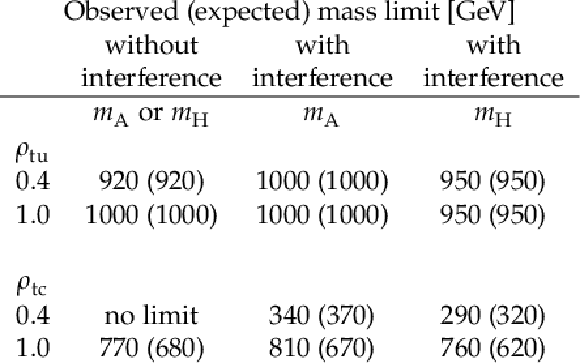
Table 3:
Observed (expected) lower limits on $ m_{\mathrm{A} } $ at 95% CL. For the scenario without interference, the limits on $ m_{\mathrm{H}} $ and $ m_{\mathrm{A} } $ are the same. |
| Summary |
| A search for new Yukawa couplings of the top quark in models with additional Higgs bosons in proton-proton collisions at a center-of-mass energy of 13 TeV has been presented. The process considered is the production of same-sign top quark pairs associated with an up or a charm quark, and resulting in a final state containing two same-sign leptons and jets. No significant excess above the background prediction is observed. When no interference between the pseudoscalar (A) and scalar (H) Higgs bosons is assumed, A or H bosons with masses below 920 GeV and 1000 GeV are excluded at the 95% confidence level (CL) for coupling values $ \rho_{\mathrm{t}\mathrm{u}} = $ 0.4 and 1.0, respectively, while all other extra Yukawa couplings are assumed to be zero. Similarly, without interference between H and A, and assuming a coupling value of $ \rho_{\mathrm{t}\mathrm{c}} = $ 1.0, A or H bosons with masses below approximately 770 GeV are excluded at the 95% CL. Under the assumption that A and H interfere in the scenario with a mass difference of $ m_{\mathrm{A} } - m_{\mathrm{H}} = $ 50 GeV, the pseudoscalar Higgs boson is excluded for $ m_{\mathrm{A} } $ values below 1000 GeV when considering coupling values $ \rho_{\mathrm{t}\mathrm{u}} > $ 0.4. Furthermore, assuming $ \rho_{\mathrm{t}\mathrm{c}} = $ 0.4, the exclusion limit for A is $ m_{\mathrm{A} } = $ 340 GeV, whereas assuming $ \rho_{\mathrm{t}\mathrm{c}} = $ 1.0, the limit extends to $ m_{\mathrm{A} } = $ 810 GeV at 95% CL. These results represent the first search based on the generalized two-Higgs-doublet model considering A-H interference. |
| References | ||||
| 1 | ATLAS Collaboration | Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 2 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 3 | ATLAS and CMS Collaborations | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}= $ 7 and 8 TeV | JHEP 08 (2016) 045 | 1606.02266 |
| 4 | E. da Silva Almeida et al. | Electroweak sector under scrutiny: A combined analysis of LHC and electroweak precision data | PRD 99 (2019) 033001 | 1812.01009 |
| 5 | E. d. S. Almeida, A. Alves, O. J. P. Éboli, and M. C. Gonzalez-Garcia | Electroweak legacy of the LHC run II | PRD 105 (2022) 013006 | 2108.04828 |
| 6 | ATLAS Collaboration | A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery | Nature 607 (2022) 52 | 2207.00092 |
| 7 | CMS Collaboration | A portrait of the Higgs boson by the CMS experiment ten years after the discovery | Nature 607 (2022) 60 | CMS-HIG-22-001 2207.00043 |
| 8 | G. C. Branco et al. | Theory and phenomenology of two-Higgs-doublet models | Phys. Rept. 516 (2012) 1 | 1106.0034 |
| 9 | M. Kohda, T. Modak, and W.-S. Hou | Searching for new scalar bosons via triple-top signature in $ cg \to ts^0 \to tt\bar t $ | PLB 776 (2018) 379 | 1710.07260 |
| 10 | W.-S. Hou | Tree level t $ \rightarrow $ ch$ ^0 $ or h$ ^0 \rightarrow $ t$ \mathrm{\bar{c}} $ decays | PLB 296 (1992) 179 | |
| 11 | W.-S. Hou and M. Kikuchi | Approximate alignment in two Higgs doublet model with extra Yukawa couplings | Eur. Phys. Lett. 123 (2018) 11001 | 1706.07694 |
| 12 | J. F. Gunion and H. E. Haber | The CP conserving two Higgs doublet model: The approach to the decoupling limit | PRD 67 (2003) 075019 | hep-ph/0207010 |
| 13 | M. Carena, I. Low, N. R. Shah, and C. E. M. Wagner | Impersonating the standard model Higgs boson: Alignment without decoupling | JHEP 04 (2014) 015 | 1310.2248 |
| 14 | P. S. Bhupal Dev and A. Pilaftsis | Maximally symmetric two Higgs doublet model with natural standard model alignment | JHEP 12 (2014) 024 | 1408.3405 |
| 15 | T. D. Lee | A theory of spontaneous T violation | PRD 8 (1973) 1226 | |
| 16 | K. Fuyuto, W.-S. Hou, and E. Senaha | Electroweak baryogenesis driven by extra top Yukawa couplings | PLB 776 (2018) 402 | 1705.05034 |
| 17 | K. Fuyuto, W.-S. Hou, and E. Senaha | Cancellation mechanism for the electron electric dipole moment connected with the baryon asymmetry of the universe | PRD 101 (2020) 011901 | 1910.12404 |
| 18 | Muon g-2 Collaboration | Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm | 2308.06230 | |
| 19 | ATLAS Collaboration | Search for heavy Higgs bosons with flavour-violating couplings in multi-lepton plus $ b $-jets final states in $ pp $ collisions at 13 TeV with the ATLAS detector | submitted to JHEP | 2307.14759 |
| 20 | CMS Collaboration | HEPData record for this analysis | link | |
| 21 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 22 | CMS Collaboration | Performance of the CMS level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 23 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 24 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 25 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 26 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 27 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 28 | CMS Collaboration | Technical proposal for the phase-II upgrade of the Compact Muon Solenoid | CMS Technical proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 29 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 30 | M. Cacciari, G. P. Salam, and G. Soyez | Fastjet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 31 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 32 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 33 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 34 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 35 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 36 | W.-S. Hou and T. Modak | Probing top changing neutral Higgs couplings at colliders | Mod. Phys. Lett. A 36 (2021) 2130006 | 2012.05735 |
| 37 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 38 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 39 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 40 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG box | JHEP 06 (2010) 043 | 1002.2581 |
| 41 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 42 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W$ ^+ $W$ ^- $, WZ and ZZ production in the POWHEG box | JHEP 11 (2011) 078 | 1107.5051 |
| 43 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 44 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: \it s- and \it t-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 45 | H. B. Hartanto, B. Jager, L. Reina, and D. Wackeroth | Higgs boson production in association with top quarks in the POWHEG BOX | PRD 91 (2015) 094003 | 1501.04498 |
| 46 | T. Sjöstrand et al. | An introduction to PYTHIA8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 47 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 48 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 49 | GEANT 4 Collaboration | GEANT 4 --- a simulation toolkit | NIM A 506 (2003) 250 | |
| 50 | CMS Collaboration | Measurement of the inclusive W and Z production cross sections in pp collisions at $ \sqrt{s}= $ 7 TeV | JHEP 10 (2011) 132 | CMS-EWK-10-005 1107.4789 |
| 51 | CMS Collaboration | Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at $ \sqrt{s} = $ 13 TeV | EPJC 81 (2021) 378 | CMS-HIG-19-008 2011.03652 |
| 52 | CMS Collaboration | Measurement of the cross section of top quark-antiquark pair production in association with a W boson in proton-proton collisions at $ \sqrt{s} $ = 13 TeV | JHEP 07 (2023) 219 | CMS-TOP-21-011 2208.06485 |
| 53 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 54 | K. Rehermann and B. Tweedie | Efficient identification of boosted semileptonic top quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 55 | CMS Collaboration | A new calibration method for charm jet identification validated with proton-proton collision events at $ \sqrt{s} $ = 13 TeV | JINST 17 (2022) P03014 | CMS-BTV-20-001 2111.03027 |
| 56 | CMS Collaboration | Performance summary of AK4 jet charm tagging with the CMS Run2 legacy dataset | CMS Detector Performance Note CMS-DP-2023-006, 2023 CDS |
|
| 57 | E. Bols et al. | Jet flavour classification using DeepJet | JINST 15 (2020) P12012 | 2008.10519 |
| 58 | CMS Collaboration | Performance summary of AK4 jet b tagging with data from proton-proton collisions at 13 TeV with the CMS detector | CMS Detector Performance Note CMS-DP-2023-005, 2023 CDS |
|
| 59 | CMS Collaboration | Evidence for associated production of a Higgs boson with a top quark pair in final states with electrons, muons, and hadronically decaying $ \tau $ leptons at $ \sqrt{s} = $ 13 TeV | JHEP 08 (2018) 066 | CMS-HIG-17-018 1803.05485 |
| 60 | J. H. Friedman | Greedy function approximation: A gradient boosting machine | Annals Statist. 29 (2001) 1189 | |
| 61 | A. Hoecker et al. | TMVA --- toolkit for multivariate data analysis | physics/0703039 | |
| 62 | The ATLAS and CMS Collaborations and the LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS Physics Analysis Summary CMS-NOTE-2011-005, ATL-PHYS-PUB-2011-11, 2011 | |
| 63 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 64 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 65 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 66 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} $ = 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 67 | S. Heinemeyer et al. | Handbook of LHC Higgs cross sections: 3. Higgs properties | CERN Report CERN-2013-004, 2013 link |
1307.1347 |
| 68 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 69 | A. L. Read | Presentation of search results: the CL$ _s $ technique | JPG 28 (2002) 2693 | |
| 70 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|